Thông tin
Quiz

Tích phân liên quan đến phương trình hàm ẩn Toán 12

Tích phân liên quan đến phương trình hàm ẩn Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề:

Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:

27 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Tích phân liên quan đến phương trình hàm ẩn Toán 12

58 29 lượt tải Tải xuống

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 731

KIẾN THỨC CẦN NHỚ:

1. Các tính chất tích phân:



     

d d d

b c b

a a c

f x x f x x f x x 

  

với

a c b 



     

d d 0

b b

a a

k f x x kf x x k 

 



   

d dx

b a

a b

f x x f x 

 



       

f x x F x F b F a  





   

 

   

d d d

b b b

a a a

f x g x x f x x g x x  

  



     

d d d

b b b

a a a

f x x f t t f z z 

  



       

f x x f x f b f a



  



2. Công thức đổi biến số:

 

     

. ,f u x u x dx f u du u u x



 

 

 

   

 

. ,

u b

a u a

f u x u x dx f u du u u x



 

 

Phương pháp đổi biến số thường được sử dụng theo hai cách sau đây:

 Giả sử cần tính

 

g x dx



. Nếu ta viết được

 

g x

dưới dạng

 

f u x u x



thì

   

 

u b

a u a

g x dx f u du

 

. Vậy bài toán quy về tính

 

u b

u a

f u du



, trong nhiều trường hợp thì tích phân mới

này đơn giản hơn .

 Giả sử cần tính

 

f x dx







. Đặt

 

x x t

thỏa mãn

   

,x a x b

 

 

thì

   

 

   

b b

a a

f x dx f x t x t dt g t dt







 

  

, trong đó

   

 

.g t f x t x t





TÍCH PHÂN LIÊN QUAN ĐẾN PHƯƠNG TRÌNH HÀM ẨN

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 732

BÀI TẬP MẪU

Cho hàm số





f x

liên tục trên



, và thỏa mãn









3 2 10 6

1 2 , .

xf x f x x x x x

       



Khi đó

 

f x dx





bằng



. B.



. C.

. D.



Phân tích hướng dẫn giải

1. DẠNG TOÁN: Tính tích phân hàm ẩn.

...................................................................................................................................................................

2. KIẾN THỨC CẦN NHỚ:

Công thức đổi biến số trong tích phân:

 

( )

( ) . ( ) d ( ) d

u b

a u a

f u x u x x f u u





 

 Tính chất tích phân:

( ) d 0

f x x





( ) d ( ) d ( ) d

b c b

a a c

f x x f x x f x x

 

  

( ) d ( ) ( ) ( )

x b

x a

f x x f x f b f a





  



...................................................................................................................................................................

3. HƯỚNG GIẢI:

B1: Nhân cả hai vế của phương trình với

, rồi sử dụng tích phân hai vế để tính

 

f x x





B2: Nhân cả hai vế của phương trình với

, rồi sử dụng tích phân hai vế để tính

 

f x dx



B3: Kết luận

 

f x dx





Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn B

Cách 1 : Dùng vi phân

Ta có:









3 2 10 6

1 2 ,xf x f x x x x x

       



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 733









2 3 2 11 7 2

1 2 ,x f x xf x x x x x

        







Khi đó:

 

     

1 1 1

2 3 2 11 7 2

1 1 1

* d 1 d 2 d ,x f x x xf x x x x x x x

  

        

  



   

1 0

1 1 4

d d

3 2 3

f t t f t t



   

 

     

1 1 1

1 4

d 0 d 4 d 4

3 3

f t t f t t f x x

  

         

  

Mặt khác:

 

     

1 1 1

2 3 2 11 7 2

0 0 0

* 1 2

x f x dx xf x dx x x x dx

      

  

   

1 0

0 1

1 1 5

d d

3 2 8

f t t f t t

   

 

 

5 5

6 8

f t t

  



 

f t t

  



 

f x dx

  



Theo tính chất tích phân ta có:

     

0 1 1

1 1 0

f x dx f x dx f x dx

 

  



  

Cách 2: (Tham khảo không giống phân tích ở trên)

Bậc cao nhất vế phải là

, bậc cao nhất vế phải là





x f x

. Kết luận:





f x

bậc 3 vì





3 10

x x x

 .

Hệ số của bậc cao nhất vế phải là



. Kết luận: Hệ số của bậc cao nhất vế trái là



Vậy





3 2

f x x ax bx c

    









3 10 3 10 7

. . ... ...

x f x x x a x x ax

       

Vế phải không có

. Vậy



Kết luận





f x x bx c

   

















3 2 10 4 2 2

. 1 1 1

x f x f x x bx cx x b x c

          

10 4 2 4 6 2

1 3 3

x bx cx x x x b bx c

          









10 6 4 2

3 3 1

x x b x b x cx b c

          

Đồng nhất hệ số được

3; 2

b c

  

Tóm lại





3 2

f x x x

   

. Suy ra

 

f x x







Bài tập tương tự và phát triển:

Câu 48.1: Cho hàm số





y f x



liên tục trên



thỏa mãn

     

2 1

3 2 2 1 e 4

x x

f x f x x

 

    

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 734

Khi đó

 

I f x x





bằng

e 4

 

. B.



. C.



. D.

e 2

 

Lời giải

Chọn C

Ta có

     

2 2

2 1

0 0

3 2 d 2 1 e 4 d

x x

f x f x x x x

 

 

    

 

 

 



     

2 2 2 2

2 1

0 0 0 0

3 d 2 d 2 1 e d 4 d

x x

f x x f x x x x x

 

    

   



     

 

2 2 2

2 1 2

0 0 0

3 d 2 d 2 e d 2 1 8

x x

f x x f x x x x

 

      

  



   

2 2

2 1

0 0

3 d d e 8

x x

f x x f x x

 

  

 



 

4 d 8

f x x







 

d 2

f x x





Câu 48.2: Cho hàm số





y f x



liên tục trên







thỏa mãn









ln 1 ln

f x f x x

  

Khi đó

 

I f x x





bằng



. B.



. C.

. D.



Lời giải

Chọn A

Ta có









ln 1 ln

f x f x x

  



   

1 1

ln 1 ln 1

f x f x

x x

  







Lấy tích phân từ

đến

cả hai vế của







, ta được

   

1 1

ln 1 ln d d

e e

f x f x x x

x x

 

  

 

 

 



   

1 1

ln d 1 ln d 1

e e

f x x f x x e

x x

   

 



       

1 1

ln d ln 1 ln d 1 ln 1

e e

f x x f x x e

    

 







NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 735

Đặt

t x



. Đổi cận

1 0

x t

x e t

  

Khi đó









     

1 1

0 0

d 1 d 1 1

f x x f t t e

    

 



   

1 1

0 0

d d 1

f x x f x x e

  

 



 

f x x







Câu 48.3: Cho hàm số





y f x



liên tục trên





\ 0; 1





thỏa mãn





 

     

1 2ln 2

2 ln 3; ,

1 .

f a b a b

x x f x f x x x



 



  







   





Tính

2 2

a b



. B.

. C.

. D.

Lời giải

Chọn B

Ta có













1 .

x x f x f x x x



   

(1)

Chia cả 2 vế của biểu thức (1) cho

 



ta được

 

1 1

x x

f x f x

x x



 

 





 

1 1

x x

f x

x x



 



 

 

 

, với





\ 0; 1

  





 

f x











 

. ln 1

f x x x C

   





 

ln 1

f x x x C



   

Mặt khác,





1 2 ln 2

f  







2 1 ln 2 2 ln 2

C   



 

Do đó

 

ln 1 1

f x x x



   

Với



thì

   

3 3 3

1 ln 3 ln 3

2 2 2

f x     . Suy ra



và

 

Vậy

2 2

a b

 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 736

Câu 48.4: Cho hàm số





y f x

 có đạo hàm liên tục trên



. Biết





1 e



và













2 . .

x f x x f x x



  

với

 



. Tính

 

f x x



1 2

e 3

 

. B.



. C.



. D.

2 4

e 3

 

Lời giải

Chọn D

Ta có:













2 . .

x f x x f x x



  















xf x x f x



 





 

f x





 



 

 







e d e

x x

f x

x C



 

   









2 2

. e

f x x C x

  

Vì





1 e





1 .e e

  



 

Do đó

 

2 2

1 . e

f x x x

 

   

 

 

Vậy

 

1 1 1 1

2 2 2 2

0 0 0 0

1 1

d 1 . e d d 1 e d

e e

x x

f x x x x x x x x x

 

   

       

   

 

   

 

   

   

1 1 1

0 0 0

1 1 1 1 1 1

1 d e 1 e 2 e d 1 2 1 d e

3 e 3 e 3 e

x x x

x x x e x

 

     

              

 

     

     

 

  

 

2 1 2 1 4 2

2 1 e d 2 1 1

3 e 3 e 3

e e x e e e e

 

   

              

 

 

   

 

   

 



Câu 48.5: Cho hàm số





y f x



liên tục trên





\ 0



và thỏa mãn

 

2 15

2 3 3

f x f

 

  

 

 

 

d 2019

f x x 



. Tính

I f x

 



 

 



688

I  

. B.

688

I 

. C.

886

I 

. D.

I 

Lời giải

Chọn A

Xét

I f x

 



 

 



. Đặt

t x





d d

x t



. Đổi cận

x t

  

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 737

Khi đó

1 2

I f t

 



 

 



Mà

 

2 15

2 3 3

f x f

 

  

 

 



 

2 5 2

2 3

f f x

 

  

 

 

hay

 

2 5 2

2 3

f f t

 

  

 

 

Nên

     

3 3 3 3

1 1 1 1

1 5 2 5 1 1

3 d d 3 d 5 3 d

2 2 3 4 3 3

I f t t t t f t t f t t

 

        

 

 

   





Đặt

u t





dt du



. Đổi cận

1 3

3 9

t u

  

Khi đó

 

1 2019 688

5 d 5

9 9 3

I f u u       



Câu 48.6: Cho hàm số





f x

có đạo hàm liên tục trên





\ 0



và thỏa mãn

 

2 2

f x f x

 

 

 

 

 

d 5

xf x x







. Giá trị

f x

 

 

 



bằng

103



. B.

103

. C.

103

. D.

103



Lời giải

Chọn D

Đặt

( )

u x

dv f x dx













( )

du dx

v f x













Ta có

     

2 2

1 1

. .

x f x dx x f x f x dx



 

 

     

5 2 2 1

f f f x dx

   



(1)

Lần lượt thay



và



vào

 

2 2

f x f x

 

 

 

 

ta được









   

2 2 1 1

2 1 2

f f

 







 





 



















Khi đó

       

1 2 2 1 5 4

f x dx f f

     



   

1 2

2 2

f x dx f x dx

   

 

Lại có

 

2 2

f x f x

 

 

 

 

 

1 1 1

2 2 2

2 2

f x dx f dx x dx

 

  

 

 

  

1 7

2.( 2)

f dx

 

   

 

 



1 7 103

24 24

f dx

 

     

 

 



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 738

Đặt

2 2

t x

x t

  

dx dt

  

ta có

2 1

1 2

2 2

( ).

f dx f t dt

x t



 



 

 

 

2 ( ).

f t dt







(2)

Đặt

1 1

u x

x u

  

dx du

  

ta có

1 1

( ).

f dx f u du

x u



 



 

 

 

1 103

( ).

f t dt



  



Thay vào (2) ta được

2 103 103

24 12

f dx

   

   

   

   



Câu 48.7: Cho hàm số





f x

có đạo hàm liên tục trên đoạn





0;1

đồng thời thỏa mãn





0 9





và

   

9 9

f x f x x

 

  

 

 

. Tính









1 0

T f f  .

2 9ln 2

 

. B.



. C.

9 ln 2

T  

. D.

2 9 ln 2

 

Lời giải

Chọn C

Ta có

   

9 9

f x f x x

 

  

 

 



   

9 1

f x f x x

 

   

   

   







 

f x

f x x





 



 

 



 

1 1

f x x



 



 





 



 

1 1

f x x











 

f x x

 







 

f x x

x C



 







0 9





nên





 

f x x



 



Vậy

   

1 0 d

T f f x x

 

   

 



 



9 ln 1

 

  

 

 

9ln 2

 

Câu 48.8: Cho hàm số





f x

nhận giá trị dương, có đạo hàm liên tục trên đoạn





0; 2

. Biết





0 1



và









2 4

. 2 e

x x

f x f x



  , với mọi





0; 2

x 



. Tính tích phân









 

3 2

x x f x

I x

f x

 





 

. B.

 

. C.

 

. D.

 

Lời giải

Chọn B

Ta có

   

2 4

. 2 e

x x

f x f x



 



   

2 4

ln . 2 ln e

x x

f x f x



  

 











ln ln 2 2 4

f x f x x x

   







NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 739

Mặt khác, với



, ta có









 

0 . 2 1

0 1

f f















nên





2 1



Xét









 

3 2

2 2

3 2

0 0

d 3 . d

x x f x

f x

I x x x x

f x f x

 



  

 

 

3 2

3 d ln

x x f x

 

 

 



 

3 2 2

3 ln 3 6 .ln d

x x f x x x f x x

   

   

   



 

3 6 .ln d

x x f x x

  



 

6 3 .ln d

x x f x x

 

 

 







Đặt

t x

 



d d

x t

 

. Đổi cận

0 2

2 0

x t

  

Do đó

   

 

0 2

2 0

3 2 .ln 2 d 6 3 .ln 2 d

I t t f t t t t f t t

      

   

   

 

Vì tích phân không phụ thuộc vào biến nên

 

6 3 .ln 2 d

I x x f x x

  

 

 







Cộng 2 vế của





và





, ta được

 

   

 

2 6 3 . ln ln 2 d

I x x f x f x x

      

   



Hay

 

   

 

6 3 . ln ln 2 d

I x x f x f x x

      

   









Thế







vào







, ta có

   

2 2

1 16

6 3 . 2 4 d

2 5

I x x x x x

    



Câu 48.9: Cho hàm số





f x

nhận giá trị dương, có đạo hàm liên tục trên







thỏa mãn

 



và













2 4 0

f x x f x



  

. Biết

 

d ln

a c

f x x





, với

, ,a b c





. Tính

S a b c

  



. B.



. C.



. D.



Lời giải

Chọn D





f x



, với mọi





0;x

 

nên













2 4 0

f x x f x



  







 

2 4

f x



  

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 740

Suy ra

 

x x C

f x

  

Mặt khác

 



nên



hay

 

4 3

f x

x x



 

Vậy

 

1 1

0 0

d 1 3

d ln

4 3 2 2

f x x

x x

 

 

 

1, 2, 3 6

a b c S

     

Câu 48.10: Cho hàm số





y f x

 có đạo hàm trên



thỏa mãn









       

0 0 1

3 1

f f

f x y f x f y xy x y



 





     





, với

,x y





. Tính

 

1 d

f x x





. B.



. C.

. D.

Lời giải

Chọn C

Lấy đạo hàm theo hàm số









3 6

f x y f y x xy

 

   

 



Cho









0 0 3

y f x f x

 

   







1 3

f x x



 











f x f x dx x x C



   



mà





0 1



 

. Do đó





f x x x

  

Vậy

 

1 d

f x x

 



 

f x x







 

1 d

x x x



  



Câu 48.11: Cho hàm số





f x

liên tục trên



và biết

 

tan d 4

f x x











d 2

x f x







Giá trị của tích phân

 

f x x



thuộc khoảng nào dưới đây?





5;9

. B.





3;6

. C.





2;5

. D.





1;4

Lời giải

Chọn A

Đặt

 

tan d d 1 tan d

cos

x t x t t t

    

Đổi cận

0 0

x t

  

;

x t



  

Khi đó

   

 

2 2

4 4

2 2

0 0 0

tan . tan

d tan 1 d tan . tan d

1 tan 1

x f x t f t

x t t t f t t

x t

 

  

 

  

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 741

 

4 4 4

2 2

0 0 0

tan

1 . tan d d tan d

cos cos

f t

f t t t f t t

t t

  

 

   

 

 

  

Suy ra

 

tan

d 6

cos

f t







Đặt

tan d d

cos

x t x t

  

Đổi cận

0 0

t x

  

;

t x



  

Khi đó

 

0 0

tan

d d

cos

f t

t f x x





 

. Vậy

 

d 6

f x x





Câu 48.12: Cho hàm số





y f x

 liên tục, đồng biến, nhận giá trị dương trên







và thỏa mãn

 



và

     

1 .

f x x f x



  

 

. Mệnh đề nào dưới đây đúng?





2613 8 2614

f  . B.





2614 8 2615

f  .





2618 8 2619

f 

. D.





2616 8 2617

f 

Lời giải

Chọn A

Hàm số





y f x

 đồng biến trên







nên suy ra









0, 0;f x x



   

Mặt khác





y f x



liên tục, nhận giá trị dương trên







nên

           

1 1

f x x f x f x x f x

 

     

 





0;x

  





 

f x



  





0;x

  

;





 

f x

dx x dx

f x



  

 

   

f x x C

   

;

Từ

 



suy ra

2 8

3 3

 

Như vậy

   

1 2 8

3 3 3

f x x

 

   

 

 

Bởi thế:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 742

   

2 2

1 2 8 2 8

8 8 1 9

3 3 3 3 3

   

      

   

   

 

2 8

8 9

3 3

 

   

 

 

Câu 48.13: Cho hàm số





y f x

 liên tục, không âm trên



thỏa mãn

     

 

. 2 1

f x f x x f x



 

và





0 0



. Giá trị lớn nhất

và giá trị nhỏ nhất

của hàm số





y f x

 trên đoạn





1;3

lần

lượt là



;



. B.

4 11

M  ;

m  .



;

m 

. D.

3 11

M 

;

m 

Lời giải

Chọn D

Ta có

     

 

. 2 1

f x f x x f x



 









 

f x f x

f x



 



Lấy nguyên hàm hai vế ta có

 

f x x C

  

, do





0 0



nên



Vậy

 

4 2 2

2 2

f x x x x x

   

trên đoạn





1;3

Ta có

 

2 0

f x x



   



với mọi





1;3

x 

nên





f x

đồng biến trên





1;3

Vậy





3 3 11

M f  ;





1 3

m f  .

Câu 48.14: Cho hàm số





y f x



có đạo hàm liên tục trên



thỏa mãn

 

sin .cos

f x f x x x

 

  

 

 

với mọi





và





0 0



. Giá trị của tích phân

 

. d

x f x x





bằng



. B.

. C.

. D.



Lời giải

Chọn D

Bài ra





0 0



và

 

sin .cos

f x f x x x

 

  

 

 

nên

 

0 0

f f

 

 

 

 

 

 

 

 

Ta có:

 

. d

I x f x x







 

x f x



 

 



   

xf x f x x

  

 



Suy ra:

 

I f x x

 



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 743

Mặt khác,

 

sin .cos

f x f x x x

 

   

 

 

 

2 2 2

0 0 0

d d sin .cos d

2 2

f x x f x x x x x

  



 

   

 

 

  

Suy ra:

 

d d (*)

2 2

f x x f x x



 

  

 

 

 

Đặt

t x dt dx



    

   

2 2

0 0

d dt

f x x f t f x dx

 



 

     

 

 

  

Nên từ (*)

 

f x x



 



Vậy

 

I f x x

   



Câu 48.15: Cho hàm số





f x

có đạo hàm liên tục trên





0;1

thỏa mãn





1 0



 

d 7

f x x





 

 



và

 

x f x x





. Tích phân

 

f x x



bằng

. B.

. C.

. D.

Lời giải

Chọn A

Ta có

     

1 1

3 3

0 0

3 3

 



 

 

 

 

x x

x f x dx f x f x dx

. Suy ra

 

3 3



 



f x dx

Hơn nữa ta dễ dàng tính được

9 63

x 



Do đó

   

1 1 1

3 6

0 0 0

d 2.21 d 21 d 0

3 9

x x

f x x f x x x

 

  

 

 

  

 

7 d 0

f x x x



 

  

 



Suy ra







 

f x x

, do đó

 

  

f x x C

. Vì





1 0



f nên



Vậy

 

1 1

0 0

7 7

d 1 d

4 5

f x x x x

   

 

Câu 48.16: Cho hàm số





f x

có đạo hàm liên tục trên



 

 

 

thỏa mãn





0 0



   

2 2

0 0

d sin d

f x x xf x x

 





 

 

 

 

. Tích phân

 

f x x





bằng

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 744



. B.



. C.

. D.

Lời giải

Chọn D

Ta có

     

2 2

0 0

sin . cos . cos .

x f x dx x f x x f x dx

 





   

 

 

. Suy ra

 

cos









x f x dx

Hơn nữa

2 2

0 0

1 cos 2 2 sin 2

cos

2 4 4

 



 

 

  

 

 

 

x x x

xdx dx

Do đó

     

2 2 2 2

2 2

0 0 0 0

2. cos cos 0 cos 0

   

  

     

   

   

   

f x dx x f x dx xdx f x x dx

Suy ra





cos





f x x

, do đó





sin

 

f x x C

. Vì





0 0



nên



C .

Ta được

 

2 2

0 0

sin 1

 

 

 

f x dx xdx

Câu 48.17: Cho hàm số





f x

có đạo hàm liên tục trên đoạn





0;1

thỏa mãn

 

2 3

3 1

f x x f x

 



Giá trị

 

1 d

x f x

 





 

 



bằng



. B.

. C.



. D.

Lời giải

Chọn D

Đặt

2 2

u x du dx

x x

dv f dx v f

  

 

 



 

   



 

   

 

   

 

         

2 2 1

0 0 0

1 2 1 . 2 6 1 2 0 4

2 2 2

x x x

x f dx x f f dx f f f u du

     



      

     

     

  

;

0 0

;

2 1

2 2

x u

u du dx

x u

    



  



 

  



 

 

   

 

1 1 1 1

2 3 2 3 2 3

0 0 0 0

3 6

6 6 6 6 1

3 1 3 1 3 1

f x x f x f x dx x f x dx x f x dx

x x x

 

      

 

  

 

   

*Tính

 

2 3

x f x dx



Đặt

3 2

3 .

t x dt x dx

   ;

0 0, 1 1

x t x t

     

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 745

 

   

1 1 1

2 3

0 0 0

6 2 2

x f x dx f t dt f x dx

 

  

(2).

*Tính

1 1

0 0

1 3 1 2

.2 3 1

3 3 3

3 1 3 1

dx dx

x x

   

 

 

(3).

Thay kết quả (2) và (3) vào (1) ta được:

     

1 1 1

0 0 0

2 6. 4

f x dx f x dx f x dx

    

  

Thay lần lượt

0; 1

x x

 

vào

 

2 3

3 1

f x x f x

 



ta được

       

0 6; 1 6 1 3 1

f f f f

     

Vậy

         

2 1

0 0

3 2

1 6 1 2 0 4 6. 2.6 4. 4

2 5 5

x f dx f f f u du

   



         

   

   

 

Câu 48.18: Cho hàm số





f x

liên tục trên



, và các tích phân

 

f x x







 

 



 

sin . d

x f x x







Biết rằng





0 0



, tính



 

 

 

3 2



 



 

 

. B.

3 2



 



 

 

. C.

3 2



 

 

 

 

. D.

3 2



 

 

 

 

Lời giải

Chọn B

 Ta có

 

sin . d

x f x x







Đặt





d sin d

u f x

v x x

















d d

cos

u f x x

v x











 





Khi đó

 

sin . d

x f x x







   

cos . cos . d

x f x x f x x





   



 

cos . d

x f x x





 



 Xét

     

2 2 2 2

2 2

0 0 0 0

cos d d 2 cos . d cos d

f x x x f x x x f x x x x

   

  

      

   

   

1 cos 2

2. d

4 4 2



 



  



sin 2

4 2 4

x x



 

    

 

 

 

cos d 0

f x x x





  

 

 







cos 0

f x x



  





cos

f x x



  .

Suy ra





sin

f x x C

 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 746

Mà





0 0 0

f C

  

Khi đó





sin

f x x



Vậy

sin

3 3 2

 

 

 

 

 

Câu 48.19: Cho hàm số





y f x

 liên tục trên đoạn





0; 1

, thỏa mãn

   

1 1

0 0

d d 1

f x x xf x x

 

 

và

 

d 4

f x x



 

 



. Giá trị của tích phân

 

f x x

 

 



bằng

A. 1. B. 8. C. 10. D. 80.

Lời giải

Chọn C

Xét

   

f x ax b x

  

 



       

1 1 1

0 0 0

d 2 . d d

f x x f x ax b x ax b x

       

   

  

     

1 1

0 0

4 2 d 2 d

a xf x x b f x x ax b

    

 

 

4 2

a b ab b

     

Cần xác định

a b

để

 

2 2 4 0

b a b b

     

. (1)

Coi (1) là phương trình bậc hai ẩn

Ta có:

 

2 2

4 4 2 4

b b b b

      

 

b 

 

2 6

b a

    

Khi đó:

   

6 2 d 0

f x x x

   

 

 







6 2

f x x

  

Suy ra

   

1 1

0 0

d 6 2 d

f x x x x

  

 

 

 

6 2 10

  

Câu 48.20: Xét hàm số





f x

có đạo hàm liên tục trên



và thỏa mãn điều kiện





1 1



và





2 4



Tính









2 1

f x f x

J x

x x



 

 

 

 

 



1 ln 4

 

. B.

4 ln 2

 

. C.

ln 2

 

. D.

ln 4

J  

Lời giải

Chọn D

Ta có









2 1

f x f x

J x

x x



 

 

 

 

 











2 2 2

2 2

1 1 1

2 1

d d d

f x f x

x x x

x x x x



 

   

 

 

  

Đặt

   

1 1

d d

u u x

x x

v f x x v f x

 

  

 



 

 



 

 









2 1

f x f x

J x

x x



 

 

 

 

 



 









2 2 2

1 1 1

1 2 1

. d d d

f x f x

f x x x x

x x x x x

 

    

 

 

  

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 747

   

1 1 1

2 1 2 ln ln 4

2 2

f f x

 

     

 

 

Câu 48.21: Cho hàm số





y f x



liên tục trên



thỏa mãn

   

f x f f x dx





 

 



và









0 1, 1 2

f f

 

. Tích phân

 

f x dx



bằng

. B.

. C.

. D.

Lời giải

Chọn A

Đặt

















; 0 0 1, 1 1 2

t f x dt f x dx x t f x t f



          

Khi đó

     

1 2

0 1

f x f f x dx f t dt



  

 

 

Vậy

 

10.

f x dx





Câu 48.22: Cho

 

1 d 10.

x f x x 



Tính

 

cos sin d .

I xf x x











. B.





. C.



. D.



Lời giải

Chọn C

 

2 2

3 2

0 0

cos sin d 1 sin . sin .cos d

I xf x x x f x x x

 

  

 

Đặt

sin d cos d

t x t x x

  

và

0 0; 1

x t x t



     

Khi đó

 

1 d 10

I t f t t

  



Câu 48.23: Cho

 

dx 1

f x





và









dx 2

x f x







. Tích phân

 

f e



bằng

. B.



. C.

. D.



Lời giải

Chọn B

Đặt

t e



dt dx dx dx

e t

    

và 0 1; 1

x t x t e

     

Do đó:

 

0 1

f e f t



 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 748

Mặt khác theo giả thiết có:

   

 

   

 

1 1 1 1

1 1

2 1 dx dx dx dx

e e e e

x f x x f x f x

f x f x

x x x

  

      

 

 

   

Vậy

 

0 1

dx 1

f e f t

  

 

Câu 48.24: Cho hàm số

 

y f x

có đạo hàm liên tục trên



. Đồ thị của hàm số

 

y f x

như hình

vẽ bên dưới

Khi đó tổng

   

4 2

0 0

2 d 2 df x x f x x

 

  

 

bằng

. B.

2

. C.

. D.

Lời giải

Chọn D

Dựa vào đồ thị hàm số có

     

1 2, 2 2, 4 4f f f     .

Đặt

2 dt dxt x   

và

         

4 2

0 2

2 dx dt 2 2 2 2 4f x f t f f



 

        

 

Đặt 2 dt dxt x    và

       

2 4

0 2

2 dx dt 4 2 4 2 2f x f t f f

 

      

 

Vậy

   

4 2

0 0

2 dx 2 dx 6f x f x

 

   

 

Câu 48.25: Cho hàm số

 

y f x

có đạo hàm và liên tục trên  . Đồ thị của hàm số

 

y f x

như

hình vẽ bên dưới

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 749

Khi đó tổng

   

0 2

2 0

2 1 d 1 df x x f x x



 

  

 

bằng

. B.

. C.

. D.

Lời giải

Chọn A

Đặt

2 1 d 2dt x t x   

Ta có

     

0 1 1

2 3 3

1 3 2 2

d 1

2 1 d d 2

2 2 2 2

f f

f x x f t f t x

  

   

  

     

  

Đặt

1 d dt x t x   

Ta có

       

2 3

0 1

1 d d 3 1 4 2 2f x x f t t f f

 

      

 

Vậy

   

0 2

2 0

2 1 d 1 df x x f x x



 

  

 

2 2 4  

Câu 48.26: Cho hàm số

 

f x

có đạo hàm liên tục trên  thỏa mãn

 

3 1 3 2f x x x   

, với mọi

x  

.Tích phân

 

dxf x x





bằng



. B.

. C.

. D.

Lời giải

Chọn C

Từ giả thiết ta có

 

3 1 3 2f x x x   

nên suy ra

 

1 2f 

 

5 5f 

Suy ra

       

5 5 5

1 1 1

d d 23 dI xf x x xf x f x x f x x



    

  

Đặt

 

3 2

3 1 d 3 3 dx t t x t t     

Với 1 0; 5 1x t x t     

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 750

Do đó

 

  

 

5 1 1

3 2 2

1 0 0

d 3 1 3 3 d 3 2 3 3 d

f x x f t t t t t t t

       

  

Vậy

59 33

4 4

I   

Câu 48.27: Cho hàm số





f x

xác định và liên tục trên



đồng thời thỏa mãn

 

   

 

/ 2

0, x

f x

f x e f x x



  



   











. Tính giá trị của





ln 2

 

ln 2



. B.

 

ln 2



. C.

 

ln 2 ln 2

 

. D.

 

ln 2 ln 2

 

Lời giải

Chọn B

Ta có

   





 

/ 2

x x

f x

f x e f x e

f x

    

(do





f x



)





   

 

1 1

x x

f x

dx e dx e C f x

f x f x e C

         



 

Thay



ta được

 

0 1.

f C

e C



   



Vậy

   

ln 2

1 1 1 1

ln 2 .

1 1 2 1 3

f x f

e e

    

  

Câu 48.28: Cho hàm số

( )

y f x



xác định và liên tục trên



thỏa mãn





2 ( ) 3 ( ) 5

f x f x x

  

với

 



. Tính

( )

I f x dx







. B.



. C.



. D.



Lời giải

Chọn B

Đặt

3 2

( ) 2 3 5 (6 3)

t f x t t x dx t dt

        và

5 2 3 5 0 0

x t t t

      

10 2 3 5 10 1

x t t t

      

Vậy

10 1

5 0

( ) (6 3) 3

I f x dx t t dt

   

 

Câu 48.29: Cho hàm số





y f x

 liên tục trên đoạn





0;1

thỏa mãn









bf a af b

 

, với mọi





, 0;1

a b 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 751

Tính

 

I f x dx









. B.



. C.





. D.



Lời giải

Chọn C

- Đặt

sin cos

x t dx tdt

  

Với



thì



; Với



thì





Ta được:

 

sin cos

I f t tdt







Đặt

cos sin

x t dx tdt

   

Với



thì





; Với



thì



Ta được:

   

cos sin cos sin

I f t tdt f t tdt



  

 

Suy ra:

   

2 2

0 0

2 sin cos cos sin

2 4

I f t t f t t dt dt I

 

     

 

 

 

Câu 48.30: Cho hàm số





f x

liên tục trên đoạn





;

a b

thỏa mãn

 

 

2 3

6 . , ;

3 1

f x x f x x a b

   



Tính

 

f x x



. B.

. C.



. D.

Lời giải

Chọn B

Ta có:

 

2 3

6 .

3 1

f x x f x

 



 

1 1 1

2 3

0 0 0

d 2 3 d 6 d

3 1

f x x x f x x x

   



  

(*)

Đặt

3 2

u x du x dx

  

Với

0 0

x u

  

và

1 1

x u

  

Khi đó

 

   

1 1 1

2 3

0 0 0

3 d du= d

x f x x f u f x x



  

thay vào (*), ta được:

   

1 1 1

0 0 0

d 2 d 6 d

3 1

f x x f x x x

  



  

 

1 1

0 0

d 6 d 4

3 1

f x x x

  



 

Câu 48.31: Cho hàm số





f x

và





g x

có đạo hàm trên





1; 2

thỏa mãn









1 1 0

f g

 

và

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 752

 

     

   

 

2017 1

, 1; 2 .

2018

g x x x f x

g x f x x





  







 







 







Tính tích phân

   

x x

I g x f x dx

x x



 

 

 



 



. B.

. C.



. D.

Lời giải

Chọn A

Từ giả thiết ta có

 

     

   

 

2017 1

, 1; 2 .

2018

g x x x f x

g x f x x





  







 







 







Suy ra

 

   

 

   

2 2

1 1

g x g x f x f x

x x x

 



 



   

 



 

 

 

g x f x

x x



 

 

  

 



 

   

x x

g x f x x C

x x



   



Mà

         

2 2

1 1

1 1 1

1 1 0 1 1 .

x x

f g C I f x f x dx x dx

x x

 

 

           

 

 

 

Câu 48.32: Cho hàm số





y f x

 liên tục trên đoạn





0;1

và thoả mãn

 

3 4

8 0

f x x f x

  



Tích phân

 

I f x x





có kết quả dạng

a b



, ,a b c





tối giản. Tính

a b c

 

. B.



. C.

. D.



Lời giải

Chọn A

Ta có:

 

3 4

8 0

f x x f x

  



 

3 4

f x x f x

  



 

1 1 1

3 4

0 0 0

d 8 d d

I f x x x f x x x

  



  





Xét

     

1 1

3 4 4 4

0 0

8 d 2

x f x x f x d x



 

 

2 d 2

f x x I

 



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 753

Xét

x 



. Đặt

2 2 2

1 1

t x t x

    

d d

t t x x

 

Đổi cận

0 1

x t

  

1 2

x t  

Nên





1 2

0 1

1 d

t t t







 

2 2

3 3 3

 

   

 

 

Do đó

 

2 2

1 2

I I

 



  

 

 

2 2



  .Nên



Vậy

a b c

  

Câu 48.33: Cho hàm số





f x

liên tục trên đoạn





0;1

thỏa mãn điều kiện













2 1 3 6 , 0;1

f x f x x x x     

. Tính

 

I f x dx

 





. B.



. C.

 

. D.



Lời giải

Chọn C

Đặt









1 , 0;1 0;1

t x x t     

Ta có

         

2 1 3 6 2 1 3 1 3

f x f x x x f x f x x

         

















2 2

1 2 3 3 2 1 3 3

f t f t t f x f x x

         

Ta có hệ phương trình









   









   

2 2

2 1 3 6 2 1 3 6

2 1 3 3 4 2 1 6 6

3 3 6 6 2 2

f x f x x x f x f x x x

f x f x x f x f x x

f x x x f x x x

 

       

 



 

       

 

 

       

Khi đó













2 2 2 4 2

1 1 2 1 2 4 1

f x x x x x

        

Suy ra

   

1 1

2 4 2

0 0

1 4 1

I f x dx x x dx

      

 

Câu 48.34: Cho hàm số





y f x

 liên tục, nhận giá trị dương trên





 

và thỏa mãn





1 1



, biểu

thức









3 1

f x f x x



 

, với mọi



. Mệnh đề nào sau đây đúng?





2 5 3

 

. B.





4 5 5

 

. C.





1 5 2

 

. D.





3 5 4

 

Lời giải

Chọn D

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 754

Theo giả thiết ta có





 

3 1

f x











 

5 5

1 1

d d

3 1

f x

x x

f x



 



 

 





d 3 1

3 1

f x



  

 





   

ln 5 ln 1 3 1

f f x

   

   

   

 

ln 5

 

 

 

 

5 3,7937

f e   .

Vậy





3 5 4

 

Câu 48.35: Cho hàm số





y f x

 liên tục trên



thỏa mãn

 





2019 2020 2

  

f x x f x x

với mọi

thuộc





0;1

. Tích phân

 

f x dx



bằng:

1020604



. B.

2017

8072



. C.

505

2021



. D.

8076



Lời giải

Chọn C

Có

 

1 1 1

2019 2020 2

0 0 0



   

  

f x dx x f x dx x dx

Đặt

2020 2019

2020.  

t x dt x dx

và

 

   

1 1 1

2019 2020

0 0 0

1 1

2020 2020

 

  

x f x dx f t dt f x dx

Vậy

 

   

1 1 1 1

2019 2020

0 0 0 0

2021 505

4 2020 4 2021

  

     

   

f x dx x f x dx f x dx f x dx

Câu 48.36: Cho hàm số





f x

có đạo hàm liên tục trên đoạn





4;8

và





f x







4;8

x  . Biết rằng

 

dx 1

f x



 

 



 

 



và

 



 



. Tính





. B.

. C.

. D.

Lời giải

Chọn D

Ta có:

( ) 1 1 1

d 2

( ) ( ) (8) (4)

f x

f x f x f f



 

     

 

 



(1).

Gọi

là một hằng số thực, ta sẽ tìm

để

( )

d 0

( )

f x

k x

f x



 

 

 

 



Ta có

 

8 8 8 8

2 2

42 2

4 4 4 4

( )

( ) ( )

d d 2 d d 1 4 4 1 2

( ) ( )

( )

f x

f x f x

k x x k x k x k k k

f x f x

f x



 

   

        

   

   

   

  

thì

8 6 6

2 2 2

4 4 4

( ) 1 ( ) 1 ( ) 1

d 0 d d

( ) 2 ( ) 2 ( ) 2

f x f x f x

x x x

f x f x f x

  

 

     

 

 

  

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 755

 

( ) 1 1 1 1 1

1 1 1 4 1 6

( ) ( ) (4) (6) (6) 3

df x

f x f x f f f

            



Chú ý:

 

f x dx





không được phép suy ra





f x



nhưng

   

0 0

f x dx f x

  

 

 



Câu 48.37: Cho hàm số





f x

liên tục trên





0;1

thỏa mãn điều kiện





 

 

2 2

4 3 1 1 , 0;1

     xf x f x x x

. Khi đó

 



f x x

bằng



. B.



. C.



. D.



Lời giải

Chọn A

Vì





f x

liên tục trên





0;1

và





 

 

2 2

4 3 1 1 , 0;1

     xf x f x x x

nên ta có

 

   

1 1 1 1 1

2 2 2 2

0 0 0 0 0

4 . 3 1 d 1 4 . 3 1 1 1

 

        

 

    

x f x f x x x dx x f x dx f x dx x dx

Lại có

     

 

1 1 1

2 2 2

0 0 0

4 . 2 2 2



  

  

t x

x f x dx f x d x f t dt I

và

       

1 1 1

0 0 0

3 1 3 1 1 3 3 .

 

      

  

u x

f x dx f x d x f u du I

Đồng thời

 

2 2 2

sin

2 2 2

0 0 0 0

1 1 sin .cos cos 1 cos 2 .

2 4

  





      

   

x t

x dx t tdt tdt t dt

Vậy

   

1 2 3 d

4 20 20

  

      



I I I f x x

Câu 48.38: Cho

 

f x dx





và





x f x







. Tính

 

tan

I f x dx









. B.

 

. C.



. D.

 

Lời giải

Chọn B

Đặt





tan 1 tan d

t x dt x x

    Và

0 0;

x t

  

x t



  

Do đó

 

   

1 1

4 4

2 2 2

0 0 0 0

tan

tan . 1 tan . .

1 tan 1 1

f x f t f x

I f x dx x dx dt dx

x t x

 

    

  

   

Ta có :

 









1 1

2 2

0 0

1 1

2 2

1 1

x f x

dx dx

x x

 

 

 

  

 

 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 756

 





1 1

0 0

2 1 2 1

f x

f x dx dx I I

        



 

Câu 48.39: Cho





f x

liên tục trên





\ 0



thỏa mãn

 

   

2 3

2 2, \ 0

xf x f x x x

      . Giá

trị của

tích phân

 

f x x



thuộc khoảng nào sau đây?





5;6

. B.





3; 4

. C.





1; 2

. D.





2;3

Lời giải

Chọn D

Ta có

 

   

2 3

2 2, \ 0

xf x f x x x

     

 

2 2

2 3

1 1

2 2

xf x f x dx x dx

 

 

    

 

 

 

 

   

2 2

1 1

1 1 1

2 2 ln 2

2 2 4 2

f x d x f x d x x x

 

    

 

 

 

       

4 4 4 4

1 2 1 2

1 1 7 1 1 1 7 1

ln 2 ln 2

2 2 4 2 2 2 4 2

u x

v x

f u du f v dv f x dx f x dx



       

   

     

2 4 4

1 2 2

1 1 7 1

ln 2

2 2 4 2

f x dx f x dx f x dx

 

    

 

 

  

   

2 2

1 1

1 7 1 7

ln 2 ln 2 2.80852819.

2 4 2 2

f x dx f x dx      

 

Câu 48.40: Cho hàm số





f x

liên tục trên



thỏa mãn





 

d cot . sin d 1

f x

x x f x x



 

 

. Tích

phân





f x



bằng

. B.

. C.

. D.

Lời giải

Chọn A

Đặt

d 2 d

t x t x x t t

    

. Đổi cận

1 1; 16 4

x t x t

     

Suy ra





     

16 4 4 4

1 1 1 1

1 d .2 d 2 d d

f x

f t f t f t

x t t t t

x t t t

    

   

Đặt

d d d

sin d 2sin cos d cot d cot .

2sin cos 2 sin 2

t t t

t x t x x x x x x

x x x t

      

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 757

Đổi cận

; 1

4 2 2

x t x t

 

     

Do đó

 









1 1 1

2 2 2

d 1 1

1 cot . sin d . d d

2 2 2

f t f t

x f x x f t t t

t t t



    

   

Đặt

4 d 4d

t x t x

  

. Đổi cận

1 1

; 1 4

8 2

x t x t

     

Suy ra





















1 4 4 1 4

1 1 1 1

8 2 2 2

4 d

d 1 5

. .d d d 2

4 2 2

f x x f t f t f t f t

t t t

x t t t

      

    

Bấm Tải xuống để xem toàn bộ.

| 1/27

| | Tải xuống

Preview text:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
TÍCH PHÂN LIÊN QUAN ĐẾN PHƯƠNG TRÌNH HÀM ẨN
KIẾN THỨC CẦN NHỚ:
1. Các tính chất tích phân: b c b
 f  x dx  f  x dx  f  x dx   
với a  c  b . a a c b b
 k f  xdx  kf  x dx k  0   a a b a
 f  x dx   f  x dx   a b b b
 f  x dx  F  x  F b  F a  a a b b b
  f x g xdx  f xdx  g xdx   a a a b b b
 f  x dx  f t  dt  f  z dz    a a a b b
 f  x dx  f  x  f b  f a  a a
2. Công thức đổi biến số:
f u  x.u x dx  f u du, u  u  x   ub b  f
 u  x.uxdx 
f u  du, u  u  x  a ua
Phương pháp đổi biến số thường được sử dụng theo hai cách sau đây: b  Giả sử cần tính
g  x dx 
. Nếu ta viết được g  x dưới dạng f u  xu x thì a ub b  u b
g  x dx 
f u  du  
. Vậy bài toán quy về tính
f u  du 
, trong nhiều trường hợp thì tích phân mới a u a u a này đơn giản hơn .   Giả sử cần tính
f  x dx 
. Đặt x  x t  thỏa mãn   x a,   x b thì   b b
f  x dx  f 
 xt xt dt  g t dt 
, trong đó g t   f  x t .xt   a a Trang 731
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 BÀI TẬP MẪU
Cho hàm số f  x liên tục trên  , và thỏa mãn xf  3 x   f  2  x  10 6 1
 x  x  2x, x   .  0 Khi đó
f  x dx  bằng 1  1  7 1  3 17 A. . B. . C. . D. 1  . 20 4 4
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Tính tích phân hàm ẩn.
...................................................................................................................................................................
2. KIẾN THỨC CẦN NHỚ: b u (b)
Công thức đổi biến số trong tích phân: f u(x).u (  x) dx  f (u) du   a u( a)  Tính chất tích phân: a
f (x) dx  0  a b c b
f (x) dx 
f (x) dx  f ( ) x dx    a a c b x b  f (
 x) dx  f (x)
 f (b)  f (a)  xa a
................................................................................................................................................................... 3. HƯỚNG GIẢI: 1
B1: Nhân cả hai vế của phương trình với x , rồi sử dụng tích phân hai vế để tính
f  x dx  . 1 1
B2: Nhân cả hai vế của phương trình với x , rồi sử dụng tích phân hai vế để tính f  xdx  . 0 0 B3: Kết luận
f  x dx  . 1 
Từ đó, ta có thể giải bài toán cụ thể như sau: Lời giải Chọn B
Cách 1 : Dùng vi phân Ta có: xf  3 x   f  2  x  10 6 1
 x  x  2 , x x    Trang 732
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2  x f  3 x   xf  2  x  11 7 2 1
 x  x  2x , x    * 1 1 1 Khi đó: * 2  x f  3
x  dx  xf  2
1 x  dx   11 7 2
x  x  2x  dx, x       1 1 1 1 0 1 1 4 
f t  dt 
f t dt     3 2 3 1  0 1 1 1 1 4 
f t  dt  0   
f t  dt  4 
f  x dx  4    3 3 1 1 1 1 1 1 Mặt khác: * 2  x f   3
x dx  xf   2
1 x dx   11 7 2
x  x  2x  dx 0 0 0 1 0 1 1 5 
f t  dt 
f t  dt     3 2 8 0 1 1 5 5 1 3 1 3 
f t dt    
f t  dt    
f  xdx    6 8 4 4 0 0 0 0 1 1 1  3
Theo tính chất tích phân ta có:
f  xdx 
f  xdx  f  xdx     4 1  1  0
Cách 2: (Tham khảo không giống phân tích ở trên)
Bậc cao nhất vế phải là 10
x , bậc cao nhất vế phải là  3 .
x f x  . Kết luận: f  x bậc 3 vì  3 3 10 . x x  x .
Hệ số của bậc cao nhất vế phải là 1. Kết luận: Hệ số của bậc cao nhất vế trái là 1  . Vậy   3 2
f x   x  ax  bx  c .
x f  x   x  x a  x 2 3 10 3 10 7 . .
 ...  x  ax  ... Vế phải không có 7
x . Vậy a  0 Kết luận   3
f x  x  bx  c .
x f  x   f   x   x  bx  cx    x 3 3 2 10 4 2  b  2 . 1 1 1 x   c 10 4 2 4 6 2
 x  bx  cx 1 3x  3x  x  b  bx  c 10 6
 x  x  b   4
x    b 2 3 3
x  cx  b  c 1
Đồng nhất hệ số được b  3; c  2  . 0 13
Tóm lại f  x 3
 x  3x  2 . Suy ra
f  xdx   . 4 1
Bài tập tương tự và phát triển:
Câu 48.1: Cho hàm số y  f  x liên tục trên  thỏa mãn f  x f  x  x  2x2x 1 3 2 2 1 e       4 . Trang 733
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 Khi đó I 
f  x dx  bằng 0
A. I  e  4 . B. I  8 . C. I  2 .
D. I  e  2 . Lời giải Chọn C 2 2
Ta có 3 f  x  f 2  x dx 
2 x   2x2x 1 1 e    4 dx       0 0 2 2 2 2
 3 f  x dx
f 2 x dx 2 x  2x2x 1 1 e      dx  4 dx     0 0 0 0 2 2 2 2
 3 f  x dx
f 2 x d 2 x x 2 x 1 e      d     2 x  2x   1  8 0 0 0 2 2 2
 3 f  x dx f  x 2 x 2 x 1 dx e     8   0 0 0 2
 4 f  xdx  8 0 2 
f  x dx  2  . 0
Câu 48.2: Cho hàm số y  f  x liên tục trên 0;  thỏa mãn f ln x  f 1 ln x  x . 1 Khi đó I 
f  x dx  bằng 0 e 1 e 1 e 2 A. . B. . C. . D. . 2 2 2 e 1 Lời giải Chọn A 1 1
Ta có f ln x  f 1 ln x  x  f ln x 
f 1 ln x  1  x x
Lấy tích phân từ 1 đến e cả hai vế của  , ta được e  1 1 e  f ln x 
f 1 ln x dx  dx    x x    1 1 e 1 e 1 
f ln x dx 
f 1 ln x dx  e 1   x x 1 1 e e 
f ln x d ln x  f 1 ln xd 1 ln x  e 1    1 1 Trang 734
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
x  1  t  0
Đặt t  ln x . Đổi cận x  e  t 1 1 1 Khi đó   
f  x dx  f 1 t  d 1 t   e 1   0 0 1 1 
f  x dx  f  x dx  e 1   0 0 1 e 1 
f  x dx   . 2 0  f   1  2 ln 2 
Câu 48.3: Cho hàm số y  f  x liên tục trên  \ 0;  
1 thỏa mãn  f 2  a  b ln 3; a,b   .
xx  1.f x f x 2  x  x  Tính 2 2 a  b . 25 9 5 13 A. . B. . C. . D. . 4 2 2 4 Lời giải Chọn B
Ta có x  x   f  x  f  x 2 1 .  x  x (1) x 1 x
Chia cả 2 vế của biểu thức (1) cho  x  2 1 ta được
. f   x  f x  2   x 1 x   1 x 1 x    x  . f  x    , với x   \ 0;   1 .  x 1    x 1 x x  . f  x  dx  x 1 x 1 x 
. f  x  x  ln x 1  C x 1 x 1
 f  x 
 x  ln x 1  C x
Mặt khác, f 1  2 ln 2  2 1 ln 2  C   2
 ln 2  C  1 . x 1
Do đó f  x 
 x  ln x 1   1 . x 3 3 3 3 3
Với x  2 thì f  x  1 ln 3   ln 3. Suy ra a  và b   . 2 2 2 2 2 9 Vậy 2 2 a  b  . 2 Trang 735
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Câu 48.4: Cho hàm số y  f  x có đạo hàm liên tục trên  . Biết f  
1  e và  x   f  x  x f  x 3 2 . .  x 1 với x    . Tính
f  xdx  . 0 1 2 2 1 2 4 A.   . B. e  . C. e  . D. e   . e 3 3 e e 3 Lời giải Chọn D 
xf  x   x  2 f  x
 ex f  x 
Ta có:  x   f  x  x f  x 3 2 . .  x   1   ex 3   x 2 x   ex f  x 
 exdx  ex   C    2     2 2 . ex f x x C x x 1 Vì f  
1  e  1 C.e  e  C  1 e  1  Do đó   2 2    1 . ex f x x x    e  1 1 1 1   1   x  1  Vậy   2 2 2 2 d    1 . e d   d  1 ex f x x x x x x x x dx             e    e  0 0 0 0 1 1 1 1 1     x 1  1  x 1  1 2     1 d    e     1 e  2 e d    1 2 1 d         ex x x x e x . 3  e  3  e  3  e  0  0  0 1 2 1     x 2  1  4 2   e  2 1 e  e dx   e  2 1 e         e   1     e  3 e 3 e       3 e  0   2  15x
Câu 48.5: Cho hàm số y  f  x liên tục trên  \   0
và thỏa mãn 2 f 3x  3 f     ,  x  2 3 9 2  1 
f  x dx  2019  . Tính I  f dx    .  x  3 1 2 688 688 886 68 A. I   . B. I  . C. I  . D. I  . 3 3 3 3 Lời giải Chọn A 3 1 x   t  1 2  1  1 2 Xét I  f dx
   . Đặt t  2x  dx  dt . Đổi cận .  x 2 3 1  x   t  3 2 2 Trang 736
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 3 1  2  Khi đó I  f dt    . 2  t  1  2  15x  2  5x 2  2  5t 2
Mà 2 f 3x  3 f      f    f   3x hay f    f   3t   x  2  x  2 3  t  2 3 3 3 3 3 1  5t 2  5 1 1 Nên I   
f 3t  dt   t dt 
f 3t  dt  5  
f 3t  dt       1 2  2 3    4 3 3 1 1 1 1 1
t  1  u  3
Đặt u  3t  dt  du . Đổi cận . 3
t  3 u  9 9 1 2019 688 Khi đó I  5 
f u du  5     . 9 9 3 3  1 
Câu 48.6: Cho hàm số f  x có đạo hàm liên tục trên  \  
0 và thỏa mãn 2 f 2x 2  f  x   ,  x  2 2  2 
xf  x dx  5  . Giá trị f dx    bằng  x  1 1 103 103 103 103 A.  . B. . C. . D.  . 48 24 48 12 Lời giải Chọn D u   x du  dx Đặt    . dv  f (  x)dx 
v  f (x)  2 2 2 2 Ta có .
x f   x dx  .
x f  x  f  x dx  
 5  2 f 2  f   1 
f  x dx  (1) 1 1 1 1 1  1 
Lần lượt thay x  1 và x 
vào 2 f 2x 2  f  x   ta được 2  x   3
2 f 2  f   1  1 f 2     4  1   . 2 f   1  f 2   1   4 f   1    2 2 1 2 1 Khi đó   1 
f  x dx  2 f 2  f   1  5  4  
f 2x dx 
f  x dx  2   . 2 1 1 1 2 1 1 1 1  1   1   1  7
Lại có 2 f 2x 2  f  x 2  
 2 f 2x dx  f dx  x dx       2.(2)  f dx      x   x  x  24 1 1  1 1 2 2 2 2 1  1  7 103  f dx  4       .  x  24 24 1 2 Trang 737
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 2 2 2 1 1  2  2 1 Đặt t   x   dx   dt ta có f dx  f (t). dt      2 f (t). dt  (2) x t 2 t 2  x  t 2 t 1 2 2 1 1 1 1 1  1  1 1 1 103 Đặt u   x   dx   du ta có f dx  f (u). du      f (t). dt    . x u 2 u 2  x  u 2 t 24 1 2 2 2 2  2   103  103 Thay vào (2) ta được f dx  2.         .  x   24  12 1
Câu 48.7: Cho hàm số f  x có đạo hàm liên tục trên đoạn 0; 
1 đồng thời thỏa mãn f 0  9 và
f  x   f  x 2 9  x  9  
. Tính T  f   1  f 0 . 1
A. T  2  9 ln 2 . B. T  9 . C. T   9 ln 2 .
D. T  2  9 ln 2 . 2 Lời giải Chọn C
f  x 1 1
Ta có f  x   f  x 2 9  x  9   
 f  x      f  x 2 9 1  x        .
 f  x 2 9  x     1  1 1 1 1 x 9       dx   
 C  f   x  x 
f  x  x 9  
f  x  x 9
f  x  x 9 x  9C 1 9
Do f  0  9 nên C 
 f  x   x 9 x  1 1 1 2  9   x  1
Vậy T  f   1  f 0   x dx     9 ln x 1     9 ln 2  .  x 1  2 2 0   0
Câu 48.8: Cho hàm số f  x nhận giá trị dương, có đạo hàm liên tục trên đoạn 0;2 . Biết f 0  1 và  3 2 2
x  3x  f  x     2 2 4 . 2 e x x f x f x   
, với mọi x 0; 2
 . Tính tích phân I  dx  . f x 0   16 16 14 32 A. I   . B. I   . C. I   . D. I   . 3 5 3 5 Lời giải Chọn B Ta có     2 2 4 . 2 e x x f x f x          2 2 4 ln . 2  ln e x x f x f x       f  x  f   x 2 ln ln 2
 2x  4x  Trang 738
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  f
 0. f  2  1
Mặt khác, với x  0 , ta có 
nên f 2  1 . f  0  1   3 2 2
x  3x  f  x 2 f  x Xét I  dx     3 2 x  3x    . dx f x f x 0   0   2   3 2
x  3x  d ln  f  x    0 2   2  3 2
x  3x ln  f  x      2
3x  6x.ln  f  x dx   0 0 2   2
3x  6x.ln f  xdx 0 2   2
6x  3x .ln  f  x dx     1 0
x  0  t  2
Đặt t  2  x  dx  dt . Đổi cận x  2  t  0 0 2
Do đó I   32  t t.ln  f 2  t  dt       2
6t  3t .ln  f 2  t  dt   2 0 2
Vì tích phân không phụ thuộc vào biến nên I   2
6x  3x .ln  f 2  x dx   2 0 2 Cộng 2 vế của  
1 và 2 , ta được 2I   2
6x  3x .ln  f  x  ln  f 2  x     dx 0 2 1 Hay I   2
6x  3x .ln  f  x  ln  f 2  x     dx  2 0 2 1 16
Thế  vào  , ta có I   2
6x  3x . 2
2x  4x dx    2 5 0 1
Câu 48.9: Cho hàm số f  x nhận giá trị dương, có đạo hàm liên tục trên 0; thỏa mãn f 2  và 15 1 a c
f  x   x   2 2
4 f  x  0 . Biết f  x dx  ln 
, với a,b,c   . Tính S  a  b  c . b 2 0 A. S  3 . B. S  4 . C. S  5 . D. S  6 . Lời giải Chọn D f  x
Do f  x  0 , với mọi x  0;  nên f  x   x   2 2
4 f  x  0    2x  4 . 2 f  x Trang 739
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 1 Suy ra 2
 x  4x  C . f  x 1 1
Mặt khác f 2 
nên C  3 hay f  x  . 15 2 x  4x  3 1 1 dx 1 3 Vậy
f  x dx   ln  
 a  1, b  2, c  3  S  6 2 x  4x  3 2 2 0 0  f
 0  f 0  1
Câu 48.10: Cho hàm số y  f  x có đạo hàm trên  thỏa mãn  f
  x  y   f  x   f  y   3xy  x  y  1  1
, với x, y   . Tính
f  x  1dx  . 0 1 1 1 7 A. . B.  . C. . D. . 2 4 4 4 Lời giải Chọn C
Lấy đạo hàm theo hàm số y
f   x  y  f  y  2
 3x  6 xy , x   .
Cho y   f  x  f   2 0
0  3x  f  x 2  1 3x       3 f x f
x dx  x  x  C 
mà f 0  1  C  1. Do đó f  x 3
 x  x  1 . 1 0 0 1 Vậy f  x   1 dx  
f  x dx    3 x  x   1 dx   . 4 0 1 1  4 1 2 x f  x
Câu 48.11: Cho hàm số f  x liên tục trên  và biết f tan xdx  4  , dx  2  . 2 x  1 0 0 1 Giá trị của tích phân
f  xdx 
thuộc khoảng nào dưới đây? 0 A. 5;9 . B. 3;6 . C.  2;5. D. 1;4 . Lời giải Chọn A 1
Đặt x  tan t  dx  dt   2 1  tan t dt 2  cos t 
Đổi cận x  0  t  0 ; x  1  t  4   1 2 x f  x 4 2
tan t. f  tan t  4 Khi đó dx 
tan t  1 dt  tan t. f tan t dt  2  2  2  2    x  1 tan t  1 0 0 0 Trang 740
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020    4 4  1  f tan t  4  1 . f  
tant dt  dt 
f  tan t dt 2  2  .  cos t  cos t 0 0 0  4 f tan t  Suy ra dt  6  2 cos t 0 1
Đặt x  tan t  dx  dt 2 cos t 
Đổi cận t  0  x  0 ; t   x  1 . 4  4 f tan t  1 1 Khi đó dt 
f  xdx  f x dx  6 2  . Vậy    . cos t 0 0 0
Câu 48.12: Cho hàm số y  f  x liên tục, đồng biến, nhận giá trị dương trên 0;  và thỏa mãn 2 2 f 3 
và  f   x   x   1 . f  x  
. Mệnh đề nào dưới đây đúng? 3 A. 2
2613  f 8  2614 . B. 2
2614  f 8  2615 . C. 2
2618  f 8  2619 . D. 2
2616  f 8  2617 . Lời giải Chọn A
Hàm số y  f  x đồng biến trên 0;  nên suy ra f  x  0, x  0; .
Mặt khác y  f  x liên tục, nhận giá trị dương trên 0;  nên
 f   x 2    x  
1 f  x  f  x   x   1 f  x   , x  0;  f  x    x   1 , x  0;  ; f  x f  x 1  dx   x   1 dx    f  x   x  3 1  C ; f  x 3 2 2 8
Từ f 3  suy ra C   3 3 3 2  1  3 2 8
Như vậy f  x    x   1     3 3 3    Bởi thế: Trang 741
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 2 4  1 2 8   2 8   2 8  f 8  2  8  3 1     9 
   f 8  9   .   3 3 3   3 3        3 3  
Câu 48.13: Cho hàm số y  f  x liên tục, không âm trên  thỏa mãn f  x f  x  x  f  x2 . 2 1 và
f 0  0 . Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y  f  x trên đoạn 1;  3 lần lượt là
A. M  20 ; m  2 .
B. M  4 11 ; m  3 .
C. M  20 ; m  2 .
D. M  3 11 ; m  3 . Lời giải Chọn D
f  x. f  x
Ta có f  x f  x  x  f  x2 . 2 1   2x .
 f x2 1
Lấy nguyên hàm hai vế ta có  f  x2 2
1  x  C , do f 0  0 nên C  1. Vậy f  x 4 2 2 
x  2x  x x  2 trên đoạn 1;  3 . 2 x
Ta có f   x 2  x  2 
 0 với mọi x 1; 
3 nên f  x đồng biến trên 1;  3 . 2 x  2
Vậy M  f 3  3 11 ; m  f   1  3 .  π 
Câu 48.14: Cho hàm số y  f  x có đạo hàm liên tục trên  thỏa mãn f  x  f  x  sin . x cos x   ,  2  π 2
với mọi x   và f 0  0 . Giá trị của tích phân .
x f   x dx  bằng 0 π 1 π 1 A.  . B. . C. . D.  . 4 4 4 4 Lời giải Chọn D  π   π   π 
Bài ra f 0  0 và f  x  f  x  sin . x cos x  
nên f 0  f  0    f  0   .  2   2   2  π π π 2 2 π 2 Ta có: I  .
x f  x dx   d
x  f  x  2 
  xf  x 
f  x dx    0 0 0 0 π 2
Suy ra: I   f  x dx  . 0 Trang 742
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Mặt khác,     π     1
f  x  f  x  sin . x cos x  2 2 2  
f  x dx  f  x dx  sin .
x cos x dx        2  0 0 0  2  2  0    1
Suy ra: 2 f  x dx     f x dx (*)     0  2  2 2    0    Đặt t 
 x  dt  dx 2        f x dx f    t  2 dt
f  x dx   2 0 0  2 2   1 Nên từ (*) 2 
f  x dx  0 4 π 2 1
Vậy I   f  x dx    . 4 0 1 2
Câu 48.15: Cho hàm số f  x có đạo hàm liên tục trên 0;  1 thỏa mãn f   1  0,
 f  x dx  7    và 0 1 1 1 2
x f  x dx   . Tích phân
f  x dx  bằng 3 0 0 7 7 A. . B. 1. C. . D. 4 . 5 4 Lời giải Chọn A 1 1 3 1 3  x  x 1 3 x 1 Ta có 2
x f  xdx    f  x  f    x  dx . Suy ra
f  x dx    . 3 3 3 3 0   0 0 0 1 6 x 1
Hơn nữa ta dễ dàng tính được dx   . 9 63 0 1 1 3 1 6 1 2 x x 2
Do đó  f  x dx  2.21 f  x 2 dx  21 dx  0  3    
  f  x  7x  dx  0  . 3 9   0 0 0 0 7 7
Suy ra f  x 3  7
 x , do đó f  x 4  
x  C . Vì f   1  0 nên C  . 4 4 1 1 7 7 Vậy
f  x dx    4 x   1 dx    . 4 5 0 0   
Câu 48.16: Cho hàm số
f  x có đạo hàm liên tục trên 0;  thỏa mãn f 0  0, 2       2 2  2
 f  x 2
 dx  sin xf  x dx      . Tích phân
f  xdx  bằng 4 0 0 0 Trang 743
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020   A. . B. . C. 2 . D.1. 4 2 Lời giải Chọn D    2  2 2  Ta có sin .
x f  x dx  cos . x f  x 2   cos .
x f  x dx     . Suy ra cos     x f x dx . 0 4 0 0 0    2 2 2 1  cos 2x
 2x  sin 2 x   Hơn nữa 2 cos xdx  dx     . 2  4    4 0 0 0     2 2 2 2 2 2
Do đó  f  x dx  2. cos x f  x 2
dx  cos xdx  0   f  x  cos x dx  0         . 0 0 0 0
Suy ra f  x  cos x , do đó f  x  sin x  C . Vì f 0  0 nên C  0 .   2 2 Ta được
f  x dx  sin xdx  1   . 0 0 6 2 3
Câu 48.17: Cho hàm số f  x có đạo hàm liên tục trên đoạn0; 
1 thỏa mãn f  x  6x f  x   . 3x 1 2  x 
Giá trị  x   1 f  dx    bằng  2  0 8 4 12 2 A.  . B. . C.  . D. . 5 5 5 5 Lời giải Chọn D u   x 1 du  dx   Đặt  x      x  dv  f  dx v  2 f         2    2  2 2 2 1  x   x   x   x   1 f  dx  2     x   1 . f  2 f dx  6 f       
1  2 f 0  4 f u du  ;  2   2   2  0 0 0 0  x 1
x  0  u  0  u   du  dx;    . 2 2
x  2  u  1    1 1 1 1 3  6  dx f  x 2  6x f  3 x    f x 2 dx  6x f    3x 2  dx  6x f    3xdx6   1  3x 1  3x 1  3x 1 0 0 0 0 1 *Tính 2 6x f  3 x dx  . 0 Đặt 3 2
t  x  dt  3x .dx ; x  0  t  0, x 1  t  1. Trang 744
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 1 1 1 2 6x f   3
x dx  2 f tdt  2 f  x dx   (2). 0 0 0 1 1 1 dx 1 3dx 1 2 *Tính   .2 3x 1    (3). 3x 1 3 3x 1 3 3 0 0 0 1 1 1 2
Thay kết quả (2) và (3) vào (1) ta được:
f  x dx  2 f  x dx  6.  f  x dx  4     . 3 0 0 0 6
Thay lần lượt x  0; x  1 vào f  x 2  6x f  3 x   ta được 3x 1 3
f 0  6; f   1  6 f   1  3  f   1   5 2 1  x   3  2 Vậy  x   1 f 
dx  6 f  
1  2 f 0  4 f u du  6.   2.6  4. 4           2   5  5 0 0   2 2 2  
Câu 48.18: Cho hàm số f  x liên tục trên  , và các tích phân  f  x dx     , sin .
x f  x dx   . 4 4 0 0   
Biết rằng f 0  0 , tính f   .  3     1    3    1    3 A. f    . B. f    . C. f     . D. f     .  3  2  3  2  3  2  3  2 Lời giải Chọn B  2   Ta có sin .
x f  x dx   . 4 0 u 
  f  x 
du  f   x dx Đặt    .
dv  sin xdx 
v   cos x    2   2  Khi đó sin .
x f  x dx     cos .
x f  x 2  cos .
x f  x dx   4 0 4 0 0  2   cos .
x f  x dx   . 4 0     2 2 2 2 2 2  Xét
 f  x  cos x dx   f  x dx  2 cos . x f   x 2 dx  cos d x x         0 0 0 0   2   1 cos 2x 2   x sin 2x    2.  dx       0   . 4 4 2 4  2 4  0 0  2
  f  x 2
 cos x dx  0   
 f  x  cos x  0  f  x  cos x . 0
Suy ra f  x  sin x  C . Trang 745
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Mà f 0  0  C  0 .
Khi đó f  x  sin x .     3 Vậy f  sin    .  3  3 2 1 1
Câu 48.19: Cho hàm số y  f  x liên tục trên đoạn 0;  1 , thỏa mãn
f  x dx  xf  x dx  1   và 0 0 1 1 3  f  x 2  dx  4    . Giá trị của tích phân
 f  x dx    bằng 0 0 A. 1. B. 8. C. 10. D. 80. Lời giải Chọn C 1 1 1 1 2 2 2
Xét  f  x  ax  b dx   
  f  x dx  2  f  x.ax  b dx  ax  b dx        0 0 0 0 1 1 1 1 2 a
 4  2a xf  xdx  2b f  x dx  ax  b3  
  a  b 2 4 2   ab  b . 3a 3 0 0 0 2 a
Cần xác định a, b để    b 2 2
a  b  2b  4  0 . (1) 3
Coi (1) là phương trình bậc hai ẩn a . 4 b  2 2 Ta có: 2
  b  4b  4   2
b  2b  4 
 0  b  2  a  6  . 3 3 1 2
Khi đó:  f  x  6x  2 dx  0   
 f  x  6x  2 . 0 1 1 1 3 3 1 Suy ra 4
 f  x dx  6x  2 dx      6x  2  10 . 24 0 0 0
Câu 48.20: Xét hàm số f  x có đạo hàm liên tục trên  và thỏa mãn điều kiện f  
1  1 và f 2  4 .
2  f  x  2
f  x 1 Tính J   dx   . 2  x x 1   1 1
A. J  1 ln 4 .
B. J  4  ln 2 .
C. J  ln 2  . D. J   ln 4 . 2 2 Lời giải Chọn D
2  f  x  2
f  x 1 2 f  x 2 f  x 2  2 1  Ta có J   dx   dx  dx   dx . 2      x x 2 2 x x  x x  1   1 1 1  1  1 u  du   dx   Đặt 2 x   x  .
dv  f  xdx v
  f  x  
2  f  x  2
f  x 1 2 2 1 f  x 2 f  x 2  2 1  J   dx    . f  x  dx  dx   dx 2      x x 2 2 2 x x x  x x  1   1 1 1 1 Trang 746
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 1  1  1 
f 2  f   1  2 ln x    ln 4   . 2  x  2 1 1 Câu 48.21:
Cho hàm số y  f  x liên tục trên  thỏa mãn
f  x f  f  x dx  10    và 0 2
f 0  1, f 1  2 . Tích phân f  x dx  bằng 1 A. 10 . B. 3 . C. 1. D. 30 . Lời giải Chọn A
Đặt t  f  x  dt  f  x dx; x  0  t  f 0  1, x  1  t  f 1  2 . 1 2 Khi đó 10 
f   x f  f  x dx  f t  dt     . 0 1 2 Vậy
f  x dx  10. 1  1 2 Câu 48.22: Cho  2
1 x  f  x dx  10. Tính 3
I  cos xf sin xd . x  . 0 0
A. I  5 .
B. I  10 . C. I  10 . D. I  5 . Lời giải Chọn C   2 2 3
I  cos xf sin x dx    2
1 sin x. f sin x.cos d x x . 0 0 
Đặt t  sin x  dt  cos d
x x và x  0  t  0; x   t  1 . 2 1 Khi đó I   2
1  t  f t dt  10 . 0 e e  x   1 f  x 1 Câu 48.23: Cho
f  x dx  1  và dx  2  . Tích phân  x f e  dx bằng x 1 1 0 A. 3 . B. 1  . C. 1. D. 3 . Lời giải Chọn B x dt Đặt x
t  e  dt  e dx  tdx  dx 
và x  0  t 1; x  1 t  e . t 1 e x dt Do đó: f
 e dx  f t  . t 0 1 Trang 747
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Mặt khác theo giả thiết có: e    1   e e    1   e x f x x f x  f  x 2 1  dx 
f  x dx   f      x dx   dx   . x x x 1 1 1   1 1 e x dt Vậy
f e  dx  f t  1    . t 0 1 Câu 48.24:
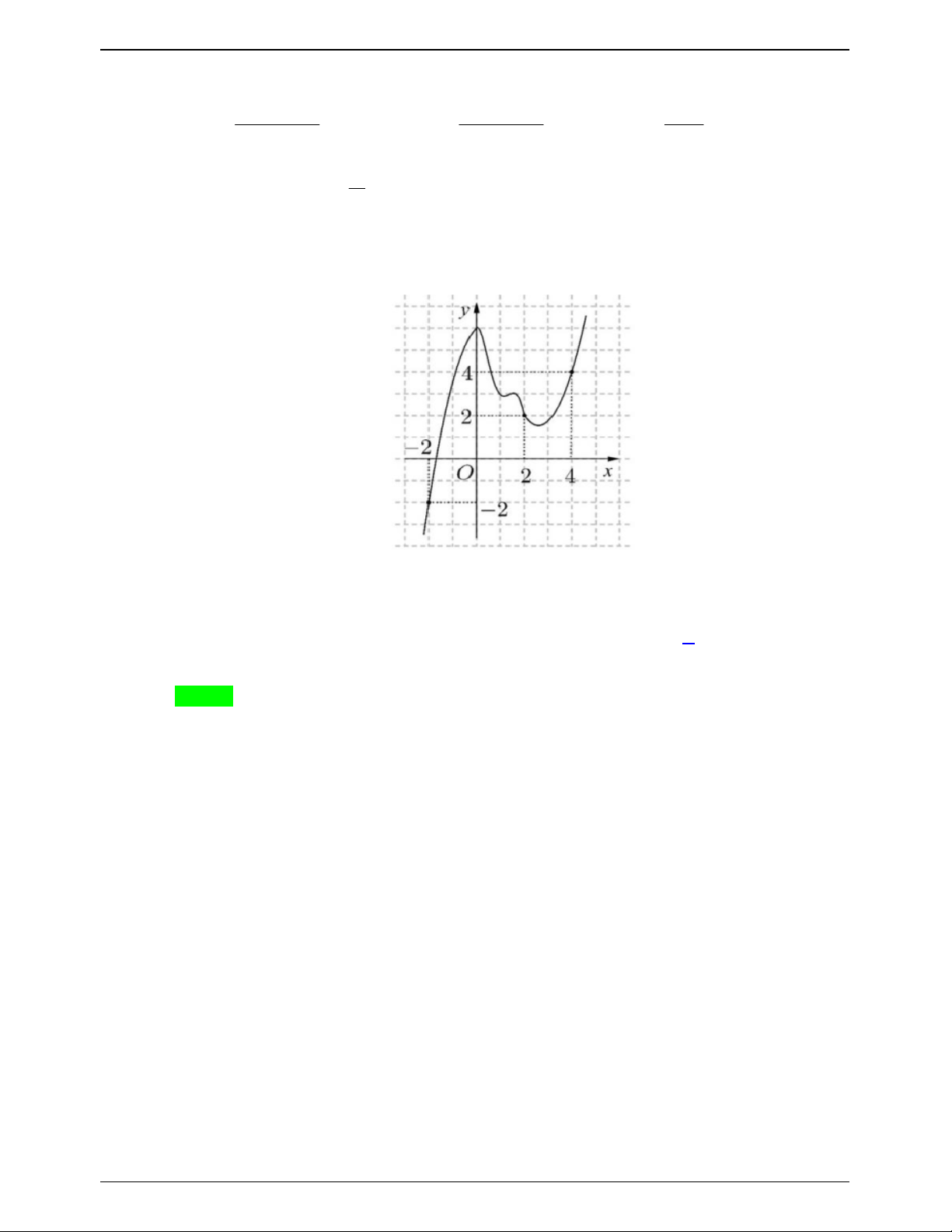
Cho hàm số y  f  x có đạo hàm liên tục trên  . Đồ thị của hàm số y  f  x như hình vẽ bên dưới 4 2 Khi đó tổng
f  x  2 dx  f  x  2 dx   bằng 0 0 A. 10 . B. 2  . C. 2 . D. 6 . Lời giải Chọn D
Dựa vào đồ thị hàm số có f  
1  2, f 2  2, f 4  4 . 4 2
Đặt t  x  2  dt  dx và f  x  2 dx 
f t  dt  f 2  f  2
   2  2  4   . 0 2  2 4
Đặt t  x  2  dt  dx và
f  x  2dx  f t  dt  f 4  f 2  4  2  2   . 0 2 4 2 Vậy
f  x  2 dx  f  x  2 dx  6   . 0 0 Câu 48.25:
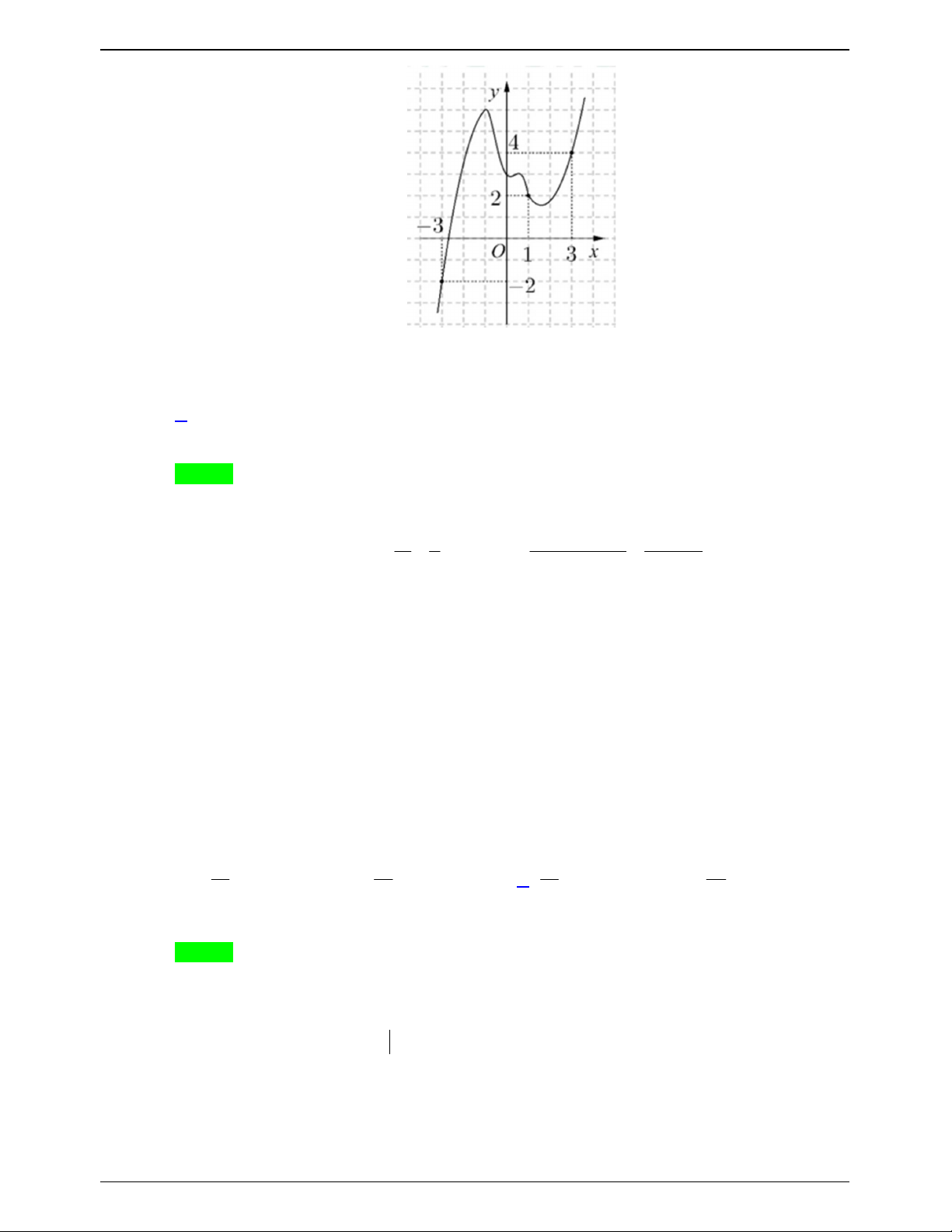
Cho hàm số y  f  x có đạo hàm và liên tục trên  . Đồ thị của hàm số y  f  x như hình vẽ bên dưới Trang 748
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 0 2 Khi đó tổng
f 2x   1 dx 
f   x   1 dx   bằng 2  0 A. 4 . B. 10 . C. 0 . D. 6 . Lời giải Chọn A
Đặt t  2 x  1  dt  2dx . 0 1 1 dt 1 f   1  f  3   2   2   Ta có
f 2x   1 dx  f t  
f t dx    2    . 2 2 2 2 2  3  3 
Đặt t  x  1  dt  dx . 2 3 Ta có
f  x   1 dx 
f  t dt  f 3  f   1  4  2  2   . 0 1 0 2 Vậy
f 2x   1 dx 
f  x   1 dx    2  2  4 . 2  0 Câu 48.26:
Cho hàm số f  x có đạo hàm liên tục trên  thỏa mãn f  3 x  3x  
1  3x  2 , với mọi 5
x   .Tích phân xf  xdx  bằng 1 31 17 33 49 A.  . B. . C. . D. . 4 4 4 4 Lời giải Chọn C
Từ giả thiết ta có f  3 x  3x  
1  3x  2 nên suy ra f 1  2 , f 5  5 . 5 5 5 5
Suy ra I  xf  x dx  xf  x  f  x dx  23  f  xdx    . 1 1 1 1 Đặt 3
x  t  t   x   2 3 1 d 3t  3dt .
Với x  1 t  0; x  5  t  1 Trang 749
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 5 1 1 59
Do đó f  x dx  f  3 t  3t   1  2
3t  3dt  3t  2 2
3t  3dt     . 4 1 0 0 59 33 Vậy I  23   . 4 4 Câu 48.27:
Cho hàm số f  x xác định và liên tục trên  đồng thời thỏa mãn 
 f  x  0, x     /  f  x  x 2
 e f  x, x
   . Tính giá trị của f ln 2  1  f 0   2 1 1 1 1
A. f ln 2  .
B. f ln 2  .
C. f ln 2  ln 2  . D. f ln 2 2  ln 2  . 4 3 2 2 Lời giải Chọn B / f x / x 2  
Ta có f  x  e f  x x 
 e (do f  x  0 ) 2 f  x / f  x x 1 x 1 
dx  e dx  
 e  C  f x  .  2    f  x f  x x e  C 1 f 0 2 1
Thay x  0 ta được f 0   C  1. 0 e  C 1 1 1 1
Vậy f  x   f    x ln 2 . ln 2 e 1 e 1 2 1 3 Câu 48.28:
Cho hàm số y  f (x) xác định và liên tục trên  thỏa mãn  f x 3 2
( )  3 f (x)  5  x với 10 x
   . Tính I  f (x)dx  . 5 A. I  0 . B. I  3 . C. I  5 . D. I  6 Lời giải Chọn B Đặt 3 2
t  f (x)  2t  3t  5  x  dx  (6t  3)dt và 3
x  5  2t  3t  5  0  t  0 3
x 10  2t  3t  5  10  t 1 10 1 Vậy 2 I 
f (x)dx  t(6t  3)dt  3   . 5 0 Câu 48.29:
Cho hàm số y  f  x liên tục trên đoạn 0; 
1 thỏa mãn bf a  af b  1 , với mọi
a, b  0;  1 . Trang 750
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 1 Tính I 
f  x dx  . 0  1  1 A. I  . B. I  . C. I  . D. I  . 2 2 4 4 Lời giải Chọn C
- Đặt x  sin t  dx  cos tdt 
Với x  0 thì t  0 ; Với x  1 thì t  2  Ta được: 2 I 
f sin t  cos tdt  . 0
Đặt x  cos t  dx   sin tdt 
Với x  0 thì t 
; Với x  1 thì t  0 2  0 Ta được: I   
 f  cos t  2 sin tdt
f cos t sin tdt   . 0 2     Suy ra: 2 2I 
 f sin t  cost  f cos t  2 sin t d  t  dt   I      . 0 0 2 4 Câu 48.30: Cho hàm số f  x liên tục trên đoạn a;b thỏa mãn 6x f  x 2  6x . f  3 x   , x  ; a b. 3x 1 1 Tính
f  xdx 0 A. 2 . B. 4 . C. 1  . D. 6 . Lời giải Chọn B 6 1 1 1 1
Ta có: f  x 2  6x . f  3 x    f  x 2 dx  2 3x f    3 x dx  6  dx  (*) 3x  1 3x 1 0 0 0 Đặt 3 2
u  x  du  3x dx
Với x  0  u  0 và x  1  u  1 1 1 1 Khi đó 2 3x f   3
x dx  f udu= f xdx   thay vào (*), ta được: 0 0 0 1 1 1 1 1 1 1
f  xdx  2 f  xdx  6 dx    
f  xdx  6 dx  4   . 3x 1 3x 1 0 0 0 0 0 Câu 48.31:
Cho hàm số f  x và g  x có đạo hàm trên 1; 2 thỏa mãn f   1  g   1  0 và Trang 751
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  x
g x  2017 x  x 1 f  x  2        x   1  , x  1; 2. 3  x
g x  f  x 2  2018x   x 1  x x 1  Tính tích phân I  g  x 
f  x dx .  x 1 x    1 3 A. . B. 4 . C. 1  . D. . 2 2 Lời giải Chọn A  x
g x  2017 x  x 1 f  x  2        x   1 Từ giả thiết ta có  , x  1; 2. 3  x
g x  f  x 2  2018x   x 1  1 x   x  1 1  /   Suy ra  g x  g x   f  x  f x  1 2        2    x   1 x  1 x x         x   x   1  x x 1  g  x  f     x 1   g  x 
f  x  x  C.  x 1  x   x 1 x 2 2  x 1 x 1  1 Mà  f   1  g  
1  0  C  1  I  f  x 
f  x dx   x   1 dx  .    x x    2 1 1 3 x Câu 48.32:
Cho hàm số y  f  x liên tục trên đoạn 0; 
1 và thoả mãn f  x 3  8x f  4 x    0 2 x 1 . 1 a  b 2 a b Tích phân I 
f  x dx  có kết quả dạng , a, , b c   ,
, tối giản. Tính a  b  c . c c c 0 A. 6 . B. 4 . C. 4 . D. 10 . Lời giải Chọn A 3 x 3 x
Ta có: f  x 3  8x f  4 x  
 0  f  x 3  8x f  4 x   . 2 x 1 2 x 1 1 1 1 3 x I  f  x 3 dx  8x f    4 x dx  dx    1 2 0 0 0 x 1 1 1 1 Xét 3 8x f   4
x dx  2 f   4 x  d  4
x   2 f  x dx  2I  0 0 0 Trang 752
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 1 3 x Xét dx  . Đặt 2 2 2 t 
x 1  t  x 1  tdt  xdx . 2 0 x 1
Đổi cận x  0  t  1, x  1  t  2 . 2 3  2 1 2 t   1 tdt x 3  t  2 2 Nên dx      t     2 t 3 3 3 0 x 1 1   1  2  2  2  2 Do đó  
1  I  2I     I  .Nên , , . 
a  2 b  1 c  3 3    3
Vậy a  b  c  6 . Câu 48.33:
Cho hàm số f  x liên tục trên đoạn 0;  1 thỏa mãn điều kiện 1
f  x  f   x 2 2 1
 3x  6 x, x  0;  1 . Tính I  f   2 1 x  dx 0 4 2 2 A. I  . B. I  1. C. I   . D. I  . 15 15 15 Lời giải Chọn C
Đặt t  1 x, x 0;  1  t  0;  1 .
Ta có f  x  f   x  x  x  f  x  f   x    x2 2 2 1 3 6 2 1 3 1  3
 f   t   f t  2  t  
f  x  f   x 2 1 2 3 3 2 1  3x  3 Ta có hệ phương trình  f
  x  2 f 1 x 2  3x  6x  f
  x  2 f 1 x 2  3x  6x    2 f 
x  f 1 x 2  3x  3 4 f  
 x  2 f 1 x 2  6x  6   3 f  x 2
 3x  6x  6  f  x 2
 x  2x  2 2 Khi đó f  2  x    2  x    2  x  4 2 1 1 2 1
 2  x  4x 1 1 1 2 Suy ra I  f  2
1 x dx   4 2 x  4x   1 dx     . 15 0 0 Câu 48.34:
Cho hàm số y  f  x liên tục, nhận giá trị dương trên 0;    và thỏa mãn f   1  1, biểu
thức f  x  f  x 3x 1 , với mọi x  0 . Mệnh đề nào sau đây đúng?
A. 2  f 5  3 .
B. 4  f 5  5 .
C. 1  f 5  2 .
D. 3  f 5  4 . Lời giải Chọn D Trang 753
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 f  x 1 5 f  x 5 1 5 5 1 d 3x   1 Theo giả thiết ta có   dx  dx  
 ln  f  x   f  x   3x 1 f x 3x 1 1 3 3x 1 1   1 1 5 4 2 4
 ln  f 5  ln  f   1   3x 1 3    
 ln  f 5   
 f 5  e  3,7937 . 3 3 1
Vậy 3  f 5  4 . Câu 48.35:
Cho hàm số y  f  x liên tục trên  thỏa mãn f  x 2019  x f  2020 x  2
 1 x với mọi x 1 thuộc 0; 
1 . Tích phân f  x dx  bằng: 0 2017 505  A. 1020604 . B. . C. . D. . 8072 2021 8076 Lời giải Chọn C 1 1 1  Có f  x 2019 dx  x f  2020 x  2 dx  1 x dx     4 0 0 0 1 1 1 1 1 Đặt 2020 2019 t  x
 dt  2020.x dx và 2019  x f  2020 x dx 
f t  dt  f  x   dx 2020 2020 0 0 0 1 1 1 1  2021  505 Vậy f  x 2019 dx  x f  2020 x dx  
f  x dx  
f  x dx      . 4 2020 4 2021 0 0 0 0 Câu 48.36:
Cho hàm số f  x có đạo hàm liên tục trên đoạn 4;8 và f  x  0 x 4;8 . Biết rằng
 f  x 2 8    1 1 dx  1  và f 4 
, f 8  . Tính f 6 .  f  x 4 4 2 4    5 2 3 1 A. . B. . C. . D. . 8 3 8 3 Lời giải Chọn D 8 8  f (  x)  1 1 1 Ta có: dx       2  (1). 2  f (x) f (x) f (8) f (4) 4   4 2 8  f (  x) 
Gọi k là một hằng số thực, ta sẽ tìm k để  k dx  0  2  f (x) 4   2  f (  x)   f (x)2 8 8 8 8  f (  x)  2 Ta có 2 2  k dx  dx  2k dx  k
dx  1 4k  4k  1 2k  2   4   2     f ( x)   f (x) f (x) 4 4   4   4 2 1 8 6 6  f (  x) 1  f (  x) 1 f (  x) 1  k   thì  dx  0    dx  dx     2 2 2 2 f (x) 2 f (x) 2 f (x) 2 4   4 4 Trang 754
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 6 6 df (x) 1 1 1 1 1   1    1    1  4   1  f 6   2   f (x) f (x) f (4) f (6) f (6) 3 4 4 b b 2k Chú ý:
f  x dx  0 
không được phép suy ra f  x  0 nhưng  f  x dx  0  f  x  0    a a Câu 48.37:
Cho hàm số f  x liên tục trên 0;  1 thỏa mãn điều kiện 1 xf  2
x   f   x 2 4 3 1
 1 x , x 0;  1 . Khi đó  d  f x x bằng 0     A. . B. . C. . D. . 20 16 6 4 Lời giải Chọn A
Vì f  x liên tục trên 0;  1 và xf  2
x   f   x 2 4 3 1
 1 x , x 0;  1 nên ta có 1 1 1 1 1 4 .  x f  2
x   3 f 1 x 2  dx  1 x dx  4 .   x f  2
x dx  3 f 1 x 2 dx  1 x dx   1     0 0 0 0 0 1 1 2 1 t  x Lại có 4 x.  f  2
x  dx  2 f  2 x  d  2
x   2 f t  dt  2  I và 0 0 0 1 1 1 u 1 x
3 f 1  x  dx  3 f 1  x  d 1  x   3 f u  du  3I .    0 0 0    1 2 2 2 xsin t 1  Đồng thời 2 2 2 1  x dx 
1 sin t .cos tdt  cos tdt 
1 cos 2t dt  .     2 4 0 0 0 0 1    Vậy  
1  2I  3I   I  
f  xdx   . 4 20 20 0  1 1 2 x f  x 4 Câu 48.38: Cho
f  x dx  1  và dx  2  . Tính I 
f tan xdx 2  . x 1 0 0 0 A. I  3 . B. I  1 . C. I  1. D. I  3 Lời giải Chọn B  Đặt t  x  dt   2 tan
1 tan x dx Và x  0  t  0; x   t  1. 4   4 4 f  tan x 1 1 f t f x Do đó I 
f tan x dx  .    2 1 tan x dx  .dt  .dx 2       2  . 2 1 tan x 1 t 1 x 0 0 0 0 1   1  2 2 x  
1 1 f  x x f x  Ta có : dx 2     dx  2  2  2 x 1 x 1 0 0 Trang 755
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 1 1 f  x 
f  xdx 
dx  2  1 I  2  I  1    . 2 x  1 0 0 1 Câu 48.39:
Cho f  x liên tục trên  \   0 thỏa mãn xf  2
x   f 2x 3  x   2, x    \   0 . Giá 2x trị của 2 tích phân
f  x dx 
thuộc khoảng nào sau đây? 1 A. 5; 6 . B. 3; 4 . C. 1; 2 . D. 2;3 . Lời giải Chọn D 1 Ta có xf  2
x   f 2x 3  x   2, x    \   0 2x 2 2    xf   1 2
x   f 2x 3 d  x  x   2 dx       2x  1 1 2 2 2 4 1    f   1 x 1 2 x  d  2 x  
f 2xd 2x   ln x  2x    2 2 4 2 1 1   1 2 4 4 4 4 u x 1 1 7 1 1 1 7 1 
f u du 
f vdv   ln 2 
f  x dx 
f  x dx   ln 2     v2x 2 2 4 2 2 2 4 2 1 2 1 2 2 4 4 1   1 7 1  f 
 x dx  f  x dx  f   
 x dx   ln 2  2 2 4 2  1 2  2 2 2 1 7 1 7 
f  x dx   ln 2  f  x dx   ln 2  2.80852819.   2 4 2 2 1 1 f x  16   Câu 48.40:
Cho hàm số f  x liên tục trên  thỏa mãn dx  cot . x f  . Tích     2 2 sin xdx 1 1 x 4 1 f  4x  phân dx 1  bằng x 8 5 3 A. . B. 2 . C. . D. 4 . 2 2 Lời giải Chọn A Đặt 2 t 
x  t  x  dx  2 d
t t . Đổi cận x  1  t  1; x  16  t  4 . f x 16   4 f t  4 f t  4 f t  1 Suy ra 1  dx  .2 d t t  2 dt  dt    2   1 1 1 1 x t t t 2 dt dt dt Đặt 2
t  sin x  dt  2 sin x cos d x x  cot d x x  cot . x   2 2 sin x cos x 2 sin x 2t Trang 756
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  1  Đổi cận x   t  ; x   t  1 4 2 2  1 1 dt 1 f t  1 f t 1 2   Do đó 2 1  cot . x f       sin xdx f t . dt dt 1   1 1    . 2t 2 t t 2 4 2 2 2 1 1
Đặt t  4x  dt  4dx . Đổi cận x   t 
; x  1  t  4 8 2
1 f  4x dx 4 f t  4 dt f t  1 f t  4 f t  1 5 Suy ra  .  .dt  dt  dt  2   1 1 1 1      . x t 1 4 t t t 2 2 8 2 2 2 4 Trang 757