Tìm cực trị của hàm số hợp f(u(x)) khi biết đồ thị hàm số f(x) Toán 12

Tìm cực trị của hàm số hợp f(u(x)) khi biết đồ thị hàm số f(x) Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

22 11 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 658

KIẾN THỨC CẦN NHỚ:

 Đạo hàm của hàm số hợp:























  

  

   

   

g x f u x g x u x f u x



 





 







 







 



 



u x

g x

f u x

 Lập bảng biến thiên của hàm số







y f x

khi biết đồ thị hàm số









y f x

B1. Xác định giao điểm của đồ thị hàm số









y f x

với trục hoành

B2: Xét dấu của hàm số









y f x

, ta làm như sau

- Phần đồ thị của





f x



nằm bên trên trục hoành trong khoảng





;

a b

thì









f x ,





;

x a b



- Phần đồ thị của





f x



nằm bên dưới trục hoành trong khoảng





;

a b

thì





f x









;

x a b



 Lập bảng biến thiên của hàm số













g x f x u x

  khi biết đồ thị hàm số









y f x

B1: Đạo hàm













g x f x u x

  

 

. Cho













g x f x u x

  

   

B2. Xác định giao điểm của đồ thị hàm số









y f x

và đồ thị hàm số





y u x



 

B3: Xét dấu của hàm số





y g x





, ta làm như sau

- Phần đồ thị của





f x



nằm bên trên đồ thị





u x





trong khoảng





;

a b

thì





g x









;

x a b



- Phần đồ thị của





f x



nằm bên dưới đồ thị





u x



 trong khoảng





;

a b

thì





g x









;

x a b



BÀI TẬP MẪU

Cho hàm số bậc bốn

( )

y f x



có đồ thị như hình bên

Số điểm cực trị của hàm số





3 2

( ) 3

g x f x x

  là

. B.

. D.

TÌM CỰC TRỊ CỦA HÀM SỐ HỢP

(

)

KHI BIẾT ĐỒ THỊ HÀM SỐ f

(

)

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 659

Phân tích hướng dẫn giải

1. DẠNG TOÁN: Đây là dạng toán tìm số cực trị của hàm hợp









f u x

khi biết đồ thị hàm số





f x

2. KIẾN THỨC CẦN NHỚ:

 Đạo hàm của hàm hợp:

 

   

f u x u x f u



 

 



 

 Định lí về cực trị của hàm số:

Cho hàm số





y f x



xác định trên

Điểm

x D



là điểm cực trị của hàm số





y f x

 khi





f x





hoặc





f x



không xác định và





f x



đổi dấu khi đi qua

 Sự tương giao của hai đồ thị:

Hoành độ giao điểm của hai đồ thị hàm số





y f x



và





y g x



là nghiệm của phương trình













f x g x

Số nghiệm của phương trình





bằng số giao điểm của hai cực trị.

 Tính chất đổi dấu của biểu thức:

Gọi





là một nghiệm của phương trình:





f x



. Khi đó

Nếu





là nghiệm bội bậc chẳn (

   

2 4

, ,...

x x

 

  ) thì hàm số





y f x



không đổi

dấu khi đi qua



Nếu





là nghiệm đơn hoặc nghiệm bội bậc lẻ (

   

, ,...

x x

 

  )thì hàm số





y f x



đổi dấu khi đi qua



3. HƯỚNG GIẢI:

B1: Tính đạo hàm của hàm số:





3 2

( ) 3

g x f x x

 

B2: Dựa vào đồ thị của hàm





f x

ta suy ra số nghiệm của phương trình :

( ) 0

g x





B3: Lập bảng biến thiên của hàm số





3 2

( ) 3

g x f x x

 

và suy ra số cực trị.

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn B

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 660

Từ đồ thị, ta có bảng biến thiên của

( )

y f x



như sau:

         

3 2 3 2 3 2 32

( ) 3 ( ) 3 3 3 6 3

g x f x x g x x x f x x x x f x x



  

        

   

 

   

 

3 2

3 6 0

0 1

( ) 0 3 6 3 0

; 2

x x

g x x x f x x

f x x

x x

  













 







 



      





 



 











 









Xét hàm số

3 2

( ) 3

h x x x

 

( ) 3 6

h x x x

   

( ) 0

h x





   



 



Bảng biến thiên

Từ bảng biến thiên, ta thấy

Đường thẳng

y a



cắt đồ thị hàm số

( )

y h x



tại 1 điểm

Đường thẳng

y b



cắt đồ thị hàm số

( )

y h x



tại 3 điểm.

Đường thẳng

y c



cắt đồ thị hàm số

( )

y h x



tại 1 điểm.

Như vậy, phương trình

( ) 0

g x

 

có tất cả 7 nghiệm đơn phân biệt.

Vậy hàm số





3 2

( ) 3

g x f x x

  có 7 cực trị.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 661

Cách trình bày khác:

Phân tích hướng dẫn giải

1. DẠNG TOÁN: Đây là dạng toán sử dụng đồ thị (hoặc bảng biến thiên) của hàm số







y f x

(hoặc









y f x

) để tìm cực trị hàm số











 

 

g x f u x

2. HƯỚNG GIẢI:

B1: Lập bảng biên thiên của hàm số







y f x

- Dựa vào đồ thị hàm số







y f x

xác định cực trị của hàm số







y f x

- Lập bảng biến thiên











f x













f x



B2: Tìm các điểm tới hạn của hàm số









3 2

g x f x x

 

- Đạo hàm













2 3 2

3 6 . 3

g x x x f x x

 

  

- Cho





g x







 

3 2

3 6 0

3 0

x x

f x x



 





 







3 2

3 ; 0

3 ; 0 4

3 ; 4







 



  



   



  



x x a a

x x b b

x x c c

B3: Khảo sát hàm số





3 2

h x x x

  để tìm số giao điểm của đồ thị





3 2

h x x x

  với các đường thẳng

, ,

  

y a y b y c

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn C

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 662

Từ đồ thị ta có bảng biến thiên của hàm số





y f x

 như sau











f x













f x



Ta có









3 2

g x f x x

 















2 3 2

3 6 . 3

g x x x f x x

 

  

Cho





g x







 

3 2

3 6 0

3 0

x x

f x x



 





 







3 2

3 ; 0

3 ; 0 4

3 ; 4







 



  



   



  



x x a a

x x b b

x x c c

Xét hàm số





3 2

h x x x

 







3 6

h x x x



 

. Cho





h x













 



Bảng biến thiên

Ta có đồ thị của hàm





3 2

h x x x

  như sau

Từ đồ thị ta thấy:

Đường thẳng

y a



cắt đồ thị hàm số





y h x



tại 1 điểm.

Đường thẳng

y b



cắt đồ thị hàm số





y h x

 tại 3 điểm.

Đường thẳng

y c



cắt đồ thị hàm số





y h x



tại 1 điểm.

Như vậy phương trình





g x





có tất cả 7 nghiệm đơn phân biệt.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 663

Vậy hàm số









3 2

g x f x x

 

có 7 cực trị.

Bài tập tương tự và phát triển:

Câu 46.1: Cho hàm số





y f x



Đồ thị hàm số





y f x





như hình bên.

Tìm số điểm cực trị của hàm số









3 .

g x f x

 

. B.

. D.

Lời giải

Chọn B

Ta có









2 3

g x xf x

 

 

 

theo do thi '

0 3 2 1 .

3 0

2 nghiem kep

3 1 nghiem kep

f x

g x x x

f x













        





 







 

 



Bảng biến thiên

Dựa vào bảng biến thiên ta thấy hàm số có 3 điểm cực trị.

Câu 46.2: Cho hàm số

( )

y f x



có đạo hàm

'( )

f x

trên



và đồ thị của hàm số

'( )

f x

như hình vẽ.

Tìm số điểm cực trụ hàm số





( 2 1)

g x f x x

  

. C.

. D.

Lời giải

Chọn D

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 664

Ta có:





' (2 2) '( 2 1)

g x x f x x

   

. Nhận xét:

 

' 0 2 1 1

2 1 2

g x x x

x x







    



  



2; 3

x x







  



 



Ta có bảng biến thiên:

Dựa vào bảng biến thiên, ta thấy hàm số có đúng ba cực trị.

Câu 46.3: Cho hàm số bậc bốn





y f x



. Đồ thị hình bên dưới là đồ thị của đạo hàm





f x

. Hàm số

 





2 2

g x f x x

  

có bao nhiêu điểm cực trị ?

. B.

. C.

. D.

Lời giải

Chọn C

Ta có

 





2 2 .

2 2

g x f x x

x x



 

  

 

Suy ra

 





 

theo do thi '

1 0

2 2 1

0 1 2.

2 2 0

2 2 1

1 2

2 2 3

f x

x x

g x x

f x x

x x

 



 





 



   





     





  



  





  





  



Bảng xét dấu

Từ đó suy ra hàm số

 





2 2

g x f x x

  

có

điểm cực trị.

Câu 46.4: Cho hàm số





y f x



có đạo hàm trên



và có bảng xét dấu của





y f x





như sau

Hỏi hàm số









g x f x x

  có bao nhiêu điểm cực tiểu ?

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 665

. B.

. D.

Lời giải

Chọn A

Ta có













2 2 2 ;

g x x f x x

 

  

 

theo BBT '

2 2 0

2 2

2 0

2 1 nghiem kep

2 3

1 2 nghiem kep

f x

x x

g x

f x x

x x







 



  





   





 







 









 







 









Bảng biến thiên

Dựa vào bảng biến thiên ta thấy hàm số có một điểm cực tiểu.

Câu 46.5: Cho hàm số





f x

, bảng biến thiên của hàm số





f x



như sau:

Số điểm cực trị của hàm số





4 4

y f x x

  là

. B.

. C.

. D.

Lời giải

Chọn B

Dựa vào bảng biến thiên ta có:





f x









 

; 1

1;0

0;1

x a

x b

x c

x d

   





  







 



   



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 666

Ta có:









8 4 4 4

y x f x x

 

  





 

8 4 0

4 4 0

f x x

 









 





 

4 4 ; 1

4 4 1;0

4 4 0;1

4 4 1;

x x a

x x b

x x c

x x d







    



    



  



    





Ta có khi

4 4 1

x x x

    

và





1 3 0



   

Mặt khác:

 

4 4 2 1 1 1

x x x

     

nên:



4 4

x x a

 

vô nghiệm.



4 4

x x b

 

có

nghiệm phân biệt



4 4

x x c

 

có

nghiệm phân biệt



4 4

x x d

 

có

nghiệm phân biệt

Vậy phương trình





có

nghiệm bội lẻ phân biệt nên hàm số có

điểm cực trị.

Câu 46.6: Cho hàm số





f x

, bảng biến thiên của hàm số





f x



như sau

Số điểm cực trị của hàm số





y f x x

 

là

. B.

. C.

. D.

Lời giải

Chọn B

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 667

Từ bảng biến thiên ta có phương trình





f x





có các nghiệm tương ứng

là





 

, ; 1

, 1;0

,c 0;1

, 1;

x a a

x b b

x c

x d d

   





  



 



  



Xét hàm số













2 2

2 2 1 2

y f x x y x f x x

 

     

Giải phương trình

 

2 2

2 1

1 0

0 2 1 2 0 2 2

2 0

2 3

2 4

x x a

y x f x x x x b

f x x

x x c

x x d







 



 





 

        





 







 



 



Vẽ đồ thị hàm số





h x x x

 

Dựa vào đồ thị ta thấy: phương trình





vô nghiệm. Các phương trình













2 ; 3 ; 4

mỗi

phương trình có 2 nghiệm. Các nghiệm đều phân biệt nhau.

Vậy phương trình





y có

nghiệm phân biệt nên hàm số





y f x x

  có

điểm cực

trị.

Câu 46.7: Cho hàm số





y f x

 có đạo hàm





f x



trên khoảng





;

 

. Đồ thị của hàm số





y f x



như hình vẽ

Đồ thị của hàm số

 





y f x



có bao nhiêu điểm cực đại, cực tiểu?

điểm cực đại,

điểm cực tiểu. B.

điểm cực đại,

điểm cực tiểu.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 668

điểm cực đại,

điểm cực tiểu. D.

điểm cực đại,

điểm cực tiểu.

Lời giải

Chọn A

Từ đồ thị hàm số ta có bảng biến thiên

 





y f x











2 . 0

y f x f x

 

  





 

f x

















Quan sát đồ thị ta có

 

0 1

f x x







  







và

 

0 1

x x

f x x

x x









  







với





0;1

x  và





1;3

x  .

Suy ra





 

f x

























 





























   

1 2

0; 1;

x x x

 





 

















1 2

0; 1; 3;x x x

    

Từ đó ta lập được bảng biến thiên của hàm số

 





y f x



Suy ra hàm số có

điểm cực đại,

điểm cực tiểu.

Câu 46.8: Cho hàm số





y f x



có đồ thị hàm số như hình bên.

Hàm số









g x f x x

   có bao nhiêu điểm cực đại ?

. B.

. D.

Lời giải

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 669

Chọn B

Ta có













2 3 . 3 ;

g x x f x x

 

    

 

theo do thi

2 3 0

3 17

0 3 2 .

3 0

f x

g x x x

f x x

x x













  











       







  







  













Bảng biến thiên

Dựa vào bảng biến thiên ta thấy hàm số có 4 điểm cực trị.

Câu 46.9: Cho hàm số





y f x



có đồ thị như hình vẽ bên.

Hàm số









g x f f x



 

 

có bao nhiêu điểm cực trị ?

. B.

. D.

Lời giải

Chọn C

Dựa vào đồ thị ta thấy





f x

đạt cực trị tại

0, 2.

x x

 

Suy ra

 





 

0 nghiem don

0 .

2 nghiem don

f x





 









Ta có

       





 

. ; 0 .

f x

g x f x f f x g x

f f x





   

   



 





 



 





 





 

0 nghiem don

0 .

2 nghiem don

f x





 











 









   

0 1

0 .

2 2

f x

f f x

f x





  



 







NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 670

Dựa vào đồ thị suy ra:

 Phương trình





có hai nghiệm



(nghiệm kép) và





2 .

x a a 

 Phương trình





có một nghiệm





x b b a

 

Vậy phương trình





g x





có

nghiệm bội lẻ là 0, 2,

x x x a

  

và

x b



Suy ra hàm số









g x f f x



 

 

có

điểm cực trị.

Câu 46.10: Cho hàm số





y f x



có bảng biến thiên như sau

Số điểm cực trị của hàm số





( )

g x f x x

  

là

. B.

. D.

Lời giải

Chọn B

Từ đồ thị, ta có bảng biến thiên của

( )

y f x



như sau:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 671

         

2 24 4 24 3 4

( ) 4 ( ) 4 4 4 8 4

g x f x x g x x x f x x x x f x x



  

             

   

 

   

 

3 4

4 8 0

( ) 0 4 8 4 0

4 0

0 1

0;4

x x

g x x x f x x

f x x

x x



 











  





 

 

        





  





 



 

 

 









Xét hàm số

( ) 4

h x x x

  

( ) 4 8

h x x x

    

( ) 0

h x





   



 



Bảng biến thiên

∞

h x( )

h' x( )

0 0 +

Từ bảng biến thiên, ta thấy

Đường thẳng

y a

 

cắt đồ thị hàm số

( )

y h x



tại 2 điểm

Đường thẳng





0; 4

y b 

cắt đồ thị hàm số

( )

y h x



tại 4 điểm.

Đường thẳng

y c

 

cắt đồ thị hàm số

( )

y h x



tại 0 điểm.

Như vậy, phương trình

( ) 0

g x

 

có tất cả 7 nghiệm đơn phân biệt.

Vậy hàm số





3 2

( ) 3

g x f x x

 

có 7 cực trị

Câu 46.11: Cho hàm số





y f x



có bảng biến thiên như sau

Tìm số điểm cực trị của hàm số









3 .

g x f x

 

. B.

. D.

Lời giải

Chọn B

Ta có









3 .

g x f x

 

  

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 672



   

theo BBT

3 0 3

0 3 0 .

3 2 1

x x

g x f x

x x

  

 

 

     

 

  

 







g x



không xác định

3 1 2.

x x

    

Bảng biến thiên

Vậy hàm số









g x f x

 

có

điểm cực trị.

Câu 46.12: Cho hàm số





y f x

 có đạo hàm liên tục trên



. Đồ thị hàm số





y f x



 như hình vẽ

sau. Số điểm cực trị của hàm số





y f x x

 

là:

. B.

. C.

. D.

Lời giải

Chọn B

Đặt









g x f x x

 

suy ra

     

0 2 0 2

g x f x f x

x x

 



  

       



  



Dựa vào đồ thị ta có: Trên





; 1

 

thì









2 2 0

f x f x

 

    

Trên







thì









2 2 0

f x f x

 

    

Trên





 

thì









2 2 0

f x f x

 

    

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 673

Vậy hàm số









g x f x x

 

có

cực trị.

Câu 46.13: Cho hàm số





y f x

 có đạo hàm trên



Đồ thị hàm số





y f x



 như hình vẽ bên

dưới. Hỏi đồ thị hàm số









g x f x x

 

có bao nhiểu điểm cực trị ?

. B.

. C.

. D.

Lời giải

Chọn B

Ta có

















3; 0 3.

g x f x g x f x

   

     

Suy ra số nghiệm của phương trình





g x





chính là số giao điểm giữa đồ thị của hàm số





f x



và đường thẳng

 

Dựa vào đồ thị ta suy ra

 

0 .

g x

 











 











Ta thấy

1, 0, 1

x x x

   

là các nghiệm đơn

và



là nghiệm kép nên đồ thị hàm số









g x f x x

 

có

điểm cực trị

Câu 46.14: Cho hàm số

( )

y f x



có đạo hàm trên



. Đồ thị của hàm số

'( )

y f x



như hình vẽ.

-2

-1

Tìm số điểm cực trị của hàm số

( ) 2 ( ) 2 2017

g x f x x x    .

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 674

. B.

. C.

. D.

Lời giải

Chọn B

Ta có





'( ) 2 '( ) 2 2 2 '( ) ( 1)

g x f x x f x x

     

Dựa vào hình vẽ ta thấy đường thẳng

y x

 

cắt đồ thị hàm số

'( )

y f x



tại 3 điểm:

( 1; 2), (1;0), (3;2).

 

-2

-1

Dựa vào đồ thị ta có

 

'( ) 0 2 '( ) ( 1) 0 1

g x f x x x

 





      







đều là các nghiệm đơn

Vậy hàm số

( )

y g x



có 3 điểm cực trị.

Câu 46.15: Cho hàm số





y f x

 có đạo hàm trên



Đồ thị hàm số





y f x



 như hình vẽ bên

dưới. Hàm số









g x f x x

 

đạt cực tiểu tại điểm

 



Lời giải

Chọn B

Ta có

















2 2 ; 0 .

g x f x x g x f x x

   

     

Suy ra số nghiệm của phương trình





g x





chính là số giao điểm giữa đồ thị của hàm số





f x



và đường thẳng

y x

 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 675

Dựa vào đồ thị ta suy ra

 

0 .

g x

 











 











Bảng biến thiên

Dựa vào bảng biến thiên ta thấy





g x

đạt cực tiểu tại



Câu 46.16: Cho hàm số





y f x

 có đạo hàm trên



Đồ thị hàm số





y f x



 như hình vẽ bên

dưới.

Hàm số

   

g x f x x x

    

đạt cực đại tại.

 

. B.



. C.



. D.



Lời giải

Chọn C

Ta có

         

2 1; 0 1 .

g x f x x x g x f x x

   

       

Suy ra số nghiệm của phương trình





g x





chính là số giao điểm giữa đồ thị của hàm số





f x



và parapol

   

: 1 .

P y x 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 676

Dựa vào đồ thị ta suy ra

 

0 1 .

g x x









  







Bảng biến thiên

Dựa vào bảng biến thiên ta thấy





g x

đạt cực đại tại



Câu 46.17: Cho hàm số





y f x

 Đồ thị hàm số





y f x



 như hình vẽ bên.

Lời giải

Số điểm cực trị của hàm số









3 15 1

g x f x x x

   

là

. B.

. C.

. D.

Lời giải

Chọn B

Ta có

















2 2

3 3 15; 0 5 .

g x f x x g x f x x

   

      

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 677

Đồ thị hàm số





f x



cắt đồ thị hàm số

y x

 

tại hai điểm









0;5 , 2;1 .

A B

Trong đó



là nghiệm bội bậc 2;



là nghiệm đơn.

Vậy hàm số có một điểm cực trị

Câu 46.18: Cho hàm số







y f x

có đồ thị như hình bên dưới. Hàm số









  

g x f x x

có bao nhiêu điểm

cực trị?

A. 3. B. 4. C. 5. D. 6.

Lời giải

Chọn C

Từ đồ thị ta có bảng biến thiên của hàm số





y f x



như sau













f x











f x







Ta có









  

g x f x x















2 3 . 3

 

    

g x x f x x

Cho





g x







 

2 3 0

3 0

  







  





f x x



3 2

3 0







   



  





x x



3 17























Như vậy phương trình





g x





có tất cả 5 nghiệm đơn phân biệt.

Vậy hàm số









  

g x f x x

có 5 cực trị.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 678

Câu 46.19: Cho hàm số





y f x



có đồ thị như hình bên dưới. Hàm số





y f x

 có bao nhiêu điểm

cực trị?

. B.

. C.

. D.

Lời giải

Chọn A

Gọi



x a

, với

1 4

 

là điểm cực tiểu của hàm số





y f x



Từ đồ thị ta có bảng biến thiên của hàm số





y f x

 như sau











f x











f x





Ta có





y f x









2 .

 



y x f x

Cho







 

2 0















f x

















x a



0





 



x a

, với

1 4

 

Bảng biến thiên của hàm số





y f x





















Vậy hàm số





y f x



có 3 cực trị.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 679

Câu 46.20: Cho hàm số





y f x



có đồ thị như hình bên dưới

Số điểm cực trị của hàm số





y f x x

 

là

. B.

. C.

. D.

Lời giải

Chọn C

Từ đồ thị ta có bảng biến thiên của hàm số





y f x



như sau













f x













f x







Ta có





y f x x

 











2 2 . 2

 

  

y x f x x

Cho







 

2 2 0

2 0

 







 





f x x



2 1

2 0

2 1

 





  



 



  



x x



1 2

 





 







  





Bảng biến thiên của hàm số





y f x x

 



1 2

 



1 2

 



















Vậy hàm số





y f x x

 

có 5 cực trị.

Câu 46.21: Cho hàm số





f x

, bảng biến thiên của hàm số





f x



như sau:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 680

Số điểm cực trị của hàm số





6 3

y f x

 

là

. B.

. C.

. D.

Lời giải

Chọn C.

Ta có





3. 6 3

y f x

 

  

. Cho







6 3 3

6 3 1

6 3 3

  





 



 



















Bảng biến thiên















Nhận xét:



đổi dấu 3 lần khi đi qua các nghiệm nên phương trình





có 3 nghiệm phân

biệt. Vậy hàm số





6 3

y f x

 

có 3 cực trị.

Câu 46.22: Cho hàm số





f x

, bảng biến thiên của hàm số





f x



như sau:

Số điểm cực trị của hàm số









g x f x

 

là

. B.

. C.

. D.

Lời giải

Chọn A.

Ta có









2 . 5

g x x f x

 

 

. Cho





g x







 

2 0

5 0

f x









 







5 , 5

5 , 5 2

5 , 2 3

5 , 3

x a a

x b b

x c c

x d d







   



     



    



  



 Phương trình

5 0

x a

  

 

nên phương trình vô nghiệm.

 Phương trình

5 0

x b

  

5 2

   

nên phương trình 2 nghiệm phân biệt.











f x



















f x









NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 681

 Phương trình

5 0

x c

  

2 3

  

nên phương trình 2 nghiệm phân biệt.

 Phương trình

5 0

x d

  



nên phương trình 2 nghiệm phân biệt.

Nhận xét: 7 nghiệm trên khác nhau đôi một nên phương trình





g x





có 7 nghiệm phân biệt.

Vậy hàm số









g x f x

 

có 7 cực trị.

Câu 46.23: Cho hàm số





f x

, bảng biến thiên của hàm số





f x



như sau:

Số điểm cực trị của hàm số

   

g x f x

 

 

 

là

. B.

. C.

. D.

Lời giải

Chọn A.

Ta có

   





1 2 1

g x f x f x x

 

    

 















2 2 . 2 1

g x x f x x

 

   

Cho





g x







 

2 2 0

2 1 0

f x x

 







  







2 1 , 0

2 1 , 0 ` 3

2 1 , 3

x x a a

x x b b

x x c c

 





   



    



    





2 1 0

x x a

   

có

4 0

  



nên phương trình vô nghiệm.



2 1 0

x x b

   

có

4 0

  

 

nên phương trình có 2 nghiệm phân biệt.



2 1 0

x x c

   

có

4 0

  



nên phương trình có 2 nghiệm phân biệt.

Nhận xét: 5 nghiệm trên khác nhau đôi một nên phương trình





g x





có 5 nghiệm phân biệt.

Vậy hàm số

   

g x f x

 

 

 

có 5 cực trị.

Câu 46.24: Cho hàm số





f x

liên tục trên



, bảng biến thiên của hàm số





f x



như sau:

Số điểm cực trị của hàm số

 

g x f

 





 

 

là

. B.

. C.

. D.

Lời giải

Chọn A.









f x















f x





NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 682

Ta có

 

2 2

1 1

x x

g x f

x x

 

 





 

 

Cho





g x















 







 



 





1 0

, 2

, 2 2

, 2

a a

b a

c c



 







  







   







 







1 0

 

có 2 nghiệm phân biệt

 

 Xét hàm số

 

h x





Tập xác định





\ 0

D 



. Ta có

 

h x





 . Cho





h x







 

Bảng biến thiên











f x













f x



Dựa vào bảng biến thiên, ta thấy







h x a



có 2 nghiệm phân biệt, với

 







h x b



vô nghiệm, với

2 2

  







h x c



có 2 nghiệm phân biệt, với



Vậy hàm số

 

g x f

 





 

 

có 6 điểm cực trị.

Câu 46.25: Cho hàm số





f x

liên tục trên



, bảng biến thiên của hàm số





f x



như sau:

Số điểm cực trị của hàm số

 

g x f



 



 



 

là

. B.

. C.

. D.

Lời giải

Chọn A











f x



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 683

Ta có

 

2 1

g x f

 

 

 



 



 



. Cho





g x









 





 



 



, 1

, 1 0

, 0 2

, 2

a a

b b

c c

d d





  











   











  

 







 





Xét hàm số

 

h x







 Tập xác định





\ 1

D 



. Ta có

 

h x x D





   



 Bảng biến thiên









f x









f x

Dựa vào bảng biến thiên, ta thấy: Phương trình





h x a







h x b







h x c







h x d



đều

có 2 nghiệm phân biệt.

Vậy hàm số

 

g x f



 



 



 

có 8 cực trị

Câu 46.26: Cho hàm số







y f x

xác định, liên tục trên



và có bảng biến thiên như sau













f x













f x



Hàm số









3 1

 

g x f x đạt cực tiểu tại điểm nào sau đây?

 

. B.



. C.

 

. D.



Lời giải

Chọn C

Ta có









 



g x f x

Do đó điểm cực tiểu của hàm số





g x

trùng với điểm cực tiểu của hàm số







y f x

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 684

Vậy điểm cực tiểu của hàm số là

 

Câu 46.27: Cho hàm số







y f x

có đồ thị hàm số









y f x

như hình vẽ

Hàm số

   

g x f x  

2020

đạt cực đại tại điểm nào sau đây?



. B.



. C.

 

. D.

 

Lời giải

Chọn D

Ta có









g x f x x

 

 

. Cho





g x











f x x



 

Nhận thấy đường thẳng

y x

 

cắt đồ thị hàm số





y f x



 lần lượt tại ba điểm

x x

  

3; 1.

Ta có bảng biến thiên của hàm số

   

g x f x  

2020

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 685

 

        



    

  

       

  

3 1 3 4

1 3 1 1 3 2 0

t x x

f t t

t x x

Câu 46.28: Cho hàm số





     

4 3 2

y f x ax bx cx dx e

, đồ thị hình bên dưới là đồ thị của hàm số









y f x

. Xét hàm số









 

g x f x

. Mệnh đề nào dưới đây sai?

A. Hàm số





g x

đạt cực tiểu tại

 

. B. Hàm số





g x

đạt cực đại tại



C. Hàm số





g x

có 5 điểm cực trị D. Hàm số





g x

nghịch biến trên khoảng





0; 2 .

Lời giải

Chọn C

Ta có:





 

 

( ) 2 . 2

g x x f x

. Cho

 

g x x x

f x

 





        





 







 

 



0 2 1 1

2 0

2 2

Ta có bảng xét dấu

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 686

Câu 46.29: Cho hàm số





y f x

 có đạo hàm





f x



trên



và đồ thị của hàm số





y f x



 như

hình vẽ. Hàm số









2 1

g x f x x

  

đạt cực đại tại giá trị nào sau đây?



. B.



. C.

 

. D.



Lời giải

Chọn D

Ta có













2 2 . 2 1

g x x f x x

 

   

. Cho

 

0 2 1 1

2 1 2

g x x x

x x









     



  









 















Ta có bảng biến thiên

Dựa vào bảng biến thiên, ta thấy hàm số đạt cực đại tại



Câu 46.30: Cho hàm số





y f x

 có đạo hàm trên



thoả mãn









2 2 0

f f

  

và đồ thị của hàm

số





y f x





có dạng như hình bên dưới. Hàm số





y f x



nghịch biến trên khoảng nào

trong các khoảng sau?

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 687

1; .

 



 

 





1;1 .







2; 1 .

 





1;2 .

Lời giải

Chọn D

Ta có

 

f x







 



 



, với









2 2 0

f f

  

Ta có bảng biến thiên











f x















f x



0 0



Ta có













2 .

y f x y f x f x

 

  

. Cho





 

1; 2

f x

x x

f x



 





  



  











Bảng xét dấu











f x















f x







y f x





Câu 46.31: Cho hàm số





y f x



Đồ thị hàm số





y f x





như hình bên dưới và









2 2 0.

f f

  

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 688

Hàm số

   

g x f x

 

 

 

nghịch biến trên khoảng nào trong các khoảng sau?





2; 1 .

 





1;2 .





2;5 .





5; .



Lời giải

Chọn C

Dựa vào đồ thị hàm số





y f x





suy ra bảng biến thiên của hàm số





f x

như sau

Từ bảng biến thiên suy ra





0, .

f x x

  



Ta có













2 3 . 3 .

g x f x f x

 

   

Cho





g x











 

3 0

f x



 





 







3 2 5

3 1 2

3 2 1

x x

   

 

 

   

 

  

 

Vì









0, 3 0, .

f x x f x x

       

 

Do đó





2 3 0

f x

  

 



Bảng biến thiên









f x















2 3

f x

 



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 689





g x











Suy ra hàm số





g x

nghịch biến trên các khoảng





;1 ,







2;5 .

Câu 46.32: Cho hàm số





y f x

 Đồ thị hàm số





y f x



 như hình bên dưới

Hàm số









g x f x

 

đồng biến trên khoảng nào trong các khoảng sau





; 1 .

 





1; 2 .







2;3 .





4;7 .

Lời giải

Chọn B

Dựa vào đồ thị ta có bảng biến thiên của hàm số





y f x













f x















f x



Ta có

 





 

3 . Khi 3

f x x

g x f x

f x x

 





  



 





 Với



khi đó









g x f x

 

  

Hàm số





g x

đồng biến







g x





   

3 1 4

3 0 3 0

1 3 4 1 2

x x

f x f x

x x

   

 

 

        

 

     

 

Kết hợp điều kiện



, ta được

1 2

  

Vậy hàm số





g x

đồng biến trên khoảng





1;2 .



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 690

 Với



khi đó









g x f x

 

 

Hàm số





g x

đồng biến







g x





 

1 3 1 2 4

3 0

3 4 7

x x

f x

x x

     

 



    

 

  

 

Kết hợp điều kiện



, ta được

3 4

 









Vậy hàm số





g x

đồng biến trên khoảng





3; 4

và







Câu 46.33: Cho hàm số





y f x



Đồ thị hàm số





y f x





như hình bên dưới

Hàm số

 





4 3

g x f x x

  

có bao nhiêu điểm cực trị?

. B.

. C.

. D.

Lời giải

Chọn A

Dựa vào đồ thị ta có bảng biến thiên của hàm số





y f x













f x















f x



Ta có

 





4 3

g x f x x

  



 





. 4 3

4 3

g x f x x

x x



 

  

 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 691

Cho

 

2 0

2 2 0

g x

f x x

 







 



  





2 2

1 0

4 3 1 4 2 0 2 2

4 6 0

2 10

4 3 3

x x x x x

x x

 



 



 





           



  

  

  







Vì





g x





có 5 nghiệm bội lẻ nên hàm số

 





4 3

g x f x x

  

có 5 điểm cực trị.

Câu 46.34: Cho hàm số





y f x

 Đồ thị hàm số





y f x



 như hình bên dưới

Hàm số

 





2 2

2 3 2 2

g x f x x x x

     

đồng biến trong khoảng nào sau đây





; 1 .

 

; .

 



 

 

; .

 



 

 





1; .

 

Lời giải

Chọn A

Dựa vào đồ thị ta có bảng biến thiên của hàm số





y f x











f x













f x





Ta có

 





2 2

2 3 2 2

g x f x x x x

     

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 692



   

 

2 2

1 1

1 . 2 3 2 2 .

2 3 2 2

g x x f x x x x

x x x x

 

 

       

 

   

 

Dễ thấy

2 2

1 1

2 3 2 2x x x x

 

   

với mọi









Đặt

 

2 2

2 3 2 2

u u x x x x x

      

Dễ thấy

2 2

2 3 2 2 0

x x x x

     







u x







Mặt khác

   

2 2

1 1

2 3 2 2 1

2 1

1 2 1 1

x x x x

x x

       



    







u x







Từ















0 1

u x

 

Kết hợp đồ thị ta suy ra





f u





, với

0 1

 





Từ





và











g x



ngược dấu với dấu của nhị thức





h x x

 

Bảng biến thiên











h x









g x











g x





Câu 46.35: Cho hàm số





y f x



có bảng biến thiên như hình vẽ











f x













f x







NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 693

Tìm tất cả các giá trị thực của tham số

để phương trình





1 3 1

f x m

  

có nhiều nghiệm

nhất?



. B.



. C.

0 2

 

. D.



Lời giải

Chọn C

Đặt









1 3 1

g x f x

  











3. 1 3

g x f x

 

  

Cho





g x











1 3 0

f x



 



1 3 1

1 3 3

  





 











 





Bảng biến thiên











g x













g x











g x



Để phương trình





1 3 1

f x m

  

có nhiều nghiệm nhất



đường thẳng

y m



cắt đồ thị





y g x

 tại nhiều điểm nhất



0 2

 

Câu 46.36: Cho hàm số





y f x



xác định trên





\ 0



và có bảng biến thiên như hình vẽ









f x











f x







NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 694

Số nghiệm của phương trình





3 2 1 10 0

f x

  

là

A. 2. B. 1. C. 4. D. 3.

Lời giải

Chọn C

Đặt

2 1

t x

 

, phương trình đã cho trở thành

 

f t



Với mỗi nghiệm của

thì có một nghiệm





nên số nghiệm của phương trình

 

f t



bằng số nghiệm của





3 2 1 10 0

f x

  

Bảng biến thiên của hàm số





y f x



là









f x



Suy ra phương trình

 

f t



có 4 nghiệm phân biệt nên phương trình





3 2 1 10 0

f x

  

có 4 nghiệm phân biệt.

Câu 46.37: Cho hàm số





y f x

 có đạo hàm





f x



trên



. Đồ thị của hàm số





y f x



 như hình

vẽ. Đồ thị của hàm số









g x f x

 có bao nhiêu điểm cực trị?

. B.

. C.

. D.

Lời giải

Chọn B

Ta có









g x f x

















3. .

g x f x f x

 



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 695

Vì





f x



, với mọi





nên









0 0 1

g x f x x

 

     

Từ đó suy ra









g x f x

 có hai điểm.

Bấm Tải xuống để xem toàn bộ.

| 1/38

| | Tải xuống

Preview text:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
TÌM CỰC TRỊ CỦA HÀM SỐ HỢP f (u (x)) KHI BIẾT ĐỒ THỊ HÀM SỐ f (x)
KIẾN THỨC CẦN NHỚ:
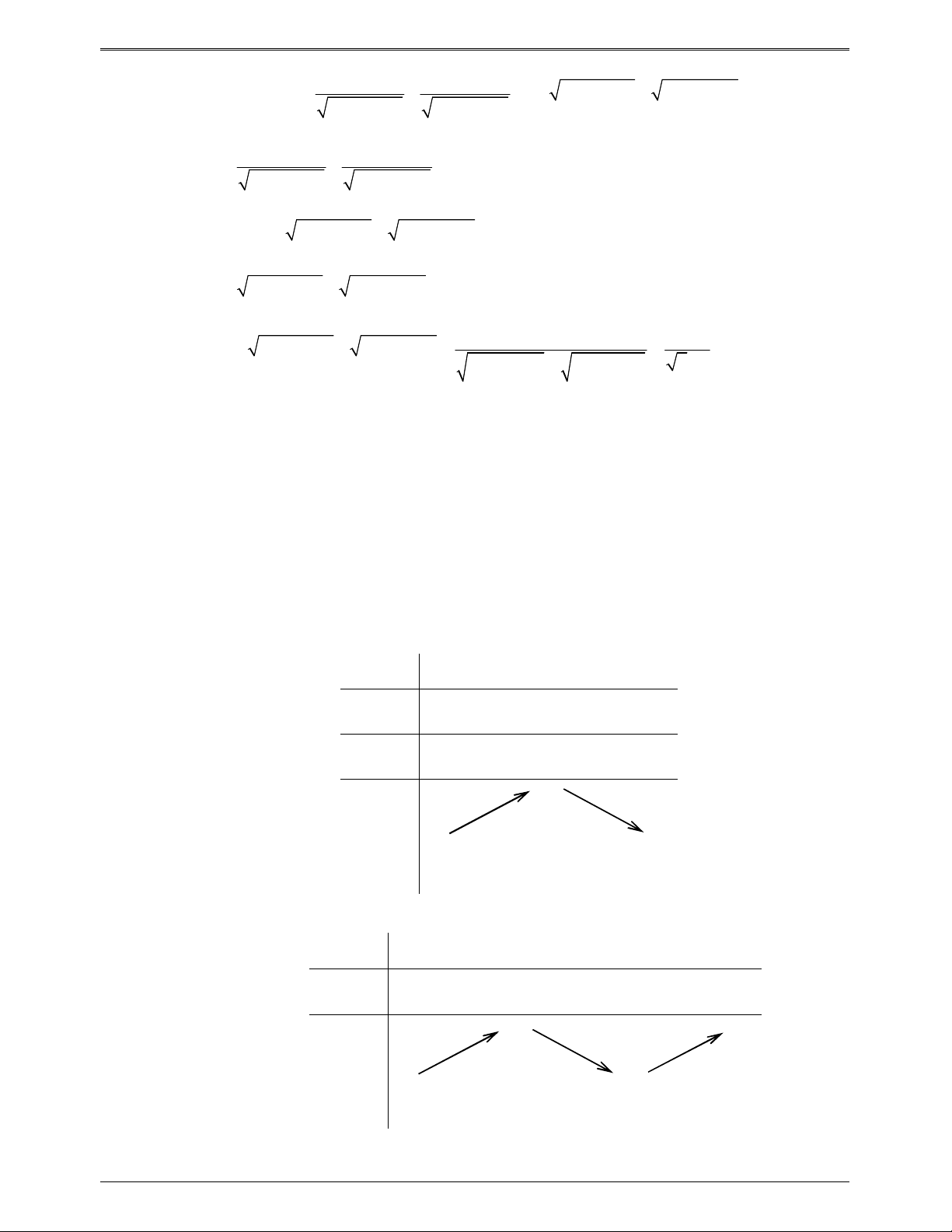
 Đạo hàm của hàm số hợp:
 g  x  f u  x  g x  u x. f  u  x     .
u  x  0
 g x  0   f  
u  x  0   
 Lập bảng biến thiên của hàm số y  f  x khi biết đồ thị hàm số y  f  x
B1. Xác định giao điểm của đồ thị hàm số y  f  x với trục hoành
B2: Xét dấu của hàm số y  f   x , ta làm như sau
- Phần đồ thị của f  x nằm bên trên trục hoành trong khoảng a;b thì f  x  0 , x  ; a b
- Phần đồ thị của f  x nằm bên dưới trục hoành trong khoảng a;b thì f  x  0 , x  ; a b
 Lập bảng biến thiên của hàm số g  x  f  x  u  x khi biết đồ thị hàm số y  f  x
B1: Đạo hàm g x  f  x  u x . Cho g x  0  f  x  u x
B2. Xác định giao điểm của đồ thị hàm số y  f  x và đồ thị hàm số y  u   x
B3: Xét dấu của hàm số y  g x , ta làm như sau
- Phần đồ thị của f  x nằm bên trên đồ thị u x trong khoảng a;b thì g x  0 , x  ; a b
- Phần đồ thị của f  x nằm bên dưới đồ thị u x trong khoảng a;b thì g x  0 , x  ; a b BÀI TẬP MẪU
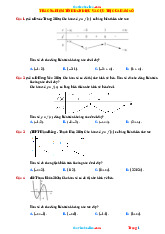
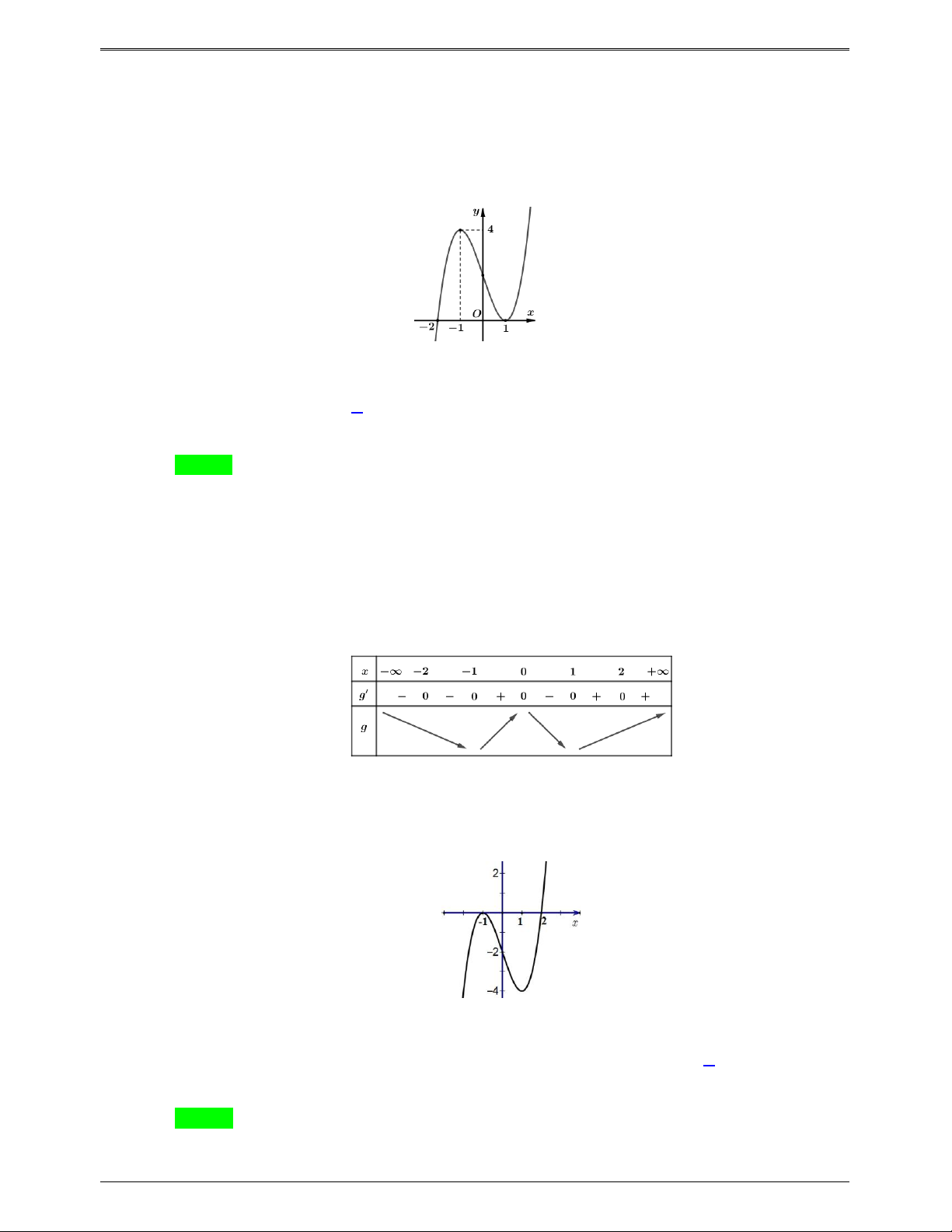
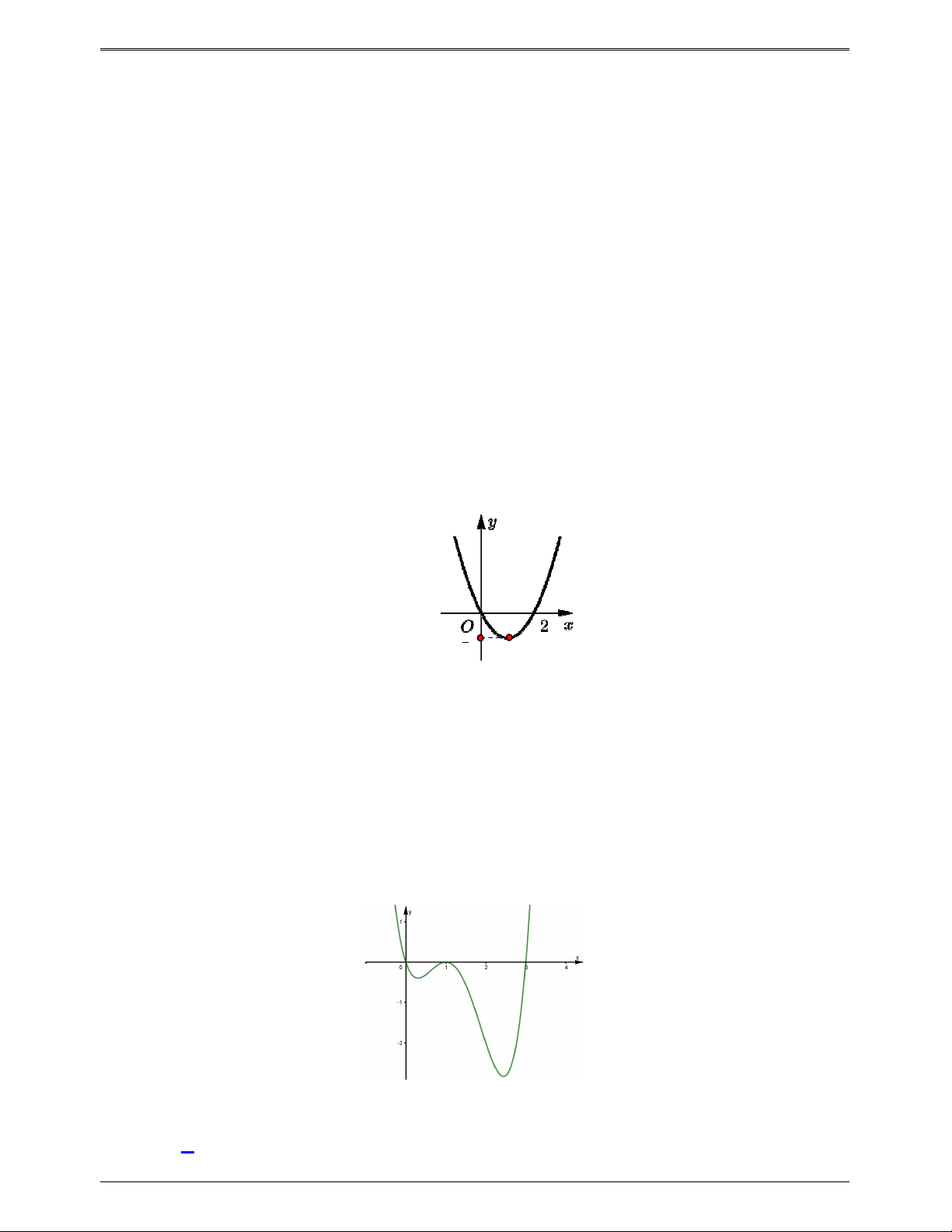
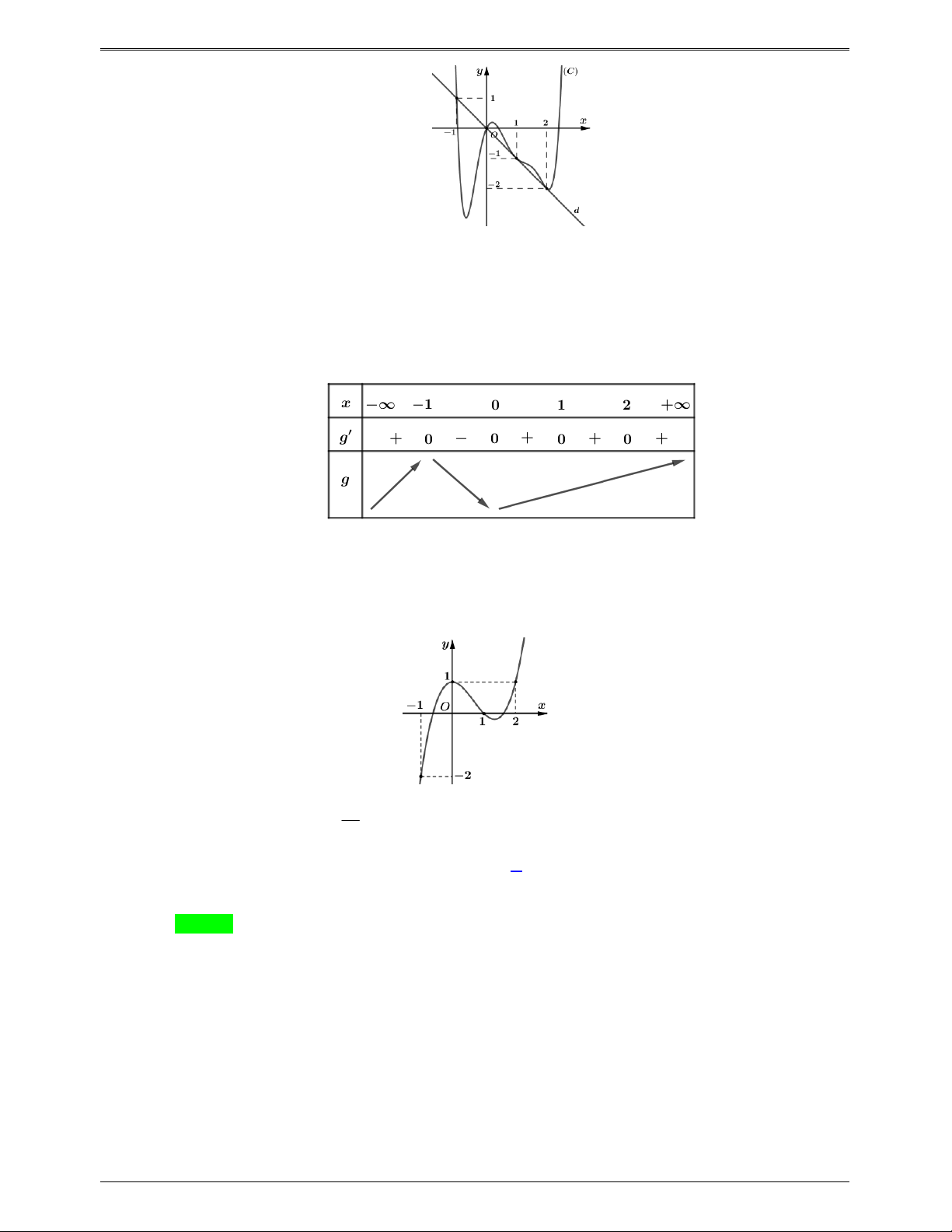
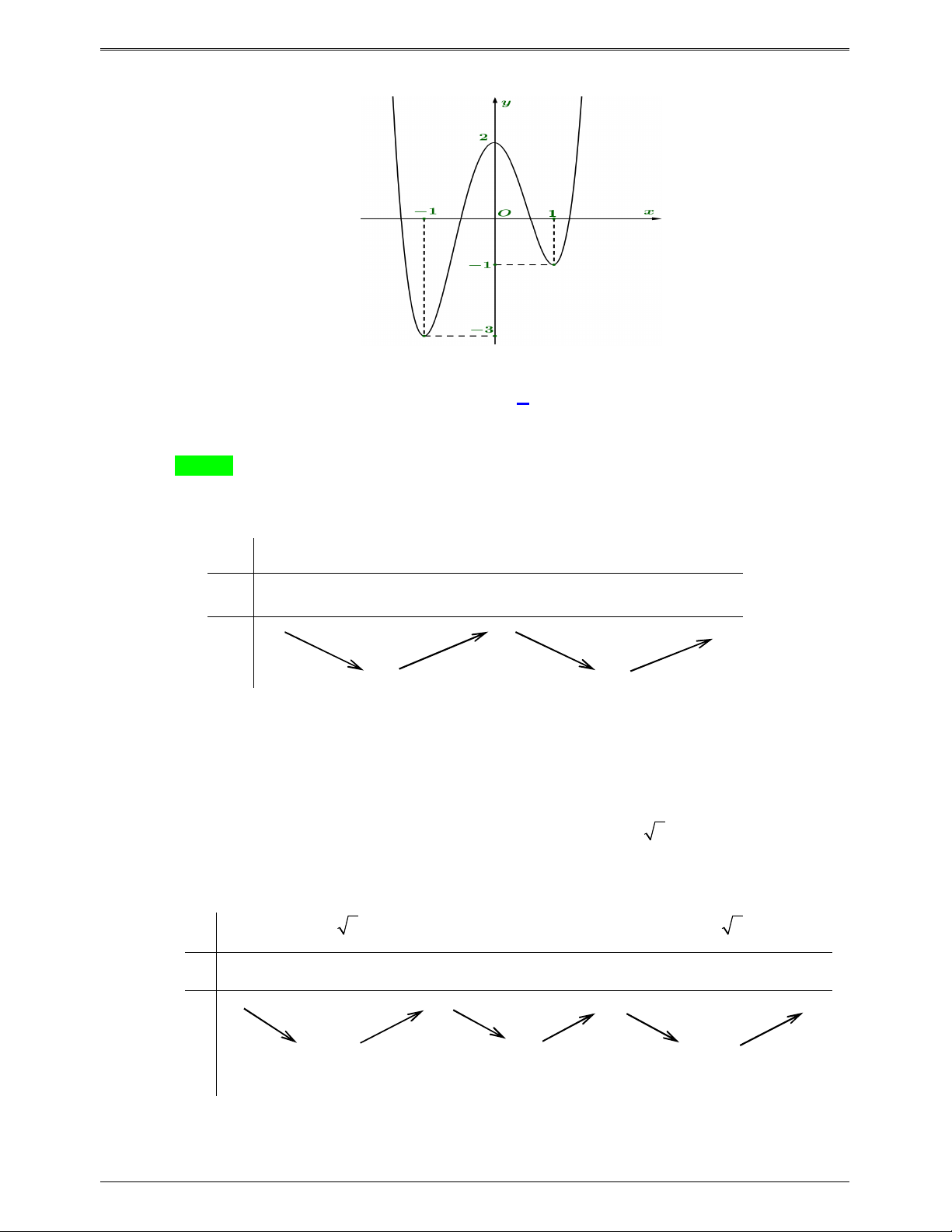
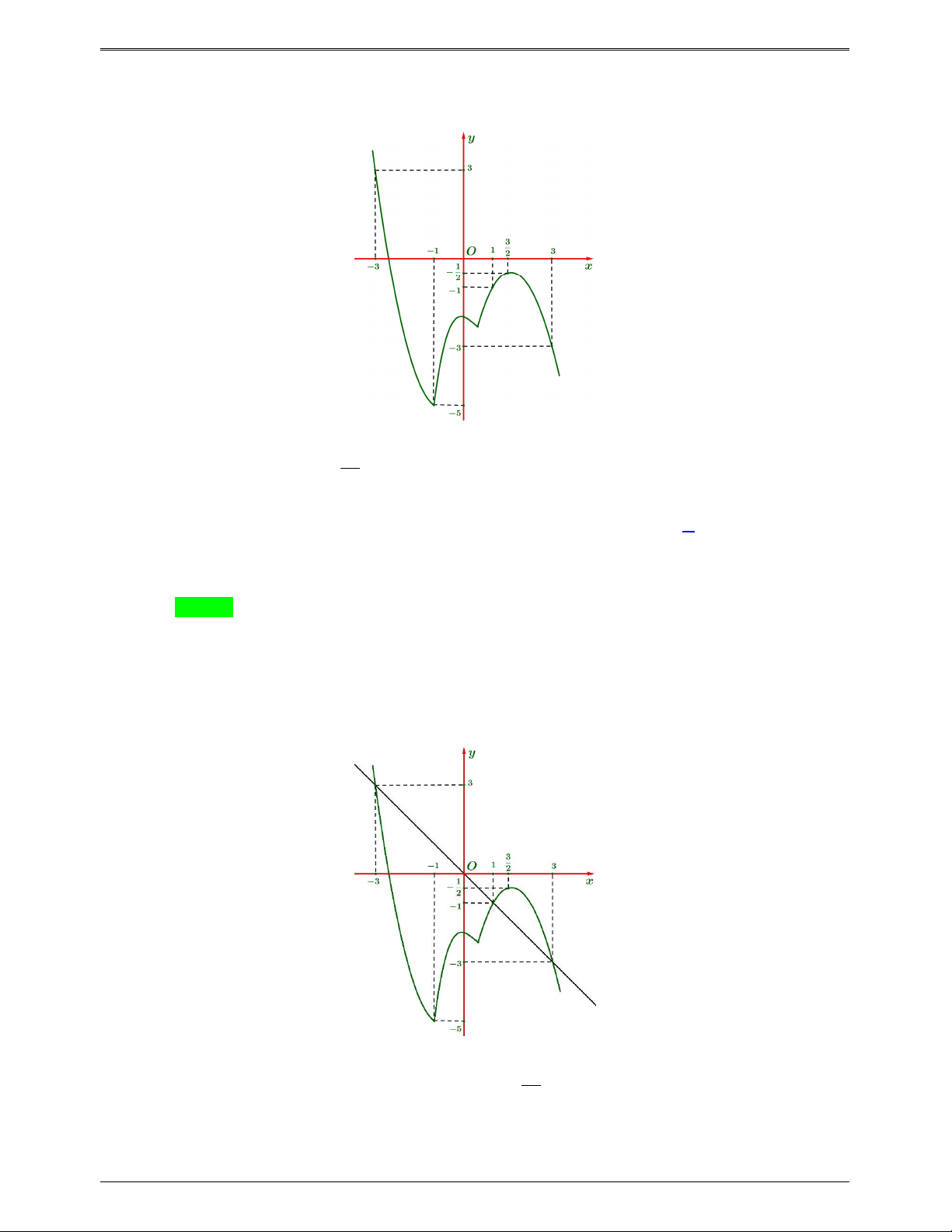
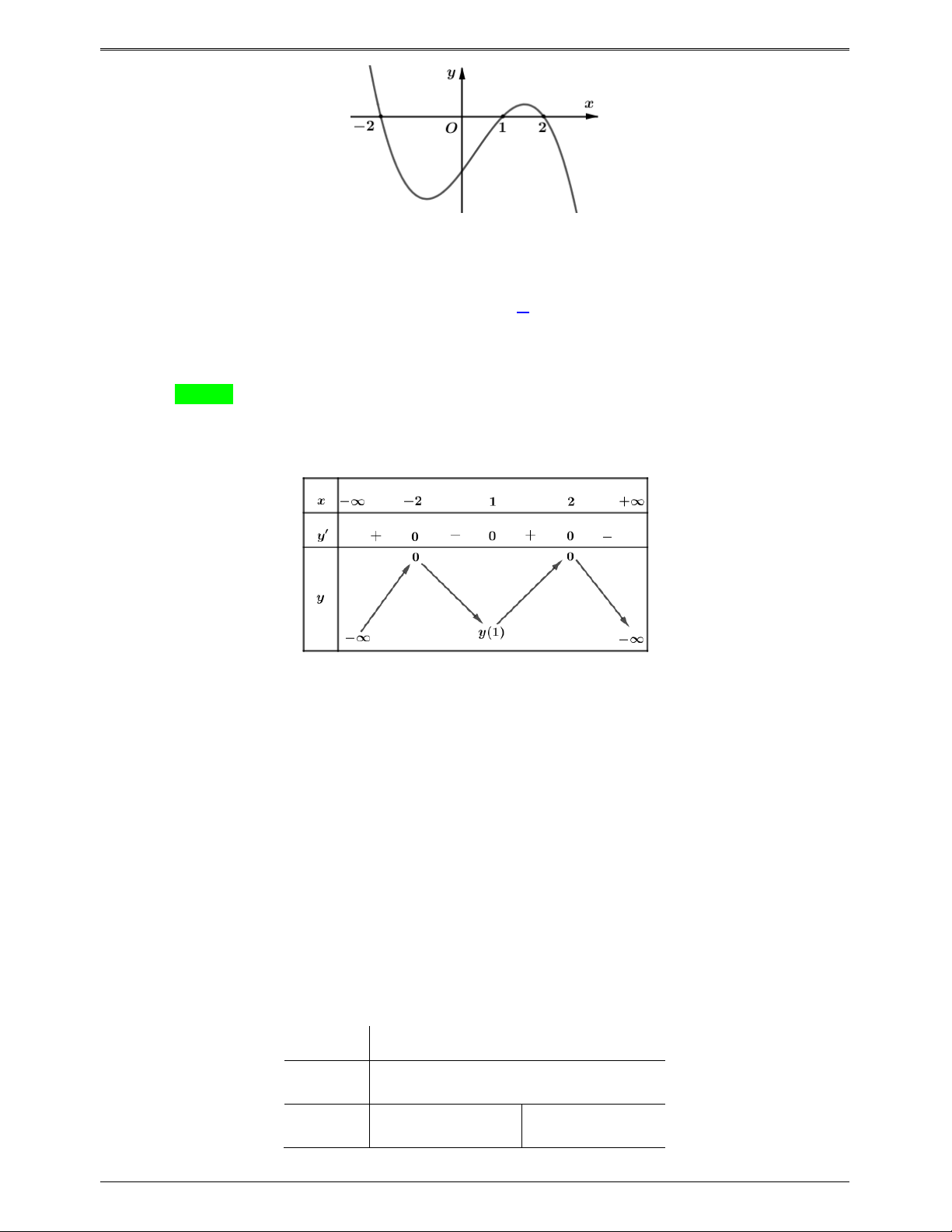
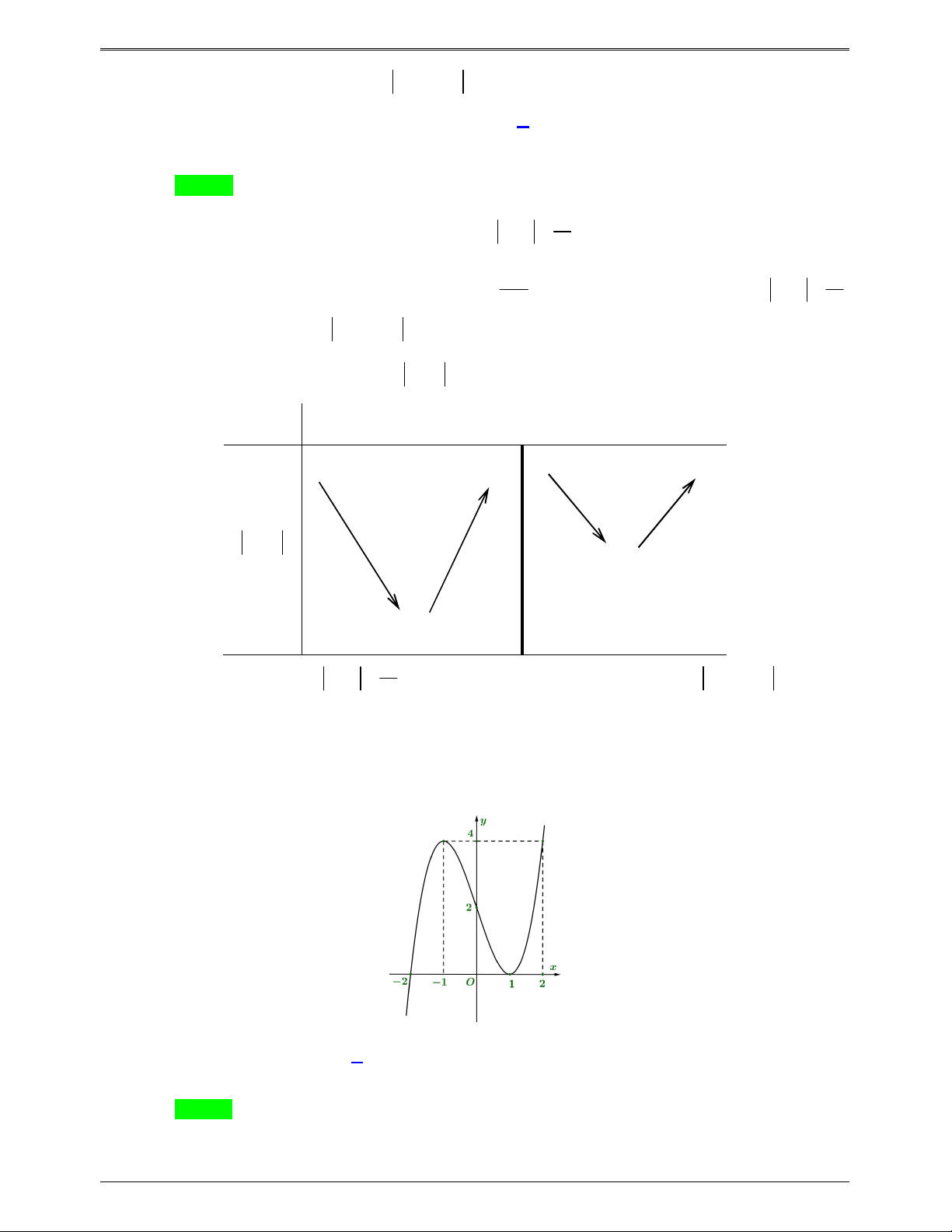
Cho hàm số bậc bốn y  f (x) có đồ thị như hình bên
Số điểm cực trị của hàm số g x  f  3 2 ( ) x  3x  là A. 5 . B. 3 C. 7 . D. 11. Trang 658
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán tìm số cực trị của hàm hợp f u  x khi biết đồ thị hàm số f  x .
2. KIẾN THỨC CẦN NHỚ:
 Đạo hàm của hàm hợp: 
 f u x  ux. f u  
 Định lí về cực trị của hàm số:
Cho hàm số y  f  x xác định trên D .
Điểm x  D là điểm cực trị của hàm số y  f  x khi f  x  0 hoặc f  x không xác định và 0  0  0
f   x đổi dấu khi đi qua x . 0
 Sự tương giao của hai đồ thị:
Hoành độ giao điểm của hai đồ thị hàm số y  f  x và y  g  x là nghiệm của phương trình
f  x  g  x   1
Số nghiệm của phương trình  
1 bằng số giao điểm của hai cực trị.
 Tính chất đổi dấu của biểu thức:
Gọi x   là một nghiệm của phương trình: f  x  0 . Khi đó 2 4
Nếu x   là nghiệm bội bậc chẳn (  x   , x   ,... ) thì hàm số y  f  x không đổi
dấu khi đi qua  .
Nếu x   là nghiệm đơn hoặc nghiệm bội bậc lẻ (  x    x  3 , ,... )thì hàm số
y  f  x đổi dấu khi đi qua  . 3. HƯỚNG GIẢI:
B1: Tính đạo hàm của hàm số: g x  f  3 2 ( ) x  3x 
B2: Dựa vào đồ thị của hàm f  x ta suy ra số nghiệm của phương trình : g (  x)  0
B3: Lập bảng biến thiên của hàm số g x  f  3 2 ( )
x  3x  và suy ra số cực trị.
Từ đó, ta có thể giải bài toán cụ thể như sau: Lời giải Chọn B Trang 659
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 a c b
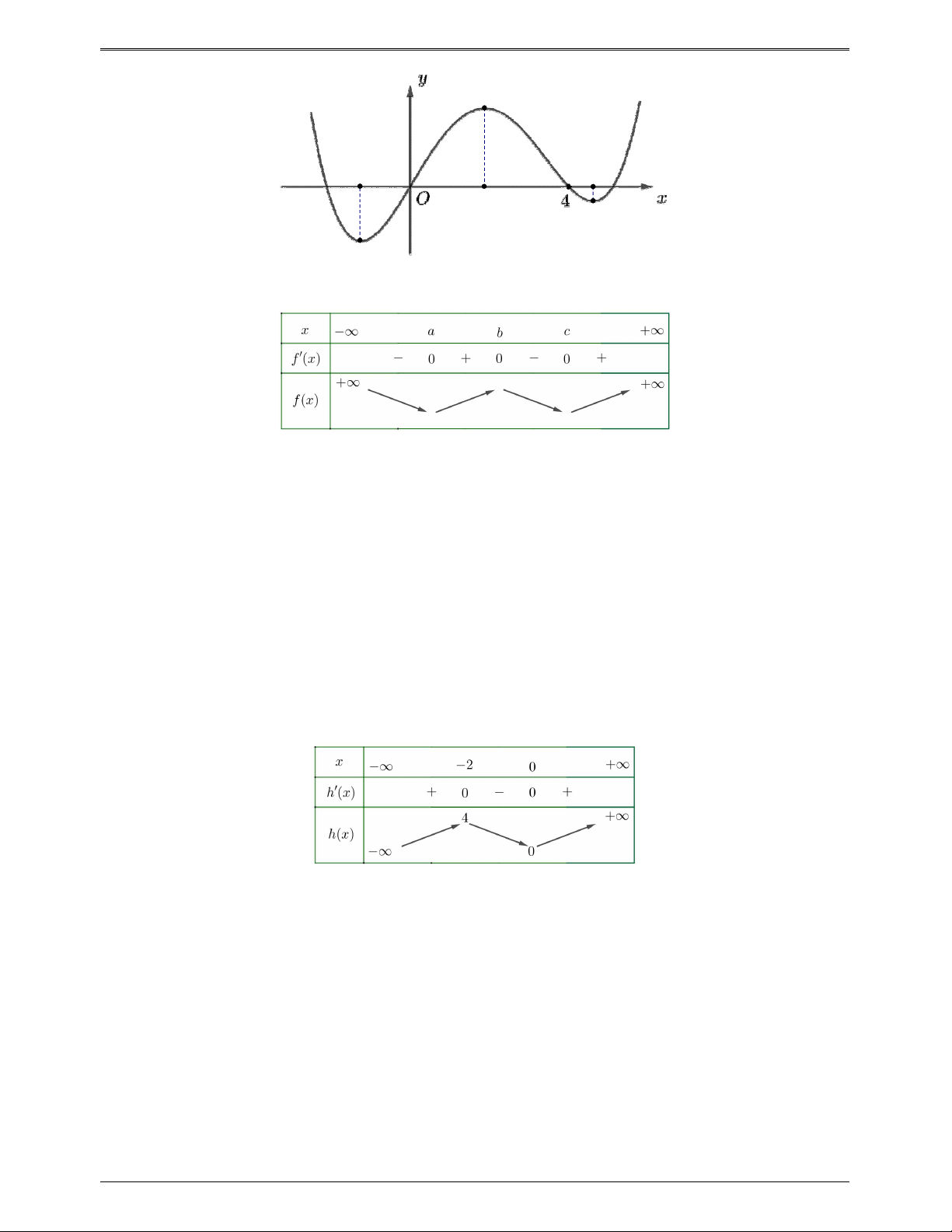
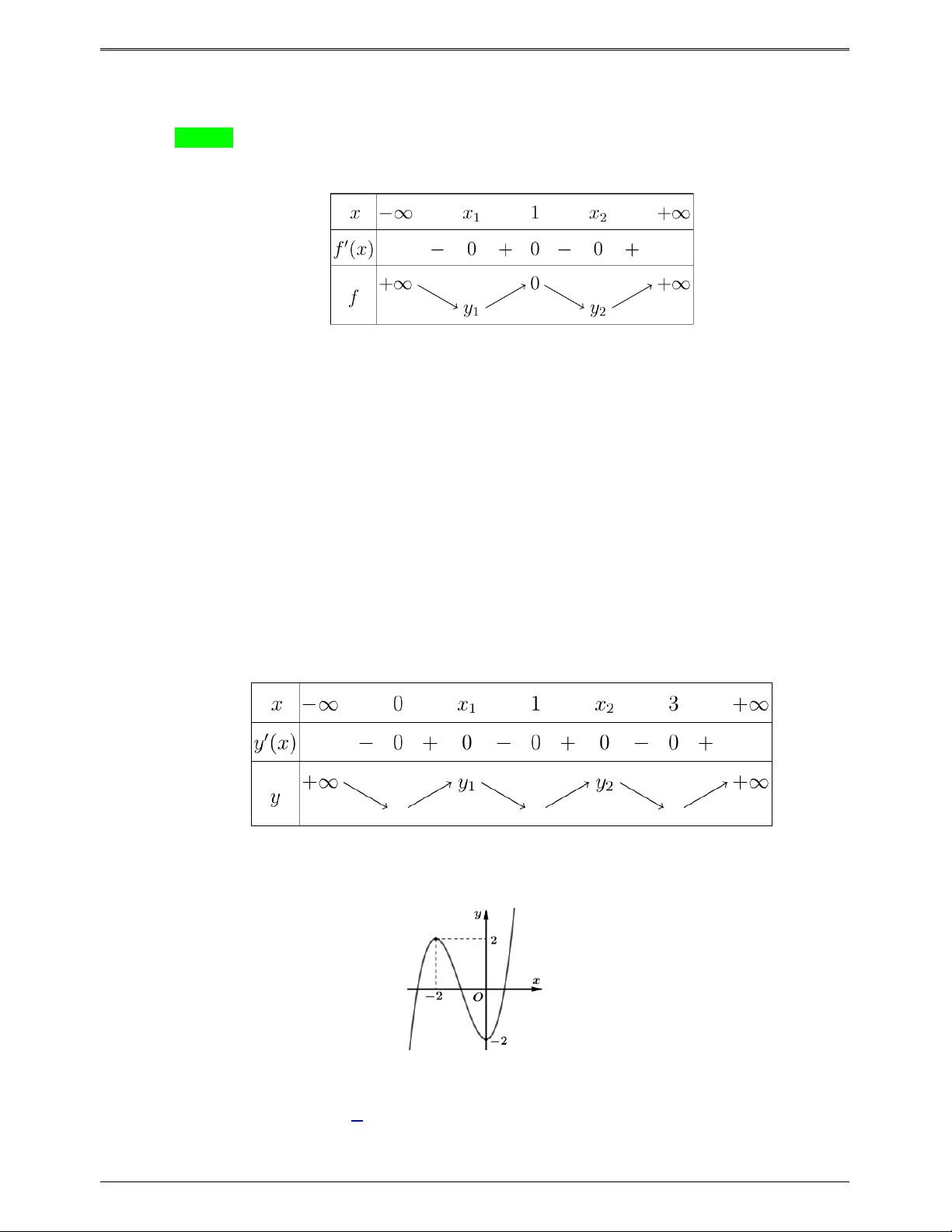
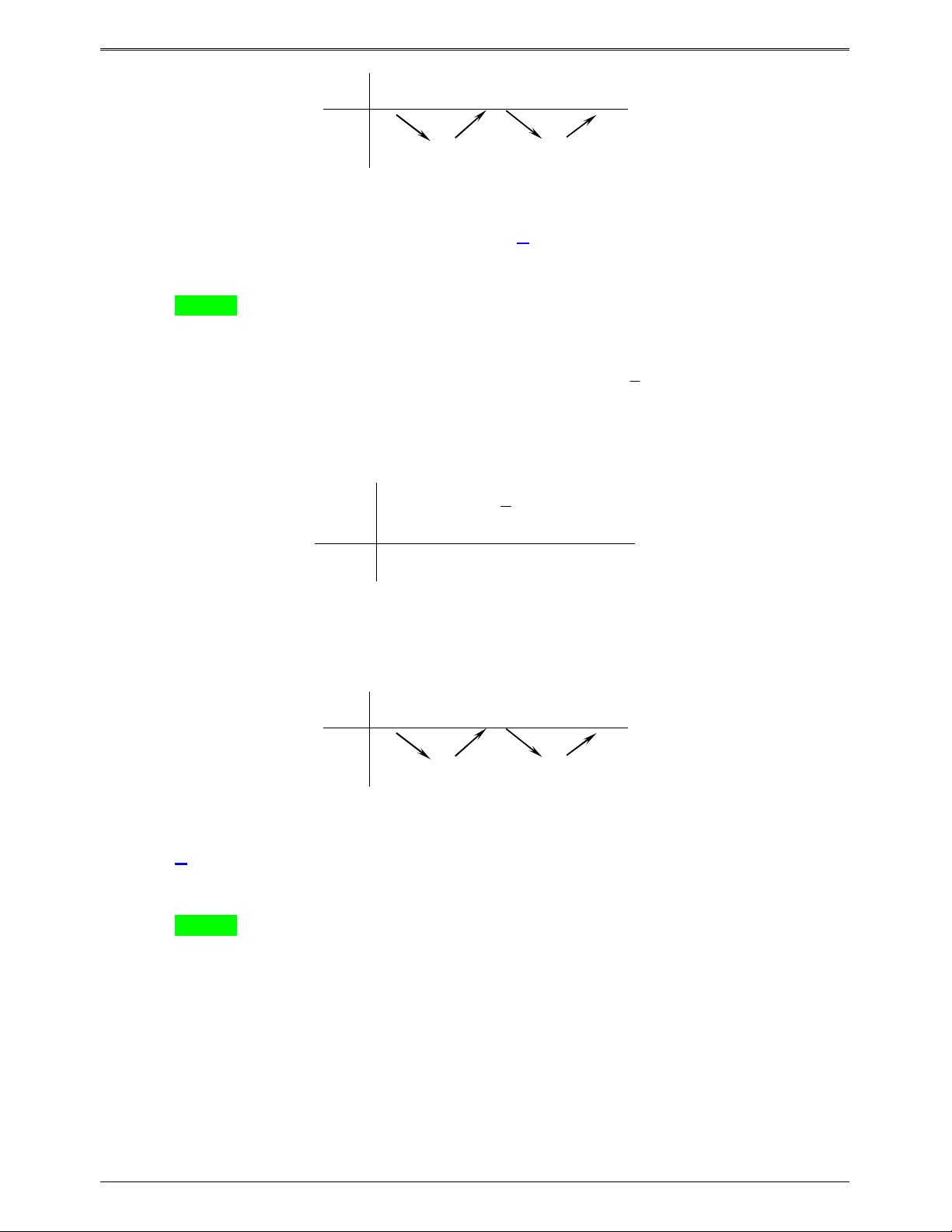
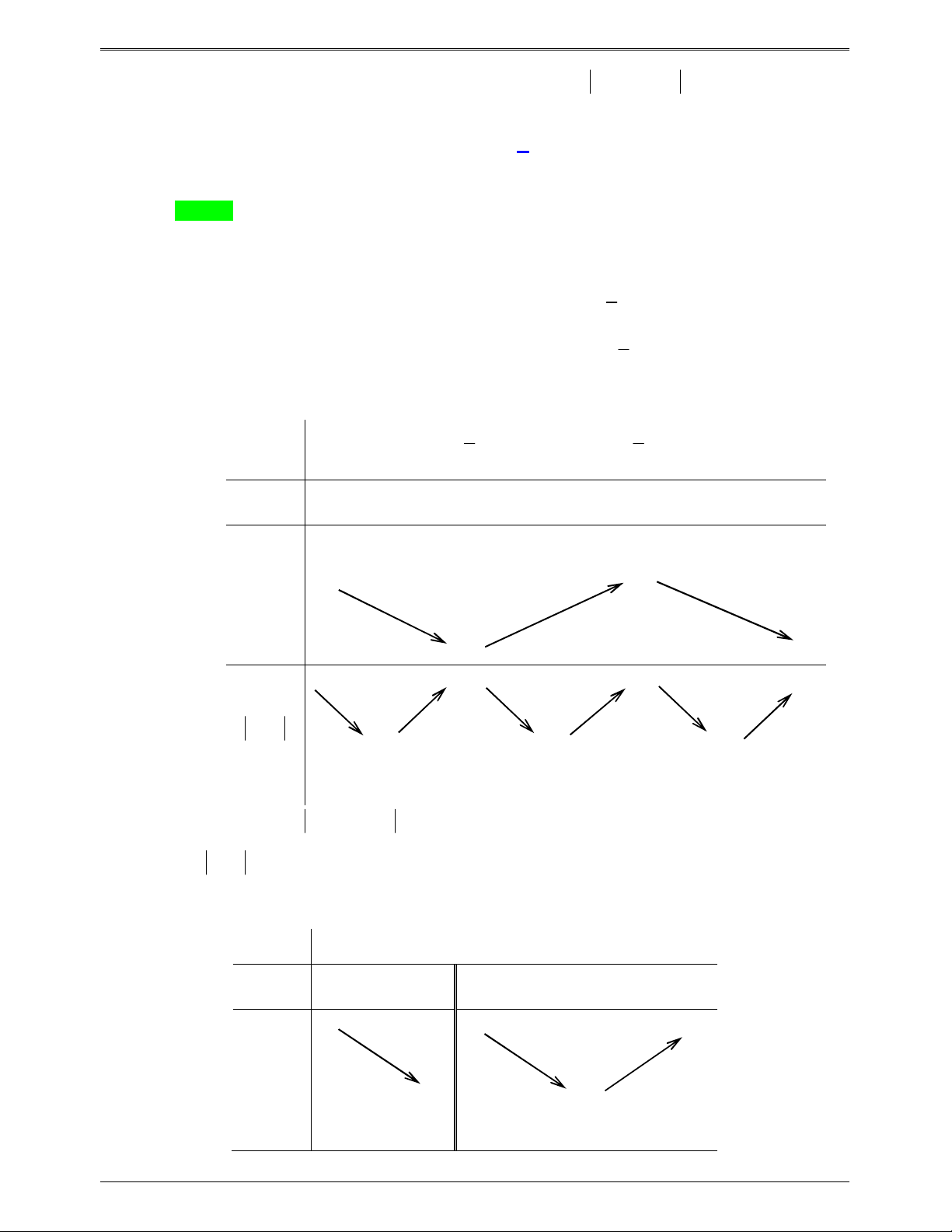
Từ đồ thị, ta có bảng biến thiên của y  f (x) như sau:  g x  f  3 2
x  x   g x   3 2
x  x  f  3 2
x  x    2
x  x  f  3 2 ( ) 3 ( ) 3 3 3 6 x  3x  x  2 x  0  2
3x  6x  0  g (  x)  0   2
3x  6x  f  x  3x  3 2 3 2  0    
x  3x  a  0   1  f  3 2
x  3x   0  3 2 
x  3x  b0;4 2  3 2
 x  3x  c  4  3  x  0 Xét hàm số 3 2
h(x)  x  3x 2  h (
 x)  3x  6x  h (
 x)  0  x  2   Bảng biến thiên
Từ bảng biến thiên, ta thấy
Đường thẳng y  a cắt đồ thị hàm số y  h(x) tại 1 điểm
Đường thẳng y  b cắt đồ thị hàm số y  h(x) tại 3 điểm.
Đường thẳng y  c cắt đồ thị hàm số y  h(x) tại 1 điểm.
Như vậy, phương trình g (
 x)  0 có tất cả 7 nghiệm đơn phân biệt.
Vậy hàm số g x  f  3 2 ( )
x  3x  có 7 cực trị. Trang 660
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Cách trình bày khác:
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán sử dụng đồ thị (hoặc bảng biến thiên) của hàm số y  f  x (hoặc
y  f  x ) để tìm cực trị hàm số g  x  f u  x   . 2. HƯỚNG GIẢI:
B1: Lập bảng biên thiên của hàm số y  f  x
- Dựa vào đồ thị hàm số y  f  x xác định cực trị của hàm số y  f  x . - Lập bảng biến thiên x  a b c  f  x  0  0  0    f  x
B2: Tìm các điểm tới hạn của hàm số g  x  f  3 2 x  3x 
- Đạo hàm g x   2
x  x f  3 2 3 6 . x  3x  x  0 x  2  2
3x  6x  0 
- Cho g x  0    3 2
x  3x  ; a a  0  f   3 2
x  3x   0   3 2
x  3x  ; b 0  b  4  3 2
x  3x  c; c  4 
B3: Khảo sát hàm số h  x 3 2
 x  3x để tìm số giao điểm của đồ thị h  x 3 2
 x  3x với các đường thẳng
y  a, y  , b y  c
Từ đó, ta có thể giải bài toán cụ thể như sau: Lời giải Chọn C Trang 661
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
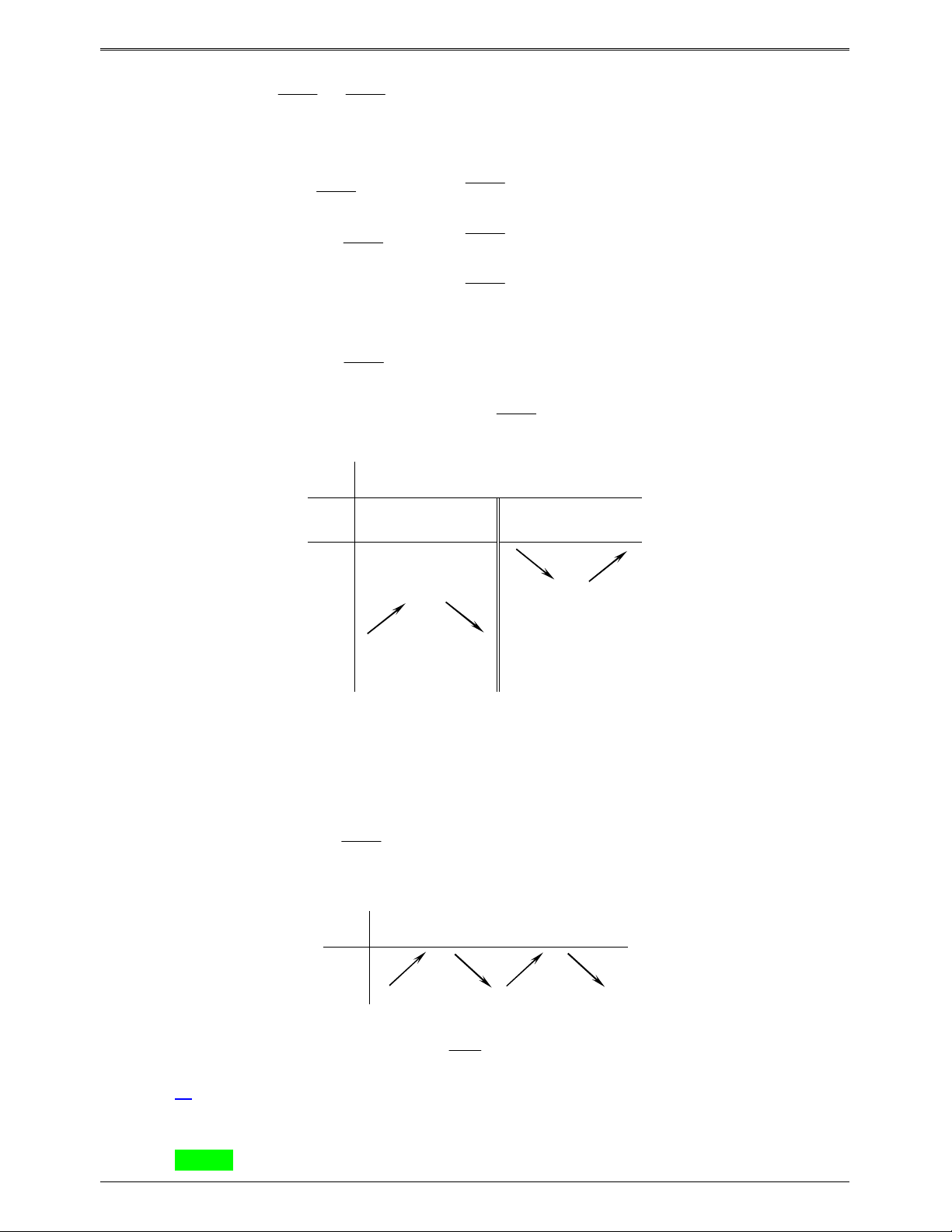
Từ đồ thị ta có bảng biến thiên của hàm số y  f x như sau x  a b c  f  x  0  0  0    f  x
Ta có g  x  f  3 2
x  3x   g x   2
x  x  f  3 2 3 6 . x  3x  x  0 x  2  2 3
 x  6x  0 
Cho g x  0    3 2
x  3x  ; a a  0  f   3 2
x  3x   0   3 2
x  3x  ; b 0  b  4  3 2
x  3x  c; c  4  x  0
Xét hàm số h  x 3 2
 x  3x  h x 2
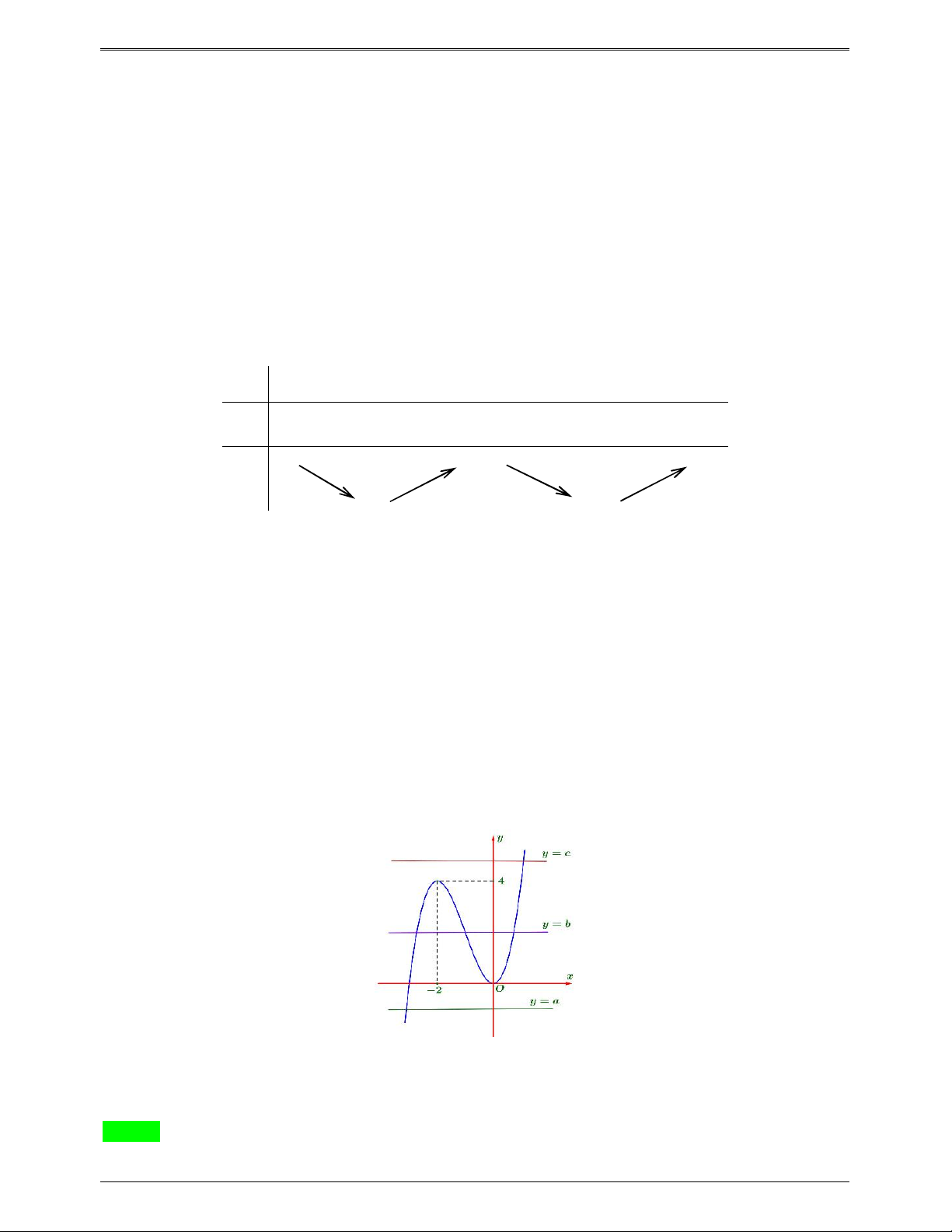
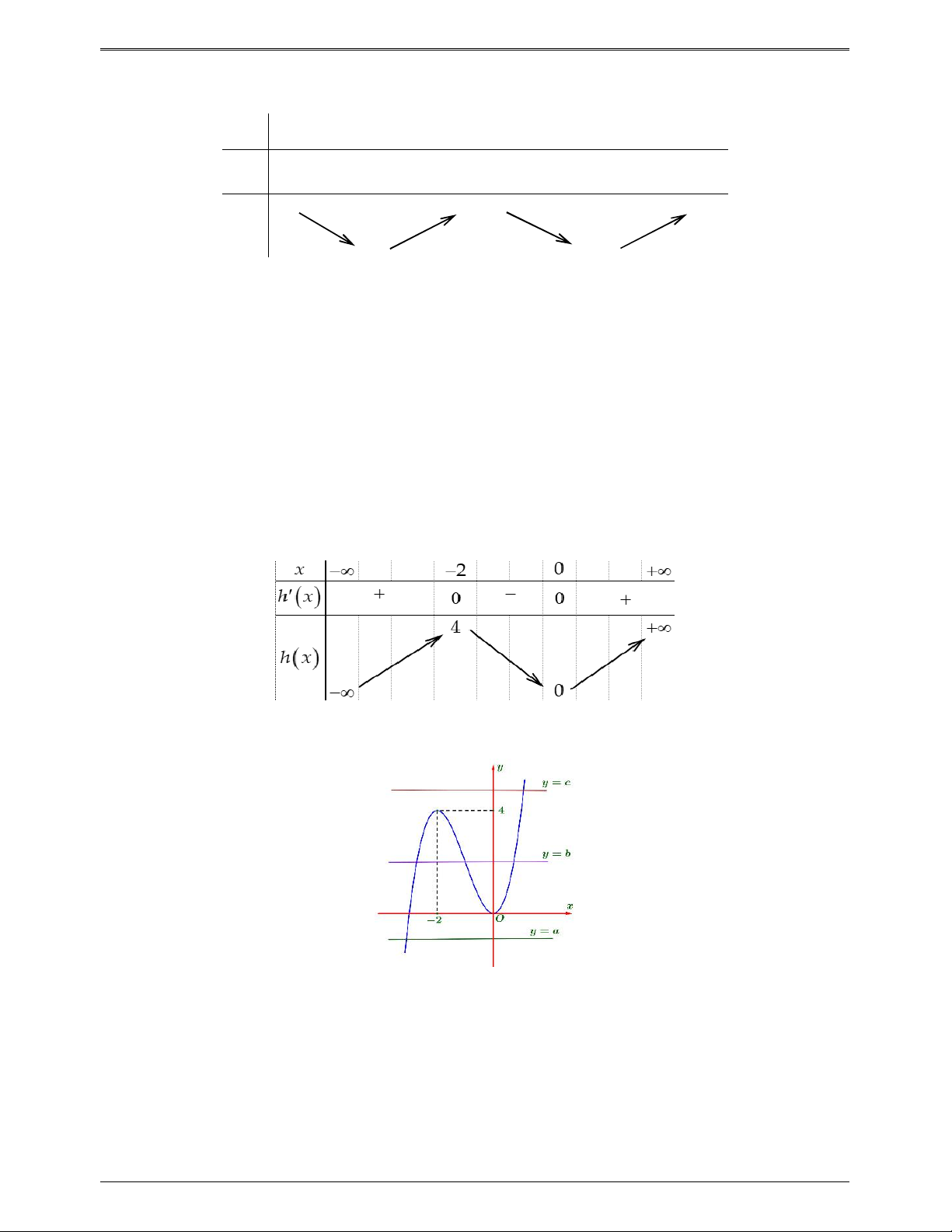
 3x  6x . Cho h x  0  x  2   Bảng biến thiên
Ta có đồ thị của hàm h  x 3 2
 x  3x như sau Từ đồ thị ta thấy:
Đường thẳng y  a cắt đồ thị hàm số y  h  x tại 1 điểm.
Đường thẳng y  b cắt đồ thị hàm số y  h  x tại 3 điểm.
Đường thẳng y  c cắt đồ thị hàm số y  h  x tại 1 điểm.
Như vậy phương trình g x  0 có tất cả 7 nghiệm đơn phân biệt. Trang 662
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Vậy hàm số g  x  f  3 2
x  3x  có 7 cực trị.
Bài tập tương tự và phát triển:
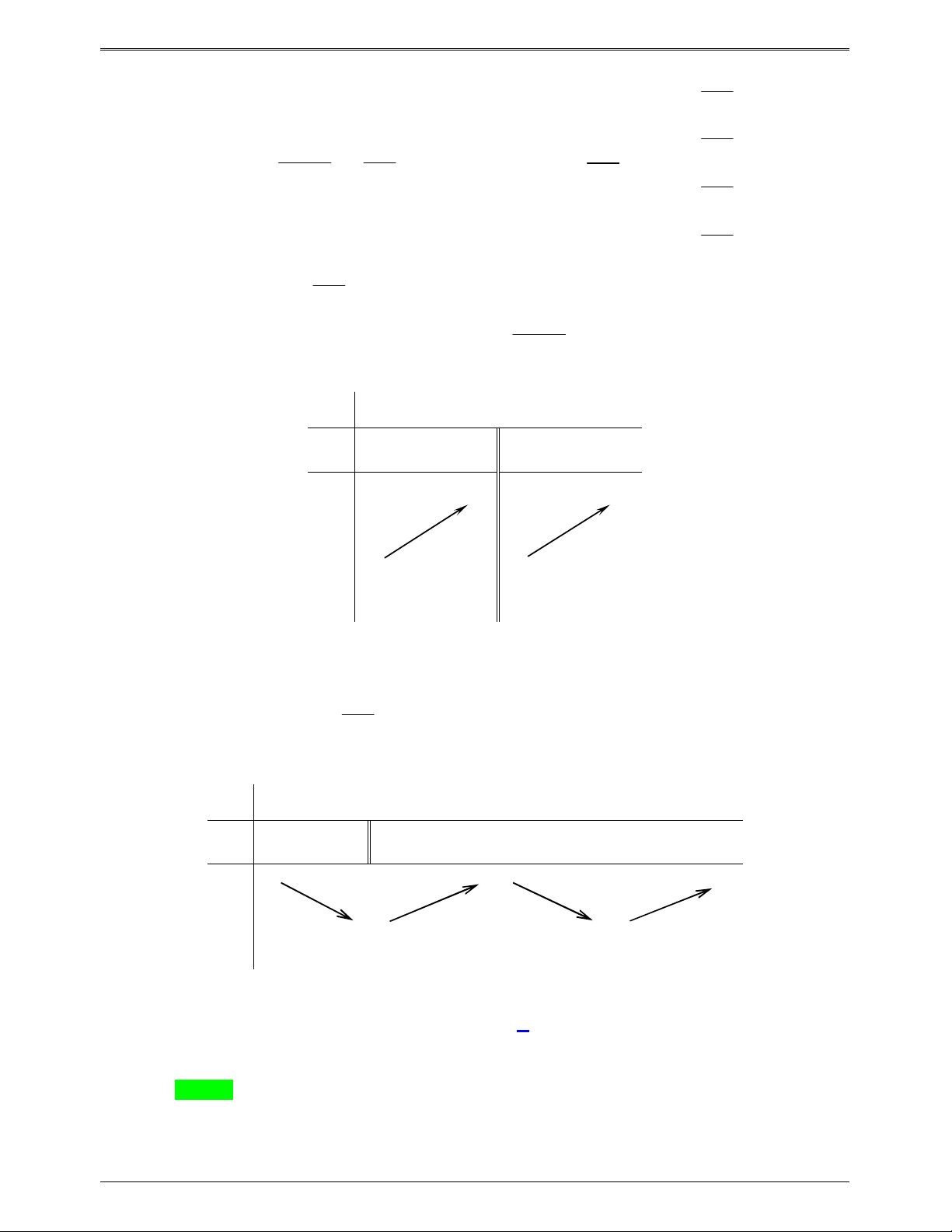
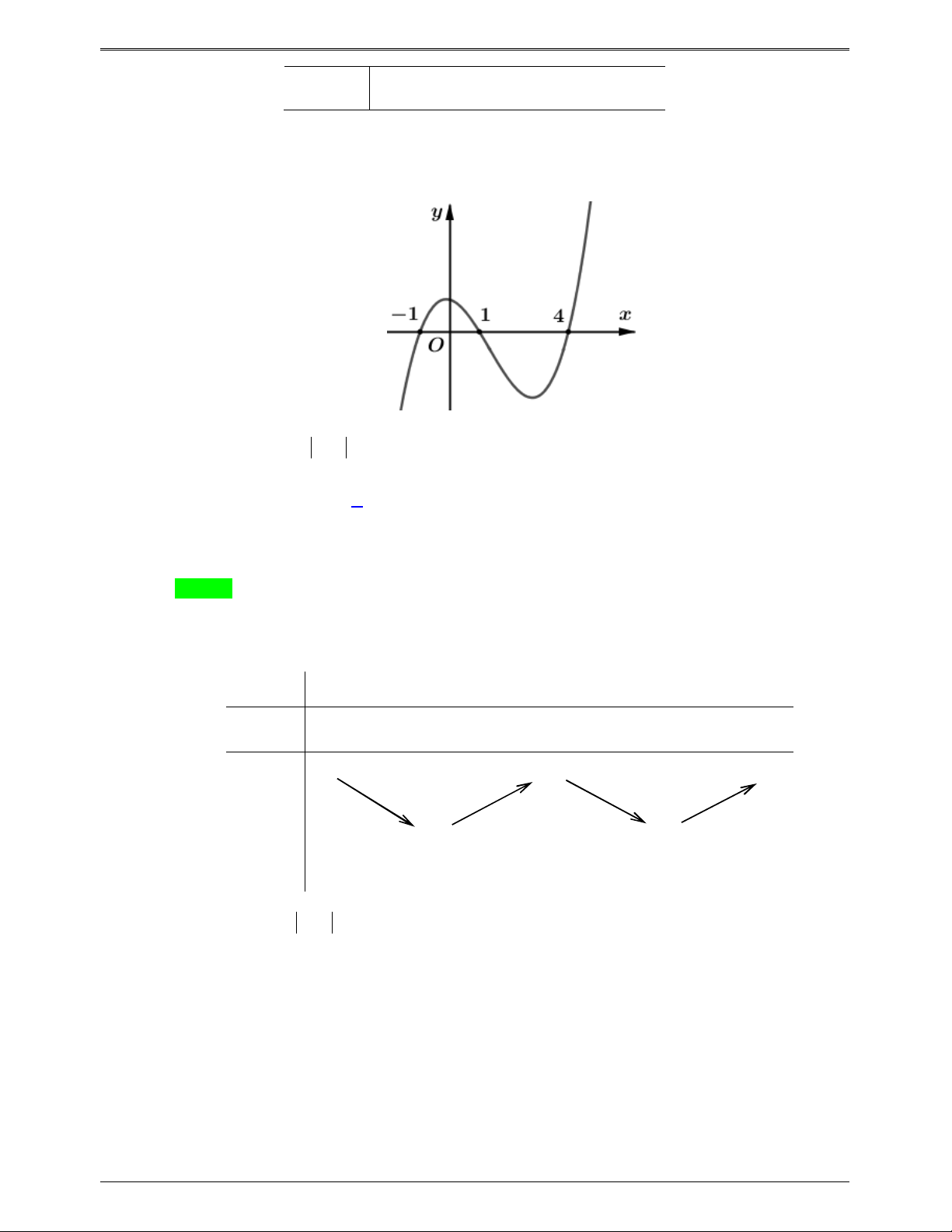
Câu 46.1: Cho hàm số y  f  x. Đồ thị hàm số y  f  x như hình bên.
Tìm số điểm cực trị của hàm số g  x  f  2 x  3. A. 2 . B. 3 C. 4 . D. 5 . Lời giải Chọn B
Ta có g x  xf  2 2 x  3 x  0  x  0 x  0   g x
theo do thi f ' x 2  0  
 x  3  2  x  1 .  f  2 x 3 0       2
x  3  1 nghiem kep
 x  2 nghiem kep   Bảng biến thiên
Dựa vào bảng biến thiên ta thấy hàm số có 3 điểm cực trị.
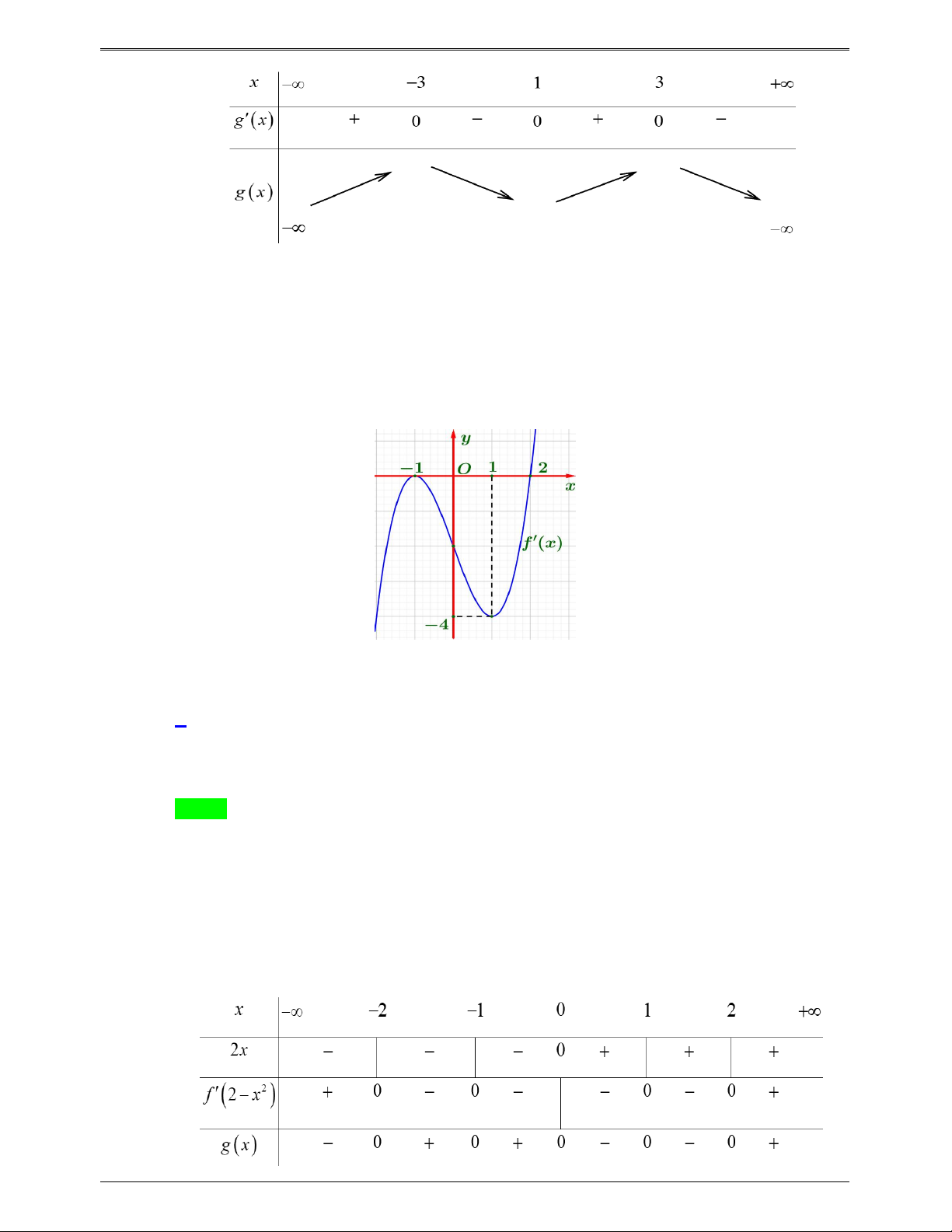
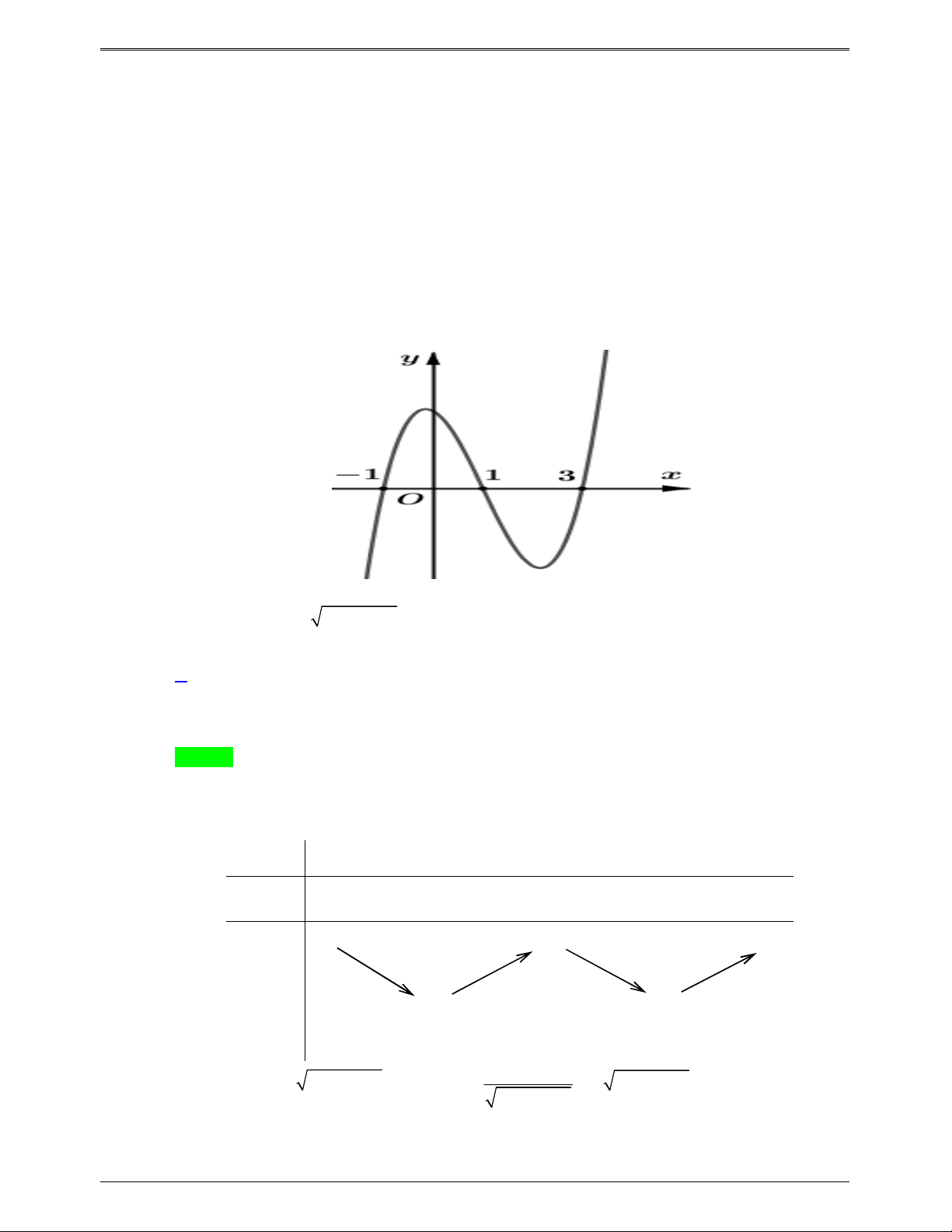
Câu 46.2: Cho hàm số y  f (x) có đạo hàm f '(x) trên  và đồ thị của hàm số f '(x) như hình vẽ.
Tìm số điểm cực trụ hàm số g  x 2
 f (x  2x 1) . A. 6. B. 5 . C. 4 . D. 3 . Lời giải Chọn D Trang 663
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 x 1 x  0  Ta có:  g  x 2 '
 (2x 2) f '(x  2x 1) . Nhận xét: g ' x 2
 0  x 2x 1   1   x  1    2  x 2x 1   2 
x  2; x  3  Ta có bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy hàm số có đúng ba cực trị.
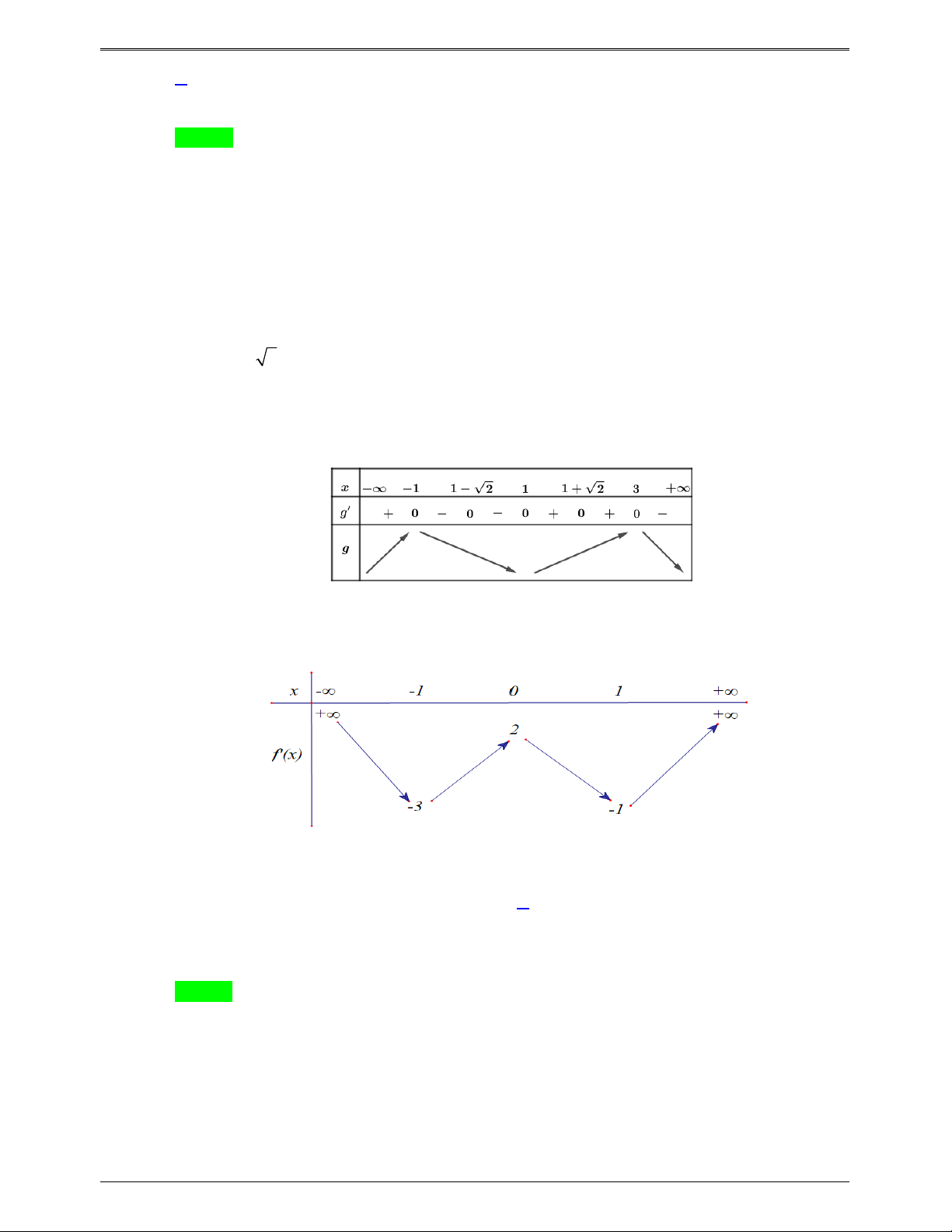
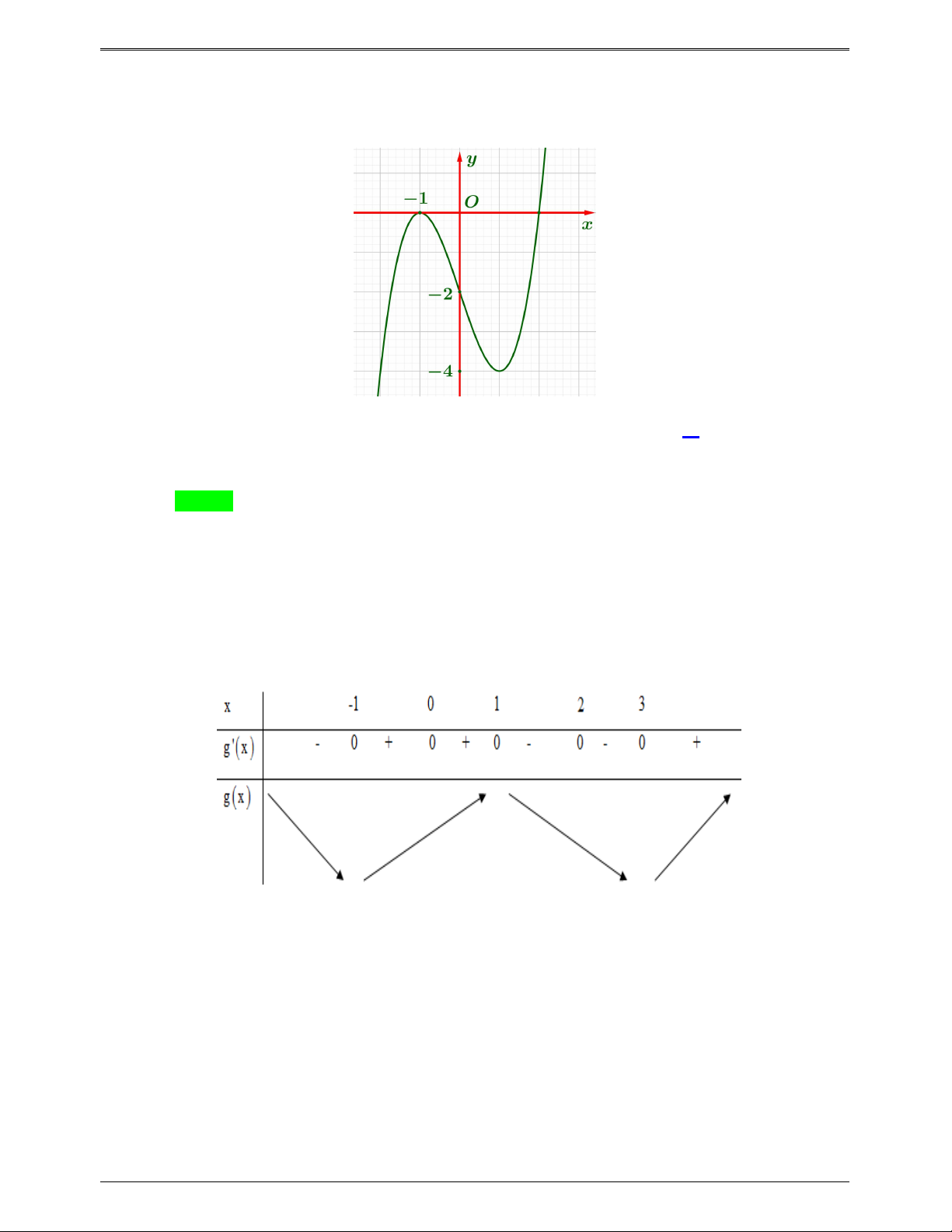
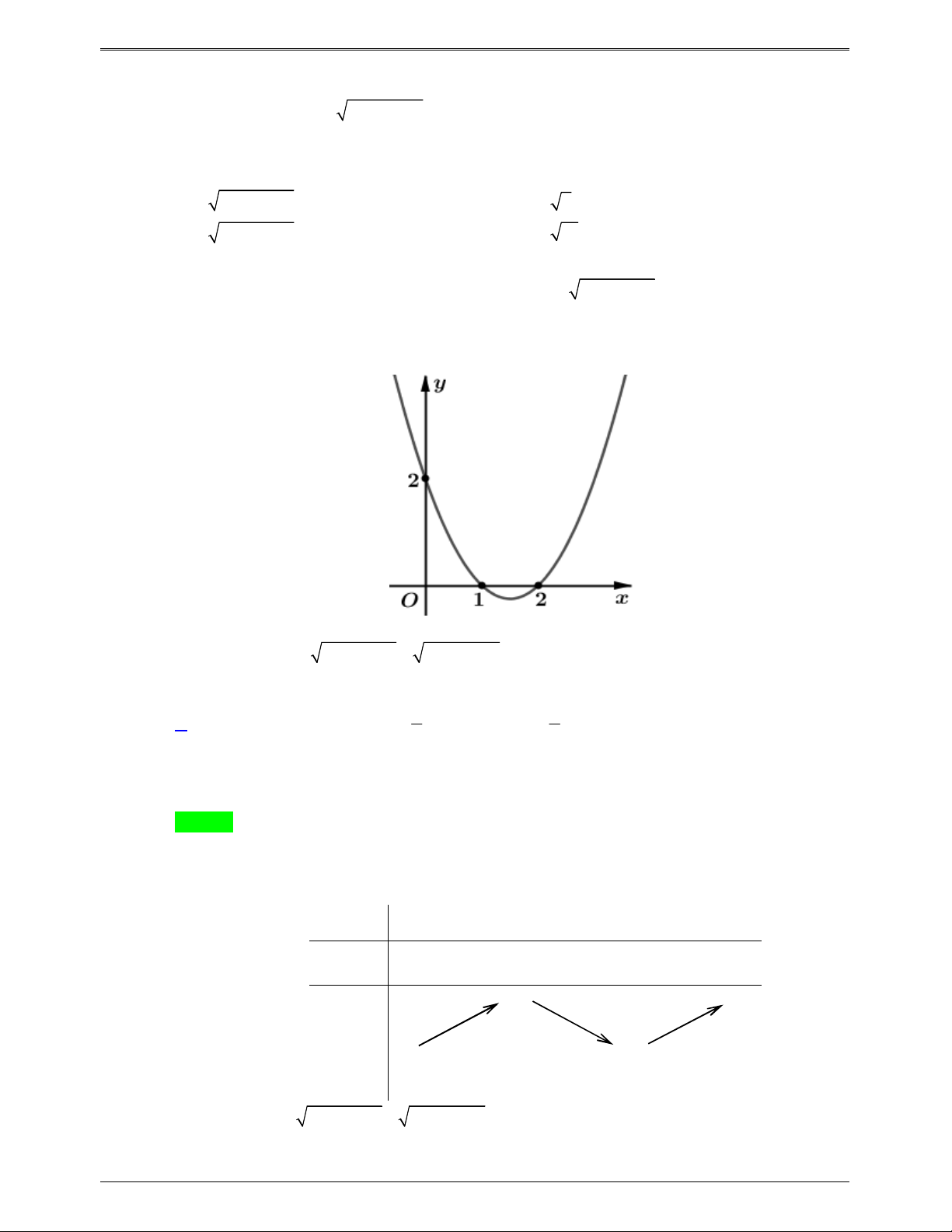
Câu 46.3: Cho hàm số bậc bốn y  f  x . Đồ thị hình bên dưới là đồ thị của đạo hàm f ' x . Hàm số
g  x  f  2
x  2x  2  có bao nhiêu điểm cực trị ? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C x 1
Ta có g x  f  2
x  2x  2 . 2  x  2x  2  x 1  0  x  1  2 x 1  0
 x  2x  2  1  
Suy ra g  x
theo do thi f ' x  0          f  x 1 2 . 2
x  2x  2  2  0
x  2x  2  1    x  1   2   2
x  2x  2  3  Bảng xét dấu
Từ đó suy ra hàm số g  x  f  2
x  2x  2 có 3 điểm cực trị.
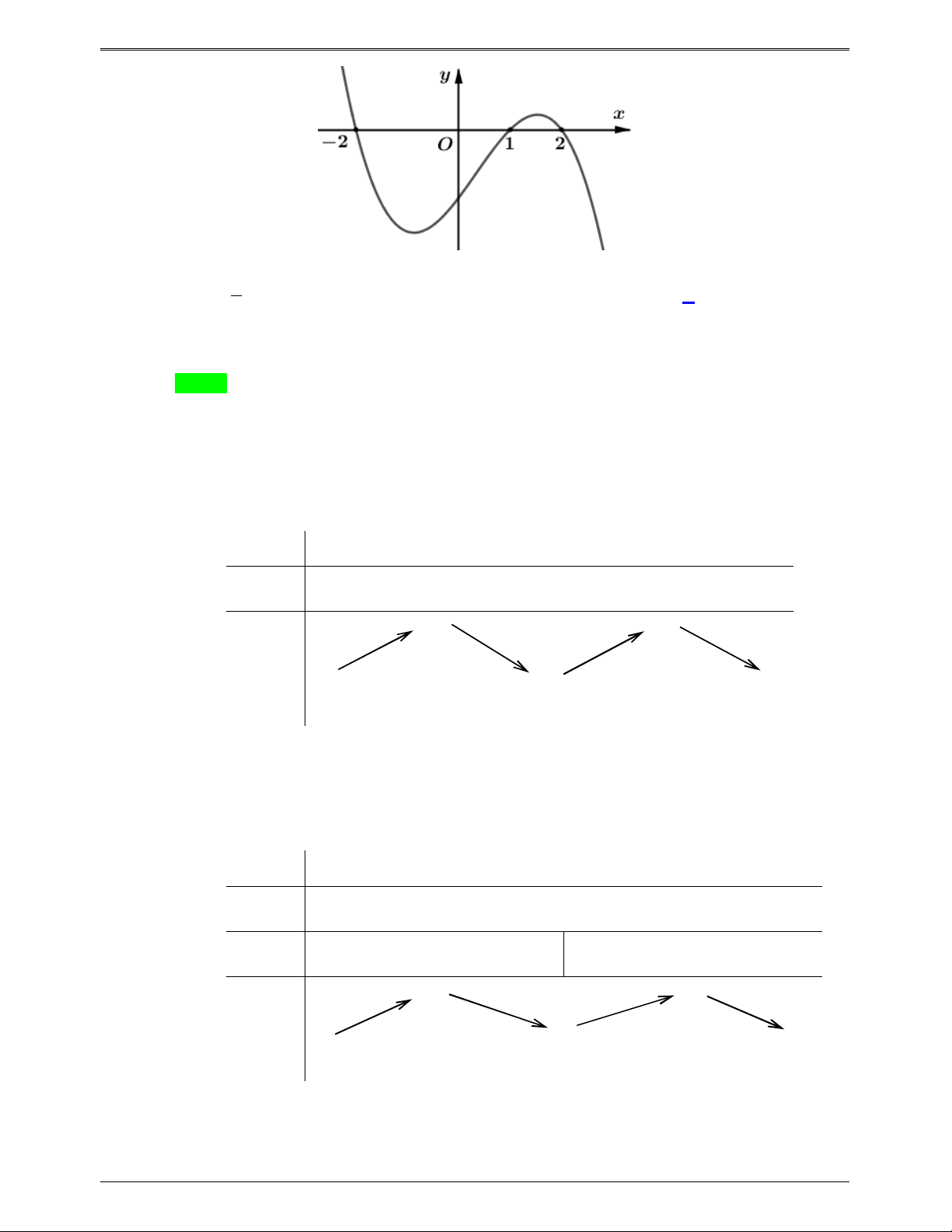
Câu 46.4: Cho hàm số y  f  x có đạo hàm trên  và có bảng xét dấu của y  f  x như sau
Hỏi hàm số g  x  f  2
x  2x có bao nhiêu điểm cực tiểu ? Trang 664
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 A. 1. B. 2 C. 3 . D. 4 . Lời giải Chọn A
Ta có g x   x   f  2 2 2 x  2x;  x  1  2 2x  2  0
x  2x  2  g x
theo BBT f ' x  0     f   2 x 2x 2 0    
x  2x  1nghiem kep   2
 x  2x  3  x  1 x 1 2  nghiem kep  . x  1  x  3  Bảng biến thiên
Dựa vào bảng biến thiên ta thấy hàm số có một điểm cực tiểu.
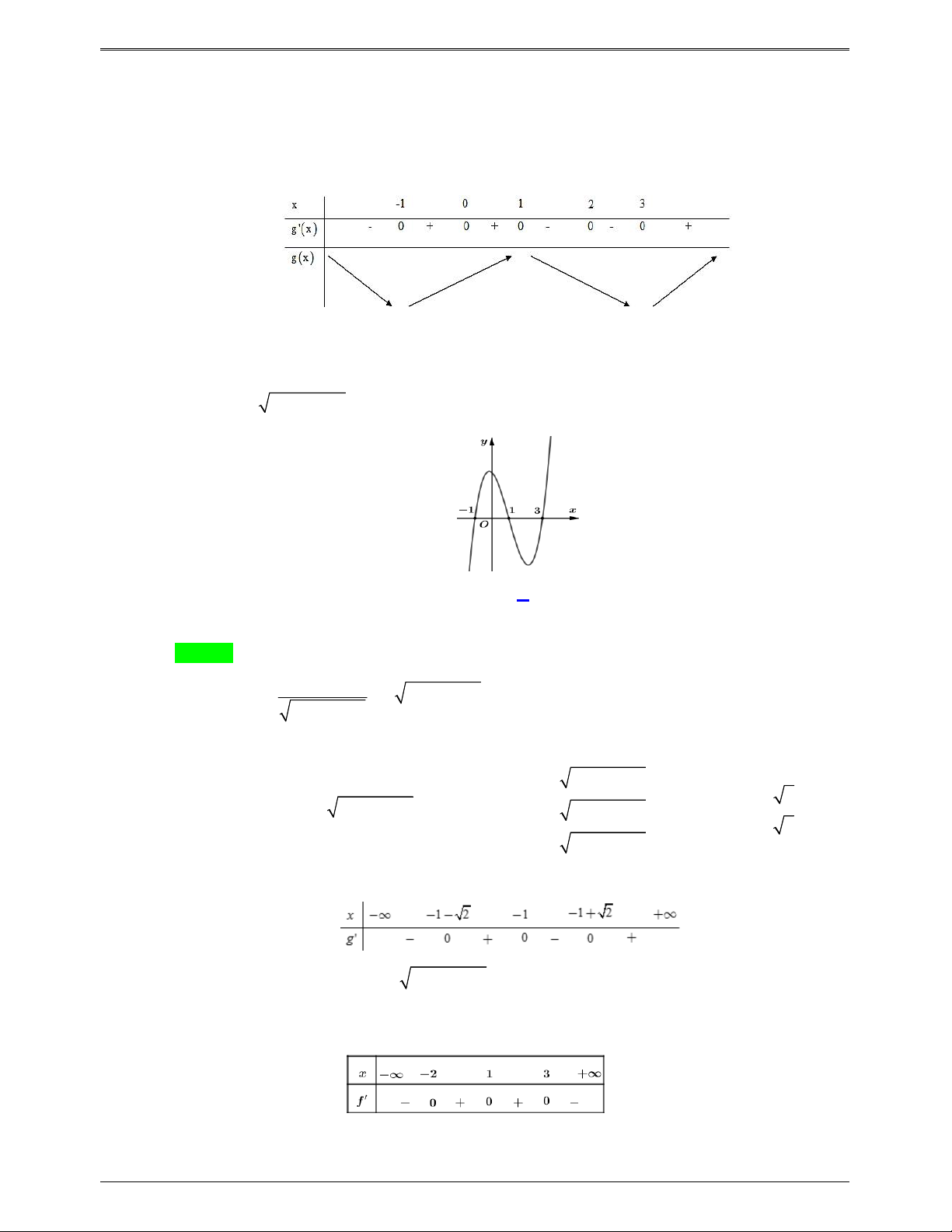
Câu 46.5: Cho hàm số f  x , bảng biến thiên của hàm số f  x như sau:
Số điểm cực trị của hàm số y  f  2 4x  4x là A. 9. B. 5. C. 7 . D. 3. Lời giải Chọn B
x  a   ;    1 x  b  1;0
Dựa vào bảng biến thiên ta có: f  x  0   .
x  c  0  ;1 
x  d 1;   Trang 665
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  1 x   2  2
4x  4x  a    ;    1 8x  4  0 
Ta có: y   x   f  2 8 4
4x  4x  , y  0   2
 4x  4x  b   1  ;0 . f     2
4x  4x   0   2
4x  4x  c  0  ;1  2
4x  4x  d 1;    1 Ta có khi 2 x 
 4x  4x  1 và f   1  3  0 2
Mặt khác: x  x   x  2 2 4 4 2 1 1  1 nên:  2
4 x  4 x  a vô nghiệm.  2
4 x  4 x  b có 2 nghiệm phân biệt x , x . 1 2  2
4 x  4 x  c có 2 nghiệm phân biệt x , x . 3 4  2
4 x  4 x  d có 2 nghiệm phân biệt x , x . 5 6
Vậy phương trình y  0 có 7 nghiệm bội lẻ phân biệt nên hàm số có 7 điểm cực trị.
Câu 46.6: Cho hàm số f  x , bảng biến thiên của hàm số f  x như sau
Số điểm cực trị của hàm số y  f  2 x  2x  là A. 9 . B. 3 . C. 7 . D. 5 . Lời giải Chọn B Trang 666
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Từ bảng biến thiên ta có phương trình f   x  0 có các nghiệm tương ứng
x  a, a   ;    1
x  b,b   1  ;0 là  .
x  c, c  0;  1 
x  d,d 1; 
Xét hàm số y  f  2
x  x   y   x   f  2 2 2 1 x  2x . x  1  2
x  2x  a    1 x 1  0 
Giải phương trình y  0  2  x   1 f   2 x  2x 2  0  
 x  2x  b 2 . 2   f  x 2x 0       2
x  2x  c 3  2
x  2x  d 4 
Vẽ đồ thị hàm số h  x 2  x  2x 1
Dựa vào đồ thị ta thấy: phương trình 1 vô nghiệm. Các phương trình 2 ; 3 ; 4 mỗi
phương trình có 2 nghiệm. Các nghiệm đều phân biệt nhau.
Vậy phương trình y  0 có 7 nghiệm phân biệt nên hàm số y  f  2
x  2x  có 7 điểm cực trị.
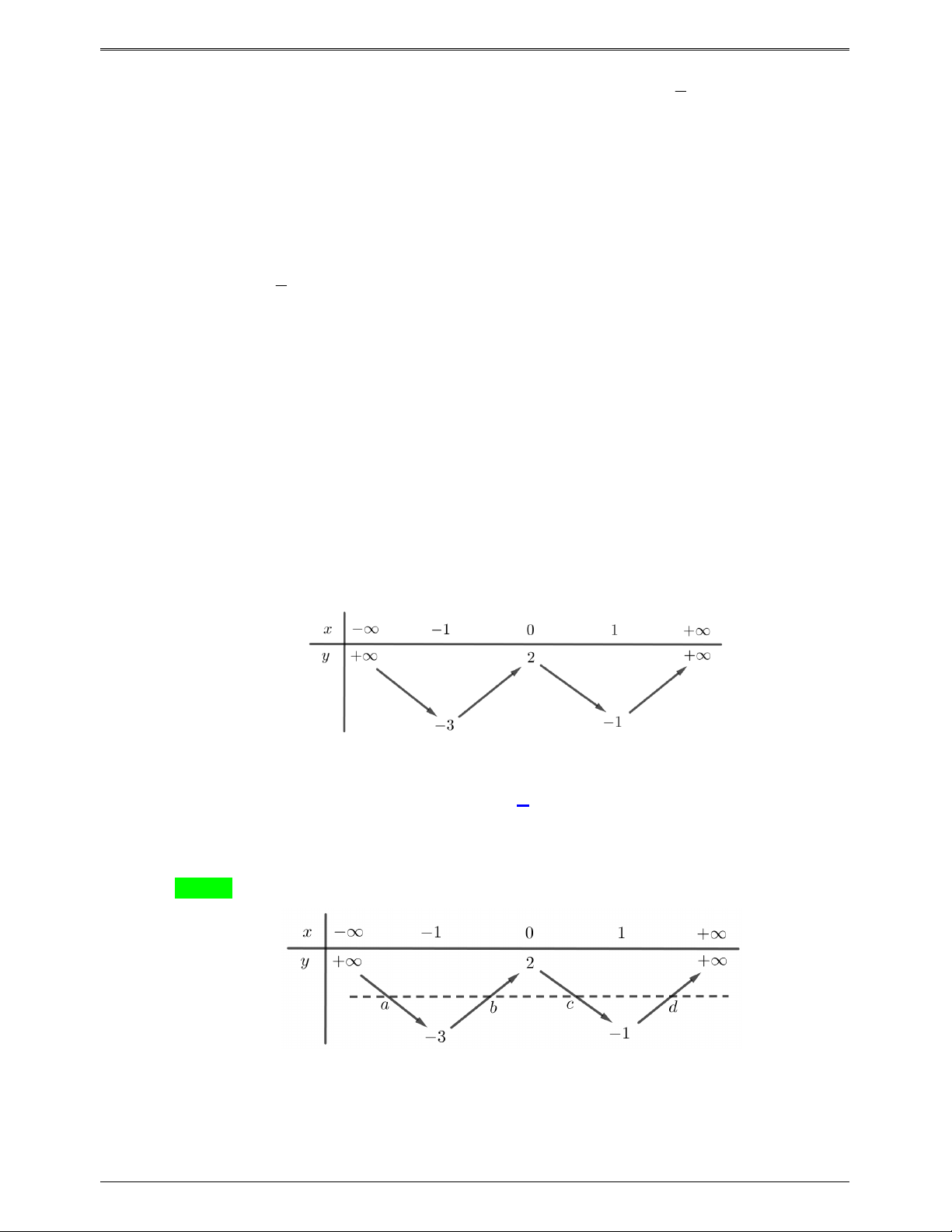
Câu 46.7: Cho hàm số y  f  x có đạo hàm f  x trên khoảng  ;
  . Đồ thị của hàm số
y  f  x như hình vẽ Đồ thị của hàm số    2 y f x
có bao nhiêu điểm cực đại, cực tiểu?
A. 2 điểm cực đại, 3 điểm cực tiểu.
B. 1 điểm cực đại, 3 điểm cực tiểu. Trang 667
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
C. 2 điểm cực đại, 2 điểm cực tiểu.
D. 3 điểm cực đại, 2 điểm cực tiểu. Lời giải Chọn A
Từ đồ thị hàm số ta có bảng biến thiên
 f  x  0    2 y f x
 y  2 f  x. f  x  0   .
 f   x   0  x  0 x  x1 
Quan sát đồ thị ta có f  x 0  
 x  1 và f   x  0  x  1 với x  0;1 và x  1;3 . 2   1     x  3  x  x  2  f   x  0   f    x  0  x  3;
Suy ra y  0    
 x 0; x  1; x  3; 1   2     f   x  0
x  0; x  1; x  1   2    f    x  0 
Từ đó ta lập được bảng biến thiên của hàm số    2 y f x
Suy ra hàm số có 2 điểm cực đại, 3 điểm cực tiểu.
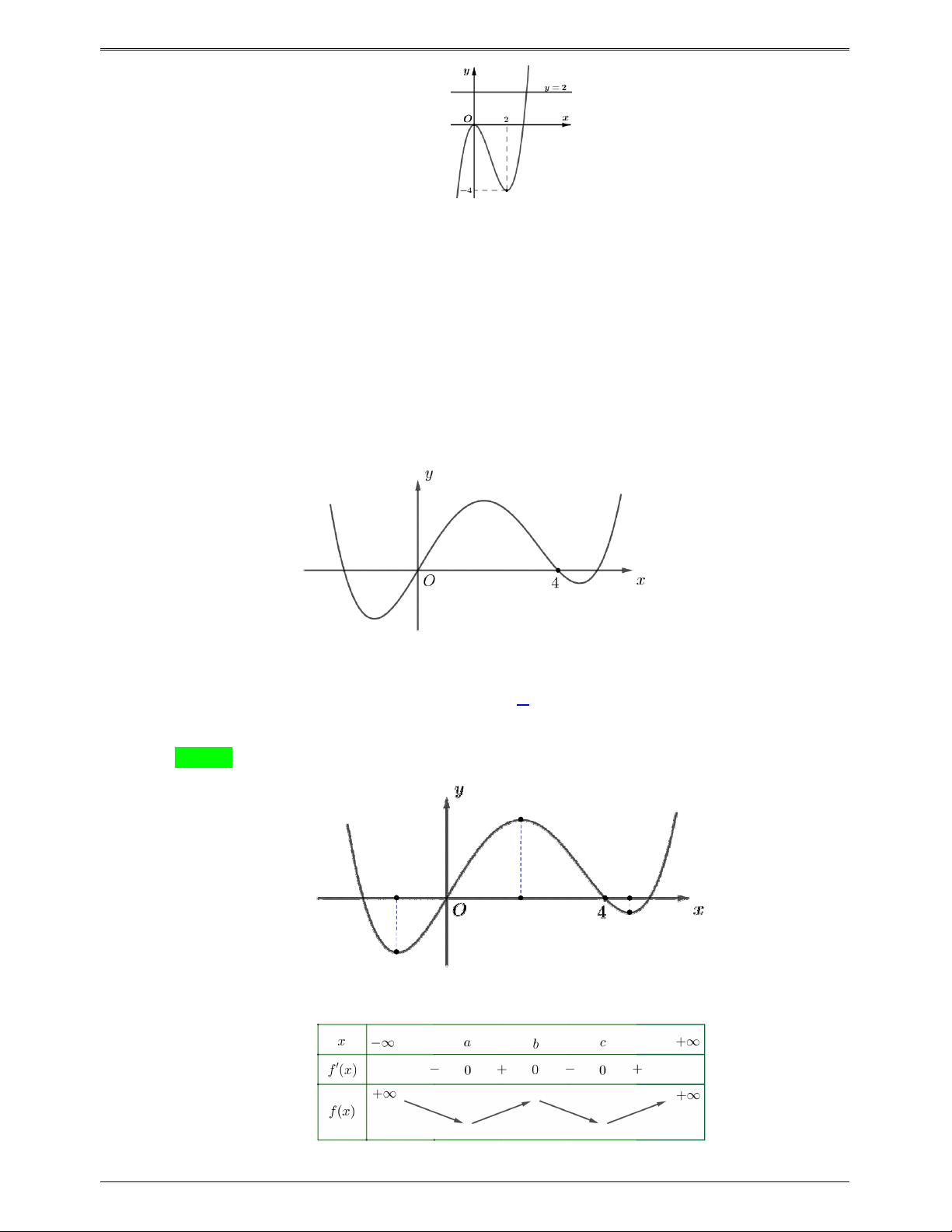
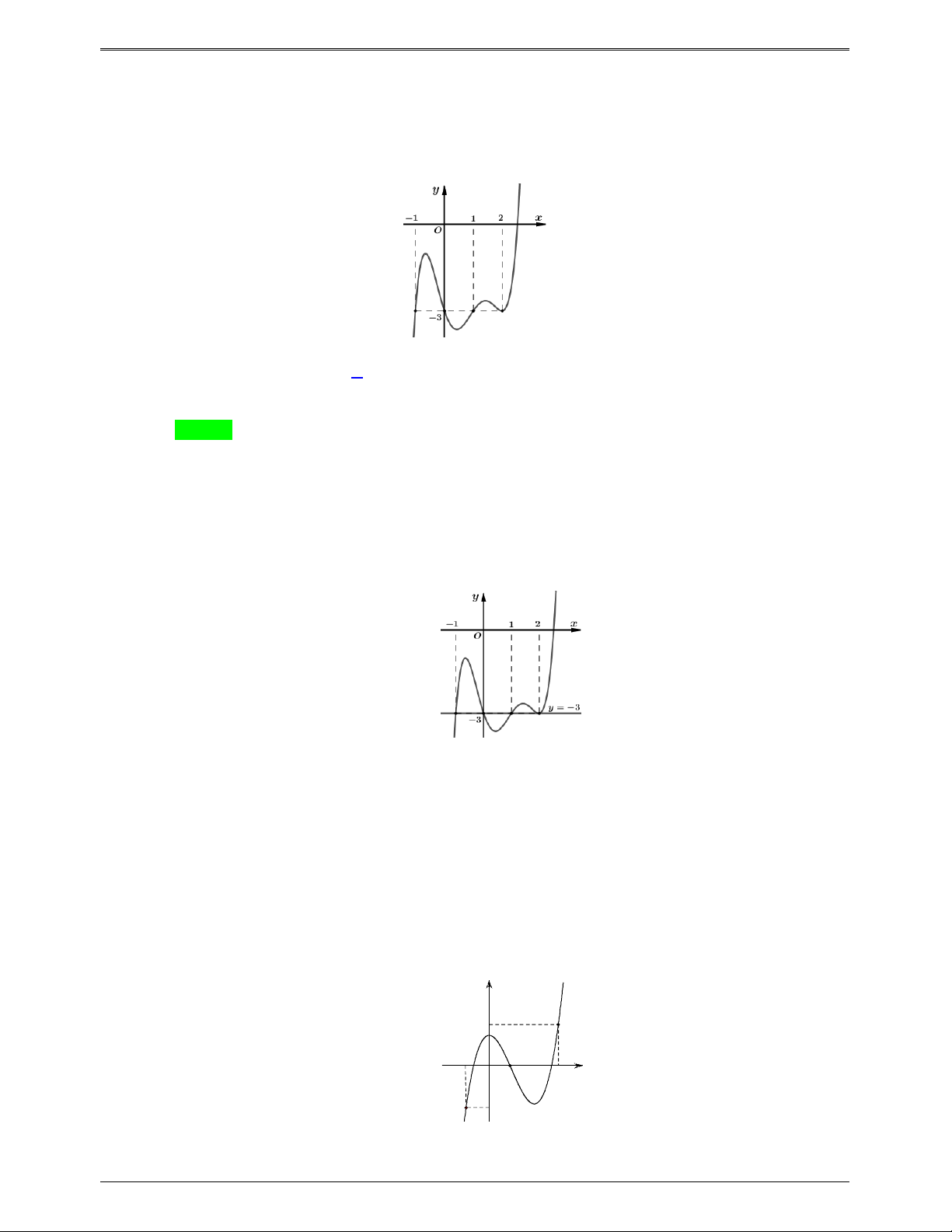
Câu 46.8: Cho hàm số y  f  x có đồ thị hàm số như hình bên.
Hàm số g  x  f  2
x  3x có bao nhiêu điểm cực đại ? A. 3 . B. 4 C. 5 . D. 6 . Lời giải Trang 668
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Chọn B
Ta có g x   x   f  2 2 3 . x  3x;  3  3 x  x   2  2   2  x  3  0  f x  3  17 g x theo do thi   2  0  
 x  3x  2   x  . f   2 x 3x 0      2   2 x 3x 0      x  0   x  3  Bảng biến thiên
Dựa vào bảng biến thiên ta thấy hàm số có 4 điểm cực trị.
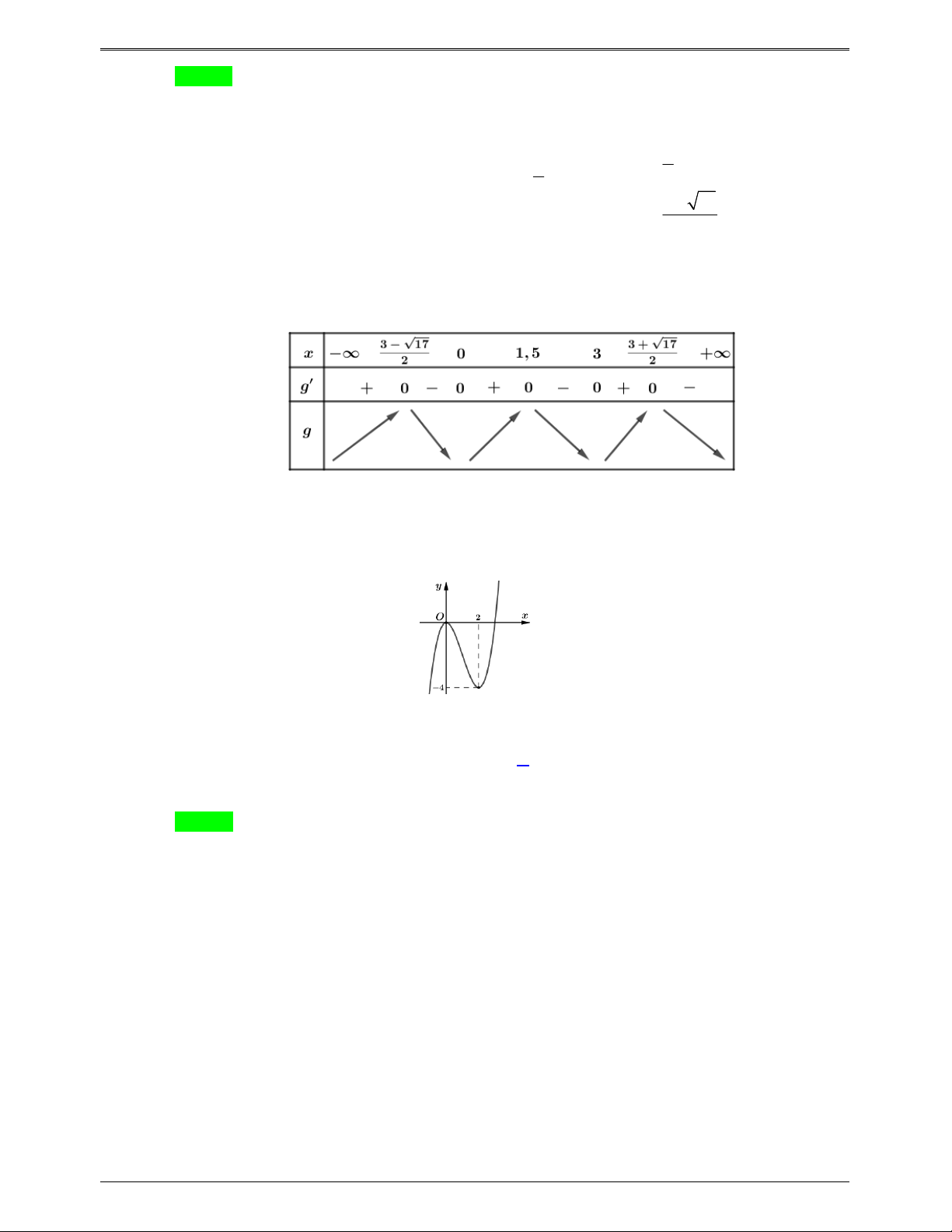
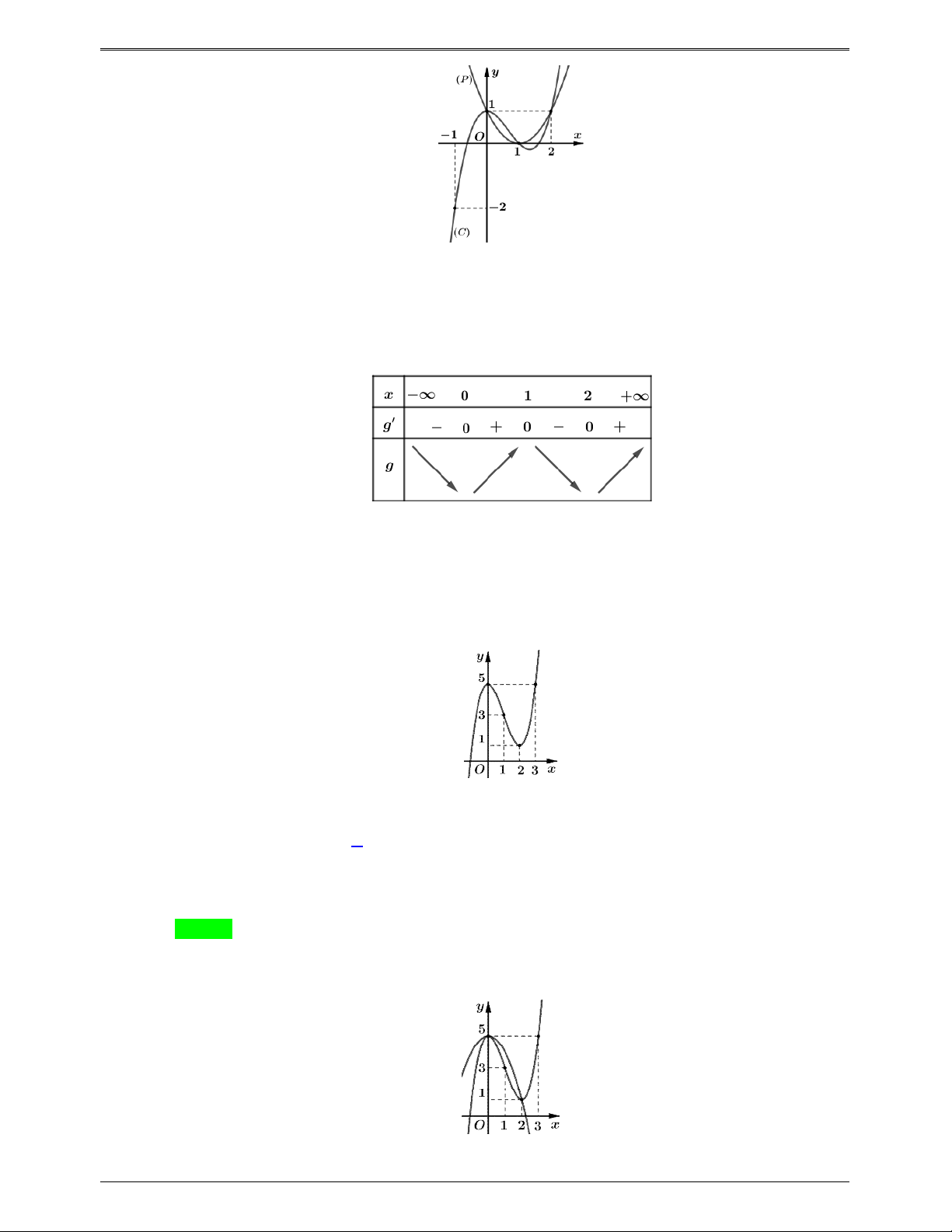
Câu 46.9: Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Hàm số g  x  f  f  x 
 có bao nhiêu điểm cực trị ? A. 3 . B. 5 . C. 4 . D. 6 . Lời giải Chọn C
Dựa vào đồ thị ta thấy f  x đạt cực trị tại x  0, x  2.
 x  0 nghiem don
Suy ra f   x  0   .
 x  2  nghiem don  
 f  x  0
Ta có g x  f  x. f   f  x ; g x  0   .  
 f   f  x  0   
 x  0 nghiem don
 f  x  0   1
 f  x  0   .
 f   f  x  0   .  
 x  2  nghiem don  
 f  x  2 2  Trang 669
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Dựa vào đồ thị suy ra:  Phương trình  
1 có hai nghiệm x  0 (nghiệm kép) và x  a a  2.
 Phương trình 2 có một nghiệm x  b b  a.
Vậy phương trình g x  0 có 4 nghiệm bội lẻ là x  0, x  2, x  a và x  . b Suy ra hàm số
g  x  f  f  x   có 4 điểm cực trị. Câu 46.10:
Cho hàm số y  f  x có bảng biến thiên như sau
Số điểm cực trị của hàm số g x  f  4 2 ( )
x  4x  là A. 5 . B. 3 C. 7 . D. 11. Lời giải Chọn B a c b
Từ đồ thị, ta có bảng biến thiên của y  f (x) như sau: Trang 670
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  g x  f  4 2
x  x   g x   4 2
 x  x  f  4 2
x  x    3
 x  x f  4 2 ( ) 4 ( ) 4 4 4 8  x  4x   x   2  x  0  3
4x  8x  0  g (  x)  0   3
4x  8x f  4 2 x  4x  4 2  0  
  x  4x  a  0    1  f   4 2
 x  4x   0    4 2
 x  4x  b  0; 4 2  4 2
 x  4x  c 4   3  x  0 Xét hàm số 4 2
h(x)  x  4x 3  h (
 x)  4x  8x  h (
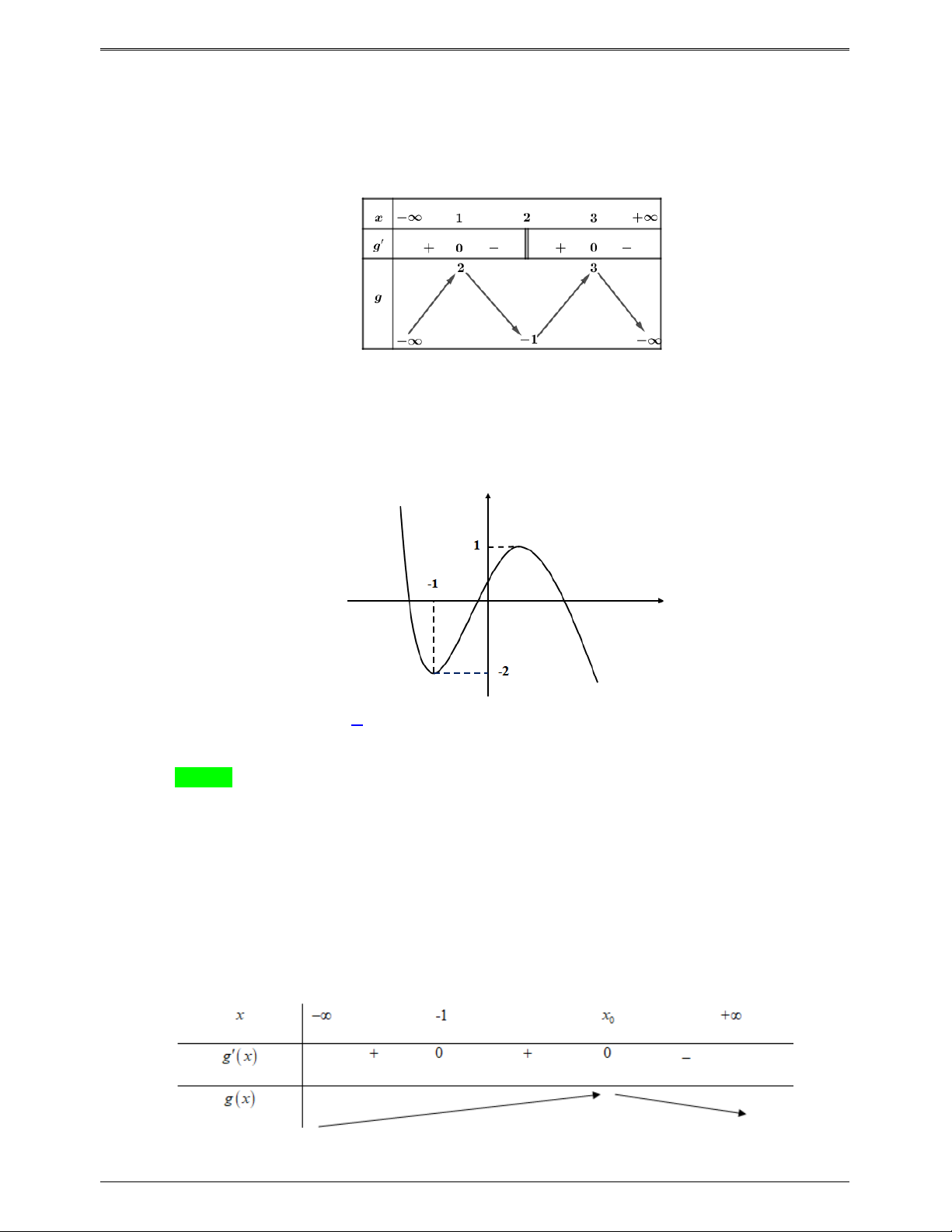
 x)  0  x   2  Bảng biến thiên x ∞ 2 0 2 + ∞ h' x ( ) + 0 0 + 0 4 4 h x ( ) ∞ 0 ∞
Từ bảng biến thiên, ta thấy
Đường thẳng y  a  0 cắt đồ thị hàm số y  h(x) tại 2 điểm
Đường thẳng y  b  0; 4 cắt đồ thị hàm số y  h(x) tại 4 điểm.
Đường thẳng y  c  4 cắt đồ thị hàm số y  h(x) tại 0 điểm.
Như vậy, phương trình g (
 x)  0 có tất cả 7 nghiệm đơn phân biệt.
Vậy hàm số g x  f  3 2 ( )
x  3x  có 7 cực trị Câu 46.11:
Cho hàm số y  f  x có bảng biến thiên như sau
Tìm số điểm cực trị của hàm số g  x  f 3  x. A. 2 . B. 3 . C. 5 . D. 6 . Lời giải Chọn B
Ta có g x   f 3  x. Trang 671
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 3   x  0 x  3
 g x  0  f 3  x theo BBT  0    .   3  x  2 x  1  
 g x không xác định  3 x  1  x  2. Bảng biến thiên
Vậy hàm số g  x  f 3  x có 3 điểm cực trị. Câu 46.12:
Cho hàm số y  f  x có đạo hàm liên tục trên  . Đồ thị hàm số y  f  x như hình vẽ
sau. Số điểm cực trị của hàm số y  f  x  2x là: A. 4 . B. 1. C. 3 . D. 2 . Lời giải Chọn B  x  1 
Đặt g  x  f  x  2x suy ra g x  0  f  x  2  0  f  x  2   . x  x  1   0
Dựa vào đồ thị ta có: Trên  ;   
1 thì f   x  2
  f  x  2  0 .
Trên 1; x thì f  x  2  f  x  2  0 . 0 
Trên  x ;   thì f  x  2  f  x  2  0 . 0  Trang 672
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Vậy hàm số g  x  f  x  2x có 1 cực trị. Câu 46.13:
Cho hàm số y  f  x có đạo hàm trên .
 Đồ thị hàm số y  f  x như hình vẽ bên
dưới. Hỏi đồ thị hàm số g  x  f  x  3x có bao nhiểu điểm cực trị ? A. 2 . B. 3 . C. 4 . D. 7 . Lời giải Chọn B
Ta có g x  f  x  3; g x  0  f  x  3  .
Suy ra số nghiệm của phương trình g x  0 chính là số giao điểm giữa đồ thị của hàm số
f   x và đường thẳng y  3. x  1  x  0
Dựa vào đồ thị ta suy ra g x  0  
. Ta thấy x  1, x  0, x  1 là các nghiệm đơn x  1 x  2 
và x  2 là nghiệm kép nên đồ thị hàm số g  x  f  x  3x có 3 điểm cực trị Câu 46.14:
Cho hàm số y  f (x) có đạo hàm trên  . Đồ thị của hàm số y  f '( x) như hình vẽ. y 2 -1 O 1 3 x -2
Tìm số điểm cực trị của hàm số 2
g(x)  2 f (x)  x  2x  2017 . Trang 673
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 A. 2 . B. 3 . C. 4 . D. 7 . Lời giải Chọn B Ta có g '( ) x  2 f '( )
x  2x  2  2 f '( )
x  (x 1).
Dựa vào hình vẽ ta thấy đường thẳng yx 1
 cắt đồ thị hàm số y  f '( ) x tại 3 điểm: ( 1  ; 2  ), (1;0), (3;2). y 2 -1 O 1 3 x -2 Dựa vào đồ thị ta có x  1  g '(x) 0
2 f '(x) (x 1) 0      
 x  1 đều là các nghiệm đơn  x  3 
Vậy hàm số y  g( )
x có 3 điểm cực trị. Câu 46.15:
Cho hàm số y  f  x có đạo hàm trên .
 Đồ thị hàm số y  f  x như hình vẽ bên
dưới. Hàm số g  x  f  x 2 2
 x đạt cực tiểu tại điểm A. x  1  . B. x  0. C. x  1. D. x  2. Lời giải Chọn B
Ta có g x  2 f  x  2 ;
x g  x  0  f  x   . x
Suy ra số nghiệm của phương trình g x  0 chính là số giao điểm giữa đồ thị của hàm số
f   x và đường thẳng y   . x Trang 674
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 x  1  x  0
Dựa vào đồ thị ta suy ra g x  0   . x  1 x  2  Bảng biến thiên
Dựa vào bảng biến thiên ta thấy g  x đạt cực tiểu tại x  0. Câu 46.16:
Cho hàm số y  f  x có đạo hàm trên .
 Đồ thị hàm số y  f  x như hình vẽ bên dưới. 3 x
Hàm số g  x  f  x 2 
 x  x  2 đạt cực đại tại. 3 A. x  1 . B. x  0 . C. x  1 . D. x  2 . Lời giải Chọn C
Ta có g x  f  x  x  x 
g x   f  x   x  2 2 2 1; 0 1 .
Suy ra số nghiệm của phương trình g x  0 chính là số giao điểm giữa đồ thị của hàm số
f   x và parapol  P y   x  2 : 1 . Trang 675
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 x  0
Dựa vào đồ thị ta suy ra g  x 0     x  1 .  x  2  Bảng biến thiên
Dựa vào bảng biến thiên ta thấy g  x đạt cực đại tại x  1. Câu 46.17:
Cho hàm số y  f  x. Đồ thị hàm số y  f  x như hình vẽ bên. Lời giải
Số điểm cực trị của hàm số g  x  f  x 3 3
 x 15x 1 là A. 2 . B. 1. C. 3 . D. 4 . Lời giải Chọn B
Ta có g x  f  x 2  x 
g x   f  x 2 3 3 15; 0  5  x . Trang 676
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Đồ thị hàm số f   x cắt đồ thị hàm số 2
y  5  x tại hai điểm A0;5, B 2  ;1 .
Trong đó x  0 là nghiệm bội bậc 2; x  2 là nghiệm đơn.
Vậy hàm số có một điểm cực trị
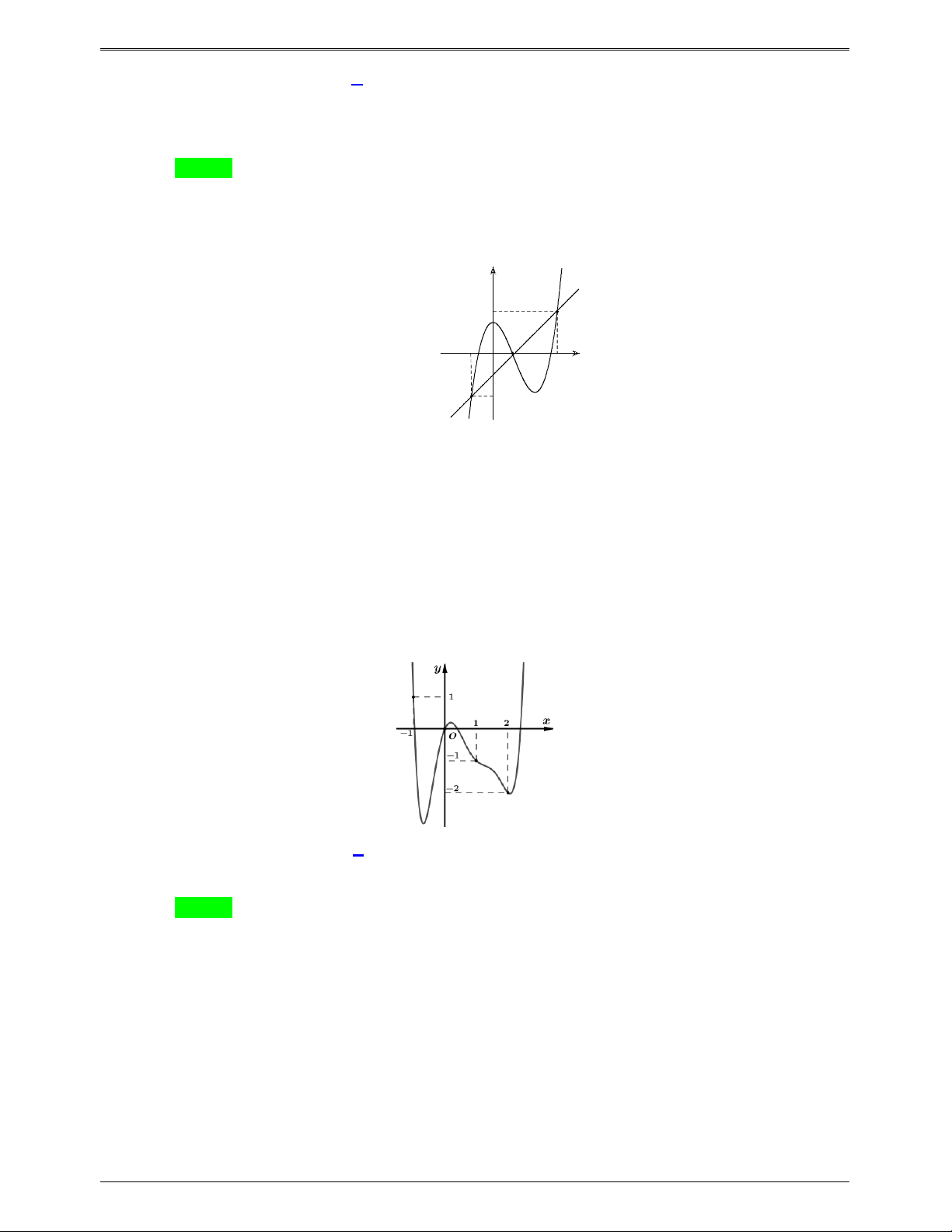
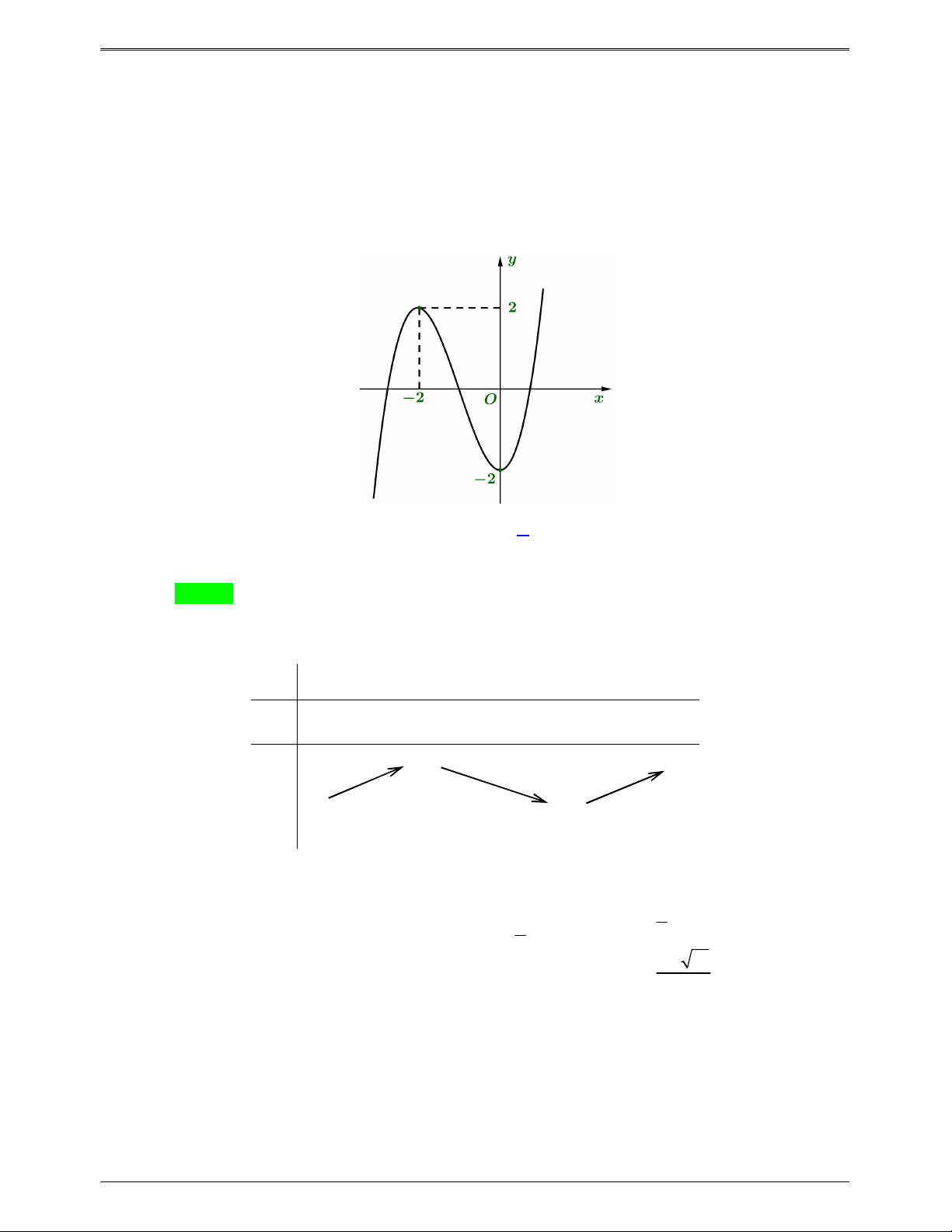
Câu 46.18: Cho hàm số y  f  x có đồ thị như hình bên dưới. Hàm số g  x  f  2
x  3x có bao nhiêu điểm cực trị? A. 3. B. 4. C. 5. D. 6. Lời giải Chọn C
Từ đồ thị ta có bảng biến thiên của hàm số y  f x như sau x  2  0  f  x  0  0  2  f  x  2 
Ta có g  x  f  2
x  3x  g x   x   f  2 2 3 . x  3x   3  3 x  x    2 2  2x  3  0   3  17
Cho g  x  0    2
x  3x  2  x  f     2
x  3x  0   2 2
x  3x  0   x  0   x  3 
Như vậy phương trình g x  0 có tất cả 5 nghiệm đơn phân biệt.
Vậy hàm số g  x  f  2
x  3x có 5 cực trị. Trang 677
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Câu 46.19:
Cho hàm số y  f  x có đồ thị như hình bên dưới. Hàm số   2 y
f x  có bao nhiêu điểm cực trị? A. 3 . B. 2 . C. 5 . D. 4 . Lời giải Chọn A
Gọi x  a , với 1  a  4 là điểm cực tiểu của hàm số y  f  x
Từ đồ thị ta có bảng biến thiên của hàm số y  f x như sau x  0 a  f  x  0  0   f  x  Ta có   2 y
f x   y  x f  2 2 . x  x  0 2x  0  x  0 Cho y  0    2 x  0   , với 1  a  4 f     2 x   0  x   a 2   x   a
Bảng biến thiên của hàm số   2 y f x  x   a 0 a  y  0  0  0    y Vậy hàm số   2 y
f x  có 3 cực trị. Trang 678
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Câu 46.20:
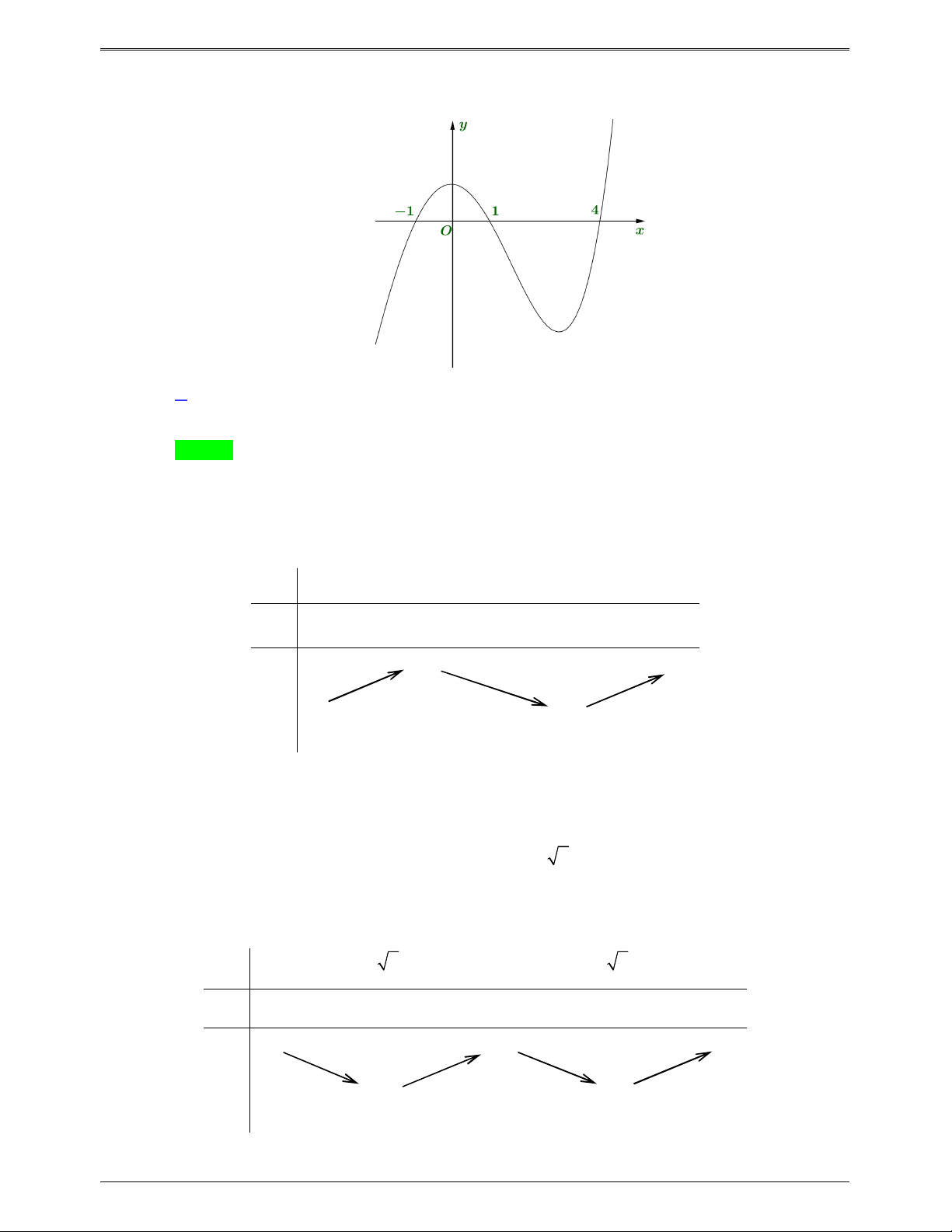
Cho hàm số y  f  x có đồ thị như hình bên dưới
Số điểm cực trị của hàm số y  f  2 x  2x là A. 3. B. 9 . C. 5 . D. 7 . Lời giải Chọn C
Từ đồ thị ta có bảng biến thiên của hàm số y  f x như sau x  1  0 1  f  x  0  0  0   2  f  x 3  1 
Ta có y  f  2
x  2x  y   x   f  2 2 2 . x  2x  x  1 x  1    2x  2  0 2
x  2x  1 x  2  Cho y  0       f  2    2
x  2x   0 x  0  x  2x  0   2
x  2x  1  x  1   2 
Bảng biến thiên của hàm số y  f  2 x  2x x  1   2 2  1  0 1   2  y  0  0  0  0  0    y
Vậy hàm số y  f  2
x  2x có 5 cực trị. Câu 46.21:
Cho hàm số f  x , bảng biến thiên của hàm số f  x như sau: Trang 679
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 x  3  1 3   3  f  x 3  2 
Số điểm cực trị của hàm số y  f 6 3x là A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C. x  3 6  3x  3    5 Ta có y  3
 . f 6 3x . Cho y  0  6  3x  1 x     3 6  3x  3  x 1  Bảng biến thiên 5 x  1 3  3 y  0  0  0 
Nhận xét: y đổi dấu 3 lần khi đi qua các nghiệm nên phương trình y  0 có 3 nghiệm phân
biệt. Vậy hàm số y  f 6 3x có 3 cực trị. Câu 46.22:
Cho hàm số f  x , bảng biến thiên của hàm số f  x như sau: x  5  2  3   3  f  x 5  1 
Số điểm cực trị của hàm số g  x  f  2 x  5 là A. 7 . B. 1. C. 5 . D. 4 . Lời giải Chọn A. x  0  2
x  5  a, a  5 2x  0 
Ta có g x  x f  2 2 .
x  5 . Cho g x  0  2 
 x  5  b,  5  b  2 f    2 x  5  0   2 x  5  ,
c  2  c  3  2
x  5  d , d  3   Phương trình 2
x  a  5  0 , a  5 nên phương trình vô nghiệm.  Phương trình 2
x  b  5  0 , 5  b  2 nên phương trình 2 nghiệm phân biệt. Trang 680
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  Phương trình 2
x  c  5  0 , 2  c  3 nên phương trình 2 nghiệm phân biệt.  Phương trình 2
x  d  5  0 , d  3 nên phương trình 2 nghiệm phân biệt.
Nhận xét: 7 nghiệm trên khác nhau đôi một nên phương trình g  x  0 có 7 nghiệm phân biệt.
Vậy hàm số g  x  f  2
x  5 có 7 cực trị. Câu 46.23:
Cho hàm số f  x , bảng biến thiên của hàm số f  x như sau: x  0 3  4  f  x
Số điểm cực trị của hàm số g  x f   x 2 1    là   A. 5 . B. 3 . C. 2 . D. 4 . Lời giải Chọn A. 2
Ta có g  x f   x      f  2 1 x  2x  
1  g x   x   f  2 2 2 . x  2x   1 .   x  1   2x  2  0 2
x  2x 1  a, a  0
Cho g x  0     f  2    2 x  2x   1  0 
x  2x 1  , b 0 `  b  3  2
x  2x 1  c, c  3   2
x  2x 1  a  0 có   4a  0 , a  0 nên phương trình vô nghiệm. 1  2
x  2x 1  b  0 có   4b  0 , 0  b 
nên phương trình có 2 nghiệm phân biệt. 2  2
x  2x 1 c  0 có   4c  0 , c  3 nên phương trình có 2 nghiệm phân biệt.
Nhận xét: 5 nghiệm trên khác nhau đôi một nên phương trình g  x  0 có 5 nghiệm phân biệt.
Vậy hàm số g  x f   x 2 1    có 5 cực trị.   Câu 46.24:
Cho hàm số f  x liên tục trên  , bảng biến thiên của hàm số f  x như sau: x  3  3  4  f  x 2  x 1
Số điểm cực trị của hàm số g  x  f   là x   A. 6 . B. 2 . C. 1. D. 4 . Lời giải Chọn A. Trang 681
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 2 x 1  x 1
Ta có g x  . f . 2   x x   2 x 1  0  2 2  x 1 x 1   a, a  2   0   2 x x
Cho g x  0     2 2 x 1   x 1   ,
b  2  a  2 f   0     x x     2 x 1   , c c  2  x  2
x 1  0 có 2 nghiệm phân biệt x  1 . 2 x 1 
Xét hàm số h  x  x 2 x 1
Tập xác định D   \  
0 . Ta có h x 
. Cho h x  0  x  1. 2 x Bảng biến thiên x  1  0 1  f  x  0   0  2 f  x 2 
Dựa vào bảng biến thiên, ta thấy 
h  x  a có 2 nghiệm phân biệt, với a  2 
h  x  b vô nghiệm, với 2  b  2 
h  x  c có 2 nghiệm phân biệt, với c  2 2  x 1
Vậy hàm số g  x  f 
 có 6 điểm cực trị. x   Câu 46.25:
Cho hàm số f  x liên tục trên  , bảng biến thiên của hàm số f  x như sau: x  1  0 2  1 2 f  x  x 1
Số điểm cực trị của hàm số g  x  f   là  x 1 A. 8 . B. 7 . C. 1. D. 3 . Lời giải Chọn A Trang 682
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
 x 1  a, a  1   x 1  x 1 
 b, 1  b  0 2   x 1  x 1   x 1
Ta có g x  . f 
 . Cho g x  0  f   0     x  2 1  x 1  x 1  x 1   , c 0  c  2  x 1  x 1   d, d  2  x 1 x 1
Xét hàm số h  x  x 1 2
 Tập xác định D   \  
1 . Ta có h x   0, x   D .  x  2 1  Bảng biến thiên x  1  f  x   f  x
Dựa vào bảng biến thiên, ta thấy: Phương trình h  x  a , h  x  b , h x  c , h  x  d đều có 2 nghiệm phân biệt.  x 1
Vậy hàm số g  x  f   có 8 cực trị  x 1 Câu 46.26:
Cho hàm số y  f  x xác định, liên tục trên  và có bảng biến thiên như sau x  1  0 1  f  x   0  0   2  f  x 1 1
Hàm số g  x  3 f x 1 đạt cực tiểu tại điểm nào sau đây? A. x  1  . B. x  1 . C. x  1  . D. x  0 . Lời giải Chọn C
Ta có g x  3 f  x
Do đó điểm cực tiểu của hàm số g  x trùng với điểm cực tiểu của hàm số y  f  x . Trang 683
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Vậy điểm cực tiểu của hàm số là x  1  . Câu 46.27:
Cho hàm số y  f x có đồ thị hàm số y  f x như hình vẽ 2
Hàm số      x g x f x 
 2020 đạt cực đại tại điểm nào sau đây? 2 A. x  3 . B. x  1 . C. x  3 . D. x  3 . Lời giải Chọn D
Ta có gx  f x  x . Cho gx  0  f  x  x
Nhận thấy đường thẳng y  x cắt đồ thị hàm số y  f  x lần lượt tại ba điểm x  3; x  1. 2
Ta có bảng biến thiên của hàm số      x g x f x   2020 2 Trang 684
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 t  3 1 x  3 x  4
f t  t       . 1  t  3 1  1  x  3 2  x     0 Câu 46.28: Cho hàm số     4  3  2 y f x ax bx
cx  dx  e , đồ thị hình bên dưới là đồ thị của hàm số
y  f  x . Xét hàm số g x  f  2
x  2 . Mệnh đề nào dưới đây sai?
A. Hàm số g x đạt cực tiểu tại x  2 .
B. Hàm số g x đạt cực đại tại x  0 .
C. Hàm số g x có 5 điểm cực trị
D. Hàm số g x nghịch biến trên khoảng 0; 2. Lời giải Chọn C x  0 x  0 x  0  2 
Ta có: g x  x f  2 ( ) 2 .
x  2 . Cho gx  0    2 1 1 2 2
 x     x   f x       0  x2   2  2 x     2 Ta có bảng xét dấu Trang 685
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Câu 46.29:
Cho hàm số y  f  x có đạo hàm f  x trên  và đồ thị của hàm số y  f  x như
hình vẽ. Hàm số g  x  f  2 x  2x  
1 đạt cực đại tại giá trị nào sau đây? A. x  2 . B. x  0 . C. x  1 . D. x  1 . Lời giải Chọn D x  0 x  1   x  1 
Ta có g x   x   f  2 2 2 . x  2x  
1 . Cho g x 2
 0  x  2x 1  1    x  2 2
x  2x 1  2  x  3  Ta có bảng biến thiên
Dựa vào bảng biến thiên, ta thấy hàm số đạt cực đại tại x  1 Câu 46.30:
Cho hàm số y  f  x có đạo hàm trên  thoả mãn f 2  f 2  0 và đồ thị của hàm
số y  f  x có dạng như hình bên dưới. Hàm số 2
y  f  x nghịch biến trên khoảng nào trong các khoảng sau? Trang 686
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  3  A. 1; .   B. 1;  1 . C. 2;   1 . D. 1; 2.  2  Lời giải Chọn D x  1
Ta có f  x  0  
, với f 2  f 2  0 . x  2  Ta có bảng biến thiên x  2  1 2 
f  x  0  0  0  0 0 f  x  
 f  x  0 x  2 Ta có 2
y  f  x  y  2 f  x. f  x . Cho y  0    
 f   x  0
x  1; x  2   Bảng xét dấu x  2 1 2 
f  x  0  0  0 
f  x  0   0  2
y  f  x   Câu 46.31:
Cho hàm số y  f  x. Đồ thị hàm số y  f  x như hình bên dưới và f 2  f 2  0. Trang 687
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Hàm số g  x   f   x 2 3  
 nghịch biến trên khoảng nào trong các khoảng sau? A. 2;  1 . B. 1;2. C. 2;5. D. 5; . Lời giải Chọn C
Dựa vào đồ thị hàm số y  f   x, suy ra bảng biến thiên của hàm số f  x như sau
Từ bảng biến thiên suy ra f  x  0, x   . 
Ta có g x  2 f 3  x. f 3  x. 3   x  2 x  5
 f  3  x  0  
Cho g x  0   
3  x  1  x  2  
 f 3  x   0  3   x  2 x  1  
Vì f  x  0, x
    f 3  x  0, x  . 
Do đó 2 f 3  x  0 , x   .  Bảng biến thiên x  1 2 5 
f 3  x  0  0  0 
2 f 3  x  0   0  Trang 688
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 g x  0  0  0 
Suy ra hàm số g  x nghịch biến trên các khoảng  ;   1 , 2;5. Câu 46.32:
Cho hàm số y  f  x. Đồ thị hàm số y  f  x như hình bên dưới
Hàm số g  x  f  3  x  đồng biến trên khoảng nào trong các khoảng sau A.  ;    1 . B. 1; 2. C. 2;3. D. 4; 7. Lời giải Chọn B
Dựa vào đồ thị ta có bảng biến thiên của hàm số y  f  x. x  1 1 4 
f  x  0  0  0    f  x  f
 3  x. Khi x  3
Ta có g  x  f  3  x    f
  x  3. Khi x  3 
 Với x  3 khi đó g x   f 3  x
Hàm số g  x đồng biến  g x  0 3   x  1 x  4
  f 3  x  0  f 3  x  0     1  3  x  4 1   x  2  
Kết hợp điều kiện x  3 , ta được 1   x  2 .
Vậy hàm số g  x đồng biến trên khoảng 1;2. Trang 689
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
 Với x  3 khi đó g x  f  x  3
Hàm số g  x đồng biến  g x  0
1  x  3  1 2  x  4
 f   x  3  0     x  3  4 x  7   3   x  4
Kết hợp điều kiện x  3, ta được  . x  7 
Vậy hàm số g  x đồng biến trên khoảng 3;4 và 7;  Câu 46.33:
Cho hàm số y  f  x. Đồ thị hàm số y  f  x như hình bên dưới
Hàm số g  x  f  2
x  4x  3  có bao nhiêu điểm cực trị? A. 5 . B. 3 . C. 2 . D. 7 . Lời giải Chọn A
Dựa vào đồ thị ta có bảng biến thiên của hàm số y  f  x. x  1 1 3 
f  x  0  0  0    f  x x  2
Ta có g  x  f  2
x  4x  3   g x  . f  2
x  4x  3 . 2  x  4x  3 Trang 690
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  x  2  0
Cho g x  0   f  2x 2x2  0  x 1  0  x 1  0  x  1    2 2
  x  4x  3  1  x  4x  2  0  x  2  2    2 2
 x  4x  6  0 
 x  4x  3  3  x  2  10  
Vì g  x  0 có 5 nghiệm bội lẻ nên hàm số g  x  f  2
x  4x  3  có 5 điểm cực trị. Câu 46.34:
Cho hàm số y  f  x. Đồ thị hàm số y  f  x như hình bên dưới
Hàm số g  x  f  2 2
x  2x  3  x  2x  2  đồng biến trong khoảng nào sau đây  1   1  A.  ;    1 . B.  ;  .   C. ;  .   D. 1;.  2   2  Lời giải Chọn A
Dựa vào đồ thị ta có bảng biến thiên của hàm số y  f  x. x  1 2 
f  x  0  0   f  x 
Ta có g  x  f  2 2
x  2x  3  x  2x  2  Trang 691
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  1 1 
 g x   x   1  . f     2 2
x  2x  3  x  2x  2 . 2 2   x  2x  3
x  2x  2  1 1 Dễ thấy 
 0 với mọi x  .    1 2 2 x  2x  3 x  2x  2
Đặt u  u  x 2 2 
x  2x  3  x  2x  2 Dễ thấy 2 2
x  2x  3  x  2x  2  0  u  x  0 2 1 1 Mặt khác 2 2
x  2x  3  x  2x  2    1
 x  2   x  2 2 1 1 2 1 1
 u  x  1 3
Từ 2 , 3  0  u  x  1
Kết hợp đồ thị ta suy ra f u  0 , với 0  u  1 4 Từ  
1 và 4  g x ngược dấu với dấu của nhị thức h  x  x 1 Bảng biến thiên x  1  h  x  
g x  0  g  x   Câu 46.35:
Cho hàm số y  f  x có bảng biến thiên như hình vẽ x  1 3 
f  x  0  0  5  f  x  3  Trang 692
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Tìm tất cả các giá trị thực của tham số m để phương trình f 1 3x 1  m có nhiều nghiệm nhất? A. m  0 . B. m  2 .
C. 0  m  2 . D. m  0 . Lời giải Chọn C
Đặt g  x  f 1 3x 1  g x  3. f 1 3x  2 x  1   3x  1  3
Cho g  x  0  f 1 3x  0     1 3x  3  2 x    3 Bảng biến thiên 2 2 x    3 3 g  x  0  0   6 g  x 2    2 6  g  x 0 0 0
Để phương trình f 1 3x 1  m có nhiều nghiệm nhất  đường thẳng y  m cắt đồ thị
y  g  x tại nhiều điểm nhất  0  m  2 . Câu 46.36:
Cho hàm số y  f  x xác định trên  \  
0 và có bảng biến thiên như hình vẽ x  0 1 
f  x   0     f  x  3 Trang 693
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Số nghiệm của phương trình 3 f 2x   1 10  0 là A. 2. B. 1. C. 4. D. 3. Lời giải Chọn C 10
Đặt t  2x 1, phương trình đã cho trở thành f t   . 3 t 1 10
Với mỗi nghiệm của t thì có một nghiệm x 
nên số nghiệm của phương trình f t   2 3
bằng số nghiệm của 3 f 2x   1 10  0 .
Bảng biến thiên của hàm số y  f  x là x  x 0 1 0      f  x 3 0 10
Suy ra phương trình f t  
có 4 nghiệm phân biệt nên phương trình 3 f 2x   1 10  0 3 có 4 nghiệm phân biệt. Câu 46.37:
Cho hàm số y  f  x có đạo hàm f  x trên  . Đồ thị của hàm số y  f  x như hình
vẽ. Đồ thị của hàm số   3
g x  f  x có bao nhiêu điểm cực trị? A. 1. B. 2 . C. 3 . D. 5 . Lời giải Chọn B Ta có   3
g x  f  x  g x  f   x 2 3. . f  x Trang 694
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Vì 2
f  x  0 , với mọi x   nên g x  0  f  x  0  x  1 Từ đó suy ra   3
g x  f  x có hai điểm. Trang 695

Tìm cực trị của hàm số hợp f(u(x)) khi biết đồ thị hàm số f(x) Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số