Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số có chứa dấu giá trị tuyệt đối Toán 12
Tài liệu gồm 20 trang, được biên soạn bởi thầy giáo Nguyễn Hữu Tình (giáo viên Toán trường THPT chuyên Võ Nguyên Giáp, tỉnh Quảng Bình), hướng dẫn phương pháp giải dạng toán tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số có chứa dấu giá trị tuyệt đối.
Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn:
Tác giả:
Tài liệu liên quan:
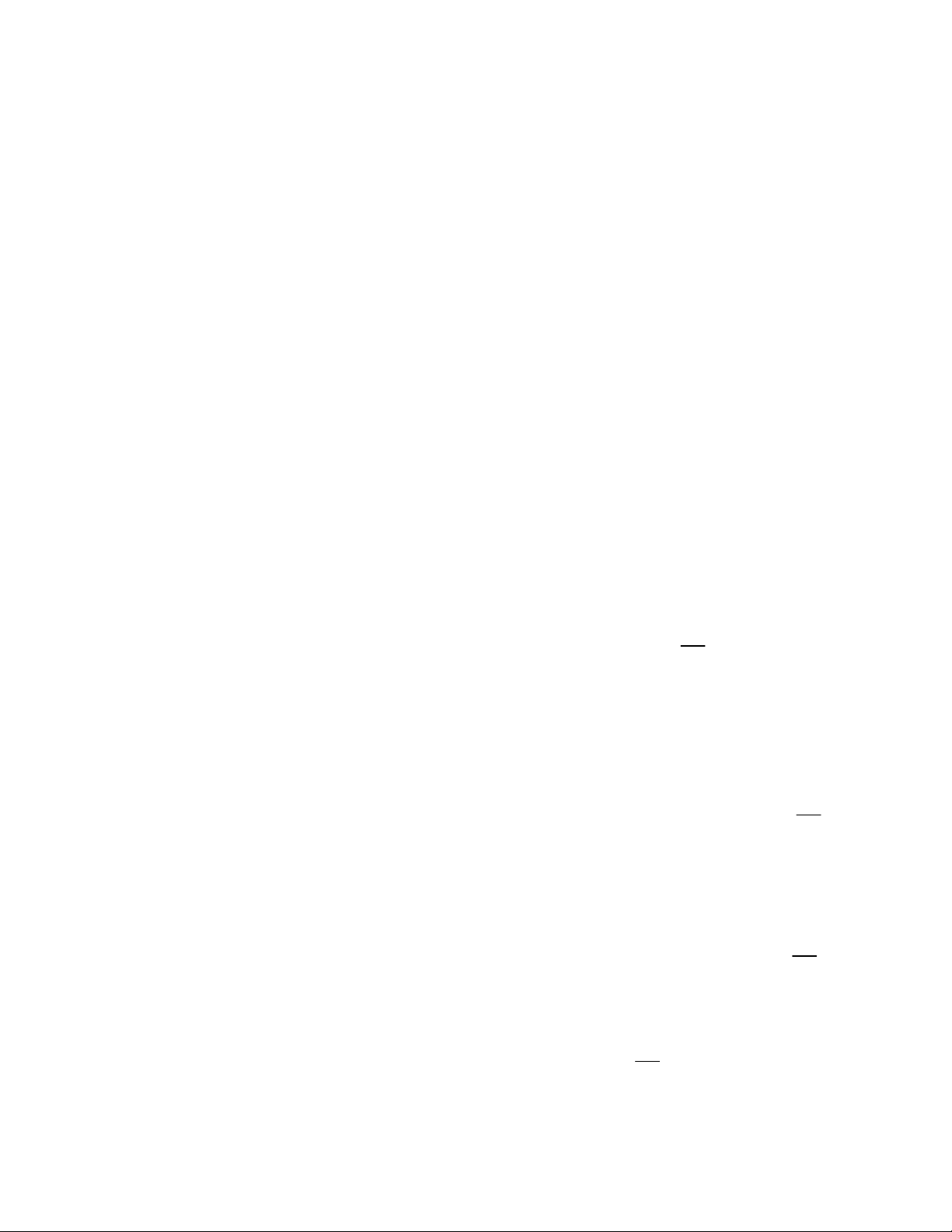
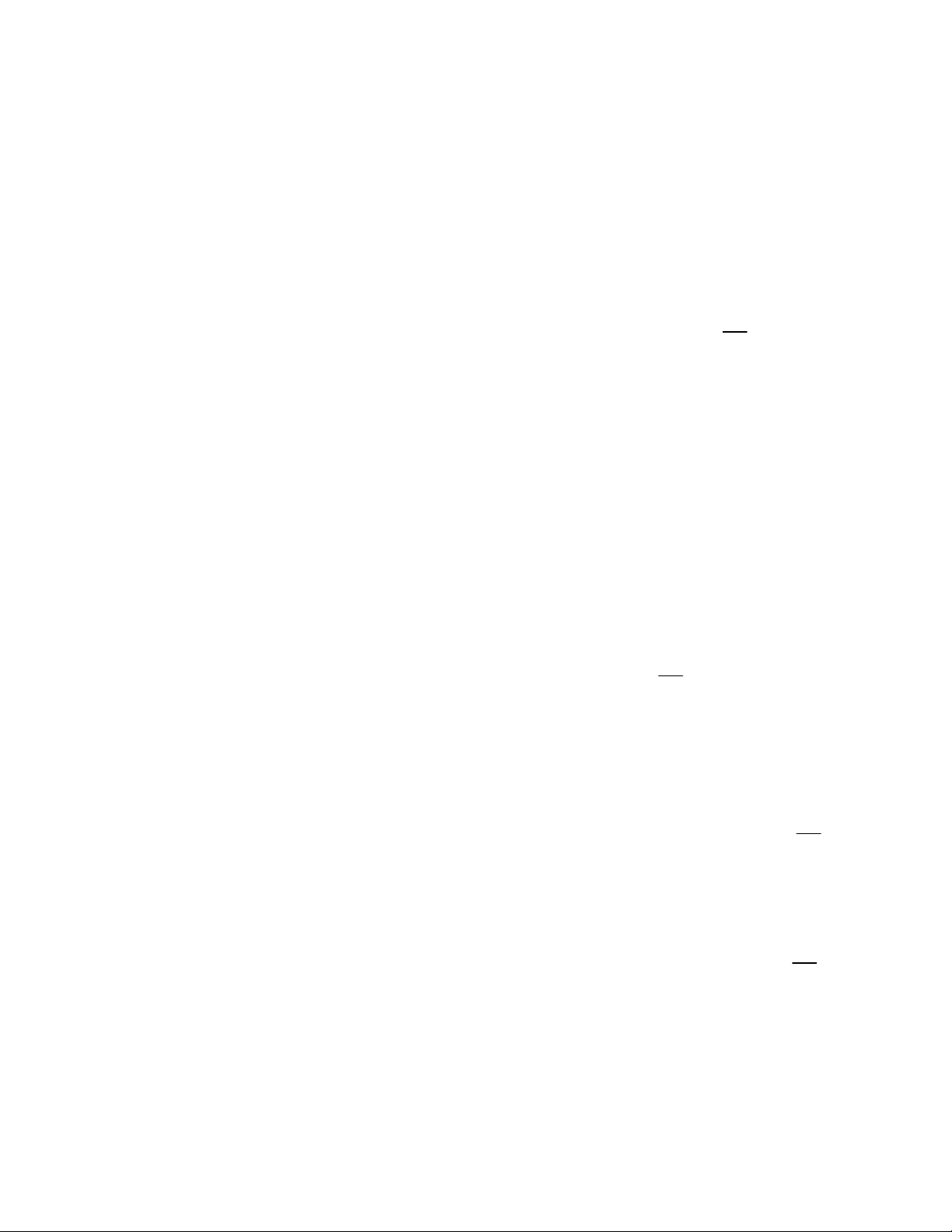
Preview text:
PHẦN MỞ ĐẦU 1.1. Lý do chọn đề tài
Bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất nói chung và bài toán tìm giá trị
lớn nhất, giá trị nhỏ nhất của hàm số có chứa dấu giá trị tuyệt đối là một trong
những bài toán khá hấp dẫn và khó trong chương trình Toán THPT. Đã có nhiều tài
liệu trình bày về kỹ thuật tìm giá trị lớn nhất, giá trị nhỏ nhất của các biểu thức
nhiều biến, lượng giác, … bằng nhiều phương pháp khác nhau như đạo hàm, bất
đẳng thức, lượng giác …(Chuyên đề Bồi dưỡng Học sinh giỏi, Phan Huy Khải).
Tuy nhiên, việc tìm giá trị lớn nhất và nhỏ nhất của một hàm số có chứa dấu giá trị
tuyệt đối thì còn hạn chế. Trong quá trình giảng dạy, thông qua việc tham khảo
nhiều tài liệu riêng lẻ, tôi thấy đây là một trong những nội dung rất hay và rất thích
hợp với việc thi Toán với hình thức thi trắc nghiệm nên tôi chọn đề tài: Tìm giá trị
lớn nhất và giá trị nhỏ nhất của hàm số có chứa dấu giá trị tuyệt đối để làm chuyên
đề chuyên môn trăng năm học này.
1.2. Điểm mới của đề tài
- Xây dựng được quy trình tính nhanh các bài toán tìm giá trị lớn nhất, giá trị
nhỏ nhất của hàm số có chứa dấu giá trị tuyệt đối. PHẦN NỘI DUNG
2.1. Thực trạng của vấn đề tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
có chứa dấu giá trị tuyệt đối.
Như đã nói trên, trong các kì thi và gần gũi nhất là kì thi Tốt nghiệp THPT
Quốc gia thường có các câu hỏi về việc tìm giá trị lớn nhất và giá trị nhỏ nhất của
các hàm số có chứa dấu giá trị tuyệt đối. Học sinh thường gặp khá nhiều khó khăn
và mất khá nhiều thời gian cho bài toán này. 2.1. Nội dung giải pháp
1. Một số kiến thức, kí hiệu ban đầu Định nghĩa:
Cho hàm f xác định trên D ,D .
+ Số M được gọi là giá trị lớn nhất của hàm số f trên D nếu f x M , x D
và tồn tại x D sao cho f x M. 0 0
Kí hiệu: max f x M hay max f M. x D D
+ Số m được gọi là giá trị nhỏ nhất của hàm số f trên D nếu f x M , x D
và tồn tại x D sao cho f x . m 0 0
Kí hiệu: min f x m hay max f . m x D D Một số định lí
Định lí 1. Cho f x xác định trên D và , A B D và A . B Giả sử
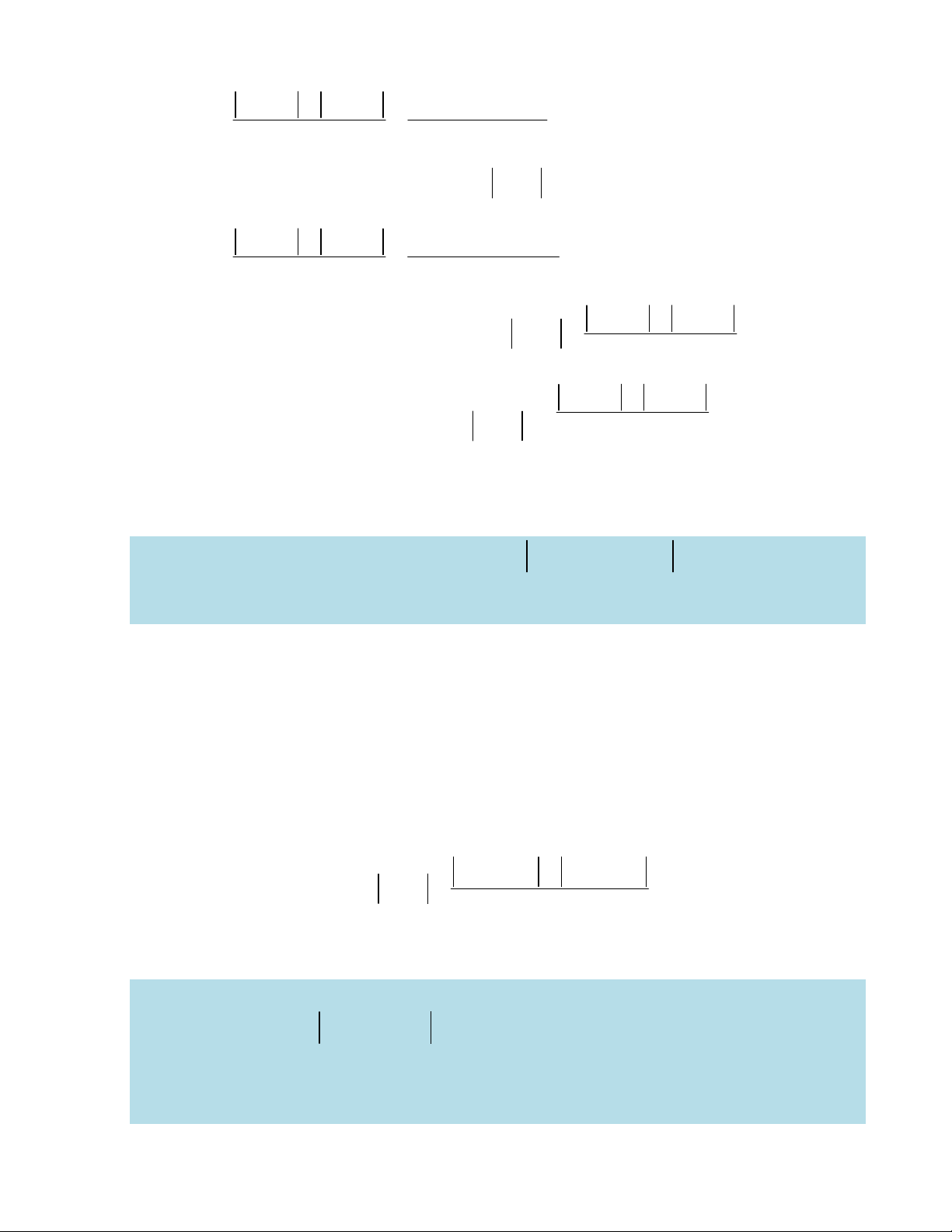
min f ;min f ;max f ;max f tồn tại. Khi đó ta có, max f max f ;min f min f . A B A B A B A B Chứng minh:
+ Giả sử, max f x f x , với x . A 0 0 A
Do x A B x B f x max f x . 0 0 0 B
+ Chứng minh tương tự cho min f min f . A B
Định lí 2. Cho f , g là hai hàm số cùng xác định trên D và f x g x, x . D
Giả sử max f ;max g tồn tại. Khi đó ta có, max f max g. D D D D Chứng minh
Giả sử max g x g x , với x . D 0 0 D
Do f x g x, x
D f x g x . 0 0
Lại có, f x max f x . Suy ra, max f max g. 0 D D D
Định lí 3. Cho f là hàm số xác định trên D D D . Giả sử, max f ,min f , (với 1 2 i D i D
i 1,2) đều tồn tại. Khi đó ta có:
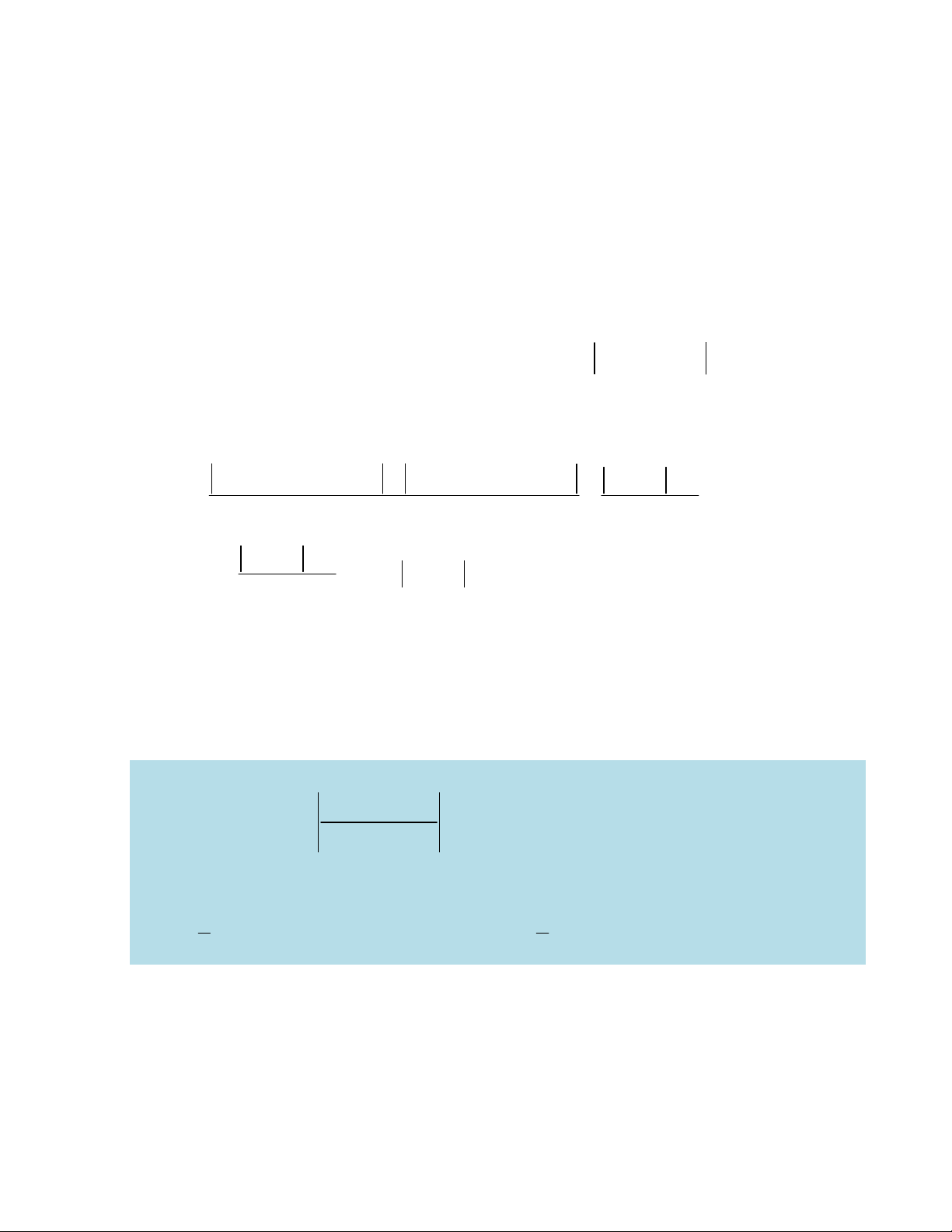
max f maxmax f ;max f , (1) D 1 D 2 D
min f minmin f ;min f . (2) D 1 D 2 D Chứng minh
Ta chứng minh (1), ((2) được chứng minh tương tự). Vì D , D D nên theo định lí 2, ta có 1 2
max f max f maxmax f ;max f max f . (3) i D D 1 D 2 D D
Giả sử, max f f x , x . D 0 0 D
Do D D D nên hoặc x D hoặc x D . 1 2 0 1 0 2
Không mất tính tổng quát, ta có thể giả sử x D . 0 1
Theo định nghĩa, ta phải có
f x max f max f f x max max f ;max f (4) 0 0 1 D D 1D 2D
Từ (3) và (4), suy ra điều phải chứng minh.
Định lí 4. Cho hàm số f xác định trên .
D Giả sử min f ,max f đều tồn tại. D D
Khi đó ta có: max f min f ;min f max f . D D D D Chứng minh
+ Giả sử, max f f x , x . D 0 0 D Suy ra, f x f x , x
D f x f x , x D 0 0
min f f x max f . Hay max f min f . 0 D D D D
+ Phần còn lại chứng minh tương tự.
Định lí 5. Cho có hàm số f , f ,..., f cùng xác định trên . D Đặt 1 2 n
f f f ... f . Giả sử min f ,min f ,max f ,max f , i
1,n đều tồn tại. Khi 1 2 n i i D D D D đó, ta có: n max f max f . i D D i 1
Dấu bằng xảy ra khi và chỉ khi x
D sao cho max f f x ,i 1, . n i i 0 0 D n và min f min f . i D D i 1
Dấu bằng xảy ra khi và chỉ khi x
D sao cho min f f x , i 1, . n i i 0 0 D Chứng minh Lấy tùy ý x .
D Khi đó ta có, f x max f , i 1, . n i i D n n
Từ đó suy ra, f f max f , x . D i i D i 1 i 1 n
Do điều này đúng với mọi x tùy ý thuộc D nên suy ra max f max f . (5) i D D i 1 n
Bây giờ ta xét điều kiện để dấu bằng xảy ra, tức max f max f . i D D i 1
Giả sử, tồn tại x D sao cho max f f x , u 1, . n Khi đó, i 0 0 D n n max f f x f x i i . 0 0 D i 1 i 1
Mặt khác, do x D nên f x max f . (6) 0 0 D n
Từ (5) và (6), suy ra max f x max f . Hơn nữa, max f f x . 0 i D D D i 1
+ Trường hợp còn lại chứng minh tương tự.
Định lí 6. Cho có hàm số f , f ,..., f cùng xác định trên D và f x x D i 0, . 1 2 n
Đặt f f . f .... f . Giả sử min f ,min f ,max f ,max f , i
1,n đều tồn tại. Khi đó, 1 2 n i i D D D D ta có:
max f max f . max f ... max f . 1 2 n D D D D
Dấu bằng xảy ra khi và chỉ khi x
D sao cho max f f x ,i 1, . n i i 0 0 D và
min f min f . min f .... min f . 1 2 n D D D D
Dấu bằng xảy ra khi và chỉ khi x
D sao cho min f f x , i 1, . n i i 0 0 D Chứng minh
Chứng minh tương tự định lí 5.
Định lí 7. Cho f , g là hai hàm số xác định trên .
D Đặt h f g. Giả sử min f ;min g;min ;
h max f ;max g;max h đều tồn tại. Khi đó ta có: D D D D D D max h max f min g. (7) D D D
Dấu bằng xảy ra khi và chỉ khi tồn tại x D sao cho max f f x và 0 0 D min g g x . 0 D min h min f max g. D D D
Dấu bằng xảy ra khi và chỉ khi tồn tại x D sao cho min f f x và 0 0 D max g g x . 0 D Chứng minh
Ta có, hx f x g x f x g x.
Theo định lí 5, ta có: max h x max f x maxg x. (8) D D D
Theo định lí 2, ta có: max g x min
g x min g x. (9) D D D
Từ (8) và (9), suy ra max h x max f x min g x. Vậy (7) đúng. D D D
Vẫn theo tính chất 5 thì dấu bằng trong (8) xảy ra khi và chỉ khi tồn tại x D sao 0
cho max f x f x ;max g x g x . 0 0 D D
Nhưng max g x g x min g x g x min g x g x . 0 0 0 D D D f
Định lí 8. Cho f , g là hai hàm số xác định và dương trên . D Đặt h . Giả sử g min f ;min g;min ;
h max f ;max g;max h đều tồn tại. Khi đó ta có: D D D D D D max f max D h . D min g D
Dấu bằng xảy ra khi và chỉ khi tồn tại x D sao cho max f f x và 0 0 D min g g x . 0 D min f min D h . D max g D
Dấu bằng xảy ra khi và chỉ khi tồn tại x D sao cho min f f x và 0 0 D max g g x . 0 D
Chứng minh tương tự định lí 7.
Định lí 9. Giả sử hàm f xác định và liên tục trên . D Khi đó, nếu đặt 0 nÕu Mn 0
M max f x,m min f x thì min f x D D D min M ; m nÕu Mn 0. Chứng minh
Trước hết, ta có f x 0, x
D và với mọi c ; m M thì tồn tại x D : f x . c (10)
1. Nếu Mm 0, khi đó m 0 M nên tồn tại x D sao cho f x 0. 0 0
Kết hợp với (10), suy ra min f x 0. D
2. Nếu M .m 0 . Không mất tính tổng quát, giả sử M m 0 khi đó f x m 0, x D nên f x , m x D và f x m nên 0
min f x min f x m minM; m min M ; m. D D
Trường hợp m M 0 , chứng minh tương tự.
Định lí 10. Cho f là hàm số xác định trên D và tồn tại max f x,min f x. Khi D D đó ta có: max f x max f x f x (11) D max ;min D . D Chứng minh Áp dụng định lí 4, thì (11) tương đương với
max f x maxmax f x ; max f x. D D D
Lấy x tùy ý thuộc D, xảy ra hai khả năng sau: 0 1. f x 0. Khi đó, 0
f x f x max f x max f x max max f x ; max f x . 0 0 D D D D 2. f x 0 . Khi đó, 0
f x f x max f x max f x max max f x ; max f x . 0 0 D D D D
Do x tùy ý thuộc D nên suy ra, max f x max f x f x (12) D
max ;max D D . 0 Bây giờ, không giảm tính tổng quát, giả sử
maxmax f x ; max f x max f x f c ,c . D (Trường hợp còn lại D D D chứng minh tương tự).
Khi đó, max f x f c max f x f x (13) D
max ;max D D
Từ (12) và (13), suy ra max f x max f x f x D
max ;max D D Định lí 11. Cho hàm số f x xác định trên D . Đặt
D x D : f x 0 ; D x D : f x 0 . Giả sử min f x và max f x đều 1 2 1 D 2 D
tồn tại. Khi đó ta có: min f x minmin f x; max f x . D 1 D 2 D Chứng minh.
Từ các giả thiết, ta suy ra min f x min f x (14) 1 D 1 D
và max f x f x , x D . (15) 2 2 D
Giả sử, max f x f x , x D nên ta có f x max f x . (16) 0 0 0 2 2 D 2 D
Từ đó (15) và (16) suy ra, min f x max f x . (17) 2 D 2 D Áp dụng tính chất 4, và (14), (17) suy ra:
min f x minmin f x;min f x min min f x ; max f x . D 1 D 2 D 1 D 2 D
Định lí 12. Cho hàm số f x xác định trên D . Giả sử min f x : ; m max f x : M ; D D Khi đó M m M m f x M m M m f x nÕu . p q 0 max ;min 2 ; D 2 D 0 nÕu .pq 0 Chứng minh
Theo định lí 10, ta có max f x max f x f x (18) D max ;min D . D + Nếu M m 0 thì M m M m M m M m
max f x maxM , m M . D 2 2 + Nếu M ,m 0 thì do M m M m và M m 0
max f x maxM , m m . D M m M m M m M m Mặt khác, . m 2 2
+ Nếu M m 0 thì max f x maxM , m M D M m M m M m M m Mặt khác, M. 2 2
+ Nếu M 0,m 0 và M m thì max f x maxM , m . m D M m M m M m M m Mặt khác, . m 2 2 M m M m
Vậy, trong mọi trường hợp, ta đều có: max f x . D 2 M m M m nÕu p q
Chứng minh tương tự cho kết quả f x . 0 min 2 ; D 0 nÕu .pq 0 2. Ví dụ
Ví dụ 1. Tìm giá trị lớn nhất của hàm số 3 2
y x 3x 9x 2 trên 0;4. A. 5. B. 25. C. 18. D. 32. Lời giải Xét hàm số f x 3 2
x 3x 9x 2 trên đoạn 0;4. Ta có, f x 2 '
3x 6x 9 f 'x 0 x 10;4, x 30;4.
Lại có f 0 2; f 3 2 5, f 4 1
8 nên max f x 2,min f x 2 5 0;4 0;4 2 25 2 2 5
Theo định lí 12, suy ra max f x 25 f 3. 0;4 2
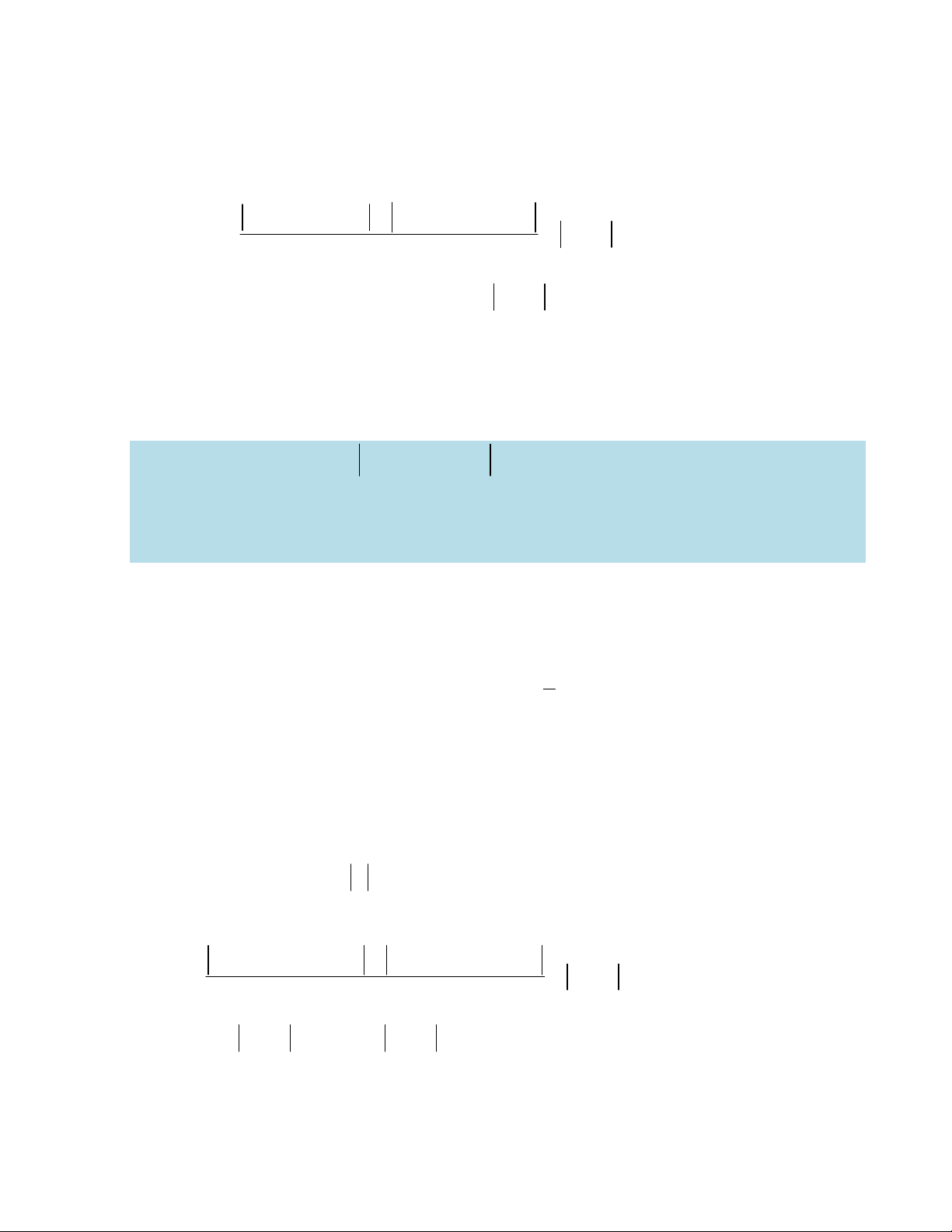
Ví dụ 2: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số 4 2
y x 2x m trên 1
;2 bằng 2. Tổng tất cả các phần tử của S bằng A. 2. B. 7. C. 14. D. 3. Lời giải Xét hàm số f x 4 2 x 2x m thì f x 2 '
4x 4x f ' x 0 x 0, x 1, x 1. Ta có f
1 m 1; f 0 ; m f
1 m 1; f 2 m 8
nên min f x: m 1;max f x: m 8; 1 ;2 1 ;2 + Nếu m 1 m 8 0 1 m 8 thì 4 2
min x 2x m 0 (không thỏa 1;2 mãn) + Nếu m 1 hoặc m 8 thì m
1 m 8 m 1 m 8 2m 7 9 max y 1;2 2 2 2m 7 9 Ta phải có:
2 2m 7 13 m 10,m 3 (thỏa mãn) 2 Vậy, S 3 ;1
0 nên tổng các phần tử của S bằng 7. Chọn B.
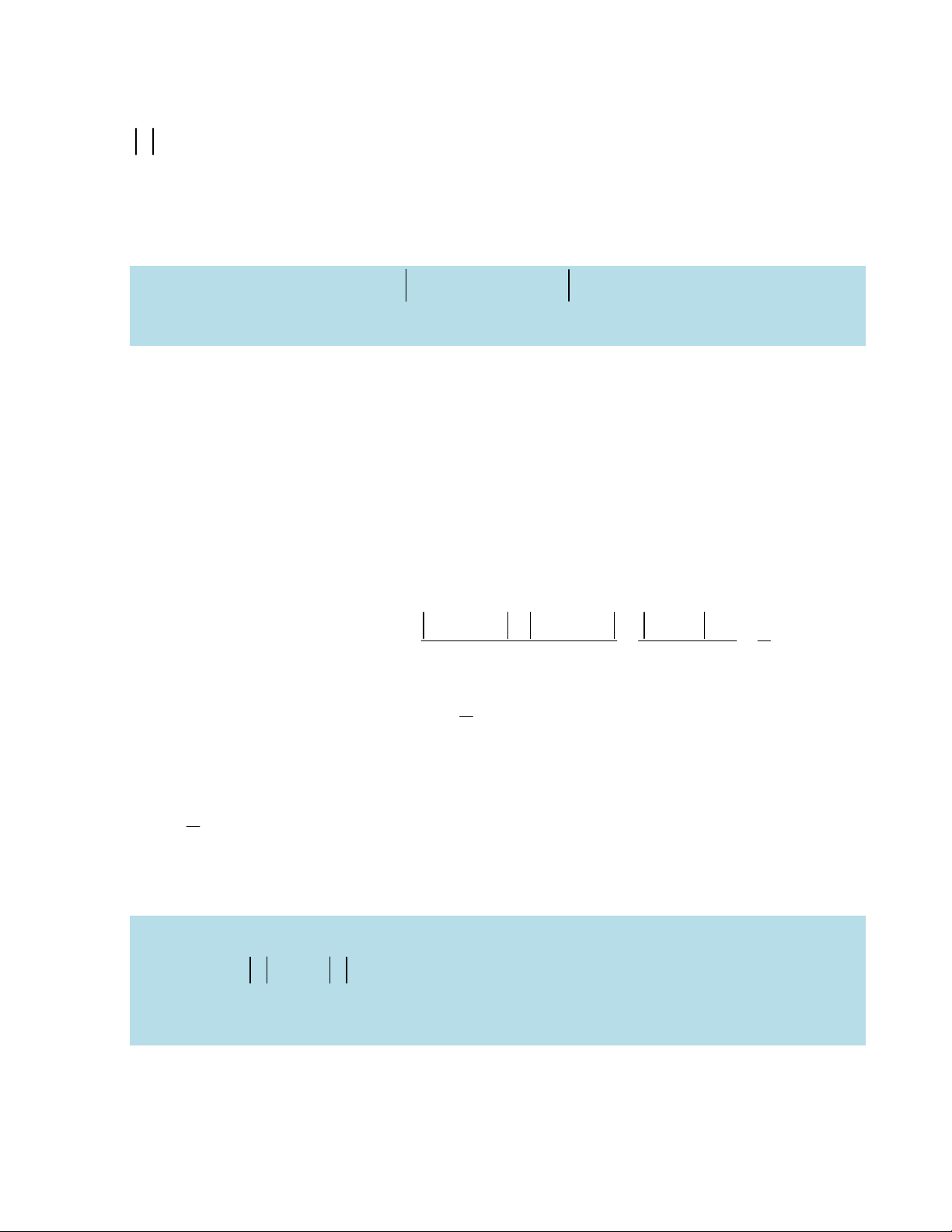
Ví dụ 3: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn 2 x mx 2m nhất của hàm số y trên 1 ;
1 bằng 3. Tổng tất cả các phần tử của x 2 S bằng 8 5 A. . B. 5. C. . D. 1. 3 3 Lời giải 2 x mx 2m Xét hàm số f x thì x 2 2 x x 4x f '
f ' x 0 x 0, x 4 1 ;2 . 2 x 1 1 Ta có f
1 m ; f 0 ; m f
1 m 1; nên min f x : m 1; 3 1 ;2 max f x: ; m 1 ;2 m
1 m m 1 m 2m 1 1 Suy ra, max y 1; 1 2 2 2m 1 1 Ta phải có:
3 2m 1 1 6 m 2,m 3 (thỏa mãn) 2 Vậy, S 3 ;
2 nên tổng các phần tử của S bằng 1.
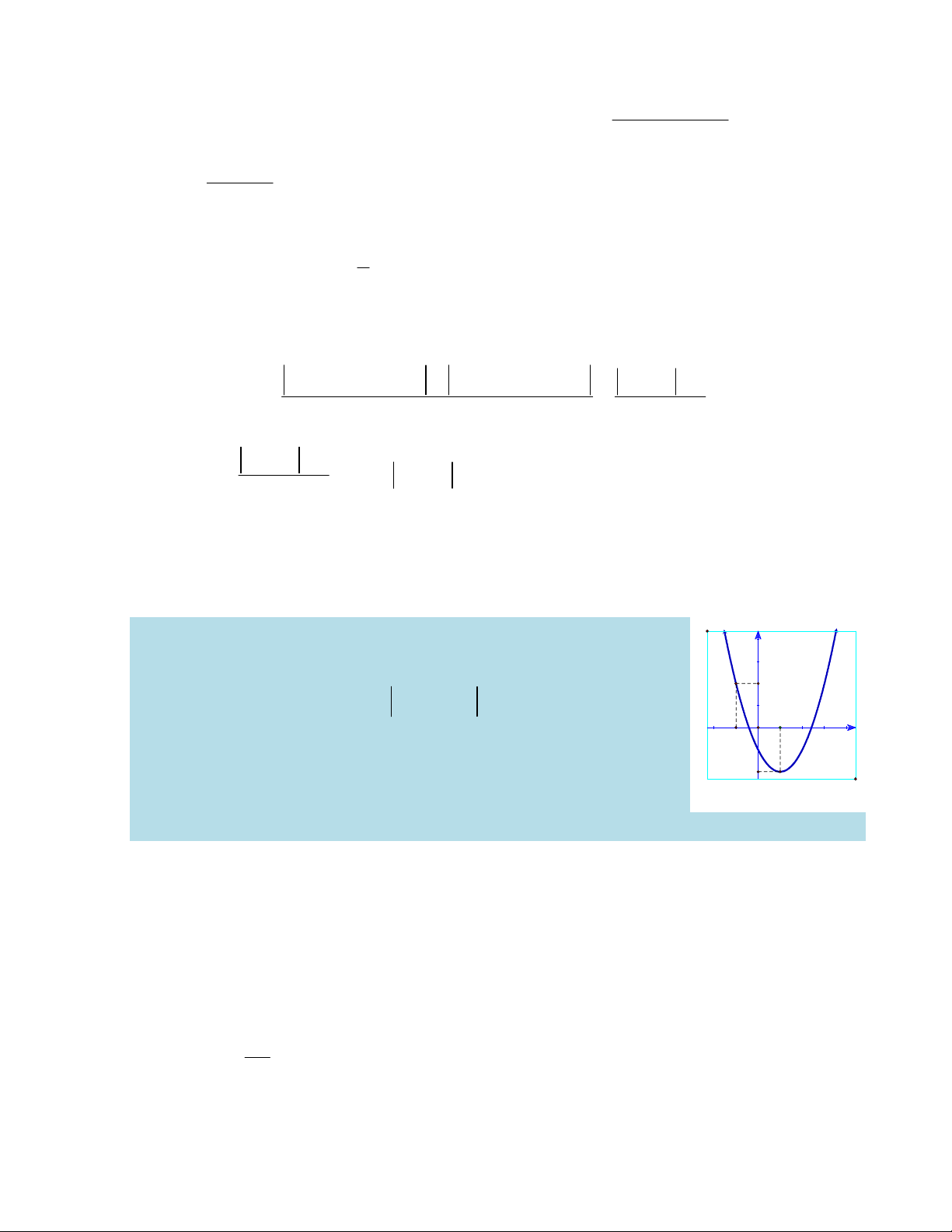
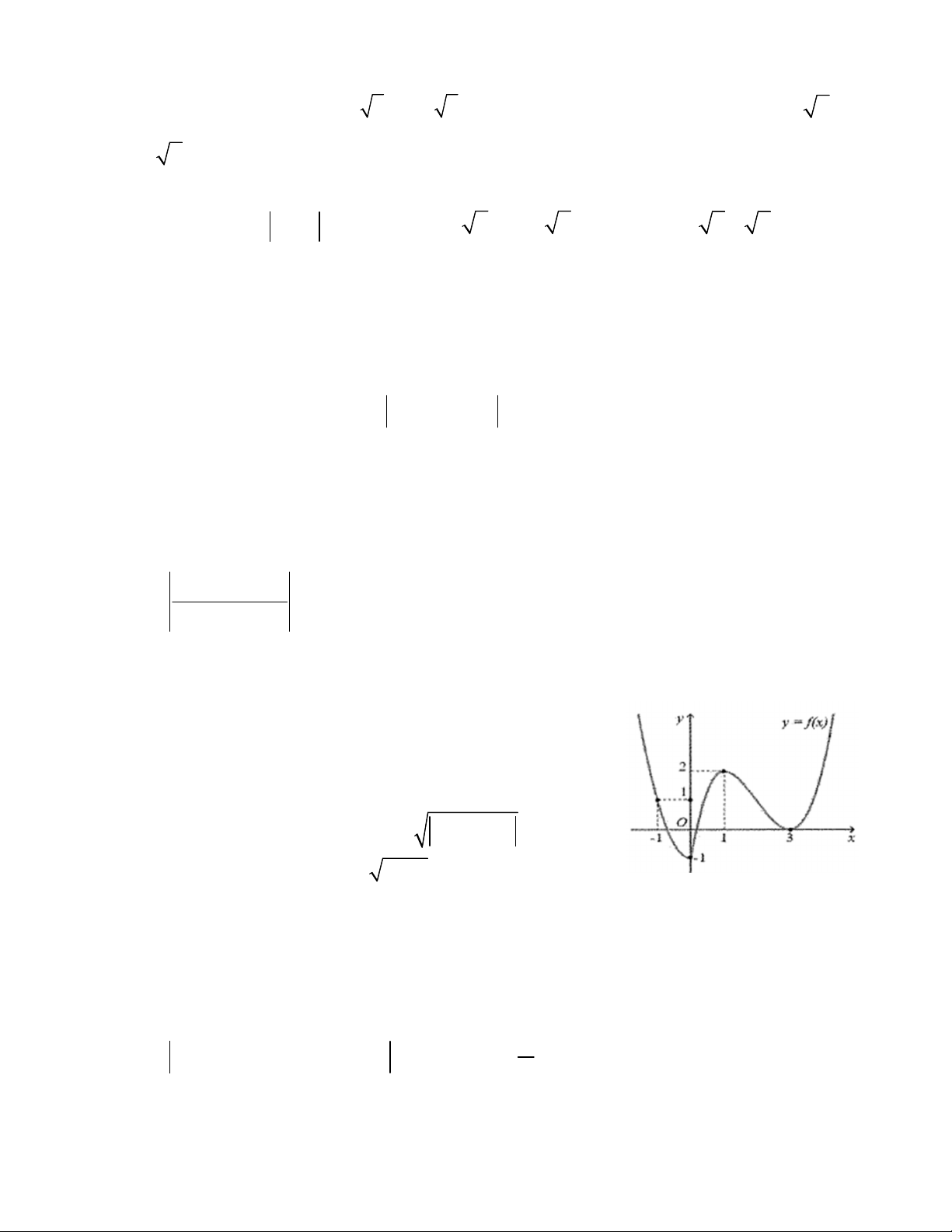
Ví dụ 4: Cho hàm số 2
f x ax bx c có đồ thị như hình y
vẽ. Gọi S là tập hợp tất cả các giá trị của tham số m để giá trị 2
lớn nhất của hàm số g x f x m trên đoạn 1 ;5 bằng O 1
10. Tính tổng các phần tử của tập S. x -1 -2 A. 12. B. 12. C. 8. D. 4. Lời giải
Ta thấy, đồ thị hàm số f x đi qua các điểm 1 ;2,1; 2
và có đỉnh là 1; 2 a b c 2
nên ta có a b c 2 a 1,b 1,c 1 nên f x 2 x 2x 1. b 1 2a Trên đoạn 1
;5, hàm số f x có một cực trị là x 1. Lại có f 1 2, f 1 2
, f 5 14 nên max f x 14,min f x 2 . 1 ; 5 1 ; 5
Xét hàm số h x f x m thì min h x m 2,max h x m 14 nên 1 ;5 1 ;5 m m m m max g x 14 2 14 2 m 6 8. 1 ;5 2
Theo đề bài, ta phải có max g x 10 m 6 8 10 m 4 ,m 8 . 1 ; 5 Vậy S 4 ;
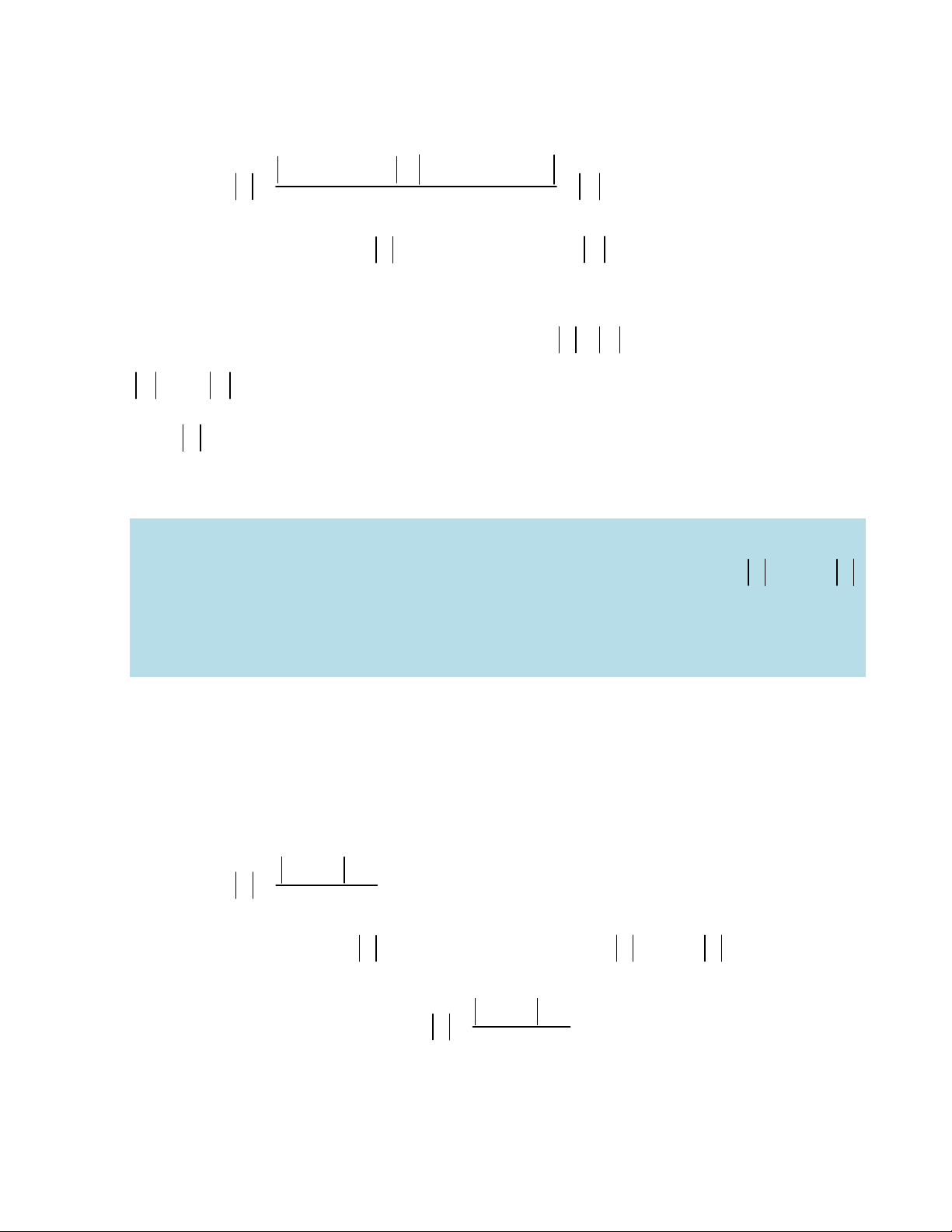
8 nên tổng các phần tử của S bằng 12. Ví dụ 5. Cho hàm số 3 2
y x x x m . Có bao nhiêu số nguyên m để min y nhỏ 1; 3 hơn 3? A. 21. B. 22. C. 4. D. 20. Lời giải Xét hàm số 3 2 f x x x x m thì f ' x 1 2
3x 2x 1 f 'x 0 x 1, x 1; 3 3 Ta có f
1 m 1; f 3 m 15 nên min f x m 1;max f x m 15; 1; 3 1; 3 + Nếu m
1 m 15 0 15 m 1 thì min y 0 (thỏa mãn). 1; 3
Vậy, trường hợp này thì S 17. + Nếu m 1 5 hoặc m 1 thì m
1 m 15 m 1 m 15 min y m 7 8 1; 3 2
Ta phải có: m 7 8 3 m 7 11 1 8 m 4.
Kết hợp với điều kiện m 1
5 hoặc m 1 thì ta được m 1 6; 1 7;2; 3 . Tức S 4 .
Vậy, có 21 số nguyên m thỏa mãn.
Ví dụ 6. Cho hàm số f x 4 3 2
x 4x 4x m . Tìm m để giá trị lớn nhất của
hàm số f x trên đoạn 0;
3 đạt giá trị nhỏ nhất. Lời giải Xét hàm f x 4 3 2 x 4x 4x m có f x 3 2 ' 4x 12x 8x, x x 0 f ' x 0 x 1 . x 2 Lại có, g 0 ; m g 1 m 1; g 2 ;
m g 3 m 9 nên max g x m 9; 0; 3
m 9 m m 9 m 2m 9 9 9
min g x m do đó max f x , m . 0; 3 0; 3 2 2 2 9
Dấu bằng xảy ra khi và chỉ khi m . 2
Vậy, giá trị lớn nhất của hàm số f x trên đoạn 0;
3 nhỏ nhất khi và chỉ khi 9 m . 2
Ví dụ 7. Cho hàm số y f x 3 x 3x .
m Gọi S là tập hợp các giá trị của tham
số m để min y max y 6. Tính số phần tử của S. 0;2 0;2 A. 0. B. 6. C. 1. D. 2. Lời giải Ta có, f x 2 '
3x 3 f 'x 0 x 0, x 1. f 0 ; m f
1 m 2; f 2 m 2 nên min y m 2;max y m 2. 0;2 0;2
m 2 m 2 m 2 m 2 Ta có, max y m 2. 0;2 2 + Nếu 2
m 2 thì min y 0 nên ta phải có m 2 0 6 m 4 (không 0;2 thỏa mãn).
+ Nếu m 2 hoặc m 2 thì min y m 2 nên ta phải có 0;2
m 2 m 2 6 m 3 (Thỏa mãn) Vậy, S 2.
Ví dụ 8 (Phú Thọ - 2020). Cho hàm số y f x 4 2
x 2x m. Gọi S là tập hợp
các giá trị nguyên của m thuộc đoạn 2
020;2020 sao cho max y 3min y . 0;2 0;2
Tổng các phần tử của S bằng A. 63. B. 51. C. 195. D. 23. Lời giải Ta có, f x 3 '
4x 4x f 'x 0 x 0, x 10;2, x 1. f 0 ; m f
1 m 1; f 2 m 8 nên max f x m 8;min f x m 1. 0;2 0;2 2m 7 9 Ta có, max y . 0;2 2
+ Nếu 8 m 1 thì min y 0 nên không thể có max y 3min y . 0;2 0;2 0;2 2m 7 9
+ Nếu m 8 hoặc m 1 thì min y 0;2 2 2m 7 9 2m 7 9 Để max y 3min y thì 3. 2m 7 18 0;2 0;2 2 2 11 2m 7 18 m 2 2m 7 1 8 25 m 2
Kết hợp với điều kiện m 8 hoặc m 1 thì ta phải có m 12,5 hoặc m 5,5 . Theo đề bài thì m , m 2 020;2020 nên m 2 020; 2 019; 2
018;...;13;6;7;...;202 0 S 7
Vậy S 6 7 8 9 10 1112 .6 12 63. 2 Chọn A.
Ví dụ 9 (Lương Gia Huy). Biết rằng hàm số 4 2
f x ax bx c có đúng ba điểm chung với trục hoành và f 1 1, f ' 1 0. Gọi
S m * f x m 12, x
0;2. Số phần tử của tập S là A. 10. B. 11. C. 12. D. 0. Lời giải
Đồ thị hàm số f x có đúng 3 điểm chung với trục hoành nên đồ thị tiếp xúc với
trục hoành tại gốc tọa độ nên f 0 0 c 0. Lại do f ' 1 0 nên 4a 2b 0. (1) f 1 1 a b 1 (2)
Từ (1) và (2), suy ra a 1,b 2. Vậy f x 4 2 x 2x . Theo đề, ta phải có
f x m 12,x0;2 max g x 12 với 0;2
g x f x . m x 1 Ta thấy, g ' x 3
4x 4x g 'x 0 và x 0 g 0 ; m g
1 m 1; g 2 m 8 nên
g x m 8 m
1 m 8 m 1 2m 7 9 max . 0;2 2 2
Suy ra, ta có: 2m 7 9 24 1 5 2m 7 15 4 m 11. Vậy, S 1;2;,...,1 1 nên S 11. Ví dụ 10. Cho hàm số 3 2 y x x 2 m
1 x 27 . Gọi S là tập tất cả các giá trị
của tham số m sao cho giá trị lớn nhất của hàm số trên đoạn 3 ; 1 có giá trị nhỏ
nhất. Khi đó, tích của các phần tử của S là A. 4. B. 4. C. 8. D. 8. Lời giải Xét hàm số f x 3 2 x x 2 m 1 x 27 có f x 2 2 ' 3x 2xm 10, x 3 ; 1. Lại có f 2 m f 2 3 6 3 , 1 26 m . Ta thấy, 2 m 2 m 2 2 2 26 6 3
20 2m 0 26 m 6 3m nên max f x 2 26 m , min f x 2 6 3m . 3; 1 3; 1 2 2 2 2
6 3m 26 m 6 3m 26 m Suy ra, max f x 2 2
2 8m m 10 g m 3 ; 1 2 + Nếu 2 8 m 0 2
2 m 2 2 thì g m 2 m 26 18, m 2 2;2 2 . + Nếu 2 8m 0 m 2 2,m 2 2 thì g m 2 3m 6 18, m ; 2 2 2 2;) .
Vậy, minmax f x 18 m 2 2,m 2 2. Hay S 2 2;2 2 nên tích 3 ; 1
tất cả các phần tử của S là 8. 3. Bài tập tự luyện Bài tập 1. Cho hàm số 4 3
y x 4x m . Có bao nhiêu giá trị của tham số m để min y 2020? 4 ; 2 A. 1. B. 2. C. 3. D. 4.
Bài tập 2. Gọi S là tập hợp các giá trị của tham số m để giá trị lớn nhất của hàm số 2 x mx 3m y trên đoạn 2
;2 bằng 5. Tính tổng các phần tử của S. x 3 A. 4. B. 5. C. 1. D. 4.
Bài tập 3. Cho hàm số y f x liên tục và có đồ thị như hình vẽ.
Gọi S là tổng các giá trị nguyên của tham số m sao cho
giá trị lớn nhất của hàm số y
f x m trên đoạn 1 ;
3 nhỏ hơn hoặc bằng 2020. Giá trị của S bằng A. 2019. B. 2018. C. 1. D. 0.
Bài tập 4. Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số 2 y 4
cos x 2sin x m 4 trên đoạn 0; nhỏ hơn hoặc bằng 4? 2 A. 12. B. 14. C. 13. D. 15.
Bài tập 5. Cho hàm số f x 2
x 2mx 3 . Có bao nhiêu giá trị nguyên của m để
giá trị lớn nhất của f x trên đoạn 1;2 không lớn hơn 3?. A. 1. B. 2. C. 3. D. 4.
Bài tập 6. Tính tổng tất cả các giá trị nguyên lớn hơn 6 của tham số m sao cho giá trị của hàm số 2 y x m 1 x m trên 2;m 1 nhỏ hơn 2020. A. 2043210. B. 2034201. C. 3421020. D. 3412020.
Bài tập 7. Cho hàm số y sin x cos x m . Có bao nhiêu giá trị của tham số m để
giá trị lớn nhất của hàm số trên bé hơn 2? A. 0. B. 1. C. 2. D. 3.
Bài tập 8. Cho hàm số f x 3 2
x 3x m . Tìm tất cả các giá trị của m thỏa mãn
3max f x 2min f x 17. 1; 3 1; 3 5 A. m9; 5 ;2 9 . B. m 9 ;5; . 3 C. m9; 5 . D. m9;5; 5 .
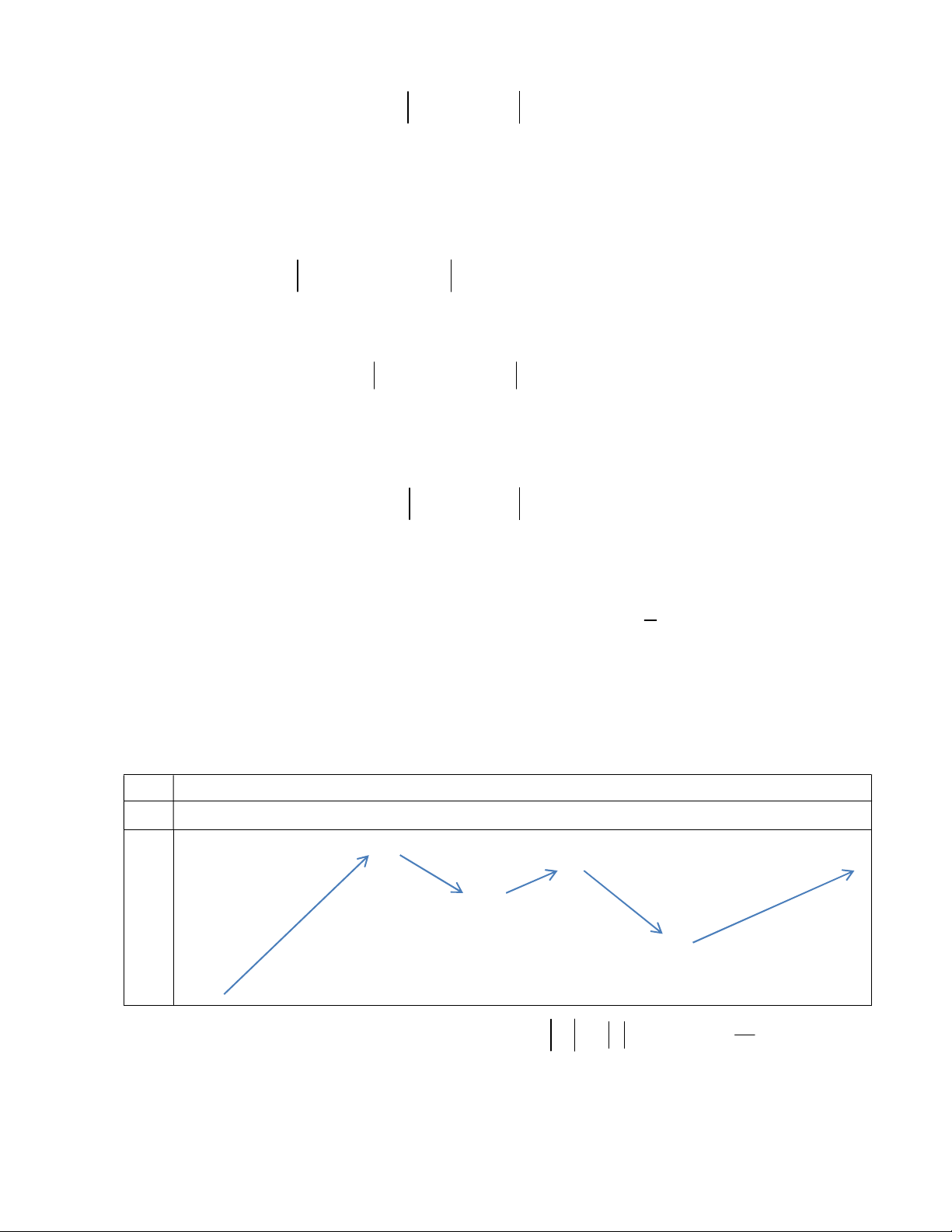
Bài tập 9. Cho hàm số f x có bảng biến thiên như sau x 4 3 1 0 2 4 f ' 0 0 0 0 4 3 2 f 1 4 3 11
Có bao nhiêu giá trị của tham số m để max f x 3 x f m . 1 ;1 3 2 A. 2. B. 3. C. 4. D. 5. PHẦN KẾT LUẬN
3.1. Ý nghĩa, phạm vi áp dụng của đề tài
Thông qua đề tài này, chúng ta thấy rằng, với một số bài toán thoạt nhìn ta
thấy việc giải bài toán đó theo cách thông thường đôi khi gặp khá nhiều khó khăn.
Tuy nhiên, bằng sự linh hoạt, sáng tạo và hiểu được bản chất của vấn đề chúng ta
có thể giải quyết nó một cách nhanh chóng và kết quả hết sức bất ngờ.
Với đề tài này, bản thân tôi đã vận dụng trong quá trình dạy học sinh ôn thi
THPT Quốc gia năm học 2020 – 2021, 2021 – 2022 và nhận thấy rằng, đa số học
sinh rất hào hứng tiếp nhận phương pháp và cũng thực hiện rất tốt các bài tập có
dạng liên quan. Vì vậy, tôi cho rằng, với đề tài này, các đồng nghiệp có thể vận
dụng trong quá trình giảng dạy và học sinh học tập trong chương trình Giải tích lớp
12, đặc biệt là chuyên đề tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số một cách có hiệu quả.
3.2. Kiến nghị, đề xuất
Trong quá trình thực hiện, chắc chắn sẽ không tránh khỏi những sơ suất. Rất
mong được quí đồng nghiệp cũng như học sinh góp ý đề tài này thực sự một tài liệu
tham khảo có giá trị cho giáo viên và học sinh trong giải toán. .