Tìm số nghiệm của phương trình hàm hợp – Đặng Việt Đông Toán 12

Tìm số nghiệm của phương trình hàm hợp – Đặng Việt Đông Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

37 19 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

TÌM SỐ NGHIỆM CỦA PHƯƠNG TRÌNH HÀM HỢP

I. KIẾN THỨC CẦN NHỚ:







 m

là phương trình hoành độ giao điểm của hai đồ thị

y  f





, y  m

. Số nghiệm của phương

trình bằng số giao điểm của hai đồ thị y  f





, y  m.







 g





là phương trình hoành độ giao điểm của hai đồ thị y  f





, y  g





. Số nghiệm của

phương trình bằng số giao điểm của hai đồ thị y  f





, y  g





II. CÁC DẠNG BÀI TẬP TƯƠNG TỰ

 Sử dụng BBT hoặc đồ thị của hàm số

 

f x để tìm số nghiệm thuộc đoạn

 

;a b của

phương trình

 

.c f g x d m  , với g(x) là hàm số lượng giác.

 Sử dụng BBT hoặc đồ thị của hàm số

 

f x để tìm số nghiệm thuộc đoạn

 

;a b của

phương trình

 

.c f g x d m  , với g(x) là hàm số căn thức, đa thức, …

 Sử dụng BBT hoặc đồ thị của hàm số





f x

để tìm số nghiệm thuộc đoạn





;

a b

của

phương trình

 

.c f g x d m  , với g(x) là hàm số mũ, hàm số logarit.

 Sử dụng BBT hoặc đồ thị của hàm số

 

f x để tìm số nghiệm thuộc đoạn

 

;a b của

phương trình

 

.c f g x d m  , với g(x) là hàm số chứa dấu giá trị tuyệt đối.

(ĐỀ MINH HỌA LẦN 2 - BDG 2019 - 2020) Cho hàm số

 

f x có bảng biến thiên như sau:

Số nghiệm thuộc đoạn



 

 

 

của phương trình

 

sin 1f x  là

A. 7 . B.

. C. 5. D. 6 .

Phân tích:

1. DẠNG TOÁN: Đây là dạng toán sử dụng BBT hoặc đồ thị của hàm số

 

f x để tìm số nghiệm thuộc

đoạn

 

;a b của PT

 

.c f g x d m  .

2. KIẾN THỨC CẦN NHỚ:

Số nghiệm thuộc đoạn

 

;a b

 

của PT

 

f t k là số giao diểm của đồ thị

 

y f t và đường thẳng

y k

với

 

;t a b

 

 ( k là tham số).

3. HƯỚNG GIẢI:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

B1: Đặt ẩn phụ

 

t g x . Với

   

; ; .x a b t a b

 

  

B2: Với

 

.c f g x d m f t k    .

B3: Từ BBT của hàm số

 

y f x suy ra BBT của hàm số

 

y f t để giải bài toán số nghiệm thuộc

đoạn

 

;a b

 

của phương trình

 

f t k .

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn C

Đặt

 

sin , 1;1t x t   thì PT

   

sin 1 1f x  trở thành

   

1 2f t  .

BBT hàm số

 

 

, 1;1y f t t   :

Dựa vào BBT ta có số nghiệm

 

1;1t   của PT

 

1 là 2 nghiệm phân biệt

   

1 2

1;0 , 0;1 .t t  

Quan sát đồ thị

siny x

và hai đường thẳng

y t

với

 

1;0t   và

y t

với

 

0;1t  .

+ Với

 

1;0t   thì PT

sin x t

có 2 nghiệm



 



 

 

+ Với

 

0;1t  thì PT

sin x t

có 3 nghiệm



 



 

 

Vậy số nghiệm thuộc đoạn



 

 

 

của phương trình

 

sin 1f x  là 2 3 5  nghiệm.

Câu 1. Cho hàm số

 

y f x

liên tục trên  có đồ thị như hình vẽ.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Phương trình

 

2 1f f x 

có tất cả bao nhiêu nghiệm thực phân biệt?

A. 3. B. 4. C. 5. D. 6.

Lời giải

Chọn A

Từ đồ thị ta có

 

2 2

2 1

f x

f f x

f x

  

  



 





 

0 0

x x x

f x

  







   















Vậy phương trình

 

2 1f f x 

có ba nghiệm phân biệt.

Câu 2. Cho hàm số

 

f x liên tục trên



và có đồ thị như hình bên.

Số nghiệm phân biệt của phương trình

 

2f f x   là

. B.

. C.

Lời giải

Chọn D

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Dựa vào hình vẽ của đồ thị hàm số





y f x

 , ta thấy đồ thị hàm số cắt trục hoành tại 3 điểm

có hoành độ lần lượt là

x x



và

x x



Đặt





t f x

 .

Phương trình









f f x

 

trở thành phương trình





f t

 

Ta có nghiệm của phương trình





f t

 

là hoành độ giao điểm của đồ thị hàm số





y f t



và đường thẳng

 

Dựa vào hình vẽ trên, ta thấy đồ thị hàm số





y f t

 cắt đường thẳng

 

tại 2 điểm phân

biệt có hoành độ lần lượt là

 

và



, hay ta có





f x

 

và





f x



Trường hợp 1:

Xét phương trình





f x

 

, ta có nghiệm của phương trình





f x

 

là hoành độ giao điểm

của đồ thị hàm số





y f x

 và đường thẳng

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Dựa vào hình vễ trên, ta thấy đồ thị hàm số





y f x

 cắt đường thẳng

 

tại 3 điểm phân

biệt có hoành độ lần lượt là





3 1 3

x x x x

   

x x



, và

x x



Vậy phương trình





f x

 

có 3 nghiệm phân biệt





Trường hợp 2:

Xét phương trình





f x



, ta có nghiệm của phương trình





f x



là hoành độ giao điểm

của đồ thị hàm số





y f x

 và đường thẳng



Dựa vào hình vẽ trên, ta thấy đồ thị hàm số





y f x

 cắt đường thẳng



tại 2 điểm phân

biệt có hoành độ lần lượt là





6 6 1

x x x x

  và



Vậy phương trình





f x



có 2 nghiệm phân biệt





Từ





và





, suy ra số nghiệm phân biệt của phương trình









f f x

 

là 5.

Câu 3. Cho hàm số





y f x



liên tục trên



và có đồ thị như hình dưới đây.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Số nghiệm phân biệt của phương trình









1 0

f f x

 

là

. B.

. C.

. D.

Lời giải

Chọn A

Xét

 

1 0 1f f x f f x     

   

2 1

0 1

1 2

f x a a

f x b b

f x c c

    



  



  



Xét

 

f x a

 

2 1a   

: Dựa vào đồ thị ta thấy

y a

cắt đồ thị tại

điểm phân biệt

 

Xét

 

f x b

 

0 1b 

: Dựa vào đồ thị ta thấy y b cắt đồ thị tại

điểm phân biệt

 

Xét





f x c







1 2

 

: Dựa vào đồ thị ta thấy

y c

cắt đồ thị tại

điểm phân biệt





Các nghiệm ở trên không có nghiệm nào trùng nhau nên

 

có

nghiệm phân biệt

Câu 4. Cho hàm số

 

y f x liên tục trên R và có đồ thị như hình vẽ sau

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Số các giá trị nguyên của tham số m để phương trình

 





 

có hai nghiệm phân

biệt là

. B.

. C.

. D.

Lời giải

Chọn C

Đặt





, 0

t t



 

, khi đó:

 





 

có hai nghiệm phân biệt.

 

f t



 

có hai nghiệm dương phân biệt.

1 1 3 3



       



m là số nguyên nên





2; 1; 0; 1; 2

m   .

Câu 5. Cho hàm số

 

132

 xxxxf

. Khi đó phương trình









0xff có bao nhiêu nghiệm

thực?

A. 9. B. 6. C. 5. D. 4.

Lời giải.

Chọn C

Bảng biến thiên của hàm số





f x

như sau:

Ở đây

 

f x





 







và

 

f x





  







Suy ra

 









   

0;1

0 1;3

3;4

f x a

f f x f x b

f x c

 



   



 



Phương trình





f x a



có 3 nghiệm.

Phương trình





f x b



có 1 nghiệm.

Phương trình





f x c



có 1 nghiệm.

Dễ thấy các nghiệm không trùng nhau nên phương trình đã cho có 5 nghiệm.

Câu 6. Cho







y f x

là hàm số bậc 3 và có đồ thị như hình vẽ bên.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Số nghiệm thuộc nửa khoảng

;

2 6

 

 







 

của phương trình

 

sin

2 1f x  là

A. 17 . B. 15. C. 10. D. 16.

Lời giải.

Chọn D

Vì

 

y f x

là hàm số bậc 3 nên điểm uốn của ĐTHS là

 

1;2I

Do đó, từ đồ thị ta có:

 

2sin 1 1;0

2sin 1 2si 1

n 1;2

2sin 2;3

x a

x x b

x c





 



   

 





 

 

 

1 1

sin 1; 1

2 2

1 1

sin 0; 2

2 2

1 1

sin ;1 3

2 2



 



   

 

 

 



 

 

 

 























 





29 / 6



/ 2





Dựa vào đồ thị hàm số siny x trên nửa khoảng

;

2 6

 

 







 

hoặc dùng đường tròn lượng giác,

ta được:

- Phương trình

 

có 5 nghiệm phân biệt.

- Phương trình

 

có 5 nghiệm phân biệt khác 5 nghiệm ở trên.

- Phương trình

 

có 6 nghiệm phân biệt khác 10 nghiệm ở trên.

Vậy phương trình đã cho có 16 nghiệm trên nửa khoảng

;

2 6

 

 







 

Câu 7. Cho hàm số

 

xfy  có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của

để phương

trình

 

mxf 1

có 4 nghiệm phân biệt?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Lời giải

Chọn C

- Hàm số





y f x

 

là hàm số chẵn nên đồ thị hàm số nhận trục

làm trục đối xứng.

- Ta có

 





 

1 0

f x khi x

f x

f x khi x

 





 



  





+) Ta vẽ đồ thị





của hàm số





y f x

 

được suy từ đồ thị





của hàm số





y f x



đã

cho bằng cách tịnh tiến





sang phải 1 đơn vị và bỏ đi phần đồ thị ở bên trái trục

+) Sau đó lấy đối xứng phần đồ thị





ở bên phải trục tung

qua trục tung thì được đồ thị của hàm số





y f x

 

Khi đó, để phương trình đã cho có 4 nghiệm phân biệt thì

ta phải có

3 1

  

Suy ra, có 3 số nguyên thỏa mãn bài toán.

Câu 8. Cho hàm số







y f x

liên tục trên



có đồ thị như hình vẽ.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Có bao nhiêu giá trị nguyên của

để phương trình

 

16cos 6sin 2 8 1   f x x f n n

có

nghiệm x ?

A. 10 B.

C. 8 D. 6

Lời giải

Chọn D

Dựa vào đồ thị hàm số ta thấy hàm số

 

y f x

đồng biến trên



Do đó:

 

2 2

16cos 6sin2 8 1 16cos 6sin2 8 1        f x x f n n x x n n

   

1 cos2

16. 6sin2 8 1 8cos2 6sin2 1



        

x n n x x n n

Phương trình có nghiệm x

   

2 2

2 2 2 2

8 6 1 1 100      n n n n

 

1 10

10 0

1 41 1 41

10 0

2 2

1 10

10 0

  



  

   

 

       

 

 

  





n n

n n n

n n

Vì n nên

 

3; 2; 1;0;1;2   n

Câu 9. Cho hàm số

 

y f x

liên tục trên  và có đồ thị như hình vẽ.

Gọi m là số nghiệm của phương trình









f f x



. Khẳng định nào sau đây là đúng?

A. 6m  . B. 7m  . C. 5m  . D. 9m  .

Lời giải

Chọn B

Đặt

 

f x u

khi đó phương trình

 

1f f x 

trở thành

   

1 1f u 

Nghiệm của phương trình (1) là hoành độ giao điểm của đồ thị hàm số





y f u



và đường

thẳng 1y  .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Dựa vào đồ thị ta có 3 nghiệm giả sử

 

1;0u  

 

0;1u 

 



 

 

Xét số giao điểm của đồ thị hàm số

 

f x

với từng đường thẳng

y u ,

y u .

Dựa vào đồ thị ta có:

Phương trình





f x u



, với





1;0

u  

cho 3 nghiệm phân biệt.

Phương trình

 

f x u

, với

 

0;1u 

cho 3 nghiệm phân biệt.

Phương trình

 

f x u

, với

 



 

 

cho 1 nghiệm duy nhất.

Suy ra phương trình ban đầu









f f x



có 7 nghiệm.

Câu 10. Cho hàm số

 

y f x có đồ thị như hình bên. Hỏi có bao nhiêu điểm trên đường tròn lượng

giác biểu diễn nghiệm của phương trình

 

cos2 0f f x

 



 

A. 1 điểm. B. 3 điểm. C. 4 điểm. D. vô số.

Lời giải

Chọn C

Ta luôn có: 1 cos2 1x   nên từ đồ thị suy ra:

 

0 cos2 1f x  .

Trên đoạn

 

0;1 :

   

cos 2 0 cos 2 0f f x f x

 

  

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Trên đoạn

 

1;1 :

 

cos2 0 cos2 0 2

2 4 2

f x x x k x k

  



        

Vậy có 4 điểm.

Câu 11. Cho hàm số

 

f x x x x   

5 3

2 5 1

. Số nghiệm thực của bất phương trình

 

sin sinf x x f  

2 3 0

trên đoạn

 

;

 

3 3

là

A. 3. B. 2. C. 0. D. vô số.

Lời giải

Chọn A

 

,f x x x x



     

4 2

5 6 5 0

 

f x

đồng biến trên  .

Khi đó, bất phương trình

 

sin sinf x x f  

2 3 0

sin sinx x   

2 3 0

sin

 











 

sin x x k k



        1 2

Nghiệm của bpt đã cho trên đoạn

 

;

 

3 3

là

 

 

2 2

và



Câu 12. Cho hàm số

 

3 1f x x x  

. Tìm số nghiệm của phương trình

 

0f f x  .

. B.

. C.

. D. 7.

Lời giải

Chọn D

Xét phương trình

 

0 3 1 0f x x x    

dùng máy tính cầm tay ta ước lượng được phương

trình có ba nghiệm và

1,879

1,532

0,347

 













Xét hàm số





3 1

f x x x

  

, ta có bảng biến thiên của





f x

như sau:

Xét phương trình

 

0 1f f x  ta ước lượng được

 

1,879

1,532

0,347

f x

  











Dựa vào bảng biến thiên của hàm số





f x

ta có:

+ Với

 

1,879f x  

phương trình

 

có

nghiệm.

+ Với





1,532

f x 

phương trình





có 3 nghiệm.

+ Với

 

0,347f x 

phương trình

 

có 3 nghiệm.

Vậy phương trình đã cho có 7 nghiệm.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Câu 13. Cho hàm số





dcxbxaxxfy 

có đồ thị như hình bên dưới.

Có bao nhiêu giá trị nguyên của tham số

để phương trình













0445

 mxfmxf

có 7 nghiệm phân biệt?

. B.

. C.

. D.

Lờigiải

Chọn C

Từ đồ thị hàm số





xfy  , vẽ được đồ thị hàm số





xfy 

như sau:

Ta có

     









   













0445

mxf

mxfmxf

Từ đồ thị hàm số





xfy 

suy ra phương trình (1) có 3 nghiệm phân biệt.

Vậy để phương trình đã cho có 7 nghiệm phân biệt thì (2) có 4 nghiệm phân biệt và khác với

các nghiệm của (1) 31410















mm . Do đó có 3 giá trị nguyên của

Câu 14. Cho hàm số

xác định trên



và cũng nhận giá trị trên tập



thỏa mãn:









4 3

2 12 4

f x f x x x

    

với mọi x, y thuộc R. Tính giá trị









1 1

 





1 1







1 9







1 9

 

Lời giải

Chọn B

Cho



ta được













2 1 1 1 12 1 4 7

f f

      

Cho

 

ta được

















4 3

2 1 1 1 12 1 4 17

f f

       

Ta có hệ









   





 

2 1 1 7 1 1

1 2 1 17 1 9

f f f

     

 



 

     

 

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Câu 15. Cho hàm số , (với ). Hàm số có

đồ thị như hình vẽ bên dưới:

Tập nghiệm của phương trình có số phần tử là

A. . B. . C. . D. .

Lời giải

Chọn B

Ta có

Dựa vào đồ thị ta thấy phương trình có ba nghiệm đơn là , , .

Do đó và .

Hay .

Từ và suy ra , và .

Khi đó phương trình

Vậy tập nghiệm của phương trình là .

Câu 16. Cho hàm số

xác định trên tập số nguyên và nhận giá trị cũng trong tập số nguyên, thỏa mãn

 

       

1 0

3 4 1

f m n f m f n mn







    





với mọi ,m n là số nguyên.

Tính

 

19f .

 

19 1999f  . B.

 

19 1998f  . C.

 

19 2000f  . D.

 

19 2001f 

Lời giải

Chọn B





4 3 2

f x mx nx px qx r

    

, , , ,

m n p q r









y f x









f x r







3 2

4 3 2



   

f x mx nx px q













y f x









f x



















1 4 5 3



   

f x m x x x







3 2

4 13 2 15



   

f x mx mx mx m













 

n m

 

p m



q m







f x r



4 3 2

   

mx nx px qx



4 3 2

15 0

 

   

 

 

m x x x x



4 3 2

3 13 3 45 0

   

x x x x



  

3 5 3 0

  

x x x









 













f x r

;0;3

 

 

 

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông









1 2 2 1 9 9

m n f f

     









2 4 2 2 45 63

m n f f

     









4 8 2 4 189 315

m n f f     









8 16 2 8 765 1395

m n f f     













2; 1 3 2 1 21 30

m n f f f

      













16; 3 19 16 3 573 1998

m n f f f      

Câu 17. Cho hàm số





y f x



liên tục trên



và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị của

tham số

để phương trình





cos 2 1

f x m

  

có nghiệm thuộc khoảng



 

 

 

là





1;1



. B.





0;1

. C.





1;1



. D.





0;1

Lời giải

Chọn B

Đặt

cos

t x



. Khi đó:

 



 

 



thì





0;1

t 

Bài toán trở thành: Tìm m để phương trình





2 1

f t m

  

có nghiệm





0;1

t 

hay phương

trình





2 1

f x m

  

có nghiệm





0;1

x

Từ đồ thị ta thấy điều kiện bài toán tương đương

1 2 1 1 0 1

m m

       

Câu 18. Cho hàm số

( )

y f x



có bảng biến thiên sau.

Tìm tất cả các giái trị của tham số m để phương trình

(2tan ) 2 1

f x m

 

có nghiệm thuộc

khoảng

(0; )



  

. B.

  

. C.

1 1

  

. D.



Lời giải

Chọn C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Đặt

2tan , (0; ) (0;2)

t x x t



   

Phương trình

(2tan ) 2 1

f x m

 

có nghiệm thuộc khoảng

(0; )





Phương trình

( ) 2 1

f t m

 

có nghiệm thuộc khoảng

(0;2)

Từ BBT ta suy ra

1 2 1 3 1 1

m m

       

Câu 19. Cho hàm số





y f x

 . Đồ thị hàm





y f x



 như hình vẽ

Đặt









3 3

g x f x x x m

   

, với

là tham số thực. Điều kiện cần và đủ để bất phương

trình





g x



đúng với

3; 3

 

  

 

là





3 3

m f . B.





3 0

m f . C.





3 1

m f

 . D.





3 3

m f  .

Lời giải

Chọn A













3 3

0 3 3 0 3 3

g x f x x x m f x x x m

         

Đặt









3 3

h x f x x x

  

. Ta có









3 3 3

h x f x x

 

  

. Suy ra









   

3 3 3 6 0

0 3 0 0

1 3 1 0

h f



 

    



 

  







 

 



 

 





Từ đó ta có bảng biến thiên

Vậy

   









3 3 3

g x m g x h f    .

Câu 20. Cho hàm số

'( )

y f x



có đồ thị như hình vẽ dưới đây.











h 











ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Xét tính đơn điệu của hàm số

( ) 2 ( ) 2

g x f x x x

  

ta được

A. Hàm số

( )

g x

nghịch biến trên













; 2 ; 1;1 ; 2;

   

; đồng biến trên









2; 1 ; 1;2

 

B. Hàm số

( )

g x

đồng biến trên













; 2 ; 1;1 ; 2;

   

; nghịch biến trên









2; 1 ; 1;2

 

C. Hàm số

( )

g x

đồng biến trên









;2 ; 1;

 

; nghịch biến trên





2;1



D. Hàm số

( )

g x

đồng biến trên

3 3

; ; 0;

2 2

   

 

   

   

; nghịch biến trên

3 3

;0 ; ;

2 2

   

 

   

   

Lời giải

Chọn B

Ta có

'( ) 2 '( ) 2 2; '( ) 0 '( ) 1

g x f x x g x f x x

 





 



       











Ta có đồ thị sau:

Hàm số đồng biến trên













; 2 ; 1;1 ; 2;

   

; nghịch biến trên









2; 1 ; 1;2

 

Câu 21. Cho hàm số





f x

xác định và liên tục trên



và có đồ thị như hình vẽ. Có bao nhiêu giá trị

nguyên của

để phương trình





2. 3 3 9 30 21 2019

f x x m      có nghiệm.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

A. 15. B. 14. C. 10. D. 13.

Lời giải

Chọn D

Điều kiện:

 



 

 

Xét phương trình:

 

2. 3 3 9 30 21 2019 1f x x m      .

Ta có:

 

9 30 21 4 3 5x x x     

   

2 2

0 4 3 5 2 3 3 3 4 3 5 3x x           

Đặt

3 3 9 30 21t x x    

 

3;3t  

Khi đó, phương trình

 

trở thành:

     

2019

2. 2019 2

f t m f t



   

Phương trình

 

có nghiệm

 



 

 



phương trình

 

có nghiệm

 

3;3t  

Dựa vào đồ thị của hàm số

 

y f x

, phương trình

 

có nghiệm

 

3;3t  

khi và chỉ

khi

2019

5 1 2009 2021



     

 

2009, 2010,..., 2021m m  

Vậy số giá trị nguyên của m là: 2021 2009 1 13   .

Câu 22. Cho hàm số

( )y f x

xác định và liên tục trên trên R có đồ thị như hình vẽ.

Có bao nhiêu giá trị nguyên của tham số m để phương trình

 

7 5 2 1 3 3 7f cosx m   

có hai nghiệm phân biệt thuộc ;

2 2

 



 

 

 

. B. 7 . C. 6 . D. 5 .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Lời giải

Chọn C

Đặt 5 2 1 3

t cosx

   (1). Vì

 

; 0 1 1;3

2 2

x cosx t

 



 

     

 

 

Phương trình đầu trở thành

 

3 7

f t



 (2)

Nhận xét:

+Với

1 1

cosx t

  

nên khi



phương trình (1) chỉ có một nghiệm thuộc

;

2 2

 



 

 

 

+Với mỗi





1;3

t 

thì phương trình (1) có hai nghiệm thuộc

;

2 2

 



 

 

 

Như vậy dựa vào đồ thị hàm số ta thấy phương trình đầu có hai nghiệm phân biệt thuộc

;

2 2

 



 

 

 

khi phương trình (2) có một nghiệm





1;3

t 

3 7

7 7

3 7

2 0

3 3





 





 









 



  







Vì





7; 2; 1;0;1;2

m Z m     

Câu 23. Cho hàm số





y f x

 có đạo hàm trên



và có đồ thị là đường cong trong hình vẽ dưới. Đặt









g x f f x



 

 

. Tìm số nghiệm của phương trình





g x





. B.

. C.

. D.

Lời giải

Chọn B

Ta có

     





 

. 0

f x

g x f f x f x

f f x







  

   



 





 



 



 

2;3

f x

x x







 



 



 





   

2;3

f x

f f x

f x x





  



 

 





 





 

1;0

0 1

3;4

x x

f x x

x x

  



  



 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

   

 

2 1

2;3

0;1

x x x

f x x

x x

 



  



 



Vậy phương trình





g x





có

nghiệm phân biệt.

Câu 24. Cho hàm số 

(



)

có bảng biến thiên của ′

(



)

như hình sau:

Đặt 

(



)

=

(



)

−









+ 2. Mệnh đề nào dưới đây đúng?

A. 

(

)

<

(

)

<

(

−1

)

. B. 

(

−1

)

<

(

)

<

(

)

C. 

(

−1

)

=

(

)

>

(

)

. D. 

(

−1

)

=

(

)

<

(

)

Lời giải

Chọn B

Ta có: ′

(



)

=′

(



)

−+ 2, ′

(



)

=0⇔′

(



)

=−2

Do đường thẳng =−2 đi qua

(

−1;−3

)

(

1;−1

)

nên dựa vào bảng biến thiên ta có

′

(



)

≥0,∀⇒

(

−1

)

<

(

)

<

(

)

Câu 25. Cho hàm số =

(



)

liên tục trên ℝ và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt

của phương trình 

(

2cos

)

=1 trên khoảng 󰇡0;





󰇢 là:

A. . B. . C. . D. .

Lời giải

Chọn C

Đặt =

2cos

∈

[

0;2

]

,∀∈󰇡0;





󰇢⇒

(



)

=1⇔



=∈

(

−2;0

)

=∈

(

0;2

)

=>2

⇔

2cos

=∈

(

0;2

)(

∗

)

Đồ thị hàm số =

2cos

trên khoảng 󰇡0;





󰇢 như hình vẽ bên.

Suy ra phương trình

(

∗

)

có 5 nghiệm thực phân biệt trên khoảng 󰇡0;





󰇢.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Câu 26. Cho hàm số =

(



)

có đồ thị như hình vẽ sau

Tìm số giao điểm của đồ thị hàm số =





(



)



và trục hoành

A. 2. B. . C. . D. .

Lời giải

Chọn D

Phương trình hoành độ giao điểm của đồ thị hàm số =





(



)



và trục hoành là: 





(



)



(

)

Ta có

(

)

⇔



(



)



(



)

=−2

Số nghiệm của phương trình

(

)

là tổng số giao điểm của đồ thị hàm số =

(



)

và hai đường

thẳng song song =2 và =−2.

Từ đồ thị hàm số =

(



)

, ta thấy tổng số giao điểm bằng 5. Suy ra phương trình

(

)

có 5n

ghiệm phân biệt.

Vậy số giao điểm của đồ thị hàm số =





(



)



và trục hoành là 5.

Câu 27. Cho hàm số có đạo hàm là hàm số với đồ thị như hình

vẽ bên.

Biết rằng đồ thị hàm số tiếp xúc với trục hoành tại điểm có hoành độ âm. Khi đó đồ

thị hàm số cắt trục tung tại điểm có tung độ là bao nhiêu?

A. B. C. D.

Lời giải

Chọn A

Ta có

Đồ thị hàm số đi qua các điểm , và nên ta có





3 2

y f x ax bx cx d

    





y f x









y f x













3 2 2

3 2

y f x ax bx cx d f x ax bx c



        





y f x









2;0

A 





0;0





1; 3

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

và .

Gọi tiếp điểm của đồ thị hàm số và trục hoành là với

Tiếp tuyến có hệ số góc

. Vì .

thuộc đồ thị hàm số

Khi đó Đồ thị hàm số cắt trục tung tại điểm có tung độ là .

Câu 28. Cho hàm số có đồ thị như hình vẽ sau:

Số nghiệm của phương trình

2 2 2

[ ( 1)] ( 1) 2 0f x f x    

là

A. 1. B. 4. C. . D. .

Lời giải

Chọn B

Đặt

1 1t x t    .

Ta thấy ứng với 1t  cho ta một giá trị của x và ứng với mỗi giá trị 1t  cho ta hai giá trị của

x .

Phương trình đã cho trở thành:

( ) 1

[ ( )] ( ) 2 0

( ) 2

f t

f t f t

f t

 



   







Từ đồ thị hàm số ( )y f t trên [1;+ ) suy ra phương trình ( ) 1f t   có nghiệm 2t 

và

phương trình ( ) 2f t  có nghiệm 2t  do đó phương trình đã cho có 4 nghiệm.

Vậy phương trình đã cho có 4 nghiệm.

Câu 29. ##Cho hàm số

 

f x

xác định trên

 

\ 0

và có bảng biến thiên như hình vẽ.

Số nghiệm của phương trình

 

3 2 1 10 0f x    là.

. B.

. C.

. D.

Lời giải

Chọn C

 

3 2

12 4 0 1

0 3 3

3 2 3 0

a b c a

c b y f x x x d

a b c c

   

 

 

       

 

 

    

 





3 6

f x x x



 





y f x







M x



 

0 0 0

0 ' 0 3 6 0

k y x x x





      



 



0 0

0 2

x x

   





2;0

M 





8 12 0 4.

y f x d d

        





3 2

3 4.

y f x x x

   







y f x



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Đặt

2 1t x 

, ta có phương trình trở thành

 

f t  . Với mỗi nghiệm t thì có một nghiệm



 nên số nghiệm t của phương trình

 

f t  bằng số nghiệm của

 

3 2 1 10 0f x    .

Bảng biến thiên của hàm số

 

y f x là

Suy ra phương trình

 

f t  có

nghiệm phân biệt nên phương trình

 

3 2 1 10 0f x   

có

nghiệm phân biệt.

Câu 30. Cho hàm số

 

y f x có đạo hàm

 

f x



trên

 

\ 0 và có bảng biến thiên như hình dưới.

Hỏi phương trình

 

2f x  có bao nhiêu nghiệm?

A. 1 nghiệm. B. 2 nghiệm. C. 3 nghiệm. D. 4 nghiệm.

Lời giải

Chọn C

Bảng biến thiên cho hàm số

 

y f x như sau:

∞

1 +

∞

Dựa vào BBT suy ra: phương trình

 

2f x  có 3 nghiệm phân biệt.

Câu 31. Cho hàm số

 

3 2

3 1f x x x  

. Số nghiệm của phương trình

   

2 4 1f f x f x    

 

là

A. 5 . B. 6 . C. 8 . D. 9 .

Lời giải

Chọn B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 24

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Đặt

 

3 2

2 3 3t f x t x x     

Khi đó phương trình trở thành

 

3 2

1 0

4 1

4 2 1

4 2 4 0

1 3

f t t

f t t t

t t t

 







    

 

   

   



















 





 







 





Xét hàm số

3 2

3x 3y t x   

 

3 6 3 2 0

y x x x x







     







Ta có bảng biến thiên

Dựa vào BBT ta có phương trình 2t  có 3 nghiệm phân biệt, phương trình 1 3t   có 3

nghiệm phân biệt.

Vây phương trình ban đầu có 6 nghiệm phân biệt.

Câu 32. Đồ thị hàm số

 

4 3 2

f x ax bx cx dx e    

có dạng như hình vẽ sau:

Phương trình

     

4 3 2

( ) ( ) ( ) ( ) 0a f x b f x c f x df x e    

(*) có số nghiệm là

12.

16.

Lời giải

Chọn C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 25

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Ta thấy đồ thị

 

y f x

cắt trục hoành tại 4 điểm phân biệt nên phương trình

 

0f x 

có 4

nghiệm phân biệt:

 

1,5; 1x   

 

1; 0,5x   

 

0;0,5x 

 

1,5;2x 

Kẻ đường thẳng y m , khi đó:

Với

 

1,5; 1m x   

có 2 giao điểm nên phương trình

 

f x x

có 2 nghiệm.

Với

 

1; 0,5m x   

có 4 giao điểm nên phương trình

 

f x x

có 4 nghiệm.

Với

 

0;0,5m x 

có 4 giao điểm nên phương trình

 

f x x

có 4 nghiệm.

Với

 

1,5;2m x 

có 2 giao điểm nên phương trình

 

f x x

có 2 nghiệm.

Vậy phương trình (*) có 12 nghiệm.

Câu 33. Cho hàm số

:f  

thỏa mãn điều kiện

   

2 2 2

3 2 3 5 6 10 17,f x x f x x x x x          

Tính

 

2018f

 

2018 2018f 

. B.

 

2018 2018f 

 

2018 4033f 

. D.

 

2018 3033f 

Lời giải

Chọn C

Ta cần thay

bởi đại lượng nào đó để bảo toàn được sự xuất hiện của

 

3f x x 

và

 

3 5f x x 

trong phương trình.

Do đó ta cần có

2 2

3 3 5 1x x x x x x       

Như vậy ta thay x bởi 1 x .

Cuối cùng ta tính được:

   

2 2 2

3 2 2 3 2 3 3f x x x x x x        

Vậy

 

2018 2.2018 3 4033f   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 26

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Câu 34. Cho hàm số





f x

có bảng biến thiên như sau:

Số nghiệm thuộc đoạn



 

 

 

của phương trình





cos



f x là

. B.

. C.

. D.

Lời giải.

Chọn B

Từ BBT ta thấy:

 





 

cos 1 :

cos 1 0

cos

cos 0 1

cos 1 :

x a a voânghieäm

x b b

x c c

x d d voânghieäm





 









   

  

 





 

cos 1 0

cos 0 1







   

  





x b b

x c c

Dựa vào đường tròn lượng giác, trên đoạn



 

 

 

thì:

- Phương trình cos



x b

có 8 nghiệm phân biệt.

- Phương trình

cos



x c

có 9 nghiệm phân biệt khác 8 nghiệm ở trên.

Vậy phương trình





cos



f x có 17 nghiệm trên đoạn

0; .



 

 

 

Câu 35. Cho hàm số





f x

liên tục trên



và có bảng biến thiên như sau:

Số nghiệm thuộc đoạn





0;2020



của phương trình





cof x



là

2021

. B.

3030

. C.

2020

. D.

3031

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 27

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Lời giải.

Chọn D

Từ BBT ta thấy:

 

cos 1

cos cos

s 1 :

x x

x a a voâ nghieäm





 







  

 

 

cos 1

cos







 







Dựa vào đường tròn lượng giác, trên đoạn





0;2020



thì:

- Phương trình

cos 1



có

1011

nghiệm phân biệt.

- Phương trình

cos

 

có

2020

nghiệm phân biệt khác

1011

nghiệm ở trên.

Vậy phương trình





cof x



có

3031

nghiệm trên đoạn





0;2020



Câu 36. ##Cho hàm số





3 2

f x ax bx bx c

   

có đồ thị như hình vẽ:

Số nghiệm nằm trong

;

2 2

 



 

 

 

của phương trình





cos 1 cos 1

f x x

  

là

. B.

. C.

. D.

Lời giải

Chọn B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 28

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Từ đồ thị ta có

 

0;1

x a

f x x x b

  



   







Do đó

 





 

cos 1 ;0

cos 1 cos 1 cos 1 0;1

cos 1 2

x a

f x x x b

   



      



 







 

cos 1 ; 1 ( )

cos 1 1;0 (1)

cos 1 (2)

x a t VN

x b t

     



     







Dựa vào đường tròn lượng giác, phương trình (1) có

nghiệm nằm trong

;

2 2

 



 

 

 

Phương trình (2) có

nghiệm nằm trong

;

2 2

 



 

 

 

Vậy phương trình ban đầu có tất cả

nghiệm nằm trong

;

2 2

 



 

 

 

Câu 37. Cho hàm số

 

y f x

có đạo hàm trên



. Biết rằng hàm số

 

'y f x

có đồ thị như hình vẽ

bên dưới. Hỏi đồ thị hàm số

 

3 4y f x 

cắt đường thẳng

y x  

tại nhiều nhất bao nhiêu điểm?

. B.

. C.

. D.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 29

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Lời giải

Chọn D

Đặt

 

3 4

t x x



   

Phương trình hoành độ giao điểm là:

   

3 4

f x x    

Số nghiệm của







là số giao điểm của đồ thị hàm số





3 4

y f x

 

và đường thẳng

y x  

. Thế

vào

 



ta có:

 

3 6

f t   

Đặt

   

3 6

g t f t  

     

1 1

' ' 0 '

3 3

g t f t f t



     

Quan sát đồ thị ta thấy

 

f t  

có 3 nghiệm thực phận biệt nên hàm

 

g t

có 3 cực trị.

Số nghiệm lớn nhất của phương trình





g t



là 4. Suy ra phương trình







có tối đa 4 nghiệm

Vậy chọn đáp án

Câu 38. Cho hàm số

 

y f x

liên tục trên



có đồ thị như hình vẽ bên. Hỏi phương trình

 

2 1f f x 

có tất cả bao nhiêu nghiệm thực phân biệt?

A. 5. B. 6 . C. 3. D.

Lời giải

Chọn C

Từ đồ thị ta suy ra:

 

2 1 1

2 1

2 2 4

f x f x

f f x

f x f x

   

   

 

   

 

 

•

 

f x

 



 







•

 

4 2f x x x    

Vậy phương trình có 3 nghiệm phân biệt.

Câu 39. Cho hàm số

 

3 1f x x x  

. Số nghiệm của phương trình

   

3 1 0f x f x   

 

là

A. 1. B. 6. C. 5. D. 7.

Lời giải

Chọn D

Đồ thị hàm số

 

3 1y f x x x   

có dạng:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 30

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Dựa vào đồ thị ta thấy phương trình

 

0f x 

có 3 nghiệm

     

1 2 3

2; 1 , 0;1 , 1;2x x x    

Nếu phương trình

   

3 1 0f x f x   

 

có nghiệm

x thì

   

0 1 2 3

, ,f x x x x

Dựa vào đồ thị ta có:

   

1 1

, 2; 1f x x x   

có 1 nghiệm duy nhất.

   

2 2

, 0;1f x x x 

có 3 nghiệm phân biệt.





3 3

( ) , 1;2

f x x x 

có 3 nghiệm phân biệt.

Vậy phương trình

   

3 1 0f x f x   

 

có 7 nghiệm phân biệt.

Câu 40. Cho hàm số 

(



)

=



+ 



+ 



+ +  có đồ thị như hình bên. Phương trình











(



)



+ 2=

(



)

+ 1 có bao nhiêu nghiệm thực phân biệt.

A. 3. B. 4. C. 2. D. 5.

Lời giải

Chọn C

Ta có:

′

(



)

=4



+ 3



+ 2+ =4

(

+ 1

)



(

−1

)

=4

(





−

)

⇒

(



)

=

(





−2



)

+ .

Và





(

)



(

−1

)

=−1

⇔

󰇥

=0

−+ =−1

⇔

󰇥

=1

3=0

⇒

(



)

=



−2



Đặt =





(



)

;

(

≥0

)

phương trình trở thành:



(



)

+ 2=



+ 1⇔







−2



+ 2=



+ 1⇔



−2



+ 2=

(





+ 1

)



⇔4



⇔=

(

≥0

)

Vậy





(



)





⇔

(



)





phương trình này có 2 nghiệm.

Câu 41. Cho hàm số

 

y f x liên tục trên  và có bảng biến thiên như sau

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 31

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Có bao nhiêu giá trị nguyên của tham số

sao cho phương trình





2 sin cos 1

f x x m

  

có hai nghiệm phân biệt trên khoảng

;

4 4

 

 



 

 

. B.

. C.

. D.

Lời giải

Chọn A

Đặt

sin cos

t x x

 

Ta có:

cos sin 2 sin 0, ;

4 4 4

t x x x x

  

   



       

   

   

Bảng biến thiên của





t t x



trên khoảng

;

4 4

 

 



 

 

Nhận xét: Dựa vào bảng biến thiên của





t x

trên khoảng

;

4 4

 

 



 

 

ta thấy với mỗi

;

4 4

 

 

 

 

 

có duy nhất một giá trị





2; 2

t   .

Do đó, phương trình





2 sin cos 1

f x x m

  

có hai nghiệm phân biệt trên khoảng

;

4 4

 

 



 

 



phương trình





2 1

f t m

 

có hai nghiệm phân biệt trên





2; 2 4 3 7 7



        

Mà





6; 5;..;5;6m m

     



có 13 giá trị nguyên

thỏa mãn yêu cầu bài toán.

Câu 42. ##Cho hàm số





y f x



liên tục trên



và có đồ thị như hình vẽ.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 32

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Số nghiệm thuộc đoạn

 

 

 của phương trình

 

2 2 sin 1 0f x   là

. B. 2 . C.

. D. 12.

Lời giải

Chọn D

Đặt 2 sint x . Xét hàm

 

2 sint g x x  trên đoạn

 

 



Ta có bảng biến thiên của hàm số

 

2 siny g x x  trên đoạn





 



Dựa vào BBT ta có

   

0,2 ;2t x

 

   

Nếu

 

0,2t  thì mỗi giá trị

cho

giá trị x thuộc đoạn





 



Phương trình

 

2 2 sin 1 0f x   trở thành

 

f t   với

 

0,2t 

Dựa vào đồ thị ta có phương trình

 

f t   có 2 nghiệm

phân biệt thuộc khoảng

 

0,2 nên phương trình ban đầu có 12 nghiệm phân biệt thuộc đoạn





 



Câu 43. Cho hàm số

( )y f x

liên tục trên R và có đồ thị như hình vẽ

Gọi

là số nghiệm của phương trình

 

( ) 0f f x  . Khẳng định nào sau đây đúng.

4m 

6m 

5m 

7m 

Lời giải

Chọn D

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 33

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Từ đồ thị ta có

 

( )

( ) 0 ( ) 1

( )

f x x

f f x f x

f x x







  







với

1 2

1 0 ; 2 3

x x

    

Trường hợp 1:

( )

f x x



có 3 nghiệm phân biệt

Trường hợp 2:

( ) 1

f x



có 3 nghiệm phân biệt

Trường hợp 3:

( )

f x x



có 1 nghiệm

Vậy phương trình





( ) 0

f f x



có 7 nghiệm hay



Câu 44. Cho hàm số



( )

liên tục trên

và có đồ thị như hình vẽ. Gọi

là tập hợp tất cả các

giá trị nguyên của

để phương trình

(sin ) 2sin

f x x m

 

có nghiệm thuộc khoảng

(0; )



. Tông các

phần tử của

bằng



Lời giải

Chọn C

Đặt





















sin 0;1 sin 2sin 2 0;1

t x t f x x m m f t t t         

Xét













2 , 0;1

g t f t t t  





















' ' 2 0 0;1 3;1

g t f t t g t        

Phương trình





sin 2sin

f x x m

 

có nghiệm









3;1 3; 2; 1;0

m m       

Vậy tổng các số là

 

Câu 45. ##Cho hàm số





f x

liên tục trên



có đồ thị





y f x



như hình vẽ dưới đây.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 34

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Số nghiệm thực của phương trình









4 2 2

f f

 

là

A. 1. B. 2. C. 3. D. 4.

Lời giải

Chọn B

Ta có:

Theo đồ thị :

 





 

4 2 2

4 2 , 4 6

f f

f a a



  



  



   



TH1)





4 2 2

  





2 6

  

 

2 2

b KTM





  



  





TH2)





4 2

f a

 





2 4,

f a

  





0 4 2

  





 

2 2

2 0 log

2 4

c KTM

d KTM x t



  



    



 





Vì



nên

2 2

log log 4 2 1

  

nên phương trình đã cho có 2 nghiệm phân biệt.

Câu 46. Cho hàm số

( )

y f x



xác định và liên tục trên



có đồ thị như hình vẽ. Có bao nhiêu giá trị

nguyên của

để phương trình





2 3 3 9 30 21 2019

f x x m      

có nghiệm.

A. 15. B. 14. C. 10. D. 13.

Lời giải

Chọn D

Ta có

 

9 30 21 3 5 4 4

x x x

       

nên

 

9 30 21 0;2

x x    .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 35

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Đặt

3 3 9 30 21

t x x

    

thì





3;3

t  

. Ta cần tìm số các giá trị nguyên của

để phương

trình

 

2019

f t



 có nghiệm





3;3

t  

Từ đồ thị suy ra đường thẳng

2019



 cắt đồ thị









; 3;3

y f t t  

khi và chỉ khi

 

 

3;3

2019

5 ; max

a a f t



    , và cũng từ đồ thị ta có

1 1,5

 

Do đó

2009 2 2019

m a

  

và

2021 2 2019 2022

  

. Mà m





nên

2009 2021

 

Vậy có tất cả

2021 2009 1 13

  

giá trị nguyên của

thỏa mãn.

Câu 47. Cho hàm số





y f x



có đồ thị như hình vẽ sau.

Số nghiệm của phương trình









e e 2 0

x x

f f

 

  

 

là:

. B.

. C.

. D.

Lời giải

Chọn B

Điều kiện



Đặt

t 

. Do

0 1

x t

  

và ứng với mỗi giá trị



chỉ cho một giá trị



Ta có phương trình trở thành:

   





 

2 0

f t

f t f t

f t

 



    



 







Từ đồ thị hàm số





y f t



trên







suy ra phương trình





f t

 

có

nghiệm và phương

trình





f t



có

nghiệm khác với nghiệm của phương trình





f t

 

Vậy phương trình đã cho có 2 nghiệm.

Câu 48. Cho hàm số





y f x

 liên tục trên



có đồ thị như hình vẽ. Phương trình









1 0

f f x

 

có tất

cả bao nhiêu nghiệm thực phân biệt?

. B.

. C.

. D.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 36

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Chọn C

Từ đồ thị hàm số ta có :

 

   

 

1 2 1 1

1 0 1 0 1 1 .

1 1 2 1

f x m m f x m

f f x f x n n f x n

f x p p f x p

 

       

 

         

 

     

 

 

+) Do 2 1 2 1 3m m         phương trình

 

1f x m  có 1 nghiệm

x .

+) Do 0 1 0 1 1n n       phương trình

 

1f x n  có 3 nghiệm

2 3 4

, ,x x x .

+) Do 1 2 1 1 0p p        phương trình

 

1f x p  có 3 nghiệm

5 6 7

, ,x x x .

Dựa vào đồ thị ta thấy 7 nghiệm này phân biệt.

Vậy phương trình đã cho có đúng 7 nghiệm phân biệt.

Câu 49. Cho hàm số bậc ba

 

y f x có đồ thị như hình vẽ.

Có bao nhiêu giá trị nguyên của tham số

để phương trình

 

cos 2 f f x f m có

nghiệm trên nửa khoảng





0; ?



A. 3 . B.

. C.

. D. 5 .

Lời giải.

Chọn A

Sử dụng đường tròn lượng giác và qua sát đồ thị ta thấy:



 



 





0; cos 1;1 cos 2;2



      x x f x

 





 





 







    

cos 2 0;4

cos 2 0;2

cos 2 2;2

2;2 \ 1 2;0;1 .

  

    

      

f x

f f x f m

m m

Vậy có tất cả 3 giá trị nguyên.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 37

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Câu 50. Cho hàm số





y f x



có đồ thị là đường cong trong hình vẽ dưới đây

Gọi

là tập hợp tất cả các giá trị nguyên của

để phương trình









f f x m

 

có

nghiệm

phân biệt thuộc đoạn





2;2



. Số phần tử của

là

. B.

. C.

. D.

Lời giải

Chọn D

Gọi





là đồ thị hàm số





y f x



Vẽ đồ thị





của đồ thị hàm số





y f x

 

bằng cách: Tịnh tiến đồ thị





của hàm số





y f x



theo phương của trục hoành sang trái

đơn vị.

Vẽ đồ thị





của hàm số





y f x

 

bằng cách: Giữ nguyên đồ thị





nằm bên phải trục

tung rồi lấy đối xứng phần đó chính phần đồ thị đó qua trục tung, ta được đồ thị





của hàm

số





y f x

 

. Do đó, ta có đồ thị hàm số





y f x

 

Đặt





t f x

 

, với









2;2 1;0

x t    

Ta có phương trình





f t m



(1).

Nếu



cho ta ba nghiệm phân biệt





2;2

x 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 38

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Nếu

 

cho ta hai nghiệm phân biệt





2;2

x 

Nếu





1;0

t  

thì mỗi giá trị của

cho ta bốn nghiệm phân biệt





2;2

x 

Vậy phương trình đã cho có bốn nghiệm phân biệt khi và chỉ phương trình





có đúng 1

nghiệm





1;0

t  









0 1

f m f

   

3 8

  

Vậy

có tất cả

phần tử.

NHẬN XÉT : Cách giải 2 : Chọn hàm

( ) ( 1)( 3)

f x x x

  

Câu 51. Cho hai hàm số





f x

và





3 2

5 2 8

g x x x x

   

. Trong đó hàm số





f x

liên tục trên



và có

đồ thị như hình vẽ dưới đây.

Số nghiệm của phương trình









g f x



là

. B.

. C.

. D.

Lời giải

Chọn C

Đặt





3 2

, 0

f x ax bx cx d a

    





3 2

f x ax bx c



   

Theo hình vẽ có:





 

1 0

1 1

0 1









 





 







3 2 0

a b c

a b c d

  





  







    





















 











3 1

f x x x

   

Ta có:





g x



3 2

5 2 8

x x x

   







 



 



Suy rA.









g f x







 

f x







 



 



3 1 4

3 1 2

3 1 1

x x



  



   



   







 

3 3 0 1

3 1 0 2

3 2 0 3

x x



  



   



  





Ta thấy:





có một nghiệm,





có ba nghiệm,





có hai nghiệm.

Vậy









g f x



có 6 nghiệm.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 39

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Câu 52. Cho hàm số





7 5 4 3 2

2 2 10

f x x x x x x x

      

và





3 2

g x x x

  

. Đặt









F x g f x



 

 

. Tìm tất cả các giá trị của tham số

để phương trình





F x m



có ba nghiệm thực

phân biệt.





1;3

m 





0;4

m





3;6

m





1;3

m

Lời giải

Chọn B

Ta có





'( ) '( ) ' ( ) .

F x f x g f x



 

6 4 3 2

7 5 4 3 4 2 0(1)

'( ) 0

'( ) 0 ( ) 1

' ( )

( ) 1

x x x x x

f x

F x f x

g f x

f x



     







   







 



(1)Vô nghiệm vì

6 4 3 2

7 5 4 3 4 2 0

x x x x x x

      

Bản biến thiên:

Vậy





F x m



có ba nghiệm thực phân bit thì





0;4

m

Câu 53. Cho hai hàm số





f x

và





g x

đều có đạo hàm trên



và thỏa mãn:













3 2 2

2 2 2 3 . 36 0

f x f x x g x x

     

, với x

 



. Tính









3 2 4 2

A f f



  .

. B.

. C.

. D.

Lời giải

Chọn D

Với x

 



, ta có









3 2 2

(2 ) 2 2 3 . 36 0

f x f x x g x x

     





Đạo hàm hai vế của





, ta được

























2 2

3 2 . 2 12 2 3 . 2 3 2 . . 36 0

f x f x f x f x x g x x g x

  

         





Từ





và





, thay



, ta có













         

3 2

2 2 2 0 3

3 2 . 2 12 2 . 2 36 0 4

f f

f f f f



 





 

   





Từ





, ta có









2 0 2 2

f f

  

Với





2 0



, thế vào





ta được

36 0



(vô lí).

Với





2 2



, thế vào





ta được





36. 2 36 0



  





2 1



 

Vậy









3 2 4 2

A f f



 

3.2 4.1

 



Câu 54. ##Cho hàm số





y f x

 có đồ thị như hình vẽ bên dưới. Số nghiệm thực của bất phương trình









3 2 2 3 2

1 3 1 2 3 1 2

f x x f x x

      

là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 40

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

. B.

. C.

. D.

Lời giải

Chọn B

Đặt





3 2

3 1

a f x x

  

ta được bất phương trình

 

2 2

1 0

1 2 2 1

1 2 2 2

1 0

a a a

 



 





      

 

   

 





Với



ta được





3 2

3 1 1

f x x

  

. Đặt

3 2

3 1

t x x

  

ta được PT









1 *

f t  .

Vẽ đường thẳng



lên đồ thị đã cho ta được PT





có 1 nghiệm





2; 1

t t

   

và 1

nghiệm





1;2

t t  .

Ta có BBT của hàm số

3 2

3 1

y x x

  

như sau

Với

t t



ta được PT

3 2

3 1

x x t

  

. Dựa vào BBT ta thấy PT này có 3 nghiệm phân biệt.

Với

t t



ta được PT

3 2

3 1

x x t

  

. Dựa vào BBT ta thấy PT này có 1 nghiệm.

Vậy BPT đã cho có 4 nghiệm thực.

Câu 55. ##Cho hàm số





y f x

 là hàm bậc 3 và có bảng biến thiên như sau

Phương trình

   

sin cos 1 sin2 2 2sin sin cos

f x x x x f x x



 

     

 

 

có mấy nghiệm

thực thuộc đoạn

5 5

;

4 4

 

 



 

 

. B.

. C.

. D.

Lời giải

Chọn B

Vì hàm số có 2 điểm cực trị là

 

nên









2 3

' 3 3 3

f x ax a f x ax ax d

     

. Theo

BBT thì đồ thị hàm số đi qua 2 điểm





1;2

 và





1; 2



nên

2 2 1

2 2 0

a d a

a d d

  

 



 

    

 

Suy ra





f x x x

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 41

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Ta có

   

sin cos 1 sin2 2 2sin sin cos

f x x x x f x x



 

     

 

 

       

sin cos sin cos 2 sin cos sin cos

f x x x x x x f x x

      

     

sin cos sin cos 0 sin cos sin cos

f x x x x f x x x x

         

 

Đặt

sin cos 2sin , 2; 2

t x x x t



 

 

     

 

 

 

ta được phương trình

 

loaïi

f t t t t t





    



 



Với



ta được 2 sin 0 ,

4 4

x x k k

 



 

      

 

 



Ta có

5 5 3

1 1, 0, 1

4 4 4 2

k k k k k

  



             

. Vậy PT có 3 nghiệm.

Câu 56. ##Cho





y f x



là hàm số bậc ba và có bảng biến thiên như hình vẽ

Có bao nhiêu giá trị nguyên





5;5

m 

để hàm số













g x f f x m

 

có

điểm cực trị?

A. 5. B. 6. C. 7. D. 8.

Lời giải

Chọn B

















. .

g x f x f f x m

  

 

 





 

f x

g x

f f x m







 





 





 

2 2

x x

f x m f x m

   

 

 

 

 

 

 

     

 

    

 

 

trong đó

 

và



là hai nghiệm bội lẻ.

Đặt









f x f x

 

và









f x f x

 

, ta có đồ thị sau

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 42

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Với

 

5;5m

 















và nhìn vào đồ thị, ta thấy hàm số

 

g x

có 4 điểm cực trị 

 

0g x





có 4

nghiệm bội lẻ

 

4; 3; 1;1;3;4 .m   

Câu 57. ##Cho hàm số

 

f x

có bảng biến thiên như sau:

Số nghiệm thuộc khoảng

 

;

 



của phương trình

   

cos cos 2f x f x 

là

. B.

. C.

. D.

Lời giải

Chọn A

Đặt

cos ,t x

 

; .x

 

 

Ta có bảng biến thiên (*)





1;1 .t  

Phương trình đã cho trở thành

   

 

2 (1)

2 0 .

1 (2)

f t

f t f t

f t



   



 





Từ bảng biến thiên của đề bài, với





1;1t  

ta có nghiệm của phương trình (1) là

 

1;0t a  

hay

 

0;1t b 

và nghiệm của phương trình (2) là

1t 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 43

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Từ bảng biến thiên (*), ta có:





1;0t a

   





 

x x



  



 









0;1t b

  





 

x x



  



 





 



Vậy, phương trình đã cho có 5 nghiệm phân biệt thuộc khoảng





; .

 



Câu 58. Cho hàm số





y f x



có đồ thị như hình vẽ dưới đây. Gọi S là tập hợp tất cả các giá trị của

tham số

để phương trình





3 4

f x m

  

có hai nghiệm phân biệt thuộc đoạn

2; 3

 



 

. Tìm tập







1; 3 2

S f



  



. B.







3 2 ;3

S f



 



 

. D.





1;3

S  

Lời giải

Chọn A

Xét phương trình





3 4

f x m

  

. Điều kiện

4 0 2 2

x x

     

Đặt

3 4

  

t x

với

2; 3

 

 

 

. Ta có







và

0 0



  

t x .

Bảng biến thiên của hàm số

3 4

  

t x

trên đoạn

2; 3

 



 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 44

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Nhận xét:

+) Mỗi



1;3 2



 



cho ta 2 giá trị

2; 3x

 

 

 

+) Mỗi



3 2;2



 



cho ta một giá trị

2; 3x

 

 

 

+) 1t cho ta 1 nghiệm duy nhất 0x .

Dựa vào đồ thị hàm số





y f x



ta suy ra đường thẳng y m chỉ cắt đồ thị hàm số

 

y f t

nhiều nhất tại một điểm trên

 

1;2

Do đó, để phương trình





3 4f x m  

có hai nghiệm phân biệt thuộc đoạn

2; 3

 



 

thì

 



1; 3 2m f



  



Vậy, các giá trị của

cần tìm là







1; 3 2

m f



  



Câu 59. Cho hàm số

 

4 3 2

y f x ax bx cx dx k     

với ( , , , , )a b c d k  . Biết đồ thị hàm số

 

y f x





có đồ thị như hình vẽ, đạt cực trị tại điểm

 

0;0O

và cắt trục hoành tại

 

3;0A

. Có bao nhiêu

giá trị nguyên của m trên

 

5;5

để phương trình

 

2f x x m k    có bốn nghiệm phân biệt?

A. 0. B. 2. C. 5. D. 7.

Lời giải

Chọn B

Từ đồ thị ta thấy

 

f x



không thể có bậc nhỏ hơn hoặc bằng 2, do đó 0a  .

Ta suy ra

   

3f x x x





 

, 0a  . Đồ thị của nó đi qua

 

2;1A

nên

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 45

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

 

1 .2 . 2 3

a a

    

Suy ra

   

f x x



  

, do đó

 

4 3

16 4

x x

f x k

   

Ta có

 

4 3

16 4

x x

f x k k k





      







Suy ra

 

2 0

2 4

x x m

f x x m k

x x m



   

    



   



Phương trình





2 0 1

x x m   

có hai nghiệm phân biệt khi

1 0 1

m m



      

Phương trình





2 4 2

x x m   

có hai nghiệm phân biệt khi

1 4 0 3

m m



      

Hai phương trình





và





nếu như có nghiệm chung

thì

0 0

2 0

4 0

2 4

x x m



   



 



   





(

Vô lí). Suy ra phương trình





và





không có nghiệm chung.

Do vậy để phương trình





f x x m k

   

có

nghiệm phân biệt thì

 



 







nguyên và





5;5

m 

nên





4;5

m

. Vậy có

giá trị của

Câu 60. Cho hàm số

( )

f x

là hàm số đa thức bậc ba có đồ thị như hình bên dưới. Số nghiệm thuộc

khoảng





0;3



của phương trình





sin 1 sin

f x x

 

là

. B.

. C.

. D.

Lời giải

Chọn C

Đặt

sin 1

t x

 

. Khi đó, phương trình đã cho trở thành

( ) 1

f t t

 

Vẽ đồ thị hàm số

( )

y f t



và đường thẳng

y t

 

trên cùng hệ trục tọa độ

Oxy

Từ đồ thị ta có

( ) 1 1

, ( 1).

f t t t

t m m

 





   



 



-1

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 46

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Với 1t  thì sin 1 1 sin 2x x     phương trình vô nghiệm.

Với

t m

thì sin 1 sin 1x m x m     . Phương trình này vô nghiệm vì 1 2m   .

Với 1t   thì sin 1 1 sin 0 , ( )x x x k k



        .

Do (0;3 )x



 và k  nên





0 3 0 3 1,2

k k k

 

      

Vậy phương trình đã cho có đúng 2 nghiệm thuộc khoảng (0;3 )



là ; 2x x

 

  .

Câu 61. Cho hàm số

 

y f x

có đồ thị như hình vẽ sau

Có bao nhiêu số nguyên m thuộc đoạn

 

2019;2019

sao cho phương trình

 

2 2 2

2 4 2 1 2 0f x m m f x m m      có đúng 8 nghiệm phân biệt.

A. 1. B. 2020. C. 2019. D. 2.

Lời giải

Chọn D

   

 

2 2

2 2 2 0f x f x m m f x m m

   

      

   

 

   

2 2 1 0

2 3

f x

f x m m f x

f x m m







 

     

 



 





Dựa vào đồ thị ta thấy phương trình





có bốn nghiệm phân biệt.

Để phương trình

 

có đúng 8 nghiệm thì phương trình

 

có 4 nghiệm phân biệt khác

nghiệm của phương trình





Yêu cầu bài toán

2 2

m m m m m       

và

1 1 1

2 2 .

4 8 8

m m m

 

     

 

 

Dựa và đồ thị ta có

2 0 0

1 1

2 1

m m

m m m

m m



 





  



 





 







  





Vậy có 2 nguyên của m thoả mãn.

Câu 62. Biết rằng đồ thị hàm số bậc bốn

 

y f x

được cho như hình vẽ sau

















2 2 2

2 4 2 1 2 0 1

f x m m f x m m     

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 47

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Tìm số giao điểm của đồ thị hàm số

       

' . "y g x f x f x f x  

 

 

và trục hoành.

. B.

. C.

. D.

Lời giải

Chọn B

Ta thấy đồ thị hàm số

 

y f x

cắt trục hoành tại 4 điểm phân biệt

1 2 3

0; ; ;x x x nên

     

1 2 3

, 0f x ax x x x x x x a    

Khi đó

              

1 2 3 2 3 1 3 1 2

'f x a x x x x x x ax x x x x ax x x x x ax x x x x            

Với

1 2 3

0; ; ;x x x x thì

 

1 2 3

1 1 1 1

f x

f x x x x x x x x

   

  

 

     

 

     

2 2 2 2

1 2 3

" . '

1 1 1 1

f x f x f x

f x

f x x

x x x x x x

f x





   

   

 

    

 

  

 

Do đó

     

2 2 2

1 2 3

1 1 1 1

' . " 0 0f x f x f x

x x x x x x

      

 

 

  

, vô nghiệm.

Vậy đồ thị hàm số

       

' . "y g x f x f x f x  

 

 

không cắt trục hoành.

Câu 63. Cho hàm số

 

f x

liên tục trên  và có đồ thị như hình vẽ bên.

Số giá trị nguyên của tham số m để phương trình

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 48

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông













cos 2019 cos 2020 0

f x m f x m

    

có đúng

nghiệm phân biệt thuộc đoạn





0;2



là

. B.

. C.

. D.

Lời giải

Chọn C

Phương trình













cos 2019 cos 2020 0

f x m f x m

    













 

cos 1

cos 2020

f x

f x m

 





 





Dựa vào đồ thị hàm số

Xét phương trình:





cos 1 cos 0

f x x

   

 

0;2





















Phương trình





có

nghiệm phân biệt khi và chỉ khi phương trình





cos 2020

f x m

 

có 4

nghiệm phân biệt khác

2 2

 

trên đoạn





0;2







2020

f t m

  

có 2 nghiệm phân biệt









1;1 \ 0

t  

với

cos

t x



1 2020 1 2019 2021

m m

       

Vậy có

giá trị nguyên của

là

2019

và

2020

Câu 64. Cho hàm số





y f x

 có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình

 

f x x

 

là

. B.

. C.

. D.

Lời giải

Chọn B

Từ đồ thị hàm số





y f x

 suy ra đồ thị hàm số





y f x

 là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 49

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Đặt

3t x x  , ta có:

 

2 2

3 3

f x x f t    .

Từ đồ thị trên suy ra phương trình

 

f t



có sáu nghiệm phân biệt

t t , (với

1,6i 

và

2t   ;

2 3

2 , 2t t   ;

4 5 6

, , 2t t t  ).

Xét hàm số

 

3t x x x  , ta có:

 

3 3t x x



  ;

 

0 1t x x



    .

Bảng biến thiên của hàm





t x

là:

Dựa vào bảng biến thiên, ta có:

- Phương trình

3x x t 

có một nghiệm (do

2t   ).

- Mỗi phương trình

3x x t 

có ba nghiệm phân biệt (do

2 3

2 , 2t t   ).

- Mỗi phương trình

3x x t 

có một nghiệm (do

4 5 6

, , 2t t t  ).

Vậy phương trình

 

f x x  có 10 nghiệm.

Câu 65. Cho hàm số

 

y f x

liên tục trên  và có đồ thị như hình vẽ.

Có bao nhiêu giá trị nguyên của tham số m để phương trình

 

2 sin

f x f

 



 

 

có đúng 12

nghiệm phân biệt thuộc đoạn

 

 



A. 3. B. 4. C. 2. D.

Lời giải

Chọn C

Ta có bảng biến thiên của hàm số

 

2 siny g x x 

trên đoạn

 

 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 50

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Phương trình

 

2 sin

f x f

 



 

 

có đúng 12 nghiệm phân biệt thuộc đoạn

 

 



khi và chỉ

khi phương trình

 

f t f

 



 

 

có 2 nghiệm phân biệt

 

0;2t 

Dựa vào đồ thị hàm số

 

y f x

suy ra phương trình

 

f t f

 



 

 

có 2 nghiệm phân biệt

 

0;2t 

khi và chỉ khi

16 2

 

  

 

 

0 2

0 4

3 3

2 2

m m



 



 





 

 













Do m nguyên nên

 

1;2m

. Vậy có 2 giá trị của m thoả mãn bài toán.

Câu 66. Cho hàm số

   

3 2

0y f x ax bx cx d a      có đồ thị như hình vẽ. Phương trình

 

0f f x 

có tất cả bao nhiêu nghiệm thực?

A. 5. B. 9. C. 7. D. 3.

Lời giải

Chọn C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 51

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Từ hình vẽ trên ta thấy

 

2; 1

0 0;1

1;2

x a

f x x b

x c



   



   



 



nên phương trình

 

     

2; 1 1

0 0;1 2

1;2 3

f x a

f f x f x b

f x c



   



   



 



Dễ thấy: *) phương trình (1) có 1 nghiệm duy nhất

2x  

*) phương trình (2) có 3 nghiệm phân biệt

*) phương trình (3) có 3 nghiệm phân biệt khác 4 nghiệm đã tìm được ở trên.

Vậy phương trình

 

0f f x 

có tất cả 7 nghiệm phân biệt.

Câu 67. Cho hàm số

 

y f x

có bảng biến thiên như sau

Hỏi có bao nhiêu điểm trên đường tròn lượng giác biểu diễn tập nghiệm của phương

trình

 

cos 2f f x 

. B.

. C.

. D.

Lời giải

Chọn D

Dựa vào bảng biến thiên ta có:

 

cos 1

cos 2

cos 1

f x

f f x

f x

 

 









 









   

1 1

2 2

cos 1 , 1

cos 1

cos 2 , 1

x t t

f x

x t t

  



  



 





Dễ thấy phương trình

 

và

 

đều vô nghiệm.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 52

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

 









   

3 3

4 4

5 5

6 6

cos 3 , 1

cos 4 , 1 0

cos 1

cos 5 , 0 1

cos 6 , 1

x t t

f x

x t t

  



   



 



  



 



Ta thấy phương trình





và





đều vô nghiệm còn phương trình





và





mỗi phương

trình tập nghiệm của nó đều được biểu diễn bởi hai điểm trên đường tròn lượng giác.

Vậy tập nghiệm của phương trình









cos 2

f f x



được biểu diễn bởi bốn điểm trên đường

tròn lượng giác.

Câu 68. Xét tất cả các số thực ,∈

(

0; 1

)

và hàm số đa thức 

(



)

có đồ thị như hình vẽ bên:

Đặt 

(



)

=





(



)



. Số nghiệm thực phân biệt của phương trình 

(



)

.



󰆓

(



)



󰆒

(



)

.



(



)

=

(



)

+ 

󰆒

(



)

là

A. 14. B. 10. C. . D. 17.

Lời giải

Chọn C

Đặt



=

(



)

=

󰆒

(



)

, phương trình đã cho thành .



+ .



=+ ⇔.

(





−1

)

.

(





−1

)

=0 (1)

Dễ thấy

󰇣

=0

=0

thỏa mãn phương trình (1).

Trường hợp

󰇥

≠0

≠0

ta có: .

(





−1

)

+ .

(





−1

)

=0⇔

















=0⇔





















=0 (2)

Mà các hàm số =



, =



đều nghịch biến với ,∈

(

0; 1

)

, do đó











<0,











0, như vậy phương trình (2) vô nghiệm.

Ta có (1) ⇔

󰇣

=0

=0

⇔

󰇩



(



)



󰆒

(



)

.

󰆒





(



)



⇔󰇯



(



)



󰆒

(



)



󰆒





(



)



⇔

󰇯

∈

{

−2,0,2

}

∈

{

,0,1,2

}



∈

(

−2;0

)





(



)

∈

{

,0,1,2

}



∈

(

−2;0

)



Từ đồ thị của hàm số 

(



)

suy ra:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 53

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

+ phương trình 

(



)

= có 1 nghiệm;

+ phương trình 

(



)

=1 có 3 nghiệm;

+ phương trình 

(



)

=2 có 3 nghiệm;

Vậy tổng số nghiệm của phương trình đã cho là 12 nghiệm.

Câu 69. Cho hàm số





4 3

y f x x x

   

có bao nhiêu giá trị nguyên của tham số

để phương trình:













6 5 0

f x m f x m

    

có 6 nghiệm thực phân biệt.

. B.

. C.

. D.

Lời giải

Chọn D

+) Ta có đồ thị hàm số:





4 3

y f x x x

   

như hình vẽ:

+) Đồ thị hàm số





4 3

y f x x x

   

như sau:

+) Ta có:













6 5 0. (1)

f x m f x m     .

 

5 (2)

f x

f x m



 



 



  



 





 



Phương trình

(1)

có 6 nghiệm thực phân biệt thì phương trình

(2)

có 4 nghiệm thực phân

biệt

 

Dựa vào đồ thị hàm số ta có:

1 5 3 4 8

m m

      

Vậy có 3 giá trị nguyên của tham số

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 54

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Câu 70. Cho hàm số , trong đó Biết rằng hàm số

có đồ thị như hình vẽ bên.

Tập nghiệm của phương trình có tất cả bao nhiêu phần tử.

A. . B. . C. . D. .

Lời giải

Chọn A

+) Ta có

4 3 2 3 2

( ) ( ) 4 3 2

y f x mx nx px qx r f x mx nx px q



          

(1)

+) Dựa đồ thị suy ra có 3 nghiệm phân biệt

Do đó

Và

(2)

Từ (1) và (2) ta được

Suy ra

+) phương trình

-9

(*)

+) Xét

(x) 0 1

g x

 







   







Bảng biên thiên





4 3 2

y f x mx nx px qx r

     

, , , ,

m n p q r R







y f x







16 8 4 2

f x m n p q r

    





y f x







' 0

f x



1; 1; 4

x x x

   



(x) 4m(x 1)(x 1)(x 4)



   

(x) 4m(x 1)(x 4)



   

3 2 3 2

(x) 4m(x 4 x 4) 4mx 16 4 16

f x mx mx m



        

3 16

2 4 2

16 16

n m

p m p m

q m q m



 



 





    

 

 

 







 

4 3 2

2 16

f x mx mx mx mx r

    





16 8 4 2

f x m n p q r

    

4 3 2

2 16 16 8 4 2

16 16

2 16 16 8.( )m 4( 2)m 2.16

3 3

mx mx mx mx r m n p q r

mx mx mx mx m m

         

         

4 3 2

16 16

2 16 16 8.( ) 4( 2) 2.16

3 3

x x x x         

4 3 2

16 8

2 16 0

3 3

x x x x

     

4 3 2 3 2

16 8

( ) 2 16 ( ) 4 16 4 16

3 3

g x x x x x g x x x x



         

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 55

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Suy ra (*) có 4 nghiệm phân biệt

Câu 71. Phương trình

   

f x f x

 

có tập nghiệm là





20;18;3

T 

. Phương trình

     

2 1 3 2 2

g x g x g x

   

có tập nghiệm





0;3;15;19

T 

. Hỏi tập nghiệm của phương trình

       

f x g x f x g x

  

có bao nhiêu phần tử?

. B.

. C.

. D.

Lời giải

Chọn C

Điều kiện:





 

0 2

f x

g x

 













Ta có

   





   

   

2 1 20;18;3

2 0

f x

f x f x f x x T

f x f x





       



  





Lại có

     

2 1 3 2 2

g x g x g x

   

       

2 1 3 2 0

g x g x g x g x

      









   









       

2 3

2 1 3 2

2 1

3 2 3 2

g x g x g x g x

g x g x

g x g x g x g x

   

  

 

    

 

 

   

       

2 2

1 1 2

2 1

3 2 3 2

g x g x g x

g x g x

g x g x g x g x

        

     

  

 

    

 

 

   

 

       

1 0

2 1

3 2 3 2

g x

g x g x

g x g x g x g x

 



 

   

 

 

 

 

 

    

 

 













1 0 1 0;3;15;19

g x g x x T       

Do đó, ta có

           

1 1 1 0

f x g x f x g x f x g x

   

       

   





 

f x

g x















ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 56

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông





 

20;18;3

0;3;15;19

x T

 





 









1 2

0;3;15;18;19;20

x T T   

Câu 72. Cho hàm số





y f x ax bx c

   

có đồ thị





(như hình vẽ). Có bao nhiêu giá trị nguyên

của tham số

để phương trình









2 ( ) 3 0

f x m f x m

    

có

nghiệm phân biệt?



. B.



. C.



. D.



Lời giải

Chọn B

* Vẽ đồ thị hàm số





của hàm số





y f x

 : Giữ nguyên phần đồ thị





nằm phía bên

phải trục

, bỏ đi phần đồ thị





bên trái trục

và lấy đối xứng phần đồ thị





phía bên

phải trục

qua trục

* Ta có









2 ( ) 3 0

f x m f x m

    





 

f x

f x m



 





 





* Từ đồ thị





, ta có:

- Phương trình





f x

 

có hai nghiệm là

2, 2

x x

  

- Yêu cầu bài toán



phương trình





f x m

 

có bốn nghiệm phân biệt khác





Đường

thẳng

: 3

d y m

 

cắt đồ thị





tại bốn điểm phân biệt khác

A B



1 3 3

   



0 4

 

. Suy ra





1,2,3

m

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 57

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Câu 73. Cho hàm số





4 3 2

=ax x x x

y f x b c d e

    

trong đó

, , , ,

a b c d e

là các hệ số thực có đồ thị

như hình vẽ sau đây.

Số nghiệm của phương trình

 





   

2 1 0

f f x f x f x

   

là

. B.

. C.

. D.

Lời giải

Chọn B

*) Phân tích: Đây là bài toán tương giao dựa vào đồ thị.

-Phương pháp chung giải bài tập loại này là ta thường biến đổi phương trình đưa về dạng





f x m







m



- Ta thấy vế trái của phương trình có chứa

   





f x f f x

, do đó để biến đổi phương trình

về dạng





f x m



ta cần đặt ẩn phụ

 

t f x



-Ngoài ra ta có thể tìm hàm số





4 3 2

f x ax bx cx dx e

    

có đồ thị như giả thiết.

Sau đây tôi xin trình bày 2 cách.

Cách 1: Biến đổi phương trình.

Điều kiện:





f x



Đặt

 

f x t



. Dựa vào đồ thị và kết hợp điều kiện ta có





0;1

t 

Phương trình trở thành





2 1 0

f t t t

   









2 1 1

f t t t    

Ta có đồ thị hàm số





y f t



và

2 1

y t t

   

như hình vẽ bên dưới.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 58

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Trên đoạn





0;1

đồ thị hàm số





y f t



và đồ thị hàm số





2 1

y g t t t

    

cắt nhau tại

một điểm duy nhất.

Do đó phương trình (1) có duy nhất nghiệm ,





0;1

t m  , với





0;1

m

Hay phương trình tương đương với





f x m



Vậy phương trình đã cho có 4 nghiệm phân biệt.

Cách 2:

Điều kiện:





f x



Đặt

 

f x t



. Dựa vào đồ thị và kết hợp điều kiện ta có





0;1

t 

Phương trình trở thành





2 1 0

f t t t

   









2 1 1

f t t t    

Đồ thị hàm số





4 3 2

f x ax bx cx dx e

    

đi qua điểm













0;0 , 1;1 , 1;1



nên

 

0 0

1 1 2

1 0

e e

a b c d a c

a b c d b d

 

 

 

      

 

 

     

 

Ta có





3 2

4 3 2

f x ax bx cx d



   

và hàm số đạt cực trị tại

 

nên

 

4 3 2 0 3 0

4 3 2 0 4 2 0

a b c d b d

a b c d a c

     

 



 

      

 

Giải hệ (2) và (3) ta có

1; 0; 2; 0; 0

a b c d e

     

Do đó





4 2

f x x x

  





4 2 2

1 2 2 1

t t t t

      





0;1

t 

4 2

3 2 1 0

t t t

     

Xét hàm số









4 2

3 2 1, 0;1

h t t t t t      

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 59

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Có





4 6 2

h t t t



   

 

1 3

h t t













   



 





Lập bảng xét dấu của





h t

Hàm số đồng biến trên





0;1

t 

nên phương trình

4 2

3 2 1 0

t t t

    

có duy nhất nghiệm.

Sử dụng MTCT ta có nghiệm

0.336



hay

   

0.336 0.11

f x f x  

Do đó phương trình đã cho có 4 nghiệm phân biệt.

Lưu ý: Việc tìm ra nghiệm thuộc





0;1

của phương trình





h t



có thể dùng MTCT với chức

năng MODE 7.

Câu 74. Cho hàm số 

(



)

có đạo hàm trên ℝ\

{



}

và hàm số 

(



)

có đạo hàm trên ℝ. Biết đồ thị của

hai hàm số =′

(



)

và =′

(



)

như hình vẽ dưới. Đặt ℎ

(



)

=

(



)

−

(



)

và =−

[

ℎ

(

+ 

)]



ℎ

(

+ 



)



1 + 2ℎ

(



)



−

[

ℎ

(



)]



với ,, là các số thực đã biết. Khẳng định đúng với mọi ≠0 là?

A. ∈

[

ℎ

(



)

;ℎ

(

+

)]

.. B. ≤ℎ

(



)

C. ∈

[

ℎ

(



)

;ℎ

(

+

)]

. D. ∈

[

ℎ

(



)

;ℎ

(



)]

Lời giải

Chọn B

Từ đồ thị đã cho ta suy ra ℎ′

(



)

=′

(



)

−′

(



)

, ℎ′

(



)

=0⇔′

(



)

=′

(



)

⇔

󰇣

=

=

Lập bảng biến thiên ta có

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 60

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Lại có =−

[

ℎ

(

+

)]



+ ℎ

(

+ 



)



1 + 2ℎ

(



)



−

[

ℎ

(



)]



⇒=−

[

ℎ

(

+ 

)

−ℎ

(



)]



+ ℎ

(

+



)

≤ℎ

(





+ 

)

v × −

[

ℎ

(

+ 

)

−ℎ

(



)]



≤0,∀

≠

Từ bảng biến thiên suy ra max

(

;

)

ℎ

(



)

=ℎ

(



)

Vì: 



+ >,∀≠0 nên ta có ℎ

(





+ 

)

≤h

(



)

,∀≠0.

Vậy ≤ℎ

(



)

,∀≠0.

Câu 75. Cho hàm số





y f x



, hàm số





y f x





liên tục trên



và có đồ thị như hình vẽ

Bất phương trình





f x m x x

  

(

là tham số thực) nghiệm đúng với mọi





2;0

x 

khi

và chỉ khi





m f

. B.





2 10

m f

  

. C.





2 10

m f

  

. D.





m f

Lời giải

Chọn D

Dựa vào đồ thị hàm số





y f x





suy ra









1, 2;0

f x x



    

Ta có

















3 3

, 2;0 , 2;0

f x m x x x f x x x m x            

(1)

Đặt









g x f x x x

  

. Khi đó













3 1 0, 2;0

g x f x x x

 

      

Bảng biến thiên

Vậy













, 2;0 0

g x m x m f    

Câu 76. Cho các số thực ,,<0 và hàm số 

(



)

có bảng biến thiên như sau:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 61

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Phương trình 











(



)



+ 

(



)





(



)



=

(

)

có số nghiệm là.

A. 3. B. 1. C. 4. D. 2.

Lời giải

Chọn A

Đặt: =





(



)

(

≥0

)

phương trình trở thành 

(



(



)

+ 



+ 

)

=

(

)

(∗).

Từ bảng biến thiên ta thấy trên trên nửa khoảng

[

0;+∞

)

hàm số 

(



)

đồng biến do đó (∗)⇔



(



)

+ 



+ =1⇔

(



)

+ 



+ −1=0(1).

Xét hàm số 

(



)

=

(



)

+ 



+ −1 trên nửa khoảng

[

0;+∞

)

có ′

(



)

=′

(



)

+ 2+1>

0,∀>0.

Mặt khác:





(

)

=−1<0



(

)

=

(

)

+ 1>0

⇒

(

)

.

(

)

<0⇒ pt (1) có nghiệm duy nhất =



∈

(

0;1

)

Vậy





(



)

=



⇔

(



)

=





∈

(

0;1

)

. Phương trình này có 3 nghiệm vì đường thẳng

=





∈

(

0;1

)

cắt đồ thị hàm số 

(



)

tại 3 điểm phân biệt.

Câu 77. Cho hàm số





y f x



và hàm số





y g x



có đạo hàm xác định trên



và có đồ thị như hình

vẽ dưới đây:

Có bao nhiêu giá trị nguyên của tham số m để phương trình





 

f x

g x



có nghiệm thuộc





2;3



A. 4. B. 5. C. 7. D. 6.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 62

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Lời giải

Chọn D

Xét hàm số

 





 

f x

h x

g x



. Dựa vào đồ thị, ta thấy các hàm số





f x

và





g x

liên tục và nhận

giá trị dương trên





2;3



, do đó





h x

liên tục và nhận giá trị dương trên





2;3



Ngoài ra với





2;3

x 

, dễ thấy





f x







g x



nên

 





 

f x

h x

g x

 

, mà

 





 

0 6

0 1

  

nên

 





2;3

max 6

h x





(1).

Lại có





h x



với mọi





2;3

x 

và





2 1

 

nên

 





2;3

0 min 1

h x



 

(2).

Phương trình





 

f x

g x



có nghiệm trên





2;3



khi và chỉ khi

 





 





2;3

min max

h x m h x



 

(3).

Từ









và





, kết hợp với m





, ta có





1;2;3;4;5;6

m

Câu 78. Cho hàm số bậc ba





y f x



có đồ thị trong hình dưới đây. Số nghiệm thực của phương trình









2 2 2

2 1 9 1 10 0

f x f x

    

là

. B.

. C.

. D.

Lời giải

Chọn C

Đặt

1, 1

t x t

   

. Ta được phương trình sau:









2 9 10 0

f t f t

  





 

f t

























 

   

 

, 3

, 1 0

2 1

1 0

t a t l

t l

t b b

t c c a l

t d d l

t e e b



  



 



   









   



    



    



Suy ra:

1 1

x b x b

x e



    





 

  





Vậy phương trình có 4 nghiệm phân biệt.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 63

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Câu 79. Cho hàm số

 

y f x

có đồ thị như hình vẽ

Số nghiệm của phương trình

 

3 2

3 2 1 0f x x    là

A. 9. B. 10. C. 11. D. 12 .

Lời giải

Chọn C

Từ đồ thị hàm số

 

y f x

suy ra đồ thị hàm số

 

y f x như sau:

   

3 2 3 2

3 2 1 0 3 2 1f x x f x x        (1)

Đặt

3 2

3 2x x t   . Dựa vào đồ thị hàm số

 

y f x , phương trình

 

1f t  có 5 nghiệm

phân biệt là:

1 2 3 4 5

, , , , t t t t t

với

1 2 3 4 5

1 3

1 0 , , 2< 3

2 2

t t t t t       

Xét hàm số

 

3 2

3 2g x x x  





3 6

g x x x

  

 

g x





  







Bảng biến thiên

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 64

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Khi đó, số nghiệm của các phương trình

3 2 3 2 3 2 3 2 3 2

1 2 3 4 5

3 2 , 3 2 , 3 2 , 3 2 , 3 2x x t x x t x x t x x t x x t              

lần lượt

bằng 3, 3, 3, 1, 1.

Vậy tổng số nghiệm của phương trình (1) bằng 11.

Câu 80. Cho hàm số 

(



)

có đạo hàm liên tục trên

[

−3;3

]

và hàm số =′

(



)

có đồ thị như hình vẽ

bên. Biết 

(

)

=6 và 

(



)

=

(



)

−

(



)





Mệnh đề nào sau đây đúng?

A. Phương trình 

(



)

=0 có đúng hai nghiệm thuộc

[

−3;3

]

B. Phương trình 

(



)

=0 có đúng một nghiệm thuộc

[

−3;3

]

C. Phương trình 

(



)

=0 không có nghiệm thuộc

[

−3;3

]

D. Phương trình 

(



)

=0 có đúng ba nghiệm thuộc

[

−3;3

]

Lời giải

Chọn B

Ta có: ()=() −

()





⇒

󰆒

()=

󰆒

() −(+ 1).

Vẽ đường thẳng =+ 1 trên cùng một hệ trục tọa độ với đồ thị hàm số =

󰆒

() (như hình

vẽ bên).

Từ đồ thị ta thấy: 

󰆒

()=

󰆒

() −(+ 1)>0, ∀∈(−3;1) (do đường cong nằm phía trên

đường thẳng), 

󰆒

()=

󰆒

() −(+1)<0, ∀∈(1;3) (do đường cong nằm phía dưới

đường thẳng).

Ta có: (1)=(1) −

()





=6 −2=4.

Bảng biến thiên:



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 65

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Dựa vào đồ thị ta thấy: diện tích 



lớn hơn 4 (trong phần bên trái có nhiều hơn 4 ô, mỗi ô có

diện tích bằng 1), do đó:

4<



∫



󰆒





()d ⇔4<()





⇔4<(1) −(−3) ⇔(−3)<0.

Mặt khác diện tích 



nhỏ hơn 4 (trong phần bên phải có ít hơn 4 ô), do đó:

4>



=−

∫



󰆒





()d ⇔4>−()





⇔4>(1) −(3) ⇔(3)>0.

Vậy phương trình ()=0 có đúng một nghiệm thuộc đoạn [−3;3] (nghiệm này nằm trong

khoảng (−3;1)).

Câu 81. Cho hàm số bậc bốn

 

y f x

có đồ thị như hình vẽ.

Gọi

 

và

 

lần lượt là đồ thị của hàm số

     

.y f x f x f x

 

   

 

và

2020

y 

. Số

giao điểm của





và





là

A. 4. B. 0. C. 1. D. 2.

Lời giải

Chọn B

Giả sử:





4 3 2

y f x ax bx cx dx e

     

với 0a  .

Từ đồ thị hàm số ta thấy phương trình

 

0f x 

có 4 nghiệm phân biệt nên ta có:





















1 2 3 4

f x a x x x x x x x x

    

với

là 4 nghiệm của phương trình

 

0f x 

Suy ra:

             

1 2 3 1 2 4 1 3 4

f x a x x x x x x x x x x x x x x x x x x



            



   

2 3 4

x x x x x x    



Do đó:

 

1 2 3 4

1 1 1 1

f x

f x x x x x x x x x



   

   

 

     

 

       

2 2 2 2 2

1 2 3 4

1 1 1 1

f x f x f x

f x

x x x x x x x x

f x



 

 

       

 

   

 

 

1 2 3 4

\ ; ; ;x x x x x  



−



′

(



)

−



(



)

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 66

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Dễ thấy tại các điểm





1 2 3 4

; ; ;

x x x x

thì

     

. 0

i i i

y f x f x f x

 

  

 

 





1,4

i 

và

2020 0



Nên:

     





. 2020

f x f x f x

 

 

vô nghiệm trên



Vậy





và





không có điểm chung.

Câu 82. Cho hàm số:

3 2

( ) 6 9

  

f x x x x

. Đặt

( ) ( ( ))

k k

f x f f x



 (với k là số tự nhiên lớn hơn 1).

Tính số nghiệm của phương trình

( ) 0

f x



729

. B.

365

. C.

730

. D.

364

Lời giải

Chọn B

Có:

 

3 2

6 9 0





    







f x x x x

( ) 0

( ) 0 ( ( )) 0

( ) 3

k k

f x

f x f f x

f x







   







Mà

( ) 3

f x



có 3 nghiệm phân biệt đều thuộc khoảng

(0;4)

( )

f x a



với a thuộc

(0;4)

cũng

có 3 nghiệm phân biệt.

Đặt

là số nghiệm của phương trình

( ) 0

f x



. Có



Đặt

là số nghiệm của phương trình

( ) 3

f x



. Có:

1 2

3; 9;...; 3

v v v

  

Ta có:

2 1 2 1

1 1

3 1

2 3 3 ... 3 1 1 3 3 ... 3

 



             

k k

k k k

u u v

Vậy

3 1

365



  .

Bấm Tải xuống để xem toàn bộ.

| 1/66

| | Tải xuống

Preview text:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
TÌM SỐ NGHIỆM CỦA PHƯƠNG TRÌNH HÀM HỢP
I. KIẾN THỨC CẦN NHỚ:
 f x   m là phương trình hoành độ giao điểm của hai đồ thị y  f x , y  m. Số nghiệm của phương
trình bằng số giao điểm của hai đồ thị y  f x, y  m.
 f x  g x là phương trình hoành độ giao điểm của hai đồ thị y  f x, y  g x. Số nghiệm của
phương trình bằng số giao điểm của hai đồ thị y  f x, y  g x.
II. CÁC DẠNG BÀI TẬP TƯƠNG TỰ
 Sử dụng BBT hoặc đồ thị của hàm số f  x để tìm số nghiệm thuộc đoạn a ;b của phương trình .
c f  g  x  d  m , với g(x) là hàm số lượng giác.
 Sử dụng BBT hoặc đồ thị của hàm số f  x để tìm số nghiệm thuộc đoạn a ;b của phương trình .
c f  g  x  d  m , với g(x) là hàm số căn thức, đa thức, …
 Sử dụng BBT hoặc đồ thị của hàm số f  x để tìm số nghiệm thuộc đoạn a ;b của phương trình .
c f  g  x  d  m , với g(x) là hàm số mũ, hàm số logarit.
 Sử dụng BBT hoặc đồ thị của hàm số f  x để tìm số nghiệm thuộc đoạn a ;b của phương trình .
c f  g  x  d  m , với g(x) là hàm số chứa dấu giá trị tuyệt đối.
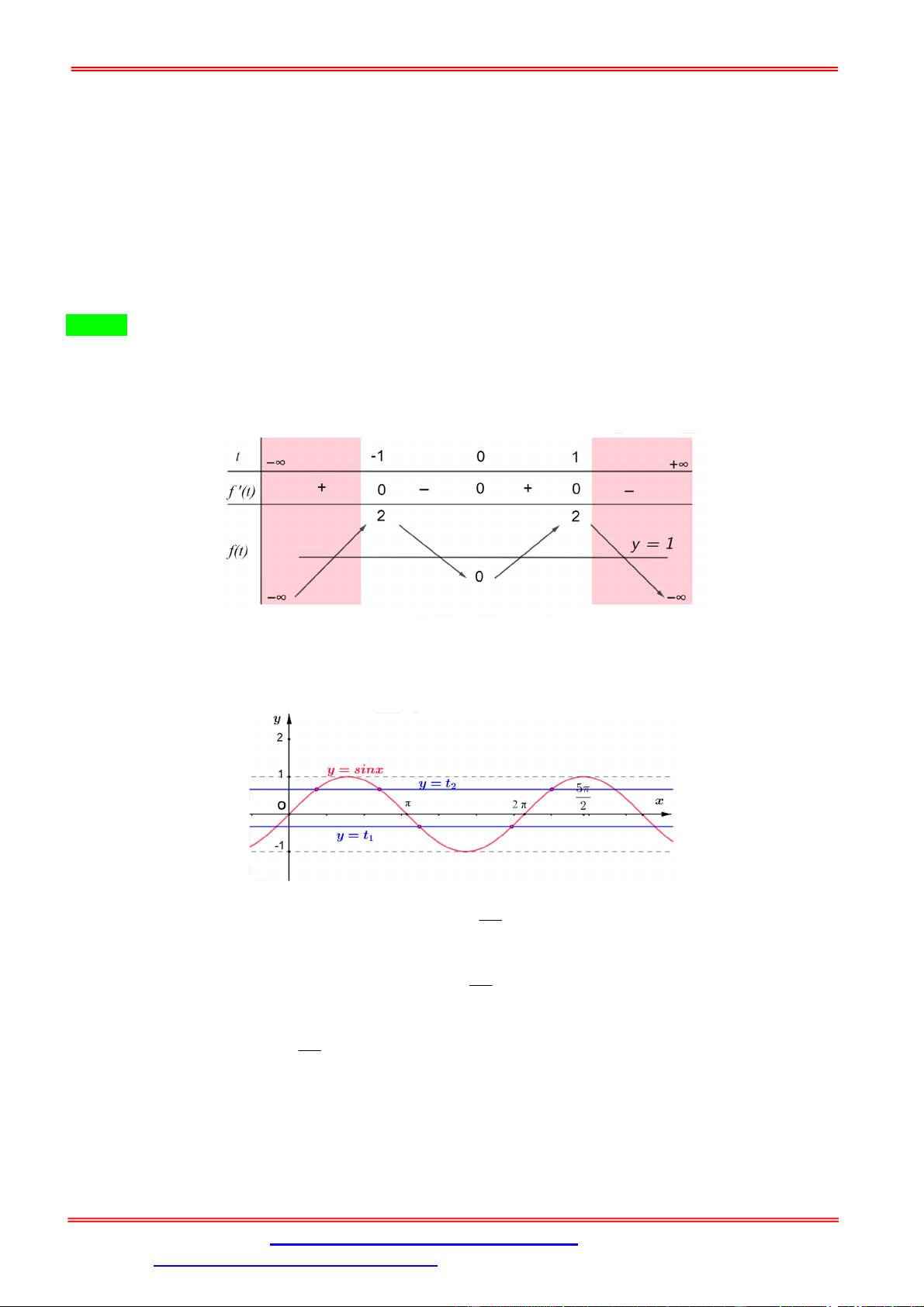
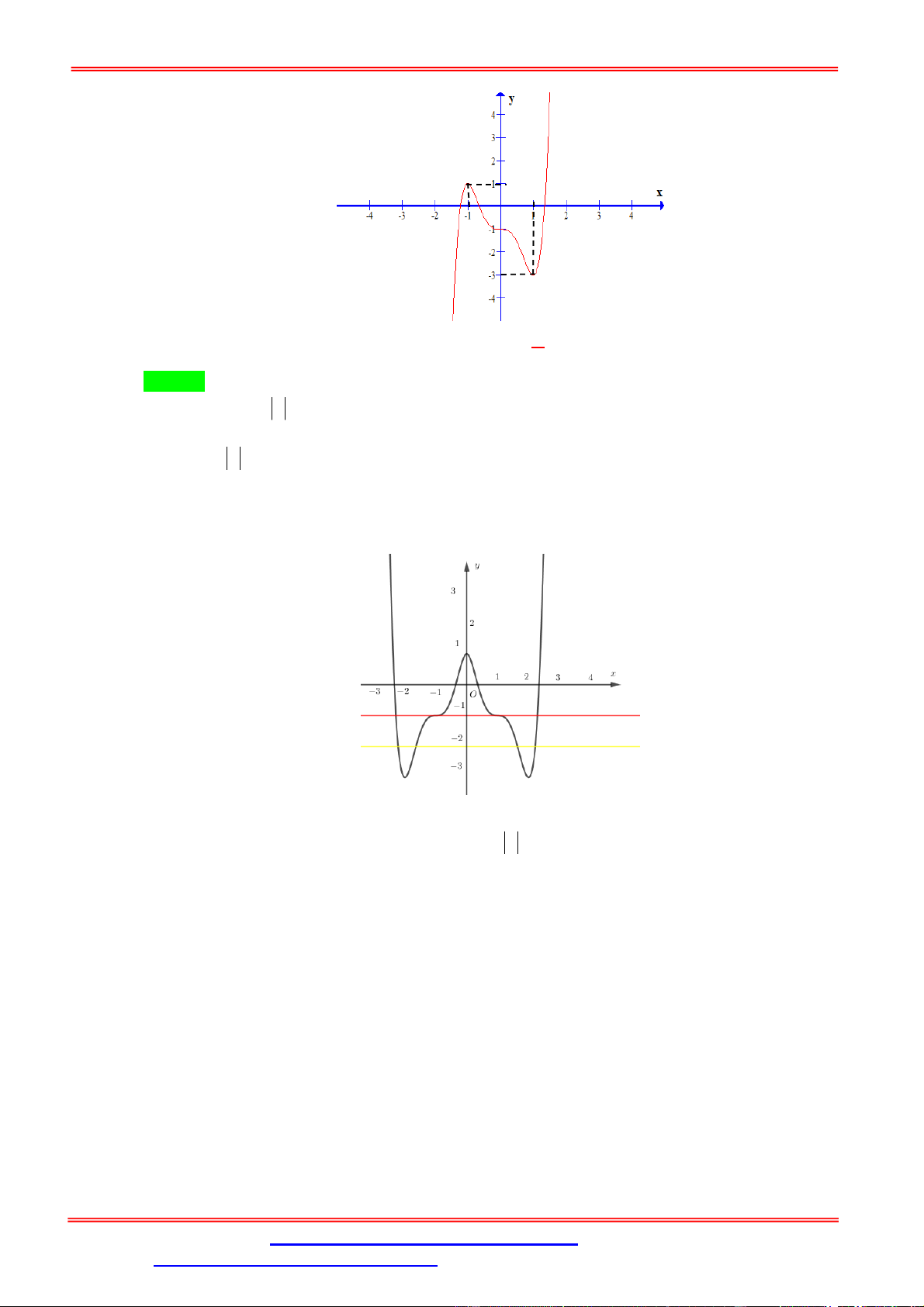
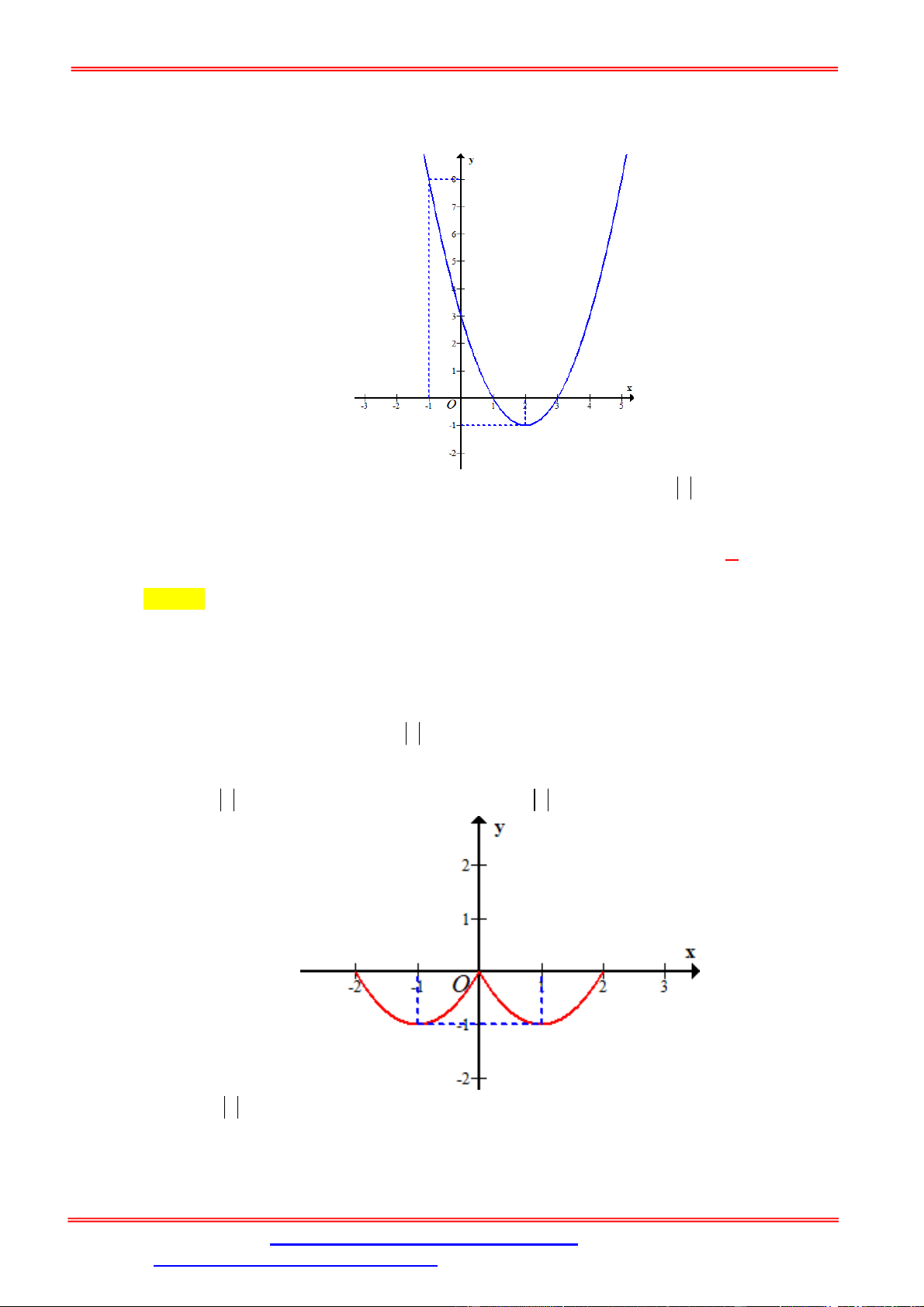
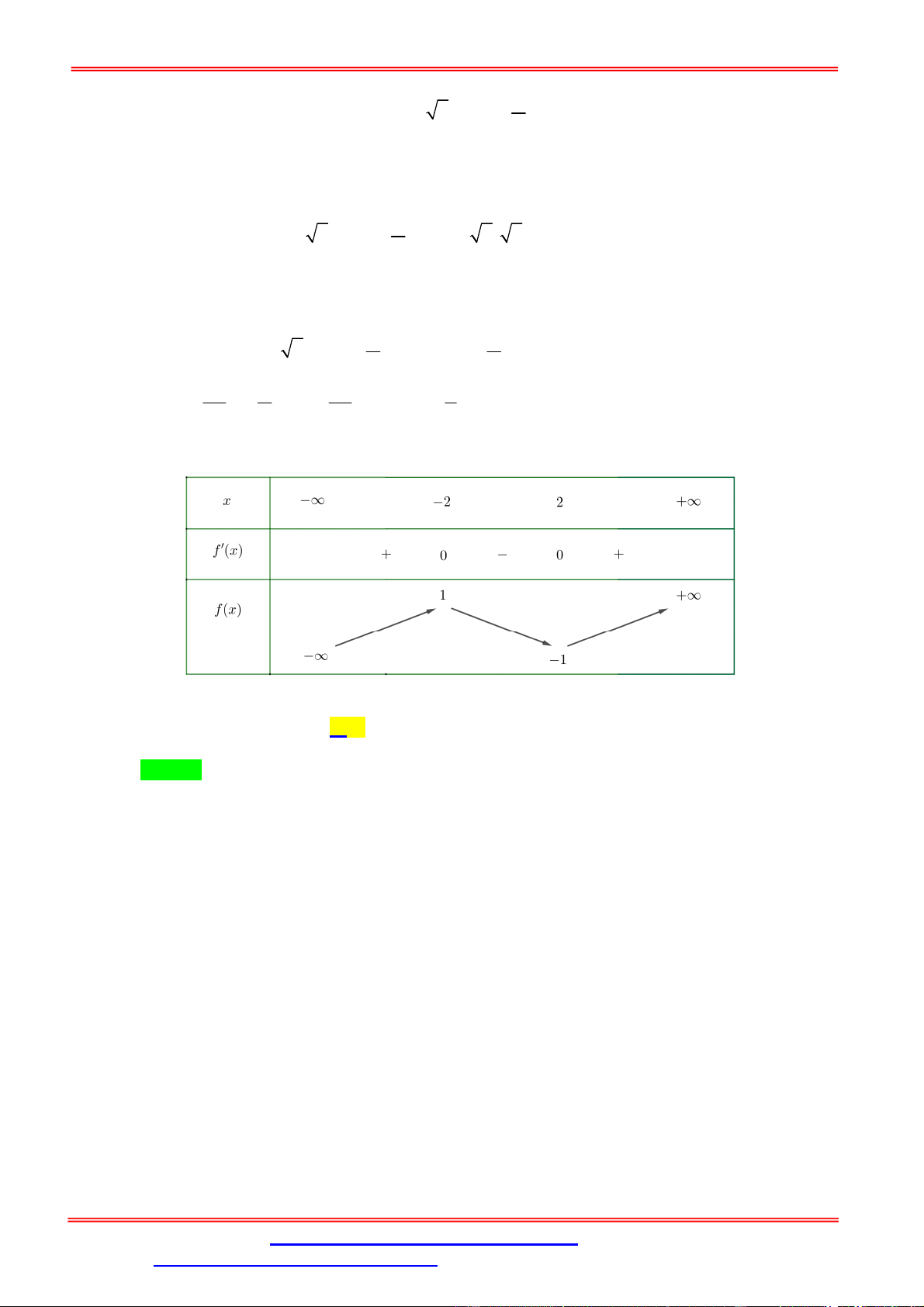
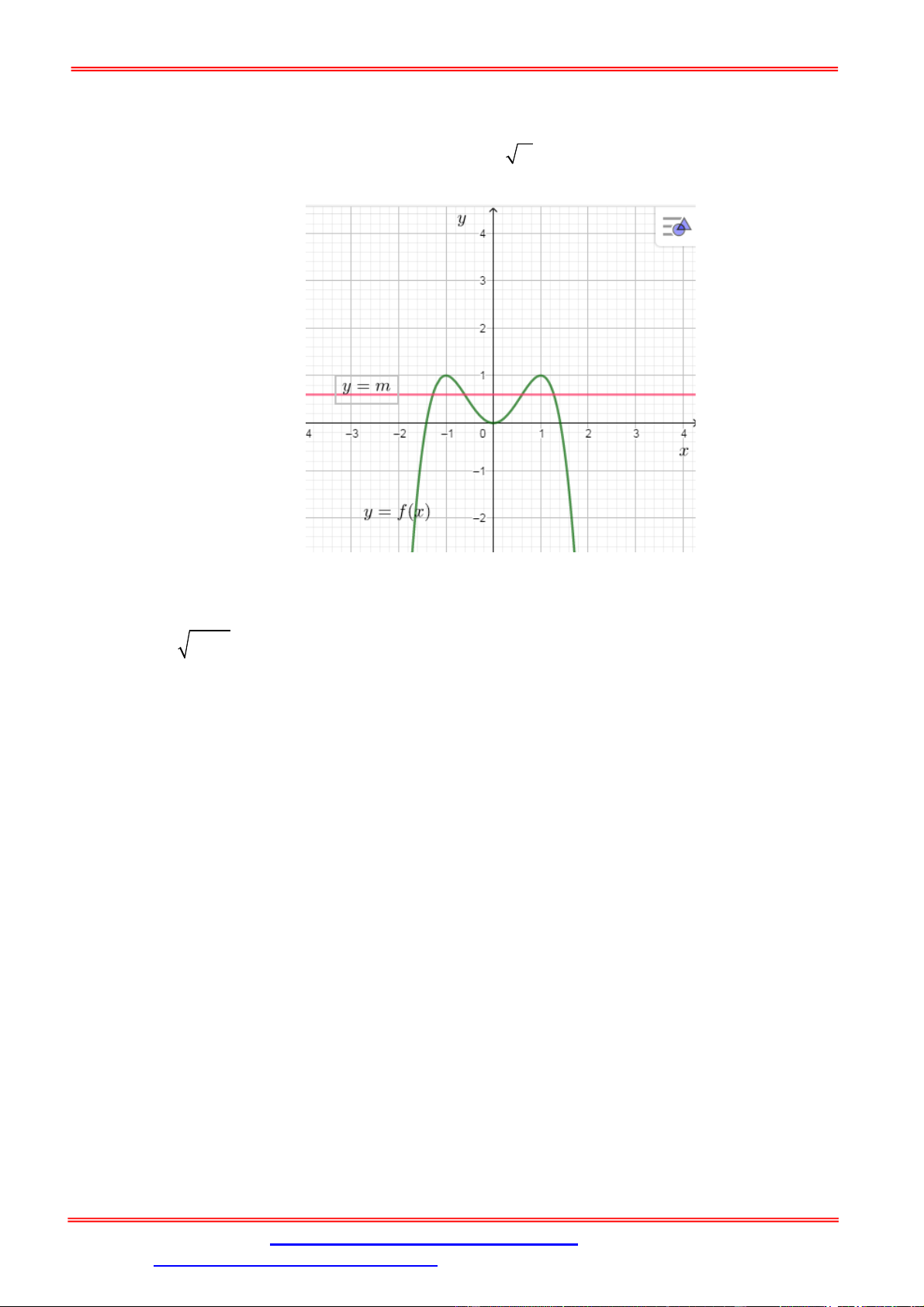
(ĐỀ MINH HỌA LẦN 2 - BDG 2019 - 2020) Cho hàm số f  x có bảng biến thiên như sau:  5 
Số nghiệm thuộc đoạn 0; 
của phương trình f sin x  1 là 2    A. 7 . B. 4 . C. 5 . D. 6 . Phân tích:
1. DẠNG TOÁN: Đây là dạng toán sử dụng BBT hoặc đồ thị của hàm số f  x để tìm số nghiệm thuộc
đoạn a ;b của PT .
c f  g  x  d  m .
2. KIẾN THỨC CẦN NHỚ:
Số nghiệm thuộc đoạn a;b của PT f t   k là số giao diểm của đồ thị y  f t  và đường thẳng
y  k với t a;b ( k là tham số). 3. HƯỚNG GIẢI:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
B1: Đặt ẩn phụ t  g  x  . Với x a ;b  t a;b   . B2: Với .
c f  g  x  d  m  f t   k .
B3: Từ BBT của hàm số y  f  x suy ra BBT của hàm số y  f t  để giải bài toán số nghiệm thuộc
đoạn a;b của phương trình f t   k .
Từ đó, ta có thể giải bài toán cụ thể như sau: Lời giải Chọn C
Đặt t  sin x, t  1  ; 
1 thì PT f sin x  1  
1 trở thành f t   1 2 .
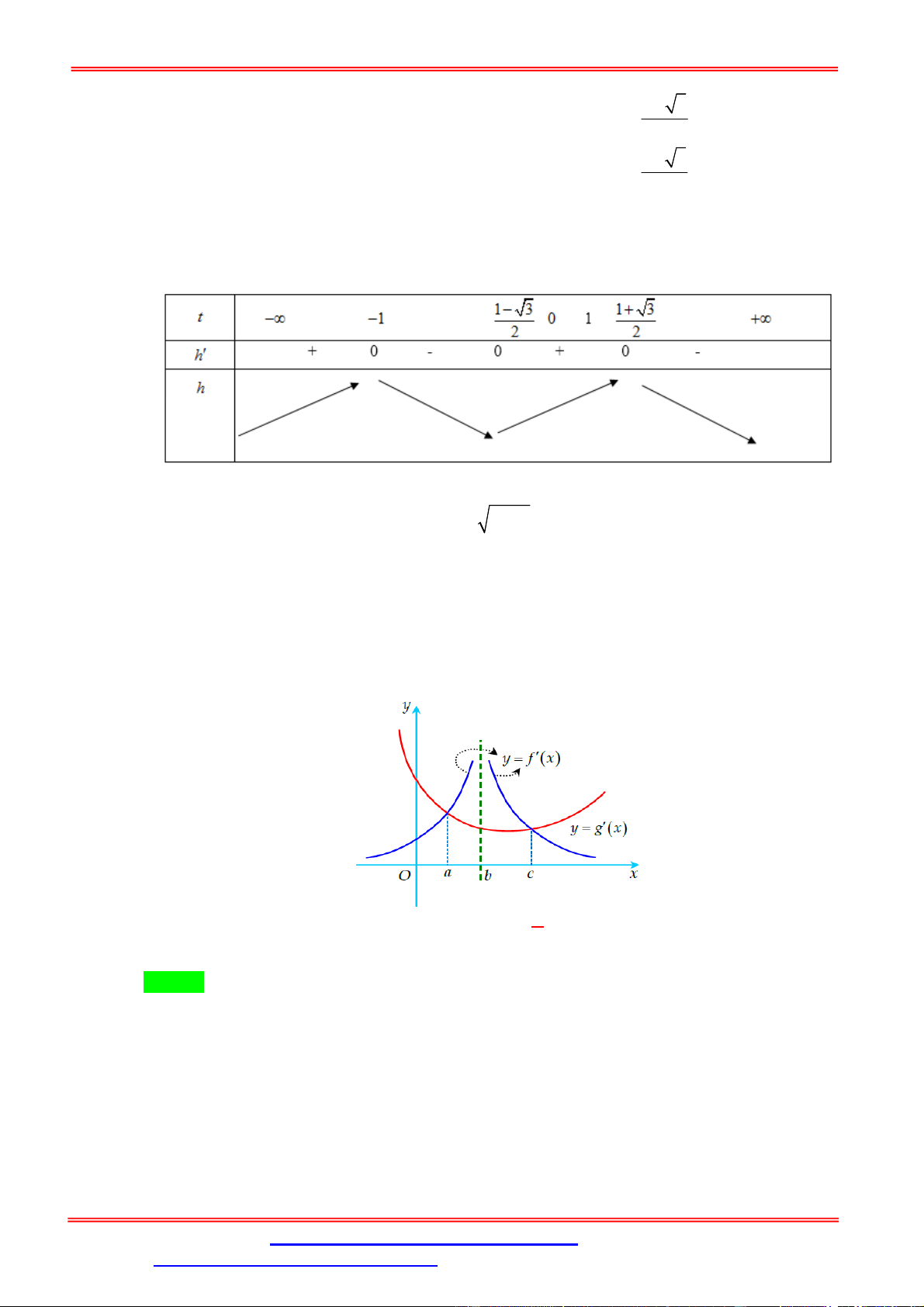
BBT hàm số y  f t , t 1;  1 :
Dựa vào BBT ta có số nghiệm t 1;  1 của PT  
1 là 2 nghiệm phân biệt t  1;0 , t  0;1 . 1   2  
Quan sát đồ thị y  sin x và hai đường thẳng y  t với t  1; 0 và y  t với t  0;1 . 2   1   1 2  5 
+ Với t  1; 0 thì PT sin x  t có 2 nghiệm x  0; . 1   1  2     5 
+ Với t  0;1 thì PT sin x  t có 3 nghiệm x  0; . 2   2  2     5 
Vậy số nghiệm thuộc đoạn 0; 
của phương trình f sin x  1 là 2  3  5 nghiệm. 2   
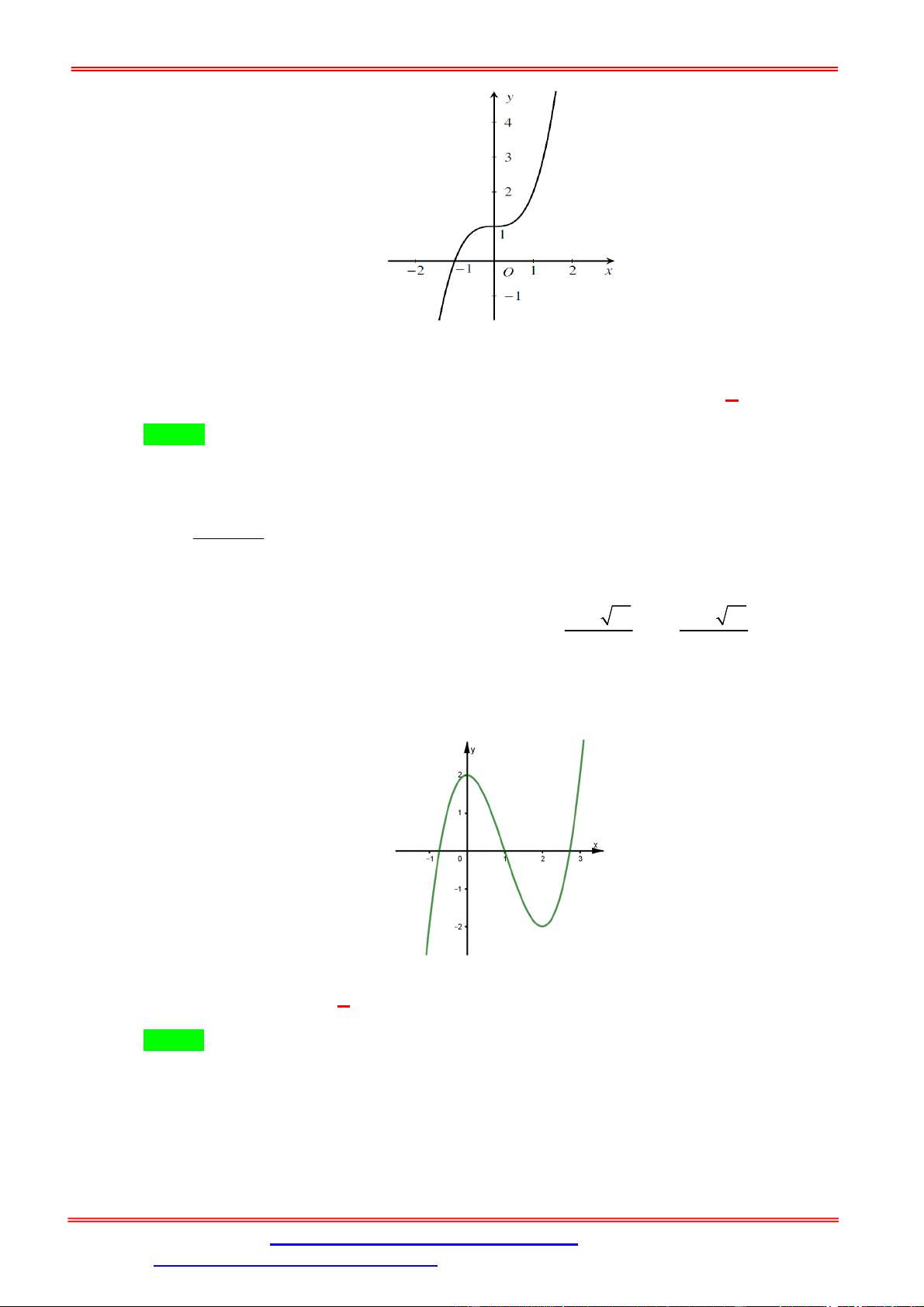
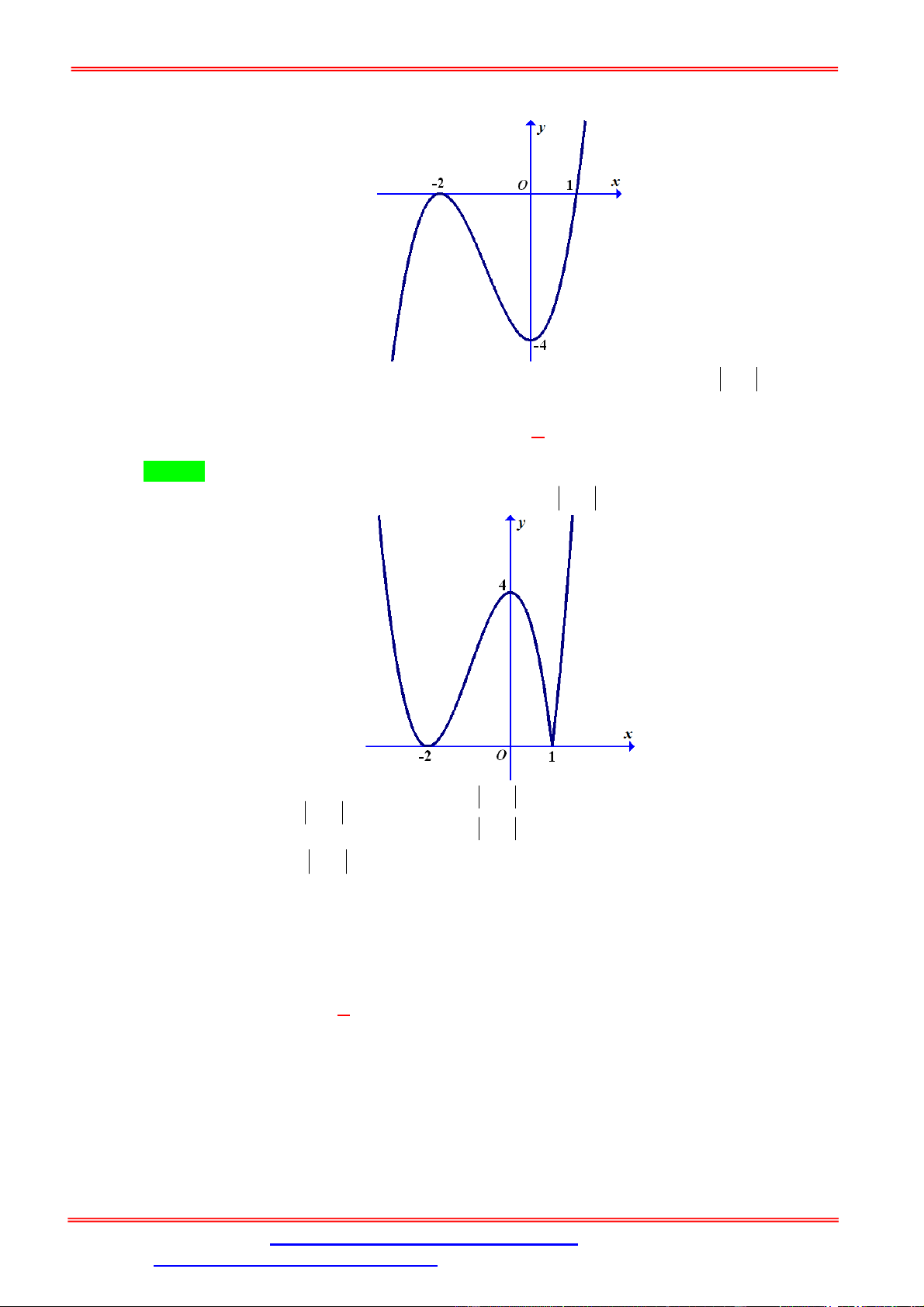
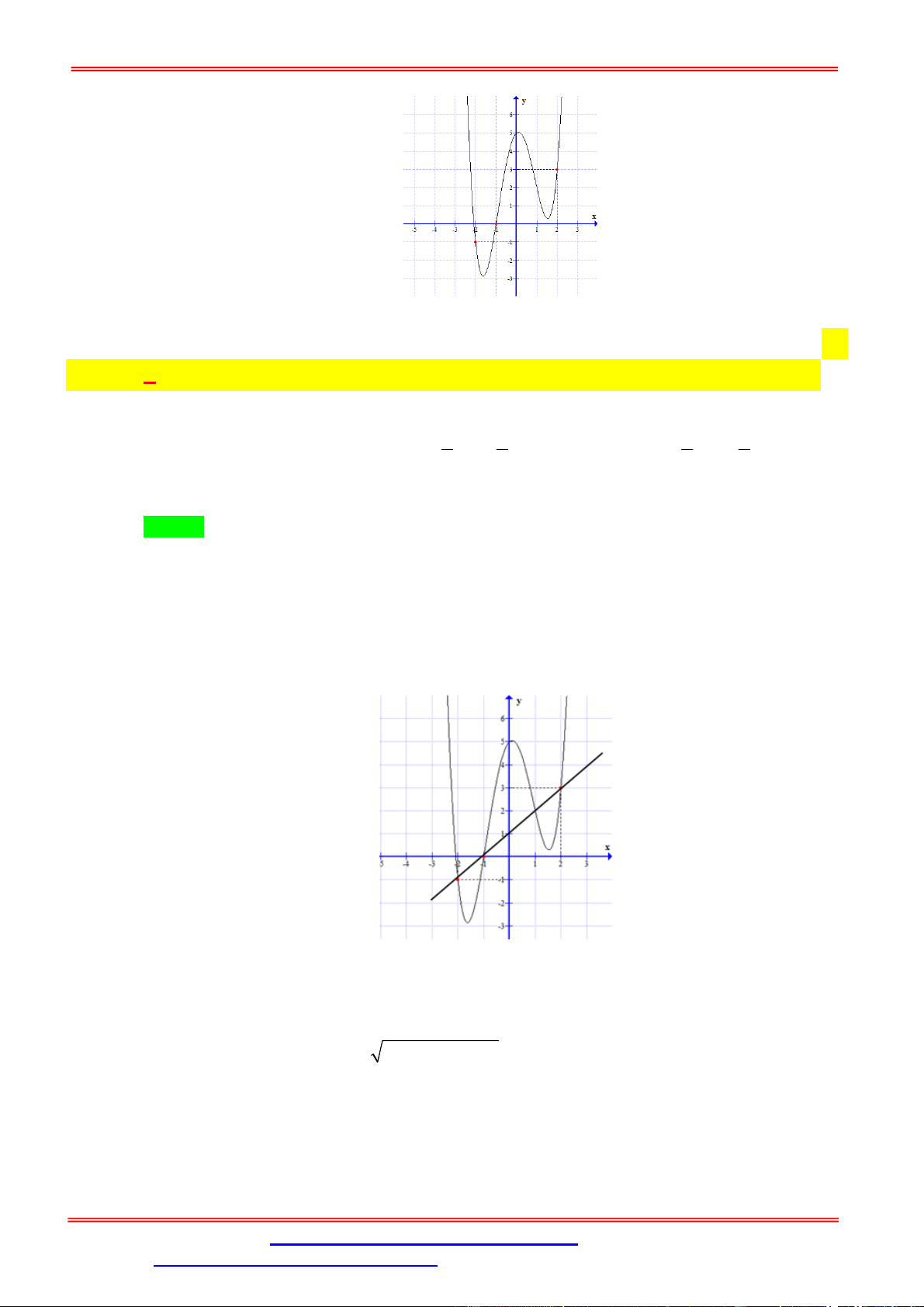
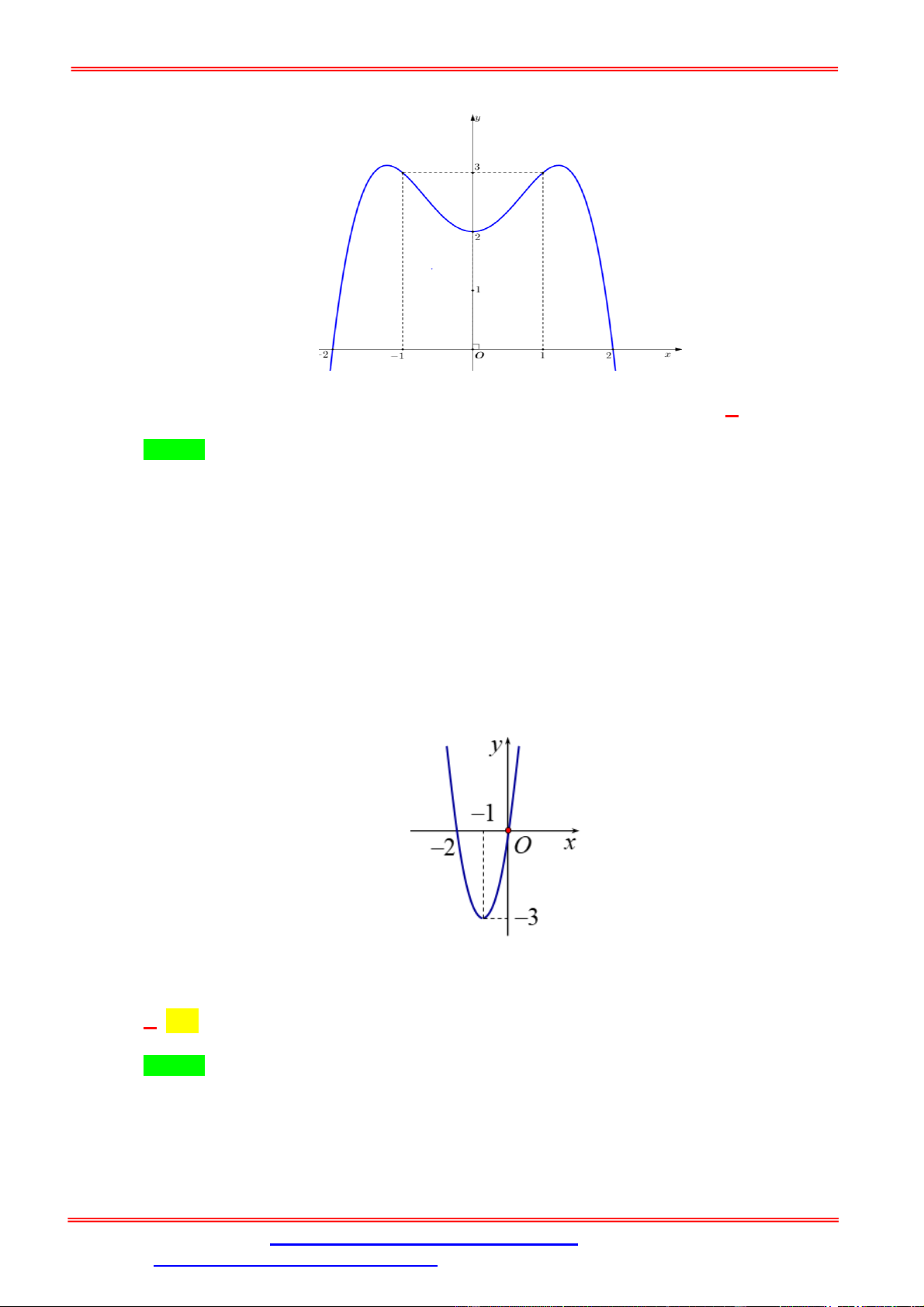
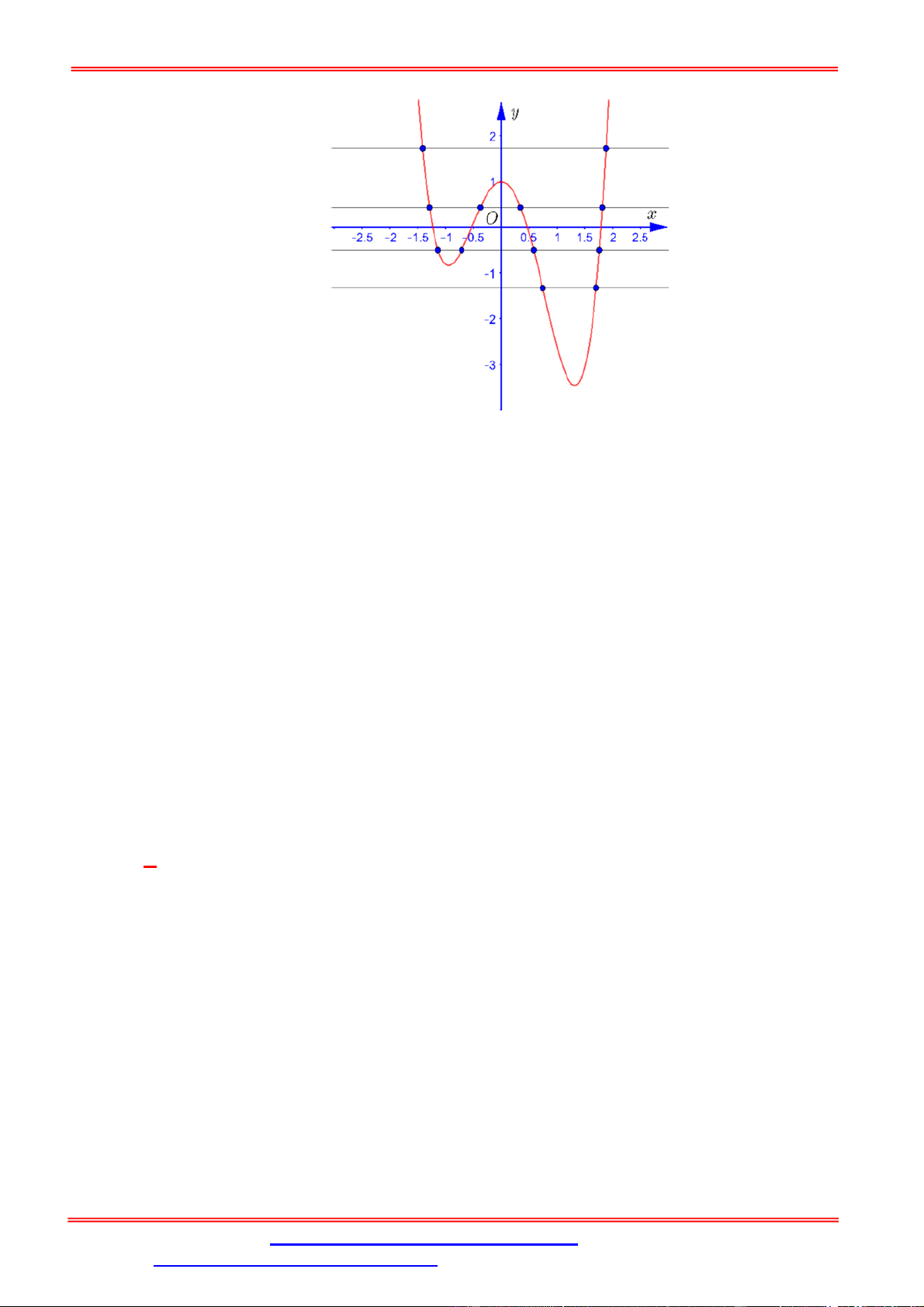
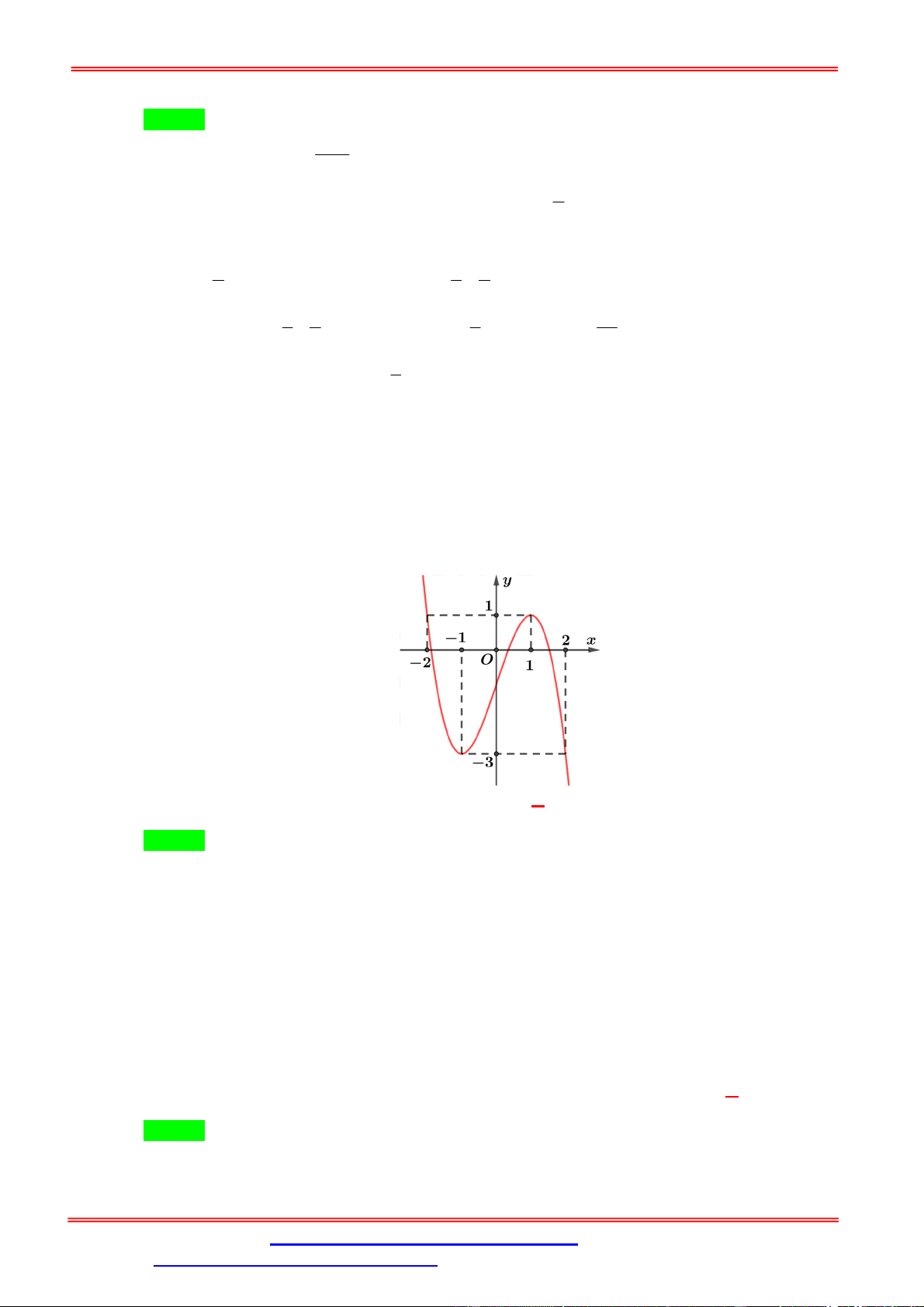
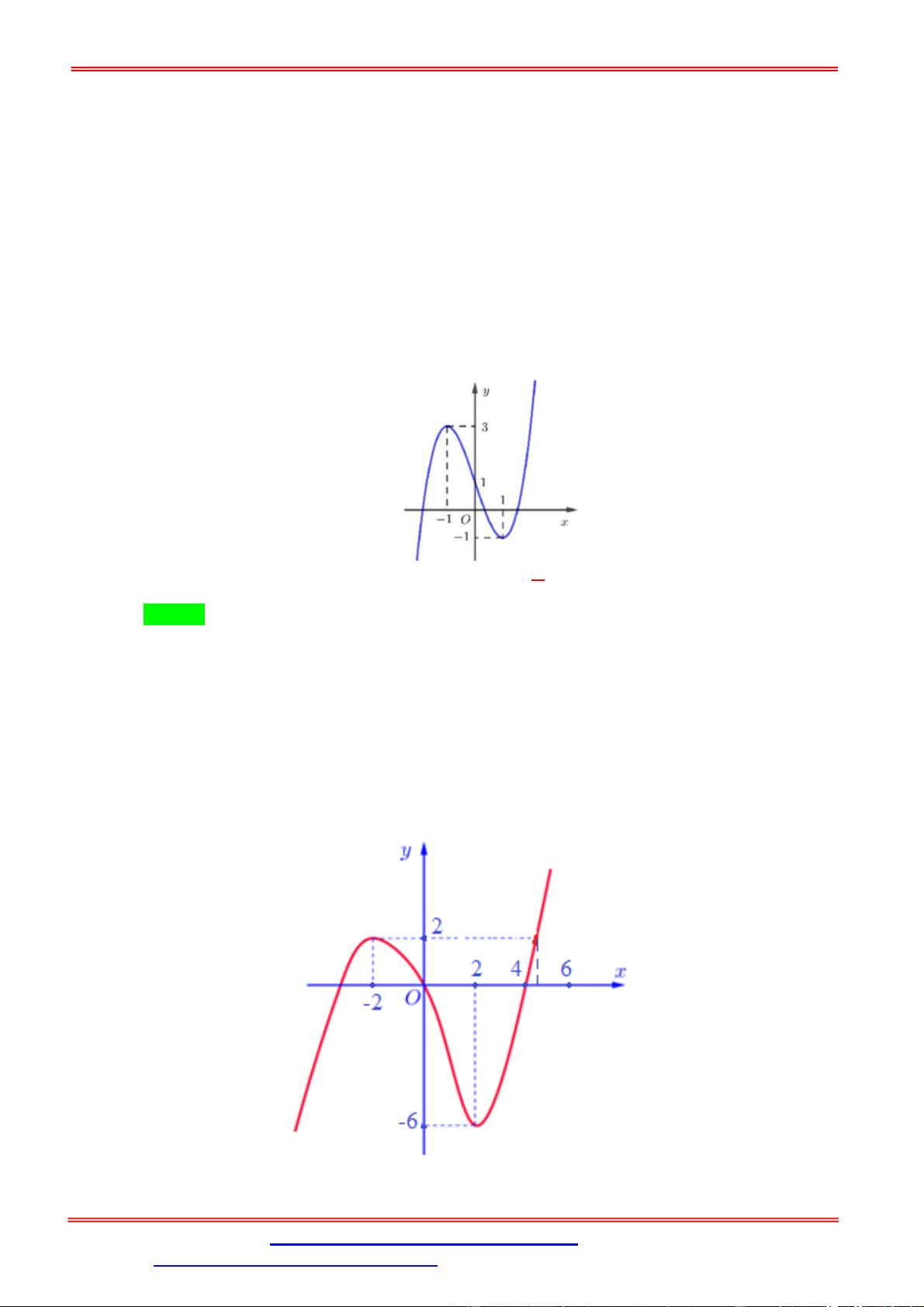
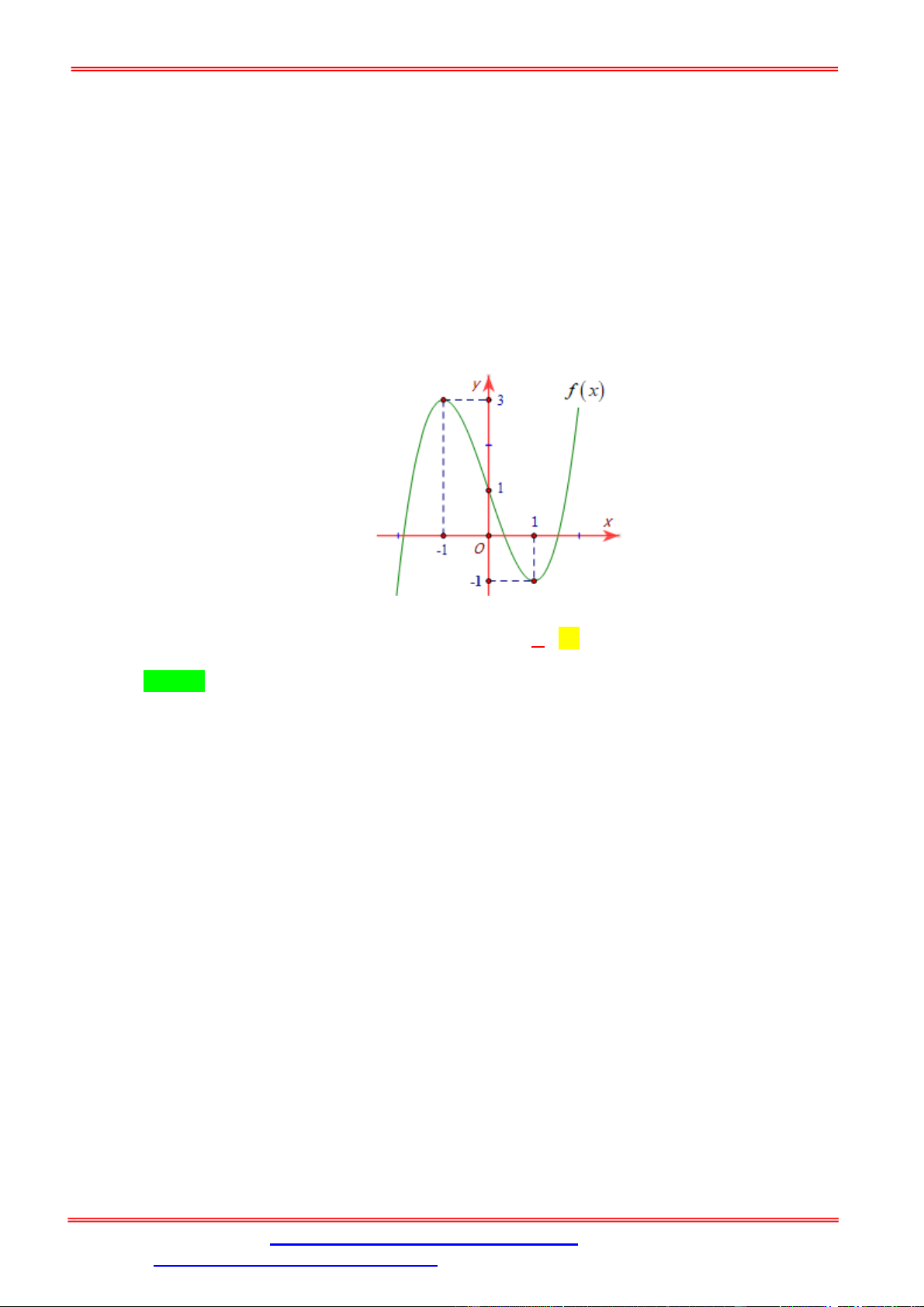
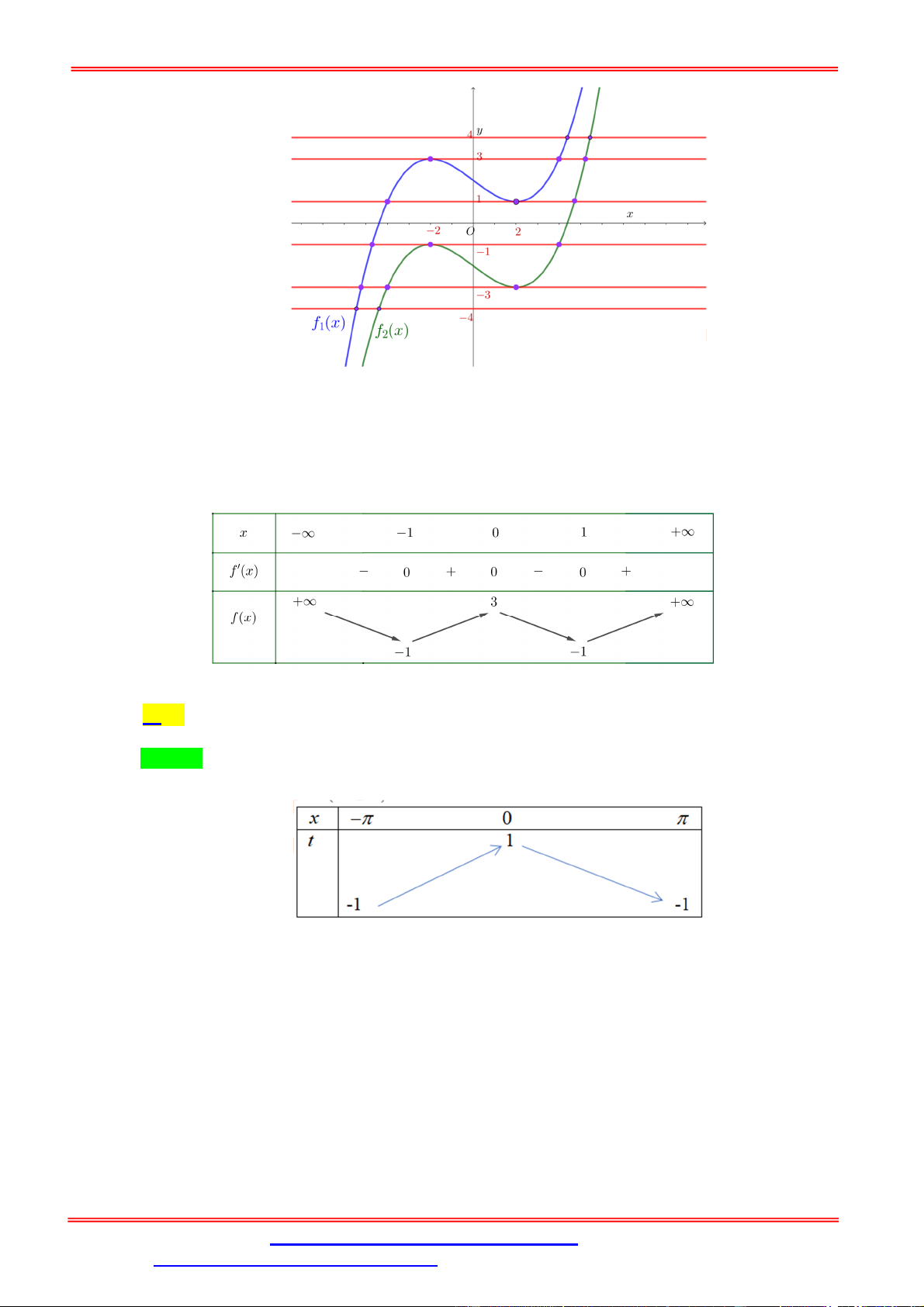
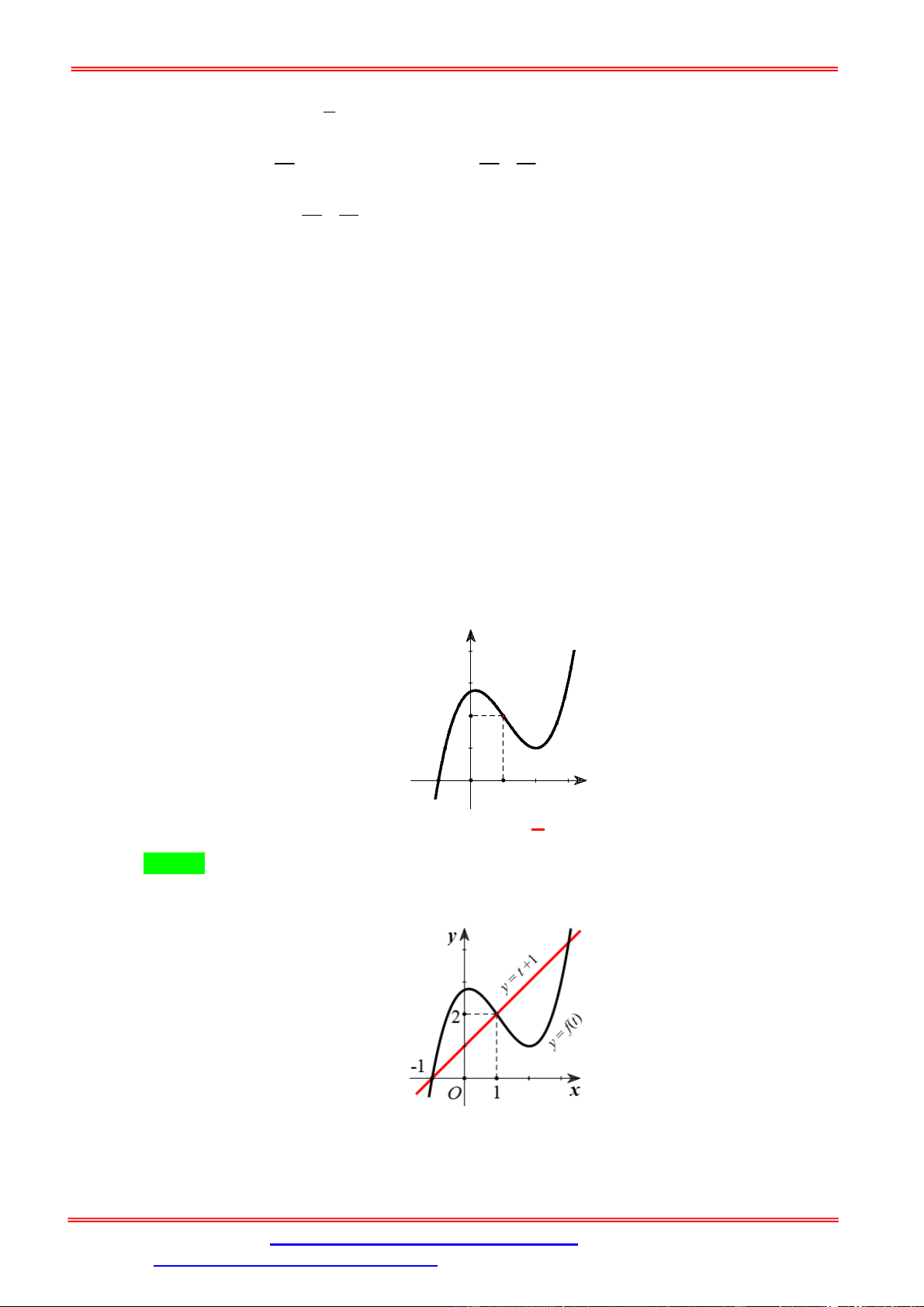
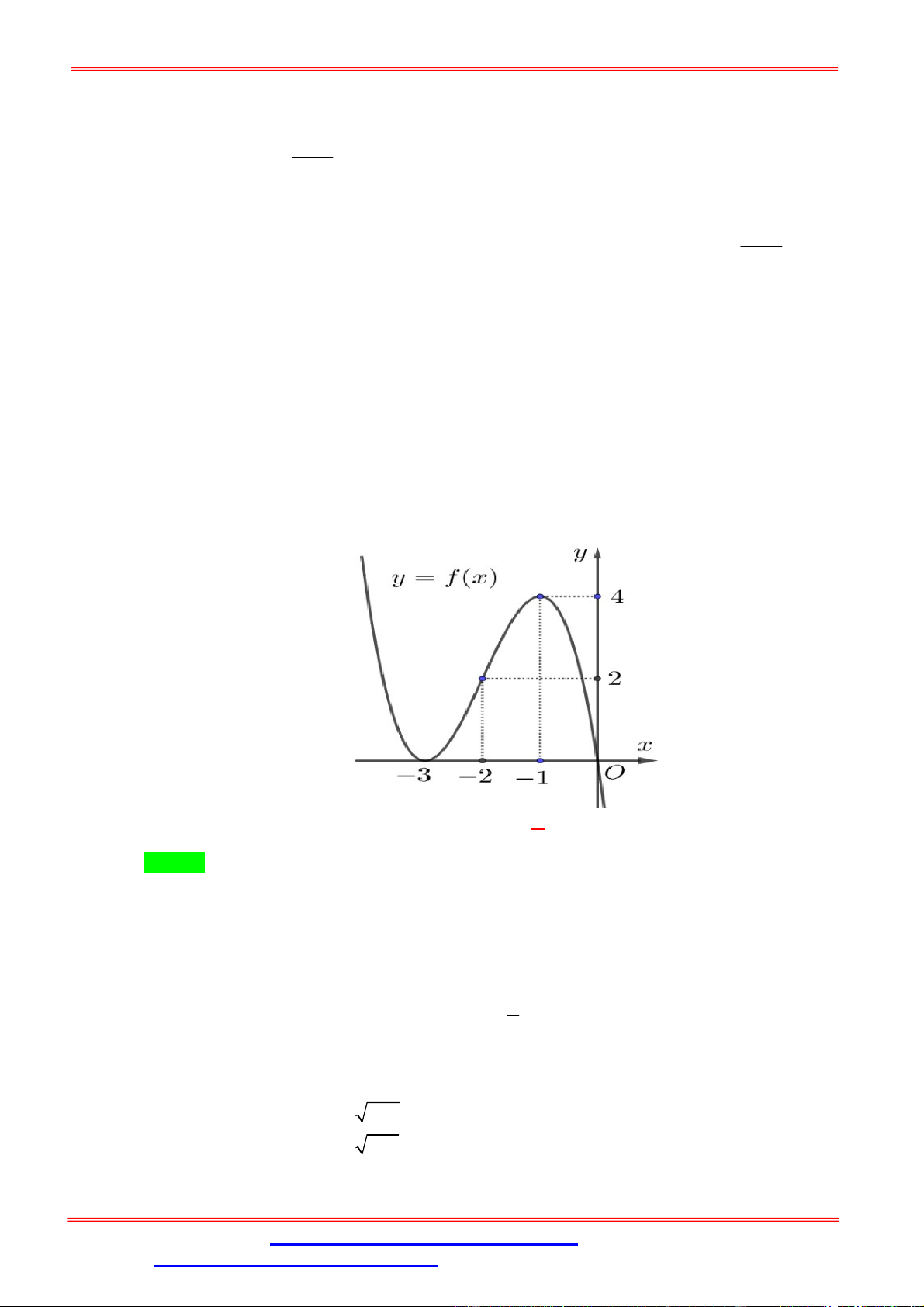
Câu 1. Cho hàm số y  f  x liên tục trên  có đồ thị như hình vẽ.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Phương trình f 2  f  x 1 có tất cả bao nhiêu nghiệm thực phân biệt? A. 3. B. 4. C. 5. D. 6. Lời giải Chọn A x  x x  2 0  0 
2  f  x  2 
 f  x  4 
Từ đồ thị ta có f 2  f  x  1      x  2   .
2  f  x  1 
 f  x  1  x 1 
Vậy phương trình f 2  f  x 1 có ba nghiệm phân biệt.
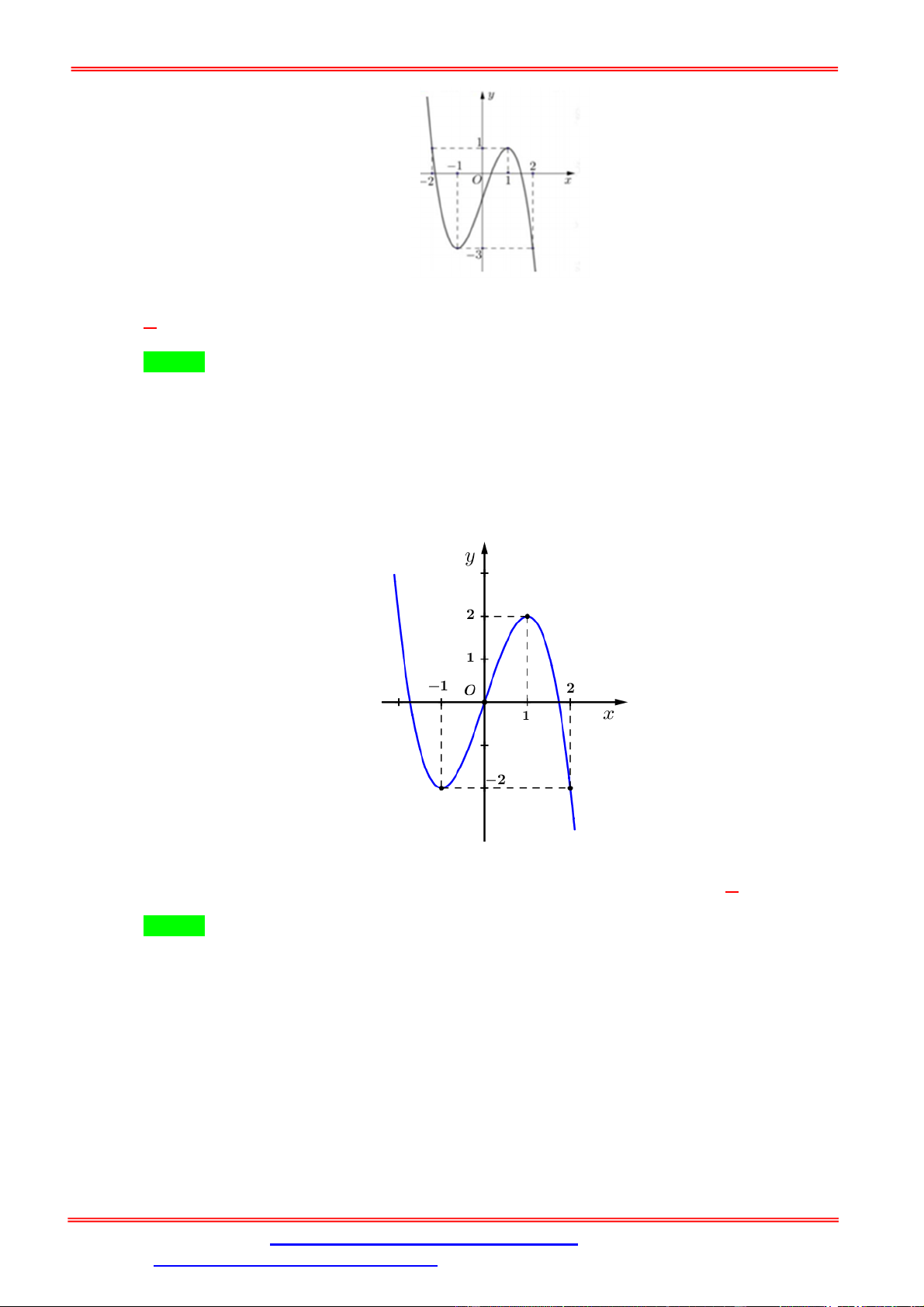
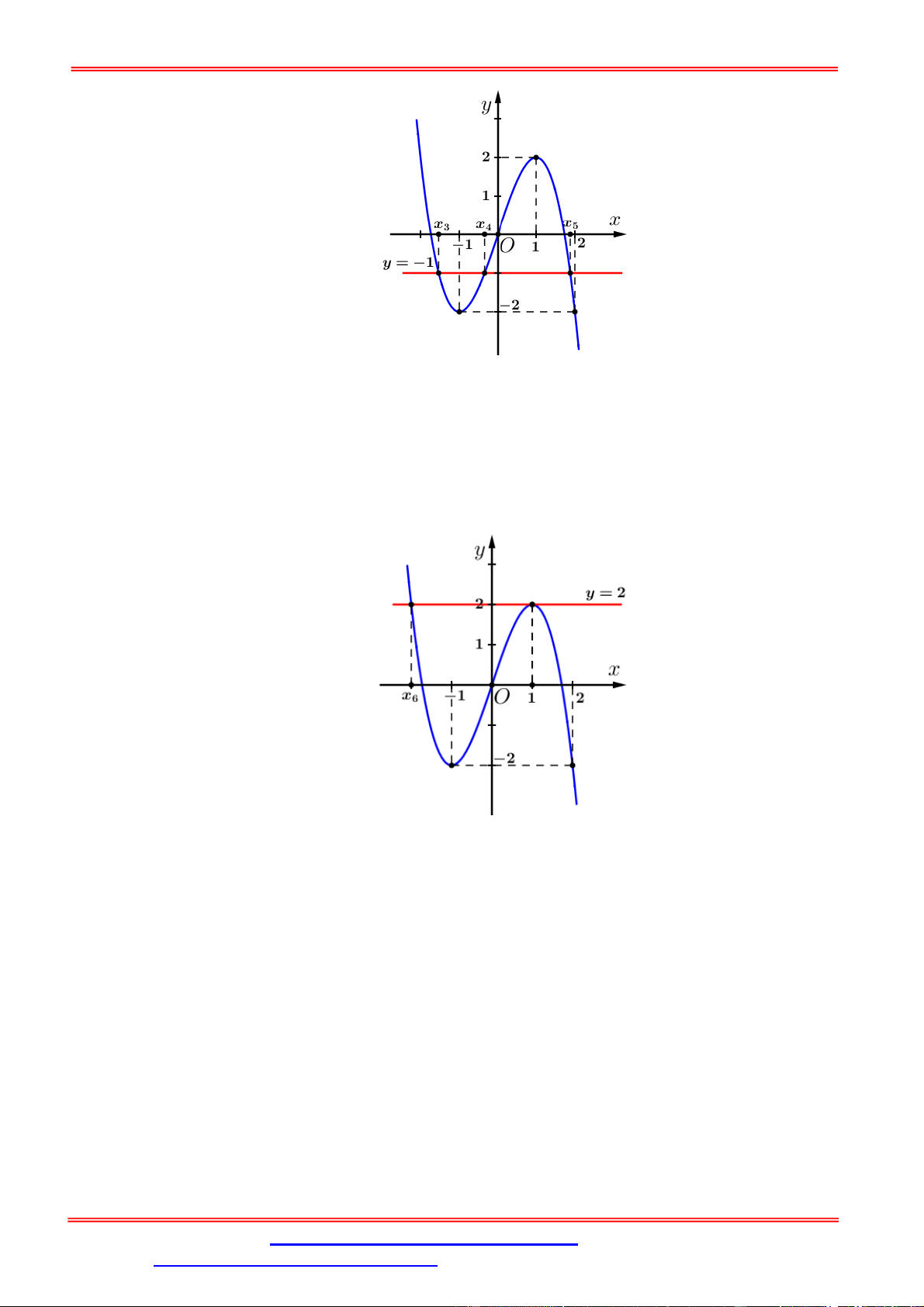
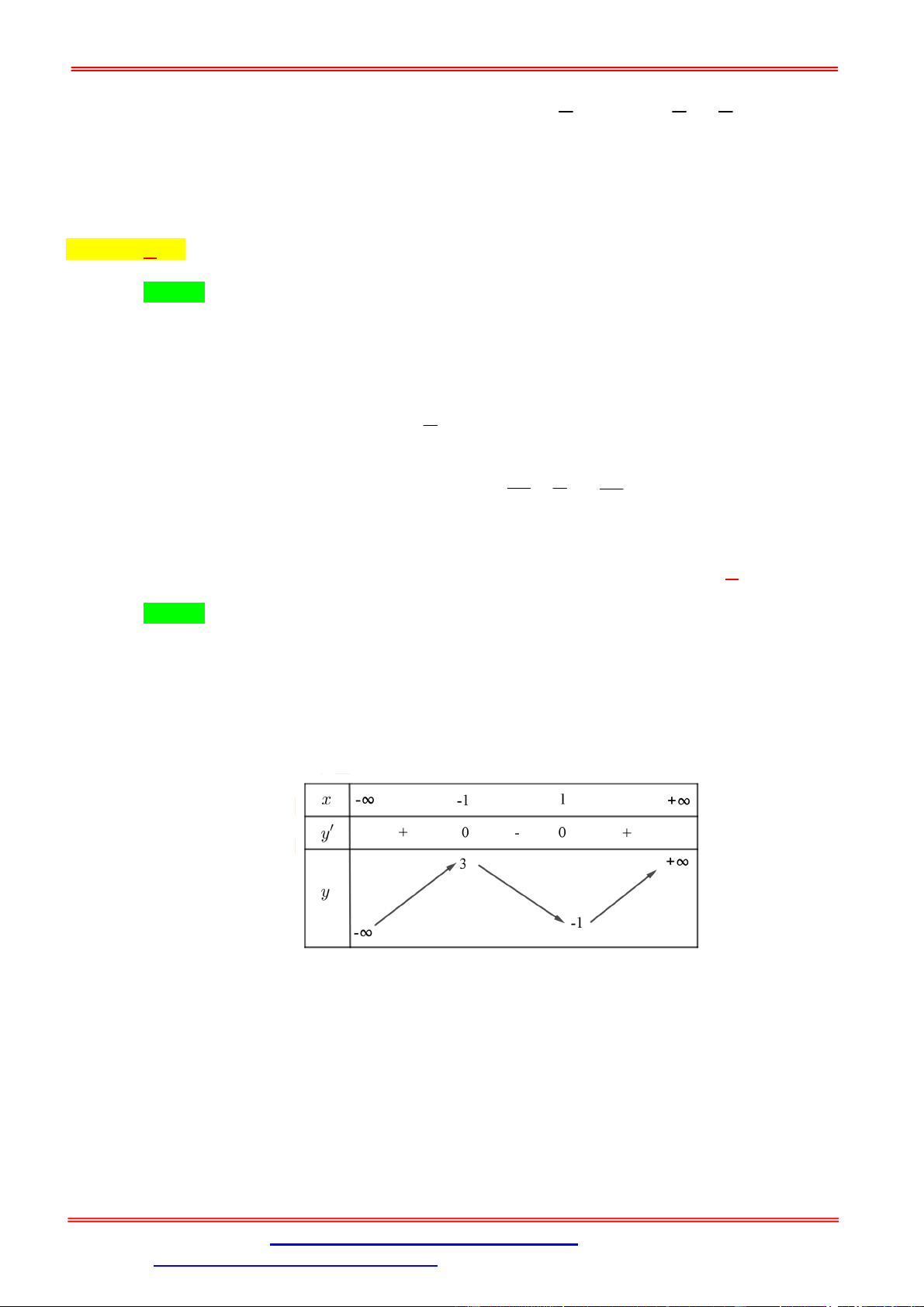
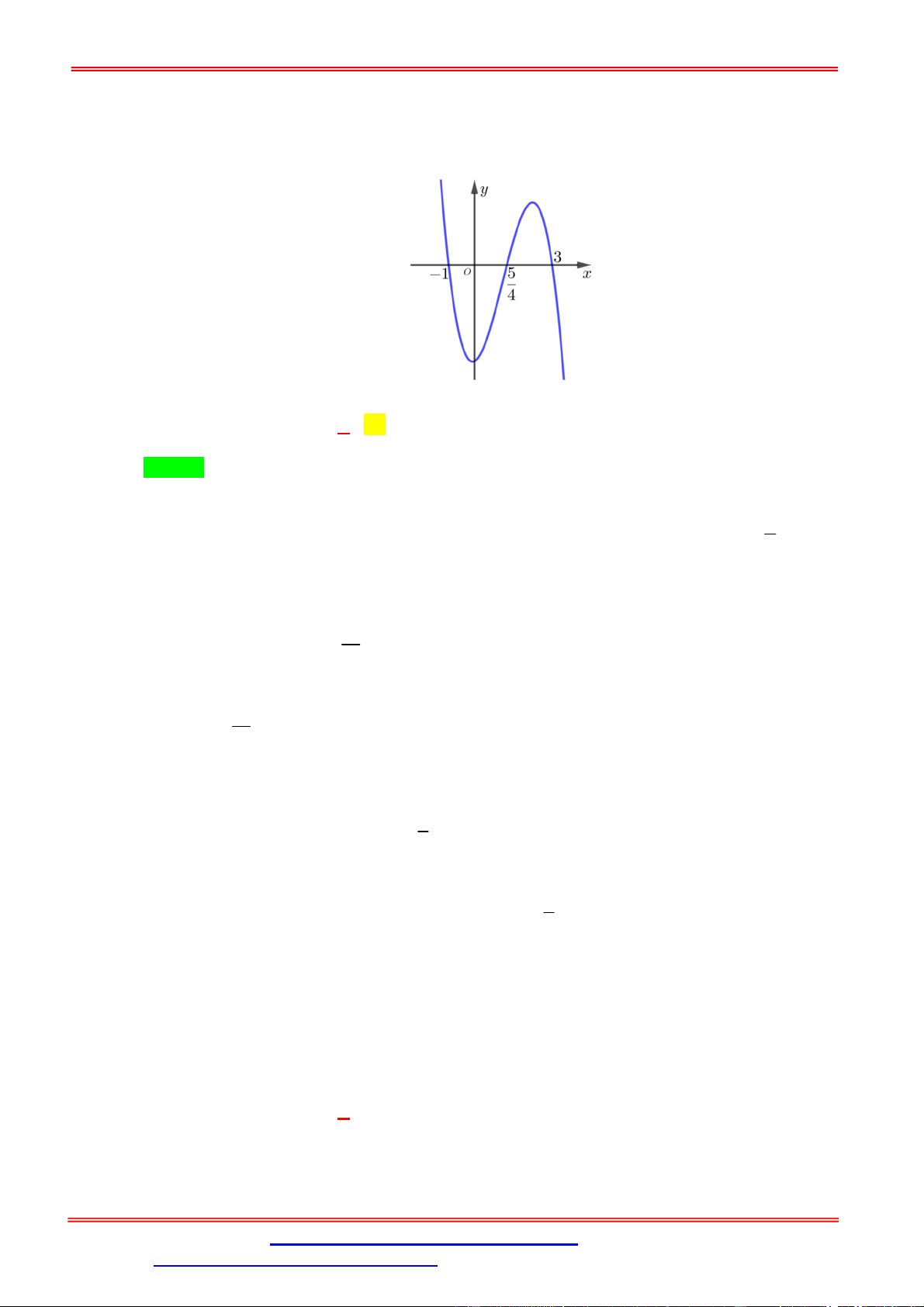
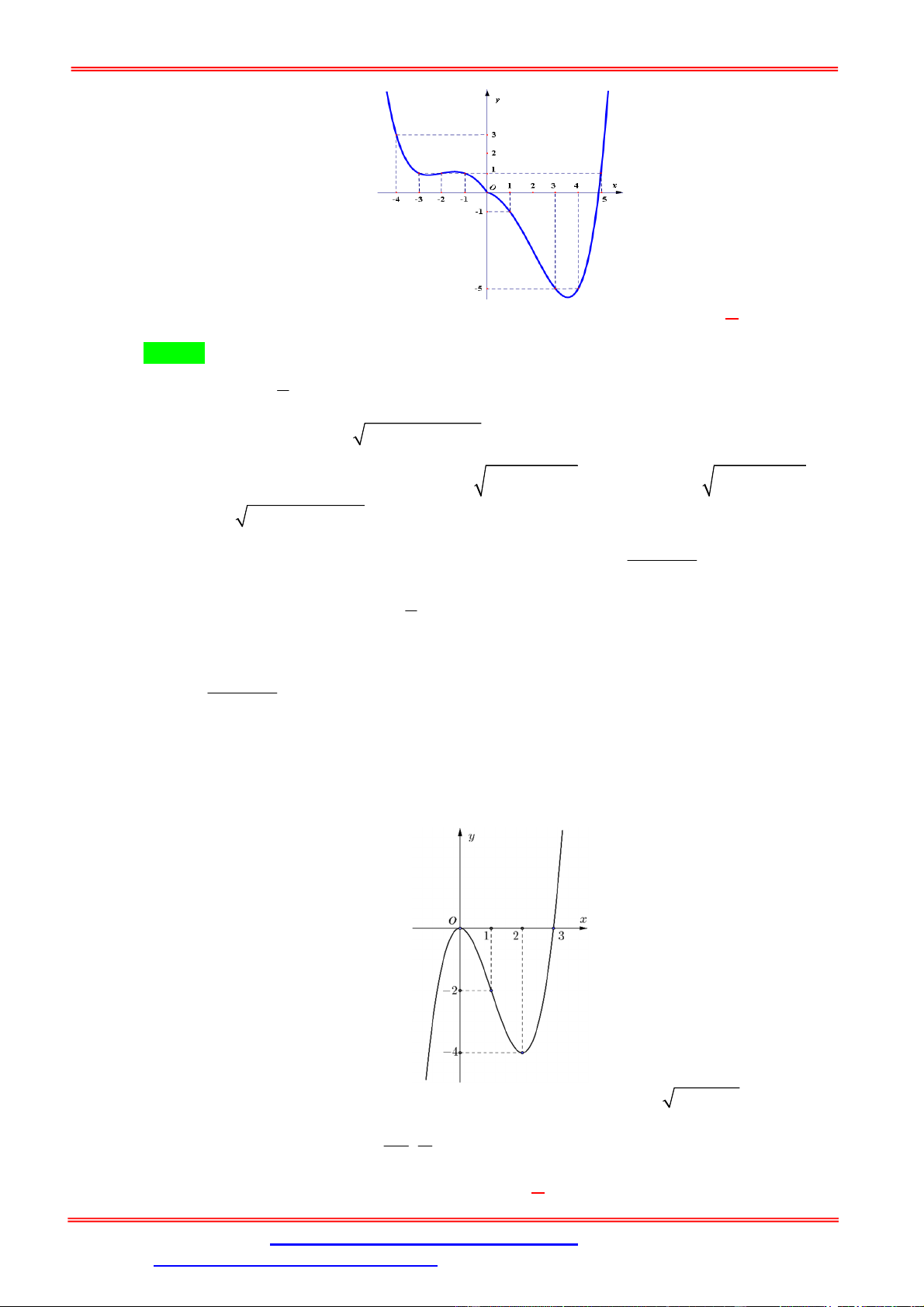
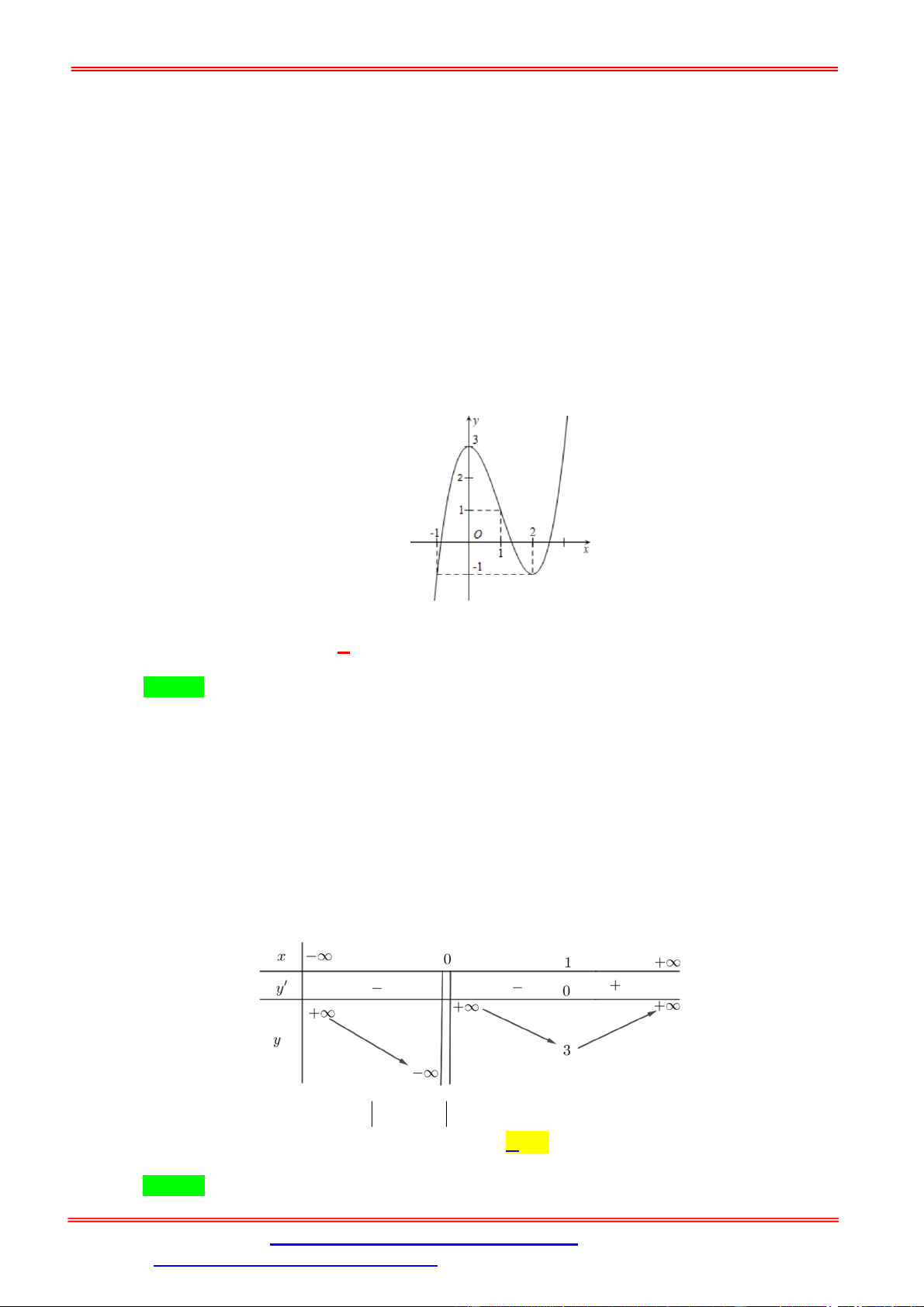
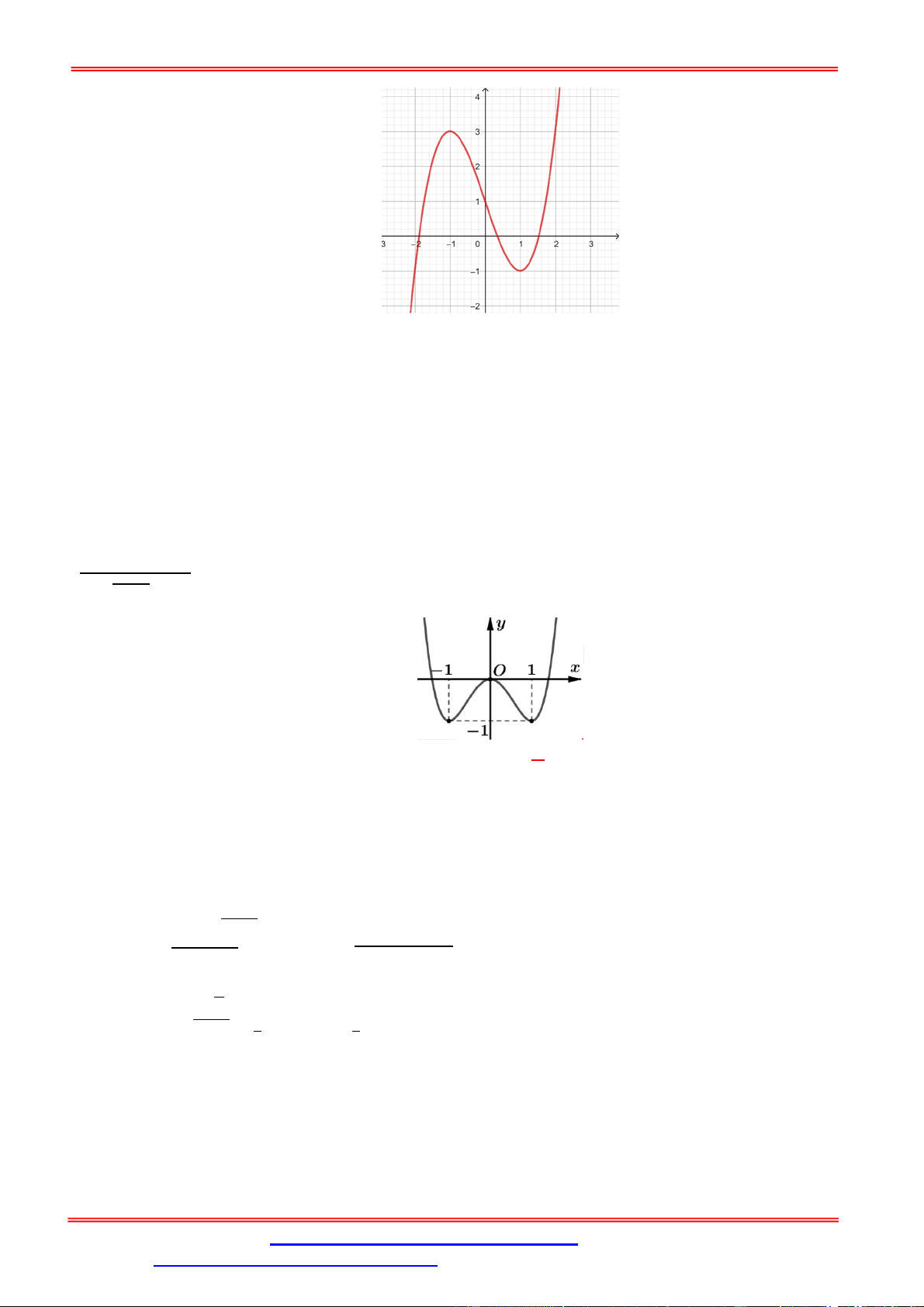
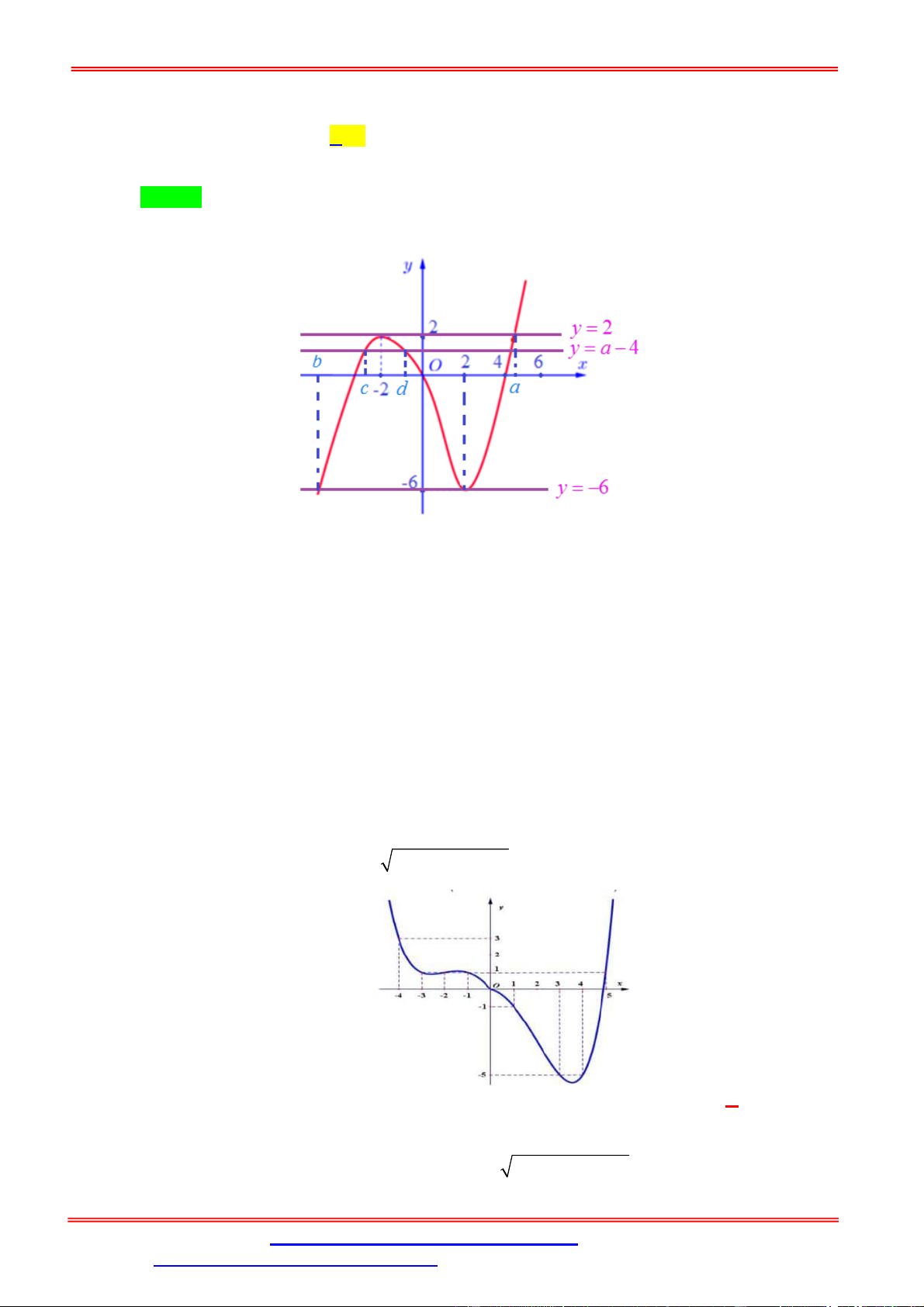
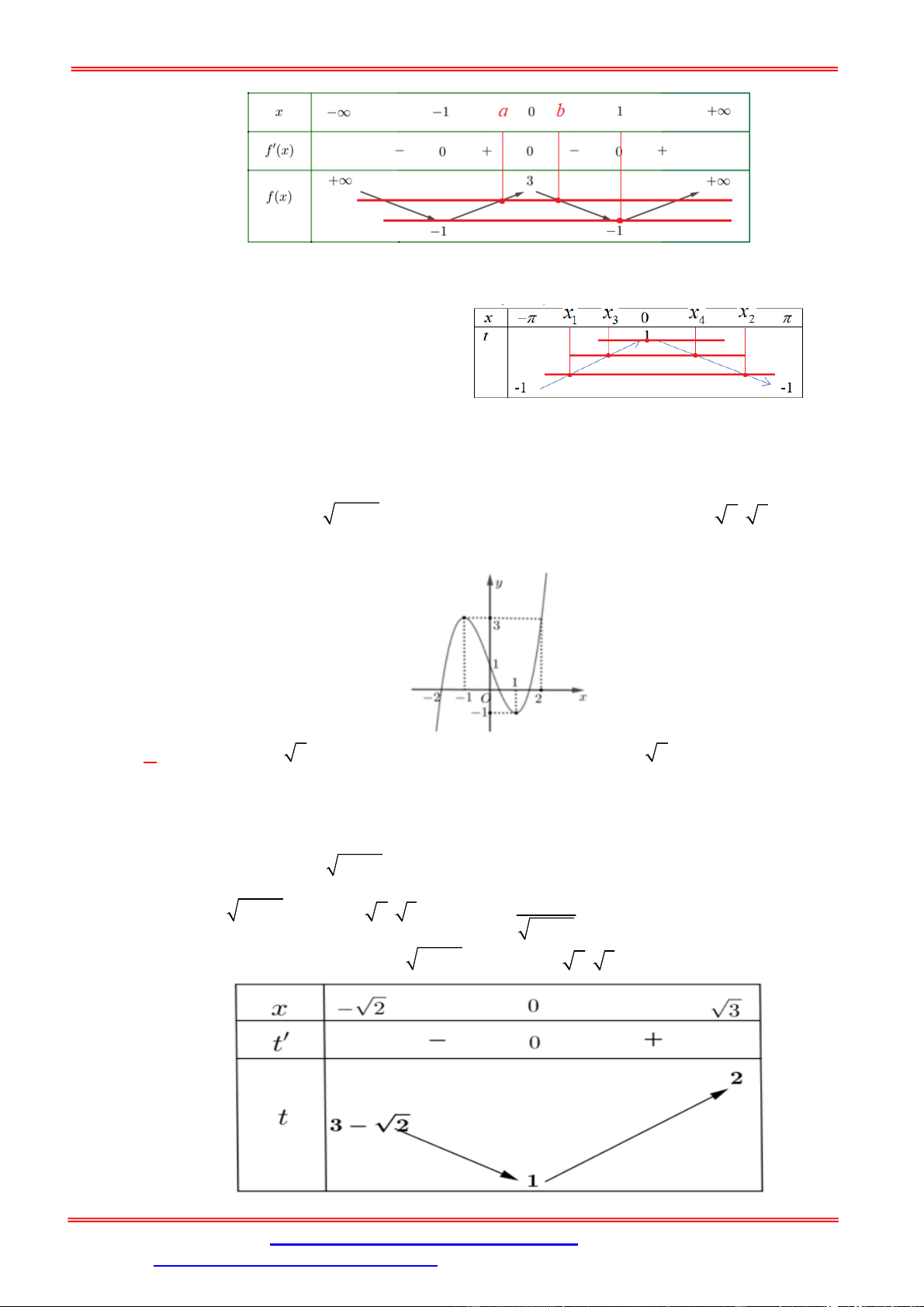
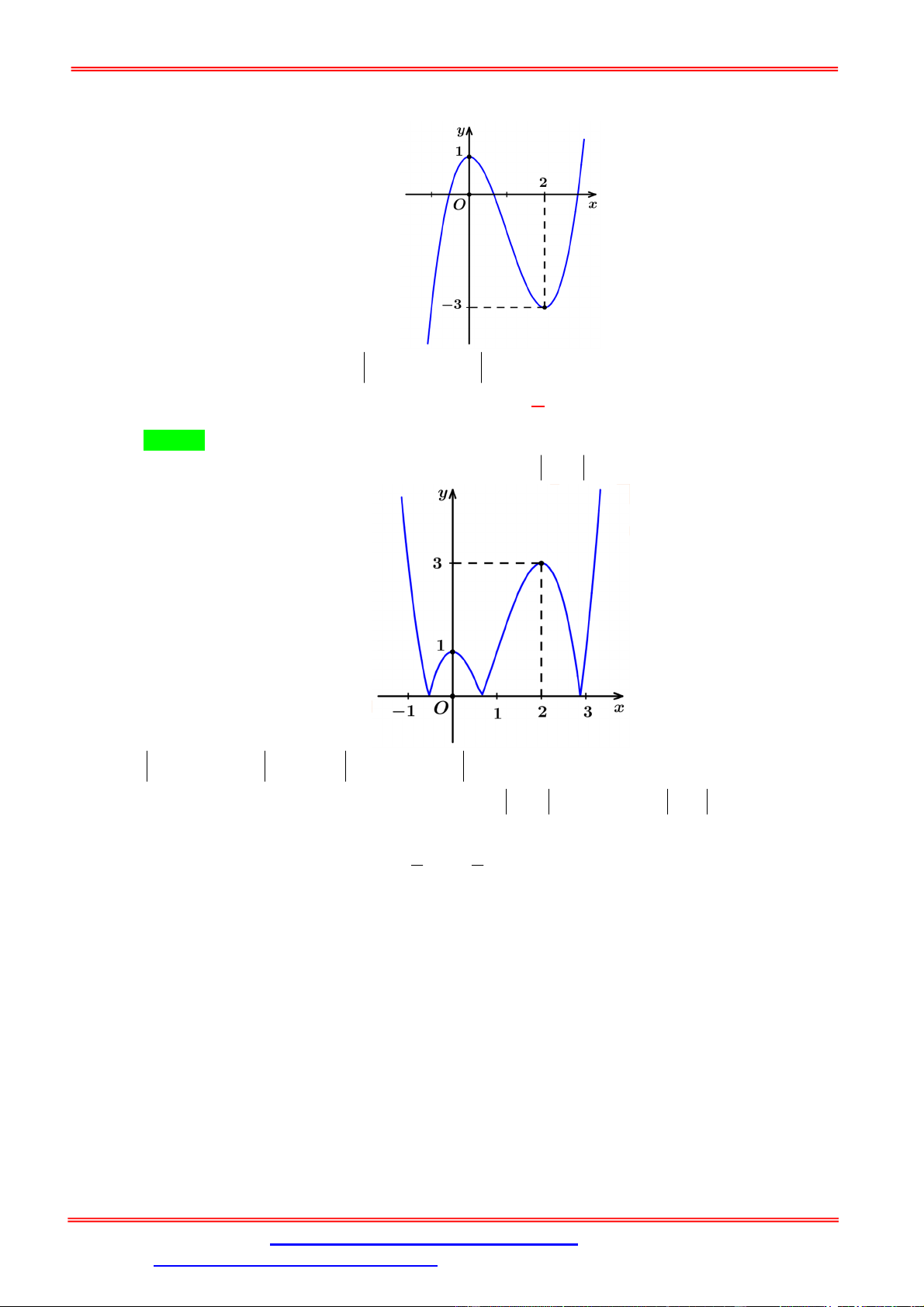
Câu 2. Cho hàm số f  x liên tục trên  và có đồ thị như hình bên.
Số nghiệm phân biệt của phương trình f  f  x  2  là A. 7 . B. 9 . C. 3 D. 5 . Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Dựa vào hình vẽ của đồ thị hàm số y  f  x , ta thấy đồ thị hàm số cắt trục hoành tại 3 điểm
có hoành độ lần lượt là x  x , x  0 và x  x . 1 2
Đặt t  f  x .
Phương trình f  f  x  2
 trở thành phương trình f t   2  .
Ta có nghiệm của phương trình f t   2
 là hoành độ giao điểm của đồ thị hàm số y  f t 
và đường thẳng y  2  .
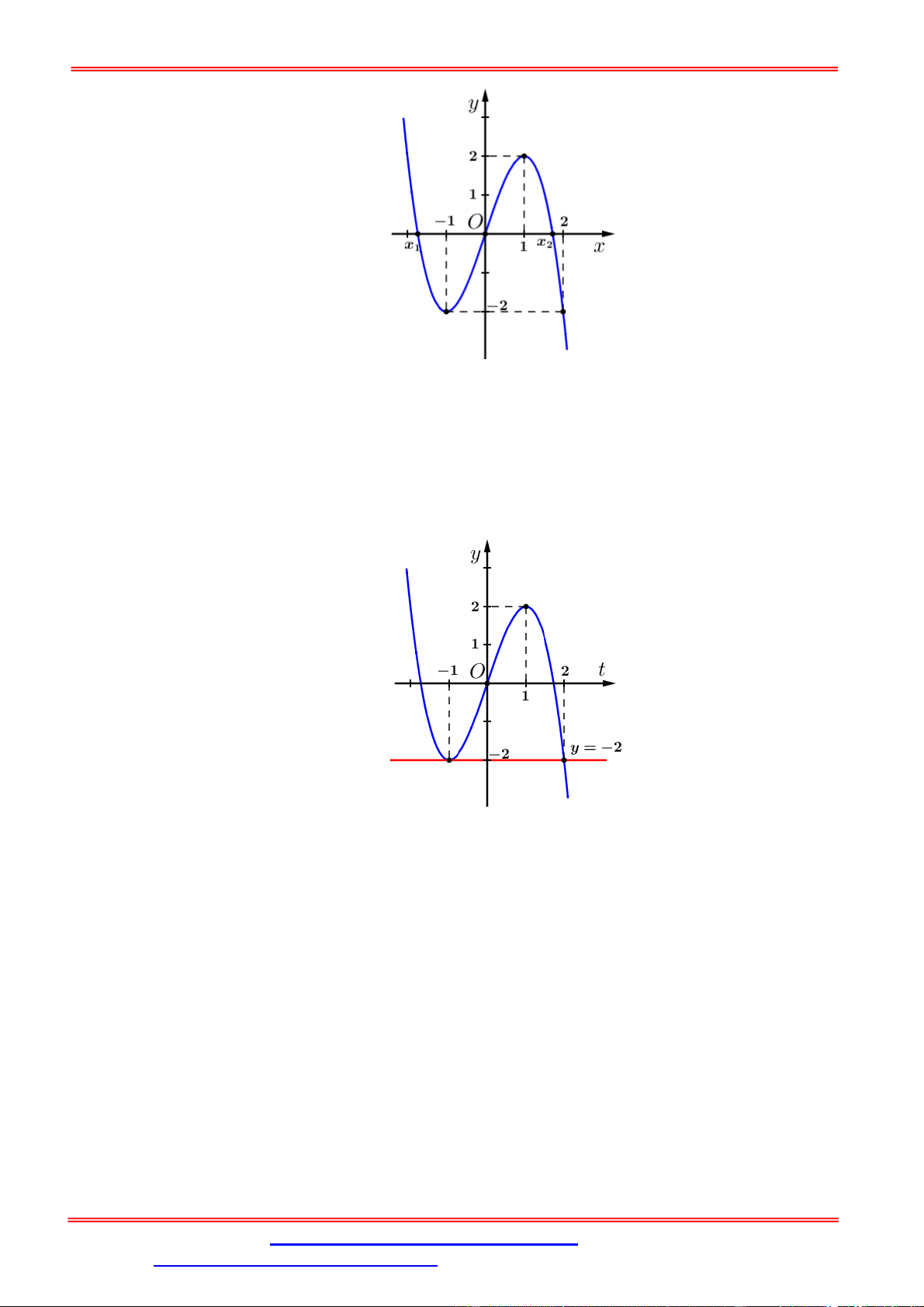
Dựa vào hình vẽ trên, ta thấy đồ thị hàm số y  f t  cắt đường thẳng y  2  tại 2 điểm phân
biệt có hoành độ lần lượt là t  1 và t  2 , hay ta có f  x  1
 và f  x  2 . Trường hợp 1:
Xét phương trình f  x  1
 , ta có nghiệm của phương trình f  x  1
 là hoành độ giao điểm
của đồ thị hàm số y  f  x và đường thẳng y  1  .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Dựa vào hình vễ trên, ta thấy đồ thị hàm số y  f  x cắt đường thẳng y  1  tại 3 điểm phân
biệt có hoành độ lần lượt là x  x x  x  1 
, x  x , và x  x . 3  1 3  4 5
Vậy phương trình f  x  1
 có 3 nghiệm phân biệt   1 . Trường hợp 2:
Xét phương trình f  x  2 , ta có nghiệm của phương trình f  x  2 là hoành độ giao điểm
của đồ thị hàm số y  f  x và đường thẳng y  2 .
Dựa vào hình vẽ trên, ta thấy đồ thị hàm số y  f  x cắt đường thẳng y  2 tại 2 điểm phân
biệt có hoành độ lần lượt là x  x
x  x và x  1 . 6  6 1 
Vậy phương trình f  x  2 có 2 nghiệm phân biệt2 . Từ  
1 và 2 , suy ra số nghiệm phân biệt của phương trình f  f  x  2  là 5.
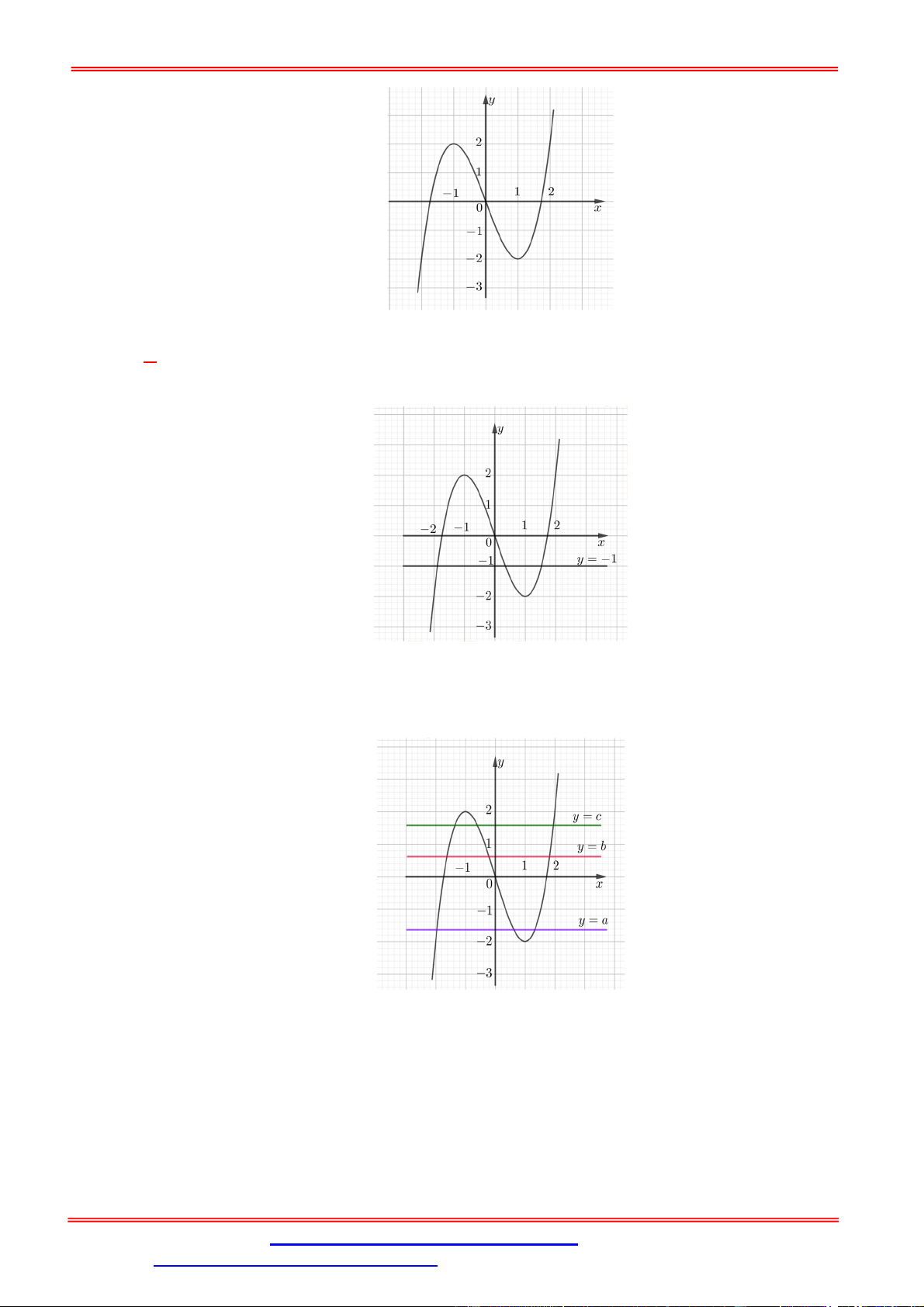
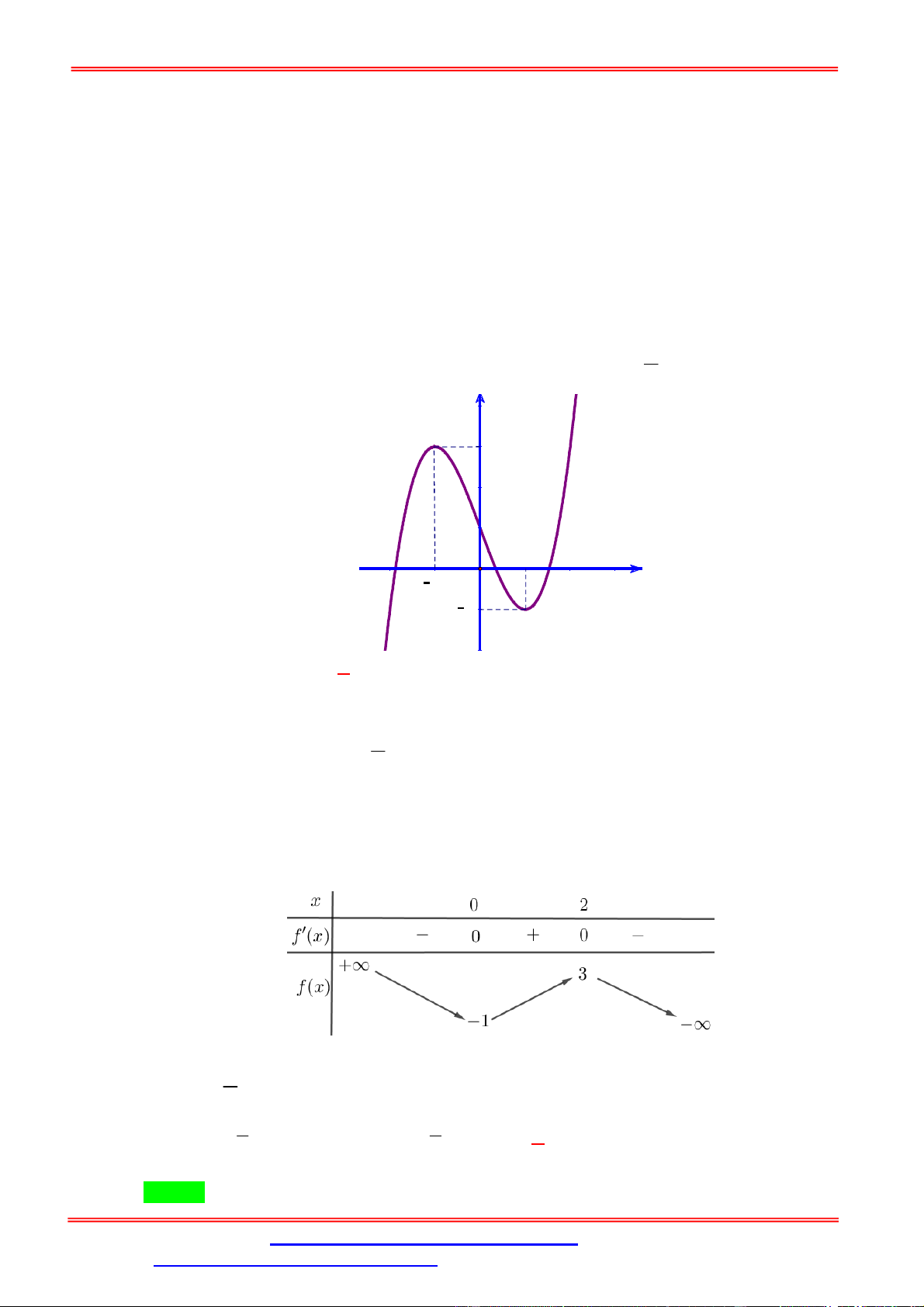
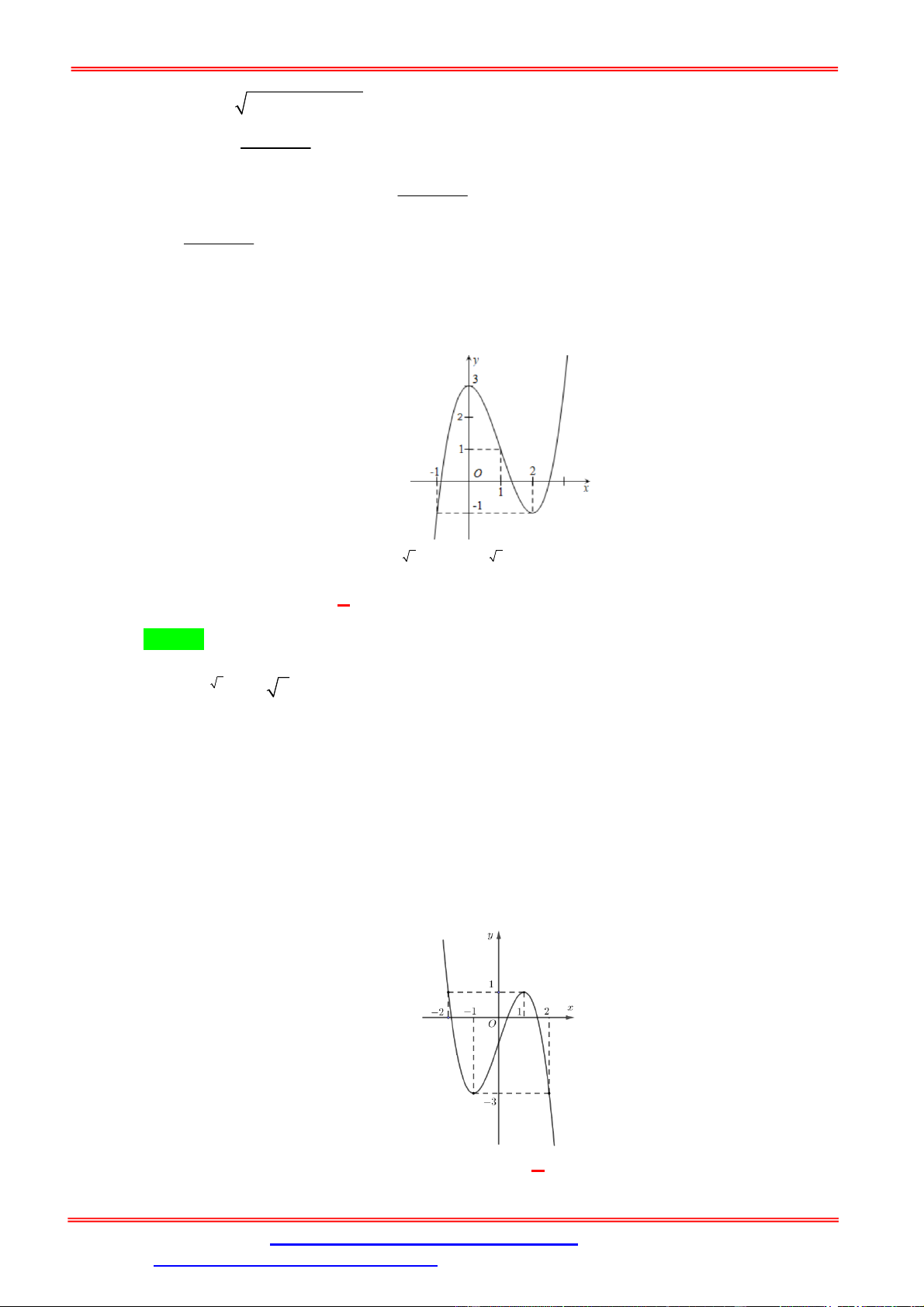
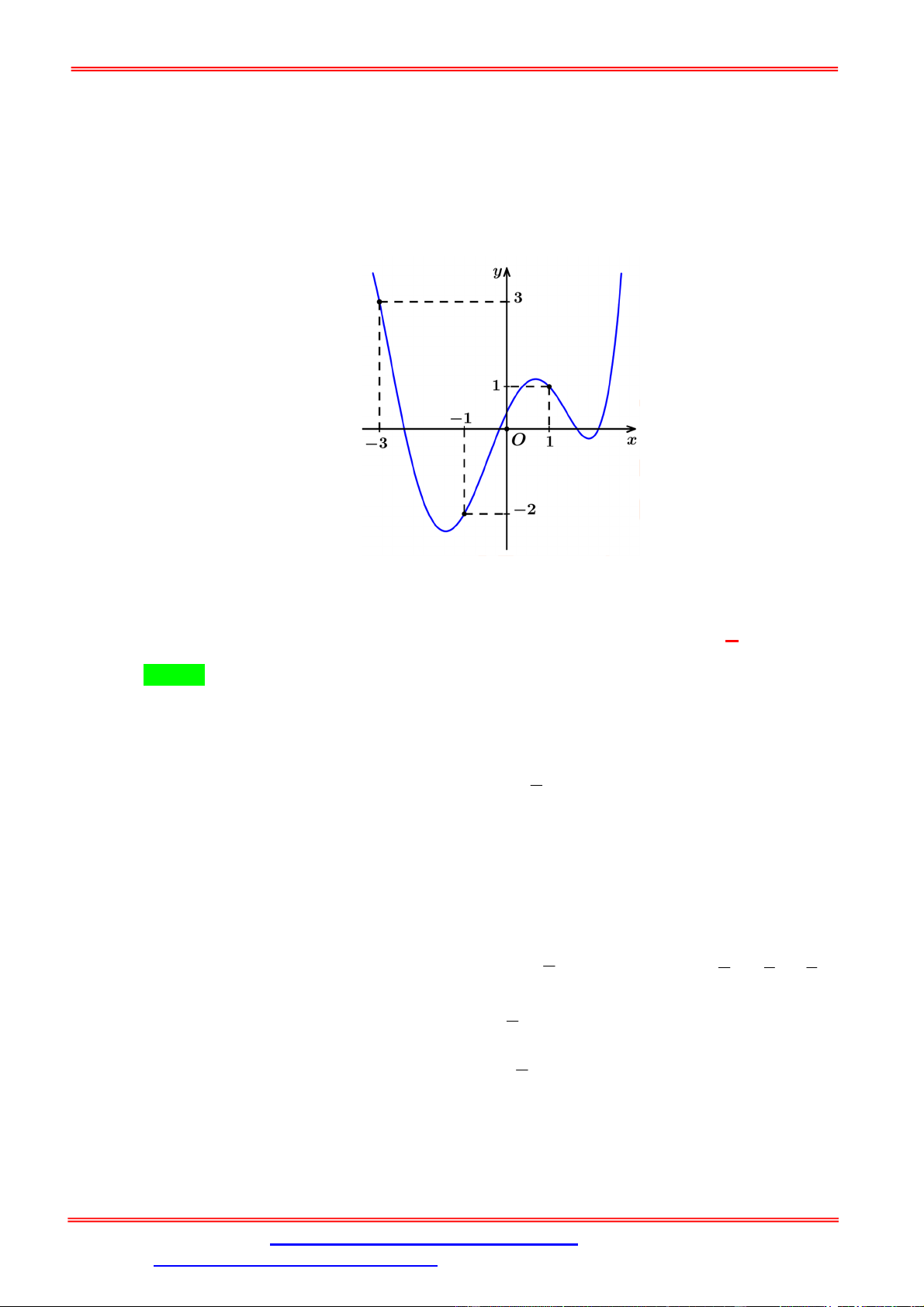
Câu 3. Cho hàm số y  f  x liên tục trên  và có đồ thị như hình dưới đây.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Số nghiệm phân biệt của phương trình f  f  x 1  0 là A. 9 . B. 8 . C. 10 . D. 7 . Lời giải Chọn A
 f  x  a  2   a    1 
Xét f  f  x 1  0  f  f  x  1  f  x  b 0  b    1 .
 f x  c 1  c  2 
Xét f  x  a  2   a   
1 : Dựa vào đồ thị ta thấy y  a cắt đồ thị tại 3 điểm phân biệt   1 .
Xét f  x  b 0  b  
1 : Dựa vào đồ thị ta thấy y  b cắt đồ thị tại 3 điểm phân biệt 2 .
Xét f  x  c 1  c  2 : Dựa vào đồ thị ta thấy y  c cắt đồ thị tại 3 điểm phân biệt 3 .
Các nghiệm ở trên không có nghiệm nào trùng nhau nên * có 9 nghiệm phân biệt
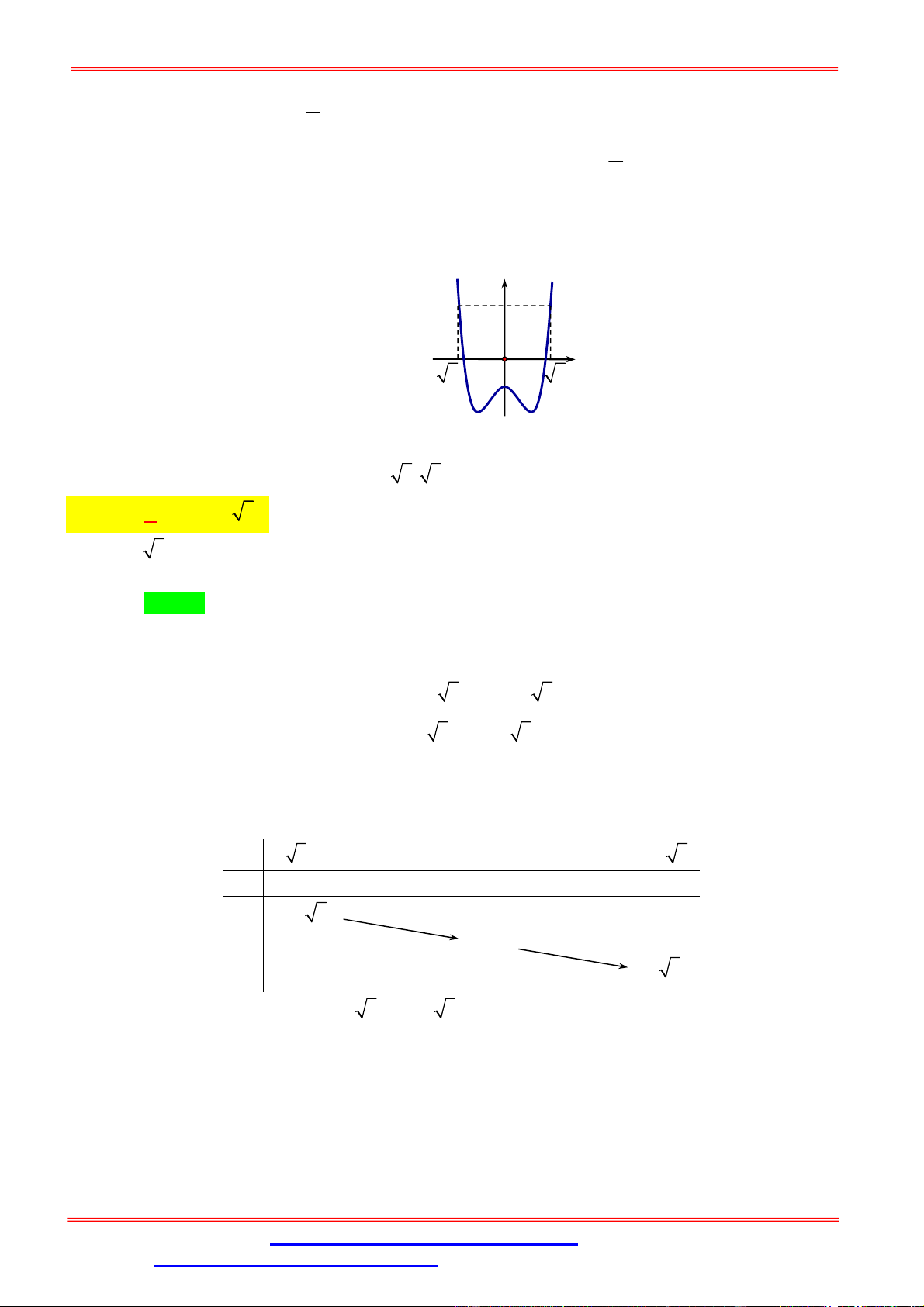
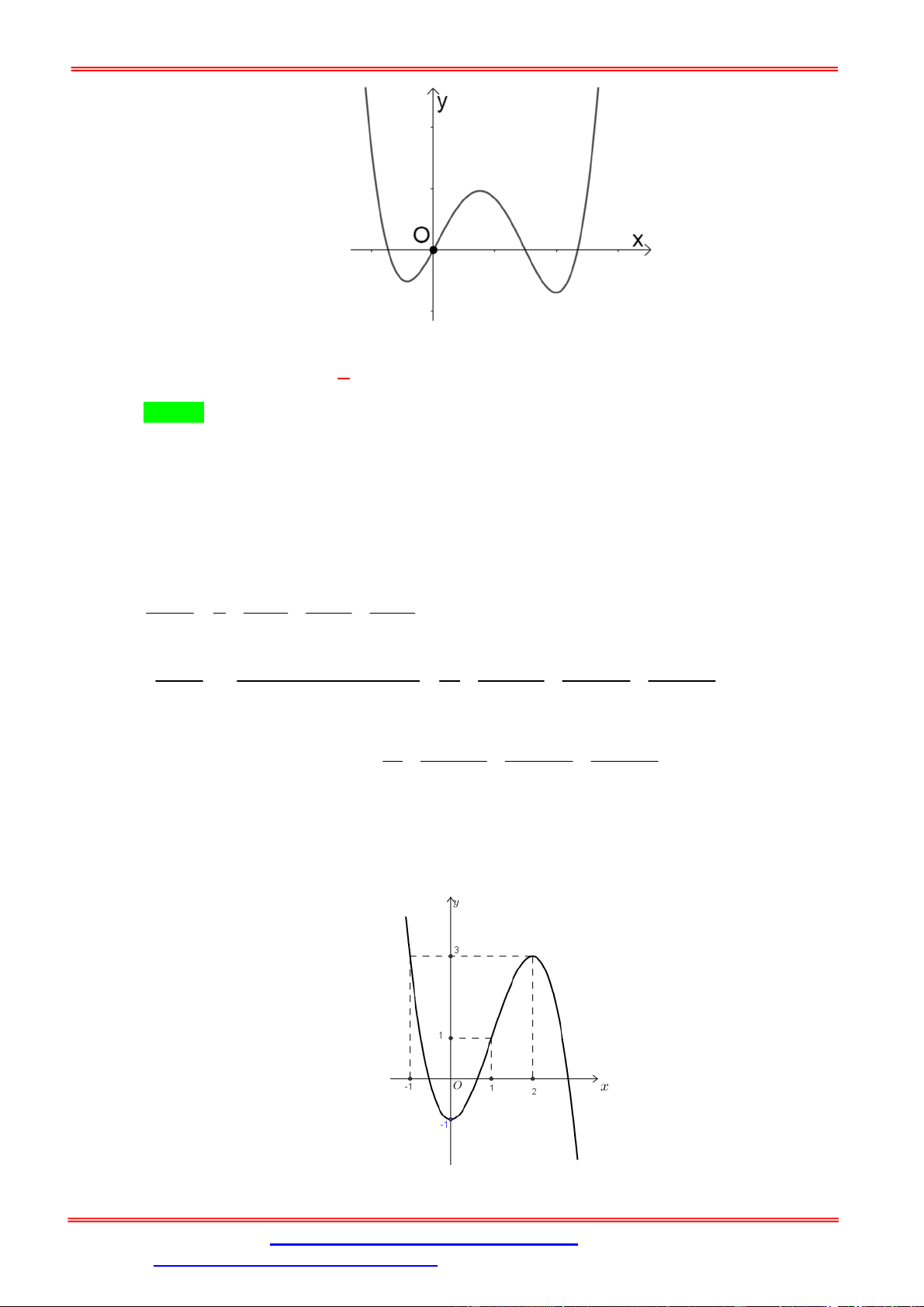
Câu 4. Cho hàm số y  f  x liên tục trên R và có đồ thị như hình vẽ sau
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 2 m  x 1
Số các giá trị nguyên của tham số m để phương trình f     0 có hai nghiệm phân 8 biệt là A. 7 . B. 6 . C. 5 . D. 4 . Lời giải Chọn C 2 m  x 1 Đặt x
t   , t  0 , khi đó: f   
 0 có hai nghiệm phân biệt. 8 2 m 1
 f t  
có hai nghiệm dương phân biệt. 8 2 m 1  1 
 1  3  m  3 . 8
 m là số nguyên nên m  2  ; 1; 0; 1;  2 . 1
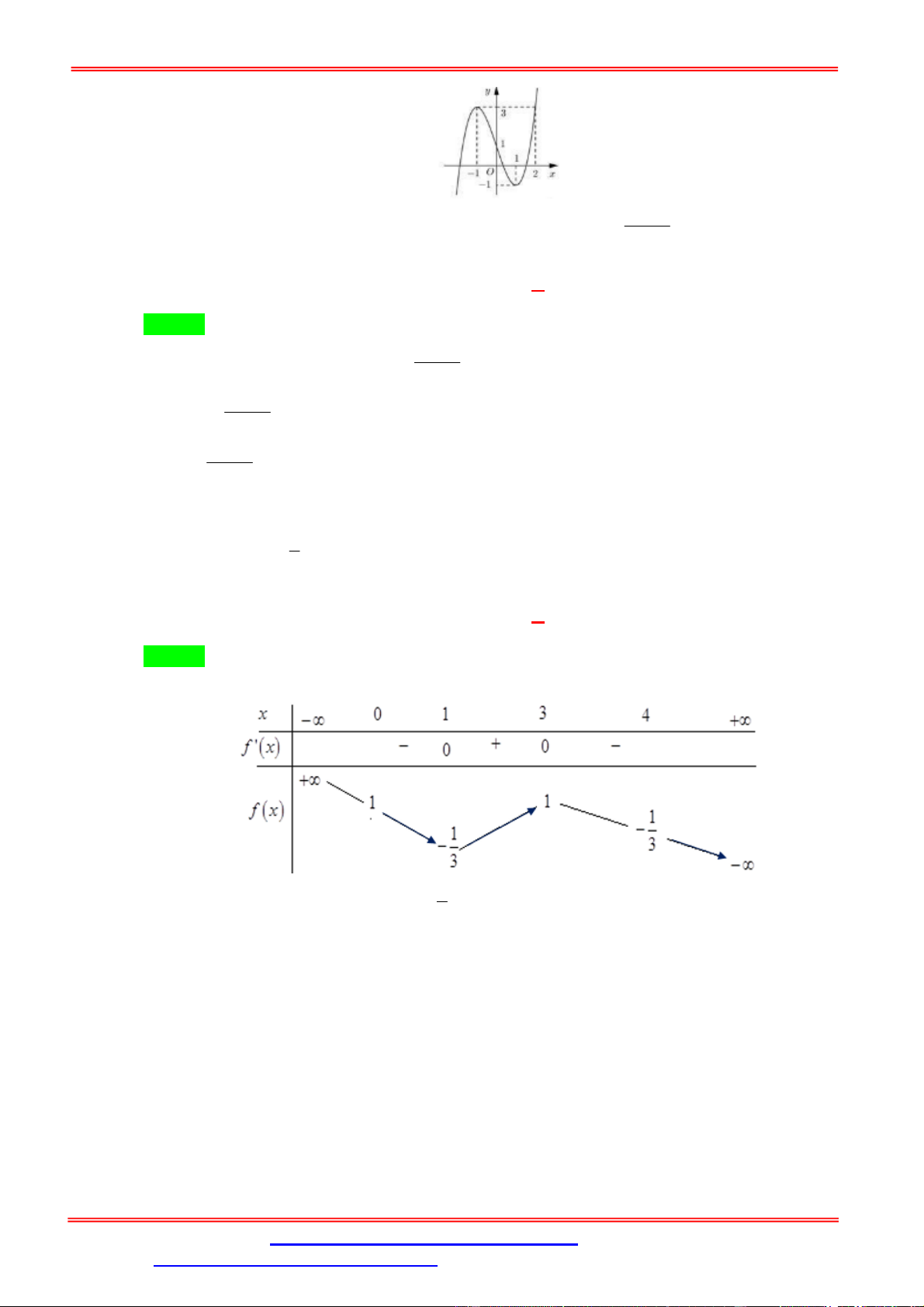
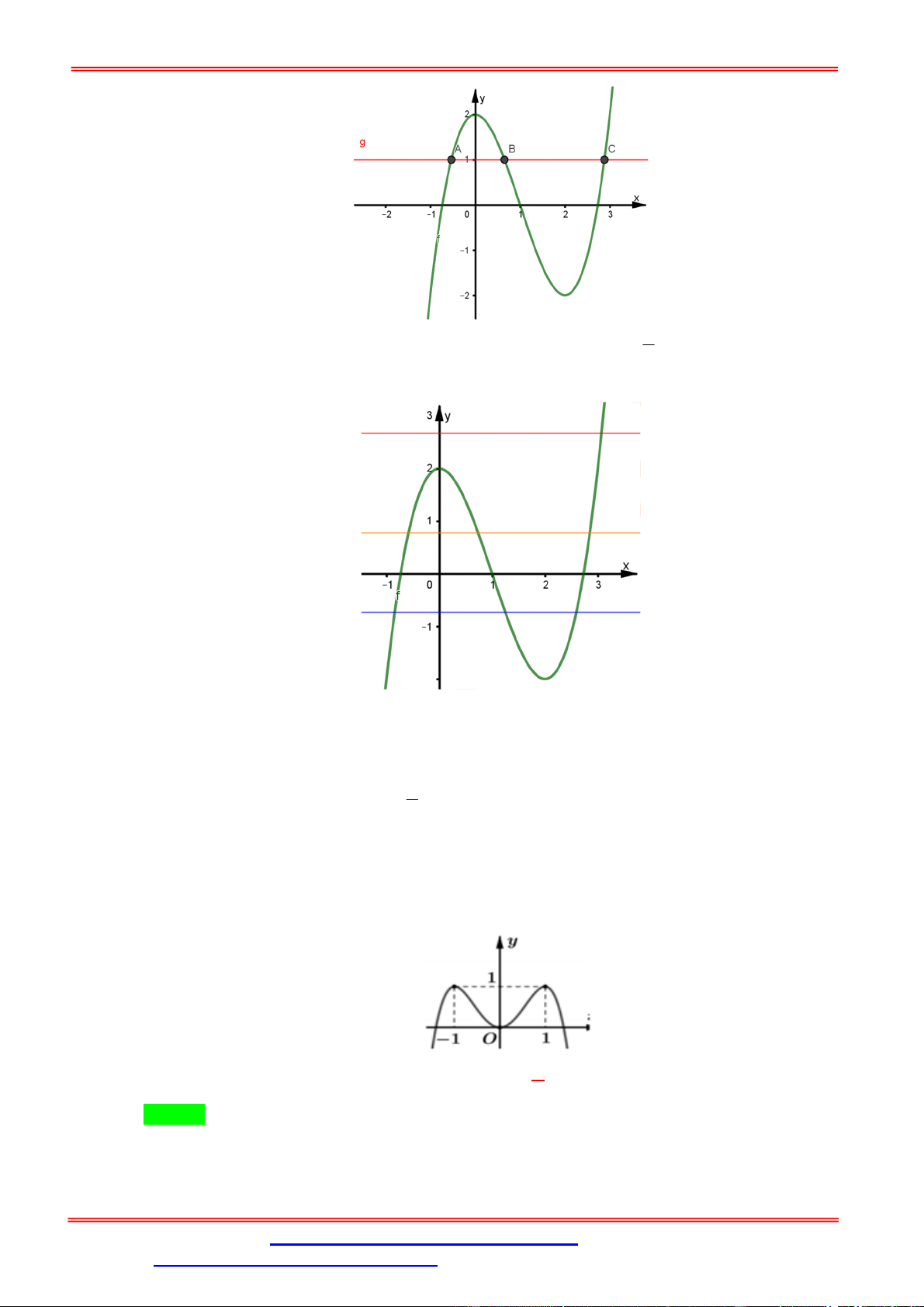
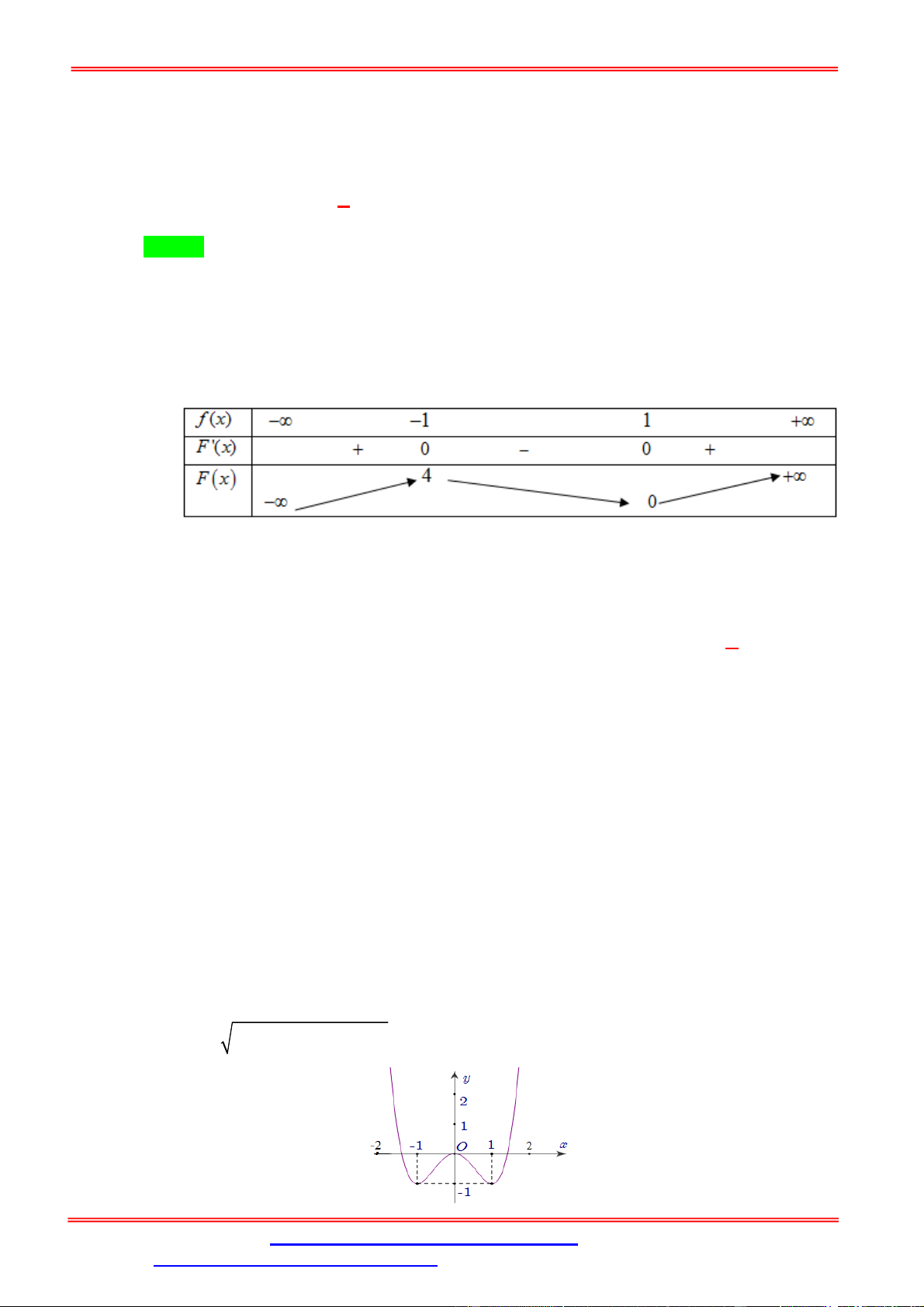
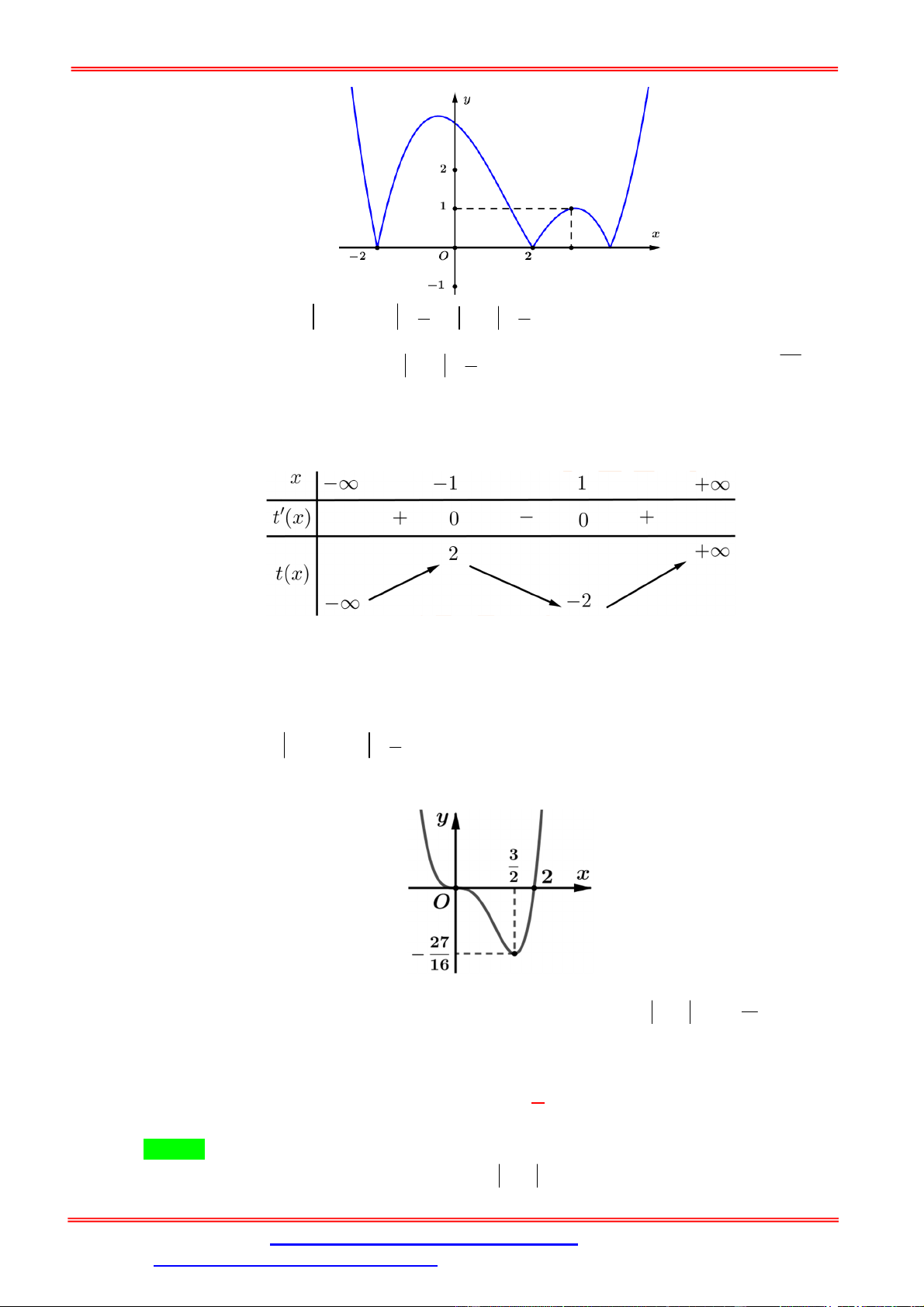
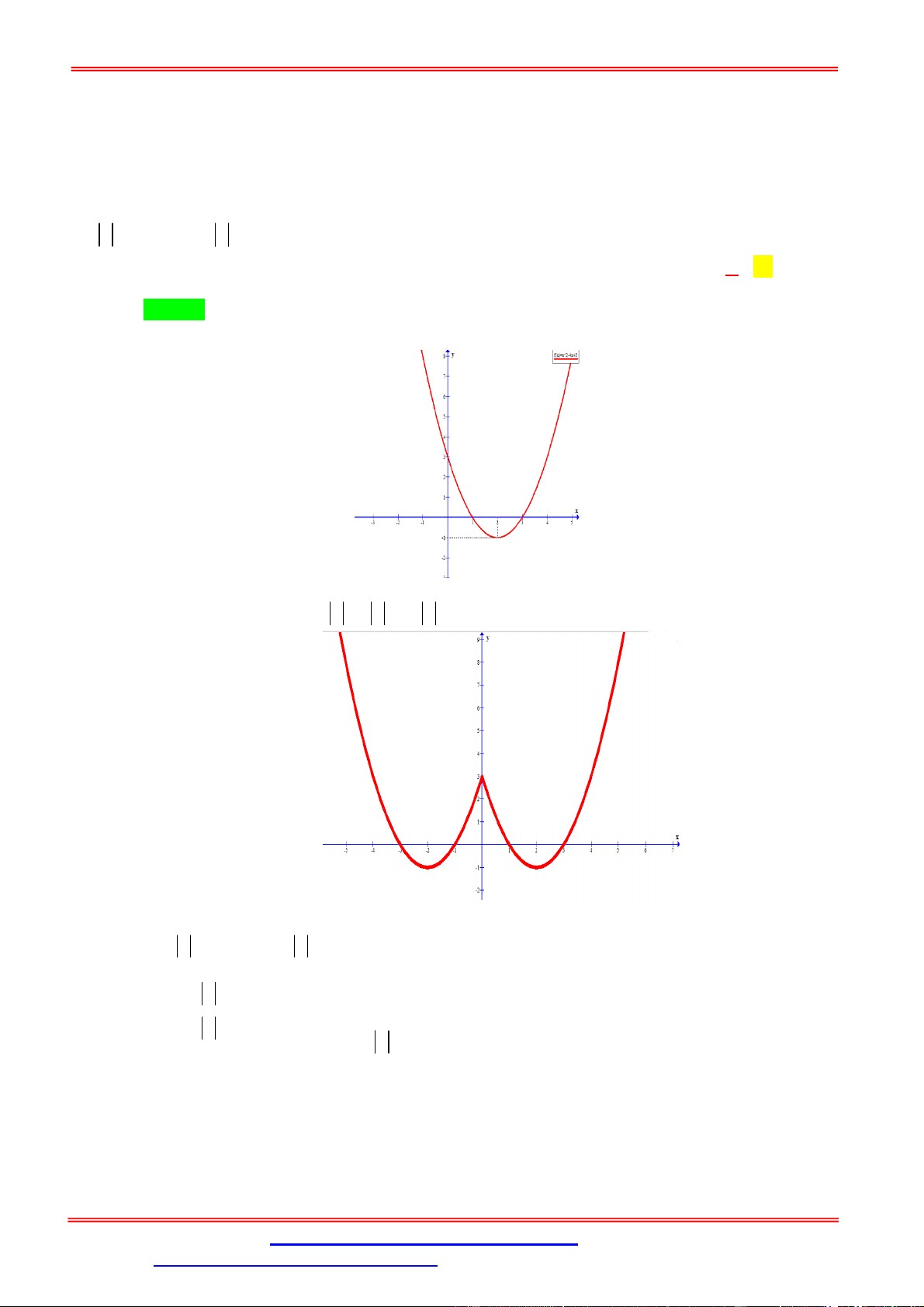
Câu 5. Cho hàm số f x 3   x  2 2
x  3x 1. Khi đó phương trình f  f x  0 có bao nhiêu nghiệm 3 thực? A. 9. B. 6. C. 5. D. 4. Lời giải. Chọn C
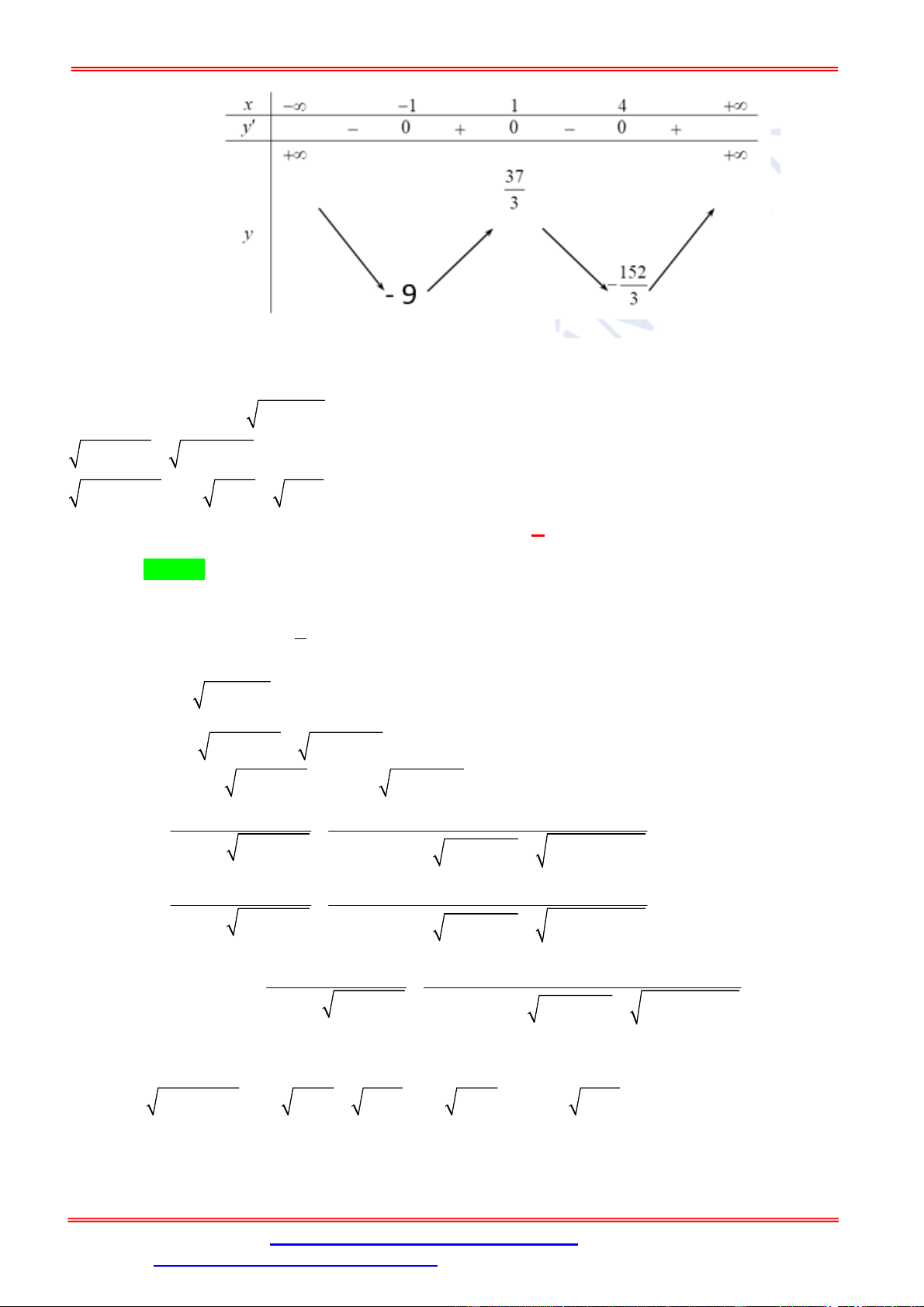
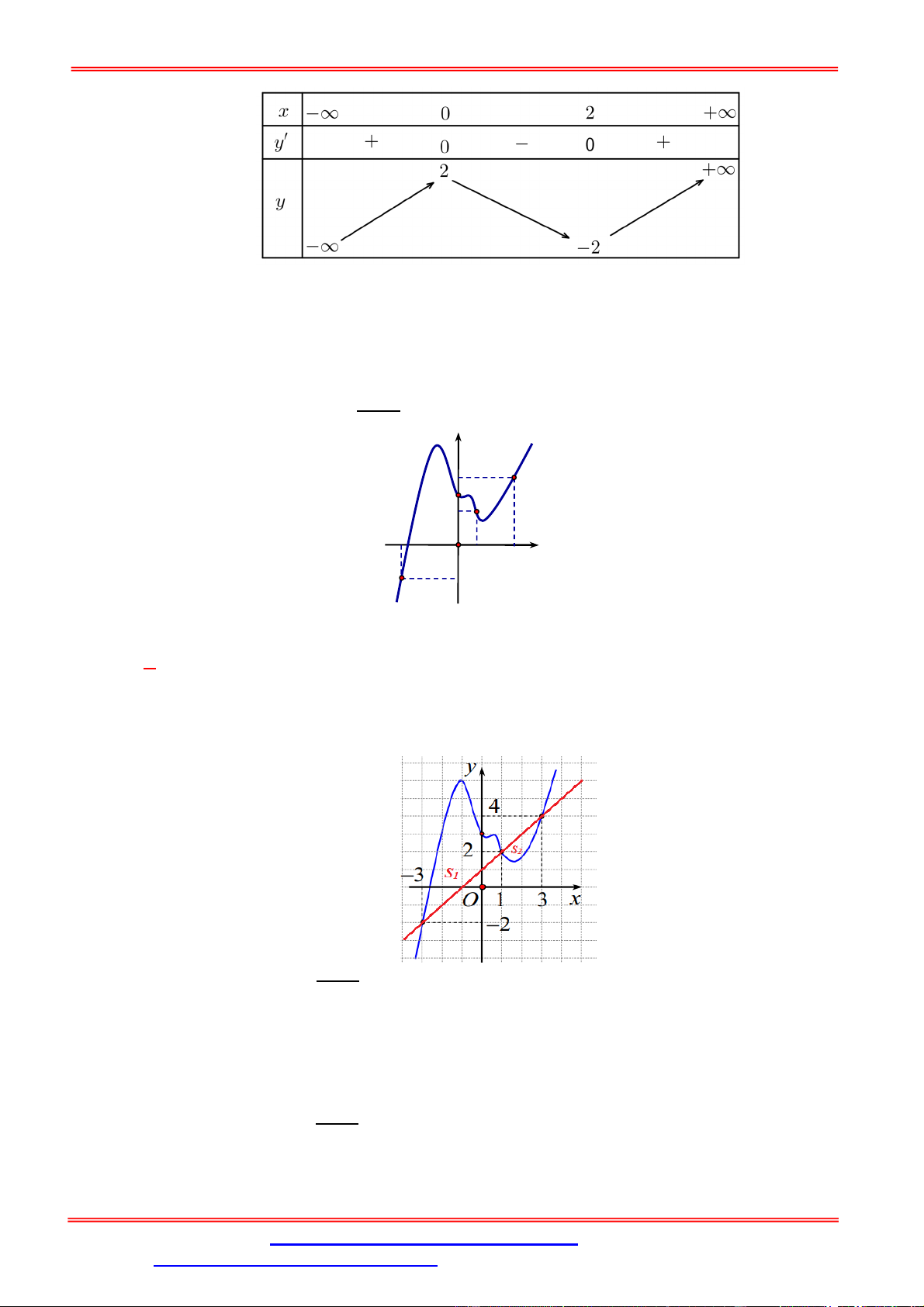
Bảng biến thiên của hàm số f  x như sau: x  0 1 x  1
Ở đây f  x 1  
và f  x     . x  3  3 x  4 
 f  x  a 0;  1 
Suy ra f  f  x  0  f  x  b   1;3 .
 f x  c3;4 
Phương trình f  x  a có 3 nghiệm.
Phương trình f  x  b có 1 nghiệm.
Phương trình f  x  c có 1 nghiệm.
Dễ thấy các nghiệm không trùng nhau nên phương trình đã cho có 5 nghiệm.
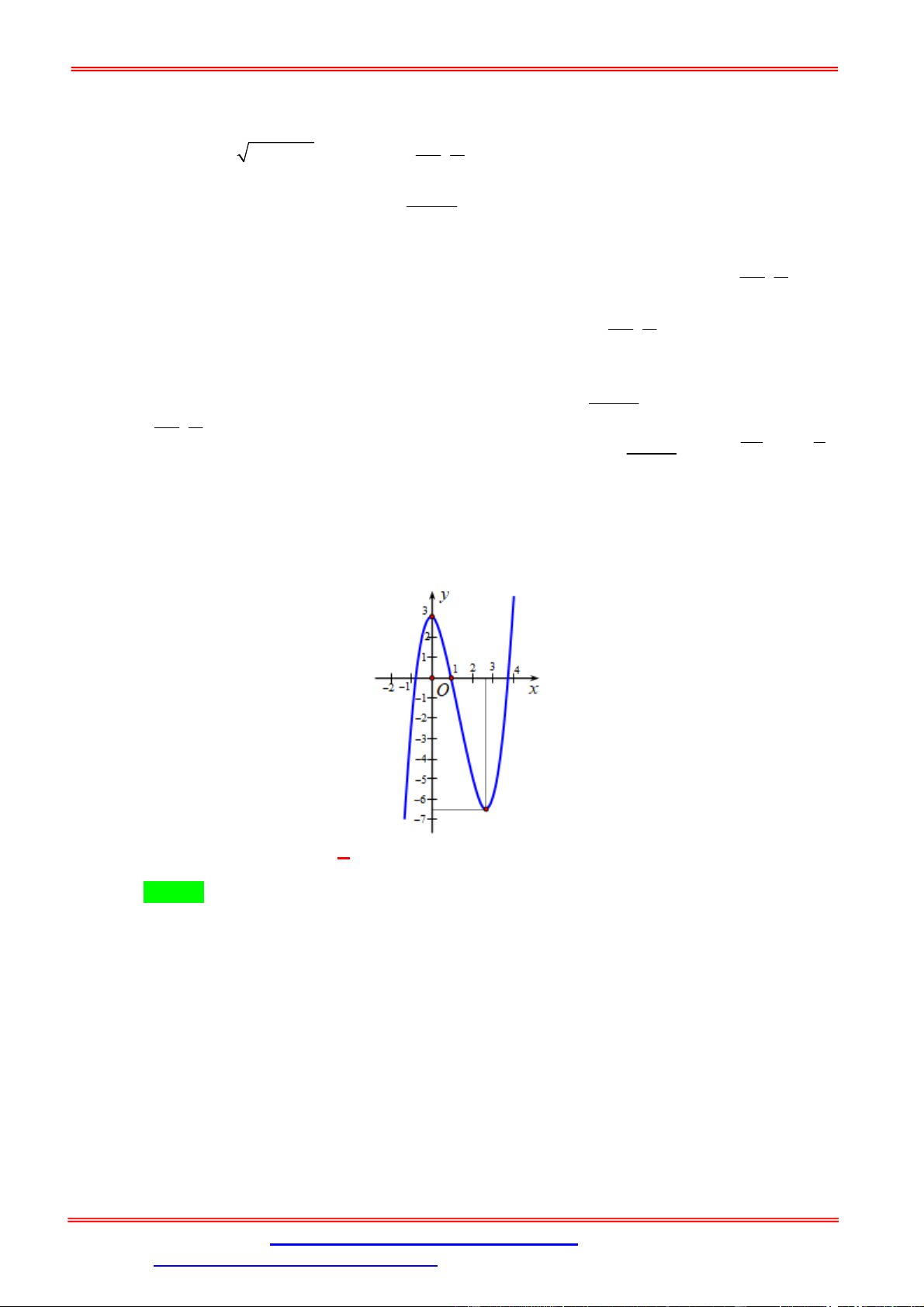
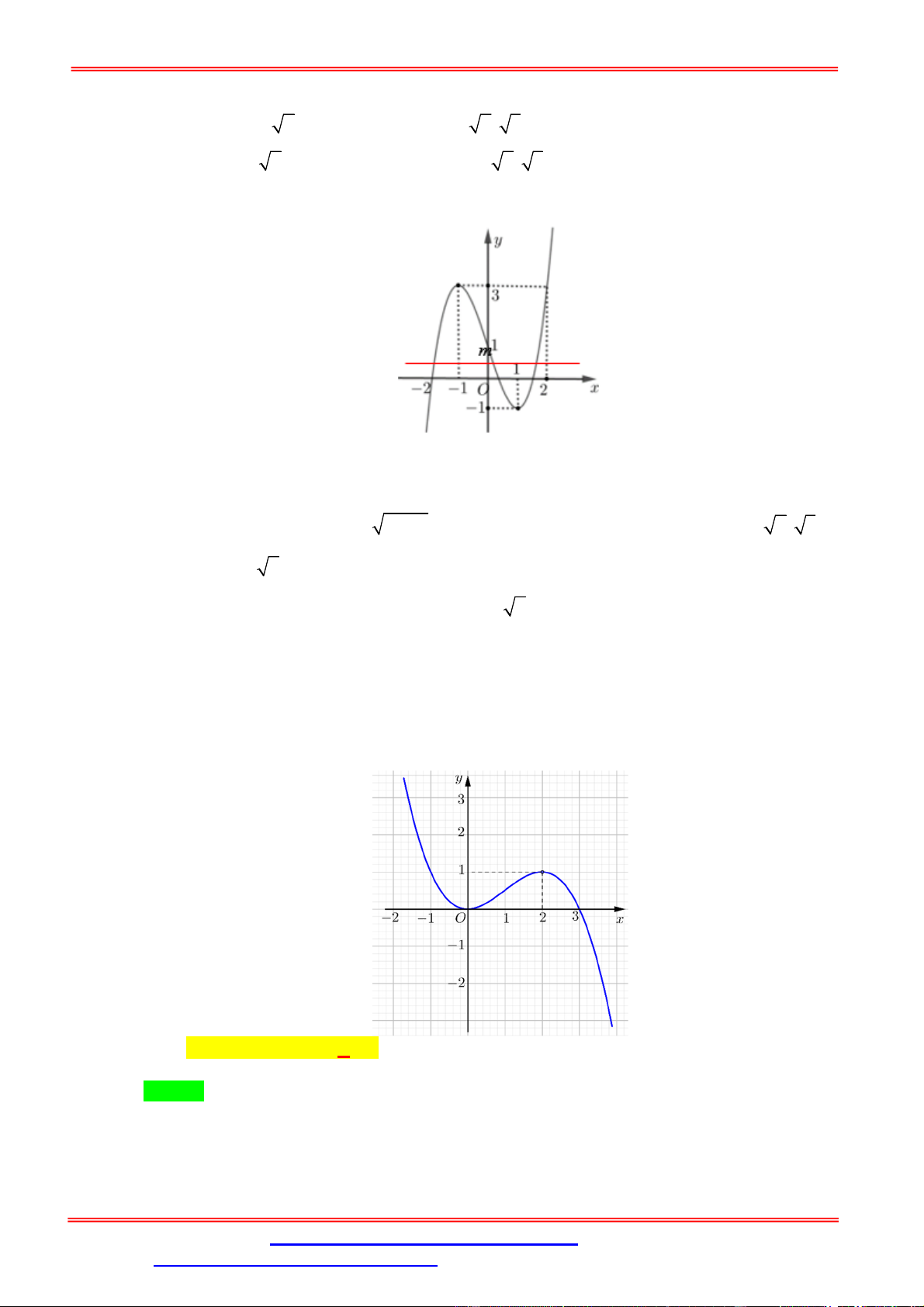
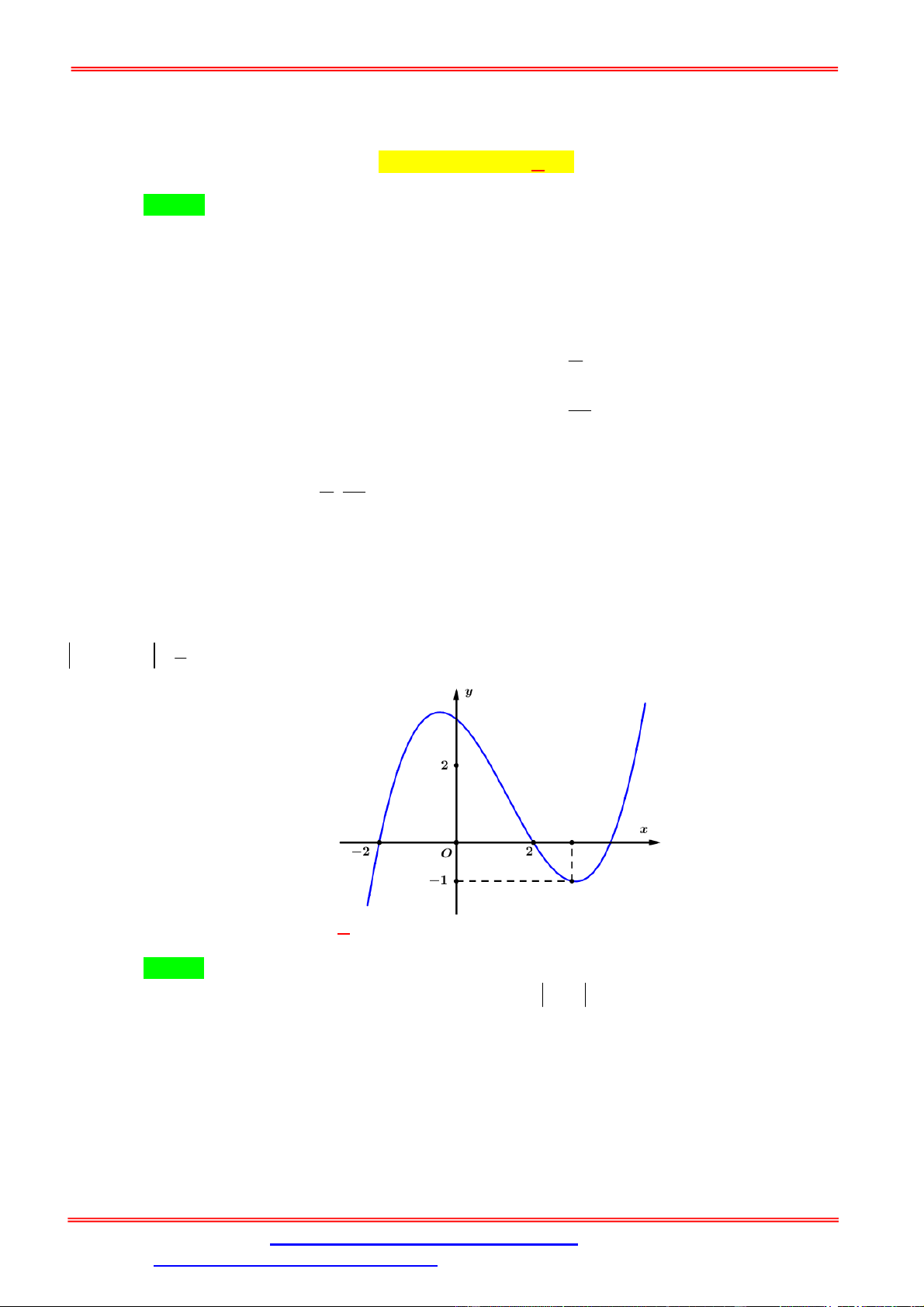
Câu 6. Cho y  f  x là hàm số bậc 3 và có đồ thị như hình vẽ bên.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
  29  19
Số nghiệm thuộc nửa khoảng  ; 
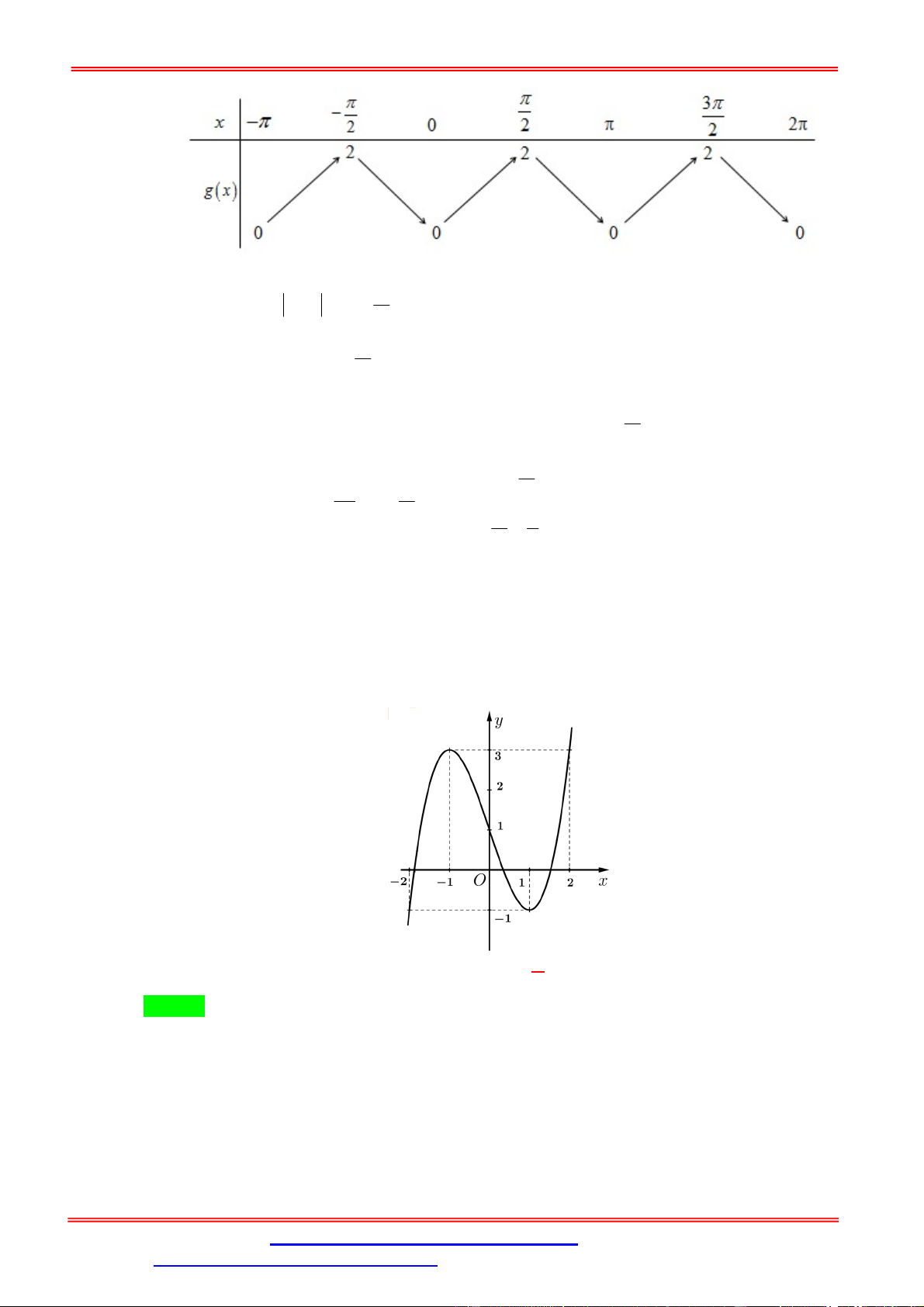
của phương trình f 2sin x   1  là 2 6    10 A. 17 . B. 15. C. 10. D. 16 . Lời giải. Chọn D
Vì y  f  x là hàm số bậc 3 nên điểm uốn của ĐTHS là I 1; 2 .  a1  1  sin x   1  ;      1 2 2 2
 sin x 1 a 1  ;  0    19   b1  1 
Do đó, từ đồ thị ta có: f 2sin x   1   2
 sin x 1 b1;2  s  in x   0;   2 10  2 2    2
 sin x 1 c2;  3   c 1  1  s  in x   ;1     3  2 2    29 / 6   / 2
  29 
Dựa vào đồ thị hàm số y  sin x trên nửa khoảng  ; 
hoặc dùng đường tròn lượng giác, 2 6    ta được:
- Phương trình 1 có 5 nghiệm phân biệt.
- Phương trình 2 có 5 nghiệm phân biệt khác 5 nghiệm ở trên.
- Phương trình 3 có 6 nghiệm phân biệt khác 10 nghiệm ở trên.
  29 
Vậy phương trình đã cho có 16 nghiệm trên nửa khoảng  ;  . 2 6   
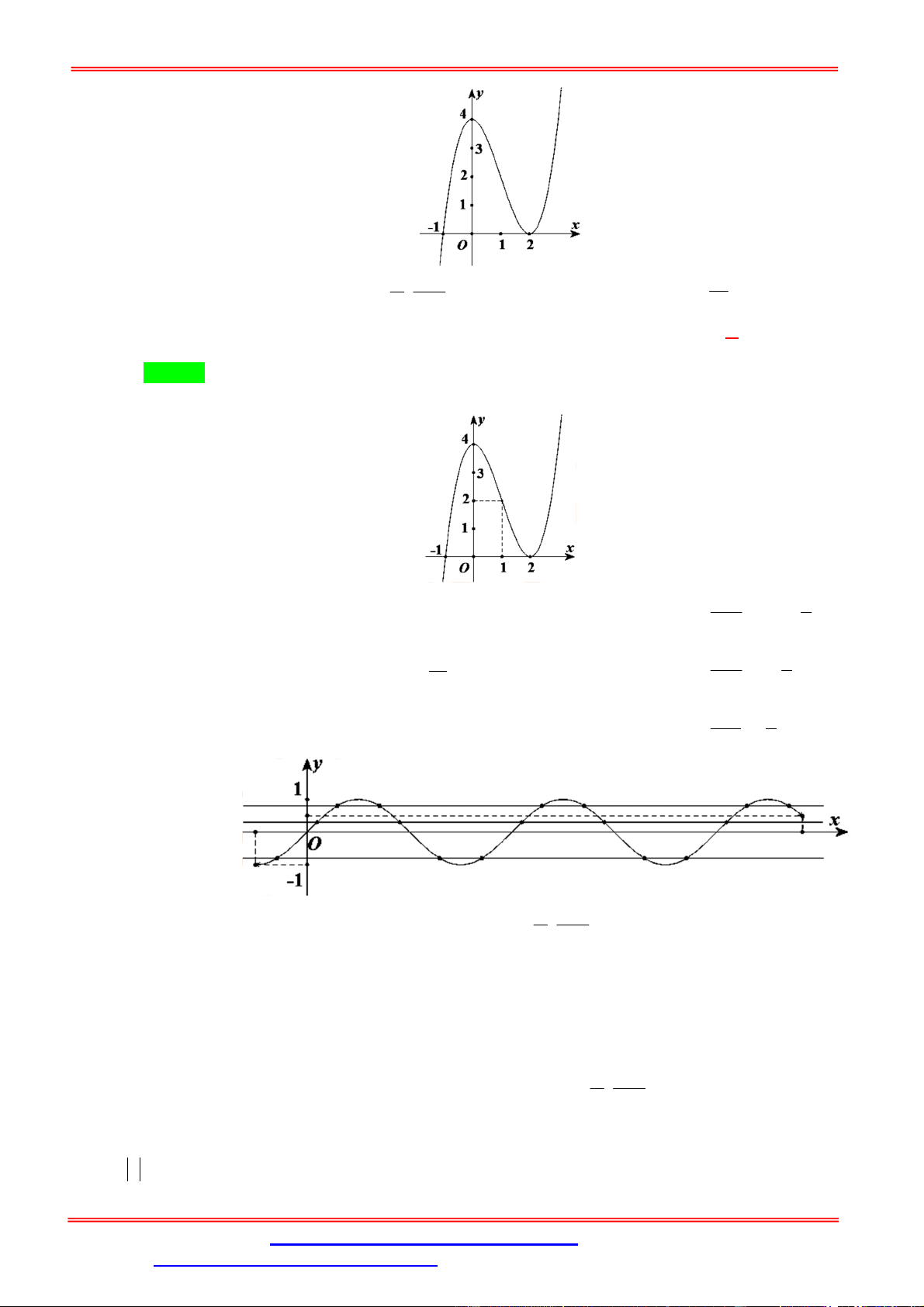
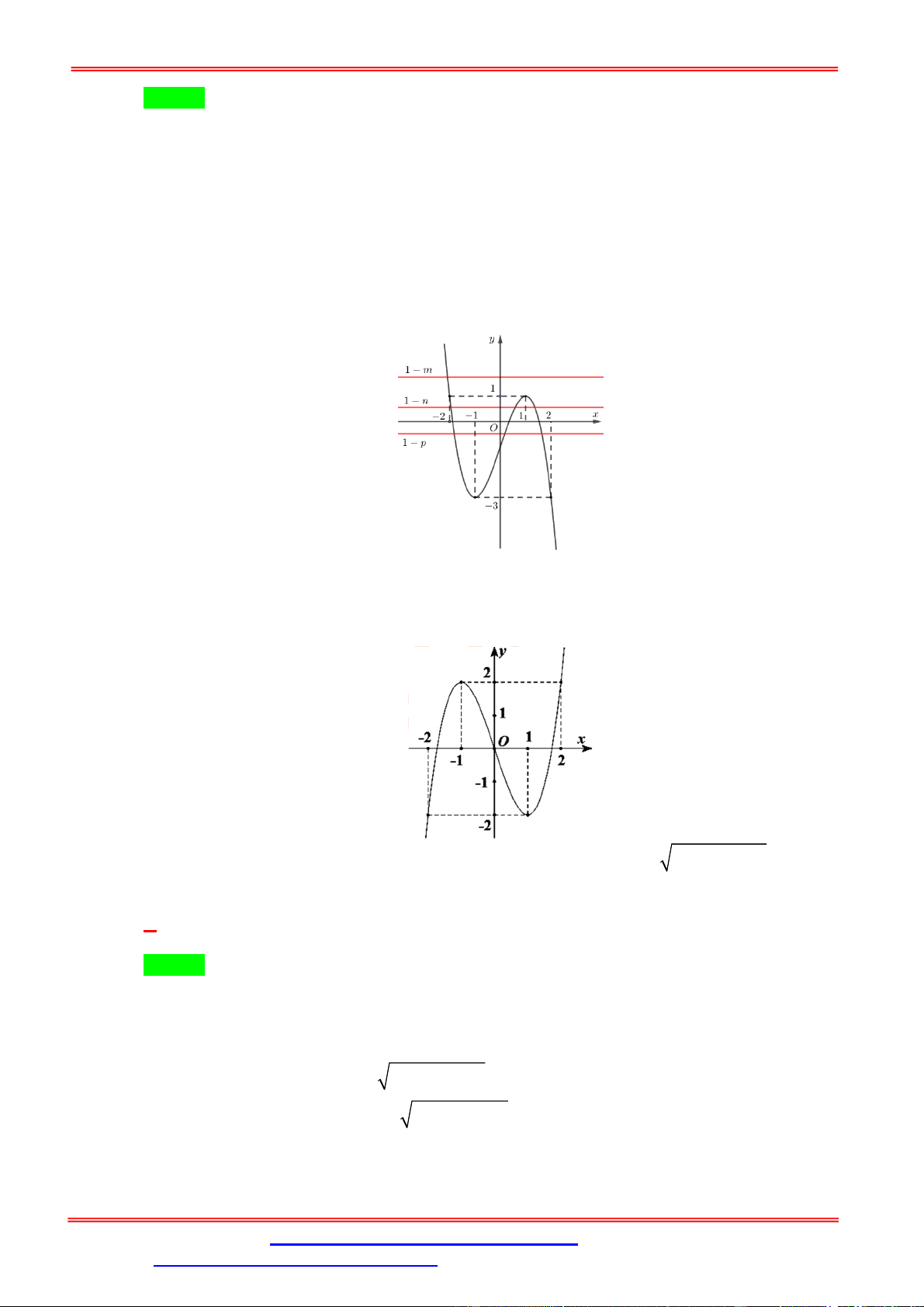
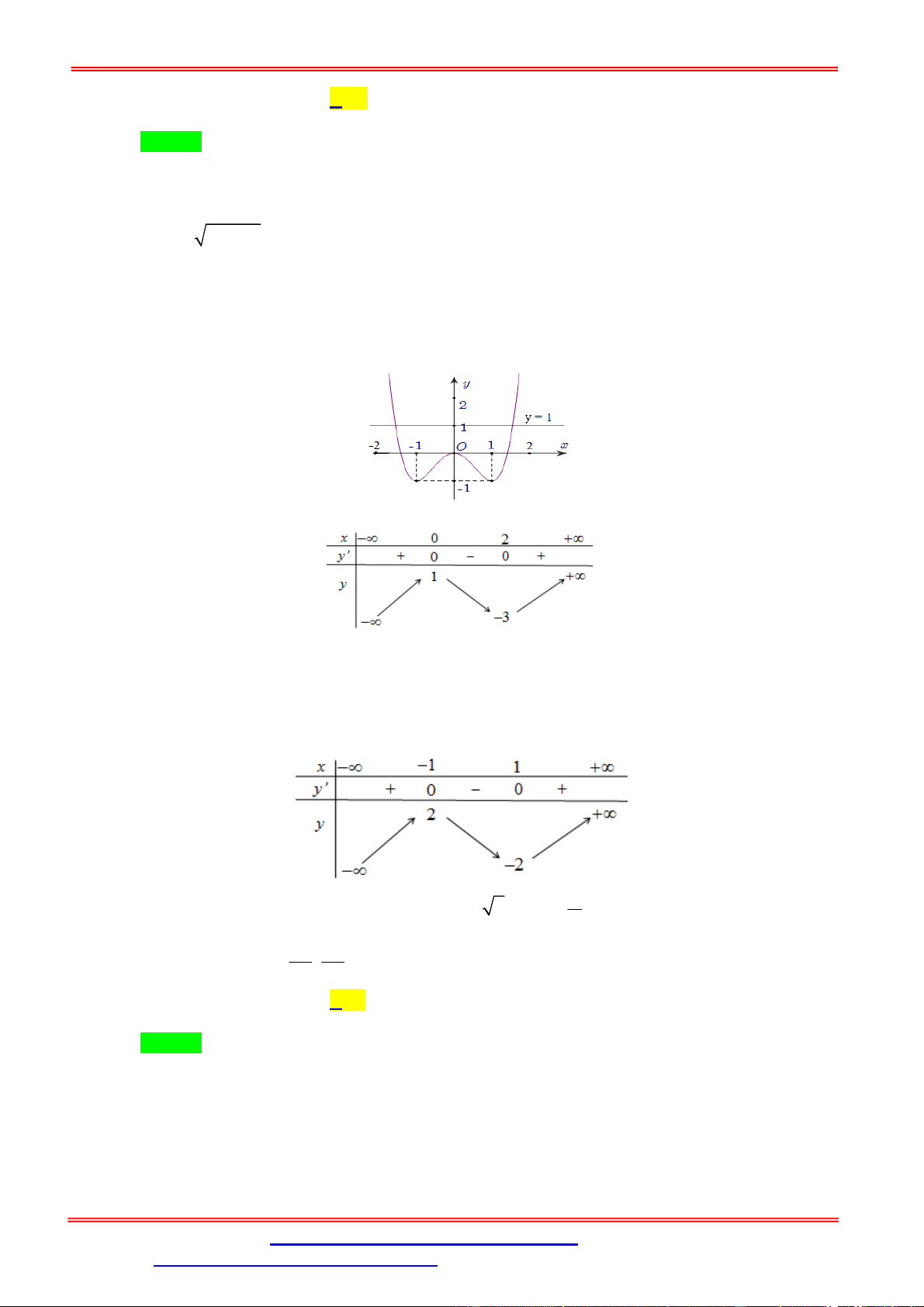
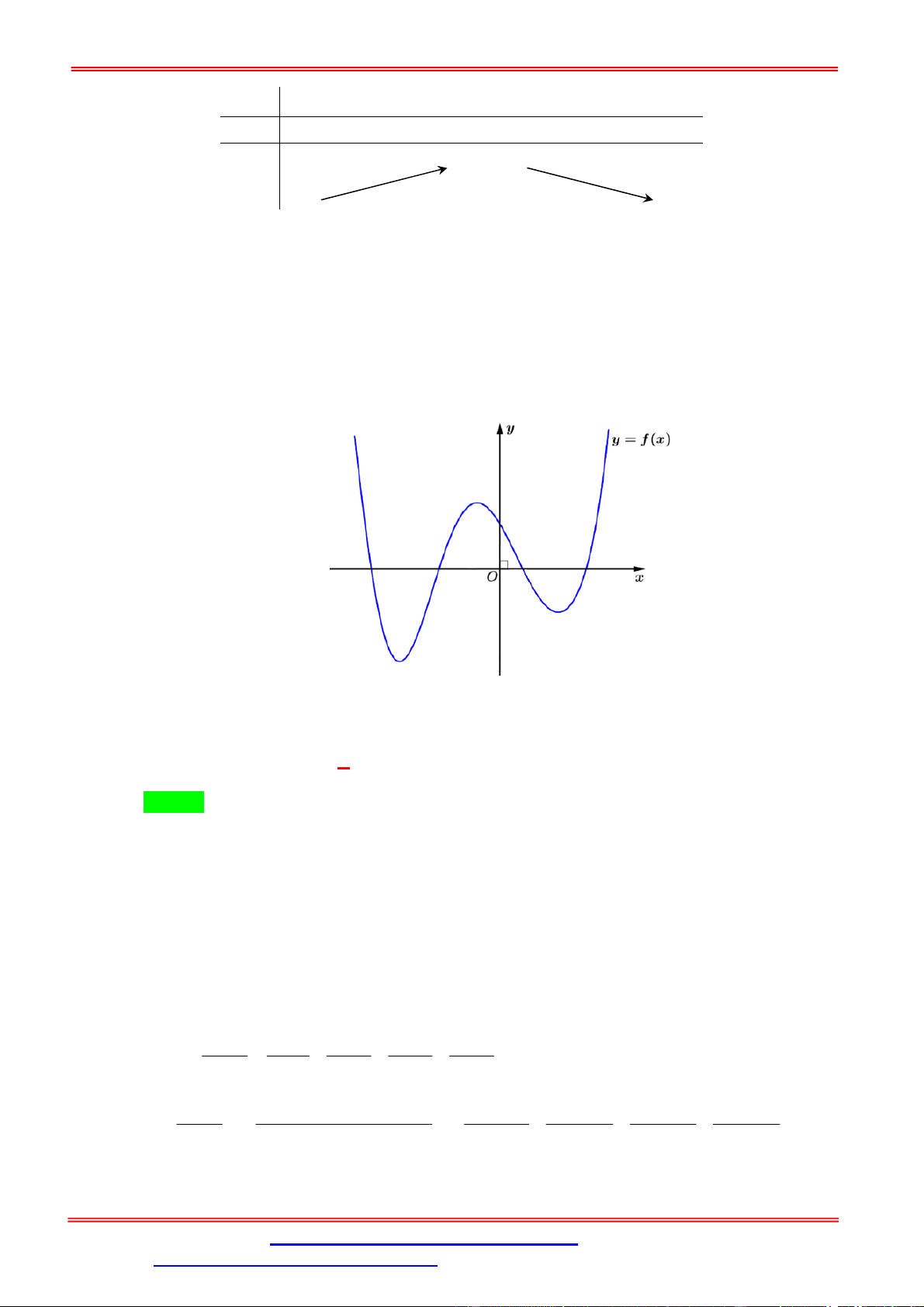
Câu 7. Cho hàm số y  f x có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của m để phương
trình f  x  
1  m có 4 nghiệm phân biệt?
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 A. 2. B. 1. C. 3. D. 4. Lời giải Chọn C
- Hàm số y  f  x  
1 là hàm số chẵn nên đồ thị hàm số nhận trục Oy làm trục đối xứng.  f   x   1 khi x  0
- Ta có f  x  
1   f x 1 khi x  0 
+) Ta vẽ đồ thị C của hàm số y  f  x  
1 được suy từ đồ thị C của hàm số y  f  x đã 1 
cho bằng cách tịnh tiến C sang phải 1 đơn vị và bỏ đi phần đồ thị ở bên trái trục Oy .
+) Sau đó lấy đối xứng phần đồ thị C ở bên phải trục tung 1 
qua trục tung thì được đồ thị của hàm số y  f  x   1 .
Khi đó, để phương trình đã cho có 4 nghiệm phân biệt thì
ta phải có 3  m  1 .
Suy ra, có 3 số nguyên thỏa mãn bài toán.
Câu 8. Cho hàm số y  f  x liên tục trên  có đồ thị như hình vẽ.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Có bao nhiêu giá trị nguyên của 2
n để phương trình f 16cos x  6sin 2x  8  f n n   1  có nghiệm x   ? A. 10 B. 4 C. 8 D. 6 Lời giải Chọn D
Dựa vào đồ thị hàm số ta thấy hàm số y  f  x đồng biến trên  . Do đó: f  2 x 
x    f nn   2 16 cos 6sin 2 8
1  16 cos x  6sin 2x  8  n n   1 1 cos 2x  16.
 6sin 2x 8  n n  
1  8cos 2x  6sin 2x  nn   1 2 2 2
Phương trình có nghiệm x   2 2 2  
 n n   2 8 6 1
 n n   1  100 
n n   2 1  10  
n  n 10  0 1 41 1   41 2   
 n  n 10  0   n  .
n n   2 1  10
n  n 10  0 2 2  
Vì n   nên n  3  ; 2; 1;0;1;  2 .
Câu 9. Cho hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ.
Gọi m là số nghiệm của phương trình f  f  x  1. Khẳng định nào sau đây là đúng? A. m  6 . B. m  7 . C. m  5 . D. m  9 . Lời giải Chọn B
Đặt f  x  u khi đó phương trình f  f  x  1trở thành f u 1  1 .
Nghiệm của phương trình (1) là hoành độ giao điểm của đồ thị hàm số y  f u và đường thẳng y  1.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020  5 
Dựa vào đồ thị ta có 3 nghiệm giả sử u  1
 ; 0 , u  0;1 , u  ;3 . 2   1   3    2 
Xét số giao điểm của đồ thị hàm số f  x với từng đường thẳng y  u , y  u , y  u . 1 2 3
Dựa vào đồ thị ta có:
Phương trình f  x  u , với u  1
 ; 0 cho 3 nghiệm phân biệt. 1   1
Phương trình f  x  u , với u  0;1 cho 3 nghiệm phân biệt. 2   2  5 
Phương trình f  x  u , với u  ;3 cho 1 nghiệm duy nhất. 3 3    2 
Suy ra phương trình ban đầu f  f  x  1 có 7 nghiệm.
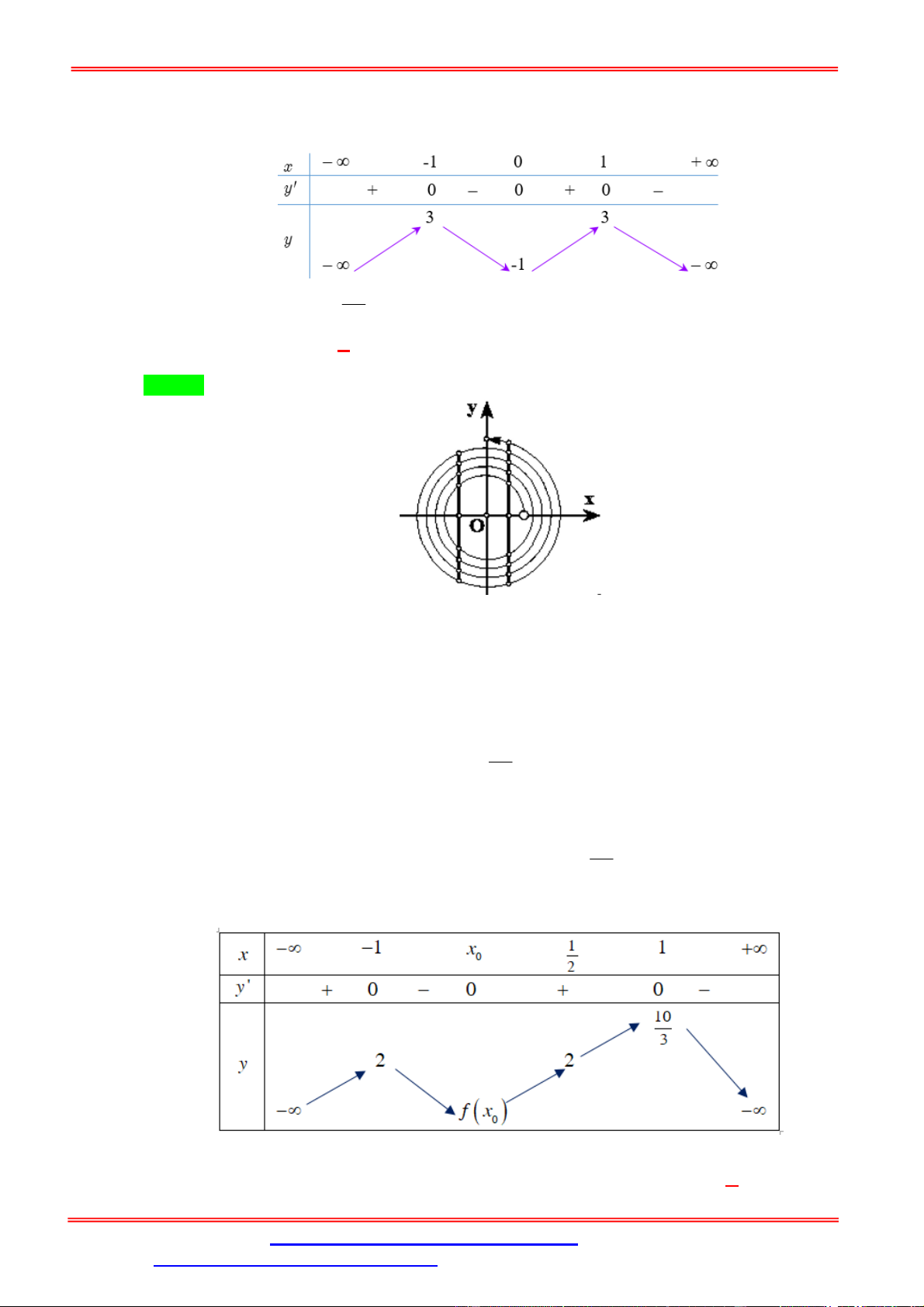
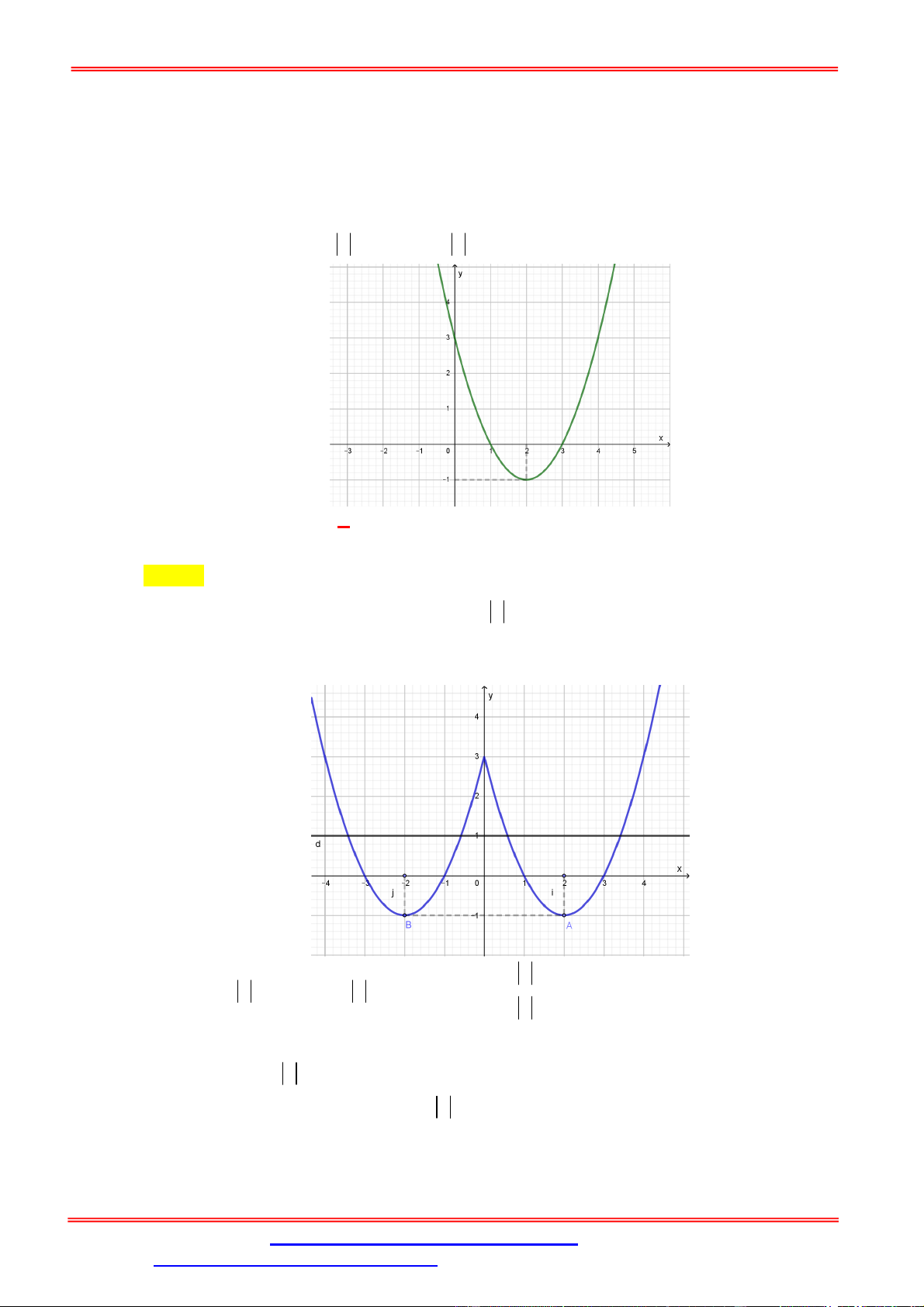
Câu 10. Cho hàm số y  f x có đồ thị như hình bên. Hỏi có bao nhiêu điểm trên đường tròn lượng
giác biểu diễn nghiệm của phương trình f  f cos 2x  0   ? A. 1 điểm. B. 3 điểm. C. 4 điểm. D. vô số. Lời giải Chọn C Ta luôn có: 1
  cos 2x 1 nên từ đồ thị suy ra: 0  f cos 2x1. Trên đoạn 0; 
1 : f  f cos 2x  0  f cos 2x  0  
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020    Trên đoạn 1; 
1 : f cos 2x 0  cos 2x  0  2x 
 k  x   k . 2 4 2 Vậy có 4 điểm.
Câu 11. Cho hàm số f  x  x5  x3 2
 5x 1. Số nghiệm thực của bất phương trình
f sin2 x  2sin x  3  f 0 trên đoạn   3 ;  3  là A. 3 . B. 2 . C. 0 . D. vô số. Lời giải Chọn A
f  x  x4  x2 5 6  5  , 0 x
    f  x đồng biến trên  .
Khi đó, bất phương trình f sin2 x  2sin x  3  f 0  sin2 x  2sin x  3  0 s  in x  1   
 sin x  1  x    k  2 k   . sin x   3 2  5   3
Nghiệm của bpt đã cho trên đoạn   3 ;  3  là  ,  và . 2 2 2
Câu 12. Cho hàm số f  x 3
 x  3x 1. Tìm số nghiệm của phương trình f  f  x  0 . A. 5. B. 9. C. 4. D. 7 . Lời giải Chọn D
Xét phương trình f  x 3
 0  x  3x 1  0 dùng máy tính cầm tay ta ước lượng được phương  x  1  ,879 1 
trình có ba nghiệm và x  1,532 . 2   x  0,347  3
Xét hàm số f  x 3
 x  3x 1, ta có bảng biến thiên của f  x như sau:
 f  x  1  ,879 
Xét phương trình f  f  x  0  
1 ta ước lượng được f
  x  1,532 .
 f x  0,347 
Dựa vào bảng biến thiên của hàm số f  x ta có:
+ Với f  x  1,879 phương trình 1 có 1 nghiệm.
+ Với f  x 1,532 phương trình 1 có 3 nghiệm.
+ Với f  x  0,347 phương trình 1 có 3 nghiệm.
Vậy phương trình đã cho có 7 nghiệm.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
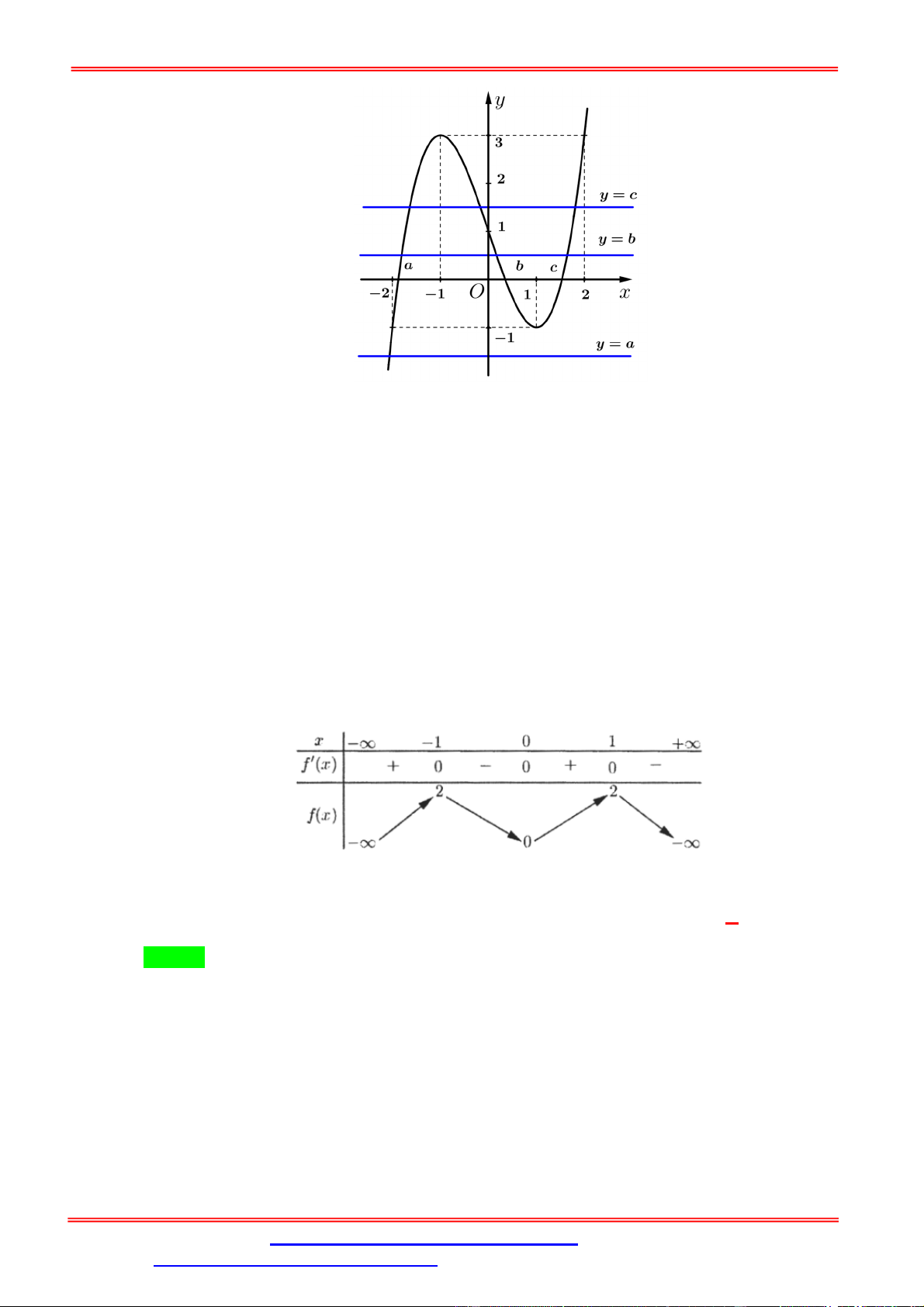
Câu 13. Cho hàm số y  f x  ax3  bx2  cx  d có đồ thị như hình bên dưới.
Có bao nhiêu giá trị nguyên của tham số 2
m để phương trình f x  m  
5 f x  4m  4  0 có 7 nghiệm phân biệt? A. 1 . B. 2 . C. 3 . D. 4 . Lờigiải Chọn C
Từ đồ thị hàm số y  f x, vẽ được đồ thị hàm số y  f x như sau:
 f x  4   1 Ta có 2
f x  m  5 f x  4m  4  0  
 f x  m  1 2 
Từ đồ thị hàm số y  f x suy ra phương trình (1) có 3 nghiệm phân biệt.
Vậy để phương trình đã cho có 7 nghiệm phân biệt thì (2) có 4 nghiệm phân biệt và khác với
các nghiệm của (1)  0  m  1  4  1  m  3 . Do đó có 3 giá trị nguyên của m .
Câu 14. Cho hàm số f xác định trên  và cũng nhận giá trị trên tập  thỏa mãn:
f  x  f x 4 3 2
 x 12x  4 với mọi x, y thuộc R. Tính giá trị f   1 . A. f   1  1 B. f   1  1 C. f   1  9 D. f   1  9  Lời giải Chọn B
Cho x  1 ta được f    f      3 4 2 1 1 1 12 1  4  7  4 3
Cho x  1 ta được 2 f   1  f   1    1 12  1  4  17 2 f    1  f   1  7  f    1  1 Ta có hệ     f    1  2 f   1  17 f     1  9 
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Câu 15. Cho hàm số   4 3 2
f x  mx  nx  px  qx  r , (với m,n, ,
p q,r   ). Hàm số y  f xcó
đồ thị như hình vẽ bên dưới:
Tập nghiệm của phương trình f x   r có số phần tử là A. 4 . B. 3 . C. 1 . D. 2 . Lời giải Chọn B
Ta có f  x 3 2
 4mx  3nx  2 px  q   1 5
Dựa vào đồ thị y  f   x ta thấy phương trình f  x  0có ba nghiệm đơn là 1  , , 3. 4
Do đó f  x  m x  
1 4x  5 x  3và m  0.
Hay f  x 3 2
 4mx 13mx  2mx 15m 2 . 13 Từ  
1 và 2 suy ra n  
m , p  mvà q  15m . 3
Khi đó phương trình f  x  r  4 3 2
mx  nx  px  qx  0  13   4 3 2 m x 
x  x 15x  0    3   4 3 2
3x 13x  3x  45x  0  x  0  5
 x  x    x  2 3 5 3
 0   x   .  3  x  3   5 
Vậy tập nghiệm của phương trình f  x  r là S    ; 0;3 .  3 
Câu 16. Cho hàm số f xác định trên tập số nguyên và nhận giá trị cũng trong tập số nguyên, thỏa mãn  f    1  0 
với mọi m, n là số nguyên.
f m  n  f m  f n  34mn    1 
Tính f 19 .
A. f 19  1999 .
B. f 19  1998 .
C. f 19  2000 . D.
f 19  2001 Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
m  n  1  f 2  2 f   1  9  9
m  n  2  f 4  2 f 2  45  63
m  n  4  f 8  2 f 4 189  315
m  n  8  f 16  2 f 8  765  1395
m  2; n  1  f 3  f 2  f   1  21  30
m  16; n  3  f 19  f 16  f 3  573  1998
Câu 17. Cho hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị của   
tham số m để phương trình f cos x  2m 1 có nghiệm thuộc khoảng 0;   là  2  y 3 1 1 x 1 1 A.  1  ;  1 . B. 0;  1 . C.  1  ;  1 . D. 0;  1 . Lời giải Chọn B   
Đặt t  cos x . Khi đó: x  0; 
 thì t  0;  1 .  2 
Bài toán trở thành: Tìm m để phương trình f t   2
 m  1 có nghiệm t  0;  1 hay phương
trình f  x  2m 1 có nghiệm x  0;  1 .
Từ đồ thị ta thấy điều kiện bài toán tương đương 1
  2m 1  1  0  m  1.
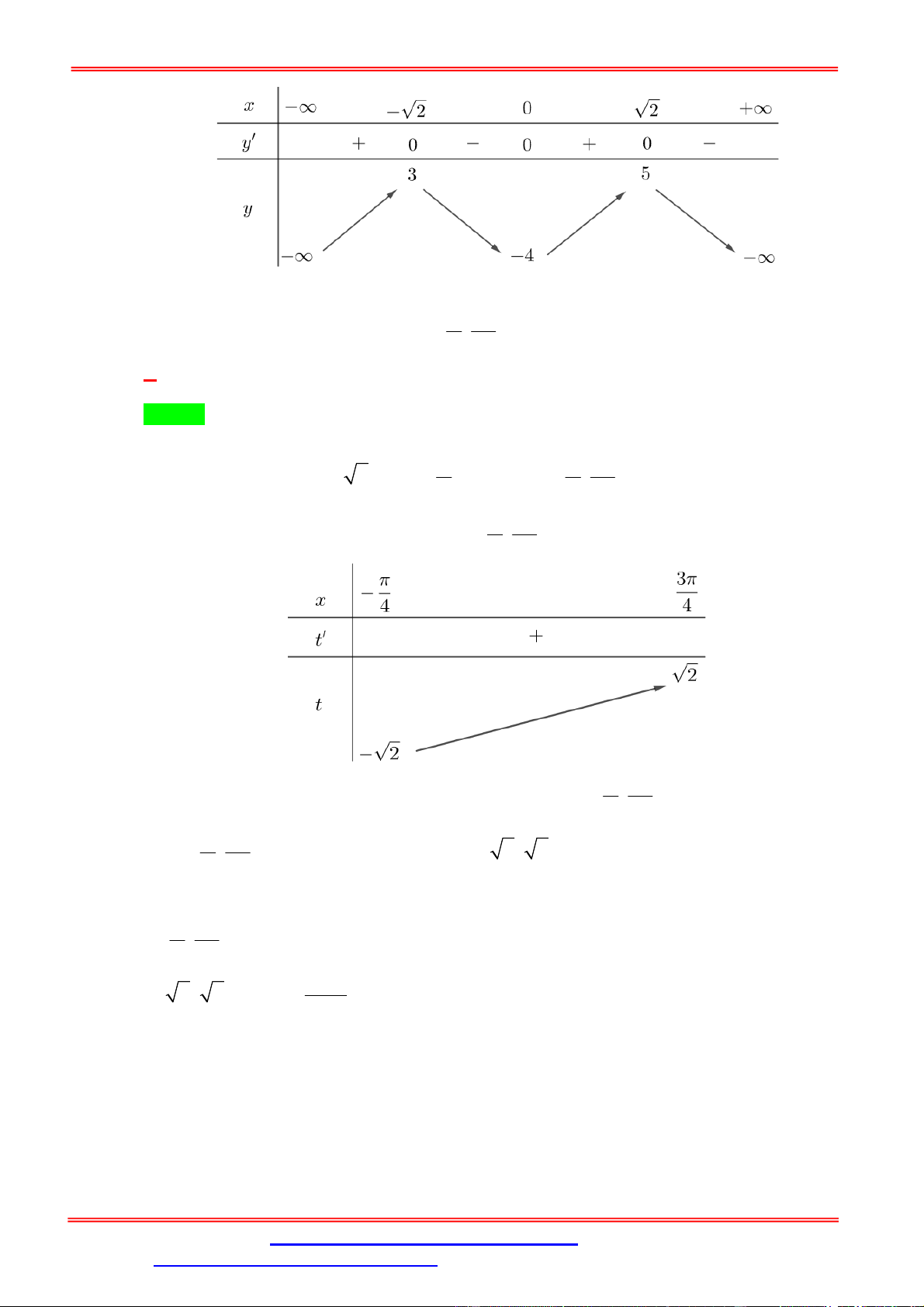
Câu 18. Cho hàm số y  f (x) có bảng biến thiên sau.
Tìm tất cả các giái trị của tham số m để phương trình f (2 tan x)  2m 1 có nghiệm thuộc  khoảng (0; ) . 4 1 1 A. 1   m  . B. 1   m  .
C. 1  m  1 . D. m  1 . 2 2 Lời giải Chọn C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 
Đặt t  2 tan x, x (0; )  t (0; 2) . 4 
Phương trình f (2 tan x)  2m 1 có nghiệm thuộc khoảng (0; ) . 4
 Phương trình f (t)  2m 1 có nghiệm thuộc khoảng (0; 2) .
Từ BBT ta suy ra 1  2m 1  3  1  m  1 .
Câu 19. Cho hàm số y  f  x . Đồ thị hàm y  f  x như hình vẽ y 2 x O  3 3 1 
Đặt g  x  f  x 3 3
 x  3x  m , với m là tham số thực. Điều kiện cần và đủ để bất phương
trình g  x  0 đúng với x    3; 3 là  
A. m  3 f  3 .
B. m  3 f 0 .
C. m  3 f   1 . D.
m  3 f  3 . Lời giải Chọn A
g  x   f  x 3
 x  x  m   f  x 3 0 3 3 0 3
 x  3x  m .
Đặt h  x  f  x 3 3
 x  3x . Ta có h x  f  x 2 3  3x  3 . Suy ra
h 3  3 f  3  6  0  
h  3  3 f  3  6  0 
h0  3 f 0  0  h   1  3 f   1  0 
Từ đó ta có bảng biến thiên x  3 0 1 3 h  0  h  3 h h 0 h  3
Vậy g  x  m  g  x  h 3  3 f  3 .
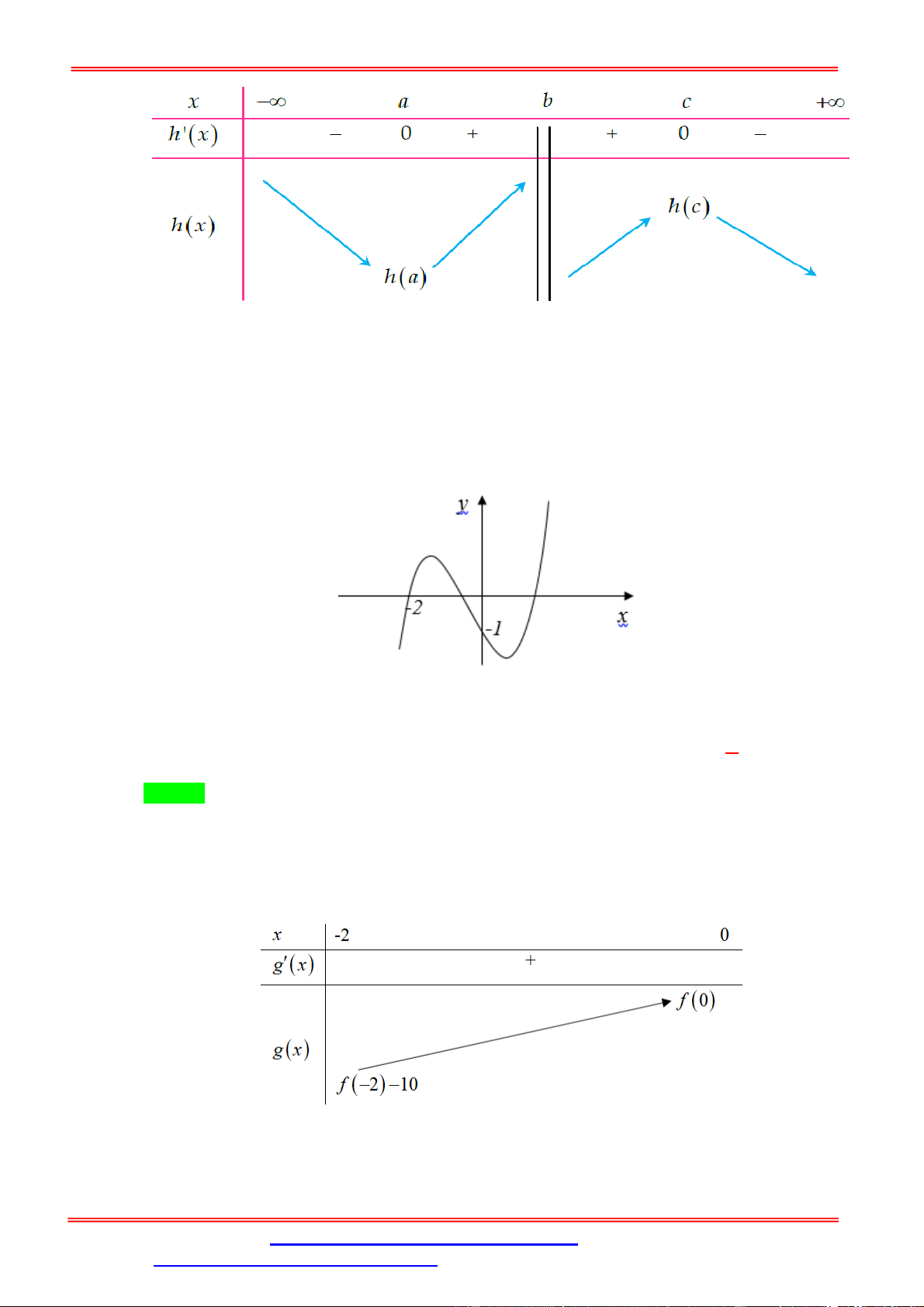
Câu 20. Cho hàm số y  f '(x) có đồ thị như hình vẽ dưới đây.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Xét tính đơn điệu của hàm số 2
g(x)  2 f (x)  x  2x ta được
A. Hàm số g ( x) nghịch biến trên  ;  2  ; 1  ; 
1 ;2;  ; đồng biến trên  2  ;   1 ;1;2 .
B. Hàm số g ( x) đồng biến trên  ;  2  ; 1  ; 
1 ;2;  ; nghịch biến trên  2  ;   1 ;1;2 .
C. Hàm số g ( x) đồng biến trên  ;
 2;1;  ; nghịch biến trên  2  ;  1 .  3   3   3   3 
D. Hàm số g ( x) đồng biến trên  ;   ; 0;   
 ; nghịch biến trên  ;0 ; ;      .  2   2   2   2  Lời giải Chọn B Ta có  x  2   x  1  g '(x)
2 f '(x) 2x 2; g '(x) 0 f '(x) x 1          .  x  1  x  2  Ta có đồ thị sau:
Hàm số đồng biến trên  ;  2  ; 1  ; 
1 ;2;  ; nghịch biến trên  2  ;   1 ;1;2 .
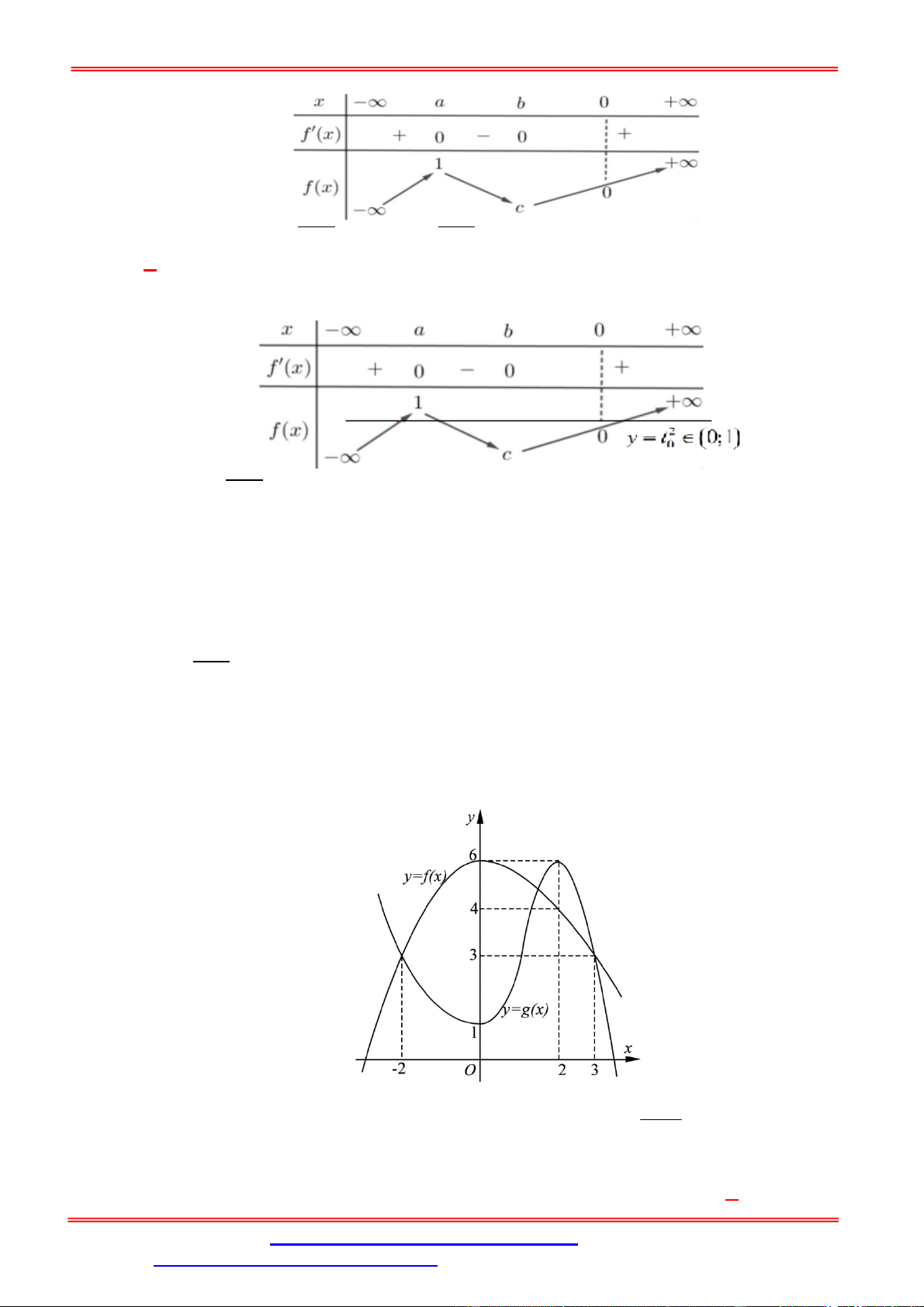
Câu 21. Cho hàm số f  x xác định và liên tục trên  và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của m để phương trình f  2 2. 3  3 9
 x  30x  21  m  2019 có nghiệm.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 A. 15 . B. 14 . C. 10 . D. 13 . Lời giải Chọn D  7 
Điều kiện: x  1;  . 3    Xét phương trình: f  2 2. 3  3 9
 x  30x  21  m  2019   1 . 2 2 Ta có:  x  x     x  2 2 9 30 21 4 3 5
 0  4  3x  5  2  3
  3  3 4  3x  5  3. Đặt 2
t  3  3 9x  30x  21 , t 3;  3 . m  2019
Khi đó, phương trình  
1 trở thành: 2. f t   m  2019  f t   2 . 2  7  Phương trình   1 có nghiệm x  1; 
 phương trình 2 có nghiệm t 3;  3 . 3   
Dựa vào đồ thị của hàm số y  f  x , phương trình 2 có nghiệm t 3;  3 khi và chỉ m  2019 khi 5  
 1  2009  m  2021. 2
Do m    m 2009, 2010,..., 202  1 .
Vậy số giá trị nguyên của m là: 2021 2009 1  13 .
Câu 22. Cho hàm số y  f (x) xác định và liên tục trên trên R có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số m để phương trình 7 f 5  2 1 3cosx   3m  7     
có hai nghiệm phân biệt thuộc ;  ? 2 2    A. 4 . B. 7 . C. 6 . D. 5 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Lời giải Chọn C     
Đặt t  5  2 1 3cosx (1). Vì x  ;
 0  cosx  1  t  1;  3  2 2    3m  7
Phương trình đầu trở thành f t   (2) 7 Nhận xét:     
+Với cosx  1  t  1 nên khi t  1 phương trình (1) chỉ có một nghiệm thuộc ;  2 2        
+Với mỗi t 1; 
3 thì phương trình (1) có hai nghiệm thuộc ;  2 2   
Như vậy dựa vào đồ thị hàm số ta thấy phương trình đầu có hai nghiệm phân biệt thuộc  3m  7  4  m  7        7 ;  
khi phương trình (2) có một nghiệm t 1;  3    7  7 2 2    3m  7   m  2   0  3 3  7
Vì m  Z m 7; 2  ; 1  ; 0;1;  2
Câu 23. Cho hàm số y  f  x có đạo hàm trên  và có đồ thị là đường cong trong hình vẽ dưới. Đặt
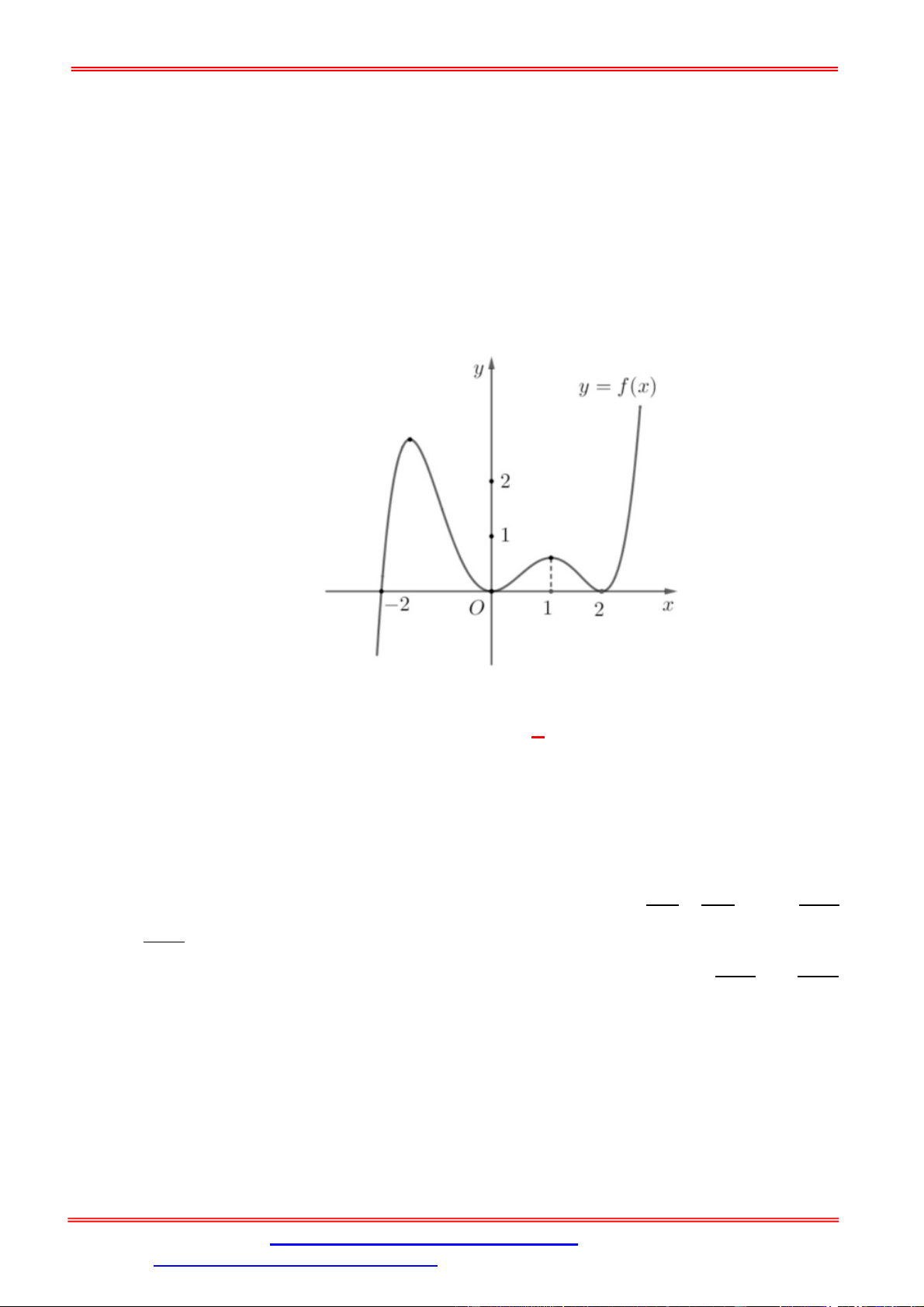
g  x  f  f  x 
 . Tìm số nghiệm của phương trình g x  0 . A. 2 . B. 8 . C. 4 . D. 6 . Lời giải Chọn B
 f  x  0
Ta có g x  f   f  x. f  x  0    
 f   f  x  0     x  0
f  x  0  x  x  2;3  3  
 f  x  0
f   f  x  0     .
 f  x  x  2;3  3  
 x  x  1;0 1   
+ f  x  0  x  1 
 x  x  3;4 3   
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
 x  x  x 2 1
+ f  x  x  2;3  . 3  
 x  x  0;1  3  
Vậy phương trình g x  0 có 8 nghiệm phân biệt.
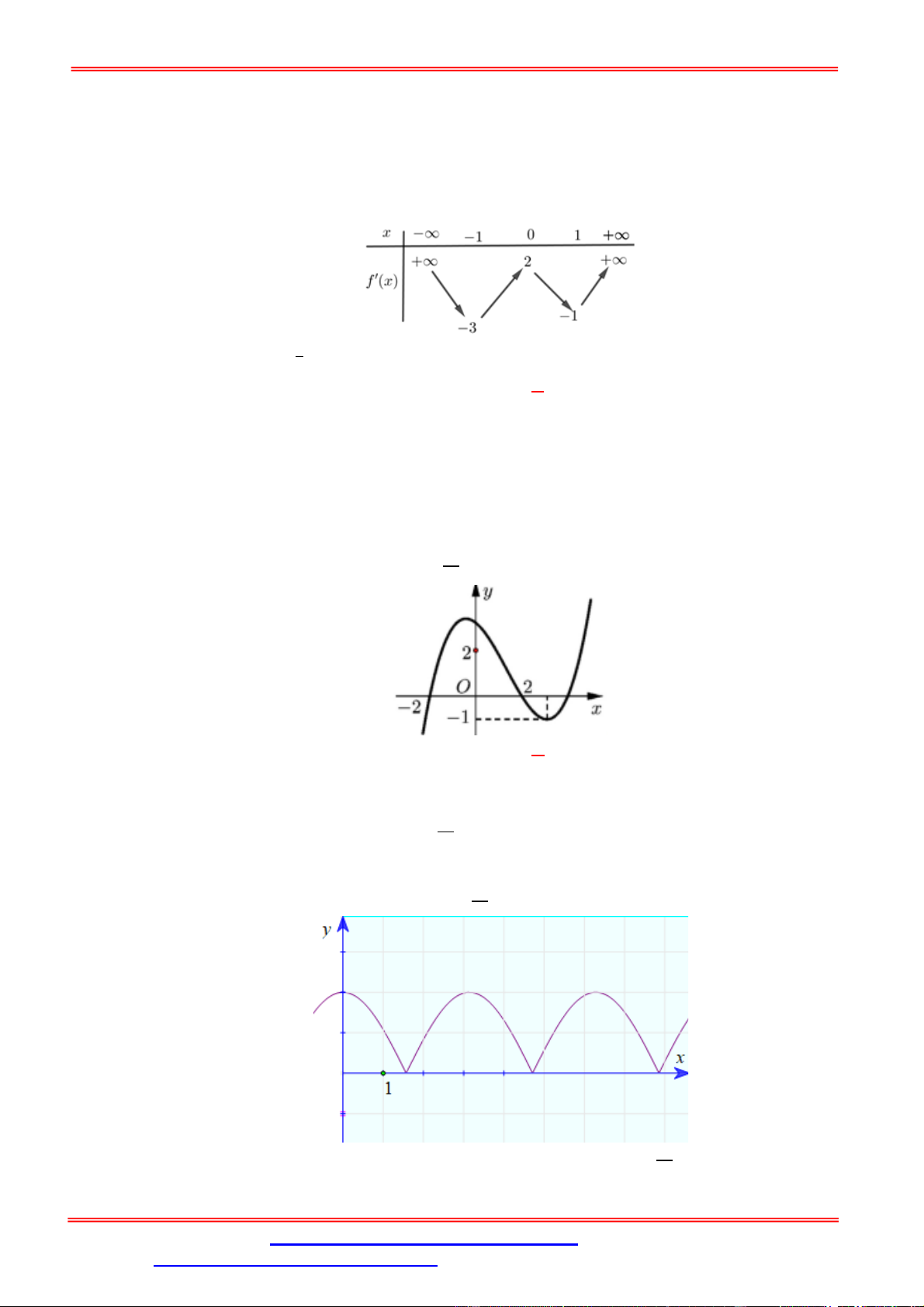
Câu 24. Cho hàm số ( ) có bảng biến thiên của ′( ) như hình sau: Đặt ( ) = ( ) −
+ 2 . Mệnh đề nào dưới đây đúng? A. (1) < (0) < (−1). B. (−1) < (0) < (1). C. (−1) = (1) > (0). D. (−1) = (1) < (0). Lời giải Chọn B
Ta có: ′( ) = ′( ) − + 2, ′( ) = 0 ⇔ ′( ) = − 2 Do đường thẳng =
− 2 đi qua (−1; −3), (1; −1) nên dựa vào bảng biến thiên ta có
′( ) ≥ 0, ∀ ⇒ (−1) < (0) < (1)
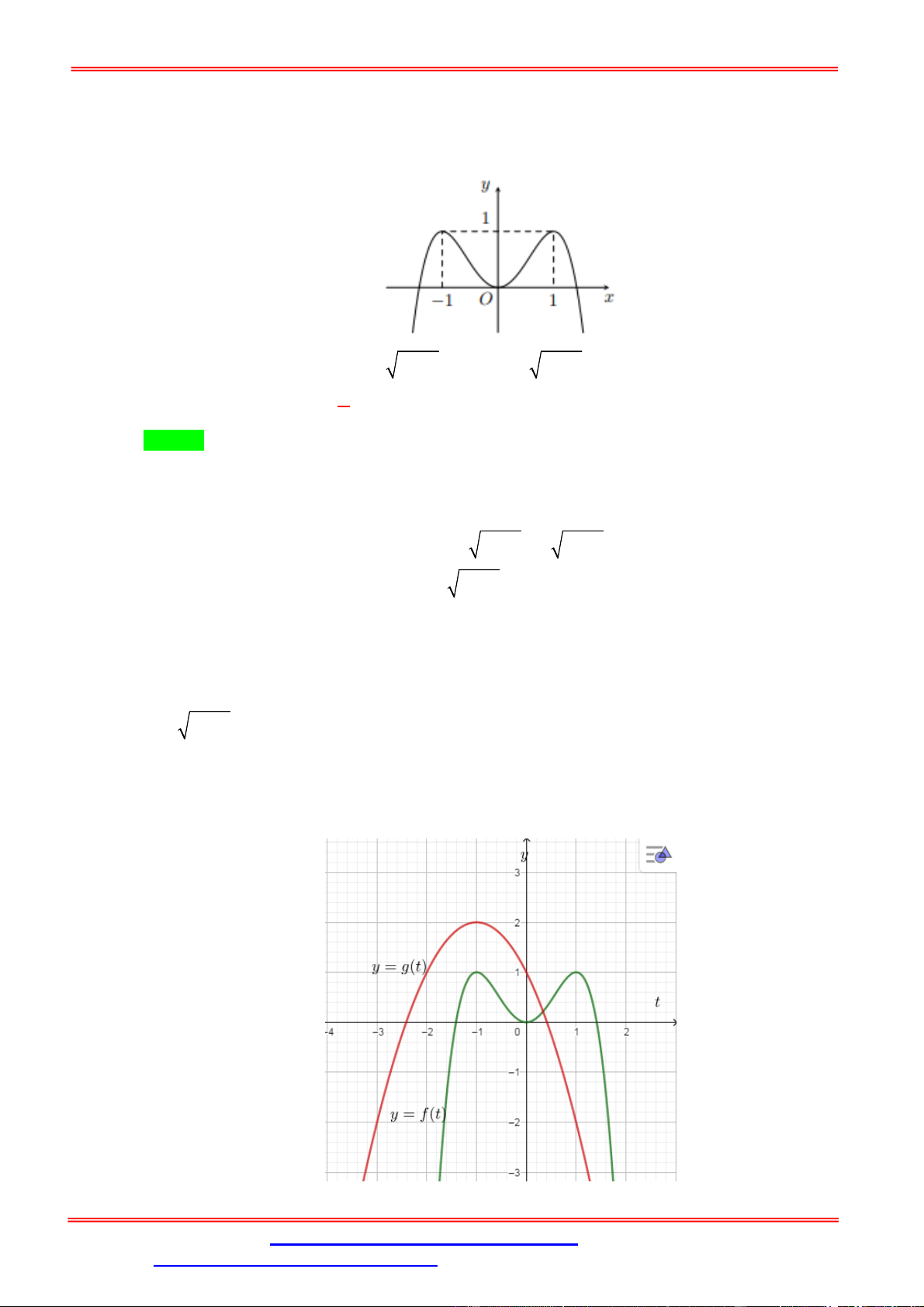
Câu 25. Cho hàm số = ( ) liên tục trên ℝ và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt
của phương trình (|2cos |) = 1 trên khoảng 0; là: A. . B. . C. . D. . Lời giải Chọn C = ∈ (−2; 0) Đặt
= |2cos | ∈ [0; 2], ∀ ∈ 0; ⇒ ( ) = 1 ⇔ = ∈ (0; 2) ⇔ |2cos | = ∈ = > 2 (0; 2)(∗).
Đồ thị hàm số = |2cos | trên khoảng 0; như hình vẽ bên.
Suy ra phương trình (∗) có 5 nghiệm thực phân biệt trên khoảng 0; .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Câu 26. Cho hàm số = ( ) có đồ thị như hình vẽ sau
Tìm số giao điểm của đồ thị hàm số = ( ) và trục hoành A. 2. B. . C. . D. . Lời giải Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số = ( ) và trục hoành là: ( ) = 0 (1). ( ) = 2 Ta có (1) ⇔ . ( ) = −2
Số nghiệm của phương trình (1) là tổng số giao điểm của đồ thị hàm số = ( ) và hai đường
thẳng song song = 2 và = −2. Từ đồ thị hàm số
= ( ), ta thấy tổng số giao điểm bằng 5. Suy ra phương trình (1) có 5n ghiệm phân biệt.
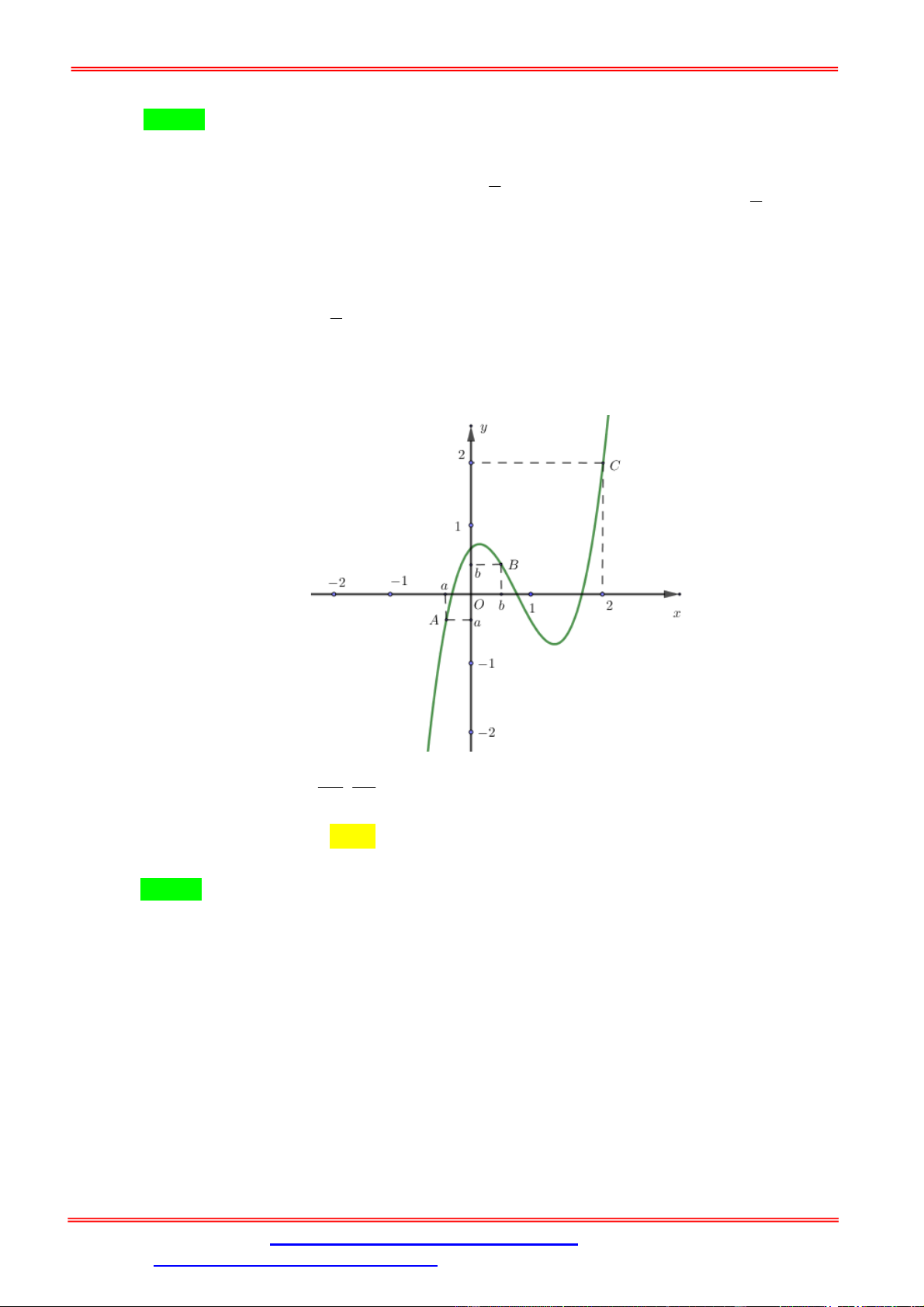
Vậy số giao điểm của đồ thị hàm số = ( ) và trục hoành là 5. Câu 27. Cho hàm số    3 2 y
f x  ax  bx  cx  d có đạo hàm là hàm số y  f  x với đồ thị như hình vẽ bên.
Biết rằng đồ thị hàm số y  f  x tiếp xúc với trục hoành tại điểm có hoành độ âm. Khi đó đồ
thị hàm số cắt trục tung tại điểm có tung độ là bao nhiêu? A. 4  . B. 1. C. 2. D. 4. Lời giải Chọn A
Ta có y  f  x 3 2
 ax  bx  cx  d  f  x 2
 3ax  2bx  c
Đồ thị hàm số y  f  x đi qua các điểm A 2
 ;0, O0;0và C 1; 3 nên ta có
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 1
 2a  4b  c  0 a  1   c  0
 b  3  y  f  x 3 2
 x  3x  d và f  x 2  3x  6x . 3  a 2b c 3      c  0  
Gọi tiếp điểm của đồ thị hàm số y  f  x và trục hoành là M  x ;0 x  0. 0  với 0
Tiếp tuyến có hệ số góc x  0
k  0  y ' x  0  3x  6x  0 
x  0  x  2  0  2 0 . Vì . 0 0 x  2  0 0  0 M  2
 ; 0 thuộc đồ thị hàm số y  f  x  8
 12  d  0  d  4  .
Khi đó y  f  x 3 2
 x  3x  4. Đồ thị hàm số cắt trục tung tại điểm có tung độ là 4 .
Câu 28. Cho hàm số y  f  x có đồ thị như hình vẽ sau:
Số nghiệm của phương trình 2 2 2
[f (x 1)]  f (x 1)  2  0 là A. 1. B. 4. C. 3 . D. 5 . Lời giải Chọn B Đặt 2
t  x  1  t  1.
Ta thấy ứng với t  1 cho ta một giá trị của x và ứng với mỗi giá trị t  1 cho ta hai giá trị của x .  f (t)  1 
Phương trình đã cho trở thành: 2
[f (t)]  f (t)  2  0   . f (t)  2 
Từ đồ thị hàm số y  f (t) trên [1;+) suy ra phương trình f (t)  1
 có 1 nghiệm t  2 và
phương trình f (t)  2 có 1 nghiệm t  2 do đó phương trình đã cho có 4 nghiệm.
Vậy phương trình đã cho có 4 nghiệm.
Câu 29. ##Cho hàm số f  x xác định trên  \ 
0 và có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình 3 f 2x   1 10  0 là. A. 2 . B. 1. C. 4 . D. 3 . Lời giải Chọn C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 10
Đặt t  2x 1, ta có phương trình trở thành f t 
. Với mỗi nghiệm t thì có một nghiệm 3 t 1 10 x 
nên số nghiệm t của phương trình f t  bằng số nghiệm của 2 3
3 f 2x   1 10  0 .
Bảng biến thiên của hàm số y  f  x là 10
Suy ra phương trình f t 
có 4 nghiệm phân biệt nên phương trình 3 f 2x   1 10  0 3 có 4 nghiệm phân biệt.
Câu 30. Cho hàm số y  f  x có đạo hàm f  x trên  \  
0 và có bảng biến thiên như hình dưới.
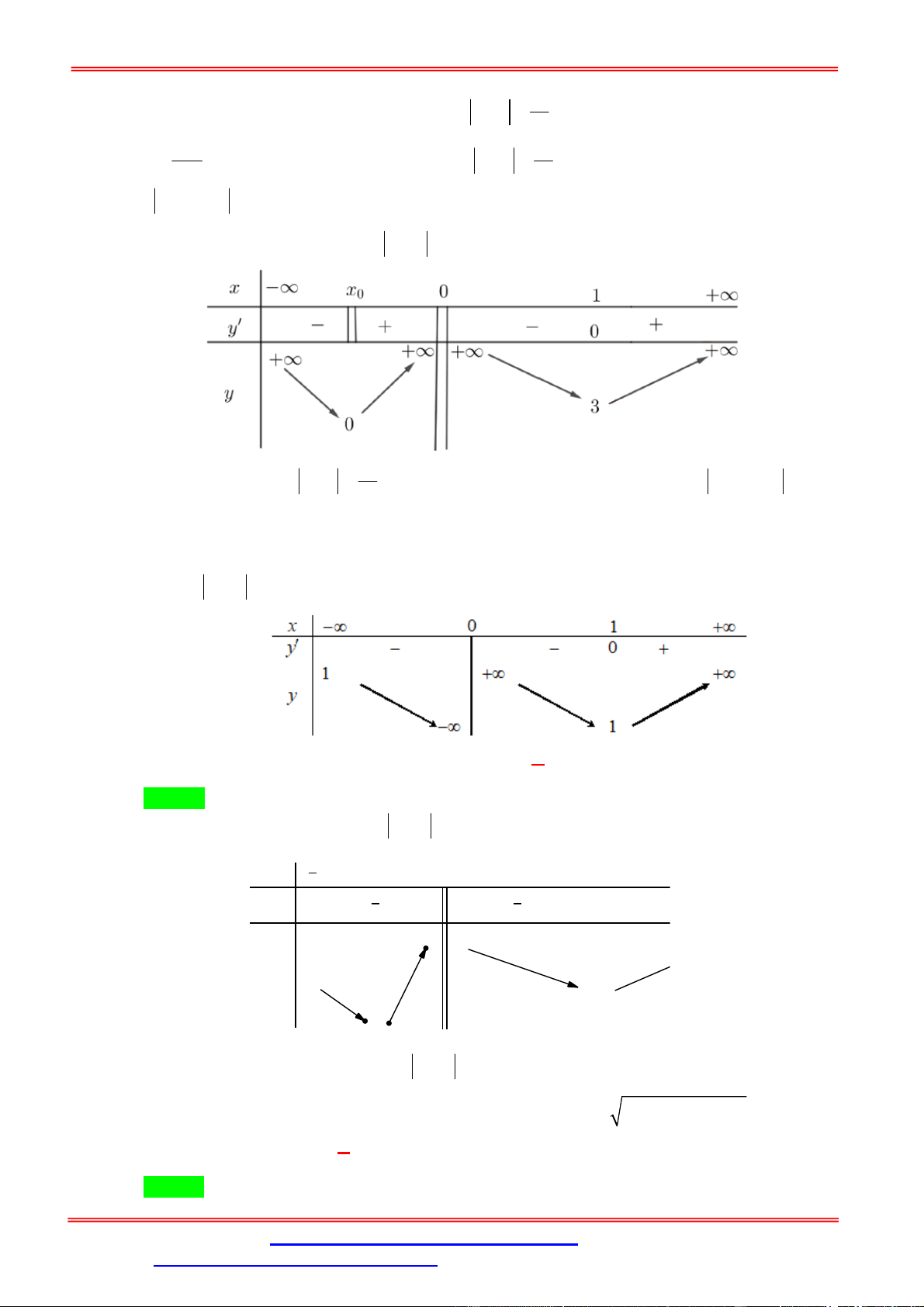
Hỏi phương trình f  x  2 có bao nhiêu nghiệm? A. 1 nghiệm. B. 2 nghiệm. C. 3 nghiệm. D. 4 nghiệm. Lời giải Chọn C
Bảng biến thiên cho hàm số y  f  x như sau: x ∞ x0 0 1 + ∞ y' 0 + + ∞ +∞ +∞ y 1 1 0
Dựa vào BBT suy ra: phương trình f  x  2 có 3 nghiệm phân biệt.
Câu 31. Cho hàm số f  x 3 2
 x  3 x 1. Số nghiệm của phương trình
f  f  x  2  4  f  x 1   là A. 5 . B. 6 . C. 8 . D. 9 . Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Đặt t  f  x 3 2
 2  t  x  3 x  3
Khi đó phương trình trở thành t 1  0 t    1
f t   4  t 1      f t  2 3 2
 4  t  2t 1
t  4t  2t  4  0   t  1  t  2  t  2     t  1 3  t  1 3  Xét hàm số 3 2
y  t  x  3x  3  x  0 2
y  3 x  6 x  3 x  x  2  0  x  2  Ta có bảng biến thiên
Dựa vào BBT ta có phương trình t  2 có 3 nghiệm phân biệt, phương trình t  1 3 có 3 nghiệm phân biệt.
Vây phương trình ban đầu có 6 nghiệm phân biệt.
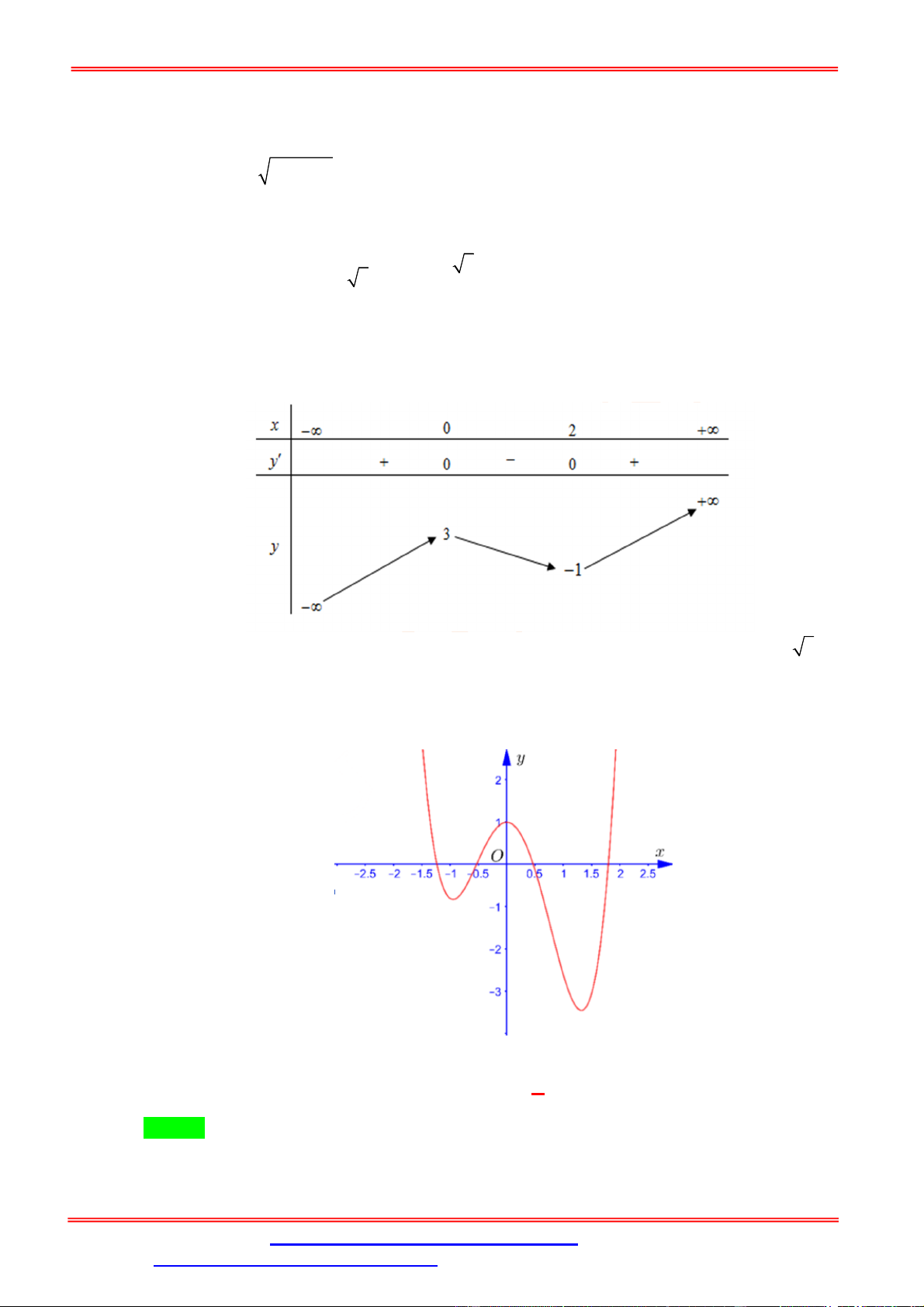
Câu 32. Đồ thị hàm số   4 3 2
f x  ax  bx  cx  dx  e có dạng như hình vẽ sau: Phương tr 4 3 2
ình a  f (x)  b  f (x)  c  f (x)  df (x)  e  0 (*) có số nghiệm là A. 2. B. 6. C. 12. D. 16. Lời giải Chọn C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Ta thấy đồ thị y  f  x cắt trục hoành tại 4 điểm phân biệt nên phương trình f  x  0 có 4
nghiệm phân biệt: x  1  ,5; 1  , x  1  ; 0
 ,5 , x  0;0,5 , x  1,5;2 . 4   3   2   1  
Kẻ đường thẳng y  m , khi đó:
Với m  x  1  ,5; 1 
có 2 giao điểm nên phương trình f  x  x có 2 nghiệm. 1   1
Với m  x  1  ; 0
 ,5 có 4 giao điểm nên phương trình f  x  x có 4 nghiệm. 2   2
Với m  x  0;0,5 có 4 giao điểm nên phương trình f  x  x có 4 nghiệm. 3   3
Với m  x  1, 5; 2 có 2 giao điểm nên phương trình f  x  x có 2 nghiệm. 4   4
Vậy phương trình (*) có 12 nghiệm.
Câu 33. Cho hàm số f :    thỏa mãn điều kiện f  2
x  x    f  2 x  x   2 3 2 3
5  6x 10x 17, x    . Tính f  2018 .
A. f 2018  2018. B. f   2 2018  2018 .
C. f 2018  4033.
D. f 2018  3033 . Lời giải Chọn C
Ta cần thay x bởi đại lượng nào đó để bảo toàn được sự xuất hiện của f  2
x  x  3 và f  2
x  3x  5 trong phương trình. Do đó ta cần có 2 2
x  x  3  x  3x  5  x  1  x .
Như vậy ta thay x bởi 1 x .
Cuối cùng ta tính được: f  2 x  x   2
 x  x    2 3 2 2 3
2 x  x  3  3 .
Vậy f 2018  2.2018  3  4033 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
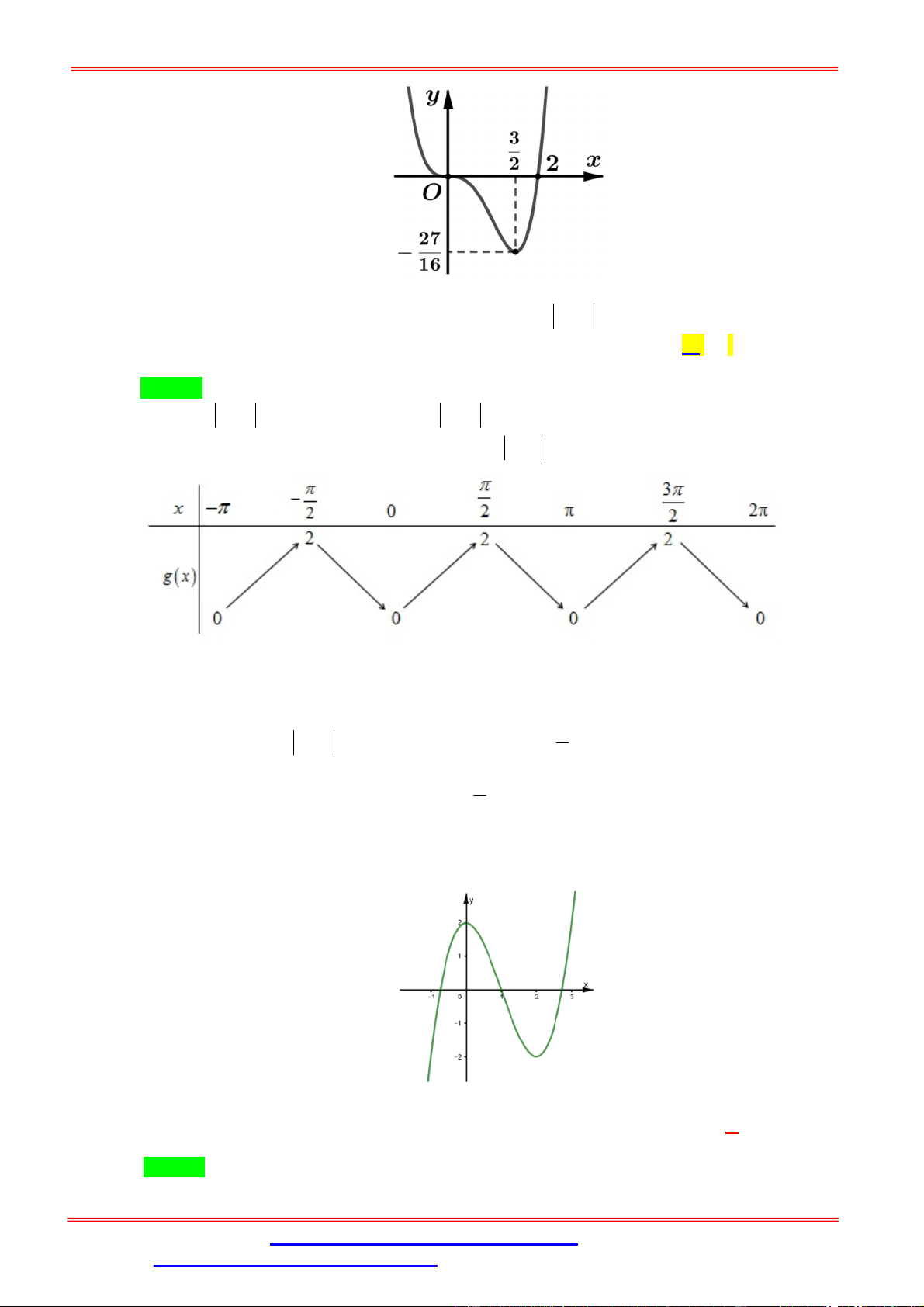
Câu 34. Cho hàm số f  x có bảng biến thiên như sau:  9 
Số nghiệm thuộc đoạn 0; 
của phương trình f cos x  2 là 2    A. 16 . B. 17 . C. 18 . D. 19 . Lời giải. Chọn B
cosx  aa    1 : voânghieäm 
cos x  b 1   b  0 c
 os x  b 1   b   0
Từ BBT ta thấy: f cos x  2    
cos x  c0  c   1 cos 
x  c0  c   1  cosx d  d   1 : voânghieäm   9 
Dựa vào đường tròn lượng giác, trên đoạn 0;  thì: 2   
- Phương trình cos x  b có 8 nghiệm phân biệt.
- Phương trình cos x  c có 9 nghiệm phân biệt khác 8 nghiệm ở trên.  9 
Vậy phương trình f cos x  2 có 17 nghiệm trên đoạn 0; .  2   
Câu 35. Cho hàm số f  x liên tục trên  và có bảng biến thiên như sau:
Số nghiệm thuộc đoạn 0; 2020 của phương trình f  co s x  2 là A. 2021 . B. 3030 . C. 2020 . D. 3031.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Lời giải. Chọn D  co s x  1  co s x  1 1
Từ BBT ta thấy: f  cos x 2     co s x    1  2 co s x     2
co s x  a a   1 : voâ nghieäm 
Dựa vào đường tròn lượng giác, trên đoạn 0; 2020 thì:
- Phương trình co s x  1có 1011 nghiệm phân biệt. 1
- Phương trình co s x  
có 2020 nghiệm phân biệt khác 1011 nghiệm ở trên. 2
Vậy phương trình f  co s x  2 có 3031 nghiệm trên đoạn 0; 2020 .
Câu 36. ##Cho hàm số   3 2
f x  ax  bx  bx  c có đồ thị như hình vẽ:    9  Số nghiệm nằm trong ; 
 của phương trình f cos x  
1  cos x 1 là  2 2  A. 6 . B. 10. C. 4 . D. 8 . Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
 x  a ;0 
Từ đồ thị ta có f  x  x  x  b   0;  1  x  2 
cos x 1  a   ;  0
cos x  a 1  t   ;  1  (VN ) 1    
Do đó f cos x  
1  cos x 1  cos x 1  b   0;  1
 cos x  b 1  t  1; 0 (1)  2   cos x 1  2   cos x  1 (2)     9 
Dựa vào đường tròn lượng giác, phương trình (1) có 4 nghiệm nằm trong ;   .  2 2     9 
Phương trình (2) có 6 nghiệm nằm trong ;   .  2 2     9 
Vậy phương trình ban đầu có tất cả 10 nghiệm nằm trong ;   .  2 2 
Câu 37. Cho hàm số y  f  x có đạo hàm trên  . Biết rằng hàm số y  f ' x có đồ thị như hình vẽ 3
bên dưới. Hỏi đồ thị hàm số y  f 3x  4 cắt đường thẳng y  x  tại nhiều nhất bao nhiêu điểm? 2 A. 5 . B. 2 . C. 3 . D. 4 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Lời giải Chọn D t  4
Đặt t  3x  4  x  . 3 3
Phương trình hoành độ giao điểm là: f 3x  4  x   2
Số nghiệm của  là số giao điểm của đồ thị hàm số y  f 3x  4 và đường thẳng 3 t 1 y   x 
. Thế t vào  ta có: f t     0 . 2 3 6 t 1 1 1
Đặt g t   f t     g 't   f 't    0  f 't   . 3 6 3 3 1
Quan sát đồ thị ta thấy f 't    có 3 nghiệm thực phận biệt nên hàm g t  có 3 cực trị. 3
Số nghiệm lớn nhất của phương trình g t   0 là 4. Suy ra phương trình  có tối đa 4 nghiệm . Vậy chọn đáp án D.
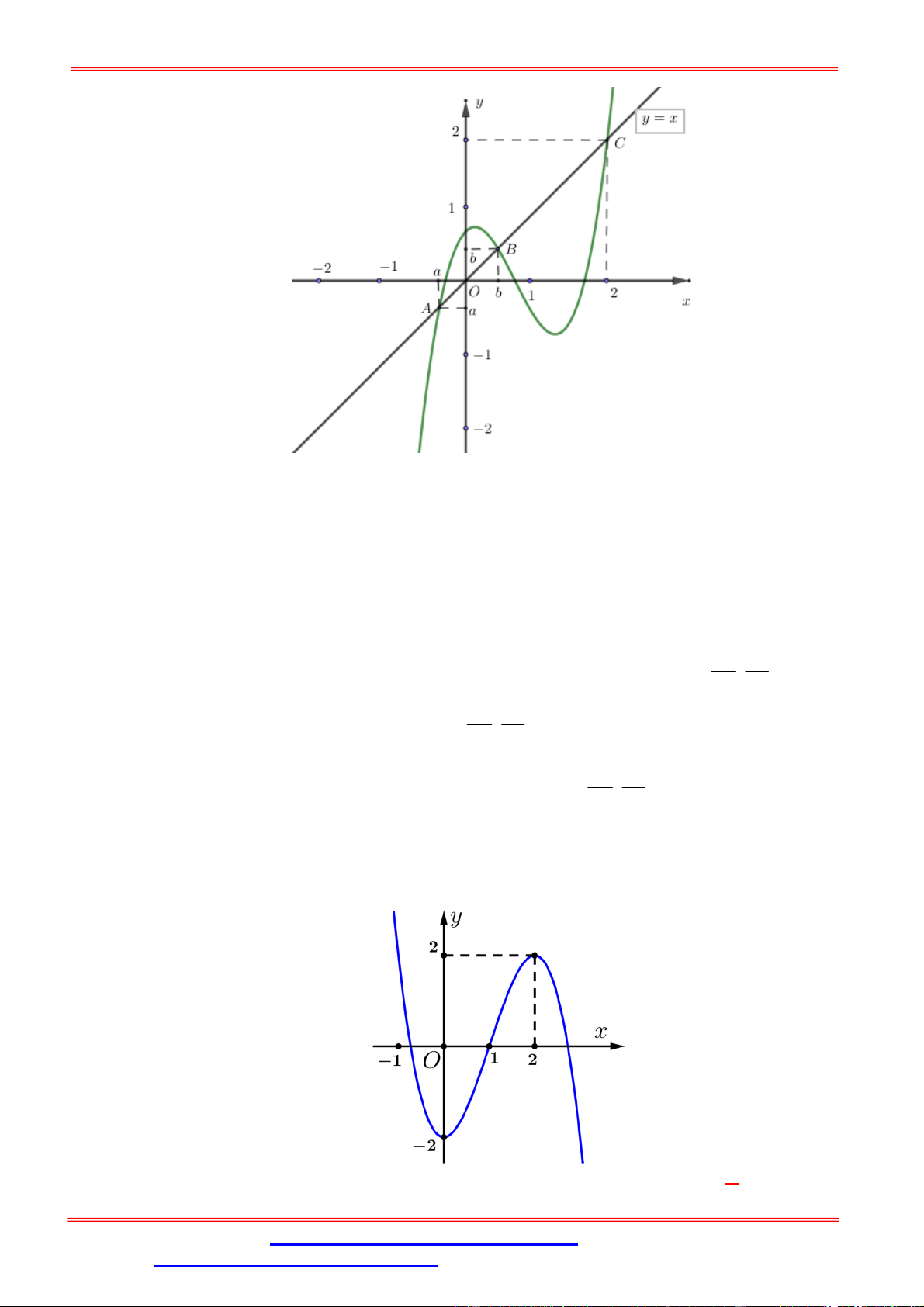
Câu 38. Cho hàm số y  f  x liên tục trên  có đồ thị như hình vẽ bên. Hỏi phương trình
f 2  f  x 1 có tất cả bao nhiêu nghiệm thực phân biệt? A. 5 . B. 6 . C. 3 . D. 4 . Lời giải Chọn C
2  f  x  1
 f  x  1
Từ đồ thị ta suy ra: f 2  f  x  1     .
2  f  x  2 
 f  x  4   x  2
• f  x  1  . x  1 
• f  x  4  x  x  2  . 3
Vậy phương trình có 3 nghiệm phân biệt. 3
Câu 39. Cho hàm số f  x 3
 x  3x 1. Số nghiệm của phương trình  f  x  3 f  x 1  0   là A. 1. B. 6. C. 5. D. 7. Lời giải Chọn D
Đồ thị hàm số y  f  x 3
 x  3x 1 có dạng:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Dựa vào đồ thị ta thấy phương trình f  x  0 có 3 nghiệm x  2  ; 1
 , x  0;1 , x  1; 2 1   2   3   3
Nếu phương trình  f  x  3 f  x 1  0  
có nghiệm x thì f  x  x , x , x . 0   1 2 3 0
Dựa vào đồ thị ta có:
+ f  x  x , x  2  ; 1  có 1 nghiệm duy nhất. 1 1  
+ f  x  x , x  0;1 có 3 nghiệm phân biệt. 2 2  
+ f (x)  x , x  1; 2 có 3 nghiệm phân biệt. 3 3   3
Vậy phương trình  f  x  3 f  x 1  0  
có 7 nghiệm phân biệt.
Câu 40. Cho hàm số ( ) = + + +
+ có đồ thị như hình bên. Phương trình
( ) + 2 = ( ) + 1 có bao nhiêu nghiệm thực phân biệt. A. 3. B. 4. C. 2. D. 5. Lời giải Chọn C Ta có: ′( ) = 4 + 3 + 2 + = 4 ( + 1) ( − 1) = 4 ( − ) ⇒ ( ) = ( − 2 ) + . (0) = 0 = 0 = 1 Và ⇔ ⇔ ⇒ ( ) = − 2 . (−1) = −1 − + = −1 3 = 0 Đặt =
( ); ( ≥ 0) phương trình trở thành: ( ) + 2 = + 1 ⇔ − 2 + 2 = + 1 ⇔ − 2 + 2 = ( + 1) ⇔ 4 = 1 1 ⇔ = ( ≥ 0). 2 Vậy
( ) = ⇔ ( ) = phương trình này có 2 nghiệm.
Câu 41. Cho hàm số y  f  x liên tục trên  và có bảng biến thiên như sau
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình 2 f sin x  cos x  m 1   3 
có hai nghiệm phân biệt trên khoảng  ;   ?  4 4  A. 13 . B. 15 . C. 12 . D. 14 . Lời giải Chọn A
Đặt t  sin x  cos x .      3 
Ta có: t  cos x  sin x  2 sin x   0, x    ;     .  4   4 4    3 
Bảng biến thiên của t  t  x trên khoảng  ;   .  4 4    3 
Nhận xét: Dựa vào bảng biến thiên của t  x trên khoảng  ;   ta thấy với mỗi  4 4    3  x   ; 
 có duy nhất một giá trị t   2 ; 2  .  4 4 
Do đó, phương trình 2 f sin x  cos x  m 1 có hai nghiệm phân biệt trên khoảng   3   ; 
  phương trình 2 f t   m 1 có hai nghiệm phân biệt trên  4 4    m 1 2 ; 2  4 
 3  7  m  7 . 2
Mà m    m 6;  5;..;5; 
6  có 13 giá trị nguyên m thỏa mãn yêu cầu bài toán.
Câu 42. ##Cho hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Số nghiệm thuộc đoạn  
 ; 2  của phương trình 2 f 2 sin x  1  0 là A. 6 . B. 2 . C. 8 . D. 12 . Lời giải Chọn D
Đặt t  2 sin x . Xét hàm t  g  x  2 sin x trên đoạn    ; 2 
Ta có bảng biến thiên của hàm số y  g  x  2 sin x trên đoạn    ; 2 
Dựa vào BBT ta có t 0, 2 x    ;2 
Nếu t  0, 2 thì mỗi giá trị t cho 6 giá trị x thuộc đoạn    ; 2  1
Phương trình 2 f 2 sin x  1  0 trở thành f t    với t 0,2 2 1
Dựa vào đồ thị ta có phương trình f t    có 2 nghiệm t phân biệt thuộc khoảng 2
0,2 nên phương trình ban đầu có 12 nghiệm phân biệt thuộc đoạn    ; 2 
Câu 43. Cho hàm số y  f (x) liên tục trên R và có đồ thị như hình vẽ
Gọi m là số nghiệm của phương trình f  f (x)  0 . Khẳng định nào sau đây đúng. A. m  4 B. m  6 C. m  5 D. m  7 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 32
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
 f (x)  x1 
Từ đồ thị ta có f  f (x)  0   f (x) 1 
với 1 x  0 ; 2  x  3 1 2
 f (x)  x  2
Trường hợp 1: f (x)  x có 3 nghiệm phân biệt 1
Trường hợp 2: f (x)  1 có 3 nghiệm phân biệt
Trường hợp 3: f (x)  x có 1 nghiệm 2
Vậy phương trình f  f (x)  0 có 7 nghiệm hay m  7 .
Câu 44. Cho hàm số y  f (x) liên tục trên R và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các
giá trị nguyên của m để phương trình f (sin x)  2 sin x  m có nghiệm thuộc khoảng (0; ) . Tông các
phần tử của S bằng A. 10 B. 8  C. 6  D. 5  Lời giải Chọn C
Đặt t  sin x  t 0; 
1  f sin x  2sin x  m  m  f t   2t t 0;  1 
Xét g t  f t   2t,t 0;  1
 g 't  f 't  2  0 t  0; 
1  g t  3  ;  1
Phương trình f sin x  2sin x  m có nghiệm  m 3  ;  1  m   3  ; 2  ; 1  ;  0 .
Vậy tổng các số là S  6 
Câu 45. ##Cho hàm số f  x liên tục trên  có đồ thị y  f  x như hình vẽ dưới đây.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 33
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Số nghiệm thực của phương trình 4 2x f f   2 là A. 1. B. 2. C. 3. D. 4. Lời giải Chọn B Ta có: Theo đồ thị :
4  f 2x   2 
f 4  f 2x   2  4 f 2x  a,4 a  6  2x  2 TH1) 4  2x f   2  2x f   6     x  1.
2x  b  2   KTM  
2x  c  2   KTM   TH2) 4  2x f
  a  2x f
  a  4, 0  a  4  2  2x  d  0KTM   x  log t . 2
2x  t  4 
Vì t  4 nên log t  log 4  2  1 2 2
nên phương trình đã cho có 2 nghiệm phân biệt.
Câu 46. Cho hàm số y  f ( )
x xác định và liên tục trên  có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của m để phương trình  f  2 2 3  3 9
 x  30x  21  m 2019 có nghiệm. A. 15. B. 14. C. 10. D. 13. Lời giải Chọn D Ta có  x  x     x  2 2 9 30 21 3 5  4  4 nên 2 9
 x  30x  21 0;2 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 34
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Đặt 2 t  3  3 9
 x  30x  21 thì t 3; 
3 . Ta cần tìm số các giá trị nguyên của m để phương m  2019
trình f t  
có nghiệm t 3;  3 . 2 m  2019
Từ đồ thị suy ra đường thẳng y 
cắt đồ thị y  f t ; t 3;  3 khi và chỉ khi 2 m  2019 5    ;
a a  max f t , và cũng từ đồ thị ta có 1  a 1,5 . 3  ;3 2
Do đó 2009  m  2a  2019 và 2021  2a  2019  2022 . Mà m   nên 2009  m  2021.
Vậy có tất cả 2021 2009 1  13 giá trị nguyên của m thỏa mãn.
Câu 47. Cho hàm số y  f  x có đồ thị như hình vẽ sau. 2
Số nghiệm của phương trình  e x   e x f f  2  0 là:   A. 1. B. 2 . C. 3. D. 5. Lời giải Chọn B
Điều kiện x  0 . Đặt e x t 
. Do x  0  t  1 và ứng với mỗi giá trị t  1 chỉ cho một giá trị x  0 .    2 f t  1
Ta có phương trình trở thành:  f t   f t   2  0     .
 f t   2 
Từ đồ thị hàm số y  f t  trên 1;  suy ra phương trình f t   1 có 1 nghiệm và phương
trình f t   2 có 1 nghiệm khác với nghiệm của phương trình f t   1.
Vậy phương trình đã cho có 2 nghiệm.
Câu 48. Cho hàm số y  f  x liên tục trên  có đồ thị như hình vẽ. Phương trình f 1 f  x  0 có tất
cả bao nhiêu nghiệm thực phân biệt? A. 5. B. 4 . C. 7 . D. 6 . Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 35
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Chọn C
Từ đồ thị hàm số ta có : 1
  f  x  m 2  m    1
 f  x  1 m  
f 1 f x  0  1
  f  x   n 0  n   1
  f  x   1 n .   1
  f  x   p 1  p  2
 f  x   1 p   +) Do 2   m  1
  2  1 m  3  phương trình f  x   1 m có 1 nghiệm x . 1
+) Do 0  n  1  0  1 n  1  phương trình f  x   1 n có 3 nghiệm x , x , x . 2 3 4
+) Do 1  p  2  1  1  p  0  phương trình f  x   1 p có 3 nghiệm x , x , x . 5 6 7
Dựa vào đồ thị ta thấy 7 nghiệm này phân biệt.
Vậy phương trình đã cho có đúng 7 nghiệm phân biệt.
Câu 49. Cho hàm số bậc ba y  f  x có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số m để phương trình f  f cos x  2  f m có
nghiệm trên nửa khoảng 0; ? A. 3 . B. 2 . C. 4 . D. 5 . Lời giải. Chọn A
Sử dụng đường tròn lượng giác và qua sát đồ thị ta thấy:
x 0;   co s x  1; 
1  f cos x  2  ; 2
 f cos x  20; 4 
f co s x  2 0;2
 f  f cos x  2   f m2;2  m  2  ; 2 \  1  m  2  ;0;  1 .
Vậy có tất cả 3 giá trị nguyên.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 36
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Câu 50. Cho hàm số y  f  x có đồ thị là đường cong trong hình vẽ dưới đây
Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f  f  x  
1   m có 4 nghiệm
phân biệt thuộc đoạn  2  ; 
2 . Số phần tử của S là A. 7 . B. 8 . C. 3 . D. 4 . Lời giải Chọn D
Gọi  P là đồ thị hàm số y  f  x
Vẽ đồ thị  P của đồ thị hàm số y  f  x  
1 bằng cách: Tịnh tiến đồ thị  P của hàm số 1 
y  f  x theo phương của trục hoành sang trái 1đơn vị.
Vẽ đồ thị  P của hàm số y  f  x  
1 bằng cách: Giữ nguyên đồ thị  P nằm bên phải trục 1  2 
tung rồi lấy đối xứng phần đó chính phần đồ thị đó qua trục tung, ta được đồ thị  P của hàm 2 
số y  f  x  
1 . Do đó, ta có đồ thị hàm số y  f  x   1
Đặt t  f  x   1 , với x  2  ;  2  t  1  ;  0 .
Ta có phương trình f t   m (1).
Nếu t  0cho ta ba nghiệm phân biệt x  2  ;  2 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 37
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Nếu t  1
 cho ta hai nghiệm phân biệt x 2  ;  2 . Nếu t  1
 ;0 thì mỗi giá trị của t cho ta bốn nghiệm phân biệt x 2  ;  2 .
Vậy phương trình đã cho có bốn nghiệm phân biệt khi và chỉ phương trình   1 có đúng 1 nghiệm t  1
 ;0  f 0  m  f   1  3  m  8.
Vậy S có tất cả 4 phần tử.
NHẬN XÉT : Cách giải 2 : Chọn hàm f (x)  (x  1)(x  3)
Câu 51. Cho hai hàm số f  x và g  x 3 2
 x  5x  2x  8. Trong đó hàm số f  x liên tục trên  và có
đồ thị như hình vẽ dưới đây.
Số nghiệm của phương trình g  f  x  0 là A. 1. B. 3 . C. 6 . D. 9 . Lời giải Chọn C
Đặt f  x 3 2
 ax  bx  cx  d ,a  0  f  x 2
 3ax  2bx  c .  f   1  0
3a  2b  c  0 a  1  f       1  0
3a  2b  c  0 b   0 Theo hình vẽ có:       f  x 3
 x  3x 1. f   1  1  
a  b  c  d  1   c  3    f 0 1 d  1 d  1     x  4
Ta có: g  x  0 3 2
 x  5x  2x  8   x  2 .   x  1 
 f  x  4 3
 x  3x 1  4 3
x  3x  3  0   1   
Suy rA. g  f  x  0  f 3 3
  x  2  x  3x 1  2 
 x  3x 1  0 2    f  x  1  3 3 
x  3x 1  1  
x  3x  2  0  3  Ta thấy:  
1 có một nghiệm, 2 có ba nghiệm, 3 có hai nghiệm.
Vậy g  f  x  0 có 6 nghiệm.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 38
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Câu 52. Cho hàm số f  x 7 5 4 3 2
 x  x  x  x  2x  2x 10 và g  x 3
 x  3x  2 . Đặt
F  x  g  f  x 
 . Tìm tất cả các giá trị của tham số m để phương trình F  x  m có ba nghiệm thực phân biệt. A. m  1  ;3
B. m  0; 4
C. m  3;6
D. m  1;3 Lời giải Chọn B 6 4 3 2
7x  5x  4x  3x  4x  2  0 (1)  f '(x)  0 
Ta có F '(x)  f '(x)g ' f (x). F '(x)  0   f (x)  1
 g ' f (x)    f (x)  1   (1)Vô nghiệm vì 6 4 3 2
7x  5x  4x  3x  4x  2  0 x  Bản biến thiên:
Vậy F  x  m có ba nghiệm thực phân bit thì m 0; 4 .
Câu 53. Cho hai hàm số f  x và g  x đều có đạo hàm trên  và thỏa mãn: 3 f   x 2
 f   x 2 2 2 2 3
 x .g  x  36x  0 , với x
   . Tính A  3 f 2  4 f 2 . A. 11. B. 13 . C. 14 . D. 10 . Lời giải Chọn D Với x    , ta có 3 2 f
 x  f   x 2 (2 ) 2 2 3
 x .g  x  36x  0   1 .
Đạo hàm hai vế của   1 , ta được 2
 f   x f   x 
f   x f   x  x g  x 2 3 2 . 2 12 2 3 . 2 3 2 .
 x .g  x  36  0 2 . 3  f  2 2  2 f 2  0 3 Từ  
1 và 2 , thay x  0 , ta có  2 3  f 
2. f 2 12 f 2. f 2  36  0 4 
Từ 3 , ta có f 2  0  f 2  2 .
Với f 2  0 , thế vào 4 ta được 36  0 (vô lí).
Với f 2  2 , thế vào 4 ta được 3
 6. f  2  36  0  f 2  1.
Vậy A  3 f 2  4 f 2  3.2  4.1  10 .
Câu 54. ##Cho hàm số y  f  x có đồ thị như hình vẽ bên dưới. Số nghiệm thực của bất phương trình  f  3 2 x  x   2  f  3 2 1 3 1 2 x  3x   1  2 là
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 39
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 A. 5 . B. 4 . C. 3 . D. 2 . Lời giải Chọn B
Đặt a  f  3 2 x  3x  
1 ta được bất phương trình 1   a  0 a  1  2  1 a  2a  2      a  1 .
1 2a  a  2a  2  a   2 2 2 1  0 
Với a  1 ta được f  3 2 x  3x   1  1. Đặt 3 2
t  x  3x 1 ta được PT f t   1 * .
Vẽ đường thẳng y  1 lên đồ thị đã cho ta được PT * có 1 nghiệm t  t  2; 1 và 1 1  
nghiệm t  t  1; 2 . 2   Ta có BBT của hàm số 3 2
y  x  3x 1 như sau
Với t  t ta được PT 3 2
x  3x  1  t . Dựa vào BBT ta thấy PT này có 3 nghiệm phân biệt. 1 1
Với t  t ta được PT 3 2
x  3x 1  t . Dựa vào BBT ta thấy PT này có 1 nghiệm. 2 2
Vậy BPT đã cho có 4 nghiệm thực.
Câu 55. ##Cho hàm số y  f  x là hàm bậc 3 và có bảng biến thiên như sau    Phương trình 2
f sin x  cos x 1 sin 2x  2 2 sin x  f  
sin x  cos x có mấy nghiệm  4 
 5 5  thực thuộc đoạn  ;  ? 4 4    A.1. B. 3 . C. 4 . D. 6 . Lời giải Chọn B
Vì hàm số có 2 điểm cực trị là x  1
 nên f  x 2
 ax  a  f  x 3 ' 3 3
 ax  3ax  d . Theo
2a  d  2 a  1
BBT thì đồ thị hàm số đi qua 2 điểm  1
 ; 2 và 1; 2 nên    2
 a  d  2 d  0  
Suy ra f  x 3  x  3x .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 40
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020    Ta có 2
f sin x  cos x 1 sin 2x  2 2 sin x  f  
sin x  cos x  4  2 2
 f sin x  cos x  sin x  cos x  2 sin x  cos x f sin x  cos x 2
  f sin x  cos x  sin x  cos x  0  f sin x  cos x  sin x  cos x     
Đặt t  sin x  cos x  2 sin x  , t   2; 2    ta được phương trình 4     t  0 f t 3
 t  t  3t  t   t  2loaïi     
Với t  0 ta được 2 sin x   0  x    k , k      4  4 5  5 3 Ta có     k   1   k 
 k  1, k  0, k  1 . Vậy PT có 3 nghiệm. 4 4 4 2
Câu 56. ##Cho y  f  x là hàm số bậc ba và có bảng biến thiên như hình vẽ
Có bao nhiêu giá trị nguyên m  5
 ;5 để hàm số g  x  f  f  x  m có 4 điểm cực trị? A. 5. B. 6. C. 7. D. 8. Lời giải Chọn B
g x  f  x. f  f  x  m.
 f  x  0
g x  0   f  f xm  0   x  2   x  2    x  2 x  2    
, trong đó x  2 và x  2 là hai nghiệm bội lẻ.
 f  x  m  2 
 f  x  2  m  
 f  x  m  2
 f  x  2  m  
Đặt f x  f x  2 và f
x  f x  2 , ta có đồ thị sau 2     1    
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 41
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020  m  5  ;5 Với 
và nhìn vào đồ thị, ta thấy hàm số g  x có 4 điểm cực trị  g x  0 có 4 m   
nghiệm bội lẻ  m  4  ; 3  ; 1  ;1;3;  4 .
Câu 57. ##Cho hàm số f  x có bảng biến thiên như sau:
Số nghiệm thuộc khoảng  
 ;  của phương trình 2
f cos x  f cos x  2 là A. 5 . B. 6 . C. 7 . D. 9 . Lời giải Chọn A
Đặt t  cos x, x   
 ; . Ta có bảng biến thiên (*)  t  1  ;  1 .
 f t   2 (1)
Phương trình đã cho trở thành 2
f t   f t   2  0   .
 f t   1 (2) 
Từ bảng biến thiên của đề bài, với t  1  ; 
1 ta có nghiệm của phương trình (1) là
t  a  1;0 hay t  b 0; 
1 và nghiệm của phương trình (2) là t  1.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 42
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Từ bảng biến thiên (*), ta có:  x  x    ; 0 1  
t  a   1  ;0   .
 x  x  0;  2    x  x    ; 0 3  
t  b  0;  1   .
 x  x  0;  4  
t  1  x  0.
Vậy, phương trình đã cho có 5 nghiệm phân biệt thuộc khoảng    ; .
Câu 58. Cho hàm số y  f  x có đồ thị như hình vẽ dưới đây. Gọi S là tập hợp tất cả các giá trị của
tham số m để phương trình f  2
3  4  x   m có hai nghiệm phân biệt thuộc đoạn  2; 3 . Tìm tập   S. A. S  1; f 3 2    . B. S  f 3 2;3   .   C. S   . D. S   1  ;  3 . Lời giải Chọn A
Xét phương trình f  2
3  4  x   m . Điều kiện 2 4  x  0  2   x  2 . x Đặt 2
t  3  4  x với x   2; 3 . Ta có t 
và t  0  x  0 .   2 4  x
Bảng biến thiên của hàm số 2
t  3  4  x trên đoạn  2; 3  
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 43
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Nhận xét:
+) Mỗi t  1;3  2 cho ta 2 giá trị x   2; 3   
+) Mỗi t  3  2;2 cho ta một giá trị x   2; 3   
+) t  1cho ta 1 nghiệm duy nhất x  0 .
Dựa vào đồ thị hàm số y  f  x ta suy ra đường thẳng y  m chỉ cắt đồ thị hàm số
y  f t  nhiều nhất tại một điểm trên 1; 2.
Do đó, để phương trình f  2
3  4  x   m có hai nghiệm phân biệt thuộc đoạn  2; 3 thì   m  1; f 3 2    
Vậy, các giá trị của m cần tìm là m  1; f 3 2    .  Câu 59. Cho hàm số    4 3 2 y
f x  ax  bx  cx  dx  k với (a, ,
b c, d, k  ) . Biết đồ thị hàm số
y  f  x có đồ thị như hình vẽ, đạt cực trị tại điểm O0;0 và cắt trục hoành tại A3;0 . Có bao nhiêu
giá trị nguyên của m trên  5  ; 
5 để phương trình f  2
x  2x  m  k có bốn nghiệm phân biệt? A. 0 . B. 2 . C. 5 . D. 7 . Lời giải Chọn B
Từ đồ thị ta thấy f  x không thể có bậc nhỏ hơn hoặc bằng 2 , do đó a  0 .
Ta suy ra f  x 2
  x  x  
3 , a  0 . Đồ thị của nó đi qua A2;  1 nên
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 44
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 1 2 1  .
a 2 .2  3  a   . 4 2 x 4 3 x x
Suy ra f   x  
 x  3 , do đó f  x     k . 4 16 4 4 3 x x  x  0
Ta có f  x  k   
 k  k   . 16 4 x  4  2
x  2x  m  0 Suy ra f  2
x  2x  m  k   . 2
x  2x  m  4  Phương trình 2
x  2x  m  0  
1 có hai nghiệm phân biệt khi   1 m  0  m  1  . 1 Phương trình 2
x  2x  m  42 có hai nghiệm phân biệt khi   1 m  4  0  m  3. 2 2
x  2x  m  0  Hai phương trình  
1 và 2 nếu như có nghiệm chung x thì 0 0   4  0 ( 0 2
x  2x  m  4  0 0
Vô lí). Suy ra phương trình  
1 và 2 không có nghiệm chung. m  1 
Do vậy để phương trình f  2
x  2x  m  k có 4 nghiệm phân biệt thì   m  3 . m  3 
Do m nguyên và m 5  ;  5 nên m4; 
5 . Vậy có 2 giá trị của m .
Câu 60. Cho hàm số f (x) là hàm số đa thức bậc ba có đồ thị như hình bên dưới. Số nghiệm thuộc
khoảng 0;3  của phương trình f sin x   1  sin x là y 2 -1 O 1 x A. 5 . B. 6 . C. 2 . D. 3 . Lời giải Chọn C
Đặt t  sin x 1 . Khi đó, phương trình đã cho trở thành f (t)  t 1 .
Vẽ đồ thị hàm số y  f (t) và đường thẳng y  t 1 trên cùng hệ trục tọa độ Oxy . t   1  
Từ đồ thị ta có f (t)  t 1  t  1  t   , m (m  1). 
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 45
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Với t  1 thì sin x 1  1  sin x  2  phương trình vô nghiệm.
Với t  m thì sin x 1  m  sin x  m 1. Phương trình này vô nghiệm vì m 1  2 . Với t  1
 thì sin x 1  1
  sin x  0  x  k , (k  ) .
Do x  (0;3 ) và k   nên 0  k  3  0  k  3  k 1,  2 .
Vậy phương trình đã cho có đúng 2 nghiệm thuộc khoảng (0;3 ) là x   ; x  2 .
Câu 61. Cho hàm số y  f  x có đồ thị như hình vẽ sau
Có bao nhiêu số nguyên m thuộc đoạn 2019;2019 sao cho phương trình 2
f  x   2
m  m   f  x 2 2 4 2 1
 2m  m  0 có đúng 8 nghiệm phân biệt. A. 1. B. 2020. C. 2019. D. 2. Lời giải Chọn D 2
f  x   2
m  m   f  x 2 2 4 2 1
 2m  m  0   1 
f  x  f  x   2
m  m   f  x   2 2 2
2m  m  0      1 f  x  2
 f  x   2
2m  m 2 f  x 1  0       2 .       f  x 2
 2m  m 3 
Dựa vào đồ thị ta thấy phương trình 2 có bốn nghiệm phân biệt. Để phương trình  
1 có đúng 8 nghiệm thì phương trình 3 có 4 nghiệm phân biệt khác
nghiệm của phương trình 2 . 1 2  1  1 1 Yêu cầu bài toán 2 2
m  2m  m  2m  m  và 2
2m  m  2 m     .   2  4  8 8  1 2 m  0, m 
2m  m  0  m  0 2 Dựa và đồ thị ta có     . 2  2m  m  1 1 m  1  m 1, m     2
Vậy có 2 nguyên của m thoả mãn.
Câu 62. Biết rằng đồ thị hàm số bậc bốn y  f  x được cho như hình vẽ sau
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 46
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 2
Tìm số giao điểm của đồ thị hàm số y  g  x   f ' x  f  x. f " x   và trục hoành. A. 4 . B. 0 . C. 6 . D. 2 . Lời giải Chọn B
Ta thấy đồ thị hàm số y  f  x cắt trục hoành tại 4 điểm phân biệt 0; x ; x ; x nên 1 2 3
f  x   ax  x  x x  x
x  x , a  0 . 1   2   3  Khi đó
f '  x  a  x  x x  x x  x  ax x  x x  x  ax x  x x  x  ax x  x x  x 1   2   3   2   3   1   3   1   2  .
Với x  0; x ; x ; x thì 1 2 3 f '  x 1 1 1 1     f  x x x  x x  x x  x 1 2 3 2 
 f '  x 
f "  x. f  x   f '  x 1  1  1 1          . f  x  
 f x2 2 x  x  x x  x x  x 1 2  2 2  3 2 Do đó 1 1 1 1
 f '  x 2
  f  x. f " x  0      0   , vô nghiệm. 2 x  x  x x  x x  x 1 2  2 2  3 2 2
Vậy đồ thị hàm số y  g  x   f ' x  f  x. f " x   không cắt trục hoành.
Câu 63. Cho hàm số f  x liên tục trên  và có đồ thị như hình vẽ bên.
Số giá trị nguyên của tham số m để phương trình
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 47
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 2
f cos x  m  2019 f cos x  m  2020  0
có đúng 6 nghiệm phân biệt thuộc đoạn 0;2  là A. 5 . B. 3 . C. 2 . D. 1. Lời giải Chọn C Phương trình 2
f cos x  m  2019 f cos x  m  2020  0   1 .
 f cos x  1   1   .
 f cos x  2020  m 
Dựa vào đồ thị hàm số   x  x   0;2   2
Xét phương trình: f cos x  1
  cos x  0   . 3  x   2 Phương trình  
1 có 6 nghiệm phân biệt khi và chỉ khi phương trình f cos x  2020  m có 4  3 nghiệm phân biệt khác ,
trên đoạn 0;2 . 2 2
 f t   2020  m có 2 nghiệm phân biệt t  1  ;  1 \  
0 với t  cos x  1
  2020  m  1  2019  m  2021.
Vậy có 2 giá trị nguyên của m là 2019 và 2020 .
Câu 64. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình f  2 3 x  3x  là 3 A. 6 . B. 10 . C. 3 . D. 9 . Lời giải Chọn B
Từ đồ thị hàm số y  f  x suy ra đồ thị hàm số y  f  x là
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 48
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 2 2 Đặt 3
t  x  3x , ta có: f  3 x  3x 
 f t   . 3 3 2
Từ đồ thị trên suy ra phương trình f t  
có sáu nghiệm phân biệt t  t , (với i  1, 6 và 3 i t  2 ; 2
  t ,t  2 ; t ,t ,t  2 ). 1 2 3 4 5 6
Xét hàm số t  x 3
 x  3x , ta có: t x 2
 3x  3; t x  0  x  1.
Bảng biến thiên của hàm t  x là:
Dựa vào bảng biến thiên, ta có: - Phương trình 3
x  3x  t có một nghiệm (do t  2 ). 1 1 - Mỗi phương trình 3
x  3x  t , 3
x  3x  t có ba nghiệm phân biệt (do 2
  t ,t  2 ). 2 3 2 3 - Mỗi phương trình 3
x  3x  t , 3
x  3x  t , 3
x  3x  t có một nghiệm (do t , t , t  2 ). 4 5 6 4 5 6 2
Vậy phương trình f  3 x  3x  có 10 nghiệm. 3
Câu 65. Cho hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ.  m 
Có bao nhiêu giá trị nguyên của tham số m để phương trình f 2 sin x   f   có đúng 12  2 
nghiệm phân biệt thuộc đoạn    ; 2  ? A. 3. B. 4. C. 2. D. 5. Lời giải Chọn C
Ta có bảng biến thiên của hàm số y  g  x  2 sin x trên đoạn    ; 2 
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 49
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020  m 
Phương trình f 2 sin x   f   có đúng 12 nghiệm phân biệt thuộc đoạn  
 ; 2  khi và chỉ  2   m 
khi phương trình f t   f   có 2 nghiệm phân biệt t 0;2 .  2   m 
Dựa vào đồ thị hàm số y  f  x suy ra phương trình f t   f   có 2 nghiệm phân biệt  2   m 0   2 27  m    0  m  4 t  0; 2 2 khi và chỉ khi   f  0       . 16  2  m 3 m  3      2 2
Do m nguyên nên m 1; 
2 . Vậy có 2 giá trị của m thoả mãn bài toán.
Câu 66. Cho hàm số y  f  x 3 2
 ax  bx  cx  d a  0 có đồ thị như hình vẽ. Phương trình
f  f  x   0 có tất cả bao nhiêu nghiệm thực? A. 5. B. 9. C. 7. D. 3. Lời giải Chọn C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 50
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 x  a 2  ; 1  1   
Từ hình vẽ trên ta thấy f  x  0  x  b 0;1  2   nên phương trình
x  c 1;2 3   
 f  x  a  2  ;  1   1 
f  f  x  0  f  x  b  0;  1 2 .
 f x  c1;2   3 
Dễ thấy: *) phương trình (1) có 1 nghiệm duy nhất x  2  1
*) phương trình (2) có 3 nghiệm phân biệt
*) phương trình (3) có 3 nghiệm phân biệt khác 4 nghiệm đã tìm được ở trên.
Vậy phương trình f  f  x   0 có tất cả 7 nghiệm phân biệt.
Câu 67. Cho hàm số y  f  x có bảng biến thiên như sau
Hỏi có bao nhiêu điểm trên đường tròn lượng giác biểu diễn tập nghiệm của phương
trình f  f cos x  2 ? A. 2 . B. 3 . C. 6 . D. 4 . Lời giải Chọn D
 f cos x  1
Dựa vào bảng biến thiên ta có: f  f cos x  2   . f  cos x   1 
cos x  t 1 , t  1  1    1 
+ f cos x  1    .
cos x  t 2 , t  1  2    2 
Dễ thấy phương trình  
1 và 2 đều vô nghiệm.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 51
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
cos x  t 3 , t  1  3    3 
cos x  t 4 , 1   t  0  4    4 
+ f cos x  1   .
cos x  t 5 , 0  t  1 5    5  
cos x  t 6 , t 1  6    6 
Ta thấy phương trình 3 và 6 đều vô nghiệm còn phương trình 4 và 5 mỗi phương
trình tập nghiệm của nó đều được biểu diễn bởi hai điểm trên đường tròn lượng giác.
Vậy tập nghiệm của phương trình f  f cos x  2 được biểu diễn bởi bốn điểm trên đường tròn lượng giác.
Câu 68. Xét tất cả các số thực ,
∈ (0; 1) và hàm số đa thức ( ) có đồ thị như hình vẽ bên: Đặt ( ) =
( ) . Số nghiệm thực phân biệt của phương trình ( ). ( ) + ( ). ( ) = ( ) + ( ) là A. 14. B. 10. C. . D. 17. Lời giải Chọn C = ( ) Đặt
, phương trình đã cho thành . + . = + ⇔ . ( − 1) + = ( ) . ( − 1) = 0 (1) = 0 Dễ thấy
thỏa mãn phương trình (1). = 0 ≠ 0 Trường hợp ta có: . ( − 1) + . ( − 1) = 0 ⇔ + = 0 ⇔ + ≠ 0 = 0 (2) Mà các hàm số = , =
đều nghịch biến với , ∈ (0; 1), do đó < 0, <
0, như vậy phương trình (2) vô nghiệm. ( ) = 0 = 0 ( ) = 0 Ta có (1) ⇔ ⇔ ⇔ ( ) = 0 ⇔ = 0 ( ). ( ) = 0 ( ) = 0 ∈ {−2,0,2} ∈ { , 0,1,2} ∈ (−2; 0) . ( ) ∈ { , 0,1,2} ∈ (−2; 0)
Từ đồ thị của hàm số ( ) suy ra:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 52
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
+ phương trình ( ) = có 1 nghiệm;
+ phương trình ( ) = 1 có 3 nghiệm;
+ phương trình ( ) = 2 có 3 nghiệm;
Vậy tổng số nghiệm của phương trình đã cho là 12 nghiệm.
Câu 69. Cho hàm số y  f  x 2
 x  4 x  3 có bao nhiêu giá trị nguyên của tham số m để phương trình: 2
f  x   m  6 f  x   m  5  0 có 6 nghiệm thực phân biệt. A. 2 . B. 4 . C. 1. D. 3 . Lời giải Chọn D
+) Ta có đồ thị hàm số: y  f  x 2
 x  4 x  3 như hình vẽ:
+) Đồ thị hàm số y  f  x  2
 x  4 x  3như sau: +) Ta có: 2
f  x   m  6 f  x   m  5  0. (1) .     f  x  x 2  1      x  2 .
 f  x   m  5 (2)  
f  x   m  5 (2) 
Phương trình (1) có 6 nghiệm thực phân biệt thì phương trình (2) có 4 nghiệm thực phân biệt x  2  .
Dựa vào đồ thị hàm số ta có: 1
  m  5  3  4  m  8 .
Vậy có 3 giá trị nguyên của tham số m .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 53
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Câu 70. Cho hàm số    4 3 2 y
f x  mx  nx  px  qx  r , trong đó , m ,
n p, q, r  R Biết rằng hàm số
y  f ' x có đồ thị như hình vẽ bên.
Tập nghiệm của phương trình f  x  16m  8n  4 p  2q  r có tất cả bao nhiêu phần tử. A. 4 . B. 3 . C. 5 . D. 6 . Lời giải Chọn A +) Ta có 4 3 2 3 2 y  f ( )
x  mx  nx  px  qx  r  f (  )
x  4mx  3nx  2 px  q (1)
+) Dựa đồ thị y  f ' x suy ra f ' x  0 có 3 nghiệm phân biệt x  1; x  1; x  4 Do đó m  0 Và f (
 x)  4 m(x1)(x1)(x 4) 2  f (
 x)  4 m(x 1)(x 4) 3 2 3 2  f (
 x)  4 m(x  4x  x 4)  4 mx 16mx  4mx 16m (2)  16 n   m 3  n  16m  3  
Từ (1) và (2) ta được 2 p  4m   p  2  m q 16m   q  16m    16
Suy ra f  x 4 3 2  mx 
mx  2mx 16mx  r 3
+) phương trình f  x 16m  8n  4 p  2q  r 16 4 3 2  mx 
mx  2mx 16mx  r  16m  8n  4 p  2q  r 3 16 16 4 3 2  mx 
mx  2mx 16mx  16m  8.( ) m 4( 2  ) m 2.16m 3 3 16 16 4 3 2  x 
x  2x 16x  16  8.( )  4(2)  2.16 -9 3 3 16 8 4 3 2  x 
x  2x 16x   0 (*) 3 3 16 8 +) Xét 4 3 2 3 2
g(x)  x 
x  2x 16x   g (
 x)  4x 16x  4x 16 3 3 x  1   g (
 x)  0  x  1  x  4  Bảng biên thiên
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 54
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Suy ra (*) có 4 nghiệm phân biệt
Câu 71. Phương trình 2  f  x  f  x có tập nghiệm là T  20;18;3 . Phương trình 1   g  x 3 2
1  3g  x  2  2g  x có tập nghiệm T  0;3;15;19 . Hỏi tập nghiệm của phương trình 2  
f  x g  x 1 
f  x  g  x có bao nhiêu phần tử? A. 4 . B. 7 . C. 6 . D. 5 . Lời giải Chọn C
0  f  x  2  Điều kiện:  1 g   x  .  2  f   x  0
Ta có 2  f  x  f  x  
 f  x  1  x T  20;18;3 . 1   2 f 
 x  f  x  2  0  Lại có g  x 3 2
1  3g  x  2  2g  x
 g  x 
g  x   g  x 3 2 1
 3g  x  2  0 2
g  x  2g  x 3 1
g  x  3g  x  2    0
g  x  2g  x 1
g  x  g  x 3 3g  x  2  3g  x 2 2 3  2    g  x 2 1  g  x 2
1  g  x  2          0
g  x  2g  x 1
g  x  g  x 3 3g  x  2  3g  x 2 2 3  2     2  1 g  x  2  g  x 1       0 
  g x 2gx 1   
g  x  g  x 3 3g  x  2  3g  x 2 2 3  2     
 g  x 1  0  g  x 1  xT  0;3;15;19 . 2   Do đó, ta có
f  x g  x 1 f  x g  x
 f x 1 1  g  x          0    
 f  x  1
 gx 1 
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 55
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
 x T  20;18;3 1    
 x T  0;3;15;19  2  
 x T T  0;3;15;18;19; 20 . 1 2   Câu 72. Cho hàm số    2 y
f x  ax  bx  c có đồ thị C  (như hình vẽ). Có bao nhiêu giá trị nguyên
của tham số m để phương trình 2
f  x   m  2 f ( x )  m  3  0 có 6 nghiệm phân biệt? A. m  4 . B. m  3 . C. m  2 . D. m 1. Lời giải Chọn B
* Vẽ đồ thị hàm số C ' của hàm số y  f  x  : Giữ nguyên phần đồ thị C  nằm phía bên
phải trục Oy , bỏ đi phần đồ thị C  bên trái trục Oy và lấy đối xứng phần đồ thịC  phía bên
phải trục Oy qua trục Oy .
 f  x   1  * Ta có 2
f  x   m  2 f ( x )  m  3  0   .
 f  x   3  m 
* Từ đồ thị C ' , ta có:
- Phương trình f  x   1 có hai nghiệm là x  2, x  2 .
- Yêu cầu bài toán  phương trình f  x   3  m có bốn nghiệm phân biệt khác 2  Đường
thẳng d : y  3  m cắt đồ thị C ' tại bốn điểm phân biệt khác , A B  1
  3  m  3  0  m  4 . Suy ra m 1, 2,  3 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 56
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Câu 73. Cho hàm số y  f  x 4 3 2 =ax  x b  x c  x
d  e trong đó a, b, c, d , e là các hệ số thực có đồ thị như hình vẽ sau đây.
Số nghiệm của phương trình f  f x  f x  2 f x 1  0 là A. 3 . B. 4 . C. 2 . D. 0 . Lời giải Chọn B
*) Phân tích: Đây là bài toán tương giao dựa vào đồ thị.
-Phương pháp chung giải bài tập loại này là ta thường biến đổi phương trình đưa về dạng
f  x  m , m  .
- Ta thấy vế trái của phương trình có chứa
f  x, f  f x , do đó để biến đổi phương trình
về dạng f  x  m ta cần đặt ẩn phụ t  f  x .
-Ngoài ra ta có thể tìm hàm số   4 3 2
f x  ax  bx  cx  dx  e có đồ thị như giả thiết.
Sau đây tôi xin trình bày 2 cách.
Cách 1: Biến đổi phương trình.
Điều kiện: f  x  0 . Đặt
f  x  t . Dựa vào đồ thị và kết hợp điều kiện ta có t 0;  1 .
Phương trình trở thành f t 2
 t  2t 1  0  f t  2  t   2t 1   1
Ta có đồ thị hàm số y  f t  và 2
y  t  2t 1 như hình vẽ bên dưới.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 57
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Trên đoạn 0; 
1 đồ thị hàm số y  f t  và đồ thị hàm số y  g t  2
 t  2t 1 cắt nhau tại một điểm duy nhất.
Do đó phương trình (1) có duy nhất nghiệm , t  m  0 
;1 , với m  0;  1 .
Hay phương trình tương đương với f  x  , m .
Vậy phương trình đã cho có 4 nghiệm phân biệt. Cách 2:
Điều kiện: f  x  0 Đặt
f  x  t . Dựa vào đồ thị và kết hợp điều kiện ta có t 0;  1 .
Phương trình trở thành f t 2
 t  2t 1  0  f t  2  t   2t 1   1 Đồ thị hàm số   4 3 2
f x  ax  bx  cx  dx  e
đi qua điểm 0;0,1;  1 , 1  ;  1 nên e  0 e  0  
a  b  c  d  1  a  c  1 2 a b c d 1 b       d  0  
Ta có f  x 3 2
 4ax  3bx  2cx  d và hàm số đạt cực trị tại x  1  nên
4a  3b  2c  d  0 3
 b  d  0    3 . 4
 a  3b  2c  d  0 4a  2c  0  
Giải hệ (2) và (3) ta có a  1; b  0; c  2; d  0; e  0 .
Do đó f  x 4 2
 x  2x .   4 2 2 1  t   2t  t
  2t 1, t 0;  1 4 2
 t  3t  2t  1  0 .
Xét hàm số h t 4 2  t
  3t  2t 1, t  0;  1 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 58
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020  1 3 t   2   1 3 Có ht  3
 4t  6t  2  ht  0  t   2  t   1   
Lập bảng xét dấu của h t
Hàm số đồng biến trên t 0;  1 nên phương trình 4 2
t  3t  2t  1  0 có duy nhất nghiệm.
Sử dụng MTCT ta có nghiệm t  0.336 hay
f  x  0.336  f  x  0.11.
Do đó phương trình đã cho có 4 nghiệm phân biệt.
Lưu ý: Việc tìm ra nghiệm thuộc 0; 
1 của phương trình ht   0 có thể dùng MTCT với chức năng MODE 7.
Câu 74. Cho hàm số ( ) có đạo hàm trên ℝ\{ } và hàm số ( ) có đạo hàm trên ℝ. Biết đồ thị của
hai hàm số = ′( ) và = ′( ) như hình vẽ dưới. Đặt ℎ( ) = ( ) − ( ) và = −[ℎ( + )] + ℎ( +
) 1 + 2ℎ( ) − [ℎ( )] với ,
, là các số thực đã biết. Khẳng định đúng với mọi ≠ 0 là? A.
∈ [ℎ( ); ℎ( + )].. B. ≤ ℎ( ). C. ∈ [ℎ( ); ℎ( + )]. D. ∈ [ℎ( ); ℎ( )]. Lời giải Chọn B =
Từ đồ thị đã cho ta suy ra ℎ′( ) = ′( ) − ′( ), ℎ′( ) = 0 ⇔ ′( ) = ′( ) ⇔ =
Lập bảng biến thiên ta có
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 59
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Lại có = −[ℎ( + )] + ℎ( + ) 1 + 2ℎ( ) − [ℎ( )] ⇒
= −[ℎ( + ) − ℎ( )] + ℎ( + ) ≤ ℎ(
+ ) v × −[ℎ( + ) − ℎ( )] ≤ 0, ∀ ≠
Từ bảng biến thiên suy ra max ℎ( ) = ℎ( ). ( ; ) Vì: +
> , ∀ ≠ 0 nên ta có ℎ( + ) ≤ h( ), ∀ ≠ 0. Vậy ≤ ℎ( ), ∀ ≠ 0.
Câu 75. Cho hàm số y  f  x , hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ Bất phương trình   3
f x  m  x  x ( m là tham số thực) nghiệm đúng với mọi x 2;0 khi và chỉ khi
A. m  f 0 .
B. m  f  2   10 .
C. m  f  2   10 .
D. m  f 0 . Lời giải Chọn D
Dựa vào đồ thị hàm số y  f  x suy ra f  x  1  , x   2;0 .
Ta có f  x 3
 m  x  x x  
  f  x 3 , 2; 0  x  x  , m x    2  ;0 (1) Đặt      3 g x
f x  x  x . Khi đó g x  f  x 2
 3x 1  0, x   2;0 . Bảng biến thiên
Vậy g  x  , m x   2
 ; 0  m  f 0
Câu 76. Cho các số thực , ,
< 0 và hàm số ( ) có bảng biến thiên như sau:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 60
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Phương trình ( ) + ( ) +
( ) = (1) có số nghiệm là. A. 3. B. 1. C. 4. D. 2. Lời giải Chọn A Đặt: =
( ), ( ≥ 0) phương trình trở thành ( ( ) + + ) = (1)(∗).
Từ bảng biến thiên ta thấy trên trên nửa khoảng [0; +∞) hàm số ( ) đồng biến do đó (∗) ⇔ ( ) + + = 1 ⇔ ( ) + + − 1 = 0(1). Xét hàm số ( ) = ( ) +
+ − 1 trên nửa khoảng [0; +∞) có ′( ) = ′( ) + 2 + 1 > 0, ∀ > 0. (0) = −1 < 0 Mặt khác:
⇒ (0). (1) < 0 ⇒ pt (1) có nghiệm duy nhất = ∈ (1) = (1) + 1 > 0 (0; 1). Vậy ( ) = ⇔ ( ) =
∈ (0; 1). Phương trình này có 3 nghiệm vì đường thẳng =
∈ (0; 1) cắt đồ thị hàm số ( ) tại 3 điểm phân biệt.
Câu 77. Cho hàm số y  f  x và hàm số y  g  x có đạo hàm xác định trên  và có đồ thị như hình vẽ dưới đây: f  x
Có bao nhiêu giá trị nguyên của tham số m để phương trình
 m có nghiệm thuộc g  x  2  ;  3 ? A. 4. B. 5. C. 7. D. 6.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 61
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Lời giải Chọn D f  x
Xét hàm số h  x 
. Dựa vào đồ thị, ta thấy các hàm số f  x và g  x liên tục và nhận g  x giá trị dương trên  2  ; 
3 , do đó h x liên tục và nhận giá trị dương trên  2  ;  3 . f  x
Ngoài ra với x  2  ;  3 , dễ thấy
f  x  6 , g  x 1 nên h x   6 , mà g  x f 0 6 h 0  
 6 nên max h  x  6 (1). g 0 1  2  ;  3
Lại có h  x  0 với mọi x  2  ; 
3 và h2  1 nên 0  min h x  1 (2). 2;  3 f  x Phương trình
 m có nghiệm trên  2  ; 
3 khi và chỉ khi min h  x  m  max h  x (3). g  x  2  ;  3  2  ;  3 Từ  
1 , 2 và 3 , kết hợp với m  , ta có m1;2;3; 4;5;  6 .
Câu 78. Cho hàm số bậc ba y  f  x có đồ thị trong hình dưới đây. Số nghiệm thực của phương trình 2 f  2
x    f  2 2 1 9 x   1 10  0 là A. 2 . B. 3 . C. 4 . D. 6 . Lời giải Chọn C Đặt 2
t  x 1, t  1
 . Ta được phương trình sau:
t  a,t  3   l    t  2  l 
 f t   2
t  b,1 b  0  2
2 f t   9 f t  10  0   5  .   f t   t  c
c  a  3 l  2 
 t  d  2   d     1 l 
 t  e  1
  e  b  0  2  x 1  b
 x   1 b Suy ra:    . 2 x 1  e 
 x   1 e 
Vậy phương trình có 4 nghiệm phân biệt.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 62
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Câu 79. Cho hàm số y  f  x có đồ thị như hình vẽ
Số nghiệm của phương trình f  3 2
x  3x  2 1  0 là A. 9 . B. 10 . C. 11. D. 12 . Lời giải Chọn C
Từ đồ thị hàm số y  f  x suy ra đồ thị hàm số y  f  x như sau: f  3 2
x  x      f  3 2 3 2 1 0
x  3x  2 1 (1) Đặt 3 2
x  3x  2  t . Dựa vào đồ thị hàm số y  f  x , phương trình f t   1 có 5 nghiệm phân biệt là: 1 3
t , t , t , t , t với 1
  t  0  t ,  t 
, 2<t  3  t . 1 2 3 4 5 1 2 3 4 5 2 2
Xét hàm số g  x 3 2
 x  3x  2 g x 2  3x  6x  x  2
g  x  0  x  0  Bảng biến thiên
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 63
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Khi đó, số nghiệm của các phương trình 3 2 3 2 3 2 3 2 3 2
x  3x  2  t , x  3x  2  t , x  3x  2  t , x  3x  2  t , x  3x  2  t lần lượt 1 2 3 4 5 bằng 3, 3, 3, 1, 1.
Vậy tổng số nghiệm của phương trình (1) bằng 11.
Câu 80. Cho hàm số ( ) có đạo hàm liên tục trên [−3; 3] và hàm số = ′( ) có đồ thị như hình vẽ ( )
bên. Biết (1) = 6 và ( ) = ( ) − . y 4 2 3  O 1 3 x 2 
Mệnh đề nào sau đây đúng?
A. Phương trình ( ) = 0 có đúng hai nghiệm thuộc [−3; 3].
B. Phương trình ( ) = 0 có đúng một nghiệm thuộc [−3; 3].
C. Phương trình ( ) = 0 không có nghiệm thuộc [−3; 3].
D. Phương trình ( ) = 0 có đúng ba nghiệm thuộc [−3; 3]. Lời giải Chọn B Ta có: ( ) = ( ) − ( ) ⇒ ( ) = ( ) − ( + 1). Vẽ đường thẳng =
+ 1 trên cùng một hệ trục tọa độ với đồ thị hàm số = ( ) (như hình vẽ bên). Từ đồ thị ta thấy: ( ) =
( ) − ( + 1) > 0, ∀ ∈ (−3; 1) (do đường cong nằm phía trên đường thẳng), ( ) =
( ) − ( + 1) < 0, ∀ ∈ (1; 3) (do đường cong nằm phía dưới đường thẳng). Ta có: (1) = (1) − ( ) = 6 − 2 = 4. Bảng biến thiên:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 64
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 −3 1 3 ′( ) + 0 − 4 ( )
Dựa vào đồ thị ta thấy: diện tích lớn hơn 4 (trong
phần bên trái có nhiều hơn 4 ô, mỗi ô có
diện tích bằng 1), do đó: 4 < = ∫
( )d ⇔ 4 < ( )| ⇔ 4 < (1) − (−3) ⇔ (−3) < 0. Mặt khác diện tích
nhỏ hơn 4 (trong phần bên phải có ít hơn 4 ô), do đó: 4 > = − ∫
( )d ⇔ 4 > − ( )| ⇔ 4 > (1) − (3) ⇔ (3) > 0.
Vậy phương trình ( ) = 0 có đúng một nghiệm thuộc đoạn [−3; 3] (nghiệm này nằm trong khoảng (−3; 1)).
Câu 81. Cho hàm số bậc bốn y  f  x có đồ thị như hình vẽ.
Gọi C và C lần lượt là đồ thị của hàm số y  f  x f  x   f  x 2 .  2  1    và 2020x y  . Số
giao điểm của C và C là 2  1  A. 4. B. 0. C. 1. D. 2. Lời giải Chọn B Giả sử:    4 3 2 y
f x  ax  bx  cx  dx  e với a  0 .
Từ đồ thị hàm số ta thấy phương trình f  x  0 có 4 nghiệm phân biệt nên ta có:
f  x  a  x  x x  x x  x x  x
với x , x , x , x là 4 nghiệm của phương trình 1   2   3   4  1 2 3 4
f  x  0 . Suy ra:
f  x  a  x  x x  x x  x  x  x x  x x  x  x  x x  x x  x   1   2   3   1   2   4   1   3   4    x  x x  x x  x  2   3   4  . f  x 1 1 1 1 Do đó:     f  x x  x x  x x  x x  x 1 2 3 4 2 
 f  x 
f  x. f  x   f  x 1 1 1 1           0 , f  x  
 f x2
 x  x 2  x  x 2  x  x 2  x  x 2 1 2 3 4
x   \ x ; x ; x ; x . 1 2 3 4 
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 65
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Dễ thấy tại các điểm x ; x ; x ; x thì
y  f  x
f x   f  x   i  1, 4 và i   i    i  2 . 0 1 2 3 4    2020x  0 . Nên:        2 .  2020x f x f x f x vô nghiệm trên  .
Vậy C và C không có điểm chung. 2  1 
Câu 82. Cho hàm số: 3 2
f (x)  x  6x  9x . Đặt k k 1 f (x) f ( f  
(x)) (với k là số tự nhiên lớn hơn 1).
Tính số nghiệm của phương trình 6
f (x)  0 . A. 729. B. 365. C. 730. D. 364. Lời giải Chọn B  x  0 Có: f  x 3 2
 x  6x  9x  0  x  3  k 1  f (x)  0 k k 1
f (x)  0  f ( f  (x))  0   k1 f (x)  3 
Mà f (x)  3 có 3 nghiệm phân biệt đều thuộc khoảng ( 0; 4) , f (x)  a với a thuộc ( 0; 4) cũng có 3 nghiệm phân biệt.
Đặt u là số nghiệm của phương trình k
f (x)  0 . Có u  2 k 1
Đặt v là số nghiệm của phương trình k
f (x)  3. Có: v  3; v  9;...; v  3k k 1 2 k k k k    3 1 Ta có: 2 1 2 1 u  u  v
 2  3  3  ...  3
 11 3  3  ...  3  k k 1  k 1  2 6 3 1 Vậy u   365 . 6 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 66
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

Tìm số nghiệm của phương trình hàm hợp – Đặng Việt Đông Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số