Tính đơn điệu của hàm ẩn cho bởi đồ thị hàm f'(x) Toán 12

Tính đơn điệu của hàm ẩn cho bởi đồ thị hàm f'(x) Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

27 14 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Caâu 50

TÍNH ÑÔN ÑIEÄU CUÛA HAØM AÅN

CHO BÔÛI ÑOÀ THÒ HAØM F’(X)

1 Định nghĩa 1

Giả sử K là một khoảng, một đoạn hoặc một nữa khoảng và

 

y f x

là một hàm số xác định trên K. Ta

nói:

+ Hàm số

 

y f x

được gọi là đồng biến (tăng) trên K nếu

   

1 2 1 2 1 2

,,    x x K x x f x f x

+ Hàm số

 

y f x

được gọi là nghịch biến (giảm) trên K nếu

   

1 2 1 2 1 2

,,    x x K x x f x f x

Hàm số đồng biến hoặc nghịch biến trên K gọi chung là đơn điệu trên K.

2 Nhận xét

Nhận xét 1

Nếu hàm số

 

và

 

cùng đồng biến (nghịch biến) trên D thì hàm số

   

f x g x

cũng đồng

biến (nghịch biến) trên D. Tính chất này có thể không đúng đối với hiệu

   

f x g x

Nhận xét 2

Nếu hàm số

 

và

 

là các hàm số dương và cùng đồng biến (nghịch biến) trên D thì hàm số

   

.f x g x

cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng khi các hàm số

   

,f x g x

không là các hàm số dương trên D.

Nhận xét 3

Cho hàm số

 

u u x

, xác định với

 

;x a b

và

   

;u x c d

. Hàm số

 





f u x

cũng xác định với

 

;x a b

. Ta có nhận xét sau:

i. Giả sử hàm số

 

u u x

đồng biến với

 

;x a b

. Khi đó, hàm số

 





f u x

đồng biến với

   

;x a b f u

đồng biến với

 

;u c d

ii. Giả sử hàm số

 

u u x

nghịch biến với

 

;x a b

. Khi đó, hàm số

 





f u x

nghịch biến với

   

;x a b f u

nghịch biến với

 

;u c d

3 Định lý 1

Giả sử hàm số

có đạo hàm trên khoảng K. Khi đó:

a) Nếu hàm số đồng biến trên khoảng K thì

 

' 0,  f x x K

b) Nếu hàm số nghịch biến trên khoảng K thì

 

' 0,  f x x K

4 Định lý 2

KIẾN THỨC CẦN NHỚ

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Giả sử hàm số

có đạo hàm trên khoảng K. Khi đó:

a) Nếu

 

' 0,  f x x K

thì hàm số

đồng biến trên K.

b) Nếu

 

' 0,  f x x K

thì hàm số

nghịch biến trên K.

c) Nếu

 

' 0,  f x x K

thì hàm số

không đổi trên K.

Chú ý

Chú ý: Khoảng K trong định lí trên ta có thể thay thế bởi đoạn hoặc một nửa khoảng. Khi đó phải có

thêm giả thuyết “ Hàm số liên tục trên đoạn hoặc nửa khoảng đó’. Chẳng hạn:

Nếu hàm số

liên tục trên đoạn

 

;ab

và

   

' 0, ;  f x x a b

thì hàm số

đồng biến trên đoạn

 

;ab

5 Định lý 3

Giả sử hàm số

có đạo hàm trên khoảng K. Khi đó:

a) Nếu

 

' 0,  f x x K

và

 

'0fx

chỉ tại hữu hạn điểm thuộc K thì hàm số

đồng biến trên K.

b) Nếu

 

' 0,  f x x K

và

 

'0fx

chỉ tại hữu hạn điểm thuộc K thì hàm số

đồng biến trên K.

Quy tắc xét tính đơn điệu của hàm số.

Giả sử hàm số

có đạo hàm trên

 Nếu

 

'0fx

với mọi

xK

và

 

'0fx

chỉ tại một số hữu hạn điểm

xK

thì hàm số

đồng

biến trên

 Nếu

 

'0fx

với mọi

xK

và

 

'0fx

chỉ tại một số hữu hạn điểm

xK

thì hàm số

nghịch

biến trên

1 Lời giải tham khảo

Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ

Câu 50. Cho hàm số

( ).y f x

Hàm số

()y f x

có đồ thị như hình vẽ bên dưới. Hàm số

( ) (1 2 )g x f x x x

nghịch biến trên khoảng nào dưới đây?

BÀI TẬP MẪU

II.

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

. B.

. C.

( 2; 1)

. D.

(2;3)

Lời giải

Chọn A

Xét hàm số

( ) (1 2 )g x f x x x

Tập xác định:

Đạo hàm:

( ) 2 (1 2 ) 2 1, .g x f x x x

Trước tiên ta cần tìm

sao cho

( ) 0.gx

Ta có

( ) 0 2 (1 2 ) 2 1 0g x f x x

(1 2 ) (1 2 )

f x x

(*)

Đặt

12tx

, bất phương trình

(*)

trở thành

( )

f t t

Từ đồ thị ta có

()

f t t

Do đó,

( ) 0gx

2 1 2 0

1 2 4

1 3 1 3

( ) 0 (1 2 ) 1 2 ; ;

2 2 2 2

g x f x x x

: hữu hạn.

Như vậy hàm số

()gx

nghịch biến trên đoạn

;

và nửa khoảng

;

Soi các phương án của đề bài, ta chọn

2 Phân tích – Bình luận

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

 Bình luận: Đây là câu vận dụng cao về vấn đề tính đơn điệu của một hàm số. Để làm được

nó hoặc những dạng tương tự mở rộng, ta cần nắm vững kiến thức cơ bản sau:

 Tính đơn điệu và dấu của đạo hàm

Điều kiện cần: Giả sử hàm số

()y f x

có đạo hàm trên khoảng

đồng biến trên khoảng

( ) 0, .K f x x K

nghịch biến trên khoảng

( ) 0, .K f x x K

Điều kiện đủ: Giả sử hàm số

()y f x

có đạo hàm trên khoảng

Nếu

( ) 0, f x x K

thì hàm số đồng biến trên khoảng

Nếu

( ) 0, f x x K

thì hàm số nghịch biến trên khoảng

Nếu

( ) 0, f x x K

thì hàm số không đổi trên khoảng

Mở rộng:

1)Nếu phương trình

( ) 0fx

có hữu hạn nghiệm trên

thì ta có điều kiện cần và đủ sau

đây:

đồng biến trên khoảng

( ) 0, .K f x x K

nghịch biến trên khoảng

( ) 0, .K f x x K

( ) ;

( ) 0, ;

f x a b

f x x a b

lieân tuïc treân

đồng biến trên

;.ab

( ) ;

( ) 0, ;

f x a b

f x x a b

lieân tuïc treân

nghịch biến trên

;.ab

( ) ;

( ) 0, ;

f x a

f x x a

lieân tuïc treân

đồng biến trên

…

 Đạo hàm hàm hợp: Giả sử hàm số

()y f x

và

u u x

có đạo hàm trên khoảng

Khi

đó:

.f u u f u

3 Phân tích hướng giải

1. Dạng toán

Đây là dạng toán tìm khoảng đơn điệu của hàm ẩn dạng

     

g x f u x v x





khi biết đồ thị của

hàm số

 

y f x





2. Hướng giải

Cách 1:

B1: Tính đạo hàm của hàm số

 

       

.g x u x f u x v x

   







B2: Sử dụng đồ thị của

 



, lập bảng xét dấu của

 



B3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số.

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Cách 2:

B1: Tính đạo hàm của hàm số

 

       

.g x u x f u x v x

   







B2: Hàm số

 

đồng biến

 

0gx





; (Hàm số

 

nghịch biến

 

0gx





) (*)

B3: Giải bất phương trình

 

(dựa vào đồ thị hàm số

 

y f x





) từ đó kết luận khoảng đồng biến,

nghịch biến của hàm số.

Cách 3: (Trắc nghiệm)

B1: Tính đạo hàm của hàm số

 

       

.g x u x f u x v x

   







B3: Hàm số

 

đồng biến trên

 

0,g x x K



   

; (Hàm số

 

nghịch biến trên

 

0,g x x K



   

) (*)

B3: Lần lượt chọn thay giá trị từ các phương án vào

 



để loại các phương án sai.

 Câu 1: Cho hàm số

 

. Hàm số

 

y f x





có đồ thị như hình sau.

Hàm số

xxxxfxg 6218)21(3)(



đồng biến trên khoảng nào dưới đây?

 

2;1

. B.

 

1;3 

. C.

 

1;0

. D.

 

2;1

 Lời giải

Chọn A

Ta có

64224)21('6)('

 xxxfxg

(*)174)21('0)('

 xxxfxg

Đặt

xtx





Ta có

(*)

trở thành

)('1

.4)('



















 tttf

Ta vẽ parapol

:)(

 xxyP

trên cùng hệ trục

Oxy

với đồ thị

 

y f x





như hình

vẽ sau, ta thấy

)(P

có đỉnh

)

;

( I

và đi qua các điểm

     

.1;1,2;1,3;3 

BÀI TẬP TƯƠNG TỰ VÀ PHÁT TRIỂN

III.

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Từ đồ thị hàm số ta thấy trên khoảng

 

1;3

ta có

)('

 ttttf

211213  xx

Vậy hàm số

)(xg

nghịch biến trên khoảng

).2;1(

 Câu 2: Cho hàm số

 

. Hàm số

 

y f x





có đồ thị như hình sau.

Có tất cả bao nhiêu giá trị nguyên dương của tham số

đề hàm số

20202)(4)(

 mxxmxfxg

đồng biến trên khoảng

).2;1(

. B.

. C.

. D.

* Ý tưởng : Phát triển thành bài toán chứa tham số.

 Lời giải

Chọn A

Ta có

mxmxfxg 22)('4)(' 

(*)

)('0)('

mxfxg





Đặt

mxt 

thì

)('(*)

tf 

Vẽ đường thẳng

y 

trên cùng hệ trục

Oxy

với đồ thị

 

y f x





như hình vẽ sau

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Từ đồ thị ta có

























)('

mxm

Hàm số

)(xg

đồng biến trên khoảng

)2;1(

 

2;10)('  xxg

























212

Vì

nguyên dương nên

 

.3;2m

Vậy có hai giá trị nguyên dương của

đề hàm số

)(xg

đồng biến trên khoảng

).2;1(

 Câu 3: Cho hàm số đa thức

)(xf

có đạo hàm tràm trên

. Biết

0)0( f

và đồ thị hàm số

 

y f x





như hình sau.

Hàm số

)(4)( xxfxg 

đồng biến trên khoảng nào dưới đây ?

 

4;0

. B.

 

0;2

. C.

 

;4

. D.

 

2;

* Ý tưởng : Phát triển thành bài toán tìm khoảng đồng biến và nghịch biến của hàm số chứa

dấu giá trị tuyệt đối.

 Lời giải

Chọn A

Xét hàm số

Rxxxfxh  ,)(4)(

Có

)('0)('2)('4)('

xfxhxxfxh 

Vẽ đường thẳng

y 

trên cùng hệ trục

Oxy

với đồ thị

 

y f x





như hình vẽ sau

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Từ đồ thị ta có BBT của

)(xh

như sau :

Chú ý ở đây

0)0(4)0(  fh

Từ đó ta có BBT của như sau :

Từ BBT ta suy ra

)(xg

đồng biến trên khoảng

 

.4;0

 Câu 4: Cho hàm số

)(xfy 

có bảng xét dấu đạo hàm như sau

Biết rằng

Rxxf  ,5)(1

. Hàm số

20203)1)(()(

 xxxffxg

nghịch biến

trên khoảng nào dưới đây

 

5;0

. B.

 

0;2

. C.

 

5;2

. D.

 

2;

* Ý tưởng : Phát triển thành bài toán tìm khoảng đồng biến và nghịch biến của hàm số

)()( xgufy 

 Lời giải

Chọn B

Ta có

xxxffxfxg 63)1)((').(')('



Vì

41)(0,5)(1  xfRxxf

Từ bảng xét dấu của

0)1)((')('  xffxf

Từ đó ta có bảng xét dấu như sau

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Do đó hàm

)(xg

nghịch biến trên khoảng

 

0;2

 Câu 5: Cho hàm số

()y f x

liên tục trên và có đồ thị hàm số

()fx

như hình bên dưới.

Hỏi hàm số

( ) (1 )

g x f x x

nghịch biến trên khoảng nào?

( 3;1)

. B.

( 2;0)

. C.

. D.

(1;3)

Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ

 Lời giải

Chọn B

( ) (1 ) 1, x .g x f x x

( ) (1 ) 1 0g x f x x

(1 ) (1 )f x x

1 1 3

( ) 0 (1 ) 1 0 2; 0; 4g x f x x x

: hữu hạn.

Hàm số

()gx

nghịch biến trên mỗi tập

2;0 , 4;

nên nghịch biến trên

( 2;0).

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

 Câu 6: Cho hàm số

5 4 3 2

f x ax bx cx dx ex f

, , , , ,a b c d e f

. Biết rằng đồ

thị hàm số

có đồ thị như hình vẽ bên. Hỏi hàm số

1 2 2 1g x f x x

đồng

biến trên khoảng nào dưới đây?

. B.

;

. C.

1;0

. D.

1;3

Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ

 Lời giải

Chọn C

Hàm số

1 2 2 1g x f x x

đồng biến

( ) 2 (1 2 ) 4 0g x f x x

(1 2 ) (1 2 ) 1f x x

1 1 2 3 1 0xx

 Câu 7: Cho hàm số

( ).y f x

Hàm số

()y f x

có đồ thị như hình vẽ bên dưới.

Có tất cả bao nhiêu giá trị nguyên

10;10m

đê hàm số

( ) 1 2 ( 1)g x f x m x m x m

nghịch biến trên khoảng

1;2

. B.

. C.

. D.

Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ

 Lời giải

Chọn B

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

( ) 2 (1 2 ) 2 1, .g x f x m x m x

( ) 0gx

(1 2 ) 1 2

f x m x m

1 2 4

2 1 2 0

1 2 4

2 1 2 0 1 3

x m m m

( ) 0gx

(1 2 ) 1 2

f x m x m

3 1 3

;;

2 2 2

m m m

: hữu hạn.

Hàm số

nghịch biến trên

1;2

( ) 0, 1;2g x x

( ) 0, 1;2

g x x

Vậy

1;7;8;9m

 Câu 8: Cho hàm số

y f x

có đạo hàm

11f x x x x

với mọi

Tìm tất

cả các giá trị của tham số

để hàm số

2 2019y g x f x x m

đồng biến

trên khoảng

. B.

. C.

. D.

Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ

 Lời giải

Chọn D

Cách 1:

Ta có

2 2 2 0y g x x f x x m

Hàm số đồng biến trên

0, x 1; .gx

2 2 2 0, 1; , 1; .x f x x m x x

2 2 2

2 2 2 2 1 2 1 0,x x x m x x m x x m

1;x

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

2 2 2

2 2 1 2 1 0x x m x x m x x m

1;x

2 2 1 0,x x m x x m

1;x

( ) 1 0 1;h t t m t m t

(

2 1 1;t x x x

)

Bảng xét dấu

Khi đó

( ) 0, 1; 1 1h t t m m

Cách 2: Ta có bảng xét dấu đạo hàm

như sau

2 2 2y g x x f x x m

Hàm số

y g x

đồng biến trên khoảng

1; 0, 1;g x x

Ta thấy

2 2 0, 1;xx

nên

0, 1 2 0, 1g x x f x x m x

2 1, 1

2 0, 1

x x m x

2 1 , 1

2 , 1

m x x u x x

m x x v x x

(do tính liên tục)

 

2 1 , 1m x x u x x      

: Không tồn tại

 

2 , 1 1 1 , 1 1.m x x x m x x m            

 Câu 9: Cho hàm số

y f x

có bảng xét dấu của đạo hàm như hình vẽ

Biết

1 3,f x x

. Hàm số

61y g x f f x x x

nghịch biến trên

khoảng nào dưới đây?

3;4

. B.

3; 2

. C.

1; 3

. D.

2;1

Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ

 Lời giải

Chọn A

( ). 2 12 .g x f x f f x x x

1 3,f x x

nên từ bảng xét dấu ta có

( ) 0f f x x

Ta xét một số khả năng có thể xảy ra

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

+ TH1:

( ) 0















2 12 0





   







Chưa xác định được dấu của

với giả thiết đã cho.

6 2 12 0x x x    

0, 6g x x

Hàm số

đồng biến trên

+ TH2:

( ) 0















Ta thấy với

34x

thì

2 12 0xx

nên

0, 3;4g x x

Hàm số

nghịch

biến trên

3;4

 Câu 10: Cho hàm số

 

có bảng xét dấu đạo hàm như sau:

Hàm số

2 1 1y f x x x

nghịch biến trên những khoảng nào dưới đây

. B.

. C.

2;0

. D.

3; 2

Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ

 Lời giải

Chọn C

( ) 2 1 1g x f x x x

( ) 2 1 1

g x f x

Để ý

1 , 1 0, .

x x x x

Ta xét một số khả năng về dấu của

2 (1 )fx





+TH1:

2 (1 ) 0 (1 ) 0

3 1 4

f x f x







      



  



: Chưa xác định được dấu của

với giả thiết đã cho.

+TH2:

1 1 3 2 0

2 (1 ) 0 (1 ) 0 .

1 4 3

f x f x

     





       



   





  

( ) 0, ; 3 2;0g x x



       

Hàm số

nghịch biến trên

2;0

 Câu 11: Cho hàm số

()y f x

có đạo hàm

2f x x x

với mọi

. Hàm số

2 1 1 3g x f x x

đồng biến trên các khoảng nào dưới đây?

2; 1

. B.

1;1

. C.

1;2

. D.

2;3

Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ

 Lời giải

Chọn A

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ta có

( ) 2 1 .

g x f x

2 1 1

Vì

2 1 1f x x x x

nên

( ) 1fx

hay

10fx

Suy ra

2 1 1 0fx

Bảng biến thiên:

∞

( )

∞

Hàm số

đồng biến trên khoảng

 Câu 12: Cho hàm số

y f x

có đồ thị của hàm số

'y f x

như hình vẽ. Hàm số

2 3 2

2 3 4

y f x x x x

nghịch biến trên khoảng nào dưới đây?

. B.

3;0

. C.

1; 3

. D.

Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ

 Lời giải

Chọn C

Ta xét

2 . 2 2 3 0y x f x x x

( 2) 0 (1)

2 3 0 (2)

xf x

Từ

(2)

nên loại A, B,. D. Vậy chọn. C.

 Câu 13: Cho hàm số

 

. Hàm số

 

y f x





có đồ thị như hình bên dưới.

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Hàm số

   

3 1 3g x f x x x   

đồng biến trên khoảng nào dưới đây?







. B.







. C.

 

1;0

. D.







 Lời giải

Chọn B

Ta có:

     

3 3 1 6 2 3g x f x x



    

Hàm

()gx

đồng biến trên khoảng

khi

 

0gx





(dấu = xảy ra tại một số hữu hạn điểm)

   

3 3 1 6 2 3 0f x x



     

(1)

Đặt

31ux

ta được:

   

3 2 3h u f u u



  

Ta có: (1)

   

3 2 3 0 1

f u u f u



      

Từ đồ thị hàm số

 

y f x





ta có đồ thị hàm số

 

y f u





và



như hình vẽ

Để

 

0hu

ta cần có đồ thị

 

y f u





phải nằm bên trên của đồ thị hàm



 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Từ đó ta có

 

0hu















0 3 1 3

3 1 3

















;

























Cho nên ta Chọn B vì

2 1 2

0; ;

3 3 3

   







   

 Câu 14: Cho hàm số

 

. Đồ thị

 

'y f x

cho như hình bên. Hàm số

   

g x f x  

nghịch biến trong khoảng nào dưới đây?

 

2;4

. B.

 

0;1

. C.

 

2;1

. D.

 

1;3

 Lời giải

Chọn A

Ta có:

   

g x f x  

   

1g x f x x



   

       

0 1 0 1 1 1g x f x x f x x

  

          

Đặt

1tx

thì

 

1f t t





Vẽ đường thẳng

1yx

trên cùng một hệ trục tọa độ với đồ thị hàm số

 

y f x





(như

hình vẽ bên).

Dựa vào đồ thị

 

' 1 3, 1, 3f t t t t t      

Hàm số nghịch biến

     

1 0 ( ; 3) (1;3)g x f x x f t t t

  

          

Do đó

( ; 2) (2;4)x   

vậy g(x) nghịch biến trên

 

2;4

 Câu 15: Cho hàm số

 

y f x

. Hàm số

 

'y f x

có đồ thị như hình bên.

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Hàm số

 

22g x f x x x x   

đồng biến trên khoảng nào dưới đây?

 

1 2; 1  

. B.

 

1 2; 1 2   

. C.

 

1; 

. D.

 

1; 1 2  

 Lời giải

Chọn A

Ta có:

 

22g x f x x x x   

   

 

2 2 2 2 2 2 1 2 1g x x f x x x x f x x



  

         



   

 

0 2 1 2 1 0 1, 1 2, 1 2g x x f x x x x x





               



Xét

 

f x x

  

















































Xét sự tương giao của đồ thị hàm số

 

y f x





và

1y 

Dựa vào đồ thị ta có:

 

2 1 2 1f x x x x



    

và

 

2 1 2 1f x x x x



    

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Xét hệ (I):

 

f x x





































    

  







  







Xét hệ (II):

 

f x x





























1 2 1 2











     





1 2 1x     

Vậy hàm số

 

đồng biến trên khoảng

 

1 2; 1  

và

 

1 2;  

 Câu 16: Cho hàm số

 

y f x

có đạo hàm trên . Hàm số

 

'y f x

có đồ thị như hình vẽ

bên. Đặt

   

y g x f x  

. Khẳng định nào sau đây là đúng?

A. Hàm số

 

y g x

đồng biến trên khoảng

 

1;2

B. Đồ thị hàm số

 

y g x

có 3 điểm cực trị.

C. Hàm số

 

y g x

đạt cực tiểu tại

1x 

D. Hàm số

 

y g x

đạt cực đại tại

1x 

 Lời giải

Chọn D

Ta có:

       

' ' ; ' 0 'g x f x x g x f x x    

(*).

Số nghiệm của phương trình (*) là số giao điểm giữa đồ thị hàm số

 

'y f x

và

đường thẳng

yx

Dựa vào hình bên ta thấy giao tại 3 điểm

     

1; 1 ; 1;1 ; 2;2

(*) 1







  







Bảng xét dấu

 

'gx



1



 

'gx



 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Từ bảng xét dấu

 

'gx

ta thấy hàm số

   

y g x f x  

Đồng biến trên khoảng

 

;1

và

 

2;

; nghịch biến trên khoảng

 

1;2

Hàm số

 

y g x

đạt cực đại tại

1x 

 Câu 17: Cho hàm số

 

có đồ thị của hàm số

 



như hình vẽ.

Hỏi hàm số

   

g x f x x   

nghịch biến trên khoảng nào dưới đây?

 

2;0

. B.

 

1;3

. C.









. D.

 

3;1

 Lời giải

Chọn A

Ta có:

   

11g x f x x



    

Hàm số

 

nghịch biến

 

0gx





 

1 1 (1)f x x



   

Đặt

1tx

. Khi đó (1) trở thành

 

f t t





(2).

Bất phương trình (2) được thỏa khi

 

f x x





hay đồ thị hàm số

 



nằm phía trên

đồ thị hàm số

yx

Từ đồ thị ta được

3 1 3 4

1 3 1 1 3 2 0

t x x

     

  



  

       

  

. Vậy chọn khoảng

 

2;0

 Câu 18: Cho hàm số

 

y f x

có đồ thị hàm số

 

y f x





được cho như hình vẽ sau.

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

-1

Hàm số

 

21g x f x

đồng biến trên khoảng nào dưới đây?

 

1;

. B.







. C.

 

;1 

. D.







 Lời giải

Chọn D

Ta có:

 

8 . 2 1g x x f x





TH1:

0x 

. Để hàm số

 

đồng biến thì

 

4 4 4 2

2 1 0 1 2 1 3 0 2 0 2 2 2f x x x x x



                

0 2 0; 2xx



    



TH2:

0x 

. Để hàm số

 

đồng biến thì

 

0( )

2 1 1 2

2 1 0

2 1 3







   



    













So sánh với điều kiện



0 2 ; 2x x x



       



Vậy hàm số

 

đồng biến trên

0; 2





và





 



. Do đó chọn khoảng







 Câu 19: Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình vẽ sau đây.

Hàm số

 

y f x x

nghịch biến trên khoảng nào?

;









. B.

;









. C.

;



 





. D.

;



 





 Lời giải

Chọn A

Xét hàm số

 

y f x x

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ta có:

 

12y x f x x



  

 

2 1 0

0 1 1 0

y x x x x VN

x x VN















        





  







Ta lại có:

1 1 1

4 2 4

x x x x R



       





Từ đồ thị của hàm số

 

y f x





 

0,f x x x R



    

Bảng biến thiên của hàm số

 

y f x x

Vậy hàm số nghịch biến trên

;









. Chọn A

 Câu 20: Cho hàm số

 

y f x

có đạo hàm trên

Đồ thị hàm số

 

y f x





như hình vẽ.

Hàm số

 

2y f x x

đồng biến trên khoảng nào sau đây?

 

1; 2

. B.

 

;3 

. C.

 

0;1

. D.

 

2; 0

 Lời giải

Chọn A

Từ đồ thị của hàm số

 

y f x





ta có bảng biến thiên của hàm số

 

y f x

như sau

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Đặt

 

2g x f x x

, ta có

 

   

 

2 2 2

2 . 2 2 1 . 2 .g x x x f x x x f x x



  

     

Hàm số

 

đồng biến khi

   

 

0 1 . 2 0g x x f x x



    

 

f x x



















hoặc

 

f x x

















· Xét

 

1 2 1 2

1 1 2

1 2 1













     



    





  

   

































· Xét

 

2 1 0

1 2 3

2 3 0





















  







  







  











  









3 1 2

















    









  





















  













  







 Câu 21: Cho hàm số

 

y f x

, biết hàm số

 

y f x





có đồ thị như hình bên dưới.

Hàm số

 

3g x f x

đồng biến trên khoảng?

 

2;3

. B.

 

1;0

. C.

 

2; 1

. D.

 

0;1

 Lời giải

Chọn B

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Dựa vào đồ thị, ta có bảng xét dấu

 

' 2 3



  g x xf x

 















  





















 

6 3 1

3 0 2 3

f x x

   



    





     









  



Bảng biến thiên:

Từ BBT suy ra hàm số đồng biến trên

 

1;0

 Câu 22: Cho hàm số

()y f x

có bảng xét dấu đạo hàm như sau:

Biết:

1 ( ) 5, .f x x R   

Khi đó, hàm số

( ) ( ( ) 1) 3 2020g x f f x x x    

nghịch biến trong

khoảng nào dưới đây:

( 2;0)

. B.

(0;5)

. C.

( 2;5)

. D.

( ; 2) 

 Lời giải

Chọn A

Ta có:

'( ) '( ). '( ( ) 1) 3 6g x f x f f x x x   

Vì

1 ( ) 5, 0 ( ) 1 4f x x R f x       

Từ bảng xét dấu của

'( ) 0 '( ( ) 1) 0f x f f x   

Từ đó, ta có bảng xét dấu như sau:

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Do đó, hàm

()gx

nghịch biến trên khoảng

( 2;0).

 Câu 23: Cho hàm số

 

y f x

có đạo hàm trên và có bảng biến thiên của đạo hàm

 

'fx

như sau :

Hỏi hàm số

 

2 2020g x f x x  

có bao nhiêu điểm cực tiểu ?

A. 1. B. 2. C. 3. D. 4.

 Lời giải

Chọn A

Ta có

2 2 2 ;g x x f x x

theo BBT '

2 2 0

f x x

Bảng biến thiên

Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta Chọn A

Chú ý: Dấu của

được xác định như sau: Ví dụ xét trên khoảng



3; 2 2 0.xx



theo BBT '

3; 2 3 2 0.

x x x f x x

Từ

và

suy ra

2 2 2 0g x x f x x

trên khoảng

nên

mang dấu

Nhận thấy các nghiệm

và

là các nghiệm bội lẻ nên

qua nghiệm đổi

dấu.

 Câu 24: Cho hàm số

 

y f x

có đạo hàm trên

Đồ thị hàm số

 

y f x





như hình vẽ bên

dưới.

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Hàm số

   

3 1 9 18 12 2021g x f x x x x     

nghịch biến trên khoảng.

 

;1

. B.

 

1;2

. C.

 

3;1

. D.







 Lời giải

Chọn D

Ta có

         

3 3 1 3(9 12 4); 0 3 1 3 2 .(1)g x f x x x g x f x x

   

         

Đặt

31tx

khi đó

   

(1) 1f t t



  

Dựa vào đồ thị ta suy ra

   

f t t







  







(vì phần đồ thị của

 

'ft

nằm phía

dưới đồ thị hàm số

 

1yt

Như vậy

   

3 1 0

3 1 3 2

1 3 1 2 2

f x x













    



  











Vậy hàm số

   

3 1 9 18 12 2021g x f x x x x     

nghịch biến trên các khoảng

;









và







 Câu 25: Cho hàm số

y f x

có bảng xét dấu của đạo hàm như sau:

Đặt

4 3 2

2 1 3

y g x f x x x x

. Khẳng định nào dưới đây là đúng?

A. Hàm số

y g x

đồng biến trên khoảng

 

;0

B. Hàm số

y g x

đồng biến trên khoảng

 

1;2

C. Hàm số

y g x

đồng biến trên khoảng

 

0;1

D. Hàm số

y g x

nghịch biến trên khoảng

 

2;

 Lời giải

Chọn C

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ta có:

   

2 1 3 2y g x f x x x x

  

      

Dựa vào bảng xét dấu

 



ta có

 













  











   

2 1 1 2 3

2 1 0 1 0

0 1 1 0 1

f x f x

      





       



    



  

3 2 1 2x x x x x x    

Bảng xét dấu

 

y g x





Vậy hàm số đồng biến trên

 

0;1

 Câu 26: Cho hàm số

 

y f x

. Hàm số

 

'y f x

có đồ thị như hình vẽ bên dưới.

f(x)=-3x^5+2x^4-2x^2+x

f(x)=2

f(x)=-2

x(t)=-1 , y(t)=t

x(t)=1 , y(t)=t

-8 -7.5 -7 -6.5 -6 -5.5 -5 -4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0.5 1 1.5

-6

-5

-4

-3

-2

-1

Hàm số

   

2 3 4 12 1g x f x x x    

đồng biến trên khoảng nào dưới đây?









; 2 .









2; .









;0 .









 Lời giải

Chọn B

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

f(x)=-3x^5+2x^4-2x^2+x

f(x)=2

f(x)=-2

x(t)=-1 , y(t)=t

x(t)=1 , y(t)=t

f(x)=-2x

-8 -7.5 -7 -6.5 -6 -5.5 -5 -4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0.5 1 1.5

-6

-5

-4

-3

-2

-1

 

'y f x

2yx

Hàm số

 

đồng biến

       

' 0 2 ' 2 3 8 12 0 ' 2 3 2 2 3g x f x x f x x           

2 3 1

0 2 3 1







  







  

   







Chọn B

 Câu 27: Cho hàm số

 

y f x

có đồ thị

 

y f x





như hình vẽ. Xét hàm số

   

1 3 3

2018

3 4 2

g x f x x x x    

. Mệnh đề nào dưới đây đúng?

A. Hàm số

 

đồng biến trên

 

1;1

. B. Hàm số

 

đồng biến trên

 

3;1

C. Hàm số

 

đồng biến

 

3; 1

. D. Hàm số

 

nghịch biến trên

 

1;1

 Lời giải

Chọn B

Ta có:

       

3 2 2

1 3 3 3 3

2018

3 4 2 2 2

g x f x x x x g x f x x x



         

3

1

2

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

   

' 0 '

g x f x x x    

. Đặt

y x x  

có đồ thị (P)

Dựa vào đồ thị

 

y f x





, ta có:

 

1 2 1 0

1 1 1 0

3 3 3 0



    







  







   



Vẽ đồ thị

 

của hàm số

y x x  

trên cùng hệ trục tọa độ như hình vẽ trên

(đường nét đứt ), Đồ thị

 

đi qua các điểm

 

3;3

 

1; 2

 

1;1

với đỉnh

3 33

;

4 16









Ta thấy: + Trên khoảng

 

1;1

thì

 

f x x x



  

, nên

   

0 1;1xgx 





+Trên khoảng

 

3; 1

thì

 

f x x x



  

, nên

   

0 3; 1xgx 



 

Từ những nhận xét trên, ta có bảng biến thiên của hàm

 

y g x





trên

 

3;1

như sau:

Vậy hàm số

 

đồng biến trên

 

1;1

. Chọn A

 Câu 28: Cho hàm số

 

. Hàm số

 

'y f x

có đồ thị như hình vẽ

3

1

2

 

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Hàm số

   

g x f x



  

đồng biến trên khoảng nào dưới đây?

 

;2 

. B.

 

3; 1

. C.

 

0;1

. D.

 

1;0

 Lời giải

Chọn B

Ta có:

       

1 ' ' 1 2

g x f x g x f x x



       

Hàm số đồng biến

   

' 0 ' 1 2g x f x x     

(1)

Đặt

1xt

. Bất phương trình (1) có dạng:

 

'1f t t

Xét hai hàm số

 

'y f t

và

1yt

Dựa vào đồ thị ta có:

 

2;0

f t t





  







 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ta có

 

2 1 0 3 1

1 2 1

       



  



  



 Câu 29: Cho hàm số

()fx

liên tục trên R và có đồ thị

'( )fx

như hình vẽ. Tìm số điểm cực trị

của hàm số

()y f x x

. B.

. C.

. D.

 Lời giải

Chọn B

Ta có

' (2 1) '( )y x f x x  

;

x x m

có nghiệm khi và chỉ khi

m 

Dựa vào đồ thị ta thấy đồ thị hàm

'( )fx

cắt trục hoành tại 5 điểm trong đó 1 điểm có

hoành độ nhỏ hơn



và có một tiệm cận.

Khi đó ứng với mỗi giao điểm có hoành độ lớn hơn



và 1 điểm không xác định thì

'0y 

có hai nghiệm. Từ đây dễ dàng suy ra hàm

()y f x x

có 11 cực trị.

 Câu 30: Cho hàm số

()y f x

có đạo hàm trên . Đồ thị của hàm số

'( )y f x

như hình vẽ.

Tìm các khoảng đơn điệu của hàm số

( ) 2 ( ) 2 2020g x f x x x   

-2

-1

Mệnh đề nào dưới đây đúng?

A. Hàm số

 

nghịch biến trên

 

1;3

. B. Hàm số

 

có 2 điểm cực trị đại.

C. Hàm số

 

đồng biến trên

 

1;1

. D. Hàm số

 

nghịch biến trên

 

3; 

 Lời giải

Chọn C

Ta có

 

'( ) 2 '( ) 2 2 2 '( ) ( 1)g x f x x f x x     

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Dựa vào hình vẽ ta thấy đường thẳng

1yx

cắt đồ thị hàm số

'( )y f x

tại 3 điểm:

( 1; 2), (1;0), (3;2).

-2

-1

Dựa vào đồ thị ta có

 

'( ) 0 2 '( ) ( 1) 0 1

g x f x x x







      







 

'( ) 0 2 '( ) ( 1) 0

g x f x x

  



     







 

'( ) 0 2 '( ) ( 1) 0

g x f x x





     







 Câu 31: Cho hàm số

 

y f x

có bảng xét dấu như hình vẽ

Tìm khoảng đồng biến của hàm số

5 4 3

( ) 2 (1 ) 3x

y g x f x x x     

 

;0

. B.

 

2;3

. C.

 

0;2

. D.

 

3; 

 Lời giải

Chọn B

Coi

      

' 2 1 1f x x x x x   

có bảng xét dấu như trên.

4 3 2

'( ) 2 '(1 ) 5 6xg x f x x x     

Ta đi xét dấu

'( )g x P Q

. Với:

          

2 ' 1 2 3 2 1 2 3 2 1P f x x x x x x x x x            

Bảng xét dấu của P

  

4 3 2 2

5 6x 2 3Q x x x x x       

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Bảng xét dấu của

Từ hai BXD của

,PQ

. Ta có

0, 0PQ

với

 

2;3x

nên

'( ) 0g x P Q  

với

 

2;3x

 Câu 32: Cho hàm số

 

y f x

có đồ thị hàm số

 

y f x





như hình vẽ

Xét hàm số

   

2 2 4 3 6 5    g x f x x x m

với

là tham số thực. Điều kiện cần và

đủ để

 

0gx

với mọi

5; 5







là

 

mf

. B.

 

mf

. C.

 

mf

. D.

 

mf

 Lời giải

Chọn A

Ta có

 

0gx

với mọi

5; 5x







 

2 2 4 3 6 5 0f x x x m     

với mọi

5; 5x







 

2 2 4 6 5 3f x x x m    

với mọi

5; 5x







 

5; 5

max 2 2 4 6 5 3f x x x m







    

với mọi

 

5; 5 *x







Đặt

   

2 2 4 6 5h x f x x x   

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ta có

   

2 6 4h x f x x



  

   

0 3 2 5

h x f x x x









       







Dựa vào đồ thị ta thấy

 

32f x x



  

với mọi

5; 5x







 

hx

luôn đồng biến

trên

5; 5







 

   

5; 5

max 5 2 5h x h f







  

Vậy

 

   

* 2 5 3 5

f m m f   

 Câu 33: Cho hàm số

()fx

có đồ thị của hàm số

’()y f x

như hình vẽ:

Hàm số

(2 1) 2

y f x x x    

nghịch biến trên khoảng nào sau đây?

 

6; 3

. B.

 

3;6

. C.

 

6;

. D.

 

1;0

 Lời giải

Chọn D

Ta có:

 

’ 2 ’(2 1) 2 2 2 ’(2 1) 1 3y f x x x f x x         

Nhận xét: Hàm số

()y f x

có

3’( ) 1 3f x x    

và

( ) 1

’













Do đó ta xét các trường hợp:

Với

6 3 13 2 1 7xx         

suy ra

0’y 

hàm số đồng biến (loại)

Với

3 6 5 2 1 11xx     

suy ra

0’y 

hàm số đồng biến (loại)

Với

6 2 1 11xx   

suy ra

0’y 

hàm số đồng biến (loại)

Với

1 0 3 2 1 1xx        

nên

22 ’(2 1)xf 

và

 

3 1 3 2x     

suy ra

0’y 

hàm số nghịch biến (nhận).

 Câu 34: Cho hàm số

 

có bảng xét dấu của đạo hàm như sau

Hàm số

   

3 2 3g x f x x x   

đồng biến trên khoảng nào dưới đây?

 

1; 

. B.

 

;1 

. C.

 

1;0

. D.

 

0;2

 Lời giải

Chọn C

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ta có

   

 

3 2 3g x f x x





   



Với

     

1;0 2 1;2 2 0x x f x



       

lại có

 

3 0 0, 1;0x y x



      

Vậy hàm số

 

đồng biến trên khoảng

 

1;0

Chú ý:

+) Ta xét

       

1;2 1; 2 3;4 2 0; 3 0x x f x x



          

Suy ra hàm số nghịch biến trên

 

1;2

nên loại hai phương án A, D.

+) Tương tự ta xét

       

; 2 2 ;0 2 0; 3 0 0, ; 2x x f x x y x



                 

Suy ra hàm số nghịch biến trên khoảng

 

;2 

nên loại phương án B.

 Câu 35: Cho hàm số

 

có đạo hàm, liên tục trên . Hàm số

 

y f x





có đồ thị như hình

sau.

Hàm số

 

2 4 2

3 2 3

g x f x x x   

đồng biến trên khoảng nào dưới đây?

 

3; 1

. B.

 

0;1

. C.

 

1;1

. D.







 Lời giải

Chọn D

Ta có

 

   

2 3 2 2

6 . 2 6 6 6 2 1g x x f x x x x f x x



  

       



 

2 1 0

f x x













   





Đặt

 

   

2 2 2

2 2 1 0 1 0 1t x f x x f t t f t t

  

              

Đồ thị của hàm số

 

y f t





và

1yt  

như hình vẽ sau

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Từ đồ thị, ta có

 

f t t







   







(

1t 

là nghiệm đơn và

1t 

là nghiệm kép).

   

2 2 1

f x x





  



       









Suy ra

 

g x x









   







(

0, 1xx  

là nghiệm đơn và

3x 

là nghiệm kép).

Bảng xét dấu

 



(vì

1 7 3

3. 0

2 4 4



   



   

   



   



Vậy hàm số đồng biến trên khoảng

 

1;0

và

 

1; 

 Câu 36: Cho hàm số

5 4 3 2

     y ax bx cx dx ex f

với

, , , , ,a b c d e f

là các số thực, đồ thị của

hàm số

 

y f x





như hình vẽ dưới đây. Hàm số

 

1 2 2 1y f x x   

đồng biến trên

khoảng nào sau đây?

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn









. B.

;









. C.

 

1;0

. D.

 

1;3

 Lời giải

Chọn C

Cách 1: Ta có:

       

1 2 2 1 2 1 2 4 .



        g x f x x g x f x x

Có:

     

0 2 1 2 4 0 ' 1 2 2 (1).



         g x f x x f x x

Đặt

1 2 ,tx

bất phương trình

 

trở thành

 

1f t t





Vẽ đường thẳng

1yx

. Trên cùng đồ thị, ta thấy đường thẳng

1yx

nằm trên đồ

thị hàm số

 



trên khoảng

   

1;3 1 1 3 1 1 2 3 1 0.



             f t t t x x

Vậy hàm số

 

đồng biến trên khoảng

 

1;0 .

Cách 2: Ta có:

       

1 2 2 1 2 1 2 4 .



        g x f x x g x f x x

Có

     

0 ' 1 2 2 ' 1 2 (1 2 ) 1.



         g x f x x f x x

Xét sự tương giao của đồ thị hàm số

 

'y f t

và

 

1, 1 2 .   y t t x

Từ đồ thị ta có

 

' 1 .













f t t

Khi đó

 

1 2 1 0

' 0 .

1 2 3 1

  



  



   



Ta có bảng xét dấu

Dựa vào bảng xét dấu ta thấy hàm số đồng biến trên các khoảng

 

1;0 .

Cách 3: Cách trắc nghiệm.

Ta có:

       

1 2 2 1 2 1 2 4 .



        g x f x x g x f x x

Ta lần lượt thử các đáp án.

Thử Chọn A Chọn

   

1,25 ; 1 ' 1,25 2 ' 3,5 5.

x g f



         





Nhìn đồ thị

 

'fx

ta thấy

   

' 3,5 0 ' 1,25 0fg    

loại đáp án A.

Thử đáp án B: Chọn

   

0,25 ; ' 0,25 2 ' 0,5 1.

x g f



      





 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Nhìn đồ thị

 

'fx

ta thấy

   

' 0,5 0 ' 0,25 0fg   

loại đáp án B.

Thử đáp án C: Chọn

     

0,5 1;0 ' 0,5 2 ' 2 2.x g f        

Nhìn đồ thị

 

'fx

ta thấy

     

' 2 0 2 ' 2 0 ' 0,5 0f f g       

Chọn đáp án C.

Thử đáp án D: Chọn

     

2 1;3 ' 2 2 ' 3 8.x g f      

Nhìn đồ thị

 

'fx

ta thấy

     

' 3 0 2 ' 3 0 ' 2 0f f g        

loại đáp án D.

 Câu 37: Cho hàm số

 

y f x

có đạo hàm

 



có đồ thị như hình dưới đây.

Hàm số

   

3 1 27 54 27 4g x f x x x x     

đồng biến trên khoảng nào dưới đây?







. B.







. C.

 

0;3

. D.

 

4;

 Lời giải

Chọn D

Cách 1:

Ta có:

               

3 2 2

3 1 3 1 3 3 1 ' 3 ' 3 1 3 1 2 3 1g x f x x x g x f x x x



            



Có

       

' 0 ' 3 1 3 1 2 3 1 (1).g x f x x x      

Đặt

3 1,tx

bất phương trình

 

trở thành

 

'2f t t t

Vẽ Parabol

2.y x x

Trên cùng đồ thị, ta thấy đồ thị hàm số

 

'fx

nằm trên đồ thị

hàm số

2y x x

trên các khoảng

 

;1 

và

 

3; .

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Suy ra

 

1 3 1 1

' 2 .

3 3 1 3

f t t t





    





    





  







Vậy hàm số

 

đông biến trên các khoảng

 

;0

và









Cách 2:

Ta có:

               

3 2 2

3 1 3 1 3 3 1 ' 3 ' 3 1 3 1 2 3 1g x f x x x g x f x x x



            



Có:

       

' 0 ' 3 1 3 1 2 3 1 .g x f x x x      

Xét sự tương giao của đồ thị hàm số

 

'y f t

và

 

2t, 3 1 .y t t x   

Từ đồ thị ta có:

 







   







' 2 1( ).

f t t t t nghieäm keùp

Khi đó

 







  



     













3 1 1

' 0 3 1 1 ( ).

3 1 3

g x x x nghieäm keùp

Ta có bảng xét dấu.

Dựa vào bảng xét dấu ta thấy hàm số đồng biến trên các khoảng

 

;0

và

 

3; .

 Câu 38: Cho hàm số

()fx

liên tục trên có

( 1) 0f 

và có đồ thị hàm số

()y f x





như

hình vẽ.

Hàm số

2 ( 1)y f x x  

đồng biến trên khoảng

 

3; 

. B.

 

1;2

. C.

 

0;

. D.

 

0;3

 Lời giải

Chọn D

Đặt

( ) 2 ( 1) ( ) 2[ ( 1) ( 1) 1]g x f x x g x f x x



        

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Dựa vào đồ thị hàm số

()y f x





và đồ thị hàm số

1yx

ta có:

( ) 0 ( 1) ( 1) 1 1 1 2 0 3g x f x x x x



             

Bảng biến thiên:

Dựa vào bảng biến thiên, hàm số

2 ( 1)y f x x  

đồng biến trên khoảng

 

0;3

 Câu 39: Cho hàm số

 

. Hàm số

 

y f x





có đồ thị như hình sau.

Hàm số

xxxxfxg 6218)21(3)(



đồng biến trên khoảng nào dưới đây?

 

2;1

. B.

 

1;3 

. C.

 

1;0

. D.

 

2;1

 Lời giải

Chọn A

Ta có

64224)21('6)('

 xxxfxg

(*)174)21('0)('

 xxxfxg

Đặt

xtx





Ta có

(*)

trở thành

)('1

.4)('



















 tttf

Ta vẽ parapol

:)(

 xxyP

trên cùng hệ trục

Oxy

với đồ thị

 

y f x





như hình

vẽ sau ( đường nét đứt), ta thấy

)(P

có đỉnh

)

;

( I

và đi qua các điểm

     

.1;1,2;1,3;3 

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Từ đồ thị hàm số ta thấy trên khoảng

 

1;3

ta có

)('

 ttttf

211213  xx

Vậy hàm số

)(xg

nghịch biến trên khoảng

).2;1(

 Câu 40: Cho hàm số

 

y f x

liên tục trên và có đạo hàm

 



thỏa mãn:

 

15f x x x



  

Hàm số

 

3 3 12y f x x x   

nghịch biến trên khoảng nào sau

đây?

 

1;5

. B.

 

2;

. C.

 

1;0

. D.

 

;1 

 Lời giải

Chọn B

Ta có:

 

15f x x x



  

suy ra

     

3 1 3 3 5f x x x





     



   

4 2 2xxx    

Mặt khác:

 

3. 3 3 12y f x x



   

   

 

3 4 2 2 4x x x x



      



   

3 2 2 5x x x    

Xét





   

3 2 2 5 0x x x     

   











Vậy hàm số

 

3 3 12y f x x x   

nghịch biến trên các khoảng

 

5; 2

và

 

2;

 Câu 41: Cho hàm số

 

y f x

, hàm số

   

,,f x x ax bx c a b c



    

có đồ thị như hình

vẽ

Hàm số

   

 

g x f f x





nghịch biến trên khoảng nào dưới đây?

 

1; 

. B.

 

;2 

. C.

 

1;0

. D.

;









 Lời giải

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Chọn B

Vì các điểm

     

1;0 , 0;0 , 1;0

thuộc đồ thị hàm số

 

y f x





nên ta có hệ:

   

1 0 0

0 1 '' 3 1

1 0 0

a b c a

c b f x x x f x x

a b c c

     







         





    



Ta có:

   

 

   

 

. ''g x f f x g x f f x f x

   

  

Xét

     

 

  

0 ' . 0 3 1 0

3 1 0

g x g x f f x f x f x x x











    

        



  







1,325



























Bảng biến thiên

Dựa vào bảng biến thiên

 

gx

nghịch biến trên

 

;2 

 Câu 42: Cho hàm số

 

y f x

có đạo hàm

 

' 2 3, .f x x x x    

Có bao nhiêu giá trị

nguyên của tham số m thuộc đoạn

 

10;20

để hàm số

 

31g x f x x m m    

đồng biến trên

 

0;2 ?

A. 16. B. 17. C. 18. D. 19.

 Lời giải

Chọn C

Ta có

   

' 2 3 0 * .

f t t t





    







Có

   

 

' 2 3 ' 3g x x f x x m   

Vì

 

2 3 0, 0;2xx   

nên

 

đồng biến trên

     

0;2 ' 0, 0;2g x x   

 

' 3 0, 0;2f x x m x     

 

3 3, 0;2 3 3, 0;2

3 1, 0;2 3 1, 0;2

x x m x x x m x



          





         





(**)

Có

 

3h x x x

luôn đồng biến trên

 

0;2

nên từ (**)



3 10 13

1 0 1

  







   



 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Vì

 

10;20m

















Có 18 giá trị của tham số m.

Vậy có 18 giá trị của tham số m cần tìm.

 Câu 43: Cho hàm số

 

y f x

có đạo hàm liên tục trên và đồ thị của hàm số

 

'y f x

như hình vẽ.

Đặt

     

1 2019

g x f x m x m     

với

là tham số thực. Gọi

là tập các giá trị

nguyên dương của

để hàm số

 

y g x

đồng biến trên khoản

 

5;6

.Tổng các phần tử

của

bằng:

. B. 11. C.

. D. 20.

 Lời giải

Chọn C

Ta có

     

' ' 1g x f x m x m    

Đặt

     

'1h x f x x  

. Từ đồ thị

 

'y f x

và đồ thị

1yx

trên hình vẽ ta suy ra

 

  











Ta có

   

1 1 1 1

x m m x m

g x h x m

x m x m

       



    



   



Do đó hàm số

 

y g x

đồng biến trên các khoảng

 

1; 1mm

và

 

3;m 

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Do vậy, hàm số

 

y g x

đồng biến trên khoảng

 

5;6

  





























nguyên dương nên

 

1;2;5;6m

, tức

 

1;2;5;6S 

Tổng các phần tử của

bằng 14.

 Câu 44: Cho hàm số

 

y f x

là hàm đa thức có đồ thị hàm số

 

y f x





như hình vẽ.

Có bao nhiêu giá trị nguyên của tham số

, 2020 2020m Z m   

để hàm số

 

2 2 2

g x f x mx x x



   





đồng biến trên khoảng

 

3;0

A. 2021. B. 2020. C. 2019. D. 2022.

 Lời giải

Chọn B

Ta có

 

   

2 4 2 3g x xf x mx x x



   

Hàm số

 

đồng biến trên khoảng

 

3;0

suy ra

   

0, 3;0g x x



   

   

 

   

 

2 2 2 2

2 4 2 3 0, 3;0 2 2 3 0, 3;0xf x mx x x x f x m x x x



               

   

 

2 2 3 , 3;0 , 3;0

2 2 3

f x m x x x m x



            

  

 

3;0

max

2 2 3







  

Ta có

 

3 0 0 9 3x x f x



        

dấu “



” khi

11xx   

   

2 3 1 4 0 2 3 4, 3;0x x x x x x               

2 3 4xx



  

dấu “



” khi

1x 

Suy ra

 

2.4 8

2 2 3







  

 

3;0x  

, dấu “



” khi

1x 

 

3;0

max

2 2 3





  



 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Vậy

m 

, mà

m

2020 2020m  

nên có 2020 giá trị của tham số

thỏa mãn

bài toán.

 Câu 45: Cho hàm số

 

. Hàm số

 

y f x





có đồ thị như hình sau.

Có tất cả bao nhiêu giá trị nguyên dương của tham số

đề hàm số

20202)(4)(

 mxxmxfxg

đồng biến trên khoảng

).2;1(

. B.

. C.

. D.

 Lời giải

Chọn A

Ta có

mxmxfxg 22)('4)(' 

(*)

)('0)('

mxfxg





Đặt

mxt 

thì

)('(*)

tf 

Vẽ đường thẳng

y 

trên cùng hệ trục

Oxy

với đồ thị

 

y f x





như hình vẽ sau

Từ đồ thị ta có

























)('

mxm

Hàm số

)(xg

đồng biến trên khoảng

)2;1(

 

2;10)('  xxg

























212

Vì

nguyên dương nên

 

.3;2m

Vậy có hai giá trị nguyên dương của

đề hàm số

)(xg

đồng biến trên khoảng

).2;1(

 Câu 46: Cho hàm số

 

có đạo hàm

     

1 1 4 ;f x x x x x



     

.Có bao nhiêu

số nguyên

2020m 

để hàm số

 

g x f m













đồng biến trên

 

2; 

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

2018

. B.

2019

. C.

2020

. D.

2021

 Lời giải

Chọn B

Ta có:

 

g x f m







  









Hàm số

 

đồng biến trên

 

2; 



   

0; 2;g x x



    

 

0; 2;

f m x







       











 

0; 2;

f m x







     







Ta có:

 

0fx







   

1 1 4 0x x x   













Do đó:

 

0; 2;

f m x







     









   

1; 2; 1

1 4; 2; 2





      











      







Hàm số

 

h x m







;

 

2;x  

có bảng biến thiên:

Căn cứ bảng biến thiên suy ra: Điều kiện

 

không có nghiệm

thỏa mãn.

Điều kiện

 



1m  



1m 

,kết hợp điều kiện

2020m 

suy ra có

2019

giá trị

thỏa mãn yêu cầu bài toán.

Nhận xét: Có thể mở rộng bài toán đã nêu như sau:

Cho hàm số

 

có đạo hàm

     

1 1 4 ;f x x x x x



     

.Có bao nhiêu số

nguyên

2020m 

để hàm số

   

g x f h m













đồng biến trên

 

2; 

 Câu 47: Cho hàm số

 

y f x

có đạo hàm

   

f x x e

, có bao nhiêu giá trị nguyên của

tham số

trong đoạn

 

2019;2019

để hàm số

   

ln 2y g x f x mx mx    

nghịch

biến trên

 

1; e

A. 2018. B. 2019. C. 2020. D. 2021.

 Lời giải

Chọn B

 Quảng Thuận – Ba Đồn – QB Khai thác và phát triển câu hỏi đề tham khảo 2020

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Trên

 

1; e

ta có

     

' . ' ln 2 ln 1 2 1g x f x mx m x x m

      

Để hàm số

 

y g x

nghịch biến trên

 

1; e

thì

   

 

' ln 1 2 1 0, 1;g x x x m x e      

 

ln 1 2 1 0, 1;

ln 1

, 1;

x x m x e

m x e

      



   



Xét hàm số

 

ln 1







trên

 

1; e

, ta có

 

2ln

' 0, 1;

h x x e



   



, từ đây

suy ra

1m 

. Vậy có 2019 giá trị nguyên của

thỏa bài toán.

Bấm Tải xuống để xem toàn bộ.

| 1/46

| | Tải xuống

Preview text:

 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” Caâu 50
TÍNH ÑÔN ÑIEÄU CUÛA HAØM AÅN
CHO BÔÛI ÑOÀ THÒ HAØM F’(X)
I. KIẾN THỨC CẦN NHỚ =I m.vn 1 Định nghĩa 1 ie gh
Giả sử K là một khoảng, một đoạn hoặc một nữa khoảng và y  f  x là một hàm số xác định trên K. Ta nói: racn it
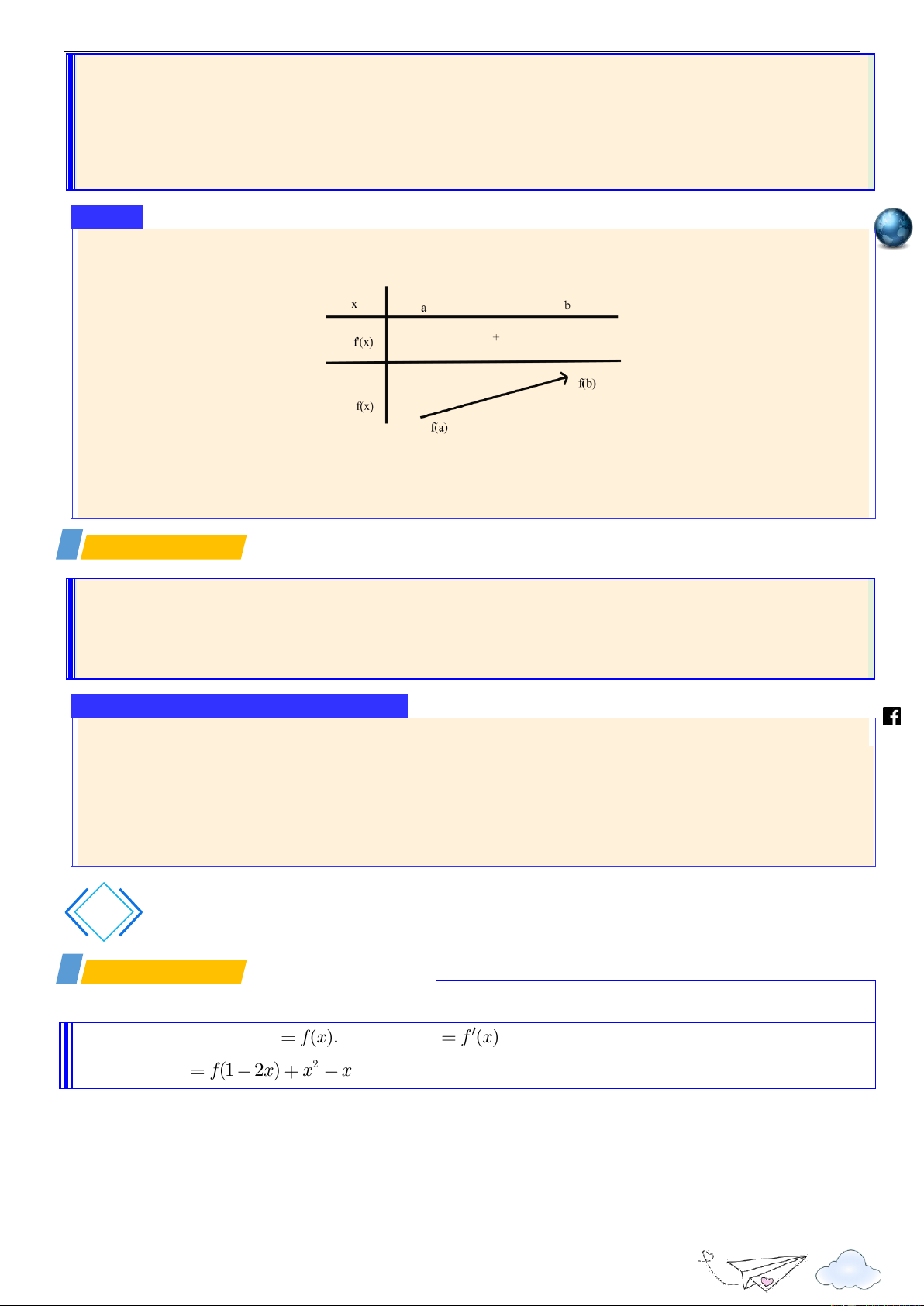
+ Hàm số y  f  x được gọi là đồng biến (tăng) trên K nếu x , x  K, x  x  f x  f x 1 2 1 2  1  2 th n
+ Hàm số y  f  x được gọi là nghịch biến (giảm) trên K nếu x , x  K, x  x  f x  f x 1 2 1 2  1  2 ye lu
Hàm số đồng biến hoặc nghịch biến trên K gọi chung là đơn điệu trên K. s:// 2 Nhận xét ttp h Nhận xét 1
Nếu hàm số f  x và g  x cùng đồng biến (nghịch biến) trên D thì hàm số f  x  g  x cũng đồng
biến (nghịch biến) trên D. Tính chất này có thể không đúng đối với hiệu f  x  g  x . Nhận xét 2
Nếu hàm số f  x và g  x là các hàm số dương và cùng đồng biến (nghịch biến) trên D thì hàm số
f  x.g  x cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng khi các hàm số
f  x, g  x không là các hàm số dương trên D.
/vietgold Nhận xét 3
k.com Cho hàm số u ux, xác định với x ;ab và ux ;cd. Hàm số f ux   cũng xác định với
ceboo x ;ab. Ta có nhận xét sau:
.fa i. Giả sử hàm số u ux đồng biến với x ;ab. Khi đó, hàm số f ux   đồng biến với x  ;
a b  f u đồng biến với u  ; c d  .
ii. Giả sử hàm số u  u  x nghịch biến với x  ;
a b . Khi đó, hàm số f u  x   nghịch biến với
https://www x ;ab f unghịch biến với u ;cd. 3 Định lý 1
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
a) Nếu hàm số đồng biến trên khoảng K thì f ' x  0,x  K .
b) Nếu hàm số nghịch biến trên khoảng K thì f ' x  0,x  K . 4 Định lý 2 1
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
a) Nếu f ' x  0,x  K thì hàm số f đồng biến trên K.
b) Nếu f ' x  0,x  K thì hàm số f nghịch biến trên K.
c) Nếu f ' x  0,x  K thì hàm số f không đổi trên K. Chú ý
Chú ý: Khoảng K trong định lí trên ta có thể thay thế bởi đoạn hoặc một nửa khoảng. Khi đó phải có h
thêm giả thuyết “ Hàm số liên tục trên đoạn hoặc nửa khoảng đó’. Chẳng hạn: ttp s:// lu ye n th it rac n gh
Nếu hàm số f liên tục trên đoạn  ;
a b và f ' x  0,x  ;
a b thì hàm số f đồng biến trên đoạn ie  ;ab. m.vn 5 Định lý 3
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
a) Nếu f ' x  0,x  K và f ' x  0 chỉ tại hữu hạn điểm thuộc K thì hàm số f đồng biến trên K.
b) Nếu f ' x  0,x  K và f ' x  0 chỉ tại hữu hạn điểm thuộc K thì hàm số f đồng biến trên K.
Quy tắc xét tính đơn điệu của hàm số.
Giả sử hàm số f có đạo hàm trên K http
 Nếu f 'x  0 với mọi xK và f 'x  0 chỉ tại một số hữu hạn điểm xK thì hàm số f đồng s://www biến trên K .
 Nếu f 'x  0 với mọi xK và f 'x  0 chỉ tại một số hữu hạn điểm xK thì hàm số f nghịch .fa biến trên K . ceboo k.com
II. BÀI TẬP MẪU =I /v
1 Lời giải tham khảo ietgold
Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ
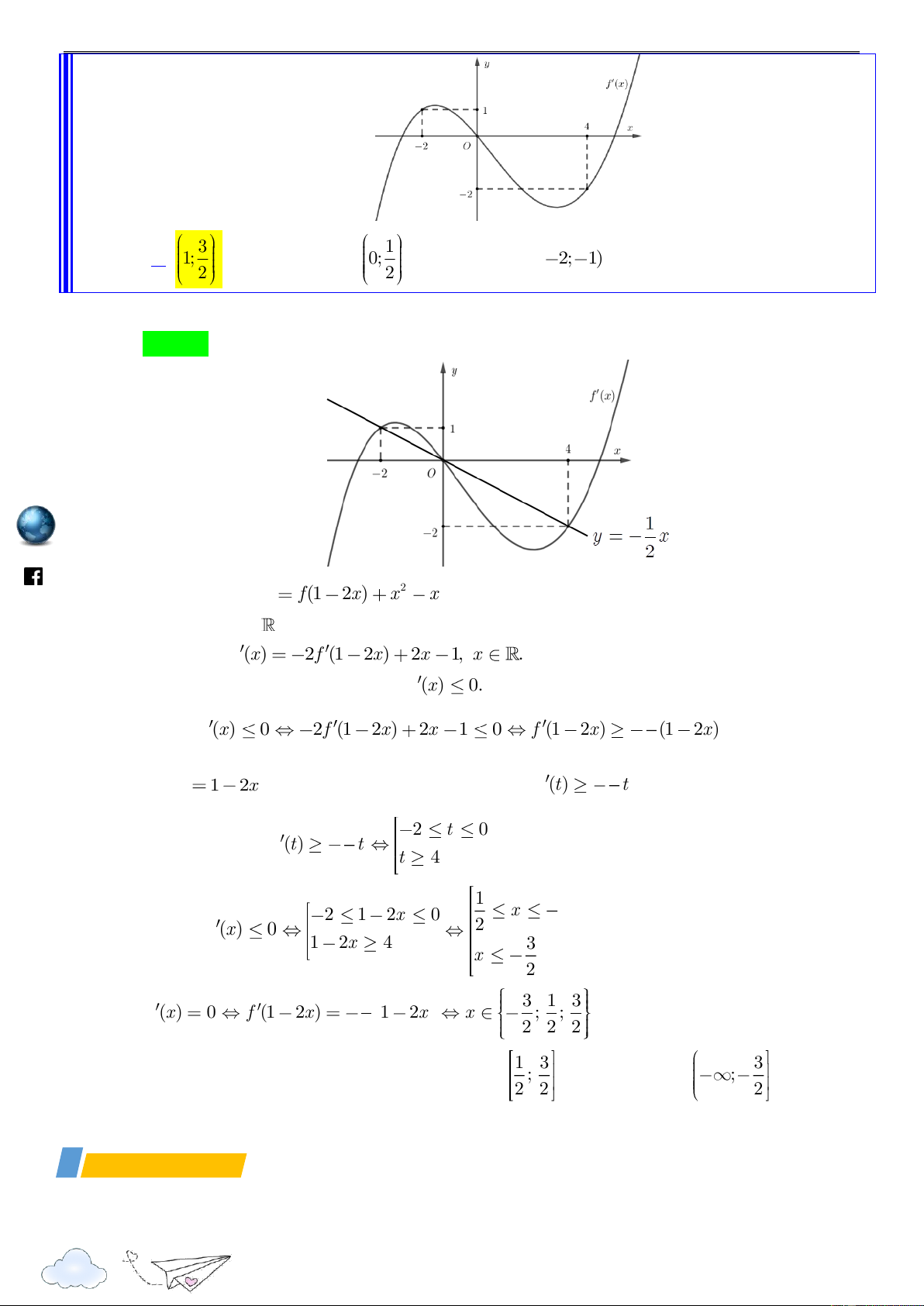
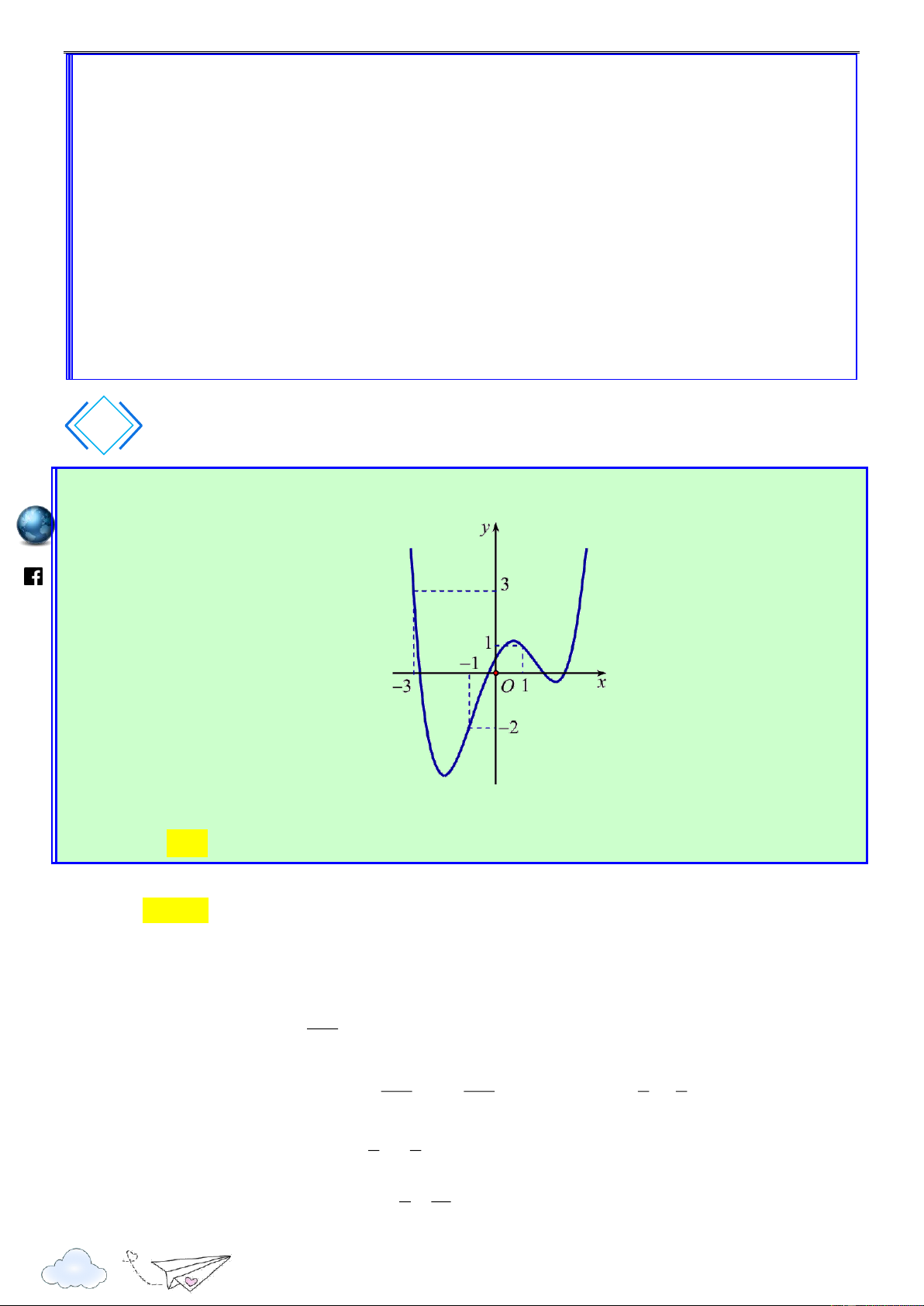
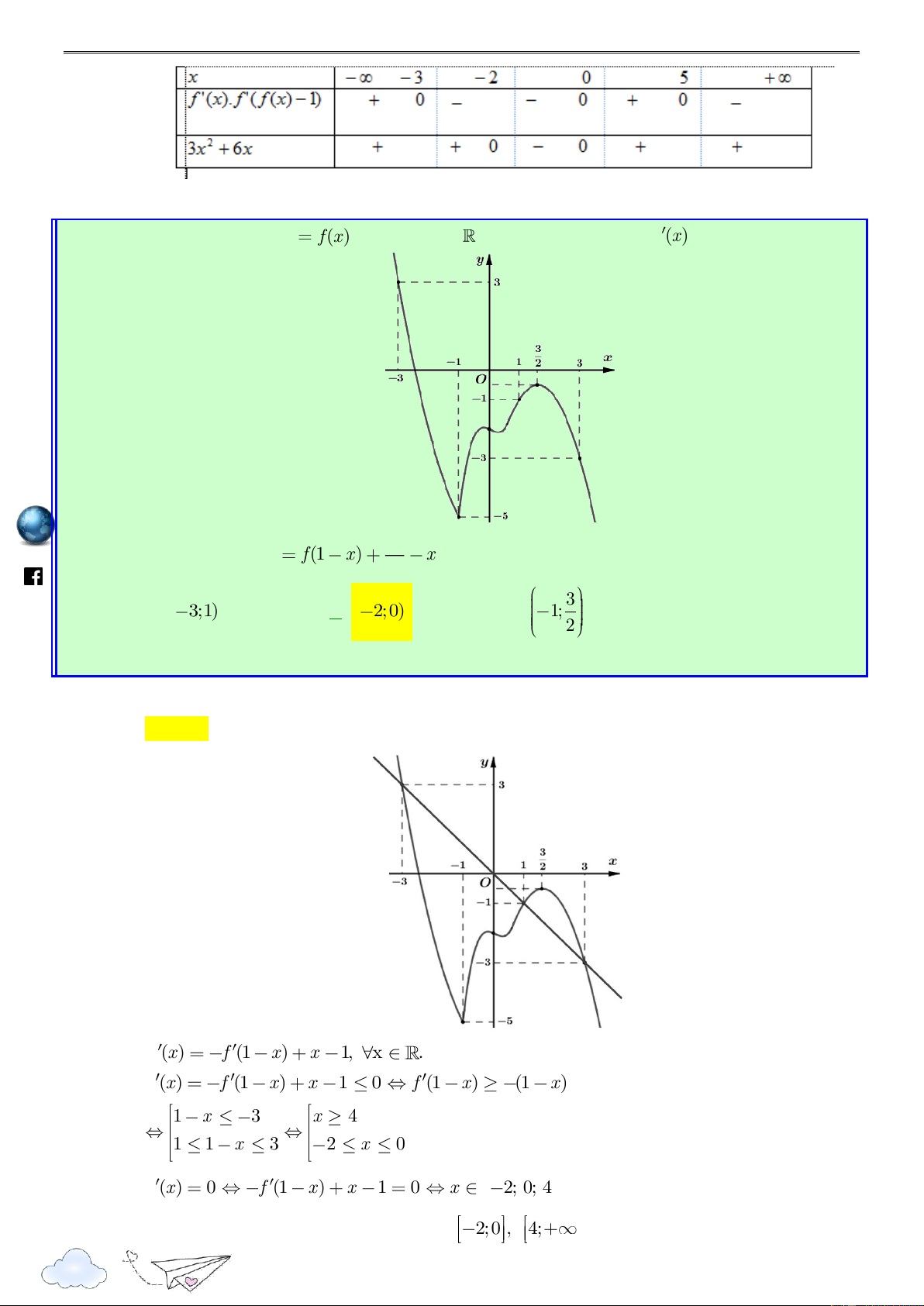
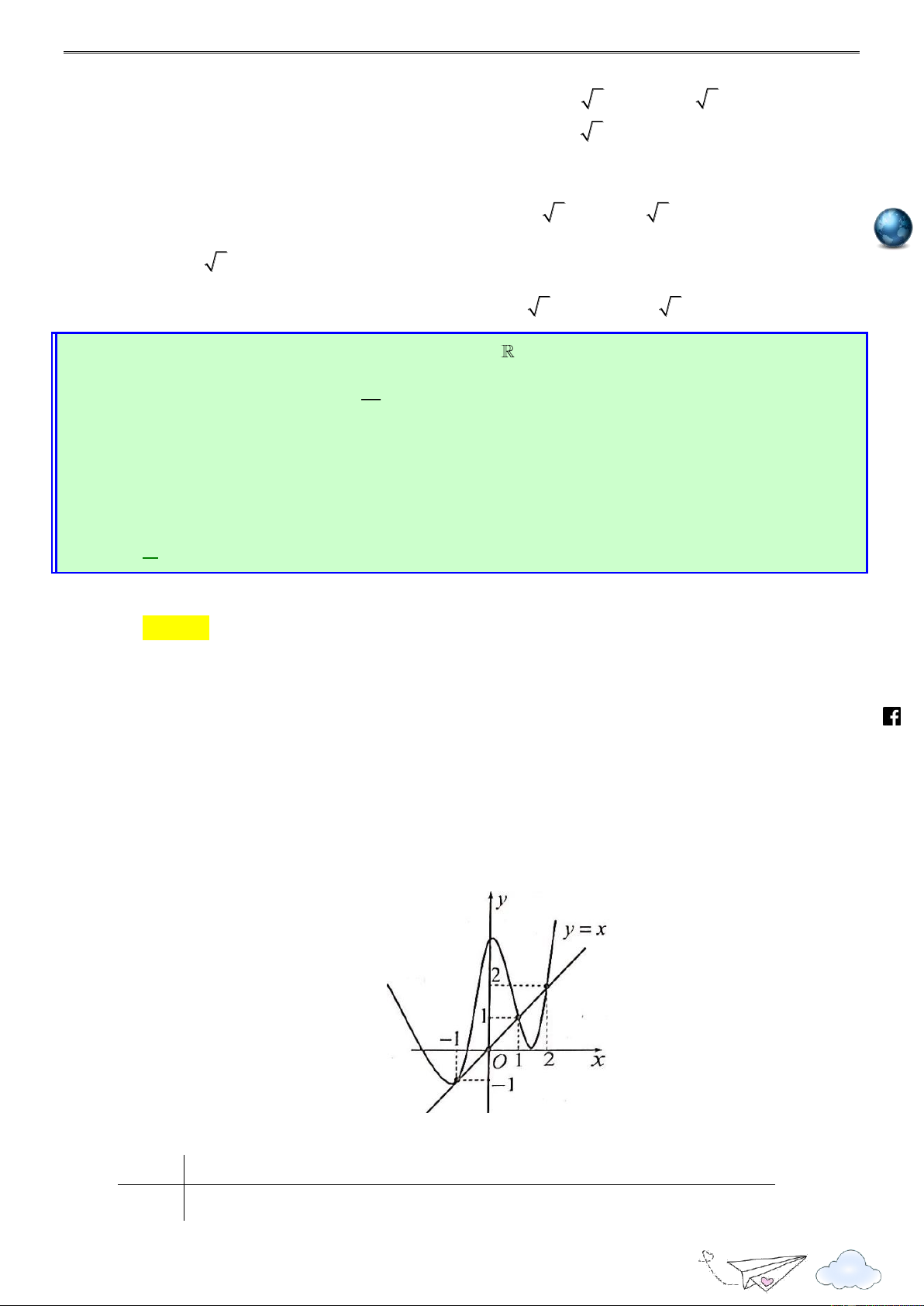
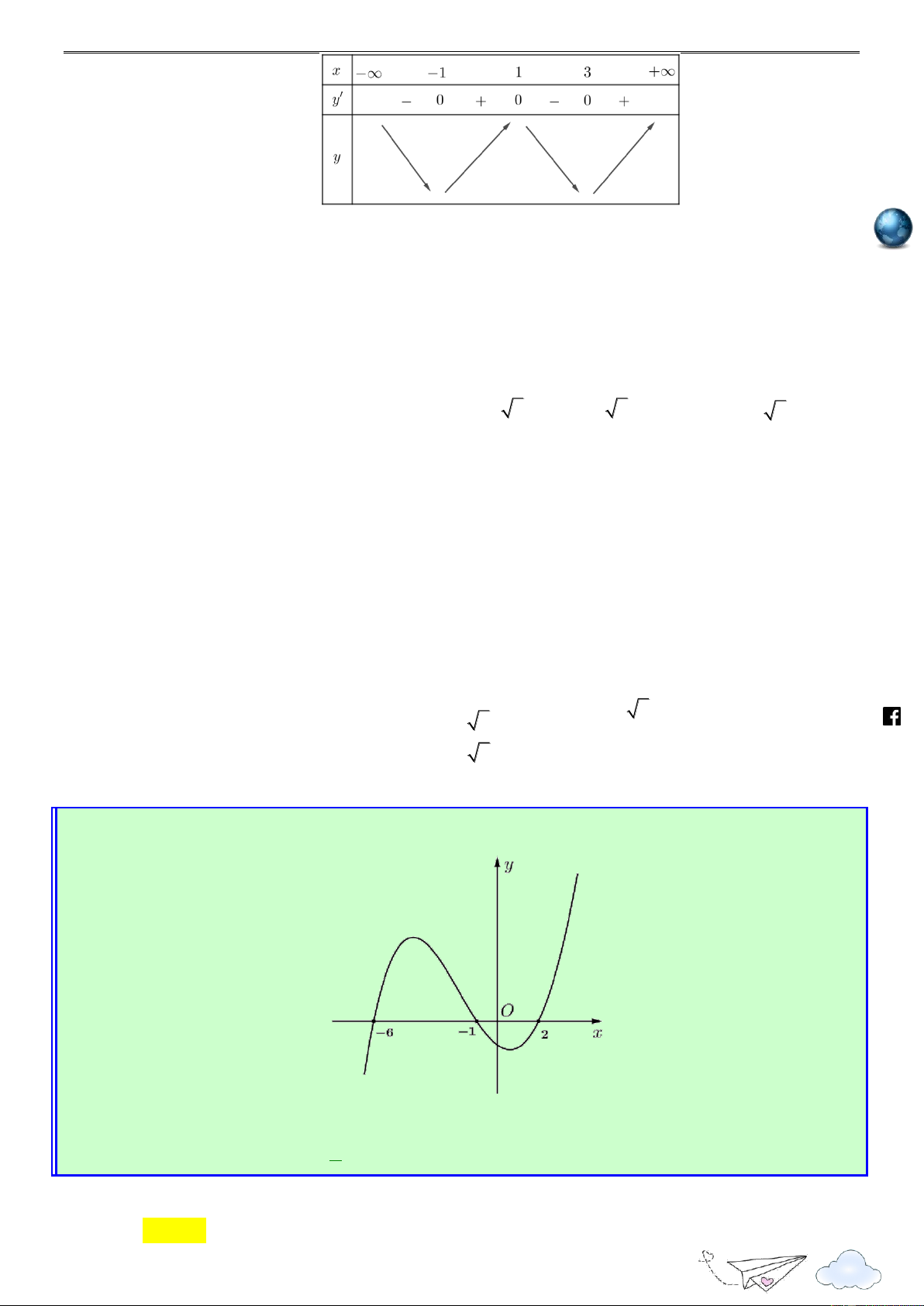
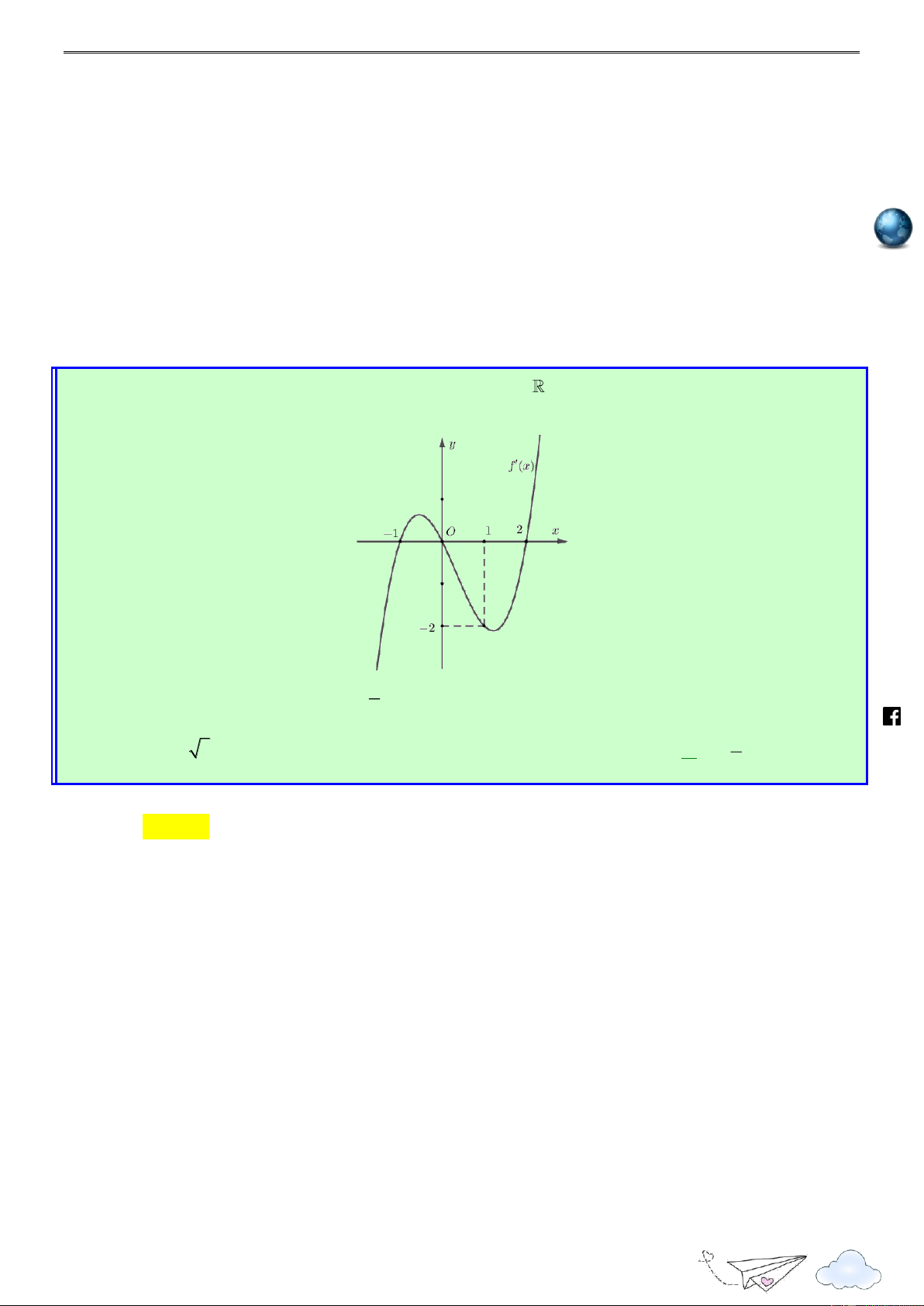
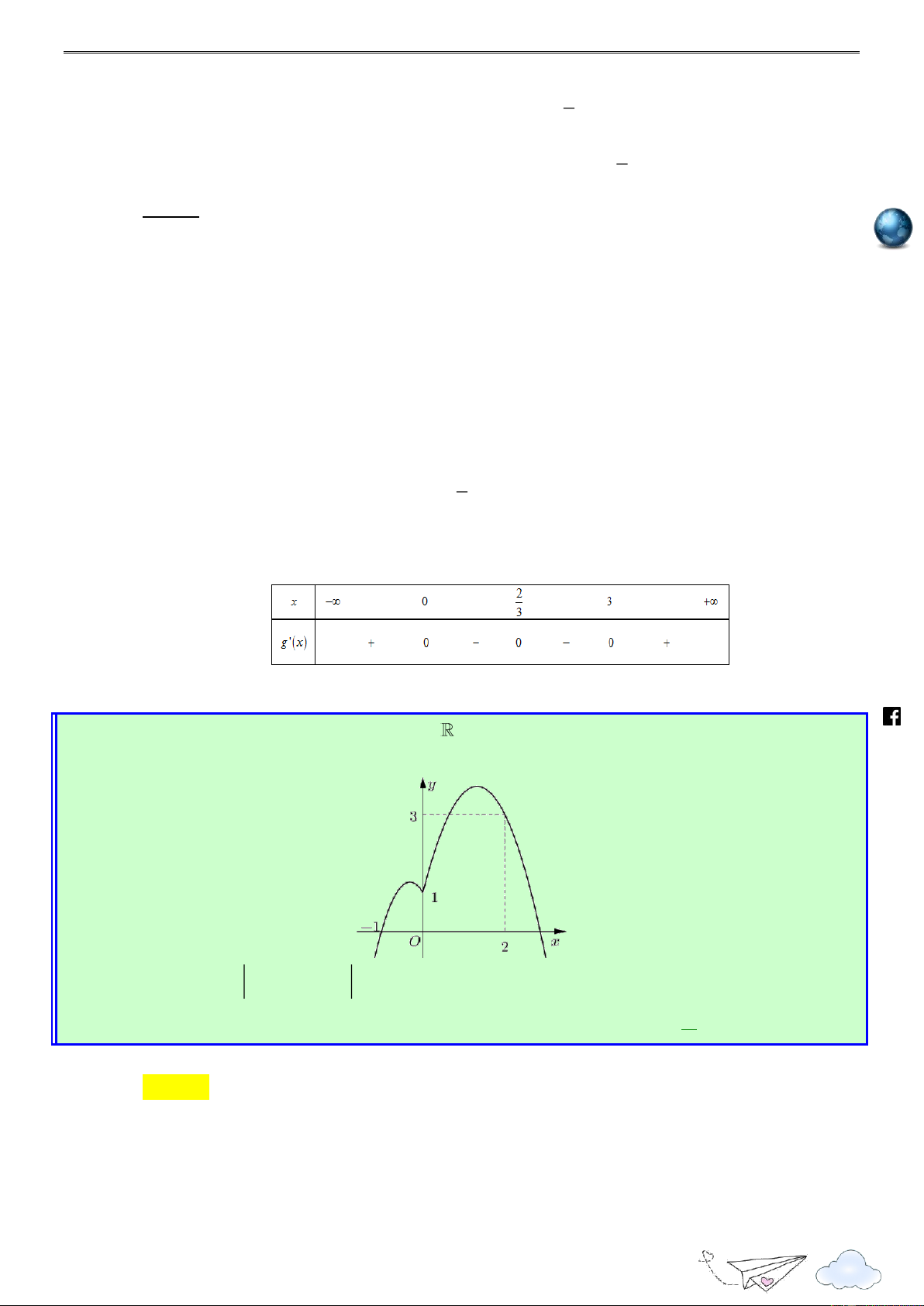
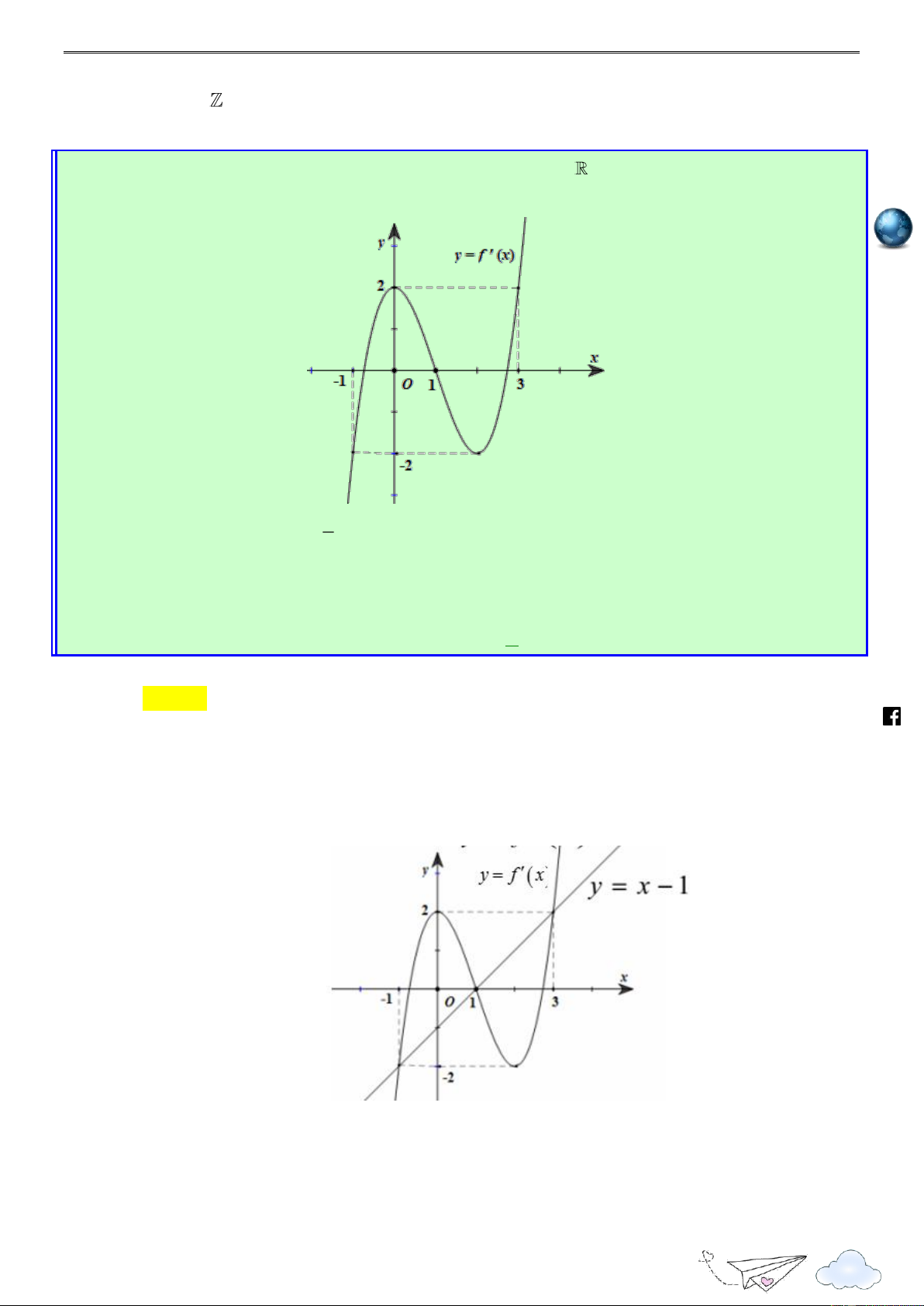
Câu 50. Cho hàm số y
f (x). Hàm số y
f (x) có đồ thị như hình vẽ bên dưới. Hàm số 2 g(x) f (1 2x) x
x nghịch biến trên khoảng nào dưới đây? 2
 Quảng Thuận – Ba Đồn – QB
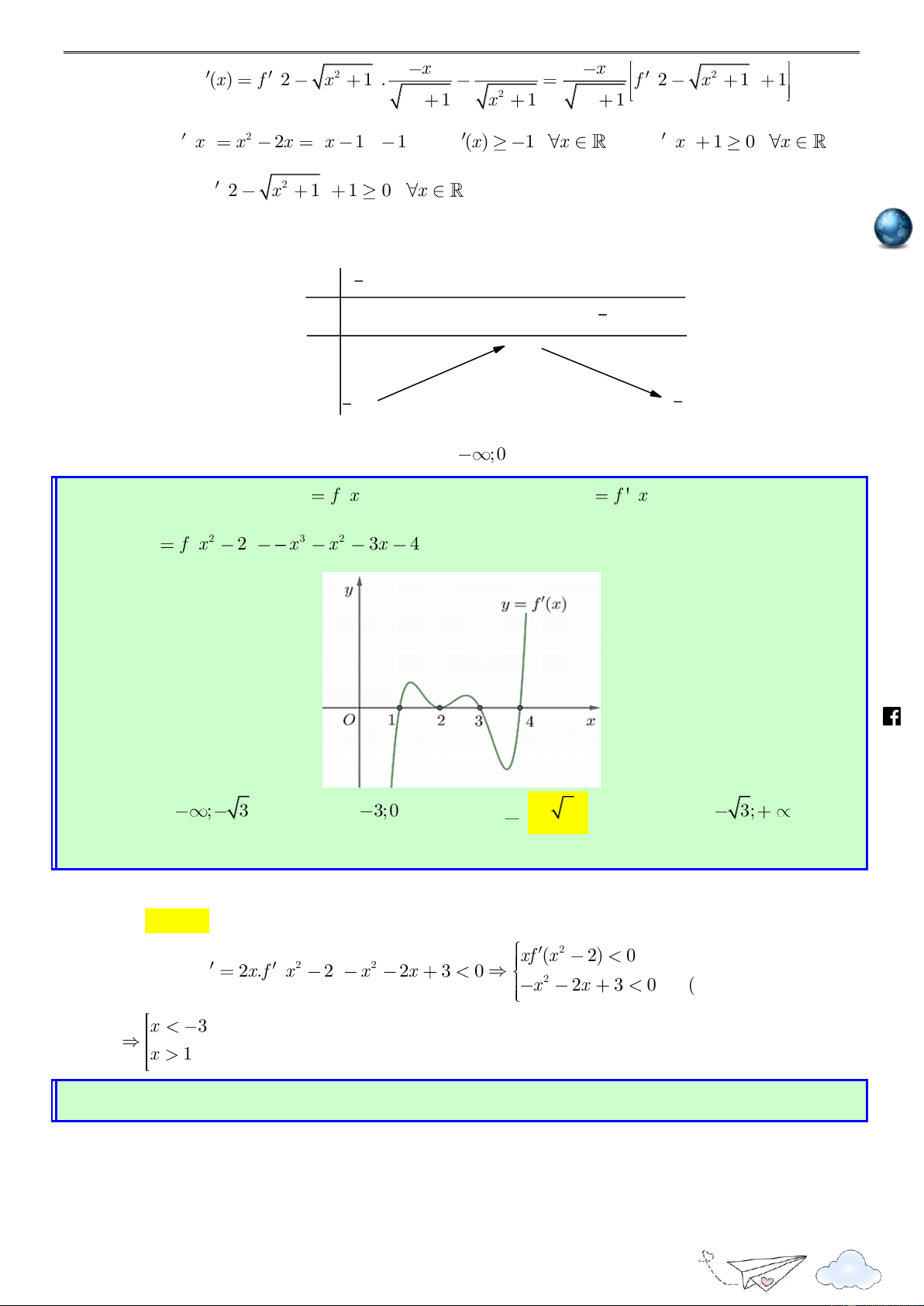
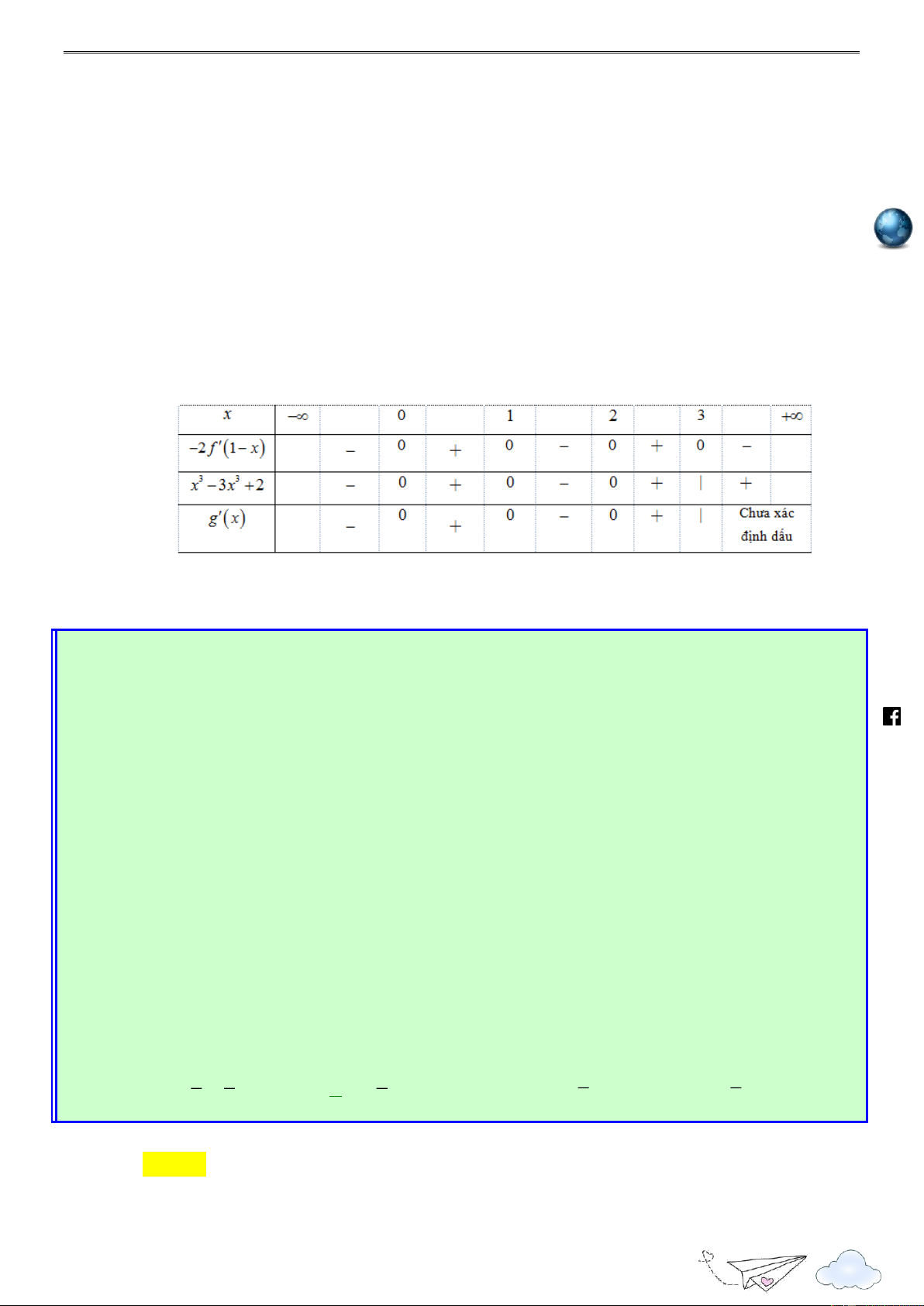
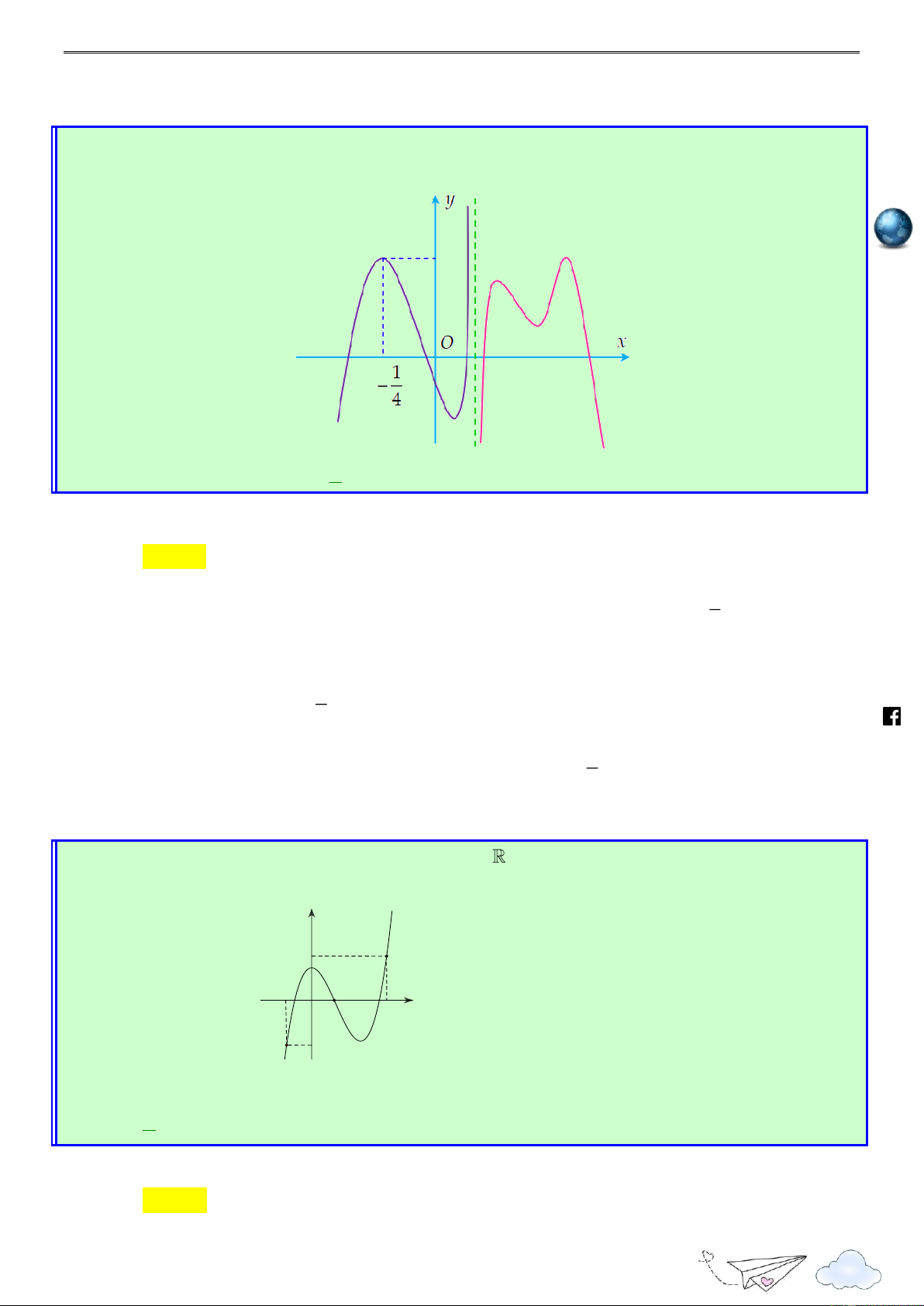
“Thành công là nói không với lười biếng” m.vn 3 1 ie A. 1; . B. 0; . C. ( 2; 1). D. (2; 3) . 2 2 gh Lời giải racn it Chọn A th n ye lu s:// ttp h Xét hàm số 2 g(x) f (1 2x) x x Tập xác định:
Đạo hàm: g (x) 2f (1 2x) 2x 1, x .
Trước tiên ta cần tìm x sao cho g (x) 0. 1 /vietgold Ta có g (x) 0 2f (1 2x) 2x 1 0 f (1 2x) (1 2x) (*) 2 k.com 1 Đặt t
1 2x , bất phương trình (*) trở thành f (t) t 2 ceboo 1 2 t 0 .fa
Từ đồ thị ta có f (t) t 2 t 4 1 3 2 1 2x 0 x Do đó, g (x) 0 2 2 . 1 2x 4 3 https://www x 2 1 3 1 3 g (x) 0 f (1 2x) 1 2x x ; ; : hữu hạn. 2 2 2 2 1 3 3
Như vậy hàm số g(x) nghịch biến trên đoạn ; và nửa khoảng ; . 2 2 2
Soi các phương án của đề bài, ta chọn . A
2 Phân tích – Bình luận 3
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020
 Bình luận: Đây là câu vận dụng cao về vấn đề tính đơn điệu của một hàm số. Để làm được
nó hoặc những dạng tương tự mở rộng, ta cần nắm vững kiến thức cơ bản sau:
 Tính đơn điệu và dấu của đạo hàm
Điều kiện cần: Giả sử hàm số y
f (x) có đạo hàm trên khoảng K.
+ f đồng biến trên khoảng K f (x) 0, x K. h
+ f nghịch biến trên khoảng K f (x) 0, x K. ttp s://
Điều kiện đủ: Giả sử hàm số y
f (x) có đạo hàm trên khoảng K. lu Nếu f (x) 0, x
K thì hàm số đồng biến trên khoảng K. ye n Nếu f (x) 0, x
K thì hàm số nghịch biến trên khoảng K. th it Nếu f (x) 0, x
K thì hàm số không đổi trên khoảng K. racn Mở rộng: gh
1)Nếu phương trình f (x)
0 có hữu hạn nghiệm trên K thì ta có điều kiện cần và đủ sau ie m.vn đây:
+ f đồng biến trên khoảng K f (x) 0, x K.
+ f nghịch biến trên khoảng K f (x) 0, x K.
f (x) lieân tuïc treân a;b 2)
f đồng biến trên a;b . f (x) 0, x a;b
f (x) lieân tuïc treân a;b
f nghịch biến trên a;b . f (x) 0, x a;b https://www
f (x) lieân tuïc treân ;a
f đồng biến trên ;a . f (x) 0, x ;a .fa … ceboo
 Đạo hàm hàm hợp: Giả sử hàm số y
f (x) và u
u x có đạo hàm trên khoảng K. Khi k.com đó: f u u .f u . /v iet
3 Phân tích hướng giải gold 1. Dạng toán
Đây là dạng toán tìm khoảng đơn điệu của hàm ẩn dạng g x  f u
 x v 
x khi biết đồ thị của
hàm số y  f x .
2. Hướng giải Cách 1:
B1: Tính đạo hàm của hàm số g  x , g x  u x. f  u
 x v  x.
B2: Sử dụng đồ thị của f  x , lập bảng xét dấu của g x .
B3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số. 4
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” Cách 2:
B1: Tính đạo hàm của hàm số g  x , g x  u x. f  u
 x v  x.
B2: Hàm số g  x đồng biến  g x  0 ; (Hàm số g  x nghịch biến  g x  0 ) (*)
B3: Giải bất phương trình * (dựa vào đồ thị hàm số y  f  x ) từ đó kết luận khoảng đồng biến,
nghịch biến của hàm số.
Cách 3: (Trắc nghiệm) m.vn g x        ie
B1: Tính đạo hàm của hàm số   , g  x u  x. f u  x v  x. gh
B3: Hàm số g  x đồng biến trên K  g x  0, x
  K ; (Hàm số g x nghịch biến trên K racn
 gx  0, x   K ) (*) it th
B3: Lần lượt chọn thay giá trị từ các phương án vào g x để loại các phương án sai. n ye lu
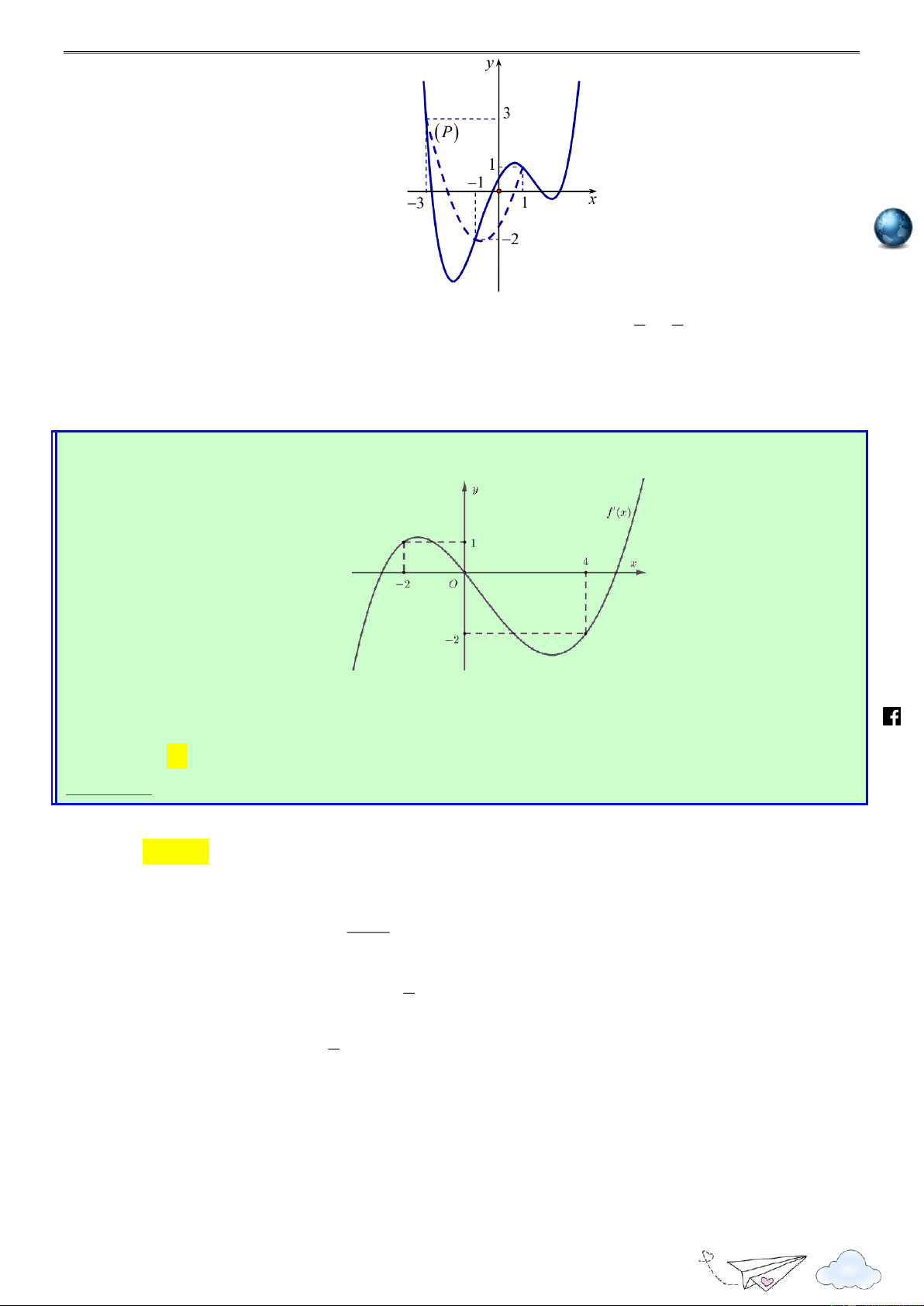
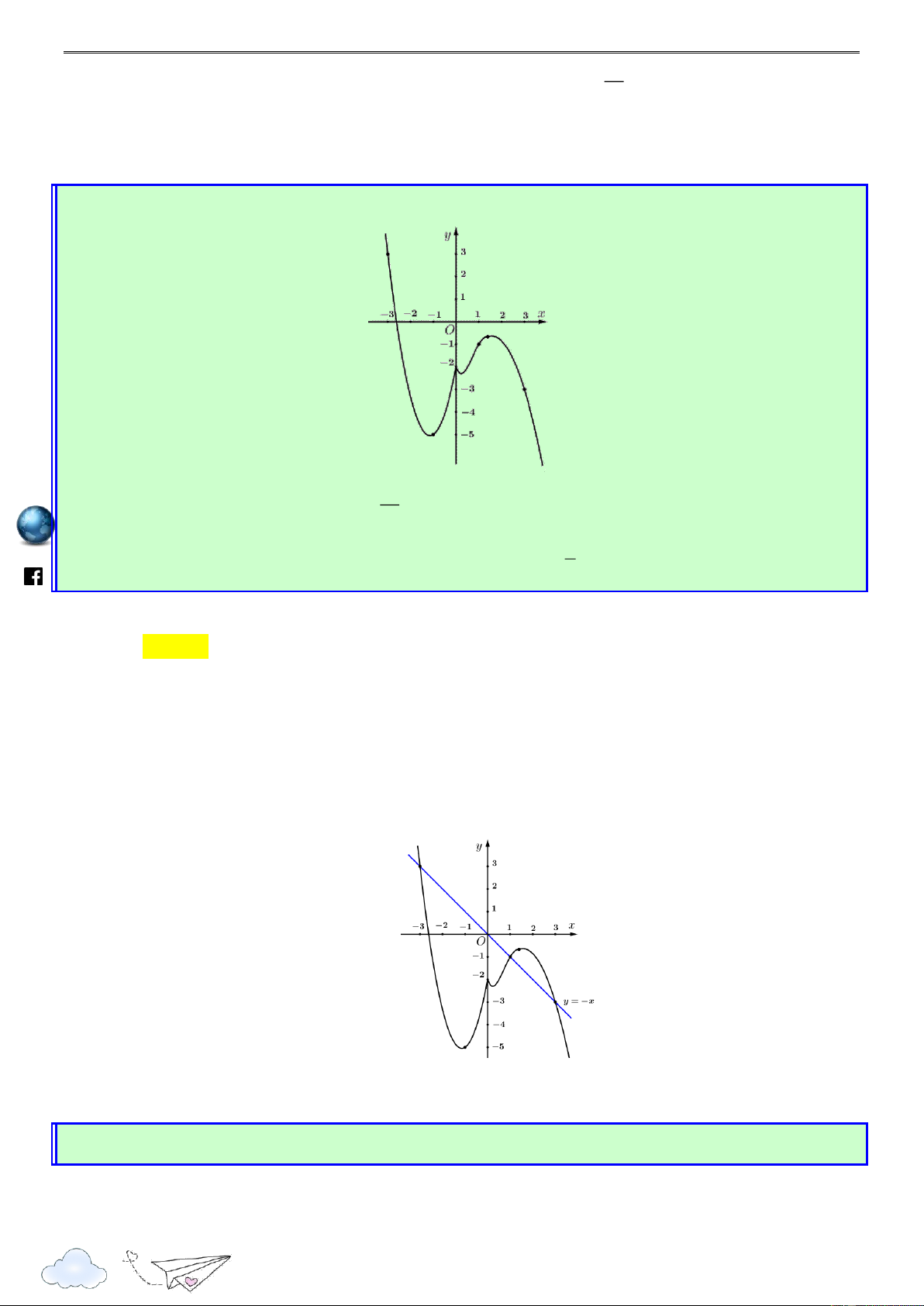
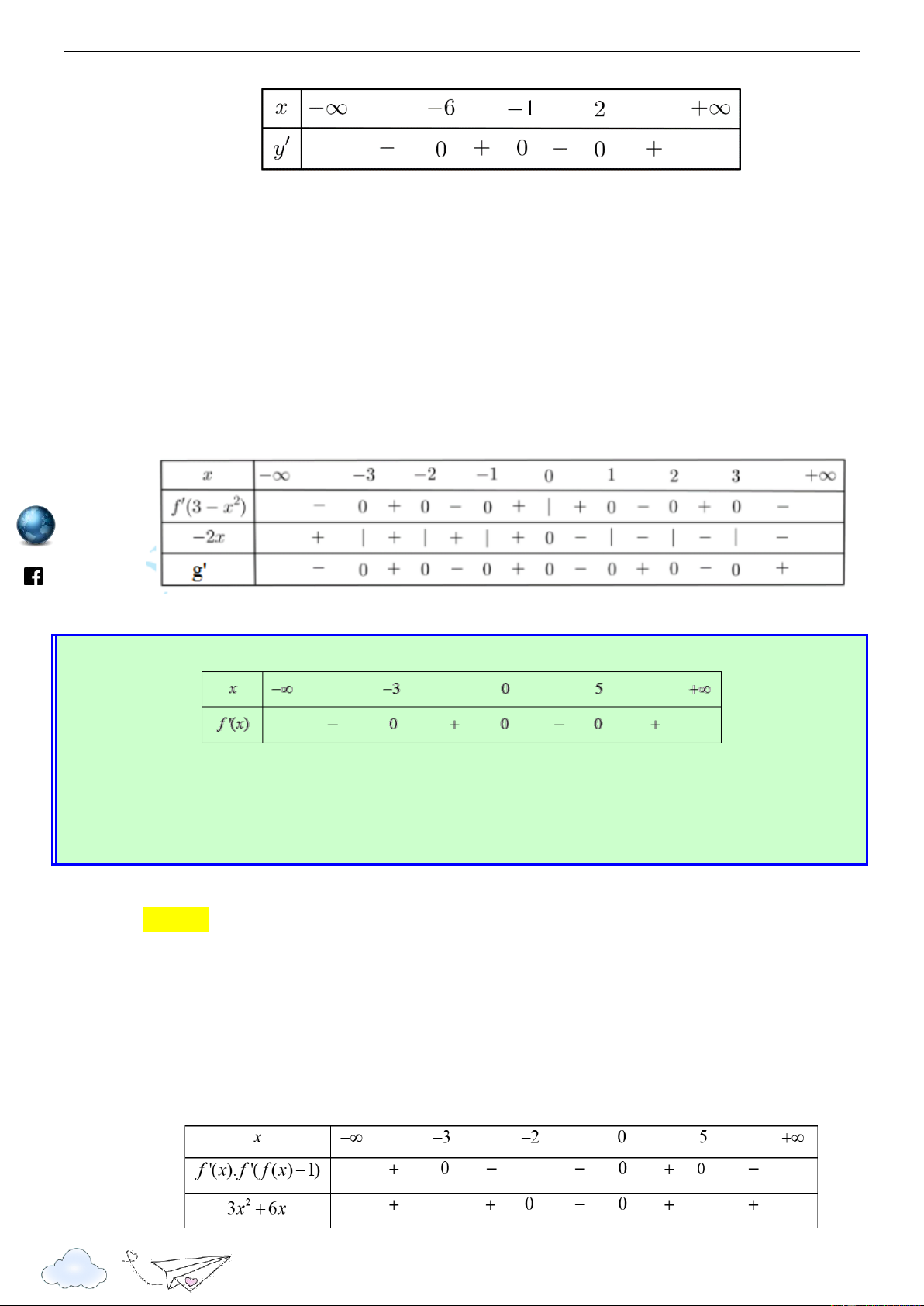
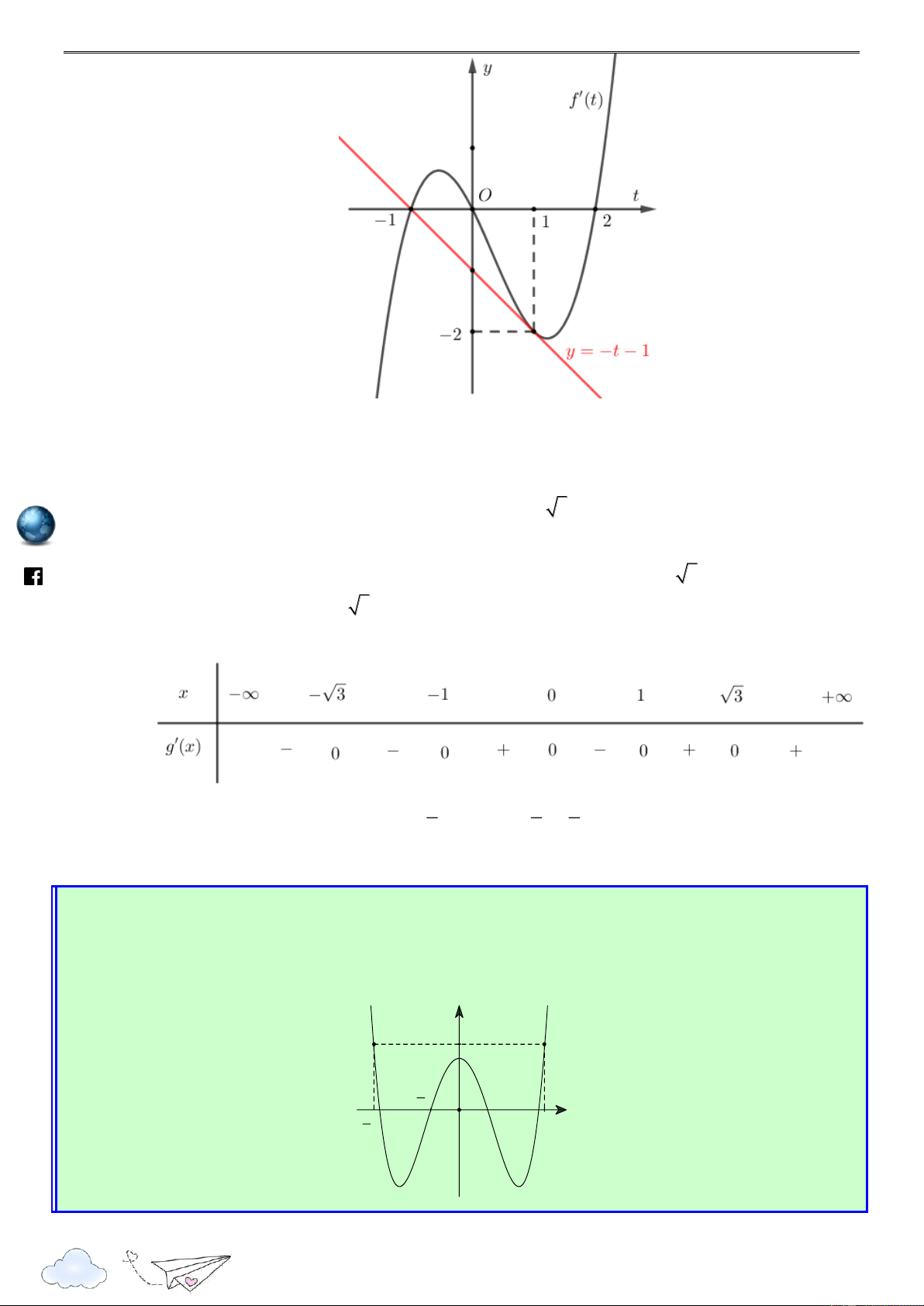
III. BÀI TẬP TƯƠNG TỰ VÀ PHÁT TRIỂN s:// =I ttp h  Câu 1:
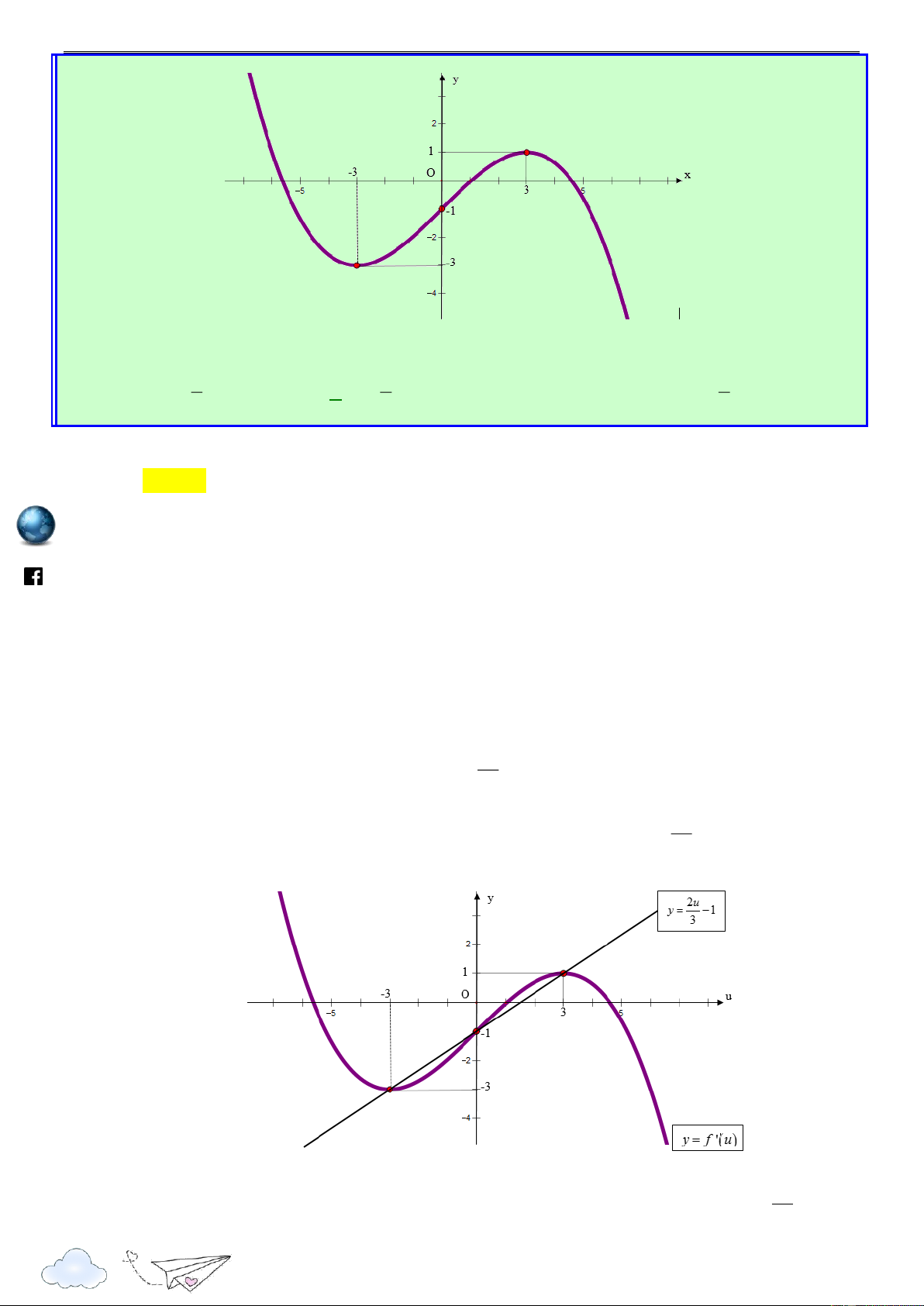
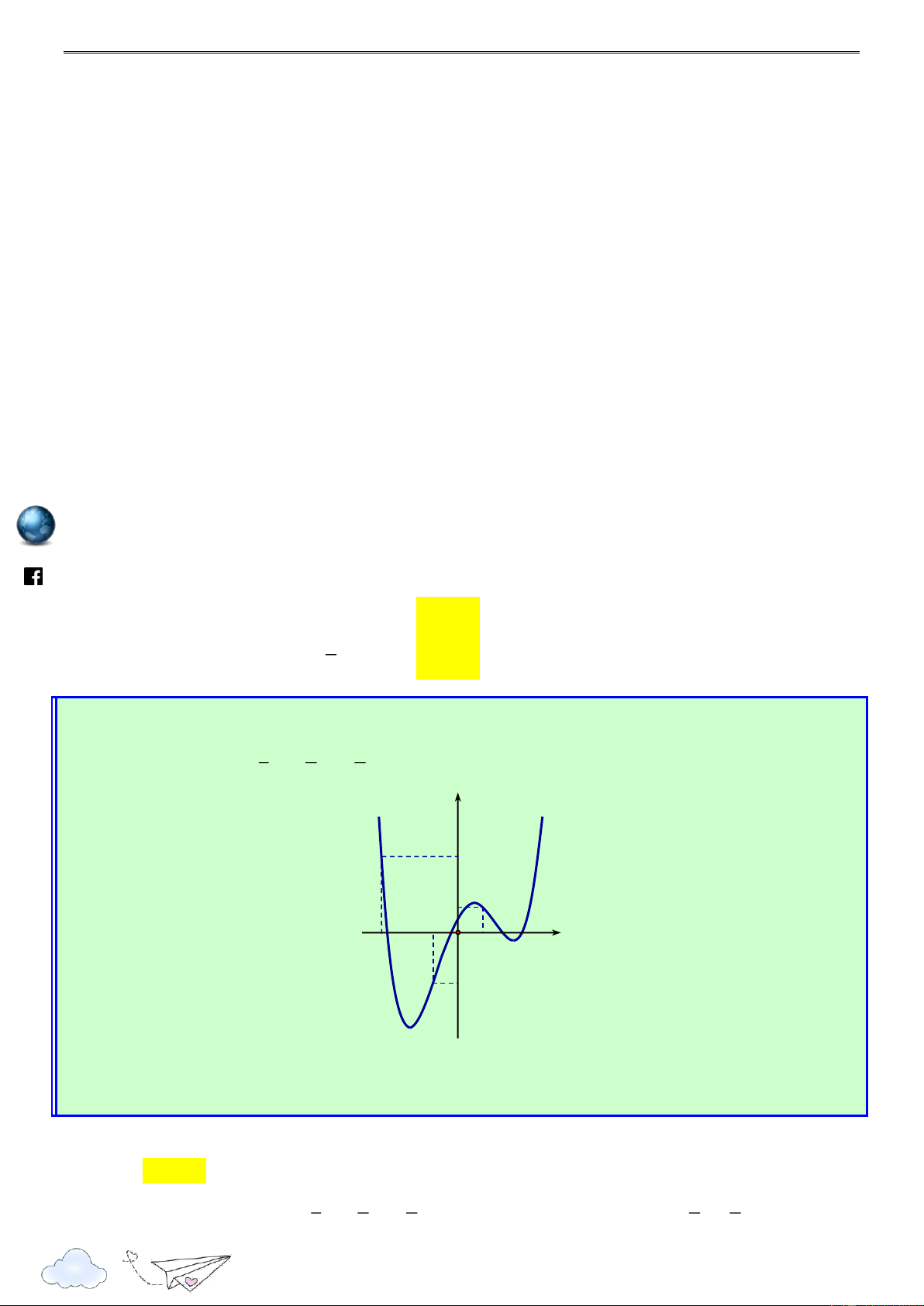
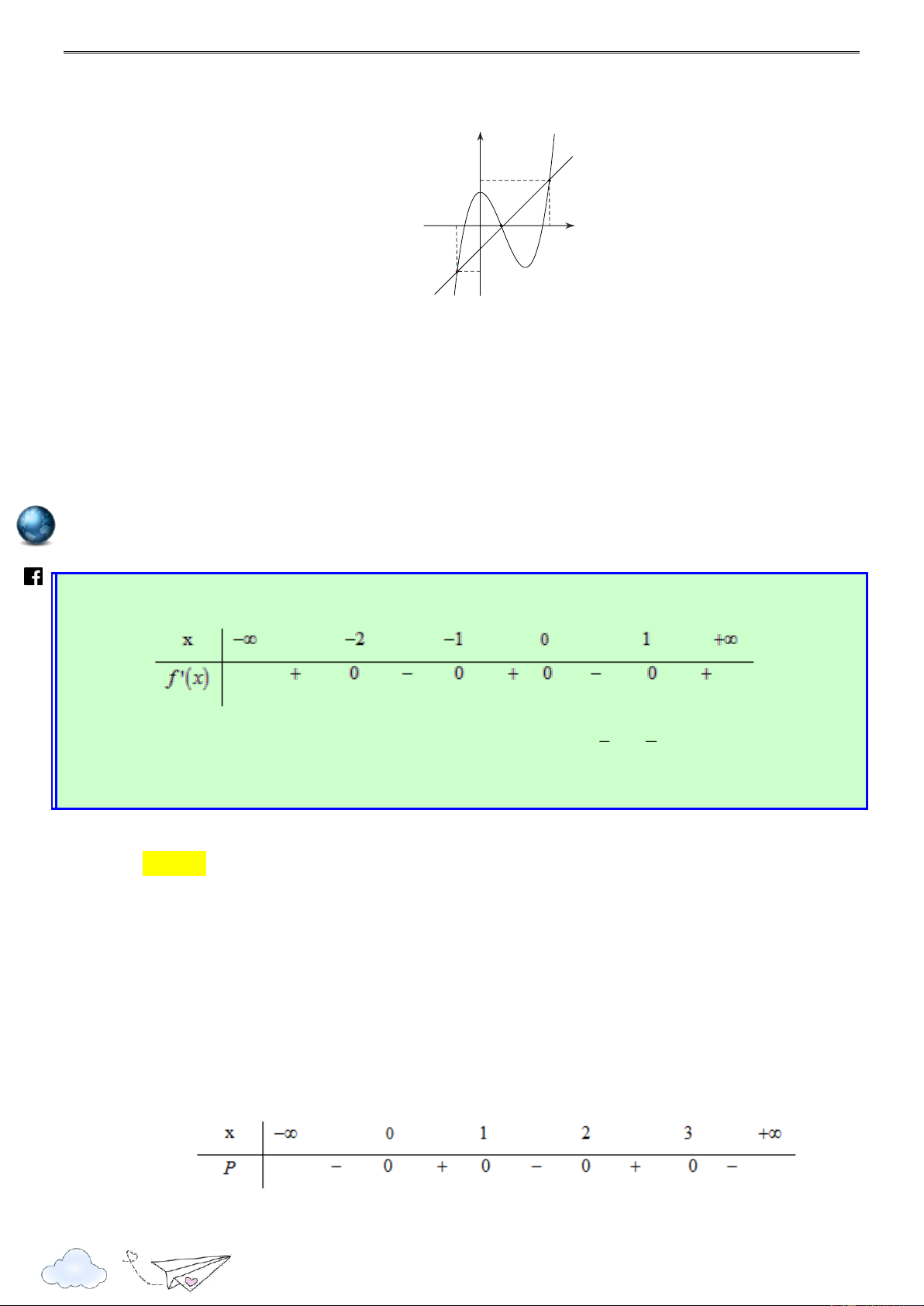
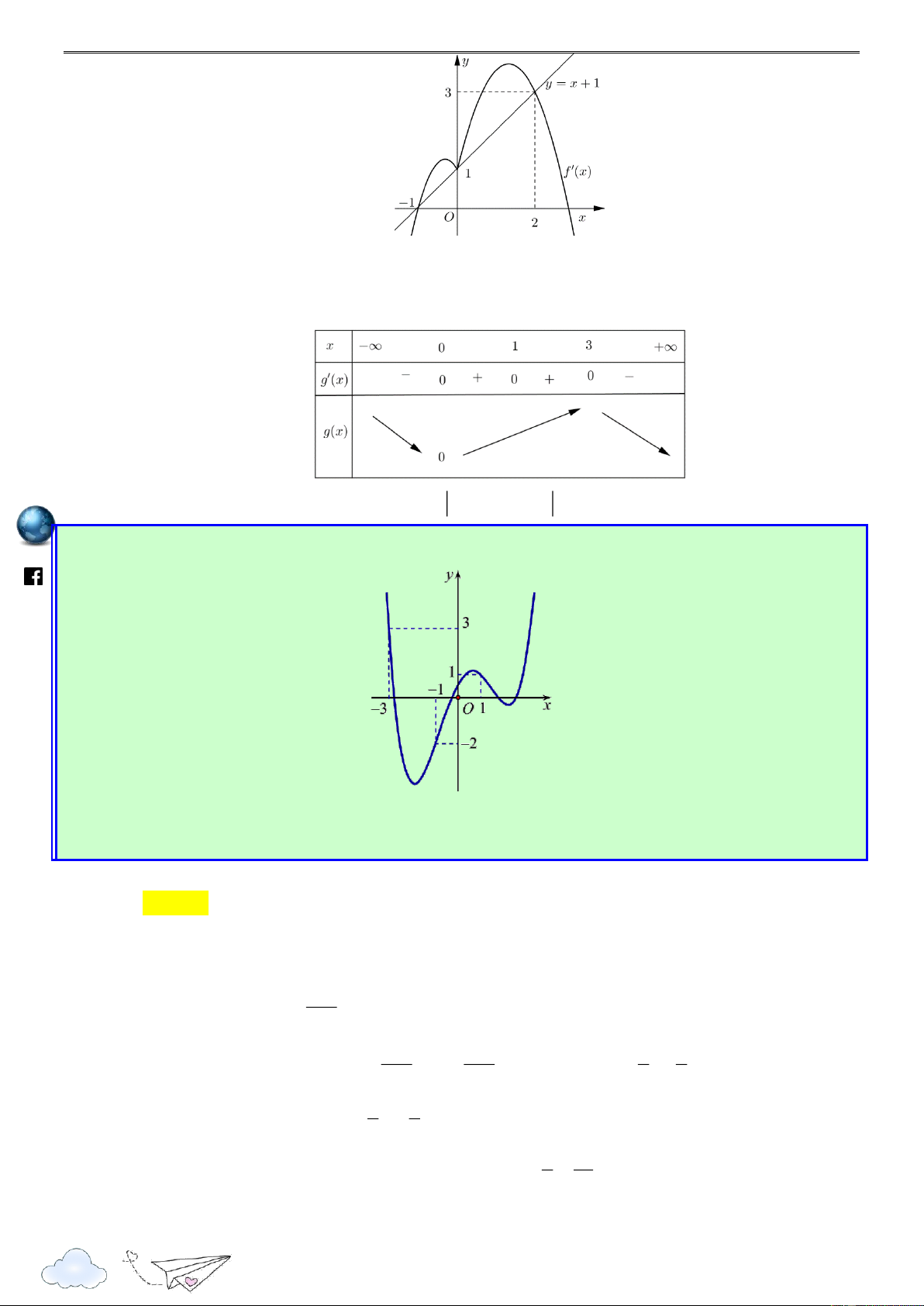
Cho hàm số f  x . Hàm số y  f  x có đồ thị như hình sau. /vietgold k.com 3 2      ceboo Hàm số g(x) 3 f 1 ( 2x) 8x x 21
6x đồng biến trên khoảng nào dưới đây? .fa A.  2 ; 1  . B.  ; 3   1 . C.  1 ; 0 . D.  2 ; 1  .  Lời giải Chọn A g'(x)  6  f ' 1 (  2x)  24 2 x  42x  https://www Ta có 6
g'(x)  0  f ' 1 (  2x)  4 2
x  7x 1 (*) 1  t
Đặt 1 2x  t  x  2 2 1 t  1  t 2 3 3
Ta có (*) trở thành f '(t)  . 4    . 7
1  f '(t)  t  t  .  2  2 2 2 2 3 3
Ta vẽ parapol (P) : y  x  x 
trên cùng hệ trục Oxy với đồ thị y  f  x như hình 2 2 3 33
vẽ sau, ta thấy (P) có đỉnh I ( ;
) và đi qua các điểm   3 ; 3 ,  ; 1 2  ,   1 ; 1 . 4 16 5
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 h ttp s:// 2 3 3
Từ đồ thị hàm số ta thấy trên khoảng  1 ; 3
ta có f '(t)  t  t   3   t  1  lu 2 2 ye n  3  1 2x  1  1 x  2 th it
Vậy hàm số g(x) nghịch biến trên khoảng ). 2 ; 1 ( racn  Câu 2:
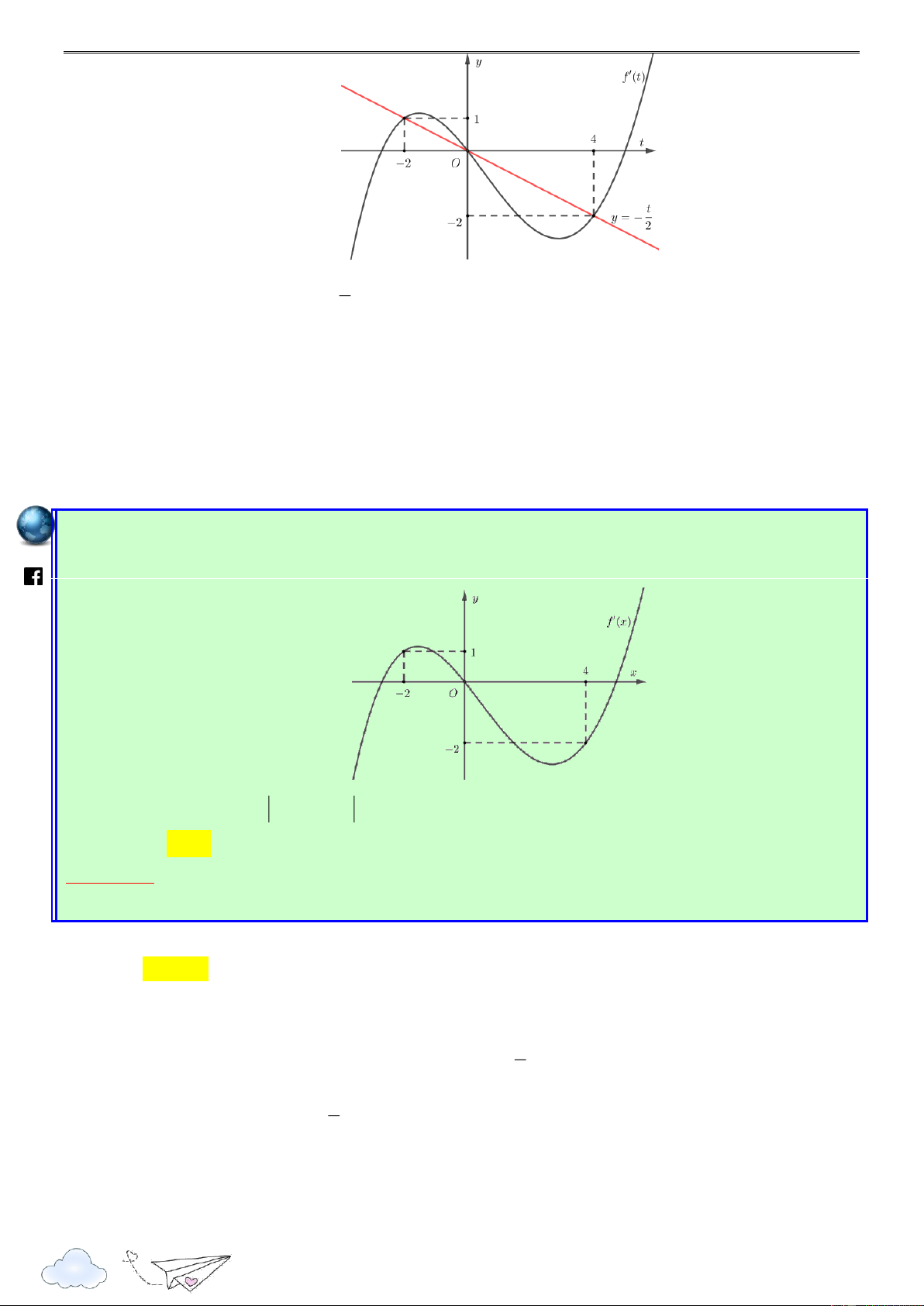
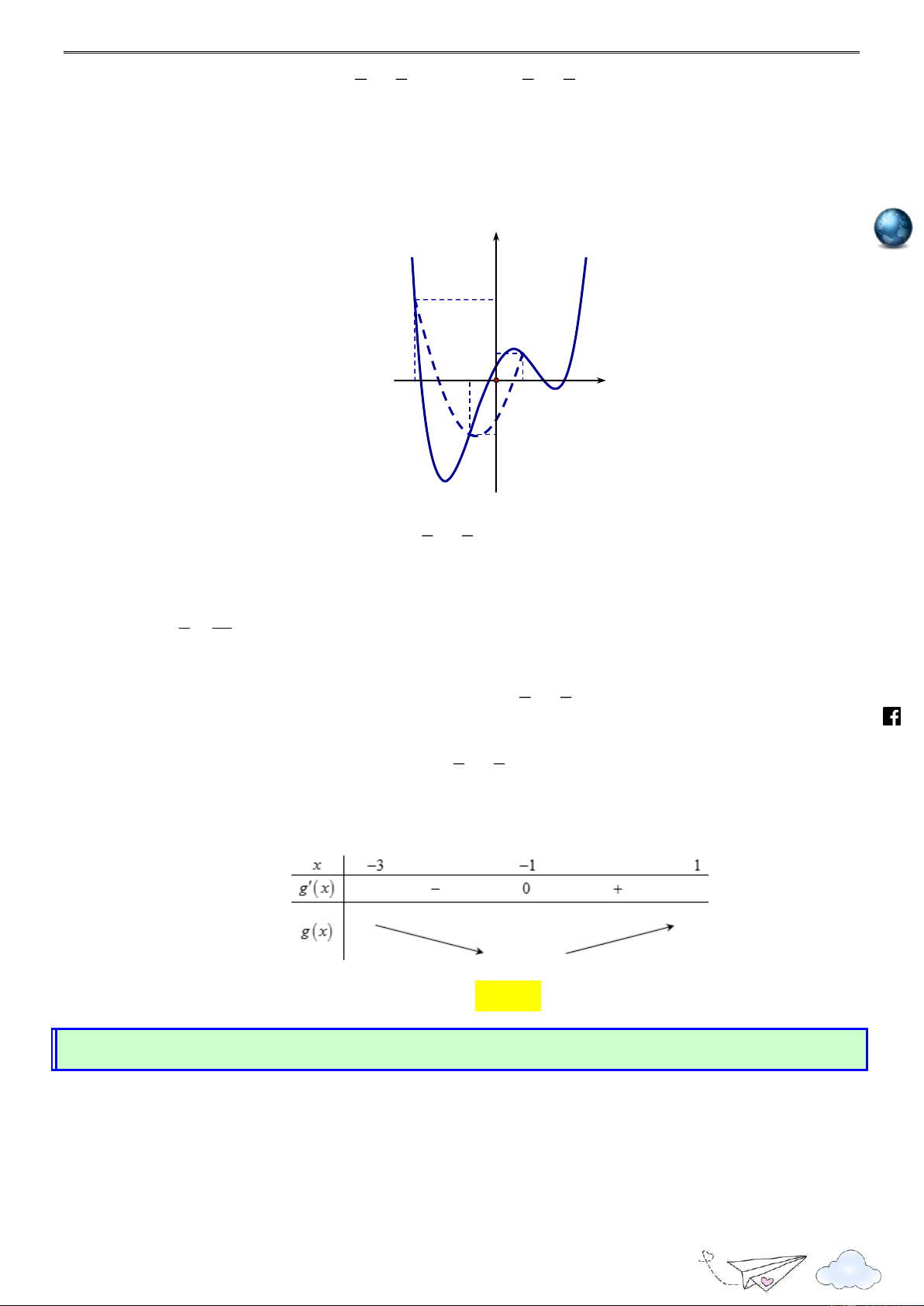
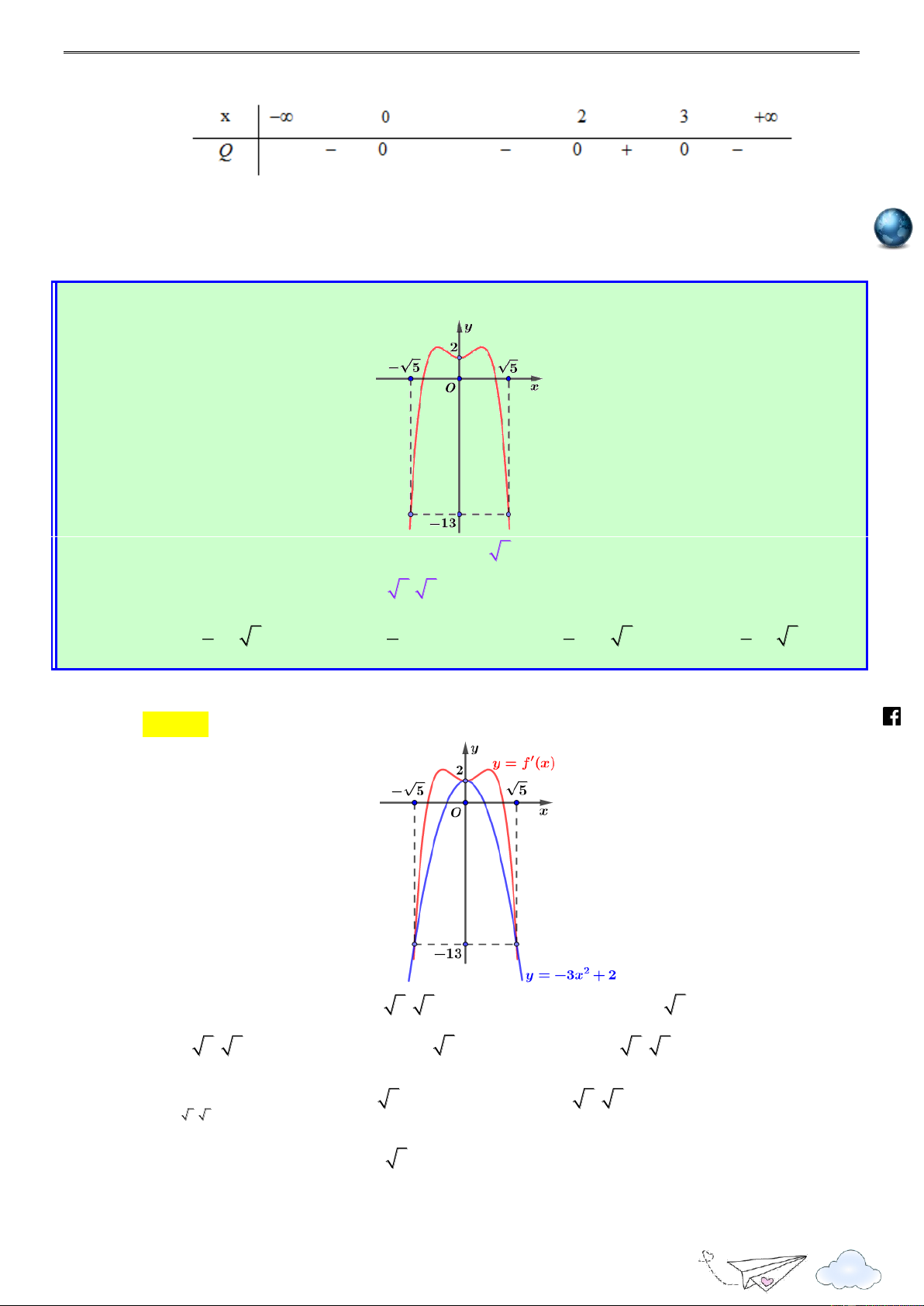
Cho hàm số f  x . Hàm số y  f  x có đồ thị như hình sau. gh ie m.vn
Có tất cả bao nhiêu giá trị nguyên dương của tham số m đề hàm số
g(x)  4 f (x  ) 2
m  x  2mx  2020 đồng biến trên khoảng ). 2 ; 1 ( http A. 2 . B. 3 . C. 0 . D. 1. s://www
* Ý tưởng : Phát triển thành bài toán chứa tham số.  Lời giải .fa Chọn A ceboo
Ta có g'(x)  4 f '(x  m)  2x  m 2 k.com x  m
g'(x)  0  f '(x  ) m   (*) 2 /viet t gold
Đặt t  x  m thì (*)  f '(t)   2 x
Vẽ đường thẳng y   trên cùng hệ trục Oxy với đồ thị y  f  x như hình vẽ sau 2 6
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” m.vn ie gh t  2  t  0
m  2  x  m
Từ đồ thị ta có f '(t)       2 t  4 x  m  4 racn it
Hàm số g(x) đồng biến trên khoảng ) 2 ; 1 (
 g'(x)  0 x  2 ; 1  th n
m  2  1  2  m 2  m  3 ye     m  4  1 m  3 lu  s://
Vì m nguyên dương nên m   3 ; 2 . ttp h
Vậy có hai giá trị nguyên dương của m đề hàm số g(x) đồng biến trên khoảng ). 2 ; 1 (  Câu 3:
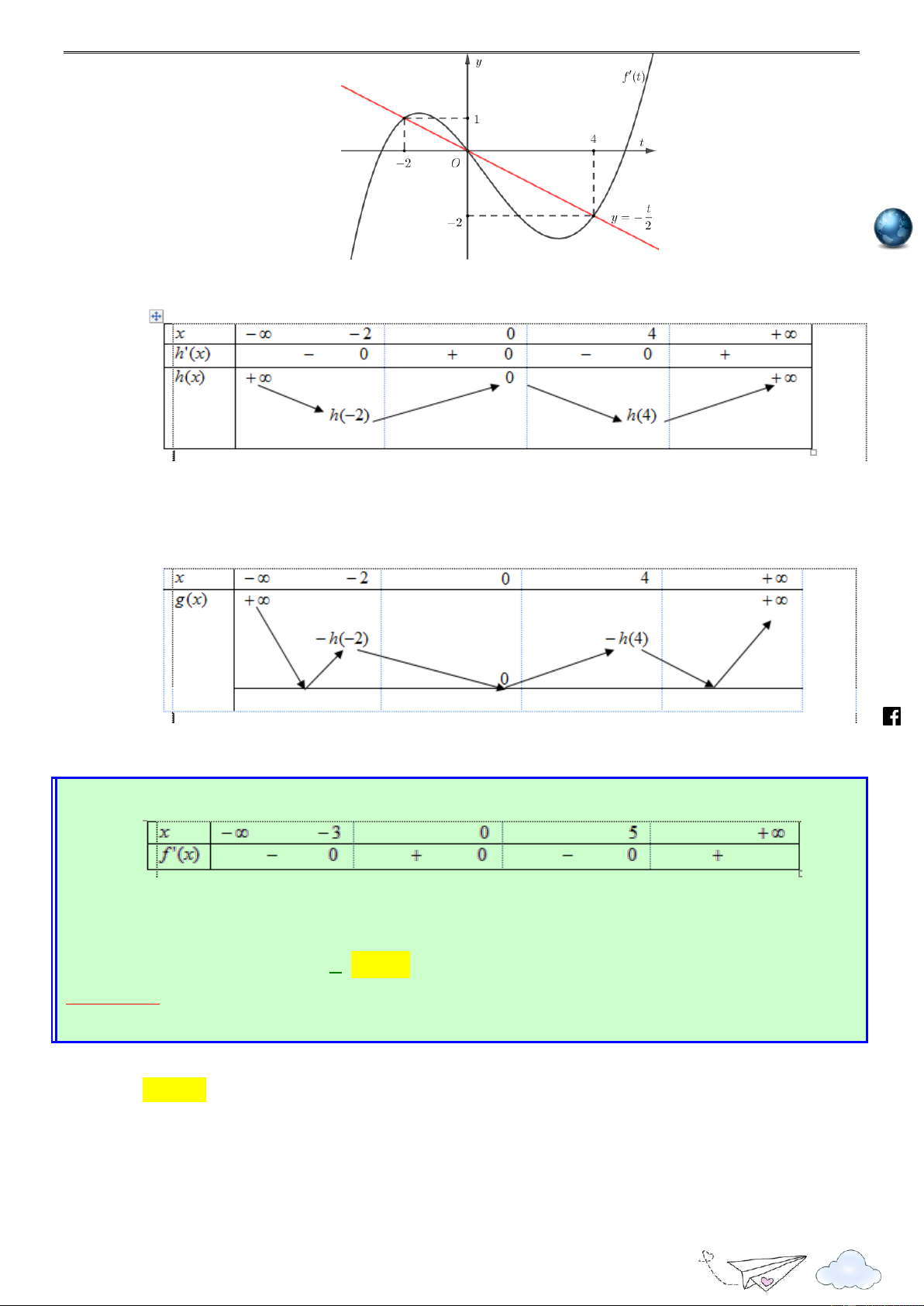
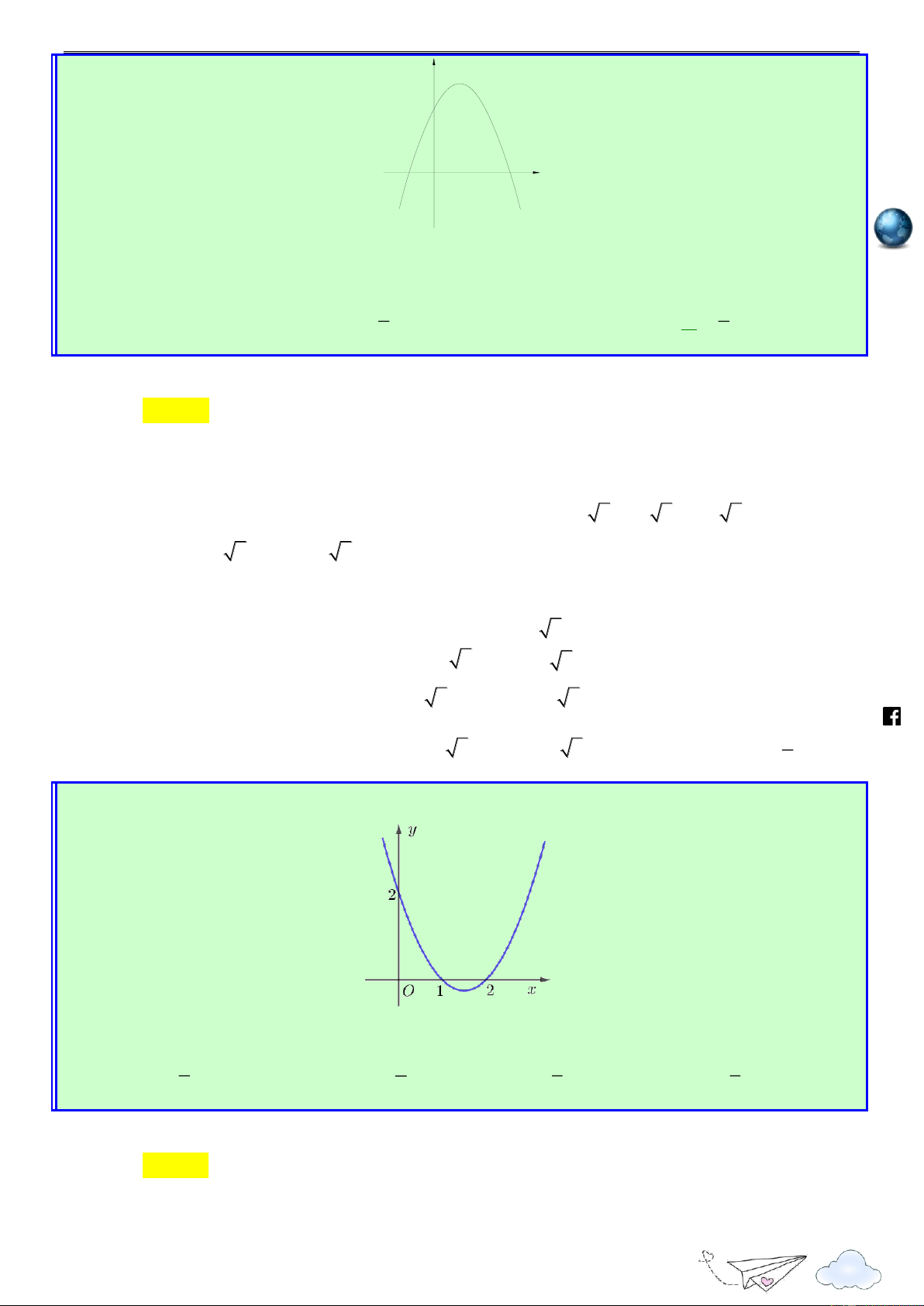
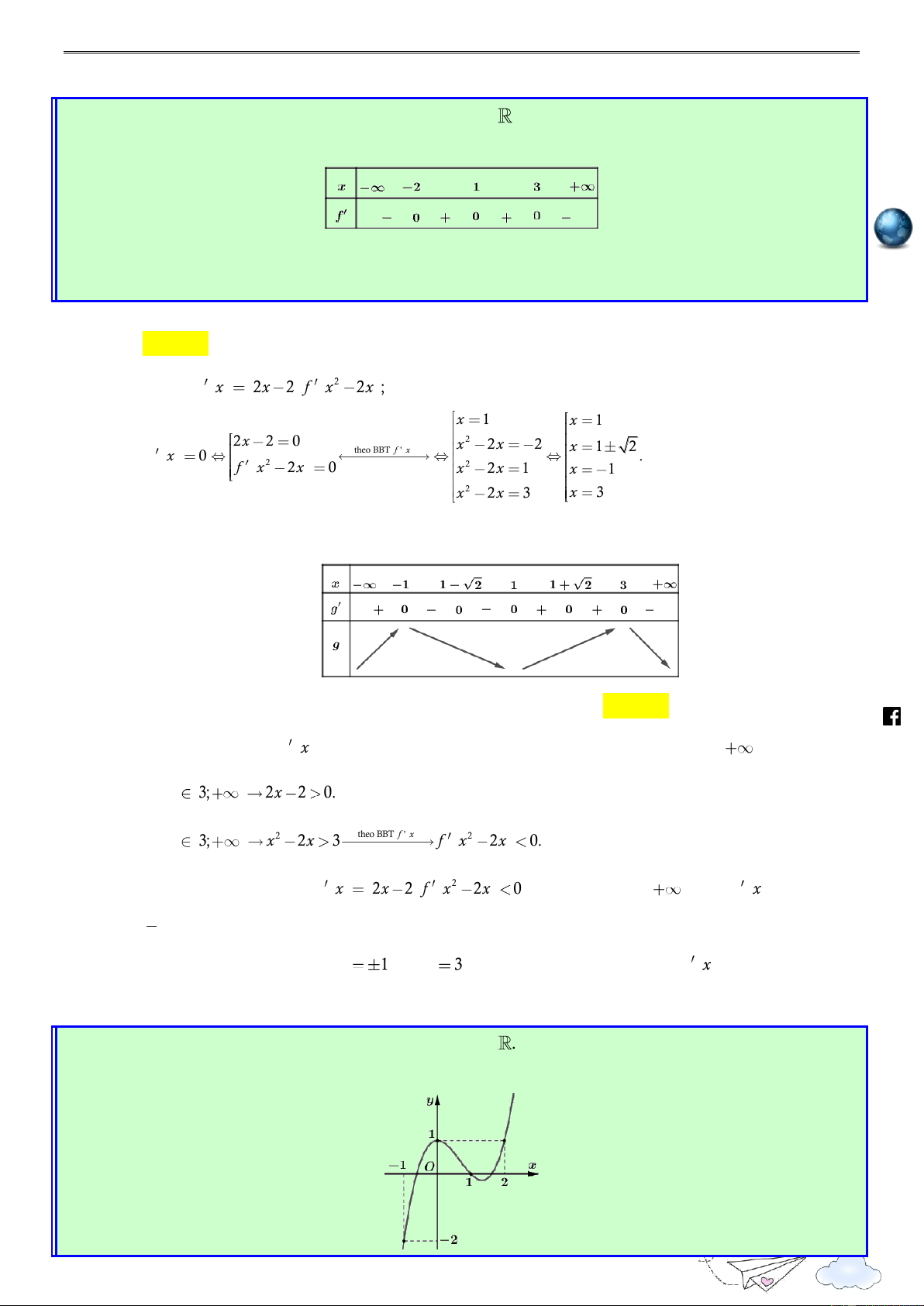
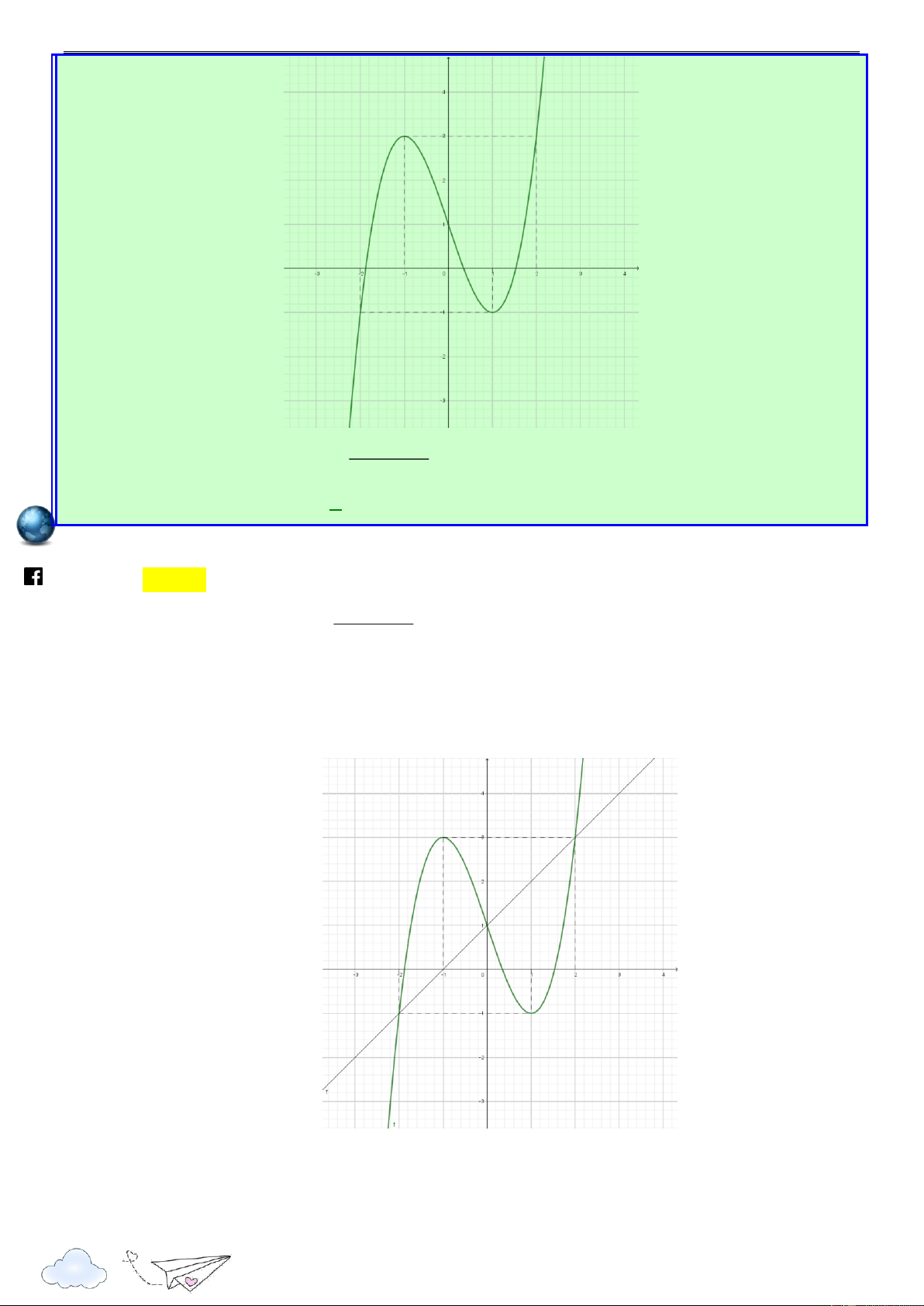
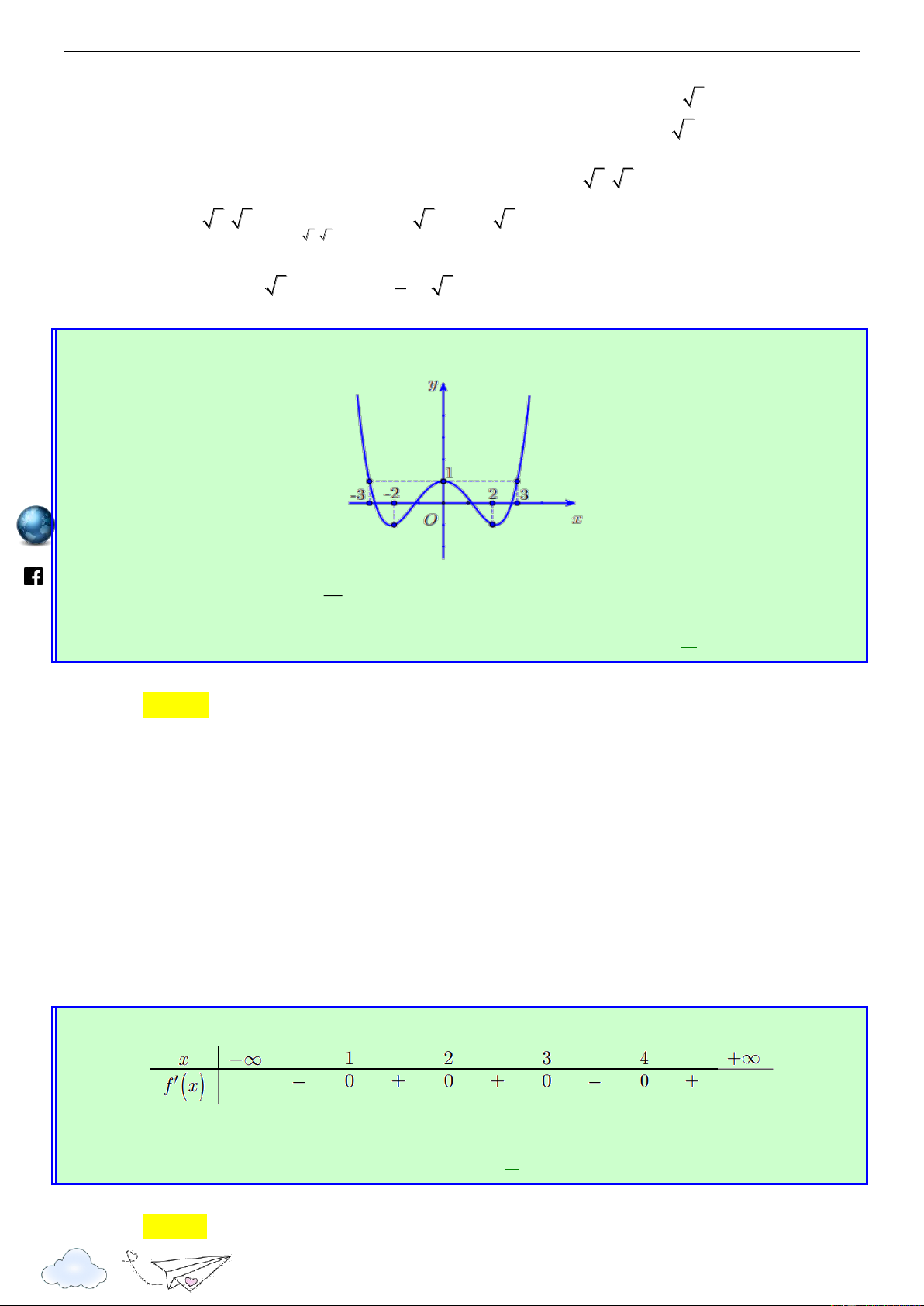
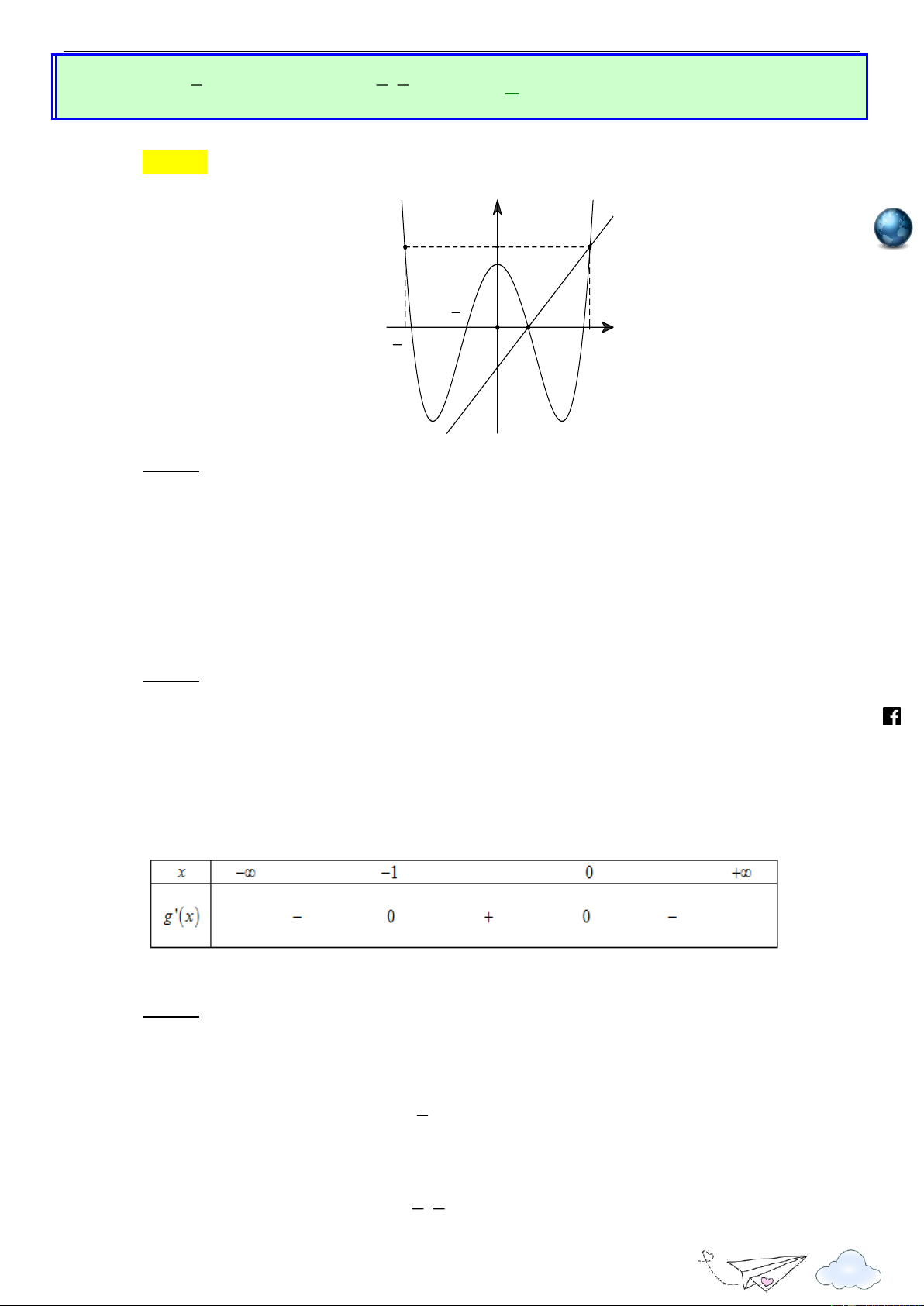
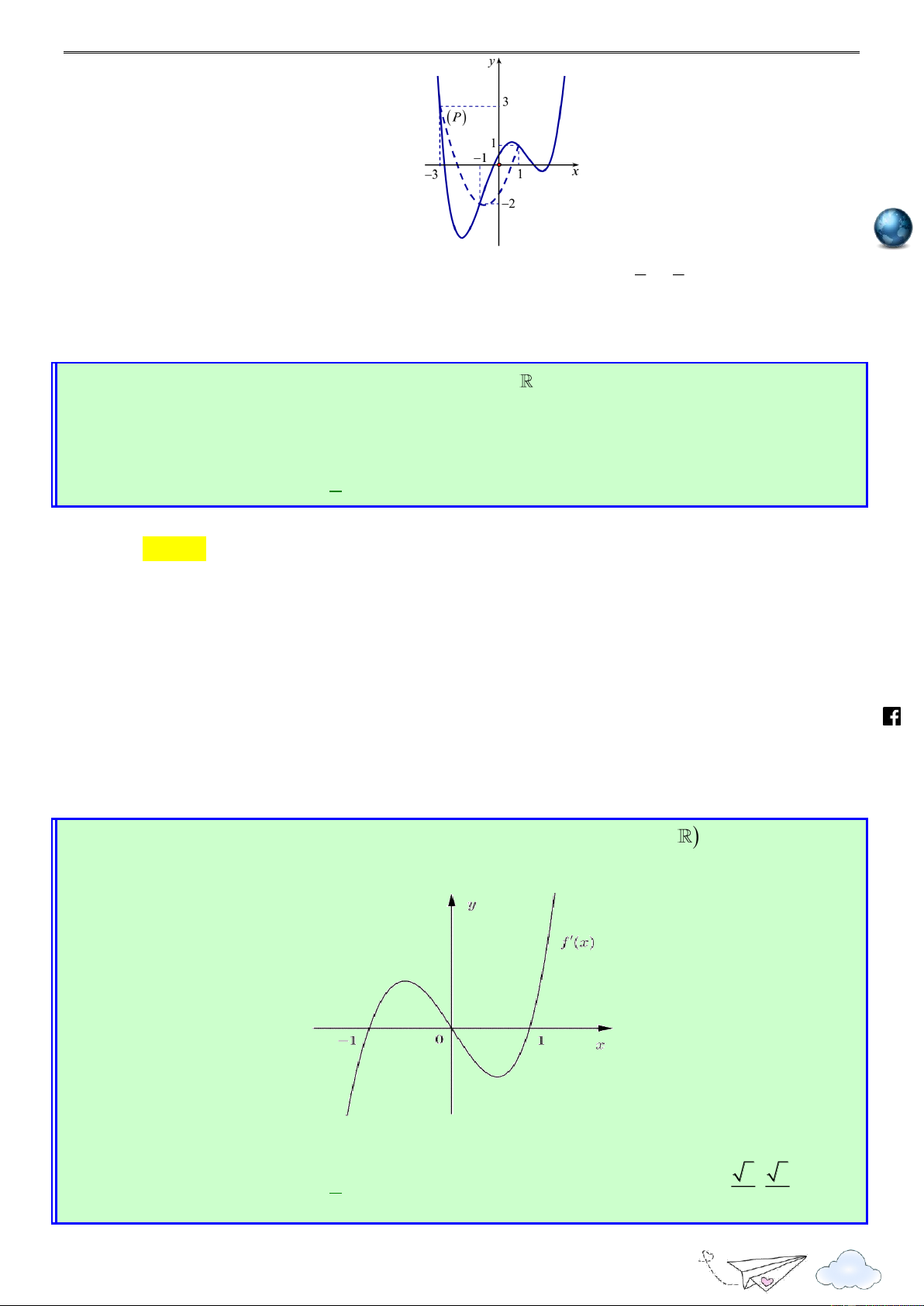
Cho hàm số đa thức f (x) có đạo hàm tràm trên R . Biết f ) 0 (
 0 và đồ thị hàm số
y  f  x như hình sau. /vietgold k.com Hàm số 2
g(x)  4 f (x)  x đồng biến trên khoảng nào dưới đây ? ceboo .fa A.  4 ; 0  . B.  0 ; 2  . C.    ; 4 . D.  ;  2  .
* Ý tưởng : Phát triển thành bài toán tìm khoảng đồng biến và nghịch biến của hàm số chứa
dấu giá trị tuyệt đối.  Lời giải https://www Chọn A
Xét hàm số h(x)  4 f (x)  x2 , x  R x
Có h'(x)  4 f '(x)  2x  h'(x)  0  f '(x)   2 x
Vẽ đường thẳng y   trên cùng hệ trục Oxy với đồ thị y  f  x như hình vẽ sau 2 7
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 h ttp
Từ đồ thị ta có BBT của h(x) như sau : s:// lu ye n th it racn gh ie Chú ý ở đây h ) 0 (  4 f ) 0 (  0 m.vn
Từ đó ta có BBT của như sau : ht
Từ BBT ta suy ra g(x) đồng biến trên khoảng  4 ; 0 . tps://www  Câu 4:
Cho hàm số y  f (x) có bảng xét dấu đạo hàm như sau .fa ceboo
Biết rằng 1  f (x)  , 5 x
  R. Hàm số g(x)  f ( f (x)  ) 1 3  x  3 2
x  2020 nghịch biến k.com
trên khoảng nào dưới đây /v A.  5 ; 0 . B.  0 ; 2  . C.  5 ; 2 . D.  ;  2  . ietgold
* Ý tưởng : Phát triển thành bài toán tìm khoảng đồng biến và nghịch biến của hàm số
y  f (u)  g(x)  Lời giải Chọn B
Ta có g'(x)  f '(x). f '( f (x)  )
1  3x2  6x Vì 1  f ( ) x  ,
5 x  R  0  f ( ) x 1  4
Từ bảng xét dấu của f '(x)  f '( f (x)  ) 1  0
Từ đó ta có bảng xét dấu như sau 8
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
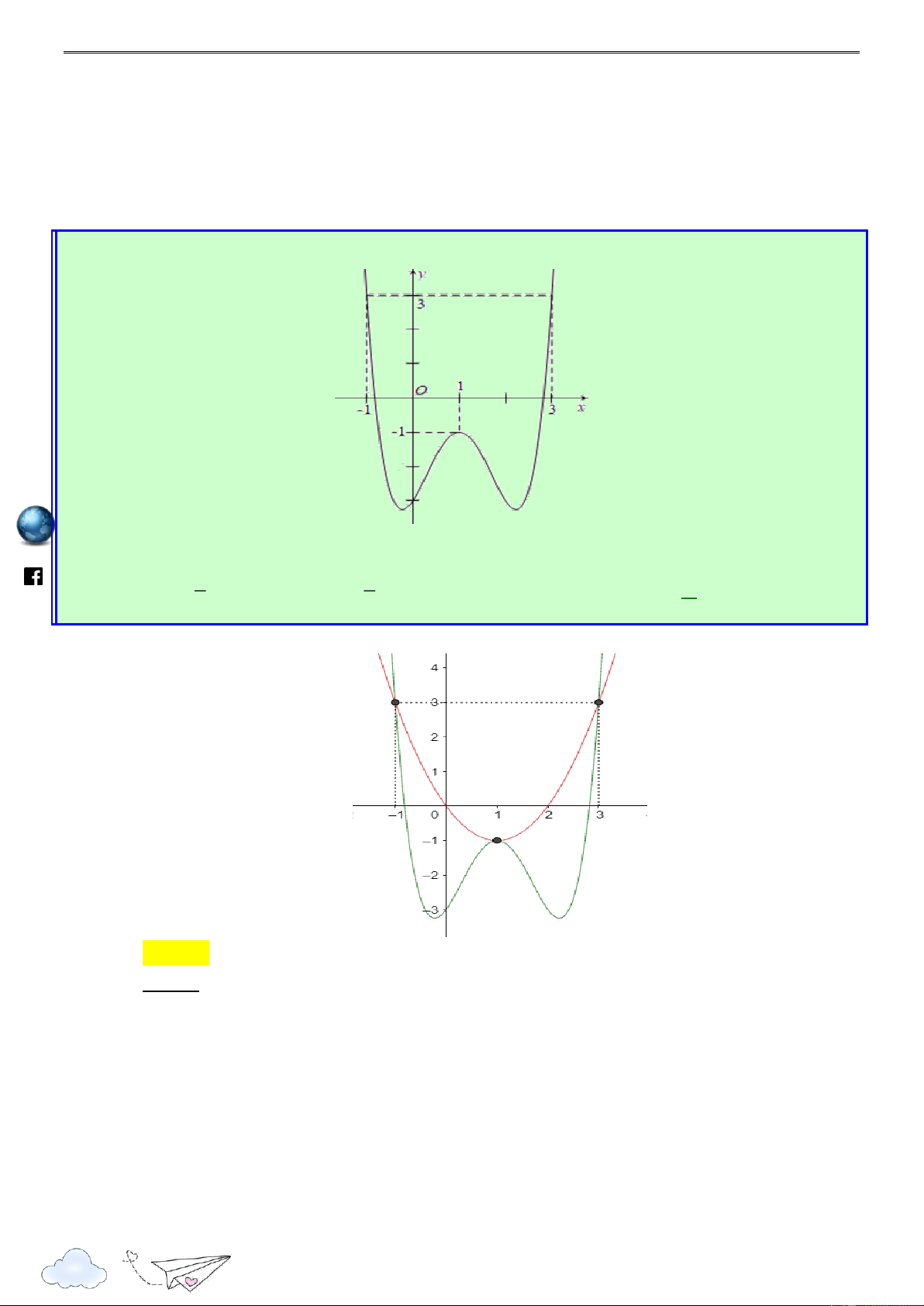
Do đó hàm g(x) nghịch biến trên khoảng  0 ; 2  . m.vn  Câu 5: Cho hàm số y
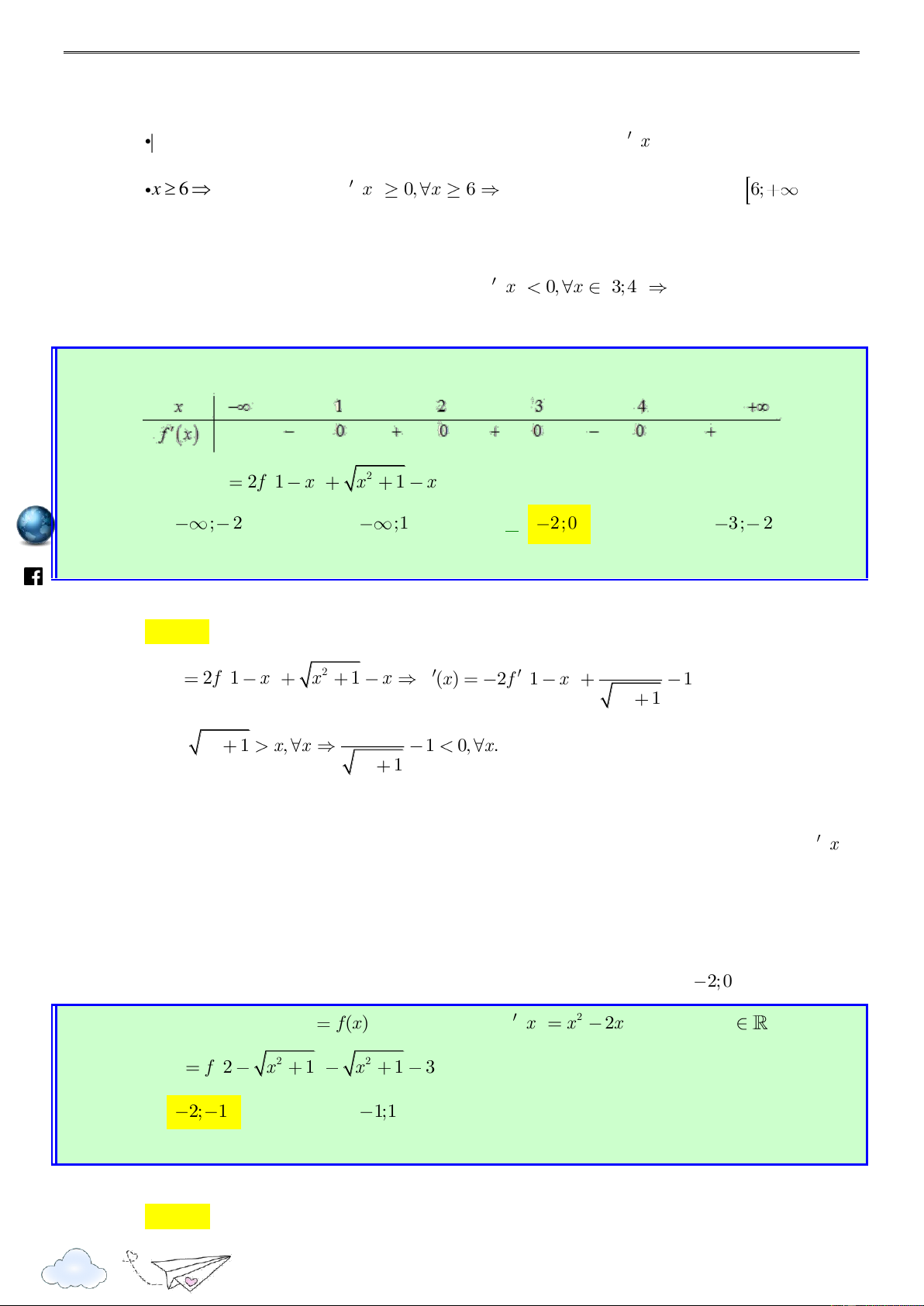
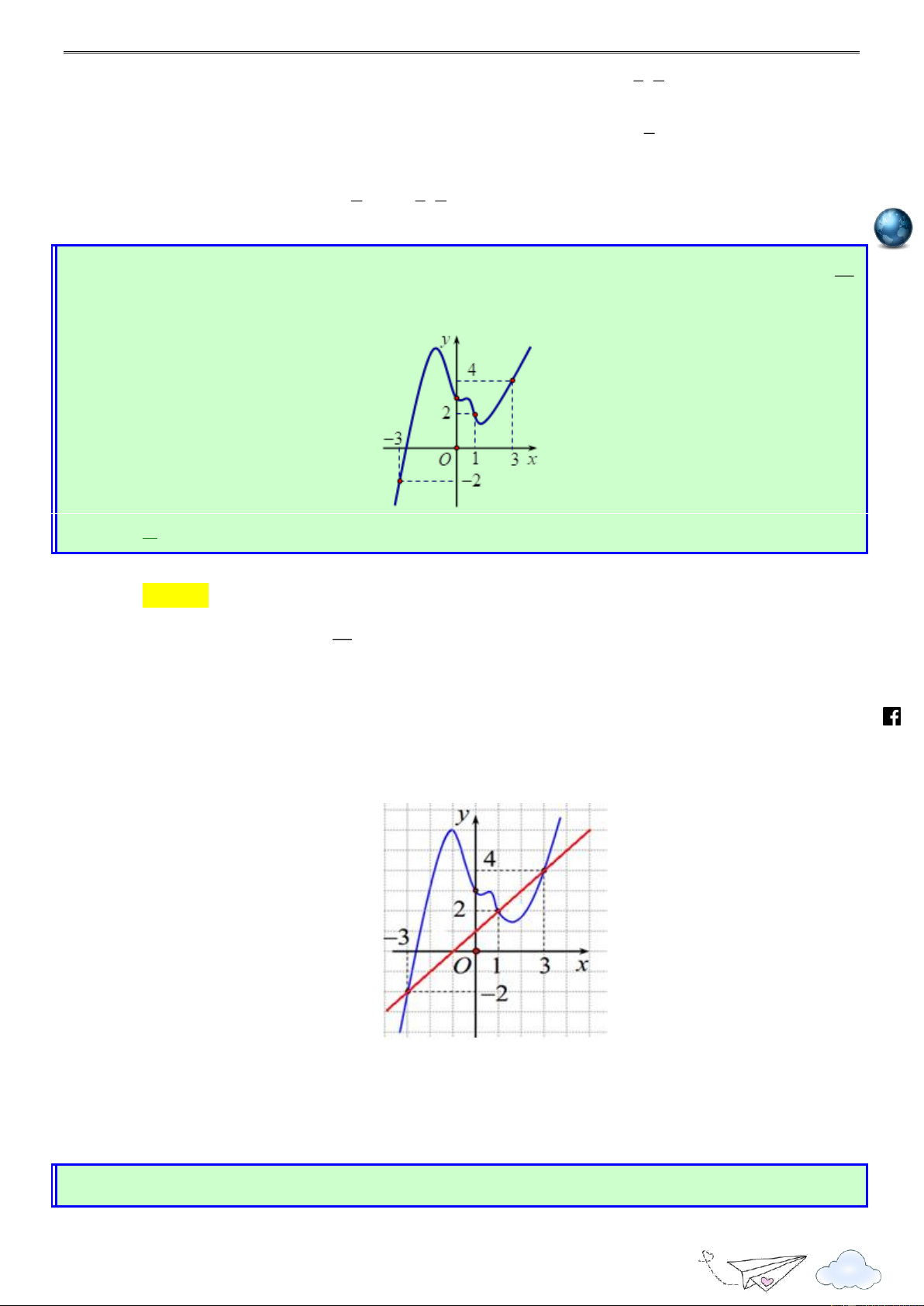
f (x) liên tục trên và có đồ thị hàm số f (x) như hình bên dưới. ie gh racn it th n ye lu s:// ttp h 2 x
Hỏi hàm số g(x) f (1 x)
x nghịch biến trên khoảng nào? 2 3 A. ( 3;1). B. ( 2; 0) . C. 1; . D. (1; 3) . 2
Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ  Lời giải /vietgold Chọn B k.com ceboo .fa https://www g (x) f (1 x) x 1, x . g (x) f (1 x) x 1 0 f (1 x) (1 x) 1 x 3 x 4 . 1 1 x 3 2 x 0 g (x) 0 f (1 x) x 1 0 x 2; 0; 4 : hữu hạn.
Hàm số g(x) nghịch biến trên mỗi tập 2;0 , 4;
nên nghịch biến trên ( 2  ;0). 9
 Quảng Thuận – Ba Đồn – QB
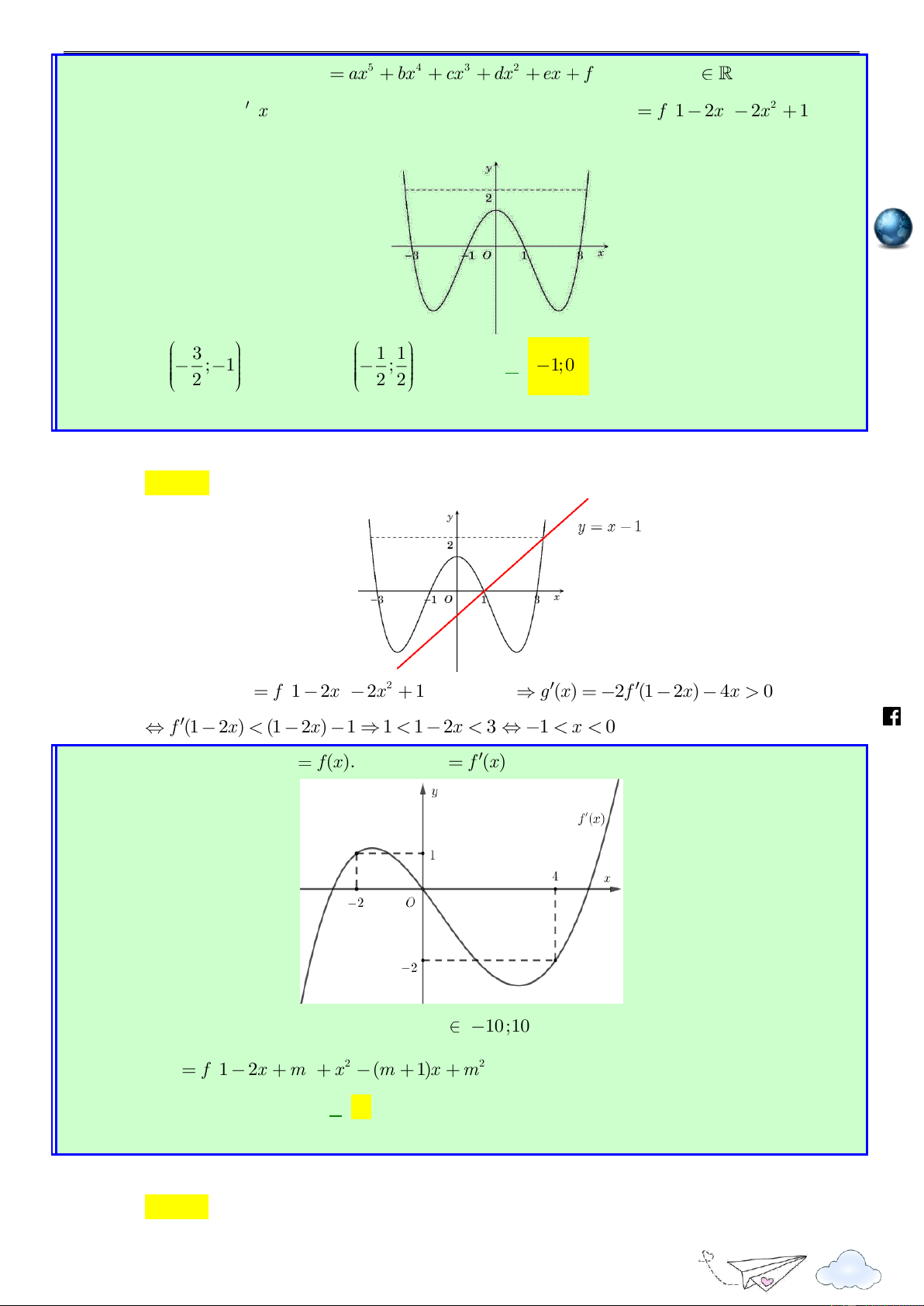
Khai thác và phát triển câu hỏi đề tham khảo 2020  Câu 6: Cho hàm số 5 4 3 2 f x ax bx cx dx ex f , a , b , c d, , e f . Biết rằng đồ
thị hàm số f x có đồ thị như hình vẽ bên. Hỏi hàm số 2 g x f 1 2x 2x 1 đồng
biến trên khoảng nào dưới đây? h ttp s:// lu ye 3 1 1 A. ; 1 . B. ; . C. 1;0 . D. 1; 3 . n 2 2 2 th it
Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ racn  Lời giải gh ie Chọn C m.vn Hàm số 2 g x f 1 2x 2x 1 đồng biến g (x)
2f (1 2x) 4x 0 f (1 2x) (1 2x) 1 1 1 2x 3 1 x 0 . http  Câu 7: Cho hàm số y
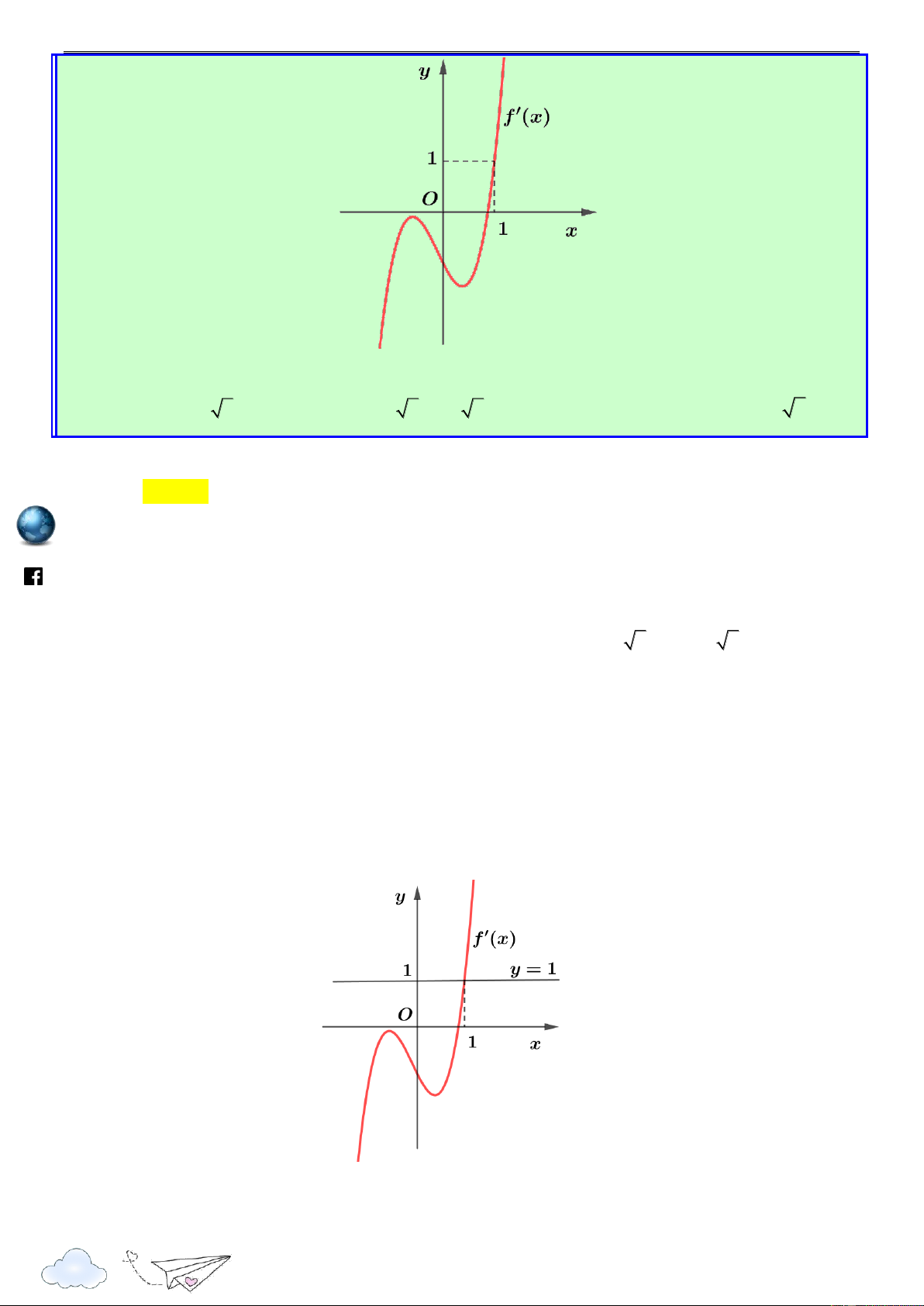
f (x). Hàm số y
f (x) có đồ thị như hình vẽ bên dưới. s://www .fa ceboo k.com /vietgold m
Có tất cả bao nhiêu giá trị nguyên 10;10 đê hàm số 2 2 g(x) f 1 2x m x (m 1)x
m nghịch biến trên khoảng 1;2 . A. 5 . B. 4 . C. 3 . D. 6 .
Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ  Lời giải Chọn B 10
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” m.vn ie gh g (x) 2f (1 2x ) m 2x m 1, x . racn it 1 2x m 4 th 1 f (1 2x m) 1 2x m n g (x) 0 2 2 1 2x m 0 ye lu m 3 1 2 4 x x m s:// 2 2 1 2x m 0 1 m 3 m ttp x h 2 2 1 m 3 1 m 3 m g (x) 0 f (1 2x m) 1 2x m x ; ; : hữu hạn. 2 2 2 2
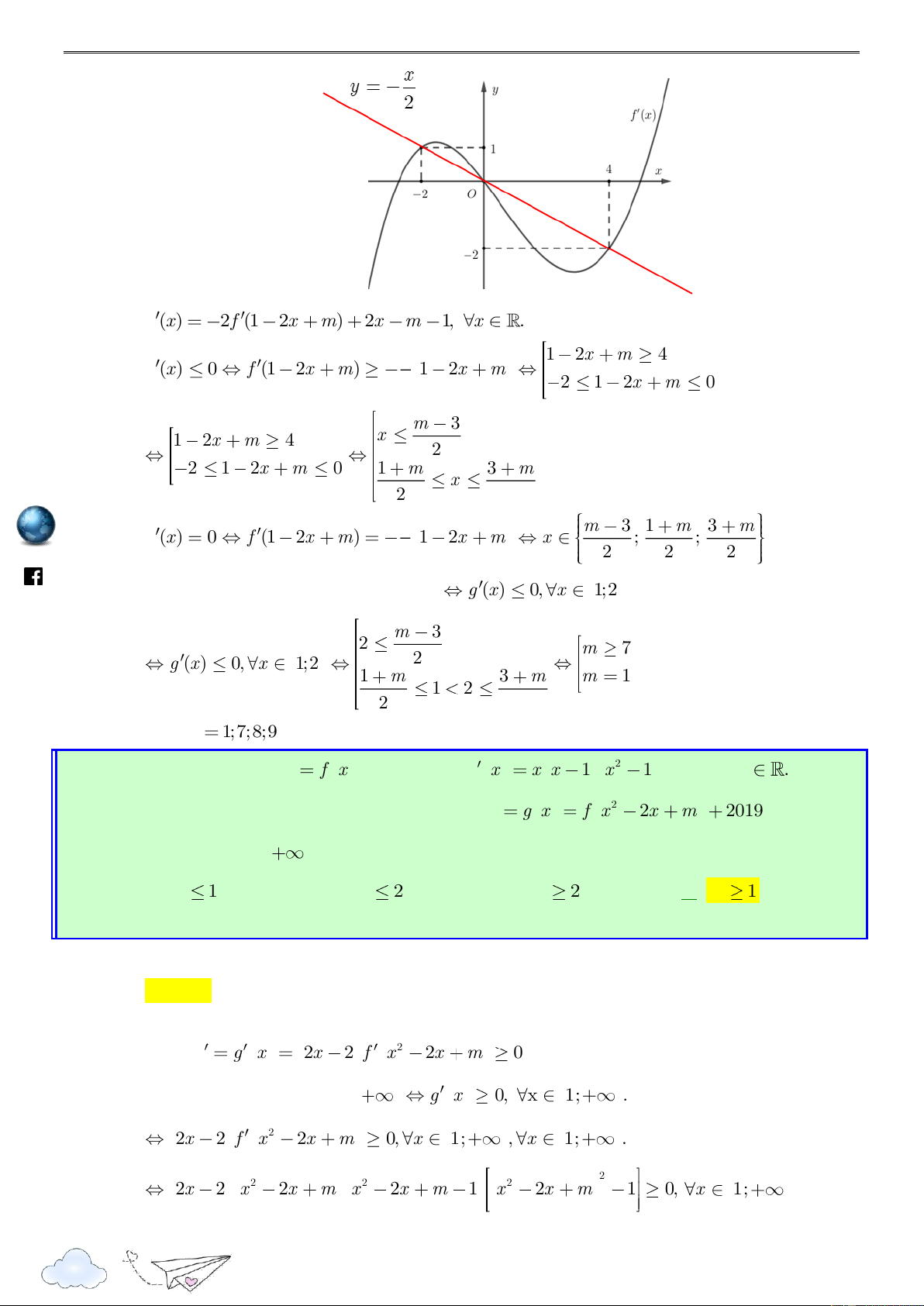
Hàm số g x nghịch biến trên 1;2 g (x) 0, x 1;2 m 3 2 m 7 2 g (x) 0, x 1;2 1 m 3 m m 1 1 2 2 2 /vietgold Vậy m 1;7;8;9 .
k.com  Câu 8: Cho hàm số y f x có đạo hàm 2 f x x x 1 x 1 với mọi x . Tìm tất y g x f x x m ceboo
cả các giá trị của tham số m để hàm số 2 2 2019 đồng biến .fa trên khoảng 1; . A. m 1. B. m 2 . C. m 2 . D. m 1 .
Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ https://www  Lời giải Chọn D Cách 1: Ta có 2 y g x 2x 2 f x 2x m 0
Hàm số đồng biến trên 1; g x 0, x 1; . 2 2x 2 f x 2x m 0, x 1; , x 1; . 2 2 2 2 2x 2 x 2x m x 2x m 1 x 2x m 1 0, x 1; . 11
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 2 2 2 2 x 2x m x 2x m 1 x 2x m 1 0 x 1; 2 2 x 2x m x 2x m 1 0, x 1; h(t) t m t m 1 0 t 1; ( 2 t x 2x 1 x 1; ) Bảng xét dấu h ttp Khi đó ( h t) 0, t 1; m 1 m 1 . s:// lu
Cách 2: Ta có bảng xét dấu đạo hàm f x như sau ye n th it ra cn 2 y g x 2x 2 f x 2x m . gh ie g x x m.vn Hàm số y
g x đồng biến trên khoảng 1; 0, 1; . x x Ta thấy 2 2 0, 1; nên 2 g x 0, x 1 f x 2x m 0, x 1. 2 x 2x m 1, x 1 2 m x 2x 1 u x , x 1 (do tính liên tục) 2 x 2x m 0, x 1 2 m x 2x v x , x 1 2
m  x  2x 1  u  x, x
 1: Không tồn tại m . http
m  x  x x
   m  x  2 2 2 , 1 1 1 , x  1 m 1. s://www  Câu 9: Cho hàm số y
f x có bảng xét dấu của đạo hàm như hình vẽ .fa ceboo Biết 1 f x 3, x . Hàm số 3 2 y g x f f x x 6x 1 nghịch biến trên k.com
khoảng nào dưới đây? /viet A. 3; 4 . B. 3; 2 . C. 1; 3 . D. 2;1 . gold
Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ  Lời giải Chọn A 2 g x
f (x).f f x 2x 12x. Do 1 f x 3, x
nên từ bảng xét dấu ta có f f (x) 0 x .
Ta xét một số khả năng có thể xảy ra 12
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” 1   x  3 + TH1: f (  x)  0   x  4 1   x  3 2
 2x 12x  0  
Chưa xác định được dấu của g x với giả thiết đã cho. 4  x  6 2
x  6  2x 12x  0  g x 0, x 6
Hàm số g x đồng biến trên 6; . 3  x  4 m.vn + TH2: f (  x)  0     ie x 1 gh
Ta thấy với 3  x  4 thì 2
2x 12x  0 nên g x 0, x 3;4
Hàm số g x nghịch racn biến trên 3; 4 . it th
 Câu 10: Cho hàm số f  x có bảng xét dấu đạo hàm như sau: n ye lu s:// ttp h Hàm số 2 y 2f 1 x x 1
x nghịch biến trên những khoảng nào dưới đây A. ; 2 . B. ;1 . C. 2;0 . D. 3; 2 .
Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ  Lời giải Chọn C 2 x g(x) 2f 1 x x 1 x g (x) 2f 1 x 1. 2 x 1 /vietgold x Để ý 2 x 1 x, x 1 0, x. 2 x 1 k.com
Ta xét một số khả năng về dấu của 2
 f (1 x) ceboo 1   x 1 .fa +TH1: 2
 f (1 x)  0  f (1 x)  0  
: Chưa xác định được dấu của g x 3 1 x  4 với giả thiết đã cho. 1  1 x  3  2   x  0 +TH2: 2
 f (1 x)  0  f (1 x)  0   .         https://www 1 x 4 x 3
 g (x)  0, x   ;    3  2
 ;0 Hàm số g x nghịch biến trên 2;0 .
 Câu 11: Cho hàm số y
f (x) có đạo hàm 2 f x x
2x với mọi x . Hàm số 2 2 g x f 2 x 1 x 1
3 đồng biến trên các khoảng nào dưới đây? A. 2; 1 . B. 1;1 . C. 1;2 . D. 2; 3 .
Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ  Lời giải Chọn A 13
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 x x x Ta có 2 g (x) f 2 x 1 . 2 f 2 x 1 1 . 2 2 x 1 x 1 2 x 1 2 Vì 2 f x x 2x x 1 1 nên f (x) 1, x hay f x 1 0 , x . Suy ra 2 f 2 x 1 1 0 , x . Bảng biến thiên: h ttp x ∞ 0 + ∞ s:// g' x ( ) + 0 lu ye 0 n g x ( ) th it ∞ ∞ r acn
Hàm số g x đồng biến trên khoảng ;0 . gh ie
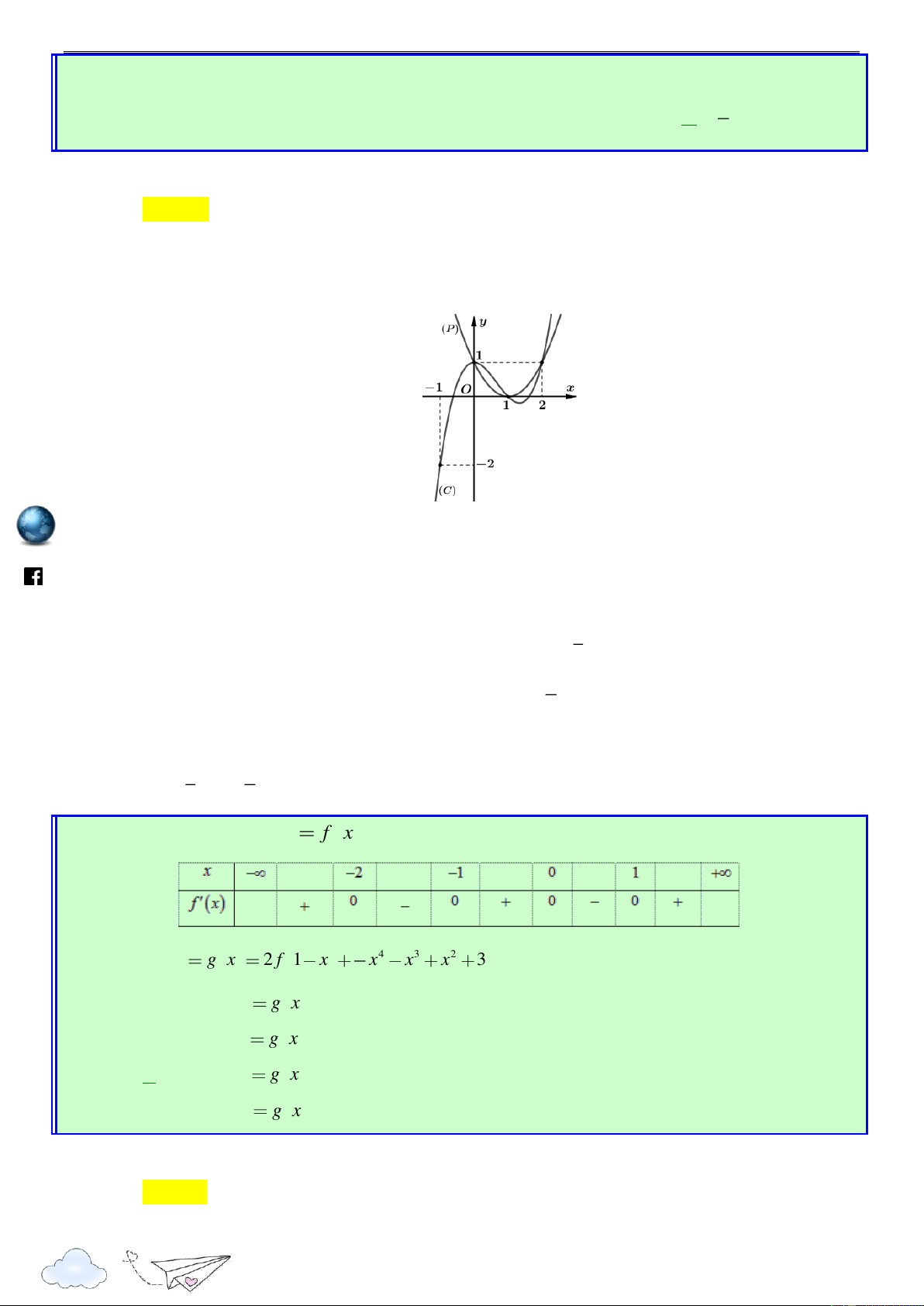
 Câu 12: Cho hàm số y
f x có đồ thị của hàm số y
f ' x như hình vẽ. Hàm số m.vn 1 2 3 2 y f x 2 x x 3x
4 nghịch biến trên khoảng nào dưới đây? 3 https://www A. ; 3 . B. 3;0 . C. 1; 3 . D. 3; . .fa
Bùi Sỹ Khanh – Nguyễn Đức Lợi – Huỳnh Đức Vũ ceboo  Lời giải k.com Chọn C 2 /v xf (x 2) 0 (1) Ta xét 2 2 y 2x.f x 2 x 2x 3 0 iet 2 x 2x 3 0 (2) gold x 3 Từ (2)
nên loại A, B,. D. Vậy chọn. C. x 1
 Câu 13: Cho hàm số f  x . Hàm số y  f x có đồ thị như hình bên dưới. 14
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” m.vn ie gh racn it
Hàm số g  x  f  x   2 3
1  3x  x đồng biến trên khoảng nào dưới đây? th n  3   2    2  ye A. 1;   . B. 0;   . C.  1;0 . D. ; 2   .  2   3   3  lu s://  Lời giải ttp h Chọn B
Ta có: g x  3 f 3x  
1  6x  2  3
Hàm g(x) đồng biến trên khoảng K khi
g x  0 (dấu = xảy ra tại một số hữu hạn điểm)
 3 f 3x  
1  6x  2  3  0 (1)
Đặt u  3x 1 ta được: hu  3 f u  2u  3 . /vietgold u        k.com Ta có: (1) f u u f u 2 3 2 3 0  1 3 ceboo 2u
y  f  x
y  f  u   .fa Từ đồ thị hàm số
  ta có đồ thị hàm số   và y 1 như hình vẽ 3 https://www 2u
Để hu  0 ta cần có đồ thị y  f u phải nằm bên trên của đồ thị hàm y  1 3 15
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020   1 2  x   ; 0  u  3 0  3x 1 3     3 3
Từ đó ta có hu  0        u  3   3x 1 3   4 x    3  2   1 2 Cho nên ta Chọn B vì 0;   ;      3   3 3 h x ttp
 Câu 14: Cho hàm số f  x . Đồ thị y  f 'x cho như hình bên. Hàm số g x  f x   2 1  2 s://
nghịch biến trong khoảng nào dưới đây? lu ye n th it racngh ie m.vn A. 2; 4 . B. 0  ;1 . C.  2   ;1 . D. 1;3 .  Lời giải Chọn A x
Ta có: g  x  f  x   2 1 
 gx  f x   1  x . 2
 gx  0  f x  
1  x  0  f  x   1   x   1 1
Đặt t  x 1 thì f t   t 1 ht   tp
Vẽ đường thẳng y  x 1 trên cùng một hệ trục tọa độ với đồ thị hàm số y
f  x (như s://www hình vẽ bên). .fa ceboo k.com /vietgold
Dựa vào đồ thị f 't  t 1  t  3
 ,t 1,t  3
Hàm số nghịch biến g x  f  x  
1  x  0  f t   t  t ( ;  3  )(1;3) Do đó x ( ;  2
 ) (2;4) vậy g(x) nghịch biến trên 2;4 .
 Câu 15: Cho hàm số y  f x . Hàm số y  f 'x có đồ thị như hình bên. 16
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” m.vn ie gh racn it th 2 2     n
Hàm số g  x f x 2x x
2x đồng biến trên khoảng nào dưới đây? ye        1  ; 1  ;1 2 lu A.  1 2; 1. B.  1 2; 1 2  . C.  . D.  . s://  Lời giải ttp h Chọn A
Ta có: g  x  f  2 x  x 2 2  x  2x
 gx   x   f  2
x  x  x   x    f    2 2 2 2 2 2 2 1
x  2x 1 .
 gx   x   f    2 0 2 1
x  2x 1  0  x  1  , x  1   2, x  1   2  x 1  0   I /vietgold  f    2 x  2x   1
Xét g x  0   . x 1 0 k.com   f    II 2 x  2x   1 ceboo .fa
Xét sự tương giao của đồ thị hàm số y  f  x và y  1. https://www
Dựa vào đồ thị ta có: f  2 x  x 2 2
1 x  2x 1 và f  2 x  x 2 2
1 x  2x 1. 17
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 x  1  x 1  0  x  1   Xét hệ (I):       x  1   2  x  1   2 . f    2
x  2x  1 2 x  2x 1 
x  1 2 x 1 0  x  1  x  1   Xét hệ (II):      f    2
x  2x  1 2 x  2x 1  1   2  x  1   2 h  1   2  x  1  . ttp s://
Vậy hàm số g  x đồng biến trên khoảng  1   2;  1 và  1   2;. lu ye
 Câu 16: Cho hàm số y  f x có đạo hàm trên . Hàm số y  f 'x có đồ thị như hình vẽ nth x
bên. Đặt y  g  x  f  x 2 
. Khẳng định nào sau đây là đúng? it 2 rac
A. Hàm số y  g  x đồng biến trên khoảng 1;2 . n gh
B. Đồ thị hàm số y  g  x có 3 điểm cực trị. ie m.vn
C. Hàm số y  g  x đạt cực tiểu tại x  1  .
D. Hàm số y  g  x đạt cực đại tại x 1.  Lời giải Chọn D
Ta có: g ' x  f ' x  ; x
g ' x  0  f ' x  x (*).
Số nghiệm của phương trình (*) là số giao điểm giữa đồ thị hàm số y  f ' x và ht
đường thẳng y  x . tps://www
Dựa vào hình bên ta thấy giao tại 3 điểm  1  ;  1 ;1;  1 ;2;2 x  1   .fa  (*)  x 1  . ceboo x  2  k.com /vietgold
Bảng xét dấu g ' x : x  1  1 2  g ' x + 0 + 0  0 + 18
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” x
Từ bảng xét dấu g ' x ta thấy hàm số y  g  x  f  x 2  . 2
Đồng biến trên khoảng   ;1
 và 2; ; nghịch biến trên khoảng 1;2 .
Hàm số y  g  x đạt cực đại tại x 1.
 Câu 17: Cho hàm số f x có đồ thị của hàm số f x như hình vẽ. m.vn ie gh racn it th n ye lu s:// ttp h x
Hỏi hàm số g  x  f   x 2 1 
 x nghịch biến trên khoảng nào dưới đây? 2  3  A.  2  ;0 . B. 1;3 . C. 1  ;   . D.  3   ;1 .  2   Lời giải Chọn A
Ta có: g x   f 1 x  x 1.
Hàm số g  x nghịch biến  g x  0  f 1 x  x 1 (1) . /vietgold
Đặt t 1 x . Khi đó (1) trở thành f t   t  (2). k.com
Bất phương trình (2) được thỏa khi f  x  x hay đồ thị hàm số f  x nằm phía trên ceboo
đồ thị hàm số y  x . .fa https://www  t  3   1 x  3   x  4 Từ đồ thị ta được      . Vậy chọn khoảng  2  ;0 . 1   t  3 1  1 x  3  2   x  0
 Câu 18: Cho hàm số y  f x có đồ thị hàm số y  f x được cho như hình vẽ sau. 19
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 y -1 O 3 x 4 h
Hàm số g  x  f 2x  
1 đồng biến trên khoảng nào dưới đây? ttp s://  3   1  A. 1; . B. 1;   . C. ;  1 . D. ;1   . lu  2   2  ye n  Lời giải th it Chọn D ra 3 4 c
Ta có: g x  8x . f 2x   1 n gh
TH1: x  0 . Để hàm số g  x đồng biến thì ie m.vn f  4 x   4 4 2 4 4 2 1  0  1
  2x 1 3  0  x  2  0  x  2   2  x  2 4 4       0 x 2 x 0; 2   .
TH2: x  0 . Để hàm số g  x đồng biến thì   x    x  L x  f 2x   4 4 2 1 1 0( ) 2 4 1  0       . 4 2 4 2x 1 3 x  2 x   2 So sánh với điều kiện 4
x   x    x 4 0 2 ; 2 . ht  1 
Vậy hàm số g  x đồng biến trên 4 0; 2   ;1 . tp   và  4 ;
2  . Do đó chọn khoảng    2  s://www
 Câu 19: Cho hàm số y  f  x . Hàm số y  f x có đồ thị như hình vẽ sau đây. .fa ceboo k.com /vietgold 2
y  f x  x Hàm số 
 nghịch biến trên khoảng nào?  1   3   3   1  A. ;   . B. ;    . C.  ;    . D.  ;    .  2   2   2   2   Lời giải Chọn A Xét hàm số   2 y f x  x  20
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Ta có: y    x f  2 1 2 x  x   1 2 1  0 x x   2   2 2
 y  0  x  x  1  
x  x 1  0VN   2  2 x  x  2 
x  x  2  0VN   m.vn ie 2   gh 2 1 1 1
Ta lại có: x  x  
 x  1, x   R 4  2    4 racn it
y  f  x  f  2
x  x   0, x   R th
Từ đồ thị của hàm số   n ye
Bảng biến thiên của hàm số   2 y f x  x  lu s:// ttp h  1 
Vậy hàm số nghịch biến trên ;  2  . Chọn A  
 Câu 20: Cho hàm số y  f x có đạo hàm trên . Đồ thị hàm số y  fx như hình vẽ. /vietgold k.com ceboo .fa
Hàm số y  f  2
x  2x đồng biến trên khoảng nào sau đây? https://www A. 1; 2 . B.  ;   3 . C. 0;  1 . D.  2  ; 0 .  Lời giải Chọn A
Từ đồ thị của hàm số y  f  x ta có bảng biến thiên của hàm số y  f x như sau 21
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 
Đặt g  x  f  2
x  2x , ta có g x   2
x  x f  2
x  x   x   f  2 2 . 2 2 1 . x  2x. h 2 ttp
Hàm số g  x đồng biến khi g x  0   x  
1 . f  x  2x  0 s:// x 1 0  x 1 0   lu  hoặc  2 f   2   1 2 x  2x    0 f 
 x  2x    0 ye n x  1  th x 1 0  it    1   2  x  1   2  1   x  1   2 r 1   1
  x  2x 1     . a · Xét   2 c  x  3   x 1 n 2
x  2x  3 gh x 1  ie m.vn x  1  x 1 0   x  1   · Xét 2 2
 x  2x  1    2  
x  2x 1 0 2 1
  x  2x  3   2
x  2x  3  0 x  1  x  1     3   x  1   2    x  1   2   .  ht   x  1  tp   x  1   2 s://www    3   x  1
 Câu 21: Cho hàm số y  f x , biết hàm số y  f x có đồ thị như hình bên dưới. .fa ceboo k.com /vietgold
Hàm số g  x  f  2
3  x  đồng biến trên khoảng? A. 2;3 . B.  1  ;0 . C.  2  ;  1 . D. 0  ;1 .  Lời giải Chọn B 22
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Dựa vào đồ thị, ta có bảng xét dấu
g  x   xf  2 ' 2 3  x   x  0 m.vn  ie   x  g  x 2 0 x  3  '  0     gh f  2 3  x   0 x  2     x  1  racn it  3   x  2  th  6   3 x  1   n
f 3  x  2 2  0    2  x  3 2  ye  2  3  x  1   x 1  lu s:// Bảng biến thiên: ttp h
Từ BBT suy ra hàm số đồng biến trên  1  ;0 .
 Câu 22: Cho hàm số y  f (x) có bảng xét dấu đạo hàm như sau: /vietgold
k.com Biết: 1 f( )x5, x   . R Khi đó, hàm số 3 2
g(x)  f ( f (x) 1)  x  3x  2020 nghịch biến trong khoảng nào dưới đây: ceboo .fa A. ( 2  ;0) . B. (0;5) . C. ( 2  ;5) . D. ( ;  2  ).  Lời giải Chọn A https://www Ta có: 2
g '(x)  f '(x). f '( f (x) 1)  3x  6x .
Vì 1 f (x)  5, x
 R  0  f (x) 1 4 .
Từ bảng xét dấu của f '(x)  0  f '( f (x) 1)  0 .
Từ đó, ta có bảng xét dấu như sau: 23
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020
Do đó, hàm g(x) nghịch biến trên khoảng ( 2  ;0).
 Câu 23: Cho hàm số y  f  x có đạo hàm trên và có bảng biến thiên của đạo hàm f ' x như sau :
Hỏi hàm số g  x  f  2
x  2x  2020 có bao nhiêu điểm cực tiểu ? h ttp A. 1. B. 2. C. 3. D. 4. s://  Lời giải lu Chọn A ye n th Ta có 2 g x 2x 2 f x 2x ; it r x 1 x 1 a 2 c 2x 2 0 x 2x 2 f x x 1 2 n theo BBT ' g x 0 . 2 gh 2 f x 2x 0 x 2x 1 x 1 ie 2 x 2x 3 x 3 m.vn Bảng biến thiên
Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta Chọn A ht
Chú ý: Dấu của g x được xác định như sau: Ví dụ xét trên khoảng 3; tps://www  x 3; 2x 2 0. 1  2 f x 2 x 3; x 2x 3 f x 2x 0. .fa theo BBT ' 2 ceboo Từ 1 và 2 , suy ra 2 g x 2x 2 f x 2x 0 trên khoảng 3; nên g x mang dấu k.com . /v
Nhận thấy các nghiệm x
1 và x 3 là các nghiệm bội lẻ nên g x qua nghiệm đổi ietgold dấu.
 Câu 24: Cho hàm số y  f x có đạo hàm trên . Đồ thị hàm số y  f x như hình vẽ bên dưới. 24
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Hàm số g  x  f  x   3 2 3
1  9x 18x 12x  2021 nghịch biến trên khoảng.  2  A.   ;1  . B. 1;2 . C.  3   ;1 . D. ;1   .  3   Lời giải Chọn D m.vn ie
Ta có g x  f  x    x  x 
g x   f  x     x  2 2 3 3 1 3(9 12 4); 0 3 1 3 2 .(1) gh
Đặt t  3x 1 khi đó
 f t  t  2 (1) 1 . racn it th n ye lu s:// ttp h t 
Dựa vào đồ thị ta suy ra f t   t  2 0 1  . 
(vì phần đồ thị của f 't  nằm phía 1   t  2
dưới đồ thị hàm số y  t  2 1 ).  1 x  3x 1 0  3
Như vậy f 3x  
1  3x  22     . 1   3x 1 2 2   x 1 3 /vietgold
Vậy hàm số g  x  f  x   3 2 3
1  9x 18x 12x  2021 nghịch biến trên các khoảng k.com  1   2  ;    và ;1   .  3   3  ceboo  .fa
Câu 25: Cho hàm số y
f x có bảng xét dấu của đạo hàm như sau: https://www 1 Đặt 4 3 2 y g x 2 f 1 x x x x
3 . Khẳng định nào dưới đây là đúng? 4 A. Hàm số y
g x đồng biến trên khoảng ;0 . B. Hàm số y
g x đồng biến trên khoảng 1; 2 . C. Hàm số y
g x đồng biến trên khoảng 0  ;1 . D. Hàm số y
g x nghịch biến trên khoảng 2;  Lời giải Chọn C 25
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020
Ta có: y  g x   f   x 3 3 2 1
 x 3x  2x . x  2 x 1
Dựa vào bảng xét dấu f  x ta có f 1 x  0   . x  0  x  3
   x     x            h f  x f  x 2 1 1 2 3 2 1 0 1 0   . ttp 0 1 x 1 0  x 1 s:// 3 3
x  3x  2x  x  x   1  x  2 lu ye
Bảng xét dấu y  g x n th it racngh ie m.vn
Vậy hàm số đồng biến trên 0  ;1 .
 Câu 26: Cho hàm số y  f x . Hàm số y  f 'x có đồ thị như hình vẽ bên dưới. f(x)=-3x^5+2x^4-2x^2+x y 3 f(x)=2 f(x)=-2 x(t)=-1 , y(t)=t ht 2 x(t)=1 , y(t)=t tps://www 1 x .fa -8 -7.5 -7 -6.5 -6 -5.5 -5 -4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 ceboo -1 k.com -2 /vietgold -3
Hàm số g x  f  x   2 2
3  4x 12x 1 đồng biến trên khoảng nào dưới đây? -4  3 1   5   3   1  A.  ;  .   B.  ; 2  .   C. 2  ; .   D.  ;0 .    2 2   2   2   2  -5  Lời giải Chọn B -6 26
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” f(x)=-3x^5+2x^4-2x^2+x y 3 f(x)=2 f(x)=-2 x(t)=-1 , y(t)=t 2 x(t)=1 , y(t)=t f(x)=-2x 1 x m.vn -8 -7.5 -7 -6.5 -6 -5.5 -5 -4.5 ie -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 gh -1 racn it th n -2 ye lu -3 s://
y  f 'x ttp y  2  x h -4
Hàm số g  x đồng biến -5
 g'x  0  2 f '2x 38x 12  0  f '2x 3  2  2x 3 -6 x  2 2x 3 1          3 . Chọn B      0 2x 3 1   x  1   2
 Câu 27: Cho hàm số y  f x có đồ thị y  f  x như hình vẽ. Xét hàm số /vietgold
g  x  f  x 1 3 3 3 2
 x  x  x  2018. Mệnh đề nào dưới đây đúng? k.com 3 4 2 y ceboo .fa 3 1 1  3  O x 1 https://www 2 
A. Hàm số g  x đồng biến trên  1   ;1 .
B. Hàm số g  x đồng biến trên  3   ;1 .
C. Hàm số g  x đồng biến  3  ;  1 .
D. Hàm số g  x nghịch biến trên  1   ;1 .  Lời giải Chọn B 1 3 3 3 3
Ta có: g  x  f  x 3 2
 x  x  x  2018  gx  f x 2  x  x  3 4 2 2 2 27
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 3 3 3 3
+ g ' x  0  f ' x 2
 x  x  . Đặt 2 y  x  x  có đồ thị (P) 2 2 2 2  f   1  2  g  1  0  
Dựa vào đồ thị y  f  x , ta có:  f   1  1  g  1  0   f    3    3 g   3    0 y h ttp 3 s:// P lu ye 1 n 1  th x 3  1 it ra 2  cngh ie m.vn 3 3
Vẽ đồ thị  P của hàm số 2 y  x  x 
trên cùng hệ trục tọa độ như hình vẽ trên 2 2
(đường nét đứt ), Đồ thị  P đi qua các điểm  3  ;3 ,  1  ; 2  , 1  ;1 với đỉnh  3 33  I  ;    .  4 16  3 3
Ta thấy: + Trên khoảng  1  
;1 thì f  x 2
 x  x  , nên gx  0 x   1  ;  1 2 2 ht 3 3 tp +Trên khoảng  3  ; 
1 thì f  x 2
 x  x  , nên gx  0 x   3  ;  1 s://www 2 2
Từ những nhận xét trên, ta có bảng biến thiên của hàm y  g x trên  3   ;1 như sau: .fa ceboo k.com /v ietgold
Vậy hàm số g  x đồng biến trên  1   ;1 . Chọn A
 Câu 28: Cho hàm số f  x . Hàm số y  f 'x có đồ thị như hình vẽ 28
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” m.vn ie gh racn it th n ye lu s:// x  x 
Hàm số g  x  f  x   2 4 3 1 
đồng biến trên khoảng nào dưới đây? ttp 2 h A.  ;  2  . B.  3  ;  1 . C. 0  ;1 . D.  1  ;0 .  Lời giải Chọn B 2 x  4x  3
Ta có: g  x  f  x   1 
 g 'x  f 'x   1  x  2 . 2
Hàm số đồng biến  g ' x  0  f ' x   1  x  2 (1)
Đặt x 1  t . Bất phương trình (1) có dạng: f 't   t 1 /vietgold
Xét hai hàm số y  f 't  và y  t 1: k.com ceboo .fa https://www t  2  ;0
Dựa vào đồ thị ta có: f 't     t 1  t  2 29
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020   x     x  
Ta có g  x 2 1 0 3 1 '  0     x 1  2 x 1
 Câu 29: Cho hàm số f (x) liên tục trên R và có đồ thị f '(x) như hình vẽ. Tìm số điểm cực trị của hàm số 2
y  f (x  x) ? h ttp s:// lu ye n th it racn gh A. 10 . B. 11. C. 12 . D. 13 . ie m.vn  Lời giải Chọn B 1 Ta có 2
y '  (2x 1) f '(x  x) ; 2
x  x  m có nghiệm khi và chỉ khi m   . 4
Dựa vào đồ thị ta thấy đồ thị hàm f '(x) cắt trục hoành tại 5 điểm trong đó 1 điểm có 1
hoành độ nhỏ hơn  và có một tiệm cận. 4 http 1  s://www
Khi đó ứng với mỗi giao điểm có hoành độ lớn hơn
và 1 điểm không xác định thì 4
y '  0 có hai nghiệm. Từ đây dễ dàng suy ra hàm 2
y  f (x  x) có 11 cực trị. .fa
 Câu 30: Cho hàm số y  f (x) có đạo hàm trên . Đồ thị của hàm số y  f '(x) như hình vẽ. ceboo
Tìm các khoảng đơn điệu của hàm số 2
g(x)  2 f (x)  x  2x  2020 . k.com y /v 2 ietgold -1 O 1 3 x -2
Mệnh đề nào dưới đây đúng?
A. Hàm số g  x nghịch biến trên 1;3 .
B. Hàm số g  x có 2 điểm cực trị đại.
C. Hàm số g  x đồng biến trên  1   ;1 .
D. Hàm số g  x nghịch biến trên 3;  .  Lời giải Chọn C
Ta có g '(x)  2 f '(x)  2x  2  2 f '(x)  (x 1). 30
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Dựa vào hình vẽ ta thấy đường thẳng y  x 1 cắt đồ thị hàm số y  f '(x) tại 3 điểm: ( 1  ; 2  ), (1;0), (3;2). y 2 -1 m.vn O 1 3 x ie -2 gh racn Dựa vào đồ thị ta có it th    n x 1  ye
g '(x)  0  2 f '(x)  (x 1)  0  x  1  . lu x  3  s://   x  ttp g x 
  f x  x   1 1 '( ) 0 2 '( ) ( 1)  0   h 3  x    g x 
  f x  x   x 1 '( ) 0 2 '( ) ( 1)  0   1   x  3
 Câu 31: Cho hàm số y  f x có bảng xét dấu như hình vẽ /vietgold 1 5
Tìm khoảng đồng biến của hàm số 5 4 3
y  g(x)  2 f (1 x)  x  x  3x . 5 4 k.com A.  ;0  . B. 2;3 . C. 0;2 . D. 3;   . ceboo  Lời giải .fa Chọn B
Coi f ' x   x  2 x   1 x x  
1 có bảng xét dấu như trên. 4 3 2 g '(x)  2
 f '(1 x)  x 5x 6x https://www
Ta đi xét dấu g '(x)  P  Q . Với: P  2
 f '1 x  2
 3 x2 x1 xx  2x3 x2 x1 x
Bảng xét dấu của P 4 3 2 2
Q  x  5x  6x  x  x  2 x  3 31
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020
Bảng xét dấu của Q
Từ hai BXD của P,Q . Ta có P  0,Q  0 với x
 2;3 nên g'(x)  P Q  0với x  2;3. h ttp s://
 Câu 32: Cho hàm số y  f x có đồ thị hàm số y  f x như hình vẽ lu ye n th it racngh ie m.vn
Xét hàm số g  x  f  x 3 2
 2x  4x 3m  6 5 với m là tham số thực. Điều kiện cần và
đủ để g  x  0 với mọi x   5; 5   là 2 2 2 2 A. m  f  5 . B. m  f 0 . C. m  f  5 . D. m  f  5 . 3 3 3 3  Lời giải Chọn A https://www .fa ceboo k.com /viet gold
Ta có g  x  0 với mọi x   5; 5 
  f x 3 2
 2x  4x 3m  6 5  0 với mọi x   5; 5    
  f x 3 2
 2x  4x  6 5  3m với mọi x  5; 5  
 max 2 f x 3
 2x  4x  6 5  3m với mọi x 5; 5   *    .  5; 5  
Đặt h x  f  x 3 2
 2x  4x  6 5 . 32
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” x  0 
Ta có h x  f  x 2 2
 6x  4 , hx  0  f x 2  3
 x  2  x   5  . x  5     
Dựa vào đồ thị ta thấy f  x 2  3
 x  2 với mọi x  5; 5 
  h x luôn đồng biến trên  5; 5 
  max h x  h 5  2 f  5 .   m.vn 5; 5   ie 2 gh Vậy  
*  2 f  5  3m  m  f  5 . 3 racn it
 Câu 33: Cho hàm số f (x) có đồ thị của hàm số y  f ’(x) như hình vẽ: th n ye lu s:// ttp h 3 x Hàm số 2
y  f (2x 1) 
 x  2x nghịch biến trên khoảng nào sau đây? 3 A.  6  ; 3   . B. 3;6 . C. 6; . D.  1  ;0 .  Lời giải Chọn D /vietgold Ta có: y  f x 
 x  x   f x   x  2 2 ’ 2 ’(2 1) 2 2 2 ’(2 1) 1  3 k.com x  3
Nhận xét: Hàm số y  f (x) có f ’(x) 1  3
  x  3và f ’(x) 1   x  3  ceboo .fa
Do đó ta xét các trường hợp: Với 6   x  3   1  3  2x 1 7  suy ra ’
y  0 hàm số đồng biến (loại)
Với 3  x  6  5  2x 111suy ra ’
y  0 hàm số đồng biến (loại)
Với x  6  2x 1 11suy ra ’
y  0 hàm số đồng biến (loại) https://www Với 1   x  0  3   2x 1 1
 nên 2 f ’(2x 1)  2 và   x  2 3 1  3  2  suy ra ’ y  0
hàm số nghịch biến (nhận).
 Câu 34: Cho hàm số f  x có bảng xét dấu của đạo hàm như sau
Hàm số g  x  f  x   3 3
2  x  3x đồng biến trên khoảng nào dưới đây? A. 1;   . B.  ;    1 . C.  1  ;0 . D. 0;2 .  Lời giải Chọn C 33
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020
Ta có g x   f  x      2 3 2 x  3 Với x  1
 ;0  x  21;2  f x  2  0 lại có 2
x  3  0  y  0, x   1  ;0 .
Vậy hàm số g  x đồng biến trên khoảng  1  ;0 . Chú ý: +) Ta xét x 
     x    f x  2 1; 2 1; 2 3; 4 2  0; x  3  0
Suy ra hàm số nghịch biến trên 1;2 nên loại hai phương án A, D. h ttp +) Tương tự ta xét s://
x     x     f  x   2 ; 2 2 ;0
2  0; x  3  0  y  0, x   ;   2. lu  ;   2 ye
Suy ra hàm số nghịch biến trên khoảng 
 nên loại phương án B. n th
 Câu 35: Cho hàm số f  x có đạo hàm, liên tục trên . Hàm số y  f x có đồ thị như hình itr sau. acngh ie m.vn 3
Hàm số g  x  3 f  2 x  2 4 2
 x 3x đồng biến trên khoảng nào dưới đây? 2 ht  3  A.  3; 1 . B. 0  ;1 . C.  1   ;1 . D. 1; . tp      2  s://www  Lời giải Chọn D .fa
Ta có g x  x f  2 x   3
 x  x  x  f    2 x   2 6 . 2 6 6 6 2  x 1 ceboo  x  0 k.com
g x  0   . f    2 x  2 2  x 1  0 /v Đặt 2
t  x   f  2 x   2 2
2  x 1  0  f t   t 1  0  f t   t  1. ietgold
Đồ thị của hàm số y  f t  và y  t  1 như hình vẽ sau 34
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” m.vn ie gh racn it th n ye lu t  
Từ đồ thị, ta có f t  1  t  1   ( t  1
 là nghiệm đơn và t 1 là nghiệm kép). s:// t 1 ttp x  2  1  x  1  h
 f x  2  x  2 2 2 2 1     2 x  2 1 x   3 x  0 
Suy ra g x  0  x  1  
( x  0, x  1
 là nghiệm đơn và x   3 là nghiệm kép).  x   3
Bảng xét dấu g x /vietgold k.com  1    7  3 ceboo (vì g  3. f     0       ).  2    4  4 .fa
Vậy hàm số đồng biến trên khoảng  1
 ;0 và 1; .
 Câu 36: Cho hàm số 5 4 3 2
y  ax  bx  cx  dx  ex  f với , a , b , c d, ,
e f là các số thực, đồ thị của
hàm số y  f  x như hình vẽ dưới đây. Hàm số y  f   x 2 1 2
 2x 1 đồng biến trên https://www khoảng nào sau đây? y 2 x 1 1 3 O 3 35
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020  3   1 1  A.  ; 1    . B.  ;   . C.  1  ;0 . D. 1;3 .  2   2 2   Lời giải Chọn C y 2 h ttp s:// x 1 1 lu ye 3 O 3 n th it rac n 2 gh
Cách 1: Ta có: g  x  f 1 2x  2x 1 g x  2
 f 1 2x 4 .x ie
Có: g x  0  2
 f 1 2x  4x  0  f '1 2x  2  x (1). m.vn Đặt t 1 2 ,
x bất phương trình  
1 trở thành f t   t 1.
Vẽ đường thẳng y  x 1. Trên cùng đồ thị, ta thấy đường thẳng y  x 1 nằm trên đồ
thị hàm số f  x trên khoảng 1; 
3  f t  t 1 1 t  3 11 2x  3  1   x  0.
Vậy hàm số g  x đồng biến trên khoảng  1  ;0.
Cách 2: Ta có: g  x  f   x 2 1 2
 2x 1 gx  2
 f 1 2x 4 .x
Có g x  0  f '1 2x  2
 x  f '1 2x  (1 2x) 1. ht
Xét sự tương giao của đồ thị hàm số y  f 't  và y  t 1,t 1 2x. tps://www t    x  x 
Từ đồ thị ta có f t  1 '  t 1  . 
Khi đó g  x 1 2 1 0 '  0   .   t  3 1   2x  3 x  1  Ta có bảng xét dấu .fa ceboo k.com /viet
Dựa vào bảng xét dấu ta thấy hàm số đồng biến trên các khoảng  1  ;0. gold
Cách 3: Cách trắc nghiệm.
Ta có: g  x  f   x 2 1 2
 2x 1 gx  2
 f 1 2x 4 .x
Ta lần lượt thử các đáp án.  3 
Thử Chọn A Chọn x  1  ,25  ; 1   g '    1  ,25  2  f '3,5 5.  2 
Nhìn đồ thị f ' x ta thấy f '3,5  0  g ' 1
 ,25  0  loại đáp án A.  1 1 
Thử đáp án B: Chọn x  0, 25  ;  g '   0,25  2  f '0,5 1.  2 2  36
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Nhìn đồ thị f ' x ta thấy f '0,5  0  g '0,25  0  loại đáp án B.
Thử đáp án C: Chọn x  0  ,5 1  ;0  g ' 0  ,5  2  f '2 2.
Nhìn đồ thị f ' x ta thấy f '2  0  2
 f '2  0  g ' 0
 ,5  0  Chọn đáp án C.
Thử đáp án D: Chọn x  21;3  g '2  2  f ' 3  8.
Nhìn đồ thị f ' x ta thấy f '  3  0  2  f ' 3
   0  g '2  0  loại đáp án D. m.vn
 Câu 37: Cho hàm số y  f x có đạo hàm f  x có đồ thị như hình dưới đây. ie gh racn it th n ye lu s:// ttp h
Hàm số g  x  f  x   3 2 3
1  27x  54x  27x  4 đồng biến trên khoảng nào dưới đây?  2   2  A. 0;  . B. ;3   . C. 0;3 . D. 4; .  3   3   Lời giải /vietgold k.com ceboo .fa https://www Chọn D Cách 1: 3 2 2
Ta có: g  x  f 3x   1  3x   1  33x  
1  g ' x  3 f '3x   1  3x   1  23x   1   
Có g  x   f  x     x  2 ' 0 ' 3 1 3 1  23x   1 (1).
Đặt t  3x 1, bất phương trình  
1 trở thành f t  2 '  t  2t . Vẽ Parabol 2 y  x  2 .
x Trên cùng đồ thị, ta thấy đồ thị hàm số f ' x nằm trên đồ thị hàm số 2
y  x  2x trên các khoảng  ;    1 và 3; . 37
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 x  0 t  1  3x 1 1  Suy ra  f 't  2  t  2t      4 . t  3 3x 1  3 x   3  4 
Vậy hàm số g  x đông biến trên các khoảng  ;  0 và ;  .    3  Cách 2: 3 2 2
Ta có: g  x  f 3x   1  3x   1  33x  
1  g ' x  3 f '3x   1  3x   1  23x   1    h ttp
Có: g  x   f  x     x  2 ' 0 ' 3 1 3 1  23x   1 . s://
Xét sự tương giao của đồ thị hàm số y  f 't  và 2
y  t  2 t,t  3x   1 . lu ye t  1 n 2  th
Từ đồ thị ta có: f 't  t  2t  t  
1(nghieäm keùp). it t  3 r  acn x  0 gh 3x 1  1   2 ie
Khi đó g ' x 0 3x 1 1       x  
(nghieäm keùp). m.vn   3 3x 1   3 x   3 Ta có bảng xét dấu.
Dựa vào bảng xét dấu ta thấy hàm số đồng biến trên các khoảng  ;
 0 và 3;.
 Câu 38: Cho hàm số f (x) liên tục trên có f ( 1
 )  0 và có đồ thị hàm số y  f (x) như http hình vẽ. s://www .fa ceboo k.com /viet Hàm số 2
y  2 f (x 1)  x đồng biến trên khoảng gold
A. 3;  . B.  1  ;2 .
C. 0;  . D. 0;3  Lời giải Chọn D Đặt 2
g(x)  2 f (x 1)  x  g (
 x)  2[ f (x 1) (x 1) 1] 38
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” m.vn     ie
Dựa vào đồ thị hàm số y
f (x) và đồ thị hàm số y x 1 ta có: gh g (  ) x  0  f (
 x 1)  (x 1) 1 1
  x 1 2  0  x  3 Bảng biến thiên: racn it th n ye lu s:// ttp h
Dựa vào bảng biến thiên, hàm số 2
y  2 f (x 1)  x đồng biến trên khoảng 0;3 .
 Câu 39: Cho hàm số f  x . Hàm số y  f x có đồ thị như hình sau. /vietgold k.com
Hàm số g(x)  3 f 1
(  2x)  8x3  x
21 2  6x đồng biến trên khoảng nào dưới đây? ceboo .fa A.  2 ; 1  . B.  ; 3   1 . C.  1 ; 0 . D.  2 ; 1  .  Lời giải Chọn A
Ta có g'(x)  6  f ' 1 (  2x)  24 2 x  42x  6 https://www
g'(x)  0  f ' 1 (  2x)  4 2
x  7x 1 (*) 1  t
Đặt 1 2x  t  x  2 2 1 t  1  t 2 3 3
Ta có (*) trở thành f '(t)  . 4    . 7
1  f '(t)  t  t  .  2  2 2 2 2 3 3
Ta vẽ parapol (P) : y  x  x 
trên cùng hệ trục Oxy với đồ thị y  f  x như hình 2 2 3 33
vẽ sau ( đường nét đứt), ta thấy (P) có đỉnh I ( ; ) và đi qua các điểm 4 16   3 ; 3 ,  ; 1 2  ,   1 ; 1 . 39
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 h 2 3 3 ttp
Từ đồ thị hàm số ta thấy trên khoảng  1 ; 3
ta có f '(t)  t  t   3   t  1  2 2 s://  3  1 2x  1  1 x  2 lu
Vậy hàm số g(x) nghịch biến trên khoảng ). 2 ; 1 ( ye n
 Câu 40: Cho hàm số y  f x liên tục trên
và có đạo hàm f  x thỏa mãn: th it 2     y  f x   x  x r
f  x 1 x  x 5 Hàm số   3 3 3
12 nghịch biến trên khoảng nào sau acn đây? gh A. 1;5 .
B. 2;  . C.  1  ;0 . D. ;  1 . ie m.vn  Lời giải Chọn B 2
Ta có: f  x   2
1 x  x  5 suy ra f  x  3  1
 x 3 x 35  
 x  4x  2x  2. Mặt khác: y 
f  x   2 3. 3  3x 12  
x  x  x     2 3 4 2 2 x  4  3
 x  2x  2x 5.   x   ht Xét y  0  3
 x  2x  2x 5  5 2 0  . tp  x  2 s://www
Vậy hàm số y  f  x   3 3
3  x 12x nghịch biến trên các khoảng  5
 ; 2 và 2;  .
 Câu 41: Cho hàm số y  f x , hàm số f x 3 2
 x  ax  bx  ca, ,
b c   có đồ thị như hình .fa ceboo vẽ k.com /vietgold
Hàm số g  x  f  f  x nghịch biến trên khoảng nào dưới đây?  3 3 
A. 1; . B.  ;  2  . C.  1  ;0 . D.   ;    . 3 3    Lời giải 40
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” Chọn B Vì các điểm  1
 ;0,0;0,1;0 thuộc đồ thị hàm số y  f x nên ta có hệ:  1
  a  b  c  0 a  0   c  0  b   1
  f x 3
 x  x  f ' x 2  3x 1  
1 a  b  c  0 c  0  
Ta có: g  x  f  f x  gx  f  f x. f ' x m.vn ie 3 x  x  0  gh 3 x  x  1 
Xét g x  0  g x  f  f ' x. f   x  0  f  3 x  x 2 3x   1  0   3    racn x x 1  it 2 3x 1 0 th n  ye x  1  lu  x  0 s://   x  1,325 ttp  h x  1  ,325   3 x    3 Bảng biến thiên
Dựa vào bảng biến thiên  g  x nghịch biến trên  ;  2  
/vietgold  Câu 42: Cho hàm số y  f x có đạo hàm f x 2 '
 x  2x  3, x
  . Có bao nhiêu giá trị k.com
nguyên của tham số m thuộc đoạn  1
 0;20 để hàm số g x  f  2
x  x  m 2 3  m 1 ceboo
đồng biến trên 0;2? .fa A. 16. B. 17. C. 18. D. 19.  Lời giải Chọn C t  3  https://www
Ta có f 't  2
 t  2t  3  0     * . t 1
Có g  x   x   f  2 ' 2 3
' x  3x  m
Vì 2x  3  0, x
 0;2 nên g x đồng biến trên 0;2  g 'x  0, x  0;2  f  2
' x  3x  m  0, x  0;2 2
x  3x  m  3  , x  0;2 2
x  3x  m 3, x  0;2     (**) 2
x  3x  m 1, x    0;2 2
x  3x  m 1, x    0;2 m  3 10 m 13 Có h x 2
 x  3x luôn đồng biến trên 0;2 nên từ (**)     m 1 0 m  1  41
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 m 1  0;20 Vì 
 Có 18 giá trị của tham số m. m
Vậy có 18 giá trị của tham số m cần tìm.
 Câu 43: Cho hàm số y  f x có đạo hàm liên tục trên và đồ thị của hàm số y  f 'x như hình vẽ. h ttp s:// lu ye n th it racngh ie m.vn 1
Đặt g  x  f  x  m   x  m  2
1  2019 với m là tham số thực. Gọi S là tập các giá trị 2
nguyên dương của m để hàm số y  g  x đồng biến trên khoản 5;6 .Tổng các phần tử
của S bằng: A. 4 . B. 11. C. 14 . D. 20.  Lời giải Chọn C
Ta có g ' x  f ' x  m   x  m   1 http
Đặt h x  f ' x   x  
1 . Từ đồ thị y  f ' x và đồ thị y  x 1 trên hình vẽ ta suy ra s://www    h  x 1 x 1  0   x  3 .fa ceboo k.com /vietgold
  x  m 
m   x  m 
Ta có g  x  h x  m 1 1 1 1 '  0     x  m  3 x  m  3
Do đó hàm số y  g  x đồng biến trên các khoảng m 1;m  
1 và m  3; 42
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” m 1 5  5  m  6
Do vậy, hàm số y  g  x đồng biến trên khoảng 5;6  m 1 6   m  2 m3  5
Do m nguyên dương nên m1;2;5; 
6 , tức S  1;2;5;  6
Tổng các phần tử của S bằng 14.
 Câu 44: Cho hàm số y  f x là hàm đa thức có đồ thị hàm số y  f x như hình vẽ. m.vn ie gh racn it th n ye lu s:// ttp h
Có bao nhiêu giá trị nguyên của tham số m , m Z,  2020 m  2020 để hàm số  
g  x  f  8 2 x  2 2
 mx x  x  6 
 đồng biến trên khoảng  3  ;0  3  A. 2021. B. 2020. C. 2019. D. 2022.  Lời giải Chọn B /vietgold
Ta có g x  xf  2
x   mx 2 2 4
x  2x  3 .
Hàm số g  x đồng biến trên khoảng  3
 ;0 suy ra gx  0, x   3  ;0 . k.com xf  2
x   mx 2
x  x    x  
  f  2x m 2 2 4 2 3 0, 3;0 2
x  2x  3  0, x   3  ;0 ceboo f  2 x 2 2  .fa
 f x   2mx  2x 3, x   3  ;0 m  x    2 , 3;0 2
x  2x  3   f  2 x   m  max .   2 2 3;0
x  2x  3 https://www Ta có 2
  x    x   f  2 3 0 0 9 x   3  dấu “  ” khi 2
x  1  x  1  .
x  x    x  2 2 2 2 3 1
 4  0  x  2x  3  4, x   3  ;0 1 1   , x   . 2 x  2x  dấu “  ” khi 1 3 4 f  2 x  3  3  Suy ra   , x   3
 ;0, dấu “  ” khi x  1  . 2 2
x  2x  3 2.4 8 f  2 x  3  max   .   2 2 3;0
x  2x  3 8 43
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 3
Vậy m   , mà m , 2
 020 m  2020 nên có 2020 giá trị của tham số m thỏa mãn 8 bài toán.
 Câu 45: Cho hàm số f  x . Hàm số y  f x có đồ thị như hình sau. h ttp s:// lu ye n th
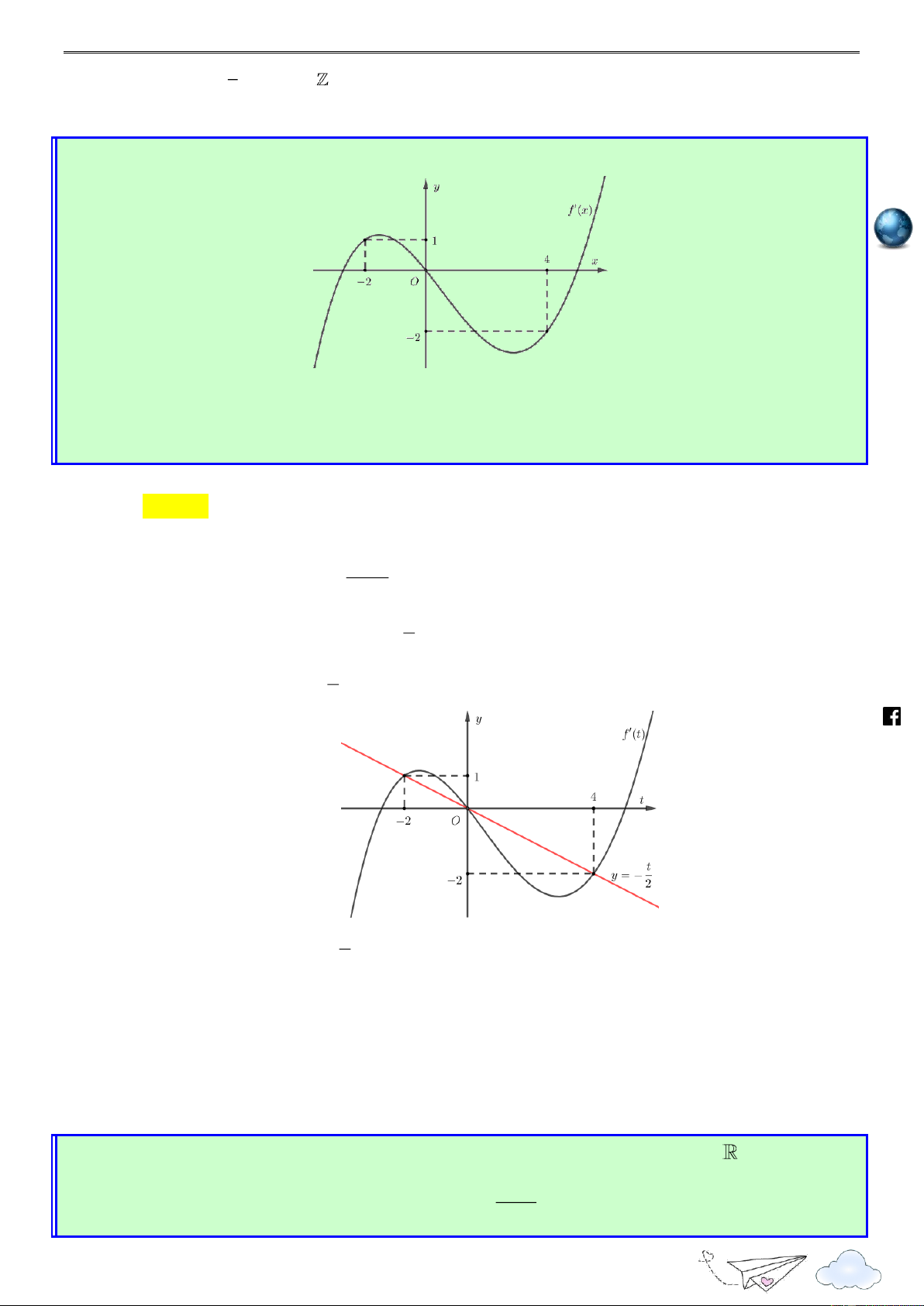
Có tất cả bao nhiêu giá trị nguyên dương của tham số m đề hàm số it
g(x)  4 f (x  ) 2
m  x  2mx  2020 đồng biến trên khoảng ). 2 ; 1 ( racn A. 2 . B. 3 . C. 0 . D. 1. gh  Lời giải ie m.vn Chọn A
Ta có g'(x)  4 f '(x  m)  2x  m 2 x  m
g'(x)  0  f '(x  ) m   (*) 2 t
Đặt t  x  m thì (*)  f '(t)   2 x
Vẽ đường thẳng y   trên cùng hệ trục Oxy với đồ thị y  f  x như hình vẽ sau 2 https://www .fa ceboo k.com t  2  t  0
m  2  x  m
Từ đồ thị ta có f '(t)       /v 2 t  4 x  m  4 ietgold
Hàm số g(x) đồng biến trên khoảng ) 2 ; 1 (
 g'(x)  0 x  2 ; 1 
m  2  1  2  m 2  m  3     m  4  1 m  3
Vì m nguyên dương nên m   3 ; 2 .
Vậy có hai giá trị nguyên dương của m đề hàm số g(x) đồng biến trên khoảng ). 2 ; 1 (
 Câu 46: Cho hàm số f  x có đạo hàm f x  x   1  x  
1  x  4; x   .Có bao nhiêu   x 
số nguyên m  2020 để hàm số g  x 2  f  m 
 đồng biến trên 2;   .  1 x  44
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” A. 2018. B. 2019 . C. 2020 . D. 2021  Lời giải Chọn B 3  2  x 
Ta có: g x   f   m .    x  2 1  1 x 
Hàm số g  x đồng biến trên 2;   m.vn ie
 gx  0; x  2;   gh 3  2  x    f   m  0; x   2;     2   racn x   1  1 x  it th    n  2 x f   m  0; x  2;      ye  1 x  lu          x s://
Ta có: f  x 0   x
1x 1x 4 0  1  1   x  4 ttp h
2  x m  1  ; x  2;      1 2  x  1 x Do đó: f   m  0; x  2;         1 x  2  x 1  m  4; x
 2;   2  1 x  x
Hàm số h x 2 
 m ; x 2;   có bảng biến thiên: 1 x /vietgold k.com
Căn cứ bảng biến thiên suy ra: Điều kiện 2 không có nghiệm m thỏa mãn. ceboo .fa Điều kiện   1  m  1
  m 1,kết hợp điều kiện m  2020 suy ra có 2019 giá trị
m thỏa mãn yêu cầu bài toán.
Nhận xét: Có thể mở rộng bài toán đã nêu như sau:
Cho hàm số f  x có đạo hàm f  x   x   1  x  
1  x  4; x   .Có bao nhiêu số https://www  2  x 
nguyên m  2020 để hàm số g  x  f  h 
m đồng biến trên 2; .  1 x 
 Câu 47: Cho hàm số y  f x có đạo hàm '      1 x f x x
e , có bao nhiêu giá trị nguyên của
tham số m trong đoạn  2  019;201 
9 để hàm số y  g  x  f  x 2 ln
 mx  mx  2 nghịch biến trên  2 1; e  . A. 2018. B. 2019. C. 2020. D. 2021.  Lời giải Chọn B 45
 Quảng Thuận – Ba Đồn – QB
Khai thác và phát triển câu hỏi đề tham khảo 2020 1 Trên  2
1; e  ta có g ' x  . f 'ln x  2mx  m  ln x 1 2x   1 m x
Để hàm số y  g  x nghịch biến trên  2
1; e  thì g  x 
x    x   m  x   2 ' ln 1 2 1 0, 1;e 
 ln x 1 2x   1 m  0, x    2 1; e  ln x  1   , m x    2 1; e  2x 1 1   2ln x h x  2 x 2 ttp
Xét hàm số h  x ln 1  1; e
, ta có h ' x   0, x
  1;e , từ đây 2   2x  trên   1 2x   1 s:// lu
suy ra m  1. Vậy có 2019 giá trị nguyên của m thỏa bài toán. ye n th it racngh ie m.vn https://www .fa ceboo k.com /vietgold 46
Document Outline

1. Dạng toán
2. Hướng giải

Tính đơn điệu của hàm ẩn cho bởi đồ thị hàm f'(x) Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số