Tính đơn điệu của hàm số liên kết Toán 12

Tính đơn điệu của hàm số liên kết Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

31 16 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 1

KIẾN THỨC CẦN NHỚ: Điều kiện để hàm số đơn điệu trên khoảng

1. Định nghĩa 1.

Giả sử K là một khoảng, một đoạn hoặc một nữa khoảng và

 

y f x

là một hàm số xác định trên K. Ta

nói:

+ Hàm số

 

y f x

được gọi là đồng biến (tăng) trên K nếu

   

1 2 1 2 1 2

, ,    x x K x x f x f x

+ Hàm số

 

y f x

được gọi là nghịch biến (giảm) trên K nếu

   

1 2 1 2 1 2

, ,    x x K x x f x f x

Hàm số đồng biến hoặc nghịch biến trên K gọi chung là đơn điệu trên K.

2. Nhận xét.

a. Nhận xét 1.

Nếu hàm số

 

f x

và

 

g x

cùng đồng biến (nghịch biến) trên D thì hàm số

   

f x g x

cũng đồng biến

(nghịch biến) trên D. Tính chất này có thể không đúng đối với hiệu

   

f x g x

b. Nhận xét 2.

Nếu hàm số

 

f x

và

 

g x

là các hàm số dương và cùng đồng biến (nghịch biến) trên D thì hàm số

   

.f x g x

cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng khi các hàm số

   

,f x g x

không là các hàm số dương trên D.

c. Nhận xét 3.

Cho hàm số

 

u u x

, xác định với

 

;x a b

và

   

;u x c d

. Hàm số

 

 

 

f u x

cũng xác định với

 

;x a b

. Ta có nhận xét sau:

i. Giả sử hàm số

 

u u x

đồng biến với

 

;x a b

. Khi đó, hàm số

 

 

 

f u x

đồng biến với

   

; x a b f u

đồng biến với

 

;u c d

ii. Giả sử hàm số

 

u u x

nghịch biến với

 

;x a b

. Khi đó, hàm số

 

 

 

f u x

nghịch biến với

   

; x a b f u

nghịch biến với

 

;u c d

3. Định lí 1.

Giả sử hàm số

có đạo hàm trên khoảng K. Khi đó:

a) Nếu hàm số đồng biến trên khoảng K thì

 

' 0,  f x x K

b) Nếu hàm số nghịch biến trên khoảng K thì

 

' 0,  f x x K

4. Định lí 2.

Giả sử hàm số

có đạo hàm trên khoảng K. Khi đó:

a) Nếu

 

' 0,  f x x K

thì hàm số

đồng biến trên K.

b) Nếu

 

' 0,  f x x K

thì hàm số

nghịch biến trên K.

c) Nếu

 

' 0,  f x x K

thì hàm số

không đổi trên K.

Chú ý: Khoảng K trong định lí trên ta có thể thay thế bởi đoạn hoặc một nửa khoảng. Khi đó phải có

thêm giả thuyết “ Hàm số liên tục trên đoạn hoặc nửa khoảng đó’. Chẳng hạn:

TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ LIÊN KẾT

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 2

Nếu hàm số

liên tục trên đoạn

 

;a b

và

   

' 0, ;  f x x a b

thì hàm số

đồng biến trên đoạn

 

;a b

Ta thường biểu diển qua bảng biến thiên như sau:

5. Định lí 3.(mở rộng của định lí 2)

Giả sử hàm số

có đạo hàm trên khoảng K. Khi đó:

a) Nếu

 

' 0,  f x x K

và

 

' 0f x

chỉ tại hữu hạn điểm thuộc K thì hàm số

đồng biến trên K.

b) Nếu

 

' 0,  f x x K

và

 

' 0f x

chỉ tại hữu hạn điểm thuộc K thì hàm số

đồng biến trên K.

Quy tắc xét tính đơn điệu của hàm số.

Giả sử hàm số

có đạo hàm trên

 Nếu

 

' 0f x 

với mọi

x K

và

 

' 0f x 

chỉ tại một số hữu hạn điểm

x K

thì hàm số

đồng

biến trên

 Nếu

 

' 0f x 

với mọi

x K

và

 

' 0f x 

chỉ tại một số hữu hạn điểm

x K

thì hàm số

nghịch

biến trên

BÀI TẬP MẪU:

(ĐỀ MINH HỌA BDG 2019-2020) Cho hàm số

 

f x

. Hàm số

 

'y f x

có đồ thị như hình bên. Hàm

số

   

1 2   g x f x x x

nghịch biến trên khoảng nào dưới đây ?

 

 

 

. B.

 

 

 

. C.

 

2; 1 

. D.

 

2;3

Phân tích hướng dẫn giải

1. DẠNG TOÁN: Đây là dạng toán tìm khoảng đơn điệu của hàm ẩn dạng

     

g x f u x v x 

 

 

khi

biết đồ thị của hàm số

 

y f x





2. HƯỚNG GIẢI:

– 2

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 3

Cách 1:

B1: Tính đạo hàm của hàm số

 

g x

       

.g x u x f u x v x

   

  

 

B2: Sử dụng đồ thị của

 

f x



, lập bảng xét dấu của

 

g x



B3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số.

Cách 2:

B1: Tính đạo hàm của hàm số

 

g x

       

.g x u x f u x v x

   

  

 

B2: Hàm số

 

g x

đồng biến

 

0g x



 

; (Hàm số

 

g x

nghịch biến

 

0g x



 

) (*)

B3: Giải bất phương trình

 

(dựa vào đồ thị hàm số

 

y f x





) từ đó kết luận khoảng đồng biến,

nghịch biến của hàm số.

Cách 3: (Trắc nghiệm)

B1: Tính đạo hàm của hàm số

 

g x

       

.g x u x f u x v x

   

 

 

 

B3: Hàm số

 

g x

đồng biến trên

 

0,g x x K



   

; (Hàm số

 

g x

nghịch biến trên

 

0,g x x K



   

) (*)

B3: Lần lượt chọn thay giá trị từ các phương án vào

 

g x



để loại các phương án sai.

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn A

Cách 1:

Ta có:

   

1 2g x f x x x   

   

2 1 2 2 1g x f x x

 

     

Hàm số nghịch biến

   

1 2

0 1 2

g x f x



 

     

Xét sự tương giao của đồ thị hàm số

 

y f t





và

y  

Dựa vào đồ thị ta có:

 

2 0

f t

  





  







Khi đó:

 

1 3

2 1 2 0

2 2

' 0

1 2 4 3

g x



 



   



  



 





 





Cách 2:

Ta có:

   

1 2g x f x x x   

   

2 1 2 2 1g x f x x

 

     

   

1 2

0 ' 1 2

g x f x





    

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 4

Xét sự tương giao của đồ thị hàm số

 

y f t





và

y  

Từ đồ thị ta có:

 

' 0

f t t

 





   







. Khi đó:

 

1 2 2

0 1 2 0

1 2 4

g x x x







  







     



 







 





Ta có bảng xét dấu:

Dựa vào bảng xét dấu, ta thấy: hàm số nghịch biến trên các khoảng

;

 

 

 

 

và

1 3

;

2 2

 

 

 

Phân tích hướng dẫn giải

1. DẠNG TOÁN:Đây là dạng toán xét tính đơn điệu của hàm liên kết

( ) ( ) ( )h x f u g x 

khi biết

BBT,BXD, đồ thị của hàm số

2. KIẾN THỨC CẦN NHỚ:

- Cách tính đạo hàm của hàm hợp

- Các bước lập bảng biến thiên của hàm số

- Đồ thị và sự tương giao hai đồ thị

3. HƯỚNG GIẢI:

Lời giải

Chọn A

Ta có :

   

1 2   g x f x x x

   

' 2 ' 1 2 2 1     g x f x x

   

' 0 2 ' 1 2 2 1 0g x f x x       

Đặt

   

1 2 0 2 ' '

t x f t t f t        

Vẽ đường thẳng

 

và đồ thị hàm số

 

'f x

trên cùng một hệ trục

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 5

Dựa vào đồ thị

 

' 2, 0, 4

f t t t t      

Hàm số

 

g x

nghịch biến

   

2 0

' 0 '

g x f t

  



     







Như vậy

 

1 3

2 1 2 0

1 2

2 2

1 2

4 1 2 3

f x



 



   







   



 







 





Vậy hàm số

   

1 2g x f x x x   

nghịch biến trên các khoảng

1 3

;

2 2

 

 

 

và

;

 

 

 

 

Mà

3 1 3

1; ;

2 2 2

   



   

   

nên hàm số

   

1 2g x f x x x   

nghịch biến trên khoảng

 

 

 

Bài tập tương tự và phát triển:

Câu 50.1: Cho hàm số

 

f x

. Hàm số

 

y f x





có đồ thị như hình bên dưới.

Hàm số

   

3 1 3g x f x x x   

đồng biến trên khoảng nào dưới đây?

 

 

 

. B.

 

 

 

. C.

 

1;0

. D.

 

 

 

Lời giải

– 2

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 6

Chọn B

Ta có:

     

3 3 1 6 2 3g x f x x

 

    

Hàm

( )g x

đồng biến trên khoảng

khi

 

0g x





(dấu = xảy ra tại một số hữu hạn điểm)

   

3 3 1 6 2 3 0f x x



     

(1)

Đặt

3 1u x 

ta được:

   

3 2 3h u f u u



  

Ta có: (1)

   

3 2 3 0 1

f u u f u

 

      

Từ đồ thị hàm số

 

y f x





ta có đồ thị hàm số

 

y f u





và

 

như hình vẽ

Để

 

0h u 

ta cần có đồ thị

 

y f u





phải nằm bên trên của đồ thị hàm

 

Từ đó ta có

 

0h u 

0 3







 







0 3 1 3

3 1 3

 







 







1 2

;

3 3



 

 



 

 







 





Cho nên ta chọn đáp án B vì

2 1 2

0; ;

3 3 3

   

 

 

 

   

Câu 50.2: Cho hàm số

 

f x

. Đồ thị

 

'y f x

cho như hình bên. Hàm số

   

g x f x   nghịch

biến trong khoảng nào dưới đây?

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 7

 

2;4

. B.

 

0;1

. C.

 

2;1

. D.

 

1;3

Lời giải

Chọn A

Ta có:

   

g x f x  

   

1g x f x x

 

   

       

0 1 0 1 1 1g x f x x f x x

  

          

Đặt

1t x 

thì

 

1f t t



 

Vẽ đường thẳng

1y x 

trên cùng một hệ trục tọa độ với đồ thị hàm số

 

y f x





(như hình

vẽ bên).

Dựa vào đồ thị

 

' 1 3, 1, 3f t t t t t      

Hàm số nghịch biến

     

1 0 ( ; 3) (1;3)g x f x x f t t t

  

          

Do đó

( ; 2) (2;4)x    

vậy g(x) nghịch biến trên

 

2;4

Câu 50.3: Cho hàm số

 

y f x

. Hàm số

 

'y f x

có đồ thị như hình bên.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 8

Hàm số

 

2 2

2 2g x f x x x x   

đồng biến trên khoảng nào dưới đây?

 

1 2; 1   . B.

 

1 2; 1 2    .

 

1; 

. D.

 

1; 1 2  

Lời giải

Chọn A

Ta có:

 

2 2

2 2g x f x x x x   

   

 

2 2

2 2 2 2 2 2 1 2 1g x x f x x x x f x x

 

  

         

 

   

 

0 2 1 2 1 0 1, 1 2, 1 2g x x f x x x x x

 

 

               

 

Xét

 

1 0

2 1

1 0

2 1

f x x

g x

f x x

  











 









 



 













 









Xét sự tương giao của đồ thị hàm số

 

y f x





và

1y 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 9

Dựa vào đồ thị ta có:

 

2 2

2 1 2 1f x x x x



    

và

 

2 2

2 1 2 1f x x x x



    

Xét hệ (I):

 

1 0

2 1

f x x

 









 





2 1

x x

 







 



1 2

 







    

  







  







Xét hệ (II):

 

1 0

2 1

f x x

 









 





2 1

x x

 







 



1 2 1 2

 









     





1 2 1x     

Vậy hàm số

 

g x

đồng biến trên khoảng

 

1 2; 1   và

 

1 2;   .

Câu 50.4: Cho hàm số

 

y f x

có đạo hàm trên



. Hàm số

 

'y f x

có đồ thị như hình vẽ bên. Đặt

   

y g x f x   . Khẳng định nào sau đây là đúng?

A. Hàm số

 

y g x

đồng biến trên khoảng

 

1;2

B. Đồ thị hàm số

 

y g x

có 3 điểm cực trị.

C. Hàm số

 

y g x

đạt cực tiểu tại

1x  

D. Hàm số

 

y g x

đạt cực đại tại

1x 

Lời giải

Chọn D

Ta có:

       

' ' ; ' 0 'g x f x x g x f x x    

(*).

Số nghiệm của phương trình (*) là số giao điểm giữa đồ thị hàm số

 

'y f x

và đường thẳng

y x

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 10

Dựa vào hình bên ta thấy giao tại 3 điểm

     

1; 1 ; 1;1 ; 2;2 

(*) 1

 





  







Bảng xét dấu

 

'g x

Từ bảng xét dấu

 

'g x

ta thấy hàm số

   

y g x f x   .

Đồng biến trên khoảng

 

;1

và

 

2;

; nghịch biến trên khoảng

 

1;2

Hàm số

 

y g x

đạt cực đại tại

1x 

Câu 50.5: Cho hàm số

 

f x

có đồ thị của hàm số

 



f x

như hình vẽ.

Hỏi hàm số

   

g x f x x   

nghịch biến trên khoảng nào dưới đây?

 

2;0

. B.

 

1;3

. C.

 



 

 

. D.

 

3;1

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 11

Lời giải

Chọn A

Ta có:

   

1 1g x f x x

 

    

Hàm số

 

g x

nghịch biến

 

0g x



 

 

1 1 (1)f x x



   

Đặt

1t x 

. Khi đó (1) trở thành

 

f t t



 

(2).

Bất phương trình (2) được thỏa khi

 

f x x



 

hay đồ thị hàm số

 

f x



nằm phía trên đồ thị

hàm số

y x 

Từ đồ thị ta được

3 1 3 4

1 3 1 1 3 2 0

t x x

     

  

 

  

       

  

. Vậy chọn khoảng

 

2;0

Câu 50.6: Cho hàm số

 

y f x

có đồ thị hàm số

 

y f x





được cho như hình vẽ sau.

Hàm số

 

2 1g x f x 

đồng biến trên khoảng nào dưới đây?

 

1;

. B.

 

 

 

. C.

 

; 1 

. D.

 

 

 

Lời giải

Chọn D

Ta có:

 

3 4

8 . 2 1g x x f x

 

 

TH1:

0x 

. Để hàm số

 

g x

đồng biến thì

-1

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 12

 

4 4 4 2

4 4

2 1 0 1 2 1 3 0 2 0 2 2 2f x x x x x



                

4 4

0 2 0; 2x x

 

    

 

TH2:

0x 

. Để hàm số

 

g x

đồng biến thì

 

0( )

2 1 1 2

2 1 0

2 1 3

x L

x x

f x







   



    





 

 





So sánh với điều kiện



4 4

0 2 ; 2x x x



       



Vậy hàm số

 

g x

đồng biến trên

0; 2

 

 

và



; 2



 



. Do đó chọn khoảng

 

 

 

Câu 50.7: Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình vẽ sau đây.

Hàm số

 

y f x x 

nghịch biến trên khoảng nào?

;

 



 

 

. B.

;

 



 

 

. C.

;

 

 

 

 

. D.

;

 

 

 

 

Lời giải

Chọn A

Xét hàm số

 

y f x x 

Ta có:

 

1 2y x f x x

 

  

 

2 2

2 1 0

0 1 1 0

2 0

y x x x x VN

x x

x x VN









 





        



 

  







Ta lại có:

1 1 1

4 2 4

x x x x R

 

       

 

 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 13

Từ đồ thị của hàm số

 

y f x





 

0,f x x x R



    

Bảng biến thiên của hàm số

 

y f x x 

Vậy hàm số nghịch biến trên

;

 



 

 

. Chọn A.

Câu 50.8: Cho hàm số

 

y f x có đạo hàm trên



Đồ thị hàm số

 

y f x



 như hình vẽ.

Hàm số

 

2y f x x 

đồng biến trên khoảng nào sau đây?

 

1; 2

. B.

 

; 3 

. C.

 

0;1

. D.

 

2; 0

Lời giải

Chọn A

Từ đồ thị của hàm số

 

y f x



 ta có bảng biến thiên của hàm số

 

y f x như sau

Đặt

 

2g x f x x 

, ta có

 

   

 

2 2 2

2 . 2 2 1 . 2 .g x x x f x x x f x x



  

     

Hàm số

 

g x

đồng biến khi

   

 

0 1 . 2 0g x x f x x

 

    

 

1 0

2 0

f x x

 











 





hoặc

 

1 0

2 0

f x x

 









 





NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 14

· Xét

 

1 0

1 2 1 2

1 1 2

1 .

1 2 1

2 3

 



 







     



    





  

   



 



 







 

 















x x

· Xét

 

1 0

2 1

2 1 0

1 2 3

2 3 0

 



 





 







 

  



 



  





 

  











  









x x

3 1 2

1 2

3 1

 





 









    







 

  











 









  













  







Câu 50.9: Cho hàm số

 

y f x

, biết hàm số

 

y f x





có đồ thị như hình bên dưới.

Hàm số

 

3 g x f x

đồng biến trên khoảng?

 

2;3

. B.

 

1;0

. C.

 

2; 1 

. D.

 

0;1

Lời giải

Chọn B

Dựa vào đồ thị, ta có bảng xét dấu

 

' 2 3



  g x xf x

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 15

 

2 0

' 0

3 0







 



 



  







 

 







 



g x

f x

 

3 2

6 3 1

3 0 2 3

2 3

1 1

f x x

   



    





     



 





  



Bảng biến thiên:

Từ BBT suy ra hàm số đồng biến trên

 

1;0

Câu 50.10: Cho hàm số

( )y f x

có bảng xét dấu đạo hàm như sau:



3



'( )

f x









Biết:

1 ( ) 5, .f x x R   

Khi đó, hàm số

3 2

( ) ( ( ) 1) 3 2020g x f f x x x    

nghịch

biến trong khoảng nào dưới đây:

( 2;0)

. B.

(0;5)

. C.

( 2;5)

. D.

( ; 2) 

Lời giải

Chọn A

Ta có:

'( ) '( ). '( ( ) 1) 3 6g x f x f f x x x   

Vì

1 ( ) 5, 0 ( ) 1 4f x x R f x       

Từ bảng xét dấu của

'( ) 0 '( ( ) 1) 0f x f f x   

Từ đó, ta có bảng xét dấu như sau:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 16

Do đó, hàm

( )g x

nghịch biến trên khoảng

( 2;0).

Câu 50.11: Cho hàm số

 

y f x

có đạo hàm trên



và có bảng biến thiên của đạo hàm

 

'f x

như

Hỏi hàm số

 

2 2020g x f x x  

có bao nhiêu điểm cực tiểu ?

A. 1. B. 2. C. 3. D. 4.

Lời giải

Chọn A

Ta có

   

 

2 2 2 ;g x x f x x

 

  

 

theo BBT '

2 2 0

2 2

1 2

0 .

2 0

2 1

2 3

f x

x x

g x

f x x

x x







 

 

  

 



 



    





 

 











 





Bảng biến thiên

Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta chọn A

Chú ý: Dấu của

 

g x



được xác định như sau: Ví dụ xét trên khoảng

 





 

3; 2 2 0.x x

    

 



 

theo BBT '

2 2

3; 2 3 2 0.

f x

x x x f x x



       

 

Từ

 

và

 

2 ,

suy ra

   

 

2 2 2 0g x x f x x

 

   

trên khoảng

 



nên

 

g x



mang dấu



Nhận thấy các nghiệm

 

và



là các nghiệm bội lẻ nên

 

g x



qua nghiệm đổi dấu.

Câu 50.12: Cho hàm số

 

y f x

có đạo hàm trên



Đồ thị hàm số

 

y f x





như hình vẽ bên dưới.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 17

Hàm số

   

3 2

3 1 9 18 12 2021g x f x x x x     

nghịch biến trên khoảng .

 

;1

. B.

 

1;2

. C.

 

3;1

. D.

 

 

 

Lời giải

Chọn D

Ta có

         

3 3 1 3(9 12 4); 0 3 1 3 2 .(1)g x f x x x g x f x x

   

         

Đặt

3 1t x 

khi đó

   

(1) 1f t t



  

Dựa vào đồ thị ta suy ra

   

1 .

1 2

f t t







  



 



(vì phần đồ thị của

 

'f t

nằm phía dưới

đồ thị hàm số

 

1y t 

) .

Như vậy

   

3 1 0

3 1 3 2

1 3 1 2 2

f x x







 





    



  





 





Vậy hàm số

   

3 2

3 1 9 18 12 2021g x f x x x x     

nghịch biến trên các khoảng

;

 



 

 

và

 

 

 

Câu 50.13: Cho hàm số

 

y f x



có bảng xét dấu của đạo hàm như sau:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 18

Đặt

   

4 3 2

2 1 3

y g x f x x x x

      

. Khẳng định nào dưới đây là đúng?

A. Hàm số

 

y g x



đồng biến trên khoảng

 

;0

B. Hàm số

 

y g x



đồng biến trên khoảng

 

1;2

C. Hàm số

 

y g x



đồng biến trên khoảng

 

0;1

D. Hàm số

 

y g x



nghịch biến trên khoảng

 

2;

Lời giải

Chọn C

Ta có:

   

3 3

2 1 3 2y g x f x x x x

  

      

Dựa vào bảng xét dấu

 

f x



ta có

 

1 0

f x













  











   

2 1 1 2 3

2 1 0 1 0

0 1 1 0 1

x x

f x f x

x x

      

 

 

       

 

    

 

  

3 3

3 2 1 2x x x x x x    

Bảng xét dấu

 

y g x

 



Vậy hàm số đồng biến trên

 

0;1

Câu 50.14: Cho hàm số

 

y f x



. Hàm số

 

'y f x



có đồ thị như hình vẽ bên dưới.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 19

-2 -1.5 -1 -0.5 0.5 1 1.5

-3

-2

-1

Hàm số









2 3 4 12 1

g x f x x x

    

đồng biến trên khoảng nào dưới đây ?

3 1

; .

2 2

 

 

 

 

; 2 .

 

 

 

 

2; .

 

 

 

 

;0 .

 



 

 

Lời giải

Chọn B

-2 -1.5 -1 -0.5 0.5 1 1.5

-3

-2

-1





y f x



y x

 

Hàm số





g x

đồng biến

















' 0 2 ' 2 3 8 12 0 ' 2 3 2 2 3

g x f x x f x x

           

2 3 1

0 2 3 1



 



  



 



  

   







Chọn đáp án B .

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 20

Câu 50.15: Cho hàm số

 

y f x

có đồ thị

 

y f x





như hình vẽ. Xét hàm số

   

3 2

1 3 3

2018

3 4 2

g x f x x x x    

. Mệnh đề nào dưới đây đúng?

A. Hàm số

 

g x

đồng biến trên

 

1;1

. B. Hàm số

 

g x

đồng biến trên

 

3;1

C. Hàm số

 

g x

đồng biến

 

3; 1 

. D. Hàm số

 

g x

nghịch biến trên

 

1;1

Lời giải

Chọn B

Ta có:

       

3 2 2

1 3 3 3 3

2018

3 4 2 2 2

g x f x x x x g x f x x x

 

         

   

3 3

' 0 '

2 2

g x f x x x    

. Đặt

3 3

2 2

y x x  

có đồ thị (P)

Dựa vào đồ thị

 

y f x





, ta có:

 

1 2 1 0

1 1 1 0

3 3 3 0

f g

 

    

 

 

 

  

 

 

 

   

 







NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 21

Vẽ đồ thị

 

của hàm số

3 3

2 2

y x x  

trên cùng hệ trục tọa độ như hình vẽ trên (đường nét

đứt ), Đồ thị

 

đi qua các điểm

 

3;3

 

1; 2 

 

1;1

với đỉnh

3 33

;

4 16

 

 

 

 

Ta thấy: + Trên khoảng

 

1;1

thì

 

3 3

2 2

f x x x



  

, nên

   

0 1;1xg x 



 

+Trên khoảng

 

3; 1 

thì

 

3 3

2 2

f x x x



  

, nên

   

0 3; 1xg x 



  

Từ những nhận xét trên, ta có bảng biến thiên của hàm

 

y g x





trên

 

3;1

như sau:

Vậy hàm số

 

g x

đồng biến trên

 

1;1

. Chọn A

Câu 50.16: Cho hàm số

 

f x

. Hàm số

 

'y f x

có đồ thị như hình vẽ

Hàm số

   

4 3

x x

g x f x

 

   đồng biến trên khoảng nào dưới đây?

 

; 2 

. B.

 

3; 1 

. C.

 

0;1

. D.

 

1;0

Lời giải

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 22

Chọn B

Ta có:

       

4 3

1 ' ' 1 2

x x

g x f x g x f x x

 

        .

Hàm số đồng biến

   

' 0 ' 1 2g x f x x     

(1)

Đặt

1x t 

. Bất phương trình (1) có dạng:

 

' 1f t t 

Xét hai hàm số

 

'y f t

và

1y t 

Dựa vào đồ thị ta có:

 

2;0

' 1

f t t

 



  







Ta có

 

2 1 0 3 1

' 0

1 2 1

x x

g x

x x

       

 

  

 

  

 

Câu 50.17: Cho hàm số

( )f x

liên tục trên R và có đồ thị

'( )f x

như hình vẽ . Tìm số điểm cực trị của

hàm số

( )y f x x  ?

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 23

. B.

. C.

. D.

Lời giải

Chọn B

Ta có

' (2 1) '( )y x f x x  

;

x x m 

có nghiệm khi và chỉ khi

m  

Dựa vào đồ thị ta thấy đồ thị hàm

'( )f x

cắt trục hoành tại 5 điểm trong đó 1 điểm có hoành độ

nhỏ hơn



và có một tiệm cận .

Khi đó ứng với mỗi giao điểm có hoành độ lớn hơn



và 1 điểm không xác định thì

' 0y 

có hai nghiệm . Từ đây dễ dàng suy ra hàm

( )y f x x 

có 11 cực trị.

Câu 50.18: Cho hàm số

( )y f x

có đạo hàm trên



. Đồ thị của hàm số

'( )y f x

như hình vẽ. Tìm

các khoảng đơn điệu của hàm số

( ) 2 ( ) 2 2020g x f x x x   

Mệnh đề nào dưới đây đúng?

A. Hàm số

 

g x

nghịch biến trên

 

1;3

. B. Hàm số

 

g x

có 2 điểm cực trị đại.

C. Hàm số

 

g x

đồng biến trên

 

1;1

. D. Hàm số

 

g x

nghịch biến trên

 

3;

Lời giải

Chọn C

Ta có

 

'( ) 2 '( ) 2 2 2 '( ) ( 1)g x f x x f x x     

Dựa vào hình vẽ ta thấy đường thẳng

1y x 

cắt đồ thị hàm số

'( )y f x

tại 3 điểm:

( 1; 2), (1;0), (3;2). 

-2

-1

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 24

Dựa vào đồ thị ta có

 

'( ) 0 2 '( ) ( 1) 0 1

g x f x x x

 





      







 

1 1

'( ) 0 2 '( ) ( 1) 0

g x f x x

  



     







 

'( ) 0 2 '( ) ( 1) 0

1 3

g x f x x

 



     



 



Câu 50.19: Cho hàm số

 

y f x

có bảng xét dấu như hình vẽ

Tìm khoảng đồng biến của hàm số

5 4 3

1 5

( ) 2 (1 ) 3x

5 4

y g x f x x x     

 

;0

. B.

 

2;3

. C.

 

0;2

. D.

 

3; 

Lời giải

Chọn B

Coi

      

' 2 1 1f x x x x x   

có bảng xét dấu như trên.

4 3 2

'( ) 2 '(1 ) 5 6xg x f x x x     

Ta đi xét dấu

'( )g x P Q 

. Với:

          

2 ' 1 2 3 2 1 2 3 2 1P f x x x x x x x x x            

Bảng xét dấu của P

-2

-1

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 25

  

4 3 2 2

5 6x 2 3Q x x x x x       

Bảng xét dấu của

Từ hai BXD của

,P Q

. Ta có

0, 0P Q 

với

 

2;3x 

nên

'( ) 0g x P Q  

với

 

2;3x 

Câu 50.20: Cho hàm số

 

y f x

có đồ thị hàm số

 

y f x





như hình vẽ

Xét hàm số

   

2 2 4 3 6 5g x f x x x m    

với

là tham số thực. Điều kiện cần và đủ

để

 

0g x 

với mọi 5; 5x

 

 

 

là

 

m f

. B.

 

m f

. C.

 

m f 

. D.

 

m f

Lời giải

Chọn A

Ta có

 

0g x 

với mọi 5; 5x

 

 

 

 

2 2 4 3 6 5 0f x x x m      với mọi

5; 5x

 

 

 

 

2 2 4 6 5 3f x x x m     với mọi 5; 5x

 

 

 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 26

 

5; 5

max 2 2 4 6 5 3f x x x m

 



 

    

với mọi

 

5; 5 *x

 

 

 

Đặt

   

2 2 4 6 5h x f x x x    .

Ta có

   

2 6 4h x f x x

 

  

   

0 3 2 5

h x f x x x







 

       







Dựa vào đồ thị ta thấy

 

3 2f x x



  

với mọi 5; 5x

 

 

 

 

h x

luôn đồng biến trên

5; 5

 



 

 

   

5; 5

max 5 2 5h x h f

 



 

  

Vậy

 

   

* 2 5 3 5

f m m f   

Câu 50.21: Cho hàm số

( )f x

có đồ thị của hàm số

’( )y f x

như hình vẽ:

Hàm số

(2 1) 2

y f x x x     nghịch biến trên khoảng nào sau đây?

 

6; 3 

. B.

 

3;6

. C.

 

6;

. D.

 

1;0

Lời giải

Chọn D

Ta có:

 

’ 2 ’(2 1) 2 2 2 ’(2 1) 1 3y f x x x f x x         

Nhận xét: Hàm số

( )y f x

có

3’( ) 1 3f x x    

và

( ) 1

’

f x





 



 



Do đó ta xét các trường hợp:

Với

6 3 13 2 1 7x x         

suy ra

0’y 

hàm số đồng biến (loại)

Với

3 6 5 2 1 11x x     

suy ra

0’y 

hàm số đồng biến (loại)

Với

6 2 1 11x x   

suy ra

0’y 

hàm số đồng biến (loại)

Với

1 0 3 2 1 1x x        

nên

22 ’(2 1)xf  

và

 

3 1 3 2x     

suy ra

0’y 

hàm số nghịch biến (nhận).

Câu 50.22: Cho hàm số

 

f x

có bảng xét dấu của đạo hàm như sau

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 27

Hàm số

   

3 2 3g x f x x x   

đồng biến trên khoảng nào dưới đây?

 

1; 

. B.

 

; 1 

. C.

 

1;0

. D.

 

0;2

Lời giải

Chọn C

Ta có

   

 

3 2 3g x f x x

 

 

   

 

Với

     

1;0 2 1;2 2 0x x f x



       

lại có

 

3 0 0, 1;0x y x



      

Vậy hàm số

 

g x

đồng biến trên khoảng

 

1;0

Chú ý:

+) Ta xét

       

1;2 1; 2 3;4 2 0; 3 0x x f x x



          

Suy ra hàm số nghịch biến trên

 

1;2

nên loại hai phương án A, D.

+) Tương tự ta xét

       

; 2 2 ;0 2 0; 3 0 0, ; 2x x f x x y x

 

                 

Suy ra hàm số nghịch biến trên khoảng

 

; 2 

nên loại phương án B.

Câu 50.23: Cho hàm số

 

f x

có đạo hàm, liên tục trên



. Hàm số

 

y f x





có đồ thị như hình

sau.

Hàm số

 

2 4 2

3 2 3

g x f x x x   

đồng biến trên khoảng nào dưới đây?

 

3; 1 

. B.

 

0;1

. C.

 

1;1

. D.

 

 

 

Lời giải

Chọn D

Ta có

 

   

2 3 2 2

6 . 2 6 6 6 2 1g x x f x x x x f x x

 

  

       

 

 

2 2

2 1 0

g x

f x x







 





   





Đặt

 

   

2 2 2

2 2 1 0 1 0 1t x f x x f t t f t t

  

              

Đồ thị của hàm số

 

y f t





và

1y t  

như hình vẽ sau

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 28

Từ đồ thị, ta có

 

f t t

 





   







(

1t  

là nghiệm đơn và

1t 

là nghiệm kép).

   

2 2

2 1

2 2 1

2 1

f x x

 



  



       



 

 



Suy ra

 

0 1

g x x









   



 



(

0, 1x x  

là nghiệm đơn và

3x  

là nghiệm kép).

Bảng xét dấu

 

g x



(vì

1 7 3

3. 0

2 4 4

g f

 

   

 

   

   

 

   

 

Vậy hàm số đồng biến trên khoảng

 

1;0

và

 

1; 

Câu 50.24: Cho hàm số

5 4 3 2

     y ax bx cx dx ex f

với

, , , , ,a b c d e f

là các số thực, đồ thị của

hàm số

 

y f x





như hình vẽ dưới đây. Hàm số

 

1 2 2 1y f x x   

đồng biến trên khoảng

nào sau đây?

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 29

; 1

 

 

 

 

. B.

1 1

;

2 2

 



 

 

. C.

 

1;0

. D.

 

1;3

Lời giải

Chọn C

Cách 1: Ta có:

       

1 2 2 1 2 1 2 4 .

 

        g x f x x g x f x x

Có:

     

0 2 1 2 4 0 ' 1 2 2 (1).

 

         g x f x x f x x

Đặt

1 2 , t x

bất phương trình

 

trở thành

 

1f t t



 

Vẽ đường thẳng

1y x 

. Trên cùng đồ thị, ta thấy đường thẳng

1y x 

nằm trên đồ thị hàm

số

 



f x

trên khoảng

   

1;3 1 1 3 1 1 2 3 1 0.



             f t t t x x

Vậy hàm số

 

g x

đồng biến trên khoảng

 

1;0 .

Cách 2: Ta có:

       

1 2 2 1 2 1 2 4 .

 

        g x f x x g x f x x

Có

     

0 ' 1 2 2 ' 1 2 (1 2 ) 1.



         g x f x x f x x

Xét sự tương giao của đồ thị hàm số

 

'y f t

và

 

1, 1 2 .   y t t x

Từ đồ thị ta có

 

' 1 .





  







f t t

Khi đó

 

1 2 1 0

' 0 .

1 2 3 1

  

 

  

 

   

 

x x

g x

x x

Ta có bảng xét dấu

Dựa vào bảng xét dấu ta thấy hàm số đồng biến trên các khoảng

 

1;0 .

Cách 3: Cách trắc nghiệm.

Ta có:

       

1 2 2 1 2 1 2 4 .

 

        g x f x x g x f x x

Ta lần lượt thử các đáp án.

Thử đáp án A: Chọn

   

1, 25 ; 1 ' 1,25 2 ' 3,5 5.

x g f

 

         

 

 

Nhìn đồ thị

 

'f x

ta thấy

   

' 3,5 0 ' 1,25 0f g    

loại đáp án#A.

Thử đáp án B: Chọn

   

1 1

0,25 ; ' 0,25 2 ' 0,5 1.

2 2

x g f

 

      

 

 

Nhìn đồ thị

 

'f x

ta thấy

   

' 0,5 0 ' 0,25 0f g   

loại đáp án B.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 30

Thử đáp án C: Chọn

     

0,5 1;0 ' 0,5 2 ' 2 2.x g f        

Nhìn đồ thị

 

'f x

ta thấy

     

' 2 0 2 ' 2 0 ' 0,5 0f f g       

Chọn đáp án C.

Thử đáp án D: Chọn

     

2 1;3 ' 2 2 ' 3 8.x g f      

Nhìn đồ thị

 

'f x

ta thấy

     

' 3 0 2 ' 3 0 ' 2 0f f g        

loại đáp án D.

Câu 50.25: Cho hàm số

 

y f x

có đạo hàm

 

f x



có đồ thị như hình dưới đây.

Hàm số

   

3 2

3 1 27 54 27 4g x f x x x x     

đồng biến trên khoảng nào dưới đây?

 

 

 

. B.

 

 

 

. C.

 

0;3

. D.

 

4;

Lời giải

Chọn D

Cách 1:

Ta có:

               

3 2 2

3 1 3 1 3 3 1 ' 3 ' 3 1 3 1 2 3 1g x f x x x g x f x x x

 

            

 

Có

       

' 0 ' 3 1 3 1 2 3 1 (1).g x f x x x      

Đặt

3 1,t x 

bất phương trình

 

trở thành

 

' 2f t t t 

Vẽ Parabol

2 .y x x 

Trên cùng đồ thị, ta thấy đồ thị hàm số

 

'f x

nằm trên đồ thị hàm số

2y x x 

trên các khoảng

 

; 1 

và

 

3; .

Suy ra

 

1 3 1 1

' 2 .

3 3 1 3

t x

f t t t

t x





    

 



    

 



  



 



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 31

Vậy hàm số

 

g x

đông biến trên các khoảng

 

;0

và

; .

 



 

 

Cách 2:

Ta có:

               

3 2 2

3 1 3 1 3 3 1 ' 3 ' 3 1 3 1 2 3 1g x f x x x g x f x x x

 

            

 

Có:

       

' 0 ' 3 1 3 1 2 3 1 .g x f x x x      

Xét sự tương giao của đồ thị hàm số

 

'y f t

và

 

2t, 3 1 .y t t x   

Từ đồ thị ta có:

 



 



   







' 2 1( ).

f t t t t nghieäm keùp

Khi đó

 







  



     



 









3 1 1

' 0 3 1 1 ( ).

3 1 3

g x x x nghieäm keùp

Ta có bảng xét dấu.

Dựa vào bảng xét dấu ta thấy hàm số đồng biến trên các khoảng

 

;0

và

 

3; .

Câu 50.26: Cho hàm số

( )f x

liên tục trên



có

( 1) 0f  

và có đồ thị hàm số

( )y f x





như hình

vẽ.

Hàm số

2 ( 1)y f x x  

đồng biến trên khoảng

 

3;

. B.

 

1;2

. C.

 

0;

. D.

 

0;3

Lời giải

Chọn D

Đặt

( ) 2 ( 1) ( ) 2[ ( 1) ( 1) 1]g x f x x g x f x x

 

        

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 32

Dựa vào đồ thị hàm số

( )y f x





và đồ thị hàm số

1y x 

ta có:

( ) 0 ( 1) ( 1) 1 1 1 2 0 3g x f x x x x

 

             

Bảng biến thiên:

Dựa vào bảng biến thiên, hàm số

2 ( 1)y f x x  

đồng biến trên khoảng

 

0;3

Câu 50.27: Cho hàm số

 

f x

. Hàm số

 

y f x





có đồ thị như hình sau.

Hàm số xxxxfxg 6218)21(3)(

 đồng biến trên khoảng nào dưới đây?

 

2;1

. B.

 

1;3 

. C.

 

1;0

. D.

 

2;1

Lời giải

Chọn A

Ta có

64224)21('6)('

 xxxfxg

(*)174)21('0)('

 xxxfxg

Đặt

xtx





Ta có

(*)

trở thành

)('1

.4)('



















 tttf

Ta vẽ parapol

:)(

 xxyP

trên cùng hệ trục

Oxy

với đồ thị

 

y f x





như hình vẽ

sau ( đường nét đứt), ta thấy

)(P

có đỉnh

)

;

( I

và đi qua các điểm

     

.1;1,2;1,3;3 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 33

Từ đồ thị hàm số ta thấy trên khoảng

 

1;3

ta có

)('

 ttttf

211213  xx

Vậy hàm số

)(xg

nghịch biến trên khoảng

).2;1(

Câu 50.28: Cho hàm số

 

y f x

liên tục trên



và có đạo hàm

 

f x



thỏa mãn:

 

1 5f x x x



  

Hàm số

 

3 3 12y f x x x   

nghịch biến trên khoảng nào sau đây?

 

1;5

. B.

 

2; 

. C.

 

1;0

. D.

 

; 1 

Lời giải

Chọn B

Ta có:

 

1 5f x x x



  

suy ra

     

3 1 3 3 5f x x x

 



     

 

   

4 2 2x x x    

Mặt khác:

 

3. 3 3 12y f x x

 

   

   

 

3 4 2 2 4x x x x

 

      

 

   

3 2 2 5x x x    

Xét





   

3 2 2 5 0x x x     

5 2

   











Vậy hàm số

 

3 3 12y f x x x   

nghịch biến trên các khoảng

 

5; 2 

và

 

2; 

Câu 50.29: Cho hàm số

 

y f x

, hàm số

   

3 2

, ,f x x ax bx c a b c



    



có đồ thị như hình vẽ

Hàm số

   

 

g x f f x





nghịch biến trên khoảng nào dưới đây?

 

1;

. B.

 

; 2 

. C.

 

1;0

. D.

3 3

;

3 3

 



 

 

Lời giải

Chọn B

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 34

Vì các điểm

     

1;0 , 0;0 , 1;0

thuộc đồ thị hàm số

 

y f x





nên ta có hệ:

   

3 2

1 0 0

0 1 '' 3 1

1 0 0

a b c a

c b f x x x f x x

a b c c

     

 

 



         

 

 

    

 

Ta có:

   

 

   

 

. ''g x f f x g x f f x f x

   

  

Xét

     

 

  

3 2

0 ' . 0 3 1 0

3 1 0

x x

g x g x f f x f x f x x x

x x



 



 



    

        



  



 



1,325





 







 



 



 





Bảng biến thiên

Dựa vào bảng biến thiên

 

g x

nghịch biến trên

 

; 2 

Câu 50.30: Cho hàm số

 

y f x

có đạo hàm

 

' 2 3, .f x x x x    



Có bao nhiêu giá trị

nguyên của tham số m thuộc đoạn

 

10;20

để hàm số

 

2 2

3 1g x f x x m m    

đồng

biến trên

 

0;2 ?

A. 16. B. 17. C. 18. D. 19.

Lời giải

Chọn C

Ta có

   

' 2 3 0 * .

f t t t

 



    







Có

   

 

' 2 3 ' 3g x x f x x m   

Vì

 

2 3 0, 0;2x x   

nên

 

g x

đồng biến trên

     

0;2 ' 0, 0;2g x x   

 

' 3 0, 0;2f x x m x     

 

2 2

3 3, 0;2 3 3, 0;2

3 1, 0; 2 3 1, 0;2

x x m x x x m x

 

          

 

 

         

 

 

(**)

Có

 

3h x x x 

luôn đồng biến trên

 

0;2

nên từ (**) 

3 10 13

1 0 1

m m

  

 



 

   

 

Vì

 

10;20m



 















Có 18 giá trị của tham số m.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 35

Vậy có 18 giá trị của tham số m cần tìm.

Câu 50.31: Cho hàm số

 

y f x

có đạo hàm liên tục trên



và đồ thị của hàm số

 

'y f x

như

hình vẽ.

Đặt

     

1 2019

g x f x m x m     

với

là tham số thực. Gọi

là tập các giá trị

nguyên dương của

để hàm số

 

y g x

đồng biến trên khoản

 

5;6

.Tổng các phần tử của

bằng:

. B. 11. C.

. D. 20.

Lời giải

Chọn C

Ta có

     

' ' 1g x f x m x m    

Đặt

     

' 1h x f x x  

. Từ đồ thị

 

'y f x

và đồ thị

1y x 

trên hình vẽ ta suy ra

 

1 1

h x

  



 







Ta có

   

1 1 1 1

' 0

3 3

x m m x m

g x h x m

x m x m

       

 

    

 

   

 

Do đó hàm số

 

y g x

đồng biến trên các khoảng

 

1; 1m m 

và

 

3;m  

Do vậy, hàm số

 

y g x

đồng biến trên khoảng

 

5;6

1 5

5 6

1 6

3 5

  



 







 

 











 



nguyên dương nên

 

1;2;5;6m

, tức

 

1;2;5;6S 

Tổng các phần tử của

bằng 14.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 36

Câu 50.32: Cho hàm số

 

y f x

là hàm đa thức có đồ thị hàm số

 

y f x





như hình vẽ.

Có bao nhiêu giá trị nguyên của tham số

, 2020 2020m Z m   

để hàm số

 

2 2 2

g x f x mx x x

 

   

 

 

đồng biến trên khoảng

 

3;0

A. 2021. B. 2020. C. 2019. D. 2022.

Lời giải

Chọn B

Ta có

 

   

2 2

2 4 2 3g x xf x mx x x

 

   

Hàm số

 

g x

đồng biến trên khoảng

 

3;0

suy ra

   

0, 3;0g x x



   



   

 

   

 

2 2 2 2

2 4 2 3 0, 3;0 2 2 3 0, 3;0xf x mx x x x f x m x x x

 

               

   

 

2 2

2 2 3 , 3;0 , 3;0

2 2 3

f x

f x m x x x m x

x x



            

  

 

3;0

max

2 2 3

f x

x x





 

  

 Ta có

 

2 2

3 0 0 9 3x x f x



        

dấu “  ” khi

1 1x x   



   

2 2

2 3 1 4 0 2 3 4, 3; 0x x x x x x               

1 1

2 3 4x x

 

  

dấu “  ” khi

1x  

Suy ra

 

3 3

2.4 8

2 2 3

f x

x x



 

 

  

 

3;0x  

, dấu “  ” khi

1x  

 

3;0

max

2 2 3

f x

x x





  

 

Vậy

m  

, mà

m 



2020 2020m  

nên có 2020 giá trị của tham số

thỏa mãn bài

toán.

Câu 50.33: Cho hàm số

 

f x

. Hàm số

 

y f x





có đồ thị như hình sau.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 37

Có tất cả bao nhiêu giá trị nguyên dương của tham số

đề hàm số

20202)(4)(

 mxxmxfxg đồng biến trên khoảng

).2;1(

. B.

. C.

. D.

Lời giải

Chọn A

Ta có

mxmxfxg 22)('4)(' 

(*)

)('0)('

mxfxg





Đặt mxt  thì

)('(*)

tf 

Vẽ đường thẳng

y 

trên cùng hệ trục

Oxy

với đồ thị

 

y f x





như hình vẽ sau

Từ đồ thị ta có

























)('

mxm

Hàm số

)(xg

đồng biến trên khoảng

)2;1(

 

2;10)('  xxg

























212

Vì

nguyên dương nên

 

.3;2m

Vậy có hai giá trị nguyên dương của

đề hàm số

)(xg

đồng biến trên khoảng

).2;1(

Câu 50.34: Cho hàm số

 

f x

có đạo hàm

     

1 1 4 ;f x x x x x



     



.Có bao nhiêu số

nguyên

2020m 

để hàm số

 

g x f m



 

 

 



 

đồng biến trên

 

2;  

2018

. B.

2019

. C.

2020

. D.

2021

Lời giải

Chọn B

Ta có:

 

3 2

g x f m



 

 

  

 



 



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 38

Hàm số

 

g x

đồng biến trên

 

2;  



   

0; 2;g x x



    

 

3 2

0; 2;

f m x



 



       

 



 





 

0; 2;

f m x



 



     

 



 

Ta có:

 

0f x







   

1 1 4 0x x x   



1 4

 





 



Do đó:

 

0; 2;

f m x



 



     

 



 



   

1; 2; 1

1 4; 2; 2

m x





      











      







Hàm số

 

h x m



 



;

 

2;x   

có bảng biến thiên:

Căn cứ bảng biến thiên suy ra: Điều kiện

 

không có nghiệm

thỏa mãn.

Điều kiện

 



1m  



1m 

,kết hợp điều kiện

2020m 

suy ra có

2019

giá trị

thỏa mãn yêu cầu bài toán.

Nhận xét: Có thể mở rộng bài toán đã nêu như sau:

Cho hàm số

 

f x

có đạo hàm

     

1 1 4 ;f x x x x x



     



.Có bao nhiêu số

nguyên

2020m 

để hàm số

   

g x f h m



 

 

 



 

đồng biến trên

 

2;  

Câu 50.35: Cho hàm số

 

y f x

có đạo hàm

   

' 1

f x x e 

, có bao nhiêu giá trị nguyên của

tham số

trong đoạn

 

2019;2019

để hàm số

   

ln 2y g x f x mx mx    

nghịch

biến trên

 

1;e

A. 2018. B. 2019. C. 2020. D. 2021.

Lời giải

Chọn B

Trên

 

1;e

ta có

     

' . ' ln 2 ln 1 2 1g x f x mx m x x m

      

Để hàm số

 

y g x

nghịch biến trên

 

1;e

thì

   

 

' ln 1 2 1 0, 1;g x x x m x e      

 

ln 1 2 1 0, 1;

ln 1

, 1;

2 1

x x m x e

m x e

      



   



NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020

Trang 39

Xét hàm số

 

ln 1

2 1

h x







trên





, ta có

 

2ln

' 0, 1;

2 1

h x x e

 

   



, từ đây suy ra



. Vậy có 2019 giá trị nguyên của

thỏa bài toán.

Bấm Tải xuống để xem toàn bộ.

| 1/39

| | Tải xuống

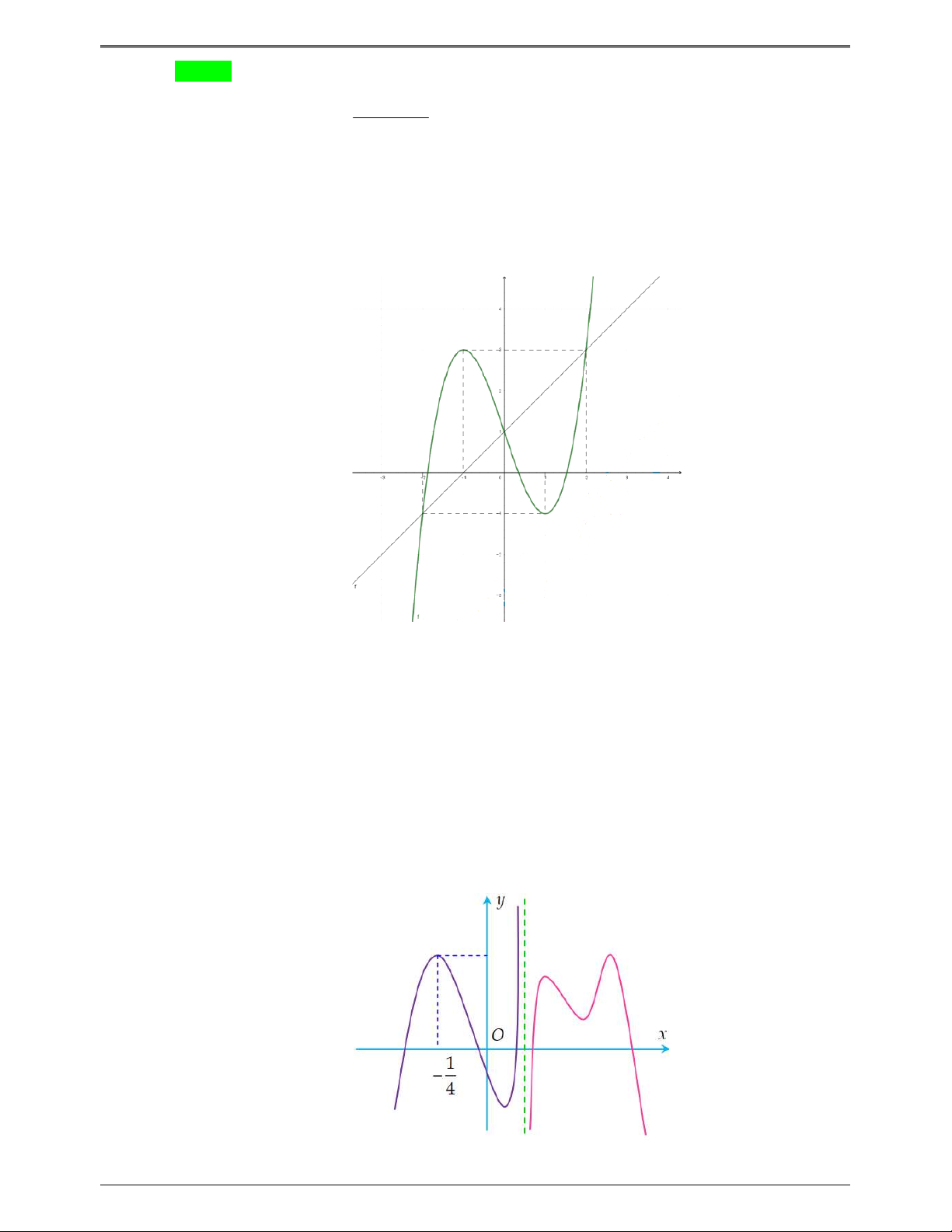
Preview text:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ LIÊN KẾT
KIẾN THỨC CẦN NHỚ: Điều kiện để hàm số đơn điệu trên khoảng K . 1. Định nghĩa 1.
Giả sử K là một khoảng, một đoạn hoặc một nữa khoảng và y  f  x là một hàm số xác định trên K. Ta nói:
+ Hàm số y  f  x được gọi là đồng biến (tăng) trên K nếu
x , x  K, x  x  f x  f x 1 2 1 2  1  2
+ Hàm số y  f  x được gọi là nghịch biến (giảm) trên K nếu
x , x  K, x  x  f x  f x 1 2 1 2  1  2 
Hàm số đồng biến hoặc nghịch biến trên K gọi chung là đơn điệu trên K. 2. Nhận xét. a. Nhận xét 1.
Nếu hàm số f  x và g  x cùng đồng biến (nghịch biến) trên D thì hàm số f  x  g  x cũng đồng biến
(nghịch biến) trên D. Tính chất này có thể không đúng đối với hiệu f  x  g  x . b. Nhận xét 2.
Nếu hàm số f  x và g  x là các hàm số dương và cùng đồng biến (nghịch biến) trên D thì hàm số
f x.g  x cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng khi các hàm số
f x, g x không là các hàm số dương trên D. c. Nhận xét 3.
Cho hàm số u  u  x , xác định với x ; a b và u  x ;
c d  . Hàm số f u x   cũng xác định với x  ;
a b . Ta có nhận xét sau:
i. Giả sử hàm số u  u  x đồng biến với x  ;
a b . Khi đó, hàm số f u x   đồng biến với x  ;
a b  f u đồng biến với u  ; c d  .
ii. Giả sử hàm số u  u  x nghịch biến với x  ;
a b . Khi đó, hàm số f u x   nghịch biến với x  ;
a b  f u nghịch biến với u  ; c d  . 3. Định lí 1.
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
a) Nếu hàm số đồng biến trên khoảng K thì f ' x  0,x  K .
b) Nếu hàm số nghịch biến trên khoảng K thì f ' x  0,x  K . 4. Định lí 2.
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
a) Nếu f ' x  0,x  K thì hàm số f đồng biến trên K.
b) Nếu f ' x  0,x  K thì hàm số f nghịch biến trên K.
c) Nếu f ' x  0,x  K thì hàm số f không đổi trên K.
Chú ý: Khoảng K trong định lí trên ta có thể thay thế bởi đoạn hoặc một nửa khoảng. Khi đó phải có
thêm giả thuyết “ Hàm số liên tục trên đoạn hoặc nửa khoảng đó’. Chẳng hạn: Trang 1
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
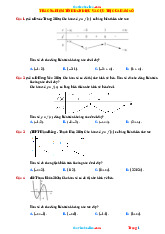
Nếu hàm số f liên tục trên đoạn  ;
a b và f ' x  0,x ;
a b thì hàm số f đồng biến trên đoạn  ;ab.
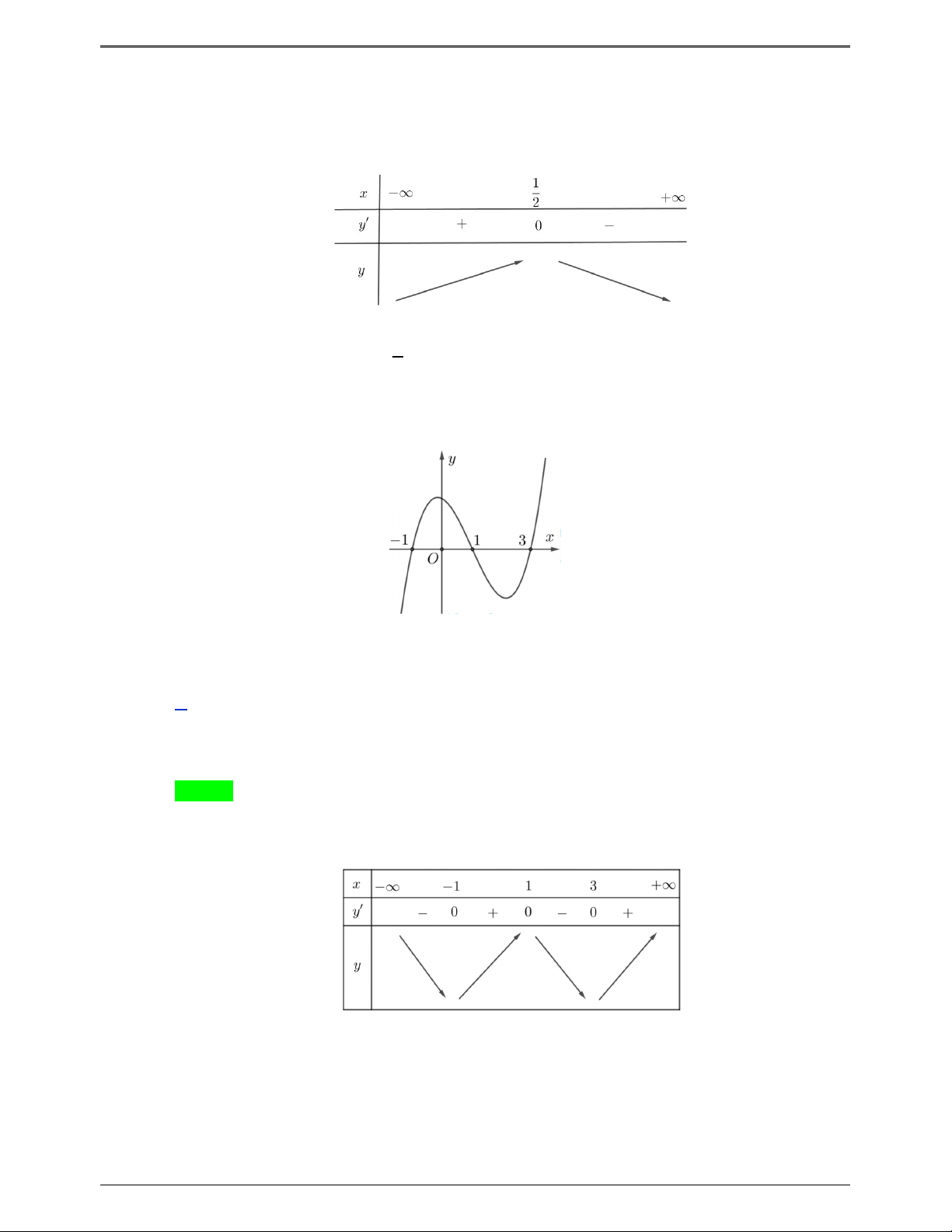
Ta thường biểu diển qua bảng biến thiên như sau:
5. Định lí 3.(mở rộng của định lí 2)
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
a) Nếu f ' x  0,x K và f ' x  0 chỉ tại hữu hạn điểm thuộc K thì hàm số f đồng biến trên K.
b) Nếu f ' x  0,x  K và f ' x  0 chỉ tại hữu hạn điểm thuộc K thì hàm số f đồng biến trên K.
Quy tắc xét tính đơn điệu của hàm số.
Giả sử hàm số f có đạo hàm trên K
 Nếu f ' x  0 với mọi xK và f 'x  0 chỉ tại một số hữu hạn điểm xK thì hàm số f đồng biến trên K .
 Nếu f ' x  0 với mọi xK và f 'x  0 chỉ tại một số hữu hạn điểm xK thì hàm số f nghịch biến trên K . BÀI TẬP MẪU:
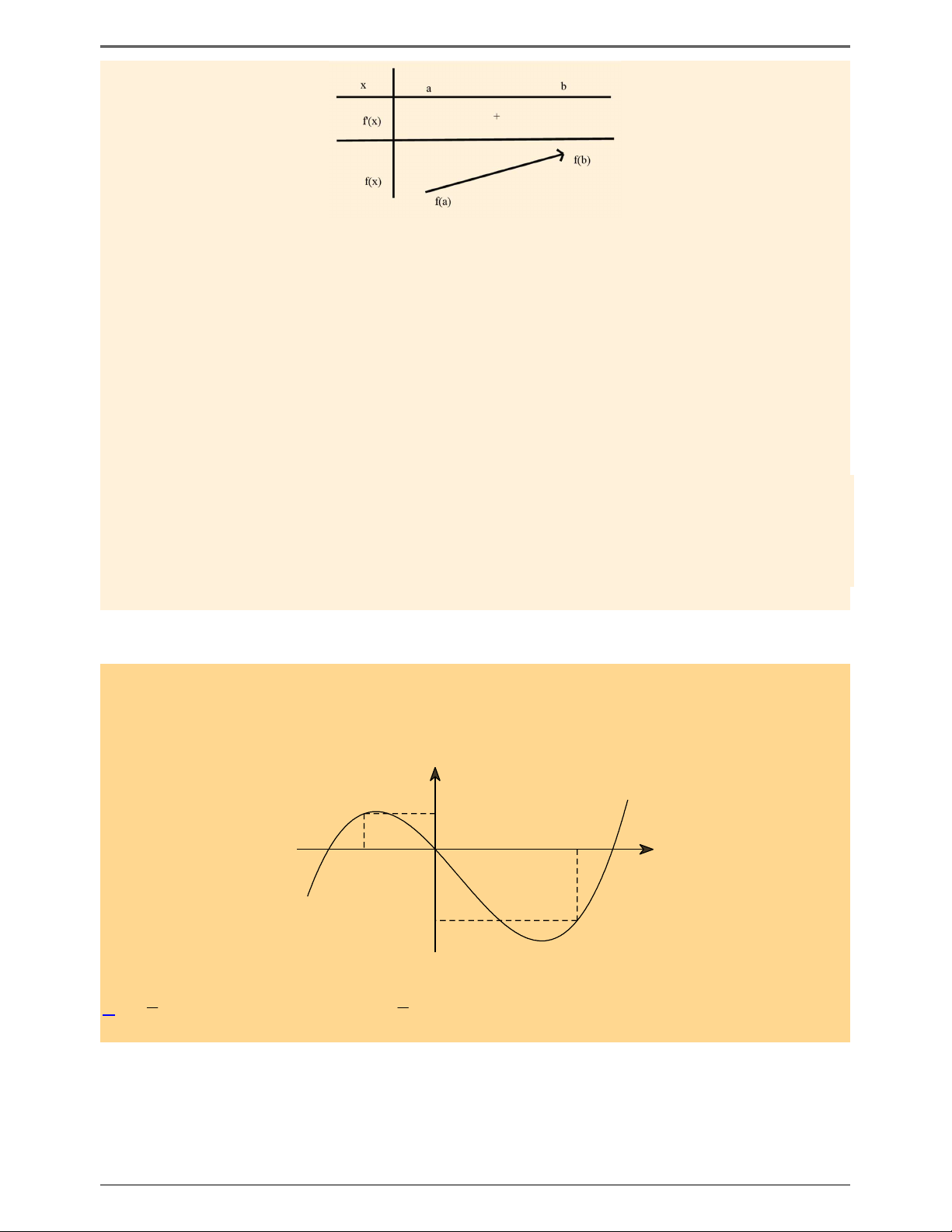
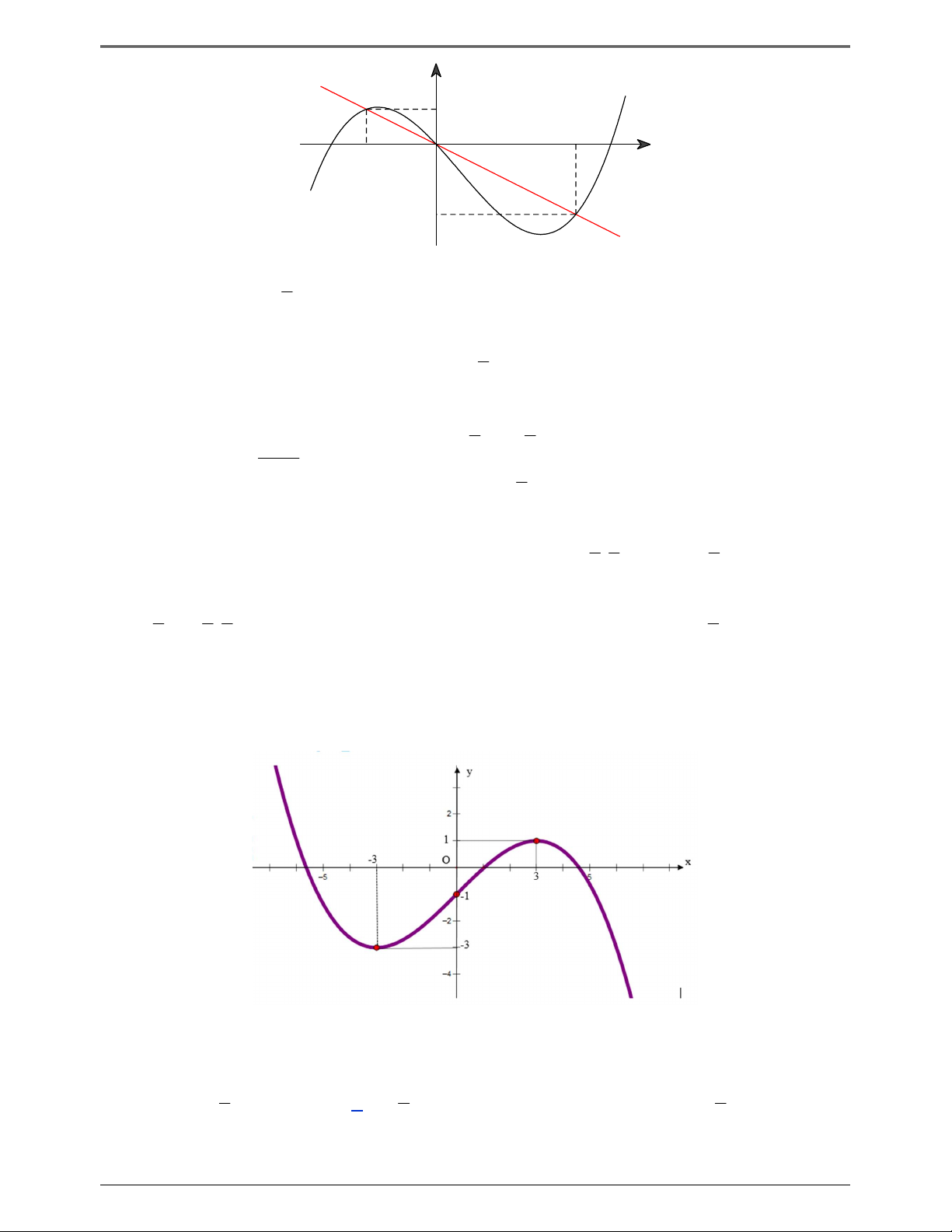
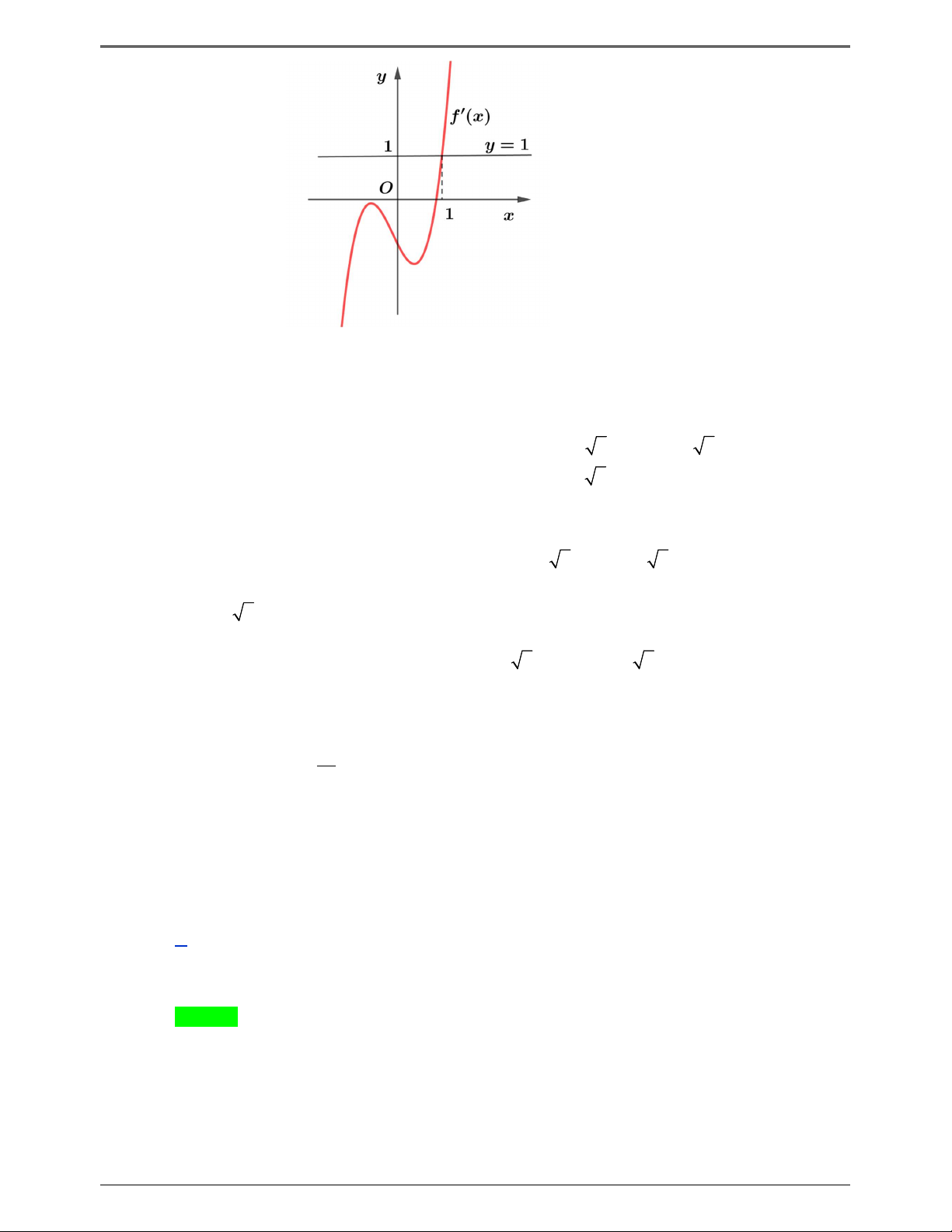
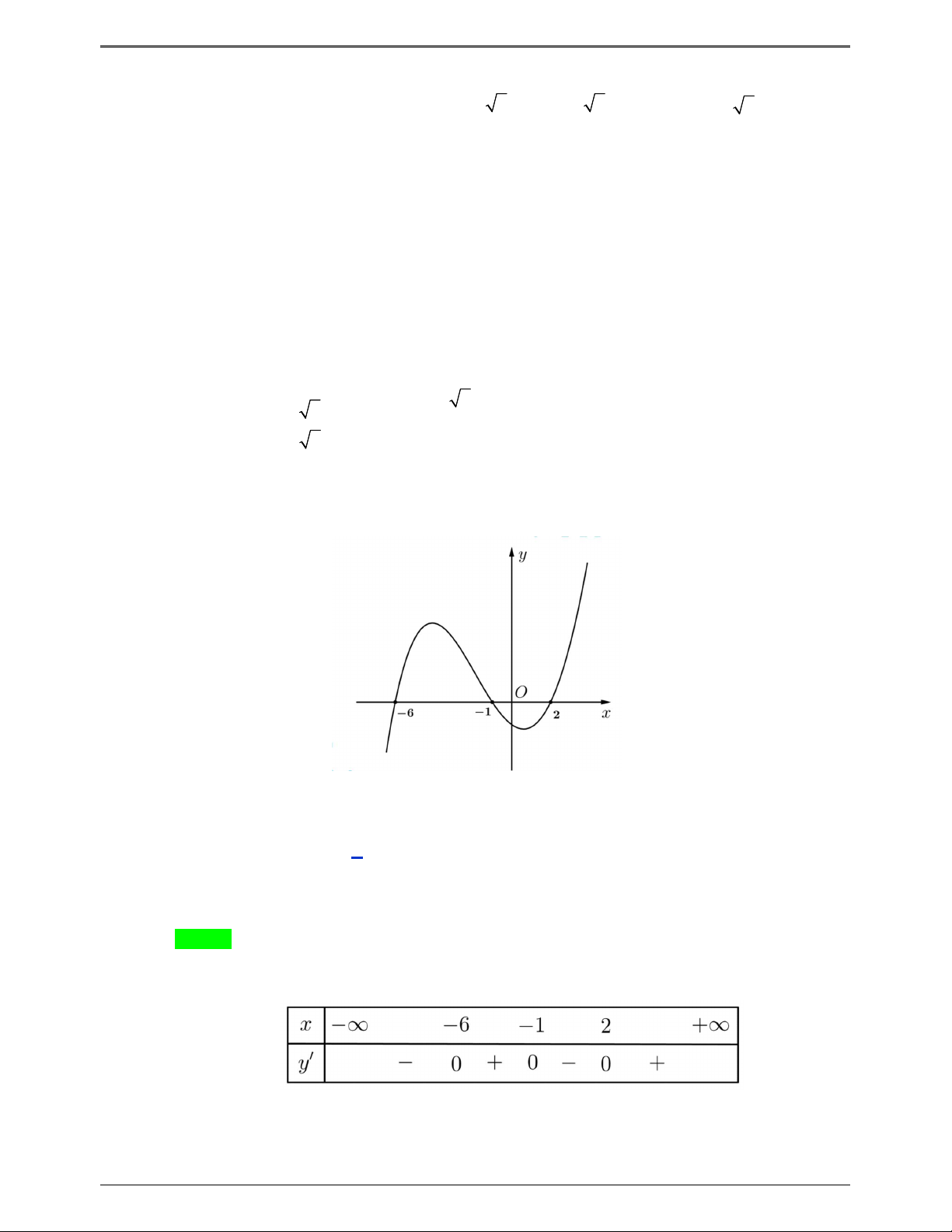
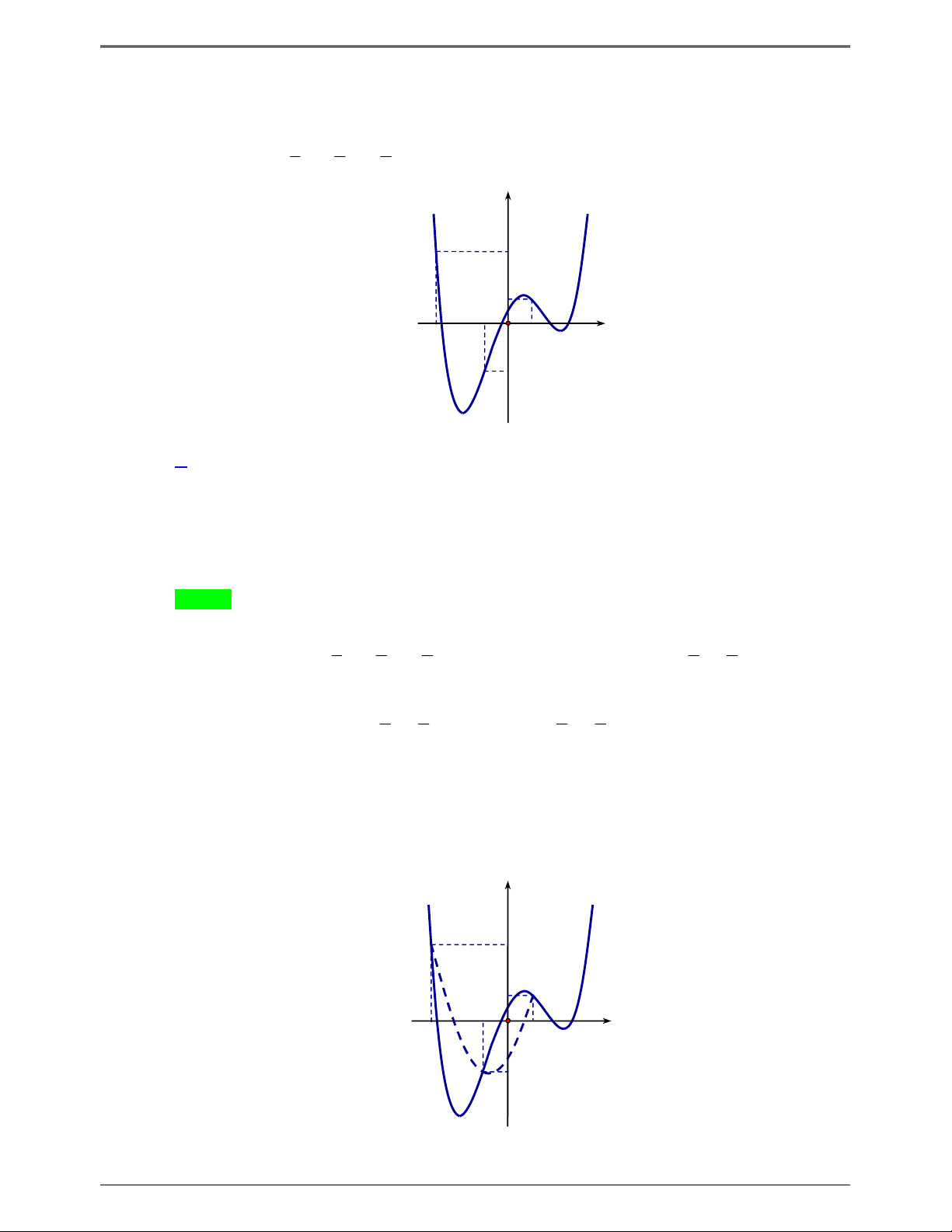
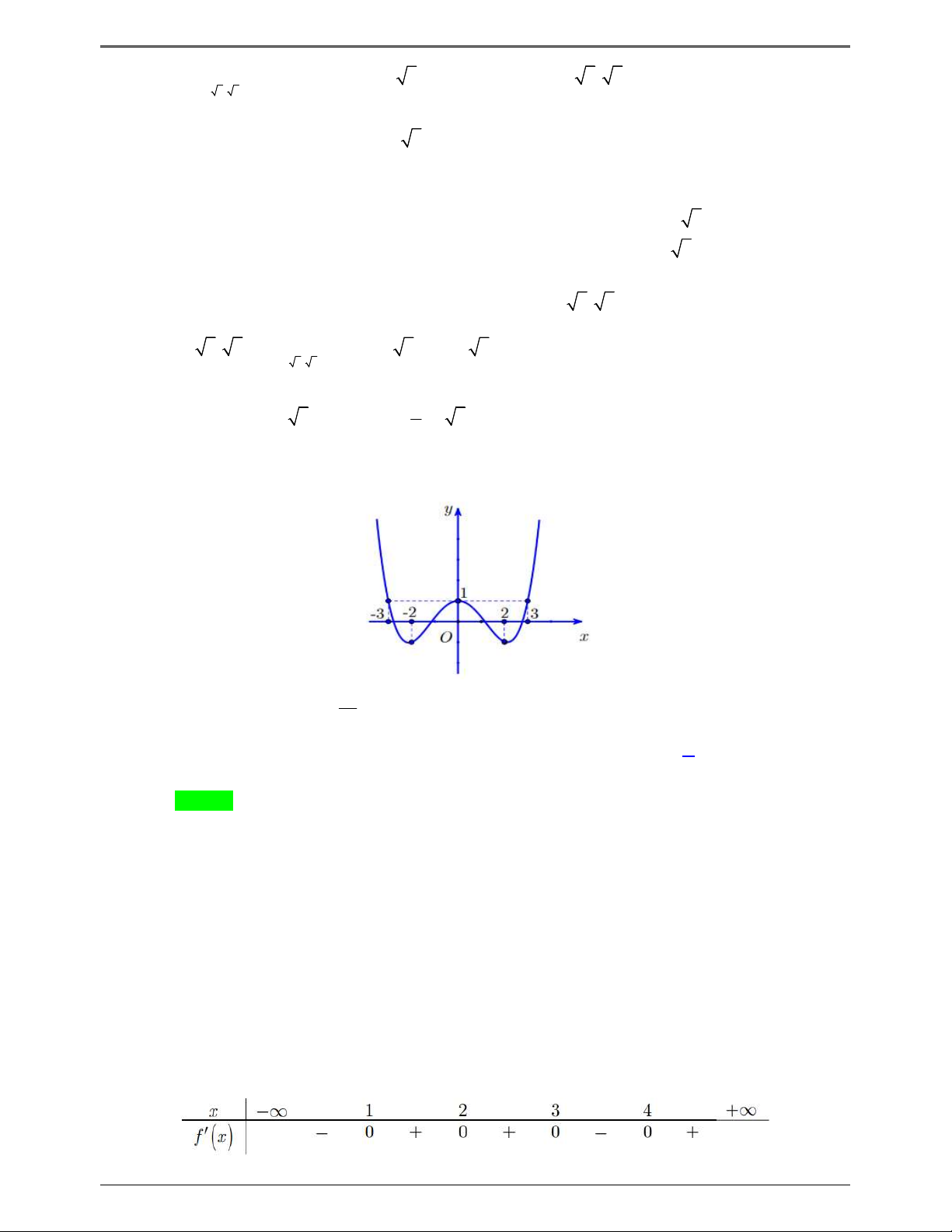
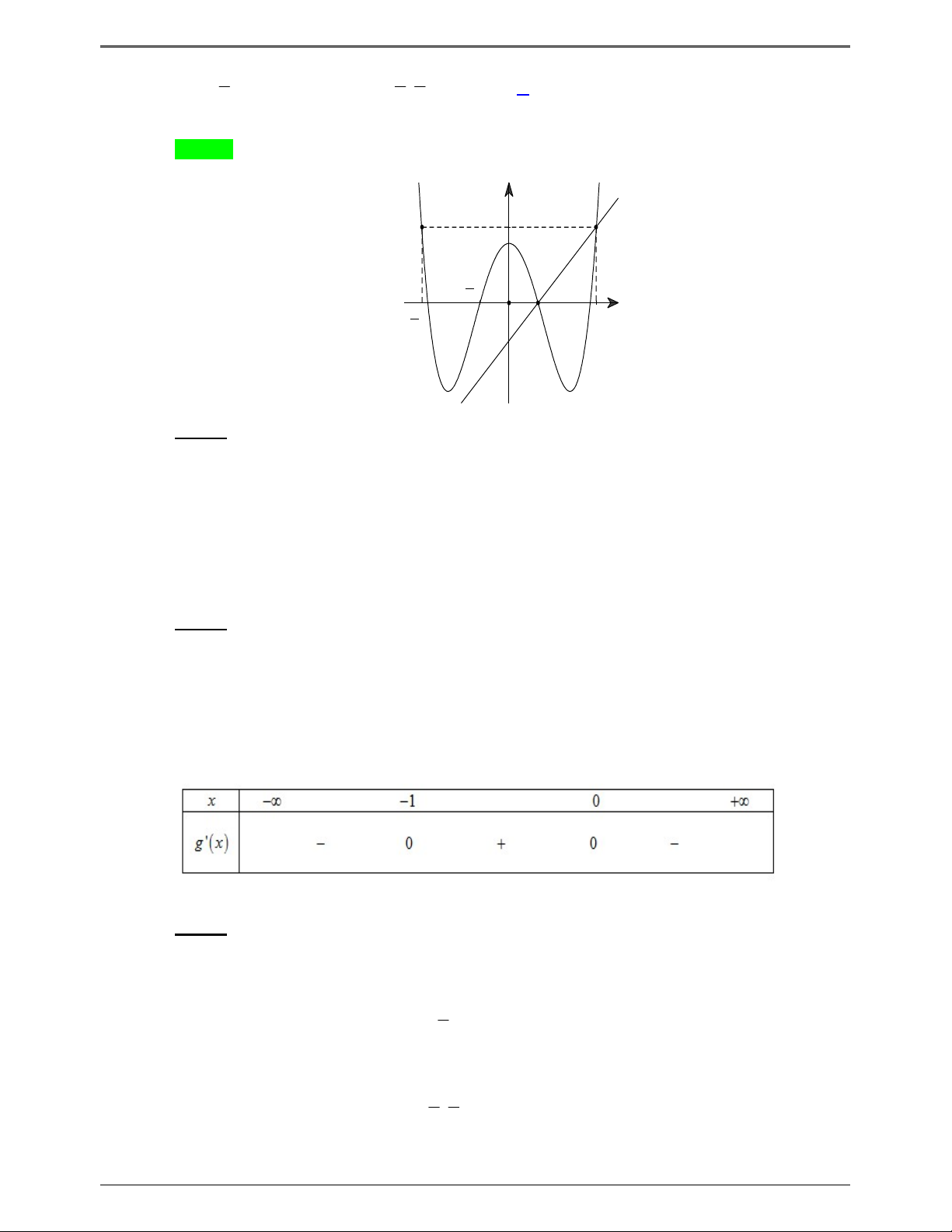
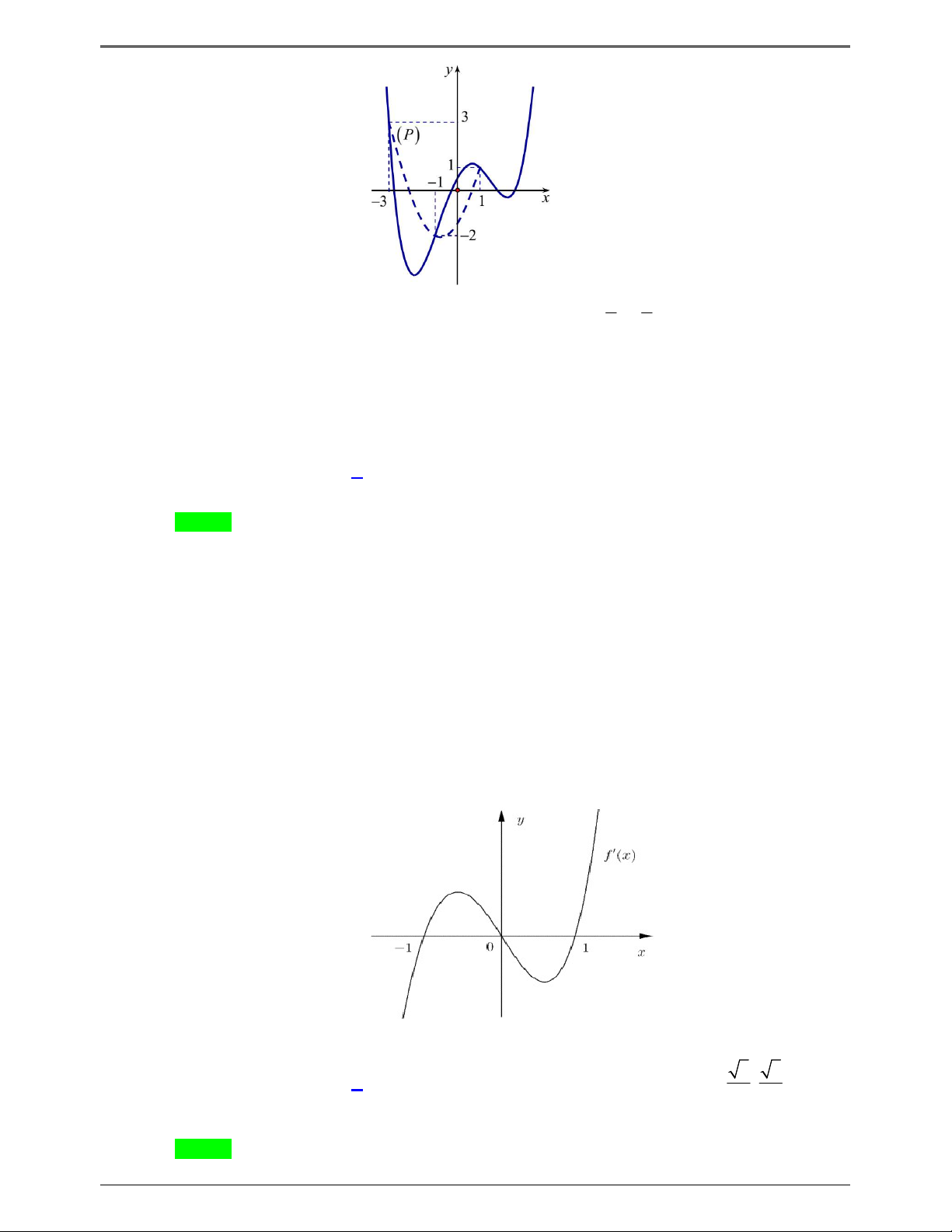
(ĐỀ MINH HỌA BDG 2019-2020) Cho hàm số f  x . Hàm số y  f ' x có đồ thị như hình bên. Hàm
số g  x  f   x 2
1 2  x  x nghịch biến trên khoảng nào dưới đây ? y 1 4 – 2 O x – 2  3   1  A. 1;   . B. 0;   . C.  2  ;  1 . D. 2;3.  2   2 
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán tìm khoảng đơn điệu của hàm ẩn dạng g  x  f u   x  v  x khi
biết đồ thị của hàm số y  f  x . 2. HƯỚNG GIẢI: Trang 2
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Cách 1:
B1: Tính đạo hàm của hàm số g  x , g x  u x. f  u   x  v  x .
B2: Sử dụng đồ thị của f  x , lập bảng xét dấu của g x .
B3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số. Cách 2:
B1: Tính đạo hàm của hàm số g  x , g x  u x. f  u   x  v  x .
B2: Hàm số g  x đồng biến  g x  0 ; (Hàm số g  x nghịch biến  g x  0 ) (*)
B3: Giải bất phương trình * (dựa vào đồ thị hàm số y  f x ) từ đó kết luận khoảng đồng biến,
nghịch biến của hàm số. Cách 3: (Trắc nghiệm)
B1: Tính đạo hàm của hàm số g  x , g x  u x. f  u   x  v  x .
B3: Hàm số g  x đồng biến trên K  g x  0, x
  K ; (Hàm số g x nghịch biến trên K  gx  0, x   K ) (*)
B3: Lần lượt chọn thay giá trị từ các phương án vào g x để loại các phương án sai.
Từ đó, ta có thể giải bài toán cụ thể như sau: Lời giải Chọn A Cách 1:
Ta có: g  x  f   x 2
1 2  x  x  g x  2
 f 1 2x  2x 1.  x
Hàm số nghịch biến  gx   f   x 1 2 0 1 2   . 2 t
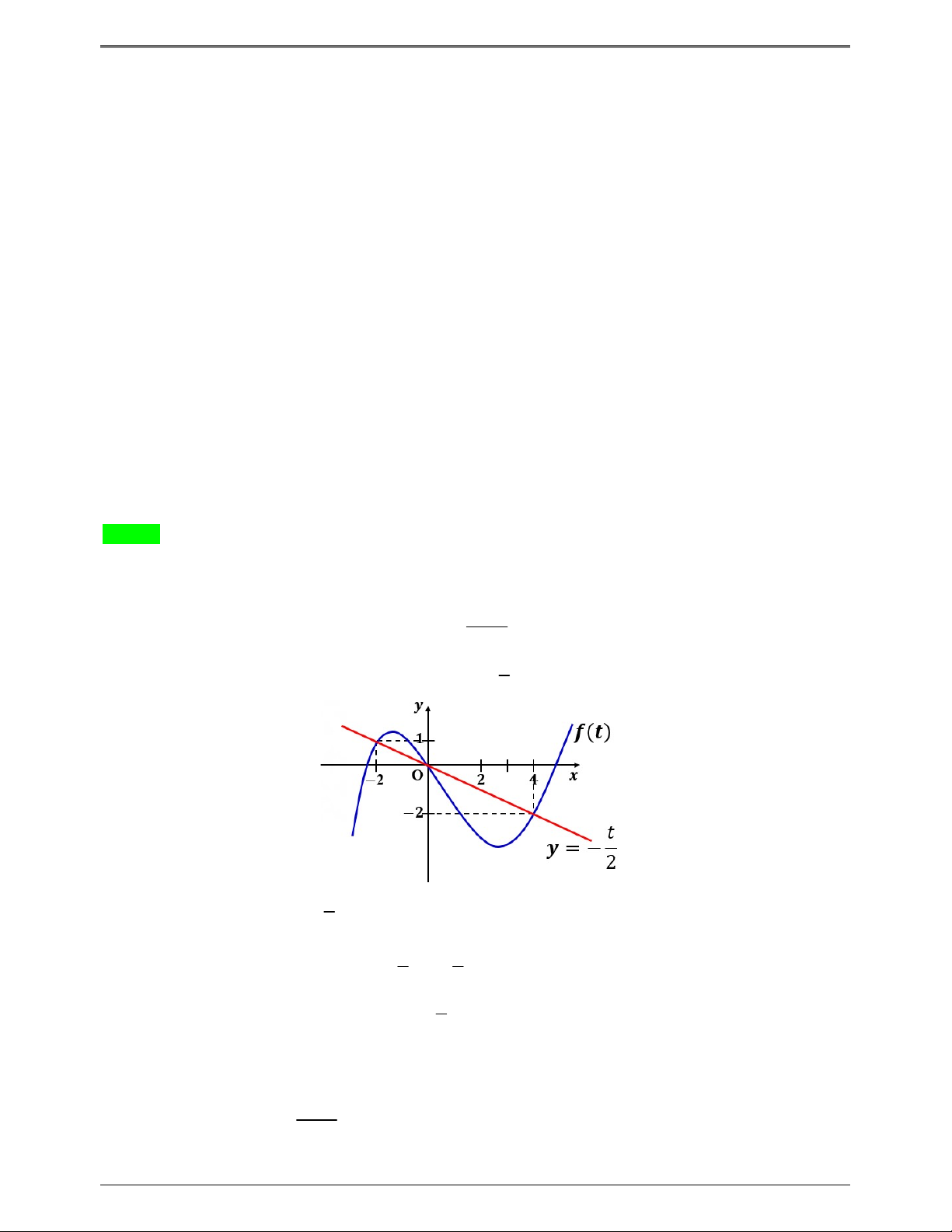
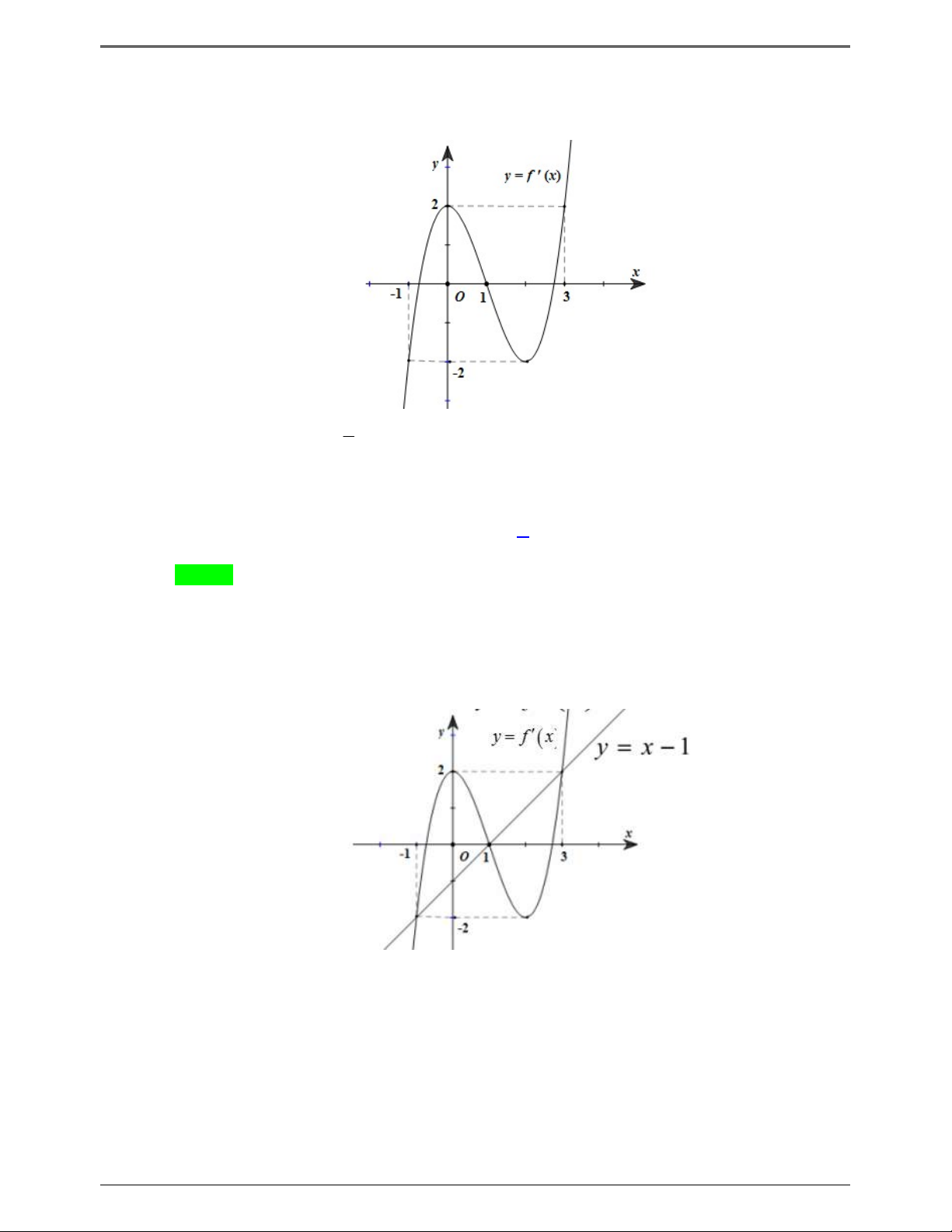
Xét sự tương giao của đồ thị hàm số y  f t  và y   . 2 t   t 
Dựa vào đồ thị ta có: f t 2 0    . 2  t  4 1 3    2   1 2  0 x x  Khi đó: g x 2 2 '  0     . 1   2x  4 3 x    2 Cách 2:
Ta có: g  x  f   x 2
1 2  x  x  g x  2
 f 1 2x  2x 1.       f   x 1 2x g x 0 ' 1 2   . 2 Trang 3
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 t
Xét sự tương giao của đồ thị hàm số y  f t  và y   . 2  3 x   t  2  2 1   2x  2   t  1
Từ đồ thị ta có: f 't 
   t  0 . Khi đó: g x 0 1 2x 0        x  . 2    2 t  4  1   2x  4   3 x    2 Ta có bảng xét dấu:  3   1 3 
Dựa vào bảng xét dấu, ta thấy: hàm số nghịch biến trên các khoảng ;    và ;   .  2   2 2 
Phân tích hướng dẫn giải
1. DẠNG TOÁN:Đây là dạng toán xét tính đơn điệu của hàm liên kết h(x)  f (u)  g(x) khi biết
BBT,BXD, đồ thị của hàm số 2. KIẾN THỨC CẦN NHỚ:
- Cách tính đạo hàm của hàm hợp
- Các bước lập bảng biến thiên của hàm số
- Đồ thị và sự tương giao hai đồ thị 3. HƯỚNG GIẢI: Lời giải Chọn A
Ta có : g  x  f   x 2
1 2  x  x  g ' x  2
 f '1 2x  2x 1  g 'x  0  2
 f '1 2x  2x 1 0 t
Đặt t  1 2x  0  2
 f 't  t  f 't   2
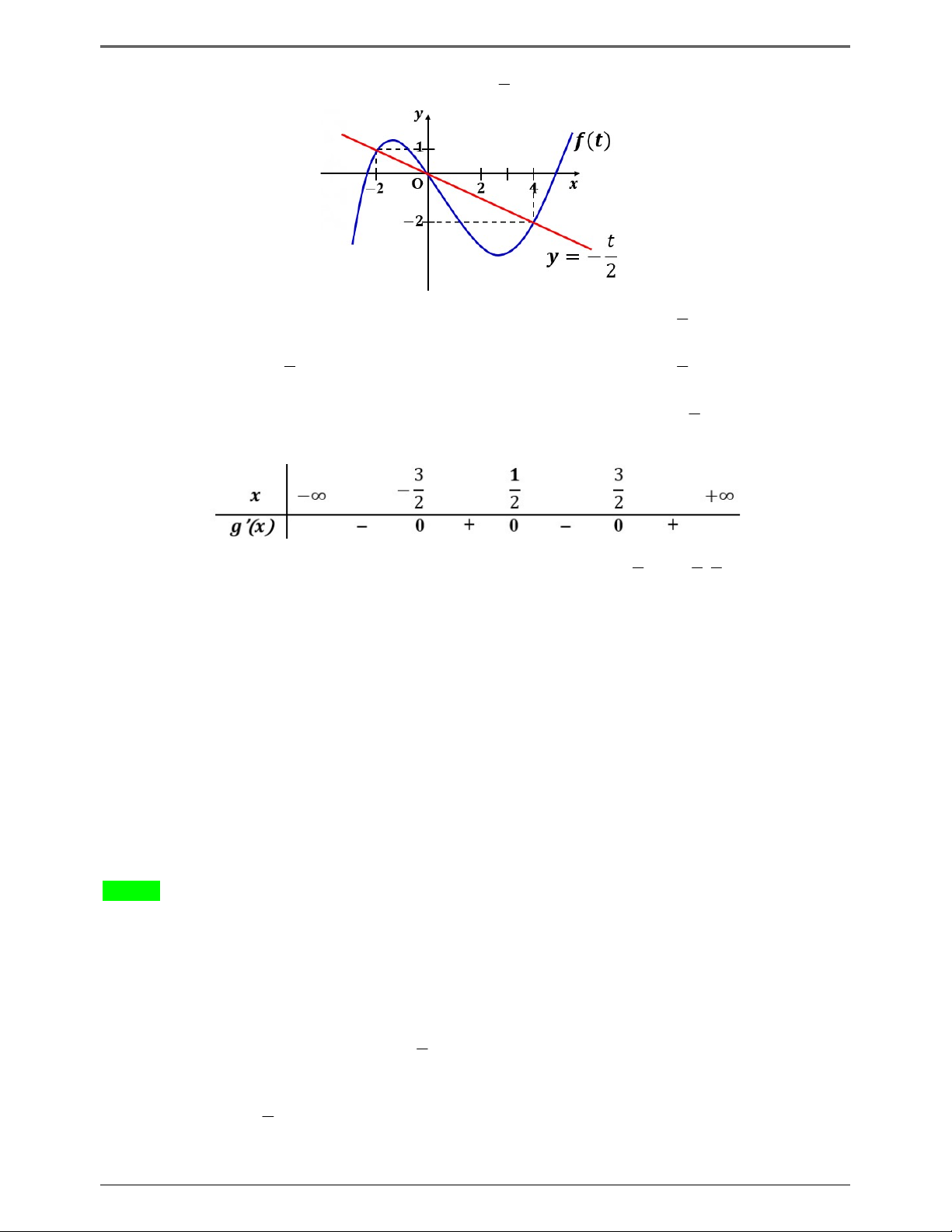
Vẽ đường thẳng   x y
và đồ thị hàm số f ' x trên cùng một hệ trục 2 Trang 4
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 y 1 4 – 2 O x – 2 t
Dựa vào đồ thị f 't    t  2,t  0,t  4 2 t   t 
Hàm số g  x nghịch biến  g x   f t  2 0 ' 0 '    2  t  4 1 3  x  1 2x  2   1 2x  0  Như vậy f   x 2 2 1 2      . 2  4  1 2x 3   x    2  1 3   3 
Vậy hàm số g  x  f   x 2
1 2  x  x nghịch biến trên các khoảng ;   và ;   .  2 2   2   3   1 3   3  Mà 1;  ;   
 nên hàm số g  x  f   x 2
1 2  x  x nghịch biến trên khoảng 1;    2   2 2   2 
Bài tập tương tự và phát triển:
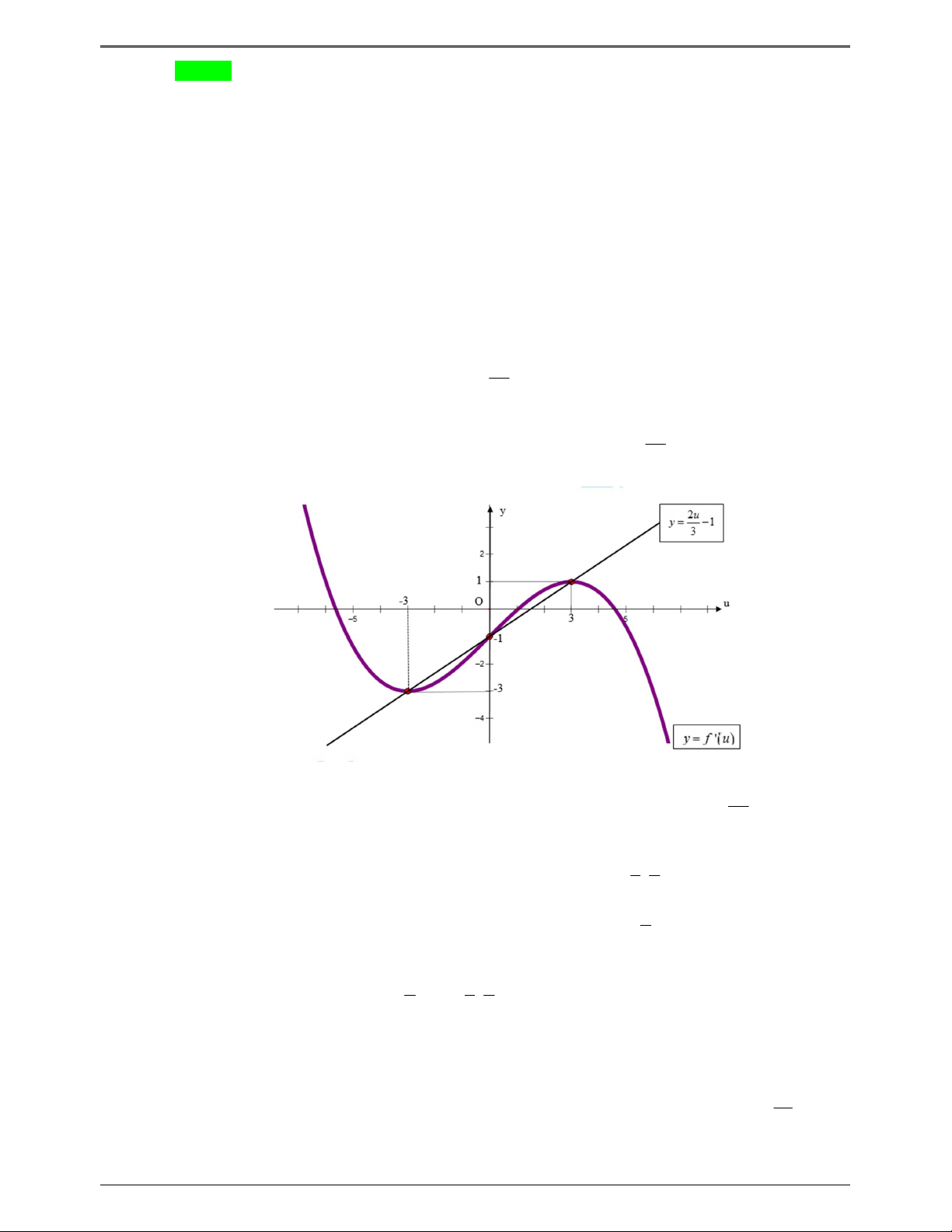
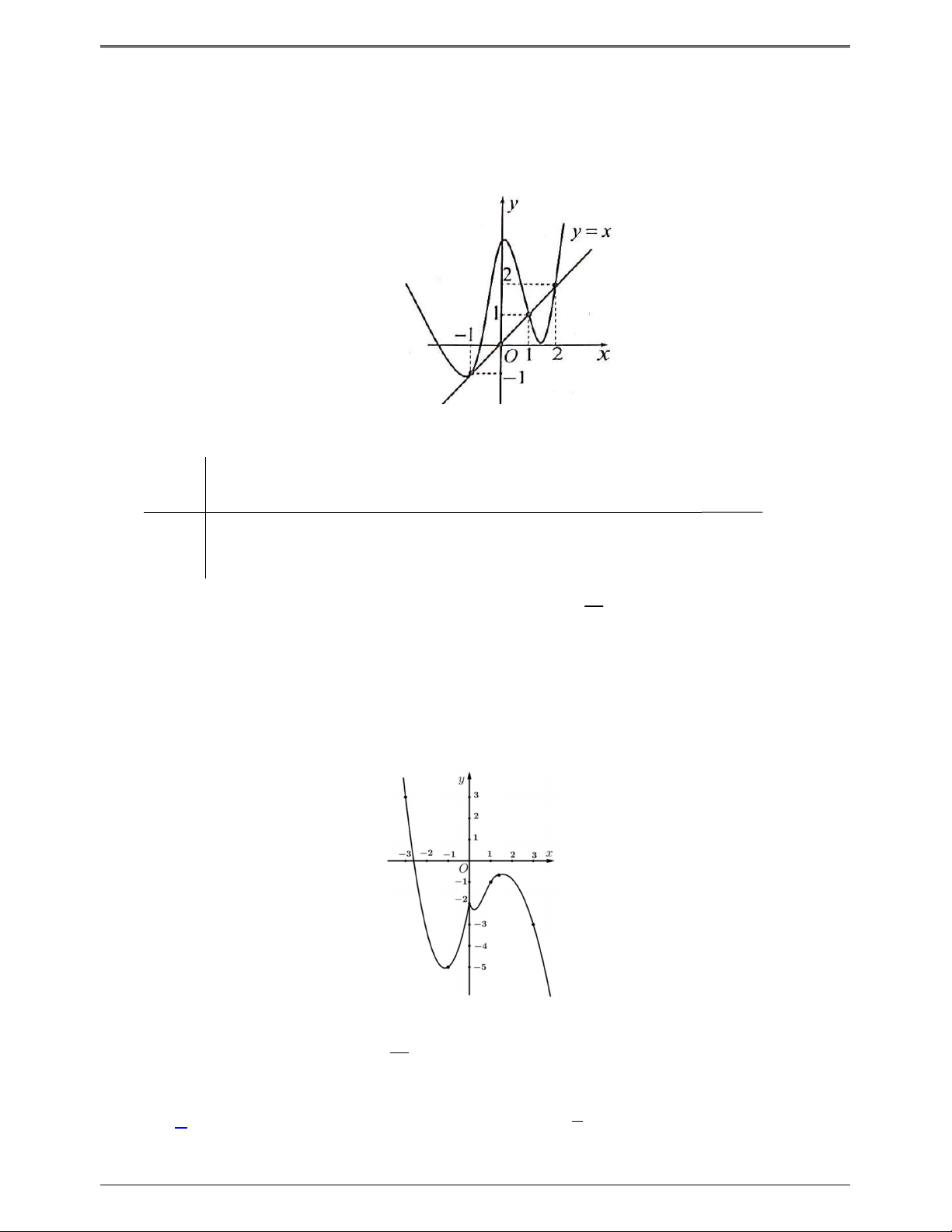
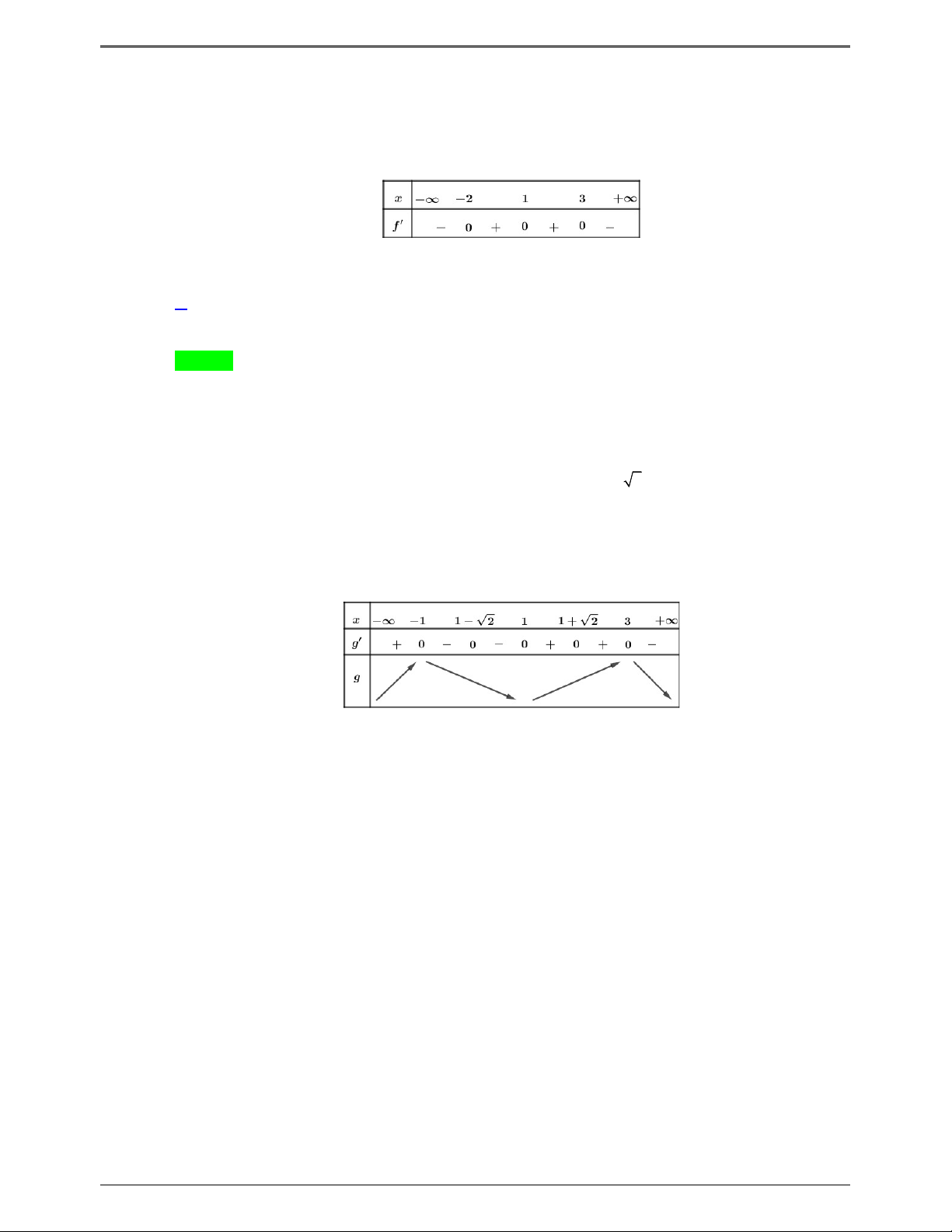
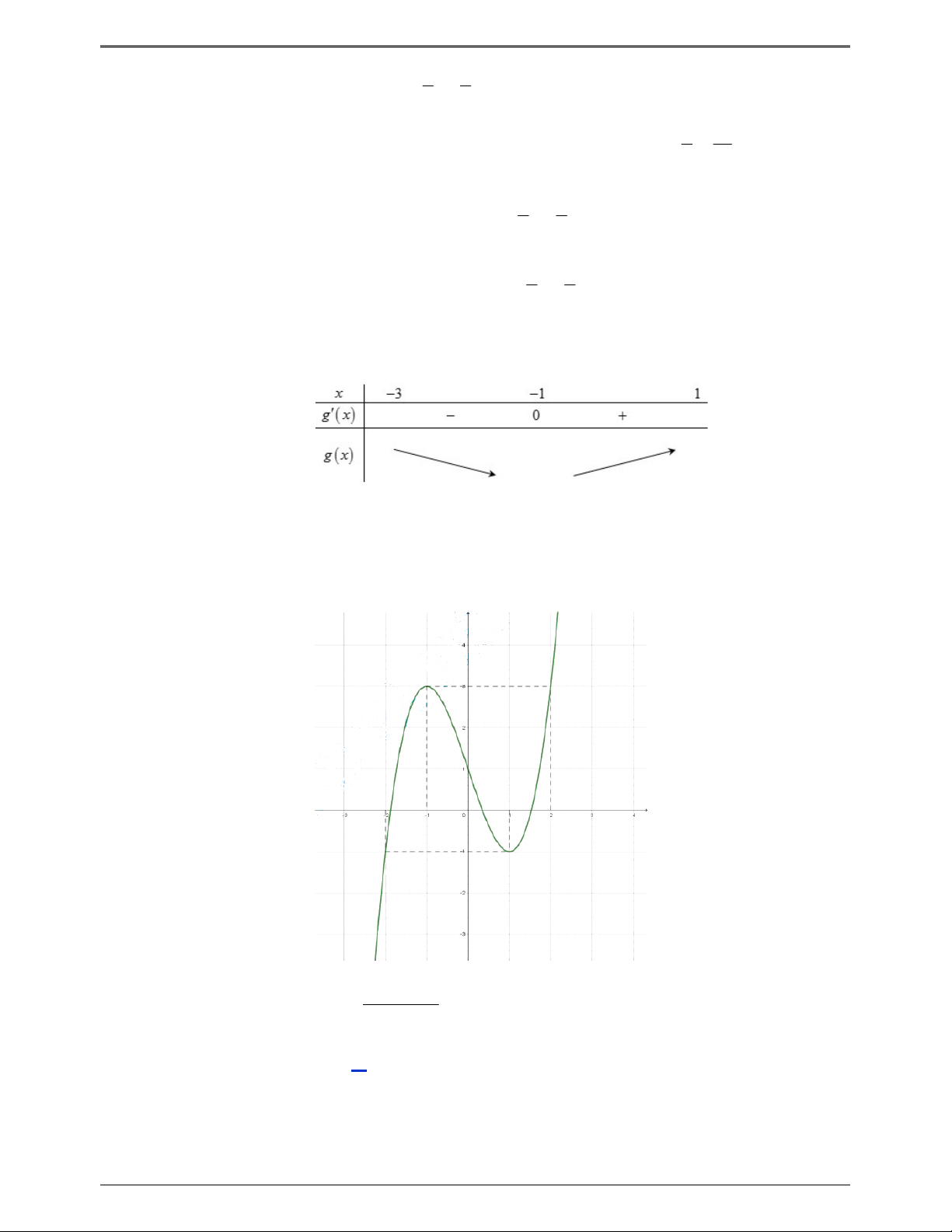
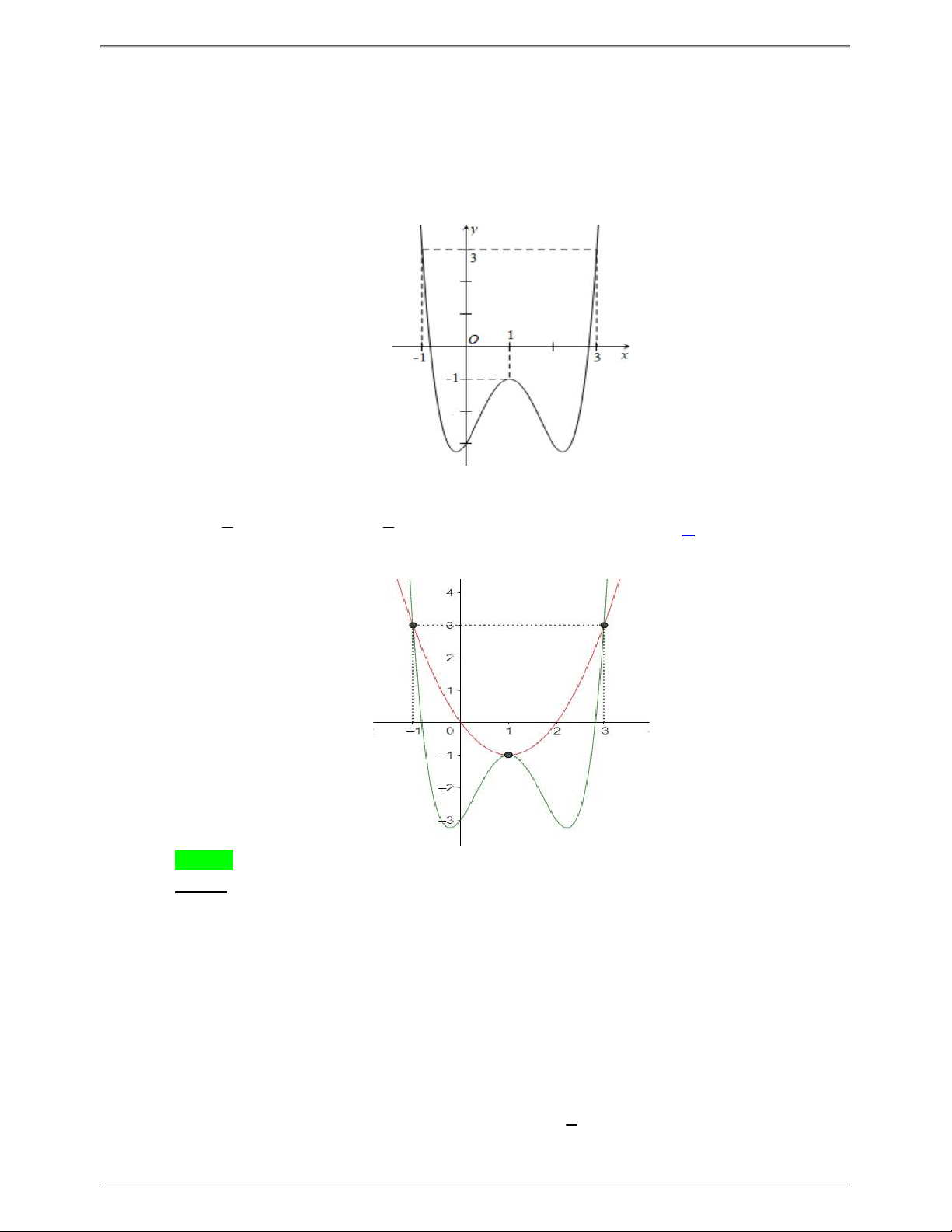
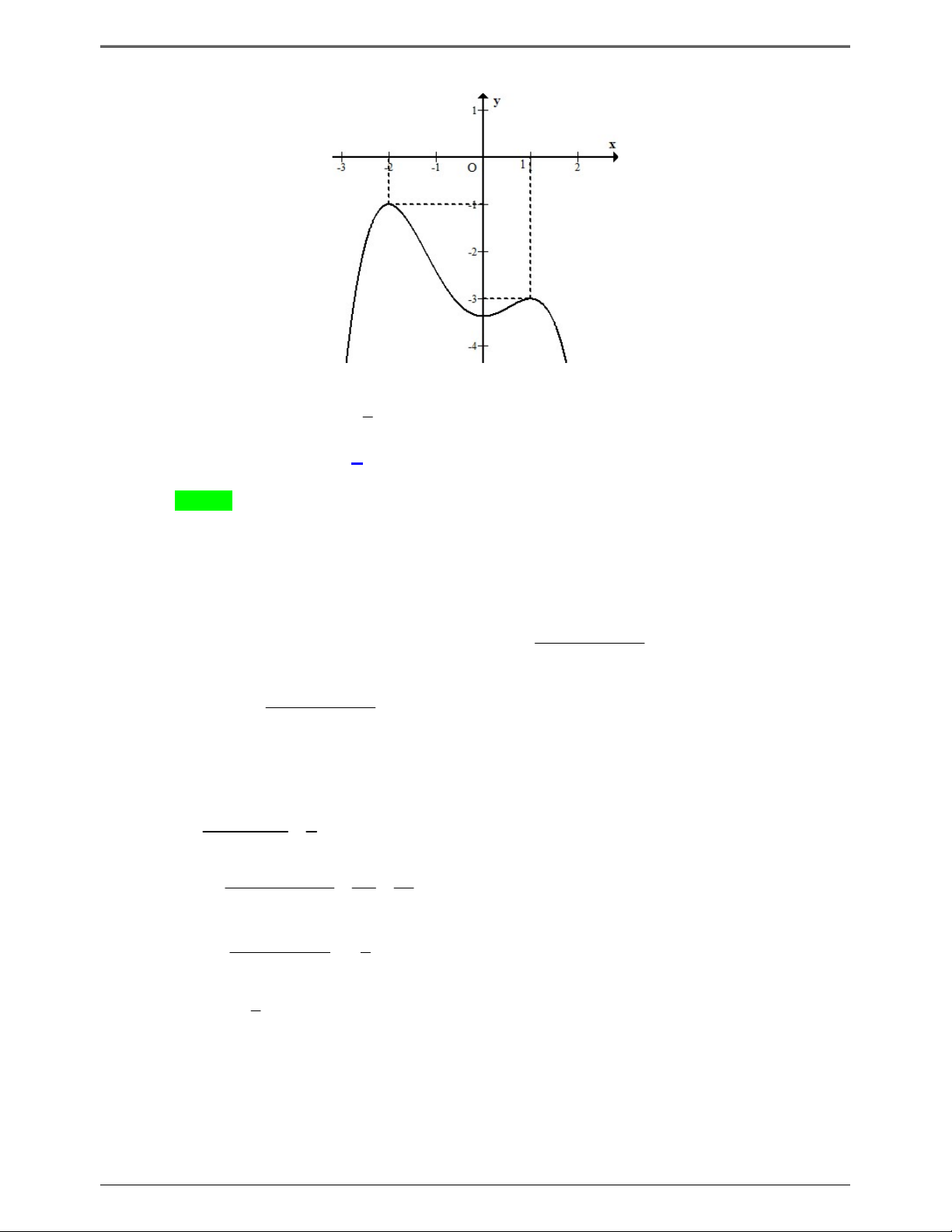
Câu 50.1: Cho hàm số f  x . Hàm số y  f x có đồ thị như hình bên dưới.
Hàm số g  x  f  x   2 3
1  3x  x đồng biến trên khoảng nào dưới đây?  3   2   2  A. 1;   . B. 0;   . C. 1  ;0 . D. ; 2   .  2   3   3  Lời giải Trang 5
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Chọn B
Ta có: g x  3 f 3x   1 6x  2  3
Hàm g(x) đồng biến trên khoảng K khi
g x  0 (dấu = xảy ra tại một số hữu hạn điểm)  3 f 3x  
1  6x  2  3  0 (1)
Đặt u  3x 1 ta được: hu  3 f u  2u  3 . u
Ta có: (1)  f u  u    f u 2 3 2 3 0  1 3 2u
Từ đồ thị hàm số y  f  x ta có đồ thị hàm số y  f u và y  1 như hình vẽ 3 2u
Để hu  0 ta cần có đồ thị y  f u phải nằm bên trên của đồ thị hàm y  1 3   1 2    x ; 0  u  3 0  3x 1  3   
Từ đó ta có hu  0   3 3       u  3  3x 1  3   4 x    3  2   1 2
Cho nên ta chọn đáp án B vì 0;   ;   3  3 3     2 x
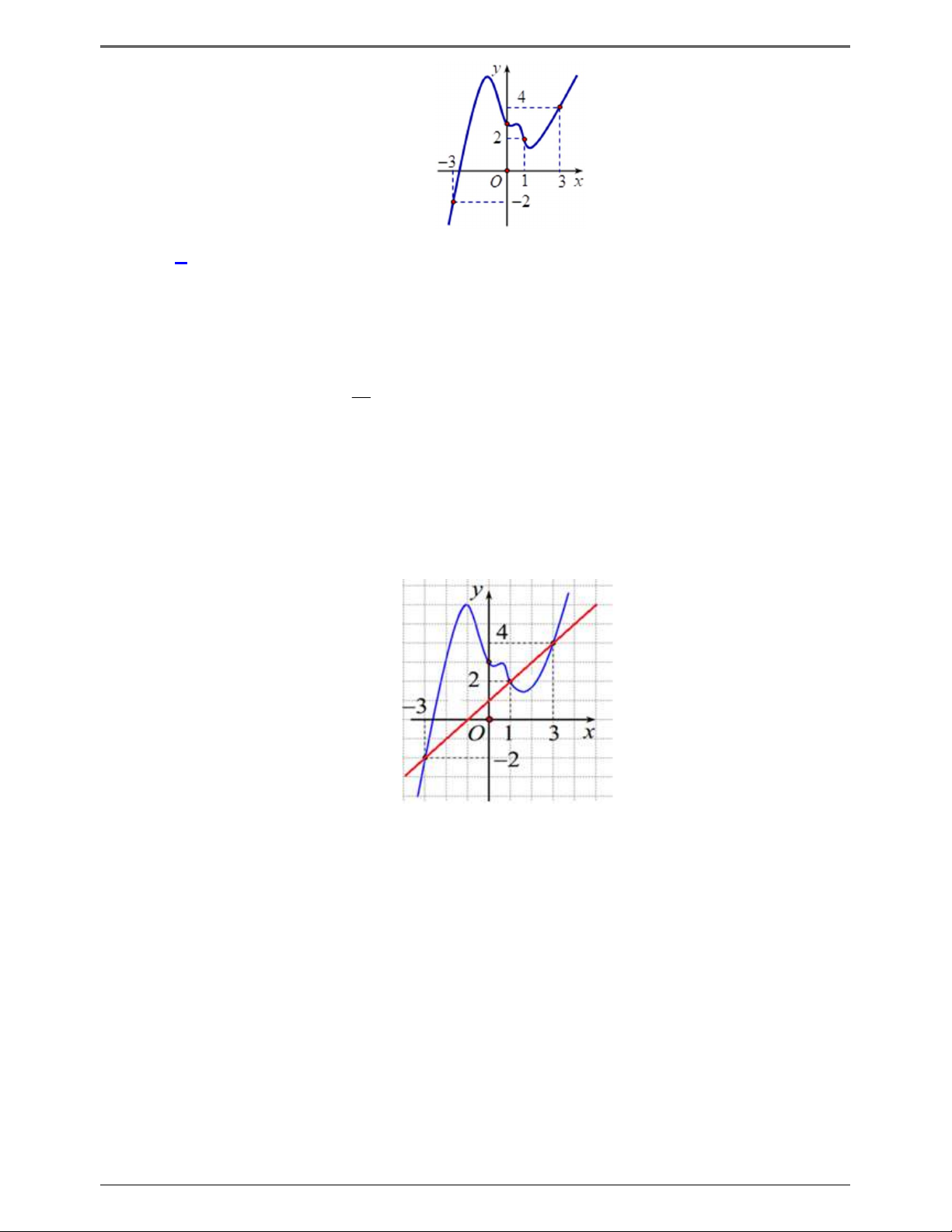
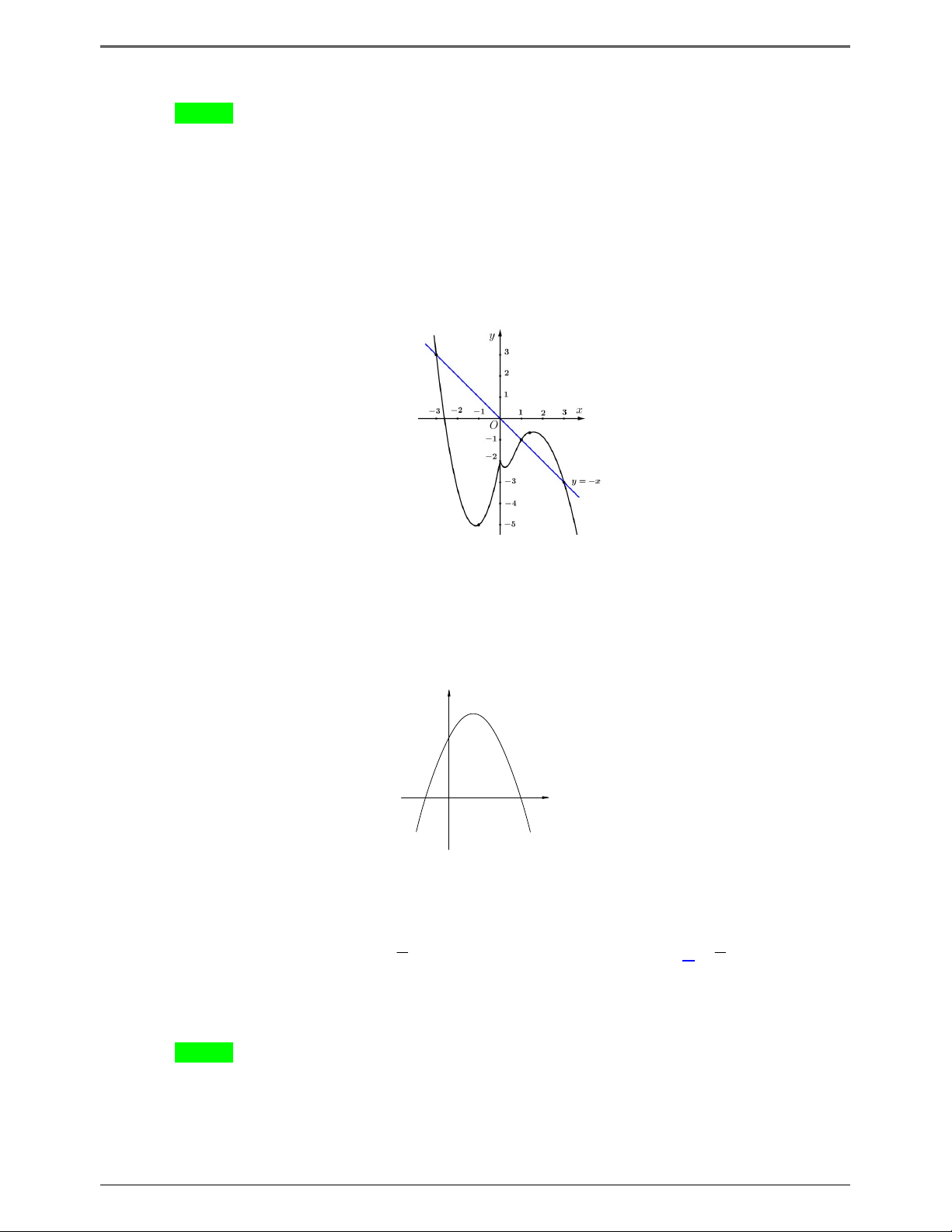
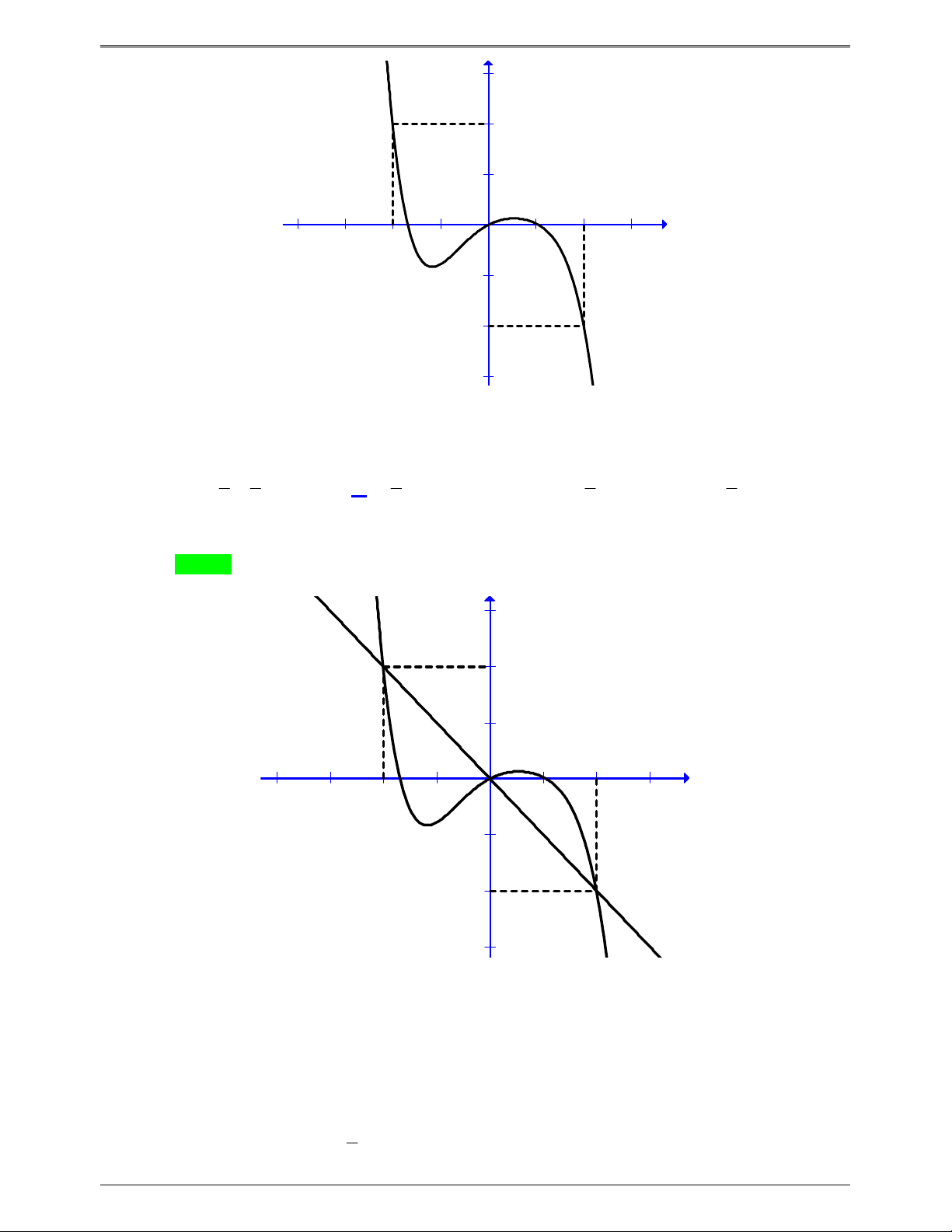
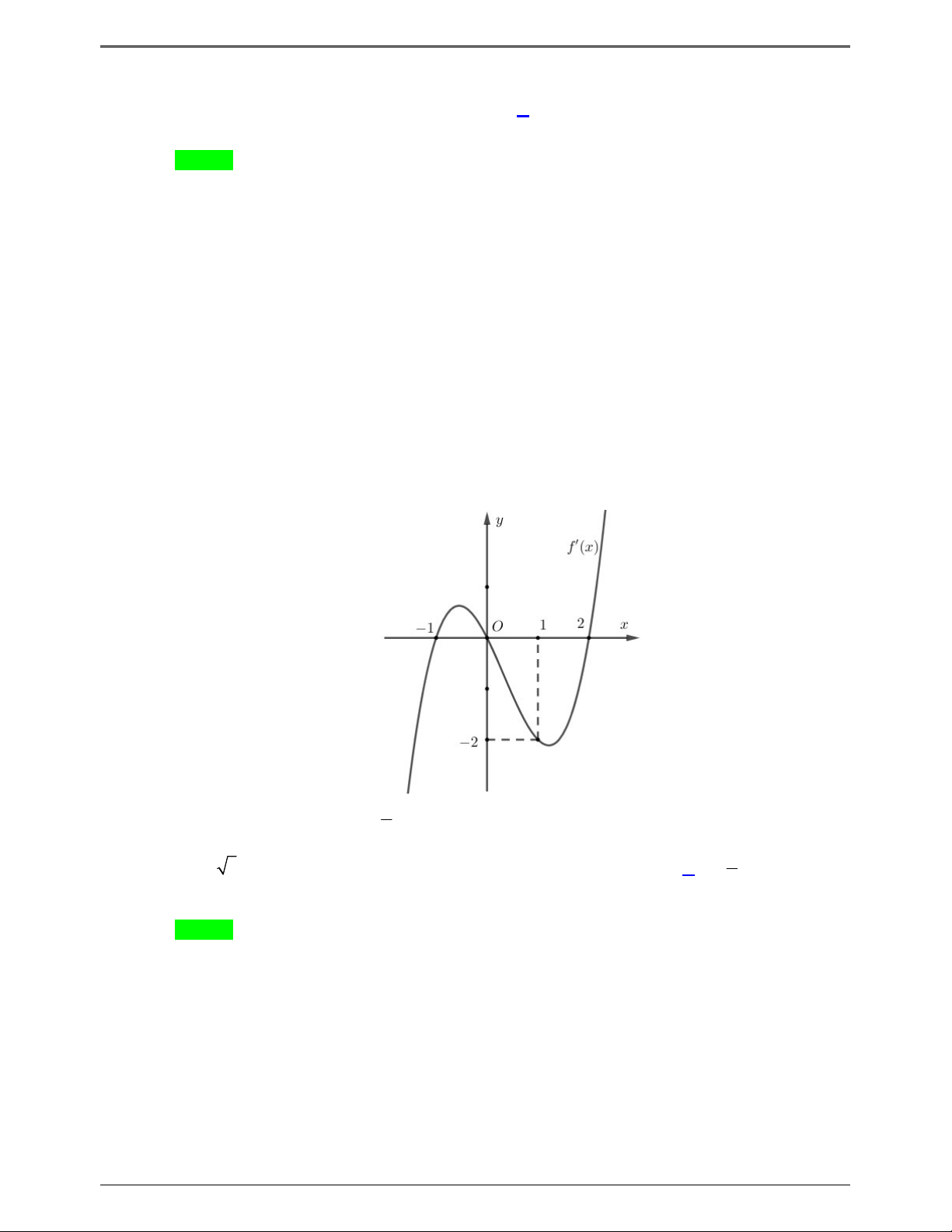
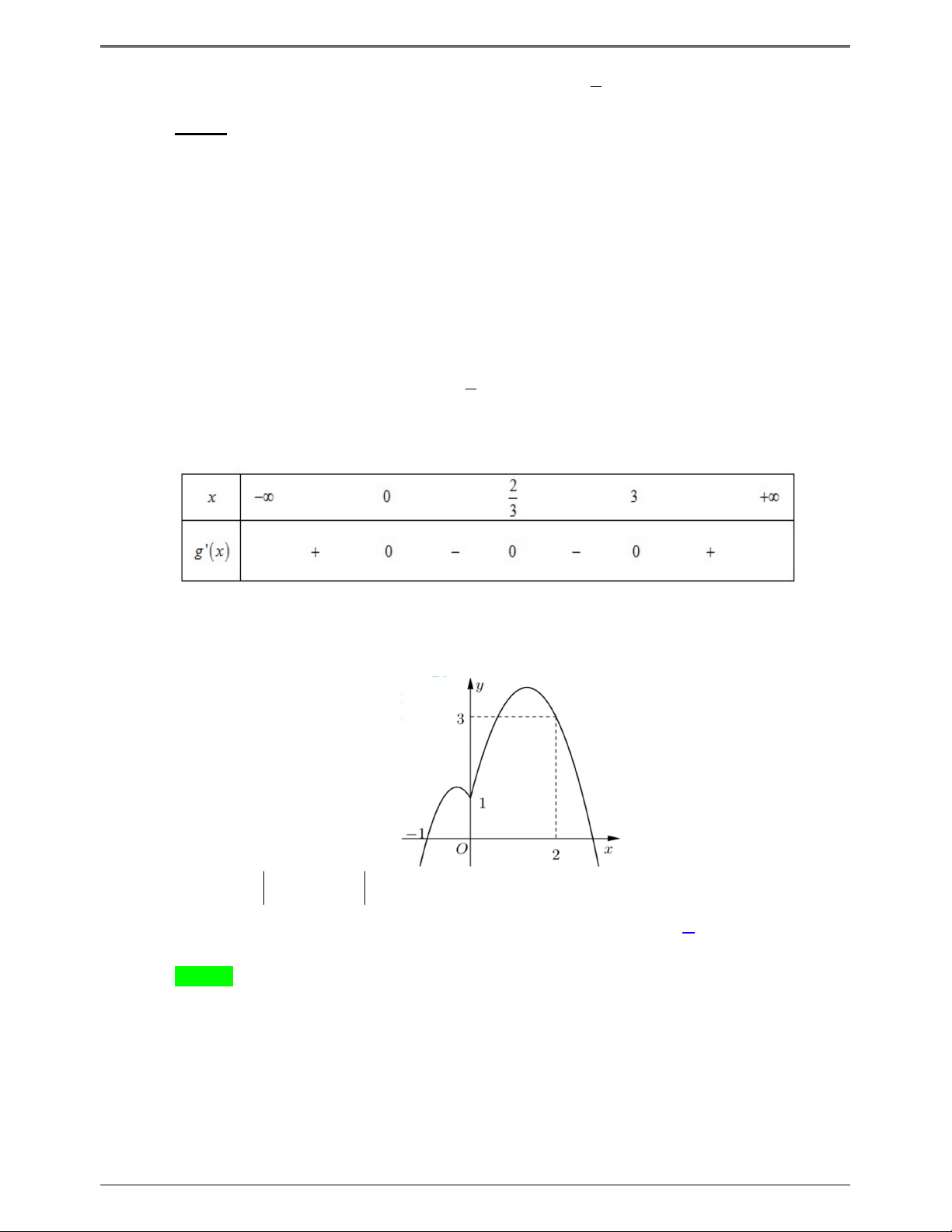
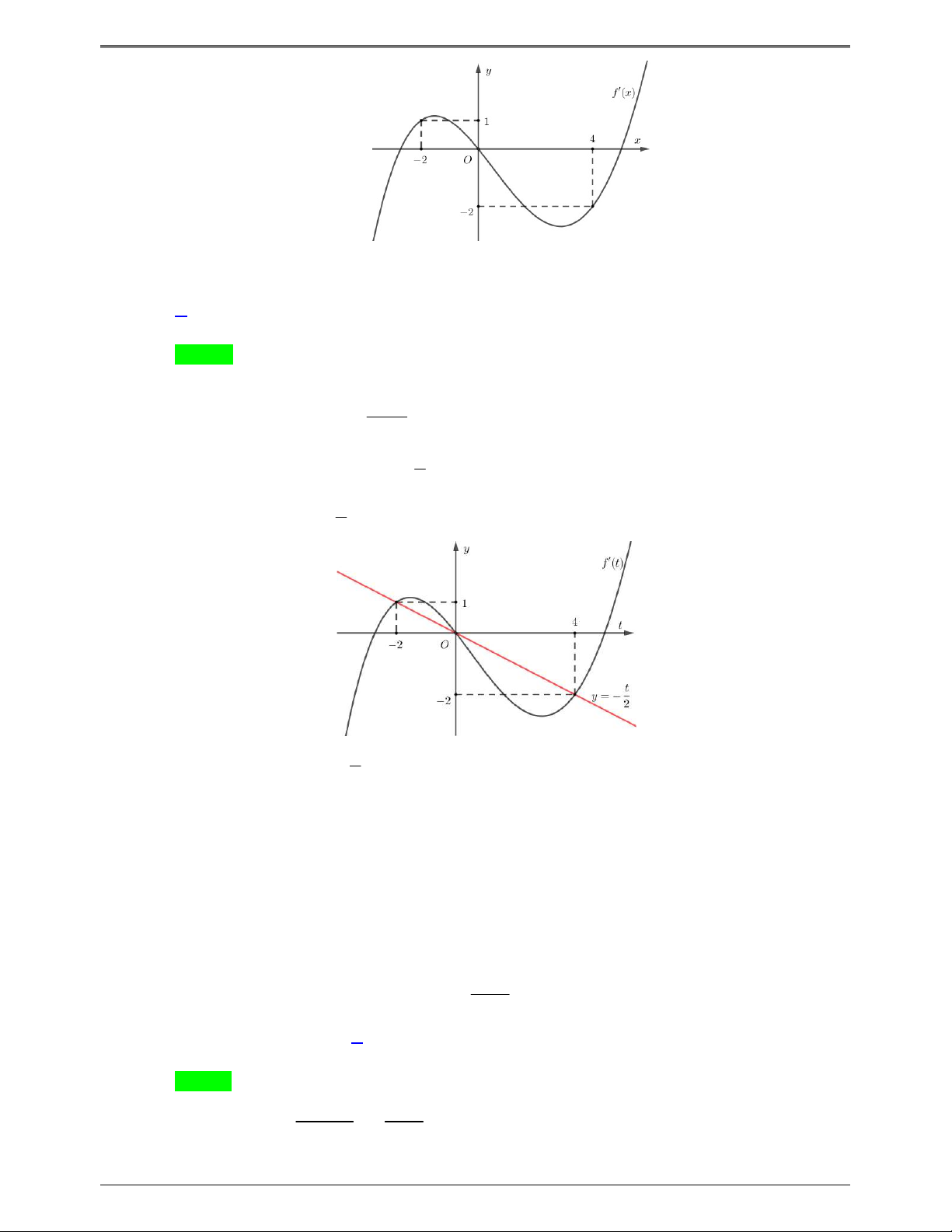
Câu 50.2: Cho hàm số f  x . Đồ thị y  f 'x cho như hình bên. Hàm số g  x  f x   1  nghịch 2
biến trong khoảng nào dưới đây? Trang 6
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 A. 2;4 . B. 0;  1 . C.  2  ;  1 . D. 1;3 . Lời giải Chọn A 2 x
Ta có: g x  f x   1 
 gx  f x   1  x . 2
 gx  0  f x  
1  x  0  f x   1  x 11
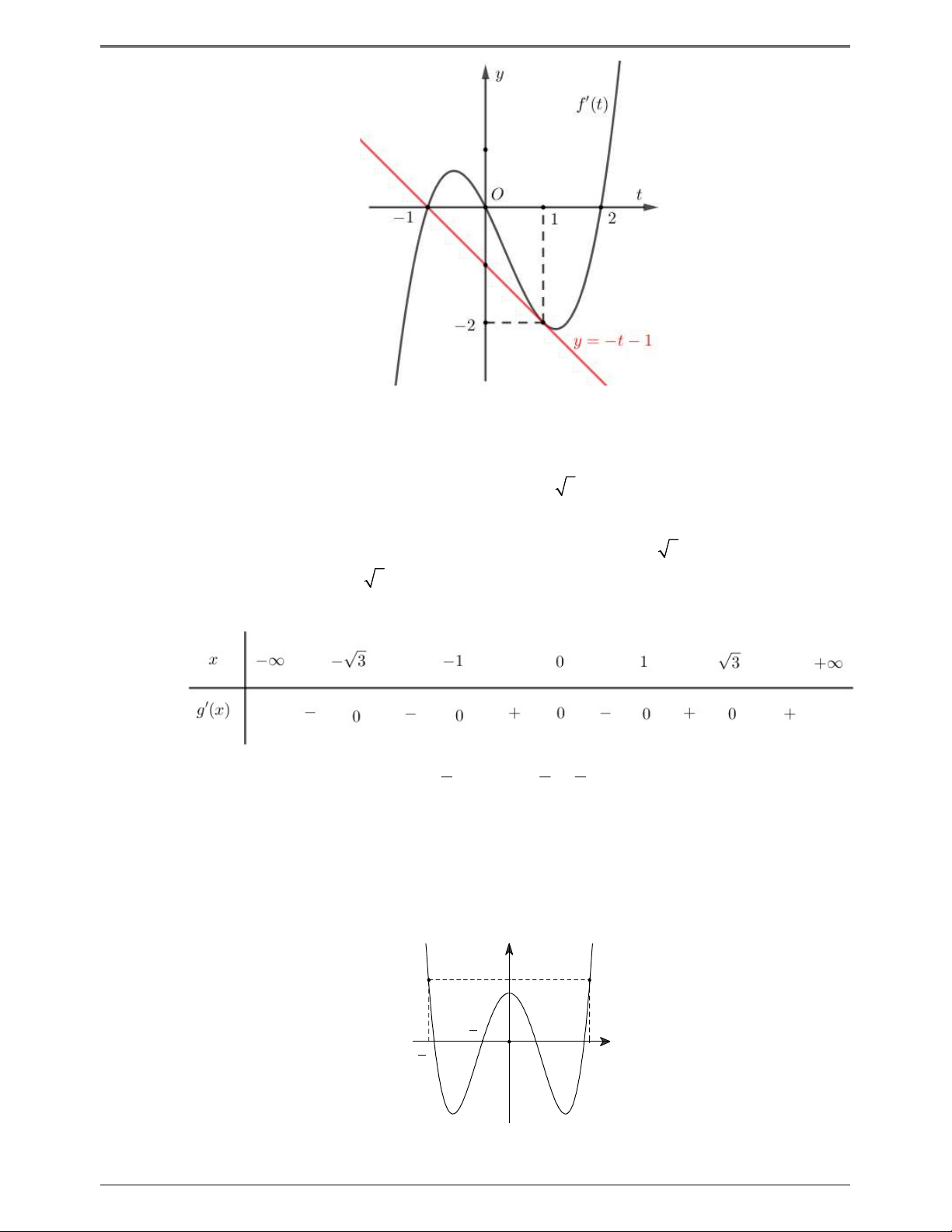
Đặt t  x 1 thì f t  t 1
Vẽ đường thẳng y  x 1 trên cùng một hệ trục tọa độ với đồ thị hàm số y  f x (như hình vẽ bên).
Dựa vào đồ thị f 't   t 1  t  3  ,t 1,t  3
Hàm số nghịch biến g x  f  x  
1  x  0  f t  t  t ( ;  3  ) (1;3)
Do đó x  (; 2)  (2;4) vậy g(x) nghịch biến trên 2;4 .
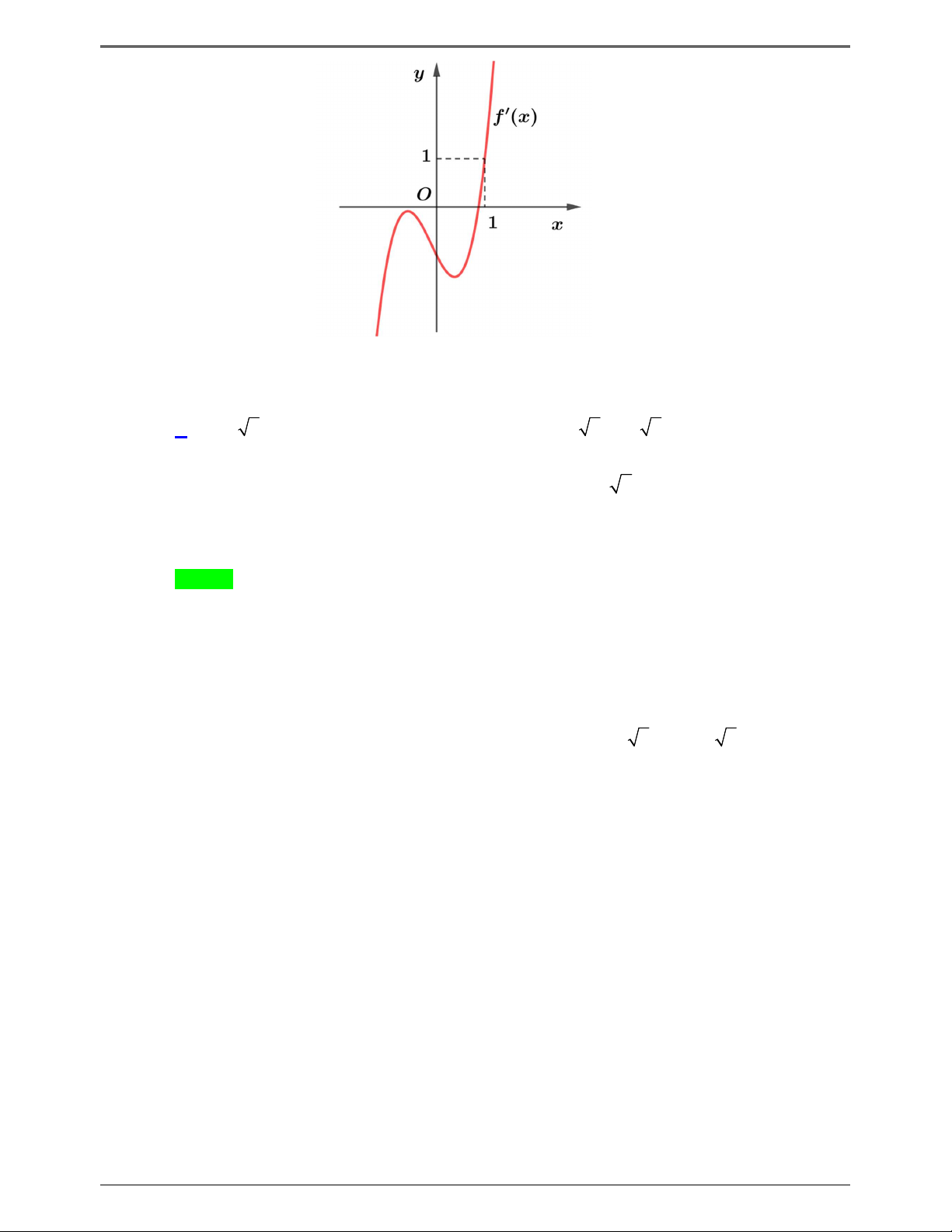
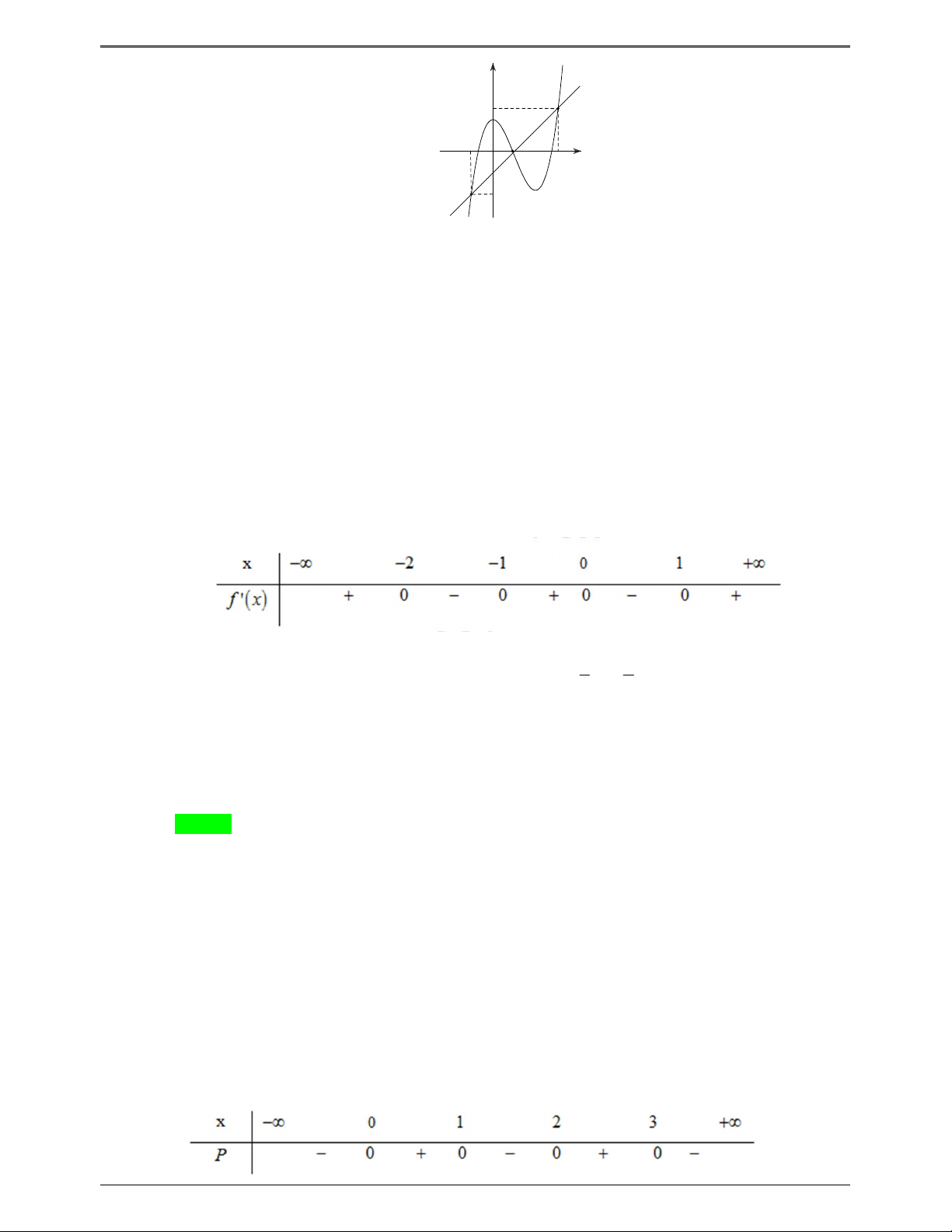
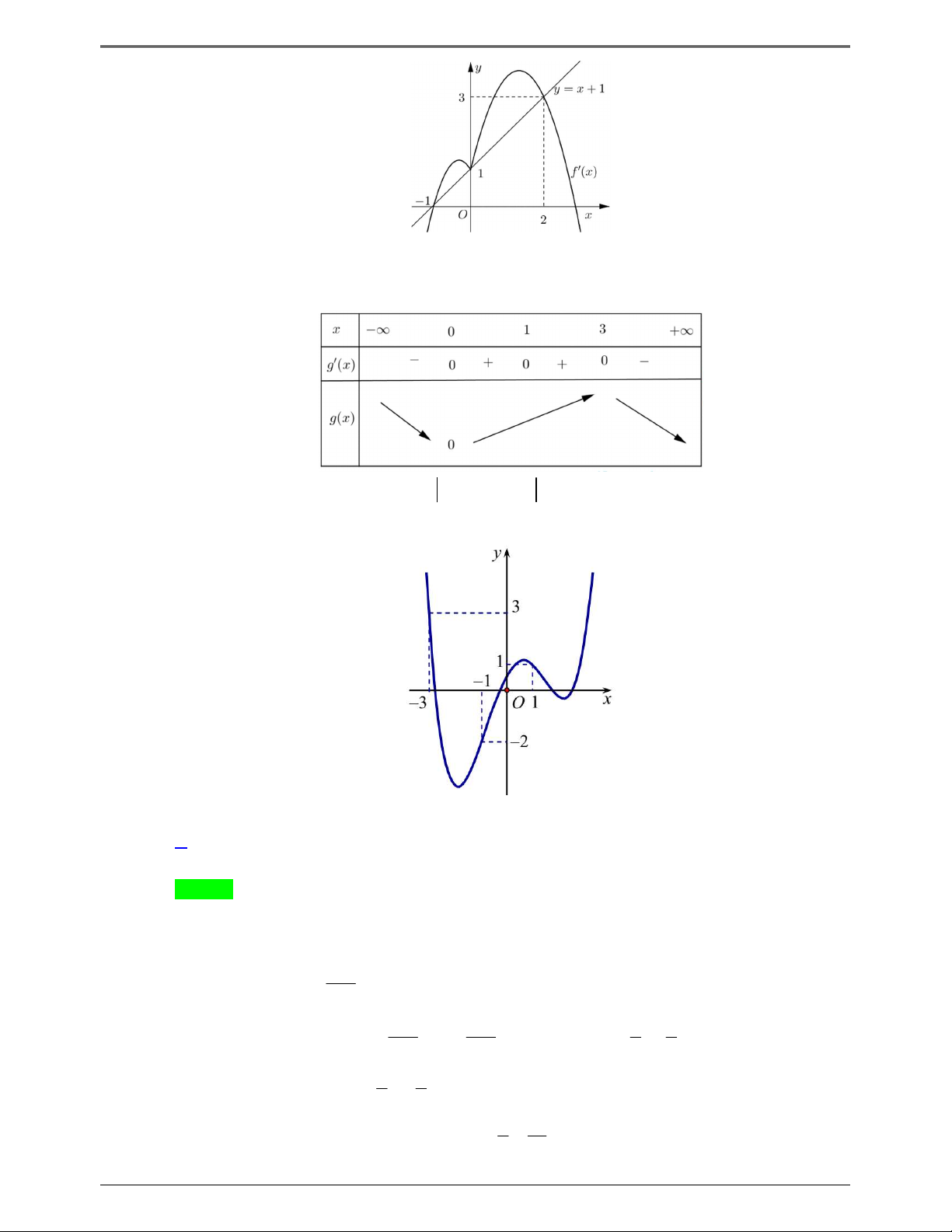
Câu 50.3: Cho hàm số y  f  x . Hàm số y  f ' x có đồ thị như hình bên. Trang 7
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Hàm số g  x  f  2 x  x 2
2  x  2x đồng biến trên khoảng nào dưới đây? A.  1   2;  1 . B. 1 2; 1   2  . C.  1  ; . D. 1;1 2 . Lời giải Chọn A Ta có: g  x  f  2 x  x 2 2  x  2x
 gx   x   f  2
x  x  x    x    f    2 2 2 2 2 2 2 1 x  2x 1 .
 gx    x    f    2 0 2 1
x  2x 1  0  x  1, x  1   2, x  1   2  x 1  0    f    I 2 x  2x   1
Xét g x  0   . x 1  0   f    II 2 x  2x   1
Xét sự tương giao của đồ thị hàm số y  f  x và y  1. Trang 8
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Dựa vào đồ thị ta có: f  2 x  x 2
2 1  x  2x 1 và f  2 x  x 2 2 1  x  2x 1. x  1 x 1  0  x  1  Xét hệ (I):       x  1
  2  x  1 2 . f   2   2 x  2x 1 x  2x 1  x  1 2 x 1  0  x  1 x  1   Xét hệ (II):      f   2   2 x  2x 1 x  2x  1
1 2  x  1 2  1   2  x  1  .
Vậy hàm số g  x đồng biến trên khoảng 1 2;  1 và  1   2; .
Câu 50.4: Cho hàm số y  f  x có đạo hàm trên  . Hàm số y  f ' x có đồ thị như hình vẽ bên. Đặt 2       x y g x f x 
. Khẳng định nào sau đây là đúng? 2
A. Hàm số y  g x đồng biến trên khoảng 1;2 .
B. Đồ thị hàm số y  g x có 3 điểm cực trị.
C. Hàm số y  g x đạt cực tiểu tại x  1  .
D. Hàm số y  g x đạt cực đại tại x 1. Lời giải Chọn D
Ta có: g ' x  f ' x  ; x
g 'x  0  f 'x  x (*).
Số nghiệm của phương trình (*) là số giao điểm giữa đồ thị hàm số y  f ' x và đường thẳng y  x . Trang 9
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Dựa vào hình bên ta thấy giao tại 3 điểm  1  ;  1 ;1;  1 ;2;2 x  1  (*)    x 1  . x  2 
Bảng xét dấu g ' x : 2 x
Từ bảng xét dấu g ' x ta thấy hàm số y  g  x  f  x  . 2
Đồng biến trên khoảng  ;  
1 và 2; ; nghịch biến trên khoảng 1;2 .
Hàm số y  g  x đạt cực đại tại x 1.
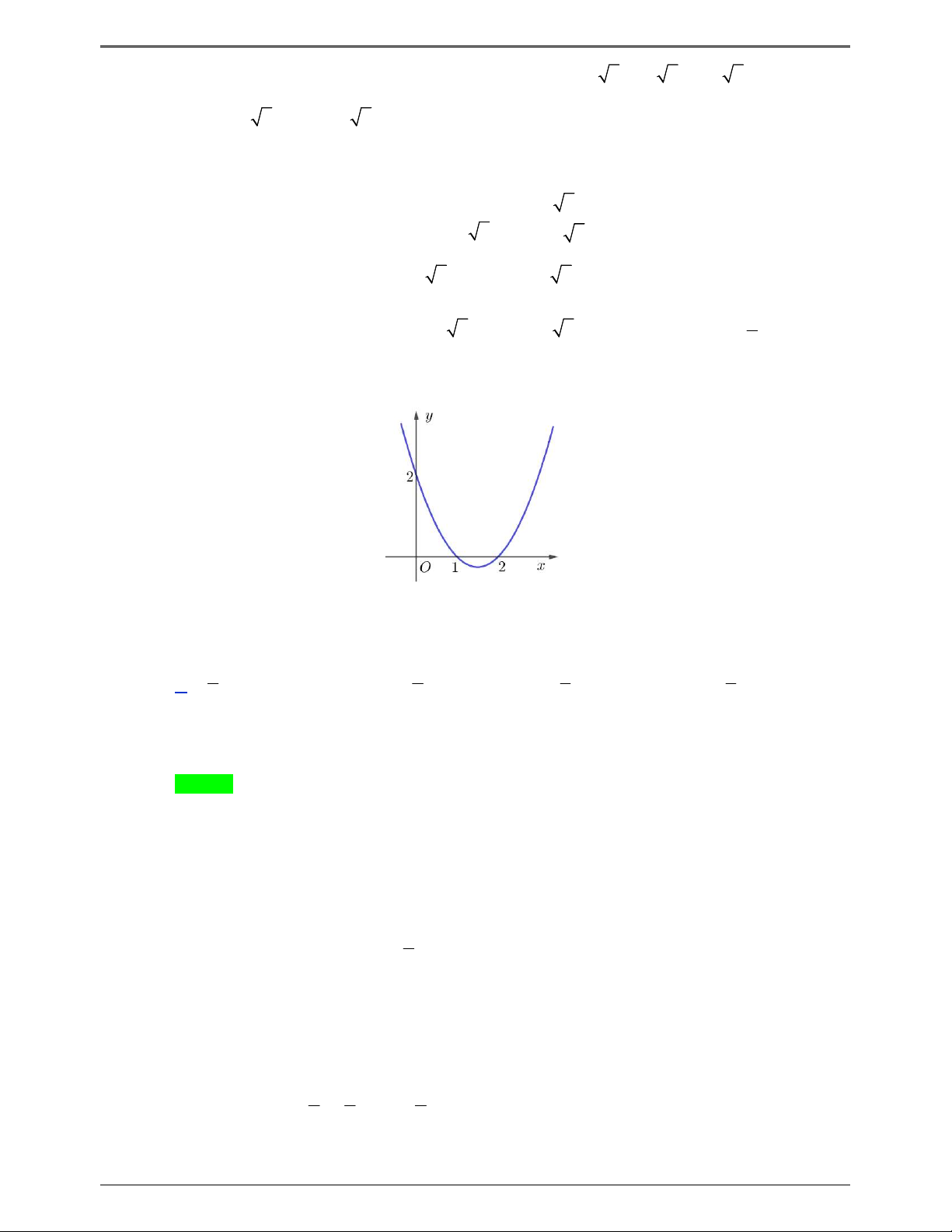
Câu 50.5: Cho hàm số f  x có đồ thị của hàm số f  x như hình vẽ. 2 x
Hỏi hàm số g  x  f 1 x 
 x nghịch biến trên khoảng nào dưới đây? 2  3  A.  2  ;0 . B. 1;3 . C. 1;   . D. 3;  1 .  2  Trang 10
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Lời giải Chọn A
Ta có: g x   f 1 x  x 1.
Hàm số g  x nghịch biến  g x  0  f 1 x  x 1 (1) .
Đặt t  1 x . Khi đó (1) trở thành f t  t  (2).
Bất phương trình (2) được thỏa khi f  x  x hay đồ thị hàm số f  x nằm phía trên đồ thị hàm số y  x .  t  3   1 x  3  x  4 Từ đồ thị ta được   . Vậy chọn khoảng  2  ;0 . 1   t 3 1   1 x 3       2  x  0
Câu 50.6: Cho hàm số y  f  x có đồ thị hàm số y  f  x được cho như hình vẽ sau. y -1 O 3 x
Hàm số g  x  f  4 2x  
1 đồng biến trên khoảng nào dưới đây?  3   1  A. 1; . B. 1;   . C. ;  1 . D. ;1   .  2   2  Lời giải Chọn D Ta có: g x 3  x f  4 8 . 2x   1
TH1: x  0 . Để hàm số g  x đồng biến thì Trang 11
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 f  4 x   4 4 2 4 4 2
1  0  1  2x 1  3  0  x  2  0  x  2   2  x  2 4 4
 0  x  2  x  0; 2   .
TH2: x  0 . Để hàm số g  x đồng biến thì   x    x  L x  f 2x   4 4 2 1 1 0( ) 2 4 1  0       . 4 2 4 2x 1 3 x  2 x   2 So sánh với điều kiện 4 x   x    x  4 0 2 ; 2 .  1 
Vậy hàm số g  x đồng biến trên 4 0; 2   và  4
; 2. Do đó chọn khoảng ;1   .  2 
Câu 50.7: Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình vẽ sau đây. Hàm số   2 y
f x  x  nghịch biến trên khoảng nào?  1   3   3   1  A. ;  . B.  ;    . C.  ;   . D.  ;   .  2   2   2   2  Lời giải Chọn A Xét hàm số   2 y f x  x 
Ta có: y    x  f  2 1 2 x  x   1 2 1  0 x x   2   2 2
 y  0  x  x  1   x  x 1  0VN   2  2 x  x  2 
x  x  2  0VN   2   Ta lại có: 2 1 1 1 x  x    x     1, x  R 4  2  4 Trang 12
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Từ đồ thị của hàm số y  f  x  f  2 x  x   0,x  R
Bảng biến thiên của hàm số   2 y f x  x   1 
Vậy hàm số nghịch biến trên ;  . Chọn A. 2   
Câu 50.8: Cho hàm số y  f x có đạo hàm trên .
 Đồ thị hàm số y  f x như hình vẽ. Hàm số y  f  2
x  2x đồng biến trên khoảng nào sau đây? A. 1; 2 . B.  ;   3 . C. 0;  1 . D. 2; 0 . Lời giải Chọn A
Từ đồ thị của hàm số y  f  x ta có bảng biến thiên của hàm số y  f x như sau Đặt  g  x  f  2
x  2x , ta có gx   2 x  x f  2
x  x   x   f  2 2 . 2 2 1 . x  2x.
Hàm số g x đồng biến khi g x    x   f  2 0 1 . x  2x  0 x 1  0  x 1  0    hoặc  2 f   2   1 2 x  2x    0 f   x  2x    0 Trang 13
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 x  1  x 1  0    1 2  x  1   2 1 x  1   2 · Xét   2 1   1
  x  2x  1     .  x  3  x  1 2 x  2x  3 x 1  x  1  x 1  0   x  1   · Xét 2 2  x  2x  1    2   x  2x 1  0 2 1   x  2x  3   2
x  2x  3  0 x  1  x  1     3   x  1   2    x  1 2   .   x  1   x  1 2   3   x  1
Câu 50.9: Cho hàm số y  f  x , biết hàm số y  f  x có đồ thị như hình bên dưới. Hàm số g  x  f  2
3 x  đồng biến trên khoảng? A. 2;3. B.  1  ;0 . C.  2  ;  1 . D. 0;  1 . Lời giải Chọn B
Dựa vào đồ thị, ta có bảng xét dấu g  x   xf  2 ' 2 3 x  Trang 14
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  x  0  2x  0  g x x  3  '  0   f      2 3  x   0 x  2   x  1 3  x  2     x   f 3 x  2 6 3 1 2 0       2  x  3  2  2 3 x     1   x 1  Bảng biến thiên:
Từ BBT suy ra hàm số đồng biến trên  1  ;0 . Câu 50.10:
Cho hàm số y  f (x) có bảng xét dấu đạo hàm như sau: x  3  0 5  f '(x)  0  0  0  Biết: 1  f (x)  5, x   . R Khi đó, hàm số 3 2
g(x)  f ( f (x) 1)  x  3x  2020 nghịch
biến trong khoảng nào dưới đây: A. ( 2  ;0) . B. (0;5) . C. ( 2  ;5) . D. ( ;  2  ). Lời giải Chọn A Ta có: 2
g '(x)  f '(x). f '( f (x) 1)  3x  6x . Vì 1  f (x)  5, x
  R  0  f (x) 1 4 .
Từ bảng xét dấu của f '(x)  0  f '( f (x) 1)  0 .
Từ đó, ta có bảng xét dấu như sau: Trang 15
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Do đó, hàm g(x) nghịch biến trên khoảng ( 2  ;0). Câu 50.11:
Cho hàm số y  f  x có đạo hàm trên  và có bảng biến thiên của đạo hàm f 'x như sau :
Hỏi hàm số g  x  f  2
x  2x  2020 có bao nhiêu điểm cực tiểu ? A. 1. B. 2. C. 3. D. 4. Lời giải Chọn A
Ta có gx x   f  2 2 2 x 2x; x 1 x 1   2 2x 2  0            g x x 2x 2 theo BBT f 'x x 1 2  0       f   . 2 x 2x 2 0 x 2x 1        x   1   2 x 2x  3 x  3   Bảng biến thiên
Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta chọn A
Chú ý: Dấu của gx được xác định như sau: Ví dụ xét trên khoảng 3;    x 3;   2x 20.  1  x    2 theo BBT f 'x
  x  x   f  2 3; 2 3 x 2x0.  2 Từ  
1 và 2, suy ra gx x  f  2 2 2
x 2x0 trên khoảng 3; 
 nên gx mang dấu  .
Nhận thấy các nghiệm x  1
 và x 3 là các nghiệm bội lẻ nên gx qua nghiệm đổi dấu. Câu 50.12:
Cho hàm số y  f  x có đạo hàm trên .
 Đồ thị hàm số y  f x như hình vẽ bên dưới. Trang 16
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Hàm số g  x  f  x   3 2 3
1  9x 18x 12x  2021 nghịch biến trên khoảng .  2  A. ;  1 . B. 1;2 . C. 3;  1 . D. ;1   .  3  Lời giải Chọn D
Ta có g x  f  x    x  x 
g x   f  x     x  2 2 3 3 1 3(9 12 4); 0 3 1 3 2 .(1) Đặt t  3x 1 khi đó
 f t   t  2 (1) 1 . t 
Dựa vào đồ thị ta suy ra f t  t  2 0 1 
.(vì phần đồ thị của f 't nằm phía dưới 1    t  2
đồ thị hàm số y  t  2 1 ) .  1 x  3x 1 0 
Như vậy f  x     x  2 3 3 1 3 2     . 1   3x 1  2 2   x 1 3  1 
Vậy hàm số g  x  f  x   3 2 3
1  9x 18x 12x  2021 nghịch biến trên các khoảng ;    3   2  và ;1   .  3  Câu 50.13:
Cho hàm số y  f x có bảng xét dấu của đạo hàm như sau: Trang 17
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 1
Đặt y  gx 2 f 1 x 4 3 2
 x  x  x 3. Khẳng định nào dưới đây là đúng? 4
A. Hàm số y  gx đồng biến trên khoảng ;0 .
B. Hàm số y  gx đồng biến trên khoảng 1;2 .
C. Hàm số y  gx đồng biến trên khoảng 0;  1 .
D. Hàm số y  gx nghịch biến trên khoảng 2; Lời giải Chọn C
Ta có: y  g x   f   x 3 3 2 1  x 3x  2x . x  2 x 1
Dựa vào bảng xét dấu f  x ta có f 1 x  0   . x  0  x  3        
 f   x   f   x 2 1 x 1 2 x 3 2 1 0 1  0    . 0 1 x 1     0  x  1 3 3
x  3x  2x  x x   1  x  2
Bảng xét dấu y  g x
Vậy hàm số đồng biến trên 0;  1 . Câu 50.14:
Cho hàm số y  f x . Hàm số y  f 'x có đồ thị như hình vẽ bên dưới. Trang 18
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 3 y 2 1 x -2 -1.5 -1 -0.5 0.5 1 1.5 -1 -2 -3
Hàm số gx  f  x   2 2
3  4x 12x 1 đồng biến trên khoảng nào dưới đây ?  3 1   5   3   1  A.  ; .   B.  ;2 .   C. 2  ; .   D.  ;0 .    2 2   2   2   2  Lời giải Chọn B 3 y 2 1 x -2 -1.5 -1 -0.5 0.5 1 1.5 -1 -2 -3 y  f 'x y  2x
Hàm số gx đồng biến  g'x  0  2 f '2x 3 8x 12  0  f '2x 3  2  2x 3 x  2 2x 3 1          3 . Chọn đáp án B . 0  2x  3 1   x  1   2 Trang 19
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Câu 50.15:
Cho hàm số y  f  x có đồ thị y  f  x như hình vẽ. Xét hàm số g  x  f x 1 3 3 3 2
 x  x  x  2018. Mệnh đề nào dưới đây đúng? 3 4 2 y 3 1 1 3 O x 1 2
A. Hàm số g  x đồng biến trên 1;  1 .
B. Hàm số g  x đồng biến trên 3;  1 .
C. Hàm số g  x đồng biến 3;  1 .
D. Hàm số g  x nghịch biến trên 1;  1 .. Lời giải Chọn B 1 3 3 3 3
Ta có: g  x  f  x 3 2
 x  x  x  2018  gx  f x 2  x  x  3 4 2 2 2 3 3 3 3
+ g ' x  0  f ' x 2  x  x  . Đặt 2
y  x  x  có đồ thị (P) 2 2 2 2  f   1  2 g  1  0  
Dựa vào đồ thị y  f  x , ta có:  f   1  1  g  1  0   f   3  3 g  3  0 y 3 P 1 1  x 3  1 2  Trang 20
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Vẽ đồ thị P của hàm số 2 3 3
y  x  x  trên cùng hệ trục tọa độ như hình vẽ trên (đường nét 2 2  3 33 
đứt ), Đồ thị P đi qua các điểm  3  ;  3 ,  1  ; 2  , 1;  1 với đỉnh I  ;   .  4 16  3 3
Ta thấy: + Trên khoảng  1  ;  1 thì f  x 2
 x  x  , nên gx  0 x   1  ;  1 2 2 3 3 +Trên khoảng  3  ;  1 thì f  x 2
 x  x  , nên gx  0 x   3  ;  1 2 2
Từ những nhận xét trên, ta có bảng biến thiên của hàm y  g x trên  3  ;  1 như sau:
Vậy hàm số g  x đồng biến trên 1;  1 . Chọn A Câu 50.16:
Cho hàm số f  x . Hàm số y  f ' x có đồ thị như hình vẽ 2 x  4x  3
Hàm số g x  f x   1 
đồng biến trên khoảng nào dưới đây? 2 A.  ;  2   . B.  3  ;  1 . C. 0;  1 . D.  1  ;0 . Lời giải Trang 21
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Chọn B 2 x  4x  3
Ta có: g  x  f  x   1 
 g 'x  f 'x   1  x  2 . 2
Hàm số đồng biến  g ' x  0  f ' x   1  x  2 (1)
Đặt x 1  t . Bất phương trình (1) có dạng: f 't  t 1
Xét hai hàm số y  f 't và y  t 1: t  2  ;0
Dựa vào đồ thị ta có: f 't    t 1 t  2   x     x   Ta có g  x 2 1 0 3 1 '  0    x 1 2    x  1 Câu 50.17:
Cho hàm số f (x) liên tục trên R và có đồ thị f '(x) như hình vẽ . Tìm số điểm cực trị của hàm số 2 y  f (x  x) ? Trang 22
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 A. 10 . B. 11. C. 12 . D. 13 . Lời giải Chọn B 1 Ta có 2
y '  (2x 1) f '(x  x) ; 2
x  x  m có nghiệm khi và chỉ khi m   . 4
Dựa vào đồ thị ta thấy đồ thị hàm f '(x) cắt trục hoành tại 5 điểm trong đó 1 điểm có hoành độ 1
nhỏ hơn  và có một tiệm cận . 4 1
Khi đó ứng với mỗi giao điểm có hoành độ lớn hơn  và 1 điểm không xác định thì y '  0 4
có hai nghiệm . Từ đây dễ dàng suy ra hàm 2
y  f (x  x) có 11 cực trị. Câu 50.18:
Cho hàm số y  f (x) có đạo hàm trên  . Đồ thị của hàm số y  f '(x) như hình vẽ. Tìm
các khoảng đơn điệu của hàm số 2
g(x)  2 f (x)  x  2x  2020 . y 2 -1 O 1 3 x -2
Mệnh đề nào dưới đây đúng?
A. Hàm số g  x nghịch biến trên 1;3 .
B. Hàm số g  x có 2 điểm cực trị đại.
C. Hàm số g  x đồng biến trên  1  ;  1 .
D. Hàm số g  x nghịch biến trên 3; . Lời giải Chọn C Ta có g '( )
x  2 f '(x)  2x  2  2 f '(x)  (x 1  ) .
Dựa vào hình vẽ ta thấy đường thẳng yx 1
 cắt đồ thị hàm số y  f '(x) tại 3 điểm: ( 1  ; 2  ), (1;0), (3;2). Trang 23
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 y 2 -1 O 1 3 x -2 Dựa vào đồ thị ta có x  1 g '(x) 0 2 f '(x) (x 1) 0        x  1  . x  3    
g x    f x  x   1 x 1 '( ) 0 2 '( ) ( 1)  0  3 x   
g x    f x  x   x 1 '( ) 0 2 '( ) (
1)  0  1 x  3
Câu 50.19: Cho hàm số y  f  x có bảng xét dấu như hình vẽ 1 5
Tìm khoảng đồng biến của hàm số 5 4 3
y  g(x)  2 f (1 x)  x  x  3x . 5 4 A.  ;  0. B. 2;  3 . C. 0;2 . D. 3;   . Lời giải Chọn B
Coi f ' x   x  2 x   1 x x  
1 có bảng xét dấu như trên. 4 3 2 g '( ) x  2
 f '(1 x)  x  5x  6x Ta đi xét dấu g '( ) x  P Q . Với: P  2  f '1 x  2
 3 x2 x1 xx  2x3 x2 x1 x Bảng xét dấu của P Trang 24
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 4 3 2 2
Q  x  5x  6x  x  x  2 x   3 Bảng xét dấu của Q Từ hai BXD của ,
P Q . Ta có P  0,Q  0 với x  2;3 nên g'( ) x  P Q  0 với x  2;3. Câu 50.20:
Cho hàm số y  f  x có đồ thị hàm số y  f  x như hình vẽ
Xét hàm số g  x  f  x 3 2
 2x  4x  3m  6 5 với m là tham số thực. Điều kiện cần và đủ
để g  x  0 với mọi x   5; 5   là 2 2 2 2 A. m  f  5 . B. m  f 0 . C. m  f  5 . D. m  f  5 . 3 3 3 3 Lời giải Chọn A
Ta có g  x  0 với mọi x   5; 5    f  x 3 2
 2x  4x  3m  6 5  0 với mọi x   5; 5       f  x 3 2
 2x  4x  6 5  3m với mọi x  5; 5   Trang 25
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  max    
với mọi x   5; 5 *   .    2 f  x  3 2x 4x 6 5 3m  5; 5  
Đặt h x  f  x 3 2  2x  4x  6 5 . x  0 
Ta có h x  f  x 2 2
 6x  4 , hx  0  f  x 2  3  x  2  x   5  . x  5 
Dựa vào đồ thị ta thấy f  x 2  3
 x  2 với mọi x   5; 5 
  h x luôn đồng biến trên  5; 5 
  max h x  h 5  2 f .    5 5; 5   2 Vậy  
*  2 f  5  3m  m  f  5 . 3 Câu 50.21:
Cho hàm số f (x) có đồ thị của hàm số y  f ’(x) như hình vẽ: 3 x Hàm số 2 y  f (2x 1) 
 x  2x nghịch biến trên khoảng nào sau đây? 3 A.  6  ;  3 . B. 3;6 . C. 6;. D.  1  ;0 . Lời giải Chọn D Ta có: y  f x   x  x   f x   x  2 2 ’ 2 ’(2 1) 2 2 2 ’(2 1) 1  3 x  3
Nhận xét: Hàm số y  f (x) có f ’(x)  1  3  x  3 và f ’(x)  1  x  3
Do đó ta xét các trường hợp: Với 6   x  3   1  3  2x 1 7  suy ra ’
y  0 hàm số đồng biến (loại)
Với 3  x  6  5  2x 1  11suy ra ’
y  0 hàm số đồng biến (loại)
Với x  6  2x 1 11suy ra ’
y  0 hàm số đồng biến (loại) Với 1   x  0  3   2x 1 1
 nên 2 f ’(2x 1)  2 và   x  2 3 1  3  2 suy ra ’ y  0
hàm số nghịch biến (nhận). Câu 50.22:
Cho hàm số f  x có bảng xét dấu của đạo hàm như sau Trang 26
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Hàm số g  x  f  x   3 3
2  x  3x đồng biến trên khoảng nào dưới đây? A. 1;  . B.  ;    1 . C.  1  ;0 . D. 0;2 . Lời giải Chọn C
Ta có gx   f x      2 3 2 x  3 Với x  1
 ;0  x  21;2  f x  2  0 lại có 2
x  3  0  y  0, x   1  ;0 .
Vậy hàm số g  x đồng biến trên khoảng  1  ;0 . Chú ý: +) Ta xét x 
     x     f x   2 1;2 1; 2 3;4 2  0; x  3  0
Suy ra hàm số nghịch biến trên 1;2 nên loại hai phương án A, D. +) Tương tự ta xét
x     x     f x   2 ; 2 2 ;0
2  0; x  3  0  y  0, x    ;   2.
Suy ra hàm số nghịch biến trên khoảng  ;
  2 nên loại phương án B. Câu 50.23:
Cho hàm số f x có đạo hàm, liên tục trên  . Hàm số y  f x có đồ thị như hình sau. 3
Hàm số g x  3 f  2 x  2 4 2
 x  3x đồng biến trên khoảng nào dưới đây? 2  3 A.   3;   1 . B. 0;1 . C.  1  ;  1 . D. 1;   .  2  Lời giải Chọn D
Ta có g x  x f  2 x   3  x  x  x  f    2 x   2 6 . 2 6 6 6 2  x 1 x  0 gx  0   . f    2 x  2 2  x 1  0 Đặt 2 t  x   f  2 x   2 2
2  x 1  0  f t   t 1  0  f t   t 1 .
Đồ thị của hàm số y  f t và y  t 1 như hình vẽ sau Trang 27
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 t  
Từ đồ thị, ta có f t 1  t  1   ( t  1
 là nghiệm đơn và t  1 là nghiệm kép). t  1         f  x x
x  2   x  2 2 2 1 1 2 2 1     2 x  2 1 x   3 x  0 
Suy ra g x  0  x  1 
( x  0, x  1 là nghiệm đơn và x   3 là nghiệm kép).  x   3 Bảng xét dấu g x  1    7  3 (vì g  3. f     0      ). 2  4 4      
Vậy hàm số đồng biến trên khoảng 1;0 và 1;  . Câu 50.24: Cho hàm số 5 4 3 2
y  ax  bx  cx  dx  ex  f với a,b, c, d,e, f là các số thực, đồ thị của
hàm số y  f  x như hình vẽ dưới đây. Hàm số y  f   x 2
1 2  2x 1 đồng biến trên khoảng nào sau đây? y 2 1 1 x 3 O 3 Trang 28
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  3   1 1  A.  ; 1    . B.  ;   . C.  1  ;0 . D. 1;3 .  2   2 2  Lời giải Chọn C y 2 1 1 x 3 O 3
Cách 1: Ta có: g  x  f   x 2
1 2  2x 1 g x  2  f 1 2x 4 .x Có: g x  0  2
 f 1 2x  4x  0  f '1 2x  2  x (1).
Đặt t  1 2x, bất phương trình  
1 trở thành f t  t 1.
Vẽ đường thẳng y  x 1. Trên cùng đồ thị, ta thấy đường thẳng y  x 1 nằm trên đồ thị hàm
số f  x trên khoảng 1;3  f t  t 1 1 t  3 11 2x  3  1   x  0.
Vậy hàm số g  x đồng biến trên khoảng 1;0.
Cách 2: Ta có: g  x  f   x 2
1 2  2x 1 gx  2  f 1 2x 4 .x
Có g x  0  f '1 2x  2
 x  f '1 2x  (1 2x) 1.
Xét sự tương giao của đồ thị hàm số y  f 't  và y  t 1,t 1 2x. t    x  x 
Từ đồ thị ta có f t  1 '  t 1  .  Khi đó g  x 1 2 1 0 '  0   .   t  3 1   2x  3 x  1  Ta có bảng xét dấu
Dựa vào bảng xét dấu ta thấy hàm số đồng biến trên các khoảng 1;0.
Cách 3: Cách trắc nghiệm.
Ta có: g  x  f   x 2
1 2  2x 1 gx  2  f 1 2x 4 .x
Ta lần lượt thử các đáp án.  3 
Thử đáp án A: Chọn x  1  ,25  ; 1   g '    1  ,25  2  f '3,  5  5.  2 
Nhìn đồ thị f ' x ta thấy f '3,5  0  g ' 1
 ,25  0  loại đáp án#A.  1 1 
Thử đáp án B: Chọn x  0, 25  ;  g '   0,25  2  f '0,5 1.  2 2 
Nhìn đồ thị f ' x ta thấy f '0,5  0  g '0,25  0  loại đáp án B. Trang 29
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Thử đáp án C: Chọn x  0  ,5 1  ;0  g ' 0  ,5  2  f '2  2.
Nhìn đồ thị f ' x ta thấy f '2  0  2
 f '2  0  g ' 0
 ,5  0  Chọn đáp án C.
Thử đáp án D: Chọn x  21;3  g '2  2  f ' 3   8.
Nhìn đồ thị f ' x ta thấy f ' 3    0  2  f ' 3
   0  g '2  0  loại đáp án D. Câu 50.25:
Cho hàm số y  f  x có đạo hàm f  x có đồ thị như hình dưới đây.
Hàm số g  x  f  x   3 2 3
1  27x  54x  27x  4 đồng biến trên khoảng nào dưới đây?  2   2  A. 0;  . B. ;3   . C. 0;3 . D. 4; .  3   3  Lời giải Chọn D Cách 1:
Ta có: g  x  f  x     x  3   x  2  g x   f  x     x  2 3 1 3 1 3 3 1 ' 3 ' 3 1 3 1  23x   1   
Có g x   f  x     x  2 ' 0 ' 3 1 3 1  2 3x   1 (1).
Đặt t  3x 1, bất phương trình   1 trở thành f t 2 '  t  2t . Vẽ Parabol 2 y  x  2 .
x Trên cùng đồ thị, ta thấy đồ thị hàm số f ' x nằm trên đồ thị hàm số 2
y  x  2x trên các khoảng  ;    1 và 3;. x  0 t  1 3x 1  1  Suy ra f 't 2 t 2t         4 . t  3 3x 1  3 x   3 Trang 30
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  4 
Vậy hàm số g  x đông biến trên các khoảng  ;  0 và ; .    3  Cách 2:
Ta có: g  x  f  x     x  3   x  2  g x   f  x     x  2 3 1 3 1 3 3 1 ' 3 ' 3 1 3 1  23x   1   
Có: g  x   f  x     x  2 ' 0 ' 3 1 3 1  2 3x 1.
Xét sự tương giao của đồ thị hàm số y  f 't  và 2
y  t  2 t,t  3x   1 . t  1 2 
Từ đồ thị ta có: f 't  t  2t  t   1(nghieäm keù ) p . t   3 x   0 3x 1  1   2
Khi đó g'x  0  3x 1  1  x   (nghieäm keùp).   3 3x 1   3 x   3 Ta có bảng xét dấu.
Dựa vào bảng xét dấu ta thấy hàm số đồng biến trên các khoảng  ;  0 và 3;. Câu 50.26:
Cho hàm số f (x) liên tục trên  có f (1)  0 và có đồ thị hàm số y  f (x) như hình vẽ. Hàm số 2
y  2 f (x 1)  x đồng biến trên khoảng A. 3; . B.  1  ;2 . C. 0; . D. 0;3 Lời giải Chọn D Đặt 2
g(x)  2 f (x 1)  x  g (x)  2[ f (  x 1) (x 1) 1] Trang 31
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Dựa vào đồ thị hàm số y  f (x) và đồ thị hàm số y  x 1 ta có: g (
 x)  0  f (x 1)  (x 1) 1  1  x 1  2  0  x  3 Bảng biến thiên:
Dựa vào bảng biến thiên, hàm số 2 y  2 f (x 1)  x
đồng biến trên khoảng 0;3 . Câu 50.27:
Cho hàm số f  x . Hàm số y  f  x có đồ thị như hình sau. Hàm số g(x)  3 f 1 (  2x)  8x3  x
21 2  6x đồng biến trên khoảng nào dưới đây? A.  2 ; 1  . B.  ; 3   1 . C.   1 ; 0 . D.  ; 1 2 . Lời giải Chọn A Ta có g'(x)  6 f ' 1 (  2x)  24 2 x  42x  6 g'(x)  0  f ' 1 (  2x)  4 2 x  7x 1 (*) 1  t
Đặt 1  2x  t  x  2 1 2  t  1  t 2 3 3
Ta có (*) trở thành f '(t)  4.   7.
1  f '(t)  t  t  .  2  2 2 2 2 3 3
Ta vẽ parapol (P) : y  x  x  trên cùng hệ trục Oxy với đồ thị y  f  x như hình vẽ 2 2 3 33
sau ( đường nét đứt), ta thấy (P) có đỉnh I ( ;
) và đi qua các điểm   3 ; 3 , ; 1 2  ,   1 ; 1 . 4 16 Trang 32
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 3 3
Từ đồ thị hàm số ta thấy trên khoảng  1 ;
3 ta có f '(t)  t  t   3  t  1 2 2  3   1 2x  1   1  x  2
Vậy hàm số g(x) nghịch biến trên khoảng ; 1 ( 2). Câu 50.28:
Cho hàm số y  f  x liên tục trên  và có đạo hàm f  x thỏa mãn: f  x   2
1 x  x  5 Hàm số y  f x   3 3
3  x 12x nghịch biến trên khoảng nào sau đây? A. 1;5 . B. 2;  . C.  1  ;0 . D. ;  1 . Lời giải Chọn B Ta có: f  x   2
1 x x  5 suy ra f  x       x  2 3 1 3   x  3  5  
  x  4 x  2 x  2.
Mặt khác: y  f x   2 3.
3  3x 12    x   x   x      2 3 4 2 2 x  4  3
 x  2x  2x  5 .  5   x  2 
Xét y  0  3 x  2 x  2 x  5  0   . x  2
Vậy hàm số y  f x   3 3
3  x 12x nghịch biến trên các khoảng  5
 ; 2 và 2;  . Câu 50.29:
Cho hàm số y  f  x , hàm số f  x 3 2
 x  ax  bx  ca, ,
b c   có đồ thị như hình vẽ
Hàm số g  x  f  f  x nghịch biến trên khoảng nào dưới đây?  3 3  A. 1; . B.  ;  2   . C.  1  ;0 . D.   ;   . 3 3    Lời giải Chọn B Trang 33
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Vì các điểm  1
 ;0,0;0,1;0 thuộc đồ thị hàm số y  f  x nên ta có hệ: 1 a  b  c  0 a  0   c  0  b   1 f  x 3  x  x  f '  x 2  3x 1 1  a b c 0      c  0  
Ta có: g  x  f  f  x  g x  f  f  x. f ' x 3 x  x  0  3 x  x  1
Xét g x  0  g x  f  f 'x. f x  0  f  3 x  x 2 3x   1  0         3x  x  1  2 3x 1 0  x  1   x  0   x 1,325  x  1  ,325   3 x    3 Bảng biến thiên
Dựa vào bảng biến thiên  g  x nghịch biến trên  ;  2   Câu 50.30:
Cho hàm số y  f  x có đạo hàm f  x 2 '  x  2x  3, x   .  Có bao nhiêu giá trị
nguyên của tham số m thuộc đoạn  10
 ;20 để hàm số g x  f  2 x  x  m 2 3  m 1 đồng biến trên 0;2? A. 16. B. 17. C. 18. D. 19. Lời giải Chọn C t  3 Ta có f 't  2
 t  2t  3  0   *. t  1
Có g  x   x   f  2 ' 2 3 ' x  3x  m Vì 2x  3  0, x
 0;2 nên g x đồng biến trên 0;2  g 'x  0, x  0;2  f  2 ' x  3x  m  0, x  0;2 2 x  3x  m  3, x  0;2 2 x  3x  m  3, x  0;2     (**) 2 x  3x  m  1, x    0;2 2 x  3x  m 1, x    0;2 m  3  10 m  13 Có h x 2
 x  3x luôn đồng biến trên 0;2 nên từ (**)    m 1 0    m  1  m 1  0;20 Vì 
 Có 18 giá trị của tham số m. m Trang 34
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Vậy có 18 giá trị của tham số m cần tìm. Câu 50.31:
Cho hàm số y  f  x có đạo hàm liên tục trên  và đồ thị của hàm số y  f ' x như hình vẽ. 1
Đặt g  x  f  x  m   x  m  2
1  2019 với m là tham số thực. Gọi S là tập các giá trị 2
nguyên dương của m để hàm số y  g  x đồng biến trên khoản 5;6.Tổng các phần tử của S bằng: A. 4 . B. 11. C. 14 . D. 20. Lời giải Chọn C
Ta có g ' x  f ' x  m   x  m   1
Đặt h x  f ' x   x  
1 . Từ đồ thị y  f ' x và đồ thị y  x 1 trên hình vẽ ta suy ra    h  x 1 x 1  0  x 3   x  m  m   x  m 
Ta có g x  h x  m 1 1 1 1 '  0    x m 3    x  m  3
Do đó hàm số y  g  x đồng biến trên các khoảng m 1;m   1 và m  3; m 1 5  5  m  6
Do vậy, hàm số y  g  x đồng biến trên khoảng 5;6  m 1 6  m  2 m 3  5
Do m nguyên dương nên m1;2;5;  6 , tức S  1;2;5;  6
Tổng các phần tử của S bằng 14. Trang 35
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Câu 50.32:
Cho hàm số y  f  x là hàm đa thức có đồ thị hàm số y  f  x như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số m , m  Z ,  2020  m  2020 để hàm số   g  x  f  2 x  2 2 8  mx x  x  6 
 đồng biến trên khoảng 3;0  3  A. 2021. B. 2020. C. 2019. D. 2022. Lời giải Chọn B
Ta có g x  xf  2 x   mx  2 2 4 x  2x  3 .
Hàm số g  x đồng biến trên khoảng 3;0 suy ra g x  0, x   3  ;0 .  xf  2 x   mx  2
x  x    x  
  f  2x  m  2 2 4 2 3 0, 3; 0 2
 x  2x  3  0,x  3;0 f  2 x 2 2 
 f x   2mx  2x  3, x   3  ;0  m  x    2 , 3;0 2 x  2x     3 f  2 x   m  max .   2 2 3;0 x  2x  3  Ta có 2
  x    x   f  2 3 0 0 9
x   3 dấu “  ” khi 2 x  1  x  1 . 
 x  x     x  2 2 2 2 3
1  4  0   x  2 x  3  4, x  3; 0 1 1 
 , dấu “  ” khi x  1  . 2 x  2x  3 4 f  2 x  3  3  Suy ra   , x   3
 ;0 , dấu “  ” khi x  1  . 2 2 x  2x  3 2.4 8 f  2 x  3  max   .   2 2 3;0 x  2x  3 8 3
Vậy m   , mà m   , 2020 m  2020 nên có 2020 giá trị của tham số m thỏa mãn bài 8 toán. Câu 50.33:
Cho hàm số f  x . Hàm số y  f  x có đồ thị như hình sau. Trang 36
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Có tất cả bao nhiêu giá trị nguyên dương của tham số m đề hàm số g(x)  4 f (x  ) 2
m  x  2mx  2020 đồng biến trên khoảng ; 1 ( 2). A. 2 . B. 3 . C. 0 . D.1. Lời giải Chọn A
Ta có g'(x)  4 f '(x  m)  2x  2m x  m
g'(x)  0  f '(x  m)   (*) 2 t
Đặt t  x  m thì (*)  f '(t)   2 x
Vẽ đường thẳng y   trên cùng hệ trục Oxy với đồ thị y  f  x như hình vẽ sau 2 t  2  t  0 m  2  x  m
Từ đồ thị ta có f '(t)       2 t  4 x  m  4
Hàm số g(x) đồng biến trên khoảng ; 1
( 2)  g'(x)  0 x   2 ; 1  m  2  1  2  m 2  m  3     m  4  1 m  3
Vì m nguyên dương nên m   3 ; 2 .
Vậy có hai giá trị nguyên dương của m đề hàm số g(x) đồng biến trên khoảng ; 1 ( 2). Câu 50.34:
Cho hàm số f  x có đạo hàm f  x   x   1  x   1  x  4; x
  .Có bao nhiêu số   x 
nguyên m  2020 để hàm số g  x 2  f  m 
 đồng biến trên 2;   .  1 x  A. 2018. B. 2019 . C. 2020 . D. 2021 Lời giải Chọn B 3  2  x  Ta có: g x        . x   f m 2 1  1 x  Trang 37
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Hàm số g  x đồng biến trên 2;    gx  0; x  2;   3  2  x    f 
 m  0; x  2;   2     x   1  1 x    2  x  f   m  0; x  2;       1 x  x  1
Ta có: f  x  0   x   1  x  
1  x  4  0  1 x  4  2  x  m  1; x   2;     1  2  x  1 x Do đó: f   m  0; x  2;         1 x  2  x 1    m  4; x  2;   2  1 x  x Hàm số h  x 2 
 m ; x 2;   có bảng biến thiên: 1 x
Căn cứ bảng biến thiên suy ra: Điều kiện 2 không có nghiệm m thỏa mãn. Điều kiện   1  m  1
  m 1,kết hợp điều kiện m  2020 suy ra có 2019 giá trị m
thỏa mãn yêu cầu bài toán.
Nhận xét: Có thể mở rộng bài toán đã nêu như sau:
Cho hàm số f  x có đạo hàm f x   x   1  x   1 x  4; x
  .Có bao nhiêu số  2  x 
nguyên m  2020 để hàm số g  x  f  h 
m đồng biến trên 2; .  1 x  Câu 50.35:
Cho hàm số y  f  x có đạo hàm '      1 x f x x
e , có bao nhiêu giá trị nguyên của
tham số m trong đoạn  2
 019;2019 để hàm số y  g x  f  x 2 ln  mx  mx  2 nghịch biến trên  2 1;e  . A. 2018. B. 2019. C. 2020. D. 2021. Lời giải Chọn B 1 Trên  2
1;e  ta có g ' x  . f 'ln x  2mx  m  ln x 1 2x   1 m x
Để hàm số y  g  x nghịch biến trên  2
1;e  thì g x  x    x  m  x   2 ' ln 1 2 1 0, 1;e   ln x 1 2x   1 m  0, x   2 1;e  ln x 1   m, x   2 1;e  2x 1 Trang 38
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 1   x  2ln x Xét hàm số h  x ln 1  trên  2 1;e  , ta có '  x h x   0, x    2 1;e , từ đây suy ra 2  2x 1 2x   1
m  1. Vậy có 2019 giá trị nguyên của m thỏa bài toán. Trang 39

Tính đơn điệu của hàm số liên kết Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số