Tính đơn điệu hàm giá trị tuyệt đối Toán 12

Tính đơn điệu hàm giá trị tuyệt đối Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

23 12 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 1

NHÓM TOÁN VD – VDC

 I

 Hàm s

 

y f x

ng bin trên





;





khi và ch khi



 





 

0, ;







    













. 

 





 

0, ;







    













 Hàm s

 

y f x

ng bin trên

 

;



khi và ch khi



   

 

0, ;

  





  













. 

   

 

0, ;

  





  













 Các dng bin

 

y f x

trên





;a

 

;



ta thc hi.

 Hàm s hi nghch bic li

TÍNH ĐƠN ĐIỆU HÀM GIÁ TRỊ TUYỆT ĐỐI

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 2

NHÓM TOÁN VD – VDC



 

y f x



 



h 

Câu 1. Có bao nhiêu giá tr nguyên ca tham s

 hàm s

 

5 5 1 8y x x m x    

nghch bin trên khong

 

;1 ?

Li gii:

Chn D

Xét hàm s

   

5 5 1 8.f x x x m x    

TH1:

 

0fx

có nghim

;1x

thì hàm s

 

y f x

không th nghch bin trên

khong

 

;1 .

TH2:

 

0fx

không có nghim

;1x

Ta có:

   

5 10 5 1 .f x x x m



   



     

5 2 2

5 5 1 8y x x m x f x f x      

nên

( ). ( )

()

f x f x

Hàm s nghch bin trên

 

;1

khi và ch khi

vi

 

;1x  

( ). ( ) 0

, ;1

f x f x

( ) 0

, ;1

( ) 0

( vì

 

lim



 

)

     

 

5 10 5 1 0, ;1

1 5 17 0

f x x x m x





       







  





 

max 2 1 1

2 1, ;1

2. 2

m x x

m x x x





     

      





















3 17

1 3.

2. 2



     

Câu 2. Có bao nhiêu giá tr a tham s

 hàm s

21y x mx  

ng

bin trên khong

 

1; ?

Li gii:

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 3

NHÓM TOÁN VD – VDC

Chn C

Xét hàm s

 

2 1.f x x mx  

TH1:

 

0fx

có nghim

1;x

thì hàm s

 

y f x

không th ng bin trên

khong

 

1; .

TH2:

 

0fx

không có nghim

1;x

Ta có:

 

6.f x x m







   

21y x mx f x f x    

nên

( ). ( )

()

f x f x

Hàm s ng bin trên khong

 

1; 

khi và ch khi

vi

 

1;x  

( ). ( ) 0

, 1;

f x f x

( ) 0

, 1;

( ) 0

( vì

 

lim



 

)

2 1 0

, 1;

x mx

2 1 0

3 1;2;3mm

Câu 3.         

  

   

4 3 2

3 4 12y x x x m   



 

;1 

. B.

. C.

. D.

Li gii

Chn D

-

 

4 3 2

3 4 12f x x x x m   

 

3 2 2

12 12 24 12 2f x x x x x x x



      

 

0fx



















BBT:



 

y f x



 

;1 

50m  

5m













 

5;6;7;8;9m







NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 4

NHÓM TOÁN VD – VDC

Câu 4. Tp hp tt c các giá tr ca tham s

 hàm s

34y x x m   

ng bin trên

khong

 

3; 

là





2;

. B.





;2

. C.





;4

. D.





4;

Li gii

Chn D

Xét hàm s

( ) 3 4f x x x m   

Ta có

( ) 3 6f x x x





( ) 0















Bng BT ca hàm s

()fx





()fx









()fx

4m



4m



8m

 th hàm s

()y f x

c bng cách gi nguyên ph th ca hàm s

()y f x

 phía trên tri xng ph th  i lên trên

qua trc

Vy hàm s

()y f x

ng bin trên

 

3; 

(3) 0f

40m  

4m

Câu 5. Tìm tt c các giá tr ca

 hàm s

22y x x mx   

ng bin trên khong

 

1; ?  

1m 

. B.

m

. C.

01m

. D.

0m 

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 5

NHÓM TOÁN VD – VDC

i

Chn C

t

 

22f x x x mx   

 

46f x x x m



   

22y x x mx   

 

fx

Ta có

 

lim



 

nên hàm s ng bin trên

 

1;  

khi và ch khi

   

 

0, 1;

f x x



     













 

4 6 0, 1;

x x m x



       













 

4 6 , 1;

m x x x



       













 

max 4 6

m x x

 



  

























01m  

Câu 6. Có bao nhiêu giá tr nguyên ca tham

thu n

 

10;10

 hàm s

     

3 2 2

3 1 3 2 3y x m x m m x m m       

ng bin trên khong

 

0;1

. B.

. C.

. D.

Li gii

Chn B

Xét hàm s

       

3 2 2

3 1 3 2 3f x m x m x mx mm      

trên khong

 

0;2

     

' 3 6 1 3 2f x x m x m m     

   

3 2 1 2x m x m m



     



 

'0fx













 

2mm

Nhn xét:

 













T bng bin thiên, suy ra hàm s

 

y f x

ng bin trên khong

 

0;1

khi

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 6

NHÓM TOÁN VD – VDC

   

0;1 ; 2

0 1 2 1 0

3 0 3

0;1 3;

m m m





      



  





   

   







Mà

nguyên thuc khong

 

10;10

nên có 10 giá tr

tha mãn yêu cu bài

toán.

Câu 7. Có bao nhiêu s nguyên

thuc khong

 

4;4

 hàm s

y x x mx   

ng

bin trên

 

1; 

. B.

. C.

. D.

Li gii

Chn A

Xét hàm s:

   

3 2 2

f x x x mx f x x x m



       

Ta có:

1 m



  

ng hp 1:

0 1 0 1mm



      

. Suy ra

   

0, 1;f x x



    

Vy yêu cu bài toán

 









  

    

  



   









Kt hp vu kin

 

; 4;4mm  

c

 

3; 2; 1;0;1m   

. Ta có 5 giá tr ca

tho mãn yêu cu bài toán .

ng hp 2:

01m



   

. Suy ra

 

'0fx

có 2 nghim phân bit

,xx

 

xx

Ta có bng bin thiên:

Vy yêu cu bài toán

 

1 1 0

(1) 0

x x m





























       

  



  

















Vy tt c có 5 giá tr ca

tho mãn yêu cu bài toán.

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 7

NHÓM TOÁN VD – VDC

Câu 8. Tng tt c các giá tr nguyên thuc

 

5;5

c hàm s

   

( ) 1 2 3

     g x x m x m x

ng bin trên

 

1;5

là:

. B.

1

. C.

. D.

Li gii

Chn B

Xét hàm s

   

( ) 1 2 3

     f x x m x m x

 

( ) 2 1 2 3



    f x x m x m

( ) 0















Hàm s

()gx

ng bin trên

 

1;5

khi và ch khi xy ra mng hp sau:

+,TH1:

 

( ) ®ång biÕn trªn 1;5

(1) 0













3 2 1

3 4 0











  























Kt hu kin

nguyên và thuc

 

5;5

c

 

2;3;4;5



+,TH2:

 

( ) nghÞch biÕn trªn 1;5

(1) 0













5 3 2

3 4 0











  





















  

Kt hu kin

nguyên và thuc

 

5;5

c

 

1; 2; 3; 4; 5

     

Vy tng tt c các s nguyên ca

 hàm s ng bin trên

 

5;5

là:

1

Tác gi 

Câu 9. Có bao nhiêu giá tr nguyên thun

 

2019;2019

ca tham s thc

 hàm s

   

3 2 3 4y x m x m m x    

ng bin trên khong

 

0;4

4033

. B.

4032

. C.

2018

. D.

2016

Li gii

Chn A

Xét hàm s

     

3 2 3 4    f x x m x m m x

trên khong

 

0;4

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 8

NHÓM TOÁN VD – VDC

     

' 3 6 2 3 4f x x m x m m    

   

3 2 2 4x m x m m



    



 

'0fx













 

4mm

Nhn xét:  th hàm s

 

y f x

m

 

0;0O

ng hp 1: Nu

0m 

T bng bin thiên, suy ra

hàm s

 

y f x

ng bin trên khong

 

0;4

   

0;4 0;m

4m

Kt hp vi

0m 

, ta có

4m 

ng hp 2: Nu

04mm  

40m   

T bng bin thiên, suy ra

hàm s

 

y f x

ng bin trên khong

 

0;4

   

0;4 0; 4m  

44m  

0m

Kt hp vi

40m  

, ta có

0m 

ng hp 3: Nu

40m

4m  

T bng bin thiên, suy ra

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 9

NHÓM TOÁN VD – VDC

hàm s

 

y f x

ng bin trên khong

 

0;

nên hàm s

 

y f x

ng

bin trên khong

 

0;4

vi mi

4m 

.Vy















Mà

nguyên thuc khong

 

2019;2019

nên có 4033 giá tr

tha mãn yêu

cu bài toán.

Câu 10. Có bao nhiêu giá tr   a

5m 

 hàm s

y x x x m



   

ng

bin trên

(0, )

i

Chn B

Xét hàm s

y x x x m



   

ta có

1 0, .y x x x R



     

Suy ra hàm s

y x x x m



   

ng bin trên

  u kin hàm s

y x x x m



   

ng bin trên

(0, )

là

(0)

0y 

0.m

Li có



5m 

vy có 4 giá tr ca

Câu 11. Có bao nhiêu s 

 hàm s

4y x mx  

ng bin trên khong

 

1; .

. B.

. C.

. D.

Li gii

Chn B

Ta có:

 

4 4 0

x mx khi x mx



    







     





 

5 4 0

x m khi x mx



   







    





TH1:

5 0 5

' , 1 , 1 5.

x m m

y x x m

x mx







  





        

  



  









NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 10

NHÓM TOÁN VD – VDC

TH2:

' , 1.

x mx



  



  



  





H vô nghim vì

 

lim 4 .

x mx



   

Vy

 

1,2,3,4,5 .















Câu 12. Có bao nhiêu s nguyên

thuc khong

 

10;10

 hàm s

2 2 3y x mx  

ng

bin trên khong

 

1;

. B.

. C.

. D.

Li gii

Chn A

Xét hàm s:

 

2 2 3f x x mx  

có

 

' 6 2f x x m

TH1: Hàm s

 

ng bin trên khong

 

1;

và

 

10f 

 

3 1;

6 2 0

5 2 0

m x x





   







    

  













Suy ra có 12 giá tr

tha yêu cu

TH2: Hàm s

 

nghch bin trên khong

 

1;

và

 

10f 

ng hp này không xy ra do

 

lim



 

Vy có tt c 12 giá tr

tha yêu c bài.

Câu 13. Cho hàm s

| 1|y x mx  

. Gi

là tp tt c các s 

sao cho hàm

s ng bin trên





1; 

. Tính tng tt c các phn t ca

Li gii

Chn A

 

' . 5

| 1|

x mx

y x m

x mx







 hàm s ng bin trên





1; 

thì

 

  

1 5 0 (*)g x x mx x m    

1x

Vi

0m 

ta có

 

0 1 .5 0, 1g x x x    

Vi

0m 

. Do

m



 

luôn có 1 nghim là

. Ta chú ý

 

lim



 

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 11

NHÓM TOÁN VD – VDC

Do vu kin c

 

0gx

1x

là





5m 

Vi

1m 

2m 

;

3m 

;

4m 

;

5m 

, thay vào (*) kim tra BXD th



nhn

1; 2mm

;

3m 

;

4m 

;

5m 

Vy

{1;2;3;4;5}S 

. Tng các phn t ca

là

Câu 14. Cho hàm s

( ) | 2 2|f x x mx m   

. Có bao nhiêu giá tr nguyên ca tham s

thuc

[ 9;9]

 hàm s ng bin trên khong

(0;2)

Li gii

Xét hàm

( ) 2 2g x x mx m   

. Ta có

'( ) 2 2g x x m

Hàm s

()fx

ng bin trên khong

(0;2)

khi và ch khi

(0) 0

, (0;2)

'( ) 0













hoc

(0) 0

, (0;2)

'( ) 0













ng hp 1.

(0) 0 2 0

, (0;2) 2 0

'( ) 0 2 0

g x m

  



      



  



ng hp 2.

(0) 0 2 0 2

, (0;2)

'( ) 0 2 0 0

g m m

g x m m

    

  

   

  

   

  

vô nghim.

Do m là nguyên thuc

[ 9;9]

nên

{-2, -1, 0}m

. Ch

Câu 15. Cho hàm s

3 2 2

1 1 2

( ) (2 3) ( 3 )

3 2 3

f x x m x m m x      

. Có bao nhiêu giá tr nguyên

ca tham s

thuc

[ 9;9]

 hàm s nghch bin trên khong

(1;2)

. B.

. C.

. D.

Li gii

Xét hàm

3 2 2

1 1 2

( ) (2 3) ( 3 )

3 2 3

g x x m x m m x      

. Ta có

'( ) (2 3) ( 3 ) ( )( 3).g x x m x m m x m x m          

Hàm s

()fx

nghch bin trên khong

(1;2)

khi và ch khi

(2) 0

, (1;2)

'( ) 0













hoc

(2) 0

, (1;2)

'( ) 0













ng hp 1.

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 12

NHÓM TOÁN VD – VDC

(2) 0 ( ; 2] [1; )

2 2 4 0

, (1;2) , (1;2) 1.

'( ) 0 [ 1;1]

( )( 3) 0

x x m

g x m

x m x m

     



   



       

  

  

    





ng hp 2.

(2) 0 [ 2;1]

2 2 4 0

, (1;2) , (1;2) 2.

'( ) 0 ( , 2] [2; )

( )( 3) 0

x x m

g x m

x m x m

  



   



        

  

     

    





Do m là nguyên thuc

[ 9;9]

nên

{1, -2}m

. Ch

Câu 16. Có bao nhiêu giá tr nguyên

 

20;20m

 hàm s

4 3 2

3 4 12   y x x x m

nghch

bin trên khong

 

1; 

. B.

. C.

. D.

Li gii

Tác gi:Nguyn Thanh Tho Facebook:Nguyn Thanh Tho

Chn D

Ta có

 

4 3 2 4 3 2

3 4 12 3 4 12 0



      







       





x x x m x x x m

Nên

 

3 2 4 3 2

12 12 24 3 4 12 0



     









      





x x x x x x m

Yêu ci

TH1:

4 3 2

12 12 24 0

3 4 12 0



  







   





x x x

x x x m

4 3 2

3 4 12 , 1 5        m x x x x m

TH2:

4 3 2

12 12 24 0

3 4 12 0



   







   





x x x

x x x m



H này vô nghim.

Vy

 

5;6;...;19m

. Có

s nguyên tha mãn.

Câu 17. Có bao nhiêu giá tr nguyên không âm

 hàm s

9  y x mx

ng bin trên

khong

 

1; 

. B.

. C.

. D.

Li gii

Chn A

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 13

NHÓM TOÁN VD – VDC

Ta có

 

4 2 4 2

9 9 0



    







     





x mx x mx

Nên

 

3 4 2

4 2 9 0



   









    





x mx x mx

Yêu ci

TH1:

4 2 0











  





x mx







  















  









 

2 0;1;2   mm

TH2:

4 2 0



  



  



  





x mx

H này vô nghim vì khi

 x

thì

9   x mx

Câu 18. Cho hàm s

   

3 2 3 1

y x m x m x     

. Gi

là tp hp tt c các giá tr



 hàm s ng bin trên khong

 

4;

. Chn m

sai?

có 4 phn t.

B. Tng các giá tr ca

thuc

bng 6.

C. Tích các giá tr ca

thuc

bng 0.

D. Giá tr

ln nht thuc

bng 4.

Li gii

Chn D

t

   

( ) 3 2 3 1

f x x m x m x     

Ta có:

 

'( ) 3 2 3f x x m x m    

Hàm s ng bin trên khong

 

4;

khi và ch khi:

 

'( ) 0, 4;

(4) 0

f x x

   













hoc

 

'( ) 0, 4;

(4) 0

f x x

   













NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 14

NHÓM TOÁN VD – VDC

TH1:

 

'( ) 0, 4;

(4) 0

f x x

   













     

 

3 2 3 0, 4;

16 4 3 2 3 0

x m x m x



       







    





 

, 4;





   





















min































  











TH2:

 

'( ) 0, 4;

(4) 0

f x x

   













H vô nghim vì

   

 

lim 3 2 3

x m x m



     

Vy

mm



 

0;1;2;3m

. Chn D.

Câu 19. Cho hàm s

   

2 5 2018f x x m x   

. Có bao nhiêu giá tr nguyên ca tham s

thuc

 

2019;2019

 hàm s ng bin trên khong

 

1;3

3032

. B.

4039

. C.

. D.

2021

Li gii

Chn A

Xét hàm s

   

2 5 2018f x x m x   

o hàm

   

3 2 5f x x m  

Hàm s

 

y f x

ng bin trên khong

 

1;3

 thì ca hàm s trong khong

 

1;3

phi có hình d

ng hp 1: Hàm s

 

ng bin trong khong

 

1;3

và không âm trên

 

1;3

tc

là :

 

   

 

2 3 5 1;3

1012

0 1;3

2024 2 0

m x x

f x x







   





   

  





  











NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 15

NHÓM TOÁN VD – VDC

ng hp 2: Hàm s

 

nghch bin trong khong

 

1;3



 

1;3

tc là :

 

   

 

2 3 5 1;3

1012.

1012

0 1;3

2024 2 0

m x x

f x x







   





   

  





  











Kt hp vu kic kt qu

   

2019;4 1012;2019m  

. Vây có

3032

giá tr ca

Câu 20. Cho hàm s

| 1|y x mx  

. Gi

là tp tt c các s t nhiên

sao cho hàm s

ng bin trên

 

1; 

. Tính tng tt c các phn t ca

Li gii

Chn A

 

' . 3

| 1|

x mx

y x m

x mx







 hàm s ng bin trên

 

1; 

thì

 

  

1 3 0 (*)g x x mx x m    

1x

Vi

0m 

ta có

 

0 1 .3 0, 1g x x x    

Vi

0m 

. Do

m



 

luôn có 1 nghim là

. Ta chú ý

 

lim



 

Do vu kin c

 

0gx

1x

là





3m 

Vi

1m 

2m 

thay vào (*) kim tra BXD th



nhn

1; 2mm

Vi

3m 

thì

 

  

3 1 3 3g x x x x   

có mt nghim

1x 



do vy trên min

 

1; x

thì

 

0gx



trái yêu cu bài toán.

Vy

{0;1;2}S 

. Tng các phn t ca

là

Bài 19. Có tt c bao nhiêu giá tr nguyên ca tham s

 hàm s

     

3 1 3 2y g x x m x m m x     

ng bin trên nn





0;

bit rng

2021 2021m  

2020

. B.

2021

. C.

2022

. D.

2019

i

Chn A

Xét hàm s:

     

3 1 3 2y f x x m x m m x     



D 

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 16

NHÓM TOÁN VD – VDC

Ta có:

   

' 3 6 1 3 2y x m x m m    

 

' 0 2,

y m m m





    







Bng bin thiên

Gi

 

là ph th ca hàm s

   

3 1 3 2y x m x m m x    

nm trên

Gi

 

là ph th ca hàm s

   

3 1 3 2y x m x m m x    

ni

Gi

 



là ph th i xng vi

 

qua

 th hàm s

     

3 1 3 2y g x x m x m m x     

gm

   





Da vào bng bin thiên ta thy: hàm s

     

3 1 3 2y g x x m x m m x     

ng

bin trên nn





0;

khi và ch khi

 















2m  

Kt hp vu kin

2021 2021m  

, ta suy ra có

2020

giá tr ca

tha mãn yêu

c bài.

Câu 21. Gi





;Sa  

là tp tt c các giá tr ca tham s

 hàm s

3 3 1y x x mx m    

ng bin trên khong

 

2;  



bng

. A.

3

. B.

. C.

. D.

2

Li gii

Chn B

t

   

3 2 2

3 3 1 3 6f x x x mx m f x x x m



        

TH1:

   

 

0, 2 ;

f x x



     













   

 

   

0, 2 ;

3 6 0, 2 ; 3 6 , 2 ;

19 19

f x x

x x m x m x x x



     





               

  



  













NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 17

NHÓM TOÁN VD – VDC

 

max 3 6

m x x

  



  







  













TH2:

   

 

0, 2 ;

f x x



     













   

 

   

0, 2 ;

3 6 0, 2 ; 3 6 , 2 ;

19 0 19

f x x

x x m x m x x x



     





               

  



  



  









 

min 3 6

m x x

 



  











Vì

 

lim 3 6



   



hàm s

36y x x  

không có giá tr nh nht. Vì vy TH2

không có giá tr

tha mãn.

Vy tp các giá tr

cn tìm là





19 ;S  



 

y f x



 





Câu 22. Tính tng

tt c các giá tr nguyên ca tham s

n

 

10;10

 hàm s







ng bin trên

 

1; 

55S

. B.

54S

. C.

3S

. D.

5S

Li gii

Tác gi: Chungthanh Vu Facebook Chungthanh Vu

Chn B.

Xét hàm s







vi

2  xm

, có

 







Hàm s







ng bin trên

 

1; 

khi xy ra mng hp sau :

+ TH 1:

 

2 3 0

, 1 1

2 1;







  





  







  





     





  







  







  



    



NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 18

NHÓM TOÁN VD – VDC

+ TH 2:

 

2 3 0

2 1;







  











    











  



    



Vy

 

1;  m

, li do

 

10;10











suy ra

 

2;3;4;5;6;7;8;9;10m

, vy

54S

Câu 23. Tìm m  hàm s

21





ng bin trên

 

1; 

m

 

1;1 \ .









  m

m

Li gii

Tác gi: Ai Pha Facebook AI Pha

Chn B

t

()









xm



 

'( )







 hàm s ng bin trên

   

'( ). ( )

1; ' 0, 1;

()

      

f x f x

 

'( ) 0, 1;

(1) 0

   













f x x

(I) hoc

 

'( ) 0, 1;

(1) 0

   













f x x

(II)

Ta có (I)

3 1 0









     















; (II)

3 1 0









    















Vy

m

Câu 24. Có bao nhiêu s nguyên ca tham s m  hàm s

2 2 2

x x m

  





ng bin trên





3; ?

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 19

NHÓM TOÁN VD – VDC

. B.

. C. vô s. D.

Li gii

Tác gi

Chn A

Tnh:

 

\ 1 .D 

Xét hàm s

 

2 2 2

x x m

  





Có

 

x x m









   

 

f x f x

y f x f x y

   

Hàm s ng bin trên









3; ' 0, 3;yx      

   

 





 





. 0 0

, 3; , 3;

0 ' 0

f x f x f x

f x f x









         









(vì

 

lim



 

)

 





2 2 2

, 3;

x x m



  









    



















2 2 2 0

, 3;

2 2 0

x x m



   



    



  













 





 

2 2 max 2

2 2 2 2 2 3

, 3;

2 min 2

m x x

m x x m

m x x





   



      





     

  

































. Vì

 

2; 1;0;1 .mm    

Vy có 4 giá tr nguyên ca tham s m tha mãn yêu cu bài toán.

Câu 25. Tìm tt c các giá thc ca tham s

 hàm s

y x m

  

ng bin trên





1; 

1.m 

1 1.m  

1.m 

0.m 

Li gii

Tác gi: Long Giang Vo Facebook Long Giang Vo

Chn C

+ Ta có:

y x m x m



     





  

  

  

  











NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 20

NHÓM TOÁN VD – VDC

+ Hàm s ng bin trên





1; 





' 0, 1;y   









, 1; 0, 1;





  





 



        

































 

0, 1; , 1;

max *

x m m x





           







   





+ Xét hàm s

 





, 1;g x x x

     

 





' 1 0, 1;       g x x





 





 

1; 1;

max max 1 1g x x g

 



     





Vy

 

* 1.m

Câu 26. Bit rng tp hp tt c các giá tr ca

sao cho hàm s



  



ng

bin trên

 

2;

là

 

;ab

.Tính

.ab

10

. B.

9

. C.

. D.

7

Li gii

Tác gi: Nguyn Hin Facebook Nguyn Hin

Chn A

Xét hàm

s

 

f x x



  



. Ta có

 











   

y x f x f x



    



nên

   

 

f x f x





Hàm s ng bin trên

 

2;

khi và ch khi





vi

 

2;x  

   

 

, 2;

f x f x









   









 

, 2;









   









( vì

 

lim



 

)

 

2 1 1

, 2; , 2;

2 1 1

m m x





  





    





       





   













NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 21

NHÓM TOÁN VD – VDC

 

2 1 1 9

2 8 0

1 11 1 11

2 10 0

2 1 min 1 9

m m max x

m m x







      





  



      



  



    





Câu 27.

Tìm tt c các giá tr thc ca m sao cho hàm s







ng bin trên khong

 

1; 

1m 

. B.

1m 

. C.

11m  

. D.

11m  

Li gii

Tác gi: Nguyn Th Huyn, Facebook: Nguyn Th Huyn

Chn D.



1x 

t

 







 









   

 

f x f x

y f x f x y

   

Hàm s ng bin trên

 

1; 

nu

 

' 0 1;yx   

     

' . 0 1;f x f x x    

TH1:

   

 

' 0 1;

f x x





   









     

  













TH2:

   

 

' 0 1;

f x x





   









    

  













Vy





1;1m

là giá tr cn tìm.

Câu 28. Tính tng tt c các giá tr a

 hàm s

x mx







ng bin

trên khong

 

2;

Li gii

Tác gi:Phc Thành Facebook: pham duc

thanh

Chn A

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 22

NHÓM TOÁN VD – VDC

Xét hàm s

 

x mx







. Ta có:

 

2 3 2 2

x x m

  









   

x mx

y f x f x



  



nên

   

 

.f x f x





Hàm s ng bin trên khong

 

2;

khi và ch khi





vi

 

2;x   

   

 

, 2;

f x f x









    









 

, 2;







    











( do

 

lim



 

)

 

2 3 2 2

0, 2;

x x m







  



    







 

10 4 0

2 3 2 2 0, 2;

x x m x











       





 

2 2 3 2, 2;

m x x x













      







 

2 max 2 3 2

m x x

 













   



































m   

Vì





nên

 

1;2m

. Vy tng các giá tr a

là 3.

Câu 29. Có bao nhiêu s nguyên

 hàm s







ng bin trên khong

 

2;

. B.

. C.

. D.

Li gii

Tác gi: Thanh Vân. Facebook: Thanh Van

Chn A

t

 







. Tnh:

 

\3Dm  

. Ta có

 









Hàm s ng bin trên khong

 

2;

   

 

0, 2;

f x f x



     

     

. 0, 2;f x f x x



    

ng hp 1:

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 23

NHÓM TOÁN VD – VDC

   

 

2 3 0

0, 2;

3 2 1 1 2

2 5 2

f x x

m m m











   





          

  









   









ng hp 2:

   

 

2 3 0

0, 2;

3 2 1

2 2 5

f x x

m m m











   





      

  









    









(không có m tha mãn).

Vy

12m  

, mà

m

 

1;0;1;2m  

. Vy có 4 s nguyên m tho mãn.

Câu 30. Có bao nhiêu giá tr nguyên âm ca

 hàm s



  



ng bin trên





5;

. B.

. C.

. D.

Li gii

Tác gi:Trn Nhung. Facebook: Trn Nhung

Chn C

Tnh:

 

\2DR

Xét hàm s

 

f x x



  



o hàm:

 

   

1 4 3

m x x m

   



  





   

y f x f x

nên

   

 

.f x f x





Hàm s ng bin trên





5;

khi và ch khi





0, 5;yx



    

   

 





 





. 0 0

, 5; , 5;

f x f x f x

f x f x









         











(vì

 

lim



 

)

 





, 5;





  







    



















, 5;

m x x



  



    



   









 





 

min 3 9

5 3.5 9

8 31

5 4.5 3

max 4 3

m x x





  



  



     



   









Mà

nguyên âm nên ta có:

 

8; 7; 6; 5; 4; 3; 2; 1m        

Vy có

giá tr nguyên âm ca

 hàm s



  



ng bin trên





5;

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 24

NHÓM TOÁN VD – VDC

Câu 31. Có tt c bao nhiêu giá tr nguyên ca tham s

 hàm s

x x m

  





ng

bin trên khong

 

3; 

. B.

. C.

. D. Vô s .

Li gii

Tác gi: Nguyn Nga Nvc. Facebook: Nguyn Nga Nvc

Chn A

t

   

 

2 3 2 2 2

x x m x x m

f x f x

     



  





   

 

.f x f x

y f x f x y



   

Hàm s ng bin trên khong

 

3; 

khi

 

0, 3;yx



    

   

 

0, 3;

f x f x



     

   

 

, 3;

f x f x









    









 

   

, 3; ,do lim









      











x f x

 

   

0, 3;

f x x













    





 

2 2 2 0, 3;

x x m x















       



 

2 2 2 , 3;

x x m x













      



 

2 2 2 , 3;

x x m x











     





      









Ta có

m

nên

 

4; 3; 2; 1;0;1;2m    

Câu 32. Tìm tt c các giá tr ca tham s

 hàm s

1xm







ng bin trên khong

 

1; 

m 

hoc

2m 

. B.

m

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 25

NHÓM TOÁN VD – VDC

2m 

. D.

m

Li gii

Tác gi:Nht Thin. Facebook: Nht Thin

Chn C

t

 

1xm







 

x m



 







 hàm s

ng bin trên khong

 

1; 

thì

   

 

' 00

f x x



  

 

1;x 

ng hp 1:

   

 

' 0, 1;

x



  











2 1 0







































 





m 

ng hp 2:

   

 

' 0, 1;

x



  











2 1 0













































m 

V hàm s ng bin trên khong

 

1; 

thì

m



 

y f x



 





Câu 33. Cho hàm s

2 2 1

y x x x     

. Có bao nhiêu giá tr

 hàm s

nghch bin trên

(0;1)

. C.

. D.

i

Chn A

t

( ) 2 2 1

f x x x x     

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 26

NHÓM TOÁN VD – VDC

Ta có

()

2 2 2 2



   



Do hàm s liên tc ti

0; 1xx

 hàm s nghch bin trên

(0;1)

ng

hp sau:

ng hp 1:

 

, 0;1

( ) 0, 0;1

2 2 2 2

(1) 0

f x x





   



  





















 

, 0;1

2 2 2 2



   

















 

0;1

min

2 2 2 2 2 3 0

x x m













      











ng hp 2:

 

, 0;1

( ) 0, 0;1

2 2 2 2

(1) 0

f x x





   



  





















 

, 0;1

2 2 2 2



   

















 

0;1

max

2 2 2 2













































(vô nghim).

nguyên nên

nhn các giá tr sau

3; 2; 1;0  

Câu 34. Có bao nhiêu giá tr nguyên ca tham s

 

5;5m

 hàm s

3 2 3y x x m   

nghch bin trên

 

2;3

. B.

. C.

. D.

Li gii

Chn B

Xét hàm s

 

3 2 3f x x x m   

Ta có:

   

x x x

f x f x





   



NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 27

NHÓM TOÁN VD – VDC

Cho

 

0 2 3 0 2



      f x x x x

Ta thy

   

0, 2;3f x x



  

nên hàm s

 

nghch bin trên

 

2;3



3 2 3y x x m   

nghch bin trên

 

2;3

thì

 

3 0 6 6 3 0

f m m



      

 

5;5m

nên

 

2; 3; 4m    

Câu 35. Có bao nhiêu giá tr nguyên ca tham s

 

0;10m

ð hàm s

23y x m x x   

ðng bin trên khong

 

1; 

. B.

. C.

. D.

Li gii

Tác gi Thúy. 

Thúy

Chn A



D 

+ Xét hàm s

 

23f x x m x x   

 

f x m









+ Hàm s ng bin trên khong

 

1; 

   

 

   

 

0, 1;

f x x







   























   

















*) TH1:

     

0, 1; 1 0, 1;

f x x m x





         



   

2 3 1 0 , 1; .x x m x x        

t

1, 0 2 0 0t x t t mt t        

m , t



   

Xét

()

f t





( ) 0 t > 0



  



.BBT:

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 28

NHÓM TOÁN VD – VDC

T BBT ta có

   

 

0, 1;

1 . 2 0

f x x









   







  

   



  













*) TH2:

     

0, 1; 1 0, 1;

f x x m x





         



   

2 3 1 0 , 1; .x x m x x        

t

 

1, 0 2 0 * , 0t x t t mt t        

+ Mà





lim 2 2 0

t mt





   

nên vi mi giá tr ca

luôn có giá

tr ca

 nh  VT ca

 

l nào ca



TH2 tha mãn.

Vy có

giá tr nguyên ca m tha mãn là

 

0;1;2;3;4;5;6;7;8;9;10

Câu 36. Cho hàm s

 

22f x x x x m    



là tham s thc.

là tp hp tt

c các giá tr nguyên ca

n

 

2019;2019

 hàm s

 

ng bin trên

khong

 

1;  

. S phn t ca tp

là

A. 2018. B. 2017. C. 2019. D. 4039.

Li gii

Tác gi:Nguy

Chn A

Xét hàm s

 

22g x x x x m    

trên khong

 

1;  

Ta có,

 

1 1 2 2

' 1 0, 1

2 2 2 2

x x x x

g x x

x x x x

    

      

   

(Do

   

1 2 2 1 1 1 0, 1x x x x x x            

)

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 29

NHÓM TOÁN VD – VDC

Vy hàm s

 

nghch bin trên khong

 

1;  

Suy ra, hàm s

   

f x g x

ng bin trên khong

 

1;  

   

0, 1 1g x x    

Do hàm s

 

liên tc trên





1;  

và nghch bin trên khong

 

1;  

nên hàm

s

 

nghch bin trên





1;  

Vy

 





 

max 0gx

 





 

1 2 0gm   

2m  

Vy

 

2019 ; 2018;...; 2S    

A.

Câu 37. 



31y x x m   





 

1; 

. B.

. C.

. D. Vô s.

Li gii

Tác gi:Nguyn Vit Tho. Facebook: Vit Tho

Chn A

-

 

31f x x x m   

 



  



Trên

 

1; 

 

0fx





BBT:



 

y f x



 

1; 

3 2 1 0m   

3 2 1m   













 

5; 4; 3; 2; 1m      







Câu 38. Có bao nhiêu giá tr nguyên ca tham s

 hàm s

4 2 3 5 5y x x x m     

ng bin trên khong

(1; )

Li gii

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 30

NHÓM TOÁN VD – VDC

Chn A

Xét hàm s

( ) 4 2 3 5 5f x x x x m     

 nh trên . Ta có

4( 1)

'( ) 5







Vi

1 '( ) 0x f x  

()fx

ng bin trên

 

1;

V  hàm s

()y f x

ng bin trên

(1; ) (1) 0 10 4 6 0fm        

10 4 6 2 6 2 6mm        

Mà

 

, 4; 3; 2 ; 1; 0 ;1; 2 ; 3; 4mm      

suy ra ch

Câu 39. Cho hàm s

( ) | 3 2 5 |y f x x x m m     

.Hi

thuc khong nào trong các

kho hàm s

()fx

ng bin trên

(1; )





;0

. B.

(1;4)

. C.

( ;2)

. D.





3;

Li gii

Chn A

t

( ) 3 2 5g x x x m m    

Ta có

( ) 2 0 (1; ).

g x x



      



+D thy

()gx

liên tc trên





1;

và

( ) 0 x (1; )gx



    

nên

()gx

ng bin trên





1;

(1) 0g

5 4 0mm   

(*)

Nên

( ) | ( )|y f x g x

ng bin trên





1;

(1) 0f

kt hp vi (*) ta có :

5 4 0





   

















 



  





.Mà









;0 ;1m   

Câu 40. 





6y x x m   



 

0;3

. B.

. C.

. D.

Li gii

Tác gi: Nguyn Th Thu Huyn. Facebook:

Thu Huyn

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 31

NHÓM TOÁN VD – VDC

Chn D



 

0;6D 

-

 

6f x x x m   

 

0 3.

f x x





    



BBT:



 

y f x

ng 

 

0;3

0m













 

0;1;2;3;4;5;6;7;8;9m





Câu 41. Tng các giá tr nguyên ca tham s

 hàm s

    

3 9 5

y x x x

có

m

cc tr là.

2016

. B.

1952

. C.

2016

. D.

496

Li gii

Xét hàm s

 

    

3 9 5

f x x x x

Ta có

 



   

3 6 9 0f x x x













Ta có bng bin thiên

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 32

NHÓM TOÁN VD – VDC

 

   

















f x f x

y f x

f x f x

nên

? Nu

  00

thì

 

 0fx

có nghim



, ta có bng bin thiên ca hàm s



ng hp này hàm s 

m cc tr.

? Nu

   32 0 64

thì

 

 0fx

có nghim



,ta có bng bin thiên ca

hàm s 

ng hp này hàm s 

m cc tr.

? Nu







  











0 64

32 0

thì

 

     

3 9 5 0

f x x x x

có ba nghim

;

vi

    

1 2 3

13x x x

, ta có bng bin thiên ca hàm s 

ng hp này hàm s 

m cc tr.

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 33

NHÓM TOÁN VD – VDC

y, các giá tr nguyên ca

 hàm s 

m cc tr là

 

 1;2;3;...;63m

Tng các giá tr nguyên này là:

 



      

63 1 63

1 2 3 ... 63 2016

Câu 42. Có bao nhiêu giá tr nguyên ca

2020;2020m







 hàm s

11y x mx   

ng

bin

trên khong

 

1; 2

4042

4039

4040

4041

Li gii

Chọn D.

t

( ) 1 1f x x mx   

. Ta có

'( )

f x m





Vì hàm s liên tc ti

1; 2xx

 hàm s

()y f x

ng bin trên khong

 

1; 2

ng hp sau:

TH1:

 

0, 1; 2

'( ) 0, 1; 2

(1) 0



   



  





















f x x

 

 

1; 2

, 1; 2

min

2 1 1







  









    













TH2:

 

0, 1; 2

'( ) 0, 1; 2

(1) 0



   



  





















f x x

 

 

1; 2

, 1; 2

max







  









   













T (1) và (2) ta có











 

2020; 2020















nên có 4041 giá tr ca

tha mãn yêu cu bài toán.

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 34

NHÓM TOÁN VD – VDC



 

y f x



 





Câu 43.

Có bao nhiêu giá tr

  hàm s

   

3 2 2 2

( ) 3 3 5 12 3 cosy f x x x m x m x      

ng bin trên

 

0;

. B.

. C.

. D. Vô s

Li gii

Chn B

t

 

   

3 2 2 2

3 3 5 12 3 cosh x x x m x m x     

Ta có

 

   

2 2 2

3 6 3 5 12 3 sinh x x x m m x



     

         

3 1 12 1 sinx 3 1 sin 0 0; .h x x m x x



          

Vy hàm s

 

ng bin trên

 

0;



()y f x

ng bin trên

 

0;

. Thì

 

 

0 0 12 3 0 2;2h m m      

Kt lun: có 5 giá tr

nguyên tha mãn.

Câu 44. Các giá tr ca tham s

 hàm s

sin cosy x x m  

ng bin trên khong

;











là

2m 

. B.

2m 

. C.

1m 

. D.

1m 

Li gii

Tác gi:Thanh Nhã. Facebook: Nhã Thanh

Chn B

Xét hàm s

 

sin cosf x x x m  

2sin





  





 

2 cos

f x x







  







   

sin cosy x x m f x f x    

. Nên

   

 

.f x f x





Hàm s

sin cosy x x m  

ng bin trên khong

;











0; ;







    





   

 

, ; 1

f x f x













   













Vi

4 2 2 4 4

    

       

cos 0, ;

4 4 2

  

   

     

   

   

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 35

NHÓM TOÁN VD – VDC

 

0, ;

f x x







    





Nên

   

1 0, ;

f x x





    









  





 

2. 1 0 2mm     

Câu 45. Cho hàm s

sin .sin 1.y x m x  

Gi

là tp hp tt c các s t nhiên

sao cho

hàm s ng bin trên

0; .









Tính s phn t ca

. B.

. C.

. D.

Li gii

Chn A

Trên khong

0; ,









hàm s

sinyx

ng bit

 

sin , 0; 0;1

t x x t





   





   

sin .sin 1y x m x  

ng bin trên khong









khi và ch khi

 

1y g t t mt   

ng bin trên

 

0;1

Xét hàm s

 

1y f t t mt   

trên khong

 

0;1

có

 

3.f t t m





+) Khi

   

0: 3 0, 1m f t t t y f t t



       

ng bin trên

 

0;1

 

 

1y f t t  

ct trc hoành tm duy nht

1t 

 

1y g t t mt    

ng bin trên

 

0;1

0m

tha mãn

+) Khi

 

0: 0m f t





có 2 nghim phân bit

tt  

Hàm s

 

1y f t t mt   

ng bin trên các khong

;



 





và

;









TH1:

0 1 0 3

m      

Hàm s

 

1y f t t mt   

nghch bin trên khong







 ng bin trên

khong









Không có giá tr ca



 

1y g t t mt   

ng bin trên

 

0;1

TH2:

0 1 3

m     



 

1y g t t mt   

ng bin trên

 

0;1

thì

 

1 0, 0;1t mt t    

   

1, 0;1 , 0;1mt t t m t t

         

m  

Không có giá tr ca

tha

mãn.

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 36

NHÓM TOÁN VD – VDC

Vy ch có giá tr

0m 

tha mãn

Câu 46. Có bao nhiêu giá tr nguyên ca

thuc

 

5;5

 hàm s

cos 3 cosy x m x

nghch bin trên









. B.

. C.

. D.

Li gii

Chn B

t

costx

, vì

 

0; 0;1





  





. Vì

costx

là hàm s nghch bin trên









nên

Yêu cu bài toán tr thành tìm

nguyên thuc

 

5;5

 hàm s

3y t m t

ng

bin trên

 

0;1

. Xét

   

3 2 2

3 ; 0;1f t t m t t  

;

 

' 3 3f t t m

TH1: Nu

     

0 ' 0; 0;1m f t t f t     

ng bin trên

 

0;1

Mà

   

00f y f t  

ng bin trên

 

0; 

 

y f t

ng bin trên

 

0;1



0m 

tha mãn bài toán

 

TH2:

 

0 ' 0

m f t





   







;

 

f t t







  







*) Vi

0m 

, ta có BBT sau:

T BBT suy ra hàm s

 

||y f t

ng bin trên

 

0;m



     

0;1 0; 1 2mm  

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 37

NHÓM TOÁN VD – VDC

*) Vi

0m 

, ta có BBT sau:

T BBT suy ra hàm s

 

||y f t

ng bin trên

 

0; m



     

0;1 0; 1 3mm    

T

     

1 ; 2 ; 3

vy có

giá tr nguyên ca

tha mãn bài toán.



 

y f x



 





Du ca du tr tuyi

Câu 47. Có bao nhiêu giá tr a



9 3 1

ym   

ng bin

 

0;1

. B.

. C.

. D.

Li gii

Tác gi:Phm Tun. Facebook: Bánh Bao Phm

t

 

3 1;3

tt  

vì

 

0;1x

 

   

2. 1 . 1

2. 1

t t m t t m

y t t m t t m y

t t m



     



          

  

 hàm s ng bin

 

1;3t 

thì

 

 

2 1 . 1

0 1;3

t t t m

t t m

   



   

  

i mi giá tr ca

 

1;3t 

thì

21t 

>0 nên



 

0 1;3yt



  

thì :

 

 

 

1 0 1;3 1 1;3t t m t m t t g t t            

 

 

1;3

1 min 2 3m g t m     

Vy có 3 giá tr nguyên

 

1;2;3

tha mãn yêu cu bài toán.

Chn C

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 38

NHÓM TOÁN VD – VDC

Câu 48. Có bao nhiêu giá tr m        hàm s

4 .2 2

y m m



   

ng bin trên khong

(0;1)

2018

. B.

2019

. C.

. D.

Li gii.

Tác gi: Nguy

Chn A

Xét hàm s

( ) 4 .2 2

f x m m



   

(1) trên khong

(0;1)

t

t 

(1;2)t 

Hàm s (1) tr thành

( ) 2 . 2h t t mt m   

trên khong

(1;2)

. Suy ra

'( ) 2 2h t t m

Ta có

()y f x

ng bin trên khong

( ) (0;1)

(0) 0

(0;1)

( ) (0;1)

(0) 0

































ñoàng bieán treân

nghòch bieán treân

(*).

Vì hàm s

t 

ng bin trên

(0;1)



2 2 0 (1;2)

( ) (1;2)

(*)

2 2 0 (1;2)

( ) (1;2)

t m t



    

















   















ñoàng bieán treân

nghòch bieán treân







































. Vy có 2018 s  a ycbt.

Câu 49. Cho hàm s

2 2 1

3 2 5 (1)

y e e m





   

. Có bao nhiêu giá tr a tham

s  hàm s nghch bin trên khong

 

2;4

234

. B. Vô s. C.

. D. Không tn ti m.

Li gii

Tác gi:Nguyn Mng Facebook Cuong Nguyen

Chn C

t







, ta có

 

. . 0 2;3 ;

t e e x t e e













      









ng thi

và

s c chiu bin thiên.

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 39

NHÓM TOÁN VD – VDC

 tr thành

 

3 2 5 3 2 5 (2)y t t m t t m       

Ta có:

 

2 3 2 5 . 2 3 3 2 5 . 2 3

2 3 2 5 3 2 5

t t m t t t m t

t t m t t m

       





     

Hàm s

(1)

nghch bin trên khong

 

2;3



hàm s

(2)

ng bin trên khong

 

;ee

 

   

2 3 2 2 3

2 3 2 5 . 2 3

0 ; 3 2 5 0 ;

2 3 2 5

t t m t

t e e t t m t e e

t t m

   

          

  

 

( ) ; .

m g t t e e



    

+) Có

 

4 2 6 4 4 2

2 3 3 5 3 5 3 5

( ) 0 ; ( )

2 2 2 2

t e e e e e e

g t t e e g t m

      



        

Vu kin m là s c 40 giá tr ca m. Chn C

Câu 50. Có bao nhiêu giá tr  

( 2019;2020)m

,  hàm s

y e e m



  

nghch bin trên

 

1; e

401

. B.

. C.

2019

. D.

2016

Li gii

Tác gi: Nguyn Th Hoa Facebook Hoa nguyen

Chn A

t

2 2 2 2

( ) ( ) 2 2

x x x x

f x e e m f x xe xe





      

Ta có

 

()

( ) ( )

f x f x

y f x f x y



   

Yêu cu bài toán

 

0, 1; .y x e



   

(*)

Vì

 

1;xe

nên

 

2 2 0, 1;

xe xe e



    



     

* 0, 1;f x x e   

 

0, 1;

, 1;

e e m x e



     

    

Ta có giá tr ln nht ca hàm s

 

, 1;

y e e x e



  

là





nên

1618,18

m e e



  

Vy có

401

giá tr 

tha mãn.

Câu 51. Giá tr ln nht c hàm s

2xx

y e e m  

ng bin trên

 

1;2

là

. B.

ee

. C.

. D.

Li gii

Chn B

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 40

NHÓM TOÁN VD – VDC

t

     

22xx

f x e e m y f x f x     

Ta có

   

 

f x f x



Hàm s ng bin trên

   

1;2 ' 0 1;2yx   

   

 

1;2

f x f x







  









Vì

   

' 2 0 1;2

f x e e x    

Nên

     

 

' 0 1;2 0 1;2

1;2

y x f x x

m e e x m e e

      

       

Câu 52. Tìm tt c các giá tr ca

 hàm s

tan tan

8 3.2 2

ym   

ng bin trên

;













m 

. B.

m 

. C.

m 

. D.

m 

Li gii

Tác gi: Lê Minh Hùng. Facebook: Lê Minh Hùng

Chn C

t

tan

t

vì

;













suy ra

tan 1x 

nên

t 

      :

32y t t m   

(1).

 hàm s   ng bin trên

;













thì hàm s (1) ph ng bin trên

;











Xét hàm s

 

32f t t t m   

Ta có:

 

3 3 0,f t t t



   



   

y f t f t

nên

   

 

.f t f t





Hàm s ng bin trên

;











khi và ch khi

0, ;





   







NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 41

NHÓM TOÁN VD – VDC

 

0, ;

f t t



    







3 2 0, ;

t t m t



       







3 2, ;

m t t t



      







 



Xét hàm s:

 

3 2, ;

g t t t t



     







 

3 3 0,g t t t



   

. Vy hàm s

 

ng bin trên nên

 

g t g









T

 



suy ra:

1 29











 

y f x



 





Câu 53. Có bao nhiêu giá tr nguyên thuc khong

 

100;100

ca tham s

 hàm s

ln3 4y x x m  

ng bin

1; e





101

. B.

102

. C.

103

. D.

100

Li gii

Tác gi Hi Thu

Chn B

ln3 4y x x m  

u kin

0x 

Xét hàm s

 

g ln3 4x x x m  

trên

1; e





 

1 1 8

g 8 0, 1;

x x x e







      



 

gx

nghch bin trên

1; e







hàm s

 

g ln3 4y x x x m   

ng bin

1; e





ln3 4 0 4 ln3mm      

Mà

nguyên thuc khong

 

100;100

nên

 

99; 98;...; 1;0;1;2m   

Vy có 102 giá tr

nguyên tha mãn yêu cu bài toán.

Câu 54. Có bao nhiêu s nguyên

2020m 

 hàm s

 

ln 2y mx x  

nghch bin trên

 

1;4

A. 2018. B. 2019. C. 1. D. vô s.

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 42

NHÓM TOÁN VD – VDC

Li gii

Chn A

Tác giả: Nguyễn Văn Hà; Facebook: Hà Nguyễn Văn

Xét

   

ln 2f x mx x  

D thy

 

1;4 : 0 0x mx m    



   

1 0, 1;4f x x



    



 

luôn nghch bin trên

 

1;4

Yêu ci

   

4 0 ln 4 2 0 1,6

f m m      

Vy

 

2;2019m

có 2018 s nguyên tha mãn.

Câu 55. Có bao nhiêu s nguyên

thuc

 

2020;2020

 hàm s

 

ln 2 2 1y x x m mx    

ng bin trên

 

0;10

4038

. B.

2020

. C.

2017

. D.

2017

i

Tác gi: Cao Tung

Chn C

Ta xét hàm s

 

ln 2 2 1f x x x m mx    

trên

 

0;10

u kin hàm s 

 

2 0, 0;10x x m x    

 

2 , 0;10x x m x    

 

Ta li có

 

2 2 0x x x x   

vi mi

 

0;10x

u kin

 

cho ta

0m 

 

o hàm

 

f x mx

x x m









0m 

và

 

0;10x

nên

0; 4 0

x x m



  



suy ra

 

0fx





hàm s ng bin trên

 

0;10

T  hàm s

 

ln 2 2 1y x x m mx f x     

ng bin trên

 

0;10

u kin

 là

 

0fx

vi mi

 

0;10x

 

+) TH1: Xét

0m 



 

ln 2 1f x x x  

có

 

lim





 

không tha mãn

 

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 43

NHÓM TOÁN VD – VDC

+) TH2: Xét

0m 

, do hàm s

 

ng bin nên ta ch cn

 

00f 

 

ln 1 0m   

m e m e     

T c:

2020 me

   









 

2019; 2018; 2017;....; 3m     

có 2017 giá tr

tha mãn bài toán.

Câu 56. Có bao nhiêu s nguyên ca tham s

 n

 

3;3

 hàm s

 

ln 2y x mx  

ng bin trên na khong





1;3 ?

. C.

. D.

Li gii

Tác gi: Hoàng Th Hng Minh  Facebook: Minh Hoang.

Chn C

u kinh:

2 0.x mx  

Xét hàm s

 

ln 2f x x mx  

. Ta có:

 

x mx









Hàm s ng bin trên na khong





1;3

 



  

 



  

, 1;3 1

, 1;3 2





















































ng hp 1:

 









ln 2 0

1 , 1;3 3 0 , 1;3

x mx

x x m x

x mx



  



  



       









  

















 

1;3

max 2

, 1;3 2.

max 3 3







    





  





      





   









ng hp 2:

 









ln 2 0

2 , 1;3 3 0 , 1;3

x mx

x x m x

x mx



  



  



       









  













1;3

3 , 1;3 27 .

max 3

m x x m m



  







         









  

    











NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 44

NHÓM TOÁN VD – VDC

T ng hp suy ra

2m 

. Vì ch ly

 

3;3m

nên

 

2; 1;0; 1; 2; 3m  

Câu 57. Cho hàm s

 

ln 1y x mx m   

. Có bao nhiêu giá tr nguyên thuc khong

 

10;10

ca tham s

 hàm s ng bin trên khong









A. 10. B. 6. C. 9. D. 5.

Li gii

Tác gi: Nguyn Th Thu Trang

Chn D

t

 

ln 1f x x mx m   

Hàm s ng bin trên khong









 

0, ;1

0, ;1 1

0, ;1

0, ;1 2

0, ;1

x mx m x

f x x

x mx m x

f x x







     





















   



















   























     





















   



















   













+ Xét

0, ;1

x mx m x



     





 

1 , ;1

x m x x



     





, ;1



    







t

 







 

, ;1 , ;1

1 2 2

m x g x m x

   

        

   



   

Ta có:

 

g x x

  



 



  



 

0 ;1

2 ;1





  

















   









BBT ca hàm s

 

y g x

trên khong









NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 45

NHÓM TOÁN VD – VDC

T BBT ca hàm s

 

y g x

suy ra

 

g x m x



   





 

00mg  

 

2 







x mx m

 

1 2 , ;1

lim 0

x m x















    















ln 1 0









  









  









ln 1















































  









 

2 2 ;1

lim 0

x m x















    















ln 1 0



















  









suy ra không tn ti

Vy





. Mà

nguyên,

10 10  m

nên có 5 giá tr

tha mãn bài toán

Câu 58. Tng các giá tr

nguyên thuc

 

5;5

sao cho hàm s

 

ln 3 1y x x m   

nghch

bin trên

 

0;1

bng

. B.

. C.

. D.

Tác gi : Phan Th Yn_Facebook Phan Yên.

Li gii

Chn C

t

 

ln 3 1f x x x m   

, ta có

 

x x m









u kinh ca

 

là

30x x m

u kin c hàm s

 

y f x

nghch bin trên

 

0;1

là

   

3 0, 0;1 3 , 0;1 2x x m x m x x x m            

(1).

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 46

NHÓM TOÁN VD – VDC

Vi mi

 

0;1x 

, ta có

3 3 0x 

 u kin (1) ta suy ra

 

 

0, 0;1

f x x

x x m





   



u ki  hàm s

 

y f x

nghch bin trên

 

0;1

là

 

 

0, 0;1f x x  

 

 

ln 3 1 0, 0;1x x m x      

 

3 , 0;1m x x x

      

2 2,37m

   

nguyên thuc

 

 

5;5 3;4;5m  

Vy tng các giá tr ca

bng 12.

Câu 59. Có bao nhiêu giá tr nguyên ca tham s

 

10;10m

 hàm s

 

log 1y x x mx   

ng bin trên





1; 

. B.

. C.

. D.

Li gii

Tác gi: Nguyn Thanh Hùng. Facebook: Hùng

Nguyn

Chn A

t

 

log 1f x x x mx   

nên

 

1 ln3

x x m

x x mx





  

Hàm s ng bin trên

 

y f x

ng bin trên





1; 

 





, 1;





















   























ng hp 1:

 





 





log 1 0

, 1; 1 0 , 1;

3 2 0

x x mx

x x x mx x

x x m



   









          









  













3 2 2

, 1; , 1;

3 2 3 2

x x mx m x x

x x m m x x



     



       



   





NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 47

NHÓM TOÁN VD – VDC





 





 

min

min 3 2

m x x













   













ng hp 2:

 





 





log 1 0

, 1; 1 0 , 1;

3 2 0

x x mx

x x x mx x

x x m



   









          









  













3 2 2

1 0, 1; , 1;

x x m

x x mx

x x mx x x x m x

x x m







   



              















Ta có:









 

, 1; max ,m x x x m x x



        

Vì

 

lim



  

nên không tn ti

tha mãn

 



ng hp 2 không tn

ti giá tr nào ca

tha mãn yêu cu bài toán.

Suy ra

2m 

tha mãn yêu cu bài toán. Mt khác

 

10;10















nên có

giá tr ca

tha mãn yêu cu bài toán.

Câu 60. Tng các giá tr nguyên ca

trên

 

10;10



 

( ) lny g x x x m x    



 

1;3

là

. B.

100

. C.

. D.

105





Chn C

Xét hàm s

 

lnf x x x m x   



 

1;3



0x x m  



 

1;3x 



 

2 1 3 1

x x x m

x x m x x m

   

  



   

NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 48

NHÓM TOÁN VD – VDC



 



 

1;3

 

3 1 0 1

ln 0

3 1 0 2

ln 0

x x m

x x m x

x x m

x x m x





  







   







   















  







   









   











 

1;3x 



 

3 1 0

ln 0

x x m

x x m x



  



   





   







 

1;3x 

Ta có:

   

0, 1;3 , 1;3x x m x m x x x            



y x x  



 

1;3

ta suy ra

Ví dụ 1.

 

1;3

max

m x x m



    



   

3 1 0, 1;3 3 1, 1;3x x m x m x x x              



31y x x   



 

1;3

ta suy ra:

 

[ 1;3

]

max 3 1 1m x x m



     

Ngoài ra

 

   

ln 0, 1;3 , 1;3

x x m x x m x x e x



              



 

2 x

k x x x e



   

   

2 1 0, 1;3

k x e x x



       





 

, 1;3

m x x e x m e



        



 



me



 



 

3 1 0 1;3 19

ln 0 ln 0

x x m

x x m x m m

x x m x x x m x









  



           





       





NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020

https:/www.facebook.com/groups/toanvd.vdc Trang 49

NHÓM TOÁN VD – VDC



 

( ) lny g x x x m x    



 

1;3

khi và ch khi

me

, mà

   

 

10;10

nên

 

3;4;5;6;7;8;9;10m

      





Bấm Tải xuống để xem toàn bộ.

| 1/49

| | Tải xuống

Preview text:

NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
TÍNH ĐƠN ĐIỆU HÀM GIÁ TRỊ TUYỆT ĐỐI N H Ó M T O
 PHƢƠNG PHÁP GIẢI Á N     V
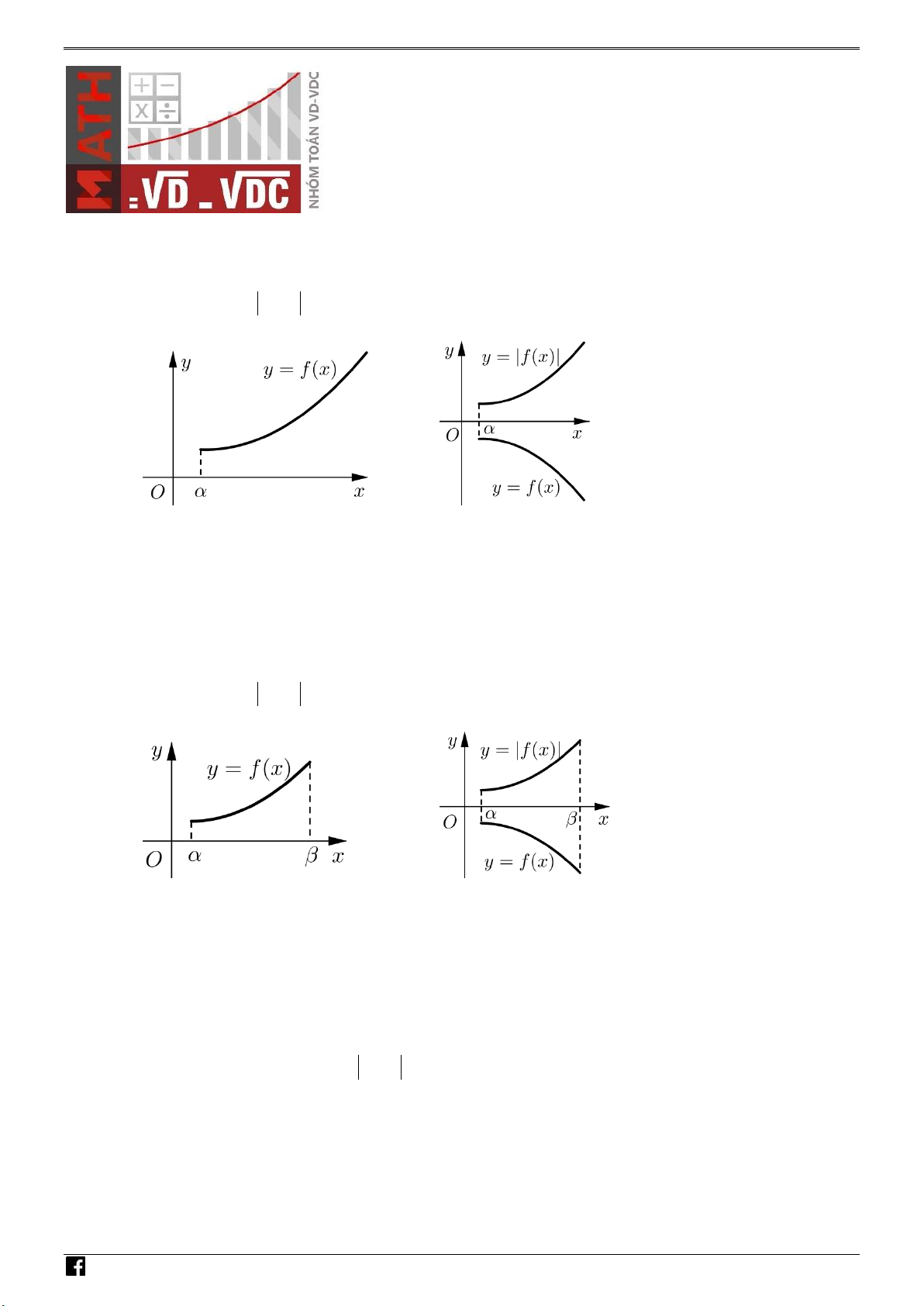
 Hàm số y
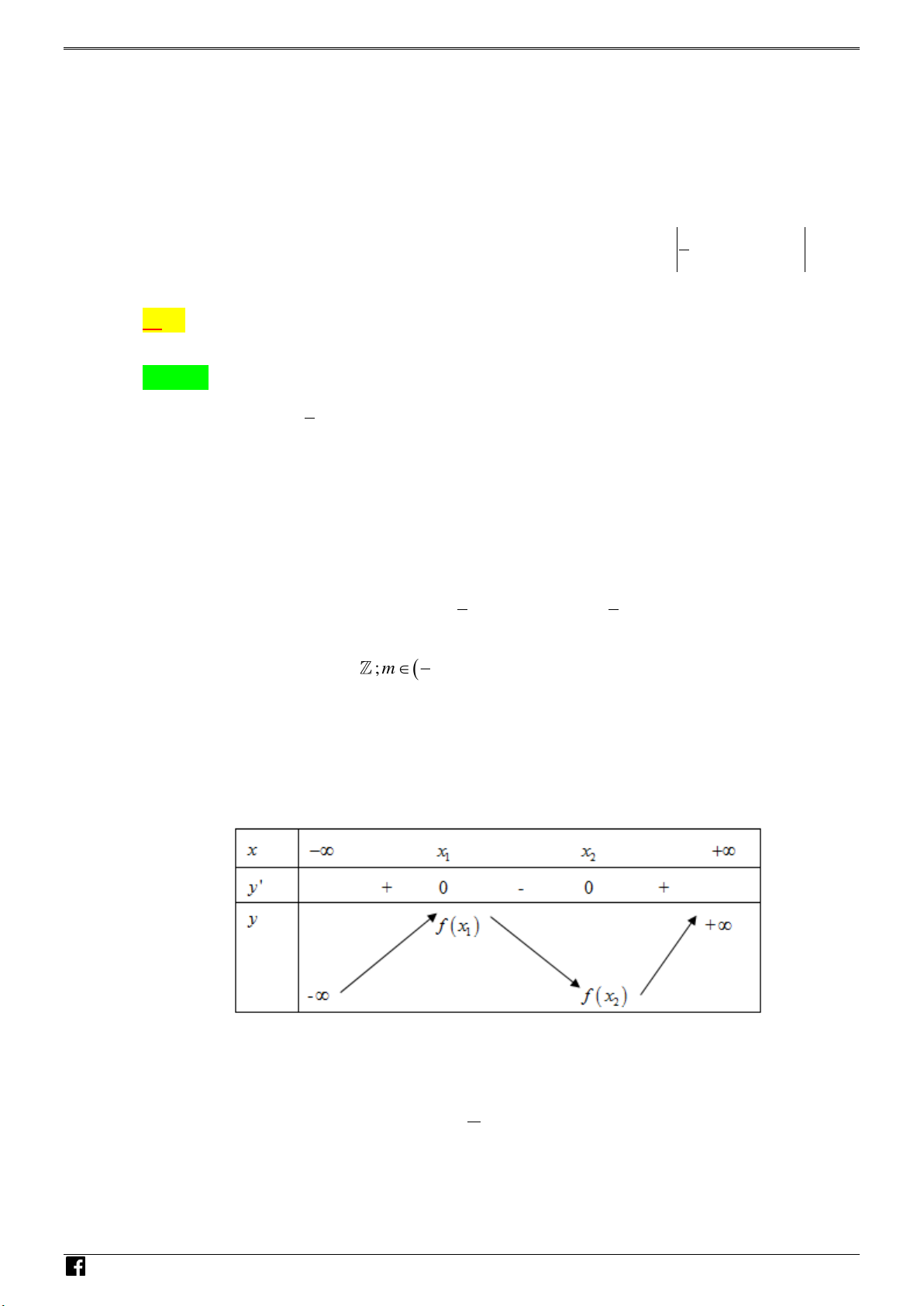
f  x đồng biến trên  ;  khi và chỉ khi D – VDC  y     0, x  ;    .   y     0  y     0, x  ;   .  y     0 N
 Hàm số y  f  x đồng biến trên ;  khi và chỉ khi H Ó M T O Á N V D – VDC  y     0, x  ;    .   y     0  y     0, x  ;   .  y     0
 Các dạng đồng biến y  f  x trên  ;
 a,;  ta thực hiện tương tự.
 Hàm số hỏi nghịch biến làm ngược lại
https:/www.facebook.com/groups/toanvd.vdc Trang 1 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
1. Dạng 1: Tìm điều kiện tham số m để hàm y  f  x với f  x là hàm số dạng đa
thức đồng biến, nghịch biến trên tập D cho trƣớc. Câu 1.
Có bao nhiêu giá trị nguyên của tham số m để hàm số 5 2
y  x  5x  5m  1 x  8 NH
nghịch biến trên khoảng ;1? Ó M A. 2. B. 0. C. 4. D. 1. T O Á Lời giải: N V Chọn D D – 5 2 VDC
Xét hàm số f x  x  5x  5m  1 x  8.
TH1: f x  0 có nghiệm x
;1 thì hàm số y  f x không thể nghịch biến trên 0 khoảng ;1.
TH2: f x  0 không có nghiệm x ;1 . 0
Ta có: f x 4
 5x 10x  5m 1.
f (x). f (x) Khi đó 5 2
y  x  x  m   x   f x 2 5 5 1 8
 f x nên y . 2 f (x)
Hàm số nghịch biến trên ;1 khi và chỉ khi y 0 với x  ;1 N H Ó
f (x). f (x) 0 f (x) 0 M T , x ;1 , x
;1 ( vì lim f x   ) f x 0 f (x) 0 x O Á 4   N
f x  5x 10x  5m 1  0, x    ;1   V f    1  5m  17   0 D – VDC  3 4
m  x  2x  1, x  ;1 m  max   4
x  2x  1   1     ;1 3 2. 2   17   m   17  5 m   5 3 17 1 m m       m  3. 3 2. 2 5 Câu 2.
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 3
y  2x  mx  1 đồng
biến trên khoảng 1; ? A. 2. B. 6. C. 3. D. 4. Lời giải:
https:/www.facebook.com/groups/toanvd.vdc Trang 2 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 Chọn C
Xét hàm số f x 3
 2x  mx  1. N  x 1;  H
TH1: f x 0 có nghiệm thì hàm số y
f x không thể đồng biến trên 0 Ó M
khoảng 1; . T O Á
TH2: f x  0 không có nghiệm x 1; . 0 N V D
Ta có: f x 2  6x  . m – VDC
f (x). f (x) Khi đó 3
y  x  mx   f x 2 2 1
 f x nên y . 2 f (x)
Hàm số đồng biến trên khoảng 1;  khi và chỉ khi y 0 với x  1;
f (x). f (x) 0 f (x) 0 , x 1; , x 1;
( vì lim f x   ) f x 0 f (x) 0 x 3 2x mx 1 0 f 1 0 2 m 1 0 , x 1; m 3 m 1; 2;3 . 2 6x m 0 f 1 0 6 m 0 Câu 3.
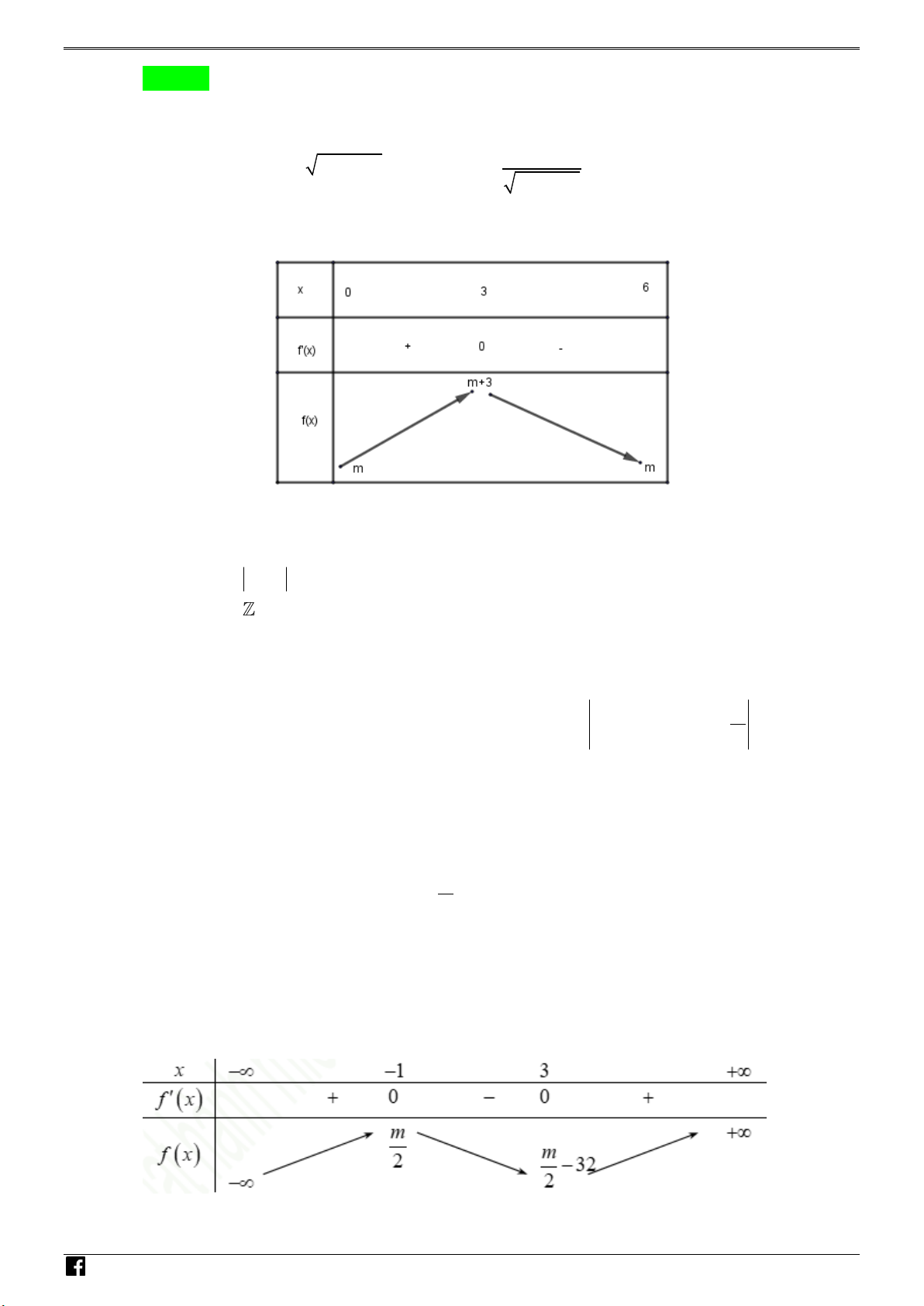
Có o nhiêu gi trị nguyên củ th m số m nhỏ hơn 10 để hàm số 4 3 2
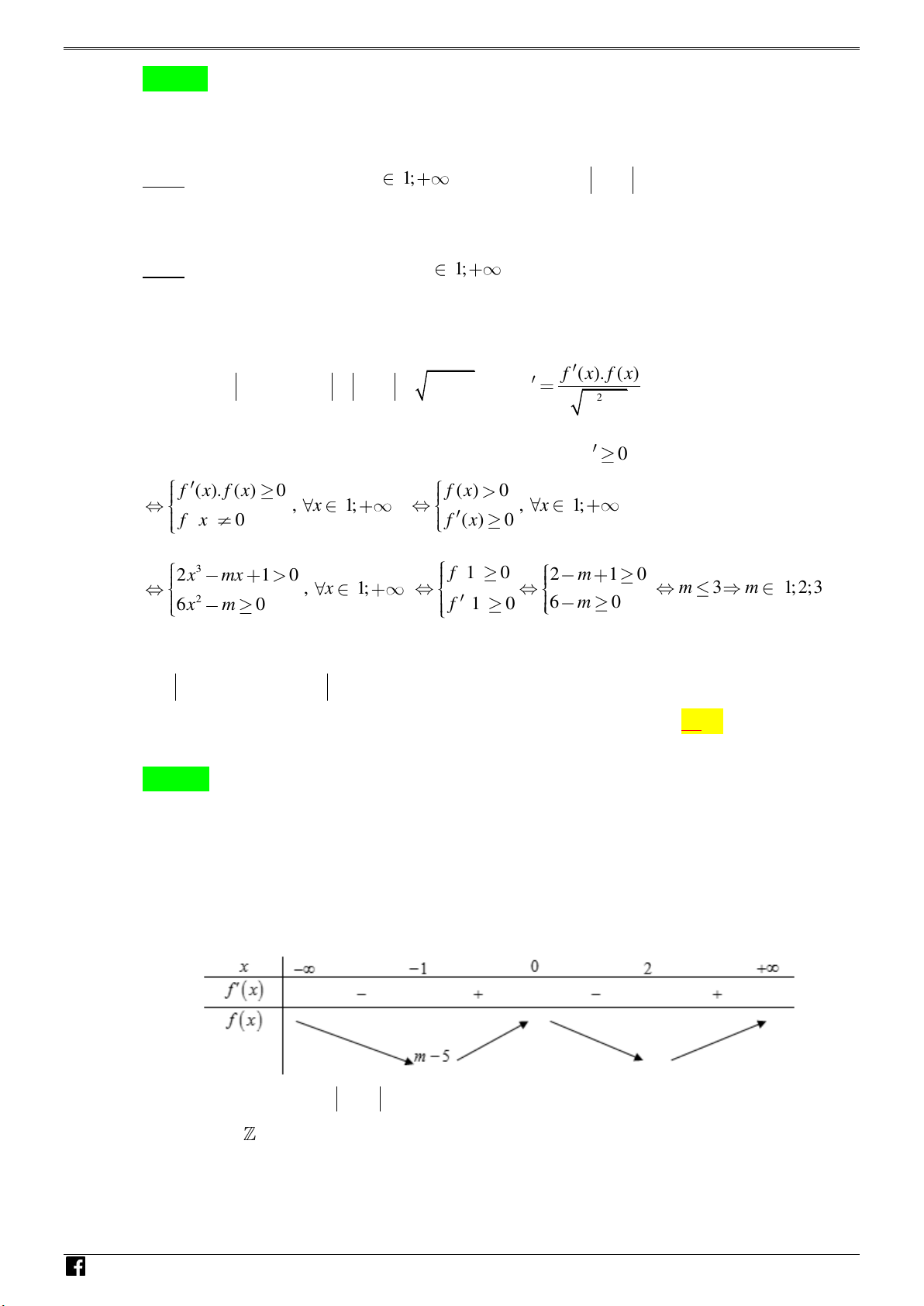
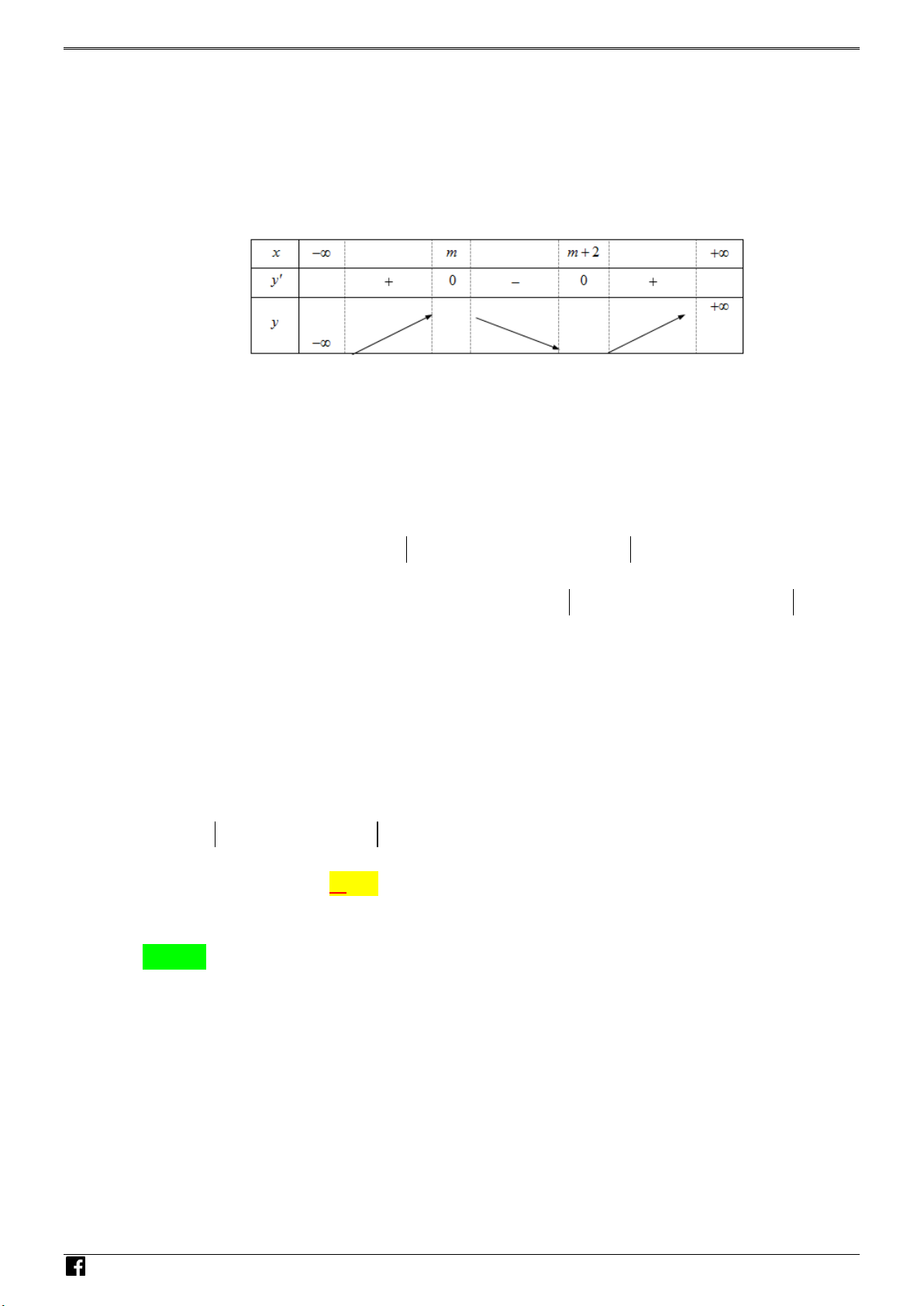
y  3x  4x 12x  m nghịch iến trên hoảng ;   1 ? N H Ó A. 6 . B. 4 . C. 3 . D. 5 . M T Lời giải O Chọn D Á 3 2 2 N
- t hàm số f  x 4 3 2
 3x  4x 12x  m  f x 12x 12x  24x 12xx  x  2 V D x  1  – 
 f  x  0  x  0 VDC  x  2  BBT:
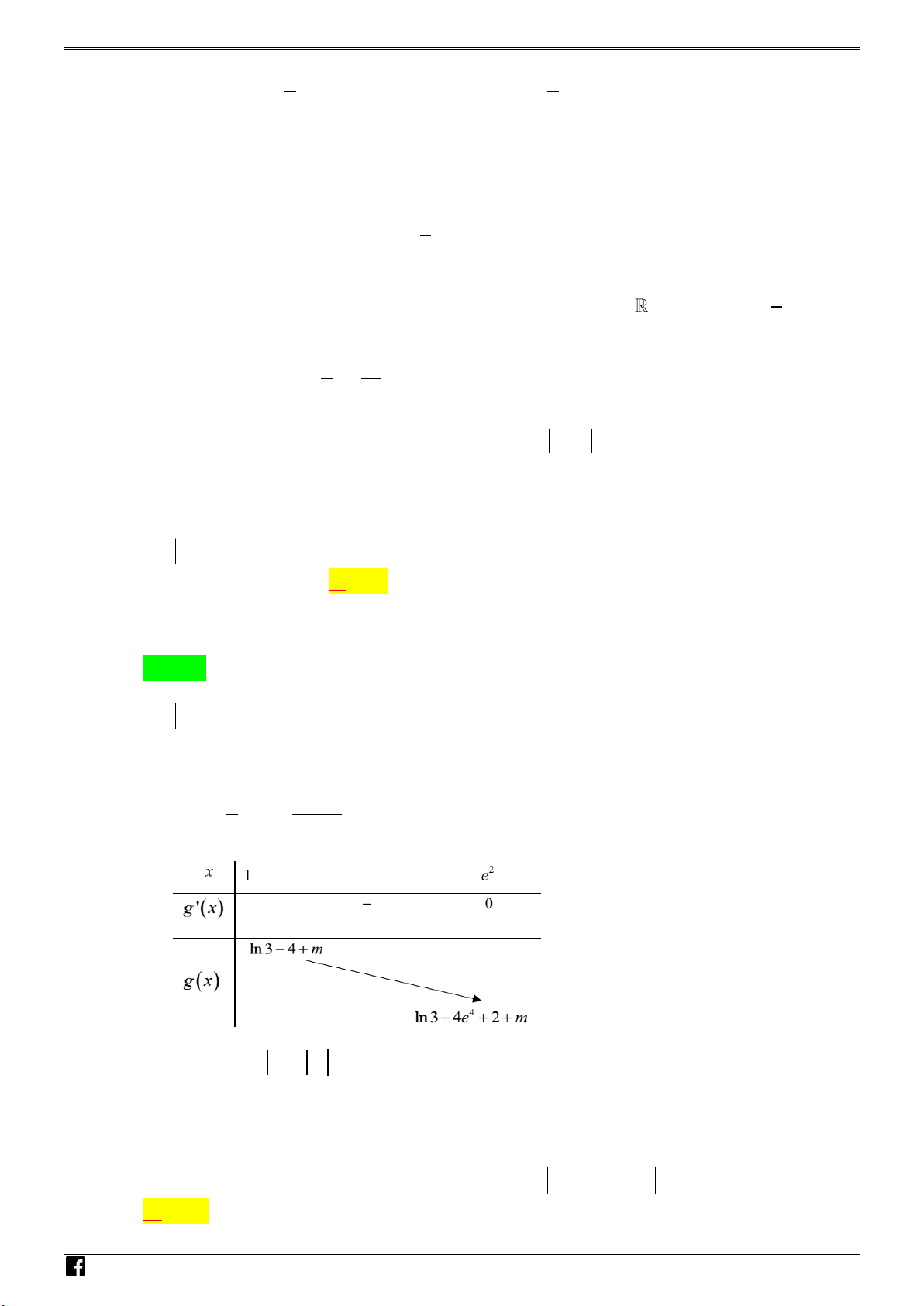
h n th y hàm số y  f  x nghịch iến trên hoảng ;  
1  m  5  0  m  5. m  ại do 
 m 5;6;7;8;  9 . m  10
y có 5 gi trị củ m thỏ m n yêu c u ài to n
https:/www.facebook.com/groups/toanvd.vdc Trang 3 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 Câu 4.
T p hợp t t cả các giá trị của tham số m để hàm số 3 2
y  x  3x  m  4 đồng biến trên khoảng 3;  là A. 2;  .
B.  ; 2 . C.  ;  4 . D. 4;   . N H Ó Lời giải M Chọn D T O Á Xét hàm số 3 2
f (x)  x  3x  m  4 N V x  0 D Ta có 2 f (
 x)  3x 6x , f (x)  0   – x  2 VDC
Bảng BT của hàm số f (x) x  0 2 3  f (  x)  0  0  m  4  f (x) m  N 4 H Ó M T O  m 8 Á N V D –
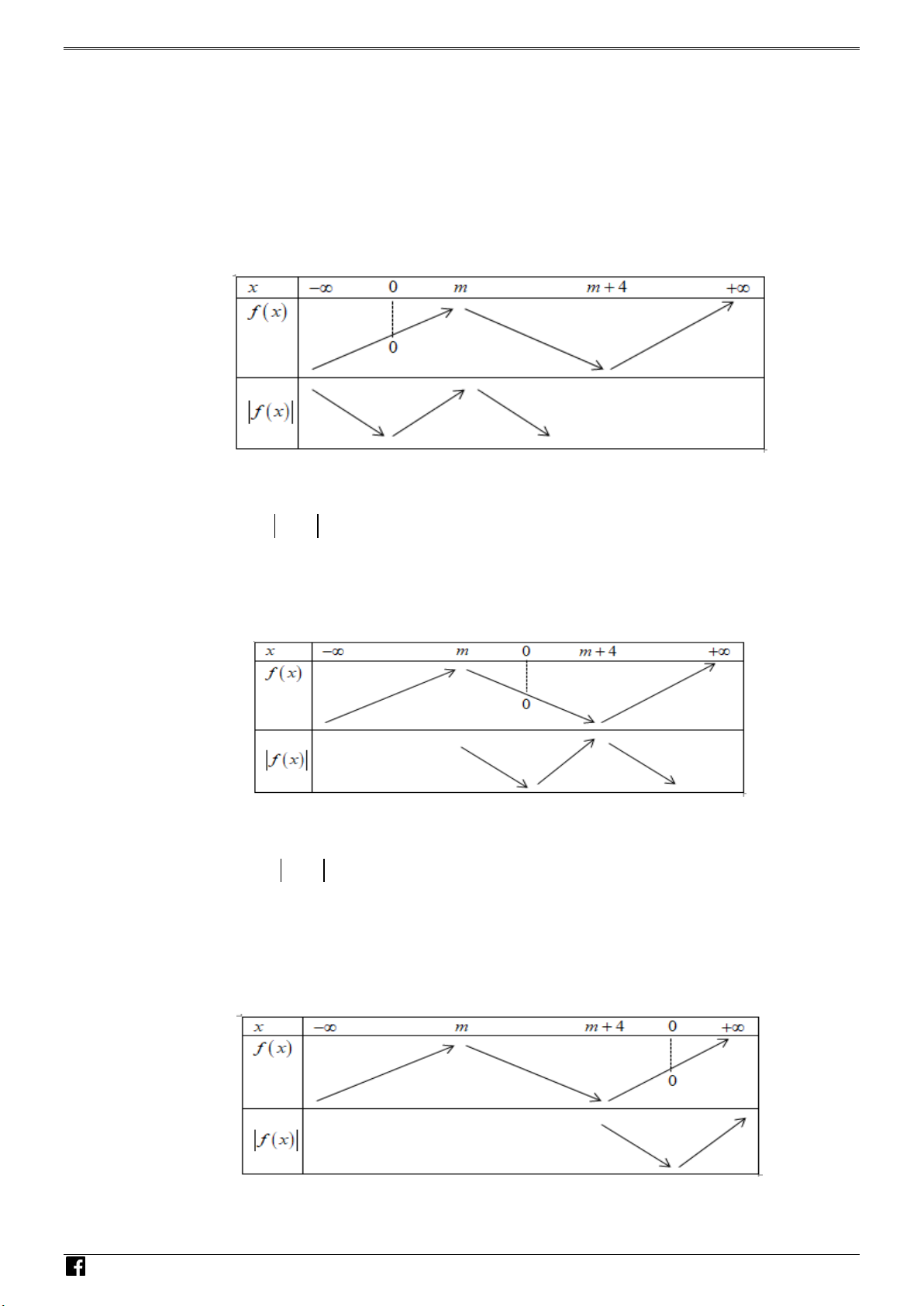
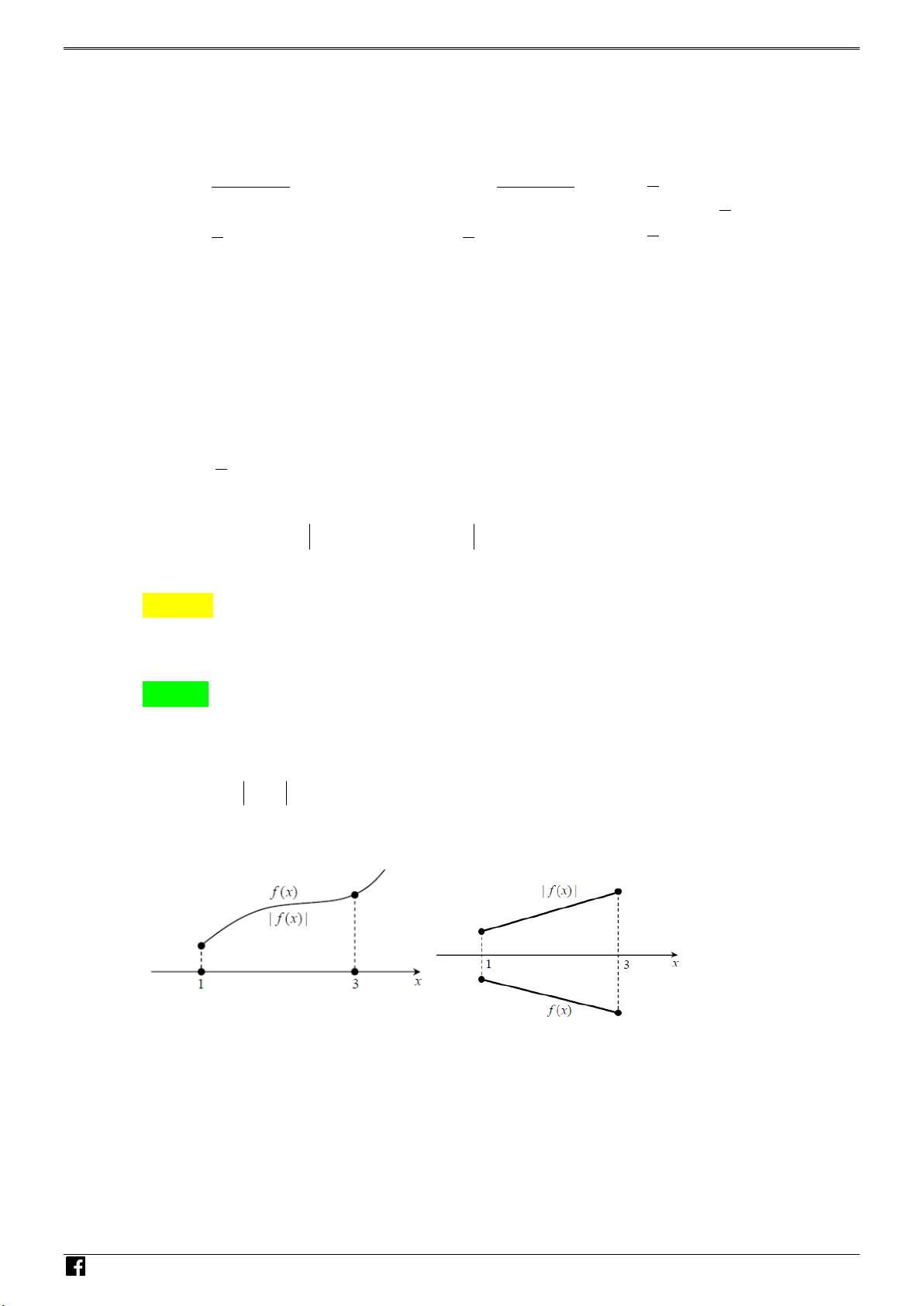
ì đồ thị hàm số y  f (x) có được bằng cách giữ nguyên ph n đồ thị của hàm số VDC
y  f (x) ở phía trên trục hoành, s u đó l y đối xứng ph n đồ thị ở phí dưới lên trên qua trục Ox .
V y hàm số y  f (x) đồng biền trên 3;   f (3)  0  m  4  0  m  4 Câu 5.
Tìm t t cả các giá trị của m để hàm số 4 3
y  x  2x  mx  2 đồng biến trên khoảng  1;   ? A. m 1. B. m .
C. 0  m 1. D. m  0 .
https:/www.facebook.com/groups/toanvd.vdc Trang 4 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 ời giải Chọn C N
Đặt f  x 4 3
 x  2x  mx  2  f x 3 2
 4x  6x  m . H Ó M 4 3
y  x  2x  mx  2  f  x . T O Á
Ta có lim f  x   nên hàm số đồng biến trên  1;
   khi và chỉ khi N x V  f 
  x  0, x   1  ;  3 2
4x  6x  m  0, x   1  ;  D    –  f    1  0 1   m  0 VDC 3 2  3 2  m  4
 x  6x , x   1  ;  m  max   4  x  6x     m 0 1;             0 m 1. 1   m  0    m 1 m 1 Câu 6.
Có bao nhiêu giá trị nguyên của tham m thuộc đoạn 10;10 để hàm số 3
y  x  m   2
x  m m   2 3 1 3
2 x  m m  3 đồng biến trên khoảng 0;  1 ? A. 21. B. 10 . C. 8 . D. 2 . Lời giải N Chọn B H Ó
Xét hàm số f  x 3
 x  m   2
x  m m   2 3 1 3
2 x  m m  3 trên khoảng 0;2 . M T 2 2 O
f ' x  3
 x  6m  
1 x  3m m  2  3
 x  2m  
1 x  m m  2   . Á N   V x m
f ' x  0 
 m  m  2  . D  x  m  2 – VDC x  m
Nhận xét: f  x  0   x  m  3
Từ bảng biến thiên, suy ra hàm số y  f  x đồng biến trên khoảng 0;  1 khi
https:/www.facebook.com/groups/toanvd.vdc Trang 5 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 0  ;1   ; m m  2
m  0 1 m  2  1   m  0   .      0 
;1  m  3;   m  3  0 m  3 
Mà m nguyên thuộc khoảng 10;10 nên có 10 giá trị m thỏa mãn yêu c u bài N H Ó toán. M T  1 4; 4     O Câu 7.
Có bao nhiêu số nguyên m thuộc khoảng   để hàm số 3 2 y x x mx 1 đồng 3 Á N biến trên 1; ? V D A. 5 . B. 4 . C. 3 . D. 6 . – Lời giải VDC Chọn A 1
Xét hàm số: f  x 3 2
 x  x  mx 1 f x 2
 x  2x  m . 3 Ta có:   1 m
+ Trƣờng hợp 1: 
  0 1 m  0  m 1. Suy ra f x  0, x  1;  . m 1 m 1 m 1   
V y yêu c u bài toán         .  f    1 1 m 1 1  0  m  0 m     3  3
Kết hợp với điều kiện m  ; m  4
 ;4 t được m  3; 2;1;0; 
1 . Ta có 5 giá trị của N
m thoả mãn yêu c u bài toán . H Ó M T
+ Trƣờng hợp 2: 
  0  m 1. Suy ra f ' x  0 có 2 nghiệm phân biệt x , x  x  x 1 2  1 2 O Á Ta có bảng biến thiên: N V D – VDC m 1    m  f   m 1 1 1  0      f   1  0
V y yêu c u bài toán  x  x  1      m   1 2 S        f    1 0 1 1 0 1  0 2   f (1)  0  f (1)  0
V y t t cả có 5 giá trị của m thoả mãn yêu c u bài toán.
https:/www.facebook.com/groups/toanvd.vdc Trang 6 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 Câu 8.
Tổng t t cả các giá trị nguyên thuộc 5;5 củ m để hàm số 1 2 3 g(x) 
x  m   2
1 x  2m  3 x  3 3 N H
đồng biến trên 1;5 là: Ó M A. 1. B. 1  . C. 0 . D. 2 . T O Lời giải Á N Chọn B V 1 2 D Xét hàm số 3 f (x) 
x  m   2
1 x  2m  3 x  – 3 3 VDC 2 f (
 x)  x  2m  
1 x  2m  3 x  1  f (  x)  0   . x  3 2m
Hàm số g(x) đồng biến trên 1;5 khi và chỉ khi xảy ra một trong h i trường hợp sau:        3 2m 1 m 1 f ( ) x ®ång biÕn trªn 1;5   13 +,TH1:       m   1 13  f(1)  0 3m  4   0  3m  9   3  3
Kết hợp điều kiện m nguyên và thuộc 5;5 t được m2;3;4;  5 N H 5  3 2m m  1  Ó  f( )
x nghÞch biÕn trªn 1;5   M T +,TH2:       m 1   1 13  f(1)  0 3m  4   0  3m    3  3 O Á N
Kết hợp điều kiện m nguyên và thuộc 5;5 t được m1;2; 3  ; 4  ;  5 V D –
V y tổng t t cả các số nguyên của m để hàm số đồng biến trên 5;5 là: 1  . VDC
Tác giả: Đào Thị Hƣơng Facebook: Hƣơng Đào Câu 9.
Có bao nhiêu giá trị nguyên thuộc đoạn 2019; 2019 của tham số thực m để hàm số 3
y  x  m   2 3
2 x  3m m  4 x đồng biến trên khoảng 0; 4 ? A. 4033. B. 4032 . C. 2018 . D. 2016 . Lời giải Chọn A
Xét hàm số f  x 3
 x  m   2 3
2 x  3m m  4 x trên khoảng 0;4
https:/www.facebook.com/groups/toanvd.vdc Trang 7 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 f  x 2 '
 3x  6m  2 x  3mm  4 2
 3x  2m  2 x  mm  4    x  m
f ' x  0  
 m  m  4  x  m  4 N H Ó
Nhận xét: Đồ thị hàm số y  f  x luôn đi qu điểm O 0;0 . M T
Trường hợp 1: Nếu m  0 O Á N V D – VDC
Từ bảng biến thiên, suy ra
hàm số y  f  x đồng biến trên khoảng 0; 4  0; 4  0; m  m  4
Kết hợp với m  0 , ta có m  4 .
Trường hợp 2: Nếu m  0  m  4  4   m  0 N H Ó M T O Á N V
Từ bảng biến thiên, suy ra D –
hàm số y  f  x đồng biến trên khoảng 0; 4  0; 4  0; m  4  m  4  4 VDC  m  0 Kết hợp với 4
  m  0 , ta có m  0.
Trường hợp 3: Nếu m  4  0  m  4 
Từ bảng biến thiên, suy ra
https:/www.facebook.com/groups/toanvd.vdc Trang 8 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
hàm số y  f  x luôn đồng biến trên khoảng 0;   nên hàm số y  f  x đồng  m  4 
biến trên khoảng 0; 4 với mọi m  4  .V y m  0  N m  4  H Ó M
Mà m nguyên thuộc khoảng 2019; 2019 nên có 4033 giá trị m thỏa mãn yêu T O c u bài toán. Á N  1 V
Câu 10. Có bao nhiêu giá trị nguyên dương của m  5 để hàm số 3 2 y  x 
x  x  m đồng D 3 2 – biến trên (0, )  ? VDC A. 2 B. 4 C. 6 D. 8 ời giải Chọn B  1 Xét hàm số 3 2 y  x 
x  x  m ta có 2
y  x  x 1  0, x   . R 3 2  1 Suy ra hàm số 3 2 y  x 
x  x  m luôn đồng biến trên R . 3 2  1
Do đó điều kiện hàm số 3 2 y  x 
x  x  m đồng biến trên (0, )  là y  0 3 2 (0) N  m  0. H Ó M T
Lại có m nguyên dương và m  5 v y có 4 giá trị của m O    Á
Câu 11. Có bao nhiêu số nguyên dương m để hàm số 5 y x mx
4 đồng biến trên khoảng N 1;. V D A. 4 . B. 5 . C. 6 . D. 7. – VDC Lời giải Chọn B 5
x  mx  4 khi 
 5x  mx  4  0 Ta có: y   5
x  mx  4 khi 
 5x mx  4  0 4 5  x  m khi 
 5x mx  4  0 y '   4  5  x  m khi 
 5x mx  4  0 4   4 m 5x 5
 x  m 0  m  5 TH1: y '   , x  1   , x   1    m  5. 4 5 4
x  mx  4 0 m  x   m  1 4  x
https:/www.facebook.com/groups/toanvd.vdc Trang 9 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 4  5  x  m 0 TH2: y '   , x
  1. Hệ vô nghiệm vì  5
lim x  mx  4   .  5
x  mx  4 0 x m  5 V y   m1,2,3,4,  5 . N m   H Ó M
Câu 12. Có bao nhiêu số nguyên m thuộc khoảng 10;10 để hàm số 3
y  2x  2mx  3 đồng TO
biến trên khoảng 1;  ? Á N A. 12 . B. 8 . C. 11. D. 7 . V D – Lời giải VDC Chọn A
Xét hàm số: f  x 3
 2x  2mx  3 có f x 2 '  6x  2m
TH1: Hàm số f  x đồng biến trên khoảng 1;  và f   1  0 2 m  3x x   1; m  3 2  
6x  2m  0   5         5 5 m 5   2m  0 m  m  2   2  2
Suy ra có 12 giá trị m thỏa yêu c u
TH2: Hàm số f  x nghịch biến trên khoảng 1;  và f   1  0 N H Ó
Trường hợp này không xảy ra do lim f  x   . M T x O
V y có t t cả 12 giá trị m thỏa yêu c u đề bài. Á N V Câu 13. Cho hàm số 5 y |
 x  mx 1|. Gọi S là t p t t cả các số nguyên dương m sao cho hàm D
số đồng biến trên 1;  . Tính tổng t t cả các ph n tử của S . – VDC A. 15 B. 14 C. 12 D. 13 Lời giải Chọn A 5 x  mx 1 y '  . 4 5x  m 5  | x  mx  1|
Để hàm số đồng biến trên 1;  thì g  x   5
x  mx   4
1 5x  m  0 (*) , x  1.
Với m  0 ta có g     5 x   4 0 1 .5x  0, x  1 . m
Với m  0. Do m  * luôn có 1 nghiệm là 4
. Ta chú ý lim g  x   . 5 x
https:/www.facebook.com/groups/toanvd.vdc Trang 10 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 m
Do v y, điều kiện c n để g  x  0 , x  1 là 4  1  m  5 . 5
Với m 1, m  2 ; m  3 ; m  4 ; m  5 , thay vào (*) kiểm tra BXD th y đúng N
 nh n m 1;m  2 ; m  3 ; m  4 ; m  5 H Ó
V y S  {1;2;3;4;5}. Tồng các ph n tử của S là 15 . M T
Câu 14. Cho hàm số 2 f (x) |
 x  2mx  m  2 | . Có bao nhiêu giá trị nguyên của tham số m thuộc OÁ
[  9;9] để hàm số đồng biến trên khoảng (0; 2) ? N A. 3 B. 2 C. 16 D. 9 V D – Lời giải VDC Xét hàm 2
g(x)  x  2mx  m  2 . Ta có g '( )
x  2x  2m .
Hàm số f (x) đồng biến trên khoảng (0;2) khi và chỉ khi g(0)  0 g(0)  0  , x  (0;2) hoặc  , x  (0;2) . g '(x)  0 g '(x)  0 Trƣờng hợp 1. g(0)  0 m  2  0  , x  (0;2)    2   m  0 . g '(x)  0  2  m  0 Trƣờng hợp 2. N         H g(0) 0 m 2 0 m 2  , x  (0;2)    vô nghiệm. Ó  g '(x)  0  2  m  0 m  0 M T O
Do m là nguyên thuộc [  9;9] nên m{-2, -1, 0}. Chọn đáp án A. Á N 1 1 2 Câu 15. Cho hàm số 3 2 2 f (x)   x 
(2m  3)x  (m  3m)x 
. Có bao nhiêu giá trị nguyên V 3 2 3 D  –
của tham số m thuộc [ 9;9] để hàm số nghịch biến trên khoảng (1;2) ? VDC A. 3 . B. 2 . C. 16 . D. 9 . Lời giải 1 1 2 Xét hàm 3 2 2 g(x)   x 
(2m  3)x  (m  3m)x  . Ta có 3 2 3 2 2 g '( )
x  x  (2m  3)x  (m  3 ) m  (  x  )
m (x  m  3).
Hàm số f (x) nghịch biến trên khoảng (1;2) khi và chỉ khi g(2)  0 g(2)  0  , x  (1;2) hoặc  , x  (1;2) .     g '(x) 0 g '(x) 0 Trƣờng hợp 1.
https:/www.facebook.com/groups/toanvd.vdc Trang 11 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 2 g(2)  0  2
 m  2m  4  0 m( ;  2  ][1;)  , x  (1;2)   , x  (1;2)    m 1. g '(x)  0
(x  m)(x  m  3)  0 m[ 1;1] Trƣờng hợp 2. N 2 H g(2)  0  2
 m  2m  4  0 m[  2;1] Ó  , x  (1;2)   , x  (1;2)    m  2  M . g '(x)  0 (x  )
m (x  m  3)  0 m( ,  2  ][2;) T
Do m là nguyên thuộc [  9;9] nên m {
 1, -2}. Chọn đáp án B. O Á N
Câu 16. Có bao nhiêu giá trị nguyên m  20; 20 để hàm số 4 3 2
y  3x  4x 12x  m nghịch VD
biến trên khoảng 1;  . – VDC A. 4 . B. 30 . C. 8 . D. 15 . Lời giải
Tác giả:Nguyễn Thanh Thảo Facebook:Nguyễn Thanh Thảo Chọn D 4 3 2 3
 x  4x 12x   m  4 3 2
3x  4x 12x  m  0 Ta có y   4 3 2  3
 x  4x 12x   m  4 3 2
3x  4x 12x  m  0 3 2 1
 2x 12x  24  x  4 3 2
3x  4x 12x  m  0 Nên y   3 2  1
 2x 12x  24  x  4 3 2
3x  4x 12x  m  0 N H
Yêu c u ài to n tương đương với Ó M T 3 2 1
 2x 12x  24x  0 TH1:  , x  1 4 3 2 O 3
 x  4x 12x  m  0 Á N 4 3 2 V m  3
 x  4x 12x ,x  1   m  5 D – 3 2
 x  x  x  VDC 12 12 24 0 TH2: 
, x  1  Hệ này vô nghiệm. 4 3 2 3
 x  4x 12x  m  0
V y m 5;6;...;1 
9 . Có 15 số nguyên thỏa mãn.
Câu 17. Có bao nhiêu giá trị nguyên không âm m để hàm số 4 2
y  x  mx  9 đồng biến trên khoảng 1;  . A. 3 . B. 6 . C. 7 . D. 4 . Lời giải Chọn A
https:/www.facebook.com/groups/toanvd.vdc Trang 12 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 4 2
x  mx  9   4 2
x  mx  9  0 Ta có y   4 2
x  mx  9   4 2
x  mx  9  0 N 3 4x  2  mx  4 2
x  mx  9  0 H y  Ó Nên  3 4 2 M  4  x  2  mx
x mx 9 0 T O Á
Yêu c u ài to n tương đương với N V 2 m  2 m  3 2x 2x D
4x  2mx  0   TH1:  , x  1   ,x  1   ,x  1 – 9 9 4 2 2 2
x  mx  9  0 m  x  m  x  VDC   2  x 2  x
 m  2  m0;1;  2 3  4
 x  2mx  0 TH2: 
, x  1  Hệ này vô nghiệm vì khi x   thì 4 2
x  mx  9   . 4 2
x  mx  9  0 1 1 Câu 18. Cho hàm số 3 y  x 
m3 2x 2m3x 1 . Gọi S là t p hợp t t cả các giá trị 3 2
nguyên dương m để hàm số đ cho đồng biến trên khoảng 4; . Chọn mệnh đề sai? N
A. S có 4 ph n tử. H Ó M T
B. Tổng các giá trị của m thuộc S bằng 6. O Á
C. Tích các giá trị của m thuộc S bằng 0. N V D
D. Giá trị m lớn nh t thuộc S bằng 4. – VDC Lời giải Chọn D 1 1 Đặt 3 f (x)  x 
m 3 2x 2m 3x 1. 3 2 Ta có: 2
f '(x)  x  m  3 x  2m  3 .
Hàm số đ cho đồng biến trên khoảng 4; khi và chỉ khi:
 f '(x)  0, x  4;
 f '(x)  0, x  4;  hoặc   f (4)  0  f (4)  0
https:/www.facebook.com/groups/toanvd.vdc Trang 13 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
 f '(x)  0, x  4; 2
x m 3 x 2m 3  0, x  4; TH1:     f (4)  0 1  6  4 
m3 2m3  0 N 2  x  3x  3 2  x  3x  3  7 H m  , x  4;   m  min  m   Ó  x  2   4; x  2   2 7    m  M   7   7   7 2 m  T m  m   O  2  2 2 Á N V
 f '(x)  0, x  4; D TH2:   f (4)  0 – VDC Hệ vô nghiệm vì  2
lim x  m  3 x  2m  3   . x 7
V y m  , m nguyên dương nên m 0;1;2;  3 . Chọn D. 2
Câu 19. Cho hàm số f  x 3
 x  2m  5 x  2018 . Có bao nhiêu giá trị nguyên của tham số m
thuộc 2019; 2019 để hàm số đồng biến trên khoảng 1;3 ? A. 3032 . B. 4039 . C. 0 . D. 2021. Lời giải N Chọn A H Ó 3 2 M T
Xét hàm số f  x  x  2m  5 x  2018 , có đạo hàm f  x  3x  2m  5 . O Á
Hàm số y  f  x đồng biến trên khoảng 1;3 thì đồ thì của hàm số trong khoảng N V
1;3phải có hình dạng như s u D – VDC
Trường hợp 1: Hàm số f  x đồng biến trong khoảng 1;3 và không âm trên 1;3 tức là :  f    2 1  0
2m  3x  5 x  1;3 m  4         f    x m  0 x  1;3 4. 2024  2m  0 m 1012
https:/www.facebook.com/groups/toanvd.vdc Trang 14 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
Trường hợp 2: Hàm số f  x nghịch biến trong khoảng 1;3 và hông dương trên 1;3 tức là : 2 N  f    1  0
2m  3x  5 x  1;3 m  4 H       m 1012. Ó  f 
  x  0 x  1;3 2024  2m  0 m 1012 M T O
Kết hợp với điều kiện t được kết quả m  20
 19;41012;2019. Vây có Á N
3032 giá trị của m . V D – Câu 20. Cho hàm số 3 y |
 x  mx 1| . Gọi S là t p t t cả các số tự nhiên m sao cho hàm số VDC
đồng biến trên 1;  . Tính tổng t t cả các ph n tử của S . A. 3 B. 1 C. 9 D. 10 Lời giải Chọn A 3 x  mx  1 y '  . 2 3x  m 3 
| x  mx  1 |
Để hàm số đồng biến trên 1;  thì g  x   3
x  mx   2
1 3x  m  0 (*) , x   1.
Với m  0 ta có g     3 x   2 0 1 .3x  0, x   1. m
Với m  0 . Do m    * luôn có 1 nghiệm là
. Ta chú ý lim g  x   . N 3 x H Ó m M T
Do v y, điều kiện c n để g  x  0, x   1 là  1  m  3. 3 O
Với m  1, m  2 thay vào (*) kiểm tra BXD th y đúng  nh n m  1;m  2 . Á N
Với m  3 thì g  x   3
x  x   2 3
1 3x  3 có một nghiệm x  1  do v y trên miền 0 V D
1;x thì g x  0  trái yêu c u bài toán. 0  – VDC
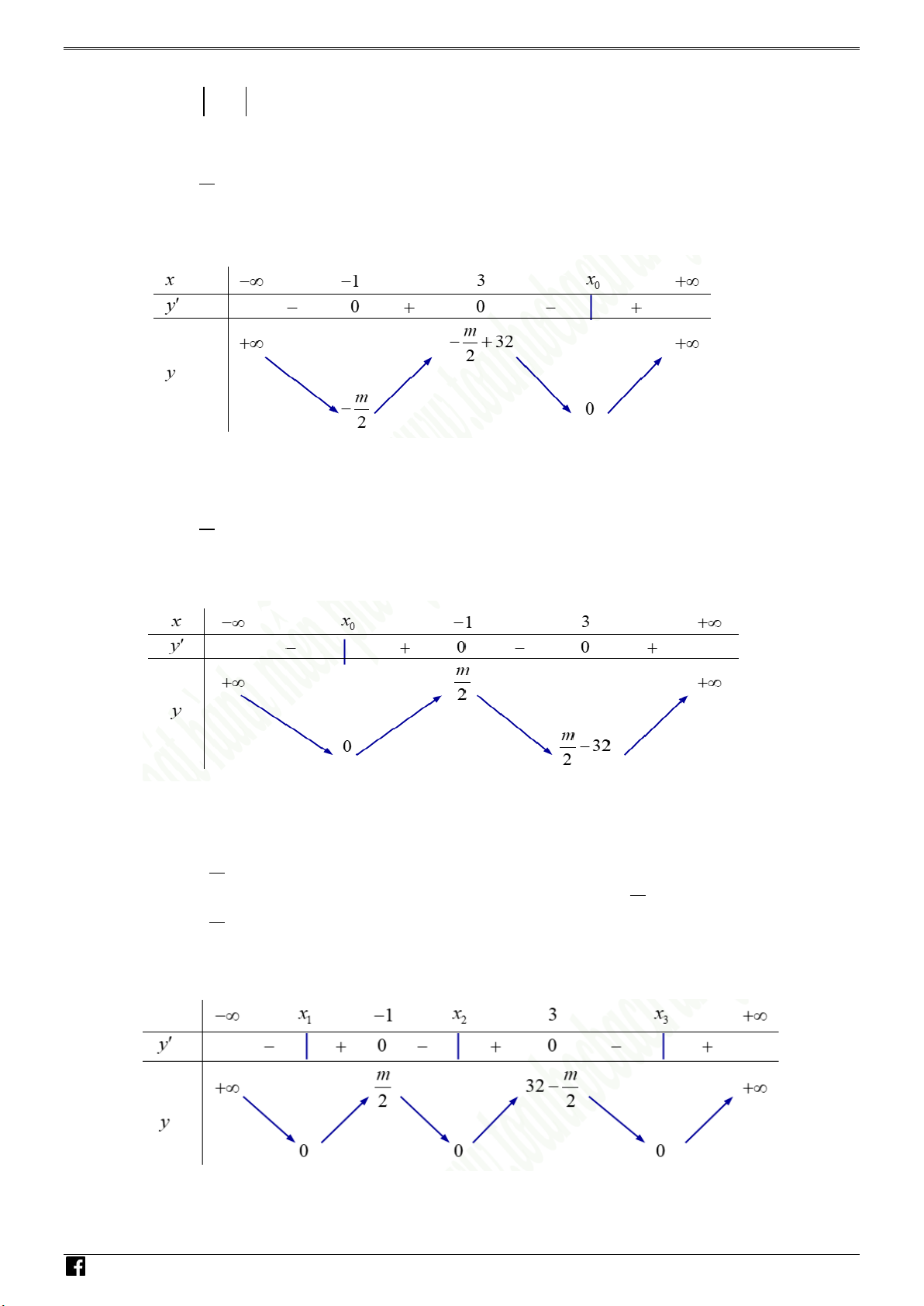
V y S  {0;1;2}. Tồng các ph n tử của S là 3 . Bài 19.
Có t t cả bao nhiêu giá trị nguyên của tham số m để hàm số
y  g  x 3
 x  m   2 3
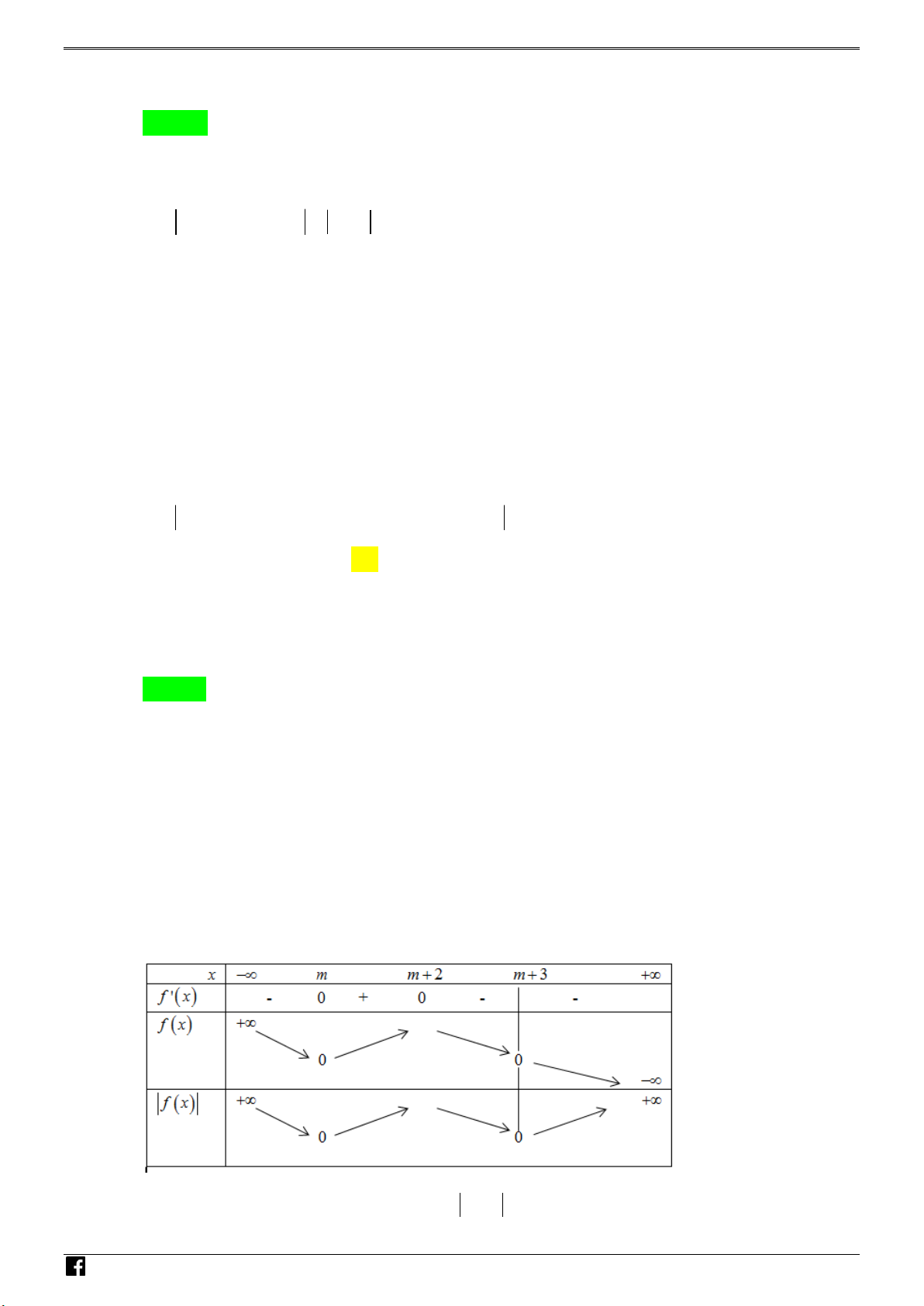
1 x  3m m  2 x đồng biến trên nử đoạn 0;  biết rằng 2  021 m  2021? A. 2020 . B. 2021. C. 2022 . D. 2019 . ời giải Chọn A
Xét hàm số: y  f  x 3
 x  m   2 3
1 x  3m m  2 x . T Đ D 
https:/www.facebook.com/groups/toanvd.vdc Trang 15 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 Ta có: 2
y '  3x  6 m  
1 x  3m m  2 . x  m y '  0 
m  m  2, m   . x  m  2 N H Ó Bảng biến thiên M T O Á N V D – . VDC
Gọi C là ph n đồ thị của hàm số 3
y  x  m   2 3
1 x  3m m  2 x nằm trên 0x . 1 
Gọi C là ph n đồ thị của hàm số 3
y  x  m   2 3
1 x  3m m  2 x nằm dưới 0x . 2 
Gọi C là ph n đồ thị đối xứng với C qua 0x . 2  2 
Suy r đồ thị hàm số y  g  x 3
 x  m   2 3
1 x  3m m  2 x gồm C  C . 1   2
Dựa vào bảng biến thiên ta th y: hàm số y  g  x 3
 x  m   2 3
1 x  3m m  2 x đồng m  2  0
biến trên nử đoạn 0;  khi và chỉ khi   m  2  .  f  0  0 N H
Kết hợp với điều kiện 2
 021 m  2021, ta suy ra có 2020 giá trị của m thỏa mãn yêu Ó M T c u đề bài. O Á
Câu 21. Gọi S  a ;   là t p t t cả các giá trị của tham số m để hàm số N V 3 2
y  x  3x  mx  3m 1 đồng biến trên khoảng  2
 ;   Khi đó a bằng D – VDC . A. 3  . B. 19 . C. 3 . D. 2  . Lời giải Chọn B
Đặt f  x 3 2
 x  x  mx  m   f  x 2 3 3 1
 3x  6x  m .  f 
  x  0, x   2  ;   TH1:  .  f   2    0  f    x  x     2
 x  x  m  x     2 0, 2 ; 3 6 0, 2 ; m  3  x  6 , x x   2  ;         f   2    0 m 19 m 19
https:/www.facebook.com/groups/toanvd.vdc Trang 16 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 m  max   2 3  x  6x m  x  3  2;       m 19 .   m 19 m 19  f 
  x  0, x   2  ;   N TH2:  . H  f   2    0 Ó M  f    x  x     2
 x  x  m  x     2 0, 2 ; 3 6 0, 2 ; m  3  x  6 , x x   2  ;   T      O  f   2    0 m 19  0 m 19 Á N V 2 D m  min   3  x  6x  2;   –  . VDC m 19 Vì  2 lim 3
 x  6x    hàm số 2 y  3
 x  6x không có giá trị nhỏ nh t. Vì v y TH2 x
không có giá trị m thỏa mãn.
V y t p các giá trị m c n tìm là S  19 ;  .
2. Dạng 2: Tìm điều kiện tham số m để hàm y  f  x với f  x là hàm số dạng phân
thức hữu tỉ đồng biến, nghịch biến trên tập D cho trƣớc.
Câu 22. Tính tổng S t t cả các giá trị nguyên của tham số m trong đoạn 10;10 để hàm số mx  3 y 
đồng biến trên 1;   . x  m  2 A. S  55. B. S  54 . C. S  3. D. S  5. N H Ó Lời giải M T
Tác giả: Chungthanh Vu Facebook Chungthanh Vu OÁN Chọn B. V D mx  3 2 m  2m  3 – Xét hàm số y 
với x  m 2 , có y '  . 2 VDC x  m  2
x  m 2 mx  3 Hàm số y 
đồng biến trên 1;   khi xảy ra một trong h i trường hợp sau : x  m  2 2  m  2m  3 2  y  
m  2m  3  0 '  x  m  m   0 2   3  2  m3  + TH 1:  x m m .  y   ,   1    0   1  1 1  0  m  3   m  
 m     3  m  2 1 2 1;
https:/www.facebook.com/groups/toanvd.vdc Trang 17 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 2  m  2m  3 2  y  
m  2m  3  0 '  
x  m  2 0 2  m3 + TH 2:  x m .  y   ,   1    0   1  0  m  3 N
 m      m  2 1 2 1; H Ó M  m  T
V y m  1;   , lại do 
suy ra m 2;3; 4;5;6;7;8;9;  10 , v y S  54 . O m    10  ;10 Á N x  m  V 2 1
Câu 23. Tìm m để hàm số y 
đồng biến trên 1;  D x  m – 1   VDC A.  m  1.
B. m   1 1;1 \  . 3 3 1 1 C. 1   m  .
D.  m  1. 3 3 Lời giải
Tác giả: Ai Pha Facebook AI Pha Chọn B x  2m 1 Đặt f (x) 
ĐK x  m x  m N 3m 1
hi đó f '(x)  H x  Ó  m2 M T
f '(x). f (x) O
Để hàm số đồng biến trên 1;  y ' 
 0,x1; Á f (x) N V D
 f '(x)  0,x1;
 f '(x)  0,x1;  (I) hoặc  (II) –  f   f  (1) 0 (1) 0 VDC   3  m 1  0 3  m 1 0  1 
Ta có (I)  m  1
  m  1; (II)  m 1  m 3   2  2  m   2 2m 0   0  1 m  1 m 1 V y  m  1. 3 2
x  2x  2m  2
Câu 24. Có bao nhiêu số nguyên của tham số m để hàm số y  đồng biến trên x 1 3; ?
https:/www.facebook.com/groups/toanvd.vdc Trang 18 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 A. 4 . B. 5 . C. vô số. D. 6 . Lời giải
Tác giả: Kiên Cao Văn Facebook Kiên Cao Văn NHÓ Chọn A M T p x c định: D  \   1 . T O
x  x  m  Á
Xét hàm số f  x 2 2 2 2  . N x  1 V 2   D x 2x 2m
Có f ' x  2 – x   1 VDC
f ' x . f x
Khi đó y  f  x 2  f x      y '  2 f  x
Hàm số đồng biến trên 3;   y '  0, x  3;   f 
  x. f  x  0      x   f  x   0 , 3;   , x
 3;  (vì lim f x   )  f   x  0  f '   x  0 x 2
 x  2x  2m  2  0   x 1 2       x 2x 2m 2 0  , x   3;    , x  3;  2  
x  2x  2m   2
x  2x  2m  0  x    0 2 1
2m  2  max 2   2 x 2x
2m  2  x  2x      3; 2m 2 3 N   , x  3;       2 2 H
2m  x  2x
2m  min x  2x 2m  3 Ó  3; M T  5 m    O  2 Á  
. Vì m   m 2; 1;0;  1 . N 3 m  V  2 D
V y có 4 giá trị nguyên của tham số m thỏa mãn yêu c u bài toán. – VDC 2
Câu 25. Tìm t t cả các giá thực của tham số m để hàm số y  x   m đồng biến trên 1;  . x A. m  1.  B. 1   m 1. C. m 1. D. m  0. Lời giải
Tác giả: Long Giang Vo Facebook Long Giang Vo Chọn C  2  2  x   m  2 1    2  2  2  x  x 
+ Ta có: y  x   m  x   m    y '  x  x  2  2  x    m   x 
https:/www.facebook.com/groups/toanvd.vdc Trang 19 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
+ Hàm số đồng biến trên 1;   y '  0,1;   2  x   m  0     x   2  N  
,  1;   x   m  0,   1; H  2    x  Ó 1  0   2  M   x  T O  2  2 Á
 x   m  0,1;  m  x  ,1;    N  x  x V  2  D
 m  max x   *  – 1;   x  VDC 2 2
+ Xét hàm số g  x  x  , x
 1;  g 'x  1  
 0,x  1; 2   x x    g  x 2 max  max x   g     1  1 1; 1;  x 
V y *  m  1. 2 m  2m 1
Câu 26. Biết rằng t p hợp t t cả các giá trị của m sao cho hàm số y  x 1 đồng x 1
biến trên 2;  là a;b .Tính . a b . A. 10  . B. 9  . C. 2 . D. 7  . N Lời giải H Ó M T
Tác giả: Nguyễn Hiền Facebook Nguyễn Hiền O Chọn A Á N Xét hàm V 2 D m  m  m  2m 1 số f  x 2 2 1  x 1 f  x  1 2 – x  . Ta có   1 x   1 VDC 2 m  2m 1
f  x. f  x
Khi đó y  x 1  f x 2
 f x nên y '  x 1 2 f  x
Hàm số đồng biến trên 2;  khi và chỉ khi y  0 với x  2;
 f x. f x  0
 f x  0        , x
  2; ( vì lim f x   )  f  x , x 2;   0  f   x    0 x 2  m  2m 1 x 1  0  2 2  x 1
m  2m 1  x 1   , x   2;   , x   2; 2       m  2m 1   
 m  2m 1  0  x 2 2 1 1  x   2 1
https:/www.facebook.com/groups/toanvd.vdc Trang 20 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
m  2m 1 max x  2 2 1   9    2       2; m 2m 8 0    
 1 11  m  1 11
 m  m   x   2 2 2 
m  2m 10  0 2 1 min 1 9  2; N H x  m Ó
Câu 27. Tìm t t cả các giá trị thực của m sao cho hàm số y 
đồng biến trên khoảng M x 1 T 1; O Á m   m    m    m  N A. 1. B. 1. C. 1 1 . D. 1 1 V D Lời giải – VDC
Tác giả: Nguyễn Thị Huyền, Facebook: Nguyễn Thị Huyền Chọn D. ĐK Đ x  1  x  m 1 m
Đặt f  x 
 f 'x  . x 1 x  2 1 f ' x f x
Khi đó t có y  f  x 2  f x      y '  2 f  x
Hàm số đồng biến trên 1;  nếu y '  0 x
 1;  f 'x. f x  0 x  1; N H     f   x  x    1 m 0 ' 0 1;  m 1 Ó TH1:   1   m    1   m 1 M T  f    1  0  0  m  1   2 O Á N     f   x  x    1 m 0 ' 0 1;  m 1 V TH2:   1   m    m   D  f    1  0  0  m  1   2 – VDC V y m  1  ;  1 là giá trị c n tìm. 3 x  2mx  2
Câu 28. Tính tổng t t cả các giá trị nguyên dương của m để hàm số y  đồng biến x 1
trên khoảng 2;   A. 3 B. 4 C. 2 D. 5 Lời giải
Tác giả:Phạm Đức Thành Facebook: pham duc thanh Chọn A
https:/www.facebook.com/groups/toanvd.vdc Trang 21 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 x  mx  3 2
2x  3x  2m  2
Xét hàm số f  x 3 2 2 
. Ta có: f  x  . x 1 x  2 1 3 x  2mx  2
f  x. f  x N Khi đó y   f x 2
 f x nên y  . H x 1 2 f  x Ó M T
Hàm số đồng biến trên khoảng 2;   khi và chỉ khi y  0 với x  2;  O Á N  f 
  x. f  x  0  f   x  0 V   , x  2;    , x
 2;  ( do lim f x   ) D  f   x  0  f    x  0 x – VDC  f 2  0  1  0  4m  0  3 2
 2x 3x  2m  2    0 , x   2;   3 2
2x  3x  2m  2  0, x     2;  2   x    1  5  5 m  m     2 2   3 2  2m  max  3 2 2
 x  3x  2 2m  2
 x  3x  2, x  2;    x    2;  5   5 m  m  5   2   2  1   m   2 2m  2  m  1  N Vì m   nên m   1; 
2 . V y tổng các giá trị nguyên dương của m là 3. H Ó M T x  m
Câu 29. Có bao nhiêu số nguyên m để hàm số y 
đồng biến trên khoảng 2;  ? x  m  3 O Á A. 4 . B. 2 . C. 3 . D. 1 . N V Lời giải D –
Tác giả: Thanh Vân. Facebook: Thanh Van VDC Chọn A x  m 2m  3
Đặt f  x  D 
\ m  3 . Ta có f  x  .
x  m  . T p x c định:   3
x  m  2 3
Hàm số đ cho đồng biến trên khoảng 2; 
f  x. f  x  y      f  x 0, x 2; 
 f x. f x  0, x  2; . Trường hợp 1:
https:/www.facebook.com/groups/toanvd.vdc Trang 22 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020   3 m        f    x  x    2m 3 0 2 0, 2;   
            .  f    m 3 2 m 1 1 m 2 2  0   2  m 5   m  2 N   0  H 5  m  Ó M Trường hợp 2: T   3 O m       Á  f    x  x    2m 3 0 2 0, 2; N   
 m  3  2  m  1 (không có m thỏa mãn). V  f  2  0   D 2  m
m  2  m  5    0 – 5  m  VDC V y 1
  m  2 , mà m  m 1;0;1; 
2 . V y có 4 số nguyên m thoả mãn. 1  m
Câu 30. Có bao nhiêu giá trị nguyên âm của m để hàm số y  x  5  x  đồng biến trên 2 5;  ? A. 11. B. 10 . C. 8 . D. 9 . Lời giải
Tác giả:Trần Nhung. Facebook: Trần Nhung Chọn C  N T p x c định: D R \   2 . H 2 Ó  m m 1
x  4x  m  3
Xét hàm số f  x 1  x  5 
Đạo hàm: f  x  1  . M T x  2 x  22 x  22 O
f  x. f  x 2 Á
Khi đó y  f  x 
f  x nên y  . N 2 f  x V D
Hàm số đồng biến trên 5;   khi và chỉ khi y  0, x  5;  –      VDC f
  x. f x 0    x   f  x   0 , 5;   , x
 5;  (vì lim f x   )  f   x  0  f    x  0 x  1  m x  5   0  x  2 2      m x 3x 9  , x  5;    , x  5;  m  1 2 1   
m  x  4x  3  x  2 0 2
m  min  2x  3x 9    2     5; m 5 3.5 9        m  . m  max  8 31 2
x  4x  3 2 m  5   4.5  3  5;
Mà m nguyên âm nên ta có: m  8
 ; 7; 6; 5; 4; 3; 2;  1 . 1  m
V y có 8 giá trị nguyên âm của m để hàm số y  x  5  5;   . x  đồng biến trên   2
https:/www.facebook.com/groups/toanvd.vdc Trang 23 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 2
x  x  2m  3
Câu 31. Có t t cả bao nhiêu giá trị nguyên của tham số m để hàm số y  đồng x 1
biến trên khoảng 3;   ? N A. 7 . B. 5 . C. 4 . D. Vô số . H Ó Lời giải M T
Tác giả: Nguyễn Nga Nvc. Facebook: Nguyễn Nga Nvc OÁN Chọn A V D 2 2
x  x  2m  3
x  2x  2  2m – f x   f  x  Đặt     VDC x 1 x  2 1
f  x . f x
Khi đó y  f  x 2  f x      y  2 f  x
Hàm số đồng biến trên khoảng 3;   khi
f  x. f  x y  0, x  3;   0, x  3;  2 f  x
 f x. f x 0        f  x , x 3;   0 N H
 f x 0 Ó   f  3 0 M T
  f x 0,x3; ,do lim f x     x   f 
  x 0, x  3;  f x  O    0 Á N 9  2m  9 V  0 m   D   2   2 – 2  2 
x  2x  2  2m  0, x  3;   
x  2x  2  2 , m x  3;    VDC  9  9 m   m    2 9 5   2      m  2
x  x   m x     5 2 2 2 2 2 , 3; m    2
Ta có m nên m  4  ; 3  ;2;1;0;1;  2 . x  m  1
Câu 32. Tìm t t cả các giá trị của tham số m để hàm số y  x 
đồng biến trên khoảng m 1;. 1 1 A. m  hoặc m  2 . B.  m  2 . 2 2
https:/www.facebook.com/groups/toanvd.vdc Trang 24 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 1 1 C.  m  2 . D.  m  2 . 2 2 Lời giải N H
Tác giả:Nhật Thiện. Facebook: Nhật Thiện ÓM T Chọn C O Á x  m  2m 1 N
Đặt f  x 1 
,  x  m  f ' x  V x  m x  m2 D – VDC
f ' x  f  x
Để hàm số y đồng biến trên khoảng 1;  thì y '  0   , x   1; f  x 0 Trường hợp 1:   1    m    2m 1 0 f '
  x  0, x  1;  2    m  1  m  1   m  f    1  0   2  m       m 1 2 m 0   m 1  Trường hợp 2:   1 m  N 2m 1  0  2 H  f '
  x  0, x  1;   1 Ó   m  1  m  1    m  2 M T  f    1  0   2 2  m      1 m 2 0  O 1 m  Á N 1 V
V y để hàm số đồng biến trên khoảng 1;  thì  m  2 . D 2 – VDC
y  f  x f  x
3. Dạng 3: Tìm điều kiện tham số m để hàm với
là hàm số chứa căn
đồng biến, nghịch biến trên tập D cho trƣớc. m
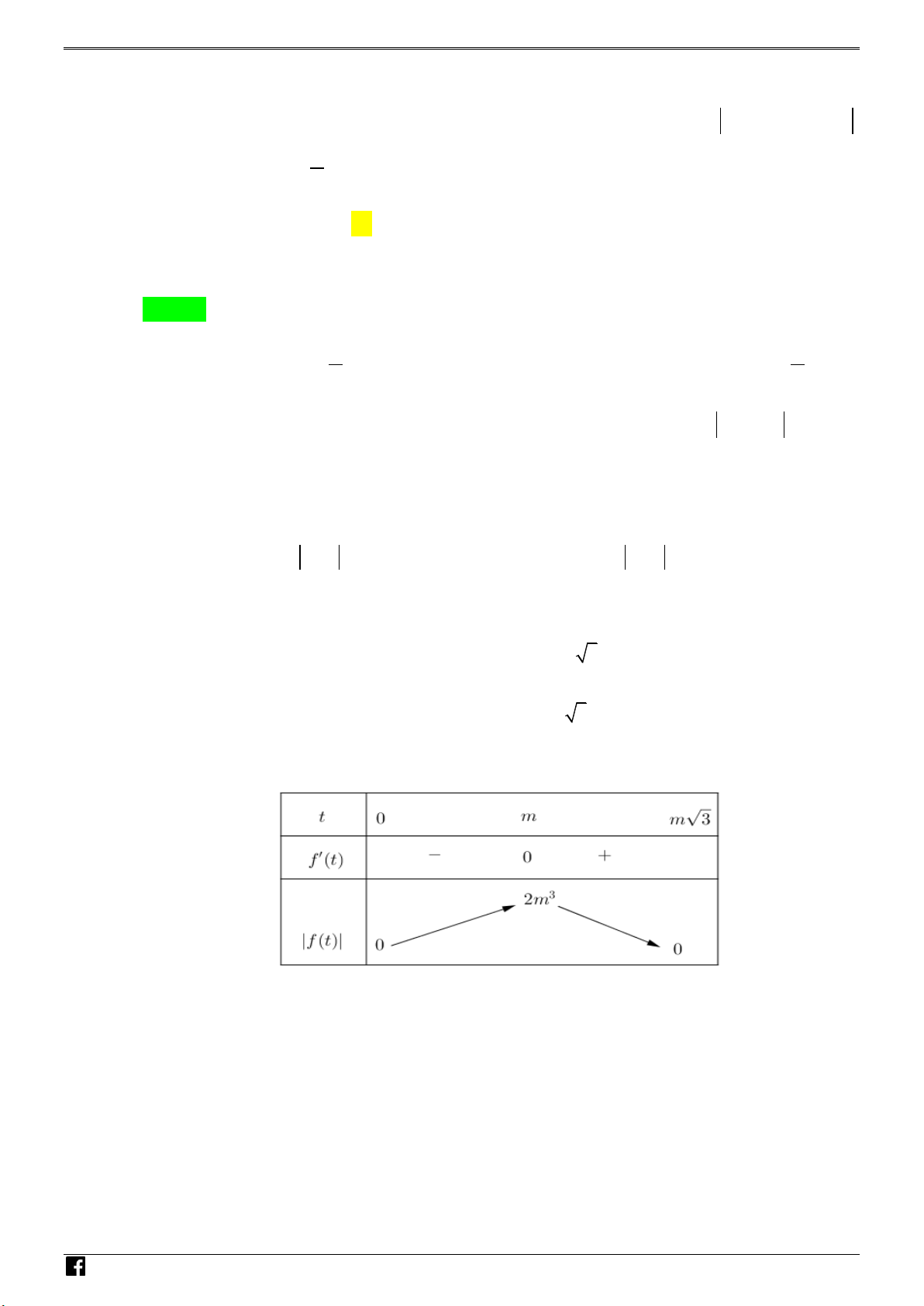
Câu 33. Cho hàm số y  2  x  x  2 
x 1 . Có bao nhiêu giá trị m nguyên để hàm số 2 nghịch biến trên (0;1) A. 4 B. 2 . C. 3 . D. 5 . ời giải Chọn A m
Đặt f (x)  2  x  x  2  x 1 2
https:/www.facebook.com/groups/toanvd.vdc Trang 25 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 1 1 m Ta có f (  x)     2 2  x 2 2  x 2
Do hàm số liên tục tại x  0; x 1 nên để hàm số nghịch biến trên (0;1) t x t 2 trường N H hợp sau: Ó M Trường hợp 1: T O Á m 1 1   N
f (x)  0, x  0  ;1    , x  0  ;1    2 2 2  x 2 2  x V  f (1)  0  D  f (1)  0 – VDC m 1 1   , x  0  ;1  m  1 1   2    min     2 2 x 2 2 x   x   0;  1  2 
2 2  x 2 2  x   2  3  m  0 m     3  m  2  3 2 Trường hợp 2: m
 f (x)  0, x  0  1 1 ;1    , x  0  ;1 
  2 2 2  x 2 2  x  f (1)  0  f (1)  0 m 1 1   m  1 1  , x  0  ;1       max  2 2 2  x 2 2  x  x    0;  1     2 2 2 x 2 2 x    N m  m H   3   3 Ó  2  2 M T  1 O m  1  Á   3 (vô nghiệm). N  V m  2  3 D –
Do m nguyên nên m nh n các giá trị sau 3  ; 2;1;0 VDC
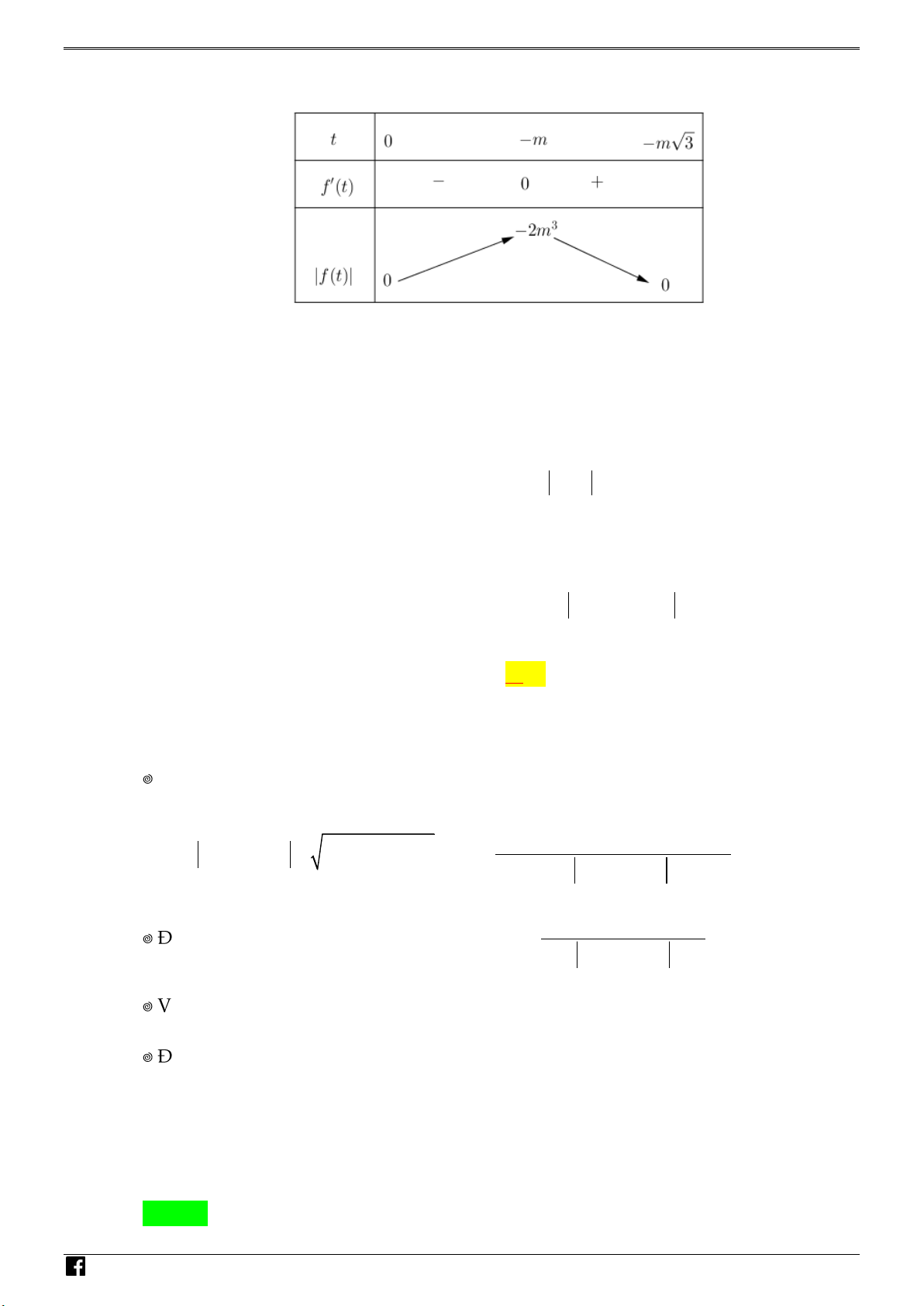
Câu 34. Có bao nhiêu giá trị nguyên của tham số m  5  ;5 để hàm số 2 y 
x  3  2x  3m
nghịch biến trên 2;3 ? A. 2 . B. 3 . C. 5 . D. 9 . Lời giải Chọn B
Xét hàm số f  x 2
 x  3  2x  3m x x  2 x  3
Ta có: f  x 
 2  f x 2  . 2 2 x  3 x  3
https:/www.facebook.com/groups/toanvd.vdc Trang 26 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
Cho f  x 2
 0  x  2 x  3  0  x  2 .
Ta th y f  x  0, x
 2;3 nên hàm số f  x nghịch biến trên 2;3 . N Để 2 y 
x  3  2x  3m nghịch biến trên 2;3 thì H Ó M  f   6 6 3  0 
6  6  3m  0  m  T 3 O Á N Do m  5
 ;5 nên m  2;3;  4 . V D
Câu 35. Có bao nhiêu giá trị nguyên của tham số m0;1  0 ðể hàm số 2
y  x  m x  2x  3 – VDC
ðồng biến trên khoảng 1;  ? A. 11 . B. 10 . C. 12 . D. 9 . Lời giải
Tác giả:Vũ Thị Thúy. Facebook: Vũ Thị Thúy Chọn A + T Đ D 
+ Xét hàm số f  x 2
 x  m x  2x  3 . x  1
+ f  x  1 m N 2 x  2x  3 H Ó M T
 f x  0, x  1;    O  f    1  0 Á
+ Hàm số đồng biến trên khoảng 1;    N  .  f 
  x  0, x  1; V  D  f    1  0 – VDC *) TH1: 
f  x  x    x 1 0, 1;  1 m  0, x  1; + 2 x  2x  3 2
 x  2x  3  m x   1  0 , x  1;. 2  t  2 + Đặt 2
t  x  1, t  0  t  2  mt  0 t   0  m  , t   0 t 2  t  2 2 Xét f (t)  , f (  t)   0 t  > 0.BBT: t 2 2 t t  2
https:/www.facebook.com/groups/toanvd.vdc Trang 27 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 N H Ó M T O Á Từ BBT ta có N V     f   x  x    m 1 0, 1; m  1  D   1       1   m  . –  f    1  0 1   . m 2  0 m  2  VDC  2 *) TH2: 
f  x  x    x 1 0, 1;  1 m  0, x  1; + 2 x  2x  3 2
 x  2x  3  m x   1  0 , x  1;. + Đặt 2
t  x  1, t  0  t  2  mt  0   * , t   0 lim      
 2t 2 mt 2 0nên với mỗi giá trị của m luôn có giá t 0  + Mà  
trị của t dương đủ nhỏ để VT của * lớn hơn 0 Suy r hông có gí trị nào của m để N TH2 thỏa mãn. H Ó M T 0;1;2;3;4;5;6;7;8;9; 
V y có 11 giá trị nguyên của m thỏa mãn là 10 . OÁ
Câu 36. Cho hàm số f  x 2
 x  2x  2  x  m , trong đó m là tham số thực. S là t p hợp t t N V
cả các giá trị nguyên của m trên đoạn 2019; 2019 để hàm số f  x đồng biến trên D – khoảng  1;
   . Số ph n tử của t p S là VDC A. 2018. B. 2017. C. 2019. D. 4039. Lời giải
Tác giả:Nguyễn Văn Toàn; Facebook: Nguyễn Văn Toàn Chọn A
Xét hàm số g  x 2
 x  2x  2  x  m trên khoảng  1;    . x 1 x 1 x  2x  2
Ta có, g ' x 2  1   0, x   1  2 2 x  2x  2 x  2x  2
(Do x   x  x    x     x  2 2 1 2 2 1 1 1  0, x   1  )
https:/www.facebook.com/groups/toanvd.vdc Trang 28 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
V y hàm số g  x nghịch biến trên khoảng  1;    .
Suy ra, hàm số f  x  g  x đồng biến trên khoảng  1;    N H
 g x  0, x   1   1 Ó M g x 1;  1;    T
Do hàm số   liên tục trên 
 và nghịch biến trên khoảng   nên hàm OÁ
số g  x nghịch biến trên 1;   . N V D V y  
1  max g  x  0  g  
1  m  2  0  m  2   1;   – VDC V y S   2019  ; 2018;...; 
2 , nên suy r đ p n là A.
Câu 37. Có o nhiêu gi trị nguyên m củ th m số m để hàm số 2
y  3 x 1  x  m đồng
iến trên hoảng 1;  ? A. 5 . B. 6 . C. 4 . D. Vô số. Lời giải
Tác giả:Nguyễn Việt Thảo. Facebook: Việt Thảo Chọn A 3x
- t hàm số f  x 2
 3 x 1  x  m  f x  1. 2 x 1 N H
Trên 1;   f  x  0 . Ó M T BBT: O Á N V D – VDC
h n th y hàm số y  f  x đồng iến trên hoảng 1;   3 2 1 m  0  m  3  2 1. m  ại do   m 5  ;4;3;2;  1 . m  0
y có 5 gi trị củ m thỏ m n yêu c u ài to n
Câu 38. Có bao nhiêu giá trị nguyên của tham số m để hàm số 2 2
y  4 x  2x  3  5x  m  5
đồng biến trên khoảng (1; )  ? A. 9 B. 6 C. 11 D. 8 Lời giải
https:/www.facebook.com/groups/toanvd.vdc Trang 29 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 Chọn A Xét hàm số 2 2
f (x)  4 x  2x  3  5x  m  5 x c định trên . Ta có 4(x 1) N f '(x)   5 H 2 x  2x  3 Ó M
Với x 1 f '( )
x  0  f (x) đồng biến trên 1;   . T O Á N
V y để hàm số y  f (x) đồng biến trên 2
(1;  )  f (1)  0  m 10  4 6  0 V 2 D
 m 10  4 6  2
  6  m  2  6 – VDC
Mà m  ,  m  4
 ;  3 ;  2 ; 1; 0 ;1; 2 ; 3 ;  4 suy ra chọn đ p n A Câu 39. Cho hàm số 2 2
y  f (x) |
 x  3  2x  m  5m |.Hỏi m thuộc khoảng nào trong các
khoảng s u để hàm số f (x) đồng biến trên (1; )  . A.  ;0 . B. (1;4) . C. (;2) . D.3;   . Lời giải Chọn A +Đặt 2 2 g(x) 
x  3  2x  m  5m . x Ta có g (  x)   2  0 x  (1; ). N 2  H x 3 Ó M T
+Dế th y g(x) liên tục trên 1;   và g (
 x)  0x(1; )nên g(x) đồng biến trên O 1;  Á N 2 V
 g(1)  0  m 5m  4  0 (*) D – VDC Nên y  f ( ) x |  g( )
x | đồng biến trên 1;    f (1)  0 kết hợp với (*) ta có :
m 1 m  ;1 2
m  5m  4  0   . 
.Mà m  ;0  ;  1 .
m  4 m  4;
Câu 40. Có o nhiêu gi trị nguyên củ th m số m nhỏ hơn 10 để hàm số 2 y 
x  6x  m
đồng iến trên hoảng 0;3 ? A. 6 . B. 4 . C. 3 . D. 10 . Lời giải
Tác giả: Nguyễn Thị Thu Huyền. Facebook: Thu Huyền
https:/www.facebook.com/groups/toanvd.vdc Trang 30 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 Chọn D T Đ D  0;6 2  x  6 N
- t hàm số f  x 2
 x  6x  m  f x   0  x  3. 2 H x  6x Ó M BBT: T O Á N V D – VDC
àm số y  f  x đồng iến trên hoảng 0;3  m  0 . m  ại do 
 m0;1;2;3;4;5;6;7;8;  9 . m  10
y có 0 gi trị củ m thỏ m n yêu c u ài to n N H 3 2 m Ó
Câu 41. Tổng các giá trị nguyên của tham số m để hàm số y  x  3x  9x  5  có 5 điểm M T 2 cực trị là. O Á A. 2016 . B. 1952 . C. 2016 . D. 496 . N V Lời giải D – VDC m
Xét hàm số f  x  3 x  2
3x  9x  5  2 . x  1
Ta có f  x  2
3x  6x  9  0  x .  3 Ta có bảng biến thiên
https:/www.facebook.com/groups/toanvd.vdc Trang 31 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
 f x , f x   0
Do y  f  x       nên 
 f  x, f  x  0 N m H ? Nếu
 0  m  0 thì f x  0 có nghiệm x  3 0
, ta có bảng biến thiên của hàm số Ó 2 M đ cho là T O Á N V D – VDC
Trường hợp này hàm số đ cho có 3 điểm cực trị. m ? Nếu
 32  0  m  64 f x x 1 2
thì    0 có nghiệm   0
,ta có bảng biến thiên của hàm số đ cho là N H Ó M T O Á N
Trường hợp này hàm số đ cho có 3 điểm cực trị. V D m –  0  VDC  2 3 2 m ? Nếu   0  m  64 f x x 3x 9x 5 0 có ba nghiệm x x 1 ; 2 ; m thì         2  32  0  2 x x 1 x 3 x 3 với      1 2
3 , ta có bảng biến thiên của hàm số đ cho là
Trường hợp này hàm số đ cho có 5 điểm cực trị.
https:/www.facebook.com/groups/toanvd.vdc Trang 32 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
hư v y, các giá trị nguyên của m để hàm số đ cho có 5 điểm cực trị là m 1;2;3;...;6  3 .
Tổng các giá trị nguyên này là: N H Ó 631 63 M
S  1 2  3  ... 63   2016 . T 2 O Á N
Câu 42. Có bao nhiêu giá trị nguyên của m   2  020;2020   để hàm số 2
y  x 1  mx 1 đồng VD biến – VDC trên khoảng 1; 2 A. 4042 B. 4039 C. 4040 D. 4041 Lời giải Chọn D. x Đặt 2
f (x)  x 1  mx 1. Ta có f '(x)   m 2 x 1
Vì hàm số liên tục tại x 1; x  2 nên để hàm số y  f (x) đồng biến trên khoảng 1; 2
t x t h i trường hợp sau: x
 f x   x  
 m  0, x   1; 2 '( ) 0, 1; 2  TH1: 2    x 1  f (1)  0  m  2 1 N H  x   x  Ó m  ,  x  
1; 2 m  min  M T 2 1; 2 2   x 1  
 x 1   m  2 1   1   O m  2 1 m  2 1 Á N  x
 f x   x
 m  0, x  1; 2 '( ) 0, 1; 2 V      TH2: 2    x 1 D  f (1)  0  – m  2 1 VDC  x   x  m  ,  x  
1; 2 m  max  2 5 2 1; 2 2   x 1  
 x 1   m  2 5   m  2 1 m  2 1  2 5 m  Từ (1) và (2) ta có 5  m  2 1 m  Do 
nên có 4041 giá trị của m thỏa mãn yêu c u bài toán. m   2  020; 2020
https:/www.facebook.com/groups/toanvd.vdc Trang 33 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
4. Dạng 4: Tìm điều kiện tham số m để hàm y  f  x với f  x là hàm số lƣợng giác
đồng biến, nghịch biến trên tập D cho trƣớc. Có bao nhiêu giá trị m nguyên để hàm số NH Câu 43. 3 2
y  f x  x  x   2
m   x   2 ( ) 3 3 5
12  3m cos x đồng biến trên 0; Ó M A. 3 . B. 5 . C. 4 . D. Vô số T O Á Lời giải N V Chọn B D – 3 2 2 2 VDC
Đặt h  x  x  3x  3m  5 x  12  3m  cos x .
Ta có h x 2
 x  x   2 m     2 3 6 3 5
12  3m sin x .
 hx  x  2     2 3 1
12 1 s inx  3m 1 sin x  0 x  0;.
V y hàm số h  x luôn đồng biến trên 0;  .
Để y  f (x) đồng biến trên 0;  . Thì h      2 0 0
12  3m   0  m 2  ;2.
Kết luận: có 5 giá trị m nguyên thỏa mãn.
Câu 44. Các giá trị của tham số m để hàm số y  sin x  cos x  m đồng biến trên khoảng NH     Ó  ;   là M T  4 2  A. m  2 . B. m  2 . C. m 1. D. m 1. O Á Lời giải N V
Tác giả:Thanh Nhã. Facebook: Nhã Thanh D – VDC Chọn B      
Xét hàm số f  x  sin x  cos x  m  2 sin x   m  
 f x  2 cos x    .  4   4 
f  x. f  x Khi đó y  x 
x  m  f  x 2 sin cos
 f x . Nên y  . 2 f  x        
Hàm số y  sin x  cos x  m đồng biến trên khoảng  ; 
  y  0; x    ;   .  4 2   4 2   f
  x. f  x  0       , x    ;    .  f   x 1  0  4 2              Với 
 x     x    cos x   0, x    ;     . 4 2 2 4 4  4   4 2 
https:/www.facebook.com/groups/toanvd.vdc Trang 34 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020    
 f x  0, x    ;   .  4 2         Nên  
1  f  x  0, x    ;    f   0    2. 
1  m  0  m  2 . N  4 2   4  H Ó    M Câu 45. Cho hàm số 3 y sin x .
m sin x 1 . Gọi S là t p hợp t t cả các số tự nhiên m sao cho T    O
hàm số đồng biến trên 0; . 
 Tính số ph n tử của S . Á  2  N A. 1. B. 2 . C. 3 . D. 0 . V D Lời giải – VDC Chọn A       Trên khoảng 0; , 
 hàm số y  sin x đồng biến Đặt t  sin x, x 0;  t    0  ;1 .  2   2     Khi đó hàm số 3
y  sin x  .
m sin x 1 đồng biến trên khoảng 0;   khi và chỉ khi  2 
y  g t  3
 t  mt 1 đồng biến trên 0;  1
Xét hàm số y  f t  3
 t  mt 1 trên khoảng 0; 
1 có f t  2  3t  . m +) Khi m  f t  2  t  t
  y  f t 3 0 : 3 0,
 t 1 đồng biến trên 0;  1 và đths
y  f t  3
 t 1 cắt trục hoành tại điểm duy nh t t  1 
 y  g t 3
 t  mt 1 đồng biến trên 0; 
1  m  0 thỏa mãn N m m
+) Khi m  0 : f t   0 có 2 nghiệm phân biệt t   , t  . H 1 2 3 3 Ó M T  m   m 
Hàm số y  f t  3
 t  mt 1 đồng biến trên các khoảng  ;      và  ;     O 3   3   Á N m m V TH1:   0  1  0  m  3 D 3 3 – VDC  m 
Hàm số y  f t  3
 t  mt 1 nghịch biến trên khoảng 0;    và đồng biến trên 3    m  khoảng  ;1   3  
 Không có giá trị của m để y  g t 3
 t  mt 1 đồng biến trên 0;  1 m m TH2:   0 1  m  3 3 3
Để y  g t  3
 t  mt 1 đồng biến trên 0;  1 thì 3
t  mt 1  0, t  0;  1 1 3 3
 mt  t 1, t  0  2
;1  m  t  , t  0  ;1  m 
 Không có giá trị của m thỏa t 3 4 mãn.
https:/www.facebook.com/groups/toanvd.vdc Trang 35 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
V y chỉ có giá trị m  0 thỏa mãn
Câu 46. Có bao nhiêu giá trị nguyên của m thuộc 5;5 để hàm số 3 2
y  cos x  3m cos x    N nghịch biến trên 0;   . H  2  Ó M A. 1. B. 11. C. 5 . D. 6 T O Á Lời giải N V Chọn B D –       VDC
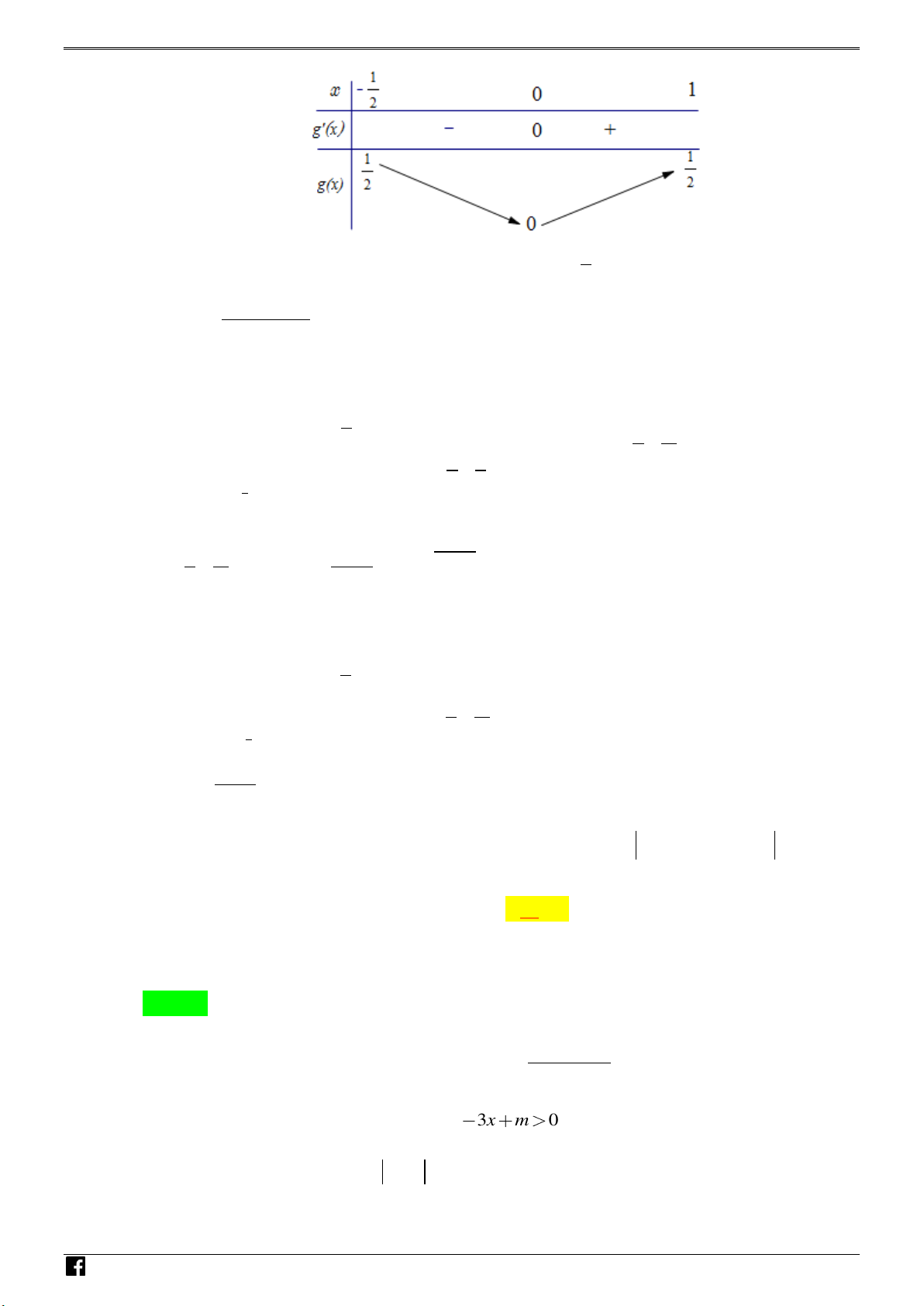
Đặt t  cos x , vì x  0;  t    0 
;1 . Vì t  cos x là hàm số nghịch biến trên 0;   nên  2   2 
Yêu c u bài toán trở thành tìm m nguyên thuộc 5;5 để hàm số 3 2
y  t  3m t đồng biến trên 0; 
1 . Xét f t  3 2 2
 t  3m t ;t 0;  1 ; f t  2 2 '  3t  3m .
TH1: Nếu m  0  f 't   0; t  0; 
1  f t  luôn đồng biến trên 0;  1 .
Mà f 0  0  y  f t  luôn đồng biến trên 0;   y  f t  đồng biến trên 0;  1 .
Do đó m  0 thỏa mãn bài toán   1 . t  m 3 t  m 
TH2: m  0  f 't   0  
; f t   0  t  0  N t  m  H t  m 3  Ó M T
*) Với m  0, ta có BBT sau: O Á N V D – VDC
Từ BBT suy ra hàm số y |
 f t | đồng biến trên 0;m .
YCBT tương đương 0; 
1  0; m  m  1 2 .
https:/www.facebook.com/groups/toanvd.vdc Trang 36 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
*) Với m  0 , ta có BBT sau: N H Ó M T O Á N V D y |  f t | 0;  m – Từ BBT suy ra hàm số
  đồng biến trên  . VDC
YCBT tương đương 0; 
1  0;  m  m  1  3 . Từ  
1 ;2;3 v y có 11 giá trị nguyên của m thỏa mãn bài toán.
5. Dạng 5: Tìm điều kiện tham số m để hàm y  f  x với f  x là hàm số mũ đồng
biến, nghịch biến trên tập D cho trƣớc.
DẠNG 5: Tính đơn điệu của hàm mũ chứa dấu trị tuyệt đối
Câu 47. Có bao nhiêu giá trị nguyên dương của m để  9x  3x y
 m 1 đồng biến trên đoạn 0; 1. A. 1. B. 4 . C. 3 . D. 6 . N H Lời giải Ó
Tác giả:Phạm Tuấn. Facebook: Bánh Bao Phạm M T x O
Đặt 3  t  t 1;  3 vì x 0;  1 . Á N V  2 2       2 2. t t m 1 . t t m 1 D 2
 y  t  t  m 1   2t t  m       1  y  2 –
2. t  t  m 1 VDC 2t   1 . 2
t  t  m   1
ể hàm số đồng biến trên đoạn t 1;3 thì y   0 t  1;  3 2
t  t  m 1
ới mọi giá trị của t 1; 
3 thì 2t 1>0 nên ể y  0 t  1;  3 thì : 2
t  t  m   t    2 1 0 1;3
 m 1 t  t  g t t  1;  3
 m 1 min g t  2  m  3. 1  ;3
V y có 3 giá trị nguyên 1; 2; 
3 thỏa mãn yêu c u bài toán. Chọn C
https:/www.facebook.com/groups/toanvd.vdc Trang 37 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
Câu 48. Có bao nhiêu giá trị m nguyên dương và nhỏ hơn 2020 để hàm số x x 1 y 4 .2 m   
 m  2 đồng biến trên khoảng (0;1) ? A. 2018 . B. 2019 . C. 2 . D. 3 . N H Lời giải. Ó M T
Tác giả: Nguyễn ăn gà F ce oo g guyen O Á Chọn A N V x x D Xét hàm số 1 f ( ) x  4  . m 2
 m  2 (1) trên khoảng (0;1) Đặt 2x t  , t (1; 2) . – VDC Hàm số (1) trở thành 2 (
h t)  t  2 .
m t  m  2 trên khoảng (1;2) . Suy ra h'(t)  2t  2m .
 f (x) ñoàng bieán treân ( 0;1)   f (0)  0
Ta có y  f (x) đồng biến trên khoảng (0;1)   (*).
 f (x) nghòch bieán treân (0;1)   f (0)  0 Vì hàm số 2x t  đồng biến trên (0;1) .
h(t) ñoàng bieán treân ( 1;2)
2t  2m  0 t  (1;2)   3   m  0 3   m  0 Do đó, (*)    
h(t) nghòch bieán treân (1;2)
2t  2m  0 t  (1;2)     N  3   m  0  3   m  0 H Ó M T m 1  O m  3 m 1 Á    
. V y có 2018 số nguyên dương nhỏ hơn 2020 thỏa ycbt.     N m 2 m 3   V m  3 D – 2 x2 x 1  VDC Câu 49. Cho hàm số x 1  x 1 y e 3e   
 2m  5 (1) . Có bao nhiêu giá trị nguyên dương của tham
số m để hàm số nghịch biến trên khoảng 2; 4 ? A. 234 . B. Vô số. C. 40 .
D. Không tồn tại m. Lời giải
Tác giả:Nguyễn Mạnh Cƣờng Facebook Cuong Nguyen Chọn C x 1  x 1   x 1   x 1 2  +) Đặt x 1 t e   , ta có x t  e  . x  e  .  0 x
 2;3  t     2 3 1 1 e ; e , đồng thời x 2   x 1 x  1
và t sẽ ngược chiều biến thiên.
https:/www.facebook.com/groups/toanvd.vdc Trang 38 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
+) Khi đó hàm số trở thành y  t  t  m   t  t  m  2 2 2 3 2 5 3 2 5 (2) 2 2
t  3t  2m  5.2t  3  2
t  3t  2m  5.2t  3 Ta có: y   . 2 2 2 2 2
t  3t  2m  5
t  3t  2m  5 N     H Ó
Hàm số (1) nghịch biến trên khoảng 2;3  hàm số (2) đồng biến trên khoảng M 2 3 T e ;e  O Á 2 2
t  3t  2m  5.2t  3 N   0 t   2 3 e ; e  2
 t  3t  2m  5  0 t   2 3 e ;e  2 V 2  2
t  3t  2m  5 D – 2 t  3t  5 VDC  m 
 g(t) t   2 3 e ; e . 2 2t  3 e  3e  5 e  3e  5 e  3e  5 +) Có g (  t)   0 t
 e ;e  4 2 6 4 4 2 2 3   g(t)   m  . 2 2 2 2
Với điều kiện m là số nguyên dương t tìm được 40 giá trị của m. Chọn C 2 2 
Câu 50. Có bao nhiêu giá trị nguyên dương x x m( 2
 019;2020) , để hàm số y  e  e  m
nghịch biến trên 1;e ? A. 401. B. 0 . C. 2019 . D. 2016 . Lời giải
Tác giả: Nguyễn Thị Hoa Facebook Hoa nguyen Chọn A 2 2 2 2  x x  x x         N
Đặt f (x) e e m f (x) 2xe 2xe H  Ó f (x) f x 2  
y  f (x) 
f (x)  y  M T Ta có 2 f  x O
 y  0, x   1;e . Á Yêu c u bài toán   (*) N 2 2 x V 2x e 1 2 2 x x   D
Vì x  1;e 2
 xe  2xe   0, 1;e 2   nên x – e VDC
Khi đó, *  f  x  0, x  1;e 2 2  x x  e
 e  m  0, x  1;e 2 2  x x  e  e  , m x  1;e 2 2 2 2
Ta có giá trị lớn nh t của hàm số  x x y  e
 e , x 1;e là e e e e  nên 2 2 e e m e e   1618,18 .
V y có 401 giá trị nguyên dương m thỏa mãn.
Câu 51. Giá trị lớn nh t củ m để hàm số x 2 x
y  e  e
 m đồng biến trên1;2 là A. e . B. 2 e  e . C. 2 e . D. 2 . Lời giải Chọn B
https:/www.facebook.com/groups/toanvd.vdc Trang 39 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 Đặt   x 2 x
f x  e  e
 m  y  f x 2  f x .
f ' x f  x Ta có y '  2 N f  x H Ó M
Hàm số đồng biến trên 1; 2  y '  0 x  1;2 T O Á  f
  x f ' x  0 N   x   1;2  f   x  0 V D – x 2 x     
Vì f ' x e 2e 0 x 1;2 VDC y '  0 x
 1;2  f x  0 x  1;2 Nên x 2 x
 m  e  e x  1;2 2
 m  e  e    
Câu 52. Tìm t t cả các giá trị của m để hàm số tan x tan  8  3.2 x y
 m  2 đồng biến trên  ;    4 2  . 29 29 29 29 A. m  . B. m  . C. m  . D. m  . 8 8 8 8 Lời giải
Tác giả: Lê Minh Hùng. Facebook: Lê Minh Hùng N Chọn C H Ó     1 M T Đặt tan
2 x  t vì x   ;   suy ra tan x  1
 nên t  Khi đó t có hàm số:  4 2  2 O 3 Á
y  t  3t  m  2 (1). N V    D 
Để hàm số n đ u đồng biến trên  ;
thì hàm số (1) phải đồng biến trên   –  4 2  VDC 1  ;    .  2 
Xét hàm số f t  3
 t  3t  m  2 .
Ta có: f t  2
 3t  3  0, t  .
f t . f t  Khi đó    2 y f t 
f t  nên y  . 2 f t  1  1 
Hàm số đồng biến trên ;  
 khi và chỉ khi y  0, t   ;    .  2  2 
https:/www.facebook.com/groups/toanvd.vdc Trang 40 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020    1  f t  1  0, t   ;    3
 t  3t  m  2  0, t   ;    2  2  1  3
 m  t  3t  2, t   ;  ,  . N   2  H Ó M 1 
Xét hàm số: g t  3
 t  3t  2, t   ;  . T   2 O  Á N   V gt  2
 3t  3  0, t
 . V y hàm số g t luôn đồng biến trên nên g t 1  g   . D  2  – VDC  1  29
Từ  suy ra: m  g    .  2  8
6. Dạng 6: Tìm điều kiện tham số m để hàm y  f  x với f  x là hàm số logarit
đồng biến, nghịch biến trên tập D cho trƣớc.
Câu 53. Có bao nhiêu giá trị nguyên thuộc khoảng  10
 0;100 của tham số m để hàm số 2
y  ln 3x  4x  m đồng biến trên đoạn 2 1  ;e    ? A. 101. B. 102 . C. 103 . D. 100 . Lời giải
Tác giả: Đỗ Hải Thu Chọn B N H 2
y  ln 3x  4x  m Điều kiện x  0 . Ó M T Xét hàm số  x 2 g
 ln 3x  4x  m trên 2 1  ;e    . O Á 1 1 8x N  gx 2 2  8x   0, x   1  ;e  
  g  x nghịch biến trên 2 1  ;e    . V x x D – VDC
 hàm số y  x 2 g
 ln 3x  4x  m đồng biến trên đoạn 2 1  ;e   
 ln3 4 m  0  m  4ln3.
Mà m nguyên thuộc khoảng  10
 0;100 nên m 99  ; 98  ;...; 1  ;0;1;  2 .
V y có 102 giá trị m nguyên thỏa mãn yêu c u bài toán.
Câu 54. Có bao nhiêu số nguyên m  2020 để hàm số y  ln mx  x  2 nghịch biến trên 1; 4 ? A. 2018. B. 2019. C. 1. D. vô số.
https:/www.facebook.com/groups/toanvd.vdc Trang 41 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 Lời giải Chọn A N
Tác giả: Nguyễn Văn Hà; Facebook: Hà Nguyễn Văn HÓM
Xét f  x  ln mx  x  2 . T O Á Dễ th y x
 1;4 : mx  0  m  0. N V 1 D
Khi đó f  x  1  0, x  1;4 . – x VDC
Do đó f  x luôn nghịch biến trên 1; 4 . e
Yêu c u ài to n tương đương với f      m 2 4 0 ln 4  2  0  m  1,6 . 4
V y m 2; 2019 có 2018 số nguyên thỏa mãn. Câu 55. Có bao nhiêu số nguyên m thuộc
2020;2020 để hàm số y 
 2x  xm 2 ln 2
 2mx 1 luôn đồng biến trên 0;10 . A. 4038 . B. 2020 . C. 2017 . D. 2017 . ời giải N H Ó
Tác giả: Cao Tung M T Chọn C O Á N
Ta xét hàm số f  x 
 2x  xm 2 ln 2
 2mx 1 trên 0;10 . V D 2 2 –
Điều kiện hàm số có nghĩ là x  2x  m  0, x
 0;10  x  2x  m, x  0;10   1 VDC Ta lại có 2
x  2x  x  x  2  0 với mọi x 0;10 nên điều kiện  
1 cho ta m  0 2 2x  2 2x  2
Đạo hàm f  x 
 4mx do m  0 và x 0;10 nên  0; 4  mx  0 2
x  2x  m 2
x  2x  m
suy ra f  x  0 hàm số đồng biến trên 0;10 .
Từ đó để hàm số y 
 2x  xm 2 ln 2
 2mx 1  f x đồng biến trên 0;10 điều kiện
đủ là f  x  0 với mọi x 0;10 3 .
+) TH1: Xét m  0 hi đó f  x   2
ln x  2x 1 có lim f  x   không thỏa mãn 3 .  x  0
https:/www.facebook.com/groups/toanvd.vdc Trang 42 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
+) TH2: Xét m  0 , do hàm số f  x đồng biến nên ta chỉ c n f 0  0  ln m 1  0
 m  e  m  e  .  2020   m  e N Từ đó t được:   m 20  19; 20  18; 20  17;....; 
3 có 2017 giá trị m H m Ó M thỏa mãn bài toán. T O  Á
Câu 56. Có bao nhiêu số nguyên của tham số m trong đoạn  3;3 để hàm số N 3
y  ln  x  mx  2 đồng biến trên nửa khoảng 1;3? V D A. 7. B. 4 . C. 6 . D. 5 . – VDC Lời giải
Tác giả: Hoàng Thị Hồng Minh – Facebook: Minh Hoang. Chọn C Điều kiện x c định: 3
x  mx  2  0. 3x  m
Xét hàm số f  x   3
ln x  mx  2 . Ta có: f  x 2  . 3 x  mx  2  f   x  0  , x  1;3    f    x 1  0
Hàm số đồng biến trên nửa khoảng 1;3   .  f   x  0  , x  1;3 2  f    x  0 N Trường hợp 1: H Ó 3 M T
  3x  mx    
x  mx  2  1 ln 2 0     1   , x  1;3 2       2 3x m 0 , x 1;3 O 3x  m Á   0  3 3   
x  mx  2  0 N x mx 2  V   1 D  2  1 2
m  max x   2         m x  – 1;3       x      x , x 1;3   m 2. VDC   m  3  x m  max  2 2 3  x   3   1;3 Trường hợp 2:
 x  mx   3 3  
x  mx  2  1 ln 2 0   2   , x  1;3 2       2 3x m 0 , x 1;3 3x  m   0  3 3   
x  mx  2  0 x mx 2   1  2 28 m  x   m   x 3     2  m  3  x , x
 1;3  m  2  7  m .    2   2 2 2
m  x 
m  max x   3     x  1;3   x 
https:/www.facebook.com/groups/toanvd.vdc Trang 43 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
Từ h i trường hợp suy ra m  2
 . Vì chỉ l y m 3  ; 
3 nên m 2; 1;0; 1; 2;  3 .
Câu 57. Cho hàm số y   2
ln x  mx  m 1 . Có bao nhiêu giá trị nguyên thuộc khoảng N   1 
10;10 của tham số m để hàm số đồng biến trên khoảng  ;1 ? H    2  Ó M A. 10. B. 6. C. 9. D. 5. T Lời giải O Á
Tác giả: Nguyễn Thị Thu Trang N V Chọn D D 2
Đặt f  x  ln  x  mx  m 1. – VDC   1  2
x  mx  m  0,  x   ;1     2     
 f  x 1  0, x    ;1     1   2    
 f  x 1  0, x    ;1    1    2 
Hàm số đồng biến trên khoảng  ;1    .  2    1  2
 x  mx  m  0, x  ;1      2     
 f x 1  0, x    ;1   2   2      f x 1  0, x    ;1     2  N H  1   1  2 Ó + Xét 2
x  mx  m  0, x    ;1 
  x  m x   1 , x    ;1   M T  2   2  2 x  1  O .  m  , x    ;1   . Á x 1  2  N 2 V x x  1   1 
Đặt g  x 2  Khi đó, m  , x    ;1  g   x  , m x    ;1 . D   x 1 x 1  2   2  – VDC 1
Ta có: g  x 1  x 1
 g x  1 . x 1 x  2 1   1  x  0   ;1      g x 2  0   .  1  x  2    ;1      2   1 
BBT của hàm số y  g  x trên khoảng  ;1   .  2 
https:/www.facebook.com/groups/toanvd.vdc Trang 44 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020 N H Ó M T O   y  g x g x  m x   
 m  g 0  0 Á Từ BBT của hàm số   suy ra   1 ;1   .  2  N V 2x  f  m D + x  . 2 x  mx  m – VDC    m  0       m 0 m 1   1    +   1  2x  , m x    ;1    m  1     1 m    2   ln  1      1 1    4 2 
lim f  x  0 ln  m 1 0     1   4 2  x  2 m  1      m 1 1 4e    1 m   e  m  .   1 4 e  m  2 4 2  2    m  0  m  0   1  
+ 2  2x  m x    ;1    m  2
suy ra không tồn tại m .   2 N    1 m H  
lim f  x  0 ln  1 0   Ó   1     4 2 M T x  2 1 4e O V y m  . Mà m nguyên, 1
 0m10 nên có 5 giá trị m thỏa mãn bài toán Á 2 N V  3 D
Câu 58. Tổng các giá trị m nguyên thuộc  5;5 sao cho hàm số y  ln  x  3x  m 1 nghịch – 0;1 VDC biến trên   bằng A. 10. B. 11. C. 12 . D. 13 .
Tác giả : Phan Thị Yến_Facebook Phan Yên. Lời giải Chọn C 3x  3
Đặt f  x   3
ln x  3x  m 1, ta có f  x 2  3 x  3x  . m
Điều kiện x c định của f  x là 3 x 3x m 0 .
Điều kiện c n để hàm số y  f  x nghịch biến trên 0;  1 là 3
x  x  m  x    3 3 0,
0;1  m  x  3 x, x  0;  1  m  2 (1).
https:/www.facebook.com/groups/toanvd.vdc Trang 45 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
Với mọi x 0;  1 , ta có 2
3x  3  0 Do đó từ điều kiện (1) ta suy ra  f  x 2 3x 3   0, x   0;1 3   x  3x  . m N H Ó
Điều kiện đủ để hàm số y  f  x nghịch biến trên 0;  1 là M T 3 O
f  x  0, x  0; 
1  ln  x  3 x  m 1 0, x  0  ;1 Á N V 1 3 D
 m   x  3x, x  0  ;1 e – VDC 1
 m   2  2,37 . e
Do m nguyên thuộc  5
 ;5  m3;4;  5 .
V y tổng các giá trị của m bằng 12.
Câu 59. Có bao nhiêu giá trị nguyên của tham số m  10  ;10 để hàm số y  log  3 2
x  x  mx 1 đồng biến trên 1;  . 3  A. 13. B.12 . C.11. D. 10 . Lời giải
Tác giả: Nguyễn Thanh Hùng. Facebook: Hùng N Nguyễn H Ó M T Chọn A O 2 Á
3x  2x  m
Đặt f  x  log  3 2
x  x  mx 1 nên f ' x  . 3  N  3 2
x  x  mx   1 ln 3 V D   f   x 0 –   VDC  f '   x  0
Hàm số đồng biến trên y  f  x đồng biến trên 1;    , x  1; .  f   x  0   f '   x  0 Trƣờng hợp 1: log  3 2
x  x  mx 1  0 3   f   x  0   , x  1; 3 2
 x  x  mx 1 0 , x
 1; .  f '   x  0  2
3x  2x  m  0  3 2 2
x  x  mx 11
m  x  x   , x  1;   , x  1;. 2 2 3
 x  2x  m
m  3x  2x
https:/www.facebook.com/groups/toanvd.vdc Trang 46 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
m  min 2x  x     1; m 2       . m   m 2 2 x  x m  5 min 3 2  1; N Trƣờng hợp 2: H 3 2 Ó
log x  x  mx 1  0 3   M  f   x  0   , x  1; 3 2
 x  x  mx 1 0 , x
 1; . T   O f '   x 0  2
3x  2x  m  0 Á  N 2 V    3 2 x x m      D x x mx 1 1    1 – 3 2
 x  x  mx 1 0, x  1; 2
 x  x   m, x
 1; . VDC x   2
3x  2x  m 2  3
 x  2x  m  Ta có: 2
m  x  x, x
 1;  m  max  2 x  x, . 1; Vì  2
lim x  x   nên không tồn tại m thỏa mãn  Do đó trường hợp 2 không tồn x
tại giá trị nào của m thỏa mãn yêu c u bài toán. m 
Suy ra m  2 thỏa mãn yêu c u bài toán. Mặt khác  nên có 13 giá trị của m   10  ;10
m thỏa mãn yêu c u bài toán.
Câu 60. Tổng các giá trị nguyên của m trên 10;10 để hàm số y  g x   2 ( )
ln x  x  m  x
đồng iến trên 1;3 là N H A. 50 . B. 100 . C. 52 . D. 105 . Ó M T ời giải O Á
Tác giả: Trƣơng Quang Phú N VD Chọn C – VDC
Xét hàm số f  x   2
ln x  x  m  x trên hoảng 1;3 .
Điều iện x c định là 2
x  x  m  0 với mọi x   1  ;3. 2x  1
x  3x  m  1
Khi đó f  x 2  1  . 2 2
x  x  m
x  x  m
https:/www.facebook.com/groups/toanvd.vdc Trang 47 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020   2
x  x  m  0   2
  x  3x  m 1  0   1    ln   2
x  x  m  x  0 N
àm số g  x đồng iến trên 1;3  
với mọi x   1  ;3. H  2
x  x  m  0 Ó  M 2
 x  3x  m 1  0  2 T  2 O ln
 x  x  m  x  0 Á N V  2
x  x  m  0 D  2 –
t hệ t phương trình  
1 :  x  3x  m 1  0 đúng với mọi x   1  ;3. VDC ln   2
x  x  m  x  0 2
x  x  m  x    2 0,
1;3  m  x  x, x  1;3 Ta có: .
Khảo s t tính iến thiên củ hàm số 2
y  x  x trên hoảng 1;3 ta suy ra Ví dụ 1. 1 m  max  2
x  x  m   1  ;3 4 2
x  x  m   x     2 3 1 0,
1;3  m  x  3x  1, x   1;3 ại có .
Khảo s t tính iến thiên củ hàm số 2
y  x  3x 1 trên hoảng 1;3 ta suy ra: m  max  2
x  3x   1  m  1 N [ 1  ;3] H Ó 2 2  x M T
ln  x  x  m  x  0, x
  1;3  m  x  x  e , x   1;3 Ngoài ra . O  x Á Đặt   2 x k x x x e    
, k  x  e  2x 1  0, x   1;3 . N V 2  x D
Do đó m  x  x  e , x
  1;3  m  e . – VDC y  
1 tương đương m  e .
ới hệ t phương trình 2 t cũng làm tương tự như trên thì được  1   2 m
x  x  m  0  4   2
 x  3x  m 1  0 x    1  ;3   m  1  9  m  .   ln   2
x  x  m  x  0 ln   2
x  x  m  x  0 
https:/www.facebook.com/groups/toanvd.vdc Trang 48 NHÓM TOÁN VD–VDC
NĂM HỌC 2019 – 2020
y hàm số y  g x   2 ( )
ln x  x  m  x đồng iến trên 1;3 khi và chỉ khi m  e , mà
m là số nguyên thuộc 10;10 nên m 3; 4;5;6;7;8;9; 
10 Do đó tổng c c gi trị
nguyên củ m thỏ m n là 52 . N H Ó M T O Á N V D – VDC N H Ó M T O Á N V D – VDC
https:/www.facebook.com/groups/toanvd.vdc Trang 49
Document Outline

1. Dạng 1: Tìm điều kiện tham số m để hàm với là hàm số dạng đa thức đồng biến, nghịch biến trên tập D cho trước.
2. Dạng 2: Tìm điều kiện tham số m để hàm với là hàm số dạng phân thức hữu tỉ đồng biến, nghịch biến trên tập D cho trước.
3. Dạng 3: Tìm điều kiện tham số m để hàm với là hàm số chứa căn đồng biến, nghịch biến trên tập D cho trước.
4. Dạng 4: Tìm điều kiện tham số m để hàm với là hàm số lượng giác đồng biến, nghịch biến trên tập D cho trước.
5. Dạng 5: Tìm điều kiện tham số m để hàm với là hàm số mũ đồng biến, nghịch biến trên tập D cho trước.
6. Dạng 6: Tìm điều kiện tham số m để hàm với là hàm số logarit đồng biến, nghịch biến trên tập D cho trước.
Word Bookmarks
- MTBlankEqn

Tính đơn điệu hàm giá trị tuyệt đối Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số