Thông tin
Quiz

Tính giá trị của hàm số khi cho trước các tích phân liên quan Toán 12

Tính giá trị của hàm số khi cho trước các tích phân liên quan Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề:

Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:

17 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Tính giá trị của hàm số khi cho trước các tích phân liên quan Toán 12

69 35 lượt tải Tải xuống

A. KIẾN THỨC CƠ BẢN

1. Tính chất nguyên hàm, tích phân thường sử dụng

   

f x x f x C



 



d du v uv v u

 

 

 

   

d df u x u x x f u u





 

   

d 0 0

f x x f x

  



Tổng quát:

 

 

   

 

0 ; , 0 0, ;

f x x a b f x dx f x x a b

       



2. Nhị thức Niuton

 

0 1 1

... ...

n n k n k k n n

n n n n

x y C x C x y C x y C y

 

      

 Lưu ý:

B. BÀI TẬP

Bài 1. Cho hàm số

 

f x

xác định trên

 

 

 



thỏa mãn

 

2 1

f x







 

0 1



và

 

1 2.



Giá trị

của biểu thức

   

1 3

f f 

Lời giải

Ta có

 

d d ln 2 1

2 1

f x x x x C



   



 

. Hàm số gián đoạn tại điểm



Nếu

   

ln 2 1

x f x x C    

mà

 

1 2 2

f C

  

. Vậy

   

ln 2 1 2

f x x

  

khi



Nếu

   

ln 1 2

x f x x C    

mà

 

0 1 1

f C

  

. Vậy

   

ln 1 2 1

f x x

  

khi



Do đó

   

1 3 ln3 1 ln 5 2 ln15 3.

f f

       

Bài 2. Cho hàm số

 

y f x



xác định trên

 

\ 1;1





và thỏa mãn

 

f x







. Biết rằng

   

3 3 0

f f

  

. Tính

     

2 0 4

T f f f

   

Lời giải

Ta có:

   

df x f x x













1 1 1

2 1 1

x x

 

 

 

 

 



1 1 1

d d

2 1 1

x x

 

 

 

 

 

 

1 1

2 1



 



CHUYÊN ĐỀ

TÍNH GIÁ TRỊ CỦA HÀM SỐ

KHI CHO TRƯỚC CÁC TÍCH PHÂN LIÊN QUAN

Do đó:

   

3 3 0

f f

  

1 1 1

ln 2 ln 0

2 2 2

C C

   

    

   

   

 

Như vậy:

 

1 1

2 1

f x







 

1 2 1

2 ln

2 2 1







ln3

 

;

 

1 0 1

0 ln 0

2 0 1



 



;

 

1 4 1

4 ln

2 4 1

 

 

 

 

ln5 ln 3

 

Từ đó:

     

2 0 4

T f f f

   

 

1 1

ln3 0 ln 5 ln 3

2 2

    

ln5 ln3

 

Bài 3. Cho hàm số

 

f x

xác định trên

 

\ 1;1





thỏa mãn

 

f x







   

2 2 0

f f

  

và

1 1

2 2

f f

   

  

   

   

. Tính

     

3 0 4

f f f  

Lời giải

Ta có

   

df x f x x













1 1

x x

 

 

 

 

 



ln 1

ln 1 1

ln 1

 

  









    









 







khi

C x

Khi đó

   

1 3

2 2

2 2 0

ln3 ln 0

1 1

ln3 ln 2

2 2



  

   



 



 

 

  

   



  



   

 

   

   







f f

C C

f f

C C

Do đó

     

1 2 3

3 6

3 0 4 ln 2 ln ln 1

5 5

         

f f f C C C

Bài 4. Cho hàm số

 

f x

xác định trên

 

\ 1

thỏa mãn

 

f x







 

0 2017

f 

 

2 2018

f 

Tính

   

3 1

S f f

  

Lời giải

Ta có

 

d d ln 1

f x x x x C

   



 

Theo giả thiết

 

0 2017

f 

 

2 2018

f 

nên

 

ln 1 2017 khi 1

ln 1 2018 khi 1

f x x x



   



   



Do đó

   

3 1

S f f

  

ln 2 2018 ln 2 2017 1    

Bài 5. Giả sử hàm số

 

y f x



liên tục, nhận giá trị dương trên

 

 

và thỏa mãn điều kiện

 

1 1



   

3 1f x f x x



 

với mọi



Tính

 

2018

Lời giải

Ta có:

   

3 1f x f x x



 

 

3 1

f x



 



 

3 1

f x



 



 

 

ln 3 1

f x x C   

 

3 1

x C

f x

 

 

Mặt khác ta lại có

 

1 1



nên

1 e



   

Vậy

 

2 4

3 1

3 3

f x

 



 

2 4

6055

3 3

2018 ef



 

Bài 6. Cho hàm số

 

f x



thỏa mãn điều kiện

     

2 1

f x x f x



 

và

 

1 .

 

Tính tổng

       

1 2 3 ... 2018

f f f f   

Lời giải

Ta có :

     

2 1

f x x f x



 

 

2 1

f x



  

 

d 2 1 d

f x

x x x

f x



  

 

 

d f x

x x C

f x

   



 

x x C

f x

    

 

f x

x x C

  

 

Mặt khác theo giả thiết ta lại có

 

 

 

1 1

2 2

    



 

Vậy

 

1 1 1

f x

x x x x

   

 

Khi đó

       

1 2 3 ... 2018

f f f f   

1 1 1 1 1 1 1

1 ...

2 3 2 2018 2017 2019 2018

        

2019

 

2018

2019

 

Bài 7. Cho hàm số

( )f x

có đạo hàm trên



thỏa mãn

2017 2018

( ) 2018 ( ) 2018. .

f x f x x e



 

với mọi



và

(0) 2018.



Tính giá trị

(1).f

Lời giải

Ta có:

2017 2018

( ) 2018 ( ) 2018. .

f x f x x e



 

   

2017

2018

2018.

f x f x





 

   

1 1

2017

2018

0 0

2018.

f x f x

dx x dx





 

 

 

Xét tích phân

   

2018

2018.

f x f x

I dx









   

1 1

2018 2018

0 0

. 2018. .

x x

f x e dx f x e dx

 



 

 

Xét

 

2018

2018. .

I f x e dx







. Đặt

   

2018 2018

2018.

x x

u f x du f x dx

dv e dx v e

 



   

 



 

  

 

 

Do đó

 

   

2018 1 2018 2018

1 0

. . 1 . 2018

x x x

I f x e f x e dx I f e

  



     



Khi đó

 

2018 2018 1

1 . 2018

f e x



  

 

2018

1 2019.

f e

 

Bài 8. Giả sử hàm số

( )f x

liên tục, dương trên



; thỏa mãn

 

0 1



và

 

f x

f x x







Tính

 

2018

f .

Lời giải

Ta có

'( )

( )

f x











 

d 1

2 1

f x

f x x







 

 

ln ln 1

f x x C   

Mặt khác

 

0 1 0

f C

  

. Do đó

 

f x x

 

. Vậy

 

2018 2019

f  .

Bài 9. Xét hàm số

 

f x

liên tục trên đoạn

 

0;1

và thỏa

   

2 3 1 1

f x f x x   

. Tính

 

df x x



Lời giải

Ta có:

   

2 3 1 df x f x x

 

 

 



1 dx x

 



A B C  

Tính:

1 dC x x

 



Đặt

sinx t

suy ra

d cos dx t t

. Đổi cận:

0 0x t  

;

x t



  

Vậy:

cos dC t t







1 cos2t









1 1

sin 2

2 4 4

t t



 

  

 

 

Tính:

 

3 1 dB f x x

 



Đặt

1 d dt x t x    

. Đổi cận:

0 1

x t

   

;

1 0x t  

Vậy:

 

3 dB f t t





 

3 df x x





Do đó:

   

2 3 d

f x f x x



 

 

 



 

5 d

f x x



 



 

f x x



 



Bài 10. Cho hàm số

 

f x

xác định trên



 

 

 

thỏa mãn

   

2 2 sin d

4 2

f x f x x x



 

  

 

  

 

 

 

 



Tính tích phân

 

df x x





Lời giải

Ta có:

2sin d

x x



 



 

 



1 cos 2 d

x x



 

 

  

 

 

 

 



 

1 sin 2 dx x



 



cos2

x x



 

 

 

 







Do đó:

   

2 2 sin d

f x f x x x



 

 

 

 

 

 

 



2sin d

x x



 

 

 

 



2 2

 

 

  

   

2 2

2 2 sin 2sin d 0

4 4

f x f x x x x



 

 

   

     

   

 

   

 



 

2 sin d 0

f x x x



 

 

   

 

 

 

 



Suy ra

 

2 sin 0

f x x



 

  

 

 

, hay

 

2 sin

f x x



 

 

 

 

Bởi vậy:

 

2 2

0 0

d 2 sin d

f x x x x

 



 

 

 

 

 

2 cos 0



 

   

 

 

Bài 11. Cho hàm số

 

f x

liên tục, không âm trên đoạn



 

 

 

, thỏa mãn

 

0 3

f và

     

. cos . 1



 

f x f x x f x



 

 

 

 

. Tìm giá trị nhỏ nhất

và giá trị lớn nhất

của

hàm số

 

f x

trên đoạn

;

6 2

 

 

 

 

Lời giải

Từ giả thiết

     

. cos . 1

f x f x x f x



 

   

 

cos



 



f x f x

f x

   

 

d sin

f x f x

x x C

f x



  





Đặt

   

2 2 2

1 1

t f x t f x

    

   

d dt t f x f x x



 

Thay vào ta được

d sin sin

t x C t x C    



 

1 sin

f x x C   

 

0 3

f 

 

Vậy

   

2 2 2

1 sin 2 sin 4sin 3f x x f x x x      

 

sin 4sin 3f x x x   

, vì hàm số

 

f x

liên tục, không âm trên đoạn



 

 

 

Ta có

sin 1

6 2 2

x x

 

    

, Do hàm số

 

4 3g t t t  

đồng biến trên

 

 

 

Suy ra

   

max 1 8

g t g

 

 

 

 

 

1 21

min

2 4

g t g

 

 

 

 

 

 

 

Vậy

 

;

6 2

max 2 2

f x f

 



 

 

 

 

 

 

 

 

;

6 2

min

6 2

f x g

 



 

 

 

 

 

 

 

Bài 12. Cho hai hàm số

 

f x

và

 

g x

có đạo hàm trên đoạn

 

1;4

và thỏa mãn hệ

thức

   

       

1 1 4

. ; .

f g

g x x f x f x x g x

 





 

   





.Tính

   

dI f x g x x

 

 

 



Lời giải

Ta có

       

f x g x x f x g x

 

   

 

 

   

f x g x

f x g x x



  

 



   

d d

f x g x

x x

f x g x x



  

 



 

   

f x g x

 

x C  

Theo giả thiết ta có

   

ln 1 ln 1 1

C f g  

ln4

 

Khi đó

   

f x g x



 



  





, vì

   

1 1 4

f g

 

nên

   

f x g x

 

Vậy

   

d 8ln 2

I f x g x x   

 



Bài 13. Cho hàm số

 

f x

có đạo hàm liên tục trên đoạn

 

0;1

thỏa

 

f x

mãn

 

1 1



 

d 9

f x x





 

 



và

 

x f x x





. Tích phân

 

df x x



Lời giải

Ta có:

 

d 9

f x x





 

 



 

- Tính

 

d .

x f x x





Đặt

 

d .d

u f x

v x x

 











 

d d

u f x x



 













 

x f x x

 



 

f x

 



 

 

 

. d

x f x x







 

1 1

. d

4 4

x f x x



 



 

. d 1

x f x x



  



 

18 . d 18

x f x x



  



 

Mặt khác

9 9

x x

 



81 d 9

x x

 



 

Cộng vế với vế các đẳng thức

 

và

 

ta được:

   

4 8

18 . 81 d 0

f x x f x x x

 

 

  

 

 



 

9 d 0

f x x x



 

  

 



 

. 9 d 0

f x x x





 

  

 



 

9 0

f x x



  

 

9f x x



  

   

.df x f x x



 



x C  

Mà

 

1 1



 

 

9 14

5 5

f x x

   

 

df x x 



9 14

5 5

x x

 

 

 

 



3 14 5

10 5 2

x x

 

   

 

 

Bài 14. Cho hàm số

 

f x

có đạo hàm liên tục trên đoạn

 

1;2

thỏa mãn

   

1 d

x f x x

  



 

2 0



và

 

d 7

f x x



 



 



. Tính

 

 

 

Lời giải

Đặt

   

d du f x u f x x



  

 

d 1 d

v x x v



   

Ta có

   

1 d

x f x x

  



 

3 3

1 1

. d

3 3

x x

f x f x x

 



 



   

1 1

1 d

3 3

x f x x



    



   

1 d 1x f x x



  



   

2.7 1 d 14

x f x x



    



Tính được

 

49 1 d 7

x x

 



 

df x x



 



 



   

2.7 1 dx f x x



 



 

49 1 d 0

x x

  



   

7 1 d 0

x f x x

 



   

 



   

7 1

f x x



  

 

7 1

f x C



  

 

2 0



 

7 1

4 4

f x



  

. Vậy

3 105

2 64



 



 

 

Bài 15. Cho hàm số

 

f x

thỏa mãn

 

   

. 15 12f x f x f x x x

 

  

  

và

   

0 0 1

f f



 

Tính

 

Lời giải

Ta có:

 

   

. 15 12f x f x f x x x

 

  

   

. 15 12f x f x x x



  

 

 

   

5 2

. 3 6

f x f x x x C



   

   

0 0 1

f f



 

nên ta có



Do đó:

   

5 2

. 3 6 1

f x f x x x



  

 

2 5 2

3 6 1

f x x x



 

   

 

 

 

2 6 3

4 2 .f x x x x C

    

Mà

 

0 1



nên ta có



Vậy

 

2 6 3

4 2 1f x x x x   

suy ra

 

1 8.



Bài 16. Cho hàm số

 

y f x



có đạo hàm liên tục trên đoạn

 

0;1

và

   

0 1 0

f f

 

. Biết

     

1 1

0 0

d , cos d

2 2

f x x f x x x





 

 

. Tính

 

lim

f x



Lời giải

Đặt

 

cos d sin d

d d

u x u x x

v f x x v f x

  

   

 



 



 

 

 

Khi đó

           

1 1

0 0

cos d cos sin df x x x x f x f x x x

   



 

 

   

 

   

1 0 sin df f f x x x

 

   



       

1 1

0 0

sin d sin d

f x x x f x x x

  

  

 

Ta có

           

1 1 1 1

2 2 2

0 0 0 0

sin d d 2 sin d sin df x k x x f x x k f x x x k x x

  

    

 

   

0 1

2 2

k k

     

Do đó

       

sin d 0 sin

f x x x f x x

 

    

 



Vậy

 

lim

f x







Bài 17. Cho

 



và

   

[ ' ' 3 ]. 5

f x f x dx

  



. Tính

(3) .

Lời giải

     

3 3

0 0

[ ' d ' 3 d 3 5

f x x f x x

    

 

   

3 3

0 0

3 5

f x f x

   

       

3 0 0 3 5

f f f f

    

 

2 3 6

 

 

3 3

 

Vậy

 

3 3



Bài 18. Cho hàm số

 

y f x



có đạo hàm và liên tục trên

 

1,2

thỏa mãn

 

f x dx







và

 

ln 2

f x







Biết rằng

 

f x



 

1,2

x 

. Tính

 

Lời giải

Ta có

       

2 1f x dx f x f f



  



 

f x dx







   

2 1 10

f f

  

 

ln 2

f x







 

ln ln 2

f x 

 

ln ln 2

 

 

 

 

(Vì

 

f x



 

1,2

x 

)

   

1 2

f f 

 

Từ

 

và

 

ta có

 

2 20



Bài 19. Cho hàm số

 

f x

xác định trên

 

\ 0

thỏa mãn

 

f x





 ,

( 1) 1

 

và

 

1 4

 

Tính giá trị của biểu thức

   

2 2

f f 

Lời giải

Ta có

 

f x







1 2

x x

  

nên

 

f x x







1 2

dx x

x x

 

  

 

 



2ln

2 2

x C

   

 

2ln 0

2 2

2ln 0

2 2

x C khi x



    









     





• Trên khoảng

 



, ta có

 

1 4

 

  

Do đó

 

2ln 4

2 2

f x x

   

. Suy ra

 

2 2 2ln 2 4

   

• Trên khoảng

 



, ta có

 

1 1

 

 

Do đó

   

2ln 1

2 2

f x x

    

. Suy ra

 

2 2 2ln 2 1

    

Vậy

   

2 2 4ln 2.

f f   

Bài 20. Cho hàm số

 

f x

xác định trên

 

\ 0;1

thỏa mãn

 

f x

x x





;

   

1 2 0

f f

  

và

 



 

 

. Tính giá trị biểu thức:

   

2 3

f f f

 

  

 

 

Lời giải

Ta có

 

f x

 

x x







1 1

x x

 

 

 



 



ln 1 ln

x x C   

Như vậy

 

f x

     

   

ln 1 ln , ;0

ln 1 ln , 0;1

ln 1 ln , 1;

x x C x

      



     





     



Trên khoảng

 



, ta có

 

1 ln 2

f C  

Trên khoảng

 

0;1

, ta có

 



 

 

1 1

ln ln 2

2 2

   

 

Do đó:

   

ln 1 ln 2

f x x x

   

. Suy ra:

1 3 1

ln ln 2

4 4 4

 

  

 

 

Trên khoảng

 

 

, ta có

 

2 ln 2

f C  

Lại có:

   

1 2 0

f f

  

1 3

ln 2 ln 2 0

C C

    

1 3

C C

  

Khi đó:

   

2 3

f f f

 

  

 

 

   

1 2 3

3 1

ln 3 ln 2 ln ln ln 2 ln3

4 4

C C C

 

        

 

 

1 2 3

ln3 ln 3 2

C C C

     

. Vậy

   

2 3

f f f

 

  

 

 

ln3 2

Bài 21. Cho

   

. ' 12 13

f x f x x

 

 

0 2



. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm

số

 

y f x

trên đoạn

 

0; 1

Lời giải

Ta có

   

. ' 12 13

f x f x x

 

     

0 0

. d 12 3 d

t t

f x f x x x x



  

 

 

7 2

6 3

f t t t C   

hay

 

7 2

42 21 7f x x x C

  

. Do

 

0 2



nên

7 2

C C

  

. Do đó

 

42 21 2

f x x x

  

 

   

0;1

Max 1f x f



 

   

0;1

Min 0

f x f

hay

 

 

0;1

Max 65

f x 

và

 

 

0;1

Min 2

f x 

Bài 22. Cho

 

f x 

với

  

và thỏa mãn điều kiện

     

. ' 2 1

f x f x x f x

 

 

0 0



. Tính giá trị lớn nhất

, giá trị nhỏ nhất

của hàm số

 

y f x

trên [1;3].

Lời giải

Đặt

     

0 0

. ' d 2 1d

t t

I f x f x x x f x x

  

 

* Ta tính

   

. ' d

I f x f x x





   

 

f x f x





 

f x



 

f t



 

* Ta tính

 

2 1d

I x f x x

 



Đặt

 

u f x

 



   

 

d d

f x f x

u x

f x







2 dx x

d 2 dv x x

chọn

v x

 

2 1d

I x f x x  



 

2 2 3

1 2 d

x f x x x

 

 

 



 

2 2

t f t

  

 

* Từ

 

và

 

ta có

   

2 2 2

2 2

f t t f t

  

   

2 2 2 4

2 1 0

f t t f t t

    

 

2 2

1 1

f t t



  







  



 

f t



với

 

nên

 

1 1

f t

 

với

 

.Vậy

 

2 2

1 1

f t t

  

hay

 

4 2

2f x x x

 

 

4 2

2 1 2

2 2

x x

f x

x x





  



với

 

1;3

Vậy

 

   

1;3

Max f x f

hay

 

 

1;3

3 11

Max f x 

 

 

1;3

Min f x 

Bài 23. Cho hàm số

 

f x

thỏa mãn

 



và

    

2 1 0

f x f x x



  

. Tính tổng

 

2018

S f k





Lời giải

Ta có

 

2 1

f x



  

 

f x





 



 

2 1 d

x x x x

f t

   



   

1 1

t t

f t f

    

 

f t

t t

 



hay

 

f x

x x





Khi đó

 

1 1

f x

x x

 



 

2018

1 1 1 1 1 1 1 1 2018

1 ... 1

2 2 3 3 4 2018 2019 2019 2019

S f k



       

           

       

       



Bài 24. Cho hàm số

 

f x

có đạo hàm liên tục trên



 

 

 

thỏa mãn



 



 

 

 

48 8

f x dx



 



 

 

 



   

sin cos

48 8

x x x f x dx



 

   



. Tính



 

 

 

Lời giải

Bằng công thức tích phân từng phần ta có:

           

2 2

0 0

sin cos sin sin

 





  

 

 

 

x x x f x dx x x f x x x f x dx

Suy ra

   

sin

48 8



 



 



x x f x dx

Hơn nữa ta tính được

 

2 2 2

2 2

0 0 0

1 cos 2

sin sin

  



 

  

x x

x x dx x x dx dx

 

2 2

2 2 2

0 0 0

1 cos 2

cos 2

2 2 2

  



  

  

x x

x x x

dx dx dx

48 8

 

 

Do đó

       

2 2 2

0 0 0

2 sin sin 0

f x dx x x f x dx x x dx

  

 

  

 

 

  

 

sin 0

f x x x dx





  

 

 



Suy ra

 

sinf x x x





, do đó

 

sin cos

f x x x x C  

. Vì



 



 

 

nên

1 

Vậy

2 2

 

 



 

 

Bài 25. Cho hàm số

 

f x

xác định trong khoảng

 

 

đồng thời

 

   

1 .

f x

x f x







Biết

 

f x



với

 

0;x

   

và

 

0 1



. Tính giá trị

 

Lời giải

Ta có

   

f x f x







   

0 0

. d d

t t

f x f x x x



 



 

   

2 2

2 1

3 3

f x x x

   

   

2 2

2 1

3 3

f x x x

   

   

2 2 2 4

1 1

3 3 3 3

f t t t

     

   

2 2 2 4

1 1

3 3 3 3

f t t t

     

   

1 1 3

f t t t

    

   

1 1 6

f t t t

 

    

 

Vậy

 



100

Bài 26. Cho hàm số

 

y f x



có

 

f x



liên tục trên nửa khoảng







thỏa mãn

   

3 1 3.e

f x f x





  

. Tính giá trị biểu thức

   

e 1 0

A f f 

Lời giải

Ta có

   

e 3

3 1 3.e

f x f x







   

 

3 2 2

e e e 3

x x x

f x



 

  

 

Lấy tích phân từ

đến

hai vế ta được

 

1 1

3 2 2

0 0

e d e e 3 d

x x x

f x x x



 

 

 

 

 





3 2

e e 3

x x

f x

 

  

 

   

 

2 2

e 3 e 3 8

e 1 0

f f

  

  

Vậy

 

2 2

e 3 e 3 8

  



Bài 27. Cho hàm số

 

4 8 d

f x t t t

 



. Gọi

,m M

lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của

hàm số

 

f x

trên đoạn

 

0;6

. Tính

M m

Lời giải

 

   

3 4 2 2

4 8 4 4 3

f x t t dt t t x x      



với



 

2 4f x x



 

 

 

0 2 1;6

f x x



   

 

0 3



;

 

2 1

 

;

 

6 15



. Suy ra

15, 1

M m

  

M m

  

Bài 28. Tìm hàm số

 

sin

f x a x b



 

thỏa mãn:

 

1 2



và

 

d 4

f x x





Lời giải

Ta có:

 

1 2 sin 2 2

f a x b b



     

   

1 1

0 0

d 4 sin 2 d 4

f x x a x x



   

 

cos

2 4

a x

x a





 

    

 

 

Vậy

 

sin 2f x x

 

 

Bài 29. Cho hàm số

 

y f x



xác định trên



, thỏa mãn

 

0, f x x

  

và

   

2 0

f x f x



 

Tính

 



, biết rằng

 

1 1



Lời giải

Ta có

       

 

2 0 2 2

f x

f x f x f x f x

f x



 

       

(do

 

f x



Lấy tích phân hai vế, ta được

 

1 1

2 ln 2

f x

dx dx f x x

f x



 



    

 

 

     

ln 1 ln 1 4 ln1 ln 1 4

f f f

         

     

     

   

ln 1 4 1f f

     

 

 

Bài 30. Cho hàm số

 

f x

có đạo hàm, liên tục trên đoạn

 

1;4

 

1 1



và

 

d 2

f x x







. Tính

 

Lời giải

Ta có

( ) 2 ( ) 2 (4) (1) 2

f x dx f x f f



     



mà

(1) 1 (4) 3

f f

  

Bài 31. Giả sử hàm số

 

y f x



liên tục, nhận giá trị dương trên

 



và có

       

3 , 1 .

f f x x f x



  

Tính

 

Lời giải

Ta có:

     

 

1 1

f x

f x x f x x

f x



    

 

8 8

3 3

d 1d

f x

x x x

f x



  

 

 

f x x  

   

8 3

f f

  

 

8 7 49

  

Bài 32. Cho hàm số

 

f x

có đạo hàm, liên tục trên

 



và thỏa mãn

 

d .cos

f t t x x









. Tính

 

Lời giải

Ta có

 

' d 0 .cos

f t t F x F x x



  



Lấy đạo hàm hai vế ta có:

 

2 . cos .sin

x f x x x x

  

 

 

4. 4 cos2 2 .sin 2 1

  

   

 

 

Bài 33. Cho hàm số

 

f x

thỏa mãn

 

d .cos

f x

t t x x







. Tính

 

Lời giải

Ta có:

 

d .cos

f x

t t x x







 

.cos

f x

x x



 

 

3 .cosf x x x



 

 

4 12.cos4 12



  

 

4 12

f  .

Bài 34. Cho hàm số

 

f x

có đạo hàm, liên tục trên đoạn

 

1;2

và thỏa mãn

 

f x



khi

 

1;2

x 

. Biết

 

d 10

f x x







và

 

d ln 2

f x







. Tính

 

Lời giải

Ta có:

   

d 10

f x x f x



 



   

2 1 10

f f

  

(1).

Ta có:

 

d ln ln 2

f x

x f x

f x



 



 

ln 2 ln 1 ln 2

f f  

 

 

(2) .

Từ (1) và (2)

 

2 20

 

Bài 35. Cho hàm số

 

f x

có đạo hàm, liên tục trên đoạn

 

1;ln3

và thỏa mãn

 



và

 

ln3

9f x x



 



. Tính

 

ln3

I f

Lời giải

Ta có:

 

ln3

9f x x



 



   

ln3 1 9

f f

   

 

ln3 9

 

Bài 36. Cho hàm số

 

y f x



liên tục và thỏa mãn

 

2017

3 2

3 6 .

f x x x x f x



   ,

 

 

Tính

 

Lời giải

 

2017

3 2

3 6 .

f x x x x f x



  

 

2017

3 2

3 6

f x

x x x

f x



   

 

0 0

2017

3 2

2 2

3 6 4 d

f x

x x x x

f x

 



    

 

Ta có:

 

2017

3 2

3 6 4 dI x x x x



   



   

 

2017

1 3 1 dx x x



   



Đặt

1 d dt x x t   

, đổi cận

2 1, 0 1x t x t       

 

2017

3I t t



  



. Xét hàm số

 

2017

3f t t t  là hàm số lẻ nên



 

f x





 



 

ln 0

f x





   

ln 0 ln 2

f f

  

 

f e 

Bài 37. Cho hàm số

 

ln d

f x t t t





. Xác định hoành độ điểm cực đại của đồ thị hàm số

 

f x

Lời giải

Tập xác định

D  

Gọi

 

F t

là một nguyên hàm của

 

lng t t t



với

0t 

. Khi đó

   

ln d

f x t t t F t

 



   

e e

x x

F F 

 

     

2 2

e e e e

x x x x

f x F F



  

 

   

2 2

e e e

x x x x

f f 

4 2

4 e

x x

 

 

2 2

4e e

x x

 

 

f x





ln 2

4 0e 1





 



 

 



Bảng biến thiên của hàm số

Vậy hoành độ điểm cực đại của đồ thị hàm số là

ln 2

 

Bài 38. Cho hàm số

 

y f x



liên tục trên





 

và

   

d sin

f t t x x







. Tính

 

Lời giải

Gọi

 

F t

là một nguyên hàm của

 

f t

     

 

   

d 0 sin

g x f t t F t F x F x x



    



 

2 sin cosg x xF x x x x

  

 

  

 

2 sin cosxf x x x x

  

  

Chọn



ta được

 

4 4

sin 2 2 cos 2

  

 





 



 

Vậy

 





Bài 39. Lấy tích phân hai vế, ta được Cho hàm số

 

f x





. Giải bất phương trình sau:

 

6 sin

f x











Lời giải

Ta có

       

1 3

3ln 3 ; 3. . 3 .

3 3

f x x f x x

x x

      







 

0 0

6 6 1 cos 3

sin sin 3

2 2

t t

dt dt t t



 

  



   

 

Khi đó

 

3 3

6 sin

3 2

3; 2

f x

x x









 

 

















  

2 1

3 2

3; 2

x x





 









 

 





 



 





Vậy nghiệm bất phương trình:

 





 



Bài 40. Chứng minh rằng

1 3 5 2 1 *

2 2 2 2

1 1 1 1 2 1

... ,

2 4 6 2 2 1

n n n n

C C C C n

n n



      







ln 2















Lời giải

* Nhận xét : Số hạng tổng quát của tổng vế trài là



với

nguyên dương lẻ và không

xuất hiện



với

chẵn. Do đó ta phải sử dụng

 



và

 



sử dụng phương

pháp tích phân hai vế.

Ta có

 

0 1 2 2 2 1 2 1 2 2

2 2 2 2 2

1 ...

n n n n

n n n n n

x C C x C x C x C x

 

      

 

0 1 2 2 2 1 2 1 2 2

2 2 2 2 2

1 ...

n n n n

n n n n n

x C C x C x C x C x

 

      

Suy ra

   

 

2 2

1 3 3 5 5 2 1 2 1

2 2 2 2

1 1 2 ...

n n

n n n n

x x C x C x C x C x

 

       

Do đó

   

 

2 2

1 1

1 3 3 5 5 2 1 2 1

2 2 2 2

0 0

1 1

... *

n n

n n n n

x x

dx C x C x C x C x dx

 

  

    

 

Mà

       

 

2 2 2 1 2 1

1 1 1 1

2 1

2 2 2 1 2 1

n n n n

x x x x

n n

 

     



 

 



và

 

2 4 6 2

1 3 3 5 5 2 1 2 1 1 3 5 2 1

2 2 2 2 2 2 2 2

... ...

2 4 6 2

n n n

n n n n n n n n

x x x x

C x C x C x C x dx C C C C

  

        



 

1 3 5 2 1

2 2 2 2

1 1 1 1

... 2

2 4 6 2

n n n n

C C C C



    

Thay (1) và (2) vào (*) ta có

1 3 5 2 1

2 2 2 2

1 1 1 1 2 1

...

2 4 6 2 2 1

n n n n

C C C C

n n



    



(đpcm)

Bài 41. Tìm số nguyên dương

thỏa mãn

 

1 3 4 5

1 1 1 1 2018

...

2 3 4 5 1 2019

n n n n n

C C C C C



    



Lời giải

Nhận xét:

* Số hạn tổng quát của tổng vế trái là

 







(



và



). Số đi chung với

là

phân số nên có thể sử dụng tích phân là phù hợp.

* Số hạng tổng quát của tổng vế trái là

 







có mẫu là phân số

1k 

. Do

1k 

lớn hơn

một đơn vị nên có khả năng ban đầu

đi chung với

tức là

k k

x C

* Dấu của các số hạng thay đổi từ dấu



sang dấu



do đó ta khai triển nhị thức

 



. Vì

chưa khớp dấu của đề nên nhân hai vế cho

1

Ta có:

   

 

1 1

0 1 3 2 3 3

0 0

1 ... 1 d

n n

n n n n n

x C C x C x C x C x x



         

 

   

1 1

0 1 2 2 3 3 4 1

1 1

1 1 1

...

1 2 3 4 1

n n

n n n n n

x n

C x C x C x C x C x

n n

 



 

 

 

        

 

 

 

 

1 2 3

1 1 1 1

1 ...

1 2 3 4 1

n n n n

C C C C

n n





        

 

 

1 2 3

1 1 1

...

1 2 3 4 1

n n n n

C C C C

n n





     

 

2018

2019 1

 



2018

 

Bài 42. Chứng minh rằng với mọi số nguyên dương n ta luôn có:

 

  

0 1 2 3

1 1 1 1 1

...

2 3 4 5 2 1 2

n n n n n

C C C C C

n n n



    

  

Lời giải

Nhận xét:

* Số hạng tổng quát của vế trái là

 





(





). Số đi chung với

là phân số

nên có thể sử dụng phương pháp tích phân.

* Số hạng tổng quát của vế trái là

 





có mẫu số là phân số

 





là



lớn hơn chỉ

số chập

đúng

đơn vị



có khả năng ban đầu

đi chung với



, tức là

k k

x C



 

* Dấu của các số đổi dấu từ



sang



Ta xét

   

0 1 2 2 3 3

1 ... 1

n n

n n n n n

x C C x C x C x C x

       

Tới đây ta nhận thấy số hạng vế phải chưa giống như ta đoán ở

 

, do đó ta nhân hai vế cho

ta được

   

0 1 2 2 3 3 4 1

1 ... 1

n n

n n n n n

x x C x C x C x C x C x



       

Khi đó

   

 

1 1

0 1 2 2 3 3 4 1

0 0

1 d ... 1 d

n n

n n n n n

x x x C x C x C x C x C x x



       

 

Xét

 

1 d

x x x





. Đặt

1 d dt x t x    

 

1 d

x x x





 

1 d

t t t

 



1 2

1 1

1 2

n n

t t

n n

 

 

 

 

 

 

1 1

1 2n n

 

 

Mặt khác

 

0 1 2 2 3 3 4 1

... 1 d

n n

n n n n n

C x C x C x C x C x x



     



 

0 2 1 3 2 4 3 5 1

1 1 1 1

...

2 3 4 5 1

n n

n n n n n

C x C x C x C x C x



 



 

     

 



 

 

1 2 3

1 1 1 1

...

2 3 4 5 1

n n n n

C C C C



     



Vậy

 

  

1 2 3

1 1 1 1 1

...

2 3 4 5 1 1 2

n n n n

C C C C

n n n



     

  

Bài 43. Tính tổng

 

1 2 3

1 1 1

1 ...

3 5 7 2 1

n n n n

S C C C C



    



với

nguyên dương.

Lời giải

Ta có

 

2 0 1 2 3 2

1 ... 1

n n

n n n n

x C C x C C x

      

 

1 1

2 0 1 2 3 2

0 0

1 d ... 1 d

n n

n n n n

x x C C x C C x x

     

 

* Ta có

 

0 1 2 3 2

... 1 d

n n

n n n n

C C x C C x x

   



 

0 1 3 2 5 3 6 2 1

1 1 1

...

3 5 7 2 1

n n

n n n n n

C x C x C x C x C x



 



 

    

 



 

 

0 1 2 3

1 1 1

...

3 5 7 2 1

n n n n n

C C C C C



    



Ta tính

 

1 d

I x x

 



Đặt

   

2 2

1 d 2 1 d

d d

n n

u x u nx x x

v x v x



 

    

 



 

 

 

 

 

1 d

x x





   

2 2 2

1 2 1 d

n n

x x nx x x



   



  

2 2

2 1 1 1 d

n x x x



     



   

1 1

2 2

0 0

2 1 d 2 1 d 2 . 2 .

n n

n x x n x x n I n I



     

 

. Do đó

2 . 2 .

n n n

I n I n I



  

2 1

n n

I I



 



2 4 8 2

. . ....

3 7 9 2 1

n o

I I

 



2 4 8 2

. . ....

3 7 9 2 1





Vậy

2 4 8 2

. . ....

3 7 9 2 1





_______________ TOANMATH.com _______________

Bấm Tải xuống để xem toàn bộ.

| 1/17

| | Tải xuống

Preview text:

CHUYÊN ĐỀ
TÍNH GIÁ TRỊ CỦA HÀM SỐ
KHI CHO TRƯỚC CÁC TÍCH PHÂN LIÊN QUAN
A. KIẾN THỨC CƠ BẢN
1. Tính chất nguyên hàm, tích phân thường sử dụng 1.
f  x dx  f  x  C  2. d u v  uv  d v u   3. f
 u  xuxdx  f udu  b 4. 2
f  x dx  0  f  x  0  . a b
Tổng quát: f  x  0 x
 a;b, f  x dx  0  f  x  0, x  a;b a 2. Nhị thức Niuton
 x  yn 0 n 1 n 1
 C x  C x  y  ... k nk k  C x y  ... n n  C y n n n n  Lưu ý: B. BÀI TẬP  1  2
Bài 1. Cho hàm số f  x xác định trên  \   thỏa mãn f  x 
, f 0  1 và f   1  2. Giá trị  2  2x 1
của biểu thức f   1  f 3 Lời giải 2 1 Ta có
f  x dx 
dx  ln 2x 1  C  
. Hàm số gián đoạn tại điểm x  2x 1 2 1 1 Nếu x 
 f  x  ln 2x  
1  C mà f  
1  2  C  2 . Vậy f  x  ln 2x   1  2 khi x  2 2 1 1 Nếu x 
 f  x  ln 1 2x  C mà f 0  1  C  1. Vậy f  x  ln 1 2x 1 khi x  2 2 Do đó f  
1  f 3  ln 3 1 ln 5  2  ln15  3. 1
Bài 2. Cho hàm số y  f  x xác định trên  \ 1; 
1 và thỏa mãn f  x  . Biết rằng 2 x 1
f 3  f 3  0 . Tính T  f 2  f 0  f 4 . Lời giải Ta có: 1 1  1 1  1  1 1 
f  x  f  x d x   d x    d x  d x  d x 2     x 1 2    x 1 x 1  2  x 1 x 1  1 x 1  ln  C . 2 x 1  1   1 1 
Do đó: f 3  f 3  0  ln 2  C  ln  C  0      C  0 .  2   2 2  1 x 1
Như vậy: f  x  ln . 2 x 1 1 2 1 1 1 0 1 1 4 1 1 f 2  ln   ln 3 ; f 0  ln
 0 ; f 4  ln  ln 5  ln 3 . 2 2 1 2 2 0 1 2 4  1 2 1 1 1
Từ đó: T  f 2  f 0  f 4   ln 3  0  ln 5  ln 3  ln 5  ln 3 . 2 2 2 2
Bài 3. Cho hàm số f  x xác định trên  \  1  
;1 thỏa mãn f  x  , f  2
   f 2  0 và 2 x 1  1   1  f   f  2     . Tính f  3
   f 0  f 4 .  2   2  Lời giải  x 1 ln
 C khi x  1   1 x 1  2  1 1   x 1
Ta có f  x  f  x dx   dx    dx  ln
 C khi 1  x  1. 2   x 1 2  x 1 x 1  x 1   x 1 ln
 C khi x  1 3 x 1 
 f    f    1 2 2  0 ln 3  C  ln  C  0 1 3    C  C  0 3 Khi đó 1 3   1   1      f   f  2 1 C  1        2 ln 3  C  ln  C  2   2   2  2 2   3 3 6
Do đó f 3  f 0  f 4  ln 2  C  C  ln  C  ln 1 . 1 2 3 5 5 1
Bài 4. Cho hàm số f  x xác định trên  \  
1 thỏa mãn f  x 
, f 0  2017 , f 2  2018 . x 1
Tính S  f 3  f   1 . Lời giải 1 Ta có
f  x dx  dx  ln  
 x 1  C . x 1
 f  x  ln  x 1   2017 khi x  1
Theo giả thiết f 0  2017 , f 2  2018 nên  .
f  x  ln  x 1   2018 khi x  1 
Do đó S  f 3  f  
1  ln 2  2018  ln 2  2017  1 .
Bài 5. Giả sử hàm số y  f  x liên tục, nhận giá trị dương trên 0;   và thỏa mãn điều kiện f  
1  1, f  x  f  x 3x 1 với mọi x  0.Tính f 2018 . Lời giải Ta có: f  x 1 f  x dx 2
f  x  f  x 3x 1    dx   
 ln f  x  3x 1  C f  x 3x 1 f  x 3x 1 3 2 3x1 C  f  x 3  e . 4  C 4
Mặt khác ta lại có f   1  1 nên 3 1  e  C   . 3 2 4 2 4 3x 1 6055  Vậy f  x 3 3  e  f   3 3 2018  e . 1
Bài 6. Cho hàm số f  x  0 thỏa mãn điều kiện f  x   x   2 2
1 f  x và f   1   . Tính tổng 2 f  
1  f 2  f 3  ...  f 2018 . Lời giải Ta có : f  x f  x
d  f  x
f   x   x   2 2 1 f  x   2x 1  dx  2x  1 dx  2 
 x  x  C 2   2   f  x f  x 2 f  x 1 2 1  
 x  x  C  f  x   . f  x 2
x  x  C 1 1 1
Mặt khác theo giả thiết ta lại có f   1    f   1      C  0 . 2 C  2 2 1 1 1
Vậy f  x     . 2 x  x x 1 x Khi đó f  
1  f 2  f 3  ...  f 2018 1 1 1 1 1 1 1 1 2018  1   ...      1   . 2 3 2 2018 2017 2019 2018 2019 2019
Bài 7. Cho hàm số f (x) có đạo hàm trên  thỏa mãn 2017 2018 (  )  2018 ( )  2018. . x f x f x x e với mọi
x   và f (0)  2018. Tính giá trị f (1). Lời giải Ta có:
f  x  2018. f  x 2017 2018 (  )  2018 ( )  2018. . x f x f x x e 2017   2018.x 2018 x e
1 f  x  2018. f  x 1 2017  dx  2018.x dx  2018 x    1 e 0 0
1 f  x  2018. f  x 1 1 Xét tích phân I  dx     2  018 . x  2018.   2018 . x f x e dx f x e dx 2018 x   e 0 0 0 1 u   f   x du  f    x dx Xét  2018.   2018 . x I f x e dx   . 1  . Đặt  2018 2018 dv  2018. x x e dx  v  e 0  1 Do đó   . 2  018 x   1    2  018 . x     2018 1 . x I f x e f x e dx I f e  2018 1 0 0 Khi đó   1  f   2018  x 2018 1 1 .e  2018  x  f   2018 1  2019.e . 0 f  x x
Bài 8. Giả sử hàm số f (x) liên tục, dương trên  ; thỏa mãn f 0  1 và  . f  x 2 x 1 Tính f  2018 . Lời giải 2 f '(x) x
d  f  x d 1 x   1 1 Ta có dx   dx     
 ln  f  x  ln  2 x   1  C . f (x) 2 x 1 f  x 2 2 x 1 2
Mặt khác f 0  1  C  0 . Do đó f  x 2 
x 1 . Vậy f  2018  2019 . 1
Bài 9. Xét hàm số f  x liên tục trên đoạn 0; 
1 và thỏa f  x  f   x 2 2 3 1  1 x . Tính
f  x dx 0 Lời giải 1 1
Ta có: 2 f  x  3 f 1 x dx  2    1 x dx 
 A  B  C . 0 0 1 Tính: 2 C  1  x dx  . 0 
Đặt x  sin t suy ra dx  cos t dt . Đổi cận: x  0  t  0 ; x  1  t  . 2    2 2 1 cos2t 2  1 1   Vậy: 2
C  cos t dt   dt   t  sin 2t    . 2  2 4  4 0 0 0 1
Tính: B  3 f 1 x dx  . 0
Đặt t  1 x  dt  d
 x . Đổi cận: x  0  t  1
 ; x  1  t  0 . 1 1
Vậy: B  3 f t  dt 
 3 f  x dx  . 0 0 1  1  1 
Do đó: 2 f  x  3 f  x dx    
 5 f  x dx   
f  x dx   . 4 4 20 0 0 0     2     2  
Bài 10. Cho hàm số f  x xác định trên 0; 2  thỏa mãn
f  x  2 2 f  xsin x  d x      . 2      4  2 0   2 Tính tích phân
f  x d x  . 0 Lời giải Ta có:     2   2     2 2  1   2 2   2sin x  d x     1 cos 2x  d x    
 1 sin 2x d x   x  cos 2x    .  4    2   2  2 0 0  0 0   2     2    2     2 Do đó: 2
f  x  2 2 f  xsin x  d x  2     2 sin x  d x       0 4      4  2 2 0  0   2 2        2     2 
f  x  2 2 f  x 2 sin x   2 sin x  d x  0       
f  x  2 sin x  d x  0     4 4          4  0  0       
Suy ra f  x  2 sin x   0  
, hay f  x  2 sin x    .  4   4     2 2    2    Bởi vậy:
f  x d x  2 sin x  d x       2 cos x   0   .  4   4  0 0 0   
Bài 11. Cho hàm số f  x liên tục, không âm trên đoạn 0; 
, thỏa mãn f 0  3 và 2      
f  x f  x 2 .  cos .
x 1 f  x , x   0; 
. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của 2      
hàm số f  x trên đoạn ;  . 6 2    Lời giải
f  x. f  x
f  x. f  x
Từ giả thiết f  x f  x 2 .  cos .
x 1 f  x   cos x 
dx  sin x  C  2 1 f  x 2 1 f  x Đặt 2 t   f  x 2 2 1
 t  1 f  x  tdt  f  x f  x dx .
Thay vào ta được dt  sin x  C  t  sin x  C  2
 1 f  x  sin x  C .
Do f 0  3  C  2 . Vậy 2  f  x 2 
x   f  x 2 1 sin 2
 sin x  4sin x  3 .     f  x 2
 sin x  4sin x  3 , vì hàm số f  x liên tục, không âm trên đoạn 0;  . 2      1  1  Ta có  x  
 sin x  1 , Do hàm số g t  2
 t  4t  3 đồng biến trên ;1 . 6 2 2  2     1  21
Suy ra max g t   g  
1  8 , min g t   g    .  1   1  ;1  2  4  ;1 2       2        21
Vậy max f  x  f  2 2  
, min f  x  g    .       ;  2   6  2  ; 6 2       6 2 
Bài 12. Cho hai hàm số f  x và g  x có đạo hàm trên đoạn 1; 4 và thỏa mãn hệ  f 4    1  g   1  4 thức 
.Tính I   f  x  g  x dx    g   x   . x f  x;
f  x   . x g x  1 Lời giải
Ta có f  x  g  x  x  f  x  g x  
f  x  g  x 1
f  x  g  x 1     dx   dx  
 ln f  x  g  x   ln x  C
f  x  g x x
f   x  g x x
Theo giả thiết ta có C  ln 1  ln f   1  g   1  C  ln 4 .  4
f  x  g  x   x 4 Khi đó  , vì f   1  g  
1  4 nên f  x  g  x  . 4  x
f  x  g  x    x 4
Vậy I   f  x  g  x dx  8ln 2    . 1
Bài 13. Cho hàm số f  x có đạo hàm liên tục trên đoạn 0; 
1 thỏa f  x mãn f   1  1, 1 1 1 1
 f  x 2  dx  9  3   và
x f  x dx   . Tích phân
f  x dx  2 0 0 0 Lời giải 1 2
Ta có:  f  x dx  9      1 0
du  f  x dx 1 1 u   f   x  - Tính 3
x f  x dx  .  Đặt  4   2 3 x 0
dv  x .dx  v   4 1 1 1 4  x  1 1 1 1 1 3 
 x f  x dx   . f 4 4   x 
x . f  x dx   
x . f  x dx  2 4 4 4 4 0   0 0 0 1 1 4
 x . f  x dx  1  4
 18 x . f  x dx  18  2 0 0 1 1 9 x 1 1 Mặt khác 8 x dx    8
 81 x dx  9  3 9 9 0 0 0
Cộng vế với vế các đẳng thức  
1 , 2 và 3 ta được: 1 1 1
 f  x 2 4
 18x . f  x 8  81x    dx  0  4 4  
  f  x  9x  dx  0  .  f  x  9x  dx  0         0 0 0 9
 f  x 4
 9x  0  f  x 4  9
 x  f  x  f  x.dx  4   x  C . 5 14 9 14 Mà f   1  1  C   f  x 5   x  5 5 5 1 1 1  9 14   3 14  5 
f  x dx   5  x  dx  6     x  x    .  5 5   10 5  2 0 0 0 2 2 1
Bài 14. Cho hàm số f  x có đạo hàm liên tục trên đoạn 1; 2 thỏa mãn  x   1
f  x dx    , 3 1 2 2  3 
f 2  0 và  f  x dx  7    . Tính f   .  2  1 Lời giải  x  3 2 1
Đặt u  f  x  du  f  x dx , dv   x   1 dx  v  3 2 2 3 3 1 2 2  x   1  x   1 Ta có    x   1
f  x dx   . f  x 
f  x dx  3 3 3 1 1 1 2 1 1 2 2 3 3      x  3 1
f  x dx    x   1
f  x dx  1 
  2.7  x   1
f  x dx  14  3 3 1 1 1 2 2 2 2 6 2 3 6
Tính được 49 x   1 dx  7 
  f  x dx     2.7  x   1
f  xdx   49 x   1 dx  0  1 1 1 1 2 2  x  4 7 1   7  x  3
1  f  x dx  0 
 f  x   x  3 7
1  f  x   C .   4 1  x  4 7 1 7  3  105
Do f 2  0  f  x   . Vậy f    . 4 4  2  64 2
Bài 15. Cho hàm số f  x thỏa mãn  f  x  f  x f   x 4 .
 15x 12x , x
   và f 0  f 0  1 Tính 2 f   1 . Lời giải Ta có:
 f x2  f x f  x 4 .
 15x 12x   f  x f  x  4 .
  15x 12x  
 f  x. f  x 5 2
 3x  6x  C1
Do f 0  f 0  1 nên ta có C  1. Do đó: 1 1   
f  x f  x 5 2 .
 3x  6x 1 2  f 2 6 3   x 5 2
 3x  6x 1 
 f  x  x  4x  2x  C . 2  2 
Mà f 0  1 nên ta có C  1. 2 Vậy 2 f  x 6 3
 x  4x  2x 1 suy ra 2 f   1  8.
Bài 16. Cho hàm số y  f  x có đạo hàm liên tục trên đoạn 0 
;1 và f 0  f   1  0 . Biết 1 1 1  f  x 2
f  x dx  , f  x cos  x dx    . Tính lim . 2 2 x0 x 0 0 Lời giải u   cos   x du    sin   xdx Đặt    . dv  f    xdx v  f    x  Khi đó 1 1
f  x cos  x dx  cos  x f  x 1   f  xsin  x dx   0 0 0 1 1 1 1    f  
1  f 0   f  xsin  x dx  .  
f  xsin  x dx  f  xsin  x dx    2 0 0 0 1 1 1 1 2 Ta có
 f  x  k sin  x 2  dx 
f  x dx  2k f  xsin  x 2 2 dx  k
sin  x dx       0 0 0 0 2 1 k   k   0  k  1. 2 2 1 2
Do đó  f  x  sin  x dx  0  f  x  sin  x    . 0 f  x Vậy lim   . x0 x 1 3
Bài 17. Cho f 0  và
[ f ' x  f '3  x].dx  5  . Tính f (3) . 2 0 Lời giải 3 3 3 3
 [ f ' xdx  f '3  xd3  x  5  
 f  x  f 3  x  5 0 0 0 0
 f 3  f 0  f 0  f 3  5  2 f 3  6  f 3  3. Vậy f 3  3. 2 Bài 18.
Cho hàm số y  f  x có đạo hàm và liên tục trên 1, 2 thỏa mãn f  x dx  10  và 1
2 f  x dx  ln 2 
Biết rằng f  x  0 , x
 1, 2 . Tính f 2 . f x 1   Lời giải 2 2 2 Ta có
f  x dx  f  x  f 2  f   1  ,
f  x dx  10 
 f 2  f   1  10   1 . 1 1 1 2 f  x  f 2  dx  ln 2 
 ln f  x 2  ln 2  ln 
  ln 2 (Vì f  x  0 , x  1, 2 ) f x 1  f   1  1     1  f   1  f 2 2 . 2 Từ  
1 và 2 ta có f 2  20 . x  2 2 1 Bài 19.
Cho hàm số f  x xác định trên  \  
0 thỏa mãn f  x 
, f (1)  1 và f   1  4  . 3 x
Tính giá trị của biểu thức f  2
   f 2 . Lời giải x  2 2 1 1 2
Ta có f  x   x   nên 3 x 3 x x x  2 2 1  1 2  2 x 1 f  x  dx   x   dx    2 ln x  C 3   x 3 2  x x  2 2x 2  x 1  
 2 ln x  C khi x  0  2  2 2x   . 2 x 1  
 2 ln x  C khi x  0 2   2 2x
• Trên khoảng 0;  , ta có f   1  4   C  4  . 2 x 1 1
Do đó f  x  
 2 ln x  4 . Suy ra f 2  2   2 ln 2  4 . 2 2 2x 8 • Trên khoảng  ;
 0 , ta có f   1  1  C  1 2 x 1 1
Do đó f  x  
 2 ln x 1. Suy ra f  2
   2   2 ln 2 1 . 2   2 2x 8 3
Vậy f 2  f 2   4 ln 2. 4 1 Bài 20.
Cho hàm số f  x xác định trên  \ 0 
;1 thỏa mãn f ' x  ; f  
1  f 2  0 và x  x   1  1   1  f  2  
. Tính giá trị biểu thức: f 2  f  f   3 .  2   4  Lời giải 1  1 1 
Ta có f  x  dx    dx  
 ln x 1  ln x  C . x  x   1  x 1 x 
ln 1 x  ln x  C , x   ;  0 1   
Như vậy f  x  ln 1 x  ln x  C , x   0;1 . 2  
lnx  1 ln x C , x   1;   3   Trên khoảng  ;
 0 , ta có f   1  ln 2  C . 1  1  1 1 Trên khoảng 0  ;1 , ta có f  2    ln  ln
 C  2  C  2 . 2 2  2  2 2  1  3 1
Do đó: f  x  ln 1 x  ln x  2 . Suy ra: f  ln  ln  2   .  4  4 4
Trên khoảng 1;   , ta có f 2   ln 2  C . 3 Lại có: f  
1  f 2  0  ln 2  C  ln 2  C  0  C  C  0 . 1 3 1 3  1   3 1 
Khi đó: f 2  f  f  
3  ln 3  ln 2  C  ln  ln  C  ln 2  ln 3  C 1   2   3   4   4 4   1 
 ln 3  C  C  C  ln 3  2 . Vậy f 2  f  f   3 = ln 3 2 . 1 2 3  4  Bài 21. Cho 6
f  x. f ' x  12x 13, f 0  2 . Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm
số y  f  x trên đoạn 0;  1 . Lời giải t t Ta có 6
f  x. f ' x  12x 13 6 
f  x. f  xdx  12x  3dx   0 0 1 7  f t  2
 6t  3t  C hay 7 f  x 2
 42x  21x  7C . Do f 0  2 nên 7 2
7C  2  C 
. Do đó f  x 7 2 
42x  21x  2 . 7
Max f  x  f  
1 , Min f  x  f 0 hay Max f  x 7
 65 và Min f  x 7  2 . 0;  1 0;  1 0;  1 0;  1 2 Bài 22.
Cho f  x  với x
   và thỏa mãn điều kiện f  x. f ' x  2x f  x 1 ,
f 0  0 . Tính giá trị lớn nhất M , giá trị nhỏ nhất m của hàm số y  f  x trên [1;3]. Lời giải t t Đặt I 
f  x. f ' x 2
dx  2x f  x 1dx   . 0 0 t t t 1 1 * Ta tính I 
f  x. f ' xdx   f  x.d 
 f  x 2  f  x 2 
f t    1 . 2 2 0 0 0 t * Ta tính 2
I  2x f  x 1dx  . 0
f  x. f  x Đặt 2 u 
f  x 1  du  dx  2 d x x , dv  2 d x x chọn 2 v  x . 2 f  x 1 t t t 4 2 t
I  2x f  x 1dx   2 2 x f  x 3 1   2x dx 2 2  t f t 1  2 .      0 2 0 0 4 1 t * Từ   1 và 2 ta có 2 f t  2 2  t
f t  1  2  f t  2 2  t f t  4 2 1  t  0 2 2 2  f t  2 1  t 1   .  2 f t  2 1  t 1  Do
f t   0 với t    nên 2
f t  1  1 với t    .Vậy 2 f t  2 1  t 1 hay 2 2 x   1 2x f  x 4 2 
x  2x  f  x   0 với 1;  3 4 2 2 x  2x
Vậy Max f  x  f 3 hay Max f  x  3 11 , Min f  x  3 . 1;  3 1;  3 1;  3 1 2018 Bài 23.
Cho hàm số f  x thỏa mãn f   1 
và f  x 2
 f  x2x  
1  0 . Tính tổng S  f  k  . 2 k 1  Lời giải t f  x
t  f  x t 1 t Ta có   2x 1  dx  2x 1 dx     2 x  x 2    f  x 2 f x f t 1   1 1   1 1 1 1 1 2  
 t  t  2  f t  
hay f  x  . f t  f   1 2 t  t 2 x  x 1 1
Khi đó f  x   . x x 1 2018  1   1 1   1 1   1 1  1 2018 S  f  k   1     ...    1          . k   2   2 3   3 4   2018 2019  2019 2019 1       Bài 24.
Cho hàm số f  x có đạo hàm liên tục trên 0;  thỏa mãn f  0   , 2     2    2 3   2 3     
 f  x 2  dx     
, sin x  x cos x f  x dx     . Tính f   . 48 8 48 8  2  0 0 Lời giải
Bằng công thức tích phân từng phần ta có:   2  2
sin x  xcos x f  xdx   xsin x f  x 2 
  xsin x f  x     dx . 0 0 0  2 3   Suy ra  sin       x x f x dx . 48 8 0    2 2 2 2 2 x 1 cos 2x
Hơn nữa ta tính được  x sin x dx   2 2 x sin x   dx     dx 2 0 0 0    2 2
x 1 cos 2x 2 2 2 2 x x cos 2x 3    dx  dx     dx   . 2 2 2 48 8 0 0 0     2 2 2 2 2 2 2
Do đó  f  x dx  2  x sin x f  x dx   x sin x dx  0     
  f  x  x sin x dx  0    0 0 0 0   
Suy ra f  x  x sin x , do đó f  x  sin x  x cos x  C . Vì f  0   nên C  1  .  2      Vậy f    .  2  2 x Bài 25.
Cho hàm số f  x xác định trong khoảng 0;   đồng thời f  x  .  x   1 . f  x
Biết f  x  0 với x
  0;   và f 0  1. Tính giá trị f 3 . Lời giải x t t x
Ta có f  x. f  x  
f  x. f  x dx  dx   x 1 x 1 0 0 t t 3 t t 2 2 3 2 2 2 
f  x   x  2 x 1 2 
f  x   x  2 x 1 3 3 3 3 0 0 0 0 3 2 2 2 4 3 2 2 2 4 2  f t    t   1 t 1  2  f t    t   1 t 1  3 3 3 3 3 3 3 3 3 2 2
 f t   t   1
t 1  3  f t  3  t   1 t 1  6 .  
Vậy f 3  3 100 . Bài 26.
Cho hàm số y  f  x có f  x liên tục trên nửa khoảng 0;  thỏa mãn      2 3  1 3.e x f x f x  
. Tính giá trị biểu thức 3
A  e f   1  f 0 . Lời giải 2   e x x 3 
Ta có 3 f  x  f  x 2  1 3.e  3x     2 x 2 e   e e x f x  3 ex   .
Lấy tích phân từ 0 đến 1 hai vế ta được 1 1 1 3 1 x 1 3  e x   2 x 2  d  e e x f x x  3 dx  3 2 x   
 e f  x  e  3   0   3 0 0 0  2 e  3 2 e  3  8 3  e f   1  f 0  . 3  2   2 e 3 e  3  8 Vậy A  3 x Bài 27.
Cho hàm số f  x    3
4t  8t dt . Gọi ,
m M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của 1
hàm số f  x trên đoạn 0;6. Tính M  m . Lời giải x x
f  x    3
4t  8t  dt   4 2 t  4t  2
 x  4x  3 với x  0 . 1 1
f  x  2x  4 , f  x  0  x  2 1;6 .
f 0  3 ; f 2  1
 ; f 6  15 . Suy ra M  15, m  1
  M  m  16 . 1 Bài 28.
Tìm hàm số f  x  a sin  x  b thỏa mãn: f   1  2 và
f  x dx  4  0 Lời giải Ta có: f  
1  2  a sin  x  b  2  b  2 1 1
 a cos x 
f  x dx  4  a sin  x  2 dx  4   
 2x  4  a     .    0 0
Vậy f  x   sin  x  2 . Bài 29.
Cho hàm số y  f  x xác định trên  , thỏa mãn f  x  0, x
   và f  x  2 f  x  0 . Tính f  
1 , biết rằng f   1  1. Lời giải f  x
Ta có f  x  2 f  x  0  f  x  2 f  x   2
 (do f x 0 ). f  x 1 f  x 1 1 1
Lấy tích phân hai vế, ta được
dx  2 dx  ln  f  x  2x   f     x 1 1   1 1  ln  f  
1   ln  f  
1   4  ln1 ln  f   1   4        ln  f  
1   4  f   4 1  e   . 4 Bài 30.
Cho hàm số f  x có đạo hàm, liên tục trên đoạn 1; 4, f   1 1 và
f  x dx  2  . Tính f 4 . 1 Lời giải 4 4 Ta có f (
 x)dx  2  f (x)  2  f (4)  f (1)  2 
mà f (1)  1  f (4)  3 . 1 1 Bài 31.
Giả sử hàm số y  f  x liên tục, nhận giá trị dương trên 0;  và có 4
f 3  , f  x   x  
1 f  x. Tính f 8 . 9 Lời giải f  x 8 f  x 8
Ta có: f  x   x   1 f  x   x 1  dx  x 1dx   f  x 3 f  x 3 8 8 3 1 19 
f  x   x 1  f 8  f 3   f   2 8  7  49 . 3 3 3 3 2 x Bài 32.
Cho hàm số f  x có đạo hàm, liên tục trên 0;  và thỏa mãn
f t  dt  . x cos x  . Tính 0 f 4 . Lời giải 2 x Ta có
f 't  dt  F   2
x   F 0  . x cos x . 0
Lấy đạo hàm hai vế ta có: x f  2 2 .
x   cos x  . x sin  x . 1
 4. f 4  cos 2  2 .sin 2  1  f 4  . 4 f  x Bài 33.
Cho hàm số f  x thỏa mãn 2 t dt  . x cos x  . Tính f 4 . 0 Lời giải f  x f  x 3 t Ta có: 2 t dt  . x cos x    . x cos x 3
 f  x  3 . x cos x 3 0 0 3
 f 4  12.cos 4  12  f   3 4  12 . Bài 34.
Cho hàm số f  x có đạo hàm, liên tục trên đoạn 1; 2 và thỏa mãn f  x  0 khi x 1; 2 . Biết 2 2 f  x
f  x dx  10  và dx  ln 2  . Tính f 2 . f x 1   1 Lời giải 2 2 Ta có:
f  x dx  f  x  10 
 f 2  f   1  10 (1). 1 1 2 f  x 2 f 2 Ta có: dx  ln 
 f x  ln 2  ln  f 2  ln  f   1   ln 2   2 (2) . f  x 1 f   1 1
Từ (1) và (2)  f 2  20 . Bài 35.
Cho hàm số f  x có đạo hàm, liên tục trên đoạn 1;ln 
3 và thỏa mãn f   2 1  e và ln 3 f  x 2 dx  9  e 
. Tính I  f ln 3 . 1 Lời giải ln 3 Ta có: f  x 2 dx  9  e   f    f   2 ln 3
1  9  e  f ln 3  9 . 1 2017 Bài 36.
Cho hàm số y  f  x liên tục và thỏa mãn f  x   3 2
x  3x  6x
. f  x , f 2 2  e . Tính f 0 ? Lời giải 2017 f  x
f  x   3 2
x  3x  6x . f  x 
  x  x  x2017 3 2 3 6 f  x 0 f  x 0   
 x  3x  6x  42017 3 2 dx f x 2    2  0 0 2017 2017 3 Ta có: I    3 2
x  3x  6x  4
dx   x   1  3 x   1  dx 2 2
Đặt t  x 1  dx  dt , đổi cận x  2
  t  1, x  0  t  1. 1
 I   t  3t2017 3
. Xét hàm số f t   t  t2017 3 3
là hàm số lẻ nên I  0 . 1  0 f  x 0   0  ln f  x
 0  ln f 0  ln f 2  f   2 0  e . f x 2  2    2 e x Bài 37.
Cho hàm số f  x  t ln t dt 
. Xác định hoành độ điểm cực đại của đồ thị hàm số f  x . ex Lời giải
Tập xác định D   .
Gọi F t  là một nguyên hàm của g t   t ln t với t  0 . Khi đó 2 e x 2 x f  x e 
t ln t dt  F t  2  e x  ex F F x      e ex
    2x    2 e
e x   ex ex f x F F  2  2 x  2 e
e x   ex ex f f  4 2
 4 e x  e x x x 2  e x  2 4e x x   1 .  x  0 x  0
f  x  0    . 2  4e x 1  0 x   ln 2  
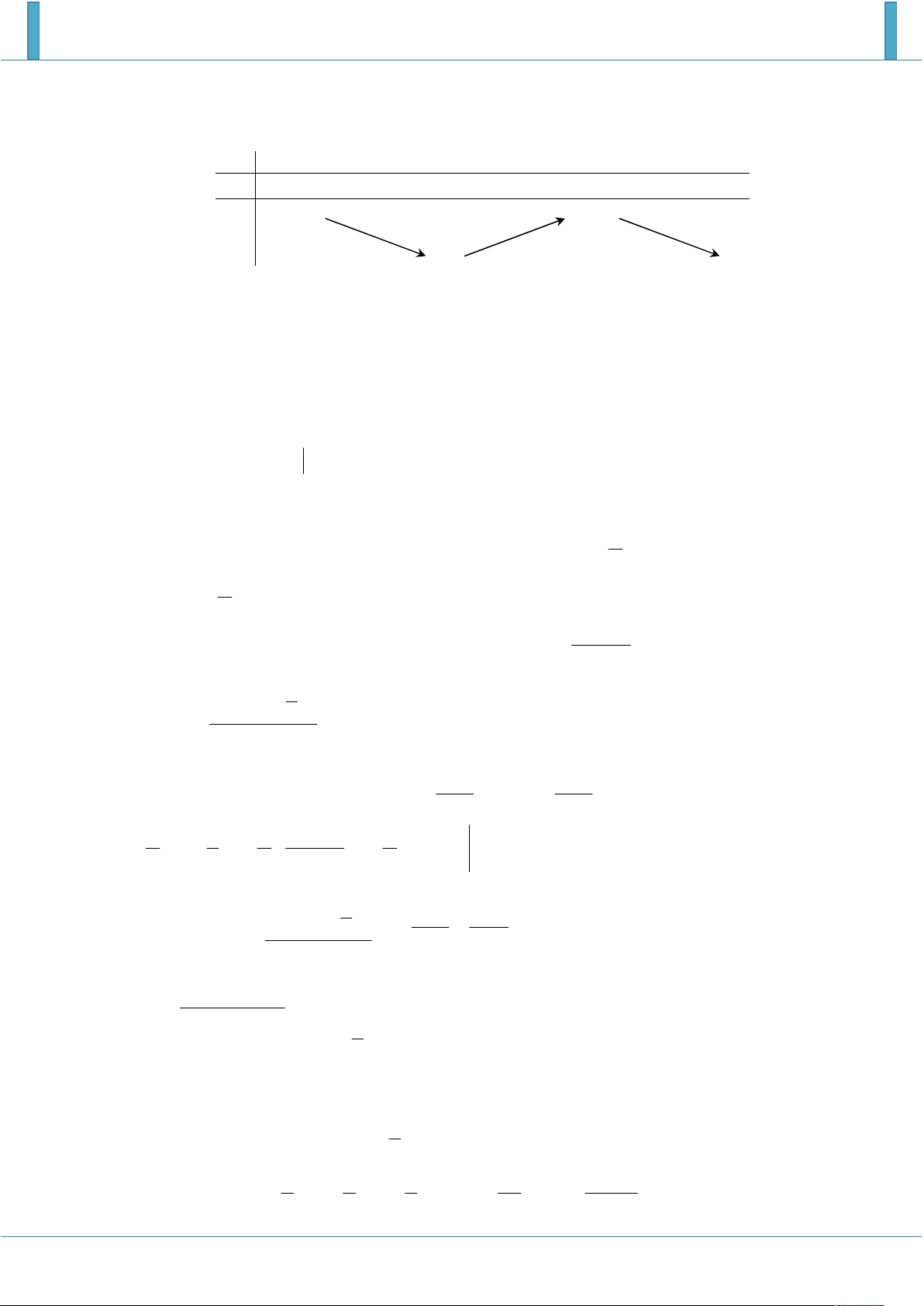
Bảng biến thiên của hàm số x   ln 2 0  y  0  0   y 
Vậy hoành độ điểm cực đại của đồ thị hàm số là x   ln 2 . 2 x Bài 38.
Cho hàm số y  f  x liên tục trên 0;   và f t  dt  x sin  x  . Tính f 4 . 0 Lời giải
Gọi F t  là một nguyên hàm của f t  . 2 x 2      x g x
f t dt  F t   F   2
x   F 0  x sin  x . 0 0
g x  xF 2 2
x   sin  x   x cos x  xf  2 2
x   sin  x   x cos x 
Chọn x  2 ta được 4 f 4  sin 2  2 cos 2  2  f 4  . 2  Vậy f 4  . 2 1 Bài 39.
Lấy tích phân hai vế, ta được Cho hàm số f  x  ln
. Giải bất phương trình sau: 3  x3  t 2 6 sin dt  f  x 0 2  . x  2 Lời giải 1 3
Ta có f  x  3ln 3  x; f  x  3. .3  x'  . 3  x 3  x    6 t 6 1  cos t 3 2 sin dt  dt 
t  sin t  3    2  2  0 0 0  t 2 6 sin dt  3 3 0  
Khi đó f  x 2   3  x x  2 x  2
 x  3; x  2   2x 1  x  2   0 
  x 3 x 2     1 .   x  3  x  3; x  2   2  x  2
Vậy nghiệm bất phương trình:  1 .   x  3  2 2 1 1 1 1   2 n n 1 Bài 40. Chứng minh rằng 1 3 5 2 1 * C 
C  C  ...  C  , n    2n 2n 2n 2 2 4 6 2 n n 2n 1 Lời giải 1
* Nhận xét : Số hạng tổng quát của tổng vế trài là k
C với k nguyên dương lẻ và không 2 k 1 n 1 x n xuất hiện k
C với k chẵn. Do đó ta phải sử dụng   x2 1 và   x2 1 sử dụng phương 2 k 1 n pháp tích phân hai vế. n Ta có 1 x2 0 1 2 2 2n 1  2n 1  2n 2
 C  C x  C x  ... n  C x  C x . 2n 2n 2n 2n 2n  n 1 x2 0 1 2 2 2n 1  2n 1  2n 2
 C  C x  C x  ... n  C x  C x 2n 2n 2n 2n 2n 2n 2n Suy ra 1 x 1 x 2 1 3 3 5 5 2n 1  2n 1 C x C x C x ... C x          2n 2n 2n 2n   n n
1 x2  1 x2 1 1 Do đó dx    1 3 3 5 5 2n 1  2n 1
C x  C x  C x  ...  C x  dx * 2n 2n 2n 2n    2 0 0 1  n n n n 1 2  1 2
1 2 1  1 2 1 1 2 2 n x x x x 1 Mà dx     1  2 2 2n 1 2n 1 0   0 1 1 2 4 6 2n   x x x  x và  1 3 3 5 5 2n 1 2n 1
C x  C x  C x  ...  C x dx  C  C  C   C n n n n  1 3 5 2n 1 ... 2 2 2 2 2n 2n 2n 2 2 4 6 n 2n 0 0 1 1 1 1 1 3 5 2n 1 C C C ... C       2 . 2n 2n 2n 2n   2 4 6 2n 2 1 1 1 1   2 n n 1
Thay (1) và (2) vào (*) ta có 1 3 5 2 1 C 
C  C  ...  C  (đpcm) 2n 2n 2n 2 2 4 6 2 n n 2n 1 n 1 1 1 1 1 n 2018 1 3 4 5   Bài 41.
Tìm số nguyên dương n thỏa mãn C  C  C  C ...  C  . 2 n 3 n 4 n 5 n n 1 n 2019 Lời giải Nhận xét:  k 1 1
* Số hạn tổng quát của tổng vế trái là n
C ( k  0 và k   ). Số đi chung với k C là k 1 k n
phân số nên có thể sử dụng tích phân là phù hợp.  k 1 1 1
* Số hạng tổng quát của tổng vế trái là n
C có mẫu là phân số . Do k 1 lớn hơn k 1 k k 1
k một đơn vị nên có khả năng ban đầu k
C đi chung với k x tức là k k x C . n n n
* Dấu của các số hạng thay đổi từ dấu  sang dấu  do đó ta khai triển nhị thức 1 x . Vì
chưa khớp dấu của đề nên nhân hai vế cho 1. 1 1 n n 1 
Ta có:  1 x    0 1 3 2 3 3
C  C x  C x  C x  ...    1 n n C x x n n n n n d 0 0 0 1  n n 1 x 1  1 1 1   1 1 n    0 1 2 2 3 3 4 n n 1     C  x  C x  C x  C x  ...  C x   n 1 n  2 n 3 n 4 n n 1 n  1   0 n 1 1 1 1   1 1 1 2 3    1 C  C  C  ... n  C n 1 2 n 3 n 4 n n 1 n n n 1 1 1   1 1 2018 n 1 2 3   C  C  C  ... n  C    n  2018 . n 1 2 n 3 n 4 n n 1 n 2019 n 1 Bài 42.
Chứng minh rằng với mọi số nguyên dương n ta luôn có: n 1 1 1 1 1 n 1 0 1 2 3   C  C  C  C ...  C  . 2 n 3 n 4 n 5 n n  2 n n   1 n  2 Lời giải Nhận xét:  k 1
* Số hạng tổng quát của vế trái là k
C ( k  0 , k   ). Số đi chung với k C là phân số k  2 n n
nên có thể sử dụng phương pháp tích phân.  k  k 1   1
* Số hạng tổng quát của vế trái là k
C có mẫu số là phân số
là k  2 lớn hơn chỉ k  2 n k  2
số chập k đúng 2 đơn vị  có khả năng ban đầu k
C đi chung với k 1
x  , tức là k 1  k x C   * . n n
* Dấu của các số đổi dấu từ  sang  . n n Ta xét   x 0 1 2 2 3 3 1
 C  C x  C x  C x  ...    1 n n C x . n n n n n
Tới đây ta nhận thấy số hạng vế phải chưa giống như ta đoán ở  
* , do đó ta nhân hai vế cho x n n ta được x  x 0 1 2 2 3 3 4 C x C x C x C x C x          . n n n n   n n 1 1 ... 1 n 1 1 n n
Khi đó x 1 x dx   0 1 2 2 3 3 4 C x C x C x C x ... C x          x . n n n n   n n 1 1 n d 0 0 1 n
Xét x 1 x dx 
. Đặt t  1 x  dt  dx 0 1 1 1  1 1 1 n 1  n 
x 1 x dx   1  n t t dt  1 n2  t  t     .  n 1 n  2  n 1 n  2 0 0 0 1 n Mặt khác  0 1 2 2 3 3 4 C x C x C x C x ... C x        x n n n n   n n 1 1 n d 0 1 n  1 1 1 1 1   0 2 1 3 2 4 3 5   n n 1
  C x  C x 
C x  C x  ...  C x    2 n 3 n 4 n 5 n n 1 n    0 n 1 1 1 1 1 1 2 3     C  C  C  ... n  C . 2 3 n 4 n 5 n n 1 n n 1 1 1 1 1 n 1 1 2 3   Vậy  C 
C  C  ...  C  . 2 3 n 4 n 5 n n 1 n n   1 n  2 n 1 1 1 1  1 2 3   Bài 43.
Tính tổng S  1 C  C  C ... n 
C với n nguyên dương. 3 n 5 n 7 n 2n 1 n Lời giải n n Ta có  2  x  0 1 2 3
 C  C x  C    n 2 1 ... 1 n C x  n n n n 1 1  n 2 n
1 x  dx   0 1 2 3
C  C x  C  ...  n 2 1 n C x x n n n n d 0 0 1 n * Ta có  0 1 2 3
C  C x  C  ...  n 2 1 n C x x n n n n d 0 1 n  n 1 1 1 1   1 1 1 1 0 1 2 3   0 1 3 2 5 3 6   n 2n 1
  C x  C x  C x  C x  ...
C x    C  C  C  C  ... n C n  3 n 5 n 7 n 2n 1 n  n 3 n 5 n 7 n 2n 1 n   0 1 n Ta tính I   x x . n  2 1  d 0  u    x n   
 u   nx   x n 1 2 2 1 d 2 1 dx Đặt    . dv  dx v  x   1 1 1 1 n n 1  n 1   n 2
1 x  dx  x  2 1 x  2  2nx   2
1 x  dx  2n  2 1 x   1  2
1 x  dx   0 0 0 0 1 1 n n
2n1 x  dx  2n1 x  1 2 2 dx  2 . n I  2 . n I . Do đó I  2 . n I  2 . n I n n 1  n n n 1  0 0 2n 2 4 8 2n 2 4 8 2n  I  I  I  . . .... I  . . .... . n n 1 2n 1  n 3 7 9 2n 1 o 3 7 9 2n 1 2 4 8 2n Vậy S  . . .... . 3 7 9 2n 1
_______________ TOANMATH.com _______________