Toán 12 bài 1: Nguyên hàm

Toán 12 bài 1: Nguyên hàm
A. Lý thuyết Nguyên hàm
1. Định nghĩa nguyên hàm
- Định nghĩa: Cho hàm số y  f  x xác định trên tập D. Hàm F  x gọi là nguyên
hàm của f x nếu đạo hàm của nó F  x bằng f x với mọi x thuộc D. Ví dụ: - Hàm   3
F x  x là nguyên hàm của hàm số y  3x trên R vì F 'x  f x 1 - Hàm F x 2
 x là nguyên hàm của hàm số y  x vì F 'x  f x 2
- Họ nguyên hàm:
- Nếu F(x) là là một nguyên hàm của hàm f(x) trên D thì F(x) + C (với C là hằng
số) cũng là một nguyên hàm của f(x) trên D.
- Nếu F(x) là một nguyên hàm của f(x) trên D thì mọi nguyên hàm của f(x) trên D
đều có dạng F(x) + C (với C là hằng số), khi đó F(x) + C được gọi là họ nguyên
hàm của f(x) trên D, kí hiệu: f
 xdx  FxC
Chú ý: Vì dF x  F 'xdx  f xdx nên biểu thức f(x) cũng chính là vi phân của F(x).
2. Tính chất của nguyên hàm
Tính chất 1: f '
 xdx  f xC
Tính chất 2: k. f
 xdx  k. f
 xdx (với k là một hằng số)
Tính chất 3:  f
 x gxdx  f 
 xdx g  xdx
Tính chất 4: Mọi hàm số f(x) liên tục trên D đều có nguyên hàm trên D.
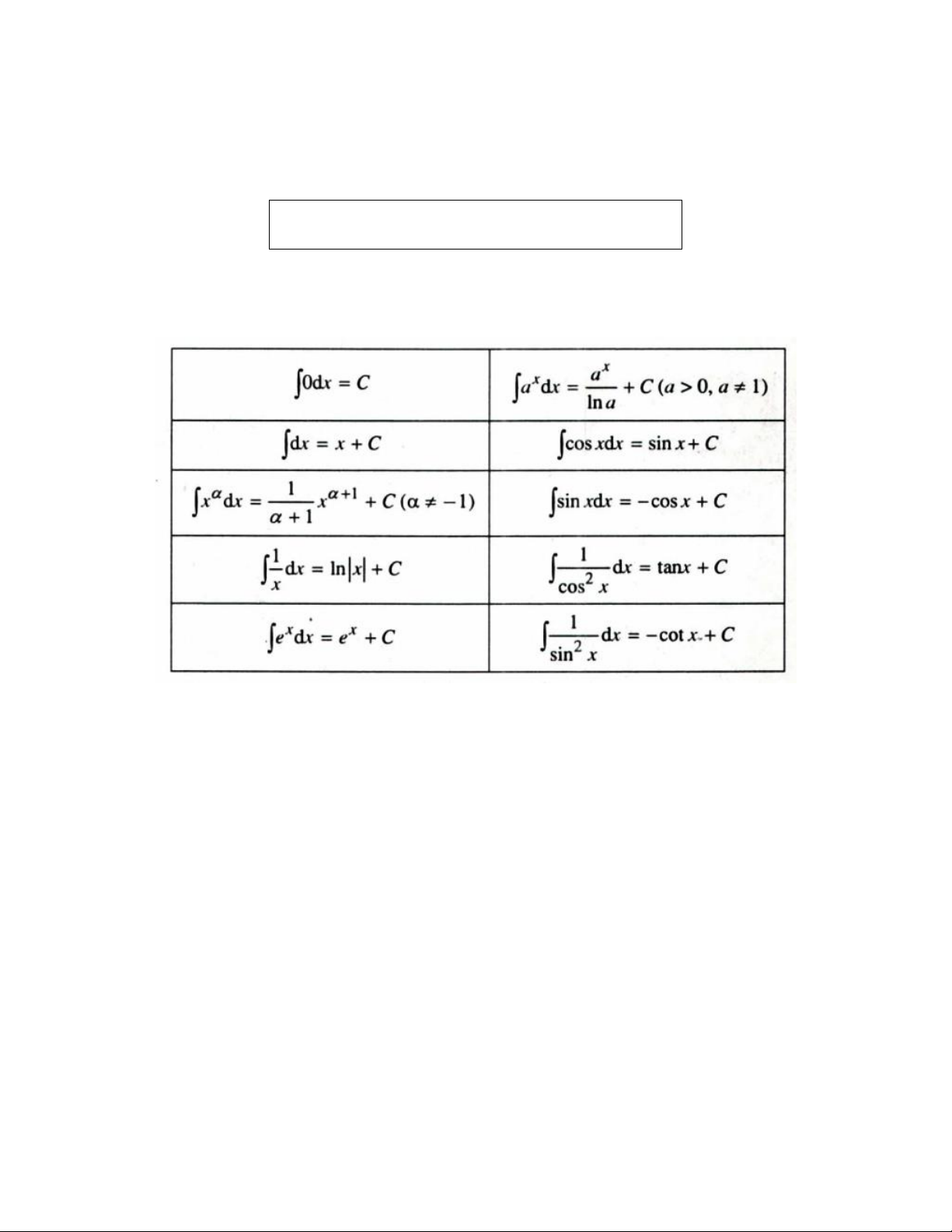
3. Bảng nguyên hàm của một số hàm thường gặp
F 'x  f x  f
 xdx  FxC
- Ta có các bảng nguyên hàm của một số hàm thường gặp dưới đây:
Bảng nguyên hàm cơ bản
Bảng nguyên hàm tích phân thường gặp
4. Phương pháp tính nguyên hàm
a. Phương pháp đổi biến số Nếu f
 udu  FuC và u  ux là hàm số có đạo hàm liên tục thì f
 uxu'xdx  FuxC
b. Phương pháp tính nguyên hàm từng phần
Nếu hai hàm số u  ux và v  vx có đạo hàm liên tục trên D thì u
 xv'xdx  uxvx u'
 xvxdx