Toán 12 Bài 2: Tích phân

Toán 12 Bài 2: Tích phân
A. Lý thuyết Tích phân
1. Diện tích hình thang
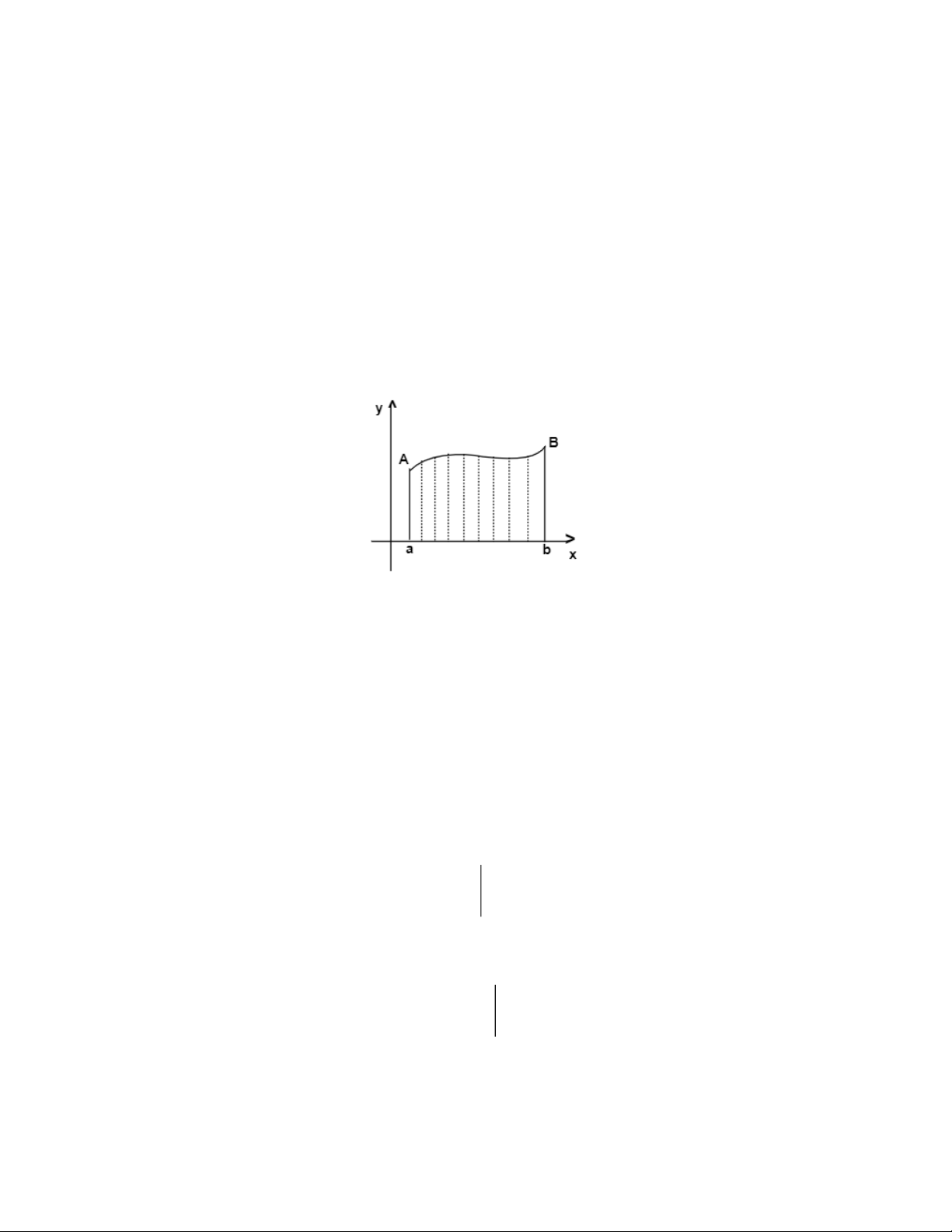
- Cho hàm số y = f(x) liên tục, không đổi dấu trên đoạn [a ; b], hình phẳng giới
hạn bởi f(x), trục hoành và hai đường thẳng x = a và x = b được gọi là hình thang cong.
- Nếu F(x) là nguyên hàm của f(x) thì ta có thể chứng minh được diện tích S của
hình thang cong được tính theo công thức
S  F b  F a
2. Định nghĩa tích phân
Hiệu F(b) – F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên
đoạn [a ; b]) của hàm số f(x) và được kí hiệu là: b
      b f x dx F x
 F b  F a a a
- Ta có công thức tính diện tích hình thang cong như sau: b
       b S f x dx F x
 F b  F a a a
3. Tính chất của tích phân b b
Tính chất 1: k. f
 xdx  k. f  xdx a a b b b
Tính chất 2:  f
 x gx dx   f 
 xdx g  xdx a a a b c b
Tính chất 3: f
 xdx  f
 xdx f
 xdx a a c
4. Phương pháp tính tích phân
a. Phương pháp đổi biến số
- Cho hàm số f(x) liên tục trên đoạn [a ; b]. Giả sử hàm số x   t có đạo hàm liên tục trên đoạn   ;   
 sao cho     a,    b và a   t  b với mọi t    ;     . Khi đó: b  f
 xdx  f
 t'tdt a 
b. Phương pháp tích phân từng phần
Nếu u  ux và v  vx là hai hàm số có đạo hàm liên tục trên đoạn [a ; b] thì b    b b
u x .v'xdx  u
 x.vx  u' 
 x.vxdx a a a b b b
Hay udv  uv  vdu   a a a