Toán 12 bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số
A. Lý thuyết khảo sát sự biến thiên và vẽ đồ thị hàm số
1. Khảo sát sự biến thiên
Bước 1: Tìm tập xác định của hàm số. Xét tính chẵn lẻ, tuần hoàn của hàm số để
thu hẹp phạm vi khảo sát.
Bước 2: Khảo sát và lập bảng biến thiên:
- Xét sự biến thiên của hàm số
+ Tìm đạo hàm bậc nhất y’
+ Tìm các điểm tai đó y’ bằng 0 xác định
+ Xét dấu y’ và suy ra chiều biến thiên của hàm số - Tìm cực trị
- Tìm giới hạn tại vô cực, các giới hạn vô cực và tìm các tiệm cận (nếu có)
Bước 3: Lập bảng biến thiên tổng kết các bước trên để hình dung ra dáng điệu của đồ thị
2. Cách vẽ đồ thị hàm số
- Vẽ các đường tiệm cận của đồ thị (nếu có)
- Tìm giao điểm của đồ thị với Ox, Oy
- Vẽ các điểm đặc biệt: cực trị, điểm uốn
- Tìm thêm điểm thuộc đồ thị hàm số (càng nhiều điểm đồ thị càng chính xác)
- Nêu tính chất đối xứng của đồ thị: trục đối xứng, tâm đối xứng.
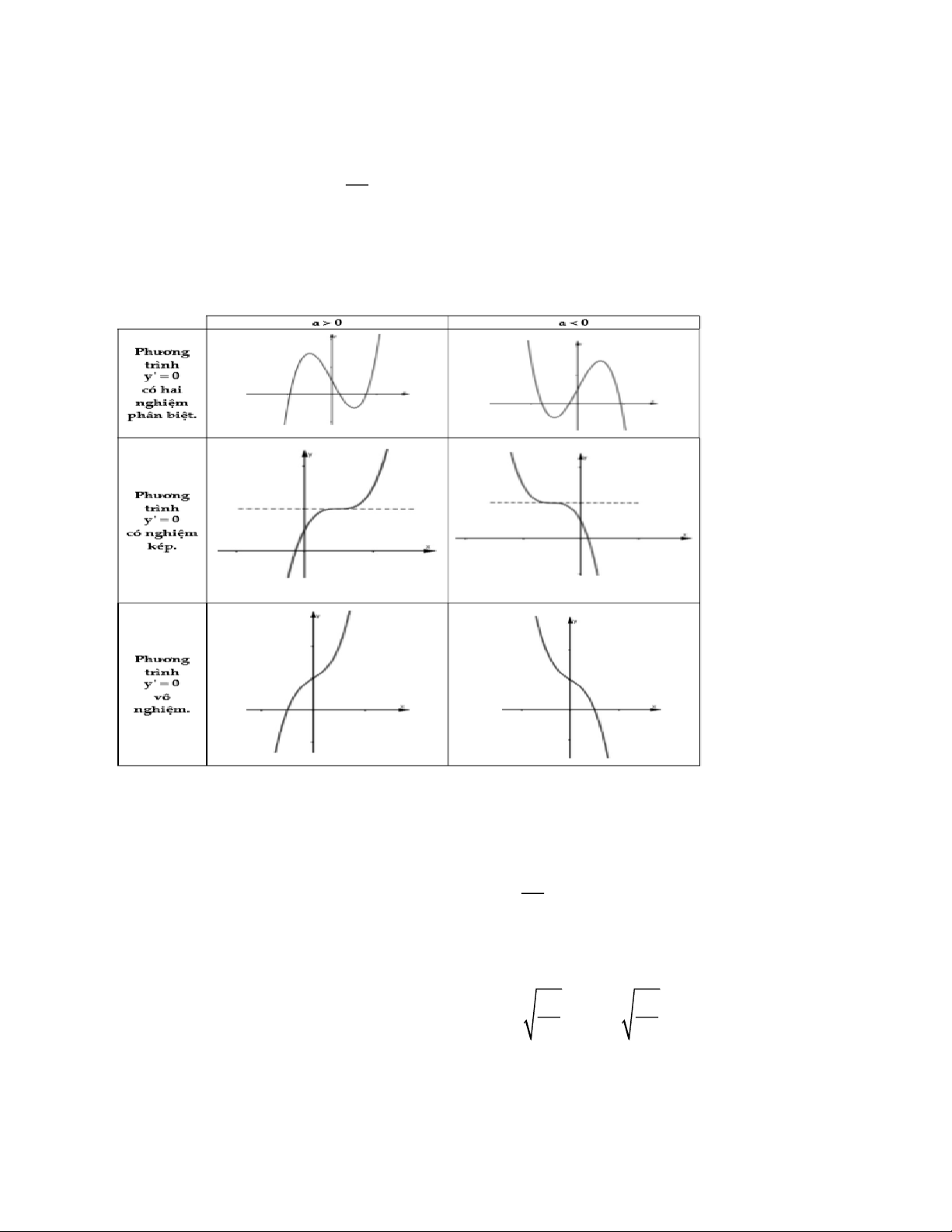
3. Khảo sát hàm đa thức bậc 3: 3 2
y  ax  bx  cx  d Ta có: 2 2
y'  3ax  2bx  c,'  b  3ac
- Hàm số có hai cực trị nếu  '  0 và không có cực trị nếu  '  0 b 
y'  6ax  2b, y'  0  x 
là hoành độ điểm uốn, đồ thị nhận điểm uốn làm 2a tâm đối xứng
Dạng đồ thị hàm số bậc 3
4. Khảo sát hàm đa thức bậc bốn trùng phương: 4 2
y  ax  bx  c  x  0 3 y' 4ax 2bx 2x 2 2ax b y' 0          2 b x   2a
+ Nếu ab  0 thì hàm số có một cực trị x  0 0 b b
+ Nếu ab  0 thì hàm số có 3 cực trị x  0, x  , x   0 1 2 2a 2a
- Đồ thị hàm số cắt trục tung tại điểm có tung độ c, cắt trục hoành tại tối đa 4
điểm và các điểm này đối xứng lẫn nhau qua gốc tọa độ O.
- Đồ thị nhận trục Oy làm trục đối xứng.
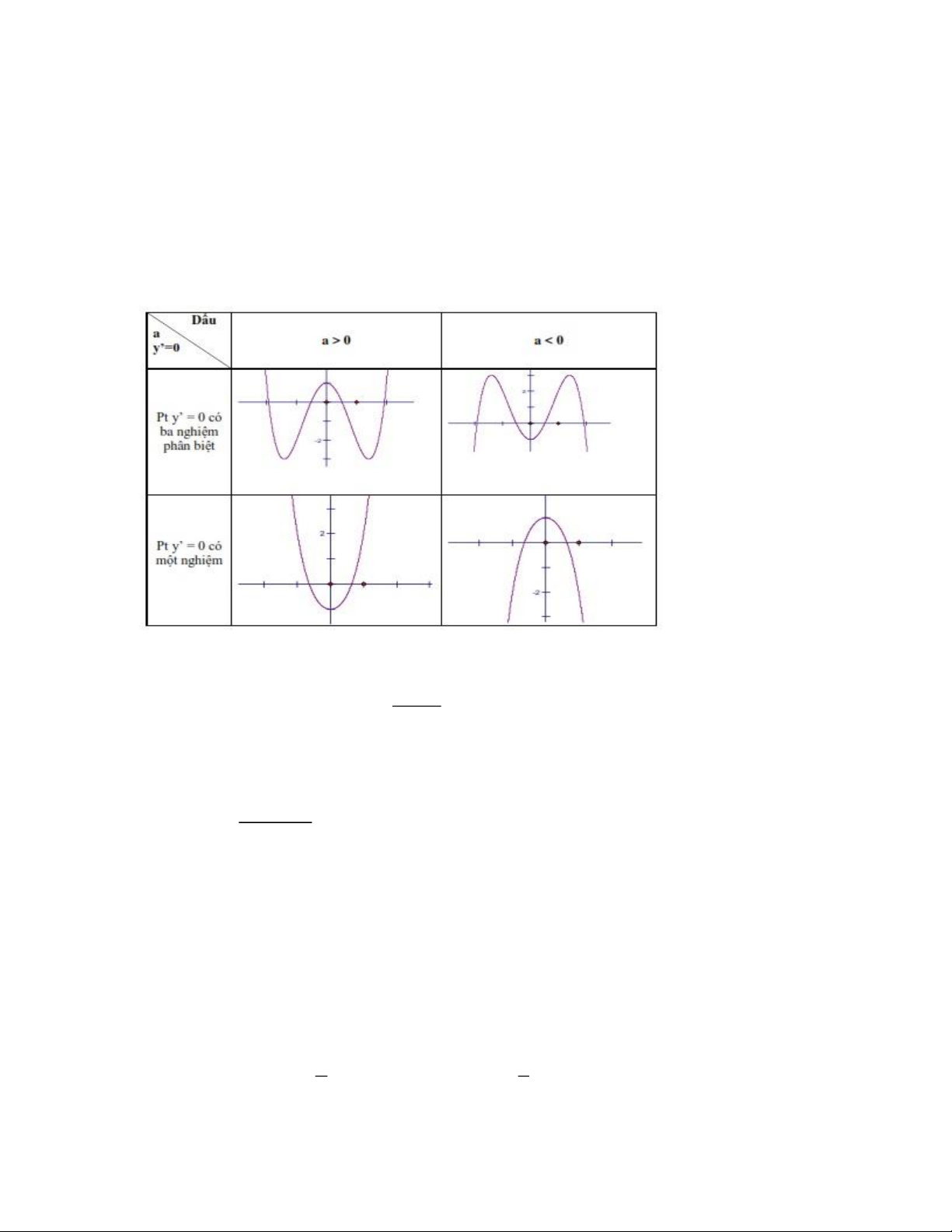
- Dạng đồ thị hàm số 4 2
y  ax  bx  c ax  b
5. Khảo sát hàm phân thức y  cx d
Điều kiện ad  bc  0,c  0 ad  bc Đạo hàm y'   cx  d2
+ Nếu ad  bc  0 hàm số đồng biến trên từng khoảng xác định. Đồ thị nằm góc
phần tư thứ (II) và thứ (IV) của hai tiệm cận.
+ Nếu ad  bc  0 hàm số nghịch biến trên từng khoảng xác định. Đồ thị nằm góc
phần tư thứ (I) và thứ (Iii) của hai tiệm cận. d a
+ Tiệm cận đứng x   , tiệm cận ngang y  c c  d a 
- Đồ thị hàm số có tâm đối xứng I  ,   c c  b
- Đồ thị cắt trục hoành tại điểm có hoành độ
, cắt trục tung tại điểm có tung a b độ d