

























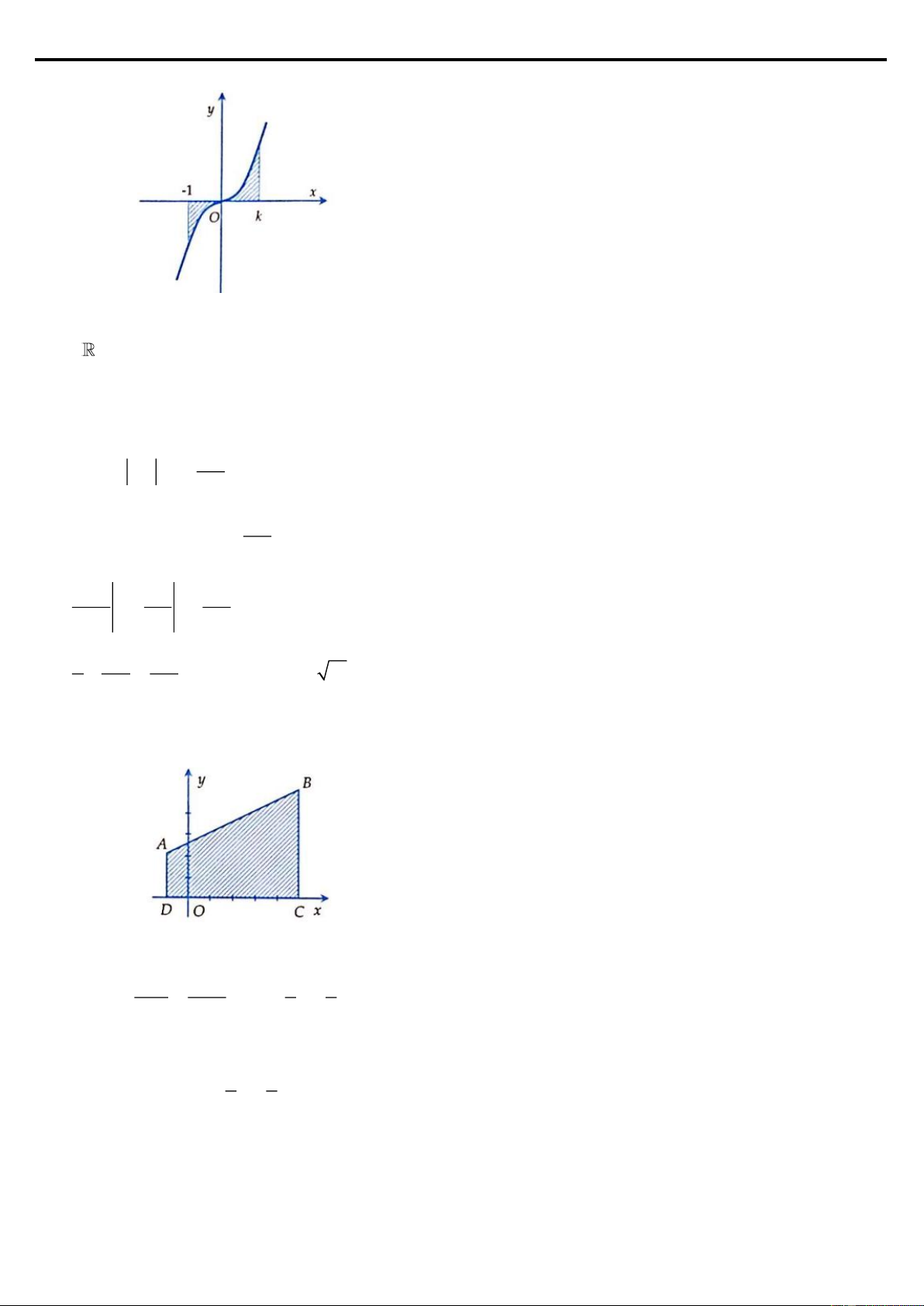





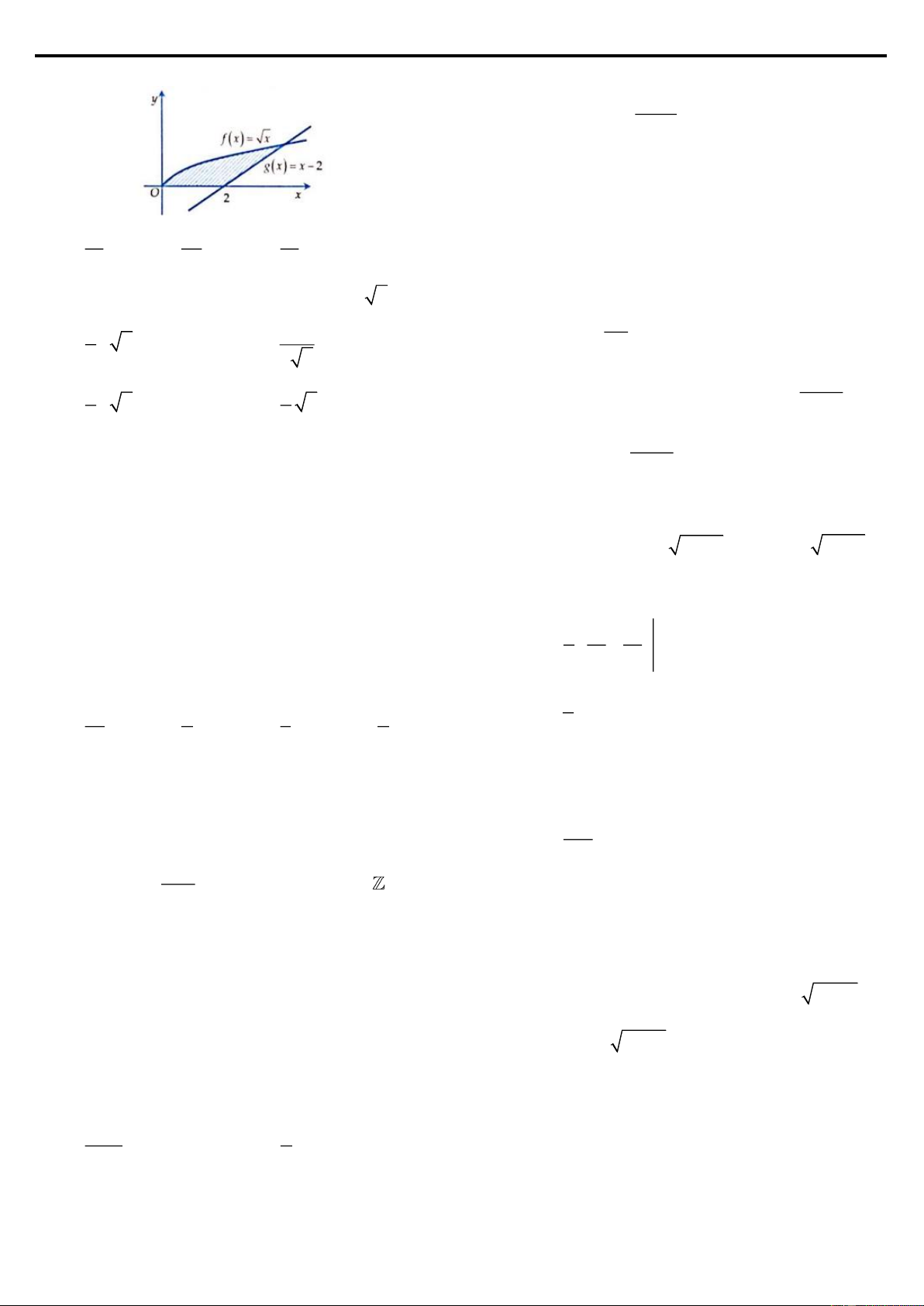



Preview text:
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng T r a n g 1 Chủ đề III
NGUYÊN HÀM – TÍCH PHÂN
I. Nguyên hàm và các tính chất cơ bản
Vấn đề cần nắm:
Kí hiệu K là một khoảng, một đoạn hay một nửa khoảng I. Nguyên hàm và các tính chất cơ 1. Định nghĩa bản II. Hai phương
Cho hàm số f ( x) xác định trên K. Hàm số F ( x) được gọi là nguyên hàm của pháp cơ bản tìm
hàm số f ( x) trên K nếu F '( x) = f ( x) với mọi x thuộc K. nguyên hàm III. Khái niệm và Định lý 1 tính chất cơ bản tích phân
1. Nếu F ( x) là một nguyên hàm của hàm số f ( x) trên K thì với mỗi hằng số IV. Hai phương
C, hàm G ( x) = F ( x) + C cũng là một nguyên hàm của hàm f ( x) trên K. pháp cơ bản tính tích phân
2. Đảo lại nếu F ( x) và G ( x) là hai nguyên hàm của hàm số f ( x) trên K thì V. Ứng dụng hình
tồn tại hằng số C sao cho F học của tích phân
(x) = G(x) +C . Định lý 2
Nếu F ( x) là một nguyên hàm của f ( x) trên K thì mọi nguyên hàm của f ( x)
trên K đều có dạng F ( x) + C , với C là một hằng số. STUDY TIP
Người ta chứng minh được rằng: “Mọi hàm số liên tục trên K đều có nguyên Từ định nghĩa nguyên hàm trên K.” hàm ta có được:
Từ hai định lý trên ta có
- Nếu F ( x) là một nguyên hàm của hàm số f ( x) trên K thì F ( x) + C,C là
họ tất cả các nguyên hàm của f ( x) trên K. Kí hiệu Chú ý f
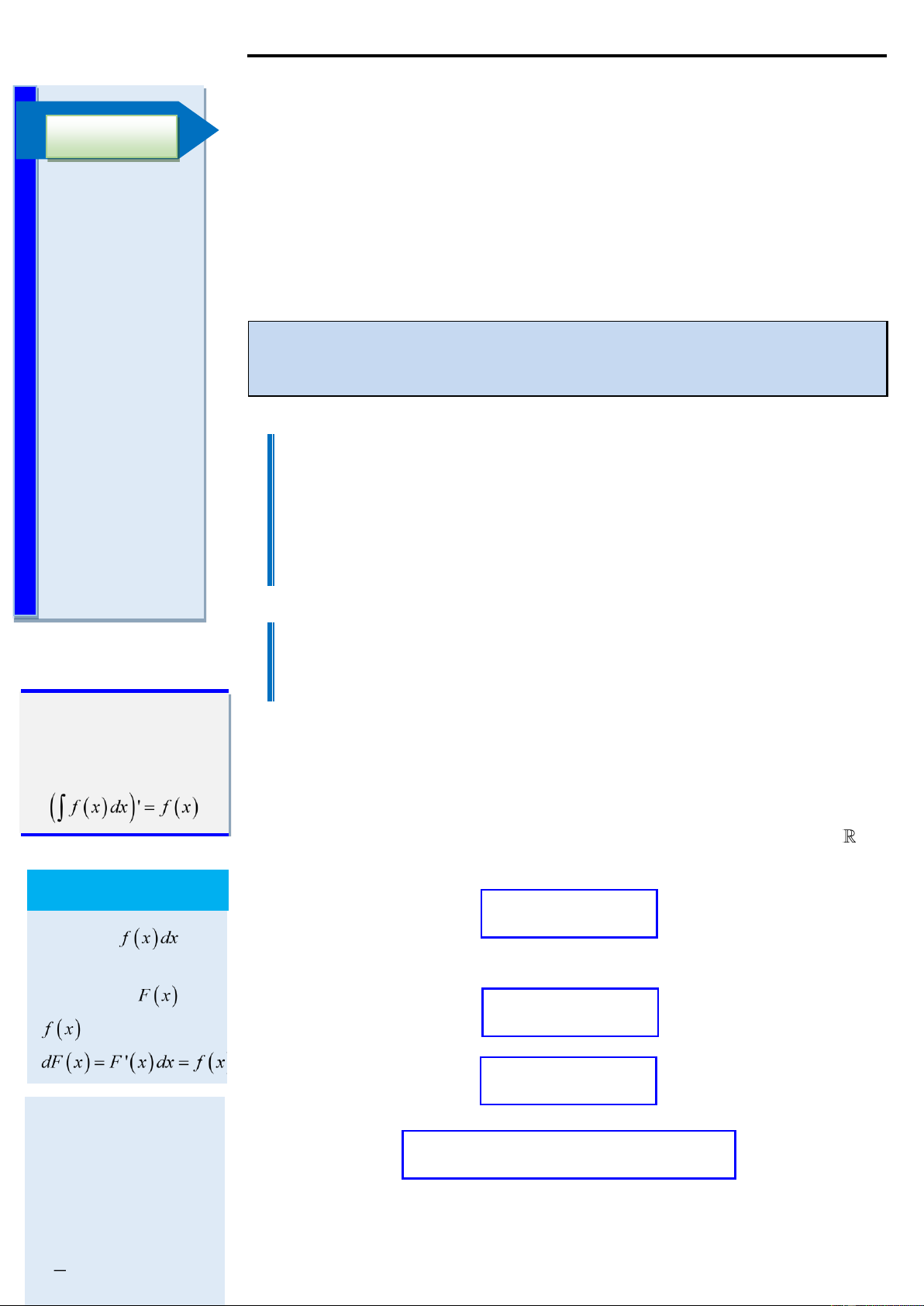
(x)dx = F (x)+C . Biểu thức
2. Tính chất của nguyên hàm chính là vi phân của Tính chất 1 nguyên hàm của f '
(x)dx = f (x)+C , vì Tính chất 2 kf
(x)dx = k f (x)dx
Từ đây ta suy ra hệ quả Tính chất 3
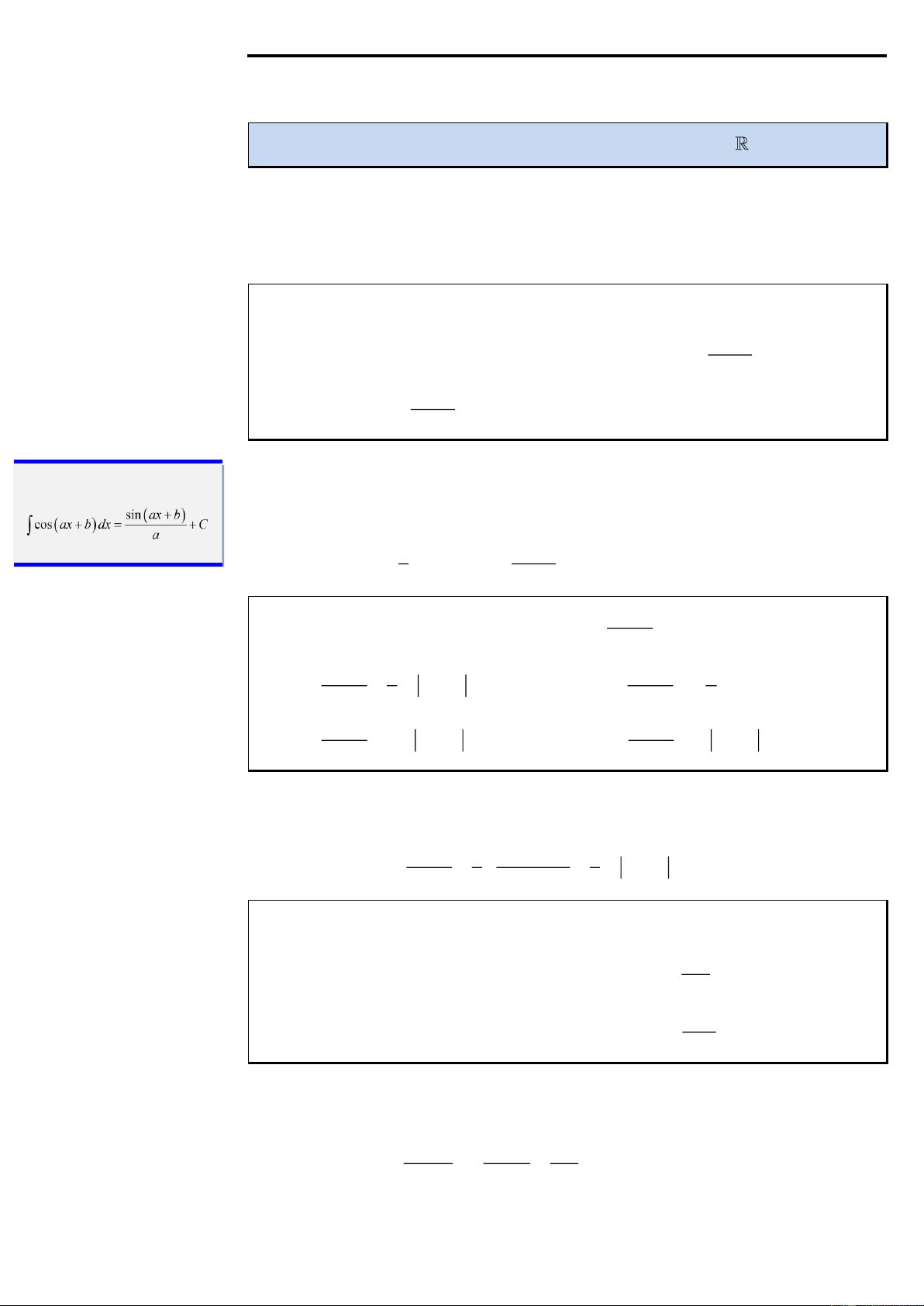
Với u = ax + b, (a 0) f
(x) g(x)dx = f
(x)dx g (x)dx ta có f
(ax +b)dx 1
= F (ax + b) + C a
Công Phá Toán – Lớp 12 Ngọc Huyền LB
II. Hai phương pháp cơ bản để tìm nguyên hàm
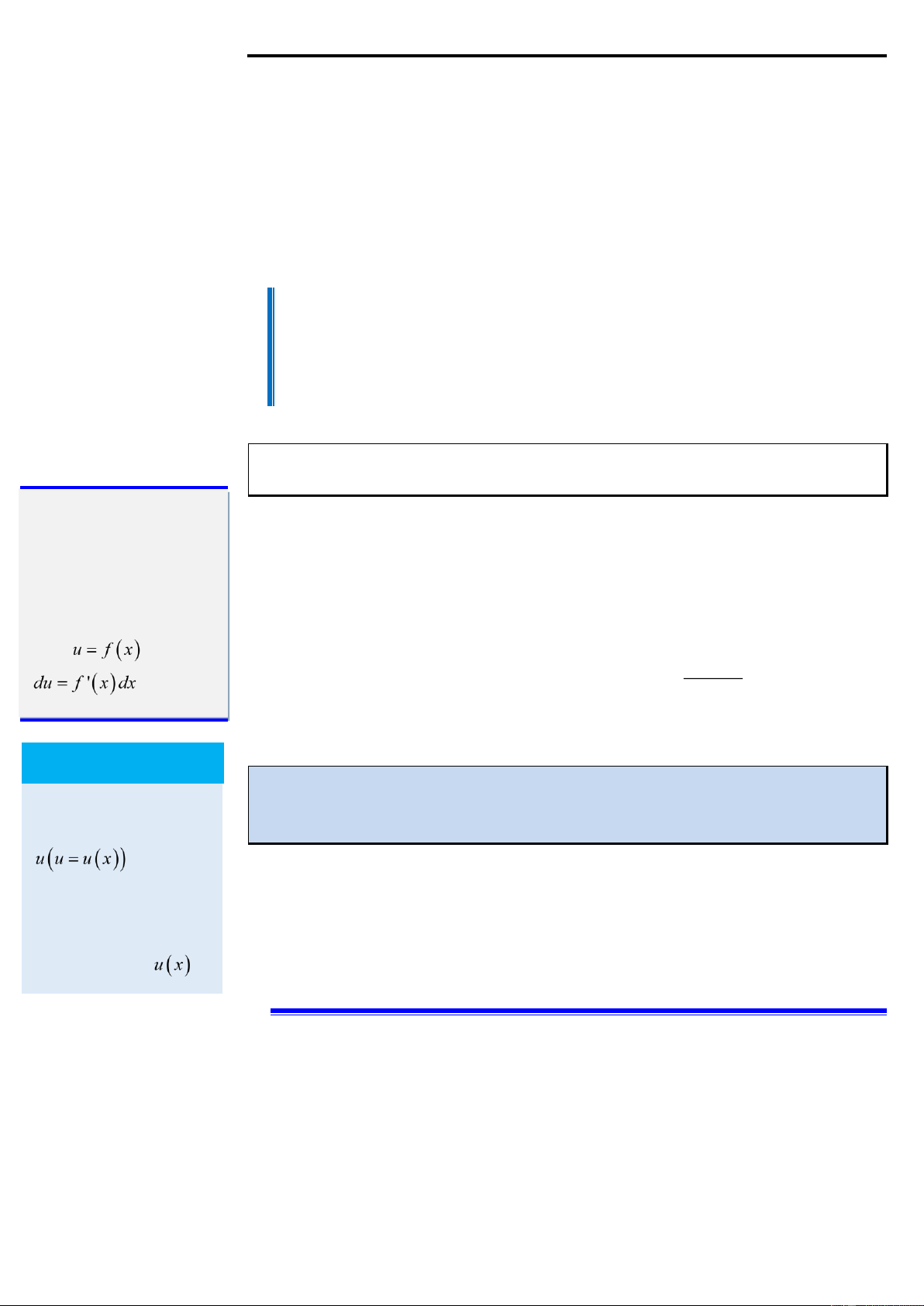
1. Phương pháp đổi biến số Định lý 3
Cho hàm số u = u ( x) có đạo hàm liên tục trên K và hàm số y = f (u) liên tục
sao cho hàm hợp f u ( x)
xác định trên K. Khi đó nếu F là một nguyên hàm của f thì f u (x)u'
( x) dx = F u ( x) + C
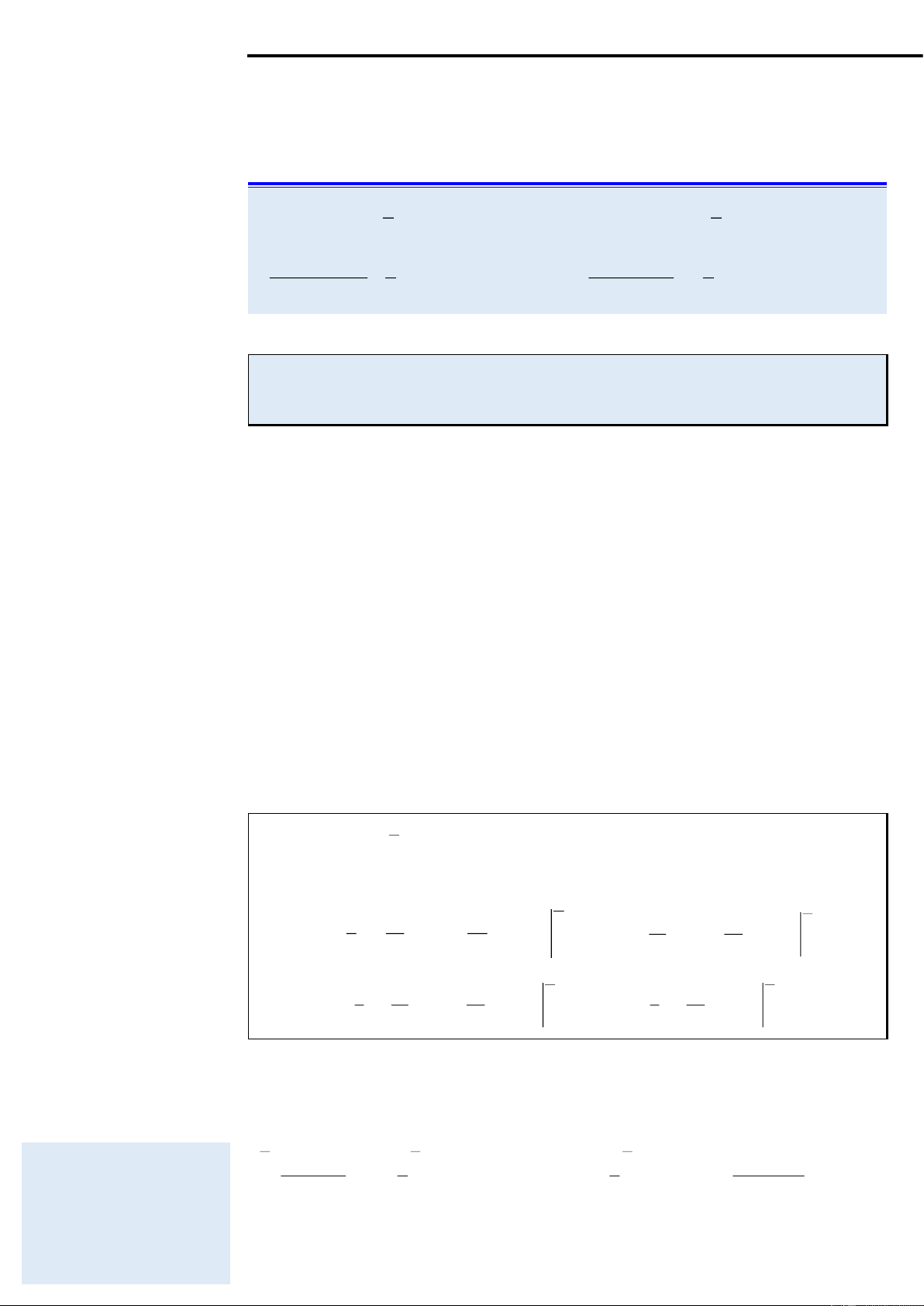
Ví dụ 1: Tìm nguyên hàm ( x − )10 1 dx . STUDY TIP Lời giải Với phương pháp đổi biến ta cần chú trọng
Theo định lý trên thì ta cần viết về dạng f (u)du . công thức mà suy ra từ định lý như sau:
Mà u ' = ( x − ) 1 ' = 1 , do vậy Nếu , khi đó ( −
x − ) dx = (x − ) (x − ) dx = (x − ) d (x − ) (x )11 10 10 10 1 1 1 . 1 ' 1 1 = + C . 11
Từ ví dụ trên ta có các bước gợi ý để xử lý bài toán tìm nguyên hàm theo phương pháp đổi biến.
Dạng 2: Gửi vào ngân hàng một số tiền a đồng với lãi suất x% = r mỗi tháng Nếu tính nguyên hàm
theo hình thức lãi kép. Gửi theo phương thức có kỳ hạn m tháng. Tính số tiền
cả gốc lẫn lãi A sau n kỳ hạn. theo biến mới thì sau
Từ “STUDY TIP” ở bên ta thấy đưa về một ghi nhớ quan trọng: Trong cùng một khi tính nguyên hàm
kỳ hạn, lãi suất sẽ giống nhau mà không được cộng dồn vào vốn để tính lãi kép. Ví xong, ta phải trở lại
dụ kỳ hạn là 3 tháng thì lãi suất tháng 1 là ar, tháng 2, tháng 3 cũng là ar, sau hết
biến x ban đầu bằng
kỳ hạn 3 tháng mà không rút ra thì số tiền lãi một kỳ hạn sẽ được cộng dồn vào tiền gốc. cách thay u bởi .
Lời giải tổng quát
1. Đặt u = g ( x).
2. Biến đổi x và dx về u và du.
3. Giải bài toán dưới dạng nguyên hàm hàm hợp f (u) du
, sau đó thay biến x
vào nguyên hàm tìm được và kiểm tra lại kết quả. Ta đến với ví dụ 2
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng T r a n g 3
Ví dụ 2: Tìm x ( − x)7 2 1 dx .
Ở bài toán này, ta thấy số mũ 7 khá cao mà lại có biểu thức trong ngoặc phức tạp hơn là 2
x . Do vậy ta sẽ đặt ( − )7
1 x để đổi biến, dưới đây là lời giải áp dụng gợi ý các bước trên. Lời giải
Đặt u = 1− x du = (1− x)'dx du = −dx 7 2 ta có 2 x
( − x) dx = ( −u) 7u (− )du = −( 7 8 9 1 1 . . 1
u − 2u + u ) du u 2u u ( − x)8
( − x)9 ( − x)10 8 9 10 1 2 1 1 = − + − + C = − + − + C 8 9 10 8 9 10
2. Phương pháp lấy nguyên hàm từng phần. Định lý 4
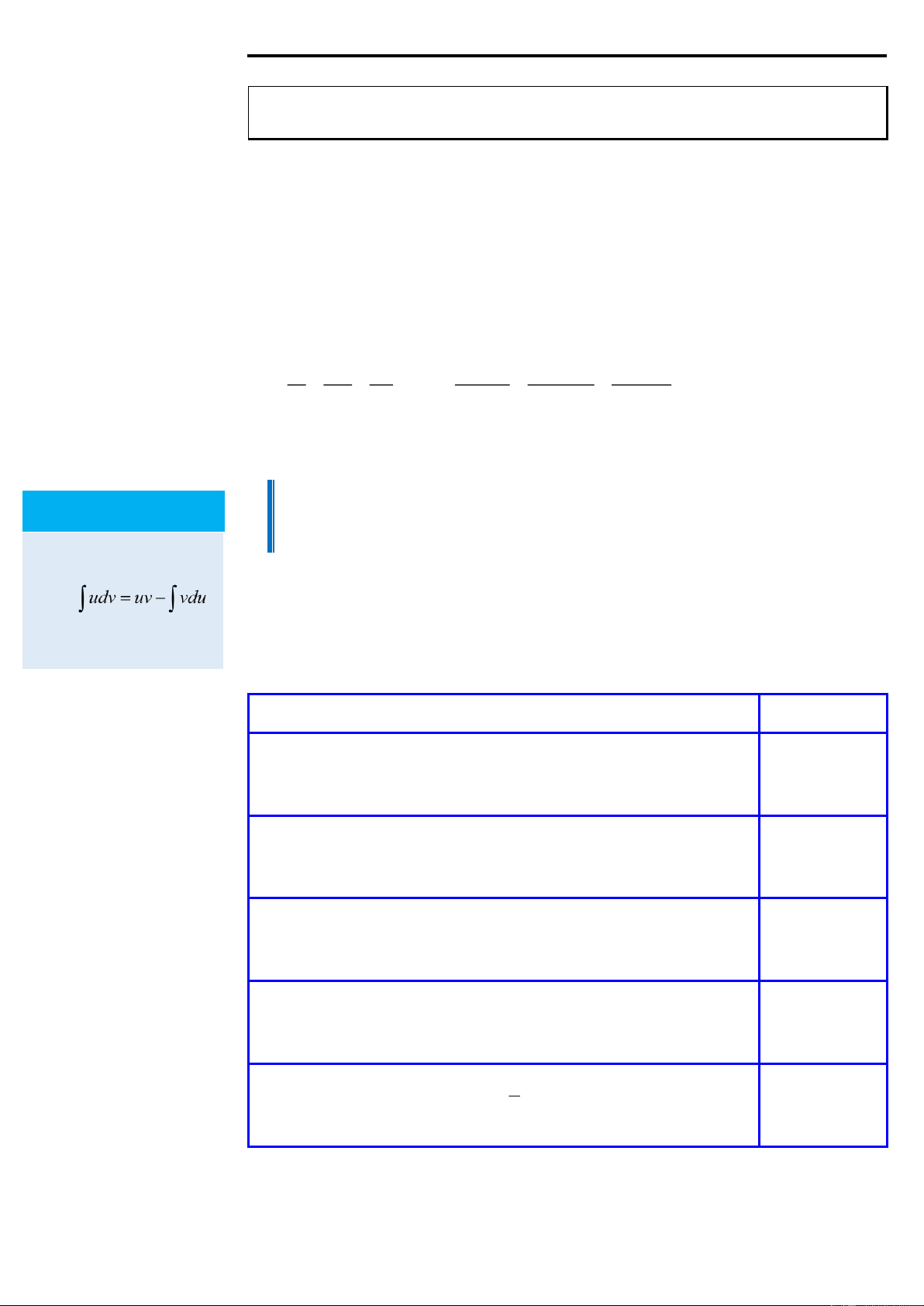
Nếu u và v là hai hàm số có đạo hàm liên tục trên K thì Chú ý u
(x)v'(x)dx = u(x).v(x)− v
(x)u'(x)dx Đẳng thức trong định lý 4 còn dc viết dưới Nếu nguyên hàm có dạng
p ( x).q ( x)dx
thì ta có thể nghĩ đến phương pháp dạng
nguyên hàm từng phần. Bảng sau gợi ý cách đặt ẩn phụ để tính nguyên hàm
p ( x).q ( x) dx .
Hàm dưới dấu tích phân Cách đặt
p ( x) là đa thức, q ( x) là hàm lượng giác u = p (x) dv = q (x)dx
p ( x) là đa thức, ( ) = '( x ). x q x f e e u = p (x) dv = q (x)dx
p ( x) là đa thức, q ( x) = f (ln x) u = q (x) dv = p (x)dx
p ( x) là hàm lượng giác, ( ) = ( x q x f e ) u = q (x) dv = p (x)dx u = p (x)
p ( x) là đa thức, q ( x) = f ( x) 1 ' ln x dv = q (x)dx
Công Phá Toán – Lớp 12 Ngọc Huyền LB
p ( x) là đa thức, q ( x) = f '(u ( x)).(u ( x))' , u ( x) là các hàm u = p (x)
lượng giác (sin x,cos x, tan x,cot x) dv = q (x)dx
Ví dụ 3: Thầy Điệp Châu cho bài toán “Tìm sin x cos xdx
” thì ba bạn Huyền, Lê
và Hằng có ba cách giải khác nhau như sau Bạn Huyền giải
bằng Bạn Lê giải bằng phương pháp lấy nguyên Bạn Minh Hằng chưa
phương pháp đổi biến số hàm từng phần như sau:
học đến hai phương như sau: “Đặt u = cos , x v ' = sin x . Ta
có pháp trên nên làm như
“Đặt u = sin x , ta có: sau: u ' = −sin ,
x v = −cos x . du = cos xdx “ sin . x cos xdx
Công thức nguyên hàm từng phần cho ta Vậy sin .
x cos xdx = udu 2
sin x cos xdx = − cos x − sin x cos xdx sin 2x = dx 2 2 2 u sin x = + C = + C ”
Giả sử F là một nguyên hàm của sin . x cos x . cos 2x 2 2 Theo đẳ = − + ng thức trên ta có C ”. 4 F ( x) 2
= − cos x − F (x) + C . x C Suy ra F ( x) 2 cos = − + . 2 2 2 Điề cos x u này chứng tỏ − là một nguyên 2 hàm của sin . x cos x . 2 cos x Vậy sin . x cos xdx = − + C .” 2
Kết luận nào sau đây là đúng?
A. Bạn Hằng giải đúng, bạn Lê và Huyền giải sai STUDY TIP
B. Bạn Lê sai, Huyền và Hằng đúng. Bài toán củng cố về
C. Ba bạn đều giải sai.
định lý 1 đã nêu ở trên,
D. Ba bạn đều giải đúng.
và củng cố các cách giải Đáp án D. nguyên hàm cơ bản.
Nhận xét: Sau khi soát kĩ cả ba lời giải, ta thấy ba lời giải trên đều không sai ở
bước nào cả, tuy nhiên, tại sao đến cuối cùng đáp án lại khác nhau? Ta xem giải thích ở lời giải sau Lời giải
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng T r a n g 5 2 sin x 2 cos x cos 2x
Cả ba đáp số đều đúng, tức là cả ba hàm số ; − và − đều là 2 2 4 nguyên hàm của sin .
x cos x do chúng chỉ khác nhau về một hằng số. Thật vậy 2 2 sin x cos x 1 − − = ; 2 2 2 2 x ( 2 2 2sin 1 2sin sin cos 2 x x x + − ) 1 − − = = . 2 4 4 4
3. Bảng một số nguyên hàm mở rộng 1 + 1 ( + cos
(ax+b)dx = sin(ax+b)+ ax + b) (ax b) dx = + − C a ( + ) C, 1 1 a dx 1 = 1
ln ax + b + C sin
(ax+b)dx = − cos(ax+b)+C ax + b a a 1 ax+b 1 ax+b e dx = e + C tan
(ax+b)dx = − ln cos(ax+b) +C a a 1 ax+b 1 ax+b m dx = m + C, (m 0) cot
(ax+b)dx = ln sin(ax+b) +C a ln m a dx 1 x = dx 1 arctan + C
= − cot ax + b + C 2 2 a + x a a 2 sin (ax + b) ( ) a dx 1 a + x − = dx 1 x a ln + C = ln + C 2 2 a − x 2a a − x 2 2 x − a 2a x + a dx = dx 1 ln ( 2 2 x + x + a + C
= tan ax + b + C 2 2 ) 2 x + a cos (ax + b) ( ) a 2 2 dx 1 a + x + a 2 2 2 − = − x a x a x ln + C 2 2 a − x dx = + arcsin + C 2 2 + a x x x a 2 2 a b dx 1 ax + b ln
(ax+b)dx = x+ ln
(ax + b) − x + C = ln tan + C a sin (ax + b) a 2 ax e a bx − b bx ax e a bx + b bx ax ( cos sin ) ax ( sin cos ) e sin bxdx = + C e cos bxdx = + C 2 2 a + b 2 2 a + b
Công Phá Toán – Lớp 12 Ngọc Huyền LB
III. Các dạng toán về nguyên hàm
Dạng 1: Tìm nguyên hàm F ( x) của hàm số f ( x) trên D .
Các bài toán ở dạng 1 thì chỉ yêu cầu độc giả nhớ bảng công thức nguyên hàm
cơ bản thường gặp. Chú ý với các nguyên hàm hàm hợp để áp dụng đúng công thức!
Ví dụ 1: Tìm nguyên hàm của hàm số f ( x) = cos 3x . sin 3x
A. cos 3xdx = 3sin 3x + C B. cos 3xdx = + C 3 sin 3x
C. cos 3xdx = − + C
D. cos 3xdx = sin 3x + C 3 Đáp án B. STUDY TIP Lời giải . 1 sin 3x Ta có cos 3xdx = d (sin3x) = + C 3 3
Ví dụ 2: Tìm nguyên hàm của hàm số f ( x) 1 = 5x− . 2 dx 1 dx 1 A.
= ln 5x − 2 + C B. = − (ln5x − 2)+C 5x − 2 5 5x − 2 2 dx dx C.
= 5ln 5x − 2 + C D.
= ln 5x − 2 + C 5x − 2 5x − 2 Đáp án A. Lời giải dx 1 d 5x − 2 1 Ta có f (x) ( ) dx = =
= ln 5x − 2 + C 5x − 2 5 5x − 2 5
Ví dụ 3: Tìm nguyên hàm của hàm số ( ) 7x f x = . x 7x A. 7x = 7x dx ln 7 + C B. 7 dx = + C ln 7 x 1 + x 7 C. x x 1 7 dx 7 + = + C D. 7 dx = + C x +1 Đáp án B. Lời giải d d x x (7x) (7x) 7x Ta có 7 dx = 7 . = = + C . 7 . x ln 7 ln 7 ln 7
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng T r a n g 7 x
Ví dụ 4: Nguyên hàm của hàm số f ( x) = ( là + x)5 1 1 1
A. F ( x) = − + C
B. F ( x) = + C 3( x + )3 1 4 ( x + )4 1 1 1 1 1
C. F ( x) = − + C
D. F ( x) = − + C 4 3 3( x + )3 1 4( x + )4 1 4( x + ) 1 3( x + ) 1 Đáp án D. Lời giải
Đặt u = x +1 thì u ' =1. − Khi đó x u 1 1 1 4 − 5 − = = − = − ( dx du du u du u du 1+ x)5 5 5 u u u 1 1 1 1 = − . + . + C . 3 4 3 u 4 u x 1 1
Thay u = x +1 ta được = − + ( x + ) dx C 5 1 4( x + )4 1 3( x + )3 1
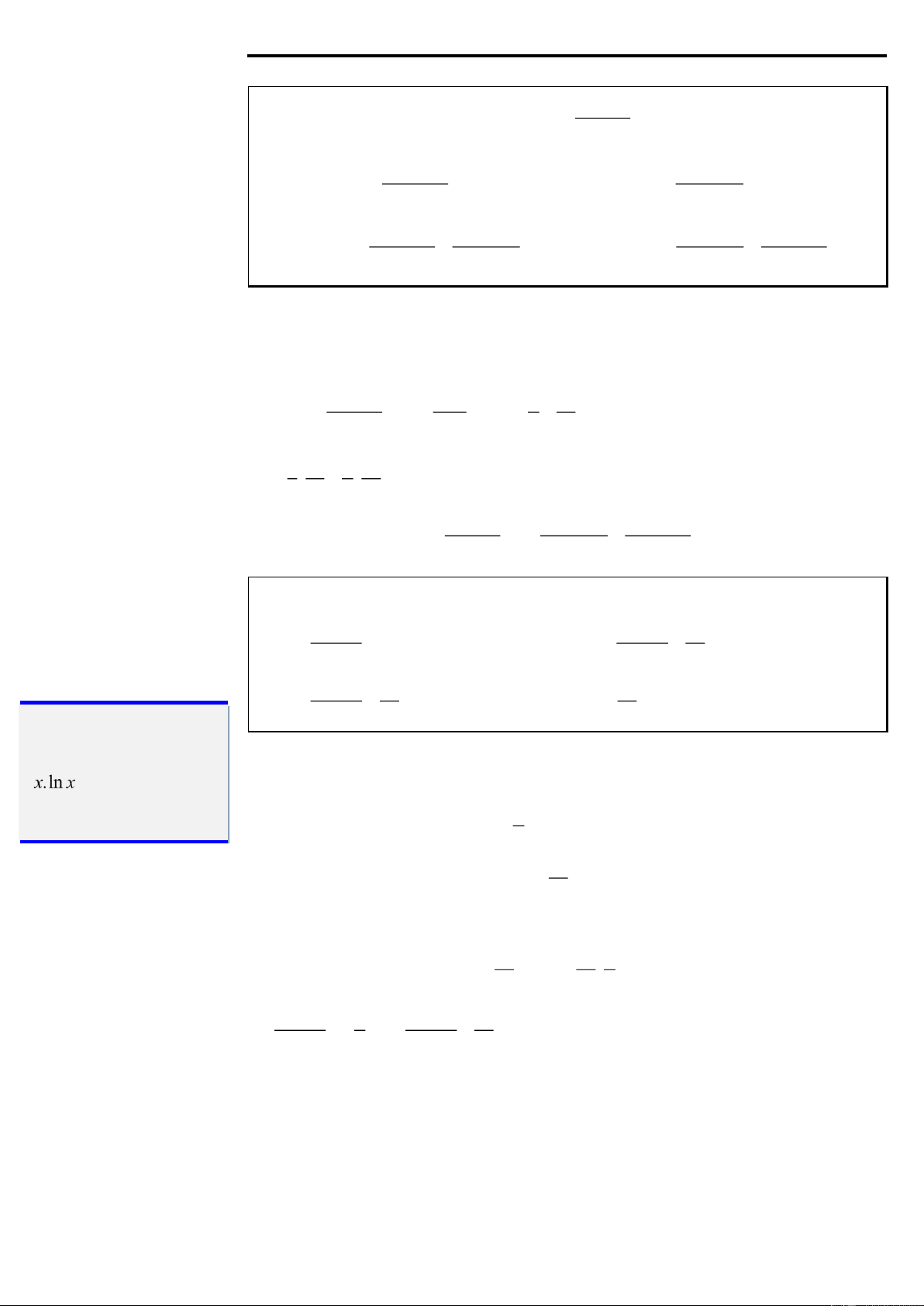
Ví dụ 5: Nguyên hàm của hàm số . x ln x là 2 x .ln x 2 2 x .ln x x A. + C B. − + C 2 2 4 2 2 x .ln x x 2 x C. + + C D. + C 2 4 4 STUDY TIP Đáp án B.
Ở đây xuất hiện tích của nên ta áp dụng Lời giải nguyên hàm từng phần. 1 ln x = u dx = du x Ta có . x ln xdx . Đặt 2 x
dv = xdx v = 2
Theo phương pháp nguyên hàm từng phần ta có 2 2 x x 1 .
x ln xdx = udv = uv − vdu = .ln x − . dx 2 2 x 2 2 2 x .ln x x x .ln x x = − dx = − + C . 2 2 2 4
Công Phá Toán – Lớp 12 Ngọc Huyền LB
Dạng 2: Chứng minh F ( x) là một nguyên hàm của hàm f ( x) trên D .
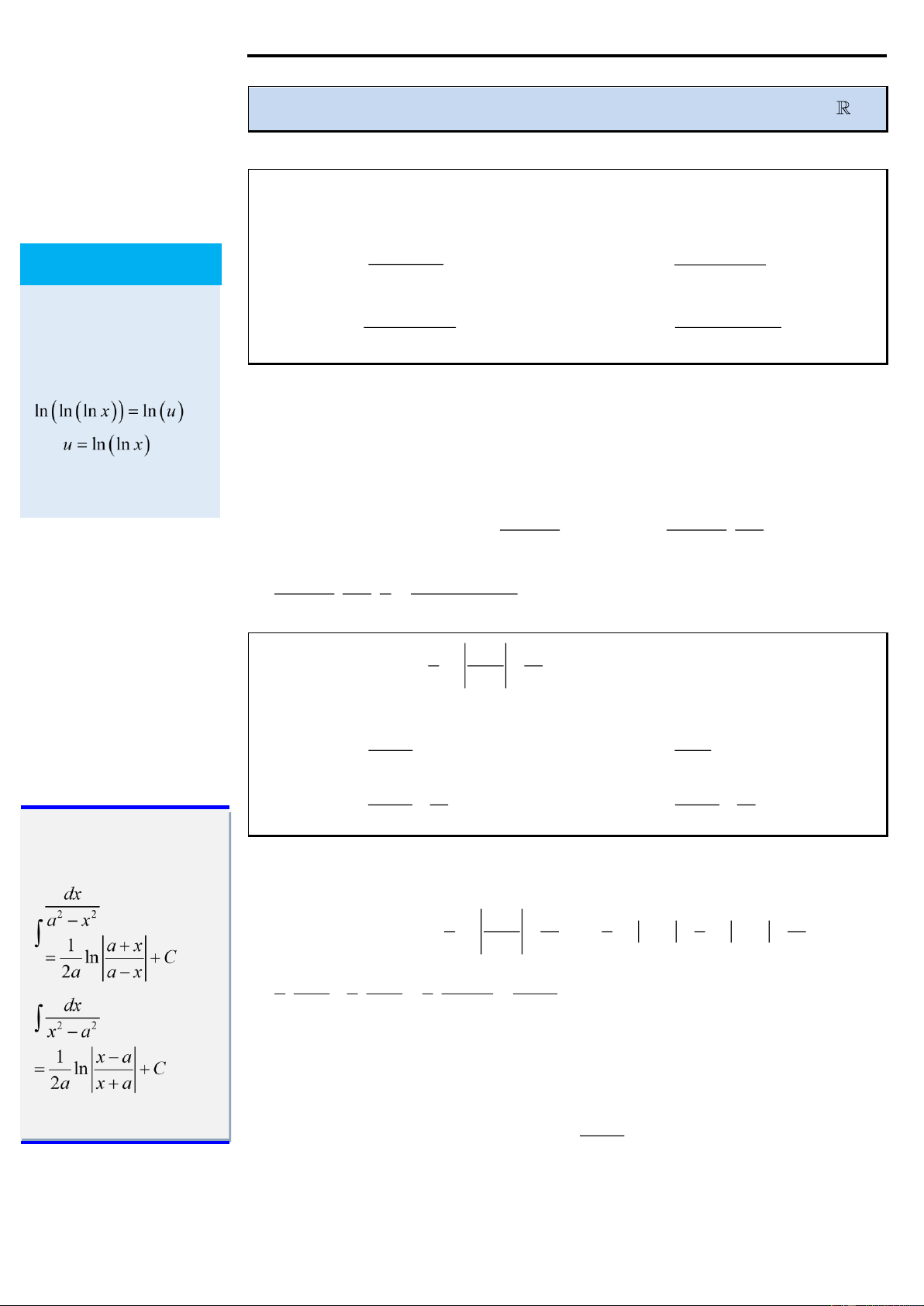
Ví dụ 1: Cho F ( x) = ln (ln (ln x)) . Hỏi F ( x) là nguyên hàm của hàm số nào dưới đây? 1 1 Chú ý
A. f ( x) =
B. f ( x) = . x ln (ln x) ln (ln (ln x)) Sai lầm thường gặp là 1 1 không biết cách đạo
C. f ( x) =
D. f ( x) = ln . x ln (ln x) . x ln . x ln (ln x) hàm hàm hợp. Ở đây ta cần đạo hàm như sau: Đáp án D. Lời giải với lần
Để tìm F ( x) là nguyên hàm của hàm số nào trong số 4 hàm số trên, ta sẽ đi đạo lượt như thế ta sẽ ra
hàm F ( x) từ đó suy ra f ( x) .
được kết quả như bên. 1 1 1
Ta có F '( x) = ln (ln (ln x)) ' = ( = x) . ln (ln x) ' ( x). (ln x)' ln ln ln ln ln x 1 1 1 1 = ( = = . x) . . f x ln ln ln x x . x ln . x ln (ln x) ( ) x −
Ví dụ 2: Cho F ( x) 1 3 1 = .ln +
. Hỏi F ( x) là nguyên hàm của hàm số nào 6 x + 3 12 dưới đây? 1
A. f ( x) = f x = 2 x − B. ( ) 1 9 x − 9 1 x 1 x
C. f ( x) = + f x = + 2 x − D. ( ) 9 12 2 x + 9 12 STUDY TIP Đáp án A. Công thức cần nhớ: Lời giải x −
Cách 1: Ta có F ( x) 1 3 1 1 1 1 ' = .ln + ' =
.ln x − 3 − .ln x + 3 + ' 6 x + 3 12 6 6 12 1 1 1 1 1 6 1 = . − . = . = 2 2 2 6 x − 3 6 x + 3 6 x − 3 x − 9
Cách 2: Thực chất đây là công thức nguyên hàm mà tôi đã giới thiệu ở bảng
nguyên hàm phía trên (dòng số 6 trong bảng). 1
Áp dụng công thức trên ta có ngay f ( x) = 2 x − . 9
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng T r a n g 9
Dạng 3: Xác định nguyên hàm của một hàm số với điều kiện ràng buộc.
Ví dụ 1: Tìm nguyên hàm F ( x) của hàm số f ( x) = sin x + cos x thỏa mãn F = 2 . 2
A. F ( x) = cos x − sin x + 3
B. F ( x) = − cos x + sin x + 3
C. F ( x) = − cos x + sin x −1
D. F ( x) = − cos x + sin x +1 Đáp án D. Lời giải Với các bài toán đơn
Ta có F ( x) = f
giải như ở ví dụ 1, ta
(x)dx = (sin x +cos x)dx = sin x −cos x +C . chỉ đi tìm nguyên hàm như thông thườ Do F = 2 ng, sau nên sin
− cos + C = 2 1+ C = 2 C = 1. 2 2 2
đó dùng điều kiện ràng buộc có sẵn để tìm
Vậy hàm số cần tìm là F ( x) = sin x − cos x +1. hằng số C.
Ví dụ 2: Cho hàm số f ( x) thỏa mãn f '( x) = 3 − 5sin x và f (0) = 10 . Mệnh đề
nào dưới đây đúng?
A. f ( x) = 3x + 5cos x + 5
B. f ( x) = 3x + 5cos x + 2
C. f ( x) = 3x − 5cos x + 2
D. f ( x) = 3x − 5cos x +15 Đáp án A. Lời giải STUDY TIP
Ta có f ( x) = f '
(x)dx = (3−5sin x)dx = 3x +5cosx +C Rõ ràng trong bài toán
này, việc sử dụng công
Do f (0) = 10 nên 3.0 + 5cos0 + C =10 C = 5 . Vậy f ( x) = 3x + 5cos x + 5 . thức nguyên hàm từng Ví dụ 3: Cho
phần sẽ mang lại kết quả ( ) 2
F x = x là một nguyên hàm của hàm số ( ) 2x f x e . Tìm nguyên nhanh hơn. Do hàm của hàm số ( ) 2 ' x f x e ? có sự xuất A. f (x) 2x 2 ' e
= −x + 2x + C B. ( ) 2 2 ' x f x e
= −x + x + C hiện của tích hai phần
tử, nếu sử dụng nguyên C. f (x) 2x 2 ' e
= 2x − 2x + C D. f (x) 2x 2 ' e = 2
− x + 2x + C
hàm từng phần sẽ xuất Đáp án hiện ngay D. Lời giải và kết
Cách 1: Sử dụng tính chất của nguyên hàm f
(x)dx = F (x) F '(x) = f (x).
hợp dữ kiện đề bài sẽ có Từ giả thiết, ta có ngay đáp án. f ( x) x x x 2 2
e dx = F ( x) f ( x) 2 e = F '(x) = ( 2
x )' = 2x f ( x) = 2 x e
Công Phá Toán – Lớp 12 Ngọc Huyền LB (2x) 2 '. x e − 2 . x ( 2x
e )' (2 − 4x) 2x e 2 − 4x Suy ra f '( x) = ( ) = = . 2 ( )2 2 2 2 x x x e e e − x x 2 4 Vậy f ' (x) 2 2 e dx = . x e dx =
− x dx = x − x + C x (2 4 ) 2 2 2 2 e
Cách 2: Sử dụng công thức nguyên hàm từng phần.
Nếu u, v là hai hàm số có đạo hàm liên tục trên K thì: u
(x)v'(x)dx = u(x).v(x)− v
(x).u'(x)dx . Ta có 2 x ( ) 2 x =
( ) − ( ) 2x = ( ) 2x − ( ) 2 . ' . .2 2 x e f x dx e f x f x e dx f x e f x e dx
Từ giả thiết: ( ) 2x = ( ) 2 = ( ) 2x f x e dx F x x f x e = F (x) = ( 2 ' x )' = 2x . Vậy f (x) 2x 2 '
e dx = 2x − 2x + C . Ví dụ 4: Cho ( ) = ( − ) 1 x F x x
e là một nguyên hàm của hàm số ( ) 2x f x e . Tìm nguyên hàm của hàm số ( ) 2 ' x f x e . − x x 2 A. ( ) 2 ' x = (4 − 2 ) x f x e dx x e + C B. f ' (x) 2 x e dx = e + C 2 C. ( ) 2 ' x = (2 − ) x f x e dx x e + C D. ( ) 2 ' x = ( − 2) x f x e dx x e + C Đáp án C. Lời giải
Cách 1: Sử dụng tính chất của nguyên hàm f
(x)dx = F (x) F '(x) = f (x).
Từ giả thiết, ta có ( ) 2x = ( ) ( ) 2x = '( ) = ( − ) 1 x ' x f x e dx F x f x e F x x e = xe ( ) x xe x f x = ( ) = . 2 x x e e
(x)'. xe − .x( xe )' xe − . x x x e e (1− x) 1− x Suy ra f '( x) = ( ) = = = . 2 ( )2 ( )2 x x x x e e e e − x x 1 Vậy f ' (x) 2 2 e dx = . x e dx =
(1− x) xedx. x e u =1− x du = −dx Đặt . x x dv = e dx v = e
(1− ) x = (1− ) x x + = (1− ) x x + + = (2 − ) x x e dx x e e dx x e e C x e + C .
Cách 2: Sử dụng công thức nguyên hàm từng phần.
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng T r a n g 11 Ta có 2 x ( ) 2 x =
( ) − ( ) 2x = ( ) 2x − ( ) 2 . ' . .2 2 x e f x dx e f x f x e dx f x e f x e dx Từ giả thiết: ( ) 2x = ( ) = ( − ) 1 x f x e dx F x x e
( ) 2x = '( ) = ( − ) 1 x ' x f x e F x x e = xe . Vậy ( ) 2 ' x x = − 2( − ) 1 x + = (2 − ) x f x e dx xe x e C x e + C .
Dạng 4: Tìm giá trị của tham số để F ( x) là một nguyên hàm của f ( x) .
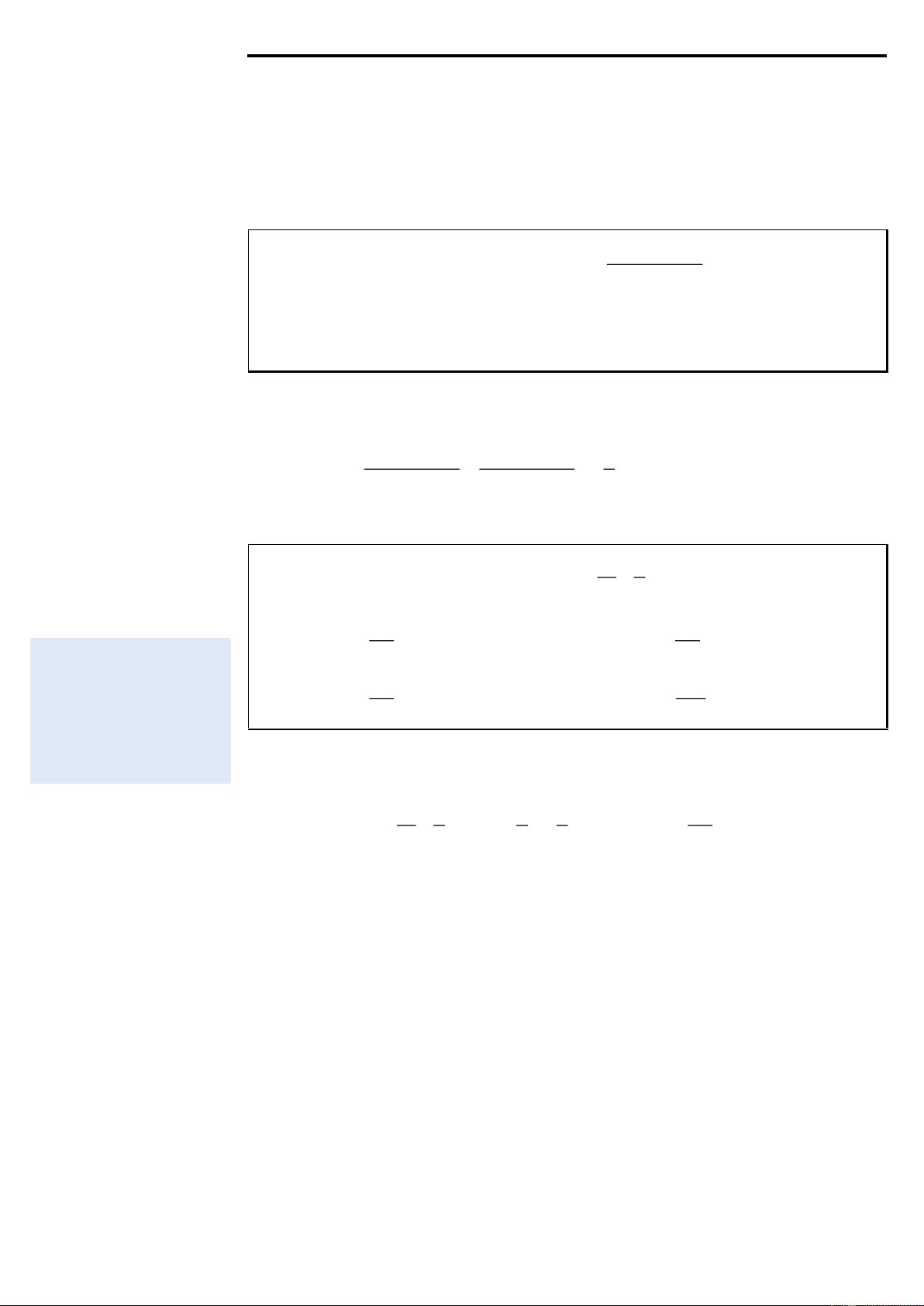
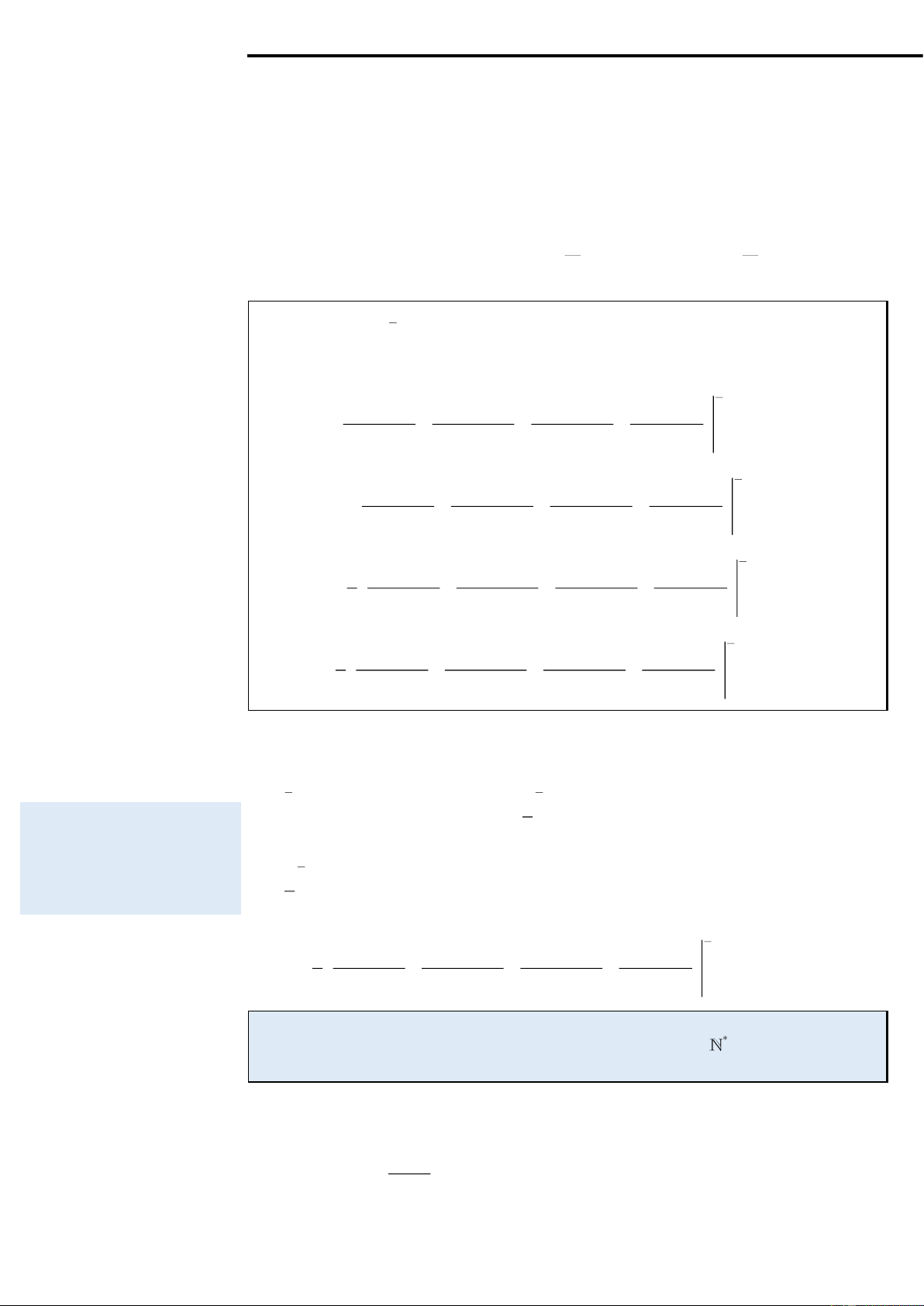
Ví dụ 1: Tìm a, b, c, d để ( ) = ( 3 2 + + + ) x F x ax bx cx
d e là một nguyên hàm của ( ) = ( 3 2 2 + 9 − 2 + 5) x f x x x x e .
A. a = 3;b = 3;c = 7 − ;d =13
B. a = 2;b = 3;c = 8 − ;d =13 Với các bài toán dạng C. a = 2 − ;b = 3;c = 8 − ;d =13
D. a = 3;b = 3;c = 8 − ;d =15
này ta chỉ cần tìm đạo Đáp án B. hàm của Lời giải
F ( x) = F '( x) sau đó Ta có = ( ) = cho F '( x) f ( x) và ( 2 + + ) +( 3 2 ' 3 2 x + + + ) x F x ax bx c e ax bx cx d e sau đó sử 3 dụng hệ số = + ( + ) 2 3 + (2 + ) + ( + ) x ax a b x b c x c d e
bất định để tìm giá trị của tham số. a = 2 a = 2 + = =
F ( x) = f ( x) 3a b 9 b 3 ' , x 2b + c = 2 − c = 8 − c + d = 5 d =13
Công Phá Toán – Lớp 12 Ngọc Huyền LB
IV. Bổ sung một số vấn đề về nguyên hàm
Nguyên hàm của các dạng hàm số đặc biệt
Dạng 1: Nguyên hàm của các hàm số dạng tích, phương.
Cho hai hàm số u = u ( x) và v = v ( x) có đạo hàm liên tục trên K. Lúc này ta có bảng sau: Dạng Cấu trúc hàm số Nguyên hàm Tổng
f ( x) = u '+ v ' = (u + v) '
F ( x) = u + v Với các bài toán dạng Hiệu
f ( x) = u '− v ' = (u − v) '
F ( x) = u − v
này ta chỉ cần tìm đạo hàm của Tích
f ( x) = u 'v + uv ' = (uv) '
F ( x) = uv = ( ) 2 2 x vdu f x e dx sau đó = / cho ( ) 2x uv f x e và − Phương u 'v uv ' u f ( x) = = ( ) u F x = 2
sau đó sử dụng hệ số v v v
bất định để tìm giá trị của tham số.
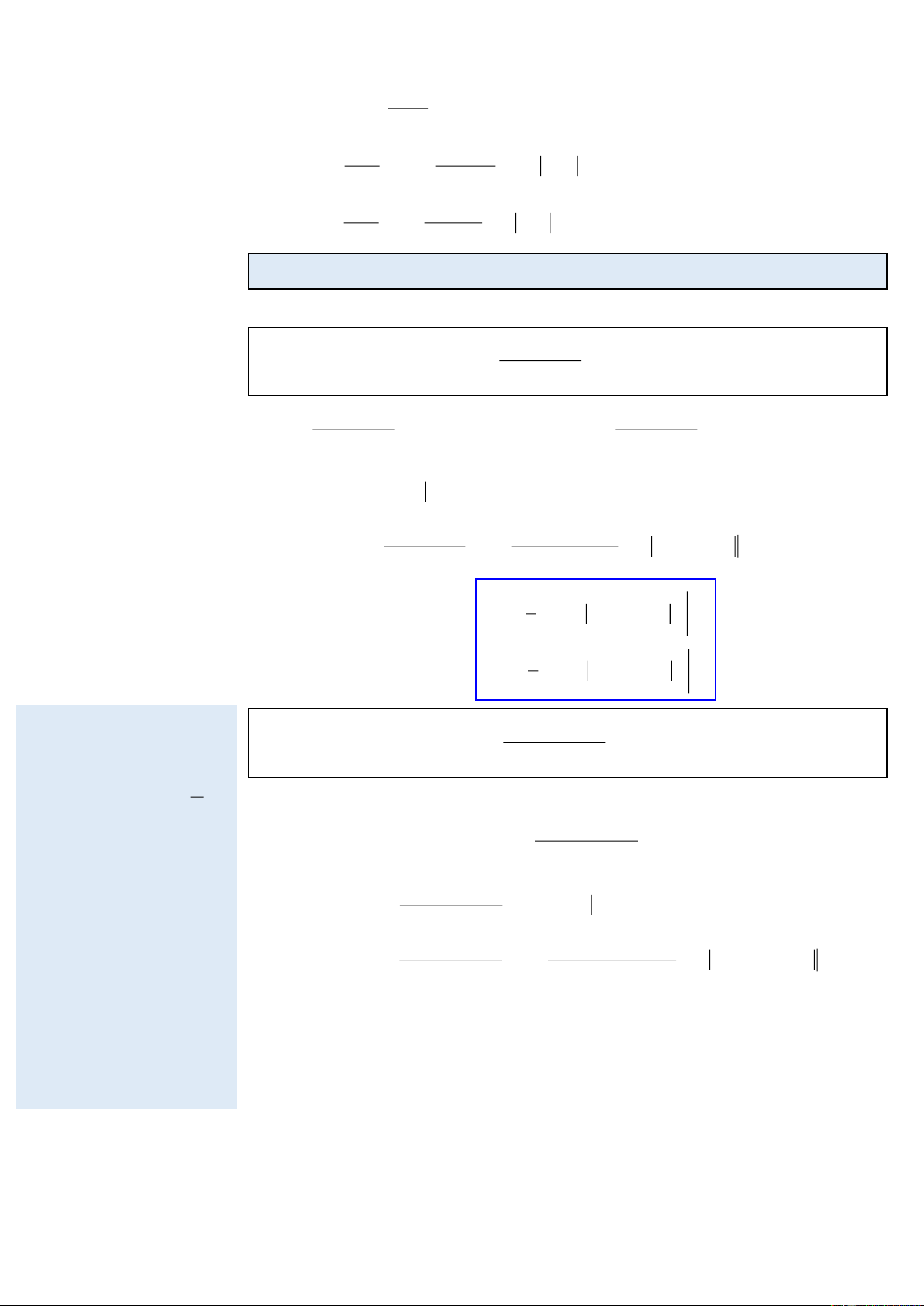
Ví dụ 1: Nguyên hàm của hàm số f ( x) 1 = 1 x + là: e
A. ( ) = − ln ( x f x dx x e + ) 1 + C
B. ( ) = ln ( x f x dx e + ) 1 + C ln ( x e + ) 1 C. f (x)dx = + C
D. ( ) = ln ( x f x dx x e + ) 1 + C x Đáp án A. Lời giải
Thay vì đi tìm nguyên hàm của hàm số theo cách truyền thống, ta có thể giải bài
toán bằng bảng ở trên như sau: (1 x + e ) x − e (1 x x + e e ) f ( x) ' 1 = = =1− = x '−
= x '− (ln( xe + x x x x )1 ' 1+ e 1+ e 1+ e 1+ e = ( −ln( x + )
1 ' ( ) = − ln ( x x e f x dx x e + ) 1 + C 1 1
Ví dụ 2: Nguyên hàm của hàm số f ( x) = − ( là ln x)2 ln x 1 1 1 1 A. f (x)dx = + + C B. f (x)dx = − + C 3 2 ln x ln x 3 2 ln x ln x
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng T r a n g 13 x −x C. f (x)dx = + C D. f (x)dx = + C ln x ln x Đáp án D. Lời giải 1 1 1− ln x
(−x)'.ln x −(−x).(ln x) / ' −x Ta có f ( x) = − = = = ( ln x)2 ln x (ln x)2 (ln x)2 ln x ( ) −x f x dx = + C . ln x
Ví dụ 3: Tìm nguyên hàm F ( x) của hàm số f ( x) = x ( 2
.ln ex ) với x 0 . A. F ( x) 2
= ex .ln (ex) + C B. F ( x) 2
= x .ln (ex) + C C. F ( x) 2
= x .ln x + C
D. F ( x) = x ln x + C Đáp án C. Lời giải Ta có f ( x) = .
x (ln e + 2ln x) = x (1+ 2ln x) 1 2 = x . + (2x) 2
ln x = x .(ln x)'+ ( 2 x )'.ln x x = ( 2 x
x) F ( x) 2 ln '
= x .ln x + C
Dạng 2: Các dạng nguyên hàm đơn giản chứa hàm x e .
Bảng nhận dạng nguyên hàm và đạo hàm của hàm số chứa x e . Đặc trưng Nguyên hàm Hàm số (đạo hàm) x e ( ) = ( ). x F x u x e '( ) = ' ( ) + ( ) x F x u x
u x e = f (x) x e− ( ) ( ). x F x u x e− = '( ) = ' ( ) − ( ) −x F x u x u x e = f (x) ax b e + ( ) ( ) ax b F x u x e + = '( ) = ' ( ) + ( ) ax+b F x u x au x e = f (x) v( x) e
F ( x) = u ( x) v(x) e
F '( x) = u '
( x) + v '( x)u ( x) v(x) e = f (x)
Ví dụ 1: Nguyên hàm của hàm số ( ) = ( 2 5 +13 + 9) x f x x x e là A. ( ) = ( 2 5 + 6) x F x x e + C B. ( ) x F x = e ( 2 x + ) 1 + 5x + C C. ( ) = ( 2 5 + 3 ) x F x x
x e + C D. ( ) = ( 2 5 + 3 + 6) x F x x x e + C Đáp án D.
Công Phá Toán – Lớp 12 Ngọc Huyền LB Lời giải Ta có ( ) = ( 2 + + + + ) x = ( 2 + + ) 2 10 3 5 3 6 5 3 6 '+ 5 + 3 + 6 x f x x x x e x x x x e
Từ bảng nhận dạng nguyên hàm phía trên ( ) = ( 2 5 + 3 + 6) x F x x x e + C là
nguyên hàm của hàm số đã cho. x x e + x e x
Ví dụ 2: Tìm nguyên hàm của hàm số f ( x) . .ln = x A. ( ) x
F x = e .ln 2x + C B. ( ) x
F x = e .ln x + C C. ( ) −x
F x = e .ln x + C D. ( ) x
F x = −e .ln x + C Đáp án B. Lời giải x e + . x x e .ln x 1+ x ln x x e 1 Ta có f ( x) ( ) = = = + ln x x e = (ln x)'+ ln x x e x x x ( ) x
F x = e .ln x + C là nguyên hàm của hàm số đã cho. 1 1
Ví dụ 3: Nguyên hàm của hàm số ( ) − x f x = − − e là 2 x x − − x e A. ( ) x e F x = + C
B. F ( x) = + C x 2 x Tương tự với hai nhận − −x
dạng còn lại, quý độc e C. ( ) x e F x = + C F x = + C
giả có thể áp dụng vào − D. ( ) x 2 − x các bài toán phức tạp Đáp án A. hơn. Lời giải 1 1 − e− −x 1 1 x
Ta có f ( x) = − − e = ' x − e F x = + C là nguyên hàm 2 ( ) x x
x x x của hàm số đã cho.
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng T r a n g 15
Nguyên hàm một số hàm lượng giác
a. Dạng sinm .cosn x xdx
trong đó m, n là các số tự nhiên.
Trường hợp 1: Trong hai số m, n có ít nhất một số lẻ.
Lũy thừa của cos x là số lẻ, n = 2k +1 thì Lũy thừa của sin x là số lẻ, m = 2k +1 thì đổi biến u = cos x
đổi biến u = sin x k x xdx = x ( k m n m 2 sin .cos sin cos x) cos xdx m n n x xdx = x ( 2 sin .cos cos sin x) sin xdx = k n 2 x ( k m 2 sin
1− sin x) .(sin x)'dx = − cos . x
(1−cos x) (cos x)'dx = k 2 n u ( k m 2 1− u ) du
= −(1−u ) .u du Ví dụ 1: Tìm 5 2 sin . x cos xdx . Lời giải
Vì lũy thừa của sin x là số lẻ nên ta đổi biến u = cos x du = (cos x)'dx . x xdx = − ( − x)2 5 2 2 2 sin .cos 1 cos .cos . x (cos)' dx = −( u u u
1− u ) .u du = (2u −u −u ) 5 3 7 2 2 2 2 4 2 6 du = − − + C 5 3 7 5 3 7 2 cos x cos x cos x = − − + C . 5 3 7
Trường hợp 2: Cả hai số m ,n đều là số chẵn: Ta sử dụng công thức hạ bậc để
giảm một nửa số mũ của sin ;
x cos x , để làm bài toán trở nên đơn giản hơn. b. Dạng sin m .
x cos nxdx, sin m .
x sin nxdx, cos m . x cos nxdx .
Ta sử dụng công thức biến đổi tích thành tổng trong lượng giác. tanm x c. Dạng dx
trong đó m, n là các số nguyên. cosn x
Lũy thừa của cos x là số nguyên dương Lũy thừa của tan x là số nguyên dương
chẵn, n = 2k thì ta đổi biến u = tan x 1
lẻ, m = 2k +1 thì ta đổi biến u = cos x tanm x tanm x 1 sin x dx = . dx Khi đó u ' = , do đó n 2k −2 2 2 cos x cos cos x cos x
Công Phá Toán – Lớp 12 Ngọc Huyền LB tanm x m 2k = tan x tan x tan x tan x ' dx dx = . dx k 1 − ( ) ( − 2 n n 1 cos x) cos x cos x cos x k − 1 m = x ( + x)k 1 2 tan . 1 tan .d (tan x) −1 2 cos x sin x = . dx − n 1 − 2 m = cos x cos x u ( +u )k 1 2 . 1 du ( k 2 u ) n 1 1 u − = − .du
Ví dụ 2: Tìm nguyên hàm 6 tan x 5 tan x a. dx b. dx 4 cos x 7 cos x Lời giải Tương tự với hai nhận
dạng còn lại, quý độc
a. Do lũy thừa của cos x là số nguyên dương chẵn nên đặt u = tan x . Từ công thức
giả có thể áp dụng vào
tổng quát đã chứng minh ở trên ta có các bài toán phức tạp 6 tan x u u x x hơn. du = u . (1+u ) 9 7 9 7 1 tan tan 6 2 du = + + C = + + C . 4 cos x 9 7 9 7 b. Do lũy thừ 1
a của tan x là một số lẻ nên ta đặt u = , do vậy, từ công thức cos x
tổng quát chứng minh ở trên ta có 5 tan x dx = (u − ) 11 9 7 2 u 2u u 2 6 1 .u du = − + + C 7 cos x 11 9 7 1 2 1 = − + + C . 11 9 7 11cos x 9 cos x 7 cos x
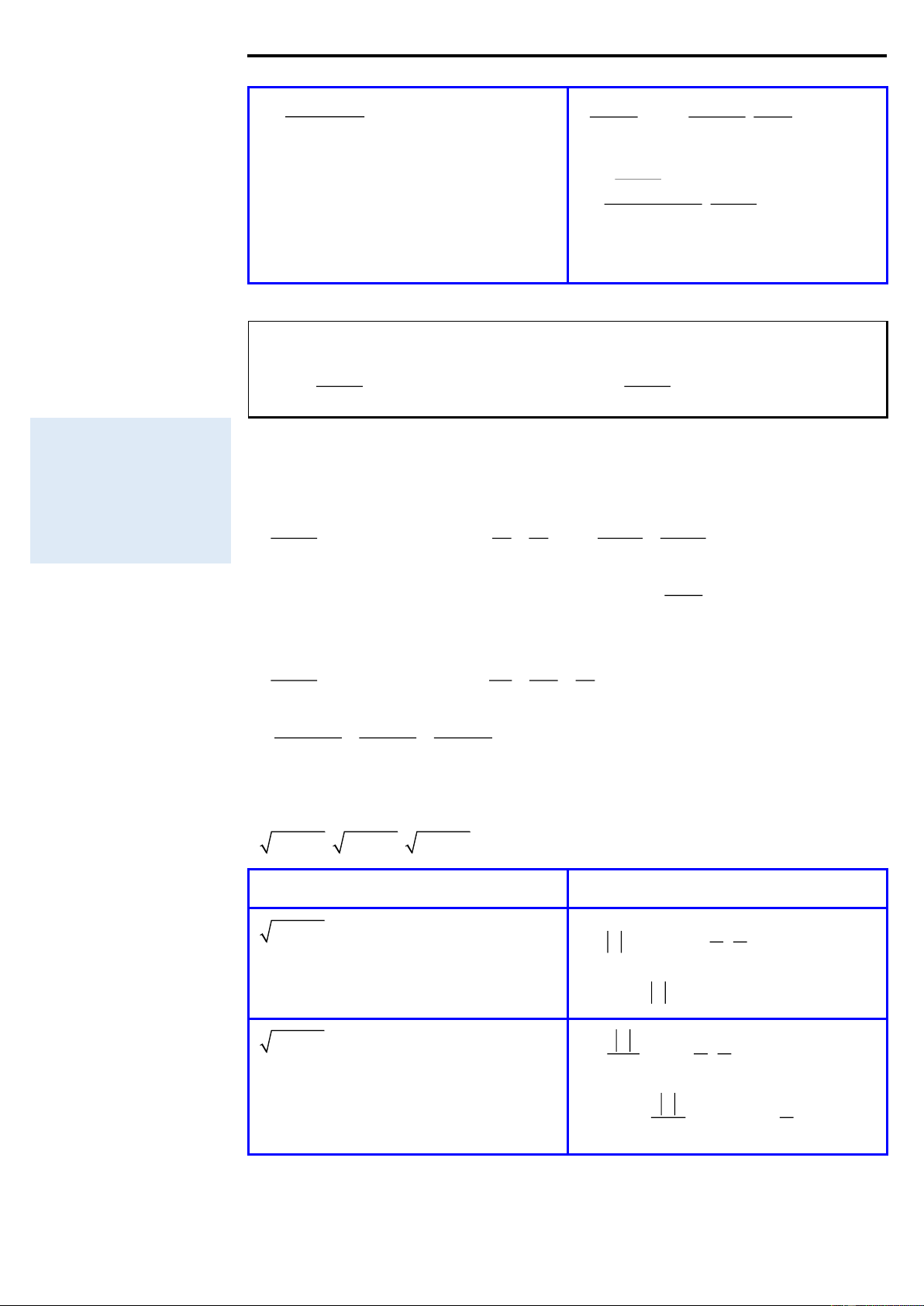
Đổi biến lượng giác
Khi nguyên hàm, tích phân của các hàm số mà biểu thức của nó có chứa các dạng 2 2 2 2 2 2
x + a , x − a , a − x , thì ta có cách biến đổi lượng giác như sau:
Biểu thức có chứa Đổi biến 2 2 x + a
x = a tan t,t − ; 2 2
Hoặc x = a cot, t (0; ) 2 2 x − a a x = , t − ; \ 0 sin t 2 2 a Hoặc x =
, t 0; \ cos t 2
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng T r a n g 17 2 2 a − x
x = a sin t,t − ; 2 2
Hoặc x = a cos t, t 0; a + x a − x
x = a cos 2t a − x a + x
(x − a)(b − x)
x = a + (b − a) 2 sin t,t 0; 2
Nguyên hàm của hàm phân thức hữu tỉ P x
Cho hàm số y = f ( x) có dạng f ( x) ( ) =
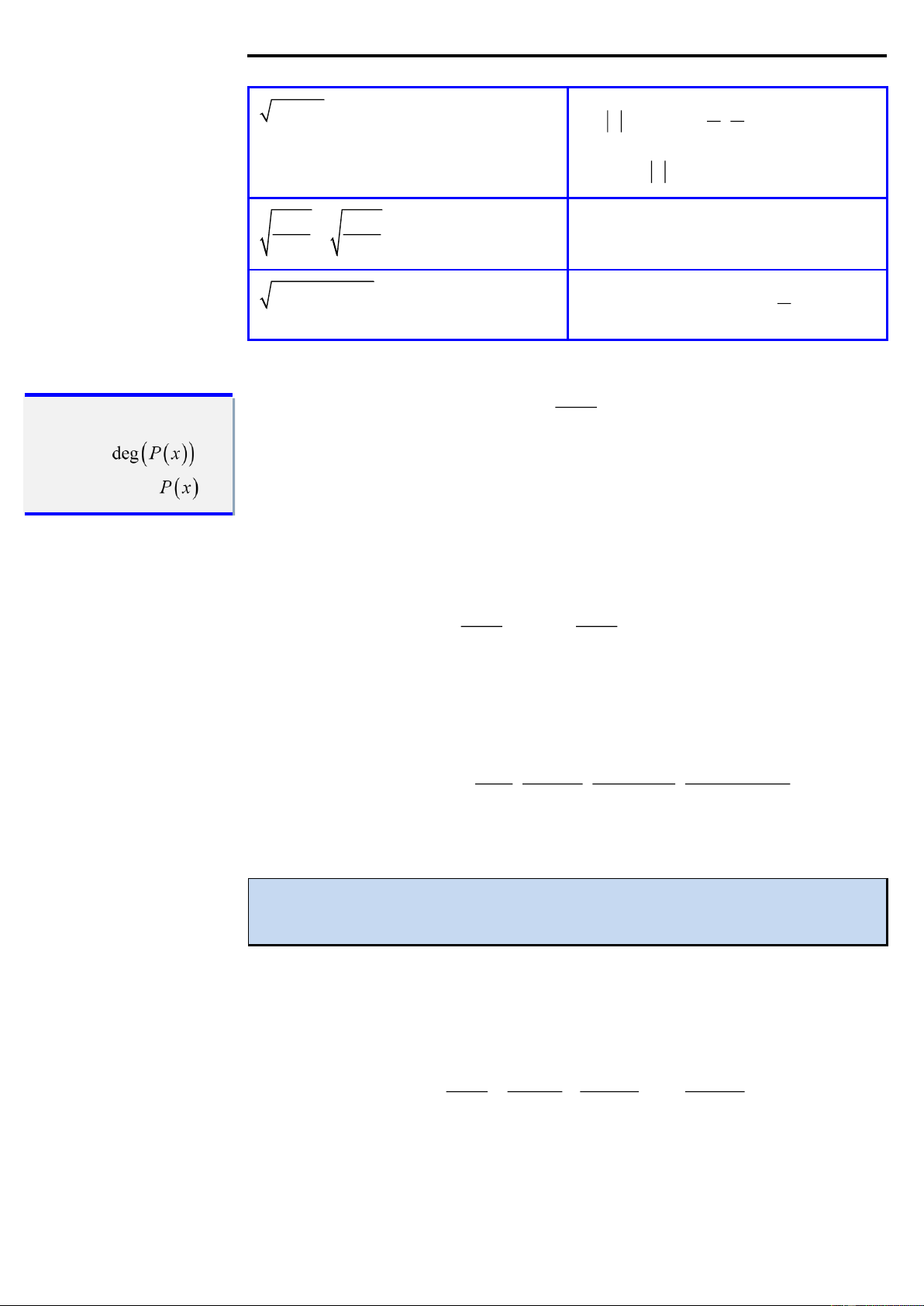
trong đó P và Q là các đa thức, và P STUDY TIP Q ( x) Kí hiệu là
không chia hết cho Q. bậc của đa thức .
Hàm f ( x) được gọi là hàm phân thức hữu tỉ thực sự nếu deg ( P) deg (Q) .
Trong các bài toán tìm nguyên hàm và tích phân của hàm phân thức hữu tỉ, nếu
f ( x) chưa phải là hàm phân thức hữu tỉ thực sự thì ta thực hiện chia tử thức cho mẫu thức để được ( ) P(x) R x f x = = + = + , Q ( x) S ( x) ( ) Q ( x)
S ( x) h ( x)
Khi đó, h ( x) sẽ là hàm phân thức hữu tỉ thực sự.
Định lý: Một phân thức thực sự luôn phân tích được thành tổng các phân thức đơn giản hơn. + + Đó là các biể 1 1 ax b ax b u thức có dạng ; là các hàm
x − a ( x − a) ; ; k 2
x + px + q ( k 2
x + px + q)
số có thể tìm nguyên hàm một cách dễ dàng. Để tách được phân thức ta dùng
phương pháp hệ số bất định.
a. Trường hợp phương trình Q ( x) = 0 không có nghiệm phức và các nghiệm đều là nghiệm đơn.
Q ( x) = (a x + b
a x + b ... a x + b 1 1 ) ( 2 2 ) ( k k k )
(Số nhân tử chính bằng bậc của đa thức Q ( x) ).
Trong trường hợp này, g có thể biểu diễn dưới dạng g ( x) R ( x) A A A 1 2 = = + + + Q ( x) ... k a x + b a x + b a x + b 1 1 2 2 k k
Sau khi biểu diễn được g ( x) về dạng này, bài toán trở thành bài toán cơ bản.
Công Phá Toán – Lớp 12 Ngọc Huyền LB 4x − 3
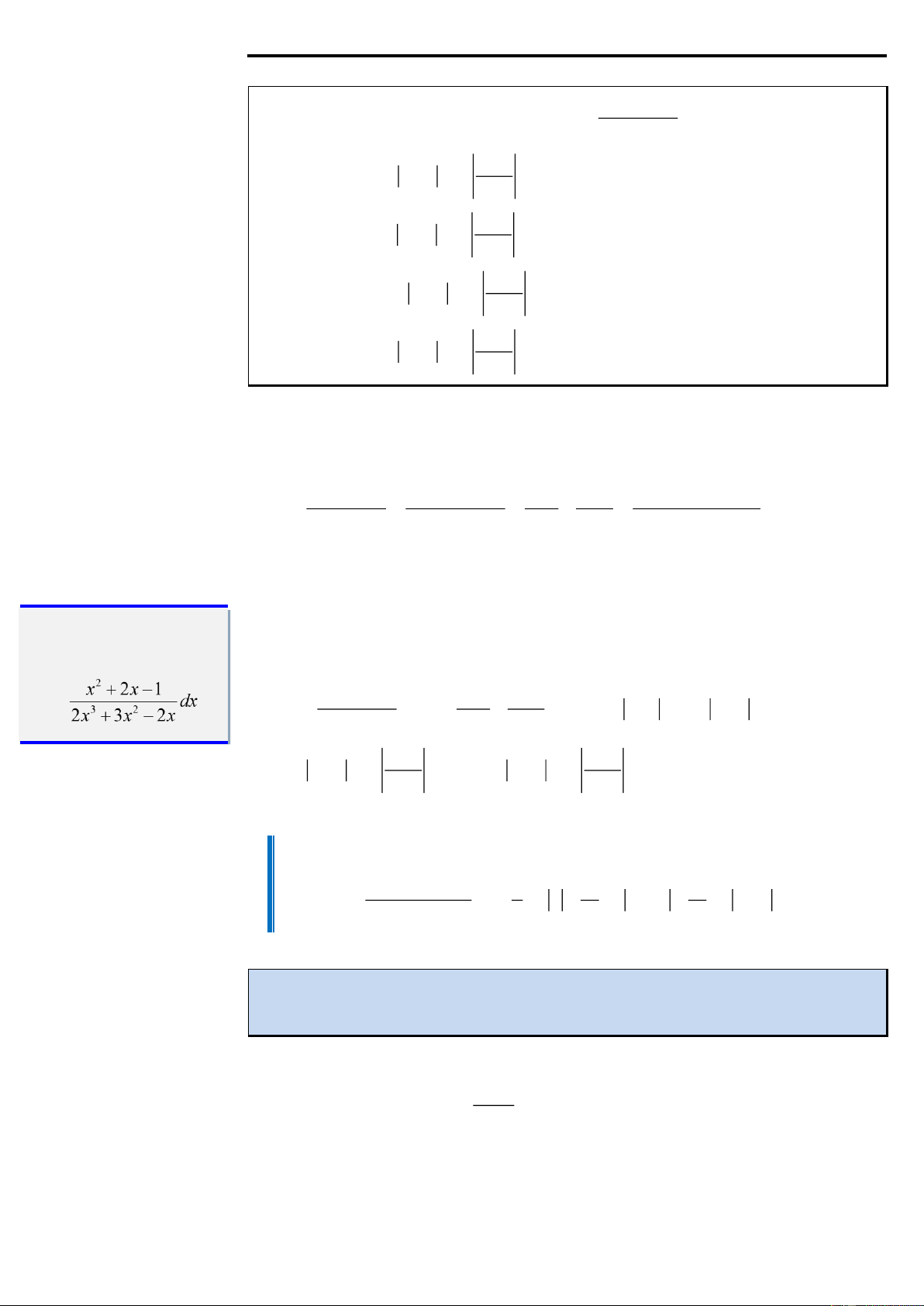
Ví dụ 3: Họ nguyên hàm của hàm số f ( x) = là 2 x − 3x + 2 x − A. F ( x) 1 = 4ln x − 2 + ln + C x − 2 x − B. F ( x) 1 = 4ln x − 2 − ln + C x − 2 x − C. F ( x) 2 = 4 − ln x − 2 − ln + C x −1 x − D. F ( x) 2 = 4ln x − 2 − ln + C x −1 Phân tích Đáp án B. 4x − 3 4x − 3 A B
Ax − 2A + Bx − B Ta có = = + = 2 x − 3x + 2
(x − 2)(x − ) 1 x −1 x − 2 (x − ) 1 ( x − 2)
Khi đó ( A + B) x − 2A − B = 4x − 3 , đồng nhất hệ số thì ta được A + B = 4 A = 1 −
Kiểm tra khả năng vận 2A + B = 3 B = 5 dụng từ ví dụ 3 Lời giải 4x − 3 Tìm 1 − 5 Ta có dx = +
dx = − ln x −1 + 5.ln x − 2 + C 2 x − 3x + 2
x −1 x − 2 x − 2 x −1 = 4.ln x − 2 + ln
+ C = 4.ln x − 2 − ln + C x −1 x − 2
Đáp số bài tập kiểm tra khả năng vận dụng: 2 x + 2x −1 1 1 1 dx = .ln x + .ln 2x −1 − .ln x + 2 + C 3 2
2x + 3x − 2x 2 10 10
b. Trường hợp Q ( x) = 0 không có nghiệm phức, nhưng có nghiệm thực là nghiệm bội.
Nếu phương trình Q ( x) = 0 có các nghiệm thực a ;a ;...;a trong đó a là nghiệm 1 2 n 1 R x
bội k thì ta phân tích g ( x) ( ) = về dạng Q ( x)
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng T r a n g 19 g ( x) A A A B B B 1 2 k 1 2 n 1 + = ( + + + + + + +
x − a ) ( x − a ) ... ... 2 k x − a x − a x − a x − a 1 ( ) 2 3 1 1 n
Trên đây là phần lý thuyết khá phức tạp, ta đến với bài tập ví dụ đơn giản sau: 2x
Ví dụ 4: Nguyên hàm của hàm số f ( x) = ( 1− x)3 2 1 2 1
A. F ( x) = + + C
B. F ( x) = − + C x −1 (x − )2 1 x −1 (x − )2 1 1 1 1 1
C. F ( x) = + + C
D. F ( x) = − + C 1− x 4(1− x)4 1− x 4 (1− x)4 Phân tích
Nhận thấy x = 1 là nghiệm bội ba của phương trình ( x − )3 1
= 0 , do đó ta biến đổi A( 2 x − 2x + ) 1 + B (1 2 − x) + C x A B C = + + = ( 1− x)3 1− x
(1− x)2 (1− x)3 (1− x)3 2 Ax + ( 2
− A − B) x + A+ B + C = ( 1− x)3 A = 0 A = 0 Từ đây ta có 2
− A − B = 2 B = 2 −
A + B + C = 0 C = 2
Kiểm tra khả năng vận Lời giải dụng từ ví dụ 4 Tìm 2x 2 2 − 2 1 Ta có = + = − + ( dx dx C 1− x)3
(1− x)2 (1− x)3 x −1 (x − )2 1
Đáp số bài tập kiểm tra khả năng vận dụng ví dụ 4: 4 2 2
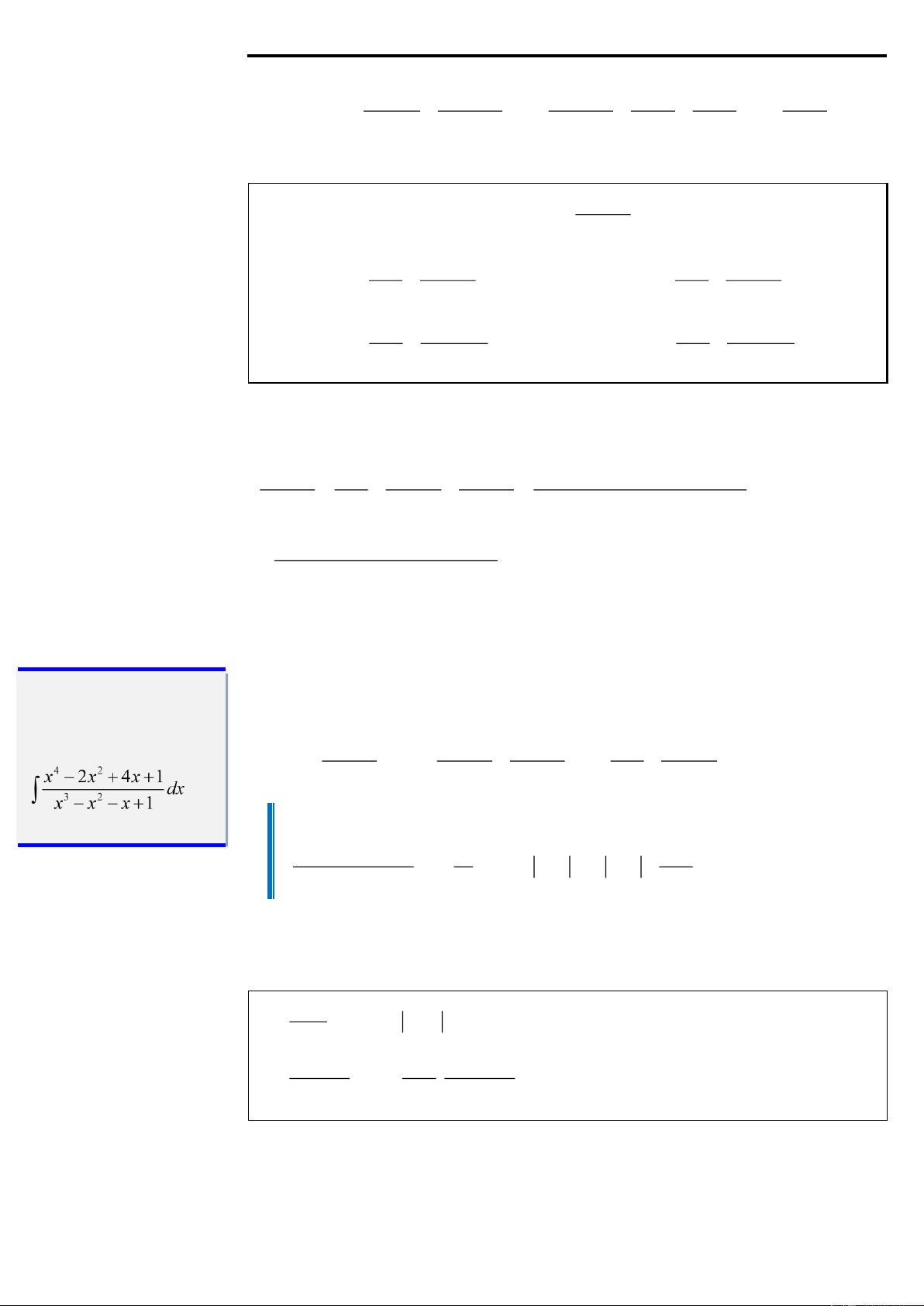
x − 2x + 4x +1 x 2 dx =
+ x − ln x +1 + ln x −1 − + C 3 2
x − x − x +1 2 x −1
TỔNG QUÁT: Việc tính nguyên hàm của hàm phân thức hữu tỉ thực sự được
đưa về các dạng nguyên hàm sau: A 1. dx = .
A ln x − a + C k 1 x − a A A 1 2. = − + ( −
x − a) dx . C k
k −1 ( x − a)k 1
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng Trang 21
Câu 5: Nguyên hàm của hàm số 2017 x f e− = là:
Bài tập rèn luyện kỹ năng 1 A. 2017 − x e + C B. 2017 − x e +C
Câu 1: Tìm nguyên hàm = (2 − ) 1 − x I x e dx . 2017 − − A. = − (2 + ) 1 x I x e + C 1 C. 2017 − 2017. − x − e +C D. 2017 x e + C 2017 − B. = − (2 − ) 1 x I x e + C
Câu 6: Tìm một nguyên hàm F ( x) của hàm số −
C. = − (2 + 3) x I x e + C f ( x) 4 = biết F = 3 . 2 − cos 3x 9
D. = − (2 − 3) x I x e + C
Câu 2: Tìm nguyên hàm I = x ln (2x − ) 1 dx . A. F ( x) 4 3 = tan 3x − 3 3 2 4x −1 x ( x + ) 1 = − A. I = ln 2x −1 + + C
B. F ( x) 4 tan 3x 3 3 8 4 2 4x +1 x ( x + ) 1 C. F ( x) 4 3 = tan 3x + B. I = ln 2x −1 + + C 3 3 8 4 2 4x −1 x ( x + ) 1 D. F ( x) 4 3 = − tan 3x − C. I = ln 2x −1 − + C 3 3 8 4 = 2
Câu 7: Tìm nguyên hàm của hàm số f ( x) x x . 4x +1 x ( x + ) 1 D. I = ln 2x −1 − + C 8 4 2 A. f (x) 2 dx = x x + C
Câu 3: Tìm nguyên hàm I = ( x − ) 1 sin 2 . x dx 5 ( = +
1− 2x) cos 2x + sin 2x B. f (x) 2 dx x x C A. I = + C 5 2 1 ( C. f (x) 2 dx = x x + C
2 − 2x) cos 2x + sin 2x 2 B. I = + C 2 ( D. f (x) 3 dx = x + C
1− 2x) cos 2x + sin 2x 2 C. I = + C 4
Câu 8: Tìm nguyên hàm của hàm số
(2− 2x)cos2x +sin 2x
f ( x) = ( x − )2 2 3 . D. I = + C 4 x −
Câu 4: Cho f ( x), g ( x) là các hàm số liên tục A. f (x) ( )3 2 3 dx = + C 3 trên
. Tìm khẳng định sai trong các khẳng định = − + sau? B. f
(x)dx ( x )3 2 3 C A. k. f
(x)dx = k. f
(x)dx với k là hằng số x − C. f (x) ( )3 2 3 dx = + C 6 B. f
(x)− g(x)dx = f
(x)dx− g (x)dx x − C. f
(x).g(x)dx = f (x) . dx g (x)dx D. f (x) ( )3 2 3 dx = + C 2 D. f
(x)+ g(x)dx = f
(x)dx + g (x)dx
Câu 9: Tìm nguyên hàm của hàm số:
f ( x) = 3sin 3x − cos 3x .
Công Phá Toán – Lớp 12 Ngọc Huyền LB A. f
(x)dx = cos3x −sin3x +C x − B. F ( x) ln 4 6 = +10 4 B. f
(x)dx = cos3x +sin3x +C x − C. F ( x) ( )2 ln 2 3 = + 5 C. f (x) 1
dx = − cos 3x − sin 3x + C 4 3 3 ln x − D. f (x) 1 1
dx = − cos 3x − sin 3x + C 2 3 3
D. F ( x) = +1 2
Câu 10: Tìm nguyên hàm của hàm số ( )
Câu 14: Tìm nguyên hàm F ( x) của hàm số x x f x e e− = − . + − f ( x) 2 x x 1 = . x e A. ( ) x − x
f x dx = e + e + C 2 x −1 B. ( ) x − x
f x dx = −e + e + C A. ( ) 2 = −1. x F x x e + C C. ( ) x − x
f x dx = e − e + C B. ( ) 2 = − −1. x F x x e + C D. ( ) x − x
f x dx = −e − e + C − C. ( ) 2 2 = 2 − −1. x F x x x e + C
Câu 11: Tìm nguyên hàm F ( x) của hàm số − D. ( ) 1 = −1. x F x x e + C
f ( x) = 3x + 4 , biết F (0) = 8.
Câu 15: Tìm nguyên hàm của hàm số x −
A. F ( x) 1 38 = 3x + 4 + f ( x) 3 7 = 3 3 x + 2 2 16 = − + +
B. F ( x) = (3x + 4) 3x + 4 + A. f
(x)dx x 13ln x 2 C 3 3 B. f
(x)dx = ln x + 2 +C 2 56
C. F ( x) = (3x + 4) 3x + 4 + 9 9 C. f
(x)dx = 3x −13ln x +2 +C 2 8
D. F ( x) = (3x + 4) 3x + 4 + = − + + 3 3 D. f
(x)dx 3x 7ln x 2 C 1
Câu 16: Tìm nguyên hàm của hàm số
Câu 12: Tìm nguyên hàm I = dx 2 4 − x + f ( x) 4 x 5 = . 1 x + 2 1 x − 2 x +1 A. I = ln
+ C B. I = ln + C 2 x − 2 2 x + 2 1 1 1 A. f ( x) dx 4 3 2
= x − x + x 1 x − 2 1 x + 2 4 3 2 C. I = ln
+ C D. I = ln + C + − + + 4 x + 2 4 x − 2 x 6 ln x 1 C B.
Câu 13: Cho hàm số f ( x) 1 =
. Gọi F ( x) là 2x − 3 f (x) 1 1 1 4 3 2 dx = x − x +
x − x + 6 ln x +1 + C
một nguyên hàm của f ( x) . Chọn phương án sai. 4 3 2 C. f (x) 4 3 2
dx = x − x + x − x + 6 ln x +1 + C x − A. F ( x) ln 2 3 = +10 2 D. f (x) 4 3 2
dx = x − x + x − x − 6 ln x +1 + C
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng Trang 23
Câu 17: Tìm nguyên hàm của hàm số 1 A. F = − B. F = − + f ( x) 1 = 2 2 4 2 x x +1 C. F = + D. F = 1 x +1 −1 2 4 2 A. f (x) 2 dx = .ln + C 2 2 x +1 +1
Câu 21: Biết F ( x) là nguyên hàm của ( ) 4x f x = x +1 −1 B. f (x) 2 dx = ln + C và F ( ) 1 1 =
. Khi đó giá trị F (2) bằng 2 x +1 +1 ln 2 7 8 1 x +1 +1 A. B. C. f (x) 2 dx = .ln + C ln 2 ln 2 2 2 x +1 −1 9 3 C. D. 1 1− x +1 ln 2 ln 2 D. f (x) 2 dx = .ln + C 2 2 1+ x +1
Câu 22: Nguyên hàm của hàm số
Câu 18: Tìm nguyên hàm của hàm số − f ( x) x e x = e 2 + là: 2 f ( x) 1 = . cos x x +1 + x −1 A. ( ) = 2 x F x
e + cot x + C 2 2 A. f
(x)dx = (x+ )3 −(x− )3 1 1 + C B. ( ) = 2 x F x
e − tan x + C 3 3 x F x = e + x + C B. C. ( ) 2 tan f
(x)dx = (x+ )2 −(x− )2 1 1 + C D. ( ) = 2 x F x e − tan x 2 3 1 C. f
(x)dx = (x+ )3 1 − (x − )2 1 + C 3
Câu 23: Tìm nguyên hàm F ( x) = (x + sin x)dx 3 3 1 biết F (0) = 19 . D. f
(x)dx = (x+ )2 1 − (x − )2 1 + C 3 1 A. F ( x) 2
= x + cos x + 20
Câu 19: Tìm nguyên hàm của hàm số 2 f ( x) 1 = . B. F ( x) 2
= x + cos x + 20 x e + 3 = − + x C. F ( x) 2 x cos x 20 e A. f (x) 1 dx = ln + C 3 x e + 3 1 D. F ( x) 2
= x − cos x + 20 2 x e B. f (x)dx = ln + C x e + 3 1
C. ( ) = ln x ( x f x dx e e + 3) + C 3 . 1
D. ( ) = ln x ( x f x dx e e + 3) + C 6
Câu 20: Biết F ( x) là một nguyên hàm của hàm số f ( x) 3 = sin .
x cos x và F (0) = . Tìm F . 2
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng Trang 25
Hướng dẫn giải chi tiết
Câu 1: Đáp án A. Câu 6: Đáp án A.
Đặt u = 2x −1 du = 2dx ; 4 4 Ta có F ( x) = dx = . tan 3x + C − 2 x −x
e dx = dv v = e − cos 3x 3 Lúc này ta có Mà ( 4 3 2 − ) 1 − x = −(2 − )
1 . −x + 2 −x x e dx x e e dx F
= 3 .tan + C = 3 C = − 9 3 3 3 = −(2 − )
1 . −x − 2 −x + = −(2 + ) 1 −x x e e C x e + C Câu 7: Đáp án A. Câu 2: Đáp án C. 3 5 2 2 2 2 2 x xdx = x dx = x + C = x x + C . Đặt 5 5 = ( Câu 8: Đáp án C. x − ) 2 2 x u ln 2 1 du = d ;
x dv = xdx v = 2x −1 2 1 Ta có f
(x)dx = (2x−3)3 +C Khi đó 3.2 Câu 9: Đáp án C. x ( x− ) 2 x dx = ( x − ) 2 x 2 ln 2 1 .ln 2 1 − . dx 2 2 2x −1 ( x − x) 3 dx = (− x) 1 3sin 3 cos 3 . cos 3
− .sin 3x + C 2 2 x x 3 3 = .ln 2x −1 − dx 2 2x −1 Câu 10: Đáp án A. Câu 11: Đáp án C. 2 x x 1 1 =
.ln 2x −1 − + + dx 1 3 2 2 4 4(2x )1 − F ( x) = 3x + 4dx = (3x+4) 2 2 dx = .(3x + 4)2 + C 9 2 2 x x x 1 = .ln 2x −1 − + + .ln (2x − ) 1 + C 2 4 4 8 2
= .(3x + 4) 3x + 4 + C 2 9 4x −1 x ( x + ) 1 = .ln 2x −1 − + C 8 4 Mà F ( ) 56 0 = 8 C = , ta chọn C. Câu 3: Đáp án D. 9 Câu 12: Đáp án D. I = ( x − ) 1 sin 2xdx Ta có
Đặt x −1= u dx = du . 1 1 dx = dx 1 2 2 a − x
(a + x)(a − x)
sin 2xdx = dv v = − .cos 2x 2 1 1 1 −(x − ) 1 = + dx Khi đó 1 I = .cos 2x + cos 2xdx
2a a − x a + x 2 2 ( 1 x + a 1− x) cos 2x 1 = .ln + C = + .sin 2x + C 2a x − a 2 4
Áp dụng vào bài ta chọn D. Câu 4: Đáp án C. Câu 13: Đáp án B. Câu 5: Đáp án D. 1 1 1 = = − − Ta có F ( x) dx . d 2x 3 x 1 Ta có 2017 2 − 017 x e dx = e + C 2x − 3 2 (2x − 3) ( ) 2017 −
Công Phá Toán – Lớp 12 Ngọc Huyền LB ln 2x − 3 = + d ( 2 x +1) d ( 2 x +1) C 2 1 x +1 −1 2 = = = .ln + C 2 x ( x + )2 2 2 2 x +1 +1 1 −1
Từ đây ta thấy A đúng. Với B ta thấy du 1 u − a (Áp dụng công thức = .ln + C ) 2 2 u − a 2a u + a ln 4x − 6 ln 2 + ln 2x − 3 +10 =
+10 F (x) , B sai. 4 4 Câu 18: Đáp án D. Câu 14: Đáp án A. Ta có + − x − + x ( x+1− x−1) x x dx dx x ( 2 2 )1 1 Ta có f ( x) = .e = . x e = 2 2 x −1 x −1 x +1 + x −1
( x+1− x−1)( x+1+ x−1) x 2 = + x −1 x
e = ( 2x −1) 2 '+ x −1 x e 3 3 2 1 1 2 x −1
= ( x +1− x −1)dx = . (x + )2 1 − (x − )2 1 + C 2 2 3 ( ) 2 = −1. x F x x
e + C (áp dụng bảng ở lý 1 ( = x + )3 1 − (x − )3 2 2 1 + C thuyết). 3 Câu 15: Đáp án C. Câu 19: Đáp án A. 3x − 7 3 x + 2 −13 d ( x x e dx e dx ) Ta có f (x) ( ) dx = dx = dx Ta có = = x + 2 x + 2 x e + 3 x e ( x e + 3) x e ( x e + 3) 13 d ( x + 2) = 3 − dx = 3dx −13 x 1 1 1 e x 1 x + 2 x + 2 = − d e = + C x x ( ) ln 3 e e + 3 3 x e + 3
= 3x −13ln x + 2 + C Câu 20: Đáp án C. Câu 16: Đáp án B.
F ( x) = f (x) 3 dx = sin . x cos . x dx + ( 4 4 x x − ) 1 + 6 5 Ta có dx = dx 1 x +1 x +1 3 = sin . x d (sin x) 4 = sin x + C 4 ( = x − ) 1 ( 6 2 x + ) 1 + dx 1 x +1
F (0) C = F ( x) 4 = sin x + 4 = ( d x +1 3 2
x − x + x − ) ( ) 1 dx + 6 1 = + x +1 F 2 4 1 1 1 4 3 2
= x − x + x − x + 6ln x +1 + C Câu 21: Đáp án A. 4 3 2 x 1 Câu 17: Đáp án A. x Ta có 4 dx = .4 + C = F (x) ln 4 d ( 2 x xdx + ) 1 1 1 dx = = Mà F ( ) 1 4 1 1 1 = + C = C = − . 2 2 2 2 2 + + 2 x x 1 x x 1 x . x +1 ln 2 ln 4 ln 2 ln 2 Do đó F (2) 1 1 16 1 7 2 = .4 − = − = . ln 4 ln 2 2 ln 2 ln 2 ln 2 Câu 22: Đáp án C.
Chủ đề 3: Nguyên hàm - tích phân và ứng dụng Trang 29 −
F ( x) = f (x) x e x dx = e 2+ dx 2 cos x dx = 2 x e dx + = 2 x
e + tan x + C 2 cos x Câu 23: Đáp án D. ( ) = ( + x) 2 x F x x sin dx = − cos x + C 2
( ) = C = F (x) 2 x F 0 19 20 = − cos x + 20 2
Công Phá Toán – Lớp 12 Ngọc Huyền LB
V. Khái niệm và các tính chất cơ bản của tích phân b 1. Định nghĩa Ta gọi là dấu tích a
Cho hàm số f ( x) là hàm số liên tục trên đoạn a;b . Giả sử F ( x) là một nguyên
phân, a là cận dưới, b hàm của f
là cận trên, f ( x) dx là
(x) trên đoạn a;b.
biểu thức dưới dấu tích
Hiệu số F (b) − F (a) được gọi là tích phân từ a đến b (hay tích phân xác định trên b
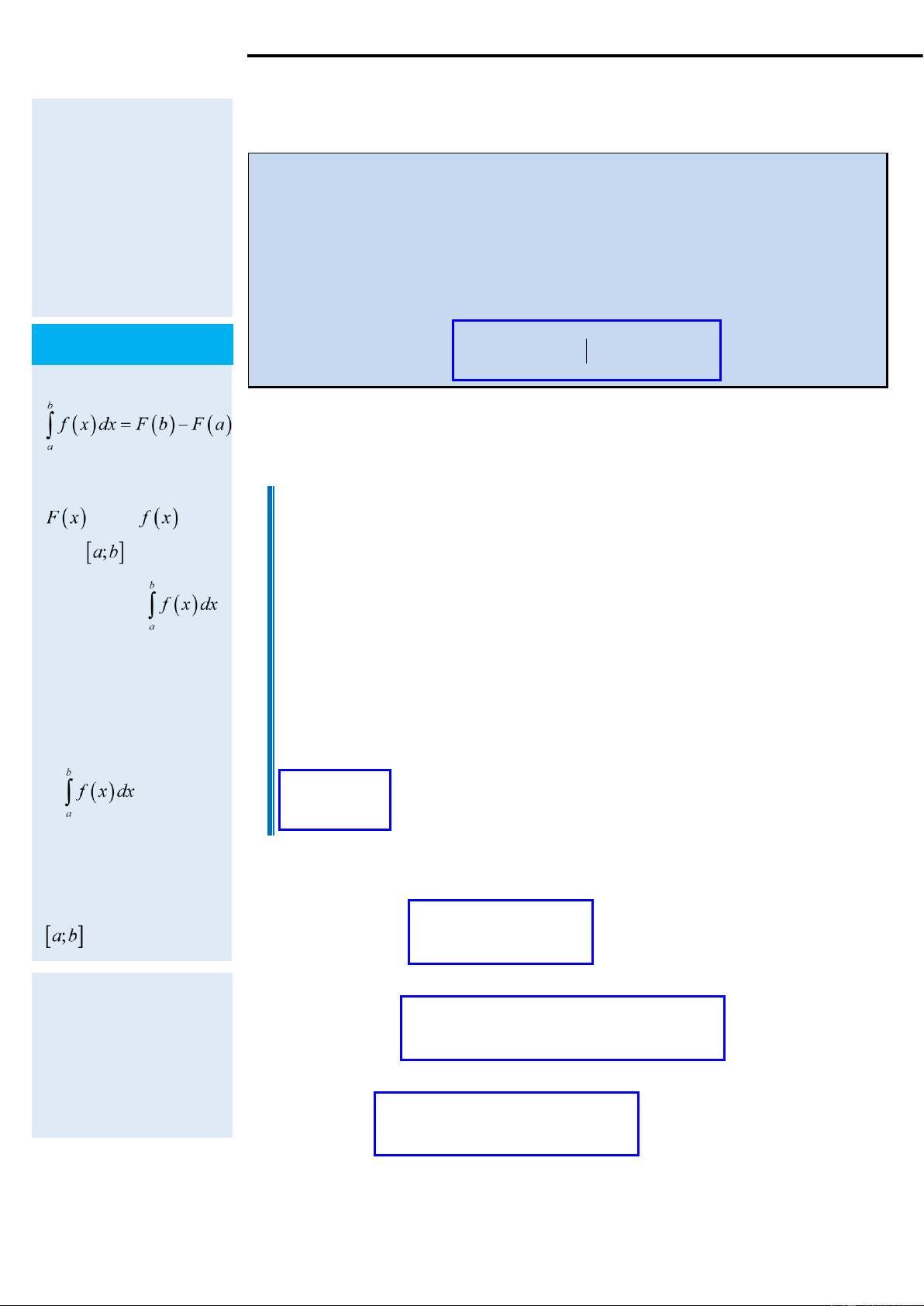
phân và f ( x) là hàm
đoạn a;b ) của hàm số f ( x) , kí hiệu là f ( x)dx .
số dưới dấu tích phân. a b b Chú ý Vậy f
(x)dx = F (x) = F (b)− F (a). a a 1. Định nghĩa tích phân
chỉ được áp dụng khi 2. Nhận xét biết một nguyên hàm b của trên
a. Tích phân của hàm số f từ a đến b có thể kí hiệu bởi f ( x) dx hay a đoạn . b f (t ) dt
. Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc a 2. Tích phân
vào biến số x hay t. là một số, còn nguyên
b. Ý nghĩa hình học của tích phân. Nếu hàm số f ( x) liên tục và không âm hàm là một (họ) hàm b
số (nó còn được gọi là
trên đoạn a;b , thì tích phân f ( x)dx
là diện tích S của hình thang cong giới tích phân không xác a định).
hạn bởi đồ thị f ( x) , trục Ox và hai đường thẳng x = ; a x = b . Vậy b 3. không S = f (x)dx . a
phụ thuộc vào chữ viết
3. Các tính chất của tích phân biến số trong dấu tích
phân, mà chỉ phụ thuộc Tính chất 1
vào hàm số f và đoạn b b kf .
(x)dx = k f
(x)dx với k là hằng số. a a Tính chất 2 Ta quy ước b b b b f f (x)dx = 0;
(x) g(x)dx = f
(x)dx g (x)dx a a a a Tính chất 3 b b f
(x)dx = − f (x)dx c b b a a f
(x)dx+ f
(x)dx = f
(x)dx với a c b. a c a LOVEBOOK.VN|30 Định lý 1
Cho f là hàm số xác định trên K và a là một điểm cố định thuộc K. Xét hàm số
G ( x) xác định trên K bởi công thức x
G ( x) = f (t)dt a
Khi đó G là một nguyên hàm của f. Định lý 2
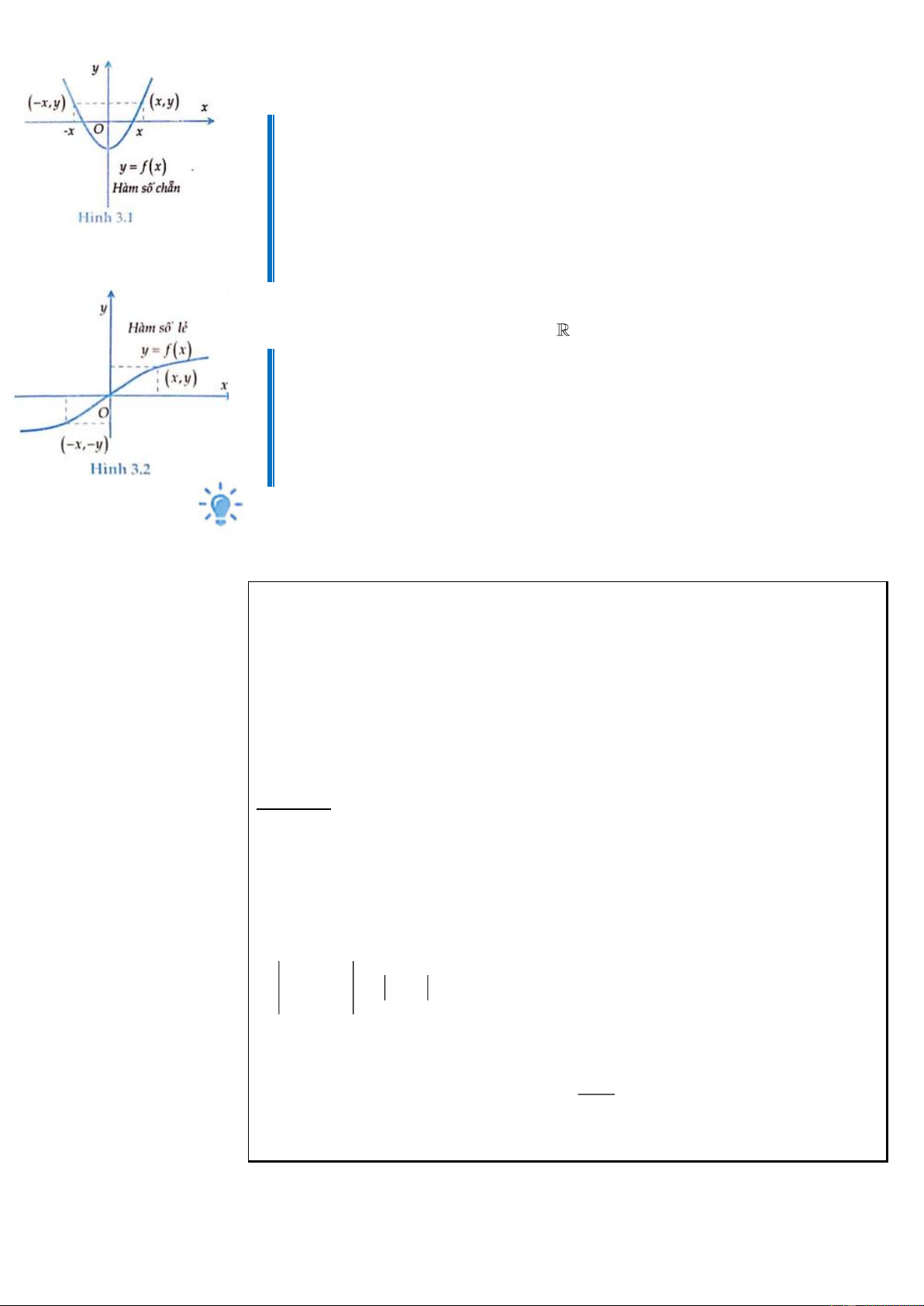
Tích phân của hàm lẻ và hàm chẵn trên . a a
1. Nếu f là một hàm số chẵn, khi đó f
(x)dx = 2 f (x)dx −a 0 a
2. Nếu f là một hàm số lẻ, khi đó f (x)dx = 0. −a Đọc thêm
Ta vừa đưa ra 3 tính chất của tích phân theo chương trình chuẩn. Dưới đây là các tính chất bổ sung: b 1. 0dx = 0 a b
2. cdx = c (b − a) a b
3. Nếu f ( x) 0, x
a,b thì f
(x)dx 0. a
Hệ quả 3: Nếu hai hàm số f ( x) và g ( x) liên tục và thỏa mãn b b
f ( x) g ( x), x
a;b thì f
(x)dx g (x)dx a a b
Chú ý: Nếu f ( x) liên tục và dương trên a;b thì f
(x)dx 0. a b b 4. f
(x)dx f
(x) dx,(a b) . a a
5. Nếu m f ( x) M , x
a;b; ,
m M là các hằng số thì b 1 b
m (b − a) f
(x)dx M (b−a) hay m f
(x)dx M . b − a a a LOVEBOOK.VN|31
Công Phá Toán – Lớp 12 Ngọc Huyền LB
VI. Hai phương pháp cơ bản để tìm tích phân
1. Phương pháo đổi biến số Định lý 1
Cho hàm số f ( x) liên tục trên đoạn a;b . Giả sử hàm số x = (t ) có đạo
hàm liên tục trên đoạn ; sao cho ( ) = ;
a (b) = b và a (t ) b với
mọi t ; . Khi đó b f
(x)dx = f
((t))'(t)dt a
Từ định lý 1 ta rút ra các bước đổi biến số
1. Đặt x = (t ) , ta xác định đoạn ; sao cho ( ) = a, ( ) = b và
a (t ) b , t ; ;
2. Biến đổi f ( x) dx = f ( (t )) '(t ) dt = g (t ) dt
3. Tìm một nguyên hàm G (t ) của g (t ) 4. Tính g
(t)dt = G()−G() b 5. Kết luận f
(x)dx = G( )−G(). a 3 2 x
Ví dụ 1: Tính tích phân I = ( ? + x) dx 3 0 1 33 4121 A. I = ln 4 + B. I = ln 4 − 32 4000 33
C. I = ln 4 −1 D. I = ln 4 − 32 Đáp án D. Lời giải
Đặt 1+ x = u dx = du .
Đổi cận x = 0 u =1; x = 3 u = 4 (u − )2 4 4 4 2 4 1 − + Khi đó u 2u 1 1 2 1 2 1 I = du = du = − + du = ln u + − 3 2 2 3 2 u u u u u u 2u 1 1 1 1 33 = ln 4 − 32 LOVEBOOK.VN|32 Định lý 2
Cho hàm số f ( x) liên tục trên đoạn a;b . Nếu hàm số u = u ( x) có đạo hàm
liên tục trên đoạn a;b và u ( x) với mọi x a;b sao cho
f ( x) = g (u ( x))u '( x), g (u) liên tục trên đoạn ; thì u(b b ) f
(x)dx = g (u)du a u(a)
Từ định lý 2 ta rút ra các bước đổi biến số
1. Đặt u = u ( x) ,
2. Biến đổi f ( x) dx = g (u ) du .
3. Tìm một nguyên hàm G (u ) của g (u ) . u(b) 4. Tính g
(u)du = G(u(b))−G(u(a)). u(a) b 5. Kết luận f
(x)dx = G(u(b))−G(u(a)) a 2
Ví dụ 2: Tính tích phân 2 I = sin . x cos xdx 0 1 1 2 1 A. I = B. I = C. I = D. I = 2 3 3 5 Đáp án B. Lời giải
Đặt u = sin x , ta có 2 2 x xdx = x ( x) 2 sin cos sin sin ' dx = u du . u Hàm số g (u ) 2
= u ;u 0; 1 do u (0) = 0;u =1
có nguyên hàm G (u) 3 = . 2 3 1 2 1 3 u 1 Vậy 2 2
sin x cos xdx = u du = = . 3 3 0 0 0
2. Phương pháp tích phân từng phần
Tương tự tính nguyên hàm từng phần, ta có định lý sau: Định lý LOVEBOOK.VN|33
Công Phá Toán – Lớp 12 Ngọc Huyền LB
Nếu u = u ( x) và v = v ( x) là hai hàm số có đạo hàm liên tục trên đoạn a;b thì b b b b b u (x) b
v '( x) dx = (u ( x)v ( x)) − u '
(x)v(x)dx hay udv = uv − vdu a a a a a a Ta có bảng sau ( ) x P x e dx
P ( x) cos xdx
P ( x) ln xdx Trong thực tế, đôi khi việc sử dụng phương u P ( x) P ( x) ln x pháp tính tích phân từng phần phải linh dv x e dx cos xdx
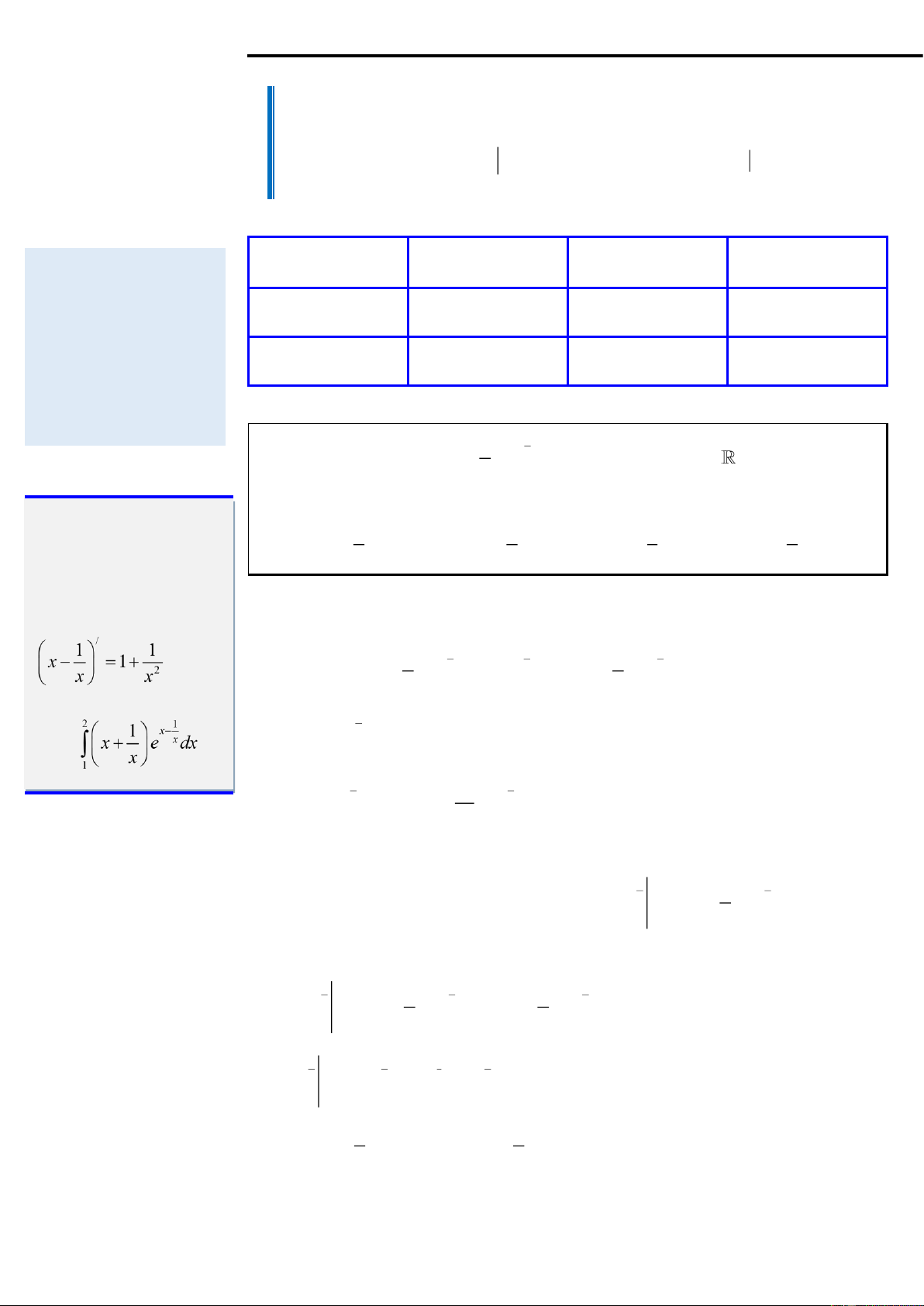
P ( x) dx hoạt, đôi khi phải dự đoán khác thường như ví dụ 1 dưới đây. 2 1 1 x− Ví dụ 3: Cho = 1 b x I + x + e
dx = ae − c với ; a ; b c ; a 0 . Lúc này x 1
S = a + b + c có giá trị bằng Ta thấy trong bài toán 1 3 1 9 bên việc sử dụng tích A. S = − B. S = − C. S = D. S = 2 2 3 2 phân từng phần ở đây rất thông minh khi phát Đáp án D. hiện được Lời giải 2 1 2 1 2 1 khi 1 x− x− 1 x− Ta có = 1 x x x I + x + e dx = e dx + x + e dx (1) x x 1 1 1
nhân thêm x sẽ triệt tiêu 2 1 x− Đặt x I = e dx được . . 1 1 1 1 x− 1 x− x = = 1 x u e du + e dx Đặ t 2 x
dv = dx v = x 2 1 2 1 x− 1 x−
Theo công thức tích phân từng phần ta có x x I = xe − x + e dx (2) 1 x 1 1 Từ (1); (2) ta có 2 1 2 1 2 1 x− 1 x− 1 x− = . x x x I x e − x + e dx + x + e dx x x 1 1 1 2 1 1 1 3 x− 2− 1− x 2 1 2 = . x e = 2.e
−1.e = 2.e −1 1 3 9
a = 2;b = ;c =1 a + b + c = . 2 2 LOVEBOOK.VN|34
VII. Ứng dụng hình học của tích phân
1. Tính diện tích hình phẳng
a. Diện tích hình phẳng giới hạn bởi một đường cong và trục hoành
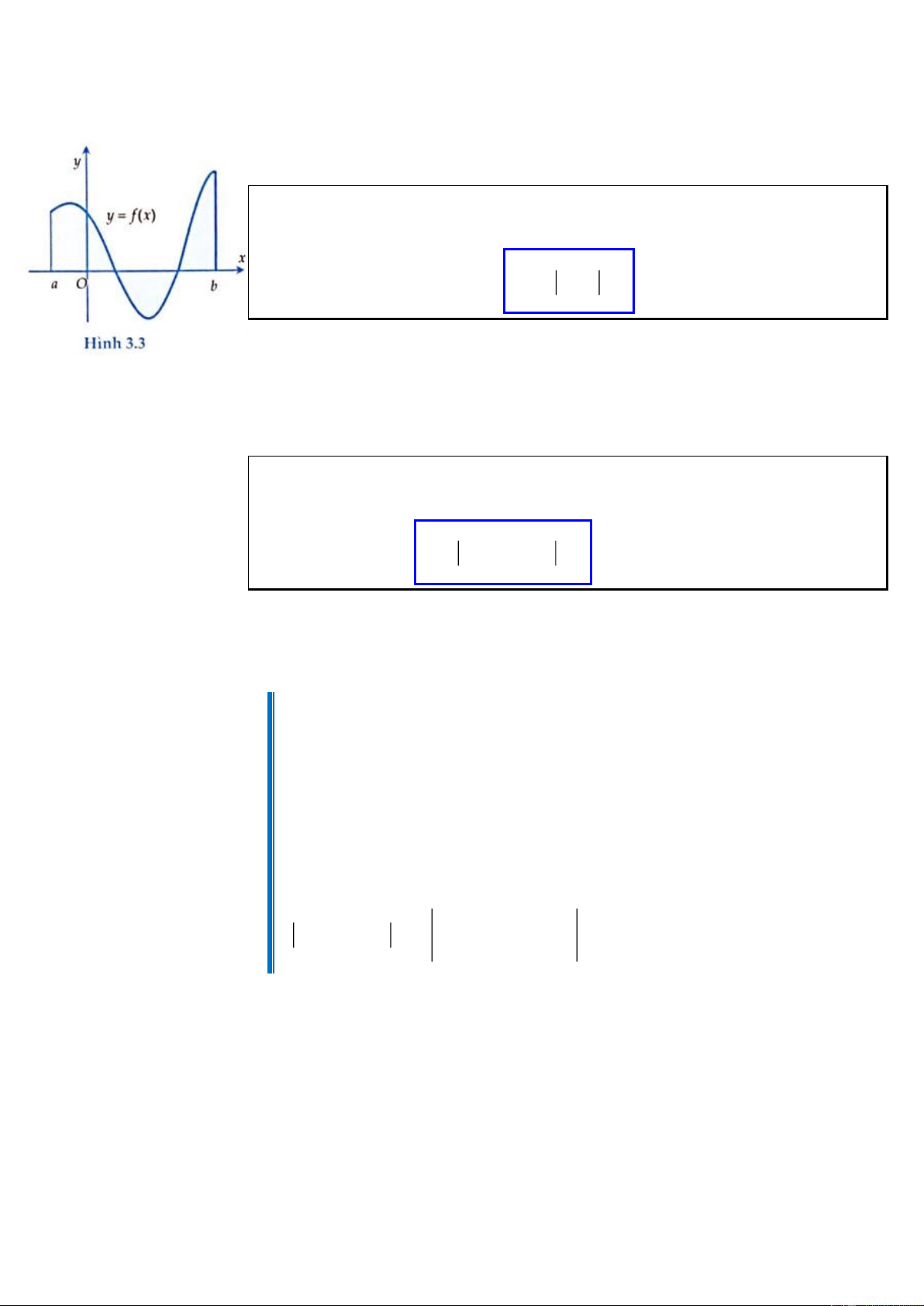
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f ( x) liên tục, trục
hoành và hai đường thẳng x = ;
a x = b được tính theo công thức b S = f (x) dx a
Chú ý: Trong trường hợp dấu của f ( x) thay đổi trên đoạn a;b thì ta phải chia
đoạn a;b thành một số đoạn con để trên đó dấu của f ( x) không đổi, do đó ta có
thể bỏ dấu giá trị tuyệt đối trên đoạn đó.
b. Diện tích hình phẳng giới hạn bởi hai đường cong
Cho hai hàm số y = f ( x) và y = g ( x) liên tục trên đoạn a;b . Khi đó diện tích S
của hình phẳng giới hạn bởi đồ thị hàm số y = f ( x) , y = g ( x) và hai đường b thẳng x = ,
a x = b là S = f
(x)− g(x) dx. a
Tương tự như chú ý ở trên thì ở bài toán này ta cũng phải xét đoạn mà dấu của
f ( x) − g ( x) không đổi. Chú ý
Khi áp dụng công thức này cần khử dấu giá trị tuyệt đối của hàm số dưới dấu
tích phân. Muốn vậy ta phải giải phương trình f ( x) − g ( x) = 0 trên đoạn a;b.
Giả sử phương trình có hai nghiệm ;
c d (c d ) . Khi đó f ( x) − g ( x) không đổi dấu trên các đoạn ; a b, ;
c d ,d;b . Trên mỗi đoạn đó, chẳng hạn trên đoạn
a;c thì ta có c c f
(x)− g(x) dx = f
(x)− g(x)dx a a LOVEBOOK.VN|35
Công Phá Toán – Lớp 12 Ngọc Huyền LB
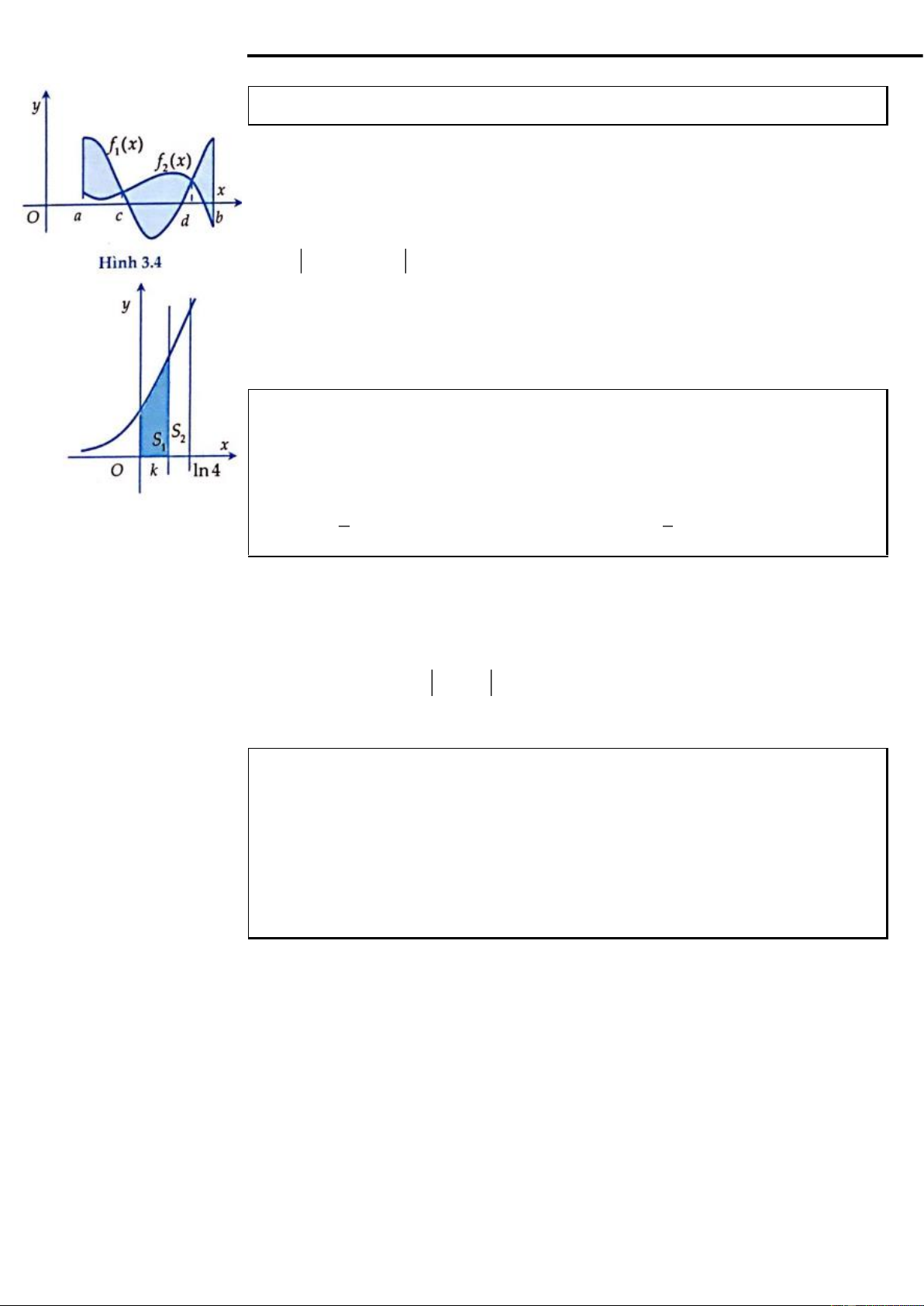
Ví dụ 4: Tính diện tích hình phẳng (hình được tô màu) ở biểu diễn ở hình 3.4. Lời giải
Nhận thấy trên a;c và d;b thì f x f x ; trên ;
c d thì f x f x 1 ( ) 2 ( ) 1 ( ) 2 ( ) Do vậy b c d S = f x − f x dx = f x − f x dx
+( f x − f x dx 2 ( ) 1( )) 1 ( ) 2 ( ) ( 1( ) 2 ( )) a a c b
+( f x − f x dx 1 ( ) 2 ( )) d
(Trên đây là cách bỏ dấu giá trị tuyệt đối)
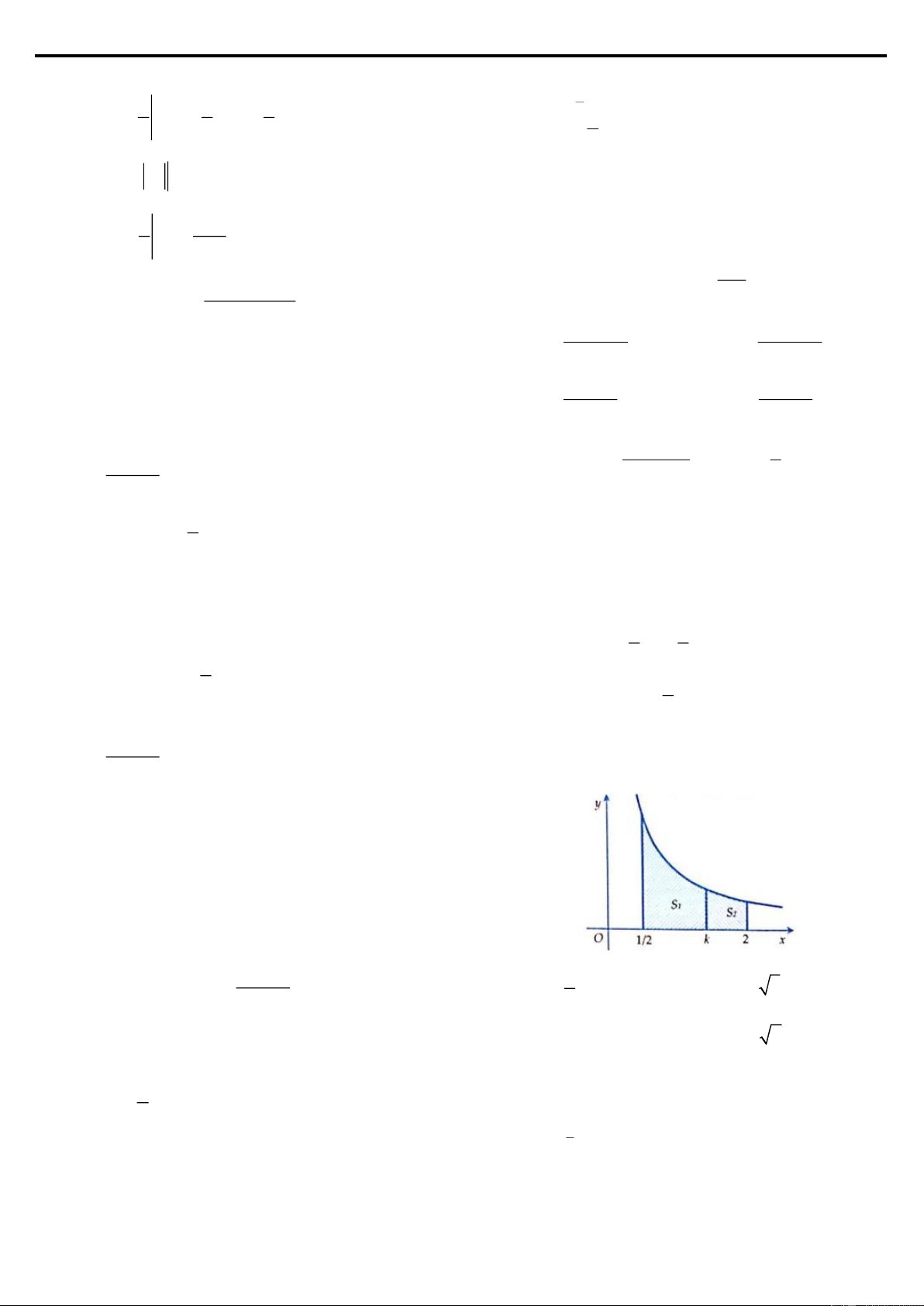
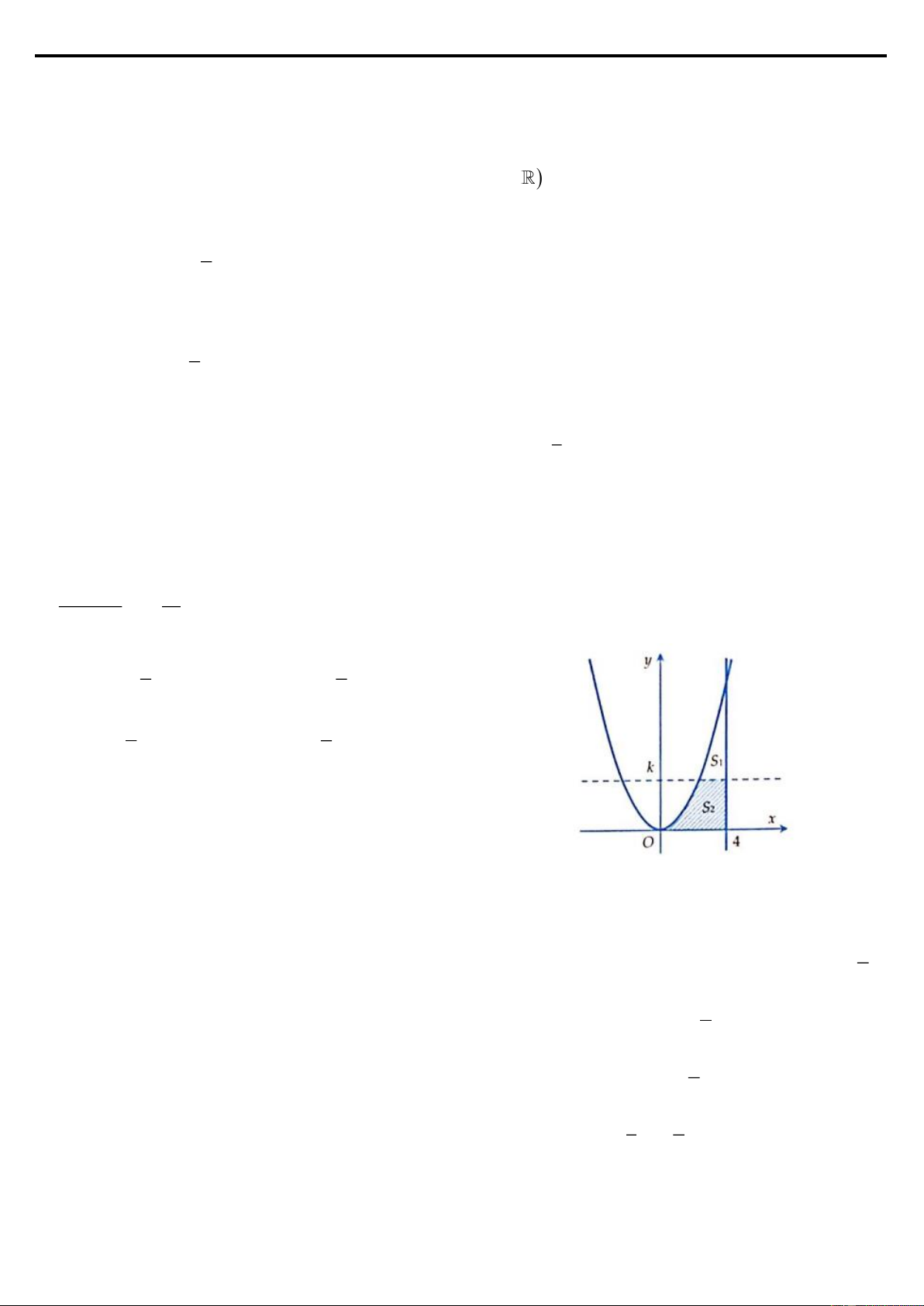
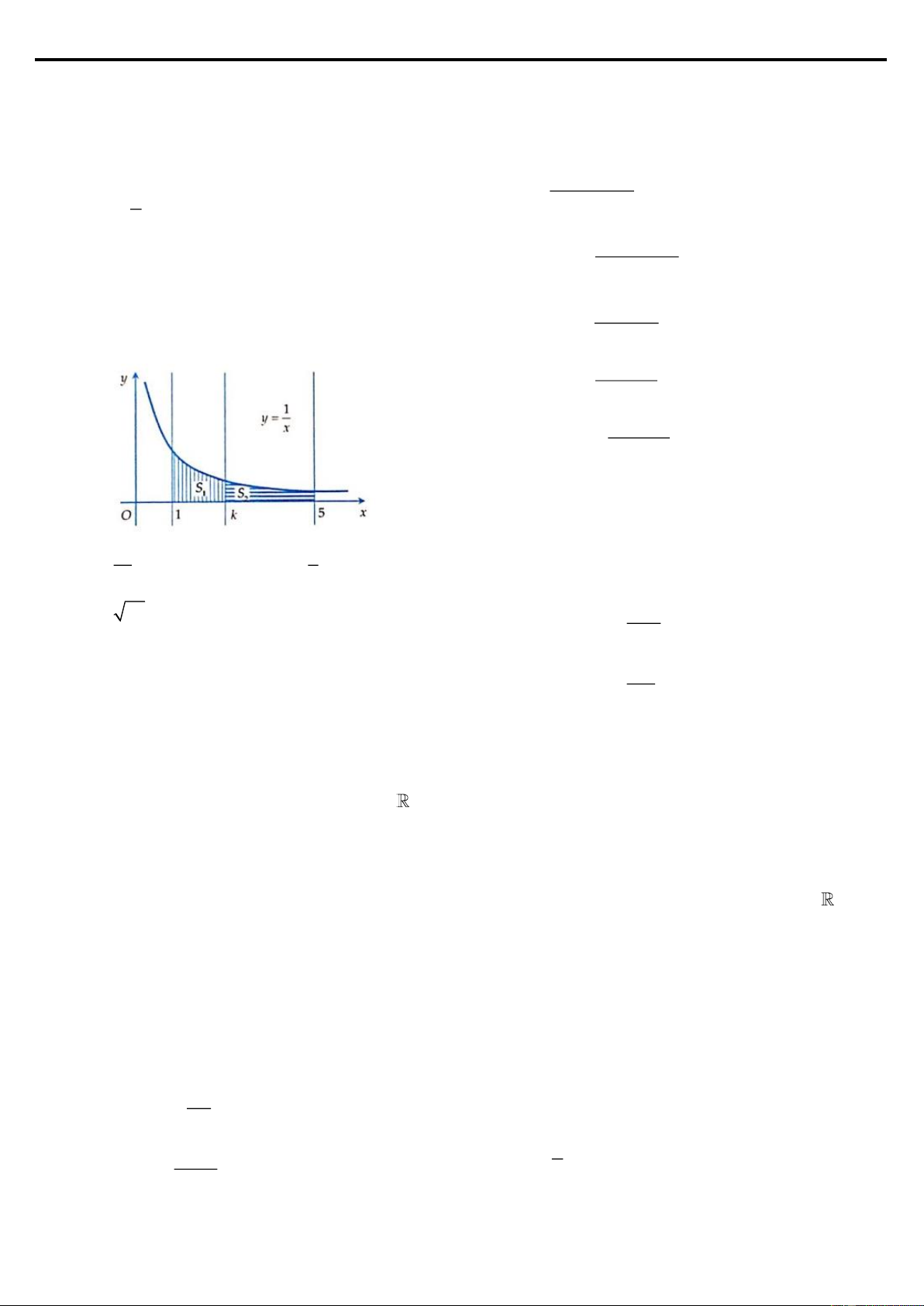
Ví dụ 5: Cho hình thang cong ( H ) giới hạn bởi các đường x
y = e , y = 0 , x = 0
và x = ln 4 . Đường thẳng x = k (0 k ln 4) chia ( H ) thành hai phần có diện tích
là S và S như hình vẽ bên. Tìm k để S = 2S . 1 2 1 2 2 8 A. k = ln 4
B. k = ln 2
C. k = ln
D. k = ln 3 3 3 Lời giải Đáp án D.
Nhìn vào hình vẽ ta có được các công thức sau: k ln 4 k ln 4 x x x x k 0 ln 4 e dx = 2. e dx e = 2.e
e − e = 2.e − 2. k e 3 k e = 9 0 k 0 k k
e = 3 k = ln3.
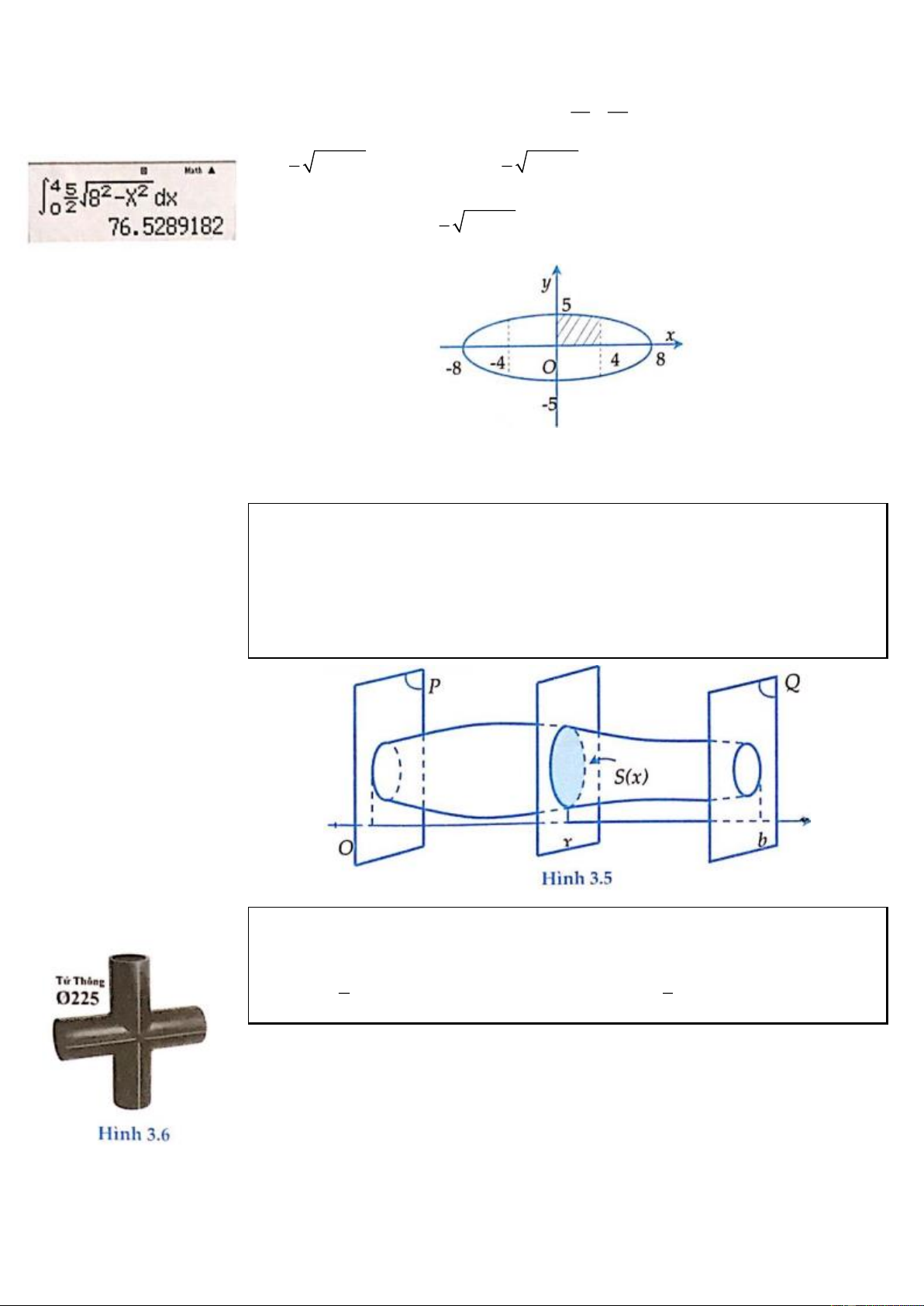
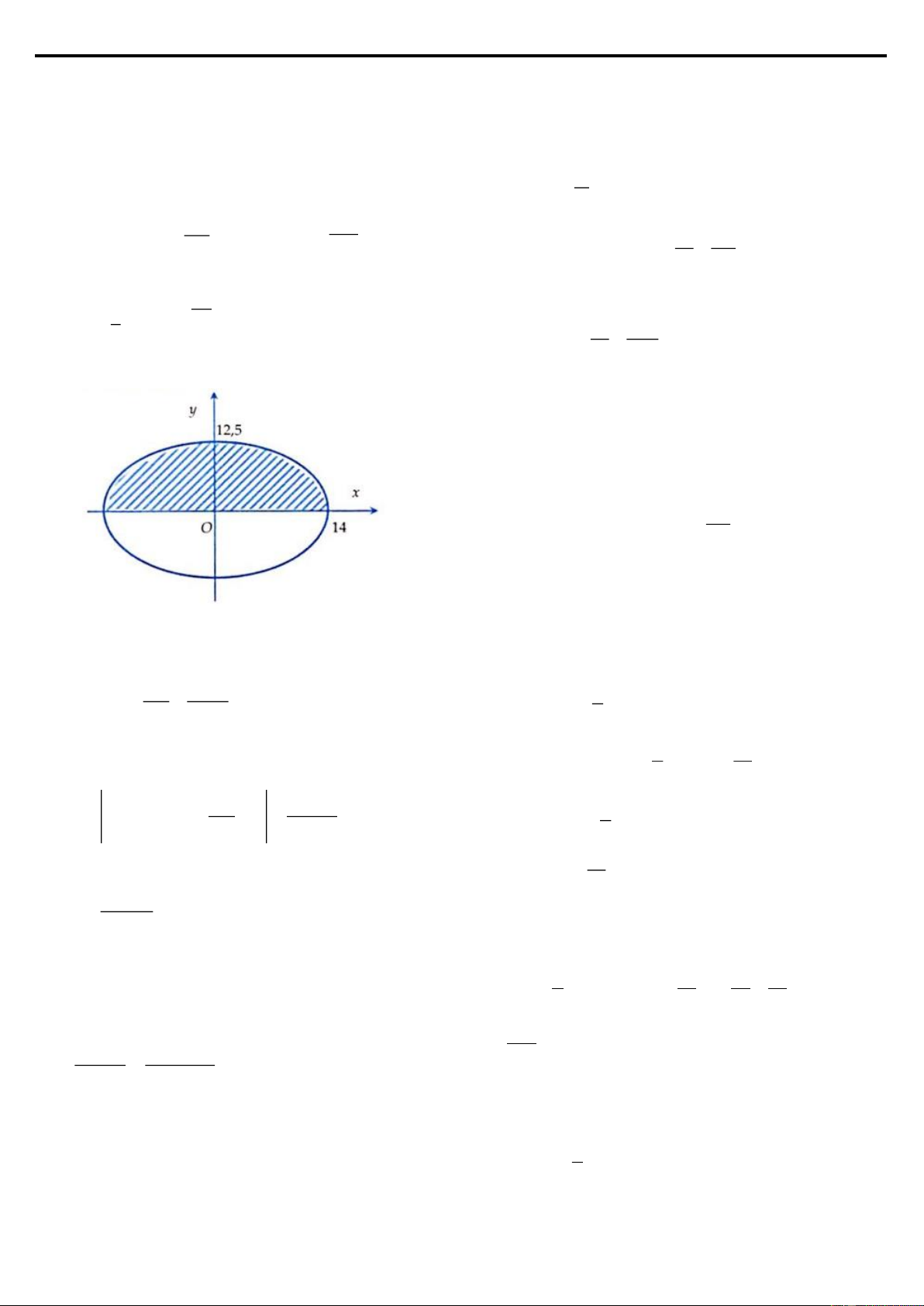
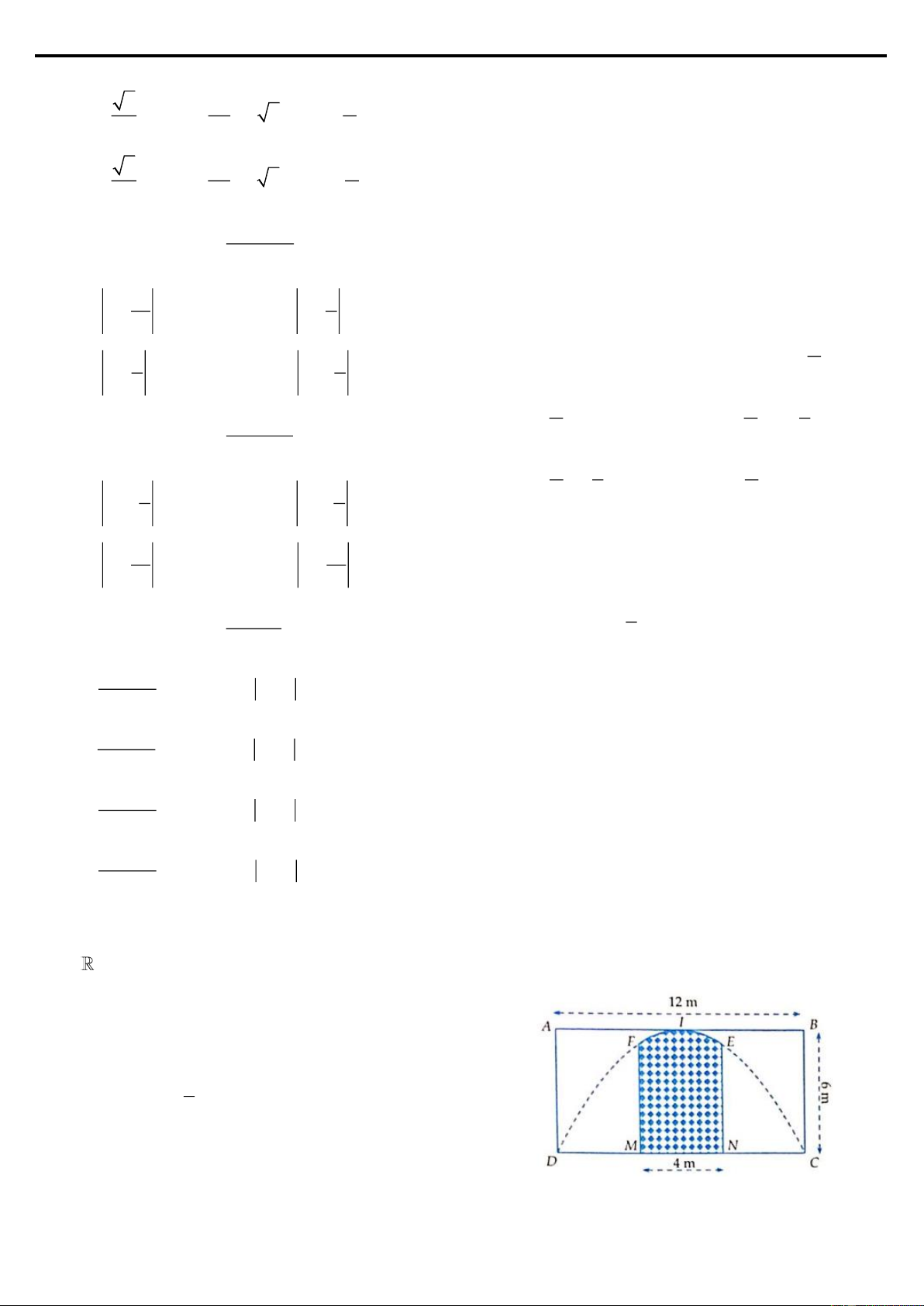
Ví dụ 6: Ông An có một mảnh vườn hình elip có độ dài trục lớn bằng 16m và độ
dài trục bé bằng 10m. Ông muốn trồng hoa trên một dải đất rộng 8m và nhận trục
bé của elip làm trục đối xứng (như hình vẽ). Biết kinh phí để trồng hoa là 100.000
đồng/1m2. Hỏi ông An cần bao nhiêu tiền để trồng hoa trên dải đất đó? (Số tiền
được làm tròn đến hàng nghìn.)
A. 7.862.000 đồng B. 7.653.000 đồng. C. 7.128.000 đồng. D. 7.826.000 đồng. Lời giải Đáp án B.
Nhận thấy đây là bài toán áp dụng ứng dụng của tích phân vào tính diện tích hình
phẳng. Ta có hình vẽ bên:
Ta thấy, diện tích hình phẳng cần tìm gấp 4 lần diện tích phần gạch chéo, do đó ta
chỉ cần đi tìm diện tích phần gạch chéo. LOVEBOOK.VN|36 2 2
Ta có phương trình đường elip đã cho là x y +
=1. Xét trên 0;4 nên y 0 thì 2 2 8 5 5 4 5 2 2 y = 8 − x . Khi đó 2 2 S = 8 − x dx
, vậy diện tích trồng hoa của ông An 8 cheo 8 0 4 5 trên mảnh đất là 2 2 S = 4.
8 − x dx 76,5289182 8 0
Khi đó số kinh phí phải trả của ông An là 76,5289182.100000 7.653.000 đồng.
c. Tính thể tích vật thể
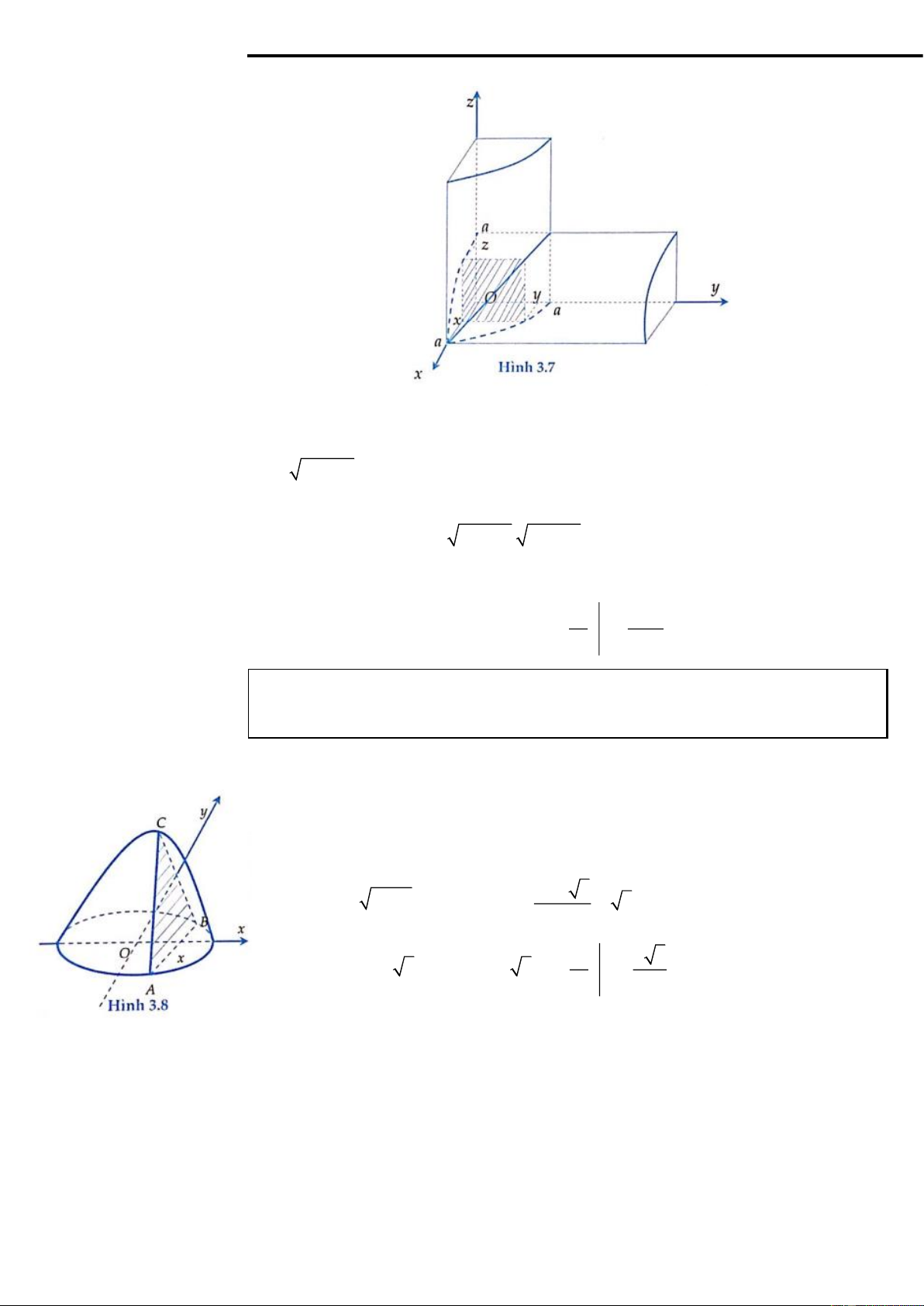
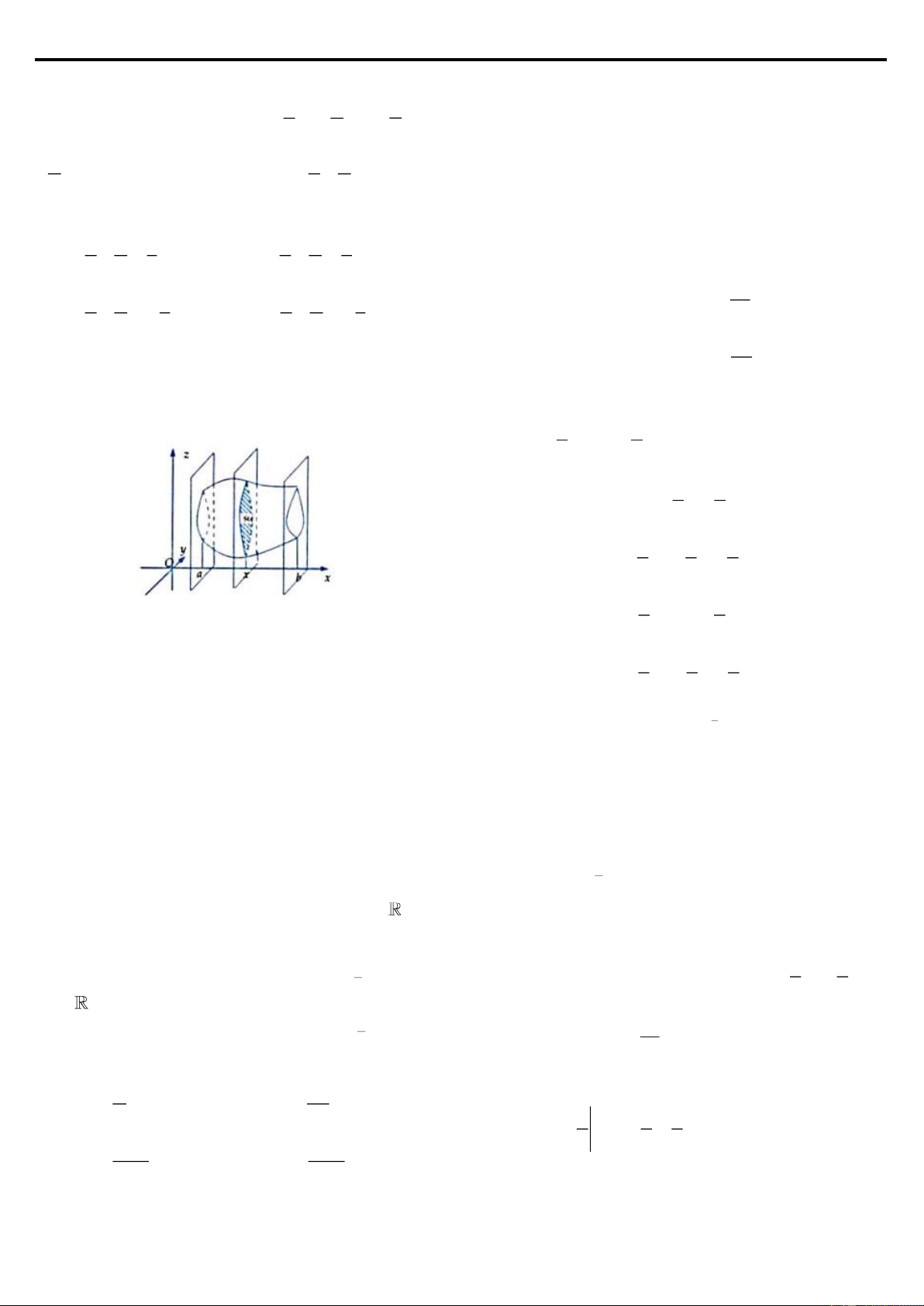
Cho H là một vật thể nằm giới hạn giữa hai mặt phẳng x = a và x = b . Gọi S ( x)
là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại
điểm có hoành độ x ( a x b ). Giả sử S ( x) là một hàm liên tục. Khi đó thể tích b
V của H là V = S
(x)dx. (hình 3.5) a
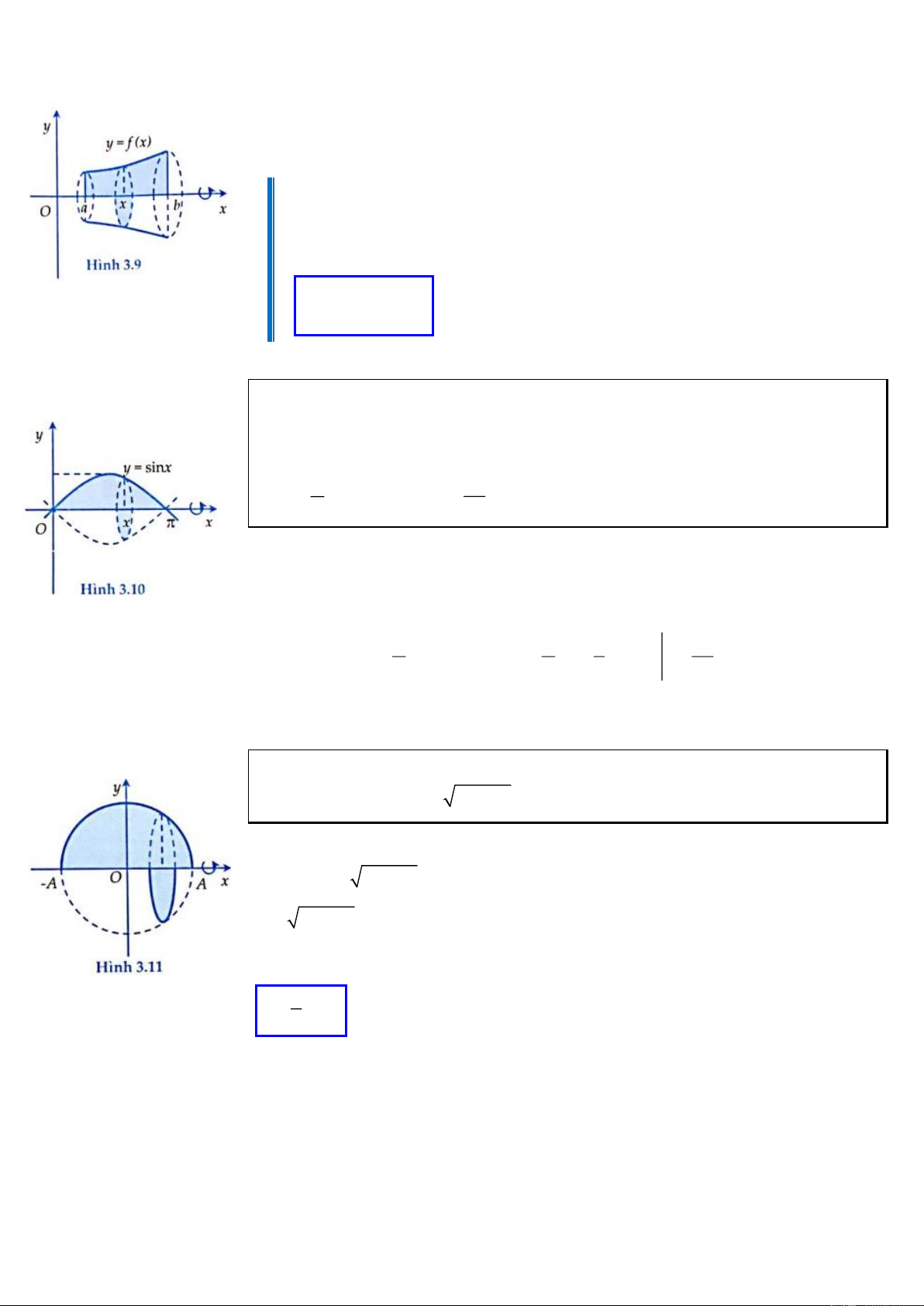
Ví dụ 7: Tính thể tích vật thể tạo được khi lấy giao vuông góc hai ống nước hình
trụ có cùng bán kính đáy bằng a. (hình 3.6) 2 8 A. k = ln 4
B. k = ln 2
C. k = ln
D. k = ln 3 3 3 Đáp án A Lời giải
Ta sẽ gắn hệ trục tọa độ Oxyz vào vật thể này, tức là ta sẽ đi tính thể tích vật thể V
giới hạn bởi hai mặt trụ: 2 2 2
x + y = a và 2 2 2
x + z = a ( a 0 ). LOVEBOOK.VN|37
Công Phá Toán – Lớp 12 Ngọc Huyền LB
Hình vẽ trên mô tả một phần tám thứ nhất của vật thể này, với mỗi x 0; a thiết
diện của vật thể (vuông góc với trục Ox) tại x là một hình vuông có cạnh 2 2 y =
a − x (chính là phần gạch chéo trong hình 3.7). Do đó diện tích thiết diện sẽ là: S ( x) 2 2 2 2 2 2
= a − x . a − x = a − x , x 0;a .
Khi đó áp dụng công thức (*) thì thể tích vật thể cần tìm sẽ bằng: a a a x a V = 8 S
(x)dx =8(a − x ) 3 3 16 2 2 2
dx = 8 a x − = 3 3 0 0 0
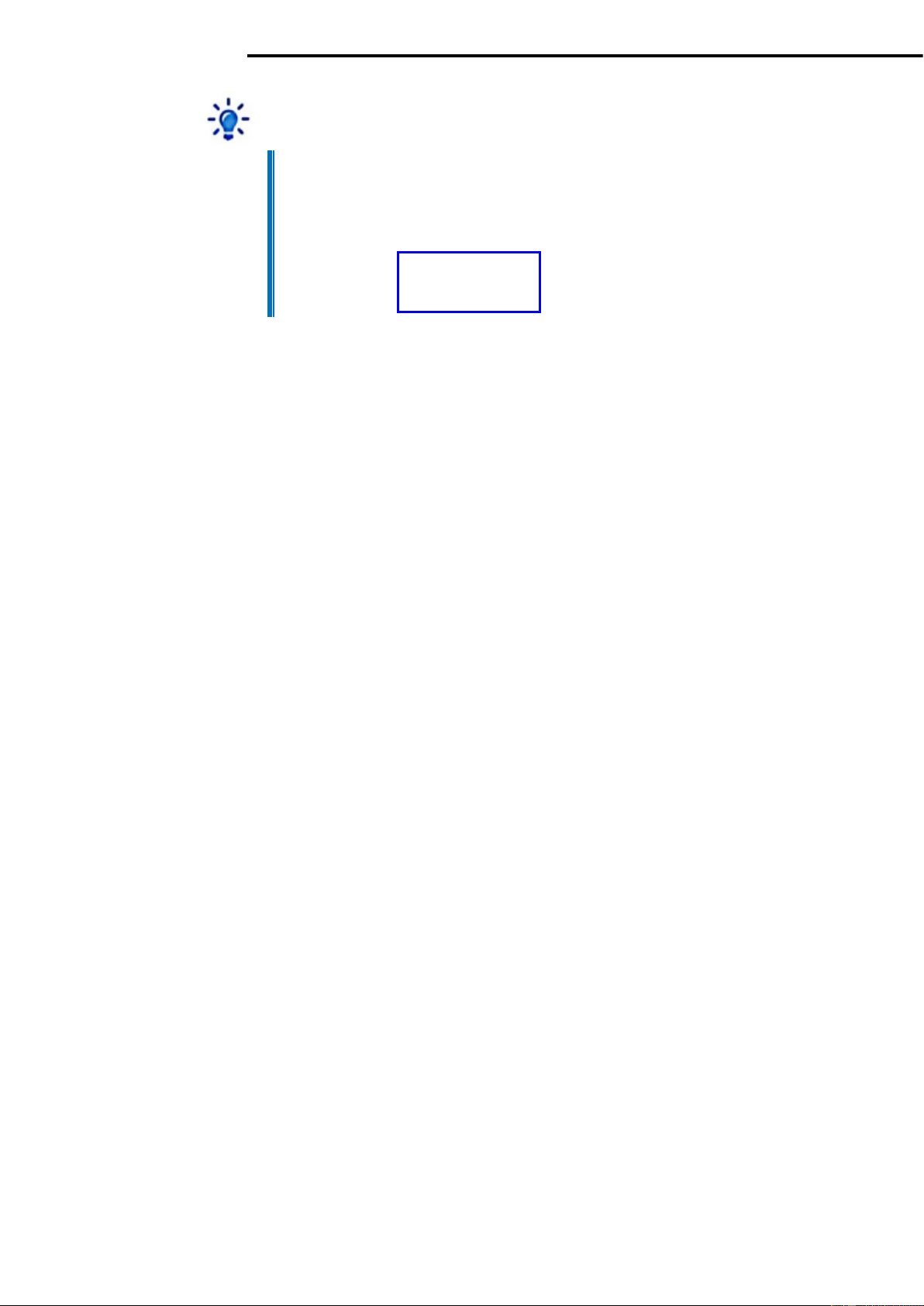
Ví dụ 8: Tính thể tích của vật thể H biết rằng đáy của H là hình tròn 2 2 x + y 1 và
thiết diện cắt bởi mặt phẳng vuông góc với trục hoành luôn là tam giác đều. Lời giải
Giả sử mặt phẳng vuông góc với trục hoành tại điểm có hoành độ là
x (−1 x )
1 cắt vật thể ( H ) theo thiết diện là tam giác ABC đều, với AB chứa
trong mặt phẳng xOy (hình 3.8). 2 AB 3 Ta có 2
AB = 2 1− x . Do đó S ( x) = = 3 ( 2 1− x ) . Vậy 4 1 1 1 = ( ) x S S x dx = 3 (1− x ) 3 4 3 2 dx = 3 x − = (đvtt). 3 3 1 − 1 − 1 − LOVEBOOK.VN|38
d. Tính thể tích khối tròn xoay Định lý Chú ý
Cho hàm số y = f ( x) liên tục, không âm trên đoạn a;b . Hình phẳng giới hạn
bởi đồ thị hàm số y = f ( x) , trục hoành và hai đường thẳng x = , a x = b quay
quanh trục hoành tạo nên một khối tròn xoay. Thể tích V của khối tròn xoay đó b là 2 V = f (x)dx. a
Ví dụ 9: Thể tích của khối tròn xoay thu được khi quay hình phẳng được giới hạn
bởi đường cong y = sin x , trục hoành và hai đường thẳng x = 0, x = (hình 3.10) quanh trục Ox là 2 A. (đvtt) B. (đvtt)
C. (đvtt) D. 2 (đvtt) 2 2 Lời giải Đáp án B.
Áp dụng công thức ở định lý trên ta có V = sin xdx = (1−cos2x) 2 1 2 dx = x − sin 2x = . 2 2 2 2 0 0 0
Tiếp theo dưới đây là một bài toán thường xuất hiện trong các đề thi thử, bài
toán có thể đưa về dạng quen thuộc và tính toán rất nhanh.
Ví dụ 10: Tính thể tích khối tròn xoay thu được khi quay hình phẳng được giới hạn bởi đường cong 2 2 y =
A − x và trục hoành quanh trục hoành.
Lời giải tổng quát Ta thấy 2 2 2 2 2 2 2 2 y =
A − x y = A − x x + y = A Do 2 2
A − x 0 với mọi x, do vậy đây là phương trình nửa đường tròn tâm O, bán
kính R = A nằm phía trên trục Ox. Khi quay quanh trục Ox thì hình phẳng sẽ tạo
nên một khối cầu tâm O, bán kính R = A (hình 3.11). Do vậy ta có luôn 4 3 V = . .A 3
Vậy với bài toán dạng này, ta không cần viết công thức tích phân mà kết luận luôn
theo công thức tính thể tích khối cầu. LOVEBOOK.VN|39
Công Phá Toán – Lớp 12 Ngọc Huyền LB Đọc thêm Định lý
Cho hàm số y = f ( x) liên tục, không âm trên đoạn a,b(a 0) . Hình phẳng
giới hạn bởi đồ thị hàm số y = f ( x) , trục hoành và hai đường thẳng x = ,
a x = b quay quanh trục tung tạo nên một khối xoay. Thể tích V của khối b
tròn xoay đó là V = 2 xf (x)dx . a LOVEBOOK.VN|40
VIII. Một số dạng tích phân thường gặp
Tích phân hàm phân thức hữu tỉ
Trong bài toán này, ta sẽ tham khảo lại phần “Nguyên hàm phân thức hữu
tỉ” phía trên để hiểu được các định nghĩa phân thức hữu tỉ, phân thức hữu tỉ thực sự
và phân thức đơn giản, cùng các định lý đã được nêu ở phần nguyên hàm ở phần trước.
Dưới đây là một số bài toán thường gặp về dạng này.
A. MỘT SỐ CÔNG THỨC VÀ KĨ NĂNG BIẾN ĐỔI du 1 u − a du 1 a + u 1. = ln + C 2. = ln + C . 2 2 u − a 2a u +1 2 2 a − u 2a a − u
Kỹ năng biến đổi tam thức bậc hai 2 2 b b − 4ac 1. 2
ax + bx + c = a x + − 2. + + = ( + )2 2 2 ax bx c mx n p 2 2a 4a B. CÁC DẠNG TOÁN dx
Dạng 1: Tích phân dạng I = . 1 2
ax + bx + c Phương pháp chung STUDY TIP Khi mẫu thức có dạng dx 1
mx + n − p Biến đổi I = = tam thức bậc hai thì ln 1 + − + + ( mx n)2 2 p 2mp mx n p thường đưa về dạng a + b 3 ln 1 dx 13
Ví dụ 1: Cho I = = , với , a ,
b c ;c 0 . Đặt 2 4x + 8x +1 c 3 0
S = a + b + c , lúc này S có giá trị bằng
A. S = 20 + 37 3 B. S = 37 + 24 3 C. S = 57 D. S = 61 Đáp án D. Lời giải
Áp dụng bài toán tổng quát trên ta có STUDY TIP 1 1 dx 1 2x + 2 − 3 I = = ( 2x + 2) ln 2 − 3 4 3 2x + 2 + 3 0 0 37 + 20 3 ln 1 2.1+ 2 − 3 2.0 + 2 − 3 13 = ln − ln = 4 3 2.1+ 2 + 3 2.0 + 2 + 3 4 3 LOVEBOOK.VN|41
Công Phá Toán – Lớp 12 Ngọc Huyền LB
S = a +b + c = 37 = 37 + 20+ 4 = 61. 0 dx 1 b − 53
Ví dụ 2: Cho I = = .ln với ;
a b ; a 0 . Tích ab 2 7 −10x − 4x + − a 53 b 53 1 có giá trị bằng A. ‒24 B. 24 C. ‒48 D. 48 Đáp án A. Lời giải
Áp dụng bài toán tổng quát trên ta có 0 0 dx dx I = = − 2 2 2 2 1 − 53 5 1 − 5 53 − 2x + 2x + − 2 2 2 2 0 + − + − − + − 1 4x 5 53 1 4.0 5 53 4.( )1 5 53 = − .ln = − . ln − ln 2 53 4x + 5 + 53 2 53 4.0 + 5 + 53 4.(− ) 1 + 5 + 53 1 − 1 12 − 53 = − .ln 2 53 12 + 53 a = 2
− ;b =12 ab = 2 − 4. mx + n
Dạng 2: Tính tích phân I = dx 2 2
ax + bx + c Phương pháp chung STUDY TIP Cách 1: Khi mẫu thức có dạng tam thức bậc hai thì m ( mb
2ax + b) + n − thường đưa về dạng 2a 2a m
(2ax +b)dx mb dx I = = + n + 2 2 2 2
ax + bx + c 2a
ax + bx + c
2a ax + bx + c d ( 2
ax + bx + c m
) mb m mb 2 = + n − I =
ln ax + bx + c + n − I 2 1 1 2a
ax + bx + c 2a 2a 2a
Cách 2: Phương pháp hệ số bất định (Sử dụng khi mẫu có nghiệm)
* Nếu mẫu số có nghiệm kép x = x tức là ax + bx + c = a ( x − x ta giả sử 0 )2 2 0 mx + n A B = + 2
ax + bx + c x − x − 0 (x x0)2
Quy đồng vế phải và đồng nhất hệ số hai vế để tìm A; B. Sau khi tìm đượ B
c A; B thì ta có I = .
A ln x − x − . 2 0 x − x 0 LOVEBOOK.VN|42
* Nếu mẫu số có 2 nghiệm phân biệt x ; x : 2
ax + bx + c = a ( x − x x − x thì ta 1 ) ( 2 ) 1 2 giả sử: mx + n A B = + 2
ax + bx + c x − x x − x 1 2
Quy đồng và đồng nhất hệ số để tìm A; B.
Sau khi tìm được A; B ta có I = Aln x − x + B ln x − x 2 1 2 . 0 2x − 9
Ví dụ 1: Cho I =
dx = a ln 3 + b ln 2 , ; a b
thì a + 2b có giá trị 2 x − 3x + 2 2 − bằng A. ‒35 B. ‒2 C. 2 D. 3 Đáp án D. Lời giải 0 (2x + 3) 0 0 − 6 2x − 3 6dx
Cách 1: Ta có I = dx = dx − 2 2 2 x − 3x + 2 x − 3x + 2 x − 3x + 2 2 − 2 − 2 − 0 ( 3 1 2 0 − − − 3 + 2) 0 x dx x x dx 2 2 2 = − 6 =
ln x − 3x + 2 − 6ln 2 2 2 x − 3x + 2 3 1 2 − 2 − 3 1 x − + x − − 2 2 2 2 2 − 0 ( − = x − )( x − ) x 2 ln 1 2 − 6 ln =
(7ln x−1 −5ln x−2 )0 2 x −1 − 2−
= 7 ln1− 5ln 2 − (7ln 3−5ln 4) = 7 − ln 3 +10ln 2 − 5ln 2 = 7 − ln 3 + 5ln 2 . a + 2b = 3. x =1 Cách 2: Ta thấy 2
x − 3x + 2 = 0 . x = 2 2x − 9 A B 2x − 9
(A+ B) x −(2A+ B) Giả sử = + = 2 2 2 x − 3x + 2 x −1 x − 2 x − 3x + 2 x − 3x + 2 A + B = 2 A = 7
Đồng nhất hệ số ta có 2A + B = 9 B = 5 − 0
Áp dụng công thức ta có I = 7 ln x −1 − 5ln x − 2 = −7 ln 3+ 5ln 2 . 2 −
Cách 3: Sử dụng máy tính cầm tay.
Trong bài toán này ta có thể sử dụng chức năng TABLE để giải quyết, tuy nhiên
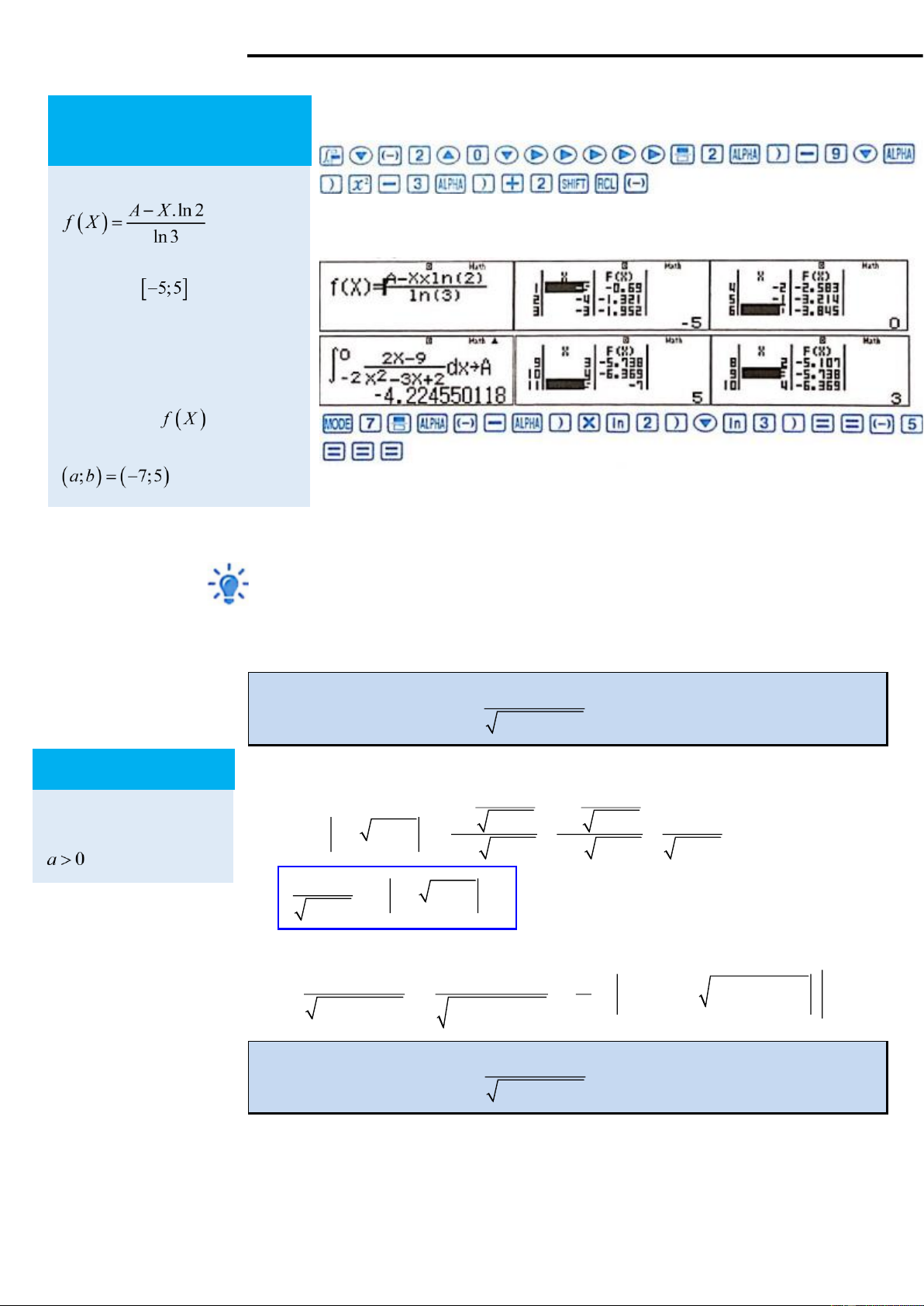
cách làm này chỉ mang tính chất “mò” (tức dự đoán khoảng của a; b). I − . b ln 2 Ta thấy I = . a ln 3 + . b ln 2 a = . ln 3 LOVEBOOK.VN|43
Công Phá Toán – Lớp 12 Ngọc Huyền LB
1. Lúc này ta nhập biểu thức tích phân vào máy tính và gán giá trị này cho
Giải thích cách sử dụng biến A. MTCT
Ta thấy khi nhập vào màn hình
2. Tiếp tục sử dụng MODE 7 TABLE để chạy biến giá trị của b từ đó tìm thì ta đã
ra bảng giá trị tương ứng của a.
coi b (biến X) chạy trong khoảng từ và step là 1.
Ở đây ta chọn STEP 1 vì đề
cho a; b nguyên. Lúc này màn
hình sẽ hiện giá trị của b (chính
là X) và giá trị tương ứng của a (chính là cột ). Do a; b nguyên nên ta sẽ chọn .
Ta thấy chỉ có trường hợp X = 5; F ( X ) = −7 là thỏa mãn 2 số nguyên, do
đó ta kết luận a = 7
− ;b = 5 a + 2b = 3 .
Đọc thêm: Tích phân hàm phân thức chứa căn ở mẫu thức dx
Dạng 1: Tính tích phân I = 3 2
ax + bx + c Chú ý Phương pháp chung u u Phương pháp này chỉ 1+ 1+ u + k u + k 1
áp dụng được khi hệ số
Ta có (ln u + u + k ) 2 2 2 ' = = = 2 2 2 u + u + k u + u + k u + k . du 2
= ln u + u + k + C 2 u + k
Áp dụng bài toán vừa chứng minh ở trên ta áp dụng vào bài toán biến đổi sau: dx dx 1 I = = = .ln
(mx + n)+ (mx + n)2 + k 3 2 + + ( + )2 + m ax bx c mx n k
(mx + n)dx
Dạng 2: Tính tích phân I = . 4 2
ax + bx + c Phương pháp chung LOVEBOOK.VN|44 (
mx + n) dx m
(2ax +b)dx mb dx Ta có I = = − 4 2 2 2 + + 2a + + 2a ax bx c ax bx c
ax + bx + c d ( 2
ax + bx + c m ) mb = − .I 3 2 2a + + 2a ax bx c dx
Dạng 3: Tính tích phân I = 5 ( px + q) 2
ax + bx + c Phương pháp chung Đặ 1 dt 1 1
t px + q = pdx = − ; x = − q . Khi đó 2 t t p t 1 p +q dx −dt I = = 5 ( px + q) 2 2
ax + bx + c 1 1 a 1 b 1 2 − + − + p +q pt . q q c 2 t p t p t 1 p +q dt =
(quay trở về bài toán dạng 1). 2 + + 1 At Bt p +q LOVEBOOK.VN|45
Công Phá Toán – Lớp 12 Ngọc Huyền LB
Tích phân hàm lượng giác
A. MỘT SỐ CÔNG THỨC VÀ KĨ NĂNG BIẾN ĐỔI
Các công thức nguyên hàm của hàm lượng giác ( 1 ax + b) 1 cos dx =
sin (ax + b) + C sin
(ax +b)dx = − cos(ax +b)+C a a dx 1 = dx 1
ax + b + C
= − cot ax + b + C
cos x (ax + b) tan ( ) 2 a sin (ax + b) ( ) 2 a B. CÁC DẠNG TOÁN 1 b 2 b
Dạng 1: Tính tích phân: n n I = sin x d ; x I = cos x dx 1 ( ) 2 ( ) a a 1 2
1. Nếu n chẵn thì ta sử dụng công thức hạ bậc.
2. Nếu n = 3 thì ta sử dụng công thức hạ bậc hoặc biến đổi theo trường hợp 3.
3. Nếu n 3 và n lẻ (n = 2 p + )
1 thì ta thực hiện biến đổi. 1 b b b b + I = ( p n p p sin x) 1 dx = (sin x) 1 2
1 dx = (sin x) 1 2 .sin xdx = − ( 2 1 − cos x d cos x 1 ) ( ) a a a a 1 1 1 1 p
Sử dụng công thức khai triển nhị thức Newton để khai triển ( 2 1 − cos x) .
Từ đây ta giải quyết dc bài toán. 2 b b b b + I = ( p n p p cos x) 2 dx = (cos x) 2 2
1 dx = (cosx) 2 2 .cos . x dx = ( 2 1 − sin x d sin x 2 ) ( ) a a a a 2 2 2 2 p
Sử dụng công thức khai triển nhị thức Newton để khai triển ( 2 1 − sin x) .
Từ đây ta giải quyết dc bài toán. 10 Ví dụ 1: Cho 4 I = cos 3xdx
. Đẳng thức nào sau đây đúng? 0 10 3 1 1 10 1 1 A. I = x + sin 6x + sin12x B. I = sin 6x + sin12x 8 12 96 12 96 0 0 10 3 1 1 10 3 1
C. I = − x + sin 6x + sin12x D. I = x − sin12x 8 12 96 8 96 0 0 Đáp án A. Lời giải Ta có 2 10 10
Ta thấy bậc của cos3x là 4 1+ cos6x 1 = ( + x dx
1+ 2cos 6x + cos 6x) 10 1 1 cos12 2 dx = 1+ 2cos 6x + dx
là một số chẵn. Từ 1 trong 2 4 4 2 0 0 0 phần phương pháp chung LOVEBOOK.VN|46
ta sẽ sử dụng công thức hạ bậc như lời giải bên. 10 3 1 1 = x + sin 6x + sin12x . 8 12 96 0
Từ đây ta giải quyết được bài toán. Ví dụ 2: Cho: 3 I = (sin5x) 3 9 1 1 3 5 7 9 dx = −
cos5x + a cos 5x + b cos 5x + c cos 5x + cos 5x . 5 9 0 0
Đặt S = a + b + c . Giá trị của S bằng 74 5 1 A. S = 3 B. S = − C. S = − D. S = 105 4 9 Đáp án B. Lời giải 3 3 4 1
Ta có I = (sin5x)8 sin5xdx = − ( 2
1 − cos 5x) d (cos5x) 5 0 0 3 1 2 4 6 8 = − 1
− 4cos 5x + 6cos 5x − 4cos 5x + cos 5x d (cos5x) 5 0 3 1 4 6 4 1 3 5 7 9 = − cos5x − cos 5x + cos 5x − cos 5x + cos 5x 5 3 5 7 9 0 4 6 4 74
a = − ;b = ;c = − S = − . 3 5 7 105 b
Dạng 2*: Tính tích phân I = sinm . x cosn xdx . a Phương pháp chung
a. Trường hợp 1: m; n là các số nguyên
1. Nếu m chẵn, n chẵn thì sử dụng công thức hạ bậc, biến đổi tích thành tổng.
2. Nếu m chẵn, n lẻ (n = 2 p + ) 1 thì biến đổi b b + I = ( x)m (
x)2 p 1dx =
( x)m ( x)2p sin cos sin cos cos xdx a a b = ( x)m ( − x)2 2 sin 1 sin d (sin x) . a
Sử dụng công thức khai triển nhị thức Newton để khai triển và giải quyết bài toán.
3. Nếu m lẻ (m = 2 p + )
1 , n chẵn thì ta biến đổi b b + I = ( x)2 p 1 ( x)n dx = ( x)2p n sin . cos sin
.(cos x) .sin xdx a a LOVEBOOK.VN|47
Công Phá Toán – Lớp 12 Ngọc Huyền LB b = −( p 2 n
1 − cos x) .(cos x) d (cos x) . a
Sử dụng công thức khai triển nhị thức Newton để khai triển và giải quyết bài toán.
4. Nếu m lẻ, n lẻ thì sử dụng biến đổi 2 hoặc 3 cho số mũ lẻ bé hơn.
b. Trường hợp 2: m; n là các số hữu tỉ b b n 1 − sin b n− m I = sinm . x cosn xdx =
(sin x) .(cos x) cos m xdx = u (1−u ) 1 2 2 2 2 du ( ) * a a sin a 3
Ví dụ 1: Cho I = (sin 2x)7 .(cos2x)100 dx . Đẳng thức nào sau đây là đúng? 0
(cos2x)101 3(cos2x)103 3(cos2x)105 (cos2x)107 3 A. I = − + − . 10 103 105 107 0
(cos2x)101 3(cos2x)103 3(cos2x)105 (cos2x)107 3 B. I = 2 − + + + 10 103 105 107 0 1 (cos 2x)101 3(cos 2x)103 3(cos 2x)105 (cos2x)107 3 C. I = − − + − 2 10 103 105 107 0 1 (cos 2x)101 3(cos 2x)103 3(cos 2x)105 (cos2x)107 3 D. I = − + − 2 101 103 105 107 0 Đáp án C. Lời giải 3 I =
Trong bài toán này, ta thấy ( x) ( x) 3 1 cos 2 . sin 2
.sin 2xdx = − (cos2x) (1− cos 2x)3 100 6 100 2 d (cos 2x) 2 0 0
m lẻ, n chẵn nên ta áp dụng phương pháp 3 trong bài 3 1
toán tổng quát phía trên. = − (cos2x)100.( 2 4 6
1− 3cos 2x + 3cos 2x − cos 2x)d (cos 2x) 2 0 1 (cos 2x)101 3(cos 2x)103 3(cos 2x)105 (cos2x)107 3 = − − + − . 2 101 103 105 107 0 1 b 2 b
Dạng 3: Tính tích phân I = ( n n tan x) d ;
x I = (cot x) dx ( * n . 1 2 ) a a 1 2 Phương pháp chung
Sử dụng các công thức sau: ( dx 2 1 + tan x)dx = = d
(tan x) = tan x +C 2 cos x LOVEBOOK.VN|48 ( dx 2 1 + cot x)dx = = − d
(cot x) = −cot x +C 2 sin x sin x d (cos x) tan xdx = dx = −
= −ln cos x + C cos x cos x cos x d (sin x) cot xdx = dx = = ln sin x + C sin x sin x
Dạng 4*: Tích phân liên kết. Phương pháp chung b cos xdx
Bài toán 1: Tính tích phân I = sin x + cos x a b cos xdx b sin xdx * I =
. Xét tích phân liên kết I = 1 sin x + cos x 2 sin x + cos x a a b b
I + I = dx = x 1 1 a Ta có a b cos x − sin b x
d (sin x + cos x) b I − I = dx =
= ln sin x + cos x 1 2 sin x + cos x sin x + cos a x a a b 1 I =
x + ln sin x + cos x 1 ( ) 2
Giải hệ phương trình ta được a b 1 I =
x − ln sin x + cos x 2 ( ) 2 a
Các trường hợp thường gặp: sin xdx
Bài toán 2: Tính tích phân I = 1 * = khi đó tính
a cos x + b sin x I I 1 2
I + I = I = I = . Phương pháp chung 1 2 1 2 2 cos xdx
* I là một tích phân đơn
Xét tính phân liên kết với I là I = 2 1 2
a cos x + bsin x
giản, thường thì các hàm số
dưới dấu tích phân f ( x) ;
a cos x + b sin x b I + aI =
dx = dx = x 1 2
g ( x) (của hai tích phân liên
a cos x + b sin x Ta có
kết) thường có tính cân xứng
b cos x − a sin x
d (a cos x + bsin x) bI − aI = dx =
= ln a cos x + bsin x 2 1
hoặc bổ sung cho nhau như
a cos x + b sin x
a cos x + b sin x
ở bài toán 1 và bài toán 2.
Giải hệ phương trình ta được I ; I . 1 2
Việc tìm được tích phân liên kết phụ thuộc vào kinh
nghiệm giải toán của người đọc. LOVEBOOK.VN|49
Công Phá Toán – Lớp 12 Ngọc Huyền LB
Từ hai bài toán trên ta đưa ra kết luận về tích phân liên kết như sau: b
Trong một số bài toán tính tích phân I = f x dx
, ta sẽ sử dụng tích phân 1 ( ) a b I = g x dx
là tích phân liên kết của I sao cho ta có thể xác lập được mối quan 2 ( ) 1 a
hệ ràng buộc giữa I và I thành hệ phương trình như sau: 1 2 mI + nI = 1 2 pI + qI = 1 2
Giải hệ phương trình ta dễ dàng tìm được I ; I . 1 2 LOVEBOOK.VN|50
Một số bài toán tích phân gốc thường gặp
Bài toán 1: Cho f là hàm số chẵn và liên tục trên − ;
b b với b 0 . Chứng minh b f ( x) b rằng dx = f
(x)dx (với a 0 và a 1) (1) x a + 1 −b 0
Lời giải tổng quát Đặt x = t
− thì dx = −dt; f ( t
− ) = f (t) nên 0 f ( x) 0 − f ( t − ) b t a f (t ) b x a f ( x) dx = dt = dt = dx x a +1 −t a +1 t a +1 x a +1 −b b 0 0 Do đó b f ( x) b x a f ( x) b f ( x) b dx = dx = dx = f (x)dx x a +1 x a +1 x a +1 −b 0 0 0 1 4 2 x + x + 1
Ví dụ 1: Tính tích phân dx 2x + 1 1 − 23 15 A. B. C. 1 D. −1 15 23 Đáp án A. Lời giải
Ta thấy hàm số f ( x) 4 2
= x + x +1 là hàm số chẵn, áp dụng bài toán 1 ở trên ta có: 1 1 4 2 1 x + x +1 x x dx = x + x + dx = + + x = . x ( ) 5 3 23 4 2 1 2 +1 5 3 15 1 − 0 0
Bài toán 2*: Cho f là hàm số liên tục trên đoạn ;
a b . Chứng minh rằng: b b f
(a +b − x)dx = f (x)dx (2) a a b b Đặc biệt f
(b − x)dx = f (x)dx (3) 0 0
Lời giải tổng quát
Đặt t = a + b − x thì dt = −dx . Khi đó b a b f
(a +b − x)dx = − f
(t)dt = f (x)dx a b a
Khi a = 0 , ta nhận được công thức (3). 4 Ví dụ 2: Cho ln
(1+ tan x)dx = .lnb , (a ;b 0). Khi đó tổng a+b bằng a 0 A. 8 B. 10 C. 5 D. 4 Đáp án B. LOVEBOOK.VN|51
Công Phá Toán – Lớp 12 Ngọc Huyền LB Lời giải
Nhận xét: f ( x) = ln(1+ tan x) liên tục trên 0;
, áp dụng (3) với bài toán này ta 4 có: 4 4 4 2 I = ln 1 + tan − x dx = ln dx =
(ln2−ln(1+ tan x))dx 4 1+ tan x 0 0 0 4 = − = 4 ln 2dx I 2I ln 2.x I = .ln 2 . 0 8 0
Vậy a + b =10 .
Bài toán 3: Cho hàm số f liên tục trên 0;
1 . Chứng minh rằng: 2 f (sin x) 2 dx = f (cosx)dx (4) 0 0
Lời giải tổng quát 2 0 2
Đặt t = − x thì dt = −dx , khi đó f
(sin x)dx = − f
(cost)dt = f (cosx)dx 2 0 0 2 2 2011 2011 sin x
Ví dụ 3: Tính tích phân: I = dx 2011 2011 2011 2011 + 0 cos x sin x A. B. 1 C. D. 2 4 8 Đáp án C. Lời giải 2 2011 2011 cos x
Sử dụng công thức (4) ta có I = dx 2011 2011 2011 2011 + 0 sin x cos x 2
Từ đây suy ra 2I = 1dx I = . 4 0
** Bài toán 4: (đọc thêm) Cho f là hàm số liên tục trên ;
a b thỏa mãn b b a + b
f ( x) = f (a + b − x) . Chứng minh rằng: xf (x)dx = f
(x)dx (8) 2 a a Đặc biệt xf (sin x)dx = f
(sin x)dx (9). 2 0 0
Lời giải tổng quát
Thực hiện phép biến đổi x = a + b − t thì LOVEBOOK.VN|52 b b b b xf
(x)dx = (a +b −t) f (t)(−dt) = (a +b) f
(x)dx − xf (x)dx a a a a
Từ đó suy ra (8). Chọn a = 0,b = ta có (9). LOVEBOOK.VN|53
Công Phá Toán – Lớp 12 Ngọc Huyền LB A. 3 B. 2 C. 4 D. 6
Bài tập rèn luyện kỹ năng 2 3 cos x
1. Bài toán tính tích phân Câu 7: Tích phân dx bằng sin x 1 4
Câu 1: Biết tích phân = (2 + )1 x I x
e dx = a + be 0 1 − 1 − − ( A. ln 2 B. ln 2
a ;b ) . Khi đó tích .
a b có giá trị bằng 4 4 1 1 A. 1 B. −1 C. 2 D. 3 C. + ln 2 D. − + ln 2 4 4 1 Câu 2: Biết f
(x)dx = 2 và f (x) là hàm số lẻ. 1 2 Câu 8: Tích phân − x xe dx bằng 0 0 0 Khi đó I = f
(x)dx có giá trị bằng e −1 e + 1 e + 1 e −1 1 − A. B. C. D. 2 2e 2 2e A. I =1 B. I = 0 C. I = 2 − D. I = 2 1 x 1
Câu 9: Tính tích phân: dx Câu 3: Tích phân 2
I = x x + 1dx có giá trị bằng x +1 0 0 1 5 A. − ln 2 B. 2ln 2 − 2 2 −1 2 A. I = B. I = 6 3 3 3 4 − 2 2 1 C. D. ln 2 − 2 2 2 C. 3 6 I = D. I = 3 3
Câu 10: Giá trị dương a sao cho 3 x
Câu 4: Cho tích phân a I = dx nếu đặt 2 2 x + 2x + 2 a = + + 1 + x +1 dx a ln 3 là 0 x + 1 2 0 2
t = x +1 thì I = f
(t)dt trong đó A. 5 B. 4 C. 3 D. 2 1 5 dx A. ( ) 2
f t = t + t B. f (t) 2 = 2t + 2t Câu 11: Giả sử = ln c
. Giá trị của c là 2x −1 1 C. ( ) 2
f t = t − t D. f (t ) 2 = 2t − 2t A. 9 B. 3 C. 81 D. 8 1 x 4 3 1 − sin x
Câu 12: Tích phân I = dx có giá trị là
Câu 5: Tính tích phân dx + 0 ( x )3 2 1 sin x 6 1 1 1 1 A. B. C. − D. 3 − 2 3 + 2 − 2 2 8 8 4 A. B. 2 2 1 3 Câu 13: Giả sử f
(t)dt = 5 và f
(r)dr = 6 . Tính 3 + 2 3 + 2 2 − 2 C. D. 1 − 1 − 2 2 3 I = f (u)du a 1 cos 2x 1 Câu 6: Cho I = dx = ln 3 . Tìm giá trị 1 + 2sin 2x 4 A. I = 4 B. I = 3 C. I = 2 D. I =1 0 của a là LOVEBOOK.VN|52
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing e
Câu 14: Tính tích phân I = cos x dx
Câu 23: Tích phân I = 2x
(1−ln x)dx bằng 0 1 A. I = 0 B. I =1 C. I = 2 D. I = 3 2 e −1 2 e 2 e − 3 2 e − 3 A. B. C. D. f ( x) 2 2 4 2 Câu 15: Cho biết 2 t dt = x cos
( x). Tính f (4) . 0
Câu 24: Hàm số nào sau đây không là nguyên hàm x x + 2 A. f (4) = 2 3 B. f (4) = 1 −
của hàm số f ( x) ( ) = ( ? x + )2 1 C. f ( ) 1 4 = D. f ( ) 3 4 = 12 2 2 2 x + x −1 x − x −1 A. + B. + a x 1 x 1
Câu 16: Đẳng thức cos ( 2
x + a ) dx = sin a xảy ra 2 x + x +1 2 x 0 C. + D. nếu x 1 x + 1 1 + A. x 2 a = B. a = Câu 25: Biết
dx = a ln 12 + b ln 7 , 2 x + 4x + 7 0 C. a = 3 D. a = 2
với a, b là các số nguyên. Tính tổng a + b bằng 2 1
Câu 17: Tính tích phân I = . x sin xdx A. −1 B. 1 C. D. 0 2 0 1 A. I = 3 B. I = 2 C. I =1 D. I = 1 − 2 5 dx n 1
Câu 26: Cho x dx = và = ln m , với n, a 64 2x −1 0 1 Câu 18: Nếu x xe dx = 1
thì giá trị của a bằng:
m là các số nguyên dương. Khi đó: 0 + A. 0 B. 1 C. 2 D. e A. n m B. 1 n m 5
C. n m
D. n = m 6 n 1
Câu 19: Nếu sin x cos xdx = thì n bằng 4 dx 64 Câu 27: Biết
= a ln 3+ bln 4 + c ln 5 , với a, 0 2 x + x 3 A. 3 B. 4 C. 5 D. 6
b, c là các số nguyên. Tính S = a + b + c n 1 + 1 A. S = 6 B. S = 2 C. S = 2 − D. S = 0
Câu 20: Giá trị của lim dx bằng →+ 1 x n + e n 1
Câu 28: Kết quả tích phân = (2 +3) x I x e dx A. −1 B. 1 C. e D. 0 0 2
được viết dưới dạng I = ae + b với a, b là các số Câu 21: Tích phân 2 4 − x xdx có giá trị bằng
hữu tỉ. Tìm khẳng định đúng. 0 A. 3 3 a + b = 28
B. a + 2b =1 2 5 8 10 A. B. C. D. 3 3 3 3
C. a − b = 2 D. ab = 3 4 2 sin 2xdx
Câu 22: Tích phân cot . x dx có giá trị bằng
Câu 29: Xét tích phân I = . Nếu đặt 1+ cos x 0 6
t = 1+ cos x , ta được:
A. − ln 2 B. ln 2 C. ln 4 D. ln 2 LOVEBOOK.VN|383
Công Phá Toán – Lớp 12 Ngọc Huyền LB 1 3 4t − 4t 2 A. I = dt B. I = 4 − ( 2t − )1dt t
B. I = − ( x − ) 4 4 1 cos 2x − cos 2xdx 2 1 0 0 1 3 4 − t + 4t 2 C. I = dx D. I = 4 ( 2 x − )1dx t 1 1 = − − + 2 1 C. I (x ) 4 4 1 cos 2x cos 2xdx 2 2 0 0
Câu 30: Có bao nhiêu giá trị của a trong đoạn a sin x 2 ; 2 thỏa mãn dx = . 1 1 4 = − − − 1+ 3cos x 3 D. I (x ) 4 4 1 cos 2x cos 2xdx 0 2 2 0 0 A. 2 B. 1 C. 4 D. 3
Câu 36: Tìm tất cả các số thực m dương thỏa mãn
Câu 31: Cho hàm số g ( x) có đạo hàm trên đoạn m 2 x dx 1 = − ln 2 : −1; 1 . Có g (− ) 1 = 3 và tích phân x +1 2 0 1 A. m = 3 B. m = 2 C. m = 1 D. m 3 I =
g '( x) dx = 2 − . Tính g ( ) 1 . 4 1 − a
Câu 37: Biết I = x ln
(2x+ )1dx = ln3−c , 3 b A. 1 B. −5 C. −6 D. − 0 2
trong đó a, b, c là các số nguyên dương và b là 2 4 x c Câu 32: Cho
f ( x) dx = 3 − , tính I = f dx . = + + 2
phân số tối giản. Tính S a b c . 1 2
A. S = 60 B. S = 70 C. S = 72 D. S = 68 3 A. −6 B. − C. −1 D. 5 2 3 dx b Câu 38: Biết = a ln , với a, b,
Câu 33: Biết rằng: c + ln 2 sin . x sin x 1 1 6 a 5 6 x + dx =
ln 2 + b ln 2 + c ln . Trong 2 x e +1 2 3 0
c là các số nguyên dương và b là phân số tối giản.
đó a, b, c là những số nguyên. Khi đó S = a + b − c c bằng
Tính S = a + b + c . A. 2 B. 3 C. 4 D. 5 A. S = 7 B. S = 8
C. S = 10 D. S = 9
Câu 34: Có bao nhiêu số a (0; 20 ) sao cho
Câu 39: Biết rằng: 2 x 2 x a e .cos 3 . x dx = e
(acos3x +bsin3x) + 2 c , trong 5 sin . x sin 2xdx = . 7
đó a, b, c là các hằng số, khi đó tổng a + b có giá 0 trị là A. 20 B. 19 C. 9 D. 10 1 5 5 1 A. − B. − C. D. 4 13 13 13 13
Câu 35: Cho I = ( x − )
1 sin 2xdx . Tìm đẳng thức 1 0
Câu 40: Biết tích phân = (2 + ) 1 x I x
e dx = a + be , đúng. 0
(a ;b ) . Khi đó tích .ab có giá trị bằng:
A. I = − ( x − ) 4 4 1 cos 2x + cos 2xdx 0 A. 1 B. −1 C. 2 D. 3 0
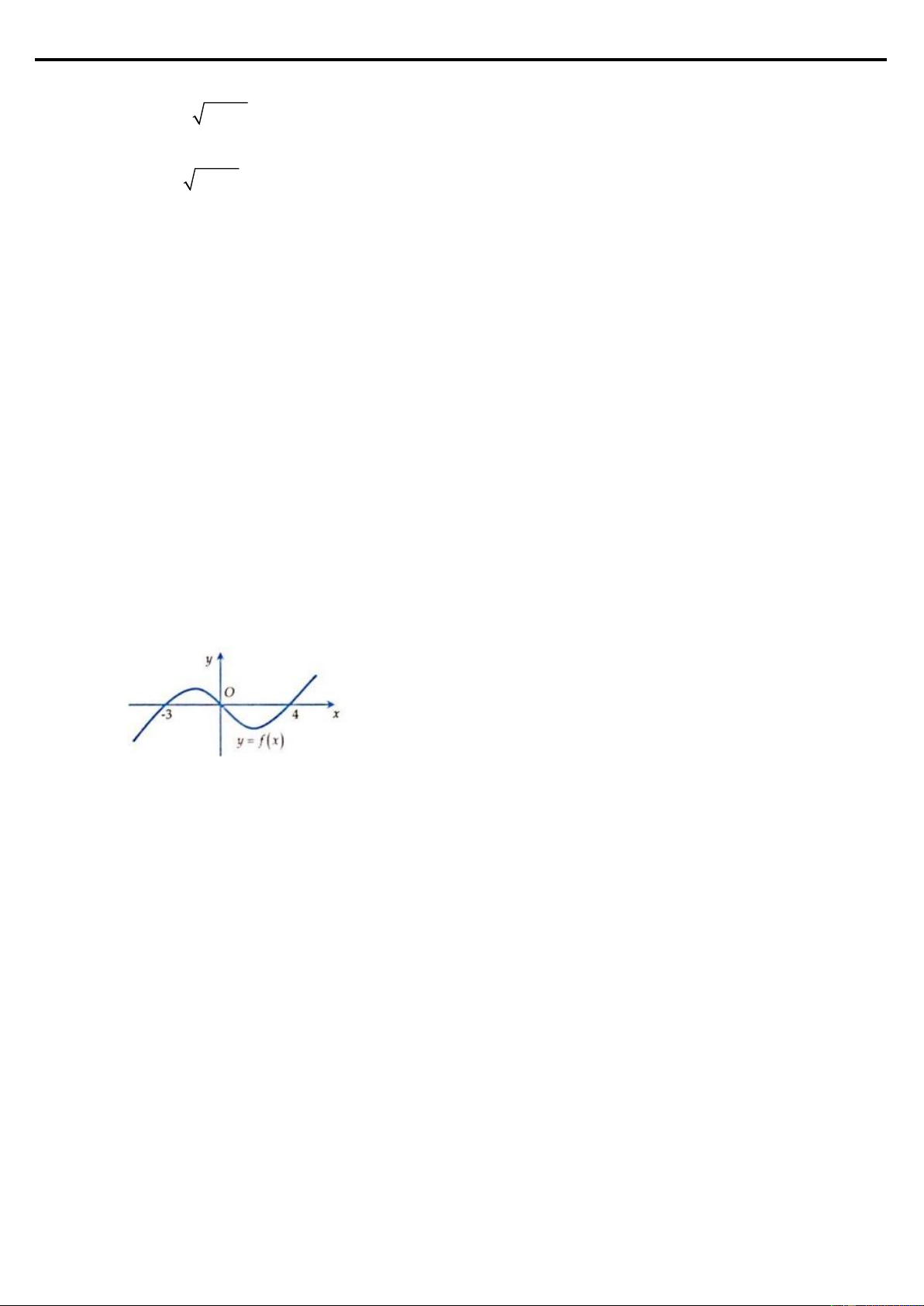
Câu 41: Cho đồ thị hàm số y = f ( x) trên đoạn 0;6 như hình vẽ. LOVEBOOK.VN|384
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing
Câu 2: Thể tích khối tròn xoay tạo thành khi quay
quanh trục Ox hình phẳng được giới hạn bởi đồ thị x
hàm số y = ( − x) 2 2
e và hai trục tọa độ là A. 2 2e −10 B. 2 2e +10
Biểu thức nào dưới đây có giá trị lớn nhất: C. ( 2 2e −10) D. ( 2 2e +10) 1 2 A. f ( x) dx B. f ( x) dx
Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ + 0 0 x 1 thị hàm số y =
và các trục tọa độ. Chọn kết − 3 6 x 2 C. f ( x) dx D. f ( x) dx quả đúng? 0 0 3 5 A. 3ln 6 B. 3ln dx
Câu 42: Tính tích phân: I = được kết 2 x 3x +1 1 3 3 C. 3ln − 2 D. 3ln −1
quả I = a ln 3 + b ln 5 . Giá trị 2 2
a + ab + 3b là 2 2 A. 4 B. 1 C. 0 D. 5
Câu 4: Cho hàm số f ( x) 3 2
= x − 3x + 2x . Tính 6 2 Câu 43: Cho
diện tích S của hình phẳng giới hạn bởi đồ thị hàm f
(x)dx =12. Tính I = f (3x)dx = 0 0 số y
f ( x) , trục tung, trục hoành và đường thẳng A. I = 6
B. I = 36 C. I = 2 D. I = 4 x = 3 2 2 10 12 11 9 Câu 44: Cho f
(x)dx = 2 và g(x)dx = 1 − . A. S = B. S = C. S = D. S = 4 4 4 4 1 − 1 − 2
Câu 5: Tính thể tích của vật thể giới hạn bởi hai Tính I = x + 2 f
(x)−3g (x)dx .
mặt phẳng x = 0 và x = 3 , biết rằng thiết diện của 1 −
vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox 5 7 17 11 A. I = B. I = C. I = D. I =
tại điểm có hoành độ x (0 x 3) là một hình chữ 2 2 2 2 −
nhật có hai kích thước là x và 2 2 9 x . 2 A. 18 B. 19 C. 20 D. 21 Câu 45: Cho f
(x)dx = 5. Tính 0
Câu 6: Tính diện tích hình phẳng S giới hạn bởi đồ thị các hàm số 2x y =
và y = 3 − x , trục hoành và 2 I = f
(x)+2sin x dx . trục tung. 0 5 1 A. S = − B. S = 2 A. I = 7 B. I = 5 + 2 ln 2 2 1 − C. I = 3 D. I = 5 + C. S = 2 D. S = 4 ln 2
2. Ứng dụng của tích phân trong hình học
Câu 7: Công thức tính diện tích S của hình thang
Câu 1: Tính diện tích hình phẳng giới hạn bởi đồ
cong giới hạn bởi hai đồ thị y = f ( x) , y = g ( x) , thị hàm số 2
y = x + 2 và y = 3x :
x = a , x = b , (a b) 1 1 1 A. 1 B. C. D. b 4 6 2
A. S = ( f (x) − g (x))dx a LOVEBOOK.VN|385
Công Phá Toán – Lớp 12 Ngọc Huyền LB b C. 2 V = 2 D. V = 12 B. S = f
(x)− g(x) dx a
Câu 13: Cho hình phẳng D giới hạn bởi đường b cong 2 y =
x +1 , trục hoành và các đường thẳng
C. S = ( f (x) − g (x))2 dx
x =1; x = 0 . Khối tròn xoay tạo thành khi quay D a
quanh trục hoành có thể tích V bằng bao nhiêu? b D. S = ( 2 f ( x) 2
− g (x))dx 4 A. V = B. V = 2 a 3
Câu 8: Diện tích hình phẳng giới hạn bởi đồ thị ( 4 C ) của hàm số 3 2 y = 2
− x + x + x + 5 và đồ thị C. V = D. V = 2 3 (C ') của hàm số 2
y = x − x + 5 bằng
Câu 14: Diện tích hình phẳng giới hạn bởi đồ thị A. 0 B. 1 C. 2 D. 3 1 hàm số y =
, trục hoành và hai đường thẳng x
Câu 9: Tính diện tích hình phẳng giới hạn bởi đồ
x =1, x = e là thị hàm số = ( − ) 2 1 x y x
e , trục hoành và các đường 1
thẳng x = 0 , x = 2 . A. 0 B. 1 C. e D. e 4 2 e e 3 4 2 e e 3 A. + − B. − −
Câu 15: Diện tích hình phẳng giới hạn bởi đường 4 2 4 4 2 4 cong 2
y = 4x và đường thẳng x =1 bằng S. Giá trị 4 2 e e 3 4 2 e e 3 của S là C. + + D. − + 4 2 4 4 2 4 3 8 A. 1 B. C. D. 16
Câu 10: Tính thể tích khối tròn xoay khi cho hình 8 3
phẳng giới hạn bởi đồ thị các hàm số 2
y = x − 2x
Câu 16: Diện tích hình phẳng giới hạn bởi nhánh và 2
y = −x quay quanh trục Ox. đường cong 2
y = x với x 0 , đường thẳng 4 4 1
y = 2 − x và trục hoành bằng A. B. C. D. 3 3 3 3 7 1 5 A. 2 B. C. D.
Câu 11: Cho hình phẳng D giới hạn bởi đường 6 3 6 cong y =
2 + cos x , trục hoành và các đường
Câu 17: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y = ax (a 0) , trục hoành và hai đường
thẳng x = 0 , x =
. Khối tròn xoay tạo thành khi 2 − = 15a
quay D quanh trục hoành có thể tích V bằng bao thẳng x = 1, x
k (k 0) bằng . Tìm k. 4 nhiêu? 1
A. V = −1
B. V = ( − ) 1 − A. k = 1 B. k = 4 C. V = ( + ) 1 D. V = +1 1 C. k = D. 4 k = 14 2
Câu 12: Cho hình phẳng D giới hạn bởi đường cong y =
2 + sin x , trục hoành và các đường
Câu 18: Trong mặt phẳng tọa độ Oxy, cho hình
thang ABCD với A(−1; 2) , B (5;5) , C (5; 0) ,
thẳng x = 0 , x = . Khối tròn xoay tạo thành khi
quay D quanh trục hoành có thể tích V bằng bao
D (−1; 0) . Quay hình thang ABCD xung quanh nhiêu?
trục Ox thì thể tích khối tròn xoay tạo thành bằng
A. V = 2 ( + ) 1
B. V = 2 ( + ) 1 bao nhiêu? A. 72 B. 74 LOVEBOOK.VN|386
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing C. 76 D. 78 LOVEBOOK.VN|387
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing
Hướng dẫn giải chi tiết
1. Bài toán tính tích phân 4 1 4 4
− sin x dx = −cot x + cos x
Câu 1: Đáp án A 2 sin x 6 6 1 1 1 6
= (2 + )1 x = 2 x x I x e dx xe dx + e dx 2 − + 2 3 3 + 2 − 2 0 0 0 = + = . 2 2 2 1 = 2 x xe dx + e −1 Câu 6: Đáp án C 0 x x a cos 2x
1 a cos 2xd 2x 1 a d (sin 2x) e dx = dv v = e Đặt I = dx = = x = u dx = du 1+ 2sin 2x 2 1+ 2sin 2x 2 1+ 2sin 2x 0 0 0 1 1 1
I = 2 udv + e −1 = 2uv − 2 vdu + e −1 0
1 a d (2sin 2x + ) 0 0 1 1 a = = ln 2 + sin 2x +1 1 4 1+ 2sin 2x 4 1 = 0 0 2 . x x x e
− e e dx + e −1 = e +1 0 0 1 2 1 = ln 2sin +1 = ln 3 .
a = b =1 ab =1. 4 a 4 Câu 2: Đáp án C 2 Suy ra: 2sin +1 = 3.
f ( x) là hàm số lẻ a
Trong các đáp án a = 4. 0 1
f (x)dx = − f (x)dx = 2 − Câu 7: Đáp án D 1 − 0 Cách 1: Thử Câu 3: Đáp án A
Cách 2: Đặt sin x = t . 1 2
I = x x +1dx Câu 8: Đáp án D 0
Cách 1: Thử bằng máy tính
Ta thử bằng máy tính để tìm ra kết quả. 1 1 2 2 − x 1 − Câu 4: Đáp án D x
Cách 2: I = . x e dx = − ( 2 − x)e dx 2 0 0 3 x I = dx 1 1 1 −x 1 −x 1 − 1 1+ x +1 2 = − e d ( 2 −x ) 2 1 = − = − + 0 e .e 2 2 2 2 0 0 2
t = x +1 t = x +1 2tdt = dx 1 1 e −1 = − = 3 x (1− x +1) 3 2 2e 2e I = dx =
( x+1− )1dx 1− x +1 Câu 9: Đáp án C 0 ( ) 0
Cách 1: Thử trực tiếp bằng máy tính 2 2 I = 2(t − )
1 tdt = ( 2t − )
1 2dt f (t ) 2 = 2t − 2t
Cách 2: Đặt x +1 = t , biến đổi 1 1 Câu 5: Đáp án B Câu 10: Đáp án D a x + 2x + 2 a ( x + )2 2 1 +1 I = dx = dx x +1 x +1 0 0 LOVEBOOK.VN|387
Công Phá Toán – Lớp 12 Ngọc Huyền LB a 1
Trong 4 phương án, chỉ có phương án D thỏa mãn. = x +1+ d (x + ) 1 x +1 Câu 17: Đáp án C 0
Cách 1: Thử bằng máy tính (x + ) a 2 1 + a (a )2 1 1 = + ln x +1 = − + ln a +1 sin xdx = dv 0 2 2 2
Cách 2: Tích phân thành phần: = 0 x u 2 a Câu 18: Đáp án B = + a + ln a +1 2
Theo như biến đổi câu 1, ta có:
a +1= 3 a = 2. a a a = . x = . x x I x e dx x e − e dx Câu 11: Đáp án B. 0 0 0 Câu 12: Đáp án B. = . a a a e − e +1 =1 Thử máy tính. a =1 1 1 1 Câu 19: Đáp án A Gợi ý: I = − d x +1 2 3 ( ) x +1 x +1 0 ( ) ( ) 6 Câu 13: Đáp án D = sinn I . x cos xdx 3 3 1 0 I = f
(u)du = f
(u)du − f
(u)du = 6−5 =1
Đặt sin x = t . Đổi cận: x = 0 t = 0 1 1 − 1 − 1 Câu 14: Đáp án C x = t = 6 2 2 1 1 I = cos x dx = cos x dx + cos x dx n 1 + 2 n 1 + 2 t n 1 1 1 I = t dt = = . = 0 0 n +1 2 n +1 64 2 0 0 n = 3. 2 = − = 2 cos xdx cos xdx sin x − sin x Câu 20: Đáp án D 0 2 0 2
Cách 1: Thử bằng máy tính =1+1= 2
Lấy giá trị n càng lớn càng tốt. Giả sử n = 100 . Câu 15: Đáp án D 101 1 Nhập biểu thức dx Ta có: 1 x + e 100 f ( x) f ( x) 3 3 t f x f x − 2 ( ) 3 ( ) Máy tính cho kết quả 44 2.35 10 0 . t dt = = = . x cos ( x) 3 3 3 0 0
Cách 2: Giải chi tiết 3 f (4) n 1 + n 1 + n 1 + x n 1 + 1 x e e Thay x = 4 = 4.cos(4 ) I = dx = 1dx − dx = 1− dx 3 1 x + e 1 x + e 1 x + e n n n n 3
f ( ) = f ( ) 3 4 12 4 = 12 . 1 + d ( x n e + ) Câu 16: Đáp 1 án D n 1 + I =1− =1− ln 1 x + e x n + a 1 e n cos ( 2
x + a ) dx = sin a n n 1 0 I 1 ln 1 e ln 1 e + = + + − + ( 2 a + a ) 2 sin
− sin a = sin a LOVEBOOK.VN|388
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing ln (1 n + e ) 2 2 x x − x −1 Ta luôn có lim =1 −1 = + + n→+ n x 1 x 1 n 1 + 1
Ta thấy 3 phương án B, C, D có cùng đạo hàm. lim dx = lim 1 + ln 1 n
+ e − ln + e + x ( n 1 1 ) n→+ 1 n + e →+ Vậy phương án A sai. n ( Câu 25: Đáp án D n + e ) n 1 ln 1 ln 1+ e + =1+ lim .n − .(n + ) 1 1 1 x + 2 1 2x + 4 n→+ n n +1 dx = . dx 2 2 x + 4x + 7 2 x + 4x + 7 = 0 0 1+ n − (n + ) 1 = 0 1 d ( 2 x + 4x + 7 1 ) 1 Câu 21: Đáp án C 1 = . = ln ( 2x +4x+7 2 ) 2 x + 4x + 7 2
Cách 1: Thử bằng máy tính 0 0 1 1 Cách 2: Đặt 2 4 − x = t
= ln12 − ln 7 = ln 12 − ln 7 2 2 Câu 22: Đáp án D a =1;b = 1
− a +b = 0
Cách 1: Thử bằng máy tính Câu 26: Đáp án D 2 2 1 1 n 1 +
Cách 2: Đặt sin x = t I = dt 2 n 1 1 1 1 t x dx = . = n = 3 1 64 2 n +1 64 2 0 Câu 23: Đáp án D 5 5 dx 1 d (2x − ) 5 1 1 = = ln 2x −1 e e e 2x −1 2 2x −1 2 I = 2x
(1−ln x)dx = − 2 .xln xdx+ 2xdx 1 1 1 1 1 1 1 1 = ln 9 − ln1 = ln 3 e 2 2 2 = e −1− 2 . x ln xdx m = n = 3 1 1 Câu 27: Đáp án D dx = du ln x = u 4 4 4 Đặ x t dx 1 1 1 I = = dx = − dx 2 xdx = dv x 2 = x + x x x +1 x x +1 3 3 ( ) v 3 2
= (ln x − ln x +1) 4 = ln 4 − ln5−(ln3− ln 4) e e e e 3
x ln xdx = udv = uv − vdu 1 = −ln3+ 2ln 4−ln5 1 1 1 e = + + = 2 e S a b c 0 x x = ln . x − dx Câu 28: Đáp án B 2 2 1 1 1 1 1 2 2 2 e e 1 e 1
I = (2x + 3) x x x = + = − + = + .e dx 2 . x e dx 3 e dx 2 4 4 4 4 0 0 0 Tương tự 2 2 các bài trên e +1 e − 3 2
I = e −1− = 1 1 2 2 1 . x = . x x x e dx x e − e dx Câu 24: Đáp án A 0 0 0 2 2 1 x x + x +1 1 1 x x x x Dễ nhận thấy +1 = I = 2 . x e + e dx = 2 . x e + e = 3e −1 x +1 x + 1 0 0 0 LOVEBOOK.VN|389
Công Phá Toán – Lớp 12 Ngọc Huyền LB a = 3;b = 1 − 2 2
I = 2 f (t)dt = 2 f (t)dt = 2.( 3 − ) = 6 −
Suy ra, đáp án B: a + 2b =1 1 1 Câu 29: Đáp án D Câu 33: Đáp án C 2 ln 2 ln 2 ln 2
t = 1+ cos x, t 0 t = 1+ cos x 1 2 x e +1− 2 x e x + dx = xdx + dx x x
2tdt = − sin xdx 2e +1 2e +1 0 0 0 Đổi cận: ln 2 ln 2 = (x + ) 2 x e 1 dx − dx 2 x e +1 x = 0 t = 2; x = t =1 0 0 2 ln 2 2 ln 2 d (2 x e x + ) 1 = + x − 2 2 sin 2xdx 2 cos . x sin x 2 2 x e +1 I = = dx 0 0 1+ cos x 1+ cos x 0 0 2 ln 2 ln 2 = + ln 2 − ln 2 x e +1 4( 2 1 t − ) 2 1 t 0 = − 2 dt = 4 (t − ) 2 2 1 dt = 4 ( 2 x − )1dx t 2 2 2 1 1 ln 2 ln 2 5 = + ln 2 − ln 5 + ln 3 = + ln 2 − ln Câu 30: Đáp án A 2 2 3 a
a = 2;b =1;c = 1
− a + b − c = 4 sin x I = dx 1+ 3cos x Câu 34: Đáp án D 0 a a
Đặt 1+ 3cos x = t,t 0 5 6 I = sin .
x sin 2xdx = 2 sin . x cos xdx 0 0 2
t =1+3cos x 2tdt = 3 − sin xdx a a 2 − tdt sin x 2sin a = = 2 sin . x d (sin x) 7 7 6 = = sin xdx 2. 3 7 7 0 0 1+3cos a 1+3cos 2 2 a tdt 2 = = = + I = − = − dt I sin a 1 a k 2 3 t 3 7 2 2 2 1 2 2 = − a 0
+ k2 0 k2 − k − 1+ 3cos a + .2 2 2 4 3 3 1 39 2 a 20
+ 2k 20 k Mà I =
1+ 3cos a =1 cos a = 0 2 4 3
k = 0;1;2;3;4;5;6;7;8;9 Có 10 giá trị của a. 3 a = ; 2 2 Câu 35: Đáp án C Suy ra, đáp án A 1 s in 2xdx = dv
− cos 2x = v Câu 31: Đáp án A Đặ t 2 x −1 = u dx = du 1 I =
g '( x) dx = 2 − g ( ) 1 − g (− ) 1 = 2 − 1 − 4 I = (x − ) 4 4 = = 4 1 sin 2xdx udv uv − vdu g ( ) 1 = 2 − + g (− ) 1 = 2 − + 3 = 1 0 0 0 0 Câu 32: Đáp án A 1 = − (x − ) 4 4 1 1 cos 2x + cos 2xdx Đặ x t
= t dx = 2dt 2 2 2 0 0 LOVEBOOK.VN|390
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing Suy ra, đáp án C. cos x + Câu 36: Đáp án C 3 3 cos x 6 I = 2 dx − 2 dx
Thử các đáp án, suy ra m = 1 sin x sin x + 6 6 6 Câu 37: Đáp án B 4 3 1 3 = − − +
I = x ln (2x + ) 1 dx 2.ln 2 ln 2 ln1 2 ln 2 2 2 0 2 3 3 3 dx = du = − = + = 4 ln 2 ln 2 2 ln 2 ln 2 2 ln ln (2x + ) 1 = u + Đặ 2x 1 2 4 2 t 2 xdx = dv x 1 − = v = + + = S 2 3 2 7 2 8 Câu 37: Đáp án C 4 4 4
I = udv = uv − vdu 2 x 0 2 x e e dx = dv = 0 0 Đặ v t 2 = 4 cos 3x u 2 4 2 x 1 x 1 2 3
− sin 3xdx = du
= − ln 2x +1 − − . dx 2 8 2 8 2x +1 0 = = − 0 I udv uv vdu 4 2 4 63 4x −1 63 1 = 2 x 2 x ln 9 − dx = ln 9 − 2x −1 dx e −e = − 8 4 2x +1 8 4 .cos 3x .3sin 3xdx 0 ( ) ( ) 0 2 2 63 1 2 x = e 3 ln 9 − (x − x)4 63 2 = ln 3 − 3 2 = .cos 3 x x + e .sin 3xdx 8 4 4 2 2 0
a = 63;b = 4;c = 3 S = 63+ 4+ 3 = 70
Đặt sin 3x = u 3cos3xdx = du 1 1 Câu 38: Đáp án A 2 x
e .sin 3xdx = u dv = u v − vdu 1 1 1 3 2 x 2 x 2 x dx e e e 3 I = = .sin 3x − .3.cos 3xdx = .sin 3x − .I 2 2 2 2 sin . x sin x + 6 6 2 x 2 .cos 3 3 x e x
e .sin 3x 3 I = + . − I Ta có: 2 2 2 2 13 x x cos 3 3 sin x + − x sin x +
.cos x − cos x + .sin x 2 I = e + .sin 3x 6 6 6 4 2 4 1 = = sin sin x x 2 cos 3 3 2 6 6 I = e + .sin 3x 13 13 2 3 5 a + b = + = . cos x + 1 1 cos x 13 13 13 6 = . − sin x Câu 40: Đáp án A sin . x sin x + sin sin x + 6 6 6 Câu 41: Đáp án B Câu 42: Đáp án D 5 dx I = x 3x +1 1 LOVEBOOK.VN|391
Công Phá Toán – Lớp 12 Ngọc Huyền LB Đặt 2
3x +1 = t 3x = t 3dx = 2tdt
Đổi cận: x =1 t = 2 x = 5 t = 4 4 4 2 tdt dt I = = 2 2 3 t −1 t −1 t +1 2 2 ( )( ) t 3 4 1 1 = − dt
t −1 t +1 2
= (ln t −1 − ln t +1) 4 = 2ln3− ln5 2 2 2 a = 2;b = 1
− a + ab + 3b = 5 Câu 43: Đáp án D
Đặt t = 3x dt = 3dx . Đổi cận:
x = 0 t = 0; x = 2 t = 6 2 6 6 I = f ( x) 1 dx = f (t) 1 3 dt = f (x)dx 3 3 0 0 0 1 = .12 = 4 3 Câu 44: Đáp án C 2 Ta có I = x + 2 f
(x)−3g (x) d x 1 − 2 2 2 = xdx + 2 f
(x)dx−3 g (x)dx 1 − 1 − 1 − 2 2 x I = + − (− ) 3 17 2.2 3 1 = + 4 + 3 = 2 2 2 1 − Câu 45: Đáp án A Ta có 2 I = f (x) 2 + 2sin x d x = f (x) 2 dx + 2 sin xdx 0 0 0 = − 2 5 2 cos x = 7 0 LOVEBOOK.VN|392
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing
2. Ứng dụng của tích phân trong hình học Câu 6: Đáp án A x Câu 1: Đáp án C Giao điể = − m 2 3 x Nhẩm được nghiệm 1 1 Giao điể 1 x 2 m tại 2
x + 2 = 3x x =1 2 x x 2 S = 2 + x − 3dx = + − 3x 2 ln 2 2 0 0 2 S = x + 2 − 3x dx 2 1 1 1 5 1 = + − 3− = − ln 2 2 ln 2 ln 2 2 2 3 2 x 3x 2 1 2
= x + 2 − 3x dx = − + 2x = Câu 7: Đáp án B 1 3 2 6 1 Câu 8: Đáp án B Câu 2: Đáp án C
Ta xét phương trình hoành độ giao điểm x y = ( − x) 2 2
e cắt trục hoành tại điểm có hoành độ 3 2 2 2
− x + x + x +5 = x − x + 5 bằng 2 x = 0 3 2
− x + 2x = 0 2 = 2 x 1 Thể tích = (2 − ) x V x e dx 0 1 Lúc này ta có 3 S = 2 − x + 2x dx =1
Sử dụng phương pháp tích phân thành phần 1 − V = ( 2 2e −10)
Ta bấm máy và cũng được kết quả như trên: Câu 3: Đáp án D 0 0 x +1 3 S = dx = 1+ dx x − 2 x − 2 1 − 1 − Câu 9: Đáp án A 0 0
= x + 3ln x − 2 1 − 1 −
Xét phương trình hoành độ giao điểm = (x − ) 2x 1+ 3ln 2 − 3ln 3 1 .e
= 0 x = 1. Vậy diện tích hình phẳng
được giới hạn bởi đồ thị hàm số = ( − ) 2 1 . x y x e , 2 3 = 1+ 3ln = 3ln −1 3 2
trục hoành và các đường thẳng x = 0 , x = 2 được tính bởi công thức: Câu 4: Đáp án C 1 2 1 = − ( − ) 2 1 . x + ( − ) 2 1 . x S x e dx x e dx 3 2 S =
x − 3x + 2x dx 0 1 0 0 2 3 = ( − ) 2 1 . x + ( − ) 2 1 . x x e dx x e dx
= (x −3x + 2x) 2 3 2 dx − ( 3 2
x − 3x + 2x)dx 1 1 0 1 0 2 3 Đặt = −1 . x I x e dx ; = −1 x I x e dx 2 ( ) 2 1 ( ) 2 +( 3 2
x − 3x + 2x) dx 1 1 2 x 1 x 1 1 9 11 Đặt 2 2
x −1 = u dx = du;vdv = e dx v = .e = + + = 2 4 4 4 4 b b Câu 5: Đáp án A 1 x 1 Khi đó 2 I = .e .( x − ) 2 1 x − e dx 0 2 2 3 a a 2
V = 2x 9 − x dx = 18 0 LOVEBOOK.VN|393
Công Phá Toán – Lớp 12 Ngọc Huyền LB b b 1
Thể tích khối tròn xoay được tạo nên bởi hình x 1 2 = .e .(x − ) 2 1 − . x e . 2 4
phẳng giới hạn bởi các đường y = 2 + sin x , a a
x = 0 , x = và trục hoành khi quay quanh Ox là: 2 1 1 1 e 3 Vậy từ đây ta có 0 2 I = − − .e − .e = − . 1 2 4 4 4 4
V = (2 + sin x) dx = (2x − cos x) = 2 ( + ) 1 x 0 4 2 0 1 1 1 e e 4 4 2 I = .e − .e − .e = + 2 (đvtt). 2 4 4 4 4 Câu 13: Đáp án A 4 2 e e 3
Suy ra I = I + I = + − 1 2
Thể tích khối tròn xoay được tạo nên bởi hình 4 2 4 phẳng giới hạn bởi các đường Câu 10: Đáp án C 2 y =
x +1, x = 0, x = 1 và trục hoành khi quay
Xét phương trình hoành độ giao điểm quanh Ox là: x = 0 2 2
x − 2x = −x 1 1 3 x =1 x V = x + dx = + x = (đvtt). x ( 4 2 )1 3 3 Khi đó thể 0
tích khối tròn xoay có được khi quay 0
hình phẳng giới hạn bởi các đồ thị hàm số Câu 14: Đáp án B 2 2 e e y = x − 2 ;
x y = −x quay quanh trục Ox được tính 1 1 e Ta có S = dx = dx = ln x = 1 . 1 bởi công thức x x 1 1 1 Câu 15: Đáp án C
V = (x − 2x)2 −(−x )2 2 2 dx
Ta có: Phương trình tung độ giao điểm 0 2 2 2 y Ta thấy trên 0; 1 thì ( 2 −x ) ( 2
x − 2x) , do vậy =1 y = 2 4 ta có công thức 2 2 2 3 1 y y 4 4 8 4
= − = − = − − =
V = −x + S 1 dy y . ( 4 3 2
x − 4x + 4x ) d x 4 12 3 3 3 2 − − 0 2 Câu 16: Đáp án B ( 4x 4x ) 1 1 4 3 2 4 3 dx = − + = . −x + x = (đvtt) 3 3
Xét phương trình hoành độ giao điểm: 0 0 Câu 11: Đáp án C 2 2
x = 2 − x x + x − 2 = 0 x =1 hoặc x = 2 − (loại vì x 0 ).
Thể tích khối tròn xoay được tạo nên bởi hình 1
phẳng giới hạn bởi các đường y = 2 + cos x , 7 Ta có 2 S =
x − (2 − x) dx = 6 0 x = 0 , x =
và trục hoành khi quay quanh Ox là: 2 Câu 17: Đáp án D 2
V = (2 + cos x) dx = (2x + sin x) 2 = ( + ) 1 x 0 0 (đvtt). Câu 12: Đáp án B LOVEBOOK.VN|394
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing Ta thấy hàm số 3
y = ax , (a 0) luôn đồng biến trên
và có tâm đối xứng là O (0;0) . Hình vẽ
minh họa ở bên ta thấy với x ( 1 − ;0) thì 3 ax 0 ,
với x (0; k ) thì 3 ax 0 . k 15a Vậy 3 S = ax dx = 4 1 − 0 ( k 15a 3 −ax ) 3 dx + ax dx = 4 1 − 0 0 k 4 4 −ax ax 15a + = (Do k 0 ). 4 4 4 1 − 0 4 a ak 15a 4 4 + =
k =14 k = 14 4 4 4 (vì k 0 ). Câu 18: Đáp án D
Phương trình đường thẳng AB là: x +1 y − 2 1 5 = y = x + 5 +1 5 − 2 2 2
Thể tích khối tròn xoay là: 5 5 2 1 5 2 V = f (x)dx = x + dx = 78 2 2 1 − 1 − LOVEBOOK.VN|395
Công Phá Toán – Lớp 12 Ngọc Huyền LB
IX. Ứng dụng nguyên hàm, tích phân trong thực tế
Ví dụ 1: Một ô tô đang chạy với vận tốc 10m/s thì tài xế đạp phanh; từ thời điểm
đó, ô tô chuyển động chậm dần đều với vận tốc v (t) = −5t +10 (m/s), trong đó t là
khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh
đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 0,2 m B. 2 m C. 10 m D. 20 m Lời giải Đáp án C.
Nguyên hàm của hàm vận tốc chính là quãng đường s (t ) mà ô tô đi được sau
quãng đường t giây kể từ lúc tài xế đạp phanh xe.
Vào thời điểm người lái xe bắt đầu đạp phanh ứng với t = 0 .
Thời điểm ô tô dừng lại ứng với t , khi đó v (t = 0 t = 2 . 1 ) 1 1
Vậy từ lúc đạp phanh đến khi dừng lại quãng đường ô tô đi được là: STUDY TIP 2 2 Hàm số thể hiện quãng − s =
đường vật đi được tính ( 5 − t +10) 5 2 dt = t +10t =10m 2 0 0
theo thời gian là biểu thức nguyên hàm của hàm số
Ví dụ 2: Một chiếc ô tô đang đi trên đường với vận tốc v (t ) = 2 t (0 t 30) vận tốc.
(m/s). Giả sử tại thời điểm t = 0 thì s = 0 . Phương trình thể hiện quãng đường
theo thời gian ô tô đi được là 4 4 A. 3 s =
t (m) B. s = 2 t (m) C. 3 s =
t (m) D. s = 2t (m) 3 3 Đáp án A. Lời giải 1 3 STUDY TIP Tương tự 1 4
như ở ví dụ 1 thì ta có s (t ) 3 2 2
= 2 tdt = 2 t dt = 2. .t = . t
Biểu thức gia tốc là đạo (m) 1 3 +1
hàm cấp một của biểu thức 2
vận tốc, và là đạo hàm cấp
hai của biểu thức quãng
Ví dụ 3: Một vật chuyển động với vận tốc đầu bằng 0, vận tốc biến đổi theo quy đường.
luật, và có gia tốc a = 0,3 (m/s2). Xác định quãng đường vật đó đi được trong 40 phút đầu tiên. A. 12000m B. 240 m C. 864000 m D. 3200 m Đáp án C. Phân tích
Nhận thấy bài toán này khác với hai ví dụ trên ở chỗ bài toán cho biểu thức gia tốc
mà không cho biểu thức vận tốc, ở đây ta có thêm một kiến thức như sau: LOVEBOOK.VN|396
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing
Biểu thức gia tốc là đạo hàm của biểu thức vận tốc, đến đây, kết hợp với 2 ví dụ
đầu ta kết luận: “Biểu thức gia tốc là đạo hàm cấp một của biểu thức vận tốc, và là
đạo hàm cấp hai của biểu thức quãng đường”. Từ đây ta có lời giải: Lời giải
Ta có v (t ) = 0,3dt = 0,3t
(do ban đầu vận tốc của vật bằng 0).
Vậy quãng đường vật đi được trong 40 phút đầu tiên là: 40.60 2400 0,3 2 0,3tdt = .t = 864000 (m) 2 0 0 LOVEBOOK.VN|397
Công Phá Toán – Lớp 12 Ngọc Huyền LB
Bài tập rèn luyện kỹ năng
trong đó t là khoảng thời gian tính bằng giây, kể từ
lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến
khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét?
Câu 1: Một vật chuyển động với vận tốc thay đổi A. 20m B. 10 m C. 22,5m D. 5m
theo thời gian được tính bởi công thức v (t ) = 3t + 2
Câu 6: Cho chuyển động thẳng xác định bởi
, thời gian tính theo đơn vị giây, quãng đường vật đi được tính theo đơn vị = − +
m. Biết tại thời điểm t = 2s phương trình 3 S 2t
t 1 , trong đó t được tính
thì vật đi được quãng đường là 10m. Hỏi tại thời
bằng giây và S được tính bằng mét. Gia tốc của điể =
m t = 30s thì vật đi được quãng đường là bao chuyển động khi t 2s là: nhiêu? A. 63 m/s2 B. 64 m/s2
A. 1410 m B. 1140 m C. 300 m D. 240 m C. 23 m/s2 D. 24 m/s2
Câu 2: Một tàu lửa đang chạy với vận tốc 200 m/s
Câu 7: Cho một vật chuyển động có phương trình
thì người lái tàu đạp phanh; từ thời điểm đó, tàu là:
chuyển động chậm dần đều với vận tốc 2 3 = − +
v (t ) = 200 − 20t (m/s). Trong đó t là khoảng thời s 2t
3 (t được tính bằng giây, S tính bằng t
gian tính bằng giây, kể từ lúc bắt đầu đạp phanh.
mét). Vận tốc của chuyển động thẳng t = 2s là:
Hỏi thời gian khi tàu đi được quãng đường 750 m 49
(kể từ lúc bắt đầu đạp phanh) ít hơn bao nhiêu giây A. 3 m/s B. m/s 2
so với lúc tàu dừng hẳn? 47 A. 5 s B. 8 s C. 15 s D. 10 s C. 12 m/s D. m/s 2
Câu 3: Giả sử một vật từ trạng thái nghỉ khi t = 0
Câu 8: Cho chuyển động thẳng xác định bởi
(s) chuyển động thẳng với vận tốc v (t ) = t (5 − t ) phương trình 4
S = 2t − t +1 , trong đó t được tính
(m/s). Tìm quãng đường vật đi được cho đến khi nó
bằng giây và S được tính bằng mét. Vận tốc của dừng lại.
chuyển động khi t = 1s là: 125 125 A. (m) B. (m) A. 24 m/s B. 23 m/s C. 7 m/s D. 8 m/s 12 9
Câu 9: Một chiếc ôtô sẽ chạy trên đường với vận 125 125 = C. (m) D. (m)
tốc tăng dần đều với vận tốc v 10t (m/s) t là 3 6
khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
Câu 4: Một người đi xe đạp dự định trong buổi
chạy. Hỏi quãng đường xe phải đi là bao nhiêu từ
lúc xe bắt đầu chạy đến khi đạt vận tốc 20 (m/s)?
sáng đi hết quãng đường 60 km. Khi đi đượ 1 c 2 A. 10m B. 20m C. 30m D. 40m
quãng đường, anh ta thấy vận tốc của mình chỉ
Câu 10: Một ôtô đang chạy với vận tốc 19m/s thì 2 ngườ bằng
vận tốc dự định, anh ta bèn đạp nhanh hơn
i lái hãm phanh, ôtô chuyển động chậm dần 3
đều với vận tốc v (t) = 38
− t +19 (m/s), trong đó t là
vận tốc dự định 3km/h, đến nơi anh ta vẫn chậm
khoảng thời gian tính bằng giây kể từ lúc bắt đầu
mất 45 phút. Hỏi vận tốc dự định của người đi xe đạ
hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng p là bao nhiêu?
hẳn, ôtô còn di chuyển bao nhiêu mét? A. 5km/h B. 12km/h A. 4,75m B. 4,5m C. 4,25m D. 5m C. 7km/h D. 18 km/h
Câu 11: Một ô tô đang chạy đều với vận tốc 15 m/s
Câu 5: Một ôtô đang chạy với vận tốc 10 m/s thì
thì phía trước xuất hiện chướng ngại vật nên người
người lái đạp phanh; từ thời điểm đó, ôtô chuyển
lái đạp phanh gấp. Kể từ thời điểm đó, ô tô chuyể
động chậm dần đều với vận tốc v = 5 − t +15 (m/s),
động chậm dần đều với gia tốc a − m/s2. Biết ô tô LOVEBOOK.VN|398
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing
chuyển động thêm được 20 m thì dừng hẳn. Hỏi a
hoành. Tính quãng đường s mà vật di chuyển được
thuộc khoảng nào dưới đây:
trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm) A. (3; 4) B. (4;5) C. (5;6) D. (6;7)
Câu 12: Bổ dọc một quả dưa hấu ta được thiết diện
là hình elip có trục lớn là 28cm, trục nhỏ 25cm.
Biết cứ 1000cm3 dưa hấu sẽ làm được cốc sinh tố
giá 20.000 đ. Hỏi từ quả dưa như trên có thể thu
được bao nhiêu tiền từ việc bán nước sinh tố? (Biết
rằng bề dày của vỏ dưa không đáng kể, kết quả đã được quy tròn) A. 183.000 đ B. 180.000 đ C. 185.000 đ D. 190.000 đ
A. s = 23, 25 (km)
B. s = 21,58 (km)
Câu 13: Một viên đạn được bắn theo phương thẳng đứ
C. s =15,50 (km)
D. s =13,83 (km)
ng với vận tốc ban đầu 29,4 m/s. Gia tốc trọng
trường là 9,8 m/s2. Tính quãng đường S viên đạn đi
Câu 17: Một vật chuyển động trong 3 giờ với vận
được từ lúc bắn lên cho đến khi chạm đất.
tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là
A. S = 88, 2m
B. S = 88,5m
một phần của đường parabol có đỉnh I (2;9) và C. S = 88 m D. S = 89 m
trục đối xứng song song với trục tung như hình
dưới. Tính quãng đường s mà vật di chuyển được
Câu 14: Một chất điểm đang chuyển động với vận trong 3 giờ đó.
tốc v = 15 m/s thì tăng vận tốc với gia tốc 0 a (t ) 2
= t + 4t (m/s2). Tính quãng đường chất điểm
đó đi được trong khoảng thời gian 3 giây kể từ lúc
bắt đầu tăng vận tốc. A. 68,25 m B. 70,25 m C. 69,75 m D. 67,25 m
Câu 15: Một ca nô đang chạy trên Hồ Tây với vận
tốc 20 m/s thì hết xăng. Từ thời điểm đó, ca nô
chuyển động chậm dần đều với vận tốc
v (t ) = −5t + 20 m/s, trong đó t là khoảng thời gian
A. s = 24, 25 (km)
B. s = 26, 75 (km)
tính bằng giây, kể từ lúc hết xăng. Hỏi từ lúc hết
xăng đến lúc dừng hẳn, ca nô đi được bao nhiêu
C. s = 24, 75 (km)
D. s = 25, 25 (km) mét?
Câu 18: Một người chạy trong thời gian 1 giờ, vận A. 10 m B. 20 m C. 30 m D. 40 m
tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là
Câu 16: Một vật chuyển động trong 3 giờ với vận 1
một phần của đường thẳng parabol với I ;8 và
tốc (km/h) phụ thuộc thời gian t (h) có đồ thị của 2
vận tốc như hình dưới. Trong khoảng thời gian 1
trục đối xứng song song với trục tung như hình bên.
giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một
Tính quãng đường s người đó chạy được trong
phần của đường parabol có đỉnh I (2;9) và trục đối
khoảng thời gian 45 phút, kể từ khi bắt đầu chạy
xứng song song với trục tung, khoảng thời gian còn
lại đồ thị là một đoạn thẳng song song với trục LOVEBOOK.VN|399
Công Phá Toán – Lớp 12 Ngọc Huyền LB
A. s = 4, 0 (km) B. s = 2,3 (km)
C. s = 4,5 (km) D. s = 5,3 (km) LOVEBOOK.VN|400
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing
Hướng dẫn giải chi tiết Câu 1: Đáp án A
Quãng đường vật đi từ lúc đạp phanh cho đến lúc dừng hẳn = ( ) = ( t + ) 2 3t S v t dt 3 2 dt = + 2t + c − + = = 2 5t 15 0 t 3 3 0 2 5 − t S ( ) 2 3.2 2 = 10
+ 2.2 + c =10 c = 0 . ( 5
− t +15)dt = +15t 2 2 3 0 2 3t S = + 2t . 5 2 = − − .3 +15.3 = 22,5 (m) 2 2
Suy ra: Khi t = 30 s, vật đi được quãng đường Câu 6: Đáp án D 2 3.30 2 s = + 2.30 =1410 m.
v = s ' = 6t −1 2
a = v ' =12t Câu 2: Đáp án A Khi t = a = ( 2 2 24 m / s )
Khi tàu dừng hẳn: v = 0 t =10 (s). Câu 7: Đáp án B S = v
(t)dt = ( − t) 2
200 2 dt s = 200t − t 2 = = +
t = 15 10 loai Ta có 2 v s ' 6t 2 2
S = 750 200t −10t = 750 t t = 5 2 49 Với 2
t = 2 v = 6.2 + = t =10 −5 = 5 (s). 2 2 2 Câu 3: Đáp án D Câu 8: Đáp án C = ( − Ta có 3
v = s ' = 8t −1 t ) 2 3 5t t S t 5 dt S = − 2 3
Khi t = 1 v = 8 −1 = 7 (m / s) .
Khi vật dừng lại v = t (5 − t ) = 0 t = 5 . Câu 9: Đáp án B 2 3 3 2 Khi đó 5.5 5 5 125 = = S = − = = (m) . s 10tdt s 5t . 2 3 6 6 = = = = Câu 4: Đáp án B Khi 2 v 20m / s t 2 s 5.2 20m . Câu 10: Đáp án A
Vận tốc dự định là v (km / h) . Khi ô tô dừng lại hẳn Thời gian đi nửa quãng đường đầu 1 30 45
v = 0 19 − 38t = 0 t = t = = h . 1 ( ) 2 2 v v 3 s = ( − t) 2
19 38 dt s = 19t −19t 30
Thời gian đi nửa quãng đường sau t = 1 1 1 19 2 t = s =19. −19. = = 4,75(m) v + . 3 2 2 4 4 Ta có phương trình Câu 11: Đáp án C 60 45 30 60 t + t = − 0,75 + = + 0,75
Từ giả thiết ta có v = (−a)dt v =15 − at 1 2 v v v + 3 v
Giải phương trình suy ra: v = 12 km/h. at Mà s = vdt = ( − at) 2 15
dt s = 15t − Câu 5: Đáp án C 2 LOVEBOOK.VN|401
Công Phá Toán – Lớp 12 Ngọc Huyền LB
Ô tô chuyển động được 20m thì dừng tại thời điểm Ta có: t 1 v = a
(t)dt = ( 2t + 4t)dt Suy ra 3 t 2 1 5 − at = 0 = + + at = 15 v 15 2t 1 1 v = 0 3 2 at 15t 1 1 s = 20 15t − = 20 15t − = 20 4 3 t 2t 1 1 2 2
Mà s = vdt s = 15t + + . 12 3 at =15 1 45
Sau 3 giây, chất điểm đi được quãng đường: a = a (5;6 8 ) t = 8 4 3 1 3 2.3 3 s (3) = 15.3 + + = 69,75(m) . 12 3 Câu 12: Đáp án A Câu 15: Đáp án D
Khi dừng hẳn v = 0 (m / s) t = 4(s) .
Phương trình quãng đường đi được của ca - nô từ khi hết xăng = ( − t) 2 5t s
20 5 dt s = 20t − 2
Tại t = 4 s = 40
Suy ra: ca - nô đi được 40 mét
Giả sử thiết diện nằm trên hệ Oxy, tâm O trùng với Câu 16: Đáp án B tâm thiết diện
Ta tìm được phương trình của parabol là 2 2 x y 5 Suy ra elip: +
=1. Thể tích quả dưa hấu (P):v(t) 2
= − t + 5t + 4 . 2 2 14 12, 5 4
chính là thể tích vật thể thu được khi quay phần = − + + =
gạch chéo quanh trục Ox.
Khi t =1 thì v ( ) 5 31 1 5 4 (km/h). 4 4 14 2 x 8750 2 V = 12,5 1− dx = 5 2 − + + 2 t 5t 4 khi 0 t 1 14 3 14 − 4
Vậy v (t ) = 31 Số tiền thu được là: khi 1 t 3 4 8750 20000. 183259 183.000 đ.
Vậy quãng đường mà vật di chuyển được trong 3 3.1000 giờ là: Câu 13: Đáp án A 1 5 31 73 31
Ta có công thức liên hệ giữa vận tốc, gia tốc và 2 s =
− t + 5t + 4 dt + .2 = + quãng đường đi đượ 4 4 12 2 c là 2 2
v − v = 2as 0 0 259 = 21,58(km) 2 2 2 v − v 0 − 29, 4 0 s = = = 44,1 12 2a 2 − .9,8 Câu 17: Đáp án C
Quãng đường đi được từ lúc bắn đến khi chạm đất
Ta tìm được phương trình của parabol là
là s = 44,1.2 = 88, 2 (m) (P) 3 2 : y = − x + 3x + 6 Câu 14: Đáp án C 4 LOVEBOOK.VN|402
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing
Như vậy, quãng đường s mà vật di chuyển được trong 3 giờ là: 3 3 3 2 3 x 3x 2 s =
− x + 3x + 6 dx = − + + 6x 4 4 2 0 0 99 = = 24,75(km) 4 Câu 18: Đáp án C
Ta tìm được phương trình của parabol là (P) v(t) 2 : = 32 − t + 32t
Quãng đường s mà người đó chạy được trong
khoảng thời gian 0,75 (h) là:
s = (−32t + 32t) 0,75 0,75 32 2 3 2 dt = − t +16t 3 0 0 = 4,5(km) LOVEBOOK.VN|403
Công Phá Toán – Lớp 12 Ngọc Huyền LB
X. Tổng ôn tập chủ đề 3
Quý độc giả vui lòng khai báo sách chính hãng tại web: congphatoan.com để nhận được đáp án chi tiết. BÀI KIỂM TRA SỐ 1 Câu 1: Nguyên hàm của hàm số 2 2 2 2 A. I = tdt B. 2 I = t dt
f ( x) = 2sin x + cos x là 3 3 1 1 A. 2
− cos x −sin x +C B. 2
− cos x +sin x +C 2 2 14 C. 3 I = t D. I =
C. 2cos x − sin x + C
D. 2cos x − sin x + C 9 9 1
Câu 2: Biết F ( x) là một nguyên hàm của hàm số e 3 a e +1 Câu 7: Biết 3 x ln xdx =
(a,b ) . Mệnh b f ( x) 1 =
F 0 = 2 . Tính F ( ) 1 1 x + và ( ) 1
đề nào sau đây đúng? A. F ( ) 1 = ln 2 − 2 B. F ( ) 1 1 = A. ab = 48 B. ab = 64 2
C. a − b = 20
D. a − b =12 C. F ( ) 1 = ln 2 + 2 D. F ( ) 1 = 2
Câu 8: Cho 0 b d a c và hàm số f ( x) b liên tục trên thỏa mãn
Câu 3: Giá trị nào của b để (2x − 6)dx = 0 ? d d ln e 1 f
(x)dx =10, f (x)dx =8 , x e f ( xe)dx = 7 .
A. b = 5 hoặc b = 0
B. b = 0 hoặc b = 3 a b ln a
C. b = 0 hoặc b =1
D. b =1 hoặc b = 5 ln c Tính x I = e f ( xe)dx e 2 x + 2 ln x ln b
Câu 4: Giá trị của tích phân I = dx là x − 1 A. I = 5 B. I = 5 2 e −1 2 e +1 C. I = 7 D. c b
I = e − e A. 2 e +1 B. 2 e C. D. 2 2
Câu 9: Nguyên hàm của hàm số ( ) = + 2x f x x là
Câu 5: Tìm nguyên hàm của hàm số x f ( x) 3 = x + sin 2x A. f (x) 2 dx = 1+ + C ln 2 x x A. (x + x) 4 3 sin 2 dx = − cos 2x + C x = + + 4 B. f (x) 2 2 dx C 2 ln 2 x 1
B. (x + sin 2x) 4 3 dx = + cos 2x + C x x = + + 4 2 C. f (x) 2 dx 2 ln 2 C 2 x C. (x + x) 4 3 sin 2 dx = + cos 2x + C x x = + + 4 D. f (x) 2 dx 2 C 2 x 1
D. (x + sin 2x) 4 3 dx = − cos 2x + C
Câu 10: Biết một nguyên hàm của hàm số 4 2
y = f ( x) là F ( x) 2
= x + 4x +1. Khi đó, giá trị của e 1+ 3ln x =
Câu 6: Cho tích phân y f x x = I = dx và đặt hàm số ( ) tại 3 là x 1 A. f (3) = 30 B. f (3) = 6
t = 1+ 3ln x . Mệnh đề nào dưới đây sai? C. f (3) = 22 D. f (3) = 10 LOVEBOOK.VN|404
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing e a c a
Câu 14: Một ô tô đang dừng và bắt đầu chuyển Câu 11: Biết rằng 2 3 x ln xdx = e + , với và b d b
động theo một đường thẳng với gia tốc 1 a (t ) = − c 6
2t (m/s2), trong đó t là khoảng thời gian
là hai phân số tối giản. Khi đó, a c + bằng bao d b d
tính bằng giây kể từ lúc ô tô bắt đầu chuyển động. nhiêu?
Hỏi quãng đường ô tô đi được kể từ lúc bắt đầu
chuyển động đến khi vận tốc của ô tô đạt giá trị a c 1 a c 1 A. + = B. + =
lớn nhất là bao nhiêu mét? b d 3 b d 9 45 a c 1 a c 1 A. 18 mét B. mét C. + = − D. + = − 2 b d 9 b d 3 27
Câu 12: Trong không gian với hệ tọa độ Oxyz, cho C. 36 mét D. mét 4
vật thể ( H ) giới hạn bởi hai mặt phẳng có phương
Câu 15: Tìm nguyên hàm của hàm số
trình x = a và x = b (a b) . ( ) 1 x f x = x + sin 2 2 1 x A. f (x) 2 dx = x + cos + C 2 2 1 1 x B. f (x) 2 dx = x − cos + C 4 4 2 1 x = − +
Gọi S ( x) là diện tích thiết diện của ( H ) bị cắt C. f (x) 2 dx x cos C 4 2
bởi mặt phẳng vuông góc với trục Ox tại điểm có 1 1 x hoành độ = − +
là x, với a x b . Giả sử hàm số D. f (x) 2 dx x cos C 4 2 2
y = S ( x) liên tục trên đoạn a;b . Khi đó, thể tích 2 x 2 = − = +
V của vật thể ( H ) được tính bởi công thức
Câu 16: Biết I
(3x )1e dx a be , với a, b 0 b b
là các số nguyên. Tính S = a + b .
A. V = S
(x) 2 dx
B. V = S
(x) 2 dx a a
A. S = 12 B. S = 8
C. S = 16 D. S = 10 b b
Câu 17: Biết F ( x) là một nguyên hàm của hàm
C. V = S (x)dx D. V = S (x)dx a a số ( ) 2
f x = xe và F (0) = 1 − . Tính F (4) .
Câu 13: Cho hàm số y = f ( x) liên tục trên và A. F ( ) 2 4 = 4e − 3 B. F (4) = 3
thỏa mãn f ( x) + f (−x) = 3 − 2 cos x , với mọi 7 3 C. F ( ) 2 4 = 4e + 3 D. F (4) 2 = e − 2 4 4 x
. Khi đó, giá trị của tích phân I = f (x)dx 2 − 1 = 2 Câu 18: Xét I dx
. Đẳng thức nào sau đây 2 x bằng bao nhiêu? 1 là đúng? 3 A. I = + 2 B. I = − 2 2 2 2 1 1 1 A. I = =1− = −1 +1 x 2 2 1 C. I = D. I = 3 2 LOVEBOOK.VN|405
Công Phá Toán – Lớp 12 Ngọc Huyền LB 2 1 1 1 B. I = − = − −1 = 4 1 x 2 2 B. I = dt 1 a 0 2 C. 2 I = ln x = ln 4 C. 2 2 2
a + x = a ( 2 1+ tan t ) 1 2 1 1
D. dx = a ( 2 1+ tan t ) dt D. I = − = − = 1 − x 2 −1 1 2 ln x ln 6
Câu 23: Tính tích phân I = dx dx 3
Câu 19: Biết I = = 3ln a − ln b với x 1 x e + 2 x e− − 3 ln 3 3 + 2 ln 2 3 − 2 ln 2
a, b là các số nguyên dương. Tính P = ab . A. I = B. I = 16 16 A. P = 15 B. P = 10 2 + ln 2 − = 2 ln 2 = C. P = 20 D. P = 10 − C. I D. I 16 16
Câu 20: Tìm nguyên hàm của hàm số 5 2 x + x +1 b Câu 24: Biết dx = a + ln với a, b là f ( x) 1 = . x +1 2 2 3 sin 2x
các số nguyên. Tính S = a − 2b . A. f (x) 1 dx = cot 2x + C A. S = 10 B. S = 5 2 C. S = 2 D. S = 2 − B. f
(x)dx = 2cot2x +C
Câu 25: Cho hình thang cong ( H ) giới hạn bởi C. f (x)dx = 2 − cot 2x + C các đườ 1 1 ng y = , x =
, x = 2 và trục hoành. x 2 D. f (x) 1
dx = − cot 2x + C 2 Đườ 1 ng thẳng x = k k 2 chia (H ) thành 2
Câu 21: Tìm nguyên hàm của hàm số
hai phần có diện tích là S và S như hình vẽ dưới 1 2 f ( x) 1 = 2 sin 2x
đây. Tìm tất cả giá trị thực của k để S = 3S . 1 2 A. ( ) = ( − ) 1 x f x dx x e + C B. ( ) 2 x
f x dx = x e + C C. ( ) x
f x dx = xe + C D. ( ) = ( + ) 1 x f x dx x e + C a dx 7 Câu 22: Cho I = a 0 và đặt A. k = B. k = 3 2 2 ( ) a + x 5 0
x = a tan t . Trong các mệnh đề sau đây, mệnh đề C. k = 1 D. k = 2
nào là mệnh đề sai? 1 a 1 Câu 26: Cho f (x)dx = 9. A. I = dt 0 a 0 6 Tính I = f
(sin3x).cos3xdx. 0 LOVEBOOK.VN|406
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing A. I = 3 B. I = 5 C. I = 2 D. I = 9
Câu 32: Cho n là số tự nhiên sao cho 1 n 1 −
Câu 27: Xét I = x ( x − )5 3 4 4
3 dx . Bằng cách đặt
( 2x − )1 xdx = . Tính tích phân 20 0 4
u = 4x − 3 , đẳng thức nào sau đây đúng? 2 1 1 n A. 5 I = u du B. 5 I = u du sin x cos xdx . 4 12 0 1 1 1 1 1 C. 5 I = u du D. 5 I = u du A. B. C. D. 16 10 15 5 20 ln m x e dx 2 Câu 28: Cho = ln 2
. Khi đó giá trị của m
Câu 33: Tính 2xdx . Chọn kết quả đúng. x e + 2 0 1 − là A. 6 B. −3 C. 3 D. −6 1 A. m = B. m = 2 dx 2 Câu 34: Tìm ta được 2x +1 C. m = 4
D. m = 0, m = 4 1 1 A. ln 2x +1 + C B. ln (2x + ) 1 + C
Câu 29: Tìm nguyên hàm F ( x) của hàm số 2 2 ( ) x ( 2 1 3 x f x e e− = − ) 2
C. ln 2x +1 + C D. − + ( C 2x + )2 1 A. ( ) x 3 = − 3 − x F x e e + C
Câu 35: Cho biết F ( x) là một nghiệm nguyên B. ( ) x = + 3 −x F x e e + C
của hàm số f ( x) . Tìm I = 3 f
(x)+1dx . C. ( ) x = − 3 −x F x e e + C
A. I = 3xF ( x) +1+ C D. ( ) x 2 = + 3 − x F x e e + C
B. I = 3F ( x) +1+ C e
Câu 30: Tính tích phân ( x + ) 1 ln xdx
C. I = 3F ( x) + x + C 1 2 = + + e + 5 2 e − 5 D. I
3xF ( x) x C A. B. 4 4
Câu 36: Một vật chuyển động với vận tốc v (t ) có 2 e + 5 2 e − 5 = + C. D.
gia tốc là a (t ) 2 3t
t (m/s2). Vận tốc ban đầu 2 4
của vật là 2 (m/s). Hỏi vận tốc của vật sau 2s bằng
Câu 31: Gọi F ( x) là một nguyên hàm của hàm số bao nhiêu? A. 12 m/s B. 10 m/s
f ( x) = cos 5x cos x thỏa mãn F = 0 . Tính 3 C. 8 m/s D. 16 m/s 1 F . + = + 6 Câu 37: Cho ln
(x )1dx a lnb , (a,b ) . 0 3 3 3 b A. B. 0 C. D. Tính (a + 3) . 12 8 6 1 1 A. 25 B. C. 16 D. 9 7
Câu 38: Diện tích hình phẳng trong hình vẽ sau là LOVEBOOK.VN|407
Công Phá Toán – Lớp 12 Ngọc Huyền LB 1 f ( x) Câu 44: Cho dx = 4 trong đó hàm số 1+ 2x 1 −
y = f ( x) là hàm số chẵn trên −1; 1 , khi đó 1 f
(x)dx bằng 1 − 16 22 10 A. B. C. D. 2 3 3 3 A. 2 B. 16 C. 4 D. 8
Câu 45: Mệnh đề nào dưới đây đúng?
Câu 39: Một nguyên hàm của hàm số y = x là 2 x e 3 1 A. 2 x e dx = + C B. 2 x 2 x e dx = e + C A. x x B. 2 2 2 x 2 x 1 e + 2 2 C. 2 x 2 = 2 x e dx e + C D. 2 x e dx = + C C. x x D. x 2x +1 3 3 5 dx
Câu 40: Cho F ( x) là một nguyên hàm của hàm Câu 46: Giả sử = ln K . Tìm K. 2x −1 1
số f ( x) . Khi đó hiệu số F ( ) 1 − F (2) bằng
A. K = 3 B. K = 9
C. K = 81 D. K = 8 2 2 4 A. f ( x) dx B. − f (x)dx
Câu 47: Cho I = x 1+ 2xdx
và u = 2x +1 . 1 1 0 1 2
Mệnh đề nào dưới đây sai? C. −F (x)dx D. −F (x)dx 3 2 1 5 3 1 u u = −
Câu 41: Diện tích hình phẳng giới hạn bởi đồ thị A. I 2 5 3 1 hàm số 2
y = x và đường thẳng y = 2x bằng 3 1 2 2 23 4 5 3 B. I = u (u − )1du A. B. C. D. 2 15 3 3 2 1 3
Câu 42: Trong các khẳng định sau, khẳng định C. 2 I = u ( 2 u − )1du nào sai? 1
A. dx = x + 2C (C là hằng số) 298 D. I = 15 n 1 x + B. n x dx = + C
(C là hằng số; n )
Câu 48: Tính thể tích V của phần vật thể giới hạn n +1
bởi hai mặt phẳng x = 0 và x = 3 , biết rằng thiết
C. 0dx = C (C là hằng số)
diện của vật thể cắt bởi mặt phẳng vuông góc với
trục Ox tại điểm có hoành độ x (0 x 3) là một D. x x
e dx = e − C (C là hằng số)
hình chữ nhật có hai kích thước là x và 2 2 9 − x . Câu 43: Cho f
(x)dx = F (x)+C . Khi đó với 3 A. 2
V = 2x 9 − x dx a 0 , ta có f
(ax +b)dx bằng 0
A. F (ax + b) + C
B. aF (ax + b) + C 3 B. V = 4 ( 2 9 − x ) dx 1 1 0 C.
F (ax + b) + C
F ax + b + C a + D. ( ) b a LOVEBOOK.VN|408
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing 3 C. V = 2( 2
x + 2 9 − x )dx 0 3 D. V = ( 2
x + 2 9 − x )dx 0
Câu 49: Sau khi phát hiện một bệnh dịch, các
chuyên gia y tế ước tính số người nhiễm bệnh kể
từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ
t được tính theo công thức f (t ) 2 3 = 45t − t ,
0 t 25 . Nếu coi f (t ) là hàm số xác định trên
đoạn 0;25 thì đạo hàm f '(t) được xem là tốc
độ truyền bệnh (người/ngày) tại thời điểm t. Xác
định ngày mà tốc độ truyền bệnh là lớn nhất? A. Ngày thứ 16 B. Ngày thứ 15 C. Ngày thứ 5 D. Ngày thứ 19
Câu 50: Cho đồ thị hàm số y = f ( x) đi qua gốc
tọa độ O, ngoài ra còn cắt trục Ox tại các điểm có
hoành độ lần lượt bằng −3 và 4 như hình bên. Tính
diện tích S của hình phẳng giới hạn bởi đồ thị hàm số và trục Ox. 4 A. S = f (x)dx 3 − 3 − 4 B. S = f
(x)dx+ f (x)dx 0 0 0 4 C. S = f
(x)dx+ f (x)dx 3 − 0 0 0 D. S = f
(x)dx+ f (x)dx 3 − 4 LOVEBOOK.VN|409
Công Phá Toán – Lớp 12 Ngọc Huyền LB BÀI KIỂM TRA SỐ 2
Câu 1: Tìm họ nguyên hàm của hàm số
(II ): k.F (x) là một nguyên hàm của kf (x)
f ( x) = sin 2x (k ) . A. sin 2xdx = 2 − cos 2x + C
(III ) : F (x).G(x) là một nguyên hàm của 1
f ( x).g ( x) . Những mệnh đề nào là mệnh đề đúng?
B. sin 2xdx = − cos 2x + C 2
A. ( I ) và ( II )
B. ( I ),( II ) và ( III )
C. sin 2xdx = 2 cos 2x + C C. ( II ) D. ( I ) 1 D. sin 2xdx = cos 2x + C 5 2 2 Câu 6: Cho f
(x)dx = 3. Tính I = f (3x− ) 1 dx . e 2 1
Câu 2: Cho tích phân I = 4 x (1+ln x) 2 dx = . a e + b 1 1 A. I = B. I =1 3
; với a, b là các số nguyên. Tính M = ab + 4 (a + b) . C. I = 9 D. I = 3 A. M = 5 − B. M = 2 −
Câu 7: Cho hình phẳng ( H ) giới hạn bởi các C. M = 5 D. M = 6 − đường 2
y = x , y = 0, x = 0, x = 4 . Đường thẳng
Câu 3: Cho m là số thực dương thỏa mãn m = x 3 y
k (0 k 16) chia hình ( H ) thành hai phần có ( dx =
. Mệnh đề nào sau đây là đúng? 1+ x )3 2 16
diện tích S , S (hình vẽ). 0 1 2 7 3 A. m 3; B. m 0; 2 2 3 7 C. m ;3 D. m ;5 2 2
Câu 4: Cho hàm số f ( x) = 2x + sin x + 2 cos x . Tìm
nguyên hàm F ( x) của hàm số f ( x) thỏa mãn F (0) = 1.
Tìm k để S = S . A. 2
x + cos x + 2sin x − 2 1 2 A. k = 3 B. k = 8 C. k = 4 D. k = 5
B. 2 + cos x + 2sin x x C. 2
x − cos x + 2sin x
Câu 8: Tìm nguyên hàm của hàm số f ( x) 2 = tan . 3 D. 2
x − cos x + 2sin x + 2 x A. f
(x)dx = −x+3tan +C
Câu 5: Cho hai hàm số f ( x), g ( x) là hàm số liên 3
tục trên R, có F ( x),G ( x) lần lượt là một nguyên x B. f
(x)dx = x−3tan +C
hàm của f ( x), g ( x) . Xét các mệnh đề sau 3 ( 1 x
I ) : F ( x) + G ( x) là một nguyên hàm của C. f (x) 3 dx = tan + C 3 3
f ( x) + g ( x) LOVEBOOK.VN|410
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing x 3 x 4 D. f
(x)dx = 3tan +C A. 3 + 3ln x + x + C 3 3 3
Câu 9: Hàm số nào sau đây không phải nguyên 3 x 4 B. 3 + 3ln x − x
hàm của hàm số f ( x) 1 = 3 3 2x + ? 1 3 x 4 3
A. F ( x) = ln 2x +1 +1 C. + 3ln x − x 3 3 3 B. F ( x) 1 = ln 2x +1 + 2 x 4 3 − − + 2 D. 3ln x x C 3 3 2 C. F ( x) 1 = ln 4x + 2 + 3 2x +1 2 Câu 14: Nguyên hàm dx bằng 2 x +1 1
D. F ( x) = ln ( 2 4x + 4x + ) 1 + 3 2 + 4 1 x A. + C B. 2
x 1+ x + C x
Câu 10: Một trường THPT dự định xây một bồn
hoa hình tròn có đường kính AB =10m. Để tạo ấn 2 + + + 1 x + tượng ngườ C. 2 2 x 1 x C D. C
i thiết kế đã tạo ra hai hình tròn nhỏ 2 x
trong hình tròn lớn bằng cách lấy điểm M giữa A và dx
B rồi dựng các hình tròn đường kính MA, MB. Trong
Câu 15: Nguyên hàm bằng 2 tan x +1
hai hình tròn nhỏ nhà trường dự định trồng hoa hồng
đỏ và phần còn lại trồng hoa hồng vàng. Biết giá x 2 A.
+ ln 2sin x + cos x + C
mỗi gốc hồng đó là 5000 đồng, giá mỗi gốc hồng 5 5
vàng là 4000 đồng và ít nhất 2
0, 5m mới trồng được 2x 1 B.
− ln 2sin x + cos x + C
một gốc hồng. Hỏi chi phí thấp nhất để trồng bồn 5 5 hoa là bao nhiêu? x 1 C.
− ln 2sin x + cos x + C A. 622000 đồng B. 702000 đồng 5 5 C. 706858 đồng D. 752000 đồng x 1 D.
+ ln 2sin x + cos x + C 2 5 5
Câu 11: Giả sử (2x − )
1 ln xdx = a ln 2 + b với a, b 10 1 (x − 2)
là số thực. Khi đó a + b bằng
Câu 16: Nguyên hàm ( bằng x + ) dx 12 1 5 3 A. B. 2 C. 1 D. 11 − − 11 − 2 2 1 x 2 1 x 2 A. . + C B. . + C 11 x +1 3 x +1 Câu 12: Cho f
(x)dx = F (x)+C , khi đó với a 11 11 1 x − 2 1 x − 2 khác 0 ta có f
(ax +b) bằng C. . + C D. . + C 11 x +1 33 x +1
A. F (ax + b) + C
B. aF (ax + b) + C sin 4x Câu 17: Nguyên hàm dx bằng 1 1 sin x + cos x C.
F (ax + b) + C D.
F (ax + b) + C a 2a 2 3 A. − cos 3x + − 2 cos x + + C
Câu 13: Tìm nguyên hàm của hàm số 3 4 4 3 2 x + − 2 x dx . 2 3 x B. − sin 3x + − 2 sin x + + C 3 4 4 LOVEBOOK.VN|411
Công Phá Toán – Lớp 12 Ngọc Huyền LB 2 3
Câu 22: Cho hàm số f ( x) có đạo hàm trên đoạn C. − sin 3x + + 2 sin x + + C 3 4 4 4
−1;4 , f (4) = 2017 , f '
(x)dx = 2016 . Tính 2 3 1 − D. − sin 3x + + 2 cos x + + C 3 4 4 f (− ) 1 . 2 x −1 A. f (− ) 1 = 3 B. f (− ) 1 = 1
Câu 18: Nguyên hàm bằng x ( dx 2 x + ) 1 C. f (− ) 1 = −1 D. f (− ) 1 = 2 1 1 A. ln x − + C B. ln x − + C
Câu 23: Biết F ( x) là một nguyên hàm của hàm số 2 x x f ( x) 3 1 1 = sin .
x cos x và F (0) = . Tìm F . C. ln x + + C D. 2 ln x − + C 2 x x 1 3 = − = − + 2x +1 A. F B. F
Câu 19: Nguyên hàm bằng 2 2 4 x ( dx 3 x − ) 1 1 C. F = + D. F = 1 1 2 4 2 A. 2 ln x − + C B. 2 ln x + + C x x
Câu 24: Tìm nguyên hàm của hàm số ( ) 2x f x = e 1 1 C. ln x − + C D. ln x + + C 2 A. ( ) 2 = + x 2 x 2 x f x dx e C 2 x sin x 1 x = + Câu 20: Nguyên hàm dx bằng B. f (x) 2 dx e C 3 cos x 2 2 = + x C. ( ) 2 x f x dx e C A.
− x tan x + ln cos x + C 2 2 cos x D. ( ) 2 x
f x dx = e ln 2 + C 2 x B.
+ x tan x − ln cos x + C
Câu 25: Một công ty quảng cáo X muốn làm một 2 2 cos x
bức tranh trang trí hình MNEIF ở chính giữa của 2 x
một bức tường hình chữ nhật ABCD có chiều cao C.
− x tan x − ln cos x + C 2 2 cos x
BC = 6 m , chiều dài CD =12 m (hình vẽ bên). Cho = 2
biết MNEF là hình chữ nhật có MN 4 m ; cung x D.
+ x tan x + ln cos x + C 2
EIF có hình dạng là một phần của cung parabol có 2 cos x
đỉnh I là trung điểm của cạnh AB và đi qua hai điểm
Câu 21: Cho f ( x) là một hàm số chẵn, liên tục
C, D. Kinh phí làm bức tranh là 900.000 đồng / m2. 2 1
Hỏi công ty X cần bao nhiêu tiền để làm bức tranh trên và f
(x)dx = 2. Tính f (2x)dx . đó? 2 − 0 1 1 A. f (2x)dx = 2 B. f (2x)dx = 4 0 0 1 1 1 C.
f (2x) dx = D. f (2x)dx =1 2 0 0 LOVEBOOK.VN|412
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing A. 20.400.000 đồng B. 20.600.000 đồng D. ( ) 2 = 2 x f x dx e + C C. 20.800.000 đồng D. 21.200.000 đồng Câu 30: Tìm các hàm số f ( x) biết
Câu 26: Cho hình thang cong ( H ) giới hạn bởi các (x) cos x f ' = đườ 1 ng y =
, y = 0, x = 1, x = 5 . Đường thẳng x = k (2+sin x)2 x
(1 k 5) chia (H ) thành hai phần là (S và sin x 1 )
A. f ( x) = + C ( (2+sin x)2 S
(hình vẽ bên). Cho hai hình (S và (S quay 2 ) 1 ) 2 )
quanh trục Ox ta thu được hai khối tròn xoay có thể B. f ( x) 1 = + C
tích lần lượt là V và V . Xác định k để V = 2V . 2 + cos x 1 2 1 2 x C. f ( x) sin = + C 2 + sin x D. f ( x) 1 = − + C 2 + sin x
Câu 31: Tìm nguyên hàm của hàm số ( ) 2x f x = . A. ( ) 1 .2x f x dx x − = + C 15 5 A. k = B. k = B. ( ) = 2x f x dx ln 2 + C 7 3 x+ C. 3 k = 25 D. k = ln 5 C. f (x) 1 2 dx = + C x +1 2
Câu 27: Biết rằng ln
(x+ )1dx = aln3+bln2+c x 1 D. f (x) 2 dx = + C
với a, b, c là các số nguyên. Tính S = a + b + c . ln 2 1 A. S = 0 B. S = 1
Câu 32: Với mỗi số tự nhiên n, ta đặt: n x I = x e dx . n C. S = 2 D. S = 2 − 0
Mệnh đề nào sau đây đúng?
Câu 28: Cho hàm số f ( x) liên tục trên và
A. I = 2e − n − I
B. I = e + nI n ( ) 1 9 n 1 − n n 1 −
F ( x) là nguyên hàm của f ( x) , biết f (x)dx = 9
C. I = 2 − nI
D. I = −e + n + I n ( ) 1 0 n n 1 − n 1 −
và F (0) = 3. Tính F (9) .
Câu 33: Cho hàm số y = f ( x) liên tục trên và là A. F (9) = 6 − B. F (9) = 6 3 hàm số chẵn. Biết rằng f (x)dx = 3 , C. F (9) = 12 D. F (9) = 12 − 0 0 f (y) =
Câu 29: Tìm nguyên hàm của hàm số ( ) 2x f x = e dx
7 . Tính giá trị của tích phân 4 − 4 A. ( ) 2 1 2 x f x dx xe − = I = f (t)dt . x 3 e B. f (x) 2 dx = + C 2 A. I = 10 B. I = 4 x 7 e + C. I = D. I = 21 C. f (x) 2 1 dx = + C 3 2x +1 LOVEBOOK.VN|413
Công Phá Toán – Lớp 12 Ngọc Huyền LB 1 dx b
Câu 34: Tính tích phân I = B.
f ( x).g '( x) dx 2 x + 4x + 3 0 a 3 1 3 b b A. I = ln B. I = ln = f
( x).g ( x) + f '
(x).g(x)dx 2 3 2 a a 1 3 1 3 b C. I = − ln D. I = ln 2 2 2 2 C.
f ( x).g '( x) dx a
Câu 35: Viết công thức tính diện tích S của hình b
phẳng D giới hạn bởi hai đồ thị hàm số y = f ( x) , = f
( x) g ( x) b − f '
(x).g(x)dx a
y = g ( x) liên tục trên đoạn a;b và các đường a b
thẳng x = a , x = b . D.
f ( x).g '( x) dx b a
A. S = f
(x)− g(x) dx b b a = f
( x).g ( x) + f
(x).g'(x)dx a b a B. S = f
(x)− g(x) dx
Câu 39: Tính nguyên hàm ( − ) 3 2 1 x x e dx a b x x −
C. S = ( f (x) − g (x) )dx 2x 1 e e x 2 A. (2x − ) ( ) 3 3 3 1 e dx = − + C a 3 9 b 2x −1 x e e x 2 x D. S = f
(x)− g(x) dx B. (2x − ) ( ) 3 3 3 1 e dx = − + C 3 3 a
Câu 36: Tính diện tích hình phẳng giới hạn bởi các x 1 C. (2 − ) 3 1 = ( 2 − ) 3x x e dx x x e + C 3 đườ x ng y =
, x = 3 và các trục tọa độ? x +1 D. ( − ) 3 = ( 2 − ) 3 2 1 x x x e dx x x e + C 8 10 7 A. B. 3 C. D.
Câu 40: Một vật chuyển động với vận tốc thay đổi 3 3 3
theo thời gian được tính bởi công thức v (t ) = 3t + 2 , 2 x
thời gian tính theo đơn vị giây, quãng đường vật đi
Câu 37: Cho hàm số G ( x) = cos tdt . Đạo hàm
được tính theo đơn vị m. Biết tại thời điểm t = 2s 0
của hàm số G ( x) là
thì vật đi được quãng đường là 10m. Hỏi tại thời
điểm t = 30 s thì vật đi được quãng đường là bao
A. G '( x) = 2x cos x
B. G '( x) = 2x cos x nhiêu?
C. G '( x) = x cos x
D. G '( x) = 2x sin x
A. 1410 m B. 1140 m C. 300 m D. 240 m
Câu 41: Tìm nguyên hàm của F ( x) của hàm số
Câu 38: Cho các hàm số f ( x), g ( x) có đạo hàm
f ( x) = 3x + 4 , biết F (0) = 8.
liên tục trên đoạn a;b . Khi đó b A. F ( x) 1 38 = 3x + 4 + A.
f ( x).g '( x) dx 3 3 a 2 16 = + + + b B. F ( x) (3x 4) 3x 4 = 3 3 f ( x) b
.g ( x) − f '
(x).g '(x)dx a a 2 56
C. F ( x) = (3x + 4) 3x + 4 + 9 9 LOVEBOOK.VN|414
Chủ đề 3: Nguyên hàm – tích phân và ứng dụng The best or nothing 2 8
D. F ( x) = (3x + 4) 3x + 4 + 4 3 3 Giá trị của I = f
(cos2x)sin xdx bằng
Câu 42: Tính diện tích hình phẳng giới hạn bởi đồ 0 thị hàm số 2
y = 2 − x và y = x . 1 1 1 1 A. B. C. − D. − 2 4 2 4 9 11 A. 5 B. 7 C. D. = 2 2
Câu 49: Xét hàm số y
f ( x) liên tục trên miền D = ; a b
Câu 43: Kí hiệu ( H ) là hình phẳng giới hạn bởi đồ
có đồ thị là một đường cong C. Gọi S là = = thị hàm số 2
y = 2x − x và y = 0 . Tính thể tích vật
phần giới hạn bởi C và các đường thẳng x ; a x b . Ngườ
thể tròn xoay được sinh ra bởi hình phẳng đó khi nó
i ta chứng minh được rằng diện tích mặt cong quay quanh trục Ox.
tròn xoay tạo thành khi xoay S quanh Ox bằng b 17 16 18 19 S = f ( x) + ( f (x))2 2 1 ' dx . A. B. C. D. 15 15 15 15 a 2
Theo kết quả trên, tổng diện tích bề mặt của khối x
Câu 44: Parabol y =
chia hình tròn có tâm tại
tròn xoay tạo thành khi xoay phần hình phẳng giới 2 x − x
gốc tọa độ, bán kính 2 2 thành 2 phần, tỉ số diện
hạn bởi đồ thị hàm số f ( x) 2 2 ln = và các 4
tích của chúng thuộc khoảng nào?
đường thẳng x =1; x = e quanh Ox là A. (0, 7;0,8) B. (0,5;0, 6) 2 2e −1 4 4e − 9 A. B. C. (0, 6;0, 7) D. (0, 4;0,5) 8 64 4 2 4e +16e + 7 4 4e − 9 6 C. D. n 1 Câu 45: Nếu sin . x cos xdx =
(n ) thì n 16 16 64 0
Câu 50: Diện tích hình phẳng giới hạn bởi hàm số bằng 2 2 y = x
x +1 , trục Ox và đường thẳng x = 1 bằng A. 3 B. 4 C. 5 D. 6
a b − ln (1+ b )
Câu 46: Nguyên hàm của hàm số 2 y = cos . x sin x là
với a, b, c là các số nguyên dương. c 1 A. 3 cos x + C B. 3 −cos x +C
Khi đó giá trị của a + b + c là 3 A. 11 B. 12 C. 13 D. 1 1 1 C. 3 − cos x + C D. 3 sin x + C 3 3
Câu 47: Cho f ( x) liên tục trên đoạn 0;10 thỏa 10 6 mãn f
(x)dx = 7; f
(x)dx = 3. Khi đó giá trị của 0 2 2 10 biểu thức P = f
(x)dx+ f (x)dx là 0 0 A. 10 B. 4 C. 3 D. −4 1 Câu 48: Cho f (x)dx = 2. 0 LOVEBOOK.VN|415
Công Phá Toán – Lớp 12 Ngọc Huyền LB LOVEBOOK.VN|86




