Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

Toán 9 Bài 1:
Một số hệ thức về cạnh và đường cao trong tam giác vuông
I. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
* Phát biểu: Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của
cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
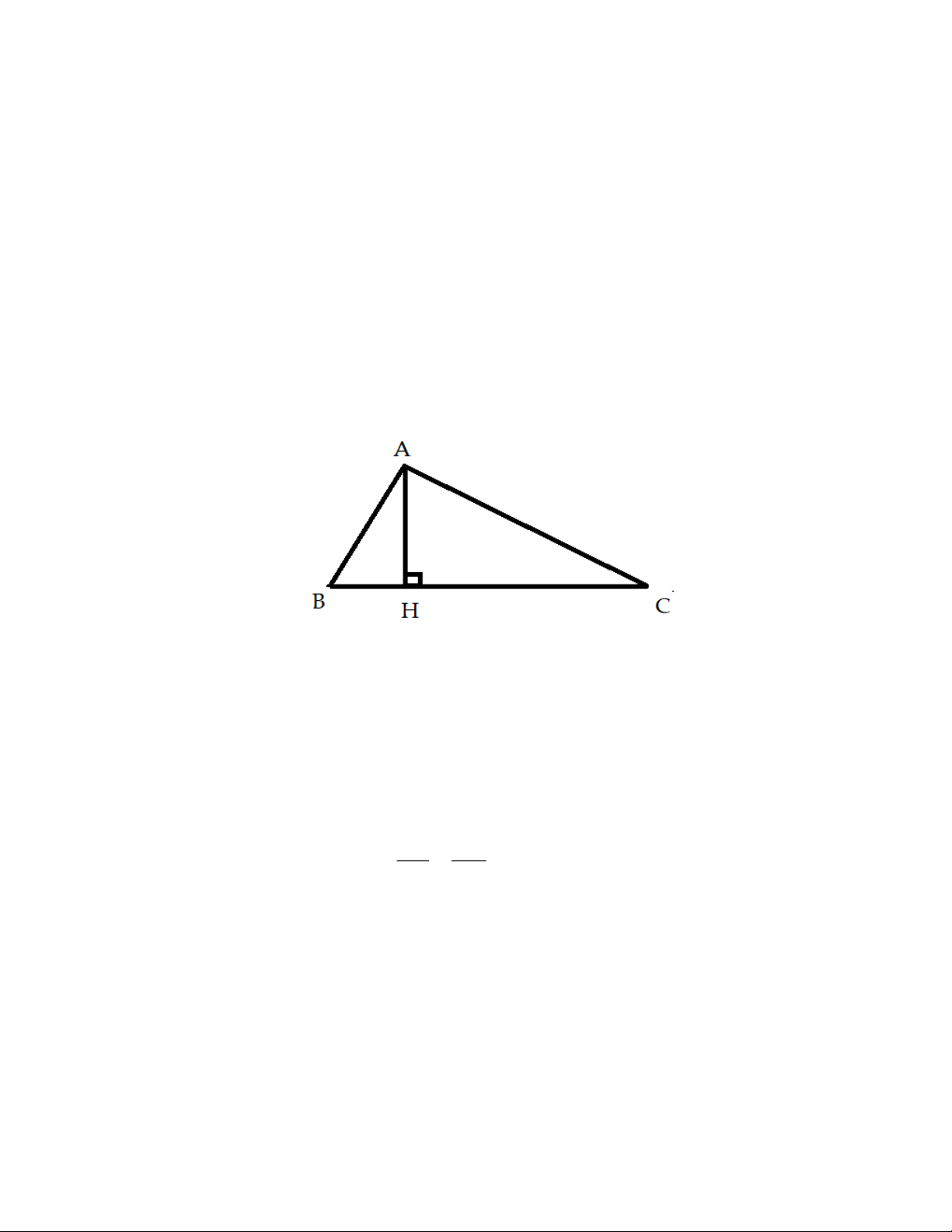
* Bài toán: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng 2
AB  BH.BC và 2
AC  CH.CB  Chứng minh: + Xét ABH  và C  BA có: ABC chung AHB  BAC  0  90  AB BH Suy ra AB  H ~ C  BA (g.g)  
(cặp cạnh tương ứng tỉ lệ) BC AB 2
 AB  BH.BC (đpcm)
II. Một số hệ thức liên quan tới đường cao 1. Định lí 1
* Phát biểu: Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền
bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
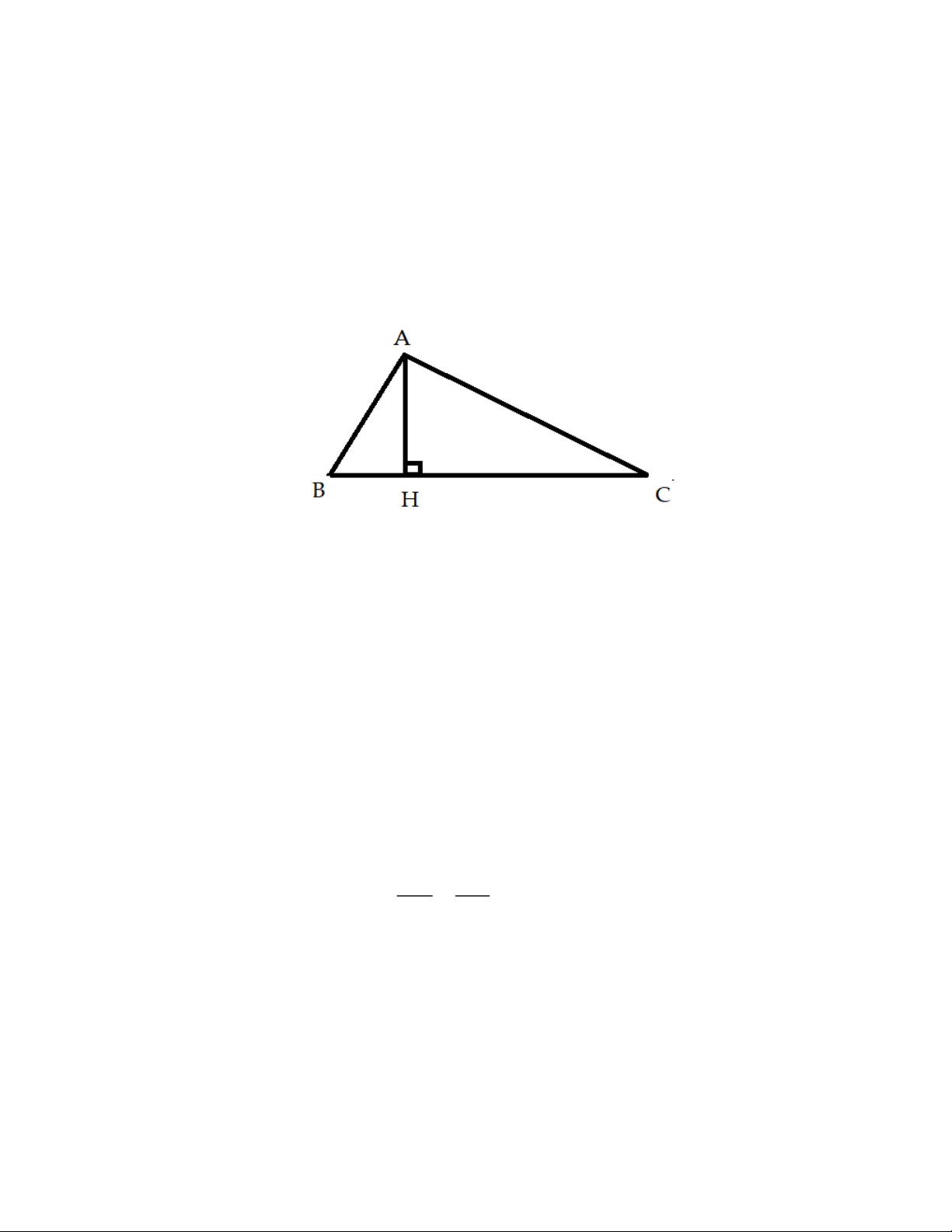
* Bài toán: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng 2
AH  BH.CH  Chứng minh: + Xét ABH  và C  BA có: ABC chung AHB  BAC  0  90  Suy ra AB  H ~ C
 BA (g.g)  BAH  BCA (cặp góc tương ứng tỉ lệ)
+ Xét AHC và B  HA có:
BAH  BCA(cmt) AHB  AHC  0  90  AH HC Suy ra AH  C ~ BH  A (g.g)  
(cặp cạnh tương ứng tỉ lệ) BH HA 2
 AH  BH.CH (đpcm) 2. Định lý 2
* Phát biểu: Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh
huyền và đường cao tương ứng.
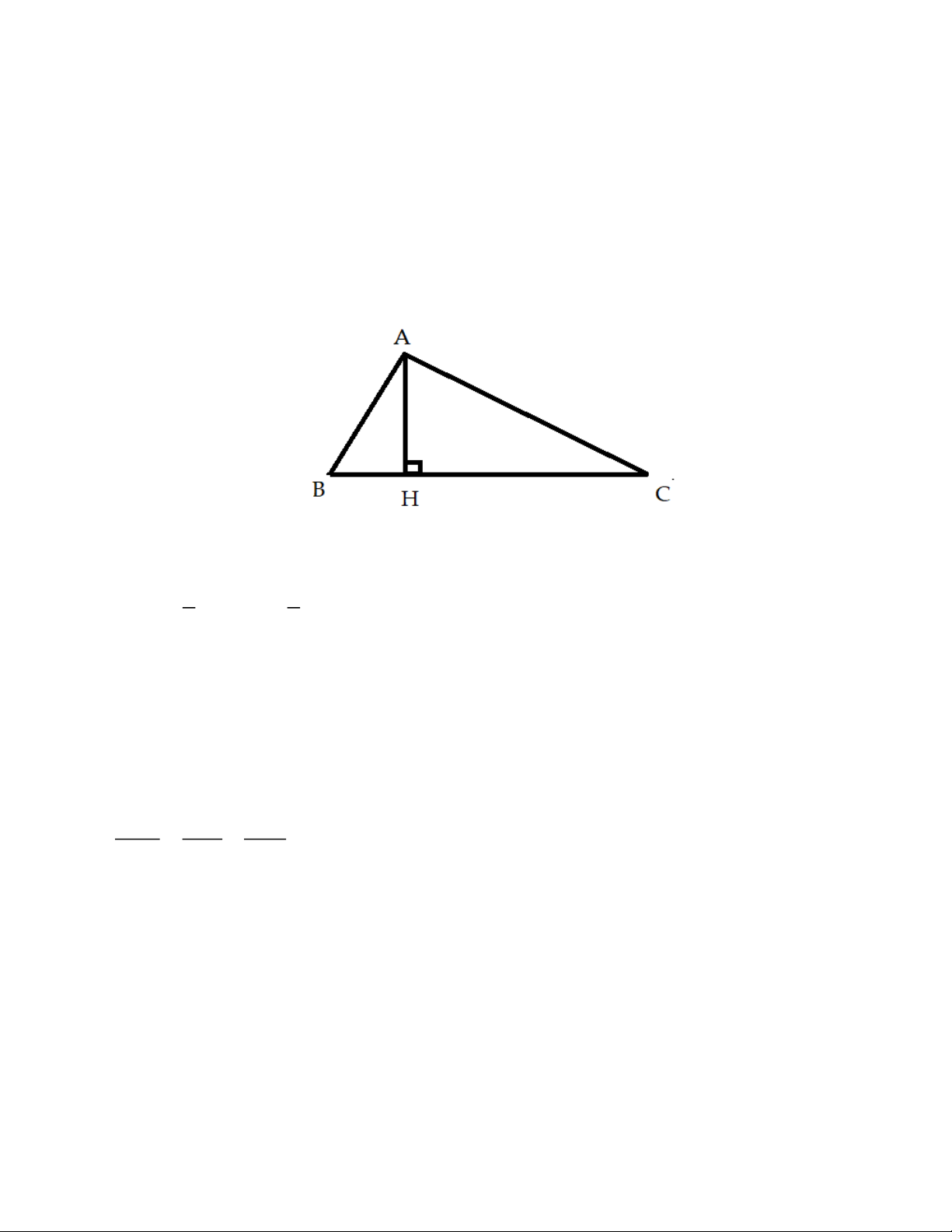
* Bài toán: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng A .
B AC  AH .BC  Chứng minh:
+ Xét tam giác ABC vuông tại A, đường cao AH có: 1 1 S  .A .
B AC  .AH.BC  A .
B AC  AH.BC (đpcm) ABC  2 2 3. Định lý 3
* Phát biểu: Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng
với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
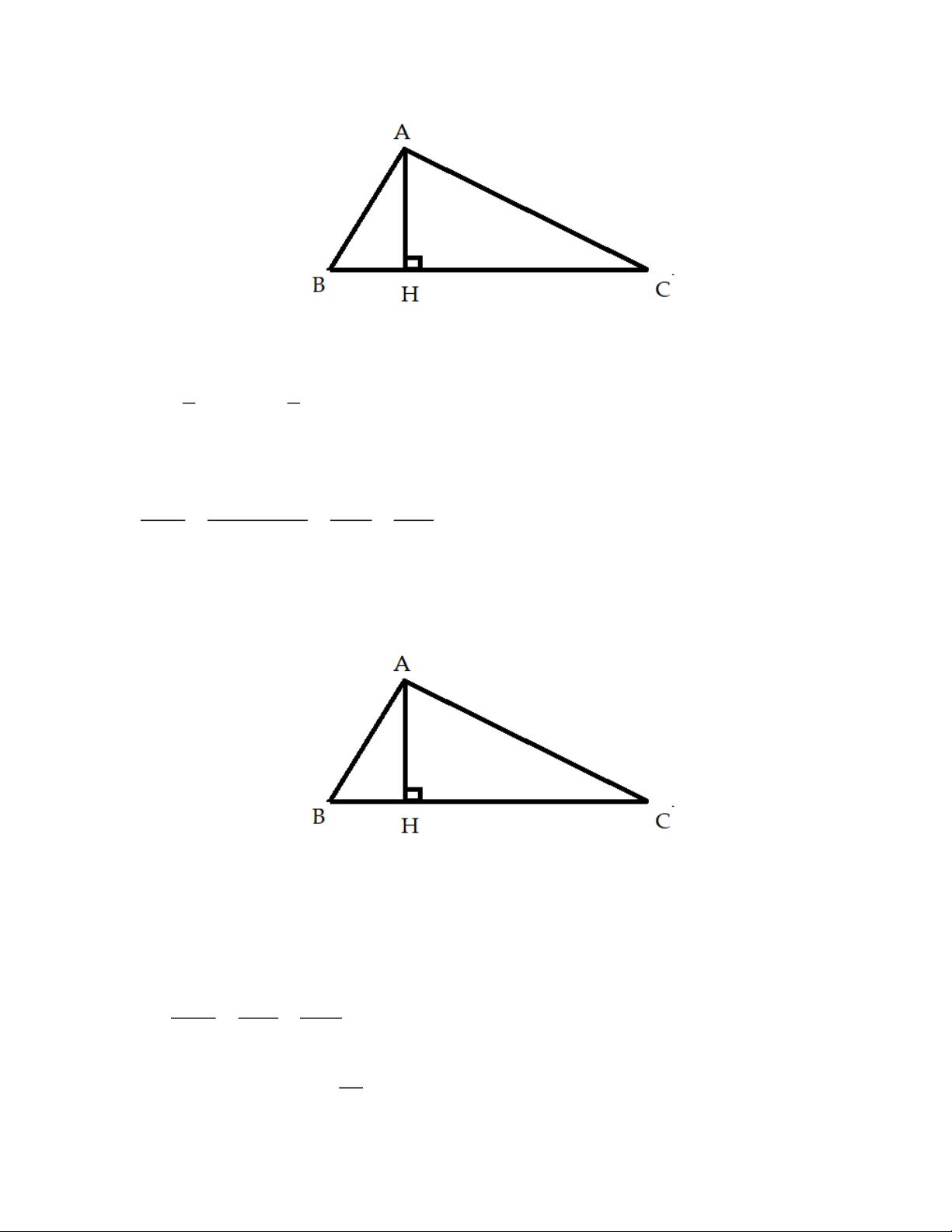
* Bài toán: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng 1 1 1   2 2 2 AH AB AC  Chứng minh:
+ Xét tam giác ABC vuông tại A, đường cao AH có: 1 1 S  .A .
B AC  .AH.BC  A .
B AC  AH.BC ABC  2 2 2 2 2 2 2 2 2 2 2
 AB .AC  AH .BC  AB .AC  AH .(AB  AC ) 2 2 1 AB  AC 1 1     (đpcm) 2 2 2 2 2 AH AB .AC AC AB
!Ví dụ: Cho tam giác ABC vuông tại A, có AB = 6cm và AC = 8cm và đường cao AH. Tính BC, AH, BH và HC.
+ Xét tam giác ABC vuông tại A, đường cao AH có:  2 2 2
AB  AC  BC (Pytago)
Thay số tính được BC = 10 (cm)  1 1 1  
(hệ thức lượng trong tam giác vuông) 2 2 2 AH AB AC 24 Thay số tính được AH = (cm) 5  2
AB  BH.BC (hệ thức lượng trong tam giác vuông) 18 Thay số tính được BH = (cm) 5  2
AH  BH.HC (hệ thức lượng trong tam giác vuông) 32 Thay số tính được HC = (cm) 5