Toán 9 Bài 2: Căn thức bậc hai và hằng đẳng thức
Qua đó giúp các bạn học sinh ôn tập, củng cố và rèn luyện thêm kiến thức đã học trong chương trình Toán 9, Mời các bạn học sinh và quý thầy cô cùng tham khảo chi tiết.
Tài liệu liên quan:
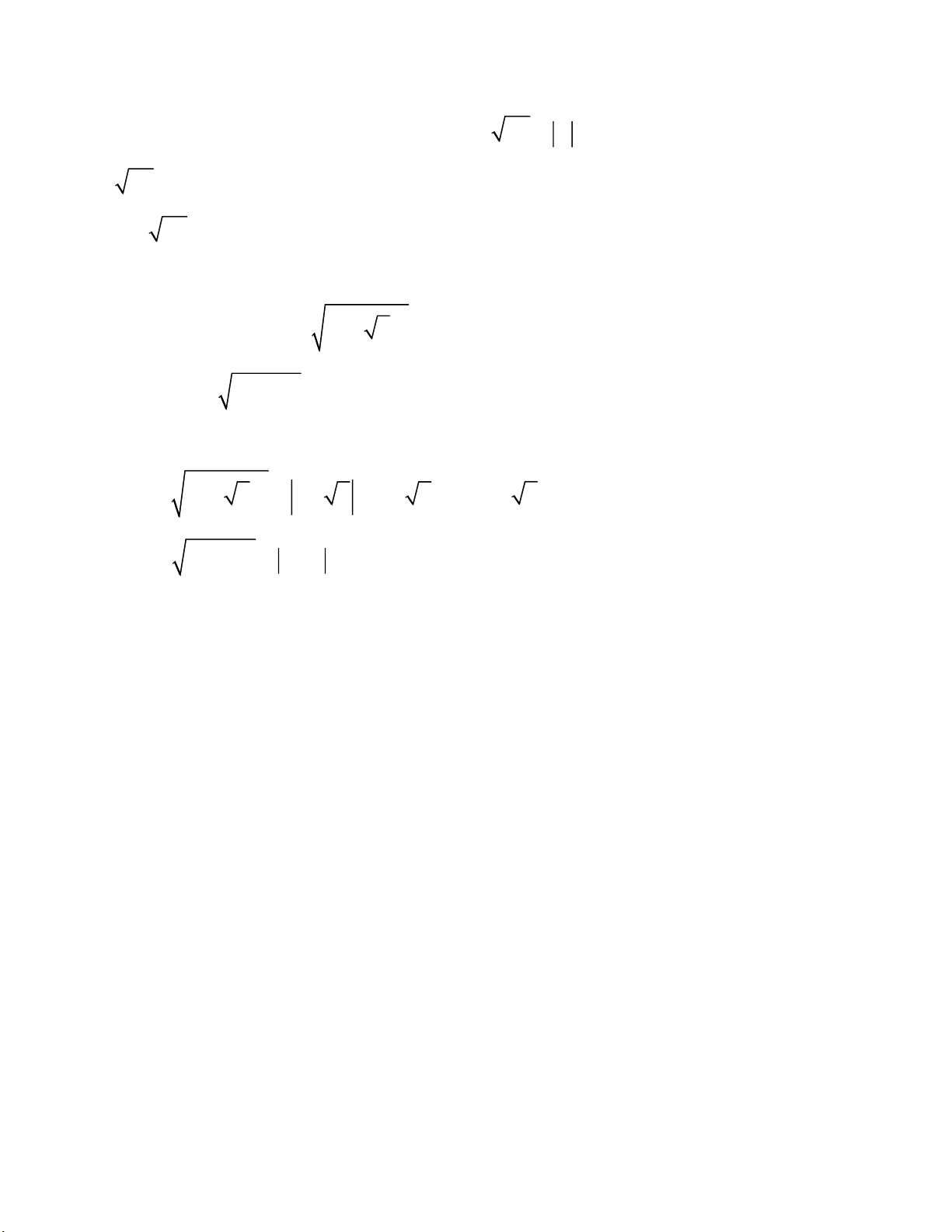
Preview text:
Toán 9 Bài 2: Căn thức bậc hai và hằng đẳng thức
I. Căn thức bậc hai
1. Nhắc lại về biểu thức đại số
+ Những biểu thức bao gồm các phép toán cộng, trừ, nhân, chia, nâng lên lũy thừa
không chỉ trên số mà còn trên chữ (đại diện cho các số) được gọi là biểu thức đại số.
2. Căn thức bậc hai
+ Định nghĩa: Với A là một biểu thức đại số, người ta gọi
A là căn thức bậc hai
của A, còn A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn. +
A xác định (hoặc có nghĩa) khi biểu thức dưới dấu căn có giá trị không âm, hay A lấy giá trị không âm
+ Ví dụ: Với giá trị nào của x thì 3x 2 xác định? Lời giải: 2 Để
3x 2 có nghĩa thì 3x 2 0 x 3
II. Hằng đẳng thức 2 A A
+ Định lý: với mọi số a, ta có 2 a a Chứng minh:
Thật vậy, theo định nghĩa giá trị tuyệt đối có a 0 a
Nếu a 0 thì a a nên 2 2 a a 2 2
Nếu a 0 thì a a nên 2 a a a Vậy 2 2 a
a với mọi số a hay a chính là căn bậc hai số học của 2 a , tức là 2
a a (điều phải chứng minh)
+ Tổng quát: với A là một biểu thức ta có 2
A A có nghĩa là: 2
A A nếu A 0 (tức là A lấy giá trị không âm) Và 2
A A nếu A 0 (tức là A lấy giá trị âm) + Ví dụ: a) Rút gọn biểu thức: 2 3 7 b) Rút gọn x 2 4 với x 4 Lời giải: a) Có 2 3 7
3 7 3 7 (vì 3 7 ) 2 b) Có
x 4 x 4 x 4(vì x < 4)