2 trang 58 lượt tải

Toán 9 Bài 4: Liên hệ giữa phép chia và phép khai phương

115

Bao gồm hướng dẫn lý thuyết và đáp án chi tiết cho từng bài tập giúp các bạn học sinh luyện tập và hiểu rõ hơn về phần Căn thức bậc hai. Qua đó giúp các bạn học sinh ôn tập, củng cố và rèn luyện thêm kiến thức đã học trong chương trình Toán 9, Mời các bạn học sinh và quý thầy cô cùng tham khảo chi tiết.

Chủ đề: Chương 1: Căn bậc hai. Căn bậc ba 90 tài liệu

Môn: Toán 9 3.5 K tài liệu

Tác giả:

Profile

VietJack

1 năm trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/2
Toán 9 Bài 4: Liên hệ giữa phép chia và phép khai phương
I. Định lý
+ Với số a không âm và số b dương, ta có:
aa
b
b
Chứng minh:
Có
0a
và
0b
nên
;ab
và
a
b
xác định và không âm
Lại có
2
2
2
a
aa
b
b
b




Vậy
a
b
là căn bậc hai số học của
, tức là
aa
b
b
+ Một cách tổng quát, với biểu thức A không âm và biểu thức B dương, ta có:
AA
B
B
II. Áp dụng
1. Quy tắc khai phương một thương
+ Muốn khai phương một thương
, trong đó số a không âm và số b dương, ta có
thể lần lượt khai phương số a và số b, rồi lấy kết quả thứ nhất chia cho kết quả thứ
hai.
+ Ví dụ 1: Áp dụng quy tắc khai phương của một thương, tính:
a,
9
1
16
b,
25
144
Lời giải:
a,
9 25 25 5
1
16 16 4
16

b,
25 25 5
144 12
144

2. Quy tắc chia hai căn bậc hai
+ Muốn chia căn bậc hai của số a không âm cho căn bậc hai của số b dương, ta có thể
chia số a cho số b rồi khai phương kết quả đó.
+ Ví dụ 2: Áp dụng quy tắc nhân các căn bậc hai, tính:
a,
4600
46
b,
37,5
1,5
Lời giải:
a,
4600 4600
100 10
46
46
b,
37,5 37,5
25 5
1,5
1,5

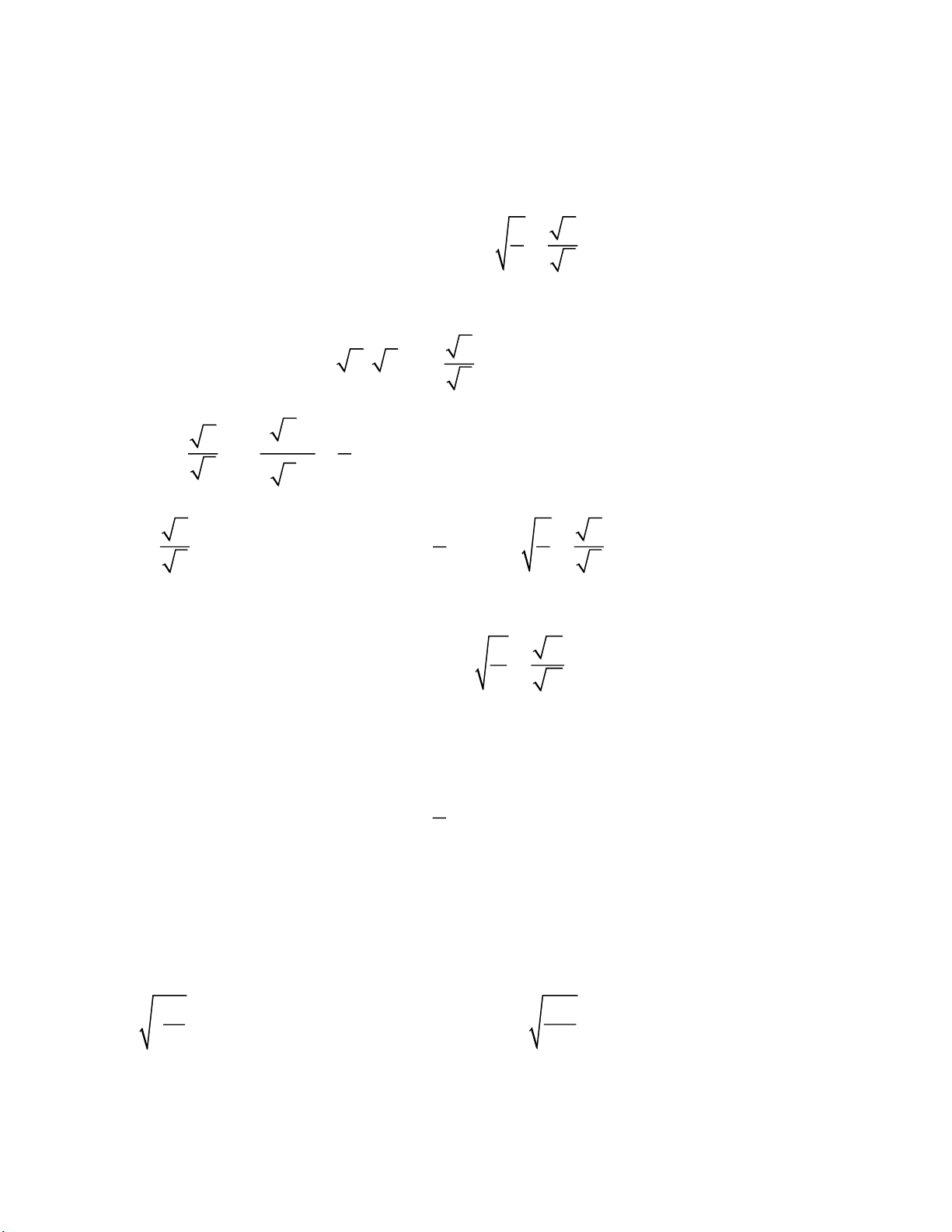
Tài liệu khác của Toán 9

Preview text:

Toán 9 Bài 4: Liên hệ giữa phép chia và phép khai phương I. Định lý a a
+ Với số a không âm và số b dương, ta có:  b b  Chứng minh: a
Có a  0 và b  0 nên a; b và xác định và không âm b    a a 2 2 a Lại có     b    b2 b a a a a Vậy
là căn bậc hai số học của , tức là  b b b b
+ Một cách tổng quát, với biểu thức A không âm và biểu thức B dương, ta có: A AB B II. Áp dụng
1. Quy tắc khai phương một thương a
+ Muốn khai phương một thương
, trong đó số a không âm và số b dương, ta có b
thể lần lượt khai phương số a và số b, rồi lấy kết quả thứ nhất chia cho kết quả thứ hai.
+ Ví dụ 1: Áp dụng quy tắc khai phương của một thương, tính: 9 25 a, 1 b, 16 144  Lời giải: 9 25 25 5 a, 1    16 16 16 4 25 25 5 b,   144 144 12
2. Quy tắc chia hai căn bậc hai
+ Muốn chia căn bậc hai của số a không âm cho căn bậc hai của số b dương, ta có thể
chia số a cho số b rồi khai phương kết quả đó.
+ Ví dụ 2: Áp dụng quy tắc nhân các căn bậc hai, tính: 4600 37,5 a, b, 46 1,5  Lời giải: 4600 4600 a,   100 10 46 46 37,5 37,5 b,   25  5 1,5 1,5

Tài liệu liên quan: