
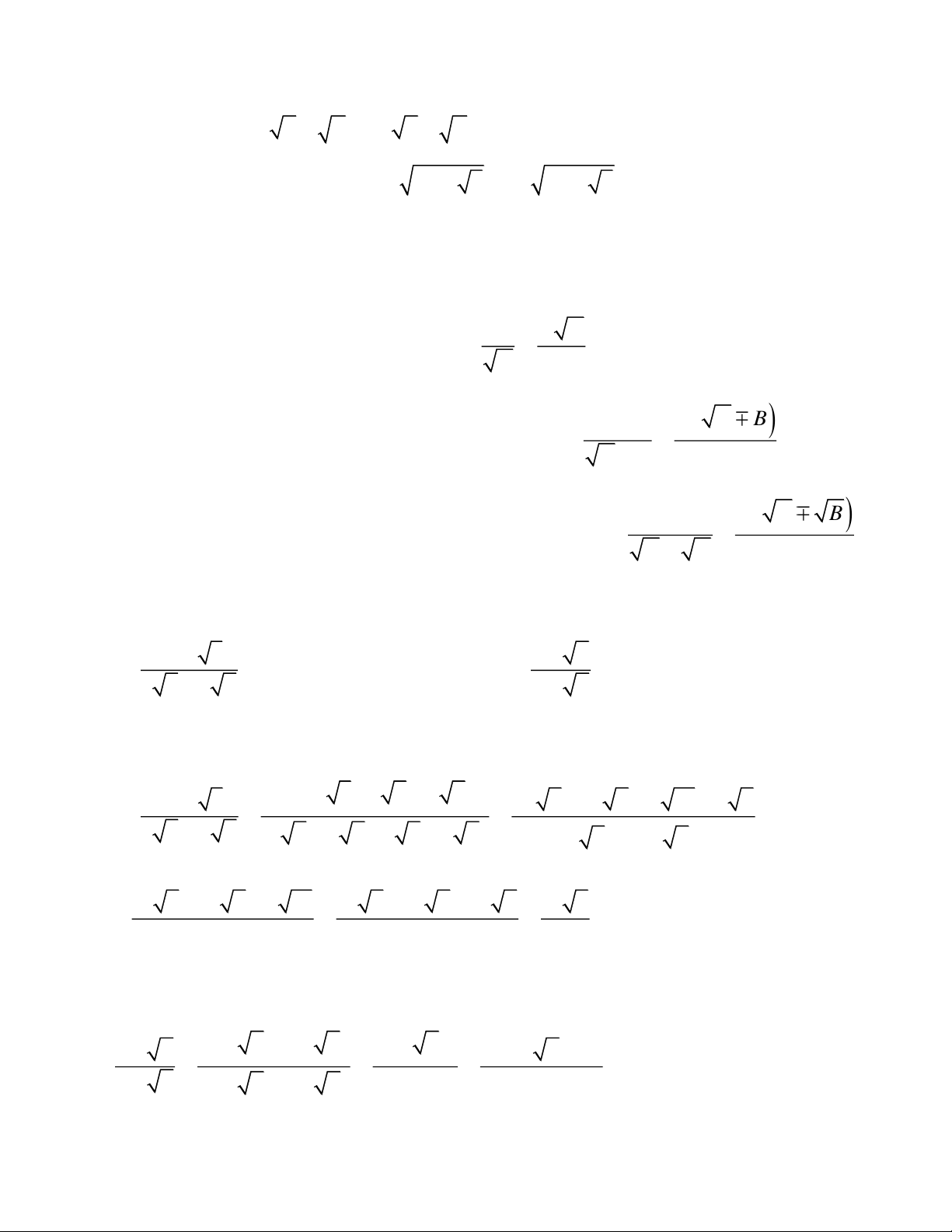
Preview text:
Toán 9 Bài 7:
Biến đổi đơn giản biểu thức chứa căn bậc hai (tiếp theo)
I. Khử mẫu của biểu thức lấy căn
* Khi biến đổi biểu thức chứa căn thức bậc hai, người ta có thể sử dụng phép khử
mẫu của biểu thức lấy căn. * Một cách tổng quát: A AB
Với các biểu thức A, B mà A.B ≥ 0 và B ≠ 0, ta có B B
* Ví dụ 1: Khử mẫu của biểu thức lấy căn: 7 6 a) b) 5xy với x > 0 và y > 0 50 xy Lời giải: 7 7 1 7 1 7.2 14 a) . . 50 25.2 5 2 5 2 10 6 6xy b) 5xy 5xy xy xy 6 6xy
Vì x > 0 và y > 0 nên x.y > 0; ta có: 5xy 5x . y 5 6xy xy xy
II. Trục căn thức ở mẫu * Hai biểu thức x y và x
y x 0; y 0 được gọi là hai biểu thức liên
hợp. Tổng quát: hai biểu thức n a b c và n a b c trong đó a, b, c là các biểu
thức gọi là hai biểu thức liên họp bậc n.
* Trục căn thức ở mẫu: A A B
a) Với các biểu thức A, B mà B > 0, ta có: B B C A B C
b) Với các biểu thức A, B, C mà 2
A 0; A B ta có: 2 A B A B C A B C
c) Với các biểu thức A, B, C mà A 0; B 0; A B ta có: A B A B
* Ví dụ 1: Trục căn thức ở mẫu: 9 2 3 5 x a) b)
với x 0; x 25 3 6 2 2 5 x Lời giải: 92 33 6 2 2 9 2 3
27 6 18 2 6 18 4 6 a) 3 6 2 2
3 6 2 23 6 2 2 3 62 2 22 31 6 18 2 6 18 31 6 18 2 18 2 31 6 46 46 46
b) Với x 0; x 25 ; ta có:
x x x x 2 5 5 5 5 x 10 x 25 5 x
5 x5 x 25 x 25 x




