
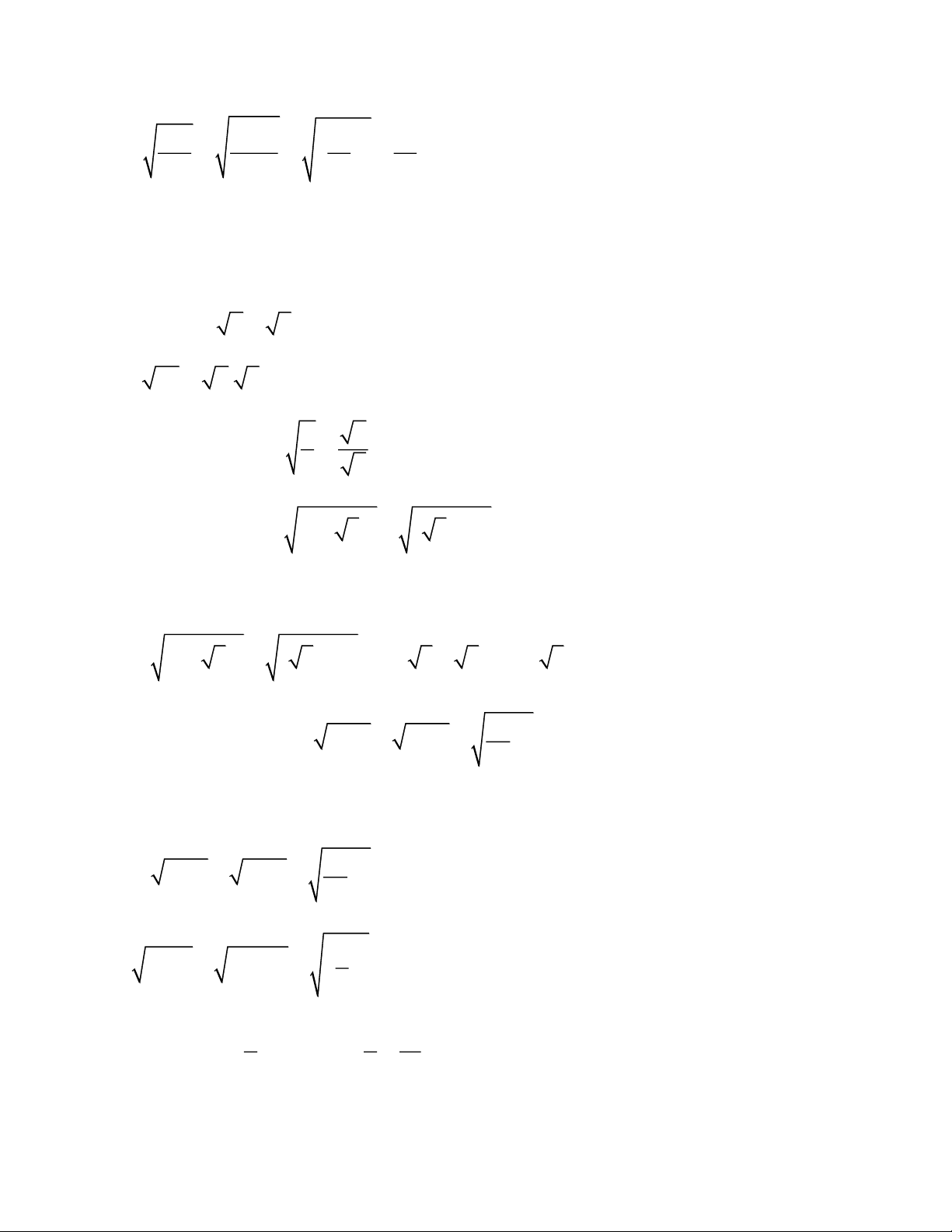
Preview text:
Toán 9 Bài 9: Căn bậc ba
I. Khái niệm căn bậc ba
+ Căn bậc ba của một số a là số x sao cho x3 = a. Kí hiệu 3 a
Ví dụ 1: 4 là căn bậc ba của 64, vì 43 = 64 + Chú ý:
a) Mỗi số a đều có duy nhất một căn bậc ba. Phép tìm căn bậc ba của một số gọi là phép khai căn bậc ba.
b) Từ định nghĩa căn bậc ba, ta có 3 a 3 3 3 a a + Nhận xét:
Căn bậc ba của số dương là số dương.
Căn bậc ba của số âm là số âm
Căn bậc ba của số 0 là số 0
Ví dụ 2: Tìm căn bậc của của mỗi số sau: 1 b) – 1 c) 125 1 a) d) 512 343 Lời giải: 3 3 1 1 1 1 a) 3 3 3 3 512 8 8 8 b) 3 3 3 1 1 1 c) 3 3 3 125 5 5 1 3 3 1 1 1 d) 3 3 3 3 343 7 7 7
II. Tính chất căn bậc ba
Tương tự như căn bậc hai, căn bậc ba cũng có các tính chất sau: a) 3 3 a b a b b) 3 3 3
ab a. b 3 a a
c) Với b 0 , ta có 3 3 b b 3 3 Ví dụ 3: Tính: 3 A 3 1 3 3 1 Lời giải: A 3 3 3 3 1 3 3 1 1 3 3 1 2 3 1
Ví dụ 4: Rút gọn: 3 3 3 3 3 3 B 27x 8 x x 27 Lời giải: 1 3 3 3 3 3 3 B 27x 8 x x 27 3
x3 x3 x 3 3 3 3 2 3
x x x x 16 3 2
3x 2x x 3 3 3




