Tóm tắt lý thuyết và bài tập trắc nghiệm đường tiệm cận của đồ thị hàm số Toán 12

Tóm tắt lý thuyết và bài tập trắc nghiệm đường tiệm cận của đồ thị hàm số Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

21 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

16 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Trang 1/16
CHỦ ĐỀ 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
8. ÑÖÔØNG TIEÄM CAÄN CUÛA ÑOÀ THÒ HAØM SOÁ
Đồ thị
ax b
y
cx d
có tiệm cận đứng
d
x
c

, tiệm cận ngang
a
y
c

.
Đồ thị
2
ax bx c r
y mx n
px q px r



có tiệm cận đứng
q
x
p

, tiệm cận xiên
y mx n
.
Đồ thị
2
ymxn ax bxc 
có các đường cận là
.
2
b
y mx n a x
a

A. BÀI TẬP TRẮC NGHIỆM
Câu 1. Đồ thị hàm số
23
1
x
y
x
−
=
−
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A.
và
3y = −
. B.
2x =
và
1y =
.
C.
và
2y
=
. D.
1x
= −
và
2y
=
.
Câu 2. Đồ thị hàm số
13
2
x
y
x
−
=
+
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A.
2x = −
và
3y
= −
. B.
2x = −
và
.
C.
2x = −
và
3y
=
. D.
2x =
và
1
y =
.
Câu 3. Đồ thị hàm số
2
23
32
x
y
xx
−
=
−+
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A.
1, 2
xx
= =
và
0
y
=
. B.
1, 2xx= =
và
2
y =
.
C.
và
0
y
=
. D.
1, 2xx= =
và
3y = −
.
Câu 4. Đồ thị hàm số
2
2
13
69
−
=
−+
x
y
xx
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A.
3x =
và
3y = −
. B.
3x =
và
0y =
.
C.
3x =
và
1y =
. D.
3y =
và
3x = −
.
Câu 5. Đồ thị hàm số
2
3
32
8
xx
y
x
++
=
−
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A.
2y =
và
0x =
. B.
2x =
và
0y =
.
C.
2x =
và
3y
=
. D.
2y
=
và
3x =
.
Câu 6. Số đường tiệm cận của đồ thị hàm số
1
32
x
y
x
−
=
+
là:
A. 4. B. 1. C. 0. D. 2.
Câu 7. Số đường tiệm cận của đồ thị hàm số
1
32
y
x
=
+
là:
A. 1. B. 3. C. 4. D. 2.
Câu 8. Số đường tiệm cận của đồ thị hàm số
2
1
4
x
y
x
+
=
−
là:
A. 4. B. 2. C. 1. D. 3.
Câu 9. Số đường tiệm cận của đồ thị hàm số
2
34
x
yx
xx
= +
−−
là:
A. 4. B. 3. C. 2. D. 5.
Câu 10. Cho hàm số
2
3
+
=
−
x
y
x
khẳng định nào sau đây là sai:
A. Đồ thị hàm số có tiệm cận đứng
3x =
.
B. Hàm số nghịch biến trên
{ }
\3
.
C. Đồ thị hàm số có tiệm cận ngang là
.
Trang 2/16
D. Đồ thị hàm số có tâm đối xứng là
(3;1)I
.
Câu 11. Đồ thị hàm số nào sau đây có ba đường tiệm cận ?
A.
12
1
x
y
x
−
=
+
. B.
2
1
4
y
x
=
−
. C.
3
51
x
y
x
+
=
−
. D.
2
9
x
y
xx
=
−+
.
Câu 12. Cho hàm số
( )
4
2
2
9
33
xx
y
x
−
=
−
. Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số có tiệm cận đứng, không có tiệm cận ngang.
B. Đồ thị hàm số có 2 tiệm cận đứng, có 1 tiệm cận ngang
3y = −
.
C. Đồ thị hàm số có 2 tiệm cận đứng, có 1 tiệm cận ngang
1y = −
.
D. Đồ thị hàm số không có tiệm cận đứng, có tiệm cận ngang.
Câu 13. Đồ thị hàm số nào sau đây không có tiệm cận đứng:
A.
2
31
1
x
y
x
−
=
+
. B.
1
y
x
−
=
. C.
3
2
x
y
x
+
=
+
. D.
2
1
21
y
xx
=
−+
.
Câu 14. Đồ thị hàm số nào sau đây không có tiệm cận ngang:
A.
23
1
x
y
x
−
=
+
. B.
42
37
21
xx
y
x
++
=
−
. C.
2
3
1
y
x
=
−
. D.
3
1
2
y
x
= +
−
.
Câu 15. Đồ thị như hình vẽ là của hàm số nào sau đây :
A.
1
1
x
y
x
−
=
+
. B.
3
1
x
y
x
−
=
−
. C.
2
1
x
y
x
+
=
−
. D.
2
1
x
y
x
−
=
−
.
Câu 16. Đồ thị hàm số
31
32
x
y
x
−
=
+
co đường tiêm cân ngang là
A.
3x =
. B.
1x =
. C.
3y =
. D.
1
y =
.
Câu 17. Đồ thị hàm số
21
2
x
y
x
−
=
+
có bao nhiêu đường tiệm cận?
A. 1. B. 2. C. 3. D. 0.
Câu 18. Số đường tiệm cận của đồ thị hàm số
2
21
32
x
y
xx
−
=
−+
là
A. 0. B. 1. C. 2. D. 3.
Câu 19. Cho hàm số
9mx
y
xm
+
=
+
có đồ thị
()C
. Kết luận nào sau đây đúng ?
A. Khi
3m =
thì
()C
không có đường tiệm cận đứng.
B. Khi
3m = −
thì
()C
không có đường tiệm cận đứng.
C. Khi
3m ≠±
thì
()C
có tiệm cận đứng
,xm
= −
tiệm cận ngang
ym=
.
D. Khi
0m =
thì
()C
không có tiệm cận ngang.
Câu 20. Tìm tất cả các đường tiệm cận của đồ thị hàm số
2
3
1
x
y
x
+
=
+
A.
1y
= ±
. B.
1x =
. C.
1y =
. D.
1
y = −
.
Trang 3/16
Câu 21. Với giá trị nào của
m
thì đồ thị (C):
1
2
mx
y
xm
−
=
+
có tiệm cận đứng đi qua điểm
2()1;M −
?
A.
2
2
m =
. B.
0m =
. C.
1
2
m =
. D.
2m =
.
Câu 22. Cho hàm số
1
mx n
y
x
+
=
−
có đồ thị (C). Biết tiệm cận ngang của (C) đi qua điểm
( 1; 2)A
−
đồng
thời điểm
(2;1)I
thuộc (C). Khi đó giá trị của
mn+
là
A.
1mn+=−
. B.
1mn
+=
. C.
3mn+=−
. D.
3mn+=
.
Câu 23. Số tiệm cận của hàm số
2
2
1
94
xx
y
x
+−
=
−−
là
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 24. Giá trị của
m
để đồ thị hàm số
1
xm
y
mx
−
=
−
không có tiệm cận đứng là
A.
0; 1mm= = ±
. B.
1
m = −
. C.
1
m = ±
. D.
1
m =
.
Câu 25. Số tiệm cận của hàm số
3
2 32
1 31
1
x xx
y
x
++ + +
=
−
là
A. 3. B. 2. C. 1. D. 4.
Câu 26. Đồ thị hàm số
2
22
2
x x mx
y
x
+ +−
=
+
có hai đường tiệm cận ngang với
A.
m∀∈
. B.
1m =
. C.
0; 1mm= =
. D.
0m =
.
Câu 27. Đồ thị hàm số
2
1
1
x x mx
y
x
−++
=
−
có đường tiệm cận đứng khi
A.
0m ≠
. B.
mR∀∈
. C.
1
m
≠−
. D.
1
m ≠
.
Câu 28. Số đường tiệm cận của đồ thị hàm số
2
2
4
34
x
y
xx
−
=
−−
là:
A. 1. B. 0. C. 2. D. 3.
Câu 29. Số tiệm cận của đồ thị hàm số
2
1
1
2
1
1
x
x
x
y
x
x
x
+
≥
=
<
−
neáu
neáu
.
A. 1. B. 2. C. 3. D. 4.
Câu 30. Xác định
m
để đồ thị hàm số
(
) (
)
2
23 2 1
2
x mxm
y
x
− ++ −
=
−
không có tiệm cận đứng.
A.
2m = −
. B.
2m =
. C.
3m =
. D.
1m =
.
Câu 31. Xác định
m
để đồ thị hàm số
( )
22
3
4 22 3 1
y
x m xm
=
+ + +−
có đúng hai tiệm cận đứng.
A.
13
12
m <−
. B.
11m−< <
. C.
3
2
m >−
. D.
13
12
m >−
.
Câu 32. Xác định
m
để đồ thị hàm số
( )
22
1
21 2
x
y
x m xm
−
=
+ − +−
có đúng hai tiệm cận đứng.
A.
3
; 1; 3
2
m mm< ≠ ≠−
. B.
3
;1
2
mm>− ≠
.
C.
3
2
m >−
. D.
3
2
m <
.
Câu 33. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
2
1y x mx=++
có tiệm cận ngang.
Trang 4/16
A.
01m<<
. B.
1
m = −
. C.
1
m >
. D.
1m =
.
Câu 34. Cho hàm số
2
32
3 21
22
xx x
y
x xx
−+− +
=
− −+
. Trong các khẳng định sau, khẳng định nào là khẳng
định đúng?
A. Đồ thị hàm số không có tiệm cận đứng, không có tiệm cận ngang.
B. Đồ thị hàm số không có tiệm cận đứng và có đúng 1 tiệm cận ngang.
C. Đồ thị hàm số có đúng 3 tiệm cận đứng và 2 tiệm cận ngang.
D. Đồ thị hàm số có đúng 2 tiệm cận đứng và 1 tiệm cận ngang.
Câu 35. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
2
1
1
x
y
mx
+
=
+
có hai tiệm
cận ngang.
A.
0m
<
. B.
0m >
.
C.
0m =
. D. Không có giá trị thực nào của
m
thỏa mãn yêu cầu đề bài.
Câu 36. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
1 x
y
xm
−
=
−
có tiệm cận
đứng.
A.
1m
>
. B.
1m
=
.
C.
1m ≤
. D. Không có
m
thỏa mãn yêu cầu đề bài.
Câu 37. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
32
1
3
x
y
x xm
+
=
−−
có đúng
một tiệm cận đứng.
A.
m ∈
. B.
0
4
m
m
>
<−
. C.
0
4
m
m
>
≤−
. D.
0
4
m
m
≥
≤−
.
Câu 38. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
22
2
2
x mx m
y
x
−−
=
−
có tiệm
cận đứng.
A. Không có
m
thỏa mãn yêu đều đề bài.. B.
2
1
m
m
≠−
≠
.
C.
m ∈
. D.
2
1
m
m
≠−
≠
Câu 39. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
2
53
21
x
y
x mx
−
=
−+
không có
tiệm cận đứng.
A.
1
1
m
m
>
<−
. B.
11m−< <
. C.
1m = −
. D.
1m =
.
Câu 40. Cho hàm số
21
1
x
y
x
+
=
−
có đồ thị
( )
C
. Gọi
M
là một điểm bất kì trên
( )
C
. Tiếp tuyến của
( )
C
tại
M
cắt các đường tiệm cận của
( )
C
tại
A
và
B
. Gọi
I
là giao điểm của các đường tiệm
cận của
( )
C
. Tính diện tích của tam giác
IAB
.
A.
2
. B.
12
. C.
4
. D.
6
.
Câu 41. Số đường tiệm cận của đồ thị hàm số
2
3
1
x
y
x
+
=
+
là:
A. 2. B. 0. C. 1. D. 3.
Câu 42. Số đường tiệm cận của đồ thị hàm số
2
1
2
x
y
x
−
=
−
là:
A. 0. B. 1. C. 3. D. 3.
Trang 5/16
Câu 43. Đồ thị hàm số
2
42
yx x x=− −+
có tiệm cận ngang là:
A.
2y
=
. B.
2y = −
. C.
2y =
. D.
2x = −
.
Câu 44. Tìm điểm M thuộc đồ thị hàm số
21
1
x
y
x
+
=
−
sao cho khoảng cách từ M đến tiệm cận đứng bằng
khoảng cách từ M đến trục hoành
A.
( ) ( )
0; 1 , 3; 2
MM
−
. B.
( ) ( )
2;1 , 4;3MM
.
C.
( ) ( )
0; 1 , 4; 3MM−
. D.
( ) ( )
2;1 , 3; 2MM
.
Câu 45. Số tiệm cận của đồ thị hàm số
2
2
2
xx
y
x
+−
=
+
là
A. 0. B. 1. C. 2. D. 3.
Câu 46. Số tiệm cận của đồ thị hàm số
(
)
2
2
2
2
xx
y
x
+−
=
+
là
A. 0. B. 1. C. 2. D. 3.
Câu 47. Số tiệm cận của đồ thị hàm số
2
2
1
x
y
x
−
=
−
là
A. 1. B. 0. C. 3. D. 2.
Câu 48. Cho hàm số
2
()
3
x
yC
x
+
=
−
. Có tất cả bao nhiêu điểm M thuộc (C) sao cho khoảng cách từ M
đến tiệm cận ngang bằng 5 lần khoảng cách từ điểm M đến tiệm cận đứng.
A. 4. B. 3. C. 2. D. 1.
Câu 49. Đồ thị hàm số
2
39
x
y
x
+
=
+
có đường tiệm cận đứng là
xa=
và đường tiệm cận ngang là
yb=
.
Giá trị của số nguyên m nhỏ nhất thỏa mãn
mab≥+
là
A.
0
. B.
3−
. C.
1−
. D.
2−
.
Câu 50. Cho hàm số
23
()
2
x
yC
x
−
=
−
. Gọi
M
là điểm bất kỳ trên (C), d là tổng khoảng cách từ
M
đến
hai đường tiệm cận của đồ thị (C). Giá trị nhỏ nhất của d là
A. 5. B. 10. C. 6. D. 2.
Câu 51. Cho hàm số
23
()
2
x
yC
x
−
=
−
. Gọi d là khoảng cách từ giao điểm của 2 tiệm cận của (C) đến một
tiếp tuyến bất kỳ của đồ thị (C). Giá trị lớn nhất của d là
A.
2
. B.
3
. C.
33
. D.
2
.
Câu 52. Cho hàm số
23
()
2
x
yC
x
−
=
−
. Gọi d là tiếp tuyến bất kì của (C), d cắt hai đường tiệm cận của đồ
thị (C) lần lượt tại A, B. Khi đó khoảng cách giữa A và B ngắn nhất bằng
A.
4
. B.
32
. C.
22
. D.
33
.
B. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM
I – ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
C
A
A
A
B
D
D
D
C
B
B
C
A
B
C
D
B
D
C
A
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
D
A
B
A
A
A
C
A
C
A
D
A
D
B
B
C
C
D
B
C
41
42
43
44
45
46
47
48
49
50
51
52
A
A
A
C
A
C
D
C
D
D
A
A
II –HƯỚNG DẪN GIẢI
Trang 6/16
Câu 1. Chọn C
Phương pháp tự luận
Ta có
1
23
lim
1
+
→
−
= −∞
−
x
x
x
và
1
23
lim
1
x
x
x
−
→
−
= +∞
−
nên đồ thị hàm số có tiệm cận đứng là
1x =
23
lim 2
1
x
x
x
→±∞
−
=
−
nên đồ thị hàm số có tiệm cận ngang là
2y =
Phương pháp trắc nghiệm
Nhập biểu thức
23
1
−
−
x
x
.
Ấn CALC
9
1 10
−
= +x
. Ấn = được kết quả bằng -999999998 nên
1
23
lim
1
+
→
−
= −∞
−
x
x
x
.
Ấn CALC
9
1 10
−
= −
x
. Ấn = được kết quả bằng 999999998 nên
1
23
lim
1
−
→
−
= +∞
−
x
x
x
.
⇒
đồ thị hàm số có tiệm cận đứng là
1
x =
Ấn CALC
10
10x
=
. Ấn = được kết quả bằng 2 nên
23
lim 2
1
→±∞
−
=
−
x
x
x
.
⇒
đồ thị hàm số có tiệm cận ngang là
2
y
=
Câu 2. Chọn A
Phương pháp tự luận
Ta có
( 2)
13
lim
2
x
x
x
+
→−
−
= +∞
+
và
( 2)
13
lim
2
x
x
x
−
→−
−
= −∞
+
nên đồ thị hàm số có tiệm cận đứng là
2x = −
Ta có
13
lim 3
2
x
x
x
→±∞
−
= −
+
nên đồ thị hàm số có tiệm cận ngang là
3y = −
Phương pháp trắc nghiệm
Nhập biểu thức
13
2
x
x
−
+
.
Ấn CALC
9
2 10x
−
=−+
. Ấn = được kết quả bằng 6999999997 nên
( 2)
13
lim
2
x
x
x
+
→−
−
= +∞
+
.
Ấn CALC
9
2 10x
−
=−−
. Ấn = được kết quả bằng -7000000003 nên
( 2)
13
lim
2
x
x
x
−
→−
−
= −∞
+
.
⇒
đồ thị hàm số có tiệm cận đứng là
2x = −
Ấn CALC
10
10x
=
. Ấn = được kết quả bằng -2,999999999 nên
13
lim 3
2
x
x
x
→±∞
−
= −
+
.
⇒
đồ thị hàm số có tiệm cận ngang là
3y
= −
Câu 3. Chọn A
Phương pháp tự luận
Ta có
2
1
23
lim
32
x
x
xx
+
→
−
= +∞
−+
và
2
1
23
lim
32
x
x
xx
−
→
−
= −∞
−+
nên đồ thị hàm số có tiệm cận đứng là
. Tính tương tự với
2x =
Ta có
2
23
lim 0
32
x
x
xx
→±∞
−
=
−+
nên đồ thị hàm số có tiệm cận ngang là
0y =
Phương pháp tự luận
Nhập biểu thức
2
23
32
x
xx
−
−+
.
Xét tại
1x =
: Ấn CALC
9
1 10x
−
= +
. Ấn = được kết quả bằng 999999998 nên
2
1
23
lim
32
x
x
xx
+
→
−
= +∞
−+
.
Ấn CALC
9
1 10x
−
= +
. Ấn = được kết quả bằng -1,000000002 nên
2
1
23
lim
32
x
x
xx
−
→
−
= −∞
−+
.
Tương tự xét với
2x =
Trang 7/16
⇒
đồ thị hàm số có tiệm cận đứng là
1
x =
và
2x
=
Ấn CALC
10
10x =
. Ấn = được kết quả bằng
10
2.10
−
nên
2
23
lim 0
32
x
x
xx
→±∞
−
=
−+
.
⇒
đồ thị hàm số có tiệm cận ngang là
0y =
Câu 4. Chọn A
Phương pháp tự luận
2
2
3
13
lim
69
x
x
xx
+
→
−
= −∞
−+
và
2
2
3
13
lim
69
x
x
xx
−
→
−
= −∞
−+
nên đồ thị hàm số có tiệm cận đứng là
3x
=
.
Ta có
2
2
13
lim 3
69
x
x
xx
→±∞
−
= −
−+
nên đồ thị hàm số có tiệm cận ngang là
3y = −
Phương pháp trắc nghiệm
Tương tự câu 3,4 nên tự tính kiểm tra
Câu 5. Chọn B
Tương tự câu 3 .
Câu 6. Chọn D
Tìm tương tự các câu trên ta được tiệm cận đứng là
3
2
x
= −
và tiệm cận ngang là
1
2
y = −
⇒
Số đường tiệm cận là 2.
Câu 7. Chọn D
Tìm tương tự các câu trên ta được tiệm cận đứng là
2
3
= −x
và tiệm cận ngang là
0=y
⇒
Số đường tiệm cận là 2
Câu 8. Chọn D
Tìm được tiệm cận đứng là
2x = ±
và tiệm cận ngang là
0y =
⇒
Số đường tiệm cận là 3
Câu 9. Chọn C
Quy đồng biến đổi hàm số đã cho trở thành
32
2
33
34
xxx
y
xx
−−
=
−−
Tìm được tiệm cận đứng là
1x = −
,
4x =
và không có tiệm cận ngang (Vì
lim
x
y
→±∞
= ±∞
)
⇒
Số đường tiệm cận là 2
Câu 10. Chọn B
Tìm được tiệm cận đứng là
3
=x
và tiệm cận ngang là
1=y
Giao điểm của hai đường tiệm cận
(3;1)
I
là tâm đối xứng của đồ thị
⇒
A,C,D đúng và chọn B
Câu 11. Chọn B
Đồ thị hàm số
2
1
4
y
x
=
−
có 3 đường tiệm cận .( TCĐ là
2
x = ±
và TCN
0y =
)
Câu 12. Chọn C
Đồ thị hàm số
( )
4
2
2
9
33
xx
y
x
−
=
−
có hai đường tiệm cận đứng
1x = ±
và một tiệm cận ngang
1y = −
Câu 13. Chọn A
Phương trình
2
10x +=
vô nghiệm nên không tìm được số
0
x
để
0
2
31
lim
1
xx
x
x
+
→
−
= ±∞
+
hoặc
0
2
31
lim
1
xx
x
x
−
→
−
= ±∞
+
⇒
đồ thị hàm số không có tiệm cận đứng
Các đồ thị hàm số ở B,C,D lần lượt có các TCĐ là
0, 2, 1xx x= =−=
Câu 14. Chọn B
Trang 8/16
Ta có
42
37
lim
21
x
xx
x
→±∞
++
= ±∞
−
⇒
đồ thị hàm số không có tiệm cận ngang.
Các đồ thị hàm số ở B,C,D lần lượt có các TCN là
2, 0, 1
yyy= = =
Câu 15. Chọn C
Từ đồ thị ta thấy có tiệm cận đứng là
và
1y =
⇒
loại A,B
Xét tiếp thấy giao điểm của đồ thị hàm số với trục tung là
(0; 2)−
⇒
chọn C.
Câu 16. Chọn D
Phương pháp tự luận
Ta có
31 31
lim lim 1
32 32
xx
xx
xx
→+∞ →−∞
−−
= =
++
.
Do đó đồ thị hàm số có đường tiệm cận ngang là
1
y =
Phương pháp trắc nghiệm
Nhập vào máy tính biểu thức
31
32
X
X
−
+
ấn CALC
12
10
ta được kết quả là 1.
Tiếp tục CALC
12
10−
ta được kết quả là 1.
Vậy đồ thị hàm số có đường tiệm cận ngang là
1y =
Câu 17. Chọn B
Phương pháp tự luận
Ta có
21 21
lim lim 2
22
xx
xx
xx
→+∞ →−∞
−−
= =
++
nên đồ thị hàm số có đường tiệm cận ngang là
2y =
.
Lại có
22
21 21
lim ; lim
22
xx
xx
xx
+−
→− →−
−−
= −∞ = +∞
++
nên đồ thị hàm số có đường tiệm cận đứng
2x = −
.
Vậy đồ thị hàm số đã cho có hai đường tiệm cận.
Phương pháp trắc nghiệm
Nhập vào máy tính biểu thức
21
2
X
X
−
+
ấn CALC
12
10
ta được kết quả là 2.
Tiếp tục CALC
12
10−
ta được kết quả là 2.
Vậy đồ thị hàm số có đường tiệm cận ngang là
2y =
.
Tiếp tục ấn CALC
12
2 10
−
−+
ta được kết quả là
12
5.10−
, ấn CALC
12
2 10
−
−−
ta được kết quả
là
12
5.10
nên có
22
21 21
lim ; lim
22
xx
xx
xx
+−
→− →−
−−
= −∞ = +∞
++
.
Do đó ta được
2x = −
là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có hai đường tiệm cận.
Câu 18. Chọn D
Phương pháp tự luận
Ta có:
22
21 21
lim 0; lim 0
32 32
xx
xx
xx xx
→−∞ →+∞
−−
= =
−+ −+
.
Do đó đồ thị hàm số có đường tiệm cận ngang
0y =
.
Lại có
22
11
21 21
lim ; lim
32 32
xx
xx
xx xx
−+
→→
−−
= +∞ = −∞
−+ −+
và
2
2
21
lim ;
32
x
x
xx
−
→
−
= −∞
−+
2
2
21
lim
32
x
x
xx
+
→
−
= +∞
−+
nên đồ thị hàm số có hai đường tiệm cận đứng là
1; 2xx= =
.
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Phương pháp trắc nghiệm
Nhập vào máy tính biểu thức
2
21
32
X
XX
−
++
ấn CALC
12
10
ta được kết quả là 0.
Tiếp tục CALC
12
10−
ta được kết quả là 0.
Vậy đồ thị hàm số có đường tiệm cận ngang là
0y =
.
Trang 9/16
Tiếp tục ấn CALC
12
1 10
−
+
ta được kết quả là
12
1.10−
, ấn CALC
12
1 10
−
−
ta được kết quả là
12
1.10
nên có
22
11
21 21
lim ; lim
32 32
xx
xx
xx xx
−+
→→
−−
= +∞ = −∞
−+ −+
do đó ta được
1
x =
là tiệm cận đứng
của đồ thị hàm số.
Tiếp tục ấn CALC
12
2 10
−
+
ta được kết quả là
12
3.10
, ấn CALC
12
1 10
−
−
ta được kết quả là
12
3.10−
nên có
22
22
21 21
lim ; lim
32 32
xx
xx
xx xx
−+
→→
−−
= −∞ = +∞
−+ −+
do đó ta được
2x =
là tiệm cận
đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có ba đường tiệm cận.
Câu 19. Chọn C
Phương pháp tự luận
Xét phương trình:
90mx +=
.
Với
xm= −
ta có:
2
90 3mm− +=⇔ =±
Kiểm tra thấy với
3m = ±
thì hàm số không có tiệm cận đứng và tiệm cận ngang.
Khi
3
m ≠±
hàm số luôn có tiệm cận đứng
xm=
hoặc
xm
= −
và tiệm cận ngang
ym=
Phương pháp trắc nghiệm
Nhập vào máy tính biểu thức
9XY
XY
+
+
ấn CALC
10
3 10 ; 3XY
−
=−+ =−
ta được kết quả
3−
.
Tiếp tục ấn CALC
10
3 10 ; 3XY
−
=−− =−
ta được kết quả -3.
Vậy khi
3m = −
đồ thị hàm số không có đường tiệm cận đứng.
Tương tự với
3m =
ta cũng có kết quả tương tự.
Vậy các đáp án A và B không thỏa mãn.
Tiếp tục ấn CALC
10
10 ; 0XY=−=
ta được kết quả
10
9 10x
−
, ấn CALC
10
10 ; 0XY= =
ta
được kết quả
10
9x10
−
.
Do đó hàm số có tiệm cận ngang
0
y =
.
Vậy đáp án D sai.
Câu 20. Chọn A
Phương pháp tự luận
Vì TXĐ của hàm số là
nên đồ thị hàm số không có tiệm cận đứng.
Lại có
2
2
3
1
3
lim lim 1
1
1
1
xx
x
x
x
x
→+∞ →+∞
+
+
= =
+
+
và
2
2
3
1
3
lim lim 1
1
1
1
xx
x
x
x
x
→−∞ →−∞
+
+
= = −
+
−+
Vậy đồ thị hàm số có hai đường tiệm cận ngang là
1y
= ±
Phương pháp trắc nghiệm
Nhập vào máy tính biểu thức
2
3
1
x
x
+
+
ấn CALC
10
10
ta được kết quả là 1.
Tiếp tục ấn CALC
10
10
−
ta được kết quả là
1−
.
Vậy có hai tiệm cận ngang là
1y = ±
.
Câu 21. Chọn D
Để đồ thị hàm số có đường tiệm cận đứng thì
2
20m +≠
luôn đúng với mọi
m
.
Khi đó đồ thị hàm số có đường tiệm cận đứng là
2
m
x = −
.
Vậy để tiệm cận đứng đi qua điểm
2()1;
M −
thì
12
2
m
m− =−⇔ =
Câu 22. Chọn A
Để hàm số có đường tiệm cận ngang thì
0mn+≠
Khi đó tiệm cận ngang của đồ thị hàm số là
ym=
do đó ta có
2m =
Mặt khác đồ thị hàm số đi qua điểm
(2;1)I
nên có
21 3mn n+=⇒=−
Trang 10/16
Vậy
1mn+=−
Câu 23. Chọn B
Điều kiện xác định
2
2
90
( ; 3] [3; ) \ { 5}
94
x
x
x
−≥
⇔ ∈ −∞ − ∪ +∞ ±
−≠
Khi đó có:
22
22
11
lim 0; lim 2
94 94
xx
xx xx
xx
→+∞ →−∞
+− +−
= =
−− −−
nên đồ thị hàm số có hai đường tiệm cận
ngang.
Mặt khác có
22
22
55
11
lim ; lim
94 94
xx
xx xx
xx
±±
→− →
+− +−
= ∞ = ±∞
−− −−
nên đồ thị hàm số có hai đường tiệm
cận đứng.
Vậy đồ thị hàm số đã cho có 4 đường tiệm cận.
Câu 24. Chọn A
Xét
0m =
thì đồ thị hàm số không có đường tiệm cận đứng.
Xét
0m ≠
khi đó đồ thị hàm số không có đường tiệm cận đứng nếu
2
01 0ad bc m− = ⇔− + =
1m⇔=±
.
Vậy giá trị của
m
cần tìm là
0; 1mm= = ±
Câu 25. Chọn A
Ta có
3
2 32
1
1 31
lim
1
x
x xx
x
→
++ + +
= ∞
−
. Vậy đồ thị hàm số có đường tiệm cận đứng là
1x
=
Mặt khác
lim 2; lim 0
xx
yy
→+∞ →−∞
= =
nên đồ thị hàm số có hai tiệm cận ngang.
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Câu 26. Chọn A
Xét
2
22
lim 1
2
x
x x mx
m
x
→−∞
+ +−
=−−
+
và
2
22
lim 1
2
x
x x mx
m
x
→+∞
+ +−
= −
+
Để hàm số có hai tiệm cận ngang thì
11
mm−− ≠−
(thỏa với mọi m) .
Vậy
mR∀∈
thì đồ thị hàm số có hai tiệm cận ngang.
Câu 27. Chọn C
Xét phương trình
2
10x x mx−++ =
.
Nếu phương trình không có nghiệm
1x =
thì đồ thị hàm số có đường tiệm cận đứng là
1x =
.
Nếu phương trình có nghiệm
1x =
hay
1m
= −
.
Khi đó xét giới hạn:
2
2
11
1 11
lim lim
12
1
xx
xx x
x
xx x
→→
−+− −
= = −
−
−++
nên trong trường hợp này đồ
thị hàm số không có đường tiệm cận đứng.
Vậy
1m ≠−
.
Câu 28. Chọn A
Điều kiện:
2
2
22
4 0 22
1
1
3 40
4
x
xx
x
x
xx
x
−≤ ≤
− ≥ −≤ ≤

⇔ ≠− ⇔

≠−
− −≠
≠
.
Ta có
( ) ( )
2
2
11
4
lim lim
34
xx
x
y
xx
++
→− →−
−
= = −∞
−−
;
( ) ( )
2
2
11
4
lim lim
34
xx
x
y
xx
−−
→− →−
−
= = +∞
−−
.
Suy ra đường thẳng
1x = −
là tiệm cận đứng của đồ thị hàm số khi
( )
1x
+
→−
và
( )
1x
−
→−
.
Vì
lim
x
y
→±∞
không tồn tại nên đồ thị hàm số không có tiệm cận ngang.
Câu 29. Chọn C
Ta có
11
2
lim lim
1
xx
x
y
x
−−
→→
= = −∞
−
nên đường thẳng
1x =
là tiệm cận đứng của đồ thị hàm số.
Trang 11/16
22
lim lim lim 2
1
1
1
xx x
x
y
x
x
→−∞ →−∞ →−∞
= = =
−
−
nên đường thẳng
2
y =
là tiệm cận ngang của đồ thị hàm số
khi
x
→ −∞
.
2
2
11
lim lim lim 1 1
xx x
x
y
xx
→+∞ →+∞ →+∞
+
= = +=
nên đường thẳng
1y =
là tiệm cận ngang của đồ thị
hàm số khi
x → +∞
.
Câu 30. Chọn A
Đồ thị hàm số
( ) ( )
2
23 2 1
2
x mxm
y
x
− ++ −
=
−
không có tiệm cận đứng
⇔
phương trình
( ) ( ) ( )
2
2 3 2 10fx x m x m= − + + −=
có nghiệm
2
x =
( ) ( ) ( )
2 0 4 22 3 2 1 0f mm⇔ =⇔− + + − =
2 40 2mm⇔− − = ⇔ =−
.
Câu 31. Chọn D
Đồ thị hàm số
( )
22
3
4 22 3 1
y
x m xm
=
+ + +−
có đúng hai tiệm cận đứng
⇔
phương trình
( )
22
4 22 3 1 0x m xm+ + + −=
có hai nghiệm phân biệt
( )
( )
2
2
'0 2 3 4 1 0mm⇔∆ > ⇔ + − − >
13
12 13
12
mm⇔ >− ⇔ >−
.
Câu 32. Chọn A
Đồ thị hàm số
(
)
22
1
21 2
x
y
x m xm
−
=
+ − +−
có đúng hai tiệm cận đứng
⇔
phương trình
( ) ( )
22
2 1 20fx x m x m= + − + −=
có 2 nghiệm phân biệt khác 1.
( )
( )
( )
( )
2
2
2
1 20
'0
10
12 1 2 0
mm
f
mm
− − −>
∆>

⇔⇔

≠
+ −+ −≠
2
3
2
2 30
1
2 30
3
m
m
m
mm
m
<
− +>
⇔ ⇔≠

+ −≠
≠−
.
Câu 33. Chọn D
- Nếu
0m =
thì
1yx
= +
. Suy ra, đồ thị của nó không có tiệm cận ngang.
- Nếu
0m <
thì hàm số xác định
2
11
10mx x
mm
−
⇔ +≥ ⇔ ≤ ≤
−−
.
Do đó,
lim
x
y
→±∞
không tồn tại nên đồ thị hàm số không có tiệm cận ngang.
- Với
01m<<
thì
2
1
lim lim 1
xx
y xm
x
→+∞ →+∞

= + + = +∞



;
2
1
lim lim 1
xx
y xm
x
→−∞ →−∞

= − + = −∞



nên
đồ thị hàm số không có tiệm cận ngang.
- Với
1
m =
thì
2
1yx x=++
2
1
lim lim 1 1
xx
yx
x
→+∞ →+∞

= + + = +∞



( )
22
2
2
1
1
lim lim lim 0
1
1
11
xx x
xx
y
xx
x
x
→−∞ →−∞ →+∞
+−
= = =

+−
− ++


.
Suy ra đường thẳng
0y =
là tiệm cận ngang của đồ thị hàm số khi
x → −∞
.
Trang 12/16
- Với
1
m
>
thì
2
1
lim lim 1
xx
y xm
x
→+∞ →+∞

= + + = +∞



2
1
lim lim 1
xx
y xm
x
→−∞ →−∞

= − + = +∞



nên đồ thị hàm số không có tiệm cận ngang.
Câu 34. Chọn B
Điều kiện:
2
32
11
30
22
2 10 2 2
11
2 20
xx
xx
x xx
xx
x xx

≥− ≥−

−+≥

+≥ ⇔≠ ⇔≠


≠± ≠
− −+≠


.
Với điều kiện trên ta có,
( )
( )
( )
( )
(
)
2
22
3 21
32 1 3 21
xx x
y
x x x xx x
−+ − +
=
− + + −++ +
( )
( )
(
)
( )
(
)
2
22 2
32 1
32 1 3 21 1 3 21
xx
x x x xx x x xx x
−+
= =
− + + −++ + + −++ +
.
Ta có
(
)
1
lim
x
y
+
→−
;
( )
1
lim
x
y
−
→−
nên đồ thị hàm số không có tiệm cận đứng.
Mặt khác
2
22
1
lim lim 0
1 13 21
11
xx
y
x
x xx xx
→+∞ →+∞
= =


+ −+ + +




nên đường thẳng
0
y =
là tiệm
cận ngang của đồ thị hàm số khi
x
→ +∞
.
lim
x
y
→−∞
không tồn tại.
Câu 35. Chọn B
Điều kiện:
2
10mx +>
.
- Nếu
0m =
thì hàm số trở thành
1yx= +
không có tiệm cận ngang.
- Nếu
0m
<
thì hàm số xác định
11
x
mm
−−
⇔ <<
−−
.
Do đó,
lim
x
y
→±∞
không tồn tại nên đồ thị hàm số không có tiệm cận ngang.
- Nếu
0m >
thì hàm số xác định với mọi
x ∈
.
2
2
1
1
11
lim lim lim
1
1
xx x
x
x
y
m
mx
m
x
→+∞ →+∞ →+∞
+
+
= = =
+
+
.
Suy ra đường thẳng
1
y
m
=
là tiệm cận ngang của đồ thị hàm số khi
x → +∞
.
2
2
1
1
11
lim lim lim
1
1
xx x
x
x
y
m
mx
m
x
→−∞ →−∞ →+∞
+
+
= = = −
+
−+
.
Suy ra đường thẳng
1
y
m
= −
là tiệm cận ngang của đồ thị hàm số khi
x → −∞
.
Vậy
0m >
thỏa mãn yêu cầu đề bài.
Câu 36. Chọn C
Điều kiện:
1x
xm
≤
≠
.
Trang 13/16
Nếu
1
m
>
thì
lim
xm
y
+
→
;
lim
xm
y
−
→
không tồn tại nên đồ thị hàm số không có tiệm cận đứng.
Nếu
1
m
=
thì hàm số trở thành
1
1
x
y
x
−
=
−
11 1
11
lim lim lim
1
1
xx x
x
y
x
x
−− −
→→ →
−−
= = = −∞
−
−
Suy ra đường thẳng
1
x
=
là tiệm cận đứng của đồ thị hàm số khi
1x
−
→
.
1
lim
x
y
+
→
không tồn tại.
Do đó,
1m =
thỏa mãn.
- Nếu
1m <
thì
1
lim lim
xm xm
x
y
xm
++
→→
−
= = +∞
−
;
1
lim lim
xm xm
x
y
xm
−−
→→
−
= = −∞
−
.
Suy ra đường thẳng
xm=
là tiệm cận đứng của đồ thị hàm số khi
xm
+
→
và
xm
−
→
.
Vậy
1m ≤
thỏa mãn yêu cầu đề bài.
Câu 37. Chọn C
TH1 : Phương trình
32
30
x xm
− −=
có một nghiệm đơn
1x = −
và một nghiệm kép.
Phương trình
32
30x xm− −=
có nghiệm
1
x
= −
nên
( ) (
)
32
1 31 0 4mm− −− −=⇔=−
.
Với
4m = −
phương trình trở thành
32
1
3 40
2
x
xx
x
= −
− +=⇔
=
(thỏa mãn vì
2
x
là nghiệm
kép).
TH2: Phương trình
32
30x xm− −=
có đúng một nghiệm
khác
1
−
32
3
x xm⇔− =
có một nghiệm khác
1−
( ) ( )
32
4
4
4
0
0
0
4
1 3. 1
m
m
m
m
m
m
m
m
<−
<−
<−
>
⇔ ⇔⇔
>

>

≠−
−−−≠
.
Vậy với
0
4
m
m
>
≤−
thỏa mãn yêu cầu đề bài.
Câu 38. Chọn D
Đồ thị của hàm số
22
2
2
−−
=
−
x mx m
y
x
có tiệm cận đứng
2⇔
không là nghiệm của
(
)
22
2
=−−f x x mx m
( )
2
2 42 2 0
⇔ =−− ≠f mm
1
2
≠
⇔
≠−
m
m
.
Câu 39. Chọn B
Đồ thị của hàm số
2
53
21
x
y
x mx
−
=
−+
không có tiệm cận đứng
2
2 10
x mx⇔ − +=
vô nghiệm
2
'0 10 1 1mm⇔∆ < ⇔ − < ⇔− < <
.
Câu 40. Chọn C
Tập xác định
{ }
\1D =
. Đạo hàm
( )
2
3
' ,1
1
yx
x
−
= ∀≠
−
.
( )
C
có tiệm cận đứng
(
)
1
1 xd=
và tiệm cận ngang
(
)
2
2 yd=
nên
( )
1; 2I
.
Gọi
( )
0
00
0
21
; ,1
1
x
Mx C x
x

+
∈≠

−

.
Tiếp tuyến
∆
của
( )
C
tại
M
có phương trình
( )( ) ( )
00 0
'y f x x x fx= −+
Trang 14/16
( )
(
)
0
0
2
0
0
21
3
1
1
x
y xx
x
x
+
−
⇔= − +
−
−
∆
cắt
1
d
tại
0
0
22
1;
1
x
A
x

+

−

và cắt
2
d
tại
( )
0
2 1; 2Bx
−
.
Ta có
0
00
22
4
2
11
x
IA
xx
+
= −=
−−
;
( )
00
2 112 1IB x x= − −= −
.
Do đó,
0
0
1 14
. . .2 1 4
2 21
S IA IB x
x
= = −=
−
.
Câu 41. Chọn A
Tập xác định
D =
Ta có
2
2
3
1
3
lim lim 1
1
1
1
xx
x
x
x
x
→+∞ →+∞
+
+
= =
+
+
;
2
2
3
1
3
lim lim 1
1
1
1
xx
x
x
x
x
→−∞ →−∞
+
+
= = −
+
−+
Do đó đồ thị hàm số có hai đường tiệm cận ngang là
1y =
và
1y = −
.
Câu 42. Chọn A
Tập xác định
[ ]
1;1
D = −
Nên không tồn tại giới hạn
2 222
22
1 111
lim ; lim ; lim ; lim
2 222
xx
xx
x xxx
x xxx
+−
→+∞ →−∞
→→
−−−−
−−−−
.
Do đó đồ thị hàm số không có tiệm cận.
Câu 43. Chọn A
Tập xác định
D =
Ta có
(
)
2
2
2
2
4
42
lim 4 2 lim lim 2
42
42
11
x xx
x
x
xx x
xx x
xx
→+∞ →+∞ →+∞
−
−
− −+= = =
+ −+
+ −+
(
)
2
2
42
lim 4 2 lim 1 1
xx
xx x x
xx
→−∞ →−∞

− − + = + − + = −∞



vì
lim
x
x
→−∞
= −∞
và
2
42
lim 1 1 2 0
x
xx
→−∞

+ −+ =>



Do đó đồ thị hàm số có hai đường tiệm cận ngang là
2y =
.
Câu 44. Chọn C
Do M thuộc đồ thị hàm số
21
1
x
y
x
+
=
−
nên
0
0
0
21
;
1
x
Mx
x

+

−

với
0
1x
≠
Phương trình tiệm cận đứng là
( )
10xd−=
.
Giải phương trình
( ) ( )
0
0
0
0
0
0
21
,, 1
4
1
x
x
dMd dMOx x
x
x
=
+
= ⇔ −= ⇔
=
−
.
Câu 45. Chọn A
Tập xác định
{ }
\2D = −
Trên TXĐ của hàm số, biến đổi được
1yx= −
.
Do đó đồ thị không có tiệm cận
Câu 46. Chọn C
Tập xác định
{ }
\2D = −
Trang 15/16
Trên TXĐ của hàm số, biến đổi được
1
2
x
y
x
−
=
+
.
Ta có
11
lim lim 1
22
xx
xx
xx
→+∞ →−∞
−−
= =
++
;
22
11
lim ; lim
22
xx
xx
xx
+−
→− →−
−−
= −∞ = +∞
++
Do đó đồ thị có 2 tiệm cận
Câu 47. Chọn D
Tập xác định
(
)
; 2 2;
D

= −∞ − ∪ +∞

Ta có
2
2
2
1
2
lim lim 1
1
1
1
xx
x
x
x
x
→+∞ →+∞
−
−
= =
−
−
;
2
2
2
1
2
lim lim 1
1
1
1
xx
x
x
x
x
→−∞ →−∞
−−
−
= = −
−
−
Do tập xác định
(
)
; 2 2;
D

= −∞ − ∪ +∞

nên không tồn tại
22
11
22
lim ; lim
11
xx
xx
xx
+−
→→
−−
−−
Do đó đồ thị có 2 tiệm cận ngang là
1y =
và
1y = −
.
Câu 48. Chọn C
Tọa độ điểm
M
có dạng
0
0
0
2
;
3
x
Mx
x

+

−

Phương trình đường tiệm cận đứng, tiệm cận ngang lần lượt là
( ) ( )
12
30 , 10
x dy d−= −=
.
Giải phương trình
( ) (
)
12
5 , ,ddMd dM=
tìm
0
x
Chọn A.
Câu 49. Chọn D
Ta có đường tiệm cận đứng là
3x = −
và đường tiệm cận ngang là
1
3
y =
Nên
1
3,
3
ab=−=
Do đó
8
2
3
mab m m≥+⇔ ≥−⇒ =−
Câu 50. Chọn D
Tọa độ điểm
M
có dạng
0
0
0
23
;
2
x
Mx
x

−

−

với
0
2
x ≠
Phương trình tiệm cận đứng, ngang lần lượt là
( )
( )
12
20 , 20
x dy d−= −=
.
Ta có
( ) ( )
1 20
0
1
,,2 2
2
d dMd d Md x
x
= + = −+ ≥
−
Câu 51. Chọn A
Tọa độ điểm
M
bất kì thuộc đồ thị có dạng
0
0
0
23
;
2
x
Mx
x

−

−

với
0
2x ≠
Do đó phương trình tiếp tuyến tại
M
là
( )
( )
00
2
0
0
23
2
2
xx x
y
x
x
−−
=− +∆
−
−
.
Tính
( )
,2dM∆≤
.
Câu 52. Chọn A
Tọa độ điểm
M
bất kì thuộc đồ thị có dạng
0
0
0
23
;
2
x
Mx
x

−

−

với
0
2x ≠
Do đó phương trình tiếp tuyến tại
M
là
( )
( )
00
2
0
0
23
2
2
xx x
yd
x
x
−−
=−+
−
−
.
Trang 16/16
Tìm tọa độ giao của tiệm cận và tiếp tuyến
(
)
0
0
0
22
2; , 2 2; 2
2
x
A Bx
x

−
−

−

Từ đó đánh giá
4AB ≥
.
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

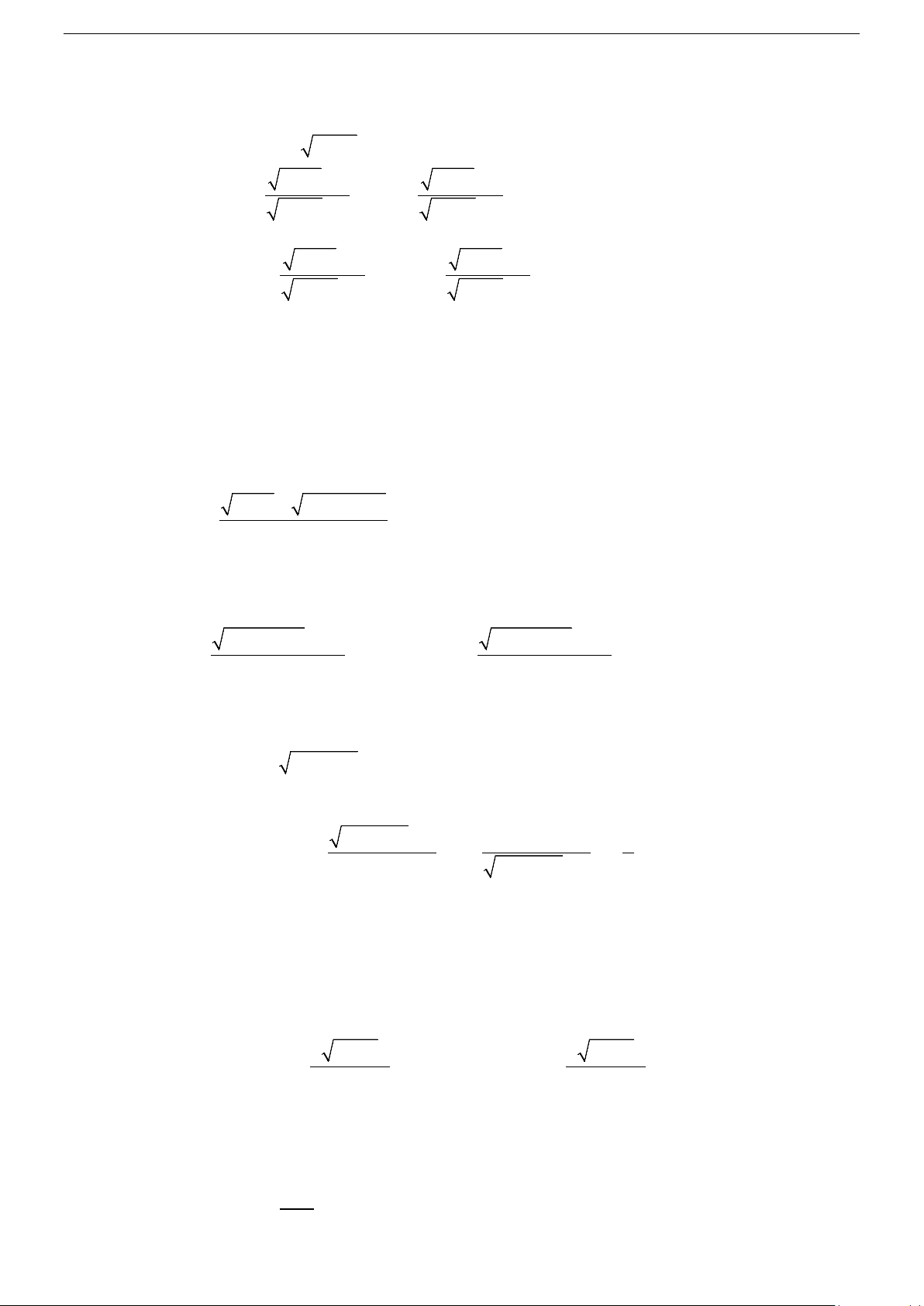
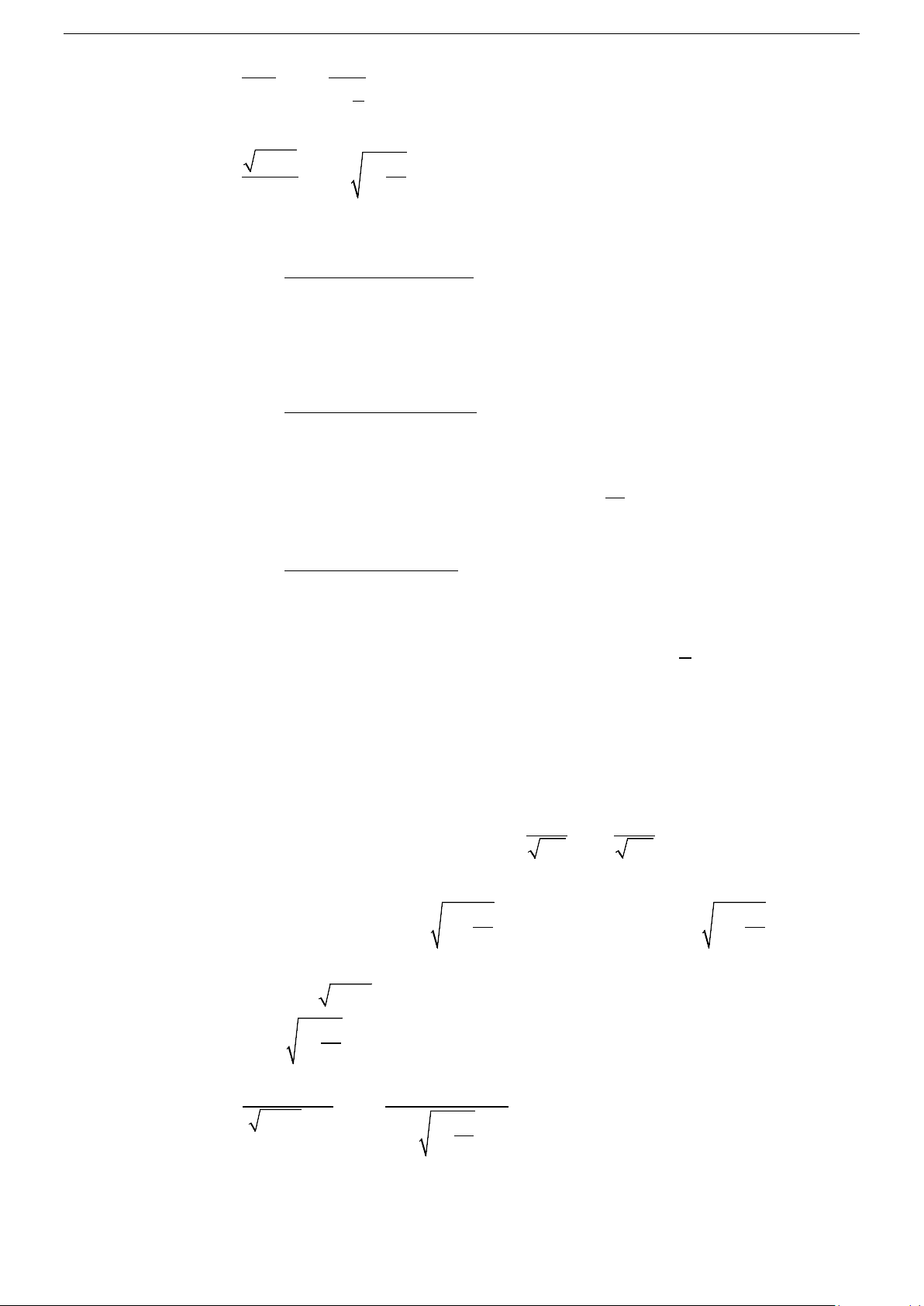
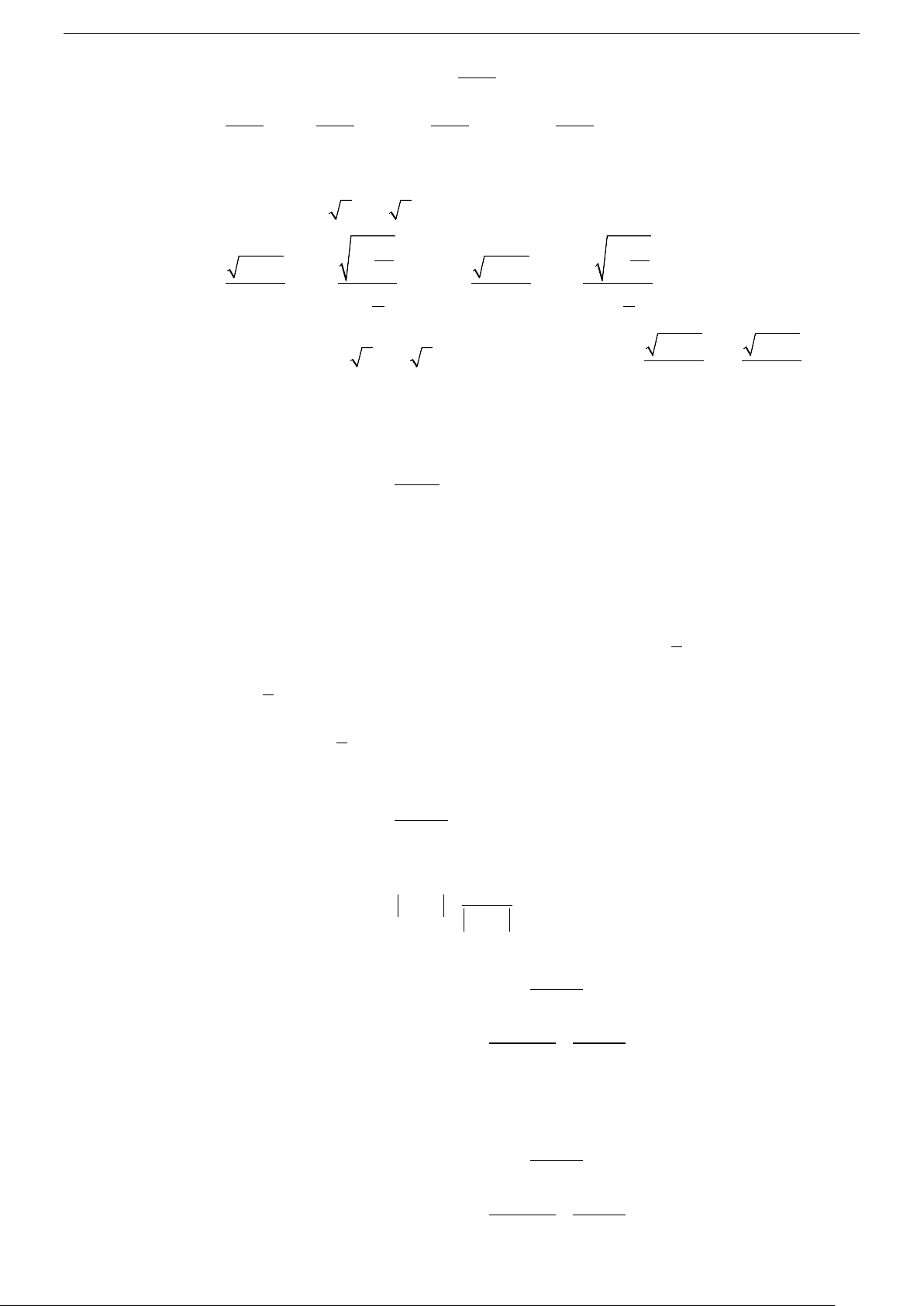
Preview text:


CHỦ ĐỀ 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
8. ÑÖÔØNG TIEÄM CAÄN CUÛA ÑOÀ THÒ HAØM SOÁ Đồ thị ax b y  có tiệm cận đứng d
x   , tiệm cận ngang a y   . cx d c c 2 Đồ thị
ax bx c r y   mx n có tiệm cận đứng q
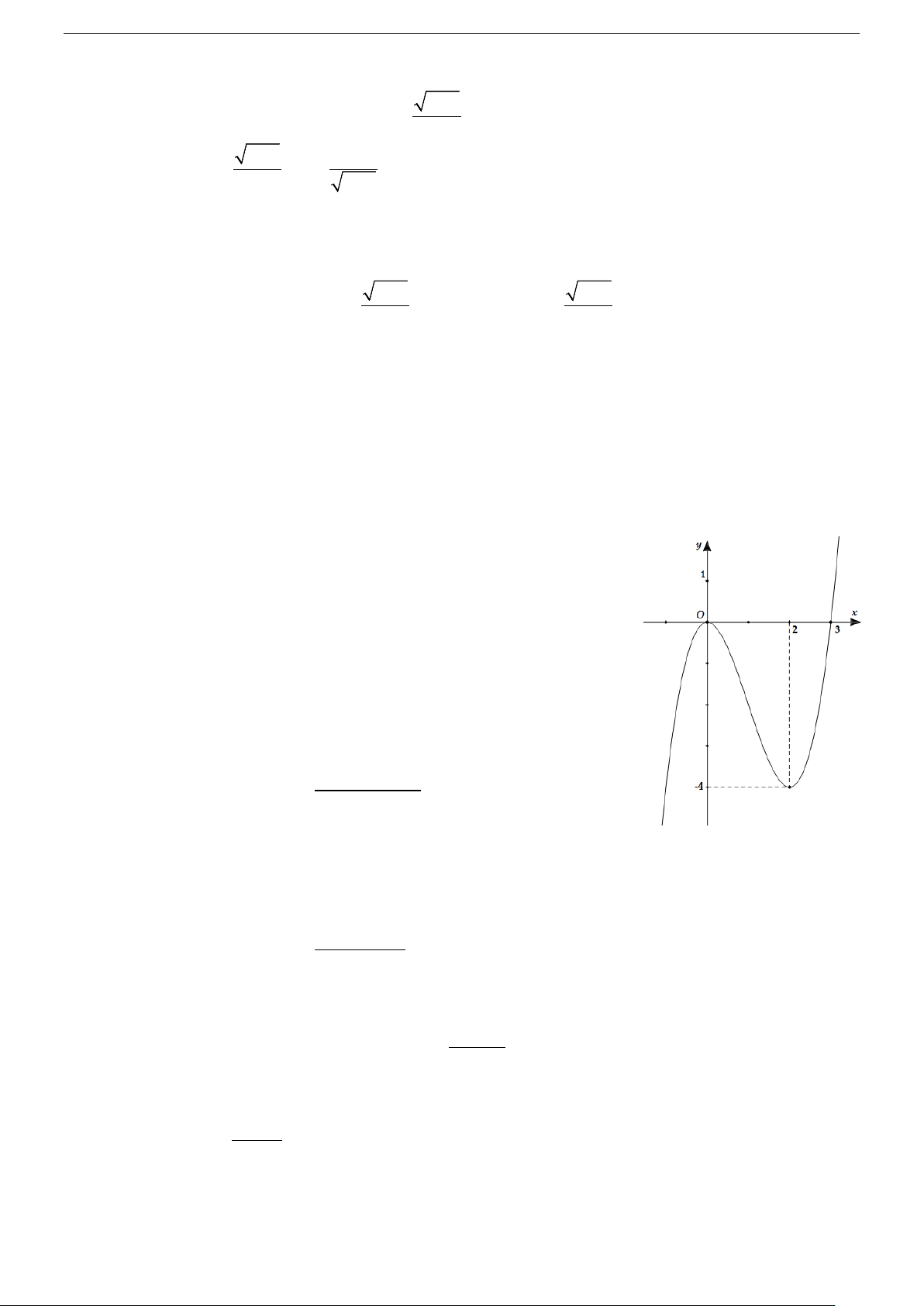
x   , tiệm cận xiên y mx n . px q px r p Đồ thị 2 y b
mx nax bx c có các đường cận là y mx na x  . 2a
A. BÀI TẬP TRẮC NGHIỆM
Câu 1. Đồ thị hàm số 2x − 3 y =
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là: x −1
A. x =1 và y = 3 − .
B. x = 2 và y =1.
C. x =1 và y = 2 . D. x = 1 − và y = 2 .
Câu 2. Đồ thị hàm số 1− 3x y =
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là: x + 2 A. x = 2 − và y = 3 − . B. x = 2 − và y =1. C. x = 2 − và y = 3.
D. x = 2 và y =1.
Câu 3. Đồ thị hàm số 2x − 3 y =
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là: 2 x − 3x + 2
A. x =1, x = 2 và y = 0.
B. x =1, x = 2 và y = 2 .
C. x =1 và y = 0.
D. x =1, x = 2 và y = 3 − . 2 Câu 4. − Đồ thị hàm số 1 3 = x y
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là: 2 x − 6x + 9
A. x = 3 và y = 3 − .
B. x = 3 và y = 0.
C. x = 3 và y =1.
D. y = 3 và x = 3 − . 2 Câu 5. + + Đồ thị hàm số 3x x 2 y =
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là: 3 x −8
A. y = 2 và x = 0 .
B. x = 2 và y = 0 .
C. x = 2 và y = 3.
D. y = 2 và x = 3.
Câu 6. Số đường tiệm cận của đồ thị hàm số 1− x y = là: 3+ 2x A. 4. B. 1. C. 0. D. 2.
Câu 7. Số đường tiệm cận của đồ thị hàm số 1 y = là: 3x + 2 A. 1. B. 3. C. 4. D. 2.
Câu 8. Số đường tiệm cận của đồ thị hàm số x +1 y = là: 2 x − 4 A. 4. B. 2. C. 1. D. 3.
Câu 9. Số đường tiệm cận của đồ thị hàm số x y = + x là: 2 x − 3x − 4 A. 4. B. 3. C. 2. D. 5. Câu 10. x + Cho hàm số 2 y =
khẳng định nào sau đây là sai: x − 3
A. Đồ thị hàm số có tiệm cận đứng x = 3.
B. Hàm số nghịch biến trên  \{ } 3 .
C. Đồ thị hàm số có tiệm cận ngang là y =1. Trang 1/16
D. Đồ thị hàm số có tâm đối xứng là I(3;1) .
Câu 11. Đồ thị hàm số nào sau đây có ba đường tiệm cận ? A. − + 1 2x y = . B. 1 y = . C. x 3 y = . D. x y = . 1+ x 2 4 − x 5x −1 2 x − x + 9 4 Câu 12. − Cho hàm số x 9x y = (
. Khẳng định nào sau đây là khẳng định đúng? 3x − 3)2 2
A. Đồ thị hàm số có tiệm cận đứng, không có tiệm cận ngang.
B. Đồ thị hàm số có 2 tiệm cận đứng, có 1 tiệm cận ngang y = 3 − .
C. Đồ thị hàm số có 2 tiệm cận đứng, có 1 tiệm cận ngang y = 1 − .
D. Đồ thị hàm số không có tiệm cận đứng, có tiệm cận ngang.
Câu 13. Đồ thị hàm số nào sau đây không có tiệm cận đứng: A. 3x −1 + y − = . B. 1 y = . C. x 3 y = . D. 1 y = . 2 x +1 x x + 2 2 x − 2x +1
Câu 14. Đồ thị hàm số nào sau đây không có tiệm cận ngang: 4 2 + + A. 2x − 3 y x 3x 7 = . B. y = . C. 3 y = . D. 3 y = +1. x +1 2x −1 2 x −1 x − 2
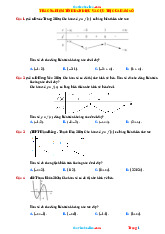
Câu 15. Đồ thị như hình vẽ là của hàm số nào sau đây : A. x −1 y − + − = . B. 3 x y = . C. x 2 y = . D. x 2 y = . x +1 x −1 x −1 x −1 Câu 16. − Đồ thị hàm số 3x 1 y =
có đường tiệm cận ngang là 3x + 2 A. x = 3. B. x =1. C. y = 3. D. y =1 . Câu 17. − Đồ thị hàm số 2x 1 y =
có bao nhiêu đường tiệm cận? x + 2 A. 1. B. 2. C. 3. D. 0. Câu 18. −
Số đường tiệm cận của đồ thị hàm số 2x 1 y = là 2 x − 3x + 2 A. 0. B. 1. C. 2. D. 3. Câu 19. + Cho hàm số mx 9 y =
có đồ thị (C) . Kết luận nào sau đây đúng ? x + m
A. Khi m = 3 thì (C)không có đường tiệm cận đứng. B. Khi m = 3
− thì (C) không có đường tiệm cận đứng. C. Khi m ≠ 3
± thì (C) có tiệm cận đứng x = − ,
m tiệm cận ngang y = m.
D. Khi m = 0 thì (C) không có tiệm cận ngang. Câu 20. +
Tìm tất cả các đường tiệm cận của đồ thị hàm số x 3 y = 2 x +1 A. y = 1 ± . B. x =1. C. y =1. D. y = 1 − . Trang 2/16 Câu 21. −
Với giá trị nào của m thì đồ thị (C): mx 1 y =
có tiệm cận đứng đi qua điểm M ( 1; − 2) ? 2x + m A. 2 m = . B. m = 0. C. 1 m = . D. m = 2 . 2 2 Câu 22. + Cho hàm số mx n y =
có đồ thị (C). Biết tiệm cận ngang của (C) đi qua điểm ( A 1; − 2) đồng x −1
thời điểm I(2;1) thuộc (C). Khi đó giá trị của m + n là
A. m + n = 1 − .
B. m + n =1.
C. m + n = 3 − .
D. m + n = 3 . 2 Câu 23. + −
Số tiệm cận của hàm số x 1 x y = là 2 x − 9 − 4 A. 2 . B. 4 . C. 3. D. 1. Câu 24. −
Giá trị của m để đồ thị hàm số x m y =
không có tiệm cận đứng là mx −1
A. m = 0;m = 1 ± . B. m = 1 − . C. m = 1 ± . D. m =1. 2 3 3 2 Câu 25. + + + +
Số tiệm cận của hàm số x 1 x 3x 1 y = là x −1 A. 3. B. 2. C. 1. D. 4. 2 Câu 26. + + − Đồ thị hàm số x 2x 2 mx y =
có hai đường tiệm cận ngang với x + 2 A. m ∀ ∈  . B. m =1.
C. m = 0;m =1. D. m = 0. 2 Câu 27. − + + Đồ thị hàm số x x 1 mx y =
có đường tiệm cận đứng khi x −1 A. m ≠ 0 . B. m ∀ ∈ R . C. m ≠ 1 − . D. m ≠ 1 . 2 Câu 28. −
Số đường tiệm cận của đồ thị hàm số 4 x y = là: 2 x − 3x − 4 A. 1. B. 0. C. 2. D. 3.  2 x +1  neáu x ≥1
Câu 29. Số tiệm cận của đồ thị hàm số  x y =  .
 2x neáu x <1  x −1 A. 1. B. 2. C. 3. D. 4. 2
x − (2m + 3) x + 2(m − ) 1
Câu 30. Xác định m để đồ thị hàm số y =
không có tiệm cận đứng. x − 2 A. m = 2 − . B. m = 2 . C. m = 3 . D. m =1.
Câu 31. Xác định m để đồ thị hàm số 3 y =
có đúng hai tiệm cận đứng. 2 4x + 2(2m + 3) 2 x + m −1 A. 13 m < − . B. 1 − < m <1. C. 3 m > − . D. 13 m > − . 12 2 12 Câu 32. −
Xác định m để đồ thị hàm số x 1 y =
có đúng hai tiệm cận đứng. 2 x + 2(m − ) 2 1 x + m − 2 A. 3
m < ;m ≠ 1;m ≠ 3 − . B. 3
m > − ;m ≠ 1. 2 2 C. 3 m > − . D. 3 m < . 2 2
Câu 33. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 2
y = x + mx +1 có tiệm cận ngang. Trang 3/16
A. 0 < m <1. B. m = 1 − . C. m >1. D. m =1. 2 Câu 34. − + − + Cho hàm số x x 3 2x 1 y =
. Trong các khẳng định sau, khẳng định nào là khẳng 3 2
x − 2x − x + 2 định đúng?
A. Đồ thị hàm số không có tiệm cận đứng, không có tiệm cận ngang.
B. Đồ thị hàm số không có tiệm cận đứng và có đúng 1 tiệm cận ngang.
C. Đồ thị hàm số có đúng 3 tiệm cận đứng và 2 tiệm cận ngang.
D. Đồ thị hàm số có đúng 2 tiệm cận đứng và 1 tiệm cận ngang. Câu 35. +
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số x 1 y = có hai tiệm 2 mx +1 cận ngang. A. m < 0 . B. m > 0. C. m = 0.
D. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài. Câu 36. −
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 1 x y = có tiệm cận x − m đứng. A. m >1. B. m =1. C. m ≤1.
D. Không có m thỏa mãn yêu cầu đề bài. Câu 37. +
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số x 1 y = có đúng 3 2
x − 3x − m một tiệm cận đứng. m > 0 m > 0 m ≥ 0 A. m∈ . B.  . C.  . D.  . m < 4 − m ≤ 4 − m ≤ 4 − 2 2 Câu 38. − −
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số x mx 2m y = có tiệm x − 2 cận đứng. m ≠ 2 −
A. Không có m thỏa mãn yêu đều đề bài. B.  . m ≠ 1 m ≠ 2 − C. m∈ . D.  m ≠ 1 Câu 39. −
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 5x 3 y = không có 2 x − 2mx +1 tiệm cận đứng. m >1 A.  . B. 1 − < m <1. C. m = 1 − . D. m =1. m < 1 − Câu 40. + Cho hàm số 2x 1 y =
có đồ thị (C). Gọi M là một điểm bất kì trên (C). Tiếp tuyến của (C) x −1
tại M cắt các đường tiệm cận của (C) tại A và B . Gọi I là giao điểm của các đường tiệm
cận của (C). Tính diện tích của tam giác IAB . A. 2 . B.12. C. 4 . D. 6 . Câu 41. +
Số đường tiệm cận của đồ thị hàm số x 3 y = là: 2 x +1 A. 2. B. 0. C. 1. D. 3. 2 Câu 42. −
Số đường tiệm cận của đồ thị hàm số 1 x y = là: x − 2 A. 0. B. 1. C. 3. D. 3. Trang 4/16
Câu 43. Đồ thị hàm số 2
y = x − x − 4x + 2 có tiệm cận ngang là: A. y = 2 . B. y = 2 − . C. y = 2 . D. x = 2 − . Câu 44. +
Tìm điểm M thuộc đồ thị hàm số 2x 1 y =
sao cho khoảng cách từ M đến tiệm cận đứng bằng x −1
khoảng cách từ M đến trục hoành A. M (0;− ) 1 , M (3;2). B. M (2; ) 1 , M (4;3) . C. M (0;− ) 1 , M (4;3). D. M (2; ) 1 , M (3;2) . 2 Câu 45. + −
Số tiệm cận của đồ thị hàm số x x 2 y = là x + 2 A. 0. B. 1. C. 2. D. 3. 2 Câu 46. + −
Số tiệm cận của đồ thị hàm số x x 2 y = là (x + 2)2 A. 0. B. 1. C. 2. D. 3. 2 Câu 47. −
Số tiệm cận của đồ thị hàm số x 2 y = là x −1 A. 1. B. 0. C. 3. D. 2. Câu 48. + Cho hàm số x 2 y =
(C) . Có tất cả bao nhiêu điểm M thuộc (C) sao cho khoảng cách từ M x − 3
đến tiệm cận ngang bằng 5 lần khoảng cách từ điểm M đến tiệm cận đứng. A. 4. B. 3. C. 2. D. 1. Câu 49. + Đồ thị hàm số x 2 y =
có đường tiệm cận đứng là x = a và đường tiệm cận ngang là y = b . 3x + 9
Giá trị của số nguyên m nhỏ nhất thỏa mãn m ≥ a + b là A. 0 . B. 3 − . C. 1 − . D. 2 − . Câu 50. − Cho hàm số 2x 3 y =
(C) . Gọi M là điểm bất kỳ trên (C), d là tổng khoảng cách từ M đến x − 2
hai đường tiệm cận của đồ thị (C). Giá trị nhỏ nhất của d là A. 5. B. 10. C. 6. D. 2. Câu 51. − Cho hàm số 2x 3 y =
(C) . Gọi d là khoảng cách từ giao điểm của 2 tiệm cận của (C) đến một x − 2
tiếp tuyến bất kỳ của đồ thị (C). Giá trị lớn nhất của d là A. 2 . B. 3 . C. 3 3 . D. 2 . Câu 52. − Cho hàm số 2x 3 y =
(C) . Gọi d là tiếp tuyến bất kì của (C), d cắt hai đường tiệm cận của đồ x − 2
thị (C) lần lượt tại A, B. Khi đó khoảng cách giữa A và B ngắn nhất bằng A. 4 . B. 3 2 . C. 2 2 . D. 3 3 .
B. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
C A A A B D D D C B B C A B C D B D C A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
D A B A A A C A C A D A D B B C C D B C
41 42 43 44 45 46 47 48 49 50 51 52 A A A C A C D C D D A A
II –HƯỚNG DẪN GIẢI Trang 5/16 Câu 1. Chọn C Phương pháp tự luận Ta có 2x − 3 − lim = −∞ và 2x 3 lim
= +∞ nên đồ thị hàm số có tiệm cận đứng là x =1 x 1+ → x −1 x 1− → x −1 2x − 3 lim
= 2 nên đồ thị hàm số có tiệm cận ngang là y = 2 x→±∞ x −1
Phương pháp trắc nghiệm x − Nhập biểu thức 2 3 . x −1 Ấn CALC 9 x 1 10− = +
. Ấn = được kết quả bằng -999999998 nên 2x − 3 lim = −∞ . x 1+ → x −1 Ấn CALC 9 x 1 10− = −
. Ấn = được kết quả bằng 999999998 nên 2x − 3 lim = +∞ . x 1− → x −1
⇒ đồ thị hàm số có tiệm cận đứng là x =1 Ấn CALC 10
x =10 . Ấn = được kết quả bằng 2 nên 2x − 3 lim = 2 . x→±∞ x −1
⇒ đồ thị hàm số có tiệm cận ngang là y = 2 Câu 2. Chọn A Phương pháp tự luận Ta có 1− 3 − lim x = +∞ và 1 3 lim
x = −∞nên đồ thị hàm số có tiệm cận đứng là x = 2 − x ( 2)+ → − x + 2 x ( 2)− → − x + 2 Ta có 1− 3 lim x = 3
− nên đồ thị hàm số có tiệm cận ngang là y = 3 − x→±∞ x + 2
Phương pháp trắc nghiệm
Nhập biểu thức 1− 3x . x + 2 Ấn CALC 9 − x 2 10− = − +
. Ấn = được kết quả bằng 6999999997 nên 1 3 lim x = +∞. x ( 2)+ → − x + 2 Ấn CALC − 9 x 2 10− = − −
. Ấn = được kết quả bằng -7000000003 nên 1 3 lim x = −∞. x ( 2)− → − x + 2
⇒ đồ thị hàm số có tiệm cận đứng là x = 2 − Ấn CALC − 10
x =10 . Ấn = được kết quả bằng -2,999999999 nên 1 3 lim x = 3 − . x→±∞ x + 2
⇒ đồ thị hàm số có tiệm cận ngang là y = 3 − Câu 3. Chọn A Phương pháp tự luận Ta có 2x − 3 − lim = +∞ và 2x 3 lim
= −∞ nên đồ thị hàm số có tiệm cận đứng là + 2 x 1 → x − 3x + 2 − 2 x 1 → x − 3x + 2
x =1 . Tính tương tự với x = 2 Ta có 2x − 3 lim
= 0 nên đồ thị hàm số có tiệm cận ngang là y = 0 2
x→±∞ x − 3x + 2
Phương pháp tự luận −
Nhập biểu thức 2x 3 . 2 x − 3x + 2
Xét tại x =1: Ấn CALC 9 x 1 10− = +
. Ấn = được kết quả bằng 999999998 nên 2x − 3 lim = +∞ . + 2 x 1 → x − 3x + 2 Ấn CALC 9 − x 1 10− = +
. Ấn = được kết quả bằng -1,000000002 nên 2x 3 lim = −∞ . − 2 x 1 → x − 3x + 2
Tương tự xét với x = 2 Trang 6/16
⇒ đồ thị hàm số có tiệm cận đứng là x =1và x = 2 Ấn CALC 10 −
x =10 . Ấn = được kết quả bằng 10 2.10− nên 2x 3 lim = 0 . 2
x→±∞ x − 3x + 2
⇒ đồ thị hàm số có tiệm cận ngang là y = 0 Câu 4. Chọn A
Phương pháp tự luận 2 1− 3 2 − lim x = −∞ và 1 3 lim x
= −∞ nên đồ thị hàm số có tiệm cận đứng là x = 3 . + 2
x→3 x − 6x + 9 − 2
x→3 x − 6x + 9 2 − Ta có 1 3 lim x = 3
− nên đồ thị hàm số có tiệm cận ngang là y = 3 − 2
x→±∞ x − 6x + 9
Phương pháp trắc nghiệm
Tương tự câu 3,4 nên tự tính kiểm tra Câu 5. Chọn B Tương tự câu 3 . Câu 6. Chọn D
Tìm tương tự các câu trên ta được tiệm cận đứng là 3
x = − và tiệm cận ngang là 1 y = − 2 2
⇒ Số đường tiệm cận là 2.
Câu 7. Chọn D
Tìm tương tự các câu trên ta được tiệm cận đứng là 2
x = − và tiệm cận ngang là y = 0 3
⇒ Số đường tiệm cận là 2
Câu 8. Chọn D
Tìm được tiệm cận đứng là x = 2
± và tiệm cận ngang là y = 0
⇒ Số đường tiệm cận là 3
Câu 9. Chọn C 3 2 − −
Quy đồng biến đổi hàm số đã cho trở thành x 3x 3x y = 2 x − 3x − 4
Tìm được tiệm cận đứng là x = 1
− , x = 4 và không có tiệm cận ngang (Vì lim y = ±∞ ) x→±∞
⇒ Số đường tiệm cận là 2 Câu 10. Chọn B
Tìm được tiệm cận đứng là x = 3 và tiệm cận ngang là y = 1
Giao điểm của hai đường tiệm cận I(3;1) là tâm đối xứng của đồ thị ⇒ A,C,D đúng và chọn B Câu 11. Chọn B Đồ thị hàm số 1 y =
có 3 đường tiệm cận .( TCĐ là x = 2 ± và TCN y = 0 ) 2 4 − x Câu 12. Chọn C 4 − Đồ thị hàm số x 9x y = (
có hai đường tiệm cận đứng x = 1
± và một tiệm cận ngang 3x − 3)2 2 y = 1 − Câu 13. Chọn A Phương trình 2 x −
+1 = 0 vô nghiệm nên không tìm được số x để 3x 1 lim = ±∞ 0 + 2 x→ 0 x x +1 hoặc 3x −1 lim
= ±∞ ⇒ đồ thị hàm số không có tiệm cận đứng − 2 x→ 0 x x +1
Các đồ thị hàm số ở B,C,D lần lượt có các TCĐ là x = 0, x = 2, − x =1 Câu 14. Chọn B Trang 7/16 4 2 + + Ta có x 3x 7 lim
= ±∞ ⇒ đồ thị hàm số không có tiệm cận ngang. x→±∞ 2x −1
Các đồ thị hàm số ở B,C,D lần lượt có các TCN là y = 2, y = 0, y =1 Câu 15. Chọn C
Từ đồ thị ta thấy có tiệm cận đứng là x =1 và y =1 ⇒ loại A,B
Xét tiếp thấy giao điểm của đồ thị hàm số với trục tung là (0; 2 − ) ⇒ chọn C. Câu 16. Chọn D
Phương pháp tự luận − − Ta có 3x 1 3x 1 lim = lim = 1. x→+∞ 3x + 2
x→−∞ 3x + 2
Do đó đồ thị hàm số có đường tiệm cận ngang là y =1
Phương pháp trắc nghiệm −
Nhập vào máy tính biểu thức 3X 1 ấn CALC 12
10 ta được kết quả là 1. 3X + 2 Tiếp tục CALC 12 10 −
ta được kết quả là 1.
Vậy đồ thị hàm số có đường tiệm cận ngang là y =1 Câu 17. Chọn B
Phương pháp tự luận − − Ta có 2x 1 2x 1 lim = lim
= 2 nên đồ thị hàm số có đường tiệm cận ngang là y = 2 . x→+∞ x + 2 x→−∞ x + 2 − − Lại có 2x 1 2x 1 lim = ; −∞ lim
= +∞ nên đồ thị hàm số có đường tiệm cận đứng x = 2 − . x 2+ + x 2 x 2 − →− →− x + 2
Vậy đồ thị hàm số đã cho có hai đường tiệm cận.
Phương pháp trắc nghiệm −
Nhập vào máy tính biểu thức 2X 1 ấn CALC 12
10 ta được kết quả là 2. X + 2 Tiếp tục CALC 12 10 −
ta được kết quả là 2.
Vậy đồ thị hàm số có đường tiệm cận ngang là y = 2 . Tiếp tục ấn CALC 12 2 10− − + ta được kết quả là 12 5.10 − , ấn CALC 12 2 10− − − ta được kết quả − − là 12 5.10 nên có 2x 1 2x 1 lim = ; −∞ lim = +∞ . x 2+ + x 2 x 2 − →− →− x + 2
Do đó ta được x = 2
− là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có hai đường tiệm cận. Câu 18. Chọn D
Phương pháp tự luận − − Ta có: 2x 1 2x 1 lim = 0; lim = 0 . 2 2
x→−∞ x − 3x + 2
x→+∞ x − 3x + 2
Do đó đồ thị hàm số có đường tiệm cận ngang y = 0. − − − Lại có 2x 1 2x 1 lim = ; +∞ lim = −∞ và 2x 1 lim = ; −∞ − 2 + 2 x 1 → − + x 1 x 3x 2 → x − 3x + 2 − 2
x→2 x − 3x + 2 2x −1 lim
= +∞ nên đồ thị hàm số có hai đường tiệm cận đứng là x =1; x = 2 . + 2
x→2 x − 3x + 2
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Phương pháp trắc nghiệm −
Nhập vào máy tính biểu thức 2X 1 ấn CALC 12
10 ta được kết quả là 0. 2 X + 3X + 2 Tiếp tục CALC 12 10 −
ta được kết quả là 0.
Vậy đồ thị hàm số có đường tiệm cận ngang là y = 0 . Trang 8/16 Tiếp tục ấn CALC 12 1 10− + ta được kết quả là 12 1.10 − , ấn CALC 12 1 10− − ta được kết quả là 12 − − 1.10 nên có 2x 1 2x 1 lim = ; +∞ lim
= −∞ do đó ta được x =1 là tiệm cận đứng − 2 + 2 x 1 → − + x 1 x 3x 2 → x − 3x + 2 của đồ thị hàm số. Tiếp tục ấn CALC 12 2 10− + ta được kết quả là 12 3.10 , ấn CALC 12 1 10− − ta được kết quả là 12 − − 3.10 − nên có 2x 1 2x 1 lim = ; −∞ lim
= +∞ do đó ta được x = 2 là tiệm cận − 2 + 2 x→2 − + x→2 x 3x 2 x − 3x + 2
đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có ba đường tiệm cận. Câu 19. Chọn C
Phương pháp tự luận
Xét phương trình: mx + 9 = 0 .
Với x = −m ta có: 2
−m + 9 = 0 ⇔ m = 3 ±
Kiểm tra thấy với m = 3
± thì hàm số không có tiệm cận đứng và tiệm cận ngang. Khi m ≠ 3
± hàm số luôn có tiệm cận đứng x = m hoặc x = −m và tiệm cận ngang y = m
Phương pháp trắc nghiệm +
Nhập vào máy tính biểu thức XY 9 ấn CALC 10 X 3 10− = − + ;Y = 3 − X +Y ta được kết quả 3 − . Tiếp tục ấn CALC 10 X 3 10− = − − ;Y = 3
− ta được kết quả -3. Vậy khi m = 3
− đồ thị hàm số không có đường tiệm cận đứng.
Tương tự với m = 3 ta cũng có kết quả tương tự.
Vậy các đáp án A và B không thỏa mãn. Tiếp tục ấn CALC 10 X = 10 −
;Y = 0 ta được kết quả 10 9 10 x − , ấn CALC 10 X =10 ;Y = 0 ta được kết quả 10 9x10− .
Do đó hàm số có tiệm cận ngang y = 0. Vậy đáp án D sai. Câu 20. Chọn A
Phương pháp tự luận
Vì TXĐ của hàm số là  nên đồ thị hàm số không có tiệm cận đứng. 3 1+ 3 + 1+ + Lại có x 3 lim = lim x =1 và x 3 lim = lim x = 1 − x→+∞ 2 x +1 x→+∞ 1 x→−∞ 2 x→−∞ 1+ x +1 1 − 1+ 2 x 2 x
Vậy đồ thị hàm số có hai đường tiệm cận ngang là y = 1 ±
Phương pháp trắc nghiệm +
Nhập vào máy tính biểu thức x 3 ấn CALC 10
10 ta được kết quả là 1. 2 x +1 Tiếp tục ấn CALC 10 10 − ta được kết quả là 1 − .
Vậy có hai tiệm cận ngang là y = 1 ± . Câu 21. Chọn D
Để đồ thị hàm số có đường tiệm cận đứng thì 2
m + 2 ≠ 0 luôn đúng với mọi m .
Khi đó đồ thị hàm số có đường tiệm cận đứng là m x = − . 2
Vậy để tiệm cận đứng đi qua điểm M ( 1; − 2) thì m − = 1 − ⇔ m = 2 2 Câu 22. Chọn A
Để hàm số có đường tiệm cận ngang thì m + n ≠ 0
Khi đó tiệm cận ngang của đồ thị hàm số là y = mdo đó ta có m = 2
Mặt khác đồ thị hàm số đi qua điểm I(2;1) nên có 2m + n =1⇒ n = 3 − Trang 9/16 Vậy m + n = 1 − Câu 23. Chọn B 2 x − 9 ≥  0
Điều kiện xác định  ⇔ x ∈( ; −∞ 3 − ]∪[3;+∞) \{± 5} 2  x − 9 ≠ 4 2 2 + − + − Khi đó có: x 1 x x 1 lim = 0; lim
x = 2 nên đồ thị hàm số có hai đường tiệm cận x→+∞ 2 x→−∞ 2 x − 9 − 4 x − 9 − 4 ngang. 2 2 + − + − Mặt khác có x 1 x x 1 lim =  ; ∞ lim
x = ±∞ nên đồ thị hàm số có hai đường tiệm x 5± 2 x 5± →− → 2 x − 9 − 4 x − 9 − 4 cận đứng.
Vậy đồ thị hàm số đã cho có 4 đường tiệm cận. Câu 24. Chọn A
Xét m = 0 thì đồ thị hàm số không có đường tiệm cận đứng.
Xét m ≠ 0 khi đó đồ thị hàm số không có đường tiệm cận đứng nếu 2
ad − bc = 0 ⇔ 1 − + m = 0 ⇔ m = 1 ± .
Vậy giá trị của m cần tìm là m = 0;m = 1 ± Câu 25. Chọn A 2 3 3 2 + + + + Ta có x 1 x 3x 1 lim
= ∞ . Vậy đồ thị hàm số có đường tiệm cận đứng là x =1 x 1 → x −1
Mặt khác lim y = 2; lim y = 0 nên đồ thị hàm số có hai tiệm cận ngang. x→+∞ x→−∞
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận. Câu 26. Chọn A 2 + + − 2 + + − Xét x 2x 2 lim mx = 1 − − m và x 2x 2 lim mx =1−m x→−∞ x + 2 x→+∞ x + 2
Để hàm số có hai tiệm cận ngang thì 1
− − m ≠ 1− m (thỏa với mọi m) . Vậy m
∀ ∈ R thì đồ thị hàm số có hai tiệm cận ngang. Câu 27. Chọn C Xét phương trình 2
x − x +1 + mx = 0 .
Nếu phương trình không có nghiệm x =1thì đồ thị hàm số có đường tiệm cận đứng là x =1.
Nếu phương trình có nghiệm x =1hay m = 1 − . 2 − + − − Khi đó xét giới hạn: x x 1 x 1 1 lim = lim
= − nên trong trường hợp này đồ x 1 → x 1 → 2 x −1
x − x +1 + x 2
thị hàm số không có đường tiệm cận đứng. Vậy m ≠ 1 − . Câu 28. Chọn A  2 − ≤ x ≤ 2 2 4 − x ≥ 0   2 − ≤ x ≤ 2 Điều kiện:  ⇔ x ≠ 1 − ⇔  . 2
x − 3x − 4 ≠ 0  x ≠ 1 − x ≠  4 2 − 2 − Ta có 4 lim = lim x y = −∞ ; 4 lim = lim x y = +∞ . x→(− )+ x→(− )+ 2 1 1 x − 3x − 4 x→(− )− x→(− )− 2 1 1 x − 3x − 4
Suy ra đường thẳng x = 1
− là tiệm cận đứng của đồ thị hàm số khi x ( ) 1 + → − và x ( ) 1 − → − .
Vì lim y không tồn tại nên đồ thị hàm số không có tiệm cận ngang. x→±∞ Câu 29. Chọn C Ta có 2 lim = lim x y
= −∞ nên đường thẳng x =1 là tiệm cận đứng của đồ thị hàm số. x 1− x 1− → → x −1 Trang 10/16 2x 2 lim y = lim = lim
= 2 nên đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số x→−∞
x→−∞ x −1 x→−∞ 1 1− x khi x → −∞ . 2 x +1 1 lim y = lim = lim 1+
= 1 nên đường thẳng y =1 là tiệm cận ngang của đồ thị 2 x→+∞ x→+∞ x x →+∞ x
hàm số khi x → +∞ . Câu 30. Chọn A 2
x − (2m + 3) x + 2(m − ) 1
Đồ thị hàm số y =
không có tiệm cận đứng x − 2
⇔ phương trình f (x) 2
= x − (2m + 3) x + 2(m − )
1 = 0 có nghiệm x = 2
⇔ f (2) = 0 ⇔ 4 − 2(2m + 3) + 2(m − ) 1 = 0 ⇔ 2
− m − 4 = 0 ⇔ m = 2 − . Câu 31. Chọn D Đồ thị hàm số 3 y =
có đúng hai tiệm cận đứng 2 4x + 2(2m + 3) 2 x + m −1 ⇔ phương trình 2 x + ( m + ) 2 4 2 2
3 x + m −1 = 0 có hai nghiệm phân biệt
⇔ ∆ > ⇔ ( m + )2 − ( 2 ' 0 2 3 4 m − ) 1 > 0 13 ⇔ 12m > 13 − ⇔ m > − . 12 Câu 32. Chọn A − Đồ thị hàm số x 1 y =
có đúng hai tiệm cận đứng 2 x + 2(m − ) 2 1 x + m − 2
⇔ phương trình f (x) 2 = x + (m − ) 2 2
1 x + m − 2 = 0 có 2 nghiệm phân biệt khác 1.  3 m <  ∆ 2  ' > 0 (  m − )2 1 − ( 2 m − 2) > 0  2 − m + 3 > 0  ⇔  ⇔ ⇔  ⇔ m ≠1 .  f  ( ) 1 0  ≠ 1  + 2 2  (m − ) 2 1 + m − 2 ≠ 0
m + 2m − 3 ≠ 0 m ≠ 3 −   Câu 33. Chọn D
- Nếu m = 0 thì y = x +1. Suy ra, đồ thị của nó không có tiệm cận ngang. −
- Nếu m < 0 thì hàm số xác định 2 1 1 ⇔ mx +1≥ 0 ⇔ ≤ x ≤ . −m −m
Do đó, lim y không tồn tại nên đồ thị hàm số không có tiệm cận ngang. x→±∞    
- Với 0 < m <1 thì 1 lim y = lim x 1 1+ m +  = +∞ 
; lim y = lim x1− m +  = −∞ nên 2 x→+∞ x→+∞ x      2 x→−∞ x→−∞ x  
đồ thị hàm số không có tiệm cận ngang. - Với m =1 thì 2
y = x + x +1  1 
lim y = lim x1+ 1+  = +∞  2 x→+∞ x→+∞ x    ( 2x + ) 2 1 − x 1 lim y = lim = lim = 0 . x→−∞ x→−∞ 2 x +1 x − x →+∞  1  −x 1+ +1 2 x   
Suy ra đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số khi x → −∞ . Trang 11/16   - Với m >1 thì 1
lim y = lim x1+ m +  = +∞  2 x→+∞ x→+∞ x     1 
lim y = lim x1− m +  = +∞ 
nên đồ thị hàm số không có tiệm cận ngang. 2 x→−∞ x→−∞ x    Câu 34. Chọn B  1  1 2  − + 3 ≥ 0 x ≥ − x x x ≥ −  2  2   
Điều kiện: 2x +1≥ 0
⇔ x ≠ 2 ⇔ x ≠ 2 .  3 2
x − 2x − x + 2 ≠  0 x 1  ≠ ± x ≠ 1    
( 2x − x+3)−(2x+ )1
Với điều kiện trên ta có, y = ( 2
x − 3x + 2)(x + )
1 ( 2x − x +3 + 2x +1) 2 x − 3x + 2 1 = ( = . 2
x − 3x + 2)(x + )
1 ( 2x − x +3 + 2x +1) (x + )1( 2x − x +3 + 2x +1)
Ta có lim y ; lim y nên đồ thị hàm số không có tiệm cận đứng. x ( ) 1 + → − x ( ) 1 − → − Mặt khác 1 lim y = lim
= 0 nên đường thẳng y = 0 là tiệm x→+∞ x→+∞    2 1 1 3 2 1 x 1+  1− + + + 2 2  x x x x x   
cận ngang của đồ thị hàm số khi x → +∞ .
lim y không tồn tại. x→−∞ Câu 35. Chọn B Điều kiện: 2 mx +1 > 0.
- Nếu m = 0 thì hàm số trở thành y = x +1 không có tiệm cận ngang. − −
- Nếu m < 0 thì hàm số xác định 1 1 ⇔ < x < . −m −m
Do đó, lim y không tồn tại nên đồ thị hàm số không có tiệm cận ngang. x→±∞
- Nếu m > 0 thì hàm số xác định với mọi x ∈ . 1 1 x 1 + + x 1 lim y = lim = lim = . x→+∞ x→+∞ 2 mx +1 x→+∞ 1 m m + 2 x Suy ra đường thẳng 1 y =
là tiệm cận ngang của đồ thị hàm số khi x → +∞ . m 1 1 x 1 + + x 1 lim y = lim = lim = − . x→−∞ x→−∞ 2 mx +1 x→+∞ 1 m − m + 2 x Suy ra đường thẳng 1 y = −
là tiệm cận ngang của đồ thị hàm số khi x → −∞ . m
Vậy m > 0 thỏa mãn yêu cầu đề bài. Câu 36. Chọn C x ≤1 Điều kiện:  . x ≠ m Trang 12/16
Nếu m >1 thì lim y ; lim y không tồn tại nên đồ thị hàm số không có tiệm cận đứng. x m+ → x m− → −
Nếu m =1 thì hàm số trở thành 1 x y = x −1 1− x 1 − lim y = lim = lim = −∞ x 1− x 1− − x 1 x 1 − → → → 1− x
Suy ra đường thẳng x =1 là tiệm cận đứng của đồ thị hàm số khi x 1− → .
lim y không tồn tại. x 1+ →
Do đó, m =1 thỏa mãn. − − - Nếu m <1 thì 1 lim = lim x y = +∞ ; 1 lim = lim x y = −∞ . x m+ x m+ → → x − m x m− x m− → → x − m
Suy ra đường thẳng x = m là tiệm cận đứng của đồ thị hàm số khi x m+ → và x m− → .
Vậy m ≤1 thỏa mãn yêu cầu đề bài. Câu 37. Chọn C TH1 : Phương trình 3 2
x − 3x − m = 0 có một nghiệm đơn x = 1 − và một nghiệm kép. Phương trình 3 2
x − 3x − m = 0 có nghiệm x = 1 − nên (− )3 − (− )2 1
3 1 − m = 0 ⇔ m = 4 − . x = 1 − Với m = 4
− phương trình trở thành 3 2
x − 3x + 4 = 0 ⇔ 
(thỏa mãn vì x  2 là nghiệm x = 2 kép). TH2: Phương trình 3 2
x − 3x − m = 0 có đúng một nghiệm khác 1 − 3 2
⇔ x − 3x = m có một nghiệm khác 1 − m < 4 − m < 4 −   m < 4 ⇔ m > 0 −
⇔ m > 0 ⇔  .   m > 0 (−  )3 1 − 3.(− )2 1 ≠ mm ≠ 4 − m > 0 Vậy với 
thỏa mãn yêu cầu đề bài. m ≤ 4 − Câu 38. Chọn D 2 2 x − mx − Đồ thị của hàm số 2 = m y có tiệm cận đứng x − 2
⇔ 2 không là nghiệm của f (x) 2 2
= x −mx − 2m m ≠ 1 ⇔ f ( ) 2
2 = 4 − 2m − 2m ≠ 0 ⇔  . m ≠ 2 − Câu 39. Chọn B − Đồ thị của hàm số 5x 3 y =
không có tiệm cận đứng 2 x − 2mx +1 2
⇔ x − 2mx +1 = 0 vô nghiệm 2
⇔ ∆ ' < 0 ⇔ m −1< 0 ⇔ 1 − < m <1. Câu 40. Chọn C − Tập xác định D = 3  \{ } 1 . Đạo hàm y ' = , x ∀ ≠ 1. (x − )2 1
(C) có tiệm cận đứng x =1 (d và tiệm cận ngang y = 2 (d nên I (1;2). 2 ) 1 )  +  Gọi 2x 1 0 M x ;
∈ C , x ≠ 1. 0 ( ) 0 x −  1 0 
Tiếp tuyến ∆ của (C) tại M có phương trình y = f '(x x − x + f x 0 ) ( 0 ) ( 0) Trang 13/16 3 − 2x +1 ⇔ y = x − x + 2 ( 0 ) 0 (x −1 x −1 0 ) 0  +  ∆ cắt d tại 2x 2 0 A1;
và cắt d tại B(2x −1;2 . 0 ) 1 x 1  −  2 0  + Ta có 2x 2 4 0 IA = − 2 =
; IB = (2x −1 −1 = 2 x −1 . 0 ) x −1 x −1 0 0 0 Do đó, 1 1 4 S = . IA IB = . .2 x −1 = 4 . 0 2 2 x −1 0 Câu 41. Chọn A
Tập xác định D =  3 1+ 3 + 1+ + Ta có x 3 lim = lim x =1 ; x 3 lim = lim x = 1 − x→+∞ 2 x +1 x→+∞ 1 x→−∞ 2 x→−∞ 1+ x +1 1 − 1+ 2 x 2 x
Do đó đồ thị hàm số có hai đường tiệm cận ngang là y =1 và y = 1 − . Câu 42. Chọn A
Tập xác định D = [ 1; − ] 1 2 2 2 2 − − − −
Nên không tồn tại giới hạn 1 x 1 x 1 x 1 lim ; lim ; lim ; lim x . x x − − x 2+ − x 2 x 2 x 2 x 2 − →+∞ →−∞ → → x − 2
Do đó đồ thị hàm số không có tiệm cận. Câu 43. Chọn A
Tập xác định D =  2 4 − − Ta có x x
x − x − x + = = = x→+∞ ( 2 ) 4 2 lim 4 2 lim lim 2 x→+∞ 2
x + x − 4x + 2 x→+∞ 4 2 1+ 1− + 2 x x  
x − x − x + = x + − +  = −∞ x→−∞ ( 2 ) 4 2 lim 4 2 lim 1 1  2 x→−∞ x x      vì lim x = −∞ và 4 2 lim 1+ 1− +  = 2 > 0 x→−∞  2 x→−∞ x x   
Do đó đồ thị hàm số có hai đường tiệm cận ngang là y = 2 . Câu 44. Chọn C +  + 
Do M thuộc đồ thị hàm số 2x 1 y = nên 2x 1 0 M x ; với x ≠ 1 x −1 0 x 1  −  0 0 
Phương trình tiệm cận đứng là x −1 = 0 (d ) . 2x +1 x = 0
Giải phương trình d (M ,d ) = d (M ,Ox) 0 0 ⇔ x −1 = ⇔ . 0 x −1  x = 4 0 0 Câu 45. Chọn A
Tập xác định D =  \{− } 2
Trên TXĐ của hàm số, biến đổi được y = x −1.
Do đó đồ thị không có tiệm cận Câu 46. Chọn C
Tập xác định D =  \{− } 2 Trang 14/16 −
Trên TXĐ của hàm số, biến đổi được x 1 y = . x + 2 − − − − Ta có x 1 x 1 lim = lim = 1; x 1 x 1 lim = ; −∞ lim = +∞ x→+∞ x + 2 x→−∞ x + 2 x 2+ + x 2 x 2 − →− →− x + 2
Do đó đồ thị có 2 tiệm cận Câu 47. Chọn D
Tập xác định D = ( ; −∞ − 2 ∪  2;+∞   ) 2 2 2 1− − 1− 2 − 2 2 − Ta có x 2 lim = lim x =1; x 2 lim = lim x = 1 − x→+∞ x −1 x→+∞ 1 1− x→−∞ x −1 x→−∞ 1 1− x x 2 2 − −
Do tập xác định D = ( ; −∞ − 2 ∪  2;+∞ x 2 x 2   ) nên không tồn tại lim ; lim x 1+ − x 1 x 1 − → → x −1
Do đó đồ thị có 2 tiệm cận ngang là y =1 và y = 1 − . Câu 48. Chọn C  + 
Tọa độ điểm M có dạng x 2 0 M x ; 0 x 3  −  0 
Phương trình đường tiệm cận đứng, tiệm cận ngang lần lượt là x − 3 = 0 (d , y −1 = 0 d . 1 ) ( 2)
Giải phương trình 5d (M ,d = d M ,d tìm x 1 ) ( 2 ) 0 Chọn A. Câu 49. Chọn D
Ta có đường tiệm cận đứng là x = 3
− và đường tiệm cận ngang là 1 y = 3 Nên 1 a = 3, − b = 3 Do đó 8
m ≥ a + b ⇔ m ≥ − ⇒ m = 2 − 3 Câu 50. Chọn D  − 
Tọa độ điểm M có dạng 2x 3 0 M x ; với x ≠ 2 0 x 2  −  0 0 
Phương trình tiệm cận đứng, ngang lần lượt là x − 2 = 0 (d , y − 2 = 0 d . 1 ) ( 2) Ta có d = d ( 1
M ,d + d M ,d = x − 2 + ≥ 2 1 ) ( 2 ) 0 x − 2 0 Câu 51. Chọn A  − 
Tọa độ điểm M bất kì thuộc đồ thị có dạng 2x 3 0 M x ; với x ≠ 2 0 x 2  −  0 0  − −
Do đó phương trình tiếp tuyến tại M là x x 2x 3 0 0 y = − + ∆ . 2 ( ) (x − 2 x − 2 0 ) 0
Tính d (M ,∆) ≤ 2 . Câu 52. Chọn A  − 
Tọa độ điểm M bất kì thuộc đồ thị có dạng 2x 3 0 M x ; với x ≠ 2 0 x 2  −  0 0  − −
Do đó phương trình tiếp tuyến tại M là x x 2x 3 0 0 y = − + d . 2 ( ) (x − 2 x − 2 0 ) 0 Trang 15/16  − 
Tìm tọa độ giao của tiệm cận và tiếp tuyến 2x 2 0 A2;
, B (2x − 2;2 0 ) x −  2 0 
Từ đó đánh giá AB ≥ 4. Trang 16/16
Document Outline

  • DS_C1_TIEM CAN
    • A. BÀI TẬP TRẮC NGHIỆM
    • B. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM