33 trang 31 lượt tải

Tóm tắt lý thuyết và bài tập trắc nghiệm nguyên hàm Toán 12

62

Tóm tắt lý thuyết và bài tập trắc nghiệm nguyên hàm Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Profile

Mai Nguyệt

1 năm trước
Danh sách Quiz
/33
Trang 1/34
CHỦ ĐỀ 1. NGUYÊN HÀM
KIẾN THỨC CƠ BẢN
I. NGUYÊN HÀM VÀ TÍNH CHẤT
1. Nguyên hàm
Định nghĩa: Cho hàm số
(
)
fx
xác định trên
K
(
K
là khoảng, đoạn hay nửa khoảng). Hàm số
(
)
Fx
được gọi là nguyên hàm của hàm số
( )
fx
trên
K
nếu
( ) ( )
'F x fx=
với mọi
xK∈
.
Định lí:
1) Nếu
là một nguyên hàm của hàm số
( )
fx
trên
K
thì với mỗi hằng số
C
, hàm số
(
) (
)
Gx Fx C
= +
cũng là một nguyên hàm của
( )
fx
trên
K
.
2) Nếu
(
)
Fx
là một nguyên hàm của hàm số
( )
fx
trên
K
thì mọi nguyên hàm của
(
)
fx
trên
K
đều
có dạng
(
)
Fx C+
, với
C
là một hằng số.
Do đó
(
)
,
F x CC+∈
là họ tất cả các nguyên hàm của
( )
fx
trên
K
. Ký hiệu
(
) ( )
f x dx F x C
= +
∫
.
2. Tính chất của nguyên hàm
Tính chất 1:
(
)
( )
(
)
fxdx fx
′
=
∫
và
( ) ( )
'f x dx f x C= +
∫
Tính chất 2:
(
) ( )
kf x dx k f x dx
=
∫∫
với
k
là hằng số khác
0
.
Tính chất 3:
(
) ( )
( ) ( )
f x g x dx f x dx g x dx
±= ±


∫ ∫∫
3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số
(
)
fx
liên tục trên
K
đều có nguyên hàm trên
K
.
4. Bảng nguyên hàm của một số hàm số sơ cấp
Nguyên hàm của hàm số sơ cấp
Nguyên hàm của hàm số hợp
( )
( )
u ux=
dx x C= +
∫
du u C= +
∫
(
)
1
1
1
1
x dx x C
α α+
= + α≠−
α+
∫
( )
1
1
1
1
u du u C
α α+
= + α≠−
α+
∫
1
ln
dx x C
x
= +
∫
1
ln
du u C
u
= +
∫
xx
e dx e C= +
∫
uu
e du e C= +
∫
( )
0, 1
ln
x
x
a
a dx C a a
a
= + >≠
∫
( )
0, 1
ln
u
u
a
a du C a a
a
= + >≠
∫
sin cosxdx x C=−+
∫
sin cosudu u C=−+
∫
cos sinxdx x C= +
∫
cos sinudu u C= +
∫
2
1
tan
cos
dx x C
x
= +
∫
2
1
tan
cos
du u C
u
= +
∫
2
1
cot
sin
dx x C
x
=−+
∫
2
1
cot
sin
du u C
u
=−+
∫
II. PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
1. Phương pháp đổi biến số
Định lí 1: Nếu
( ) ( )
f u du F u C= +
∫
và
(
)
u ux=
là hàm số có đạo hàm liên tục thì
( )
( )
( ) ( )
( )
'fux u xdx Fux C= +
∫
Hệ quả: Nếu
( )
0u ax b a
=+≠
thì ta có
( ) ( )
1
f ax b dx F ax b C
a
+ = ++
∫
2. Phương pháp nguyên hàm từng phần
Định lí 2: Nếu hai hàm số
( )
u ux=
và
( )
v vx=
có đạo hàm liên tục trên
K
thì
Trang 2/34
( ) ( ) ( ) ( ) ( ) ( )
''uxv xdx uxvx u xvxdx= −
∫∫
Hay
udv uv vdu
= −
∫∫
A. KỸ NĂNG CƠ BẢN
- Tìm nguyên hàm bằng phương pháp biến đổi trực tiếp.
- Tìm nguyên hàm bằng phương pháp đổi biến số.
- Tìm nguyên hàm bằng phương pháp nguyên hàm từng phần.
B. BÀI TẬP TRẮC NGHIỆM
Câu 1. Nguyên hàm của hàm số
( )
3
32fx x x=++
là hàm số nào trong các hàm số sau?
A.
( )
42
3
2
42
xx
Fx x C=+ ++
. B.
( )
4
2
32
3
x
Fx x x C=+ ++
.
C.
( )
42
2
42
xx
Fx x C=+++
. D.
( )
2
33Fx x x C= ++
.
Hướng dẫn giải: Sử dụng bảng nguyên hàm.
Câu 2. Hàm số
( )
32
5 4 7 120Fx x x x C= + −+ +
là họ nguyên hàm của hàm số nào sau đây?
A.
(
)
2
15 8 7
fx x x= +−
. B.
( )
2
5 47
fx x x= ++
.
C.
( )
232
547
432
xxx
fx=+−
. D.
( )
2
5 47fx x x= +−
.
Hướng dẫn giải: Lấy đạo hàm của hàm số
( )
Fx
ta được kết quả.
Câu 3. Họ nguyên hàm của hàm số:
2
1
3yx x
x
=−+
là
A.
( )
3
2
3
ln
32
=−++
x
Fx x x C
. B.
( )
3
2
3
ln
32
=− ++
x
Fx x x C
.
C.
( )
3
2
3
ln
32
=+ ++
x
Fx x x C
. D.
( )
2
1
23
= −− +Fx x C
x
.
Hướng dẫn giải: Sử dụng bảng nguyên hàm.
Câu 4. Tìm nguyên hàm của hàm số
( ) ( )( )
12fx x x
=++
A.
( )
3
2
3
2
32
=+ ++
x
Fx x x C
. B.
( )
3
2
2
2
33
=+ ++
x
Fx x x C
.
C.
( )
23= ++Fx x C
. D.
( )
3
2
2
2
33
=− ++
x
Fx x x C
.
Hướng dẫn giải:
( ) ( )( )
2
1 2 32fx x x x x=+ +=++
. Sử dụng bảng nguyên hàm.
Câu 5. Nguyên hàm
của hàm số
( )
2
2 23
52
fx
xxx
= ++
−
là hàm số nào?
A.
( )
3
ln 5 2 2lnFx x x C
x
=− − + −+
. B.
( )
3
ln 5 2 2lnFx x x C
x
=− − + ++
.
C.
( )
3
ln 5 2 2lnFx x x C
x
= − + −+
. D.
( )
3
ln 5 2 2lnFx x x C
x
=− − − ++
.
Hướng dẫn giải: Sử dụng bảng nguyên hàm.
4.1.2. NGUYÊN HÀM CỦA HÀM SỐ LƯỢNG GIÁC.
Câu 6. Tìm nguyên hàm của hàm số
( ) sin 2fx x=
A.
1
sin 2 cos 2
2
xdx x C=−+
∫
. B.
1
sin 2 cos 2
2
xdx x C= +
∫
.
C.
sin 2 cos 2xdx x C= +
∫
. D.
sin 2 cos 2xdx x C=−+
∫
.
Hướng dẫn giải
11
sin 2 sin 2 (2 ) cos 2
22
xdx xd x x C= =−+
∫∫
.
Trang 3/34
Câu 7. Tìm nguyên hàm của hàm số
( ) cos 3
6
fx x
π

= +


.
A.
1
( ) sin 3
36
f x dx x C

= ++


∫
π
. B.
( ). sin 3
6
f x dx x C

= ++


∫
π
.
C.
1
( ) sin 3
36
f x dx x C

=− ++


∫
π
. D.
1
( ) sin 3
66
f x dx x C

= ++


∫
π
.
Hướng dẫn giải:
11
( ) cos 3 3 sin 3
3 6 63 6
f x dx x d x x C

= + += ++


∫∫
ππ π
.
Câu 8. Tìm nguyên hàm của hàm số
2
a(
2
) 1 tn+=f
x
x
.
A.
( ) 2 tan
2
x
f x dx C= +
∫
. B.
( ) tan
2
x
f x dx C= +
∫
.
C.
1
( ) tan
22
x
f x dx C
= +
∫
. D.
( ) 2 tan
2
x
f x dx C=−+
∫
.
Hướng dẫn giải:
2
2
1
() 1 t
s
an
o
2
2
c
x
fx
x
=+=
nên
22
2
2 2 tan
2
cos cos
22
x
d
dx x
C
xx



= = +
∫∫
.
Câu 9. Tìm nguyên hàm của hàm số
2
1
()
sin
3
fx
x
π
=

+


.
A.
( ) cot
3
f x dx x C

=− ++


∫
π
. B.
1
( ) cot
33
f x dx x C

=− ++


∫
π
.
C.
( ) cot
3
f x dx x C

= ++


∫
π
. D.
1
( ) cot
33
f x dx x C

= ++


∫
π
.
Hướng dẫn giải:
22
3
cot
3
sin sin
33
dx
dx
xC
xx

+



= =− ++

 

++
 
 
∫∫
π
π
ππ
.
Câu 10. Tìm nguyên hàm của hàm số
3
( ) sin .cosfx x x=
.
A.
4
sin
()
4
x
f x dx C= +
∫
. B.
4
sin
()
4
x
f x dx C=−+
∫
.
C.
2
sin
()
2
x
f x dx C= +
∫
. D.
2
sin
()
2
x
f x dx C=−+
∫
.
Hướng dẫn giải
4
33
sin
sin .cos . sin . (sin )
4
x
x xdx xd x C= = +
∫∫
.
4.1.3. NGUYÊN HÀM CỦA HÀM SỐ MŨ, LÔGARIT.
Câu 11. Tìm nguyên hàm của hàm số
()
xx
fx e e
−
= −
.
A.
( )
xx
f x dx e e C
−
=++
∫
. B.
( )
xx
f x dx e e C
−
=−+ +
∫
.
C.
( )
xx
f x dx e e C
−
=−+
∫
. D.
( )
xx
f x dx e e C
−
=−− +
∫
.
Hướng dẫn giải:
( )
xx xx
e e dx e e C
−−
− =++
∫
.
Câu 12. Tìm nguyên hàm của hàm số
2
( ) 2 .3
xx
fx
−
=
.
A.
( )
21
.
9 ln 2 ln 9
x
f x dx C

= +

−

∫
. B.
( )
91
.
2 ln 2 ln 9
x
f x dx C

= +

−

∫
.
Trang 4/34
C.
( )
21
.
3 ln 2 ln 9
x
f x dx C

= +

−

∫
. D.
( )
21
.
9 ln 2 ln 9
x
f x dx C

= +

+

∫
.
Hướng dẫn giải:
2
2 21
2 .3 .
9 9 ln 2 ln 9
xx
xx
dx dx C
−
 
= = +
 
−
 
∫∫
Câu 13. Họ nguyên hàm của hàm số
( ) (3 )
xx
fx e e
−
= +
là
A.
() 3
x
Fx e x C= ++
. B.
( ) 3 ln
xx x
Fx e e e C=++
.
C.
1
() 3
x
x
Fx e C
e
= −+
. D.
() 3
x
Fx e x C= −+
.
Hướng dẫn giải:
F( ) (3 ) (3 1) 3
xx x x
x e e dx e dx e x C
−
= + = + = ++
∫∫
Câu 14. Hàm số
( )
7 tan
x
Fx e x= −
là một nguyên hàm của hàm số nào sau đây?
A.
( )
2
7
cos
x
x
e
fx e
x
−

= −


. B.
( )
2
1
7
cos
x
fx e
x
= +
.
C.
( )
2
7 tan 1
x
fx e x=+−
. D.
( )
2
1
7
cos
x
fx e
x

= −


.
Hướng dẫn giải: Ta có
22
1
'() 7 (7 ) ()
cos cos
x
xx
e
gx e e fx
xx
−
=−=− =
Câu 15. Tìm nguyên hàm của hàm số
42
()
x
fx e
−
=
.
A.
(
)
21
1
2
x
f x dx e C
−
= +
∫
. B.
( )
21x
f x dx e C
−
= +
∫
.
C.
( )
42
1
2
x
f x dx e C
−
= +
∫
. D.
( )
21
1
2
x
f x dx e C
−
= +
∫
.
Hướng dẫn giải:
42 21 21
1
2
xxx
e dx e dx e C
−−−
= = +
∫∫
.
4.1.4. NGUYÊN HÀM CỦA HÀM SỐ CHỨA CĂN THỨC.
Câu 16. Nguyên hàm của hàm số
1
()
21
=
−
fx
x
là
A.
( )
21
f x dx x C= −+
∫
. B.
( )
22 1f x dx x C
= −+
∫
.
C.
( )
21
2
x
f x dx C
−
= +
∫
. D.
(
)
22 1f x dx x C=− −+
∫
.
Hướng dẫn giải:
( )
21
11
21
2
21 21
−
= = −+
−−
∫∫
dx
dx x C
xx
.
Câu 17. Tìm nguyên hàm của hàm số
1
()
3
=
−
fx
x
.
A.
( )
23f x dx x C=− −+
∫
. B.
( )
3f x dx x C
=− −+
∫
.
C.
( )
23f x dx x C= −+
∫
. D.
( )
33f x dx x C=− −+
∫
.
Hướng dẫn giải:
( )
3
1
23
33
−
=− =− −+
−−
∫∫
dx
dx x C
xx
.
Câu 18. Tìm nguyên hàm của hàm số
() 2 1= +fx x
.
A.
( ) ( )
1
2121
3
f x dx x x C= + ++
∫
. B.
( ) ( )
2
2121
3
f x dx x x C= + ++
∫
.
C.
( )
1
21
3
f x dx x C=− ++
∫
. D.
( )
1
21
2
f x dx x C= ++
∫
.
Hướng dẫn giải: Đặt
21t x dx tdt= +⇒ =
Trang 5/34
(
)
3
2
1
21 2121
33
t
x dx= t dt C x x C
⇒ + = + = + ++
∫∫
.
Câu 19. Tìm nguyên hàm của hàm số
() 5 3= −
fx x
.
A.
( ) ( )
2
53 53
9
f x dx x x C=− − −+
∫
. B.
( ) ( )
2
53 53
3
f x dx x x=−− −
∫
.
C.
( ) (
)
2
53 53
9
f x dx x x=−−
∫
. D.
( )
2
53
3
f x dx x C
=− −+
∫
.
Hướng dẫn giải: Đặt
2
53
3
tdt
t x dx=−⇒=−
( )
2
53 53 53
9
xdx x x C
− =− − −+
∫
.
Câu 20. Tìm nguyên hàm của hàm số
3
() 2= −fx x
.
A.
( ) ( )
3
3
22
4
f x dx x x C= − −+
∫
. B.
( ) ( )
3
3
22
4
f x dx x x C=− − −+
∫
.
C.
( ) ( )
2
22
3
f x dx x x=−−
∫
. D.
( ) ( )
2
3
1
2
3
f x dx x C
−
=−+
∫
.
Hướng dẫn giải: Đặt
2
3
23
t x dx t dt= −⇒ =
. Khi đó
(
)
33
3
2 22
4
x dx x x C− = − −+
∫
Câu 21. Tìm nguyên hàm của hàm số
3
() 1 3= −fx x
.
A.
( )
( )
3
1
13 13
4
f x dx x x C=− − −+
∫
. B.
( )
( )
3
3
13 13
4
f x dx x x C=− − −+
∫
.
C.
( ) ( )
3
1
13 13
4
f x dx x x C= − −+
∫
. D.
( ) ( )
2
3
13f x dx x C
−
=−− +
∫
.
Hướng dẫn giải: Đặt
2
3
13t x dx t dt=−⇒=−
. Khi đó
( )
33
1
13 13 13
4
xdx x x C− =− − −+
∫
Câu 22. Tìm nguyên hàm của hàm số
(
)
3
=
x
fx e
.
A.
( )
3
2
3
x
e
f x dx C= +
∫
B.
( )
3
3
2
x
f x dx C
e
= +
∫
C.
( )
3
3
2
x
e
f x dx C= +
∫
D.
( )
32
2
2
32
x
e
f x dx C
x
+
= +
+
∫
Hướng dẫn giải:
33
3
3
22
2 32 2
..
3 23 3
xx
x
x
xe
e dx e d e C C

= = += +


∫∫
Câu 23. Hàm số
( ) ( )
2
1 1 2016Fx x x= + ++
là một nguyên hàm của hàm số nào sau đây?
A.
( ) ( )
5
11
2
fx x x=++
B.
( ) ( )
5
11
2
fx x x C= + ++
C.
( ) (
)
2
11
5
fx x x=++
D.
( ) ( )
11fx x x C= + ++
Hướng dẫn giải:
( )
( )
5
' 11
2
Fx x x=++
Câu 24. Biết một nguyên hàm của hàm số
( )
1
1
13
fx
x
= +
−
là hàm số
( )
Fx
thỏa mãn
( )
2
1
3
F −=
.
Khi đó
( )
Fx
là hàm số nào sau đây?
A.
( )
2
13 3
3
Fx x x=− −+
B.
( )
2
13 3
3
Fx x x=− −−
Trang 6/34
C.
( )
2
13 1
3
Fx x x=− −+
D.
( )
2
4 13
3
Fx x=−−
Hướng dẫn giải
( )
( )
13
11 2
1 13
33
13 13
dx
F x dx x x x C
xx
−

= + =− +=− − +

−−

∫∫
( ) ( )
22
1 3 13 3
33
F C Fx x x−=⇒=⇒ =− − +
Câu 25. Biết
() 61
Fx x= −
là một nguyên hàm của hàm số
()
1
a
fx
x
=
−
. Khi đó giá trị của
a
bằng
A.
3
−
. B.
3
. C.
6
. D.
1
6
.
Hướng dẫn giải:
(
)
3
'( ) 6 1
1
Fx x
x
−
′
= −=
−
3a⇒=−
4.1.5. PHƯƠNG PHÁP NGUYÊN HÀM TỪNG PHẦN
Câu 26. Tính
( ) sinF x x xdx
=
∫
bằng
A.
( ) sin cosFx x x x C=−+
. B.
( ) sin cosFx x x x C= −+
.
C.
( ) sin cosFx x x x C=++
. D.
( ) sin cosFx x x x C
= ++
.
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần
Phương pháp trắc nghiệm:
Cách 1: Dùng định nghĩa, sử dụng máy tính nhập
( )
() ()
d
Fx f x
dx
−
, CALC ngẫu nhiên tại một
số điểm
0
x
thuộc tập xác định, kết quả xấp xỉ bằng 0 chọn.
Cách 2: Sử dụng phương pháp bảng
u
và đạo hàm của
u
dv
và nguyên hàm của
v
x
sin x
1
cos x−
0
sin x
−
Vậy
( ) sin cosFx x x x C=−+
.
Câu 27. Tính
2
lnx xdx
∫
. Chọn kết quả đúng:
A.
( )
22
1
2ln 2ln 1
4
xx xC− ++
. B.
( )
22
1
2ln 2ln 1
2
xx xC− ++
.
C.
( )
22
1
2ln 2ln 1
4
xx xC+ ++
. D.
( )
22
1
2ln 2ln 1
2
xx xC+ ++
.
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần 2 lần.
Phương pháp trắc nghiệm
Cách 1: Sử dụng định nghĩa
'() () '() () 0F x fx F x fx=⇔ −=
.
Nhập máy tính
( )
() ()
d
Fx f x
dx
−
. CALC
x
tại một số giá trị ngẫu nhiên
0
x
trong tập xác định,
nếu kết quả xấp xỉ bằng
0
thì chọn.
Cách 2: Sử dụng phương pháp bảng:
u
và đạo hàm của
u
dv
và nguyên hàm của
v
2
ln x
x
2
2
x
+
-
+
Trang 7/34
ln x
(chuyển
2
x
qua
dv
)
x
(nhận
2
x
từ
u
)
1
x
2
2
x
1 (chuyển
1
x
qua
dv
)
2
x
(nhận
1
x
từ
u
)
0
2
4
x
Do đó
2 22 2 2
1 11
ln ln ln
2 24
xxdx x x xx xC= − ++
∫
=
( )
22
1
2ln 2ln 1
4
xx xC− ++
.
Câu 28. Tính
( ) sin cosF x x x xdx=
∫
. Chọn kết quả đúng:
A.
1
( ) sin 2 cos 2
84
x
Fx x x C=−+
. B.
1
( ) cos 2 sin 2
42
x
Fx x x C= −+
.
C.
1
( ) sin 2 cos 2
48
x
Fx x x C=++
. D.
1
( ) sin 2 cos 2
48
x
Fx x x C
−
= −+
.
Hướng dẫn giải:
Phương pháp tự luận: Biến đổi
1
sin cos sin 2
2
xx x=
rồi sử dụng phương pháp nguyên hàm
từng phần.
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa
'() () '() () 0
F x fx F x fx=⇔ −=
Nhập máy tính
( )
() ()
d
Fx f x
dx
−
. CALC
x
tại một số giá trị ngẫu nhiên
0
x
trong tập xác định,
nếu kết quả xấp xỉ bằng
0
thì chọn.
Cách 2: Sử dụng phương pháp bảng.
Câu 29. Tính
3
()
x
F x xe dx=
∫
. Chọn kết quả đúng
A.
3
( ) 3( 3)
x
Fx x e C=−+
B.
3
( ) ( 3)
x
Fx x e C
=++
C.
3
3
()
3
x
x
Fx e C
−
= +
D.
3
3
()
3
x
x
Fx e C
+
= +
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với
3
,
x
u x dv e dx
= =
.
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa
'() () '() () 0F x fx F x fx=⇔ −=
.
Nhập máy tính
( )
() ()
d
Fx f x
dx
−
. CALC
x
tại một số giá trị ngẫu nhiên
0
x
trong tập xác định,
nếu kết quả xấp xỉ bằng
0
thì chọn.
Cách 2: Sử dụng phương pháp bảng.
Câu 30. Tính
2
()
cos
x
F x dx
x
=
∫
. Chọn kết quả đúng
A.
( ) tan ln | cos |Fx x x x C=++
. B.
( ) cot ln | cos |Fx x x x C=−+ +
.
C.
( ) tan ln | cos |Fx x x x C=−+ +
. D.
( ) cot ln | cos |Fx x x x C=−− +
.
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với
2
1
co
,
s
u x dv dx
x
= =
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa
'() () '() () 0F x fx F x fx=⇔ −=
.
+
-
Trang 8/34
Nhập máy tính
( )
() ()
d
Fx f x
dx
−
. CALC
x
tại một số giá trị ngẫu nhiên
0
x
trong tập xác định,
nếu kết quả xấp xỉ bằng
0
thì chọn.
Cách 2: Sử dụng phương pháp bảng.
Câu 31. Tính
2
( ) cos
F x x xdx
=
∫
. Chọn kết quả đúng
A.
2
( ) ( 2)sin 2 cosFx x x x x C=−+ +
. B.
2
( ) 2 sin cos sinFx x x x x x C= − ++
.
C.
2
( ) sin 2 cos 2sinFx x x x x x C= − ++
. D.
2
( ) (2 ) cos sin
Fx x x x x x C
=+ −+
.
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần 2 lần với
2
; cosu x dv xdx= =
, sau đó
11
; sinu x dv xdx= =
.
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa
'() () '() () 0F x fx F x fx=⇔ −=
Nhập máy tính
( )
() ()
d
Fx f x
dx
−
. CALC
x
tại một số giá trị ngẫu nhiên
0
x
trong tập xác định,
nếu kết quả xấp xỉ bằng
0
thì chọn.
Cách 2: Sử dụng phương pháp bảng.
Câu 32. Tính
( ) sin 2F x x xdx=
∫
. Chọn kết quả đúng
A.
1
( ) (2 cos 2 sin 2 )
4
Fx x x x C=− −+
. B.
1
( ) (2 cos 2 sin 2 )
4
Fx x x x C
= −+
.
C.
1
( ) (2 cos 2 sin 2 )
4
Fx x x x C=− ++
. D.
1
( ) (2 cos 2 sin 2 )
4
Fx x x x C= ++
.
Hướng dẫn giải: Sử dụng phương pháp nguyên hàm từng phần với
; sin 2u x dv xdx= =
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng hoặc sử dụng máy tính: Nhập
( ()) ()
d
Fx f x
dx
−
, CALC ngẫu nhiên tại một số điểm
0
x
bất kỳ, nếu kết quả xấp xỉ bằng
0
thì
chọn đáp án đó.
Câu 33. Hàm số
( ) sin cos 2017Fx x x x= ++
là một nguyên hàm của hàm số nào?
A.
( ) cosfx x x
=
. B.
( ) sinfx x x=
.
C.
( ) cos
fx x x= −
. D.
( ) sinfx x x= −
.
Hướng dẫn giải:
Phương pháp tự luận: Tính
'( )Fx
có kết quả trùng với đáp án chọn.
Phương pháp trắc nghiệm: Sử dụng định nghĩa
'() () '() () 0F x fx F x fx=⇔ −=
Nhập máy tính
(
)
() ()
d
Fx f x
dx
−
. CALC
x
tại một số giá trị ngẫu nhiên
0
x
trong tập xác định,
nếu kết quả xấp xỉ bằng
0
chọn.
Câu 34. Tính
2
1 ln( 1)x
dx
x
++
∫
. Khẳng định nào sau đây là sai?
A.
1 ln( 1)
ln
1
xx
C
xx
−+ +
++
+
B.
1 ln( 1)
ln
1
xx
C
xx
++
− ++
+
C.
( )
1
1 ln( 1) ln | |
x
x xC
x
+
− + ++ +
D.
1 ln( 1)
ln ln1
x
x
x
x C
++
− − +++
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với
2
1
1 ln( 1);u x dv dx
x
=++ =−
hoặc biến đổi rồi đặt
2
1
ln( 1);u x dv dx
x
=+==−
.
Phương pháp trắc nghiệm: Sử dụng máy tính kiểm tra bằng định nghĩa.
4.1.6. ÔN TẬP
Câu 35. Hãy chọn mệnh đề đúng
Trang 9/34
A.
( )
01
ln
x
x
a
a dx C a
a
= + <≠
∫
. B.
1
,
1
x
x dx C R
α
α
α
α
+
= + ∀∈
+
∫
.
C.
().() () .g()f x g x dx f x dx x dx=
∫ ∫∫
. D.
()
()
()
g( )
f x dx
fx
dx
gx
x dx
=
∫
∫
∫
.
Hướng dẫn giải: A đúng. B sai vì thiếu điều kiện
1
α
= −
/
; C, D sai vì không có tính chất.
Câu 36. Mệnh đề nào sau đây sai?
A.
sin cosxdx x C
= +
∫
. B.
1
ln , 0
dx x C x
x
= +≠
∫
.
D.
, (0 1)
ln
x
x
a
a dx C a
a
= + <≠
∫
. C.
xx
e dx e C= +
∫
.
Hướng dẫn giải:
sin cosxdx x C=−+
∫
Câu 37. Hàm số
32
1
() 3fx x x
x
= − ++
có nguyên hàm là
A.
43
( ) 3 ln
43
xx
Fx x x C
= −++ +
. B.
3
4
( ) 3 ln
3
x
Fx x x x C=−++ +
.
C.
2
2
1
() 3 2
Fx x x C
x
= −−+
. D.
43
( ) 3 lnFx x x x x C=−++ +
.
Hướng dẫn giải:
43
32
1
( ) ( 3 ) 3 ln
43
xx
F x x x dx x x C
x
= − ++ = − + + +
∫
Câu 38. Họ nguyên hàm của hàm số
2
( ) tanfx x=
là
A.
( )
tanFx x x C= −+
. B.
( )
tanFx x x C
=− ++
.
C.
( )
tanFx x x C= ++
. D.
( )
tanFx x x C=− −+
.
Hướng dẫn giải:
2
1
( ) 1 tan
cos
f x dx dx x x C
x

= − = −+


∫∫
Câu 39. Hàm số
( ) 7sin cos 1Fx x x= −+
là một nguyên hàm của hàm số nào sau đây?
A.
( )
sin 7cosfx x x= +
. B.
( )
sin 7cosfx x x=−+
.
C.
( )
sin 7cosfx x x= −
. D.
( )
sin 7cosfx x x=−−
.
Hướng dẫn giải:
'( ) 7 cos sin
Fx x x= +
Câu 40. Kết quả tính
22
1
sin cos
dx
xx
∫
là
A.
tan cotx xC−+
. B.
cot 2xC+
.
C.
tan 2xxC−+
. D.
tan cotx xC−++
.
Hướng dẫn giải:
22 2 2
1 11
tan cot
sin cos cos sin
dx dx x x C
xx x x

= + =−+


∫∫
Câu 41. Hàm số
2
2
11
() 3 1Fx x
x
x
= − +−
có một nguyên hàm là
A.
3
1
() 2fx x x x
x
= − −−
. B.
3
1
()fx x x x
x
= − −−
.
C.
3
1
() 2fx x x
x
=−+
. D.
3
11
()
2
fx x x x
x
= − −−
.
Hướng dẫn giải: Ta có
23
22
11 1
() 3 1 2F x dx x dx x x x C
xx
x

= − + − = − − −+


∫∫
Câu 42. Hàm số
5
cos
()
sin
x
fx
x
=
có một nguyên hàm
()Fx
bằng
Trang 10/34
A.
4
1
4sin x
−
. B.
4
1
4sin x
. C.
4
4
sin x
. D.
4
4
sin x
−
.
Hướng dẫn giải:
55 4
cos 1 1
( ) (sin )
sin sin 4sin
x
f x dx dx d x C
xx x
= = =−+
∫∫ ∫
Câu 43. Kết quả tính
2
2 54x x dx−
∫
bằng
A.
( )
3
2
1
54
6
xC−−+
. B.
( )
2
3
54
8
xC− −+
.
C.
( )
3
2
1
54
6
xC−+
. D.
( )
3
2
1
54
12
xC
− −+
.
Hướng dẫn giải: Đặt
2
54 4t x tdt xdx=− ⇒=−
Ta có
( )
3
2 23 2
11 1
2 54 54
26 6
x x dx t dt t C x C− =− =− +=− − +
∫∫
Câu 44. Kết quả
sin
cos
x
e xdx
∫
bằng
A.
sin
x
eC
+
. B.
sin
cos .
x
xe C
+
. C.
cos x
eC+
. D.
sin x
eC
−
+
.
Hướng dẫn giải: Ta có
sin sin sin
cos (sin )
x xx
e xdx e d x e C= = +
∫∫
Câu 45. Tính
tan
xdx
∫
bằng
A.
ln cos xC−+
. B.
ln cos xC+
. C.
2
1
cos
C
x
+
. D.
2
1
cos
C
x
−
+
.
Hướng dẫn giải: Ta có
1
tan (cos ) ln cos
cos
xdx d x x C
x
=− =−+
∫∫
Câu 46. Tính
cot xdx
∫
bằng
A.
ln sin xC+
. B.
ln sin xC−+
. C.
2
1
sin
C
x
−
+
. D.
2
1
sin
C
x
−
.
Hướng dẫn giải: Ta có
1
cot (sin ) ln sin
sin
xdx d x x C
x
= = +
∫∫
Câu 47. Nguyên hàm của hàm số
3
1
x
y
x
=
−
là
A.
32
11
ln 1
32
x xx x C+ ++ −+
. B.
32
11
ln 1
32
x xx x C+ ++ ++
.
C.
32
11
ln 1
62
x xx x C+ ++ −+
. D.
32
11
ln 1
34
x xx x C+ ++ −+
.
Hướng dẫn giải: Ta có
3
2
1
1
11
x
xx
xx
= + ++
−−
. Sử dụng bảng nguyên hàm suy ra đáp án.
Câu 48. Một nguyên hàm của hàm số
( )
2
23
1
xx
fx
x
−+
=
+
là
A.
2
3 6ln 1
2
x
xx−+ +
. B.
2
3 6ln 1
2
x
xx++ +
.
C.
2
3 6ln 1
2
x
xx+− +
. D.
( )
2
3 6ln 1
2
x
xx
−+ +
.
Hướng dẫn giải:
(
)
2
23 6
3
11
xx
fx x
xx
−+
= =−+
++
. Sử dụng bảng nguyên hàm.
Câu 49. Kết quả tính
( )
1
3
dx
xx+
∫
bằng
A.
1
ln
33
x
C
x
+
+
. B.
1
ln
33
x
C
x
−+
+
.
Trang 11/34
C.
23
ln
3
x
C
x
+
+
. D.
2
ln
33
x
C
x
+
+
.
Hướng dẫn giải:
( )
1 11 1
33 3
xx x x

= −

++

. Sử dụng bảng nguyên hàm.
Câu 50. Kết quả tính
( )
1
3
dx
xx−
∫
bằng
A.
13
ln
3
x
C
x
−
+
. B.
13
ln
3
x
C
x
+
+
.
C.
1
ln
33
x
C
x
+
+
. D.
1
ln
33
x
C
x
+
−
.
Hướng dẫn giải:
( )
1 11 1
33 3xx x x

= −

+−

. Sử dụng bảng nguyên hàm.
Câu 51. Họ nguyên hàm của hàm số
( )
2
1
2
fx
xx
=
+−
là
A.
( )
11
ln
32
x
Fx C
x
−
= +
+
. B.
( )
12
ln
31
x
Fx C
x
+
= +
−
.
C.
( )
1
ln
2
x
Fx C
x
−
= +
+
. D.
( )
2
ln 2Fx x x C= +−+
.
Hướng dẫn giải:
( )
2
1 11 1
23 1 2
fx
xx x x

= = −

+− − +

. Sử dụng bảng nguyên hàm.
Câu 52. Họ nguyên hàm của hàm số
( )
2
1 x
fx
x
−

=


là
A.
(
)
1
2lnFx x x C
x
=−− ++
. B.
( )
1
2lnFx x x C
x
=−− ++
.
C.
( )
1
2lnFx x x C
x
= − ++
. D.
( )
1
2lnFx x x C
x
=−− −+
.
Hướng dẫn giải:
( )
2
2
22
1 12 1 2
1
x xx
fx
x x xx
− −+

= = = −+


. Sử dụng bảng nguyên hàm.
Câu 53. Nguyên hàm của hàm số
(
)
22
1
fx
xa
=
−
với
0a ≠
là
A.
1
ln
2
xa
C
a xa
−
+
+
. B.
1
ln
2
xa
C
a xa
+
+
−
.
C.
1
ln
xa
C
a xa
−
+
+
. D.
1
ln
xa
C
a xa
+
+
−
.
Hướng dẫn giải:
22
1 11 1
2x a axa xa

= −

− −+

. Sử dụng bảng nguyên hàm.
Câu 54. Biết
( )
Fx
là một nguyên hàm của hàm số
(
)
2
8
x
fx
x
=
−
thoả mãn
( )
20
F =
. Khi đó phương
trình
( )
Fx x=
có nghiệm là
A.
13x = −
. B.
1x =
. C.
1x = −
. D.
0x =
.
Hướng dẫn giải: Đặt
22 2
88t x t x tdt xdx= − ⇒ = − ⇒− =
2
2
8
8
x tdt
dx t C x C
t
x
=− =−+ =− − +
−
∫∫
.
Vì
( )
20F =
nên
2C =
. Ta có phương trình
2
8 2 13x xx− − +=⇔=−
Trang 12/34
Câu 55. Nếu
( )
Fx
là một nguyên hàm của hàm số
1
()
1
fx
x
=
−
và
( )
21F =
thì
( )
3
F
bằng
A.
ln 2 1+
. B.
3
ln
2
. C.
ln 2
. D.
1
2
.
Hướng dẫn giải:
1
ln 1
1
dx x C
x
= −+
−
∫
, vì
( )
21F
=
nên
1C =
.
( )
ln 1 1
Fx x= −+
, thay
3x =
ta có đáp án.
Câu 56. Biết
( )
Fx
là một nguyên hàm của hàm số
( )
2
ln
ln 1.
x
fx x
x
= +
thoả mãn
( )
1
1
3
F =
. Giá trị
của
( )
2
Fe
là
A.
8
9
. B.
1
9
. C.
8
3
. D.
1
3
.
Hướng dẫn giải: Đặt
2
ln
ln 1
x
t x tdt dx
x
= +⇒ =
(
)
3
2
3
22
ln 1
ln
ln 1.
33
x
xt
x dx t dt C C
x
+
+ = = += +
∫∫
. Vì
( )
1
1
3
F =
nên
Vậy
( )
2
8
9
Fe=
.
Câu 57. Nguyên hàm
của hàm số
(
)
2
1
2
sin
fx x
x
= +
thỏa mãn
1
4
F

= −


π
là
A.
2
2
cot
16
xx− +−
π
. B.
2
2
cot
16
xx−+
π
.
C.
2
cot xx
−+
. D.
2
2
cot
16
xx−−
π
.
Hướng dẫn giải:
2
2
1
2 cot
sin
x dx x x C
x

+ =−+


∫
.
1
4
F

= −


π
nên
2
16
C
= −
π
.
4.1.2. NGUYÊN HÀM CỦA HÀM SỐ LƯỢNG GIÁC.
Câu 58. Tìm nguyên hàm của hàm số
2
( ) cos .sinfx x x=
.
A.
3
cos
()
3
x
f x dx C=−+
∫
. B.
3
cos
()
3
x
f x dx C= +
∫
.
C.
2
sin
()
2
x
f x dx C=−+
∫
. D.
2
sin
()
2
x
f x dx C= +
∫
.
Hướng dẫn giải:
3
22
cos
cos sin cos (cos )
3
x
x xdx xd x C
=− =−+
∫∫
Câu 59. Tìm nguyên hàm của hàm số
sin 2
()
cos 2 1
x
fx
x
=
−
.
A.
( ) ln sinf x dx x C=−+
∫
. B.
( ) ln cos 2 1f x dx x C= −+
∫
.
C.
( ) ln sin 2f x dx x C= +
∫
. D.
( ) ln sinf x dx x C= +
∫
.
Hướng dẫn giải
( )
2
sin
sin 2 2sin cos cos
ln sin
cos2 1 1 2sin 1 sin sin
dx
xdx x x x
dx dx x C
x x xx
= =− =− =−+
−− +
∫∫ ∫∫
Câu 60. Tìm nguyên hàm của hàm số
( ) sin .cos 2 .f x x x dx=
.
A.
3
2 cos
( ) cos
3
x
f x dx x C
−
= ++
∫
. B.
11
( ) cos3 sin
62
f x dx x x C= ++
∫
.
C.
3
cos
( ) cos
3
x
f x dx x C= ++
∫
. D.
11
( ) cos3 sin
62
f x dx x x C= −+
∫
.
Trang 13/34
Hướng dẫn giải
(
)
(
)
(
)
3
22
2 cos
sin .cos 2 2cos 1 sin 2cos 1 cos cos
3
x
x xdx x xdx x d x x C
−
= − =− − = ++
∫∫ ∫
Câu 61. Tìm nguyên hàm của hàm số
( ) 2sin .cos3
fx x x=
.
A.
11
( ) cos 2 cos 4
24
f x dx x x C
=−+
∫
. B.
11
( ) cos 2 cos 4
24
f x dx x x C=++
∫
.
C.
42
( ) 2cos 3cosf x dx x x C=++
∫
. D.
42
( ) 3cos 3cosf x dx x x C=−+
∫
.
Hướng dẫn giải:
( )
11
2sin .cos3 sin 4 sin 2 cos 2 cos 4
24
x xdx x x dx x x C=− =−+
∫∫
.
Câu 62. Tìm nguyên hàm của hàm số
3
( ) sin .sin 3
fx x x=
.
A.
3 sin 2 sin 4 1 sin 6
()
82 4 8 6
xx x
f x dx x C

= − −− +


∫
.
B.
3 sin 2 sin 4 1 sin 6
()
82 4 8 6
xx x
f x dx x C

= − +− +


∫
.
C.
1 sin 2 sin 4 3 sin 6
()
82 4 8 6
xx x
f x dx x C

= − −− +


∫
.
D.
3 sin 2 sin 4 1 sin 6
()
82 4 8 6
xx x
f x dx x C

= + −+ +


∫
.
Hướng dẫn giải
( ) ( )
3
2
3sin sin 3
sin .sin 3 .sin3
4
3 13 1
2sin .sin 3 2sin 3 cos 2 cos 4 1 cos6
8 88 8
3 sin 2 sin 4 1 sin 6
82 4 8 6
xx
x xdx xdx
x xdx xdx x x dx x dx
xx x
xC
−
=
= − = − −−

= − −− +


∫∫
∫ ∫∫ ∫
Câu 63. Tìm nguyên hàm của hàm số
33
( ) sin .cos3 cos .sin 3fx x x x x
= +
.
A.
3
( ) cos 4
16
f x dx x C
−
= +
∫
. B.
3
( ) cos 4
16
f x dx x C= +
∫
.
C.
3
( ) sin 4
16
f x dx x C
−
= +
∫
. D.
3
( ) sin 4
16
f x dx x C= +
∫
.
Hướng dẫn giải:
( )
33
sin .cos3 cos .sin 3 .x x x x dx+
∫
3sin sin 3 cos3 3cos
.cos3 .sin 3
44
xx x x
x x dx
−+

= +


∫
33
sin .cos3 sin 3 .cos3 sin 3 .cos sin 3 .cos3
44
xx xx xx xxdx

= −+ +


∫
( )
3 33
sin .cos3 sin 3 .cos sin 4 cos 4
4 4 16
x x x x dx xdx x C
−
= +==+
∫∫
Câu 64. Tìm một nguyên hàm
()Fx
của hàm số
2
( ) sin
2
x
fx=
biết
24
F

=


ππ
.
A.
( )
sin 1
222
xx
Fx=−+
. B.
( )
sin 3
222
xx
Fx=++
.
C.
( )
sin 1
222
xx
Fx=++
. D.
( )
sin 5
222
xx
Fx=++
.
Hướng dẫn giải
•
( )
2
11
( ) sin 1 cos sin
2 2 22
xx
F x dx x dx x C= =− =−+
∫∫
Trang 14/34
•
11
sin
2 4 42 2 4 2
F CC

=⇔− +=⇔=


πππ π π
4.1.3. NGUYÊN HÀM CỦA HÀM SỐ MŨ, HÀM SỐ LÔGARIT.
Câu 65. Hàm số
2
( ) ln 2
sin
x
x
e
fx e
x
−

= +


có họ nguyên hàm là
A.
(
)
ln 2 cot
x
Fx e x C= −+
. B.
(
)
ln 2 cot
x
Fx e x C= ++
.
C.
( )
2
1
ln 2
cos
x
Fx e C
x
=++
. D.
( )
2
1
ln 2
cos
x
Fx e C
x
=−+
.
Hướng dẫn giải:
2
1
( ) ln 2 ln 2 cot
sin
xx
f x dx e dx e x C
x

= + = −+


∫∫
Câu 66. Hàm số
( ) 3 2 .3
x xx
fx= −
có nguyên hàm bằng
A.
36
ln 3 ln 6
xx
C−+
. B.
3 ln 3(1 2 ln 2)
xx
C
++
.
C.
3 3 .2
ln 3 ln 6
x xx
C++
. D.
36
ln 3 ln 3.ln 2
xx
C
++
.
Hướng dẫn giải:
( )
36
() 3 6
ln 3 ln 6
xx
xx
f x dx dx C=+ =++
∫∫
Câu 67. Một nguyên hàm
()
Fx
của hàm số
2
() ( )
xx
fx e e
−
= +
thỏa mãn điều kiện
(0) 1F =
là
A.
22
11
() 2 1
22
xx
Fx e e x
−
=− + ++
. B.
22
() 2 2 2 1
xx
Fx e e x
−
=− + ++
.
C.
22
11
() 2
22
xx
Fx e e x
−
=− ++
. D.
22
11
() 2 1
22
xx
Fx e e x
−
=− + +−
.
Hướng dẫn giải: Ta có
22
11
( ) 2 , (0) 1 1
22
xx
Fx e e x CF C
−
=− + + + =⇔=
Câu 68. Tìm nguyên hàm của hàm số
21
()
1
x
fx
x
−
=
+
.
A.
( )
2 3ln 1Fx x x C
= − ++
. B.
( )
2 3ln 1Fx x x C= + ++
.
C.
( )
2 ln 1Fx x x C= − ++
. D.
( )
2 ln 1F x x+ x C
= ++
.
Hướng dẫn giải:
21 3
2 2 3ln 1
11
x
dx dx x x C
xx
−

= − = − ++

++

∫∫
Câu 69. Tìm nguyên hàm của hàm số
2
2 23
()
21
xx
fx
x
++
=
+
.
A.
( ) ( )
2
15
21 ln21
84
Fx x x C= + + ++
. B.
( ) (
)
2
1
21 5ln21
8
Fx x x C
= + + ++
.
C.
( ) ( )
2
21 ln21Fx x x C= + + ++
. D.
( ) ( )
2
21 ln21Fx x x C= + − ++
.
Hướng dẫn giải:
( )
( )
2
2
2 23 21 5 1 5
21 ln21
21 2 221 8 4
xx x
dx dx x x C
xx

++ +
= + = + + ++


++

∫∫
Câu 70. Tìm nguyên hàm của hàm số
3
2
()
1
xx
fx
x
−
=
+
.
A.
( )
( )
2
2
ln 1
2
x
Fx x C= − ++
. B.
( )
( )
2
2
ln 1
2
x
Fx x C= + ++
.
C.
( )
( )
22
ln 1Fx x x C= − ++
. D.
( )
( )
22
ln 1Fx x x C= + ++
.
Hướng dẫn giải:
( )
( )
2
3 22
2
22 2
1
2
ln 1
1 1 2 12
dx
xx x x x
dx x dx x C
xx x
+
−

= − = − = − ++

++ +

∫∫ ∫
Trang 15/34
Câu 71. Tìm nguyên hàm của hàm số
1
()
ln
fx
x xx
=
+
.
A.
( )
ln ln 1Fx x C= ++
. B.
( )
ln ln 1Fx x C= −+
.
C.
(
)
ln 1
Fx x C= ++
. D.
( )
ln 1Fx x C= ++
.
Hướng dẫn giải:
( )
( )
( )
ln 1
1
ln ln 1
ln 1 ln 1
dx
dx x C
xx x
+
= = ++
++
∫∫
Câu 72. Tìm nguyên hàm của hàm số
2
()
1
x
x
e
fx
e
=
+
.
A.
( )
(
)
ln 1
xx
Fx e e C= − ++
. B.
( )
( )
ln 1
xx
Fx e e C= + ++
.
C.
( )
( )
ln 1
x
Fx e C= ++
. D.
( )
2xx
Fx e e C
= −+
.
Hướng dẫn giải:
( )
( )
2
1
ln 1
11 1
x
xx
x x xx
xx x
de
ee
dx e dx e e e C
ee e
+

= − = − = − ++

++ +

∫∫ ∫
4.1.4. NGUYÊN HÀM CỦA HÀM SỐ CHỨA CĂN THỨC.
Câu 73. Tìm nguyên hàm của hàm số
1
()
1
fx
x
=
+
.
A.
( )
( )
2 2ln 1f x dx x x C= − ++
∫
. B.
( )
( )
2 2 ln 1f x dx x x C= + ++
∫
.
C.
( )
( )
ln 1f x dx x C=++
∫
. D.
( )
( )
2 2ln 1f x dx x C=+ ++
∫
.
Hướng dẫn giải
Đặt
( ) ( )
2
1 1 21t x x t dx t dt=+ ⇒=− ⇒ = −
.
Khi đó
(
)
( )
1
21
11
2 1 2 ln
1
t dt
dx dt t t C
tt
x
−

= =−=−+

+

∫∫ ∫
( )
( )
1
2 1 ln 1 2 2ln 1x x C x xC= +− + + = − + +
. (Với
1
2CC= +
và
10x+>
)
Câu 74. Tìm nguyên hàm của hàm số
2
()
1
x
fx
x
+
=
+
.
A.
( ) ( )
2
41
3
f x dx x x C= + ++
∫
. B.
( ) ( )
41f x dx x x C= + ++
∫
.
C.
( )
( )
21 1
x
f x dx C
xx
= +
++
∫
. D.
( )
1
1
1
f x dx x C
x
= ++ +
+
∫
.
Hướng dẫn giải:
( ) ( )
2 12
1 1 41
3
11
x
dx x d x x x C
xx
+

= ++ + = + ++

++

∫∫
Câu 75. Tìm nguyên hàm của hàm số
21
()
1
x
fx
x
−
=
−
.
A.
( ) ( )
2
2 11
3
f x dx x x C=− + −+
∫
. B.
( )
( )
2
2 11
3
f x dx x x C= + −+
∫
.
C.
( ) ( )
2
2 11
3
f x dx x x C=− − −+
∫
. D.
( )
1
21
1
f x dx x C
x
=− −+ +
−
∫
.
Hướng dẫn giải
(
)
(
) ( )
( )
31
22
21 1
21 1
11
22
1 21 2 1 1
33
x
dx x d x
xx
x x C x xC
−

=− − −+ −

−−

=−−−+=− + −+
∫∫
Câu 76. Tìm nguyên hàm của hàm số
2
()
32
x
fx
x
=
+
.
Trang 16/34
A.
( )
2
1
32
3
f x dx x C= ++
∫
. B.
( )
2
1
32
3
f x dx x C=− ++
∫
.
C.
( )
2
1
32
6
f x dx x C= ++
∫
. D.
( )
2
2
32
3
f x dx x C= ++
∫
.
Hướng dẫn giải:
(
)
2
2
22
32
11
32
63
32 32
dx
x
dx x C
xx
+
= = ++
++
∫∫
Câu 77. Tìm nguyên hàm của hàm số
3
2
()
4
x
fx
x
=
−
.
A.
( )
(
)
22
1
84
3
f x dx x x C=− + −+
∫
. B.
( )
( )
22
1
84
3
f x dx x x C= + −+
∫
.
C.
( )
2
1
4
3
f x dx x C=− −+
∫
. D.
( )
( )
22
2
84
3
f x dx x x C=− + −+
∫
.
Hướng dẫn giải: Đặt
22 2
44
t x x t xdx tdt= − ⇒ =−⇒ =−
. Khi đó
( )
( )
( )
2
33
2
2
4
44
3
4
t tdt
xt
dx t dt t C
t
x
−−
= = − =−+
−
∫∫ ∫
(
)
( )
3
2
2 22
4
1
44 8 4
33
x
xC x xC
−
= − −+=− + −+
4.1.5. PHƯƠNG PHÁP NGUYÊN HÀM TỪNG PHẦN
Câu 78. Tính
( )
11
(2 1) ( )
xx
F x x e dx e Ax B C
−−
= − = ++
∫
. Giá trị của biểu thức
AB+
bằng:
A.
3−
. B.
3
. C.
0
. D.
5
.
Hướng dẫn giải:
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng.
u
và đạo hàm của
u
dv
và nguyên hàm của
v
21x −
1 x
e
−
2
1 x
e
−
−
0
1 x
e
−
Do đó
11 1
( ) (2 1) 2 ( 2 1)
xx x
Fx x e e C e x C
−− −
=− − − += − −+
.
Vậy
3AB+=−
.
Câu 79. Tính
( ) cos ( cos sin )
xx
F x e xdx e A x B x C= = ++
∫
. Giá trị của biểu thức
AB
+
bằng
A.
1
. B.
1−
. C.
2
. D.
2
−
.
Hướng dẫn giải:
Phương pháp trắc nghiệm: Sử dụng bảng
u
và đạo hàm của
u
dv
và nguyên hàm của
v
x
e
cos
x
x
e
sin x
x
e
cos x−
Do đó
1
() sin cos ()
xx
Fx e x e x Fx C= + −+
hay
( )
1
( ) sin cos
2
xx
Fx e x e x C= ++
.
Vậy
1AB+=
.
Câu 80. Tính
6 87
( ) 2 (3 2) (3 2) (3 2)Fx xx dx Ax Bxx C= − = −+ −+
∫
. Giá trị của biểu thức
12 11AB+
là
A.
1
. B.
1−
. C.
12
11
. D.
12
11
−
.
Hướng dẫn giải:
Phương pháp trắc nghiệm: Sử dụng bảng
+
-
+
-
+
Trang 17/34
u
và đạo hàm của
u
dv
và nguyên hàm của
v
2
x
6
(3 2)x −
2
7
1
(3 2)
21
x −
0
8
1
(3 2)
504
x −
Do đó
78
21
( ) (3 2) (3 2)
21 252
Fx x x x C= −− −+
. Vậy
12 11 1AB+=
.
Câu 81. Tính
2 232
( ) 1 ( 1) 1 ( 1) 1 ( 1) 1F x x x dx ax x x bx x x c x x C= − = − −+ − −+ − −+
∫
. Giá trị của
biểu thức
abc++
bằng:
A.
2
7
B.
7
2−
C.
142
105
D.
5
142
10
−
Hướng dẫn giải:
Phương pháp tự luận:
Đặt
2
,1u x dv x dx= = −
ta được
22 23
2 8 16
( ) 1 ( 1) 1 ( 1) 1 ( 1) 1
3 15 105
F x x x dx x x x x x x x x C= − = − −− − −+ − −+
∫
Vậy
82
105
abc
−
++=
.
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
u
và đạo hàm của
u
dv
và nguyên hàm của
v
2
x
1
2
( 1)
x −
2
x
-
3
2
2
( 1)
3
x −
2
+
5
2
4
( 1)
15
x −
0
7
2
8
( 1)
105
x −
22 23
2 8 16
( ) 1 ( 1) 1 ( 1) 1 ( 1) 1
3 15 105
F x x x dx x x x x x x x x C= − = − −− − −+ − −+
∫
Vậy
2
7
abc++=
.
Câu 82. Tính
( )
(
)
2
ln 1F x x x dx= ++
∫
. Chọn kết quả đúng:
A.
(
)
22
( ) ln 1 1Fx x x x x C= ++ −++
. B.
2
1
()
1
Fx C
x
= +
+
.
C.
(
)
22
( ) ln 1 1Fx x x x x C
= ++ +++
. D.
(
)
22
( ) ln 1 1Fx x x x x C= ++ − ++
.
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với
(
)
2
ln 1 ;u x x dv dx= ++ =
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
u
và đạo hàm của
u
dv
và nguyên hàm của
v
(
)
2
ln 1xx++
1
+
+
-
+
Trang 18/34
2
1
1
x
+
(Chuyển
2
1
1
x
+
qua
dv
)
x
1
2
1
x
x+
(Nhận
2
1
1
x+
từ
u
)
0
2
1 x+
Câu 83. Hàm số
()fx
có đạo hàm
2
3
'( )
x
f x xe=
và đồ thị hàm số
()fx
đi qua gốc tọa độ
O
. Chọn kết
quả đúng:
A.
22
2
1 11
()
2 22
xx
f x xe e= −+
. B.
22
2
1 11
()
2 22
xx
f x xe e= +−
.
C.
22
2
1 11
()
2 22
xx
f x xe e= −−
. D.
22
2
1 11
()
2 22
xx
f x xe e= ++
.
Hướng dẫn giải:
Phương pháp tự luận: Đặt
2
2
,
x
u x dv xe= =
chọn
2
1
2,
2
x
du xdx v e= =
ta được
22
2
11
()
22
xx
f x xe e C
= −+
. Đồ thị đi qua
(0; 0)O
nên
1
2
C =
.
Phương pháp trắc nghiệm:
u
và đạo hàm của
u
dv
và nguyên hàm của
v
2
x
2
x
xe
2
x
(chuyển 2
x
qua
dv
)
2
1
2
x
e
1
2
x
xe
(nhận 2
x
từ
u
)
0
2
1
2
x
e
22
2
11
()
22
xx
f x xe e C
= −+
. Đồ thị đi qua
(0; 0)O
nên
1
2
C
=
.
Câu 84. Tính
2
() 1F x x dx= −
∫
bằng:
A.
( )
22
11
1 ln 1
22
Fx xx x x C= −− + − +
. B.
( )
22
11
1 ln 1
22
Fx xx x x C= −+ + − +
.
C.
( )
22
11
1 ln 1
22
Fx xx x x C= −− − − +
. D.
( )
22
11
1 ln 1
22
Fx xx x x C= −+ − − +
.
Hướng dẫn giải:
Cách 1: Sử dụng định nghĩa
'() () '() () 0F x fx F x fx=⇔ −=
Nhập máy tính
( )
() ()
d
Fx f x
dx
−
. CALC
x
tại một số giá trị ngẫu nhiên trong tập xác định,
nếu kết quả xấp xỉ bằng
0
thì chọn.
Cách 2: Đặt
2
1,u x dv dx=−=
ta được
2
() 1 () ()
Fx x x Fx Jx= −− −
với
1
()
1
dx
Jx
x
=
−
∫
, bằng cách đặt
2
1ux x=+−
ta được
2
( ) ln 1Jx x x C= + −+
Vậy
22
11
( ) 1 ln 1
22
Fx x x x x C= −− + − +
.
4.1.6. ÔN TẬP
+
-
-
Trang 19/34
Câu 85. Kết quả của
2
sin cosx xdx
∫
bằng
A.
3
1
sin
3
xC+
. B.
3
sin xC+
. C.
3
1
sin
3
xC−+
. D.
3
sin xC
−+
.
Hướng dẫn giải: Ta có
22 3
1
sin cos sin (sin ) sin
3
x xdx xd x x C= =−+
∫∫
.
Câu 86. Tính
2
cos sin
x xdx
∫
bằng
A.
3
1
cos
3
xC−+
. B.
3
cos
xC−+
. C.
3
1
cos
3
xC
+
. D.
3
cos xC
+
.
Hướng dẫn giải: Ta có
22 3
1
cos sin cos (cos ) cos
3
x xdx xd x x C=− =−+
∫∫
.
Câu 87. Kết quả của
3
sin
xdx
∫
bằng
A.
3
co s
cos
3
x
xC−+
. B.
3
co s
cos
3
x
xC
− −+
.
C.
2
3sin .cosx xC+
. D.
3
co s
cos
6
x
xC
−+
.
Hướng dẫn giải:
32 2 3
1
sin (1 cos )sin (1 cos ) (cos ) cos cos
3
xdx x xdx x d x x x C= − =−− = − +
∫∫ ∫
.
Câu 88. Kết quả của
3
cos xdx
∫
bằng
A.
3
sin
sin
3
x
xC−+
. B.
3
sin
sin
3
x
xC++
.
C.
2
3sin .cos
x xC+
. D.
3
sin
sin
3
x
xC−− +
.
Hướng dẫn giải:
32 2 3
1
cos (1 sin )cos (1 sin ) (sin ) sin sin
3
xdx x xdx x d x x x C=− =− =−+
∫∫ ∫
.
Câu 89. Kết quả của
4
sin cosx xdx
∫
bằng
A.
5
1
sin
5
xC+
. B.
5
1
sin
5
xC−+
. C.
5
sin xC+
. D.
5
sin
xC−+
.
Hướng dẫn giải: Ta có
44 5
1
sin cos sin (sin ) sin
5
x xdx xd x x C= = +
∫∫
.
Câu 90. Tính
tan
2
cos
x
e
dx
x
∫
bằng
A.
tan x
eC+
. B.
tan
tan .
x
xe C+
. C.
tan x
eC
−
+
. D.
tan x
eC−+
.
Hướng dẫn giải:
tan
tan tan
2
(tan )
cos
x
xx
e
dx e d x e C
x
= = +
∫∫
.
Câu 91. Tính
2
1
cos
dx
xx
∫
bằng:
A.
2 tan xC+
. B.
tan xC+
. C.
2
tan xC+
. D.
1
tan
2
xC+
.
Hướng dẫn giải:
22
11
2 ( ) 2 tan
cos cos
dx d x x C
xx x
= = +
∫∫
.
Câu 92. Tính
2
3
3
1
x
dx
x +
∫
bằng
A.
3
ln 1xC++
. B.
3
4
4
4
x
C
xx
+
+
. C.
3
ln( 1)xC
++
. D.
3
4
x
C
xx
+
+
.
Trang 20/34
Hướng dẫn giải:
2
33
33
31
( 1) ln 1
11
x
dx d x x C
xx
= + = ++
++
∫∫
.
Câu 93. Tính
2
32
6 12
36
xx
dx
xx
−
−+
∫
bằng
A.
32
2ln 3 6xx C− ++
. B.
32
ln 3 6xx C− ++
.
C.
32
1
ln 3 6
2
xx C− ++
. D.
32
2ln( 3 6)
xx C− ++
.
Hướng dẫn giải:
2
32 32
32 32
6 12 1
2 (36)2ln 36
36 36
xx
dx dxx xx C
xx xx
−
= −+= −++
−+ −+
∫∫
.
Câu 94. Tính
3
42
42
3
xx
dx
xx
+
++
∫
bằng
A..
42
ln 3xx C
+ ++
. B.
42
2ln 3xx C+ ++
.
C.
42
1
ln 3
2
xx C+ ++
. D.
42
2 ln( 3)xx C− + ++
.
Hướng dẫn giải:
3
42 42
42 42
42 1
( 3) ln 3
33
xx
dx dxx xx C
xx xx
+
= ++= +++
++ ++
∫∫
.
Câu 95. Tính
2
3
1
31
x
dx
xx
+
+−
∫
bằng
A.
3
1
ln 3 1
3
xx C
+ −+
. B.
3
ln 3 1xx C+ −+
.
C.
3
ln 3 1
xx C+ −+
. D.
3
1
ln( 3 1)
3
xx C
+ −+
.
Hướng dẫn giải:
2
33
33
1 11 1
( 31) ln 31
31 3 31 3
x
dx dxx xx C
xx xx
+
= +−= +−+
+− +−
∫∫
.
Câu 96. Tính
65
x
e dx
−
∫
bằng
A.
65
1
6
x
eC
−
+
. B.
65x
eC
−
+
. C.
65
6
x
eC
−
+
. D.
65x
eC
+
−
.
Hướng dẫn giải:
65 65 65
11
(6 5)
66
xx x
edx edx e C
−− −
= −= +
∫∫
.
Câu 97. Tính
5x
e dx
−−
∫
bằng
A.
5x
eC
−−
−+
. B.
5x
eC
−−
+
. C.
5x
eC
+
+
. D.
5x
eC
+
−+
.
Hướng dẫn giải:
55 5
( 5)
xx x
edx edx e C
−− −− −−
=− −− =− +
∫∫
.
Câu 98. Tính
( )
12
59x dx−
∫
bằng
A.
13
(5 9 )
117
x
C
−
−+
. B.
13
(5 9 )
117
x
C
−
+
. C.
13
(5 9 )
13
x
C
−
+
. D.
13
(5 9 )
9
x
C
−
+
.
Hướng dẫn giải:
( ) ( )
13
12 12
1 (5 9 )
59 59 (59)
9 117
x
xdx xd x C
−
− =− − −=− +
∫∫
.
Câu 99. Tính
cos 5
4
x dx
π

+


∫
bằng
A.
1
sin 5
54
xC
π

++


. B.
sin 5
4
xC
π

++


.
C.
5sin 5
4
xC
π

− ++


. D.
1
sin 5
54
xC
π

− ++


.
Trang 21/34
Hướng dẫn giải:
11
cos 5 cos 5 5 sin 5
4 5 4 45 4
xdx xdx x C
π ππ π
 
+ = + += ++
 
 
∫∫
.
Câu 100. Tính
2
1
cos
4
dx
x
π

+


∫
bằng
A.
tan
4
xC
π

++


. B.
4 tan
4
xC
π

++


.
C.
tan
4
xC
π

− ++


. D.
1
tan
44
xC
π

++


.
Hướng dẫn giải:
22
11
tan
44
cos cos
44
dx d x x C
xx
ππ
ππ

= += ++

 

++
 
 
∫∫
.
Câu 101. Tính
2
1
(cos sin )
dx
xx+
∫
bằng
A.
1
cot
24
xC
π

− ++


. B.
1
cot
24
xC
π

++


.
C.
cot
4
xC
π

− ++


. D.
1
cot
44
xC
π

− ++


.
Hướng dẫn giải
2
22
1 1 1 11 1
cot
(cos sin ) 2 2 4 2 4
sin sin
44
dx dx d x x C
xx
xx
ππ
ππ
 
= = +=− ++
 
+
 
 
++
 
 
∫ ∫∫
Câu 102. Tính
12 5
31
x
dx
x
+
+
∫
bằng
A.
1
4 ln 3 1
3
x xC+ ++
. B.
2
3
65xx
C
xx
+
+
+
.
C.
4 ln 3 1x xC+ ++
. D.
1
4 ln(3 1)
3
x xC+ ++
.
Hướng dẫn giải:
12 5 1 1
4 4 ln 3 1
31 31 3
x
dx dx x x C
xx
+

= + = + ++

++

∫∫
.
Câu 103. Tính
2
2
21
xx
dx
x
+
−
∫
bằng
A.
2
1
ln 2 1
22
x
x xC++ −+
. B.
2
ln 2 1
2
x
x xC++ −+
.
C.
2
1
ln(2 1)
22
x
x xC++ −+
. D.
2
2 ln(2 1)
2
x
x xC++ −+
.
Hướng dẫn giải:
22
2 11
1 21
21 21 2 2
xx x
dx x dx x x C
xx
+

= ++ = + + − +

−−

∫∫
.
Câu 104. Tính
2
( 1)
x
dx
x
−
+
∫
bằng
A.
1
ln 1
1
xC
x
− − ++
+
. B.
1
ln 1
1
xC
x
− ++
+
.
C.
1
ln 1
1
xC
x
− + ++
+
. D.
1
ln( 1)
1
xC
x
− − ++
+
.
Hướng dẫn giải:
22
11 1
ln 1
( 1) ( 1) 1 1
x
dx dx x C
x xx x

−
= − =− − ++

+ ++ +

∫∫
.
Trang 22/34
Câu 105. Tính
sin (2 cos )x x dx
+
∫
bằng
A.
1
2 cos cos 2
4
x xC−− +
B.
1
2 cos cos 2
4
x xC
−+
C.
1
2 cos cos 2
4
x xC
++
D.
1
2 cos cos 2
2
x xC
++
Hướng dẫn giải:
11
sin (2 cos ) (2sin sin 2 ) 2cos cos 2
24
x x dx x x dx x x C+ = + =−− +
∫∫
.
Câu 106. Tính
.2
x
x dx
∫
bằng:
A.
2
.2 2
ln 2 ln 2
xx
x
C−+
. B.
( )
21
ln 2
x
x
C
−
+
.
C.
2 ( 1)
x
xC++
. D.
2 ( 1)
x
xC−+
.
Hướng dẫn giải
Đặt
2
2
ln 2
x
x
du dx
ux
dv dx
v
=
=
⇒

=
=
. Ta có
2
.2 2 .2 2
2
ln 2 ln 2 ln 2 ln 2
x x xx
x
xx
x dx dx C
=− =−+
∫∫
.
Câu 107. Tính
ln xdx
∫
bằng:
A.
lnx xxC−+
. B.
2
ln ln
2
x
x x xC−+
.
C.
1
ln xxC
x
−+
. D.
1
ln
xx C
x
−+
.
Hướng dẫn giải
Đặt
1
ln
ux
du dx
x
dv dx
vx
=
=
⇒

=
=
. Ta có
ln ln lnxdx x x dx x x x C
= − = −+
∫∫
.
Câu 108. Tính
2 ln( 1)x x dx−
∫
bằng:
A.
2
2
( 1) ln( 1)
2
x
x x xC− −− −+
. B.
2
2
ln( 1)
2
x
x x xC− − −+
.
C.
2
2
( 1) ln( 1)
2
x
x x xC+ − − −+
. D.
2
2
( 1) ln( 1)
2
x
x x xC− −− ++
.
Hướng dẫn giải
Đặt
2
1
ln( 1)
1
2
1
du dx
ux
x
dv xdx
vx
=
= −
⇒
−

=
= −
Ta có
2
22
2 ln( 1) ( 1) ln( 1) ( 1) ( 1) ln( 1)
2
x
x x dx x x x dx x x x C− = − −− + = − −− −+
∫∫
.
Câu 109. Tính
2
1
sin
cos
x dx
x

+


∫
bằng:
A.
cos tan
x xC−++
. B.
cos tan
x xC++
.
C.
cos tan
x xC−+
. D.
1
cos
cos
xC
x
−− +
.
Hướng dẫn giải: Ta có
2
1
sin cos tan
cos
x dx x x C
x

+ =−++


∫
Câu 110. Hàm số
( ) ln sin cosFx x x= −
là một nguyên hàm của hàm số
A.
sin cos
()
sin cos
xx
fx
xx
+
=
−
. B.
sin cos
()
sin cos
xx
fx
xx
−
=
+
.
Trang 23/34
C.
1
()
sin cos
fx
xx
=
+
. D.
1
()
sin cos
fx
xx
=
−
.
Hướng dẫn giải: Ta có
(sin cos )' cos sin
'( )
sin cos sin cos
x x xx
Fx
xx xx
−+
= =
−−
.
Câu 111. Một nguyên hàm
()Fx
của hàm số
32
() 3 2 1fx x x=−+
thỏa mãn điều kiện
( 2) 3F −=
là:
A.
43
3 2 37
()
43 3
Fx x x x= − +−
. B.
43
32
()
43
Fx x x x C= − ++
.
C.
43
32
()
43
Fx x x x=−+
. D.
43
3 2 37
()
43 3
Fx x x x= − ++
.
Hướng dẫn giải
Ta có
32 4 3
32
( ) (3 2 1)
43
Fx x x x x x C= − + = − ++
∫
và
37
( 2) 3
3
FC−=⇔=−
Vậy
43
3 2 37
()
43 3
Fx x x x= − +−
.
VẬN DỤNG CAO
4.1.1. NGUYÊN HÀM CỦA HÀM SỐ ĐA THỨC, PHÂN THỨC.
Câu 112. Kết quả tính
3
2
52
4
xx
dx
x
−+ +
−
∫
bằng
A.
2
ln 2
2
x
xC− −+
. B.
2
ln 2
2
x
xC+ −+
.
C.
3
ln 2
3
x
xC− −+
. D.
3
ln 2
3
x
xC+ −+
.
Hướng dẫn giải
( )
( )
( )( )
2
33
22
2 21
52 52 1
4 4 22 2
x xx
xx xx
x
x x xx x
+ −−
−+ + − −
= = = −
− − +− −
. Sử dụng bảng nguyên hàm.
Câu 113. Họ nguyên hàm của
(
)
(
)
5
23
1fx x x
= +
là
A.
( )
( )
6
3
1
1
18
Fx x C= ++
. B.
( )
( )
6
3
18 1Fx x C= ++
.
C.
( )
( )
6
3
1Fx x C= ++
. D.
( )
( )
6
3
1
1
9
Fx x C= ++
.
Hướng dẫn giải: Đặt
32
13t x dt x dx= +⇒ =
. Khi đó
( )
( )
56
23 5 6 3
11 1
11
3 18 18
x x dx t dt t C x C+ = = += + +
∫∫
.
Câu 114. Họ nguyên hàm của hàm số
( )
23
3
1x xx
fx
x
++ +
=
là hàm số nào?
A.
( )
2
11
ln
2
Fx x x C
xx
= − +− +
. B.
( )
2
11
ln
2
Fx x x C
xx
= + +− +
.
C.
( )
32
3
ln
32
xx
Fx x C=−+ +
. D.
( )
32
3
ln
32
xx
Fx x C=+++
.
Hướng dẫn giải:
( )
23
3 23
11 1 1
1
x xx
fx
x xx x
++ +
= = + ++
. Sử dụng bảng nguyên hàm.
Câu 115. Giá trị
m
để hàm số
( ) ( )
32
3 2 43F x mx m x x= + + −+
là một nguyên hàm của hàm số
( )
2
3 10 4
fx x x=+−
là:
A.
1m =
. B.
0m =
. C.
2m =
. D.
3m
=
.
Hướng dẫn giải:
( )
2 32
3 10 4 5 4x x dx x x x C+ − =+ −+
∫
, nên
1m =
.
Trang 24/34
Câu 116. Gọi
là nguyên hàm của hàm số
( ) ( )
4
sin 2fx x=
thoả mãn
( )
3
0
8
F =
. Khi đó
là:
A.
( ) ( )
31 1
1 sin 4 sin8
8 8 64
Fx x x x= +− +
. B.
( )
31 1
sin 4 sin8
8 8 64
Fx x x x=−+
.
C.
( )
31 1 3
sin 2 sin 4
8 8 64 8
Fx x x x=−+ +
. D.
( )
3
sin 4 sin 6
8
Fxxxx=−++
.
Hướng dẫn giải
( )
( )
2
42
1 cos 4 1 1 1 cos8
sin 2 1 2cos 4 cos 4 1 2cos 4
24 4 2
3 cos 4 cos8
82 8
xx
x xx x
xx
−+

= =−+ =−+


=−+
Nên
( )
4
3 cos 4 cos8 3 sin 4 sin 8
sin 2
8 2 8 8 8 64
x x xx
x dx dx x C

=− + =−++


∫∫
.
Vì
(
)
3
0
8
F =
nên suy ra đáp án.
Câu 117. Biết hàm số
2
( ) (6 1)fx x= +
có một nguyên hàm là
32
()F x ax bx cx d= + ++
thoả mãn điều
kiện
( 1) 20.F −=
Tính tổng
abcd+++
.
A.
46
. B.
44
. C.
36
. D.
54
.
Hướng dẫn giải
(
)
(
)
2
2 32
6 1 36 12 1 12 6
x dx x x dx x x x C+ = + + = + ++
∫∫
nên
12; 6; 1a bc= = =
Thay
( 1) 20.F
−=
27d =
, cộng lại và chọn đáp án.
Câu 118. Hàm số
( )
1fx xx
= +
có một nguyên hàm là
( )
Fx
. Nếu
( )
02F =
thì
( )
3F
bằng
A.
146
15
. B.
116
15
. C.
886
105
. D.
105
886
.
Hướng dẫn giải: Đặt
12t x tdt dx= +⇒ =
( )
( ) ( )
53
42 5 3
22 2 2
1 22 1 1
53 5 3
x x dx t t dt t t C x x C
+ = − = − += + − + +
∫∫
Vì
( )
02
F =
nên
34
15
C =
. Thay
3x =
ta được đáp án.
Câu 119. Gọi
( )
Fx
là một nguyên hàm của hàm số
( ) cosfx x x
=
thỏa mãn
( )
01F =
. Khi đó phát biểu
nào sau đây đúng?
A.
( )
Fx
là hàm số chẵn.
B.
( )
Fx
là hàm số lẻ.
C. Hàm số
tuần hoàn với chu kì là
2
π
.
D. Hàm số
không là hàm số chẵn cũng không là hàm số lẻ.
Hướng dẫn giải
cos sin cosx xdx x x x C= ++
∫
(
)
01F =
nên
0
C =
. Do đó
là hàm số chẵn.
Câu 120. Một nguyên hàm
( )
Fx
của hàm số
2
sin 2
()
sin 3
x
fx
x
=
+
thỏa mãn
( )
00F =
là
A.
2
sin
ln 1
3
x
+
. B.
2
ln 1 sin x+
. C.
2
ln 2 sin
3
x+
. D.
2
ln cos x
.
Hướng dẫn giải: Đặt
2
sin 3 2sin cost x dt x xdx
= +⇒ =
2
2
sin 2
ln ln sin 3
sin 3
x dt
dx t C x C
xt
= = + = ++
+
∫∫
Trang 25/34
vì
( )
00F =
nên
ln 3C = −
. Chọn đáp án.
Câu 121. Cho
( )
2
4
sin
m
fx x= +
π
. Tìm
m
để nguyên hàm
của hàm số
( )
fx
thỏa mãn
( )
01F =
và
48
F

=


ππ
.
A.
3
4
−
. B.
3
4
. C.
4
3
−
D.
4
3
.
Hướng dẫn giải:
2
4 4 sin 2
sin
24
m mx x
x dx x C

+ = +− +


∫
ππ
vì
( )
01F =
nên
1C =
48
F

=


ππ
nên tính được
3
4
m = −
4.1.2. NGUYÊN HÀM CỦA HÀM SỐ LƯỢNG GIÁC.
Câu 122. Tìm nguyên hàm của hàm số
1
()
sin .cos
fx
xx
=
.
A.
2
1
( ) ln sin ln 1 sin
2
f x dx x x C
= −− +
∫
. B.
2
1
( ) ln sin ln 1 sin
2
f x dx x x C= +− +
∫
.
C.
2
11
( ) ln sin ln 1 sin
22
f x dx x x C= −− +
∫
. D.
2
1
( ) ln sin ln 1 sin
2
f x dx x x C=− −− +
∫
.
Hướng dẫn giải
( )
( )
2
2
sin
cos
sin .cos sin .cos
sin . 1 sin
dx
dx xdx
xx x x
xx
= =
−
∫∫ ∫
( ) ( ) ( )
sin sin sin
11
2 1 sin sin 2 1 sin
dxdx dx
xx x
= +−
−+
∫∫ ∫
2
11 1
ln 1 sin ln sin ln 1 sin ln sin ln 1 sin
22 2
x x xC x xC
−
= −+ −++= −− +
Câu 123. Tìm nguyên hàm của hàm số
3
2sin
()
1 cos
x
fx
x
=
+
.
A.
2
( ) cos 2cosf x dx x x C=−+
∫
. B.
2
1
( ) cos 2cos
2
f x dx x x C= −+
∫
.
C.
2
( ) cos cos
f x dx x x C= ++
∫
. D.
2
1
( ) cos 2cos
2
f x dx x x C= ++
∫
.
Hướng dẫn giải
( )
32 2
2sin 2sin 2cos 2
.sin cos
1 cos 1 cos 1 cos
xx x
dx xdx d x
xx x
−
= =
++ +
∫∫ ∫
(
) ( )
2
2 cos 1 cos cos 2 cosx d x x xC= − =−+
∫
Câu 124. Tìm nguyên hàm của hàm số
3
5
cos
()
sin
x
fx
x
=
.
A.
4
cot
( ).
4
x
f x dx C
−
= +
∫
. B.
4
cot
( ).
4
x
f x dx C= +
∫
.
C.
2
cot
( ).
2
x
f x dx C= +
∫
. D.
4
tan
( ).
4
x
f x dx C= +
∫
.
Hướng dẫn giải
( )
34
33
52
cos cot
cot . cot . cot
sin sin 4
xdx dx x
x xd x C
xx
−
==−=+
∫∫ ∫
Câu 125. Tìm nguyên hàm của hàm số:
( )
44
( ) cos 2 sin cosfx x x x= +
.
A.
3
11
( ). sin 2 sin 2
2 12
f x dx x x C=−+
∫
. B.
3
11
( ). sin 2 sin 2
2 12
f x dx x x C=++
∫
.
C.
3
1
( ). sin 2 sin 2
4
f x dx x x C=−+
∫
. D.
3
11
( ). sin 2 sin 2
24
f x dx x x C=−+
∫
.
Trang 26/34
Hướng dẫn giải
( )
44
cos 2 sin cos
x x x dx+
∫
( )
2 2 22
cos 2 sin cos 2sin .cos
x x x x x dx

= +−

∫
(
)
22
23
11
cos 2 1 sin 2 cos 2 sin 2 .cos 2
22
1 11
cos2 sin 2 . sin 2 sin 2 sin 2
4 2 12
x x dx xdx x xdx
xdx x d x x x C

=−=−


= − =−+
∫ ∫∫
∫∫
Câu 126. Tìm nguyên hàm của hàm số
( )
2sin
( ) tan cos
x
fx x e x= +
.
A.
2sin
1
( ) cos
2
x
f x dx x e C=−+ +
∫
. B.
2sin
1
( ) cos
2
x
f x dx x e C=++
∫
.
C.
2sin
( ) cos
x
f x dx x e C=−++
∫
. D.
2sin
1
( ) cos
2
x
f x dx x e C=−− +
∫
.
Hướng dẫn giải
( )
( )
2sin 2sin 2sin
1
tan cos sin sin cos
2
x xx
x e xdx xdx e d x x e C+ = + =−+ +
∫ ∫∫
Câu 127. Tìm nguyên hàm của hàm số
1
()
sin cos 2
fx
xx
=
++
.
A.
13
( ) cot
28
2
x
f x dx C

=− ++


∫
π
. B.
13
( ) cot
28
2
x
f x dx C

= ++


∫
π
.
C.
13
( ) cot
24
2
x
f x dx C

=− ++


∫
π
. D.
13
( ) cot
28
2
x
f x dx C

=− −+


∫
π
.
Hướng dẫn giải
1
sin cos 2 2
2 sin 2 sin 1
44
dx dx dx
xx
xx
= =
 
++
++ ++
 
 
∫∫ ∫
ππ
2
2
1 1 13
cot
3
28
2 22
2sin
sin cos
28
28 28
dx dx x
C
x
xx

= = =− ++





+

++ +





∫∫
π
π
ππ
4.1.3. NGUYÊN HÀM CỦA HÀM SỐ MŨ, LÔGARIT.
Câu 128. Hàm số
( ) ln sin cosFx x x= −
là một nguyên hàm của hàm số
A.
sin cos
()
sin cos
xx
fx
xx
+
=
−
. B.
sin cos
()
sin cos
xx
fx
xx
−
=
+
.
C.
1
()
sin cos
fx
xx
=
+
. D.
1
()
sin cos
fx
xx
=
−
.
Hướng dẫn giải:
(sin cos )' cos sin
'( )
sin cos sin cos
x x xx
Fx
xx xx
−+
= =
−−
Câu 129. Kết quả tính
2 ln( 1)x x dx−
∫
bằng:
A.
2
2
( 1) ln( 1)
2
x
x x xC− −− −+
. B.
2
2
ln( 1)
2
x
x x xC− − −+
.
C.
2
2
( 1) ln( 1)
2
x
x x xC+ − − −+
. D.
2
2
( 1) ln( 1)
2
x
x x xC− −− ++
.
Hướng dẫn giải
Đặt
2
1
ln( 1)
1
2
1
du dx
ux
x
dv xdx
vx
=
= −
⇒
−

=
= −
Ta có
2
22
2 ln( 1) ( 1) ln( 1) ( 1) ( 1) ln( 1)
2
x
x x dx x x x dx x x x C− = − −− + = − −− −+
∫∫
Trang 27/34
Câu 130. Kết quả tính
tan
2
cos
x
e
dx
x
∫
bằng:
A.
tan x
eC+
. B.
tan
tan .
x
xe C+
. C.
tan x
eC
−
+
. D.
tan x
eC−+
.
Hướng dẫn giải:
tan
tan tan
2
(tan )
cos
x
xx
e
dx e d x e C
x
= = +
∫∫
.
Câu 131. Tính
2
cos
e sin 2
x
xdx
∫
bằng:
A.
2
cos x
eC−+
. B.
sin 2
x
eC
−
+
. C.
2sin
x
eC
−
+
. D.
sin 2x
eC−+
.
Hướng dẫn giải:
22 2
cos cos 2 cos
e sin 2 e (cos ) e
xx x
xdx d x C
=− =−+
∫∫
.
Câu 132. Tính
2
sin
e sin 2
x
xdx
∫
bằng:
A.
2
sin
x
eC+
. B.
sin 2x
eC+
. C.
2
cos x
eC+
. D.
2sin x
eC+
.
Hướng dẫn giải:
2 22
sin sin 2 sin
e sin 2 e (sin ) e
x xx
xdx d x C
= = +
∫∫
.
Câu 133. Kết quả
cos
sin
x
e xdx
∫
bằng:
A.
cos x
eC−+
. B.
cos
x
eC+
. C.
cos x
eC
−
−+
. D.
sin x
eC
−
+
.
Hướng dẫn giải:
cos cos cos
sin (cos )
x xx
e xdx e d x e C=− =−+
∫∫
.
4.1.4. NGUYÊN HÀM CỦA HÀM SỐ CHỨA CĂN THỨC.
Câu 134. Biết hàm số
( ) 1 2 2017Fx x x
=− −+
là một nguyên hàm của hàm số
()
12
ax b
fx
x
+
=
−
. Khi đó
tổng của
a
và
b
là
A.
2
. B.
2−
. C.
0
. D.
1
.
Hướng dẫn giải:
( )
31
'( ) 1 2 2017 '
12
x
Fx x x
x
−
=− −+ =
−
( )
3 12ab⇒ + = +− =
Câu 135. Tìm nguyên hàm của hàm số
3
2
2
()
1
xx
fx
x
−
=
+
.
A.
( )
( )
22
1
81
3
Fx x x C= − ++
. B.
(
)
22 2
1
1 81
3
Fx x x x C= ++ ++
.
C.
( )
( )
22
1
81
3
Fx x x C= − ++
. D.
( )
( )
22
2
81
3
Fx x x C= − ++
.
Hướng dẫn giải:
(
)
2
3
22
2
2
11
x xdx
xx
dx
xx
−
−
=
++
∫∫
Đặt
2 22
11t x x t xdx tdt= +⇒ = −⇒ =
. Khi đó
(
)
( )
( )
2
33
2
2
3
2
33
3
1
t tdt
xx t
dx t dt t C
t
x
−
−
= = − = −+
+
∫∫ ∫
(
)
( )
3
2
2 22
1
1
31 8 1
33
x
xCx xC
+
= − ++ = − ++
Câu 136. Tính
( )
22
sin 2
4sin 2cos 3
x
F x dx
xx
=
++
∫
. Hãy chọn đáp án đúng.
A.
( )
6 cos 2Fx x C=−+
. B.
( )
6 sin 2Fx x C=−+
.
C.
( )
6 cos 2Fx x C=++
. D.
( )
6 sin 2Fx x C=−− +
.
Hướng dẫn giải
Trang 28/34
( )
22
6 cos 2
sin 2 sin 2
6 cos 2
6 cos 2 2 6 cos 2
4sin 2cos 3
dx
xx
dx dx= x C
xx
xx
−
= =−+
−−
++
∫ ∫∫
Câu 137. Biết hàm số
( )
() x 2 1Fx m n x=+−
là một nguyên hàm của hàm số
1
()
21
x
fx
x
−
=
−
. Khi đó
tích của
m
và
n
là
A.
2
9
−
. B.
2−
. C.
2
3
−
. D.
0
.
Hướng dẫn giải
Cách 1: Tính
1 12
2x 1
33
2x 1
x
dx x C
−

=− + −+

−

∫
. Suy ra
12 2
;.
33 9
m n mn=−=⇒=−
Cách 2: Tính
( )
3
'
21
mx m n
Fx
x
−+
=
−
. Suy ra
1
31
2
3
.
12
9
3
m
m
mn
nm
n
= −
= −
⇒ ⇒=−

−=
=
Câu 138. Biết hàm số
()Fx
là một nguyên hàm của hàm số
2
ln
()
ln 3
x
fx
xx
=
+
có đồ thị đi qua điểm
( )
;2016e
. Khi đó hàm số
( )
1
F
là
A.
3 2014+
. B.
3 2016+
.
C.
2 3 2014+
. D.
2 3 2016+
.
Hướng dẫn giải: Đặt
2
ln 3tx= +
và tính được
(
)
2
ln 3
Fx x C= ++
.
( ) ( )
( )
2
2016 2014 ln 3 2014 1 3 2014Fe C Fx x F= ⇒ = ⇒ = ++ ⇒ = +
4.1.5. PHƯƠNG PHÁP NGUYÊN HÀM TỪNG PHẦN
Câu 139. Tính
3 32
()
xx
x e dx e ax bx cx d C
= + +++
∫
. Giá trị của
abcd+++
bằng
A.
2−
. B.
10
. C.
2
. D.
9−
.
Hướng dẫn giải:
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
Kết quả:
3 3 2 32
3 6 6 ( 3 6 6)
x x x xx x
xedx xe xe xe e C e x x x C= − + − += − + −+
∫
.
Vậy
2abcd+++ =−
.
Câu 140. Tính
2 22 2
( ) ln( 3) ( 3) ln( 3)F x x x dx A x x Bx C= + = + ++ +
∫
. Giá trị của biểu thức
AB+
bằng
A.
0
. B.
1
. C.
1−
. D.
2
.
Hướng dẫn giải
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
u
và đạo hàm của
u
dv
và nguyên hàm của
v
2
ln( 3)x +
x
2
2
3
x
x +
2
3
2
x +
1
(Chuyển
2
2
3
x
x
+
qua
dv
)
x
(Nhận
2
2
3
x
x +
từ
u
)
0
2
2
x
Do đó
2 22 2
11
( ) ln( 3) ( 3) ln( 3)
22
F x x x dx x x x C= + = + +− +
∫
.
Vậy
0AB+=
.
Câu 141. Tính
22
cos 2 sin 2 cos 2 sinx xdx ax x bx x c x C= + ++
∫
. Giá trị của
4ab c++
bằng
+
-
Trang 29/34
A.
0
. B.
3
4
. C.
3
4
−
. D.
1
2
.
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần 2 lần.
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
Kết quả:
22
1 11
cos 2 sin 2 cos 2 sin 2
2 24
x xdx x x x x x C
= + −+
∫
.
Vậy
40ab c++ =
.
Câu 142. Tính
34
ln 2 ( ln 2 )x xdx x A x B C= ++
∫
. Giá trị của
54
AB+
bằng:
A.
1
. B.
1
4
−
. C.
1
4
. D.
1−
.
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với
3
ln 2 ,u x dv x dx
= =
.
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
Kết quả:
3 4 44
1 1 11
ln 2 ln 2 ln 2
4 16 4 16
x xdx x x x C x x C

= − += − +


∫
.
Vậy
541AB+=
.
Câu 143. Tính
1
( ) ln
1
x
F x x dx
x
+
=
−
∫
. Chọn kết quả đúng:
A.
2
1
( ) ln
21
1
xx
Fx x C
x
+
= ++
−
−
B.
2
1
( ) ln
21
1xx
Fx x C
x
+
= ++
−
+
C.
2
11
( ) ln
21
xx
Fx x C
x
++
= −+
−
D.
2
11
( ) ln
21
xx
Fx x C
x
−+
= −+
−
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần và nguyên hàm của hàm
số hữu tỉ.
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
Kết quả:
2
1 11
ln ln
1 21
xx x
x dx x C
xx
+ −+
= ++
−−
∫
.
Câu 144. Cho hàm số
3
( ) (1 )F x x x dx= −
∫
. Biết
(0) 1
F =
, khi đó
(1)F
bằng:
A.
21
20
. B.
19
20
. C.
0
21
2
−
. D.
19
20
−
.
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp đổi biến số với
1ux= −
.
Sử dụng phương pháp từng phần với
3
; (1 )u x dv x dx= = −
.
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng với
3
; (1 )u x dv x dx= = −
Kết quả
3
54
(1 ) (1 )
( ) (1 )
4 20
xx x
F x x x dx C
−− −
=−= − +
∫
(0) 1F =
suy ra
21
20
C =
. Do đó
21
(1)
20
F =
.
Câu 145. Tính
(2 1)sin cos cos sinx xdx ax xb xc xC+ = + ++
∫
. Giá trị của biểu thức
abc++
bằng
A.
1−
. B.
1
. C.
5
. D.
5−
.
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần.
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng.
Kết quả
( ) (2 1)sin 2 cos cos 2sinF x x xdx x x x x C=+ =− −+ +
∫
nên
1abc++=−
.
Câu 146. Cho hàm số
( ) ln( 1)F x x x dx= +
∫
có
(1) 0F =
. Khi đó giá trị của
(0)F
bằng
Trang 30/34
A.
1
4
−
. B.
1
4
. C.
1
2
−
. D.
1
2
.
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với
ln( 1),u x dv xdx=+=
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
Kết quả
( ) ln( 1)F x x x dx= +
∫
22
11
( 1) ln( 1) ( 2 )
24
x x x xC= − +− − +
.
Từ
(1) 0F =
suy ra
1
4
C
−
=
. Vậy
1
(0)
4
F
−
=
.
Câu 147. Hàm số
2
( ) ( 1) lnF x x xdx= +
∫
thỏa mãn
5
(1)
9
F
−
=
là
A.
3
3
1
( 3 )ln
6 18 2
xx
x xx+ −−
. B.
3
3
1
( 3 )ln 1
6 18 2
xx
x xx+ − −−
.
C.
3
3
1 10
( 3 )ln
6 18 2 9
xx
x xx+ − −+
. D.
3
3
1
( 3 )ln 1
6 18 2
xx
x xx+ − −+
.
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp từng phần.
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
Kết quả
3
23
1
( ) ( 1) ln ( 3 )ln
6 18 2
xx
F x x xdx x x x C= + = + − −+
∫
Với
5
(1)
9
F
−
=
suy ra
0C =
nên
3
3
1
( ) ( 3 ) ln
6 18 2
xx
Fx x x x= + −−
.
Câu 148. Hàm số
()fx
có đạo hàm
2
'( )
( 1)
x
xe
fx
x
=
+
và có đồ thị đi qua điểm
(0;1)A
. Chọn kết quả đúng
A.
()
1
x
e
fx
x
=
+
B.
() 1
1
x
e
fx
x
= +
+
C.
() 1
1
x
e
fx
x
= −
+
D.
() 2
1
x
e
fx
x
= +
+
Hướng dẫn giải: Sử dụng phương pháp từng phần với
2
1
,
( 1)
x
u xe dv dx
x
= =
+
u
và đạo hàm của
u
dv
và nguyên hàm của
v
x
xe
2
1
( 1)x +
( 1)
x
xe+
(Chuyển
( 1)
x
xe+
qua
dv
)
1
1
x
−
+
1
x
e−
(nhận
( 1)
x
xe+
từ
u
)
0
x
e−
Kết quả
2
()
( 1) 1
xx
xe e
f x dx C
xx
= = +
++
∫
. Với
(0) 1f
=
suy ra
. Vậy
()
1
x
e
fx
x
=
+
Câu 149. Một nguyên hàm
()Fx
của hàm số
(
)
2
( ) ln 1fx x x= ++
thỏa mãn
(0) 1F =
. Chọn kết quả
đúng
A.
(
)
22
( ) ln 1 1 2Fx x x x x= + + − ++
. B.
(
)
22
( ) ln 1 1 2Fx x x x x= + + − +−
.
C.
(
)
22
( ) ln 1 1 1Fx x x x x= + + − ++
. D.
(
)
22
( ) ln 1 1Fx x x x x= + +− +
.
Hướng dẫn giải:
+
-
Trang 31/34
Đặt
(
)
2
ln 1 ,u x x dv dx= ++ =
ta được
(
)
22
( ) ln 1 1
Fx x x x x C
= + + − ++
. Vì
(0) 1F
=
nên
2C
=
Vậy
(
)
22
( ) ln 1 1 2Fx x x x x= + + − ++
.
Câu 150. Một nguyên hàm
()Fx
của hàm số
2
()
cos
x
fx
x
=
thỏa mãn
( ) 2017
F
π
=
. Khi đó
(
)
Fx
là
hàm số nào dưới đây?
A.
( ) tan ln | cos | 2017Fx x x x=++
. B.
( ) tan ln | cos | 2018Fx x x x=−+
.
C.
( ) tan ln | cos | 2016
Fx x x x=++
. D.
( ) tan ln | cos | 2017
Fx x x x=−+
.
Hướng dẫn giải: Đặt
2
1
,
cos
u x dv dx
x
= =
ta được
, tandu dx v x= =
Kết quả
2
( ) tan tan tan ln | cos |
cos
x
F x dx x x xdx x x x C
x
= =−=+ +
∫∫
.
Vì
( ) 2017F
π
=
nên
2017C =
. Vậy
( ) tan ln | cos | 2017
Fx x x x
=++
.
Câu 151. Tính
2
( ) (1 sin 2 ) cos 2 sin 2F x x x dx Ax Bx x C x D
=+ =+ ++
∫
. Giá trị của biểu thức
ABC++
bằng
A.
1
4
. B.
1
4
−
. C.
5
4
. D.
3
4
−
.
Hướng dẫn giải:
Cách 1: Sử dụng phương pháp nguyên hàm từng phần.
Cách 2: Sử dụng phương pháp bảng với
, (1 sin 2 )
u x dv x dx= = +
ta được
2
11 1
( ) cos 2 sin 2
22 4
Fxxxx xD=− ++
. Vậy
1
4
ABC++=
.
Câu 152. Tính
2
1 sin
()
cos
xx
F x dx
x
+
=
∫
. Chọn kết quả đúng
A.
1 sin 1
( ) tan ln
cos 2 sin 1
xx
Fx x C
xx
−
=++ +
+
. B.
1 sin 1
( ) tan ln
cos 2 sin 1
xx
Fx x C
xx
−
=−+ +
+
.
C.
1 sin 1
( ) tan ln
cos 2 sin 1
xx
Fx x C
xx
−
=+− +
+
. D.
1 sin 1
( ) tan ln
cos 2 sin 1
xx
Fx x C
xx
−
=−− +
+
.
Hướng dẫn giải
Cách 1: Biến đổi
22
sin
() tan ()
cos cos
dx x x
F x dx x I x
xx
=+=+
∫∫
Tính
()Ix
bằng cách đặt
2
sin
;
cos
x
u x dv dx
x
= =
ta được
()
cos cos
x dx
Ix
xx
= −
∫
Tính
2
cos (sin ) sin 1
( ) ln
cos sin 1 (sin 1)(sin 1) sin 1
dx xdx d x x
Jx C
x x xx x
−
=−= = = +
− −+ +
∫∫ ∫
Kết quả
( )
1 sin 1
tan ln
cos 2 sin 1
xx
Fx x C
xx
−
=++ +
+
Phương pháp trắc nghiệm: Sử dụng máy tính kiểm tra
( ()) () 0
d
Fx f x
dx
−=
tại một số điểm
ngẫu nhiên
0
x
.
4.1.6. ÔN TẬP
Câu 153. Một nguyên hàm
()Fx
của hàm số
2
1
( ) sin
cos
fx x
x
= +
thỏa mãn điều kiện
2
42
F

=


π
là
A.
( ) cos tan 2 1Fx x x=−++−
. B.
( ) cos tan 2 1Fx x x= + +−
.
Trang 32/34
C.
( ) cos tan 1 2Fx x x
=−++−
. D.
( ) cos tanFx x x=−+
.
Hướng dẫn giải
Ta có
2
1
sin x cos tan ( ) cos tan
cos
x d x xC Fx x xC
x

+ =−++⇒ =−++


∫
2
21
42
FC
π

= ⇔= −


. Vậy
( ) cos tan 2 1Fx x x
=−++−
Câu 154. Một nguyên hàm
()Fx
của hàm số
3
( ) 2sin5
5
fx x x= ++
thỏa mãn đồ thị của hai hàm số
()Fx
và
()fx
cắt nhau tại một điểm nằm trên trục tung là
A.
2 23
( ) cos5 1
5 35
Fx x x x x=− + ++
. B.
2 23
( ) cos5 1
5 35
Fx x x x x= + ++
.
C.
13
( ) 10cos5 1
5
2
Fx x x
x
= + ++
. D.
2 23
( ) cos5
5 35
Fx x x x x=− ++
.
Hướng dẫn giải
Ta có
2 23
( ) cos5
5 35
Fx x x x x C=− + ++
và
(0) (0) 1Ff C= ⇔=
Vậy
2 23
( ) cos5 1
5 35
Fx x x x x=− + ++
Câu 155. Hàm số
2
() ( )
x
F x ax bx c e= ++
là một nguyên hàm của hàm số
2
()
x
f x xe=
thì
abc++
bằng:
A.
1
. B.
2
. C.
3
. D.
2−
.
Hướng dẫn giải
Ta có
22
11
'() () (2 ) 2 0 2
02
aa
Fx fx ax abxbc x ab b
bc c
= =


= ⇔ + + ++= ⇔ +=⇔ =−


+= =

Vậy
1abc++=
Câu 156. Một nguyên hàm
()
Fx
của hàm số
( ) cos 2fx a b x= +
thỏa mãn
(0)
2
F
π
=
,
26
F
ππ

=


,
12 3
F
ππ

=


là
A.
27
( ) sin 2
39 2
Fx x x
ππ
=−+ +
. B.
27
( ) sin 2
39
Fx x x
π
=−+
.
C.
27
( ) sin 2
39 2
Fx x x
ππ
=−− +
. D.
27
( ) sin 2
39 2
Fx x x
ππ
=−+ −
.
Hướng dẫn giải
Ta có
( ) sin 2
2
b
F x ax x C=++
và
2
(0)
2
3
7
26 9
2
12 3
F
a
Fb
C
F
π
ππ π
π
ππ
=
= −

=⇔=






=
=



Vậy
27
( ) sin 2
39 2
Fx x x
ππ
=−+ +
Câu 157. Cho hàm số
32
() 1F x ax bx cx= + ++
là một nguyên hàm của hàm số
()fx
thỏa mãn
(1) 2,f =
(2) 3, (3) 4ff= =
. Hàm số
()Fx
là
A.
2
1
() 1
2
Fx x x= ++
. B.
2
1
() 1
2
Fx x x=− ++
.
Trang 33/34
C.
2
1
() 1
2
Fx x x=− −+
. D.
2
1
() 1
2
Fx x x= −+
.
Hướng dẫn giải
Ta có
2
() '() 3 2f x F x ax bx c= = ++
và
0
(1) 2 3 2 2
1
(2) 3 12 4 3
2
(3) 4 27 6 4
1
a
f a bc
f a bc b
f a bc
c
=
= + +=


=⇔ + += ⇔ =


= + +=

=
Vậy
2
1
() 1
2
Fx x x
= ++
.
Câu 158. Một nguyên hàm
()Fx
của hàm số
( ) tan .sin 2fx x x=
thỏa mãn điều kiện
0
4
F
π

=


là
A.
11
( ) sin 2
2 24
Fx x x
π
=− +−
. B.
1
( ) cos 2 1
24
Fx x x
π
=+ +−
.
C.
3
22
( ) cos
32
Fx x= +
. D.
1
sin 2
24
xx
π
+−
.
Hướng dẫn giải
Ta có
11
tan .sin 2 (1 cos2 ) sin 2 ( ) sin 2
22
x xdx x dx x x C F x x x C=− =−+⇒=−+
∫∫
và
1
0
4 24
FC
ππ

=⇔=−


Vậy
11
( ) sin 2
2 24
Fx x x
π
=− +−
.
Câu 159. Cho hàm số
2
( ) tan
fx x=
có nguyên hàm là
()Fx
. Đồ thị hàm số
()y Fx=
cắt trục tung tại
điểm
(0; 2)A
. Khi đó
()Fx
là
A.
( ) tan 2Fx x x= −+
. B.
( ) tan 2Fx x= +
.
C.
3
1
( ) tan 2
3
Fx x= +
. D.
( ) cot 2Fx x x= −+
.
Hướng dẫn giải
2
( ) ( ) tan tanF x f x dx xdx x x C= = = −+
∫∫
.
Vì đồ thị hàm số
()y Fx=
đi qua điểm
(0; 2)A
nên
2
C =
.
Vậy
( ) tan 2Fx x x= −+
.
Câu 160. Cho hàm số
()
Fx
là một nguyên hàm của hàm số
2
( ) tan
fx x=
. Giá trị của
(0)
4
FF
π

−


bằng
A.
1
4
π
−
. B.
4
π
. C.
1
4
π
+
. D.
3
4
π
−
.
Hướng dẫn giải:
( )
tan (0) 1
44
Fx x x C F F

= −+ ⇒ − =−


ππ
.

Tài liệu khác của Toán 12

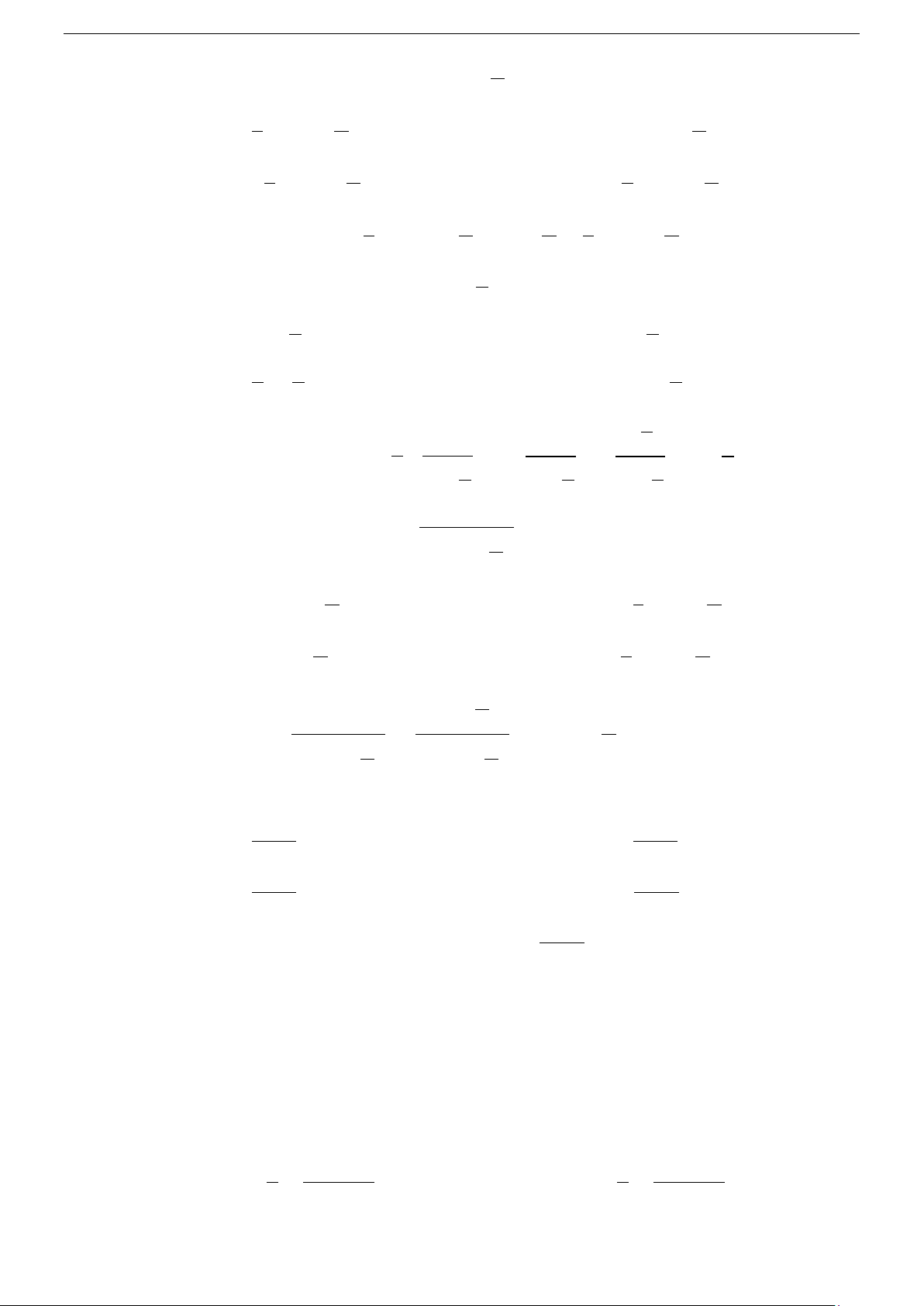
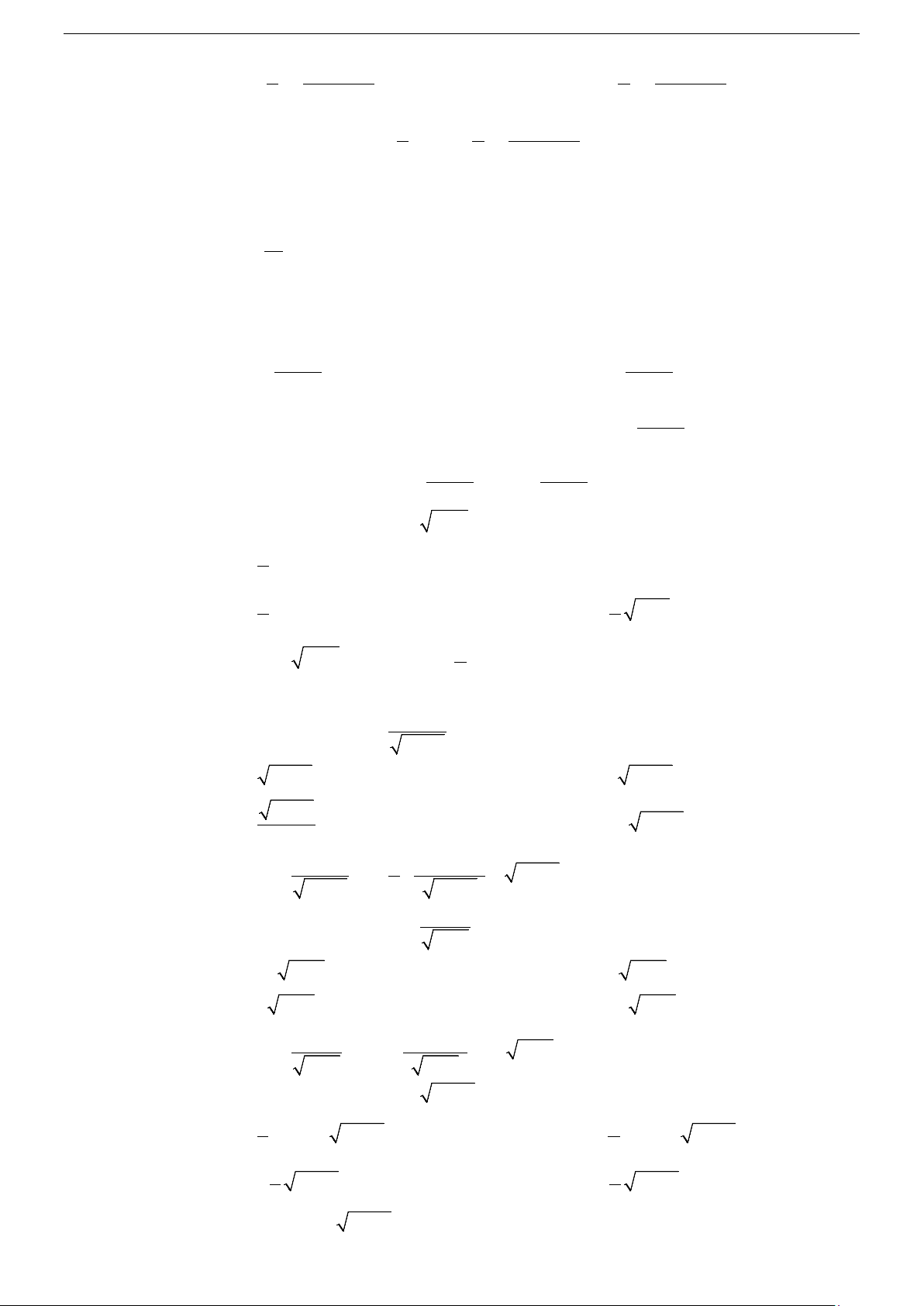
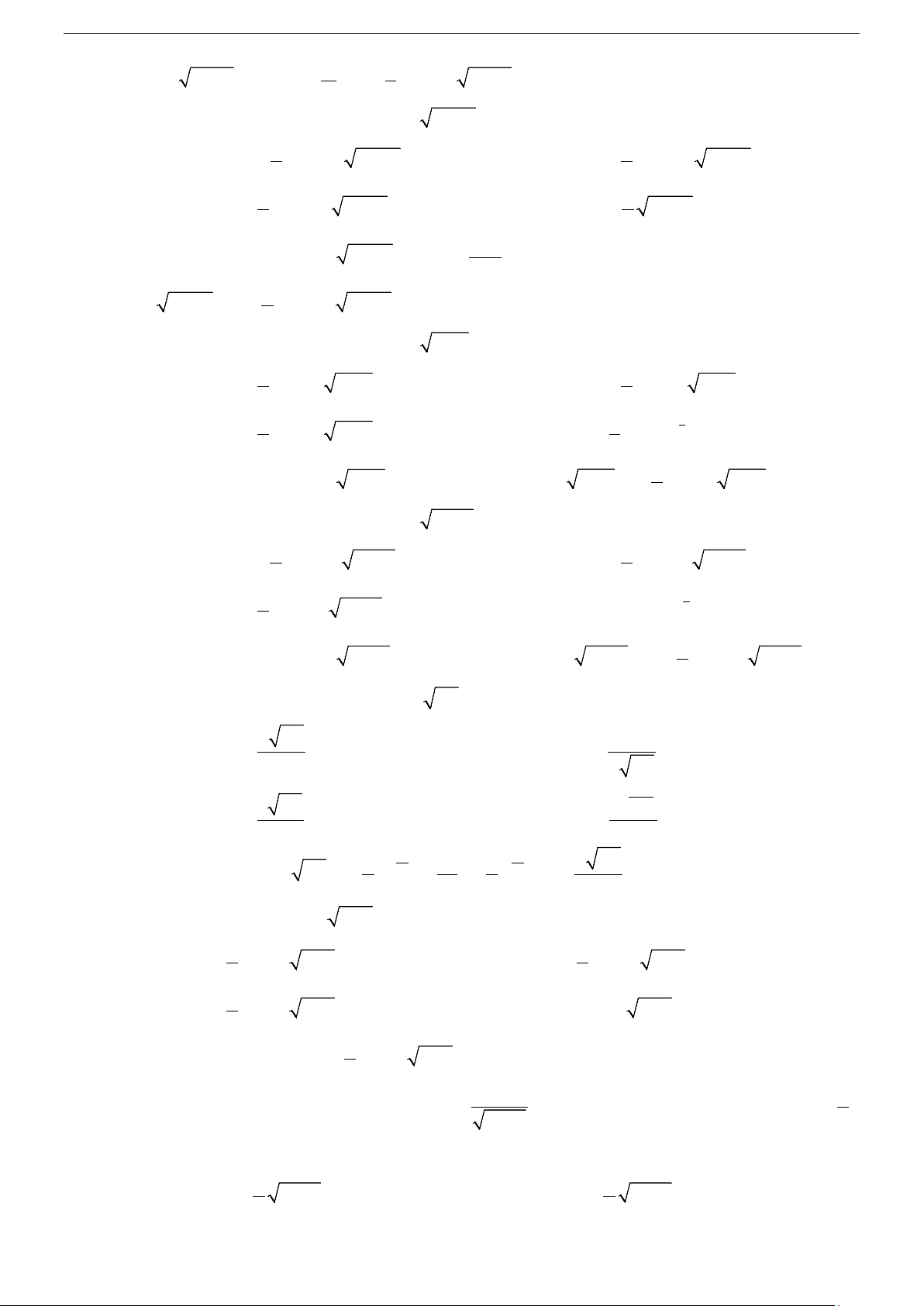
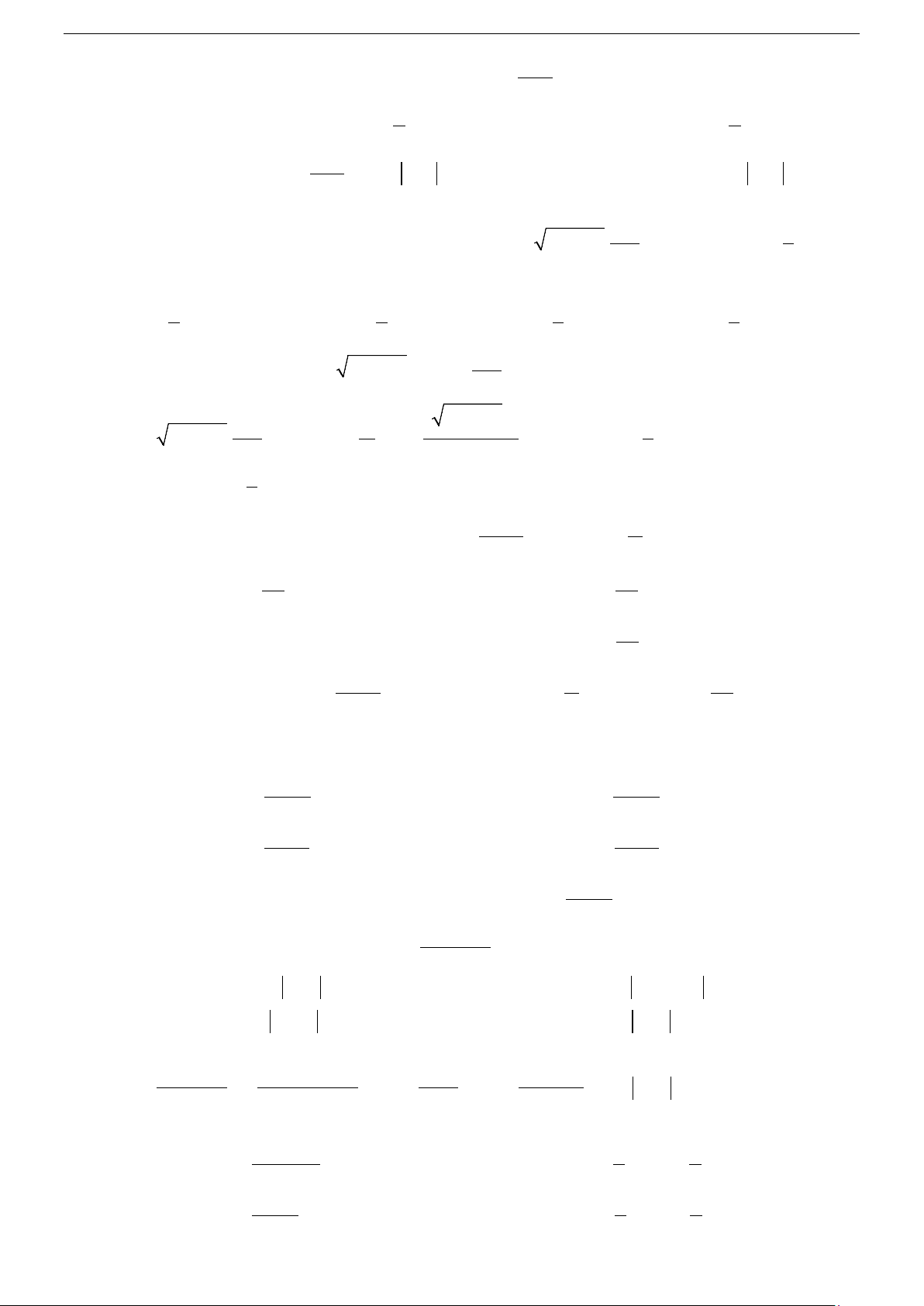
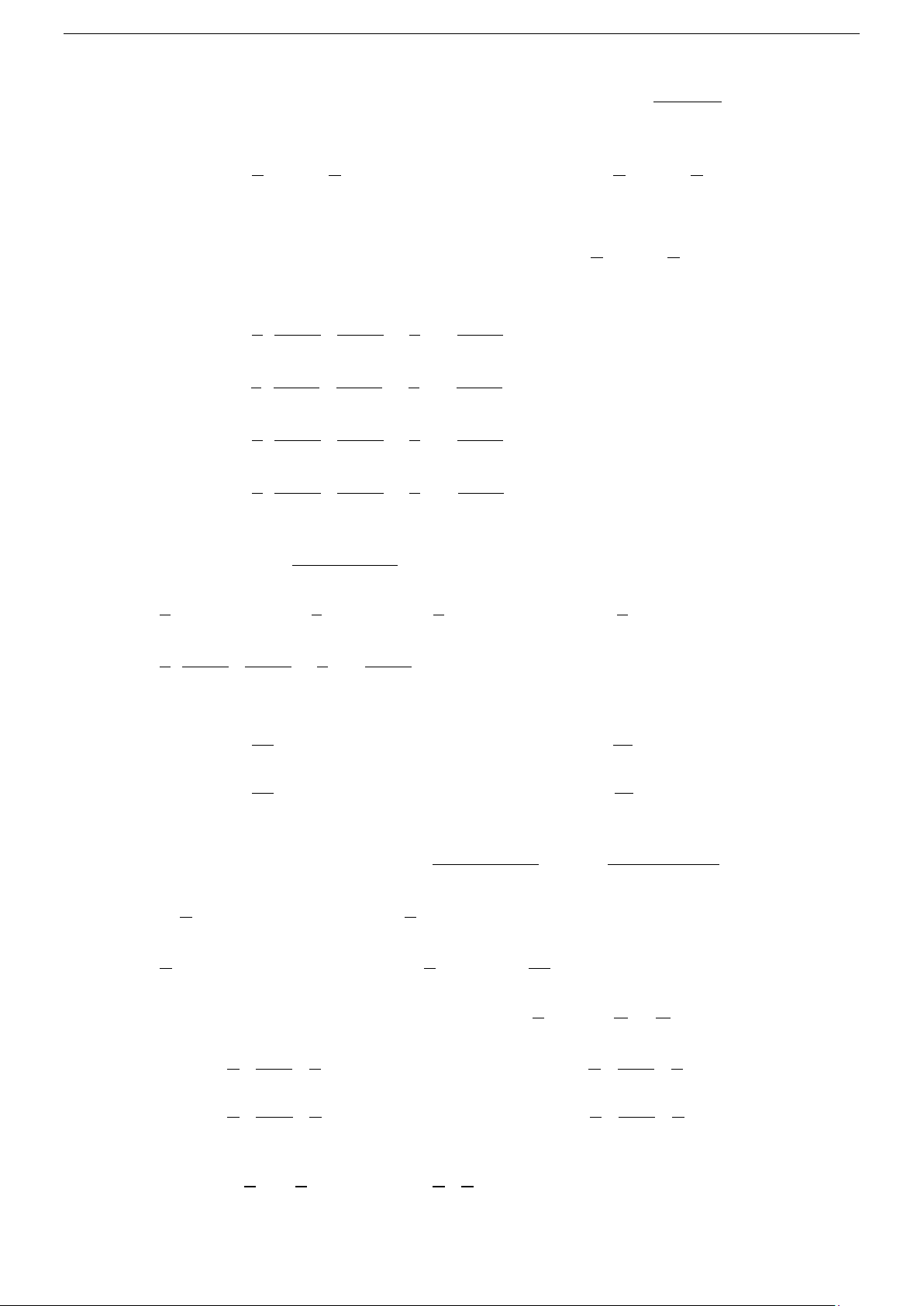
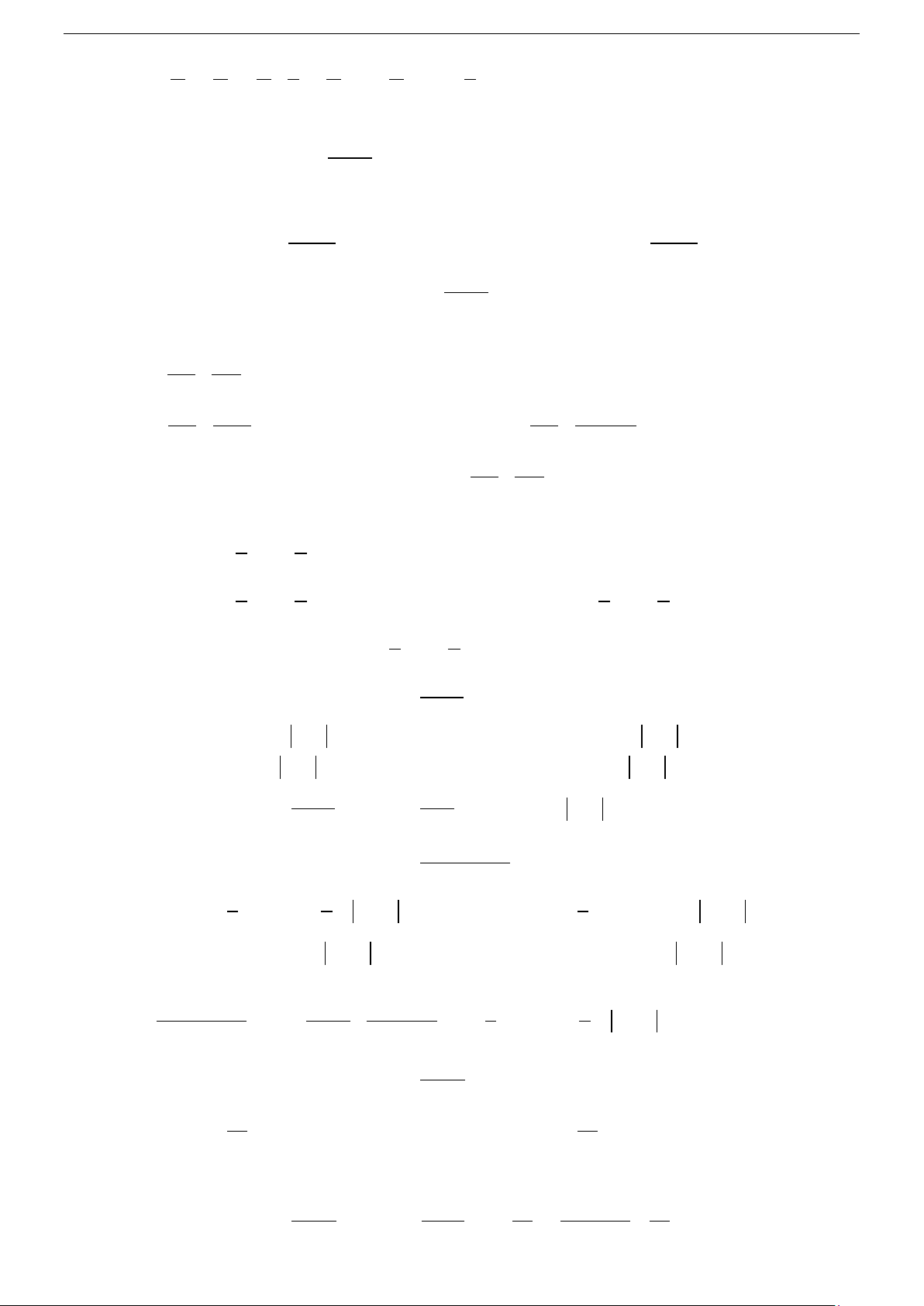
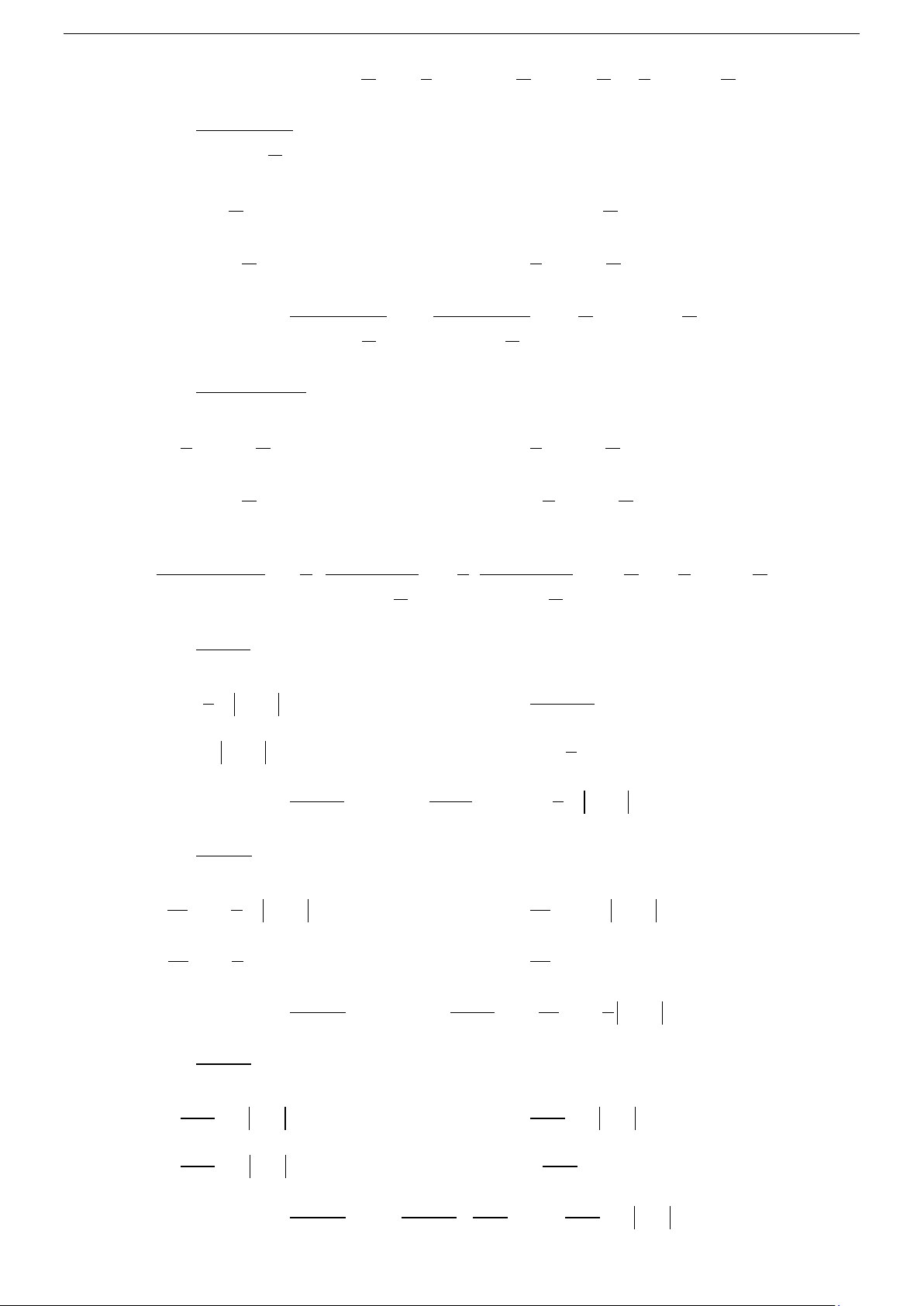
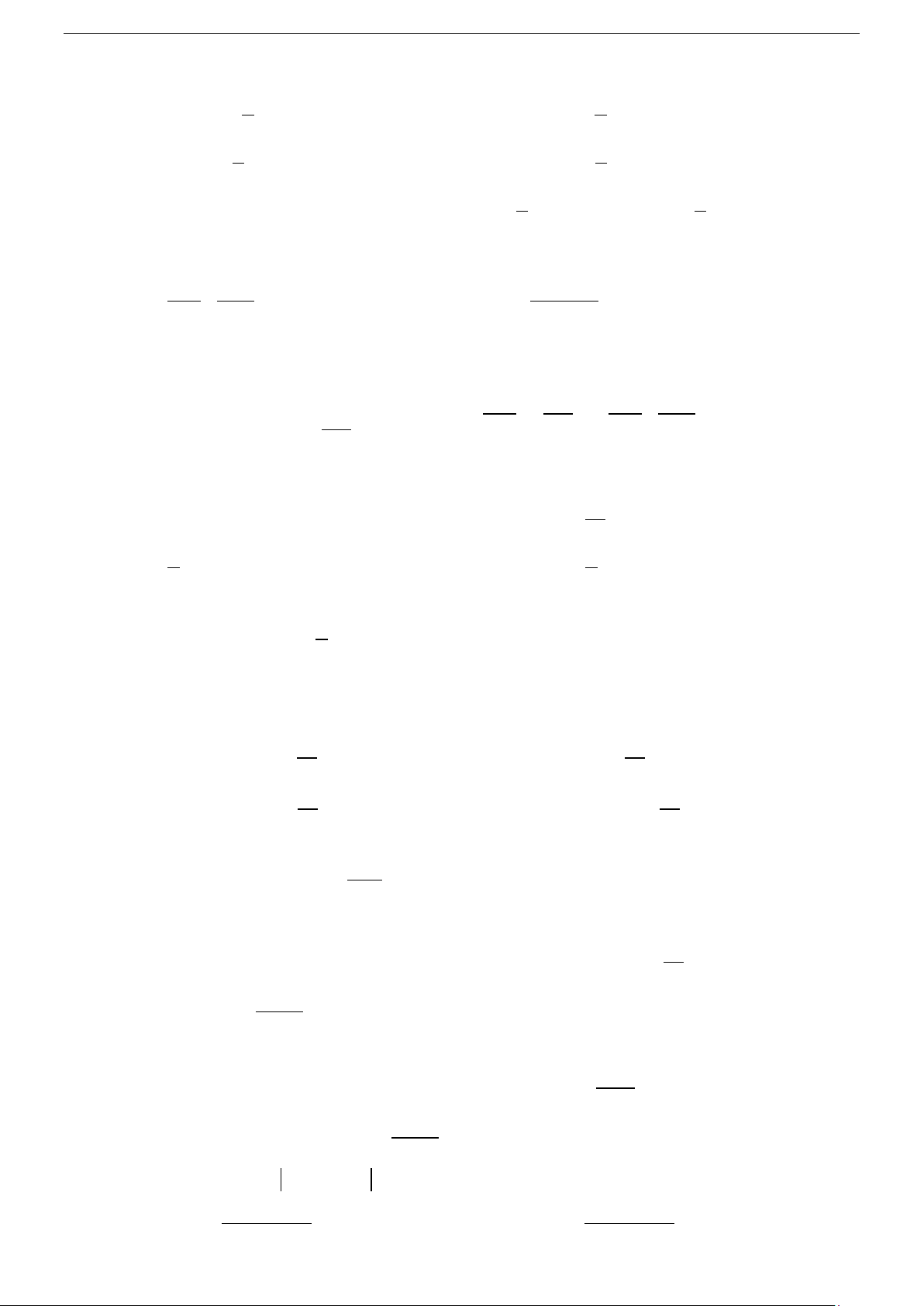
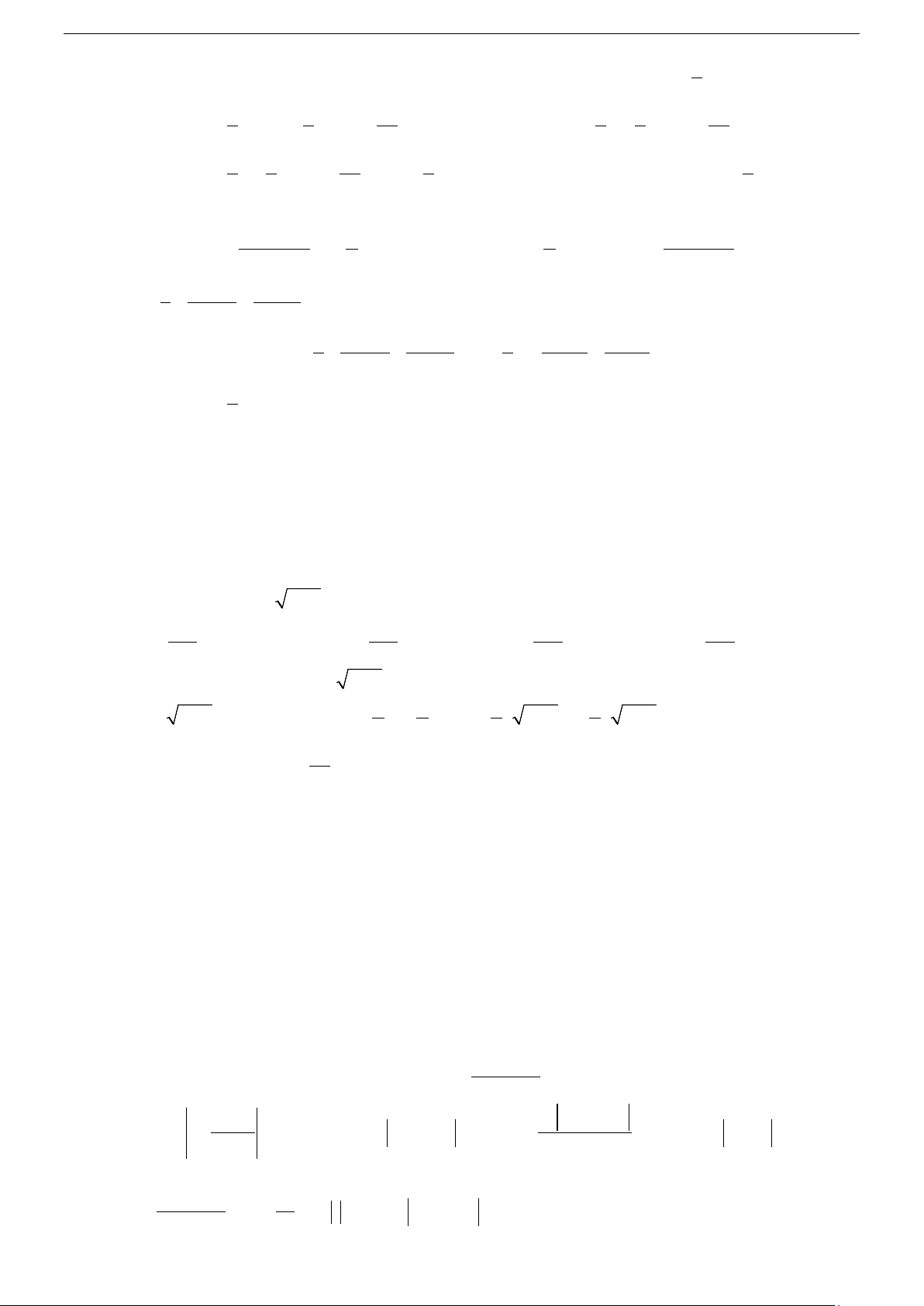
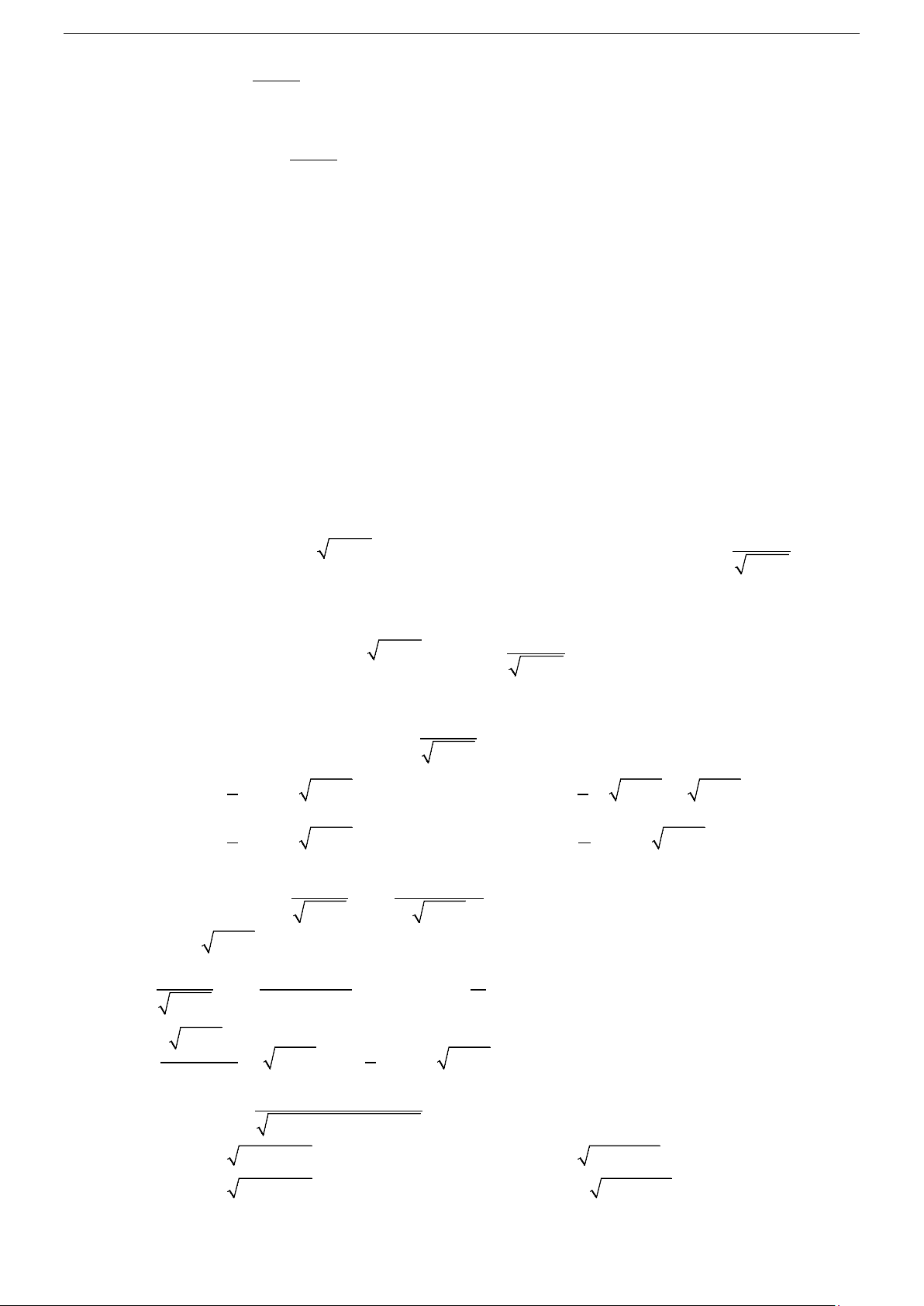
Preview text:


CHỦ ĐỀ 1. NGUYÊN HÀM
KIẾN THỨC CƠ BẢN
I. NGUYÊN HÀM VÀ TÍNH CHẤT 1. Nguyên hàm
Định nghĩa: Cho hàm số f (x) xác định trên K ( K là khoảng, đoạn hay nửa khoảng). Hàm số F (x)
được gọi là nguyên hàm của hàm số f (x) trên K nếu F '(x) = f (x) với mọi x∈ K . Định lí:
1) Nếu F (x) là một nguyên hàm của hàm số f (x) trên K thì với mỗi hằng số C , hàm số
G (x) = F (x) + C cũng là một nguyên hàm của f (x) trên K .
2) Nếu F (x) là một nguyên hàm của hàm số f (x) trên K thì mọi nguyên hàm của f (x) trên K đều
có dạng F (x) + C , với C là một hằng số.
Do đó F (x) + C,C ∈ là họ tất cả các nguyên hàm của f (x) trên K . Ký hiệu f
∫ (x)dx = F (x)+C .
2. Tính chất của nguyên hàm
Tính chất 1: ( f
∫ (x)dx)′ = f (x) và f '
∫ (x)dx = f (x)+C
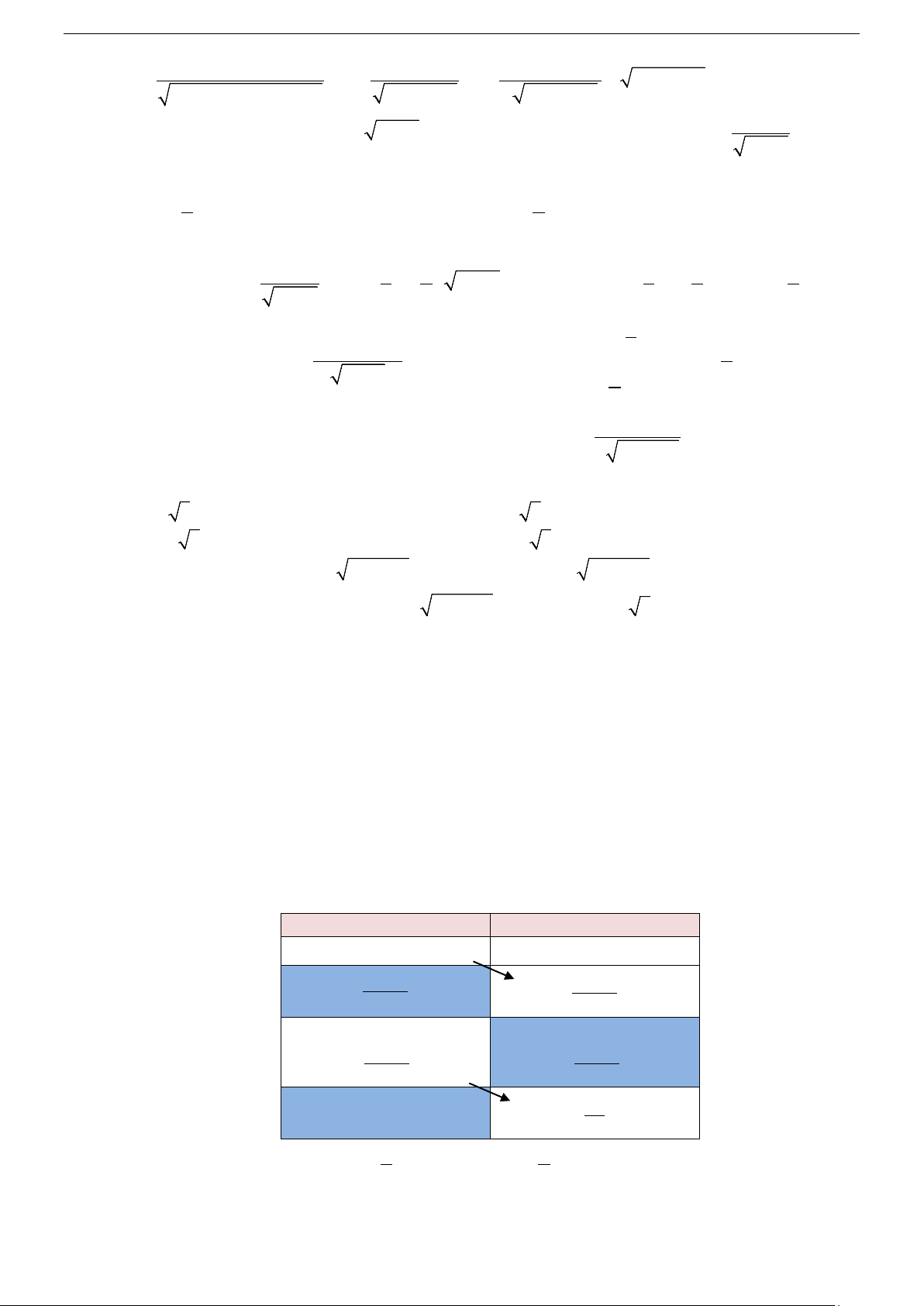
Tính chất 2: kf
∫ (x)dx = k f
∫ (x)dx với k là hằng số khác 0 .
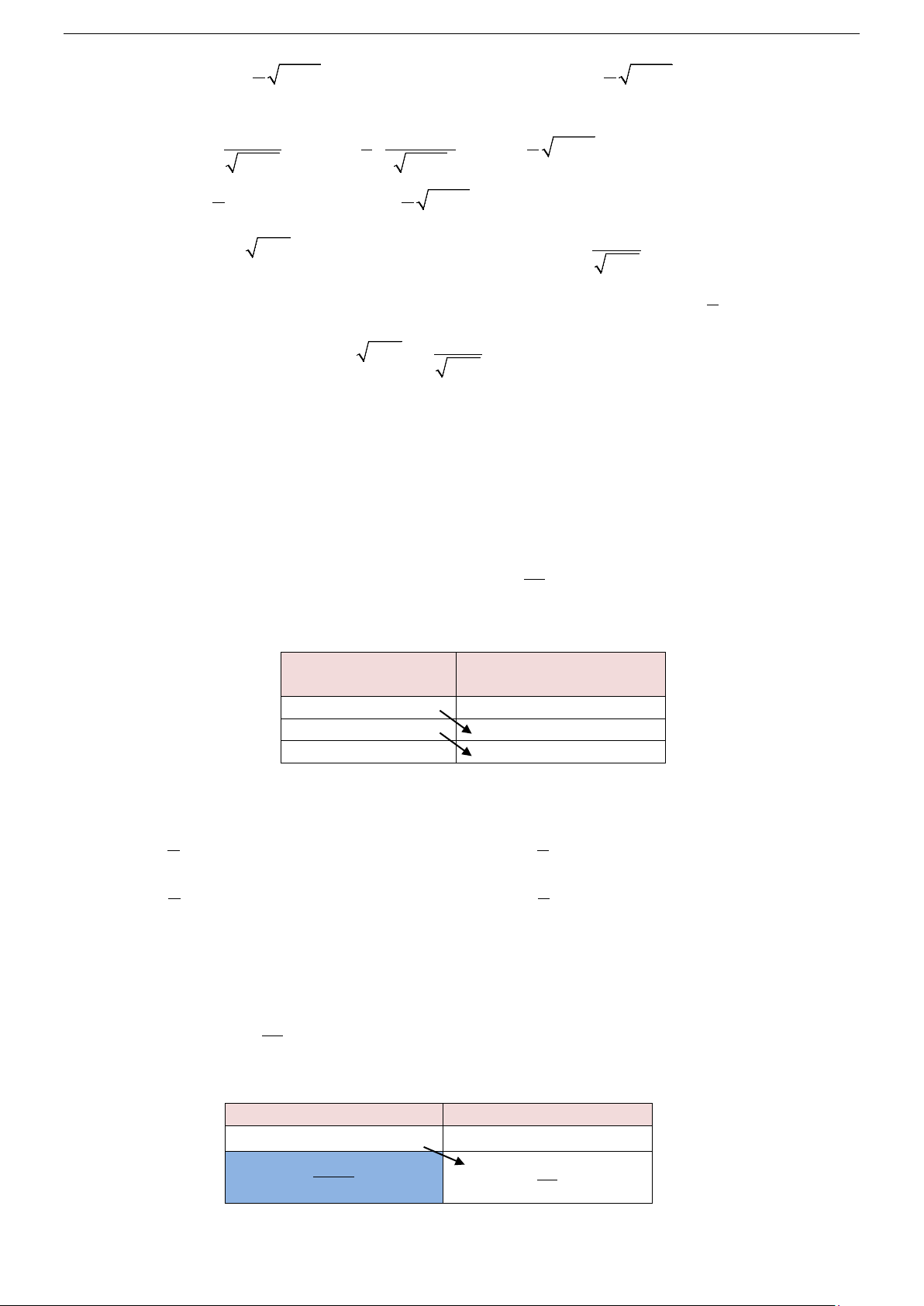
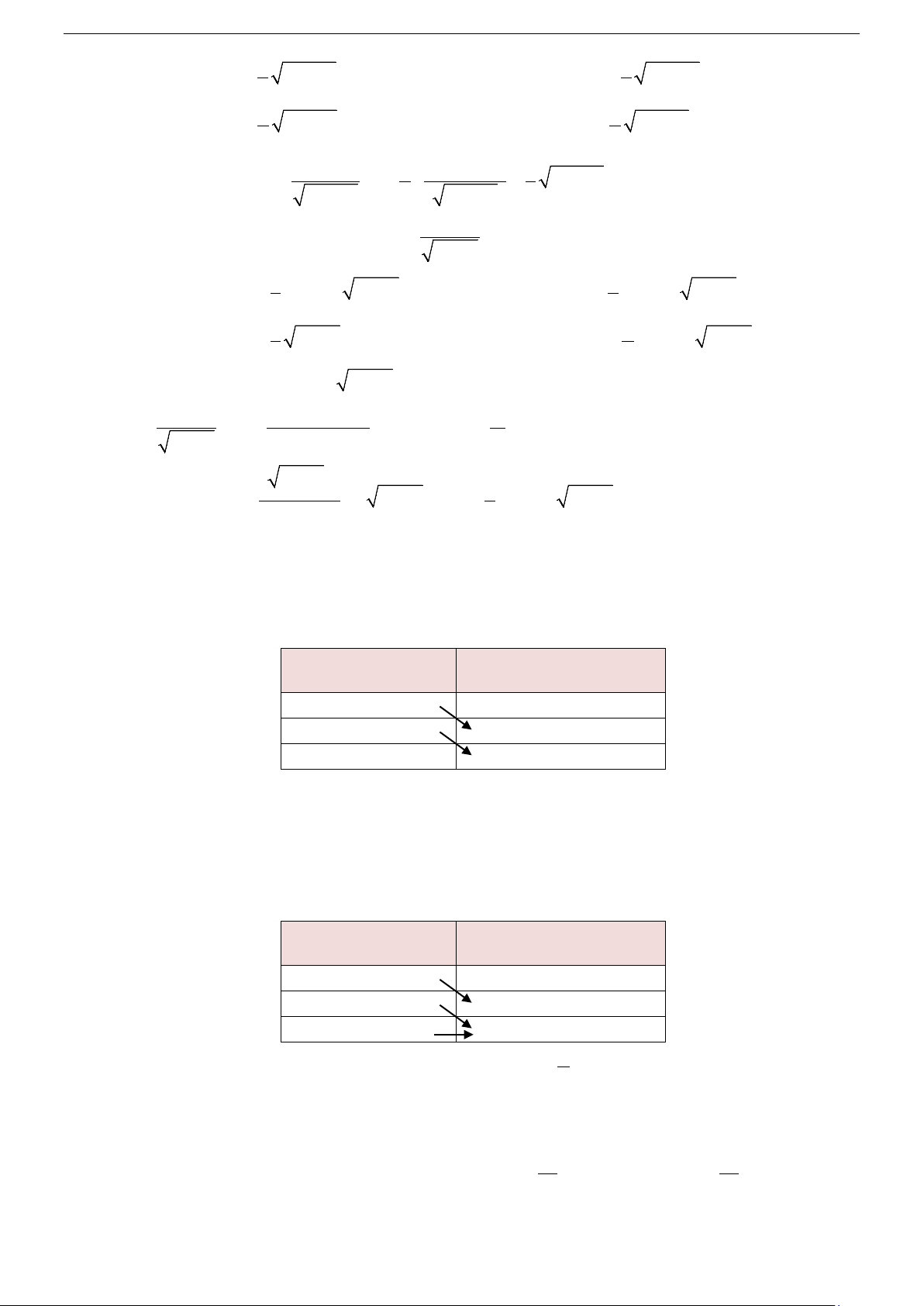
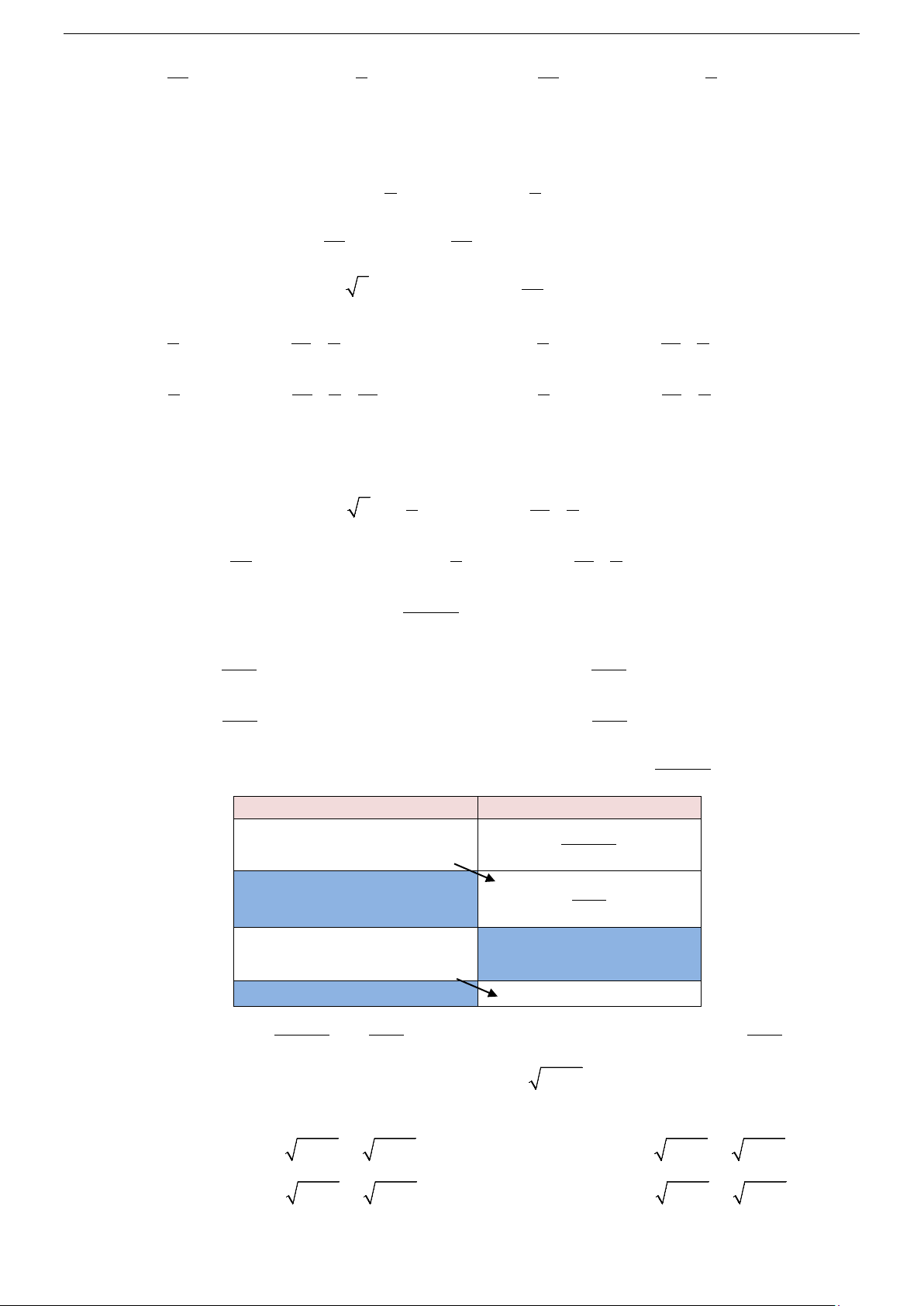
Tính chất 3: f
∫ (x)± g(x)dx = f
∫ (x)dx± g
∫ (x)dx
3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f (x) liên tục trên K đều có nguyên hàm trên K .
4. Bảng nguyên hàm của một số hàm số sơ cấp
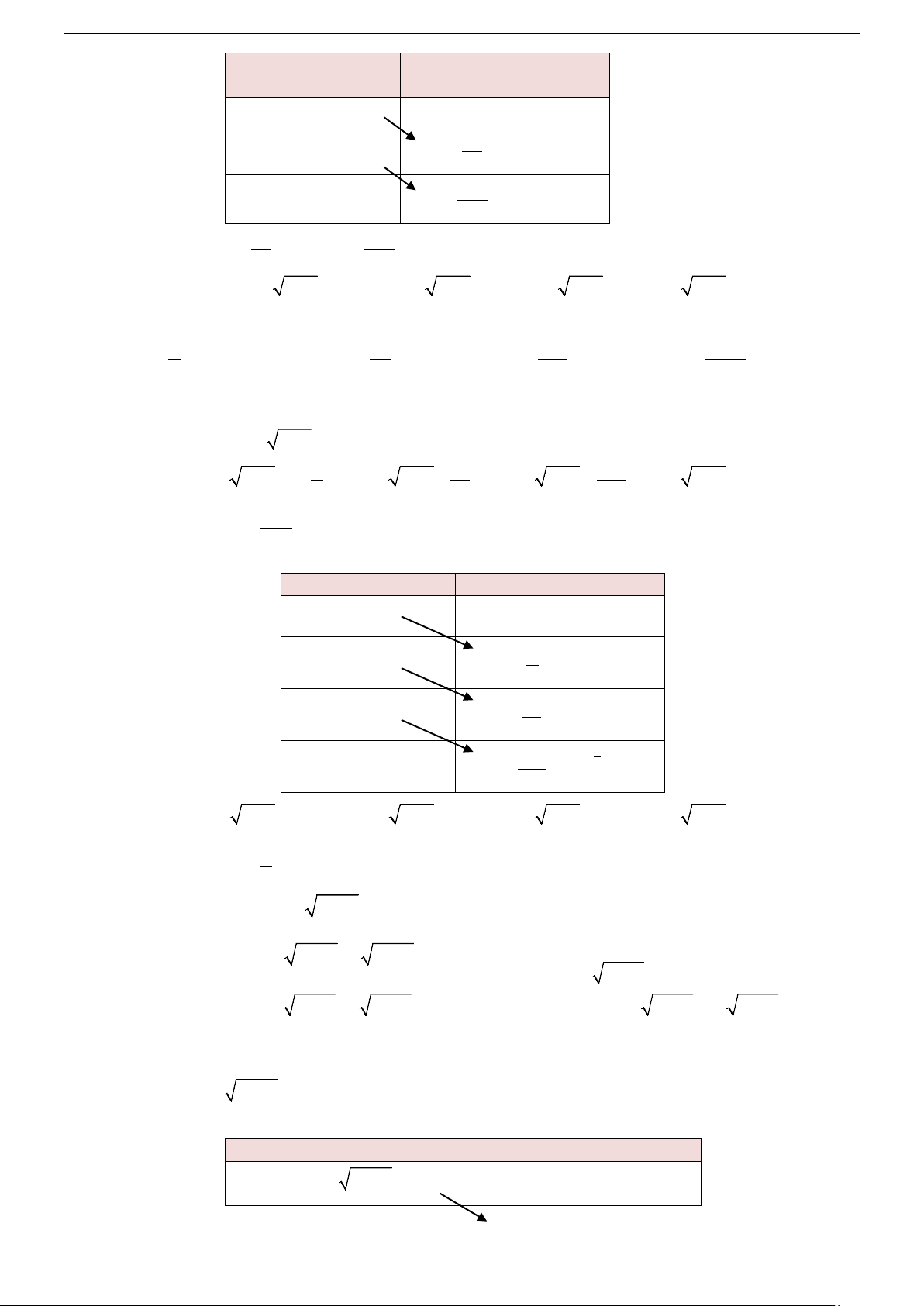
Nguyên hàm của hàm số sơ cấp
Nguyên hàm của hàm số hợp (u = u(x))
dx = x + C ∫
du = u + C ∫ α 1 1 x dx xα+ = + C ∫ (α ≠ − ) 1 α 1 1 u du uα+ = + C ∫ (α ≠ − ) 1 α +1 α +1
1 dx = ln x +C ∫
1 du = ln u +C x ∫ u x x
e dx = e + C ∫ u u
e du = e + C ∫ x u x a a dx =
+ C (a > 0,a ≠ ∫ )1 u a a du =
+ C (a > 0,a ≠ ∫ ) 1 ln a ln a
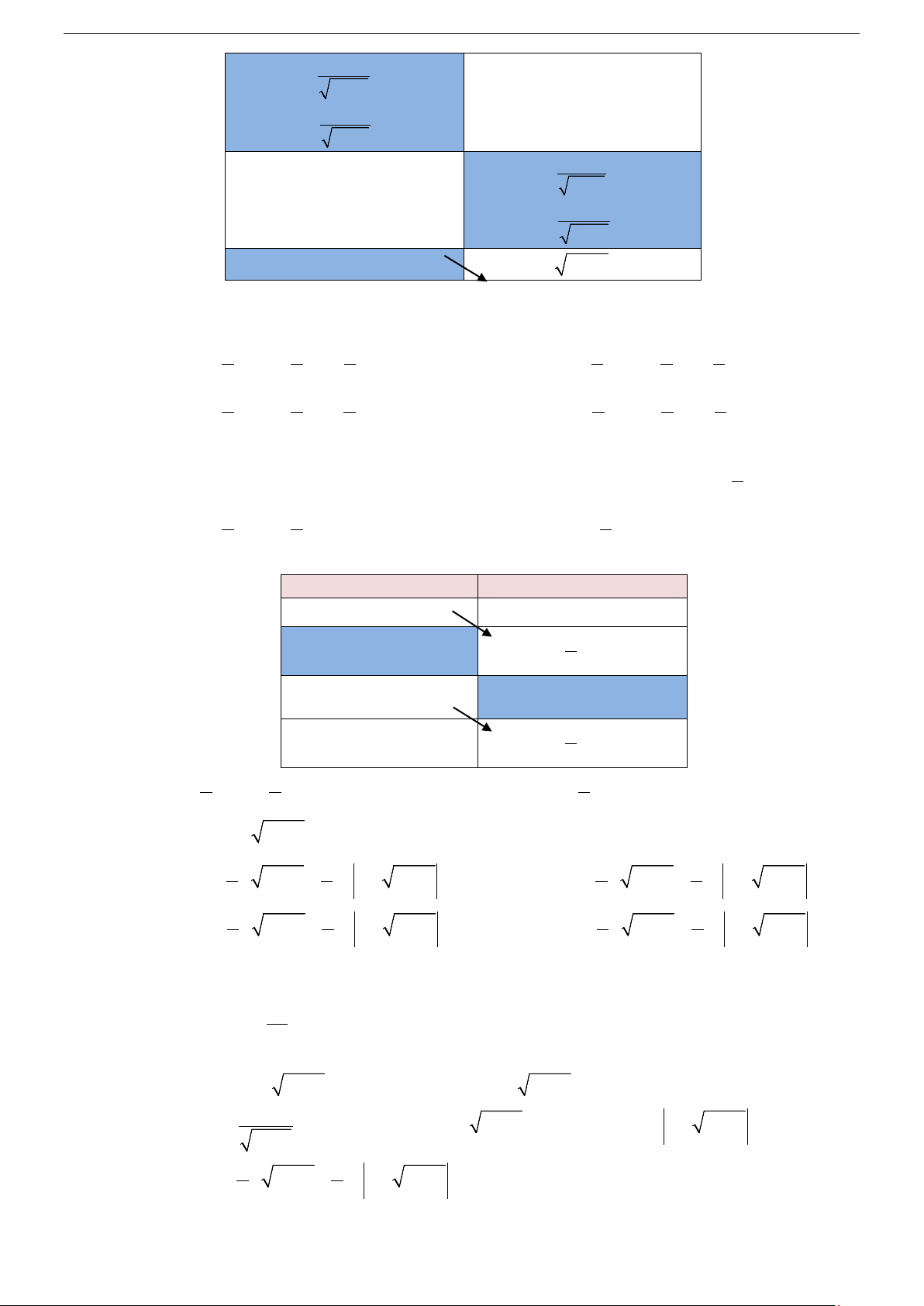
sin xdx = −cos x + C ∫
sin udu = −cosu + C ∫
cos xdx = sin x + C ∫
cosudu = sin u + C ∫
1 dx = tan x+C ∫
1 du = tanu +C 2 ∫ cos x 2 cos u
1 dx = −cot x+C ∫
1 du = −cotu +C 2 ∫ sin x 2 sin u
II. PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
1. Phương pháp đổi biến số
Định lí 1: Nếu f
∫ (u)du = F (u)+C và u = u(x) là hàm số có đạo hàm liên tục thì f
∫ (u(x))u'(x)dx = F (u(x))+C
Hệ quả: Nếu u = ax + b(a ≠ 0) thì ta có ∫ ( + ) 1
f ax b dx = F (ax + b) + C a
2. Phương pháp nguyên hàm từng phần
Định lí 2: Nếu hai hàm số u = u (x) và v = v(x) có đạo hàm liên tục trên K thì Trang 1/34 u
∫ (x)v'(x)dx = u(x)v(x)− u'
∫ (x)v(x)dx Hay
udv = uv − vdu ∫ ∫
A. KỸ NĂNG CƠ BẢN
- Tìm nguyên hàm bằng phương pháp biến đổi trực tiếp.
- Tìm nguyên hàm bằng phương pháp đổi biến số.
- Tìm nguyên hàm bằng phương pháp nguyên hàm từng phần.
B. BÀI TẬP TRẮC NGHIỆM
Câu 1. Nguyên hàm của hàm số f (x) 3
= x + 3x + 2 là hàm số nào trong các hàm số sau? 4 2 4 A. ( ) x 3x F x = + + 2x + C .
B. F (x) x 2 =
+ 3x + 2x + C . 4 2 3 4 2 C. ( ) x x F x = + + 2x + C . D. F (x) 2
= 3x + 3x + C . 4 2
Hướng dẫn giải: Sử dụng bảng nguyên hàm.
Câu 2. Hàm số F (x) 3 2
= 5x + 4x − 7x +120 + C là họ nguyên hàm của hàm số nào sau đây? A. f (x) 2
= 15x + 8x − 7 . B. f (x) 2 = 5x + 4x + 7 . 2 3 2 C. ( ) 5x 4x 7x f x = + − . D. f (x) 2
= 5x + 4x − 7 . 4 3 2
Hướng dẫn giải: Lấy đạo hàm của hàm số F (x) ta được kết quả.
Câu 3. Họ nguyên hàm của hàm số: 2 1
y = x − 3x + là x 3 3
A. F (x) x 3 2 =
− x + ln x + C .
B. F (x) x 3 2 =
− x + ln x + C . 3 2 3 2 3
C. F (x) x 3 2 =
+ x + ln x + C . D. F (x) 1 = 2x − 3− + C . 3 2 2 x
Hướng dẫn giải: Sử dụng bảng nguyên hàm.
Câu 4. Tìm nguyên hàm của hàm số f (x) = (x + ) 1 (x + 2) 3 3
A. F (x) x 3 2 =
+ x + 2x + C .
B. F (x) x 2 2 =
+ x + 2x + C . 3 2 3 3 3
C. F (x) = 2x + 3+ C .
D. F (x) x 2 2 =
− x + 2x + C . 3 3
Hướng dẫn giải: f (x) = (x + )(x + ) 2 1
2 = x + 3x + 2 . Sử dụng bảng nguyên hàm.
Câu 5. Nguyên hàm F (x) của hàm số f (x) 2 2 3 = + + là hàm số nào? 2 5 − 2x x x A. F (x) 3
= − ln 5 − 2x + 2ln x − + C . B. F (x) 3
= − ln 5 − 2x + 2ln x + + C . x x C. F (x) 3
= ln 5 − 2x + 2ln x − + C . D. F (x) 3
= − ln 5 − 2x − 2ln x + + C . x x
Hướng dẫn giải: Sử dụng bảng nguyên hàm.
4.1.2. NGUYÊN HÀM CỦA HÀM SỐ LƯỢNG GIÁC.
Câu 6. Tìm nguyên hàm của hàm số f (x) = sin 2x A. 1
sin 2xdx = − cos 2x + C ∫ . B. 1
sin 2xdx = cos 2x + C ∫ . 2 2
C. sin 2xdx = cos 2x + C ∫ .
D. sin 2xdx = −cos 2x + C ∫ . Hướng dẫn giải 1 1 sin 2xdx =
sin 2xd(2x) = − cos 2x + C ∫ ∫ . 2 2 Trang 2/34  π
Câu 7. Tìm nguyên hàm của hàm số f (x) cos 3x  = +  . 6    A. 1 f (x)dx sin 3x  = + + ∫ π     C .
B. f (x).dx = sin 3x + + ∫ π   C . 3  6   6  C. 1 f (x)dx sin 3x  = − + + ∫ π     C . D. 1
f (x)dx = sin 3x + + ∫ π   C . 3  6  6  6  Hướng dẫn giải: 1     1 f (x)dx cos 3x d 3x sin 3x  = + + = + + ∫ ∫ π π π       C . 3  6   6  3  6 
Câu 8. Tìm nguyên hàm của hàm số 2 f ( ) =1+ tan x x . 2 A. ( ) = 2 tan x f x dx + C ∫ . B. ( ) = tan x f x dx + C ∫ . 2 2 C. 1 ( ) = tan x f x dx + C ∫ . D. ( ) = 2 − tan x f x dx + C ∫ . 2 2 2  x d    Hướng dẫn giải: 2 x 1 f (x) =1+ tan = nên dx  2 2  = = 2 tan x + C 2 ∫ ∫ . 2 o c s x 2 x 2 x 2 cos cos 2 2 2
Câu 9. Tìm nguyên hàm của hàm số 1 f (x) = . 2  π sin x  +  3   
A. f (x)dx cot  x  = − + + ∫ π     C . B. 1
f (x)dx = − cot x + + ∫ π   C .  3  3  3 
C. f (x)dx cot  x  = + + ∫ π     C . D. 1
f (x)dx = cot x + + ∫ π   C .  3  3  3  π d x  +   π Hướng dẫn giải: dx  3  = = − cot  x  + + ∫ ∫   C . 2  π  2  π   3 sin x  sin  x  + +  3 3     
Câu 10. Tìm nguyên hàm của hàm số 3 f (x) = sin . x cos x . 4 4 A. sin ( ) x f x dx = + C ∫ . B. sin ( ) x f x dx = − + C ∫ . 4 4 2 2 C. sin ( ) x f x dx = + C ∫ . D. sin ( ) x f x dx = − + C ∫ . 2 2 4 Hướng dẫn giải 3 3 sin sin .cos . = sin . (sin ) x x x dx x d x = + C ∫ ∫ . 4
4.1.3. NGUYÊN HÀM CỦA HÀM SỐ MŨ, LÔGARIT.
Câu 11. Tìm nguyên hàm của hàm số ( ) x x f x e e− = − . A. ∫ ( ) x − x
f x dx = e + e + C . B. ∫ ( ) x − x
f x dx = −e + e + C . C. ∫ ( ) x − x
f x dx = e − e + C . D. ∫ ( ) x − x
f x dx = −e − e + C .
Hướng dẫn giải: ∫( x −x − ) x − x
e e dx = e + e + C .
Câu 12. Tìm nguyên hàm của hàm số x 2 ( ) 2 .3 x f x − = . x x A. f ∫ (x)  2  1 dx = . +     C . B. f ∫ (x) 9 1 dx = . +   C .  9  ln 2 − ln 9  2  ln 2 − ln 9 Trang 3/34 x x C. f ∫ (x)  2  1 dx = . +     C . D. f ∫ (x) 2 1 dx = . +   C .  3  ln 2 − ln 9  9  ln 2 + ln 9 x x
Hướng dẫn giải: x 2−x  2   2  1 2 .3 dx = dx = . + ∫ ∫    C  9   9  ln 2 − ln 9
Câu 13. Họ nguyên hàm của hàm số ( ) x (3 x f x e e− = + ) là A. ( ) = 3 x F x
e + x + C . B. ( ) = 3 x x + ln x F x e e e + C . C. 1
F(x) = 3 x e − + C . D. ( ) = 3 x F x
e − x + C . x e
Hướng dẫn giải: F( ) x = (3 − x +
) = (3 x +1) = 3 x x e e dx e dx e + x + C ∫ ∫
Câu 14. Hàm số ( ) = 7 x F x
e − tan x là một nguyên hàm của hàm số nào sau đây? − x   A. ( ) x = x 1 7 e f x e − .
B. f (x) = 7e + . 2 cos x    2 cos x C. f (x) x 2
= 7e + tan x −1. D. f (x)  x 1 7 e  = −  . 2 cos x    − x
Hướng dẫn giải: Ta có x 1 '( ) = 7 x − = (7 e g x e e − ) = f (x) 2 2 cos x cos x
Câu 15. Tìm nguyên hàm của hàm số 4 2 ( ) x f x e − = . A. f ∫ (x) 1 2x 1 dx e − = + C . B. f ∫ (x) 2x 1 dx e − = + C . 2 C. f ∫ (x) 1 4x−2 dx = e + C . D. f ∫ (x) 1 2x 1 dx e − = + C . 2 2 Hướng dẫn giải: 4x−2 2x 1 − 1 2x 1 e dx e dx e − = = + C ∫ ∫ . 2
4.1.4. NGUYÊN HÀM CỦA HÀM SỐ CHỨA CĂN THỨC.
Câu 16. Nguyên hàm của hàm số 1 f (x) = là 2x −1 A. f
∫ (x)dx = 2x−1+C . B. f
∫ (x)dx = 2 2x−1+C . C. − f ∫ (x) 2x 1 dx = + C . D. f ∫ (x)dx = 2
− 2x −1 + C . 2 1 1 (2 − ) 1 Hướng dẫn giải: = = 2 −1 + ∫ ∫ d x dx x C . 2x −1 2 2x −1
Câu 17. Tìm nguyên hàm của hàm số 1 f (x) = . 3− x A. f ∫ (x)dx = 2
− 3− x + C . B. f
∫ (x)dx = − 3− x +C . C. f
∫ (x)dx = 2 3− x +C . D. f ∫ (x)dx = 3
− 3− x + C . 1 (3− ) Hướng dẫn giải: = − = 2 − 3− + ∫ ∫ d x dx x C . 3− x 3− x
Câu 18. Tìm nguyên hàm của hàm số f (x) = 2x +1 . A. f ∫ (x) 1 dx = (2x + ) 1 2x +1 + C . B. f ∫ (x) 2 dx = (2x + ) 1 2x +1 + C . 3 3 C. f ∫ (x) 1 dx = − 2x +1 + C . D. f ∫ (x) 1 dx = 2x +1 + C . 3 2
Hướng dẫn giải: Đặt t = 2x +1 ⇒ dx = tdt Trang 4/34 3 2 t 1 ⇒
2x +1dx= t dt = + C = ∫ ∫ (2x + )
1 2x +1 + C . 3 3
Câu 19. Tìm nguyên hàm của hàm số f (x) = 5 −3x . A. f ∫ (x) 2
dx = − (5 − 3x) 5 − 3x + C . B. f ∫ (x) 2
dx = − (5 − 3x) 5 − 3x . 9 3 C. f ∫ (x) 2
dx = (5 −3x) 5 −3x . D. f ∫ (x) 2 dx = − 5 − 3x + C . 9 3
Hướng dẫn giải: Đặt 2 = 5 − 3 tdt t x ⇒ dx = − 3 2 5 − 3xdx = − ∫
(5−3x) 5−3x +C . 9
Câu 20. Tìm nguyên hàm của hàm số 3
f (x) = x − 2 . A. f ∫ (x) 3
dx = (x − 2) 3 x − 2 + C . B. f ∫ (x) 3
dx = − (x − 2) 3 x − 2 + C . 4 4 C. f ∫ (x) 2
dx = (x − 2) x − 2 . D. f ∫ (x) 1 dx (x 2) 2− = − 3 + C . 3 3
Hướng dẫn giải: Đặt 3 3 2
t = x − 2 ⇒ dx = 3t dt . Khi đó 3 x − 2dx = ∫
(x − 2) 3 x − 2 +C 4
Câu 21. Tìm nguyên hàm của hàm số 3
f (x) = 1− 3x . A. f ∫ (x) 1
dx = − (1− 3x) 3 1− 3x + C . B. f ∫ (x) 3
dx = − (1− 3x) 3 1− 3x + C . 4 4 C. f ∫ (x) 1
dx = (1− 3x) 3 1− 3x + C . D. f
∫ (x)dx ( x) 2− = − − 3 1 3 + C . 4
Hướng dẫn giải: Đặt 1 3 2
t = 1− 3x ⇒ dx = t
− dt . Khi đó 3 1− 3xdx = − ∫
(1−3x) 3 1−3x +C 4
Câu 22. Tìm nguyên hàm của hàm số ( ) 3 = x f x e . 3x A. ∫ ( ) 2 e f x dx = + C B. f ∫ (x) 3 dx = + C 3 3 2 x e 3x+2 3x 2 C. ∫ ( ) 3 e f x dx = + C D. ∫ ( ) 2e f x dx = + C 2 3x + 2 3x 3x 3x Hướng dẫn giải: 3x 2  3x  2 2 e 2 2 e dx = e .d = .e + C = + ∫ ∫   C 3  2  3 3
Câu 23. Hàm số F (x) = (x + )2 1
x +1 + 2016 là một nguyên hàm của hàm số nào sau đây?
A. f (x) 5 = (x + ) 1 x +1
B. f (x) 5 = (x + ) 1 x +1 + C 2 2
C. f (x) 2 = (x + ) 1 x +1
D. f (x) = (x + ) 1 x +1 + C 5
Hướng dẫn giải: F (x) 5 ' = (x + ) 1 x +1 2
Câu 24. Biết một nguyên hàm của hàm số f (x) 1 =
+1 là hàm số F (x) thỏa mãn F (− ) 2 1 = . 1− 3x 3
Khi đó F (x) là hàm số nào sau đây? A. F (x) 2 = x − 1− 3x + 3 B. F (x) 2 = x − 1− 3x − 3 3 3 Trang 5/34 C. F (x) 2 = x − 1− 3x +1 D. F (x) 2 = 4 − 1− 3x 3 3 Hướng dẫn giải   − F (x) 1 1 d (1 3x) 2 = +1 dx = − + x = x − 1− 3x + ∫  C ∫  1− 3x  3 1− 3x 3 F (− ) 2
= ⇒ C = ⇒ F (x) 2 1 3 = x − 1− 3x + 3 3 3
Câu 25. Biết F(x) = 6 1− x là một nguyên hàm của hàm số ( ) a f x =
. Khi đó giá trị của a bằng 1− x A. 3 − . B. 3. C. 6 . D. 1 . 6
Hướng dẫn giải: F x = ( − x )′ 3 − '( ) 6 1 = ⇒ a = 3 − 1− x
4.1.5. PHƯƠNG PHÁP NGUYÊN HÀM TỪNG PHẦN
Câu 26. Tính F(x) = xsin xdx ∫ bằng
A. F(x) = sin x − x cos x + C .
B. F(x) = xsin x − cos x + C .
C. F(x) = sin x + x cos x + C .
D. F(x) = xsin x + cos x + C . Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần
Phương pháp trắc nghiệm:
Cách 1: Dùng định nghĩa, sử dụng máy tính nhập d (F(x)) − f (x) , CALC ngẫu nhiên tại một dx
số điểm x thuộc tập xác định, kết quả xấp xỉ bằng 0 chọn. 0
Cách 2: Sử dụng phương pháp bảng
u và đạo hàm của dv và nguyên hàm của u v + x sin x 1 - − cos x 0 −sin x
Vậy F(x) = sin x − x cos x + C . Câu 27. Tính 2 x ln xdx ∫ . Chọn kết quả đúng: A. 1 2 x ( 2
2ln x − 2ln x + ) 1 + C . B. 1 2 x ( 2
2ln x − 2ln x + ) 1 + C . 4 2 C. 1 2 x ( 2
2ln x + 2ln x + ) 1 + C . D. 1 2 x ( 2
2ln x + 2ln x + ) 1 + C . 4 2 Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần 2 lần.
Phương pháp trắc nghiệm
Cách 1: Sử dụng định nghĩa F '(x) = f (x) ⇔ F '(x) − f (x) = 0 .
Nhập máy tính d (F(x)) − f (x) . CALC x tại một số giá trị ngẫu nhiên x trong tập xác định, dx 0
nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng:
u và đạo hàm của u
dv và nguyên hàm của v 2 ln x x + 2ln x 2 x x 2 Trang 6/34
ln x (chuyển 2 qua dv )
x (nhận 2 từ u ) x x - 1 2 x x 2 1 (chuyển 1 qua dv )
x (nhận 1 từ u ) x + 2 x 0 2 x 4 Do đó 2 1 2 2 1 2 1 2
x ln xdx = x ln x − x ln x + x + C ∫ = 1 2 x ( 2
2ln x − 2ln x + ) 1 + C . 2 2 4 4
Câu 28. Tính F(x) = xsin xcos xdx ∫ . Chọn kết quả đúng: A. 1 ( ) = sin 2 x F x
x − cos 2x + C . B. 1 ( ) = cos 2 x F x
x − sin 2x + C . 8 4 4 2 C. − 1 ( ) = sin 2 x F x
x + cos 2x + C . D. 1 ( ) = sin 2 x F x
x − cos 2x + C . 4 8 4 8 Hướng dẫn giải:
Phương pháp tự luận: Biến đổi 1
sin x cos x = sin 2x rồi sử dụng phương pháp nguyên hàm 2 từng phần.
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F '(x) = f (x) ⇔ F '(x) − f (x) = 0
Nhập máy tính d (F(x)) − f (x) . CALC x tại một số giá trị ngẫu nhiên x trong tập xác định, dx 0
nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng. x Câu 29. Tính 3
F(x) = xe dx ∫ . Chọn kết quả đúng x x A. 3
F(x) = 3(x − 3)e + C B. 3
F(x) = (x + 3)e + C x x C. − + x 3 x 3 3 F(x) = e + C D. 3 F(x) = e + C 3 3 Hướng dẫn giải: x
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với 3
u = x,dv = e dx .
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F '(x) = f (x) ⇔ F '(x) − f (x) = 0 .
Nhập máy tính d (F(x)) − f (x) . CALC x tại một số giá trị ngẫu nhiên x trong tập xác định, dx 0
nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng. Câu 30. Tính ( ) x F x = dx ∫ . Chọn kết quả đúng 2 cos x
A. F(x) = x tan x + ln | cos x | +C .
B. F(x) = −x cot x + ln | cos x | +C .
C. F(x) = −x tan x + ln | cos x | +C .
D. F(x) = −x cot x − ln | cos x | +C . Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với 1
u = x,dv = dx 2 cos x
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F '(x) = f (x) ⇔ F '(x) − f (x) = 0 . Trang 7/34
Nhập máy tính d (F(x)) − f (x) . CALC x tại một số giá trị ngẫu nhiên x trong tập xác định, dx 0
nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng. Câu 31. Tính 2
F(x) = x cos xdx ∫ . Chọn kết quả đúng A. 2
F(x) = (x − 2)sin x + 2x cos x + C . B. 2
F(x) = 2x sin x − x cos x + sin x + C . C. 2
F(x) = x sin x − 2x cos x + 2sin x + C . D. 2
F(x) = (2x + x )cos x − xsin x + C . Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần 2 lần với 2
u = x ;dv = cos xdx , sau đó u = ;
x dv = sin xdx . 1 1
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F '(x) = f (x) ⇔ F '(x) − f (x) = 0
Nhập máy tính d (F(x)) − f (x) . CALC x tại một số giá trị ngẫu nhiên x trong tập xác định, dx 0
nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng.
Câu 32. Tính F(x) = xsin 2xdx ∫ . Chọn kết quả đúng A. 1
F(x) = − (2x cos 2x − sin 2x) + C . B. 1
F(x) = (2x cos 2x − sin 2x) + C . 4 4 C. 1
F(x) = − (2x cos 2x + sin 2x) + C . D. 1
F(x) = (2x cos 2x + sin 2x) + C . 4 4
Hướng dẫn giải: Sử dụng phương pháp nguyên hàm từng phần với u = ;
x dv = sin 2xdx
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng hoặc sử dụng máy tính: Nhập
d (F(x))− f (x), CALC ngẫu nhiên tại một số điểm x bất kỳ, nếu kết quả xấp xỉ bằng0thì dx 0 chọn đáp án đó.
Câu 33. Hàm số F(x) = xsin x + cos x + 2017 là một nguyên hàm của hàm số nào?
A. f (x) = x cos x .
B. f (x) = xsin x .
C. f (x) = −x cos x .
D. f (x) = −xsin x . Hướng dẫn giải:
Phương pháp tự luận: Tính F '(x) có kết quả trùng với đáp án chọn.
Phương pháp trắc nghiệm: Sử dụng định nghĩa F '(x) = f (x) ⇔ F '(x) − f (x) = 0
Nhập máy tính d (F(x)) − f (x) . CALC x tại một số giá trị ngẫu nhiên x trong tập xác định, dx 0
nếu kết quả xấp xỉ bằng 0 chọn. Câu 34. + +
Tính 1 ln(x 1) dx ∫
. Khẳng định nào sau đây là sai? 2 x A. − + + + +
1 ln(x 1) + ln x + C B. 1 ln(x 1) − + ln x + C x x +1 x x +1 C. + + + x 1 −
(1+ ln(x +1))+ ln | x | +C D. 1 ln(x 1) −
− ln x +1 + ln x + C x x Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với 1
u =1+ ln(x +1);dv = −
dx hoặc biến đổi rồi đặt 1
u = ln(x +1);dv == − dx . 2 x 2 x
Phương pháp trắc nghiệm: Sử dụng máy tính kiểm tra bằng định nghĩa. 4.1.6. ÔN TẬP
Câu 35. Hãy chọn mệnh đề đúng Trang 8/34 x α 1 + A. x a a dx =
+ C (0 < a ≠ ∫ ) 1 . B. α x x dx = + C, α ∀ ∈ R ∫ . ln a α +1 f (x) f (x)dx ∫
C. f (x).g(x)dx = f (x) . dx g(x)dx ∫ ∫ ∫ . D. dx = ∫ . g(x) g(x)dx ∫
Hướng dẫn giải: A đúng. B sai vì thiếu điều kiện α =/ 1
− ; C, D sai vì không có tính chất.
Câu 36. Mệnh đề nào sau đây sai?
A. sin xdx = cos x + C ∫ .
B. 1dx = ln x + C, x ≠ 0 ∫ . x x D. x a a dx =
+ C,(0 < a ≠ 1) ∫ . C. x x
e dx = e + C ∫ . ln a
Hướng dẫn giải: sin xdx = −cos x + C ∫ Câu 37. Hàm số 3 2 1
f (x) = x − x + 3+ có nguyên hàm là x 4 3 3 A. ( ) x x F x = −
+ 3x + ln x + C . B. 4 ( ) x F x = x −
+ 3x + ln x + C . 4 3 3 C. 2 1
F(x) = 3x − 2x − + C . D. 4 3
F(x) = x − x + 3x + ln x + C . 2 x 4 3 Hướng dẫn giải: 3 2 1 ( ) = ( − + 3+ ) x x F x x x dx = −
+ 3x + ln x + C ∫ x 4 3
Câu 38. Họ nguyên hàm của hàm số 2
f (x) = tan x là
A. F (x) = tan x − x + C .
B. F (x) = − tan x + x + C .
C. F (x) = tan x + x + C .
D. F (x) = − tan x − x + C . Hướng dẫn giải:  1 f (x)dx 1 =
− dx = tan x − x + ∫ ∫  C 2  cos x
Câu 39. Hàm số F(x) = 7sin x − cos x +1 là một nguyên hàm của hàm số nào sau đây?
A. f (x) = sin x + 7cos x .
B. f (x) = −sin x + 7cos x .
C. f (x) = sin x − 7cos x .
D. f (x) = −sin x − 7cos x .
Hướng dẫn giải: F '(x) = 7cos x + sin x
Câu 40. Kết quả tính 1 dx ∫ là 2 2 sin x cos x
A. tan x − cot x + C .
B. cot 2x + C .
C. tan 2x − x + C .
D. − tan x + cot x + C . Hướng dẫn giải: 1  1 1 dx  = +
dx = tan x − cot x + ∫ ∫  C 2 2 2 2 sin x cos x
 cos x sin x Câu 41. Hàm số 2 1 1
F(x) = 3x − +
−1 có một nguyên hàm là 2 x x A. 3 1
f (x) = x − 2 x − − x . B. 3 1
f (x) = x − x − − x . x x C. 3 1
f (x) = x − 2 x + . D. 3 1 1
f (x) = x − x − − x . x 2 x
Hướng dẫn giải: Ta có  2 1 1  3 1
F(x)dx = 3x − +
−1 dx = x − 2 x − − x + ∫ ∫  C 2 2  x xx Câu 42. Hàm số cos ( ) x f x =
có một nguyên hàm F(x) bằng 5 sin x Trang 9/34 A. 1 − − . B. 1 . C. 4 . D. 4 . 4 4sin x 4 4sin x 4 sin x 4 sin x Hướng dẫn giải: cos x 1 1 f (x)dx = dx = d(sin x) = − + C ∫ ∫ 5 ∫ 5 4 sin x sin x 4sin x
Câu 43. Kết quả tính 2 2x 5 − 4x dx ∫ bằng A. 1 − (5−4x )3 2 + C . B. 3 − ( 2
5 − 4x ) + C . 6 8 C. 1 (5− 4x )3 2 + C . D. 1 − (5−4x )3 2 + C . 6 12
Hướng dẫn giải: Đặt 2
t = 5 − 4x ⇒ tdt = 4 − xdx Ta có 1 1 1
2x 5 − 4x dx = −
t dt = − t + C = − ∫ ∫ (5−4x )3 2 2 3 2 + C 2 6 6
Câu 44. Kết quả sinx e cos xdx ∫ bằng A. sinx e + C . B. sin cos . x x e + C . C. cosx e + C . D. −sinx e + C .
Hướng dẫn giải: Ta có sinx sin x sin cos = (sin ) x e xdx e d x e = + C ∫ ∫
Câu 45. Tính tan xdx ∫ bằng A. −
− ln cos x + C .
B. ln cos x + C . C. 1 + C . D. 1 +C. 2 cos x 2 cos x
Hướng dẫn giải: Ta có 1 tan xdx = −
d(cos x) = −ln cos x + C ∫ ∫ cos x
Câu 46. Tính cot xdx ∫ bằng A. − ln sin x + C .
B. −ln sin x + C . C. 1 +C . D. 1 − C . 2 sin x 2 sin x
Hướng dẫn giải: Ta có 1 cot xdx =
d(sin x) = ln sin x + C ∫ ∫ sin x 3
Câu 47. Nguyên hàm của hàm số x y = là x −1 A. 1 3 1 2
x + x + x + ln x −1 + C . B. 1 3 1 2
x + x + x + ln x +1 + C . 3 2 3 2 C. 1 3 1 2
x + x + x + ln x −1 + C . D. 1 3 1 2
x + x + x + ln x −1 + C . 6 2 3 4 3
Hướng dẫn giải: Ta có x 2 1 = x + x +1+
. Sử dụng bảng nguyên hàm suy ra đáp án. x −1 x −1 2 Câu 48. − +
Một nguyên hàm của hàm số f (x) x 2x 3 = là x +1 2 2
A. x − 3x + 6ln x +1 .
B. x + 3x + 6ln x +1 . 2 2 2 2
C. x + 3x − 6ln x +1 .
D. x − 3x + 6ln (x + ) 1 . 2 2 2
Hướng dẫn giải: f (x) x − 2x + 3 6 = = x − 3+
. Sử dụng bảng nguyên hàm. x +1 x +1
Câu 49. Kết quả tính 1 ∫ ( dx bằng x x + 3)
A. 1 ln x + C . B. 1 − ln x + C . 3 x + 3 3 x + 3 Trang 10/34 C. + 2 x 3 ln + C .
D. 2 ln x + C . 3 x 3 x + 3 Hướng dẫn giải: 1 1  1 1  = −
. Sử dụng bảng nguyên hàm.
x(x 3) 3  x x 3  + + 
Câu 50. Kết quả tính 1 ∫ ( dx bằng x x − 3) A. − + 1 x 3 ln + C . B. 1 x 3 ln + C . 3 x 3 x
C. 1 ln x + C .
D. 1 ln x + C . 3 x + 3 3 x − 3 Hướng dẫn giải: 1 1  1 1  = −
. Sử dụng bảng nguyên hàm.
x(x 3) 3  x 3 x  + − 
Câu 51. Họ nguyên hàm của hàm số f (x) 1 = là 2 x + x − 2 A. − + F (x) 1 x 1 = ln + C .
B. F (x) 1 x 2 = ln + C . 3 x + 2 3 x −1 C. − F (x) x 1 = ln + C . D. F (x) 2
= ln x + x − 2 + C . x + 2
Hướng dẫn giải: f (x) 1 1  1 1  = = −
. Sử dụng bảng nguyên hàm. 2 x
x 2 3  x 1 x 2  + − − +  2 Câu 52.  −
Họ nguyên hàm của hàm số ( ) 1 x f x  =  là x    A. F (x) 1
= − − 2ln x + x + C . B. F (x) 1
= − − 2ln x + x + C . x x
C. F (x) 1
= − 2ln x + x + C . D. F (x) 1
= − − 2ln x − x + C . x x 2 2
Hướng dẫn giải: f (x) 1− x  1− 2x + x 1 2 = = = − +  
1. Sử dụng bảng nguyên hàm. 2 2  x x x x
Câu 53. Nguyên hàm của hàm số ( ) 1 f x = với a ≠ 0 là 2 2 x − a A. − + 1 ln x a + C .
B. 1 ln x a + C . 2a x + a 2a x − a C. − + 1 ln x a + C .
D. 1 ln x a + C . a x + a a x − a Hướng dẫn giải: 1 1  1 1  = −
. Sử dụng bảng nguyên hàm. 2 2 x a
2a  x a x a  − − + 
Câu 54. Biết F (x) là một nguyên hàm của hàm số ( ) x f x =
thoả mãn F (2) = 0 . Khi đó phương 2 8 − x
trình F (x) = x có nghiệm là A. x =1− 3 . B. x =1. C. x = 1 − . D. x = 0 .
Hướng dẫn giải: Đặt 2 2 2
t = 8 − x ⇒ t = 8 − x ⇒ t − dt = xdx x tdt 2 dx = − = t
− + C = − 8 − x + C ∫ ∫ . 2 8 − x t
Vì F (2) = 0 nên C = 2 . Ta có phương trình 2
− 8 − x + 2 = x ⇔ x =1− 3 Trang 11/34
Câu 55. Nếu F (x) là một nguyên hàm của hàm số 1 f (x) =
và F (2) =1 thì F (3) bằng x −1 A. ln 2 +1. B. 3 ln . C. ln 2 . D. 1 . 2 2 Hướng dẫn giải:
1 dx = ln x−1 +C ∫
, vì F (2) =1nên C =1. F (x) = ln x −1 +1, thay x −1
x = 3 ta có đáp án.
Câu 56. Biết F (x) là một nguyên hàm của hàm số ( ) 2 ln = ln +1. x f x x thoả mãn F ( ) 1 1 = . Giá trị x 3 của 2 F (e) là A. 8 . B. 1 . C. 8 . D. 1 . 9 9 3 3
Hướng dẫn giải: Đặt 2 ln = ln +1 x t x ⇒ tdt = dx x x t ( ln x+1 ln )3 2 3 2 2 ln x +1.
dx = t dt = + C = + C ∫ F = nên C = 0 x ∫ . Vì ( ) 1 1 3 3 3 Vậy 2 F (e) 8 = . 9 π
Câu 57. Nguyên hàm F (x) của hàm số f (x) 1 = 2x + thỏa mãn F   =   1 − là 2 sin x  4  2 π 2 π A. 2
− cot x + x − . B. 2 cot x − x + . 16 16 2 π C. 2 −cot x + x . D. 2 cot x − x − . 16 π 2 π
Hướng dẫn giải:  1  2 2x +
dx = x − cot x + ∫  C . F   =   1 − nên C = − . 2  sin x   4  16
4.1.2. NGUYÊN HÀM CỦA HÀM SỐ LƯỢNG GIÁC.
Câu 58. Tìm nguyên hàm của hàm số 2 f (x) = cos . x sin x . 3 3 A. cos ( ) x f x dx = − + C ∫ . B. cos ( ) x f x dx = + C ∫ . 3 3 2 2 C. sin ( ) x f x dx = − + C ∫ . D. sin ( ) x f x dx = + C ∫ . 2 2 3 Hướng dẫn giải: 2 2 cos cos sin = − cos (cos ) x x xdx xd x = − + C ∫ ∫ 3
Câu 59. Tìm nguyên hàm của hàm số sin 2 ( ) x f x = . cos 2x −1
A. f (x)dx = −ln sin x + C ∫ .
B. f (x)dx = ln cos 2x −1 + C ∫ .
C. f (x)dx = ln sin 2x + C ∫ .
D. f (x)dx = ln sin x + C ∫ . Hướng dẫn giải sin 2xdx 2sin x cos x cos x d (sin x) = dx = − dx = −
= − ln sin x + C ∫ ∫ 2 ∫ ∫ cos 2x −1 1− 2sin x +1 sin x sin x
Câu 60. Tìm nguyên hàm của hàm số f (x) = sin .xcos 2 .xdx . 3 A. − 2cos ( ) x f x dx = + cos x + C ∫ . B. 1 1
f (x)dx = cos3x + sin x + C ∫ . 3 6 2 3 C. cos ( ) x f x dx = + cos x + C ∫ . D. 1 1
f (x)dx = cos3x − sin x + C ∫ . 3 6 2 Trang 12/34 Hướng dẫn giải = ∫ ∫( − ) = −∫( − ) 3 2 2 ( ) 2 − cos sin .cos 2 2cos 1 sin 2cos 1 cos x x xdx x xdx x d x = + cos x + C 3
Câu 61. Tìm nguyên hàm của hàm số f (x) = 2sin .xcos3x . A. 1 1
f (x)dx = cos 2x − cos 4x + C ∫ . B. 1 1
f (x)dx = cos 2x + cos 4x + C ∫ . 2 4 2 4 C. 4 2
f (x)dx = 2cos x + 3cos x + C ∫ . D. 4 2
f (x)dx = 3cos x − 3cos x + C ∫ . Hướng dẫn giải: x xdx = ∫ ∫( x − x) 1 1 2sin .cos3 sin 4
sin 2 dx = cos 2x − cos 4x + C . 2 4
Câu 62. Tìm nguyên hàm của hàm số 3 f (x) = sin . x sin 3x . A.
3  sin 2x sin 4x  1  sin 6 ( ) x f x dx x  = − − − + ∫     C . 8  2 4  8  6  B.
3  sin 2x sin 4x  1  sin 6 ( ) x f x dx x  = − + − + ∫     C . 8  2 4  8  6  C.
1  sin 2x sin 4x  3  sin 6 ( ) x f x dx x  = − − − + ∫     C . 8  2 4  8  6  D.
3  sin 2x sin 4x  1  sin 6 ( ) x f x dx x  = + − + + ∫     C . 8  2 4  8  6  Hướng dẫn giải 3 3sin x − sin 3 sin .sin 3 x x xdx = .sin 3xdx ∫ ∫ 4 3 1 2 3 = x xdx − xdx = ∫ ∫ ∫( x − x) 1 2sin .sin 3 2sin 3 cos 2
cos 4 dx − ∫(1−cos6x)dx 8 8 8 8
3  sin 2x sin 4x  1  sin 6x x  = − − − +     C 8  2 4  8  6 
Câu 63. Tìm nguyên hàm của hàm số 3 3 f (x) = sin . x cos3x + cos . x sin 3x . A. − 3 f (x)dx = cos 4x + C ∫ . B. 3 f (x)dx = cos 4x + C ∫ . 16 16 C. − 3 f (x)dx = sin 4x + C ∫ . D. 3 f (x)dx = sin 4x + C ∫ . 16 16 Hướng dẫn giải: ∫( 3 3  − + sin . x cos3x + cos .
x sin 3x).dx 3sin x sin 3x cos3x 3cos .cos3 x x .sin 3x = + ∫  dx  4 4   3 3 sin . x cos3x sin 3 . x cos3x sin 3 . x cos x sin 3 . x cos3x = − + + ∫  dx  4 4  − 3 = ∫( x x + x x) 3 3 sin .cos3 sin 3 .cos dx = sin 4xdx = cos 4x + C ∫ 4 4 16 π π
Câu 64. Tìm một nguyên hàm F(x) của hàm số 2 ( ) sin x f x = biết F   = . 2  2    4
A. F (x) x sin x 1 = − + .
B. F (x) x sin x 3 = + + . 2 2 2 2 2 2
C. F (x) x sin x 1 = + + .
D. F (x) x sin x 5 = + + . 2 2 2 2 2 2
Hướng dẫn giải • 2 x 1 F x = dx = ∫ ∫( − x) x 1 ( ) sin
1 cos dx = − sin x + C 2 2 2 2 Trang 13/34 π π π π π •   1 1 F = ⇔ − 
sin + C = ⇔ C =   2  4 4 2 2 4 2
4.1.3. NGUYÊN HÀM CỦA HÀM SỐ MŨ, HÀM SỐ LÔGARIT. − x   Câu 65. Hàm số ( ) x = ln 2 e f x e + có họ nguyên hàm là 2 sin x    A. ( ) x
F x = e ln 2 − cot x + C . B. ( ) x
F x = e ln 2 + cot x + C . C. F (x) x 1 = e ln 2 + + C . D. F (x) x 1 = e ln 2 − + C . 2 cos x 2 cos x Hướng dẫn giải: x 1 ( ) = ln 2  x f x dx e +
dx = e ln 2 − cot x + ∫ ∫  C 2  sin x
Câu 66. Hàm số ( ) 3x 2x.3x f x = − có nguyên hàm bằng x x A. 3 6 − + C .
B. 3x ln 3(1+ 2x ln 2) + C . ln 3 ln 6 x x x x x C. 3 3 .2 + + C . D. 3 6 + + C . ln 3 ln 6 ln 3 ln 3.ln 2 x x Hướng dẫn giải: = ∫ ∫( x x f x dx + ) 3 6 ( ) 3 6 dx = + + C ln 3 ln 6
Câu 67. Một nguyên hàm F(x) của hàm số − x x 2
f (x) = (e + e ) thỏa mãn điều kiện F(0) =1 là A. 1 2−x 1 2 ( ) x
F x = − e + e + 2x +1. B. 2 − x 2 ( ) = 2 − + 2 x F x e e + 2x +1. 2 2 C. 1 2−x 1 2 ( ) x
F x = − e + e + 2x . D. 1 2−x 1 2 ( ) x
F x = − e + e + 2x −1. 2 2 2 2
Hướng dẫn giải: Ta có 1 2−x 1 2 ( ) x
F x = − e + e + 2x + C, F(0) =1 ⇔ C =1 2 2 Câu 68. −
Tìm nguyên hàm của hàm số 2x 1 f (x) = . x +1
A. F (x) = 2x −3ln x +1 + C .
B. F (x) = 2x + 3ln x +1 + C .
C. F (x) = 2x − ln x +1 + C .
D. F (x) = 2x+ln x +1 + C .
Hướng dẫn giải: 2x −1  3 dx 2  = −
dx = 2x − 3ln x +1 + ∫ ∫  C x +1  x +1 2 Câu 69. + +
Tìm nguyên hàm của hàm số 2x 2x 3 f (x) = . 2x +1
A. F (x) 1 = ( x + )2 5
2 1 + ln 2x +1 + C .
B. F (x) 1 = (2x + )2
1 + 5ln 2x +1 + C . 8 4 8
C. F (x) = ( x + )2
2 1 + ln 2x +1 + C .
D. F (x) = ( x + )2
2 1 − ln 2x +1 + C . Hướng dẫn giải: 2 2x + 2x + 3  2x +1 5  1 2 5 dx = ∫ ∫ +  = + + + + x   ( x ) dx (2x )1 ln 2x 1 C 2 1 2 2 2 1  + + 8 4  3 Câu 70. −
Tìm nguyên hàm của hàm số ( ) x x f x = . 2 x +1 2 2 A. ( ) x F x = − ( 2 ln x + ) 1 + C . B. ( ) x F x = + ( 2 ln x + ) 1 + C . 2 2 C. F (x) 2 = x − ( 2 ln x + ) 1 + C . D. F (x) 2 = x + ( 2 ln x + ) 1 + C . x − x  2x x d ( 2 3 2 x + ) 2 1 Hướng dẫn giải: x dx = x − dx = − = − ln ∫ ∫ ∫ ( 2x +1 +   C 2 2 2 ) x +1  x +1 2 x +1 2 Trang 14/34
Câu 71. Tìm nguyên hàm của hàm số 1 f (x) = .
x ln x + x
A. F (x) = ln ln x +1 + C .
B. F (x) = ln ln x −1 + C .
C. F (x) = ln x +1 + C .
D. F (x) = ln x +1+ C . 1 d (ln x + ) 1
Hướng dẫn giải: ∫ ( = = + + x ∫ + ) dx
( x + ) ln ln x 1 C x ln 1 ln 1 2x
Câu 72. Tìm nguyên hàm của hàm số ( ) e f x = . x e +1 A. ( ) x = − ln ( x F x e e + ) 1 + C . B. ( ) x = + ln ( x F x e e + ) 1 + C . C. ( ) = ln ( x F x e + ) 1 + C . D. ( ) 2x x
F x = e − e + C . 2 ee d ( x x x e + x x )1 Hướng dẫn giải: x dx = ∫ ∫e −  dx = e − = e − ln ∫
( xe + +C x x x )1 e +1  e +1 e +1
4.1.4. NGUYÊN HÀM CỦA HÀM SỐ CHỨA CĂN THỨC.
Câu 73. Tìm nguyên hàm của hàm số 1 f (x) = . x +1 A. f
∫ (x)dx = 2 x −2ln(1+ x)+C . B. f
∫ (x)dx = 2 x + 2ln(1+ x)+C . C. f
∫ (x)dx = ln(1+ x)+C . D. f
∫ (x)dx = 2+ 2ln(1+ x)+C . Hướng dẫn giải
Đặt t = + x ⇒ x = (t − )2 1
1 ⇒ dx = 2(t − ) 1 dt . 1 2(t − ) 1 dt Khi đó  1 dx 2 1  = = − dt = 2 ∫ ∫ ∫ (t −ln t )+   C 1 1+ x tt
= 2( x +1−ln 1+ x )+C = 2 x − 2ln 1+ x +C . (Với C = 2+C và 1+ x > 0) 1 ( ) 1 Câu 74. +
Tìm nguyên hàm của hàm số x 2 f (x) = . x +1 A. f ∫ (x) 2
dx = (x + 4) x +1 + C . B. f
∫ (x)dx = (x+ 4) x+1+C . 3 C. ∫ ( ) x f x dx = + C . D. f ∫ (x) 1 dx = x +1 + + C . 2(x + ) 1 x +1 x +1
Hướng dẫn giải: x + 2  1 dx x  = + + d ∫ ∫ (x + ) 2 1
1 = (x + 4) x +1 +   C x +1  x +1  3 Câu 75. −
Tìm nguyên hàm của hàm số 2x 1 f (x) = . 1− x A. f ∫ (x) 2 dx = − (2x + ) 1 1− x + C . B. f ∫ (x) 2 dx = (2x + ) 1 1− x + C . 3 3 C. f ∫ (x) 2
dx = − (2x − ) 1 1− x + C . D. f ∫ (x) 1 dx = 2 − 1− x + + C . 3 1− x Hướng dẫn giải 2x −1  1 dx 2 1 x  = − − − + d ∫ ∫ (1−   x) 1− x  1− x 2
= (1− x)3 − 2(1− x)1 2 2
2 + C = − (2x + ) 1 1− x + C 3 3
Câu 76. Tìm nguyên hàm của hàm số ( ) x f x = . 2 3x + 2 Trang 15/34 A. f ∫ (x) 1 2 dx = 3x + 2 + C . B. f ∫ (x) 1 2 dx = − 3x + 2 + C . 3 3 C. f ∫ (x) 1 2 dx = 3x + 2 + C . D. f ∫ (x) 2 2 dx = 3x + 2 + C . 6 3 x 1 d ( 2 3x + 2) Hướng dẫn giải: 1 2 dx = = 3x + 2 + C ∫ ∫ 2 2 3x + 2 6 3x + 2 3 3
Câu 77. Tìm nguyên hàm của hàm số ( ) x f x = . 2 4 − x A. f ∫ (x) 1 dx = − ( 2 x + 8) 2 4 − x + C . B. f ∫ (x) 1 dx = ( 2 x + 8) 2 4 − x + C . 3 3 C. f ∫ (x) 1 2 dx = − 4 − x + C . D. f ∫ (x) 2 dx = − ( 2 x + 8) 2 4 − x + C . 3 3
Hướng dẫn giải: Đặt 2 2 2
t = 4 − x ⇒ x = 4 − t ⇒ xdx = t
− dt . Khi đó x ( 2 3 4 − t )( t − dt) = = ∫ ∫ ∫( −4) 3 2 t dx t
dt = − 4t + C 2 4 − x t 3 ( 4−x )32 2 1 =
− 4 4 − x + C = − ( 2 x + 8) 2 4 − x + C 3 3
4.1.5. PHƯƠNG PHÁP NGUYÊN HÀM TỪNG PHẦN Câu 78. Tính ( ) 1−x 1 = (2 −1) −x F x x
e dx = e (Ax + B) + C ∫
. Giá trị của biểu thức A + B bằng: A. 3 − . B. 3. C. 0 . D. 5. Hướng dẫn giải:
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng.
u và đạo hàm của
dv và nguyên hàm của u v + 2x −1 1 x e − 2 1 x - e − − 0 1 x e − Do đó 1−x 1−x 1 ( ) = −(2 −1) − 2 −x F x x e
e + C = e ( 2
− x −1) + C . Vậy A + B = 3 − . Câu 79. Tính ( ) x = cos x F x e
xdx = e (Acos x + Bsin x) + C ∫
. Giá trị của biểu thức A + B bằng A. 1. B. 1 − . C. 2 . D. 2 − . Hướng dẫn giải:
Phương pháp trắc nghiệm: Sử dụng bảng
u và đạo hàm của
dv và nguyên hàm của u v + x e cos x x e - sin x x e + − cos x Do đó ( ) x = sin x F x e
x + e cos x − F(x) + C hay 1 ( ) = ( x sin x F x e
x + e cos x) + C . 1 2 Vậy A + B =1. Câu 80. Tính 6 8 7
F(x) = 2x(3x − 2) dx = (3
A x − 2) + Bx(3x − 2) + C ∫
. Giá trị của biểu thức 12A +11B là A. 1. B. 1 − . C. 12 . D. 12 − . 11 11 Hướng dẫn giải:
Phương pháp trắc nghiệm: Sử dụng bảng Trang 16/34
u và đạo hàm của
dv và nguyên hàm của u v 2 x 6 (3x − 2) + 2 1 7 (3x − 2) - 21 0 1 8 (3x − 2) 504 Do đó 2 7 1 8 F(x) = x(3x − 2) −
(3x − 2) + C . Vậy 12A +11B =1. 21 252 Câu 81. Tính 2 2 2 3
F(x) = x x −1dx = ax (x −1) x −1 + bx(x −1) x −1 + c(x −1) x −1 + C ∫ . Giá trị của
biểu thức a + b + c bằng: A. − 2 B. 2 − C. 142 D. 142 7 7 105 5 10 Hướng dẫn giải:
Phương pháp tự luận: Đặt 2
u = x ,dv = x −1dx ta được 2 2 2 8 2 16 3
F(x) = x x −1dx = x (x −1) x −1 −
x(x −1) x −1 +
(x −1) x −1 + C ∫ 3 15 105 Vậy 82 a b c − + + = . 105
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
u và đạo hàm của u dv và nguyên hàm của v 2 x 1 2 + (x −1) 2 x 3 2 - 2 (x −1) 3 2 5 4 + 2 (x −1) 15 0 7 8 2 (x −1) 105 2 2 2 8 2 16 3
F(x) = x x −1dx = x (x −1) x −1 −
x(x −1) x −1 +
(x −1) x −1 + C ∫ 3 15 105 Vậy 2
a + b + c = . 7
Câu 82. Tính F (x) = ∫ ( 2
ln x + 1+ x )dx . Chọn kết quả đúng:
A. F x = x ( 2 x + + x ) 2 ( ) ln 1 − 1+ x + C . B. 1 F(x) = + C . 2 1+ x
C. F x = x ( 2 x + + x ) 2 ( ) ln 1 + 1+ x + C . D. F x = ( 2 x + + x ) 2 ( ) ln 1
− x 1+ x + C . Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với u = ( 2
ln x + 1+ x );dv = dx
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
u và đạo hàm của u
dv và nguyên hàm của v ( 2 ln x + 1+ x ) 1 + Trang 17/34 1 2 1+ x x (Chuyển 1 qua dv ) 2 1+ x x 2 1+ x 1 (Nhận 1 từ u ) 2 1+ x 0 - 2 1+ x
Câu 83. Hàm số f (x) có đạo hàm 2 3 '( ) x
f x = x e và đồ thị hàm số f (x) đi qua gốc tọa độ O . Chọn kết quả đúng: A. 1 2 x 1 2 2 x 1
f (x) = x e − e + . B. 1 2 x 1 2 2 x 1
f (x) = x e + e − . 2 2 2 2 2 2 C. 1 2 x 1 2 2 x 1
f (x) = x e − e − . D. 1 2 x 1 2 2 x 1
f (x) = x e + e + . 2 2 2 2 2 2 Hướng dẫn giải:
Phương pháp tự luận: Đặt 2 2 = , x
u x dv = xe chọn 1 2 = 2 , x du
xdx v = e ta được 2 1 2 x 1 2 2 ( ) x
f x = x e − e + C . Đồ thị đi qua O(0;0) nên 1 C = . 2 2 2
Phương pháp trắc nghiệm:
u và đạo hàm của u
dv và nguyên hàm của v 2 x 2 x + xe
2 x (chuyển 2 x qua dv ) 1 2x e 2 1 2 x
xe (nhận 2 x từ u ) - 0 1 2x e 2 1 2 x 1 2 2 ( ) x
f x = x e − e + C . Đồ thị đi qua O(0;0) nên 1 C = . 2 2 2 Câu 84. Tính 2 F(x) = x −1dx ∫ bằng:
A. F (x) 1 2 1 2
= x x −1 − ln x + x −1 + C .
B. F (x) 1 2 1 2
= x x −1 + ln x + x −1 + C . 2 2 2 2
C. F (x) 1 2 1 2
= x x −1 − ln x − x −1 + C .
D. F (x) 1 2 1 2
= x x −1 + ln x − x −1 + C . 2 2 2 2 Hướng dẫn giải:
Cách 1: Sử dụng định nghĩa F '(x) = f (x) ⇔ F '(x) − f (x) = 0
Nhập máy tính d (F(x)) − f (x) . CALC x tại một số giá trị ngẫu nhiên trong tập xác định, dx
nếu kết quả xấp xỉ bằng 0 thì chọn. Cách 2: Đặt 2
u = x −1,dv = dx ta được 2
F(x) = x x −1 − F(x) − J (x) với ( ) dx J x = ∫ , bằng cách đặt 2
u = x + x −1 ta được 2
J (x) = ln x + x −1 + C 1 x −1 Vậy 1 2 1 2
F(x) = x x −1 − ln x + x −1 + C . 2 2 4.1.6. ÔN TẬP Trang 18/34
Câu 85. Kết quả của 2 sin x cos xdx ∫ bằng A. 1 3 sin x + C . B. 3 sin x + C . C. 1 3 − sin x + C . D. 3 −sin x + C . 3 3
Hướng dẫn giải: Ta có 2 2 1 3
sin x cos xdx = sin xd(sin x) = − sin x + C ∫ ∫ . 3 Câu 86. Tính 2 cos xsin xdx ∫ bằng A. 1 3 − cos x + C . B. 3 − cos x + C . C. 1 3 cos x + C . D. 3 cos x + C . 3 3
Hướng dẫn giải: Ta có 2 2 1 3
cos xsin xdx = − cos xd(cos x) = − cos x + C ∫ ∫ . 3
Câu 87. Kết quả của 3 sin xdx ∫ bằng 3 3
A. cos x − cos x + C . B. cos x − − cos x + C . 3 3 3 C. 2 3sin .
x cos x + C .
D. cos x − cos x + C . 6 Hướng dẫn giải: 3 2 2 1 3
sin xdx = (1− cos x)sin xdx = − (1− cos x)d(cos x) = cos x − cos x + C ∫ ∫ ∫ . 3
Câu 88. Kết quả của 3 cos xdx ∫ bằng 3 3 A. sin sin x x − + C . B. sin sin x x + + C . 3 3 3 C. 2 3sin .
x cos x + C . D. sin −sin x x − + C . 3 Hướng dẫn giải: 3 2 2 1 3
cos xdx = (1− sin x)cos xdx = (1− sin x)d(sin x) = sin x − sin x + C ∫ ∫ ∫ . 3
Câu 89. Kết quả của 4 sin x cos xdx ∫ bằng A. 1 5 sin x + C . B. 1 5 − sin x + C . C. 5 sin x + C . D. 5 −sin x + C . 5 5
Hướng dẫn giải: Ta có 4 4 1 5
sin x cos xdx = sin xd(sin x) = sin x + C ∫ ∫ . 5 tan x Câu 90. Tính e dx ∫ bằng 2 cos x A. tanx e + C . B. tan tan . x x e + C . C. −tanx e + C . D. tanx −e + C . tan x
Hướng dẫn giải: e tan x tan
dx = e d(tan x) x = e + C ∫ 2 ∫ . cos x Câu 91. Tính 1 dx ∫ bằng: 2 x cos x
A. 2 tan x + C .
B. tan x + C . C. 2 tan x + C .
D. 1 tan x + C . 2 Hướng dẫn giải: 1 1 dx = 2
d( x) = 2 tan x + C ∫ ∫ . 2 2 x cos x cos x 2
Câu 92. Tính 3x dx ∫ bằng 3 x +1 3 3 A. 3 ln x +1 + C . B. 4x + C . C. 3 ln(x +1) + C . D. x + C . 4 x + 4x 4 x + x Trang 19/34 2
Hướng dẫn giải: 3x 1 3 3 dx =
d(x +1) = ln x +1 + C ∫ 3 ∫ . 3 x +1 x +1 2 Câu 93. −
Tính 6x 12x dx ∫ bằng 3 2 x − 3x + 6 A. 3 2
2ln x − 3x + 6 + C . B. 3 2
ln x − 3x + 6 + C . C. 1 3 2
ln x − 3x + 6 + C . D. 3 2
2ln(x − 3x + 6) + C . 2 2 Hướng dẫn giải − : 6x 12x 1 3 2 3 2 dx = 2
d(x − 3x + 6) = 2ln x − 3x + 6 + C ∫ 3 2 ∫ . 3 2 x − 3x + 6 x − 3x + 6 3 Câu 94. +
Tính 4x 2x dx ∫ bằng 4 2 x + x + 3 A.. 4 2
ln x + x + 3 + C . B. 4 2
2ln x + x + 3 + C . C. 1 4 2
ln x + x + 3 + C . D. 4 2 2
− ln(x + x + 3) + C . 2 3 Hướng dẫn giải + : 4x 2x 1 4 2 4 2 dx =
d(x + x + 3) = ln x + x + 3 + C ∫ 4 2 ∫ . 4 2 x + x + 3 x + x + 3 2 Câu 95. + Tính x 1 dx ∫ bằng 3 x + 3x −1 A. 1 3
ln x + 3x −1 + C . B. 3
ln x + 3x −1 + C . 3 C. 3
ln x + 3x −1 + C . D. 1 3
ln(x + 3x −1) + C . 3 2 Hướng dẫn giải + : x 1 1 1 3 1 3 dx =
d(x + 3x −1) = ln x + 3x −1 + C ∫ 3 ∫ . 3 x + 3x −1 3 x + 3x −1 3
Câu 96. Tính 6x−5 e dx ∫ bằng A. 1 6x−5 e + C . B. 6x−5 e + C . C. 6 −5 6 x e + C . D. 6x+5 e − C . 6
Hướng dẫn giải: 6x−5 1 6x−5 1 6x−5 e dx = e
d(6x − 5) = e + C ∫ ∫ . 6 6
Câu 97. Tính −x−5 e dx ∫ bằng A. −x−5 −e + C . B. −x−5 e + C . C. x+5 e + C . D. x+5 −e + C .
Hướng dẫn giải: −x−5 − x−5 − x−5 e dx = − e
d(−x − 5) = −e + C ∫ ∫ . Câu 98. Tính ( − ∫ )12 5 9x dx bằng 13 13 13 13 A. − − − − (5 9x) − + C .
B. (5 9x) + C .
C. (5 9x) + C .
D. (5 9x) + C . 117 117 13 9 13 Hướng dẫn giải − : ∫( − x)12 1
dx = − ∫( − x)12 (5 9x) 5 9 5 9
d(5 − 9x) = − + C . 9 117  π
Câu 99. Tính cos 5x dx  + ∫  bằng 4     π  π A. 1 sin 5x  + +    C . B. sin 5x + +   C . 5  4   4   π  π C. 5sin 5x  − + +    C . D. 1 − sin 5x + +   C .  4  5  4  Trang 20/34  π   π   π   π Hướng dẫn giải: 1 1 cos 5x dx cos 5x d 5x sin 5x  + = + + = + + ∫   ∫       C .  4  5  4   4  5  4  Câu 100. Tính 1 dx ∫ bằng 2  π cos x  +  4     π  π A. tan x  + +    C . B. 4 tan x + +   C .  4   4   π  π C. tan x  − + +    C . D. 1 tan x + +   C .  4  4  4   π   π Hướng dẫn giải: 1 1 dx d x tan x  = + = + + ∫ ∫     C . 2  π  2  π   4   4 cos x  cos  x  + +  4 4      Câu 101. Tính 1 dx ∫ bằng 2 (cos x + sin x)  π  π A. 1 cot x  − + +    C . B. 1 cot x + +   C . 2  4  2  4   π  π C. cot x  − + +    C . D. 1 − cot x + +   C .  4  4  4  Hướng dẫn giải 1 1 1 1 1  π  1  π dx dx d x cot x  = = + = − + + ∫ ∫ ∫     C 2 (cos x + sin x) 2 2  π  2 2  π   4  2  4 sin x  sin  x  + +  4 4      Câu 102. +
Tính 12x 5 dx ∫ bằng 3x +1 2 A. + 1
4x + ln 3x +1 + C .
B. 6x 5x + C . 3 3 x + x
C. 4x + ln 3x +1 + C . D. 1
4x + ln(3x +1) + C . 3 Hướng dẫn giải + : 12x 5  1  1 dx = 4 +
dx = 4x + ln 3x +1 + ∫ ∫  C . 3x +1  3x +1 3 2 Câu 103. + Tính 2x xdx ∫ bằng 2x −1 2 2 A. x 1
+ x + ln 2x −1 + C .
B. x + x + ln 2x −1 + C . 2 2 2 2 2 C. x 1
+ x + ln(2x −1) + C .
D. x + x + 2ln(2x −1) + C . 2 2 2 2 2 Hướng dẫn giải + : 2x x  1  x 1 dx = x +1+ dx = + x + 2x −1 + ∫ ∫  C . 2x −1  2x −1 2 2 Câu 104. − Tính x dx ∫ bằng 2 (x +1) A. 1 −
− ln x +1 + C .
B. 1 − ln x +1 + C . x +1 x +1 C. 1 − + ln x +1 + C . D. 1 −
− ln(x +1) + C . x +1 x +1 −   Hướng dẫn giải: x 1 1 1 dx = − dx = − − ln x +1 + ∫ ∫  C . 2 2 (x +1)  (x +1) x +1 x +1 Trang 21/34
Câu 105. Tính sin x(2 + cos x)dx ∫ bằng A. 1 2
− cos x − cos 2x + C B. 1
2cos x − cos 2x + C 4 4 C. 1
2cos x + cos 2x + C D. 1
2cos x + cos 2x + C 4 2 Hướng dẫn giải: 1 1
sin x(2 + cos x)dx = (2sin x + sin 2x)dx = − 2cos x − cos 2x + C ∫ ∫ . 2 4
Câu 106. Tính .2x x dx ∫ bằng: x x 2x (x − ) 1 A. .2 x 2 − + C . B. + C . 2 ln 2 ln 2 ln 2
C. 2x(x +1) + C .
D. 2x(x −1) + C . Hướng dẫn giảidu = dx u  = x x x x x Đặt  x .2 x 2 .2 x 2  ⇒  . Ta có x2 dx = − dx = − + C ∫ ∫ . x 2xdv = 2 dxv = 2 ln 2 ln 2 ln 2 ln 2  ln 2
Câu 107. Tính ln xdx ∫ bằng: 2
A. x ln x − x + C . B. ln x x x − ln x + C . 2
C. 1 ln x − x + C . D. 1
x ln x − + C . x x Hướng dẫn giải  1 u  = ln xdu = dx Đặt  ⇒ 
x . Ta có ln xdx = x ln x − dx x
= ln x − x + C ∫ ∫ . dv = dx v = x
Câu 108. Tính 2xln(x −1)dx ∫ bằng: 2 2 A. 2 ( −1)ln( −1) x x x − − x + C . B. 2 ln( −1) x x x − − x + C . 2 2 2 2 C. 2 ( +1)ln( −1) x x x − − x + C . D. 2 ( −1)ln( −1) x x x − + x + C . 2 2 Hướng dẫn giải  1 u  = ln(x −1) du = dx Đặt  ⇒  x −1 dv = 2xdx  2 v = x −1 2 Ta có 2 2
2 ln( −1) = ( −1)ln( −1) − ( +1) =( −1)ln( −1) x x x dx x x x dx x x − − x + C ∫ ∫ . 2 Câu 109. Tính  1 sin x  + ∫  dx bằng: 2  cos x
A. −cos x + tan x + C .
B. cos x + tan x + C .
C. cos x − tan x + C . D. 1 − cos x − + C . cos x
Hướng dẫn giải: Ta có  1 sin x  +
dx = −cos x + tan x + ∫  C 2  cos x
Câu 110. Hàm số F(x) = ln sin x − cos x là một nguyên hàm của hàm số A. + − sin x cos ( ) x f x = . B. sin x cos ( ) x f x = . sin x − cos x sin x + cos x Trang 22/34 C. 1 f (x) = . D. 1 f (x) = . sin x + cos x sin x − cos x Hướng dẫn giải − + : Ta có
(sin x cos x)' cos x sin '( ) x F x = = . sin x − cos x sin x − cos x
Câu 111. Một nguyên hàm F(x) của hàm số 3 2
f (x) = 3x − 2x +1 thỏa mãn điều kiện F( 2) − = 3 là: A. 3 4 2 3 37
F(x) = x − x + x − . B. 3 4 2 3
F(x) = x − x + x + C . 4 3 3 4 3 C. 3 4 2 3
F(x) = x − x + x . D. 3 4 2 3 37
F(x) = x − x + x + . 4 3 4 3 3 Hướng dẫn giải Ta có 3 2 3 4 2 3
F(x) = (3x − 2x +1) = x − x + x + C ∫ và 37 F( 2) − = 3 ⇔ C = − 4 3 3 Vậy 3 4 2 3 37
F(x) = x − x + x − . 4 3 3 VẬN DỤNG CAO
4.1.1. NGUYÊN HÀM CỦA HÀM SỐ ĐA THỨC, PHÂN THỨC. 3 Câu 112. − + + Kết quả tính x 5x 2 dx ∫ bằng 2 4 − x 2 2
A. x − ln 2 − x + C .
B. x + ln 2 − x + C . 2 2 3 3
C. x − ln 2 − x + C .
D. x + ln x − 2 + C . 3 3 Hướng dẫn giải
−x + 5x + 2 x − 5x − 2 ( x + 2)( 2 3 3 x − 2x − ) 1 1 = = = x −
. Sử dụng bảng nguyên hàm. 2 2 4 − x x − 4 (x + 2)(x − 2) x − 2
Câu 113. Họ nguyên hàm của f (x) = x (x + )5 2 3 1 là
A. F (x) 1 = (x + )6 3 1 + C .
B. F (x) = (x + )6 3 18 1 + C . 18
C. F (x) = (x + )6 3 1 + C .
D. F (x) 1 = (x + )6 3 1 + C . 9
Hướng dẫn giải: Đặt 3 2
t = x +1⇒ dt = 3x dx . Khi đó x ∫ (x + )5 1 1 1 1 dx = t dt = t + C = ∫ (x + )6 2 3 5 6 3 1 + C . 3 18 18 2 3 Câu 114. + + +
Họ nguyên hàm của hàm số f (x) x x x 1 = là hàm số nào? 3 x A. F (x) 1 1
= ln x − + x − + C . B. F (x) 1 1 = ln x + + x − + C . 2 x 2x 2 x 2x 3 2 3 2 C. ( ) x 3x F x = − + ln x + C . D. ( ) x 3x F x = + + ln x + C . 3 2 3 2 2 3
Hướng dẫn giải: f (x) x + x + x +1 1 1 1 = = + +1+
. Sử dụng bảng nguyên hàm. 3 2 3 x x x x
Câu 115. Giá trị m để hàm số F (x) 3 = mx + ( m + ) 2 3
2 x − 4x + 3 là một nguyên hàm của hàm số f (x) 2
= 3x +10x − 4 là: A. m =1. B. m = 0. C. m = 2 . D. m = 3 .
Hướng dẫn giải: ∫( 2x + x − ) 3 2 3 10
4 dx = x + 5x − 4x + C , nên m =1. Trang 23/34
Câu 116. Gọi F (x) là nguyên hàm của hàm số f (x) 4
= sin (2x) thoả mãn F ( ) 3
0 = . Khi đó F (x) là: 8
A. F (x) 3 = (x + ) 1 1 1 − sin 4x + sin8x .
B. F (x) 3 1 1 = x − sin 4x + sin8x . 8 8 64 8 8 64
C. F (x) 3 1 1 3 = x − sin 2x + sin 4x + . D. F (x) 3
= x − sin 4x + sin 6x + . 8 8 64 8 8 Hướng dẫn giải 2
4 ( ) 1− cos 4x  1  ( 2 ) 1 1+ cos8 sin 2 1 2cos 4 cos 4 1 2cos 4 x x x x x  = = − + = − +  2 4 4 2      3 cos 4x cos8x = − + 8 2 8 Nên 4 ∫ ( )
 3 cos 4x cos8x  3 sin 4x sin8 sin 2 x x dx = − + dx = x − + + ∫  C .  8 2 8  8 8 64 Vì F ( ) 3 0 = nên suy ra đáp án. 8
Câu 117. Biết hàm số 2
f (x) = (6x +1) có một nguyên hàm là 3 2
F(x) = ax + bx + cx + d thoả mãn điều kiện F( 1
− ) = 20. Tính tổng a + b + c + d . A. 46 . B. 44 . C. 36. D. 54. Hướng dẫn giải
∫( x+ )2 dx = ∫( 2x + x+ ) 3 2 6 1 36 12
1 dx =12x + 6x + x + C nên a =12;b = 6;c =1 Thay F( 1
− ) = 20. d = 27 , cộng lại và chọn đáp án.
Câu 118. Hàm số f (x) = x x +1 có một nguyên hàm là F (x) . Nếu F (0) = 2thì F (3) bằng A. 146 . B. 116 . C. 886 . D. 105 . 15 15 105 886
Hướng dẫn giải: Đặt t = x +1 ⇒ 2tdt = dx x x + dx = ∫ ∫( t − t ) 2 2 2
dt = t − t + C = ( x + )5 2 1 2 2 1 − ( x +1)3 4 2 5 3 + C 5 3 5 3 Vì F (0) = 2 nên 34 C =
. Thay x = 3 ta được đáp án. 15
Câu 119. Gọi F (x) là một nguyên hàm của hàm số f (x) = xcos x thỏa mãn F (0) =1. Khi đó phát biểu nào sau đây đúng?
A. F (x) là hàm số chẵn.
B. F (x) là hàm số lẻ.
C. Hàm số F (x) tuần hoàn với chu kì là 2π .
D. Hàm số F (x) không là hàm số chẵn cũng không là hàm số lẻ. Hướng dẫn giải
x cos xdx = xsin x + cos x + C ∫
F (0) =1 nên C = 0 . Do đó F (x) là hàm số chẵn.
Câu 120. Một nguyên hàm F (x) của hàm số sin 2 ( ) x f x =
thỏa mãn F (0) = 0 là 2 sin x + 3 2 2 ln 2 + sin x A. sin ln 1 x + . B. 2 ln 1+ sin x . C. . D. 2 ln cos x . 3 3
Hướng dẫn giải: Đặt 2
t = sin x + 3 ⇒ dt = 2sin x cos xdx sin 2x dt 2 dx =
= ln t + C = ln sin x + 3 + C ∫ 2 ∫ sin x + 3 t Trang 24/34
vì F (0) = 0 nên C = −ln 3 . Chọn đáp án.
Câu 121. Cho f (x) 4m 2 =
+ sin x . Tìm m để nguyên hàm F (x) của hàm số f (x) thỏa mãn F (0) =1 π π π và F   =  . 4    8 A. 3 − . B. 3 . C. 4 − D. 4 . 4 4 3 3
Hướng dẫn giải:  4m 2  4m x sin 2 + sin x x dx = x + − + ∫ 
C vì F (0) =1 nên C =1  π  π 2 4 π π F   =  nên tính được 3 m = − 4    8 4
4.1.2. NGUYÊN HÀM CỦA HÀM SỐ LƯỢNG GIÁC.
Câu 122. Tìm nguyên hàm của hàm số 1 f (x) = . sin . x cos x A. 1 2
f (x)dx = ln sin x − ln 1− sin x + C ∫ . B. 1 2
f (x)dx = ln sin x + ln 1− sin x + C ∫ . 2 2 C. 1 1 2
f (x)dx = ln sin x − ln 1− sin x + C ∫ . D. 1 2
f (x)dx = −ln sin x − ln 1− sin x + C ∫ . 2 2 2 Hướng dẫn giải dx cos xdx d (sin x) 1 d (sin x)
d (sin x) 1 d (sin x) = = ∫ ∫ = + − 2 ∫ ∫ ∫ ∫ sin . x cos x sin . x cos x sin . x ( 2
1− sin x) 2 1−sin x sin x 2 1+ sin x 1 − 1 1 2 =
ln 1− sin x + ln sin x − ln 1+ sin x + C = ln sin x − ln 1− sin x + C 2 2 2 3
Câu 123. Tìm nguyên hàm của hàm số 2sin ( ) x f x = . 1+ cos x A. 2
f (x)dx = cos x − 2cos x + C ∫ . B. 1 2
f (x)dx = cos x − 2cos x + C ∫ . 2 C. 2
f (x)dx = cos x + cos x + C ∫ . D. 1 2
f (x)dx = cos x + 2cos x + C ∫ . 2 Hướng dẫn giải 3 2 2 2sin x 2sin x 2cos x − 2 dx = .sin xdx = d ∫ ∫ ∫ (cos x) 1+ cos x 1+ cos x 1+ cos x
= ∫ ( x − )d ( x) 2 2 cos 1
cos = cos x − 2cos x + C 3
Câu 124. Tìm nguyên hàm của hàm số cos ( ) x f x = . 5 sin x 4 4 A. − cot ( ). x f x dx = + C ∫ . B. cot ( ). x f x dx = + C ∫ . 4 4 2 4 C. cot ( ). x f x dx = + C ∫ . D. tan ( ). x f x dx = + C ∫ . 2 4 3 4
Hướng dẫn giải cos xdx 3 dx 3 − cot = cot . = − cot . cot x x x d x = + C ∫ 5 ∫ 2 ∫ ( ) sin x sin x 4
Câu 125. Tìm nguyên hàm của hàm số: f x = x( 4 4
( ) cos 2 sin x + cos x) . A. 1 1 3
f (x).dx = sin 2x − sin 2x + C ∫ . B. 1 1 3
f (x).dx = sin 2x + sin 2x + C ∫ . 2 12 2 12 C. 1 3
f (x).dx =sin 2x − sin 2x + C ∫ . D. 1 1 3
f (x).dx = sin 2x − sin 2x + C ∫ . 4 2 4 Trang 25/34 Hướng dẫn giải x ∫ ( 4 4
cos 2 sin x + cos x)dx = x  ∫ ( 2 2 x + x) 2 2 cos 2 sin cos − 2sin .
x cos xdx   1 2  1 2
= cos 2x 1− sin 2x dx = cos 2xdx − ∫   sin 2 . x cos 2xdx ∫ ∫  2  2 1 2 = cos 2xdx − sin 2 . x d ∫ ∫ (sin 2x) 1 1 3
= sin 2x − sin 2x + C 4 2 12
Câu 126. Tìm nguyên hàm của hàm số = ( 2sin ( ) tan x f x x + e )cosx. A. 1 2sin ( ) = − cos x f x dx x + e + C ∫ . B. 1 2sin ( ) =cos x f x dx x + e + C ∫ . 2 2 C. 2sin ( ) = − cos x f x dx x + e + C ∫ . D. 1 2sin ( ) = − cos x f x dx x − e + C ∫ . 2 Hướng dẫn giải ∫( 2sin tan x + ) 2sin cos = sin x + ∫ ∫ (sin ) 1 2sin = −cos x x e xdx xdx e d x x + e + C 2
Câu 127. Tìm nguyên hàm của hàm số 1 f (x) = .
sin x + cos x + 2 A. 1  x 3 f (x)dx cot  = − + + ∫ π  x    C . B. 1 3 f (x)dx = cot + + ∫ π   C . 2  2 8  2  2 8  C. 1  x 3 f (x)dx cot  = − + + ∫ π  x    C . D. 1 3
f (x)dx = − cot − + ∫ π   C . 2  2 4  2  2 8  Hướng dẫn giải dx dx 1 dx = = ∫ ∫ ∫
sin x + cos x + 2  π  2 π 2 sin x + + 2 sin  x  + +     1  4   4  1 dx 1 dx 1  x 3 cot  = = = − + + ∫ ∫ π   C 2 2   x   x  2 2  x 3π π π  2  2 8 + + + 2sin  sin   cos +     2 8   2 8 2 8     
4.1.3. NGUYÊN HÀM CỦA HÀM SỐ MŨ, LÔGARIT.
Câu 128. Hàm số F(x) = ln sin x − cos x là một nguyên hàm của hàm số A. + − sin x cos ( ) x f x = . B. sin x cos ( ) x f x = . sin x − cos x sin x + cos x C. 1 f (x) = . D. 1 f (x) = . sin x + cos x sin x − cos x Hướng dẫn giải − + :
(sin x cos x)' cos x sin '( ) x F x = = sin x − cos x sin x − cos x
Câu 129. Kết quả tính 2xln(x −1)dx ∫ bằng: 2 2 A. 2 ( −1)ln( −1) x x x − − x + C . B. 2 ln( −1) x x x − − x + C . 2 2 2 2 C. 2 ( +1)ln( −1) x x x − − x + C . D. 2 ( −1)ln( −1) x x x − + x + C . 2 2 Hướng dẫn giải  1 u  = ln(x −1) du = dx Đặt  ⇒  x −1 dv = 2xdx  2 v = x −1 2 Ta có 2 2
2 ln( −1) = ( −1)ln( −1) − ( +1) =( −1)ln( −1) x x x dx x x x dx x x − − x + C ∫ ∫ 2 Trang 26/34 tan x
Câu 130. Kết quả tính e dx ∫ bằng: 2 cos x A. tanx e + C . B. tan tan . x x e + C . C. −tanx e + C . D. tanx −e + C . tan x
Hướng dẫn giải: e tan x tan
dx = e d(tan x) x = e + C ∫ 2 ∫ . cos x Câu 131. Tính 2 cos e xsin 2xdx ∫ bằng: A. 2 cos x −e + C . B. −sin2x e + C . C. 2−sinx e + C . D. sin2x −e + C . Hướng dẫn giải: 2 2 2 cos x cos x 2 cos e sin 2 = − e (cos ) = −e x xdx d x + C ∫ ∫ . Câu 132. Tính 2 sin e xsin 2xdx ∫ bằng: A. 2 sin x e + C . B. sin2x e + C . C. 2 cos x e + C . D. 2sinx e + C . Hướng dẫn giải: 2 2 2 sin x sin x 2 sin e sin 2 = e (sin ) =e x xdx d x + C ∫ ∫ .
Câu 133. Kết quả cosx e sin xdx ∫ bằng: A. cosx −e + C . B. cosx e + C . C. −cosx −e + C . D. −sinx e + C .
Hướng dẫn giải: cosx cos x cos sin = − (cos ) x e xdx e d x = −e + C ∫ ∫ .
4.1.4. NGUYÊN HÀM CỦA HÀM SỐ CHỨA CĂN THỨC. Câu 134. +
Biết hàm số F(x) = −x 1− 2x + 2017 là một nguyên hàm của hàm số ( ) ax b f x = . Khi đó 1− 2x
tổng của a và b là A. 2 . B. 2 − . C. 0 . D. 1. Hướng dẫn giải −
: F x = (−x − x + ) 3x 1 '( ) 1 2 2017 ' = 1− 2x
⇒ a + b = 3+ (− ) 1 = 2 3 Câu 135. −
Tìm nguyên hàm của hàm số x 2 ( ) x f x = . 2 x +1
A. F (x) 1 = ( 2 x −8) 2 x +1 + C .
B. F (x) 1 2 2 2
= x 1+ x + 8 1+ x + C . 3 3
C. F (x) 1 = ( 2 8 − x ) 2 x +1 + C .
D. F (x) 2 = ( 2 x −8) 2 1+ x + C . 3 3 x − 2x ( 2 3 x − 2) xdx Hướng dẫn giải: dx = ∫ ∫ 2 2 x +1 x +1 Đặt 2 2 2
t = x +1 ⇒ x = t −1⇒ xdx = tdt . Khi đó x − 2x ( 2 3 t − 3)(tdt) = = ∫ ∫ ∫( −3) 3 2 t dx t
dt = − 3t + C 2 x +1 t 3 ( x +1)3 2 2 1 =
− 3 x +1 + C = ( 2 x −8) 2 x +1 + C 3 3 Câu 136. Tính ( ) sin 2x F x = dx ∫
. Hãy chọn đáp án đúng. 2 2
4sin x + 2cos x + 3
A. F (x) = 6 − cos 2x + C .
B. F (x) = 6 −sin 2x + C .
C. F (x) = 6 + cos 2x + C .
D. F (x) = − 6 −sin 2x + C . Hướng dẫn giải Trang 27/34 sin 2x sin 2x d (6 − cos 2x) dx = dx=
= 6 − cos 2x + C ∫ ∫ ∫ 2 2
4sin x + 2cos x + 3 6 − cos 2x 2 6 − cos 2x Câu 137. −
Biết hàm số F(x) = ( x
m + n) 2x −1 là một nguyên hàm của hàm số 1 ( ) x f x = . Khi đó 2x −1
tích của m và n là A. 2 − . B. 2 − . C. 2 − . D. 0 . 9 3
Hướng dẫn giải − Cách 1: Tính 1 x  1 2 dx x  = − + 2x −1 + ∫   C . Suy ra 1 2 2
m = − ;n = ⇒ . m n = − 2x −1  3 3  3 3 9  1 3  = 1 m m = − −  Cách 2: − + Tính ( ) 3 ' mx m n F x = . Suy ra  3 2  ⇒  ⇒ . m n = − 2x −1 n − m = 1 2 9 n =  3
Câu 138. Biết hàm số F(x) là một nguyên hàm của hàm số ln ( ) x f x =
có đồ thị đi qua điểm 2 x ln x + 3
( ;e2016). Khi đó hàm số F ( ) 1 là A. 3 + 2014 . B. 3 + 2016 . C. 2 3 + 2014 . D. 2 3 + 2016 .
Hướng dẫn giải: Đặt 2
t = ln x + 3 và tính được F (x) 2
= ln x + 3 + C . F (e) = ⇒ C = ⇒ F (x) 2 2016 2014
= ln x + 3 + 2014 ⇒ F ( ) 1 = 3 + 2014
4.1.5. PHƯƠNG PHÁP NGUYÊN HÀM TỪNG PHẦN Câu 139. Tính 3 x x 3 2
x e dx = e (ax + bx + cx + d) + C ∫
. Giá trị của a + b + c + d bằng A. 2 − . B. 10. C. 2 . D. 9 − . Hướng dẫn giải:
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng Kết quả: 3 x 3 x 2 x x x x 3 2
x e dx = x e − 3x e + 6xe − 6e + C = e (x − 3x + 6x − 6) + C ∫ .
Vậy a + b + c + d = 2 − . Câu 140. Tính 2 2 2 2
F(x) = x ln(x + 3)dx = (
A x + 3)ln(x + 3) + Bx + C ∫
. Giá trị của biểu thức A + B bằng A. 0 . B. 1. C. 1 − . D. 2 . Hướng dẫn giải
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
u và đạo hàm của u
dv và nguyên hàm của v 2 ln(x + 3) x + 2x 2 x + 3 2 x + 3 2 1 x
(Chuyển 2x qua dv )
(Nhận 2x từ u ) 2 x + 3 2 - x + 3 2 0 x 2 Do đó 2 1 2 2 1 2
F(x) = x ln(x + 3)dx = (x + 3)ln(x + 3) − x + C ∫ . 2 2
Vậy A + B = 0. Câu 141. Tính 2 2
x cos 2xdx = ax sin 2x + bx cos 2x + csin x + C ∫
. Giá trị của a + b + 4c bằng Trang 28/34 − A. 0 . B. 3 . C. 3 . D. 1 . 4 4 2 Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần 2 lần.
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng Kết quả: 2 1 2 1 1
x cos 2xdx = x sin 2x + x cos 2x − sin 2x + C ∫ . 2 2 4
Vậy a + b + 4c = 0 . Câu 142. Tính 3 4
x ln 2xdx = x (Aln 2x + B) + C ∫
. Giá trị của 5A + 4B bằng: A. − 1. B. 1. C. 1 . D. 1 − . 4 4 Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với 3
u = ln 2x,dv = x dx .
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng Kết quả: 3 1 4 1 4 4  1 1 x ln 2xdx x ln 2x x C x ln 2x  = − + = − + ∫   C . 4 16  4 16 
Vậy 5A + 4B =1. Câu 143. + Tính 1 ( ) = ln x F x x dx ∫ . Chọn kết quả đúng: 1− x 2 2 A. − + + + x 1 1 ( ) = ln x F x + x + C B. x 1 1 ( ) = ln x F x + x + C 2 1− x 2 1− x 2 2 C. + + − + x 1 1 ( ) = ln x F x − x + C D. x 1 1 ( ) = ln x F x − x + C 2 1− x 2 1− x Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần và nguyên hàm của hàm số hữu tỉ.
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng 2 Kết quả: 1+ x x −1 1+ ln = ln x x dx + x + C ∫ . 1− x 2 1− x
Câu 144. Cho hàm số 3
F(x) = x(1− x) dx ∫
. Biết F(0) =1, khi đó F(1) bằng: A. − − 21 . B. 19 . C. 21 . D. 19 . 20 20 0 2 20 Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp đổi biến số với u =1− x .
Sử dụng phương pháp từng phần với 3 u = ;
x dv = (1− x) dx .
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng với 3 u = ;
x dv = (1− x) dx 4 5 Kết quả − − − 3 x(1 x) (1 x)
F(x) = x(1− x) dx = − + C ∫ 4 20 F(0) =1 suy ra 21 C = . Do đó 21 F(1) = . 20 20
Câu 145. Tính (2x +1)sin xdx = a xcos x + bcos x + csin x + C ∫
. Giá trị của biểu thức a + b + c bằng A. 1 − . B. 1. C. 5. D. 5 − . Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần.
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng.
Kết quả F(x) = (2x +1)sin xdx = 2
− x cos x − cos x + 2sin x + C ∫
nên a + b + c = 1 − .
Câu 146. Cho hàm số F(x) = xln(x +1)dx ∫
có F(1) = 0 . Khi đó giá trị của F(0) bằng Trang 29/34 A. − − 1 . B. 1 . C. 1 . D. 1 . 4 4 2 2
Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần vớiu = ln(x +1),dv = xdx
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng
Kết quả F(x) = x ln(x +1)dx ∫ 1 2 1 2
= (x −1)ln(x +1) − (x − 2x) + C . 2 4 Từ F(1) = 0 suy ra 1 C − = . Vậy 1 F − (0) = . 4 4 Câu 147. Hàm số 2
F(x) = (x +1)ln xdx ∫ thỏa mãn 5 F − (1) = là 9 3 3 A. 1 3 ( + 3 )ln x x x x x − − . B. 1 3 ( + 3 )ln x x x x x − − −1. 6 18 2 6 18 2 3 3 C. 1 3 x x 10
(x + 3x)ln x − − + . D. 1 3 ( + 3 )ln x x x x x − − +1. 6 18 2 9 6 18 2 Hướng dẫn giải:
Phương pháp tự luận: Sử dụng phương pháp từng phần.
Phương pháp trắc nghiệm: Sử dụng phương pháp bảng 3 Kết quả 2 1 3 ( ) = ( +1)ln = ( + 3 )ln x x F x x xdx x x x − − + C ∫ 6 18 2 3 Với 5 F − (1) = suy ra C = 0 nên 1 3 ( ) = ( + 3 )ln x x F x x x x − − . 9 6 18 2 x
Câu 148. Hàm số f (x) có đạo hàm '( ) xe f x =
và có đồ thị đi qua điểm (
A 0;1) . Chọn kết quả đúng 2 (x +1) x x A. ( ) e f x = B. ( ) e f x = +1 x +1 x +1 x x C. ( ) e f x = −1 D. ( ) e f x = + 2 x +1 x +1
Hướng dẫn giải: Sử dụng phương pháp từng phần với x 1
u = xe ,dv = dx 2 (x +1)
u và đạo hàm của u
dv và nguyên hàm của v x xe 1 2 + (x +1) ( +1) x x e 1 − (Chuyển ( +1) x x e qua dv ) x +1 1 x −e - (nhận ( +1) x x e từ u ) 0 x −e x x x Kết quả ( ) xe e f x = dx = + C ∫
. Với f (0) =1 suy ra C = 0 . Vậy ( ) e f x = 2 (x +1) x +1 x +1
Câu 149. Một nguyên hàm F(x) của hàm số f x = ( 2
( ) ln x + x +1) thỏa mãn F(0) =1. Chọn kết quả đúng
A. F x = x ( 2 x + x + ) 2 ( ) ln 1 − x +1 + 2 .
B. F x = x ( 2 x + x + ) 2 ( ) ln 1 − x +1 − 2 .
C. F x = x ( 2 x + x + ) 2 ( ) ln 1 − x +1 +1.
D. F x = x ( 2 x + x + ) 2 ( ) ln 1 − x +1 . Hướng dẫn giải: Trang 30/34 Đặt u = ( 2
ln x + x +1),dv = dx ta được F x = x ( 2 x + x + ) 2 ( ) ln
1 − x +1 + C . Vì F(0) =1 nên C = 2 Vậy F x = x ( 2 x + x + ) 2 ( ) ln 1 − x +1 + 2 .
Câu 150. Một nguyên hàm F(x) của hàm số ( ) x f x =
thỏa mãn F(π ) = 2017 . Khi đó F (x) là 2 cos x hàm số nào dưới đây?
A. F(x) = x tan x + ln | cos x | 2017 + .
B. F(x) = x tan x − ln | cos x | 2018 + .
C. F(x) = x tan x + ln | cos x | 2016 + .
D. F(x) = x tan x − ln | cos x | 2017 + .
Hướng dẫn giải: Đặt 1
u = x,dv =
dx ta được du = dx,v = tan x 2 cos x Kết quả ( ) x F x =
dx = x tan x − tan xdx = x tan x + ln | cos x | +C ∫ 2 ∫ . cos x
Vì F(π ) = 2017 nên C = 2017 . Vậy F(x) = x tan x + ln | cos x | 2017 + . Câu 151. Tính 2
F(x) = x(1+ sin 2x)dx = Ax + Bx cos 2x + C sin 2x + D ∫
. Giá trị của biểu thức A + B + C bằng A. 1 . B. 1 − . C. 5 . D. 3 − . 4 4 4 4 Hướng dẫn giải:
Cách 1: Sử dụng phương pháp nguyên hàm từng phần.
Cách 2: Sử dụng phương pháp bảng với u = x,dv = (1+ sin 2x)dx ta được 1 2 1 1
F(x) = x − x cos 2x + sin 2x + D . Vậy 1
A + B + C = . 2 2 4 4 Câu 152. + Tính 1 xsin ( ) x F x = dx ∫ . Chọn kết quả đúng 2 cos x A. − − x 1 sin x 1
F(x) = tan x + + ln + C . B. x 1 sin x 1
F(x) = tan x − + ln + C . cos x 2 sin x +1 cos x 2 sin x +1 C. − − x 1 sin x 1
F(x) = tan x + − ln + C . D. x 1 sin x 1
F(x) = tan x − − ln + C . cos x 2 sin x +1 cos x 2 sin x +1 Hướng dẫn giải Cách 1: Biến đổi dx xsin ( ) x F x = +
dx = tan x + I(x) ∫ 2 ∫ 2 cos x cos x
Tính I(x) bằng cách đặt sin = ; x u x dv = dx ta được ( ) x dx I x = − 2 ∫ cos x cos x cos x − Tính dx cos xdx d(sin x) sin x 1 J (x) = − = = = ln + C ∫ ∫ 2 ∫ cos x sin x −1
(sin x −1)(sin x +1) sin x +1
Kết quả F (x) x 1 sin x −1 = tan x + + ln + C cos x 2 sin x +1
Phương pháp trắc nghiệm: Sử dụng máy tính kiểm tra d (F(x)) − f (x) = 0 tại một số điểm dx ngẫu nhiên x . 0 4.1.6. ÔN TẬP π
Câu 153. Một nguyên hàm F(x) của hàm số 1
f (x) = sin x + thỏa mãn điều kiện 2 F   = là 2 cos x  4    2
A. F(x) = −cos x + tan x + 2 −1.
B. F(x) = cos x + tan x + 2 −1. Trang 31/34
C. F(x) = −cos x + tan x +1− 2 .
D. F(x) = −cos x + tan x . Hướng dẫn giải Ta có  1 sin x d  +
x = −cos x + tan x + C ⇒ F(x) = −cos x + tan x + ∫  C 2  cos x   π  2 F = ⇔ C = 2 −  
1. Vậy F(x) = −cos x + tan x + 2 −1  4  2
Câu 154. Một nguyên hàm F(x)của hàm số 3
f (x) = 2sin 5x + x + thỏa mãn đồ thị của hai hàm số 5
F(x) và f (x) cắt nhau tại một điểm nằm trên trục tung là A. 2 2 3
F(x) = − cos5x + x x + x +1. B. 2 2 3
F(x) = cos5x + x x + x +1. 5 3 5 5 3 5 C. 1 3
F(x) =10cos5x + + x +1. D. 2 2 3
F(x) = − cos5x + x x + x . 2 x 5 5 3 5 Hướng dẫn giải Ta có 2 2 3
F(x) = − cos5x + x x + x + C và F(0) = f (0) ⇔ C =1 5 3 5 Vậy 2 2 3
F(x) = − cos5x + x x + x +1 5 3 5 Câu 155. Hàm số 2 ( ) = ( + + ) x F x
ax bx c e là một nguyên hàm của hàm số 2 ( ) x
f x = x e thì a + b + c bằng: A. 1. B. 2 . C. 3. D. 2 − . Hướng dẫn giảia =1 a =1 Ta có 2 2
F '(x) f (x)
ax (2a b)x b c x  2a b 0 b  = ⇔ + + + + = ⇔ + = ⇔  = 2 − bc 0  + = c =   2
Vậy a + b + c =1 π  π  π
Câu 156. Một nguyên hàm F(x) của hàm số f (x) = a + bcos 2x thỏa mãn F(0) = , F = , 2  2    6  π  π F =  là 12    3 π π π A. 2 7
F(x) = − x + sin 2x + . B. 2 7
F(x) = − x + sin 2x . 3 9 2 3 9 π π π π C. 2 7
F(x) = − x − sin 2x + . D. 2 7
F(x) = − x + sin 2x − . 3 9 2 3 9 2 Hướng dẫn giải  π  2 F(0) = a = − 2   3    π  π  π Ta có ( ) b
F x = ax + sin 2x + C và 7 F = ⇔   b  = 2   2  6 9    π  π  π F C = =     12  3  2 π π Vậy 2 7
F(x) = − x + sin 2x + 3 9 2
Câu 157. Cho hàm số 3 2
F(x) = ax + bx + cx +1 là một nguyên hàm của hàm số f (x) thỏa mãn f (1) = 2,
f (2) = 3, f (3) = 4. Hàm số F(x) là A. 1 2
F(x) = x + x +1. B. 1 2
F(x) = − x + x +1. 2 2 Trang 32/34 C. 1 2
F(x) = − x − x +1. D. 1 2
F(x) = x − x +1. 2 2 Hướng dẫn giảia = 0  f (1) = 2 3
a + 2b + c = 2  Ta có 2
f (x) = F '(x) = 3ax + 2bx + c và    1  f (2) = 3 ⇔ 12
a + 4b + c = 3 ⇔ b  = 2
f (3) 4 27a 6b c 4  = + + =   c =1  Vậy 1 2
F(x) = x + x +1. 2  π
Câu 158. Một nguyên hàm F(x) của hàm số f (x) = tan .xsin 2x thỏa mãn điều kiện F  =   0 là  4  π π A. 1 1
F(x) = x − sin 2x + − . B. 1
F(x) = x + cos 2x + −1. 2 2 4 2 4 π C. 2 3 2
F(x) = cos x + . D. 1
x + sin 2x − . 3 2 2 4 Hướng dẫn giải Ta có 1 1 tan .
x sin 2xdx = (1− cos 2x)dx = x − sin 2x + C ⇒ F(x) = x − sin 2x + C ∫ ∫ 2 2  π  π và 1 F =  0 ⇔ C = −   4  2 4 π Vậy 1 1
F(x) = x − sin 2x + − . 2 2 4
Câu 159. Cho hàm số 2
f (x) = tan x có nguyên hàm là F(x) . Đồ thị hàm số y = F(x) cắt trục tung tại điểm (
A 0;2) . Khi đó F(x) là
A. F(x) = tan x − x + 2 .
B. F(x) = tan x + 2 . C. 1 3
F(x) = tan x + 2.
D. F(x) = cot x − x + 2. 3 Hướng dẫn giải 2
F(x) = f (x)dx = tan xdx = tan x − x + C ∫ ∫ .
Vì đồ thị hàm số y = F(x) đi qua điểm (
A 0;2) nên C = 2 .
Vậy F(x) = tan x − x + 2 .  π
Câu 160. Cho hàm số F(x) là một nguyên hàm của hàm số 2
f (x) = tan x . Giá trị của F  −   F(0) bằng  4  π π π π A. 1− . B. . C. 1+ . D. 3 − . 4 4 4 4 π π
Hướng dẫn giải: F (x) tan x x C F   = − + ⇒ −  F(0) = 1−  .  4  4 Trang 33/34
Document Outline

  • DS_C3_NGUYEN HAM
    • CHỦ ĐỀ 1. NGUYÊN HÀM
    • KIẾN THỨC CƠ BẢN
    • A. KỸ NĂNG CƠ BẢN
    • B. BÀI TẬP TRẮC NGHIỆM

Tài liệu liên quan: