Tóm tắt lý thuyết và bài tập trắc nghiệm sự tương giao giữa hai đồ thị hàm số Toán 12

Tóm tắt lý thuyết và bài tập trắc nghiệm sự tương giao giữa hai đồ thị hàm số Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

27 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Trang 1/28
CHỦ ĐỀ 6. SỰ TƯƠNG GIAO GIỮA HAI ĐỒ THỊ HÀM SỐ
I. SỰ TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VÀ ĐỒ THỊ HÀM SỐ BẬC BA
1. KIẾN THỨC TRỌNG TÂM
Xét hàm số bậc ba
( )
32
0y ax bx cx d a= + ++ ≠
có đồ thị
( )
C
và hàm số bậc nhất
y kx n= +
có đồ thị
d
.
Lập phương trình hoành độ giao điểm của
( )
C
và
d
:
32
(1)ax bx cx d kx n+ + += +
Phương trình
(
)
1
là phương trình bậc ba nên có ít nhất một nghiệm. Ta có 2 trường hợp:
• Trường hợp 1: Phương trình
(
)
1
có “nghiệm đẹp”
.
Thường thì đề hay cho nghiệm
0
0; 1; 2;...
= ±±x
thì khi đó:
(
)
(
)
( )
0
2
0
2
0
(1) 0
0 2
xx
x x Ax Bx C
Ax Bx C
−=
⇔− ++ =⇔
+ +=
Khi đó:
+
( )
C
và
d
có ba giao điểm
⇔
phương trình
( )
1
có ba nghiệm phân biệt
⇔
phương trình
( )
2
có hai nghiệm phân biệt khác nghiệm
0
x
. (Đây là trường hợp thường gặp)
+
( )
C
và
d
có hai giao điểm
⇔
phương trình
( )
1
có hai nghiệm phân biệt
⇔
phương trình
( )
2
có hai nghiệm phân biệt, trong đó có một nghiệm
0
x
hoặc phương trình
( )
2
có nghiệm
kép khác
0
x
.
+
(
)
C
và
d
có một giao điểm
⇔
phương trình
( )
1
có một nghiệm
⇔
phương trình
( )
2
vô
nghiệm hoặc phương trình
( )
2
có nghiệm kép là
.
• Trường hợp 2: Phương trình
(
)
1
không thể nhẩm được “nghiệm đẹp” thì ta biến đổi
phương trình
( )
1
sao cho hạng tử chứa
x
tất cả nằm bên vế trái, các hạng tử chứa tham số
nằm bên vế phải, nghĩa là
(
)
1 () ( )f x gm⇔=
.
Ta khảo sát và vẽ bảng biến thiên hàm số
( )
=y fx
và biện luận số giao điểm của
( )
C
và
d
theo tham số
.
2. CÁC VÍ DỤ
Ví dụ 1: Tìm giao điểm của đồ thị
32
( ): 3 2 1Cyx x x
=− ++
và đường thẳng
1y =
.
Hướng dẫn giải
Phương trình hoành độ giao điểm:
32 32
3211 320xx x xx x−++=⇔−+=
0
1
2
x
x
x
=
⇔=
=
. Vậy có
ba giao điểm
(
) ( )
( )
0;1 , 1;1 , 2;1 .A BC
Ví dụ 2: Cho hàm số
32
28y mx x x m= −−+
có đồ thị là
( )
m
C
. Tìm m đồ thị
( )
m
C
cắt trục
hoành tại ba điểm phân biệt.
Hướng dẫn giải
Phương trình hoành độ giao điểm
32
28 0mx x x m−−+ =
(1)
⇔
( )
2
2 (2 1) 4 0x mx m x m

+ − ++ =

⇔
2
2
(2 1) 4 0 (2)
x
mx m x m
= −
− ++=
( )
m
C
cắt trục hoành tại ba điểm phân biệt
⇔
( )
1
có ba nghiệm phân biệt.
⇔
( )
2
có hai nghiệm phân biệt khác
2−
Trang 2/28
⇔
2
0
12 4 1 0
12 2 0
m
mm
m
≠
∆=− + + >
+≠
⇔
0
11
62
1
6
m
m
m
≠
−< <
≠−
⇔
0
11
62
m
m
≠
−< <
.
Vậy
{ }
11
; \0
62

∈−


m
thỏa yêu cầu bài toán.
Ví dụ 3: Cho hàm số
( )
32
23 11= − +− +
y x mx m x
có đồ thị
( )
C
. Tìm
m
để đường thẳng
:1dy x=−+
cắt đồ thị
(
)
C
tại ba điểm phân biệt.
Hướng dẫn giải
Phương trình hoành độ giao điểm của
( )
C
và
d
:
( )
( )
( )
32 2
2
0
23 11 1 23 0
2 3 0*
=
− + − +=−+⇔ − + = ⇔
− +=
x
x mx m x x x x mx m
x mx m
Yêu cầu bài toán
( )
*⇔
có hai nghiệm phân biệt khác 0
2
9 80
0
mm
m
∆= − >
⇔
≠
( )
8
;0 ;
9

⇔ ∈ −∞ ∪ +∞


m
.
Vậy
( )
8
;0 ;
9

∈ −∞ ∪ +∞


m
thỏa yêu cầu bài toán.
Ví dụ 4: Tìm m để đồ thị hàm số
3
2y x mx=++
cắt trục hoành tại một điểm duy nhất.
Hướng dẫn giải
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là
3
20x mx+ +=
.
Vì
0x =
không là nghiệm của phương trình, nên phương trình tương đương với
( )
2
2
0mx x
x
=−− ≠
Xét hàm số
2
2
()fx x
x
=−−
với
0x ≠
, suy ra
3
22
2 22
'( ) 2
x
fx x
xx
−+
=−+ =
. Vậy
'( ) 0 1fx x=⇔=
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy đồ thị cắt trục hoành tại một điểm duy nhất
3m⇔ >−
. Vậy
3m >−
thỏa yêu cầu bài toán.
Ví dụ 5: Tìm m để đồ thị
( )
C
của hàm số
32
39y x x xm=− −+
cắt trục hoành tại ba điểm
phân biệt.
Hướng dẫn giải
x
−∞
0
1
+∞
( )
fx
′
+
+
0
–
( )
fx
−∞
+∞
−∞
3
−
−∞
Trang 3/28
Phương trình hoành độ giao điểm của đồ thị và trục hoành:
( )
32 32
39 0 39 1xxxm xxxm−−+=⇔−−=−
Phương trình
( )
1
là phương trình hoành độ giao điểm của đường
( )
32
: 39Cyx x x=−−
và
đường thẳng
:
dy m
= −
. Số nghiệm của
( )
1
bằng số giao điểm của
( )
C
và
d
.
Khảo sát và vẽ bảng biến thiên của hàm số
32
39yx x x=−−
.
Tập xác định
D =
.
Đạo hàm
22
3
3 69; 0 3 690
1
x
yxxy xx
x
=
′′
= −− =⇔ −−=⇔
= −
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy
( )
1
có ba nghiệm phân biệt
27 5 5 27mm⇔− <− < ⇔− < <
.
Ví dụ 6: Gọi
d
là đường thẳng đi qua điểm
( )
1; 0−A
với hệ số góc
k
()k ∈
. Tìm
k
để
đường thẳng
d
cắt đồ thị hàm số
( ):C
32
34yx x=−+
tại ba điểm phân biệt
, , ABC
và tam
giác
OBC
có diện tích bằng
1
(O là gốc tọa độ).
Hướng dẫn giải
Đường thẳng
d
đi qua
( 1; 0)A −
và có hệ số góc
k
nên có dạng
( 1)y kx= +
, hay
0
kx y k−+=
.
Phương trình hoành độ giao điểm của
()C
và
d
là:
( )
( )
32 2
2
1
3 4 1 44 0
( ) 4 4 0 (*)
x
x x kx k x x x k
gx x x k
= −
− += +⇔ + − +− =⇔
= − +−=
d
cắt
()C
tại ba điểm phân biệt
⇔
phương trình (*) có hai nghiệm phân biệt khác
1
−
'0 0
( 1) 0 9
k
gk
∆> >

⇔⇔

−≠ ≠

.
Khi đó
() 0 2 ; 2
gx x kx k=⇔=− =+
. Vậy các giao điểm của hai đồ thị lần lượt là
(
)
( )
( 1;0), 2 ;3 , 2 ;3
A B kkkk C kkkk− −− ++
.
Tính được
2
2
2 1 , (, ) (,)
1
k
BC k k d O BC d O d
k
=+==
+
. Khi đó
23
2
1
. .2 . 1 1 1 1 1
2
1
OBC
k
S k k kk k k
k
∆
= + =⇔ =⇔ =⇔=
+
.
Vậy
1k =
thỏa yêu cầu bài toán.
II. SỰ TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VỚI ĐỒ THỊ HÀM SỐ TRÙNG PHƯƠNG
1. KIẾN THỨC TRỌNG TÂM
Cho hàm số
( )
42
0y ax bx c a
=++ ≠
có đồ thị
( )
C
và đường thẳng
yk=
có đồ thị
d
.
Lập phương trình hoành độ giao điểm của
( )
C
và
d
:
( )
42
1ax bx c k+ +=
Đặt
( )
2
0= ≥tx t
ta có phương trình
( )
2
0 2at bt c k+ +−=
x
−∞
1
−
3
+∞
y
′
+
0
−
0
+
y
−∞
5
27−
+∞
Trang 4/28
•
( )
C
và
d
có bốn giao điểm
⇔
(
)
1
có bốn nghiệm phân biệt
⇔
( )
2
có hai nghiệm dương
phân biệt
⇔
phương trình
(
)
2
thỏa
0
0
0
P
S
∆>
>
>
. (Trường hợp này thường gặp)
•
( )
C
và
d
có ba giao điểm
⇔
(
)
1
có ba nghiệm phân biệt
⇔
(
)
2
có hai nghiệm phân biệt,
trong đó có một nghiệm dương và một nghiệm
0
t =
.
•
( )
C
và
d
có hai giao điểm
⇔
( )
1
có hai nghiệm phân biệt
⇔
(
)
2
có nghiệm kép dương
hoặc có hai nghiệm trái dấu.
•
( )
C
và
d
không có giao điểm
⇔
( )
1
vô nghiệm
⇔
( )
2
vô nghiệm hoặc chỉ có nghiệm âm.
•
( )
C
và
d
có một giao điểm
⇔
( )
1
có một nghiệm
⇔
( )
2
có nghiệm
0t
=
và một nghiệm
âm.
2. CÁC VÍ DỤ
Ví dụ 1: Tìm giao điểm của đồ thị
42
( ): 2 3Cyx x=+−
và trục hoành.
Hướng dẫn giải
Phương trình hoành độ giao điểm:
2
42
2
1
2 3 0 1 1.
3
=
+ −=⇔ ⇒ =∨=−
= −
x
xx x x
x
Vậy có hai giao điểm:
(
) (
)
1; 0 , 1; 0 .
AB
−
Ví dụ 2: Tìm
m
để phương trình
42
2 30x xm− − +=
có bốn nghiệm phân biệt.
Hướng dẫn giải
Phương trình:
( )
42 42
2 30 2 3 1
xxm xx m
− − +=⇔ − +=
Phương trình
(
)
1
là phương trình hoành độ giao điểm của hai đường
( )
42
: 23Cyx x=−+
và
đường thẳng
:
dy m=
. Số nghiệm của
( )
1
bằng số giao điểm của
(
)
C
và
d
.
Khảo sát và vẽ bảng biến thiên của hàm số
42
23yx x=−+
.
Tập xác định
D =
.
Đạo hàm
33
0
4 4; 04 40 1
1
=
′′
= − =⇔ −=⇔=
= −
x
yxxy xx x
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy
(
)
1
có bốn nghiệm phân biệt
23
m⇔< <
. Vậy
23m<<
thỏa
yêu cầu bài toán.
Ví dụ 3: Cho hàm số
( ) ( )
4 22
2 1 3 2
m
yx m x m m C=− + +−−
. Định m để đồ thị (C
m
) cắt đường
thẳng
:2dy= −
tại bốn điểm phân biệt.
Lời giải
Phương trình hoành độ giao điểm của
()
m
C
và
d
:
( ) ( ) ( )
4 22 4 22
21 322 21 301x m xm m x m xm m− + +−−=−⇔− + +−=
.
Đặt
( )
2
0= ≥tx t
, phương trình trở thành
( ) ( )
22
2 1 3 0 2− ++−=t m tm m
.
x
–∞
1−
0
1
+∞
–
0
+
0
–
0
+
y
+∞
2
3
3
+∞
Trang 5/28
()
m
C
và
d
có bốn giao điểm
( )
1⇔
có bốn nghiệm phân biệt
(
)
2⇔
có hai nghiệm dương phân
biệt.
( )
2
1
5 10
'0
1
5
0
0 3 0 0, 3
5
3
01
2 10
m
m
m
P mm mm
m
Sm
m
>−
+>
∆>
−< <
⇔ > ⇔ − > ⇔ < >⇔


>
> >−
+>
.
Vậy
( )
1
; 0 3;
5

∈ − ∪ +∞


m
thỏa yêu cầu bài toán.
Ví dụ 4: Cho hàm số
( ) ( )
42
32 3
y x m x mC=−+ +
. Tìm m để đường thẳng
:1dy= −
cắt đồ
thị
()
C
tại bốn điểm phân biệt có hoành độ đều nhỏ hơn 2.
Hướng dẫn giải
Phương trình hoành độ giao điểm của
()C
và
d
:
1y = −
là
(
) (
)
42 42
32 3 1 32 310x m xm x m xm
−+ +=−⇔−+ ++=
.
Đặt
( )
2
0t xt= ≥
, ta có phương trình
(
)
2
1
3 2 3 10
31
t
t m tm
tm
=
− + + += ⇔
= +
Khi đó
2
2
1
31
x
xm
=
= +
. Yêu cầu bài toán
03 14
1
1
3 11
3
m
m
m
< +<
⇔ ⇔− < <
+≠
và
0m ≠
. Vậy
1
1
3
m−< <
và
0
m
≠
thỏa yêu cầu bài toán.
Ví dụ 5: Cho hàm số
( )
4 22
34=−+ +yx m x m
có đồ thị là
( )
m
C
. Tìm m để đồ thị
( )
m
C
cắt
trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng.
Hướng dẫn giải
Phương trình hoành độ giao điểm:
( )
4 22
34 0− + +=
x m xm
( )
1
Đặt
2
tx=
( )
0t ≥
, phương trình
( )
1
trở thành:
( )
22
34 0− ++=t m tm
( )
2
( )
m
C
cắt trục hoành tại bốn điểm phân biệt
⇔
( )
1
có bốn nghiệm phân biệt
⇔
( )
2
có hai nghiệm dương phân biệt
⇔
2
2
5 24 16 0
0
3 40
mm
Pm
Sm
∆= + + >
= >
= +>
⇔
4
4
5
0
4
3
mm
m
m
<− ∨ >−
≠
>−
⇔
4
5
0
m
m
>−
≠
(*)
Khi đó phương trình
( )
2
có hai nghiệm
12
0 tt<<
. Suy ra phương trình
( )
1
có bốn nghiệm
phân biệt là
1 22 13 14 2
x t x tx tx t=− <=− <= <=
. Bốn nghiệm
1234
,,,xxxx
lập thành cấp
số cộng
⇔
21 32 43
xxxxxx−=−=−
⇔
12 1
2tt t−+ =
⇔
21
3tt=
21
9tt⇔=
(3)
Theo định lý Viet ta có
12
2
12
3 4 (4)
(5)
tt m
tt m
+= +
=
Trang 6/28
Từ
( )
3
và
(
)
4
ta suy ra được
( )
1
2
34
10
93 4
10
+
=
+
=
m
t
m
t
( )
6.
Thay
(
)
6
vào
( )
5
ta được
( )
2
2
9
34
100
mm+=
⇔
( )
( )
12
3 3 4 10
12
3 3 4 10
19
m
mm
m
mm
=
+=
⇔
= −
+=−
(thỏa (*))
Vậy giá trị
cần tìm là
12
12; .
19
= = −mm
III. SỰ TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VỚI ĐỒ THỊ HÀM SỐ
ax b
y
cx d
+
=
+
1. KIẾN THỨC TRỌNG TÂM
Cho hàm số
( )
0
ax b
y ad bc
cx d
+
= −≠
+
có đồ thị
()C
và đường thẳng
y kx n= +
có đồ thị
d
.
Lập phương trình hoành độ giao điểm của
()C
và
d
:
( )
2
0 1Ax Bx C
ax b
kx n
d
cx d
x
c
+ +=
+
= +⇔
+
≠−
()C
và
d
có hai giao điểm
⇔
( )
1
có hai nghiệm phân biệt khác
d
c
−
.
2. CÁC VÍ DỤ
Ví dụ 1: Tìm tọa độ giao điểm của đồ thị
()C
:
21
21
x
y
x
+
=
−
và đường thẳng
: 2.dy x= +
Lời giải
Phương trình hoành độ giao điểm:
21
2
21
x
x
x
+
= +
−
( )
1
Điều kiện:
1
2
x
≠
. Khi đó
(1)
⇔
(
)( )
2121 2+= − +x xx
2
2 30xx⇔ +−=
⇔
31
22
13
xy
xy
=−⇒=
=⇒=
Vậy tọa độ giao điểm cần tìm là
31
;
22

−


và
( )
1; 3
.
Ví dụ 2. Cho hàm số
21
1
x
y
x
−
=
−
có đồ thị là
()
C
. Tìm m để đường thẳng
:dy x m=−+
cắt đồ
thị
()
C
tại hai điểm phân biệt.
Lời giải
Phương trình hoành độ giao điểm:
21
1
x
xm
x
−
=−+
−
( )
1
Điều kiện:
1x ≠
. Khi đó
(1)
⇔
( )
( )
21 1−=−+ −
x xmx
⇔
( )
2
1 10− − + −=x m xm
( )
2
d
cắt
()
C
tại hai điểm phân biệt
⇔
( )
1
có hai nghiệm phân biệt
⇔
(2) có hai nghiệm phân biệt khác
1
⇔
( ) ( )
( )
2
1 4 10
1 1 .1 1 0
mm
mm
∆= − − − − >


− − + −≠
Trang 7/28
⇔
2
6 50mm− +>
( ) ( )
;1 5; .⇔ ∈ −∞ ∪ +∞m
Vậy giá trị
cần tìm là
( ) ( )
;1 5; .∈ −∞ ∪ +∞
m
Ví dụ 3: Cho hàm số
1
2
mx
y
x
−
=
+
có đồ thị là
( )
m
C
. Tìm m để đường thẳng
: 21dy x= −
cắt đồ
thị
( )
m
C
tại hai điểm phân biệt
, AB
sao cho
10AB =
.
Lời giải
Phương trình hoành độ giao điểm:
1
21
2
mx
x
x
−
= −
+
( )
1
Điều kiện:
2x
≠−
. Khi đó
(1)
⇔
( )( )
121 2
−= − +
mx x x
⇔
( )
2
2 3 10− − −=xm x
( )
2
d
cắt
( )
m
C
tại hai điểm phân biệt
, AB
⇔
( )
1
có hai nghiệm phân biệt
⇔
(2) có hai nghiệm phân biệt khác
2−
⇔
( )
2
3 80
82 61 0
m
m
∆= − − + >


+ −−≠
⇔
1
2
m ≠−
(*)
Đặt
( ) ( )
11 2 2
;2 1 ; ;2 1−−Ax x Bx x
với
12
,
xx
là hai nghiệm của phương trình
( )
2
.
Theo định lý Viet ta có
12
12
3
2
1
2
m
xx
xx
−
+=
= −
, khi đó
( ) ( )
22
12 12
4 10AB xx xx= −+− =
⇔
( )
2
1 2 12
5 4 10x x xx

+− =

⇔
2
3
22
2
m −

+=


⇔
3m =
(thỏa (*))
Vậy giá trị
cần tìm là
3m =
.
Ví dụ 4: Cho hàm số
21
1
x
y
x
+
=
+
()C
. Tìm m để đường thẳng
:2dy x m=−+
cắt
()C
tại hai
điểm phân biệt
,
AB
sao cho tam giác
OAB
có diện tích là
3
.
Lời giải
Phương trình hoành độ giao điểm của
()C
và
d
:
( )( )
21
2 21 12
1
x
xm x x xm
x
+
=−+⇔ +=+ −+
+
( điều kiện:
1x
≠−
)
( ) ( )
2
2 4 1 0 1⇔ + − +− =x mx m
( điều kiện:
1x
≠−
).
d
cắt
()C
tại hai điểm
, AB
phân biệt
⇔
(1) có hai nghiệm phân biệt khác
1−
.
( ) ( )( )
2
2
8 0
2. 1 4 1 1 0
∆= + > ∀
⇔
− + − − +− ≠
mm
mm
.
Suy ra
d
luôn cắt
()C
tại hai điểm
, AB
phân biệt với mọi m.
Gọi
( ) ( )
11 2 2
; ; ;Ax y Bx y
, trong đó
1 12 2
2 ; 2y x my x m=−+ =−+
và
12
, xx
là các nghiệm của
( )
1
. Theo định lý Viet ta có
12
12
4
2
1
2
m
xx
m
xx
−
+=
−
=
. Tính được:
( )
( ) ( )
( )
( )
2
22 2
1 2 1 2 1 2 12
58
; ; 5 20
2
5
+
= = − +− = + − =
m
m
d O AB AB x x y y x x x x
Trang 8/28
( )
2
8
1
. ; 3 2 2.
24
+
= = = ⇔=∨=−
OAB
mm
S AB d O AB m m
Vậy các giá trị
m
cần tìm là
2; 2.= = −mm
Ví dụ 5: Cho hàm số
21
1
x
y
x
+
=
+
()
C
. Tìm k để đường thẳng
: 21d y kx k=++
cắt
()C
tại hai
điểm phân biệt
, AB
sao cho khoảng các từ
A
và
B
đến trục hoành bằng nhau.
Lời giải
Phương trình hoành độ giao điểm của
()C
và
d
:
( )
(
)
21
2121 1 21
1
x
kx k x x kx k
x
+
= + +⇔ += + + +
+
(điều kiện:
1x ≠−
)
(
) ( )
2
3 1 2 01kx k x k⇔ + − +=
. (điều kiện:
1
x ≠−
)
d
cắt
()C
tại hai điểm
, AB
phân biệt
⇔
(1) có hai nghiệm phân biệt khác
1−
( ) ( )( )
2
2
0
0
6 10
3 22 3 22
1 31 12 0
≠
≠

⇔ ∆= − + > ⇔

<− ∨>+
− + − −+ ≠
k
k
kk
kk
kk k
Khi đó:
( ) (
)
11 2 2
; 21, ; 21++ ++A x kx k B x kx k
với
12
,
xx
là nghiệm của (1).
Theo định lý Viet ta có
12
12
31
2
k
xx
k
xx
−+
+=
=
. Tính được
(
) ( )
12
; ; 21 21= ⇔ ++= ++d A Ox d B Ox kx k kx k
⇔
12
12
21 21
21 21
kx k kx k
kx k kx k
++= ++
+ +=− − −
⇔
( )
( )
12
12
4 20
xx
kx x k
=
+ + +=
loaïi
(
)
12
4 20 3
kx x k k
⇔ + + +=⇔=−
.
Vậy
3
k = −
thỏa yêu cầu bài toán.
A. BÀI TẬP TRẮC NGHIỆM
Câu 1. Số giao điểm của đồ thị hàm số
42
21yx x=−+ −
với trục
Ox
là
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 2. Số giao điểm của đồ thị hàm số
( )
( )
2
3 32=+ ++
yx x x
với trục
Ox
là
A.
1
.
B.
3.
C.
0.
D.
2.
Câu 3. Số giao điểm của đồ thị hàm số
32
2 12yx x x= − +−
và trục
Ox
là
A. 2. B. 1. C. 3. D. 0.
Câu 4. Đường thẳng
1yx
= −
cắt đồ thị hàm số
21
1
x
y
x
−
=
+
tại các điểm có tọa độ là
A.
( )
0; 2 .
B.
( ) ( )
1; 0 ; 2;1 .−
C.
( ) (
)
0; 1 ; 2;1 .−
D.
( )
1; 2 .
Câu 5. Đồ thị
( )
21
:
1
x
Cy
x
−
=
+
cắt đường thẳng
: 23dy x= −
tại các điểm có tọa độ là
A.
(
)
2; 1−
;
( )
1
; 2.
2
−−
B.
( )
2; 1
;
( )
1
; 4.
2
−−
C.
( )
1; 5−−
;
( )
3
;0 .
2
D.
( )
1
; 2.
2
−
Câu 6. Đồ thị hàm số
432
2y xxx= ++
cắt trục hoành tại mấy điểm?
Trang 9/28
A.
2.
B.
3.
C.
1 .
D.
0
.
Câu 7. Cho hàm số
32
231yx x=−+
có đồ thị
()C
và đường thẳng
d
:
1yx= −
. Số giao điểm của
()C
và
d
là
A.
0
. B.
1 .
C.
D.
3.
Câu 8. Số giao điểm của đồ thị hàm số
2
43
2
−+
=
+
xx
y
x
và trục hoành là
A. 0. B.
1 .
C.
D.
2.
Câu 9. Số giao điểm của đồ thị hàm số
( )
( )
2
1 32yx x x=− −+
và trục hoành là
A. 0. B.
1 .
C.
D. 2.
Câu 10. Giao điểm giữa đồ thị
2
23
( ):
1
xx
Cy
x
−−
=
−
và đường thẳng
( )
:1
dyx= +
là
A.
( )
2; 1 .A
−
B.
( )
0; 1 .A −
C.
( )
1; 2 .A
−
D.
( )
1; 0 .A −
Câu 11. Cho hàm số
42
42
yx x=−−
có đồ thị
()C
và đồ thị
()P
:
2
1yx= −
. Số giao điểm của
()P
và
đồ thị
()C
là
A. 1. B. 2. C. 3. D. 4.
Câu 12. Cho hàm số
21
1
x
y
x
−
=
+
có đồ thị
()C
và đường thẳng
: 23dy x= −
. Số giao điểm của
( )
C
và
d
là
A.
2.
B.
1 .
C.
D.
0.
Câu 13. Tọa độ giao điểm giữa đồ thị
21
( ):
2
x
Cy
x
−
=
+
và đường thẳng
:2dy x= −
là
A.
( ) ( )
1; 3 ; 3; 1 .−−AB
B.
( ) ( )
1;1; 0;2.−−AB
C.
( ) ( )
1;3; 0;2.−− −AB
D.
(
)
(
)
1; 1 ; 3; 1 .
−
AB
Câu 14. Cho hàm số
21
1
x
y
x
−
=
+
có đồ thị
()C
và đường thẳng
d
:
23yx= −
. Đường thằng
d
cắt
()C
tại hai điểm A và B. Khi đó hoành độ trung điểm I của đoạn thẳng AB là
A.
=
I
x
4
.
3
B.
= −
I
x
3
.
4
C.
=
I
x
3
.
4
D.
= −
I
x
4
.
3
Câu 15. Tọa độ trung điểm
I
của đoạn thẳng
MN
với
, MN
là giao điểm của đường thẳng
d
:
1yx= +
và đồ thị hàm số
()
C
:
22
1
x
y
x
+
=
−
là
A.
( )
1; 2 .I −−
B.
( )
1; 2 .I −
C.
( )
1; 2 .I −
D.
( )
1; 2 .
I
Câu 16. Gọi
, MN
là hai giao điểm của đường thẳng
:1dy x= +
và
( )
24
:
1
x
Cy
x
+
=
−
. Hoành độ trung
điểm
I
của đoạn thẳng
MN
là
A.
2.
B.
1.
C.
5
.
2
D.
5
.
2
−
Câu 17. Đồ thị hàm số
42
22y xx= −+
cắt đuờng thẳng
6y =
tại bao nhiêu điểm?
A.
2.
B.
0.
C.
4.
D.
3.
Câu 18. Tiệm cận ngang của đồ thị hàm số
2
( ):
1
+
=
+
x
Hy
x
cắt đồ thị hàm số
( )
42
:2Cy x x= −
tại các
điểm có tọa độ là
A.
( ) ( )
1;1 ; 1; 1 .−
B.
( )
1;1 .
C.
( )
1;1 .−
D.
( )
0;1 .
Câu 19. Đồ thị hàm số
32
31yx x=−+
cắt đường thẳng
ym=
tại ba điểm phân biệt thì tất cả các giá trị
tham số
m
thỏa mãn là
Trang 10/28
A.
1 .m >
B.
3 1 .
m−≤ ≤
C.
3 1 .
m−< <
D.
3.m <−
Câu 20. Đường thẳng
ym=
không cắt đồ thị hàm số
42
242y xx
=−+ +
thì tất cả các giá trị tham số
là
A.
4
m >
. B.
4
m ≥
.
C.
2
m ≤
. D.
24m<<
.
Câu 21. Với tất cả giá trị nào của tham số
m
thì phương trình
42
23x xm−=+
có bốn nghiệm phân
biệt?
A.
( )
4; 3 .
m
∈− −
B.
3m = −
hoặc
4.m = −
C.
( )
3; .m ∈ − +∞
D.
( )
; 4.m ∈ −∞ −
Câu 22. Tất cả giá trị của tham số
m
để phương trình
3
3 10x xm− − +=
có ba nghiệm phân biệt là
A.
1 3.m−< <
B.
1 3.m−≤ ≤
C.
1.m
=
D.
1m <−
hoặc
3.m
>
Câu 23. Tất cả giá trị của tham số
m
để đồ thị
(
)
32
: 32Cyx x
=−+
cắt đường thẳng
:dy m=
tại ba
điểm phân biệt là
A.
2 0.m−< <
B.
2 2.m
−< <
C.
0 1.m<<
D.
1 2.m<<
Câu 24. Tất cả giá trị của tham số
để đồ thị
( )
42
: 23Cyx x=−−
cắt đường thẳng
:dy m=
tại bốn
điểm phân biệt là
A.
4 3.
m− < <−
B.
4.m
<−
C.
3.m
>−
D.
7
4.
2
m− < <−
Câu 25. Cho hàm số
42
42yx x=−−
có đồ thị
()C
và đường thẳng
:dy m=
. Tất cả các giá trị của
tham số
m
để
d
cắt
()C
tại bốn điểm phân biệt là
A.
6 2.m− ≤ ≤−
B.
2 6.
m<<
C.
6 2.m− < <−
D.
2 6.
m
≤≤
Câu 26. Tất cả các giá trị của tham số
m
để phương trình
42
30x xm
− +=
có bốn nghiệm phân biệt là
A.
13
1.
4
m<<
B.
9
0.
4
m<<
C.
9
0.
4
m−< <
D.
13
1.
4
m−< <
Câu 27. Cho hàm số
42
2y x xm=−+ +
. Tất cả giá trị của tham số
để đồ thị hàm số đã cho cắt trục
hoành tại ít nhất ba điểm phân biệt là
A.
0 1.m<<
B.
1 0.m−< ≤
C.
1 0.m−< <
D.
1 0.m−≤ <
Câu 28. Cho hàm số
( )
22
( 2) 3y x x mx m=− ++−
. Tất cả giá trị của thma số
để đồ thị hàm số đã cho
cắt trục hoành tại ba điểm phân biệt là
A.
2 1.m− < <−
B.
22
.
1
m
m
−< <
≠−
C.
1 2.m−< <
D.
12
.
1
m
m
−< <
≠
Câu 29. Tất cả giá trị của tham số
m
để phương trình
42
2 30
x xm− − +=
có bốn nghiệm phân biệt là
A.
2 3.m<<
B.
2 3.m≤≤
C.
2.m ≥
D.
2.m >
Câu 30. Tất cả giá trị của tham số
m
để phương trình
42
2 30x xm− − +=
có hai nghiệm phân biệt là
A.
3.m >
B.
3.m ≥
C.
3m >
hoặc
2.m =
D.
3m =
hoặc
2.m =
Câu 31. Tất cả giá trị của tham số
m
để đồ thị hàm số
42
221=−+ +y xx
cắt đường thẳng
3ym=
tại
ba điểm phân biệt là
A.
11
.
32
m≤≤
B.
1
.
2
m =
C.
1
.
3
m ≤
D.
1
.
3
m =
Câu 32. Tất cả giá trị của tham số
m
để đồ thị hàm số
( )
32
: 2 3 21Cy x x m=−+ +−
cắt trục hoành tại
ba điểm phân biệt là
A.
11
.
42
m≤<
B.
11
.
22
m−< <
C.
1
0.
2
m<<
D.
1
0.
2
m≤≤
Trang 11/28
Câu 33. Tìm tất cả các giá trị của tham số m để phương trình
32
34 0xx m− ++ =
có nghiệm duy nhất lớn hơn
2
.
Biết rằng đồ thị của hàm số
32
34yx x=−+ −
là hình
bên.
A.
0.m >
B.
4.m ≤−
C.
4.m <−
D.
4m
≤−
hoặc
0.
m ≥
Câu 34. Tất cả giá trị của thm số
m
để phương trình
3
3 10x xm− − +=
có ba nghiệm phân biệt, trong
đó có hai nghiệm dương là
A.
1 1.m−≤ ≤
B.
1 1.m−< ≤
C.
1 3.m−< <
D.
1 1.m−< <
Câu 35. Cho hàm số
32
231y xx=−+ −
có đồ thị
( )
C
như hình vẽ. Dùng
đồ thị
(
)
C
suy ra tất cả giá trị tham số
m
để phương trình
32
2320xxm−+=
( )
1
có ba nghiệm phân biệt là
A.
1
0
2
m<<
. B.
10m−< <
.
C.
01m≤ ≤−
. D.
10m−≤ ≤
.
Câu 36. Cho phương trình
32
31 0xx m− +− =
(1)
. Điều kiện của tham số
m
để
(1)
có ba nghiệm phân
biệt thỏa
1 23
1x xx<< <
khi
A.
1.m = −
B.
1 3.
m
−< <
C.
3 1.m− < <−
D.
3 1.m− ≤ ≤−
Câu 37. Cho hàm số
32
231yx x=−+
có đồ thị
()
C
và đường thẳng
:1dy x= −
. Giao điểm của
()C
và
d
lần lượt là
( )
1; 0
A
,
B
và
C
. Khi đó khoảng cách giữa
B
và
C
là
A.
30
.
2
BC =
B.
34
.
2
BC =
C.
32
.
2
BC =
D.
14
.
2
BC =
Câu 38. Cho hàm số
21
1
x
y
x
−
=
+
có đồ thị
()
C
và đường thẳng
d
:
23yx= −
. Đường thằng
d
cắt
()C
tại hai điểm
A
và
B
. Khoảng cách giữa
A
và
B
là
A.
2
.
5
AB =
B.
5
.
2
AB
=
C.
25
.
5
AB =
D.
55
.
2
AB =
Câu 39. Cho hàm số
21
1
x
y
x
−
=
+
có đồ thị
()C
và đường thẳng
d
:
2y xm= −
. Đường thằng
d
cắt
()C
tại hai điểm
A
và
B
khi giá trị của tham số
thỏa
A.
4 26 4 26.m−− ≤ ≤−+
B.
4 26m ≤− −
hoặc
4 26m
≥− +
.
C.
4 26 4 26.
m−− < <−+
D.
4 26
m <− −
hoặc
4 26
m >− +
.
Câu 40. Cho hàm số
( )
:
1
x
Cy
x
=
−
và đường thẳng
:
dy x m= +
. Tập tất cả các giá trị của tham số m
sao cho
( )
C
và
d
cắt nhau tại hai điểm phân biệt là
A.
( )
2; 2−
. B.
( ) ( )
; 2 2;∞∪
−− +∞
.
C.
.
D.
Câu 41. Tập tất cả các giá trị của tham số
m
để đường thẳng
2
:dy x m= +
cắt đồ thị hàm số
( )
3
:4Cy x x=−+
tại ba điểm phân biệt là
A.
(
)
1;1−
.
B.
(
]
;1−∞
. C.
.
D.
( )
2; 2−
.
Câu 42. Tất cả giá trị tham số
m
để đồ thị
( )
4
:Cyx=
cắt đồ thị
( )
( )
22
: 34Py m x m=+−
tại bốn điểm
phân biệt là
2
2
-1
O
Trang 12/28
A.
(
)
(
)
(
)
5
; 4 ; 0 0;
4
m
∈ −∞ − ∪ − ∪ +∞
. B.
(
) ( )
1; 0 0;
m
∈ − ∪ +∞
.
C.
( )
(
)
4
; 0 0;
5
m∈ − ∪ +∞
. D.
{ }
\ 0.m∈
Câu 43. Cho đồ thị
( )
32
:231Cy x x=−−
. Gọi
d
là đường thẳng qua
(
)
0; 1
A
−
có hệ số góc bằng
k
.
Tất cả giá trị
k
để
( )
C
cắt
d
tại ba điểm phân biệt là
A.
9
.
8
0
k
k
<
≠
B.
9
.
8
0
k
k
>−
≠
C.
9
.
8
0
k
k
<−
≠
D.
9
.
8
0
k
k
>
≠
Câu 44. Cho hàm số
32
34yx x=−+
có đồ thị
( )
C
. Gọi
d
là đường thẳng qua
( )
1; 2I
với hệ số góc
k
.
Tập tất cả các giá trị của
k
để
d
cắt
( )
C
tại ba điểm phân biệt I, A, B sao cho I là trung điểm
của đoạn thẳng AB là
A.
{ }
0
. B.
. C.
{ }
3−
. D.
( )
3;−+∞
.
Câu 45. Với những giá trị nào của tham số m thì
( ) ( )
( )
( )
3 22
: 3 1 2 41 4 1
m
C y x m x m m x mm=− + + ++− +
cắt trục hoành tại ba điểm phân biệt
có hoành độ lớn hơn 1?
A.
1
1.
2
m
<≠
B.
1
.
2
m
>
C.
1
.
2
m ≥
D.
1.
m ≠
Câu 46. Cho đồ thị
3
( ): 4 3 1Cy x x
= −+
và đường thẳng
( )
: 12d y mx= −+
. Tất cả giá trị tham số
m
để
()C
cắt
d
tại một điểm là
A.
9.m =
B.
0.m ≤
C.
0m ≤
hoặc
9.m =
D.
0.m <
Câu 47. Cho hàm số
21
1
x
y
x
+
=
+
có đồ thị
()C
và đường thẳng
d
:
y xm= +
. Giá trị của tham số m để
d
cắt
()C
tại hai điểm phân biệt
,AB
sao cho
10AB =
là
A.
0m =
hoặc
6.m =
B.
0.m =
C.
6.m =
D.
0 6.
m
≤≤
Câu 48. Cho hàm số
21
1
x
y
x
+
=
+
có đồ thị
()C
và
:dy x m= +
. Giá trị của tham số
m
để
d
cắt
()C
tại
hai điểm phân biệt
A
,
B
sao cho tiếp tuyến tại
A
và
B
song song với nhau.
A. Không tồn tại. B.
0.m =
C.
3.m = −
D.
3.m =
Câu 49. Cho
( )
22
:2Py x xm
=−−
và
: 21dy x= +
. Giả sử
( )
P
cắt
d
tại hai điểm phân biệt
,AB
thì
tọa độ trung điểm
I
của đoạn thẳng
AB
là
A.
( )
2
2;
Im
−
. B.
( )
2
1; 1Im−−
. C.
( )
1; 3I
. D.
( )
2; 5I
.
Câu 50. Giá trị nào của tham số m để đồ thị
( ) ( )
32
:1
m
C ym xxm= − +−
chỉ có một điểm chung với
trục hoành?
A.
1.m =
B.
0m <
hoặc
4
.
3
m
>
C.
0.m
<
D.
4
.
3
m >
Câu 51. Cho hàm số
32
31
yx x m= − −−
có đồ thị
()C
. Giá trị của tham số
để đồ thị
()C
cắt trục
hoành tại ba điểm phân biệt lập thành cấp số cộng là
A.
0.m =
B.
3.m =
C.
3.m = −
D.
6.m = ±
Câu 52. Cho hàm số
21
1
x
y
x
+
=
−
có đồ thị
()C
và đường thẳng
:dy x m= +
. Đường thẳng
()d
cắt đồ
thị
()C
tại hai điểm
A
và
B
. Với
( 2; 5)C −
, giá trị của tham số
m
để tam giác
ABC
đều là
Trang 13/28
A.
1.m
=
B.
1
m =
hoặc
5.m =
C.
5.m
=
D.
5.m = −
Câu 53. Cho hàm số
(
)
42
21 2yx m x m=−−+
có đồ thị
()C
. Tất cả các giá trị của tham số
để đường
thẳng
d
:
2y =
cắt đồ thị
()
C
tại bốn điểm phân biệt đều có hoành độ lớn hơn
3
là
A.
3
.
2
m ≠
B.
11
1.
2
m
<<
C.
3
.
2
12
m
m
≠
<<
D.
3
2
.
11
1
2
m
m
≠
<<
Câu 54. Cho hàm số:
32
2 3( 1) 2y x mx m x=+ + −+
có đồ thị
()C
. Đường thẳng
:2
dy x
=−+
cắt đồ thị
()C
tại ba điểm phân biệt
(
)
0; 2 ,
AB−
và
C
. Với
(3;1)M
, giá trị của tham số
để tam giác
MBC
có diện tích bằng
27
là
A.
1.m = −
B.
1m = −
hoặc
4.m =
C.
4.m =
D. Không tồn tại
.m
Câu 55. Cho đồ thị
(
)
( )
32
: 21
m
C y x x mx m
= − +− +
. Tất cả giá trị của tham số
m
để
( )
m
C
cắt trục
hoành tại ba điểm phân biệt có hoành độ
123
,,xxx
thỏa
222
1 23
4xxx++=
là
A.
1.m =
B.
0.
m ≠
C.
2.
m =
D.
1
4
m >−
và
0.m
≠
Câu 56. Cho hàm số
32
12
:
33
y x mx x m= − −+ +
có đồ thị
( )
m
C
. Tất cả các giá trị của tham số m để
( )
m
C
cắt trục
Ox
tại ba điểm phân biệt có hoành độ
123
, , xxx
thỏa
222
1 23
15xxx
++>
là
A.
1m >
hoặc
1.m <−
B.
1m <−
. C.
0m >
. D.
1m >
.
Câu 57. Cho đồ thị
( )
2
1
:
1
xx
Cy
x
−+
=
−
và đường thẳng
:dy m=
. Tất cả các giá trị tham số
m
để
( )
C
cắt
d
tại hai điểm phân biệt
A
,
B
sao cho
2AB
=
là
A.
1 6.m = +
B.
16m = −
hoặc
1 6.m = +
C.
1 6.
m = −
D.
1m <
hoặc
3
m >
.
B. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM
I – ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
C
B
B
C
B
C
D
D
D
D
B
A
A
C
D
B
A
A
C
A
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
A
A
B
A
C
B
B
B
A
C
D
C
C
D
A
C
B
D
D
C
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
D
C
B
D
A
D
A
A
D
B
C
B
D
B
A
A
B
II –HƯỚNG DẪN GIẢI
Câu 1. Chọn C.
Phương trình hoành độ giao điểm:
42
2 10
xx− + −=
⇔
2
1x =
⇔
1 1.xx=∨=−
Vậy số giao điểm là
2
.
Câu 2. Chọn B.
Giải phương trình
( )
( )
2
1
3 320 2
3
x
x xx x
x
= −
+ ++=⇔ =−
= −
Vậy số giao điểm là
3
.
Câu 3. Chọn B.
Trang 14/28
Lập phương trình hoành độ giao điểm:
32
2 12 0x xx− +− =
3x
⇔=
Vậy có một giao điểm duy nhất.
Câu 4. Chọn C.
Lập phương trình hoành độ giao điểm
2
21
1 20 0 2
1
x
x xx x x
x
−
= −⇔ − = ⇔ = ∨ =
+
.
Thế vào phương trình
1yx= −
được tung độ tương ứng
1
1
y
y
= −
=
.
Vậy chọn
( )
( )
0; 1 , 2;1 .
−
Câu 5. Chọn B.
Phương trình hoành độ giao điểm:
21
23
1
x
x
x
−
= −
+
⇔
2
1
2 3 20
x
xx
≠−
− −=
⇔
2
1
2
x
x
=
= −
Thế vào phương trình
23
x
−
được tung độ tương ứng:
1
4
y
y
=
= −
.
Vậy chọn
( )
(
)
1
2; 1 ; 4
2
−− vaø
.
Câu 6. Chọn C.
Phương trình hoành độ giao điểm
432 22
2
0
2 0 ( 2 1) 0
2 1 0( )
x
xxx xxx
x x VN
=
+ + =⇔ ++ =⇔
++=
Vậy đồ thị hàm số cắt trục hoành tại một điểm.
Câu 7. Chọn D.
Phương trình hoành độ giao điểm
( )
( )
32 32 2
1
1 17
231 123 20 12 20
4
1 17
4
x
x x x x xx x xx x
x
=
−
− +=−⇔ − −+=⇔ − −− =⇔ =
+
=
Vậy số giao điểm là 3.
Câu 8. Chọn D
Phương trình hoành độ giao điểm
2
1
43
0
3
2
x
xx
x
x
=
−+
= ⇔
=
+
.
Vậy số giao điểm là
2
.
Câu 9. Chọn D.
Phương trình hoành độ giao điểm
( )
( )
2
1
1 320
2
x
x xx
x
=
− −+=⇔
=
.
Vậy số giao điểm là
2
.
Câu 10. Chọn D.
Lập phương trình hoành độ giao điểm
2
23
1 10
1
xx
xx y
x
−−
= +⇔ =−⇒ =
−
.
Vậy chọn
( )
1; 0−
.
Câu 11. Chọn B.
Phương trình hoành độ giao điểm:
Trang 15/28
2
42 2 42
2
3 21 3 21 3 21
222
4 2 1 3 30
3 21
0
2
x xx
xx x xx
x
+++
= ⇔= ∨=−
− − =− +⇔ − −= ⇔
−
= <
Vậy số giao điểm là 2.
Câu 12. Chọn A.
Phương trình hoành độ giao điểm:
2
2
1
21
23 .
1
1
2 3 20
2
x
x
x
x
x
x
xx
=
≠−
−
= −⇔ ⇔
+
= −
− −=
Vậy số giao điểm là 2.
Câu 13. Chọn A.
Lập phương trình hoành độ giao điểm
31
21
2
13
2
xy
x
x
xy
x
=⇒=
−
=−⇔
=−⇒ =−
+
.
Vậy chọn
( )
( )
1; 3 , 3; 1 .AB−−
Câu 14. Chọn C
Phương trình hoành độ giao điểm:
2
2
21 3
23 .
1
1 24
2 3 20
1
2
AB
I
x
x
xx
x
xx
x
x
xx
=
+
−
= −⇔ ⇔ ⇒ = =
+
= −
− −=
≠−
Câu 15. Chọn D.
Lập phương trình hoành độ giao điểm
( )
34
22
1 1; 2 .
10
1
xy
x
xI
xy
x
=⇒=
+
= +⇔ ⇒
=−⇒ =
−
Vậy chọn
( )
1; 2 .I
Câu 16. Chọn B.
Lập phương trình hoành độ giao điểm
16
24
1 1.
1
16
I
x
x
xx
x
x
= +
+
= +⇔ ⇒ =
−
= −
Câu 17. Chọn A.
Lập phương trình hoành độ giao điểm:
2
42
2
1 33
1 33 1 33
4
2 26 .
44
1 33
4
x
xx x x
x
+
=
++
− +=⇔ ⇒= ∨=−
−
=
Vậy số giao điểm là 2.
Câu 18. Chọn A.
Tiệm cận ngang của đồ thị hàm số
(
)
'C
là
1.y =
Phương trình hoành độ giao điểm
42 2
1
2 1 1 1.
1
x
xx x y
x
=
− =⇔ =⇔ ⇒=
= −
Vậy chọn
( ) ( )
1;1 , 1;1 .−
Câu 19. Chọn C.
Lập phương trình hoành độ giao điểm:
32
31xx m− +=
Ta có:
2
'3 6yxx= −
;
' 0 0 2.y xx=⇔=∨=
Bảng biến thiên:
Trang 16/28
Do đó, đồ thị cắt đường thẳng
ym=
tại ba điểm phân biệt khi
3 1 m−< <
.
Vậy chọn
31m−< <
.
Câu 20. Chọn A.
Lập phương trình hoành độ giao điểm:
42
242xx m− + +=
Ta có:
3
'8 8
y xx
=−+
;
' 0 0 1 1.y x xx=⇔=∨=∨=−
Bảng biến thiên:
Do đó, đường thẳng
ym=
không cắt đồ thị hàm số khi
4m
>
.
Vậy chọn
4m >
.
Câu 21. Chọn A.
Ta khảo sát hàm số
( )
42
:2Cyx x= −
tìm được
1, 0
CT
yy
=−=
C§
.
Yêu cầu bài toán
1 30 4 3mm⇔− < + < ⇔− < <−
.
Vậy chọn
( )
4; 3m ∈− −
.
Câu 22. Chọn A.
Phương pháp tự luận:
Ta khảo sát hàm số
( )
3
: 31Cyx x=−+
tìm được
3, 1.
CT
yy= = −
C§
Yêu cầu bài toán
13m⇔− < <
. Vậy chọn
1 3.m−< <
Phương pháp trắc nghiệm: Ta kiểm tra trực tiếp đáp án
+Với
2,m
=
giải phương trình
3
3 10xx− −=
ta bấm máy được ba nghiệm
⇒
loại C, D.
+Với
1m
= −
, giải phương trình
3
3 20
xx− +=
ta bấm máy được hai nghiệm
⇒
loại B.
Vậy chọn
13m−< <
Câu 23. Chọn B.
Bảng biến thiên:
Đường thẳng
:dy m=
cắt
( )
C
tại ba điểm phân biệt khi:
22m−< <
.
Vậy chọn
22
m−< <
.
Câu 24. Chọn A.
Bảng biến thiên
x
–∞
1−
0
1
+∞
y
′
+
0
–
0
+
0
–
y
−∞
4
2
4
−∞
x
−∞
0
2
+∞
y'
+
0
−
0
+
y
−∞
1
3−
+∞
x
−∞
0
2
+∞
y'
+
0
−
0
+
y
−∞
2
2−
+∞
Trang 17/28
Đường thẳng
:dy m=
cắt
( )
C
tại bốn điểm phân biệt khi
43
m− < <−
.
Vậy chọn
43m− < <−
Câu 25. Chọn C.
Xét hàm số
42
42
yx x
=−−
Tính
3
'4 8yxx= −
Cho
3
02
'0 4 8 0 2 6
26
xy
y xx x y
xy
=⇒=−
=⇔ − =⇔ = ⇒=−
=− ⇒=−
.
Bảng biến thiên:
Dựa vào bảng biến thiên suy ra
62m− < <−
.
Vậy chọn
62
m− < <−
.
Câu 26. Chọn B.
Phương trình ⇔
42
3mx x
=−+
. Đặt
( )
42
:3Cy x x
=−+
và
:dy m=
Xét hàm số
42
3yx x=−+
. Ta có
3
'4 6
y xx=−+
;
66
'0 0 .
22
y xx x=⇔=∨= ∨=−
Bảng biến thiên:
Phương trình có bốn nghiệm phân biệt ⇔
d
cắt
(
)
C
tại bốn điểm phân biệt ⇔
9
0
4
m<<
.
Vậy chọn
9
0
4
m<<
.
Câu 27. Chọn B.
Phương trình hoành độ giao điểm:
42
20x xm−+ +=
⇔
42
2
mx x= −
.
Đặt
( )
42
:2Cyx x= −
và
:dy m=
Xét hàm số
42
2yx x= −
.
Ta có
3
'4 4yxx= −
;
' 0 0 1 1.y xx x= ⇔ = ∨ =−∨ =
Bảng biến thiên:
x
'
y
y
−∞
+∞
0
2
0
0
6−
−
+
+
+∞
2
−
0
−
2−
6−
+∞
x
–∞
1−
0
1
+∞
y
′
–
0
+
0
–
0
+
y
+∞
4
−
3−
4−
+∞
x –∞
6
2
−
0
6
2
+∞
y
′
+
0
–
0
+
0
–
y
−∞
9
4
0
9
4
−∞
Trang 18/28
Đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt khi
10m−< ≤
.
Vậy chọn
10m−< ≤
.
Câu 28. Chọn B.
Phương trình hoành độ giao điểm:
( )
( )
22
2 3 0 (1)x x mx m− + + −=
⇔
22
2
3 0 (2)
x
x mx m
=
+ + −=
Để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt ⇔ Phương trình
( )
1
có ba
nghiệm phân biệt ⇔ Phương trình
( )
2
có hai nghiệm phân biệt khác
2
⇔
2
0
42 30mm
∆>
+ + −≠
⇔
2
2
3 12 0
2 10
m
mm
− +>
+ +≠
⇔
22
1
m
m
−< <
≠−
. Vậy chọn
22
1
m
m
−< <
≠−
.
Câu 29. Chọn A.
Tương tự ta khảo sát hàm số
( )
42
: 23Cyx x=−+
ta tìm được
2, 3
CT CD
yy= =
.
Yêu cầu bài toán
23m⇔< <
. Vậy chọn
23m<<
.
Câu 30. Chọn C.
Phương pháp tự luận:
Tương tự ta khảo sát hàm số
( )
42
: 23Cyx x=−+
ta tìm được
2, 3
CT CD
yy
= =
.
Yêu cầu bài toán
23mm⇔=∨>
. Vậy chọn
23mm=∨>
.
Phương pháp trắc nghiệm:
+Với
3,m =
ta giải phương trình
42
20 0 2 2xx x x x− =⇔=∨= ∨=− ⇒
loại B, D.
+Với
2,m =
ta giải phương trình
42
21011xx x x− += ⇔ =∨ =−⇒
loại A.
Câu 31. Chọn D.
Phương pháp tự luận:
Khảo sát hàm số
( )
42
: 221Cy x x=−+ +
tìm được
3
1,
2
CT
yy= =
C§
.
Yêu cầu bài toán
1
31
3
mm⇔ =⇔=
. Vậy chọn
1
3
m
=
.
Phương pháp trắc nghiệm:
+ Với
1
2
m =
, ta giải phương trình
42
1 22
22 0
2 22
xx x x− + −=⇔= ∨=− ⇒
loại B, A.
+ Với
0m =
, ta giải phương trình
2
42
2
13
13 13
2
2 2 10
22
13
2
x
xx x x
x
+
=
++
− + += ⇔ ⇔ = ∨ =−
−
=
⇒
loại C.
Vậy chọn
1
.
3
m =
Câu 32. Chọn C.
Phương pháp tự luận:
x
–∞
1−
0
1
+∞
y
′
–
0
+
0
–
0
+
y
+∞
1
−
0
1
−
+∞
Trang 19/28
Phương trình hoành độ giao điểm của
()C
và trục
Ox
:
32
2 3 2 10
xxm
− + + −=
. Ta khảo sát
hàm số
( )
32
': 2 3 1Cy x x=−+
và cũng chỉ là tìm
,
CD CT
yy
. Cụ thể
1, 0
CD CT
yy= =
. Do đó yêu
cầu bài toán
1
02 1 0
2
mm⇔< <⇔< <
. Vậy chọn
1
0
2
m<<
Phương pháp trắc nghiệm:
+ Với
0,
m
=
ta có phương trình
32
1
2 3 10
2
1
x
xx
x
−
=
− + −= ⇔
=
⇒
loại B, D.
+ Với
0.1
m
=
, ta có phương trình
32
2 3 0.8 0xx−+ −=
có 3 nghiệm
⇒
loại C.
Câu 33. Chọn C.
Ta có
(
)
32
3 4 0 * .xx m
− ++ =
Xem phương trình (*) là phương trình hoành độ giao điểm của
đồ thị hàm số
()C
:
32
34yx x=−+ −
và đường thẳng
d
:
ym=
. Số giao điểm của
()C
và
d
là
số nghiệm của (*). Dựa vào đồ thị hàm số, yêu cầu bài toán
⇔
4m <−
. Vậy chọn
4m <−
.
Câu 34. Chọn D.
Phương pháp tự luận:
Ta có đồ thị của hàm số
3
31yx x=−+
như hình bên.
Dựa vào đồ thị ta tìm được kết quả để đồ thị cắt hàm số tại ba điểm phân biệt là
1 3.m−< <
Với
01xy
=⇒=
nên yêu cầu bài toán
11m⇔− < <
. Vậy chọn
1 1.m−< <
Phương pháp trắc nghiệm: Xét
1
m =
, ta được phương trình
3
0
30
3
x
xx
x
=
−=⇔
= ±
không đủ hai nghiệm dương
⇒
loại A, B, C. Vậy
chọn
1 1.m
−< <
Câu 35. Chọn A.
Phương trình
( )
1
⇔
32
2 3 12 1xx m− + −= −
là phương
trình hoành độ giao điểm của đồ thị
(
)
C
và
: 21dy m
= −
(là đường thẳng song song hoặc trùng
với
Ox
).
Phương trình có ba nghiệm phân biệt ⇔
(
)
C
cắt
d
tại
ba điểm phân biệt ⇔
12 10
m−< −<
⇔
1
0
2
m<<
.
Vậy chọn
1
0
2
m<<
.
Câu 36. Chọn C.
Phương pháp tự luận
Ta có
32
31 0xx m− +− =
là phương trình hoành độ giao điểm giữa hai đồ thị hàm số
32
31yx x=−+
và
ym
=
(là đường thẳng song song hoặc trùng với
Ox
).
Xét
32
31yx x=−+
. Tập xác định:
.D =
Tính
2
' 3 6.yxx= −
Ta có
2
'0 3 6 0y xx=⇔ −=
01
23
xy
xy
=⇒=
⇔
=⇒=−
.
Ta có
11xy=⇒=−
Dựa vào đồ thị, số nghiệm của phương trình
(1)
chính là số giao điểm của đồ thị
32
31yx x=−+
và đường thẳng
ym=
.
Trang 20/28
Do đó, yêu cầu bài toán
31m⇔− < <−
.
Phương pháp trắc nghiệm
Chọn
2
m
=
thay vào
(1)
tìm nghiệm bằng máy tính. Ta nhận thấy
(1)
chỉ có một nghiệm. Suy
ra loại được đáp án B.
Tiếp tục thử
1m = −
thay vào
(1)
tìm nghiệm bằng máy tính. Ta nhận thấy
(1)
có ba nghiệm
nhưng có một nghiệm bằng 1. Suy ra loại A.
Tiếp tục thử
2m = −
thay vào
(1)
tìm nghiệm bằng máy tính. Ta nhận thấy
(1)
có ba nghiệm
thỏa yêu cầu bài toán. Suy ra loại D.
Vậy C là đáp án cần tìm.
Câu 37. Chọn B.
Phương pháp tự luận
Phương trình hoành độ giao điểm của đồ thị
()C
và đường thẳng
d
32 32
231 123 20xx x xxx−+=−⇔−−+=
2
2
1
( 1)(2 2) 0
2 2 0 (1)
x
x xx
xx
=
⇔ − −− =⇔
−−=
Khi đó ta có
11
(1; 0) , ( ; 1)A Bx x−
và
22
( ; 1)
Cx x
−
(
12
,xx
là nghiệm của (1))
Ta có
2121
(; )BC xxxx=−−

, suy ra
22 2 2
21 21 21 21 12
1 34
()()2()2()4 24
42
BC xx xx xx xx xx

= −+−= −= +− = +=


.
Vậy chọn B.
Phương pháp trắc nghiệm
Phương trình hoành độ giao điểm
32 32
231 123 20xx x xxx
−+=−⇔−−+=
.
- Nhập máy tính tìm nghiệm phương trình bậc ba.
- Gán hai nghiệm khác 1 vào
B
và
C
.
- Nhập máy
1X −
. Dùng lệnh CALC tìm tung độ của điểm
B
và
C
gán vào hai biến
D
và
E
.
Khi đó
22
34
( )( )
2
BC C B E D= − +− =
.
Vậy chọn B.
Câu 38. Chọn D.
Phương pháp tự luận
Phương trình hoành độ giao điểm của đồ thị
()C
và đường thẳng
d
2
2 1 (2;1)
21
23
11
1
4 ; 4
2 3 20
22
1
xy A
x
x
x
x
xy B
xx
=⇒= ⇒
−
= −⇔ ⇔

+
=−⇒=−⇒ −−
− −=


≠−
Ta có
5
;5
2
AB

=−−



. Suy ra
55
2
AB =
. Vậy chọn
55
2
AB =
.
Phương pháp trắc nghiệm
Phương trình hoành độ giao điểm:
21
2 3 ( 1)
1
x
xx
x
−
= − ≠−
+
.
Dùng lệnh CALC của máy tính, ta tìm được hai nghiệm của phương trình lần lượt là
2x
=
và
1
2
x = −
. Suy ra
(2;1)
A
và
1
;4
2
B

−−


. Dùng máy tính thu được
55
2
AB =
.
Vậy chọn
55
2
AB =
.
Câu 39. Chọn D.
Phương pháp tự luận
Phương trình hoành độ giao điểm của đồ thị
()C
và đường thẳng
d
:
Trang 21/28
2
21
2 ( 1) 2 1 0 (1)
1
x
x m x x mx m
x
−
= − ≠− ⇔ − + − =
+
Yêu cầu bài toán
⇔
(1)
có hai nghiệm phân biệt khác
1−
2
8(1 ) 0
4 26 4 26
21 0
mm
mm
mm
∆= − − >
⇔ ⇔ <− − ∨ >− +
+ +− ≠
.
Vậy chọn
4 26m <− −
hoặc
4 26
m >− +
.
Phương pháp trắc nghiệm
Phương trình hoành độ giao điểm của đồ thị
()C
và đường thẳng
d
:
2
21
2 ( 1) 2 1 0 (1)
1
x
x m x x mx m
x
−
= − ≠− ⇔ − + − =
+
Chọn
0m =
thay vào
(1)
tìm nghiệm bằng máy tính, ta nhận thấy
(1)
vô nghiệm. Suy ra loại
được A và C.
Tiếp tục chọn
4 26m =−+
thay vào
(1)
tìm nghiệm bằng máy tính, ta nhận thấy
(1)
có
nghiệm kép. Suy ra loại B.
Vậy chọn
4 26
m <− −
hoặc
4 26m
>− +
.
Câu 40. Chọn C.
Phương trình hoành độ giao điểm của đồ thị
()C
và đường thẳng
d
:
( ) ( )
2
2 01
1
x
xm x m xm
x
=+⇔ + − −=
−
( )
C
cắt
d
tại hai điểm phân biệt
( )
1⇔
có hai nghiệm phân biệt
2
0 40m⇔∆> ⇔ + >
(đúng với mọi m).
Vậy chọn
.
Câu 41. Chọn D.
Phương pháp tự luận:
Phương trình hoành độ giao điểm của đồ thị
()C
và
đường thẳng
d
:
3 23 2
43
x x xm x xm−+ =+ ⇔−+ =
Ta khảo sát hàm số
( )
3
:3Cy x x=−+
có đồ thị sau
như hình bên.
Tìm được
2, 2
CT
yy=−=
C§
nên yêu cầu bài toán
2
2 22 2mm⇔− < < ⇔− < <
.
Vậy chọn
2 2.m
− <<
Phương pháp trắc nghiệm:
+ Với
3,m = −
ta có phương trình
3
3 90xx− + −=
, bấm máy tính ta chỉ tìm được một nghiệm
⇒
loại B, C.
+ Với
1.4,
m =
ta có phương trình
32
3 1, 4 0xx−+ − =
, bấm máy tính ta ra được ba nghiệm
⇒
loại A.
Vậy chọn
22m− <<
.
Câu 42. Chọn C.
Phương trình hoành độ giao điểm của
( )
C
và
( )
P
là:
( )
4 22
34x m xm=+−
⇔
( )
4 22
34 0x m xm− + +=
(1)
.
( )
C
cắt
( )
P
tại bốn điểm phân biệt ⇔ Phương trình
( )
1
có bốn nghiệm phân biệt
⇔
0
0
0
P
S
∆>
>
>
⇔
2
2
5 24 16 0
0
3 40
mm
m
m
+ +>
>
+>
⇔
4
4
5
0
4
3
mm
m
m
<− ∨ >−
≠
>−
⇔
4
5
0
m
m
>−
≠
.
Trang 22/28
Vậy chọn
4
5
0
m
m
>−
≠
.
Câu 43. Chọn B.
Phương trình đường thẳng
:1d y kx
= −
.
Phương trình hoành độ giao điểm của đồ thị
()C
và đường thẳng
d
:
32
231 1x x kx− −= −
⇔
( )
2
23 0x x xk−−=
⇔
2
0 (1)
2 3 (2)
x
x xk
=
−−
( )
C
cắt
d
tại ba điểm phân biệt
⇔
Phương trình
(
)
2
có hai nghiệm phân biệt khác
0
⇔
0
00
k
∆>
−≠
⇔
9
8
0
k
k
>−
≠
.
Vậy chọn
9
8
0
k
k
>−
≠
.
Câu 44. Chọn D.
Phương pháp tự luận:
Phương trình
( )
: 12d y kx= −+
.
Phương trình hoành độ giao điểm của đồ thị
()
C
và đường thẳng
d
:
32
34 2x x kx k
− += −+
( )
32
3 20 1x x kx k⇔ − − ++=
(
)
( )
2
2
()
1
1 2 20
2 2 0 (*)
gx
x
x x xk
x xk
=
⇔ − − −− =⇔
− −−=

d
cắt
(
)
C
tại ba điểm phân biệt
⇔
Phương trình
(*)
có hai nghiệm phân biệt
12
;xx
khác
1
( )
'
0
30
3
30
10
g
k
k
k
g
∆>
+>
⇔ ⇔ ⇔ >−

−− ≠
≠
Hơn nữa theo Viet ta có
( )
12
12 12
22
2 442
I
I
xx x
y y kx x k y
+==
+ = + − +==
nên I là trung điểm AB.
Vậy chọn
3k >−
, hay
( )
3;−+∞
.
Phương pháp trắc nghiệm:
Ta tính toán đến phương trình
( )
1
+ Với
2k = −
, ta giải phương trình
32
3 20xx x− +=
thu được
12
2, 0, 1
I
xxx= = =
.
+ Hơn nữa
12
12
22
42
I
I
xx x
yy y
+==
+==
nên I là trung điểm AB
⇒
loại A, C từ đó ta loại được B.
Vậy chọn
3k >−
.
Câu 45. Chọn A.
Phương trình hoành độ giao điểm của đồ thị
()C
và trục
Ox
:
( )
( )
( )
3 22
3 1 2 4 1 4 10x m x m m x mm− + + + + − +=
( ) ( )
( )
22
2 31 2 2 0x x m xm m⇔− − + + + =
22
20
(3 1) 2 2 0
x
x m xm m
−=
⇔
− ++ +=
2
2
1
x
xm
xm
=
⇔=
= +
Trang 23/28
Yêu cầu bài toán
1
1
12 2
2
1
1 12 0 1 1
2
21 1
m
m
m mm
mm m
<≠
<≠
⇔<+≠⇔ <≠⇔<≠


≠+ ≠
.
Vậy chọn
1
1
2
m<≠
.
Câu 46. Chọn D.
Phương trình hoành độ giao điểm
( )
C
và
d
là
( )
3
4 3 1 12x x mx− += − +
⇔
(
)
3
4 3 10x m xm− + + −=
⇔
2
1
4 4 1 0 (1)
x
x xm
=
+ − +=
( )
C
cắt
d
tại một điểm ⇔ Phương trình
( )
1
vô nghiệm hay phương trình
( )
1
có nghiệm kép
bằng
1
⇔
0
0
44 10m
′
∆<
′
∆=
+ − +=
⇔
40
40
9
m
m
m
<
=
=
⇔
0m <
.
Vậy chọn
0m <
.
Câu 47. Chọn A.
Phương pháp tự luận
Phương trình hoành độ giao điểm của đồ thị
()C
và đường thẳng
d
2
21
1
( 1) 1 0 (1)
1x
x
xm
x
x m xm
+
=+⇔
+
+ − + −=
≠−
Khi đó
d
cắt
()C
tại hai điểm phân biệt
A
,
B
khi và chi khi phương trình
(1)
có hai nghiệm
phân biệt khác
1−
2
2
( 1) 4( 1) 0
1 5 (*)
( 1) ( 1) 1 0
mm
mm
mm
− − −>
⇔ ⇔ <∨ >
− − − + −≠
Khi đó ta lại có
2
11 22 2121 21 21
( ; ), ( ; ) ( ; ) 2( ) 2AxxmBxxm ABxxxx AB xx xx+ +⇒=− −⇒= − = −

,
và
12
12
1
1
xx m
xx m
+=−
= −
. Từ đây ta có
2
2 1 2 1 12
10 5 ( ) 4 5AB x x x x x x= ⇔−= ⇔ + − =
22
0
(1 ) 4( 1) 5 6 0
6
m
m m mm
m
=
⇔− − −=⇔ − =⇔
=
(thỏa
(*)
)
Vậy chọn
06mm=∨=
.
Phương pháp trắc nghiệm
Chọn
0m =
thay vào
d
. Ta được
21
( 1)
1
x
xx
x
+
= ≠−
+
.
Dùng lệnh SHIFT CALC tìm được
15
2
x
+
=
hoặc
15
2
x
−
=
.
Suy ra
1 51 5 1 51 5
; , ; ( 5, 5) 10
22 22
A B AB AB

++ −−
⇒ −− ⇒ =





.
Nhận thấy
0m =
thỏa yêu cầu.
Tượng tự chọn
6m =
kiểm tra tương tự
0m =
nhận thấy
6m =
thỏa yêu cầu bài toán.
Vậy chọn
06mm=∨=
.
Câu 48. Chọn A.
Phương trình hoành độ giao điểm của đồ thị
()C
và đường thẳng
d
Trang 24/28
2
21
( 1) ( 1) 1 0 (1)
1
x
xmx x m xm
x
+
= + ≠− ⇔ + − + − =
+
Khi đó
d
cắt
()C
tại hai điểm phân biệt
A
,
B
khi và chi khi phương trình
(1)
có hai nghiệm
phân biệt khác
1−
2
2
( 1) 4( 1) 0 1 5
15
1
1 ( 1)
0
10
m m mm
mm
mm
− − − > <∨ >
⇔ ⇔ ⇔ <∨ >

− − + −≠
≠
Ta có
2
1
'( )
( 1)
fx
x
=
+
. Gọi
11 2 2
( ; ), ( ; )
Ax y Bx y
trong đó
12
,xx
là nghiệm của
(1)
(nên ta có
12
1xx m+=−
). Suy ra hệ số góc của các tiếp tuyến tại điểm
A
và
B
lần lượt là
2
1
1
( 1)
A
k
x
=
+
và
2
2
1
( 1)
B
k
x
=
+
Vì tiếp tuyến tại
A
và
B
song song, đồng thời
12
xx≠
nên phải có
22
12
11
( 1) ( 1)xx
=
++
, suy ra
1 2 12
1 1 20 1 20 3()x x xx m m l+=− −⇔ + +=⇔− +=⇔ =
.
Vậy chọn không tồn tại.
Câu 49. Chọn D.
Phương trình hoành độ giao điểm của đồ thị
()P
và đường thẳng
d
:
22
2 21x xm x−−=+
⇔
22
4 10x xm− − −=
(
)
1
( )
P
cắt
d
tại hai điểm phân biệt ⇔ Phương trình
( )
1
có hai nghiệm phân biệt
⇔
0
′
∆>
⇔
2
50m +>
(đúng với mọi
)
Hoành độ của điểm
,AB
là nghiệm
12
,xx
của phương trình
( )
1
và tung độ trung điểm
I
thỏa
phương trình
d
, nên tọa độ trung điểm
I
là
12
2
2
2 15
I
II
xx
x
yx
+
= =
= +=
.
Vậy chọn
( )
2; 5
I
.
Câu 50. Chọn B.
Phương pháp tự luận: Xét
1
m =
, phương trình
2
10x
−=
có hai nghiệm (loại).
Khi
1
m ≠
ta thấy đồ thị hàm luôn có có hai điểm cực trị. Vậy ta tìm giá trị cực đại và cực tiểu
của hàm số như sau:
( )
( )
( )
2
32
2
0
'3 1 2 0
2 27 54 27 4
31
27 1
x ym
y mx x
mmm
xy
m
m
=⇒=−
= − +=⇔
− − + −+
= ⇒=
−
−
( )
m
C
có 1 điểm chung với
Ox
(
)
( )
32
2
27 54 27 4
. 0 0.
27 1
CD CT
mm m m
yy
m
− +−
⇔ >⇔ >
−
4
0
3
mm⇔ <∨ >
.
Vậy chọn
4
0
3
mm<∨ >
.
Phương pháp trắc nghiệm: Ta kiểm tra trực tiếp các đáp án của đề bài
+ Với
1m = −
, phương trình
32
2 10xx− + +=
thu được
1x =
là nghiệm duy nhất
⇒
loại A,
D.
+ Với
2m =
, phương trình
32
20xx+ −=
thu được
1x =
là nghiệm duy nhất
⇒
loại C.
Vậy chọn
4
0
3
mm<∨ >
.
Trang 25/28
Câu 51. Chọn C.
Phương pháp tự luận
Đồ thị
()C
cắt trục hoành tại điểm phân biệt tạo thành cấp số cộng khi và chỉ khi phương trình
32
31xx m− −=
có ba nghiệm phân biệt lập thành cấp cố cộng.
Suy ra đường thẳng
ym=
đi qua điểm uốn của đồ thị
32
31yx x=−−
(do đồ thị
()C
nhận
điểm uốn làm tâm đối xứng). Mà điểm uốn của
32
31yx x=−−
là
(1; 3)I −
. Suy ra
3m
= −
. Vậy
chọn
3m = −
.
Phương pháp trắc nghiệm
Chọn
3
m
= −
thay vào phương trình
32
3 10x xm− − −=
.
Ta được
32
3 20xx− +=
. Dùng chức năng tìm nghiệm phương trình bậc ba ta được ba nghiệm
13,1,13x xx=−==+
thỏa cấp số cộng.
Vậy chọn
3
m = −
.
Câu 52. Chọn B.
Phương pháp tự luận
Phương trình hoành độ giao điểm của
()C
và đường thẳng
d
:
2
21
( 1) ( 3) 1 0 (1)
1
x
x mx x m x m
x
+
= + ≠ ⇔ + − − −=
−
Khi đó
d
cắt
()C
tại hai điểm phân biệt
A
,
B
khi và chi khi phương trình
(1)
có hai nghiệm
phân biệt khác
1−
2
2
2
( 3) 4( 1) 0
2 13 0
1
1 ( 3) 1
0
0
mm
mm
mm
− + +>
− +>
⇔⇔

−
+ −−−
≠
≠
đúng
.m∀∈
Gọi
11 2 2
( ; ), ( ; )Ax x m Bx x m++
trong đó
12
,xx
là nghiệm của
(1)
, theo Viet ta có
12
12
3
1
xx m
xx m
+=−
=−−
.
Gọi
1212
2
;
22
xxxx m
I
+ ++



là trung điểm của
AB
, suy ra
33
;
22
mm
I
−+



, nên
22
33 1
2 ;5 ( 7) (7 )
22 2
mm
CI CI m m
−+

−− − ⇒ = − + −



.
Mặt khác
22
2121 21
( ; ) 2( ) 2( 2 13)ABxxxx AB xx m m=− −⇒ = − = −+

. Vậy tam giác
ABC
đều khi và chỉ khi
22
31 3
2( 7) 2( 2 13)
22 2
CI AB m m m
= ⇔ − = −+
22 2
1
( 7) 3( 2 13) 2 8 10 0
5
m
m mm mm
m
=
⇔ − = − + ⇔ + −=⇔
= −
.
Vậy chọn
15mm=∨=−
.
Câu 53. Chọn D.
Phương trình hoành độ giao điểm của
()C
và đường thẳng
d
:
2
42 42
2
1
(2 1) 2 2 ( 2 1) 2 2 0
2 2 (1)
x
x mx m x mx m
xm
=
−−+=⇔−−+−=⇔
= −
Đường thẳng
d
cắt
()C
tại bốn điểm phân biệt có hoành độ nhỏ hơn 3 khi và chỉ khi phương
trình
(1)
có hai nghiệm phân biệt nhỏ hơn 3.
3
2 21
2
0 2 2 9 11
1
2
m
m
m
m
≠
−≠
⇔⇔

< −<
<<
. Vậy chọn
3
2
11
1
2
m
m
≠
<<
.
Câu 54. Chọn B.
Phương trình hoành độ giao điểm
Trang 26/28
( )
32 2
2
2 3( 1) 2 2 2 3( 1) 0
0
2 3( 1) 0(1)
x mx m x x x x mx m
x
x mx m
+ + − +=−+⇔ + + − =
=
⇔
+ + −=
Đường thẳng
d
cắt
()C
tại ba điểm phân biệt khi và chỉ khi phương trình
(1)
có hai nghiệm
phân biệt khác
0
2
3 30
1
1
10
m
mm
m
m
m
∀∈
− +>
⇔ ⇔ ⇔≠

≠
−≠
.
Khi đó ta có:
11 2 2
( ; 2), ( ; 2)Cx x Bx x
−+ −+
trong đó
12
,xx
là nghiệm của
(1)
, nên theo Viet thì
12
12
2
33
xx m
xx m
+=−
= −
. Vậy
22
21 21 21
( ; ) 2( ) 8( 3 3)
312
( ; ( )) 2
2
CB x x x x CB x x m m
dM d
= − −+ ⇒ = − = − +
−−+
= =

Diện tích tam giác
MBC
bằng
27
khi và chỉ khi
22
1
8( 33).227 337
2
mm mm−+ = ⇔−+=
1
4
m
m
= −
⇔
=
( thỏa
1m ≠
)
Vậy chọn
14mm=−∨ =
.
Câu 55. Chọn A.
Phương pháp tự luận
Phương trình hoành độ giao điểm của
( )
m
C
và trục hoành là
( )
32
21 0
x x mx m− +− +=
⇔
( )
( )
2
10x x xm− −− =
⇔
2
1
0 (1)
x
x xm
=
−− =
( )
m
C
cắt trục hoành tại ba điểm phân biệt ⇔ Phương trình
( )
1
có hai nghiệm phân biệt khác
1
⇔
0
11 0m
∆>
−− ≠
⇔
14 0
0
m
m
+>
≠
⇔
1
(*)
4
0
m
m
>−
≠
Gọi
3
1x =
còn
12
,xx
là nghiệm phương trình
( )
1
nên theo Vi-et ta có
12
12
1xx
xx m
+=
= −
. Vậy
222
123
4xx x++=
⇔
22
12
14
xx+ +=
⇔
( )
2
1 2 12
2 30
x x xx+ − −=
⇔
1m =
(thỏa (*))
Vậy chọn
1m =
.
Câu 56. Chọn A.
Phương pháp tự luận:
Phương trình hoành độ giao điểm của
()C
và đường thẳng
d
:
(
) ( )
32 2
12
0 1 31 3 20
33
x mx x m x x m x m

− − + + = ⇔ − +− + − − =

(
)
2
()
1
3 1 3 2 0 (1)
gx
x
x m xm
=
⇔
+− + − − =

(
)
m
C
cắt
Ox
tại ba điểm phân biệt
⇔
phương trình
(1)
có hai nghiệm phân biệt khác
1
( )
2
0
9 6 90
0
10
60
g
mm
m
g
m
∆>
+ +>
⇔ ⇔ ⇔≠

≠
−≠
.
Gọi
1
1x =
còn
23
,xx
là nghiệm phương trình
( )
1
nên theo Viet ta có
23
23
31
32
xx m
xx m
+= −
=−−
.
Vậy
Trang 27/28
( )
(
) ( )
2
222
1 2 3 2 3 23
2
2
15 1 2 15
3 1 23 2 140 9 90 1 1
xxx xx xx
m m m mm
+ + > ⇔+ + − >
⇔ − + + − >⇔ −>⇔ >∨ <−
Vậy chọn
11mm> ∨ <−
.
Phương pháp trắc nghiệm: Ta kiểm tra ngay trên đáp án
+ Với
2m = −
, ta giải phương trình bậc ba:
32
14
20
33
x xx+ −− =
thu được 3 nghiệm
1 23
6.37..., 1, 0.62...x xx=−==−
Ta chọn những giá trị nhỏ hơn các nghiệm này và kiểm tra
điều kiện của bài toán.
Cụ thể ta tính
( ) ( )
22
2
6.4 1 0.63 42.3569 15− + +− = >
⇒
loại C, D.
+ Với
2m =
, ta làm tương tự thu được 3 nghiệm
1 23
6.27..., 1, 1.27...x xx= = = −
Tính
( )
2
22
6.2 1 1.3 41.13 15+ +− = >
⇒
loại B.
Vậy chọn
11mm> ∨ <−
.
Câu 57. Chọn B.
Phương trình hoành độ giao điểm
( )
C
và
d
là
2
1
1
xx
m
x
−+
=
−
⇔
( )
2
1
1 1 0 (1)
x
x m xm
≠
− + + +=
( )
C
cắt
d
tại hai điểm phân biệt ⇔ Phương trình
(
)
1
có hai nghiệm phân biệt khác
1
⇔
( )( )
1 30
1 1 10
mm
mm
∆= + − >
− −+ +≠
⇔
1 3 (*)mm
<− ∨ >
Hoành độ giao điểm
12
,xx
là nghiệm của phương trình (1) nên theo Vi-et ta có:
12
12
1
1
xx m
xx m
+=+
= +
. Khi đó:
( )
1
;Ax m
,
( )
2
;Bx m
, suy ra
2AB =
⇔
2
2AB =
⇔
( )
2
21
2xx−=
⇔
( )
2
1 2 12
4 20x x xx+ − −=
⇔
12 6
12 6
m
m
+= +
+= −
⇔
16
16
m
m
= +
= −
( thỏa (*))
Vậy chọn
1 6 1 6.
mm=+ ∨=−
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


CHỦ ĐỀ 6. SỰ TƯƠNG GIAO GIỮA HAI ĐỒ THỊ HÀM SỐ
I. SỰ TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VÀ ĐỒ THỊ HÀM SỐ BẬC BA
1. KIẾN THỨC TRỌNG TÂM Xét hàm số bậc ba 3 2
y = ax + bx + cx + d (a ≠ 0) có đồ thị (C) và hàm số bậc nhất
y = kx + n có đồ thị d .
Lập phương trình hoành độ giao điểm của (C)và d : 3 2
ax + bx + cx + d = kx + n (1) Phương trình ( )
1 là phương trình bậc ba nên có ít nhất một nghiệm. Ta có 2 trường hợp:
• Trường hợp 1: Phương trình ( )
1 có “nghiệm đẹp” x . 0
Thường thì đề hay cho nghiệm x = 0; 1 ± ; ±2;. . thì khi đó: 0 x − x =
(1) ⇔ (x − x )( Ax + Bx + C) 0 0 2 = 0 ⇔ 0  2
Ax + Bx + C = 0  (2) Khi đó:
+ (C) và d có ba giao điểm ⇔ phương trình ( )
1 có ba nghiệm phân biệt ⇔ phương trình
(2) có hai nghiệm phân biệt khác nghiệm x . (Đây là trường hợp thường gặp) 0
+ (C) và d có hai giao điểm ⇔ phương trình ( )
1 có hai nghiệm phân biệt ⇔ phương trình
(2) có hai nghiệm phân biệt, trong đó có một nghiệm x hoặc phương trình (2) có nghiệm 0 kép khác x . 0
+ (C) và d có một giao điểm ⇔ phương trình ( )
1 có một nghiệm ⇔ phương trình (2) vô
nghiệm hoặc phương trình (2) có nghiệm kép là x . 0
• Trường hợp 2: Phương trình ( )
1 không thể nhẩm được “nghiệm đẹp” thì ta biến đổi phương trình ( )
1 sao cho hạng tử chứa x tất cả nằm bên vế trái, các hạng tử chứa tham số
m nằm bên vế phải, nghĩa là ( )
1 ⇔ f (x) = g(m) .
Ta khảo sát và vẽ bảng biến thiên hàm số y = f (x) và biện luận số giao điểm của (C) và
d theo tham số m . 2. CÁC VÍ DỤ
Ví dụ 1: Tìm giao điểm của đồ thị 3 2
(C) : y = x − 3x + 2x +1 và đường thẳng y =1. Hướng dẫn giải x = 0
Phương trình hoành độ giao điểm: 3 2 3 2
x − 3x + 2x +1 =1 ⇔ x − 3x + 2x = 0  ⇔ x =1  . Vậy có x =  2 ba giao điểm A(0 ) ;1 , B(1 ) ;1 ,C (2 ) ;1 .
Ví dụ 2: Cho hàm số 3 2
y = mx − x − 2x + 8m có đồ thị là (C . Tìm m đồ thị (C cắt trục m ) m )
hoành tại ba điểm phân biệt. Hướng dẫn giải
Phương trình hoành độ giao điểm 3 2
mx − x − 2x + 8m = 0 (1) x = 2 − ⇔ (x + ) 2
2 mx − (2m +1)x + 4m = 0   ⇔  2
mx − (2m +1)x + 4m = 0 (2)
(C cắt trục hoành tại ba điểm phân biệt ⇔ ( )
1 có ba nghiệm phân biệt. m )
⇔ (2) có hai nghiệm phân biệt khác 2 − Trang 1/28 m ≠ 0 ⇔  2 ∆ = 12
− m + 4m +1 > 0 12  m + 2 ≠ 0   m ≠ 0  m ≠ 0 ⇔  1 1  − < m < ⇔ . 6 2  1 1  − < m <   1  6 2 m ≠ −  6 Vậy  1 1 m ;  ∈ −   \{ }
0 thỏa yêu cầu bài toán.  6 2 
Ví dụ 3: Cho hàm số 3 2
y = 2x − 3mx + (m − )
1 x +1 có đồ thị (C). Tìm m để đường thẳng
d : y = −x +1 cắt đồ thị (C) tại ba điểm phân biệt. Hướng dẫn giải
Phương trình hoành độ giao điểm của (C)và d : x = 0 3 2
2x − 3mx + (m − )
1 x +1 = −x +1 ⇔ x( 2
2x − 3mx + m) = 0 ⇔  2
2x − 3mx + m = 0  (*)
Yêu cầu bài toán ⇔ (*) có hai nghiệm phân biệt khác 0 2
∆ = 9m −8m > 0 ⇔  m ≠ 0 m ( )  8 ;0 ;  ⇔ ∈ −∞ ∪ +∞  . 9    Vậy m ( )  8 ;0 ;  ∈ −∞ ∪ +∞ 
thỏa yêu cầu bài toán. 9   
Ví dụ 4: Tìm m để đồ thị hàm số 3
y = x + mx + 2 cắt trục hoành tại một điểm duy nhất. Hướng dẫn giải
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là 3
x + mx + 2 = 0 .
Vì x = 0 không là nghiệm của phương trình, nên phương trình tương đương với 2 2
m = −x − (x ≠ 0) x 3 − + Xét hàm số 2 2
f (x) = −x − với x ≠ 0 , suy ra 2 2 2 '( ) = 2 x f x − x + = . Vậy x 2 2 x x
f '(x) = 0 ⇔ x =1. Bảng biến thiên: x −∞ 0 1 +∞
f ′(x) + + 0 – +∞ 3 − f (x) −∞ −∞ −∞
Dựa vào bảng biến thiên ta thấy đồ thị cắt trục hoành tại một điểm duy nhất ⇔ m > 3 − . Vậy m > 3
− thỏa yêu cầu bài toán.
Ví dụ 5: Tìm m để đồ thị (C) của hàm số 3 2
y = x − 3x − 9x + m cắt trục hoành tại ba điểm phân biệt. Hướng dẫn giải Trang 2/28
Phương trình hoành độ giao điểm của đồ thị và trục hoành: 3 2 3 2
x − 3x − 9x + m = 0 ⇔ x − 3x − 9x = −m ( ) 1 Phương trình ( )
1 là phương trình hoành độ giao điểm của đường (C) 3 2
: y = x − 3x − 9x và
đường thẳng d : y = −m . Số nghiệm của ( )
1 bằng số giao điểm của (C)và d .
Khảo sát và vẽ bảng biến thiên của hàm số 3 2
y = x − 3x − 9x .
Tập xác định D =  . x = 3 Đạo hàm 2 2
y′ = 3x − 6x − 9; y′ = 0 ⇔ 3x − 6x − 9 = 0 ⇔  . x = 1 − Bảng biến thiên: x −∞ 1 − 3 +∞ y′ + 0 − 0 + 5 +∞ y −∞ 27 −
Dựa vào bảng biến thiên ta thấy ( )
1 có ba nghiệm phân biệt ⇔ 27
− < −m < 5 ⇔ 5 − < m < 27 .
Ví dụ 6: Gọi d là đường thẳng đi qua điểm A( 1;
− 0) với hệ số góc k (k ∈) . Tìm k để
đường thẳng d cắt đồ thị hàm số (C) : 3 2
y = x − 3x + 4tại ba điểm phân biệt ,
A B, C và tam
giác OBC có diện tích bằng 1 (O là gốc tọa độ). Hướng dẫn giải
Đường thẳng d đi qua ( A 1;
− 0) và có hệ số góc k nên có dạng y = k(x +1) , hay
kx − y + k = 0 .
Phương trình hoành độ giao điểm của (C) và d là: x = 1 − 3 2
x − 3x + 4 = kx + k ⇔ (x + ) 1 ( 2
x − 4x + 4 − k ) = 0 ⇔  2
g(x) = x − 4x + 4 − k = 0 (*)
d cắt (C) tại ba điểm phân biệt ⇔ phương trình (*) có hai nghiệm phân biệt khác 1 − ∆ ' > 0 k > 0 ⇔  ⇔ . g( 1) 0  − ≠ k ≠ 9
Khi đó g(x) = 0 ⇔ x = 2 − k ; x = 2 + k . Vậy các giao điểm của hai đồ thị lần lượt là ( A 1
− ;0), B(2 − k ;3k − k k ), C (2 + k ;3k + k k ) . k Tính được 2
BC = 2 k 1+ k , d(O, BC) = d(O,d) = . Khi đó 2 1+ k 1 k 2 3 S = + = ⇔ = ⇔ = ⇔ = . ∆ k k k k k k OBC . .2 . 1 1 1 1 1 2 2 1+ k
Vậy k =1 thỏa yêu cầu bài toán.
II. SỰ TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VỚI ĐỒ THỊ HÀM SỐ TRÙNG PHƯƠNG
1. KIẾN THỨC TRỌNG TÂM Cho hàm số 4 2
y = ax + bx + c ( 0
a ≠ ) có đồ thị (C)và đường thẳng y = k có đồ thị d .
Lập phương trình hoành độ giao điểm của (C)và d : 4 2
ax + bx + c = k ( ) 1 Đặt 2 t = x ( 0
t ≥ ) ta có phương trình 2
at + bt + c − k = 0 (2) Trang 3/28
• (C) và d có bốn giao điểm ⇔ ( )
1 có bốn nghiệm phân biệt ⇔ (2) có hai nghiệm dương ∆ > 0
phân biệt ⇔ phương trình (2) thỏa P > 0 . (Trường hợp này thường gặp)S >  0
• (C) và d có ba giao điểm ⇔ ( )
1 có ba nghiệm phân biệt ⇔ (2) có hai nghiệm phân biệt,
trong đó có một nghiệm dương và một nghiệm t = 0.
• (C) và d có hai giao điểm ⇔ ( )
1 có hai nghiệm phân biệt ⇔ (2) có nghiệm kép dương
hoặc có hai nghiệm trái dấu.
• (C) và d không có giao điểm ⇔ ( )
1 vô nghiệm ⇔ (2) vô nghiệm hoặc chỉ có nghiệm âm.
• (C) và d có một giao điểm ⇔ ( )
1 có một nghiệm ⇔ (2) có nghiệm t = 0 và một nghiệm âm. 2. CÁC VÍ DỤ
Ví dụ 1: Tìm giao điểm của đồ thị 4 2
(C) : y = x + 2x − 3 và trục hoành. Hướng dẫn giải 2 x =1
Phương trình hoành độ giao điểm: 4 2
x + 2x − 3 = 0 ⇔ 
⇒ x =1∨ x = 1. − 2 x = 3 −
Vậy có hai giao điểm: A( 1; − 0), B( 1;0).
Ví dụ 2: Tìm m để phương trình 4 2
x − 2x − m + 3 = 0 có bốn nghiệm phân biệt. Hướng dẫn giải Phương trình: 4 2 4 2
x − 2x − m + 3 = 0 ⇔ x − 2x + 3 = m ( ) 1 Phương trình ( )
1 là phương trình hoành độ giao điểm của hai đường (C) 4 2
: y = x − 2x + 3 và
đường thẳng d : y = m . Số nghiệm của ( )
1 bằng số giao điểm của (C) và d .
Khảo sát và vẽ bảng biến thiên của hàm số 4 2
y = x − 2x + 3 .
Tập xác định D =  . x = 0 Đạo hàm 3 3 y = 4x − 4 ;
x y = 0 ⇔ 4x − 4x = 0  ′ ′ ⇔ x =1  . x = 1 −  Bảng biến thiên: x –∞ 1 − 0 1 +∞ y′ – 0 + 0 – 0 + +∞ 3 +∞ y 2 3
Dựa vào bảng biến thiên ta thấy ( )
1 có bốn nghiệ m phân biệt ⇔ 2 < m < 3. Vậy 2 < m < 3 thỏa yêu cầu bài toán.
Ví dụ 3: Cho hàm số 4
y = x − (m + ) 2 2 2
1 x + m − 3m − 2 (C . Định m để đồ thị (C m ) m) cắt đường
thẳng d : y = 2
− tại bốn điểm phân biệt. Lời giải
Phương trình hoành độ giao điểm của (C và d : m ) 4 x − (m + ) 2 2 4
x + m − m − = − ⇔ x − (m + ) 2 2 2 1 3 2 2 2
1 x + m − 3m = 0 ( ) 1 . Đặt 2 t = x ( 0
t ≥ ) , phương trình trở thành 2 t − (m + ) 2 2
1 t + m − 3m = ( 0 2) . Trang 4/28
(C và d có bốn giao điểm ⇔ ( )
1 có bốn nghiệm phân biệt ⇔ (2)có hai nghiệm dương phân m ) biệt.  1 ∆ ' > 0 5  +1 > 0 m m > −  5  1    − < m < 0 2 P 0 m 3m 0 m 0, m 3  ⇔ > ⇔ − > ⇔ < > ⇔ 5 .   S > 0 2  (m + ) 1 > 0 m > 1 − m > 3   Vậy  1 m ;0 ∈ − ∪ (3;+∞  
) thỏa yêu cầu bài toán.  5 
Ví dụ 4: Cho hàm số 4
y = x − ( m + ) 2 3
2 x + 3m (C) . Tìm m để đường thẳng d : y = 1 − cắt đồ
thị (C) tại bốn điểm phân biệt có hoành độ đều nhỏ hơn 2. Hướng dẫn giải
Phương trình hoành độ giao điểm của (C) và d : y = 1 − là 4 x − ( m + ) 2 4
x + m = − ⇔ x − ( m + ) 2 3 2 3 1 3
2 x + 3m +1 = 0 . Đặt 2
t = x (t ≥ 0) , ta có phương trình t =1 2
t − (3m + 2)t + 3m +1 = 0 ⇔  t = 3m +1 2 x =1 0 < 3m +1 < 4 Khi đó 1 
. Yêu cầu bài toán ⇔ 
⇔ − < m <1 và m ≠ 0 . Vậy 2 x = 3m +1 3  m +1 ≠ 1 3 1
− < m <1 và m ≠ 0 thỏa yêu cầu bài toán. 3
Ví dụ 5: Cho hàm số 4
y = x − ( m + ) 2 2 3
4 x + m có đồ thị là (C . Tìm m để đồ thị (C cắt m ) m )
trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng. Hướng dẫn giải
Phương trình hoành độ giao điểm: 4 x − ( m + ) 2 2 3 4 x + m = 0 ( )1 Đặt 2
t = x (t ≥ 0), phương trình ( )
1 trở thành: 2t − ( m + ) 2 3 4 t + m = 0 (2)
(C cắt trục hoành tại bốn điểm phân biệt ⇔ ( )
1 có bốn nghiệm phân biệt m ) 2
∆ = 5m + 24m +16 > 0 
⇔ (2) có hai nghiệm dương phân biệt ⇔ 2 P = m > 0
S = 3m + 4 > 0   4 m < 4 − ∨ m > −  5   4 m > − ⇔ m ≠ 0 ⇔  5 (*)  4 m ≠ 0 m > −  3
Khi đó phương trình (2) có hai nghiệm 0 < t < t . Suy ra phương trình ( ) 1 có bốn nghiệm 1 2
phân biệt là x = − t < x = − t < x = t < x = t . Bốn nghiệm x , x , x , x lập thành cấp 1 2 2 1 3 1 4 2 1 2 3 4 số cộng
⇔ x − x = x − x = x − x ⇔ − t + t = 2 t ⇔ t = 3 t ⇔ t = 9t (3) 2 1 3 2 4 3 1 2 1 2 1 2 1 t
 + t = 3m + 4 (4)
Theo định lý Viet ta có 1 2  2 t t =  m (5) 1 2 Trang 5/28  3m + 4 t =  1
Từ (3) và (4) ta suy ra được  10  (6). 9  (3m + 4) t = 2  10
Thay (6) vào (5) ta được 9 (3m + 4)2 2 = m 100  ( m + ) m =12 3 3 4 =10m ⇔   (thỏa (*))  ( ⇔ m + ) 12 3 3 4 = 10 − mm = −  19
Vậy giá trị m cần tìm là 12 m =12; . m = − 19 III. +
SỰ TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VỚI ĐỒ THỊ HÀM SỐ ax b y = cx + d
1. KIẾN THỨC TRỌNG TÂM + Cho hàm số ax b y = ( 0
ad − bc ≠ ) có đồ thị (C) và đường thẳng y = kx + n có đồ thị d . cx + d
Lập phương trình hoành độ giao điểm của (C) và d : 2
Ax + Bx + C = 0 ( ) 1 ax + b kx n  = + ⇔  d cx + dx ≠ −  c
(C) và d có hai giao điểm ⇔ ( )
1 có hai nghiệm phân biệt khác d − . c 2. CÁC VÍ DỤ Ví dụ 1: +
Tìm tọa độ giao điểm của đồ thị (C): 2x 1 y =
và đường thẳng d : y = x + 2. 2x −1 Lời giải +
Phương trình hoành độ giao điểm: 2x 1 = x + 2 ( ) 1 2x −1 Điều kiện: 1
x ≠ . Khi đó (1) ⇔ 2x +1 = (2x − ) 1 (x + 2) 2
⇔ 2x + x − 3 = 0 2  3 1 x = − ⇒ y = ⇔  2 2 
x = 1⇒ y = 3
Vậy tọa độ giao điểm cần tìm là  3 1 ;  −  và (1;3) . 2 2    Ví dụ 2. − Cho hàm số 2x 1 y =
có đồ thị là (C) . Tìm m để đường thẳng d : y = −x + m cắt đồ x −1
thị (C) tại hai điểm phân biệt. Lời giải −
Phương trình hoành độ giao điểm: 2x 1 = −x + m ( )1 x −1
Điều kiện: x ≠ 1. Khi đó (1) ⇔ 2x −1 = (−x + m)(x − ) 1 ⇔ 2 x − (m − )
1 x + m −1 = 0 (2)
d cắt (C) tại hai điểm phân biệt ⇔ ( )
1 có hai nghiệm phân biệt ∆ = −  (m − ) 2 1  − 4  (m − )1 > 0
⇔ (2) có hai nghiệm phân biệt khác 1 ⇔  1  −  (m − ) 1 .1+ m −1 ≠ 0 Trang 6/28 ⇔ 2
m − 6m + 5 > 0 ⇔ m∈( ; −∞ ) 1 ∪(5;+∞).
Vậy giá trị m cần tìm là m∈( ; −∞ ) 1 ∪(5;+∞). Ví dụ 3: − Cho hàm số mx 1 y =
có đồ thị là (C . Tìm m để đường thẳng d : y = 2x −1 cắt đồ m ) x + 2
thị (C tại hai điểm phân biệt ,
A B sao cho AB = 10 . m ) Lời giải −
Phương trình hoành độ giao điểm: mx 1 = 2x −1 ( )1 x + 2 Điều kiện: x ≠ 2 − . Khi đó
(1) ⇔ mx −1 = (2x − ) 1 (x + 2) ⇔ 2
2x − (m − 3) x −1 = 0 (2)
d cắt (C tại hai điểm phân biệt , A B ⇔ ( )
1 có hai nghiệm phân biệt m )
⇔ (2) có hai nghiệm phân biệt khác 2 − ∆ = −  (m − 3) 2  + > ⇔ 8 0   ⇔ 1 m ≠ − (*) 8
 + 2m − 6 −1 ≠ 0 2
Đặt A(x ;2x −1 ; ;2
B x x −1 với x , x là hai nghiệm của phương trình (2) . 1 1 ) ( 2 2 ) 1 2  m − 3 x + x =  1 2
Theo định lý Viet ta có  2  , khi đó 1 x x = − 1 2  2
AB = (x − x )2 + 4(x − x )2 = 10 ⇔ 5(x + x − 4x x  =10 1 2 )2 1 2 1 2 1 2   2
⇔  m − 3  + 2 =   2 ⇔ m = 3 (thỏa (*))  2 
Vậy giá trị m cần tìm là m = 3 . Ví dụ 4: + Cho hàm số 2x 1 y =
(C) . Tìm m để đường thẳng d : y = 2
− x + m cắt (C) tại hai x +1 điểm phân biệt ,
A B sao cho tam giác OAB có diện tích là 3 . Lời giải
Phương trình hoành độ giao điểm của (C) và d : 2x +1 = 2
− x + m ⇔ 2x +1 = (x + ) 1 ( 2
− x + m) ( điều kiện: x ≠ 1 − ) x +1 2
⇔ 2x + (4 − m) x +1− m = 0 ( )
1 ( điều kiện: x ≠ 1 − ).
d cắt (C) tại hai điểm ,
A B phân biệt ⇔ (1) có hai nghiệm phân biệt khác 1 − . 2
∆ = m + 8 > 0 ∀  m ⇔  . 2.  (− )2 1 + (4 − m)(− ) 1 +1− m ≠ 0
Suy ra d luôn cắt (C) tại hai điểm ,
A B phân biệt với mọi m.
Gọi A(x ; y ; ;
B x y , trong đó y = 2 − x + ; 2
m y = − x +m và x , x là các nghiệm của 1 1 ) ( 2 2) 1 1 2 2 1 2  m − 4 x + x =  ( ) 1 2
1 . Theo định lý Viet ta có  2  . Tính được: 1− mx x = 1 2  2 m 5( 2 m + 8 2 2 2 ) d ( ; O AB) = ; AB = ( 5 x − x + y − y = x + x − 20x x = 1 2 ) ( 1 2) ( 1 2) 1 2 5 2 Trang 7/28 2 1 m m + S = A . B d ( ; O AB) 8 =
= 3 ⇔ m = 2 ∨ m = 2. − OAB 2 4
Vậy các giá trị m cần tìm là m = 2; 2 m = − . Ví dụ 5: + Cho hàm số 2x 1 y =
(C) . Tìm k để đường thẳng d : y = kx + 2k +1 cắt (C) tại hai x +1 điểm phân biệt ,
A B sao cho khoảng các từ A và B đến trục hoành bằng nhau. Lời giải
Phương trình hoành độ giao điểm của (C) và d :
2x +1 = kx+2k +1⇔ 2x+1= (x+ )1(kx+2k + )1(điều kiện: x ≠ 1 − ) x +1 2
⇔ kx + (3k − ) 1 x + 2k = 0 ( )
1 . (điều kiện: x ≠ 1 − )
d cắt (C) tại hai điểm ,
A B phân biệt ⇔ (1) có hai nghiệm phân biệt khác 1 − k ≠ 0  k ≠  0 2
⇔ ∆ = k − 6k +1 > 0 ⇔  
k < 3− 2 2 ∨ k > 3+ 2 2 k (− )2 1 + (3k − ) 1 (− ) 1 + 2k ≠ 0
Khi đó: A(x ;kx + 2k +1 , B x ;kx + 2k +1 với x , x là nghiệm của (1). 1 1 ) ( 2 2 ) 1 2  3 − k +1 x + x = Theo định lý Viet ta có 1 2  k . Tính được x x =  2 1 2 d ( ; A Ox) = d ( ;
B Ox) ⇔ kx + 2k +1 = kx + 2k +1 1 2
kx + 2k +1= kx + 2k +1 ⇔ 1 2 
kx + 2k +1= −kx − 2k −1 1 2
x = x (loaïi) ⇔ 1 2 
k (x + x + 4k + 2 =  0 1 2 )
⇔ k (x + x + 4k + 2 = 0 ⇔ k = 3 − . 1 2 ) Vậy k = 3
− thỏa yêu cầu bài toán.
A. BÀI TẬP TRẮC NGHIỆM
Câu 1. Số giao điểm của đồ thị hàm số 4 2
y = −x + 2x −1 với trục Ox là A. 3. B. 1 . C. 2 . D. 4 .
Câu 2. Số giao điểm của đồ thị hàm số y = (x + )( 2
3 x + 3x + 2) với trục Ox là A. 1. B. 3. C. 0. D. 2.
Câu 3. Số giao điểm của đồ thị hàm số 3 2
y = x − 2x + x −12 và trục Ox là A. 2. B. 1. C. 3. D. 0. Câu 4. −
Đường thẳng y = x −1 cắt đồ thị hàm số 2x 1 y =
tại các điểm có tọa độ là x +1 A. (0;2). B. ( 1; − 0); ( 2; ) 1 . C. (0;− ) 1 ; ( 2; ) 1 . D. (1;2).
Câu 5. Đồ thị (C) 2x −1 : y =
cắt đường thẳng d : y = 2x − 3 tại các điểm có tọa độ là x +1 A. (2; − ) 1 ; ( 1 − ; − 2). B. (2; ) 1 ; ( 1 − ; − 4 2 ). 2 C. ( 1; − − 5); (3; 0). D. (1; −2 2 ). 2
Câu 6. Đồ thị hàm số 4 3 2
y = 2x + x + x cắt trục hoành tại mấy điểm? Trang 8/28 A. 2. B. 3. C. 1 . D. 0 . Câu 7. Cho hàm số 3 2
y = 2x − 3x +1 có đồ thị (C) và đường thẳng d : y = x −1. Số giao điểm của (C) và d là A. 0 . B. 1 . C. 2. D. 3. 2 Câu 8. x − x +
Số giao điểm của đồ thị hàm số 4 3 y = và trục hoành là x + 2 A. 0. B. 1 . C. 3. D. 2.
Câu 9. Số giao điểm của đồ thị hàm số y = (x − )( 2
1 x − 3x + 2) và trục hoành là A. 0. B. 1 . C. 3. D. 2. 2
Câu 10. Giao điểm giữa đồ thị x − 2x − 3 (C) : y =
và đường thẳng (d ) : y = x +1 x −1 là A. A(2;− ) 1 . B. A(0;− ) 1 . C. A( 1; − 2). D. A( 1; − 0). Câu 11. Cho hàm số 4 2
y = x − 4x − 2 có đồ thị (C) và đồ thị (P) : 2
y =1− x . Số giao điểm của (P) và đồ thị (C) là A. 1. B. 2. C. 3. D. 4. Câu 12. − Cho hàm số 2x 1 y =
có đồ thị (C) và đường thẳng d : y = 2x − 3. Số giao điểm của (C) và x +1 d là A. 2. B. 1 . C. 3. D. 0. Câu 13. −
Tọa độ giao điểm giữa đồ thị 2x 1 (C) : y =
và đường thẳng d : y = x − 2 là x + 2 A. A( 1; − 3 − ); B( 3; ) 1 . B. A(1;− ) 1 ; B(0; 2 − ). C. A( 1 − ; 3 − ); B(0; 2 − ). D. A(1;− ) 1 ; B( 3; ) 1 . − Câu 14. Cho hàm số 2x 1 y = có đồ thị (C)
y = x − . Đường thằng d C x +1
và đường thẳng d : 2 3 cắt ( )
tại hai điểm A và B. Khi đó hoành độ trung điểm I của đoạn thẳng AB là A. x 4 = I . B. x 3 = − . C. x 3 = . D. x 4 = − . 3 I 4 I 4 I 3
Câu 15. Tọa độ trung điểm I của đoạn thẳng MN với M , N là giao điểm của đường thẳng +
d : y = x +1 và đồ thị hàm số (C): 2x 2 y = là x −1 A. I ( 1; − 2 − ). B. I ( 1; − 2). C. I (1; 2 − ). D. I (1;2). Câu 16. +
Gọi M , N là hai giao điểm của đường thẳng d : y = x +1 và (C) 2x 4 : y = . Hoành độ trung x −1
điểm I của đoạn thẳng MN là A. 2. B. 1. C. 5 . D. 5 − . 2 2
Câu 17. Đồ thị hàm số 4 2
y = 2x − x + 2 cắt đuờng thẳng y = 6 tại bao nhiêu điểm? A. 2. B. 0. C. 4. D. 3. Câu 18. x +
Tiệm cận ngang của đồ thị hàm số 2 (H ) : y =
cắt đồ thị hàm số (C) 4 2
: y = 2x − x tại các x +1 điểm có tọa độ là A. (1; ) 1 ; ( 1; − ) 1 . B. (1; ) 1 . C. ( 1; − ) 1 . D. (0; ) 1 .
Câu 19. Đồ thị hàm số 3 2
y = x − 3x +1 cắt đường thẳng y = m tại ba điểm phân biệt thì tất cả các giá trị
tham số m thỏa mãn là Trang 9/28 A. m >1 . B. 3 − ≤ m ≤1 . C. 3 − < m <1 . D. m < 3. −
Câu 20. Đường thẳng y = m không cắt đồ thị hàm số 4 2 y = 2
− x + 4x + 2 thì tất cả các giá trị tham số m là A. m > 4 . B. m ≥ 4 . C. m ≤ 2.
D. 2 < m < 4 .
Câu 21. Với tất cả giá trị nào của tham số m thì phương trình 4 2
x − 2x = m + 3 có bốn nghiệm phân biệt? A. m∈( 4; − 3 − ). B. m = 3 − hoặc m = 4. − C. m∈( 3 − ;+∞). D. m∈( ; −∞ 4 − ).
Câu 22. Tất cả giá trị của tham số m để phương trình 3
x − 3x − m +1 = 0 có ba nghiệm phân biệt là A. 1 − < m < 3. B. 1 − ≤ m ≤ 3. C. m =1. D. m < 1 − hoặc m > 3.
Câu 23. Tất cả giá trị của tham số m để đồ thị (C) 3 2
: y = x − 3x + 2 cắt đường thẳng d : y = m tại ba điểm phân biệt là A. 2 − < m < 0. B. 2 − < m < 2.
C. 0 < m <1.
D. 1< m < 2.
Câu 24. Tất cả giá trị của tham số m để đồ thị (C) 4 2
: y = x − 2x − 3 cắt đường thẳng d : y = m tại bốn điểm phân biệt là A. 4 − < m < 3. − B. m < 4. − C. m > 3. − D. 7 4
− < m < − . 2 Câu 25. Cho hàm số 4 2
y = x − 4x − 2 có đồ thị (C) và đường thẳng d : y = m . Tất cả các giá trị của
tham số m để d cắt (C) tại bốn điểm phân biệt là A. 6 − ≤ m ≤ 2. −
B. 2 < m < 6. C. 6 − < m < 2. −
D. 2 ≤ m ≤ 6.
Câu 26. Tất cả các giá trị của tham số m để phương trình 4 2
x − 3x + m = 0 có bốn nghiệm phân biệt là A. 13 1< m < . B. 9 0 < m < . C. 9
− < m < 0. D. 13 1
− < m < . 4 4 4 4 Câu 27. Cho hàm số 4 2
y = −x + 2x + m . Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục
hoành tại ít nhất ba điểm phân biệt là
A. 0 < m <1. B. 1
− < m ≤ 0. C. 1
− < m < 0. D. 1
− ≤ m < 0.
Câu 28. Cho hàm số y = x − ( 2 2 (
2) x + mx + m − )
3 . Tất cả giá trị của thma số m để đồ thị hàm số đã cho
cắt trục hoành tại ba điểm phân biệt là  2 − < m < 2  1 − < m < 2 A. 2 − < m < 1. − B.  . C. 1
− < m < 2. D.  . m  ≠ 1 − m  ≠1
Câu 29. Tất cả giá trị của tham số m để phương trình 4 2
x − 2x − m + 3 = 0 có bốn nghiệm phân biệt là
A. 2 < m < 3.
B. 2 ≤ m ≤ 3.
C. m ≥ 2.
D. m > 2.
Câu 30. Tất cả giá trị của tham số m để phương trình 4 2
x − 2x − m + 3 = 0 có hai nghiệm phân biệt là
A. m > 3.
B. m ≥ 3.
C. m > 3 hoặc m = 2.
D. m = 3 hoặc m = 2.
Câu 31. Tất cả giá trị của tham số m để đồ thị hàm số 4 2 y = 2
− x + 2x +1 cắt đường thẳng y = 3m tại ba điểm phân biệt là A. 1 1 ≤ m ≤ . B. 1 m = . C. 1 m ≤ . D. 1 m = . 3 2 2 3 3
Câu 32. Tất cả giá trị của tham số m để đồ thị hàm số (C) 3 2 : y = 2
− x + 3x + 2m −1 cắt trục hoành tại ba điểm phân biệt là A. 1 1 ≤ m < . B. 1 1
− < m < . C. 1 0 < m < . D. 1 0 ≤ m ≤ . 4 2 2 2 2 2 Trang 10/28
Câu 33. Tìm tất cả các giá trị của tham số m để phương trình 3 2
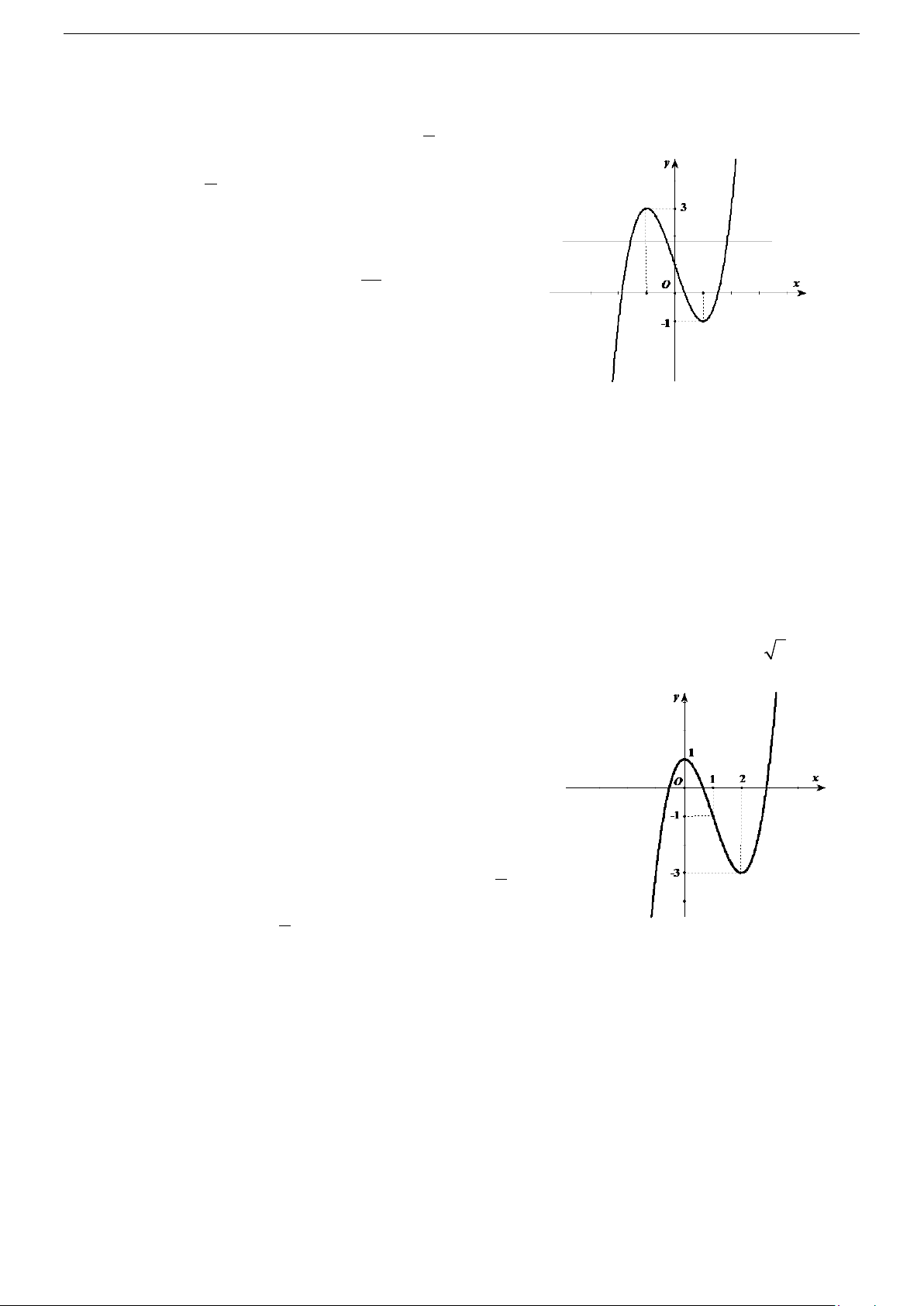
x − 3x + 4 + m = 0 có nghiệm duy nhất lớn hơn 2 .
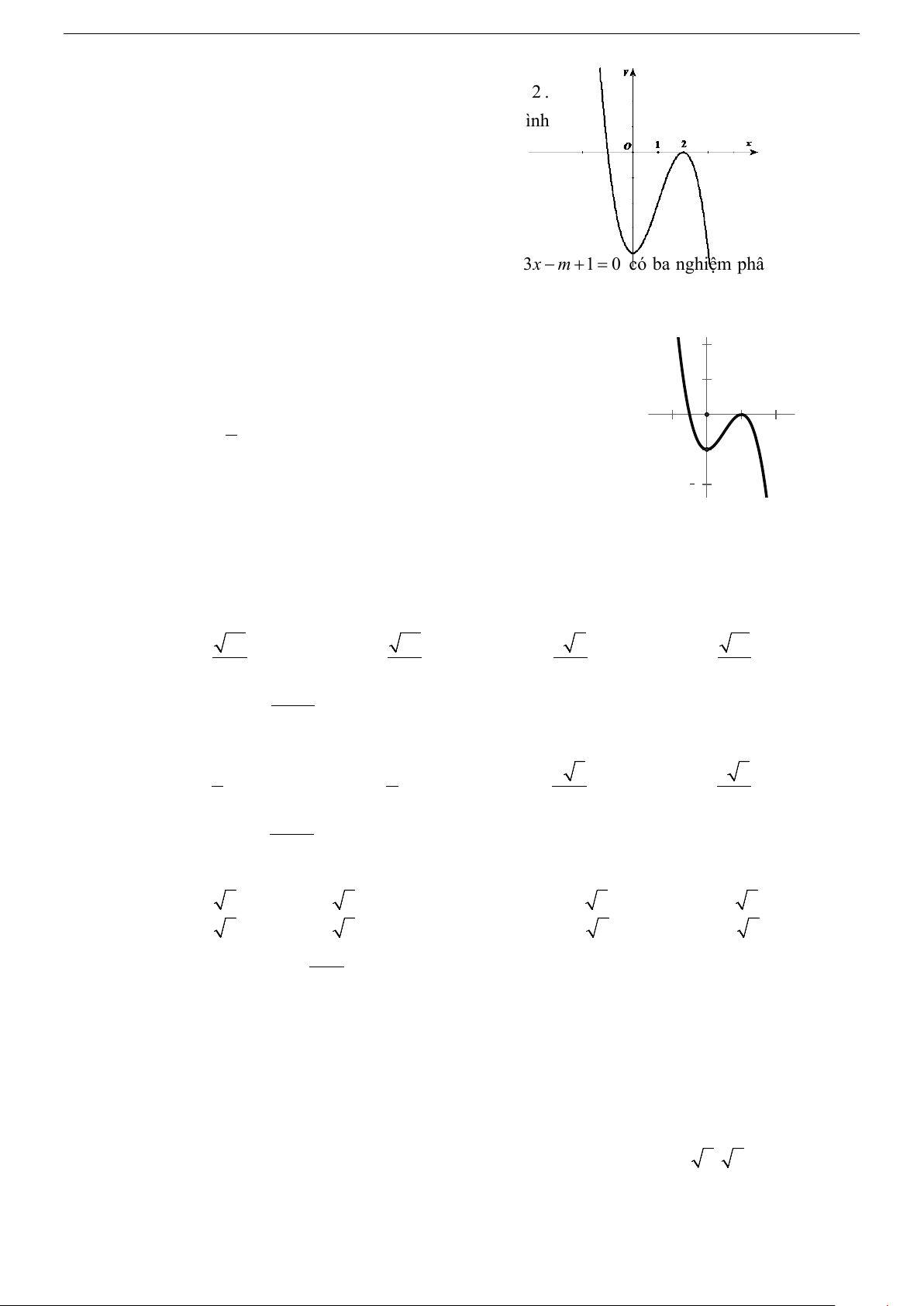
Biết rằng đồ thị của hàm số 3 2
y = −x + 3x − 4 là hình bên.
A. m > 0. B. m ≤ 4. − C. m < 4. − D. m ≤ 4
− hoặc m ≥ 0.
Câu 34. Tất cả giá trị của thm số m để phương trình 3
x − 3x − m +1 = 0 có ba nghiệm phân biệt, trong
đó có hai nghiệm dương là A. 1 − ≤ m ≤1. B. 1
− < m ≤1. C. 1
− < m < 3. D. 1
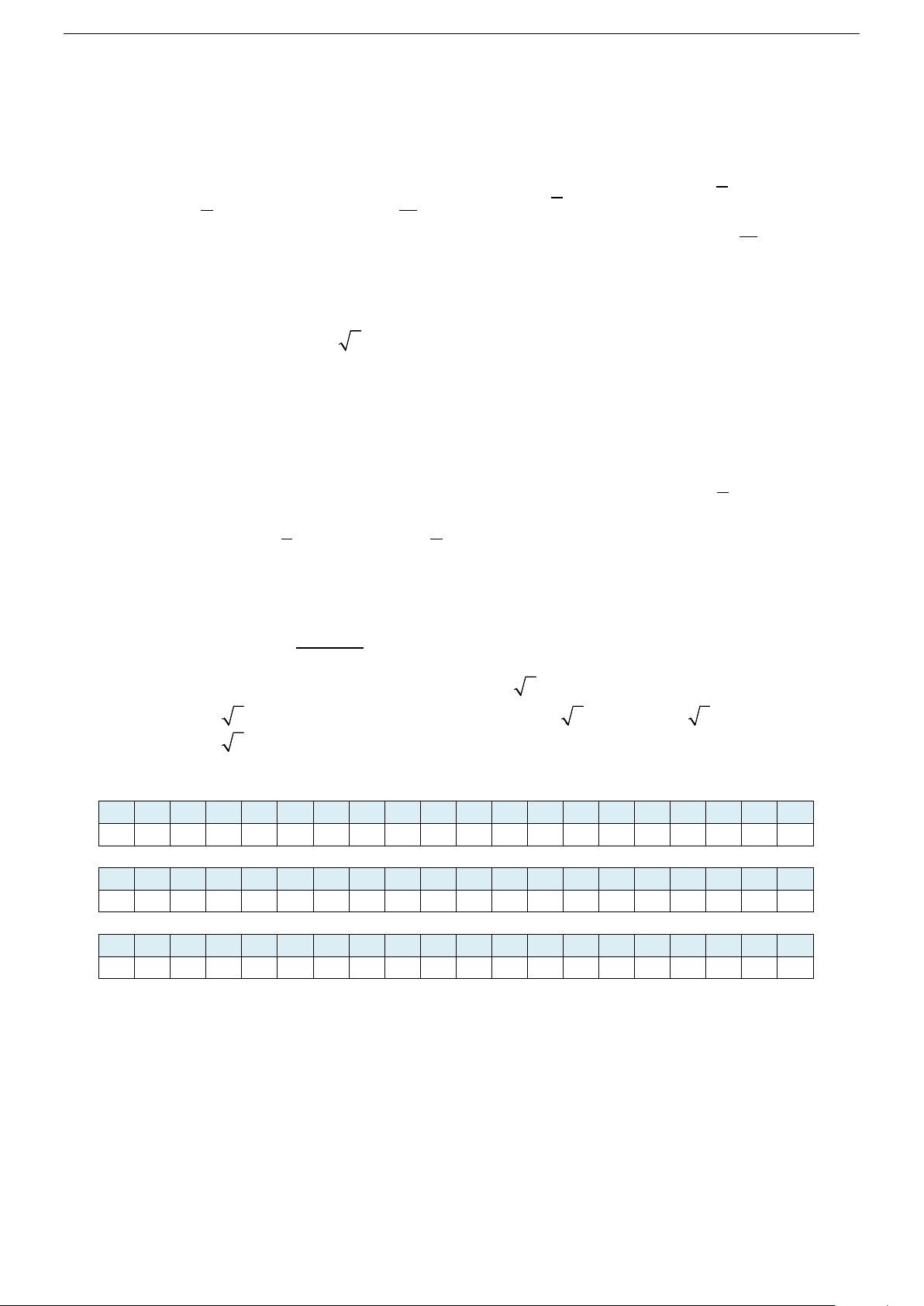
− < m <1. Câu 35. Cho hàm số 3 2 y = 2
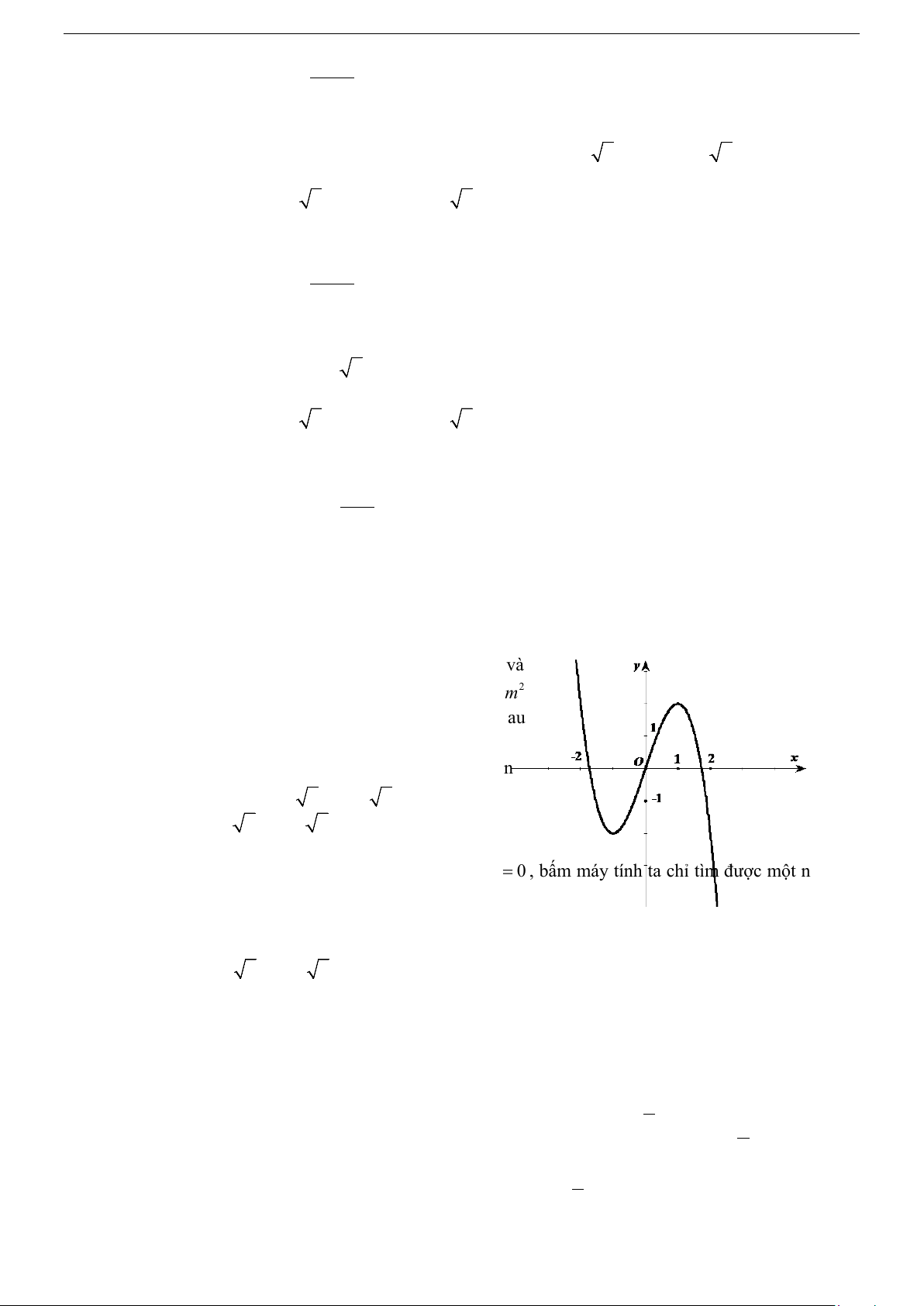
− x + 3x −1 có đồ thị (C) như hình vẽ. Dùng 2
đồ thị (C) suy ra tất cả giá trị tham số m để phương trình 3 2
2x − 3x + 2m = 0 ( )
1 có ba nghiệm phân biệt là O A. 1 0 < m < . B. 1
− < m < 0 . 2 C. 0 ≤ m ≤ 1 − . D. 1
− ≤ m ≤ 0 . -1
Câu 36. Cho phương trình 3 2
x − 3x +1− m = 0 (1) . Điều kiện của tham số m để (12) có ba nghiệm phân
biệt thỏa x <1< x < x khi 1 2 3 A. m = 1. − B. 1
− < m < 3. C. 3 − < m < 1. − D. 3 − ≤ m ≤ 1. − Câu 37. Cho hàm số 3 2
y = 2x − 3x +1 có đồ thị (C)và đường thẳng d : y = x −1. Giao điểm của (C) và
d lần lượt là A(1;0), B và C . Khi đó khoảng cách giữa B và C là A. 30 BC = . B. 34 BC = . C. 3 2 BC = . D. 14 BC = . 2 2 2 2 Câu 38. − Cho hàm số 2x 1 y =
có đồ thị (C) và đường thẳng d : y = 2x − 3 . Đường thằng d cắt (C) x +1
tại hai điểm A và B . Khoảng cách giữa A và B là A. 2 AB = . B. 5 AB = . C. 2 5 AB = . D. 5 5 AB = . 5 2 5 2 Câu 39. − Cho hàm số 2x 1 y =
có đồ thị (C) và đường thẳng d : y = 2x − m . Đường thằng d cắt (C) x +1
tại hai điểm A và B khi giá trị của tham số m thỏa A. 4 − − 2 6 ≤ m ≤ 4 − + 2 6. B. m ≤ 4
− − 2 6 hoặc m ≥ 4 − + 2 6 . C. 4
− − 2 6 < m < 4 − + 2 6. D. m < 4
− − 2 6 hoặc m > 4 − + 2 6 .
Câu 40. Cho hàm số ( ) : x C y =
và đường thẳng d : y = x + m . Tập tất cả các giá trị của tham số m x −1
sao cho (C) và d cắt nhau tại hai điểm phân biệt là A. ( 2; − 2) . B. (− ; ∞ 2 − ) ∪(2;+∞) . C. .  D. ∅
Câu 41. Tập tất cả các giá trị của tham số m để đường thẳng 2
d : y = x + m cắt đồ thị hàm số (C) 3
: y = −x + 4x tại ba điểm phân biệt là A. ( 1; − ) 1 . B. (−∞ ] ;1 . C. .  D. (− 2; 2) .
Câu 42. Tất cả giá trị tham số m để đồ thị (C) 4
: y = x cắt đồ thị (P) y = ( m + ) 2 2 : 3
4 x − m tại bốn điểm phân biệt là Trang 11/28
A. m∈(−∞ − ) ∪( 5 ; 4 − ;0 ∪ +∞ . B. m∈( 1; − 0) ∪(0;+∞) . 4 ) (0; ) C. m∈( 4 − ;0 ∪ +∞ . D. m∈ \{ } 0 . 5 ) (0; )
Câu 43. Cho đồ thị (C) 3 2
: y = 2x − 3x −1. Gọi d là đường thẳng qua A(0; − )
1 có hệ số góc bằng k .
Tất cả giá trị k để (C) cắt d tại ba điểm phân biệt là  9 k  9  9  9  < k  > − k  < − k  > A.  8. B.  8. C.  8. D.  8. k  ≠ 0 k  ≠ 0 k  ≠ 0 k  ≠ 0 Câu 44. Cho hàm số 3 2
y = x − 3x + 4 có đồ thị (C)
. Gọi d là đường thẳng qua I (1;2) với hệ số góc k .
Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm
của đoạn thẳng AB là A. { } 0 . B.  . C. { } 3 − . D. ( 3 − ;+∞) . Câu 45. Với những giá trị nào của tham số m thì
(C y = x − m + x + m + m + x − m m + cắt trục hoành tại ba điểm phân biệt m ) 3 ( ) 2 ( 2 : 3 1 2 4 )1 4 ( ) 1
có hoành độ lớn hơn 1?
A. 1 < m ≠ 1. B. 1 m > . C. 1 m ≥ .
D. m ≠ 1. 2 2 2
Câu 46. Cho đồ thị 3
(C): y = 4x − 3x +1 và đường thẳng d : y = m(x − )
1 + 2 . Tất cả giá trị tham số m để
(C) cắt d tại một điểm là
A. m = 9.
B. m ≤ 0.
C. m ≤ 0 hoặc m = 9. D. m < 0. Câu 47. + Cho hàm số 2x 1 y =
có đồ thị (C) và đường thẳng d : y = x + m . Giá trị của tham số m để x +1
d cắt (C) tại hai điểm phân biệt ,
A B sao cho AB = 10 là
A. m = 0 hoặc m = 6.
B. m = 0.
C. m = 6.
D. 0 ≤ m ≤ 6. Câu 48. + Cho hàm số 2x 1 y =
có đồ thị (C) và d : y = x + m . Giá trị của tham số m để d cắt (C) tại x +1
hai điểm phân biệt A , B sao cho tiếp tuyến tại A và B song song với nhau.
A. Không tồn tại.
B. m = 0. C. m = 3. −
D. m = 3. Câu 49. Cho (P) 2 2
: y = x − 2x − m và d : y = 2x +1. Giả sử (P) cắt d tại hai điểm phân biệt , A B thì
tọa độ trung điểm I của đoạn thẳng AB là A. I ( 2 2; − m ) . B. I ( 2 1; − m − ) 1 . C. I (1; ) 3 .
D. I (2; 5) .
Câu 50. Giá trị nào của tham số m để đồ thị (C
y = m − x + x − m chỉ có một điểm chung với m ) ( ) 3 2 : 1 trục hoành?
A. m =1.
B. m < 0 hoặc 4 m > . 3
C. m < 0. D. 4 m > . 3 Câu 51. Cho hàm số 3 2
y = x − 3x − m −1 có đồ thị (C). Giá trị của tham số m để đồ thị (C) cắt trục
hoành tại ba điểm phân biệt lập thành cấp số cộng là
A. m = 0.
B. m = 3. C. m = 3. − D. m = 6. ± Câu 52. + Cho hàm số 2x 1 y =
có đồ thị (C) và đường thẳng d : y = x + m . Đường thẳng (d) cắt đồ x −1
thị (C) tại hai điểm A và B . Với C( 2;
− 5) , giá trị của tham số m để tam giác ABC đều là Trang 12/28
A. m =1.
B. m =1 hoặc m = 5.
C. m = 5. D. m = 5. − Câu 53. Cho hàm số 4
y = x − ( m − ) 2 2
1 x + 2m có đồ thị (C) . Tất cả các giá trị của tham số m để đường
thẳng d : y = 2 cắt đồ thị (C) tại bốn điểm phân biệt đều có hoành độ lớn hơn 3 là  3  3 m ≠ m ≠  A. 3 m ≠ . B. 11 1< m < . C.  2  2 . D.  . 2 2 1  11  < m < 2 1  < m <  2
Câu 54. Cho hàm số: 3 2
y = x + 2mx + 3(m −1)x + 2 có đồ thị (C). Đường thẳng d : y = −x + 2 cắt đồ thị
(C) tại ba điểm phân biệt A(0; 2
− ), B và C . Với M (3;1) , giá trị của tham số m để tam giác
MBC có diện tích bằng 2 7 là A. m = 1. − B. m = 1
− hoặc m = 4.
C. m = 4.
D. Không tồn tại . m
Câu 55. Cho đồ thị (C
y = x − x + − m x + m. Tất cả giá trị của tham số m để (C cắt trục m ) m ) 3 2 : 2 (1 )
hoành tại ba điểm phân biệt có hoành độ x , x , x thỏa 2 2 2
x + x + x = 4 là 1 2 3 1 2 3 A. m =1.
B. m ≠ 0.
C. m = 2. D. 1
m > − và m ≠ 0. 4 Câu 56. Cho hàm số 1 3 2 2
: y = x − mx − x + m + có đồ thị (C . Tất cả các giá trị của tham số m để m ) 3 3
(C cắt trục Ox tại ba điểm phân biệt có hoành độ x , x, x thỏa 2 2 2
x + x + x >15 là m ) 1 2 3 1 2 3
A. m >1 hoặc m < 1. − B. m < 1 − .
C. m > 0.
D. m >1. 2
Câu 57. Cho đồ thị (C) x − x +1 : y =
và đường thẳng d : y = m . Tất cả các giá trị tham số m để (C) x −1
cắt d tại hai điểm phân biệt A , B sao cho AB = 2 là
A. m =1+ 6.
B. m =1− 6 hoặc m =1+ 6.
C. m =1− 6.
D. m <1 hoặc m > 3.
B. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
C B B C B C D D D D B A A C D B A A C A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
A A B A C B B B A C D C C D A C B D D C
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57
D C B D A D A A D B C B D B A A B
II –HƯỚNG DẪN GIẢI Câu 1. Chọn C.
Phương trình hoành độ giao điểm: 4 2
−x + 2x −1= 0 ⇔ 2
x =1 ⇔ x =1∨ x = 1. −
Vậy số giao điểm là 2 . Câu 2. Chọn B. x = 1 −
Giải phương trình (x 3)( 2 x 3x 2) 0  + + + = ⇔ x = 2 −  x = 3 − 
Vậy số giao điểm là 3. Câu 3. Chọn B. Trang 13/28
Lập phương trình hoành độ giao điểm: 3 2
x − 2x + x −12 = 0 ⇔ x = 3
Vậy có một giao điểm duy nhất. Câu 4. Chọn C. −
Lập phương trình hoành độ giao điểm 2x 1 2
= x −1 ⇔ x − 2x = 0 ⇔ x = 0 ∨ x = 2. x +1 y = 1 −
Thế vào phương trình y = x −1 được tung độ tương ứng  . y =1 Vậy chọn (0;− ) 1 , ( 2; ) 1 . Câu 5. Chọn B. x ≠ 1 − x = 2
Phương trình hoành độ giao điểm: 2x −1 = 2x − 3 ⇔ ⇔  x +1  2 2 1
x − 3x − 2 = 0 x = −  2 y =1
Thế vào phương trình 2x − 3 được tung độ tương ứng:  . y = 4 − Vậy chọn ( ) vaø ( 1 2;1 − ; − 4 . 2 ) Câu 6. Chọn C.
Phương trình hoành độ giao điểm x = 0 4 3 2 2 2
2x + x + x = 0 ⇔ x (2x + x +1) = 0 ⇔  2
2x + x +1 = 0(VN)
Vậy đồ thị hàm số cắt trục hoành tại một điểm. Câu 7. Chọn D.
Phương trình hoành độ giao điểm  x =1  3 2 3 2
x − x + = x − ⇔ x − x − x + = ⇔ (x − )( 2 x − x − )  1− 17 2 3 1 1 2 3 2 0 1 2 2 = 0 ⇔ x =  4   1+ 17 x =  4
Vậy số giao điểm là 3. Câu 8. Chọn D 2 x − 4x + 3 x =1
Phương trình hoành độ giao điểm = 0 ⇔ . x + 2  x = 3
Vậy số giao điểm là 2 . Câu 9. Chọn D. x =1
Phương trình hoành độ giao điểm (x − ) 1 ( 2
x − 3x + 2) = 0 ⇔  . x = 2
Vậy số giao điểm là 2 . Câu 10. Chọn D. 2
Lập phương trình hoành độ giao điểm x − 2x − 3 = x +1 ⇔ x = 1 − ⇒ y = 0 . x −1 Vậy chọn ( 1; − 0) . Câu 11. Chọn B.
Phương trình hoành độ giao điểm: Trang 14/28  2 3+ 21 3+ 21 3+ 21 x = ⇔ x = ∨ x = − 4 2 2 4 2  2 2 2
x − 4x − 2 = −x +1 ⇔ x − 3x − 3 = 0 ⇔  2 3− 21 x = < 0  2
Vậy số giao điểm là 2. Câu 12. Chọn A.
Phương trình hoành độ giao điểm: x = 2 2x −1 x ≠ 1 − 2x 3  = − ⇔  ⇔ 1 . 2 x +1
2x − 3x − 2 = 0 x = −  2
Vậy số giao điểm là 2. Câu 13. Chọn A. 2x −1
x = 3 ⇒ y =1
Lập phương trình hoành độ giao điểm = x − 2 ⇔ . x + 2  x = 1 − ⇒ y = 3 − Vậy chọn A( 1; − 3 − ), B( 3; ) 1 . Câu 14. Chọn C
Phương trình hoành độ giao điểm: x = 2 2x −1 x ≠ 1 − x + xA B 3 = 2x − 3 ⇔  ⇔ 1 ⇒ x = = I . 2 x +1
2x − 3x − 2 = 0 x = − 2 4  2 Câu 15. Chọn D. 2x + 2
x = 3 ⇒ y = 4
Lập phương trình hoành độ giao điểm = x +1 ⇔ ⇒  I (1;2) . x −1 x = 1 − ⇒ y = 0 Vậy chọn I (1;2). Câu 16. Chọn B.
Lập phương trình hoành độ giao điểm 2x + 4 x =1+ 6 = x +1 ⇔  ⇒ x =1. x −1 x =1− 6 I Câu 17. Chọn A.
Lập phương trình hoành độ giao điểm:  2 1+ 33 x = 4 2 4 1+ 33 1+ 33
2x − x + 2 = 6 ⇔  ⇒ x = ∨ x = − .  1− 33 4 4 2 x =  4
Vậy số giao điểm là 2. Câu 18. Chọn A.
Tiệm cận ngang của đồ thị hàm số (C ') là y =1. Phương trình hoành độ giao điểm x = 1 4 2 2
2x − x =1 ⇔ x =1 ⇔ ⇒ y =  1. x = 1 − Vậy chọn (1; ) 1 , ( 1; − ) 1 . Câu 19. Chọn C.
Lập phương trình hoành độ giao điểm: 3 2
x − 3x +1= m Ta có: 2
y' = 3x − 6x ; y' = 0 ⇔ x = 0 ∨ x = 2. Bảng biến thiên: Trang 15/28 x −∞ 0 2 +∞ y' + 0 − 0 + +∞ y 1 3 − −∞
Do đó, đồ thị cắ t đường thẳng y = m tại ba điểm phân biệt khi 3 − < m <1 . Vậy chọn 3 − < m <1. Câu 20. Chọn A.
Lập phương trình hoành độ giao điểm: 4 2 2
− x + 4x + 2= m Ta có: 3 y' = 8
− x + 8x ; y' = 0 ⇔ x = 0 ∨ x =1∨ x = 1. − Bảng biến thiên: x –∞ 1 − 0 1 +∞ y′ + 0 – 0 + 0 – 4 4 y −∞ 2 −∞
Do đó, đường thẳng y = m không cắt đồ thị hà m số khi m > 4 .
Vậy chọn m > 4 . Câu 21. Chọn A.
Ta khảo sát hàm số (C) 4 2
: y = x − 2x tìm được y = − y = . CT 1, C§ 0 Yêu cầu bài toán ⇔ 1
− < m + 3 < 0 ⇔ 4 − < m < 3 − . Vậy chọn m∈( 4; − 3 − ) . Câu 22. Chọn A.
Phương pháp tự luận:
Ta khảo sát hàm số (C) 3
: y = x − 3x +1 tìm được y = 3, y = − C§ CT 1. Yêu cầu bài toán ⇔ 1
− < m < 3 . Vậy chọn 1 − < m < 3.
Phương pháp trắc nghiệm: Ta kiểm tra trực tiếp đáp án
+Với m = 2, giải phương trình 3
x − 3x −1 = 0 ta bấm máy được ba nghiệm ⇒ loại C, D. +Với m = 1 − , giải phương trình 3
x − 3x + 2 = 0 ta bấm máy được hai nghiệm ⇒ loại B. Vậy chọn 1 − < m < 3 Câu 23. Chọn B. Bảng biến thiên: x −∞ 0 2 +∞ y' + 0 − 0 + +∞ y 2 −∞ 2 −
Đường thẳng d : y = m cắt (C) tại ba điểm phân biệt khi: 2 − < m < 2 . Vậy chọn 2 − < m < 2 . Câu 24. Chọn A. Bảng biến thiên Trang 16/28 x –∞ 1 − 0 1 +∞ y′ – 0 + 0 – 0 + +∞ 3 − +∞ y 4 − 4 −
Đường thẳng d : y = m cắt (C) tại bốn điểm phân biệt khi 4 − < m < 3 − . Vậy chọn 4 − < m < 3 − Câu 25. Chọn C. Xét hàm số 4 2
y = x − 4x − 2 Tính 3
y ' = 4x −8x
x = 0 ⇒ y = 2 −  Cho 3
y ' = 0 ⇔ 4x −8x = 0 ⇔ x = 2 ⇒ y = 6 −  .
x = − 2 ⇒ y = 6 −  Bảng biến thiên: x −∞ − 2 0 2 +∞ y ' − 0 + 0 − 0 + y +∞ +∞ 2 − 6 − 6 −
Dựa vào bảng biến thiên suy ra 6 − < m < 2 − . Vậy chọn 6 − < m < 2 − . Câu 26. Chọn B. Phương trình ⇔ 4 2
m = −x + 3x . Đặt (C) 4 2
: y = −x + 3x và d : y = m Xét hàm số 4 2
y = −x + 3x . Ta có 3 y' = 4 − x + 6x ; 6 6
y' = 0 ⇔ x = 0 ∨ x = ∨ x = − . 2 2 Bảng biến thiên: 6 x –∞ − 2 0 6 +∞ 2 y′ + 0 – 0 + 0 – 9 9 4 4 y −∞ 0 −∞
Phương trình có bốn nghiệm phân biệt ⇔ d cắt (C) tại bốn điểm phân biệt ⇔ 9 0 < m < . 4 Vậy chọn 9 0 < m < . 4 Câu 27. Chọn B.
Phương trình hoành độ giao điểm: 4 2
−x + 2x + m = 0 ⇔ 4 2
m = x − 2x . Đặt (C) 4 2
: y = x − 2x và d : y = m Xét hàm số 4 2
y = x − 2x . Ta có 3
y' = 4x − 4x ; y' = 0 ⇔ x = 0 ∨ x = 1 − ∨ x =1. Bảng biến thiên: Trang 17/28 x –∞ 1 − 0 1 +∞ y′ – 0 + 0 – 0 + +∞ 0 +∞ y 1 − 1 −
Đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt khi 1 − < m ≤ 0 . Vậy chọn 1 − < m ≤ 0 . Câu 28. Chọn B.
Phương trình hoành độ giao điểm: (x − )( 2 2
2 x + mx + m − ) 3 = 0 (1) x = 2 ⇔  2 2
x + mx + m − 3= 0 (2)
Để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt ⇔ Phương trình ( ) 1 có ba
nghiệm phân biệt ⇔ Phương trình (2) có hai nghiệm phân biệt khác 2 ∆  > 0 2  3 − m +12 > 0  2 − < m < 2  2 − < m < 2 ⇔  ⇔  ⇔  . Vậy chọn  . 2 4
 + 2m + m − 3 ≠ 0 2 m  + 2m +1≠ 0 m  ≠ 1 − m  ≠ 1 − Câu 29. Chọn A.
Tương tự ta khảo sát hàm số (C) 4 2
: y = x − 2x + 3 ta tìm được y = y = . CT 2, CD 3
Yêu cầu bài toán ⇔ 2 < m < 3. Vậy chọn 2 < m < 3. Câu 30. Chọn C.
Phương pháp tự luận:
Tương tự ta khảo sát hàm số (C) 4 2
: y = x − 2x + 3 ta tìm được y = y = . CT 2, CD 3
Yêu cầu bài toán ⇔ m = 2 ∨ m > 3. Vậy chọn m = 2 ∨ m > 3 .
Phương pháp trắc nghiệm:
+Với m = 3, ta giải phương trình 4 2
x − 2x = 0 ⇔ x = 0 ∨ x = 2 ∨ x = − 2 ⇒ loại B, D.
+Với m = 2, ta giải phương trình 4 2
x − 2x +1 = 0 ⇔ x =1∨ x = 1 − ⇒ loại A. Câu 31. Chọn D.
Phương pháp tự luận:
Khảo sát hàm số (C) 4 2 : y = 2
− x + 2x +1 tìm được 3 y = y = . CT 1, C§ 2 Yêu cầu bài toán 1
⇔ 3m =1 ⇔ m = . Vậy chọn 1 m = . 3 3
Phương pháp trắc nghiệm: + Với 1
m = , ta giải phương trình 4 2 1 2 2 2
− x + 2x − = 0 ⇔ x = ∨ x = − ⇒ loại B, A. 2 2 2 2
+ Với m = 0, ta giải phương trình  2 1+ 3 x = 4 2 2 1+ 3 1+ 3 2
− x + 2x +1 = 0 ⇔  ⇔ x = ∨ x = − ⇒ loại C.  1− 3 2 2 2 x =  2 Vậy chọn 1 m = . 3 Câu 32. Chọn C.
Phương pháp tự luận: Trang 18/28
Phương trình hoành độ giao điểm của (C) và trục Ox : 3 2 2
− x + 3x + 2m −1 = 0. Ta khảo sát hàm số (C ) 3 2
' : y = 2x − 3x +1 và cũng chỉ là tìm y
y . Cụ thể y = y = . Do đó yêu CD 1, CT 0 CD , CT cầu bài toán 1
⇔ 0 < 2m <1 ⇔ 0 < m < . Vậy chọn 2 1 0 < m < 2
Phương pháp trắc nghiệm:
+ Với m = 0, ta có phương trình  1 x − = 3 2 2x 3x 1 0  − + − = ⇔ 2 ⇒ loại B, D.  x = 1
+ Với m = 0.1, ta có phương trình 3 2 2
− x + 3x − 0.8 = 0 có 3 nghiệm ⇒ loại C. Câu 33. Chọn C. Ta có 3 2
x − 3x + 4 + m = (
0 *). Xem phương trình (*) là phương trình hoành độ giao điểm của
đồ thị hàm số (C) : 3 2
y = −x + 3x − 4 và đường thẳng d : y = m. Số giao điểm của (C) và d là
số nghiệm của (*). Dựa vào đồ thị hàm số, yêu cầu bài toán ⇔ m < 4
− . Vậy chọn m < 4 − . Câu 34. Chọn D.
Phương pháp tự luận:
Ta có đồ thị của hàm số 3
y = x − 3x +1như hình bên.
Dựa vào đồ thị ta tìm được kết quả để đồ thị cắt hàm số tại ba điểm phân biệt là 1 − < m < 3.
Với x = 0 ⇒ y =1 nên yêu cầu bài toán ⇔ 1
− < m <1. Vậy chọn 1 − < m <1. x = 0
Phương pháp trắc nghiệm: Xét m =1, ta được phương trình 3
x − 3x = 0 ⇔  x = ± 3
không đủ hai nghiệm dương ⇒ loại A, B, C. Vậy chọn 1 − < m <1. Câu 35. Chọn A. Phương trình ( ) 1 ⇔ 3 2 2
− x + 3x −1= 2m −1 là phương
trình hoành độ giao điểm của đồ thị (C) và
d : y = 2m −1 (là đường thẳng song song hoặc trùng với Ox ).
Phương trình có ba nghiệm phân biệt ⇔ (C) cắt d tại ba điểm phân biệt ⇔ 1
− < 2m −1< 0 ⇔ 1 0 < m < . 2 Vậy chọn 1 0 < m < . 2 Câu 36. Chọn C.
Phương pháp tự luận Ta có 3 2
x − 3x +1− m = 0 là phương trình hoành độ giao điểm giữa hai đồ thị hàm số 3 2
y = x − 3x +1 và y = m (là đường thẳng song song hoặc trùng với Ox ). Xét 3 2
y = x − 3x +1. Tập xác định: D = .  Tính 2 y ' = 3x − 6 . x
x = 0 ⇒ y =1 Ta có 2
y ' = 0 ⇔ 3x − 6x = 0 ⇔  .
x = 2 ⇒ y = 3 −
Ta có x =1⇒ y = 1 −
Dựa vào đồ thị, số nghiệm của phương trình (1) chính là số giao điểm của đồ thị 3 2
y = x − 3x +1 và đường thẳng y = m. Trang 19/28
Do đó, yêu cầu bài toán ⇔ 3 − < m < 1 − .
Phương pháp trắc nghiệm
Chọn m = 2 thay vào (1) tìm nghiệm bằng máy tính. Ta nhận thấy (1) chỉ có một nghiệm. Suy
ra loại được đáp án B.
Tiếp tục thử m = 1
− thay vào (1) tìm nghiệm bằng máy tính. Ta nhận thấy (1) có ba nghiệm
nhưng có một nghiệm bằng 1. Suy ra loại A.
Tiếp tục thử m = 2
− thay vào (1) tìm nghiệm bằng máy tính. Ta nhận thấy (1) có ba nghiệm
thỏa yêu cầu bài toán. Suy ra loại D.
Vậy C là đáp án cần tìm. Câu 37. Chọn B.
Phương pháp tự luận
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d 3 2 3 2
2x − 3x +1 = x −1 ⇔ 2x − 3x − x + 2 = 0 x =1 2
⇔ (x −1)(2x − x − 2) = 0 ⇔  2
2x − x − 2 = 0 (1) Khi đó ta có (
A 1;0), B(x ; x −1) và C(x ; x −1) ( x , x là nghiệm của (1)) 1 1 2 2 1 2 
Ta có BC = (x − x ; x − x ) , suy ra 2 1 2 1 2 2 2 2  1  34
BC = (x − x ) + (x − x ) = 2(x − x ) = 2(x + x ) − 4x x = 2 + 4 = . 2 1 2 1 2 1 2 1 1 2  4  2 Vậy chọn B.
Phương pháp trắc nghiệm
Phương trình hoành độ giao điểm 3 2 3 2
2x − 3x +1 = x −1 ⇔ 2x − 3x − x + 2 = 0.
- Nhập máy tính tìm nghiệm phương trình bậc ba.
- Gán hai nghiệm khác 1 vào B và C .
- Nhập máy X −1. Dùng lệnh CALC tìm tung độ của điểm B và C gán vào hai biến D và E . Khi đó 2 2 34
BC = (C − B) + (E − D) = . 2 Vậy chọn B. Câu 38. Chọn D.
Phương pháp tự luận
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d  = 2 ⇒ =1 ⇒ (2;1) 2x −1  ≠ 1 x y A x − 2x 3  = − ⇔  ⇔ 2 1  1 x +1
2x − 3x − 2 = 0
x = − ⇒ y = 4 − ⇒ B− ; 4  −   2  2   Ta có 5 AB  ; 5 = − −  . Suy ra 5 5 AB = . Vậy chọn 5 5 AB = .  2  2 2
Phương pháp trắc nghiệm −
Phương trình hoành độ giao điểm: 2x 1 = 2x − 3 (x ≠ 1) − . x +1
Dùng lệnh CALC của máy tính, ta tìm được hai nghiệm của phương trình lần lượt là x = 2 và 1 x = − . Suy ra ( A 2;1) và 1 B ; 4 −
− . Dùng máy tính thu được 5 5 AB = . 2  2  2 Vậy chọn 5 5 AB = . 2 Câu 39. Chọn D.
Phương pháp tự luận
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d : Trang 20/28 2x −1 2
= 2x − m (x ≠ 1)
− ⇔ 2x − mx +1− m = 0 (1) x +1
Yêu cầu bài toán ⇔ (1) có hai nghiệm phân biệt khác 1 − 2
∆ = m −8(1− m) > 0 ⇔  ⇔ m < 4
− − 2 6 ∨ m > 4 − + 2 6 .
2 + m +1− m ≠ 0 Vậy chọn m < 4
− − 2 6 hoặc m > 4 − + 2 6 .
Phương pháp trắc nghiệm
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d : 2x −1 2
= 2x − m (x ≠ 1)
− ⇔ 2x − mx +1− m = 0 (1) x +1
Chọn m = 0 thay vào (1) tìm nghiệm bằng máy tính, ta nhận thấy (1) vô nghiệm. Suy ra loại được A và C.
Tiếp tục chọn m = 4
− + 2 6 thay vào (1) tìm nghiệm bằng máy tính, ta nhận thấy (1) có
nghiệm kép. Suy ra loại B. Vậy chọn m < 4
− − 2 6 hoặc m > 4 − + 2 6 . Câu 40. Chọn C.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d : x 2
= x + m ⇔ x + (m − 2) x − m = 0 ( ) 1 x −1
(C) cắt d tại hai điểm phân biệt⇔ ( )
1 có hai nghiệm phân biệt 2
⇔ ∆ > 0 ⇔ m + 4 > 0 (đúng với mọi m). Vậy chọn  . Câu 41. Chọn D.
Phương pháp tự luận:
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d : 3 2 3 2
−x + 4x = x + m ⇔ −x + 3x = m
Ta khảo sát hàm số (C) 3
: y = −x + 3x có đồ thị sau như hình bên.
Tìm được y = − y = nên yêu cầu bài toán CT 2, C§ 2 2 ⇔ 2
− < m < 2 ⇔ − 2 < m < 2 .
Vậy chọn − 2 < m < 2.
Phương pháp trắc nghiệm: + Với m = 3, − ta có phương trình 3
−x + 3x − 9 = 0 , bấm máy tính ta chỉ tìm được một nghiệm ⇒ loại B, C.
+ Với m =1.4, ta có phương trình 3 2
−x + 3x −1,4 = 0 , bấm máy tính ta ra được ba nghiệm ⇒ loại A.
Vậy chọn − 2 < m < 2 . Câu 42. Chọn C.
Phương trình hoành độ giao điểm của (C) và (P) là: 4 x = ( m + ) 2 2 3 4 x − m ⇔ 4 x − ( m + ) 2 2 3
4 x + m = 0 (1) .
(C) cắt (P) tại bốn điểm phân biệt ⇔ Phương trình ( )
1 có bốn nghiệm phân biệt  4 ∆  > 0 2 5
m + 24m +16 > 0 m < 4 − ∨ m > −   5  4 m  > − ⇔   P > 0 ⇔ 2 m  > 0 ⇔ m  ≠ 0 ⇔  5 .   S > 0 3  m + 4 > 0  4 m  ≠ 0 m  > −  3 Trang 21/28  4 m  > − Vậy chọn  5 . m  ≠ 0 Câu 43. Chọn B.
Phương trình đường thẳng d : y = kx −1.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d : x = 0 (1) 3 2
2x − 3x −1= kx −1 ⇔ x( 2
2x − 3x − k) = 0 ⇔  2
2x − 3x − k (2)
(C) cắt d tại ba điểm phân biệt ⇔ Phương trình (2) có hai nghiệm phân biệt khác 0 ∆  > 0  9 k  > − ⇔ ⇔  8 . 0   − k ≠ 0 k  ≠ 0  9 k  > − Vậy chọn  8 . k  ≠ 0 Câu 44. Chọn D.
Phương pháp tự luận:
Phương trình d : y = k (x − ) 1 + 2 .
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d : 3 2
x − 3x + 4 = kx − k + 2 3 2
⇔ x − 3x − kx + k + 2 = 0 ( ) 1 x =1 ⇔ (x − ) 1 ( 2
x − 2x − k − 2) = 0 ⇔  2
x − 2x − k − 2 = 0 (*)   g (x)
d cắt (C) tại ba điểm phân biệt ⇔ Phương trình (*) có hai nghiệm phân biệt x ; x khác 1 1 2 ' ∆ >  g 0 k + 3 > 0 ⇔  ⇔  ⇔ > − g  ( ) k 3 1 ≠ 0  3 − − k ≠ 0
x + x = 2 = 2x Hơn nữa theo Viet ta có 1 2 I
nên I là trung điểm AB.
y + y = k x + x − 2k + 4 = 4 = 2y  1 2 ( 1 2) I Vậy chọn k > 3 − , hay ( 3 − ;+∞) .
Phương pháp trắc nghiệm:
Ta tính toán đến phương trình ( ) 1 + Với k = 2
− , ta giải phương trình 3 2
x − 3x + 2x = 0 thu được x = 2, x = 0, x = . I 1 1 2
x + x = 2 = 2x + Hơn nữa 1 2 I
nên I là trung điểm AB ⇒ loại A, C từ đó ta loại được B. y + y = 4 =  2y 1 2 I Vậy chọn k > 3 − . Câu 45. Chọn A.
Phương trình hoành độ giao điểm của đồ thị (C) và trục Ox : 3 x − (m + ) 2 x + ( 2 3 1 2 m + 4m + )
1 x − 4m(m + ) 1 = 0 ⇔ (x − )( 2 x − ( m + ) 2 2 3
1 x + 2m + 2m) = 0 x = 2 x − 2 = 0 ⇔   ⇔ x = 2m 2 2
x − (3m +1)x + 2m + 2m = 0  x = m +  1 Trang 22/28 1 < m ≠1 1  < 2m ≠ 2 2   Yêu cầu bài toán 1 ⇔ 1
 < m +1 ≠ 2 ⇔ 0 < m ≠ 1 ⇔ < m ≠ 1. 2 2m m 1  ≠ + m ≠  1  
Vậy chọn 1 < m ≠ 1. 2 Câu 46. Chọn D.
Phương trình hoành độ giao điểm (C) và d là 3
4x − 3x +1= m(x − ) 1 + 2 x =1 ⇔ 3 4x − (m + )
3 x + m −1= 0 ⇔  2
4x + 4x − m +1= 0 (1)
(C) cắt d tại một điểm ⇔ Phương trình ( )
1 vô nghiệm hay phương trình ( ) 1 có nghiệm kép bằng 1  ′ ∆ < 0 4m < 0 ⇔  ′ ∆ = 0   ⇔ 4  m = 0  ⇔ m < 0.   4   + 4 − m +1= 0  m  = 9 Vậy chọn m < 0. Câu 47. Chọn A.
Phương pháp tự luận
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d 2x +1 x ≠ 1 − = x + m ⇔  2 x +1
x + (m −1)x + m −1 = 0 (1)
Khi đó d cắt (C) tại hai điểm phân biệt A , B khi và chi khi phương trình (1) có hai nghiệm 2
(m −1) − 4(m −1) > 0 phân biệt khác 1 − ⇔ 
⇔ m <1∨ m > 5 (*) 2 ( 1) −
− (m −1) + m −1 ≠ 0 Khi đó ta lại có  2 (
A x ; x + m), B(x ; x + m) ⇒ AB = (x − x ; x − x ) ⇒ AB = 2(x − x ) = 2 x − x , 1 1 2 2 2 1 2 1 2 1 2 1
x + x =1− m và 1 2  . Từ đây ta có x x = m −  1 1 2 2
AB = 10 ⇔ x − x = 5 ⇔ (x + x ) − 4x x = 5 2 1 2 1 1 2 m = 0 2 2
⇔ (1− m) − 4(m −1) = 5 ⇔ m − 6m = 0 ⇔  (thỏa (*) ) m = 6
Vậy chọn m = 0 ∨ m = 6 .
Phương pháp trắc nghiệm +
Chọn m = 0 thay vào d . Ta được 2x 1 = x (x ≠ 1) − . x +1
Dùng lệnh SHIFT CALC tìm được 1 5 x + = hoặc 1 5 x − = . 2 2  + +   − −   Suy ra 1 5 1 5 1 5 1 5 A ; , B  ;
 ⇒ AB(− 5, − 5) ⇒ AB = 10 . 2 2  2 2     
Nhận thấy m = 0 thỏa yêu cầu.
Tượng tự chọn m = 6 kiểm tra tương tự m = 0 nhận thấy m = 6 thỏa yêu cầu bài toán.
Vậy chọn m = 0 ∨ m = 6 . Câu 48. Chọn A.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d Trang 23/28 2x +1 2
= x + m (x ≠ 1)
− ⇔ x + (m −1)x + m −1 = 0 (1) x +1
Khi đó d cắt (C) tại hai điểm phân biệt A , B khi và chi khi phương trình (1) có hai nghiệm phân biệt khác 1 − 2
(m −1) − 4(m −1) > 0
m <1∨ m > 5 ⇔  ⇔ 
⇔ m <1∨ m > 5 2 1
 − (m −1) + m −1 ≠ 0 1  ≠ 0 Ta có 1 f '(x) = . Gọi (
A x ; y ), B(x ; y ) trong đó x , x là nghiệm của (1) (nên ta có 2 (x +1) 1 1 2 2 1 2
x + x =1− m ). Suy ra hệ số góc của các tiếp tuyến tại điểm A và B lần lượt là 1 k = 1 2 A 2 (x +1) 1 và 1 k = B 2 (x +1) 2
Vì tiếp tuyến tại A và B song song, đồng thời x ≠ x nên phải có 1 1 = , suy ra 1 2 2 2 (x +1) (x +1) 1 2
x +1 = −x −1 ⇔ x + x + 2 = 0 ⇔ 1− m + 2 = 0 ⇔ m = 3 (l) . 1 2 1 2
Vậy chọn không tồn tại. Câu 49. Chọn D.
Phương trình hoành độ giao điểm của đồ thị (P) và đường thẳng d : 2 2
x − 2x − m = 2x +1⇔ 2 2
x − 4x − m −1= 0 ( ) 1
(P) cắt d tại hai điểm phân biệt ⇔ Phương trình ( )
1 có hai nghiệm phân biệt ⇔ ′ ∆ > 0 ⇔ 2
m + 5 > 0 (đúng với mọi m ) Hoành độ của điểm ,
A B là nghiệm x , x của phương trình ( )
1 và tung độ trung điểm I thỏa 1 2  x + x 1 2 x = = I 2
phương trình d , nên tọa độ trung điểm I là  2 . y = x + = I 2 I 1 5
Vậy chọn I (2; 5) . Câu 50. Chọn B.
Phương pháp tự luận: Xét m =1, phương trình 2
x −1 = 0 có hai nghiệm (loại).
Khi m ≠ 1 ta thấy đồ thị hàm luôn có có hai điểm cực trị. Vậy ta tìm giá trị cực đại và cực tiểu của hàm số như sau:
x = 0 ⇒ y = −m
y ' = 3(m − ) 2  3 2 1 x + 2x = 0 ⇔ 2 − 27
− m + 54m − 27m + 4 x = ⇒ y =  3(m − ) 1 27(m −  )2 1 m( 3 2
27m − 54m + 27m − 4)
(C có 1 điểm chung với Ox ⇔ y y > ⇔ > CD . CT 0 0. m ) 27(m − )2 1 4
⇔ m < 0 ∨ m > . 3 Vậy chọn 4
m < 0 ∨ m > . 3
Phương pháp trắc nghiệm: Ta kiểm tra trực tiếp các đáp án của đề bài + Với m = 1 − , phương trình 3 2 2
− x + x +1 = 0 thu được x =1 là nghiệm duy nhất ⇒ loại A, D.
+ Với m = 2 , phương trình 3 2
x + x − 2 = 0 thu được x =1 là nghiệm duy nhất ⇒ loại C. Vậy chọn 4
m < 0 ∨ m > . 3 Trang 24/28 Câu 51. Chọn C.
Phương pháp tự luận
Đồ thị (C) cắt trục hoành tại điểm phân biệt tạo thành cấp số cộng khi và chỉ khi phương trình 3 2
x − 3x −1 = m có ba nghiệm phân biệt lập thành cấp cố cộng.
Suy ra đường thẳng y = m đi qua điểm uốn của đồ thị 3 2
y = x − 3x −1 (do đồ thị (C) nhận
điểm uốn làm tâm đối xứng). Mà điểm uốn của 3 2
y = x − 3x −1 là I(1; 3 − ) . Suy ra m = 3 − . Vậy chọn m = 3 − .
Phương pháp trắc nghiệm Chọn m = 3
− thay vào phương trình 3 2
x − 3x − m −1 = 0 . Ta được 3 2
x − 3x + 2 = 0 . Dùng chức năng tìm nghiệm phương trình bậc ba ta được ba nghiệm
x =1− 3, x =1, x =1+ 3 thỏa cấp số cộng. Vậy chọn m = 3 − . Câu 52. Chọn B.
Phương pháp tự luận
Phương trình hoành độ giao điểm của (C) và đường thẳng d : 2x +1 2
= x + m (x ≠ 1) ⇔ x + (m − 3)x − m −1 = 0 (1) x −1
Khi đó d cắt (C) tại hai điểm phân biệt A , B khi và chi khi phương trình (1) có hai nghiệm 2 2
(m −3) + 4(m +1) > 0
m − 2m +13 > 0 phân biệt khác 1 − ⇔  ⇔  đúng m ∀ ∈ .  2 1
 + (m − 3) − m −1 ≠ 0  1 − ≠ 0 Gọi (
A x ; x + m), B(x ; x + m) trong đó x , x là nghiệm của (1) , theo Viet ta có 1 1 2 2 1 2
x + x = 3 − m 1 2  . x x = −m −  1 1 2  + + + Gọi x x x x 2mm m 1 2 1 2 I ;   
 là trung điểm của AB , suy ra 3 3 I − +  ; , nên  2 2   2 2    3− m 3+ m  1 2 2 CI  2 − − ;5 −  ⇒ CI =
(m − 7) + (7 − m) .  2 2  2  Mặt khác 2 2
AB = (x − x ; x − x ) ⇒ AB = 2(x − x ) = 2(m − 2m +13) . Vậy tam giác ABC 2 1 2 1 2 1 đều khi và chỉ khi 3 1 2 3 2 CI = AB ⇔ 2(m − 7) = 2(m − 2m +13) 2 2 2 m =1 2 2 2
⇔ (m − 7) = 3(m − 2m +13) ⇔ 2m + 8m −10 = 0 ⇔  . m = 5 −
Vậy chọn m =1∨ m = 5 − . Câu 53. Chọn D.
Phương trình hoành độ giao điểm của (C) và đường thẳng d : 2 x =1 4 2 4 2
x − (2m −1)x + 2m = 2 ⇔ x − (2m −1)x + 2m − 2 = 0 ⇔  2
x = 2m − 2 (1)
Đường thẳng d cắt (C) tại bốn điểm phân biệt có hoành độ nhỏ hơn 3 khi và chỉ khi phương
trình (1) có hai nghiệm phân biệt nhỏ hơn 3.  3  3 ≠ 2 − 2 ≠ 1 m m ≠  m  2  ⇔  2  ⇔ . Vậy chọn  . 0 2m 2 9  < − < 11 1  < m < 11  < <  1 m  2  2 Câu 54. Chọn B.
Phương trình hoành độ giao điểm Trang 25/28 3 2
x + 2mx + 3(m −1)x + 2 = −x + 2 ⇔ x( 2
x + 2mx + 3(m −1)) = 0 x = 0 ⇔  2
x + 2mx + 3(m −1) = 0(1)
Đường thẳng d cắt (C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm 2
m − 3m + 3 > 0  m ∀ ∈  phân biệt khác 0 ⇔  ⇔  ⇔ m ≠ 1. m −1 ≠ 0 m ≠ 1
Khi đó ta có: C(x ;−x + 2), B(x ;−x + 2) trong đó x , x là nghiệm của (1) , nên theo Viet thì 1 1 2 2 1 2 x + x = 2 − m 1 2  . Vậy x x = 3m −  3 1 2  2 2
CB = (x − x ;−x + x ) ⇒ CB = 2(x − x ) = 8(m − 3m + 3) 2 1 2 1 2 1 3 − −1+ 2
d(M ;(d)) = = 2 2
Diện tích tam giác MBC bằng 2 7 khi và chỉ khi 1 m = 1 − 2 2
8(m − 3m + 3). 2 = 2 7 ⇔ m − 3m + 3 = 7 ⇔ ( thỏa m ≠ 1) 2  m = 4 Vậy chọn m = 1 − ∨ m = 4 . Câu 55. Chọn A.
Phương pháp tự luận
Phương trình hoành độ giao điểm của (C và trục hoành là 3 2
x − 2x + (1− m) x + m = 0 m ) x =1 ⇔(x − )( 2
1 x − x − m) = 0 ⇔  2
x − x − m = 0 (1)
(C cắt trục hoành tại ba điểm phân biệt ⇔ Phương trình ( )
1 có hai nghiệm phân biệt khác 1 m ) ∆  > 0 1  + 4m > 0  1 m  > − ⇔ ⇔ ⇔  4 (*) 1    −1− m ≠ 0 m  ≠ 0 m  ≠ 0 x + x =1
Gọi x =1 còn x , x là nghiệm phương trình ( ) 1 nên theo Vi-et ta có 1 2 . Vậy 3 1 2 x x = −  m 1 2 2 2 2
x + x + x = 4 ⇔ 2 2
x + x +1= 4 ⇔(x + x − 2x x − 3 = 0 ⇔ m =1 (thỏa (*)) 1 2 )2 1 2 3 1 2 1 2 Vậy chọn m =1. Câu 56. Chọn A.
Phương pháp tự luận:
Phương trình hoành độ giao điểm của (C) và đường thẳng d : 1 3 2 2
x − mx − x + m + = 0 ⇔ (x − ) 2 1 x +  ( 3 − m + )
1 x − 3m − 2 = 0 3 3  x =1  2 ⇔ x +  ( 3 − m + )
1 x − 3m − 2 = 0 (1)
  g (x)
(C cắt Ox tại ba điểm phân biệt⇔ phương trình (1) có hai nghiệm phân biệt khác 1 m ) 2 ∆ >  g 0 9
m + 6m + 9 > 0 ⇔  ⇔  ⇔ ≠ . g  ( ) m 0 1 ≠ 0  6 − m ≠ 0
x + x = 3m −1
Gọi x =1 còn x , x là nghiệm phương trình ( ) 1 nên theo Viet ta có 2 3 . 1 2 3 x x = 3 − m −  2 2 3 Vậy Trang 26/28 2 2 2
x + x + x >15 ⇔ 1+ x + x − 2x x >15 1 2 3 ( 2 3)2 2 3 ⇔ (3m − )2 1 + 2(3m + 2) 2
−14 > 0 ⇔ 9m − 9 > 0 ⇔ m >1∨ m < 1 −
Vậy chọn m >1∨ m < 1 − .
Phương pháp trắc nghiệm: Ta kiểm tra ngay trên đáp án + Với m = 2
− , ta giải phương trình bậc ba: 1 3 2 4
x + 2x − x − = 0 thu được 3 nghiệm 3 3 x = 6.37..., −
x =1, x = 0.62... −
Ta chọn những giá trị nhỏ hơn các nghiệm này và kiểm tra 1 2 3
điều kiện của bài toán. Cụ thể ta tính (− )2 2 6.4 +1 + ( 0.63 −
)2 = 42.3569 >15 ⇒ loại C, D.
+ Với m = 2 , ta làm tương tự thu được 3 nghiệm x = 6.27..., x =1, x = 1.27... − 1 2 3 Tính 2 2 6.2 +1 + ( 1.3 −
)2 = 41.13 >15 ⇒ loại B.
Vậy chọn m >1∨ m < 1 − . Câu 57. Chọn B. 2
Phương trình hoành độ giao điểm (C) và d là x − x +1 = m x −1 x ≠1 ⇔  2 x − (m + )
1 x + m +1= 0 (1)
(C) cắt d tại hai điểm phân biệt ⇔ Phương trình ( )
1 có hai nghiệm phân biệt khác 1 ∆  = (m + ) 1 (m − ) 3 > 0 ⇔  ⇔ m < 1 − ∨ m > 3 (*) 1
 − m −1+ m +1≠ 0
Hoành độ giao điểm x , x là nghiệm của phương trình (1) nên theo Vi-et ta có: 1 2
x + x = m +1 1 2 
. Khi đó: A(x ; m , B(x ; m , suy ra 2 ) 1 ) x x = m +  1 1 2 m +1= 2 + 6 AB = 2 ⇔ 2
AB = 2⇔(x − x )2 = 2 ⇔(x + x − 4x x − 2 = 0 ⇔ 1 2 )2 2 1 1 2  m +1= 2 − 6 m =1+ 6 ⇔  ( thỏa (*)) m =1− 6
Vậy chọn m =1+ 6 ∨ m =1− 6. Trang 27/28
Document Outline

  • DS_C1_TUONG GIAO
    • A. BÀI TẬP TRẮC NGHIỆM
    • B. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM