














































Preview text:
CHỦ ĐỀ 2. TÍCH PHÂN
A. KIẾN THỨC CƠ BẢN 1. Định nghĩa
Cho f là hàm số liên tục trên đoạn [ ;
a b]. Giả sử F là một nguyên hàm của f trên [ ; a b]. Hiệu số
F(b) − F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [ ; a b] của hàm số b
f (x),kí hiệu là f (x) . dx ∫ a b
Ta dùng kí hiệu F(x) b = F(b) − F(a) để chỉ hiệu số F(b) − F(a) . Vậy f (x)dx = F(x) b = F(b) − F(a) a ∫ . a a b b
Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi f (x)dx ∫
hay f (t)dt. ∫ Tích phân đó a a
chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
Ý nghĩa hình học của tích phân: Nếu hàm số f liên tục và không âm trên đoạn [ ; a b] thì tích phân b f (x)dx ∫
là diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f (x) , trục Ox và hai đường a b
thẳng x = a, x = .
b Vậy S = f (x) . dx ∫ a
2. Tính chất của tích phân a b a
1. f (x)dx = 0 ∫
2. f (x)dx = − f (x)dx ∫ ∫ a a b b c c b b
3. f (x)dx + f (x)dx = f (x)dx ∫ ∫ ∫
( a < b < c ) 4. k. f (x)dx = k. f (x)dx (k ∈ ) ∫ ∫ a b a a a b b b
5. [ f (x) ± g(x)]dx = f (x)dx ± g(x)dx ∫ ∫ ∫ . a a a
B. KỸ NĂNG CƠ BẢN
1. Một số phương pháp tính tích phân
I. Dạng 1: Tính tích phân theo công thức
Ví dụ 1: Tính các tính phân sau: 1 1 1 1 a) + I dx = ∫ . b) I x = dx 2x 9 I = dx I x = dx 3 ∫ . c) ∫ . d) ∫ . (1+ x) x +1 x + 3 2 4 − x 0 0 0 0 Hướng dẫn giải 1 1 1 a) dx d(1+ x) 1 3 I = = = − = ∫ 3 ∫ . 3 2 (1+ x) (1+ x) 2(1+ x) 8 0 0 0 1 1 b) x 1 I dx 1 = = − dx = ∫ ∫
(x − ln(x +1)) 10 =1− ln 2 . x +1 x +1 0 0 1 1 c) 2x + 9 3 I dx 2 = = + dx = ∫ ∫
(2x + 3ln(x + 3))1 = 3+ 6ln2 − 3ln3 . 0 x + 3 x + 3 0 0 d ( 2 1 1 4 1 − x x ) d) 1 2 3 I = dx = − = ln | 4 − x | = ln ∫ 2 ∫ . 2 0 4 − x 2 4 − x 4 0 0 Bài tập áp dụng 1 1 1) 3 4 5
I = x (x −1) dx ∫ . 2) I = ( 3 2x + x + ∫ )1dx. 0 0 Trang 1/80 1 16
3) I = x 1− xdx ∫ . 4) I dx = ∫ . + − 0 0 x 9 x
II. Dạng 2: Dùng tính chất cận trung gian để tính tích phân b b b
Sử dụng tính chất [f (x) + g(x)]dx = f (x)dx + g(x)dx ∫ ∫ ∫
để bỏ dấu giá trị tuyệt đối. a a a 2
Ví dụ 2: Tính tích phân I = | x +1| dx ∫ . 2 − Hướng dẫn giải + − ≤ ≤ Nhận xét: x 1, 1 x 2 x +1 = . Do đó
−x −1, − 2 ≤ x < 1 − 1 − 2 2 1 − 2 1 − 2 2 2 = | +1| = | +1| + | +1| = − ∫ ∫ ∫ ∫ ( + )1 + ∫ ( + )1 x x I x dx x dx x dx x dx x dx = − + x + + x = 5. 2 2 2 − 2 − 1 − 2 − 1 − 2 − 1− Bài tập áp dụng 3 2 1) 2
I = | x − 4 | dx ∫ . 2) 3 2
I = | x − 2x − x + 2 | dx ∫ . 4 − 1 − π 3 2 π 3) = | 2x I − 4 | dx ∫ .
4) I = 2 | sin x | dx ∫ .
5) I = 1+ cos2xdx ∫ . 0 π − 0 2
III. Dạng 3: Phương pháp đổi biến số
1) Đổi biến số dạng 1
Cho hàm số f liên tục trên đoạn [ ;
a b].Giả sử hàm số u = u(x) có đạo hàm liên tục trên đoạn
[a;b] và α ≤ u(x) ≤ β. Giả sử có thể viết f (x) = g(u(x))u '(x), x∈[a;b], với g liên tục trên đoạn [α;β ]. Khi đó, ta có b u(b)
I = f (x)dx = g(u)du. ∫ ∫ a u(a) π 2
Ví dụ 3: Tính tích phân 2
I = sin xcos xdx ∫ . 0 Hướng dẫn giải Đặt π π u = sin .
x Ta có du = cos x .
dx Đổi cận: x 0 u(0) 0; x u = ⇒ = = ⇒ = 1. 2 2 π 2 1 Khi đó 2 2 1 3 1 1
I = sin xcos xdx = u du = u = . ∫ ∫ 3 0 3 0 0 Bài tập áp dụng 1 1 1) 2
I = x x +1dx ∫ . 2) 3
I = x x +1dx ∫ . 0 0 e 2 e 3) 1+ ln x I = dx ∫ . 4) dx I = x ∫ . + 1 e 2x 2 ln x
Dấu hiệu nhận biết và cách tính tính phân Dấu hiệu Có thể đặt Ví dụ 3 1 Có f (x)
t = f (x) 3 x dx I = ∫
. Đặt t = x +1 0 x +1 Trang 2/80 2 Có ( + )n ax b
t = ax + b 1 2016
I = x(x +1) dx ∫
. Đặt t = x −1 0 π tan x+3 3 Có f (x) e a
t = f (x) 4 I = dx ∫
. Đặt t = tan x + 3 2 0 cos x e ln xdx
4 Có dx và ln x
t = ln x hoặc biểu thức I = ∫
. Đặt t = ln x +1 x chứa ln x 1 x(ln x +1) x ln 2 5 = hoặc biểu thức 2x x x Có x t e e dx I = e 3e +1dx ∫
. Đặt t = 3e +1 chứa x e 0 π 6 Có sin xdx t = cos x 3 2 I = sin xcos xdx ∫
. Đặt t = sin x 0 3 7 Có cos xdx t = sin xdx π sin x I = dx ∫
Đặt t = 2cos x +1 0 2cos x +1 π π dx 1 2 1 4 4 8 Có = = + t = x I dx (1 tan x) dx ∫ 4 ∫ 2 2 tan 0 0 cos x cos x cos x
Đặt t = tan x dx π cot x cot x e e 9 Có t = x 4 I = = = π dx dx ∫ ∫
. Đặt t cot x 2 cot sin x 2 1− cos2x 2sin x 6
2) Đổi biến số dạng 2
Cho hàm số f liên tục và có đạo hàm trên đoạn [ ;
a b]. Giả sử hàm số x = ϕ(t) có đạo hàm và liên tục trên đoạn (*)
[α;β ] sao cho ϕ(α) = a,ϕ(β ) = b và a ≤ ϕ(t) ≤ b với mọi t ∈[α;β ]. Khi đó: b β
f (x)dx = f (ϕ(t))ϕ '(t)dt. ∫ ∫ a α
Một số phương pháp đổi biến: Nếu biểu thức dưới dấu tích phân có dạng 1. 2 2 π π
a − x : đặt x | a | sint; t ; = ∈ − 2 2 2. 2 2 π π
x − a : đặt | a | x ; t ; = ∈ − \{0} sint 2 2 3. 2 2 π π
x + a : x | a | tant; t ; = ∈ − 2 2
4. a + x hoặc a − x : đặt x = . a cos2t a − x a + x
Lưu ý: Chỉ nên sử dụng phép đặt này khi các dấu hiệu 1, 2, 3 đi với x mũ chẵn. Ví dụ, để tính 3 2 3 tích phân x dx I = ∫
thì phải đổi biến dạng 2 còn với tích phân 3 x dx I = ∫ thì nên đổi 2 0 2 0 x +1 x +1 biến dạng 1.
Ví dụ 4: Tính các tích phân sau: 1 1 a) 2 I = 1− x dx ∫ . b) dx I = ∫ . 2 1+ x 0 0 Hướng dẫn giải a) Đặt π
x = sint ta có dx = costdt. Đổi cận: x = 0 ⇒ t = 0; x =1⇒ t = . 2 π π 1 2 2 π Vậy 2 2 I =
1− x dx = | cost |dt = costdt = sint ∫ ∫ ∫ 0 | =1. 0 0 0
x = 0 → t = 0
b) Đặt x = tant, ta có dx = ( 2
1+ tan t)dt . Đổi cận: π . x =1→ t = 4 Trang 3/80 π 1 4 π Vậy dx π 4 I = = dt = t | = . ∫ 2 ∫ 0 1+ x 4 0 0
IV. Dạng 4: Phương pháp tính tích phân từng phần.
Định lí : Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm và liên tục trên đoạn [ ; a b] thì b b
u(x)v'(x)dx = ∫
(u(x)v(x)) b − u'(x)v(x)dx ∫ , a a a b b b
hay viết gọn là udv = uv |b ∫ a − vdu
∫ . Các dạng cơ bản: Giả sử cần tính I = P(x).Q(x)dx ∫ a a a
Dạng P(x): Đa thức
P(x): Đa thức P(x): Đa thức
hàm Q(x): sin(kx) hay
P(x): Đa thức
Q(x): ln(ax + b) Q(x): 1 hay 1
Q(x): kx cos(kx) e 2 sin x 2 cos x
* u = P(x)
* u = P(x)
* u = P(x)
Cách * dv là Phần còn lại * dv là Phần còn * u = ln(ax + b) * dv là Phần còn lại của đặt
của biểu thức dưới lại của biểu thức * dv = P(x)dx biểu thức dưới dấu tích dấu tích phân dưới dấu tích phân phân
Thông thường nên chú ý: “Nhất log, nhì đa, tam lượng, tứ mũ”. π 2 e 1 −
Ví dụ 5: Tính các tích phân sau : a) I = xsin xd .x ∫
b) I = xln(x +1)dx ∫ . 0 0 Hướng dẫn giải = = a) Đặt u x du dx ta có . dv = sin xdx v = −cos x π π 2 π 2 π
Do đó I = xsin xdx = ∫ (−xcos x) 2 2 0
| + cos xdx = 0 + sin x ∫ 0 | =1. 0 0 1 du = dx = +
b) Đặt u ln(x 1) x +1 ta có dv = xdx 2 x − 1 v = 2e 1 e 1 2 − − e 1 − 2 2 x −1 1
e − 2e + 2 1 x e 1
I = xln(x +1)dx = ∫ ln(x +1) − (x −1)dx = − ∫ − x − 0 2 2 2 2 2 0 0 0 2 2 2
e − 2e + 2 1 e − 4e + 3 e +1 = − = . 2 2 2 4 Bài tập áp dụng π 1 2 2π 1 1) = (2 + 2) x I x e dx ∫ .
2) I = 2 .xcos xdx ∫ . 3) 2 = .sin x I x dx ∫ . 4) 2 2 = ( +1) x I x e dx ∫ . 2 0 0 0 0 Trang 4/80
BÀI TẬP TRẮC NGHIỆM
NHẬN BIẾT – THÔNG HIỂU
Câu 1. Cho hai hàm số f , g liên tục trên đoạn [ ;
a b] và số thực k tùy ý. Trong các khẳng định sau,
khẳng định nào sai? b b b b a
A. ∫[ f (x)+ g(x)]dx = f (x)dx + g(x)dx ∫ ∫ .
B. f (x)dx = − f (x)dx ∫ ∫ . a a a a b b b b b
C. kf (x)dx = k f (x)dx ∫ ∫ .
D. xf (x)dx = x f (x)dx ∫ ∫ . a a a a
Câu 2. Cho hàm số f liên tục trên và số thực dương a . Trong các khẳng định sau, khẳng định nào luôn đúng? a a a a
A. f (x)dx = 0 ∫ .
B. f (x)dx =1 ∫ .
C. f (x)dx = 1 − ∫ .
D. f (x)dx = f (a) ∫ . a a a a 1
Câu 3. Tích phân dx ∫ có giá trị bằng 0 A. 1 − . B. 1. C. 0 . D. 2 . a
Câu 4. Cho số thực a thỏa mãn x 1+ 2 e dx = e −1 ∫
, khi đó a có giá trị bằng 1 − A. 1. B. 1 − . C. 0 . D. 2 .
Câu 5. Trong các hàm số dưới đây, hàm số nào có tích phân trên đoạn [0;π ] đạt giá trị bằng 0 ?
A. f (x) = cos3x .
B. f (x) = sin 3x . π π C. ( ) cos x f x = x + .
D. f (x) = sin + . 4 2 4 2
Câu 6. Trong các tích phân sau, tích phân nào có giá trị khác 2 ? 2 e 1 π 2 A. ln xdx ∫ . B. 2dx ∫ . C. sin xdx ∫ . D. xdx ∫ . 1 0 0 0 1 2
Câu 7. Trong các hàm số dưới đây, hàm số nào thỏa mãn f (x)dx = f (x)dx ∫ ∫ ? 1 − 2 − A. ( ) x f x = e .
B. f (x) = cos x .
C. f (x) = sin x .
D. f (x) = x +1. 5 Câu 8. Tích phân dx
I = ∫ có giá trị bằng x 2 A. 3ln 3 . B. 1 ln 3 . C. 5 ln . D. 2 ln . 3 2 5 π 2 Câu 9. Tích phân x I d = ∫ có giá trị bằng π sin x 3 A. 1 1 ln . B. 2ln 3 . C. 1 ln 3. D. 1 2ln . 2 3 2 3 0 Câu 10. Nếu ( − x/2 4 − e
)dx = K − 2e ∫
thì giá trị của K là 2 − A. 12,5. B. 9. C. 11. D. 10. 1 Câu 11. Tích phân 1 I = dx ∫ có giá trị bằng 2 x − x − 2 0 Trang 5/80 A. 2ln 2 . B. 2ln 2 − . C. 2 − ln 2 . D. 2ln 2. 3 3 5 5
Câu 12. Cho hàm số f và g liên tục trên đoạn [1;5] sao cho f (x)dx = 2 ∫
và g(x)dx = 4 − ∫ . Giá trị 1 1 5
của ∫[g(x)− f (x)]dx là 1 A. 6 − . B. 6 . C. 2 . D. 2 − . 3 3
Câu 13. Cho hàm số f liên tục trên đoạn [0;3]. Nếu f (x)dx = 2 ∫
thì tích phân ∫[x − 2 f (x)]dx có giá 0 0 trị bằng A. 7 . B. 5 . C. 5. D. 1 . 2 2 5 3 5
Câu 14. Cho hàm số f liên tục trên đoạn [0;6] . Nếu f (x)dx = 2 ∫
và f (x)dx = 7 ∫
thì f (x)dx ∫ có giá 1 1 3 trị bằng A. 5. B. 5 − . C. 9. D. 9 − .
Câu 15. Trong các phép tính sau đây, phép tính nào sai? 3 2 − A. 3 x = ( x e dx e ) ∫ 1 2 − = 1 . B. dx (ln x) ∫ 3 . − x − 1 3 2π 2 2 2 C. xdx = ( x) 2 cos sin π ∫ x π . D. (x + ) 1 dx = ∫ + x . 2 π 1 1
Câu 16. Cho hàm số f liên tục trên đoạn [ ;
a b] có một nguyên hàm là hàm F trên đoạn [ ; a b]. Trong
các phát biểu sau, phát biểu nào sai ? b
A. f (x)dx = F(b) − F(a) ∫ . a
B. F '(x) = f (x) với mọi x ∈( ; a b) . b
C. f (x)dx = f (b) − f (a) ∫ . a b
D. Hàm số G cho bởi G(x) = F(x) + 5 cũng thỏa mãn f (x)dx = G(b) − G(a) ∫ . a
Câu 17. Xét hàm số f liên tục trên và các số thực a , b , c tùy ý. Trong các khẳng định sau, khẳng định nào sai? b b a b c b
A. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ .
B. f (x)dx = f (x)dx + f (x)dx ∫ ∫ ∫ . a c c a a c b c b b c c
C. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ .
D. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ . a a c a a b
Câu 18. Xét hai hàm số f và g liên tục trên đoạn [ ;
a b] . Trong các mệnh đề sau, mệnh đề nào sai? b
A. Nếu m ≤ f (x) ≤ M x ∀ ∈[ ;
a b] thì m(b − a) ≤ f (x)dx ≤ M (a − b) ∫ . a Trang 6/80 b
B. Nếu f (x) ≥ m x ∀ ∈[ ;
a b] thì f (x)dx ≥ m(b − a) ∫ . a b
C. Nếu f (x) ≤ M x ∀ ∈[ ;
a b] thì f (x)dx ≤ M (b − a) ∫ . a b
D. Nếu f (x) ≥ m x ∀ ∈[ ;
a b] thì f (x)dx ≥ m(a − b) ∫ . a
Câu 19. Cho hai hàm số f và g liên tục trên đoạn [ ;
a b] sao cho g(x) ≠ 0 với mọi x ∈[ ; a b] . Xét các khẳng định sau: b b b
I. ∫[ f (x)+ g(x)]dx = f (x)dx + g(x)dx ∫ ∫ . a a a b b b
II. ∫[ f (x)− g(x)]dx = f (x)dx − g(x)dx ∫ ∫ . a a a b b b
III. ∫[ f (x).g(x)]dx = f (x) . dx g(x)dx ∫ ∫ . a a a b f (x)dx b ∫ IV. f (x) a dx = ∫ . g(x) b a g(x)dx ∫a
Trong các khẳng định trên, có bao nhiêu khẳng định sai? A. 1. B. 2 . C. 3. D. 4 . 3
Câu 20. Tích phân x(x −1)dx ∫
có giá trị bằng với giá trị của tích phân nào trong các tích phân dưới 0 đây? 2 3π ln 10 π A. ( 2
x + x − 3)dx ∫ . B. 3 sin xdx ∫ . C. 2x e dx ∫ .
D. cos(3x +π )dx ∫ . 0 0 0 0
Câu 21. Trong các mệnh đề sau, mệnh đề nào đúng? b
A. Nếu hàm số f liên tục trên đoạn [ ;
a b] , sao cho f (x)dx ≥ 0 ∫
thì f (x) ≥ 0 x ∀ ∈[ ; a b]. a 3
B. Với mọi hàm số f liên tục trên đoạn [ 3
− ;3], luôn có f (x)dx = 0 ∫ . 3 − b a
C. Với mọi hàm số f liên tục trên , ta có f (x)dx = f (x)d(−x) ∫ ∫ . a b 5 D. f (x)
Với mọi hàm số f liên tục trên đoạn [1;5] thì [ f (x)]2 [ ] 5 3 dx = ∫ . 3 1 1
Câu 22. Trong các mệnh đề sau, mệnh đề nào đúng? 1 0
A. Nếu f là hàm số chẵn trên thì f (x)dx = f (x)dx ∫ ∫ . 0 1 − 0 1
B. Nếu f (x)dx = f (x)dx ∫ ∫
thì f là hàm số chẵn trên đoạn [ 1; − 1] . 1 − 0 Trang 7/80 1
C. Nếu f (x)dx = 0 ∫
thì f là hàm số lẻ trên đoạn [ 1; − 1]. 1 − 1
D. Nếu f (x)dx = 0 ∫
thì f là hàm số chẵn trên đoạn [ 1; − 1]. 1 −
Câu 23. Giả sử F là một nguyên hàm của hàm số 6 5
y = x sin x trên khoảng (0;+∞). Khi đó 2 6 5 x sin xdx ∫ có giá trị bằng 1
A. F(2) − F(1) . B. −F(1) . C. F( ) 2 .
D. F(1) − F(2) . b
Câu 24. Cho hàm số f liên tục trên và hai số thực a < b . Nếu f (x)dx = α ∫ thì tích phân a
b 2 f (2x)dx ∫ có giá trị bằng a 2 α A. . B. 2α . C. α . D. 4α . 2
Câu 25. Giả sử F là một nguyên hàm của hàm số 3 5
y = x sin x trên khoảng (0;+∞). Khi đó tích phân 2 3 5 81x sin 3xdx ∫ có giá trị bằng 1
A. 3[F(6) − F(3)] .
B. F(6) − F(3) .
C. 3[F(2) − F(1)].
D. F(2) − F(1) . 2
Câu 26. Giả sử hàm số f liên tục trên đoạn [0;2] thỏa mãn f (x)dx = 6 ∫
. Giá trị của tích phân 0
π 2 f (2sin x)cosxdx ∫ là 0 A. 6 − . B. 6 . C. 3 − . D. 3. e Câu 27. +
Bài toán tính tích phân ln x 1ln x I = dx ∫
được một học sinh giải theo ba bước sau: x 1
I. Đặt ẩn phụ t = ln x +1, suy ra 1 dt = dx và x x 1 e t 1 2 e 2 + II. ln x 1ln x I = dx = t (t − ) 1 dt ∫ x ∫ 1 1 2 2 III. I t (t ) 5 2 1 dt t = − = − = 1+ ∫ 3 2 . 1 t 1
Học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào? A. Bài giải đúng.
B. Sai từ Bước II. C. Sai từ Bước I.
D. Sai ở Bước III. π 3
Câu 28. Xét tích phân sin 2x I = dx ∫
. Thực hiện phép đổi biến t = cos x , ta có thể đưa I về dạng 1+ cos x 0 nào sau đây π 4 π 4 1 1 A. 2t I = − dt ∫ . B. 2t I = dt ∫ . C. 2t I = − dt ∫ . D. 2t I = dt ∫ . 1+ t 1+ t 1+ t 1+ t 0 0 1 1 2 2 Trang 8/80
Câu 29. Cho hàm số y = f (x) liên tục trên đoạn [ ;
a b]. Trong các bất đẳng thức sau, bất đẳng thức nào luôn đúng? b b b b
A. f (x) dx > f (x)dx ∫ ∫ . B. f
∫ (x)dx ≥ f (x) dx ∫ . a a a a b b b b
C. f (x) dx ≥ f (x)dx ∫ ∫ . D. f
∫ (x)dx > f (x) dx ∫ . a a a a
Câu 30. Trong các khẳng định dưới đây, khẳng định nào sai? 1 1 1
A. sin(1− x)dx = sin xdx ∫ ∫ . B. (1+ )x x dx = 0 ∫ . 0 0 0 π π 2 1
C. sin x dx = 2 sin xdx ∫ ∫ . D. 2017 2
x (1+ x)dx = ∫ . 2 − 2019 0 0 1
Câu 31. Cho hàm số y = f (x) lẻ và liên tục trên đoạn [ 2;
− 2] . Trong các đẳng thức sau, đẳng thức nào luôn đúng? 2 2 2
A. f (x)dx = 2 f (x)dx ∫ ∫ .
B. f (x)dx = 0 ∫ . 2 − 0 2 − 2 0 2 2
C. f (x)dx = 2 f (x)dx ∫ ∫ .
D. f (x)dx = 2 − f (x)dx ∫ ∫ . 2 − 2 − 2 − 0 1
Câu 32. Bài toán tính tích phân 2
I = (x +1) dx ∫
được một học sinh giải theo ba bước sau: 2 − I. Đặt ẩn phụ 2
t = (x +1) , suy ra dt = 2(x +1)dx ,
II. Từ đây suy ra dt dt = dx ⇒ = dx . Đổi cận 2(x +1) 2 t x 2 − 1 t 1 4 1 4 4 III. Vậy 2 t 1 3 7
I = (x +1) dx = dt = t = ∫ ∫ . − 2 t 3 1 3 2 1
Học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào? A. Sai từ Bước I.
B. Sai ở Bước III.
C. Sai từ Bước II. D. Bài giải đúng.
Câu 33. Một học sinh được chỉ định lên bảng làm 4 bài toán tích phân. Mỗi bài giải đúng được 2,5
điểm, mỗi bài giải sai (sai kết quả hoặc sai bước tính nguyên hàm) được 0 điểm. Học sinh đã
giải 4 bài toán đó như sau: Bài Đề bài Bài giải của học sinh 1 2 1 1 1 x 1 2 x e xdx ∫ 2 x 1 2 x e xdx = e d ( 2 x ) e e −1 = = ∫ ∫ 0 2 2 0 2 0 0 1 1 1 1 1 2 dx ∫ dx = [ 2
ln x − x − 2 ] = ln 2 − ln 2 = 0 2 x ∫ − x − 2 2 0 x − x − 2 0 0
Đặt t = cos x , suy ra dt = −sin xdx . Khi x = 0 thì t =1; khi π
x = π thì t = 1 − . Vậy 3 sin 2x cos xdx ∫ 1 π π 1 − 3 t 0 2 2 2 4
sin 2x cos xdx = 2 sin x cos xdx = 2 − t dt = = ∫ ∫ ∫ 3 1− 3 0 0 1 Trang 9/80
e 1+ (4 − 2e)ln e x
e 1+ (4 − 2e)ln x dx = ∫
∫[1+(4−2e)ln x]d (ln x) 4 dx ∫ x x 1 1 1 2 e
= x + (4 − 2e)ln x = 3− e 1
Số điểm mà học sinh này đạt được là bao nhiêu? A. 5,0 điểm. B. 2,5 điểm. C. 7,5 điểm. D. 10,0 điểm.
Câu 34. Cho hai hàm số liên tục f và g liên tục trên đoạn [ ;
a b]. Gọi F và G lần lượt là một nguyên
hàm của f và g trên đoạn [ ;
a b]. Đẳng thức nào sau đây luôn đúng? b b
A. f (x)G(x)dx = ∫
[F(x)g(x)]b − F(x)G(x)dx ∫ . a a a b b
B. f (x)G(x)dx = ∫
[F(x)G(x)]b − F(x)g(x)dx ∫ . a a a b b
C. f (x)G(x)dx = ∫
[ f (x)g(x)]b − F(x)g(x)dx ∫ . a a a b b
D. f (x)G(x)dx = ∫
[F(x)G(x)]b − f (x)g(x)dx ∫ . a a a 0 Câu 35. Tích phân − x I = xe dx ∫ có giá trị bằng 2 − A. 2 −e +1. B. 2 3e −1. C. 2 −e −1. D. 2 2 − e +1.
Câu 36. Cho hai hàm số f và g liên tục trên đoạn [ ;
a b] và số thực k bất kỳ trong . Trong các phát
biểu sau, phát biểu nào sai? b b b b a
A ∫[ f (x)+ g(x)]dx = f (x)dx + g(x)dx ∫ ∫ .
B. f (x)dx = − f (x)dx ∫ ∫ . a a a a b b b b b
C. kf (x)dx = k f (x)dx ∫ ∫ .
D. xf (x)dx = x f (x)dx ∫ ∫ . a a a a
Câu 37. Cho hàm số f liên tục trên và số thực dương a . Trong các đẳng thức sau, đẳng thức nào luôn đúng? a a a a
A. f (x)dx =1 ∫ .
B. f (x)dx = 0 ∫ .
C. f (x)dx = 1 − ∫ .
D. f (x)dx = f (a) ∫ . a a a a 1
Câu 38. Tích phân dx ∫ có giá trị bằng 0 A. 2 . B. 1 − . C. 0 . D. 1. a
Câu 39. Cho số thực a thỏa mãn x 1+ 2 e dx = e −1 ∫
, khi đó a có giá trị bằng 1 − A. 0 . B. 1 − . D. 1. D. 2 .
Câu 40. Trong các hàm số dưới đây, hàm số nào có tích phân trên đoạn [0;π ] đạt giá trị bằng 0 ?
A. f (x) = cos3x .
B. f (x) = sin 3x . π π C. ( ) cos x f x = x + .
D. f (x) = sin + . 4 2 4 2
Câu 41. Tích phân nào trong các tích phân sau có giá trị khác 2 ? π 1 2 e 2 A. sin xdx ∫ . B. 2dx ∫ . B. ln xdx ∫ . D. xdx ∫ . 0 0 1 0 Trang 10/80 1 2
Câu 42. Trong các hàm số dưới đây, hàm số nào thỏa mãn f (x)dx = f (x)dx ∫ ∫ ? 1 − 2 −
A. f (x) = cos x .
B. f (x) = sin x . C. ( ) x f x = e .
D. f (x) = x +1. 5 Câu 43. Tích phân dx
I = ∫ có giá trị bằng x 2 A. 1 ln 3 . B. 5 ln . C. 3ln 3 . D. 2 ln . 3 2 5 π 2 Câu 44. Tích phân x I d = ∫ có giá trị bằng π sin x 3 A. 1 2ln . B. 2ln 3 . C. 1 ln 3. D. 1 1 ln . 3 2 2 3 0 Câu 45. Nếu ( − x/2 4 − e
)dx = K − 2e ∫
thì giá trị của K là 2 − A. 9. B. 10. C. 11. D. 12,5. 1 Câu 46. Tích phân 1 I = dx ∫ có giá trị bằng 2 x − x − 2 0 A. 2 − ln 2 . B. 2ln 2 . C. 2ln 2 − .
D. Không xác định. 3 3 5 5
Câu 47. Cho hàm số f và g liên tục trên đoạn [1;5] sao cho f (x)dx = 2 ∫
và g(x)dx = 4 − ∫ . Giá trị 1 1 5
của ∫[g(x)− f (x)]dx là 1 A. 2 − . B. 6 . C. 2 . D. 6 − . 3 3
Câu 48. Cho hàm số f liên tục trên đoạn [0;3]. Nếu f (x)dx = 2 ∫
thì tích phân ∫[x −2 f (x)]dx có giá 0 0 trị bằng A. 7 . B. 5 . C. 5. D. 1 . 2 2 5 3 5
Câu 49. Cho hàm số f liên tục trên đoạn [0;6] . Nếu f (x)dx = 2 ∫
và f (x)dx = 7 ∫
thì f (x)dx ∫ có giá 1 1 3 trị bằng A. 9 − . B. 5. C. 9. D. 5 − .
Câu 50. Trong các phép tính sau đây, phép tính nào sai? 2 2 2 3 A. 3 ( + ) 1 x x dx = ∫ + x .
B. x = ( x e dx e ) ∫ . 2 1 1 1 1 2π 2 − C. xdx = ( x) 2 cos sin π ∫ 1 2 − π . D. dx = (ln x) ∫ 3 . − x − π 3
Câu 51. Cho hàm số f liên tục trên đoạn [ ;
a b] có một nguyên hàm là hàm F trên đoạn [ ; a b]. Trong
các phát biểu sau, phát biểu nào sai ?
A. F '(x) = f (x) với mọi x ∈( ; a b) . Trang 11/80 b
B. f (x)dx = f (b) − f (a) ∫ . a b
C. f (x)dx = F(b) − F(a) ∫ . a b
D. Hàm số G cho bởi G(x) = F(x) + 5 cũng thỏa mãn f (x)dx = G(b) − G(a) ∫ . a
Câu 52. Xét hàm số f liên tục trên và các số thực a , b , c tùy ý. Trong các phát biểu sau, phát biểu nào sai? b c b b c b
A. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ .
B. f (x)dx = f (x)dx + f (x)dx ∫ ∫ ∫ . a a c a a c b b a b c c
C. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ .
D. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ . a c c a a b
Câu 53. Xét hai hàm số f và g liên tục trên đoạn [ ;
a b] .Trong các mệnh đề sau, mệnh đề nào sai? b
A. Nếu f (x) ≥ m x ∀ ∈[ ;
a b] thì f (x)dx ≥ m(a − b) ∫ . a b
B. Nếu f (x) ≥ m x ∀ ∈[ ;
a b] thì f (x)dx ≥ m(b − a) ∫ . a b
C. Nếu f (x) ≤ M x ∀ ∈[ ;
a b] thì f (x)dx ≤ M (b − a) ∫ . a b
D. Nếu m ≤ f (x) ≤ M x ∀ ∈[ ;
a b] thì m(b − a) ≤ f (x)dx ≤ M (a − b) ∫ . a
Câu 54. Cho hai hàm số f và g liên tục trên đoạn [ ;
a b] sao cho g(x) ≠ 0 với mọi x ∈[ ; a b] . Một học
sinh lên bảng và phát biểu các tính chất sau: b b b b b b
I. ∫[ f (x)+ g(x)]dx = f (x)dx + g(x)dx ∫ ∫ .
II. ∫[ f (x)− g(x)]dx = f (x)dx − g(x)dx ∫ ∫ . a a a a a a b f (x)dx b b b b ∫
III. ∫[ f (x).g(x)]dx = f (x) . dx g(x)dx ∫ ∫ . IV. f (x) a dx = ∫ . g(x) b a a a a g(x)dx ∫a
Trong số các phát biểu trên, có bao nhiêu phát biểu sai? A. 3. B. 1. C. 2 . D. 4 . 3
Câu 55. Tích phân x(x −1)dx ∫
có giá trị bằng với tích phân nào trong các tích phân dưới đây ? 0 π 3π 2 ln 10
A. cos(3x +π )dx ∫ . B. 3 sin xdx ∫ . C. ( 2
x + x − 3)dx ∫ . D. 2x e dx ∫ . 0 0 0 0
Câu 56. Trong các mệnh đề sau, mệnh đề nào đúng? 3
A. Với mọi hàm số f liên tục trên đoạn [ 3
− ;3], luôn có f (x)dx = 0 ∫ . 3 − b a
B. Với mọi hàm số f liên tục trên , ta có f (x)dx = f (x)d(−x) ∫ ∫ . a b Trang 12/80 b
C. Nếu hàm số f liên tục trên đoạn [ ;
a b] , sao cho f (x)dx ≥ 0 ∫
thì f (x) ≥ 0 x ∀ ∈[ ; a b]. a 5 D. f (x)
Với mọi hàm số f liên tục trên đoạn [1;5] thì [ f (x)]2 [ ] 5 3 dx = ∫ . 3 1 1
Câu 57. Trong các mệnh đề sau, mệnh đề nào đúng? 1 0
A. Nếu f là hàm số chẵn trên thì f (x)dx = f (x)dx ∫ ∫ . 0 1 − 0 1
B. Nếu f (x)dx = f (x)dx ∫ ∫
thì f là hàm số chẵn trên đoạn [ 1; − 1] . 1 − 0 1
C. Nếu f (x)dx = 0 ∫
thì f là hàm số lẻ trên đoạn [ 1; − 1]. 1 − 1
D. Nếu f (x)dx = 0 ∫
thì f là hàm số chẵn trên đoạn [ 1; − 1]. 1 − 2
Câu 58. Giả sử F là một nguyên hàm của hàm số sin x y =
trên khoảng (0;+∞). Khi đó sin x dx x ∫ có x 1 giá trị bằng
A. F(2) − F(1) . B. −F(1) . C. F( ) 2 .
D. F(2) + F(1) . b
Câu 59. Cho hàm số f liên tục trên và hai số thực a < b . Nếu f (x)dx = α ∫ thì tích phân a
b 2 f (2x)dx ∫ có giá trị bằng a 2 α A. α . B. 2α . C. . D. 4α . 2 2
Câu 60. Giả sử F là một nguyên hàm của hàm số sin x y =
trên khoảng (0;+∞). Khi đó sin 3x dx x ∫ có x 1 giá trị bằng
A. F(6) − F(3) .
B. 3[F(6) − F(3)] .
C. 3[F(2) − F(1)].
D. F(2) − F(1) . 2
Câu 61. Giả sử hàm số f liên tục trên đoạn [0;2] thỏa mãn
f (x)dx = 6 ∫ . Giá trị của 0
π 2 f (2sin x)cosxdx ∫ là 0 A. 3. B. 6 . C. 3 − . D. 6 − . e Câu 62. +
Bài toán tính tích phân ln x 1ln x I = dx ∫
được một học sinh giải theo ba bước sau: x 1
I. Đặt ẩn phụ t = ln x +1, suy ra 1 dt = dx và x x 1 e t 1 2 e 2 + II. ln x 1ln x I = dx = t (t − ) 1 dt ∫ x ∫ 1 1 Trang 13/80 2 2 III. I t (t ) 5 2 1 dt t = − = − = 1+ ∫ 3 2 . 1 t 1
Vây học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào?
A. Bài giải đúng.
B. Sai từ Bước II. C. Sai từ Bước I.
D. Sai ở Bước III. π 3
Câu 63. Xét tích phân sin 2x I = dx ∫
. Thực hiện phép đổi biến t = cos x , ta có thể đưa I về dạng 1+ cos x 0 nào sau đây 1 π 4 1 π 4 A. 2t I = dt ∫ . B. 2t I = dt ∫ . C. 2t I = − dt ∫ . D. 2t I = − dt ∫ . + + + + 1 1 t 1 t 1 t 1 t 0 1 0 2 2
Câu 64. Cho hàm số y = f (x) bất kỳ liên tục trên đoạn [ ;
a b]. Trong các bất đẳng thức sau, bất đẳng
thức nào luôn đúng? b b b b A. f
∫ (x)dx ≥ f (x) dx ∫ .
B. f (x) dx ≥ f (x)dx ∫ ∫ . a a a a b b b b
C. f (x) dx > f (x)dx ∫ ∫ . D. f
∫ (x)dx > f (x) dx ∫ . a a a a
Câu 65. Trong các khẳng định dưới đây, khẳng định nào sai? 1 1 1 A. (1+ )x x dx = 0 ∫ .
B. sin(1− x)dx = sin xdx ∫ ∫ . 0 0 0 π π 2 1
C. sin x dx = 2 sin xdx ∫ ∫ . D. 2017 2
x (1+ x)dx = ∫ . 2 − 2019 0 0 1
Câu 66. Cho hàm số y = f (x) lẻ và liên tục trên đoạn [ 2;
− 2] . Trong các đẳng thức sau, đẳng thức nào luôn đúng? 2 2 2 2
A. f (x)dx = 2 − f (x)dx ∫ ∫ .
B. f (x)dx = 2 f (x)dx ∫ ∫ . 2 − 0 2 − 0 2 0 2
C. f (x)dx = 2 f (x)dx ∫ ∫ .
D. f (x)dx = 0 ∫ . 2 − 2 − 2 − 1
Câu 67. Bài toán tính tích phân 2
I = (x +1) dx ∫
được một học sinh giải theo ba bước sau: 2 − I. Đặt ẩn phụ 2
t = (x +1) , suy ra dt = 2(x +1)dx ,
II. Từ đây suy ra dt dt = dx ⇒
= dx . Bảng giá trị 2(x +1) 2 t x 2 − 1 t 1 4 1 4 4 III. Vậy 2 t 1 3 7
I = (x +1) dx = dt = t = ∫ ∫ . − 2 t 3 1 3 2 1
Vây học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào?
A. Sai ở Bước III. B. Sai từ Bước II. C. Sai từ Bước I. D. Bài giải đúng. Trang 14/80
Câu 68. Một học sinh được chỉ định lên bảng làm 4 bài toán tích phân. Mỗi bài giải đúng được 2,5
điểm, mỗi bài giải sai (sai kết quả hoặc sai bước tính nguyên hàm) được 0 điểm. Học sinh đã
giải 4 bài toán đó như sau: Bài Đề bài Bài giải của học sinh 1 2 1 1 1 x 1 2 x e xdx ∫ 2 x 1 2 x e xdx = e d ( 2 x ) e e −1 = = ∫ ∫ 0 2 2 0 2 0 0 1 1 1 1 1 2 dx ∫ dx = [ 2
ln x − x − 2 ] = ln 2 − ln 2 = 0 2 x ∫ − x − 2 2 0 x − x − 2 0 0
Đặt t = cos x , suy ra dt = −sin xdx . Khi x = 0 thì t =1; khi π
x = π thì t = 1 − . Vậy 3 sin 2x cos xdx ∫ 1 π π 1 − 3 t 0 2 2 2 4
sin 2x cos xdx = 2 sin x cos xdx = 2 − t dt = = ∫ ∫ ∫ 3 1− 3 0 0 1
e 1+ (4 − 2e)ln e x
e 1+ (4 − 2e)ln x dx = ∫
∫[1+(4−2e)ln x]d (ln x) 4 dx ∫ x x 1 1 1 2 e
= x + (4 − 2e)ln x = 3− e 1
Số điểm mà học sinh này đạt được là bao nhiêu? A. 7,5 điểm. B. 2,5 điểm. C. 5,0 điểm. D. 10,0 điểm.
Câu 69. Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [ ; a b]. Đẳng
thức nào sau đây luôn đúng? b b
A. f (x)G(x)dx = ∫
[F(x)g(x)]b − F(x)G(x)dx ∫ . a a a b b
B. f (x)G(x)dx = ∫
[F(x)G(x)]b − F(x)g(x)dx ∫ . a a a b b
C. f (x)G(x)dx = ∫
[ f (x)g(x)]b − F(x)g(x)dx ∫ . a a a b b
D. f (x)G(x)dx = ∫
[F(x)G(x)]b − f (x)g(x)dx ∫ . a a a 0 Câu 70. Tích phân − x I = xe dx ∫ có giá trị bằng 2 − A. 2 2 − e +1. B. 2 3e −1. C. 2 −e +1. D. 2 −e −1. b b
Câu 71. Ta đã biết công thức tích phân từng phần F(x)g(x)dx = ∫
[F(x)G(x)]b − f (x)G(x)dx ∫ , trong a a a
đó F và G là các nguyên hàm của f và g . Trong các biến đổi sau đây, sử dụng tích phân
từng phần ở trên, biến đổi nào là sai? 2 e e e A. ( x) x 1 ln xdx = ∫ ln x − xdx
∫ , trong đó F(x) = ln x , g(x) = x. 2 2 1 1 1 1 1 B. 1 x = ( x ) x xe dx xe − ∫ = = 0 e dx ∫
, trong đó F(x) x , ( ) x g x e . 0 0 π π
C. xsin xdx = (x cos x) π − ∫ = = 0 cos xdx ∫
, trong đó F(x) x , g(x) sin x . 0 0 Trang 15/80 1 x 1 1 + 1 x 1 + D. x 1 + 2 2 x2 dx = ∫ x − dx ∫
, trong đó F(x) = x , 1 ( ) 2x g x + = . ln 2 ln 2 0 0 0 π π
Câu 72. Tích phân xcos ∫ x
+ dx có giá trị bằng 4 0 (π − 2) (π − 2) (π + 2) (π + 2) A. 2 . B. 2 − . C. 2 . D. 2 − . 2 2 2 2
Câu 73. Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [0;2]. Biết rằng 2 2
F(0) = 0 , F(2) =1, G(0) = 2
− , G(2) =1 và F(x)g(x)dx = 3 ∫
. Tích phân f (x)G(x)dx ∫ có 0 0 giá trị bằng A. 3. B. 0 . C. 2 − . D. 4 − .
Câu 74. Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [1;2] . Biết rằng 2 2
F(1) =1, F(2) = 4 , 3
G(1) = , G(2) = 2 và 67
f (x)G(x)dx = ∫
. Tích phân F(x)g(x)dx ∫ có 2 12 1 1 giá trị bằng A. 11 . B. 145 − . C. 11 − . D. 145 . 12 12 12 12 b
Câu 75. Cho hai số thực a và b thỏa mãn a < b và xsin xdx = π ∫
, đồng thời a cos a = 0 và a b bcosb = π
− . Tích phân cos xdx ∫ có giá trị bằng a A. 145 . B. π . C. π − . D. 0 . 12 e Câu 76. − Cho tích phân: 1 ln x I = dx ∫
.Đặt u = 1− ln x .Khi đó I bằng 2x 1 0 0 0 2 1 A. 2 I = u du ∫ . B. 2 I = − u du ∫ . C. u I = du ∫ . D. 2 I = − u du ∫ . 2 1 1 1 0 2 2 Câu 77. Tích phân x I = dx ∫ có giá trị bằng 2 x − 7x +12 1 A. 5ln 2 − 6ln 3 .
B. 1+ 2ln 2 − 6ln 3 .
C. 3+ 5ln 2 − 7ln 3. D. 1+ 25ln 2 −16ln 3 . 2 Câu 78. Tích phân 5 I = x dx ∫ có giá trị là: 1 A. 19 . B. 32 . C. 16 . D. 21 . 3 3 3 2 1 Câu 79. Tích phân xdx I = ∫ bằng 3 (x +1) 0 A. 1 − . B. 1 . C. 1 . D. 12. 7 6 8 Trang 16/80 π 2
Câu 80. Cho tích phân I = (2 − x)sin xdx ∫
. Đặt u = 2 − x, dv = sin xdx thì I bằng 0 π π π 2 π 2 A. − − 2
(2 x)cos x − cos xdx − − 2
(2 x)cos x + cos xdx 0 ∫ . B. 0 ∫ . 0 0 π π π 2 π 2 C. − 2
(2 x)cos x + cos xdx − 2 (2 x) + cos xdx 0 ∫ . D. 0 ∫ . 0 0 1 7 Câu 81. Tích phân x dx ∫ bằng 2 5 (1+ x ) 0 2 3 3 3 2 3 4 3 A − − − − . 1 (t 1) dt ∫ .
B. (t 1) dt 1 (t 1) dt 3 (t 1) dt 5 ∫ . C. ∫ . D. ∫ . 2 t 5 t 4 2 t 4 2 t 1 1 1 1 4 3 Câu 82. Tích phân 1 I = dx ∫ bằng 4 x(x +1) 1 A. 3 ln . B. 1 3 ln . C. 1 3 ln . D. 1 3 ln . 2 3 2 5 2 4 2 2 2
Câu 83. Cho hai tích phân 3 I = x dx ∫ , J = xdx
∫ .Tìm mối quan hệ giữa I và J 0 0
A. I.J = 8. B. 32 I.J = . C. 128 I − J = . D. 64 I + J = . 5 7 9 a
Câu 84. Cho số thực a thỏa mãn x 1+ 4 2
e dx = e − e ∫
, khi đó a có giá trị bằng 1 A. 1 − . B. 3. C. 0 . D. 2. 2 Câu 85. Tích phân x ke dx ∫
(với k là hằng số )có giá trị bằng 0 A. 2 k(e −1) . B. 2 e −1. C. 2
k(e − e) . D. 2 e − e .
Câu 86. Với hằng số k , tích phân nào sau đây có giá trị khác với các tích phân còn lại ? 2 2 1 2 3 3 A. 2 k(e −1)dx ∫ . B. x ke dx ∫ . C. 3 3 x ke dx ∫ . D. 2x ke dx ∫ . 0 0 0 0
Câu 87. Với số thực k , xét các phát biểu sau: 1 1 1 1 (I) dx = 2 ∫ ; (II) kdx = 2k ∫ ; (III) xdx = 2x ∫ ; (IV) 2 3kx dx = 2k ∫ . 1 − 1 − 1 − 0 Số phát biểu đúng là A. 4. B. 3. C. 1. D. 2. 5 5
Câu 88. Cho hàm số f và g liên tục trên đoạn [1;5] sao cho f (x)dx = 7 − ∫
và g(x)dx = 5 ∫ và 1 1
5∫[g(x)−kf(x)]dx =19 Giá trị của k là: 1 A. 2 . B. 6 . C. 2. D. 2 − . Trang 17/80 5 3 5
Câu 89. Cho hàm số f liên tục trên . Nếu 2 f (x)dx = 2 ∫
và f (x)dx = 7 ∫
thì f (x)dx ∫ có giá trị 1 1 3 bằng: A. 5. B. 6 − . C. 9. D. 9 − . 2 2
Câu 90. Cho hàm số f liên tục trên đoạn [0;3]. Nếu f (x)dx = 4 ∫
và tích phân [kx − f (x)]dx = 1 − ∫ 1 1 giá trị k bằng A. 7 . B. 5 . C. 5. D. 2. 2 e
Câu 91. Tích phân (2x −5)ln xdx ∫ bằng 1 e e A. 2 − ( − 5 )ln e x x
x − (x − 5)dx ∫ . B. 2 ( − 5 )ln e x x
x + (x − 5)dx ∫ . 1 1 1 1 e e C. 2 ( − 5 )ln e x x
x − (x − 5)dx ∫ . D. e 2
(x − 5)ln x − (x − 5x)dx ∫ . 1 1 1 1 π 2 Câu 92. Tích phân 2
I = cos x cos 2xdx ∫ có giá trị bằng 0 − π π π π A. 5 . B. . C. 3 . D. . 8 2 8 8 π 3 Câu 93. Tích phân 4sin x 2 I = dx ∫ có giá trị bằng 0 1+ cos x A. 4. B. 3. C. 2. D. 1. 2π
Câu 94. Tích phân I = 1+ sin xdx ∫ có giá trị bằng 0 A. 4 2 . B. 3 2 . C. 2 . D. − 2 . π 3 Câu 95. Tích phân 2
I = sin x tan xdx ∫ có giá trị bằng 0 A 3 ln 3− . B. ln 2 − 2. C. 3 ln 2 − . D. 3 ln 2 − . 5 4 8
Câu 96. Cho hàm số f(x) liên tục trên và 4
f (x) + f (−x) = cos x với mọi x∈ . Giá trị của tích phân π 2 I = f (x)dx ∫ là −π 2 π A. 2 − . B. 3 . C. 3 ln 2 − . D. 3 ln 3− . 16 4 5 0
Câu 97. Nếu (5 −x − e ) 2
dx = K − e ∫
thì giá trị của K là: 2 − A. 11. B. 9. C. 7. D. 12,5. π 2
Câu 98. Cho tích phân I =
1+ 3cos x.sin xdx ∫
.Đặt u = 3cos x +1 .Khi đó I bằng 0 Trang 18/80 3 2 2 3 A. 2 2 u du ∫ . B. 2 2 u du ∫ . C. 2 3 u . D. 2 u du ∫ . 3 3 9 1 0 1 1 e Câu 99. + Tích phân 8ln x 1 I = dx ∫ bằng x 1 A. 2 − . B. 13 . C. 3 ln 2 − . D. 3 ln 3− . 6 4 5 5 Câu 100. Tích phân 2
x − 2x − 3dx ∫ có giá trị bằng 1 − A. 0. B. 64 . C. 7. D. 12,5. 3 2
Câu 101. Tìm a để (3− ax)dx = 3 − ∫ ? 1 A. 2. B. 9. C. 7. D. 4. 5 Câu 102. Nếu 2 k ( 3
5 − x )dx = 549 − ∫
thì giá trị của k là: 2 A. 2 ± B. 2. C. 2 − . D. 5. 3 2 Câu 103. − +
Tích phân x x 4dx ∫ bằng x +1 2 A. 1 4 + 6ln . B. 1 4 + 6ln . C. 1 4 − ln . D. 1 4 + ln . 3 3 2 3 2 3 2 3
Câu 104. Cho hàm số f liên tục trên thỏa f (x) + f (−x) = 2 + 2cos 2x , với mọi x∈ . Giá trị của π 2 tích phân I = f (x)dx ∫ là −π 2 A. 2. B. 7 − . C. 7. D. 2 − . 2
Câu 105. Tìm m để 4 122 (3− 2x) dx = ∫ ? 5 m A. 0. B. 9. C. 7. D.2. 4.2 TÍCH PHÂN I. VẬN DỤNG THẤP 1 2
Câu 106. Giá trị của tích phân 1 I = dx ∫ là 2 0 1− x π π π π A. . B. . C. . D. . 6 4 3 2 1
Câu 107. Giá trị của tích phân dx I = ∫ là 2 1+ x 0 π π π π A I = . B. 3 I = . C. I = . D. 5 I = . 2 4 4 4 3 1 −
Câu 108. Giá trị của tích phân dx I = ∫ là 2 x + 2x + 2 0 π π π π A. 5 I = . B. I = . C. 3 I = . D. I = . 12 6 12 12 Trang 19/80 1 Câu 109. Tích phân 2 3
I = x x + 5dx ∫ có giá trị là 0 A. 4 10 6 − 3 . B. 4 10 7 − 5 . C. 4 10 6 − 5 . D. 2 10 6 − 5 . 3 9 3 9 3 9 3 9 2 Câu 110. Tích phân 2 4 − x dx ∫ có giá trị là 0 π π π A. . B. . C. . D. π . 4 2 3 1 Câu 111. Tích phân 2
I = x x +1dx ∫ có giá trị là 0 A − − − − . 3 2 1. B. 2 2 1 . C. 2 2 1 . D. 3 2 1. 3 3 2 2 0 Câu 112. Tích phân 3
I = x x +1dx ∫ có giá trị là 1 − A. 9 − . B. 3 − . C. 3 . D. 9 . 28 28 28 28 1 2
Câu 113. Giá trị của tích phân = 2 x dx I ∫ là + + 0 (x 1) x 1 A − − − − . 16 10 2 . B. 16 11 2 . C. 16 10 2 . D. 16 11 2 . 3 4 4 3 1
Câu 114. Giá trị của tích phân I = x ∫ (1− x )6 5 3 dx là 0 A. 1 . B. 1 . C. 1 . D. 1 . 167 168 166 165 3 2 Câu 115. + −
Giá trị của tích phân 2x x 1 I = dx ∫ là + 0 x 1 A. 53 . B. 54 . C. 52 . D. 51. 5 5 5 5 1 Câu 116. −
Giá trị của tích phân 3 x I = dx ∫ là 1+ x 0 π π π π A. − 2 + 2 . B. − 2 + 2 . C. − 3 + 2 . D. − 3 + 2 . 2 3 3 2 1
Câu 117. Giá trị của tích phân (2x + ∫ )5 1 dx là 0 A. 1 30 . B. 1 60 . C. 2 60 . D. 2 30 . 3 3 3 3 1 Câu 118. +
Giá trị của tích phân 4x 2 dx ∫ là 2 x + x +1 0 A. ln 2 . B. ln 3. C. 2ln 2. D. 2ln 3 . 2
Câu 119. Giá trị của tích phân dx ∫ là 2 (2x −1) 1 Trang 20/80 A 1 . B. 1 . C. 1 . D. 2 . 2 3 4 3 3 Câu 120. −
Giá trị của tích phân x 3 dx ∫ là + + + 0 3. x 1 x 3 A. 3 3+ 3ln . B. 3 3+ 6ln . B. 3 3 − + 6ln . D. 3 3 − + 3ln . 2 2 2 2 4 Câu 121. +
Giá trị của tích phân: I x 1 = ∫ ( dx là 1+ 1+ 2x )2 0 A. 1 2ln 2 − . B. 1 2ln 2 − . C. 1 2ln 2 − . D. 1 ln 2 − . 2 3 4 2 1 (7x − )99
Câu 122. Giá trị của tích phân: 1 I = dx ∫ là (2x + )101 0 1 A. 1 100 2 −1 1 2 −1 1 2 −1 1 2 −1 900 . B. 101 900 . C. 99 900 . D. 98 900 . 2 2001 Câu 123. Tích phân x I = dx ∫ có giá trị là 2 1002 (1+ x ) 1 A. 1 . B. 1 . C. 1 . D. 1 . 1001 2002.2 1001 2001.2 1002 2001.2 1002 2002.2 2π 3 π
Câu 124. Giá trị của tích phân 2 cos(3x − )dx ∫ là π 3 3 A. 3 − . B. 2 − . C. 2 3 − . D. 2 2 − . 3 3 3 3 π 2
Câu 125. Giá trị của tích phân 2
I = cos x cos 2xdx ∫ là 0 π π π π A. . B. . C. . D. . 6 8 4 2 π
Câu 126. Giá trị của tích phân: x sin x I = dx ∫ là 2 1 + cos x 0 2 π 2 π 2 π 2 π A. . B. . C. . D. . 2 6 8 4 π 2
Câu 127. Giá trị tích phân J = ( 4 sin x + ∫ )1cosxdx là 0 A. 2 . B. 3 . C. 4 . D. 6 . 5 5 5 5 π 2 Câu 128. −
Giá trị tích phân sin x cos x I = dx ∫ là π 1+ sin 2x 4 A. 3 ln 2 . B. 1 ln 3. C. ln 2 . D. 1 ln 2 . 2 2 2 Trang 21/80 π 2
Câu 129. Giá trị tích phân sin x I = dx ∫ là 1+ 3cos x 0 A. 2 ln 2 . B. 2 ln 4 . C. 1 ln 4. D. 1 ln 2. 3 3 3 3 2
Câu 130. Giá trị của tích phân 6 3 5
I = 2 1− cos x.sin . x cos xdx ∫ là 1 A. 21 . B. 12 . C. 21 . D. 12 . 91 91 19 19 π 4
Câu 131. Giá trị của tích phân cos x I = dx ∫ là 3 (sin x + cos x) 0 A. 1 . B. 3 . C. 5 . D. 7 . 8 8 8 8 π 2
Câu 132. Giá trị của tích phân I = sin xdx ∫ là 3 (sin x + cos x) 0 A 1 . B. 1 . C. 1 . D. 1 . 4 3 2 6 π 2
Câu 133. Giá trị của tích phân 4 2
I = cos xsin xdx ∫ là 0 π π π π A. I = . B. I = . C. I = . D. I = . 32 16 8 4 π 2
Câu 134. Giá trị của tích phân 4 4 6 6
I = (sin x + cos x)(sin x + cos x)dx ∫ là 0 A. 32 I = π . B. 33 I = π . C. 31 I = π . D. 30 I = π . 128 128 128 128 π 4
Câu 135. Giá trị của tích phân sin 4x I = dx ∫ là 6 6 0 sin x + cos x A. 4 . B. 1 . C. 2 . D. 5 . 3 3 3 3 π
Câu 136. Giá trị của tích phân xdx I = ∫ là sin x +1 0 π π π A. I = . B. I = . C. I = . D. I = π . 4 2 3 π 2 2007
Câu 137. Giá trị của tích phân sin x I = dx ∫ là 2007 2007 sin x + cos x 0 π π π π A. I = . B. I = . C. 3 I = . D. 5 I = . 2 4 4 4 π 2
Câu 138. Giá trị của tích phân 11 cos xdx ∫ là 0 Trang 22/80 A. 250 . B. 254 . C. 252 . D. 256 . 693 693 693 693 π 2
Câu 139. Giá trị của tích phân 10 sin xdx ∫ là 0 π π π π A. 67 . B. 61 . C. 63 . D. 65 . 512 512 512 512 1
Câu 140. Giá trị của tích phân dx I = ∫ là 1 x + e 0 A. 2 ln e e e e . B. ln . C. 2ln . D. 2 2ln . e 1 + e +1 e +1 e +1 ln5 2x
Câu 141. Giá trị của tích phân e dx I = ∫ là x ln 2 e −1 A. 5 . B. 10 . C. 20 . D. 2 . 3 3 3 3 ln 2
Câu 142. Giá trị của tích phân x I = e −1dx ∫ là 0 −π −π −π −π A. 4 . B. 4 . C. 5 . D. 5 . 3 2 3 2 ln3 x
Câu 143. Giá trị của tích phân e I = ∫ ( dx là x e + )3 0 1 A. 2 2 −1. B. 2 −1. C. 2 − 2 . D. 2 2 − 2. 2 e
Câu 144. Giá trị của tích phân dx I = ∫ là x ln x e A. 2ln 3 . B. ln 3. C. ln 2 . D. 2ln 2. ln3 2x
Câu 145. Giá trị của tích phân: e dx I = ∫ là x x ln 2 e −1+ e − 2 A. 2ln 2 −1. B. 2ln3 – 1. C. ln 3−1. D. ln 2 −1. ln 2 3x 2x Câu 146. + − Cho 2e e 1 M = dx ∫ . Giá trị của M e là 3x 2x x
e + e − e +1 0 A. 7 . B. 9 . C. 11. D. 5 . 4 4 4 4 e 3 2 Câu 147. + ln x 2 ln x I = dx ∫ . x 1 A 3 3 5 3 5 3 2 − 3 3 5 4 3 2 − 3 3 4 5 3 2 − 3 3 4 4 3 2 − 8 . B. 3 8 . C. 3 8 . D. 3 8 . 1 Câu 148. +
Giá trị của tích phân ln(1 x) I = dx ∫ là 2 1+ x 0 π π π π A. I = ln 3 . B. I = ln 2 . C. I = ln 3. D. I = ln 2 . 8 4 8 8 Trang 23/80
Câu 149. Cho hàm số f(x) liên tục trên và thỏa f (−x) + 2 f (x) = cos x . Giá trị của tích phân π 2 I = f (x)dx ∫ là π − 2 A. 1 I = . B. 4 I = . C. 2 I = . D. I =1. 3 3 3 II. VẬN DỤNG CAO 2
Câu 150. Tìm hai số thực ,
A B sao cho f (x) = Asinπ x + B , biết rằng f '(1) = 2 và f (x)dx = 4 ∫ . 0 A = 2 − A = 2 A = 2 − 2 A = − A. 2 . B. . C. . D. π . B = − 2 2 B = − B = π π π B = 2 2 4
Câu 151. Giá trị của a để đẳng thức 2 3
a + (4 − 4a)x + 4x dx = 2xdx ∫ ∫ là đẳng thức đúng 1 2 A. 4. B. 3. C. 5. D. 6. a
Câu 152. Giá trị của tích phân dx I = (a > 0) ∫ là 2 2 x + a 0 π 2 π 2 π π A. . B. . C. − . D. − . 4a 4a 4a 4a π 3
Câu 153. Giá trị của tích phân cos x I = dx ∫ là + 0 2 cos 2x π π π π A. − . B. . C. 4 . D. . 4 2 2 2 2 2 1 Câu 154. Cho dt I = ∫
. Tích phân nào sau đây có giá trị bằng với giá trị của tích phân đã cho. 2 1+ t x 1 1 x x x x A. −∫ dt . B. dt dt . D. − dt . 2 ∫ . C. ∫ ∫ 1+ t 2 1+ t 2 1+ t 2 1+ t 1 1 1 1 π 2
Câu 155. Giá trị của tích phân 1 I = ln(sin x)dx ∫ là 2 π sin x 6 π π A − 3 ln 2 + 3 + . B. 3 ln 2 + 3 − . 3 3 π π
C. − 3 ln 2 − 3 − .
D. − 3 ln 2 + 3 − . 3 3 2
Câu 156. Giá trị của tích phân I = min ∫ { 2 1, x }dx là 0 A. 4 . B. 3 . C. 4 . D. 3 − . 4 3 4 3 −
Câu 157. Giá trị của tích phân = ∫ dx I dx là x − 8 − 1 x Trang 24/80 A. 2 ln . B. 2 . C. −ln 2 . D. 2ln 2. 3 a 3 Câu 158. − Biết x 2ln x 1 I = dx = + ln 2 ∫
. Giá trị của a là 2 x 2 1 A. 2. B. ln 2 . C. π . D. 3. π π 2 2
Câu 159. Cho I = cos x 3sin x +1dx sin 2x I = dx 1 ∫ , 2 ∫
. Khẳng định nào sau đây là sai ? 2 (sin x + 2) 0 0 A. 14 I = .
B. I > I . B. 3 3 I = 2ln + . D. 3 2 I = 2ln − . 1 9 1 2 2 2 2 2 2 3 m
Câu 160. Tất cả các giá trị của tham số m thỏa mãn ∫(2x +5)dx = 6 là 0
A. m =1,m = 6 − . B. m = 1, − m = 6 − . C. m = 1, − m = 6 .
D. m =1,m = 6 . π 2
Câu 161. Cho hàm số sin 2 ( ) x h x = . Tìm để a cos x bcos ( ) x h x = +
và tính I = h(x)dx 2 ∫ (2 + sin x) 2 (2 + sin x) 2 + sin x 0 A. 2 3 a = 4
− , b = 2; I = + 2ln . B. 2 3 a = 4, b = 2; − I = − − 2ln . 3 2 3 2 C. 1 3
a = 2, b = 4; I = − + 4ln . D. 1 3 a = 2
− , b = 4; I = + 4ln . 3 2 3 2
Câu 162. Giá trị trung bình của hàm số y = f (x) trên [a;b], kí hiệu là m( f ) được tính theo công thức m( f ) 1 b = f
∫ (x)dx. Giá trị trung bình của hàm số f (x) = sin x trên [0;π] là b − a a A. 4 . B. 3 . C. 1 . D. 2 . π π π π π 1 4 2
Câu 163. Cho ba tích phân dx I = ∫ , J = ∫( 4 4
sin x − cos x)dx và K = ( 2 x + 3x + ∫ )1dx. Tích phân 3x +1 0 0 1 −
nào có giá trị bằng 21 ? 2 A. K. B. I. C. J.
D. J và K. a
Câu 164. Với 0 < a <1, giá trị của tích phân sau ∫ dx dx là: 2 x − 3x + 2 0 A. a − 2 − − − ln . B. a 2 ln . C. a 2 ln . D. a 2 ln . 2a −1 a −1 2(a − ) 1 2a +1 1 3 Câu 165. Cho 4 2 3 x m − dx = 0 ∫ . Khi đó giá trị của 2 144m −1 bằng 4 2 (x + 2) 0 A. 2 − . B. 4 3 −1. C. 2 3 . D. 2 3 − . 3 3 3
Câu 166. Cho hàm số f liên tục trên đoạn [ ;
a b] và có đạo hàm liên tục trên ( ;
a b), đồng thời thỏa mãn
f (a) = f (b) . Lựa chọn khẳng định đúng trong các khẳng định sau b b A. f (x)
f '(x).e dx = 2 ∫ . B. f (x)
f '(x).e dx =1 ∫ . a a Trang 25/80 b b C. f (x)
f '(x).e dx = 1 − ∫ . D. f (x)
f '(x).e dx = 0 ∫ . a a 5
Câu 167. Kết quả phép tính tích phân dx I = ∫
có dạng I = a ln 3 + b ln 5 (a,b ∈ ) . Khi đó + 1 x 3x 1 2 2
a + ab + 3b có giá trị là A. 1. B. 5. C. 0. D. 4. π 2
Câu 168. Với n ∈ ,n ≥ 1, tích phân = ∫(1−cos )n I
x sin xdx có giá trị bằng 0 A. 1 . B. 1 . C. 1 . D. 1 . 2n n −1 n +1 n π 2 n
Câu 169. Với n ∈ sin x
, n > 1, giá trị của tích phân dx ∫ là n n + 0 cos x sin x π π π π A. − . B. . C. 3 . D. 3 − . 4 4 4 4 2017π
Câu 170. Giá trị của tích phân 1− cos 2xdx ∫ là 0 A. 3034 2 . B. 4043 − 2 . C. 3043 2 . D. 4034 2 . π 2 1+cos + x x
Câu 171. Giá trị của tích phân (1 sin ) ln ∫ dx là 1 cos + x 0 A. 2ln 3−1. B. 2 − ln 2 −1. C. 2ln 2 −1. D. 2 − ln 3−1. b
Câu 172. Có mấy giá trị của b thỏa mãn 2
(3x −12x +11)dx = 6 ∫ 0 A. 4. B. 2. C. 1. D. 3. b a
Câu 173. Biết rằng 6dx = 6 ∫ và x xe dx = a ∫ . Khi đó biểu thức 2 3 2
b + a + 3a + 2a có giá trị bằng 0 0 A. 5. B. 4. C. 7. D. 3. a bπ
Câu 174. Biết rằng dx = A ∫ , 2dx = B
a b > ). Khi đó giá trị của biểu thức 4 B aA + bằng 2 2 x ∫ (với , 0 + a 2b 0 0 A. 2π . B. π . C. 3π . D. 4π . Trang 26/80
C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
D A B A A A C D C D B A D B B C C D B C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
C A A A B D D D C B B C A B C D B D C A
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
C B B C B C D D D D B A A C D B A A C A
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
A D A B A D B C B D C D C A D B D A C B
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
A D A B A D B C B D C D C A D B D D C A
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
A D A B A D B C B D C D C A D B A C B B
101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120
D A B A A A C D C D B A D B B C C D B C
121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140
C A A A B D D D C B B C A B C D B D C A
141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
C B B C B C D D C D B A A C D B A A C A
161 162 163 164 165 166 167 168 169 170 171 172 173 174 A D A B A D B C B D C D C A
II –HƯỚNG DẪN GIẢI
Câu 1. Cho hai hàm số f , g liên tục trên đoạn [ ;
a b] và số thực k tùy ý. Trong các khẳng định sau,
khẳng định nào sai? b b b b a
A. ∫[ f (x)+ g(x)]dx = f (x)dx + g(x)dx ∫ ∫ .
B. f (x)dx = − f (x)dx ∫ ∫ . a a a a b b b b b
C. kf (x)dx = k f (x)dx ∫ ∫ .
D. xf (x)dx = x f (x)dx ∫ ∫ . a a a a
Câu 2. Cho hàm số f liên tục trên và số thực dương a . Trong các khẳng định sau, khẳng định nào luôn đúng? a a a a
A. f (x)dx = 0 ∫ .
B. f (x)dx =1 ∫ .
C. f (x)dx = 1 − ∫ .
D. f (x)dx = f (a) ∫ . a a a a 1
Câu 3. Tích phân dx ∫ có giá trị bằng 0 A. 1 − . B. 1. C. 0 . D. 2 . a
Câu 4. Cho số thực a thỏa mãn x 1+ 2 e dx = e −1 ∫
, khi đó a có giá trị bằng 1 − A. 1. B. 1 − . C. 0 . D. 2 . Trang 27/80 Hướng dẫn giải a Ta có 1 + 1 a x x+ a 1 e dx = e + 1 − = e − e ∫
. Vậy yêu cầu bài toán tương đương 1 − a 1 + 2
e −1 = e −1 ⇔ a =1.
Câu 5. Trong các hàm số dưới đây, hàm số nào có tích phân trên đoạn [0;π ] đạt giá trị bằng 0 ?
A. f (x) = cos3x .
B. f (x) = sin 3x . π π C. ( ) cos x f x = x + .
D. f (x) = sin + . 4 2 4 2 Hướng dẫn giải
Tính tích phân cho từng hàm số trong các đáp án: π π • 1
cos3xdx = sin 3x = 0 ∫ , 3 0 0 π π • 1
sin 3xdx = − cos3x = 2 ∫ , 3 0 0 π π π π • cos x ∫ 4sin x dx + = + = 2( 2 − 2) , 4 2 4 2 0 0 π π π π • sin x ∫ 4cos x dx + = − + = 2 2 . 4 2 4 2 0 0
Vậy chọn f (x) = cos3x .
Câu 6. Trong các tích phân sau, tích phân nào có giá trị khác 2 ? 2 e 1 π 2 A. ln xdx ∫ . B. 2dx ∫ . C. sin xdx ∫ . D. xdx ∫ . 1 0 0 0 Hướng dẫn giải
Dù giải bằng máy tính hay làm tay, ta không nên thử tính lần lượt từng đáp án từ A đến D, mà
nên chọn các tích phân đơn giản để thử trướC. Ví dụ 1 • 1 2dx = 2x 0 = 2 ∫ , 0 2 2 2 • x xdx = = 2 ∫ 2 0 0 π • sin xdx cos x π = − 0 = 2 ∫ , 0 2 e nên nhận ln xdx ∫ . 1 1 2
Câu 7. Trong các hàm số dưới đây, hàm số nào thỏa mãn f (x)dx = f (x)dx ∫ ∫ ? 1 − 2 − A. ( ) x f x = e .
B. f (x) = cos x .
C. f (x) = sin x .
D. f (x) = x +1. Hướng dẫn giải
Cách 1: Phương pháp tự luận
Tính lần lượt từng tích phân (cho đến khi nhận được kết quả đúng), ta được: 1 2 • 1
sin xdx = −cos x 1− = 0 = sin xdx ∫ ∫ nhận, 1 − 2 − Trang 28/80 1 2 • 1 cos xdx = sin x 2 1 − = 2 sin1 ∫
, và cos xdx = sin x 2− = 2sin 2 ∫ loại, 1 − 2 − 1 2 • 1 x x 1 e dx = e − 2 x x 2 2 − 1 − = e − e ∫
, và e dx = e 2− = e − e ∫ loại, 1 − 2 − 1 1 2 + 2 2 2 + • (x 1) (x +1)dx = = 2 ∫ , và (x 1) (x +1)dx = = 4 ∫ loại. 2 1 2 1 − − 2 2 − −
Vậy ta nhận đáp án f (x) = sin x .
Cách 2: Phương pháp tự luận a
Ta đã biết nếu f là hàm số lẻ và liên tục trên thì f (x)dx = 0 ∫
với mọi số thực a . Trong −a
các lựa chọn ở đây, chỉ có hàm số y f (x) sin x là lẻ, nên đó là đáp án của bài toán.
Cách 3: Phương pháp trắc nghiệm
Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng 0 thì ngưng) Phép tính Kết quả 1 2
sin xdx − sin xdx ∫ ∫ 0 1 − 2 − 1 2
cos xdx − cos xdx ∫ ∫ ≠ 0 1 − 2 − 1 2 x x e dx − e dx ∫ ∫ ≠ 0 1 − 2 − 1 2
(x +1)dx − (x +1)dx ∫ ∫ ≠ 0 1 − 2 −
Vậy ta nhận đáp án f (x) = sin x . 5 Câu 8. Tích phân dx
I = ∫ có giá trị bằng x 2 A. 3ln 3 . B. 1 ln 3 . C. 5 ln . D. 2 ln . 3 2 5 Hướng dẫn giải
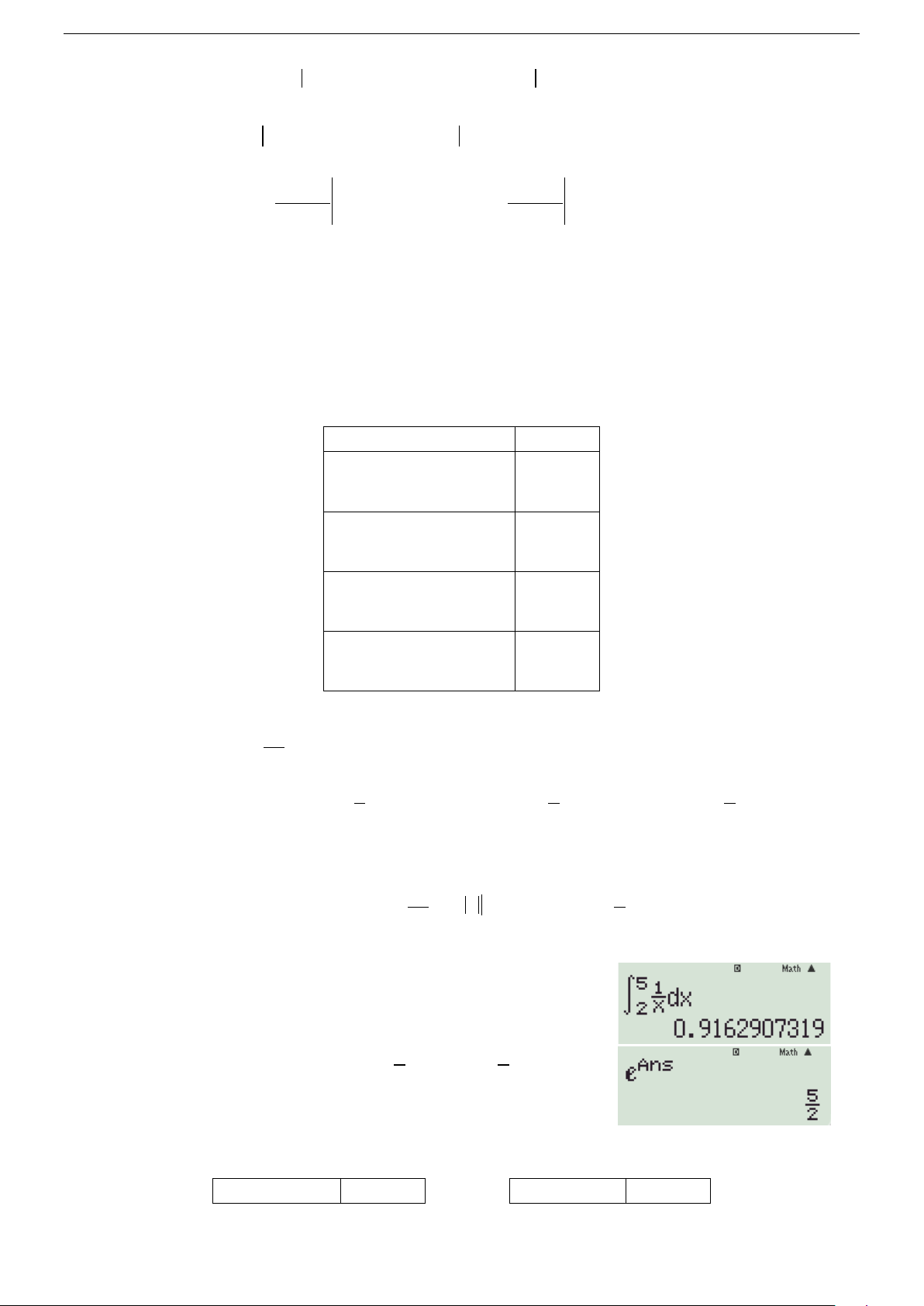
Cách 1: Phương pháp tự luận 5 dx 5 5 I = = ln x = − = ∫ 2 ln 5 ln 2 ln . x 2 2
Cách 2: Phương pháp trắc nghiệm
Bước 1: Dùng máy tính như hình bên, thu được giá trị 0,91629...
Bước 2: Lấy 0,91629.. e
cho kết quả 5 chọn 5 ln . 2 2
Cách 3: Phương pháp trắc nghiệm
Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng 0 thì ngưng) Phép tính Kết quả Phép tính Kết quả Trang 29/80 5 dx 5 5 − ln ∫ dx 0 − 3ln 3 ≠ x ∫ 0 2 x 2 2 5 dx 1 5 − ln 3 ∫ dx 2 ≠ 0 − ln ≠ x ∫ 0 3 x 5 2 2 chọn 5 ln . 2 π 2 Câu 9. Tích phân x I d = ∫ có giá trị bằng π sin x 3 A. 1 1 ln . B. 2ln 3 . C. 1 ln 3. D. 1 2ln . 2 3 2 3 Hướng dẫn giải
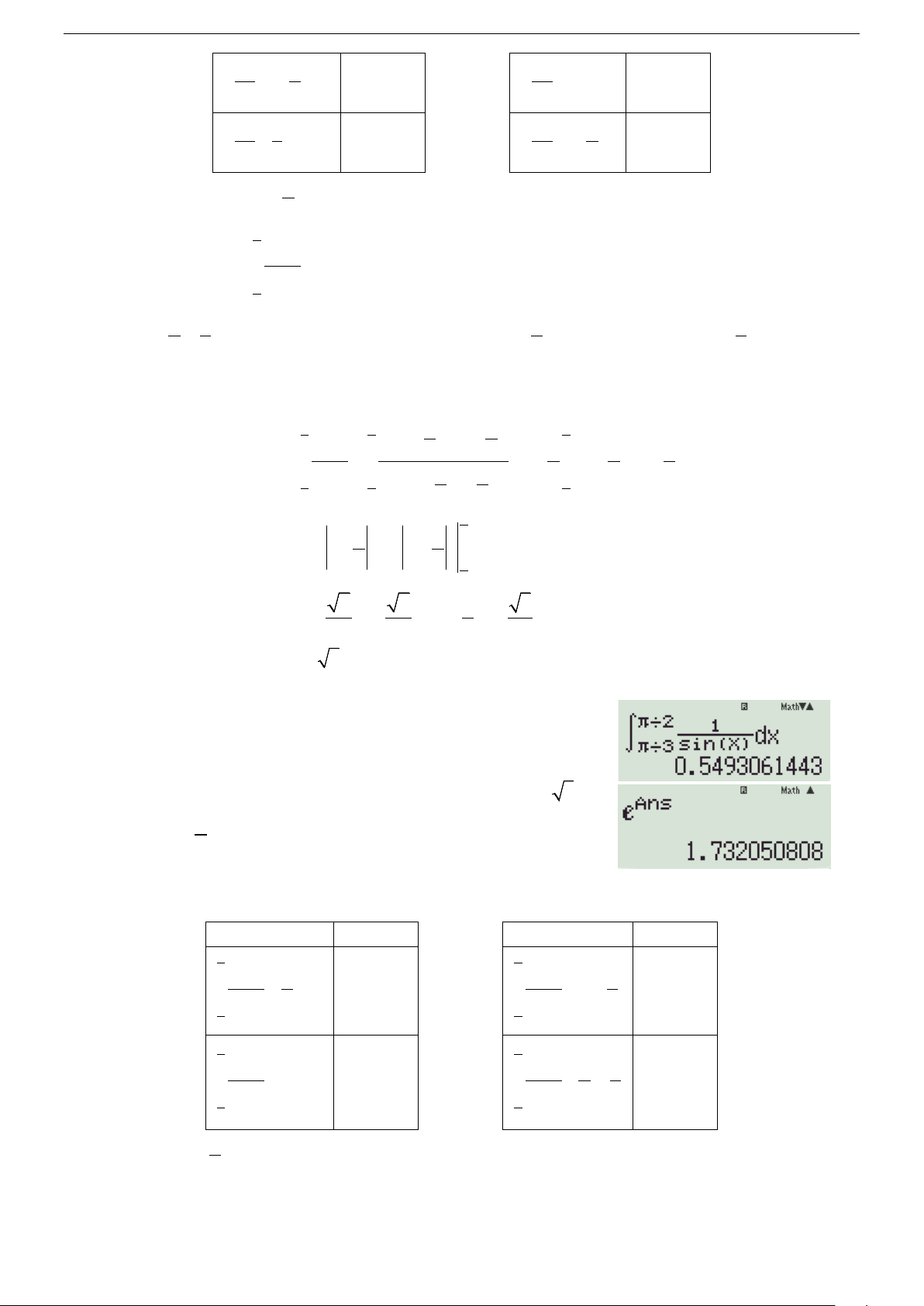
Cách 1: Phương pháp tự luận π π 2 x 2 x π 2 2 cos + sin 2 dx 2 2 1 I = = dx = ∫ ∫
∫cot x + tan x dx π sin x x x π 2 π 2 2 2sin cos 3 3 3 2 2 π 2 = ln sin x − ln cos x 2 2 π3 2 2 1 3 = ln − ln − ln − ln 2 2 2 2 = ln 3.
Cách 2: Phương pháp trắc nghiệm
Bước 1: Dùng máy tính như hình bên, thu được giá trị 0,549306...
Bước 2: Lấy 0,549306.. e
cho kết quả 1,732050808... ≈ 3 chọn 1 ln 3. 2
Cách 3: Phương pháp trắc nghiệm
Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng 0 thì ngưng) Phép tính Kết quả Phép tính Kết quả π π 2 dx 1 2 − ln 3 ∫ dx 1 0 − 2ln ∫ ≠ 0 π sin x 2 π sin x 3 3 3 π π 2 dx 2 − 2ln 3 ∫ dx 1 1 ≠ 0 − ln ∫ ≠ 0 π sin x π sin x 2 3 3 3 chọn 1 ln 3. 2
Nhận xét: Ở bài này cách làm bằng máy tính có vẻ nhanh hơn. Trang 30/80 0 Câu 10. Nếu ( − x/2 4 − e
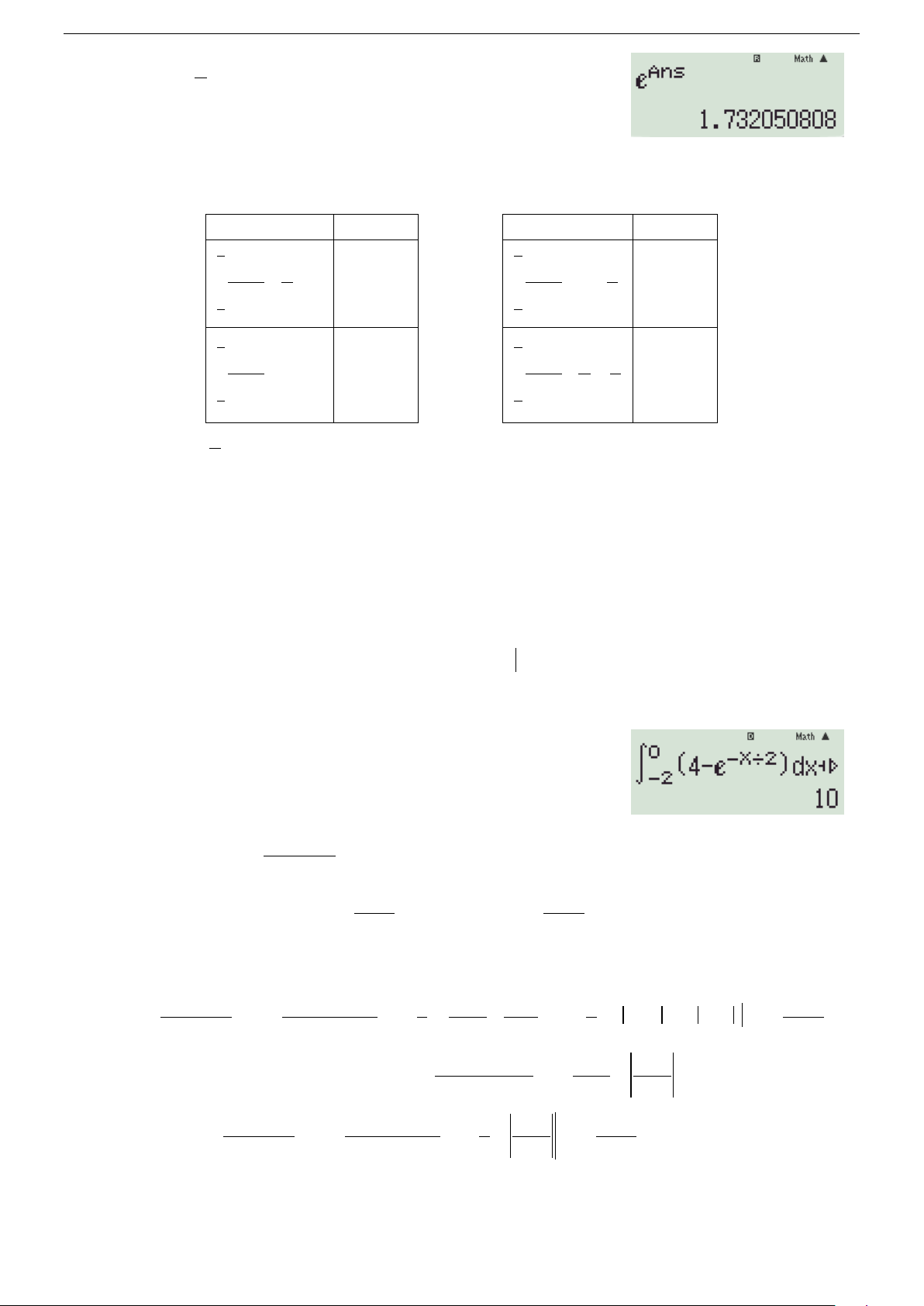
)dx = K − 2e ∫
thì giá trị của K là 2 − A. 12,5. B. 9. C. 11. D. 10. Hướng dẫn giải
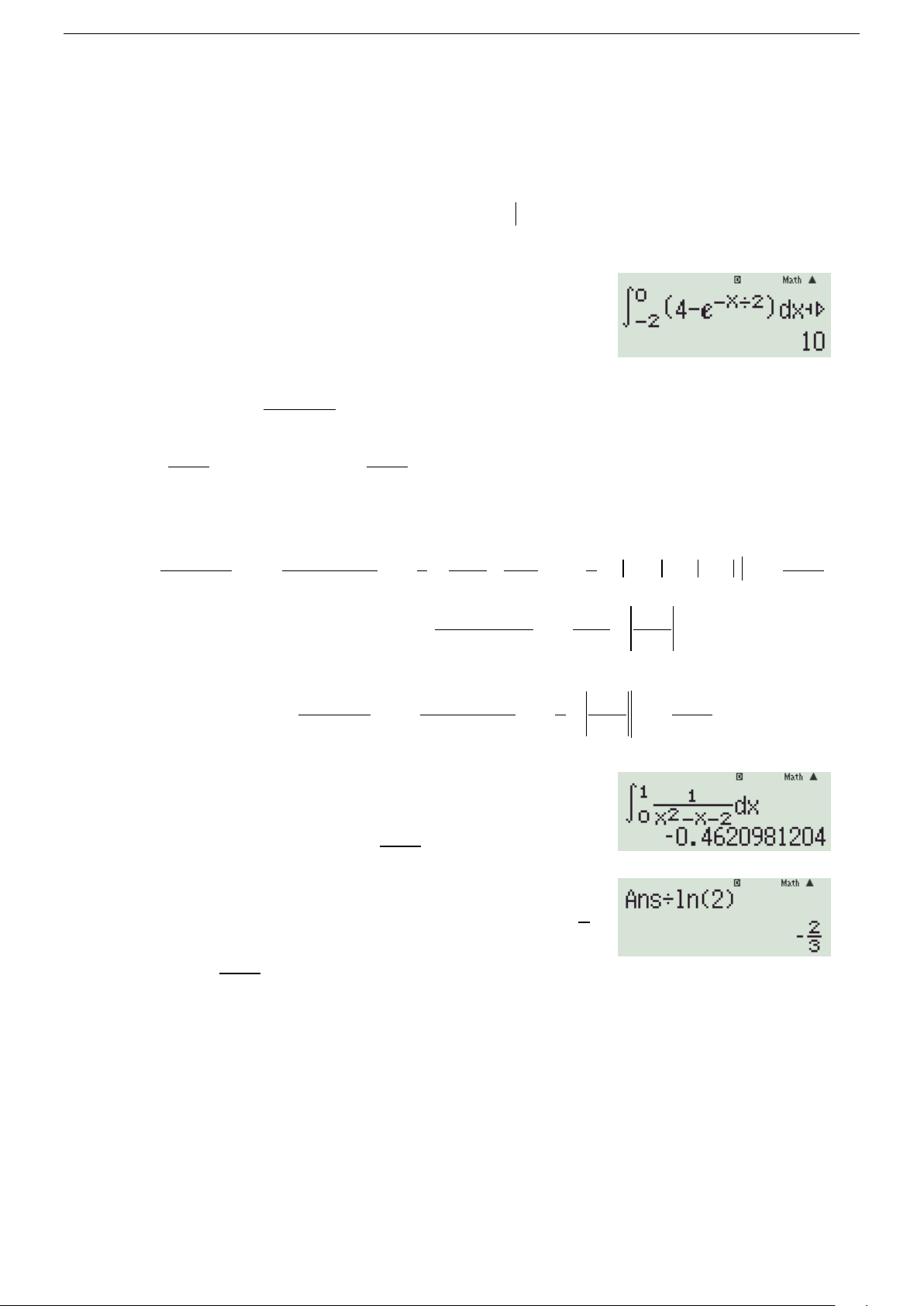
Phương pháp tự luận 0 = (4 − x − ) + 2 = (4 + 2 −x K e dx e x e ) 0 /2 /2 + = − − + + = ∫ − 2e 2 ( 8 2e) 2 2e 10. 2 −
Phương pháp trắc nghiệm 0 Dùng máy tính tính ( − x/2 4 − e )dx + 2e ∫ như hình 2 −
bên, thu được giá trị K =10 . 1 Câu 11. Tích phân 1 I = dx ∫ có giá trị bằng 2 x − x − 2 0 A. 2ln 2 . B. 2ln 2 − . C. 2 − ln 2 . D. 2ln 2. 3 3 Hướng dẫn giải
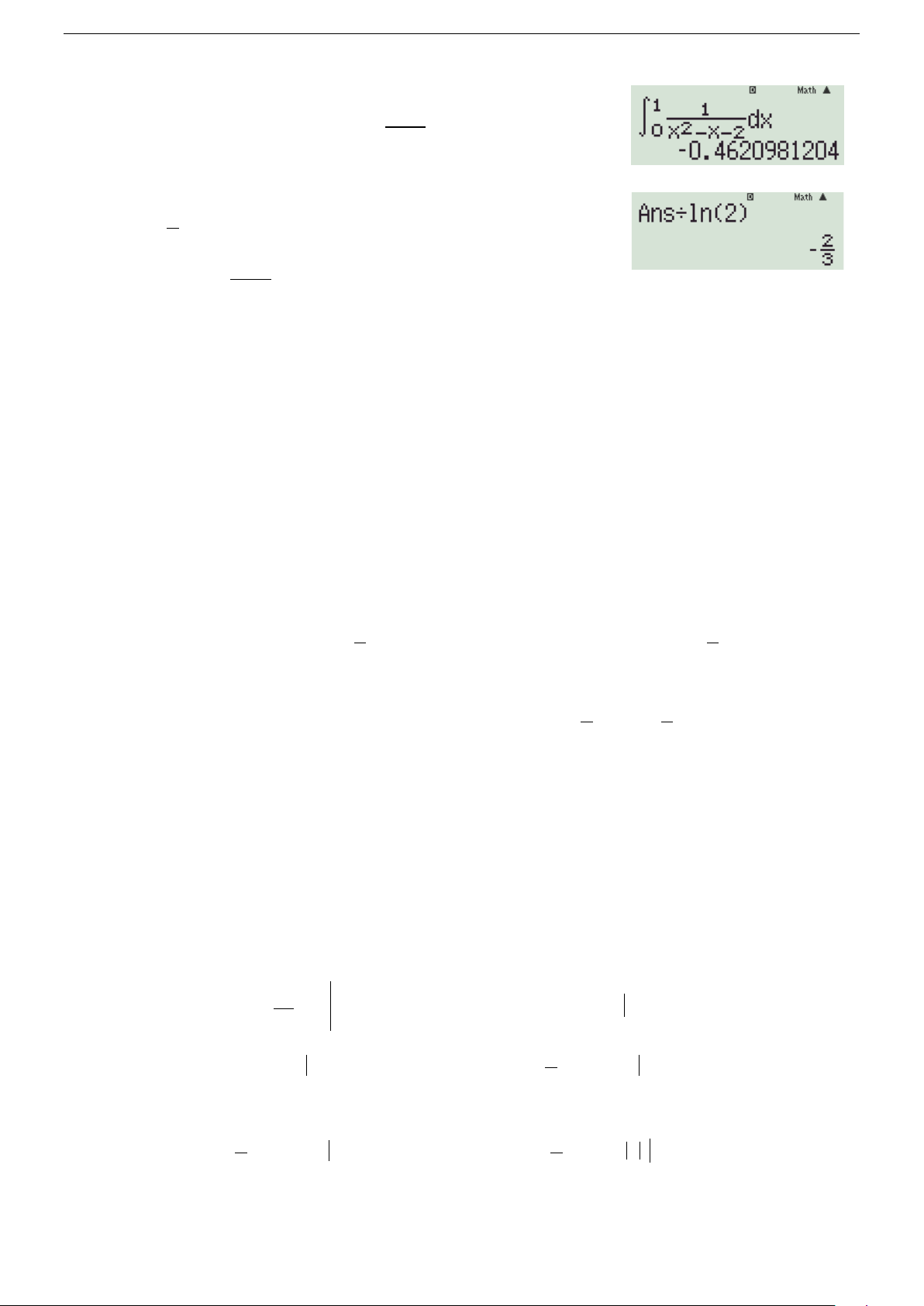
Phương pháp tự luận 1 1 1 dx dx = = −
dx = [ x − − x + ]1 1 1 1 1 1 1 2ln 2 ln 2 ln 1 = − ∫ . 2 ∫ ∫ 0 x − x − 2 (x − 2)(x +1)
3 x − 2 x +1 3 3 0 0 0 −
Học sinh có thể áp dụng công thức 1 1 = ln x a dx + C ∫
để giảm một bước
(x − a)(x − b) a − b x − b tính: 1 1 1 1 1 1 x − 2 2ln 2 I = dx = dx = ln = − ∫ 2x ∫ . − x − 2 (x − 2)(x +1) 3 x +1 3 0 0 0
Phương pháp trắc nghiệm
Bước 1: Dùng máy tính như hình bên, thu được giá trị 0.4620981... −
Bước 2: Loại đáp án dương 2ln 2 và loại đáp án nhiễu 3 “Không xác định”.
Bước 3: Chia giá trị 0.4620981... − cho ln 2 , nhận được 2 − 3 chọn 2ln 2 − . 3 5 5
Câu 12. Cho hàm số f và g liên tục trên đoạn [1;5] sao cho f (x)dx = 2 ∫
và g(x)dx = 4 − ∫ . Giá trị 1 1 5
của ∫[g(x)− f (x)]dx là 1 A. 6 − . B. 6 . C. 2 . D. 2 − . Hướng dẫn giải 5 5 5
[g(x) − f (x)]dx = g(x)dx − f (x)dx = 4 − − 2 = 6 − ∫ ∫ ∫ . 1 1 1 Trang 31/80 3 3
Câu 13. Cho hàm số f liên tục trên đoạn [0;3]. Nếu f (x)dx = 2 ∫
thì tích phân ∫[x −2 f (x)]dx có giá 0 0 trị bằng A. 7 . B. 5 . C. 5. D. 1 . 2 2 Hướng dẫn giải 3 3 3 [x − f x ] 9 1
2 ( ) dx = xdx − 2 f (x)dx = − 2× 2 = ∫ ∫ ∫ . 2 2 0 0 0 5 3 5
Câu 14. Cho hàm số f liên tục trên đoạn [0;6] . Nếu f (x)dx = 2 ∫
và f (x)dx = 7 ∫
thì f (x)dx ∫ có giá 1 1 3 trị bằng A. 5. B. 5 − . C. 9. D. 9 − . Hướng dẫn giải 5 1 5 3 5
f (x)dx = f (x)dx + f (x)dx = − f (x)dx + f (x)dx = 7 − + 2 = 5 − ∫ ∫ ∫ ∫ ∫ . 3 3 1 1 1
Câu 15. Trong các phép tính sau đây, phép tính nào sai? 3 2 − A. 3 x = ( x e dx e ) ∫ 1 2 − = 1 . B. dx (ln x) ∫ 3 . − x − 1 3 2π 2 2 2 C. xdx = ( x) 2 cos sin π ∫ x π . D. (x + ) 1 dx = ∫ + x . 2 π 1 1 Hướng dẫn giải 2 − 2 −
Phép tính 1 dx = (ln x) 2− ∫ 1 2 − =
3 là sai. Phép tính đúng là dx (ln x ) ∫ . 3 − x − − x − 3 3
Câu 16. Cho hàm số f liên tục trên đoạn [ ;
a b] có một nguyên hàm là hàm F trên đoạn [ ; a b]. Trong
các phát biểu sau, phát biểu nào sai ? b
A. f (x)dx = F(b) − F(a) ∫ . a
B. F '(x) = f (x) với mọi x ∈( ; a b) . b
C. f (x)dx = f (b) − f (a) ∫ . a b
D. Hàm số G cho bởi G(x) = F(x) + 5 cũng thỏa mãn f (x)dx = G(b) − G(a) ∫ . a
Câu 17. Xét hàm số f liên tục trên và các số thực a , b , c tùy ý. Trong các khẳng định sau, khẳng định nào sai? b b a b c b
A. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ .
B. f (x)dx = f (x)dx + f (x)dx ∫ ∫ ∫ . a c c a a c b c b b c c
C. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ .
D. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ . a a c a a b
Câu 18. Xét hai hàm số f và g liên tục trên đoạn [ ;
a b] . Trong các mệnh đề sau, mệnh đề nào sai? Trang 32/80 b
A. Nếu m ≤ f (x) ≤ M x ∀ ∈[ ;
a b] thì m(b − a) ≤ f (x)dx ≤ M (a − b) ∫ . a b
B. Nếu f (x) ≥ m x ∀ ∈[ ;
a b] thì f (x)dx ≥ m(b − a) ∫ . a b
C. Nếu f (x) ≤ M x ∀ ∈[ ;
a b] thì f (x)dx ≤ M (b − a) ∫ . a b
D. Nếu f (x) ≥ m x ∀ ∈[ ;
a b] thì f (x)dx ≥ m(a − b) ∫ . a Hướng dẫn giải b
Mệnh đề “Nếu f (x) ≥ m x ∀ ∈[ ;
a b] thì f (x)dx ≥ m(a − b) ∫
” sai, mệnh đề đúng phải là a b
“Nếu f (x) ≥ m x ∀ ∈[ ;
a b] thì f (x)dx ≥ m(b − a) ∫ ”. a
Câu 19. Cho hai hàm số f và g liên tục trên đoạn [ ;
a b] sao cho g(x) ≠ 0 với mọi x ∈[ ; a b] . Xét các khẳng định sau: b b b
I. ∫[ f (x)+ g(x)]dx = f (x)dx + g(x)dx ∫ ∫ . a a a b b b
II. ∫[ f (x)− g(x)]dx = f (x)dx − g(x)dx ∫ ∫ . a a a b b b
III. ∫[ f (x).g(x)]dx = f (x) . dx g(x)dx ∫ ∫ . a a a b f (x)dx b ∫ IV. f (x) a dx = ∫ . g(x) b a g(x)dx ∫a
Trong các khẳng định trên, có bao nhiêu khẳng định sai? A. 1. B. 2 . C. 3. D. 4 . Hướng dẫn giải b f (x)dx b ∫ b b b
Các công thức f (x) a dx = ∫
và ∫[ f (x).g(x)]dx = f (x) . dx g(x)dx g ∫ ∫ là sai. (x) b a g(x)dx ∫ a a a a 3
Câu 20. Tích phân x(x −1)dx ∫
có giá trị bằng với giá trị của tích phân nào trong các tích phân dưới 0 đây? 2 3π ln 10 π A. ( 2
x + x − 3)dx ∫ . B. 3 sin xdx ∫ . C. 2x e dx ∫ .
D. cos(3x +π )dx ∫ . 0 0 0 0 Hướng dẫn giải Phương pháp tự luận
Tính rõ từng phép tính tích phân để tìm ra kết quả đúng (chỉ tính đến khi nhận được kết quả đúng thì dừng lại): Trang 33/80 ln 10 ln 10 2x 2ln 10 • 2x e e 1 9 e dx − = = = ∫ , 2 0 2 2 0 3π • 3 3 sin xdx 3cos x π = − 0 = 6 ∫ , 0 2 2 3 2 • ( 2 x + x − 3) x x 8 4 dx = ∫ +
− 3x = + 2 − 6 = − , 3 2 3 3 0 0 π • 1 π 1
cos(3x +π )dx = sin(3x +π ) = (sin 4π − sinπ ) = 0 ∫ . 0 3 3 0 ln 10 Vậy chọn 2x e dx ∫ . 0
Phương pháp trắc nghiệm
Nhập các phép tính sau vào máy tính để thu kết quả: Phép tính Kết quả 3 ln 10 2 ( −1) x x x dx − e dx ∫ ∫ 0 0 0 3 3π
x(x −1)dx − sin xdx ∫ ∫ 3 − 0 0 2 3 2
x(x −1)dx − ( 2
x + x − 3)dx ∫ ∫ 35 0 0 6 3 π
x(x −1)dx − cos(3x +π )dx ∫ ∫ 9 0 0 2 ln 10 Vậy chọn 2x e dx ∫ . 0
Câu 21. Trong các mệnh đề sau, mệnh đề nào đúng? b
A. Nếu hàm số f liên tục trên đoạn [ ;
a b] , sao cho f (x)dx ≥ 0 ∫
thì f (x) ≥ 0 x ∀ ∈[ ; a b]. a 3
B. Với mọi hàm số f liên tục trên đoạn [ 3
− ;3], luôn có f (x)dx = 0 ∫ . 3 − b a
C. Với mọi hàm số f liên tục trên , ta có f (x)dx = f (x)d(−x) ∫ ∫ . a b 5 D. f (x)
Với mọi hàm số f liên tục trên đoạn [1;5] thì [ f (x)]2 [ ] 5 3 dx = ∫ . 3 1 1 Hướng dẫn giải b a a a
Vì d(−x) = ( 1)
− dx nên f (x)dx = − f (x)dx = f (x)( 1
− )dx = f (x)d(−x) ∫ ∫ ∫ ∫ . a b b b
Câu 22. Trong các mệnh đề sau, mệnh đề nào đúng? 1 0
A. Nếu f là hàm số chẵn trên thì f (x)dx = f (x)dx ∫ ∫ . 0 1 − Trang 34/80 0 1
B. Nếu f (x)dx = f (x)dx ∫ ∫
thì f là hàm số chẵn trên đoạn [ 1; − 1] . 1 − 0 1
C. Nếu f (x)dx = 0 ∫
thì f là hàm số lẻ trên đoạn [ 1; − 1]. 1 − 1
D. Nếu f (x)dx = 0 ∫
thì f là hàm số chẵn trên đoạn [ 1; − 1]. 1 − Hướng dẫn giải 0 1 1 • Hàm số 3 x
y = x − thỏa f (x)dx = f (x)dx ∫ ∫
và f (x)dx = 0 ∫
, nhưng nó là hàm lẻ trên 2 1 − 0 1 − [ 1; − 1]. 1 • Hàm số 2 1
y = x − thỏa f (x)dx = 0 ∫
, nhưng nó làm hàm chẵn trên [ 1; − 1]. 3 1 −
• Còn khi f là hàm chẵn trên thì f (x) = f (−x) với mọi x∈ . Đặt t = −x ⇒ dt = −dx và suy ra 1 1 1 1 1 − 0
f (x)dx = − f (x)( 1
− )dx = − f (x)d(−x) = − f (−x)d(−x) = − f (t)dt = f (t)dt. ∫ ∫ ∫ ∫ ∫ ∫ 0 0 0 0 0 1 −
Câu 23. Giả sử F là một nguyên hàm của hàm số 6 5
y = x sin x trên khoảng (0;+∞). Khi đó 2 6 5 x sin xdx ∫ có giá trị bằng 1
A. F(2) − F(1) . B. −F(1) . C. F( ) 2 .
D. F(1) − F(2) . Hướng dẫn giải b
Áp dụng công thức f (x)dx = F(b) − F(a) ∫
, trong đó F là một nguyên hàm của f trên đoạn a 2 [ ; a b], ta có 6 5 x sin dx
x = F(2) − F( ) 1 ∫ . 1 b
Câu 24. Cho hàm số f liên tục trên và hai số thực a < b . Nếu f (x)dx = α ∫ thì tích phân a
b 2 f (2x)dx ∫ có giá trị bằng a 2 α A. . B. 2α . C. α . D. 4α . 2 Hướng dẫn giải Phương pháp tự luận
Đặt t = 2x ⇒ dt = 2dx và x a 2 b 2 t a b b 2 b 2 b α Vậy 1 1
f (2x)dx =
f (2x)2dx = f (t)dt = ∫ ∫ ∫ . 2 2 2 a 2 a 2 a
Phương pháp trắc nghiệm
Phương pháp tự luận tốt hơn cả, nhưng nếu học sinh không nắm rõ, có thể thay f bởi một hàm
số đơn giản, xác định trên [0;1] và tính toán. Trang 35/80
Ví dụ f (x) = x với x ∈[0;1]. Khi đó 1 1 1
α = f (x)dx = xdx = ∫ ∫ , 2 0 0 suy ra 1/2 1/2 1 α
f (2x)dx = 2xdx = = ∫ ∫ . 4 2 0 0
Câu 25. Giả sử F là một nguyên hàm của hàm số 3 5
y = x sin x trên khoảng (0;+∞). Khi đó tích phân 2 3 5 81x sin 3xdx ∫ có giá trị bằng 1
A. 3[F(6) − F(3)] .
B. F(6) − F(3) .
C. 3[F(2) − F(1)].
D. F(2) − F(1) . Hướng dẫn giải
Đăt t = 3x ⇒ dt = 3dx và đổi cận x 1 2 t 3 6 2 2 6 Vậy 3 5 3 5 3 5 81x sin 3 dx x = (3x) si
( n 3x)3dx = t sin tdt = F(6) − F(3) ∫ ∫ ∫ . 1 1 3 2
Câu 26. Giả sử hàm số f liên tục trên đoạn [0;2] thỏa mãn f (x)dx = 6 ∫
. Giá trị của tích phân 0
π 2 f (2sin x)cosxdx ∫ là 0 A. 6 − . B. 6 . C. 3 − . D. 3. Hướng dẫn giải
Đặt t = 2sin x ⇒ dt = 2cos xdx và x 0 π 2 t 0 2 π 2 2 2 Vậy f (t) 1
f (2sin x)cos xdx = dt =
f (t)dt = 3 ∫ ∫ ∫ . 2 2 0 0 0 e Câu 27. +
Bài toán tính tích phân ln x 1ln x I = dx ∫
được một học sinh giải theo ba bước sau: x 1
I. Đặt ẩn phụ t = ln x +1, suy ra 1 dt = dx và x x 1 e t 1 2 e 2 + II. ln x 1ln x I = dx = t (t − ) 1 dt ∫ x ∫ 1 1 2 2 III. I t (t ) 5 2 1 dt t = − = − = 1+ ∫ 3 2 . 1 t 1
Học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào? A. Bài giải đúng.
B. Sai từ Bước II. C. Sai từ Bước I.
D. Sai ở Bước III. Hướng dẫn giải 2 2 2 2 4( 2 )
Bước III sai. Phép tính đúng là I = t (t − ) 5 3 1 1 dt = ∫ t − t + = . 5 3 15 1 1 Trang 36/80 π 3
Câu 28. Xét tích phân sin 2x I = dx ∫
. Thực hiện phép đổi biến t = cos x , ta có thể đưa I về dạng 1+ cos x 0 nào sau đây π 4 π 4 1 1 A. 2t I = − dt ∫ . B. 2t I = dt ∫ . C. 2t I = − dt ∫ . D. 2t I = dt ∫ . 1+ t 1+ t 1+ t 1+ t 0 0 1 1 2 2 Hướng dẫn giải π
Ta có t = cos x ⇒ dt = −sin xdx . Khi x = 0 thì t =1, khi x = thì 1 t = . Vậy 3 2 π 3 π 3 1 2 1 sin 2x 2sin x cos x 2t 2t I = dx = dx = − dt = dt ∫ ∫ ∫ ∫ . 1+ cos x 1+ cos x 1+ t 1+ t 0 0 1 1 2
Câu 29. Cho hàm số y = f (x) liên tục trên đoạn [ ;
a b]. Trong các bất đẳng thức sau, bất đẳng thức nào luôn đúng? b b b b
A. f (x) dx > f (x)dx ∫ ∫ . B. f
∫ (x)dx ≥ f (x) dx ∫ . a a a a b b b b
C. f (x) dx ≥ f (x)dx ∫ ∫ . D. f
∫ (x)dx > f (x) dx ∫ . a a a a
Câu 30. Trong các khẳng định dưới đây, khẳng định nào sai? 1 1 1
A. sin(1− x)dx = sin xdx ∫ ∫ . B. (1+ )x x dx = 0 ∫ . 0 0 0 π π 2 1
C. sin x dx = 2 sin xdx ∫ ∫ . D. 2017 2
x (1+ x)dx = ∫ . 2 − 2019 0 0 1 Hướng dẫn giải
Cách 1: Tính trực tiếp các tích phân 1 0 1
• Đặt t =1− x ⇒ dt = −dx ⇒ sin(1− x)dx = − sin tdt = sin tdt ∫ ∫ ∫ 0 1 0 π π 2 • Đặt x 1 = ⇒ = ⇒ sin x t dt dx dx = 2sin tdt ∫ ∫ 2 2 2 0 0 1 1 2018 2019 2018 2019 2018 2019 − − • 2017 x x 1 1 ( 1) ( 1) 2
x (1+ x)dx = ∫ + = + − + = − 2018 2019 − 2018 2019 2018 2019 2019 1 1 1 Vậy (1+ )x x dx = 0 ∫ sai. 0
Cách 2: Nhận xét tích phân 1 1 1 Ta thấy (1+ )x
x ≥1 với mọi x ∈[0;1] nên (1+ )x x dx ≥ 1dx =1 ∫ ∫ , vậy “ (1+ )x x dx = 0 ∫ ” là 0 0 0 khẳng định sai.
Cách 3: Phương pháp trắc nghiệm
Nhập các phép tính sau vào máy tính để thu kết quả: Phép tính Kết quả 1 (1+ )x x dx ∫ > 0 0 Trang 37/80 1 1
sin(1− x)dx − sin xdx ∫ ∫ 0 0 0 π π 2
sin x dx − 2 sin xdx ∫ ∫ 0 2 0 0 1 2017 2
x (1+ x)dx − ∫ 0 − 2019 1 1 suy ra (1+ )x x dx = 0 ∫ là khẳng định sai. 0
Câu 31. Cho hàm số y = f (x) lẻ và liên tục trên đoạn [ 2;
− 2] . Trong các đẳng thức sau, đẳng thức nào luôn đúng? 2 2 2
A. f (x)dx = 2 f (x)dx ∫ ∫ .
B. f (x)dx = 0 ∫ . 2 − 0 2 − 2 0 2 2
C. f (x)dx = 2 f (x)dx ∫ ∫ .
D. f (x)dx = 2 − f (x)dx ∫ ∫ . 2 − 2 − 2 − 0 Hướng dẫn giải Phương pháp tự luận
Với hàm số f bất kỳ và số thực dương a , ta luôn nằm lòng 2 tính chất sau đây: a
• Nếu f là hàm số lẻ trên đoạn [- ;
a a] thì f (x)dx = 0 ∫ , −a a a
• Nếu f là hàm số chẵn trên đoạn [- ;
a a] thì f (x)dx = 2 f (x)dx ∫ ∫ . −a 0 2
Vậy trong bài này ta chọn f (x)dx = 0 ∫ . 2 −
Phương pháp trắc nghiệm
Nếu học sinh không nắm rõ hai tính chất kể trên, có thể thay f bởi một hàm số đơn giản, xác định trên [ 2;
− 2] và tính toán. Ví dụ f (x) = x với x ∈[ 2; − 2]. Khi đó 2 2 2
f (x)dx = 0 ∫ ,
f (x)dx ≠ 2 f (x)dx ∫ ∫ , 2 − 2 − 0 2 0 2 2
f (x)dx ≠ 2 f (x)dx ∫ ∫ ,
f (x)dx ≠ 2 − f (x)dx ∫ ∫ . 2 − 2 − 2 − 0 2
Vậy chọn f (x)dx = 0 ∫ . 2 − 1
Câu 32. Bài toán tính tích phân 2
I = (x +1) dx ∫
được một học sinh giải theo ba bước sau: 2 − I. Đặt ẩn phụ 2
t = (x +1) , suy ra dt = 2(x +1)dx ,
II. Từ đây suy ra dt dt = dx ⇒ = dx . Đổi cận 2(x +1) 2 t x 2 − 1 t 1 4 1 4 4 III. Vậy 2 t 1 3 7
I = (x +1) dx = dt = t = ∫ ∫ . − 2 t 3 1 3 2 1 Trang 38/80
Học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào? A. Sai từ Bước I.
B. Sai ở Bước III.
C. Sai từ Bước II. D. Bài giải đúng. Hướng dẫn giải Khi đặt 2
t = (x +1) với 2
− ≤ x ≤1 thì không suy ra t = x +1 được, vì x +1 có thể bị âm khi 2 − ≤ x ≤ 1 − .
Câu 33. Một học sinh được chỉ định lên bảng làm 4 bài toán tích phân. Mỗi bài giải đúng được 2,5
điểm, mỗi bài giải sai (sai kết quả hoặc sai bước tính nguyên hàm) được 0 điểm. Học sinh đã
giải 4 bài toán đó như sau: Bài Đề bài Bài giải của học sinh 1 2 1 1 1 x 1 2 x e xdx ∫ 2 x 1 2 x e xdx = e d ( 2 x ) e e −1 = = ∫ ∫ 0 2 2 0 2 0 0 1 1 1 1 1 2 dx ∫ dx = [ 2
ln x − x − 2 ] = ln 2 − ln 2 = 0 2 x ∫ − x − 2 2 0 x − x − 2 0 0
Đặt t = cos x , suy ra dt = −sin xdx . Khi x = 0 thì t =1; khi π
x = π thì t = 1 − . Vậy 3 sin 2x cos xdx ∫ 1 π π 1 − 3 0 2 2 2t 4
sin 2x cos xdx = 2 sin x cos xdx = 2 − t dt = = ∫ ∫ ∫ 3 1− 3 0 0 1
e 1+ (4 − 2e)ln e x
e 1+ (4 − 2e)ln x dx = ∫
∫[1+(4−2e)ln x]d (ln x) 4 dx ∫ x x 1 1 1 2 e
= x + (4 − 2e)ln x = 3− e 1
Số điểm mà học sinh này đạt được là bao nhiêu? A. 5,0 điểm. B. 2,5 điểm. C. 7,5 điểm. D. 10,0 điểm. Hướng dẫn giải
Bài toán 2 giải sai. Cách giải đúng là 1 1 1 1 1 1 x − 2 2 dx = dx = ln = − ln 2 ∫ 2x ∫ − x − 2 (x +1)(x − 2) 3 x +1 3 0 0 0
Bài toán 4 ra kết quả đúng, nhưng cách tính nguyên hàm sai hoàn toàn. Lời giải đúng là: e 1+ (4 − 2 )ln e = ∫ ∫[ e e
x dx 1+(4−2e)ln x]d(ln x) 2
= ln x + (2 − e)ln x = 3− e 1 x 1 1 Kinh nghiệm
Kết quả đúng thì chưa chắc bài giải đúng.
Câu 34. Cho hai hàm số liên tục f và g liên tục trên đoạn [ ;
a b]. Gọi F và G lần lượt là một nguyên
hàm của f và g trên đoạn [ ;
a b]. Đẳng thức nào sau đây luôn đúng? b b
A. f (x)G(x)dx = ∫
[F(x)g(x)]b − F(x)G(x)dx ∫ . a a a b b
B. f (x)G(x)dx = ∫
[F(x)G(x)]b − F(x)g(x)dx ∫ . a a a b b
C. f (x)G(x)dx = ∫
[ f (x)g(x)]b − F(x)g(x)dx ∫ . a a a b b
D. f (x)G(x)dx = ∫
[F(x)G(x)]b − f (x)g(x)dx ∫ . a a a Trang 39/80 0 Câu 35. Tích phân − x I = xe dx ∫ có giá trị bằng 2 − A. 2 −e +1. B. 2 3e −1. C. 2 −e −1. D. 2 2 − e +1. Hướng dẫn giải Phương pháp tự luận
Sử dụng tích phân từng phần, ta được 0 − x I = xe dx ∫2− 0 0 0 = − xd ( −x e ) = − ( −x ∫ xe ) 0 − x − ∫ = − + = − − = − − − e dx ( −x xe ) 0 − x − e dx ( −x xe ) 0 ( −x ∫ − e ) 0 2 2 2 2 2 − e 1. 2 − 2 − 2 −
Phương pháp trắc nghiệm 0 Dùng máy tính tính − x xe dx ∫
như hình bên, thu được kết quả 2 −
như hình bên. Loại được đáp án 2
3e −1. Sau đó thử từng đáp án
còn lại để tìm ra kết quả.
Câu 36. Cho hai hàm số f và g liên tục trên đoạn [ ;
a b] và số thực k bất kỳ trong . Trong các phát
biểu sau, phát biểu nào sai? b b b b a
A ∫[ f (x)+ g(x)]dx = f (x)dx + g(x)dx ∫ ∫ .
B. f (x)dx = − f (x)dx ∫ ∫ . a a a a b b b b b
C. kf (x)dx = k f (x)dx ∫ ∫ .
D. xf (x)dx = x f (x)dx ∫ ∫ . a a a a
Câu 37. Cho hàm số f liên tục trên và số thực dương a . Trong các đẳng thức sau, đẳng thức nào luôn đúng? a a a a
A. f (x)dx =1 ∫ .
B. f (x)dx = 0 ∫ .
C. f (x)dx = 1 − ∫ .
D. f (x)dx = f (a) ∫ . a a a a 1
Câu 38. Tích phân dx ∫ có giá trị bằng 0 A. 2 . B. 1 − . C. 0 . D. 1. a
Câu 39. Cho số thực a thỏa mãn x 1+ 2 e dx = e −1 ∫
, khi đó a có giá trị bằng 1 − A. 0 . B. 1 − . D. 1. D. 2 . Hướng dẫn giải
[Phương pháp tự luận] a Ta có 1 + 1 a x x+ a 1 e dx = e + 1 − = e − e ∫
. Vậy yêu cầu bài toán tương đương 1 − a 1 + 2
e −1 = e −1 ⇔ a =1.
Câu 40. Trong các hàm số dưới đây, hàm số nào có tích phân trên đoạn [0;π ] đạt giá trị bằng 0 ?
A. f (x) = cos3x .
B. f (x) = sin 3x . π π C. ( ) cos x f x = x + .
D. f (x) = sin + . 4 2 4 2 Hướng dẫn giải
Tính tích phân cho từng hàm số trong các đáp án: Trang 40/80 π π • 1
cos3xdx = sin 3x = 0 ∫ 3 0 0 π π • 1
sin 3xdx = − cos3x = 2 ∫ 3 0 0 π π π π • cos x ∫ 4sin x dx + = + = 2( 2 − 2) 4 2 4 2 0 0 π π π π • sin x ∫ 4cos x dx + = − + = 2 2 . 4 2 4 2 0 0
Vậy chọn f (x) = cos3x .
Câu 41. Tích phân nào trong các tích phân sau có giá trị khác 2 ? π 1 2 e 2 A. sin xdx ∫ . B. 2dx ∫ . B. ln xdx ∫ . D. xdx ∫ . 0 0 1 0 1 2
Câu 42. Trong các hàm số dưới đây, hàm số nào thỏa mãn f (x)dx = f (x)dx ∫ ∫ ? 1 − 2 −
A. f (x) = cos x .
B. f (x) = sin x . C. ( ) x f x = e .
D. f (x) = x +1. Hướng dẫn giải
[Phương pháp tự luận]
Tính lần lượt từng tích phân (cho đến khi nhận được kết quả đúng), ta được: 1 2 • 1
sin xdx = −cos x 1− = 0 = sin xdx ∫ ∫ nhận, 1 − 2 − 1 2 • 1 cos xdx = sin x 2 1 − = 2 sin1 ∫
, và cos xdx = sin x 2− = 2sin 2 ∫ loại, 1 − 2 − 1 2 • 1 x x 1 e dx = e − 2 x x 2 2 − 1 − = e − e ∫
, và e dx = e 2− = e − e ∫ loại, 1 − 2 − 1 1 2 + 2 2 2 + • (x 1) (x +1)dx = = 2 ∫ , và (x 1) (x +1)dx = = 4 ∫ loại. 2 1 2 1 − − 2 2 − −
Vậy ta nhận đáp án f (x) = sin x .
[Phương pháp trắc nghiệm]
Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng 0 thì ngưng) Phép tính Kết quả 1 2
sin xdx − sin xdx ∫ ∫ 0 1 − 2 − 1 2
cos xdx − cos xdx ∫ ∫ ≠ 0 1 − 2 − 1 2 x x e dx − e dx ∫ ∫ ≠ 0 1 − 2 − 1 2
(x +1)dx − (x +1)dx ∫ ∫ ≠ 0 1 − 2 −
Vậy ta nhận đáp án f (x) = sin x . Trang 41/80 5 Câu 43. Tích phân dx
I = ∫ có giá trị bằng x 2 A. 1 ln 3 . B. 5 ln . C. 3ln 3 . D. 2 ln . 3 2 5 Hướng dẫn giải
[Cách 1: Phương pháp tự luận] 5 dx 5 5 I = = ln x = − = ∫ 2 ln 5 ln 2 ln . x 2 2
[Cách 2: Phương pháp trắc nghiệm]
Bước 1: Dùng máy tính như hình bên, thu được giá trị 0,91629...
Bước 2: Lấy 0,91629.. e
cho kết quả 5 chọn 5 ln . 2 2
[Cách 3: Phương pháp trắc nghiệm]
Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng 0 thì ngưng) Phép tính Kết quả Phép tính Kết quả 5 dx 5 5 − ln ∫ dx 0 − 3ln 3 ≠ x ∫ 0 2 x 2 2 5 dx 1 5 − ln 3 ∫ dx 2 ≠ 0 − ln ≠ x ∫ 0 3 x 5 2 2 chọn 5 ln . 2 π 2 Câu 44. Tích phân x I d = ∫ có giá trị bằng π sin x 3 A. 1 2ln . B. 2ln 3 . C. 1 ln 3. D. 1 1 ln . 3 2 2 3 Hướng dẫn giải
[Cách 1: Phương pháp tự luận] π π 2 x 2 x π 2 2 cos + sin 2 dx 2 2 1 I = = dx = ∫ ∫
∫cot x + tan x dx π sin x x x π 2 π 2 2 2sin cos 3 3 3 2 2 . π 2 x x 2 2 1 3 = ln sin −ln cos = ln − ln − ln − ln = ln 3. 2 2 π 2 2 2 2 3
[Cách 2: Phương pháp trắc nghiệm]
Bước 1: Dùng máy tính như hình bên, thu được giá trị 0,549306...
Bước 2: Lấy 0,549306.. e
cho kết quả 1,732050808... ≈ 3 Trang 42/80 chọn 1 ln 3. 2
[Cách 3: Phương pháp trắc nghiệm]
Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng 0 thì ngưng) Phép tính Kết quả Phép tính Kết quả π π 2 dx 1 2 − ln 3 ∫ dx 1 0 − 2ln ∫ ≠ 0 π sin x 2 π sin x 3 3 3 π π 2 dx 2 − 2ln 3 ∫ dx 1 1 ≠ 0 − ln ∫ ≠ 0 π sin x π sin x 2 3 3 3 chọn 1 ln 3. 2
Nhận xét: Ở bài này cách làm bằng máy tính có vẻ nhanh hơn. 0 Câu 45. Nếu ( − x/2 4 − e
)dx = K − 2e ∫
thì giá trị của K là 2 − A. 9. B. 10. C. 11. D. 12,5. Hướng dẫn giải
[Phương pháp tự luận] 0 = (4 − x − ) + 2 = (4 + 2 −x K e dx e x e ) 0 /2 /2 + = − − + + = ∫ − 2e 2 ( 8 2e) 2 2e 10. 2 −
[Phương pháp trắc nghiệm] 0 Dùng máy tính tính ( − x/2 4 − e )dx + 2e ∫ như hình bên, thu 2 −
được giá trị K =10 . 1 Câu 46. Tích phân 1 I = x d ∫ có giá trị bằng 2 x − x − 2 0 A. 2 − ln 2 . B. 2ln 2 . C. 2ln 2 − .
D. Không xác định. 3 3 Hướng dẫn giải
[Phương pháp tự luận] 1 1 1 dx dx = = −
dx = [ x − − x + ]1 1 1 1 1 1 1 2ln 2 ln 2 ln 1 = − ∫ . 2 ∫ ∫ 0 x − x − 2 (x − 2)(x +1)
3 x − 2 x +1 3 3 0 0 0 −
Học sinh có thể áp dụng công thức 1 1 = ln x a dx + C ∫
để giảm một bước
(x − a)(x − b) a − b x − b 1 1 1 − tính: 1 1 1 x 2 2ln 2 I = dx = dx = ln = − ∫ 2x ∫ − x − 2 (x − 2)(x +1) 3 x +1 3 0 0 0
[Phương pháp trắc nghiệm] Trang 43/80
Bước 1: Dùng máy tính như hình bên, thu được giá trị 0.4620981... −
Bước 2: Loại đáp án dương 2ln 2 và loại đáp án nhiễu 3 “Không xác định”.
Bước 3: Chia giá trị 0.4620981... − cho ln 2 , nhận được 2 − 3 chọn 2ln 2 − . 3 5 5
Câu 47. Cho hàm số f và g liên tục trên đoạn [1;5] sao cho f (x)dx = 2 ∫
và g(x)dx = 4 − ∫ . Giá trị 1 1 5
của ∫[g(x)− f (x)]dx là 1 A. 2 − . B. 6 . C. 2 . D. 6 − . Hướng dẫn giải 5 5 5
[g(x) − f (x)]dx = g(x)dx − f (x)dx = 4 − − 2 = 6 − ∫ ∫ ∫ . 1 1 1 3 3
Câu 48. Cho hàm số f liên tục trên đoạn [0;3]. Nếu f (x)dx = 2 ∫
thì tích phân ∫[x −2 f (x)]dx có giá 0 0 trị bằng A. 7 . B. 5 . C. 5. D. 1 . 2 2 Hướng dẫn giải 3 3 3 [x − f x ] 9 1
2 ( ) dx = xdx − 2 f (x)dx = − 2× 2 = ∫ ∫ ∫ . 2 2 0 0 0 5 3 5
Câu 49. Cho hàm số f liên tục trên đoạn [0;6] . Nếu f (x)dx = 2 ∫
và f (x)dx = 7 ∫
thì f (x)dx ∫ có giá 1 1 3 trị bằng A. 9 − . B. 5. C. 9. D. 5 − . Hướng dẫn giải 5 1 5 3 5
f (x)dx = f (x)dx + f (x)dx = − f (x)dx + f (x)dx = 7 − + 2 = 5 − ∫ ∫ ∫ ∫ ∫ . 3 3 1 1 1
Câu 50. Trong các phép tính sau đây, phép tính nào sai? 2 2 2 3 A. 3 ( + ) 1 x x dx = ∫ + x .
B. x = ( x e dx e ) ∫ . 2 1 1 1 1 2π 2 − C. xdx = ( x) 2 cos sin π ∫ 1 2 − π . D. dx = (ln x) ∫ 3 . − x − π 3 Hướng dẫn giải 2 − 2 −
Phép tính 1 dx = (ln x) 2− ∫ 1 2 − =
3 là sai. Phép tính đúng là dx (ln x ) ∫ . 3 − x − − x − 3 3
Câu 51. Cho hàm số f liên tục trên đoạn [ ;
a b] có một nguyên hàm là hàm F trên đoạn [ ; a b]. Trong
các phát biểu sau, phát biểu nào sai ? Trang 44/80
A. F '(x) = f (x) với mọi x ∈( ; a b) . b
B. f (x)dx = f (b) − f (a) ∫ . a b
C. f (x)dx = F(b) − F(a) ∫ . a b
D. Hàm số G cho bởi G(x) = F(x) + 5 cũng thỏa mãn f (x)dx = G(b) − G(a) ∫ . a
Câu 52. Xét hàm số f liên tục trên và các số thực a , b , c tùy ý. Trong các phát biểu sau, phát biểu nào sai? b c b b c b
A. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ .
B. f (x)dx = f (x)dx + f (x)dx ∫ ∫ ∫ . a a c a a c b b a b c c
C. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ .
D. f (x)dx = f (x)dx − f (x)dx ∫ ∫ ∫ . a c c a a b
Câu 53. Xét hai hàm số f và g liên tục trên đoạn [ ;
a b] .Trong các mệnh đề sau, mệnh đề nào sai? b
A. Nếu f (x) ≥ m x ∀ ∈[ ;
a b] thì f (x)dx ≥ m(a − b) ∫ . a b
B. Nếu f (x) ≥ m x ∀ ∈[ ;
a b] thì f (x)dx ≥ m(b − a) ∫ . a b
C. Nếu f (x) ≤ M x ∀ ∈[ ;
a b] thì f (x)dx ≤ M (b − a) ∫ . a b
D. Nếu m ≤ f (x) ≤ M x ∀ ∈[ ;
a b] thì m(b − a) ≤ f (x)dx ≤ M (a − b) ∫ . a Hướng dẫn giải b
Mệnh đề “Nếu f (x) ≥ M x ∀ ∈[ ;
a b] thì f (x)dx ≥ M (a − b) ∫
” sai, mệnh đề đúng phải là a b
“Nếu f (x) ≥ M x ∀ ∈[ ;
a b] thì f (x)dx ≥ M (b − a) ∫ ”. a
Câu 54. Cho hai hàm số f và g liên tục trên đoạn [ ;
a b] sao cho g(x) ≠ 0 với mọi x ∈[ ; a b] . Một học
sinh lên bảng và phát biểu các tính chất sau: b b b b b b
I. ∫[ f (x)+ g(x)]dx = f (x)dx + g(x)dx ∫ ∫ .
II. ∫[ f (x)− g(x)]dx = f (x)dx − g(x)dx ∫ ∫ . a a a a a a b f (x)dx b b b b ∫
III. ∫[ f (x).g(x)]dx = f (x) . dx g(x)dx ∫ ∫ . IV. f (x) a dx = ∫ . g(x) b a a a a g(x)dx ∫a
Trong số các phát biểu trên, có bao nhiêu phát biểu sai? A. 3. B. 1. C. 2 . D. 4 . Hướng dẫn giải Trang 45/80 b f (x)dx b ∫ b b b
Các phát biểu f (x) a dx = ∫
và ∫[ f (x).g(x)]dx = f (x) . dx g(x)dx g ∫ ∫ là sai. (x) b a g(x)dx ∫ a a a a 3
Câu 55. Tích phân x(x −1)dx ∫
có giá trị bằng với tích phân nào trong các tích phân dưới đây ? 0 π 3π 2 ln 10
A. cos(3x +π )dx ∫ . B. 3 sin xdx ∫ . C. ( 2
x + x − 3)dx ∫ . D. 2x e dx ∫ . 0 0 0 0 Hướng dẫn giải
[Phương pháp tự luận]
Tính rõ từng phép tính tích phân để tìm ra kết quả đúng (Chỉ tính đến khi nhận được kết quả đúng thì dừng lại): ln 10 ln 10 2x 2ln 10 • 2x e e 1 9 e dx − = = = ∫ , 2 0 2 2 0 3π • 3 3 sin xdx 3cos x π = − 0 = 6 ∫ , 0 2 2 3 2 • ( 2 x + x − 3) x x 8 4 dx = ∫ +
− 3x = + 2 − 6 = − , 3 2 3 3 0 0 π • 1 π 1
cos(3x +π )dx = sin(3x +π ) = (sin 4π − sinπ ) = 0 ∫ . 0 3 3 0 ln 10 Vậy chọn 2x e dx ∫ . 0
[Phương pháp trắc nghiệm]
Nhập các phép tính sau vào máy tính để thu kết quả: Phép tính Kết quả 3 ln 10 2 ( −1) x x x dx − e dx ∫ ∫ 0 0 0 3 3π
x(x −1)dx − sin xdx ∫ ∫ 3 − 0 0 2 3 2
x(x −1)dx − ( 2
x + x − 3)dx ∫ ∫ 35 0 0 6 3 π
x(x −1)dx − cos(3x +π )dx ∫ ∫ 9 0 0 2 ln 10 Vậy chọn 2x e dx ∫ . 0
Câu 56. Trong các mệnh đề sau, mệnh đề nào đúng? 3
A. Với mọi hàm số f liên tục trên đoạn [ 3
− ;3], luôn có f (x)dx = 0 ∫ . 3 − Trang 46/80 b a
B. Với mọi hàm số f liên tục trên , ta có f (x)dx = f (x)d(−x) ∫ ∫ . a b b
C. Nếu hàm số f liên tục trên đoạn [ ;
a b] , sao cho f (x)dx ≥ 0 ∫
thì f (x) ≥ 0 x ∀ ∈[ ; a b]. a 5 f x D. ( )
Với mọi hàm số f liên tục trên đoạn [1;5] thì [ f (x)]2 [ ] 5 3 dx = ∫ . 3 1 1 Hướng dẫn giải b a a a
Vì d(−x) = ( 1)
− dx nên f (x)dx = − f (x)dx = f (x)( 1
− )dx = f (x)d(−x) ∫ ∫ ∫ ∫ . a b b b
Câu 57. Trong các mệnh đề sau, mệnh đề nào đúng? 1 0
A. Nếu f là hàm số chẵn trên thì f (x)dx = f (x)dx ∫ ∫ . 0 1 − 0 1
B. Nếu f (x)dx = f (x)dx ∫ ∫
thì f là hàm số chẵn trên đoạn [ 1; − 1] . 1 − 0 1
C. Nếu f (x)dx = 0 ∫
thì f là hàm số lẻ trên đoạn [ 1; − 1]. 1 − 1
D. Nếu f (x)dx = 0 ∫
thì f là hàm số chẵn trên đoạn [ 1; − 1]. 1 − Hướng dẫn giải 0 1 1 • Hàm số 3 x
y = x − thỏa f (x)dx = f (x)dx ∫ ∫
và f (x)dx = 0 ∫
, nhưng nó là hàm lẻ trên 2 1 − 0 1 − [ 1; − 1]. 1 • Hàm số 2 1
y = x − thỏa f (x)dx = 0 ∫
, nhưng nó làm hàm chẵn trên [ 1; − 1]. 3 1 −
• Còn khi f là hàm chẵn trên thì f (x) = f (−x) với mọi x∈ . Đặt t = −x ⇒ dt = −dx và suy ra 1 1 1
f (x)dx = − f (x)( 1
− )dx = − f (x)d(−x) ∫ ∫ ∫ 0 0 0 1 1 − 0
= − f (−x)d(−x) = − f (t)dt = f (t)dt. ∫ ∫ ∫ 0 0 1 − 2
Câu 58. Giả sử F là một nguyên hàm của hàm số sin x y =
trên khoảng (0;+∞). Khi đó sin x dx x ∫ có x 1 giá trị bằng
A. F(2) − F(1) . B. −F(1) . C. F( ) 2 .
D. F(2) + F(1) . Hướng dẫn giải b
Áp dụng công thức f (x)dx = F(b) − F(a) ∫
, trong đó F là một nguyên hàm của f trên đoạn a 2 [ ;
a b], ta có sin x dx = F(2) − F(1) ∫ . x 1 Trang 47/80 b
Câu 59. Cho hàm số f liên tục trên và hai số thực a < b . Nếu f (x)dx = α ∫ thì tích phân a
b 2 f (2x)dx ∫ có giá trị bằng a 2 α A. α . B. 2α . C. . D. 4α . 2 Hướng dẫn giải
[Phương pháp tự luận]
Đăt t = 2x ⇒ dt = 2dx và x a 2 b 2 t a b b 2 b 2 b α Vậy 1 1
f (2x)dx =
f (2x)2dx = f (t)dt = ∫ ∫ ∫ . 2 2 2 a 2 a 2 a
[Phương pháp trắc nghiệm]
Phương pháp tự luận tốt hơn cả, nhưng nếu học sinh không nắm rõ, có thể thay f bởi một hàm
số đơn giản, xác định trên [0;1] và tính toán. 1 1
Ví dụ f (x) = x với x ∈[0;1]. Khi đó 1
α = f (x)dx = xdx = ∫ ∫ 2 0 0 1/2 1/2 α suy ra 1
f (2x)dx = 2xdx = = ∫ ∫ . 4 2 0 0 2
Câu 60. Giả sử F là một nguyên hàm của hàm số sin x y =
trên khoảng (0;+∞). Khi đó sin 3x dx x ∫ có x 1 giá trị bằng
A. F(6) − F(3) .
B. 3[F(6) − F(3)] .
C. 3[F(2) − F(1)].
D. F(2) − F(1) . Hướng dẫn giải
Đăt t = 3x ⇒ dt = 3dx và x 1 2 t 3 6 2 2 6 Vậy sin 3x sin 3x sin = 3 t dx dx =
dt = F(6) − F(3) ∫ x ∫ ∫ . 3x t 1 1 3 2
Câu 61. Giả sử hàm số f liên tục trên đoạn [0;2] thỏa mãn
f (x)dx = 6 ∫ . Giá trị của 0
π 2 f (2sin x)cosxdx ∫ là 0 A. 3. B. 6 . C. 3 − . D. 6 − . Hướng dẫn giải
Đăt t = 2sin x ⇒ dt = 2cos xdx và x 0 π 2 t 0 2 π 2 2 2 Vậy f (t) 1
f (2sin x)cos xdx = dt =
f (t)dt = 3 ∫ ∫ ∫ . 2 2 0 0 0 Trang 48/80 e Câu 62. +
Bài toán tính tích phân ln x 1ln x I = dx ∫
được một học sinh giải theo ba bước sau: x 1
I. Đặt ẩn phụ t = ln x +1, suy ra 1 dt = dx và x x 1 e t 1 2 e 2 + II. ln x 1ln x I = dx = t (t − ) 1 dt ∫ x ∫ 1 1 2 2 III. I t (t ) 5 2 1 dt t = − = − = 1+ ∫ 3 2 . 1 t 1
Vây học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào?
A. Bài giải đúng.
B. Sai từ Bước II. C. Sai từ Bước I.
D. Sai ở Bước III. Hướng dẫn giải 2 2 2 2 4( 2 )
Bước III sai. Phép tính đúng là I = t (t − ) 5 3 1 1 dt = ∫ t − t + = . 5 3 15 1 1 π 3
Câu 63. Xét tích phân sin 2x I = dx ∫
. Thực hiện phép đổi biến t = cos x , ta có thể đưa I về dạng 1+ cos x 0 nào sau đây 1 π 4 1 π 4 A. 2t I = dt ∫ . B. 2t I = dt ∫ . C. 2t I = − dt ∫ . D. 2t I = − dt ∫ . + + + + 1 1 t 1 t 1 t 1 t 0 1 0 2 2 Hướng dẫn giải π
Ta có t = cos x ⇒ dt = −sin xdx . Khi x = 0 thì t =1, khi x = thì 1 t = . Vậy 3 2 π 3 π 3 1 2 1 sin 2x 2sin x cos x 2t 2t I = dx = dx = − dt = dt ∫ ∫ ∫ ∫ . 1+ cos x 1+ cos x 1+ t 1+ t 0 0 1 1 2
Câu 64. Cho hàm số y = f (x) bất kỳ liên tục trên đoạn [ ;
a b]. Trong các bất đẳng thức sau, bất đẳng
thức nào luôn đúng? b b b b A. f
∫ (x)dx ≥ f (x) dx ∫ .
B. f (x) dx ≥ f (x)dx ∫ ∫ . a a a a b b b b
C. f (x) dx > f (x)dx ∫ ∫ . D. f
∫ (x)dx > f (x) dx ∫ . a a a a
Câu 65. Trong các khẳng định dưới đây, khẳng định nào sai? 1 1 1 A. (1+ )x x dx = 0 ∫ .
B. sin(1− x)dx = sin xdx ∫ ∫ . 0 0 0 π π 2 1
C. sin x dx = 2 sin xdx ∫ ∫ . D. 2017 2
x (1+ x)dx = ∫ . 2 − 2019 0 0 1 Hướng dẫn giải
[Cách 1: Tính trực tiếp các tích phân] Trang 49/80 1 0 1
• Đặt t =1− x ⇒ dt = −dx ⇒ sin(1− x)dx = − sin tdt = sin tdt ∫ ∫ ∫ 0 1 0 π π 2 • Đặt x 1 = ⇒ = ⇒ sin x t dt dx dx = 2sin tdt ∫ ∫ 2 2 2 0 0 1 1 2018 2019 2018 2019 2018 2019 − − • 2017 x x 1 1 ( 1) ( 1) 2
x (1+ x)dx = ∫ + = + − + = − 2018 2019 − 2018 2019 2018 2019 2019 1 1 1 Vậy (1+ )x x dx = 0 ∫ sai. 0
[Cách 2: Nhận xét tích phân] 1 1 1 Ta thấy (1+ )x
x ≥1 với mọi x ∈[0;1] nên (1+ )x x dx ≥ 1dx =1 ∫ ∫ , vậy “ (1+ )x x dx = 0 ∫ ” là 0 0 0 khẳng định sai.
[Cách 3: Phương pháp trắc nghiệm]
Nhập các phép tính sau vào máy tính để thu kết quả: Phép tính Kết quả 1 (1+ )x x dx ∫ > 0 0 1 1
sin(1− x)dx − sin xdx ∫ ∫ 0 0 0 π π 2
sin x dx − 2 sin xdx ∫ ∫ 0 2 0 0 1 2017 2
x (1+ x)dx − ∫ 0 − 2019 1 1 suy ra (1+ )x x dx = 0 ∫ là khẳng định sai. 0
Câu 66. Cho hàm số y = f (x) lẻ và liên tục trên đoạn [ 2;
− 2] . Trong các đẳng thức sau, đẳng thức nào luôn đúng? 2 2 2 2
A. f (x)dx = 2 − f (x)dx ∫ ∫ .
B. f (x)dx = 2 f (x)dx ∫ ∫ . 2 − 0 2 − 0 2 0 2
C. f (x)dx = 2 f (x)dx ∫ ∫ .
D. f (x)dx = 0 ∫ . 2 − 2 − 2 − Hướng dẫn giải
[Phương pháp tự luận]
Với hàm số f bất kỳ và số thực dương a , ta luôn nằm lòng 2 tính chất sau đây: a
• Nếu f là hàm số lẻ trên đoạn [- ;
a a] thì f (x)dx = 0 ∫ , −a a a
• Nếu f là hàm số chẵn trên đoạn [- ;
a a] thì f (x)dx = 2 f (x)dx ∫ ∫ . −a 0 2
Vậy trong bài này ta chọn f (x)dx = 0 ∫ . 2 −
[Phương pháp trắc nghiệm] Trang 50/80
Nếu học sinh không nắm rõ hai tính chất kể trên, có thể thay f bởi một hàm số đơn giản, xác định trên [ 2;
− 2] và tính toán. Ví dụ f (x) = x với x ∈[ 2; − 2]. Khi đó 2 2 2
f (x)dx = 0 ∫ ,
f (x)dx ≠ 2 f (x)dx ∫ ∫ , 2 − 2 − 0 2 0 2 2
f (x)dx ≠ 2 f (x)dx ∫ ∫ ,
f (x)dx ≠ 2 − f (x)dx ∫ ∫ . 2 − 2 − 2 − 0 2
Vậy chọn f (x)dx = 0 ∫ . 2 − 1
Câu 67. Bài toán tính tích phân 2
I = (x +1) dx ∫
được một học sinh giải theo ba bước sau: 2 − I. Đặt ẩn phụ 2
t = (x +1) , suy ra dt = 2(x +1)dx ,
II. Từ đây suy ra dt dt = dx ⇒
= dx . Bảng giá trị 2(x +1) 2 t x 2 − 1 t 1 4 1 4 4 III. Vậy 2 t 1 3 7
I = (x +1) dx = dt = t = ∫ ∫ . − 2 t 3 1 3 2 1
Vây học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào?
A. Sai ở Bước III. B. Sai từ Bước II. C. Sai từ Bước I. D. Bài giải đúng. Hướng dẫn giải Khi đặt 2
t = (x +1) với 2
− ≤ x ≤1 thì không suy ra t = x +1 được, vì x +1 có thể bị âm khi 2 − ≤ x ≤ 1 − .
Câu 68. Một học sinh được chỉ định lên bảng làm 4 bài toán tích phân. Mỗi bài giải đúng được 2,5
điểm, mỗi bài giải sai (sai kết quả hoặc sai bước tính nguyên hàm) được 0 điểm. Học sinh đã
giải 4 bài toán đó như sau: Bài Đề bài Bài giải của học sinh 1 2 1 1 1 x 1 2 x e xdx ∫ 2 x 1 2 x e xdx = e d ( 2 x ) e e −1 = = ∫ ∫ 0 2 2 0 2 0 0 1 1 1 1 1 2 dx ∫ dx = [ 2
ln x − x − 2 ] = ln 2 − ln 2 = 0 2 x ∫ − x − 2 2 0 x − x − 2 0 0
Đặt t = cos x , suy ra dt = −sin xdx . Khi x = 0 thì t =1; khi π
x = π thì t = 1 − . Vậy 3 sin 2x cos xdx ∫ 1 π π 1 − 3 t 0 2 2 2 4
sin 2x cos xdx = 2 sin x cos xdx = 2 − t dt = = ∫ ∫ ∫ 3 1− 3 0 0 1
e 1+ (4 − 2e)ln e x
e 1+ (4 − 2e)ln x dx = ∫
∫[1+(4−2e)ln x]d (ln x) 4 dx ∫ x x 1 1 1 2 e
= x + (4 − 2e)ln x = 3− e 1
Số điểm mà học sinh này đạt được là bao nhiêu? A. 7,5 điểm. B. 2,5 điểm. C. 5,0 điểm. D. 10,0 điểm. Hướng dẫn giải Trang 51/80
Bài toán 2 giải sai. Cách giải đúng là 1 1 1 1 1 1 x − 2 2 dx = dx = ln = − ln 2 ∫ 2x ∫ − x − 2 (x +1)(x − 2) 3 x +1 3 0 0 0
Bài toán 4 ra kết quả đúng, nhưng cách tính nguyên hàm sai hoàn toàn. Cách tính đúng là: e 1+ (4 − 2 )ln e = ∫ ∫[ e e
x dx 1+(4−2e)ln x]d(ln x) 2
= ln x + (2 − e)ln x = 3− e 1 x 1 1 [Kinh nghiệm]
Kết quả đúng thì chưa chắc bài giải đúng.
Câu 69. Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [ ; a b]. Đẳng
thức nào sau đây luôn đúng? b b
A. f (x)G(x)dx = ∫
[F(x)g(x)]b − F(x)G(x)dx ∫ . a a a b b
B. f (x)G(x)dx = ∫
[F(x)G(x)]b − F(x)g(x)dx ∫ . a a a b b
C. f (x)G(x)dx = ∫
[ f (x)g(x)]b − F(x)g(x)dx ∫ . a a a b b
D. f (x)G(x)dx = ∫
[F(x)G(x)]b − f (x)g(x)dx ∫ . a a a 0 Câu 70. Tích phân − x I = xe dx ∫ có giá trị bằng 2 − A. 2 2 − e +1. B. 2 3e −1. C. 2 −e +1. D. 2 −e −1. Hướng dẫn giải
[Phương pháp tự luận]
Sử dụng tích phân từng phần, ta được 0 − x I = xe dx ∫2− 0 0 0 = − xd ( −x e ) = − ( −x ∫ xe ) 0 − x − ∫ = − + = − − = − − − e dx ( −x xe ) 0 − x − e dx ( −x xe ) 0 ( −x ∫ − e ) 0 2 2 2 2 2 − e 1. 2 − 2 − 2 −
[Phương pháp trắc nghiệm] 0 Dùng máy tính tính − x xe dx ∫
như hình bên, thu được kết 2 −
quả như hình bên. Loại được đáp án 2
3e −1. Sau đó thử
từng đáp án còn lại để tìm ra kết quả. b b
Câu 71. Ta đã biết công thức tích phân từng phần F(x)g(x)dx = ∫
[F(x)G(x)]b − f (x)G(x)dx ∫ , trong a a a
đó F và G là các nguyên hàm của f và g . Trong các biến đổi sau đây, sử dụng tích phân
từng phần ở trên, biến đổi nào là sai? 2 e e e A. ( x) x 1 ln xdx = ∫ ln x − xdx
∫ , trong đó F(x) = ln x , g(x) = x. 2 2 1 1 1 1 1 B. 1 x = ( x ) x xe dx xe − ∫ F x = x = 0 e dx ∫ , trong đó ( ) , ( ) x g x e . 0 0 Trang 52/80 π π
C. xsin xdx = (x cos x) π − ∫ = = 0 cos xdx ∫
, trong đó F(x) x , g(x) sin x . 0 0 1 x 1 1 + 1 x 1 + D. x 1 + 2 2 x2 dx = ∫ x − dx ∫
, trong đó F(x) = x , 1 ( ) 2x g x + = . ln 2 ln 2 0 0 0 π π
Câu 72. Tích phân xcos ∫ x
+ dx có giá trị bằng 4 0 (π − 2) (π − 2) (π + 2) (π + 2) A. 2 . B. 2 − . C. 2 . D. 2 − . 2 2 2 2 Hướng dẫn giải
Áp dụng công thức tích phân từng phần, ta có π π π π π π π π π x cos ∫
x + dx = xsin x + − sin
∫ x+ dx =π sin 5 + cos x + 4 4 4 4 4 0 0 0 0 π 2 5π π (π + 2) 2 = − + cos − cos = − . 2 4 4 2
[Phương pháp trắc nghiệm] π π
Dùng máy tính tính x cos ∫ x
+ dx như hình bên, thu 4 0
được kết quả như hình bên. Loại được các đáp án dương (π + 2) 2 (π − 2) và
2 . Sau đó thử từng đáp án còn lại 2 2 để tìm ra kết quả.
Câu 73. Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [0;2]. Biết rằng 2 2
F(0) = 0 , F(2) =1, G(0) = 2
− , G(2) =1 và F(x)g(x)dx = 3 ∫
. Tích phân f (x)G(x)dx ∫ có 0 0 giá trị bằng A. 3. B. 0 . C. 2 − . D. 4 − . Hướng dẫn giải
Áp dụng công thức tích phân từng phần, ta có 2 2 2
f (x)G(x)dx = ∫
[F(x)G(x)]2 − F(x)g(x)dx = F(2)G(2) − F(0)G(0) − F(x)g(x)dx ∫ ∫ 0 0 0 0 = 1×1− 0×( 2) − − 3 = 2. −
Câu 74. Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [1;2] . Biết rằng 2 2
F(1) =1, F(2) = 4 , 3
G(1) = , G(2) = 2 và 67
f (x)G(x)dx = ∫
. Tích phân F(x)g(x)dx ∫ có 2 12 1 1 giá trị bằng A. 11 . B. 145 − . C. 11 − . D. 145 . 12 12 12 12 Hướng dẫn giải
Áp dụng công thức tích phân từng phần, ta có 2 2 2
F(x)g(x)dx = ∫
[F(x)G(x)]2 − f (x)G(x)dx = F(2)G(2) − F(1)G(1) − f (x)G(x)dx ∫ ∫ 1 1 1 1 3 67 11 = 4× 2 −1× − = . 2 12 12 Trang 53/80 b
Câu 75. Cho hai số thực a và b thỏa mãn a < b và xsin xdx = π ∫
, đồng thời a cos a = 0 và a b bcosb = π
− . Tích phân cos xdx ∫ có giá trị bằng a A. 145 . B. π . C. π − . D. 0 . 12 Hướng dẫn giải
Áp dụng công thức tích phân từng phần, ta có b b b b xsin xdx = − ∫
[xcos x]b + cos xdx ⇒ cos xdx = ∫ ∫
[xcos x]b + xsin xdx ∫ a a a a a a
= bcosb − a cos a +π = π − − 0 +π = 0. e Câu 76. − Cho tích phân: 1 ln x I = dx ∫
.Đặt u = 1− ln x .Khi đó I bằng 2x 1 0 0 0 2 1 A. 2 I = u du ∫ . B. 2 I = − u du ∫ . C. u I = du ∫ . D. 2 I = − u du ∫ . 2 1 1 1 0 Hướng dẫn giải
[Phương pháp tự luận] Đặt 2
u = 1− ln x ⇒ u =1− ln x dx ⇒ = 2
− udu . Với x =1⇒ u =1, x = e ⇒ u = 0 . x 0 Khi đó 2 I = − u du ∫ . 1
[Phương pháp trắc nghiệm] e Bước 1 −
: Bấm máy tính để tính 1 ln x dx ∫ 2x 1
Bước 2: Bấm SHIFT STO A để lưu vào biến A. 0 Bước 3: Bấm 2
A − − u du ∫
= 0 . Vậy đáp án là A. 1 2 2 Câu 77. Tích phân x I = dx ∫ có giá trị bằng 2 x − 7x +12 1 A. 5ln 2 − 6ln 3 .
B. 1+ 2ln 2 − 6ln 3 .
C. 3+ 5ln 2 − 7ln 3. D. 1+ 25ln 2 −16ln 3 . Hướng dẫn giải
[Phương pháp tự luận] 2 Ta có 16 9 I ∫1 = + −
dx = ( x +16ln x − 4 − 9ln x − 3 ) 2 = 1+ 25ln 2 −16ln 3 . 1
x − 4 x − 3 1
[Phương pháp trắc nghiệm] 2 2 Bấm máy tính x
dx − (1+ 25ln 2 −16ln 3) ∫ được đáp số là 0. 2 x − 7x +12 1 2 Câu 78. Tích phân 5 I = x dx ∫ có giá trị là: 1 A. 19 . B. 32 . C. 16 . D. 21 . 3 3 3 2 Hướng dẫn giải Trang 54/80 2 2 6 Ta có: 5 x 21 I = x dx = = ∫ . 6 1 2 1 1 Câu 79. Tích phân xdx I = ∫ bằng 3 (x +1) 0 A. 1 − . B. 1 . C. 1 . D. 12. 7 6 8 Hướng dẫn giải + − 1 Ta có x x 1 1 2 − 3 =
= (x +1) − (x +1)− 2 − 3 − 1 ⇒ I =
∫(x+1) −(x+1) dx = . 3 3 (x +1) (x +1) 8 0 π 2
Câu 80. Cho tích phân I = (2 − x)sin xdx ∫
. Đặt u = 2 − x, dv = sin xdx thì I bằng 0 π π π 2 π 2 A. − − 2
(2 x)cos x − cos xdx − − 2
(2 x)cos x + cos xdx 0 ∫ . B. 0 ∫ . 0 0 π π π 2 π 2 C. − 2
(2 x)cos x + cos xdx − 2 (2 x) + cos xdx 0 ∫ . D. 0 ∫ . 0 0 Hướng dẫn giải π u = 2 − x du = −dx π 2 Đặt ⇒ . Vậy = − − 2 I
(2 x)cos x − cos xdx ∫ . dv sin xdx = v = − cos x 0 0 1 7 Câu 81. Tích phân x dx ∫ bằng 2 5 (1+ x ) 0 2 3 3 3 2 3 4 3 A − − − − . 1 (t 1) dt ∫ .
B. (t 1) dt 1 (t 1) dt 3 (t 1) dt 5 ∫ . C. ∫ . D. ∫ . 2 t 5 t 4 2 t 4 2 t 1 1 1 1 Hướng dẫn giải 2 3 − Đặt 2
t =1+ x ⇒ dt = 2xdx . Vậy 1 (t 1) 1 1 1 I = dt = . = ∫ . 5 5 2 t 4 2 128 1 4 3 Câu 82. Tích phân 1 I = dx ∫ bằng 4 x(x +1) 1 A. 3 ln . B. 1 3 ln . C. 1 3 ln . D. 1 3 ln . 2 3 2 5 2 4 2 Hướng dẫn giải 3 Đặt 2
t = x ⇒ dt = 2xdx . Vậy 1 1 t 1 3 I = − dt = ∫ ln . 2 2 t t +1 4 2 1 2 2
Câu 83. Cho hai tích phân 3 I = x dx ∫ , J = xdx
∫ .Tìm mối quan hệ giữa I và J 0 0
A. I.J = 8. B. 32 I.J = . C. 128 I − J = . D. 64 I + J = . 5 7 9 Hướng dẫn giải 2 2 3 I = x dx = 4 ∫ và J = xdx = 2 ∫
, suy ra I.J = 8. 0 0 Trang 55/80 a
Câu 84. Cho số thực a thỏa mãn x 1+ 4 2
e dx = e − e ∫
, khi đó a có giá trị bằng 1 A. 1 − . B. 3. C. 0 . D. 2. Hướng dẫn giải
[Phương pháp tự luận] a a Ta có x 1+ x 1 + a 1 + 2 4 2 e dx = e
= e − e = e − e ⇒ a = 3 ∫ . 1 1
[Phương pháp trắc nghiệm]
Thế từng đáp án vào và bấm máy 3 1 − x 1 e + dx − ∫ ( 4 2 e − e ) = 0 x 1 e + dx − ∫ ( 4 2 e − e ) ≈ 53 − ,5981 1 1 0 2 x 1 e + dx − ∫ ( 4 2 e − e ) ≈ 51 − ,8798 x 1 e + dx − ∫ ( 4 2 e − e ) ≈ 34 − ,5126 . 1 1 2 Câu 85. Tích phân x ke dx ∫
(với k là hằng số )có giá trị bằng 0 A. 2 k(e −1) . B. 2 e −1. C. 2
k(e − e) . D. 2 e − e . Hướng dẫn giải 2 Ta có x x π 2
ke dx = ke 0 = k(e −1) ∫ . 0
Câu 86. Với hằng số k , tích phân nào sau đây có giá trị khác với các tích phân còn lại ? 2 2 1 2 3 3 A. 2 k(e −1)dx ∫ . B. x ke dx ∫ . C. 3 3 x ke dx ∫ . D. 2x ke dx ∫ . 0 0 0 0 Hướng dẫn giải 2 2 3 4 2 Ta có 3 k k π 2x 2x 3 ke dx = e = (e −1) ∫ x x 2
ke dx = ke = k(e −1) ∫ 2 0 0 2 0 0 2 3 2 1 1 3x 3x 3 2 3ke dx = ke = − ∫ 2 2 2 − = − = − 0 k(e 1)
k(e 1)dx kx(e 1) k(e 1) ∫ . 0 0 0
Câu 87. Với số thực k , xét các phát biểu sau: 1 1 1 1 (I) dx = 2 ∫ ; (II) kdx = 2k ∫ ; (III) xdx = 2x ∫ ; (IV) 2 3kx dx = 2k ∫ . 1 − 1 − 1 − 0 Số phát biểu đúng là A. 4. B. 3. C. 1. D. 2. Hướng dẫn giải (III): sai 5 5
Câu 88. Cho hàm số f và g liên tục trên đoạn [1;5] sao cho f (x)dx = 7 − ∫
và g(x)dx = 5 ∫ và 1 1
5∫[g(x)−kf(x)]dx =19 Giá trị của k là: 1 A. 2 . B. 6 . C. 2. D. 2 − . Hướng dẫn giải 5 5 5
Ta có ∫[g(x)−kf (x)]dx =19 ⇔ g(x)dx − k f (x)dx =19 ∫ ∫ ⇔ 5 − k ( 7
− ) =19 ⇔ k = 2. 1 1 1 Trang 56/80 5 3 5
Câu 89. Cho hàm số f liên tục trên . Nếu 2 f (x)dx = 2 ∫
và f (x)dx = 7 ∫
thì f (x)dx ∫ có giá trị 1 1 3 bằng: A. 5. B. 6 − . C. 9. D. 9 − . Hướng dẫn giải
[Phương pháp tự luận] 5 1 5 3 5 Ta có 2
f (x)dx = f (x)dx + f (x)dx = − f (x)dx + f (x)dx = 7 − + = 6 − ∫ ∫ ∫ ∫ ∫ . 2 3 3 1 1 1 2 2
Câu 90. Cho hàm số f liên tục trên đoạn [0;3]. Nếu f (x)dx = 4 ∫
và tích phân [kx − f (x)]dx = 1 − ∫ 1 1 giá trị k bằng A. 7 . B. 5 . C. 5. D. 2. 2 Hướng dẫn giải 2 2 2
Ta có ∫[kx − f x ] 3 ( ) dx = 1
− ⇔ k xdx − f (x)dx = k − 4 = 1 − ⇔ k = 2 ∫ ∫ . 2 1 1 1 e
Câu 91. Tích phân (2x −5)ln xdx ∫ bằng 1 e e A. 2 − ( − 5 )ln e x x
x − (x − 5)dx ∫ . B. 2 ( − 5 )ln e x x
x + (x − 5)dx ∫ . 1 1 1 1 e e C. 2 ( − 5 )ln e x x
x − (x − 5)dx ∫ . D. e 2
(x − 5)ln x − (x − 5x)dx ∫ . 1 1 1 1 Hướng dẫn giải u 1 = ln x du = dx e e Đặt e ⇒ x . Vậy 2
(2x − 5)ln xdx = (x − 5x)ln x − (x − 5)dx ∫ ∫ .
dv = (2x − 5)dx 1 2
v = x − 5x 1 1 π 2 Câu 92. Tích phân 2
I = cos x cos 2xdx ∫ có giá trị bằng 0 − π π π π A. 5 . B. . C. 3 . D. . 8 2 8 8 Hướng dẫn giải
[Phương pháp tự luận] π π π 2 2 2 2 1 1
I = cos x cos 2xdx =
(1+ cos 2x)cos 2xdx =
(1+ 2cos 2x + cos 4x)dx ∫ ∫ ∫ 2 4 0 0 0 π 2 1 1 π
= (x + sin 2x + sin 4x) = . 4 4 0 8
[Phương pháp trắc nghiệm]
Chuyển chế độ radian: SHIFT MODE 4. π 2 π π Bấm máy 2
I = cos x cos 2xdx − = 0 ∫ . Vậy đáp án là . 8 8 0 Trang 57/80 π 3 Câu 93. Tích phân 4sin x 2 I = dx ∫ có giá trị bằng 0 1+ cos x A. 4. B. 3. C. 2. D. 1. Hướng dẫn giải
[Phương pháp tự luận] 3 3 4sin x
4sin x(1− cos x) =
= 4sin x − 4sin x cos x = 4sin x − 2sin 2x 2 1+ cos x sin x π 2 ⇒ I =
(4sin x − 2sin 2x)dx = 2. ∫ 0
[Phương pháp trắc nghiệm]
Chuyển chế độ radian: SHIFT MODE 4 π 3 Bấm máy tính 4sin x 2 dx − 2 = 0 ∫ . Vậy đáp án là 2. 0 1+ cos x 2π
Câu 94. Tích phân I = 1+ sin xdx ∫ có giá trị bằng 0 A. 4 2 . B. 3 2 . C. 2 . D. − 2 . Hướng dẫn giải
[Phương pháp tự luận] 2π 2 2π 2π π
∫ sin x cos x sin x cos x 2 sin x I dx dx = + = + = ∫ ∫ + dx 2 2 2 2 2 4 0 0 0 3π 2 2π π π 2 sin x ∫ sin x dx ∫ dx = + − + = 4 2 2 4 π 2 4 0 3 2
[Phương pháp trắc nghiệm] 2π Bấm máy tính I = 1+ sin xdx − 4 2 ∫
được đáp số là 0. Vậy đáp án là 4 2 . 0 π 3 Câu 95. Tích phân 2
I = sin x tan xdx ∫ có giá trị bằng 0 A 3 ln 3− . B. ln 2 − 2. C. 3 ln 2 − . D. 3 ln 2 − . 5 4 8 Hướng dẫn giải
[Phương pháp tự luận] π π 1 3 3 2 − 2 2 − Ta có 2 sin x (1 cos x)sin = sin . x I x dx = dx ∫ ∫
. Đặt t = cos x 1 u 3 ⇒ I = − du = ln 2 − ∫ . cos x cos x u 8 0 0 1
[Phương pháp trắc nghiệm] π 3 Bấm máy tính 2 3 I sin x tan xdx ∫ ln 2 = − −
được đáp số là 0. Vậy đáp án là 3 ln 2 − . 8 8 0
Câu 96. Cho hàm số f(x) liên tục trên và 4
f (x) + f (−x) = cos x với mọi x∈ . Giá trị của tích phân π 2 I = f (x)dx ∫ là −π 2 π A. 2 − . B. 3 . C. 3 ln 2 − . D. 3 ln 3− . 16 4 5 Trang 58/80 Hướng dẫn giải
[Phương pháp tự luận] π π π π − 2 2 2 2 Đặt x = t − ⇒ f (x)dx = f ( t − )(−dt) = f ( t − )dt =
f (−x)dx ∫ ∫ ∫ ∫ −π π π π − − 2 2 2 2 π π π 2 2 2 π
⇒ 2 f (x)dx = ∫
∫ [ f (x)+ f (−x)] 4 dx = cos xdx ∫ 3 ⇒ I = . −π π −π 16 − 2 2 2
[Phương pháp trắc nghiệm] π 2 π π Bấm máy tính 4 3 cos xdx − ∫
được đáp số là 0. Vậy đáp án là 3 . −π 16 16 2 0
Câu 97. Nếu (5 −x − e ) 2
dx = K − e ∫
thì giá trị của K là: 2 − A. 11. B. 9. C. 7. D. 12,5. Hướng dẫn giải 0 = (5 − x − ) + = (5 − x K e dx e x + e ) 0 2 2 + = ∫ 2 − e 11. 2 − π 2
Câu 98. Cho tích phân I =
1+ 3cos x.sin xdx ∫
.Đặt u = 3cos x +1 .Khi đó I bằng 0 3 2 2 3 A. 2 2 u du ∫ . B. 2 2 u du ∫ . C. 2 3 u . D. 2 u du ∫ . 3 3 9 1 0 1 1 Hướng dẫn giải π
Đặt u = 3cos x +1 ⇒ 2udu = 3
− sin xdx . Khi x = 0 ⇒ u = 2; x = ⇒ u =1. 2 2 2 Khi đó 2 2 2 3 I = u du = u ∫ . 3 9 1 1 e Câu 99. + Tích phân 8ln x 1 I = dx ∫ bằng x 1 A. 2 − . B. 13 . C. 3 ln 2 − . D. 3 ln 3− . 6 4 5 Hướng dẫn giải
[Phương pháp tự luận] 3 3 3 Đặt 4
t = 8ln x +1 ⇒ tdt = dx . Với x =1⇒ t =1, x = e ⇒ t = 3. Vậy 1 2 t 13 I = t dt = = x ∫ . 4 12 1 6 1
[Phương pháp trắc nghiệm] e + Bấm máy tính 8ln x 1 I = dx ∫
được đáp số là 13 . Vậy đáp án là 13 . x 6 6 1 5 Câu 100. Tích phân 2
x − 2x − 3dx ∫ có giá trị bằng 1 − A. 0. B. 64 . C. 7. D. 12,5. 3 Trang 59/80 Hướng dẫn giải 5 5 3 5 2
x − 2x − 3 dx = (x − 3)(x +1) dx = − ( 2
x − 2x − 3)dx + ( 2
x − 2x − 3)dx ∫ ∫ ∫ ∫ 1 − 1 − 1 − 3 3 3 3 5 x 2 x 2 64
= − − x −3x + − x −3x = . 3 1 − 3 3 3 2
Câu 101. Tìm a để (3− ax)dx = 3 − ∫ ? 1 A. 2. B. 9. C. 7. D. 4. Hướng dẫn giải 2 2 a 2 (3 ax)dx 3 3x x − = − ⇔ − = 3 − ⇔ a = 4 ∫ . 2 1 1 5 Câu 102. Nếu 2 k ( 3
5 − x )dx = 549 − ∫
thì giá trị của k là: 2 A. 2 ± B. 2. C. 2 − . D. 5. Hướng dẫn giải
[Phương pháp tự luận] 5 5 k ( − x ) 4 2 3 2 x 2 549 − 5 dx = 549 − ⇔ k ∫ 5x − = 549 − ⇔ k = = 4 ⇔ k = 2. ± 4 549 − 2 2 4 3 2 Câu 103. − +
Tích phân x x 4dx ∫ bằng x +1 2 A. 1 4 + 6ln . B. 1 4 + 6ln . C. 1 4 − ln . D. 1 4 + ln . 3 3 2 3 2 3 2 3 Hướng dẫn giải 3 3 2 3 2 x − x + 4 6 x 1 4 dx = ∫ ∫ x−2+ dx =
− 2x + 6ln x +1 = + 6ln . x +1 x +1 2 2 3 2 2 2
[Phương pháp trắc nghiệm] 3 2 Bước 1 − +
: Bấm máy tính để tính x x 4dx ∫ x +1 2
Bước 2: Bấm SHIFT STO A để lưu vào biến A. Bước 3: Bấm 1 4 A 6ln − + = 0 . Vậy đáp án là 1 4 + 6ln . 2 3 2 3
Câu 104. Cho hàm số f liên tục trên thỏa f (x) + f (−x) = 2 + 2cos 2x , với mọi x∈ . Giá trị của π 2 tích phân I = f (x)dx ∫ là −π 2 A. 2. B. 7 − . C. 7. D. 2 − . Hướng dẫn giải
[Phương pháp tự luận] π π 2 0 2 Ta có I = f (x)dx =
f (x)dx + f (x)dx ∫ ∫ ∫ (1) π π 0 − − 2 2 Trang 60/80 π π 0 2 2 Tính I = f (x)dx = − ⇒
= − ⇒ I = f ( t
− )dt = f (−x)dx 1 ∫ . Đặt x t dx dt 1 ∫ ∫ . π − 0 0 2 π π π π 2 2 2 2
Thay vào (1), ta được I = ∫[ f (−x)+ f (x)]dx = 2
∫ (1+cos2x) = 2 cos x dx = 2 cos xdx = 2 ∫ ∫ . 0 0 0 0 2
Câu 105. Tìm m để 4 122 (3− 2x) dx = ∫ ? 5 m A. 0. B. 9. C. 7. D.2. Hướng dẫn giải 2 1 2 4 5 1 5 5 122
A = (3− 2x) dx = − (3− 2x) = −
(3− 4) − (3− 2m) = ⇒ m = 0 ∫ . 10 m 10 5 m 4.3 TÍCH PHÂN I. VẬN DỤNG THẤP 1 2
Câu 106. Giá trị của tích phân 1 I = dx ∫ là 2 0 1− x π π π π A. . B. . C. . D. . 6 4 3 2 Hướng dẫn giải π π π
Đặt x sin t, t ; = ∈ − ⇒ dx = costdt . Đổi cận : 1
x = 0 ⇒ t = 0, x = ⇒ t = . 2 2 2 6 π π π 6 6 6 π π π Vậy cost cost = = = = 6 I dt dt dt t = − 0 = ∫ ∫ ∫ . 2 0 1− sin t cost 6 6 0 0 0 1
Câu 107. Giá trị của tích phân dx I = ∫ là 2 1+ x 0 π π π π A I = . B. 3 I = . C. I = . D. 5 I = . 2 4 4 4 Hướng dẫn giải π π Đặt 2
x = tan t, t ∈ − ;
⇒ dx = (tan x + 1)dt . 2 2 π π π 4 2 4 + π
Đổi cận x = 0 ⇒ t = 0, 1
x = ⇒ t = , suy ra tan t 1 I = dt = dt = ∫ ∫ . 4 2 1+ tan t 4 0 0 3 1 −
Câu 108. Giá trị của tích phân dx I = ∫ là 2 x + 2x + 2 0 π π π π A. 5 I = . B. I = . C. 3 I = . D. I = . 12 6 12 12 Hướng dẫn giải 3 1 − 3 1 dx − dx I = = ∫ x + = t 2 ∫ . Đặt 1 tan 2 x + 2x + 2 1+ (x +1) 0 0 1 Câu 109. Tích phân 2 3
I = x x + 5dx ∫ có giá trị là 0 Trang 61/80 A. 4 10 6 − 3 . B. 4 10 7 − 5 . C. 4 10 6 − 5 . D. 2 10 6 − 5 . 3 9 3 9 3 9 3 9 Hướng dẫn giải Ta có 3 2
t = x + 5 ⇒ dt = 3x dx . Khi x = 0 thì t = 5 ; khi x =1 thì t = 6. 1 1 1 6 6 + 1 2 dt 1 1 (t) 6 2 6 Vậy 2 3
I = x x + 5dx = t = ∫ ∫ ∫(t) 4 10 2 dt = = t t = 6 − 5 . 3 3 3 1 5 9 5 3 9 0 5 5 +1 2 2 Câu 110. Tích phân 2 4 − x dx ∫ có giá trị là 0 π π π A. . B. . C. . D. π . 4 2 3 Hướng dẫn giải π π π
Đặt x 2sin t, t ; = ∈ −
. Khi x = 0 thì t = 0. Khi x = 2 thì t = . 2 2 2
Từ x = 2sin t ⇒ dx = 2costdt π π 2 2 2 Vậy 2 2 2 4 − x dx =
4 − 4sin t.2costdt = 4 cos tdt = π ∫ ∫ ∫ . 0 0 0 1 Câu 111. Tích phân 2
I = x x +1dx ∫ có giá trị là 0 A − − − − . 3 2 1. B. 2 2 1 . C. 2 2 1 . D. 3 2 1. 3 3 2 2 Hướng dẫn giải Đặt 2 2 2 2 2 = +1 ⇒ = +1⇒ = −1 tdt t x t x x t ⇒ dx = . x 2 3 Vậy 2 t 2 2 2 1 I t dt − = = = . ∫ 3 1 3 1 0 Câu 112. Tích phân 3
I = x x +1dx ∫ có giá trị là 1 − A. 9 − . B. 3 − . C. 3 . D. 9 . 28 28 28 28 Hướng dẫn giải Đặt 3 3 2
t = x +1 ⇒ t = x +1⇒ dx = 3t dt . 1 7 4 t t 1 Vậy 3 I = t ∫ ( 3t − ) 9 3
1 dt = 3 − = − . 7 4 0 28 0 1 2
Câu 113. Giá trị của tích phân = 2 x dx I ∫ là + + 0 (x 1) x 1 A − − − − . 16 10 2 . B. 16 11 2 . C. 16 10 2 . D. 16 11 2 . 3 4 4 3 Hướng dẫn giải Đặt 2
t = x +1 ⇒ t = x +1⇒ 2tdt = dx . Trang 62/80 2 (t − )2 2 2 2 3 1 − Ta có 1 t 1 2 16 11 2 I = .2tdt =2 ∫
∫ t − dt = 2 −2t − = 3 t t 3 t 1 3 1 1 1
Câu 114. Giá trị của tích phân I = x ∫ (1− x )6 5 3 dx là 0 A. 1 . B. 1 . C. 1 . D. 1 . 167 168 166 165 Hướng dẫn giải − Đặt 3 2 = 1− ⇒ = 3 dt t x
dt − x dx ⇒ dx = , ta có 2 3x 1 1 7 8 1 6 I = t ∫ ( −t) 1 dt = ∫( 6 7 t − t ) 1 t t 1 1 dt = − = . 3 3 3 7 8 168 0 0 3 2 Câu 115. + −
Giá trị của tích phân 2x x 1 I = dx ∫ là + 0 x 1 A. 53 . B. 54 . C. 52 . D. 51. 5 5 5 5 Hướng dẫn giải Đặt 2
x +1 = t ⇒ x = t −1⇒ dx = 2tdt . Khi x = 0 t = 1, x = 3 t = 2. 2 2(t − )2 2 1 + ( 2t − ) 2 5 1 −1 Vậy I = tdt = ∫ ∫( 4 2 t − t ) 4t 3 2 128 4 54 2 2 2 3 dt = − 2t = − −16 + 2 = . 1 t 5 5 5 5 1 1 1 Câu 116. −
Giá trị của tích phân 3 x I = dx ∫ là 1+ x 0 π π π π A. − 2 + 2 . B. − 2 + 2 . C. − 3 + 2 . D. − 3 + 2 . 2 3 3 2 Hướng dẫn giải 3 2 − π Đặt 3 x = ⇒ = 8 t dt t I ∫ ; đặt t = tan ....
u ĐS: I = − 3 + 2 . 2 2 1+ x (t +1) 3 1 1 Chú ý: − Phân tích 3 x I = dx ∫
, rồi đặt t = 1+ x sẽ tính nhanh hơn. + 0 1 x 1
Câu 117. Giá trị của tích phân (2x + ∫ )5 1 dx là 0 A. 1 30 . B. 1 60 . C. 2 60 . D. 2 30 . 3 3 3 3 Hướng dẫn giải
Đặt u = 2x +1 khi x = 0 thìu =1. Khi x =1 thì u = 3 Ta có: = 2 du du dx ⇒ dx = . 2 1 3 6 1 u 3 Do đó: ∫( x + )5 5 1 6 2 2 1 dx = u du = = (3 −1) = 60 ∫ . 2 12 1 12 3 0 1 1 Câu 118. +
Giá trị của tích phân 4x 2 dx ∫ là 2 x + x +1 0 A. ln 2 . B. ln 3. C. 2ln 2. D. 2ln 3 . Trang 63/80 Hướng dẫn giải Đặt 2
u = x + x +1. Khi x = 0 thìu =1. Khi x =1 thìu = 3.
Ta có: du = (2x +1)dx . 1 3 4x + 2 2du 3 Do đó: dx =
= 2 ln | u | = 2(ln 3 − ln1) = 2 ln 3 ∫ 2x ∫ . + x + 1 u 1 0 1 2
Câu 119. Giá trị của tích phân dx ∫ là 2 (2x −1) 1 A 1 . B. 1 . C. 1 . D. 2 . 2 3 4 3 Hướng dẫn giải
Đặt u = 2x −1. Khi x =1thì u =1. Khi x = 2 thì u = 3. Ta có = 2 du du dx ⇒ dx = . 2 2 3 dx 1 du 1 3 Do đó 1 1 1 = = − = − ( −1) = ∫ 2 ∫ . 2 (2x −1) 2 u 2u 1 2 3 3 1 1 3 Câu 120. −
Giá trị của tích phân x 3 dx ∫ là + + + 0 3. x 1 x 3 A. 3 3+ 3ln . B. 3 3+ 6ln . B. 3 3 − + 6ln . D. 3 3 − + 3ln . 2 2 2 2 Hướng dẫn giải
x = 0 ⇒ u =1 Đặt 2
u = x +1 ⇒ u −1 = x ⇒ 2udu = dx ; đổi cận:
x = 3 ⇒ u = 2 Ta có 3 2 3 2 2 x − 3 2u −8u 1 dx =
du = (2u − 6)du + 6 du ∫ ∫ 2 ∫ ∫ 3 x +1 + x + 3 u + 3u + 2 u +1 0 1 1 1 = (u − u) 2 2 2 3 6 + 6ln u +1 = 3 − + 6ln . 1 1 2 4 Câu 121. +
Giá trị của tích phân: I x 1 = ∫ ( dx là 1+ 1+ 2x )2 0 A. 1 2ln 2 − . B. 1 2ln 2 − . C. 1 2ln 2 − . D. 1 ln 2 − . 2 3 4 2 Hướng dẫn giải 2 Đặt =1+ 1+ 2 dx t x ⇒ dt =
⇒ dx = (t −1)dt và t 2t x − = 1+ 2x 2 Đổi cận: x 0 4 t 2 4 Ta có 4 2 4 3 2 4
1 (t − 2t + 2)(t −1)
1 t − 3t + 4t − 2 1 4 2 I dt dt ∫ ∫ ∫t 3 dt = = = − + − 2 2 2 2 t 2 t 2 t t 2 2 2 2 1 t 2 1
= −3t + 4ln t + = 2ln 2 − 2 2 t 4 Trang 64/80 1 (7x − )99
Câu 122. Giá trị của tích phân: 1 I = dx ∫ là (2x + )101 0 1 A. 1 100 2 −1 1 2 −1 1 2 −1 1 2 −1 900 . B. 101 900 . C. 99 900 . D. 98 900 . Hướng dẫn giải 1 99 1 99 100 7x −1 dx 1 7x −1
7x −1 1 1 7x −1 1 1 I = ∫ = ∫ d = ⋅ = [ 100 2 − ] 1
2x +1 (2x + )2 1 9 2x +1
2x +1 9 100 2x +1 0 900 0 0 2 2001 Câu 123. Tích phân x I = dx ∫ có giá trị là 2 1002 (1+ x ) 1 A. 1 . B. 1 . C. 1 . D. 1 . 1001 2002.2 1001 2001.2 1002 2001.2 1002 2002.2 Hướng dẫn giải 2 2004 2 x 1 I = .dx = .dx ∫ 1 2 t = +1 ⇒ dt = − dx . 3 2 1002 ∫ . Đặt 1002 x (1+ x ) 2 3 x x 1 1 3 1 x 1 + 2 x 2π 3 π
Câu 124. Giá trị của tích phân 2 cos(3x − )dx ∫ là π 3 3 A. 3 − . B. 2 − . C. 2 3 − . D. 2 2 − . 3 3 3 3 Hướng dẫn giải π π π π π Đặt 2 u = 3x −
. Khi x = thì u = , khi 2 x = thì 4 u = . 3 3 3 3 3 Ta có = 3 du du dx ⇒ dx = . 3 Do đó: 2π 4π 4π 3 3 π 3 2 1 1 1 4π π 1 3 3 3 cos(3x − )dx = cosudu = sin u = ∫ ∫ sin − sin = − − = − . 3 3 3 π π π 3 3 3 3 2 2 3 3 3 3 π 2
Câu 125. Giá trị của tích phân 2
I = cos x cos 2xdx ∫ là 0 π π π π A. . B. . C. . D. . 6 8 4 2 Hướng dẫn giải π π π 2 2 2 2 1 1
I = cos x cos 2xdx =
(1+ cos 2x)cos 2xdx =
(1+ 2cos 2x + cos 4x)dx ∫ ∫ ∫ 2 4 0 0 0 1 1 π π /2
= (x + sin 2x + sin 4x) | = 0 4 4 8 π
Câu 126. Giá trị của tích phân: x sin x I = dx ∫ là 2 1 + cos x 0 Trang 65/80 2 π 2 π 2 π 2 π A. . B. . C. . D. . 2 6 8 4 Hướng dẫn giải π (π −t)sint π sin t
x = π − t ⇒ dx = −dt ⇒ I = dt = π dt − I ∫ 2 ∫ 2 1+ cos t 1+ cos t 0 0 π π 2 sin t d(cost) π π π ⇒ 2I = π dt = π − = π + ⇒ ∫ ∫ I = 2 2 1+ cos t 1+ cos t 4 4 4 0 0 π 2
Câu 127. Giá trị tích phân J = ( 4 sin x + ∫ )1cosxdx là 0 A. 2 . B. 3 . C. 4 . D. 6 . 5 5 5 5 Hướng dẫn giải π π 2 J = ∫( x + ) 2 4 1 5 6 sin 1 cos xdx = sin x + sin x = 5 5 0 0 π 2 Câu 128. −
Giá trị tích phân sin x cos x I = dx ∫ là π 1+ sin 2x 4 A. 3 ln 2 . B. 1 ln 3. C. ln 2 . D. 1 ln 2 . 2 2 2 Hướng dẫn giải Đặt 2
t = 1+ sin 2x ⇒ t =1+ sin 2x ⇒ 2tdt = 2cos 2xdx 2 tdt 1 2 1 ⇒ dx = ⇒ = = = = t ( x ∫ − ) I dt ln t ln( 2) ln 2 cos sinx t 1 2 1 π 2
Câu 129. Giá trị tích phân sin x I = dx ∫ là 1+ 3cos x 0 A. 2 ln 2 . B. 2 ln 4 . C. 1 ln 4. D. 1 ln 2. 3 3 3 3 Hướng dẫn giải 4 −dt 1 1 ln t Đặt 1
t =1+ 3cos x ⇒ dt = 3
− sin xdx ⇒ dx = ⇒ I = dt = = ln 4 ∫ 3sin x 3 t 3 3 1 2
Câu 130. Giá trị của tích phân 6 3 5
I = 2 1− cos x.sin . x cos xdx ∫ là 1 A. 21 . B. 12 . C. 21 . D. 12 . 91 91 19 19 Hướng dẫn giải Đặt 6 3 6 3 5 2 t = 1− os
c x ⇔ t =1− os
c x ⇒ 6t dt = 3cos xsin xdx 5 1 2t dt ⇒ dx = ⇒ I = t ∫ ( −t ) 7 13 t t 1 6 6 12 2 1
dt = 2 − = 2 cos xsin x 7 13 0 91 0 π 4
Câu 131. Giá trị của tích phân cos x I = dx ∫ là 3 (sin x + cos x) 0 Trang 66/80 A. 1 . B. 3 . C. 5 . D. 7 . 8 8 8 8 Hướng dẫn giải π π 4 4 cos x 1 I = dx = dx ∫ t = x + 3 ∫ . Đặt tan 1 3 2 (sin x + cos x) (tan x +1) cos x 0 0 π 2
Câu 132. Giá trị của tích phân I = sin xdx ∫ là 3 (sin x + cos x) 0 A 1 . B. 1 . C. 1 . D. 1 . 4 3 2 6 Hướng dẫn giải π π π
Đặt: x = − u ⇒ dx = −du . Đổi cận: x = 0 ⇒ u = ; x = ⇒ u = 0. 2 2 2 π π π 2
sin − u du 2 Vậy 2 cos xdx I = = ∫ 3 ∫ π π (sin x+cos x)3 0 0 sin − u + cos − u 2 2 π π π π tan x − π 2 2 2 Vậy: 2I = sin x + cos x dx dx = ∫ dx 4 = ∫ 2 =1 ( ∫ = sin x + cos x)2 2 (sin x + cos x) π 2 0 0 2 0 2 os c x − 0 4 π 2
Câu 133. Giá trị của tích phân 4 2
I = cos xsin xdx ∫ là 0 π π π π A. I = . B. I = . C. I = . D. I = . 32 16 8 4 Hướng dẫn giải π π π π 2 2 2 2 4 2 1 2 2
I = cos xsin xdx = cos xsin 2xdx ∫ ∫ 1 1 2 =
(1− cos 4x)dx + cos 2xsin 2xdx ∫ ∫ 4 16 4 0 0 0 0 π 3 2 x 1 sin 2 π = − sin 4 x x + = . 16 64 24 32 0 π 2
Câu 134. Giá trị của tích phân 4 4 6 6
I = (sin x + cos x)(sin x + cos x)dx ∫ là 0 A. 32 I = π . B. 33 I = π . C. 31 I = π . D. 30 I = π . 128 128 128 128 Hướng dẫn giải Ta có: 4 4 6 6
(sin x + cos x)(sin x + cos x) 33 7 3 = + cos 4x + cos8x ⇒ 33 I = π . 64 16 64 128 π 4
Câu 135. Giá trị của tích phân sin 4x I = dx ∫ là 6 6 0 sin x + cos x A. 4 . B. 1 . C. 2 . D. 5 . 3 3 3 3 Trang 67/80 Hướng dẫn giải π 1 4 sin 4x 4 1 I = dx ∫ . Đặt 3 2
t =1− sin 2x ⇒ I = 2 1 ∫ 4 2 dt − = t = . 4 3 1 3 3 0 3 2 1− sin 2x 1 t 4 4 π
Câu 136. Giá trị của tích phân xdx I = ∫ là sin x +1 0 π π π A. I = . B. I = . C. I = . D. I = π . 4 2 3 Hướng dẫn giải
Đặt: x = π − t ⇒ dx = −dt Đổi cận: x = 0 ⇒ t = π ,
x = π ⇒ t = 0 0 (π − t)dt π π t π π π I ⇒ = − = − ∫ ∫ dt dt dt = π − I ⇒ I = π ∫ ∫ − + + + sin t +1 2 sin t +1 π sin( t) 1 sin t 1 sin t 1 0 0 0 t π π d − dt π π π dt π π π π π = = ∫ 2 4 = = tan t − = π 2 ∫ ∫ . 2 t t 4 2 t π 2 t π 2 2 4 0 0 2 sin + cos cos − 0 0 cos − 2 2 2 4 2 4 π π π
Tổng quát: xf (sin x)dx =
f (sin x)dx ∫ ∫ . 2 0 0 π 2 2007
Câu 137. Giá trị của tích phân sin x I = dx ∫ là 2007 2007 sin x + cos x 0 π π π π A. I = . B. I = . C. 3 I = . D. 5 I = . 2 4 4 4 Hướng dẫn giải π π π
Đặt x = − t ⇒ dx = −dt . Đổi cận x = 0 ⇒ t = , x = ⇒ t = 0 . Vậy 2 2 2 2007 π π − 0 sin t 2 2007 2 cos t I = − dx = dx = J ∫ ∫ (1). 2007 2007 π π + π 2007 2007 sin t cos t 0 sin − t + cos − t 2 2 2 π 2 π π
Mặt khác I + J = dx = ∫
(2). Từ (1) và (2) suy ra I = . 2 4 0 π π 2 n 2 n π Tổng quát: sin x cos x dx dx ,n + = = ∈ ∫ ∫ . sinn x + cosn x sinn x + cosn x 4 0 0 π 2
Câu 138. Giá trị của tích phân 11 cos xdx ∫ là 0 A. 250 . B. 254 . C. 252 . D. 256 . 693 693 693 693 Hướng dẫn giải π 2 11 10!! 2.4.6.8.10 256 cos xdx = = = ∫ . 11!! 1.3.5.7.9.11 693 0 Trang 68/80 π 2
Câu 139. Giá trị của tích phân 10 sin xdx ∫ là 0 π π π π A. 67 . B. 61 . C. 63 . D. 65 . 512 512 512 512 Hướng dẫn giải π 2 π π π 10 9!! 1.3.5.7.9 63 sin xdx = . = . = ∫ 10!! 2 2.4.6.8.10 2 512 0
Công thức Walliss (dùng cho trắc nghiệm): π π
(n −1)!!, neáu n leû 2 2 n n n!!
cos xdx = sin xdx = ∫ ∫ . (n −1)!! π 0 0 . , neáu n chaün n!! 2
Trong đó: n!! đọc là n walliss và được định nghĩa dựa vào n lẻ hay chẵn. Chẳng hạn:
0!!=1; 1!!=1; 2!!= 2; 3!!=1.3; 4!!= 2.4; 5!!=1.3.5;
6!!= 2.4.6; 7!!=1.3.5.7; 8!!= 2.4.6.8; 9!!=1.3.5.7.9; 10!!= 2.4.6.8.10 . 1
Câu 140. Giá trị của tích phân dx I = ∫ là 1 x + e 0 A. 2 ln e e e e . B. ln . C. 2ln . D. 2 2ln . e 1 + e +1 e +1 e +1 Hướng dẫn giải 1 1 1 e d (1 x x + e ) 1 Vì x 2 1 1 ln 1 1 ln(1 ) ln 2 ln e I dx e e = − ⇒ = − = − + = − + + = ∫ ∫ 1 x e 1 x e 1 x e 0 e 1 + + + + 0 0 ln5 2x
Câu 141. Giá trị của tích phân e dx I = ∫ là x ln 2 e −1 A. 5 . B. 10 . C. 20 . D. 2 . 3 3 3 3 Hướng dẫn giải 2 3 x x 2tdt t 2 Đặt 2
t = e − ⇔ t = e − ⇒ dx = ⇒ I = t + dt = ∫ + t = x ( 2 ) 20 1 1 2 1 2 e 3 1 3 1 ln 2
Câu 142. Giá trị của tích phân x I = e −1dx ∫ là 0 −π −π −π −π A. 4 . B. 4 . C. 5 . D. 5 . 3 2 3 2 Hướng dẫn giải Đặt x 2 x x 2tdt 2 = −1 ⇒ = −1⇒ 2 tdt t e t e
tdt = e dx ⇒ dx = = x 2 e t +1 1 2 1 2t 1 4 −π ⇒ I = dt = 2 ∫ ∫1− dt = 2 2 t 1 t 1 + + 2 0 0 ln3 x
Câu 143. Giá trị của tích phân e I = ∫ ( dx là x e + )3 0 1 Trang 69/80 A. 2 2 −1. B. 2 −1. C. 2 − 2 . D. 2 2 − 2. Hướng dẫn giải 2 x x x 2tdt tdt 1 2 Đặt 2
t = e +1 ⇔ t = e +1 ⇔ 2tdt = e dx ⇒ dx = ⇒ I = 2 = 2. − = 2 −1 x ∫ 3 e t t 2 2 2 e
Câu 144. Giá trị của tích phân dx I = ∫ là x ln x e A. 2ln 3 . B. ln 3. C. ln 2 . D. 2ln 2. Hướng dẫn giải 2
Đặt t = ln x ; 2
x = e ⇒ t =1,
x = e ⇒ t = 2 dt 2 ⇒ I = = ln t = ln 2 ∫ . 1 t 1 ln3 2x
Câu 145. Giá trị của tích phân: e dx I = ∫ là x x ln 2 e −1+ e − 2 A. 2ln 2 −1. B. 2ln3 – 1. C. ln 3−1. D. ln 2 −1. Hướng dẫn giải Đặt x
t = e − 2 , Khi x 2
= 2 ⇒ = 0; = 3 ⇒ =1; = + 2 ⇒ x x ln t x ln t e t e dx = 2tdt 1 2 + 1 + 1 1 2 + + I = 2 (t 2)tdt ∫ = 2 2t 1 (t −1+ )dt (t −1)dt d(t t 1) 2 t ∫ = 2 ∫ + 2 ∫ + t +1 2 t + t +1 2 t + t +1 0 0 0 0 = 2 1
(t − 2t) 0 + 2ln(t2 + t + 1) 10 = 2ln3 – 1. ln 2 3x 2x Câu 146. + − Cho 2e e 1 M = dx ∫ . Giá trị của M e là 3x 2x x
e + e − e +1 0 A. 7 . B. 9 . C. 11. D. 5 . 4 4 4 4 Hướng dẫn giải ln 2 3x 2x ln 2 3x 2x x 3x 2 2e + e −1
3e + 2e − e − ( x x
e + e − e +1) M = dx = dx ∫ 3x 2x x ∫ 3x 2
e + e − e +1 x x
e + e − e +1 0 0 ln 2 3x 2 3e + 2 x x e − e = ∫ − dx = ( 3x 2x x
e + e − e + ) ln2 ln 2 11 M 11 1 ln 1 − x = ln ⇒ e = 3x 2x x 0 0
e + e − e +1 4 4 0 e 3 2 Câu 147. + ln x 2 ln x I = dx ∫ . x 1 A 3 3 5 3 5 3 2 − 3 3 5 4 3 2 − 3 3 4 5 3 2 − 3 3 4 4 3 2 − 8 . B. 3 8 . C. 3 8 . D. 3 8 . Hướng dẫn giải e 3 2 e e 1 ln x 2 + ln x 3 2 I = dx = x + xd ∫ ∫ ( x) 1 ln 2 ln ln = ∫ ( 2 2 + ln x)3 d ( 2 2 + ln x) x 2 1 1 1 3 e 3 3 . (2 ln x)4 2 3 4 3 4 3 2 = + = − 8 1 8 1 Câu 148. +
Giá trị của tích phân ln(1 x) I = dx ∫ là 2 1+ x 0 π π π π A. I = ln 3 . B. I = ln 2 . C. I = ln 3. D. I = ln 2 . 8 4 8 8 Hướng dẫn giải Trang 70/80 π Đặt 2
x = tan t ⇒ dx = (1+ tan t)dt . Đổi biến: x = 0 ⇒ t = 0, 1 x = ⇒ t = 4 π π 4 ln(1+ tan t) ⇒ I = ∫ (1+ tan t) 4 2
dt = ln(1+ tan t)dt 2 ∫ . 1+ tan t 0 0 π π π
Đặt t = − u ⇒ dt = −du ; Đổi cận: t = 0 ⇒ u = , t = ⇒ u = 0 4 4 4 π 4 0 π ⇒ I
= ln(1+ tan t)dt = − ln 1+ ∫ ∫ tan − u du π 4 0 4 π π π π 4 4 1− tan u 2 4 4 π ln 1 du ln = + = ∫ ∫
du = ln 2du − ln ∫
∫ (1+ tanu)du = ln2− I . 1+ tan u 1+ tan u 4 0 0 0 0 π Vậy I = ln 2 . 8
Câu 149. Cho hàm số f(x) liên tục trên và thỏa f (−x) + 2 f (x) = cos x . Giá trị của tích phân π 2 I = f (x)dx ∫ là π − 2 A. 1 I = . B. 4 I = . C. 2 I = . D. I =1. 3 3 3 Hướng dẫn giải π 2 Xét tích phân J =
f (−x)dx ∫ . Đặt x = t
− ⇒ dx = −dt . π − 2 π π π π
Đổi cận: x = − ⇒ t = , x = ⇒ t = − . 2 2 2 2 π π π − 2 2 2 Suy ra: J =
f (−x)dx = − f (t)dt =
f (t)dt = I ∫ ∫ ∫ . π π π − − 2 2 2 π π π 2 2 2
Do đó: 3I = J + 2I = ∫ [ f (−x) + 2 f (x)]dx = cos xdx = 2 cos xdx = 2 ∫ ∫ . π π 0 − − 2 2 Vậy 2 I = . 3 II. VẬN DỤNG CAO 2
Câu 150. Tìm hai số thực ,
A B sao cho f (x) = Asinπ x + B , biết rằng f '(1) = 2 và f (x)dx = 4 ∫ . 0 A = 2 − A = 2 A = 2 − 2 A = − A. 2 . B. . C. . D. π . B = − 2 2 B = − B = π π π B = 2 Hướng dẫn giải Trang 71/80
f (x) = Asinπ x + B ⇒ f '(x) = Acosπ x 2 f '(1) = 2 ⇒ π
A cosπ = 2 ⇒ A = − π 2 2 ( ) = 4 ⇒ ( sinπ + ) = 4 A ⇒ − cos 2π + 2 A f x dx A x B dx
B + cos0 = 4 ⇒ B = 2 ∫ ∫ π π 0 0 2 4
Câu 151. Giá trị của a để đẳng thức 2 3
a + (4 − 4a)x + 4x dx = 2xdx ∫ ∫ là đẳng thức đúng 1 2 A. 4. B. 3. C. 5. D. 6. Hướng dẫn giải 2 2 2 3 2 2 4
12 = a + (4 − 4a)x + 4x dx = ∫
a x + (2 − 2a)x + x ⇒ a = 3. 1 1 a
Câu 152. Giá trị của tích phân dx I = (a > 0) ∫ là 2 2 x + a 0 π 2 π 2 π π A. . B. . C. − . D. − . 4a 4a 4a 4a Hướng dẫn giải
x = 0 ⇒ t = 0 π π Đặt 2
x = a tan t; t ∈
;− ⇒ dx = a(1+ tan t)dt . Đổi cận π . 2 2
x = a ⇒ t = 4 π π 4 2 4 + π Vậy a(1 tan t) 1 I = dt = dt = ∫ 2 2 2 a ∫ . tan t + a a 4a 0 0 π 3
Câu 153. Giá trị của tích phân cos x I = dx ∫ là + 0 2 cos 2x π π π π A. − . B. . C. 4 . D. . 4 2 2 2 2 2 Hướng dẫn giải
x = 0 ⇒ t = 0
Đặt t = sin x ⇒ dt = cos xdx . Đổi cận : π 3 . x = ⇒ t = 3 2 π 3 3 3 2 2 Vậy cos x dt 1 dt I = dx = = . ∫ ∫ ∫ 2 + 0 2 cos 2x 0 3− 2t 2 0 3 2 − t 2 π t = 0 → u = Đặt 3 3 t =
cosu ⇒ dt = −
sin udu . Đổi cận : 2 , suy ra 2 2 3 π t = → u = 2 4 π 3 π 3 π 2 2 2 sin udu 4 1 dt 1 2 1 1 π I = = = du = u = ∫ ∫ ∫ 2 0 3 2 2 π 3 2 π 2 4 2 − t 1− cos u 4 ( 2 ) 4 2 2 π 4 Trang 72/80 1 Câu 154. Cho dt I = ∫
. Tích phân nào sau đây có giá trị bằng với giá trị của tích phân đã cho. 2 1+ t x 1 1 x x x x A. −∫ dt . B. dt dt . D. − dt . 2 ∫ . C. ∫ ∫ 1+ t 2 1+ t 2 1+ t 2 1+ t 1 1 1 1 Hướng dẫn giải Đặt 1 1 1
u = ⇒ t = ⇒ dt = − du . Đổi cận 1
t = x ⇒ u = ;t =1⇒ u =1 2 t u u x 1 1 1 1 1 − du 1 x 1 2 dt − x = u =
du = du ⇒ dt = ∫ dt 2 ∫ ∫ 2 ∫ 2 ∫ 2 ∫ 2 1+ t 1 u + u + + t + t x 1 1 1 1 1 1 + 1 x 1 1 2 x x u π 2
Câu 155. Giá trị của tích phân 1 I = ln(sin x)dx ∫ là 2 π sin x 6 π π A − 3 ln 2 + 3 + . B. 3 ln 2 + 3 − . 3 3 π π
C. − 3 ln 2 − 3 − .
D. − 3 ln 2 + 3 − . 3 3 Hướng dẫn giải 2
u = ln(sin x) ⇒ du = cot xdx 1 dv = dx ⇒ v = − cot x 2 sin x π π 2 π 2 1 2 2 I =
ln(sinx)dx = −cot x ln(sin x) − ∫ π cot xdx 2 ∫ π sin x 6 π 6 6 π 2 1 π π 2 = 3 ln − cot x − x = − + − π 3 ln 2 3 2 π 3 6 6 2
Câu 156. Giá trị của tích phân I = min ∫ { 2 1, x }dx là 0 A. 4 . B. 3 . C. 4 . D. 3 − . 4 3 4 Hướng dẫn giải Xét hiệu số 2
1 − x trên đoạn [0;2] để tìm { 2 min 1, x }. 2 2 1 2 3 Vậy I = ∫ { x } x 2 2 2 4 min 1,
dx = x dx + dx = + x = . ∫ ∫ 1 3 3 0 0 1 0 3 −
Câu 157. Giá trị của tích phân = ∫ dx I dx là x − 8 − 1 x A. 2 ln . B. 2 . C. −ln 2 . D. 2ln 2. 3 Hướng dẫn giải Trang 73/80 x = 8 − ⇒ t = 3 Đặt 2
t = 1− x ⇒ x =1− t ⇒ dx = 2
− tdt . Đổi cận . x = 3 − ⇒ t = 2 − 3 3 2 3 3 − + Vậy dx 2tdt tdt dt t 1 2 I = dx = = = = = ∫ ∫ ∫ ∫ − − − − − − x 1 x ( 2 2 ln ln . 2 1 t )t ( 2 1 t t 1 t t 1 3 8 3 2 ) 2 2 2 a 3 Câu 158. − Biết x 2ln x 1 I = dx = + ln 2 ∫
. Giá trị của a là 2 x 2 1 A. 2. B. ln 2 . C. π . D. 3. Hướng dẫn giải a 3 − 2ln 1 a a x x ln x 1 I =
dx = + ln 2 = xdx − 2 dx = + ln 2 ∫ 2 ∫ ∫ 2 x 2 x 2 1 1 1 2 a 1 1 1 1
= − − 2 ln a + −1 = + ln 2 ⇒ a = 2 2 2 a a 2 2 3 − HD casio: Nhập x 2 ln x 1 dx − − ln 2 = 0 ∫ nên a = 2 . 2 x 2 1 π π 2 2
Câu 159. Cho I = cos x 3sin x +1dx sin 2x I = dx 1 ∫ , 2 ∫
. Khẳng định nào sau đây là sai ? 2 (sin x + 2) 0 0 A. 14 I = .
B. I > I . B. 3 3 I = 2ln + . D. 3 2 I = 2ln − . 1 9 1 2 2 2 2 2 2 3 Hướng dẫn giải π 2 4 t 14
I = cos x 3sin x +1dx = dt = 1 ∫ ∫ 3 9 0 1 π 2 3 sin 2x 1 2 3 2 I = dx = 2 − ∫ ∫ dt = 2ln − 2 2 2 (sin x + 2) t t 2 3 0 2 m
Câu 160. Tất cả các giá trị của tham số m thỏa mãn ∫(2x +5)dx = 6 là 0
A. m =1,m = 6 − . B. m = 1, − m = 6 − . C. m = 1, − m = 6 .
D. m =1,m = 6 . Hướng dẫn giải m ∫(2x+5) 2 m 2
dx = 6 ⇒ (x + 5x) = 6 ⇒ m + 5m − 6 = 0 ⇒ m =1, m = 6 − . 0 0
Hướng dẫn casio: Thay m =1 và m = 6
− vào thấy thỏa mãn. π 2
Câu 161. Cho hàm số sin 2 ( ) x h x = . Tìm để a cos x bcos ( ) x h x = +
và tính I = h(x)dx 2 ∫ (2 + sin x) 2 (2 + sin x) 2 + sin x 0 A. 2 3 a = 4
− , b = 2; I = + 2ln . B. 2 3 a = 4, b = 2; − I = − − 2ln . 3 2 3 2 C. 1 3
a = 2, b = 4; I = − + 4ln . D. 1 3 a = 2
− , b = 4; I = + 4ln . 3 2 3 2 Hướng dẫn giải
Sử dụng đồng nhất thức, ta thấy Trang 74/80 b a cos x bcos x
a cos x + bcos x(2 + sin x) sin 2x = 1 a = 4 − h(x) = + = = ⇒ 2 ⇒ . 2 2 2 (2 + sin x) 2 + sin x (2 + sin x) (2 + sin x) b = 2 a + 2b = 0 π π π 2 2 2 − Vậy 4cos x 2cos x 4 h(x)dx ∫ ∫ dx 2ln 2 sin x = + = − + + 2 (2 + sin x) 2 + sin x 2 + sin x 0 0 0 4 2 3
= − + 2ln 3+ 2 − 2ln 2 = + 2ln . 3 3 2
Câu 162. Giá trị trung bình của hàm số y = f (x) trên [ ;
a b], kí hiệu là m( f ) được tính theo công thức m( f ) 1 b = f
∫ (x)dx. Giá trị trung bình của hàm số f (x) = sin x trên [0;π] là b − a a A. 4 . B. 3 . C. 1 . D. 2 . π π π π Hướng dẫn giải π m( f ) 1 2 = sin xdx = . π ∫ − 0 π 0 π 1 4 2
Câu 163. Cho ba tích phân dx I = ∫ , J = ∫( 4 4
sin x − cos x)dx và K = ( 2 x + 3x + ∫ )1dx. Tích phân 3x +1 0 0 1 −
nào có giá trị bằng 21 ? 2 A. K. B. I. C. J.
D. J và K. Hướng dẫn giải 1 1 dx 1 1 I = = ln 3x +1 = ln 4 ∫ 3x +1 3 4 0 0 π π 4 J = ( x − x) 4 4 4 dx = − ( 2 2 x − x) 1 sin cos cos sin dx = ∫ ∫ 2 0 0 2
K = ∫ ( 2x + x + ) 21 3 1 dx = . − 2 1 a
Câu 164. Với 0 < a <1, giá trị của tích phân sau ∫ dx dx là: 2 x − 3x + 2 0 A. a − 2 − − − ln . B. a 2 ln . C. a 2 ln . D. a 2 ln . 2a −1 a −1 2(a − ) 1 2a +1 Hướng dẫn giải a a dx 1 1 x − 2 a a − 2 = − dx = ln = ∫ ∫ ln 2 x − 3x + 2
x − 2 x −1 x −1 a −1 0 0 0 1 3 Câu 165. Cho 4 2 3 x m − dx = 0 ∫ . Khi đó giá trị của 2 144m −1 bằng 4 2 (x + 2) 0 A. 2 − . B. 4 3 −1. C. 2 3 . D. 2 3 − . 3 3 3 Hướng dẫn giải Trang 75/80 1 1 4 d(x + 2) 1 1 1 1 2 3.m − = 0 ⇔ 2 3.m +
= 0 ⇔ 2 3m + − = 0 ⇔ m = ∫ . 4 2 4 (x + 2) (x + 2) 3 2 0 12 3 0 2 Vậy 2 1 2 144m − −1 =144 −1 = . 12 3 3
Câu 166. Cho hàm số f liên tục trên đoạn [ ;
a b] và có đạo hàm liên tục trên ( ;
a b), đồng thời thỏa mãn
f (a) = f (b) . Lựa chọn khẳng định đúng trong các khẳng định sau b b A. f (x)
f '(x).e dx = 2 ∫ . B. f (x)
f '(x).e dx =1 ∫ . a a b b C. f (x)
f '(x).e dx = 1 − ∫ . D. f (x)
f '(x).e dx = 0 ∫ . a a Hướng dẫn giải b b ( ) ( ) ( ) b f x f x f x f (b) f (a) e
f '(x)dx = e d( f (x)) = e = e − e = 0. ∫ ∫ a a a 5
Câu 167. Kết quả phép tính tích phân dx I = ∫
có dạng I = a ln 3 + b ln 5 (a,b ∈ ) . Khi đó + 1 x 3x 1 2 2
a + ab + 3b có giá trị là A. 1. B. 5. C. 0. D. 4. Hướng dẫn giải 5 4 4 Ta có dx 1 1 1 I 2 dt = = = − dt = 2ln 3− ∫ ∫ ∫ ln 5, 2 x 3x +1 t −1 t −1 t +1 1 2 2
suy ra a = 2,b = 1 − . Vậy 2 2
a + ab + 3b = 4 − 2 + 3 = 5 . π 2
Câu 168. Với n ∈ ,n ≥ 1, tích phân = ∫(1−cos )n I
x sin xdx có giá trị bằng 0 A. 1 . B. 1 . C. 1 . D. 1 . 2n n −1 n +1 n Hướng dẫn giải π 1 2 n 1 + I = ∫( − x) 1 n n t 1 1 cos sin xdx = t dt = = ∫ . 0 n +1 n +1 0 0 π 2 n
Câu 169. Với n ∈ sin x
, n > 1, giá trị của tích phân dx ∫ là n n + 0 cos x sin x π π π π A. − . B. . C. 3 . D. 3 − . 4 4 4 4 Hướng dẫn giải π
Đặt t = − x ⇒ dx = −dt 2 Trang 76/80 π π π 2 0 2 2 π f
(sin x)dx = − f ∫
∫ sin −tdt = f (cost)dt = f (cos x)dx ∫ ∫ π 2 0 0 0 2 π π 2 n 2 sin x π
dx = 2I = dx ⇒ I = ∫ ∫ n cos n x + sin x 4 0 0 2017π
Câu 170. Giá trị của tích phân 1− cos 2xdx ∫ là 0 A. 3034 2 . B. 4043 − 2 . C. 3043 2 . D. 4034 2 . Hướng dẫn giải
Do hàm số f (x) = 1− cos 2x là hàm liên tục và tuần hoàn với chu kì T = π nên ta có T 2T 3T nT
f (x)dx = f (x)dx = f (x)dx = . . = f (x) ∫ ∫ ∫ ∫ dx 0 T 2T (n 1) − T nT T 2T nT T ⇒
f (x)dx = f (x)dx + f (x)dx + . . +
f (x)dx = n f (x) ∫ ∫ ∫ ∫ ∫ dx 0 0 T (n 1) − T 0 2017π π π ⇒
1− cos2xdx = 2017 1− cos2xdx = 2017 2 sin xdx = 4034 2 ∫ ∫ ∫ 0 0 0 π 2 1+cos + x x
Câu 171. Giá trị của tích phân (1 sin ) ln ∫ dx là 1 cos + x 0 A. 2ln 3−1. B. 2 − ln 2 −1. C. 2ln 2 −1. D. 2 − ln 3−1. Hướng dẫn giải π π π 2 2 2 1+cos ln(1+ sin ) x x
− ln(1+ cos x) dx = (1+ cos x)ln(1+ sin x)dx − ln(1+ cos x)dx ∫ ∫ ∫ 0 0 0 π π π
Đặt x = − t ⇒ dx = −dt . Đổi cận x = 0 ⇒ t = ; x = ⇒ t = 0 2 2 2 π π π 2 0 2 2 π I = ln
∫ (1+cos x)dx = − ln ∫ 1+cos −t dt = ln
∫ (1+sint)dt = ln(1+ sin x)dx ∫ π 2 0 0 0 2 π π π 2 2 2
⇒ I = (1+ cos x)ln(1+ sin x)dx − ln(1+ sin x)dx = cos x ln(1+ sin x)dx = 2ln 2 −1 ∫ ∫ ∫ 0 0 0 b
Câu 172. Có mấy giá trị của b thỏa mãn 2
(3x −12x +11)dx = 6 ∫ 0 A. 4. B. 2. C. 1. D. 3. Hướng dẫn giải b =1 b 2
(3x 12x 11)dx ∫ ( 3 2
x 6x 11x) b 3 2
b 6b 11b 6 0 − + = − + = − + − = ⇔ b = 2 . 0 0 b = 3 b a
Câu 173. Biết rằng 6dx = 6 ∫ và x xe dx = a ∫ . Khi đó biểu thức 2 3 2
b + a + 3a + 2a có giá trị bằng 0 0 A. 5. B. 4. C. 7. D. 3. Trang 77/80 Hướng dẫn giải b
+Ta có 6dx = 6 ⇒ b =1 ∫ . 0 a +Tính x xe dx ∫ 0 u = x du = dx a a Đặt a ⇒ . Khi đó, x x x a a xe dx = xe
− e dx = e − e +1 = a ⇒ a =1 ∫ ∫ . x x dv = e dx v = e 0 0 0 Vậy 2 3 2
b + a + 3a + 2a = 7 . a bπ
Câu 174. Biết rằng dx = A ∫ , 2dx = B
a b > ). Khi đó giá trị của biểu thức 4 B aA + bằng 2 2 x ∫ (với , 0 + a 2b 0 0 A. 2π . B. π . C. 3π . D. 4π . Hướng dẫn giải a +Tính dx ∫ 2 2 x + a 0 π π Đặt 2 t = a tan ;
x a ∈ ;− ⇒ dx = a(1+ tan t)dt 2 2 π π π 4 2 4 + π
Đổi cận : x = 0 ⇒ t = 0; x = a ⇒ t = . Vậy a(1 tan t) 1 dt = dt = 4 ∫ 2 2 2 a ∫ tan t + a a 4a 0 0 bπ
+Tính: 2dx = 2bπ ∫ , suy ra B = π . 2b 0 Trang 78/80
Document Outline
- DS_C3_TICH PHAN
- A. KIẾN THỨC CƠ BẢN
- B. KỸ NĂNG CƠ BẢN
- C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM




