Tóm tắt lý thuyết và bài tập trắc nghiệm tiếp tuyến của đồ thị hàm số Toán 12

Tóm tắt lý thuyết và bài tập trắc nghiệm tiếp tuyến của đồ thị hàm số Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

25 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Trang 1/25
CHỦ ĐỀ 7. TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ
A. KỸ NĂNG CƠ BẢN
Bài toán 1: Các dạng phương trình tiếp tuyến thường gặp.
Cho hàm số
( )
y fx=
, gọi đồ thị của hàm số là
( )
C
.
Dạng 1. Viết phương trình tiếp tuyến của đồ thị hàm số
( ) ( )
:C y fx=
tại
(
)
;.
oo
Mx y
Phương pháp
o Bước 1. Tính
(
)
y fx
′′
=
suy ra hệ số góc của phương trình tiếp tuyến là
( )
0
k yx
′
=
.
o Bước 2. Phương trình tiếp tuyến của đồ thị
( )
C
tại điểm
(
)
00
;
Mx y
có dạng
.
Chú ý:
o Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại điểm có hoành độ
0
x
thì khi đó ta tìm
0
y
bằng cách thế vào hàm số ban đầu, tức
( )
00
.y fx=
Nếu đề cho
0
y
ta thay vào hàm số để
giải ra
0
x
.
o Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm của đồ thị
( ) ( )
:C y fx=
và
đường thẳng
:.d y ax b= +
Khi đó các hoành độ tiếp điểm là nghiệm của phương trình hoành
độ giao điểm giữa
d
và
( )
.C
Sử dụng máy tính:
Phương trình tiếp tuyến cần tìm có dạng
:.d y ax b
= +
o Bước 1: Tìm hệ số góc tiếp tuyến
( )
0
k yx
′
=
. Nhập
(
)
(
)
0
xx
d
fx
dx
=
bằng cách nhấn
SHIFT
∫
sau đó nhấn
=
ta được
.a
o Bước 2: Sau đó nhân với
X−
tiếp tục nhấn phím
+
( )
fx
CALC
o
Xx=
nhấn phím
=
ta
được b.
Ví dụ minh họa
Ví dụ 1. Cho hàm số
( )
32
3 : Cyx x= +
. Phương trình tiếp tuyến của đồ thị
( )
C
tại điểm
( )
1; 4
M
là
A.
9 5.yx=−+
B.
9 5.yx= +
C.
9 5.yx=−−
D.
9 5.yx= −
Hướng dẫn giải
Ta có
2
'3 6yxx= +
( )
19ky
′
⇒= =
. Phương trình tiếp tuyến tại
( )
1; 4M
là
(
)( ) ( )
0 00
: 9 1 49 5dy yx x x y x x
′
= − + = −+= −
. Chọn đáp án D.
Sử dụng máy tính:
o Nhập
( )
32
1
3
x
d
XX
dx
=
+
nhấn dấu
=
ta được 9.
o Sau đó nhân với
( )
X−
nhấn dấu
+
32
3XX+
CALC
1X =
=
ta được
5−
.
Vậy phương trình tiếp tuyến tại
M
là
95yx= −
.
Ví dụ 2. Cho hàm số
32
265y xx=−+ −
. Phương trình tiếp tuyến của
( )
C
tại điểm
M
thuộc
( )
C
và có hoành độ bằng
3.
A.
18 49.yx=−+
B.
18 49.yx=−−
C.
18 49.yx= +
D.
18 49.yx= −
Hướng dẫn giải
Ta có
2
6 12yxx
′
=−+
. Với
( )
00
3 5 3; 5xy M= ⇒ =−⇒ −
và hệ số góc
( )
3 18ky
′
= = −
. Vậy
phương trình tiếp tuyến tại
M
là
( )
18 3 5 18 49yx x=− − −=− +
. Chọn đáp án A.
Trang 2/25
Sử dụng máy tính:
o Nhập
( )
32
3
265
x
d
XX
dx
=
−+ −
nhấn dấu
=
ta được
18−
.
o Sau đó nhân với
( )
X−
nhấn dấu
+
32
265XX
−+ −
CALC
3X =
nhấn dấu
=
ta được
49
. Vậy phương trình tiếp tuyến tại
M
là
18 49.
yx=−+
Ví dụ 3. Cho hàm số
( )
42
1
:2
4
Cy x x
= −
. Phương trình tiếp tuyến của
( )
C
tại điểm
M
có hoành
độ
0
0,x >
biết
( )
0
1yx
′′
= −
là
A.
3 2.yx=−−
B.
3 1.yx=−+
C.
5
3.
4
yx
=−+
D.
1
3.
4
yx
=−+
Hướng dẫn giải
Ta có
3
4yx x
′
= −
,
2
3 4
yx
′′
= −
. Mà
( )
0
1yx
′′
= −
2
0
3 41 x −=−⇒
2
0
1
x⇔
=
0
1x⇔ =
(vì
0
0x >
).
Vậy
0
7
4
y = −
, suy ra
( )
13ky
′
= = −
. Vậy phương trình tiếp tuyến tại
M
là
( )
75
: 31 3
44
dy x y x=− −−⇒=− +⋅
Chọn đáp án C.
Sử dụng máy tính:
o Nhập
42
1
1
2
4
x
d
XX
dx
=

−


nhấn dấu
=
ta được
3−
.
o Sau đó nhân với
( )
−X
nhấn dấu
+
42
1
2
4
XX
−
CALC
1X =
=
ta được
5
4
.
Vậy phương trình tiếp tuyến là
5
:3
4
dy x=− +⋅
Dạng 2. Viết phương trình tiếp tuyến của đồ thị hàm số
( )
( )
:
C y fx=
có hệ số góc
k
cho
trước.
Phương pháp
o Bước 1. Gọi
( )
00
;Mx y
là tiếp điểm và tính
(
)
y fx
′′
=
.
o Bước 2. Hệ số góc tiếp tuyến là
( )
0
'k fx=
. Giải phương trình này tìm được
0
,x
thay vào hàm
số được
0
.y
o Bước 3. Với mỗi tiếp điểm ta tìm được các tiếp tuyến tương ứng
( )( )
0 00
:dy y f x x x
′
−= −
Chú ý: Đề bài thường cho hệ số góc tiếp tuyến dưới các dạng sau:
• Tiếp tuyến
// :d y ax b∆ = +⇒
hệ số góc của tiếp tuyến là
.ka=
• Tiếp tuyến
( )
: , 0d y ax b a⊥∆ = + ≠ ⇔
hệ số góc của tiếp tuyến là
1
k
a
=−⋅
• Tiếp tuyến tạo với trục hoành một góc
α
thì hệ số góc của tiếp tuyến
d
là
tan .k
α
= ±
Sử dụng máy tính:
Nhập
( ) ( )
k X fx−+
CALC
0
Xx=
nhấn dấu
=
ta được
b
. Phương trình tiếp tuyến là
:.d y kx b
= +
Trang 3/25
Ví dụ minh họa
Ví dụ 1. Cho hàm số
( )
3
: 32Cyx x=−+
. Phương trình tiếp tuyến của
(
)
C
biết hệ số góc của tiếp
tuyến đó bằng 9 là:
A.
9 14
.
9 18
yx
yx
= −
= +
B.
9 15
.
9 11
yx
yx
= +
= −
C.
91
.
94
yx
yx
= −
= +
D.
98
.
95
yx
yx
= +
= +
Hướng dẫn giải
Ta có
2
33
yx
′
= −
. Vậy
( )
0
9k yx
′
= =
2
0
3 39
x
⇔ −=
2
0 00
4 2 2.x xx⇔ =⇔=∨=−
.
+ Với
00
24xy=⇒=
ta có tiếp điểm
( )
2; 4M
.
Phương trình tiếp tuyến tại
M
là
( )
9 2 4 9 14y x yx= − +⇒ = −
.
+ Với
00
20xy=−⇒ =
ta có tiếp điểm
( )
2; 0N
−
.
Phương trình tiếp tuyến tại
N
là
( )
9 2 0 9 18
y x yx= + +⇒ = +
.
Vậy có hai tiếp tuyến cần tìm là
9 14
yx
= −
và
9 18yx= +
. Chọn đáp án A.
Sử dụng máy tính:
+ Với
0
2x =
ta nhập
( )
32
9 32 2X X X CALC X−+ − + =
nhấn dấu
=
ta được
14 −
9 14.
yx
⇒= −
+ Với
0
2x = −
ta nhập
(
)
32
9 32 2
X X X CALC X
−+ − + =−
nhấn dấu
=
ta được
18
9 18.yx
⇒= +
Ví dụ 2. Cho hàm số
( )
21
:
2
x
Cy
x
+
= ⋅
+
Viết phương trình tiếp tuyến của
( )
C
biết tiếp tuyến song
song với đường thẳng có phương trình
:3 2 0xy
∆ −+=
.
A.
3 2.yx= −
B.
3 14yx
= +
C.
3 5.yx= +
D.
3 8.yx= −
Hướng dẫn giải
Ta có
( )
2
3
'
2
y
x
=
+
,
:3 2 0xy
∆ −+=
32yx⇒= +
. Do tiếp tuyến song song với đường thẳng
∆
nên
(
)
( )
2
00
0
2
00
0
21 1
3
3 21
21 3
2
xx
kx
xx
x
+= =−

= =⇔+=⇔ ⇔

+=− =−
+

.
+ Với
0
1
x = −
nhập
( )
21
31
2
X
X CALC X
X
+
−+ =−
+
nhấn dấu
=
ta được 2, suy ra
: 32dy x
= +
(loại do trùng với
∆
).
+ Với
0
3x = −
3CALC X = −
nhấn dấu
=
ta được
14
: 3 14dy x⇒=+
.
Vậy phương trình tiếp tuyến là
: 3 14dy x
= +
. Chọn đáp án B.
Dạng 3. Viết phương trình tiếp tuyến của đồ thị hàm số
( ) ( )
:C y fx=
biết tiếp tuyến đi qua
điểm
( )
;.
AA
Ax y
Phương pháp
Cách 1.
o Bước 1: Phương trình tiếp tuyến đi qua
( )
;
AA
Ax y
hệ số góc
k
có dạng
( )
:
AA
d y kx x y= −+
()∗
o Bước 2:
d
là tiếp tuyến của
( )
C
khi và chỉ khi hệ sau có nghiệm:
( ) ( )
( )
AA
f x kx x y
fx k
= −+
′
=
.
o Bước 3: Giải hệ này tìm được
x
suy ra
k
và thế vào phương trình
()∗
, ta được tiếp tuyến
cần tìm.
Trang 4/25
Cách 2.
o Bước 1. Gọi
(
)
(
)
00
;
Mx fx
là tiếp điểm và tính hệ số góc tiếp tuyến
( ) ( )
00
k yx f x
′′
= =
theo
0
.x
o Bước 2. Phương trình tiếp tuyến có dạng:
( ) ( )
0 00
:.dy yx x x y
′
= −+
()∗∗
. Do điểm
( )
;
AA
Ax y d∈
nên
( ) ( )
0 00
.
AA
y yx x x y
′
= −+
giải phương trình này ta tìm được
x
0
.
o Bước 3. Thế
0
x
vào
()∗∗
ta được tiếp tuyến cần tìm.
Chú ý: Đối với dạng viết phương trình tiếp tuyến đi qua điểm việc tính toán tương đối mất thời
gian. Ta có thể sử dụng máy tính thay các đáp án: Cho
( )
fx
bằng kết quả các đáp án. Vào
54MODE
→→
nhập hệ số phương trình. Thông thường máy tính cho số nghiệm thực nhỏ
hơn số bậc của phương trình là 1 thì ta chọn đáp án đó.
Ví dụ minh họa
Ví dụ. Cho hàm số
( )
3
: 4 3 1.
Cy x x=− ++
Viết phương trình tiếp tuyến của
( )
C
biết tiếp tuyến đi
qua điểm
( )
1; 2 .A −
A.
97
.
2
yx
y
=−−
=
B.
42
.
1
yx
yx
= +
= +
C.
7
.
35
yx
yx
= −
= −
D.
5
.
22
yx
yx
=−−
= −
Hướng dẫn giải
Ta có
2
' 12 3
yx
=−+
.
+ Tiếp tuyến của
( )
C
đi qua
(
)
1; 2A −
với hệ số góc
k
có phương trình là
( )
: 12d y kx= ++
.
+
d
là tiếp tuyến của
( )
C
khi và chỉ khi hệ sau có nghiệm:
( ) ( )
( )
3
2
4
31 12 1
12 3 2k
x x kx
x
− + += + +
−+=
Thay
k
từ
( )
2
vào
(
)
1
ta được
(
)
(
)
32
4 3 1 12 3 1 2
xx x x− + +=− + + +
( )
2
32
1
1
8 12 4 0 1 0
1
2
2
x
xx x x
x
= −

⇔ + −=⇔ − + =⇔

=

.
+ Với
19xk=−⇒ =−
. Phương trình tiếp tuyến là
9 7.
yx=−−
+ Với
1
0
2
xk=⇒=
. Phương trình tiếp tuyến là
2.y =
Chọn đáp án A.
Dạng 4. Viết phương trình tiếp tuyến chung của hai đồ thị hàm số
( )
( )
1
:C y fx=
và
(
)
( )
2
:C y gx=
.
Phương pháp
o Bước 1. Gọi
d
tiếp tuyến chung của
(
) ( )
12
,CC
và
0
x
là hoành độ tiếp điểm của
d
và
( )
1
C
thì phương trình
d
có dạng
( ) ( ) ( )
000
.
y f x x x fx
′
= −+
( )
***
o Bước 2. Dùng điều kiện tiếp xúc của
d
và
( )
2
C
, tìm được
0
x
.
o Bước 3. Thế
0
x
vào
( )
***
ta được tiếp tuyến cần tìm.
Ví dụ minh họa
Ví dụ. Cho hai hàm số:
( ) ( ) ( )
1
: 2, 0C y fx x x= = >
và
( ) ( )
( )
2
2
1
: 8 , 22 22.
2
C y gx x x
= = − − <<
Phương trình tiếp tuyến chung của hai đồ thị hàm số là:
Trang 5/25
A.
1
5.
2
yx= +
B.
1
1.
2
yx
= −
C.
1
2
2
yx
= +
D.
1
3.
2
yx
= −
Hướng dẫn giải
+ Gọi
d
là phương trình tiếp tuyến chung của
(
)
( )
12
,
CC
và
0
xa=
(
0
a >
và
22 22a− <<
)
là hoành độ tiếp điểm của
d
với
(
)
1
C
thì phương trình
d
là
( )( )
( )
0
1
2y fxxa y xa a
a
′
= −+= −+
.
+
d
tiếp xúc với
(
)
2
C
khi và chỉ khi hệ sau có nghiệm:
( )
( )
2
2
1
81
2
1
2
28
x
xa
a
x
a
x
−= +
−
=
−
Thay
( )
2
vào
(
)
1
ta được phương trình hoành độ tiếp điểm của
d
và
( )
2
.C
( ) (
)
22
2
2
23 2
22 22
1 28
80
2
28
8 48
x
xx
xx
x
x
xx x x
− <<
−
−=− − ⇔≠
−
− =−− −
2
22 22
0 2.
2 80
x
xx
xx
− <<
⇔ ≠ ⇔=−
− −=
Thay
2x = −
vào
( )
2
ta được
0
11
4 4.
2
ax
a
=⇔=⇒ =
Vậy phương trình tiếp tuyến chung
cần tìm là
1
2
2
yx= +
. Chọn đáp án C.
Trang 6/25
Bài toán 2: Một số công thức nhanh và tính chất cần biết.
Bài toán 2.1: Cho hàm số
0,
ax b d
y cx
cx d c
+

= ≠ ≠−

+

có đồ thị
( )
C
. Phương trình tiếp
tuyến
∆
tại
M
thuộc
(
)
C
và
I
là giao điểm 2 đường tiệm cận. Ta luôn có:
• Nếu
IM∆⊥
thì chỉ tồn tại 2 điểm
M
thuộc 2 nhánh của đồ thị
( )
C
đối xứng qua
I
và
M
ad bc d
x
c
± −−
=
. Cách nhớ:
M
cx d ad bc+=± −


maãu soá cuûa haøm soá
töû soá cuûa ñaïo haøm
.
(I).
M
luôn là trung điểm của
AB
(với
,AB
là giao điểm của
∆
với 2 tiệm cận).
(II). Diện tích tam giác
IAB
không đổi với mọi điểm
M
và
2
2
IAB
bc ad
S
c
∆
−
=
.
(III). Nếu
,
EF
thuộc 2 nhánh của đồ thị
( )
C
và
, EF
đối xứng qua
I
thì tiếp tuyến tại
,
EF
song song với nhau. (suy ra một đường thẳng
d
đi qua
, EF
thì đi qua tâm
I
).
Chứng minh:
• Ta có
( )
2
ad bc
y
cx d
−
′
=
+
;
;
da
I
cc

−


là giao điểm của 2 tiệm cận.
• Gọi
; ( ) ;
M
MM
M
ax b
d
Mx C x
cx d c

+

∈ ≠−


+


. Phương trình tiếp tuyến tại
M
có dạng
2
: ()
()
M
M
MM
ax b
ad bc
y xx
cx d cx d
+
−
∆= − +
++
.
Chứng minh (I).
•
( )
;
M
M
d bc ad
IM x
c c cx d

−
+


+


;
( )
2
1;
M
ad bc
u
cx d
∆

−


+

•
( )
( )
2
.0 . 0
M
M
M
d bc ad ad bc
IM IM u x
c c cx d
cx d
∆
−−
∆⊥ ⇒ = ⇔ + + =
+
+

( ) ( )
( )
42
3
0
M
M
M
ad bc d
cx d ad bc
x
c
c cx d
± −−
+−−
⇔ =⇔=
+
.
Chứng minh (II).
• Giao điểm của
∆
với tiệm cận ngang là
2;
M
da
Ax
cc

+


.
• Giao điểm của
∆
với tiệm cận đứng là
( )
2
;
M
M
ac x bc ad
d
B
c c cx d

+−
−


+

.
• Xét
( )
22
2
2. 2
AB M M
MM
AB M
MM
dd
xx x x
cc
ac x bc ad ax b
a
yy y
c ccxd cxd
+ = +−=
+− +
+=+ = =
++
.
Vậy
M
luôn là trung điểm của
AB
.
Chứng minh (III).
•
( )
2
;
M
cx d
IA c
c
+




và
( )
( )
2
0;
M
bc ad
IB
c cx d

−


+


.
•
IAB∆
vuông tại
I
Trang 7/25
( ) ( )
( )
2
2
22
11
.. .
22
M
IAB
M
bc ad
cx d bc ad
S IA IB
c c cx d c
∆
−
+−
⇒= = = =
+
 
hằng số.
Vậy diện tích
IAB∆
không đổi với mọi điểm
M
.
Chứng minh (IV):
• Gọi
22
; () ;
EE
EE E
EE
axb axb
d da
Ex C x F x
cx d c c c cx d

++

∈ ≠− ⇒ − − −


++


(
,EF
đối xứng qua
I
).
• Phương trình tiếp tuyến tại
E
có hệ số góc
(
)
2
(1)
E
E
ad bc
k
cx d
−
=
+
.
• Phương trình tiếp tuyến tại
F
có hệ số góc
( ) ( ) ( )
2 2 22
(2)
2
2
F
E EE
E
ad bc ad bc ad bc ad bc
k
d cx d d cx cx d
d
c xd
c
− − −−
= = = =
− − + −− +


−− +




.
• Từ (1) và (2) suy ra
EF
kk=
.
Bài toán 2.2: Cho hàm số
ax b
y
cx d
+
=
+
có đồ thị là
( )
C
,
( )
0, 0c ad bc≠ −≠
. Gọi điểm
( )
00
;Mx y
trên
( )
,C
biết tiếp tuyến của
( )
C
tại điểm
M
cắt các trục
,
Ox Oy
lần lượt tại
,AB
sao cho
.OA n OB=
. Khi đó
0
x
thoả
0
.cx d n ad bc+=± −
.
Hướng dẫn giải
• Xét hàm số
ax b
y
cx d
+
=
+
,
( )
0, 0c ad bc
≠ −≠
. Ta có
( )
2
'.
ad bc
y
cx d
−
=
+
• Gọi
( )
0
0
0
;
ax b
Mx C
cx d

+
∈

+

là điểm cần tìm. Gọi
∆
tiếp tuyến với
(
)
C
tại
M
ta có phương trình
∆
:
(
)( )
0
00
0
'
ax b
y f x xx
cx d
+
= −+
+
( )
(
)
0
0
2
0
0
ax b
ad bc
y xx
cx d
cx d
+
−
⇒= − +
+
+
.
• Gọi
A Ox=∆∩
⇒
2
00
2
;0
acx bcx bd
A
ad bc

++
−

−

.
B Oy=∆∩
⇒
( )
2
00
2
0
2
0;
acx bcx bd
B
cx d

++


+

.
• Ta có
2
2
00
00
2
2
acx bcx bd
acx bcx bd
OA
ad bc ad bc
++
++
= =
−−
( )
( )
2
2
00
00
22
00
2
2
acx bcx bd
acx bcx bd
OB
cx d cx d
++
++
= =
++
(vì
,AB
không trùng
O
nên
2
00
2acx bcx bd++
0≠
).
• Ta có
( )
22
00 00
2
0
22
..
acx bcx bd acx bcx bd
OA n OB n
ad bc
cx d
++ ++
=⇔=
−
+
( )
( )
2
00
2
0
11
. . ..n cx d n ad bc cx d n ad bc
ad bc
cx d
⇔ = ⇔ + = − ⇔ +=± −
−
+
Trang 8/25
B. BÀI TẬP TRẮC NGHIỆM
Câu 1. Phương trình tiếp tuyến của đồ thị hàm số
32
31yx x=−+
tại điểm
( )
3;1A
là
A.
9 26yx=−−
. B.
9 26yx= −
. C.
93
yx=−−
. D.
92yx= −
.
Câu 2. Phương trình tiếp tuyến của đồ thị hàm số
42
41yx x
=−+
tại điểm
( )
1; 2B −
là
A.
46yx= +
. B.
42yx= +
. C.
46yx=−+
. D.
42yx
=−+
.
Câu 3. Phương trình tiếp tuyến của đồ thị hàm số
1
1
x
y
x
−
=
+
tại điểm
( )
2; 3C −
là
A.
21yx= +
. B.
27yx=−+
. C.
27yx= +
. D.
21
yx=−−
.
Câu 4. Tiếp tuyến của đồ thị hàm số
3
32yx x
=−+ −
tại điểm D có hoành độ bằng 2 có phương trình
là
A.
9 14
yx=−+
. B.
9 14yx= +
. C.
9 22yx=−+
. D.
9 22
yx= +
.
Câu 5. Tiếp tuyến của đồ thị hàm số
42
8yx x=−+
tại điểm E có hoành độ bằng –3 có phương trình là
A.
60 171
yx
= +
. B.
60 171yx=−+
.
C.
60 189.yx= +
D.
60 189yx=−+
.
Câu 6. Tiếp tuyến của đồ thị hàm số
21
1
x
y
x
−
=
−
tại điểm F có hoành độ bằng 2 có phương trình là
A.
5yx
=−+
. B.
5yx= +
. C.
1yx=−−
. D.
1yx= −
.
Câu 7. Tiếp tuyến của đồ thị hàm số
32
23yx x= +
tại điểm G có tung độ bằng 5 có phương trình là
A.
12 7yx
= −
. B.
12 7yx=−−
. C.
12 17yx= +
. D.
12 17
yx=−+
.
Câu 8. Tiếp tuyến của đồ thị hàm số
42
23yx x=+−
tại điểm H có tung độ bằng 21 có phương trình
là
A.
40 101
40 59
yx
yx
= −
=−−
. B.
40 59
40 101
yx
yx
= −
=−−
.
C.
40 59
40 101
yx
yx
= +
=−+
. D.
40 59
40 101
yx
yx
=−−
= +
.
Câu 9. Tiếp tuyến của đồ thị hàm số
2
21
x
y
x
+
=
−
tại điểm I có tung độ bằng 1 có phương trình là
A.
18
55
yx= +
. B.
12
55
yx=−−
. C.
18
55
yx=−+
. D.
12
55
yx= −
.
Câu 10. Tiếp tuyến của đồ thị hàm số
32
32yx x=−−
có hệ số góc
3k
= −
có phương trình là
A.
37yx=−−
. B.
37yx=−+
. C.
31
yx=−+
. D.
31yx=−−
.
Câu 11. Tiếp tuyến của đồ thị hàm số
42
1
2
4
y xx=−+
có hệ số góc bằng
48k = −
có phương trình là
A.
48 192yx=−+
. B.
48 160yx=−+
. C.
48 160yx
=−−
. D.
48 192yx=−−
.
Câu 12. Viết phương trình tiếp tuyến của đồ thị hàm số
3
1
x
y
x
+
=
−
biết tiếp tuyến có hệ số góc bằng 4.
A.
43
4 13
yx
yx
= −
= +
. B.
43
4 13
yx
yx
= −
= −
. C.
43
4 13
yx
yx
= +
= +
. D.
43
4 13
yx
yx
= +
= −
.
Câu 13. Có bao nhiêu tiếp tuyến của đồ thị hàm số
32
2yx x=−+
song song với đường thẳng
yx=
?
A. 2. B. 1. C. 3. D. 4.
Câu 14. Tiếp tuyến song song với đường thẳng
36 5yx=−+
của đồ thị hàm số
42
2yx x=+−
có
phương trình là
A.
36 54yx=−−
. B.
36 54yx=−+
. C.
36 90yx=−−
. D.
36 90yx=−+
.
Trang 9/25
Câu 15. Cho hàm
5
2
x
y
x
−+
=
+
có đồ thị là
()C
. Viết phương trình tiếp tuyến của
()
C
sao cho tiếp tuyến
đó song song với đường thẳng
15
:
77
dy x
=−+
.
A.
15
77
1 23
77
yx
yx
=−+
=−−
. B.
15
77
1 23
77
yx
yx
=− +−
=−+
. C.
1 23
77
yx=−−
. D.
1 23
77
yx=−+
.
Câu 16. Cho hàm
3
2 31yx x= −−
có đồ thị là
()C
. Tiếp tuyến của đồ thị
()
C
vuông góc với đường
thẳng
21 2 0xy+ −=
có phương trình là:
A.
1
33
21
1
31
21
yx
yx
= −
= +
. B.
21 33
21 31
yx
yx
=−−
=−+
. C.
21 33
21 31
yx
yx
= −
= +
. D.
1
33
21
1
31
21
yx
yx
−
= −
−
= +
.
Câu 17. Tiếp tuyến của đồ thị hàm số
42
23yx x=−− +
vuông góc với đường thẳng
8 2017 0xy
−+ =
có phương trình là
A.
1
8
8
yx=−+
. B.
88yx= +
. C.
88yx=−+
. D.
1
8
8
yx= −
.
Câu 18. Phương trình tiếp tuyến của đồ thị hàm số
22
2
x
y
x
−
=
+
biết tiếp tuyến vuông góc với đường
thẳng
61yx=−+
là
A.
11
63
yx= +
. B.
1
1
6
yx
= −
. C.
11
63
1
1
6
yx
yx
=−+
=−−
. D.
11
63
1 13
63
yx
yx
= +
= +
.
Câu 19. Có bao nhiêu tiếp tuyến của đồ thị hàm số
42
4yx x= −
tại giao điểm của đồ thị với trục Ox ?
A. 4. B. 2. C. 1. D. 3.
Câu 20. Cho hàm số
3
32yx x
=−+ −
có đồ thị (C). Tiếp tuyến của đồ thị (C) tại giao điểm của
()C
với trục hoành có phương trình là
A.
9 18yx
=−−
. B.
0
9 18
y
yx
=
=−−
. C.
9 18yx=−+
. D.
0
9 18
y
yx
=
=−+
.
Câu 21. Gọi
d
là tiếp tuyến của đồ thị hàm số (C):
5
1
x
y
x
−
=
−+
tại giao điểm A của (C) và trục hoành.
Khi đó, phương trình của đường thẳng
d
là
A.
15
44
yx= −
. B.
15
44
yx=−−
. C.
15
44
yx= +
. D.
15
44
yx=−+
.
Câu 22. Tại giao điểm của đồ thị hàm số (C):
3
2 61yx x= −+
và trục Oy ta lập được tiếp tuyến có
phương trình là
A.
61yx= −
. B.
61yx=−−
. C.
61yx= +
. D.
61yx
=−+
.
Câu 23. Phương trình tiếp tuyến của đồ thị hàm số (C):
42
1
32
4
y xx=− +−
tại giao điểm M của (C)
với trục tung là
A.
2
2
y
y
= −
=
. B.
2y =
. C.
2y = −
. D.
2
0
y
y
= −
=
.
Trang 10/25
Câu 24. Gọi
d
là tiếp tuyến của đồ thị hàm số (C):
21
3
x
y
x
+
=
−
tại giao điểm A của
()
C
và trục tung.
Khi đó, phương trình của đường thẳng
d
là
A.
71
93
yx
= −
. B.
71
93
yx=−+
. C.
71
93
yx
=−−
. D.
71
93
yx
= +
.
Câu 25. Tiếp tuyến của đồ thị hàm số
3
2
( ): 2 3 1
3
x
Cy x x=− ++
song song với đường thẳng
3 2016yx= +
có phương trình là
A.
2
3
3
38
yx
yx
= −
= −
. B.
2
3
3
38
yx
yx
= −
= +
. C.
38
2
3
3
yx
yx
= −
= +
. D.
2
3
3
38
yx
yx
= +
= +
.
Câu 26. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
3
2
2 35
3
x
y xx=− +−
sẽ
A. song song với đường thẳng
1x
=
. B. song song với trục hoành.
C. có hệ số góc dương. D. có hệ số góc bằng
1−
.
Câu 27. Phương trình tiếp tuyến với đồ thị hàm số
2
1
x
y
x
=
−
tại điểm có tung độ bằng 3 là
A.
2 70xy− −=
. B.
80xy+−=
.
C.
2 90xy−−=
. D.
2 90xy+ −=
.
Câu 28. Cho đường cong
32
( ): 3Cyx x= −
. Viết phương trình tiếp tuyến của
()C
tại điểm thuộc
()C
và có hoành độ
0
1x = −
.
A.
95
yx=−+
. B.
95yx= +
. C.
95yx= −
. D.
95yx
=−−
.
Câu 29. Phương trình tiếp tuyến của đồ thị hàm số
32
3 71y xx x= −−+
tại điểm
( )
0;1A
là
A.
1yx
= +
. B.
71yx=−+
. C.
1
y =
. D.
0y =
.
Câu 30. Cho hàm số
32
31yx x=−+
có đồ thị
()C
. Khi đó phương trinh tiêp tuyên cua đô thi
()C
tại
điểm có hoành độ bằng 5 là
A.
45 276
yx=−+
. B.
45 174yx=−+
.
C.
45 276yx= +
. D.
45 174yx= −
.
Câu 31. Cho hàm số
32
3 61yx x x=− ++
có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ
số góc nhỏ nhất có phương trình là
A.
32yx=−+
. B.
32yx= +
. C.
38yx=−+
. D.
38yx= +
.
Câu 32. Cho hàm số
32
6 31yx x x=−+ + −
có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có
hệ số góc lớn nhất có phương trình là
A.
15 55yx= +
. B.
15 5yx=−−
. C.
15 5yx
= −
. D.
15 55yx=−+
.
Câu 33. Cho hàm số
3
1yx x= ++
có đồ thị (C). Khẳng định nào sau đây là khẳng định sai?
A. Hàm số luôn đồng biến trên
.
B. Trên (C) tồn tại hai điểm
11 2 2
( ; ), ( ; )Ax y Bx y
sao cho hai tiếp tuyến của (C) tại A và B vuông
góc.
C. Tiếp tuyến của (C) tại điểm có hoành độ bằng 1 có phương trình là
41yx= −
.
D. Đồ thị (C) chỉ cắt trục hoành tại một điểm duy nhất.
Câu 34. Đường thẳng
y ax b= −
tiếp xúc với đồ thị hàm số
32
22yx x x= + −+
tại điểm
( )
1; 0M
. Khi
đó ta có
A.
36ab =
. B.
6ab = −
. C.
36ab = −
. D.
5ab = −
.
Câu 35. Cho hàm số
32
25yx x x=−++
có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ
số góc nhỏ nhất, thì hệ số góc của tiếp tuyến đó là
Trang 11/25
A.
1
3
. B.
2
3
. C.
4
3
. D.
5
3
.
Câu 36. Cho hàm số
3
1
x
y
x
=
−
có đồ thị (C). Tiếp tuyến của (C) tạo với trục hoành góc
0
60
có phương
trình là
A.
3 43
3
yx
yx
=−+
=
. B.
3 43
3
yx
yx
= −
=
.
C.
3 43
3
yx
yx
=−+
= −
. D.
3 43
3
yx
yx
=−−
= −
.
Câu 37. Cho hàm số
32
3 3( 1) 1y x mx m x
=− + ++
(1)
, m là tham số. Kí hiệu
()
m
C
là đồ thị hàm số (1)
và K là điểm thuộc
()
m
C
, có hoành độ bằng
1−
. Tập tất cả các giá trị của tham số m để tiếp
tuyến của
()
m
C
tại điểm K song song với đường thẳng
:3 0d xy+=
là
A.
{ }
1−
. B.
∅
. C.
{ }
1
;1
3
−−
. D.
{ }
1
3
−
.
Câu 38. Cho hàm số
42
1
1
2
y x mx m= + +−
có đồ thị (C). Biết tiếp tuyến của (C) tại điểm có hoành độ
bằng –1 vuông góc với đường thẳng có phương trình
3 10xy− +=
. Khi đó giá trị của
m
là
A.
1m = −
. B.
0m =
. C.
13
3
m = −
. D.
11
3
m = −
.
Câu 39. Cho hàm số
21yx= +
có đồ thị (C). Biết tiếp tuyến
d
của đồ thị (C) vuông góc với đường
thẳng
3 2017yx
=−+
. Hỏi hoành độ tiếp điểm của
d
và (C) bằng bao nhiêu?
A.
4
9
−
. B. 1. C. 4. D. – 4.
Câu 40. Cho hàm số
3
34yxx= −
có đồ thị (C). Từ điểm
(
)
1; 3
M
có thể kẻ được bao nhiêu tiếp tuyến
với đồ thị hàm số (C) ?
A. 0. B. 3. C. 2. D. 1.
Câu 41. Cho hàm số
3
2yx x= ++
có đồ thị (C). Tiếp tuyến tại điểm
( )
1; 4N
của (C) cắt đồ thị (C) tại
điểm thứ hai là M. Khi đó tọa độ điểm M là
A.
( )
1; 0
M −
. B.
( )
2; 8M −−
. C.
( )
0; 2M
. D.
( )
2;12
M
.
Câu 42. Cho hàm số
32
1yx x x= − ++
có đồ thị (C). Tiếp tuyến tại điểm
N
của (C) cắt đồ thị (C) tại
điểm thứ hai là
( )
1; 2M
−−
. Khi đó tọa độ điểm N là
A.
( )
1; 4−−
. B.
( )
2;5
. C.
( )
1; 2
. D.
( )
0;1
.
Câu 43. Cho hàm số
( )
32
3 11y x mx m x=+ ++ +
có đồ thị (C). Với giá trị nào của
m
thì tiếp tuyến
với đồ thị (C) tại điểm có hoành độ bằng –1 đi qua
(
)
1; 3A
?
A.
7
9
m =
. B.
1
2
m =
. C.
1
2
m = −
. D.
7
9
m = −
.
Câu 44. Cho hàm số
1
xm
y
x
−
=
+
có đồ thị
()
m
C
. Với giá trị nào của
m
thì tiếp tuyến của (C) tại điểm có
hoành độ bằng 0 song song với đường thẳng
31yx= +
?
A.
3m =
. B.
1m =
. C.
2m = −
. D.
2m =
.
Trang 12/25
Câu 45. Cho hàm số
1
x
y
x
=
+
có đồ thị (C) và gốc tọa độ O. Gọi
∆
là tiếp tuyến của (C), biết
∆
cắt
trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân. Phương trình
∆
là
A.
1yx= +
. B.
4.yx= +
C.
4yx= −
. D.
yx
=
.
Câu 46. Cho hàm số
42
6y xx=−− +
có đồ thị (C). Tiếp tuyến của đồ thị (C) cắt các trục Ox, Oy lần
lượt tại hai điểm A, B sao cho OB = 36OA có phương trình là:
A.
36 4 0
36 4 0
xy
xy
− −=
+ −=
. B.
36 86
36 86
yx
yx
=−−
= −
.
C.
36 58
36 58
yx
yx
=−+
= +
. D.
36 14 0
36 14 0
xy
xy
− +=
+ +=
.
Câu 47. Cho hàm số
(
)
1
21
x
y
x
−
=
+
có đồ thị là
( )
C
. Gọi điểm
( )
00
;Mx y
với
0
1x >−
là điểm thuộc
( )
,C
biết tiếp tuyến của
(
)
C
tại điểm
M
cắt trục hoành, trục tung lần lượt tại hai điểm phân
biệt
,AB
và tam giác
OAB
có trọng tâm
G
nằm trên đường thẳng
:4 0
d xy+=
. Hỏi giá trị
của
00
2xy
+
bằng bao nhiêu?
A.
7
2
−
. B.
7
2
. C.
5
2
. D.
5
2
−
.
Câu 48. Cho hàm số
42
2y x mx m=−+
(1) , m là tham số thực. Kí hiệu
( )
m
C
là đồ thị hàm số (1); d
là tiếp tuyến của
( )
m
C
tại điểm có hoành độ bằng 1. Tìm m để khoảng cách từ điểm
3
;1
4
B



đến đường thẳng d đạt giá trị lớn nhất?
A.
1
m = −
. B.
1m =
. C.
2
m =
. D.
2m = −
.
Câu 49. Cho hàm số
23
1
x
y
x
+
=
+
có đồ thị là
( )
C
. Có bao nhiêu tiếp tuyến của đồ thị
( )
C
tại những
điểm thuộc đồ thị có khoảng cách đến đường thẳng
1
:3 4 2 0dxy+ −=
bằng 2.
A. 2. B. 3. C. 4. D. 0.
Câu 50. Cho hàm số
21
1
x
y
x
−
=
−
có đồ thị là
(
)
C
. Gọi
I
là giao điểm hai tiệm cận của
( )
C
. Tìm điểm
M
thuộc
( )
C
có hoành độ lớn hơn 1 sao cho tiếp tuyến của
( )
C
tại
M
vuông góc với đường
thẳng
MI
?
A.
7
4;
3
M



. B.
5
3;
2
M



. C.
( )
2; 3M
. D.
( )
5; 3M
.
Câu 51. Cho hàm số
1
21
x
y
x
−+
=
−
có đồ thị là
( )
C
, đường thẳng
:dy x m= +
. Với mọi
m
ta luôn có
d
cắt
( )
C
tại 2 điểm phân biệt
,AB
. Gọi
12
,kk
lần lượt là hệ số góc của các tiếp tuyến với
( )
C
tại
,AB
. Tìm
m
để tổng
12
kk+
đạt giá trị lớn nhất.
A.
1m = −
. B.
2m = −
. C.
3m =
. D.
5m = −
.
Câu 52. Cho hàm số
( )
2
1
23
x
y
x
+
=
+
.Viết phương trình tiếp tuyến của đồ thị hàm số
( )
1
, biết tiếp tuyến
đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt
,AB
và tam giác
OAB
cân tại gốc
tọa độ
O
.
A.
2yx=−−
. B.
.yx= −
C.
2.yx=−+
D.
1.yx=−+
Trang 13/25
Câu 53. Cho hàm số
21
1
x
y
x
−
=
−
có đồ thị
( )
C
. Lập phương trình tiếp tuyến của đồ thị
( )
C
sao cho tiếp
tuyến này cắt các trục
, Ox Oy
lần lượt tại các điểm
A
và
B
thoả mãn
4
OA OB=
.
A.
15
44
1 13
44
yx
yx
=−+
=−+
. B.
15
44
1 13
42
yx
yx
=−+
=−+
.
C.
15
42
1 13
42
yx
yx
=−+
=−+
. D.
15
42
1 13
44
yx
yx
=−+
=−+
.
Câu 54. Cho hàm số
1
x
y
x
=
−
có đồ thị
( )
C
. Gọi
∆
là tiếp tuyến tại điểm
(
)
00
;Mx y
(với
0
0x >
)
thuộc đồ thị
( )
C
. Để khoảng cách từ tâm đối xứng
I
của đồ thị
(
)
C
đến tiếp tuyến
∆
là lớn
nhất thì tung độ của điểm
M
gần giá trị nào nhất?
A.
7
2
π
. B.
3
2
π
. C.
5
2
π
. D.
2
π
.
Câu 55. Cho hàm số
21
1
x
y
x
−
=
+
có đồ thị
( )
C
. Biết khoảng cách từ
(
)
1; 2
I −
đến tiếp tuyến của
( )
C
tại
M
là lớn nhất thì tung độ của điểm
M
nằm ở góc phần tư thứ hai, gần giá trị nào nhất?
A.
3e
. B.
2e
. C.
e
. D.
4e
.
Câu 56. Cho hàm số
23
2
x
y
x
−
=
−
có đồ thị
( )
C
. Biết tiếp tuyến tại
M
của
(
)
C
cắt hai tiệm cận của
( )
C
tại
A
,
B
sao cho
AB
ngắn nhất. Khi đó, độ dài lớn nhất của vectơ
OM

gần giá trị nào nhất ?
A. 7. B. 5. C. 6. D. 4.
Câu 57. Cho hàm số
2
1
x
y
x
−
=
+
có đồ thị
(
)
C
. Phương trình tiếp tuyến
∆
của đồ thị hàm số
( )
C
tạo với
hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó, khoảng cách
từ tâm đối xứng của đồ thị
( )
C
đến
∆
bằng?
A.
3
. B.
26
. C.
23
. D.
6
.
Câu 58. Cho hàm số
21
1
x
y
x
+
=
−
có đồ thị
( )
C
. Gọi
I
là giao điểm của hai tiệm cận. Tiếp tuyến
∆
của
( )
C
cắt 2 tiệm cận tại
A
và
B
sao cho chu vi tam giác
IAB
đạt giá trị nhỏ nhất. Khoảng cách
lớn nhất từ gốc tọa độ đến tiếp tuyến
∆
gần giá trị nào nhất?
A. 6. B. 4. C. 3. D. 5.
Câu 59. Cho hàm số
21
2
x
y
x
−
=
−
có đồ thị
( )
C
. Gọi
I
là giao điểm của hai đường tiệm cận. Tiếp tuyến
∆
của
( )
C
tại
M
cắt các đường tiệm cận tại
A
và
B
sao cho đường tròn ngoại tiếp tam giác
IAB
có diện tích nhỏ nhất. Khi đó tiếp tuyến
∆
của
( )
C
tạo với hai trục tọa độ một tam giác
có diện tích lớn nhất thuộc khoảng nào?
A.
( )
27; 28
. B.
( )
28; 29
. C.
( )
26; 27
. D.
( )
29; 30
.
C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM
I – ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
B
D
C
A
A
A
A
B
C
D
B
D
B
A
C
C
C
D
D
B
Trang 14/25
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
D
D
C
C
A
B
D
B
B
D
B
A
B
A
D
C
B
A
C
C
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
B
C
B
D
B
C
A
B
C
C
A
A
A
D
C
D
D
D
A
II –HƯỚNG DẪN GIẢI
Câu 1. Chọn B.
Tính
(
)
2
' 3 6 '3 9y x xy= −⇒ =⇒
phương trình tiếp tuyến là
9 26yx= −
.
Câu 2. Chọn D.
Tính
( )
3
' 4 8 '1 4y x xy= − ⇒ =−⇒
phương trình tiếp tuyến là
42yx=−+
.
Câu 3. Chọn C.
Tính
( )
( )
2
2
' '2 2
1
yy
x
= ⇒ −=⇒
+
phương trình tiếp tuyến là
27yx= +
.
Câu 4. Chọn A.
Tính
0
(2) 4yy= = −
và
( )
2
' 3 3 '2 9yx y=− +⇒ =−
. Vậy phương trình tiếp tuyến là
9 14yx
=−+
.
Câu 5. Chọn A.
Tính
0
( 3) 9yy= −=−
và
( )
3
' 4 16 ' 3 60y x xy=− + ⇒ −=
. Vậy phương trình tiếp tuyến là
60 171yx= +
.
Câu 6. Chọn A.
Tính
0
(2) 3yy= =
và
( )
( )
2
1
' '2 1
1
yy
x
−
= ⇒=−
−
. Vậy phương trình tiếp tuyến là
5
yx=−+
.
Câu 7. Chọn A.
Giải phương trình
32
00 0
23 5 1
xx x+ =⇔=
, và
( )
2
' 6 6 ' 1 12y x xy= +⇒ =
. Vậy phương trình
tiếp tuyến là
12 7yx= −
.
Câu 8. Chọn B.
Giải phương trình
0
42
00
0
2
2 3 21
2
x
xx
x
=
+ −= ⇔
= −
. Đồng thời
3
'4 4yxx= +
, suy ra
( )
( )
' 2 40
' 2 40
y
y
=
−=−
. Vậy có hai tiếp tuyến cần tìm là
40 59yx= −
và
40 101yx=−−
.
Câu 9. Chọn C.
Giải phương trình
0
0
0
2
13
21
x
x
x
+
=⇔=
−
và
( )
( )
2
51
' '3
5
21
yy
x
−−
= ⇒=
−
. Phương trình tiếp
tuyến là
18
55
yx=−+
.
Câu 10. Chọn D.
Giải phương trình
( )
2
0 00 0
' 3 3 6 30 1yx x x x=−⇔ − + = ⇔ =
. Đồng thời
( )
14y = −
nên phương
trình tiếp tuyến là
31yx=−−
.
Câu 11. Chọn B.
Giải phương trình
( )
3
0 00 0
' 48 4 48 0 4
yx x x x=− ⇔− + + = ⇔ =
. Đồng thời
( )
4 32y = −
nên
phương trình tiếp tuyến cần tìm là
48 160yx=−+
.
Câu 12. Chọn D.
Giải phương trình
Trang 15/25
( )
( )
(
)
(
)
0
0
2
0
0
0 03 : 43
4
'4 4
2 2 5 : 4 13
1
x y pttt y x
yx
x y pttt y x
x
=⇒=⇒ =+
=⇔=⇔
= ⇒ =−⇒ = −
−
.
Câu 13. Chọn B.
Giải phương trình
( )
( )
0
2
0 00
0
1 1 1 : (trùng)
' 1 3 4 10
1 15 4
:
3 3 27 27
x y pttt y x
yx x x
x y pttt y x
=⇒=⇒ =
= ⇔− + − = ⇔

=⇒=⇒ =−


.
Câu 14. Chọn A.
Giải phương trình
( )
3
0 00 0
' 36 4 2 36 0 2yx x x x=−⇔ + + =⇔=−
. Đồng thời
( )
2 18y −=
nên
phương trình tiếp tuyến cần tìm là
36 54yx=−−
.
Câu 15. Chọn C.
Giải phương trình
(
)
(
)
( )
( )
0
0
2
0
0
15
5 5 0 : ( trùng)
1 71
77
'
1 23
77
2
9 92 :
77
x y pttt y x
yx
x
x y pttt y x
=⇒ =⇒ =−+
−−
=−⇔ = ⇔
+
=−⇒ − =−⇒ =− −
.
Câu 16. Chọn C.
Giải phương trình
( )
( )
( )
0
0
0
2 2 9 : 21 33
' 21
2 2 11 : 21 31
x y pttt y x
yx
x y pttt y x
=⇒= ⇒ =−
= ⇔
=−⇒ − =− ⇒ = +
.
Câu 17. Chọn C.
Giải phương trình
( )
00
'81yx x=−⇔ =
. Đồng thời
(
)
10y =
nên phương trình tiếp tuyến cần
tìm là
88yx=−+
.
Câu 18. Chọn D.
Giải phương trình
( )
(
)
( )
0
0
0
11
4 41 :
1
63
'
1 13
6
8 83 :
63
x y pttt y x
yx
x y pttt y x
=⇒= ⇒ =+
= ⇔
=−⇒ − = ⇒ = +
.
Câu 19. Chọn D.
Giải phương trình
42
0 '(0) 0 : 0
4 0 2 '(2) 16 : 16 32
2 '( 2) 16 : 16 32
x y pttt y
x x x y pttt y x
x y pttt y x
=⇒= ⇒ =
− =⇔= ⇒ = ⇒ = −
=−⇒ −=−⇒ =− −
.
Câu 20. Chọn B.
Ta giải phương trình
3
1 '(1) 0 : 0
3 20
2 '( 2) 9 : 9 18
x y pttt y
xx
x y pttt y x
=⇒= ⇒ =
− + −=⇔
=− ⇒ − =−⇒ =− −
.
Câu 21. Chọn D.
Ta giải phương trình
5
05
1
x
x
x
−
=⇔=
−+
. Đồng thời
1
'(5)
4
y = −
nên phương trình tiếp tuyến
cần tìm là
15
44
yx=−+
.
Câu 22. Chọn D.
Giao điểm của
()C
và Oy là
( )
0;1 '(0) 6Ay⇒=−
nên phương trình tiếp tuyến là
61yx=−+
.
Câu 23. Chọn C.
Giao điểm của
()C
và Oy là
( )
0; 2 '(0) 0My−⇒ =
nên phương trình tiếp tuyến là
2y = −
.
Trang 16/25
Câu 24. Chọn C.
Giao điểm của
()C
và Oy là
17
0; '(0)
39
Ay

−⇒ =−


nên phương trình tiếp tuyến là
71
93
yx
=−−
.
Câu 25. Chọn A.
Ta giải phương trình
( )
( )
( )
0
0
0
72
1 1 :3
33
'3
3 31 : 38
x y pttt y x
yx
x y pttt y x
=⇒= ⇒ =−
= ⇔
=⇒= ⇒ =−
.
Câu 26. Chọn B.
Ta có
(
)
(
) (
)
0
0
11
11
3
'0
3 3 5, ' 3 0
xy
y
xy y
−
=⇒=
= ⇔
=⇒=− =
. Vậy tiếp tuyến song song trục hoành.
Câu 27. Chọn D.
Theo giả thiết ta có
00
33yx=⇒=
và
1
'(3)
2
y = −
. Vậy phương trình tiếp tuyến là
2 90xy+ −=
.
Câu 28. Chọn B.
Theo giả thiết ta có
00
14xy
=−⇒ =−
và
'( 1) 9y −=
. Vậy phương trình tiếp tuyến là
95yx
= +
.
Câu 29. Chọn B.
Theo giả thiết ta có
00
01xy=⇒=
và
'(0) 7y = −
. Vậy phương trình tiếp tuyến là
71yx=−+
.
Câu 30. Chọn D.
Theo giả thiết ta có
00
5 51
xy=⇒=
và
'(5) 45y
=
. Vậy phương trình tiếp tuyến là
45 174
yx= −
.
Câu 31. Chọn B.
Ta có
22
'3 6 63( 1) 33 min'3yxx x y= − += − +≥⇒ =
khi
00
1 (1) 5xx y y==⇒= =
.
Khi đó phương trình tiếp tuyến
3( 1) 5 3 2yx x= − += +
.
Câu 32. Chọn A.
Ta có
22
' 3 12 3 3( 2) 15 15 max ' 15yxx x y=− + +=− + + ≤ ⇒ =
khi
0
2xx
= = −
. Lúc đó
0
( 2) 25
yy=−=
.
Khi đó phương trình tiếp tuyến
15( 2) 25 15 55yx x= ++ = +
.
Câu 33. Chọn B.
[Phương pháp tự luận]
Ta có
2
11
2 .,
12
2
22
'( ) 3 1 0
' 3 1 0 ( ). ( ) 0
'( ) 3 1 0
yx x
y x yx yx
yx x
= +>
= +> ⇒ ⇒ >
= +>
hay
12
'( ). '( ) 1yx yx ≠−
. Suy ra 2 tiếp tuyến
A
và
B
không vuông góc.
[Phương pháp trắc nghiệm]
Ta có
2
' 3 1 0,yx x= + > ∀∈
.
Suy ra hàm số đồng biến trên
và cắt trục hoành tại một điểm duy nhất
→
A, D đúng.
Với
00
1 '(1) 4, 3xyy=⇒==
. Vậy phương trình tiếp tuyến
4( 1) 3 4 1yx x
= − += −→
C đúng.
Câu 34. Chọn A.
Trang 17/25
Ta có
2
' 3 4 1 '(1) 6yxx y= + −⇒ =
. Khi đó phương trình tiếp tuyến tại
(1; 0)
M
là
6( 1) 6 6yx x= −= −
, nên
6
36
6
a
ab
b
=
⇒=
=
.
Câu 35. Chọn D.
Ta có
2
22
2 1 5 1 55 5
' 3 2 2 3 3 min '
3 9 3 3 33 3
yxx x x x y

= − += − + += − +≥⇒ =




khi
0
1
.
3
xx= =
Câu 36. Chọn C.
Ta có
2
3
' 0, 1
( 1)
yx
x
−
= < ∀≠
−
. Tiếp tuyến tại điểm
00
( ; ) ()
Mx y C∈
tạo với
Ox
góc
0
60
'0
0
00
'() tan60 3 '() 3
y
yx yx
<
⇒ = ± = ± → = −
2
0
2
0
3
3 ( 1) 1
( 1)
x
x
−
⇒ =−⇔ −=
−
00
00
2 23
00
xy
xy
=⇒=
⇔
=⇒=
. Các tiếp tuyến tương ứng có phương trình là
3 43
3
yx
yx
=−+
= −
.
Câu 37. Chọn B.
Ta có
2
' 3 6 3( 1)y x mx m=− ++
. Do
()
m
KC
∈
và có hoành độ bằng
1−
, suy ra
( )
1; 6 3Km−− −
.
Khi đó tiếp tuyến tại K có phương trình
: '( 1)( 1) 6 3 (9 6) 3 3yy x m m x m∆ = − + − −= + + +
.
Đường thẳng
∆
song song với đường thẳng
d
963 1
30 3
3 30 1
mm
xy y x
mm
+=− =−

⇒ +=⇔=− ⇔ ⇔

+ ≠ ≠−

.
Vậy không tồn tại
m
, ta chọn
∅
.
Câu 38. Chọn A.
Ta có
3
'4y x mx= +
và đường thẳng
3 10xy
− +=
viết thành
11
33
yx= +
.
Theo yêu cầu bài toán, phải có
( )
'1 3 4 3 1y mm− =−⇔−− =−⇔ =−
.
Câu 39. Chọn C.
Ta có
1
'
21
y
x
=
+
. Gọi
0
x
là hoành độ tiếp điểm của
d
và (C).
Theo yêu cầu bài toán, ta có
( )
0 00
0
1 11
' 2 19 4
33
21
yx x x
x
= ⇔ = ⇔ += ⇔ =
+
.
Câu 40. Chọn C.
Đường thẳng đi qua
( )
1; 3M
có hệ số góc
k
có dạng
( )
: 13d y kx= −+
.
d
là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:
( ) ( )
( )
3
2
3 4 1 3 1
3 12 2
x x kx
xk
− = −+
−=
. Thay
(2) vào (1) ta được
(
)
( )
3 2 32
0
3
3 4 3 12 1 3 8 12 0 .
3
24
2
x
k
xx xx x x
k
x
=
=
− = − − +⇔ − =⇔ ⇒
= −
=
Vậy có 2 tiếp tuyến.
Câu 41. Chọn B.
Phương pháp tự luận
Ta có
( )
2
' 3 1 '1 4
yx y= +⇒ =
, suy ra tiếp tuyến tại
( )
1; 4N
là
:4yx
∆=
.
Phương trình hoành độ giao điểm của
∆
và (C) là
Trang 18/25
33
1
24 3 20
28
x
xx x x x
xy
=
++= ⇔ − +=⇔
=−⇒ =−
.
Phương pháp trắc nghiệm
2
NM
b
xx
a
+=−
(Với
32
y ax bx cx d
= + ++
là hàm số ban đầu)
( )
2 0 2 2; 8
MM
xx M⇔ + = ⇔ =−⇒ −−
.
Câu 42. Chọn C.
Phương pháp tự luận
Đường thẳng
∆
đi qua điểm
( )
1; 2
M −−
có hệ số góc k có dạng
( )
: 12y kx∆ = +−
.
∆
là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:
( ) ( )
( )
32
2
1 1 2 1
3 21 2
x x x kx
xx k
− + += + −
− +=
.
Thay (2) vào (1) ta được
( )
( ) ( ) ( ) ( )
2
32 2
1
1 3 2 1 1 2 1 1 0 1; 2 .
12
x
xxx x x x x x N
xy
= −
− + += − + + − ⇔ + − = ⇔ ⇒
=⇒=
Phư
ơng pháp trắc nghiệm
2
NM
b
xx
a
+=−
(Với
32
y ax bx cx d= + ++
là hàm số ban đầu)
( )
2 ( 1) 1 1 1; 2
NN
x xN⇔ +− = ⇔ = ⇒
.
Câu 43. Chọn B.
Ta có
2
'3 6 1yxmxm= + ++
. Gọi
(
)
00
;Mx y
là tiếp điểm của tiếp tuyến cần lập.
Khi đó
( )
0
0
' 1 45
1
21
ym
x
ym
−=−
=−⇒
= −
, suy ra phương trình tiếp tuyến là
( )( )
: 45 1 2 1y mx m∆ = − ++ −
.
Do
( ) ( )( )
1
1; 3 3 4 5 1 1 2 1
2
A m mm
∈∆⇒ = − + + − ⇔ =
.
Câu 44. Chọn D.
Ta có
( )
2
1
'
1
m
y
x
+
=
+
khi đó
( )
'0 3 1 3 2y mm= ⇔+ = ⇔ =
.
Câu 45. Chọn B.
Ta có
( )
2
1
' 0, 1
1
yx
x
= > ∀ ≠−
+
. Gọi
( )
00
;Mx y
là tiếp điểm của
()C
với tiếp tuyến cần lập.
Tam giác OAB cân tại O nên OA = OB, suy ra
( ) ( )
( )
0
'0
00
2
0
0
0
1
' 1 '1 1
2
1
y
x
yx yx
x
x
>
=
= ± → = ⇔ = ⇔
= −
+
.
• Với
00
00xy=⇒=
(loại, do
(
)
0; 0MO≡
).
• Với
00
22xy=−⇒ =
, suy ra phương trình tiếp tuyến
:4yx∆=+
.
Câu 46. Chọn C.
Do
0
36 '( ) 36
OB
yx
OA
=⇒=±
.
• Với
33
0 0 00
'( ) 36 4 2 36 4 2 36 0yx x x x x=−⇔− − =−⇔ + − =
0
2x⇔=
.
Vậy
0
(2) 14yy= = −
. Suy ra phương trình tiếp tuyến
36 58
yx=−+
.
• Với
33
0 0 00
'( ) 36 4 2 36 4 2 36 0yx x x x x= ⇔− − = ⇔ + + =
0
2x⇔=−
.
Trang 19/25
Vậy
0
( 2) 14yy=−=−
. Suy ra phương trình tiếp tuyến
36 58yx= +
.
Câu 47. Chọn A.
• Gọi
( )
( )
0
0
0
1
;
21
x
Mx C
x

−
∈


+

với
0
1x ≠−
là điểm cần tìm.
• Gọi
∆
tiếp tuyến của
( )
C
tại
M
ta có phương trình.
( )
00
00 0
2
00
0
11
1
: '()() ()
2( 1) 2( 1)
1
xx
y fx xx xx
xx
x
−−
∆= −+ = −+
++
+
.
• Gọi
A Ox=∆∩
⇒
2
00
21
;0
2
xx
A

−−
−


và
B Oy=∆∩
⇒
2
00
2
0
21
0;
2( 1)
xx
B
x

−−

+

.
• Khi đó
∆
tạo với hai trục tọa độ
OAB∆
có trọng tâm là
22
00 00
2
0
21 21
;
6 6( 1)
xx xx
G
x

−− −−
−

+

.
• Do
G
thuộc đường thẳng
40xy+=
⇒
22
00 00
2
0
21 21
4. 0
6 6( 1)
xx xx
x
−− −−
− +=
+
⇔
( )
2
0
1
4
1x
=
+
(vì
,AB
không trùng
O
nên
2
00
2 10xx
− −≠
)
00
00
11
1
22
13
1
22
xx
xx

+= =−

⇔⇔


+=− =−


.
• Vì
0
1x
>−
nên chỉ chọn
0 00
1 13 7
;2
2 22 2
x M xy

=−⇒ − − ⇒ + =−


.
Câu 48. Chọn B.
•
(
)
m
AC∈
nên
( )
1; 1Am−
. Ngoài ra
( )
3
' 4 4 '1 4 4y x mx y m=−⇒ =−
.
• Phương trình tiếp tuyến của
( )
m
C
tại
A
là
( ) ( )
1 1. 1y my x
′
−+ = −
, hay
(
) ( )
4 4 31 0mx y m− −− − =
.
• Khi đó
( )
(
)
2
1
;1
16 1 1
dB
m
−
∆= ≤
−+
, Dấu ‘=’ xảy ra ⇔ khi
1m =
.
• Do đó
( )
;dB
∆
lớn nhất bằng 1 khi và chỉ khi
1m =
.
Câu 49. Chọn C.
• Giả sử
( ) ( )
00
;Mx y C∈
⇒
0
0
0
23
1
x
y
x
+
=
+
.
• Ta có
( )
00
00
1
22
00
3 4 12 0
342
,2 2
3 4 80
34
xy
xy
dMd
xy
+ −=
+−
=⇔=⇔
+ +=
+
.
• Với
( )
01
0
00 0
0
02
0 0;3
23
3 4 12 0 3 4 12 0
1 1 11
1
;
3 34
xM
x
xy x
x
xM
= ⇒

+
+ −=⇔ + −=⇔


+
= ⇒



Trang 20/25
• Với
03
0
00 0
0
04
7
5 5;
23
4
3 4 80 3 4 80
1
44
;1
33
xM
x
xy x
x
xM

=−⇒ −


+

+ +=⇔ + +=⇔

+


=−⇒ − −


.
Suy ra có 4 tiếp tuyến.
Câu 50. Chọn C.
Phương pháp tự luận.
• Giao điểm của hai tiệm cận là
( )
1; 2I
. Gọi
( ) ( )
;M ab C∈
⇒
( )
21
1
1
a
ba
a
−
= >
−
.
• Phương trình tiếp tuyến của
( )
C
tại
M
là
( )
2
1 21
( 1) 1
a
y xa
aa
−
=− −+
−−
.
• Phương trình đường thẳng
MI
là
2
1
( 1) 2
( 1)
yx
a
= −+
−
.
• Tiếp tuyến tại
M
vuông góc với
MI
nên ta có
( ) ( )
22
11
.1
11aa
−=−
−−
⇔
01
23
ab
ab
=⇒=
=⇒=
.
Vì yêu cầu hoành độ lớn hơn 1 nên điểm cần tìm là
( )
2; 3M
.
Phương pháp trắc nghiệm
Gọi
( ) ( )
00
;Mx y C∈
, điểm
M
thoả yêu cầu bài toán có hoành độ được tính như sau:
( ) ( )
00
00
0
23
1 2. 1 1. 1 1 1
0( )
xy
xx
xL
=⇒=
−=± − − − ⇔ −=±⇔
=
.
Vậy
(
)
2; 3M
.
Câu 51. Chọn A.
• Phương trình hoành độ giao điểm của
d
và
( )
C
là
1
21
x
xm
x
−+
= +
−
⇔
( )
2
1
2
2 2 1 0 (*)
x
g x x mx m
≠
= + − −=
.
• Theo định lí Viet ta có
1 2 12
1
;
2
m
x x m xx
−−
+=− =
. Giả sử
( ) ( )
11 2 2
;, ;Ax y Bx y
.
• Ta có
( )
2
1
21
y
x
−
′
=
−
, nên tiếp tuyến của
( )
C
tại
A
và
B
có hệ số góc lần lượt là
( )
1
2
1
1
21
k
x
= −
−
và
( )
2
2
2
1
21
k
x
= −
−
. Vậy
[ ]
( )
( )
22
1 2 12
12
2
22
12
12 1 2
2
2
4( ) 4( ) 2
11
(2 1) ( 2 1)
4 2( ) 1
4 86 4 122
x x xx
kk
xx
xx x x
mm m
+− ++
+=− − =−
−−
− ++
=− + + =− + − ≤−
• Dấu "=" xảy ra ⇔
1m = −
.
Vậy
12
kk+
đạt giá trị lớn nhất bằng
2−
khi
1
m = −
.
Câu 52. Chọn A.
Phương pháp tự luận
• Gọi
( )
00
;Mx y
là toạ độ của tiếp điểm ⇒
( )
0
2
0
1
'( ) 0
23
yx
x
−
= <
+
.
Trang 21/25
•
OAB
∆
cân tại
O
nên tiếp tuyến ∆ song song với đường thẳng
yx= −
(vì tiếp tuyến có hệ
số góc âm). Nghĩa là
( )
( )
0
2
0
1
1
23
yx
x
−
′
= = −
+
⇒
00
00
11
20
xy
xy
=−⇒ =
=−⇒ =
.
• Với
00
1; 1xy=−=
⇒ ∆:
( )
11y x yx−=− + ⇔ =−
(loại).
• Với
00
2; 0
xy
=−=
⇒ ∆:
( )
02 2y x yx
− =− + ⇔ =−−
(nhận).
Vậy phương trình tiếp tuyến cần tìm là
2yx=−−
.
Phương pháp trắc nghiệm
• Tam giác
OAB
cân tại gốc tọa độ
O
nên ta có
1OA OB n
= ⇒=
.
22
0 0 00 0 0
2 0 2 8 6 0 1; 3acx bcx bd x x x x+ + ≠ ⇒ + + ≠ ⇔ ≠− ≠−
( )
( )
0
00
0
1
. 2 3 1. 1
2
xL
cx d n ad bc x
xN
=−
+ =± − ⇒ +=± −⇔
= −
.
• Với
00
2; 0
xy=−=
⇒ ∆:
( )
02 2y x yx− =− + ⇔ =−−
(nhận).
Câu 53. Chọn A.
• Giả sử tiếp tuyến d của
( )
C
tại
00
( ; ) ()
Mx y C∈
cắt
Ox
tại
A
,
Oy
tại
B
sao cho
4
OA OB=
.
• Do
OAB∆
vuông tại
A
nên
1
tan
4
OB
A
OA
= =
⇒ Hệ số góc của
d
bằng
1
4
hoặc
1
4
−
.
• Vì
( )
( )
0
2
0
1
'0
1
yx
x
=−<
−
nên hệ số góc của
d
bằng
1
4
−
, suy ra
( )
00
2
0
00
3
1
11
2
5
4
1
3
2
xy
x
xy
=−⇒ =
− =−⇔
−
=⇒=
.
• Khi đó có 2 tiếp tuyến thoả mãn là:
( )
( )
1 3 15
1
4 2 44
1 5 1 13
3
4 2 44
y x yx
y x yx

=− ++ =− +

⇔


=− −+ =− +


.
Câu 54. Chọn D.
Phương pháp tự luận
• Ta có
( )
2
1
1
y
x
−
′
=
−
;
( )
1;1I
.
• Gọi
( ) ( )
0
00
0
; ,1
1
x
Mx C x
x

∈≠

−

. Phương trình tiếp tuyến tại
M
có dạng
0
0
2
00
1
: ()
( 1) 1
x
y xx
xx
∆=− − +
−−
22
00
( 1) 0x x yx⇔+ − − =
.
•
( )
( )
( )
( )
0
4
2
0
0
2
0
21
22
,2
12
11
1
1
x
dI
x
x
x
−
∆= = ≤ =
+−
+−
−
.
• Dấu
""=
xảy ra khi và chỉ khi
( )
( )
( )
( )
2
00
00
2
0
0
22
1
1 11
0
1
x yN
xx
xL
x
=⇒=
= − ⇔ −=⇔
=
−
.
Trang 22/25
Tung độ này gần với giá trị
2
π
nhất trong các đáp án.
Phương pháp trắc nghiệm
Ta có
IM ⊥∆⇒
( )
(
)
00
00
0
22
1 10
0
x yN
cx d ad bc x
xL
=⇒=
+ =± − ⇒ −=± −− ⇔
=
.
Câu 55. Chọn C.
Phương pháp tự luận
• Ta có
( )
2
3
1
y
x
′
=
+
.
• Gọi
( )
( )
0
00
0
21
; ,1
1
x
Mx C x
x

−
∈ ≠−

+

. Phương trình tiếp tuyến tại
M
là
0
0
2
00
21
3
()
( 1) 1
x
y xx
xx
−
= −+
++
22
0 00
3 ( 1) 2 2 1 0xx y x x⇔ − + + − −=
.
•
(
)
0
4
2
0
0
2
0
61
66
,6
9
9 ( 1)
29
( 1)
( 1)
x
dI
x
x
x
+
∆= = ≤ =
++
++
+
.
• Dấu
""=
xảy ra khi và chỉ khi
( )
( )
( )
2
00
2
00
2
0
00
13 23
9
( 1) 1 3
( 1)
13 23
x yL
xx
x
x yN
=−+ ⇒ = −
=+⇔ +=⇔
+
=−− ⇒ = +
.
Tung độ này gần với giá trị
e
nhất trong các đáp án.
Phương pháp trắc nghiệm
Ta có
IM ⊥∆⇒
00
1 21
cx d ad bc x+=± −⇒+=±+
( )
( )
0
0
13 23
13 23
x yL
x yN
=−+ ⇒ = −
⇔
=−− ⇒ = +
.
Câu 56. Chọn D.
Phương pháp tự luận
• Gọi
(
) ( )
0
00
0
23
; ,2
2
x
Mx C x
x

−
∈≠

−

. Phương trình tiếp tuyến tại
M
có dạng
0
2
00
11
: ( )2
( 2) 2
y xx
xx
∆ =− − ++
−−
.
• Giao điểm của
∆
với tiệm cận đứng là
0
2
2; 2
2
A
x

+

−

.
• Giao điểm của
∆
với tiệm cận ngang là
( )
0
2 2; 2Bx−
.
• Ta có
( )
( )
2
2
0
2
0
1
42 8
2
AB x
x

= −+ ≥

−


. Dấu
""=
xảy ra khi
( )
( )
2
0
2
0
1
2
2
x
x
−=
−
( ) ( )
( )
( )
00
00
3 3 3; 3 3 2
1 1 1; 1 2
x y OM OM N
x y OM OM L
=⇒=⇒ ⇒ =
⇔
=⇒=⇒ ⇒ =
 
 
.
Phương pháp trắc nghiệm
Trang 23/25
•
AB
ngắn nhất suy ra khoảng cách từ
I
đến tiếp tuyến
∆
tại
M
ngắn nhất
IM⇒ ⊥∆⇒
33
2 43
11
MM
MM
MM
xy
cx d ad bc x
xy
=⇒=
+ =± − ⇒ − =± −+ ⇔
=⇒=
32OM⇒=

.
Câu 57. Chọn D.
Phương pháp tự luận
• Gọi
( ) ( ) ( )
0
00
0
2
; , 1 , 1;1
1
x
Mx C x I
x

−
∈ ≠− −

+

. Phương trình tiếp tuyến tại
M
có dạng
( )
0
0
2
0
0
2
3
: ()
1
1
x
y xx
x
x
−
∆= −+
+
+
.
• Giao điểm của
∆
với tiệm cận đứng là
0
0
5
1;
1
x
A
x

−
−

+

.
• Giao điểm của
∆
với tiệm cận ngang là
( )
0
2 1; 1
Bx+
.
• Ta có
0
0
6
, 2 1 . 12
1
IA IB x IA IB
x
= = +⇒ =
+
. Bán kính đường tròn ngoại tiếp
IAB∆
là
IAB
S pr
=
, suy ra
22
.. .
23 6
2 . 2. .
IAB
S
IA IB IA IB IA IB
r
p IA IB AB
IA IB IA IB
IA IB IA IB
=== ≤=−
++
+
++ +
.
• Suy ra
2
0
max 0
0
13 13
23 6 1 3
13 13
M
M
xy
r IA IB x
xy
=−+ ⇒ =−
= − ⇔= ⇔ −=⇔
=−− ⇒ = +
.
•
(
)
3; 3 6
IM IM−⇒ =
 
.
Phương pháp trắc nghiệm
•
IA IB= ⇒
IAB∆
vuông cân tại
I IM⇒ ⊥∆
.
•
13 13
1 12
13 13
MM
MM
MM
xy
cx d ad bc x
xy
=−+ ⇒ =−
+ =± − ⇒ +=± + ⇔
=−− ⇒ =+
6IM⇒=

.
Câu 58. Chọn D.
Phương pháp tự luận
• Gọi
(
) (
)
00
0
3
;2 , 1
1
Mx C x
x

+∈ ≠

−

. Phương trình tiếp tuyến tại
M
có dạng
(
)
0
2
0
0
33
: ( )2
1
1
y xx
x
x
−
∆ = − ++
−
−
.
• Giao điểm của
∆
với tiệm cận đứng là
0
6
1; 2
1
A
x

+

−

.
• Giao điểm của
∆
với tiệm cận ngang là
( )
0
2 1; 2Bx−
.
• Ta có
0
0
1 16
. 2 1 2.3 6
2 21
IAB
S IA IB x
x
∆
= = ⋅ ⋅ −= =
−
.
•
IAB
∆
vuông tại I có diện tích không đổi ⇒ chu vi
IAB∆
đạt giá trị nhỏ nhất khi
Trang 24/25
IA IB=
0
0
0
0
13
6
21
1
13
x
x
x
x
= +
⇔ = −⇒
−
= −
.
• Với
0
13
x = +
thì phương trình tiếp tuyến là
: 3 23yx∆ =−++
. Suy ra
( )
3 23
,
2
dO
+
∆=
.
• Với
0
13x = −
thì phương trình tiếp tuyến là
: 3 23yx∆ =−+−
. Suy ra
( )
3 23
,
2
dO
−+
∆=
.
Vậy khoảng cách lớn nhất là
3 23
2
+
gần với giá trị
5
nhất trong các đáp án.
Phương pháp trắc nghiệm
•
IA IB= ⇒
13 23
1 21
13 23
M
MM
M
xy
cx d ad bc x
xy
=+ ⇒=+
+ =± − ⇒ −=± −− ⇔
=− ⇒=−
( )
( )
3 23
,
2
dO N
+
⇒ ∆=
.
Câu 59. Chọn A.
Phương pháp tự luận
• Gọi
( ) ( )
0
00
0
21
; ,2
2
x
Mx C x
x

−
∈≠

−

. Phương trình tiếp tuyến tại
M
có dạng
0
0
2
00
21
3
: ()
( 2) 2
x
y xx
xx
−
∆=− −+
−−
.
• Giao điểm của
∆
với tiệm cận đứng là
0
0
22
2;
2
x
A
x

+

−

.
• Giao điểm của
∆
với tiệm cận ngang là
( )
0
2 2; 2Bx−
.
• Xét
00
00
0
00
22 2 2
2 2 21
2 2. 2
22
AB
AB
xx x x
xx
yy y
xx
+ =+ −=
⇒
+−
+ = += =
−−
M
là trung điểm của
AB
.
•
IAB∆
vuông tại
I
nên
M
là tâm đường tròn ngoại tiếp tam giác
IAB
.
2
22 2 2
0
00
2
00
21
9
( 2) 2 ( 2) 6
2 ( 2)
x
S R IM x x
xx
ππ π π π


−

⇒= = = −+ − = −+ ≥


−−



• Dấu
""=
xảy ra khi
00
2
0
2
0
00
32 32
9
( 2)
( 2)
32 32
xy
x
x
xy
= +⇒ = +
−= ⇔
−
=−+⇒=−+
.
• Với
0
32 : 234
x yx= + ⇒∆ =− + +
cắt 2 trục tọa độ tại
( )
0; 2 3 4E +
và
( )
2 3 4; 0F +
, suy ra
1
. 14 8 3 27,8564
2
OEF
S OE OF= =+≈
• Với
0
32 : 234x yx=− + ⇒∆ =− − +
cắt 2 trục tọa độ tại
( )
0; 2 3 4E −+
và
( )
2 3 4; 0F −+
, suy ra
1
. 14 8 3 0,1435
2
OEF
S OE OF= =−≈
Phương pháp trắc nghiệm
Trang 25/25
•
IM
lớn nhất
IM
⇔ ⊥∆⇒
00
2 41cx d ad bc x
+ =± − ⇒ − =± −+
.
00
00
32 32
32 32
xy
xy
= +⇒ = +
⇔
=−+⇒=−+
. Giải tương tự như trên.
| 1/25
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


CHỦ ĐỀ 7. TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ
A. KỸ NĂNG CƠ BẢN
Bài toán 1: Các dạng phương trình tiếp tuyến thường gặp.
Cho hàm số y = f (x) , gọi đồ thị của hàm số là (C).
Dạng 1. Viết phương trình tiếp tuyến của đồ thị hàm số (C ) : y = f ( x) tại M ( x y
o; o ) .Phương pháp
o Bước 1. Tính y′ = f ′(x) suy ra hệ số góc của phương trình tiếp tuyến là k = y′(x . 0 )
o Bước 2. Phương trình tiếp tuyến của đồ thị (C) tại điểm M (x ; y có dạng 0 0 ) /
y − y = f x x − x . 0 ( 0)( 0 )  Chú ý:
o Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại điểm có hoành độ x thì khi đó ta tìm 0
y bằng cách thế vào hàm số ban đầu, tức y = f x . Nếu đề cho y ta thay vào hàm số để 0 ( 0) 0 0 giải ra x . 0
o Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm của đồ thị (C): y = f (x) và
đường thẳng d : y = ax + .
b Khi đó các hoành độ tiếp điểm là nghiệm của phương trình hoành
độ giao điểm giữa d và (C).
Sử dụng máy tính:
Phương trình tiếp tuyến cần tìm có dạng d : y = ax + . b
o Bước 1: Tìm hệ số góc tiếp tuyến d
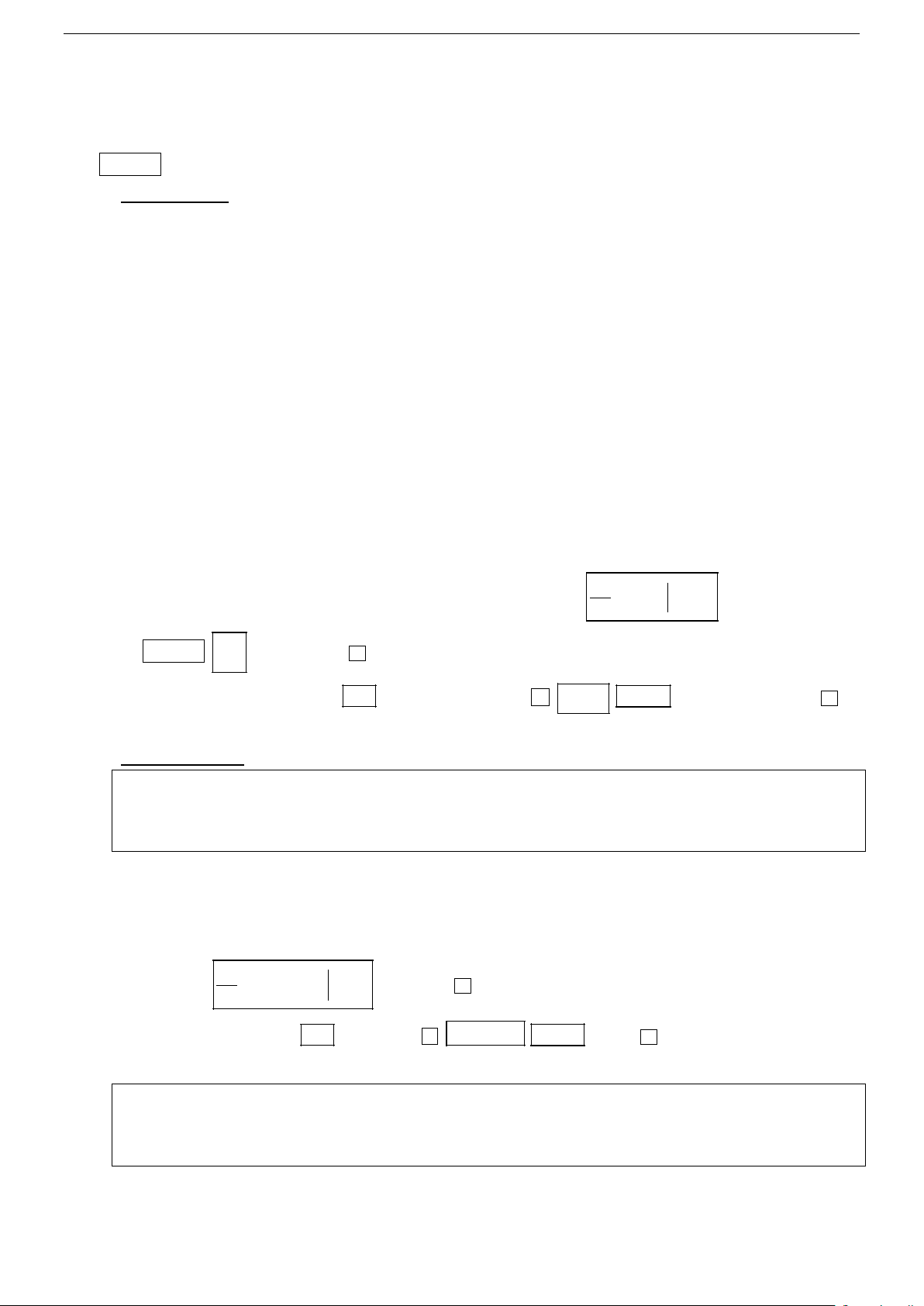
k = y′(x . Nhập ( f (x)) bằng cách nhấn 0 ) x dx = 0 x
SHIFT ∫ sau đó nhấn = ta được .a
o Bước 2: Sau đó nhân với −X tiếp tục nhấn phím + f (x) CALC X = x nhấn phím = ta o được b.
Ví dụ minh họa
Ví dụ 1. Cho hàm số (C) 3 2
: y = x + 3x . Phương trình tiếp tuyến của đồ thị (C) tại điểm M (1;4) là A. y = 9 − x + 5.
B. y = 9x + 5. C. y = 9 − x − 5.
D. y = 9x − 5. Hướng dẫn giải Ta có 2
y ' = 3x + 6x ⇒ k = y′( )
1 = 9 . Phương trình tiếp tuyến tại M (1;4) là
d : y = y′(x x − x + y = 9 x −1 + 4 = 9x − 5 . Chọn đáp án D. 0 ) ( 0 ) 0 ( )
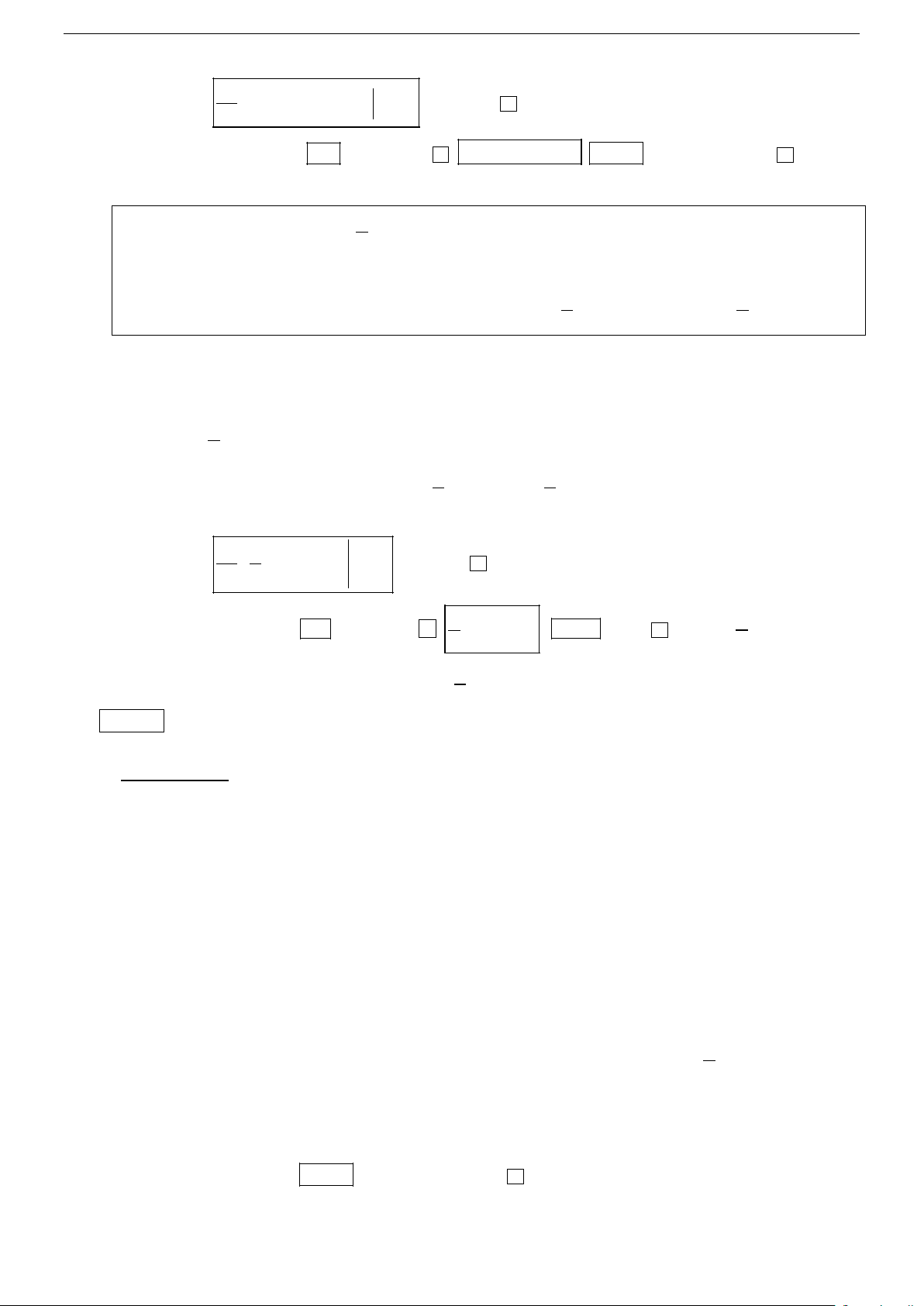
Sử dụng máy tính: o Nhập d ( 3 2 X + 3X )
nhấn dấu = ta được 9. dx x = 1
o Sau đó nhân với ( −X ) nhấn dấu + 3 2
X + 3X CALC X =1 = ta được 5 − .
Vậy phương trình tiếp tuyến tại M là y = 9x − 5 .
Ví dụ 2. Cho hàm số 3 2 y = 2
− x + 6x − 5. Phương trình tiếp tuyến của (C) tại điểm M thuộc (C)
và có hoành độ bằng 3. A. y = 18
− x + 49. B. y = 18 − x − 49.
C. y =18x + 49.
D. y =18x − 49. Hướng dẫn giải Ta có 2 y′ = 6
− x +12x . Với x = 3 ⇒ y = 5 − ⇒ M 3; 5 −
và hệ số góc k = y′(3) = 18 − . Vậy 0 0 ( )
phương trình tiếp tuyến tại M là y = 18
− (x − 3) − 5 = 18
− x + 49 . Chọn đáp án A. Trang 1/25
Sử dụng máy tính: o Nhập d ( 3 2 2
− X + 6X − 5) nhấn dấu = ta được 18 − . dx x = 3
o Sau đó nhân với ( −X ) nhấn dấu + 3 2 2
− X + 6X − 5 CALC X = 3 nhấn dấu = ta được
49 . Vậy phương trình tiếp tuyến tại M là y = 18 − x + 49.
Ví dụ 3. Cho hàm số (C) 1 4 2
: y = x − 2x . Phương trình tiếp tuyến của (C) tại điểm M có hoành 4
độ x > 0, biết y′′(x = 1 − 0 ) 0 là A. y = 3 − x − 2. B. y = 3 − x +1. C. 5 y = 3 − x + .
y = − x + 4 D. 1 3 . 4 Hướng dẫn giải Ta có 3
y′ = x − 4x , 2
y′′ = 3x − 4 . Mà y′′(x = 1 − 2 ⇒ 3x − 4 = 1 − 2 ⇔ x =1 ⇔ = (vì x > 0 ). 0 ) x 0 0 1 0 0 Vậy 7
y = − , suy ra k = y′( ) 1 = 3
− . Vậy phương trình tiếp tuyến tại M là 0 4
d y = − (x − ) 7 5 : 3 1 − ⇒ y = 3
− x + ⋅ Chọn đáp án C. 4 4
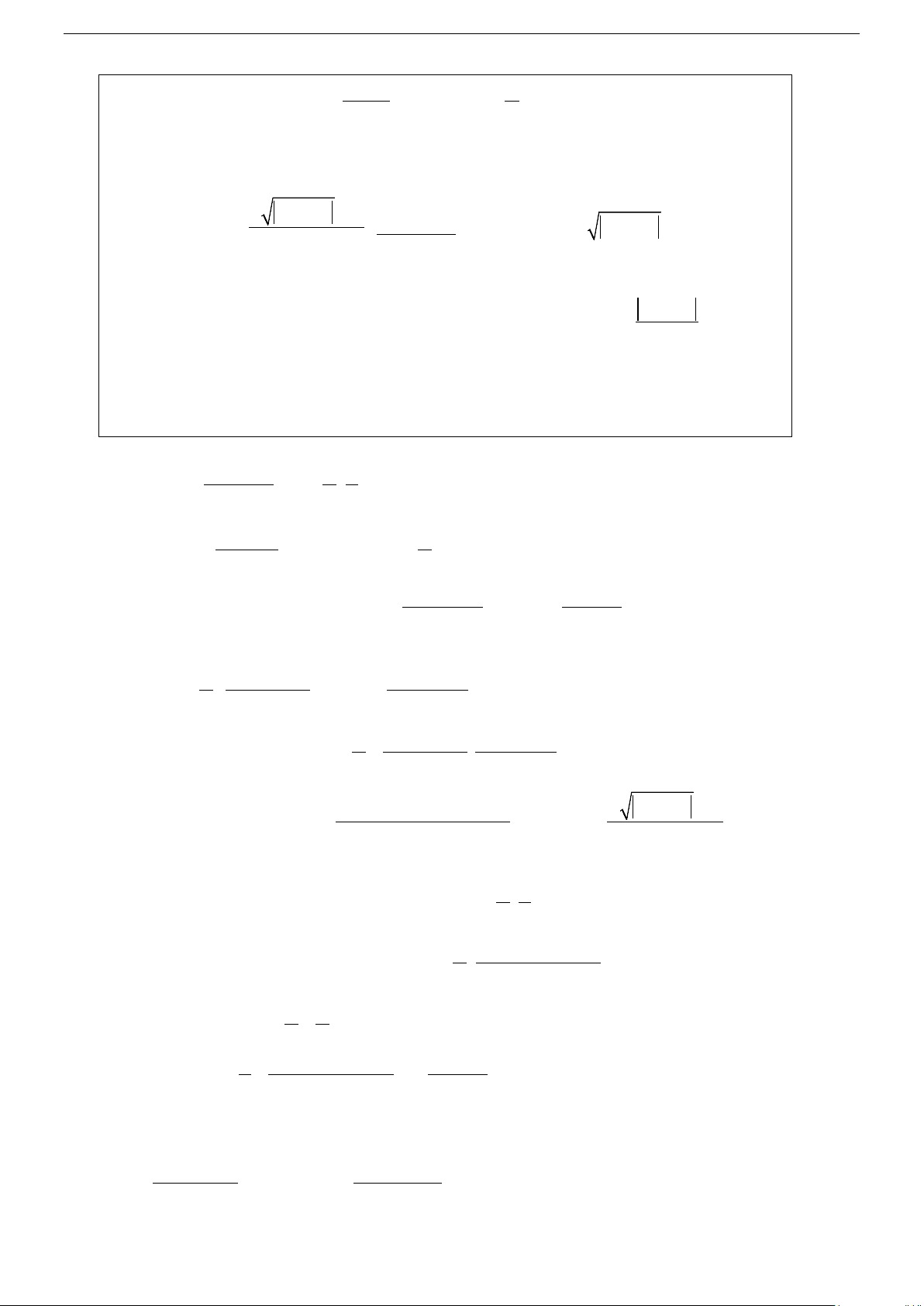
Sử dụng máy tính: o Nhập d  1 4 2 X 2X  −   nhấn dấu = ta được dx 3 − .  4  x = 1 o Sau đó nhân với ( 1 5 −X ) nhấn dấu + 4 2
X − 2X CALC X =1 = ta được . 4 4
Vậy phương trình tiếp tuyến là 5 d : y = 3 − x + ⋅ 4
Dạng 2. Viết phương trình tiếp tuyến của đồ thị hàm số (C ) : y = f ( x) có hệ số góc k cho trước. Phương pháp
o Bước 1. Gọi M (x ; y là tiếp điểm và tính y′ = f ′(x) . 0 0 )
o Bước 2. Hệ số góc tiếp tuyến là k = f '(x . Giải phương trình này tìm được x , thay vào hàm 0 ) 0 số được y . 0
o Bước 3. Với mỗi tiếp điểm ta tìm được các tiếp tuyến tương ứng
d : y − y = f ′ x x − x 0 ( 0)( 0 )
Chú ý: Đề bài thường cho hệ số góc tiếp tuyến dưới các dạng sau:
• Tiếp tuyến d // ∆ : y = ax + b ⇒ hệ số góc của tiếp tuyến là k = . a
• Tiếp tuyến d ⊥ ∆ : y = ax + ,
b (a ≠ 0) ⇔ hệ số góc của tiếp tuyến là 1 k = − ⋅ a
• Tiếp tuyến tạo với trục hoành một góc α thì hệ số góc của tiếp tuyến d là k = ± tanα.
Sử dụng máy tính:
Nhập k (−X ) + f (x) CALC X = x nhấn dấu = ta được b . Phương trình tiếp tuyến là 0
d : y = kx + . b Trang 2/25
Ví dụ minh họa
Ví dụ 1. Cho hàm số (C) 3
: y = x − 3x + 2 . Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến đó bằng 9 là:  y = 9x −14  y = 9x +15  y = 9x −1  y = 9x + 8 A.  . B.  . C.  . D.  . y = 9x +18  y = 9x −11  y = 9x + 4  y = 9x + 5 Hướng dẫn giải Ta có 2
y′ = 3x − 3 . Vậy k = y′(x = 9 2 ⇔ 3x − 3 = 9 2
⇔ x = 4 ⇔ x = 2 ∨ x = 2. − . 0 ) 0 0 0 0
+ Với x = 2 ⇒ y = 4 ta có tiếp điểm M (2;4) . 0 0
Phương trình tiếp tuyến tại M là y = 9(x − 2) + 4 ⇒ y = 9x −14. + Với x = 2
− ⇒ y = 0 ta có tiếp điểm N ( 2; − 0) . 0 0
Phương trình tiếp tuyến tại N là y = 9(x + 2) + 0 ⇒ y = 9x +18.
Vậy có hai tiếp tuyến cần tìm là y = 9x −14 và y = 9x+18. Chọn đáp án A.
Sử dụng máy tính:
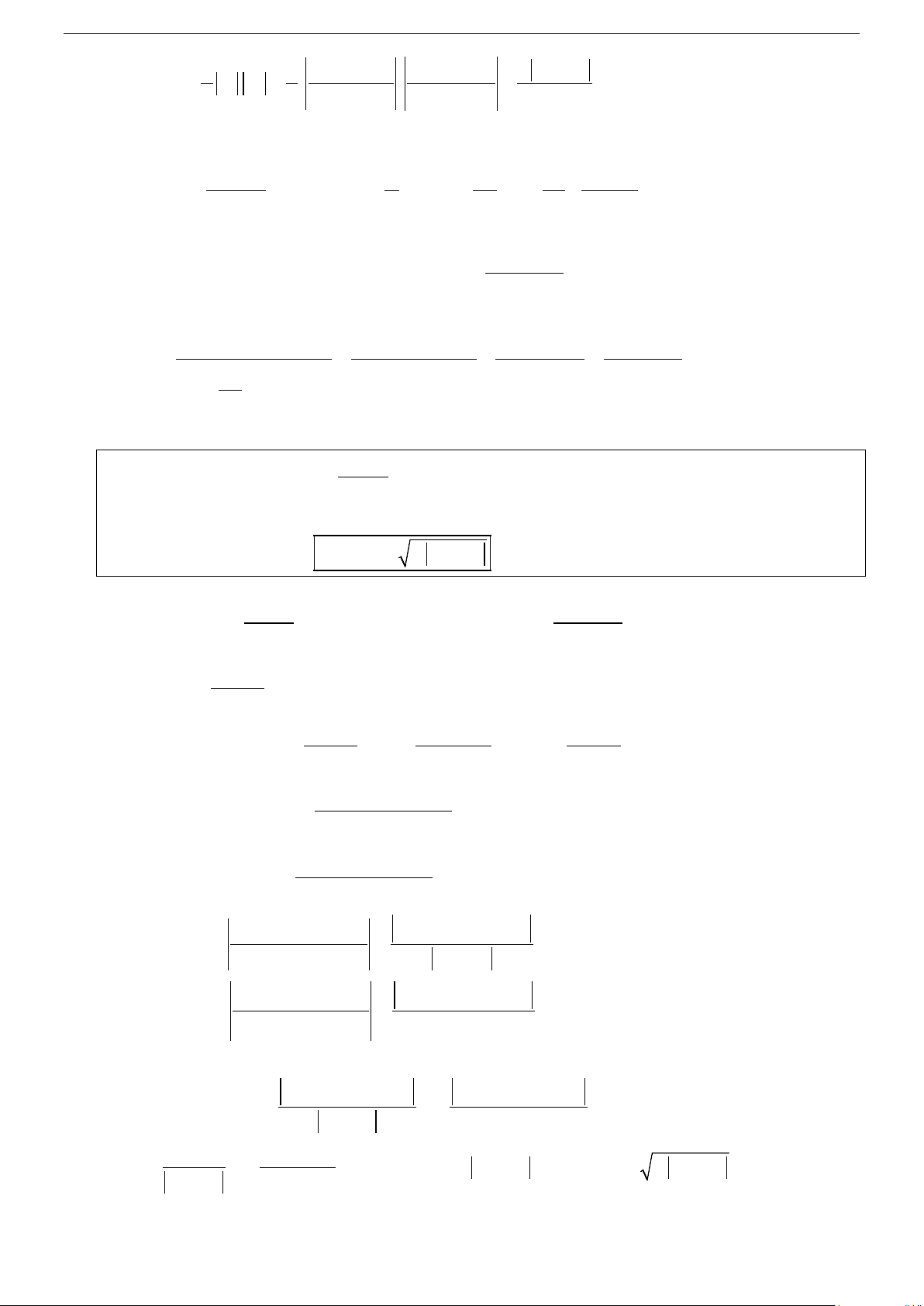
+ Với x = 2 ta nhập (−X ) 3 2 9
+ X − 3X + 2 CALC X = 2 nhấn dấu = ta được 0 14
− ⇒ y = 9x −14. + Với x = 2 − ta nhập (−X ) 3 2 9
+ X − 3X + 2 CALC X = 2
− nhấn dấu = ta được 0
18 ⇒ y = 9x +18.
Ví dụ 2. Cho hàm số (C) 2x +1 : y =
⋅ Viết phương trình tiếp tuyến của (C) x + 2 biết tiếp tuyến song
song với đường thẳng có phương trình ∆ :3x − y + 2 = 0 .
A. y = 3x − 2.
B. y = 3x +14
C. y = 3x + 5.
D. y = 3x −8. Hướng dẫn giải Ta có 3 y ' =
, ∆ :3x − y + 2 = 0 ⇒ y = 3x + 2 . Do tiếp tuyến song song với đường thẳng ∆ (x + 2)2 3 x + 2 =1 x = 1 − nên k = = 3 ⇔ x + 2 =1 ⇔ ⇔ . 2 ( 0 )2 0 0 (   x + 2) x + 2 = 1 − x = 3 − 0 0 0 + Với x = 1 − nhập + 3(−X ) 2X 1 + CALC X = − 0 1 X + 2
nhấn dấu = ta được 2, suy ra
d : y = 3x + 2 (loại do trùng với ∆ ). + Với x = 3 − CALC X = 3 − ⇒ d y = x + . 0
nhấn dấu = ta được 14 : 3 14
Vậy phương trình tiếp tuyến là d : y = 3x +14 . Chọn đáp án B.
Dạng 3. Viết phương trình tiếp tuyến của đồ thị hàm số (C ) : y = f ( x) biết tiếp tuyến đi qua
điểm A( x y
A; A ) .Phương pháp Cách 1.
o Bước 1: Phương trình tiếp tuyến đi qua A(x y hệ số góc k có dạng A; A )
d : y = k (x − x + y ( ) ∗ A ) A
o Bước 2: d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:
f (x) = k (x − x +  y A ) A  .  f ′  ( x) = k
o Bước 3: Giải hệ này tìm được x suy ra k và thế vào phương trình ( )∗, ta được tiếp tuyến cần tìm. Trang 3/25 Cách 2.
o Bước 1. Gọi M (x ; f x là tiếp điểm và tính hệ số góc tiếp tuyến k = y′(x = f ′ x 0 ) ( 0) 0 ( 0)) theo x . 0
o Bước 2. Phương trình tiếp tuyến có dạng: d : y = y′(x . x − x + y 0 ) ( 0 ) 0 ( ) ∗∗ . Do điểm
A(x y ∈d nên y = y′ x
x − x + y . A ( . 0 ) ( A 0 ) A; A )
0 giải phương trình này ta tìm được x0
o Bước 3. Thế x vào ( )
∗∗ ta được tiếp tuyến cần tìm. 0
Chú ý: Đối với dạng viết phương trình tiếp tuyến đi qua điểm việc tính toán tương đối mất thời
gian. Ta có thể sử dụng máy tính thay các đáp án: Cho f (x) bằng kết quả các đáp án. Vào
MODE → 5 → 4 nhập hệ số phương trình. Thông thường máy tính cho số nghiệm thực nhỏ
hơn số bậc của phương trình là 1 thì ta chọn đáp án đó.
Ví dụ minh họa
Ví dụ. Cho hàm số (C) 3 : y = 4
− x + 3x +1. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đi qua điểm A( 1; − 2).  y = 9 − x − 7  y = 4x + 2  y = x − 7
y = −x − 5 A.  . B.  . C.  . D.  . y = 2  y = x +1  y = 3x − 5  y = 2x − 2 Hướng dẫn giải Ta có 2 y ' = 12 − x + 3 .
+ Tiếp tuyến của (C) đi qua A( 1;
− 2) với hệ số góc k có phương trình là d : y = k (x + ) 1 + 2 .
+ d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm: 3  4
− x + 3x +1 = k (x + ) 1 +  2 ( ) 1  2  12 − x + 3 = k  (2)
Thay k từ (2) vào ( ) 1 ta được 3 − x + x + = ( 2 4 3 1 12 − x + 3)(x + ) 1 + 2 x = 1 −  1 8x 12x 4 0 x (x )2 3 2 1 0  ⇔ + − = ⇔ − + = ⇔   1 .  2  x =  2 + Với x = 1 − ⇒ k = 9
− . Phương trình tiếp tuyến là y = 9 − x − 7. + Với 1
x = ⇒ k = 0 . Phương trình tiếp tuyến là y = 2. Chọn đáp án A. 2
Dạng 4. Viết phương trình tiếp tuyến chung của hai đồ thị hàm số (C : y = f x và 1 ) ( )
(C : y = g x . 2 ) ( )  Phương pháp
o Bước 1. Gọi d tiếp tuyến chung của (C , C và x là hoành độ tiếp điểm của d và (C 1 ) 1 ) ( 2 ) 0
thì phương trình d có dạng y = f ′(x . x − x + f x (***) 0 ) ( 0 ) ( 0)
o Bước 2. Dùng điều kiện tiếp xúc của d và (C , tìm được x . 2 ) 0
o Bước 3. Thế x vào (***) ta được tiếp tuyến cần tìm. 0
Ví dụ minh họa
Ví dụ. Cho hai hàm số:
(C : y = f x = 2 x , x > 0 và (C ): y = g (x) 1 2 = 8 − x , 2
− 2 < x < 2 2 . 2 ( ) 1 ) ( ) ( ) 2
Phương trình tiếp tuyến chung của hai đồ thị hàm số là: Trang 4/25 A. 1 y = x + 5. B. 1 y = x −1. C. 1 y = x + 2 D. 1 y = x − 3. 2 2 2 2 Hướng dẫn giải
+ Gọi d là phương trình tiếp tuyến chung của (C , C
x = a ( a > 0 và 2
− 2 < a < 2 2 ) 1 ) ( 2 ) và 0
là hoành độ tiếp điểm của d với (C thì phương trình d là 1 )
y = f ′(x)(x − a) 1 + y =
x − a + 2 a . 0 ( ) a 1 2 8 x − x = + a ( )1 
+ d tiếp xúc với (C khi và chỉ khi hệ sau có nghiệm: 2 a 2 )  −x 1  = (2) 2 2 8− x a Thay (2) vào ( )
1 ta được phương trình hoành độ tiếp điểm của d và (C . 2 )  2 − 2 < x < 2 2 2 2 1 −  2 x 2 8 8 x x  − = − − ⇔ x ≠ 0 2 2 2 8 − x xx  ( 2 8 − x ) 3 = −x − 4( 2 8 −  x )  2 − 2 < x < 2 2  ⇔ x ≠ 0 ⇔ x = 2. −  2
x − 2x −8 = 0  Thay x = 2 − vào (2) ta được 1 1
= ⇔ a = 4 ⇒ x = 4. Vậy phương trình tiếp tuyến chung 0 a 2 cần tìm là 1
y = x + 2 . Chọn đáp án C. 2 Trang 5/25
Bài toán 2: Một số công thức nhanh và tính chất cần biết. Bài toán 2.1: + Cho hàm số ax b  0, d y c x  = ≠ ≠ −
có đồ thị (C). Phương trình tiếp cx d c  +  
tuyến ∆ tại M thuộc (C) và I là giao điểm 2 đường tiệm cận. Ta luôn có:
• Nếu ∆ ⊥ IM thì chỉ tồn tại 2 điểm M thuộc 2 nhánh của đồ thị (C) đối xứng qua
± ad − bc − d I và x =
. Cách nhớ: cx + d = ± ad − bc . M c M     maãu soá cuûa haøm soá töû soá cuûa ñaïo haøm
(I). M luôn là trung điểm của AB (với ,
A B là giao điểm của ∆ với 2 tiệm cận). bc − ad
(II). Diện tích tam giác IAB không đổi với mọi điểm M và S = . IA ∆ B 2 2 c
(III). Nếu E, F thuộc 2 nhánh của đồ thị (C) và E, F đối xứng qua I thì tiếp tuyến tại
E, F song song với nhau. (suy ra một đường thẳng d đi qua E, F thì đi qua tâm I ). Chứng minh: − • Ta có ad bc y′ = ;  d  ; a I  −
là giao điểm của 2 tiệm cận. (  cx + d )2  c c   + 
• Gọi M x ; a x bd MCx  ∈ ≠ −
. Phương trình tiếp tuyến tại M có dạng M ( ) ; Mcx d   c  + M  − + ∆ : ad bc y = ( ax b x − x + . M ) M 2 (cx + d cx + d M ) M Chứng minh (I).   −     − • d bc ad IM ad bcx + ; u∆ 1;  M ;   c c(cx d  +    M )   (cx + d M )2    − − • ∆ ⊥ ⇒ . ∆ = 0 d bc ad ad bc IM IM u ⇔ x + + = M
c c(cx + d M ). 0 (cx + d M )2
(cx + d − ad −bc
± ad − bc − d M )4 ( )2 ⇔ = 0 ⇔ x = . c(cx + d c M )3 M Chứng minh (II).
• Giao điểm của ∆ với tiệm cận ngang là  2 d a A x  +  . M ; c c     + − 
• Giao điểm của ∆ với tiệm cận đứng là d ac x 2 B− ; bc ad M   . c c(c x d  +  M )   d d
x + x = x + − = xA B 2 M 2 Mc c • Xét 
a ac x + bc − ad ax + b . M 2 My + y = + = = y A Bc c  (c x + d ) 2. 2 M cx + d M M
Vậy M luôn là trung điểm của AB . Chứng minh (III).
  2(cx + d   
2(bc − ad )  M ) • IA ; c và IB0;  . c     c(c x d  +  M ) 
• ∆ IAB vuông tại I Trang 6/25
1   1 2(cx + d bc − ad bc − ad M ) 2( ) 2 ⇒ S = = = = hằng số. ∆ IA IB IAB . . . 2 2 c c(c x + d c M ) 2
Vậy diện tích ∆ IAB không đổi với mọi điểm M . Chứng minh (IV):  +     +  • Gọi a x b d d a ax b E 2 2 E x ;
∈(C)  x ≠ − ⇒  F − − x ; E − E E Ecx + d   c   c c cx + d E E
( E, F đối xứng qua I ). −
• Phương trình tiếp tuyến tại E có hệ số góc ad bc k = . E (1) (cx + d E )2
• Phương trình tiếp tuyến tại F có hệ số góc ad − bc ad − bc ad − bc ad − bc k = = = = F (2) . 2   2d   ( 2
− d − cx + d −d − cx cx + d E )2 ( E )2 ( E )2 c − − x +    d E    c  
• Từ (1) và (2) suy ra k = k . E F +
Bài toán 2.2: Cho hàm số ax b y =
có đồ thị là (C), (c ≠ 0, ad − bc ≠ 0) . Gọi điểm M (x ; y 0 0 ) cx + d
trên (C), biết tiếp tuyến của (C) tại điểm M cắt các trục Ox,Oy lần lượt tại ,ABsao cho OA = .
n OB . Khi đó x thoả cx + d = ± . n ad − bc . 0 0
Hướng dẫn giải + − • Xét hàm số ax b y = , (c ad bc
≠ 0, ad − bc ≠ 0) . Ta có y ' = . cx + d (cx + d )2  +  • Gọi 0  ; ax b M x
∈ C là điểm cần tìm. Gọi ∆
C tại M ta có phương trình 0 ( ) cx + tiếp tuyến với ( )  d 0  + − + ∆ ax b ad bc ax b
: y = f '(x )(x − x ) 0 + ⇒ y = x − x + . 2 ( 0 ) 0 0 0 cx + d cx + d cx + d 0 ( 0 ) 0 2  + +  • Gọi A acx bcx bd = ∆ ∩ Ox ⇒ 2 0 0 A −  ;0 . ad bc  −    2  + +
B = ∆ ∩ Oy ⇒ 2 0 0 0; acx bcx bd B   . (cx d )2  +  0  2 2
acx + 2bcx + bd
acx + 2bcx + bd • Ta có 0 0 0 0 OA = = ad − bc ad − bc 2 2
acx + 2bcx + bd
acx + 2bcx + bd 0 0 0 0 OB = = (cx + d cx + d 0 )2 ( 0 )2 (vì ,
A B không trùng O nên 2
acx + 2bcx + bd ≠ 0). 0 0 2 2
acx + 2bcx + bd
acx + 2bcx + bd • Ta có 0 0 0 0 OA = . n OB ⇔ = . n ad − bc (cx + d )2 0 1 1 ⇔ = . n ⇔ cx + d = .
n ad − bc ⇔ cx + d = ± . n ad − bc . 2 ( 0 )2 ad − bc (cx + d 0 ) 0 Trang 7/25
B. BÀI TẬP TRẮC NGHIỆM
Câu 1. Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x + 1 tại điểm A(3; ) 1 là
A. y = −9x − 26 .
B. y = 9x − 26 .
C. y = −9x − 3.
D. y = 9x − 2 .
Câu 2. Phương trình tiếp tuyến của đồ thị hàm số 4 2
y = x − 4x + 1 tại điểm B (1;−2) là
A. y = 4x + 6 .
B. y = 4x + 2 .
C. y = −4x + 6 .
D. y = −4x + 2 . Câu 3. −
Phương trình tiếp tuyến của đồ thị hàm số x 1 y = tại điểm C ( 2 − ;3) là x + 1
A. y = 2x + 1.
B. y = −2x + 7 .
C. y = 2x + 7 .
D. y = −2x −1.
Câu 4. Tiếp tuyến của đồ thị hàm số 3
y = −x + 3x − 2 tại điểm D có hoành độ bằng 2 có phương trình là
A. y = −9x + 14 .
B. y = 9x + 14 .
C. y = −9x + 22 .
D. y = 9x + 22 .
Câu 5. Tiếp tuyến của đồ thị hàm số 4 2
y = −x + 8x tại điểm E có hoành độ bằng –3 có phương trình là
A. y = 60x + 171.
B. y = −60x + 171.
C. y = 60x + 189. D. y = 60 − x +189 . Câu 6. −
Tiếp tuyến của đồ thị hàm số 2x 1 y =
tại điểm F có hoành độ bằng 2 có phương trình là x −1
A. y = −x + 5.
B. y = x + 5.
C. y = −x −1.
D. y = x −1.
Câu 7. Tiếp tuyến của đồ thị hàm số 3 2
y = 2x + 3x tại điểm G có tung độ bằng 5 có phương trình là
A. y = 12x − 7 .
B. y = −12x − 7 .
C. y = 12x + 17 .
D. y = −12x + 17 .
Câu 8. Tiếp tuyến của đồ thị hàm số 4 2
y = x + 2x − 3 tại điểm H có tung độ bằng 21 có phương trình là
y = 40x − 101
y = 40x − 59 A.  . B.  .
y = −40x − 59
y = −40x − 101  y = 40x + 59
y = −40x − 59 C.  . D.  .
y = −40x + 101
y = 40x + 101 Câu 9. +
Tiếp tuyến của đồ thị hàm số x 2 y =
tại điểm I có tung độ bằng 1 có phương trình là 2x −1 A. 1 8 y = x + . B. 1 2 y = − x − . C. 1 8 y = − x + . D. 1 2 y = x − . 5 5 5 5 5 5 5 5
Câu 10. Tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x − 2 có hệ số góc k = 3 − có phương trình là
A. y = −3x − 7 .
B. y = −3x + 7 .
C. y = −3x + 1.
D. y = −3x −1.
Câu 11. Tiếp tuyến của đồ thị hàm số 1 4 2
y = − x + 2x có hệ số góc bằng k = −48 có phương trình là 4
A. y = −48x + 192 . B. y = −48x + 160. C. y = −48x −160. D. y = −48x −192. Câu 12. +
Viết phương trình tiếp tuyến của đồ thị hàm số x 3 y =
biết tiếp tuyến có hệ số góc bằng 4. 1 − xy = 4x − 3  y = 4x − 3  y = 4x + 3  y = 4x + 3 A.  . B.  . C.  . D.  .  y = 4x + 13  y = 4x −13  y = 4x + 13
y = 4x − 13
Câu 13. Có bao nhiêu tiếp tuyến của đồ thị hàm số 3 2
y = −x + 2x song song với đường thẳng y = x ? A. 2. B. 1. C. 3. D. 4.
Câu 14. Tiếp tuyến song song với đường thẳng y = −36x + 5 của đồ thị hàm số 4 2
y = x + x − 2 có phương trình là
A. y = −36x − 54 .
B. y = −36x + 54. C. y = −36x − 90.
D. y = −36x + 90 . Trang 8/25 Câu 15. − + Cho hàm x 5 y =
có đồ thị là (C). Viết phương trình tiếp tuyến của (C) sao cho tiếp tuyến x + 2
đó song song với đường thẳng 1 5
d : y = − x + . 7 7  1 5 y = − x +  1 5  y = − x + −  A. 7 7  . B. 7 7  . C. 1 23 y = − x − . D. 1 23 y = − x + . 1 23
y = − x − 1 23  = − + 7 7 7 7  y x  7 7  7 7 Câu 16. Cho hàm 3
y = 2x − 3x −1 có đồ thị là (C). Tiếp tuyến của đồ thị (C) vuông góc với đường
thẳng x + 21y − 2 = 0 có phương trình là:  1 y  − = x − 33 1  = −
y = −21x − 33
y = 21x − 33 y x 33  A. 21  . B. . C. . D. 21  . 1    y  = − +  = + − = x + 31 y 21x 31 y 21x 31 1   y = x + 31  21  21
Câu 17. Tiếp tuyến của đồ thị hàm số 4 2
y = −x − 2x + 3 vuông góc với đường thẳng x − 8y + 2017 = 0 có phương trình là A. 1 y = − x + 8 .
B. y = 8x + 8 .
C. y = −8x + 8 . D. 1 y = x − 8 . 8 8 Câu 18. −
Phương trình tiếp tuyến của đồ thị hàm số 2x 2 y =
biết tiếp tuyến vuông góc với đường x + 2 thẳng y = 6 − x +1 là  1 1 y = − x +  1 1  y = x +  A. 1 1 y = x + . B. 1 y = x −1. C. 6 3  . D. 6 3  . 6 3 6 1
y = − x −1  1 13 = +  y x  6  6 3
Câu 19. Có bao nhiêu tiếp tuyến của đồ thị hàm số 4 2
y = x − 4x tại giao điểm của đồ thị với trục Ox ? A. 4. B. 2. C. 1. D. 3. Câu 20. Cho hàm số 3
y = −x + 3x − 2 có đồ thị (C). Tiếp tuyến của đồ thị (C) tại giao điểm của (C)
với trục hoành có phương trình là  y = 0  y = 0
A. y = −9x −18. B.
. C. y = −9x + 18 . D.  .
y = −9x − 18
y = −9x + 18 Câu 21. −
Gọi d là tiếp tuyến của đồ thị hàm số (C): x 5 y =
tại giao điểm A của (C) và trục hoành. −x + 1
Khi đó, phương trình của đường thẳng d là A. 1 5 y = x − . B. 1 5 y = − x − . C. 1 5 y = x + . D. 1 5 y = − x + . 4 4 4 4 4 4 4 4
Câu 22. Tại giao điểm của đồ thị hàm số (C): 3
y = 2x − 6x + 1 và trục Oy ta lập được tiếp tuyến có phương trình là
A. y = 6x −1.
B. y = −6x −1.
C. y = 6x + 1.
D. y = −6x + 1.
Câu 23. Phương trình tiếp tuyến của đồ thị hàm số (C): 1 4 2
y = − x + 3x − 2 tại giao điểm M của (C) 4 với trục tung là  y = −2  y = −2 A.  . B. y = 2 . C. y = −2 . D.  .  y = 2  y = 0 Trang 9/25 Câu 24. +
Gọi d là tiếp tuyến của đồ thị hàm số (C): 2x 1 y =
tại giao điểm A của (C) và trục tung. x − 3
Khi đó, phương trình của đường thẳng d là A. 7 1 y = x − . B. 7 1 y = − x + . C. 7 1 y = − x − . D. 7 1 y = x + . 9 3 9 3 9 3 9 3 3
Câu 25. Tiếp tuyến của đồ thị hàm số x 2 (C) : y =
− 2x + 3x + 1 song song với đường thẳng 3
y = 3x + 2016 có phương trình là  2 y  = − = 3x −  2 y = 3x − y 3x 8  2 y = 3x + A.  3 . B.  . C.  . D.  .  3  2  3 y = 3x +   y = 3x − 8  y = 3x + 8  3  y = 3x + 8 3
Câu 26. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số x 2 y =
− 2x + 3x − 5 sẽ 3
A. song song với đường thẳng x =1.
B. song song với trục hoành.
C. có hệ số góc dương.
D. có hệ số góc bằng 1 − .
Câu 27. Phương trình tiếp tuyến với đồ thị hàm số 2x y =
tại điểm có tung độ bằng 3 là x −1
A. x − 2y − 7 = 0 .
B. x + y − 8 = 0 .
C. 2x − y − 9 = 0 .
D. x + 2y − 9 = 0.
Câu 28. Cho đường cong 3 2
(C) : y = x − 3x . Viết phương trình tiếp tuyến của (C) tại điểm thuộc
(C) và có hoành độ x = 1 − . 0 A. y = 9 − x + 5 .
B. y = 9x + 5 .
C. y = 9x − 5 .
D. y = −9x − 5.
Câu 29. Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = 3x − x − 7x + 1 tại điểm A(0; ) 1 là
A. y = x +1. B. y = 7 − x +1. C. y =1. D. y = 0. Câu 30. Cho hàm số 3 2
y = x − 3x + 1 có đồ thị (C) . Khi đó phương trình tiếp tuyến của đồ thị (C) tại
điểm có hoành độ bằng 5 là
A. y = −45x + 276.
B. y = −45x + 174.
C. y = 45x + 276 .
D. y = 45x −174 . Câu 31. Cho hàm số 3 2
y = x − 3x + 6x + 1 có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ
số góc nhỏ nhất có phương trình là
A. y = −3x + 2 .
B. y = 3x + 2.
C. y = −3x + 8 .
D. y = 3x + 8 . Câu 32. Cho hàm số 3 2
y = −x + 6x + 3x −1 có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có
hệ số góc lớn nhất có phương trình là
A. y =15x + 55 .
B. y = −15x − 5 .
C. y = 15x − 5 .
D. y = −15x + 55 . Câu 33. Cho hàm số 3
y = x + x + 1 có đồ thị (C). Khẳng định nào sau đây là khẳng định sai?
A. Hàm số luôn đồng biến trên  .
B. Trên (C) tồn tại hai điểm (
A x ; y ), B(x ; y ) sao cho hai tiếp tuyến của (C) tại A và B vuông 1 1 2 2 góc.
C. Tiếp tuyến của (C) tại điểm có hoành độ bằng 1 có phương trình là y = 4x −1.
D. Đồ thị (C) chỉ cắt trục hoành tại một điểm duy nhất.
Câu 34. Đường thẳng y = ax − b tiếp xúc với đồ thị hàm số 3 2
y = x + 2x − x + 2 tại điểm M (1;0). Khi đó ta có A. ab = 36. B. ab = −6 . C. ab = −36 . D. ab = −5 . Câu 35. Cho hàm số 3 2
y = x − x + 2x + 5 có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ
số góc nhỏ nhất, thì hệ số góc của tiếp tuyến đó là Trang 10/25 A. 1 . B. 2 . C. 4 . D. 5 . 3 3 3 3 Câu 36. Cho hàm số 3x y =
có đồ thị (C). Tiếp tuyến của (C) tạo với trục hoành góc 0 60 có phương x −1 trình là
y = − 3x + 4 3
y = 3x − 4 3 A.  . B.  .  y = 3x  y = 3x
y = − 3x + 4 3
y = − 3x − 4 3 C.  . D.  .
 y = − 3x
 y = − 3x Câu 37. Cho hàm số 3 2
y = x − 3mx + 3(m + 1)x + 1 (1) , m là tham số. Kí hiệu (C là đồ thị hàm số (1) m )
và K là điểm thuộc (C , có hoành độ bằng 1
− . Tập tất cả các giá trị của tham số m để tiếp m )
tuyến của (C tại điểm K song song với đường thẳng d :3x + y = 0 là m ) A. { } 1 − . B. ∅ . C. { 1 − ;− }1. D. { 1 − . 3} 3 Câu 38. Cho hàm số 4 1 2
y = x + mx + m −1 có đồ thị (C). Biết tiếp tuyến của (C) tại điểm có hoành độ 2
bằng –1 vuông góc với đường thẳng có phương trình x − 3y + 1 = 0 . Khi đó giá trị của m là A. m = −1. B. m = 0 . C. 13 m = − . D. 11 m = − . 3 3
Câu 39. Cho hàm số y = 2x +1 có đồ thị (C). Biết tiếp tuyến d của đồ thị (C) vuông góc với đường
thẳng y = −3x + 2017 . Hỏi hoành độ tiếp điểm của d và (C) bằng bao nhiêu? A. 4 − . B. 1. C. 4. D. – 4. 9 Câu 40. Cho hàm số 3
y = 3x − 4x có đồ thị (C). Từ điểm M (1;3) có thể kẻ được bao nhiêu tiếp tuyến
với đồ thị hàm số (C) ? A. 0. B. 3. C. 2. D. 1. Câu 41. Cho hàm số 3
y = x + x + 2 có đồ thị (C). Tiếp tuyến tại điểm N (1;4) của (C) cắt đồ thị (C) tại
điểm thứ hai là M. Khi đó tọa độ điểm M là A. M (−1;0) .
B. M (−2;−8) . C. M (0;2). D. M (2;12) . Câu 42. Cho hàm số 3 2
y = x − x + x + 1 có đồ thị (C). Tiếp tuyến tại điểm N của (C) cắt đồ thị (C) tại
điểm thứ hai là M (−1;−2) . Khi đó tọa độ điểm N là A. ( 1; − 4 − ). B. (2;5) . C. (1;2) . D. (0; ) 1 . Câu 43. Cho hàm số 3 2
y = x + 3mx + (m + )
1 x + 1 có đồ thị (C). Với giá trị nào của m thì tiếp tuyến
với đồ thị (C) tại điểm có hoành độ bằng –1 đi qua A(1;3) ? A. 7 m = . B. 1 m = . C. 1 m = − . D. 7 m = − . 9 2 2 9 Câu 44. − Cho hàm số x m y =
có đồ thị (C . Với giá trị nào của m thì tiếp tuyến của (C) tại điểm có m ) x + 1
hoành độ bằng 0 song song với đường thẳng y = 3x + 1 ? A. m = 3 . B. m = 1. C. m = −2 . D. m = 2. Trang 11/25 Câu 45. Cho hàm số x y =
có đồ thị (C) và gốc tọa độ O. Gọi ∆ là tiếp tuyến của (C), biết ∆ cắt x + 1
trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân. Phương trình ∆ là
A. y = x + 1.
B. y = x + 4.
C. y = x − 4 .
D. y = x . Câu 46. Cho hàm số 4 2
y = −x − x + 6 có đồ thị (C). Tiếp tuyến của đồ thị (C) cắt các trục Ox, Oy lần
lượt tại hai điểm A, B sao cho OB = 36OA có phương trình là:
x − 36y − 4 = 0
y = −36x − 86 A.  . B.  .
x + 36y − 4 = 0
y = 36x − 86
y = −36x + 58
x − 36y + 14 = 0 C.  . D.  .  y = 36x + 58
x + 36y + 14 = 0 Câu 47. − Cho hàm số x 1 y =
có đồ thị là (C). Gọi điểm M (x ; y với x > −1 là điểm thuộc 0 0 ) 2 (x + ) 1 0
(C), biết tiếp tuyến của (C) tại điểm M cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt ,
A B và tam giác OAB có trọng tâm G nằm trên đường thẳng d : 4x + y = 0. Hỏi giá trị
của x + 2y bằng bao nhiêu? 0 0 A. 7 − . B. 7 . C. 5 . D. 5 − . 2 2 2 2 Câu 48. Cho hàm số 4 2
y = x − 2mx + m (1) , m là tham số thực. Kí hiệu (C là đồ thị hàm số (1); d m )
là tiếp tuyến của (C tại điểm có hoành độ bằng 1. Tìm m để khoảng cách từ điểm 3 B  ; 1 m ) 4   
đến đường thẳng d đạt giá trị lớn nhất? A. m = −1. B. m = 1. C. m = 2. D. m = −2 . Câu 49. + Cho hàm số 2x 3 y =
có đồ thị là (C). Có bao nhiêu tiếp tuyến của đồ thị (C) tại những x + 1
điểm thuộc đồ thị có khoảng cách đến đường thẳng d : 3x + 4y − 2 = 0 bằng 2. 1 A. 2. B. 3. C. 4. D. 0. Câu 50. − Cho hàm số 2x 1 y =
có đồ thị là (C). Gọi I là giao điểm hai tiệm cận của (C). Tìm điểm x −1
M thuộc (C)có hoành độ lớn hơn 1 sao cho tiếp tuyến của (C)tại M vuông góc với đường thẳng MI ? A. 7 M 4;    . B. 5 M 3; . C. M (2;3) . D. M (5;3) . 3      2  Câu 51. − + Cho hàm số x 1 y =
có đồ thị là (C), đường thẳng d : y = x + m . Với mọi m ta luôn có d 2x −1
cắt (C) tại 2 điểm phân biệt ,
A B . Gọi k , k lần lượt là hệ số góc của các tiếp tuyến với (C) 1 2 tại ,
A B . Tìm m để tổng k + k đạt giá trị lớn nhất. 1 2 A. m = −1. B. m = −2 . C. m = 3 . D. m = −5 . Câu 52. + Cho hàm số x 2 y = ( )
1 .Viết phương trình tiếp tuyến của đồ thị hàm số ( ) 1 , biết tiếp tuyến 2x + 3
đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt ,
A B và tam giác OAB cân tại gốc tọa độ O .
A. y = −x − 2 . B. y = − . x
C. y = −x + 2.
D. y = −x + 1. Trang 12/25 Câu 53. − Cho hàm số 2x 1 y =
có đồ thị (C). Lập phương trình tiếp tuyến của đồ thị (C) sao cho tiếp x −1
tuyến này cắt các trục Ox, Oy lần lượt tại các điểm A và B thoả mãn OA = 4OB .  1 5 y = − x +  1 5  y = − x +  A. 4 4  . B. 4 4  . 1 13  y = − x + 1 13  = − +  y x  4 4  4 2  1 5 y = − x +  1 5  y = − x +  C. 4 2  . D. 4 2  . 1 13  y = − x + 1 13  = − +  y x  4 2  4 4 Câu 54. Cho hàm số x y =
có đồ thị (C). Gọi ∆ là tiếp tuyến tại điểm M (x ; y (với x > 0 ) 0 0 ) x −1 0
thuộc đồ thị (C). Để khoảng cách từ tâm đối xứng I của đồ thị (C) đến tiếp tuyến ∆ là lớn
nhất thì tung độ của điểm M gần giá trị nào nhất? π π π π A. 7 . B. 3 . C. 5 . D. . 2 2 2 2 − Câu 55. 2x 1
Cho hàm số y =
có đồ thị (C). Biết khoảng cách từ I ( 1; − 2) C tại x +1
đến tiếp tuyến của ( )
M là lớn nhất thì tung độ của điểm M nằm ở góc phần tư thứ hai, gần giá trị nào nhất? A. 3e. B. 2e . C. e . D. 4e . Câu 56. − Cho hàm số 2x 3 y =
có đồ thị (C). Biết tiếp tuyến tại M của (C) cắt hai tiệm cận của (C) x − 2 
tại A , B sao cho AB ngắn nhất. Khi đó, độ dài lớn nhất của vectơ OM gần giá trị nào nhất ? A. 7. B. 5. C. 6. D. 4. Câu 57. − Cho hàm số x 2 y =
có đồ thị (C). Phương trình tiếp tuyến ∆ của đồ thị hàm số (C) tạo với x +1
hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó, khoảng cách
từ tâm đối xứng của đồ thị (C) đến ∆ bằng? A. 3 . B. 2 6 . C. 2 3 . D. 6 . Câu 58. + Cho hàm số 2x 1 y =
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến ∆ của x −1
(C) cắt 2 tiệm cận tại A và B sao cho chu vi tam giác IAB đạt giá trị nhỏ nhất. Khoảng cách
lớn nhất từ gốc tọa độ đến tiếp tuyến ∆ gần giá trị nào nhất? A. 6. B. 4. C. 3. D. 5. Câu 59. − Cho hàm số 2x 1 y =
có đồ thị (C). Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến x − 2
∆ của (C) tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác
IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến ∆ của (C) tạo với hai trục tọa độ một tam giác
có diện tích lớn nhất thuộc khoảng nào? A. (27; 28). B. (28; 29). C. (26; 27) . D. (29; 30) .
C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B D C A A A A B C D B D B A C C C D D B Trang 13/25
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
D D C C A B D B B D B A B A D C B A C C
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59
B C B D B C A B C C A A A D C D D D A
II –HƯỚNG DẪN GIẢI Câu 1. Chọn B. Tính 2
y ' = 3x − 6x ⇒ y '(3) = 9 ⇒ phương trình tiếp tuyến là y = 9x − 26 . Câu 2. Chọn D. Tính 3
y ' = 4x −8x ⇒ y '( ) 1 = 4
− ⇒ phương trình tiếp tuyến là y = 4 − x + 2. Câu 3. Chọn C. Tính 2 y ' = ⇒ y ' 2
− = 2 ⇒ phương trình tiếp tuyến là y = 2x + 7 . 2 ( ) (x + ) 1 Câu 4. Chọn A.
Tính y = y(2) = 4 − và 2 y ' = 3
− x + 3 ⇒ y '(2) = 9
− . Vậy phương trình tiếp tuyến là 0 y = 9 − x +14 . Câu 5. Chọn A. Tính y = y( 3) − = 9 − và 3 y ' = 4
− x +16x ⇒ y '( 3
− ) = 60 . Vậy phương trình tiếp tuyến là 0 y = 60x +171. Câu 6. Chọn A. −
Tính y = y(2) = 3 và 1 y ' = ⇒ y ' 2 = 1
− . Vậy phương trình tiếp tuyến là y = −x + 5 . 2 ( ) 0 (x − )1 Câu 7. Chọn A. Giải phương trình 3 2
2x + 3x = 5 ⇔ x =1, và 2
y ' = 6x + 6x ⇒ y '( ) 1 =12 . Vậy phương trình 0 0 0
tiếp tuyến là y =12x − 7 . Câu 8. Chọn B. x = 2 Giải phương trình 4 2 0
x + 2x − 3 = 21 ⇔ . Đồng thời 3
y ' = 4x + 4x , suy ra 0 0 x = 2 −  0  y '(2) = 40 
. Vậy có hai tiếp tuyến cần tìm là y = 40x − 59 và y = 40 − x −101.  y '  ( 2 − ) = 40 − Câu 9. Chọn C. + − −
Giải phương trình x 2 5 1 0
= 1 ⇔ x = 3 và y ' = ⇒ y ' 3 = . Phương trình tiếp 2 ( ) 0 2x −1 2x −1 5 0 ( ) tuyến là 1 8 y = − x + . 5 5 Câu 10. Chọn D.
Giải phương trình y '(x ) 2 = 3
− ⇔ 3x − 6x + 3 = 0 ⇔ x =1. Đồng thời y ( ) 1 = 4 − nên phương 0 0 0 0
trình tiếp tuyến là y = 3 − x −1. Câu 11. Chọn B.
Giải phương trình y '(x ) 3 = 48
− ⇔ −x + 4x + 48 = 0 ⇔ x = 4 . Đồng thời y (4) = 32 − nên 0 0 0 0
phương trình tiếp tuyến cần tìm là y = 48 − x +160 .
Câu 12. Chọn D. Giải phương trình Trang 14/25 4
x = 0 ⇒ y 0 = 3 ⇒ pttt : y = 4x + 3 0 ( ) y '(x = 4 ⇔ = 4 ⇔ . 0 ) (  1 − x
x = 2 ⇒ y 2 = −5 ⇒ pttt : y = 4x − 13 0 )2  0 ( ) Câu 13. Chọn B. Giải phương trình
x =1⇒ y 1 =1⇒ pttt : y = x (trùng) 0 ( ) y '(x ) 2 1 3x 4x 1 0  = ⇔ − + − = ⇔ . 0 0 0  1  1  5 4 x = ⇒ y = ⇒  
pttt : y = x − 0  3  3  27 27 Câu 14. Chọn A.
Giải phương trình y '(x ) 3 = 36
− ⇔ 4x + 2x + 36 = 0 ⇔ x = 2
− . Đồng thời y ( 2 − ) =18 nên 0 0 0 0
phương trình tiếp tuyến cần tìm là y = 36 − x − 54 . Câu 15. Chọn C. Giải phương trình  1 5
x = 5 ⇒ y 5 = 0 ⇒ pttt : y = − x + ( trùng )  0 ( ) y ( 1 7 − 1 − 7 7 ' x = − ⇔ = ⇔  . 0 ) 7 (x + 2)2 7  1 23 0 x = 9 − ⇒ y 9 − = 2
− ⇒ pttt : y = − x − 0 ( )  7 7 Câu 16. Chọn C. Giải phương trình
x = 2 ⇒ y 2 = 9
⇒ pttt : y = 21x − 33 0 ( ) y '(x = 21 ⇔ . 0 ) 
x = −2 ⇒ y −2 = −11⇒ pttt : y = 21x + 31  0 ( ) Câu 17. Chọn C.
Giải phương trình y '(x = 8
− ⇔ x =1. Đồng thời y ( )
1 = 0 nên phương trình tiếp tuyến cần 0 ) 0 tìm là y = 8 − x + 8. Câu 18. Chọn D.  1 1 x = 4 ⇒ y 4 =1
⇒ pttt : y = x +  0 ( )
Giải phương trình y ( 1 6 3 ' x = ⇔  . 0 ) 6  1 13 x = 8 − ⇒ y 8
− = 3 ⇒ pttt : y = x + 0 ( )  6 3 Câu 19. Chọn D.
x = 0 ⇒ y '(0) = 0 ⇒ pttt : y = 0 Giải phương trình 4 2 x 4x 0  −
= ⇔ x = 2 ⇒ y '(2) =16 ⇒ pttt : y =16x − 32  . x = 2 − ⇒ y '( 2) − = 16
− ⇒ pttt : y = 16 − x −  32 Câu 20. Chọn B. Ta giải phương trình
x = 1 ⇒ y '(1) = 0 ⇒ pttt : y = 0 3
−x + 3x − 2 = 0 ⇔  .
x = −2 ⇒ y '(−2) = −9 ⇒ pttt : y = −9x − 18 Câu 21. Chọn D. −
Ta giải phương trình x 5 = 0 ⇔ x = 5 . Đồng thời 1
y '(5) = − nên phương trình tiếp tuyến −x +1 4 cần tìm là 1 5 y = − x + . 4 4 Câu 22. Chọn D.
Giao điểm của (C) và Oy là A(0; ) 1 ⇒ y '(0) = 6
− nên phương trình tiếp tuyến là y = 6 − x +1 . Câu 23. Chọn C.
Giao điểm của (C) và Oy là M (0; 2
− ) ⇒ y '(0) = 0 nên phương trình tiếp tuyến là y = 2 − . Trang 15/25 Câu 24. Chọn C.
Giao điểm của (C) và Oy là  1  7 A 0;− ⇒  y '(0) = − 
nên phương trình tiếp tuyến là  3  9 7 1 y = − x − . 9 3 Câu 25. Chọn A.  7 2 x =1⇒ y 1 =
⇒ pttt : y = 3x −
Ta giải phương trình y '(x 3  = ⇔ 3 3 . 0 ) 0 ( ) 
x = 3 ⇒ y 3 =1
⇒ pttt : y = 3x −8  0 ( ) Câu 26. Chọn B.  11 x − = 1⇒ y 1 =  0 ( ) Ta có y ' = 0 ⇔ 3 
. Vậy tiếp tuyến song song trục hoành.
x = 3 ⇒ y 3 = 5, − y ' 3 = 0  0 ( ) ( ) Câu 27. Chọn D.
Theo giả thiết ta có y = 3 ⇒ x = 3 và 1
y '(3) = − . Vậy phương trình tiếp tuyến là 0 0 2
x + 2y − 9 = 0 . Câu 28. Chọn B.
Theo giả thiết ta có x = 1 − ⇒ y = 4 − và y '( 1)
− = 9. Vậy phương trình tiếp tuyến là 0 0 y = 9x + 5 . Câu 29. Chọn B.
Theo giả thiết ta có x = 0 ⇒ y =1 và y '(0) = 7
− . Vậy phương trình tiếp tuyến là y = 7 − x +1. 0 0 Câu 30. Chọn D.
Theo giả thiết ta có x = 5 ⇒ y = 51 và y '(5) = 45. Vậy phương trình tiếp tuyến là 0 0
y = 45x −174 . Câu 31. Chọn B. Ta có 2 2
y ' = 3x − 6x + 6 = 3(x −1) + 3 ≥ 3 ⇒ min y ' = 3 khi x = x = 1 ⇒ y = y(1) = 5. 0 0
Khi đó phương trình tiếp tuyến y = 3(x −1) + 5 = 3x + 2. Câu 32. Chọn A. Ta có 2 2 y ' = 3
− x +12x + 3 = 3
− (x + 2) +15 ≤15 ⇒ max y ' =15 khi x = x = 2 − . Lúc đó 0 y = y( 2) − = 25 . 0
Khi đó phương trình tiếp tuyến y = 15(x + 2) + 25 = 15x + 55 . Câu 33. Chọn B.
[Phương pháp tự luận] 2
y '(x ) = 3x +1> 0 Ta có 2 1 1 . ,
y ' = 3x +1 > 0 ⇒ 
⇒ y (x ).y (x ) > 0 1 2 2
y '(x ) = 3x +1 > 0 2 2
hay y '(x ).y '(x ) ≠ 1
− . Suy ra 2 tiếp tuyến A và B không vuông góc. 1 2
[Phương pháp trắc nghiệm] Ta có 2
y ' = 3x +1 > 0, x ∀ ∈  .
Suy ra hàm số đồng biến trên  và cắt trục hoành tại một điểm duy nhất→ A, D đúng.
Với x =1⇒ y '(1) = 4, y = 3 . Vậy phương trình tiếp tuyến y = 4(x −1) + 3 = 4x −1→ C đúng. 0 0 Câu 34. Chọn A. Trang 16/25 Ta có 2
y ' = 3x + 4x −1⇒ y '(1) = 6 . Khi đó phương trình tiếp tuyến tại M (1;0) là a = 6
y = 6(x −1) = 6x − 6 , nên  ⇒ ab = 36 . b  = 6 Câu 35. Chọn D. 2 Ta có 2  2 2 1  5  1  5 5 5
y ' = 3x − 2x + 2 = 3 1
x − x +  + = 3 x − + ≥ ⇒ 
min y ' = khi x = x = .  3 9  3  3  3 3 3 0 3 Câu 36. Chọn C. − Ta có 3 y ' = < 0, x
∀ ≠ 1. Tiếp tuyến tại điểm M (x ; y )∈(C) tạo với Ox góc 0 60 2 (x −1) 0 0 0 y'<0 −
⇒ y '(x ) = ± tan 60 = ± 3 
→ y '(x ) = − 3 3 2 ⇒ = − 3 ⇔ (x −1) =1 0 0 2 0 (x −1) 0
x = 2 ⇒ y = 2 3
y = − 3x + 4 3 0 0 ⇔ 
. Các tiếp tuyến tương ứng có phương trình là  .
x = 0 ⇒ y = 0 0 0
 y = − 3x Câu 37. Chọn B. Ta có 2
y ' = 3x − 6mx + 3(m +1) . Do K ∈(C và có hoành độ bằng 1 − , suy ra m ) K ( 1; − 6 − m − 3).
Khi đó tiếp tuyến tại K có phương trình
∆ : y = y '( 1)
− (x +1) − 6m − 3 = (9m + 6)x + 3m + 3 .
Đường thẳng ∆ song song với đường thẳng d 9m+6= 3− m= 1−
⇒ 3x + y = 0 ⇔ y = 3 − x ⇔  ⇔ . 3  m 3 0  + ≠ m ≠ 1 −
Vậy không tồn tại m , ta chọn ∅ . Câu 38. Chọn A. Ta có 3
y ' = 4x + mx và đường thẳng x − 3y + 1 = 0 viết thành 1 1 y = x + . 3 3
Theo yêu cầu bài toán, phải có y '(− )
1 = −3 ⇔ −4 − m = −3 ⇔ m = −1. Câu 39. Chọn C. Ta có 1 y ' =
. Gọi x là hoành độ tiếp điểm của d và (C). 2x + 1 0
Theo yêu cầu bài toán, ta có y ( 1 1 1 ' x = ⇔
= ⇔ 2x + 1 = 9 ⇔ x = 4 . 0 ) 0 0 3 2x + 1 3 0 Câu 40. Chọn C.
Đường thẳng đi qua M (1;3) có hệ số góc k có dạng d : y = k (x − ) 1 + 3. 3
3x − 4x = k (x − ) 1 +  3 ( ) 1
d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:  . Thay 2
3 − 12x = k  (2) (2) vào (1) ta được x = 0 k = 3 3 3x 4x ( 2 3 12x )(x ) 3 2 1 3 8x 12x 0  − = − − + ⇔ − = ⇔ 3 ⇒  . x = k = 24 −  2 Vậy có 2 tiếp tuyến. Câu 41. Chọn B.
Phương pháp tự luận Ta có 2
y ' = 3x + 1 ⇒ y '( )
1 = 4 , suy ra tiếp tuyến tại N (1;4) là ∆ : y = 4x .
Phương trình hoành độ giao điểm của ∆ và (C) là Trang 17/25 x = 1 3 3
x + x + 2 = 4x ⇔ x − 3x + 2 = 0 ⇔  .
x = −2 ⇒ y = −8
Phương pháp trắc nghiệm 2 b
x + x = − (Với 3 2
y = ax + bx + cx + d là hàm số ban đầu) N M a
⇔ 2 + x = ⇔ x = − ⇒ M − − . M 0 M 2 ( 2; 8) Câu 42. Chọn C.
Phương pháp tự luận
Đường thẳng ∆ đi qua điểm M (−1;−2) có hệ số góc k có dạng ∆ : y = k (x + ) 1 − 2.
∆ là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm: 3 2
x − x + x +1 = k (x + ) 1 −  2 ( ) 1  . 2 3
x − 2x +1 = k  (2) Thay (2) vào (1) ta được x = −
x − x + x +1 = (3x − 2x + ) 1 (x + ) 1 − 2 ⇔ (x + )2 1 3 2 2 1 (x − ) 1 = 0 ⇔ ⇒  N (1;2).Phư
x = 1⇒ y = 2
ơng pháp trắc nghiệm 2 b
x + x = − (Với 3 2
y = ax + bx + cx + d là hàm số ban đầu) N M a
⇔ 2x + − = ⇔ x = ⇒ N . N ( 1) 1 N 1 (1;2) Câu 43. Chọn B. Ta có 2
y ' = 3x + 6mx + m + 1. Gọi M (x ; y là tiếp điểm của tiếp tuyến cần lập. 0 0 ) y '(− ) 1 = 4 − 5m Khi đó x = −1 ⇒
, suy ra phương trình tiếp tuyến là 0 
 y = 2m −1 0
∆ : y = (4 − 5m)(x + ) 1 + 2m −1.
Do A( ) ∈ ∆ ⇒ = ( − m)( + ) 1 1;3 3 4 5
1 1 + 2m −1 ⇔ m = . 2 Câu 44. Chọn D. + Ta có 1 ' m y =
khi đó y '(0) = 3 ⇔ 1+ m = 3 ⇔ m = 2 . (x + )2 1 Câu 45. Chọn B. Ta có 1 y ' = > 0, x
∀ ≠ −1. Gọi M (x ; y là tiếp điểm của (C) với tiếp tuyến cần lập. 0 0 ) (x + )2 1
Tam giác OAB cân tại O nên OA = OB, suy ra  = > x y '(x ) y 1 0 ' 0 = ±1 
→ y ' x = 1 ⇔ = 1 ⇔ . 0 ( 0 ) 0 (  x + )2 1 x = −2 0 0
• Với x = 0 ⇒ y = 0 (loại, do M (0;0) ≡ O ). 0 0
• Với x = −2 ⇒ y = 2 , suy ra phương trình tiếp tuyến ∆ : y = x + 4 . 0 0 Câu 46. Chọn C.
Do OB = 36 ⇒ y '(x ) = 36 ± . 0 OA • Với 3 3 y '(x ) = 36 − ⇔ 4
− x − 2x = 36
− ⇔ 4x + 2x − 36 = 0 ⇔ x = 2 . 0 0 0 0 0
Vậy y = y(2) = 14
− . Suy ra phương trình tiếp tuyến y = 36 − x + 58 . 0 • Với 3 3
y '(x ) = 36 ⇔ 4
− x − 2x = 36 ⇔ 4x + 2x + 36 = 0 ⇔ x = 2 − . 0 0 0 0 0 Trang 18/25 Vậy y = y( 2) − = 14
− . Suy ra phương trình tiếp tuyến y = 36x + 58 . 0 Câu 47. Chọn A.  −  • Gọi x 1 0 M x ;
∈ C với x ≠ 1 − là điểm cần tìm. 0  2(x 1  + 0  0 ) ( ) 
• Gọi ∆ tiếp tuyến của (C) tại M ta có phương trình. x −1 1 x −1 0 0
∆ : y = f '(x )(x − x ) + = (x − x ) + . 0 0 2(x +1) x +1 2(x +1) 0 ( 0 )2 0 0 2  − −  2  − − 
• Gọi A = ∆ ∩ Ox ⇒ x 2x 1 x 2x 1 0 0 A − 
;0 và B = ∆ ∩ Oy ⇒ 0 0 B 0; . 2     2 2(x +  1) 0 
• Khi đó ∆ tạo với hai trục tọa độ OA ∆
B có trọng tâm là 2 2
x − 2x −1 x − 2x −1 0 0 0 0 G − ; . 2 6 6(x 1)  +  0  2 2 − − − −
• Do G thuộc đường thẳng 4x + y = 0 ⇒ x 2x 1 x 2x 1 0 0 0 0 4. − + = 0 2 6 6(x + 1) 0 1 ⇔ 4 = (vì ,
A B không trùng O nên 2
x − 2x −1 ≠ 0) (x + )2 1 0 0 0  1  1 x + 1 = x = −  0  0 2 2 ⇔  ⇔  . 1 3 x 1  + = − x = − 0 0  2  2
• Vì x > −1 nên chỉ chọn 1  1 3  7
x = − ⇒ M − ;−  ⇒ x + 2y = − . 0 0 0 0 2  2 2  2 Câu 48. Chọn B.
• A∈(C nên A(1;1− m) . Ngoài ra 3
y ' = 4x − 4mx ⇒ y '( ) 1 = 4 − 4m . m )
• Phương trình tiếp tuyến của (C tại A là y −1+ m = y′( ) 1 .(x − ) 1 , hay m )
(4 − 4m) x − y − 3(1− m) = 0 . −1
• Khi đó d (B;∆) =
≤ 1, Dấu ‘=’ xảy ra ⇔ khi m = 1. 16(1− m)2 + 1
• Do đó d (B;∆) lớn nhất bằng 1 khi và chỉ khi m = 1. Câu 49. Chọn C. +
• Giả sử M (x ; y x ∈ C ⇒ 2 3 0 y = . 0 0 ) ( ) 0 x + 1 0 3x + 4y − 2
3x + 4y −12 = 0
• Ta có d (M ,d = 2 ⇔ = 2 ⇔ . 1 ) 0 0 0 0  2 2 3 + 4
3x + 4y + 8 = 0 0 0
x = 0 ⇒ M 0;3 0 1 ( )  +  • Với 2x 3 0 3x 4y 12 0 3x 4  12 0  + − = ⇔ + − = ⇔ 0 0 0  1  1 11  x +1  0  x = ⇒ M  ; 0 2  3 3 4     Trang 19/25   7 x 5 M  5;  = − ⇒ − 0 3   +  • Với 2x 3   0 4
3x + 4y + 8 = 0 ⇔ 3x + 4  + 8 = 0 ⇔  . 0 0 0  x +1 0   4  4 x = − ⇒ M   − ; 1 − 0 4  3  3  
Suy ra có 4 tiếp tuyến. Câu 50. Chọn C.
Phương pháp tự luận. −
• Giao điểm của hai tiệm cận là I (1;2). Gọi M (a;b) ∈ (C) ⇒ 2a 1 b = (a > )1 . a −1 −
• Phương trình tiếp tuyến của (C) tại M là 1 2a 1 y = − x − a + . 2 ( ) (a −1) a −1
• Phương trình đường thẳng MI là 1 y = (x −1) + 2 . 2 (a −1)
• Tiếp tuyến tại M vuông góc với MI nên ta có 1 1
a = 0 ⇒ b = 1 − . = −1 ⇔ . (a − )2 1 (a − )2 1 
a = 2 ⇒ b = 3
Vì yêu cầu hoành độ lớn hơn 1 nên điểm cần tìm là M (2;3) .
Phương pháp trắc nghiệm
Gọi M (x ; y ∈ C , điểm M thoả yêu cầu bài toán có hoành độ được tính như sau: 0 0 ) ( ) x = ⇒ y = x −1 = ± 2.(− ) 1 −1.(− ) 2 3 0 0 1 ⇔ x −1 = 1 ± ⇔ . 0 0 x =  0 (L) 0 Vậy M (2;3) . Câu 51. Chọn A.
• Phương trình hoành độ giao điểm của d và (C) là  1 −x + 1 x ≠ = x + m ⇔  2 . 2x −1 g  ( x) 2
= 2x + 2mx − m −1 = 0 (*)
• Theo định lí Viet ta có m 1 x x ; m x x − − + = − =
. Giả sử A(x ; y , B x ; y . 1 1 ) ( 2 2 ) 1 2 1 2 2 − • Ta có 1 y′ =
, nên tiếp tuyến của (C) tại A và B có hệ số góc lần lượt là (2x − )2 1 1 k = − và 1 k = − . Vậy 1 (2x − )2 1 2 (2x −1 2 )2 1 2 2 1 1
4(x + x ) − 4(x + x ) + 2 1 2 1 2 k + k = − − = − 1 2 2 2 2 (2x −1) (2x −1) 1 2
[4x x − 2(x + x )+1 1 2 1 2 ]
= −(4m +8m + 6) = 4 − (m + )2 2 1 − 2 ≤ 2 −
• Dấu "=" xảy ra ⇔ m = −1.
Vậy k + k đạt giá trị lớn nhất bằng −2 khi m = −1. 1 2 Câu 52. Chọn A.
Phương pháp tự luận −
• Gọi M (x ; y là toạ độ của tiếp điểm ⇒ 1 y '(x ) = < 0 . 0 0 ) 0 (2x +3)2 0 Trang 20/25 • OA ∆
B cân tại O nên tiếp tuyến ∆ song song với đường thẳng y = −x (vì tiếp tuyến có hệ −
x = −1 ⇒ y = 1
số góc âm). Nghĩa là y ( 1 ′ x = = −1 ⇒ 0 0  . 0 ) (2x + 3)2 0
x = −2 ⇒ y = 0 0 0
• Với x = −1; y = 1 ⇒ ∆: y −1 = − (x + )
1 ⇔ y = −x (loại). 0 0
• Với x = −2; y = 0 ⇒ ∆: y − 0 = − (x + 2) ⇔ y = −x − 2 (nhận). 0 0
Vậy phương trình tiếp tuyến cần tìm là y = −x − 2 .
Phương pháp trắc nghiệm
• Tam giác OAB cân tại gốc tọa độ O nên ta có OA = OB ⇒ n = 1. 2 2
acx + 2bcx + bd ≠ 0 ⇒ 2x + 8x + 6 ≠ 0 ⇔ x ≠ −1; x ≠ −3 0 0 0 0 0 0 x = −1 L 0 ( ) cx + d = ± .
n ad − bc ⇒ 2x + 3 = ± 1. −1 ⇔ . 0 0  x = −2 N  0 ( )
• Với x = −2; y = 0 ⇒ ∆: y − 0 = − (x + 2) ⇔ y = −x − 2 (nhận). 0 0 Câu 53. Chọn A.
• Giả sử tiếp tuyến d của (C) tại M (x ; y ) ∈ (C) cắt Ox tại A , Oy tại B sao cho 0 0 OA = 4OB . • Do OA ∆
B vuông tại A nên OB 1 tan A =
= ⇒ Hệ số góc của d bằng 1 hoặc 1 − . OA 4 4 4 • Vì y ( 1 ' x = −
< 0 nên hệ số góc của d bằng 1 − , suy ra 0 ) (x − )2 1 4 0  3 x = 1 − ⇒ y =  0 0 1 1 2 − = − ⇔ . (  x − )2 1 4  5 0 x = 3 ⇒ y = 0 0  2  1 y = − (x + ) 3  1 5 1 + y = − x +  
• Khi đó có 2 tiếp tuyến thoả mãn là: 4 2 4 4  ⇔  . 1  y (x ) 5 1 13 3  = − − + y = − x +  4 2  4 4 Câu 54. Chọn D.
Phương pháp tự luận − • Ta có 1 y′ = ; I (1; ) 1 . (x − )2 1   • Gọi x0 M x ;
∈ C , x ≠ 1 . Phương trình tiếp tuyến tại M có dạng 0 ( ) ( 0 ) x −  1 0  1 x0 ∆ : y = − (x − x ) + 2 2
⇔ x + (x −1) y − x = 0 . 2 0 (x −1) x −1 0 0 0 0 2 x −1 • d (I ∆) 0 2 2 , = = ≤ = 2 . + (x − )4 1 2 1 1 + x −1 2 ( 0 )2 0 (x −1 0 )
• Dấu " = " xảy ra khi và chỉ khi 1
x = 2 ⇒ y = 2 N 2 0 0 ( )
= x −1 ⇔ x −1 =1 ⇔  . 2 ( 0 ) (x −1 x = 0 L 0 ) 0  0 ( ) Trang 21/25 π
Tung độ này gần với giá trị nhất trong các đáp án. 2
Phương pháp trắc nghiệm
x = 2 ⇒ y = 2 N 0 0 ( )
Ta có IM ⊥ ∆ ⇒ cx + d = ± ad − bc ⇒ x −1 = ± 1 − − 0 ⇔ . 0 0  x = 0 L  0 ( ) Câu 55. Chọn C. Phương pháp tự luận • Ta có 3 y′ = . (x + )2 1  −  • Gọi 2x 1 0 M x ;
∈ C , x ≠ 1
− . Phương trình tiếp tuyến tại M là 0 ( ) ( 0 ) x +  1 0  3 2x −1 0 y = (x − x ) + 2 2
⇔ 3x − (x +1) y + 2x − 2x −1 = 0 . 2 0 (x +1) x +1 0 0 0 0 0 6 x +1 • d (I ∆) 0 6 6 , = = ≤ = 6 . 4 9 + (x +1) 9 2 0 2 9 + (x +1) 2 0 (x +1) 0
• Dấu " = " xảy ra khi và chỉ khi 9 x = 1
− + 3 ⇒ y = 2 − 3 L 2 2 0 0 ( )
= (x +1) ⇔ x +1 = 3 ⇔  . 2 0 ( 0 ) (x +1) 0 x = 1
− − 3 ⇒ y = 2 + 3 N  0 0 ( )
Tung độ này gần với giá trị e nhất trong các đáp án.
Phương pháp trắc nghiệm
Ta có IM ⊥ ∆ ⇒ cx + d = ± ad − bc ⇒ x +1 = ± 2 +1 0 0  = − + ⇒ = − x 1 3 y 2 3 L 0 ( ) ⇔  . x = 1
− − 3 ⇒ y = 2 + 3 N  0 ( ) Câu 56. Chọn D.
Phương pháp tự luận  −  • Gọi 2x 3 0 M x ;
∈ C , x ≠ 2 . Phương trình tiếp tuyến tại M có dạng 0 ( ) ( 0 ) x −  2 0  1 1 ∆ : y = − (x − x ) + 2 + . 2 0 (x − 2) x − 2 0 0  
• Giao điểm của ∆ với tiệm cận đứng là 2 A2;2 + . x 2  −  0 
• Giao điểm của ∆ với tiệm cận ngang là B(2x − 2;2 . 0 )   • Ta có 2 AB = 1 ( 1 4 x − 2 +
 ≥ 8. Dấu " = " xảy ra khi ( x − 2 = 0 )2 0 )2  (x − 2)2 (x − 2 0 )2 0      
x = 3 ⇒ y = 3 ⇒ OM 3;3 ⇒ OM = 3 2 N 0 0 ( ) ( )  ⇔    .
x =1⇒ y =1 ⇒ OM 1;1 ⇒ OM = 2 L 0 0 ( ) ( ) 
Phương pháp trắc nghiệm Trang 22/25
• AB ngắn nhất suy ra khoảng cách từ I đến tiếp tuyến ∆ tại M ngắn nhất x = ⇒ y = M 3 M 3
⇒ IM ⊥ ∆ ⇒ cx + d = ± ad − bc ⇒ x − = ± − + ⇔ M M 2 4 3 x = ⇒ y =  M 1 M 1  ⇒ OM = 3 2 . Câu 57. Chọn D.
Phương pháp tự luận  −  • Gọi x 2 0 M x ;
∈ C , x ≠ 1 − , I 1;
− 1 . Phương trình tiếp tuyến tại M có dạng 0 ( ) ( 0 ) ( ) x +  1 0  3 x − 2 0 ∆ : y = (x − x ) + . (x +1 x +1 0 )2 0 0  − 
• Giao điểm của ∆ với tiệm cận đứng là x 5 0 A 1; − . x 1  +  0 
• Giao điểm của ∆ với tiệm cận ngang là B(2x +1;1 . 0 ) • Ta có 6 IA =
, IB = 2 x +1 ⇒ .
IA IB =12 . Bán kính đường tròn ngoại tiếp ∆ IAB là 0 x +1 0 S = pr , suy ra IAB S IA IB IA IB IA IB IAB . . . r = = = ≤ = 2 3 − 6 . 2 2 p
IA + IB + AB IA+ IB + IA + IB 2 . IA IB + 2. . IA IBx = − + ⇒ y = − M 1 3 1 3 • Suy ra 2 0
r = 2 3 − 6 ⇔ IA = IB ⇔ x −1 = 3 ⇔  . max 0 x = − − ⇒ y = + M 1 3 1 3 0  
• IM ( 3;− 3) ⇒ IM = 6 .
Phương pháp trắc nghiệm
• IA = IB ⇒ ∆ IAB vuông cân tại I ⇒ IM ⊥ ∆ . x = − + ⇒ y = − M 1 3 M 1 3
• cx + d = ± ad − bc ⇒ x + = ± + ⇔  M M 1 1 2 x = − − ⇒ y = + M 1 3 M 1 3  ⇒ IM = 6 . Câu 58. Chọn D.
Phương pháp tự luận   • Gọi 3 M x ;2 +
∈ C , x ≠ 1 . Phương trình tiếp tuyến tại M có dạng 0 ( ) ( 0 ) x −  1 0  3 − 3 ∆ : y = (x − x ) + 2 + . (x −1 x −1 0 )2 0 0  
• Giao điểm của ∆ với tiệm cận đứng là 6 A1; 2 + . x 1 −  0 
• Giao điểm của ∆ với tiệm cận ngang là B(2x −1; 2 . 0 ) 1 1 6 • Ta có S = = ⋅ ⋅ − = = ∆ IA IB x IAB . 2 1 2.3 6 0 . 2 2 x −1 0
• ∆ IAB vuông tại I có diện tích không đổi ⇒ chu vi ∆ IAB đạt giá trị nhỏ nhất khi Trang 23/25 6 x =1+ 3 IA = IB 0 ⇔ = 2 x −1 ⇒  0 . x −1 0 x =1− 3 0
• Với x =1+ 3 thì phương trình tiếp tuyến là ∆ : y = −x + 3+ 2 3 . Suy ra 0 d (O ∆) 3+ 2 3 , = . 2
• Với x =1− 3 thì phương trình tiếp tuyến là ∆ : y = −x + 3− 2 3 . Suy ra 0 d (O ∆) 3 − + 2 3 , = . 2 +
Vậy khoảng cách lớn nhất là 3 2 3 gần với giá trị 5 nhất trong các đáp án. 2
Phương pháp trắc nghiệm x = + ⇒ y = + M 1 3 2 3
• IA = IB ⇒ cx + d = ± ad − bc ⇒ x − = ± − − ⇔  M M 1 2 1 x = − ⇒ y = − M 1 3 2 3
⇒ d (O ∆) 3+ 2 3 , = (N ) . 2 Câu 59. Chọn A.
Phương pháp tự luận  −  • Gọi 2x 1 0 M x ;
∈ C , x ≠ 2 . Phương trình tiếp tuyến tại M có dạng 0 ( ) ( 0 ) x −  2 0  3 2x −1 0 ∆ : y = − (x − x ) + . 2 0 (x − 2) x − 2 0 0  + 
• Giao điểm của ∆ với tiệm cận đứng là 2x 2 0 A2; . x 2  −  0 
• Giao điểm của ∆ với tiệm cận ngang là B(2x − 2; 2 . 0 )
x + x = + x − = x A B 2 2 2 2 0 0 • Xét  2x + 2 2x −1
⇒ M là trung điểm của AB . 0 0 y + y = + = = yA B 2 2. 2 0 x − 2 x −  2 0 0
• ∆ IAB vuông tại I nên M là tâm đường tròn ngoại tiếp tam giác IAB . 2    −    2 2 2 2x 1 9 0 2
⇒ S = π R = π IM = π (x − 2) + 
− 2  = π (x − 2) + ≥  6π 0 0 2   x − 2    (x − 2) 0 0    9
x = 3 + 2 ⇒ y = 3 + 2 • Dấu " = " xảy ra khi 2 0 0 (x − 2) = ⇔  . 0 2 (x − 2) 0
x = − 3 + 2 ⇒ y = − 3 + 2 0 0 • Với x =
3 + 2 ⇒ ∆ : y = −x + 2 3 + 4 cắt 2 trục tọa độ tại E (0; 2 3 + 4) và 0 F ( 2 3 + 4; 0), suy ra 1 S = OE OF = + ≈ OEF . 14 8 3 27,8564 2
• Với x = − 3 + 2 ⇒ ∆ : y = −x − 2 3 + 4 cắt 2 trục tọa độ tại E (0; − 2 3 + 4) và 0
F ( − 2 3 + 4; 0) , suy ra 1 S = OE OF = − ≈ OEF . 14 8 3 0,1435 2
Phương pháp trắc nghiệm Trang 24/25
• IM lớn nhất ⇔ IM ⊥ ∆ ⇒ cx + d = ± ad − bc ⇒ x − 2 = ± 4 − +1 . 0 0
x = 3 + 2 ⇒ y = 3 + 2 0 0 ⇔ 
. Giải tương tự như trên.
x = − 3 + 2 ⇒ y = − 3 + 2 0 0 Trang 25/25
Document Outline

  • DS_C1_TIEP TUYEN
    • A. KỸ NĂNG CƠ BẢN
    • B. BÀI TẬP TRẮC NGHIỆM
    • C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM