Tóm tắt lý thuyết và bài tập trắc nghiệm tính đơn điệu của hàm số Toán 12
Tóm tắt lý thuyết và bài tập trắc nghiệm tính đơn điệu của hàm số Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn:
Tác giả:
Tài liệu liên quan:
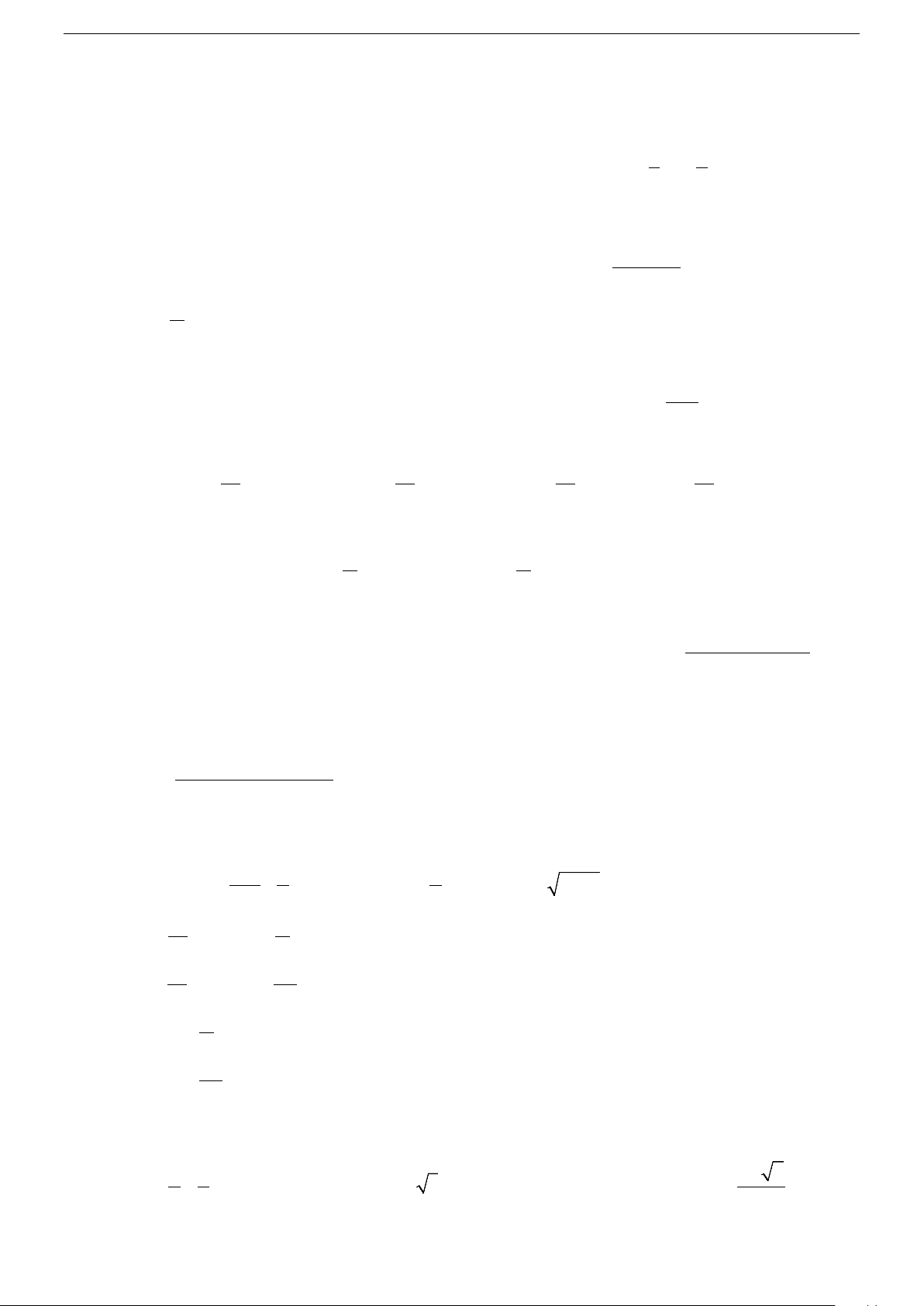
Preview text:
CHỦ ĐỀ 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
§ 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
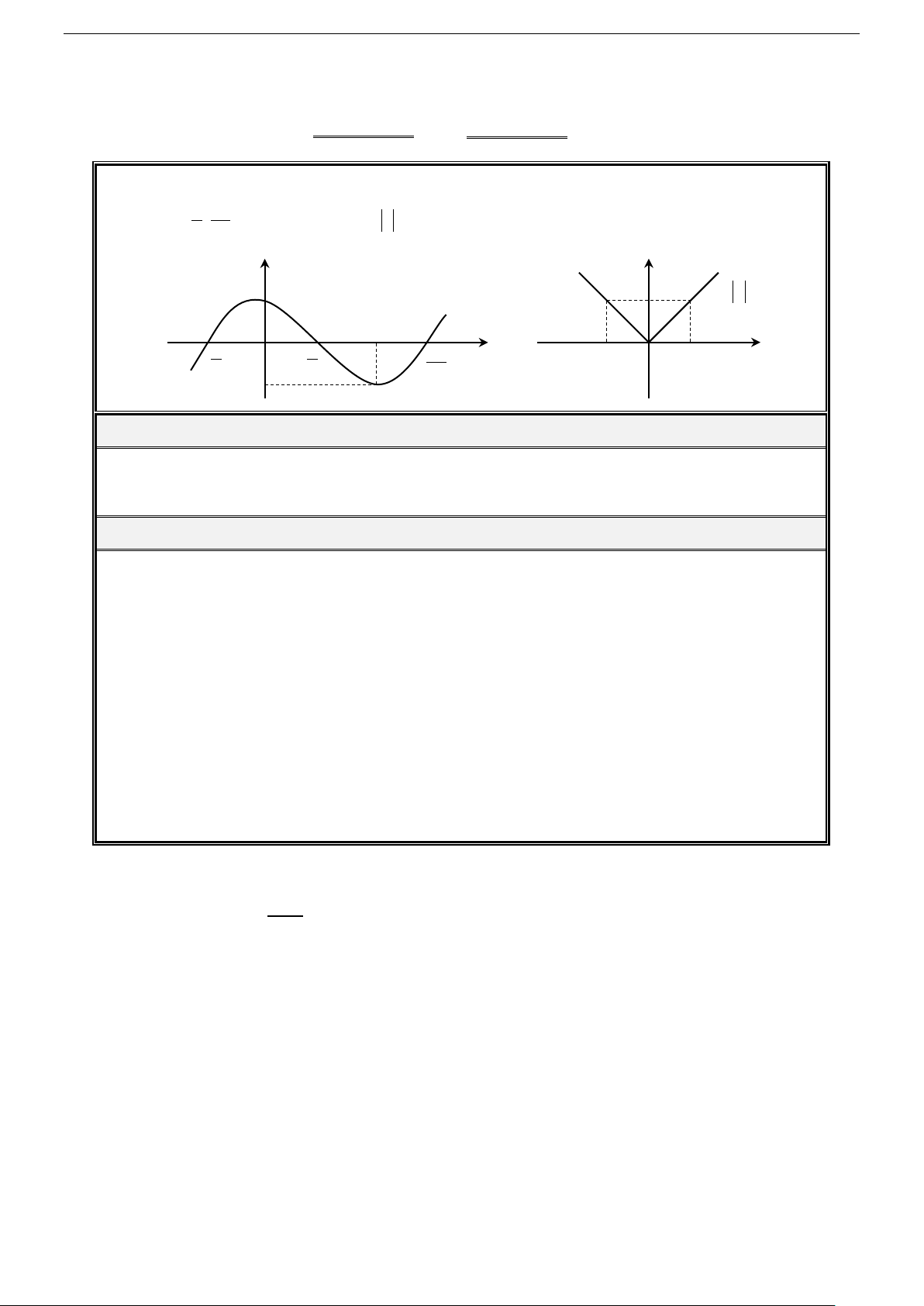
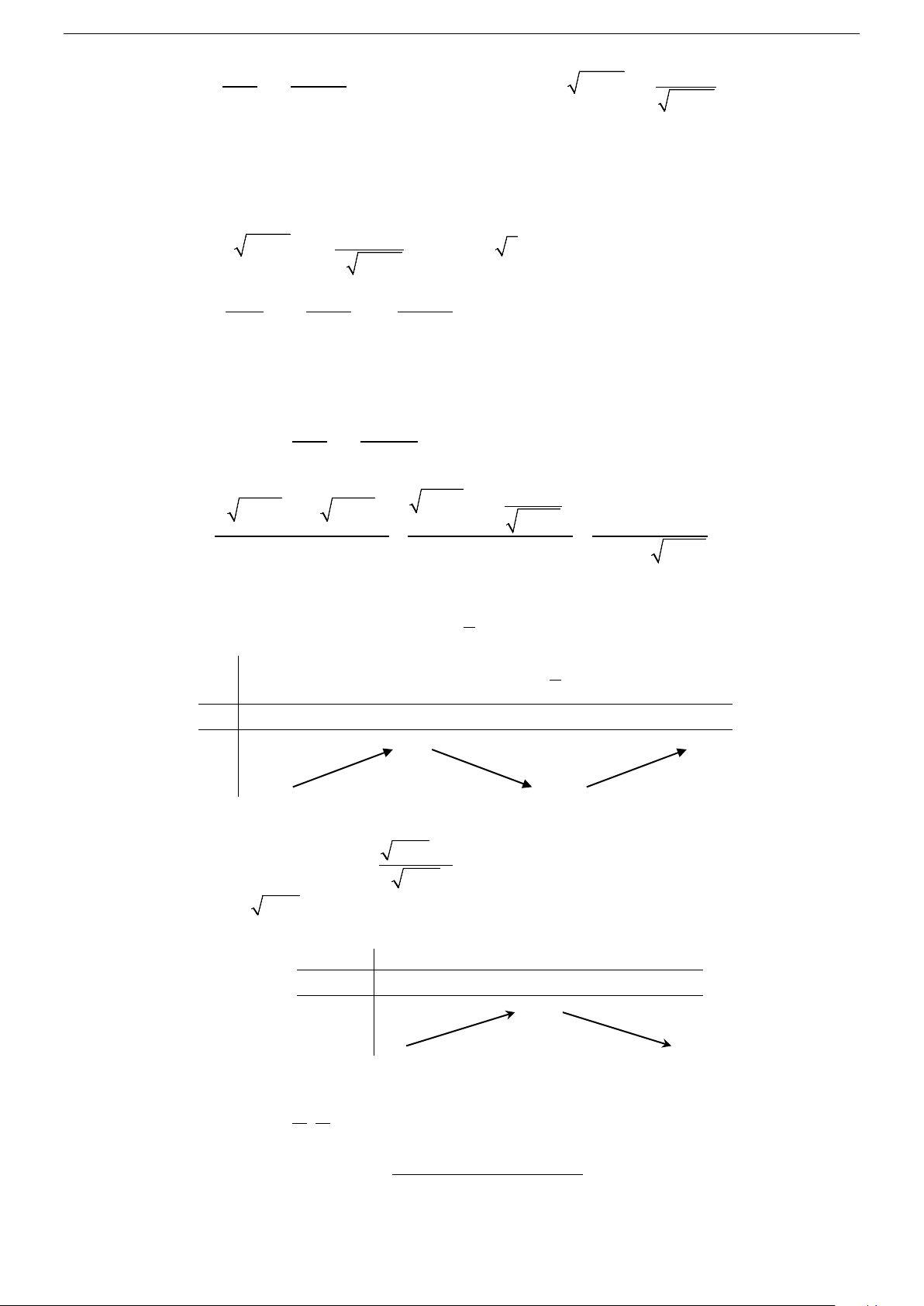
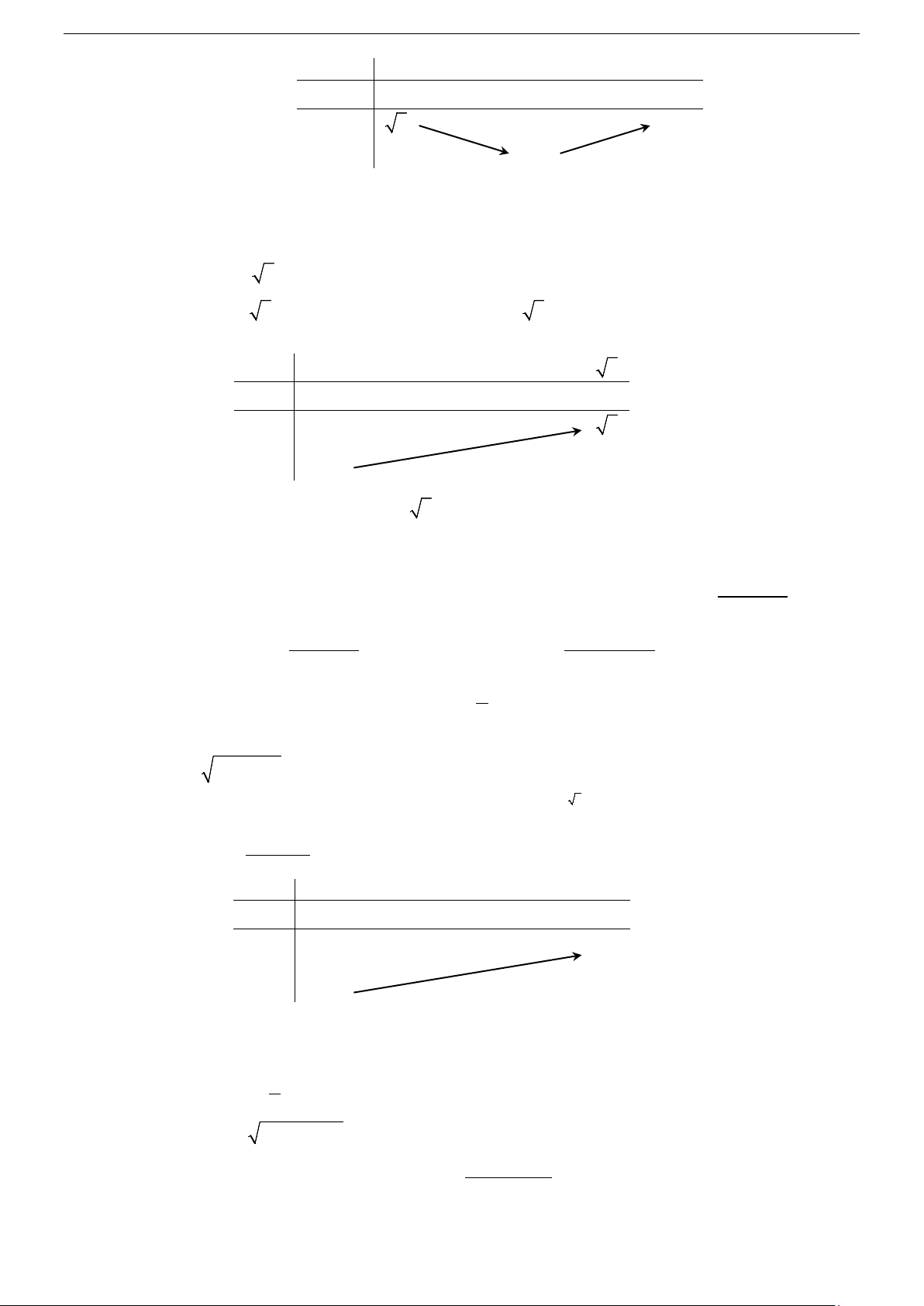
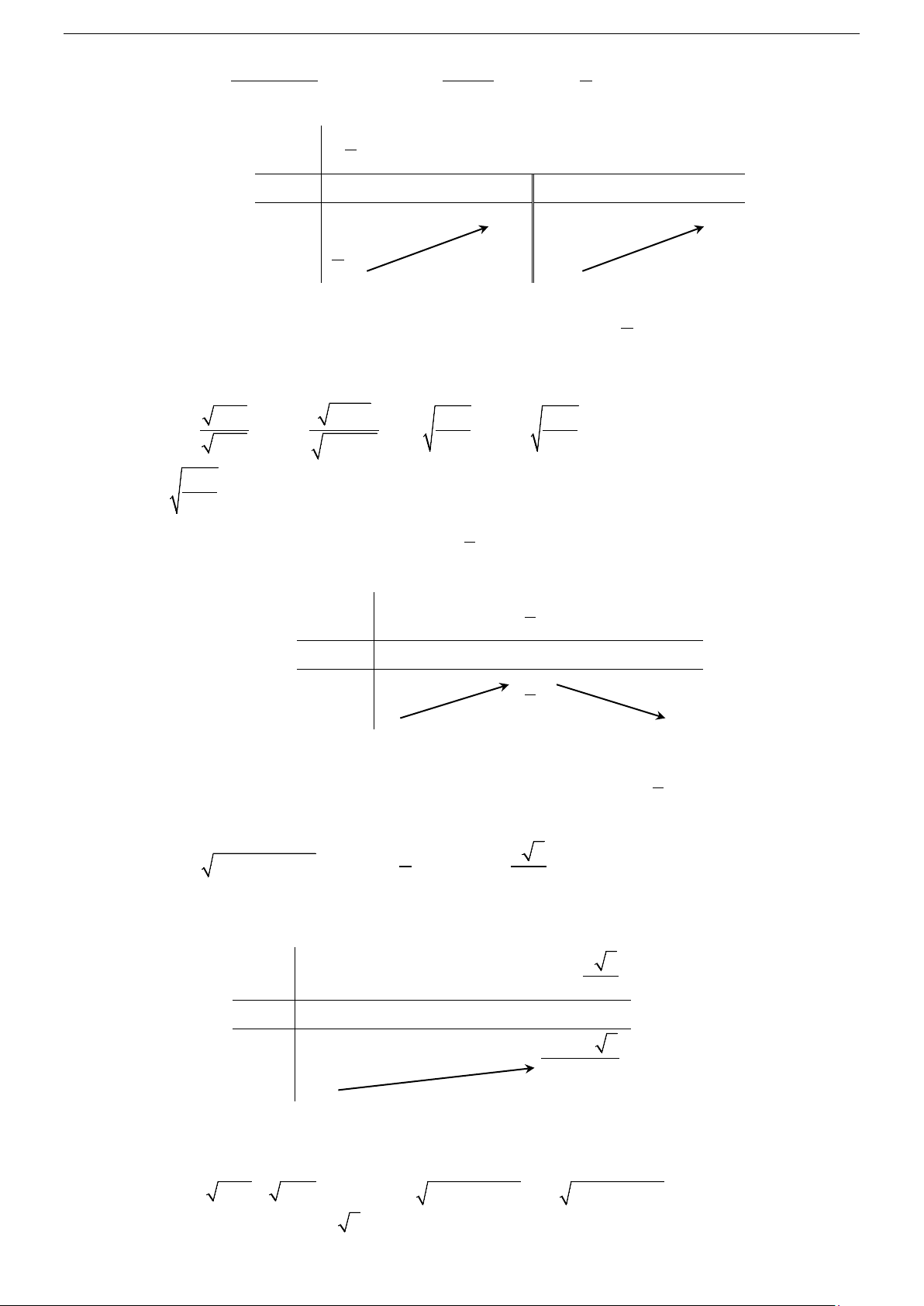
Từ đồ thị hình 1 và hình 2 bên dưới, hãy chỉ ra các khoảng tăng, giảm của hàm số y = cos x trên đoạn π 3 ; π −
và của hàm số y = x trên khoảng (−∞;+∞) ? 2 2 y y (Hình (Hình 1 1 y = x y = cos x π x x π O π − 3π 1 − O 1 2 2 2 1 − Định nghĩa
• Hàm số y = f (x) được gọi là đồng biến trên miền D ⇔ x
∀ , x ∈ D và x < x ⇒ f (x ) < f (x ). 1 2 1 2 1 2
• Hàm số y = f (x) được gọi là nghịch biến trên miền D ⇔ x
∀ , x ∈ D và x < x ⇒ f (x ) > f (x ). 1 2 1 2 1 2 Định lý
Giả sử y = f (x) có đạo hàm trên khoảng (a;b), thì:
• Nếu f (′x) > 0, ( x
∀ ∈ a;b) ⇒ hàm số f (x) đồng biến trên khoảng (a;b).
Nếu f (′x) < 0, ( x
∀ ∈ a;b) ⇒ hàm số f (x) nghịch biến trên khoảng (a;b).
• Nếu f (x) đồng biến trên khoảng (a;b) ⇒ f (′x) ≥ 0, x ∀ ∈(a;b).
Nếu f (x) nghịch biến trên khoảng (a;b) ⇒ f (′x) ≤ 0, x ∀ ∈(a;b).
Khoảng (a;b) được gọi chung là khoảng đơn điệu của hàm số. • Lưu ý:
+ Nếu f (′x) = 0, ( x
∀ ∈ a;b) thì f (x) không đổi trên (a;b).
+ Nếu thay đổi khoảng (a;b) bằng một đoạn hoặc nửa khoảng thì phải bổ sung thêm giả thiết
hàm số xác định và liên tục trên đoạn hoặc nửa khoảng đó. BÀI TẬP TRẮC NGHIỆM Câu 1. x +
Cho hàm số y =
1 . Khẳng định nào sao đây là khẳng đinh đúng? 1− x
A. Hàm số nghịch biến trên khoảng ( ; −∞ ) 1 ∪(1;+∞) .
B. Hàm số đồng biến trên khoảng (−∞; ) 1 ∪(1;+∞) .
C. Hàm số nghịch biến trên các khoảng ( ) ;1 −∞ và (1;+∞).
D. Hàm số đồng biến trên các khoảng ( ) ;1 −∞ và (1;+∞). Câu 2. Cho hàm số 3 2
y = −x + 3x − 3x + 2 . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số luôn nghịch biến trên .
B. Hàm số nghịch biến trên các khoảng ( ) ;1 −∞ và (1;+∞).
C. Hàm số đồng biến trên khoảng (−∞ )
;1 và nghịch biến trên khoảng (1;+∞).
D. Hàm số luôn đồng biến trên . Câu 3. Cho hàm số 4 2
y = −x + 4x +10 và các khoảng sau: Trang 1/16 (I): ( ; −∞ − 2) ; (II): (− 2;0) ; (III): (0; 2);
Hỏi hàm số đồng biến trên các khoảng nào? A. Chỉ (I). B. (I) và (II). C. (II) và (III). D. (I) và (III). Câu 4. − Cho hàm số 3x 1 y =
. Khẳng định nào sau đây là khẳng định đúng? 4 − + 2x
A. Hàm số luôn nghịch biến trên .
B. Hàm số luôn nghịch biến trên từng khoảng xác định.
C. Hàm số đồng biến trên các khoảng ( ;2 −∞ ) và (2;+∞) .
D. Hàm số nghịch biến trên các khoảng ( ; −∞ − 2) và( 2; − +∞) .
Câu 5. Hỏi hàm số nào sau đây luôn nghịch biến trên ? A. 4 2
h(x) = x − 4x + 4 . B. 3 2
g(x) = x + 3x +10x +1. C. 4 5 4 3
f (x) = − x + x − x . D. 3 2
k(x) = x +10x − cos x . 5 3 2 Câu 6. − + Hỏi hàm số x 3x 5 y =
nghịch biến trên các khoảng nào ? x +1 A. ( ; −∞ 4) − và (2;+∞) . B. ( 4; − 2) . C. ( ; −∞ − ) 1 và ( 1; − +∞) . D. ( 4; − − ) 1 và ( 1; − 2) . 3
Câu 7. Hỏi hàm số x 2 y =
− 3x + 5x − 2 nghịch biến trên khoảng nào? 3 A. (5;+∞) B. (2;3) C. ( ) ;1 −∞ D. (1;5) Câu 8. Hỏi hàm số 3 5 4 3
y = x − 3x + 4x − 2 đồng biến trên khoảng nào? 5 A. ( ; −∞ 0). B. . C. (0;2) . D. (2;+∞) . Câu 9. Cho hàm số 3 2
y = ax + bx + cx + d . Hỏi hàm số luôn đồng biến trên khi nào?
a = b = 0,c > 0
a = b = 0,c > 0 A. . B. . 2
a > 0;b − 3ac ≤ 0 2
a > 0;b − 3ac ≥ 0
a = b = 0,c > 0
a = b = c = 0 C. . D. . 2
a < 0;b − 3ac ≤ 0 2
a < 0;b − 3ac < 0 Câu 10. Cho hàm số 3 2
y = x + 3x − 9x +15 . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng ( 3 − ; ) 1 .
B. Hàm số đồng biến trên .
C. Hàm số đồng biến trên ( 9; − 5 − ) .
D. Hàm số đồng biến trên khoảng (5;+∞) .
Câu 11. Cho hàm số y = 2 x − 3 3
x . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng (0;2) .
B. Hàm số đồng biến trên các khoảng (−∞;0);(2;3) .
C. Hàm số nghịch biến trên các khoảng ( ; −∞ 0);(2;3) .
D. Hàm số nghịch biến trên khoảng (2;3).
Câu 12. Cho hàm số = x y + 2
sin x, x ∈[0;π ]. Hỏi hàm số đồng biến trên các khoảng nào? 2 π π π π A. 7 11 0; và ;π . B. 7 11 ; . 12 12 12 12 Trang 2/16 π π π π π π C. 7 7 11 0; và ; . D. 7 11 11 ; và ;π . 12 12 12 12 12 12 Câu 13. Cho hàm số 2
y = x + cos x . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số luôn đồng biến trên . π π
B. Hàm số đồng biến trên kπ; + +∞
và nghịch biến trên khoảng ; −∞ + kπ . 4 4 π π
C. Hàm số nghịch biến trên kπ; + +∞
và đồng biến trên khoảng ; −∞ + kπ . 4 4
D. Hàm số luôn nghịch biến trên .
Câu 14. Cho các hàm số sau: 1 3 2 −
(I) : y = x − x + 3x + 4; x 1 (II) : y = ; 2
(III) : y = x + 4 3 x +1 3
(IV) : y = x + 4x − sin x ; 4 2
(V) : y = x + x + 2 .
Có bao nhiêu hàm số đồng biến trên những khoảng mà nó xác định? A. 2. B. 4. C. 3. D. 5.
Câu 15. Cho các hàm số sau: 3 2
(I) : y = −x + 3x − 3x +1;
(II) : y = sin x − 2x ; 3 −
(III) : y = − x + 2 ; x 2 (IV) : y = 1− x
Hỏi hàm số nào nghịch biến trên toàn trục số? A. (I), (II).
B. (I), (II) và (III). C. (I), (II) và (IV). D. (II), (III).
Câu 16. Xét các mệnh đề sau: (I). Hàm số 3
y = −(x −1) nghịch biến trên . (II). Hàm số = ln( −1) x y x −
đồng biến trên tập xác định của nó. x −1 (III). Hàm số x y = đồng biến trên . 2 x +1
Hỏi có bao nhiêu mệnh đề đúng? A. 3. B. 2. C. 1. D. 0.
Câu 17. Cho hàm số y = x +1 (x − 2) . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng 1 1; − . 2
B. Hàm số nghịch biến trên khoảng ( ; −∞ 1) − .
C. Hàm số đồng biến trên các khoảng ( ; −∞ 1) − và 1 ; +∞. 2
D. Hàm số nghịch biến trên khoảng 1 1; −
và đồng biến trên khoảng 1 ;+∞ . 2 2
Câu 18. Cho hàm số y = x + 3+ 2 2 − x . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số nghịch biến trên khoảng ( ; −∞ 2
− ) và đồng biến trên khoảng ( 2; − 2) .
B. Hàm số đồng biến trên khoảng ( ; −∞ 2
− ) và nghịch biến trên khoảng ( 2; − 2) .
C. Hàm số đồng biến trên khoảng ( ) ;1
−∞ và nghịch biến trên khoảng (1;2) .
D. Hàm số nghịch biến trên khoảng ( ) ;1
−∞ và đồng biến trên khoảng (1;2) . π π
Câu 19. Cho hàm số y cos 2x sin 2 .xtan x, x ; = + ∀ ∈ −
. Khẳng định nào sau đây là khẳng định 2 2 đúng? Trang 3/16 π π
A. Hàm số luôn giảm trên ; − . 2 2 π π
B. Hàm số luôn tăng trên ; − . 2 2 π π
C. Hàm số không đổi trên ; − . 2 2
D. Hàm số luôn giảm trên Câu 20. − +
Tìm tất cả các giá trị thực của tham số m sao cho hàm số x m 2 y = giảm trên các khoảng x +1 mà nó xác định ? A. m < 3 − . B. m ≤ 3 − . C. m ≤1. D. m <1.
Câu 21. Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn nghịch biến trên ? 1 3 2
y = − x − mx + (2m − 3)x − m + 2 3 A. 3 − ≤ m ≤1. B. m ≤1. C. 3 − < m <1. D. m ≤ 3 − ;m ≥1. 2 Câu 22. − + + −
Tìm tất cả các giá trị thực của tham số m sao cho hàm số
x (m 1) 2m 1 y = tăng trên x − m
từng khoảng xác định của nó? A. m >1. B. m ≤1. C. m <1. D. m ≥1.
Câu 23. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = f (x) = x + mcos x luôn đồng biến trên ? A. m ≤1. B. 3 m > . C. m ≥1. D. 1 m < . 2 2
Câu 24. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = (m−3)x −(2m+1)cos x luôn nghịch biến trên ? m > 3 A. 2 4 − ≤ m ≤ . B. m ≥ 2 . C. . D. m ≤ 2 . 3 m ≠ 1
Câu 25. Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn đồng biến trên ? 3 2
y = 2x − 3(m + 2)x + 6(m +1)x − 3m + 5 A. 0. B. –1 . C. 2. D. 1. 3
Câu 26. Tìm giá trị nhỏ nhất của tham số m sao cho hàm số x 2 y =
+ mx − mx − m luôn đồng biến trên 3 ? A. m = −5 . B. m = 0. C. m = −1. D. m = −6 . Câu 27. + −
Tìm số nguyên m nhỏ nhất sao cho hàm số (m 3)x 2 y =
luôn nghịch biến trên các khoảng x + m xác định của nó? A. m = −1 . B. m = −2 . C. m = 0.
D. Không có m . Câu 28. mx +
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = 4 giảm trên khoảng x + m (−∞ ) ;1 ?
A. −2 < m < 2 .
B. −2 ≤ m ≤ −1.
C. −2 < m ≤ −1.
D. −2 ≤ m ≤ 2 .
Câu 29. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = 3 x − 2
6x + mx +1 đồng biến trên khoảng (0;+∞) ? A. m ≤ 0 . B. m ≤ 12 . C. m ≥ 0 . D. m ≥ 12 . Trang 4/16
Câu 30. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 4 2
y = x − 2(m −1)x + m − 2 đồng biến trên khoảng (1;3) ? A. m∈[ 5; − 2) . B. m∈( ;2 −∞ ]. C. m∈(2,+∞) . D. m∈( ; −∞ 5 − ) .
Câu 31. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = 1 3 x − 1 2
mx + 2mx − 3m + 4 3 2
nghịch biến trên một đoạn có độ dài là 3?
A. m = −1;m = 9. B. m = −1 . C. m = 9 .
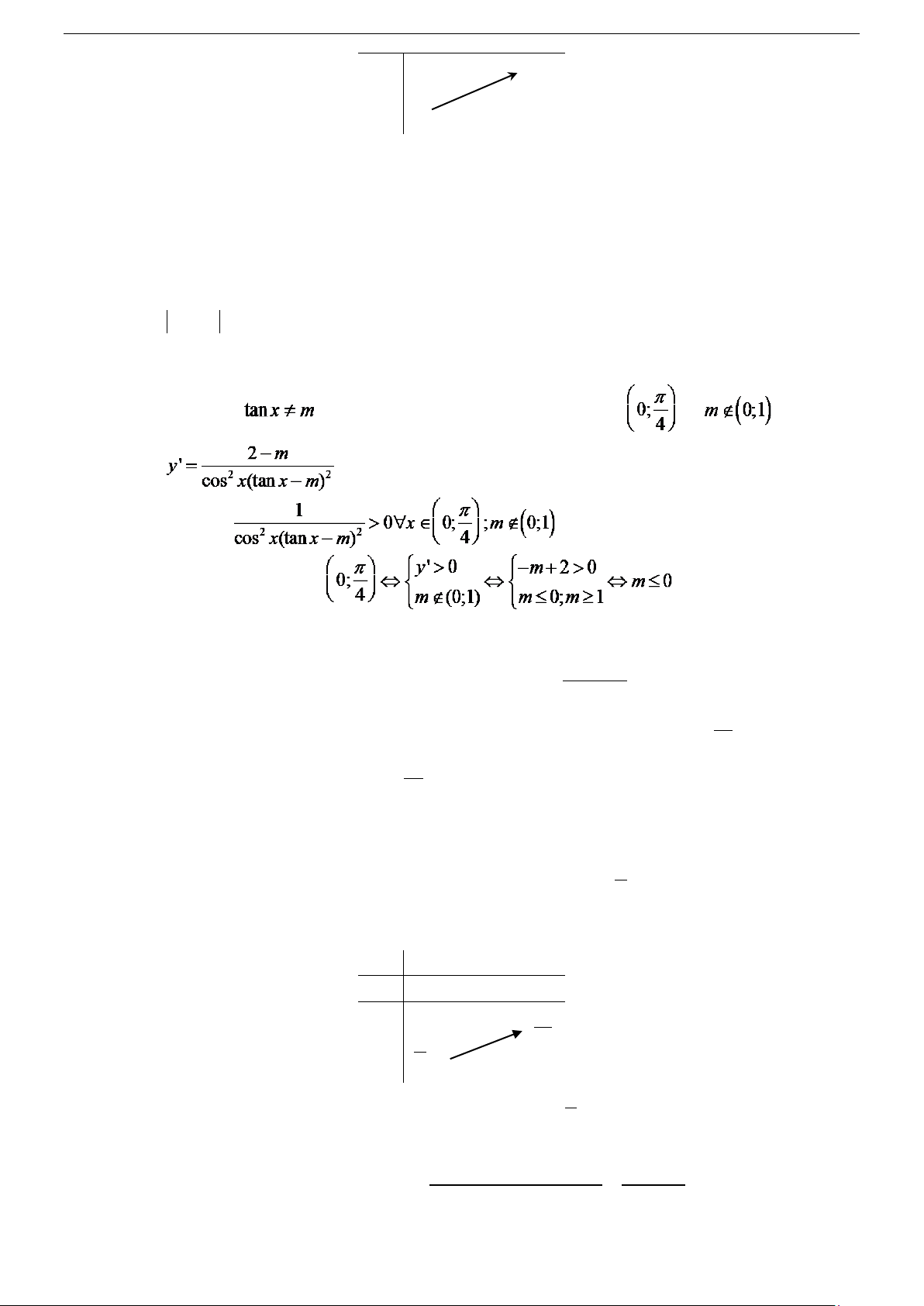
D. m = 1;m = −9 . Câu 32. tan x −
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y =
2 đồng biến trên khoảng tan x − m π 0; ? 4
A. 1 ≤ m < 2 .
B. m ≤ 0;1 ≤ m < 2 . C. m ≥ 2 . D. m ≤ 0 . 3
Câu 33. Tìm tất cả các giá trị thực của tham số m sao cho hàm số mx 2
y = f (x) =
+ 7mx +14x − m + 2 3
giảm trên nửa khoảng [1;+∞) ? A. 14 ; −∞ − . B. 14 ; −∞ − . C. 14 2; − − . D. 14 − ;+∞ . 15 15 15 15
Câu 34. Tất cả các giá trị thực của tham số m sao cho hàm số 4 2
y = −x + (2m − 3)x + m nghịch biến trên khoảng (1;2) là ; p −∞
, trong đó phân số p tối giản và q > 0 . Hỏi tổng p + q là? q q A. 5. B. 9. C. 7. D. 3. 2 Câu 35. − + +
Hỏi có bao nhiêu giá trị nguyên của tham số m sao cho hàm số x 2mx m 2 y = đồng x − m
biến trên từng khoảng xác định của nó? A. Hai. B. Bốn. C. Vô số. D. Không có.
Câu 36. Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số 2
2x + (1− m)x +1+ m y =
đồng biến trên khoảng (1;+∞) ? x − m A. 3. B. 1. C. 2. D. 0.
Câu 37. Tìm tất cả các giá trị thực của tham số α và β sao cho hàm số 3 −x 1 2 3
y = f (x) =
+ (sinα + cosα)x − xsinαcosα − β − 2 luôn giảm trên ? 3 2 2 π π A.
+ kπ ≤ α ≤ + kπ ,k ∈ và β ≥ 2 . 12 4 π π B. 5 + kπ ≤ α ≤
+ kπ ,k ∈ và β ≥ 2 . 12 12 π
C. α ≤ + kπ ,k ∈ và β ≥ 2 . 4π D. 5 α ≥
+ kπ ,k ∈ và β ≥ 2 . 12
Câu 38. Tìm mối liên hệ giữa các tham số a và b sao cho hàm số y = f (x) = 2x + asin x + bcosx luôn tăng trên ? A. 1 1 + =1.
B. a + 2b = 2 3 . C. 2 2 a + b ≤ 4 . D. 1 2 a 2b + + ≥ . a b 3 Trang 5/16
Câu 39. Tìm tất cả các giá trị thực của tham số m sao cho phương trình 3 2
x − 3x − 9x − m = 0 có đúng 1 nghiệm? A. 27 − ≤ m ≤ 5. B. m < 5 − hoặc m > 27 . C. m < 27 − hoặc m > 5 . D. 5 − ≤ m ≤ 27 .
Câu 40. Tìm tất cả các giá trị thực của tham số m sao cho phương trình 2 x +1 = x + m có nghiệm thực? A. m ≥ 2. B. m ≤ 2. C. m ≥ 3 . D. m ≤ 3 .
Câu 41. Tìm tất cả các giá trị thực của tham số m sao cho phương trình 2 2
x − 4x + 5 = m + 4x − x có đúng 2 nghiệm dương?
A. 1≤ m ≤ 3. B. 3 − < m < 5 .
C. − 5 < m < 3 . D. 3 − ≤ m < 3 .
Câu 42. Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: 2
x − 3x + 2 ≤ 0 cũng là nghiệm của bất phương trình 2 mx + (m + )
1 x + m +1≥ 0? A. m ≤ 1 − . B. 4 m ≤ − . C. 4 m ≥ − . D. m ≥ 1 − . 7 7
Câu 43. Tìm tất cả các giá trị thực của tham số m sao cho phương trình: 2 2
log x + log x +1 − 2m −1 = 0 có ít nhất một nghiệm trên đoạn 3 1; 3 3 3 ? A. 1 − ≤ m ≤ 3.
B. 0 ≤ m ≤ 2 .
C. 0 ≤ m ≤ 3. D. 1 − ≤ m ≤ 2 .
Câu 44. Tìm tất cả các giá trị thực của tham số m sao cho phương trình 2
x + mx + 2 = 2x +1 có hai nghiệm thực? A. 7 m ≥ − . B. 3 m ≥ . C. 9 m ≥ . D. m ∀ ∈ . 2 2 2
Câu 45. Tìm tất cả các giá trị thực của tham số m sao cho phương trình 4 2
3 x −1 + m x +1 = 2 x −1 có hai nghiệm thực?
A. 1 ≤ m <1. B. 1 1 − ≤ m ≤ . C. 1 2 − < m ≤ . D. 1 0 ≤ m < . 3 4 3 3
Câu 46. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình 2
(1+ 2x)(3− x) > m + 2x − 5x − 3 nghiệm đúng với mọi 1 x ;3 ∈ − ? 2 A. m >1. B. m > 0. C. m <1. D. m < 0 .
Câu 47. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình
3( 1+ x + 3− x)− 2 (1+ x)(3− x) ≥ m nghiệm đúng với mọi x∈[ −1;3]? A. m ≤ 6 . B. m ≥ 6 .
C. m ≥ 6 2 − 4 .
D. m ≤ 6 2 − 4 .
Câu 48. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình 2 2
3+ x + 6 − x − 18 + 3x − x ≤ m − m +1 nghiệm đúng x ∀ ∈[ 3, − 6] ? A. m ≥ 1 − . B. 1 − ≤ m ≤ 0 .
C. 0 ≤ m ≤ 2 . D. m ≤ 1 − hoặc m ≥ 2 .
Câu 49. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình x m + (m − ) x+2 .4 1 .2
+ m −1 > 0 nghiệm đúng x ∀ ∈ ? A. m ≤ 3 . B. m ≥1. C. 1 − ≤ m ≤ 4 . D. m ≥ 0 .
Câu 50. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình: 3 1
−x + 3mx − 2 < − 3 x nghiệm đúng x ∀ ≥ 1 ? A. 2 m < . B. 2 m ≥ . C. 3 m ≥ . D. 1 3 − ≤ m ≤ . 3 3 2 3 2 Trang 6/16
Câu 51. Tìm giá trị lớn nhất của tham số m sao cho bất phương trình 2 2 2 cos x sin x cos 2 + 3 ≥ .3 x m có nghiệm? A. m = 4 . B. m = 8 . C. m =12 . D. m =16 .
Câu 52. Bất phương trình 3 2
2x + 3x + 6x +16 − 4 − x ≥ 2 3 có tập nghiệm là [a;b]. Hỏi tổng a + b
có giá trị là bao nhiêu? A. 2 − . B. 4. C. 5. D. 3.
Câu 53. Bất phương trình 2 2
x − 2x + 3 − x − 6x +11 > 3− x − x −1 có tập nghiệm ( ; a b] . Hỏi hiệu
b − a có giá trị là bao nhiêu? A. 1. B. 2. C. 3. D. 1 − .
A. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
D A D B C D D B A B B A A C A A B C C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
A B A A A C D C D B A B B C C D B C C B
41 42 43 44 45 46 47 48 49 50 51 52 53 B C B C D D D D B A A C A
II –HƯỚNG DẪN GIẢI Câu 1. Chọn D. TXĐ: D = 2 \{ } 1 . Ta có y ' = > 0, 1 ∀x ≠ 2 (1− x)
Hàm số đồng biến trên các khoảng ( ; −∞ 1) và (1;+∞) Câu 2. Chọn A. TXĐ: D = . Ta có 2 2 y ' = 3
− x + 6x − 3 = 3
− (x −1) ≤ 0 , x ∀ ∈ Câu 3. Chọn D. x = 0 TXĐ: D = . 3 2 y ' = 4
− x + 8x = 4x(2 − x ) . Giải y ' = 0 ⇔ x = ± 2 Trên các khoảng ( ;
−∞ − 2) và (0; 2), y' > 0 nên hàm số đồng biến. Câu 4. Chọn B. TXĐ: D = 10 \{ } 2 . Ta có y ' = − < 0, x ∀ ∈ D . 2 ( 4 − + 2x) Câu 5. Chọn C. Ta có: 4 2 2 2 f '(x) = 4
− x + 4x −1 = −(2x −1) ≤ 0, x ∀ ∈ . Câu 6. Chọn D. 2 + − x = 2 TXĐ: D = x 2x 8 \{− } 1 . y ' = . Giải 2
y ' = 0 ⇒ x + 2x −8 = 0 ⇒ 2 (x +1) x = 4 −
y ' không xác định khi x = 1 − . Bảng biến thiên: x −∞ 4 − 1 − 2 +∞ y′ + 0 – – 0 + 11 − +∞ +∞ y −∞ −∞ 1 Trang 7/16
Hàm số nghịch biến trên các khoảng ( 4; − − ) 1 và ( 1; − 2) Câu 7. Chọn D. x =1 TXĐ: D = . 2
y ' = x − 6x + 5 = 0 ⇔ x =5 Trên khoảng(1;5), '
y < 0 nên hàm số nghịch biến Câu 8. Chọn B. TXĐ: D = . 4 3 2 2 2
y ' = 3x −12x +12x = 3x (x − 2) ≥ 0 , x ∀ ∈ Câu 9. Chọn A.
a = b = 0,c > 0 2
y ' = 3ax + 2bx + c ≥ 0, x ∀ ∈ ⇔ 2
a > 0;b − 3ac ≤ 0 Câu 10. Chọn B. TXĐ: D = . Do 2
y ' = 3x + 6x − 9 = 3(x −1)(x + 3) nên hàm số không đồng biến trên . Câu 11. Chọn B. 2 − HSXĐ: 2 3
3x − x ≥ 0 ⇔ x ≤ 3 6x 3x suy ra D = ( ; −∞ 3]. y ' = , ∀x ∈( ; −∞ 3) . 2 3 2 3x − x x = 0 x = 0 Giải y ' = 0 ⇒ . y ' . x = 2
không xác định khi x = 3 Bảng biến thiên: x −∞ 0 2 3 y′ − || + 0 − | +∞ 2 y 0 0 Hàm số nghịch biến ( ; −∞ 0)và (2;3) . H
àm số đồng biến (0;2) Câu 12. Chọn A. π x = − + kπ TXĐ: D = . 1
y ' = + sin 2x . Giải 1 12
y ' = 0 ⇔ sin 2x = − ⇔ ,(k ∈) 2 2 7π x = + kπ 12 π π
Vì x ∈[0;π ] nên có 2 giá trị 7 x = và 11 x = thỏa mãn điều kiện. 12 12 Bảng biến thiên: π π x 7 11 0 π 12 12 y′ || + 0 − 0 + || y π π Hàm số đồng biến 7 0; và 11 ;π 12 12 Câu 13. Chọn A.
TXĐ: D = ; y′ =1− sin 2x ≥ 0 ∀x∈ suy ra hàm số luôn đồng biến trên Câu 14. Chọn C . (I): 2
y′ = x − 2x + 3 = (x − )2
1 + 2 > 0, ∀x ∈ . Trang 8/16 ′ x − ′ (II): 1 2 y′ = = > 0, ∀x ≠ 1 − x
(III): y′ = ( 2x + 4) = 2 x +1 (x +1) 2 x + 4 (IV): 2
y′ = 3x + 4 − cos x > 0,∀x ∈ (V): 3 2
y′ = 4x + 2x = 2x(2x +1) Câu 15. Chọn A. (I): 3 2 2 2
y ' = (−x + 3x − 3x +1)' = 3
− x + 6x − 3 = 3
− (x −1) ≤ 0, ∀x ∈ ;
(II): y ' = (sin x − 2x)' = cos x − 2 < 0,∀x ∈ ; 2 ′ (III) ′ = −( 3 + ) 3 2 = − x y x ≤ 0,∀x ∈( 3 − 2;+∞ ; 3 ) 2 x + 2 ′ ′ − − (IV) x 2 x 2 1 y ' = = = − < 0, 1 x ∀ ≠ 2 1− x −x +1 (1− x) Câu 16. Chọn A. (I) y′ = ( 3 − x − )′ 2 ( 1) = 3
− (x −1) ≤ 0,∀x ∈ ′ (II) ln( 1) x ′ = − − = x y x > 0,∀x > 1
x −1 (x − )2 1 x x ( x ) ′ 2 x 2 2 x +1 − . 1. 1 . 1 x + − + 2 (III) x +1 y′ = = 1 = > 0,∀x ∈ 2 2 x +1 x +1 ( 2x + ) 2 1 x +1 Câu 17. Chọn B.
2x −1 khi x ≥ 1 − y′ = ; 1 y′ = 0 ⇔ x = 2
− x +1 khi x < 1 − 2 x 1 −∞ 1 − +∞ 2 y′ + || − 0 + y Câu 18. Chọn C. − x − TXĐ: D = ( ;2
−∞ ] . Ta có 2 1 y′ = ,∀x ∈( ;2 −∞ ) . 2 − x
Giải y′ = 0 ⇒ 2 − x =1⇒ x =1; y ' không xác định khi x = 2 Bảng biến thiên: x −∞ 1 2 y′ + 0 − || 6 y −∞ 5 Câu 19. Chọn C. π π Xét trên khoảng ; − . 2 2 x x + Ta có: cos 2 .cos sin 2 . x sin = cos 2 + sin 2 .tan = x y x x x = 1⇒ y′ = 0 cos x Trang 9/16 π π Hàm số không đổi trên ; − . 2 2 Câu 20. Chọn D m − Tập xác định: D = 1 \{− } 1 . Ta có y′ = (x + )2 1
Để hàm số giảm trên các khoảng mà nó xác định ⇔ y′ < 0,∀x ≠ 1 − ⇔ m <1 Câu 21. Chọn A
Tập xác định: D = . Ta có 2
y′ = −x − 2mx + 2m − 3 . Để hàm số nghịch biến trên thì ay′ < 0 1 − < 0 (hn)
y′ ≤ 0, ∀x ∈ ⇔ ⇔ ⇔ 3 − ≤ m ≤1 ∆′ ≤ 0 2
m + 2m − 3 ≤ 0 Câu 22. Chọn B. 2 2
x − mx + m − m + Tập xác định: D = 2 1 \{ }
m . Ta có y′ = 2 (x − m)
Để hàm số tăng trên từng khoảng xác định của nó 2 2 1 ≥ 0(hn)
⇔ y′ ≥ 0, ∀x ∈ D ⇔ x − 2mx + m − m +1≥ 0,∀x ∈ D ⇔ ⇔ m ≤1 m −1 ≤ 0 Câu 23. Chọn A.
Tập xác định: D = . Ta có y′ =1− msin x .
Hàm số đồng biến trên ⇔ y ' ≥ 0, x
∀ ∈ ⇔ msin x ≤1, x ∀ ∈
Trường hợp 1: m = 0 ta có 0 ≤1, x
∀ ∈ . Vậy hàm số luôn đồng biến trên
Trường hợp 2: m > 0 ta có 1 1 sin x ≤ , x
∀ ∈ ⇔ ≥1 ⇔ m ≤1 m m
Trường hợp 3: m < 0 ta có 1 1 sin x ≥ , x ∀ ∈ ⇔ ≤ 1 − ⇔ m ≥ 1 − m m Vậy m ≤1 Câu 24. Chọn A.
Tập xác định: D = . Ta có: y ' = m −3+ (2m +1)sin x
Hàm số nghịch biến trên ⇔ y ' ≤ 0, x
∀ ∈ ⇔ (2m +1)sin x ≤ 3− , m x ∀ ∈ Trường hợp 1: 1 m = − ta có
. Vậy hàm số luôn nghịch biến trên . 2 − − Trường hợp 2: 1 m < − ta có 3 m 3 sin ≥ , m x x ∀ ∈ ⇔ ≤ 1 − 2 2m +1 2m +1 ⇔ 3− m ≥ 2
− m −1 ⇔ m ≥ 4 − Trường hợp 3: 1 m > − ta có: 2 3− m 3− 2 sin ≤ , m x x ∀ ∈ 2 ⇔
≥ 1 ⇔ 3− m ≥ 2m +1 ⇔ m ≤ . Vậy m∈ 4 − ; 2m +1 2m +1 3 3 Câu 25. Chọn A. x =1 Tính nhanh, ta có 2
f (′x) = 0 ⇔ 6x − 6(m + 2) x + 6(m + ) 1 = 0 ⇔ x = m +1
Phương trình f (′x) = 0 có nghiệm kép khi m = 0, suy ra hàm số luôn đồng biến trên .
Trường hợp m ≠ 0 , phương trình f (′x) = 0 có hai nghiệm phân biệt (không thỏa yêu cầu bài toán). Câu 26. Chọn C.
Tập xác định: D = . Ta có 2
y′ = x + 2mx − m Trang 10/16 1 > 0(hn)
Hàm số đồng biến trên ⇔ y′ ≥ 0,∀x∈ ⇔ ⇔ 1 − ≤ m ≤ 0 2
m + m ≤ 0
Vậy giá trị nhỏ nhất của m để hàm số đồng biến trên là m = 1 − Câu 27. Chọn D. 2 m + m + Tập xác định: D = 3 2 \{− }
m . Ta có y′ = (x + m)2 Yêu cầu đề bài 2
⇔ y′ < 0,∀x ∈ D ⇔ m + 3m + 2 < 0 ⇔ 2 − < m < 1 −
Vậy không có số nguyên m nào thuộc khoảng ( 2; − − ) 1 . Câu 28. Chọn C 2 m − Tập xác định D = 4 \{− }
m . Ta có y′ =
. Để hàm số giảm trên khoảng ( ) ;1 −∞ (x + m)2 2 m
⇔ y′ < ∀x ∈(−∞ ) − 4 < 0 0, ;1 ⇔ ⇔ 2 − < m ≤ 1 − 1 ≤ −m Câu 29. Chọn D.
Cách 1:Tập xác định: D = . Ta có 2
y′ = 3x −12x + m • Trường hợp 1: 3 > 0 (hn)
Hàm số đồng biến trên ⇔ y′ ≥ 0, ∀x ∈ ⇔ ⇔ m ≥12 36 − 3m ≤ 0
• Trường hợp 2: Hàm số đồng biến trên (0;+∞) ⇔ y′ = 0 có hai nghiệm 1x, 2 x thỏa 1 x < 2 x ≤ 0 (*)
Trường hợp 2.1: y′ = 0 có nghiệm x = 0 suy ra m = 0 . Nghiệm còn lại của y′ = 0 là
x = 4 (không thỏa (*))
Trường hợp 2.2: y′ = 0 có hai nghiệm 1 x , 2 x thỏa ∆′ > 0 36 − 3m > 0 1 x < 2
x < 0 ⇔ S < 0 ⇔ 4 < 0(vl) ⇒ không có m .Vậy m ≥12 P > 0 m > 0 3
Cách 2:Hàm số đồng biến trên (0;+∞) 2
⇔ m ≥12x − 3x = g(x), x
∀ ∈(0;+∞) .
Lập bảng biến thiên của g(x) trên (0;+∞). x 0 2 +∞ g′ + 0 – 12 g 0 –∞ Câu 30. Chọn B.
Tập xác định D = . Ta có 3
y ' = 4x − 4(m −1)x .
Hàm số đồng biến trên (1;3) 2 ⇔ y ' ≥ 0, x
∀ ∈(1;3) ⇔ g(x) = x +1≥ , m x ∀ ∈(1;3) .
Lập bảng biến thiên của g(x) trên (1;3) . x 1 3 g′ + 0 Trang 11/16 10 g 2
Dựa vào bảng biến thiên, kết luận: m ≤ min g(x) ⇔ m ≤ 2 . Câu 31. Chọn A.
Tập xác định: D = . Ta có 2
y′ = x − mx + 2m
Ta không xét trường hợp y′ ≤ 0,∀x ∈ vì a =1 > 0
Hàm số nghịch biến trên một đoạn có độ dài là 3 ⇔ y′ = 0 có 2 nghiệm 1x, 2 x thỏa 2 ∆ >
0 ⇔ m −8m > 0
m > 8 hay m < 0 m = 1 − 1 x − 2 x = 3 ⇔ ⇔ ⇔ ( x − x
= 9 ⇔ S − 4P = 9 m − 8m = 9 m = 9 1 2 )2 2 2 Câu 32. Chọn B. +) Điều kiện
. Điều kiện cần để hàm số đồng biến trên là +) . +) Ta thấy:
+) Để hs đồng biến trên hoặc 1≤ m < 2 Câu 33. Chọn B.
Tập xác định D = , yêu cầu của bài toán đưa đến giải bất phương trình 2 mx −
+14mx +14 ≤ 0, x
∀ ≥ 1, tương đương với 14 g(x) = ≥ m (1) 2 x +14x
Dễ dàng có được g(x) là hàm tăng x ∀ ∈[1;+∞) , suy ra 14
min g(x) = g(1) = − x 1 ≥ 15 Kết luận: (1) 14
⇔ min g(x) ≥ m ⇔ − ≥ m x 1 ≥ 15 Câu 34. Chọn C.
Tập xác định D = . Ta có 3 y′ = 4
− x + 2(2m − 3)x .
Hàm số nghịch biến trên (1;2) 2 3
⇔ y′ ≤ 0,∀x ∈(1;2) ⇔ m ≤ x + = g(x),∀x ∈(1;2) . 2
Lập bảng biến thiên của g(x) trên (1;2) . g (′x) = 2x = 0 ⇔ x = 0 Bảng biến thiên x 1 2 g′ + 0 11 g 5 2 2
Dựa vào bảng biến thiên, kết luận: 5
m ≤ min g(x) ⇔ m ≤ . Vậy p + q = 5 + 2 = 7 . 2 Câu 35. Chọn C. 2 2
x − mx + m − m − Tập xác định D = 2 2 2 g(x) \{ }
m . Ta có y′ = = . 2 2 (x − m) (x − m)
Hàm số đồng biến trên từng khoảng xác định khi và chỉ khi g(x) ≥ 0, x ∀ ∈ D . Trang 12/16 m ≤ 1 −
Điều kiện tương đương là 2
∆g(x) = −m + m + 2 ≤ 0 ⇔ m≥ 2
Kết luận: Có vô số giá trị nguyên của m thỏa yêu cầu bài toán. Câu 36. Chọn D. 2 2
x − mx + m − m − Tập xác định D = 2 4 2 1 g(x) \{ }
m . Ta có y′ = = 2 2 (x − m) (x − m)
Hàm số đồng biến trên (1;+∞) khi và chỉ khi g(x) ≥ 0, x
∀ >1 và m ≤1 (1) Vì 2 ∆ ′ = 2( +1) ≥ 0,∀ g m
m nên (1) ⇔ g(x) = 0 có hai nghiệm thỏa 1x ≤ 2 x ≤1 2
2g(1) = 2(m − 6m +1) ≥ 0
Điều kiện tương đương là
⇔ m ≤ 3− 2 2 ≈ 0,2 S . = m ≤ 1 2
Do đó không có giá trị nguyên dương của m thỏa yêu cầu bài toán. Câu 37. Chọn B.
Điều kiện xác định: β ≥ 2
Yêu cầu của bài toán đưa đến giải bất phương trình 1 ≤ sin 2α ≤1 2 π π Kết luận: 5 + kπ ≤ α ≤
+ kπ ,k ∈ và β ≥ 2 . 12 12 Câu 38. Chọn C.
Tập xác định D = . Ta có: y′ = 2 + c
a osx − bsin x
Áp dụng bất đẳng thức Schwartz ta có 2 2 2 2
2 − a + b ≤ y′ ≤ 2 + a + b
Yêu cầu của bài toán đưa đến giải bất phương trình 2 2 2 2
y′ ≥ 0,∀x ⇔ 2 − a + b ≥ 0 ⇔ a + b ≤ 4 . Câu 39. Chọn C. 3 2
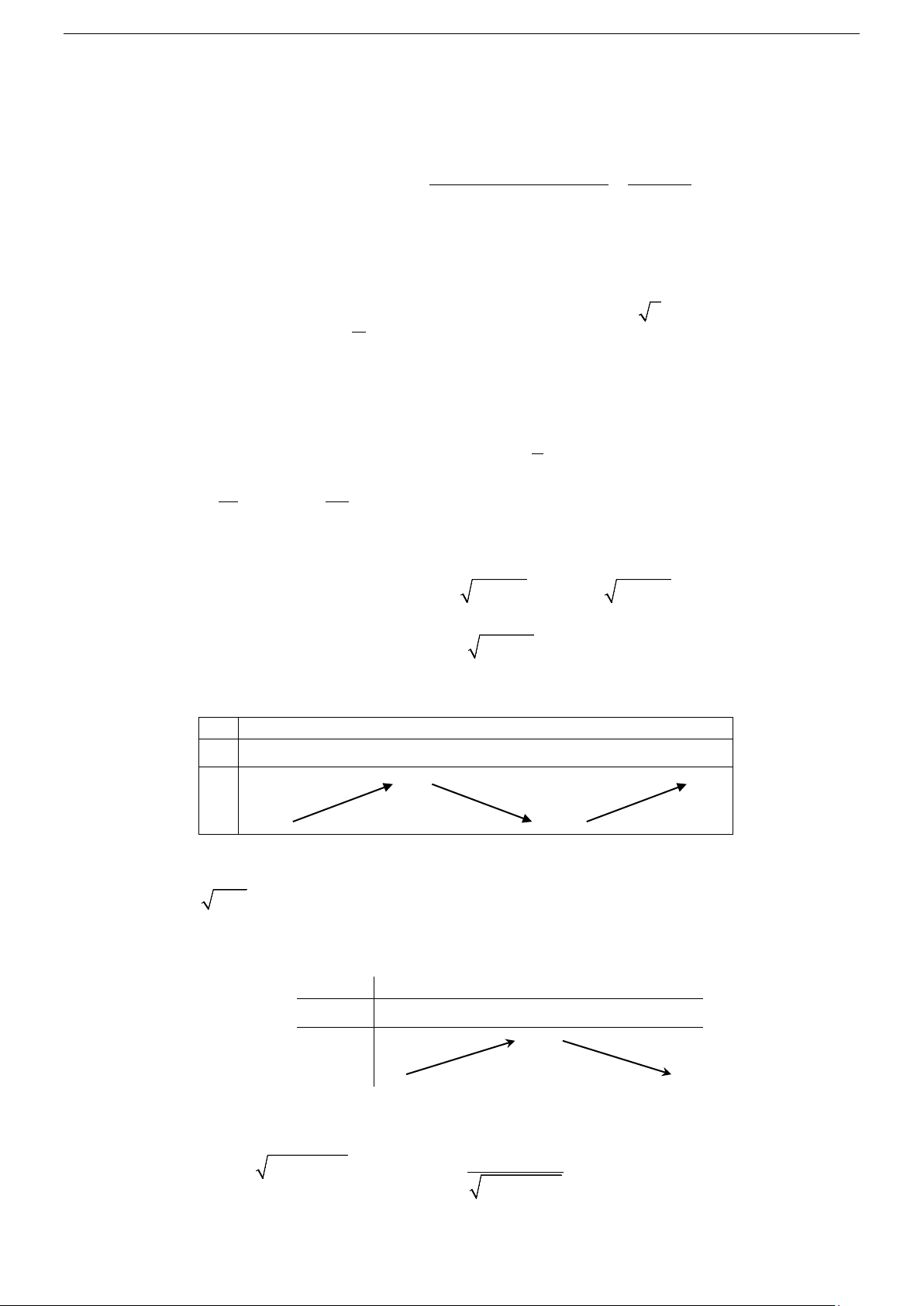
(1) ⇔ m = x − 3x − 9x = f (x) . Bảng biến thiên của f (x) trên . x −∞ 1 − 3 +∞ y′ + 0 − 0 + 5 +∞ y −∞ 27 −
Từ đó suy ra pt có đúng 1 nghiệm khi m < 27 − hoặc m > 5 Câu 40. Chọn B.
Đặt t = x +1,t ≥ 0 . Phương trình thành: 2 2
2t = t −1+ m ⇔ m = t − + 2t +1 Xét hàm số 2
f (t) = −t + 2t +1,t ≥ 0; f (′t) = 2 − t + 2
Bảng biến thiên của f (t) : t 0 1 +∞ f ′(t) + 0 − 2 f (t) 1 −∞
Từ đó suy ra phương trình có nghiệm khi m ≤ 2. Câu 41. Chọn B x − Đặt 2
t = f (x) = x − 4x + 5 . Ta có 2 f (′x) =
. f (′x) = 0 ⇔ x = 2 2 x − 4x + 5
Xét x > 0 ta có bảng biến thiên Trang 13/16 x 0 2 +∞ f ′(x) − 0 + 5 +∞ f (x) 1
Khi đó phương trình đã cho trở thành 2 2
m = t + t − 5 ⇔ t + t − 5 − m = 0 (1).
Nếu phương trình (1) có nghiệm 1t,t2 thì 1t + t2 = 1
− . (1) có nhiều nhất 1 nghiệm t ≥1.
Vậy phương trình đã cho có đúng 2 nghiệm dương khi và chỉ khi phương trình (1) có đúng 1
nghiệm t ∈(1; 5) . Đặt 2
g(t) = t + t − 5. Ta đi tìm m để phương trình g(t) = m có đúng 1
nghiệm t ∈(1; 5) . Ta có g (′t) = 2t +1> 0,∀t ∈(1; 5) .
Bảng biến thiên: t 1 5
g′(t) + 5 g (t) 3 −
Từ bảng biến thiên suy ra 3
− < m < 5 là các giá trị cần tìm. Câu 42. Chọn C. Bất phương trình 2
x − 3x + 2 ≤ 0 ⇔ 1≤ x ≤ 2 . − − Bất phương trình 2 mx + (m + ) 1 x + m +1≥ 0 2 x 2
⇔ m(x + x +1) ≥ −x − 2 ⇔ m ≥ 2 x + x +1 − − 2 x + + Xét hàm số x 2 f (x) =
với 1≤ x ≤ 2 . Có 4x 1 f (′x) = > 0,∀x ∈[1;2] 2 x + x +1 2 2 (x + x +1)
Yêu cầu bài toán ⇔ m ≥ max f (x) 4 ⇔ m ≥ − [1;2] 7 Câu 43. Chọn B. Đặt 2
t = log x +1 . Điều kiện: t ≥1. 3 Phương trình thành: 2
t + t − 2m − 2 = 0 (*) . Khi 3 x ∈ 1;
3 ⇒ t ∈[1;2] 2 t + t − 2 (*) ⇔ f (t) =
= m . Bảng biến thiên : 2 t 1 2
f ′(t) + 2 f (t) 0
Từ bảng biến thiên ta có : 0 ≤ m ≤ 2 Câu 44. Chọn C Điều kiện: 1 x ≥ − 2 Phương trình 2
x + mx + 2 = 2x +1 2
⇔ 3x + 4x −1= mx (*) 2 + −
Vì x = 0 không là nghiệm nên (*) 3x 4x 1 ⇔ m = x Trang 14/16 2 + − 2 + Xét 3 4 1 ( ) x x f x = . Ta có 3x 1 1 f (′x) = > 0 x ∀ ≥ − ; x ≠ 0 x 2 x 2 Bảng biến thiên x 1 − 0 +∞ 2
f ′(x) + + +∞ +∞
f (x) 9 2 −∞
Từ bảng biến thiên ta có để phương trình có hai nghiệm thì 9 m ≥ . 2 Câu 45. Chọn D.
Điều kiện : x ≥1 4 2 − − − − Pt x 1 x 1 ⇔ 3 + m = 2 x 1 x 1 ⇔ + = 4 3 m 2 + 4 2 x 1 (x +1) x +1 x +1 x −1 = 4 t
với x ≥1 ta có 0 ≤ t <1. Thay vào phương trình ta được 2
m = 2t − 3t = f (t) x +1
Ta có: f (′t) = 2 − 6t ta có: 1
f (′t) = 0 ⇔ t = 3 Bảng biến thiên: t 1 0 1 3 f ′(t) + 0 − 1 f (t) 0 3 1 −
Từ bảng biến thiên ta có để phương trình có hai nghiệm khi 1 0 ≤ m < 3 Câu 46. Chọn D.
Đặt t = (1+ 2x)(3− x) khi 1 7 2
x ∈ − ;3 ⇒ t ∈ 0; 2 4
Thay vào bất phương trình ta được 2
f (t) = t + t > m Bảng biến thiên t 0 7 2 4
f ′(t) + 49 +14 2 f (t) 8 0
Từ bảng biến thiên ta có : m < 0 Câu 47. Chọn D. Đặt 2 2
t = 1+ x + 3− x ⇒ t = 4 + 2 (1+ x)(3− x) ⇔ 2 (1+ x)(3− x) = t − 4
Với x ∈[ −1;3] => t ∈[2;2 2]. Thay vào bất phương trình ta được: 2 m ≤ t − + 3t + 4 Trang 15/16 Xét hàm số 2
f (t) = −t + 3t + 4; f (′t) = 2 − t + 3 ; 3
f (′t) = 0 ⇔ t = < 2 2 t 2 2 2
f ′(t) - 6 f (t) 6 2 − 4
Từ bảng biến thiên ta có m ≤ 6 2 − 4 thỏa đề bài Câu 48. Chọn D. Đặt t 2
= 3 + x + 6 − x > 0 2
⇒ t = ( 3 + x + 6 − x ) = 9 + 2 (3 + x)(6 − x) 2
⇒ 9 ≤ t = 9 + 2 (3 + x)(6 − x) ≤ 9 + (3 + x) + (6 − x) =18 2 ⇒
+ x − x = ( + x)( − x) 1 18 3 3 6 = ( 2
t − 9);t ∈ 3;3 2 2 Xét f (t) 1 2 9
= − t + t + ; f ′(t) =1− t < 0; t
∀ ∈ 3;3 2 ⇒ max f (t) = f (3) = 3 2 2 3;3 2
ycbt ⇔ max f (t) 2 2
= 3 ≤ m − m +1 ⇔ m − m − 2 ≥ 0 ⇔ m ≤ 1 − hoặc m ≥ 2 3;3 2 Câu 49. Chọn B Đặt 2x t = > 0 thì x m + (m − ) x+2 .4 1 .2
+ m −1 > 0, đúng x ∀ ∈ 2
⇔ m t + (m − ) t + (m − ) > t ∀ > ⇔ m( 2 . 4 1 . 1 0, 0 t + 4t + ) 1 > 4t +1, t ∀ > 0 ⇔ g (t) 4t +1 = < , m t ∀ > 0 . 2 t + 4t +12 Ta có ′( ) 4 − t − 2t g t =
< 0 nên g (t) nghịch biến trên [0;+∞) (t + 4t + )2 2 1
ycbt ⇔ max g (t) = g (0) =1≤ m t≥0 Câu 50. Chọn A. Bpt 3 1 2 1 2
⇔ 3mx < x − + 2, x
∀ ≥1 ⇔ 3m < x −
+ = f (x), x ∀ ≥1. 3 4 x x x Ta có f ′(x) 4 2 4 2 4 2 − 2 = 2x + − ≥ 2 2x − =
> 0 suy ra f (x) tăng. 5 2 x x ( 5x) 2 2 x x
Ycbt ⇔ f (x) > m x ∀ ≥ ⇔
f (x) = f ( ) 2 3 , 1 min
1 = 2 > 3m ⇔ > m x 1 ≥ 3 Câu 51. Chọn A. 2 2 cos x cos x (1) ⇔ 2 1 3 + ≥ m . Đặt 2
t = cos x,0 ≤ t ≤1 3 9 t t t t (1) trở thành 2 1 3 + ≥ m (2). Đặt 2 1 f (t) = + 3 . 3 9 3 9
Ta có (1) có nghiệm ⇔ (2) có nghiệm t ∈[0;1] ⇔ m ≤ Max f (t) ⇔ m ≤ 4 t [ ∈ 0;1] Câu 52. Chọn C Điều kiện: 2 − ≤ x ≤ 4 . Xét 3 2
f (x) = 2x + 3x + 6x +16 − 4 − x trên đoạn [ 2; − 4]. 3( 2 x + x + ) 1 Có 1 f (′x) = + > 0, x ∀ ∈( 2; − 4) . 3 2
2x + 3x + 6x +16 2 4 − x
Do đó hàm số đồng biến trên[ 2;
− 4], bpt ⇔ f (x) ≥ f (1) = 2 3 ⇔ x ≥1.
So với điều kiện, tập nghiệm của bpt là S = [1;4] ⇒ a + b = 5. Câu 53. Chọn A. Trang 16/16
Điều kiện: 1≤ x ≤ 3 ; bpt ⇔ (x − )2 + + x − > ( − x)2 1 2 1 3 + 2 + 3− x Xét 2
f (t) = t + 2 + t với t ≥ 0 . Có t 1 f '(t) = + > 0, t ∀ > 0 . 2 2 t + 2 2 t
Do đó hàm số đồng biến trên [0;+∞) . (1) ⇔ f (x −1) > f (3− x) ⇔ x −1 > 3 ⇔ x > 2
So với điều kiện, bpt có tập nghiệm là S = (2;3]. Trang 17/16
Document Outline
- DS_C1_DON DIEU
- CHỦ ĐỀ 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
- § 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
- BÀI TẬP TRẮC NGHIỆM
- A. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM