Ôn tập XSTK
ÔN TẬP XÁC SUẤT THỐNG KÊ ỨNG DỤNG
CHƯƠNG 2: PHÉP TÍNH XÁC SUẤT
2.1 Không gian mẫu và biến cố:
- Phép thử: là một nhóm các hành động hoặc thí nghiệm do ta tiến hành hoặc dự định
tiến hành nhằm nghiên cứu một vấn đề nào đó.
- Không gian mẫu : Tập hợp tất cả các kết quả của một phép thử
- Biến cố: một tập hợp con của không gian mẫu . Thường kí hiệu bằng chữ in: A, B,…
Biến cố sơ cấp : kết quả đơn giản nhất có thể xảy ra khi thực hiện phép thử .
Biến cố chắc chắn: là biến cố luôn xảy ra khi thực hiện phép thử. Kí hiệu :
Biến cố không thể: là biến cố không thể xảy ra. Kí hiệu là
Biến cố kép: là biến cố chứa nhiều hơn một kết quả.
- Mối quan hệ của lý thuyết tập hợp:
a. Hợp của hai biến cố: Kí hiệu: C = A + B hay C
( chỉ cần ít nhất một biến cố xảy ra)
b. Giao của hai biến cố: Kí hiệu : C = A.B hay C
(hai biến cố đồng thời xảy ra) c. Đối ậ
l p (phần bù) :. Kí hiệu A A : . A A
d. Xung khắc (rời nhau) : . A B .
e. Độc lập: Biến cố A độc lập với biến có B khi khả năng xảy ra của biến cố này
không ảnh hưởng đến biến cố kia và ngược lại.  + ++ =  f. H A A A
ệ đầy đủ: Hệ 
A ,A ,…,A gọi là hệ đầy đủ nếu 1 2 n  1 2 n
 A A =    i  j  n  i j 1 1 Ôn tập XSTK
2.2 Xác suất cổ điển
- Định nghĩa xc suất theo lối cổ điển: ( ) m P A n
- Tính chất: A : 0  P( ) A  1 ; P( )
 = 1, P() = 0 ; P(A)
2.3 Công thức cộng
- Công thức cộng xác suất: P(A + B) = P(A) + P(B) − P(AB)
Mở rộng : P(A + B+C) = P(A)+ P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)
Nếu A, B là hai biến cố xung khắc thì P(A + B) = P(A) + P(B) .
2.4 Xác suất có điều kiện: P(AB)
- Công thức xác suất điều kiện: P(A|B) = P(B)
(Xác suất xảy ra A với điều kiện B đã xảy ra).
2.5 Công thức nhân xác suất: P(AB) = P(A) . P(B|A)
Mở rộng :P(ABC) = P(A) . P(B|A) . P(C|AB)
Hai biến cố A và B gọi là độc lập thì : P(AB) = P(A)P(B)
2.6 Công thức xác suất đầy đủ
- Công thức xc suất đầy đủ (toàn phần): n
P(B) = P(A )P(B | A ) = P(A )P(B | A ) ++ P(A )P(B | A ) . i i 1 1 n n i=1
- Công thức Bayes:
P(A )P(B | A )
P (A | B ) i i = i  =  n i , 1, , P(B) 2 Ôn tập XSTK
Ví dụ 1: Ở một trạm xăng nào đó có 30% người sử dụng Gas thông thường
(A1), 45% sử dụng Gas + (A2) và 25% sử dụng Gas premium (A3). Trong số những
khách hàng sử dụng Gas thông thường thì chỉ có 30% người đổ đầy bình chứa của họ
(B), tương tự cho người sử dụng Gas + và Gas premium là 50% và 70%.
a. Tính xác suất khách hàng tiếp theo sẽ yêu cầu đổ Gas + đầy vào bình chứa của họ.
b. Tính xác suất khách hàng tiếp theo sẽ yêu cầu đổ đầy vào bình chứa của họ?
c. Nếu khách hàng tiếp theo đổ đầy vào bình chứa của họ, xác suất họ yêu cầu đổ Gas thông thường
( gợi ý áp dụng ctxsđđ cho hệ 3 biến cố đầy đủ A1, A2, A3 )
Ví dụ 2: Tại một vùng quê có 3 hãng taxi hoạt động là Vina, Mai linh và
Phương trang. Một khách hàng gọi taxi thì xác suất gọi hãng Vina ( A1) là 25%,
hãng Mai linh (A2) là 30% và Phương trang (A3) là 45%. Khi đi taxi các hãng trên
xác suất tài xế được bo thêm lần lượt là 20%, 35% và 20%. Một khách hàng gọi xe,
tính xác suất khách hàng đó có bo thêm cho tài xế taxi ( áp dụng ctxsđđ cho hệ 3 biến cố A1, A2,A3).
Ví dụ 3: Một xí nghiệp có 3 phân xưởng với tỷ lệ phế phẩm tương ứng là 3% ,
5% và 2%. Biết rằng phân xưởng I sản xuất ra 40% sản phẩm, xưởng II sản xuất ra
25% sản phẩm, xưởng III sản xuất ra 35% sản phẩm.
a. Chọn ngẫu nhiên 1sp. Tính xác suất lấy được phế phẩm.
b. Biết sản phẩm lấy ra là phế phẩm. Tính xác suất đó là phế phẩm
Ví dụ 4: Lô thứ nhất có 35 sản phẩm loại I, 5 sản phẩm loại II. Lô thứ hai có
40 sản phẩm loại I, 15 sản phẩm loại II. Lấy ngẫu nhiên 2 sản phẩm từ lô thứ nhất bỏ
sang lô thứ hai, rồi từ lô thứ hai lấy ngẫu nhiên ra 1 sản phẩm. Tính xác suất sản
phẩm vừa lấy ra là sản phẩm loại I ( gợi ý: lấy lô I bỏ qua lô II 2 sản phẩm xảy ra 3
trường hợp đây là hệ đầy đủ với 3 biến cố là 3 TH )
Ví dụ 5: Có 2 hộp bi, hộp 1 có 15 bi thì có 5 bi trắng, hộp 2 có 30 bi thì có 8
bi trắng. Lấy ngẫu nhiên mỗi hộp 1 bi, từ 2 bi lấy được đó lấy ngẫu nhiên 1 bi. Tính
xác suất bi lấy ra sau cùng là bi trắng. 3 Ôn tập XSTK
Ví dụ 6: Có 3 xạ thủ cùng bắn vào một con mồi ( mỗi người bắn 1 viên đạn)
với xác suất bắn trúng lần lượt là 0,6; 0,8; 0,7. Biết rằng nếu con thú trúng 1 viên đạn
thì xác suất nó bị tiêu diệt là 0,4; trúng 2 viên là 0,7; trúng 3 viên thì chắc chắn bị tiêu diệt.
a. Tính xác suất con thú bị tiêu diệt
b. Giả sử con thú bị tiêu diệt, tính xác suất ể đ nó trúng 2 phát đạn
Bài tập chương
1. Khả năng mỗi khách mời A, B, C đến dự sự kiện E là như nhau và bằng 0,3. Biết
A xung khắc với B, C nên khả năng A và B hay A và C cùng tới là bằng 0. Khả
năng B và C cùng tới là 0,2. Biết có ít nhất 1 người trong 3 khách A, B, C tới dự.
Tính xác suất đó là khách mời A.
2. Trong bữa tiệc giáng sinh, trung tâm X có 1 phần quà đặc biệt là học phí 1 khóa
học và 3 phần quà là chuyến tham quan miễn phí tại Snow house. Các phần quà
được tặng cho 4 trong 50 học viên tham dự bằng cách chọn ngẫu nhiên lần lượt
từng học viên tham dự. Tính xác suất 2 chị em A, B tham gia bữa tiệc này có một
người nhận được phần quà đặc biệt và một người không nhận được phần quà nào.
3. Tỷ lệ học viên của các trung tâm ngoại ngữ A, B, C có kết quả thi IELTS từ 6.0
trở lên lần lượt là 0,55; 0,6 và 0,48.
a. Tính xác suất trong 20 học viên trung tâm A đi thi IELTS có ít nhất 8 người đạt
kết quả từ 6.0 trở lên. ( 0,941965903 )
b. Tính xác suất trong số 2 học viên trung tâm A, 3 học viên trung tâm B và 4 học
viên trung tâm C thi IELTS có đúng 1 người đạt được 6.0 trở lên.
(YÊU CẦU: LÀM CÂU b) 0,01007923139. 4 Ôn tập XSTK
4. Công ty M đầu tư vào 2 dự án A, B một cách độc lập, với xác suất dự án A, B
mang lại lợi nhuận lần lượt là 0,7 và 0,8. Biết chỉ có một dự án mang lại lợi nhuận,
tính xác suất đó là dự án A. 5.
ột dây chuyền lắp ráp nhận được các chi tiết do hai nhà máy sản xuất. Nhà máy M
thứ nhất cung cấp 65% và nhà máy thứ hai cung cấp 35% tổng số chi tiết. Tỷ lệ
chi tiết đạtchuẩn của nhà máy thứ nhất là 90% và tỷ lệ chi tiết đạt chuẩn của nhà
máy thứ hai là95%. Kiểm tra ngẫu nhiên từ dây chuyền 1 chi tiết và thấy chi tiết
đạt chuẩn. Tính xác suất để chi tiết đạt chuẩn đó do nhà máy thứ nhất cung cấp.
6. Có hai lô hàng, mỗi lô chứa 15 sản phẩm, trong đó lô I gồm 10 sản phẩm tốt và 5
sản phẩm xấu; lô II gồm 8 sản phẩm tốt và 7 sản phẩm xấu. Chọn ngẫu nhiên 2 sản
phẩm từ lô I bỏ sang lô II, sau đó từ lô thứ II lấy ra 2 sản phẩm. Giả sử đã chọn
được một sản phẩm tốt và một sản phẩm xấu từ lô II. Tính xác suất để trong hai
sản phẩm chọn ra từ lô I có một sản phẩm tốt và một sản phẩm xấu.
7. Trong một kho hàng chứa sản phẩm của 3 công ty A, B và C. Số sản phẩm của
công ty A gấp đôi số sản phẩm của công ty B và số sản phẩm của công ty B gấp
đôi số sản phẩm của công ty C. Mỗi sản phẩm của công ty A, B và C có xác suất
đạt chuẩn tương ứng là 0,90; 0,95 và 0,87. Lấy ngẫu nhiên 1 sản phẩm từ kho
hàng này và được sản phẩm không đạt chuẩn. Tính xác suất ể đ sản phẩm không
đạt chuẩn này là sản phẩm của công ty B.
8. Trong kho hàng có 58% sản phẩm của công ty A, còn lại là của công ty B và C.
Xác suất đạt chuẩn của mỗi sản phẩm do công ty A, B, C sản xuất lần lượt là 0,92;
0,96; 0,96. Lấy ngẫu nhiên 1 sản phẩm từ kho đem kiểm tra và thấy sản phẩm
không đạt chuẩn. Tính xác suất để sản phẩm đó không phải của công ty A.
9. Moät traïm tín hieäu chæ phaùt hai loaïi tín hieäu A vaø B vôùi xaùc suaát töông öùng laø 0,8
vaø 0,2. Do coù nhieãu treân ñöôøng truyeàn neân 1/6 tín hieäu A bò meùo vaø thu ñöôïc nhö
tín hieäu B, coøn 1/8 tín hieäu B bò meùo thaønh tín hieäu A.
a. Tìm xaùc suaát thu ñöôïc tín hieäu A. (83/120)
b. Giaû söû thu ñöôïc tín hieäu A, tìm xaùc suaát ñeå thu ñöôïc ñuùng tín hieäu luùc phaùt.(80/83) 5 Ôn tập XSTK
10.Moät nöõ coâng nhaân quaûn lyù 5 maùy deät. Xaùc suaát ñeå moät maùy deät trong khoaûng
thôøi gian t caàn ñeán söï chaêm soùc cuûa nöõ coâng nhaân baèng 1/3. Tìm xaùc suaát ñeå :
a. Trong khoaûng thôøi gian t coù 2 maùy caàn ñeán söï -chaêm soùc.
b. Trong khoaûng thôøi gian t soá maùy caàn ñeán söï chaêm soùc khoâng beù hôn 2 vaø khoâng lôùn hôn 3.
11. Một lô hàng chứa 60 sản phẩm của nhà máy A và 40 sản phẩm của nhà máy B
được đem bán. Người mua lấy ngẫu nhiên 2 sản phẩm từ lô hàng này để kiễm tra
và mua lô hàng nếu cả 2 sản phẩm đều đạt chuẩn. Tính xác suất bán được lô hàng
này, biết xác suất mỗi sản phẩm của nhà máy A đạt chuẩn là 0,92 và xác suất mỗi
sản phẩm của nhà máy B đạt chuẩn là 0,96.
12. Có 2 học sinh giỏi, 3 học sinh khá và 4 học sinh trung bình thi tốt nghiệp phổ
thông, xác suất thi đậu của mỗi học sinh tương ứng là: 0,99; 0,95; 0,90. Khi công
bố kết quả chỉ có 1 học sinh trong 9 học sinh này thi hỏng. Tính xác suất để học
sinh thi hỏng là học sinh giỏi.
13.Moät xí nghieäp vôùi 2 phaân xöôûng vôùi caùc tyû leä pheá phaåm töông öùng laø 1% vaø 2%.
Bieát raèng phaân xöôûng I saûn xuaát 40%, coøn phaân xöôûng II saûn xuaát 60% saûn phaåm.
a. Tìm xaùc suaát ñeå töø kho cuûa xí nghieäp choïn ngaãu nhieân ñöôïc moät pheá
phaåm. Baïn coù nhaän xeùt gì veà xaùc suaát naøy (ñs : 1.6%)
b. Giaû söû laáy ñöôïc moät pheá phaåm, tìm xaùc suaát ñeå noù do phaân xöôûng I saûn
xuaát ra. (ñs : 0,25) 6 Ôn tập XSTK
CHƯƠNG 3: BIẾN NGẪU NHIÊN VÀ PHÂN PHỐI XÁC SUẤT
3.1 Biến ngẫu nhiên ( đại lượng ngẫu nhiên): 2 loại ĐLNN (BNN)
- BNN rời rạc: tập giá trị của nó là hữu hạn hay đếm được.
- BNN liên tục: tập giá trị của nó lấp đầy một khoảng nào đó tên trục số và xác suất của
một điểm bất kì luôn là 0.
3.2 Bảng phân phối xc suất của biến ngẫu nhiên rời rạc:
Bảng phân phối xác suất: X x1 …. xn p(x ) p(x ) … p(x ) i 1 n
3.3 Hàm phân phối tích luỹ (CDF) : kí hiệu F(x)
(cả biến rời rạc và biến liên tục đều có hàm phân phối xác suất tích luỹ) F (x) = ( P X  x)
Chú ý: ý nghĩa là toàn bộ xác suất tích lũy được ở bên trái giá trị x bất kỳ.
3.4 Hàm mật độ của biến n ẫ
g u nhiên liên tục (pdf) : kí hiệu f ( x)
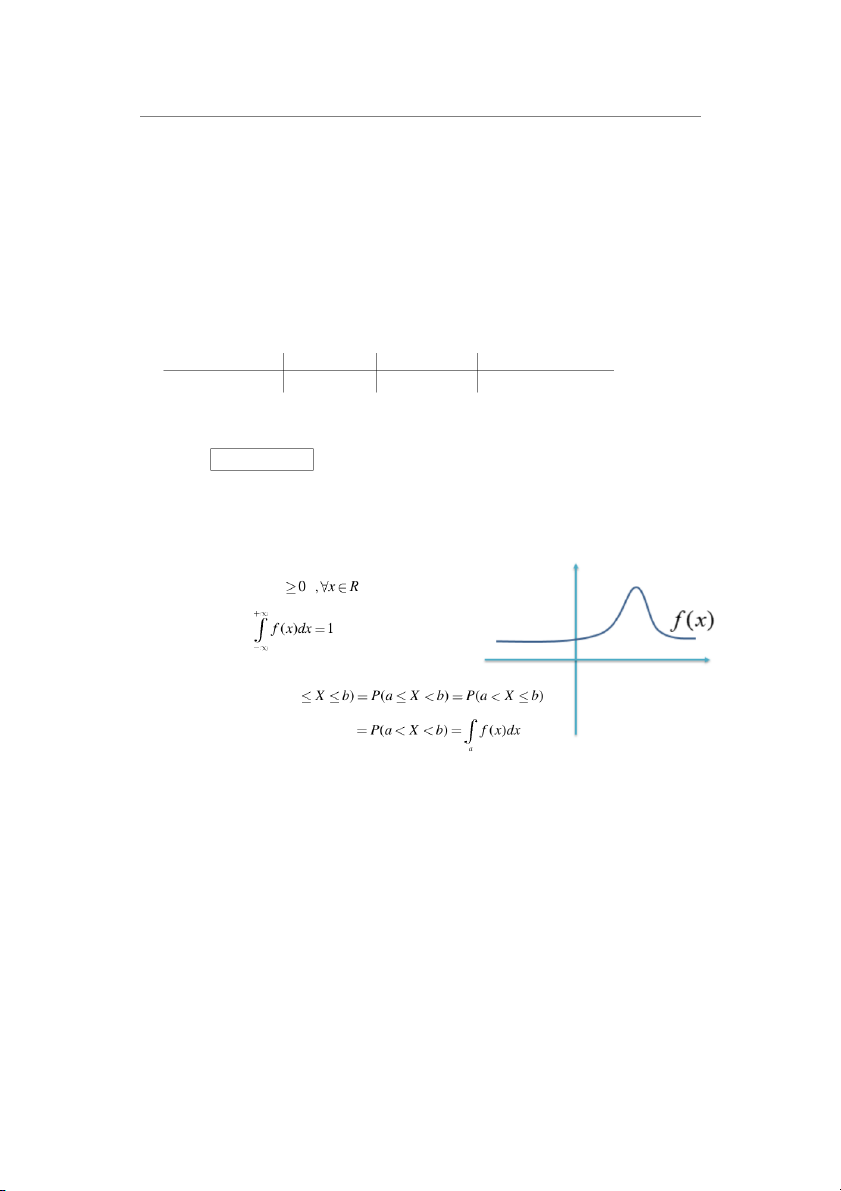
X là biến ngẫu nhiên liên tục có hàm mật độ thoả 2 điều kiện : 1/ f (x) 2/ ❖ Tính chất P (a b
3.5 Kỳ vọng và phương sai:
a/ Kỳ vọng (trung bình) của BNN X : ký hiệu : E (X ) là gi trị trung bình của X. n
- Nếu X là BNN rời rạc thì E (X ) = p x  = p x + + p x i i ... 1 1 n x i 1 = 7 Ôn tập XSTK +
- Nếu X là BNN liên tục thì E ( X ) = . x f 
(x) , với f (x) là hàm mật độ xc dx − suất đề cho.
Tnh cht: 1/ ( E ) c 2 / E( . c X) 3/ E(X
4 / E(X.Y)
(Y) nếu như X và Y độc lập.
5 / E [h( X )] = h  (x). (px) x D 
b/ Phương sai: Phương sai của BNN X ký hiệu: V ( X ) hay Var ( X ) V (X ) với 2
E(X ) xác định như sau:
- Nếu X là BNN rời rạc thì E ( 2 X ) 2 =  . p x i i +
- Nếu X là BNN liên tục thì ( 2 ) 2 E X = x f (x )  . −
- Độ lệch chuẩn của X:  ( X ) = V (X ) Tính cht : 1/ V (X ) 2 / V( ) c 3 / V( . c X ) ) 4 / V( X u X, Y doc lap 8 Ôn tập XSTK
Ví dụ 1: Tuổi thọ X của một loại côn trùng ( đơn vị: thng) là BNN có hàm mật độ : 2 k
 x (4 − x), 0  x  4 f (x) =  0, x [0;4]. a. Tìm k
b. Tính xác suất một con côn trùng chết trước khi nó 1 tháng tuổi
c. Tìm tuổi thọ trung bình của loại côn trùng trên
d. Tính độ lệch chuẩn về tuổi thọ của loại côn trùng đó.
e. Biết nó sống quá 1 tháng tuổi, tính xác suất nó chết trước 2 tháng tuổi.
Hướng dẫn giải +
a. Tìm k ta cần xét điều kiện f
 (x) =1 theo đề bài 0  x  4 nên tích phân chỉ cần − xét từ 0; 
4 và thay f (x ) 2
= kx (4 − x ) vào 4  64 3 2
kx (4 − x)dx =1  k =1  k =  . 3 64 0
b. ( Chết trước 1 tháng là tuổi thọ nhỏ hơn 1 tháng nghĩa là X < 1 ) 1 1 3 13
- P (X 1) = f  (x ) 2 = x  (4 −x ) = dx 64 256 − 0
c. ( Tính tuổi thọ trung bình là tính E (X ) áp dụng công thức ở trên ) + 4 3
- E (X ) = xf  (x) 2 = x .x 
(4 −x )dx = 2.4 64 − 0
d. ( Tính độ lệch chuẩn là tính  (X ) = V (X ), mà ( )= ( ) −  ( ) 2 2 V X E X E X    ) 9 Ôn tập XSTK + 4 3 - E ( 2 X ) 2 = x f  (x) 2 2 = x .x 
(4 −x )dx = 6.4 64 − 0
- V (X ) = E( X ) − E  (X ) 2 2 2  = − = 6.4 2.4 0.64 
-  (X ) = V ( X ) = 0.64 = 0.8
e. Cho biết X>1, tính X<2, xác suất có đk : 2 f (x)dx 
P (X  2)(X 1) P(1  X  2) -
P( X  2) / ( X  1)   1 = = = 4 ( P X 1) ( P X 1) f ( ) x dx 1
Ví dụ 2 : Chiều cao X( đơn vị: m ) của cây bắp sau khi trồng 2 tháng là biến ngẫu nhiên
có hàm mật độ xác suất f (x )= k(x +1) nếu x3;7 , f (x ) = 0 nếu x3;7. a. Tìm k
b. Tính chiều cao trung bình và độ lệch chuẩn về chiều cao của bắp.
c. Tính xác suất một cây bắp có chiều cao từ 4m-6m
d. Tính xác suất 1 cây bắp có chiều cao trên 4m.
e. Tính xác suất 1 cây bắp có chiều cao dưới 4m.
f. Tính xác suất 1 cây bắp có chiều cao lớn hơn chiều cao trung bình tối đa 1 m
g. Tính xác suất 1 cây bắp có chiều cao sai lệch so với chiều cao trung bình 2 lần độ lệch chuẩn. 10 Ôn tập XSTK
3.6 Các phân phối xác suất thường gặp ( biến NN rời rạc)
1/ Phân phối nhị thức: Kí hiệu: X p)
Phép thử nhị thức gồm có n phép thử độc lập nhau và trong mỗi phép thử chỉ xét
đến biến cố A nào đó có xảy ra hay không xảy ra với xác suất p không đổi.
Trong phép thử nhị thức, đặt X là số lần A xảy ra trong n phép thử thì khi đó X là BNN
có phân phối nhị thức, ký hiệu: X −
- Khi đó P (X =k ) =C p − p
(công thức Bernoulli hay ct xs nhị thức) n (1 )n k k k EX Tính cht: V (X )
Ví dụ 1: Xác suất 1 sản phẩm của nhà máy A bị lỗi là 10%. Nhân viên kiểm tra ngẫu nhiên 50 sản phẩm
a. Tính xác suất kiểm tra được 4 sản phẩm lỗi.
b. Tính trung bình số sản phẩm lỗi kiểm tra được.
Ví dụ 2 : Hàng đóng thành kiện, mỗi kiện có 20 sản phẩm thì trong đó có 3 sản phẩm lỗi.
Khách hàng kiểm tra mỗi kiện 2 sản phẩm, nếu không phát hiện sản phẩm lỗi sẽ nhận kiện
hàng đó. Khách hàng kiểm tra 40 kiện hàng, tính xác suất có 30 lô được nhận. 2/ Ph
ân phối nhị thức âm: (khác với trong sách)
Trong phép thử nhị thức đặt Y là số phép thử phải thực hiện cho đến khi biến cố A xuất
hiện r lần thì ngừng, khi đó Y có phân phối nhị thức âm r 1 − r 1
P (Y =n ) =C
.p − .(1−p ) n− .r p
for n r n . −1 r ( r 1− ) p Tính cht : EY = ; V (Y ) = 2 p p
Ví dụ : Mỗi lô hàng có 50 sản phẩm thì có 15 sản phẩm kém chất lượng. Một k hách hàng
kiểm tra ngẫu nhiên mỗi lô 2 sản phẩm. Nếu không phát hiện sản phẩm kém chất lượng sẽ nhận lô hàng đó. 11 Ôn tập XSTK
a. Giả sử khách hàng muống lấy 10 lô hàng, tính xác suất ể đ khách hàng đó phải
kiểm tra đến lô hàng thứ 20.
b. Tính trung bình số lô hàng phải ểm tra ể đ lấy đủ 20 lô. ki
3/ Phân phối siêu bội:
- Xét tập hợp có N phần tử, trong đó có M phần tử mang tính chất A. Lấy ngẫu
nhiên n phần tử từ tập hợp đó. Đặt X là số phần tử mang tính chất A có trong
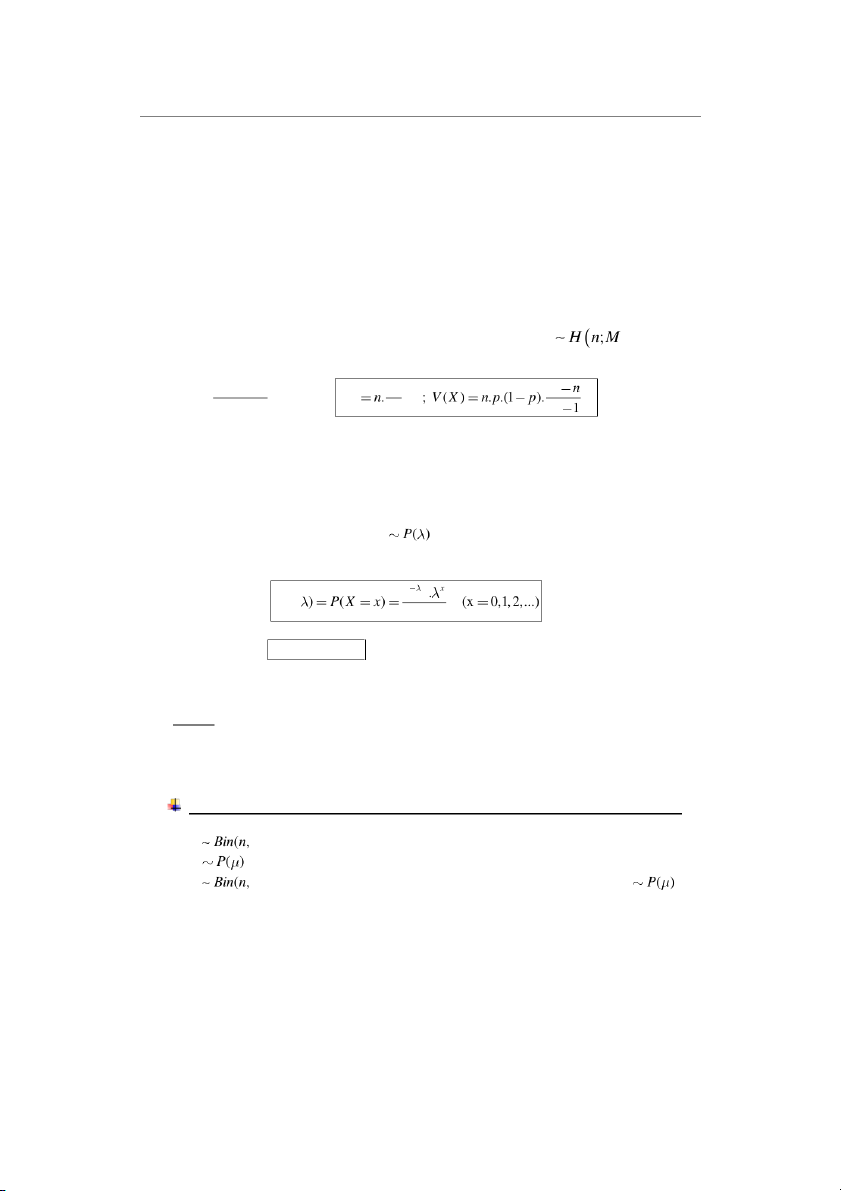
n phần tử lấy ra, thì X có phân phối siêu bội, ký hiệu X ;N ) k C C − M . n k
P (X = k ) N − M = và M N EX n C N N N
Ví dụ: Trong một giỏ mận có 30 trái thì có 10 trái bị hư. Lấy ngẫu nhiên 8 trái.
a. Tính xác suất trong 8 trái lấy ra đó có 2 trái hư.
b. Tính trung bình số trái mận hư lấy ra được.
4/ Phân phối Poisson: Kí hiệu : X tham số   0
X là số phép thử xảy ra. e p(x; x !
Tính cht: EX = V (X ) = 
Ví dụ: Tại một bến cảng, trung bình mỗi ngày có 10 tàu hàng cập bến.
a. Tính xác suất 1 ngày có 12 tàu cập bến
b. Tính xác suất một ngày có ít nhất 2 tàu cập bến.
c. Tính xác suất trong hai ngày có 18 tàu cập bến. ố ể ấ ỉ ố ị
Một s trường hợp có th x p x phân ph i nh thức sang phân phối Poission - X
p) , biết n và p . Trong đó n lớn ( n > 50) ; p nhỏ; tích np =  5 . Xem X - X
p) , chưa biết n và p mà chỉ biết trung bình np =  . Xem X 12 Ôn tập XSTK
Ví dụ: Xác suất một sản phẩm bị lỗi là p. Nhân viên kiểm tra một số sản phẩm và
biết được trung bình số sản phẩm lỗi k ể
i m tra được là 20. Tính xác suất nhân viên
đó kiểm tra phát hiện 24 sản phẩm bị lỗi.
HD: đặt X là số sản phẩm ỗ
l i phát hiện được thì X nhưng p và n chưa biết
nên không thể tính P( X = 2 )
4 bằng ct xs nhị thức nhưng biết E ( X ) = np = 20
Ta đặt  = np = 20 thì khi đó X −20 24 P (X = ) e 20 24 = = ....... 24!
3.7 Các phân phối xác suất của biến ngẫu nhiên liên tục
a. Phân phối đều
Biến ngẫu nhiên X có phân phối đều trên  ;
A B nếu hàm mật độ có dạng  1  , x ; A B
f ( x) =  B − A  0 , x ; A B 
Ví dụ: Thời gian X (phút) cho một trợ lý phòng thí nghiệm chuẩn bị thiết bị cho
một thử nghiệm nhất định được cho là có phân phối đều với A=25 và B=35.
a. Xác định hàm mật độ xác suất của X.
b. Tính xác suất thời gian chuẩn bị ít hơn 33 phút.
c. Tính xác suất thời gian chuẩn bị ít hơn thời gian chuẩn bị trung bình 2 phút.
d. Biết trợ lý đã chuẩn bị được 22 phút tính xác suất thời gian chuẩn bị không quá 30 phút.
b. Phân phối mũ
X có phân phối mũ với tham số   -
0 , thì hàm mật độ của X là t   −   .e ; x 0 f (x) =  . 0  ; x  0 1 −  x  −e ; x  0
Hàm phân phối xác suất của X là F (x) = P(X  x) =  0 ; x  0 Tính chất: 1 2 1  = ; = . 2  
Ví dụ: Thời gian sử dụng của một loại sản phẩm M là biến ngẫu nhiên X (đơn vị: -
năm) có phân phối mũ với thời gian sử dụng trung bình là 4 năm. Tính tỷ lệ sản
phẩm M có thời gian sử dụng từ 3 đến 5 năm. 13 Ôn tập XSTK Bài giải: E ( X ) 1 1 = 4 =   =  4 5 1 1 − x 4 - P (3  X  ) 5 = e dx = ..........  4 3 Hoặc: -  1 1 − .5   − .3    = − =  − 4  − − 4 P(3 X 5) F(5) F(3) 1 e 1 e  =     ...    
c. Phân phối chuẩn :
Biến ngẫu nhiên X có phân phối chuẩn với 2 tham số là  và 2  nếu hàm mật độ - có dạng: 1 2 2 −(x  − ) /(2 ) f ( ) x = e 2 b −(x− )2 1 Kí hiệu 2 2 X
), khi đó P(a  X b) 2 = - e dx    a 2
Phân phối chuẩn chuẩn tắc:
Nếu phân phối chuẩn có  = 0 và 2  1
= thì gọi là phân phối chuẩn tắc, kí hiệu - X 1 Hàm mật độ có dạng: 2 − x /2 f ( ) = - x e 2 2 x 1 − t
Đặt  ( x) = P( X  x) 2 =
 x gọi là hàm phân phối xác suất - e dt  thì ( ) − 2
của phân phối chuẩn tắc và giá trị của  ( x) được tính sẵng trong bảng 1 và 2 ( bảng z). Ví dụ : c ho biết P X  1.96 - X . Tính ( )
Ta có: P( X 1.96) = (1.96) = 0.975 ( mở bảng z bảng số thứ 2 tra hàng 1.9 và
cột 0.06 giao nhau tại đáp án cần tìm ) 14 Ôn tập XSTK
Tính chất : cho BNN X có phân phối chuẩn với trung bình  và phương sai 2  Kí hiệu 2 X ) , khi đó E ( X ) =  - và ( ) 2 V X =  X −  Đặt Z = thì - Z   −   - (  ) a P X a =       −    −   - (   ) b a P a X b =    −           −   - (  ) =1 a P X a −     
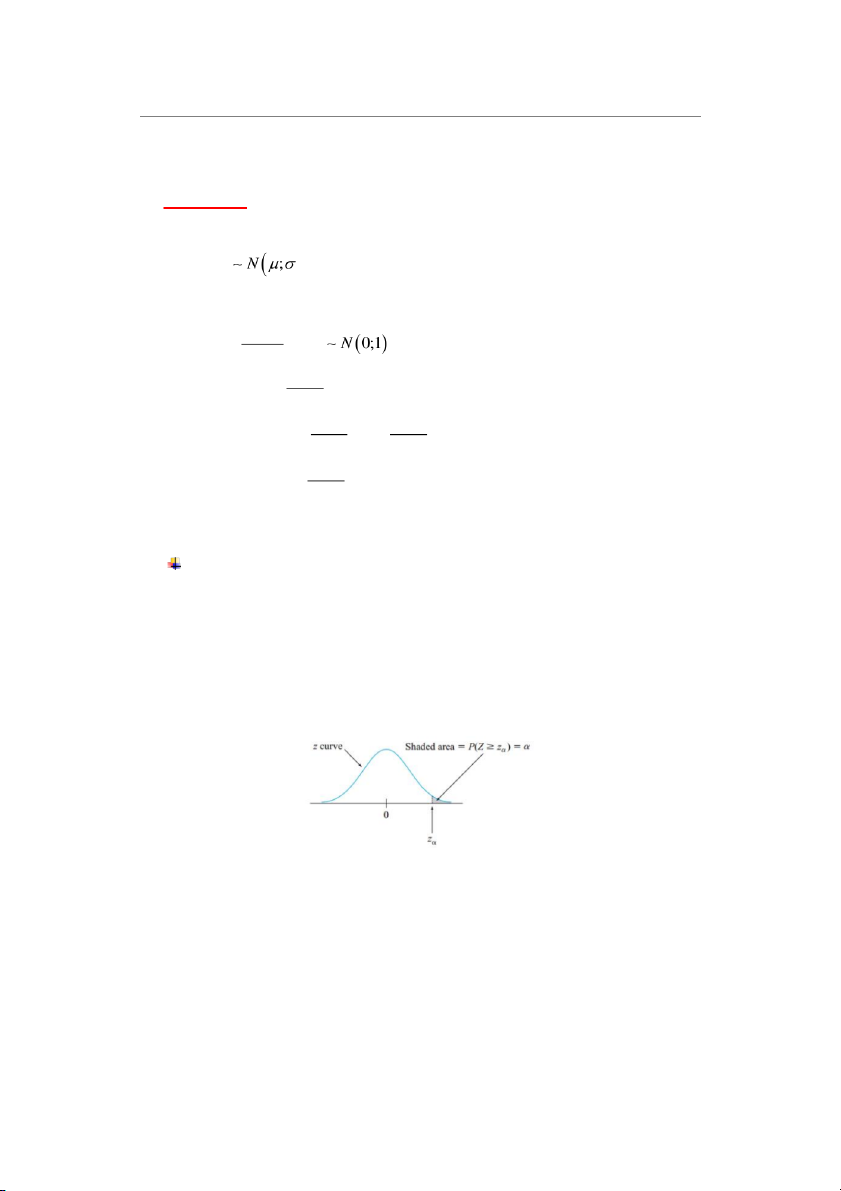
Phân vị của phân phối chuẩn:
z biểu thị giá trị trên trục z mà  là diện tích 
vùng dưới đường cong z nằm bên phải z . Khi đó chính là phân vị thứ 100(1-  z
 ) của phân phối chuẩn. 15 Ôn tập XSTK
Xấp xỉ phân phối nhị thức về phân phối chuẩn: cho X
Nếu đồ thị của phân phối nhị thức không quá lệch ( không quá mất đối xứng) ( np 10 ; (
n 1− p)  10 ) thì có thể xấp xỉ X như một phân phối chuẩn X bằng  x+ 0.5−  cách đặt và (  ) np P X x  . np (1 p )  −  
Ví dụ 1: Khối lượng X ( đv: kg ) của heo xuất chuồng là BNN tuân theo luật phân phối
chuẩn với khối lượng trung bình 95kg và độ lệch chuẩn 3kg.
a. Tính xác suất một con heo có khối lượng nhỏ hơn 94kg ( P(X<94)= ? )
b. Tính xác suất 1 con heo có khối lượng từ 94kg – 97kg. ( P(94
c. Tính xác suất 1 con heo có khối lượng lớn hơn 96kg. ( P(X>96)=? )
d. Tính xác suất 1 con heo có khối lượng lớn hơn khối lượng trung bình tối đa 2kg.
P(  X   + ) 2 = ?
e. Tính xác suất 1 con heo có khối lượng sai lệch với khối lượng trung bình không quá
1.4 lần độ lệch chuẩn. P( − 1.4  X   + 1.4 ) = ?
f. Bắt ngẫu nhiên 20 con heo. Tính xác suất có từ 3-6 con có khối lượng lớn hơn 96kg.
( đặt Y là số con heo có Kl trên 96 kg bắt được thì Y
) , P = P( X  96) 6 −
tính ở câu c, khi đó P (3 Y  ) 6 = C p  (1− p)20 k k k 20 . k=3 16 Ôn tập XSTK
BÀi tập chương 3
Bài 1. Hai người C, D lên một tàu điện gồm 3 toa một cách độc lập. Gọi 𝑋 là số người
trong hai người C, D lên toa số 1.
Lập bảng ppxs của X. Tính 𝐸(𝑋) và 𝑉(𝑋).
Bài 2. Theo dõi trọng lượng thực tế của một loại sản phẩm được quy định có trọng lượng
là 5 gam. Biết trọng lượng của loại sản phẩm này là biến ngẫu nhiên liên tục có hàm mật độ xác suất 2 k  1
 − (x − 5) , x  [4;6]   f ( ) x =  0,  x [4;6]
Tính xác suất một sản phẩm thuộc loại này trong thực tế có trọng lượng cao hơn trọng lượng quy định.
Bài 3. Tuổi thọ X (đơn vị : năm) của sản phẩm nhà máy H là biến ngẫu nhiên có có hàm mật độ xác suất  k , x   (0;9) 3 f ( ) x =  (10 − ) x 0  , x  (0;9 ) 
a. Nhà máy H bảo hành sản phẩm trong 2 năm, tính tỷ lệ sản phẩm phải bảo hành của nhà máy H.
b. Tính kỳ vọng và độ lệch chuẩn của X.
Bài 4. Tuổi thọ X (đv: giờ) của một thiết bị là biến ngẫu nhiên có hàm mật độ xác suất  A  , x  1000 3 f (x) =  x . 0, x  1000
Tính tuổi thọ trung bình của loại thiết bị này và xác suất để một thiết bị loại này
có tuổi thọ trên tuổi thọ trung bình. 17 Ôn tập XSTK
Bài 5. Xe buýt xuất hiện tại bến đợi 7 giờ sáng và cứ 15 phút có một chuyến. Thời gian đi
từ nhà đến bến đợi của cô H là biến ngẫu nhiên X(đv: phút) có hàm mật độ xác suất  1  , x 10;20 f (x) = 1  0 0, x    10;2  0
Cô H rời nhà đi đến bến đợi lúc 7 giờ, tính xác suất cô H phải đợi xe buýt không đến 3 phút.
Bài 6. Tuổi thọ của 1 loại sản phẩm là biến ngẫu nhiên X (đơn vị: năm) có hàm mật độ xác suất 2
cx (5 −x), x 0;5 f (x) =  . 0  , x   0;5
Một người mua một sản phẩm đã sử dụng được 9 tháng.
Tính xác suất để có thể sử dụng được sản phẩm này thêm 2 năm nữa
Bài 7 . Thời gian hoạt động của một máy do công ty A sản xuất là biến ngẫu nhiên X
(đơn vi: năm) có hàm mật độ xác suất 0  , x  0 f (x) =  . −0,2 0,2 x e , x   0
Một người mua 1 máy do công A sản xuất và đã sử dụng được 1 năm.
Tính xác suất máy này hoạt động được thêm 6 năm nữa.
Bài 8. Một hộp có 10 viên bi, trong đó có 6 viên đỏ, 4 bi xanh. Lấy ra 3 viên, nếu số bi đỏ
nhiều hơn số bi xanh thì lấy tiếp 1 viên nữa. Gọi X là số viên đỏ được lấy ra. Lập bảng ppxs của X.
Bài 9. Một hộp có 10 viên bi, trong đó có 6 viên đỏ, 4 bi xanh. Lấy ra 3 viên, nếu toàn là
bi đỏ thì lấy tiếp 1 viên nữa. Gọi X là số viên đỏ được lấy ra. Lập bảng ppxs của X. 18 Ôn tập XSTK
Bài 10. Tiến hành thử 5 máy, mỗi máy chỉ được thử nếu máy thử trước chịu đựng được
phép thử. Biết xs sức chịu đựng phép thử của mỗi máy là 0,9. Gọi X là số máy được thử. Lập bảng ppxs của X.
Bài 11. Thống kê cho thấy 40% khách hàng tới cửa hàng S mua bột giặt chọn loại bột
giặt E và số còn lại chọn loại bột giặt H. Trên kệ của cửa hàng lúc này còn 8 gói bột giặt
E và 8 gói bột giặt H. Tính xác suất số bột giặt này đáp ứng được nhu cầu của 10 khách
hàng mua bột giặt tiếp theo.
Bài 12. Nhà máy Q sản xuất một loại trục máy A có đường kính là biến ngẫu nhiên X có
phân phối chuẩn với đường kính trung bình là 1,55 cm và độ lệch chuẩn là 0,04 cm. Trục
máy A có đường kính chênh lệch so với đường kính trung bình không quá 0,03 cm là trục
đạt chuẩn. Tính tỷ lệ trục máy A đạt chuẩn của nhà máy M.
Bài 13. Thời gian sử dụng của một loại sản phẩm M là biến ngẫu nhiên X (đơn vị: năm)
có phân phối mũ với thời gian sử dụng trung bình là 3 năm. Một người mua 20 sản phẩm
M về sử dụng. Tính xác suất có ít nhất 15 sản phẩm trong 20 sản phẩm này có thời gian
sử dụng vượt quá thời gian sử dụng trung bình.
Bài 14. Một nhà máy đã sản xuất 10000 sản phẩm với xác suất ạ
đ t loại A của mỗi sản
phẩm là 0,842. Tính xác suất ể
đ trong 10000 sản phẩm này có ít nhất 8500 sản phẩm loại A.
Bài 15. Công ty Đất Xanh Miền Nam chính thức mở bán 926 căn hộ của Chung cư Sài
Gòn Gateway Quận 9. Xác suất bán được của mỗi căn ộ
h là 0,6. Tính xác suất công ty
bán được ít nhất 400 căn trong lần mở bán này.
Bài 16. Trọng lượng sản phẩm của nhà máy H là biến ngẫu nhiên X có phân phối chuẩn
với trọng lượng trung bình là 100 gam và độ lệch chuẩn là 0,45 gam. Sản phẩm có trọng lượng từ
99 gam đến 101 gam là sản phẩm có trọng lượng đạt chuẩn.
a. Tính tỷ lệ sản phẩm có trọng lượng đạt chuẩn của nhà máy H. b. Tính xác suất ể
đ trong 1000 sản phẩm chọn ngẫu nhiên của nhà máy H có ít nhất 950
sản phẩm có trọng lượng đạt chuẩn.
Bài 17. Thời gian X(đv: phút) đi từ nhà đến trường của sinh viên M là biến ngẫu nhiên X có pp chuẩn N(21; 10,24).
a. Sinh viên M rời nhà lúc 6 giờ 45 phút để điđến trường. Tính xs sinh viên M đến trường trước 7 giờ. 19 Ôn tập XSTK
b. Trong 1 tuần sinh viên M phải đến trường 6 ngày và ngày nào sinh viên M cũng
rời nhà lúc 6 giờ 45 phút để đi đến trường. Gọi Y là số ngày sinh viên M đến trường
sau 7 giờ trong 1 tuần. Tính EY, VY
Bài 18. Thời gian hoạt động của một máy do công ty A sản xuất là biến ngẫu nhiên X(đv:
năm) có phân phối chuẩn N(5; 3,24). Công ty A bảo hành sản phẩm trong 3 năm. Một
người mua một máy loại này đã hết han bảo hành. Tính xs máy này hoạt động được thêm 2 năm nữa.
Bài 19. Thời gian cần thiết để sản xuất một sản phẩm của nhà máy H là biến ngẫu nhiên
X(đv: phút) có pp chuẩn N(10;1). Tính xác suất để trong 5 sp của nhà máy H có nhiều nhất
1 sp có thời gian sản xuất không quá 9 phút .
Bài 20. Tuổi thọ của một loại sản phẩm là biến ngẫu nhiên X (đv: năm) có phân phối chuẩn
N(8; 2,89). Mua 10 sản phẩm loại này. Tính xác suất mua được ít nhất 9 sản phẩm có tuổi thọ trên 6 năm tuổi. Tương tự bài 19.
Bài 21. Tuổi thọ một thiết bị điện là X (năm) có phân phối chuẩn N(25;9). Quan sát một
thiết bị điện đã sử dụng 10 năm và vẫn còn hoạt động. Tính xác suất thiết bị đó có tuổi thọ dưới 30 năm Tương tự bài 18.
Bài 22. Một lô hàng chứa 10000 sản phẩm, trong đó có 8000 sản phẩm tốt và 2000 sản
phẩm xấu. Chọn ngẫu nhiên từ lô hàng ra 10 sản phẩm. Gọi X là số sản phẩm tốt trong 10
sản phẩm được chọn. Tính kỳ vọng, phương sai của X GIẢI.
HD: X có phân phối siêu bội
Bài 23. Nhà máy M sản xuất một loại trục máy có đường kính là biến ngẫu nhiên X có
phân phối chuẩn với đường kính trung bình là 1,2 cm và độ lệch chuẩn là 0,01 cm . Nhà
máy M đã sản xuất 10000 trục máy loại này. Gọi Y là số t ụ
r c có đường kính từ 1,18 cm
đến 1,22 cm trong 10000 trục đã sản xuất . Tính kỳ vọng, phương sai của Y và P (Y≥ 9500).
XẤP XĨ PP NHỊ THỨC SANG PP POISION X
khi n → , p → 0
Khi đó, X được xấp xĩ sang phân phối Poision X với  = np. 20