Tổng hợp bài giảng Tin học ứng dụng trong QLCL| Bài giảng Tin học ứng dụng trong QLCL| Trường Đại học Bách Khoa Hà Nội

TIN HỌC TRONG QLCL
Vũ Hồng Sơn - ðHBK Hà nội 1 CHƯƠNG 1 MỞ ðẦU 1.
Thống kê và nhu cầu sử dụng trong XLSL
ðiều kiện tiên quyết: Toán cao cấp, lý thuyết xác suất
Lý thuyết xác suất: khoa học về các quy luật của các hiện tượng ngẫu nhiên
Thống kê toán học: là một bộ phận của lý thuyết xác suất. Nội dung bao gồm:
Thu thập số liệu, cách thu thập số liệu
Sắp xếp số liệu, tìm tham số ñặc trưng của bộ số liệu
Phân tích quy luật biến thiên của số liệu, xây dựng mô hình lý thuyết
So sánh các tập hợp số liệu xem có cùng bản chất không
Xác ñịnh mối liên hệ giữa các bộ số liệu
Vũ Hồng Sơn - ðHBK Hà nội 2 1 2.
Những tiến bộ về sử dụng tin học trong XLSL và QLCL
Thống kê cổ ñiển ñã chuyển thành thống kê hiện ñại
Sử dụng phương tiện tính toán hiện ñại:
Thế hệ máy vi tính mới nhất
Ngôn ngữ lập trình mạnh nhất
Cho phép giải các bài toán hệ thống phức tạp, ñòi hỏi việc
truyền ñạt kiến thức toán học phải ñược kết hợp với phương
pháp tư duy, phương pháp tính toán bằng phương tiện mới
Cho phép mô phỏng quá trình sản xuất
Giám sát quá trình sản xuất
ðiều khiển quá trình sản xuất
Tối ưu hóa quá trình sản xuất
Vũ Hồng Sơn - ðHBK Hà nội 3 3.
Các sản phẩm tin học ứng dụng trong XLSL IRRISTAT SPSS R STATISTICA MATLAB MINITAB SAS SPAD NEMRODW DESIGN-EXPERT
Vũ Hồng Sơn - ðHBK Hà nội 4 2 CHƯƠNG 2
CÁC DẠNG BIẾN SỐ THƯỜNG GẶP 1. Các dạng biến số
Biến mô tả ñặc tính ñịnh tính (biến ñịnh tính): màu sắc, mùi, vị,
ngon hoặc không ngon, thích không thích, tốt hoặc xấu…
Biến mô tả ñặc tính ñịnh lượng (biến ñịnh lượng)
Biến ñịnh hạng: so sánh mức ñộ biểu hiện tương ñối của
ñặc tính (so hàng ñặc tính, ví dụ so hàng thị hiếu…)
Biến ñịnh lượng rời rạc (biến tần suất): số lần xuất hiện
của ñặc tính, biểu diễn bằng số nguyên
Biến ñịnh lượng liên tục (biến liên tục): lấy một trị số bất kỳ, số nguyên hay hữu tỷ
Vũ Hồng Sơn - ðHBK Hà nội 5 2. Các dạng bảng số liệu
Bảng mô tả ñặc tính ñịnh tính Bảng số liệu 1 chiều Bảng số liệu 2 chiều …
Bảng số liệu ñặc tính ñịnh lượng Giới tính Uống Vang Giới tính Vang ñỏ Vang trắng Trai Trai Gái Gái
Vũ Hồng Sơn - ðHBK Hà nội 6 3 3.
Trình bày số liệu bằng biểu ñồ Nguyên tắc:
Biểu ñồ rõ ràng, bỏ qua chi tiết không cần thiết
Chỉ dẫn trên biểu ñồ phải ñược hiểu dễ dàng
ðơn vị của biểu ñồ, phân biệt các thành phần khác nhau
của biểu ñồ bằng màu sắc, nền, ký tự…khác nhau Các dạng biểu ñồ:
Biểu ñồ hình chữ nhật (biểu ñồ cột) Biểu ñồ hình quạt
ðồ thị ñường liên tục
Vũ Hồng Sơn - ðHBK Hà nội 7 4.
Các phần mềm hay dùng trong QLCL SPSS SPAD DESIGN-EXPERT NEMRODW
Vũ Hồng Sơn - ðHBK Hà nội 8 4 CHƯƠNG 3
ỨNG DỤNG CÁC CHUẨN THỐNG KÊ Arithmetic Mean or Average
The mean of a set of observations is their average - the sum of
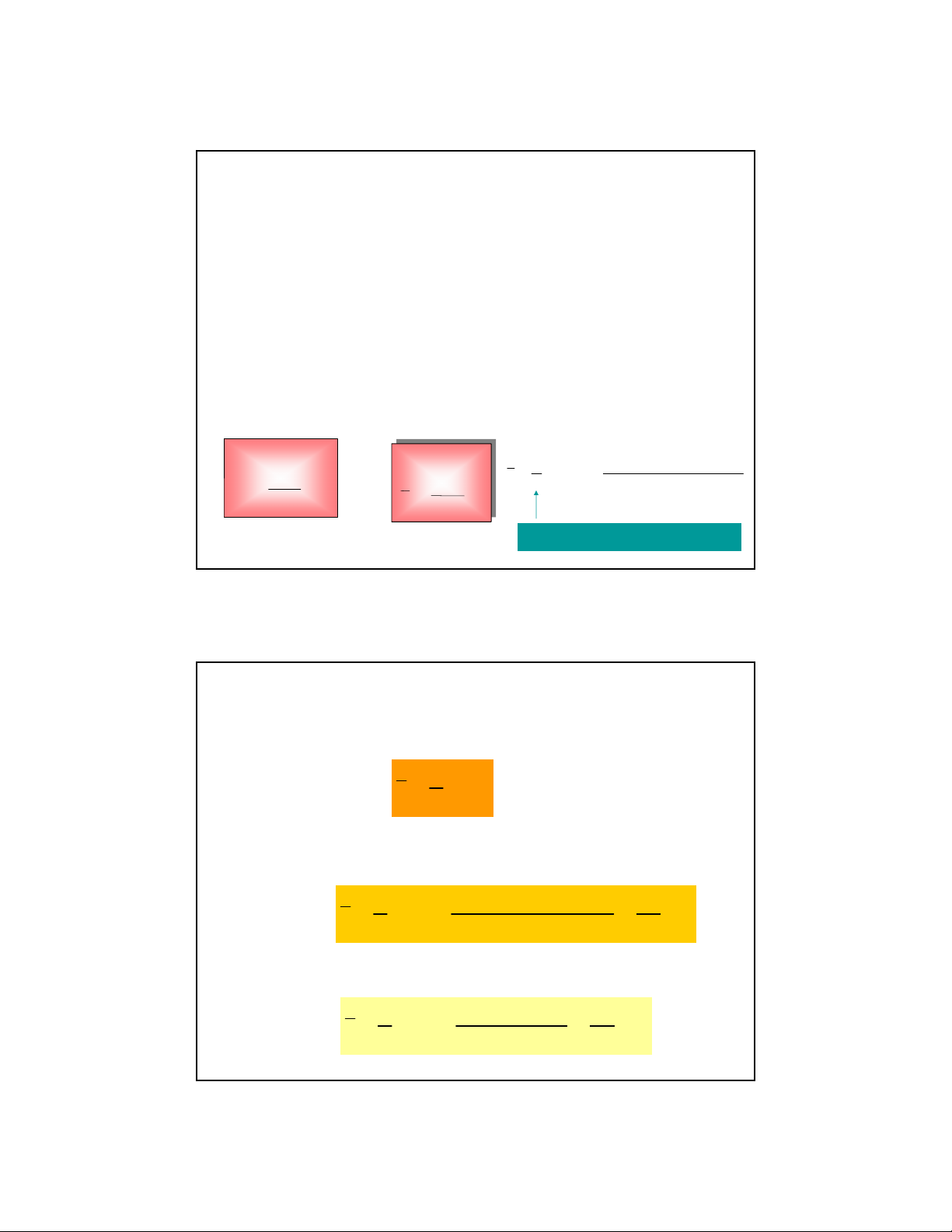
the observed values divided by the number of observations. Population Mean Sample Mean ∑N n x ∑ k 1 f x 1 1 + f x 2 + K 2 + f x x = ∑ f x k k = µ x = i i i =1 n i=1 n i = =1 N x n Vũ Hồng Sơn - ðHBK Hà n S ội ample size 9
• Given a series of values xi (i = 1, … , n): x1, x2, …, xn, the mean is: n 1 x = ∑ xi n i=1
• Study 1: the color scores of 6 consumers are: 6, 7, 8, 4, 5, and 6. The mean is: 1 n 6 + 7 + 8 + 4 + 5 + 6 36 x = ∑ xi = = = 6 n i 1 = 6 6
• Study 2: the color scores of 4 consumers are: 10, 2, 3, and 9. The mean is: 1 n 10 + 2 + 3 + 9 24 x = ∑ xi = = = 6 n i 1 = 4 4
Vũ Hồng Sơn - ðHBK Hà nội 10 5 Variation
• The mean does not adequately describe the data. We need to
know the variation in the data.
• An obvious measure is the sum of difference from the mean:
• For study 1, the scores 6, 7, 8, 4, 5, and 6, we have: •
(6-6) + (7-6) + (8-6) + (4-6) + (5-6) + (6-6)
• = 0 + 1 + 2 – 2 – 1 + 0 • = 0 • NOT SATISFACTORY!
Vũ Hồng Sơn - ðHBK Hà nội 11 Sum of squares
• We need to make the difference positive by squaring them.
This is called “Sum of squares” (SS)
• For study 1: 6, 7, 8, 4, 5, 6, we have: •
SS = (6-6)2 + (7-6)2 + (8-6)2 + (4-6)2 + (5-6)2 + (6-6)2 = 10
• For study 2: 10, 2, 3, 9, we have: •
SS= (10-6)2 + (2-6)2 + (3-6)2 + (9-6)2 = 50 • This is better!
• But it does not take into account sample size n.
Vũ Hồng Sơn - ðHBK Hà nội 12 6 Variance
• We have to divide the SS by sample size n. But in each square
we use the mean to calculate the square, so we lose 1 degree
of freedom. Therefore the correct denominator is n-1. This
is called variance (denoted by s2) x − x
+ x − x + + xn − 2 ( )2 1 ( 2 )2 ... ( x )2 s = n −1 • Or, in the sum notation: n 1 s2 = ∑ ( 2 i x − x) n −1 i=1
Vũ Hồng Sơn - ðHBK Hà nội 13
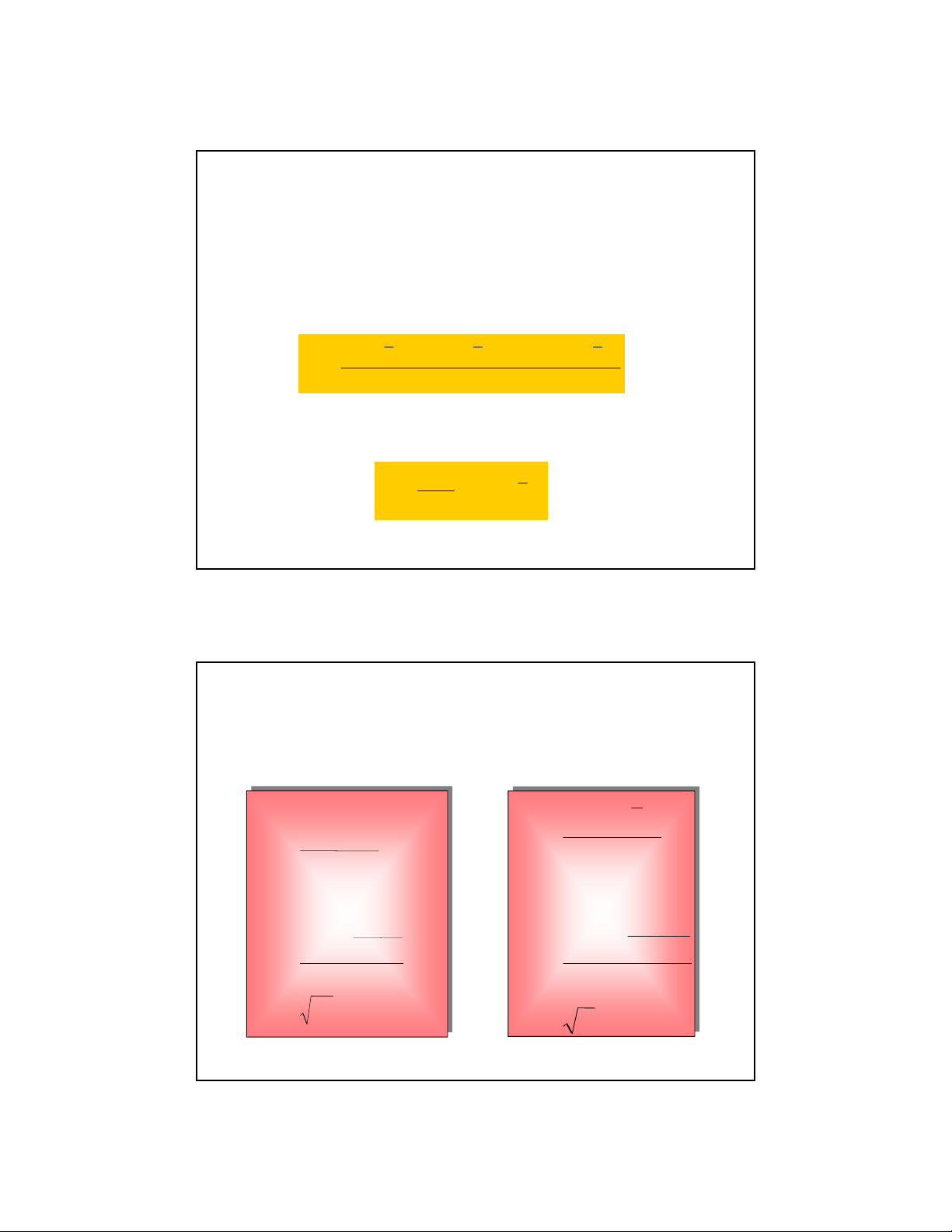
Variance and Standard Deviation Population Variance Sample Variance n ∑ N ∑ (x − x 2) (x − µ 2 ) 2 i =1 σ s = 2 i 1 = = (n − ) 1 N 2 N n x ∑ ( x) N ( ∑ )2 n = 2 i 1 ∑ 2 i 1 x − = ∑ x − = i 1 = = N i 1 n = N (n − ) 1 σ = σ2 s = s2
Vũ Hồng Sơn - ðHBK Hà nội 14 7 Variance - example
• For study 1: 6, 7, 8, 4, 5, and 6, the variance is:
(6−6)2 + − + − + − + − 2 (7 6)2 (8 6)2 (5 6)2 (6 6)2 10 s = = = 2 6 −1 5
• For study 2: 10, 2, 3, 9, the variance is: (10−6)2 + − + − + − 2 (2 6)2 (3 6)2 (9 6)2 50 s = = =16 7 . 4 −1 3
• The scores in study 2 were much more variable than those in study 1.
Vũ Hồng Sơn - ðHBK Hà nội 15 Standard deviation
• The problem with variance is that it is expressed in unit squared,
whereas the mean is in the actual unit. We need a way to convert
variance back to the actual unit of measurement.
• We take the square root of variance – this is called “standard deviation” (denote by s)
• For study 1, s = sqrt(2) = 1.41
• For study 2, s = sqrt(16.7) = 4.1
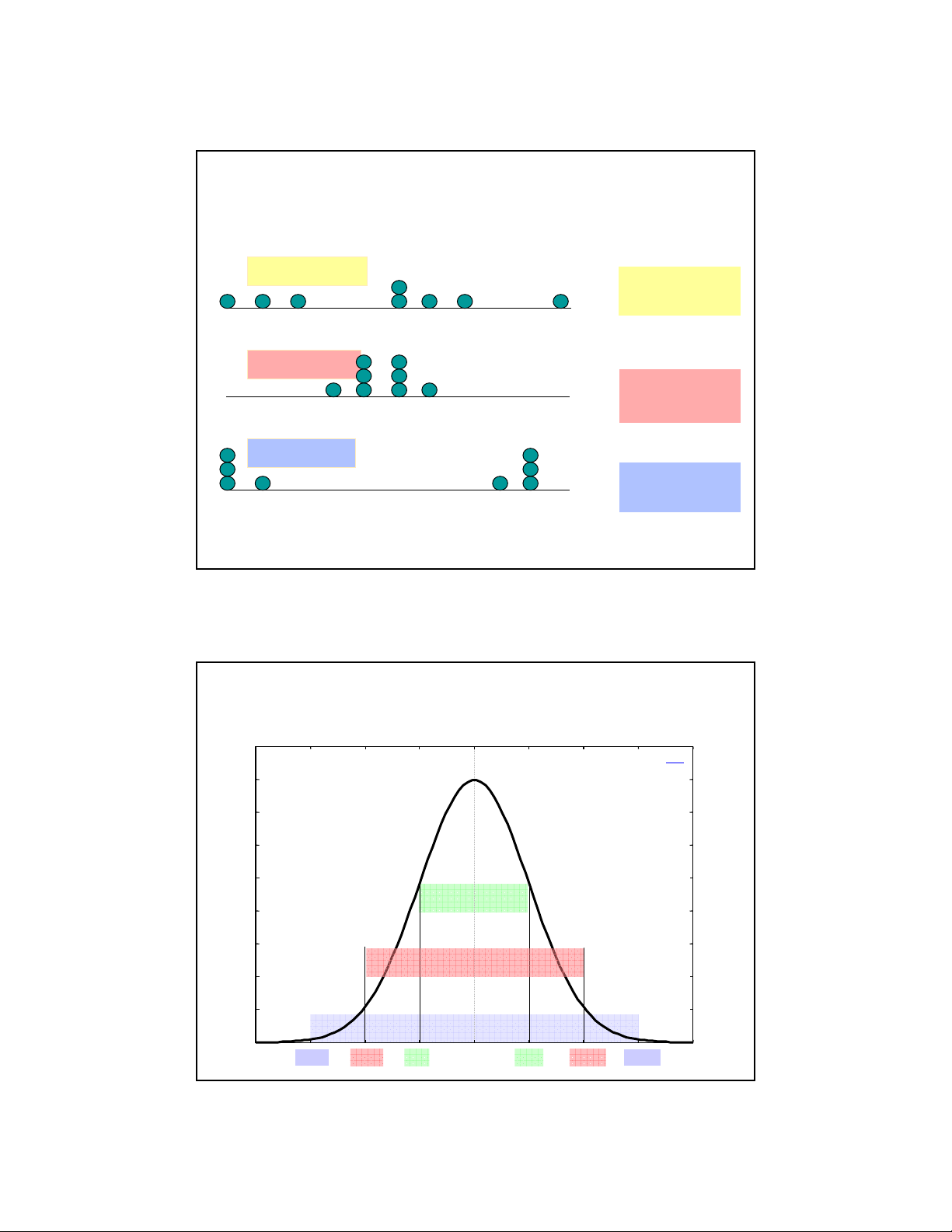
Vũ Hồng Sơn - ðHBK Hà nội 16 8 Standard Deviation Data A Mean = 15.5 s = 3.338
11 12 13 14 15 16 17 18 19 20 21 Data B Mean = 15.5
11 12 13 14 15 16 17 18 19 20 21 s = .9258 Data C Mean = 15.5
11 12 13 14 15 16 17 18 19 20 21 s = 4.57
Vũ Hồng Sơn - ðHBK Hà nội 17 Standard Deviation 0.45 normal(x) 0.4 0.35 0.3 0.25 68 % 0.2 0.15 95 % 0.1 0.05 99.7 % 0
Vũ Hồng Sơn - ðHBK Hà nội 18 µ -3σ µ -2σ µ -σ µ µ +σ µ +2σ µ +3σ 9
Kiểm ñịnh thống kê : khi- bình phương χ2 O = tần số quan sát = Σ(O - T)2 T T = tần số lý thuyết Tổng hàng x Tổng cột Tần số lý thuyết = Tổng lớn
Vũ Hồng Sơn - ðHBK Hà nội 19 Sản phẩm Trả lời Tổng A non A A 32.5 27.5 60 Non A 32.5 27.5 60 Tổng 65 55 120 χ2 = 7,55 > χ2 = 2,71, pour α = 0,05 calculé théorique
Vũ Hồng Sơn - ðHBK Hà nội 20 10
Xử lý 2 giá trị trung bình-kiểm ñịnh t-Student
Trường hợp 2 mẫu ñộc lập
1. Kim ñnh phng sai 2 S1 F = 2
với qui ước phương sai1 >phương sai 2 S2 2 n 1 2 1 2 2 ∑ S = ( ∑ xi − )   ( xi)  với x = ∑xi −   n−1 1 i=1 n−  n 
F tra bảng mức α=5%, bậc tự do f =n -1, f =n -1 b 1 1 2 2
Nếu F2 phương sai bằng nhau b Nếu F≥F 2 phương sai khác nhau b
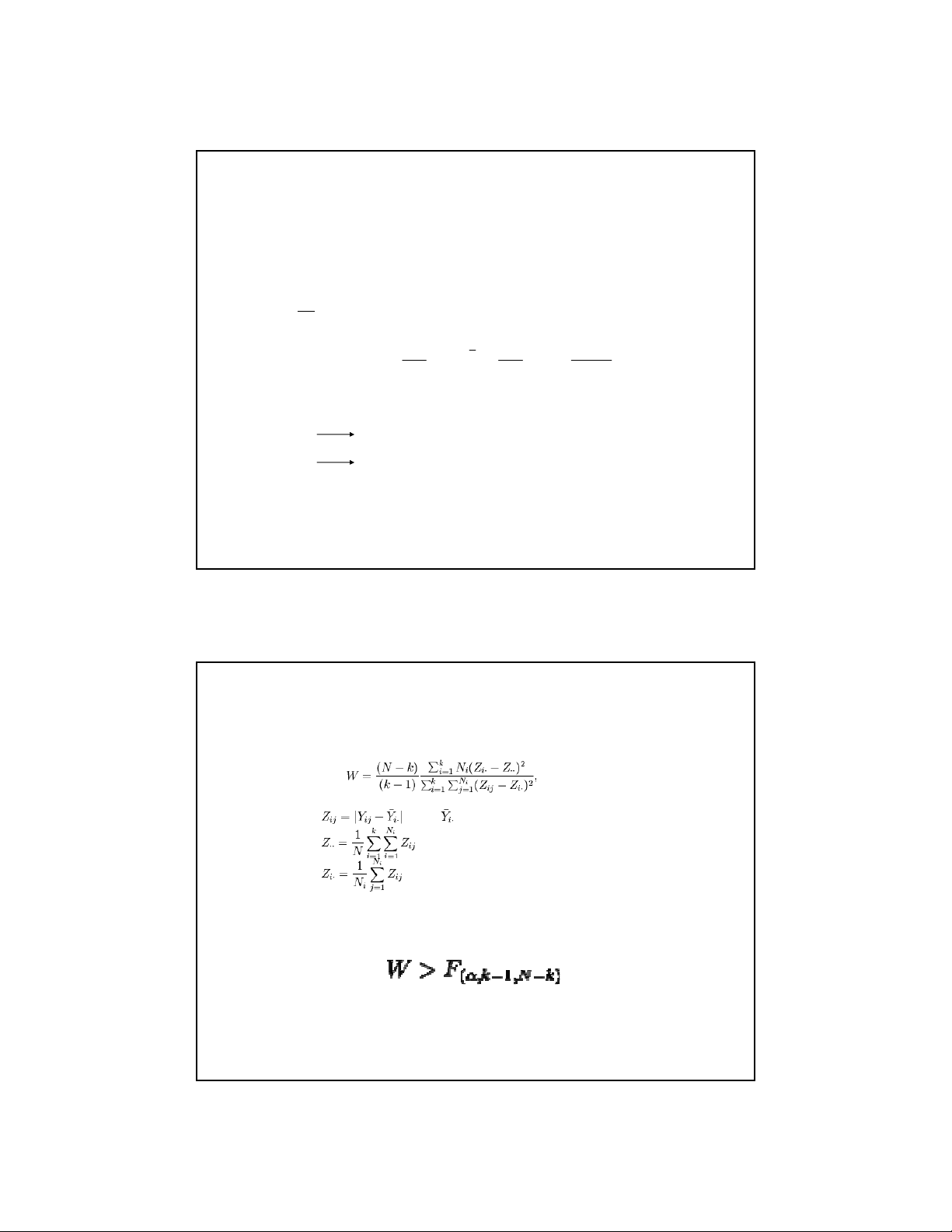
Vũ Hồng Sơn - ðHBK Hà nội 21 Levene’s test where • with the mean of group i, • is the mean of all Z , ij •
is the mean of the Z for group i. ij
The Levene test rejects the hypothesis that the variances are equal if
Vũ Hồng Sơn - ðHBK Hà nội 22 11
Giá trị xác suất (p Values)
• Giá trị p value ñược so sánh với mức ý nghĩa (significant
level - α), và dựa trên kết quả này ñể bác bỏ hay không bác bỏ giả thiết.
• Nếu giá trị p value nhỏ hơn mức ý nghĩa, giả thiết bị bác
bỏ (p value < α, bác bỏ giả thiết H ). 0
• Nếu giá trị p value bằng hoặc lớn hơn mức ý nghĩa,
không bác bỏ giả thiết H (p value > α, không bác bỏ giả o thiết H ). 0
Vũ Hồng Sơn - ðHBK Hà nội 23
2. Hai mu ñc lp có phng sai bng nhau Group 1 Group2 Mean difference: x x 11 21 x x
D = x – x 1 2 12 22 x x 13 23 Variance of D: x x 14 24 x x
n − s + n − s 2 ( 1 )1 21 ( 2 )1 2 15 25 2 s = … n + n − 2 1 2 x x 1n 2n T-statistic: Sample size n n 1 2 x x 1 − 2 Mean x x t = 1 2  1 1  2 s  +  SD s s  n n 1 2  1 2
Vũ Hồng Sơn - ðHBK Hà nội 24 12 Produc A Product B Mean difference: 106 110
D = 119.0 – 107.1 = 11.9 98 134 108 122 Variance of D: 104 104 (8 .949)2 + 2 (610 8.8)2 s = =10 . 2 2 120 118 9 + 7 − 2 124 131 108 114 T-statistic: 11.9 96 t = = 2.34  1 1  100 102 2 .  +   9 7  N 9 7 Mean 107.1 119.0 t =2.15 SD 9.49 10.88 b,5%,14 Conclusion: Significant difference
Vũ Hồng Sơn - ðHBK Hà nội 25
3. Hai mu ñc lp có phng sai khác nhau Mean difference: Group 1 Group2
D = x – x 1 2 x x 11 21 x x Variance of D: 12 22 2 2 x x S S 13 23 2 1 2 s = + x x 14 24 n n 1 2 x x 15 25 T-statistic: … x x 1 − 2 x x t = 1n 2n  2 2  S S  1 + 2  Sample size n n  n n 1 2  1 2 Mean x x 2 2 2  S S  1 2 1 2  +   n n 1 2  f = SD s s 2 2 2 2  S   S  1 2 1 2      n n 1   2  + n −1 n −1 1 2
Vũ Hồng Sơn - ðHBK Hà nội 26 13 Produc A Product B Mean difference: 28 12 D = 26.2 – 10.2 = 16 17 7 36 11 T-statistic: 23 10 26 . 2 − 10 . 2 t = = 5 . 01 27 11  6 . 98 2 1 . 92 2   +  N 5 5  5 5  Mean 26.2 10.2 ( 2 6.982 1.922 + 5 5 ) SD 6.98 1.92 f = ( = ≈ 2 2 6.982 2 5 ) (1.92 5) 4.6 5 + 4 4 t =2.57 b,5%,5 Conclusion: Significant difference
Vũ Hồng Sơn - ðHBK Hà nội 27
Trường hợp 2 mẫu tương quan, so sánh cặp Subject Before After Diff. Mean difference: 1 x x x -x 01 11 01 11
D = x – x 2 x x x -x 1 2 02 12 02 12 3 x x x -x 03 13 03 13 4 x x x -x 04 14 04 14 x t d = 5 x x x -x 05 15 05 15 s / n d … n x x x -x 0n 1n 0n 1n Mean x x x 0 1 d SD s s s 0 1 d
Vũ Hồng Sơn - ðHBK Hà nội 28 14 Paired samples
• The problem: Viewing certain meats under red light might
enhance judges preferences for meat. 12 judges were asked to
score the redness of meat under red light and white light Results: Judge Red White Judge Red White 1 20 22 8 16 20 2 18 19 9 21 22 3 19 17 10 17 20 4 22 18 11 23 27 5 17 21 12 18 24 6 20 23 7 19 19
• Question: Was there an effect of light?
Vũ Hồng Sơn - ðHBK Hà nội 29 Paired samples – analysis Judge Red light White light Difference
Mean difference: 1.83, SD: 2.82 1 20 22 2 2 18 19 1 Standard error (SE): 3 19 17 -2 SD/sqrt(n) = 2.82/sqrt(12) = 4 22 18 -4 0.81 5 17 21 4 6 20 23 3 7 19 19 0 t-test = |1.83|/0.81 = 2.23 8 16 20 4 t 9 21 22 1 b,5%= 2.201 10 17 20 3 Conclusion: there was a 11 23 27 4
significant effect of light colour. 12 18 24 6 Mean 19.2 21 1.83 SD 2.1 2.8 2.82
Vũ Hồng Sơn - ðHBK Hà nội 30 15 Tin UD trong QLCL Anova PHÂ P N HÂ N TÍ CH C PHƯ P ƠN HƯ G ƠN SAI SA (A ( N A OV N A OV ) A
Mục tiêu của phân tích phương sai là so sánh trung
bình của nhiều nhóm (tổng thể) dựa trên các số trung bình
của các mẫu quan sát từ các nhóm này và thông qua kiểm
định giả thuyết để kết luận về sự bằng nhau của các số trung bình này.
Trong nghiên cứu, phân tích phương sai được dùng
như là một công cụ để xem xét ảnh hưởng của một hay một
số yếu tố nguyên nhân (định tính) đến một yếu tố kết quả (định lượng). PHÂ PH N Â N T ÍCH T ÍCH PHƯ PH ƠN Ơ G N G SAI SA Ví dụ:
 Nghiên cứu ảnh hưởng của phương pháp đánh
giá của giáo viên đến kết quả học tập của sinh viên.
 Nghiên cứu ảnh hưởng của bậc thợ tới năng suất lao động.
 Nghiên cứu ảnh hưởng của phương pháp bán
hàng, trình độ (kinh nghiệm) của nhân viên bán hàng đến doanh số PhD.VHSơn-Hust 1 Tin UD trong QLCL Anova PHÂ PH N Â N T ÍCH T ÍCH PHƯ PH ƠN Ơ G N G SAI SA
 Phân tích phương sai một yếu tố
 Phân tích phương sai hai yếu tố Phân Ph ân tích h ph p ư h ơng n sai m ột y ếu u t ố
Phân tích phương sai một yếu tố là phân tích
ảnh hưởng của một yếu tố nguyên nhân (dạng
biến định tính) đến một yếu tố kết quả (dạng
biến định lượng) đang nghiên cứu. PhD.VHSơn-Hust 2 Tin UD trong QLCL Anova Phân Ph ân tích h ph p ư h ơng n sai m ột y ếu u t ố
Giả sử cần so sánh số trung bình của k tổng
thể độc lập. Ta lấy k mẫu có số quan sát là n , 1
n … n ; tuân theo phân phối chuẩn. Trung bình 2 k
của các tổng thể được ký hiệu là μ ; μ ….μ 1 2 k
thì mô hình phân tích phương sai một yếu tố
ảnh hưởng được mô tả dưới dạng kiểm định giả thuyết như sau: H : μ = μ =….=μ o 1 2 k
H : Tồn tại ít nhất 1 cặp có μ ≠μ ; i ≠ j 1 i j Phân Ph ân tích h ph p ư h ơng n sai m ột y ếu u t ố
Để kiểm định ta đưa ra 3 giả thiết sau: 1)
Mỗi mẫu tuân theo phân phối chuẩn N(μ, σ2) 2)
Các phương sai tổng thể bằng nhau
3) Ta lấy k mẫu độc lập từ k tổng thể. Mỗi mẫu được quan sát n lần. i PhD.VHSơn-Hust 3 Tin UD trong QLCL Anova Các bư Các ớc ớ t c i t ế i n ế hành: Bướ ư c ớ c 1 : : T ín í h c á c c á c tr t u r ng b ìn ì h m ẫ m u ẫ và à t r t u r ng b ìn ì h c h c ung củ c a a k m ẫ m u ẫ
 Ta lập bảng tính toán như sau: TT k mẫu quan sát 1 2 3 … k 1 X X X X 11 21 31 k1 2 X X X X 12 22 32 k2 3 X X X X 13 23 33 k3 … … n X X X X i 1n1 2n2 3n3 knk Trung bình mẫu x x x x 1 2 3 k Bư B ớc ư 1 ớc : : T í T nh c í á nh c c á c trung bì t nh rung bì mẫ m u ẫ và và trung bì t nh rung bì chung c c hung ủa c ủa k mẫ k m u ẫ
Trung bình mẫu x  x  x được tính theo công thức: 1 2 k i n X ∑ ij j 1 = x = (i = 1, 2,..k) i ni
Trung bình chung của k mẫu được tính theo công thức: k n x ∑ i i i 1 x = = (i = 1, 2,..k) k n ∑ i i 1 = PhD.VHSơn-Hust 4 Tin UD trong QLCL Anova Bư B ớc 2 ớc : T í T nh các tổng đ ộ l ệch b ình p hươn ươ g
Tổng các độ lệch bình phương trong nội bộ nhóm
(nội bộ từng mẫu - SSW) được tính theo công thức sau: Nhóm 1 Nhóm 2 Nhóm k 1 n n k n 2 2 SS = (X ∑ 2 − 2 =∑ − =∑ − 1) x SS (X x) SS (X x) k 1 1 j 2 2 2 j k jk j 1 = j 1 = j 1 = k i n 2 SSW S = S S + S . +.. S + S = (X ∑∑ − ix) 1 2 k ij i 1 = ij 1 = 1 Bư B ớc ư 2 ớc : : T í T nh c í á nh c c á c tổng t độ lệ độ l c ệ h c bình phươ bì ng nh phươ
Tổng các độ lệch bình phương giữa các nhóm(SSB) k 2 S S B = n ( x ∑ − x ) i i i = 1
Tổng các độ lệch bình phương của toàn bộ tổng thể(SST) k ni 2
S S T = S S W + S S B = ( X ∑ ∑ − x ) i j i =1 j =1 PhD.VHSơn-Hust 5