Tổng hợp bài tập nguyên hàm, tích phân và ứng dụng – Nhóm Toán 12

Tổng hợp bài tập nguyên hàm, tích phân và ứng dụng – Nhóm Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

67 34 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

251 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Group Nhóm Toán | Trắc nghiệm 2016-2017
1
TÍCH PHÂN VÀ ỨNG DỤNG CỦA TÍCH PHÂN
(TỰ LUẬN)
Hoàng Văn Quý – GV trường THPT Lương Tài số 2
1. Kiến thức liên quan
1.1. Công thức nguyên hàm cơ bản
Nguyên hàm của hàm số cơ bản
Nguyên hàm mở rộng
dx x C
. , aa dx ax C
1
, 1
1
x
x dx C
1
1 ( )
( ) .
1
ax b
ax b dx C
a
1
.ln
dx
ax b C
ax b a
xx
e dx e C
1
.
ax b ax b
e dx e C
a


ln
x
x
a
a dx C
a

1
.
ln
x
x
a
a dx C
a



cos sinxdx x C
1
cos( ) .sin( )ax b dx ax b C
a
sin cosxdx x C
1
sin( ) .cos( )ax b dx ax b C
a
2
11
tan( )
cos ( )
dx ax b C
ax b a
2
1
sin
dx cotx C
x
2
11
()
sin ( )
dx cot ax b C
ax b a
1.2. Công thức tích phân
F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a;b] thì
Group Nhóm Toán | Trắc nghiệm 2016-2017
2
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x F b F a
1.3. Phương pháp đổi biến số
1.3.1. Dạng 1 : Tính I =
'
( ) ( )
b
a
f x x dx

+ Đặt t =
()x
'
( ).dt x dx

+ Đổi cận :
()
()
()
( ). ( )
()
b
a
b
f t dt F t
a
I =
1.3.2. Dạng 2 : Tính I =
()
b
a
f x dx
bằng cách đặt x =
()t
Dạng chứa
22
ax
: Đặt x = asint, t
;
22





(a>0)
1.4. Phương pháp tích phân từng phần
* Công thức tính :
()
b b b
b
a
a a a
f x dx udv uv vdu
Đặt
Ta thường gặp hai loại tích phân như sau:
* Loại 1:
)(...
)(...
...
...
hamnguyenlayv
hamdaolaydxdu
dv
u
x
a b
t
()a
()b
Group Nhóm Toán | Trắc nghiệm 2016-2017
3
()
( ).sin ( ).
( ).cos ( ). ( )
( ). .
b
a
b
a
b
fx
a
P x f x dx
P x f x dx u P x
P x e dx

, trong đó
()Px
là đa thức bậc n.
*Loại 2:
( ).ln ( ). ln ( )
b
a
P x f x dx u f x
1.5. Tính chất tích phân
Tính chất 1:
( ) ( )
bb
aa
kf x dx k f x dx

, k: hằng số
Tính chất 2:
( ) ( ) ( ) ( )
b b b
a a a
f x g x dx f x dx g x dx
Tính chất 3:
( ) ( ) ( ) ( )
b c b
a a c
f x dx f x dx f x dx a c b
1.6. Diện tích hình phẳng
1.6.1. Dạng 1: Cho hàm số y = f(x) liên tục trên [a; b]. khi đó diện tích hình phẳng giới hạn bởi đồ thị
hàm số y = f(x), trục Ox và hai đường thẳng x = a và x = b là:
()
b
a
S f x dx
(*)
Lưu ý:
( ) 0fx
vô nghiệm trên (a;b) thì
( ) ( )
bb
aa
S f x dx f x dx

( ) 0fx
có 1 nghiệm
( ; )c a b
thì
( ) ( ) ( )
b c b
a a c
S f x dx f x dx f x dx
Group Nhóm Toán | Trắc nghiệm 2016-2017
4
1.6.2. Dạng 2: Cho hai hàm số y = f
1
(x) và y = f
2
(x) liên tục trên [a; b]. Khi đó diện tích của hình phẳng
giới hạn bởi đồ thị hai hàm số f
1
(x), f
2
(x) và hai đường thẳng x = a, x = b là:
12
( ) ( )
b
a
S f x f x dx
(**)
Lưu ý: Khử dấu giá trị tuyệt đối của công thức (**) thực hiện tương tự đối với công thức (*).
1.7. Thể tích vật thể tròn xoay
Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi các đường
y = f(x), trục Ox và hai đường thẳng x = a, x = b quay xung quanh trục Ox là:
2
()
b
a
V f x dx
Lưu ý: Diện tích, thể tích đều là những giá trị dương.
2. Ví dụ minh họa
Ví dụ 1: Tính các tích phân sau
11
0 0 0
4
2
3
10
1/ (2x+e ) x 2 / 2 3 3/ sinx+cos
23
4 / 5/ sin2
x x x
A d B e dx C x dx
xx
D dx E x x dx
x





Lời giải
1 1 1
11
2
00
0 0 0
1/ 2 2 1 0 1
x x x
A x e dx xdx e dx x e e e
1
1
1 1 1
0 0 0
0
0
2
2 2 1 3
2 / 2 3 2 3 2 3
ln2 ln2 ln2 ln2
x
x
x
x x x
e
e
B e dx e dx dx
ee



00
0 0 0
3/ sinx cos sinx cos cos sin 2C x dx dx xdx x x

Group Nhóm Toán | Trắc nghiệm 2016-2017
5
4
44
53
4
4
32
22
33
1
1
11
1
1 3 1 2 3
4 / 3 ln
32
x
D dx x x dx x x x
x x x x









2
2
00
0 0 0
11
5/ sin2 sin2 cos2
2 2 2
E x x dx xdx xdx x x

Ví dụ 2. Tính các tích phân sau
61
10
ln2
10
21
1/ 3 x 2 / x
1 3 1
1 2ln 1 1
3/ 4 /
ln 1 2 1
e
x
x
I x x d J d
x
x
K dx L x dx
x x e
x











Lời giải
6
1
1/ 3I x x dx
Đặt
3xt
ta được
2
32x t dx tdt
Đổi cận:
1 2; 6 3x t x t
Khi đó
3
3
4 2 5 3
2
2
2 232
2 6 2
55
I t t dt t t



1
0
21
2/
1 3 1
x
J dx
x

Đặt
31xt
ta được
2
12
33
t
x dx tdt
Đổi cận
0 1; 1 2x t x t
Khi đó
22
3
2
11
2 2 2 3 28 2 3
2 2 3 ln
9 1 9 1 27 3 2
tt
J dt t t dt
tt





1
1 2ln 1
3/
ln 1
e
x
K dx
xx
x





Tính
1
1
1
e
K dx
x
ta được kết quả
1
21Ke
Group Nhóm Toán | Trắc nghiệm 2016-2017
6
Đặt
ln xt
ta được
dx
dt
x
Đổi cận
1 0; 1x t x e t
Khi đó
1
1
2
0
0
21
2 ln 1 2 ln2
1
t
K dt t t
t
Vậy ta được
12
2 ln2K K K e
ln2
0
1
4/
21
x
L x dx
e




Tính
ln2
1
0
L xdx
ta được kết quả
2
1
ln 2
2
I
Tính
ln2
2
0
1
21
x
L dx
e
Đặt
x
et
ta được
x
e dx dt
Đổi cận
0 1; ln2 2x t x t
Khi đó
2
2
2
1
1
56
ln ln 2 1 ln2 ln ln
2 1 3 5
dt
L t t
tt
Vậy ta được
2
12
16
ln 2 ln
25
L L L
Ví dụ 3. Tính các tích phân sau
4
3
24
00
6
1
1/ 1 sin cos 2 / 3/ sinx sin
sin cos
I x xdx J dx K x xdx
xx

Lời giải
2
3
0
1/ 1 sin cosI x xdx

Đặt
sin cosx t dt xdx
Đổi cận
0 0; 1
2
x t x t
Group Nhóm Toán | Trắc nghiệm 2016-2017
7
Khi đó
1
1
4
3
0
0
3
1
44
t
I t dt t



4
24
6
1
2/
sin cos
J dx
xx
Đặt
2
1
cot
sin
x t dt dx
x
Đổi cận
3; 1
64
x t x t

Khi đó
3
2
33
2 2 4 3
11
1
1 2 1 2 1 8 3 4
11
3 27 3
J dt dt t
t t t t t

2
0 0 0
3/ sinx sin sin sinK x xdx xdx x xdx
Đặt
2
1
00
1 cos2 1
sin
22
x
K xdx dx


2
0
sinK x xdx
sin cos
u x du dx
dv xdx v x




2
00
0
cos cos sinxK x x xdx


* Chú ý: Ta thường đặt t là căn, mũ, mẫu.
- Nếu hàm có chứa dấu ngoặc kèm theo luỹ thừa thì đặt t là phần bên trong dấu ngoặc nào có luỹ
thừa cao nhất.
- Nếu hàm chứa mẫu số thì đặt t là mẫu số.
- Nếu hàm số chứa căn thức thì đặt t = căn thức.
- Nếu tích phân chứa
dx
x
thì đặt
lntx
.
- Nếu tích phân chứa
x
e
thì đặt
x
te
.
- Nếu tích phân chứa
dx
x
thì đặt
tx
.
Group Nhóm Toán | Trắc nghiệm 2016-2017
8
- Nếu tích phân chứa
2
dx
x
thì đặt
1
t
x
.
- Nếu tích phân chứa
cosxdx
thì đặt
sintx
.
- Nếu tích phân chứa
sin xdx
thì đặt
costx
.
- Nếu tích phân chứa
2
cos
dx
x
thì đặt
tantx
.
- Nếu tích phân chứa
2
sin
dx
x
thì đặt
cottx
.
Ví dụ 3. Tính các tích phân
a)
2
0
sinI x xdx
1
) ln
e
b J x xdx
1
0
)
x
c K xe dx
Lời giải
a)
2
0
sinI x xdx
sin cos
u x du dx
dv xdx v x




2
22
00
0
cos cos 0 0 sinx 1I x x xdx

1
) ln
e
b J x xdx
2
1
ln
2
du dx
ux
x
dv xdx
x
v

2 2 2 2
1
1 1 1
1
ln ln
2 2 2 4 4
e e e
e
x x x x e
J x dx x
Group Nhóm Toán | Trắc nghiệm 2016-2017
9
1
0
)
x
c K xe dx
xx
u x du dx
dv e dx v e





1
11
00
0
1
x x x
K xe e dx e e
Ví dụ 4. Tính các tích phân sau
2 ln4 2
22
2
32
1 0 1
1 1 1
1/ 2 / 3/ ln
2
x
x
xx
I x dx J e dx K xdx
x x x
e







Lời giải
2 2 2
22
22
32
1 1 1
11
1/
xx
I x dx x dx dx
x x x x





Tính
2
2
23
1
1
1
17
33
I x dx x
2
2 2 2
2
2
2
3
1 1 1
1
1
1
1
1 1 4
ln ln
11
5
dx
x
x
x
I dx dx dx x
x x x
xx
xx







Vậy
12
74
ln
35
I I I
ln4 ln4 ln4
0 0 0
11
2/
22
xx
xx
J e dx e dx dx
ee




ln4
ln4
1
0
0
3
xx
J e dx e
Group Nhóm Toán | Trắc nghiệm 2016-2017
10
ln4
2
2
0
2
2
2
1
1
12
;2
2
23
ln ln
2 2 2
x x x
x
J dx t e t e tdt e dx dx dt
t
e
t
J dt
t t t




Vậy
12
3
3 ln
2
J J J
2
2
2
1
1
3/ ln
x
K xdx
x
Đặt
2
2
2
1
1
2
1
ln
1 1 1
ln
1
1
ux
du dx
x
K x x x dx
x
x x x
dv dx
vx
x
x




22
11
1 1 5 3
ln ln2
22
K x x x
xx
Group Nhóm Toán | Trắc nghiệm 2016-2017
11
Ví dụ 5. Tính diện tích hình phẳng giới hạn bởi các đường sau
a)
2
yx
, trục hoành và hai đường thẳng x=0, x=2.
b)
2
yx
,
23yx
và hai đường thẳng x =0, x=2.
c)
2
,2y x y x
Lời giải
a)
2
yx
, trục hoành và hai đường thẳng x= 0, x=2.
Trên [0; 2] ta có
2
0 0 [0;2]xx
Diện tích của hình phẳng đã cho:
2
2
23
0
0
18
33
S x dx x
b) Đặt
2
12
( ) , ( ) 2 3f x x f x x
Ta có:
22
12
1 [0;2]
( ) ( ) 0 ( 2 3) 0 2 3 0
3 [0;2]
x
f x f x x x x x
x

Diện tích hình phẳng đã cho
2
2
0
| 2 3|S x x dx
Group Nhóm Toán | Trắc nghiệm 2016-2017
12
12
22
01
12
33
22
01
( 2 3) ( 2 3)
33
33
1 8 1 5 7
2 4 6 1 3 4
3 3 3 3 3
x x dx x x dx
xx
x x x x

c) Ta có:
22
1
( 2) 0 2 0
2
x
x x x x
x

Diện tích hình phẳng
2
2
32
2
1
1
8 1 1 9
| 2| x 2x 2 4 2
3 2 3 3 2 2
xx
S x x d



Ví dụ 6. Tính thể tích vật thể tròn xoay sinh ra khi quay hình (D) quanh trục Ox biết (D) giới hạn bởi
2
1 , 0y x y
Lời giải
Ta có:
2
1 0 1xx
Áp dụng công thức:
2
()
b
a
V f x dx
Ta có:
1
22
1
(1 )V x dx

1
1
35
24
1
1
2x
1 2x
35
x
x dx x




2 1 2 1 4 2 16
1 1 2
3 5 3 5 3 5 15




Bài Tập tự luyện
Bài 1: Tính các tích phân sau
Group Nhóm Toán | Trắc nghiệm 2016-2017
13
1.
1
3
0
( 1)x x dx
2.
2
2
1
11
()
e
x x dx
xx
3.
2
1
1x dx
4.
2
3
(2sin 3 )x cosx x dx

5.
1
0
()
x
e x dx
6.
1
3
0
()x x x dx
7.
2
1
( 1)( 1)x x x dx
8.
2
3
1
(3sin 2 )x cosx dx
x

9.
1
2
0
( 1)
x
e x dx
10.
3
3
1
( 1). x dx
11.
2
1
7 2 5
e
xx
dx
x

12.
2
2
( 3)x x dx
13.
4
2
3
( 4)x dx
14.
2
23
1
11
dx
xx



15.
2
2
3
1
2xx
dx
x
16.
8
2
3
1
1
4
3
x dx
x



Bài 2: Tính các tích phân sau
1.
2
32
3
sin xcos xdx
2.
6
0
1 4sin xcosxdx
3.
1
2
0
1x x dx
4.
1
2
0
1x x dx
5.
1
2
3
0
1
x
dx
x
6.
1
22
0
(1 3 )
x
dx
x
7.
2
sin
4
x
e cosxdx
8.
2
23
0
sin2 (1 sin )x x dx
9.
1
5 3 6
0
(1 )x x dx
Group Nhóm Toán | Trắc nghiệm 2016-2017
14
12.
6
2
0
cos
6 5sin sin
x
dx
xx

11.
9
4
1
x
dx
x
12.
6
0
1 4sin .cosx xdx
13.
2
1
2
0
x
e xdx
14.
1
1 ln
e
x
dx
x
15.
1
sin(ln )
e
x
dx
x
16.
1
0
1x x dx
17.
1
23
0
5x x dx
18.
8
2
3
1
1
dx
xx
19.
ln5
ln3
23
xx
dx
ee

20.
1
0
x
e dx
21.
3
3
0
sin
x
cos
x
d
x
22.
1
2
0
1 x dx
23.
1
2
0
1
4
dx
x
24.
1
2
0
1
1
dx
x
Bài 3: Tính các tích phân sau
1.
2
2
0
cosx xdx
2.
1
0
sin
x
e xdx
3.
2
0
(2 1) osxx c dx
4.
1
0
x
xe dx
5.
1
ln
e
x xdx
6.
2
2
0
( 1)sin xx dx
7.
2
2
0
( os )sinxx c x dx
8.
2
2
0
sin3x
x
e dx
9.
1
2
0
( 2)
x
x e dx
10.
1
2
0
ln(1 )x x dx
11.
1
(2 2)ln
e
x xdx
12.
2
0
cosx x dx
13.
2
0
(2 7)ln( 1)x x dx
14.
1
2
0
( 2)
x
x e dx
Bài 4: Tính diện tích hình phẳng giới hạn bởi các đường sau:
Group Nhóm Toán | Trắc nghiệm 2016-2017
15
a)
32
12
33
y x x
, trục hoành, x = 0 và x = 2.
b)
2
1, 1, 2y x x x
và trục hoành.
c)
32
12 ,y x x y x
d)
3
1yx
và tiếp tuyến của nó tại điểm có tung độ bằng -2.
e)
2
4 , 0, 0, 3y x x y x x
f)
3
sinx, y=0, x=0, x=
2
y
g)
, Ox, 0, 3
x
y e x x
Bài 5: Tính thể tích vật tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục
hoành:
a)
2
4 , 0, 0, 3y x x y x x
b)
cos , 0, 0,y x y x x
c)
tan , 0, 0,
4
y x y x x
d)
2
2 , 1y x y
e)
1
ln , , , 0y x x x e y
e
TỔNG HỢP CÁC CÂU HỎI TRẮC NGHIỆM - NGUYÊN HÀM – TÍCH PHÂN
PHẦN 1 :
Câu1: Tính
2
3
(x 2 )x dx
x

Group Nhóm Toán | Trắc nghiệm 2016-2017
16
A.
3
3
4
3ln
33
x
x x C
B.
3
3
4
3ln
33
x
xx
C.
3
3
4
3ln
33
x
x x C
D.
3
3
4
3ln
33
x
x x C
Câu 2: Tìm họ nguyên hàm của hàm số f(x)=
1
( 3)xx
A.
2
ln
33
x
C
x
B.
1
ln
33
x
C
x
C.
1
ln
33
x
C
x
D.
2
ln
33
x
C
x
Câu 3: Tính
(1 sinx)dx
A.
cosxxC
C.
cosx C
B.
cosxxC
D.
cosx C
Câu 4: Tìm họ nguyên hàm của hàm số f(x)=
1
1
dx
x
A.
1
C
x
B. -2
1 xC
C.
2
1 x
D.C
1 x
Câu 5: Tính
3
(2 )
x
e dx
A. 2x +
3x
eC
B. 2x -
3x
eC
C. 2 x -
1
3
3x
eC
D. 2x+
1
3
3x
eC
Câu 6: ChoF(x) là một nguyên hàm của hàm số y=
2
1
cos x
và F(0)=1.Khi đóF(x) là:
A. -tan x B. –tanx +1 C.tanx+1 D. tanx-1
Câu 7: Tìm họ nguyên hàm
2
1x
xe dx
Group Nhóm Toán | Trắc nghiệm 2016-2017
17
A.
2
1x
eC
B.
1
2
2
x
eC
C.
1
2
2
1x
eC
D.
2
1x
eC
Câu 8: Tìm họ nguyên hàm
2ln 1
dx
xx
A. F(x) =
1
ln 1
2
xC
B.
1
ln 2ln 1
2
xC
C.
2ln 1xC
D.
ln 2ln 1xC
Câu 9: Tìm họ nguyên hàm
2
(2 )
cos
x
x
e
e dx
x
Lời giải:
2
1
(2 ) 2
cos
xx
e dx e
x

+ tanx +C
A. 2
x
e
+tanx+C B. 2
x
e
+tanx C.2
x
e
-tanx+C D. Đáp án khác
Câu 9: Hàm số f(x)= x
1x
có một nguyên hàm là F(x).Nếu F(0)=2 thì giá trị của F(3) là :
A.
116
15
B.
146
15
C.
886
105
D. Một đáp án khác
Lời giải:
2
( 1)
1 ( 1)
2
x
x x dx x C
F(0)= 2
2C
2
(3 1)
(3) (3 1) 2 6
2
F
PHẦN 2 :
Mức 1: Nhận biết
Câu 1: Cho f(x) là hàm số liên tục trên đoạn
;ab
. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn
;ab
.
Công thức nào sau đây đúng:
A.
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x F b F a
C.
( ) ( ) (a) (b)
b
b
a
a
f x dx F x F F
B.
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x F b F a
D.
( ) ( ) (a) (b)
b
b
a
a
f x dx F x F F
Lời giải:
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x F b F a
Phương án nhiễu:
+) Phương án B: Nhầm dấu.
Group Nhóm Toán | Trắc nghiệm 2016-2017
18
+) Phương án C: Thay nhầm cận a,b.
,+) Phương án D: Nhầm trong việc thay cận trên hay dưới và dấu.
Câu 2: Tích phân
1
0
2
I x dx

bằng:
A.
5
2
I
B.
5
2
I
C.
5
I
D.
13
2
I
Lời giải:
1
2
0
2
5
.
22
x
I

Phương án nhiễu:
+) Phương án A: Nhầm
()
b
a
F x F a F b
+) Phương án C: Nhầm
1
2
0
2 5.Ix
+) Phương án D:
()
b
a
F x F a F b
Câu 3: Tích phân
3
0
cos .sin
I x xdx
A.
0
I
B.
1
2
I
C.
4
I
D.
4
I
Lời giải:
4
3
0
0
cos
cos cos 0
4
x
I xd x
.
Phương án nhiễu:
+) Phương án B: Đổi dấu sai trong công đoạn thay cận
+) Phương án C,D: Thay cận sai.
Mức 2: Thông hiểu
Câu 4: Cho biết
55
22
( ) 3; g(t) 9
f x dx dt


. Giá trị của
5
2
( ) g( )
A f x x dx



A.
27
I
B.
12
I

C.
12
I
D. Không xác định được
Group Nhóm Toán | Trắc nghiệm 2016-2017
19
Lời giải: Do tích phân của hàm số trên
;
ab
cho trước không phụ thuộc vào biến số nên:
5 5 5
2 2 2
( ) 12I f x g x dx f x dx g t dt


Phương án nhiễu:
+) Phương án D không xác định do học sinh không nắm được “tích phân của hàm số trên
;
ab
cho trước
không phụ thuộc vào biến số”
+) Phương án A,C. Áp dụng sai công thức tích phân của một tổng.
Câu 5: Giá trị tích phân
5
2016
1
1
21
I dx
x
là:
A.
2015
11
1
4030 9



B.
2015
11
1
4030 9



C.
2015
11
1
2015 9



D.
2015
11
1
2015 9



Lời giải:
5
2016
2015
1
21
1 1 1
1
2 4030 9
21
dx
I
x



Phương án nhiễu:
+) Phương án B: Sai tại công đoạn thay cận đổi dấu.
+) Phương án C: Đưa dx thành d(2x -1), không chia 2.
+) Phương án D. Đưa dx thành d(2x -1), không chia 2 và thay cận sai.
Câu 6: Nếu
( ) 5; ( ) 2,
dd
ab
f x dx f x dx

với
a d b
thì
b
a
I f x dx
bằng:
A.
7
I
B.
3
I
C.
10
I
D. Đáp án khác
Lời giải:
3
b d b
a a d
I f x dx f x dx f x dx
Phương án nhiễu:
+) Phương án A: Nhầm lẫn
db
bd
f x dx f x dx

.
Group Nhóm Toán | Trắc nghiệm 2016-2017
20
+) Phương án C: Nhầm lẫn
. 10
b d b
a a d
I f x dx f x dx f x dx
+) Phương án D: Gây nhiễu
Mức 3: Vận dụng thấp
Câu 7: Giả sử
4
0
2
sin3 .sin2 ,
2
I x xdx a b a b
. Khi đó, giá trị của
ab
là:
A.
1
6
I
B.
3
10
I
C.
3
10
I
D.
3
5
I
Lời giải:
4
4
0
0
1 1 1 3 2
cos cos5 sinx sin5 .
2 2 5 5 2
I x x dx x



Suy ra
3
0,
5
ab
và
3
.
5
ab
Phương án nhiễu:
+) Phương án B: Biến đổi sai công thức tích thành tổng.
+) Phương án C: đổi sai công thức tích thành tổng và sai bước đổi dấu thay cận.
+)Phương án A: Không xác đinh được a,b.
Câu 8: Biến đổi
3
0
11
x
dx
x

thành
2
1
( ) vôùi 1
f t dt t x

. Khi đó
()
ft
là hàm số nào trong các
hàm số sau:
A.
2
( ) 2 2
f t t t

B.
2
()
f t t t

C.
2
()
f t t t

D.
2
( ) 2 2
f t t t

Lời giải: Đặt
2
1 1 2t x t x tdt dx
Đổi cận
0 1; 3 2x t x t
. Khi đó
2
2
1
2 2 .I t t dt
Phương án nhiễu:
+) Phương án B,C,D tính sai dt.
Mức 3: Vận dụng cao
Group Nhóm Toán | Trắc nghiệm 2016-2017
21
Câu 9: . Giá trị tích phân
2
2016
2
1
x
x
I dx
e
là:
A.
2017
2
2017
B.
2018
2
2017
C. 0
D.
2018
2
2
21
2017
e
e

Lời giải: Đặt
x t dx dt
Đổi cận: Với
2 2; 2 2x t x t
Khi đó:
22
2016 2016
22
11
x
tx
t x e dx
I dt
ee



, suy ra
2
2
2017 2018
2016
2
2
2
2
2017 2017
x
I x dx
.
+)Phương án B: Sai lầm để 2I và chọn đáp án B
+) Phương án C: Biến đổi sai lầm sau phép đặt được
2
2016
2
1
x
x
I dx
e

và kết luận I = 0.
+) Phương án D: Nhớ sai công thức
2 2 2
2016
2016
2 2 2
dx: 1
1
x
x
x
I dx x e dx
e
và tính ra D.
Câu 10: Cho
31
3
1
ln
22
4
sin 2sin cos 3cos
0
c
dx
ab
x x x x

và a, b, c nguyên dương. Tổng
abc
bằng:
A.
9
B.
8
C. 7
D. Không xác định
Lời giải: Ta cã
2
33
cos
2 2 2
00
sin 2sin cos 3cos tan 2tan 3
dx
dx
x
I
x x x x x x



§Æt
tan
2
cos
dx
t x dt
x
3
3 3 1
33
1 1 1
ln ln
2
00
1 3 4 3 4
33
23
0
dt dt t
I
t t t
tt


Suy ra
9abc
.
+) Phương án B,C,D: Gây nhiễu
Group Nhóm Toán | Trắc nghiệm 2016-2017
22
PHẦN 3 :
Câu nhận biết
Câu 1. Diện tích hình phẳng giới hạn bởi đường
yx
và 2 đường
Thẳng x =0, x= 1, trục hoành là.
A.
1
2
S
(đvdt) B.
1S
(đvdt) C.
2S
(đvdt) D.
2
S
(đvdt)
Câu 2. Diện tích hình phẳng giới hạn bởi đồ thị hs y=f(x) nằm phía trên trục hoành và 2 đường x=a,x=b với a<b và trục
hoành là.
A.
S f a f b
(đvdt) B.
S f b f a
(đvdt) C.
()S f b f a

(đvdt) D.
( ) f(b)S f a

(đvdt)
Câu 3. Diện tích hình phẳng giới hạn bởi 2 đường
0, siny y x
và 2 đường thẳng
,
2
x o x

là
A.
0S
(đvdt) B.
S
(đvdt) C.
1S
(đvdt) D.
2S
(đvdt)
Câu thông hiểu
Câu 4. Diện tích hình phẳng giới hạn bỏi 2 đường thẳng x=1,
3yx
trục ox là.
A.
2S
B.
4S
C.
4S
D.
2S
Câu 5.Tính diện tích hình phẳng giới hạn bởi
.lny x x
,trục hoành và hai đường thẳng x = 1, x = e.
A.
2
1
( 1)
4
Se
B.
2
1
( 1)
4
Se
C.
2
1
(1 )
4
Se
D.
2
(1 )Se
Câu 6. Thể tích hình phẳng giới hạn bởi các đường
,2y x y
trục oy khi xoay quanh trục hoành là.
A.
8
()
3
V dvtt
B.
8 ( )V dvtt
C.
8
3
V
D. Các kết quả trên đều sai.
Group Nhóm Toán | Trắc nghiệm 2016-2017
23
Câu vận dụng thấp
Câu 7.Tính diện tích hình phẳng giới hạn bởi
2
.lny x x
,trục hoành và hai đường thẳng x = 1, x = e.
A.
2
1
( 1)
4
Se
B.
2
1
( 1)
4
Se
C.
2
1
(1 )
4
Se
D.
2
(1 )Se
Câu 8.Thể tích hình phẳng giới hạn bởi các đường
2
( 2), 0y x y
,x=o,x=2 khi xoay quanh trục hoành là.
A.
32
5
V
(dvtt) B.
32 ( )V dvtt
C.
32
. ( )
5
V dvtt
D.32
Câu vận dụng cao
Câu 9. Diện tích hình phẳng giới hạn bỏi trục tung và 2 đường
2 , 3
x
y y x
là.
A.
5
ln2
2
S 
B.
3
2
S
C.
5 ln2S 
D.
51
2 ln2
S 
Câu 10. Cho hình phẳng giới hạn bởi các đường
2
( 2) , 4y x y
khi xoay quanh trục hoành là.
A.
256
()
5
V dvtt
B.
256
()
5
V dvtt
C.
256. ( )V dvtt
D. Các kết quả trên đều sai.
PHẦN 4 :
Câu 1. Tính
0
sin cosx xdx



bằng:
A. 0 B. 1 C.
D.
3
2
Câu 2. Cho tích phân
2
2
1
2 1.I x x dx
. Đặt
2
1ux
. Chọn khẳng định sai trong các khẳng định sau:
A.
3
0
I udu
B.
2
. 27
3
I
C.
2
1
I udu
D.
3
0
2
.
3
I u u
Câu 3. Cho a<b<c thỏa mãn:
( ) 8
b
a
f x dx
và
( ) 2
c
b
f x dx
khi đó giá trị của tích phân
()
c
a
f x dx
bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
24
A. 6 B. 10 C. 4 D. 16
Câu 4. Tính tích phân
2
3
1
ln x
dx
x
A.
2 ln2
16
B.
3 2ln2
16
C.
3 ln2
16
A.
3 2ln2
16
Câu 5. Biết rằng
(x)f
có đạo hàm
'(x)f
liên tục trên R và
(0) 2fe
, :
0
'( ) 5
e
f x dx e
. Tính
()fe
.
A.
( ) 0fe
B.
( ) 3efe
C.
( ) 7efe
D.
( ) 3efe
Câu 6. Giả sử
5
1
ln
21
dx
Ia
x

khi đó a nhận giá trị:
A. 9 B. 3 C. 8 D. 81
Câu 7. Cho
0a
. Với giá trị nào của a để biểu thức
1
(2 4)
a
I x dx
đạt giá trị nhỏ nhất:
A.
1a
B.
4a
C.
2a
D.
3a
Câu 8. Tính tích phân
1
0
(|3 1| 2| |)I x x dx
bằng:
A.
1
6
B.
7
6
C.
1
2
D. 0
Câu 9. Tìm giá trị thực của m để I=4, biết I=
2
1
(2 1)mx dx
.
A. m=-1 B.m= - 2 C. m=1 D. m=2
Câu 10. Với hàm số
()y f x
liên tục trên miền
[ ; ]D a b
có đồ thị là đường cong (C), ta có thể tính độ dài đường
cong (C) bằng công thức:
2
1 ( '( ))
b
a
f x dx
. Tính độ dài đường cong (C) cho bởi hàm số
2
ln
8
x
yx
trên [1; 2]
bằng:
A.
3
ln2
8
B.
1 ln2
C.
3
ln2
8
D.
1 ln2
Group Nhóm Toán | Trắc nghiệm 2016-2017
25
HƯỚNG DẪN
Câu 1. Tính
0
cos 2x xdx


suy ra
0
sin cosx xdx



=0
Đáp án A
Câu 2. Đáp án C
Câu 3.
( ) ( ) ( ) 8 2 10
c b c
a a b
f x dx f x dx f x dx
- Đáp án B
Câu 4. Đặt
3
ln ;
dx
u x dv
x

. Tính được
2
3
1
ln x
dx
x
=
3 2ln2
16
Đáp án B
Câu 5.
0
'( ) ( ) (0) 5 ( ) 3
e
f x dx f e f e f e e
Đáp án 5
Câu 6.
5
5
1
1
1
ln| 2 1| ln3 ln 3
2 1 2
dx
I x a a
x
- Đáp án B
- Phương án gây nhiễu 1:
5
5
1
1
ln | 2 1| ln9 ln 9
21
dx
I x a a
x
HS chọn A
- Phương án gây nhiễu 2:
5
5
1
1
ln| 2 1| ln(2.5 1 (2.1 1)) ln8 ln 8
21
dx
I x a a
x
HS chọn C
- Phương án gây nhiễu 2:
5
5
2
1
1
2ln |2 1| ln9 ln 81
21
dx
I x a a
x
HS chọn D
Group Nhóm Toán | Trắc nghiệm 2016-2017
26
Câu 7.
2 2 2
1
1
(2 4) ( 4 ) 4 3 ( 2) 1 1
a
a
I x dx x x a a a
suy GTNN min I=-1 khi a=2
Đáp án: C
Phương án gây nhiễu: A
2 2 2
1
1
(2 4) (2 4 ) (2 4 ) 2 2( 1) 2 2 1
a
a
I x dx x x a a a a
Phương án gây nhiễu: B
2
1
1
(2 4) ( 4 ) ( 4) 3 3 4
a
a
I x dx x x a a a
Phương án gây nhiễu: D
2
1
1
(2 4) ( 4 ) ( 4) 3 3 3
a
a
I x dx x x a a a
Câu 8.
1 1 1
0 0 0
51
(|3 1| 2| |) |3 1| 2| | 1
66
I x x dx x dx x dx
Đáp án A
- Phương án gây nhiễu: B
1 1 1
0 0 0
57
(|3 1| 2| |) |3 1| 2| | 1
66
I x x dx x dx x dx
- Phương án gây nhiễu: 0
1
11
2
00
0
1
(|3 1| 2| |) ( 1) ( )
22
x
I x x dx x dx x

- Phương án gây nhiễu: C
11
1
2
0
00
(|3 1| 2| |) ( 1) ( ) 0I x x dx x dx x x

Câu 9. I=
2
1
(2 1) 3 1 4 1mx dx m m
.
Đáp án C
Group Nhóm Toán | Trắc nghiệm 2016-2017
27
- Phương án gây nhiễu 1:
2
22
1
1
(2 1) ( )| 4 2 4 2mx dx mx x m m m
HS chọn D
- Phương án gây nhiễu 2:
2
2
2
1
1
(2 1) ( )| 2 2 (m 1) 4 1
2
mx
mx dx x m m
HS chọn A
- Phương án gây nhiễu 3:
2
22
1
1
(2 1) ( ) | 4 2 4 2mx dx mx x m m m
HS chọn B
Câu 10. Học sinh phải nắm ngay công thức tính và áp dụng
2 2 2
22
1 1 1
1 1 1 3
1 ( ) ( ) ( ) ln2
4 4 4 8
x x x
dx dx dx
x x x
Đáp án: C
- Phương án gây nhiễu 1:
2 2 2
22
1 1 1
1 1 1 3
1 ( ) ( ) ( ) ln2
4 4 4 8
x x x
dx dx dx
x x x
HS chọn A
- Phương án gây nhiễu 2:
2
2 2 2
2
22
1 1 1
1
1 1 1
1 ( ) ( ) ( ) ( ln ) 1 ln2
4 4 4 8
x x x x
dx dx dx x
x x x
HS chọn B
- Phương án gây nhiễu 3:
2
2 2 2
2
22
1 1 1
1
1 1 1
1 ( ) ( ) ( ) ( ln ) 1 ln2
4 4 4 8
x x x x
dx dx dx x
x x x
HS chọn D
PHẦN 5 :
Câu 1.(Mức độ 2) Tìm nguyên hàm của hàm số
1
12
fx
x
A.
ln(1 2 )f x dx x C
B.
1
ln 1 2
2
f x dx x C
C.
2ln 1 2f x dx x C
D.
1
ln(1 2 )
2
f x dx x C
Giải thích phương án nhiễu:
A. Nhầm lẫn do không nhớ công thức
C. Nhầm lẫn công thức
D. Thiếu dấu giá trị tuyệt đối
Group Nhóm Toán | Trắc nghiệm 2016-2017
28
Lời giải
Áp dụng nguyên hàm
1
ln
dx
ax b C
ax b a
. Ta có
11
ln 1 2 ln 1 2
1 2 2 2
dx
x C x C
x

.
Câu 2. (Mức độ 1) Cho hàm số
sin2f x x
khi đó:
A.
2cos2f x dx x C
B.
2cos2f x dx x C
C.
1
cos2
2
f x dx x C
D.
1
cos2
2
f x dx x C
Giải thích phương án nhiễu:
A. Nhầm lẫn với đạo hàm
B. Nhầm lẫn với đạo hàm và lấy dấu “-“ của nguyên hàm
D. Nhầm dấu
Câu 3. (Mức độ 2) Tìm nguyên hàm của hàm số
2
x
f x xe
A.
2 x
f x dx x e C
B.
22
xx
f x dx e xe C
C.
( 1)
x
f x dx x e C
D.
( 1)
x
f x dx x e C
Giải thích phương án nhiễu:
A. Nhầm lẫn do hiểu là nguyên hàm của một tích bằng tích các nguyên hàm
B. Nhầm lẫn với đạo hàm
C. Nhầm dấu trong tich phân từng phần
Câu 4. (Mức độ 2) Tìm nguyên hàm của hàm số
cosf x x x
A.
2
1
sin
2
f x dx x x C
B.
sinf x dx x C
C.
cos sinf x dx x x x C
D.
sin cosf x dx x x x C
Câu 5. (Mức độ 2) Nguyên hàm của hàm số
22
1
()
-
fx
xa
là:
A.
1
ln
2
xa
C
a x a
B.
1
ln
2
xa
C
a x a
C.
1-
ln
xa
C
a x a
D.
1
ln
xa
C
a x a
Group Nhóm Toán | Trắc nghiệm 2016-2017
29
Câu 6. (Mức độ 2) Nguyên hàm của hàm số
22
1
()
sin .cos
fx
xx
là:
A.
tan cot F x x x C
B.
cot tan F x x x C
C.
tan cot F x x x C
D.
22
tan cot F x x x C
Câu 7. (Mức độ 3) Nguyên hàm của hàm số:
3
( ) lnf x x x
là:
A.
44
11
.ln
4 16
x x x C
B.
4 2 4
11
.ln
4 16
x x x C
C.
43
11
.ln
4 16
x x x C
D.
44
11
.ln
4 16
x x x C
Câu 8. (Mức độ 3) Nguyên hàm của hàm số
( ) 2sin3 cos2f x x x
là:
A.
Cxx cos5cos
5
1
B. F(x) =
11
cos5 cos
32
x x C
C.
11
cos5 cos
23
x x C
D. F(x) =
1
cos5 cos
5
x x C
Câu 9. (Mức độ 3) Nguyên hàm của hàm số
3
()
1
x
fx
x
là:
A.
32
11
ln 1
32
x x x x C
B.
32
11
ln 1
32
x x x x C
C.
32
11
ln 1
62
x x x x C
D.
32
11
ln 1
34
x x x x C
Câu 10. (Mức độ 4) Nguyên hàm của hàm số: y =
x
1
()
2 +5
fx
là:
A.
12
ln
2ln5
25
x
x
C
B.
12
ln
5ln2
25
x
x
C
C.
12
ln
10ln2
25
x
x
C
D.
12
ln
ln2
25
x
x
C
PHẦN 6 :
KIỂM TRA 45 PHÚT - CHƯƠNG III
Group Nhóm Toán | Trắc nghiệm 2016-2017
30
I. Mục tiêu:
+ Kiểm tra các kiến thức trong chương 3 giải tích gồm có các nội dung chính: nguyên hàm; tích phân; ứng dụng của
tích phân.
+ Học sinh cần ôn tập trước các kiến thức trong chương 3 thật kỹ, tự giác tích cực làm bài. Qua đó giáo viên nắm được
mức độ lĩnh hội kiến thức của học sinh.
+Phát triển năng lực học sinh theo 4 mức độ nhận thức
II. Chuẩn bị:
- GV: ra đề kiểm tra.
- HS: Ôn tập, chuẩn bị kiểm tra.
III. Nội dung kiểm tra:
1. Kiến thức: Kiểm tra việc nắm bắt kiến thức của Hs về phần nguyên hàm, tích phân và ứng dụng của tích phân.
2. Kĩ năng:
Rèn kỹ năng tính nguyên hàm, tích phân và giải các bài toán ứng dụng tích phân.
Rèn tư duy lôgic và tính tự giác cho học sinh.
3. Mức độ: Nhận biết ( 4,8 điểm ) + Thông hiểu ( 4.0 điểm) + Vận dụng ( 0,8 điểm).
VI. Ma trận đề kiểm tra:
Mức độ
Nội dung
Nhận biết
Thông hiểu
Vận dụng
mức độ thấp
Vận dụng
mức độ cao
Tổng
Nguyên hàm
3
1,2
2
0,8
5
2.0
Phương pháp tính tích phân
6
2,4
5
2,0
2
0,8
13
5,2
Ứng dụng tích phân tính diện
tích hình phẳng
5
2.0
2
0,8
7
2,8
Tổng
9
3,6
12
4,8
2
0,8
2
0,8
25
10
Câu 1:Tìm nguyên hàm
Fx
của hàm số
3
1
3f x x x
x
Group Nhóm Toán | Trắc nghiệm 2016-2017
31
A.
x
F x x x C
4
2
3
ln
42
B.
3
2
1
33
F x x x C
x
C.
4
2
2
ln
43
x
F x x x C
D.
4
2
3
ln
42
x
F x x x C
Câu 2:Tìm nguyên hàm
Fx
của hàm số
23
xx
fx
. Chọn đáp án sai
A.
2 3 1
ln2 ln3 ln 2
xx
Fx
B.
2 3 1
ln2 ln3
2
xx
x
Fx
C.
2 3 1
ln2 ln3 ln3
xx
Fx
D.

23
ln 2 ln3
xx
Fx
Câu 3:Tìm nguyên hàm
Fx
của hàm số
2
1
()
x
fx
x
A.
1
( ) ln
F x x C
x
B.
1
( ) ln
F x x C
x
C.
1
( ) ln
F x x C
x
D.
1
( ) ln
F x x C
x
Câu 4:Tìm nguyên hàm
Fx
của hàm số f(x)=
2
tan
cos
xdx
x
A.
2
cot
xC
B.
2
cos
xC
C.
2
sin
xC
D.
2
tan
xC
Câu 5:Tìm nguyên hàm
Fx
của hàm số f(x)=
2
sinx xdx
A.
2
11
( ) sin2 cos2
22
F x x x x x C
B.
2
11
( ) sin2 cos2
42
F x x x x x C
C.
2
11
( ) ( )cos2
42
F x x x x C
D.
2
11
( ) sin2 cos2
42
F x x x x x C
Câu 6:Tính tích phân:I=
2
1
2 5 7
e
xx
dx
x

A.
4 7 8ee
B.
7 4 8ee
C.
8 7 4ee
D.
4 7 8ee
Group Nhóm Toán | Trắc nghiệm 2016-2017
32
Câu 7:Tính tích phân: I=
2
1
1x dx
A.
2
3 2 2 3
3
B.
3
3 3 2 2
2
C.
2
3 3 2 2
3
D.
2
2 2 3 3
3
Câu 8:Tính tích phân: I=
1
2
0
1
xdx
x
A.
1
ln2
2
B.
2ln2
C.
ln2
D.
ln2
Câu 9:Tính tích phân: I=
1
2 ln
2
e
x
dx
x
A.
3 2 2 3
3
B.
3 3 2 2
3
C.
3 3 2 2
2
D.
3 3 2 2
3
Câu 10 Tính
2
0
2
cos
xdx
A.
2
B.
4
C.
3
2
D.
3
Câu 11 Tính
2
2
2
1J x dx

A. 3 B. 4 C. 9 D.
2
9
Câu 12 Tính
1
ln
e
x xdx
A.
2
1
2
e
B.
2
1
2
e
C.
2
1
2
e
D.
2
1
2
e
Group Nhóm Toán | Trắc nghiệm 2016-2017
33
Câu 13: Tính
5
2
0
4I x x dx
A.
3
19
B. 1 C.
3
19
D.
3
28
Câu 14: Tính:
1
22
0
x
K x e dx
A.
2
4
e
K
B.
2
1
4
e
K
C.
2
1
4
e
K
D.
1
4
K
Câu 15: Tính:
3
2
1
3 lnx
I dx
(x 1)
A.
2ln)3ln1(
4
3
I
B.
2ln)3ln1(
4
3
I
C.
2ln)3ln1(
4
3
I
D.
3
I (1 ln3) ln2
4
Câu 16: Tính:
2
sin
0
.cos
x
I e x xdx

.
A.
2
2
e

B.
2
2
e
C.
2
2
e
D.
2
2
e
Câu 17 Tính
2
2
0
4 x dx
,
Group Nhóm Toán | Trắc nghiệm 2016-2017
34
A.
2
1
2
B.
2
1
2
C.
2
D.
.
Câu 18 Tính,
1
2
0
1
dx
x
A.
2
1
2
B.
2
C.
4
D.
Câu 19: Số đo diện tích hình phẳng giới hạn bởi hai đường y = x
3
– x và y = 3x bằng :
A. 4 B. 8 C. 16 D. 32
Câu 20: Số đo diện tích hình phẳng giới hạn bởi các đường y =

; y = 0; x = 0 ; x = 1 bằng:
A. 2ln2 B. 1- ln2 C. 2 + ln2 D. 2
Câu 21: Số đo diện tích hình phẳng giới hạn bởi các đường: y =
xxx 2
23
và trục hoành
bằng:
A.


B.


C. 37 D. 12
Câu 22. Số đo diện tích hình phẳng giới hạn bởi các đường y = e
x
; y = e
-x
; x = 1 bằng:
A. 1 +
B. 2e C. e + 1 D. e +
- 2
Câu 23: Cho hình phẳng ( H) giới hạn bởi đồ thị hàm số y =
-1, trục Ox; đường thẳng x =
1; x = 4. Thể tích của khối tròn xoay tạo thành khi quay (H) quanh trục Ox bằng:
A.

B. 2π C.

D.
Group Nhóm Toán | Trắc nghiệm 2016-2017
35
Câu 24: Cho hình phẳng (H) giới hạn bởi các đường y = sin
2
x ; y = 0 ; x = 0 ; x = π. Thể tích
của khối tròn xoay tạo thành khi quay (H) quanh trục Ox bằng:
A.
B.
C.
D.

Câu 25: Cho hình phẳng (H) giới hạn bởi các đường: y =
; y = 1; y = 4 ; x = 0. Thể tích của
khối tròn xoay tạo thành khi quay (H) quanh trục Oy bằng:
A.π B. 2π C.3π D. 5π
ĐÁP ÁN
1A
2B
3C
4D
5B
6A
7C
8A
9B
10B
11B
12B
13A
14C
15D
16A
17D
18C
19B
20B
21A
22D
23C
24D
25C
ĐÁP ÁN CHI TIẾT
ĐS: 1a) 2b)
3c.

22
1 1 1 1
( ) ln
x
dx dx x C
xx
xx
4D.
2
tan
cos
xdx
x
.Đặt t = tanx

2
cos
dx
dt
x
.

22
2
tan
t tan
cos
xdx
dt t C x C
x
Group Nhóm Toán | Trắc nghiệm 2016-2017
36
5B.
2
sinx xdx
. Đặt


2
1
sin2
sin .
2
du dx
ux
v x x
dv x dx
2 2 2 2
1 1 1 1 1
sin ( sin2 ) ( sin2 ). ( sin2 ) ( cos2 )
2 2 2 4 2
x xdx x x x x x dx x x x x x C

2
11
sin2 cos2
42
x x x x C
6a
22
2
1
11
2 5 7 2 5
( 7) (4 5ln 7 )
ee
e
xx
dx dx x x x
xx
x


=
4 7 8ee
7C
8A
9B
1
2 ln
2
e
x
dx
x
. Đặt t=
2
1
2 ln 2 ln
2
x t x tdt dx
x
I=
2
3
3
3
2
2
3
t
t dt
=
3 2 2 3
3
Câu 10 Tính
2
0
2
cos
xdx
I =
22
2
00
1
cos x.dx (1 cos2x).dx
2



=
11
x sin 2x
2
2 2 4
0




A.
2
B.
4
C.
3
2
D.
3
Group Nhóm Toán | Trắc nghiệm 2016-2017
37
Câu 11 TÝnh
2
2
2
1J x dx

A. 3 B. 4 C. 9 D.
2
9
Xét dấu
2
1x
trên đoạn
2;2
x
-2 -1 1 2
2
1x
+ 0 - 0 +
2 1 1 2
2 2 2 2
2 2 1 1
1 1 1 1I x dx x dx x dx x dx
3 3 3
1 1 2
4
2 1 1
3 3 3
x x x
x x x

.
Câu 12 Tính
1
ln
e
x xdx
A.
2
1
2
e
B.
2
1
2
e
C.
2
1
2
e
D.
2
1
2
e
Đặt
lnux
dv xdx
2
2
dx
du
x
x
v
2 2 2 2
11
11
ln ln
11
2 2 2 4 4
ee
ee
x e x e
x xdx x xdx

Group Nhóm Toán | Trắc nghiệm 2016-2017
38
Câu 13: Tính
5
2
0
4I x x dx
A.
3
19
B. 1 C.
3
19
D.
3
28
5
2
0
4I x x dx
Đặt
2 2 2
44u x u x
22udu xdx udx xdx
Đổi cận:
02xu
53xu
3
2
2
I u du
3
3
2
3
u
I
19
3
=>CHỌN A
Câu 14: Tính:
1
22
0
x
K x e dx
A.
2
4
e
K
B.
2
1
4
e
K
C.
2
1
4
e
K
D.
1
4
K
Đặt
x
x
ev
xdxdu
dxedv
xu
2
2
2
2
1
2
LedxxeexK
xx
2
1
0
21
0
22
2
1
).
2
1
.(
Group Nhóm Toán | Trắc nghiệm 2016-2017
39
x
x
ev
dxdu
dxedv
xu
2
2
2
1
222
1
0
21
0
2
4
1
4
1
)
4
1
4
1
(
2
1
2
2
1
)
2
1
(
eee
dxeexL
xx
=> CHỌN C
Câu 15: Tính:
3
2
1
3 lnx
I dx
(x 1)
A.
2ln)3ln1(
4
3
I
B.
2ln)3ln1(
4
3
I
C.
2ln)3ln1(
4
3
I
D.
3
I (1 ln3) ln2
4
3 3 3
2 2 2
1 1 1
3
3
1
2
1
1
3
2
2
1
3 ln x dx ln x
I dx 3 dx
(x 1) (x 1) (x 1)
dx 3 3
I3
(x 1) (x 1) 4
ln x
I dx
(x 1)

Đặt u = lnx
dx
du
x

2
dx
dv .
(x 1)
Chọn
1
v
x1
3
3 3 3
2
1
1 1 1
lnx dx ln3 dx dx ln3 3
I ln
x 1 x(x 1) 4 x x 1 4 2
Vậy :
3
I (1 ln3) ln2
4
Group Nhóm Toán | Trắc nghiệm 2016-2017
40
.
Câu 16: Tính:
2
sin
0
.cos
x
I e x xdx

.
A.
2
2
e

B.
2
2
e
C.
2
2
e
D.
2
2
e
22
sin
00
cos .cos
x
I e xdx x xdx



2
22
sin sin sin
10
00
cos sin 1
x x x
I e xdx e d x e e


22
22
2
00
00
.cos sin sin cos 1
22
I x xdx x x xdx x




12
I I I
=
2
2
e

Câu 17 Tính
2
2
0
4 x dx
,
A.
2
1
2
B.
2
1
2
C.
2
D.
Đặt
2sin , ;
22
x t t




. Khi x = 0 thì t = 0. Khi
2x
thì
2
t
.
2sinxt
2cosdx tdt
4
22
2 2 2
0 0 0
4 4 4sin .2cos 4 cos
x dx t tdt tdt

.
Group Nhóm Toán | Trắc nghiệm 2016-2017
41
Câu 18 Tính,
1
2
0
1
dx
x
A.
2
1
2
B.
2
C.
4
D.
Đặt
tan , ;
22
x t t




. Khi
0x
thì
0t
, khi
1x
thì
4
t
.
Ta có
2
tan
cos
dt
x t dx
t
.
1
44
2 2 2
0 0 0
1
..
4
1 1 tan cos 4
0
dx dt
dt t
x t t


Câu 19: Số đo diện tích hình phẳng giới hạn bởi hai đường y = x
3
– x và y = 3x bằng :
A. 4 B. 8 C. 16 D. 32
Phương trình HĐGĐ : x
3
– x = 3x x = 0 ; x = -2 ; x = 2
S=
󰇛
󰇜



=



=



+


=
󰇻
󰇛

󰇜


󰇻 + 󰇻
󰇛

󰇜

󰇻 = 󰇻󰇣

󰇤

󰇻 + 󰇻󰇣

󰇤
󰇻 = 8
ĐA: B
Câu 20: Số đo diện tích hình phẳng giới hạn bởi các đường y =

; y = 0; x = 0 ; x = 1 bằng:
A. 2ln2 B. 1- ln2 C. 2 + ln2 D. 2
S=
󰇻

󰇻
=
󰇻

󰇻
= 󰇻
󰇡

󰇢

󰇻 = 󰇻
󰇟
󰇛 󰇜
󰇠
󰇻 =1- ln2
ĐA : B
Câu 21: Số đo diện tích hình phẳng giới hạn bởi các đường: y =
xxx 2
23
và trục hoành
bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
42
A.


B.


C. 37 D. 12
Câu 21: Phương trình hoành độ giao điểm của đồ thị hàm số y =
xxx 2
23
và trục hoành.
xxx 2
23
= 0
x = -2 ; x = 0 ; x = 1
S =
dxxxx
1
2
23
2
=
0
2
23
2 dxxxx
+
1
0
23
2 dxxxx
I
1
=
0
2
23
)2( dxxxx
=
0
2
234
)
3
1
4
1
(
xxx
=
3
8
I
2
=
1
0
23
)2( dxxxx
=
1
0
234
)
3
1
4
1
( xxx
=
12
5
S =
12
5
3
8
=
12
37
ĐA: A
Câu 22. Số đo diện tích hình phẳng giới hạn bởi các đường y = e
x
; y = e
-x
; x = 1 bằng:
A. 1 +
B. 2e C. e + 1 D. e +
- 2
Câu 22: Phương trình HĐGĐ : e
x
= e
-x
x = 0
S=


= 󰇻
󰇛

󰇜

󰇻 = 󰇻
󰇟

󰇠
󰇻= e +
- 2
Đ A: D
Câu 23: Cho hình phẳng ( H) giới hạn bởi đồ thị hàm số y =
-1, trục Ox; đường thẳng x =
1; x = 4. Thể tích của khối tròn xoay tạo thành khi quay (H) quanh trục Ox bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
43
A.

B. 2π C.

D.
Câu23: V= π
󰇛
󰇜

= π
󰇛
󰇜 
= π
4
1
32
)
3
4
2
1
( xxx
=

Đ A : C
Câu 24: Cho hình phẳng (H) giới hạn bởi các đường y = sin
2
x ; y = 0 ; x = 0 ; x = π. Thể tích
của khối tròn xoay tạo thành khi quay (H) quanh trục Ox bằng:
A.
B.
C.
D.

Câu 24: V= π
󰇛
󰇜

= π


=
󰇛
 
󰇜

=
0
)4sin
2
1
2sin3( xxx
=

Đ A : D
Câu 25: Cho hình phẳng (H) giới hạn bởi các đường: y =
; y = 1; y = 4 ; x = 0. Thể tích của
khối tròn xoay tạo thành khi quay (H) quanh trục Oy bằng:
A.π B. 2π C.3π D. 5π
Câu 25: y = 2/x x= 2/y
V = π
󰇛
󰇜

= 

= -4π
4
1
)
1
(
y
= 3π
Đ A : C
PHẦN 7 :
Câu 1. (Nhận biết) Đẳng thức nào sau đây là sai?
A.
( ) ( )f x dx f x C

. B.
( ) ( )f x dx f x
.
C.
(t) (t)f dt f
. D.
( ) ( )f x dx f x C

.
LỜI GIẢI
DIỄN GIẢNG NHIỄU
Group Nhóm Toán | Trắc nghiệm 2016-2017
44
HS nhầm qua họ nguyên hàm phải cộng thêm số C → Chọn câu B
HS nghĩ nguyên hàm chỉ có ẩn số là x → Chọn câu C
HS quên tính chất 1 của nguyên hàm → Chọn câu D
Câu 2. (Nhận biết) Cho
,F x G x
lần lượt là một nguyên hàm của
,f x g x
trên tập
K
và
,kh
. Kết
luận nào sau đây là sai?
A.
f x g x dx F x G x C


. B.
kf x hg x dx kF x hG x C


.
C.
..f x g x dx F x G x C
. D.
',F x f x x K
.
LỜI GIẢI
DIỄN GIẢNG NHIỄU
HS quên tính chất 2 của nguyên hàm → Chọn câu A
HS không biết kết hợp tính chất 2 và 3 → Chọn câu B
HS nghĩ nguyên hàm phải cộng thêm số C → Chọn câu D
Câu 3. (Thông hiểu) Biết
2
f y dy x xy C
, thì
fy
bằng
A.
x
B.
.xy
C.
.y
D.
2.xy
LỜI GIẢI
DIỄN GIẢNG NHIỄU
Công thức nguyên hàm theo ẩn y, x
xem là 1 hằng số giống số C
HS nhằm qua ẩn x → Chọn câu B
HS nhằm qua ẩn x → Chọn câu C
HS lấy nguyên hàm theo ẩn x → Chọn câu D
Câu 4. (Nhận biết) Trong các đẳng thức sau, đẳng thức nào sai?
A.
( ) ' ( )f x dx f x C
B.
( ) ( ) ( ). ( ) ( ). ( )u x v x dx u x v x v x u x dx



C.
( ) ' ( )f x dx f x
D.
( ) ( )f x g x dx f x dx g x dx


ĐÁP ÁN, HƯỚNG DẪN GIẢI
DIỄN GIẢNG NHIỄU
Đáp án B
A. Đúng (T/c1)
B. Sai
A .Hs chọn vì có thể nhớ nhầm công thức
C. Hs chọn vì nghĩ theo họ nguyên hàm thì phải cộng
hằng số C
Group Nhóm Toán | Trắc nghiệm 2016-2017
45
C. Đúng (theo đ.nghĩa nguyên hàm)
( ) ' ( ( ) ) ( )f x dx F x C f x
D. Đúng (t/c 3)
D. Hs chọn vì quên công thức
Câu 5. (Nhận biết) Hàm số
3
()
x
f x e
có nguyên hàm là hàm số nào sau đây?
A.
3x
y e C
B.
3
3
x
y e C
C.
3
1
3
x
y e C
D.
3
x
y e C
LỜI GIẢI TÓM TẮT
DIỄN GIẢNG NHIỄU
- A: HS nhầm lẫn
xx
e dx e C
- B: HS nhầm với công thức đạo hàm
Câu 6. (Thông hiểu) Hàm số nào sau đây không phải là nguyên hàm của hàm số
x
ye
A.
1
x
c
e

B.
1
x
c
e
C.
x
ec

D.
1
1
x
x
e
c
e

ĐÁP ÁN
DIỄN GIẢNG NHIỄU
xx
e dx e c

C) Theo công thức chọn C là nguyên hàm của hàm số
x
ye
, A, D là
biến đổi của C
Câu 7. (thông hiểu) Hàm số
cot
x
F x e x C
là nguyên hàm của hàm số
fx
nào?
A.
2
1
sin
x
f x e
x

B.
2
1
sin
x
f x e
x

C.
2
1
cos
x
f x e
x

D.
2
1
sin
x
f x e
x

ĐÁP ÁN, HƯỚNG DẪN GIẢI
DIỄN GIẢNG NHIỄU
Ta có:
( ) cot
x
f x F x e x C
B. Hs nhớ nhầm
2
1
(cot )
sin
x
x
Group Nhóm Toán | Trắc nghiệm 2016-2017
46
2
1
sin
x
f x e
x

Đáp án A
C. Hs nhớ nhầm
2
1
(cot )
cos
x
x
D. Hs nhớ nhầm
2
1
(cot )
cos
x
x

Câu 8. (vận dụng thấp ) Tìm hàm số F(x) biết rằng
32
( ) 4 3 2F x x x
và
( 1) 3F 
A.
43
( ) 2 5F x x x x
B.
43
( ) 2 5F x x x x
C.
43
( ) 2 3F x x x x
D.
2
( ) 12 6 15F x x x
ĐÁP ÁN, HƯỚNG DẪN GIẢI
DIỄN GIẢNG NHIỄU
Đáp án C
32
( ) ( ) 4 3 2F x f x dx x x dx

43
2x x x C
( 1) 3F 
43
3 ( ) 2 3C F x x x x
A. Tìm C sai
B. Tìm C sai
D. Nhầm:
1
.x dx x C
Câu 9. (Thông hiểu) Nguyên hàm của hàm số
2
3sinf x x
x

trên khoảng
0;
là:
A.
2
2
( ) 3cosG x x C
x
B.
( ) 3cos 2lnG x x x C
C.
( ) 3cos 2lnG x x x C
D.
2
2
( ) 3cosG x x C
x
ĐÁP ÁN
DIỄN GIẢNG NHIỄU
( ) 3cos 2lnG x x x C
Đáp án A: Nhầm giữa đạo hàm và nguyên hàm
Đáp án B: Nhầm nguyên hàm sinx
Đáp án D: Nhầm nguyên hàm
2
x
với đạo hàm
Câu 10. (Thông hiểu)Tìm nguyên hàm của hàm số f(x) = cos3x.cosx ta có:
Group Nhóm Toán | Trắc nghiệm 2016-2017
47
A.
( ).f x dx
=
1
sin3 .sinx
3
xC
B.
( ).f x dx
=
C.
( ).f x dx
=
11
sin2 sin4
48
x x C
D.
( ).f x dx
=
11
sin2 sin4
48
x x C
LỜI GIẢI TÓM TẮT
DIỄN GIẢNG NHIỄU
f(x) =
1
(cos2 cos4 )
2
xx
( ).f x dx
=
1 1 1
( (cos2 cos4 ) sin2 sin4
2 4 8
x x dx x x C
- A: HS không biến đổi tích thành tổng tìm luôn nguyên
hàm
- B: sai dấu khi tìm nguyên hàm
- D: Sử dụng công thức biến đổi sai dấu
Câu 11. (Vận dụng cao)
Hàm số
2
1
()
6
fx
xx

có nguyên hàm là:
A.
2
ln 6x x C
B.
ln 3 ln 2x x C
C.
1
(ln 3 ln 2)
5
x x C
D.
1
(ln 3 ln 2)
5
x x C
DIỄN GIẢNG NHIỄU
2
1 1 1 1
( ) ( )
5 3 2
6
fx
xx
xx


Nguyên hàm của f(x) là:
1
(ln 3 ln 2)
5
x x C
- A: HS nhầm lẫn với công thức
1
lndx x C
x

- B: Tìm sai hệ số
- C: HS tìm sai dấu
Câu 12. (Nhận biết) Gọi
( ), ( )F x G x
lần lượt là nguyên hàm của hai hàm số
()fx
và
()gx
trên đoạn
;ab
. Trong
các đẳng thức sau, đẳng thức nào đúng?
A.
( ) ( )
b
a
f x dx F a F b
B.
. ( ) ( )
b
a
k f x dx k F b F a


C.
( ) ( ) ( )
b c c
a b a
f x dx f x dx f x dx
D.
( ) ( )
ba
ab
f x dx f x dx

ĐÁP ÁN, HƯỚNG DẪN GIẢI
DIỄN GIẢNG NHIỄU
Group Nhóm Toán | Trắc nghiệm 2016-2017
48
Đáp án B
A. sai
B. Đúng vì
. ( ) ( ) . ( ) ( )
bb
b
a
aa
k f x dx k f x dx k F x k F b F a



C. Sai
D. Sai
A. Hs chọn vì không thuộc công thức
C. Hs chọn vì nhớ nhầm công thức
D. Hs chọn vì nhớ nhầm công thức
Câu 13. (Thông hiểu) Biết
2
1
2f x dx
và
3
1
3f x dx
. Hỏi
2
3
f x dx
bằng bao nhiêu?
A. -1 B.
5
2
C. 1 D. 3
ĐÁP ÁN
DIỄN GIẢNG NHIỄU
A.
2
3
f x dx
=-(
3
1
f x dx
-
2
1
f x dx
)=-1
Đáp án B: sai khi cộng chia trung bình
Đáp án C: không chú ý cận đề bài yêu cầu
Câu 14. (Thông hiểu) Giả sử
1 4 4
0 1 0
2; 3; 4f x dx f x dx g x dx
. Khẳng định nào sau đây là sai?
A.
44
00
.f x dx g x dx

B.
4
0
1.f x g x dx


C.
4
0
5f x dx
D.
44
00
.f x dx g x dx

Câu 15. (thông hiểu) Giả sử
9
0
37f x dx
và
0
9
16g x dx
. Khi đó,
9
0
2 3 ( )I f x g x dx


bằng
A. I = 122 B. I = 58 C. I = 143 D. I = 26
ĐÁP ÁN, HƯỚNG DẪN GIẢI
DIỄN GIẢNG NHIỄU
Group Nhóm Toán | Trắc nghiệm 2016-2017
49
Đáp án D
99
00
2 3 ( ) 2.37 3.( 16) 26I f x dx g x dx

A.
99
00
2 3 ( ) 2.37 3.16 122I f x dx g x dx

B.
99
00
2 ( ) 2.37 16 58I f x dx g x dx

C.
99
00
2 ( ) 2.16 3.37 143I f x dx g x dx

Câu 16. (thông hiểu) Tính tích phân
2
0
cos .sin .I x xdx
A.
2
3
I 
B.
3
2
I
C.
2
3
I
D.
0I
ĐÁP ÁN, HƯỚNG DẪN GIẢI
DIỄN GIẢNG NHIỄU
Đáp án C
Sử dụng MTCT
2
2
0
2
cos .sin
3
I x xdx
Hoặc Đặt
cos sinu x du xdx
1
1
23
1
1
12
33
I u du u



A.
cos sinu x du xdx
1
1
23
1
1
12
33
I u du u



B. Hs đọc sai kết quả
D.
cos sinu x du xdx
1
1
23
1
1
1 1 1
0
3 3 3
I u du u



Câu 17. (vận dụng) Cho
1
1
a
x
dx e
x
, giá trị a>1 thõa mãn đẳng thức nào sau đây:
A.
ln 1a a e
B.
2
ln 1a a e
C.
2
1
1 e
a
D.
ln ae
ĐÁP ÁN
DIỄN GIẢNG NHIỄU
Group Nhóm Toán | Trắc nghiệm 2016-2017
50
1
1
1
ln ln 1
a
a
x
dx x x a a
x
Theo đề bài:
ln 1a a e
Đáp án B: sai khi viết
11x
x
xx

Đáp án C: Nhầm đạo hàm với nguyên hàm
Đáp án D: sai khi nhầm nguyên hàm của 1 bằng 0.
Câu 18. (Vận dụng)
0
1
sin .cos .
4
a
x x dx
khi đó giá trị của a = ?
A.
2
a
B.
6
a
C.
4
a
D. Không tồn tại a
LỜI GIẢI TÓM TẮT
DIỄN GIẢNG NHIỄU
0
1
sin .cos .
4
a
x x dx
0
11
sin2 .
24
a
x dx
11
cos2
0
44
a
x
1 1 1
cos2
4 4 4
a
cos2 0a
a=
4
- A: Thế cận vào sai dẫn đến sai
- D: Tìm nguyên hàm sai dấu dẫn đến
cos2a = 2 nên không tồn tại A
Câu 19. (Vận dụng) Biết rằng tích phân
1
0
2 1 .
x
x e dx a b e
, tích
ab
bằng
A. 1. B.
1
. C.
15.
D. 20.
LỜI GIẢI
DIỄN GIẢNG NHIỄU
Đặt:
2 1 2u x du dx
xx
dv e dx v e
11
1
0
00
2 1 2 1 2
x x x
x e dx x e e dx

→ Chọn câu C
Group Nhóm Toán | Trắc nghiệm 2016-2017
51
11
1
0
00
2 1 2 1 2
x x x
x e dx x e e dx

11
00
2 1 2
1
xx
x e e
e

B, D chọn ngẫu nhiên
Câu 20. (Vận dụng thấp)
5
1
ln
21
dx
c
x
. Giá trị của c là
A. 9 B. 3 C. 81 D. 8
ĐÁP ÁN
DIỄN GIẢNG NHIỄU
5
1
5
11
ln 2 1 ln9 3
1
2 1 2 2
dx
x
x
A) Quên
1
a
trong công thức
B) Đem
1
a
vào làm lũy thừa bị sai
C)Đem
9
=3 làm lũy thừa của 2
Câu 21. (vận dụng cao) Cho tích phân
2
sin
0
sin2 .
x
I x e dx
. Một học sinh giải như sau:
* Bước 1: Đặt
sin cost x dt xdx
.
Đổi cận:
1
2
00
xt
xt
1
0
2 . 2
t
I t e dt K
* Bước 2: Đặt
tt
u t du dt
dv e dt v e





* Bước 3:
11
11
00
00
. . 1
t t t t
K t e dt t e e dt e e

Group Nhóm Toán | Trắc nghiệm 2016-2017
52
1
0
2 . 2
t
I t e dt
Hỏi bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
A. Bài giải trên sai từ bước 1 B Bài giải trên sai từ bước 2
C. Bài giải trên sai từ bước 3 D. Bài giải trên hoàn toàn đúng
ĐÁP ÁN, HƯỚNG DẪN GIẢI
DIỄN GIẢNG NHIỄU
Đáp án D
2
sin
0
2sin cos .
x
I x x e dx
nên bước 1 đúng
bước 2 đúng
bước 3 đúng
Vậy bài giải đúng hoàn toàn
A. Hs chọn vì
2
sin
0
2sin cos .
x
I x x e dx
Đặt
sin cost x dt xdx
Hoặc Vì
2
sin
0
sin cos .
x
I x x e dx
Đặt
sin cost x dt xdx
1
0
.
t
I t e dt
B. Hs nhớ nhầm cách đặt
t
ue
dv tdt
C.
11
11
00
00
. . 2 1
t t t t
K t e dt t e e dt e e e

Câu 22. (Nhận biết) Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
y f x
, trục Ox, đường thẳng
x=a, x=b (a<b) là:
A.
b
a
S f x dx
B.
b
a
S f x dx
C.
2
b
a
S f x dx
D.
a
b
S f x dx
ĐÁP ÁN
DIỄN GIẢNG NHIỄU
Group Nhóm Toán | Trắc nghiệm 2016-2017
53
A.
b
a
S f x dx
Đáp án B: học sinh thiếu dấu giá trị tuyệt đối
Đáp án C: nhầm công thức tính thể tích
Đáp án D: sai vị trí cận
Câu 23. : (Vận dụng)
Nếu gọi S là diện tích hình phẳng giới hạn bởi các đường x =0, x = 3, y = 0, y = x - 1 thì khẳng định nào sau đây là đúng?
A. S =
3
2
. B. S=
1
2
. C. S = 2. D. S =
5
2
.
LỜI GIẢI TÓM TẮT
DIỄN GIẢNG NHIỄU
Phương trình: x – 1 = 0
x=1
[0;3]
3 1 3
0 0 1
1 ( 1) ( 1)S x dx x dx x dx
=
22
13
( ) ( )
01
22
xx
xx
=
1
2
2

=
5
2
- A: HS
33
00
1 ( 1)S x dx x dx

=…=
3
2
- B: HS chỉ tính trên đoạn [0;1]
- C: HS chỉ tính trên đoạn [1;3]
Câu 24. (Vận dụng thấp) Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
32
32y x x x
, trục tung, trục
hoành, đường thẳng
3
2
x
?
A.
1
2
B.
9
64
C.
23
64
D. 0
ĐÁP ÁN
DIỄN GIẢNG NHIỄU
Giải phương trình hoành độ giao điểm
ra 3 nghiệm 0, 1, 2 (loại 2)
3
2
32
0
32
hp
S x x xdx
=
A) Giải phương trình hoành độ giao điểm ra 3 nghiệm 0, 1, 2 chon cận
từ 0 đến 2
B)Quên dấu trị tuyệt đối
D) Chon cận từ 0 đên 2 nhưng quên dấu trị tuyệt đối
Group Nhóm Toán | Trắc nghiệm 2016-2017
54
44
3 2 3 2
3
1
( ) ( )
2
0
44
1
xx
x x x x
=
23
64
Câu 25. (vận dụng thấp) Diện tích S của hình phẳng (H) giới hạn bởi đồ thị hàm số
32
32y x x
, hai trục tọa độ
và đường thẳng
2x
là
A. S =
19
2
(đvdt) B. S =
5
2
(đvdt) C. S =
1
3
(đvdt) D. S =
9
2
(đvdt)
ĐÁP ÁN, HƯỚNG DẪN GIẢI
DIỄN GIẢNG NHIỄU
Đáp án B
Ta có: S =
2
32
0
5
32
2
x x dx
A. S =
1
32
0
19
( 3 2)
2
x x dx
C. S =
12
3 2 3 2
01
1
3 2 3 2
3
x x dx x x dx

D. S =
2
32
1
13
32
12
x x dx
Câu 26. (Vận dụng) Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
32
34y x x
và đường thẳng
10xy
.
A. 8 (đvdt). B. 4 (đvdt). C. 6 (đvdt). D. 0 (đvdt).
LỜI GIẢI
DIỄN GIẢNG NHIỄU
32
32
3 4 1
3 3 0
1, 3, 1
x x x
x x x
x x x
3
32
1
3 3 8S x x x dx
Tính cận sai → chọn câu B
3
32
1
33S x x x dx
→ Chọn câu C
3
32
1
33S x x x dx
→ Chọn câu D
Group Nhóm Toán | Trắc nghiệm 2016-2017
55
Câu 27. (Thông hiểu) Cho hình phẳng giới hạn bởi đồ thị hàm số
x
ye
, trục Ox, 2 đường thẳng x = 0,
x = 1 . Thể tích khối tròn xoay khi quay hình đó xung quanh trục hoành được cho bởi công thức
A.
1
2
0
x
e dx
B.
1
2
0
x
e dx
C.
2
1
0
x
e dx



D.
2
1
0
x
e dx



ĐÁP ÁN
DIỄN GIẢNG NHIỄU
V=
1
2
0
x
e dx
B) Quên
C) Sử dụng dấu bình phương sai vị trí
D) Sử dụng dấu bình phương sai vị trí
Câu 28. ( Thông hiểu)
Nếu gọi V là thể của khối tròn xoay có được khi quay hình phẳng giới hạn bởi các đường
0 0 inx
4
x ,x , y ,y s
xung quanh trục Ox thì khẳng định nào sau đây là đúng?
A.
11
2 4 2
V ( )

. B.
1
2 4 2
V ( )


.
C.
1
24
V ( )


. D.
1
2 4 2
V ( )


.
LỜI GIẢI TÓM TẮT
DIỄN GIẢNG NHIỄU
44
2
00
sin x. (1 os2x.)
2
V dx c dx


=
11
( sin2 ) ( )
4
2 2 2 4 2
0
xx
- A: HS áp dụng công thức sai
- B: HS dùng công thức hạ bậc sai dấu
- C: HS tìm nguyên hàm sai
Câu 29. (Vận dụng) Thể tích khối tròn xoay khi quay hình phẳng
H
giới hạn bởi
2
yx
và
2yx
quanh trục
Ox
là
A.
72
5
(đvtt). B.
81
10
(đvtt). C.
81
5
(đvtt). D.
72
10
(đvtt).
Group Nhóm Toán | Trắc nghiệm 2016-2017
56
LỜI GIẢI
DIỄN GIẢNG NHIỄU
2
2 0 1, 2x x x x
22
2
2 2 4
11
( ) ( ) 2V f x g x dx x x dx



72
5
22
2
2
2
11
( ) ( ) 2V f x g x dx x x dx



→ Chọn câu B
22
2
2
2
11
11
( ) ( ) 2
22
V f x g x dx x x dx



→ Chọn câu C
22
2
2 2 4
11
11
( ) ( ) 2
22
V f x g x dx x x dx



→ Chọn câu D
Câu 30. (vận dụng cao) Cho hình phẳng (H) giới hạn bởi
2
2 , 0y x x y
. Tính thể tích của khối tròn xoay thu
được khi quay (H) xung quanh trục Ox ta được
1
a
V
b



. Khi đó
A. a = 1, b = 15 B. a = – 7, b = 15 C. B. a = 241, b = 15 D. a = 16, b = 15
ĐÁP ÁN, HƯỚNG DẪN GIẢI
DIỄN GIẢNG NHIỄU
Đáp án A
2
0
20
2
x
xx
x
2
22
0
16
(2 )
15
16
1 1, 15
15
Ox
V x x dx
a
ab
b



B.
1
22
0
87
(2 ) 1
15 15
Ox
V x x dx



C.
22
2 2 2 4
00
(2 ) (4 )
Ox
V x x dx x x dx

256 241
1
15 15



D.
2
22
0
16
(2 )
15
Ox
V x x dx
PHẦN 8 :
Group Nhóm Toán | Trắc nghiệm 2016-2017
57
Câu 1: Họ nguyên hàm của hàm số
sin2f x x
là
1
. cos2
2
A F x x C
. cos2B F x x C
1
. cos2
2
C F x x C
. cos2D F x x C
Câu 2: Nếu
( ) d sin
x
f x x e x C
thì
()fx
bằng:
. sin
x
A e x
. sin
x
B e x
. cos
x
C e x
s. o
x
D e c x
Câu 3:
2
3
( 2 )x x dx
x

3
3
4
. 3ln
33
x
A x x C
3
3
4
. 3ln
33
x
B x x C
3
3
4
. 3lnX
33
x
C x C
3
3
4
. 3ln
33
x
D x x C
Câu 4:
5
1
ln .
21
dx
K
x
Gia ùtrò cuûa K laø :
A. 3 B. 8 C. 81 D. 9
Câu 5: Tìm khẳng định sai trong các khẳng định sau:
2
0
. sinxdx 1A
1
2
0
. 1 x 0B dx
11
00
. sin(1 x) sinxdxC dx

1
2016
0
1
. 1 x
4770306
D x dx
Câu 6:
1
dx
x
.
1
C
A
x
. 2 1B x C
2
.
1
CC
x
.1D C x
Câu 7:
3
23x dx
4
23
1
..
24
x
AC
4
23
.
4
x
BC
4
23
1
..
34
x
CC
3
23
1
D. .
23
x
C
Câu 8: Hàm số F(x) =
2
x
e
là nguyên hàm của hàm số nào?
Group Nhóm Toán | Trắc nghiệm 2016-2017
58
A.
2
()
2
x
e
fx
x
B.
2
()
x
f x e
C.
2
( ) 2 .
x
f x xe
D.
2
2
( ) 1
x
f x x e
Câu 9:Họ nguyên hàm của hàm số :
22
2
()
( 9)
x
y f x
x

là:
A.
25
1
5( 9)
C
x

B.
23
1
3( 9)
C
x

C.
25
4
( 9)
C
x

D.
23
1
( 9)
C
x

Câu 10:Cho hình phẳng (S) giới hạn bởiOx, Oy, y = 3x+2. Tính thể tích của khối tròn xoay khi quay
(S) quanh Oy là :
A.
8
3
B.
4
3
C.
2
3
D.
16
3
Câu 11:Một nguyên hàm của hàm số
2
( ) . 1f x x x
là :
A.
23
1
( ) ( 1 )
3
F x x
B.
22
1
( ) ( 1 )
3
F x x
C.
2
22
( ) ( 1 )
2
x
F x x
D.
22
1
( ) ( 1 )
2
F x x
Câu 12: Tìm nguyên hàm của hàmsố f(x) thỏa điều kiện:
( ) 2 3cos , ( ) 3
2
f x x x F
A.
2
2
( ) 3sin 6
4
F x x x
B.
2
2
( ) 3sin 6
4
F x x x
C.
2
2
( ) 3sin
4
F x x x
D.
2
2
( ) 3sin 6
4
F x x x
Câu 13: Tính :
6
0
tanI xdx
là :
A.
23
ln
3
B.
23
ln
3
C.
3
ln
2
D.
1
ln
2
Câu 14: Diện tích hình phẳng giới hạn bởi:
2
43y x x
, x = 0, x = 3 và trục Ox là
A.
1
3
B.
2
3
C.
10
3
D.
8
3
Câu 15:Diện tích hình phẳng giới hạn bởi các đường cong:
2
2y x x
và
6yx
Group Nhóm Toán | Trắc nghiệm 2016-2017
59
A.
95
6
B.
265
6
C.
125
6
D.
65
6
Group Nhóm Toán | Trắc nghiệm 2016-2017
60
Câu 16:
22
d
sin cos
x
xx
A.
1 C
B.
tan cotx x C
C.
tan cotx x C
D.
11
cos sin
C
xx
Câu 17:
4
2
2
d
9
x
x
x
A.
5
2
1
59
C
x

B.
3
2
1
39
C
x

C.
5
2
4
9
C
x

D.
3
2
1
9
C
x

Câu 18:
Họ nguyên hàm của hàm số: y = sin
3
x.cosx là:
A.
tg
3
x + C
B.
cos
2
x + C
C.
3
1
cos
3
xC
D.
4
1
sin
4
xC
Câu 19:
sin cos2 dx x x
A.
11
cos3 cos
22
x x C
B.
11
cos3 cos
62
x x C
C.
11
sin3 sin
62
x x C
D.
11
cos3 cos
22
x x C
Câu 20:
Nguyên hàm
cosx xdx
A.
sin cosx x x C
B.
sin cosx x x C
C.
sin cosx x x
+C
D.
sin cosx x x
Câu 21:
Nguyên hàm của (với C hằng số) là
2
2
1
x
dx
x
A.
1
1
x
C
x
B.
1
x
C
x
C.
1
1
C
x
D.
2
ln 1 xC
Câu 22:
Họ nguyên hàm của hàm số
sin2f x x
là
A.
1
cos2
2
F x x C
B.
cos2F x x C
Group Nhóm Toán | Trắc nghiệm 2016-2017
61
C.
1
cos2
2
F x x C
D.
cos2F x x C
Câu 23:
Trong các mệnh đề sau, mệnh đề nào sai?
3
2
sin
( ): sin d
3
x
I x x C
2
2
42
( ): d 2ln 3
3
x
II x x x C
xx

6
( ): 3 2 3 d
ln6
x
x x x
III x x C
A.
()III
B.
()I
C.
Cả 3 đều sai.
D.
()II
Câu 24:
Nguyên hàm của hàm số: y = sin
3
x.cosx là:
A.
4
1
cos
4
xC
B.
4
1
sin
4
xC
C.
cos
2
x + C
D.
3
1
sin
3
xC
Câu 25:
Nguyên hàm
()Fx
của hàm số
2
sin2
sin 3
x
y
x
khi
(0) 0F
là
A.
2
ln 1 sin x
B.
2
ln 2 sin
3
x
C.
2
ln cos x
D.
2
sin
ln 1
3
x
Câu 26:
Họ nguyên hàm của hàm số
cos
x
f x e x
là
A.
1
sin cos
2
x
F x e x x C
B.
1
sin cos
2
x
F x e x x C
C.
1
sin cos
2
x
F x e x x C
D.
1
sin cos
2
x
F x e x x C
Câu 27:
Một nguyên hàm của hàm số: y = cos5x.cosx là:
A.
F(x) = cos6x
B.
F(x) = sin6x
C.
1 sin6 sin4
2 6 4




xx
D
.
1 1 1
sin6 sin4
2 6 4



xx
Group Nhóm Toán | Trắc nghiệm 2016-2017
62
PHẦN 9 :
Câu 1. Tìm nguyên hàm của hàm số f(x) = 3sinx+1 là
A.-3cosx+x +c B.
3cosxx
+c C. -
cosx
+c D.
cosxx
+c
Câu 2. Nguyên hàm của hàm số f(x) = 2
x
2
.
ln2
x
Ac
. 2 ln2
x
Bc
.2
x
CC
2
.
ln2
x
D
Câu 3. Nguyên hàm của hàm số f(x) = sin3x
1
. cos3
3
A x C
. 3cos3B x C
1
. cos3
3
C x C
. cos3D x C
Câu 4:Tìm nguyên hàm của hàm số:
󰇛
󰇜

A.
󰇛
󰇜
 
 C B
󰇛
󰇜
 

C
C
󰇛
󰇜
 
C D.
󰇛
󰇜



C
Câu 5. Tính nguyên hàm
4
2
52
()
x
fx
x
.
Câu 28:
Cho hình phẳng (S) giới hạn bởi ox, oy, y=3x+2. Thể tích khối tròn xoay khi quay (S) xung
quanh oy là:
A.
8
3
B.
4
3
C.
2
3
D
.
16
3
Câu 29:
Cho hình phẳng (S) giới hạn bởi ox,
2
1yx
. Thể tích khối tròn xoay khi quay (S) xung
quanh oy là:
A.
3
2
B.
4
2
C.
3
4
D
.
2
3
Câu 30:
Diện tích hình phẳng giới hạn bởi (P) :
3
3yx
, tiếp tuyến của (P) tại điểm x=2 và trục oy
là:
A.
2
3
B.
8
C.
4
3
D
.
8
3
Group Nhóm Toán | Trắc nghiệm 2016-2017
63
3
25
.
3
x
AC
x

4
3
10
.12B x C
x

3
25
.
3
x
CC
x

3
2
.5
3
x
D x C
Câu 6. Tìm nguyên hàm:
32
(2 )
x
e dx
36
41
.4
36
xx
A x e e C
36
41
.4
36
xx
B x e e C
36
41
. 4 .
36
xx
x
C x e e C
36
.12 6
xx
D e e C
Câu 7:Tìm nguyên hàm của hàm số:
󰇛
󰇜

A.
󰇛
󰇜



C B.
󰇛
󰇜





C
C
󰇛
󰇜
 
C D.
󰇛
󰇜
 
 C
Câu 8:Tìm nguyên hàm của hàm số:
󰇛
󰇜


là:
A.
󰇛
󰇜

 
B.
󰇛
󰇜

 
C.
󰇛
󰇜

 
D.
󰇛
󰇜

 
Câu 9. Nguyên hàm
cosx xdx
si c. n osA x x x C
2
..
2
x
B xinx C
. sin cosC x x x C
2
..
2
x
D xinx C
Câu 10. Tìm nguyên hàm:
32
(2 )
x
e dx
36
41
.4
36
xx
A x e e C
36
41
.4
36
xx
B x e e C
36
41
. 4 .
36
xx
x
C x e e C
36
.12 6
xx
D e e C
Câu 11. Tính
2
sin 2xdx
Group Nhóm Toán | Trắc nghiệm 2016-2017
64
A.
11
sin4
28
x x C
B.
1
2sin 4
2
x x C
C.
11
sin4
28
x x C
D.
1
sin4
8
xC
TÍCH PHÂN
Câu 12: Tìm khẳng định sai trong các khẳng định sau:
A.
11
22
00
22x dx x dx

B.
11
00
21
( 2)
33
x
dx x dx


C.
11
00
(2 1) 2 ( 1)x dx x dx

D.
22
11
1
x dx dx
x

Câu 13: Giả sử A =
5
1
21
dx
x
= lnK. Khi đó giá trị của K là:
A. 3 B. 4 C.81 D.9
Câu 14: Biết
0
(2 4) 0
b
x dx
. Khi đó giá trị của b là:
A. b = - 2 hoặc b = 2 B. b =
22
hoặc b = -
22
C. b = 0 hoặc b = - 4 D. b = 0 hoặc b = 4
Câu 15: Cho biết
( ) 5, ( ) 2
dd
ab
f x dx f x dx

và a< d< b. Khi đó tích phân A =
()
b
a
f x dx
bằng:
A.- 3 B. 7 C. 3 D. 10
Câu 16 : Biến đổi
3
0
11
x
dx
x
thành
2
1
()f t dt
với t =
1 x
. Khi đó f(t) là hàm nào trong các hàm sau:
A.
2
( ) 2 2f t t t
B.
2
( ) 2 2f t t t
C.
2
()f t t t
D.
2
()f t t t
Câu 17: Biết
0
1
sin cos
4
a
x xdx
. Khi đó giá trị của a là:
A.
1
arcsin( )
4
x 
B.
4
C.
3
D.
2
Group Nhóm Toán | Trắc nghiệm 2016-2017
65
Câu 18: Cho tích phân
2
2
sin 3
0
sin cos
x
e x xdx
. Nếu đổi biến số
2
sintx
thì:
A.
11
00
1
[]
2
tt
e dt te dt

B.
11
00
1
[]
2
tt
e dt te dt

C.
11
00
2[ ]
tt
e dt te dt

D.
11
00
2[ ]
tt
e dt te dt

Câu 19: Tìm khẳng định sai trong các khẳng định sau:
A.
11
22
00
22x dx x dx

B.
11
00
21
( 2)
33
x
dx x dx


C.
11
00
(2 1) 2 ( 1)x dx x dx

D.
22
11
1
x dx dx
x

Câu 20: Cho biết
55
22
( ) 3, ( ) 9f x dx g x dx

. Khi đó tích phân A =
5
2
[ ( ) ( )]f x g x dx
bằng:
A.- 6 B.
1
3
C. 6 D. 3
Câu 21: Cho tích phân I =
2
2
1
21x x dx
và u =
2
1x
. Chọn khẳng định sai trong các khẳng định sau:
A. I=
2
27
3
B.
3
2
0
2 u du
C.
2
2
1
2 u du
D. I =
3
3
0
2
3
u
Câu 22: Cho biết
( ) 5, ( ) 2
dd
ab
f x dx f x dx

và a< d< b. Khi đó tích phân A =
()
b
a
f x dx
bằng:
A.- 3 B. 7 C. 3 D. 10
Câu 23: Tính tích phân:
I =
1
x
2
dx
1
2
ò
Group Nhóm Toán | Trắc nghiệm 2016-2017
66
A.
-
1
2
B.
-
3
2
C.
-
7
8
D.
1
2
ỨNG DỤNG TÍCH PHÂN
Câu 24: Công thức diên tích hình thang cong giới hạn bỡi đồ thị hàm số
y f x
, trục hoành và hai đường thẳng
;x a x b
là
A.
b
a
S f x dx
B.
2
b
a
S f x dx
C.
b
a
S f x dx
D.
b
a
S f x dx
Câu 25: Công thức diên tích hình phằng giới hạn bỡi đồ thị
y f x
,
y g x
và hai đường thẳng
;x a x b
là
A.
b
a
S f x g x dx
B.
b
a
S f x g x dx
C.
b
a
S f x g x dx


D
b
a
S f x g x dx


Câu 26: Diện tích hình phẳng giới hạn đường cong
3
32y x x
và đường thẳng
2yx
là
A. S= 4 B. S= 40 C. S= 2 D. S= 8
Câu 27: Thể tích vật thể tròn xoay sinh ra bỡi hình phẳng giới hạn bỡi đường cong
cosyx
, y = 0,
0;
2
xx

quay
quanh trục Ox là
A.
2
4
B.
4
C.
D. 1
Câu 28: Diện tích hình phẳng giới hạn đường cong
21
1
x
y
x
;
0y
và
0; 1xx
là
A.
3ln2 2
B.
9
3ln
8
C.
2 3ln2
D.
2 ln2
Câu 29: Thể tích vật thể tròn xoay sinh ra bỡi hình phẳng giới hạn bỡi đường cong
lnyx
, y = 0,
xe
quay quanh
trục Ox là
A.
2e
B.
C.
2e
D.
1e
Câu 30: Diện tích hình phẳng giới hạn bởi đường cong y = x
2
+ 1, tiếp tuyến với đường thẳng này tại điểm M(2,5) và
trục Oy là
a.
4
3
b.
8
3
c.9 d.
14
3
Group Nhóm Toán | Trắc nghiệm 2016-2017
67
TRẢ LỜI
Câu 1. Tìm nguyên hàm của hàm số f(x) = 3sinx+1 là
A.-3cosx+x +c B.
3cosxx
+c C. -
cosx
+c D.
cosxx
+c
Giải
+Chọn A đúng
+ Chọn B sai vì nhầm công thức đạo hàm cosx là sinx
+ Chọn C sai. Vì nhầm lấy đạo hàm của 1 là 0
+ Chọn D sai. Quên còn hệ số 3
Câu 2. Nguyên hàm của hàm số f(x) = 2
x
2
.
ln2
x
Ac
. 2 ln2
x
Bc
.2
x
CC
2
.
ln2
x
D
Giải
+ Chọn A đúng
+ Chọn B sai vì công thức đạo hàm
+ Chọn C sai, nhầm công thức nguyên hàm của e
x
+ Chọn D sai, vì chỉ tìm 1 nguyên hàm
Câu 3. Nguyên hàm của hàm số f(x) = sin3x
1
. cos3
3
A x C
. 3cos3B x C
1
. cos3
3
C x C
. cos3D x C
Giải
+ Chọn A đúng
Câu 4:Tìm nguyên hàm của hàm số:
󰇛
󰇜

Group Nhóm Toán | Trắc nghiệm 2016-2017
68
A.
󰇛
󰇜
 
 C B
󰇛
󰇜
 

C
C
󰇛
󰇜
 
C D.
󰇛
󰇜



C
Câu 5. Tính nguyên hàm
4
2
52
()
x
fx
x
.
3
25
.
3
x
AC
x

4
3
10
.12B x C
x

3
25
.
3
x
CC
x

3
2
.5
3
x
D x C
Giải
+ Chọn A đúng
+Chọn B sai. Tính đạo hàm của f(x)
+ Chọn C sai. Tính sai nguyên hàm của
2
5
x
+ Chọn D sai . Chia đa thức sai
4
2
2
52
( ) 5 2
x
f x x
x
Câu 6. Tìm nguyên hàm:
32
(2 )
x
e dx
36
41
.4
36
xx
A x e e C
36
41
.4
36
xx
B x e e C
36
41
. 4 .
36
xx
x
C x e e C
36
.12 6
xx
D e e C
Giải
+ Chọn A sai, khai triển hằng đẳng thức sai dấu
+ Chọn B đúng
+ Chọn C sai, tính nguyên hàm của 4 nhân nguyên hàm của
3x
e
Group Nhóm Toán | Trắc nghiệm 2016-2017
69
+ Chọn D sai, nhầm công thức nguyên hàm với công thức đạo hàm
Câu 7:Tìm nguyên hàm của hàm số:
󰇛
󰇜

A.
󰇛
󰇜



C B.
󰇛
󰇜





C
C
󰇛
󰇜
 
C D.
󰇛
󰇜
 
 C
HD:A
󰇛
󰇜




 =


C
Câu 8:Tìm nguyên hàm của hàm số:
󰇛
󰇜


là:
A.
󰇛
󰇜

 
B.
󰇛
󰇜

 
C.
󰇛
󰇜

 
D.
󰇛
󰇜

 
HD: B.



󰇛

󰇜
 
Câu 9. Nguyên hàm
cosx xdx
c. sin osxxA xC
2
..
2
x
B xinx C
. sin cosC x x x C
2
..
2
x
D xinx C
Giải
+ Chọn A đúng
+ Chọn B sai, tách thành tích của 2 nguyên hàm
+ Chọn C sai. Tính sai nguyên hàm của sinx
cosx xdx
sin sin sin cosx x xdx x x x C
+Chọn D sai. Tách thành tích của 2 nguyên hàm và tính sai nguyên hàm của cosx
Mức 4
Câu 10. Tìm nguyên hàm:
32
(2 )
x
e dx
Group Nhóm Toán | Trắc nghiệm 2016-2017
70
36
41
.4
36
xx
A x e e C
36
41
.4
36
xx
B x e e C
36
41
. 4 .
36
xx
x
C x e e C
36
.12 6
xx
D e e C
Câu 11. Tính
2
sin 2xdx
A.
11
sin4
28
x x C
B.
1
2sin 4
2
x x C
C.
11
sin4
28
x x C
D.
1
sin4
8
xC
Giải
+ Chọn A sai. Công thức hạ bậc sai
22
1 cos4 1 cos4
sin 2 sin 2
22
xx
xx





+ Chọn B sai. Công thức nguyên hàm sai
cos4 4sin4xx
+ Chọn C đúng
+ Chọn D sai. Công thức nguyên hàm của
1
2
sai
Câu 12: Tìm khẳng định sai trong các khẳng định sau:
A.
11
22
00
22x dx x dx

B.
11
00
21
( 2)
33
x
dx x dx


C.
11
00
(2 1) 2 ( 1)x dx x dx

D.
22
11
1
x dx dx
x

Câu 13: Giả sử A =
5
1
21
dx
x
= lnK. Khi đó giá trị của K là:
A. 3 B. 4 C.81 D.9
Giải
Group Nhóm Toán | Trắc nghiệm 2016-2017
71
Ta có
5
5
1
1
11
ln 2 1 ln9
2 1 2 2
dx
Ax
x
Suy ra
1
ln ln9 3
2
KK
Câu A đúng
Câu B sai vì đúng công thức nhưng sai kết quả (nhầm ln5-ln1=ln4)
Câu C sai vì tính sai công thức tích phân (nhân u’)
Câu D sai vì tính tích phân sai công thức (quên chia u’)
Câu 14: Biết
0
(2 4) 0
b
x dx
. Khi đó giá trị của b là:
A. b = - 2 hoặc b = 2 B. b =
22
hoặc b = -
22
C. b = 0 hoặc b = - 4 D. b = 0 hoặc b = 4
Giải
Ta có
22
0
0
(2 4) ( 4 ) 4
b
b
I x dx x x b b
Khi đó
2
0
40
4
b
bb
b
Câu D đúng
Câu A sai vì nhận dạng ptr bậc hai sai (khuyết b)
Câu B sai vì tính tích phân sai công thức
22
0
0
(2 4) ( 4) 8
b
b
I x dx x b
Câu C sai vì tính tích phân nhầm dấu +
Câu15: Cho biết
( ) 5, ( ) 2
dd
ab
f x dx f x dx

và a< d< b. Khi đó tích phân A =
()
b
a
f x dx
bằng:
A.- 3 B. 7 C. 3 D. 10
Giải
Group Nhóm Toán | Trắc nghiệm 2016-2017
72
Ta có A =
( ) ( ) ( ) ( ) ( ) 3
b d b d d
a a d a b
f x dx f x dx f x dx f x dx f x dx
Câu C đúng
Câu A lấy hiệu 2 tích phân (
( ) ( )
bd
da
f x dx f x dx

)
Câu B sai vì áp dụng sai công thức (không đổi cận )
Câu D vì lấy tích 2 tích phân
Câu 16 : Biến đổi
3
0
11
x
dx
x
thành
2
1
()f t dt
với t =
1 x
. Khi đó f(t) là hàm nào trong các hàm sau:
A.
2
( ) 2 2f t t t
B.
2
( ) 2 2f t t t
C.
2
()f t t t
D.
2
()f t t t
Giải
Với t =
1 x
Ta có A =
3 2 2
2
2
0 1 1
( 1)2
(2 2 )
1
11
x t tdt
dx t t dt
t
x

Câu A đúng
Câu B sai vì sai dấu
Câu C, D sai vì tính nguyên hàm sai và chyển từ biến x sang t bị sai
Câu 17: Biết
0
1
sin cos
4
a
x xdx
. Khi đó giá trị của a là:
A.
1
arcsin( )
4
x 
B.
4
C.
3
D.
2
Giải
Ta có
0
00
1 1 1
sin cos sin2 cos2 (cos2 1)
2 4 4
a
aa
x xdx xdx x a

Mà
11
(cos2 1) cos2 0
4 4 4
a a a
Câu B đúng
Group Nhóm Toán | Trắc nghiệm 2016-2017
73
Câu A, C, D sai vì sai công thức nguyên hàm
Câu 18: Cho tích phân
2
2
sin 3
0
sin cos
x
e x xdx
. Nếu đổi biến số
2
sintx
thì:
B.
11
00
1
[]
2
tt
e dt te dt

B.
11
00
1
[]
2
tt
e dt te dt

C.
11
00
2[ ]
tt
e dt te dt

D.
11
00
2[ ]
tt
e dt te dt

Giải
Với
2
sintx
Ta có A =
1 1 1
0 0 0
11
(1 ) [ ]
22
t t t
e t dt e dt te dt
Câu B đúng
Câu A sai vì lấy nguyên hàm sai dấu
Câu C, D sai vì sai công thức nguyên hàm và bị sai dấu
Câu 19: Tìm khẳng định sai trong các khẳng định sau:
A.
11
22
00
22x dx x dx

B.
11
00
21
( 2)
33
x
dx x dx


C.
11
00
(2 1) 2 ( 1)x dx x dx

D.
22
11
1
x dx dx
x

Câu 20: Cho biết
55
22
( ) 3, ( ) 9f x dx g x dx

. Khi đó tích phân A =
5
2
[ ( ) ( )]f x g x dx
bằng:
A.- 6 B.
1
3
C. 6 D. 3
Câu 21: Cho tích phân I =
2
2
1
21x x dx
và u =
2
1x
. Chọn khẳng định sai trong các khẳng định sau:
Group Nhóm Toán | Trắc nghiệm 2016-2017
74
A. I=
2
27
3
B.
3
2
0
2 u du
C.
2
2
1
2 u du
D. I =
3
3
0
2
3
u
Giải
Với u =
2
1x
Ta có
3
3
23
0
0
22
2 27
33
I u du u
Câu C sai vì chưa đổi cận
Câu 22: Cho biết
( ) 5, ( ) 2
dd
ab
f x dx f x dx

và a< d< b. Khi đó tích phân A =
()
b
a
f x dx
bằng:
A.- 3 B. 7 C. 3 D. 10
Giải
Ta có A =
( ) ( ) ( ) ( ) ( ) 3
b d b d d
a a d a b
f x dx f x dx f x dx f x dx f x dx
Câu C đúng
Câu A lấy hiệu 2 tích phân (
( ) ( )
bd
da
f x dx f x dx

)
Câu B sai vì áp dụng sai công thức (không đổi cận )
Câu D vì lấy tích 2 tích phân
Câu 23: Tính tích phân:
I =
1
x
2
dx
1
2
ò
A.
-
1
2
B.
-
3
2
C.
-
7
8
D.
1
2
Phân tích:
A. Sai vì học sinh quên dấu “-” trong công thức.
I =
1
x
æ
è
ç
ö
ø
÷
1
2
=
1
2
-
1
1
= -
1
2
Group Nhóm Toán | Trắc nghiệm 2016-2017
75
B. Sai vì học sinh quên đổi dấu trong lúc tính cận.
I = -
1
x
æ
è
ç
ö
ø
÷
1
2
= -
1
2
-
1
1
= -
3
2
C. Sai vì học sinh áp dụng sai công thức.
I =
1
x
3
æ
è
ç
ö
ø
÷
1
2
=
1
8
-
1
1
= -
7
8
D. Đúng
Câu 24: Công thức diên tích hình thang cong giới hạn bỡi đồ thị
y f x
, trục hoành và hai đường thẳng
;x a x b
là
A.
b
a
S f x dx
B.
2
b
a
S f x dx
C.
b
a
S f x dx
D.
b
a
S f x dx
Đáp án đúng C
Nếu thiếu trị tuyệt đối chọn A
Nhớ nhầm công thức thể tích chọn B
Đặt trị tuyệt đối ra ngoài chọn D
Câu 25: Công thức diên tích hình phằng giới hạn bỡi đồ thị
y f x
,
y g x
và hai đường thẳng
;x a x b
là
A.
b
a
S f x g x dx
B.
b
a
S f x g x dx
C.
b
a
S f x g x dx


D
b
a
S f x g x dx


Đáp án đúng A
Nhớ nhầm dấu + chọn B
Đặt trị tuyệt đối ra ngoài chọn C
Nhớ nhầm dấu + và đặt trị tuyệt đối ra ngoài chọn D
Câu 26: Diện tích hình phẳng giới hạn đường cong
3
32y x x
và đường thẳng
2yx
là
A. S= 4 B. S= 40 C. S= 2 D. S= 8
Giải
Group Nhóm Toán | Trắc nghiệm 2016-2017
76
Phương trình hoành độ giao điểm
3
4 0 0, 2, 2x x x x x
2
3
2
48s x xdx
Đáp án đúng D
Giải sai nghiệm x= 0, x= 4 chọn B
Giải sai nghiệm x= 0, x= 2 chọn A
Nếu áp dụng
2
3
0
2S x xdx
chọn C
Câu 27: Thể tích vật thể tròn xoay sinh ra bỡi hình phẳng giới hạn bỡi đường cong
cosyx
, y = 0,
0;
2
xx

quay
quanh trục Ox là
A.
2
4
B.
4
C.
D. 1
Giải
2
2
2
0
cos
4
V x dx

Đáp án đúng A
Thiếu
chọn B
Thiếu bình phương chọn C
Thiếu cả hai chọn D
Câu 28: Diện tích hình phẳng giới hạn đường cong
21
1
x
y
x
;
0y
và
0; 1xx
là
A.
3ln2 2
B.
9
3ln
8
C.
2 3ln2
D.
2 ln2
Giải
Group Nhóm Toán | Trắc nghiệm 2016-2017
77
1
11
2
1
00
2
2 1 2 1 2 1 9
3ln
1 1 1 8
x x x
S dx dx dx
x x x
Đáp án đúng B
Không tách cận chọn A
Không tách cận, không hiểu trị tuyệt đối chọn C
Nguyên hàm sai chọn D
Câu 29: Thể tích vật thể tròn xoay sinh ra bỡi hình phẳng giới hạn bỡi đường cong
lnyx
, y = 0,
xe
quay quanh
trục Ox là
A.
2e
B.
C.
2e
D.
1e
Giải
ln 0 1xx
2
1
ln 2
e
V x dx e

Đáp án đúng C
Công thức thiếu
chọn A
Thiếu bình phương chọn B
Giải thiếu 2 chọn D
Câu 30: Diện tích hình phẳng giới hạn bởi đường cong y = x
2
+ 1, tiếp tuyến với đường thẳng này tại điểm M(2,5) và
trục Oy là
a.
4
3
b.
8
3
c.9 d.
14
3
Giải
Tiếp tuyến tại M: y = 4x -3
Pt hđgđ: x
2
-4x + 4 = 0 => x = 2
Group Nhóm Toán | Trắc nghiệm 2016-2017
78
S =
2
2
0
x 4x 4dx
=
8
3
PHẦN 10 :
Phần nhận biết
Câu 1: Nguyên hàm của hàm số
2
( ) 2x 1fx
là:
A.
3
2x xC
B.
3
2x
3
xC
C.
3
x
3
xC
D.
3
x
1
3
C
Câu 2: Nguyên hàm của hàm số
( ) sinxfx
là:
A.
cosx C
B.
cosx+1C
C.
-cosxC
D.
tanxC
Câu 3: Nguyên hàm của hàm số
2
1
()
cos
fx
x
là:
A.
cotxC
B.
cosx C
C.
-tanxC
D.
tanxC
Câu 4: Nguyên hàm của hàm số f(x) = x
3
-
2
3
2
x
x
là:
A.
B.
3
3
1
2
3
x
x
C
x
C.
4
32
4 ln2
x
x
C
x
D.
4
3
2 .ln2
4
x
x
C
x
Câu 5: Nguyên hàm của hàm số
( ) sin(2x 1)fx
là:
A.
1
- cos(2x 1)
2
C
B.
1
cos(2x 1)
2
C
C.
2cos(2x 1)C
D.
-2cos(2x 1)C
Câu 6: Cho hàm số y=f(x) liên tục trên [a;b].Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x),trục
hoành, hai đường thẳng x=a và x=b được xác định bởi công thức:
A.
()
b
a
f x dx
B.
()
b
a
f x dx
C.
()
a
b
f x dx
D.
()
b
a
f x dx
Câu 7:Cho hai hàm số y = f(x), y = g(x) liên tục trên [a;b].Hình phẳng giới hạn bởi đồ thị 2 hàm số y=f(x),
y=g(x) và đường thẳng x = a, x = b có diện tích S đươc tính bởi công thức
A.S=


b
a
f x g x dx
B. S=


b
a
f x g x dx
Group Nhóm Toán | Trắc nghiệm 2016-2017
79
C.S=
[ ( )]
b
a
g x f x dx
D.S=
b
a
f x g x dx
Câu 8: Thể tích V của khối trn xoay tạo thành khi ta cho hình phẳng D giới hạn bởi các đường
()y f x
,trục Ox , x=a, x = b (a< b) quay quanh trục ox được tính bởi công thức
A.
2
()
b
a
V f x dx
B.
2
()
b
a
V f x dx
C.
2
()
b
a
V f x dx
D.
2
()
a
b
V f x dx
Câu 9: Thể tích của khối tròn xoay tạo thành khi quay hình phẳng D giới hạn bởi các đường ,
trục hoành, x=2 và x=5 quanh trục Ox bằng:
A.
5
2
1
x dx
B.
5
2
1
x dx
C.
5
2
1
x dx
D.
5
2
2
1
x dx
Câu 10: Công thức nào sau đây dùng để tính diện tích hình phẳng giới hạn bởi các đường y=2
x
,y=2,x=0,x=1
cho kết quả sai ?
A.S=
1
0
22
x
dx
B.
1
0
22
x
S dx
C.
1
0
22
x
S dx
D.
0
1
22
x
S dx
Giải thích
Công thức tính diện tích hình phẳng giới hạn bởi các đường y=2
x
,y=2,x=0,x=1 là S=
1
0
22
x
dx
= L
+
0;1 :2 2 2 2 2 2
x x x
x
.A đúng
+
0;1 :2 2 2 2 (2 2)
x x x
x
.B sai
+
11
00
0;1 :2 2 2 2 0 2 2 2 2

x x x x
x dx L dx L
.C đúng
+
1 1 0
0 0 1
0;1 :2 2 2 2 0 2 2 2 2 2 2
x x x x x
x dx L dx dx L
.D đúng
Phần thông hiểu
Câu1) Cho biết
25
11
( ) 4; ( ) 6

f x dx f x dx
. Khi đó
5
2
()
f x dx
có kết quả là :
A. 2 B. 10 C. 10 D. 7
Giải thích:
2 5 5 5 5 2
1 2 1 2 1 1
( ) ( ) ( ) ( ) ( ) ( ) 10
f x dx f x dx f x dx f x dx f x dx f x dx
Câu 2) Giả sử
5
1
ln
21
dx
c
x
. Khi đó giá trị của c là:
1yx
Group Nhóm Toán | Trắc nghiệm 2016-2017
80
A. 81 B. 9 C. 8 D. 3
Giải thích:
5
1
5
21
1
ln 3
21
dx
xdx
c c e
x
Câu3) Diện tích hình phẳng giới hạn bởi các đường cong
3
yx
và
5
yx
bằng:
A. 0 B. 4 C.
1
6
D.
1
12
Giải thích:
Phương trình hoành độ giao điểm :
3 5 3 2
0
(1 ) 0
1

x
x x x x
x
Diện tích hình phẳng là:
1
35
1
1
6

x x dx
Câu4) Diện tích hình phẳng giới hạn bởi các đường cong
siny x x
và
yx
với
02x
bằng:
A. 4 B. 4 C. 0 D. 1
Giải thích:
Phương trình hoành độ giao điểm :
0
sin sin 0 ( ) (0 2 )
2
x
x x x x x k k x x
x
Diện tích hình phẳng là:
2
0
sin 4
xdx
Câu5) Cho hình phẳng giới hạn bởi các đường
yx
và y = x quay xung quanh trục Ox. Thể tích của khối
tròn xoay tạo thành bằng:
A. 0 B.
C.
6
D.
30
Giải thích:
Group Nhóm Toán | Trắc nghiệm 2016-2017
81
Phương trình hoành độ giao điểm :
0
1

x
xx
x
Thể tích khối tròn xoay là:
1
2
0
30

x x dx
Câu 6: Nguyên hàm của hàm số f(x) = x
3
2
3
2
x
x
là:
A.
B.
3
3
1
2
3
x
x
C
x
C.
4
32
4 ln2
x
x
C
x
D.
4
3
2 .ln2
4
x
x
C
x
Đáp án: C
Câu A, B, D học sinh có thể hiểu sai công thức giữa nguyên hàm và đạo hàm.
Câu 7: Biết F(x) là nguyên hàm của hàm số
1
1
y
x
và F(2)=1. Khi đó F(3) bằng bao nhiêu:
A.
ln2 1
B.
1
2
C.
3
ln
2
D.
ln2
Đáp án: A
Câu 8: Một nguyên hàm của
2
2x 3
1

x
fx
x
là
A.
2
3x 6ln 1
2
x
x
B.
2
3x-6ln 1
2

x
x
C.
2
3x+6ln 1
2

x
x
D.
2
3x+6ln 1
2

x
x
Đáp án : C
Câu A, B, D là đáp án nhiễu khi các em chia đa thức sai
Câu 9 :
2
2
3
1
x
dx
x
bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
82
A.
3
2
1
2ln
32
x
xC
x
B.
3
2
1
2ln
3
x
xC
x
C.
3
2
1
2ln
32
x
xC
x
D.
3
2
1
2ln
33
x
xC
x
Đáp án: C
Câu 10: Một nguyên hàm của hàm số:
2
( ) 1f x x x
là:
A.
2
2
1
( ) 1
2
F x x
B.
3
2
1
( ) 1
3
F x x
C.
2
2
2
( ) 1
2

x
F x x
D.
2
2
1
( ) 1
3
F x x
Đáp án: B
Phần vận dụng thấp
Câu 1: Cho
2
4
sin
m
f x x
. Tìm tham số m để nguyên hàm
Fx
của
fx
thỏa
0 1,
48




FF

a/
5
4
m
b/
1
4
m
c/
3
4
m
d/
1
4
m
Lời giải:
4 1 1
sin2
24
m
F x x x x C
Sử dụng điều kiện được:
1
0 1; 0
84



F C F m C
nên giải hệ được
3
4
m
Đáp án: c/
Phân tích đáp án nhiễu:
Lấy sai đạo hàm
4 1 1
sin2
24
m
F x x x x C
nên giải ra được đáp án a/
Giải thiếu thế C=1nên được đáp án b/
Lấy sai đạo hàm và thiếu thế C=1 nên được đáp án d/
Câu 2: Giả sử
4
0
sin3 sin2 2
I x xdx a b
. Khi đó, giá trị
ab
là:
a/
6
5
b/
3
10
c/
3
10
d/
1
2
Group Nhóm Toán | Trắc nghiệm 2016-2017
83
Lời giải:
4
4
0
0
1 1 1 3
cos5 cos sin5 sin 2
2 2 5 10



I x x dx x x
Đáp án: b/
Phân tích đáp án nhiễu:
Lấy sai đạo hàm
4
4
0
0
1 1 1 3
cos5 cos sin5 sin 2
2 2 5 10




I x x dx x x
nên chọn c/
Lấy sai đạo hàm
4
4
0
0
1 1 1
cos5 cos sin5 sin 2
2 2 2
I x x dx x x
nên chọn d/
Áp dụng sai công thức:
4
4
0
0
16
2 cos5 cos 2 sin5 sin 2
55



I x x dx x x
nên chọn a/
Câu 3: Tích phân
2
2
sin 3
0
sin .cos .
x
J e x x dx
có giá trị bằng với tích phân nào sau đây?
a/
1
0
1
1
2

t
I e t dt
b/
11
00
1
2





tt
I e dt te dt
c/
1
0
1
1
2

t
I e t dt
d/
11
00
1
2





tt
I e dt te dt
Lời giải: Đặt
2
sin 2sin .cos t x dt x xdx
. Đổi cận được t=0, t=1
Nên
1
0
1
2

t
dt
J e t
. Đáp án a/
Phân tích đáp án nhiễu:
Tính sai đạo hàm
sin ' cosxx
nên được
1
2
dx dt
do đó chọn c/
Do áp dụng sai công thức
22
cos 1 sinxx
nên được đáp án d/
Vừa sai đạo hàm, vừa sai công thức nên được đáp án b/
Câu 4: Diện tích hình phẳng giới hạn bởi các đường
2
3 5 1
, 0, 0, 1
2

xx
y y x x
x
bằng
2
ln
3
ab
. Khi
đó,
2ab
là:
a/ 2 b/ 40 c/
61
2
d/ -2
Lời giải:
0
0
2
1
1
21 3 2 19
3 11 11 21ln 2 21ln
2 2 3 2
S x dx x x x
x
nên
2 40ab
. Đáp án: b/
Phân tích đáp án nhiễu:
Group Nhóm Toán | Trắc nghiệm 2016-2017
84
Tính toán sai
0
0
2
1
1
21 3 2 19
3 11 11 21ln 2 21ln
2 2 3 2
S x dx x x x
x
do đó
22 ab
nên
chọn d/
0
0
2
1
1
21 3 2 19
3 11 11 21ln 2 21ln
2 2 3 2
S x dx x x x
x
mà tính
61
2
ab
nên chọn c/
Giải:
0
0
2
1
1
21 3 3 2 19
3 11 11 21ln 2 21ln2 21ln3 11 21ln
2 2 2 3 2
S x dx x x x
x
nên
22ab
chọn đáp án a/
Câu 5: Thể tích của vật thể tròn xoay tạo bởi hình phẳng giới hạn bởi các đường
3
ln , 1, y x x x x e
khi
quay quanh trục Ox có dạng
31
a
e
V
b
. Hãy chọn khẳng định sai trong các khẳng định sau?
a/
64ab
b/
2
logab
c/
18ab
d/
28 ab
Lời giải:
4
3 4 4
11
1
1 1 3 1
ln ln
4 16 16




ee
e
e
V x xdx x x x
nên a=4, b=16 do đó chọn c/
Bài giải hạn chế bấm máy tính, cần áp dụng tính phân từng phần, xác định a, b và chọn đáp án đúng.
Phần vận dụng cao
Câu 1.
2
2 .3 .7
x x x
dx
bằng :
A.
2
2 .3 .7
ln 4.ln 3.ln 7
x x x
C
B.
84
ln 84
x
C
C.
84 ln84
x
C
D.
2
48xC
Giải thích
Đáp án A sai do hs hiểu nhầm tính chất nguyên hàm
Đáp án A sai là do hs nhầm với công thức tính đạo hàm
Đáp án C sai do hs không thuộc công thức lũy thừa.
Câu 2. Cho
a,b
là hai số dương. Gọi H là hình phẳng nằm trong góc phần tư thứ hai, giới hạn bởi parapol
2
y ax
va đường thẳng
y bx
. Thể tích khối tròn xoay tạo được khi quay H xung quanh trục hoành là một
số không phụ thuộc vào giá trị của
a
và
b
thỏa mãn điều kiện sau:
A.
46
b 2a
B.
35
b 2a
C.
53
b 2a
D.
42
b 2a
Giải thích
Group Nhóm Toán | Trắc nghiệm 2016-2017
85
Ta có
00
5
2
2
2
3
bb
aa
2b
V bx dx ax dx
15a


Câu D sai do học sinh tính tổng hai bài và không lấy NH và thế cận vào.
Câu B sai do giải PT hoành độ giao điểm ra sai nghiệm là-a/b
Câu A sai do học sinh tính tổng hai bài và không lấy NH và thế cận vào và qui đồng mẫu số sai.
Câu 3. Một ô tô đang chạy với vận tốc
20m / s
thì người lái đạp phanh. Sau khi đạp phanh, ôtô chuyển động
chậm dần đều với vận tốc
v t 40t 20(m / s)
, trong đó
t
là khoảng thời gian tính bằng giây kể từ úc bắt
đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét?
A.
0m
B.
5m
C.
20 m
D.
40
Giải thích
Câu A sai là do thế vận tốc vào phương trình và tìm ra t
Câu C sai là do thế
t0
vào phương trình.
Câu D sai là hiểu tìm quảng đường là tính đạo hàm.
Câu 4. Tính diện tích
S
của hình phẳng
H
giới hạn bởi đồ thị hàm số
yx
, trục hoành, và đường thẳng
y x 2
được kết quả là:
A.
16
3
B.
2
C.
4
D.
10
3
Giải thích
Câu A, B, C sai là do học lấy đôi một tính kết quả mà không có vẽ hình để phân chia bài và cận
Câu 5.Tính diện tích
S
của hình phẳng
H
nằm trong phần tư thứ nhất và được giới hạn bởi đồ thị hàm số
y 8x
,
yx
, và đường thẳng
3
yx
được kết quả là:
A.12 B.15,75 C.6,75 D.4
PHẦN 11 :
Câu 1. Hãy chọn mệnh đề đúng dưới đây:
A.
..f x g x dx f x dx g x dx
Group Nhóm Toán | Trắc nghiệm 2016-2017
86
B.
f x dx
fx
dx
gx
g x dx
C.
1
1
x
x dx C

D.
f x dx F x C
.
Câu 2. Hãy chọn mệnh đề đúng dưới đây:
A. Nếu
Fx
là một nguyên hàm của hàm số
fx
thì
1
Fx
là một nguyên hàm của
1
fx
.
B. Nếu
f x dx F x C
thì
.f u x u x dx F u x C

.
C. Nếu
f x g x x
thì
f x dx g x dx

.
D. Nếu
Fx
và
Gx
cùng là nguyên hàm của hàm số
fx
thì ta có
F x G x C
(hằng số).
Câu 3. Câu nào sau đây đúng?
A.
2
11
cos sin2
22
xdx x x C



B.
2
1 cot cotx dx x C
C.
1
22
2
dx x C
x

D.
2
11
ln
x
dx x C
xx
.
Câu 4. Cho hàm số
4
2
23x
fx
x
. Khi đó nguyên hàm của hàm số
fx
là:
A.
3
23
32
x
C
x

B.
3
23
3
x
C
x

C.
3
3
2xC
x

D.
3
23
3
x
C
x

.
Câu 5. Cho hàm số
24
xx
fx
. Khi đó nguyên hàm của hàm số
fx
là:
A.
2
2
2
ln2 ln2
x
x
C
B.
1
2
12
ln2
x
x
C

Group Nhóm Toán | Trắc nghiệm 2016-2017
87
C.
24
1
ln2 ln2
xx
C




D.
2
12
2ln2
x
x
C
.
Câu 6. Hàm số
1
1fx
x

có nguyên hàm là:
A.
2
1
xC
x

B.
2
1
xC
x

C.
lnx x C
D.
lnx x C
.
Câu 7. Nguyên hàm của hàm số
2
4
cos
fx
x

là:
A.
2
4 1 tan xC
B.
4tan xC
C.
4cot xC
D.
4tan xC
.
Câu 8. Nguyên hàm của hàm số
2
3f x x x
là:
A.
4 3 2
1
69
4
x x x C
B.
4 3 2
19
2
42
x x x C
C.
4 3 2
1
29
4
x x x C
D.
4 3 2
9
2
2
x x x C
.
Câu 9. Hàm số
1x
fx
x
có nguyên hàm là:
A.
2
3
x x x C
B.
3
2
2
x x x C
C.
3
2
x x x C
D.
1
21
3
x x C




.
Câu 10. Hàm số
2
2
1
x
x
e
fx
e
có nguyên hàm là:
A.
2
1
2
x
xC
e

B.
2
1
2
x
x e C
C.
2
1
2
x
xC
e

D.
2
1
2
x
x e C

.
Group Nhóm Toán | Trắc nghiệm 2016-2017
88
Câu 11. Nguyên hàm của hàm số
11
11
fx
xx


là:
A.
2
ln 1xC
B.
1
ln
1
x
C
x
C.
1
ln
1
x
C
x
D.
2
2
1
x
C
x
.
Câu 12. Hàm số
2
31
x
fx
có nguyên hàm là:
A.
2
33
ln3 ln3
xx
xC
B.
3
34
2ln3
x
x
xC
C.
3
32
ln3
x
x
xC
D.
3
31
2ln3
x
x
xC
.
Câu 13. Nguyên hàm của hàm số
2
1
32
fx
xx

là:
A.
ln 2 1x x C
B.
2
ln
1
x
C
x
C.
1
ln
2
x
C
x
D.
2
2
23
ln
32
x
C
xx

.
Câu 14. Nguyên hàm của hàm số
22
22
cos sin
sin .cos
xx
fx
xx
là:
A.
tan cotx x C
B.
tan cotx x C
C.
cot tanx x C
D.
1
tan cot
4
x x C
.
Câu 15. Nguyên hàm của hàm số
2
sin cosf x x x
là:
A.
3
sin cos
3
xx
C
B.
2
cos sinx x C
C.
1
sin2
2
x x C
D.
1
cos2
2
x x C
.
Câu 16. Nguyên hàm của hàm số
sinf x x x
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
89
A.
cos sinx x x C
B.
sin cosx x x C
C.
cos sinx x x C
D.
sin cosx x x C
.
Câu 17. Tìm một nguyên hàm
Fx
của hàm số
.
x
f x x e
là:
A.
1
x
F x x e
B.
1
x
F x x e

C.
1
x
F x x e
D.
1
x
F x x e

.
Câu 18. Nếu
1
4
fx
x
và
Fx
là một nguyên hàm của
fx
thỏa
01F
thì
Fx
là:
A.
ln 4 1x 
B.
ln 4 1 ln4x
C.
ln 4 1 ln4x
D.
1 ln4
ln 4 1
44
x
.
Câu 19. Tìm một nguyên hàm
Fx
của hàm số
2
1f x x
, biết rằng khi
1x
thì nguyên hàm
đó bằng
1
. Ta có kết quả nào sau đây?
A.
2
1
2
F x x x
B.
2
1
2
F x x x
C.
2
1
22
x
F x x
D.
2
1
22
x
F x x
.
Câu 20. Hàm số
2
1 ln x
fx
x
có nguyên hàm là:
A.
3
ln lnx x C
B.
2
1
ln ln 3
3
x x C
C.
3
11
ln ln
33
x x C
D.
2
1
ln ln 1
3
x x C




.
Câu 21. Hàm số
2
2
1
x
x
e
fx
e
có nguyên hàm là:
A.
2
ln 1
x
eC
B.
2
2ln 1
x
eC
C.
2
ln 1
x
eC
D.
2
ln 1
x
x e C
.
Group Nhóm Toán | Trắc nghiệm 2016-2017
90
Câu 22. Một nguyên hàm
Fx
của hàm số
tan .sin2f x x x
thỏa điều kiện
0
4
F



là:
A.
1
cos2
24
xx

B.
11
cos2
2 2 4
xx
C.
3
22
cos
32
x
D.
sin2
4
x
.
Câu 23. Hàm số
3
x
F x e
là nguyên hàm của hàm số:
A.
3
2
3
x
xe
B.
3
2
3
x
e
x
C.
4
1
4
x
e
D.
3
3
x
e
.
Câu 24. Hàm số
1 lnF x x x
là nguyên hàm của hàm số:
A.
1 lnx
B.
lnxx
C.
ln x
x
D.
lnxx
.
Câu 25. Nếu
1
sin3 sin
2
f x dx x x C
thì
fx
bằng:
A.
1
3cos3 cos
2
xx
B.
3cos3 sinxx
C.
3sin3 cosxx
D.
1
3sin3 cos
2
xx
.
Câu 26. Cho
2
tanf x x
có nguyên hàm là
Fx
. Nếu đồ thị
y F x
cắt trục
Oy
tại điểm
0;2
thì
Fx
là:
A.
tan 2x
B.
tan 2xx
C.
cot 2x
D.
cot 1xx
.
Câu 27. Nếu
22
cos sinf x x x
có nguyên hàm
Fx
thỏa
1
4
F




thì giá trị của
2
F



bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
91
A.
2
B.
1
2
C.
5
2
D.
3
2
.
Câu 28. Cho hàm số
22
1
cos .sin
fx
xx
và
Fx
là một nguyên hàm của
fx
thỏa
1
4
F



thì
Fx
là hàm số nào sau đây:
A.
tan cot 1xx
B.
cot tan 1xx
C.
tan cot 3xx
D.
tan cot 1xx
.
Câu 29. Cho
Fx
là một nguyên hàm của hàm số
2
tanf x x
. Giá trị của
0
4
FF



bằng:
A.
4
B.
1
4
C.
1
4
D.
3
4
.
Câu 30. Một nguyên hàm của
fx
là
1
1
x
Fx
x
thì
1fx
là:
A.
2
2x
B.
2
2
x
C.
2
1
ln
x
x

D.
2
2
1x
.
ĐÁP ÁN
1D
2B
3A
4D
5B
6C
7D
8B
9D
10A
11C
12B
13B
14C
15D
16A
17C
18C
19C
20D
21C
22B
23A
24A
25A
26B
27D
28A
29C
30B
TÍCH PHÂN
Group Nhóm Toán | Trắc nghiệm 2016-2017
92
ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN
TÍCH
Câu 1: Cho hình phẳng giới hạn bởi đường cong
y f x
, trục hoành và hai đường thẳng
, ( )x a x b a b
quay quanh trục trục hoành tạo thành một khối tròn xoay. Công thức tính thể tích
của khối tròn xoay nói trên:
A.
2
b
a
V f x dx
B.
2
b
a
V f x dx
C.
2
a
b
V f x dx
D.
2
b
a
V f x dx

Câu 2: Cho hình phẳng giới hạn bởi đường cong
sinyx
, trục hoành và hai đường thẳng
0,xx

. Thể tích của khối trn xoay thu được khi quay hình này quanh trục trục Ox:
A.
3
0
sinV xdx
B.
2
0
sinV xdx
C.
2
0
sinV xdx
D.
2
0
sinV xdx

Câu 3: Cho hình phẳng giới hạn bởi đường cong
x f y
, trục tung và hai đường thẳng
, ( )y a y b a b
quay quanh trục trục tung tạo thành một khối tròn xoay. Công thức tính thể tích của
khối tròn xoay nói trên:
A.
2
b
a
V f y dy
B.
2
b
a
V f y dy
C.
3
b
a
V f y dy
D.
2
b
a
V f y dy

Câu 4: Cho hình phẳng giới hạn bởi đường cong
sinyx
, trục hoành và hai đường thẳng
0,xx

. Thể tích của khối trn xoay thu được khi quay hình này quanh trục trục Ox:
A.
2
B.
2
2
Group Nhóm Toán | Trắc nghiệm 2016-2017
93
C.
2
3
D.
2
3
Câu 5: Cho hình phẳng giới hạn bởi đường cong
2
4x 4, 0, 0, 3y x y x x
. Thể tích của khối
trn xoay thu được khi quay hình này quanh trục trục Ox:
A.
31
5
B.
2
32
6
C.
33
5
D.
2
32
3
Câu 6: Cho hình phẳng giới hạn bởi đường cong
2
2 , 1y x y
. Thể tích của khối tròn xoay thu
được khi quay hình này quanh trục trục Ox:
A.
56
25
B.
2
56
6
C.
33
5
D.
56
15
Câu 7: Cho hình phẳng giới hạn bởi đường cong
2
2,y x x y x
. Thể tích của khối tròn xoay thu
được khi quay hình này quanh trục trục Ox:
A.
25
B.
6
C.
5
D.
6
5
Câu 8: Cho hình phẳng giới hạn bởi đường cong
2
1 , 0y x y
. Thể tích của khối tròn xoay thu
được khi quay hình này quanh trục trục Ox:
A.
1
2
2
1
1V x dx

B.
1
2
2
1
1V x dx

C.
1
2
1
1V x dx

D.
1
4
1
1V x dx

Câu 9: Cho hình phẳng giới hạn bởi đường cong
2
1 , 0, 0, 2y x y x x
. Thể tích của khối tròn
xoay thu được khi quay hình này quanh trục trục Ox:
Group Nhóm Toán | Trắc nghiệm 2016-2017
94
A.
82
3
B.
2
5
C.
5
2
D.
2
Câu 10: Cho hình phẳng giới hạn bởi đường cong
22
,y x x y
. Thể tích của khối trn xoay thu được
khi quay hình này quanh trục trục Ox:
A.
8
3
B.
2
5
C.
2
D.
3
10
Câu 11: Cho hình phẳng giới hạn bởi đường cong
1
3
2 1 , 0, 3y x x y
. Thể tích của khối tròn
xoay thu được khi quay hình này quanh trục trục Oy:
A.
480
7
B.
481
7
C.
48
7
D.
488
7
Câu 12: Cho hình phẳng giới hạn bởi đường cong
2
1, 0y x x
và tiếp tuyến với
2
1yx
tại điểm
(1;2)M
. Thể tích của khối trn xoay thu được khi quay hình này quanh trục trục Ox:
A.
8
7
B.
11
15
C.
8
15
D.
4
7
Câu 13: Cho hình phẳng giới hạn bởi đường cong
,y x y x
. Thể tích của khối trn xoay thu được
khi quay hình này quanh trục trục Ox:
A. 0 B.
C.
D.
6
Group Nhóm Toán | Trắc nghiệm 2016-2017
95
Câu 14: Cho hình phẳng giới hạn bởi đường cong
ln , 0,y x y x e
. Thể tích của khối tròn xoay thu
được khi quay hình này quanh trục trục Oy:
A.
2
1
2
e
B.
2
1
2
e
C.
2
21
2
e
D.
2
2
2
e
Câu 15: Cho hình phẳng giới hạn bởi đường cong
2
3
,0y x x
và tiếp tuyến với
2
3
yx
tại điểm có
hoành độ bằng 1. Thể tích của khối trn xoay thu được khi quay hình này quanh trục trục Oy:
A.
5
26
B.
26
C.
7
36
D.
36
Câu 16: Cho hình phẳng giới hạn bởi đường cong
1
1, 0, 2y y y x
x
. Thể tích của khối tròn xoay
thu được khi quay hình này quanh trục trục Ox:
A.
5 6ln2
3
B.
1 6ln2
3
C.
5 6ln2
3
D.
5 6ln2
3
Câu 17: Cho hình phẳng giới hạn bởi đường cong
2
2x , 0, 3y x y x
. Thể tích của khối tròn xoay
thu được khi quay hình này quanh trục trục Ox:
A.
3
5
B.
18
5
C.
7
5
D.
5
Câu 18: Cho hình phẳng giới hạn bởi đường cong
2
2x , 0, 3y x y x
. Thể tích của khối tròn xoay
thu được khi quay hình này quanh trục trục Oy:
Group Nhóm Toán | Trắc nghiệm 2016-2017
96
A.
6
B.
17
6
C.
7
6
D.
59
6
Câu 19: Cho hình phẳng giới hạn bởi đường cong
2
2 1 , 2 1y x y x
. Thể tích của khối tròn
xoay thu được khi quay hình này quanh trục trục Ox:
A.
6
B.
3
C.
4
3
D.
5
6
Câu 20: Cho hình phẳng giới hạn bởi đường cong
1
, 0, 1, ( 1)y y x x a a
x
. Thể tích của khối tròn
xoay thu được khi quay hình này quanh trục trục Ox:
A.
1
3
a
B.
1a
a
C.
1
3
a
D.
1a
a
ỨNG DỤNG TÍCH PHÂN TÍNH THỂ
TÍCH
Câu 1. Công thức nào diện tích hình phẳng giới hạn bởi đồ thị hàm số
y f x
liên tục, trục hoành
và hai đường thẳng
,x a x b
A .
b
a
f x dx
B.
b
a
f x dx
C.
b
a
f x dx
D.
2
b
a
f x dx
Câu 2. Công thức nào diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
,y f x y g x
liên
tục và hai đường thẳng
,x a x b
Group Nhóm Toán | Trắc nghiệm 2016-2017
97
A .
b
a
f x g x dx
B.
b
a
f x g x dx
C.
b
a
f x g x dx
D.
b
a
f x g x dx
Câu 3. Trong các tích phân sau, tích phân nào là công thúc tính diện tích giới hạn bởi đồ thị hàm số
sin 2cosxyx
trục hoảnh và hai đường thẳng
0,
2
xx

là
A .
2
0
sin 2cosxx dx
B.
2
0
sin 2cosxx dx
C.
2
0
sin 2cosxx dx
D.
2
0
sin 2cosxx dx
Câu 4. Diện tích hình phẳng được giới hạn bởi đồ thị hàm sồ
3
yx
trục hoành và hai đường thẳng
1, 2xx
A.
17
4
S
B.
4S
C.
1
4
S
D.
15
4
S
Câu 5. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
2
2 4 6y x x
, trục hoành và hai
đường thẳng
2, 4xx
là:
A.
12
B.
40
3
C.
92
3
D.
50
3
Câu 6. Diện tích hình phẳng được giới hạn bởi hai đường thẳng
0,xx

và hai đồ thị hàm sồ
sin , cosy x y x
A.
2S
B.
4S
C.
0S
D.
22S
Câu 7. Diện tích hình phẳng được giới hạn bởi hai đường thẳng
0, 1xx
và hai đồ thị hàm sồ
,2
x
y e y
A.
2S
B.
1Se
C.
1Se
D.
3Se
Câu 8. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
3
yx
và
5
yx
là:
A.
1
12
B.
1
6
C.
2
6
D. 0
Câu 9. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
siny x x
,
yx
và
02x

A. 3 B. 4 C. 2 D. 1
Group Nhóm Toán | Trắc nghiệm 2016-2017
98
Câu 10. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
3
3 3 1y x x
vàđường thẳng
3y
là:
B.
57
4
B.
45
4
C.
27
4
D.
21
4
Câu 11. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
1y e x
và
1
x
y e x
là:
A.
2
2
e
B. 2 C.
1
2
e
D.
3
1
e
Câu 12. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
2
yx
,
1
ln
1
y
x
và đường thẳng
1x
là:
A.
8 31
ln2
3 18

B.
8 31
ln2
3 18
C.
8 23
ln2
3 18

D.
8 31
ln2
3 18

Câu 13. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
3
y x x
và
2
y x x
là:
A.
8
3
B.
33
12
C.
37
12
D.
5
12
Câu 14. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
2
23y x x
và trục hoành là:
C.
125
24
B.
125
34
C.
125
14
D.
125
44
Câu 15. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
2
43y x x
và
3yx
là:
A.
55
6
B.
205
6
C.
109
6
D.
126
6
Câu 16. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
2
2yx
,
2
1yx
và trục hoành là:
D.
3 2 2
B.
22
2
C.
82
32
D.
42
Câu 17. Anh An muốn làm cửa rào sắt có hình dạng
và kích thước giống như hình vẽ kế bên, biết
đường cong phía trên là một parabol. Giá
2
1m
cửa rào sắt có giá là 700000 đồng. Vậy anh An
phải trả bao nhiêu tiền để làm cài cửa rào sắt như
vậy. (làm trn đền trục hàng nghìn)
Group Nhóm Toán | Trắc nghiệm 2016-2017
99
A. 6420000 B. 6320000 C. 6520000 D. 66200000
Câu 18. Một quán café muốn lảm cái bảng hiệu là
một phần của Elip có kích thước, hình dạng
giống như hình vẽ và có chất lượng bằng gổ.
Diện tích gổ bề mặt bảng hiệu là (làm trn đến
hàng phần chục)
A. 2.3
B. 2.4
C. 2.5
D. 2.6
Câu 19. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
2
1yx
, tiếp tuyến của parapol đã cho
tại điểm
2;5M
và trục tung là:
E.
7
3
B.
5
3
C.
8
3
D.
2
Câu 20. Cho hàm số
32
32y x x
có đồ thị (C). Diện tích hình phẳng giới hạn bởi (C) và tiếp
tuyến của (C) tại điểm có hoành độ
0
1.9x
là (làm trn đến hàng phần chục)
A 4.1 B. 4.2 C. 4.3 D. 4.4
PHẦN 12 :
I. NHẬN BIẾT
Câu 1. Một nguyên hàm F(x) của hàm số
1
()
25
fx
x
là :
A.
1
( ) ln 2 5 2016
2
F x x
C.
F(x) ln 2 5
x
B.

2
2
()
25
Fx
x
D.

2
1
()
25
Fx
x
Câu 2. Một nguyên hàm F(x) của hàm số
3
1
( ) sin10
2
f x x
là :
Group Nhóm Toán | Trắc nghiệm 2016-2017
10
0
A.




4
1
sin10
42
x
x
C.
4
4
x
B.
4
1
( ) ln 2 cos10
4
F x x
D.
2
( ) 3
F x x
Câu 3. Hàm số
1
()Fx
x
là một nguyên hàm của hàm số nào sau đây ?
A.
f(x) ln 2
x
B.

2
1
()
fx
x
C.
1
D.
2
2
x
Câu 4. Một nguyên hàm F(x) của hàm số
( ) 3
x
fx
là :
A.
3
()
ln 3
x
Fx
B.
1
3
()
1
x
Fx
x
C.
( ) 3
x
Fx
D.
3
()
1
x
Fx
x
Câu 5. Một nguyên hàm F(x) của hàm số
2
3
( ) 2
f x x x
x
là :
A.
3
3
4
( ) 3ln
33
x
F x x x
C.
3
3
4
( ) 3lnx
33
x
F x x
B.
3
3
2
34
()
33
x
F x x
x
D.
3
3
4
( ) 3ln
33
x
F x x x
Câu 6. Kết quả của
2
tan
xdx
là :
A.
tan x x C
B.
tan 1xC
C.
2
cot xC
D.
2
2
1 tanxC
Câu 8. Một nguyên hàm của hàm số
2
()
x
f x e
là :
A.
2x
e
B.
2
2
x
e
C.
21
21
x
e
x
D.
2
1
2
x
e
Câu 9. Kết quả của
3
sin
2
x
dx
là :
A.
23
cos
32

x
C
B.
23
cos
32
x
C
C.
33
cos
22

x
C
D.
33
cos
22
x
C
Câu 10. Tìm hàm số
()fx
biết
'( ) sin cosf x x x
và
0
4



f
, ta được kết quả là :
Group Nhóm Toán | Trắc nghiệm 2016-2017
10
1
A.
( ) cos sin 2 f x x x
C.
2
( ) cos sin
2
f x x x
B.
( ) cos sin 2 f x x x
D.
2
( ) cos sin
2
f x x x
II. THÔNG HIỂU
Câu 11. Nguyên hàm của hàm số: y = sin
3
x.cosx là:
A.
4
1
sin
4
xC
B.

4
1
sin
4
xC
C.
4
1
cos
4
xC
D.

4
1
cos
4
xC
Câu 12. Một nguyên hàm của hàm số: y = cos5x.cosx là:
A.
1 1 1
sin6 sin4
2 6 4



xx
B. cos6x C. F(x) = sin6x D.
1 sin6 sin4
2 6 4




xx
Câu 13. Họ nguyên hàm F(x) của hàm số
2
()
1
x
fx
x
là :
A.
2
1
( ) ln 1
2
F x x C
C.
2 xC
B.
2
( ) ln 1 F x x C
D.
11
ln
21
x
C
x
Câu 14. Kết quả của
ln
xdx
là :
A.
ln x x x C
B.
ln x x x C
C.
ln x x C
D.
1
C
x
Câu 15. Kết quả của
5
2
3



x
x
e dx
xe
là :
A.
4
1
3
2

x
eC
x
B.
4
1
3
2
x
eC
x
4
1
.3
2

x
C e C
x
D.
4
1
3
2
x
eC
x
Câu 16. Nguyên hàm F(x) của hàm số
2
( ) tanf x x
thỏa
(0) 3F
là :
A.
tan 3xx
B.
tan 3xx
C.
tan 3xx
D.
tan 3xx
Câu 17. Kết quả của
20
cos
sin
x
dx
x
là :
Group Nhóm Toán | Trắc nghiệm 2016-2017
10
2
A.
19
11
19
19sin

x
B.
19
11
19
19sin
x
C.
19
11
19
19sin

x
D.
19
11
19
19sin
x
Câu 18. Kết quả của
sin
x xdx
là
A.
cos sin x x x C
. cos sinB x x x C
. sin cos C x x x C
. sin cosD x x x C
Câu 19. Nếu
2
'( ) cos
4




f x x
và
13
(0)
4
f
thì :
A.
1 1 7
( ) cos2 3 . ( ) sin
2 2 2



f x x x C f x x
B.
11
( ) cos2 4 . ( ) cos2 3
22
f x x x D f x x
Câu 20. Hàm số
2
()
x
F x e
là một nguyên hàm của hàm số nào sau đây ?
A.
2
( ) 2
x
f x xe
B.
2
()
x
f x e
C.
2
()
2
x
e
fx
x
D.
2
2
x
x
e
III. VẬN DỤNG THẤP
Câu 21. Hàm số nào dưới đây là một nguyên hàm của hàm số
2
1
4
y
x
?
A.
2
( ) ln 4 F x x x
B.
C.
2
( ) 2 4F x x
D.
2
( ) 2 4 F x x x
Câu 22. Họ nguyên hàm F(x) của hàm số
2
( ) sinf x x
là :
A.
1 sin2
()
22



x
F x x C
B.
1 cos2
()
22



x
F x x C
C.
1 sin2
()
22



x
F x x C
D.
1
( ) sin2
2
F x x x C
Câu 23. Một nguyên hàm F(x) của hàm số
()
1
x
x
e
fx
e
thỏa
(0) ln3F
là :
A.
ln 2 ln3
x
e
C.
ln 2 2ln3
x
e
Group Nhóm Toán | Trắc nghiệm 2016-2017
10
3
B.
ln 2 ln3
x
e
D.
ln 2 2ln3
x
e
Câu 24. Hàm số
F( ) ln sin 3cos
x x x
là một nguyên hàm của hàm số nào sau đây ?
A.
cos 3sin
()
sin 3cos
xx
fx
xx
C.

cosx 3sin
()
sin 3cos
x
fx
xx
B.
( ) cos 3 sin
f x x x
D.
sin 3cos
()
cos 3sin
xx
fx
xx
Câu 25. Kết quả của
tan
xdx
là :
A.
cot xC
C.
ln cos xC
B.
ln cosxC
D.
ln sin xC
IV. VẬN DỤNG CAO
Câu 26. Họ nguyên hàm F(x) của hàm số

2
1
()
43
fx
xx
là :
A.
2
( ) ln 4 3
F x x x C
C.

3
F(x) ln
1
x
C
x
B.

11
( ) ln
23
x
F x C
x
D.

13
( ) ln
21
x
F x C
x
Câu 27. Kết quả của
22
1
sin .cos
dx
xx
là :
A.
tan .cot x x C
C.
1
tan .cot
C
xx
B.
tan cotx x C
D.
tan cotx x C
Câu 28. Nguyên hàm F(x) của hàm số
23
( ) sin 2 .cos 2f x x x
thỏa
0
2



F
là :
A.
35
11
sin 2 sin 2
6 10
xx
C.
35
1 1 4
sin 2 sin 2
6 10 15
xx
B.
35
11
sin 2 sin 2
6 10
xx
D.
35
1 1 1
sin 2 sin 2
6 10 15
xx
Câu 29. Họ nguyên hàm của hàm số
là :
Group Nhóm Toán | Trắc nghiệm 2016-2017
10
4
A.
1
cos2
2
xC
C.
1
cos2
2
xC
B.
cos2xC
D.
cos2 xC
Câu 30. Kết quả của
2
1
cos ln
dx
xx
là :
A.
tan ln x x C
C.
tan lnx x C
B.
tan lnx x C
D.
tan ln xC
1A
2A
3A
4A
5A
6A
7A
8A
9A
10A
11A
12A
13A
14A
15A
16A
17A
18A
19A
20A
21A
22A
23A
24A
25A
26A
27A
28A
29A
30A
TÍCH PHÂN
I/ CẤP ĐỘ NHẬN BIẾT
Câu 1. Tích phân
2
0
sinI xdx
bằng
A. 1 B. -1
C. 0 D. -2
Câu 2. Cho hàm số f(x) xác định trên đoạn [a; b] và F(x) là nguyên hàm của f(x) trên khoảng (a; b). Kết luận
nào sau đây là đúng: F(x) là một nguyên hàm của f(x) trên đọan [a; b] khi và chỉ khi
A.
/
( ) ( )F a f a
và
/
( ) ( )F b f b
B.
/
( ) ( )F a f a
và
/
( ) ( )F b f b
C.
/
( ) ( )F a f a
và
/
( ) ( )F b f b
D.
/
( ) ( )F a f a
và
/
( ) ( )F b f b
Group Nhóm Toán | Trắc nghiệm 2016-2017
10
5
Câu 3. Tích phân
3
2
0
(1 tan )I x dx

bằng
A.
3
B.
3
3
C.
3
D. 1
Câu 4. Hàm số nào sau đây không có tích phân trên đoạn [0; 1]
A.
( ) ln( 1)f x x
B.
( ) lnf x x
C.
( ) ln( 2)f x x
D.
( ) ln( 3)f x x
Câu 5. Kết quả của
1
1
dx
I
x
là
A. 0 B. -1
C. 1 D. Không tồn tại
Câu 6. Đẳng thức nào sau đây là đúng
A.
0
2
0
2
sin sinxdx xdx

B.
22
00
sin sinxdx tdt


C.
22
00
sin cosxdx xdx


D.
0
2
0
2
sin cos2xdx xdx

Câu 7. Tích phân
2
0
cos
3
x
I dx
bằng
A.
3
6
B.
33
2
C.
2
6
D.
3
2
Câu 8. Tích phân
2
0
sin .cosI x xdx
bằng
Group Nhóm Toán | Trắc nghiệm 2016-2017
10
6
A.
1
2
B.
1
2
C.
3
2
D.
3
2
Câu 9. Tích phân
1
0
1
dx
I
x
bằng
A.
1 2ln2
B.
1 ln2
C.
1 ln2
D.
ln2
Câu 10. Tích phân
2
1
1
x
x
e
I dx
e
bằng
A.
ln( 1)e
B.
ln( 1)e
C.
ln( 1)e
D.
2
ln( 1)e
II/ CẤP ĐỘ THÔNG HIỂU
Câu 11. Biết
1
0
( 1) 3a dx
. Khi đó số thực a bằng
A. – 2 B. 2
C.
1
2
D.
1
2
Câu 12. Cho biết
2
0
( sin 2) 2t x dx
. Khi đó số thực t bằng
A.
3
B.
3
C.
D.
1
2
Câu 13. Tích phân
5
2
2
1
1
xx
I dx
x

bằng
A.
6 ln3
B.
6 ln3
C.
6 ln3
D.
6 ln3
Group Nhóm Toán | Trắc nghiệm 2016-2017
10
7
Câu 14. Chọn mệnh đề đúng trong các mệnh đề sau
A.Hàm số
1
()
2
fx
x
có tích phân trên đoạn [0;2].
B. Hàm số
1
()
2
fx
x
không có tích phân trên đoạn [0;1].
C. Nếu f(x) không liên tục trên đoạn [a; b] thì f(x) có tích phân trên [a; b].
D. Nếu f(x) liên tục trên đoạn [a; b] thì f(x) có tích phân trên [a; b].
Câu 15. Tích phân của tan x trên đoạn
[0; ]
4
là
A.
1
ln
2
B.
2
1 ln
2
C.
2
ln
2
D.
2
ln
2
Câu 16. Tích phân
2
2
1
2
xdx
I
x
bằng
A.
1
ln2
2
B.
2ln2
C.
1
ln
2
D.
1
2ln
2
Câu 17. Tích phân
3
3
0
cosI xdx
bằng
A.
33
B.
33
2
C.
33
4
D.
33
8
Câu 18. Tích phân
4
2
0
tanI xdx
bằng
A.
1
4
B.
1
4

Group Nhóm Toán | Trắc nghiệm 2016-2017
10
8
C.
1
4
D. 1
Câu 19. Tích phân
1
2
0
1
dx
I
x
bằng
A.
4
B.
6
C.
3
D.
2
Câu 20. Tích phân
6
0
4sin 1.cosI x xdx

bằng
A.
33
B.
33
C.
3 3 1
6
D.
3 3 1
2
III/ CẤP ĐỘ VẬN DỤNG THẤP
Câu 21. Một nguyên hàm của hàm số
4
2
1
()
1
x
x
e
fx
e
là
A.
2
1
2
x
ex
B.
2
1
2
x
ex
C.
2
2
x
ex
D.
2
2
x
ex
Câu 22. Biết F(x) là một nguyên hàm của
1
()
1
fx
x
và
(2) 1F
. Khi đó F(3) bằng
A.
ln2
B. ln2 + 1
C.
3
ln
2
D.
1
2
Câu 23. Các số thực x sau đây thỏa mãn đẳng thức
0
(1 ) 0
x
t dt
A. x = 0 hoặc x = - 2. B. x = 0 hoặc x = 2.
C. x = 0 hoặc x = 1. D. x = 0 hoặc x = -1.
Group Nhóm Toán | Trắc nghiệm 2016-2017
10
9
Câu 24. Tích phân
1
0
1
dx
I
x
bằng
A.
2(1 ln2)
B.
2(1 ln2)
C.
1 2ln2
D.
1 2ln2
Câu 25. Tích phân
ln2
0
2
x
x
e dx
I
e
bằng
A.
23
B.
2( 3 2)
C.
2(2 3)
D.
2( 3 2)
IV/ CẤP ĐỘ VẬN DỤNG CAO
Câu 26.
2
2 .3 .7
x x x
dx
bằng
A.
2
2 .3 .7
ln4.ln3.ln7
x x x
C
B.
84
ln84
x
C
C.
84 ln84
x
C
D.
2
48xC
Câu 27. Đẳng thức nào sau đây là sai
A.
22
00
(sin ,cos ) (cos ,sin )f x x dx f x x dx


B.
0
2
0
2
(sin ,cos ) (cos ,sin )f x x dx f x x dx


C.
00
( sin ) (sin )
2
f x x dx f x dx


D.
00
( sin ) (sin )f x x dx f x dx



Câu 28. Cho phương trình
2
2
, ( 2)
12
1
t
dx
t
xx

. Khi đó nghiệm thực t của phương trình đã cho là
A.
1
2
B.
1
2
C. 2 D. -2
Câu 29. Tích phân
2
7
77
0
sin
sin cos
x
I dx
xx
bằng
Group Nhóm Toán | Trắc nghiệm 2016-2017
11
0
A.
2
B.
4
C.
8
D.
12
Câu 30. Tích phân
1
1
( 1)( 3)
x
dx
I
ex

bằng
A.
1
ln2
2
B.
1
ln3
2
1A
2D
3C
4B
5A
6B
7D
8A
9D
10A
11B
12A
13A
14D
15D
16A
17D
18C
19A
20C
21B
22B
23B
24B
25C
26B
27D
28C
29B
30A
ỨNG DỤNG TÍCH PHÂN
NHẬN BIẾT
Câu 1. Cho hàm số
()y f x
liên tục trên
[ ; ]ab
. Khi đó, diện tích S của hình phẳng giới hạn bởi đồ thị hàm
số
( ),y f x
trục hoành và hai đường thẳng
,x a x b
được tính theo công thức:
A.
()
b
a
S f x dx
B.
()
b
a
S f x dx
C.
()
b
a
S f x dx
D.
()
b
a
S f x dx
Câu 2. Cho hai hàm số
()y f x
và
()y g x
liên tục trên
[ ; ]ab
. Khi đó, diện tích S của hình phẳng giới hạn
bởi đồ thị hai hàm số
( ),y f x
()y g x
và hai đường thẳng
,x a x b
được tính theo công thức:
A.
( ) ( )
b
a
S f x g x dx

B.
( ) ( )
b
a
S f x g x dx
C.
( ) ( )
b
a
S f x g x dx

D.
( ) ( )
b
a
S f x g x dx
Câu 3. Diện tích hình phẳng giới hạn bởi các đường
sinx, 0, 0,y y x x
bằng:
A.
6
7
B. 2 C. 2
D.
6
7
Câu 4. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
y x x
, trục hoành, trục tung và đường thẳng
2x
bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
11
1
A.
2
3
B.
C. 1 D.
2
3
Câu 5. Cho đồ thị hàm số
()y g x
. Diện tích hình phẳng ( phần gạch trong hình vẽ) bằng:
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
x
y
A.
3
1
()g x dx
B.
3
0
()g x dx
C.
3
1
()g x dx
D.
0
8
()g x dx
THÔNG HIỂU
Câu 6. Cho hàm số
()y f x
liên tục trên
[ ; ]ab
. Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị hàm số
( ),y f x
trục hoành và hai đường thẳng
,.x a x b
Nếu đồ thị hàm số
()y f x
cắt trục hoành tại một
điểm duy nhất có hoành độ
( ; )c a b
. Khi đó, diện tích S được tính theo công thức:
A.
()
b
a
S f x dx
B.
( ) ( )
cb
ac
S f x dx f x dx

C.
( ) ( )
cb
ac
S f x dx f x dx



D.
( ) ( )
cb
ac
S f x dx f x dx

Group Nhóm Toán | Trắc nghiệm 2016-2017
11
2
Câu 7. Cho hai hàm số
()y f x
và
()y g x
liên tục trên
[ ; ]ab
. Gọi S là diện tích của hình phẳng giới hạn
bởi đồ thị hai hàm số
( ),y f x
()y g x
và hai đường thẳng
,x a x b
. Nếu phương trình
( ) ( ) 0f x g x
có một nghiệm duy nhất
( ; )c a b
. Khi đó, diện tích S được tính theo công thức:
A.
( ) ( )
b
a
S f x g x dx
B.
( ) ( )
b
a
S f x g x dx
C.
( ) ( )
cb
ac
S f x dx g x dx

D.
( ) ( ) ( ) ( )
cb
ac
S f x g x dx f x g x dx

Câu 8. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
2y x x
và trục hoành bằng :
A.
4
3
B.
4
3
C.
D. 1
Câu 9. Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số
2
y x x
và
3yx
bằng :
A.
32
3
B.
40
3
C.
32
3
D.
40
3
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
lnyx
, trục hoành và đường thẳng
xe
bằng :
A.
e
B.
e
C.
1
D.
VẬN DỤNG THẤP
Câu 11. Diện tích hình phẳng giới hạn bởi các đường
3
, 1, 8x y y x
bằng :
A.
5
4
B.
7
4
C.
11
4
D.
17
4
Câu 12. Diện tích hình phẳng giới hạn bởi đường cong (C):
21
1
x
y
x
, tiệm cận ngang của (C) và hai đường
thẳng
1, 3xx
bằng :
A.
ln2
B.
4ln2
C.
1 ln2
D.
1
Câu 13. Diện tích hình phẳng giới hạn bởi các đường
4
, 0, 2, 6
1
x
y y x x
x
không được tính bởi công
thức nào sau đây :
A.
6
2
4
1
x
dx
x
B.
46
24
44
11
xx
dx dx
xx



Group Nhóm Toán | Trắc nghiệm 2016-2017
11
3
C.
46
24
44
11
xx
dx dx
xx



D.
46
24
44
11
xx
dx dx
xx



Câu 14. Cho đồ thị hàm số
()y f x
. Diện tích hình phẳng ( phần gạch trong hình vẽ) bằng:
A.
02
20
( ) ( )f x dx f x dx


B.
2
2
()f x dx
C.
02
20
( ) ( )f x dx f x dx

D.
2
0
2 ( )f x dx
Câu 15. Cho đồ thị hàm số
()y h x
. Diện tích hình phẳng ( phần gạch trong hình vẽ) bằng:
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-5
-4
-3
-2
-1
1
2
3
4
5
x
y
Group Nhóm Toán | Trắc nghiệm 2016-2017
11
4
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8
-3
-2
-1
1
2
3
x
y
A.
1
1
()g x dx
B.
00
11
( ) ( )h x dx h x dx

C.
01
10
( ) ( )h x dx h x dx

D.
01
10
( ) ( )h x dx h x dx


VẬN DỤNG CAO
Câu 16. Số đo diện tích hình phẳng giới hạn bởi parabol (P):
2
22y x x
, tiếp tuyến của (P) tại điểm
(3;5)M
và trục tung bằng:
A.
9
B.
8
C.
9
D.
8
Câu 17. Số đo diện tích hình phẳng giới hạn bởi đường
4xy
, trục hoành và hai đường thẳng
, 3 ( 0)x a x a a
bằng :
A.
4 ln3
B.
4ln3
C.
4ln2a
D.
4 ln2a
Câu 18. Số đo diện tích hình phẳng giới hạn bởi các đường
,1y x y
và
2
4
x
y
trong miền
0, 1xy
bằng :
A.
3
2
B.
3
2
C.
5
6
D.
5
6
Câu 19. Cho đồ thị hai hàm số
1
()y f x
( đường vẽ màu đỏ) và
2
()y f x
( đường vẽ màu hồng). Diện tích
hình phẳng ( phần gạch trong hình vẽ) bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
11
5
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9
-7
-6
-5
-4
-3
-2
-1
x
y
A.
1
12
2
( ) ( )f x f x dx
B.
01
1 2 1 2
20
( ) ( ) ( ) ( )f x f x dx f x f x dx

C.
01
1 2 1 2
10
( ) ( ) ( ) ( )f x f x dx f x f x dx

D.
01
1 2 2 1
20
( ) ( ) ( ) ( )f x f x dx f x f x dx

Câu 20. Cho parabol (P):
2
1yx
và đường thẳng
( ): 2d y mx
. Với giá trị thực m nào dưới đây thì diện
tích hình phẳng giới hạn bởi (P) và (d) đạt giá trị nhỏ nhất
A.
1
2
B.
3
4
C.1 D.0
1.C
2.D
3.B
4.C
5.C
6.D
7.D
8.B
9.A
10C
11.D
12.A
13.B
14.D
15.B
16.A
17.B
18.D
19.D
20.D
PHẦN 13 :
NGUYÊN HÀM
Mức độ nhận biết.
Câu 1: Nguyên hàm của hàm số f(x) = x
2
– 3x +
x
1
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
11
6
A.
32
3
32
ln
xx
xC
B.
32
2
31
32
xx
C
x
C.
32
3 lnx x x C
D.
32
3
32
ln
xx
xC
Câu 2: Họ nguyên hàm của
2
( ) 2 1f x x x
là
A.
3
1
( ) 2
3
F x x x C
B.
( ) 2 2F x x C
C.
D.
32
1
( ) 2
3
F x x x x C
Câu 3: Nguyên hàm của hàm số
2
11
()fx
x
x

là :
A.
2
ln lnx x C
B. lnx -
x
1
+ C C. ln|x| +
x
1
+ C D. Kết quả khác
Câu 4: Nguyên hàm của hàm số
2
()
xx
f x e e
là:
A.
Cee
xx
2
2
1
B.
2
2
xx
e e C
C.
()
xx
e e x C
D. Kết quả khác
Câu 5: Nguyên hàm của hàm số
f x cos3x
là:
A.
1
3
3
xCsin
B.
1
sin3
3
xC
C.
sin3xC
D.
3sin3xC
Câu 6: Nguyên hàm của hàm số
2
1
2()
cos
x
f x e
x

là:
A.2e
x
+ tanx + C B. e
x
(2x -
)
cos
2
x
e
x
C. e
x
+ tanx + C D. Kết quả khác
Câu 7: Tính
sin(3 1)x dx
, kết quả là:
A.
1
cos(3 1)
3
xC
B.
1
cos(3 1)
3
xC
C.
cos(3 1)xC
D. Kết quả khác
Câu 8: Tìm
(cos6 cos4 )
x x dx
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
11
7
A.
11
sin6 sin4
64
x x C
B.
6sin6 5sin4
x x C
C.
11
sin6 sin 4
64
x x C
D.
6sin6 sin 4
x x C
Câu 9: Tính nguyên hàm
1
21
dx
x
ta được kết quả sau:
A.
1
21
2
ln xC
B.
21ln xC
C.
1
21
2
ln xC
D.
21ln xC
Câu 10: Tính nguyên hàm
1
12
dx
x
ta được kết quả sau:
A.
12ln xC
B.
2 1 2ln xC
C.
1
12
2
ln xC
D.
2
2
12()
C
x
Câu 11: Công thức nguyên hàm nào sau đây không đúng?
A.
1
lndx x C
x

B.
1
1
1
()
x
x dx C
C.
01()
ln
x
x
a
a dx C a
a
D.
2
1
tan
cos
dx x C
x

Câu 12: Tính
(3cos 3 )
x
x dx
, kết quả là:
A.
3
3sin
ln3
x
xC
B.
3
3sin
ln3
x
xC
C.
3
3sin
ln3
x
xC
D.
3
3sin
ln3
x
xC
Câu 13: Trong các hàm số sau:
(I)
2
( ) tan 2f x x
(II)
2
2
()
cos
fx
x
(III)
2
( ) tan 1f x x
Hàm số nào có một nguyên hàm là hàm số g(x) = tanx
A. (I), (II), (III) B. Chỉ (II), (III)
C. Chỉ (III) D. Chỉ (II)
Group Nhóm Toán | Trắc nghiệm 2016-2017
11
8
Câu 14: Trong các mệnh đề sau, tìm mệnh đề sai
A.
3
2
()
'( ) ( )
3
fx
f x f x dx C
B.
( ). ( ) ( ) . ( )f x g x dx f x dx g x dx
C.
( ) ( ) ( ) ( )f x g x dx f x dx g x dx
D.
( ) ( )kf x dx k f x dx
(k là hằng số)
Câu 15: Nguyên hàm của hàm số
3
21f x x( ) ( )
là:
A.
4
1
21
2
xC()
B.
4
21xC()
C.
4
2 2 1xC()
D. Kết quả khác
Câu 16: Nguyên hàm của hàm số
5
12f x x( ) ( )
là:
A.
6
1
12
2
xC ()
B.
6
12xC()
C.
6
5 1 2xC()
D.
4
5 1 2xC()
Câu 17: Chọn câu khẳng định sai?
A.
1
xdx C
x

ln
B.
2
2xdx x C
C.
xdx x C
sin cos
D.
2
1
dx x C
x
cot
sin
Câu 18: Nguyên hàm của hàm số f(x) =
2
3
2x
x
là :
A.
2
3
xC
x

B.
2
2
3
xC
x

C.
22
3lnx x C
D. Kết quả khác
Group Nhóm Toán | Trắc nghiệm 2016-2017
11
9
Câu 19: Hàm số
tan
x
F x e x C
là nguyên hàm của hàm số
f( )x
nào?
A.
2
1
x
f x e
x
()
sin
B.
2
1
x
f x e
x
()
sin
C.
2
1
x
f x e
x
()
cos
D. Kết quả khác
Câu 20: Nếu
( ) sin2
x
f x dx e x C
thì
()fx
bằng
A.
cos2
x
ex
B.
cos2
x
ex
C.
2cos2
x
ex
D.
1
cos2
2
x
ex
Câu 21. Trong các hàm số sau đây , hàm số nào là nguyên hàm của
( ) sin2f x x
A.
2cos2x
B.
2cos2x
C.
1
cos2
2
x
D.
1
cos2
2
x
Câu 22. Trong các hàm số sau đây , hàm số nào là nguyên hàm của
32
( ) 3 2 1f x x x x
A.
2
3 6 2xx
B.
4 3 2
1
4
x x x x
C.
4 3 2
1
4
x x x
D.
2
3 6 2xx
Câu 23. Trong các hàm số sau đây , hàm số nào là nguyên hàm của
1
()
2 2016
fx
x
A.
ln 2 2016x
B.
1
ln 2 2016
2
x
C.
1
ln 2 2016
2
x
D.2
ln 2 2016x
Câu 24. Trong các hàm số sau đây , hàm số nào là nguyên hàm của
33
()
x
f x e
A.
33x
e
B. 3
33x
e
C.
33
1
3
x
e
D. -3
33x
e
Câu 25. Nguyên hàm của hàm số:
1
J x dx
x




là:
A. F(x) =
2
ln x x C
B. F(x) =
2
1
ln x x C
2

Group Nhóm Toán | Trắc nghiệm 2016-2017
12
0
C. F(x) =
2
1
ln x x C
2

D. F(x) =
2
ln x x C
.
Câu 26. Một nguyên hàm của hàm số: y = cos5x là:
A. cos5x+C B. sin5x+C C.
1
sin6
6
x
+C D.
1
sin5
5
x
+C
Câu 27. Nguyên hàm của hàm số:

xx
J 2 3 dx
là:
A F(x) =

xx
23
C
ln 2 ln 3
B. F(x) =

xx
23
C
ln 2 ln 3
C. F(x) =

xx
23
C
ln 2 ln3
D. F(x) =

xx
2 3 C
Câu 28. Nguyên hàm của hàm số:
2
I (x 3x 1)dx
là:
A. F(x)
32
13
x x C
32
B. F(x)
32
13
x x x C
32
C. F(x)
32
13
x x x C
32
D.
32
31
F(x) x x x C
22
.
Câu 29. Nguyên hàm
Fx
của hàm số
4
2
23
0
x
f x x
x
là
A.
B.
3
3
3
x
F x C
x
C.
3
3
3F x x C
x
D.
3
23
3
x
F x C
x
Câu 30. Trong các hàm số sau đây , hàm số nào là nguyên hàm của
( ) cos
x
f x e x
A.
sin
x
ex
B.
sin
x
ex
C.
sin
x
ex
D.
sin
x
ex
Câu 31. Tính:
5
P (2x 5) dx
A.
6
(2x 5)
PC
6

B.
6
1 (2x 5)
P . C
26

Group Nhóm Toán | Trắc nghiệm 2016-2017
12
1
C.
6
(2x 5)
PC
2

D.
6
(2x 5)
PC
5

.
Câu 32: Hàm số nào sau đây là một nguyên hàm của sin2x
A.
2
sin x
B. 2cos2x C. -2cos2x D. 2sinx
Câu 33. Tìm
x
3x 1
d
ta được
A.

2
3
3x 1
C
B.

1
ln 3x 1
3
C
C.
ln 3x 1
C
D.
ln 3x 1
C
Câu 34. Tìm
5
2x 1 x
d
ta được
A.

6
1
2x 1
12
C
B.

6
1
2x 1
6
C
C.

4
2x 1
C
D.

4
5 2x 1
C
Câu 35. Nguyên hàm của hàm số
2
( ) 1
f x x x
là
A.
23
23
xx
xC
B.
23
23
xx
C
C.
12
xC
D.
23
x x x C
Mức độ thông hiểu.
Câu 36. Một nguyên hàm của hàm số:
4
I sin xcosxdx
là:
A.
5
sin x
IC
5

B.
5
cos x
IC
5

C.
5
sin x
IC
5
D.
5
I sin x C
Câu 37. Trong các hàm số sau đây , hàm số nào là nguyên hàm của
2
1
()
cos (2 1)
fx
x
A.
2
1
sin (2 1)x
B.
2
1
sin (2 1)x
C.
1
tan(2 1)
2
x
D.
1
cot(2 1)
2
x
Câu 38. Nguyên hàm
Fx
của hàm số
3
3
1
0
x
f x x
x
là
Group Nhóm Toán | Trắc nghiệm 2016-2017
12
2
A.
2
31
3 ln
2
F x x x C
x
x
B.
2
31
3 ln
2
F x x x C
x
x
C.
2
31
3 ln
2
F x x x C
x
x
D.
2
31
3 ln
2
F x x x C
x
x
Câu 39.
Fx
là nguyên hàm của hàm số
2
23
0
x
f x x
x
, biết rằng
11F
.
Fx
là
biểu thức nào sau đây
A.
3
22F x x
x
B.
3
2 ln 2F x x
x
C.
3
24F x x
x
D.
3
2 ln 4F x x
x
Câu 40. Tìm một nguyên hàm
Fx
của hàm số
2
0
b
f x ax x
x
, biết rằng
11F
,
14F
,
10f
.
Fx
là biểu thức nào sau đây
A.
2
1
4F x x
x
B.
2
1
2F x x
x
C.
2
17
22
x
Fx
x
D.
2
15
22
x
Fx
x
Câu 41. Hàm số
2
x
F x e
là nguyên hàm của hàm số
A.
2
2.
x
f x x e
B.
2x
f x e
C.
2
2
x
e
fx
x
D.
2
2
.1
x
f x x e
Câu 42. Hàm số nào dưới đây không là nguyên hàm của hàm số
2
2
1
xx
fx
x
Group Nhóm Toán | Trắc nghiệm 2016-2017
12
3
A.
2
1
1
xx
x
B.
2
1
1
xx
x
C.
2
1
1
xx
x
D.
2
1
x
x
Câu 43. Nguyên hàm
Fx
của hàm số
2
2
1
0
x
f x x
x
là
A.
3
1
2
3
x
F x x C
x
B.
3
1
2
3
x
F x x C
x
C.
3
2
3
2
x
x
F x C
x
D.
3
3
2
3
2
x
x
F x C
x
Câu 44. Một nguyên hàm của hàm số: y = sinx.cosx là:
A.
1
cos2
2
x
+C B.
cos .sinxx
+C C. cos8x + cos2x+C D.
1
cos2
4
x
+C .
Câu 45. Một nguyên hàm của hàm số: y = cos5x.cosx là:
A. cos6x B. sin6x C.
1 1 1
sin6 sin4
2 6 4



xx
D.
1 sin6 sin4
2 6 4




xx
Câu 46: Nguyên hàm của hàm số f(x) = 2sin3xcos2x
A.
Cxx cos5cos
5
1
B.
1
cos5 cos
5
x x C
C.
5cos5 cosx x C
D. Kết quả khác
Câu 47: Tìm hàm số f(x) biết rằng f’(x) = 2x + 1 và f(1) = 5
A. x
2
+ x + 3 B. x
2
+ x - 3 C. x
2
+ x D. Kết quả khác
Câu 48: Tìm hàm số f(x) biết rằng f’(x) = 4
xx
và f(4) = 0
Group Nhóm Toán | Trắc nghiệm 2016-2017
12
4
A.
3
40
23
8
2
xxx
B.
2
8 40
3 2 3
xx

C.
2
8 40
3 2 3
x x x

D. Kết quả khác
Câu 49: Nguyên hàm của hàm số
2
x
xe dx
là
A.
2
x
xe C
B.
2
2
x
e
C
C.
2
x
eC
D.
2
x
xe
Câu 50: Tìm hàm số
()
y f x
biết
2
( ) ( )( 1)
f x x x x
và
(0) 3
f
A.
B.
42
( ) 3
42
xx
y f x
C.
42
( ) 3
42
xx
y f x
D.
2
( ) 3 1
y f x x
Câu 51: Tìm
3
(sin 1) cos
x xdx
là:
A.
4
(cos 1)
4
x
C
B.
4
sin
4
x
C
C.
4
(sin 1)
4
x
C
D.
3
4(sin 1)
xC
Câu 52: Tìm
2
32
dx
xx
là:
A.
11
ln ln
21
C
xx
B.
2
ln
1
x
C
x
C.
1
ln
2
x
C
x
D.
ln( 2)( 1)
x x C
Câu 53: Tìm
cos2
x xdx
là:
A.
11
sin2 cos2
24
x x x C
B.
11
sin2 cos2
22
x x x C
C.
2
sin2
4
xx
C
D.
sin2
xC
Group Nhóm Toán | Trắc nghiệm 2016-2017
12
5
Câu 54: Lựa chọn phương án đúng:
A.
cot ln sinxdx x C
B.
sin cosxdx x C
C.
2
11
dx C
x
x

D.
cos sinxdx x C
Câu 55: Tính nguyên hàm
3
sin cosx xdx
ta được kết quả là:
A.
4
sin xC
B.
4
1
4
sin xC
C.
4
sin xC
D.
4
1
4
sin xC
Câu 56: Cho
2
3 2 3()f x x x
có một nguyên hàm triệt tiêu khi
1x
. Nguyên hàm đó là kết quả
nào sau đây?
A.
32
3()F x x x x
B.
32
31()F x x x x
C.
32
32()F x x x x
D.
32
31()F x x x x
Câu 57. Hàm số nào sau đây không phải là nguyên hàm của hàm số
2
2
1
()
()
()
xx
fx
x
A.
2
1
1
xx
x

B.
2
1
1
xx
x

C.
2
1
1
xx
x

D.
2
1
x
x
Câu 58: Kết quả nào sai trong các kết quả sau:
A.
11
2 5 1 1
10 5 2 2 5 5. .ln .ln
xx
x x x
dx C

B.
44
34
21
4
ln
xx
dx x C
xx

C.
2
2
11
21
1
ln
xx
dx x C
x
x
D.
2
tan tanxdx x x C
Câu 59: Tìm nguyên hàm
3
2
4
x dx
x



A.
3
5
5
4
3
lnx x C
B.
3
5
3
4
5
lnx x C
Group Nhóm Toán | Trắc nghiệm 2016-2017
12
6
C.
3
5
3
4
5
lnx x C
D.
3
5
3
4
5
lnx x C
Câu 60: Kết quả của
2
1
x
dx
x
là:
A.
2
1 xC
B.
2
1
1
C
x
C.
2
1
1
C
x
D.
2
1 xC
Câu 61: Tìm nguyên hàm
2
1( sin )x dx
A.
21
22
34
cos sinx x x C
B.
21
22
34
cos sinx x x C
C.
21
2 2 2
34
cos sinx x x C
D.
21
22
34
cos sinx x x C
Câu 62: Tính
2
tan xdx
, kết quả là:
A.
tanx x C
B.
tanx x C
C.
tanx x C
D.
3
1
tan
3
xC
Câu 63: Trong các mệnh đề sau đây, mệnh đề nào sai ?
23
2
2
11
( ) sin sin3 (sin2 - sin 4 )
42
1
( ) tan tan
3
11
( ) ln( 2 3)
2 3 2
I x xdx x x C
II xdx x C
x
III dx x x C
xx
A. Chỉ (I) và (II) B. Chỉ (III) C. Chỉ (II) và (III) D. Chỉ (II)
Câu 64. Trong các hàm số sau đây , hàm số nào là nguyên hàm của
41
( ) 5
13
2
fx
x
x
A.
4
ln 1 3 5
3
x x x
B.
4
ln 1 3
3
x
C.
4
ln 1 3 5
3
xx
D.
4
ln 1 3
3
xx
Câu 65. Nguyên hàm của hàm số
()
f x x
là
Group Nhóm Toán | Trắc nghiệm 2016-2017
12
7
A.
xC
B.
1
2
C
x
C.
2
3
x x C
D.
3
2
x x C
Câu 66. Hàm số
( ) t anx
x
F x e C
là nguyên hàm của hàm số
()
fx
nào ?
A.

2
1
()
sin
x
f x e
x
B.

2
1
()
sin
x
f x e
x
C.

2
1
()
os
x
f x e
cx
D.

2
1
()
os
x
f x e
cx
Câu 67. Nguyên hàm F(x) của hàm số
32
( ) 4 3x 2
f x x
trên R thoả mãn điều kiện
( 1) 3
F
là
A.
43
2x 3
xx
B.
43
24
x x x
C.
43
2x 4
xx
D.
43
23
x x x
Câu 68. Một nguyên hàm của hàm số
( ) 2sin3 . os3
f x x c x
là
A.
1
cos2x
4
B.
1
cos6x
6
C.
cos3 .sin3
xx
D.
1
sin2
4
x
Câu 69: Một nguyên hàm của hàm số
2
1y x x
là:
A.
2
2
2
1
2
x
F x x
B.
2
2
1
1
2
F x x
C.
2
2
1
1
3
F x x
D.
3
2
1
1
3
F x x
Câu 70: Một nguyên hàm của hàm số
3
sin .cosy x x
là:
A.
4
sin
1
4
x
Fx
B.
42
sin cos
42
xx
Fx
C.
24
cos cos
24
xx
Fx
D.
24
cos cos
24
xx
Fx
Câu 71: Một nguyên hàm của hàm số
2
3.
x
y x e
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
12
8
A.
2
3
x
F x e
B.
2
3
2
x
F x e
C.
2
2
3
2
x
x
F x e
D.
3
2
2
x
x
F x e
Câu 72: Một nguyên hàm của hàm số
2ln x
y
x
là:
A.
2
2lnF x x
B.
2
ln
2
x
Fx
C.
2
lnF x x
D.
2
lnF x x
Câu 73: Một nguyên hàm của hàm số
21
x
y x e
là:
A.
2
21
x
F x e x x
B.
2
2 1 4
x
F x e x x
C.
2
2 1 4
x
F x e x x
D.
2
21
x
F x e x x
Câu 74: Một nguyên hàm của hàm số
sin2y x x
là:
A.
1
cos2 sin2
24
x
F x x x
B.
1
cos2 sin2
22
x
F x x x
C.
1
cos2 sin2
22
x
F x x x
D.
1
cos2 sin2
24
x
F x x x
Câu 75: Một nguyên hàm của hàm số
2
ln2x
y
x
là:
A.
1
ln2 2F x x
x
B.
1
ln2 2F x x
x

C.
1
ln2 2F x x
x
D.
1
2 ln2F x x
x
Câu 76: Một nguyên hàm của hàm số f(x) =
tanx
2
os
e
cx
là:
A.
tanx
2
os
e
cx
B.
tanx
e
C.
tanx
tanxe
D.
tanx
.tanxe
Group Nhóm Toán | Trắc nghiệm 2016-2017
12
9
Câu 77: Nguyên hàm của hàm số
2
(tanx cot )yx
là:
A.
3
1
(tanx cot )
3
F x x C
B.
tanx-cotF x x C
C.
22
11
2(tanx cot )( )
os sin
F x x C
c x x
D.
tanx+cotF x x C
Câu 78: Nguyên hàm của hàm số: y =
22
1
os sinc x x
là:
A.
t anx.cot
xC
B.
t anx- cot
xC
C.
t anx- cot
xC
D.
1
sin
22
x
C
.
Câu 79: Nguyên hàm của hàm số: y =
10
3
1
14x
là:
A.

7
3
3
14
7
xC
B.

7
3
12
14
7
xC
C.

7
3
3
14
28
xC
D.
7
3
3
14
28
xC
.
Câu 80: Một nguyên hàm của hàm số: y =
2
3
71
x
x
là:
A.
3
ln 7 1x
B.
3
1
ln 7 1
7
x
C.
3
1
ln 7 1
21
x
D.
3
1
ln 7 1
14
x
Câu 81: Nguyên hàm của hàm số f(x) =
(2 )
xx
ee
là:
A.
2
x
e x C
B.
xx
e e C

C.
2
x
e x C
D.
22
x
e x C
Mức độ vận dụng.
Câu 82: Một nguyên hàm của hàm số: y =
cos
5sin 9
x
x
là:
A.
ln 5sin 9x
B.
1
ln 5sin 9
5
x
C.
1
ln 5sin 9
5
x
D.
5ln 5sin 9x
Group Nhóm Toán | Trắc nghiệm 2016-2017
13
0
Câu 83: Tính:
.
x
P x e dx
A.
.
x
P xe C
B.
x
P e C
C.
.
xx
P xe e C
D.
.
xx
P xe e C
.
Câu 84: Tìm hàm số f(x) biết rằng
'( ) ax+ , '( ) , ( ) , ( )
b
f x f f f
x
2
1 0 1 4 1 2
A.
2
51
2
2
x
x
B.
2
15
22
x
x

C.
2
15
22
x
x

D. Kết quả khác
Lược giải:
Sử dụng máy tính kiểm tra từng đáp án:
- Nhập hàm số
- Dùng phím CALC để kiểm tra các điều kiện
- Đáp án đúng: B
Câu 85: Hàm số nào sau đây là một nguyên hàm của hàm số
2
()f x x k
với
0?k
A.
22
( ) ln
22
xk
f x x k x x k
B.
22
1
( ) ln
22
x
f x x k x x k
C.
2
( ) ln
2
k
f x x x k
D.
2
1
()fx
xk
Lược giải:
'(1) 0, (1) 4, ( 1) 2f f f
Group Nhóm Toán | Trắc nghiệm 2016-2017
13
1
2
2 2 2 2
22
x
1
x k 1 x x k
xk
x k ln x x k x k x k
2 2 2 2 2
x k x x k
Câu 86: Nếu
2
( ) ( ) 2 -1f x ax bx c x
là một nguyên hàm của hàm số
2
10 -7 2
()
2 -1
xx
gx
x
trên
khoảng
1
;
2
thì a+b+c có giá trị là
A. 3 B. 0
C. 4 D. 2
Lược giải:
22
2
5ax ( 2a 3b)x b c 10x 7x 2
(ax bx c) 2x 1
2x 3 2x 3
a2
b 1 a b c 2
c1
Câu 87: Xác định a, b, c sao cho
2
( ) ( ) 2 -3g x ax bx c x
là một nguyên hàm của hàm số
2
20 -30 7
()
2 -3
xx
fx
x
trong khoảng
3
;
2
A.a=4, b=2, c=2 B. a=1, b=-2, c=4
C. a=-2, b=1, c=4 D. a=4, b=-2, c=1
Lược giải:
22
2
5ax ( 6a 3b)x 3b c 20x 30x 7
(ax bx c) 2x 3
2x 3 2x 3
a4
b2
c1
Group Nhóm Toán | Trắc nghiệm 2016-2017
13
2
Câu 88: Một nguyên hàm của hàm số:
2
( ) sin 1f x x x
là:
A.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
B.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
C.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
D.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
Lược giải:
Đặt
2
( sin 1 )I x x dx
- Dùng phương pháp đổi biến, đặt
2
1tx
ta được
sinI t tdt
- Dùng phương pháp nguyên hàm từng phần, đặt
, sinu t dv tdt
- Ta được
2 2 2
cos cos 1 cos 1 sin 1I t t tdt x x x C
Câu 89: Trong các hàm số sau:
(I)
2
( ) 1f x x
(II)
2
( ) 1 5f x x
(III)
2
1
()
1
fx
x
(IV)
2
1
( ) -2
1
fx
x
Hàm số nào có một nguyên hàm là hàm số
2
( ) ln 1F x x x
A. Chỉ (I) B. Chỉ (III)
C. Chỉ (II) D. Chỉ (III) và (IV)
Lược giải:
2
2
22
x
1
1
x1
ln x x 1
x x 1 x 1
Câu 90: Một nguyên hàm của hàm số
2
3
1
()f x x
x
là hàm số nào sau đây:
A.
36
25
3 12
( ) ln
55
F x x x x x
B.
3
3
11
()
3
F x x
x
C.
2
3
()F x x x x
D.
35
26
3 12
( ) ln
55
F x x x x x
Group Nhóm Toán | Trắc nghiệm 2016-2017
13
3
Lược giải:
2
36
25
3
3 12 1
x x x ln x x
55
x
Câu 91: Xét các mệnh đề
(I)
( ) cosF x x x
là một nguyên hàm của
2
( ) sin -cos
22
xx
fx
(II)
4
( ) 6
4
x
F x x
là một nguyên hàm của
3
3
()f x x
x
(III)
( ) tanF x x
là một nguyên hàm của
( ) -ln cosf x x
Mệnh đề nào sai ?
A. (I) và (II) B. Chỉ (III)
C. Chỉ (II) D. Chỉ (I) và (III)
Lược giải:
ln cosx tanx
(vì
ln cosx
là một nguyên hàm của tanx)
Câu 92: Trong các mệnh đề sau đây mệnh đề nào đúng ?
(I)
2
2
1
ln( 4)
42
xdx
xC
x
(II)
2
1
cot -
sin
xdx C
x
(III)
2cos 2cos
1
sin -
2
xx
e xdx e C
A. Chỉ (I) B. Chỉ (III)
C. Chỉ (I) và (II) D. Chỉ (I) và (III)
Group Nhóm Toán | Trắc nghiệm 2016-2017
13
4
Lược giải:
2
2
22
xdx 1 d(x 4) 1
ln(x 4) C
x 4 2 x 4 2
2cosx 2cosx 2cosx
11
e sinxdx e d(cosx) e C
22
Câu 93: Tìm nguyên hàm
22
( ) ( tan tan )
x
F x e a x b x c
là một nguyên hàm của
23
( ) tan
x
f x e x
trên khoản
;
22
A.
22
1 2 2
( ) ( tan tan )
2 2 2
x
F x e x x
B.
22
1 2 1
( ) ( tan tan )
2 2 2
x
F x e x x
C.
22
1 2 1
( ) ( tan tan )
2 2 2
x
F x e x x
D.
22
1 2 2
( ) ( tan tan )
2 2 2
x
F x e x x
Lược giải:
- Có thể dùng đạo hàm để kiểm tra từng đáp án.
- Hoặc tìm đạo hàm của
22
( ) ( tan tan )
x
F x e a x b x c
rồi đồng nhất với
23
( ) tan
x
f x e x
2 2 2 2 2
'( ) 2 ( tan tan ) 2 (1 tan )tan (1 tan )
xx
F x e a x b x c e a x x b x
2 3 2
2 tan ( 2 )tan (2 2 )tan 2
x
e a x a b x a b x b c
()Fx
là nguyên hàm của f(x) nên
'( ) ( )F x f x
Suy ra
1
21
2
20
2
2
2 2 0
1
20
2
a
a
ab
b
ab
bc
c
Đáp án đúng: B
Group Nhóm Toán | Trắc nghiệm 2016-2017
13
5
Câu 94: Nguyên hàm của hàm số: y =
2
x
x
e
là:
A.
2 ln 2
x
x
e
C
B.
(1 ln 2)2
x
x
e
C
C.
.2
x
x
e
C
x
D.
ln 2
2
x
x
e
C
Câu 95: Nguyên hàm của hàm số: y =
2
os
2
x
c
là:
A.

1
( sin )
2
x x C
B.

1
(1 os )
2
c x C
C.
1
os
22
x
cC
D.
1
sin
22
x
C
.
Câu 96: Nguyên hàm của hàm số: y = cos
2
x.sinx là:
A.
3
1
cos
3
xC
B.
3
cos
xC

C.
3
1
sin
3
xC
D.

3
1
cos
3
xC
.
Câu 97: Một nguyên hàm của hàm số: y =
2
x
x
e
e
là:
A.2
ln( 2)
x
e
+ C B.
ln( 2)
x
e
+ C C.
e ln( 2)
xx
e
+ C D.
2
x
e
+ C.
Câu 98: Tính:
3
sinP xdx
A.
2
3sin .cosP x x C
B.
3
1
sin sin
3
P x x C
C.
3
1
cos os
3
P x c x C
D.
3
1
os sin
3
P c x x C
.
Câu 99: Một nguyên hàm của hàm số:
3
2
2
x
y
x
là:
A.
2
2xx
B.
22
1
42
3
xx
C.
22
1
2
3
xx
D.
22
1
42
3
xx
TÍCH PHÂN
Mức độ nhận biết
Group Nhóm Toán | Trắc nghiệm 2016-2017
13
6
Câu 1: Tích phân
1
2
0
(3 2 1)I x x dx
bằng:
A.
1I
B.
2I
C.
3I
D. Đáp án khác
Câu 2: Tích phân
2
0
sin xI dx
bằng:
A. -1 B. 1 C. 2 D. 0
Câu 3: Tích phân
1
2
0
( 1)I x dx
bằng:
A.
8
3
B. 2 C.
7
3
D. 4
Câu 4: Tích phân
1
1
0
x
I e dx
bằng:
A.
2
ee
B.
2
e
C.
2
1e
D. e + 1
Câu 5: Tích phân
4
3
1
2
x
I dx
x
bằng:
A. -1 + 3ln2 B.
2 3ln2
C.
4ln2
D.
1 3ln2
Câu 6: Tích phân
1
2
0
1
25
x
I dx
xx

bằng:
A.
8
ln
5
B.
18
ln
25
C.
8
2ln
5
D.
8
2ln
5
Câu 7: Tích phân
1
1
e
I dx
x
bằng:
A.
e
B. 1 C. -1 D.
1
e
Câu 8: Tích phân
1
0
x
I e dx
bằng :
Group Nhóm Toán | Trắc nghiệm 2016-2017
13
7
A.
1e
B.
1 e
C.
e
D. 0
Câu 9: Tích phân
2
2
0
2
x
I e dx
bằng :
A.
4
e
B.
4
1e
C.
4
4e
D.
4
31e
Câu 10: Tích phân
2
2
4
1
1
I x dx
x




bằng:
A.
19
8
B.
23
8
C.
21
8
D.
25
8
Câu 11: Tích phân
1
1
3
e
I dx
x
bằng:
A.
ln 2e
B.
ln 7e
C.
3
ln
4
e



D.
ln 4 3e


Câu 12: Tích phân
3
3
1
1I x dx

bằng:
A. 24 B. 22 C. 20 D. 18
Câu 13: Tích phân
2
2
1
1
21
I dx
x
bằng:
A. 1 B.
1
2
C.
1
15
D.
1
4
Câu 14: Tích phân
1
2
0
56
dx
I
xx

bằng:
A. I = 1 B.
4
ln
3
I
C. I = ln2 D. I = ln2
Câu 15: Tích phân:
1
3
0
( 1)
xdx
J
x
bằng:
A.
1
8
J
B.
1
4
J
C. J =2 D. J = 1
Câu 16: Tích phân
3
2
2
1
x
K dx
x
bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
13
8
A. K = ln2 B. K = 2ln2 C.
8
ln
3
K
D.
18
ln
23
K
Câu 17: Tích phân
3
2
1
1I x x dx
bằng:
A.
42
3
B.
8 2 2
3
C.
42
3
D.
8 2 2
3
Câu 18: Tích phân
1
19
0
1I x x dx
bằng:
A.
1
420
B.
1
380
C.
1
342
D.
1
462
Câu 19: Tích phân
1
2 ln
2
e
x
I dx
x
bằng:
A.
32
3
B.
32
3
C.
32
6
D.
3 3 2 2
3
Câu 20: Tích phân
6
0
tanI xdx
bằng:
A.
3
ln
2
B. -
3
ln
2
C.
23
ln
3
D. Đáp án khác.
Câu 21. Tích phân
1
0
2x
dx
bằng:
A.
2ln
B.
3ln
C.
3ln
D.
2ln
Câu 22. Tích phân
a
x
dx
ln
23
2
1
0
. Giá trị của
a
bằng:
A. 1 B. 2 C. 3 D. 4
Group Nhóm Toán | Trắc nghiệm 2016-2017
13
9
Câu 23. Cho tích phân
dxx
1
0
3
1
, với cách đặt
3
1 xt
thì tích phân đã cho bằng với tích phân nào
?
A.
1
0
3
3 dtt
B.
1
0
2
3 dtt
C.
1
0
3
dtt
D.
1
0
3 tdt
Câu 24. Tích phân
dx
x
x
e
1
ln
bằng:
A.
3
B. 1 C.
2ln
D.
2
1
Câu 25. Tích phân I =
1
0
xdx
có giá trị là:
A.
3
2
B.
1
2
C.
2
3
D. 2
Câu 26. Tích phân I =
4
0
cos2xdx
có giá trị là:
A.
1
2
B. 1 C. -2 D. -1
Câu 27. Tích phân I =
1
3
0
( 1)
x
dx
x
có giá trị là:
A.
1
2
B.
1
4
C.
1
8
D.
1
8
Câu 28. Tích phân I =
2
0
sin3 .cosx xdx
có giá trị là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
14
0
A.
1
2
B.
1
3
C.
1
2
D.
1
4
Câu 29. Tích phân I =
1
0
23
2
32
dx
x
xx
bằng:
A.
2
3
ln3
3
1
B.
3
2
ln3
3
1
C.
3
2
ln3
3
1
D.
Câu 30. I =
1
0
22
)1)(1( dxxx
A.
5
4
B.
5
6
C.
5
4
D.
5
1
Câu 31. Tích phân I =
6
0
2
sin
xdx
có giá trị là:
A.
8
3
12
B.
8
3
12
C.
8
3
12
D.
4
3
12
Câu 32. Tích phân I =
2
1
2323
132143 dxxxxxxx
có giá trị là:
A.
12
13
B.
12
5
C.
3
2
D.
12
5
Câu 33. Tích phân
4
0
2
2
sin2
x
bằng:
A.
2
2
4
B.
2
2
4
C.
2
2
4
D.
2
2
4
Câu 34. Cho tích phân
dxx
1
0
3
1
, với cách đặt
3
1 xt
thì tích phân đã cho bằng với tích phân nào
Group Nhóm Toán | Trắc nghiệm 2016-2017
14
1
?
A.
1
0
3
3 dtt
B.
1
0
2
3 dtt
C.
1
0
3
dtt
D.
1
0
3 tdt
Câu 35. Tích phân
dx
x
xdx
1
0
12
bằng:
A.
3
1
B. 1 C.
2ln
D.
2
1
Câu 36. Gía trị của
1
3
0
3
x
e dx
bằng :
A. e
3
- 1 B. e
3
+ 1 C. e
3
D. 2e
3
Câu 37. Tích Phân
1
2
0
( 1)
x dx
bằng :
A.
1
3
B. 1 C. 3 D. 4
Câu 38. Tích Phân
1
0
31
x dx
bằng :
A.
14
9
B. 0 C. 9 D.
14
3
Câu 39. Tích Phân
1
0
31
x x dx
bằng
A. 9 B.
7
9
C. 3 D. 1
Group Nhóm Toán | Trắc nghiệm 2016-2017
14
2
Câu 40. Tích Phân

2
2
0
5 13
56
x
dx
xx
bằng
A.
43 4
ln
73
B.
43 3
ln
74
C.
43 4
ln
73
D.
47 4
ln
33
Mức độ thông hiểu.
Câu 41: Tích phân
4
2
0
tanI xdx
bằng:
A. I = 2 B. ln2 C.
1
4
I

D.
3
I
Câu 42: Tích phân
1
2
0
1L x x dx
bằng:
A.
1L 
B.
1
4
L
C.
1L
D.
1
3
L
Câu 43: Tích phân
2
1
(2 1)lnK x xdx
bằng:
A.
1
3ln2
2
K 
B.
1
2
K
C. K = 3ln2 D.
1
2ln2
2
K 
Câu 44: Tích phân
0
sinL x xdx
bằng:
A. L = B. L =  C. L = 2 D. K = 0
Câu 45: Tích phân
3
0
cosI x xdx
bằng:
A.
31
6
B.
31
2
C.
31
62
D.
3
2
Group Nhóm Toán | Trắc nghiệm 2016-2017
14
3
Câu 46: Tích phân
ln2
0
x
I xe dx
bằng:
A.
1
1 ln2
2
B.
1
1 ln2
2
C.
1
ln2 1
2
D.
1
1 ln2
4
Câu 47: Tích phân
2
2
1
ln x
I dx
x
bằng:
A.
1
1 ln2
2
B.
1
1 ln2
2
C.
1
ln2 1
2
D.
1
1 ln2
4
Câu 48: Giả sử
5
1
ln
21
dx
K
x
. Giá trị của K là:
A. 9 B. 8 C. 81 D. 3
Câu 49: Biến đổi
3
0
11
x
dx
x
thành
2
1
f t dt
, với
1tx
. Khi đó f(t) là hàm nào trong các hàm
số sau:
A.
2
22f t t t
B.
2
f t t t
C.
2
f t t t
D.
2
22f t t t
Câu 50: Đổi biến x = 2sint tích phân
1
2
0
4
dx
x
trở thành:
A.
6
0
tdt
B.
6
0
dt
C.
6
0
1
dt
t
D.
3
0
dt
Câu 51: Tích phân
2
2
4
sin
dx
I
x
bằng:
A. 4 B. 3 C. 1 D. 2
Câu 52: Cho
2
1
cos ln
e
x
I dx
x
, ta tính được:
A. I = cos1 B. I = 1 C. I = sin1 D. Một kết quả khác
Group Nhóm Toán | Trắc nghiệm 2016-2017
14
4
Câu 53: Tích phân
23
2
2
3
3
I dx
xx
bằng:
A.
6
B.
C.
3
D.
2
Câu 54: Giả sử
( ) 2
b
a
f x dx
và
( ) 3
b
c
f x dx
và a < b < c thì
()
c
a
f x dx
bằng?
A. 5 B. 1 C. -1 D. -5
Câu 55: Tính thể tích khối tròn xoay tạo nên do quay quanh trục Ox hình phẳng giới hạn bởi các
đường y = (1 – x
2
), y = 0, x = 0 và x = 2 bằng:
A.
82
3
B. 2
C.
46
15
D.
5
2
Câu 56: Cho
16
1
I xdx
và
4
0
cos2J xdx
. Khi đó:
A. I < J B. I > J C. I = J D. I > J > 1
Câu 57: Tích phân
4
0
2I x dx
bằng:
A. 0 B. 2 C. 8 D. 4
Câu 58: Tích phân
2
0
sinI x xdx
bằng :
A.
2
4
B.
2
4
C.
2
23
D.
2
23
Câu 59: Kết quả của
1
1
dx
x
là:
A.
0
B.-1 C.
1
2
D. Không tồn tại
Câu 60: Cho
2
0
3f x dx
.Khi đó
2
0
43f x dx


bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
14
5
A. 2 B. 4 C. 6 D. 8
Câu 61. Tích phân I =
3
2
2
1
x
dx
x
có giá trị là:
A.
22
B.
2 2 3
C.
2 2 3
D.
3
Câu 62. Tích phân I =
1
2
0
1
43
dx
xx
có giá trị là:
A.
13
ln
32
B.
13
ln
32
C.
13
ln
22
D.
13
ln
22
Câu 63. Tích phân I =
3
2
2
1
x
dx
x
có giá trị là:
A.
22
B.
2 2 3
C.
2 2 3
D.
3
Câu 64. Cho
143
23
xxxxf
và
. Tích phân
dxxgxf
2
1
bằng với
tích phân:
A.
2
1
23
22 dxxxx
B.
1
1
23
22 dxxxx
2
1
23
22 dxxxx
C.
1
1
23
22 dxxxx
2
1
23
22 dxxxx
D. tích phân khác
Câu 65. Tích phân
dx
x
xx
2
0
2
3
1cos
cos.sin
bằng:
A.
2ln
2
1
3
1
B.
2ln
2
1
2
1
C.
2ln
3
1
2
1
D.
2ln
2
1
2
1
Group Nhóm Toán | Trắc nghiệm 2016-2017
14
6
Câu 66. Cho tích phân
dx
x
x
I
1
0
3
và
dx
x
x
J
2
0
12sin3
cos
, phát biểu nào sau đây đúng:
A.
JI
B.
2I
C.
5ln
3
1
J
D.
JI 2
Câu 67. Cho tích phân
dxxxI
1
0
2
1
bằng:
A.
dxxx
1
0
3
4
B.
1
0
43
43
xx
C.
1
0
3
2
)
3
(
x
x
D.
2
Câu 68. Tích phân
0
0
222
adxxax
a
bằng:
A.
8
.
4
a
B.
16
.
4
a
C.
16
.
3
a
D.
8
.
3
a
Câu 69. Tích phân
dx
x
x
8
1
3
1
bằng:
A.
10
141
B.
10
142
C.
5
8
D. một kết quả khác
Câu 70. Tích phân I =
e
dx
x
x
1
2
ln1
có giá trị là:
A.
3
1
B.
3
2
C.
3
4
D.
3
4
Câu 71. Tích phân I =
1
0
1
2
. dxex
x
có giá trị là:
A.
2
2
ee
B.
3
2
ee
C.
2
2
ee
D.
3
2
ee
Group Nhóm Toán | Trắc nghiệm 2016-2017
14
7
Câu 72. Tích phân I =
1
0
1 dxex
x
có giá trị là:
A. e + 2 B. 2 - e C. e - 2 D. e
Câu 73. Tích phân I =
0
2
sin2
cos
dx
x
x
có giá trị là:
A. ln3 B. 0 C. - ln2 D. ln2
Câu 74. Tích Phân
6
3
0
sin .cos
x xdx
bằng:
A. 6 B. 5 C. 4 D.
1
64
Câu 75. Nếu
1
0
()
f x dx
=5 và
1
2
()
f x dx
= 2 thì
2
0
()
f x dx
bằng :
A. 8 B. 2 C. 3 D. -3
Câu 76. Tích Phân I =
3
0
tan
xdx
là :
A. ln2 B. –ln2 C.
1
2
ln2 D. -
1
2
ln2
Câu 77. Cho tích phân
dxxxI
1
0
1
bằng:
A.
dxxx
1
0
32
B.
1
0
32
32
xx
C.
1
0
3
2
)
3
(
x
x
D.
2
Group Nhóm Toán | Trắc nghiệm 2016-2017
14
8
Câu 78. Tích Phân I =
3
2
2
ln( )
x x dx
là :
A. 3ln3 B. 2ln2 C. 3ln3-2 D. 2-3ln3
Câu 79. Tích Phân I =
4
0
.cosx
x dx
là :
A.
1
4
B.
3
2
C.
22
1
82

D.
22
1
82

Câu 80. Tích phân I =
3
2
2
ln[2 x(x 3)]dx
có giá trị là:
A.
4ln2 3
B.
5ln5 4ln2 3
C.
5ln5 4ln2 3
D.
5ln5 4ln2 3
Mức độ vận dụng.
Câu 81: Biết
0
2 4 0
b
x dx
.Khi đó b nhận giá trị bằng:
A.
0b
hoặc
2b
B.
0b
hoặc
4b
C.
1b
hoặc
2b
D.
1b
hoặc
4b
Câu 82: Để hàm số
sinf x a x b

thỏa mãn
12f
và
1
0
4f x dx
thì a, b nhận giá trị :
A.
,0ab

B.
,2ab

C.
2 , 2ab

D.
2 , 3ab

Group Nhóm Toán | Trắc nghiệm 2016-2017
14
9
Câu 83:
4
42
0
cos 1 tan
dx
I
xx
bằng
A. 1 B. 0 C.
1
2
D. Không tồn tại
Câu 84: Giả sử
4
0
2
sin3 sin2
2
I x xdx a b
khi đó a+b là
A.
1
6
B.
3
10
C.
3
10
D.
1
5
Câu 85: Giả sử
0
2
1
3 5 1 2
ln
23
xx
I dx a b
x

. Khi đó giá trị
2
ab
là
A. 30 B. 40 C. 50 D. 60
Câu 86. Tập hợp giá trị của m sao cho
0
(2 4)
m
x dx
= 5 là :
A. {5} B. {5 ; -1} C. {4} D. {4 ; -1}
Câu 87. Biết rằng
5
1
1
21
dx
x
= lna . Gía trị của a là :
A. 9 B. 3 C. 27 D. 81
Câu 88. Biết tích phân
N
M
dxxx
1
0
3
1
, với
N
M
là phân số tối giản. Giá trị
NM
bằng:
A.
35
B.
36
C.
37
D.
38
Câu 89. Tìm các hằng số A , B để hàm số f(x) = A.sinx + B thỏa các điều kiện:
Group Nhóm Toán | Trắc nghiệm 2016-2017
15
0
f ' (1) = 2 ;
4)(
2
0
dxxf
A.
2
2
B
A
B.
2
2
B
A
C.
2
2
B
A
D.
2
2
B
A
HD: f ' (x) = A.cosx f ' (1) = - A mà f ' (1) = 2 A =
2
2
0
)( dxxf
...= 2B mà
4)(
2
0
dxxf
B = 2
Câu 90. Tìm a>0 sao cho
2
0
.4
a
x
x e dx
A.
4
B.
1
4
C.
1
2
D. 2
HD:
Sử dụng phương pháp tích phân từng phần tính được
2
2 ( 2) 4
a
I e a
Vì I=4 =>a=2
Câu 91. Giá trị nào của b để
0
(2 6) 0
b
x dx
A. b = 2 hay b = 3 B. b = 0 hay b = 1
C. b = 5 hay b = 0 D. b = 1 hay b = 5
Câu 92. Giá trị nào của a để
0
(4 4) 0
b
x dx
A. a = 0 B. a = 1
Group Nhóm Toán | Trắc nghiệm 2016-2017
15
1
C. a = 2 D. a = -1
Câu 93. Tích phân I =
3
2
0
sin
1 cos
x
dx
x
có giá trị là:
A.
1
3
B.
1
4
C.
1
2
D. 2
Câu 94. Tích phân I =
1
2
0
1
1
dx
xx
có giá trị là:
A.
3
3
B.
3
6
C.
3
4
D.
3
9
Câu 95. Tích phân I =
7
3
0
1
11
dx
x
có giá trị là:
A.
93
3ln
22
B.
93
3ln
22
C.
92
3ln
23
D.
92
3ln
23
ỨNG DỤNG CỦA TÍCH PHÂN
Mức độ nhận biết.
Câu 1. Thể tích của khối tròn xoay được giới hạn bởi đồ thị hàm số f(x) liên tục trên đoạn
;ab
trục
Ox và hai đường thẳng
,x a x b
quay quanh trục Ox , có công thức là:
A.
2
b
a
V f x dx
B.
2
b
a
V f x dx
Group Nhóm Toán | Trắc nghiệm 2016-2017
15
2
C.
b
a
V f x dx
D.
b
a
V f x dx
Câu 2. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số
y f x
liên tục, trục hoành và
hai đường thẳng
,x a x b
được tính theo công thức:
A.
b
a
S f x dx
B.
b
a
S f x dx
C.
0
0
b
a
S f x dx f x dx

D.
0
0
b
a
S f x dx f x dx

Câu 3.Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số
12
,y f x y f x
liên tục và
hai đường thẳng
,x a x b
được tính theo công thức:
A.
12
b
a
S f x f x dx
B.
12
b
a
S f x f x dx
C.
12
b
a
S f x f x dx



D.
12
bb
aa
S f x dx f x dx

Câu 4. Thể tích khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các
đường sau:
y f x
, trục Ox và hai đường thẳng
,x a x b
xung quanh trục Ox là:
A.
2
b
a
V f x dx
B.
2
b
a
V f x dx
C.
b
a
V f x dx
D.
2
2
b
a
V f x dx
Câu 5. Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số
2
yx
, trục hoành và hai
đường thẳng
13,xx
là :
Group Nhóm Toán | Trắc nghiệm 2016-2017
15
3
A.
28
9
dvdt
B.
28
3
dvdt
C.
1
3
dvdt
D. Tất cả đều sai.
Câu 6. Thể tích khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi các đường
3
yx
, trục Ox,
1x
,
1x
một vòng quanh trục Ox là :
A. B.
2
C.
6
7
D.
2
7
Câu 7. Diện tích hình phẳng được giới hạn bởi đường
2
3y x x
và đường thẳng
21yx
là :
A.
7
6
dvdt
B.
1
6
dvdt
C.
1
6
dvdt
D.
5 dvdt
Câu 8. Thể tích của khối tròn xoay được giới hạn bởi đường
s inxy
, trục hoành và hai đường
thẳng
0,xx
là :
A.
2
4
B.
2
2
C.
2
D.
3
3
Câu 9. Diện tích hình phẳng được giới hạn bởi các đường
2
1y x x
và
4
1y x x
là :
A.
8
15
dvdt
B.
7
15
dvdt
C. -
7
15
dvdt
D.
4
15
dvdt
Câu 10. Diện tích hình phẳng được giới hạn bởi các đường
2
2y x x
và đường thẳng
2xy
là :
Group Nhóm Toán | Trắc nghiệm 2016-2017
15
4
A.
1
6
dvdt
B.
5
2
dvdt
C.
6
5
dvdt
D.
1
2
dvdt
Câu 11. Diện tích hình phẳng được giới hạn bởi các đường
lnyx
, trục hoành và hai đường
thẳng
1
,x x e
e
là :
A.
1
e dvdt
e
B.
1
dvdt
e
C.
1
e dvdt
e
D.
1
e dvdt
e
Câu 12. Diện tích hình phẳng được giới hạn bởi các đường
3
3y x x
,
yx
và đường
thẳng
2x
là :
A.
5
99
dvdt
B.
99
4
dvdt
C.
99
5
dvdt
D.
87
4
dvdt
Câu 13. Diện tích hình phẳng giới hạn bởi
3
, 0, 1, 2y x y x x
có kết quả là:
A.
17
4
B.
4
C.
15
4
D.
14
4
Câu 14. Diện tích hình phẳng giới hạn bởi
42
1, 2 1y y x x
có kết quả là
A.
62
5
B.
28
3
C.
16 2
15
D.
27
4
Câu 15. Diện tích hình phẳng giới hạn bởi
2
,2y x y x x
có kết quả là
A.
4
B.
9
2
C.5 D.
7
2
Câu 16. Diện tích hình phẳng giới hạn bởi
2
3, 4 3y x y x x
có kết quả là :
Group Nhóm Toán | Trắc nghiệm 2016-2017
15
5
A.
2
5
6
B.
3
5
6
C.
4
5
6
D.
3
51
6
Câu 17. Thể tích khối tròn xoay giới hạn bởi
2
2 , 0y x x y
quay quanh trục ox có kết quả là:
A.
B.
16
15
C.
14
15
D.
13
15
Câu 18. Diện tích hình phẳng giới hạn bởi
2
5x 6, 0, 0, 2y x y x x
có kết quả là:
A.
58
3
B.
56
3
C.
55
3
D.
52
3
Câu 19. Cho hình phẳng (H) được giới hạn bởi parabol
2
( ) : 2P y x x
, trục Ox và các đường
thẳng
1, 3xx
. Diện tích của hình phẳng (H) là :
A.
2
3
B.
4
3
C.2 D.
8
3
Câu 20. Cho hình phẳng (H) được giới hạn bởi đường cong
2
3y x x
và đường thẳng
21yx
. Diện tích của hình (H) là:
A.
23
6
B.4 C.
5
6
D.
1
6
Câu 21. Để tìm diện tích của hình phẳng giới hạn bởi
3
: ; 0; -1; 2C y x y x x
một học sinh thực
hiện theo các bước như sau:
Bước I.
2
3
1
S x dx
Bước II.
2
4
1
4
x
S
Bước III.
1 15
4
44
S
Cách làm trên sai từ bước nào?
A. Bước I B. Bước II
C. Bước III D. Không có bước nào sai.
Câu 22. Diện tích của hình phẳng giới hạn bởi
3
: ; 0; 1; 2C y x y x x
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
15
6
A.
1
4
B.
17
4
C.
15
4
D.
19
4
Câu 23. Diện tích của hình phẳng giới hạn bởi
42
: 3 4 5; ; 1; 2C y x x Ox x x
là:
A.
212
15
B.
213
15
C.
214
15
D.
43
3
Câu 24. Cho hai hàm số
fx
và
gx
liên tục trên
;ab
và thỏa mãn:
0 , ;g x f x x a b
.
Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh
Ox
hình phẳng
H
giới hạn bởi các
đường:
,y f x y g x
,
;x a x b
. Khi đó V dược tính bởi công thức nào sau đây?
A.
2
b
a
f x g x dx

B.
22
b
a
f x g x dx


C.
2
b
a
f x g x dx




D.
b
a
f x g x dx
Câu 25. Diện tích của hình phẳng giới hạn bởi
2
: 6 5; 0 ; 0; 1C y x x y x x
là:
A.
5
2
B.
7
3
C.
7
3
D.
5
2
Câu 26. Diện tích của hình phẳng giới hạn bởi
: sin ; ; 0;C y x Ox x x
là:
A. 1 B. 2 C. 3 D. 4
Câu 27. Gọi
H
là hình phẳng giới hạn bởi các đường:
sin ; ; 0;y x Ox x x
. Quay
H
xung
quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
2
B.
2
2
C.
D.
2
Câu 28. Diện tích hình phẳng giới hạn bởi các đường
2
4yx
;
Ox
bằng ?
A.
32
3
B.
16
3
C. 12 D.
32
3
Group Nhóm Toán | Trắc nghiệm 2016-2017
15
7
Câu 29. Diện tích hình phẳng giới hạn bởi các đường
3
4y x x
;
Ox
;
3x
4x
bằng ?
A.
119
4
B.
44
C. 36 D.
201
4
Câu 30. Diện tích hình phẳng giới hạn bởi các đường
2
yx
;
2yx
bằng ?
A.
15
2
B.
9
2
C.
9
2
D.
15
2
Câu 31. Diện tích hình phẳng giới hạn bởi các đường
42
4;y x x Ox
bằng ?
A.
128
B.
1792
15
C.
128
15
D.
128
15
Câu 32. Diện tích hình phẳng giới hạn bởi các đường
3
4 ; ; 1 y x x Ox x
bằng ?
A.
24
B.
9
4
C.
1
D.
9
4
Câu 33. Diện tích hình phẳng giới hạn bởi các đường
cos ; ; ;
y x Ox Oy x
bằng ?
A.
1
B.
2
C.
3
D. Kết quả khác
Câu 34. Diện tích hình phẳng giới hạn bởi các đường
3
;y x x Ox
bằng ?
A.
1
2
B.
1
4
C.
2
D.
1
4
Câu 35. Gọi
H
là hình phẳng giới hạn bởi các đường
2
2;y x x Ox
. Quay
H
xung quanh trục
Ox
ta được khối tròn xoay có thể tích bằng ?
A.
16
15
B.
4
3
C.
4
3
D.
16
15
Câu 36. Gọi
H
là hình phẳng giới hạn bởi các đường
tan ; ; 0;
4
y x Ox x x
. Quay
H
xung
quanh trục
Ox
ta được khối tròn xoay có thể tích bằng ?
A.
1
4
B.
2
C.
2
4
D.
2
4
Group Nhóm Toán | Trắc nghiệm 2016-2017
15
8
Câu 37. Gọi
H
là hình phẳng giới hạn bởi các đường
2
1;y x Ox
. Quay
H
xung quanh trục
Ox
ta được khối tròn xoay có thể tích bằng ?
A.
16
15
B.
16
15
C.
4
3
D.
4
3
Câu 38. Diện tích hình phẳng giới hạn bởi các đường
x
ye
;
1y
và
1x
là:
A.
1e
B.
e
C.
1e
D.
1 e
Câu 39. Diện tích hình phẳng giới hạn bởi các đường
3yx
;
4x
;
Ox
là:
A.
16
3
B.
24
C.
72
D.
16
Câu 40. Cho hình (H) giới hạn bởi các đường
2
yx
;
1x
; trục hoành. Quay hình (H) quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
5
B.
3
C.
2
3
D.
2
5
Mức độ thông hiểu.
Câu 41. Thể tích của khối tròn xoay được giới hạn bởi các đường
1
3
21yx
,
0x
,
3y
, quay quanh trục Oy là:
A.
50
7
B.
480
9
C.
480
7
D.
48
7
Câu 42. Diện tích hình phẳng được giới hạn bởi các đường
1y e x
,
1
x
y e x
là:
A.
2
2
e
dvdt
B.
1
2
e
dvdt
C.
1
3
e
dvdt
D.
1
2
e
dvdt
Group Nhóm Toán | Trắc nghiệm 2016-2017
15
9
Câu 43. Thể tích của khối tròn xoay được giới hạn bởi các đường
2
. os siny x c x x
,
00
2
,,y x y
là:
A.
34
4
B.
54
4
C.
34
4
D.
34
5
Câu 44. Diện tích hình phẳng được giới hạn bởi các đường
2sin , osy x y c x
và hai đường
thẳng
0
2
,xx
là :
A.
1
4
dvdt
B.
1
6
dvdt
C.
3
2
dvdt
D.
1
2
dvdt
Câu 45. Diện tích hình phẳng giới hạn bởi
2
, siny x y x x
0 x

có kết quả là
A.
B.
2
C.
2
D.
3
Câu 46. Thể tích khối tròn xoay giới hạn bởi
ln , 0,y x y x e
quay quanh trục ox có kết quả là:
A.
e
B.
1e
C.
2e
D.
1e
Câu 47. Thể tích khối tròn xoay giới hạn bởi
ln , 0,x 1,x 2y x y
quay quanh trục ox có kết quả
là:
A.
2
2 ln2 1
B.
2
2 ln2 1
C.
2
2ln 2 1
D.
2
2ln 2 1
Group Nhóm Toán | Trắc nghiệm 2016-2017
16
0
Câu 48. Diện tích hình phẳng được giới hạn bởi các đường
2
2y x x
và
yx
là :
A.
9
2
dvdt
B.
7
2
dvdt
C. -
9
2
dvdt
D.
0 dvdt
Câu 49. Cho hình phẳng (H) được giới hạn bởi đường cong
3
( ) :C y x
, trục Ox và đường thẳng
3
2
x
. Diện tích của hình phẳng (H) là :
A.
65
64
B.
81
64
C.
81
4
D.4
Câu 50. Thể tích vật thể quay quanh trục ox giới hạn bởi
3
, 8, 3y x y x
có kết quả là:
A.
75
3 9.2
7
B.
76
3 9.2
7
C.
77
3 9.2
7
D.
78
3 9.2
7
Câu 51. Cho hình phẳng (H) được giới hạn bởi đường cong
( ) :
x
C y e
, trục Ox, trục Oy và đường
thẳng
2x
. Diện tích của hình phẳng (H) là :
A.
4e
B.
2
2ee
C.
2
3
2
e
D.
2
1e
Câu 52. Cho hình phẳng (H) được giới hạn bởi đường cong
21
( ) :
1
x
Cy
x
, trục Ox và trục Oy.
Thể tích của khối tròn xoay khi cho hình (H) quay quanh trục Ox là :
A.
3
B.
4 ln2
C.
(3 4 ln2)
D.
(4 3 ln2)
Câu 53. Cho hình phẳng (H) được giới hạn bởi đường cong
( ) : lnC y x
, trục Ox và đường thẳng
xe
. Diện tích của hình phẳng (H) là :
Group Nhóm Toán | Trắc nghiệm 2016-2017
16
1
A.1 B.
1
1
e
C.
e
D.2
Câu 54. Cho hình phẳng (H) được giới hạn đường cong
32
( ) : 2C y x x
và trục Ox. Diện tích của
hình phẳng (H) là :
A.
4
3
B.
5
3
C.
11
12
D.
68
3
Câu 55. Diện tích hình phẳng được giới hạn bởi hai đường
yx
và
2
yx
là :
A.
1
2
B.
1
4
C.
1
5
D.
1
3
Câu 56. Hình phẳng giới hạn bởi đường cong
2
yx
và đường thẳng
4y
quay một vòng quanh
trục Ox. Thể tích khối tròn xoay được sinh ra bằng :
A.
64
5
B.
128
5
C.
256
5
D.
152
5
Câu 57. Diện tích hình phẳng giới hạn bởi
sin ; cos ;x 0;xy x y x
là:
A. 2 B. 3 C.
32
D. 2
2
Câu 58. Cho hình phẳng (H) được giới hạn bởi đường cong
( ) : sinC y x
, trục Ox và các đường
thẳng
0,xx
. Thể tích của khối tròn xoay khi cho hình (H) quay quanh trục Ox là :
A.2 B.3 C.
2
3
D.
3
2
Câu 59. Diện tích hình phẳng giới hạn bởi
sin ; 0 2y x x y x x
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
16
2
A. 1 B. 2 C. 3 D. 4
Câu 60. Diện tích hình phẳng giới hạn bởi
3
2
;
1
x
y y x
x

là:
A. 1 B. 1 – ln2 C. 1 + ln2 D. 2 – ln2
Câu 61. Diện tích của hình phẳng giới hạn bởi
2
: 4 ;C y x x Ox
là:
A.
31
3
B.
31
3
C.
32
3
D.
33
3
Câu 62. Gọi
H
là hình phẳng giới hạn bởi các đường:
2
3;y x x Ox
. Quay
H
xung quanh
trục
Ox
ta được khối tròn xoay có thể tích là:
A.
81
11
B.
83
11
C.
83
10
D.
81
10
Câu 63. Diện tích của hình phẳng giới hạn bởi
2
: 2 ; 2C y x x y x
là:
A.
5
2
B.
7
2
C.
9
2
D.
11
2
Câu 64. Diện tích của hình phẳng giới hạn bởi
1
: ; : 2 3C y d y x
x
là:
A.
3
ln2
4
B.
1
25
C.
3
ln2
4
D.
1
24
Câu 65. Diện tích của hình phẳng giới hạn bởi
2
: ; : 2C y x d x y
là:
A.
7
2
B.
9
2
C.
11
2
D.
13
2
Câu 66. Diện tích của hình phẳng giới hạn bởi
2
: ; :C y x d y x
là:
A.
2
3
B.
4
3
C.
5
3
D.
1
3
Group Nhóm Toán | Trắc nghiệm 2016-2017
16
3
Câu 67. Gọi
H
là hình phẳng giới hạn bởi các đường:
1; ; 4y x Ox x
. Quay
H
xung
quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
7
6
B.
5
6
C.
2
7
6
D.
2
5
6
Câu 68. Gọi
H
là hình phẳng giới hạn bởi các đường:
3 ; ; 1y x y x x
. Quay
H
xung
quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
8
3
B.
2
8
3
C.
2
8
D.
8
Câu 69. Diện tích hình phẳng giới hạn bởi các đường
2
33yx
với
0x
;
Ox
;
Oy
là:
A.
4
B. 2 C.
4
D.
44
Câu 70. Cho hình (H) giới hạn bởi các đường
yx
;
4x
; trục hoành. Quay hình (H) quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
15
2
B.
14
3
C.
8
D.
16
3
Câu 71. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
32
3y x x
và trục hoành là:
A.
27
4
B.
3
4
C.
27
4
D.
4
Câu 72. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
4
55yx
và trục hoành là:
A. 4 B. 8 C. 3108 D. 6216
Câu 73. Diện tích hình phẳng giới hạn bởi hai đường
3
11 6y x x
và
2
6yx
là:
A.
52
B.
14
C.
1
4
D.
1
2
Câu 74. Diện tích hình phẳng giới hạn bởi hai đường
3
yx
và
4yx
là:
A.
4
B.
8
C.
40
D.
2048
105
Group Nhóm Toán | Trắc nghiệm 2016-2017
16
4
Câu 75. Diện tích hình phẳng giới hạn bởi các đường
2yx
;
8
y
x
;
3x
là:
A.
5 8ln6
B.
2
5 8ln
3
C.
26
D.
14
3
Câu 76. Cho hình (H) giới hạn bởi các đường
1yx
;
6
y
x
;
1x
. Quay hình (H) quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
13
6
B.
125
6
C.
35
3
D.
18
Câu 77. Diện tích hình phẳng giới hạn bởi các đường
cosy mx x
;
Ox
;
0;xx

bằng
3
. Khi đó
giá trị của
m
là:
A.
3m 
B.
3m
C.
4m 
D.
3m 
Câu 78. Cho hình (H) giới hạn bởi các đường
2
2y x x
, trục hoành. Quay hình (H) quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
16
15
B.
4
3
C.
496
15
D.
32
15
Câu 79. Diện tích hình phẳng giới hạn bởi các đường
21yx
;
6
y
x
;
3x
là:
A.
4 6ln6
B.
2
4 6ln
3
C.
443
24
D.
25
6
Câu 80. Cho hình (H) giới hạn bởi các đường
4
y
x
và
5yx
. Quay hình (H) quanh trục
Ox
ta
được khối tròn xoay có thể tích là:
A.
9
2
B.
15
4ln4
2
C.
33
4ln4
2
D.
9
Mức độ vận dụng.
Group Nhóm Toán | Trắc nghiệm 2016-2017
16
5
Câu 81. Cho (C) :
32
11
22
33
y x mx x m
. Giá trị
5
0
6
;m
sao cho hình phẳng
giới hạn bởi đồ thị (C) ,
0 0 2,,y x x
có diện tích bằng 4 là:
A.
1
2
m
B.
1
2
m
C.
3
2
m
D.
3
2
m
Câu 82. Diện tích hình phẳng giới hạn bởi
22
,y ax x ay
0a
có kết quả là
A.
2
a
B.
2
1
2
a
C.
2
1
3
a
D.
2
1
4
a
Câu 83. Thể tích khối tròn xoay khi cho Elip
22
22
1
xy
ab

quay quanh trục ox :
A.
2
4
3
ab
B.
2
4
3
ab
C.
2
2
3
ab
D.
2
2
3
ab
Câu 84. Diện tích hình phẳng giới hạn bởi
2
sin x sinx 1; 0; 0; / 2y y x x
là:
A.
3
4
B.
3
1
4
C.
3
1
4
D.
3
4
Câu 85. Diện tích hình phẳng giới hạn bởi
; ; 1
xx
y e e Ox x
là:
A. 1 B.
1
1e
e

C.
1
e
e
D.
1
2e
e

Group Nhóm Toán | Trắc nghiệm 2016-2017
16
6
Câu 86. Thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi các đường
22
11
0 ; 3 ( 2); 0
42
x y y x y y y x
quay quanh Ox:
A. 32
B.
32
C.
2
32
D.
33
Câu 87. Diện tích hình phẳng được giới hạn bởi đường cong
2
( ) : sinC y x
, trục Ox và các đường
thẳng
0,xx
bằng :
A. B.
2
C.
3
D.
4
Câu 88. Diện tích hình phẳng giới hạn bởi
2
5 , 1, 0, 1y x y x x x
có kết quả là:
A.
55
3
B.
26
3
C.
25
3
D.
27
3
Câu 89. Diện tích hình phẳng giới hạn bởi
|ln |; 1y x y
là:
A.
2
22ee
B.
3
2e
e

C.
2
21ee
D. 3
Câu 90. Diện tích hình phẳng được giới hạn bởi các đường:
2
4
4
x
y
;
2
42
x
y
là:
A.
4
2
3
dvdt
B.
24
3
dvdt
C.
4
3
dvdt
Group Nhóm Toán | Trắc nghiệm 2016-2017
16
7
D.
4
2
3
dvdt
Câu 91. Diện tích của hình phẳng giới hạn bởi:
: ; : 2;C y x d y x Ox
là:
A.
10
3
B.
16
3
C.
122
3
D.
128
3
Câu 92. Diện tích của hình phẳng giới hạn bởi:
: ln ; : 1; ;C y x d y Ox Oy
là:
A.
2e
B.
2e
C.
1e
D.
e
Câu 93. Diện tích của hình phẳng giới hạn bởi:
12
: ln ; : 1; : 1C y x d y d y x
là:
A.
1
2
e
B.
3
2
e
C.
1
2
e
D.
3
2
e
Câu 94. Diện tích của hình phẳng giới hạn bởi:
: ; : 1; 1
x
C y e d y x x
là:
A.
e
B.
1
2
e
C.
1e
D.
3
2
e
Câu 95. Diện tích của hình phẳng giới hạn bởi:
12
: ; : ; : 1 1
x
C y e d y e d y e x
là:
A.
1
2
e
B.
1
2
e
C.
3
2
e
D.
2
e
Câu 96. Cho đường cong
:C y x
. Gọi
d
là tiếp tuyến của
C
tại điểm
4,2M
. Khi đó diện
tích của hình phẳng giới hạn bởi :
;;C d Ox
là:
A.
8
3
B.
2
3
C.
16
3
D.
22
3
Câu 97. Cho đường cong
: 2 lnC y x
. Gọi
d
là tiếp tuyến của
C
tại điểm
1,2M
. Khi đó
diện tích của hình phẳng giới hạn bởi :
;;C d Ox
là:
A.
2
3e
B.
2
1e
C.
2
e
D.
2
5e
Group Nhóm Toán | Trắc nghiệm 2016-2017
16
8
Câu 98. Gọi
H
là hình phẳng giới hạn bởi
1
: ; :
2
C y x d y x
. Quay
H
xung quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
8
B.
16
3
C.
8
3
D.
8
15
Câu 99. Gọi
H
là hình phẳng giới hạn bởi
3
: ; : 2;C y x d y x Ox
. Quay
H
xung
quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
4
21
B.
10
21
C.
7
D.
3
Câu 100. Gọi
H
là hình phẳng giới hạn bởi
1
: 2 ; : ; 4
2
C y x d y x x
. Quay
H
xung
quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
80
3
B.
112
3
D.
16
3
D.
32
PHẦN 14 :
A. MỨC ĐỘ NHẬN BIẾT: 20 câu
Câu 1: Nguyên hàm của hàm số f(x) = x
2
– 3x +
x
1
là:
A.
32
3
32
ln
xx
xC
B.
32
2
31
32
xx
C
x
C.
32
3 lnx x x C
D.
32
3
32
ln
xx
xC
Câu 2: Họ nguyên hàm của
2
( ) 2 1f x x x
là
A.
3
1
( ) 2
3
F x x x C
B.
( ) 2 2F x x C
C.
D.
32
1
( ) 2
3
F x x x x C
Câu 3: Nguyên hàm của hàm số
2
11
()fx
x
x

là :
A.
2
ln lnx x C
B. lnx -
x
1
+ C C. ln|x| +
x
1
+ C D. Kết quả khác
Câu 4: Nguyên hàm của hàm số
2
()
xx
f x e e
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
16
9
A.
Cee
xx
2
2
1
B.
2
2
xx
e e C
C.
()
xx
e e x C
D. Kết quả khác
Câu 5: Nguyên hàm của hàm số
f x cos3x
là:
A.
1
3
3
xCsin
B.
1
sin3
3
xC
C.
sin3xC
D.
3sin3xC
Câu 6: Nguyên hàm của hàm số
2
1
2()
cos
x
f x e
x

là:
A.2e
x
+ tanx + C B. e
x
(2x -
)
cos
2
x
e
x
C. e
x
+ tanx + C D. Kết quả khác
Câu 7: Tính
sin(3 1)x dx
, kết quả là:
A.
1
cos(3 1)
3
xC
B.
1
cos(3 1)
3
xC
C.
cos(3 1)xC
D. Kết quả khác
Câu 8: Tìm
(cos6 cos4 )
x x dx
là:
A.
11
sin6 sin4
64
x x C
B.
6sin6 5sin4
x x C
C.
11
sin6 sin 4
64
x x C
D.
6sin6 sin 4
x x C
Câu 9: Tính nguyên hàm
1
21
dx
x
ta được kết quả sau:
A.
1
21
2
ln xC
B.
21ln xC
C.
1
21
2
ln xC
D.
21ln xC
Câu 10: Tính nguyên hàm
1
12
dx
x
ta được kết quả sau:
A.
12ln xC
B.
2 1 2ln xC
C.
1
12
2
ln xC
D.
2
2
12()
C
x
Câu 11: Công thức nguyên hàm nào sau đây không đúng?
A.
1
lndx x C
x

B.
1
1
1
()
x
x dx C
C.
01()
ln
x
x
a
a dx C a
a
D.
2
1
tan
cos
dx x C
x

Câu 12: Tính
(3cos 3 )
x
x dx
, kết quả là:
A.
3
3sin
ln3
x
xC
B.
3
3sin
ln3
x
xC
C.
3
3sin
ln3
x
xC
D.
3
3sin
ln3
x
xC
Câu 13: Trong các hàm số sau:
(I)
2
( ) tan 2f x x
(II)
2
2
()
cos
fx
x
(III)
2
( ) tan 1f x x
Hàm số nào có một nguyên hàm là hàm số g(x) = tanx
Group Nhóm Toán | Trắc nghiệm 2016-2017
17
0
A. (I), (II), (III) B. Chỉ (II), (III)
C. Chỉ (III) D. Chỉ (II)
Câu 14: Trong các mệnh đề sau, tìm mệnh đề sai
A.
3
2
()
'( ) ( )
3
fx
f x f x dx C
B.
( ). ( ) ( ) . ( )f x g x dx f x dx g x dx
C.
( ) ( ) ( ) ( )f x g x dx f x dx g x dx
D.
( ) ( )kf x dx k f x dx
(k là hằng số)
Câu 15: Nguyên hàm của hàm số
3
21f x x( ) ( )
là:
A.
4
1
21
2
xC()
B.
4
21xC()
C.
4
2 2 1xC()
D. Kết quả khác
Câu 16: Nguyên hàm của hàm số
5
12f x x( ) ( )
là:
A.
6
1
12
2
xC ()
B.
6
12xC()
C.
6
5 1 2xC()
D.
4
5 1 2xC()
Câu 17: Chọn câu khẳng định sai?
A.
1
xdx C
x

ln
B.
2
2xdx x C
C.
xdx x C
sin cos
D.
2
1
dx x C
x
cot
sin
Câu 18: Nguyên hàm của hàm số f(x) =
2
3
2x
x
là :
A.
2
3
xC
x

B.
2
2
3
xC
x

C.
22
3lnx x C
D. Kết quả khác
Câu 19: Hàm số
tan
x
F x e x C
là nguyên hàm của hàm số
f( )x
nào?
A.
2
1
x
f x e
x
()
sin
B.
2
1
x
f x e
x
()
sin
C.
2
1
x
f x e
x
()
cos
D. Kết quả khác
Câu 20: Nếu
( ) sin2
x
f x dx e x C
thì
()fx
bằng
A.
cos2
x
ex
B.
cos2
x
ex
C.
2cos2
x
ex
D.
1
cos2
2
x
ex
B. MỨC ĐỘ THÔNG HIỂU: 20 câu
Group Nhóm Toán | Trắc nghiệm 2016-2017
17
1
Câu 21: Nguyên hàm của hàm số f(x) =
2
4
32
x
x
là :
A.
C
x
x
3
3
2
3
B.
3
2
23
3
x
C
x

C.
3
2
2
3ln
3
x
xC
D. Kết quả khác
Câu 22: Nguyên hàm của hàm số f(x) = 2sin3xcos2x
A.
Cxx cos5cos
5
1
B.
1
cos5 cos
5
x x C
C.
5cos5 cosx x C
D. Kết quả khác
Câu 23: Tìm hàm số f(x) biết rằng f’(x) = 2x + 1 và f(1) = 5
A. x
2
+ x + 3 B. x
2
+ x - 3 C. x
2
+ x D. Kết quả khác
Câu 24: Tìm hàm số f(x) biết rằng f’(x) = 4
xx
và f(4) = 0
A.
3
40
23
8
2
xxx
B.
2
8 40
3 2 3
xx

C.
2
8 40
3 2 3
x x x

D. Kết quả khác
Câu 25: Nguyên hàm của hàm số
2
x
xe dx
là
A.
2
x
xe C
B.
2
2
x
e
C
C.
2
x
eC
D.
2
x
xe
Câu 26: Tìm hàm số
()
y f x
biết
2
( ) ( )( 1)
f x x x x
và
(0) 3
f
A.
B.
42
( ) 3
42
xx
y f x
C.
42
( ) 3
42
xx
y f x
D.
2
( ) 3 1
y f x x
Câu 27: Tìm
3
(sin 1) cos
x xdx
là:
A.
4
(cos 1)
4
x
C
B.
4
sin
4
x
C
C.
4
(sin 1)
4
x
C
D.
3
4(sin 1)
xC
Câu 28: Tìm
2
32
dx
xx
là:
A.
11
ln ln
21
C
xx
B.
2
ln
1
x
C
x
C.
1
ln
2
x
C
x
D.
ln( 2)( 1)
x x C
Câu 29: Tìm
cos2
x xdx
là:
A.
11
sin2 cos2
24
x x x C
B.
11
sin2 cos2
22
x x x C
C.
2
sin2
4
xx
C
D.
sin2
xC
Câu 30: Lựa chọn phương án đúng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
17
2
A.
cot ln sinxdx x C
B.
sin cosxdx x C
C.
2
11
dx C
x
x

D.
cos sinxdx x C
Câu 31: Tính nguyên hàm
3
sin cosx xdx
ta được kết quả là:
A.
4
sin xC
B.
4
1
4
sin xC
C.
4
sin xC
D.
4
1
4
sin xC
Câu 32: Cho
2
3 2 3()f x x x
có một nguyên hàm triệt tiêu khi
1x
. Nguyên hàm đó là kết quả nào sau đây?
A.
32
3()F x x x x
B.
32
31()F x x x x
C.
32
32()F x x x x
D.
32
31()F x x x x
Câu 33. Hàm số nào sau đây không phải là nguyên hàm của hàm số
2
2
1
()
()
()
xx
fx
x
A.
2
1
1
xx
x

B.
2
1
1
xx
x

C.
2
1
1
xx
x

D.
2
1
x
x
Câu 34: Kết quả nào sai trong các kết quả sau:
A.
11
2 5 1 1
10 5 2 2 5 5. .ln .ln
xx
x x x
dx C

B.
44
34
21
4
ln
xx
dx x C
xx

C.
2
2
11
21
1
ln
xx
dx x C
x
x
D.
2
tan tanxdx x x C
Câu 35: Tìm nguyên hàm
3
2
4
x dx
x



A.
3
5
5
4
3
lnx x C
B.
3
5
3
4
5
lnx x C
C.
3
5
3
4
5
lnx x C
D.
3
5
3
4
5
lnx x C
Câu 36: Kết quả của
2
1
x
dx
x
là:
A.
2
1 xC
B.
2
1
1
C
x
C.
2
1
1
C
x
D.
2
1 xC
Câu 37: Tìm nguyên hàm
2
1( sin )x dx
A.
21
22
34
cos sinx x x C
B.
21
22
34
cos sinx x x C
C.
21
2 2 2
34
cos sinx x x C
D.
21
22
34
cos sinx x x C
Câu 38: Tính
2
tan xdx
, kết quả là:
A.
tanx x C
B.
tanx x C
C.
tanx x C
D.
3
1
tan
3
xC
Group Nhóm Toán | Trắc nghiệm 2016-2017
17
3
Câu 39: Trong các mệnh đề sau đây, mệnh đề nào sai ?
23
2
2
11
( ) sin sin3 (sin2 - sin 4 )
42
1
( ) tan tan
3
11
( ) ln( 2 3)
2 3 2
I x xdx x x C
II xdx x C
x
III dx x x C
xx
A. Chỉ (I) và (II) B. Chỉ (III) C. Chỉ (II) và (III) D. Chỉ (II)
Câu 40: Hàm số nào sau đây là một nguyên hàm của sin2x
A.
2
sin x
B. 2cos2x C. -2cos2x D. 2sinx
C. MỨC ĐỘ VẬN DỤNG: 10 câu
Câu 41: Tìm hàm số f(x) biết rằng
'( ) ax+ , '( ) , ( ) , ( )
b
f x f f f
x
2
1 0 1 4 1 2
A.
2
51
2
2
x
x
B.
2
15
22
x
x

C.
2
15
22
x
x

D. Kết quả khác
Lược giải:
Sử dụng máy tính kiểm tra từng đáp án:
- Nhập hàm số
- Dùng phím CALC để kiểm tra các điều kiện
'(1) 0, (1) 4, ( 1) 2f f f
- Đáp án đúng: B
Câu 42: Hàm số nào sau đây là một nguyên hàm của hàm số
2
()f x x k
với
0?k
A.
22
( ) ln
22
xk
f x x k x x k
B.
22
1
( ) ln
22
x
f x x k x x k
C.
2
( ) ln
2
k
f x x x k
D.
2
1
()fx
xk
Lược giải:
2
2 2 2 2
22
x
1
x k 1 x x k
xk
x k ln x x k x k x k
2 2 2 2 2
x k x x k
Group Nhóm Toán | Trắc nghiệm 2016-2017
17
4
Câu 43: Nếu
2
( ) ( ) 2 -1f x ax bx c x
là một nguyên hàm của hàm số
2
10 -7 2
()
2 -1
xx
gx
x
trên khoảng
1
;
2
thì a+b+c có giá trị là
A. 3 B. 0
C. 4 D. 2
Lược giải:
22
2
5ax ( 2a 3b)x b c 10x 7x 2
(ax bx c) 2x 1
2x 3 2x 3
a2
b 1 a b c 2
c1
Câu 44: Xác định a, b, c sao cho
2
( ) ( ) 2 -3g x ax bx c x
là một nguyên hàm của hàm số
2
20 -30 7
()
2 -3
xx
fx
x
trong khoảng
3
;
2
A.a=4, b=2, c=2 B. a=1, b=-2, c=4
C. a=-2, b=1, c=4 D. a=4, b=-2, c=1
Lược giải:
22
2
5ax ( 6a 3b)x 3b c 20x 30x 7
(ax bx c) 2x 3
2x 3 2x 3
a4
b2
c1
Câu 45: Một nguyên hàm của hàm số:
2
( ) sin 1f x x x
là:
A.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
B.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
C.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
D.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
Lược giải:
Đặt
2
( sin 1 )I x x dx
- Dùng phương pháp đổi biến, đặt
2
1tx
ta được
sinI t tdt
- Dùng phương pháp nguyên hàm từng phần, đặt
, sinu t dv tdt
- Ta được
2 2 2
cos cos 1 cos 1 sin 1I t t tdt x x x C
Câu 46: Trong các hàm số sau:
Group Nhóm Toán | Trắc nghiệm 2016-2017
17
5
(I)
2
( ) 1f x x
(II)
2
( ) 1 5f x x
(III)
2
1
()
1
fx
x
(IV)
2
1
( ) -2
1
fx
x
Hàm số nào có một nguyên hàm là hàm số
2
( ) ln 1F x x x
A. Chỉ (I) B. Chỉ (III)
C. Chỉ (II) D. Chỉ (III) và (IV)
Lược giải:
2
2
22
x
1
1
x1
ln x x 1
x x 1 x 1
Câu 47: Một nguyên hàm của hàm số
2
3
1
()f x x
x
là hàm số nào sau đây:
A.
36
25
3 12
( ) ln
55
F x x x x x
B.
3
3
11
()
3
F x x
x
C.
2
3
()F x x x x
D.
35
26
3 12
( ) ln
55
F x x x x x
Lược giải:
2
36
25
3
3 12 1
x x x ln x x
55
x
Câu 48: Xét các mệnh đề
(I)
( ) cosF x x x
là một nguyên hàm của
2
( ) sin -cos
22
xx
fx
(II)
4
( ) 6
4
x
F x x
là một nguyên hàm của
3
3
()f x x
x
(III)
( ) tanF x x
là một nguyên hàm của
( ) -ln cosf x x
Mệnh đề nào sai ?
A. (I) và (II) B. Chỉ (III)
C. Chỉ (II) D. Chỉ (I) và (III)
Lược giải:
ln cosx tanx
(vì
ln cosx
là một nguyên hàm của tanx)
Câu 49: Trong các mệnh đề sau đây mệnh đề nào đúng ?
(I)
2
2
1
ln( 4)
42
xdx
xC
x
(II)
2
1
cot -
sin
xdx C
x
Group Nhóm Toán | Trắc nghiệm 2016-2017
17
6
(III)
2cos 2cos
1
sin -
2
xx
e xdx e C
A. Chỉ (I) B. Chỉ (III)
C. Chỉ (I) và (II) D. Chỉ (I) và (III)
Lược giải:
2
2
22
xdx 1 d(x 4) 1
ln(x 4) C
x 4 2 x 4 2
2cosx 2cosx 2cosx
11
e sin xdx e d(cosx) e C
22
Câu 50: Tìm nguyên hàm
22
( ) ( tan tan )
x
F x e a x b x c
là một nguyên hàm của
23
( ) tan
x
f x e x
trên khoản
;
22
A.
22
1 2 2
( ) ( tan tan )
2 2 2
x
F x e x x
B.
22
1 2 1
( ) ( tan tan )
2 2 2
x
F x e x x
C.
22
1 2 1
( ) ( tan tan )
2 2 2
x
F x e x x
D.
22
1 2 2
( ) ( tan tan )
2 2 2
x
F x e x x
Lược giải:
- Có thể dùng đạo hàm để kiểm tra từng đáp án.
- Hoặc tìm đạo hàm của
22
( ) ( tan tan )
x
F x e a x b x c
rồi đồng nhất với
23
( ) tan
x
f x e x
2 2 2 2 2
'( ) 2 ( tan tan ) 2 (1 tan )tan (1 tan )
xx
F x e a x b x c e a x x b x
2 3 2
2 tan ( 2 )tan (2 2 )tan 2
x
e a x a b x a b x b c
()Fx
là nguyên hàm của f(x) nên
'( ) ( )F x f x
Suy ra
1
21
2
20
2
2
2 2 0
1
20
2
a
a
ab
b
ab
bc
c
Đáp án đúng: B
PHẦN 15 :
NHẬN BIẾT
Group Nhóm Toán | Trắc nghiệm 2016-2017
17
7
Câu 1. Để tìm diện tích của hình phẳng giới hạn bởi
3
: ; 0; -1; 2C y x y x x
một học sinh thực
hiện theo các bước như sau:
Bước I.
2
3
1
S x dx
Bước II.
2
4
1
4
x
S
Bước III.
1 15
4
44
S
Cách làm trên sai từ bước nào?
A. Bước I B. Bước II
C. Bước III D. Không có bước nào sai.
Câu 2. Diện tích của hình phẳng giới hạn bởi
3
: ; 0; 1; 2C y x y x x
là:
A.
1
4
B.
17
4
C.
15
4
D.
19
4
Câu 3. Diện tích của hình phẳng giới hạn bởi
42
: 3 4 5; ; 1; 2C y x x Ox x x
là:
A.
212
15
B.
213
15
C.
214
15
D.
43
3
Câu 4. Cho hai hàm số
fx
và
gx
liên tục trên
;ab
và thỏa mãn:
0 , ;g x f x x a b
.
Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh
Ox
hình phẳng
H
giới hạn bởi
các đường:
,y f x y g x
,
;x a x b
. Khi đó V dược tính bởi công thức nào sau
đây?
A.
2
b
a
f x g x dx

B.
22
b
a
f x g x dx


C.
2
b
a
f x g x dx




D.
b
a
f x g x dx
Câu 5. Diện tích của hình phẳng giới hạn bởi
2
: 6 5; 0 ; 0; 1C y x x y x x
là:
A.
5
2
B.
7
3
C.
7
3
D.
5
2
Câu 6. Diện tích của hình phẳng giới hạn bởi
: sin ; ; 0;C y x Ox x x
là:
A. 1 B. 2 C. 3 D. 4
Group Nhóm Toán | Trắc nghiệm 2016-2017
17
8
Câu 7. Gọi
H
là hình phẳng giới hạn bởi các đường:
sin ; ; 0;y x Ox x x
. Quay
H
xung
quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
2
B.
2
2
C.
D.
2
Câu 8. Diện tích hình phẳng giới hạn bởi các đường
2
4yx
;
Ox
bằng ?
A.
32
3
B.
16
3
C. 12 D.
32
3
Câu 9. Diện tích hình phẳng giới hạn bởi các đường
3
4y x x
;
Ox
;
3x
4x
bằng ?
A.
119
4
B.
44
C. 36 D.
201
4
Câu 10. Diện tích hình phẳng giới hạn bởi các đường
2
yx
;
2yx
bằng ?
A.
15
2
B.
9
2
C.
9
2
D.
15
2
Câu 11. Diện tích hình phẳng giới hạn bởi các đường
42
4;y x x Ox
bằng ?
A.
128
B.
1792
15
C.
128
15
D.
128
15
Câu 12. Diện tích hình phẳng giới hạn bởi các đường
3
4 ; ; 1 y x x Ox x
bằng ?
A.
24
B.
9
4
C.
1
D.
9
4
Câu 13. Diện tích hình phẳng giới hạn bởi các đường
cos ; ; ;
y x Ox Oy x
bằng ?
A.
1
B.
2
C.
3
D. Kết quả khác
Câu 14. Diện tích hình phẳng giới hạn bởi các đường
3
;y x x Ox
bằng ?
A.
1
2
B.
1
4
C.
2
D.
1
4
Câu 15. Gọi
H
là hình phẳng giới hạn bởi các đường
2
2;y x x Ox
. Quay
H
xung quanh trục
Ox
ta được khối tròn xoay có thể tích bằng ?
A.
16
15
B.
4
3
C.
4
3
D.
16
15
Câu 16. Gọi
H
là hình phẳng giới hạn bởi các đường
tan ; ; 0;
4
y x Ox x x
. Quay
H
xung
quanh trục
Ox
ta được khối tròn xoay có thể tích bằng ?
Group Nhóm Toán | Trắc nghiệm 2016-2017
17
9
A.
1
4
B.
2
C.
2
4
D.
2
4
Câu 17. Gọi
H
là hình phẳng giới hạn bởi các đường
2
1;y x Ox
. Quay
H
xung quanh trục
Ox
ta được khối tròn xoay có thể tích bằng ?
A.
16
15
B.
16
15
C.
4
3
D.
4
3
Câu 18. Diện tích hình phẳng giới hạn bởi các đường
x
ye
;
1y
và
1x
là:
A.
1e
B.
e
C.
1e
D.
1 e
Câu 19. Diện tích hình phẳng giới hạn bởi các đường
3yx
;
4x
;
Ox
là:
A.
16
3
B.
24
C.
72
D.
16
Câu 20. Cho hình (H) giới hạn bởi các đường
2
yx
;
1x
; trục hoành. Quay hình (H) quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
5
B.
3
C.
2
3
D.
2
5
THÔNG HIỄU
Câu 1. Diện tích của hình phẳng giới hạn bởi
2
: 4 ;C y x x Ox
là:
A.
31
3
B.
31
3
C.
32
3
D.
33
3
Câu 2. Gọi
H
là hình phẳng giới hạn bởi các đường:
2
3;y x x Ox
. Quay
H
xung quanh
trục
Ox
ta được khối tròn xoay có thể tích là:
A.
81
11
B.
83
11
C.
83
10
D.
81
10
Câu 3. Diện tích của hình phẳng giới hạn bởi
2
: 2 ; 2C y x x y x
là:
A.
5
2
B.
7
2
C.
9
2
D.
11
2
Câu 4. Diện tích của hình phẳng giới hạn bởi
1
: ; : 2 3C y d y x
x
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
18
0
A.
3
ln2
4
B.
1
25
C.
3
ln2
4
D.
1
24
Câu 5. Diện tích của hình phẳng giới hạn bởi
2
: ; : 2C y x d x y
là:
A.
7
2
B.
9
2
C.
11
2
D.
13
2
Câu 6. Diện tích của hình phẳng giới hạn bởi
2
: ; :C y x d y x
là:
A.
2
3
B.
4
3
C.
5
3
D.
1
3
Câu 7. Gọi
H
là hình phẳng giới hạn bởi các đường:
1; ; 4y x Ox x
. Quay
H
xung
quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
7
6
B.
5
6
C.
2
7
6
D.
2
5
6
Câu 8. Gọi
H
là hình phẳng giới hạn bởi các đường:
3 ; ; 1y x y x x
. Quay
H
xung quanh
trục
Ox
ta được khối tròn xoay có thể tích là:
A.
8
3
B.
2
8
3
C.
2
8
D.
8
Câu 9. Diện tích hình phẳng giới hạn bởi các đường
2
33yx
với
0x
;
Ox
;
Oy
là:
A.
4
B. 2 C.
4
D.
44
Câu 10. Cho hình (H) giới hạn bởi các đường
yx
;
4x
; trục hoành. Quay hình (H) quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
15
2
B.
14
3
C.
8
D.
16
3
Câu 11. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
32
3y x x
và trục hoành là:
A.
27
4
B.
3
4
C.
27
4
D.
4
Câu 12. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
4
55yx
và trục hoành là:
A. 4 B. 8 C. 3108 D. 6216
Câu 13. Diện tích hình phẳng giới hạn bởi hai đường
3
11 6y x x
và
2
6yx
là:
A.
52
B.
14
C.
1
4
D.
1
2
Group Nhóm Toán | Trắc nghiệm 2016-2017
18
1
Câu 14. Diện tích hình phẳng giới hạn bởi hai đường
3
yx
và
4yx
là:
A.
4
B.
8
C.
40
D.
2048
105
Câu 15. Diện tích hình phẳng giới hạn bởi các đường
2yx
;
8
y
x
;
3x
là:
A.
5 8ln6
B.
2
5 8ln
3
C.
26
D.
14
3
Câu 16. Cho hình (H) giới hạn bởi các đường
1yx
;
6
y
x
;
1x
. Quay hình (H) quanh trục
Ox
ta
được khối tròn xoay có thể tích là:
A.
13
6
B.
125
6
C.
35
3
D.
18
Câu 17. Diện tích hình phẳng giới hạn bởi các đường
cosy mx x
;
Ox
;
0;xx

bằng
3
. Khi đó
giá trị của
m
là:
A.
3m 
B.
3m
C.
4m 
D.
3m 
Câu 18. Cho hình (H) giới hạn bởi các đường
2
2y x x
, trục hoành. Quay hình (H) quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
16
15
B.
4
3
C.
496
15
D.
32
15
Câu 19. Diện tích hình phẳng giới hạn bởi các đường
21yx
;
6
y
x
;
3x
là:
A.
4 6ln6
B.
2
4 6ln
3
C.
443
24
D.
25
6
Câu 20. Cho hình (H) giới hạn bởi các đường
4
y
x
và
5yx
. Quay hình (H) quanh trục
Ox
ta
được khối tròn xoay có thể tích là:
A.
9
2
B.
15
4ln4
2
C.
33
4ln4
2
D.
9
VẬN DỤNG
Câu 1. Diện tích của hình phẳng giới hạn bởi:
: ; : 2;C y x d y x Ox
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
18
2
A.
10
3
B.
16
3
C.
122
3
D.
128
3
Câu 2. Diện tích của hình phẳng giới hạn bởi:
: ln ; : 1; ;C y x d y Ox Oy
là:
A.
2e
B.
2e
C.
1e
D.
e
Câu 3. Diện tích của hình phẳng giới hạn bởi:
12
: ln ; : 1; : 1C y x d y d y x
là:
A.
1
2
e
B.
3
2
e
C.
1
2
e
D.
3
2
e
Câu 4. Diện tích của hình phẳng giới hạn bởi:
: ; : 1; 1
x
C y e d y x x
là:
A.
e
B.
1
2
e
C.
1e
D.
3
2
e
Câu 5. Diện tích của hình phẳng giới hạn bởi:
12
: ; : ; : 1 1
x
C y e d y e d y e x
là:
A.
1
2
e
B.
1
2
e
C.
3
2
e
D.
2
e
Câu 6. Cho đường cong
:C y x
. Gọi
d
là tiếp tuyến của
C
tại điểm
4,2M
. Khi đó diện
tích của hình phẳng giới hạn bởi :
;;C d Ox
là:
A.
8
3
B.
2
3
C.
16
3
D.
22
3
Câu 7. Cho đường cong
: 2 lnC y x
. Gọi
d
là tiếp tuyến của
C
tại điểm
1,2M
. Khi đó
diện tích của hình phẳng giới hạn bởi :
;;C d Ox
là:
A.
2
3e
B.
2
1e
C.
2
e
D.
2
5e
Câu 8. Gọi
H
là hình phẳng giới hạn bởi
1
: ; :
2
C y x d y x
. Quay
H
xung quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
8
B.
16
3
C.
8
3
D.
8
15
Câu 9. Gọi
H
là hình phẳng giới hạn bởi
3
: ; : 2;C y x d y x Ox
. Quay
H
xung quanh
trục
Ox
ta được khối tròn xoay có thể tích là:
A.
4
21
B.
10
21
C.
7
D.
3
Group Nhóm Toán | Trắc nghiệm 2016-2017
18
3
Câu 10. Gọi
H
là hình phẳng giới hạn bởi
1
: 2 ; : ; 4
2
C y x d y x x
. Quay
H
xung
quanh trục
Ox
ta được khối tròn xoay có thể tích là:
A.
80
3
B.
112
3
D.
16
3
D.
32
LƯỢC GIẢI CÂU HỎI VẬN DỤNG
Câu 1.
Group Nhóm Toán | Trắc nghiệm 2016-2017
18
4
24
02
10
2
3
S xdx x x dx



hoặc
4
0
10
1
3
S xdx
Câu 2.
Group Nhóm Toán | Trắc nghiệm 2016-2017
18
5
1
1 1 ln 1
e
S x dx e
Câu 3.
1
13
1 ln
22
e
S x dx e
Câu 4.
Chứng minh PT
1
x
ex
có nghiệm duy nhất
0x
.
Group Nhóm Toán | Trắc nghiệm 2016-2017
18
6
1
0
3
1
2
x
S e x dx e


Câu 5.
01
10
1
11
2
x
e
S e e x dx e e dx



Group Nhóm Toán | Trắc nghiệm 2016-2017
18
7
Câu 6.
Group Nhóm Toán | Trắc nghiệm 2016-2017
18
8
Phương trình của d:
1
1
4
yx
.
4
0
18
21
43
S x x dx



.
Câu 7.
Phương trình của d:
3yx
Group Nhóm Toán | Trắc nghiệm 2016-2017
18
9
2
2
1
2 ln 2 5
e
S x dx e
Group Nhóm Toán | Trắc nghiệm 2016-2017
19
0
Câu 8.
44
2
00
8
43
V xdx x dx


Câu 9.
12
2
6
01
10
2
21
V x dx x dx


Group Nhóm Toán | Trắc nghiệm 2016-2017
19
1
Group Nhóm Toán | Trắc nghiệm 2016-2017
19
2
Câu 10.
4
2
0
2 32V x dx

PHẦN 16 :
Câu 1: Tích phân
1
2
0
(3 2 1)I x x dx
bằng:
A.
1I
B.
2I
C.
3I
D. Đáp án khác
Group Nhóm Toán | Trắc nghiệm 2016-2017
19
3
Câu 2: Tích phân
2
0
sin xI dx
bằng:
A. -1 B. 1 C. 2 D. 0
Câu 3: Tích phân
1
2
0
( 1)I x dx
bằng:
A.
8
3
B. 2 C.
7
3
D. 4
Câu 4: Tích phân
1
1
0
x
I e dx
bằng:
A.
2
ee
B.
2
e
C.
2
1e
D. e + 1
Câu 5: Tích phân
4
3
1
2
x
I dx
x
bằng:
A. -1 + 3ln2 B.
2 3ln2
C.
4ln2
D.
1 3ln2
Câu 6: Tích phân
1
2
0
1
25
x
I dx
xx

bằng:
A.
8
ln
5
B.
18
ln
25
C.
8
2ln
5
D.
8
2ln
5
Câu 7: Tích phân
1
1
e
I dx
x
bằng:
A.
e
B. 1 C. -1 D.
1
e
Câu 8: Tích phân
1
0
x
I e dx
bằng :
A.
1e
B.
1 e
C.
e
D. 0
Câu 9: Tích phân
2
2
0
2
x
I e dx
bằng :
Group Nhóm Toán | Trắc nghiệm 2016-2017
19
4
A.
4
e
B.
4
1e
C.
4
4e
D.
4
31e
Câu 10: Tích phân
2
2
4
1
1
I x dx
x




bằng:
A.
19
8
B.
23
8
C.
21
8
D.
25
8
Câu 11: Tích phân
1
1
3
e
I dx
x
bằng:
A.
ln 2e
B.
ln 7e
C.
3
ln
4
e



D.
ln 4 3e


Câu 12: Tích phân
3
3
1
1I x dx

bằng:
A. 24 B. 22 C. 20 D. 18
Câu 13: Tích phân
2
2
1
1
21
I dx
x
bằng:
A. 1 B.
1
2
C.
1
15
D.
1
4
Câu 14: Tích phân
1
2
0
56
dx
I
xx

bằng:
A. I = 1 B.
4
ln
3
I
C. I = ln2 D. I = ln2
Câu 15: Tích phân:
1
3
0
( 1)
xdx
J
x
bằng:
A.
1
8
J
B.
1
4
J
C. J =2 D. J = 1
Câu 16: Tích phân
3
2
2
1
x
K dx
x
bằng:
A. K = ln2 B. K = 2ln2 C.
8
ln
3
K
D.
18
ln
23
K
Group Nhóm Toán | Trắc nghiệm 2016-2017
19
5
Câu 17: Tích phân
3
2
1
1I x x dx
bằng:
A.
42
3
B.
8 2 2
3
C.
42
3
D.
8 2 2
3
Câu 18: Tích phân
1
19
0
1I x x dx
bằng:
A.
1
420
B.
1
380
C.
1
342
D.
1
462
Câu 19: Tích phân
1
2 ln
2
e
x
I dx
x
bằng:
A.
32
3
B.
32
3
C.
32
6
D.
3 3 2 2
3
Câu 20: Tích phân
6
0
tanI xdx
bằng:
A.
3
ln
2
B. -
3
ln
2
C.
23
ln
3
D. Đáp án khác.
Câu 21: Tích phân
4
2
0
tanI xdx
bằng:
A. I = 2 B. ln2 C.
1
4
I

D.
3
I
Câu 22: Tích phân
1
2
0
1L x x dx
bằng:
A.
1L 
B.
1
4
L
C.
1L
D.
1
3
L
Câu 23: Tích phân
2
1
(2 1)lnK x xdx
bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
19
6
A.
1
3ln2
2
K 
B.
1
2
K
C. K = 3ln2 D.
1
2ln2
2
K 
Câu 24: Tích phân
0
sinL x xdx
bằng:
A. L = B. L =  C. L = 2 D. K = 0
Câu 25: Tích phân
3
0
cosI x xdx
bằng:
A.
31
6
B.
31
2
C.
31
62
D.
3
2
Câu 26: Tích phân
ln2
0
x
I xe dx
bằng:
A.
1
1 ln2
2
B.
1
1 ln2
2
C.
1
ln2 1
2
D.
1
1 ln2
4
Câu 27: Tích phân
2
2
1
ln x
I dx
x
bằng:
A.
1
1 ln2
2
B.
1
1 ln2
2
C.
1
ln2 1
2
D.
1
1 ln2
4
Câu 28: Giả sử
5
1
ln
21
dx
K
x
. Giá trị của K là:
A. 9 B. 8 C. 81 D. 3
Câu 29: Biến đổi
3
0
11
x
dx
x
thành
2
1
f t dt
, với
1tx
. Khi đó f(t) là hàm nào trong các hàm số
sau:
A.
2
22f t t t
B.
2
f t t t
C.
2
f t t t
D.
2
22f t t t
Câu 30: Đổi biến x = 2sint tích phân
1
2
0
4
dx
x
trở thành:
Group Nhóm Toán | Trắc nghiệm 2016-2017
19
7
A.
6
0
tdt
B.
6
0
dt
C.
6
0
1
dt
t
D.
3
0
dt
Câu 31: Tích phân
2
2
4
sin
dx
I
x
bằng:
A. 4 B. 3 C. 1 D. 2
Câu 32: Cho
2
1
cos ln
e
x
I dx
x
, ta tính được:
A. I = cos1 B. I = 1 C. I = sin1 D. Một kết quả khác
Câu 33: Tích phân
23
2
2
3
3
I dx
xx
bằng:
A.
6
B.
C.
3
D.
2
Câu 34: Giả sử
( ) 2
b
a
f x dx
và
( ) 3
b
c
f x dx
và a < b < c thì
()
c
a
f x dx
bằng?
A. 5 B. 1 C. -1 D. -5
Câu 35: Tính thể tích khối tròn xoay tạo nên do quay quanh trục Ox hình phẳng giới hạn bởi các
đường y = (1 – x
2
), y = 0, x = 0 và x = 2 bằng:
A.
82
3
B. 2
C.
46
15
D.
5
2
Câu 36: Cho
16
1
I xdx
và
4
0
cos2J xdx
. Khi đó:
A. I < J B. I > J C. I = J D. I > J > 1
Câu 37: Tích phân
4
0
2I x dx
bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
19
8
A. 0 B. 2 C. 8 D. 4
Câu 38: Tích phân
2
0
sinI x xdx
bằng :
A.
2
4
B.
2
4
C.
2
23
D.
2
23
Câu 39: Kết quả của
1
1
dx
x
là:
A.
0
B.-1 C.
1
2
D. Không tồn tại
Câu 40: Cho
2
0
3f x dx
.Khi đó
2
0
43f x dx


bằng:
A. 2 B. 4 C. 6 D. 8
Câu 41: Biết
0
2 4 0
b
x dx
.Khi đó b nhận giá trị bằng:
A.
0b
hoặc
2b
B.
0b
hoặc
4b
C.
1b
hoặc
2b
D.
1b
hoặc
4b
Câu 42: Để hàm số
sinf x a x b

thỏa mãn
12f
và
1
0
4f x dx
thì a, b nhận giá trị :
A.
,0ab

B.
,2ab

C.
2 , 2ab

D.
2 , 3ab

Câu 43:
4
42
0
cos 1 tan
dx
I
xx
bằng
Group Nhóm Toán | Trắc nghiệm 2016-2017
19
9
A. 1 B. 0 C.
1
2
D. Không tồn tại
Câu 44: Diện tích hình phẳng giới hạn bởi các đường
2
;2
y x y x x
có kết quả là:
A. 4 B.
9
2
C.5 D.
7
2
Câu 45: Thể tích khối tròn xoay giới hạn bởi các đường
ln , 0,
y x y x e
khi quay quanh trục Ox
bằng:
A.
e
B.
1
e
C.
2
e
D.
1
e
Câu 46: Tính diện tích giới hạn bởi
3
2 ; 0; 1; 1
y x y x x
. Một học sinh tính theo các bước sau
I.
2
3
1
2
S x dx
II.
2
4
1
2
x
S
III.
1 15
8
22
S
Cách làm trên sai từ bước nào?
A. I B. II C. III D. Không có bước nào sai
Câu 47: Cho đồ thị hàm số
y f x
. Diện tích hình phẳng (phần gạch trong hình) là:
A.
00
34
f x dx f x dx

B.
14
31
f x dx f x dx

C.
34
00
f x dx f x dx

D.
4
3
f x dx
Group Nhóm Toán | Trắc nghiệm 2016-2017
20
0
Câu 48: Giả sử
4
0
2
sin3 sin2
2
I x xdx a b
khi đó a+b là
A.
1
6
B.
3
10
C.
3
10
D.
1
5
Câu 49: Giả sử
0
2
1
3 5 1 2
ln
23
xx
I dx a b
x

. Khi đó giá trị
2
ab
là
B. 30 B. 40 C. 50 D. 60
Câu 50: Diện tích hình phẳng giới hạn bởi đường cong
2
1
yx

, tiếp tuyến với đường này tại điểm
M(2;5) và trục Oy là
A.
7
3
B.
5
3
C. 2 D.
8
3
PHẦN 17 :
ỨNG DỤNG TÍCH PHÂN
Câu 1. Kí hiệu
S
là diện tích hình thang cong giới hạn bởi đồ thị của hàm số liên tục
y f x
, trục
hoành và hai đường thẳng
, x a x b
như trong hình vẽ bên. Khẳng định nào sai?
A.
d.
b
a
S f x x
B.
d.


b
a
S f x x
Group Nhóm Toán | Trắc nghiệm 2016-2017
20
1
C.
d.
b
a
S f x x
D.
d.
b
a
S f x x
Câu 2. Kí hiệu
S
là diện tích hình thang cong giới hạn bởi đồ thị của hàm số liên tục
y f x
, trục
hoành và hai đường thẳng
, x a x b
như trong hình vẽ bên. Khẳng định nào đúng?
A.
d.
b
a
S f x x
B.
d.
b
a
S f x x
C.
d.
b
a
S f x x
D.
d.
b
a
S f x x
Câu 3. Kí hiệu
S
là diện tích hình thang cong giới hạn bởi đồ thị của hàm số
3
yx
, trục hoành và hai
đường thẳng
1, 2 xx
như trong hình vẽ bên. Tìm khẳng định đúng?
A.
2
3
1
d.
S x x
B.
02
33
10
dd

S x x x x
C.
2
3
1
d.
S x x
D. Không có khẳng định nào đúng.
Câu 4. Kí hiệu
St
là diện tích của hình thang vuông T giới hạn bởi đường thẳng
21yx
, trục hoành
và hai đường thẳng
1, 1 5 . x x t t
Khẳng định nào sai?
Group Nhóm Toán | Trắc nghiệm 2016-2017
20
2
A.
2 1 . S t t t
B.
St
là một nguyên hàm của
2 1, 1;5 . f t t t
C. Hình thang vuông giới hạn bởi đường thẳng
2 1,yx
trục hoành và hai đường thẳng
1, 5xx
có diện tích là
5
1
2 1 d .
S x x
D. Hình thang vuông giới hạn bởi đường thẳng
2 1,yx
trục hoành và hai đường thẳng
1, 3xx
có diện tích là 30.
Câu 5. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
cos , siny x y x
và hai đường thẳng
0, .
2
xx
A.
2 2 1 .S
B.
2 1 2 .S
C.
2 2.S
D.
2 2 1.S
Câu 6. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
2 3 1 y x x
và parabol
2
2 y x x
.
Tính
cos .



S
A.
cos 0.



S
B.
2
cos .
2




S
C.
2
cos .
2



S
D.
3
cos .
2



S
Câu 7. Gọi
S
là số đo diện tích hình phẳng giới hạn bởi đường
sin ,y x x
trục hoành và hai đường thẳng
0,
xx
. Khẳng định nào sai?
A.
sin 1.
2
S
B.
cos2 1.S
C.
tan 1.
4
S
D.
sin 1.S
Câu 8. Kí hiệu
12
, SS
lần lượt là diện tích hình vuông cạnh bằng 1 và diện tích hình phẳng giới hạn bởi các
đường
2
1, 0, 1, 2 y x y x x
. Chọn khẳng định đúng.
A.
12
.SS
B.
12
.SS
C.
12
1
.
2
SS
D.
1
2
6.
S
S
Group Nhóm Toán | Trắc nghiệm 2016-2017
20
3
Câu 9. Biết rằng diện tích
S
của hình phẳng giới hạn bởi các đường
1
ln , 0, , y x x y x x e
e
có thể
được viết dưới dạng
1
1.




Sa
e
Tìm khẳng định sai?
A.
2
3 2 0. aa
B.
2
2 0. aa
C.
2
3 2 0. aa
D.
2
2 3 2 0. aa
Câu 10. Tính diện tích
S
của hình phẳng giới hạn bởi đường parabol
2
32 y x x
và hai đường thẳng
1, 0. y x x
A.
111
.
42
S
B.
4
.
3
S
C.
799
.
300
S
D.
2.S
Câu 11. Tính diện tích
S
của hình phẳng giới hạn bởi hai đường
2
50 yx
,
3 0. xy
A.
3.S
B.
4.S
C.
4,5.S
D.
5.S
Câu 12. Câu 66. Hình phẳng
H
có diện tích
S
gấp 30 làn diện tích hình phẳng giới hạn bởi các đường
2
2 , 2 2 0, 0. y x x y y
Tính
.S
A.
20.S
B.
30.S
C.
40.S
D.
50.S
Câu 13. Kí hiệu
1 2 3
, , S S S
lần lượt là diện tích hình vuông đơn vị (có cạnh bằng đơn vị), hình trn đơn vị
(có bán kính bằng đơn vị), hình phẳng giới hạn bởi hai đường
2
2 1 , 2 1 . y x y x
Tính tỉ số
13
2
.
SS
S
A.
13
2
1
.
3
SS
S
B.
13
2
1
.
4
SS
S
C.
13
2
1
.
2
SS
S
D.
13
2
1
.
5
SS
S
Câu 14. Kí hiệu
V
là thể tích khối tròn xoay tạo thành khi quay hình thang cong giới hạn bởi đồ thị hàm số
,y f x
trục
Ox
và hai đường thẳng
, x a x b
(như trong hình vẽ bên) xung quang trục
.Ox
Khẳng định nào đúng?
A.
d.
b
a
V f x x
B.
d.
b
a
V f x x
Group Nhóm Toán | Trắc nghiệm 2016-2017
20
4
C.
2
d.



b
a
V f x x
D.
2
d.
b
a
V f x x
Câu 15. Gọi
V
là thẻ tích hình cầu bán kính
R
. Khẳng định nào sai?
A. Hình cầu bán kính
R
là khối trn xoay thu được khi quay nữa hình tròn giới hạn bởi đường
22
y R x R x R
và đường thẳng
0y
xung quanh trục
.Ox
B.
2
22
d.

R
R
V R x x
C.
3
2
.
3




R
R
x
V R x
D. Không có khẳng định nào đúng.
Câu 16. Tính thể tích
V
của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
3
, 0, 1, 8 y x y x x
xung quanh trục
Ox
.
A.
2
.
V
B.
9
.
4
V
C.
18,6.V
D.
93
.
5
V
Câu 17. Tính thể tích
V
của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
tan , 0, 0,
4
y x y x x
xung quanh trục
Ox
.
A.
.
4
V
B.
2
.
4
V
C.
.
4
V
D.
ln2
.
2
V
Câu 18. Tính thể tích
V
của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
2
4 , 0 y x y
xung quanh trục
Ox
.
A.
2.
V
B.
71
.
82
V
C.
512
.
15
V
D.
2
8
.
3
V
Câu 19. Kí hiệu
12
, VV
lần lượt là thể tích hình cầu đơn vị và thể tích khối tròn xoay sinh ra khi quay hình
phẳng giới hạn bởi đường thẳng
22 yx
và đường cong
2
21yx
xung quanh trục
.Ox
Hãy
so sánh
12
, .VV
A.
12
.VV
B.
12
.VV
C.
12
.VV
D.
12
2.VV
Câu 20. Kí hiệu
12
, VV
lần lượt là thể tích hình cầu đơn vị và thể tích khối tròn xoay sinh ra khi quay hình
phẳng
H
giới hạn bởi đường thẳng
2
2
y
x
và các đường
0, 0, 1y x x
xung quanh trục
.Ox
Hãy tính tỉ số
1
2
.
V
V
Group Nhóm Toán | Trắc nghiệm 2016-2017
20
5
A.
1
2
3
.
2
V
V
B.
1
2
2
.
3
V
V
C.
1
2
1
.
2
V
V
D.
1
2
2.
V
V
PHẦN 18 :
Câu 1. Nguyên hàm của hàm số
4
2
23x
fx
x
là:
A.
3
23
.
3
x
C
x
B.
3
2
23
.
3
x
C
x
C.
3
2
2
3ln .
3
x
xC
D.
3
2
2
ln .
3
x
xC
Câu 2. Nguyên hàm của hàm số
2sin3 .cos2 f x x x
là:
A.
1
cos5 cos .
5
x x C
B.
1
cos5 cos .
5
x x C
C.
5cos5 cos .x x C
D.
5cos5 cos .x x C
Giải:
2sin3 .cos2 sin5 sin .xf x x xx
Câu 3. Tìm hàm số
fx
biết rằng
21f x x
và
15f
.
A.
2
3.xx
B.
2
3.xx
C.
2
.xx
D.
2
2.xx
Câu 4. Tìm hàm số
fx
biết rằng
4f x x x
và
40f
.
A.
2
8 40
.
3 2 3
xx
B.
2
8 40
.
3 2 3
xx
C.
2
8 40
.
3 2 3
x x x
D.
2
8 40
.
3 2 3
x x x
Câu 5. Nguyên hàm của hàm số
2
x
xe dx
là:
A.
2
.
x
eC
B.
2
.
2
x
e
C
C.
2
.
x
xe C
D.
2
.
x
xe
Giải:
2 2 2
2
11
.
22
x x x
xe dx e d x e C
Câu 6. Nguyên hàm của hàm số
5
( ) (1 2 )f x x
là:
A.
6
1
(1 2 ) .
2
xC
B.
6
(1 2 ) .xC
C.
6
1
(1 2 ) .
6
xC
D.
6
1
(1 2 ) .
12
xC
Câu 7. Trong các khẳng định sau, khẳng định nào sai?
A.
2
2.xdx x C
B.
1
ln .xdx C
x
C.
sin cos .xdx x C
D.
2
1
cot .
sin
dx x C
x
Câu 8. Nguyên hàm của hàm số
2
3
2f x x
x
là:
A.
22
3ln .x x C
B.
2
2
3
.xC
x
C.
2
3
.xC
x
D.
2
3ln .x x C
Câu 9. Hàm số
tan
x
F x e x C
là nguyên hàm của hàm số
()fx
nào?
A.
2
1
( ) .
sin
x
f x e
x
B.
2
1
( ) .
sin
x
f x e
x
C.
2
1
( ) .
cos
x
f x e
x
D.
2
1
( ) .
cos
x
f x e
x
Câu 10. Nếu
thì
()fx
bằng:
A.
cos 2 .
x
ex
B.
1
cos2 .
2
x
ex
C.
1
cos2 .
2
x
ex
D.
2cos2 .
x
ex
Câu 11. Nguyên hàm của hàm số
2
1
( ) 2
cos
x
f x e
x
là:
A.
2 tan .
x
e x C
B.
2
2.
cos
x
x
e
e x C
x
C.
tan .
x
e x C
D.
2
.
cos
x
x
e
e x C
x
Group Nhóm Toán | Trắc nghiệm 2016-2017
20
6
Câu 12. Tính
sin(3 1) x dx
.
A.
cos(3 1) .xC
B.
1
cos(3 1) .
3
xC
C.
cos(3 1) .xC
D.
1
cos(3 1) .
3
xC
Câu 13. Tính
(cos 6 cos4 ) x x dx
.
A.
11
sin 6 sin 4 .
64
x x C
B.
6sin6 5sin 4 .x x C
C.
11
sin 6 sin 4 .
64
x x C
D.
6sin6 sin4 .x x C
Câu 14. Tính
1
21
dx
x
.
A.
ln 2 1 .xC
B.
1
ln 2 1 .
2
xC
C.
1
ln 2 1 .
2
xC
D.
ln 2 1 .xC
Câu 15. Tính
1
12
dx
x
.
A.
ln 1 2 .xC
B.
2 ln 1 2 .xC
C.
1
ln 1 2 .
2
xC
D.
2
2
.
(1 2 )
C
x
Câu 16. Nguyên hàm của hàm số
2
1
3f x x x
x
là:
A.
32
3 ln .x x x C
B.
32
2
31
.
32
xx
C
x
C.
32
3
ln .
32
xx
xC
D.
32
3
ln .
32
xx
xC
Câu 17. Nguyên hàm của hàm số
2
( ) 2 1f x x x
là:
A.
3
1
( ) 2 .
3
F x x x C
B.
( ) 2 2 .F x x C
C.
32
1
( ) 2 .
3
F x x x x C
D.
32
1
( ) .
3
F x x x x C
Câu 18. Nguyên hàm của hàm số
2
11
()fx
x
x
là :
A.
2
ln ln .x x C
B.
1
ln .xC
x
C.
1
ln .xC
x
D.
2
ln ln .x x C
Câu 19. Nguyên hàm của hàm số
2
()
xx
f x e e
là:
A.
2
1
.
2
xx
e e C
B.
2
2.
xx
e e C
C.
( ) .
xx
e e x C
D.
2
.
xx
e e C
Câu 20. Nguyên hàm của hàm số
cos3f x x
là:
A.
1
sin3 .
3
xC
B.
1
sin3 .
3
xC
C.
sin 3 .xC
D.
3sin3 .xC
Câu 21. Công thức nguyên hàm nào sau đây không đúng?
A.
1
ln .dx x C
x
B.
1
( 1).
1
x
x dx C
C.
(0 1).
ln
x
x
a
a dx C a
a
D.
2
1
tan .
cos
dx x C
x
Câu 22. Tính
(3cos 3 )
x
x dx
.
A.
3
3sin .
ln3
x
xC
B.
3
3sin .
ln3
x
xC
C.
3
3sin .
ln3
x
xC
D.
3
3sin .
ln3
x
xC
Câu 23. Trong các hàm số sau:
Group Nhóm Toán | Trắc nghiệm 2016-2017
20
7
(I)
2
( ) tan 2f x x
(II)
2
2
()
cos
fx
x
(III)
2
( ) tan 1f x x
Hàm số nào có một nguyên hàm là hàm số
tang x x
A. (I), (II), (III). B. Chỉ (II), (III). C. Chỉ (III). D. Chỉ (II).
Câu 24. Trong các mệnh đề sau, mệnh đề nào sai?
A.
3
2
()
( ) ( ) .
3
fx
f x f x dx C
B.
( ). ( ) ( ) . ( ) .f x g x dx f x dx g x dx
C.
( ) ( ) ( ) ( ) .f x g x dx f x dx g x dx
D.
( ) ( )kf x dx k f x dx
(
k
là hằng số).
Câu 25. Nguyên hàm của hàm số
3
( ) (2 1)f x x
là:
A.
4
1
(2 1) .
8
xC
B.
4
1
(2 1) .
2
xC
C.
4
2(2 1) .xC
D.
4
1
(2 1) .
4
xC
PHẦN 19 :
I. NHẬN BIẾT
Câu 1. Cặp hàm số nào sau đây có tính chất: Có một hàm số là nguyên hàm của hàm số còn lại?
A.
sin2x
và
2
cos x
B.
2
tan x
và
22
1
cos x
C.
x
e
và
x
e
D.
sin2x
và
2
sin x
Câu 2. Nguyên hàm của hàm số
3
f x x
trên
R
là
A.
4
4
x
xC
B.
2
3xC
C.
2
3x x C
D.
4
4
x
C
Câu 3. Một nguyên hàm của hàm số
2
4
()
cos
fx
x
là:
A.
2
4
sin
x
x
B.
4tan x
C.
4 tan x
D.
3
4
4 tan
3
xx
Câu 4. Diện tích hình phẳng giới hạn bởi các đường
2
4y x x
và
2yx
là:
A.
4
2
0
(2 )dx x x
B.
2
2
0
( 2 )dx x x
C.
2
2
0
(2 )dx x x
D.
4
2
0
( 2 )dx x x
Câu 5. Một nguyên hàm
Fx
của
2
( ) 3 1f x x
thỏa
10F
là:
4
(2;4)
O
y
x
Group Nhóm Toán | Trắc nghiệm 2016-2017
20
8
A.
3
1x
B.
3
2xx
C.
3
4x
D.
3
22x
Câu 6. Hàm số
fx
có nguyên hàm trên K nếu
A.
fx
xác định trên K B.
fx
có giá trị lớn nhất trên K
C.
fx
có giá trị nhỏ nhất trên K D.
fx
liên tục trên K
Câu 7. Giá trị của tích phân
4
2
1
I d
21
x
x
là :
A.
17
ln
25
B.
17
ln
25
C. Không tồn tại D.
7
2ln
5
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
D
D
B
C
B
D
C
Group Nhóm Toán | Trắc nghiệm 2016-2017
20
9
II. THÔNG HIỂU
Câu 1. Tìm d để diện tích hình phẳng giới hạn bởi đường cong
2
, , 1, 1y Ox x x d d
x
bằng 2:
A.
2
e
B.
e
C.
2e
D.
1e
Câu 2. Tính các hằng số A và B để hàm số
( ) sinf x A x B

thỏa mãn đồng thời các điều kiện
'(1) 2f
và
2
0
( )d 4f x x
A.
2
,2AB
B.
2
,2AB

C.
2, 2AB
D.
2, 2AB
Câu 3. Nguyên hàm
Fx
của hàm số
23
24f x x x
thỏa mãn điều kiện
00F
là
A.4 B.
34
24xx
C.
4
3
2
4
34
x
xx
D.
34
2x x x
Câu 4. Để tìm nguyên hàm của
45
sin cosf x x x
thì nên:
A.Dùng phương pháp đổi biến số, đặt
costx
B.Dùng phương pháp lấy nguyên hàm từng phần, đặt
44
cos
d sin cos d
ux
v x x x
C.Dùng phương pháp lấy nguyên hàm từng phần, đặt
4
5
sin
d cos d
ux
v x x
D.Dùng phương pháp đổi biến số, đặt
sintx
Câu 5. Tính
5
3
1
d
x
x
x
ta được kết quả nào sau đây?
y = 2/x
O
y
x
1
d
Group Nhóm Toán | Trắc nghiệm 2016-2017
21
0
A.Một kết quả khác B.
32
32
xx
C
C.
6
4
6
4
x
x
C
x
D.
3
2
1
32
x
C
x

Câu 6. Cho tích phân
3
0
I 2 4 d
x
x
, trong các kết quả sau:
(I).
32
20
I 2 4 d 2 4 d
xx
xx

(II).
32
20
I 2 4 d 2 4 d
xx
xx

(III).
3
2
I 2 2 4 d
x
x
kết quả nào đúng?
A.Chỉ II. B. Chỉ III. C.Cả I, II, III. D.Chỉ I.
Câu 7. Tính
2
0
I 2 1 sin2 dx x x

Lời giải sau sai từ bước nào:
Bước 1: Đặt
2 1;d sin2 du x v x x
Bước 2: Ta có
d 2 d ; cos2u x v x
Bước 3:
2
2 2 2
0 0 0
0
I 2 1 cos2 2cos2 d 2 1 cos2 2sin2x x x x x x x
Bước 4: Vậy
I2
A.Bước 4 B. Bước 3 C.Bước 2 D.Bước 1
Câu 8. Giả sử
5
1
d
ln
21
x
c
x
. Giá trị của
c
là
A. 9 B. 8 C.3 D.81
Câu 9. Giá trị của
2
2
0
2d
x
ex
là
A.
4
4e
B.
4
e
C.
4
1e
D.
4
31e
Câu 10. Biểu thức nào sau đây bằng với
2
sin 3 dxx
?
A.
11
( sin6 )
26
x x C
B.
11
( sin6 )
26
x x C
C.
11
( sin3 )
23
x x C
D.
11
( sin3 )
23
x x C
Group Nhóm Toán | Trắc nghiệm 2016-2017
21
1
Câu 11. Cho hình phẳng giới hạn bởi các đường
cos4 , , 0,
8
y x Ox x x
quay xung quanh trục
Ox
.
Thể tích của khối tròn xoay tạo thành bằng:
A.
2
2
B.
2
16
C.
4
D.
3
Câu 12. Diện tích hình phẳng giới hạn bởi hai parabol
22
2 , 4y x x y x x
là giá trị nào sau đây ?
A.12 (đvdt) B. 27 (đvdt) C.4 (đvdt) D.9 (đvdt)
Câu 13. Cho hàm số
32
( ) 2 1f x x x x
. Gọi
Fx
là một nguyên hàm của biết rằng
14F
thì
A.
43
2
49
()
4 3 12
xx
F x x x
B.
43
2
( ) 1
43
xx
F x x x
C.
43
2
( ) 2
43
xx
F x x x
D.
43
2
()
43
xx
F x x x
Câu 14. Tích phân
4
0
cos2 dxx
bằng:
A.1 B.
1
2
C.2 D.0
Câu 15. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số
2
2, 3y x y x
là:
A.
1
2
B.
1
4
C.
1
6
D.
1
3
Câu 16. Tính diện tích hình phẳng giới hạn bởi các đường
32
2y x x x
và
4yx
.
A.
71
6
B.
2
3
C.
24
D.
53
7
Câu 17. Cho đồ thị hàm số
y f x
trên đoạn
0;6
như hình vẽ.
Biểu thức nào dưới đây có giá trị lớn nhất:
A.
1
0
( )df x x
B.
2
0
( )df x x
C.
3
0
( )df x x
D.
6
0
( )df x x
O
2
x
4
6
y=f(x)
y
Group Nhóm Toán | Trắc nghiệm 2016-2017
21
2
Câu 18. Biết rằng
33
12
( )d 5; ( )d 3f x x f x x

. Tính
2
1
()f x dx
?
A.
2
B.
2
C.
1
D.
5
Câu 19. Biểu thức nào sau đây bằng với
tan dxx
?
A.
1
ln( tan )
sinx
xC
B.
ln(cos )xC
C.
2
tan
2
x
C
D.
2
1
cos
C
x
Câu 20. Cho hàm số F(x) là một nguyên hàm của hàm số
cos3f x x
và
14
()
23
F
thì
A.
1 13
sin3
33
F x x
B.
1
sin3 5
3
F x x
C.
1
sin3 5
3
F x x
D.
1 13
sin3
33
F x x
Câu 21. Một học sinh tính tích phân
1
0
d
1
x
x
I
e
tuần tự như sau:
(I). Ta viết lại
1
0
d
I
1
x
xx
ex
ee
(II). Đặt
x
ue
thì
1 1 1
d d d
I ln ln 1
1
(1 ) 1
e e e
e
u u u
uu
u u u u

(III).
I ln ln( 1) ln1 ln 1 1 ln
1
e
ee
e
Lý luận trên, nếu sai thì sai từ giai đoạn nào?
A.III B. I C.II D.Lý luận đúng.
Câu 22. Nguyên hàm của hàm số
2
( ) (1 3 )
xx
f x e e

bằng:
A.
( ) 3
xx
F x e e C
B.
3
( ) 3
xx
F x e e C
C.
2
( ) 3
xx
F x e e C
D.
( ) 3
xx
F x e e C
Câu 23. Tìm họ nguyên hàm của hàm số
3
4
()f x x x x
?
A.
4
35
3
24
234
()
3 4 5
F x x x x C
B.
24
5
33
4
234
()
3 4 5
F x x x x C
C.
24
5
33
4
2 4 5
()
334
F x x x x C
D.
1
35
3
24
2 1 4
()
3 3 5
F x x x x C
Câu 24. Một nguyên hàm của
( ) cos3 cos2f x x x
bằng
A.
11
sin sin5
22
xx
B.
11
sin sin5
2 10
xx
C.
11
cos cos5
2 10
xx
D.
1
sin3 sin2
6
xx
Group Nhóm Toán | Trắc nghiệm 2016-2017
21
3
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
B
A
C
D
D
A
C
C
C
B
B
D
A
B
C
A
B
A
B
C
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
A
D
A
B
Group Nhóm Toán | Trắc nghiệm 2016-2017
21
4
III. VẬN DỤNG THẤP
Câu 1. Cho hình phẳng giới hạn bởi các đường
2
; 0; 0; 1
x
y xe y x x
. Thể tích của khối tròn xoay sinh
bởi hình phẳng trên khi quay quanh trục hoành là
A.
2
2e
B.
2
2e
C.
2e
D.
2e
Câu 2. Diện tích hình phẳng giới hạn bởi đường cong
32
: 3 2C y x x
, hai trục tọa độ và đường
thẳng
2x
là:
A.
3
2
(đvdt) B.
7
2
(đvdt) C.4 (đvdt) D.
5
2
(đvdt)
Câu 3. Gọi
Fx
là nguyên hàm của hàm số
2
1
()
32
fx
xx

thỏa mãn
3
0
2
F


. Khi đó
3F
bằng:
A.
2 ln2
B.
ln2
C.
2 ln2
D.
ln2
Câu 4. Tìm họ nguyên hàm
2
()
x
F x x e dx
?
A.
2
( ) ( 2 2)
x
F x x x e C
B.
2
( ) (2 2)
x
F x x x e C
C.
2
( ) ( 2 2)
x
F x x x e C
D.
2
( ) ( 2 2)
x
F x x x e C
Câu 5. Cho hình phẳng giới hạn bởi các đường
1 , , 0, 4y x Ox x x
quay xung quanh trục
Ox
. Thể
tích của khối tròn xoay tạo thành bằng:
A.
2
28
.
3
B.
68
.
3
C.
28
3
D.
2
68
.
3
Câu 6. Giá trị của
2
2
2
1x dx
là
A.2 B. 3 C.4 D.5
Câu 7. Họ nguyên hàm của hàm số
cos3 tanf x x x
là
A.
3
4
cos 3cos
3
x x C
B.
3
1
sin 3sin
3
x x C
C.
3
4
cos 3cos
3
x x C
D.
3
1
cos 3cos
3
x x C
Câu 8. Tính
2
0
cosI x xdx
A.I =
2
B. I =
2
- 1 C.I =
3
D.I =
1
32
Câu 9. Thể tích vật thể tròn xoay sinh ra bởi hình phẳng giới hạn parabol
2
:1P y x
và trục hoành khi
quay xung quanh trục
Ox
bằng bao nhiêu đơn vị thể tích?
A.
7
2
B.
5
2
C.
8
3
D.
16
15
Group Nhóm Toán | Trắc nghiệm 2016-2017
21
5
Câu 10. Nguyên hàm
Fx
của hàm số
4
sin 2f x x
thỏa mãn điều kiện
3
0
8
F
là:
A.
3 1 1 3
sin2 sin4
8 8 64 8
x x x
B.
3 1 1
sin4 sin8
8 8 64
x x x
C.
3 1 1
1 sin4 sin8
8 8 64
x x x
D.
3
sin4 sin6x
8
xx
Câu 11. Họ nguyên hàm của hàm số
3
2ln 3x
fx
x
là
A.
2
2ln 3
2
x
C
B.
2ln 3
8
x
C
C.
4
2ln 3
8
x
C
D.
4
2ln 3
2
x
C
Câu 12. Một nguyên hàm của
3
1
()
1
x
x
e
fx
e
là:
A.
2
1
()
2
xx
F x e e x
B.
2
1
()
2
xx
F x e e
C.
2
1
()
2
xx
F x e e
D.
2
1
( ) 1
2
xx
F x e e
Câu 13. Tính tích phân
2
2
0
I dx x x
ta được kết quả:
A.ln2 B. 6 C.1 D.
ln8
Câu 14. Họ nguyên hàm của hàm số
1
18
x
fx
là
A.
18
ln
ln12 1 8
x
x
F x C
B.
18
ln
12 1 8
x
x
F x C
C.
18
ln
ln8 1 8
x
x
F x C
D.
8
ln
18
x
x
F x C
Câu 15. Nếu
4
3
1
d ln
12
xm
xx

thì m bằng
A.
12
B.
4
3
C.
1
D.
3
4
Câu 16. Gọi (H) là đồ thị của hàm số
1
()
x
fx
x
. Diện tích giới hạn bởi (H), trục hoành và hai đường
thẳng có phương trình
1, 2xx
bằng bao nhiêu đơn vị diện tích?
A.
2ln2
B.
ln2 1
C.
1 ln2
D.
1 ln2
Câu 17. Diện tích hình phẳng giới hạn bởi đồ thị có phương trình
2
2 0 ; 0x x y x y
là:
A.8 B.
11
2
C.
9
2
D.
7
2
Group Nhóm Toán | Trắc nghiệm 2016-2017
21
6
Câu 18. Diện tích hình phẳng giới hạn bởi các đường
yx
và
1
2
yx
là:
A.
2
B.
4
3
C.
16
3
D.
5
12
Câu 19. Diện tích hình phẳng giới hạn bởi hai parabol
2
:P y x
và
2
' : 2P y x x
là bao nhiêu đơn
vị diện tích?
A.1 B.
1
3
C.
1
2
D.3
Câu 20. Tích phân
1
0
d
1
x
x
e
bằng:
A.
ln
22
e
e
B.
2
ln
1
e
e
C.
ln
21
e
e
D.
ln 1 ln2e 
Câu 21. Biểu thức nào sau đây bằng với
2
sinx xdx
?
A.
2
2 cos cos dx x x x x
B.
2
cos 2 cos dx x x x x
C.
2
cos 2 cos dx x x x x
D.
2
2 cos cos dx x x x x
Câu 22. Cho hàm số F(x) là một nguyên hàm của hàm số
2
1
32
fx
xx

và
30F
thì
A.
1
ln ln2
2
x
Fx
x

B.
2
ln ln2
1
x
Fx
x

C.
2
ln ln2
1
x
Fx
x

D.
1
ln ln2
2
x
Fx
x

Câu 23. Tính
1
2
0
2
dx
I
xx

A.
2
I ln2
3

B.
I 3 ln2
C.
1
I ln3
2
D.
I 2ln3
Câu 24. Diện tích hình phẳng giới hạn bởi hai đường
2
, sin y x y x x
và hai đường thẳng
0, xx

là:
A.S =
2
(đvdt) B. S =
1
2
(đvdt) C.S =
1
2
(đvdt) D.S =
(đvdt)
Câu 25. Tính
3
cos dxx
ta được kết quả là :
A.
4
cos x
C
x
B.
1 3sin
sin3
12 4
x
xC
C.
4
cos .sin
4
xx
C
D.
1 sin3
3sin
43
x
xC




Group Nhóm Toán | Trắc nghiệm 2016-2017
21
7
Câu 26. Bằng cách đổi biến số
2sinxt
thì tích phân
1
0
2
d
4
x
x
là:
A.
1
0
dt
B.
6
0
dt
C.
6
0
dtt
D.
3
0
dt
t
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
C
D
D
A
B
C
C
B
D
A
C
D
C
C
D
D
C
B
B
B
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
B
C
A
A
D
B
Group Nhóm Toán | Trắc nghiệm 2016-2017
21
8
IV. VẬN DỤNG CAO
Câu 1. Gọi F
1
(x) là nguyên hàm của hàm số
2
1
( ) sinf x x
thỏa mãn
1
00F
và
2
Fx
là nguyên hàm
của hàm số
2
2
( ) cosf x x
thỏa mãn
2
00F
.
Khi đó phương trình
12
F x F x
có nghiệm là:
A.
2xk
B.
xk
C.
2
xk

D.
2
k
x
Câu 2. Diện tích hình phẳng giới hạn bởi
2
20y y x
,
0xy
là:
A.Đáp số khác B.
11
2
C.5 D.
9
2
Câu 3. Tính thể tích vật thể trn xoay được tạo thành khi quay hình phẳng (H) giới hạn bởi các đường cong
2
yx
và
yx
quanh trục
Ox
.
A.
3
V
10
B.
13
V
15
C.
13
V
5
D.
3
V
5
Câu 4. Tính tích phân
23
2
5
d
I
4
x
xx
A.
3
3ln
4
B.
5
2ln
3
C.
15
ln
43
D.
13
ln
25
Câu 5. Hình phẳng D giới hạn bởi
2
2yx
và
24yx
khi quay D xung quanh trục hoành thì thể tích
khối tròn xoay tạo thành là:
A.V =
288
5
(đvtt) B. V =
2
(đvtt) C.V = 72
(đvtt) D.V =
4
5
(đvtt)
Câu 6. Các đường cong
sin , cosy x y x
với
0
2
x

và trục
Ox
tạo thành một hình phẳng. Diện
tích của hình phẳng là:
A.
22
B. 2 C.
22
D.Đáp số khác.
Câu 7. Gọi F(x) là nguyên hàm của hàm số
2
()
8
x
fx
x
thỏa mãn
20F
. Khi đó phương trình F(x)
= x có nghiệm là:
A.
0x
B.
1x
C.
1x 
D.
13x 
Câu 8. Diện tích hình phẳng nằm trong góc phần tư thứ nhất, giới hạn bởi đường thẳng
4yx
và đồ thị
hàm số
3
yx
là:
A.5 B. 3 C.4 D.
7
2
Câu 9. Tính
1
2
0
1dI x x
Group Nhóm Toán | Trắc nghiệm 2016-2017
21
9
A.I =
4
B. I =
1
2
C.I = 2 D.I =
3
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số
2
; 2y x y x
là:
A.2 B.
5
3
C.
7
3
D.3
Câu 11. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bới các đường
yx
,
2yx
,
0y
quay quanh trục
Oy
, có giá trị là kết quả nào sau đây ?
A.
1
3
(đvtt) B.
3
2
(đvtt) C.
11
6
(đvtt) D.
32
15
(đvtt)
Câu 12. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
32
3 3 1y x x x
và tiếp tuyến của đồ thị
tại giao điểm của đồ thị và trục tung.
A.
27
S
4
B.
5
S
3
C.
23
S
4
D.
4
S
7
Câu 13. Tính
1
4
1
Id
21
x
x
x
A.I =
1
5
B. I =
5
7
C.I =
7
5
D.I = 5
Câu 14. Cho (H) là hình phẳng giới hạn bởi đường cong (L):
3
ln 1y x x
, trục Ox và đường thẳng
1x
. Tính thể tích của vật thể trn xoay tạo ra khi cho (H) quay quanh trục Ox.
A.
V ln4 1
3

B.
V ln4 2
3

C.
V ln3 2
3

D.
V ln3
3
Câu 15. Với giá trị nào của
0m
thì diện tích hình phẳng giới hạn bởi hai đường
2
yx
và
y mx
bằng
4
3
đơn vị diện tích ?
A.
2m
B.
1m
C.
3m
D.
4m
Câu 16. Tích phân
2
0
d
a
x
x
ax
bằng
A.
1
2
a



B.
2
4
a



C.
1
2
a



D.
2
4
a



Câu 17. Với t thuộc
1;1
ta có
2
0
d1
ln3
12
t
x
x

. Khi đó giá trị t là:
A.
1
3
B.
1
3
C.0 D.
1
2
Câu 18. Tìm a sao cho
2
23
1
I [ (4 - ) 4 ]d 12a a x x x
A.Đáp án khác B.
3a 
C.
5a
D.
3a
Group Nhóm Toán | Trắc nghiệm 2016-2017
22
0
Câu 19. Cho
ln
0
d
ln2
2
m
x
x
ex
A
e

. Khi đó giá trị của m là:
A.
0; 4mm
B. Kết quả khác C.
2m
D.
4m
Câu 20. Cho S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
32
69y x x x
và trục Ox. Số nguyên
lớn nhất không vượt quá S là:
A.10 B. 7 C.27 D.6
Câu 21. Vận tốc của một vật chuyển động là
3 5 /v t t m s
. Quãng đường vật đó đi được từ giây thứ 4
đến giây thứ 10 là :
A.36m B. 252m C.120m D.156m
Câu 22. Diện tích hình phẳng giới hạn bởi
2
4yx
và
3yx
là:
A.
17
6
B.
3
2
C.
5
2
D.
13
3
Câu 23. Tính tích phân
2
2
0
1
Id
- 2 2
x
xx
ta được kết quả:
A.
4
B.
2
C.
4
D.
3
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
D
D
A
C
A
D
D
C
A
C
D
A
A
A
A
B
A
A
D
D
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
D
D
B
PHẦN 20 :
TÍCH PHÂN - ỨNG DỤNG
(PHẦN 4)
Mức độ nhận biết, thông hiểu
Group Nhóm Toán | Trắc nghiệm 2016-2017
22
1
Câu 1. Giá trị của
d
2
2
0
2
x
ex
là :
A.
4
e
B.
4
1e
C.
4
4e
D.
4
31e
:
Câu 2. Nếu
6
0
( ) 10f x dx
và
4
0
( ) 7f x dx
, thì
6
4
()f x dx
bằng :
A.
3
B.
17
C.
170
D.
3
Câu 3. Giả sử
d
5
1
ln
21
x
c
x
. Giá trị đúng của
c
là :
A. 9 B. 3 C. 81 D. 8
Câu 4. Khẳng định nào sau đây đúng về kết quả
1
3
4
0
1
ln 2
1
x
dx
a
x
?
A.
2a
B.
4a
C.
4a
D.
2a
Câu 5. Tính tích phân
1
2
0
(3 1)
69
x dx
I
xx

A.
45
3ln
36
B. C.
45
3ln
36
D.
47
3ln
36
Câu 6. Nguyên hàm của hàm số
2
– 3
1
f x x x
x

là:
A. F(x) =
32
3
ln
32
xx
xC
B. F(x) =
Cx
xx
ln
2
3
3
23
C. F(x) =
32
3
ln
32
xx
xC
D. F(x) =
32
3
ln
32
xx
xC
Câu 7. Thể tích của khối tròn xoay sinh ra khi quay quanh trục Oy hình phẳng giới hạn bởi các đường:
2
y x 4x 3
và Ox bằng :
A.
16
5
B.
5
C.
5
D.
16
3
Câu 8. Cho
2
2
1
x
fx
x
. Khi đó:
A.
2
2ln 1f x dx x C
B.
2
3ln 1f x dx x C
35
3ln
46
Group Nhóm Toán | Trắc nghiệm 2016-2017
22
2
C.
2
4ln 1f x dx x C
D.
2
ln 1f x dx x C
Câu 9. Cho hai hàm số y = f(x), y = g(x) có đồ thị (C1) và (C2) liên tục trên [a;b] thì công thức tính diện tích
hình phẳng giới hạn bởi (C1), (C2) và hai đường thẳng x = a, x = b là
A.
b
a
S f(x) g(x) dx
B.
b
a
S g(x) f(x) dx
C.
bb
aa
S f(x)dx g(x)dx

D.
b
a
S f(x) g(x) dx
Câu 10. Khẳng định nào sau đây sai về kết quả
0
1
1
ln 1
2
xb
dx a
xc
?
A.
. 3( 1)a b c
B.
3ac b
C.
2 10a b c
D.
1ab c
Câu 11. Tính tích phân
1
2
0
( 4)
32
x dx
I
xx

A.
5ln2 3ln2
B.
5ln2 2ln3
C.
5ln2 2ln3
D.
2ln5 2ln3
Câu 12. Cho hàm số
y = f(x)
liên tục và chỉ triệt tiêu khi
x = c
trên
[a; b].
Các kết quả sau, câu nào đúng?
A.
bb
aa
f(x) dx f(x)dx

B.
b c b
a a c
f(x) dx f(x) dx f(x) dx
C.
b c b
a a a
f(x) dx f(x) dx f(x)dx
D. A, B, C đều đúng
Câu 13. Diện tích phẳng giới hạn bởi:
2
1; 2; 0; 2x x y y x x
A.
4
3
B. 1 C. 0 D.
8
3
Câu 14. Tìm một nguyên hàm F(x) của hàm số
32
2
x 3x 3x 1
f(x)
x 2x 1

biết
1
F(1)
3
A.
B.
2
2 13
F(x) x x
x 1 6
C.
2
x 2 13
F(x) x
2 x 1 6
D.
2
x2
F(x) x 6
2 x 1
Câu 15. Tính diện tích
S
hình phẳng được giới hạn bởi các đường:
2
1
; ln ; 1
1
y x y x
x
Group Nhóm Toán | Trắc nghiệm 2016-2017
22
3
A.
8 31
ln2
3 18
S
B.
8 23
ln2
3 18
S 
C.
8 17
ln2
3 18
S 
D.
8 23
ln2
3 18
S 
Câu 16. Gọi
2008
x
dx F x C
, với C là hằng số. Khi đó hàm số
Fx
bằng
A.
2008 ln2008
x
B.
1
2008
x
C.
2008
x
D.
2008
ln2008
x
Câu 17. Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi các đường
ln , 0,y x x y x e
có giá trị bằng:
3
(b 2)e
a
trong đó a,b là hai số thực nào dưới đây?
A.
a=27; b=5
B.
a=24; b=6
C.
a=27; b=6
D.
a=24; b=5
Câu 18. Cho đồ thị hàm số
y f x
. Diện tích hình phẳng (phần tô đậm trong hình) là:
A.
d
4
3
f x x
B.
dd
00
34
f x x f x x
C.
dd
14
31
f x x f x x
D.
dd
34
00
f x x f x x
Câu 19. Tích phân
d
2
0
cos .sinx x x
bằng:
A.
2
3
B.
2
3
C.
3
2
D.0
Câu 20. Cho tích phân
1
2
2
0
1 x dx
bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
22
4
A.
3
64




B.
13
2 6 4




C.
3
64




D.
13
2 6 4




Câu 21.
0
I 1 cos2x dx

bằng :
A.
2
B. 0 C. 2 D.
22
Câu 22. Tìm họ nguyên hàm:
3
4
()
1
x
F x dx
x
A.
4
( ) ln 1F x x C
B.
4
1
( ) ln 1
4
F x x C
C.
4
1
( ) ln 1
2
F x x C
D.
4
1
( ) ln 1
3
F x x C
Câu 23. Nếu
9
0
( ) 37f x dx
và
9
0
g( ) 16x dx
thì
9
0
2 ( ) 3g( )f x x dx
bằng :
A.
122
B.
74
C.
48
D.
53
Câu 24. Giá trị của tích phân
1
3
34
0
1.x x dx
bằng?
A.
3
16
B. 2 C.
6
13
D. Đáp án khác
Câu 25. Tính
d
ln 2
2
x
x
x
, kết quả là:
A.
2 2 1
x
C
B.
2
x
C
C.
2 2 1
x
C
D.
1
2
x
C
Câu 26. Tính
d
1
x
x
, kết quả là :
A.
1
C
x
B.
21 xC
C.
2
1
C
x
D.
1Cx
Group Nhóm Toán | Trắc nghiệm 2016-2017
22
5
Câu 27. Diện tích hình phẳng giới hạn bởi
2
xln(x 2)
y
4x
và trục hoành là :
A.
23
3

B.
2ln2 2
4

C.
ln2 2 3
3
D.
2ln2 2 3
3
Câu 28. Một nguyên hàm của
2
2
xln x x 1
f(x)
x1

là:
A.
2
xln x x 1 x C
B.
2
ln x x 1 x C
C.
2
xln x 1 x C
D.
22
x 1ln x x 1 x C
Câu 29. Cho hình phẳng giới hạn bởi các đường y = 2x – x
2
và y = 0. Thì thể tích vật thể tròn xoay được sinh
ra bởi hình phẳng đó khi nó quay quanh trục Ox có giá trị bằng ?
A.
16
15
B.
15
16
C.
5
6
D.
6
5
Câu 30. Khẳng định nào sau đây sai về kết quả
2
0
1
(2 1 sin ) 1x x dx
ab
A.
28ab
B.
5ab
C.
2 3 2ab
D.
2ab
Câu 31. Một nguyên hàm của hàm số
sin3yx
A.
1
os3
3
cx
B.
3 os3cx
C.
3 os3cx
D.
1
os3
3
cx
Câu 32. Nếu
2
()
6 2 , 0
x
a
ft
dt x x
t
thì hệ số
a
bằng
A.
9
B.
19
C.
5
D.
29
Câu 33. Biết tích phân
1
0
23
2
x
dx
x
=aln2 +b . Thì giá trị của a là:
A. 7 B. 2 C. 3 D. 1
Group Nhóm Toán | Trắc nghiệm 2016-2017
22
6
Câu 34. Thể tích hình khối do hình phẳng giới hạn bởi các đường
2
y x 4,
y 2x 4,x 0,x 2
quay
quanh trục Ox bằng
A.
32
5
B.
6
C.
6
D.
32
5
:
Câu 35. Nguyên hàm của hàm số
4
2
23x
y
x
là:
A.
C
x
x
3
3
2
3
B.
3
3
3xC
x

C.
3
3
3
x
C
x

D.
3
23
3
x
C
x

Mức độ vận dụng thấp
Câu 36. Tính
dxex
x 1
2
.
A.
2
1x
eC
B.
2
1
2
x
eC
C.
2
1
1
2
x
eC
D.
2
1
1
2
x
eC
:
Câu 37. Thể tích của khối tròn xoay tạo thành khi quay hình phẳng D giới hạn bởi các đường
1yx
,
trục hoành,
2, 5xx
quanh trục Ox bằng :
A.
d
5
2
1xx
B.
d
5
2
1xx
C.
d
2
2
2
1
1yx
D.
d
5
2
1xx
:
Câu 38. Cho tích phân
4
2
0
6tan
cos 3tan 1
x
I dx
xx
. Giả sử đặt
3tan 1ux
thì ta được:
A.
2
2
1
4
21
3
I u du
B.
2
2
1
4
1
3
I u du
C.
2
2
1
4
1
3
I u du
D.
2
2
1
4
21
3
I u du
Câu 39. Họ nguyên hàm của hàm số
3
2
1
x
fx
x
là:
A.
22
1
21
3
x x C
B.
22
1
11
3
x x C
C.
22
1
11
3
x x C
D.
22
1
21
3
x x C
Group Nhóm Toán | Trắc nghiệm 2016-2017
22
7
Câu 40. Nếu
(1) 12, '( )f f x
liên tục và
4
1
'( ) 17f x dx
, giá trị của
(4)f
bằng
A.
29
B.
5
C.
19
D.
9
Câu 41. Nếu
()fx
liên tục và
4
0
( ) 10f x dx
, thì
2
0
(2 )f x dx
bằng :
A.
5
B.
29
C.
19
D.
9
Câu 42. Biết
0
2 4 0
b
x dx
, khi đó b nhận giá trị bằng:
A.
1b
hoặc
4b
B.
0b
hoặc
2b
C.
1b
hoặc
2b
D.
0b
hoặc
4b
Câu 43. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
yx
và đường thẳng
2yx
bằng:
A.
23
15
B.
4
3
C.
3
2
D.
5
3
Câu 44. Thể tích của khối tròn xoay tạo lên bởi lên hình phẳng (H) giới hạn bởi các đường
2
2yx
;
1y
và trục Ox khí quay xung quanh Ox là;
A.
11
22
11
( 1)x dx dx



B.
11
22
11
( 2)x dx dx



C.
11
22
11
( 2)x dx dx



D.
1
22
1
( 2)x dx

Câu 45. Cho
2
4
( ) sin
m
f x x

. Tìm m để nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 và
48
F




A. B. C. D. :
Câu 46. Một nguyên hàm
( ) cos3 1
( 2) sin 3 sin3 2017
x a x
x xdx x
bc
thì tổng
.S a b c
bằng
A.
14S
B.
15S
C.
3S
D.
10S
Câu 47. Tìm họ nguyên hàm:
()
2ln 1
dx
Fx
xx
A.
( ) 2 2ln 1F x x C
B.
( ) 2ln 1F x x C
4
3
m 
3
4
m
3
4
m 
4
3
m
Group Nhóm Toán | Trắc nghiệm 2016-2017
22
8
C.
1
( ) 2ln 1
4
F x x C
D.
1
( ) 2ln 1
2
F x x C
Câu 48. Cho hàm
4
sin 2f x x
. Khi đó:
A.
11
3 sin4 sin8
88
f x dx x x x C



B.
11
3 cos4 sin8
88
f x dx x x x C



C.
11
3 cos4 sin8
88
f x dx x x x C



D.
11
3 sin4 sin8
88
f x dx x x x C



Câu 49. Diện tích hình phẳng giới hạn bởi hai đường cong
(1 )
x
y e x
và
( 1)y e x
là?
A.
1
2
e
B.
2
2
e
C.
2
2
e
D.
1
2
e
Câu 50. Cho tích phân
sin
2
0
sin2 .
x
I xe dx
: .một học sinh giải như sau:
Bước 1: Đặt
sin cost x dt xdx
. Đổi cận:
00
1
2
xt
xt
1
0
2.
t
I t e dt
.
Bước 2: chọn
tt
u t du dt
dv e dt v e





11
11
00
00
. . 1
t t t t
t e dt t e e dt e e

Bước 3:
1
0
2 . 2
t
I t e dt
.
Hỏi bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
A.Bài giải trên sai từ bước 1.
B.Bài giải trên sai từ bước 2 .
C. Bài giải trên hoàn toàn đúng.
D.Bài gaiir trên sai ở bước 3
.
Câu 51. Tính diện tích hình phẳng tạo bởi các đường: Parabol
2
: 4 5P y x x
và 2 tiếp tuyến tại các
điểm
1;2 , 4;5AB
nằm trên
P
A.
7
2
S
B.
11
6
S
C.
9
4
S
D.
13
8
S
Group Nhóm Toán | Trắc nghiệm 2016-2017
22
9
Câu 52. Tìm hàm số F(x) biết rằng F’(x) = 4x
3
– 3x
2
+ 2 và F(-1) = 3
A.
43
F(x) = x - x - 2x -3
B.
43
F(x) = x - x - 2x +3
C.
43
F(x) = x - x + 2x + 3
D.
Câu 53. Biết rằng
x;
43





thì
3 cot x 4
.
x


Gọi
3
4
cot x
I dx.
x
Kết luận nào sau đây là đúng
A.
31
I
12 4

B.
11
I
43

C.
11
I
54

D.
31
I
12 3

Câu 54. Tính
ln x
A.
lnx x x C
B.
ln x x C
C.
lnx x x C
D.
lnx x x C
?
Câu 55. Thể tích của vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi các đường y = x
2
– 2x, y = 0,
x = 0, x = 1 quanh trục hoành Ox có giá trị bằng?
A.
8
15
B.
7
8
C.
8
15
D.
8
7
Câu 56. Tìm nguyên hàm của:
35
()
dx
Fx
xx
A.
2
2
11
( ) ln ln 1
22
F x x x C
x
B.
2
2
11
( ) ln ln 1
22
F x x x C
x
C.
2
2
11
( ) ln ln 1
22
F x x x C
x
D.
2
2
11
( ) ln ln 1
25 6
F x x x C
x
Câu 57. Cho hình phẳng
H
được giới hạn bởi các đường:
ln , 0,y x x y x e
. Tính thể tích khối tròn
xoay tạo thành khi hình
H
quay quanh trục
Ox
.
A.
3
52
25
Ox
e
V
B.
3
52
27
Ox
e
V
C.
3
52
27
Ox
e
V
D.
3
52
25
Ox
e
V
Mức độ vận dụng cao.
Group Nhóm Toán | Trắc nghiệm 2016-2017
23
0
Câu 58. Cho hình phẳng
H
được giới hạn bởi các đường:
ln , 0,y x x y x e
. Tính thể tích khối tròn
xoay tạo thành khi hình
H
quay quanh trục
Ox
.
A.
3
52
25
Ox
e
V
B.
3
52
27
Ox
e
V
C.
3
52
27
Ox
e
V
D.
3
52
25
Ox
e
V
Câu 59. Tính diện tích
S
hình phẳng được giới hạn bởi các đường:
22
4;
4
42
xx
yy
A.
2
2
3
S

B.
5
2
3
S

C.
4
2
3
S

D.
1
2
3
S

Câu 60. Cho
d
6
0
1
sin cos
64
n
I x x x
. Khi đó
n
bằng:
A. 5 B. 3 C. 4 D. 6
Câu 61. Khẳng định nào sau đây đúng về kết quả
3
1
31
ln
e
a
e
x xdx
b
?
A.
. 64ab
B.
. 46ab
C.
12ab
D.
4ab
Câu 62. Cho các hàm số:
2
20 30 7
()
23
xx
fx
x

;
2
23F x ax bx x x
với
3
2
x
. Để hàm số
Fx
là một nguyên hàm của hàm số
()fx
thì giá trị của
,,abc
là
A.
4; 2; 1abc
B.
4; 2; 1a b c
C.
4; 2; 1a b c
D.
4; 2; 1abc
Câu 63. Cho hình phẳng giới hạn bởi:
tan ; 0; ; 0
3
D y x x x y



Thể tích vật tròn xoay khi D quay
quanh Ox:
A.
3
3



B.
3
3
C.
3
3
D.
3
3



Câu 64. Nguyên hàm của hàm số
31yx
trên
1
;
3
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
23
1
A.
2
3
2
x x C
B.
3
2
31
9
xC
C.
3
2
31
9
xC
D.
2
3
2
x x C
Câu 65. Cho hàm
2
1
32
fx
xx

.Khi đó
A.
1
ln
2
x
f x dx C
x

B.
1
ln
2
x
f x dx C
x

C.
2
ln
1
x
f x dx C
x

D.
2
ln
1
x
f x dx C
x

Câu 66. Cho hình phẳng
H
được giới hạn bởi các đường:
ln , 0,y x x y x e
. Tính thể tích khối tròn
xoay tạo thành khi hình
H
quay quanh trục
Ox
.
A.
1
ln
2
x
f x dx C
x

B.
1
ln
2
x
f x dx C
x

C.
1
ln
2
x
f x dx C
x

D.
2
ln
1
x
f x dx C
x

Câu 67. Trong các khẳng định sau khẳng định đúng?
A. Nếu
'( )wt
là tốc độ tăng trưởng cân nặng/năm của một đứa trẻ, thì
10
5
'( )w t dt
là sự cân nặng của
đứa trẻ giữa
5
và
10
tuổi
B. Nếu dầu rò rỉ từ
1
cái thùng với tốc độ
()rt
tính bằng galông/phút tại thời gian
t
, thì
120
0
()r t dt
biểu thị lượng galông dầu rò rỉ trong
2
giờ đầu tiên
C. Nếu
()rt
là tốc độ tiêu thụ dầu của thế giới, trong đó
t
được bằng năm, bắt đầu tại
0t
vào
ngày
1
tháng
1
năm
2000
và
()rt
được tính bằng thùng/năm,
17
0
()r t dt
biểu thị số lượng thùng
dầu tiêu thụ từ ngày
1
tháng
1
năm
2000
đến ngày
1
tháng
1
năm
2017
.
D. Cả
,,A B C
đều đúng
Group Nhóm Toán | Trắc nghiệm 2016-2017
23
2
Câu 68. BIết :
4
4
0
1
3
a
dx
cos x
. Mệnh đề nào sau đây đúng?
A. a là một số chẵn B. a là số lớn hơn 5
C. a là số nhỏ hơn 3 D. a là một số lẻ
--------------------HẾT-----------------
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
B
A
B
B
C
C
D
D
D
D
C
D
D
C
B
D
A
B
B
D
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
D
B
A
A
B
B
D
D
A
B
B
A
A
D
A
C
B
C
D
A
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
50
A
D
B
C
C
B
B
D
A
C
C
C
D
C
A
B
C
B
C
B
61
62
63
64
65
66
67
68
A
C
D
B
D
C
D
A
PHẦN 21 :
TÍCH PHÂN VÀ ỨNG DỤNG
(PHẦN 3)
NHẬN BIẾT
Câu 18. Họ nguyên hàm của
tan x
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
23
3
A.
ln cosx C
B.
ln cosx C
C.
2
tan x
C
2
D.
ln(cosx) C
Câu 2. Cho hai hàm số
f(x),g(x)
là hàm số liên tục ,có
F(x),G(x)
lần lượt là nguyên hàm của
f(x),g(x)
.Xét các mệnh đề sau :
(I):
F(x) G(x)
là một nguyên hàm của
f(x) g(x)
(II):
k.F x
là một nguyên hàm của
kf x ,(k R)
(III):
F(x).G(x)
là một nguyên hàm của
f(x).g(x)
Mệnh đề nào là mệnh đề đúng?
A.
I
B.
I
và
II
C.
I,II,III
D.
II
Câu 3. Diện tích hình phẳng phần bôi đen trong hình sau được tính theo công thức:
A.
( )d ( )d

bc
ab
S f x x f x x
. B.
( )d ( )d

cb
ba
S f x x f x x
.
C.
( )d
c
a
S f x x
. D.
( )d
c
a
S f x x
Group Nhóm Toán | Trắc nghiệm 2016-2017
23
4
Câu 4.
Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay
tạo thành được tính theo công thức nào?
A.
b
2
a
V f(x) g(x) dx
B.
b
22
a
V f (x) g (x) dx


C.
b
2
a
V f(x) g(x) dx
D.
b
a
V f(x) g(x) dx
Câu 5. Tìm công thức sai:
A.
xx
e dx e C
B.
x
x
a
a dx C 0 a 1
lna
C.
cosxdx sinx C
D.
sinxdx cosx C
Câu 6. Gọi
F(x)
là một nguyên hàm của hàm
y xx.cos
mà
F(0) 1
. Phát biểu nào sau đây là
đúng:
A.
F(x)
là hàm chẵn
B.
F(x)
là hàm lẻ
C.
F(x)
là hàm tuần hoàn chu kỳ
2
D.
F(x)
không là hàm chẵn cũng không là hàm lẻ
Câu 7. Mệnh đề nào sau đây sai?
A.Nếu
F(x)
là một nguyên hàm của
f(x)
trên
a;b
và C là hằng số thì
f(x)dx F(x) C
.
Group Nhóm Toán | Trắc nghiệm 2016-2017
23
5
B.Mọi hàm số liên tục trên
a;b
đều có nguyên hàm trên
a;b
.
C.
F(x)
là một nguyên hàm của
f(x)
trên
a;b F (x) f(x), x a;b .
D.
f(x)dx f(x)
THÔNG HIỂU
Câu 8. Nếu
Fx
là một nguyên hàm của
xx
f(x) e (1 e )

và
F(0) 3
thì
F(x)
là ?
A.
x
ex
B.
x
e x 2
C.
x
e x C
D.
x
e x 1
Câu 9. Diện tích hình phẳng giới hạn bởi
2
y x 3x 2
và trục
Ox
là:
A.
1
6
B.
3
4
C.
729
35
D.
27
4
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
yx
và đường thẳng
y x 2
là
A.
13
2
(đvdt) B.11 (đvdt) C.7 (đvdt) D.Một kết quả khác
Câu 11. Tính diện tích hình phẳng được giới hạn bởi đường cong
3x 1
(C):f(x)
x1

và hai
trục tọa độ.
A.
4
1 4ln
3

B.
1 ln7
C.
1 2ln2
D.
5
1 ln
3

Câu 12. Tính
0
1
2x 1
dx
1x
bằng:
A.
ln2 2
B.
ln2 2
C.
ln2 2
D.
ln2 2
Câu 13. Nếu
x2
f(x)dx e sin x C
thì
f(x)
là hàm nào ?
A.
x2
e cos x
B.
x
e sin2x
C.
x
e cos2x
D.
x
e 2sinx
Câu 14. Thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi
2
y x 2x
và trục
Ox
quanh trục
Ox
là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
23
6
A.
16
15
B.
4
3
C.
3
16
15
D.
72
5
Câu 15. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y 4x x
và trục hoành bằng:
A.4 B.0 C.2 D.8
Câu 16. Hàm nào không phải nguyên hàm của hàm số
2
2
y
(x 1)
:
A.
x1
x1

B.
2x
x1
C.
2
x1
D.
x1
x1
Câu 17.
3
cosx.sin xdx
bằng
A.
4
cos x
C
4
B.
4
sin x
C
4
C.
4
sin x C
D.
4
cos x C
Câu 18. Tính tích phân sau
2
0
I x 1 dx
A.1 B.11 C.6
D.3
Câu 19. Cho
2
0
f x dx 5
. Khi đó
2
0
f x 2sin x .dx


bằng:
A.
5
B.
5
2
C.7 D.3
Câu 20. Họ nguyên hàm của
1
sin x
là:
A.
x
ln cot C
2
B.
x
ln tan C
2
C.
x
ln tan C
2

D.
ln sinx C
Câu 21. Tìm diện tích hình phẳng giới hạn bởi các đường
2
yx
và
y x 2
A.9 B.
9
8
C.
9
2
D.
9
4
Câu 22. Hàm số
x
F(x) e tanx C
là nguyên hàm của hàm số
f(x)
nào
A.
x
2
1
f(x) e
sin x

B.Đáp án khác
Group Nhóm Toán | Trắc nghiệm 2016-2017
23
7
C.
x
2
1
f(x) e
sin x

D.
x
x
2
e
f(x) e 1
cos x




Câu 23. Nguyên hàm của hàm số
f x 2sinx cosx
là:
A.
2cosx sinx C
B.
2cosx sinx C
C.
2cosx sinx C
D.
2cosx sinx C
Câu 24. Họ nguyên hàm của
2
sin x
là:
A.
1
x 2cos2x C
2

B.
1 sin2x
x
22



C.
x sin2x
C
24

D.
1
x 2cos2x C
2

Câu 25. Họ nguyên hàm của
1
f(x)
x(x 1)
là:
A.
x1
F(x) ln C
x

B.
x
F(x) ln C
x1

C.
1x
F(x) ln C
2 x 1

D.
F(x) ln x(x 1) C
Câu 26.
x1
2 dx
bằng
A.
x1
2
ln 2
B.
x1
2C
C.
x1
2
C
ln2
D.
x1
2 .ln2 C
Câu 27. Diện tích hình phẳng giới hạn bởi
2
yx
và
y 2x 3
là
A.
512
15
B.
88
3
C.
32
3
D.
32
3
Câu 28. Tính diện tích hình phẳng giới hạn bởi
2
(P):y 4x
và
d: y 2x 4
(VAN DUNG)
A.
9
B.
3
C.
7
D.
5
Câu 29. Thể tích khối tròn xoay khi quay hình phẳng
(H)
giới hạn bởi
2
yx
và
y x 2
quanh trục
Ox
là:
A.
72
5
B.
138
5
C.
9
2
D.
72
5
Group Nhóm Toán | Trắc nghiệm 2016-2017
23
8
Câu 30. Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi các đường
3
x
y
3
và
2
yx
là
A.
436
35
(đvtt) B.
9
2
(đvtt) C.
468
35
(đvtt) D.
486
35
(đvtt)
Câu 31. Một nguyên hàm của
2
x
f(x)
x1
là:
A.
1
ln( 1)
2
x
B.
2
2ln( 1)x
C.
2
1
ln( 1)
2
x
D.
2
ln( 1)x
Câu 32. Họ nguyên hàm của hàm số
5
y (2x 1)
là:
A.
6
1
(2x 1) C
12

B.
6
1
(2x 1) C
6

C.
6
1
(2x 1) C
2

. D.
4
10(2x 1) C
Câu 33. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
yx
, trục hoành và các đường
thẳng
x 1,x 3
là
A.
45
2
(đvdt) B.
27
2
(đvdt) C.
17
3
(đvdt) D.
41
2
(đvdt)
Câu 34.
2
0
dx
I
1 cosx

A.
1
4
B.
1
2
C.
1
D.
2
Câu 35. Tính tích phân sau:
2
2
1
2x 2
I dx
x
(SAI)
A.
I 3 2ln2
B.
I 3 2ln2
C.
I 2 2ln3
D.Đáp án khác
Câu 36. Tìm một nguyên hàm
Fx
của hàm số
2
f x 2 x
biết
7
F2
3
A.
3
x1
F x 2x
33
B.
3
19
F x 2x x
3
Group Nhóm Toán | Trắc nghiệm 2016-2017
23
9
C.
3
x
F x 2x 1
3
D.
3
x
F x 2x 3
3
VẬN DỤNG
Câu 37. Tìm diện tích hình phẳng giới hạn bởi các đường
2
x 4x 4
y
x3

;
y x 1;x 2;x 0
;
y x 2
(SAI)
A.
3
ln
2
B.
1
ln3
2
C.
1
D.
1
ln3
4
.
Câu 38. Tính diện tích hình phẳng giới hạn bởi
2
y x 4x 5
và hai tiếp tuyến tại
A(1;2)
và
B(4;5)
A.
9
4
B.
7
4
C.
3
4
D.
5
4
Câu 39. Gọi
F(x)
là một nguyên hàm của hàm
2
lnx
ln x 1.y
x
mà
1
F(1)
3
. Giá trị
2
F (e)
bằng:
A.
8
9
B.
1
9
. C.
8
3
. D.
1
3
.
Câu 40. Họ nguyên hàm của
2
f(x) x.cosx
là:
A.
2
cosx C
B.
2
sinx C
C.
2
1
sin x C
2
D.
2
2sinx C
Câu 41. Một nguyên hàm của
2
x
f(x) xe
là:
A.
2
x
e
B.
2
x
1
e
2
C.
2
x
e
D.
2
x
1
e
2
Câu 42. Tính tích phân sau
12
12
I tan x.tan( x).tan( x)dx
33

A.
1
ln2
3
B.
2
ln 2
3
C.
2
ln 3
3
D.
1
ln3
3
Câu 43. Cho hàm số
2
x
f x 2sin
2
Khi đó
f(x)dx
bằng
Group Nhóm Toán | Trắc nghiệm 2016-2017
24
0
A.
x sin x C
B.
x sinx C
C.
x cosx C
D.
x cosx C
Câu 44. Họ nguyên hàm của
3
f(x) sin x
A.
3
cos x
cosx C
3

B.
3
cos x
cosx C
3
C.
1
cosx c
cosx
D.
4
sin x
C
4
Câu 45.
2
2
0
I 4 x dx
bằng (SAI)
A.
B.
3
C.
2
D.
6
Câu 46.
1
2
0
dx
I
1x
bằng:
A.
6
B.
3
C.
4
D.
2
Câu 47. Biết rằng tích phân
x
1
0
(2x 1)e dx a b.e
, tích
ab
bằng:
A.
1
B.
1
C.
15
D.
5
Câu 48. Tính tích phân sau:
2
0
I x a xdx
A.Cả 3 đáp án trên B.
8
2x
3
C.
3
18
a 2a
33

D.
8
2a
3
Câu 49. Cho
t
4
0
3
f(x) 4sin x dx
2




.Giải phương trình
f(x) 0
A.
k2 ,k Z
B.
k
,k Z
2
C.
k ,k Z
D.
k ,k Z
2
Câu 50. Tính tích phân
2
2
0
sin cos d
x x x
Group Nhóm Toán | Trắc nghiệm 2016-2017
24
1
A.
1
4
B.
1
C.
1
3
D.
1
2
Câu 51. Tính diện tích hình phẳng giới hạn bởi đường cong
2
(C): y x 4x 3
và
d: y x 3
A.
109
6
B.
105
6
C.
107
6
D.
103
6
Câu 52. Diện tích giới hạn bởi đồ thị hàm
32
y x 3x 4
và đường thẳng
x y 1 0
A.10 B.8 C.6 D.4
Câu 53. Cho
2
2
2
1
x2
M .dx
2x
. Giá trị của
M
là:
A.
2
B.
5
2
C.
1
D.
11
2
Câu 54. Thể tích khối tròn xoay trong không gian
Oxyz
giới hạn bởi hai mặt phẳng
x x0; 
và có thiết diện cắt bởi mặt phẳng vuông góc với
Ox
tại điểm
(x;0;0)
bất kỳ là
đường tròn bán kính
sin x
là
A.
2
. B.
. C.
2
D.
4
.
Câu 55. Thể tích khối tròn xoay tạo thành khi cho đường
22
x (y 1) 1
quay quanh trục
hoành là
A.
2
6
(đvtt) B.
2
8
(đvtt) C.
2
4
(đvtt) D.
2
2
(đvtt)
Câu 56. Diện tích hình phẳng giới hạn bởi đường thẳng
2
y 2x
và đường thẳng
yx
bằng:
A.
9
2
B.
10
3
C.
11
2
D.
17
3
Câu 57. Tính tích phân
1
3
2
0
x
dx
1x
A.
5
16
B.
3
8
C.
3
16
D.
5
8
Câu 58. Tính diện tích hình phẳng giới hạn bởi các đường
1
(C ):f(x) (e 1)x
và
x
2
(C ):g(x) (e 1)x
Group Nhóm Toán | Trắc nghiệm 2016-2017
24
2
A.
e
1
2
B.
2
e2
C.
3
e3
D.
2
e
2
2
Câu 59. Tính tích phân sau
3
8
8
I cot x tan x dx

A.
ln2
B.
ln3
C.
ln 2
D.
ln 3
Câu 60.
3
3
0
I cos xdx
bằng:
A.
33
2
B.
33
4
C.
33
8
D.
33
Câu 61. Nguyên hàm của hàm số
x
f x xe
là:
A.
xx
xe e C
B.
x
eC
C.
2
x
x
eC
2
D.
xx
xe e C
Câu 62. Để
k
1
k 4x dx 3k 1 0
thì giá trị của
k
là bao nhiêu ?
A.
1
B.3 C.2 D.4
Câu 63. Cho
e
1
k
I ln dx
x
.Xác định
k
để
I e 2
A.
k e 2
B.
ke
C.
k e 1
D.
k e 1
Câu 64. Tích phân
3
1
2x 1
dx a 2
x1
nbl

. Tổng của
ab
bằng:
A.1. B.
7
C.
3
D.
2
Câu 65. Tìm nguyên hàm của hàm số
f(x)
biết
2
2x 3
f(x)
x 4x 3

A.
2
2
2
x 3x
C
x 4x 3


B.
2
(2x 3)ln x 4x 3 C
C.
2
2
x 3x
C
x 4x 3

D.
1
ln x 1 3ln x 3 C
2
Group Nhóm Toán | Trắc nghiệm 2016-2017
24
3
Câu 66.
2
d
(1 )
x
xx
bằng
A.
2
x
ln C
1x
B.
2
x
ln C
1x
C.
2
ln x 1 x C
D.
2
ln x (1 x ) C
Câu 67. Tìm nguyên hàm của hàm số
f(x)
biết
1 ln x
f(x)
x
A.Đáp án khác B.
x lnx C
C.
2
1
lnx ln x C
2

D.
2
1
lnx ln x C
4

Câu 68. Đặt
m
0
f m cosx.dx
. Nghiệm của phương trình
f m 0
là
A.
m k2 ,k Z
B.
m k ,k Z
2
C.
m k ,k Z
D.
m k2 ,k Z
2
Câu 69. Một nguyên hàm của
1
x
f(x) (2x 1).e
là:
A.
1
x
F(x) x.e
B.
1
x
F(x) e
C.
1
2
x
F(x) x .e
D.
1
2
x
F(x) x 1 .e
Câu 70. Hàm số nào là nguyên hàm của
1
f(x)
1 sin x
A.
x
F(x) 1 cot( )
24
B.
2
F(x)
x
1 tan
2

C.
F(x) ln(1 sin x)
D.
x
F(x) 2tan
2
Câu 71. Xét các mệnh đề
Group Nhóm Toán | Trắc nghiệm 2016-2017
24
4
31
46
31
1d 1d

I x x x x
3 1 1
4 4 4
0 0 3
1d 1d 1d
II x x x x x x
A.(I) đúng, (II) sai B.(I) sai, (II) đúng
C.Cả (I) và (II) đều đúng D.Cả (I) và (II) đều sai
Câu 72. Hàm số nào là nguyên hàm của
2
f(x) x. x 5
:
A.
3
2
2
F(x) (x 5)
B.
3
2
2
1
F(x) (x 5)
3

C.
3
2
2
1
F(x) (x 5)
2

D.
3
2
2
F(x) 3(x 5)
Câu 73. Tìm nguyên hàm của hàm số
f(x)
biết
1
f(x)
x 9 x

A.
3
3
2
x 9 x C
27
B.Đáp án khác
C.
3
3
2
C
3( x 9 x )

D.
3
3
2
x 9 x C
27
Câu 74. Tìm nguyên hàm của hàm số
f(x)
biết
2
f(x) tan x
A.
3
tan
3
x
C
B. Đáp án khác
C.
tanx 1 C
D.
sinx xcosx
C
cosx
Câu 75. Nguyên hàm của hàm số
2ln x x
f x ,x 0
x

là:
A.
2
ln x
C
x
B.
2lnx 1 C
C.
2
ln x x C
D.
2
ln x
xC
x

Group Nhóm Toán | Trắc nghiệm 2016-2017
24
5
Câu 76. Họ nguyên hàm của
x
2x
e
e1
là:
A.
2x
ln e 1 C
B.
x
x
1 e 1
ln C
2 e 1
C.
x
x
e1
ln C
e1
D.
x
x
1 e 1
ln C
2 e 1
Câu 77. Tìm
m
biết
m
0
2x 5 .dx 6
A.
m 1,m 6
B.
m 1,m 6
C.
m 1,m 6
D.
m 1,m 6
VẬN DỤNG CAO
Câu 78. Gọi S là diện tích giới hạn bởi đồ thị hàm số
2
2x 5x 3
y
x2

,tiệm cận xiên của đồ thi
và các đường thẳng
x 1,x m m 1
.Tìm giá trị
m
để
S6
A.
6
e4
B.
6
e2
C.
6
e1
D.
6
e3
Câu 79. Cho hình phẳng
(H)
giới hạn bởi các đường
4 2 2
y x 2mx m ,x 0,x 1
. Tìm
m
để
diện tích hình phẳng đó bằng
1
5
A.
m 1,m 2
B.
m 0;m 2/3
C.
m 2/3,m 1
D.
m 0,m 2/3
Câu 80. Cho hàm số
2
sin2x
h(x)
(2 sin x)
. Tìm
a,b
để
2
acosx bcosx
h(x)
(2 sinx) 2 sinx


và tính
0
2
I h(x)dx
A.
a4
và
b 2;I 2ln2 2
B.
a4
và
b 2;I 2 ln2 2
C.
a2
và
b 4;I 2ln2 2
D.
a2
và
b 4;I ln2 2
Group Nhóm Toán | Trắc nghiệm 2016-2017
24
6
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
B
B
A
B
D
D
B
B
A
D
A
D
B
C
D
A
B
A
D
C
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
C
D
D
C
B
A
D
A
D
D
C
A
D
C
A
C
C
A
A
C
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
B
A
B
B
A
C
A
B
B
C
A
B
C
B
D
A
A
A
A
C
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
D
B
B
A
D
B
D
C
C
B
C
B
B
D
C
D
C
B
D
A
PHẦN 22 :
NGUYÊN HÀM – TÍCH PHÂN
THÔNG HIỂU
Câu 1. Với
( ), ( )f x g x
là 2 hàm số liên tục trên
K
và
0k
thì mệnh đề nào sau đây là sai
A.

( ) ( ) .f x dx f x C
B.

( ) ( ) .kf x dx k f x dx
C.
( ) ( ) ( ) ( ) .f x g x dx f x dx g x dx

D.

( ). ( ) ( ) . ( ) .f x g x dx f x dx g x dx
Câu 2. Chọn phát biểu sai trong số các phát biểu sau
A. Cho hàm số
()fx
xác định trên
.K
Hàm số
()Fx
được gọi là nguyên hàm của hàm số
()fx
trên
K
nếu:
( ) ( ), .F x f x x K
Group Nhóm Toán | Trắc nghiệm 2016-2017
24
7
B. Nếu
()Fx
là một nguyên hàm của
()fx
trên
K
thì họ nguyên hàm của hàm số
()fx
trên
K
là:
( ) ( ) , .f x dx F x C const C K
C.Nếu
()Fx
là một nguyên hàm của
()fx
trên
K
thì họ nguyên hàm của hàm số
()fx
trên
K
là:
( ) ( ) , .f x dx F x C const C
D. Cho hàm số
()fx
xác định trên R Hàm số
()Fx
được gọi là nguyên hàm của hàm số
()fx
trên
K
nếu:
( ) ( ), .F x f x x R
Câu 3. Tìm nguyên hàm của các hàm số
3
( ) 4 5f x x x
thỏa mãn điều kiện
(1) 3.F
A.
4
2
( ) 5 3
4
x
F x x x
B.
42
15
( ) 4
54
F x x x x
C.
4
2
5
( ) 5
44
x
F x x x
D.
42
1
( ) 4 3
5
F x x x x
Câu 4. Tìm điều kiện của tham số m để
32
( ) (3 2) 4 3F x mx m x x
,
()Fx
là một nguyên hàm của hàm số
2
( ) 3 10 4f x x x
A.
1m
B.
1m 
C.
3m
D.
2m
Câu 5. Tính nguyên hàm sau:

( 1)
dx
I
xx
A.

1
ln .
( 1)
IC
xx
B.

ln .
1
x
IC
x
C.

1
ln
x
IC
x
D.

ln .
1
x
IC
x
Câu 6. Cho I=
1
dx
x
nguyên hàm là.
A.
ln xC
B.
2
1
C
x
C.
ln x
D.
ln xC
Câu 7. Nguyên hàm của I=
cos .sin .x x dx
là.
A.–cos2x + C B.
1
cos2
4
xC
C.
1
cos2
2
xC
D.
1
cos2
4
xC
Group Nhóm Toán | Trắc nghiệm 2016-2017
24
8
Câu 8. Giá trị của
2
2
0
2?
x
I e dx
A.
4
4Ie
B.
4
44Ie
C.
4
Ie
D.
4
1Ie
Câu 9. Tính:
1
2
0
43
dx
I
xx

A.
3
ln
2
I
B.
13
ln
32
I
C.
13
ln
22
I 
D.
13
ln
22
I
Câu 10. Diện tích của hình phẳng giới hạn bởi
ln , 0,y x y x e
là
A. e B. 3 C. 2 D. 1
VẬN DỤNG
Câu 11. Trong số các mệnh đề sau, có bao nhiêu mệnh đề đúng
1. Cho hàm số
()fx
liên tục trên
K
và
, .a b K
Hàm số
()Fx
được gọi là nguyên hàm của
()fx
trên
K
thì
( ) ( )F b F a
được gọi là tích phân của
()fx
từ
a
đến
b
2. Tích phân của
()fx
từ
a
đến
b
và được kí hiệu là
()
b
a
f x dx
. Khi đó:
( ) ( ) ( ) ( ) ,
b
b
a
a
I f x dx F x F b F a
với
ab
3. Đối với biến số lấy tích phân, ta có thể chọn bất kì một chữ khác nhau thay cho
x
, nghĩa là:
( ) ( ) ( ) ( ) ( ).
b b b
a a a
I f x dx f t dt f u du F b F a
4. Nếu hàm số
()y f x
liên tục và không âm trên đoạn
;ab

thì diện tích
S
của hình thang cong giới hạn
bởi đồ thị của
( ),y f x
trục
Ox
và hai đường thẳng
, x a x b
là:
()
b
a
S f x dx
5. Nếu hàm số
()y f x
liên tục và không âm trên đoạn
;ab

thì diện tích
S
của hình thang cong giới hạn
bởi đồ thị của
( ),y f x
trục
Oy
và hai đường thẳng
, x a x b
là:
()
b
a
S f x dx
A.1 B.2 C.3 D.4
Câu 12. Tìm nguyên hàm sau

41
.
2 1 2
x
I dx
x
Group Nhóm Toán | Trắc nghiệm 2016-2017
24
9
A.
2 1 5ln 2 1 2 .I x x C
B.
2 1 4 2 1 5ln 2 1 2 .I x x x C
C.
2 1 4 2 1 5ln 2 1 2 .I x x x C
D.
2 1 4 2 1 5ln 2 1 2 .I x x x C
Câu 13. Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số
2yx
,
2
yx
và trục hoành trong miền
0x
.
A.
5
6
B.
1
3
C.
1
2
D.
1
6
Câu 14. Dòng điện xoay chiều hình sin chạy qua một đoạn mạch LC có biểu thức có biểu thức cường độ là
. Biết
'
iq
với
q
là điện tích tức thời ở tụ điện. Tính từ lúc t = 0, điện lượng chuyển
qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian bằng
là
A.
0
2I
ω
B.
0
C.
0
I
ω2
D.
0
2I
ω
Câu 15. Trong kinh tế học, thặng dư tiêu dùng của hàng hóa được tính bằng công thức

0
( ) . .
a
I p x P dx
Với
()px
là hàm biểu thị biểu thị giá mà một công ty đưa ra để bán được x đơn vị hàng hóa, a là số lượng
sản phẩm đã bán ra,
()P p a
là mức giá bán ra ứng với số lượng sản phẩm là a.
Cho
2
1200 0,2 0,0001p x x
, (đơn vị tính là USD). Tìm thặng dư tiêu dùng khi số lượng sản phẩm bán
là 500
A.33333,3 USD B.1108333,3 USD C.570833,3 USD D.Đáp án khác
Câu 16. Cho:
0
sinL x xdx k
. Giá trị của
k
là:
A.2 B.1 C.0 D.-1
Câu 17. Tính thể tích sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi trục Ox và Parabol
2
(C): y ax x (a 0)
A.
5
10
a
B.
5
20
a
C.
4
5
a
D.
5
30
a
o
i I cos( t )A
2
Group Nhóm Toán | Trắc nghiệm 2016-2017
25
0
Câu 18. Tìm
,,abc
để
2
( ) ( ).
x
F x ax bx c e
là một nguyên hàm của
2
( ) ( 2 7 4).
x
f x x x e
A.
2, 3, 1a b c
a=2,b=-3,c=-1 B.
2, 3, 1a b c
C.
2, 3, 1a b c
D.
2, 3, 1a b c
Câu 19. Diện tích hình phẳng giới hạn bởi trục tung và 2 đồ thị
2 , 3
x
y y x
là.
A.
5
1/ ln2
2
S 
B.
5
ln2
2
S 
C.
5 ln2S 
D.
5
ln2
2
S 
Câu 20. Tích phân
( ) 0
a
a
f x dx
thì ta có :
A.
()fx
là hàm số chẵn trên
;aa
B.
()fx
không liên tục trên đoạn
;aa
C.
()fx
là hàm số lẻ trên
;aa
D.Các đáp án đều sai
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
D
B
C
A
B
D
B
D
D
D
B
B
A
D
A
B
D
A
A
C
Group Nhóm Toán | Trắc nghiệm 2016-2017
25
1
| 1/251
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TÍCH PHÂN VÀ ỨNG DỤNG CỦA TÍCH PHÂN (TỰ LUẬN)
Hoàng Văn Quý – GV trường THPT Lương Tài số 2
1. Kiến thức liên quan
1.1. Công thức nguyên hàm cơ bản
Nguyên hàm của hàm số cơ bản Nguyên hàm mở rộng
dx x C .
a dx ax C, a    1   1   x  1 (ax b) x dx   C,   1       (ax b) dx . C 1 a  1 dx dx 1
ln x C, x  0 
 .ln ax b C x ax b a x x
e dx e C axb 1  . axb e dx eC a x   a   a x 1 x x a dx   C a dx  .  C ln a  ln a
cos xdx  sin x C 1
cos(ax b)dx
.sin(ax b)  C a
sin xdx  cos x C 1
sin(ax b)dx   .cos(ax b)  C a 1 1 1
dx  tan x C dx
tan(ax b)  C 2 cos x 2 cos (ax b) a 1 1 1
dx  cotx C
dx   cot(ax b)  C 2 sin x 2 sin (ax b) a 1
1.2. Công thức tích phân
F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a;b] thì
Group Nhóm Toán | Trắc nghiệm 2016-2017 b b
f (x)dx F (x)  F (b)  F (a)  a a
1.3. Phương pháp đổi biến số b
1.3.1. Dạng 1 : Tính I = f   x  '
( )  (x)dx a + Đặt t = (x) '
dt   (x).dx + Đổi cận : x a b  (b) t (a) (b) (b)  I =
f (t).dt F (t)   (a)  (a) b
1.3.2. Dạng 2 : Tính I = f (x)dx
bằng cách đặt x = (t) a     Dạng chứa 2 2
a x : Đặt x = asint, t  ; 
(a>0)  2 2 
1.4. Phương pháp tích phân từng phần b b b
* Công thức tính : b
f (x)dx udv uv vdu    a a a au  ... du    ...dx (lay dao ) ham Đặt    dv  ... v  ... (lay nguyen ) ham
Ta thường gặp hai loại tích phân như sau: * Loại 1: 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 b
P(x).sin f (x).dx  ab
P(x).cos f (x).dx
u P(x) 
, trong đó P(x) là đa thức bậc n. ab f ( x)
P(x).e .dx  a b
*Loại 2: P(x).ln f (x).dx u  ln f (x)  a
1.5. Tính chất tích phân b b
Tính chất 1: kf (x)dx k f (x)dx   , k: hằng số a a b b b
Tính chất 2:  f (x)  g(x)dx f (x)dx g(x)dx   a a a b c b
Tính chất 3: f (x)dx f (x)dx f (x)dx
(a c b)    a a c
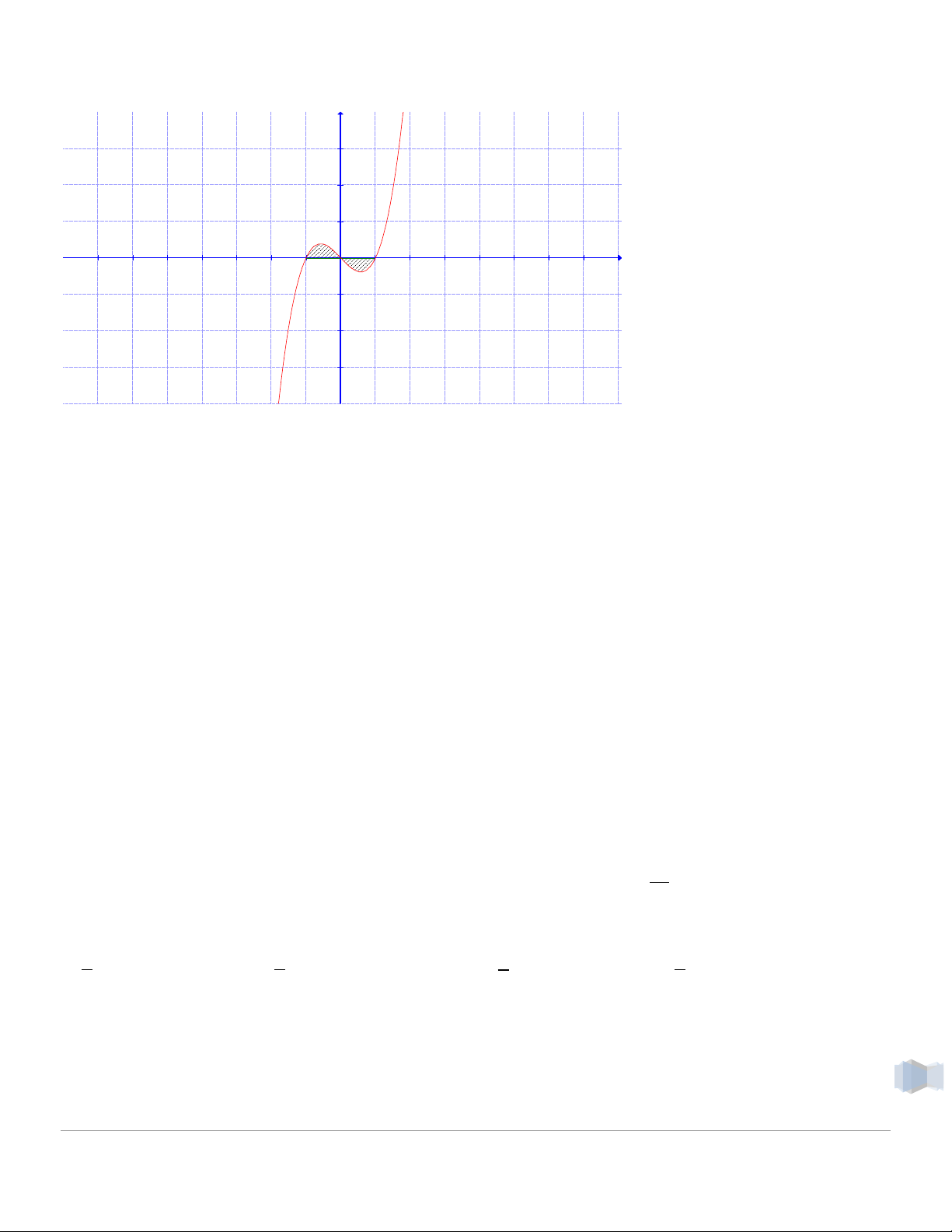
1.6. Diện tích hình phẳng
1.6.1. Dạng 1: Cho hàm số y = f(x) liên tục trên [a; b]. khi đó diện tích hình phẳng giới hạn bởi đồ thị
hàm số y = f(x), trục Ox và hai đường thẳng x = a và x = b là: b S f (x) dx  (*) a Lưu ý:
f (x)  0 vô nghiệm trên (a;b) thì b b S
f (x) dx f (x)dx   a a
f (x)  0 có 1 nghiệm c ( ; a ) b thì 3 b c b S
f (x) dx
f (x)dx f (x)dx    a a c
Group Nhóm Toán | Trắc nghiệm 2016-2017
1.6.2. Dạng 2: Cho hai hàm số y = f1(x) và y = f2(x) liên tục trên [a; b]. Khi đó diện tích của hình phẳng
giới hạn bởi đồ thị hai hàm số f1(x), f2(x) và hai đường thẳng x = a, x = b là: b S
f (x)  f (x) dx  (**) 1 2 a
Lưu ý: Khử dấu giá trị tuyệt đối của công thức (**) thực hiện tương tự đối với công thức (*).
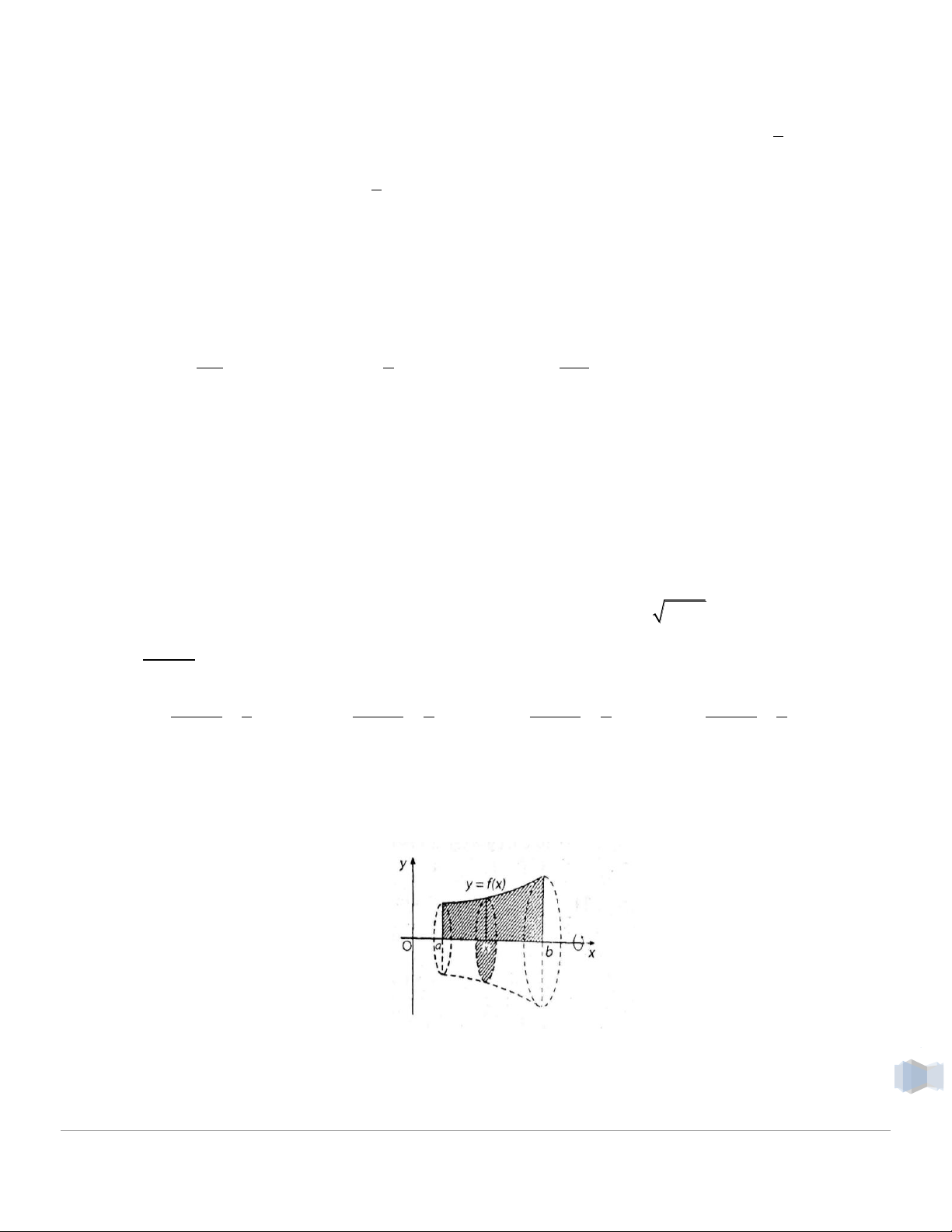
1.7. Thể tích vật thể tròn xoay
Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi các đường
y = f(x), trục Ox và hai đường thẳng x = a, x = b quay xung quanh trục Ox là: b 2 V   f (x)dxa
Lưu ý: Diện tích, thể tích đều là những giá trị dương. 2. Ví dụ minh họa
Ví dụ 1: Tính các tích phân sau 1 1  1 /  (2x+ex) x 2 /  2x    x A d B e  3dx
3 / C  sinx+cos xdx 0 0 0 4 2 
x  2 x  3  4 / D   dx 5 / E x  sin 2x dx  3   x 1   0 Lời giải 1 1 /  2 x   1 1 1 1 x 2  2 x A x e dx
xdx e dx xe
1 0  e 1  e   0 0 0 0 0   
B   e   x
dx   e 2e 1 1 1 1 1 2x x e x x x 2 1 3 2 / 2 3 2 dx 3 2 dx   3      ln 2e ln 2  ln 2e  ln 2 0 0 0 0 0    4  
3 / C  sinx  cos xdx  sinxdx  cos xdx  cos x  sin x  2   0 0 0 0 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 4 4 4 5 3  1 x 3   1   4  4  2 3 3 2 2 2 4 / D    
dx    x  3x dx  ln x xx  3 3 1 1 x x x x 3 2      1 1 1      
5 / E   x  sin 2x 2 1 1 2
dx xdx  sin 2xdx x  cos2x     2 2 2 0 0 0 0 0
Ví dụ 2. Tính các tích phân sau 6 1 2x 1
1 / I x x  3 x d 2 / J  x d  1 3x1 1 0 e ln 2  1 2ln x 1   1  3 / K    dx 4 / L x dx      x x ln x 1    2 x e 1  1   0 Lời giải 6
1 / I x x  3dx  1
 Đặt x  3  t ta được 2
x  3  t dx  2tdt
 Đổi cận: x 1 t  2;x  6  t  3    2 232
Khi đó I  2t  6t  3 3 4 2 5 3 dt t  2t     5  5 2 2 1 2x 1 2 / J dx 1 3x1 0 2   t 1 2
Đặt 3x 1  t ta được x   dx tdt 3 3
 Đổi cận x  0  t 1; x 1 t  2 2 3 2     2 2t t 2 3 28 2 3 Khi đó 2 J dt
2t  2t  3  dt   ln    9 1 t 9  t 1 27 3 2 1 1 e  1 2ln x 1  3 / K    dx   x x ln x 1 1     5 e  1 Tính K dx
ta được kết quả K  2 e 1 1   1 x 1
Group Nhóm Toán | Trắc nghiệm 2016-2017  dx
Đặt ln x t ta được dt x
 Đổi cận x 1 t  0; x e t 1 1   1 2t 1 Khi đó K
dt  2t  ln t 1  2  ln 2  2   0 t 1 0
 Vậy ta được K K K  2 e  ln 2 1 2 ln 2  1  4 / L x dx     2 x e 1  0 ln 2  1 Tính L xdx  ta được kết quả 2 I  ln 2 1 2 0 ln 2  1 Tính L dx  2 2 x e 1 0  Đặt x
e t ta được x e dx dt
 Đổi cận x  0  t 1; x  ln 2  t  2 2  2 dt 5 6 Khi đó L
 lnt  ln 2t 1  ln 2  ln  ln  2   t 2t     1 1 3 5 1  1 6 Vậy ta được 2
L L L  ln 2  ln 1 2 2 5
Ví dụ 3. Tính các tích phân sau   
1 / I  1 sin x 4 1 3
cos xdx 2 / J dx 3 / K
sinx  x sin xdx   2 4    sin x cos x 0 0 6 Lời giải  2 1/ I   3
1 sin xcos xdx 0
 Đặtsin x t dt  cos xdx
 Đổi cận x  0  t  0; x   t 1 6 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 4    t 3 Khi đó I   3
1 t dt  t     4  4 0 0  4 1 2 / J dx  2 4  sin x cos x 6  1 
Đặt cot x t dt dx 2 sin x  
 Đổi cận x   t  3; x   t 1 6 4 3 2 3 3   1   2 1   2 1  8 3 4 Khi đó J  1 dt  1  dt t             2 2 4 3  t   t t   t 3t  27 3 1 1 1   
3 / K  sinx  x 2
sin xdx  sin xdx xsin xdx   0 0 0    1 cos 2x 1 Đặt 2
K  sin xdx dx     1 2 2 0 0 
K xsin xdx 2 0 u   xdu dx    
dv  sin xdx v   cos x    
K  x cos x  cos xdx    sinx    2 0 0 0
* Chú ý: Ta thường đặt t là căn, mũ, mẫu.
- Nếu hàm có chứa dấu ngoặc kèm theo luỹ thừa thì đặt t là phần bên trong dấu ngoặc nào có luỹ thừa cao nhất.
- Nếu hàm chứa mẫu số thì đặt t là mẫu số.
- Nếu hàm số chứa căn thức thì đặt t = căn thức.
- Nếu tích phân chứa dx thì đặt t  ln x . x
- Nếu tích phân chứa x e thì đặt x t e . 7
- Nếu tích phân chứa dx thì đặt t x . x
Group Nhóm Toán | Trắc nghiệm 2016-2017 dx - Nếu tích phân chứa thì đặt 1 t  . 2 x x
- Nếu tích phân chứa cos xdx thì đặt t  sin x .
- Nếu tích phân chứa sin xdx thì đặt t  cos x . dx - Nếu tích phân chứa
thì đặt t  tan x . 2 cos x dx - Nếu tích phân chứa
thì đặt t  cot x . 2 sin x
Ví dụ 3. Tính các tích phân  2 e 1
a) I x sin xdx
b) J x ln xdx  ) x c K xe dx  0 1 0 Lời giải  2
a) I xsin xdx  0 u   xdu dx    
dv  sin xdx v   cos x   2     2     2 I x cos x cos xdx 0 0 sinx 1  0 0 0 e
b) J x ln xdx  1  1 du dx u   ln x   x    2 dv xdx xv   2 e e e 2 e 2 2 2 8   x x x x e 1 J  ln x dx  ln x    2 2 2 4 4 1 1 1 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 ) x c K xe dx  0 u   xdu dx     x xdv e dxv e 1  1 1 x x x K xe
e dx e e  1  0 0 0
Ví dụ 4. Tính các tích phân sau 2 2 ln 4 2 2  1 x    x x 1 1 2
1 / I   x
dx 2 / J   e dx 3 / K  ln xdx 3 2 xx x    x  1 0 e 2 1 Lời giải 2 2 2 2 2  1 x  1 x 2 2
1 / I   x
dx x dx dx   3 2  x x x x 1 1 1 2 2 1 7 Tính 2 3 I x dx x   1 3 3 1 1 1  1   dx 2 2 2 2 1 2   2 1 x xx   1  4 I dx dx   dx   ln  x  ln    2   3 x x 1 1  x  5 1 1 1   1 x x x x 7 4
Vậy I I I   ln 1 2 3 5 ln 4 ln 4 ln 4   x 1 x 1
2 / J   e d
x e dx dx   x x     0 e 2 0 0 e 2 9 ln 4 ln 4 x x J e dx e  3  1 0 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 ln 4 1 x x x 2 2 J d ;
x t e t e  2tdt e dx dx dt  2 x t 0 e 2 2 2 2  t  3  J dt  ln  ln  2   t t  2  t  2  2 1   1 3
Vậy J J J  3  ln 1 2 2 2 2 x 1 3 / K  ln xdx  2x 1  1 u   ln x du dx 2 2    x  1   1  1 Đặt 2      K x  ln 1 x x dx x     dv dx 1    x   x x 2 1 1 v x x    x 2 2  1   1  5 3  K x  ln x x   ln 2       x   x  2 2 1 1 10
Group Nhóm Toán | Trắc nghiệm 2016-2017
Ví dụ 5. Tính diện tích hình phẳng giới hạn bởi các đường sau a) 2
y x , trục hoành và hai đường thẳng x=0, x=2. b) 2
y x , y  2
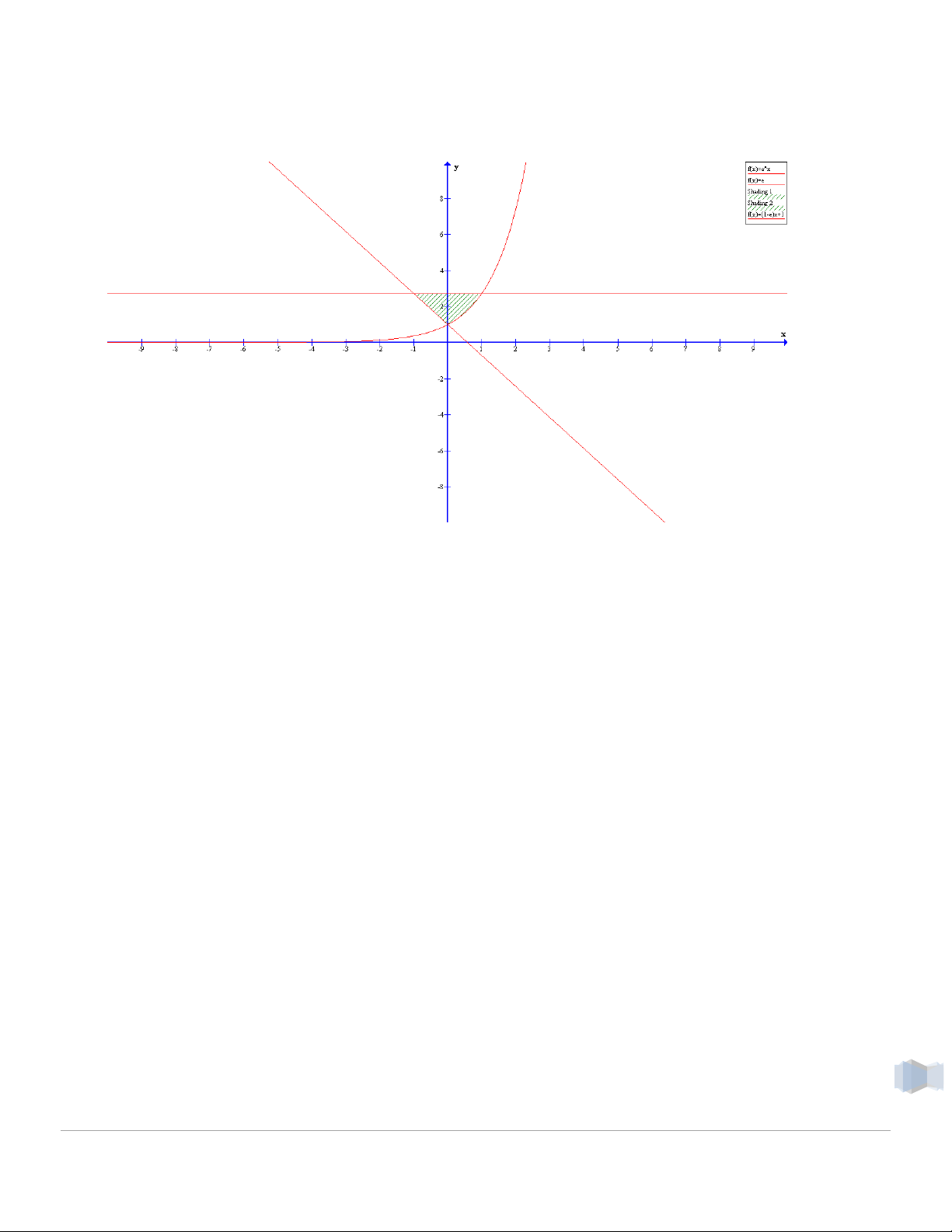
x  3 và hai đường thẳng x =0, x=2. c) 2
y x , y x  2 Lời giải a) 2
y x , trục hoành và hai đường thẳng x= 0, x=2.  Trên [0; 2] ta có 2
x  0  x  0 [0;2]
 Diện tích của hình phẳng đã cho: 2 2 1 8 2 3 S x dx x   3 3 0 0 b) Đặt 2
f (x)  x , f (x)  2  x  3 1 2 x 1[0;2] Ta có: 2 2
f (x)  f (x)  0  x  ( 2
x  3)  0  x  2x  3  0  1 2  x  3  [0;2]
 Diện tích hình phẳng đã cho 2 2
S  | x  2x  3 | dx  0 11
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 2 2 2
 (x  2x  3)dx  (x  2x  3)dx   0 1 1 2 3 3  x   x  2 2
   x  3x    x  3x  3   3  0 1 1 8 1 5 7
  2   4  6  1 3    4 3 3 3 3 3 x  1  c) Ta có: 2 2
x  (x  2)  0  x x  2  0   x  2 Diện tích hình phẳng 2 2 3 2  x x  8 1 1 9 2
S  | x x  2 | x d    
 2x    2  4    2   3 2  3 3 2 2 1  1 
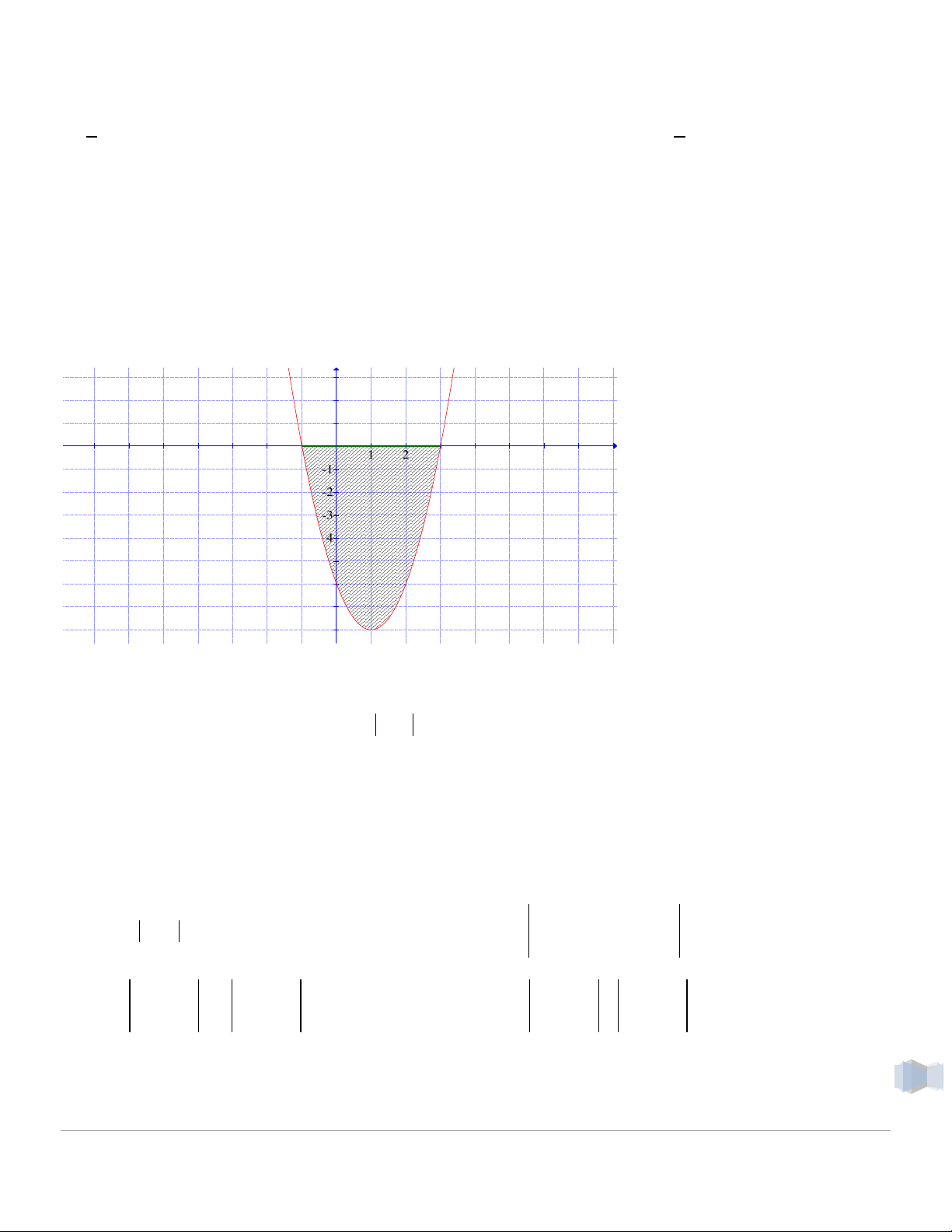
Ví dụ 6. Tính thể tích vật thể tròn xoay sinh ra khi quay hình (D) quanh trục Ox biết (D) giới hạn bởi 2
y  1 x , y  0 Lời giải  Ta có: 2
1 x  0  x  1  b  Áp dụng công thức: 2 V   f (x)dxa 1 1 1 3 5    2x x Ta có: 2 2
V   (1 x ) dx     2 4
1 2x  x dx    x     3 5  1  1  1   2 1   2 1   4 2  16   1   1      2           3 5   3 5   3 5  15 12
Bài Tập tự luyện
Bài 1: Tính các tích phân sau
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 e 1 1 2 1. 3
(x x 1)dx  2. 2 (x    x )dx  3. x 1dx  2 x x 0 1 1  2 1 1
4. (2sin x  3cosx x)dx  5. ( x
e x)dx  6. 3
(x x x )dx   0 0 3  2 2 1 1
7. ( x 1)(x x 1)dx
8. (3sin x  2cosx  )dx 9. x 2
(e x 1)dx   x 1 0 3 3 2
e 7x  2 x  5 2 10. 3 (x 1).dx  11. dx
12. x(x  3)dxx 1  1 2  4 2  1 1  2 2 x  2x 13. 2 (x  4)dx  14.  dx   15. dx  2 3  x x  3 x 3  1 1 8  1  16. 4x dx 3 2   1 3 x
Bài 2: Tính các tích phân sau   2 6 1 1. 3 2 sin xcos xdx  2. 1 4sin xcosxdx  3. 2 x x 1dx   0 0 3 1 1 2 x 1 x 4. 2 x 1 x dx  5. dx  6. dx  3 2 2 (1 3x ) 0 0 x 1 0   2 2 1 7. sin x e cosxdx  8. 2 3
sin 2x(1 sin x) dx  9. 5 3 6
x (1 x ) dx   0 0 4 13
Group Nhóm Toán | Trắc nghiệm 2016-2017   6 cos x 9 x 6 12. dx  11. dx  12.
1 4sin x.cos xdx  2
6  5sin x  sin x x 1 0 4 0 1 ee 2 1 ln x sin(ln x) 13. x 2 e xdx  14. dx  15. dxx x 0 1 1 1 1 8 1 16. x x 1dx  17. 2 3 x x  5dx  18. dx  2 0 0 3 x x 1  ln 5 dx 1 3 sin x 19.  20.  x e dx  21. x dx e 2 x e   3 3 cos x ln 3 0 0 1 1 1 1 1 22. 2 1 x dx  23. dx  24. dx  2  2 1 x 0 0 4 x 0
Bài 3: Tính các tích phân sau   2 1 2 1. 2 x cos xdx  2. x e sin xdx  3. (2x 1) o c sxdx  0 0 0  1 e 2 4. x xe dx  5. x ln xdx  6. 2 (x 1)sin xdx  0 1 0   2 2 1 7. 2 (x  o
c s x)sin xdx  8. 2 x e sin 3xdx  9. 2 (  2) x x e dx  0 0 0  1 e 2 10. 2
x ln(1 x )dx
11. (2x  2)ln xdx  12. x cos x dx  0 1 0 2 1
13. (2x  7)ln(x 1)dx  14. 2 (  2) x x e dx  14 0 0
Bài 4: Tính diện tích hình phẳng giới hạn bởi các đường sau:
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 2 a) 3 2
y   x x
, trục hoành, x = 0 và x = 2. 3 3 b) 2
y x 1, x  1
 , x  2 và trục hoành. c) 3 2 y x 12 , x y x d) 3
y x 1 và tiếp tuyến của nó tại điểm có tung độ bằng -2. e) 2 y x  4 ,
x y  0, x  0, x  3 3
f) y  sinx, y=0, x=0, x= 2 g) x
y e , Ox, x  0, x  3
Bài 5: Tính thể tích vật tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục hoành: a) 2 y x  4 ,
x y  0, x  0, x  3 b) y  cos ,
x y  0, x  0, x   
c) y  tan x, y  0, x  0, x  4 d) 2
y  2  x , y  1 1
e) y  ln x, x  , x  , e y  0 e
TỔNG HỢP CÁC CÂU HỎI TRẮC NGHIỆM - NGUYÊN HÀM – TÍCH PHÂN PHẦN 1 : Câu1: Tính 15 3 2 (x   2 x)dxx
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 x 4 3 x 4 3 x 4 A. 3  3ln x x C B. 3  3ln x x C. 3  3ln x x C 3 3 3 3 3 3 3 x 4 D. 3  3ln x x C 3 3 1
Câu 2: Tìm họ nguyên hàm của hàm số f(x)= x(x  3) 2 x 1  x A. ln  C B. ln  C 3 x  3 3 x  3 1 x 2  x C. ln  C D. ln  C 3 x  3 3 x  3
Câu 3: Tính (1 s inx)dxx  cosx C  A. C. cosx C x  cosx C   B. D. cosx C 1
Câu 4: Tìm họ nguyên hàm của hàm số f(x)= dx 1 x C 2 A.
B. -2 1 x C C. D.C 1 x 1 x 1 x Câu 5: Tính 3 (2  xe )dx  1 1 A. 2x + 3  x eC B. 2x - 3  x eC C. 2 x - 3  x eC D. 2x+ 3  x eC 3 3 1 
Câu 6: ChoF(x) là một nguyên hàm của hàm số y= và F(0)=1.Khi đóF(x) là: 2 cos x
A. -tan x B. –tanx +1 C.tanx+1 D. tanx-1
Câu 7: Tìm họ nguyên hàm 16 2  x 1 xe dx
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 1 2 1 2 2 A. x 1 e   C B. x e C C. x 1
e   C D. x 1 e   C 2 2 dx
Câu 8: Tìm họ nguyên hàm  x 2 ln x 1 1 1 A. F(x) =
ln x 1 C B.
ln 2 ln x 1  C C. 2ln x 1  C D. ln 2ln x 1  C 2 2 x e
Câu 9: Tìm họ nguyên hàm x e (2  )dx  2 cos x x 1 Lời giải: (2  )  2 x e dx e  + tanx +C 2 cos x A. 2 x
e +tanx+C B. 2 x e +tanx C.2 x
e -tanx+C D. Đáp án khác Câu 9: Hàm số f(x)= x
x 1 có một nguyên hàm là F(x).Nếu F(0)=2 thì giá trị của F(3) là : 116 146 886 A. B. C. D. Một đáp án khác 15 15 105 2 (x 1)
Lời giải: x x 1dx
 (x 1)  C  2 2 (3 1)
F(0)= 2  C  2  F (3)   (31)  2  6 2 PHẦN 2 : Mức 1: Nhận biết
Câu 1: Cho f(x) là hàm số liên tục trên đoạn  ;
a b . Giả sử F(x) là một nguyên hàm của f(x) trên đoạn  ; a b .
Công thức nào sau đây đúng: b b b b A.
f (x)dx F (x)  F (b)  F (a)  C.
f (x)dx F (x)  F (a)  F (b)  a a a a b b b b B.
f (x)dx F (x)  F (b)  F (a)  D.
f (x)dx F (x)  F (a)  F (b)  a a a a b b Lời giải:
f (x)dx F (x)  F (b)  F (a)  a 17 a Phương án nhiễu:
+) Phương án B: Nhầm dấu.
Group Nhóm Toán | Trắc nghiệm 2016-2017
+) Phương án C: Thay nhầm cận a,b.
,+) Phương án D: Nhầm trong việc thay cận trên hay dưới và dấu. 1
Câu 2: Tích phân I  x  2dx bằng: 0 5 5 13 A. I  I  I I 2 B. 2 C.  5 D.  2 x  2 1 2 5
Lời giải: I   . 2 2 0 Phương án nhiễu: +) Phương án A: Nhầ b
m F(x)  F a  F ba
+) Phương án C: Nhầm I   x  2 1 2  5. 0 +) Phương án D: b
F(x)  F a  F ba  3
Câu 3: Tích phân I  cos . x sin xdx  0 1 A. I  0 B. I  4 I   I    2 C. D. 4   cos x
Lời giải: I   cos xd  cos x 4 3   0. 4 0 0 Phương án nhiễu:
+) Phương án B: Đổi dấu sai trong công đoạn thay cận
+) Phương án C,D: Thay cận sai. Mức 2: Thông hiểu 5 5 5 Câu 4: Cho biết f( ) x dx  3; g(t)dt  9 A  f( ) x  g( ) x d  x 18   . Giá trị của   2 2 2 A. I  27 B. I  12  C. I  12
D. Không xác định được
Group Nhóm Toán | Trắc nghiệm 2016-2017
Lời giải: Do tích phân của hàm số trên  ;
a b cho trước không phụ thuộc vào biến số nên: 5 5 5 I   f
 x gxdx f (x)dxg  
 tdt 12 2 2 2 Phương án nhiễu:
+) Phương án D không xác định do học sinh không nắm được “tích phân của hàm số trên  ; a b cho trước
không phụ thuộc vào biến số”
+) Phương án A,C. Áp dụng sai công thức tích phân của một tổng. 5 1
Câu 5: Giá trị tích phân I    dx là: 2x  2016 1 1 1   1  1   1  1   1  1   1  A. 1   B. 1   C. 1   D. 1   2015 4030  9  2015 4030  9  2015 2015  9  2015 2015  9  5 1 d 2x   1 1   1  Lời giải: I       2 2x   1 2016 2015 1 4030  9  1 Phương án nhiễu:
+) Phương án B: Sai tại công đoạn thay cận đổi dấu.
+) Phương án C: Đưa dx thành d(2x -1), không chia 2.
+) Phương án D. Đưa dx thành d(2x -1), không chia 2 và thay cận sai. d d b Câu 6: Nếu
f (x)dx  5; f (x)dx  2,  
với a d b thì I f
 xdx bằng: a b a A. I  7 B. I  3 C. I  10 D. Đáp án khác b d b Lời giải: I f
 xdx f
 xdxf
 xdx  3 a a d Phương án nhiễu: d b
+) Phương án A: Nhầm lẫn f
 xdx f  xdx. 19 b d
Group Nhóm Toán | Trắc nghiệm 2016-2017 b d b
+) Phương án C: Nhầm lẫn I f
 xdx f
 xd .x f
 xdx  1  0 a a d
+) Phương án D: Gây nhiễu
Mức 3: Vận dụng thấp  4 2
Câu 7: Giả sử I  sin 3 . x sin2xdx  a  b a,b  . Khi đó, giá trị  2 của a b là: 0 1 3 3 3 A. I   I  I   I  6 B. 10 C. 10 D. 5   4 4 1 1  1  3 2
Lời giải: I   cos x  cos5xdx  s inx  sin 5x  .   2 2  5  5 2 0 0 3 3
Suy ra a  0,b
và a b  . 5 5 Phương án nhiễu:
+) Phương án B: Biến đổi sai công thức tích thành tổng.
+) Phương án C: đổi sai công thức tích thành tổng và sai bước đổi dấu thay cận.
+)Phương án A: Không xác đinh được a,b. 3 x 2 Câu 8: Biến đổi dx  thành f(t)dt vôùi t  1 x 
. Khi đó f (t) là hàm số nào trong các 0 1  x 1 1 hàm số sau: 2 2 2 2 A. f (t)  2t  2t B. f (t)  t  t C. f (t)  t  t D. f (t)  2t  2t Lời giải: Đặt 2 t
x 1  t x 1 2tdt dx 2
Đổi cận x  0  t 1; x  3  t  2. Khi đó I   2
2t  2t dt. 1 Phương án nhiễu: 20
+) Phương án B,C,D tính sai dt.
Mức 3: Vận dụng cao
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 2016 x
Câu 9: . Giá trị tích phân I dx  là: x e 1 2  2017 2 2018 2 C. 0 2018 2 1 A. B. D. 2   e 2017 2017 2 2017 e
Lời giải: Đặt x t   dx dt
Đổi cận: Với x  2  t  2  ; x  2   t  2 2  2 2016 2 2016 x  2 2017 2018 Khi đó: t x e dx x 2 I dt   2016      , suy ra 2I x dx  . t e 1 1 xe 2017 2017 2 2  2  2 
+)Phương án B: Sai lầm để 2I và chọn đáp án B 2 2016
+) Phương án C: Biến đổ x
i sai lầm sau phép đặt được I   dx  và kết luận I = 0. x e 1 2  2 2016 2 2 +) Phương án D: Nhớ x sai công thức 2016 I dx x dx :  
  xe dx và tính ra D. x 1 e 1 2  2  2   3 3  1  c dx 1 Câu 10: Cho   ln
và a, b, c nguyên dương. Tổng a b c bằng: 2 2
0 sin x2sin x cos x3cos x 4 a b A. 9 B. 8 C. 7 D. Không xác định dx   3 dx 3 2 cos x
Lời giải: Ta cã I     2 2 2
0 sin x  2 sin x cos x  3cos x
0 tan x  2 tan x  3 dx
§Æt t  tan x dt  2 cos x 3 3 3 3  dt dt 1 t  1 1  3 1  I       t  2t  3
t  t   ln ln 2 0 0 1 3 4 t  3 4 3  3 0 21
Suy ra a b c  9 .
+) Phương án B,C,D: Gây nhiễu
Group Nhóm Toán | Trắc nghiệm 2016-2017 PHẦN 3 : Câu nhận biết
Câu 1. Diện tích hình phẳng giới hạn bởi đường y x và 2 đường
Thẳng x =0, x= 1, trục hoành là. 1  A. S  (đvdt)
B. S  1(đvdt) C. S  2 (đvdt) D. S  (đvdt) 2 2
Câu 2. Diện tích hình phẳng giới hạn bởi đồ thị hs y=f(x) nằm phía trên trục hoành và 2 đường x=a,x=b với ahoành là.
A. S f a  f b (đvdt)
B. S f b  f a (đvdt)
C. S   ( f b  f a) (đvdt) D.
S    f (a)  f(b) (đvdt)
Câu 3. Diện tích hình phẳng giới hạn bởi 2 đường y  0,
y  sin x và 2 đường thẳng  x  , o x  là 2 A. S  0 (đvdt)
B. S   (đvdt) C. S  1(đvdt) D. S  2 (đvdt) Câu thông hiểu
Câu 4. Diện tích hình phẳng giới hạn bỏi 2 đường thẳng x=1,
y  3  x trục ox là. A. S  2 B. S  4 C. S  4 D. S  2
Câu 5.Tính diện tích hình phẳng giới hạn bởi y  .
x ln x ,trục hoành và hai đường thẳng x = 1, x = e. 1 1 1 A. 2 S  (e 1) B. 2 S  (e 1) C. 2 S  (1 e ) D. 2 S  (1 e ) 4 4 4
Câu 6. Thể tích hình phẳng giới hạn bởi các đường y  ,
x y  2 trục oy khi xoay quanh trục hoành là. 8 8 A.V  (dvtt) B.V  8 (dvtt) C.V   3 3
D. Các kết quả trên đều sai. 22
Group Nhóm Toán | Trắc nghiệm 2016-2017 Câu vận dụng thấp
Câu 7.Tính diện tích hình phẳng giới hạn bởi 2 y  .
x ln x ,trục hoành và hai đường thẳng x = 1, x = e. 1 1 1 A. 2 S  (e 1) B. 2 S  (e 1) C. 2 S  (1 e ) D. 2 S  (1 e ) 4 4 4
Câu 8.Thể tích hình phẳng giới hạn bởi các đường 2
y  (x  2), y  0 ,x=o,x=2 khi xoay quanh trục hoành là. 32 32 A.V  (dvtt) B.V  32 (dvtt) C.V  . (dvtt) D.32 5 5 Câu vận dụng cao
Câu 9. Diện tích hình phẳng giới hạn bỏi trục tung và 2 đường  2x y ,
y  3  x là. 5 3 5 1 A. S   ln 2 B. S  C. S  5  ln 2 D. S   2 2 2 ln 2
Câu 10. Cho hình phẳng giới hạn bởi các đường 2
y  (x  2) ,
y  4 khi xoay quanh trục hoành là. 256 256 A.V  (dvtt) B.V   (dvtt) C.V  256. (dvtt) 5 5
D. Các kết quả trên đều sai. PHẦN 4 :   
Câu 1. Tính sin   x cos xdx   bằng:  0  3 A. 0 B. 1 C.  D. 2 2
Câu 2. Cho tích phân 2
I  2x x 1.dx  . Đặt 2
u x 1. Chọn khẳng định sai trong các khẳng định sau: 1 3 3 2 2 2 A. I udu  B. I  . 27 C. I udu  D. I  .u u 3 3 0 1 0 23 b c c
Câu 3. Cho af (x)dx  8 
và f (x)dx  2 
khi đó giá trị của tích phân f (x)dx  bằng: a b a
Group Nhóm Toán | Trắc nghiệm 2016-2017 A. 6 B. 10 C. 4 D. 16 2 ln x
Câu 4. Tính tích phân dx 3 x 1 2  ln 2 3  2 ln 2 3  ln 2 3  2 ln 2 A. B. C. A. 16 16 16 16 e
Câu 5. Biết rằng f (x) có đạo hàm f '(x) liên tục trên R và f (0)  2e , : f '(x)dx  5e  . Tính f ( ) e . 0 A. f ( ) e  0 B. f ( ) e  3  e C. f ( ) e  7 e D. f ( ) e  3e 5 dx
Câu 6. Giả sử I   ln a
khi đó a nhận giá trị: 2x 1 1 A. 9 B. 3 C. 8 D. 81 a
Câu 7. Cho a  0 . Với giá trị nào của a để biểu thức I  (2x  4)dx
đạt giá trị nhỏ nhất: 1 A. a  1 B. a  4 C. a  2 D. a  3 1
Câu 8. Tính tích phân I  (| 3x 1| 2  | x |)dx  bằng: 0 1 7 1 A.  B. C. D. 0 6 6 2 2
Câu 9. Tìm giá trị thực của m để I=4, biết I= (2mx 1)dx  . 1 A. m=-1 B.m= - 2 C. m=1 D. m=2
Câu 10. Với hàm số y f (x) liên tục trên miền D  [ ; a ]
b có đồ thị là đường cong (C), ta có thể tính độ dài đường b 2 x cong (C) bằng công thức: 2
1 ( f '(x)) dx
. Tính độ dài đường cong (C) cho bởi hàm số y   ln x trên [1; 2] 8 a bằng: 24 3 3 A.  ln 2 B. 1 ln 2 C.  ln 2 D. 1 ln 2 8 8
Group Nhóm Toán | Trắc nghiệm 2016-2017 HƯỚNG DẪN    
Câu 1. Tính x cos xdx  2   
suy ra sin   x cos xdx   =0 0  0  Đáp án A Câu 2. Đáp án C c b c Câu 3.
f (x)dx
f (x)dx f (x)dx  8  2 10    a a b - Đáp án B dx 2 ln x 3  2 ln 2
Câu 4. Đặt u  ln ; x dv  . Tính được dx= 3 x 3 x 16 1 Đáp án B e
Câu 5. f '(x)dx f (e)  f (0)  5e f (e)  3e  0 Đáp án 5 5 dx 1 5 Câu 6. I
 ln | 2x 1|  ln 3  ln a a  3  1 2x 1 2 1 - Đáp án B 5 dx 5 -
Phương án gây nhiễu 1: I
 ln | 2x 1|  ln 9  ln a a  9  HS chọn A 1 2x 1 1 5 dx 5 -
Phương án gây nhiễu 2: I
 ln | 2x 1|  ln(2.5 1 (2.11))  ln8  ln a a  8  HS chọn C 1 2x 1 1 25 5 dx 5 - Phương án gây nhiễu 2: 2 I
 2ln | 2x 1|  ln 9  ln a a  81  HS chọn D 1 2x 1 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 a a Câu 7. 2 2 2
I  (2x  4)dx  (x  4x)  a  4a  3  (a  2) 1  1   suy GTNN min I=-1 khi a=2 1 1 Đáp án: C Phương án gây nhiễu: A a a 2 2 2
I  (2x  4)dx  (2x  4x)  (2a  4a)  2  2(a 1)  2  2   a 1  1 1 Phương án gây nhiễu: B a a 2
I  (2x  4)dx  (x  4x)  a(a  4)  3  3  a  4  1 1 Phương án gây nhiễu: D a a 2
I  (2x  4)dx  (x  4x)  a(a  4)  3  3  a  3  1 1 1 1 1 5 1 
Câu 8. I  (| 3x 1| 2
 | x |)dx  | 3x 1| dx  2 | x | dx  1     6 6 0 0 0 Đáp án A 1 1 1 5 7
- Phương án gây nhiễu: B I  (| 3x 1| 2
 | x |)dx  | 3x 1| dx  2 | x | dx  1     6 6 0 0 0
- Phương án gây nhiễu: 0 1 1 1 2 x 1
I  (| 3x 1| 2
 | x |)dx  (x 1)dx  (  x)     2 2 0 0 0
- Phương án gây nhiễu: C 1 1 1 2
I  (| 3x 1| 2
 | x |)dx  (x 1)dx  (x x)  0   0 0 0 2 26
Câu 9. I= (2mx 1)dx  3m 1  4  m  1  . 1 Đáp án C
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 - Phương án gây nhiễu 1: 2 2
(2mx 1)dx  (mx x) |  4m  2  m  4  m  2  HS chọn D 1 1 2 2 mx - Phương án gây nhiễu 2: 2
(2mx 1)dx  (  x) |  2
m  2  (m1)  4  m  1   HS chọn A 1 2 1 2 - Phương án gây nhiễu 3: 2 2
(2mx 1)dx  (mx x) |  4
m  2  m  4  m  2   HS chọn B 1 1
Câu 10. Học sinh phải nắm ngay công thức tính và áp dụng 2 2 2 x 1 x 1 x 1 3 2 2 1 (  ) dx
(  ) dx  (  )dx   ln 2    4 x 4 x 4 x 8 1 1 1 Đáp án: C 2 2 2 x 1 x 1 x 1 3 - Phương án gây nhiễu 1: 2 2 1 (  ) dx
(  ) dx  (  )dx   ln 2    HS chọn A 4 x 4 x 4 x 8 1 1 1 - Phương án gây nhiễu 2: 2 2 2 2 2 x 1 x 1 x 1 x 2 2 1 (  ) dx
(  ) dx  (  )dx  (  ln x) 1 ln 2    HS chọn B 4 x 4 x 4 x 8 1 1 1 1 - Phương án gây nhiễu 3: 2 2 2 2 2 x 1 x 1 x 1 x 2 2 1 (  ) dx
(  ) dx  (  )dx  (  ln x) 1 ln 2    HS chọn D 4 x 4 x 4 x 8 1 1 1 1 PHẦN 5 :
Câu 1.(Mức độ 2) Tìm nguyên hàm của hàm số f x 1  1 2x A. f
 xdx ln(12x)C  B. f  x 1 dx
ln 1 2x C 2 C. f
 xdx  2ln 12x C D. f  x 1 dx  
ln(1 2x)  C 2
Giải thích phương án nhiễu:
A. Nhầm lẫn do không nhớ công thức C. Nhầm lẫn công thức 27
D. Thiếu dấu giá trị tuyệt đối
Group Nhóm Toán | Trắc nghiệm 2016-2017 Lời giải dx 1 dx 1 1  Áp dụng nguyên hàm
 ln ax b C  . Ta có 
ln 1 2x C  ln 1 2x C  . ax b a 1 2x 2  2
Câu 2. (Mức độ 1) Cho hàm số f x  sin 2x khi đó: A. f
 xdx  2cos2xC B. f
 xdx  2
 cos 2x C C. f  x 1 dx   cos 2x C D. f  x 1 dx  cos 2x C 2 2
Giải thích phương án nhiễu:
A. Nhầm lẫn với đạo hàm
B. Nhầm lẫn với đạo hàm và lấy dấu “-“ của nguyên hàm D. Nhầm dấu
Câu 3. (Mức độ 2) Tìm nguyên hàm của hàm số    2 x f x xe A.    2 x f x dx xe C
B.    2 x  2 x f x dx e xe C
C.     ( 1) x f x dx x e C
D.     ( 1) x f x dx x e C
Giải thích phương án nhiễu:
A. Nhầm lẫn do hiểu là nguyên hàm của một tích bằng tích các nguyên hàm
B. Nhầm lẫn với đạo hàm
C. Nhầm dấu trong tich phân từng phần
Câu 4. (Mức độ 2) Tìm nguyên hàm của hàm số f x  x cos x 1    A. f  x 2 dx
x sin x C B. f
 xdx sin x C 2 C. f
 xdx  cosxxsin xC D. f
 xdx xsin xcosxC 1
Câu 5. (Mức độ 2) Nguyên hàm của hàm số f (x)  là: 2 2 x - a 1 x a 1 x a A. ln  C B. ln  C 2a x a 2a x a 28 1 x - a 1 x a C. ln  C D. ln  C a x a a x a
Group Nhóm Toán | Trắc nghiệm 2016-2017 1
Câu 6. (Mức độ 2) Nguyên hàm của hàm số f (x)  là: 2 2 sin . x cos x
A. F x  tan x  cot x C
B. F x  cot x tan xC
C. F x  tan x  cot x C D. F x 2 2
 tan x cot x C
Câu 7. (Mức độ 3) Nguyên hàm của hàm số: 3
f (x)  x ln x là: 1 1 1 1 A. 4 4 x .ln x x C B. 4 2 4 x .ln x x C 4 16 4 16 1 1 1 1 C. 4 3 x .ln x x C D. 4 4 x .ln x x C 4 16 4 16
Câu 8. (Mức độ 3) Nguyên hàm của hàm số f ( )
x  2sin 3xcos 2x là: 1 1 1 A. 
cos 5x  cos x C
B. F(x) =  cos 5x  cos x C 5 3 2 1 1 1
C.  cos 5x  cos x C
D. F(x) = cos 5x  cos x C 2 3 5 3 x
Câu 9. (Mức độ 3) Nguyên hàm của hàm số f (x)  là: x 1 1 3 1 2 1 1 A. x
x x  ln x 1  C B. 3 2 x
x x  ln x 1  C 3 2 3 2 1 1 1 3 1 2 C. 3 2 x
x x  ln x 1  C D. x
x x  ln x 1  C 6 2 3 4 1
Câu 10. (Mức độ 4) Nguyên hàm của hàm số: y = f (x)  là: x 2 + 5 1 2 x 1 2 x A. ln  C B. ln  C 2ln 5 2 x  5 5ln 2 2 x  5 1 2 x 1 2 x C. ln  C D. ln  C x x 29 10ln 2 2  5 ln 2 2  5 PHẦN 6 :
KIỂM TRA 45 PHÚT - CHƯƠNG III
Group Nhóm Toán | Trắc nghiệm 2016-2017 I. Mục tiêu:
+ Kiểm tra các kiến thức trong chương 3 giải tích gồm có các nội dung chính: nguyên hàm; tích phân; ứng dụng của tích phân.
+ Học sinh cần ôn tập trước các kiến thức trong chương 3 thật kỹ, tự giác tích cực làm bài. Qua đó giáo viên nắm được
mức độ lĩnh hội kiến thức của học sinh.
+Phát triển năng lực học sinh theo 4 mức độ nhận thức II. Chuẩn bị: - GV: ra đề kiểm tra.
- HS: Ôn tập, chuẩn bị kiểm tra.
III. Nội dung kiểm tra:
1. Kiến thức: Kiểm tra việc nắm bắt kiến thức của Hs về phần nguyên hàm, tích phân và ứng dụng của tích phân. 2. Kĩ năng:
Rèn kỹ năng tính nguyên hàm, tích phân và giải các bài toán ứng dụng tích phân.
Rèn tư duy lôgic và tính tự giác cho học sinh.
3. Mức độ: Nhận biết ( 4,8 điểm ) + Thông hiểu ( 4.0 điểm) + Vận dụng ( 0,8 điểm).
VI. Ma trận đề kiểm tra: Mức độ Nhận biết Thông hiểu Vận dụng Vận dụng mức độ thấp mức độ cao Tổng Nội dung Nguyên hàm 3 2 5 2.0 1,2 0,8
Phương pháp tính tích phân 6 5 2 13 2,4 2,0 0,8 5,2
Ứng dụng tích phân tính diện 5 2 7 tích hình phẳng 2.0 0,8 2,8 Tổng 9 12 2 2 25 3,6 4,8 0,8 0,8 10 30 1
Câu 1:Tìm nguyên hàm F x của hàm số f x 3
x  3x x
Group Nhóm Toán | Trắc nghiệm 2016-2017 x4 3 1 A. F x   x2  ln x  C B. F x  3 3x 3x   C 4 2 2 x 4 x 2 4 x 3 C. F x   2 x  ln x C D. F x   2 x  ln x C 4 3 4 2
Câu 2:Tìm nguyên hàm F x của hàm số   2x 3x f x   . Chọn đáp án sai 2x 3x 1 2x 3x 1 A. F x    B. F x    ln2 ln3 ln2 ln2 ln3 2x 2x 3x 1 2x 3x C. F x    D. F x   ln2 ln3 ln3 ln 2 ln3 x 1
Câu 3:Tìm nguyên hàm F x của hàm số f ( ) x  2 x 1 1 A. F( ) x  ln x  C F( ) x ln x C x B.    x 1 1 C. F( ) x  ln x  C F( ) x ln x C x D.     x tan xdx
Câu 4:Tìm nguyên hàm F x của hàm số f(x)=  2 cos x A. 2 cot x C B. 2 cos x C C. 2 sin x C D. 2 tan x C
Câu 5:Tìm nguyên hàm F x của hàm số f(x)= 2 x sin xdx  1 1 1 1 A. 2 F (x) 
x x sin 2x  cos 2x C B. 2 F (x) 
x x sin 2x  cos 2x C 2 2 4 2 1 1 1 1 C. 2 F (x) 
x  (x  ) cos 2x C D. 2 F (x) 
x x sin 2x  cos 2x C 4 2 4 2 2
e 2 x  5  7x Câu 6:Tính tích phân:I= dxx 1 31
A. 4 e  7e  8
B. 7 e  4e  8
C. 8 e  7e  4
D. 4 e  7e  8
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 Câu 7:Tính tích phân: I= x 1dx  1 2 3 2 2
A. 3 2  2 3 B. 3 3  2 2 C. 3 3  2 2 D. 2 2 3 3 3 2 3 3 1 xdx
Câu 8:Tính tích phân: I=  2 x 1 0 1 A. ln 2 B. 2ln 2 C. ln 2 D. ln 2 2 e 2  ln x Câu 9:Tính tích phân: I= dx  2x 1 3 2  2 3 3 3  2 2 3 3  2 2 3 3  2 2 A. B. C. D. 3 3 2 3  2 Câu 10 Tính  2 cos xdx 0   2   A. B. C. D. 2 4 3 3 2 Câu 11 Tính 2 J x 1 dx  2  9 A. 3 B. 4 C. 9 D. 2 e Câu 12 Tính x ln xdx  32 1 1 2  e 2 e  1 2 e  1 2  e 1 A. B. C. D. 2 2 2 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 5 Câu 13: Tính 2 I x x  4dx 0 19 19 28 A. B. 1 C.  D.  3 3 3 1 Câu 14: Tính: 2 2 x K x e dx  0 2 e 2 e 1 2 e  1 1 A. K  B. K  C. K  D. K  4 4 4 4 3 3  ln x Câu 15: Tính: I  dx  2 (x 1) 1 3 3 3 A. I  1 (  ln ) 3  ln 2 B. I  1 (  ln ) 3  ln 2 C. I  1 (  ln ) 3  ln 2 D. 4 4 4 3 I  (1  ln 3)  ln 2 4  2
Câu 16: Tính:   sinx I e
x.cos xdx . 0     A. e   2 B. e   2 C. e   2 D. e   2 2 2 2 2 2 2 33 Câu 17 Tính 4  x dx, 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 2  1 2  1  A. B. C. D.  2 2 2 . 1 dx Câu 18 Tính,  2 1  x 0 2  1   A. B. C. D.  2 2 4
Câu 19: Số đo diện tích hình phẳng giới hạn bởi hai đường y = x3 – x và y = 3x bằng : A. 4 B. 8 C. 16 D. 32 𝑥
Câu 20: Số đo diện tích hình phẳng giới hạn bởi các đường y =
; y = 0; x = 0 ; x = 1 bằng: 𝑥+1
A. 2ln2 B. 1- ln2 C. 2 + ln2 D. 2
Câu 21: Số đo diện tích hình phẳng giới hạn bởi các đường: y = x3  x2  2x và trục hoành bằng: 37 12 A. B. C. 37 D. 12 12 37
Câu 22. Số đo diện tích hình phẳng giới hạn bởi các đường y = ex ; y = e-x ; x = 1 bằng: 2 1
A. 1 + B. 2e C. e + 1 D. e + - 2 𝑒 𝑒 34
Câu 23: Cho hình phẳng ( H) giới hạn bởi đồ thị hàm số y = √𝑥 -1, trục Ox; đường thẳng x =
1; x = 4. Thể tích của khối tròn xoay tạo thành khi quay (H) quanh trục Ox bằng: 2𝜋 𝜋 A. B. 2π C. 7𝜋 D. 3 6 6
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 24: Cho hình phẳng (H) giới hạn bởi các đường y = sin2x ; y = 0 ; x = 0 ; x = π. Thể tích
của khối tròn xoay tạo thành khi quay (H) quanh trục Ox bằng: 𝜋2
A. B. 𝜋2 C. 𝜋2 D. 3𝜋2 8 4 2 8 2
Câu 25: Cho hình phẳng (H) giới hạn bởi các đường: y = ; y = 1; y = 4 ; x = 0. Thể tích của 𝑥
khối tròn xoay tạo thành khi quay (H) quanh trục Oy bằng: A.π B. 2π C.3π D. 5π ĐÁP ÁN 1A 2B 3C 4D 5B 6A 7C 8A 9B 10B 11B 12B 13A 14C 15D 16A 17D 18C 19B 20B 21A 22D 23C 24D 25C ĐÁP ÁN CHI TIẾT ĐS: 1a) 2b) x 1 1 1 1 3c. dx  (  )dx ln x    C 2  2 x x x x tan xdx dx  .Đặt t = tanx  dt  . 2 2 4D. cos x cos x
tan xdx  tdt  t C  tan x   2 2 C 2 cos x 35
Group Nhóm Toán | Trắc nghiệm 2016-2017 du     dx u x 5B. 2 x sin xdx  . Đặt   2  1 dv  sin . x dx v  x   sin 2x  2 1 1 1 1 1 2 2 2 2
x sin xdx  ( x x sin 2x)  ( x  sin 2x).dx (
x xsin 2x)  ( x  cos 2x)  C   2 2 2 4 2 1 1 2
x xsin 2x  cos 2x C 4 2 6a 2 2 e e 2 2  5  7 2 5 e x x dx  (
  7)dx  (4 x  5ln x  7x)  
= 4 e  7e  8 1 x x x 1 1 7C 8A e 2  ln x 1 9B dx  . Đặt t= 2
2  ln x t  2  ln x tdt dx 2x 2x 1 3 3 3 t 3 2  2 3 I= 2 t dt   = 3 3 2 2  2 Câu 10 Tính  2 cos xdx 0    2 2 1 1  1   I = 2 cos x.dx  (1 cos2x).dx   = x  sin 2x 2    2 2  2  4 0 0 0   2   A. B. C. D. 2 4 3 3 36
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 Câu 11 TÝnh 2 J x 1 dx  2  9 A. 3 B. 4 C. 9 D. 2 Xét dấu 2
x 1 trên đoạn  2  ;2 x -2 -1 1 2 2 x 1 + 0 - 0 + 2 1  1 2 2 I
x 1 dx   2 x   1 dx   2
1 x dx   2 x   1 dx     2  2  1  1 3 3 3  x  1   x  1  x  2   xx    x  4       .  3  2   3  1   3  1 e Câu 12 Tính x ln xdx  1 1 2  e 2 e  1 2 e  1 2  e 1 A. B. C. D. 2 2 2 2  dx du u   ln x  Đặ x t    dv xdx 2 xv   2 e e 37 2 2 2 2 x e 1 e x e e 1 x ln xdx  ln x xdx      2 1 2 2 4 1 4 1 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 5 Câu 13: Tính 2 I x x  4dx 0 19 19 28 A. B. 1 C.  D.  3 3 3 5 2 I x x  4dx  0 Đặt 2 2 2 u
x  4  u x  4
 2udu  2xdx udx xdx Đổi cận: x  0  u  2 3 3 3 u
x  5  u  3 2 I u duI  19  =>CHỌN A 3 3 2 2 1 Câu 14: Tính: 2 2 x K x e dx  0 2 e 2 e 1 2 e  1 1 A. K  B. K  C. K  D. K  4 4 4 4 2 du   2 u xdx Đặ  x  t     1 dv  2x e dxv  2 x e  2 1 1 1 K  (x2. e2x 1 . )  xe2xdx e L 0  2 0 2 2 38
Group Nhóm Toán | Trắc nghiệm 2016-2017 du  u xdx    1 dv  2x e dxv  2 x e  2 1 1 x 1 2 1 2 L  (x e )  e x dx  2  0 0 2 2 => CHỌN C 1 1 1 1 1 2 2 2
e  ( e  )   e 2 4 4 4 4 3 3  ln x Câu 15: Tính: I  dx  2 (x 1) 1 3 3 3 A. I  1 (  ln ) 3  ln 2 B. I  1 (  ln ) 3  ln 2 C. I  1 (  ln ) 3  ln 2 D. 4 4 4 3 I  (1  ln 3)  ln 2 4 3 3 3 3  ln x dx ln x I  dx  3  dx    2 2 2 (x 1) (x 1) (x 1) 1 1 1 3 3 dx 3  3 I  3    1 2 (x 1) (x 1) 4 1 1 3 ln x I  dx  2 2 (x 1) 1 dx Đặt u = lnx  du  x dx 1  dv  . Chọn v  2 (x 1) x 1 3 3 3 3 ln x dx ln 3 dx dx ln 3 3 I           ln    2 x  1 x(x 1) 4 x x 1 4 2 1 1 1 1 39 3
Vậy : I  (1 ln 3)  ln 2 4
Group Nhóm Toán | Trắc nghiệm 2016-2017 .  2
Câu 16: Tính:   sinx I e
x.cos xdx . 0     A. e   2 B. e   2 C. e   2 D. e   2 2 2 2 2   2 2 sin x I e cos xdx  . x cos xdx   0 0       2 2  2 2 2 2   sin x sin  cos x    sin  2 sin x I e xdx e d x ee 1 I  .
x cos xdx x sin x
 sin xdx   cos x  1   1 0 2 2 2 0 0 0 0 0 0 
I I I = e   2 1 2 2 2 Câu 17 Tính 2 4  x dx, 0 2  1 2  1  A. B. C. D.  2 2 2     
Đặt x  2sint, t   ; 
 . Khi x = 0 thì t = 0. Khi x  2 thì t  .  2 2  2
x  2sin t dx  2costdt   4 2 2 2 2 2 4  x dx
4  4sin t.2costdt  4 cos tdt      . 0 0 0 40
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 dx Câu 18 Tính,  2 1  x 0 2  1   A. B. C. D.  2 2 4     
Đặt x  tan t, t    ;
 . Khi x  0 thì t  0, khi x 1 thì t  .  2 2  4 dt
Ta có x  tan t dx  . 2 cos t    1 4 4 dx 1 dt       . dt t 4 .    2 2 2 1  x
1  tan t cos t 4 0 0 0 0
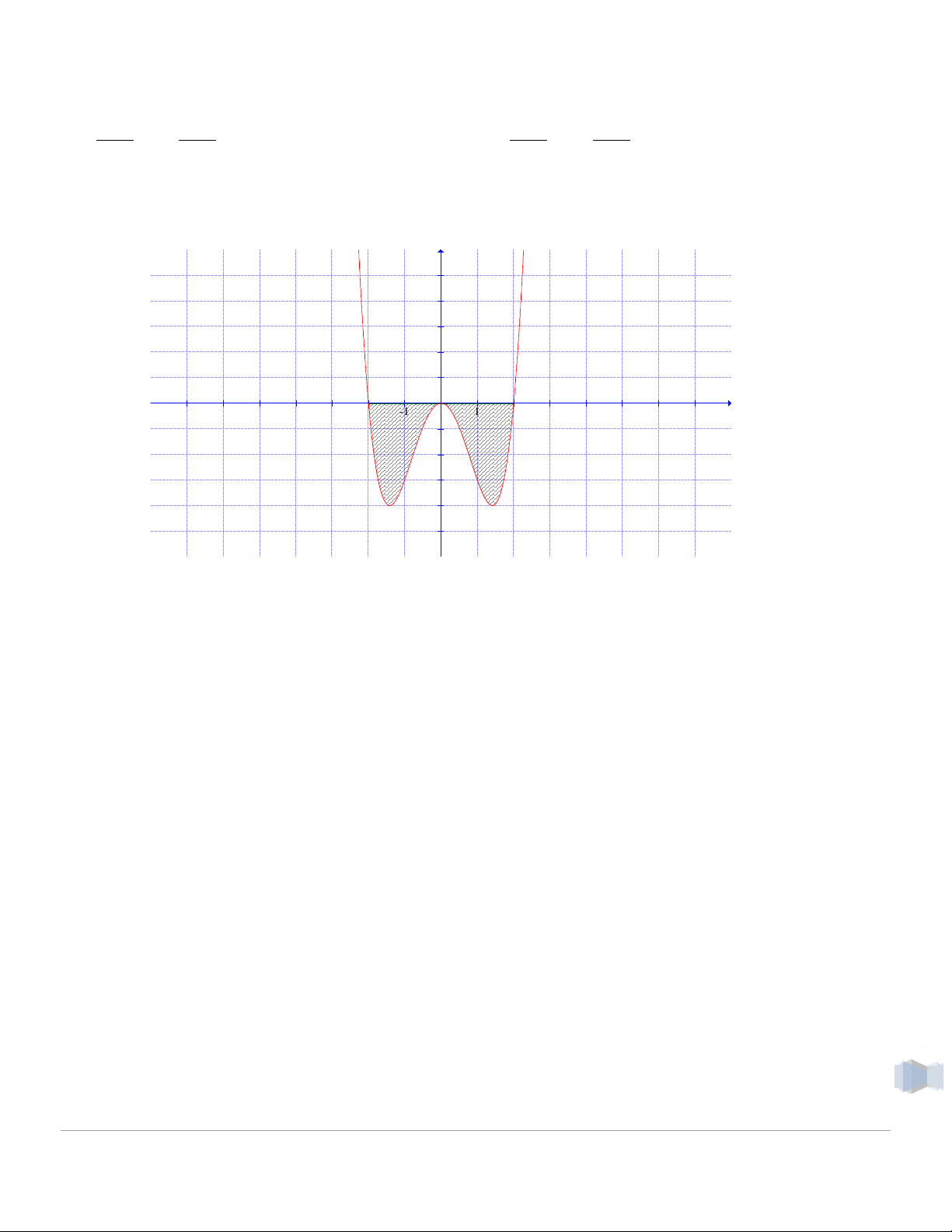
Câu 19: Số đo diện tích hình phẳng giới hạn bởi hai đường y = x3 – x và y = 3x bằng : A. 4 B. 8 C. 16 D. 32
Phương trình HĐGĐ : x3 – x = 3x ⇔ x = 0 ; x = -2 ; x = 2 2 2 0 2
S= ∫ |(𝑥3 − 𝑥) − 3𝑥|𝑑𝑥 −2
=∫ |𝑥3 − 4𝑥|𝑑𝑥 −2
= ∫ |𝑥3 − 4𝑥|𝑑𝑥 −2
+ ∫ |𝑥3 − 4𝑥|𝑑𝑥 0 =
|∫0 (𝑥3 − 4𝑥)𝑑𝑥| 2 | − 2𝑥2] 0 | − 2𝑥2] 2| −2
+ |∫ (𝑥3 − 4𝑥)𝑑𝑥 0 = |[𝑥4 + |[𝑥4 = 8 4 −2 4 0 ĐA: B 𝑥
Câu 20: Số đo diện tích hình phẳng giới hạn bởi các đường y =
; y = 0; x = 0 ; x = 1 bằng: 𝑥+1
A. 2ln2 B. 1- ln2 C. 2 + ln2 D. 2 1 1 1 S= ∫ | 𝑥 | 𝑑𝑥 | 𝑑𝑥 ) 𝑑𝑥| | 0 = ∫ |1 − 1
= |[𝑥 − ln (𝑥 + 1)]1 =1- ln2 𝑥+1 0 = |∫ (1 − 1 𝑥+1 0 𝑥+1 0 ĐA : B 41
Câu 21: Số đo diện tích hình phẳng giới hạn bởi các đường: y = x3  x2  2x và trục hoành bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017 37 12 A. B. C. 37 D. 12 12 37
Câu 21: Phương trình hoành độ giao điểm của đồ thị hàm số y = x3  x2  2x và trục hoành.
x3  x2  2x = 0  x = -2 ; x = 0 ; x = 1 1 0 1
S = x3  x2  2xdx  =  3 x  2
x  2xdx +   3 x  2
x  2xdx 2 2 0 0 0 1 1 8 I 3 (x  2 x  4 3 2 x x  1 =  2x)dx = ( x ) =  4 3 3 2 2 1 1 1 1 5 I 3 (x  2 4 3 2    2 = 
x  2x)dx = ( x x x ) = 4 3 12 0 0 8 5 37 S =   = 3 12 12 ĐA: A
Câu 22. Số đo diện tích hình phẳng giới hạn bởi các đường y = ex ; y = e-x ; x = 1 bằng: 2 1
A. 1 + B. 2e C. e + 1 D. e + - 2 𝑒 𝑒
Câu 22: Phương trình HĐGĐ : ex = e-x ⇔ x = 0 1 1 1
S= ∫ |𝑒𝑥 − 𝑒−𝑥|𝑑𝑥 | | 0
= |∫ (𝑒𝑥 − 𝑒−𝑥)𝑑𝑥 0 = |[𝑒𝑥 + 𝑒−𝑥]1 0 = e + - 2 𝑒 Đ A: D 42
Câu 23: Cho hình phẳng ( H) giới hạn bởi đồ thị hàm số y = √𝑥 -1, trục Ox; đường thẳng x =
1; x = 4. Thể tích của khối tròn xoay tạo thành khi quay (H) quanh trục Ox bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017 2𝜋 𝜋 A. B. 2π C. 7𝜋 D. 3 6 6 4 Câu23: V= π∫ ( 4 √𝑥 − 1)2𝑑𝑥 4 1 4 7𝜋 2 3   1
= π∫ (𝑥 − 2√𝑥 + 1) 𝑑𝑥 1 = π ( x x x ) = 2 3 6 1 Đ A : C
Câu 24: Cho hình phẳng (H) giới hạn bởi các đường y = sin2x ; y = 0 ; x = 0 ; x = π. Thể tích
của khối tròn xoay tạo thành khi quay (H) quanh trục Ox bằng: 𝜋2
A. B. 𝜋2 C. 𝜋2 D. 3𝜋2 8 4 2 8
Câu 24: V= π∫𝜋(sin2 𝑥)2𝑑𝑥 𝜋
𝜋 ∫𝜋(3 − 2𝑐𝑜𝑠2𝑥 + 𝑐𝑜𝑠4𝑥)𝑑𝑥 0 = π∫ sin4 𝑥 𝑑𝑥 0 = 8 0  𝜋 1 = 3
( x  sin 2x  sin 4x) = 3𝜋2 8 2 8 0 Đ A : D 2
Câu 25: Cho hình phẳng (H) giới hạn bởi các đường: y = ; y = 1; y = 4 ; x = 0. Thể tích của 𝑥
khối tròn xoay tạo thành khi quay (H) quanh trục Oy bằng: A.π B. 2π C.3π D. 5π Câu 25: y = 2/x ⇔ x= 2/y 4 V = π∫ ( 4 2)2𝑑𝑦 4 𝑑𝑦 1 1 = 4𝜋 ∫ 1 ( ) = 3π 𝑦 1 = -4π 𝑦2 y 1 Đ A : C PHẦN 7 :
Câu 1. (Nhận biết) Đẳng thức nào sau đây là sai?  
A.  f (x)dx
  f (x)C .
B.  f (x)dx    f (x) .   C.  f (t)dt    f (t).
D.  f (x) dx f (x) C . 43 LỜI GIẢI DIỄN GIẢNG NHIỄU
Group Nhóm Toán | Trắc nghiệm 2016-2017
HS nhầm qua họ nguyên hàm phải cộng thêm số C → Chọn câu B
HS nghĩ nguyên hàm chỉ có ẩn số là x → Chọn câu C
HS quên tính chất 1 của nguyên hàm → Chọn câu D
Câu 2. (Nhận biết) Cho F x,G x lần lượt là một nguyên hàm của f x, g x trên tập K  và k, h  . Kết
luận nào sau đây là sai? A.  f
 x gxdx F
xGxC . B. kf
 xhgxdx kF
xhGxC . C. f
 x.gxdx Fx.GxC .
D. F ' x  f x, x   K . LỜI GIẢI DIỄN GIẢNG NHIỄU
HS quên tính chất 2 của nguyên hàm → Chọn câu A
HS không biết kết hợp tính chất 2 và 3 → Chọn câu B
HS nghĩ nguyên hàm phải cộng thêm số C → Chọn câu D
Câu 3. (Thông hiểu) Biết    2
f y dy x xy C , thì f y bằng A. x B. . xy C. . y D. 2x  . y LỜI GIẢI DIỄN GIẢNG NHIỄU
Công thức nguyên hàm theo ẩn y, x HS nhằm qua ẩn x → Chọn câu B
xem là 1 hằng số giống số C
HS nhằm qua ẩn x → Chọn câu C
HS lấy nguyên hàm theo ẩn x → Chọn câu D
Câu 4. (Nhận biết) Trong các đẳng thức sau, đẳng thức nào sai?
A.  f (x)'dx f (x) C
B. u(x)v (
x)dx u(x).v(x)  v(x).u (x)dx  
C.  f (x)dx  ' f (x) D.  f
 x gxdx f (x)dxg(x)dx   
ĐÁP ÁN, HƯỚNG DẪN GIẢI DIỄN GIẢNG NHIỄU Đáp án B
A .Hs chọn vì có thể nhớ nhầm công thức 44 A. Đúng (T/c1)
C. Hs chọn vì nghĩ theo họ nguyên hàm thì phải cộng hằng số C B. Sai
Group Nhóm Toán | Trắc nghiệm 2016-2017
C. Đúng (theo đ.nghĩa nguyên hàm)
D. Hs chọn vì quên công thức
f (x)dx
'(F(x)C) f (x) D. Đúng (t/c 3)
Câu 5. (Nhận biết) Hàm số 3 ( ) x
f x e có nguyên hàm là hàm số nào sau đây? 1 x A. 3x y eC B. 3  3 x y eC C. 3x y eC
D. y  3e  C 3 LỜI GIẢI TÓM TẮT DIỄN GIẢNG NHIỄU - A: HS nhầm lẫn x x
e dx e C
- B: HS nhầm với công thức đạo hàm
Câu 6. (Thông hiểu) Hàm số nào sau đây không phải là nguyên hàm của hàm số x y e  1 1 x e 1 A.   c B.  c C. x e   c D. 1 c x e x e x e ĐÁP ÁN DIỄN GIẢNG NHIỄU xx e dx e   c
C) Theo công thức chọn C là nguyên hàm của hàm số x y e  , A, D là biến đổi của C
Câu 7. (thông hiểu) Hàm số   x
F x e  cot x C là nguyên hàm của hàm số f x nào? x 1 x 1
A. f x  e
B. f x  e  2 sin x 2 sin x x 1 x 1
C. f x  e
D. f x  e  2 cos x 2 sin x
ĐÁP ÁN, HƯỚNG DẪN GIẢI DIỄN GIẢNG NHIỄU 45  1 Ta có: ( )      x f x F x
e  cot x C
B. Hs nhớ nhầm (cot x)  2 sin x
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 x 1
f x  e
C. Hs nhớ nhầm (cot x)  2 sin x 2 cos x Đáp án A 1
D. Hs nhớ nhầm (cot x)   2 cos x
Câu 8. (vận dụng thấp ) Tìm hàm số F(x) biết rằng 3 2 F (
x)  4x 3x  2 và F( 1  )  3 A. 4 3
F(x)  x x  2x  5 B. 4 3
F(x)  x x  2x  5 C. 4 3
F(x)  x x  2x  3 D. 2
F(x)  12x  6x 15
ĐÁP ÁN, HƯỚNG DẪN GIẢI DIỄN GIẢNG NHIỄU Đáp án C A. Tìm C sai F x f x dx    3 2 ( ) ( )
4x  3x  2dx B. Tìm C sai D. Nhầm:   1 x dx .x     C  4 3
x x  2x C F( 1  )  3 4 3
C  3  F(x)  x x  2x  3
Câu 9. (Thông hiểu) Nguyên hàm của hàm số f x 2
 3sin x  trên khoảng 0; là: x 2
A. G(x)  3cos x   C B. G( )
x  3cos x  2ln x C 2 x 2 C. G( ) x  3
 cos x  2ln x C D. G(x)  3  cos x   C 2 x ĐÁP ÁN DIỄN GIẢNG NHIỄU G( ) x  3
 cos x  2ln x C
Đáp án A: Nhầm giữa đạo hàm và nguyên hàm
Đáp án B: Nhầm nguyên hàm sinx 2
Đáp án D: Nhầm nguyên hàm với đạo hàm x
Câu 10. (Thông hiểu)Tìm nguyên hàm của hàm số f(x) = cos3x.cosx ta có: 46
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 1 A. f (x).dx  = sin 3 . x s inx  C
B. f (x).dx
=  sin 2x  sin 4x C C. 3 4 8 1 1 1 1 f (x).dx
= sin 2x  sin 4x C D. f (x).dx
= sin 2x  sin 4x C 4 8 4 8 LỜI GIẢI TÓM TẮT DIỄN GIẢNG NHIỄU 1
- A: HS không biến đổi tích thành tổng tìm luôn nguyên
f(x) = (cos 2x  cos 4x) 2 hàm 
- B: sai dấu khi tìm nguyên hàm f (x).dx  = 1 1 1
- D: Sử dụng công thức biến đổi sai dấu
( (cos 2x  cos 4x)dx  sin 2x  sin 4x C  2 4 8
Câu 11. (Vận dụng cao) 1
Hàm số f (x)  có nguyên hàm là: 2 x x  6 A. 2
ln x x  6  C
B. ln x  3  ln x  2  C 1 1
C.  (ln x  3  ln x  2 )  C D. (ln x  3  ln x  2 )  C 5 5 DIỄN GIẢNG NHIỄU 1 1 1 1 1 f (x)   (  )
- A: HS nhầm lẫn với công thức
dx  ln x C  2 x x  6 5 x  3 x  2 x
 Nguyên hàm của f(x) là: - B: Tìm sai hệ số
1 (ln x 3  ln x  2)  C - C: HS tìm sai dấu 5
Câu 12. (Nhận biết) Gọi F(x), ( G )
x lần lượt là nguyên hàm của hai hàm số f (x) và g(x) trên đoạn  ; a b . Trong
các đẳng thức sau, đẳng thức nào đúng? b b A.
f (x)dx F
a F(b)
B. k. f (x)dx k F
b F(a)   a a b c c b a C.
f (x)dx
f (x)dx f (x)dx   
D. f (x)dx f (x)dx   47 a b a a b
ĐÁP ÁN, HƯỚNG DẪN GIẢI DIỄN GIẢNG NHIỄU
Group Nhóm Toán | Trắc nghiệm 2016-2017 Đáp án B
A. Hs chọn vì không thuộc công thức A. sai
C. Hs chọn vì nhớ nhầm công thức b b
D. Hs chọn vì nhớ nhầm công thức b
B. Đúng vì k. f (x)dx k f (x)dx k. F (x)  k F  
b F(a)   a a a C. Sai D. Sai 2 3 2
Câu 13. (Thông hiểu) Biết f
 xdx  2 và f
 xdx  3. Hỏi f xdx  bằng bao nhiêu? 1 1 3 5 A. -1 B. C. 1 D. 3 2 ĐÁP ÁN DIỄN GIẢNG NHIỄU A.
Đáp án B: sai khi cộng chia trung bình 2 3 2
Đáp án C: không chú ý cận đề bài yêu cầu
f xdx  =-(
f xdx  -
f xdx  )=-1 3 1 1 1 4 4
Câu 14. (Thông hiểu) Giả sử f
 xdx  2; f
 xdx  3; g
 xdx  4. Khẳng định nào sau đây là sai? 0 1 0 4 4 4 A. f
 xdx g
 xd .x B.  f
 x gxdx 1.  0 0 0 4 4 4 C. f
 xdx  5 D. f
 xdx g
 xd .x 0 0 0 9 0 9
Câu 15. (thông hiểu) Giả sử f
 xdx  37 và g
 xdx 16. Khi đó, I  2 f
 x3g(x)dx  bằng 0 9 0 A. I = 122 B. I = 58 C. I = 143 D. I = 26 48
ĐÁP ÁN, HƯỚNG DẪN GIẢI DIỄN GIẢNG NHIỄU
Group Nhóm Toán | Trắc nghiệm 2016-2017 Đáp án D 9 9 A. I  2 f
 xdx3 g(x)dx  2.373.16 122  0 0 9 9 9 9 I  2 f
 xdx3 g(x)dx  2.373.( 1  6)  26  B. I  2 f
 xdxg(x)dx  2.3716  58  0 0 0 0 9 9 C. I  2 f
 xdxg(x)dx  2.163.37 143  0 0 
Câu 16. (thông hiểu) Tính tích phân 2 I  cos . x sin xd . x  0 2 3 2 A. I   B. I  C. I  D. I  0 3 2 3
ĐÁP ÁN, HƯỚNG DẪN GIẢI DIỄN GIẢNG NHIỄU Đáp án C
A. u  cos x du  sin xdx 1 1     1  2 2 3
I u du u    2   2  3  3 Sử dụng MTCT 2 I  cos . x sin xdx   1 1 3 0 B. Hs đọc sai kết quả
Hoặc Đặt u  cos x du  sin xdx
D. u  cos x du  sin xdx 1 1  1  1 1 2 3
I u du u    0    1  3  3 3 1  1  2 1  1  2 3
I u du u      3  3 1  1  a x 1
Câu 17. (vận dụng) Cho dx e
, giá trị a>1 thõa mãn đẳng thức nào sau đây: x 1 1
A. a  ln a 1  e B. 2
a  ln a 1  e C. 
1  e D. ln a e 2 a 49 ĐÁP ÁN DIỄN GIẢNG NHIỄU
Group Nhóm Toán | Trắc nghiệm 2016-2017 a x 1 x 1 1 dx    a
x  ln x  a  ln a 1 Đáp án B: sai khi viết  x  1 x x x 1
Đáp án C: Nhầm đạo hàm với nguyên hàm Theo đề bài:
Đáp án D: sai khi nhầm nguyên hàm của 1 bằng 0.
a  ln a 1  e
Câu 18. (Vận dụng) a 1 sin . x cos . x dx  
khi đó giá trị của a = ? 4 0    A. a  B. a  C. a  D. Không tồn tại a 2 6 4 LỜI GIẢI TÓM TẮT DIỄN GIẢNG NHIỄU a 1 a 1 1
- A: Thế cận vào sai dẫn đến sai sin . x cos . x dx    sin 2 . x dx   4 2 4 0 0
- D: Tìm nguyên hàm sai dấu dẫn đến  1 a 1  1 1 1
cos2a = 2 nên không tồn tại A cos 2x    cos 2a   4 0 4 4 4 4   cos2a  0  a= 4 1
Câu 19. (Vận dụng) Biết rằng tích phân 2   1 x x e dx a  .
b e , tích ab bằng 0 A. 1. B. 1  . C. 15.  D. 20. LỜI GIẢI DIỄN GIẢNG NHIỄU
Đặt: u  2x   1  du  2dx 1 1 x x 1 x x x 50
dv e dx v e 2x  
1 e dx   2x  
1 e   2 e dx  → Chọn câu C 0 0 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1  B, D chọn ngẫu nhiên 2   1 x   2   1 x 1  2 x x e dx x e e dx  0 0 0  2   1 1 1 x  2 x x e e 0 0  e 1 5 dx
Câu 20. (Vận dụng thấp)  ln c  . Giá trị của c là 2x 1 1 A. 9 B. 3 C. 81 D. 8 ĐÁP ÁN DIỄN GIẢNG NHIỄU 5 dx 1 5 1 1
 ln 2x 1  ln 9  3  A) Quên trong công thức 2x 1 2 1 2 a 1 1 B) Đem
vào làm lũy thừa bị sai a
C)Đem 9 =3 làm lũy thừa của 2  2
Câu 21. (vận dụng cao) Cho tích phân sin  sin 2 . x I x e dx
. Một học sinh giải như sau: 0
* Bước 1: Đặt t  sin x dt  cos xdx .  x   t 1 1 Đổi cận: 2   2 . t I t e dt  2K
x  0  t  0 0 u   tdu dt * Bước 2: Đặt    t tdv e dtv e 1 1 1 1 * Bước 3:  . t  . t t t K t e dt t e
e dt e e 1 51   0 0 0 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 1   2 . t I t e dt  2  0
Hỏi bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
A. Bài giải trên sai từ bước 1
B Bài giải trên sai từ bước 2
C. Bài giải trên sai từ bước 3
D. Bài giải trên hoàn toàn đúng
ĐÁP ÁN, HƯỚNG DẪN GIẢI DIỄN GIẢNG NHIỄU Đáp án D  2 sin   A. Hs chọn vì 2sin cos . x I x x e dx  2 0 sin  2sin cos . x I x x e dx  nên bước 1 đúng 0
Đặt t  sin x dt  cos xdx bước 2 đúng  2 sin  bước 3 đúng Hoặc Vì sin cos . x I x x e dx  0
Vậy bài giải đúng hoàn toàn 1
Đặt t  sin x dt  cos xdx   . t I t e dt  0 t u   e
B. Hs nhớ nhầm cách đặt  dv tdt 1 1 1 1 C.  . t  . t t t K t e dt t e
e dt e e  2e 1   0 0 0 0
Câu 22. (Nhận biết) Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x , trục Ox, đường thẳng x=a, x=b (ab b b a A. S f
 xdx B. S f  xdx C. 2 S   f
 xdx D. S f  xdx a a a b 52 ĐÁP ÁN DIỄN GIẢNG NHIỄU
Group Nhóm Toán | Trắc nghiệm 2016-2017 b
Đáp án B: học sinh thiếu dấu giá trị tuyệt đối A. S f  xdx a
Đáp án C: nhầm công thức tính thể tích
Đáp án D: sai vị trí cận
Câu 23. : (Vận dụng)
Nếu gọi S là diện tích hình phẳng giới hạn bởi các đường x =0, x = 3, y = 0, y = x - 1 thì khẳng định nào sau đây là đúng? 3 1 5 A. S = . B. S= . C. S = 2. D. S = . 2 2 2 LỜI GIẢI TÓM TẮT DIỄN GIẢNG NHIỄU
Phương trình: x – 1 = 0  x=1[0;3] 3 3 3 - A: HS S x 1 dx  (x 1)dx   =…= 3 1 3 2 S x 1 dx  (x 1)dx  (x 1)dx    0 0 0 0 1
- B: HS chỉ tính trên đoạn [0;1] 2 2 x 1 x 3 1 5 = (  x)  (  x) =   2 =
- C: HS chỉ tính trên đoạn [1;3] 2 0 2 1 2 2
Câu 24. (Vận dụng thấp) Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y x  3x  2x , trục tung, trục 3
hoành, đường thẳng x  ? 2 1 9 23 A. B. C. D. 0 2 64 64 ĐÁP ÁN DIỄN GIẢNG NHIỄU
Giải phương trình hoành độ giao điểm
A) Giải phương trình hoành độ giao điểm ra 3 nghiệm 0, 1, 2 chon cận
ra 3 nghiệm 0, 1, 2 (loại 2) từ 0 đến 2 3
B)Quên dấu trị tuyệt đối 2 3 2 S
x  3x  2xdxhp
D) Chon cận từ 0 đên 2 nhưng quên dấu trị tuyệt đối 0 53 =
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 4 4 x 1 x 3 2 3 2 (
x x )  (  x x ) 2 4 0 4 1 23 = 64
Câu 25. (vận dụng thấp) Diện tích S của hình phẳng (H) giới hạn bởi đồ thị hàm số 3 2
y  x  3x  2 , hai trục tọa độ
và đường thẳng x  2 là 19 5 1 9 A. S = (đvdt) B. S = (đvdt) C. S = (đvdt) D. S = (đvdt) 2 2 3 2
ĐÁP ÁN, HƯỚNG DẪN GIẢI DIỄN GIẢNG NHIỄU Đáp án B 1 19 A. S = 3 2
(x  3x  2)dx   2 2 5 0 Ta có: S = 3 2
x  3x  2dx   2 0 1 2 1 C. S = 3 2 3 2
x  3x  2dx  x  3x  2dx    3 0 1 2 13 D. S = 3 2
x  3x  2dx   12 1
Câu 26. (Vận dụng) Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y x  3x  4 và đường thẳng
x y 1  0 . A. 8 (đvdt). B. 4 (đvdt). C. 6 (đvdt). D. 0 (đvdt). LỜI GIẢI DIỄN GIẢNG NHIỄU 3 2
x  3x  4  x 1
Tính cận sai → chọn câu B 3 2
x  3x x  3  0 3  3 2     x  1
 , x  3, x 1 S x 3x x 3 dx  → Chọn câu C 1 54 3 3 2 3 S
x  3x x  3 dx  8  S    3 2
x  3x x  3dx → Chọn câu D 1  1 
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 27. (Thông hiểu) Cho hình phẳng giới hạn bởi đồ thị hàm số x
y e , trục Ox, 2 đường thẳng x = 0,
x = 1 . Thể tích khối tròn xoay khi quay hình đó xung quanh trục hoành được cho bởi công thức 1 1 2 2 1   1   A. 2 xe dx  B. 2 x e dx  C. x   e dx   D. x  e dx   0 0  0   0  ĐÁP ÁN DIỄN GIẢNG NHIỄU 1 B) Quên  V= 2 xe dx  0
C) Sử dụng dấu bình phương sai vị trí
D) Sử dụng dấu bình phương sai vị trí
Câu 28. ( Thông hiểu) 
Nếu gọi V là thể của khối tròn xoay có được khi quay hình phẳng giới hạn bởi các đường x  0, x
, y  0, y s inx 4
xung quanh trục Ox thì khẳng định nào sau đây là đúng? 1  1   1 A. V () . B. V (). 2 4 2 2 4 2     1 V ( 1) V () C. 2 4 . D. 2 4 2 . LỜI GIẢI TÓM TẮT DIỄN GIẢNG NHIỄU  
- A: HS áp dụng công thức sai 4 4  2
V   s in x.dx  (1  o c s2x.)dx   2
- B: HS dùng công thức hạ bậc sai dấu 0 0  - C: HS tìm nguyên hàm sai  1   1 = (x  sin 2x) 4  (  ) 2 2 2 4 2 0
Câu 29. (Vận dụng) Thể tích khối tròn xoay khi quay hình phẳng  H  giới hạn bởi 2
y x và y x  2 quanh trục Ox là 72 81 81 72 55 A. (đvtt). B. (đvtt). C. (đvtt). D. (đvtt). 5 10 5 10
Group Nhóm Toán | Trắc nghiệm 2016-2017 LỜI GIẢI DIỄN GIẢNG NHIỄU 2
x x  2  0  x  1  , x  2 2 2
V     f (x)  g(x) dx    x x  22 2 2 dx 1  1  2 2 V  
f (x)  g (x) dx   x    x 22 2 2 4 dx → Chọn câu B 1  1  2 2 72 2 1 1  2 2 V
   f (x) g(x) dx    x x2 dx 5 2 2 1  1  → Chọn câu C 2 2 1 1 V
f (x)  g (x) dx   x    x 22 2 2 4 dx 2 2 1  1  → Chọn câu D
Câu 30. (vận dụng cao) Cho hình phẳng (H) giới hạn bởi 2
y  2x x , y  0 . Tính thể tích của khối tròn xoay thu  a
được khi quay (H) xung quanh trục Ox ta được V   1   . Khi đó  b
A. a = 1, b = 15 B. a = – 7, b = 15 C. B. a = 241, b = 15 D. a = 16, b = 15
ĐÁP ÁN, HƯỚNG DẪN GIẢI DIỄN GIẢNG NHIỄU Đáp án A 1 8  7   B. 2 2 V
  (2x x ) dx     1  Ox    15  15  x  0 0 2
2x x  0  x  2 2 2 C. 2 2 2 4       V (2x x ) dx (4x x )dx   Ox 2 16 0 0 2 2 V
  (2x x ) dx    Ox 15 0   256 241      16  a  1       
1  a  1, b  15   15  15  15  b  2 16 2 2      D. V (2x x ) dxOx 15 0 56 PHẦN 8 :
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 1: Họ nguyên hàm của hàm số f x  sin 2x là A F x 1 .
  cos2x C .
B F x  cos 2x C C F x 1 .  cos2x C .
D F x  cos 2x C 2 2 Câu 2: Nếu ( ) d x f x
x e  sin x C
thì f (x) bằng: . x A e  sin x x x x . B e  sin x . C e  cos x . D e c s o x 3 Câu 3: 2 (x   2 x)dxx 3 x 4 3 x 4 3 . A  3ln x x C 3 . B  3ln x x C 3 3 3 3 3 x 4 3 x 4 3 C.  3lnX x C 3 . D  3ln x x C 3 3 3 3 5 dx Câu 4:  ln K .  Gia ùtrò cuûa K laø : 2x 1 1 A. 3 B. 8 C. 81 D. 9
Câu 5: Tìm khẳng định sai trong các khẳng định sau:  2 1 1 1 1 2 1 . A sinxdx  1  . B
1 x dx  0 C. sin(1x)dx  sinxdx   2016 . D x 1 xdx   4770306 0 0 0 0 0 dx Câu 6:   1 x C 2 . A . B
 2 1 x C C.  C . D C 1 x 1 x 1 x
Câu 7: x  3 2 3 dx   1  x  4 2 3  x  4 2 3 1  x  4 2 3 1  x  3 2 3 . A .  C . BC C. .  C D. .  C 2 4 4 3 4 2 3 57 2
Câu 8: Hàm số F(x) = x
e là nguyên hàm của hàm số nào?
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 x e 2 2 A. f (x)  B. 2 ( ) x
f x e C. ( )  2 . x f x x e D. 2 ( ) x
f x x e 1 2x 2x
Câu 9:Họ nguyên hàm của hàm số : y f (x)  là: 2 2 (x  9) 1 1 4 1 A.   C B.   C C.   C D.   C 2 5 5(x  9) 2 3  2 5  2 3  3(x 9) (x 9) (x 9)
Câu 10:Cho hình phẳng (S) giới hạn bởiOx, Oy, y = 3x+2. Tính thể tích của khối tròn xoay khi quay (S) quanh Oy là : 8 4 2 16 A.  B.  C.  D.  3 3 3 3
Câu 11:Một nguyên hàm của hàm số 2 f (x)  . x 1 x là : 1 1 2 x 1 A. 2 3 F (x)  ( 1 x ) B. 2 2 F (x)  ( 1 x ) C. 2 2 F (x)  ( 1 x ) D. 2 2 F (x)  ( 1 x ) 3 3 2 2 
Câu 12: Tìm nguyên hàm của hàmsố f(x) thỏa điều kiện: f (x)  2x  3cos , x F( )  3 2 2  2  A. 2
F (x)  x  3sin x  6  B. 2
F (x)  x  3sin x  6  4 4 2  2  C. 2
F (x)  x  3sin x  D. 2
F (x)  x  3sin x  6  4 4  6
Câu 13: Tính : I  tan xdx  là : 0 2 3 2 3 3 1 A. ln B.  ln C. ln D. ln 3 3 2 2
Câu 14: Diện tích hình phẳng giới hạn bởi: 2
y  x  4x  3 , x = 0, x = 3 và trục Ox là 1 2 10 8 A. B. C. D. 58 3 3 3 3
Câu 15:Diện tích hình phẳng giới hạn bởi các đường cong: 2
y x  2x   và y x 6
Group Nhóm Toán | Trắc nghiệm 2016-2017 95 265 125 65 A. B. C. D. 6 6 6 6 59
Group Nhóm Toán | Trắc nghiệm 2016-2017 Câu 16: dx   2 2 sin x cos x 1 1 A. 1   C
B. tan x  cot x C
C.  tan x  cot x C D.    C cos x sin x Câu 17: 2x   x x  9 d 4 2 1   1 4 1       A. C B. C C. C D. C 5 x  95 2 3 x  93 2 x 95 2 x 93 2
Câu 18: Họ nguyên hàm của hàm số: y = sin3x.cosx là: 1 1 A. tg3x + C B. cos2x + C C. 3 cos x  C D. 4 sin x  C 3 4 Câu 19:
sinx cos 2x dx   1 1 1 1
A.  cos 3x  cos x C
B.  cos 3x  cos x C 2 2 6 2 1 1 1 1 C. sin 3x  sin x C D. cos 3x  cos x C 6 2 2 2
Câu 20: Nguyên hàm xcos xdx  
A. xsin x  cos x C B. xsin x  cos x C C. xsin x  cos x +C
D. xsin x  cos x Câu 21: 2  x
Nguyên hàm của (với C hằng số) là dx  2 1  x 1  x x 1 2 A. CC C. C
ln 1  x C 1  B. x 1  x 1  D. x
Câu 22: Họ nguyên hàm của hàm số f x  sin 2x là 60
A. F x 1
  cos2x C
B. F x  cos 2x C 2
Group Nhóm Toán | Trắc nghiệm 2016-2017
C. F x 1
 cos2x C
D. F x  cos2x C 2
Câu 23: Trong các mệnh đề sau, mệnh đề nào sai? 3 sin x 2
(I ) : sin x dx   C  3 4x  2 (II ) : dx  2 ln 
 2x x3 C 2  x x  3 x   x x III   6x ( ) : 3 2 3 dx   x C ln 6 A. (III ) B. (I ) C. Cả 3 đều sai. D. (II )
Câu 24: Nguyên hàm của hàm số: y = sin3x.cosx là: 1 1 1 A. 4 cos x  C B. 4 sin x  C C. cos2x + C D. 3 sin x  C 4 4 3 Câu 25: sin 2x
Nguyên hàm F(x) của hàm số y F  là 2 sin x  khi (0) 0 3 2 2 sin x 2 ln 2  sin x 2
A. ln 1  sin x B. C. ln cos x D. ln 1  3 3 Câu 26: f x x
Họ nguyên hàm của hàm số e cos x là 1 1 A.    x F x
e sin x  cos x  C B.    x F x
e sin x  cos x  C 2 2 1 1 C.    x
F x   e sin x  cos x  C D.    x
F x   e sin x  cos x  C 2 2
Câu 27: Một nguyên hàm của hàm số: y = cos5x.cosx là: 1  sin 6x sin 4x    1  1 1    D sin 6x  sin 4  x 61 
A. F(x) = cos6x
B. F(x) = sin6x C. 2  6 4  2  6 4  .
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 28: Cho hình phẳng (S) giới hạn bởi ox, oy, y=3x+2. Thể tích khối tròn xoay khi quay (S) xung quanh oy là: 8 4 2 D 16 A. B. C.   3 3 3 . 3
Câu 29: Cho hình phẳng (S) giới hạn bởi ox, 2
y  1 x . Thể tích khối tròn xoay khi quay (S) xung quanh oy là: 3 4 3 D 2 A. B. C.   2 2 4 . 3
Câu 30: Diện tích hình phẳng giới hạn bởi (P) : 3
y x  3, tiếp tuyến của (P) tại điểm x=2 và trục oy là: 2 4 D 8 A. B. 8 C. 3 3 . 3 PHẦN 9 :
Câu 1. Tìm nguyên hàm của hàm số f(x) = 3sinx+1 là
A.-3cosx+x +c B. 3cos x x +c C. - cos x +c D. cos x x +c
Câu 2. Nguyên hàm của hàm số f(x) = 2x 2x 2x . Ac . 2x B ln 2  c . 2x CC . D ln 2 ln 2
Câu 3. Nguyên hàm của hàm số f(x) = sin3x 1 1 .
A  cos3x C .
B 3cos3x C C. cos3x C .
D  cos3x C 3 3
Câu 4:Tìm nguyên hàm của hàm số: 𝑓(𝑥) = 2017𝑥
A. ∫ 𝑓(𝑥). 𝑑𝑥 = 2017𝑥. 𝑙𝑛2016 +C B ∫ 𝑓(𝑥). 𝑑𝑥 = 2017𝑥+1. +C
C ∫ 𝑓(𝑥). 𝑑𝑥 = 2017𝑥. +C D. ∫ 𝒇(𝒙). 𝒅𝒙 = 𝟐𝟎𝟏𝟕𝒙 +C 𝒍𝒏𝟐𝟎𝟏𝟕 4 5  2x
Câu 5. Tính nguyên hàm f (x)  . 62 2 x
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 2x 5 10 . A   C 4 . B 12x   C 3 x 3 x 3 2x 5 3 2x C.   C . D  5x C 3 x 3
Câu 6. Tìm nguyên hàm: 3x 2 (2  e ) dx  4 x 1 3 6 4 x 1 . 4 x A x e e C 3 6 . 4 x B x e e C 3 6 3 6 4x x 1 3 6 C. 4x  . x e e C 3x 6 . 12  6 x D e e C 3 6
Câu 7:Tìm nguyên hàm của hàm số: 𝑓(𝑥) = 22𝑥. 3𝑥. 7𝑥
A. ∫ 𝒇(𝒙). 𝒅𝒙 = 𝟖𝟒𝒙 +C B. ∫ 𝑓(𝑥). 𝑑𝑥 = 22𝑥.3𝑥.7𝑥 +C 𝒍𝒏𝟖𝟒 𝑙𝑛4.𝑙𝑛3.𝑙𝑛7
C ∫ 𝑓(𝑥). 𝑑𝑥 = 84𝑥. +C D. ∫ 𝑓(𝑥). 𝑑𝑥 = 84𝑥. 𝑙𝑛84 +C
Câu 8:Tìm nguyên hàm của hàm số: 𝑓(𝑥) = 𝑥2−2𝑥+3 là: 𝑥+1
A.∫ 𝑓(𝑥). 𝑑𝑥 = 𝑥2 + 3𝑥 − 6𝑙𝑛|𝑥 + 1| + 𝐶 B. ∫ 𝑓(𝑥). 𝑑𝑥 = 𝑥2 − 3𝑥 + 6𝑙𝑛|𝑥 + 1| + 𝐶 2 2
C. ∫ 𝑓(𝑥). 𝑑𝑥 = 𝑥2 + 3𝑥 + 6𝑙𝑛|𝑥 + 1| + 𝐶 D. ∫ 𝑓(𝑥). 𝑑𝑥 = 𝑥2 + 3𝑥 − 6𝑙𝑛|𝑥 + 1| + 𝐶 2 2
Câu 9. Nguyên hàm x cos xdx  2 x 2 x .
A xsin x  cos x C . B .xinx C .
C xsin x  cos x C . D  .xinx C 2 2
Câu 10. Tìm nguyên hàm: 3x 2 (2  e ) dx  4 x 1 3 6 4 x 1 . 4 x A x e e C 3 6 . 4 x B x e e C 3 6 3 6 4x x 1 3 6 C. 4x  . x
e e C 3x 6 . 12  6 x D e e C 3 6 63 Câu 11. Tính 2 sin 2xdx
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 1 1 1 1 A.
x  sin 4x C B.
x  2sin 4x C C.
x  sin 4x C D.  sin 4x C 2 8 2 2 8 8 TÍCH PHÂN
Câu 12: Tìm khẳng định sai trong các khẳng định sau: 1 1 1 1 x  2 1 A. 2 2 2x dx  2 x dx   B. dx  (x  2)dx   3 3 0 0 0 0 1 1 2 2 1
C. (2x 1)dx  2 (x 1)dx   D. x dx dx   x 0 0 1 1 5 dx
Câu 13: Giả sử A = 
= lnK. Khi đó giá trị của K là: 2x 1 1 A. 3 B. 4 C.81 D.9 b
Câu 14: Biết (2x  4)dx  0 
. Khi đó giá trị của b là: 0 A. b = - 2 hoặc b = 2 B. b = 2 2 hoặc b = - 2 2 C. b = 0 hoặc b = - 4 D. b = 0 hoặc b = 4 d d b Câu 15: Cho biết
f (x)dx  5 , f ( ) x dx  2  
và a< d< b. Khi đó tích phân A = f (x)dx  bằng: a b a A.- 3 B. 7 C. 3 D. 10 3 x 2
Câu 16 : Biến đổi dx
thành f (t)dt
với t = 1 x . Khi đó f(t) là hàm nào trong các hàm sau: 1 1 x 0 1 A. 2
f (t)  2t  2t B. 2
f (t)  2t  2t C. 2
f (t)  t t D. 2
f (t)  t t a 1
Câu 17: Biết sin x cos xdx  
. Khi đó giá trị của a là: 4 0 64 1    A. x  arcsin( ) B. C. D. 4 4 3 2
Group Nhóm Toán | Trắc nghiệm 2016-2017  2 2
Câu 18: Cho tích phân sin x 3 e sin x cos xdx  . Nếu đổi biến số 2
t  sin x thì: 0 1 1 1 1 1 1 A. [ t t e dt te dt]   B. [ t t e dt te dt]   2 2 0 0 0 0 1 1 1 1 2[ t t e dt te dt]   2[ t t e dt te dt]   C. 0 0 D. 0 0
Câu 19: Tìm khẳng định sai trong các khẳng định sau: 1 1 1 1 x  2 1 A. 2 2 2x dx  2 x dx   B. dx  (x  2)dx   3 3 0 0 0 0 1 1 2 2 1
C. (2x 1)dx  2 (x 1)dx   D. x dx dx   x 0 0 1 1 5 5 5
Câu 20: Cho biết f (x)dx  3 , g(x)dx  9  
. Khi đó tích phân A = [ f (x)  g(x)]dx  bằng: 2 2 2 1 A.- 6 B. C. 6 D. 3 3 2
Câu 21: Cho tích phân I = 2 2x x 1dx  và u = 2
x 1 . Chọn khẳng định sai trong các khẳng định sau: 1 3 2 3 2 2 A. I= 27 B. 2 2 u du  C. 2 2 u du  D. I = 3 u 3 3 0 1 0 d d b Câu 22: Cho biết
f (x)dx  5 , f ( ) x dx  2  
và a< d< b. Khi đó tích phân A = f (x)dx  bằng: a b a A.- 3 B. 7 C. 3 D. 10 2 65
Câu 23: Tính tích phân: I = 1 dx ò x2 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 A. - 1 B. - 3 C. - 7 D. 2 2 8 2
ỨNG DỤNG TÍCH PHÂN
Câu 24: Công thức diên tích hình thang cong giới hạn bỡi đồ thị hàm số y f x , trục hoành và hai đường thẳng x  ; a x b là b b b b A. S f  xdx B. 2 S   f
 xdx C.S f
 xdx D.S f  xdx a a a a
Câu 25: Công thức diên tích hình phằng giới hạn bỡi đồ thị y f x , y g x và hai đường thẳng x  ; a x b là b b b b A. S f
 x gxdx B. S f
 x gxdx C. S   f
 x gxdx  D S   f
 x gxdxa a a a
Câu 26: Diện tích hình phẳng giới hạn đường cong 3
y  x  3x  2 và đường thẳng y  x  2 là
A. S= 4 B. S= 40 C. S= 2 D. S= 8 
Câu 27: Thể tích vật thể tròn xoay sinh ra bỡi hình phẳng giới hạn bỡi đường cong y  cos x , y = 0, x  0; x  quay 2 quanh trục Ox là 2   A. B. C.  D. 1 4 4 2x 1
Câu 28: Diện tích hình phẳng giới hạn đường cong y
; y  0 và x  0; x  1là x 1 9 A. 3ln 2  2 B. 3ln C. 2  3ln 2 D. 2  ln 2 8
Câu 29: Thể tích vật thể tròn xoay sinh ra bỡi hình phẳng giới hạn bỡi đường cong y  ln x , y = 0, x e quay quanh trục Ox là
A. e  2 B.  C.  e  2 D. e   1
Câu 30: Diện tích hình phẳng giới hạn bởi đường cong y = x2 + 1, tiếp tuyến với đường thẳng này tại điểm M(2,5) và 66 trục Oy là 4 8 14 a. b. c.9 d. 3 3 3
Group Nhóm Toán | Trắc nghiệm 2016-2017 TRẢ LỜI
Câu 1. Tìm nguyên hàm của hàm số f(x) = 3sinx+1 là
A.-3cosx+x +c B. 3cos x x +c C. - cos x +c D. cos x x +c Giải +Chọn A đúng
+ Chọn B sai vì nhầm công thức đạo hàm cosx là sinx
+ Chọn C sai. Vì nhầm lấy đạo hàm của 1 là 0
+ Chọn D sai. Quên còn hệ số 3
Câu 2. Nguyên hàm của hàm số f(x) = 2x 2x 2x . Ac . 2x B ln 2  c . 2x CC . D ln 2 ln 2 Giải + Chọn A đúng
+ Chọn B sai vì công thức đạo hàm
+ Chọn C sai, nhầm công thức nguyên hàm của ex
+ Chọn D sai, vì chỉ tìm 1 nguyên hàm
Câu 3. Nguyên hàm của hàm số f(x) = sin3x 1 1 .
A  cos3x C .
B 3cos3x C C. cos3x C .
D  cos3x C 3 3 Giải + Chọn A đúng 67
Câu 4:Tìm nguyên hàm của hàm số: 𝑓(𝑥) = 2017𝑥
Group Nhóm Toán | Trắc nghiệm 2016-2017
A. ∫ 𝑓(𝑥). 𝑑𝑥 = 2017𝑥. 𝑙𝑛2016 +C B ∫ 𝑓(𝑥). 𝑑𝑥 = 2017𝑥+1. +C
C ∫ 𝑓(𝑥). 𝑑𝑥 = 2017𝑥. +C D. ∫ 𝒇(𝒙). 𝒅𝒙 = 𝟐𝟎𝟏𝟕𝒙 +C 𝒍𝒏𝟐𝟎𝟏𝟕 4 5  2x
Câu 5. Tính nguyên hàm f (x)  . 2 x 3 2x 5 10 . A   C 4 . B 12x   C 3 x 3 x 3 2x 5 3 2x C.   C . D  5x C 3 x 3 Giải + Chọn A đúng
+Chọn B sai. Tính đạo hàm của f(x) 5
+ Chọn C sai. Tính sai nguyên hàm của 2 x
+ Chọn D sai . Chia đa thức sai 4 5  2x 2 f (x)   5  2x 2 x
Câu 6. Tìm nguyên hàm: 3x 2 (2  e ) dx  4 x 1 3 6 4 x 1 . 4 x A x e e C 3 6 . 4 x B x e e C 3 6 3 6 4x x 1 3 6 C. 4x  . x
e e C 3x 6 . 12  6 x D e e C 3 6 Giải
+ Chọn A sai, khai triển hằng đẳng thức sai dấu 68 + Chọn B đúng
+ Chọn C sai, tính nguyên hàm của 4 nhân nguyên hàm của 3x e
Group Nhóm Toán | Trắc nghiệm 2016-2017
+ Chọn D sai, nhầm công thức nguyên hàm với công thức đạo hàm
Câu 7:Tìm nguyên hàm của hàm số: 𝑓(𝑥) = 22𝑥. 3𝑥. 7𝑥
A. ∫ 𝒇(𝒙). 𝒅𝒙 = 𝟖𝟒𝒙 +C B. ∫ 𝑓(𝑥). 𝑑𝑥 = 22𝑥.3𝑥.7𝑥 +C 𝒍𝒏𝟖𝟒 𝑙𝑛4.𝑙𝑛3.𝑙𝑛7
C ∫ 𝑓(𝑥). 𝑑𝑥 = 84𝑥. +C D. ∫ 𝑓(𝑥). 𝑑𝑥 = 84𝑥. 𝑙𝑛84 +C 84𝑥
HD:A ∫ 𝒇(𝒙). 𝒅𝒙 = ∫ 22𝑥. 3𝑥. 7𝑥. 𝑑𝑥 = ∫ 84xdx = +C 𝑙𝑛84
Câu 8:Tìm nguyên hàm của hàm số: 𝑓(𝑥) = 𝑥2−2𝑥+3 là: 𝑥+1
A.∫ 𝑓(𝑥). 𝑑𝑥 = 𝑥2 + 3𝑥 − 6𝑙𝑛|𝑥 + 1| + 𝐶 B. ∫ 𝑓(𝑥). 𝑑𝑥 = 𝑥2 − 3𝑥 + 6𝑙𝑛|𝑥 + 1| + 𝐶 2 2
C. ∫ 𝑓(𝑥). 𝑑𝑥 = 𝑥2 + 3𝑥 + 6𝑙𝑛|𝑥 + 1| + 𝐶 D. ∫ 𝑓(𝑥). 𝑑𝑥 = 𝑥2 + 3𝑥 − 6𝑙𝑛|𝑥 + 1| + 𝐶 2 2
HD: B. ∫ 𝒙𝟐−𝟐𝒙+𝟑 𝒅𝒙 = ∫(𝒙 − 𝟑 + 𝟔 )𝒅𝒙 = 𝒙𝟐 − 𝟑𝒙 + 𝟔𝒍𝒏|𝒙 + 𝟏| + 𝑪 𝒙+𝟏 𝒙+𝟏 𝟐
Câu 9. Nguyên hàm x cos xdx  2 x 2 x .
A xsin x  cos x C . B .xinx C .
C xsin x  cos x C . D  .xinx C 2 2 Giải + Chọn A đúng
+ Chọn B sai, tách thành tích của 2 nguyên hàm
+ Chọn C sai. Tính sai nguyên hàm của sinx x cos xdx  
xsin x  sin xdx x sin x  cos x C
+Chọn D sai. Tách thành tích của 2 nguyên hàm và tính sai nguyên hàm của cosx Mức 4 69
Câu 10. Tìm nguyên hàm: 3x 2 (2  e ) dx
Group Nhóm Toán | Trắc nghiệm 2016-2017 4 x 1 3 6 4 x 1 . 4 x A x e e C 3 6 . 4 x B x e e C 3 6 3 6 4x x 1 3 6 C. 4x  . x e e C 3x 6 . 12  6 x D e e C 3 6 Câu 11. Tính 2 sin 2xdx  1 1 1 1 1 1 A.
x  sin 4x C B.
x  2sin 4x C C.
x  sin 4x C D.  sin 4x C 2 8 2 2 8 8 Giải
+ Chọn A sai. Công thức hạ bậc sai 1 cos 4x  1 cos 4x  2 2 sin 2x  sin 2x    2  2 
+ Chọn B sai. Công thức nguyên hàm sai
cos 4x  4sin 4x  + Chọn C đúng 1
+ Chọn D sai. Công thức nguyên hàm của 2 sai
Câu 12: Tìm khẳng định sai trong các khẳng định sau: 1 1 1 1 x  2 1 A. 2 2 2x dx  2 x dx   B. dx  (x  2)dx   3 3 0 0 0 0 1 1 2 2 1
C. (2x 1)dx  2 (x 1)dx   D. x dx dx   x 0 0 1 1 5 dx
Câu 13: Giả sử A = 
= lnK. Khi đó giá trị của K là: 2x 1 1 70 A. 3 B. 4 C.81 D.9 Giải
Group Nhóm Toán | Trắc nghiệm 2016-2017 5 5 dx 1 1 1 Ta có A   ln 2x 1  ln 9  Suy ra ln K  ln 9  K  3 2x 1 2 2 2 1 1 Câu A đúng
Câu B sai vì đúng công thức nhưng sai kết quả (nhầm ln5-ln1=ln4)
Câu C sai vì tính sai công thức tích phân (nhân u’)
Câu D sai vì tính tích phân sai công thức (quên chia u’) b
Câu 14: Biết (2x  4)dx  0 
. Khi đó giá trị của b là: 0 A. b = - 2 hoặc b = 2 B. b = 2 2 hoặc b = - 2 2 C. b = 0 hoặc b = - 4 D. b = 0 hoặc b = 4 Giải b   b b 0 Ta có 2 2
I  (2x  4)dx  (x  4x)  b  4b  Khi đó 2
b  4b  0   0 b  4 0 Câu D đúng
Câu A sai vì nhận dạng ptr bậc hai sai (khuyết b) b b 2 2
I  (2x  4)dx  (x  4)  b  8  0
Câu B sai vì tính tích phân sai công thức 0
Câu C sai vì tính tích phân nhầm dấu + d d b Câu15: Cho biết
f (x)dx  5 , f (x)dx  2  
và a< d< b. Khi đó tích phân A = f (x)dx  bằng: a b a A.- 3 B. 7 C. 3 D. 10 71 Giải
Group Nhóm Toán | Trắc nghiệm 2016-2017 b d b d d Ta có A =
f (x)dx
f (x)dx
f (x)dx
f (x)dx
f (x)dx  3      a a d a b Câu C đúng b d
Câu A lấy hiệu 2 tích phân (
f (x)dx f (x)dx   ) d a
Câu B sai vì áp dụng sai công thức (không đổi cận )
Câu D vì lấy tích 2 tích phân 3 x 2
Câu 16 : Biến đổi dx
thành f (t)dt
với t = 1 x . Khi đó f(t) là hàm nào trong các hàm sau: 1 1 x 0 1 A. 2
f (t)  2t  2t B. 2
f (t)  2t  2t C. 2
f (t)  t t D. 2
f (t)  t t Giải 3 2 2 2 x (t 1)2tdt
Với t = 1 x Ta có A = 2 dx
 (2t  2t)dt    1 1 x 1 t 0 1 1 Câu A đúng Câu B sai vì sai dấu
Câu C, D sai vì tính nguyên hàm sai và chyển từ biến x sang t bị sai a 1
Câu 17: Biết sin x cos xdx  
. Khi đó giá trị của a là: 4 0 1    A. x  arcsin( ) B. C. D. 4 4 3 2 Giải a a a 1 1 1
Ta có sin x cos xdx
sin 2xdx   cos 2x   (cos 2a 1)   2 4 4 0 0 0 1 1 
 (cos 2a 1)   cos 2a  0  a  72 4 4 4 Mà Câu B đúng
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu A, C, D sai vì sai công thức nguyên hàm  2 2
Câu 18: Cho tích phân sin x 3 e sin x cos xdx  . Nếu đổi biến số 2
t  sin x thì: 0 1 1 1 1 1 1 B. [ t t e dt te dt]   B. [ t t e dt te dt]   2 2 0 0 0 0 1 1 1 1 C. 2[ t t e dt te dt]   D. 2[ t t e dt te dt]   0 0 0 0 Giải 1 1 1 1 t 1 Với 2
t  sin x Ta có A = (1 )  [ t t e t dt e dt te dt]    2 2 0 0 0 Câu B đúng
Câu A sai vì lấy nguyên hàm sai dấu
Câu C, D sai vì sai công thức nguyên hàm và bị sai dấu
Câu 19: Tìm khẳng định sai trong các khẳng định sau: 1 1 1 1 x  2 1 A. 2 2 2x dx  2 x dx   B. dx  (x  2)dx   3 3 0 0 0 0 1 1 2 2 1
C. (2x 1)dx  2 (x 1)dx   D. x dx dx   x 0 0 1 1 5 5 5
Câu 20: Cho biết f (x)dx  3 , g(x)dx  9  
. Khi đó tích phân A = [ f (x)  g(x)]dx  bằng: 2 2 2 1 A.- 6 B. C. 6 D. 3 3 2 2 73
Câu 21: Cho tích phân I = 2x x 1dx  và u = 2
x 1 . Chọn khẳng định sai trong các khẳng định sau: 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 2 3 2 2 A. I= 27 B. 2 2 u du  C. 2 2 u du  D. I = 3 u 3 3 0 1 0 Giải 3 3 2 2 Với u = 2 x 1 Ta có 2 3 I  2 u du u  27  3 3 0 0
Câu C sai vì chưa đổi cận d d b Câu 22: Cho biết
f (x)dx  5 , f ( ) x dx  2  
và a< d< b. Khi đó tích phân A = f (x)dx  bằng: a b a A.- 3 B. 7 C. 3 D. 10 Giải b d b d d Ta có A =
f (x)dx
f (x)dx
f (x)dx
f (x)dx
f (x)dx  3      a a d a b Câu C đúng b d
Câu A lấy hiệu 2 tích phân (
f (x)dx f (x)dx   ) d a
Câu B sai vì áp dụng sai công thức (không đổi cận )
Câu D vì lấy tích 2 tích phân 2
Câu 23: Tính tích phân: I = 1 dx ò x2 1 1 A. - 1 B. - 3 C. - 7 D. 2 2 8 2 Phân tích:
A. Sai vì học sinh quên dấu “-” trong công thức. 74 æ ö 2 I = 1 ç ÷ = 1 - 1 = - 1 è x ø 2 1 2 1
Group Nhóm Toán | Trắc nghiệm 2016-2017
B. Sai vì học sinh quên đổi dấu trong lúc tính cận. æ ö 2
I = ç- 1÷ = - 1 - 1 = - 3 è x ø 2 1 2 1
C. Sai vì học sinh áp dụng sai công thức. æ ö 2 I = 1 ç ÷ = 1 - 1 = - 7 è x3 ø 8 1 8 1 D. Đúng
Câu 24: Công thức diên tích hình thang cong giới hạn bỡi đồ thị y f x , trục hoành và hai đường thẳng x  ; a x b là b b b b A. S f  xdx B. 2 S   f
 xdx C.S f
 xdx D.S f  xdx a a a a Đáp án đúng C
Nếu thiếu trị tuyệt đối chọn A
Nhớ nhầm công thức thể tích chọn B
Đặt trị tuyệt đối ra ngoài chọn D
Câu 25: Công thức diên tích hình phằng giới hạn bỡi đồ thị y f x , y g x và hai đường thẳng x  ; a x b là b b b b A. S f
 x gxdx B. S f
 x gxdx C. S   f
 x gxdx  D S   f
 x gxdxa a a a Đáp án đúng A Nhớ nhầm dấu + chọn B
Đặt trị tuyệt đối ra ngoài chọn C
Nhớ nhầm dấu + và đặt trị tuyệt đối ra ngoài chọn D
Câu 26: Diện tích hình phẳng giới hạn đường cong 3
y  x  3x  2 và đường thẳng y  x  2 là 75
A. S= 4 B. S= 40 C. S= 2 D. S= 8 Giải
Group Nhóm Toán | Trắc nghiệm 2016-2017
Phương trình hoành độ giao điểm 3
x  4x  0  x  0, x  2  , x  2 2 3 s
x  4xdx  8  2  Đáp án đúng D
Giải sai nghiệm x= 0, x= 4 chọn B
Giải sai nghiệm x= 0, x= 2 chọn A 2 Nếu áp dụng 3 S  x  2xdx  chọn C 0 
Câu 27: Thể tích vật thể tròn xoay sinh ra bỡi hình phẳng giới hạn bỡi đường cong y  cos x , y = 0, x  0; x  quay 2 quanh trục Ox là 2   A. B. C.  D. 1 4 4 Giải  2  2
V   cos x 2 dx   4 0 Đáp án đúng A Thiếu  chọn B
Thiếu bình phương chọn C Thiếu cả hai chọn D 2x 1
Câu 28: Diện tích hình phẳng giới hạn đường cong y
; y  0 và x  0; x  1là x 1 9 A. 3ln 2  2 B. 3ln C. 2  3ln 2 D. 2  ln 2 8 Giải 76
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 2 1 2x 1 2x 1 2x 1 9 S dx dx dx  3ln    x 1 x 1 x 1 8 0 0 1 2 Đáp án đúng B Không tách cận chọn A
Không tách cận, không hiểu trị tuyệt đối chọn C Nguyên hàm sai chọn D
Câu 29: Thể tích vật thể tròn xoay sinh ra bỡi hình phẳng giới hạn bỡi đường cong y  ln x , y = 0, x e quay quanh trục Ox là
A. e  2 B.  C.  e  2 D. e   1 Giải
ln x  0  x 1 e
V   ln x2dx   e  2 1 Đáp án đúng C
Công thức thiếu  chọn A
Thiếu bình phương chọn B Giải thiếu 2 chọn D
Câu 30: Diện tích hình phẳng giới hạn bởi đường cong y = x2 + 1, tiếp tuyến với đường thẳng này tại điểm M(2,5) và trục Oy là 4 8 14 a. b. c.9 d. 3 3 3 Giải
Tiếp tuyến tại M: y = 4x -3 77
Pt hđgđ: x2 -4x + 4 = 0 => x = 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 8 S = 2 x  4x  4dx  = 3 0 PHẦN 10 :
Phần nhận biết
Câu 1: Nguyên hàm của hàm số 2
f (x)  2x 1 là: 3 2x 3 x 3 x A. 3
2x  x C B.  x C C.  x C D. 1 C 3 3 3
Câu 2: Nguyên hàm của hàm số f (x)  sinx là:
A. cosx  C B. cosx+1 C C. -cosx  C D. tanx  C 1
Câu 3: Nguyên hàm của hàm số f (x)  là: 2 cos x
A. cotx  C B. cosx  C C. -tanx  C D. tanx  C 3
Câu 4: Nguyên hàm của hàm số f(x) = x3 -  2x là: 2 x 4 x 3 x 1 A. 2
 3ln x  2 .xln 2  C B.   2x C 4 3 3 x 4 3 2x x 4 x 3 C.    C D.
  2 .xln 2  C 4 x ln 2 4 x
Câu 5: Nguyên hàm của hàm số f ( )
x  sin(2x 1) là: 1 1
A. - cos(2x 1)  C B. cos(2x 1)  C
C. 2cos(2x 1)  C D. -2cos(2x 1)  C 2 2
Câu 6: Cho hàm số y=f(x) liên tục trên [a;b].Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x),trục
hoành, hai đường thẳng x=a và x=b được xác định bởi công thức: b b a b f (x)  dx f (x)  dx f (x)  dx f (x)  dx A. a B. a C. b D. a
Câu 7:Cho hai hàm số y = f(x), y = g(x) liên tục trên [a;b].Hình phẳng giới hạn bởi đồ thị 2 hàm số y=f(x), 78
y=g(x) và đường thẳng x = a, x = b có diện tích S đươc tính bởi công thức b b A.S= 
f x gx   dx B. S= 
f x gx   dx a a
Group Nhóm Toán | Trắc nghiệm 2016-2017 b b C.S= [
gx f (x)]dx D.S= f x  
g xdx a a
Câu 8: Thể tích V của khối tròn xoay tạo thành khi ta cho hình phẳng D giới hạn bởi các đường y f (x)
,trục Ox , x=a, x = b (a< b) quay quanh trục ox được tính bởi công thức b b 2 b a A. 2 V f (x)  dx B. 2 V   f (x)  dx
C. V   f (x) dx D. 2 V   f (x)  dx a a a b
Câu 9: Thể tích của khối tròn xoay tạo thành khi quay hình phẳng D giới hạn bởi các đường y x 1 ,
trục hoành, x=2 và x=5 quanh trục Ox bằng: 5 5 5 5 A. 1  x dx B.    x 1dx C.     x 1dx D. 2     x 1dx 2 2 2 2
Câu 10: Công thức nào sau đây dùng để tính diện tích hình phẳng giới hạn bởi các đường y=2x ,y=2,x=0,x=1 cho kết quả sai ? 1 1 1 0
A.S= 2  2x dx B.  2x S  2dx C.  2x S  2dx D.  2x S  2dx 0 0 0 1 Giải thích 1
Công thức tính diện tích hình phẳng giới hạn bởi các đường y=2x ,y=2,x=0,x=1 là S= 2  2  x dx = L 0 + 0; 
1 : 2x  2  2  2x  2  2x x .A đúng + 0; 
1 : 2x  2  2  2x  (  2x x  2) .B sai 1 1 + 0; 
1 : 2x  2  2x  2  0  2x  2    2x x dx L  2dx    L .C đúng 0 0 1 1 0 + 0; 
1 : 2x  2  2x  2  0  2x  2    2x  2   2x x dx L dx  2dx     L .D đúng 0 0 1
Phần thông hiểu 2 5 5
Câu1) Cho biết f (x)dx  4
 ; f (x)dx  6   . Khi đó ( )
f x dx có kết quả là : 1 1 2 A. 2 B. 10 C. 10 D. 7 Giải thích: 2 5 5 5 5 2
f (x)dx
f (x)dx
f (x)dx f (x)dx
f (x)dx
f (x)dx  10       1 2 1 2 1 1 79 5 Câu 2) Giả sử  ln  dx
c . Khi đó giá trị của c là: 2x 1 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 A. 81 B. 9 C. 8 D. 3 Giải thích: 5 dx 5  dx 2 x 1  1
 ln c c e  3  2x 1 1
Câu3) Diện tích hình phẳng giới hạn bởi các đường cong 3 y x và 5
y x bằng: 1 1 A. 0 B. 4 C. D. 6 12 Giải thích: x  0
Phương trình hoành độ giao điểm : 3 5 3 2
x x x (1 x )  0   x  1  1 1
Diện tích hình phẳng là: 3 5    x x dx 6 1 
Câu4) Diện tích hình phẳng giới hạn bởi các đường cong y x  sin x và y x với 0  x  2 bằng: A. 4 B. 4 C. 0 D. 1 Giải thích: x  0 
Phương trình hoành độ giao điểm : x  sin x x  sin x  0  x k (k  )  x   (0  x  2 )  x  2   2
Diện tích hình phẳng là: sin  4  xdx 0
Câu5) Cho hình phẳng giới hạn bởi các đường y
x và y = x quay xung quanh trục Ox. Thể tích của khối
tròn xoay tạo thành bằng:   A. 0 B.  C. D. 6 30 80 Giải thích:
Group Nhóm Toán | Trắc nghiệm 2016-2017 x  0
Phương trình hoành độ giao điểm : x x   x 1 1 2 
Thể tích khối tròn xoay là:       x x dx 30 0 3
Câu 6: Nguyên hàm của hàm số f(x) = x3   2x là: 2 x 4 x 3 x 1 A. 2
 3ln x  2 .xln 2  C B.   2x C 4 3 3 x 4 3 2x x 4 x 3 C.    C D.
  2 .xln 2  C 4 x ln 2 4 x Đáp án: C
Câu A, B, D học sinh có thể hiểu sai công thức giữa nguyên hàm và đạo hàm. 1
Câu 7: Biết F(x) là nguyên hàm của hàm số y
và F(2)=1. Khi đó F(3) bằng bao nhiêu: x 1 1 3 A. ln 2 1 B. C. ln D. ln 2 2 2 Đáp án: A x  
Câu 8: Một nguyên hàm của f x 2 2x 3  là x 1 2 x 2 x A.  3x  6ln x 1 B.
 3x-6ln x 1 2 2 2 x 2 x C.
 3x+6ln x 1 D.  3x+6ln x 1 2 2 Đáp án : C
Câu A, B, D là đáp án nhiễu khi các em chia đa thức sai 81   2 2 1 Câu 9 :x dx bằng: 3 x
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 x 1 3 x 1 A.  2ln x   C B.  2ln x   C 2 3 2x 2 3 x 3 x 1 3 x 1 C.  2ln x   C D.  2ln x   C 2 3 2x 2 3 3x Đáp án: C
Câu 10: Một nguyên hàm của hàm số: 2
f (x)  x 1 x là: 1 1
A. F(x)   1 x 2 2
B. F(x)   1 x 3 2 2 3 2 2 x 1 C. F x   2 ( ) 1 x
D. F(x)   1 x 2 2 2 3 Đáp án: B
Phần vận dụng thấp 4m    
Câu 1: Cho f x 2   sin x FF  
. Tìm tham số m để nguyên hàm F x của f x thỏa 0 1,    4  8 5  1 3  1  a/ m  b/ m  c/ m  d/ m  4 4 4 4 m
Lời giải: F x 4 1 1  x x  sin 2x C  2 4    3
Sử dụng điều kiện được: F   1 0  C  1; F
m   C  0  
nên giải hệ được m    8  4 4 Đáp án: c/
Phân tích đáp án nhiễu: m
Lấy sai đạo hàm F x 4 1 1  x x  sin 2x C
nên giải ra được đáp án a/ 2 4
Giải thiếu thế C=1nên được đáp án b/
Lấy sai đạo hàm và thiếu thế C=1 nên được đáp án d/  4
Câu 2: Giả sử I
sin 3x sin 2xdx  a  
b 2 . Khi đó, giá trị a b là: 0 82 6 3 3 1 a/ b/ c/  d/ 5 10 10 2
Group Nhóm Toán | Trắc nghiệm 2016-2017   4 4 1 1   1  3
Lời giải: I  
 cos5xcosxdx  sin 5x  sin x  2   Đáp án: b/ 2 2  5  10 0 0
Phân tích đáp án nhiễu:   4 4 1 1   1  3 
Lấy sai đạo hàm I  
 cos5xcosxdx
 sin 5x  sin x  2   nên chọn c/ 2 2  5  10 0 0  4 1 1   1
Lấy sai đạo hàm I  
 cos5xcosxdx  sin5xsin x 4  2 nên chọn d/ 0 2 2 2 0   4 4  1  6
Áp dụng sai công thức: I  2
  cos5x cos xdx  2  sin 5x  sin x  2   nên chọn a/  5  5 0 0  2 2 Câu 3: Tích phân sin 3  sin .cos .  x J e x
x dx có giá trị bằng với tích phân nào sau đây? 0 1 1 1 1 1    a/  1  t I e t dt b/   t    t I e dt te dt  2 2   0 0 0 1 1 1 1  1   c/  1  t I e t dt d/   t    t I e dt te dt  2 2   0 0 0 Lời giải: Đặt 2
t  sin x dt  2sin .
x cos xdx . Đổi cận được t=0, t=1 1 dt
Nên J e 1
t t . Đáp án a/ 2 0
Phân tích đáp án nhiễu: 1 
Tính sai đạo hàm sin x'  cos x nên được dx dt do đó chọn c/ 2
Do áp dụng sai công thức 2 2
cos x  1 sin x nên được đáp án d/
Vừa sai đạo hàm, vừa sai công thức nên được đáp án b/ 2 3x  5x 1 2
Câu 4: Diện tích hình phẳng giới hạn bởi các đường y
, y  0, x  0, x  1
 bằng a ln  b . Khi x  2 3
đó, a  2b là: 61 a/ 2 b/ 40 c/ d/ -2 2 0 0  21   3  2 19 Lời giải: 2 S  3x 11 dx
x 11x  21ln x  2  21ln     
nên a  2b  40 . Đáp án: b/  x  2   2  3 2 1  1  83
Phân tích đáp án nhiễu:
Group Nhóm Toán | Trắc nghiệm 2016-2017 0 0  21   3  2 19 Tính toán sai 2 S  3x 11 dx
x 11x  21ln x  2  2  1ln     
do đó a  2b  2  nên  x  2   2  3 2 1  1  chọn d/ 0 0  21   3  2 19 61 2 S  3x 11 dx
x 11x  21ln x  2  21ln     
mà tính a b   nên chọn c/ x  2   2  3 2 2 1  1  0 0  21   3  3 2 19 Giải: 2 S  3x 11 dx
x 11x  21ln x  2
 21ln 2  21ln 3 11  21ln      nên  x  2   2  2 3 2 1  1 
a  2b  2 chọn đáp án a/
Câu 5: Thể tích của vật thể tròn xoay tạo bởi hình phẳng giới hạn bởi các đường 3 y
x ln x, x  1, x e khi 3 a e 1
quay quanh trục Ox có dạng V  
. Hãy chọn khẳng định sai trong các khẳng định sau? b a/ ab  64 b/ a  log b
c/ a b 18
d/ 2a b  8  2 e e e 4  1 1  3e 1 Lời giải: 3 4 4
V   x ln xdx    x ln x x     
nên a=4, b=16 do đó chọn c/ 4 16  16 1  1 1 
Bài giải hạn chế bấm máy tính, cần áp dụng tính phân từng phần, xác định a, b và chọn đáp án đúng.
Phần vận dụng cao Câu 1. 2
2 x.3x.7xdx bằng : 2 2 x.3x.7x 84x A. C B. C ln 4.ln 3.ln 7 ln 84 C. 84x ln 84 C D. 2 48x C Giải thích
Đáp án A sai do hs hiểu nhầm tính chất nguyên hàm
Đáp án A sai là do hs nhầm với công thức tính đạo hàm
Đáp án C sai do hs không thuộc công thức lũy thừa.
Câu 2. Cho a, b là hai số dương. Gọi H là hình phẳng nằm trong góc phần tư thứ hai, giới hạn bởi parapol 2
y  ax va đường thẳng y  bx . Thể tích khối tròn xoay tạo được khi quay H xung quanh trục hoành là một
số không phụ thuộc vào giá trị của a và b thỏa mãn điều kiện sau: A. 4 6 b  2a B. 3 5 b  2a C. 5 3 b  2a D. 4 2 b  2a 84 Giải thích
Group Nhóm Toán | Trắc nghiệm 2016-2017 0 0 5 2 2 2 b 
Ta có V   bx dx    2 ax  dx    3   15a b b a a
Câu D sai do học sinh tính tổng hai bài và không lấy NH và thế cận vào.
Câu B sai do giải PT hoành độ giao điểm ra sai nghiệm là-a/b
Câu A sai do học sinh tính tổng hai bài và không lấy NH và thế cận vào và qui đồng mẫu số sai.
Câu 3. Một ô tô đang chạy với vận tốc 20m / s thì người lái đạp phanh. Sau khi đạp phanh, ôtô chuyển động
chậm dần đều với vận tốc vt  4
 0t  20(m / s) , trong đó t là khoảng thời gian tính bằng giây kể từ úc bắt
đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét? A. 0m B. 5m C. 20m D. 40  Giải thích
Câu A sai là do thế vận tốc vào phương trình và tìm ra t
Câu C sai là do thế t  0 vào phương trình.
Câu D sai là hiểu tìm quảng đường là tính đạo hàm.
Câu 4. Tính diện tích S của hình phẳng H giới hạn bởi đồ thị hàm số y  x , trục hoành, và đường thẳng
y  x  2 được kết quả là: 16 10 A. B. 2 C. 4 D. 3 3 Giải thích
Câu A, B, C sai là do học lấy đôi một tính kết quả mà không có vẽ hình để phân chia bài và cận
Câu 5.Tính diện tích S của hình phẳng H nằm trong phần tư thứ nhất và được giới hạn bởi đồ thị hàm số
y  8x , y  x , và đường thẳng 3
y  x được kết quả là: A.12 B.15,75 C.6,75 D.4 PHẦN 11 : 85
Câu 1. Hãy chọn mệnh đề đúng dưới đây: A. f
 x.gxdx f
 xd .x g  xdx
Group Nhóm Toán | Trắc nghiệm 2016-2017 f xf  xdx B.    dx g x g  xdx  1   x C. x dx   C   1 D. f
 xdx FxC.
Câu 2. Hãy chọn mệnh đề đúng dưới đây: 1 1
A. Nếu F x là một nguyên hàm của hàm số f x thì là một nguyên hàm của . F xf x B. Nếu f
 xdx FxC thì f
 ux.uxdx FuxC .
C. Nếu f x  g xx   thì f
 xdx g  xdx.
D. Nếu F x và G x cùng là nguyên hàm của hàm số f x thì ta có F x  Gx  C (hằng số).
Câu 3. Câu nào sau đây đúng? 1  1  A. 2 cos xdx x  sin 2x C    B.  2
1 cot xdx  cot x C 2  2  1 x 1 1 C.
dx  2 2x C  D. dx  ln x   C  . 2x 2 x x 2x  3
Câu 4. Cho hàm số f x 4 
. Khi đó nguyên hàm của hàm số f x là: 2 x 3 2x 3 3 2x 3 A.   C B.   C 3 2x 3 x 3 3 2x 3 C. 3 2x   C D.   C . x 3 x Câu 5. Cho hàm số   2x 4x f x
 . Khi đó nguyên hàm của hàm số f x là: x x x 86  2 2 2 2  A.   C B.  x 1 1 2 C ln 2 ln 2 ln 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 2x  4x  2x C. 1   C D.
12xC. ln 2  ln 2  2ln 2
Câu 6. Hàm số f x 1 1 có nguyên hàm là: x 1 1 A. x   C B. x   C 2 x 2 x
C. x  ln x C
D. x  ln x C . 4
Câu 7. Nguyên hàm của hàm số f x   là: 2 cos x A.   2
4 1 tan x  C
B. 4 tan x C C. 4
 cot x C D. 4
 tan x C .
Câu 8. Nguyên hàm của hàm số f x  xx  2 3 là: 1 1 9 A. 4 3 2
x  6x  9x C B. 4 3 2 x  2x x C 4 4 2 1 9 C. 4 3 2
x  2x  9x C D. 4 3 2 x  2x x C . 4 2 x
Câu 9. Hàm số f x 1  có nguyên hàm là: x 2 3 A.
x x x C B.
x x  2 x C 3 2 3  1  C.
x x x C D. 2 x x 1  C   . 2  3  x e 1
Câu 10. Hàm số f x 2  có nguyên hàm là: 2 x e 1 1 A. x   C B. 2 x x eC 2 2 x e 2 87 1 1  C. x   C x x eC . 2 D. 2 2 x e 2
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 11. Nguyên hàm của hàm số f x 1 1   là: x 1 x 1 x 1 A. 2
ln x 1  C B. ln  C x 1 x 1 2x C. ln  C D.  C x 1 2 x  . 1 Câu 12. Hàm số    x f x   2 3 1 có nguyên hàm là: 2 3 x 3x 3x A.   x C B.
3x 4 xC ln 3 ln 3 2ln 3 3x 3x C.
3x 2 xC x D.
3  1 xC. ln 3 2ln 3 1
Câu 13. Nguyên hàm của hàm số f x  là: 2 x  3x  2 x  2
A. ln  x  2 x   1  C B. ln  C x 1 x 1 2x  3 C. ln  C D. ln  C . x  2
x 3x22 2 cos x  sin x
Câu 14. Nguyên hàm của hàm số f x 2 2  là: 2 2 sin . x cos x
A. tan x  cot x C
B. tan x  cot x C 1
C. cot x  tan x C
D. tan x  cot x  C . 4
Câu 15. Nguyên hàm của hàm số f x   x x2 sin cos là:  x x3 sin cos A.  C B.  x x2 cos sin  C 3 1 1 88 C. x  sin 2x C D. x  cos 2x C . 2 2
Câu 16. Nguyên hàm của hàm số f x  xsin x là:
Group Nhóm Toán | Trắc nghiệm 2016-2017
A. x cos x  sin x C
B. xsin x  cos x C
C. x cos x  sin x C
D. xsin x  cos x C .
Câu 17. Tìm một nguyên hàm F x của hàm số   . x f x x e  là: A.    1 x F x x e    B.    1 x F x x e   C.    1 x F x x e    D.    1 x F x x e   .
Câu 18. Nếu f x 1 
và F x là một nguyên hàm của f x thỏa F 0  1 thì F x là: x  4 A. ln x  4 1
B. ln x  4 1 ln 4 1 ln 4
C. ln x  4 1 ln 4 D. ln x  4 1 . 4 4
Câu 19. Tìm một nguyên hàm F x của hàm số f x 2
1 x , biết rằng khi x 1 thì nguyên hàm
đó bằng 1. Ta có kết quả nào sau đây? 1 1 A. F x 2  x x  B. F x 2  x x  2 2 x x C. F x 2 1  x   D. F x 2 1  x   . 2 2 2 2  Câu 20. Hàm số   2 1 ln x f x  có nguyên hàm là: x 1 A. 3
ln x  ln x C B. ln x  2
ln x  3  C 3 1 1  1  C. 3
ln x  ln x C D. 2 ln x ln x 1  C   . 3 3  3  x e
Câu 21. Hàm số f x 2  2 1 x  có nguyên hàm là: e A.  2 ln 1 xe  C B.  2 2ln 1 xe  C 89 C. 2 ln 1 xe C 2 D.  ln 1 x x
e  C .
Group Nhóm Toán | Trắc nghiệm 2016-2017   
Câu 22. Một nguyên hàm F x của hàm số f x  tan .
x sin 2x thỏa điều kiện F  0   là:  4  1  1 1  A. x  cos 2x  B. x  cos 2x   2 4 2 2 4 2 2  C. 3 cos x  D. sin 2x  . 3 2 4 Câu 23. Hàm số   3 x
F x e là nguyên hàm của hàm số: 3 x 3 e A. 2 3 x x e B. 2 3x 4 1 3 C. x e D. 3 x e . 4
Câu 24. Hàm số F x  1 xln x là nguyên hàm của hàm số: A. 1 ln x B. x  ln x ln x C. D. x  ln x . x 1 Câu 25. Nếu f
 xdx  sin3x sin xC thì f x bằng: 2 1
A. 3cos3x  cos x
B. 3cos3x  sin x 2 1
C. 3sin 3x  cos x
D. 3sin 3x  cos x. 2
Câu 26. Cho f x 2
 tan x có nguyên hàm là F x. Nếu đồ thị y F x cắt trục Oy tại điểm
0;2 thì F x là: A. tan x  2
B. tan x x  2 C. cot x  2
D. cot x x 1.      
Câu 27. Nếu f x 2 2
 cos x  sin x có nguyên hàm F x thỏa F  1   
thì giá trị của F    4   2  90 bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 5 3 A. 2  B. C. D.  . 2 2 2 1   
Câu 28. Cho hàm số f x 
và F x là một nguyên hàm của f x thỏa F 1   thì 2 2 cos . x sin x  4 
F x là hàm số nào sau đây:
A. tan x  cot x 1
B. cot x  tan x 1
C. tan x  cot x  3
D. tan x  cot x 1.   
Câu 29. Cho F x là một nguyên hàm của hàm số f x 2
 tan x . Giá trị của FF   0 bằng:  4    A. B. 1  4 4   C. 1  D. 3  . 4 4 x
Câu 30. Một nguyên hàm của f x là F x 1 
thì f x   1 là: x 1 2 A. 2 2x B. 2 x 2 2 C. x 1 D. . ln xx  2 1 ĐÁP ÁN 1D 2B 3A 4D 5B 6C 7D 8B 9D 10A 11C 12B 13B 14C 15D 16A 17C 18C 19C 20D 21C 22B 23A 24A 25A 26B 27D 28A 29C 30B TÍCH PHÂN 91
Group Nhóm Toán | Trắc nghiệm 2016-2017
ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH
Câu 1: Cho hình phẳng giới hạn bởi đường cong y f x , trục hoành và hai đường thẳng x  , a x  ( b a  )
b quay quanh trục trục hoành tạo thành một khối tròn xoay. Công thức tính thể tích
của khối tròn xoay nói trên: b b A. 2 V   f  xdx B. 2 V f  xdx a a a b C. 2
V    f xdx D. 2 V    f  xdx b a
Câu 2: Cho hình phẳng giới hạn bởi đường cong y  sin x , trục hoành và hai đường thẳng x  0, x  
. Thể tích của khối tròn xoay thu được khi quay hình này quanh trục trục Ox:   A. 3
V   sin xdx  B. 2 V  sin xdx  0 0   C. 2
V   sin xdx  D. 2 V    sin xdx  0 0
Câu 3: Cho hình phẳng giới hạn bởi đường cong x f y , trục tung và hai đường thẳng y  , a y  ( b a  )
b quay quanh trục trục tung tạo thành một khối tròn xoay. Công thức tính thể tích của khối tròn xoay nói trên: b b A. 2 V   f  ydy B. 2 V f  ydy a a b b C. 3 V   f  ydy D. 2 V    f  ydy a a
Câu 4: Cho hình phẳng giới hạn bởi đường cong y  sin x , trục hoành và hai đường thẳng x  0, x  
. Thể tích của khối tròn xoay thu được khi quay hình này quanh trục trục Ox: 92  2  A. B. 2 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 2  2  C. D.  3 3
Câu 5: Cho hình phẳng giới hạn bởi đường cong 2
y x  4x  4, y  0, x  0, x  3 . Thể tích của khối
tròn xoay thu được khi quay hình này quanh trục trục Ox: 31 2 32 A. B. 5 6 33 2 32 C. D. 5 3
Câu 6: Cho hình phẳng giới hạn bởi đường cong 2
y  2  x , y  1. Thể tích của khối tròn xoay thu
được khi quay hình này quanh trục trục Ox: 56 2 56 A. B. 25 6 33 56 C. D. 5 15
Câu 7: Cho hình phẳng giới hạn bởi đường cong 2
y  2x x , y x . Thể tích của khối tròn xoay thu
được khi quay hình này quanh trục trục Ox:   A. B. 25 6  6 C. D. 5 5
Câu 8: Cho hình phẳng giới hạn bởi đường cong 2
y  1 x , y  0 . Thể tích của khối tròn xoay thu
được khi quay hình này quanh trục trục Ox: 1 1 2 2 A. V    2 1 x dx B. V     2 1 x dx 1  1  1 1 C. V     2 1 x dx D. V     4 1 x dx 1  1  93
Câu 9: Cho hình phẳng giới hạn bởi đường cong y    x2 1
, y  0, x  0, x  2 . Thể tích của khối tròn
xoay thu được khi quay hình này quanh trục trục Ox:
Group Nhóm Toán | Trắc nghiệm 2016-2017 8 2 2 A. B. 3 5 5 C. D. 2 2
Câu 10: Cho hình phẳng giới hạn bởi đường cong 2 2
y x , x y . Thể tích của khối tròn xoay thu được
khi quay hình này quanh trục trục Ox: 8 2 A. B. 3 5  3 C. D. 2 10
Câu 11: Cho hình phẳng giới hạn bởi đường cong y   x  13 2
1 , x  0, y  3 . Thể tích của khối tròn
xoay thu được khi quay hình này quanh trục trục Oy: 480 481 A. B. 7 7 48 488 C. D. 7 7
Câu 12: Cho hình phẳng giới hạn bởi đường cong 2
y x 1, x  0 và tiếp tuyến với 2
y x 1 tại điểm
M (1; 2) . Thể tích của khối tròn xoay thu được khi quay hình này quanh trục trục Ox: 8 11 A. B. 7 15 8 4 C. D. 15 7
Câu 13: Cho hình phẳng giới hạn bởi đường cong y x, y x . Thể tích của khối tròn xoay thu được
khi quay hình này quanh trục trục Ox: A. 0 B.   C.   D. 94 6
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 14: Cho hình phẳng giới hạn bởi đường cong y  ln ,
x y  0, x e . Thể tích của khối tròn xoay thu
được khi quay hình này quanh trục trục Oy:  2e  1  2e  1 A. B. 2 2  2 2e   1   2e 2 C. D. 2 2 2 2
Câu 15: Cho hình phẳng giới hạn bởi đường cong 3
y x , x  0 và tiếp tuyến với 3
y x tại điểm có
hoành độ bằng 1. Thể tích của khối tròn xoay thu được khi quay hình này quanh trục trục Oy: 5  A. B. 26 26 7  C. D. 36 36 1
Câu 16: Cho hình phẳng giới hạn bởi đường cong y
1, y  0, y  2x . Thể tích của khối tròn xoay x
thu được khi quay hình này quanh trục trục Ox: 56ln 2 16ln 2 A. B. 3 3 56ln 2 5 6ln 2 C. D. 3 3
Câu 17: Cho hình phẳng giới hạn bởi đường cong 2
y  2x  x , y  0, x  3. Thể tích của khối tròn xoay
thu được khi quay hình này quanh trục trục Ox: 3 18 A. B. 5 5 7  C. D. 5 5
Câu 18: Cho hình phẳng giới hạn bởi đường cong 2
y  2x  x , y  0, x  3. Thể tích của khối tròn xoay 95
thu được khi quay hình này quanh trục trục Oy:
Group Nhóm Toán | Trắc nghiệm 2016-2017  17 A. B. 6 6 7 59 C. D. 6 6
Câu 19: Cho hình phẳng giới hạn bởi đường cong 2
y  2 1 x , y  21 x . Thể tích của khối tròn
xoay thu được khi quay hình này quanh trục trục Ox:   A. B. 6 3 4 5 C. D. 3 6 1
Câu 20: Cho hình phẳng giới hạn bởi đường cong y
, y  0, x  1, x a(a  1) . Thể tích của khối tròn x
xoay thu được khi quay hình này quanh trục trục Ox: a   1  a   1  A. B. 3 aa   1  a   1  C. D. 3 a
ỨNG DỤNG TÍCH PHÂN TÍNH THỂ TÍCH
Câu 1. Công thức nào diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x liên tục, trục hoành
và hai đường thẳng x  , a x b b b b b
A . f xdx  B.
f xdx  C.  f  xdx D. 2  f  xdx a a a a
Câu 2. Công thức nào diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y f x, y g x liên 96
tục và hai đường thẳng x  , a x b
Group Nhóm Toán | Trắc nghiệm 2016-2017 b b
A .  f x  g xdx
B.  f x  g xdx a a b b C. f
 x gxdx D. f
 x gxdx a a
Câu 3. Trong các tích phân sau, tích phân nào là công thúc tính diện tích giới hạn bởi đồ thị hàm số 
y  sin x  2cosx trục hoảnh và hai đường thẳng x  0, x  là 2   2 2
A .  sin x  2cosxdx B.
sin x  2cosx dx  0 0   2 2 C.
sin x  2cosx dx
D.  sin x  2cosxdx 0 0
Câu 4. Diện tích hình phẳng được giới hạn bởi đồ thị hàm sồ 3
y x trục hoành và hai đường thẳng x  1  , x  2 17 1 15 A. S  B. S  4 C. S  D. S  4 4 4
Câu 5. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 2
y  2x  4x  6 , trục hoành và hai
đường thẳng x  2  , x  4  là: 40 92 50 A. 12 B. C. D. 3 3 3
Câu 6. Diện tích hình phẳng được giới hạn bởi hai đường thẳng x  0, x   và hai đồ thị hàm sồ y  sin , x y  cos x A. S  2 B. S  4 C. S  0 D. S  2 2
Câu 7. Diện tích hình phẳng được giới hạn bởi hai đường thẳng x  0, x  1 và hai đồ thị hàm sồ x
y e , y  2 A. S  2 B. S e 1 C. S e 1
D. S  3  e
Câu 8. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 3 y x và 5 y x là: 1 1 2 A. B. C. D. 0 12 6 6
Câu 9. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y x  sin x , y x và 0  x  2 97 A. 3 B. 4 C. 2 D. 1
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 10. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 3 y  3
x  3x 1 vàđường thẳng y  3 là: 57 45 27 21 B. B. C. D. 4 4 4 4
Câu 11. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y  e   1 x và  1 x ye x là: e e 3 A. 2  B. 2 C. 1 D. 1 2 2 e 1
Câu 12. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 2
y x , y  ln và đường thẳng x 1 x  1 là: 8 31 8 31 8 23 8 31 A.  ln 2  B. ln 2  C.  ln 2  D.  ln 2  3 18 3 18 3 18 3 18
Câu 13. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 3
y x x và 2
y x x là: 8 33 37 5 A. B. C. D. 3 12 12 12
Câu 14. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 2 y  2
x x  3 và trục hoành là: 125 125 125 125 C. B. C. D. 24 34 14 44
Câu 15. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 2
y x  4x  3 và y x  3 là: 55 205 109 126 A. B. C. D. 6 6 6 6
Câu 16. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 2 y  2  x , 2
y  1 x và trục hoành là:  8 2  D. 3 2  2 B. 2 2  C.  D. 4 2   2 3 2
Câu 17. Anh An muốn làm cửa rào sắt có hình dạng
và kích thước giống như hình vẽ kế bên, biết
đường cong phía trên là một parabol. Giá 2 1m
cửa rào sắt có giá là 700000 đồng. Vậy anh An
phải trả bao nhiêu tiền để làm cài cửa rào sắt như
vậy. (làm tròn đền trục hàng nghìn) 98
Group Nhóm Toán | Trắc nghiệm 2016-2017 A. 6420000
B. 6320000 C. 6520000 D. 66200000
Câu 18. Một quán café muốn lảm cái bảng hiệu là
một phần của Elip có kích thước, hình dạng
giống như hình vẽ và có chất lượng bằng gổ.
Diện tích gổ bề mặt bảng hiệu là (làm tròn đến hàng phần chục) A. 2.3 B. 2.4 C. 2.5 D. 2.6
Câu 19. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 2
y x 1, tiếp tuyến của parapol đã cho
tại điểm M 2;5 và trục tung là: 7 5 8 E. B. C. D. 2 3 3 3 Câu 20. Cho hàm số 3 2
y x  3x  2 có đồ thị (C). Diện tích hình phẳng giới hạn bởi (C) và tiếp
tuyến của (C) tại điểm có hoành độ x  1.9 là (làm tròn đến hàng phần chục) 0 A 4.1 B. 4.2 C. 4.3 D. 4.4 PHẦN 12 : I. NHẬN BIẾT 1
Câu 1. Một nguyên hàm F(x) của hàm số f ( ) x  là : 2x  5 1 A. F( ) x  ln 2x  5  2016 C. F(x)  ln 2x  5 2 2 1 B. F( ) x   F( ) x    D. 2 2x  52 2x5 99 1
Câu 2. Một nguyên hàm F(x) của hàm số f ( ) x  3 x   sin10 là : 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 4 x  1  4 x A.    sin10 x C. 4  2  4 1 B. F( ) x  4 x  ln 2  cos10 D. F x  2 ( ) 3x 4 1
Câu 3. Hàm số F(x) 
là một nguyên hàm của hàm số nào sau đây ? x 1 2 A. f(x)  ln x  2 B. f ( ) x   C. 1 D. 2 x 2 x
Câu 4. Một nguyên hàm F(x) của hàm số ( )  3x f x là : x x1 3 3x A. F x  3 ( ) B. F( ) x  C. ( )  3x F x D. F( ) x  ln 3 x 1 x 1 3
Câu 5. Một nguyên hàm F(x) của hàm số f ( ) x  2 x   2 x là : x 3 x 4 3 x 4 A. F( ) x   3ln x  3 x C. F( ) x   3lnx 3 x 3 3 3 3 3 x 3 4 3 x 4 B. F( ) x    3 x D. F( ) x   3ln x  3 x 2 3 x 3 3 3
Câu 6. Kết quả của 2 tan  xdx là :
A. tan x x C
B. tan x 1 C C. 2 cot x C D.   x2 2 1 tan  C
Câu 8. Một nguyên hàm của hàm số 2 ( )  x f x e là : 2 x 1  e 1 A. 2x e B. 2 2 x e C. D. 2 x e 2x 1 2 x
Câu 9. Kết quả của  3 sin dx là : 2 2 3x 2 3x 3 3x 3 3x A.  cos
C B. cos C C.  cos  C D. cos  C 3 2 3 2 2 2 2 2 10 0   
Câu 10. Tìm hàm số f (x) biết f '( )
x  sin x  cos x và f  0  
, ta được kết quả là :  4 
Group Nhóm Toán | Trắc nghiệm 2016-2017 2
A. f (x)   cos x  sin x  2
C. f (x)  cos x  sin x  2 2
B. f (x)  cos x  sin x  2
D. f (x)   cos x  sin x  2 II. THÔNG HIỂU
Câu 11. Nguyên hàm của hàm số: y = sin3x.cosx là: 1 1 1 1 A. 4 sin x  C B.  4 sin x  C C. 4 cos x  C D.  4 cos x  C 4 4 4 4
Câu 12. Một nguyên hàm của hàm số: y = cos5x.cosx là: 1  1 1  1  sin 6x sin 4x  A. sin 6x  sin 4  x  B. cos6x
C. F(x) = sin6x D.     2  6 4  2  6 4  x
Câu 13. Họ nguyên hàm F(x) của hàm số f (x)  là : 2 x 1 1 A. F(x)  ln  2 x   1  C C. 2x C 2 1 x 1 B. F x   2 ( ) ln x   1  C D. ln  C 2 x 1
Câu 14. Kết quả của ln  xdx là : 1
A. x ln x x C
B. x ln x x C
C. x ln x C D.  C x  2 
Câu 15. Kết quả của e 3   x dx là : x  5  x e x 1 x 1 x 1 x 1 A. 3e   C B. 3  e   C C. 3e   C D. 3  e   C 4 2x 4 2x 4 4 2x 2x
Câu 16. Nguyên hàm F(x) của hàm số 2
f (x)  tan x thỏa F(0)  3 là :
A. tan x x  3
B. tan x x  3
C. tan x x  3
D. tan x x  3 10 cos
Câu 17. Kết quả của là : 1  x dx 20 sin x
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 1 1 1 1 1 1 A.   B.  C.   D.  19 19sin x 19 19 19sin x 19 19 19sin x 19 19 19sin x 19
Câu 18. Kết quả của sin  x xdx là
A. x cos x  sin x C .
B x cos x  sin x C .
C x sin x  cos x C .
D x sin x  cos x C    13 Câu 19. Nếu 2 f '(x)  cos x    và f (0)  thì :  4  4 1  1  7 A. f (x)  x  cos 2x  3
C. f (x)  sin x    2  2  2 1 1
B. f (x)  x  cos 2x  4 . D f (x)  cos 2x  3 2 2 2
Câu 20. Hàm số ( )  x F x
e là một nguyên hàm của hàm số nào sau đây ? 2 x 2 e 2 x A. ( )  2 x f x xe B. 2 ( )  x f x e C. f (x)  D. x e 2x 2
III. VẬN DỤNG THẤP 1
Câu 21. Hàm số nào dưới đây là một nguyên hàm của hàm số y  ? 2 4  x A. F x   2 ( )
ln x  4  x  B. F x   2 ( )
ln x  4  x  C. 2
F(x)  2 4  x D. 2
F(x)  x  2 4  x
Câu 22. Họ nguyên hàm F(x) của hàm số 2
f (x)  sin x là : 1  sin 2x  1  cos 2x  A. F (x)  x     C B. F (x)  x     C 2  2  2  2  1  sin 2x  1 C. F(x)  x     C
D. F(x)   x  sin 2x  C 2  2  2 x e
Câu 23. Một nguyên hàm F(x) của hàm số f (x) 
thỏa F(0)  ln 3 là : 10 x e 1 2 A. ln  x e  2  ln3 C. ln  x e  2  2ln3
Group Nhóm Toán | Trắc nghiệm 2016-2017 B. ln  x e  2  ln3 D. ln  x e  2  2ln3 Câu 24. Hàm số F( )
x  ln sin x  3cos x là một nguyên hàm của hàm số nào sau đây ? cos x  3sin x cosx 3sin x A. f ( ) x  C. f ( ) x  sin x  3cos x sin x  3cos x sin x  3cos x B. f ( ) x  cos x  3sin x D. f ( ) x  cos x  3sin x
Câu 25. Kết quả của tan  xdx là : A. cot x C
C. ln cos x C
B.  ln cos x C
D. ln sin x C IV. VẬN DỤNG CAO 1
Câu 26. Họ nguyên hàm F(x) của hàm số f ( ) x  là : 2 x  4x  3 x  3 A. F x  2 ( ) ln x  4x  3  C C. F(x)  ln  C x 1 1 x 1 1 x  3 B. F( ) x  ln  C D. F( ) x  ln  C 2 x  3 2 x 1 1
Câu 27. Kết quả của  dx là : 2 2 sin . x cos x 1 A. tan .
x cot x C C.  C tan . x cot x
B. tan x  cot x C
D. tan x  cot x C   
Câu 28. Nguyên hàm F(x) của hàm số 2 3
f (x)  sin 2 .
x cos 2x thỏa F  0   là :  2  1 1 1 1 4 A. 3 5 sin 2x  sin 2x C. 3 5 sin 2x  sin 2x  6 10 6 10 15 1 1 1 1 1 B. 3 5 sin 2x  sin 2x D. 3 5 sin 2x  sin 2x  6 10 6 10 15 10 sin . x cos x 3
Câu 29. Họ nguyên hàm của hàm số f (x)  là : 2 2 cos x  sin x
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 A.  cos 2x C C. cos 2x C 2 2
B.  cos 2x C
D. cos 2x C 1
Câu 30. Kết quả của  dx là : 2 x cos ln x
A. x tan ln x  C
C. x  tan ln x  C
B. x  tan ln x  C
D. tan ln x  C 1A 2A 3A 4A 5A 6A 7A 8A 9A 10A 11A 12A 13A 14A 15A 16A 17A 18A 19A 20A 21A 22A 23A 24A 25A 26A 27A 28A 29A 30A TÍCH PHÂN
I/ CẤP ĐỘ NHẬN BIẾT  2
Câu 1. Tích phân I  sin xdx  bằng 0 A. 1 B. -1 C. 0 D. -2
Câu 2. Cho hàm số f(x) xác định trên đoạn [a; b] và F(x) là nguyên hàm của f(x) trên khoảng (a; b). Kết luận
nào sau đây là đúng: F(x) là một nguyên hàm của f(x) trên đọan [a; b] khi và chỉ khi A. /
F (a)  f (a) và / F ( ) b f ( ) b B. /
F (a )  f (a) và /
F (b )  f ( ) b 10     4 C. /
F (a )  f (a) và /
F (b )  f ( ) b D. /
F (a )  f (a) và /
F (b )  f ( ) b
Group Nhóm Toán | Trắc nghiệm 2016-2017  3 Câu 3. Tích phân 2
I  (1 tan x)dx  bằng 0 3 A.  3 B. 3 C. 3 D. 1
Câu 4. Hàm số nào sau đây không có tích phân trên đoạn [0; 1]
A. f (x)  ln(x 1)
B. f (x)  ln x
C. f (x)  ln(x  2)
D. f (x)  ln(x  3) 1 dx
Câu 5. Kết quả của I   là x 1 A. 0 B. -1 C. 1 D. Không tồn tại
Câu 6. Đẳng thức nào sau đây là đúng    2 0 2 2
A. sin xdx  sin xdx  
B. sin xdx  sin tdt   0  0 0 2    2 2 2 0
C. sin xdx  cos xdx  
D. sin xdx  cos 2xdx   0 0 0  2  2 x
Câu 7. Tích phân I  cos dx  bằng 3 0 3 3 3 A. B. 6 2 2 3 C. D. 6 2 10  5 2
Câu 8. Tích phân I  sin . x cos xdx  bằng 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 A. B.  2 2 3 3 C. D.  2 2 1 dx
Câu 9. Tích phân I   bằng x 1 0 A.1 2ln 2 B. 1 ln 2 C. 1 ln 2 D. ln 2 2 x e
Câu 10. Tích phân I dx  bằng x e 1 1 A. ln(e 1) B. ln(e 1) C. ln(e 1) D. 2 ln(e 1)
II/ CẤP ĐỘ THÔNG HIỂU 1
Câu 11. Biết (a 1)dx  3 
. Khi đó số thực a bằng 0 A. – 2 B. 2 1 1 C. D.  2 2  2
Câu 12. Cho biết (t sin x  2)dx  2 
. Khi đó số thực t bằng 0 A.   3 B.   3 1 C.  D. 2 5 2 x x 1
Câu 13. Tích phân I dx  bằng x 1 2 10 A. 6  ln 3 B. 6  ln 3 6 C. 6   ln3 D. 6   ln3
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 14. Chọn mệnh đề đúng trong các mệnh đề sau 1
A.Hàm số f (x) 
có tích phân trên đoạn [0;2]. x  2 1
B. Hàm số f (x) 
không có tích phân trên đoạn [0;1]. x  2
C. Nếu f(x) không liên tục trên đoạn [a; b] thì f(x) có tích phân trên [a; b].
D. Nếu f(x) liên tục trên đoạn [a; b] thì f(x) có tích phân trên [a; b]. 
Câu 15. Tích phân của tan x trên đoạn [0; ] là 4 1 2 A.  ln B. 1 ln 2 2 2 2 C. ln D.  ln 2 2 2 xdx
Câu 16. Tích phân I   bằng 2 x  2 1  1 A. ln 2 B. 2ln 2 2 1 1 C. ln D. 2 ln 2 2  3 Câu 17. Tích phân 3 I  cos xdx  bằng 0 3 3 A. 3 3 B. 2 3 3 3 3 C. D. 4 8  4 Câu 18. Tích phân 2 I  tan xdx  bằng 10 0 7   A.1 B. 1   4 4
Group Nhóm Toán | Trắc nghiệm 2016-2017  C. 1 D. 1 4 1 dx
Câu 19. Tích phân I   bằng 2 1 x 0   A. B. 4 6   C. D. 3 2  6
Câu 20. Tích phân I
4sin x 1.cos xdx  bằng 0 A. 3  3 B. 3  3 3 3 1 3 3 1 C. D. 6 2
III/ CẤP ĐỘ VẬN DỤNG THẤP 4 x e 1
Câu 21. Một nguyên hàm của hàm số f (x)  là 2 x e 1 1 1 A. 2 x ex B. 2 x ex 2 2 C. 2 2 x ex D. 2 2 x ex 1
Câu 22. Biết F(x) là một nguyên hàm của f (x) 
và F(2) 1. Khi đó F(3) bằng x 1 A. ln 2 B. ln2 + 1 3 1 C. ln D. 2 2 x
Câu 23. Các số thực x sau đây thỏa mãn đẳng thức (1 t)dt  0  0 10
A. x = 0 hoặc x = - 2.
B. x = 0 hoặc x = 2. 8
C. x = 0 hoặc x = 1.
D. x = 0 hoặc x = -1.
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 dx
Câu 24. Tích phân I   bằng 1 x 0 A. 2(1 ln 2) B. 2(1 ln 2) C. 1 2ln 2 D. 1 2ln 2 ln 2 x e dx
Câu 25. Tích phân I   bằng x  0 e 2 A. 2  3 B. 2( 3  2) C. 2(2  3) D. 2( 3  2)
IV/ CẤP ĐỘ VẬN DỤNG CAO Câu 26. 2 2 .
x 3 .x7x dx  bằng 2 2 . x 3 .x7x 84x A.  C B.  C ln 4.ln 3.ln 7 ln 84
C. 84x ln 84  C D. 2 48x C
Câu 27. Đẳng thức nào sau đây là sai    2 2 2 0
A. f (sin x, cos x)dx f (cos ,
x sin x)dx  
B. f (sin x, cos x)dx   f (cos ,
x sin x)dx   0 0 0  2     
C. f (x sin x)dx
f (sin x)dx  
D. f (x sin x)dx   f (sin x)dx   2 0 0 0 0 t dx
Câu 28. Cho phương trình  , (t  2) 
. Khi đó nghiệm thực t của phương trình đã cho là 2  12 2 x x 1 1 1 A. B.  2 2 C. 2 D. -2  2 10 7 sin x
Câu 29. Tích phân I dx 9  bằng 7 7 sin x  cos x 0
Group Nhóm Toán | Trắc nghiệm 2016-2017   A. B. 2 4   C. D. 8 12 1 dx
Câu 30. Tích phân I   bằng ( x e 1)(x  3) 1  1 1 A. ln 2 B. ln 3 2 2 1A 2D 3C 4B 5A 6B 7D 8A 9D 10A 11B 12A 13A 14D 15D 16A 17D 18C 19A 20C 21B 22B 23B 24B 25C 26B 27D 28C 29B 30A
ỨNG DỤNG TÍCH PHÂN NHẬN BIẾT
Câu 1. Cho hàm số y f (x) liên tục trên [ ; a ]
b . Khi đó, diện tích S của hình phẳng giới hạn bởi đồ thị hàm
số y f (x), trục hoành và hai đường thẳng x  ,
a x b được tính theo công thức: b b b b
A. S   f (x)dx  B. S f (x)dx  C. S f (x) dx  D. S   f (x) dxa a a a
Câu 2. Cho hai hàm số y f (x) và y g(x) liên tục trên [ ; a ]
b . Khi đó, diện tích S của hình phẳng giới hạn
bởi đồ thị hai hàm số y f (x), y g(x) và hai đường thẳng x  ,
a x b được tính theo công thức: b b
A. S    f (x)  g(x)dx
B. S   f (x)  g(x)dx a a b b C. S  
f (x)  g(x) dx  D. S
f (x)  g(x) dxa a
Câu 3. Diện tích hình phẳng giới hạn bởi các đường y  sinx, y  0, x  0, x   bằng: 6 6 A.  B. 2 C. 2 D. 7 7 11
Câu 4. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x x , trục hoành, trục tung và đường thẳng 0 x  2 bằng:
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 2 A. B.  C. 1 D.  3 3
Câu 5. Cho đồ thị hàm số y g(x) . Diện tích hình phẳng ( phần gạch trong hình vẽ) bằng: y 3 2 1 x -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 -1 -2 -3 -4 -5 -6 -7 -8 3 3 3 0 A. g(x)dx
B. g(x) dx
C.  g(x)dx
D.  g(x)dx  1  0 1  8  THÔNG HIỂU
Câu 6. Cho hàm số y f (x) liên tục trên [ ; a ]
b . Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị hàm số
y f (x), trục hoành và hai đường thẳng x  , a x  . b
Nếu đồ thị hàm số y
f (x) cắt trục hoành tại một
điểm duy nhất có hoành độ c ( ; a )
b . Khi đó, diện tích S được tính theo công thức: b c b A. S   f (x) dx  B. S
f (x)dx f (x)dx   a a c c b c b C. S  
f (x)dx   f (x)dx   D. S
f (x)dx f (x)dx   a c a c 11 1
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 7. Cho hai hàm số y f (x) và y g(x) liên tục trên [ ; a ]
b . Gọi S là diện tích của hình phẳng giới hạn
bởi đồ thị hai hàm số y f (x), y g(x) và hai đường thẳng x  ,
a x b . Nếu phương trình f (x)  g( ) x  0
có một nghiệm duy nhất c ( ; a )
b . Khi đó, diện tích S được tính theo công thức: b b
A. S   f (x)  g(x)dx
B. S   f (x)  g(x)dx a a c b c b C. S
f (x)dx g(x)dx  
D. S   f (x)  g(x)dx   f (x)  g(x)dx a c a c
Câu 8. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x  2x và trục hoành bằng : 4 4 A.  B. C.  D. 1 3 3
Câu 9. Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số 2
y x x và y  3x bằng : 32 40 32 40 A. B. C.  D.  3 3 3 3
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  ln x , trục hoành và đường thẳng x e bằng : A. e B. e C. 1 D.  VẬN DỤNG THẤP
Câu 11. Diện tích hình phẳng giới hạn bởi các đường 3
x y , y  1, x  8 bằng : 5 7 11 17 A. B. C. D. 4 4 4 4 2x 1
Câu 12. Diện tích hình phẳng giới hạn bởi đường cong (C): y
, tiệm cận ngang của (C) và hai đường x 1
thẳng x 1, x  3bằng : A. ln 2 B. 4ln 2 C. 1 ln 2 D. 1 4  x
Câu 13. Diện tích hình phẳng giới hạn bởi các đường y
, y  0, x  2, x  6 không được tính bởi công x 1 thức nào sau đây : 6 4  x 4 6 4  x 4  x 11 A. dx  B. dx dx   x 1 x 1 x 1 2 2 2 4
Group Nhóm Toán | Trắc nghiệm 2016-2017 4 6 4  x 4  x 4 6 4  x x  4 C. dx dx   D. dx dx   x 1 x 1 x 1 x 1 2 4 2 4
Câu 14. Cho đồ thị hàm số y f (x) . Diện tích hình phẳng ( phần gạch trong hình vẽ) bằng: y 5 4 3 2 1 x -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 0 2 2
A.  f (x)dx f (x)dx   B. f (x)dx  2  0 2  0 2 2 C.
f (x)dx f (x)dx   D. 2  f (x)dx  2  0 0
Câu 15. Cho đồ thị hàm số y  (
h x) . Diện tích hình phẳng ( phần gạch trong hình vẽ) bằng: 11 3
Group Nhóm Toán | Trắc nghiệm 2016-2017 y 3 2 1 x -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 -1 -2 -3 1 0 0 A. g(x)dx
B. h(x)dx h(x)dx   1  1  1 0 1 0 1
C. h(x)dx h(x)dx  
D.  h(x)dx h(x)dx   1  0 1  0 VẬN DỤNG CAO
Câu 16. Số đo diện tích hình phẳng giới hạn bởi parabol (P): 2
y x  2x  2 , tiếp tuyến của (P) tại điểm
M (3;5) và trục tung bằng: A. 9 B. 8 C. 9 D. 8
Câu 17. Số đo diện tích hình phẳng giới hạn bởi đường xy  4 , trục hoành và hai đường thẳng x  ,
a x  3a (a  0) bằng : A. 4 ln 3 B. 4ln 3 C. 4ln 2a D. 4 ln 2a 2 x
Câu 18. Số đo diện tích hình phẳng giới hạn bởi các đường y  ,
x y  1và y
trong miền x  0, y  1 4 bằng : 3 3 5 5 A. B.  C.  D. 2 2 6 6
Câu 19. Cho đồ thị hai hàm số y f (x) ( đường vẽ màu đỏ) và y f (x) ( đường vẽ màu hồng). Diện tích 1 2 11
hình phẳng ( phần gạch trong hình vẽ) bằng: 4
Group Nhóm Toán | Trắc nghiệm 2016-2017 y x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 -1 -2 -3 -4 -5 -6 -7 1 0 1
A.   f (x)  f (x) dx
B.   f (x)  f (x) dx f (x)  f (x) dx  1 2   1 2  1 2  2  2  0 0 1 0 1
C.   f (x)  f (x) dx f (x)  f (x) dx
D.   f (x)  f (x) dx f (x)  f (x) dx  1 2   2 1  1 2   1 2  1  0 2  0
Câu 20. Cho parabol (P): 2
y x 1 và đường thẳng (d) : y mx  2 . Với giá trị thực m nào dưới đây thì diện
tích hình phẳng giới hạn bởi (P) và (d) đạt giá trị nhỏ nhất 1 3 A. B. C.1 D.0 2 4 1.C 2.D 3.B 4.C 5.C 6.D 7.D 8.B 9.A 10C 11.D 12.A 13.B 14.D 15.B 16.A 17.B 18.D 19.D 20.D PHẦN 13 : NGUYÊN HÀM
Mức độ nhận biết. 11 1 5
Câu 1: Nguyên hàm của hàm số f(x) = x2 – 3x + là: x
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 2 3 2 x 3x x 3x 1 3 2 x 3x A. 
 ln x C B.    C C. 3 2
x  3x  ln x C D.   ln x C 3 2 2 3 2 x 3 2
Câu 2: Họ nguyên hàm của 2
f (x)  x  2x 1 là 1 A. 3 F (x) 
x  2  x C B. F( )
x  2x  2  C 3 1 1 C. 3 2 F (x) 
x x x C D. 3 2 F (x) 
x  2x x C 3 3 1 1
Câu 3: Nguyên hàm của hàm số f (x)   là : 2 x x 1 1 A. 2 ln x ln x C B. lnx - + C C. ln|x| + + C D. Kết quả khác x x
Câu 4: Nguyên hàm của hàm số 2 ( ) x x f x ee là: 1
A. e2x ex C B. 2 2 x x
e e C C. x ( x
e e x)  C D. Kết quả khác 2
Câu 5: Nguyên hàm của hàm số f x cos 3x là: 1 1
A. sin 3x C
B.  sin 3x C
C. sin 3x C D. 3
 sin3x C 3 3 x 1
Câu 6: Nguyên hàm của hàm số f (x)  2e  là: 2 cos x ex A.2ex + tanx + C B. ex(2x - ) C. ex + tanx + C D. Kết quả khác cos 2 x
Câu 7: Tính sin(3x 1)dx  , kết quả là: 1 1
A.  cos(3x 1)  C
B. cos(3x 1)  C
C. cos(3x 1)  C D. Kết quả khác 3 3 11 6 Câu 8: Tìm (cos6x cos4 ) x dx là:
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 A. sin6x sin 4x C x x C 6 4 B. 6sin 6 5sin4 1 1 C. sin 6x sin 4x C x x C 6 4 D. 6sin 6 sin4 1
Câu 9: Tính nguyên hàm dx  ta được kết quả sau: 2x 1 1 1
A. ln 2x 1  C
B.  ln 2x 1  C
C.  ln 2x 1  C
D. ln 2x 1  C 2 2 1
Câu 10: Tính nguyên hàm dx  ta được kết quả sau: 1 2x 1 2
A. ln 1 2x C B. 2
 ln 1 2x C
C.  ln 1 2x C D.  C 2 2 1 (  2x)
Câu 11: Công thức nguyên hàm nào sau đây không đúng? 1  1   x A.
dx  ln x C  B. x dx   C (  1  )  x  1 x a 1 C. x a dx
C (0  a  1)  dx  tan  ln D. x Ca 2 cos x
Câu 12: Tính (3cos  3x x )dx  , kết quả là: 3x 3x 3x 3x A. 3sin x   C B. 3  sin x   C C. 3sin x   C D. 3  sin x   C ln 3 ln 3 ln 3 ln 3
Câu 13: Trong các hàm số sau: 2 (I) 2 f (x) tan x 2 (II) f (x) (III) 2 f (x) tan x 1 2 cos x
Hàm số nào có một nguyên hàm là hàm số g(x) = tanx A. (I), (II), (III) B. Chỉ (II), (III) 11 7 C. Chỉ (III) D. Chỉ (II)
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 14: Trong các mệnh đề sau, tìm mệnh đề sai 3 f (x) A. 2
f '(x) f (x)dx C 3 B.
f (x).g(x) dx f (x)d . x g(x)dx C. f (x) g(x) dx f (x)dx g(x)dx D.
kf (x)dx k
f (x)dx (k là hằng số)
Câu 15: Nguyên hàm của hàm số 3
f (x)  (2x 1) là: 1 A. 4
(2x 1)  C B. 4
(2x 1)  C C. 4
2(2x 1)  C D. Kết quả khác 2
Câu 16: Nguyên hàm của hàm số 5 f (x)  1 (  2x) là: 1 A. 6  1
(  2x)  C B. 6 1
(  2x)  C C. 6 5 1
(  2x)  C D. 4 5 1
(  2x)  C 2
Câu 17: Chọn câu khẳng định sai? 1 A. xdx   C ln B. 2
2xdx x Cx 1 C. xdx   x C sin cos D. dx   x C  cot 2 sin x 3
Câu 18: Nguyên hàm của hàm số f(x) = 2x  là : 2 x 3 3 A. 2 x   C B. 2 x   C C. 2 2
x  3ln x C D. Kết quả khác x 2 x 11 8
Group Nhóm Toán | Trắc nghiệm 2016-2017 Câu 19: Hàm số x F x e tan x
C là nguyên hàm của hàm số f (x) nào? x 1 x 1
A. f (x)  e
B. f (x)  e  2 sin x 2 sin x x 1
C. f (x)  e  D. Kết quả khác 2 cos x Câu 20: Nếu ( ) x f x dx e sin 2x
C thì f (x) bằng x 1 A. x e cos 2x B. x e cos 2x C. x e 2cos 2x D. e cos 2x 2
Câu 21. Trong các hàm số sau đây , hàm số nào là nguyên hàm của f (x)  sin 2x 1 1  A. 2cos 2x B. 2
 cos2x C. cos 2x D. cos 2x 2 2
Câu 22. Trong các hàm số sau đây , hàm số nào là nguyên hàm của 3 2
f (x)  x  3x  2x 1 1 1 A. 2 3x  6x  2 B. 4 3 2
x x x x C. 4 3 2
x x x D. 2 3x  6x  2 4 4 1
Câu 23. Trong các hàm số sau đây , hàm số nào là nguyên hàm của f (x)  2x  2016 1 1 A. ln 2x  2016 B. ln 2x  2016
C.  ln 2x  2016 D.2 ln 2x  2016 2 2
Câu 24. Trong các hàm số sau đây , hàm số nào là nguyên hàm của 3 3 ( ) x f x e   1 A. 3x 3 e  B. 3 3x 3 e  C. 3x 3 e  D. -3 3x 3 e  3  1 
Câu 25. Nguyên hàm của hàm số: J   x dx   là:  x  11 1 A. F(x) = 2 ln x  x  C B. F(x) = ln x 2  x  C 9 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 C. F(x) = 2 ln x  x  C D. F(x) =   2 ln x  x  C . 2
Câu 26. Một nguyên hàm của hàm số: y = cos5x là: 1 1 A. cos5x+C B. sin5x+C C. sin 6x +C D. sin 5x +C 6 5
Câu 27. Nguyên hàm của hàm số:     x x J 2 3 dx là: A F(x) = B. F(x) = C. F(x) = x x x x 2  x x x x  3  2 3 2 3
D. F(x) = 2  3  C C   C   C ln 2 ln 3 ln 2 ln 3 ln 2 ln 3
Câu 28. Nguyên hàm của hàm số: 2 I  (x  3x 1)dx  là: 1 3 1 3 A. F(x) 3 2  x  x  C B. F(x) 3 2  x  x  x  C 3 2 3 2 1 3 3 1 C. F(x) 3 2  x  x  x  C D. 3 2 F(x)  x  x  x  C . 3 2 2 2 4 2x 3
Câu 29. Nguyên hàm F x của hàm số f x x 0 là 2 x 3 2x 3 3 x 3 A. F x C B. F x C 3 x 3 x 3 3 2x 3 C. 3 F x 3x C D. F x C x 3 x
Câu 30. Trong các hàm số sau đây , hàm số nào là nguyên hàm của ( ) x
f x e  cos x A. x
e  sin x B. x e  sin x C. x e   sin x D. x e  sin x Câu 31. Tính: 5 P  (2x  5) dx  6 (2x  5) 6 1 (2x  5) A. P   C B. P  .  C 12 6 2 6 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 6 (2x  5) 6 (2x  5) C. P   C D. P   C . 2 5
Câu 32: Hàm số nào sau đây là một nguyên hàm của sin2x A. 2 sin x B. 2cos2x C. -2cos2x D. 2sinx d
Câu 33. Tìm  x ta được 3x 1 3 1 A.   ln 3x 1   C
B. ln 3x 1  C C. ln 3x 1  C D.   C 3x  2 1 3 5 Câu 34. Tìm 2x   1 x d ta được 1 6 1 6 4 4 A. 2x   1  C B. 2x   1  C C. 2x   1  C D. 52x   1  C 12 6
Câu 35. Nguyên hàm của hàm số f x   x  2 ( ) 1 x là 2 3 x x 2 3 x x A. x    C B.    C C. 1 2x C D.  2  3 x x x  C 2 3 2 3
Mức độ thông hiểu.
Câu 36. Một nguyên hàm của hàm số: 4 I  sin x cos xdx  là: 5 sin x 5 cos x 5 sin x A. I   C B. I   C C. I    C D. 5 I  sin x  C 5 5 5 1
Câu 37. Trong các hàm số sau đây , hàm số nào là nguyên hàm của f (x)  2 cos (2x 1) 1 1  1 1 A. B. C. tan(2x 1) D. co t(2x 1) 2 sin (2x 1) 2 sin (2x 1) 2 2 3 12 x 1 1
Câu 38. Nguyên hàm F x của hàm số f x x 0 là 3 x
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 1 3 1 A. F x x 3 ln x C B. F x x 3 ln x C 2 x 2x 2 x 2x 3 1 3 1 C. F x x 3 ln x C D. F x x 3 ln x C 2 x 2x 2 x 2x 2x 3
Câu 39. F x là nguyên hàm của hàm số f x x 0 , biết rằng F 1 1. F x là 2 x biểu thức nào sau đây 3 3 A. F x 2x 2 B. F x 2 ln x 2 x x 3 3 C. F x 2x 4 D. F x 2 ln x 4 x x b
Câu 40. Tìm một nguyên hàm F x của hàm số f x ax x 0 , biết rằng F 1 1 , 2 x F 1 4 , f 1
0 . F x là biểu thức nào sau đây 1 1 A. 2 F x x 4 B. 2 F x x 2 x x 2 x 1 7 2 x 1 5 C. F x D. F x 2 x 2 2 x 2 2 Câu 41. Hàm số x F x
e là nguyên hàm của hàm số 2 A. 2 . x f x x e B. 2x f x e 2 x e 2 C. f x D. 2. x f x x e 1 2x x 2 x
Câu 42. Hàm số nào dưới đây không là nguyên hàm của hàm số f x 2 12 x 1 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 x x 1 2 x x 1 A. B. x 1 x 1 2 x x 1 2 x C. D. x 1 x 1 2 2 x 1
Câu 43. Nguyên hàm F x của hàm số f x x 0 là x 3 x 1 3 x 1 A. F x 2x C B. F x 2x C 3 x 3 x 3 3 x 3 x x x 3 3 C. F x C D. F x C 2 x 2 x 2 2
Câu 44. Một nguyên hàm của hàm số: y = sinx.cosx là: 1 1 A.  cos 2x +C B. cos . x sin x +C
C. cos8x + cos2x+C D.  cos 2x +C . 2 4
Câu 45. Một nguyên hàm của hàm số: y = cos5x.cosx là: 1  1 1  1  sin 6x sin 4x  A. cos6x B. sin6x C. sin 6x  sin 4  x  D.     2  6 4  2  6 4 
Câu 46: Nguyên hàm của hàm số f(x) = 2sin3xcos2x 1 1
A.  cos 5x  cos x C
B. cos5x  cos x C 5 5
C. 5cos5x  cos x C D. Kết quả khác
Câu 47: Tìm hàm số f(x) biết rằng f’(x) = 2x + 1 và f(1) = 5 12 3 A. x2 + x + 3 B. x2 + x - 3 C. x2 + x D. Kết quả khác
Câu 48: Tìm hàm số f(x) biết rằng f’(x) = 4 x x và f(4) = 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 2 8 2 x x 40 8 x x 40 8x x x 40 A.  x  B.   C.   D. Kết quả khác 3 2 3 3 2 3 3 2 3 2
Câu 49: Nguyên hàm của hàm số x xe dx  là 2 x 2 e 2 2 A. x xe C B.  C C. x e C D. x x e 2
Câu 50: Tìm hàm số y f( ) x biết 2 f ( ) x (x ) x (x 1) và f(0) 3 4 2 x x 4 2 x x A. y f( ) x 3 y f( ) x 3 4 2 B. 4 2 4 2 x x C. y f( ) x 3 y f x x 4 2 D. 2 ( ) 3 1 Câu 51: Tìm 3 (sin x 1) cos xdx là: 4 (cos x 1) 4 sin x A. C C 4 B. 4 4 (sin x 1) C. C x C 4 D. 3 4(sin 1) dx Câu 52: Tìm 2 x 3x là: 2 1 1 x 2 A. ln ln C ln C x 2 x 1 B. x 1 x 1 C. ln C x x C x 2 D. ln( 2)( 1) Câu 53: Tìm xcos2xdx là: 1 1 1 1 A. xsin 2x cos2x C xsin2x cos2x C 2 4 B. 2 2 12 4 2 x sin2x C. C 4 D. sin 2x C
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 54: Lựa chọn phương án đúng:
A. cot xdx  ln sin x C
B. sin xdx  cos x C  1 1 C. dx   C
D. cos xdx  sin x C  2 x x
Câu 55: Tính nguyên hàm 3 sin x cos xdx  ta được kết quả là: 1 1 A. 4 sin x C B. 4 sin x C C. 4 sin x C D. 4
 sin x C 4 4 Câu 56: Cho 2
f (x)  3x  2x  3 có một nguyên hàm triệt tiêu khi x  1. Nguyên hàm đó là kết quả nào sau đây? A. 3 2
F(x)  x x  3x B. 3 2
F(x)  x x  3x 1 C. 3 2
F(x)  x x  3x  2 D. 3 2
F(x)  x x  3x 1 x(2  x)
Câu 57. Hàm số nào sau đây không phải là nguyên hàm của hàm số f (x)  2 (x 1) 2 x x 1 2 x x 1 2 x x 1 2 x A. B. C. D. x 1 x 1 x 1 x 1
Câu 58: Kết quả nào sai trong các kết quả sau: x 1  x 1 2 5   1 1 4 4 x x   2 1 A. dx    C  B. dx  ln x   C  10x 5.2x.ln 2 5x.ln 5 3 4 x 4x 2 x 1 x 1 C. dx  ln  x C  D. 2
tan xdx  tan x x C  2 1 x 2 x 1  4 
Câu 59: Tìm nguyên hàm 3 2 x dx    x  5 3
x  4 ln x C
x  4 ln x C 12 A. 3 5 B. 3 5 3 5 5
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 3 C. 3 5
x  4 ln x C D. 3 5
x  4 ln x C 5 5 x
Câu 60: Kết quả của dx  là: 2 1 x 1  1 A. 2 1 x C B.  C C.  C D. 2
 1 x C 2 1 x 2 1 x
Câu 61: Tìm nguyên hàm 2 1 (  sin x) dx  2 1 2 1
A. x  2 cos x  sin 2x C
B. x  2 cos x  sin 2x C 3 4 3 4 2 1 2 1
C. x  2 cos 2x  sin 2x C
D. x  2 cos x  sin 2x C 3 4 3 4 Câu 62: Tính 2 tan xdx  , kết quả là: 1
A. x  tan x C
B. x  tan x C
C. x  tan x C D. 3 tan x C 3
Câu 63: Trong các mệnh đề sau đây, mệnh đề nào sai ? 1 1 (I ) sin x sin 3xdx
(sin 2x - sin 4x) C 4 2 1 2 3 (II ) tan xdx tan x C 3 x 1 1 2 (III ) dx ln(x 2x 3) C 2 x 2x 3 2 A. Chỉ (I) và (II) B. Chỉ (III) C. Chỉ (II) và (III) D. Chỉ (II) 4 1
Câu 64. Trong các hàm số sau đây , hàm số nào là nguyên hàm của f (x)    5 1 3x 2 x 4  4 4 4 12 A. ln 1 3x
x  5x B. ln 1 3x C. ln 1 3x  5x D. ln 1 3x x 3 3 3 3 6
Câu 65. Nguyên hàm của hàm số f ( ) x  x là
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 2 3 A. x  C B.  C C. x x  C D. x x  C 2 x 3 2
Câu 66. Hàm số ( )  x F x
e  t anx  C là nguyên hàm của hàm số f ( ) x nào ? x 1 x 1 A. f ( ) x  e  B. f ( ) x  e  2 sin x 2 sin x x 1 x 1 C. f ( ) x  e  D. f ( ) x  e  2 os c x 2 os c x
Câu 67. Nguyên hàm F(x) của hàm số f x  3 x  2 ( ) 4
3x  2 trên R thoả mãn điều kiện F(1)  3 là A. 4 x  3 x  2x  3 B. 4 x  3 x  2x  4 C. 4 x  3 x  2x  4 D. 4 x  3 x  2x  3
Câu 68. Một nguyên hàm của hàm số f ( ) x  2sin 3 . x o c s3x là 1 A. cos 2x B.  1 cos 6x C.  cos3 . x sin3x D.  1 sin 2x 4 6 4
Câu 69: Một nguyên hàm của hàm số 2
y x 1 x là: 2 2 x 1
A. F x   2 1 x
B. F x   1 x 2 2 2 2 1 1
C. F x   1 x 2 2
D. F x   1 x 3 2 3 3
Câu 70: Một nguyên hàm của hàm số 3 y  sin . x cos x là: x x x A. F x 4 sin  1 B. F x 4 2 sin cos  4 4 2 x x x x C. F x 2 4 cos cos   D. F x 2 4 cos cos    2 4 2 4 12 7 2
Câu 71: Một nguyên hàm của hàm số  3 . x y x e là:
Group Nhóm Toán | Trắc nghiệm 2016-2017 A.   2  3 x F x e B.   2 3 x F x e 2 2 3x 2 x C. F x 2 xe D. F x 3 xe 2 2 2 ln x
Câu 72: Một nguyên hàm của hàm số y  là: x x A. F x 2  2ln x B. F x 2 ln  2 C. F x 2  ln x D. F x 2  ln x
Câu 73: Một nguyên hàm của hàm số  2  x y x e   1 là: A.   x
F x e x   2 2 1  x B.   x
F x e x   2 2 1  4x C.   x
F x e   x 2 2 1  4x D.   x
F x e   x 2 2 1  x
Câu 74: Một nguyên hàm của hàm số y xsin 2x là: x x A. F x 1
 cos 2x  sin 2x B. F x 1
  cos 2x  sin 2x 2 4 2 2 x x C. F x 1
  cos 2x  sin 2x D. F x 1
  cos 2x  sin 2x 2 2 2 4 ln 2x
Câu 75: Một nguyên hàm của hàm số y  là: 2 x 1 1
A. F x   ln 2x  2
B. F x  ln 2x  2 x x 1 1
C. F x   ln 2x  2
D. F x   2  ln 2xx x t anx e
Câu 76: Một nguyên hàm của hàm số f(x) = là: 2 os c x 12 t anx 8 e A. B. tanx e C. tanx e  t anx D. tanx e .t anx 2 os c x
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 77: Nguyên hàm của hàm số 2
y  (t anx  cot x) là: 1 A. F x 3
 (t anx  cot x)  C
B. F x  t anx-cot x C 3 1 1
C. F x  2(t anx  cot x)(  )  C
D. F x  t anx+cot x C 2 2 o c s x sin x 1
Câu 78: Nguyên hàm của hàm số: y = là: 2 2 o
c s x sin x 1 x A. t anx.cot x  C B.  t anx- cot x  C C. t anx- cot x  C D. sin  C . 2 2 1
Câu 79: Nguyên hàm của hàm số: y = là: 1 4x10 3 7 3 7 12 A. 1 4x   3  C B. 1 4x  3  C 7 7 7 3 7 3 C. 1 4x  3  C D. 1 4x   3  C . 28 28 2 x
Câu 80: Một nguyên hàm của hàm số: y = là: 3 7x 1 1 1 1 A. 3 ln 7x 1 B. 3 ln 7x 1 C. 3 ln 7x 1 D. 3 ln 7x 1 7 21 14
Câu 81: Nguyên hàm của hàm số f(x) = x (2 x e e  ) là: A. 2 x
e x C B. xx e eC C. 2 x
e x C D. 2 x
e  2x C
Mức độ vận dụng. cos x
Câu 82: Một nguyên hàm của hàm số: y = là: 5sin x  9 12 1 1 A. ln 5sin x  9 B. ln 5sin x  9 C.  ln 5sin x  9 D. 5ln 5sin x  9 9 5 5
Group Nhóm Toán | Trắc nghiệm 2016-2017 Câu 83: Tính:  . x P x e dx  A.  . x P x e C B. x
P e C C.  . x x P
x e e C D.  . x x P
x e e C . b
Câu 84: Tìm hàm số f(x) biết rằng f '(x)  ax+ , f '( ) 1  , 0 f ( ) 1  , 4 f ( ) 1  2 2 x 2 2 2 x 1 5 x 1 5 x 1 5 A.   B.   C.   D. Kết quả khác 2 x 2 2 x 2 2 x 2 Lược giải:
Sử dụng máy tính kiểm tra từng đáp án: - Nhập hàm số
- Dùng phím CALC để kiểm tra các điều kiện f '(1) 0, f (1) 4, f ( 1) 2 - Đáp án đúng: B
Câu 85: Hàm số nào sau đây là một nguyên hàm của hàm số 2 f (x) x k với k 0? x k A. 2 2 f (x) x k ln x x k 2 2 1 x B. 2 2 f (x) x k ln x x k 2 2 k C. 2 f (x) ln x x k 2 1 D. f (x) 2 x k 13 Lược giải: 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 x 1 2 x k 1 x x k 2 2 2 x k 2 x k ln x x k x k x k 2 2 2 2 2 2 2 x k x x k 2 10x - 7x 2 Câu 86: Nếu 2 f (x) (ax bx
c) 2x -1 là một nguyên hàm của hàm số g(x) trên 2x -1 1 khoảng ;
thì a+b+c có giá trị là 2 A. 3 B. 0 C. 4 D. 2 Lược giải: 2 2 5ax ( 2a 3b)x b c 10x 7x 2 2 (ax bx c) 2x 1 2x 3 2x 3 a 2 b 1 a b c 2 c 1
Câu 87: Xác định a, b, c sao cho 2 g(x) (ax bx
c) 2x - 3 là một nguyên hàm của hàm số 2 20x - 30x 7 3 f (x) trong khoảng ; 2x - 3 2 A.a=4, b=2, c=2 B. a=1, b=-2, c=4 C. a=-2, b=1, c=4 D. a=4, b=-2, c=1 Lược giải: 2 2 5ax ( 6a 3b)x 3b c 20x 30x 7 2 (ax bx c) 2x 3 2x 3 2x 3 a 4 b 2 13 c 1 1
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 88: Một nguyên hàm của hàm số: 2
f (x)  x sin 1  x là: A. 2 2 2
F(x)   1 x cos 1  x  sin 1  x B. 2 2 2
F(x)   1 x cos 1  x  sin 1  x C. 2 2 2
F(x)  1 x cos 1  x  sin 1  x D. 2 2 2
F(x)  1  x cos 1  x  sin 1  x Lược giải: Đặt 2 I (x sin 1 x )dx
- Dùng phương pháp đổi biến, đặt 2 t 1 x ta được I t sin tdt
- Dùng phương pháp nguyên hàm từng phần, đặt u , t dv sin tdt - Ta được 2 2 2 I t cos t cos tdt 1 x cos 1 x sin 1 x C
Câu 89: Trong các hàm số sau: (I) 2 f (x) x 1 (II) 2 f (x) x 1 5 1 1 (III) f (x) (IV) f (x) - 2 2 x 1 2 x 1
Hàm số nào có một nguyên hàm là hàm số 2 F (x) ln x x 1 A. Chỉ (I) B. Chỉ (III) C. Chỉ (II) D. Chỉ (III) và (IV) Lược giải: x 1 2 x 1 1 2 ln x x 1 2 2 x x 1 x 1 2 1
Câu 90: Một nguyên hàm của hàm số 3 f (x) x
là hàm số nào sau đây: x 3 3 12 1 1 A. 3 2 6 5 F (x) x x x ln x B. 3 F (x) x 5 5 3 x 13 2 2 3 12 C. 3 F (x) x x x D. 3 2 5 6 F (x) x x ln x x 5 5
Group Nhóm Toán | Trắc nghiệm 2016-2017 Lược giải: 2 3 12 1 3 2 6 5 3 x x x ln x x 5 5 x
Câu 91: Xét các mệnh đề 2 x x (I) F(x) x
cos x là một nguyên hàm của f (x) sin - cos 2 2 4 x 3 (II) F(x)
6 x là một nguyên hàm của 3 f (x) x 4 x (III) F(x)
tan x là một nguyên hàm của f (x) -ln cos x Mệnh đề nào sai ? A. (I) và (II) B. Chỉ (III) C. Chỉ (II) D. Chỉ (I) và (III) Lược giải: ln cos x
tan x (vì ln cos x là một nguyên hàm của tanx)
Câu 92: Trong các mệnh đề sau đây mệnh đề nào đúng ? xdx 1 (I) 2 ln(x 4) C 2 x 4 2 1 (II) cot xdx - C 2 sin x x 1 (III) 2cos 2cos sin - x e xdx e C 2 A. Chỉ (I) B. Chỉ (III) 13 3 C. Chỉ (I) và (II) D. Chỉ (I) và (III)
Group Nhóm Toán | Trắc nghiệm 2016-2017 Lược giải: 2 xdx 1 d(x 4) 1 2 ln(x 4) C 2 2 x 4 2 x 4 2 1 1 2cos x 2cos x 2cos x e sin xdx e d(cos x) e C 2 2
Câu 93: Tìm nguyên hàm x 2 2 F(x) e (a tan x b tan x
c) là một nguyên hàm của x 2 3 f (x) e tan x trên khoản ; 2 2 x 1 2 1 x 1 2 2 A. 2 2 F (x) e ( tan x tan x ) B. 2 2 F (x) e ( tan x tan x ) 2 2 2 2 2 2 x 1 2 2 x 1 2 1 C. 2 2 F (x) e ( tan x tan x ) D. 2 2 F (x) e ( tan x tan x ) 2 2 2 2 2 2 Lược giải:
- Có thể dùng đạo hàm để kiểm tra từng đáp án.
- Hoặc tìm đạo hàm của x 2 2 F(x) e (a tan x b tan x
c) rồi đồng nhất với x 2 3 f (x) e tan x x 2 2 x 2 2 2 F '(x) 2e (a tan x b tan x c) e 2a(1 tan x) tan x ( b 1 tan x) x 2 3 2 e 2a tan x ( 2a ) b tan x (2a 2 ) b tan x b 2c
F (x) là nguyên hàm của f(x) nên F '(x) f (x) Suy ra 1 2 1 a a 2 2a b 0 2 b Đáp án đúng: B 2a 2b 0 2 1 b 2c 0 c 2 13 4
Group Nhóm Toán | Trắc nghiệm 2016-2017 x e
Câu 94: Nguyên hàm của hàm số: y = là: 2x x e x e x e x e ln 2 A.  C B.  C C.  C D.  C x 2x ln 2 (1  ln 2)2 .2x x 2x x
Câu 95: Nguyên hàm của hàm số: y = 2 os c là: 2 1 1 1 x 1 x A. (x  sin ) x  C B. (1  os c ) x  C C. os c  C D. sin  C . 2 2 2 2 2 2
Câu 96: Nguyên hàm của hàm số: y = cos2x.sinx là: 1 1 1 A. 3 cos x  C B. 3 cos x  C C. 3 sin x  C D.  3 cos x  C . 3 3 3 x e
Câu 97: Một nguyên hàm của hàm số: y = là: x e  2 A.2 ln( x e  2) + C B. ln( x e  2) + C C. exln( x e  2) + C D. 2x e + C. Câu 98: Tính: 3 P  sin xdx  1 A. 2 P  3sin .
x cos x C B. 3
P   sin x  sin x C 3 1 1 C. 3
P   cos x  o
c s x C D. 3 P  o
c sx  sin x C . 3 3 3 x
Câu 99: Một nguyên hàm của hàm số: y  là: 2 2  x 1 A. 2
x 2  x B.   2 x  4 2 2  x 3 1 1 C. 2 2  x 2  x D.   2 x  4 2 2  x 3 3 13 5 TÍCH PHÂN
Mức độ nhận biết
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 Câu 1: Tích phân 2
I  (3x  2x 1)dx  bằng: 0 A. I  1 B. I  2 C. I  3 D. Đáp án khác  2
Câu 2: Tích phân I  sin xdx  bằng: 0 A. -1 B. 1 C. 2 D. 0 1 Câu 3: Tích phân 2
I  (x 1) dx  bằng: 0 8 7 A. B. 2 C. D. 4 3 3 1 Câu 4: Tích phân x 1 I e   dx  bằng: 0 A. 2 e e B. 2 e C. 2 e 1 D. e + 1 4 x 1
Câu 5: Tích phân I dx  bằng: x  2 3 A. -1 + 3ln2 B. 2
  3ln 2 C. 4ln 2 D. 1 3ln 2 1 x 1
Câu 6: Tích phân I dx  bằng: 2 x  2x  5 0 8 1 8 8 8 A. ln B. ln C. 2 ln D. 2  ln 5 2 5 5 5 e 1
Câu 7: Tích phân I dx  bằng: x 1 1 A. e B. 1 C. -1 D. e 13 1 6 Câu 8: Tích phân x I e dx  bằng : 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 A. e 1 B. 1 e C. e D. 0 2 Câu 9: Tích phân 2  2 x I e dx  bằng : 0 A. 4 e B. 4 e 1 C. 4 4e D. 4 3e 1 2  1  Câu 10: Tích phân 2 I x dx   bằng: 4  x  1 19 23 21 25 A. B. C. D. 8 8 8 8 e 1
Câu 11: Tích phân I dx  bằng: x  3 1  3 e  A. ln e  2 B. ln e  7 C. ln   D. ln 4  e  3   4  3
Câu 12: Tích phân I   3 x   1dx bằng: 1  A. 24 B. 22 C. 20 D. 18 2 1
Câu 13: Tích phân I    dx bằng: 2x  2 1 1 1 1 1 A. 1 B. C. D. 2 15 4 1 dx
Câu 14: Tích phân I   bằng: 2 x  5x  6 0 4 A. I = 1 B. I  ln C. I = ln2 D. I = ln2 3 1 xdx
Câu 15: Tích phân: J   bằng: 3 (x  1) 0 1 1 13 A. J  B. J  C. J =2 D. J = 1 8 4 7 3 x
Câu 16: Tích phân K dx  bằng: 2 x 1 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 8 1 8 A. K = ln2
B. K = 2ln2 C. K  ln D. K  ln 3 2 3 3 Câu 17: Tích phân 2 I x 1 x dx  bằng: 1 4  2 8  2 2 4  2 8  2 2 A. B. C. D. 3 3 3 3 1
Câu 18: Tích phân I x
 1 x19 dx bằng: 0 1 1 1 1 A. B. C. D. 420 380 342 462 e 2  ln x
Câu 19: Tích phân I dx  bằng: 2x 1 3  2 3  2 3  2 3 3  2 2 A. B. C. D. 3 3 6 3  6
Câu 20: Tích phân I  tanxdx  bằng: 0 3 3 2 3 A. ln B. - ln C. ln D. Đáp án khác. 2 2 3 1 dx
Câu 21. Tích phân  bằng: x  2 0 A.  ln 2 B. ln 3 C.  ln 3 D. ln 2 1 2dx Câu 22. Tích phân  ln a
. Giá trị của a bằng: 3  2x 0 13 A. 1 B. 2 C. 3 D. 4 8
Group Nhóm Toán | Trắc nghiệm 2016-2017 1
Câu 23. Cho tích phân 3 1 xdx   , với cách đặt 3
t  1  x thì tích phân đã cho bằng với tích phân nào 0 ? 1 1 1 1 A.  3 3 t dt B.  2 3 t dt C.  3tdt D. 3tdt 0 0 0 0 e ln x Câu 24. Tích phân dx  bằng: x 1 1 A.  3 B. 1 C. ln 2 D. 2 1
Câu 25. Tích phân I = xdx  có giá trị là: 0 3 1 2 A. B. C. D. 2 2 2 3  4
Câu 26. Tích phân I = cos 2xdx  có giá trị là: 0 1 A. B. 1 C. -2 D. -1 2 1 x
Câu 27. Tích phân I = dx  có giá trị là: 3 (x 1) 0 1 1 1 1 A. B. C. D. 2 4 8 8  2
Câu 28. Tích phân I = sin 3 . x cos xdx  có giá trị là: 13 0 9
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 1 1 A. B. C. D. 2 3 2 4 1 3 x  2 2x  3
Câu 29. Tích phân I =  dx bằng: x  2 0 1 3 1 2 1 2
A.  3ln B.  3ln C.  3ln D. 3 2 3 3 3 3 1 Câu 30. I =  2 (x  2 )( 1 x  ) 1 dx 0 4 6 4 1 A. B. C.  D. 5 5 5 5  6
Câu 31. Tích phân I =  2
sin xdx có giá trị là: 0  3  3  3  3 A.  B.  C.   D.  12 8 12 8 12 8 12 4 2
Câu 32. Tích phân I =   3 3x  2 x  4x   1   3 2x  2 x  3x  
1 dx có giá trị là: 1 13 5 2 5 A. B. C. D.  12 12 3 12  4 x
Câu 33. Tích phân  2 2 sin bằng: 2 0  2  2  2  2 A.  B.  C.   D.   4 2 4 2 4 2 4 2 14 1 0
Câu 34. Cho tích phân 3 1 xdx   , với cách đặt 3
t  1  x thì tích phân đã cho bằng với tích phân nào 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 ? 1 1 1 1 A.  3 3 t dt B.  2 3 t dt C.  3tdt D. 3tdt 0 0 0 0 1 xdx Câu 35. Tích phân dx  bằng: 2x  1 0 1 1 A. B. 1 C. ln 2 D. 3 2 1 3
Câu 36. Gía trị của 3 x e dx bằng : 0 A. e3 - 1 B. e3 + 1 C. e3 D. 2e3 1 2
Câu 37. Tích Phân (x   1) dx bằng : 0 1 A. 3 B. 1 C. 3 D. 4 1 Câu 38. Tích Phân 3x   1dx bằng : 0 14 14 A. 9 B. 0 C. 9 D. 3 1
Câu 39. Tích Phân x 3x   1dx bằng 0 7 A. 9 B. 9 C. 3 D. 1 14 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 5x 13
Câu 40. Tích Phân  dx 2 x 5x 6 bằng 0   43 4 43 3 43 4 47 4 A. ln B. ln C.  ln D. ln 7 3 7 4 7 3 3 3
Mức độ thông hiểu.  4 Câu 41: Tích phân 2 I  tan xdx  bằng: 0   A. I = 2 B. ln2 C. I  1  D. I  4 3 1 Câu 42: Tích phân 2
L x 1 x dx  bằng: 0 1 1 A. L  1  B. L  C. L  1 D. L  4 3 2
Câu 43: Tích phân K  (2x 1) ln xdx  bằng: 1 1 1 1 A. K  3ln 2  B. K
C. K = 3ln2 D. K  2ln 2  2 2 2 
Câu 44: Tích phân L x sin xdx  bằng: 0 A. L =  B. L =  C. L = 2 D. K = 0  3
Câu 45: Tích phân I x cos xdx  bằng: 0  3 1  3 1  3 1   3 A. B. C.  D. 14 6 2 6 2 2 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 ln 2 Câu 46: Tích phân x I xe dx  bằng: 0 1 1 1 1 A. 1 ln 2 B. 1 ln 2 C. ln 2   1 D. 1 ln 2 2 2 2 4 2 ln x
Câu 47: Tích phân I dx  bằng: 2 x 1 1 1 1 1 A. 1 ln 2 B. 1 ln 2 C. ln 2   1 D. 1 ln 2 2 2 2 4 5 dx Câu 48: Giả sử  ln K  . Giá trị của K là: 2x 1 1 A. 9 B. 8 C. 81 D. 3 3 x 2 Câu 49: Biến đổi dx
thành f t dt
, với t  1 x . Khi đó f(t) là hàm nào trong các hàm 1 1 x 0 1 số sau: A. f t 2  2t  2t B.   2
f t t t C.   2
f t t t D. f t 2  2t  2t 1 dx
Câu 50: Đổi biến x = 2sint tích phân  trở thành: 2  0 4 x     6 6 6 1 3 A. tdt  B. dt  C. dt  D. dtt 0 0 0 0  2 dx
Câu 51: Tích phân I   bằng: 2  sin x 4 A. 4 B. 3 C. 1 D. 2  2 e cos ln x
Câu 52: Cho I dx 14  , ta tính được: x 1 3 A. I = cos1 B. I = 1 C. I = sin1 D. Một kết quả khác
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 3 3
Câu 53: Tích phân I dx  bằng: 2  2 x x 3    A. B.  C. D. 6 3 2 b b c
Câu 54: Giả sử f (x)dx  2 
và f (x)dx  3 
và a < b < c thì f (x)dx  bằng? a c a A. 5 B. 1 C. -1 D. -5
Câu 55: Tính thể tích khối tròn xoay tạo nên do quay quanh trục Ox hình phẳng giới hạn bởi các
đường y = (1 – x2), y = 0, x = 0 và x = 2 bằng: 8 2 46 5 A. B. 2 C. D. 3 15 2  16 4
Câu 56: Cho I xdx
và J  cos 2xdx  . Khi đó: 1 0 A. I < J B. I > J C. I = J D. I > J > 1 4
Câu 57: Tích phân I x  2 dx  bằng: 0 A. 0 B. 2 C. 8 D. 4  Câu 58: Tích phân 2
I x sin xdx  bằng : 0 A. 2   4 B. 2   4 C. 2 2  3 D. 2 2  3 1 dx
Câu 59: Kết quả của  là: 1 x 1
A. 0 B.-1 C. 2 D. Không tồn tại 14 4 2 2 Câu 60: Cho f
 xdx  3.Khi đó 4 f
 x3dx  bằng: 0 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 A. 2 B. 4 C. 6 D. 8 3 x
Câu 61. Tích phân I = dx  có giá trị là: 2 2 x 1 A. 2 2 B. 2 2  3 C. 2 2  3 D. 3 1 1
Câu 62. Tích phân I = dx  có giá trị là: 2 x  4x  3 0 1 3 1 3 1 3 1 3 A.  ln B. ln C. ln D.  ln 3 2 3 2 2 2 2 2 3 x
Câu 63. Tích phân I = dx  có giá trị là: 2 2 x 1 A. 2 2 B. 2 2  3 C. 2 2  3 D. 3 2
Câu 64. Cho f x  3 3 2
x x  4x 1 và gx  2 3 2
x x  3x 1. Tích phân
f x  gxdx  bằng với 1 tích phân: 2 1 2 A.  3 x  2
2x x  2dx B.  3 x  2
2x x  2dx    3 x  2
2x x  2dx 1 1 1 1 2 C.  3 x  2
2x x  2dx    3 x  2
2x x  2dx D. tích phân khác 1 1  2 sin x 3 .cos x Câu 65. Tích phân dx  bằng: 2 cos x  1 0 1 1 1 1 1 1 1 1 A.  ln 2 B.  ln 2 C.  ln 2 D.  ln 2 3 2 2 2 2 3 2 2 14 5
Group Nhóm Toán | Trắc nghiệm 2016-2017  1 x 2 cos x
Câu 66. Cho tích phân I dx  và J dx
, phát biểu nào sau đây đúng: x  3 3sin x  12 0 0 1 A. I J B. I  2 C. J  ln 5 D. I  2J 3 1
Câu 67. Cho tích phân I x2 1 xdx   bằng: 0 1 1 1 3 4  x  3 x
A. x3  x4dx B.   x  C. 2 (x  ) D. 2 3 4   3 0 0 0 a Câu 68. Tích phân 2 2 2 x
a x dx   0  a bằng: 0 . 4 a . 4 a . 3 a . 3 a A. B. C. D. 8 16 16 8 8 x 1 Câu 69. Tích phân dx   bằng: 3 x 1 141 142 8 A. B. C. D. một kết quả khác 10 10 5 e 2 1 ln x
Câu 70. Tích phân I =  
dx có giá trị là: x 1 1 2 4 4 A. B. C.  D. 3 3 3 3 1 2
Câu 71. Tích phân I =  x 1 . x e
dx có giá trị là: 0 2 2 2 2 14 e e e e e e e e A. B. C. D. 6 2 3 2 3
Group Nhóm Toán | Trắc nghiệm 2016-2017 1
Câu 72. Tích phân I = 1 x
  exdx có giá trị là: 0
A. e + 2 B. 2 - e C. e - 2 D. e 0 cos x
Câu 73. Tích phân I = 
dx có giá trị là:  2  sin x  2 A. ln3 B. 0 C. - ln2 D. ln2  6 3
Câu 74. Tích Phân sin . x cos xdx bằng: 0 1 A. 6 B. 5 C. 4 D. 64 1 1 2 Câu 75. Nếu f ( ) x dx  =5 và f ( ) x dx  = 2 thì  f ( ) x dx bằng : 0 2 0 A. 8 B. 2 C. 3 D. -3  3
Câu 76. Tích Phân I = tan xdx  là : 0 1 1 A. ln2 B. –ln2 C. 2 ln2 D. - 2 ln2 1
Câu 77. Cho tích phân I x1 xdx   bằng: 0 1 1 1 2 3  x  3 x
A.  x2  x3 dx B.  x C. 2 (x  ) D. 2 14   2 3   3 0 0 0 7
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 2
Câu 78. Tích Phân I = ln(x   ) x dx là : 2 A. 3ln3 B. 2ln2 C. 3ln3-2 D. 2-3ln3  4
Câu 79. Tích Phân I =  . x cosx dx là : 0  2  2 2  2 2 A. 1 B. C.  1 D.  1 4 3 8 2 8 2 3
Câu 80. Tích phân I = 2 ln[2  x(x  3)]dx  có giá trị là: 2 A. 4  ln 2 3 B. 5ln 5  4ln 2 3 C. 5ln 5  4ln 2 3 D. 5ln 5  4ln 2  3
Mức độ vận dụng. b
Câu 81: Biết 2x  4dx  0 .Khi đó b nhận giá trị bằng: 0
A. b  0 hoặc b  2
B. b  0 hoặc b  4
C. b  1 hoặc b  2
D. b  1 hoặc b  4 1
Câu 82: Để hàm số f x  asin x b thỏa mãn f   1  2 và f
 xdx  4 thì a, b nhận giá trị : 0
A. a   ,b  0
B. a   ,b  2 14
C. a  2 ,b  2
D. a  2 ,b  3 8
Group Nhóm Toán | Trắc nghiệm 2016-2017  dx Câu 83: 4 I   bằng 0 4 cos x 2 1 tan x 1
A. 1 B. 0 C. 2 D. Không tồn tại  4 2
Câu 84: Giả sử I  sin 3xsin 2xdx  a  b  2 khi đó a+b là 0 1 3 3 1 A.   6 B. 10 C. 10 D. 5 0 2 3x  5x 1 2
Câu 85: Giả sử I  dx  aln  b  a  b x  2 3 . Khi đó giá trị 2 là 1  A. 30 B. 40 C. 50 D. 60 m
Câu 86. Tập hợp giá trị của m sao cho (2x  4)dx  = 5 là : 0 A. {5} B. {5 ; -1} C. {4} D. {4 ; -1} 5 1 Câu 87. Biết rằng dx
 2x1 = lna . Gía trị của a là : 1 A. 9 B. 3 C. 27 D. 81 1 M M
Câu 88. Biết tích phân x3 1  xdx   , với
là phân số tối giản. Giá trị M N bằng: N N 0 A. 35 B. 36 C. 37 D. 38
Câu 89. Tìm các hằng số A , B để hàm số f(x) = A.sinx + B thỏa các điều kiện: 14 9
Group Nhóm Toán | Trắc nghiệm 2016-2017 2
f ' (1) = 2 ; f (x)  4  dx 0       2 2 A   2 A  A   A  A.   B.   C.  2 D.   B  2 B  2 B  2 B  2 2
HD: f ' (x) = A.cosx  f ' (1) = - A mà f ' (1) = 2  A =   2 2
f (x)dx  
...= 2B mà f (x)  4  dx  B = 2 0 0 a x
Câu 90. Tìm a>0 sao cho 2 . x e dx  4  0 1 1 A. 4 B. C. D. 2 4 2 HD: a
Sử dụng phương pháp tích phân từng phần tính được 2
I  2e (a  2)  4 Vì I=4 =>a=2 b
Câu 91. Giá trị nào của b để (2x  6)dx  0  0 A. b = 2 hay b = 3 B. b = 0 hay b = 1
C. b = 5 hay b = 0 D. b = 1 hay b = 5 b
Câu 92. Giá trị nào của a để (4x  4)dx  0  0 15 0 A. a = 0 B. a = 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 C. a = 2 D. a = -1  2 3 sin x
Câu 93. Tích phân I = dx  có giá trị là: 1 cos x 0 1 1 1 A. B. C. D. 2 3 4 2 1 1
Câu 94. Tích phân I = dx  có giá trị là: 2 x x 1 0  3  3  3  3 A. B. C. D. 3 6 4 9 7 1
Câu 95. Tích phân I = dx  có giá trị là: 3 1 x 1 0 9 3 9 3 9 2 9 2 A.  3ln B.  3ln C.  3ln D.  3ln 2 2 2 2 2 3 2 3
ỨNG DỤNG CỦA TÍCH PHÂN
Mức độ nhận biết.
Câu 1. Thể tích của khối tròn xoay được giới hạn bởi đồ thị hàm số f(x) liên tục trên đoạn a;b trục
Ox và hai đường thẳngx a ,x
b quay quanh trục Ox , có công thức là: b b A. 2 V f x dx B. 2 V f x dx 15 a a 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 b b C.V f x dx D. V f x dx a a
Câu 2. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y f x  liên tục, trục hoành và
hai đường thẳng x a ,x b được tính theo công thức: b b A. S f  xdx B. S f  xdx a a 0 b 0 b C. S f
 xdx f
 xdx D. S f
 xdx f  xdx a 0 a 0
Câu 3.Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y f x ,y f x 1   2   liên tục và
hai đường thẳng x a ,x b được tính theo công thức: b b A. S f x f x dx  B. S f x f x dx  1   2   1   2   a a b b b C. S
f x f x dx  D. S
f x dx f x dx   1   2   1    2   a a a
Câu 4. Thể tích khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các
đường sau: y f x  , trục Ox và hai đường thẳng x a ,x b xung quanh trục Ox là: b b 2 2 A. V   f  xdx B. V f  xdx a a b b 2 C. V   f  xdx D. V  2 f  xdx a a 15 2
Câu 5. Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y
x , trục hoành và hai 2 đường thẳng x 1, x 3 là :
Group Nhóm Toán | Trắc nghiệm 2016-2017 28 28 1 A. dvdt B. dvdt C. dvdt D. Tất cả đều sai. 9 3 3
Câu 6. Thể tích khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi các đường 3 y x , trục Ox, x 1, x
1 một vòng quanh trục Ox là : 6 2 A. B. 2 C. D. 7 7 2
Câu 7. Diện tích hình phẳng được giới hạn bởi đường y x x 3 và đường thẳng y 2x 1 là : 7 1 1 A. dvdt B. dvdt C. dvdt D. 5 dvdt 6 6 6
Câu 8. Thể tích của khối tròn xoay được giới hạn bởi đường y
s inx , trục hoành và hai đường thẳng x 0, x là : 2 2 3 A. B. C. D. 4 2 2 3 2 4
Câu 9. Diện tích hình phẳng được giới hạn bởi các đường y x x 1 và y x x 1 là : 8 7 7 4 A. dvdt B. dvdt C. - dvdt D. dvdt 15 15 15 15 2
Câu 10. Diện tích hình phẳng được giới hạn bởi các đường y 2x
x và đường thẳng x y 2 là : 15 3
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 5 6 1 A. dvdt B. dvdt C. dvdt D. dvdt 6 2 5 2
Câu 11. Diện tích hình phẳng được giới hạn bởi các đường y
ln x , trục hoành và hai đường 1 thẳng x ,x e là : e 1 1 1 1 A. e dvdt B. dvdt C. e dvdt D. e dvdt e e e e 3
Câu 12. Diện tích hình phẳng được giới hạn bởi các đường y x 3x ,y x và đường thẳng x 2 là : 5 99 99 87 A. dvdt B. dvdt C. dvdt D. dvdt 99 4 5 4
Câu 13. Diện tích hình phẳng giới hạn bởi 3
y x , y  0, x  1
 , x  2 có kết quả là: 17 15 14 A. B. 4 C. D. 4 4 4
Câu 14. Diện tích hình phẳng giới hạn bởi 4 2 y  1
 , y x  2x 1 có kết quả là 6 2 28 16 2 27 A. B. C. D. 5 3 15 4
Câu 15. Diện tích hình phẳng giới hạn bởi 2 y   ,
x y  2x x có kết quả là 9 7 A. 4 B. C.5 D. 2 2 15
Câu 16. Diện tích hình phẳng giới hạn bởi 2
y x  3, y x  4x  3 có kết quả là : 4
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 5 3 5 4 5 3 5 1 A. B. C. D. 6 6 6 6
Câu 17. Thể tích khối tròn xoay giới hạn bởi 2
y  2x x , y  0 quay quanh trục ox có kết quả là: 16 14 13 A. B. C. D. 15 15 15
Câu 18. Diện tích hình phẳng giới hạn bởi 2
y  x  5x 6, y  0, x  0, x  2 có kết quả là: 58 56 55 52 A. B. C. D. 3 3 3 3
Câu 19. Cho hình phẳng (H) được giới hạn bởi parabol 2 (P) : y x
2x , trục Ox và các đường thẳng x 1, x
3. Diện tích của hình phẳng (H) là : 2 4 8 A. B. C.2 D. 3 3 3
Câu 20. Cho hình phẳng (H) được giới hạn bởi đường cong 2 y x x 3 và đường thẳng y 2x
1. Diện tích của hình (H) là: 23 5 1 A. B.4 C. D. 6 6 6
Câu 21. Để tìm diện tích của hình phẳng giới hạn bởi C 3
: y x ; y  0; x  -1; x  2 một học sinh thực
hiện theo các bước như sau: 2 2 4 x 1 15 Bước I. 3 S x dx  Bước II. S
Bước III. S  4   4 4 4 1  1 
Cách làm trên sai từ bước nào? A. Bước I B. Bước II 15 C. Bước III
D. Không có bước nào sai. 5
Câu 22. Diện tích của hình phẳng giới hạn bởi C 3
: y x ; y  0; x  1  ; x  2 là:
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 17 15 19 A. B. C. D. 4 4 4 4
Câu 23. Diện tích của hình phẳng giới hạn bởi C 4 2
: y  3x  4x  5;Ox ; x  1; x  2 là: 212 213 214 43 A. B. C. D. 15 15 15 3
Câu 24. Cho hai hàm số f x và g x liên tục trên  ;
a b và thỏa mãn: 0  g x  f x, x   ; a b.
Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh Ox hình phẳng  H  giới hạn bởi các
đường: y f x, y g x , x a; x b . Khi đó V dược tính bởi công thức nào sau đây? b b A.   f
 x gx 2 dx  B. 2   f  x 2
g x dx   a a 2 b   b C.    f
 x gxdx   D. f
 x gxdxaa
Câu 25. Diện tích của hình phẳng giới hạn bởi C 2
: y  x  6x  5; y  0 ; x  0; x  1 là: 5 7 7 5 A. B. C.  D.  2 3 3 2
Câu 26. Diện tích của hình phẳng giới hạn bởi C : y  sin ;
x Ox; x  0; x   là: A. 1 B. 2 C. 3 D. 4
Câu 27. Gọi  H  là hình phẳng giới hạn bởi các đường: y  sin x;Ox; x  0; x   . Quay  H  xung
quanh trục Ox ta được khối tròn xoay có thể tích là:  2  A. B. C.  D. 2  2 2
Câu 28. Diện tích hình phẳng giới hạn bởi các đường 2
y x  4 ; Ox bằng ? 15 6 32 16 32 A. B. C. 12 D. 3 3 3
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 29. Diện tích hình phẳng giới hạn bởi các đường 3
y x  4x ; Ox ; x  3  x  4 bằng ? 119 201 A. B. 44 C. 36 D. 4 4
Câu 30. Diện tích hình phẳng giới hạn bởi các đường 2
y x ; y x  2 bằng ? 15 9 9 15 A. B. C. D. 2 2 2 2
Câu 31. Diện tích hình phẳng giới hạn bởi các đường 4 2
y x  4x ; Ox bằng ? 1792 128 128 A. 128 B. C. D.  15 15 15
Câu 32. Diện tích hình phẳng giới hạn bởi các đường 3 y x  4 ; x O ; x x  1  bằng ? 9 9 A. 24 B. C. 1 D.  4 4
Câu 33. Diện tích hình phẳng giới hạn bởi các đường y  cos ; x O ; x O ; y x   bằng ? A. 1 B. 2 C. 3 D. Kết quả khác
Câu 34. Diện tích hình phẳng giới hạn bởi các đường 3 y x  ; x Ox bằng ? 1 1 1 A. B. C. 2 D. 2 4 4
Câu 35. Gọi  H  là hình phẳng giới hạn bởi các đường 2
y  2x x ; Ox . Quay  H  xung quanh trục
Ox ta được khối tròn xoay có thể tích bằng ? 16 4 4 16 A. B. C. D. 15 3 3 15 
Câu 36. Gọi  H  là hình phẳng giới hạn bởi các đường y  tan ; x O ; x x  0; x  . Quay  H  xung 4
quanh trục Ox ta được khối tròn xoay có thể tích bằng ? 2 2 15    A. 1 B. 2  C.   D.  7 4 4 4
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 37. Gọi  H  là hình phẳng giới hạn bởi các đường 2
y  1 x ; Ox . Quay  H  xung quanh trục
Ox ta được khối tròn xoay có thể tích bằng ? 16 16 4 4 A. B. C. D. 15 15 3 3
Câu 38. Diện tích hình phẳng giới hạn bởi các đường x
y e ; y  1 và x  1 là: A. e 1 B. e C. e 1 D. 1 e
Câu 39. Diện tích hình phẳng giới hạn bởi các đường y  3 x ; x  4 ; Ox là: 16 A. B. 24 C. 72 D. 16 3
Câu 40. Cho hình (H) giới hạn bởi các đường 2
y x ; x  1; trục hoành. Quay hình (H) quanh trục
Ox ta được khối tròn xoay có thể tích là:   2 2 A. B. C. D. 5 3 3 5
Mức độ thông hiểu. 1
Câu 41. Thể tích của khối tròn xoay được giới hạn bởi các đường 3 y 2x 1 ,x 0 , y 3 , quay quanh trục Oy là: 50 480 480 48 A. B. C. D. 7 9 7 7
Câu 42. Diện tích hình phẳng được giới hạn bởi các đường y e 1 x , 1 x y e x là: e e e e A. 2 dvdt B. 1 dvdt C. 1 dvdt D. 1 dvdt 2 2 3 2 15 8
Group Nhóm Toán | Trắc nghiệm 2016-2017 2
Câu 43. Thể tích của khối tròn xoay được giới hạn bởi các đường y x. o c s x sin x , y 0, x 0, y là: 2 3 4 5 4 A. B. 4 4 3 4 3 4 C. D. 4 5
Câu 44. Diện tích hình phẳng được giới hạn bởi các đường y sin 2x,y o
c sx và hai đường thẳng x 0, x là : 2 1 1 3 1 A. dvdt B. dvdt C. dvdt D. dvdt 4 6 2 2
Câu 45. Diện tích hình phẳng giới hạn bởi 2
y x, y  sin x x 0  x    có kết quả là   A. B. C. 2 D. 2 3
Câu 46. Thể tích khối tròn xoay giới hạn bởi y  ln ,
x y  0, x e quay quanh trục ox có kết quả là: A. e B. e   1 C. e  2 D. e   1
Câu 47. Thể tích khối tròn xoay giới hạn bởi y  ln ,
x y  0, x 1, x  2 quay quanh trục ox có kết quả là:         15 A.  2 2 ln 2 1 B.  2 2 ln 2 1 C.  2 2 ln 2 1 D.  2 2ln 2 1 9
Group Nhóm Toán | Trắc nghiệm 2016-2017 2
Câu 48. Diện tích hình phẳng được giới hạn bởi các đường y x 2x và y x là : 9 7 9 A. dvdt B. dvdt C. - dvdt D. 0 dvdt 2 2 2
Câu 49. Cho hình phẳng (H) được giới hạn bởi đường cong 3 (C) : y
x , trục Ox và đường thẳng 3 x
. Diện tích của hình phẳng (H) là : 2 65 81 81 A. B. C. D.4 64 64 4
Câu 50. Thể tích vật thể quay quanh trục ox giới hạn bởi 3
y x , y  8, x  3 có kết quả là:     A.  7 5 3  9.2  B.  7 6 3  9.2  C.  7 7 3  9.2  D.  7 8 3  9.2  7 7 7 7
Câu 51. Cho hình phẳng (H) được giới hạn bởi đường cong ( ) : x C y
e , trục Ox, trục Oy và đường thẳng x
2 . Diện tích của hình phẳng (H) là : 2 e A.e 4 B. 2 e e 2 C. 3 D. 2 e 1 2 2x 1
Câu 52. Cho hình phẳng (H) được giới hạn bởi đường cong (C ) : y , trục Ox và trục Oy. x 1
Thể tích của khối tròn xoay khi cho hình (H) quay quanh trục Ox là : A. 3 B. 4 ln 2 C.(3 4 ln 2) D.(4 3 ln 2)
Câu 53. Cho hình phẳng (H) được giới hạn bởi đường cong (C ) : y
ln x , trục Ox và đường thẳng 16 x
e . Diện tích của hình phẳng (H) là : 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 A.1 B. 1 C.e D.2 e
Câu 54. Cho hình phẳng (H) được giới hạn đường cong 3 2 (C) : y x
2x và trục Ox. Diện tích của hình phẳng (H) là : 4 5 11 68 A. B. C. D. 3 3 12 3
Câu 55. Diện tích hình phẳng được giới hạn bởi hai đường y x và 2 y x là : 1 1 1 1 A. B. C. D. 2 4 5 3
Câu 56. Hình phẳng giới hạn bởi đường cong 2 y
x và đường thẳng y 4 quay một vòng quanh
trục Ox. Thể tích khối tròn xoay được sinh ra bằng : 64 128 256 152 A. B. C. D. 5 5 5 5
Câu 57. Diện tích hình phẳng giới hạn bởi y  sin ; x y  cos ;
x x  0; x   là: A. 2 B. 3 C. 3 2 D. 2 2
Câu 58. Cho hình phẳng (H) được giới hạn bởi đường cong (C ) : y
sin x , trục Ox và các đường thẳng x 0,x
. Thể tích của khối tròn xoay khi cho hình (H) quay quanh trục Ox là : 2 3 A.2 B.3 C. D. 3 2 16
Câu 59. Diện tích hình phẳng giới hạn bởi y x  sin ;
x y x 0  x  2 là: 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 A. 1 B. 2 C. 3 D. 4 3 x
Câu 60. Diện tích hình phẳng giới hạn bởi y  ; y x là: 2 1 x A. 1 B. 1 – ln2 C. 1 + ln2 D. 2 – ln2
Câu 61. Diện tích của hình phẳng giới hạn bởi C 2
: y  4x x ;Ox là: 31 31 32 33 A. B.  C. D. 3 3 3 3
Câu 62. Gọi  H  là hình phẳng giới hạn bởi các đường: 2
y  3x x ;Ox . Quay  H  xung quanh
trục Ox ta được khối tròn xoay có thể tích là: 81 83 83 81 A.  B.  C.  D.  11 11 10 10
Câu 63. Diện tích của hình phẳng giới hạn bởi C 2
: y x  2x; y x  2 là: 5 7 9 11 A. B. C. D. 2 2 2 2
Câu 64. Diện tích của hình phẳng giới hạn bởi C 1 : y  ; d : y  2  x  3 là: x 3 1 3 1 A.  ln 2 B. C. ln 2  D. 4 25 4 24
Câu 65. Diện tích của hình phẳng giới hạn bởi C 2
: y x ;d  : x y  2 là: 7 9 11 13 A. B. C. D. 2 2 2 2
Câu 66. Diện tích của hình phẳng giới hạn bởi C 2
: y x ;d  : y x là: 16 2 4 5 1 2 A. B. C. D. 3 3 3 3
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 67. Gọi  H  là hình phẳng giới hạn bởi các đường: y x 1;Ox; x  4 . Quay  H  xung
quanh trục Ox ta được khối tròn xoay có thể tích là: 7 5 7 5 A.  B.  C. 2  D. 2  6 6 6 6
Câu 68. Gọi  H  là hình phẳng giới hạn bởi các đường: y  3x; y x ; x 1. Quay  H  xung
quanh trục Ox ta được khối tròn xoay có thể tích là: 8 2 8 A. B. C. 2 8 D. 8 3 3
Câu 69. Diện tích hình phẳng giới hạn bởi các đường 2 y  3
x  3 với x  0 ;Ox ;Oy là: A. 4  B. 2 C. 4 D. 44
Câu 70. Cho hình (H) giới hạn bởi các đường y x ; x  4 ; trục hoành. Quay hình (H) quanh trục
Ox ta được khối tròn xoay có thể tích là: 15 14 16 A. B. C. 8 D. 2 3 3
Câu 71. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y x  3x và trục hoành là: 27 3 27 A.  B. C. D. 4 4 4 4
Câu 72. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 4 y  5
x  5 và trục hoành là: A. 4 B. 8 C. 3108 D. 6216
Câu 73. Diện tích hình phẳng giới hạn bởi hai đường 3
y x 11x  6 và 2 y  6x là: 1 1 A. 52 B. 14 C. D. 4 2
Câu 74. Diện tích hình phẳng giới hạn bởi hai đường 3
y x và y  4x là: 16 2048 A. 4 B. 8 C. 40 D. 3 105
Group Nhóm Toán | Trắc nghiệm 2016-2017 8
Câu 75. Diện tích hình phẳng giới hạn bởi các đường y  2x ; y  ; x  3 là: x 2 14 A. 5 8ln 6 B. 5  8ln C. 26 D. 3 3 6
Câu 76. Cho hình (H) giới hạn bởi các đường y x 1; y
; x  1. Quay hình (H) quanh trục Ox x
ta được khối tròn xoay có thể tích là: 13 125 35 A. B. C. D. 18 6 6 3
Câu 77. Diện tích hình phẳng giới hạn bởi các đường y mx cos x ; Ox ; x  0; x   bằng 3 . Khi đó
giá trị của m là: A. m  3  B. m  3 C. m  4  D. m  3 
Câu 78. Cho hình (H) giới hạn bởi các đường 2
y  x  2x , trục hoành. Quay hình (H) quanh trục
Ox ta được khối tròn xoay có thể tích là: 16 4 496 32 A. B. C. D. 15 3 15 15 6
Câu 79. Diện tích hình phẳng giới hạn bởi các đường y  2x 1; y  ; x  3 là: x 2 443 25 A. 4  6ln 6 B. 4  6 ln C. D. 3 24 6 4
Câu 80. Cho hình (H) giới hạn bởi các đường y
và y  x  5 . Quay hình (H) quanh trục Ox ta x
được khối tròn xoay có thể tích là: 9 15 33 A. B.  4ln 4 C.  4ln 4 D. 9 2 2 2
Mức độ vận dụng. 16 4
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 5 Câu 81. Cho (C) : 3 2 y x mx 2x 2m . Giá trị m 0; sao cho hình phẳng 3 3 6
giới hạn bởi đồ thị (C) , y 0, x 0, x
2 có diện tích bằng 4 là: 1 1 3 3 A. m B. m C. m D. m 2 2 2 2
Câu 82. Diện tích hình phẳng giới hạn bởi 2 2
y ax , x ay a  0 có kết quả là 1 1 1 A. 2 a B. 2 a C. 2 a D. 2 a 2 3 4 2 2 x y
Câu 83. Thể tích khối tròn xoay khi cho Elip  1 quay quanh trục ox : 2 2 a b 4 4 2 2 A. 2  a b B. 2  ab C. 2  a b D. 2   ab 3 3 3 3
Câu 84. Diện tích hình phẳng giới hạn bởi 2 y  sin x sinx 1
 ; y 0; x 0; x  / 2 là: 3 3 3 3 A. B. 1 C. 1 D. 4 4 4 4
Câu 85. Diện tích hình phẳng giới hạn bởi xx
y e e ;O ; x x 1 là: 1 1 1 16 A. 1 B. e  1 C. e  D. e   2 e e e 5
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 86. Thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi các đường 1 1 2 x y y  0 2 ; x  
y  3y ( y  2); x  0 quay quanh Ox: 4 2 A. 32  B. 32 C. 2 32 D. 33
Câu 87. Diện tích hình phẳng được giới hạn bởi đường cong 2 (C) : y
sin x , trục Ox và các đường thẳng x 0,x bằng : A. B. C. D. 2 3 4
Câu 88. Diện tích hình phẳng giới hạn bởi 2
y  5  x , y x 1 , x  0, x 1 có kết quả là: 55 26 25 27 A. B. C. D. 3 3 3 3
Câu 89. Diện tích hình phẳng giới hạn bởi y |
 ln x |; y 1 là: 3 A. 2 e  2e  2 B. e   2 C. 2 e  2e 1 D. 3 e
Câu 90. Diện tích hình phẳng được giới hạn bởi các đường: 2 x 2 x y 4 ; y là: 4 4 2 4 2 4 4 A. 2 dvdt B. dvdt C. dvdt 3 3 3 16 6
Group Nhóm Toán | Trắc nghiệm 2016-2017 4 D. 2 dvdt 3
Câu 91. Diện tích của hình phẳng giới hạn bởi: C : y x;d  : y x  2;Ox là: 10 16 122 128 A. B. C. D. 3 3 3 3
Câu 92. Diện tích của hình phẳng giới hạn bởi: C : y  ln ;
x d : y  1;O ; x Oy là: A. e  2 B. e  2 C. e 1 D. e
Câu 93. Diện tích của hình phẳng giới hạn bởi: C : y  ln ;
x d : y  1; d : y  x 1 là: 1 2 1 3 1 3 A. e  B. e  C. e  D. e  2 2 2 2
Câu 94. Diện tích của hình phẳng giới hạn bởi:   : x C
y e ;d : y  x 1; x  1 là: 1 3 A. e B. e  C. e 1 D. e  2 2
Câu 95. Diện tích của hình phẳng giới hạn bởi:   : x C
y e ;d : y  ;
e d : y  1 e x 1 là: 1 2   e 1 e  1 e  3 e A. B. C. D. 2 2 2 2
Câu 96. Cho đường cong C : y x . Gọi d là tiếp tuyến của C  tại điểm M 4,2 . Khi đó diện
tích của hình phẳng giới hạn bởi : C;d;Ox là: 8 2 16 22 A. B. C. D. 3 3 3 3
Câu 97. Cho đường cong C : y  2  ln x . Gọi d là tiếp tuyến của C  tại điểm M 1, 2 . Khi đó
diện tích của hình phẳng giới hạn bởi : C;d;Ox là: 16 7 A. 2 e  3 B. 2 e 1 C. 2 e D. 2 e  5
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 98. Gọi  H  là hình phẳng giới hạn bởi C  1 : y
x;d : y
x . Quay  H  xung quanh trục 2
Ox ta được khối tròn xoay có thể tích là: 16 8 8 A. 8 B. C. D. 3 3 15
Câu 99. Gọi  H  là hình phẳng giới hạn bởi C 3
: y x ;d : y  x  2;Ox . Quay  H  xung
quanh trục Ox ta được khối tròn xoay có thể tích là: 4 10   A. B. C. D. 21 21 7 3
Câu 100. Gọi  H  là hình phẳng giới hạn bởi C  1 : y  2
x;d : y  ;
x x  4 . Quay  H  xung 2
quanh trục Ox ta được khối tròn xoay có thể tích là: 80 112 16 A. B. D. D. 32 3 3 3 PHẦN 14 :
A. MỨC ĐỘ NHẬN BIẾT: 20 câu 1
Câu 1: Nguyên hàm của hàm số f(x) = x2 – 3x + là: x 3 2 3 2 x 3x x 3x 1 3 2 x 3x A. 
 ln x C B.    C C. 3 2
x  3x  ln x C D.   ln x C 3 2 2 3 2 x 3 2
Câu 2: Họ nguyên hàm của 2
f (x)  x  2x 1 là 1 A. 3 F (x) 
x  2  x C B. F( )
x  2x  2  C 3 1 1 C. 3 2 F (x) 
x x x C D. 3 2 F (x) 
x  2x x C 3 3 1 1
Câu 3: Nguyên hàm của hàm số f (x)   là : 2 x x 16 1 1 A. 2 ln x ln x C B. lnx - + C C. ln|x| + + C D. Kết quả khác 8 x x
Câu 4: Nguyên hàm của hàm số 2 ( ) x x f x ee là:
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 A.
e2x e x C B. 2 2 x x
e e C C. x ( x
e e x)  C D. Kết quả khác 2
Câu 5: Nguyên hàm của hàm số f x cos 3x là: 1 1
A. sin 3x C
B.  sin 3x C
C. sin 3x C D. 3
 sin3x C 3 3 x 1
Câu 6: Nguyên hàm của hàm số f (x)  2e  là: 2 cos x ex A.2ex + tanx + C B. ex(2x - ) C. ex + tanx + C D. Kết quả khác cos 2 x
Câu 7: Tính sin(3x 1)dx  , kết quả là: 1 1
A.  cos(3x 1)  C
B. cos(3x 1)  C
C.  cos(3x 1)  C D. Kết quả khác 3 3 Câu 8: Tìm (cos6x cos4 ) x dx là: 1 1 A. sin6x sin 4x C x x C 6 4 B. 6sin 6 5sin4 1 1 C. sin 6x sin 4x C x x C 6 4 D. 6sin 6 sin4 1
Câu 9: Tính nguyên hàm dx  ta được kết quả sau: 2x 1 1 1 A.
ln 2x 1  C
B.  ln 2x 1  C C. 
ln 2x 1  C
D. ln 2x 1  C 2 2 1
Câu 10: Tính nguyên hàm dx  ta được kết quả sau: 1 2x 1 2
A. ln 1 2x C B. 2
 ln 1 2x C
C.  ln 1 2x C D.  C 2 2 1 (  2x)
Câu 11: Công thức nguyên hàm nào sau đây không đúng? 1  1   x A.
dx  ln x C  B. x dx   C (  1  )  x  1 x a 1 C. x a dx
C (0  a  1)  dx  tan  ln D. x Ca 2 cos x
Câu 12: Tính (3cos  3x x )dx  , kết quả là: 3x 3x 3x 3x A. 3sin x   C B. 3  sin x   C C. 3sin x   C D. 3  sin x   C ln 3 ln 3 ln 3 ln 3
Câu 13: Trong các hàm số sau: 16 2 f x x f x x 9 (I) 2 ( ) tan 2 (II) f (x) (III) 2 ( ) tan 1 2 cos x
Hàm số nào có một nguyên hàm là hàm số g(x) = tanx
Group Nhóm Toán | Trắc nghiệm 2016-2017 A. (I), (II), (III) B. Chỉ (II), (III) C. Chỉ (III) D. Chỉ (II)
Câu 14: Trong các mệnh đề sau, tìm mệnh đề sai 3 f (x) A. 2
f '(x) f (x)dx C 3 B.
f (x).g(x) dx f (x)d . x g(x)dx C. f (x) g(x) dx f (x)dx g(x)dx D.
kf (x)dx k
f (x)dx (k là hằng số)
Câu 15: Nguyên hàm của hàm số 3
f (x)  (2x 1) là: 1 A. 4
(2x 1)  C B. 4
(2x 1)  C C. 4
2(2x 1)  C D. Kết quả khác 2
Câu 16: Nguyên hàm của hàm số 5 f (x)  1 (  2x) là: 1 A. 6  1
(  2x)  C B. 6 1
(  2x)  C C. 6 5 1
(  2x)  C D. 4 5 1
(  2x)  C 2
Câu 17: Chọn câu khẳng định sai? 1 A. xdx   C ln B. 2
2xdx x Cx 1 C. xdx   x C sin cos D. dx   x C  cot 2 sin x 3
Câu 18: Nguyên hàm của hàm số f(x) = 2x  là : 2 x 3 3 A. 2 x   C B. 2 x   C C. 2 2
x  3ln x C D. Kết quả khác x 2 x Câu 19: Hàm số x F x e tan x
C là nguyên hàm của hàm số f (x) nào? x 1 x 1
A. f (x)  e
B. f (x)  e  2 sin x 2 sin x x 1
C. f (x)  e  D. Kết quả khác 2 cos x Câu 20: Nếu ( ) x f x dx e sin 2x
C thì f (x) bằng x 1 A. x e cos 2x B. x e cos 2x C. x e 2cos 2x D. e cos 2x 2 17 0
B. MỨC ĐỘ THÔNG HIỂU: 20 câu
Group Nhóm Toán | Trắc nghiệm 2016-2017 4 2x  3
Câu 21: Nguyên hàm của hàm số f(x) = là : 2 x 3 3 2x3 2x 3 2x A.  3  C B.   C C. 2
 3ln x C D. Kết quả khác 3 x 2 3 x 3
Câu 22: Nguyên hàm của hàm số f(x) = 2sin3xcos2x 1 1
A.  cos 5x  cos x C
B. cos 5x  cos x C
C. 5cos5x  cos x C D. Kết quả khác 5 5
Câu 23: Tìm hàm số f(x) biết rằng f’(x) = 2x + 1 và f(1) = 5 A. x2 + x + 3 B. x2 + x - 3 C. x2 + x D. Kết quả khác
Câu 24: Tìm hàm số f(x) biết rằng f’(x) = 4 x x và f(4) = 0 2 2 8 2 x x 40 8 x x 40 8x x x 40 A.  x  B.   C.   D. Kết quả khác 3 2 3 3 2 3 3 2 3 2
Câu 25: Nguyên hàm của hàm số x xe dx  là 2 x 2 e 2 2 A. x xe C B.  C C. x e C D. x x e 2
Câu 26: Tìm hàm số y f( ) x biết 2 f ( ) x (x ) x (x 1) và f(0) 3 4 2 x x 4 2 x x A. y f( ) x 3 y f( ) x 3 4 2 B. 4 2 4 2 x x C. y f( ) x 3 y f x x 4 2 D. 2 ( ) 3 1 Câu 27: Tìm 3 (sin x 1) cos xdx là: 4 (cos x 1) 4 sin x A. C C 4 B. 4 4 (sin x 1) C. C x C 4 D. 3 4(sin 1) dx Câu 28: Tìm 2 x 3x là: 2 1 1 x 2 A. ln ln C ln C x 2 x 1 B. x 1 x 1 C. ln C x x C x 2 D. ln( 2)( 1) Câu 29: Tìm xcos2xdx là: 1 1 1 1 A. xsin2x cos2x C xsin2x cos2x C 2 4 B. 2 2 17 2 x sin2x 1 C. C 4 D. sin 2x C
Câu 30: Lựa chọn phương án đúng:
Group Nhóm Toán | Trắc nghiệm 2016-2017
A. cot xdx  ln sin x C
B. sin xdx  cos x C  1 1 C. dx   C
D. cos xdx  sin x C  2 x x
Câu 31: Tính nguyên hàm 3 sin x cos xdx  ta được kết quả là: 1 1 A. 4 sin x C B. 4 sin x C C. 4 sin x C D. 4
 sin x C 4 4 Câu 32: Cho 2
f (x)  3x  2x  3 có một nguyên hàm triệt tiêu khi x  1 . Nguyên hàm đó là kết quả nào sau đây? A. 3 2
F(x)  x x  3x B. 3 2
F(x)  x x  3x 1 C. 3 2
F(x)  x x  3x  2 D. 3 2
F(x)  x x  3x 1 x(2  x)
Câu 33. Hàm số nào sau đây không phải là nguyên hàm của hàm số f (x)  2 (x 1) 2 x x 1 2 x x 1 2 x x 1 2 x A. B. C. D. x 1 x 1 x 1 x 1
Câu 34: Kết quả nào sai trong các kết quả sau: x 1  x 1 2 5   1 1 4 4 x x   2 1 A. dx    C  B. dx  ln x   C  10x 5.2x.ln 2 5x.ln 5 3 4 x 4x 2 x 1 x 1 C. dx  ln  x C  D. 2
tan xdx  tan x x C  2 1 x 2 x 1  4 
Câu 35: Tìm nguyên hàm 3 2 x dx    x  5 3 A. 3 5
x  4 ln x C B. 3 5 
x  4 ln x C 3 5 3 3 C. 3 5
x  4 ln x C D. 3 5
x  4 ln x C 5 5 x
Câu 36: Kết quả của dx  là: 2 1 x 1  1 A. 2 1 x C B.  C C.  C D. 2
 1 x C 2 1 x 2 1 x
Câu 37: Tìm nguyên hàm 2 1 (  sin x) dx  2 1 2 1 A.
x  2 cos x  sin 2x C B.
x  2 cos x  sin 2x C 3 4 3 4 2 1 2 1 C.
x  2 cos 2x  sin 2x C D.
x  2 cos x  sin 2x C 3 4 3 4 17 Câu 38: Tính 2 tan xdx  , kết quả là: 2 1
A. x  tan x C
B. x  tan x C
C. x  tan x C D. 3 tan x C 3
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 39: Trong các mệnh đề sau đây, mệnh đề nào sai ? 1 1 (I ) sin x sin 3xdx
(sin 2x - sin 4x) C 4 2 1 2 3 (II ) tan xdx tan x C 3 x 1 1 2 (III ) dx ln(x 2x 3) C 2 x 2x 3 2 A. Chỉ (I) và (II) B. Chỉ (III) C. Chỉ (II) và (III) D. Chỉ (II)
Câu 40: Hàm số nào sau đây là một nguyên hàm của sin2x A. 2 sin x B. 2cos2x C. -2cos2x D. 2sinx
C. MỨC ĐỘ VẬN DỤNG: 10 câu b
Câu 41: Tìm hàm số f(x) biết rằng f '(x)  ax+ , f '( ) 1  , 0 f ( ) 1  , 4 f ( ) 1  2 2 x 2 2 2 x 1 5 x 1 5 x 1 5 A.   B.   C.   D. Kết quả khác 2 x 2 2 x 2 2 x 2 Lược giải:
Sử dụng máy tính kiểm tra từng đáp án: - Nhập hàm số -
Dùng phím CALC để kiểm tra các điều kiện f '(1) 0, f (1) 4, f ( 1) 2 - Đáp án đúng: B
Câu 42: Hàm số nào sau đây là một nguyên hàm của hàm số 2 f (x) x k với k 0? x k A. 2 2 f (x) x k ln x x k 2 2 1 x B. 2 2 f (x) x k ln x x k 2 2 k C. 2 f (x) ln x x k 2 1 D. f (x) 2 x k Lược giải: x 1 2 x k 1 x x k 2 2 2 x k 2 x k ln x x k x k x k 17 2 2 2 2 2 2 2 x k x x k 3
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 10x - 7x 2 Câu 43: Nếu 2 f (x) (ax bx
c) 2x -1 là một nguyên hàm của hàm số g(x) trên khoảng 2x -1 1 ;
thì a+b+c có giá trị là 2 A. 3 B. 0 C. 4 D. 2 Lược giải: 2 2 5ax ( 2a 3b)x b c 10x 7x 2 2 (ax bx c) 2x 1 2x 3 2x 3 a 2 b 1 a b c 2 c 1
Câu 44: Xác định a, b, c sao cho 2 g(x) (ax bx
c) 2x - 3 là một nguyên hàm của hàm số 2 20x - 30x 7 3 f (x) trong khoảng ; 2x - 3 2 A.a=4, b=2, c=2 B. a=1, b=-2, c=4 C. a=-2, b=1, c=4 D. a=4, b=-2, c=1 Lược giải: 2 2 5ax ( 6a 3b)x 3b c 20x 30x 7 2 (ax bx c) 2x 3 2x 3 2x 3 a 4 b 2 c 1
Câu 45: Một nguyên hàm của hàm số: 2
f (x)  x sin 1  x là: A. 2 2 2
F(x)   1 x cos 1  x  sin 1  x B. 2 2 2
F(x)   1 x cos 1  x  sin 1  x C. 2 2 2
F(x)  1 x cos 1  x  sin 1  x D. 2 2 2
F(x)  1  x cos 1  x  sin 1  x Lược giải: Đặt 2 I (x sin 1 x )dx -
Dùng phương pháp đổi biến, đặt 2 t 1 x ta được I t sin tdt -
Dùng phương pháp nguyên hàm từng phần, đặt u , t dv sin tdt 17 - Ta được 2 2 2 I t cos t cos tdt 1 x cos 1 x sin 1 x C 4
Câu 46: Trong các hàm số sau:
Group Nhóm Toán | Trắc nghiệm 2016-2017 (I) 2 f (x) x 1 (II) 2 f (x) x 1 5 1 1 (III) f (x) (IV) f (x) - 2 2 x 1 2 x 1
Hàm số nào có một nguyên hàm là hàm số 2 F (x) ln x x 1 A. Chỉ (I) B. Chỉ (III) C. Chỉ (II) D. Chỉ (III) và (IV) Lược giải: x 1 2 x 1 1 2 ln x x 1 2 2 x x 1 x 1 2 1
Câu 47: Một nguyên hàm của hàm số 3 f (x) x
là hàm số nào sau đây: x 3 3 12 1 1 A. 3 2 6 5 F (x) x x x ln x B. 3 F (x) x 5 5 3 x 2 3 12 C. 3 F (x) x x x D. 3 2 5 6 F (x) x x ln x x 5 5 Lược giải: 2 3 12 1 3 2 6 5 3 x x x ln x x 5 5 x
Câu 48: Xét các mệnh đề 2 x x (I) F(x) x
cos x là một nguyên hàm của f (x) sin - cos 2 2 4 x 3 (II) F (x)
6 x là một nguyên hàm của 3 f (x) x 4 x (III) F(x)
tan x là một nguyên hàm của f (x) -ln cos x Mệnh đề nào sai ? A. (I) và (II) B. Chỉ (III) C. Chỉ (II) D. Chỉ (I) và (III) Lược giải: ln cos x tan x (vì
ln cos x là một nguyên hàm của tanx)
Câu 49: Trong các mệnh đề sau đây mệnh đề nào đúng ? xdx 1 (I) 2 ln(x 4) C 2 x 4 2 17 1 5 (II) cot xdx - C 2 sin x
Group Nhóm Toán | Trắc nghiệm 2016-2017 x 1 (III) 2cos 2cos sin - x e xdx e C 2 A. Chỉ (I) B. Chỉ (III) C. Chỉ (I) và (II) D. Chỉ (I) và (III) Lược giải: 2 xdx 1 d(x 4) 1 2 ln(x 4) C 2 2 x 4 2 x 4 2 1 1 2cos x 2cos x 2cos x e sin xdx e d(cos x) e C 2 2
Câu 50: Tìm nguyên hàm x 2 2 F(x) e (a tan x b tan x
c) là một nguyên hàm của x 2 3 f (x) e tan x trên khoản ; 2 2 x 1 2 1 x 1 2 2 A. 2 2 F (x) e ( tan x tan x ) B. 2 2 F (x) e ( tan x tan x ) 2 2 2 2 2 2 x 1 2 2 x 1 2 1 C. 2 2 F (x) e ( tan x tan x ) D. 2 2 F (x) e ( tan x tan x ) 2 2 2 2 2 2 Lược giải: -
Có thể dùng đạo hàm để kiểm tra từng đáp án. - Hoặc tìm đạo hàm của x 2 2 F(x) e (a tan x b tan x
c) rồi đồng nhất với x 2 3 f (x) e tan x x 2 2 x 2 2 2 F '(x) 2e (a tan x b tan x c) e 2a(1 tan x) tan x ( b 1 tan x) x 2 3 2 e 2a tan x ( 2a ) b tan x (2a 2 ) b tan x b 2c
F (x) là nguyên hàm của f(x) nên F '(x) f (x) Suy ra 1 2 1 a a 2 2a b 0 2 b Đáp án đúng: B 2a 2b 0 2 1 b 2c 0 c 2 PHẦN 15 : 17 6 NHẬN BIẾT
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 1. Để tìm diện tích của hình phẳng giới hạn bởi C 3
: y x ; y  0; x  -1; x  2 một học sinh thực
hiện theo các bước như sau: 2 2 4 x 1 15 Bước I. 3 S x dx  Bước II. S
Bước III. S  4   4 4 4 1  1 
Cách làm trên sai từ bước nào? A. Bước I B. Bước II C. Bước III
D. Không có bước nào sai.
Câu 2. Diện tích của hình phẳng giới hạn bởi C 3
: y x ; y  0; x  1  ; x  2 là: 1 17 15 19 A. B. C. D. 4 4 4 4
Câu 3. Diện tích của hình phẳng giới hạn bởi C 4 2
: y  3x  4x  5;Ox ; x  1; x  2 là: 212 213 214 43 A. B. C. D. 15 15 15 3
Câu 4. Cho hai hàm số f x và g x liên tục trên  ;
a b và thỏa mãn: 0  g x  f x, x   ; a b.
Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh Ox hình phẳng H  giới hạn bởi
các đường: y f x, y g x , x a; x b . Khi đó V dược tính bởi công thức nào sau đây? b b A.   f
 x gx 2 dx  B. 2   f  x 2
g x dx   a a 2 b   b C.    f
 x gxdx   D. f
 x gxdxaa
Câu 5. Diện tích của hình phẳng giới hạn bởi C 2
: y  x  6x  5; y  0 ; x  0; x  1 là: 5 7 7 5 A. B. C.  D.  2 3 3 2 17
Câu 6. Diện tích của hình phẳng giới hạn bởi C : y  sin ;
x Ox; x  0; x   là: 7 A. 1 B. 2 C. 3 D. 4
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 7. Gọi  H  là hình phẳng giới hạn bởi các đường: y  sin x;Ox; x  0; x   . Quay  H  xung
quanh trục Ox ta được khối tròn xoay có thể tích là:  2  A. B. C.  D. 2  2 2
Câu 8. Diện tích hình phẳng giới hạn bởi các đường 2
y x  4 ; Ox bằng ? 32 16 32 A. B. C. 12 D. 3 3 3
Câu 9. Diện tích hình phẳng giới hạn bởi các đường 3
y x  4x ; Ox ; x  3  x  4 bằng ? 119 201 A. B. 44 C. 36 D. 4 4
Câu 10. Diện tích hình phẳng giới hạn bởi các đường 2
y x ; y x  2 bằng ? 15 9 9 15 A. B. C. D. 2 2 2 2
Câu 11. Diện tích hình phẳng giới hạn bởi các đường 4 2
y x  4x ; Ox bằng ? 1792 128 128 A. 128 B. C. D.  15 15 15
Câu 12. Diện tích hình phẳng giới hạn bởi các đường 3 y x  4 ; x O ; x x  1  bằng ? 9 9 A. 24 B. C. 1 D.  4 4
Câu 13. Diện tích hình phẳng giới hạn bởi các đường y  cos ; x O ; x O ; y x   bằng ? A. 1 B. 2 C. 3 D. Kết quả khác
Câu 14. Diện tích hình phẳng giới hạn bởi các đường 3 y x  ; x Ox bằng ? 1 1 1 A. B. C. 2 D. 2 4 4
Câu 15. Gọi  H  là hình phẳng giới hạn bởi các đường 2
y  2x x ; Ox . Quay  H  xung quanh trục
Ox ta được khối tròn xoay có thể tích bằng ? 16 4 4 16 A. B. C. D. 15 3 3 15 
Câu 16. Gọi  H  là hình phẳng giới hạn bởi các đường y  tan ; x O ; x x  0; x  . Quay  H  xung 17 4 8
quanh trục Ox ta được khối tròn xoay có thể tích bằng ?
Group Nhóm Toán | Trắc nghiệm 2016-2017  2  2  A. 1 B. 2  C.   D.  4 4 4
Câu 17. Gọi  H  là hình phẳng giới hạn bởi các đường 2
y  1 x ; Ox . Quay  H  xung quanh trục
Ox ta được khối tròn xoay có thể tích bằng ? 16 16 4 4 A. B. C. D. 15 15 3 3
Câu 18. Diện tích hình phẳng giới hạn bởi các đường x
y e ; y  1 và x  1 là: A. e 1 B. e C. e 1 D. 1 e
Câu 19. Diện tích hình phẳng giới hạn bởi các đường y  3 x ; x  4 ; Ox là: 16 A. B. 24 C. 72 D. 16 3
Câu 20. Cho hình (H) giới hạn bởi các đường 2
y x ; x  1; trục hoành. Quay hình (H) quanh trục Ox
ta được khối tròn xoay có thể tích là:   2 2 A. B. C. D. 5 3 3 5 THÔNG HIỄU
Câu 1. Diện tích của hình phẳng giới hạn bởi C 2
: y  4x x ;Ox là: 31 31 32 33 A. B.  C. D. 3 3 3 3
Câu 2. Gọi  H  là hình phẳng giới hạn bởi các đường: 2
y  3x x ;Ox . Quay  H  xung quanh
trục Ox ta được khối tròn xoay có thể tích là: 81 83 83 81 A.  B.  C.  D.  11 11 10 10
Câu 3. Diện tích của hình phẳng giới hạn bởi C 2
: y x  2x; y x  2 là: 5 7 9 11 A. B. C. D. 17 2 2 2 2 9
Câu 4. Diện tích của hình phẳng giới hạn bởi C 1 : y  ; d : y  2  x  3 là: x
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 1 3 1 A.  ln 2 B. C. ln 2  D. 4 25 4 24
Câu 5. Diện tích của hình phẳng giới hạn bởi C 2
: y x ;d  : x y  2 là: 7 9 11 13 A. B. C. D. 2 2 2 2
Câu 6. Diện tích của hình phẳng giới hạn bởi C 2
: y x ;d  : y x là: 2 4 5 1 A. B. C. D. 3 3 3 3
Câu 7. Gọi  H  là hình phẳng giới hạn bởi các đường: y x 1;Ox; x  4 . Quay  H  xung
quanh trục Ox ta được khối tròn xoay có thể tích là: 7 5 7 5 A.  B.  C. 2  D. 2  6 6 6 6
Câu 8. Gọi  H  là hình phẳng giới hạn bởi các đường: y  3x; y x ; x 1. Quay  H  xung quanh
trục Ox ta được khối tròn xoay có thể tích là: 8 2 8 A. B. C. 2 8 D. 8 3 3
Câu 9. Diện tích hình phẳng giới hạn bởi các đường 2 y  3
x  3 với x  0 ;Ox ;Oy là: A. 4  B. 2 C. 4 D. 44
Câu 10. Cho hình (H) giới hạn bởi các đường y x ; x  4 ; trục hoành. Quay hình (H) quanh trục
Ox ta được khối tròn xoay có thể tích là: 15 14 16 A. B. C. 8 D. 2 3 3
Câu 11. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y x  3x và trục hoành là: 27 3 27 A.  B. C. D. 4 4 4 4
Câu 12. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 4 y  5
x  5 và trục hoành là: A. 4 B. 8 C. 3108 D. 6216
Câu 13. Diện tích hình phẳng giới hạn bởi hai đường 3
y x 11x  6 và 2 y  6x là: 18 1 1 0 A. 52 B. 14 C. D. 4 2
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 14. Diện tích hình phẳng giới hạn bởi hai đường 3
y x và y  4x là: 2048 A. 4 B. 8 C. 40 D. 105 8
Câu 15. Diện tích hình phẳng giới hạn bởi các đường y  2x ; y  ; x  3 là: x 2 14 A. 5 8ln 6 B. 5  8ln C. 26 D. 3 3 6
Câu 16. Cho hình (H) giới hạn bởi các đường y x 1; y
; x 1. Quay hình (H) quanh trục Ox ta x
được khối tròn xoay có thể tích là: 13 125 35 A. B. C. D. 18 6 6 3
Câu 17. Diện tích hình phẳng giới hạn bởi các đường y mx cos x ; Ox ; x  0; x   bằng 3 . Khi đó
giá trị của m là: A. m  3  B. m  3 C. m  4  D. m  3 
Câu 18. Cho hình (H) giới hạn bởi các đường 2
y  x  2x , trục hoành. Quay hình (H) quanh trục Ox
ta được khối tròn xoay có thể tích là: 16 4 496 32 A. B. C. D. 15 3 15 15 6
Câu 19. Diện tích hình phẳng giới hạn bởi các đường y  2x 1; y  ; x  3 là: x 2 443 25 A. 4  6ln 6 B. 4  6ln C. D. 3 24 6 4
Câu 20. Cho hình (H) giới hạn bởi các đường y
và y  x  5 . Quay hình (H) quanh trục Ox ta x
được khối tròn xoay có thể tích là: 9 15 33 A. B.  4ln 4 C.  4ln 4 D. 9 2 2 2 VẬN DỤNG 18
Câu 1. Diện tích của hình phẳng giới hạn bởi: C : y x;d  : y x  2;Ox là: 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 10 16 122 128 A. B. C. D. 3 3 3 3
Câu 2. Diện tích của hình phẳng giới hạn bởi: C : y  ln ;
x d : y  1;O ; x Oy là: A. e  2 B. e  2 C. e 1 D. e
Câu 3. Diện tích của hình phẳng giới hạn bởi: C : y  ln ;
x d : y  1; d : y  x 1 là: 1 2 1 3 1 3 A. e  B. e  C. e  D. e  2 2 2 2
Câu 4. Diện tích của hình phẳng giới hạn bởi:   : x C
y e ;d : y  x 1; x 1 là: 1 3 A. e B. e  C. e 1 D. e  2 2
Câu 5. Diện tích của hình phẳng giới hạn bởi:   : x C
y e ;d : y  ;
e d : y  1 e x 1 là: 1 2   e 1 e  1 e  3 e A. B. C. D. 2 2 2 2
Câu 6. Cho đường cong C : y x . Gọi d là tiếp tuyến của C  tại điểm M 4,2 . Khi đó diện
tích của hình phẳng giới hạn bởi : C;d;Ox là: 8 2 16 22 A. B. C. D. 3 3 3 3
Câu 7. Cho đường cong C : y  2  ln x . Gọi d là tiếp tuyến của C  tại điểm M 1, 2 . Khi đó
diện tích của hình phẳng giới hạn bởi : C;d;Ox là: A. 2 e  3 B. 2 e 1 C. 2 e D. 2 e  5
Câu 8. Gọi  H  là hình phẳng giới hạn bởi C  1 : y
x;d : y
x . Quay  H  xung quanh trục 2
Ox ta được khối tròn xoay có thể tích là: 16 8 8 A. 8 B. C. D. 3 3 15
Câu 9. Gọi  H  là hình phẳng giới hạn bởi C 3
: y x ;d : y  x  2;Ox . Quay  H  xung quanh 18
trục Ox ta được khối tròn xoay có thể tích là: 2 4 10   A. B. C. D. 21 21 7 3
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 10. Gọi  H  là hình phẳng giới hạn bởi C  1 : y  2
x;d : y  ;
x x  4 . Quay  H  xung 2
quanh trục Ox ta được khối tròn xoay có thể tích là: 80 112 16 A. B. D. D. 32 3 3 3
LƯỢC GIẢI CÂU HỎI VẬN DỤNG Câu 1. 18 3
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 4 4 10 S
xdx   x    x   10 2  dx    hoặc S xdx 1   3 3 0 2 0 Câu 2. 18 4
Group Nhóm Toán | Trắc nghiệm 2016-2017 e
S  1  1 ln xdx e 1 1 Câu 3. 1 e S     x 3 1 ln dx e   2 2 1 Câu 4. Chứng minh PT x
e  x 1 có nghiệm duy nhất x  0 . 18 5
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 x S  e   x   3
1  dx e    2 0 Câu 5. 18 0 1 e x 1 6 S  e
  1ex 1dx  
ee dx  2 1  0
Group Nhóm Toán | Trắc nghiệm 2016-2017 18 Câu 6. 7
Group Nhóm Toán | Trắc nghiệm 2016-2017 1
Phương trình của d: y x 1. 4 4  1  8 S  2  x 1 x dx    .  4  3 0 Câu 7. 18 8
Phương trình của d: y  x  3
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 e
S   2  ln x 2
dx  2  e  5 1 18 9
Group Nhóm Toán | Trắc nghiệm 2016-2017 Câu 8. 4 4  8 2
V   xdx x dx    4 3 0 0 Câu 9. 19 1 2  2 10 6 0
V   x dx   2  xdx    21 0 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 19 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 Câu 10. 4 V    2 
x 2 dx  32 0 PHẦN 16 : 1 Câu 1: Tích phân 2
I  (3x  2x 1)dx  bằng: 0 19 2 A. I 1 B. I  2 C. I  3 D. Đáp án khác
Group Nhóm Toán | Trắc nghiệm 2016-2017  2
Câu 2: Tích phân I  sin xdx  bằng: 0 A. -1 B. 1 C. 2 D. 0 1 Câu 3: Tích phân 2
I  (x 1) dx  bằng: 0 8 7 A. B. 2 C. D. 4 3 3 1 Câu 4: Tích phân x 1 I e   dx  bằng: 0 A. 2 e e B. 2 e C. 2 e 1 D. e + 1 4 x 1
Câu 5: Tích phân I dx  bằng: x  2 3 A. -1 + 3ln2 B. 2   3ln 2 C. 4ln 2 D. 1 3ln 2 1 x 1
Câu 6: Tích phân I dx  bằng: 2 x  2x  5 0 8 1 8 8 8 A. ln B. ln C. 2 ln D. 2  ln 5 2 5 5 5 e 1
Câu 7: Tích phân I dx  bằng: x 1 1 A. e B. 1 C. -1 D. e 1 Câu 8: Tích phân x I e dx  bằng : 0 A. e 1 B. 1 e C. e D. 0 19 2 3 Câu 9: Tích phân 2  2 x I e dx  bằng : 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 A. 4 e B. 4 e 1 C. 4 4e D. 4 3e 1 2  1  Câu 10: Tích phân 2 I x dx   bằng: 4  x  1 19 23 21 25 A. B. C. D. 8 8 8 8 e 1
Câu 11: Tích phân I dx  bằng: x  3 1  3 e  A. ln e  2 B. ln e  7 C. ln   D. ln 4  e  3   4  3
Câu 12: Tích phân I   3 x   1dx bằng: 1  A. 24 B. 22 C. 20 D. 18 2 1
Câu 13: Tích phân I    dx bằng: 2x  2 1 1 1 1 1 A. 1 B. C. D. 2 15 4 1 dx
Câu 14: Tích phân I   bằng: 2 x  5x  6 0 4 A. I = 1 B. I  ln C. I = ln2 D. I = ln2 3 1 xdx
Câu 15: Tích phân: J   bằng: 3 (x  1) 0 1 1 A. J  B. J  C. J =2 D. J = 1 8 4 3 x
Câu 16: Tích phân K dx  bằng: 2 x 1 2 8 1 8 19 A. K = ln2
B. K = 2ln2 C. K  ln D. K  ln 3 2 3 4
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 Câu 17: Tích phân 2 I x 1 x dx  bằng: 1 4  2 8  2 2 4  2 8  2 2 A. B. C. D. 3 3 3 3 1
Câu 18: Tích phân I x
 1 x19 dx bằng: 0 1 1 1 1 A. B. C. D. 420 380 342 462 e 2  ln x
Câu 19: Tích phân I dx  bằng: 2x 1 3  2 3  2 3  2 3 3  2 2 A. B. C. D. 3 3 6 3  6
Câu 20: Tích phân I  tanxdx  bằng: 0 3 3 2 3 A. ln B. - ln C. ln D. Đáp án khác. 2 2 3  4 Câu 21: Tích phân 2 I  tan xdx  bằng: 0   A. I = 2 B. ln2 C. I  1 D. I  4 3 1 Câu 22: Tích phân 2
L x 1 x dx  bằng: 0 1 1 A. L  1  B. L  C. L 1 D. L  4 3 19 2 5
Câu 23: Tích phân K  (2x 1) ln xdx  bằng: 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 1 A. K  3ln 2  B. K
C. K = 3ln2 D. K  2ln 2  2 2 2 
Câu 24: Tích phân L x sin xdx  bằng: 0 A. L =  B. L =  C. L = 2 D. K = 0  3
Câu 25: Tích phân I x cos xdx  bằng: 0  3 1  3 1  3 1   3 A. B. C.  D. 6 2 6 2 2 ln 2 Câu 26: Tích phân x I xe dx  bằng: 0 1 1 1 1 A. 1 ln 2 B. 1 ln 2 C. ln 2   1 D. 1 ln 2 2 2 2 4 2 ln x
Câu 27: Tích phân I dx  bằng: 2 x 1 1 1 1 1 A. 1 ln 2 B. 1 ln 2 C. ln 2   1 D. 1 ln 2 2 2 2 4 5 dx Câu 28: Giả sử  ln K  . Giá trị của K là: 2x 1 1 A. 9 B. 8 C. 81 D. 3 3 x 2 Câu 29: Biến đổi dx
thành f t dt
, với t  1 x . Khi đó f(t) là hàm nào trong các hàm số 1 1 x 0 1 sau: A. f t 2  2t  2t B.   2
f t t t C.   2
f t t t D. f t 2  2t  2t 19 1 dx 6
Câu 30: Đổi biến x = 2sint tích phân  trở thành: 2  0 4 x
Group Nhóm Toán | Trắc nghiệm 2016-2017     6 6 6 1 3 A. tdt  B. dt  C. dt  D. dtt 0 0 0 0  2 dx
Câu 31: Tích phân I   bằng: 2  sin x 4 A. 4 B. 3 C. 1 D. 2  2 e cos ln x
Câu 32: Cho I dx  , ta tính được: x 1 A. I = cos1 B. I = 1 C. I = sin1 D. Một kết quả khác 2 3 3
Câu 33: Tích phân I dx  bằng: 2  2 x x 3    A. B.  C. D. 6 3 2 b b c
Câu 34: Giả sử f (x)dx  2 
và f (x)dx  3 
và a < b < c thì f (x)dx  bằng? a c a A. 5 B. 1 C. -1 D. -5
Câu 35: Tính thể tích khối tròn xoay tạo nên do quay quanh trục Ox hình phẳng giới hạn bởi các
đường y = (1 – x2), y = 0, x = 0 và x = 2 bằng: 8 2 46 5 A. B. 2 C. D. 3 15 2  16 4
Câu 36: Cho I xdx
và J  cos 2xdx  . Khi đó: 1 0 A. I < J B. I > J C. I = J D. I > J > 1 4 19
Câu 37: Tích phân I x  2 dx 7  bằng: 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 A. 0 B. 2 C. 8 D. 4  Câu 38: Tích phân 2
I x sin xdx  bằng : 0 A. 2   4 B. 2   4 C. 2 2  3 D. 2 2  3 1 dx
Câu 39: Kết quả của  là: 1 x 1
A. 0 B.-1 C. 2 D. Không tồn tại 2 2 Câu 40: Cho f
 xdx  3.Khi đó 4 f
 x3dx  bằng: 0 0 A. 2 B. 4 C. 6 D. 8 b
Câu 41: Biết 2x  4dx  0 .Khi đó b nhận giá trị bằng: 0
A. b  0 hoặc b  2
B. b  0 hoặc b  4
C. b 1 hoặc b  2
D. b 1 hoặc b  4 1
Câu 42: Để hàm số f x  asin x b thỏa mãn f   1  2 và f
 xdx  4 thì a, b nhận giá trị : 0
A. a   ,b  0
B. a   ,b  2
C. a  2 ,b  2
D. a  2 ,b  3  19 dx Câu 43: 4 I   bằng 0 4 2 8 cos x1 tan x
Group Nhóm Toán | Trắc nghiệm 2016-2017 1
A. 1 B. 0 C. 2 D. Không tồn tại
Câu 44: Diện tích hình phẳng giới hạn bởi các đường 2 y   ;
x y  2x  x có kết quả là: 9 7 A. 4 B. 2 C.5 D. 2
Câu 45: Thể tích khối tròn xoay giới hạn bởi các đường y  ln ,
x y  0,x  e khi quay quanh trục Ox bằng: A.  e B.  e  
1 C.  e 2 D.  e  1
Câu 46: Tính diện tích giới hạn bởi 3 y  2x ;y  0;x  1
 ;x 1. Một học sinh tính theo các bước sau 2 2 4 x 1 15 I. 3 S  2x dx  II. S  S  8   2 III. 2 2 1  1 
Cách làm trên sai từ bước nào?
A. I B. II C. III D. Không có bước nào sai
Câu 47: Cho đồ thị hàm số y  f  x. Diện tích hình phẳng (phần gạch trong hình) là: 0 0 1 4 A. f  xdx f  xdx B. f  xdx f  xdx 3  4 3  1 3  4 4 C. f  xdx f  xdx D. f  xdx 19 0 0 3  9
Group Nhóm Toán | Trắc nghiệm 2016-2017  4 2
Câu 48: Giả sử I  sin3xsin 2xdx  a  b  2 khi đó a+b là 0 1 3 3 1 A.   6 B. 10 C. 10 D. 5 0 2 3x  5x 1 2
Câu 49: Giả sử I  dx  aln  b  a  b x . Khi đó giá trị 2 là  2 3 1  B. 30 B. 40 C. 50 D. 60
Câu 50: Diện tích hình phẳng giới hạn bởi đường cong 2
y  x 1, tiếp tuyến với đường này tại điểm M(2;5) và trục Oy là 7 5 8 A. 3 B. 3 C. 2 D. 3 PHẦN 17 :
ỨNG DỤNG TÍCH PHÂN
Câu 1. Kí hiệu S là diện tích hình thang cong giới hạn bởi đồ thị của hàm số liên tục y f x , trục
hoành và hai đường thẳng x  ,
a x b như trong hình vẽ bên. Khẳng định nào sai? b b
A. S   f xd .x B. S  
 f xd .x 20  a a 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 b b
C. S   f x d .x
D. S   f xdx . a a
Câu 2. Kí hiệu S là diện tích hình thang cong giới hạn bởi đồ thị của hàm số liên tục y f x , trục
hoành và hai đường thẳng x  ,
a x b như trong hình vẽ bên. Khẳng định nào đúng? b b
A. S   f xd .x
B. S   f xd .x a a b b
C. S   f x d .x
D. S   f xdx . a a
Câu 3. Kí hiệu S là diện tích hình thang cong giới hạn bởi đồ thị của hàm số 3
y x , trục hoành và hai
đường thẳng x  1
 , x  2 như trong hình vẽ bên. Tìm khẳng định đúng? 2 0 2 A. 3 S x d .  x B. 3 3
S   x dx x d   x 1  1  0 2 C. 3 S x dx . 
D. Không có khẳng định nào đúng. 1 
Câu 4. Kí hiệu S t là diện tích của hình thang vuông T giới hạn bởi đường thẳng y  2x 1, trục hoành
và hai đường thẳng x 1, x t 1 t  5. Khẳng định nào sai? 20 1
Group Nhóm Toán | Trắc nghiệm 2016-2017
A. S t   t  2t   1 .
B. S t  là một nguyên hàm của f t   2t 1, t 1;5.
C. Hình thang vuông giới hạn bởi đường thẳng y  2x 1, trục hoành và hai đường thẳng 5
x  1, x  5 có diện tích là S  2x   1d .x 1
D. Hình thang vuông giới hạn bởi đường thẳng y  2x 1, trục hoành và hai đường thẳng
x  1, x  3 có diện tích là 30.
Câu 5. Tính diện tích S của hình phẳng giới hạn bởi parabol y  cos ,
x y  sin x và hai đường thẳng  x  0, x  . 2
A. S  2 2   1 .
B. S  21 2. C. S  2 2.
D. S  2 2 1.
Câu 6. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
y  2x  3x 1 và parabol 2
y x x  2 .    Tính cos .    S        2    2    3 A. cos  0.   B. cos   .   C. cos  .   D. cos  .    S   S  2  S  2  S  2
Câu 7. Gọi S là số đo diện tích hình phẳng giới hạn bởi đường y xsin ,
x trục hoành và hai đường thẳng
x  0, x   . Khẳng định nào sai? S S A. sin 1.
B. cos 2S  1. C. tan 1. D. sin S  1. 2 4
Câu 8. Kí hiệu S , S lần lượt là diện tích hình vuông cạnh bằng 1 và diện tích hình phẳng giới hạn bởi các 1 2 đường 2
y x 1, y  0, x  1
 , x  2. Chọn khẳng định đúng. 1 S
A. S S .
B. S S . C. S S . D. 1  6. 1 2 1 2 1 2 20 2 S2 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 Câu 9. 1
Biết rằng diện tích S của hình phẳng giới hạn bởi các đường y x ln ,
x y  0, x
, x e có thể e   đượ 1
c viết dưới dạng S a 1 . 
 Tìm khẳng định sai?  e A. 2
a  3a  2  0. B. 2
a a  2  0. C. 2
a  3a  2  0. D. 2
2a  3a  2  0.
Câu 10. Tính diện tích S của hình phẳng giới hạn bởi đường parabol 2
y x  3x  2 và hai đường thẳng
y x 1, x  0. 111 4 799 A. S  . B. S  . C. S  . D. S  2. 42 3 300
Câu 11. Tính diện tích S của hình phẳng giới hạn bởi hai đường 2
y x  5  0 , x y  3  0. A. S  3. B. S  4. C. S  4,5. D. S  5.
Câu 12. Câu 66. Hình phẳng H có diện tích S gấp 30 làn diện tích hình phẳng giới hạn bởi các đường 2 y  2 ,
x x  2y  2  0, y  0. Tính S. A. S  20. B. S  30. C. S  40. D. S  50.
Câu 13. Kí hiệu S , S , S lần lượt là diện tích hình vuông đơn vị (có cạnh bằng đơn vị), hình tròn đơn vị 1 2 3
(có bán kính bằng đơn vị), hình phẳng giới hạn bởi hai đường 2
y  2 1 x , y  21 x. Tính tỉ số S S 1 3 . S2 S S 1 S S 1 S S 1 S S 1 A. 1 3  . B. 1 3  . C. 1 3  . D. 1 3  . S 3 S 4 S 2 S 5 2 2 2 2
Câu 14. Kí hiệu V là thể tích khối tròn xoay tạo thành khi quay hình thang cong giới hạn bởi đồ thị hàm số
y f x, trục Ox và hai đường thẳng x  ,
a x b (như trong hình vẽ bên) xung quang trục . Ox Khẳng định nào đúng? 20 b b 3
A. V   f xd .x
B. V    f xd .x a a
Group Nhóm Toán | Trắc nghiệm 2016-2017 2  bb
C. V     f xdx . D. 2
V    f xd . x aa
Câu 15. Gọi V là thẻ tích hình cầu bán kính R . Khẳng định nào sai?
A. Hình cầu bán kính R là khối tròn xoay thu được khi quay nữa hình tròn giới hạn bởi đường 2 2 y
R x R x R và đường thẳng y  0 xung quanh trục . Ox R B. V    R   x 2 2 2 d . x R R 3  x C. 2
V    R x   .  3  R
D. Không có khẳng định nào đúng.
Câu 16. Tính thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 3 y
x, y  0, x  1, x  8 xung quanh trục Ox . 9 93 A. 2 V   . B. V  . C. V  18, 6. D. V  . 4 5
Câu 17. Tính thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường  y
tan x, y  0, x  0, x
xung quanh trục Ox . 4  2    ln 2 A. V  . B. V  . C. V  . D. V  . 4 4 4 2
Câu 18. Tính thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 2
y  4  x , y  0 xung quanh trục Ox . 71 512 2 8 A. V  2. B. V  . C. V  . D. V  . 82 15 3
Câu 19. Kí hiệu V , V lần lượt là thể tích hình cầu đơn vị và thể tích khối tròn xoay sinh ra khi quay hình 1 2
phẳng giới hạn bởi đường thẳng y  2
x  2 và đường cong 2
y  2 1 x xung quanh trục . Ox Hãy
so sánh V , V . 1 2
A. V V .
B. V V .
C. V V .
D. V  2V . 1 2 1 2 1 2 1 2
Câu 20. Kí hiệu V , V lần lượt là thể tích hình cầu đơn vị và thể tích khối tròn xoay sinh ra khi quay hình 1 2 2
phẳng H giới hạn bởi đường thẳng y
và các đường y  0, x  0, x 1 xung quanh trục 2  x 20 V 4 .
Ox Hãy tính tỉ số 1 . V2
Group Nhóm Toán | Trắc nghiệm 2016-2017 V 3 V 2 V 1 V A. 1  . B. 1  . C. 1  . D. 1  2. V 2 V 3 V 2 V 2 2 2 2 PHẦN 18 : 4 2x 3
Câu 1. Nguyên hàm của hàm số f x là: 2 x 3 2x 3 3 2x 3 3 2x 3 2x A. C. B. C. C. 2 3ln x C. D. 2 ln x C. 3 x 2 3 x 3 3
Câu 2. Nguyên hàm của hàm số f x
2sin3x.cos 2x là: 1 1 A.
cos5x cos x C. B. cos5x cos x C. C. 5cos5x cos x C. D. 5cos5x cos x C. 5 5 Giải: f x
2sin3x.cos2x sin5x sin x.
Câu 3. Tìm hàm số f x biết rằng f x 2x 1 và f 1 5 . A. 2 x x 3. B. 2 x x 3. C. 2 x x. D. 2 x x 2.
Câu 4. Tìm hàm số f x biết rằng f x 4 x x và f 4 0 . 2 8 x x 40 2 8 x x 40 2 8x x x 40 2 8x x x 40 A. . B. . C. . D. . 3 2 3 3 2 3 3 2 3 3 2 3 2
Câu 5. Nguyên hàm của hàm số x xe dx là: 2 x 2 e 2 2 A. x e C. B. C. C. x xe C. D. x x e . 2 2 x 1 2 x 1 2 Giải: 2 x xe dx e d x e C. 2 2
Câu 6. Nguyên hàm của hàm số 5 f (x) (1 2x) là: 1 1 1 A. 6 (1 2x) C. B. 6 (1 2x) C. C. 6 (1 2x) C. D. 6 (1 2x) C. 2 6 12
Câu 7. Trong các khẳng định sau, khẳng định nào sai? 1 1 A. 2 2xdx x C. B. ln xdx C. C. sin xdx cos x C . D. dx cot x C. x 2 sin x 3
Câu 8. Nguyên hàm của hàm số f x 2x là: 2 x 3 3 A. 2 2 x 3ln x C. B. 2 x C. C. 2 x C. D. 2 x 3ln x C. 2 x x Câu 9. Hàm số x F x e
tan x C là nguyên hàm của hàm số f (x) nào? x 1 x 1 x 1 x 1 A. f (x) e . B. f (x) e . C. f (x) e . D. f (x) e . 2 sin x 2 sin x 2 cos x 2 cos x Câu 10. Nếu ( ) x f x dx e
sin 2x C thì f (x) bằng: x 1 x 1 A. x e cos2x. B. e cos 2x. C. e cos 2x. D. x e 2cos2x. 2 2 x 1
Câu 11. Nguyên hàm của hàm số f (x) 2e là: 2 cos x 20 x x x e x e 5 A. 2e tan x C. B. x e 2x C. C. e tan x C. D. x e x C. 2 cos x 2 cos x
Group Nhóm Toán | Trắc nghiệm 2016-2017 Câu 12. Tính sin(3x 1) dx . 1 1
A. cos(3x 1) C.
B. cos(3x 1) C.
C. cos(3x 1) C. D.
cos(3x 1) C. 3 3 Câu 13. Tính
(cos 6x cos 4x) dx . 1 1 A. sin 6x sin 4x C. B. 6sin 6x 5sin 4x C. 6 4 1 1 C. sin 6x sin 4x C. D. 6sin 6x sin 4x C. 6 4 1 Câu 14. Tính dx . 2x 1 1 1 A. ln 2x 1 C. B. ln 2x 1 C. C.
ln 2x 1 C. D. ln 2x 1 C. 2 2 1 Câu 15. Tính dx . 1 2x 1 2 A. ln 1 2x C. B. 2 ln 1 2x C. C. ln 1 2x C. D. C. 2 2 (1 2x) 1
Câu 16. Nguyên hàm của hàm số 2 f x x 3x là: x 3 2 x 3x 1 3 2 x 3x 3 2 x 3x A. 3 2 x 3x ln x C. B. C. C. ln x C. ln x C. 2 3 2 x 3 2 D. 3 2
Câu 17. Nguyên hàm của hàm số 2 f (x) x 2x 1 là: 1 A. 3 F (x) x 2 x C. B. F (x) 2x 2 C. 3 1 1 C. 3 2 F (x) x 2x x C. D. 3 2 F (x) x x x C. 3 3 1 1
Câu 18. Nguyên hàm của hàm số f (x) là : 2 x x 1 1 A. 2 ln x ln x C. B. ln x C. C. ln x C. D. 2 ln x ln x C. x x
Câu 19. Nguyên hàm của hàm số 2 ( ) x x f x e e là: 1 A. 2x x e e C. B. 2 2 x x e e C. C. x ( x e e x) C. D. 2x x e e C. 2
Câu 20. Nguyên hàm của hàm số f x cos3x là: 1 1 A. sin 3x C. B. sin 3x C. C. sin 3x C. D. 3sin3x C. 3 3
Câu 21. Công thức nguyên hàm nào sau đây không đúng? 1 1 x A. dx ln x C. B. x dx C ( 1). x 1 x a 1 C. x a dx C (0 a 1). D. dx tan x C. ln a 2 cos x Câu 22. Tính (3cos 3x x ) dx . 20 x x x x 6 3 3 3 3 A. 3sin x C. B. 3sin x C. C. 3sin x C. D. 3sin x C. ln 3 ln 3 ln 3 ln 3
Câu 23. Trong các hàm số sau:
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 (I) 2 f (x) tan x 2 (II) f (x) (III) 2 f (x) tan x 1 2 cos x
Hàm số nào có một nguyên hàm là hàm số g x tan x A. (I), (II), (III). B. Chỉ (II), (III). C. Chỉ (III). D. Chỉ (II).
Câu 24. Trong các mệnh đề sau, mệnh đề nào sai? 3 f (x) A. 2
f (x) f (x)dx C. B.
f (x).g(x) dx
f (x)dx. g(x)dx. 3 C. f (x) g(x) dx f (x)dx g(x)dx. D.
kf (x)dx k
f (x)dx ( k là hằng số).
Câu 25. Nguyên hàm của hàm số 3 f (x) (2x 1) là: 1 1 1 A. 4 (2x 1) C. B. 4 (2x 1) C. C. 4 2(2x 1) C. D. 4 (2x 1) C. 8 2 4 PHẦN 19 : I. NHẬN BIẾT Câu 1.
Cặp hàm số nào sau đây có tính chất: Có một hàm số là nguyên hàm của hàm số còn lại? 1 A. sin 2x và 2 cos x B. 2 tan x và 2 2 cos x C. x e và x eD. sin 2x và 2 sin x Câu 2. Nguyên hàm của hàm số   3
f x x trên R là 4 x 4 x A.x C B. 2 3x C C. 2
3x x C D.C 4 4 4 Câu 3.
Một nguyên hàm của hàm số f (x)  là: 2 cos x 4x 4 A. B. 4 tan x C. 4  tan x D. 3 4x  tan x 2 sin x 3 Câu 4.
Diện tích hình phẳng giới hạn bởi các đường 2
y  4x x và y  2x là: y (2;4) x O 4 20 4 2 2 4 A. 2
(2x x )dxB. 2
(x  2x)dxC. 2
(2x x )dxD. 2
(x  2x)dx  7 0 0 0 0 Câu 5.
Một nguyên hàm F x của 2
f (x)  3x 1 thỏa F   1  0 là:
Group Nhóm Toán | Trắc nghiệm 2016-2017 A. 3 x 1 B. 3 x x  2 C. 3 x  4 D. 3 2x  2 Câu 6.
Hàm số f x có nguyên hàm trên K nếu
A. f x xác định trên K
B. f x có giá trị lớn nhất trên K
C. f x có giá trị nhỏ nhất trên K
D. f x liên tục trên K 4 1 Câu 7.
Giá trị của tích phân I  dx  là : 2x 1 2  1 7 1 7 7 A. ln B.  ln
C. Không tồn tại D. 2 ln 2 5 2 5 5 ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 D D B C B D C 20 8
Group Nhóm Toán | Trắc nghiệm 2016-2017 II. THÔNG HIỂU 2 Câu 1.
Tìm d để diện tích hình phẳng giới hạn bởi đường cong y  ,O ,
x x  1, x d d   1 bằng 2: x y y = 2/x x O 1 d A. 2 e B. e C. 2e D. e 1 Câu 2.
Tính các hằng số A và B để hàm số f (x)  Asin x B thỏa mãn đồng thời các điều kiện f '(1)  2 2 và
f (x)dx  4  0 2 2 A. A   , B  2  
A   B   A B   B. A , B 2  C. 2, 2 D. 2, 2 Câu 3.
Nguyên hàm F x của hàm số f x 2 3
 2x x  4 thỏa mãn điều kiện F 0  0 là 4 2 x A.4 B. 3 4 2x  4x C. 3 x   4x D. 3 4
x x  2x 3 4 Câu 4.
Để tìm nguyên hàm của f x 4 5
 sin xcos x thì nên:
A.Dùng phương pháp đổi biến số, đặt t  cos x u   cos x
B.Dùng phương pháp lấy nguyên hàm từng phần, đặt  4 4
dv  sin x cos d x x 4 u   sin x
C.Dùng phương pháp lấy nguyên hàm từng phần, đặt  5 dv  cos d x x
D.Dùng phương pháp đổi biến số, đặt t  sin x 5 x 1 Câu 5. Tính dx
ta được kết quả nào sau đây? 3 x 20 9
Group Nhóm Toán | Trắc nghiệm 2016-2017 6 x  3 2 x x x 3 x 1
A.Một kết quả khác B.   C C. 6  C D.   C 3 2 4 x 2 3 2x 4 3 Câu 6. Cho tích phân I  2x  4 dx
, trong các kết quả sau: 0 3 2
(I). I  2x  4d  2x x  4dx 2 0 3 2
(II). I  2x  4d  2x x  4dx 2 0 3
(III). I  22x  4dx 2 kết quả nào đúng? A.Chỉ II. B. Chỉ III. C.Cả I, II, III. D.Chỉ I.  2 Câu 7. Tính I  2x    1 sin 2 d x x 0
Lời giải sau sai từ bước nào:
Bước 1: Đặt u  2x 1;dv  sin 2 d x x
Bước 2: Ta có du  2 d ; x v  cos 2x   2  
Bước 3: I  2x   2 1 cos 2x  2cos 2 d x x   2x   2  2 1 cos 2x 2sin 2x 0 0 0 0 Bước 4: Vậy I     2 A.Bước 4 B. Bước 3 C.Bước 2 D.Bước 1 5 dx Câu 8. Giả sử  ln c
. Giá trị của c là 1 2x 1 A. 9 B. 8 C.3 D.81 2 Câu 9. Giá trị của 2 2 x e dx  là 0 A. 4 4e B. 4 e C. 4 e 1 D. 4 3e 1
Câu 10. Biểu thức nào sau đây bằng với 2 sin 3 d x x  ? 1 1 1 1 A. (x  sin 6x)  C B. (x  sin 6x)  C 2 6 2 6 21 1 1 1 1 0 C.
(x  sin 3x)  C D.
(x  sin 3x)  C 2 3 2 3
Group Nhóm Toán | Trắc nghiệm 2016-2017 
Câu 11. Cho hình phẳng giới hạn bởi các đường y  cos 4 , x O , x x  0, x
quay xung quanh trục Ox . 8
Thể tích của khối tròn xoay tạo thành bằng: 2  2    A. B. C. D. 2 16 4 3
Câu 12. Diện tích hình phẳng giới hạn bởi hai parabol 2 2 y x  2 ,
x y  x  4x là giá trị nào sau đây ? A.12 (đvdt) B. 27 (đvdt) C.4 (đvdt) D.9 (đvdt) Câu 13. Cho hàm số 3 2
f (x)  x x  2x 1. Gọi F x là một nguyên hàm của biết rằng F   1  4 thì 4 3 x x 49 4 3 x x A. 2 F (x)    x x B. 2 F (x)  
x x 1 4 3 12 4 3 4 3 x x 4 3 x x C. 2 F (x)  
x x  2 D. 2 F (x)    x x 4 3 4 3 
Câu 14. Tích phân 4 cos 2 d x x  bằng: 0 1 A.1 B. C.2 D.0 2
Câu 15. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2
y x  2, y  3x là: 1 1 1 1 A. B. C. D. 2 4 6 3
Câu 16. Tính diện tích hình phẳng giới hạn bởi các đường 3 2
y x  2x x và y  4x . 71 2 53 A. B. C. 24 D. 6 3 7
Câu 17. Cho đồ thị hàm số y f x trên đoạn 0;6 như hình vẽ. y y=f(x) O 2 4 6 x 21
Biểu thức nào dưới đây có giá trị lớn nhất: 1 1 2 3 6 A. f (x)dx  B. f (x)dx  C. f (x)dx  D. f (x)dx  0 0 0 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 3 2 Câu 18. Biết rằng
f (x)dx  5;
f (x)dx  3   . Tính f (x)dx  ? 1 2 1 A. 2 B. 2  C.1 D. 5
Câu 19. Biểu thức nào sau đây bằng với tan d x x  ? 1 2 tan x 1 A. ln(
 tan x)  C B. ln(cos ) x C C.C D.C s inx 2 2 cos x  14
Câu 20. Cho hàm số F(x) là một nguyên hàm của hàm số f x  cos3x và F( )  thì 2 3
A. F x 1 13  sin 3x
B. F x 1   sin 3x  5 3 3 3
C. F x 1  sin 3x  5
D. F x 1 13   sin 3x 3 3 3 1 dx
Câu 21. Một học sinh tính tích phân I   tuần tự như sau: 1 xe 0 1 x e dx (I). Ta viết lại I   x e 1 xe 0   e d e u d e u du e (II). Đặt x
u e thì I       
ln u ln 1u u(1 u) u 1 u 1 1 1 1 e
(III). I  ln e  ln(e 1)  ln1 ln 11  ln e 1
Lý luận trên, nếu sai thì sai từ giai đoạn nào? A.III B. I C.II D.Lý luận đúng.
Câu 22. Nguyên hàm của hàm số x 2 ( ) (1 3 x f x e e   ) bằng: A. ( ) x  3 x F x e eC B. x 3 ( )  3  x F x e eC C. x 2 ( )   3  x F x e eC D. ( ) x   3 x F x e eC
Câu 23. Tìm họ nguyên hàm của hàm số 3 4 f (x) 
x x x ? 3 4 5 2 3 4 2 4 5 2 3 4 A. 2 3 4 F (x)  x x x C B. 3 3 4 F (x)  x x x C 3 4 5 3 4 5 2 4 5 2 4 5 3 1 5 2 1 4 C. 3 3 4 F (x)  x x x C D. 2 3 4 F (x)  x x x C 3 3 4 3 3 5
Câu 24. Một nguyên hàm của f (x)  cos3x cos 2x bằng 1 1 1 1 A. sin x  sin 5x B. sin x  sin 5x 2 2 2 10 21 1 1 1 2 C. cos x  cos 5x
D. sin 3x sin 2x 2 10 6
Group Nhóm Toán | Trắc nghiệm 2016-2017 ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 B A C D D A C C C B B D A B C A B A B C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 A D A B 21 3
Group Nhóm Toán | Trắc nghiệm 2016-2017
III. VẬN DỤNG THẤP x Câu 1.
Cho hình phẳng giới hạn bởi các đường 2
y xe ; y  0; x  0; x  1. Thể tích của khối tròn xoay sinh
bởi hình phẳng trên khi quay quanh trục hoành là A. 2  e  2 B. 2  e  2
C. e  2
D. e  2 Câu 2.
Diện tích hình phẳng giới hạn bởi đường cong C 3 2
: y  x  3x  2 , hai trục tọa độ và đường thẳng x  2 là: 3 7 5 A. (đvdt) B. (đvdt) C.4 (đvdt) D. (đvdt) 2 2 2 1  3  Câu 3.
Gọi F x là nguyên hàm của hàm số f (x)  thỏa mãn F  0  
. Khi đó F 3 bằng: 2 x  3x  2  2  A. 2 ln 2 B. ln 2 C. 2  ln 2 D.  ln 2 Câu 4. Tìm họ nguyên hàm 2 ( ) x F x x e dx ? A. 2 ( )  (  2  2) x F x x x e C B. 2 ( )  (2   2) x F x x x e C C. 2 ( )  (  2  2) x F x x x e C D. 2 ( )  (  2  2) x F x x x e C Câu 5.
Cho hình phẳng giới hạn bởi các đường y  1 x, O ,
x x  0, x  4 quay xung quanh trục Ox . Thể
tích của khối tròn xoay tạo thành bằng: 28 68 28 68 A. 2  . B.  . C.D. 2  . 3 3 3 3 2 Câu 6. Giá trị của 2 x 1 dx  là 2  A.2 B. 3 C.4 D.5 Câu 7.
Họ nguyên hàm của hàm số f x  cos3x tan x là 4 1 A. 3
 cos x  3cos x C B. 3
sin x  3sin x C 3 3 4 1 C. 3
 cos x  3cos x C D. 3
cos x  3cos x C 3 3  2 Câu 8.
Tính I x cos xdx  0     1 A.I = B. I = - 1 C.I = D.I =  2 2 3 3 2 Câu 9.
Thể tích vật thể tròn xoay sinh ra bởi hình phẳng giới hạn parabol  P 2
: y x 1 và trục hoành khi 21
quay xung quanh trục Ox bằng bao nhiêu đơn vị thể tích? 4 7 5 8 16 A.B. C. D.  2 2 3 15
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 10. Nguyên hàm F x của hàm số f x 4
 sin 2x thỏa mãn điều kiện F   3 0  là: 8 3 1 1 3 3 1 1 A. x  sin 2x  sin 4x B. x  sin 4x  sin 8x 8 8 64 8 8 8 64 3 1 1 3 C. x   1  sin 4x  sin 8x
D. x  sin 4x  sin 6 x 8 8 64 8 x
Câu 11. Họ nguyên hàm của hàm số f x  3 2 ln 3  là xx  2 2 ln 3 2 ln x  3  x  4 2 ln 3  x  4 2 ln 3 A.C B. C C.C D.C 2 8 8 2 3x e 1
Câu 12. Một nguyên hàm của f (x)  là: x e 1 1 1 A. 2 ( ) x x F x ee x B. 2 ( ) x x F x ee 2 2 1 1 C. 2 ( ) x x F x ee D. 2 ( ) x x F x ee 1 2 2 2
Câu 13. Tính tích phân 2 I 
x x dx  ta được kết quả: 0 A.ln2 B. 6 C.1 D. ln 8
Câu 14. Họ nguyên hàm của hàm số f x 1  là 1 8x x x
A. F x 1 8  ln  C
B. F x 1 8  ln  C ln12 1 8x 12 1 8x x x
C. F x 1 8  ln  C
D. F x 8  ln  C ln 8 1 8x 1 8x 4 1 Câu 15. Nếu dx  ln m  thì m bằng 3  x   1  x  2   4 3 A.12 B. C.1 D. 3 4 x 1
Câu 16. Gọi (H) là đồ thị của hàm số f (x) 
. Diện tích giới hạn bởi (H), trục hoành và hai đường x
thẳng có phương trình x  1, x  2 bằng bao nhiêu đơn vị diện tích? A. 2ln 2 B. ln 2 1 C. 1 ln 2 D.1 ln 2
Câu 17. Diện tích hình phẳng giới hạn bởi đồ thị có phương trình 2
x  2x y  0 ; x y  0 là: 21 11 9 7 A.8 B. C. D. 5 2 2 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 1
Câu 18. Diện tích hình phẳng giới hạn bởi các đường y x và y x là: 2 4 16 5 A. 2 B. C. D. 3 3 12
Câu 19. Diện tích hình phẳng giới hạn bởi hai parabol  P 2
: y x và P  2
' : y  x  2x là bao nhiêu đơn vị diện tích? 1 1 A.1 B. C. D.3 3 2 1 dx
Câu 20. Tích phân  bằng: 0 x e  1 e 2e e A. ln B. ln C. ln
D. ln e   1  ln 2 2e  2 e 1 2e   1
Câu 21. Biểu thức nào sau đây bằng với 2 x sin xdx  ? A. 2 2
xcos x x cos d x xB. 2
x cos x  2x cos d x xC. 2
x cos x  2xcos d x xD. 2 2
xcos x x cos d x x  1
Câu 22. Cho hàm số F(x) là một nguyên hàm của hàm số f x 
và F 3  0 thì 2 x  3x  2 x x
A. F x 1  ln  ln 2
B. F x 2  ln  ln 2 x  2 x 1 x x
C. F x 2  ln  ln 2
D. F x 1  ln  ln 2 x 1 x  2 1 dx
Câu 23. Tính I   2 x x  2 0 2 1 A. I   ln 2 B. I  3   ln 2 C. I  ln 3 D. I  2ln 3 3 2
Câu 24. Diện tích hình phẳng giới hạn bởi hai đường 2 y  ,
x y x  sin x và hai đường thẳng x  0, x   là:   1 A.S = (đvdt) B. S =
1 (đvdt) C.S = (đvdt) D.S =  (đvdt) 2 2 2 Câu 25. Tính 3 cos d x x
ta được kết quả là : 4 cos x 1 3sin x A.C B. sin 3x   C x 12 4 4 cos . x sin x 1  sin 3x  21 C.C D.  3sin x C   4 4  3  6
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 dx
Câu 26. Bằng cách đổi biến số x  2sin t thì tích phân  là: 0 2 4  x    1 dt A. dtB. 6 dtC. 6 tdtD. 3  0 0 0 0 t ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 C D D A B C C B D A C D C C D D C B B B
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 B C A A D B 21 7
Group Nhóm Toán | Trắc nghiệm 2016-2017 IV. VẬN DỤNG CAO Câu 1. Gọi F  
1(x) là nguyên hàm của hàm số 2 f (x)
sin x thỏa mãn F 0
0 và F x là nguyên hàm 2   1   1 của hàm số 2
f (x)  cos x thỏa mãn F 0  0 . 2   2
Khi đó phương trình F x F x có nghiệm là: 1   2    k
A. x k2
B. x kC. x   kD. x  2 2 Câu 2.
Diện tích hình phẳng giới hạn bởi 2
y  2y x  0 , x y  0 là: 11 9 A.Đáp số khác B. C.5 D. 2 2 Câu 3.
Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng (H) giới hạn bởi các đường cong 2
y x và y
x quanh trục Ox . 3 13 13 3 A. V  B. V  C. V  D. V  10 15 5 5 2 3 dx Câu 4. Tính tích phân I   2  5 x x 4 3 5 1 5 1 3 A. 3ln B. 2 ln C. ln D. ln 4 3 4 3 2 5 Câu 5.
Hình phẳng D giới hạn bởi 2
y  2x và y  2x  4 khi quay D xung quanh trục hoành thì thể tích
khối tròn xoay tạo thành là: 288 4 A.V =  (đvtt)
B. V = 2   (đvtt) C.V = 72  (đvtt) D.V = (đvtt) 5 5  Câu 6.
Các đường cong y  sin ,
x y  cos x với 0  x
và trục Ox tạo thành một hình phẳng. Diện 2
tích của hình phẳng là: A. 2  2 B. 2 C. 2 2 D.Đáp số khác. x Câu 7.
Gọi F(x) là nguyên hàm của hàm số f (x) 
thỏa mãn F 2  0 . Khi đó phương trình F(x) 2 8  x = x có nghiệm là: A. x  0 B. x  1 C. x  1  D. x  1 3 Câu 8.
Diện tích hình phẳng nằm trong góc phần tư thứ nhất, giới hạn bởi đường thẳng y  4x và đồ thị hàm số 3 y x là: 7 A.5 B. 3 C.4 D. 2 1 21 Câu 9. Tính 2 I  1  x dx  8 0
Group Nhóm Toán | Trắc nghiệm 2016-2017  1  A.I = B. I = C.I = 2 D.I = 4 2 3
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2
y x ; y  2  x là: 5 7 A.2 B. C. D.3 3 3
Câu 11. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bới các đường y
x , y  x  2 , y  0
quay quanh trục Oy , có giá trị là kết quả nào sau đây ? 1 3 11 32 A.  (đvtt) B.  (đvtt) C.  (đvtt) D.  (đvtt) 3 2 6 15
Câu 12. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y  x  3x  3x 1và tiếp tuyến của đồ thị
tại giao điểm của đồ thị và trục tung. 27 5 23 4 A. S  B. S  C. S  D. S  4 3 4 7 1 4 x Câu 13. Tính I  dx  2x 1 1  1 5 7 A.I = B. I = C.I = D.I = 5 5 7 5
Câu 14. Cho (H) là hình phẳng giới hạn bởi đường cong (L): y x  3
ln 1 x  , trục Ox và đường thẳng
x  1 . Tính thể tích của vật thể tròn xoay tạo ra khi cho (H) quay quanh trục Ox.     A. V  ln 4   1 B. V 
ln 4  2 C.V  ln3  2 D. V  ln 3 3 3 3 3
Câu 15. Với giá trị nào của m  0 thì diện tích hình phẳng giới hạn bởi hai đường 2
y x và y mx bằng 4 đơn vị diện tích ? 3 A. m  2 B. m  1 C. m  3 D. m  4 a x Câu 16. Tích phân 2 dx  bằng 0 a x  1     2   1     2  A. a     B. a   C. a     D. a    2   4   2   4  t dx 1
Câu 17. Với t thuộc  1   ;1 ta có   ln 3 
. Khi đó giá trị t là: 2 x 1 2 0 1 1 1 A. B. C.0 D. 3 3 2 2 21
Câu 18. Tìm a sao cho 2 3
I  [a  (4 - a)x  4x ]dx  12  9 1 A.Đáp án khác B. a  3  C. a  5 D. a  3
Group Nhóm Toán | Trắc nghiệm 2016-2017 ln m x e dx
Câu 19. Cho A   ln 2 
. Khi đó giá trị của m là: x e  2 0
A. m  0; m  4
B. Kết quả khác C. m  2 D. m  4
Câu 20. Cho S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y x  6x  9x và trục Ox. Số nguyên
lớn nhất không vượt quá S là: A.10 B. 7 C.27 D.6
Câu 21. Vận tốc của một vật chuyển động là v t   3t  5m / s . Quãng đường vật đó đi được từ giây thứ 4 đến giây thứ 10 là : A.36m B. 252m C.120m D.156m
Câu 22. Diện tích hình phẳng giới hạn bởi 2
y  4  x và y  3 x là: 17 3 5 13 A. B. C. D. 6 2 2 3 2 1
Câu 23. Tính tích phân I  dx  ta được kết quả: 2 x - 2x  2 0     A.B. C. D. 4 2 4 3 ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 D D A C A D D C A C D A A A A B A A D D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 D D B PHẦN 20 : TÍCH PHÂN - ỨNG DỤNG (PHẦN 4) 22
Mức độ nhận biết, thông hiểu 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 2 Câu 1. Giá trị của 2 x e dx là : 0 4 4 4 4 A. e B. e 1 C. 4e D. 3e 1: 6 4 6 Câu 2. Nếu f (x)dx 10 và f (x)dx 7 , thì
f (x)dx bằng : 0 0 4 A. 3 B. 17 C. 170 D. 3 5 dx Câu 3. Giả sử
lnc . Giá trị đúng của c là : 2x 1 1 A. 9 B. 3 C. 81 D. 8 1 3 x 1 Câu 4.
Khẳng định nào sau đây đúng về kết quả dx ln 2 ? 4 x 1 a 0 A. a 2 B. a 4 C. a 4 D. a 2 1 (3x 1)dx Câu 5.
Tính tích phân I   2 x  6x  9 0 4 5 3 5 4 5 4 7 A. 3ln  B. 3ln  C. 3ln  D. 3ln  3 6 4 6 3 6 3 6 Câu 6.
Nguyên hàm của hàm số f x 2
x – 3x  1 là: x 3 2 3 2 x 3x x 3x A. F(x) =   ln x C B. F(x) =   ln x C 3 2 3 2 3 2 x 3x 3 2 x 3x C. F(x) =   ln x C D. F(x) =   ln x C 3 2 3 2 Câu 7.
Thể tích của khối tròn xoay sinh ra khi quay quanh trục Oy hình phẳng giới hạn bởi các đường: 2
y  x  4x  3 và Ox bằng : 16  16 A. B. 5 C. D. 5 5 3 2x Câu 8.
Cho f x  . Khi đó: 2 x 1 22 A. f
 xdx   2
2 ln 1 x   C B. f
 xdx   2
3ln 1 x   C 1
Group Nhóm Toán | Trắc nghiệm 2016-2017 C. f
 xdx   2
4 ln 1 x   C D. f
 xdx   2
ln 1 x   C Câu 9.
Cho hai hàm số y = f(x), y = g(x) có đồ thị (C1) và (C2) liên tục trên [a;b] thì công thức tính diện tích
hình phẳng giới hạn bởi (C1), (C2) và hai đường thẳng x = a, x = b là b b
A. S  f (x)  g(x)dx
B. S  g(x)  f (x)dx a a b b b C. S  f (x)dx  g(x)dx   D. S  f (x)  g(x) dx  a a a 0 x 1 b
Câu 10. Khẳng định nào sau đây sai về kết quả dx a ln 1 ? x 2 c 1 A. . a b 3(c 1) B. ac b 3 C. a b 2c 10 D. ab c 1 1 (x  4)dx
Câu 11. Tính tích phân I   2 x  3x  2 0 A. 5ln 2  3ln 2 B. 5ln 2  2ln3 C. 5ln 2  2ln3 D. 2ln5  2ln3
Câu 12. Cho hàm số y = f(x) liên tục và chỉ triệt tiêu khi x = c trên [a; b]. Các kết quả sau, câu nào đúng? b b b c b A. f (x) dx  f(x)dx   B. f (x) dx  f(x) dx  f(x) dx    a a a a c b c b C. f (x) dx  f(x) dx  f (x)dx    D. A, B, C đều đúng a a a
Câu 13. Diện tích phẳng giới hạn bởi: 2 x  1
 ; x  2; y  0; y x  2x 4 8 A. B. 1 C. 0 D. 3 3 3 2 x  3x  3x 1 1
Câu 14. Tìm một nguyên hàm F(x) của hàm số f (x)  F(1)  2 x  2x  biết 1 3 2 2 13 A. 2 F(x)  x  x   6 F(x)  x  x   x  B. 2 1 x  1 6 2 x 2 13 2 x 2 C. F(x)   x   F(x)   x   6 22 2 x  D. 1 6 2 x  1 2 1
Câu 15. Tính diện tích S  hình phẳng được giới hạn bởi các đường: 2
y x ; y  ln ; x  1 x  1
Group Nhóm Toán | Trắc nghiệm 2016-2017 8 31 8 23 A. S   ln 2  B. S  ln 2  3 18 3 18 8 17 8 23 C. S  ln 2  D. S  ln 2  3 18 3 18
Câu 16. Gọi 2008xdx F
xC , với C là hằng số. Khi đó hàm số F x bằng 2008x A. 2008x ln 2008 B. 1 2008x C. 2008x D. ln 2008
Câu 17. Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi các đường  y x ln ,
x y  0, x e có giá trị bằng: 3
(b e  2) trong đó a,b là hai số thực nào dưới đây? a A. a=27; b=5 B. a=24; b=6 C. a=27; b=6 D. a=24; b=5
Câu 18. Cho đồ thị hàm số y
f x . Diện tích hình phẳng (phần tô đậm trong hình) là: 4 0 0 A. f x dx B. f x dx f x dx 3 3 4 1 4 3 4 C. f x dx f x dx D. f x dx f x dx 3 1 0 0 2 Câu 19. Tích phân
cos x.sin xdx bằng: 0 2 2 3 A. B. C. D.0 3 3 2 22 1 3 2
Câu 20. Cho tích phân 2 1 x dx  bằng: 0
Group Nhóm Toán | Trắc nghiệm 2016-2017   3  1   3    3  1   3  A.      B.      C.      D.      6 4   2 6 4   6 4   2 6 4    Câu 21. I  1 cos 2x dx  bằng : 0 A. 2 B. 0 C. 2 D. 2 2 3 x
Câu 22. Tìm họ nguyên hàm: F (x)  dx  4 x 1 1 A. 4
F(x)  ln x 1  C B. 4 F (x) 
ln x 1  C 4 1 1 C. 4 F (x) 
ln x 1  C D. 4 F (x) 
ln x 1  C 2 3 9 9 9 Câu 23. Nếu f (x)dx
37 và g(x)dx 16 thì
2 f (x) 3g(x) dx bằng : 0 0 0 A. 122 B. 74 C. 48 D. 53 1
Câu 24. Giá trị của tích phân 3 3 4 x 1 x d . x  bằng? 0 3 6 A. B. 2 C. D. Đáp án khác 16 13 ln 2 Câu 25. Tính 2 x dx , kết quả là: x x A. 2 2 1 C B. 2x C x 1 C. 2 2 1 C D. 2 x C dx Câu 26. Tính , kết quả là : 1 x C A. B. 2 1 x C 1 x 22 4 2 C. C D. C 1 x 1 x
Group Nhóm Toán | Trắc nghiệm 2016-2017 x ln(x  2)
Câu 27. Diện tích hình phẳng giới hạn bởi y 
và trục hoành là : 2 4  x   A. 2   3 B. 2 ln 2  2  3 4   C. ln 2  2   3 D. 2 ln 2  2   3 3 3 x ln  2 x  x 1
Câu 28. Một nguyên hàm của f (x)  là: 2 x 1 A.  2
x ln x  x 1  x  C B.  2
ln x  x 1  x  C C. 2 x ln x 1  x  C D. 2   2 x
1 ln x  x 1  x  C
Câu 29. Cho hình phẳng giới hạn bởi các đường y = 2x – x2 và y = 0. Thì thể tích vật thể tròn xoay được sinh
ra bởi hình phẳng đó khi nó quay quanh trục Ox có giá trị bằng ? 16 15 5 6 A. B. C. D. 15 16 6 5 2 1
Câu 30. Khẳng định nào sau đây sai về kết quả
(2x 1 sin x)dx 1 a b 0 A. a 2b 8 B. a b 5 C. 2a 3b 2 D. a b 2
Câu 31. Một nguyên hàm của hàm số y  sin 3x 1 1 A.  o c s3x B. 3  o c s3x C. 3 o c s3x D. o c s3x 3 3 x f (t) Câu 32. Nếu dt 6 2 x , x
0 thì hệ số a bằng 2 t a A. 9 B. 19 C. 5 D. 29 1 2x  3
Câu 33. Biết tích phân dx
=aln2 +b . Thì giá trị của a là: 2  x 0 22 A. 7 B. 2 C. 3 D. 1 5
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 34. Thể tích hình khối do hình phẳng giới hạn bởi các đường 2
y  x  4, y  2x  4, x  0, x  2 quay
quanh trục Ox bằng 32 32 A.  B. 6 C. 6   D. : 5 5 4 2x  3
Câu 35. Nguyên hàm của hàm số y  là: 2 x 2x3 3 3 x 3 3 2x 3 A.  3  C B. 3 3  xC C.   C D.   C 3 x x 3 x 3 x
Mức độ vận dụng thấp 2
Câu 36. Tính  x x e 1 . dx 2 2 1 2 1 2 1 A. x 1 e   C B. x eC C. x 1 e   C D. x 1 e   C : 2 2 2
Câu 37. Thể tích của khối tròn xoay tạo thành khi quay hình phẳng D giới hạn bởi các đường y x 1 , trục hoành, x 2,x 5 quanh trục Ox bằng : 5 5 2 5 2 2 A. x d 1 x B. x 1 dx C. y 1 dx D. x 1 dx : 2 2 1 2  6 tan x
Câu 38. Cho tích phân 4 I dx
. Giả sử đặt u  3tan x 1 thì ta được: 2 0
cos x 3 tan x 1 2 4 2 4 A. I   2 2u   1du B. I   2u   1du 1 3 1 3 2 4 2 4 C. I   2u   1du D. I   2 2u   1du 1 3 1 3 x
Câu 39. Họ nguyên hàm của hàm số f x 3  là: 2 1 x 1 1 A.  2 x  2 2 1 x C B.   2 x   2 1 1 x C 3 3 22 1 1 C.  2 x   2 1 1 x C D.   2 x  2 2 1 x C 6 3 3
Group Nhóm Toán | Trắc nghiệm 2016-2017 4
Câu 40. Nếu f (1) 12, f '(x) liên tục và f '(x)dx
17 , giá trị của f (4) bằng 1 A. 29 B. 5 C. 19 D. 9 4 2
Câu 41. Nếu f (x) liên tục và f (x)dx 10 , thì
f (2x)dx bằng : 0 0 A. 5 B. 29 C. 19 D. 9 b
Câu 42. Biết 2x  4dx  0 , khi đó b nhận giá trị bằng: 0
A. b  1 hoặc b  4
B. b  0 hoặc b  2
C. b  1 hoặc b  2
D. b  0 hoặc b  4 2
Câu 43. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y
x và đường thẳng y 2x bằng: 23 4 3 5 A. B. C. D. 15 3 2 3
Câu 44. Thể tích của khối tròn xoay tạo lên bởi lên hình phẳng (H) giới hạn bởi các đường 2
y  x  2 ; y 1
và trục Ox khí quay xung quanh Ox là; 1 1 1 1 A. 2 2
 (x 1) dx   dx   B. 2 2
 (x  2) dx   dx   1  1  1  1  1 1 1 C. 2 2
 (x  2) dx  dx   D. 2 2
 (x  2) dx  1  1  1  4m     Câu 45. Cho 2 f (x)   sin x  
. Tìm m để nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 và F    4  8 4 A. m   3 B. m  3 C. m   4 D. m  : 3 4 4 3 (x a) cos3x 1
Câu 46. Một nguyên hàm (x 2) sin 3xdx
sin 3x 2017 thì tổng S . a b c bằng b c A. S 14 B. S 15 C. S 3 D. S 10 dx
Câu 47. Tìm họ nguyên hàm: F(x)   x 2 ln x 1 22
A. F(x)  2 2ln x 1  C
B. F(x)  2ln x 1  C 7
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 C. F(x) 
2 ln x 1  C D. F(x) 
2 ln x 1  C 4 2
Câu 48. Cho hàm f x 4
 sin 2x . Khi đó:     A. f  x 1 1 dx
3x  sin 4x  sin 8x C   B. f  x 1 1 dx
3x  cos 4x  sin 8x C   8  8  8  8      C. f  x 1 1 dx
3x  cos 4x  sin 8x C   D. f  x 1 1 dx
3x  sin 4x  sin 8x C   8  8  8  8 
Câu 49. Diện tích hình phẳng giới hạn bởi hai đường cong  (1 x y
e )x và y  (e 1)x là? e e e e A. 1 B.  2 C.  2 D. 1 2 2 2 2 
Câu 50. Cho tích phân sin 2  sin 2 . x I x e dx
: .một học sinh giải như sau: 0
x  0  t  0 1
Bước 1: Đặt t  sin x dt  cos xdx . Đổi cận:    2 . t I t e dt  . x   t 1 0 2  u tdu dt Bước 2: chọn    t tdv e dtv e 1 1 1 1  . t  . t t t t e dt t e
e dt e e 1   0 0 0 0 1 Bước 3:  2 . t I t e dt  2  . 0
Hỏi bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
A.Bài giải trên sai từ bước 1.
B.Bài giải trên sai từ bước 2 . .
C. Bài giải trên hoàn toàn đúng.
D.Bài gaiir trên sai ở bước 3
Câu 51. Tính diện tích hình phẳng tạo bởi các đường: Parabol P 2
: y x  4x  5 và 2 tiếp tuyến tại các A 1; 2 , B 4;5 P 22 điểm 
   nằm trên   8 7 11 9 13 A. S  B. S  C. S  D. S  2 6 4 8
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 52. Tìm hàm số F(x) biết rằng F’(x) = 4x3 – 3x2 + 2 và F(-1) = 3 4 3 4 3 A. F(x) = x - x - 2x -3 B. F(x) = x - x - 2x +3 4 3 4 3 C. F(x) = x - x + 2x + 3 D. F(x) = x + x + 2x + 3    3 cot x 4 3 cot x
Câu 53. Biết rằng x   ;   thì   . Gọi I  dx. 
Kết luận nào sau đây là đúng  4 3   x   x 4 3 1 1 1 1 1 3 1 A.  I  B.  I  C.  I  D.  I  12 4 4 3 5 4 12 3
Câu 54. Tính ln x
A. xln x x C
B. ln x x C
C. xln x x C
D. xln x x C ?
Câu 55. Thể tích của vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi các đường y = x2 – 2x, y = 0,
x = 0, x = 1 quanh trục hoành Ox có giá trị bằng? 8 8 15 7 A. B. C. D. 15 7 8 8 dx
Câu 56. Tìm nguyên hàm của: F(x)   3 5 x x 1 1 1 1 A. F(x)   ln x  ln  2 1 xC B. F(x)    ln x  ln  2 1 xC 2  2  2x 2 2x 2 1 1 1 1 C. F(x)    ln x  ln  2 1 xC D. F(x)    ln x  ln  2 1 xC 2  2  2x 2 25x 6
Câu 57. Cho hình phẳng  H  được giới hạn bởi các đường: y x ln ,
x y  0, x e . Tính thể tích khối tròn
xoay tạo thành khi hình  H  quay quanh trục Ox .   3 5e  2   3 5e  2 A. V  B. VOx 25 Ox 27   3 5e  2   3 5e  2 C. V  D. VOx 27 Ox 25 22 9
Mức độ vận dụng cao.
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 58. Cho hình phẳng  H  được giới hạn bởi các đường: y x ln ,
x y  0, x e . Tính thể tích khối tròn
xoay tạo thành khi hình  H  quay quanh trục Ox .   3 5e  2   3 5e  2 A. V  B. VOx 25 Ox 27   3 5e  2   3 5e  2 C. V  D. V Ox 27 Ox 25 2 2 x x
Câu 59. Tính diện tích S  hình phẳng được giới hạn bởi các đường: y  4  ; y  4 4 2 2 5 4 1 A. S  2  B. S  2  C. S  2  D. S  2  3 3 3 3 6 n 1 Câu 60. Cho I
sin x cos xdx . Khi đó n bằng: 64 0 A. 5 B. 3 C. 4 D. 6 e 3 a e 1
Câu 61. Khẳng định nào sau đây đúng về kết quả 3 x ln xdx ? b 1 A. . a b 64 B. . a b 46 C. a b 12 D. a b 4 2
20x  30x  7 3
Câu 62. Cho các hàm số: f (x) 
; F x   2
ax bx x 2x  3 với x  . Để hàm số F x 2x  3 2
là một nguyên hàm của hàm số f (x) thì giá trị của a, , b c là
A. a  4;b  2;c  1
B. a  4;b  2  ;c  1 
C. a  4;b  2  ;c 1
D. a  4;b  2;c  1    
Câu 63. Cho hình phẳng giới hạn bởi: D  y  tan ; x x  0; x
; y  0 Thể tích vật tròn xoay khi D quay  3  quanh Ox:     A.    3    B. 3  C. 3  D.    3     3  3 3  3  1 23
Câu 64. Nguyên hàm của hàm số y 3x 1 trên ; là: 3 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 2 2 3 A. x x C B. 3x 1 C 2 9 2 3 3 2 C. 3x 1 C D. x x C 9 2 1
Câu 65. Cho hàm f x  .Khi đó 2 x  3x  2 x x  A. f  x 1 dx  ln  C B. f  x 1 dx  ln  C x  2 x  2 x x  C. f  x 2 dx  ln  C D. f  x 2 dx  ln  C x 1 x 1
Câu 66. Cho hình phẳng  H  được giới hạn bởi các đường: y x ln ,
x y  0, x e . Tính thể tích khối tròn
xoay tạo thành khi hình  H  quay quanh trục Ox . x x  A. f  x 1 dx  ln  C B. f  x 1 dx  ln  C x  2 x  2 x x  C. f  x 1 dx  ln  C D. f  x 2 dx  ln  C x  2 x 1
Câu 67. Trong các khẳng định sau khẳng định đúng? 10
A. Nếu w '(t) là tốc độ tăng trưởng cân nặng/năm của một đứa trẻ, thì
w '(t)dt là sự cân nặng của 5
đứa trẻ giữa 5 và 10 tuổi 120
B. Nếu dầu rò rỉ từ 1 cái thùng với tốc độ r (t) tính bằng galông/phút tại thời gian t , thì r (t)dt 0
biểu thị lượng galông dầu rò rỉ trong 2 giờ đầu tiên
C. Nếu r (t) là tốc độ tiêu thụ dầu của thế giới, trong đó t được bằng năm, bắt đầu tại t 0 vào 17
ngày 1 tháng 1 năm 2000 và r (t) được tính bằng thùng/năm,
r (t)dt biểu thị số lượng thùng 0
dầu tiêu thụ từ ngày 1 tháng 1 năm 2000 đến ngày 1 tháng 1 năm 2017 . 23 D. Cả , A , B C đều đúng 1
Group Nhóm Toán | Trắc nghiệm 2016-2017  4 1 a Câu 68. BIết : dx  
. Mệnh đề nào sau đây đúng? 4 cos x 3 0 A. a là một số chẵn B. a là số lớn hơn 5 C. a là số nhỏ hơn 3 D. a là một số lẻ
--------------------HẾT----------------- ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 B A B B C C D D D D C D D C B D A B B D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 D B A A B B D D A B B A A D A C B C D A
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 50 A D B C C B B D A C C C D C A B C B C B 61 62 63 64 65 66 67 68 A C D B D C D A PHẦN 21 :
TÍCH PHÂN VÀ ỨNG DỤNG (PHẦN 3) 23 2 NHẬN BIẾT
Câu 18. Họ nguyên hàm của tan x là:
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 tan x
A. ln cosx  C
B. ln cosx  C C.  C
D. ln(cosx)  C 2
Câu 2. Cho hai hàm số f (x),g(x) là hàm số liên tục ,có F(x),G(x) lần lượt là nguyên hàm của
f (x), g(x).Xét các mệnh đề sau :
(I): F(x)  G(x) là một nguyên hàm của f (x)  g(x)
(II): k.Fx là một nguyên hàm của kf x,(k R)
(III): F(x).G(x) là một nguyên hàm của f (x).g(x)
Mệnh đề nào là mệnh đề đúng? A. I B. I và II C. I, II, III D. II
Câu 3. Diện tích hình phẳng phần bôi đen trong hình sau được tính theo công thức: b c c b A. S
f (x)dx f (x)d   x . B. S
f (x)dx f (x)d   x . a b b a c c
C. S f (x)d  x . D. S f (x)d  x a a 23 3
Group Nhóm Toán | Trắc nghiệm 2016-2017 Câu 4.
Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay
tạo thành được tính theo công thức nào? b b
A. V  f(x) g(x)2 dx B. 2 2 V   f (x)  g (x) d  x   a a b b
C. V  f(x) g(x)2 dx
D. V  f(x) g(x)dx a a
Câu 5. Tìm công thức sai: x a A. x x e dx  e  C  B. x a dx   C 0  a    1 ln a
C. cos xdx  sin x  C 
D. sin xdx  cos x  C 
Câu 6. Gọi F(x) là một nguyên hàm của hàm y  x.cos x mà F(0) 1. Phát biểu nào sau đây là đúng:
A. F(x) là hàm chẵn B. F(x) là hàm lẻ
C. F(x) là hàm tuần hoàn chu kỳ 2
D. F(x) không là hàm chẵn cũng không là hàm lẻ
Câu 7. Mệnh đề nào sau đây sai? 23 4
A.Nếu F(x) là một nguyên hàm của f (x) trên a;b và C là hằng số thì f (x)dx  F(x)  C  .
Group Nhóm Toán | Trắc nghiệm 2016-2017
B.Mọi hàm số liên tục trên a;b đều có nguyên hàm trên a;b .
C. F(x) là một nguyên hàm của f (x) trên a;b  F (x)  f (x), x  a;b.  D.  f (x)dx   f(x) THÔNG HIỂU
Câu 8. Nếu Fx là một nguyên hàm của x x
f (x)  e (1 e ) và F(0)  3 thì F(x) là ? A. x e  x B. x e  x  2 C. x e  x  C D. x e  x 1
Câu 9. Diện tích hình phẳng giới hạn bởi 2
y  x  3x  2 và trục Ox là: 1 3 729 27 A. B. C. D. 6 4 35 4
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  x và đường thẳng y  x  2 là 13 A. (đvdt) B.11 (đvdt) C.7 (đvdt)
D.Một kết quả khác 2 3  x 1
Câu 11. Tính diện tích hình phẳng được giới hạn bởi đường cong (C) : f (x)  và hai x 1 trục tọa độ. 4 5 A. 1   4ln B. 1   ln 7 C. 1   2ln 2 D. 1   ln 3 3 0 2x 1 Câu 12. Tính dx  bằng: 1 x 1 
A. ln 2  2 B. ln 2  2 C. ln 2  2 D. ln 2  2 Câu 13. Nếu x 2 f (x)dx  e  sin x  C  thì f (x) là hàm nào ? A. x 2 e  cos x B. x e  sin 2x C. x e  cos 2x D. x e  2sin x 23
Câu 14. Thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi 2
y  x  2x và trục Ox 5 quanh trục Ox là:
Group Nhóm Toán | Trắc nghiệm 2016-2017 16 4 3 16 72 A. B. C. D. 15 3 15 5
Câu 15. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y  x  4x và trục hoành bằng: A.4 B.0 C.2 D.8 2
Câu 16. Hàm nào không phải nguyên hàm của hàm số y  : 2 (x 1) x 1 2x 2 x 1 A. B. C. D. x 1 x 1 x 1 x 1 Câu 17. 3 cos x.sin xdx  bằng 4 cos x 4 sin x A.  C B.  C C. 4 sin x  C D. 4 cos x  C 4 4 2
Câu 18. Tính tích phân sau I  x 1 dx  0 A.1 B.11 C.6 D.3   2 2 Câu 19. Cho f
 xdx  5. Khi đó f  x2sinx .dx  bằng: 0 0  A. 5   B. 5  C.7 D.3 2 1
Câu 20. Họ nguyên hàm của là: sin x x x x A. ln cot  C B. ln tan  C C.  ln tan
 C D. ln sin x  C 2 2 2
Câu 21. Tìm diện tích hình phẳng giới hạn bởi các đường 2 y  x và y  x  2 9 9 9 A.9 B. C. D. 8 2 4 Câu 22. Hàm số x
F(x)  e  tan x  C là nguyên hàm của hàm số f (x) nào 1 23 A. x f (x)  e  B.Đáp án khác 2 sin x 6
Group Nhóm Toán | Trắc nghiệm 2016-2017  1 x  e  C. x f (x)  e  D. x f (x)  e 1  2 sin x 2  cos x 
Câu 23. Nguyên hàm của hàm số f x  2sin x  cos x là:
A. 2cos x sinx  C B. 2cos x sinx C C. 2  cos x sinx  C D. 2  cos x  sinx  C
Câu 24. Họ nguyên hàm của 2 sin x là: 1 1  sin 2x 
A. x  2cos 2x  C B. x    2 2  2  x sin 2x 1 C.   C
D. x  2cos 2x  C 2 4 2 1
Câu 25. Họ nguyên hàm của f (x)  là: x(x 1) x 1 x A. F(x)  ln  C B. F(x)  ln  C x x 1 1 x C. F(x)  ln  C
D. F(x)  ln x(x 1)  C 2 x 1 Câu 26. x 1 2  dx  bằng x 1 2  x 1 2  A. B. x 1 2   C C.  C D. x 1 2  .ln 2  C ln 2 ln 2
Câu 27. Diện tích hình phẳng giới hạn bởi 2 y  x và y  2x  3là 512 88 32 32 A. B. C. D. 15 3 3 3
Câu 28. Tính diện tích hình phẳng giới hạn bởi 2
(P) : y  4x và d : y  2x  4 (VAN DUNG) A. 9 B. 3 C. 7 D. 5
Câu 29. Thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi 2 y  x và y  x  2 quanh trục Ox là: 23    7 72 138 9 72 A. B. C. 5 5 2 D. 5
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 30. Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn 3 x bởi các đường y  và 2 y  x là 3 436 9 468 486 A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt) 35 2 35 35 x
Câu 31. Một nguyên hàm của f (x)  là: 2 x 1 1 1 A. ln(x 1) B. 2 2ln(x 1) C. 2 ln(x 1) D. 2 ln(x 1) 2 2
Câu 32. Họ nguyên hàm của hàm số 5 y  (2x 1) là: 1 1 A. 6 (2x 1)  C B. 6 (2x 1)  C 12 6 1 C. 6 (2x 1)  C . D. 4 10(2x 1)  C 2
Câu 33. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y  x , trục hoành và các đường thẳng x  1  , x  3 là 45 27 17 41 A. (đvdt) B. (đvdt) C. (đvdt) D. (đvdt) 2 2 3 2  2 dx Câu 34. I    1 cos x 0 1 1 A. B. C.1 D. 2 4 2 2 2 2x  2
Câu 35. Tính tích phân sau: I  dx  (SAI) x 1
A. I  3 2ln 2 B. I  3 2ln 2 C. I  2  2ln 3 D.Đáp án khác
Câu 36. Tìm một nguyên hàm Fx của hàm số   2
f x  2  x biết   7 F 2  3 23 19 8 A.   3 x 1 F x  2x   B. Fx 3  2x  x  3 3 3
Group Nhóm Toán | Trắc nghiệm 2016-2017 C.   3 x F x  2x  1 D.   3 x F x  2x   3 3 3 VẬN DỤNG 2 x  4x  4
Câu 37. Tìm diện tích hình phẳng giới hạn bởi các đường y  ; y  x 1; x  2  ;x  0 ; x  3 y  x  2 (SAI) 3 1 1 A. ln B. ln 3 C.1 D. ln 3. 2 2 4
Câu 38. Tính diện tích hình phẳng giới hạn bởi 2
y  x  4x  5 và hai tiếp tuyến tại A(1; 2) và B(4;5) 9 7 3 5 A. B. C. D. 4 4 4 4 ln x 1
Câu 39. Gọi F(x) là một nguyên hàm của hàm 2 y  ln x 1. mà F(1)  . Giá trị 2 F (e) x 3 bằng: 8 1 8 1 A. B. . C. . D. . 9 9 3 3
Câu 40. Họ nguyên hàm của 2 f (x)  x.cos x là: 1 A. 2 cos x  C B. 2 sin x  C C. 2 sin x  C D. 2 2sin x  C 2 2
Câu 41. Một nguyên hàm của x f (x) xe  là: 2 1 2 1 A. x e B. 2 x  e C. x e  D. 2 x e 2 2  12  
Câu 42. Tính tích phân sau I 
tan x.tan(  x).tan(  x)dx   3 3 12 1 2 2 1 A. ln 2 B. ln 2 C. ln 3 D. ln 3 23 3 3 3 3 9 x
Câu 43. Cho hàm số f x 2  2sin Khi đó f (x)dx  bằng 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 A. x  sin x  C B. x sin x  C C. x  cos x  C D. x  cos x  C
Câu 44. Họ nguyên hàm của 3 f (x)  sin x 3 cos x 3 cos x 1 4 sin x A. cos x   C B.  cos x   C C.  cos x   c D.  C 3 3 cos x 4 2 Câu 45. 2 I  4  x dx  bằng (SAI) 0    A. B. C. D. 3 2 6 1 dx Câu 46. I   bằng: 2 1 x 0     A. B. C. D. 6 3 4 2 1
Câu 47. Biết rằng tích phân x (2x 1)e dx  a  b.e  , tích ab bằng: 0 A.1 B. 1  C. 15  D. 5 2
Câu 48. Tính tích phân sau: I  x a  x dx  0 8 1 8 8
A.Cả 3 đáp án trên B. 2x  C. 3 a   2a D.  2a 3 3 3 3 t  3  Câu 49. Cho 4 f (x)  4sin x  dx 
 .Giải phương trình f (x)  0  2  0 k  A. k2 ,  k Z B. , k  Z C. k ,  k Z D.  k ,  k  Z 2 2  24 2 0 Câu 50. Tính tích phân 2 sin cos d  x x x 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 1 1 1 A. B.1 C. D. 4 3 2
Câu 51. Tính diện tích hình phẳng giới hạn bởi đường cong 2
(C) : y  x  4x  3 và d : y  x  3 109 105 107 103 A. B. C. D. 6 6 6 6
Câu 52. Diện tích giới hạn bởi đồ thị hàm 3 2
y  x  3x  4 và đường thẳng x  y 1  0 A.10 B.8 C.6 D.4 2 2 x  2 Câu 53. Cho M  .dx 
. Giá trị của M là: 2 2x 1 5 11 A. 2 B. C.1 D. 2 2
Câu 54. Thể tích khối tròn xoay trong không gian Oxyz giới hạn bởi hai mặt phẳng
x  0; x   và có thiết diện cắt bởi mặt phẳng vuông góc với Ox tại điểm (x;0;0) bất kỳ là
đường tròn bán kính sin x là A. 2 . B.  . C. 2 D. 4 .
Câu 55. Thể tích khối tròn xoay tạo thành khi cho đường 2 2
x  (y 1)  1 quay quanh trục hoành là A. 2 6 (đvtt) B. 2 8 (đvtt) C. 2 4 (đvtt) D. 2 2 (đvtt)
Câu 56. Diện tích hình phẳng giới hạn bởi đường thẳng 2
y  x  2 và đường thẳng y  x bằng: 9 10 11 17 A. B. C. D. 2 3 2 3 1 x
Câu 57. Tính tích phân   1 x  dx 3 2 0 5 3 3 5 A. B. C. D. 16 8 16 8   24
Câu 58. Tính diện tích hình phẳng giới hạn bởi các đường (C ) : f (x) (e 1)x và 1 1 x (C ) : g(x)  (e 1)x 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 e 2 e A. 1 B. 2 e  2 C. 3 e  3 D.  2 2 2 3 8
Câu 59. Tính tích phân sau I  cot x  tan x dx   8 A. ln 2 B. ln 3 C. ln 2 D. ln 3  3 Câu 60. 3 I  cos xdx  bằng: 0 3 3 3 3 3 3 A. B. C. D. 3 3 2 4 8
Câu 61. Nguyên hàm của hàm số   x f x  xe là: 2 x A. x x xe  e  C B. x e  C C. x e  C D. x x xe  e  C 2 k
Câu 62. Để k  4xdx 3k 1 0 thì giá trị của k là bao nhiêu ? 1 A.1 B.3 C.2 D.4 e k Câu 63. Cho I  ln dx 
.Xác định k để I  e  2 1 x A. k  e  2 B. k  e C. k  e 1 D. k  e 1 3 2x 1 Câu 64. Tích phân dx  a  b n l 2 
. Tổng của a  b bằng: x 1 1 A.1. B. 7 C. 3  D. 2 2x  3
Câu 65. Tìm nguyên hàm của hàm số f (x) biết f (x)  2 x  4x  3 2 x  3x A.    B. 2
(2x  3) ln x  4x  3  C x  4x  3 C 2 2 2 24 x  3x 1 C.  C
D. ln x 1  3ln x  3   C 2 2 x  4x  3 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 d Câu 66.  x bằng 2 (1 x )x x x A. ln  C B. ln  C 2 1 x 2 1 x C. 2 ln x 1 x  C D. 2 ln x (1 x )  C 1 ln x
Câu 67. Tìm nguyên hàm của hàm số f (x) biết f (x)  x A.Đáp án khác B. x  ln x  C 1 1 C. 2 ln x  ln x  C D. 2 ln x  ln x  C 2 4 m
Câu 68. Đặt f m  cos x.dx 
. Nghiệm của phương trình f m  0 là 0  A. m  k2 ,  k Z B. m   k ,  k  Z 2  C. m  k ,  k Z D. m   k2 ,  k  Z 2 1
Câu 69. Một nguyên hàm của x f (x)  (2x  1).e là: 1 1 A. x F(x)  x.e B. x F(x)  e 1 C. 2 x F(x)  x .e D.     1 2 x F(x) x 1 .e 1
Câu 70. Hàm số nào là nguyên hàm của f (x)  1 sin x x  2
A. F(x) 1 cot(  ) B. F(x)   2 4 x 1 tan 2 x
C. F(x)  ln(1 sin x) D. F(x)  2 tan 2 24 3
Câu 71. Xét các mệnh đề
Group Nhóm Toán | Trắc nghiệm 2016-2017 3 1 I  4 6 x 1dx x 1d   x 3 1 3 1 1 II  4 4 4 x 1dx x 1dx x 1d    x 0 0 3 A.(I) đúng, (II) sai B.(I) sai, (II) đúng
C.Cả (I) và (II) đều đúng
D.Cả (I) và (II) đều sai
Câu 72. Hàm số nào là nguyên hàm của 2 f (x)  x. x  5 : 3 3 1 A. 2 2 F(x)  (x  5) B. 2 2 F(x)  (x  5) 3 3 1 3 C. 2 2 F(x)  (x  5) D. 2 2 F(x)  3(x  5) 2 1
Câu 73. Tìm nguyên hàm của hàm số f (x) biết f (x)  x  9  x 2 A.  x93 3  x C B.Đáp án khác 27 2 2 C.  3 C D.    27   x 9 3 x  C 3( x  93 3  x )
Câu 74. Tìm nguyên hàm của hàm số f (x) biết 2 f (x)  tan x 3 tan x A.C B. Đáp án khác 3 sin x  x cos x C. tan x 1 C D.  C cos x 
Câu 75. Nguyên hàm của hàm số   2ln x x f x  , x  0 là: x 2 ln x A.  C B. 2ln x 1 C x 24 2 ln x 4 C. 2 ln x  x  C D.  x  C x
Group Nhóm Toán | Trắc nghiệm 2016-2017 x e
Câu 76. Họ nguyên hàm của là: 2x e 1 x 1 e 1 A. 2x ln e 1  C B. ln  C x 2 e 1 x e 1 x 1 e 1 C. ln  C D. ln  C x e 1 x 2 e 1 m
Câu 77. Tìm m biết 2x 5.dx  6 0 A. m  1  ,m  6 B. m  1  ,m  6  C. m 1, m  6  D. m 1, m  6 VẬN DỤNG CAO 2 2x  5x  3
Câu 78. Gọi S là diện tích giới hạn bởi đồ thị hàm số y 
,tiệm cận xiên của đồ thi x  2
và các đường thẳng x  1  , x  mm   
1 .Tìm giá trị m để S  6 A. 6 e  4 B. 6 e  2 C. 6 e 1 D. 6 e  3
Câu 79. Cho hình phẳng (H) giới hạn bởi các đường 4 2 2
y  x  2mx  m , x  0, x 1. Tìm m để 1
diện tích hình phẳng đó bằng 5 A. m 1, m  2 B. m  0;m  2 / 3 C. m  2 / 3, m 1 D. m  0, m  2  / 3 sin 2x a cos x b cos x
Câu 80. Cho hàm số h(x)  . Tìm a, b để h(x)   và tính 2 (2  sin x) 2 (2  sinx) 2  sin x 0 I  h(x)dx    2            24 A. a 4 và b 2;I 2ln 2 2 B. a 4 và b 2; I 2 ln 2 2 5
C. a  2 và b  4;I  2ln 2  2 D. a  2
và b  4;I  ln 2 2
Group Nhóm Toán | Trắc nghiệm 2016-2017 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
B B A B D D B B A D A D B C D A B A D C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
C D D C B A D A D D C A D C A C C A A C
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
B A B B A C A B B C A B C B D A A A A C
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
D B B A D B D C C B C B B D C D C B D A PHẦN 22 :
NGUYÊN HÀM – TÍCH PHÂN THÔNG HIỂU Câu 1. Với f ( ) x , ( g )
x là 2 hàm số liên tục trên K và k  0 thì mệnh đề nào sau đây là sai
A. f x dx f x   ( ) ( ) . C B. kf ( ) x dx  
kf(x)d . x C.  f ( ) x  ( g ) x dx f ( ) x dx  ( g ) x d . x     D.  f ( ) x . ( g ) x dx   
f( )xdx . (g )xd .x Câu 2.
Chọn phát biểu sai trong số các phát biểu sau 24
A. Cho hàm số f (x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f (x) trên K nếu: 6 F (  ) x f ( ) x , x   . K
Group Nhóm Toán | Trắc nghiệm 2016-2017
B. Nếu F(x) là một nguyên hàm của f (x) trên K thì họ nguyên hàm của hàm số f (x) trên K là:
f x dx F x C const C   ( ) ( ) , . K
C.Nếu F(x) là một nguyên hàm của f (x) trên K thì họ nguyên hàm của hàm số f (x) trên K là:
f x dx F x C const C   ( ) ( ) , .
D. Cho hàm số f (x) xác định trên R Hàm số F(x) được gọi là nguyên hàm của hàm số f (x) trên K nếu: F( ) x f ( ) x ,  x . R Câu 3.
Tìm nguyên hàm của các hàm số f x  3 ( )
x  4x  5 thỏa mãn điều kiện ( F 1)  3. 4 x 1 5 A. F x   2 ( )
x  5x  3  B. F(x)  4 4x  2 x x   4 5 4 4 x 1 C. 2 5 F(x) 
x  5x   D. F(x)  4 4x  2
x x  3  4 4 5 Câu 4.
Tìm điều kiện của tham số m để F x  3 mx m  2 ( ) (3
2)x  4x  3 , F(x) là một nguyên hàm của hàm số f x  2
( ) 3x  10x  4 A. m  1 B. m  1  C. m  3 D. m  2 dx Câu 5.
Tính nguyên hàm sau: I    ( x x  1) 1 x A. I  ln  C. B. I  ln  C. ( x x  1) x  1 x  1 C. I  ln  C D.  x I ln  C. x x  1 1 Câu 6. Cho I= dx  nguyên hàm là. x 1  A. ln x C B.  C C. ln x  2 D. ln x C x Câu 7. Nguyên hàm của I= cos . x sin . x dx  là. 1  A.–cos2x + C B. cos 2x C 4 1   1  24 C. cos 2x C D. cos 2x C 2 4 7
Group Nhóm Toán | Trắc nghiệm 2016-2017 2 Câu 8. Giá trị của 2  2 x I e dx  ?  0 A. 4 I  4e B. 4 I  4e  4 C. 4 I e D. 4 I e 1 1 dx Câu 9. Tính: I   2 x  4x  3 0 3 1 3 1 3 1 3 A. I  ln B. I  ln C. I   ln D. I  ln 2 3 2 2 2 2 2
Câu 10. Diện tích của hình phẳng giới hạn bởi y  ln ,
x y  0, x e là A. e B. 3 C. 2 D. 1 VẬN DỤNG
Câu 11. Trong số các mệnh đề sau, có bao nhiêu mệnh đề đúng
1. Cho hàm số f (x) liên tục trên K và a, b .
K Hàm số F(x) được gọi là nguyên hàm của f (x) trên K thì ( F ) b  ( F )
a được gọi là tích phân của f (x) từ a đến b b b b
2. Tích phân của f (x) từ a đến b và được kí hiệu là f (x)dx
. Khi đó: I f (x)  dx F(x)  F( ) b F( ) a ,  a a a với a b
3. Đối với biến số lấy tích phân, ta có thể chọn bất kì một chữ khác nhau thay cho x , nghĩa là: b b b
I f (x)  dx f (t)  dt f ( )
u du    F( )
b F(a).    a a a
4. Nếu hàm số y f ( )
x liên tục và không âm trên đoạn  ; a b 
 thì diện tích S của hình thang cong giới hạn b
bởi đồ thị của y f ( )
x , trục Ox và hai đường thẳng x a, x b là: S f (x)  dx  a
5. Nếu hàm số y f ( )
x liên tục và không âm trên đoạn  ; a b 
 thì diện tích S của hình thang cong giới hạn b
bởi đồ thị của y f ( )
x , trục Oy và hai đường thẳng x a, x b là: S f (x)  dx  a 24 A.1 B.2 C.3 D.4 8 x
Câu 12. Tìm nguyên hàm sau I   4 1 d . x 2x  1  2
Group Nhóm Toán | Trắc nghiệm 2016-2017
A. I  2x  1  5ln 2x  1  2  . C
B. I  2x  1  4 2x  1  5ln 2x  1  2  . C
C. I  2x  1  4 2x  1  5ln 2x  1  2  . C
D. I  2x  1  4 2x  1  5ln 2x  1  2  C.   2 
Câu 13. Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số y 2
x , y x và trục hoành trong miền x  0 . 5 1 1 1 A. B. C. D. 6 3 2 6
Câu 14. Dòng điện xoay chiều hình sin chạy qua một đoạn mạch LC có biểu thức có biểu thức cường độ là  i  I cos( t   )A o
. Biết i  q ' với q là điện tích tức thời ở tụ điện. Tính từ lúc t = 0, điện lượng chuyển 2 
qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian bằng  là  2I  I 2I A. 0 B. 0 D. 0 ω C. 0 ω 2 ω a I   ( p x)  P  .d . x
Câu 15. Trong kinh tế học, thặng dư tiêu dùng của hàng hóa được tính bằng công thức 0
Với p(x) là hàm biểu thị biểu thị giá mà một công ty đưa ra để bán được x đơn vị hàng hóa, a là số lượng
sản phẩm đã bán ra, P p(a) là mức giá bán ra ứng với số lượng sản phẩm là a. Cho 2
p  1200  0, 2x  0, 0001x , (đơn vị tính là USD). Tìm thặng dư tiêu dùng khi số lượng sản phẩm bán là 500 A.33333,3 USD B.1108333,3 USD C.570833,3 USD D.Đáp án khác 
Câu 16. Cho: L x sin xdx k 
. Giá trị của k là: 0 A.2 B.1 C.0 D.-1
Câu 17. Tính thể tích sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi trục Ox và Parabol 2 (C) : y  ax x (a  0) 24 5 5 4 5 9  aaaa A. B. C. D. 10 20 5 30
Group Nhóm Toán | Trắc nghiệm 2016-2017
Câu 18. Tìm a, , b c để 2 ( ) ( ). x F x ax bx c e    là một nguyên hàm của 2 ( ) ( 2 7 4). x f x x x e    
A. a  2,b  3  ,c  1  a=2,b=-3,c=-1 B. a  2
 ,b  3,c 1
C. a  2,b  3  ,c 1
D. a  2,b  3,c  1 
Câu 19. Diện tích hình phẳng giới hạn bởi trục tung và 2 đồ thị  2x y
, y  3  x là. 5 5 5 A. S  1/ ln 2 B. S   ln 2 C. S  5  ln 2 D. S   ln 2 2 2 2 a Câu 20. Tích phân
f (x)dx  0  thì ta có : a
A. f (x) là hàm số chẵn trên  ; a a
B. f (x) không liên tục trên đoạn  ; a a
C. f (x) là hàm số lẻ trên  ; a a D.Các đáp án đều sai ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 D B C A B D B D D D B B A D A B D A A C 25 0
Group Nhóm Toán | Trắc nghiệm 2016-2017 25 1
Group Nhóm Toán | Trắc nghiệm 2016-2017