































Preview text:
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ
ĐỔI MỘT SỐ ĐƠN VỊ CƠ BẢN Khối lượng
Năng lượng hạt nhân 1g = 10-3kg 1u = 931,5MeV 1kg = 103g 1eV = 1,6.10-19J 1 tấn = 103kg 1MeV = 1,6.10-13J 1ounce = 28,35g 1u = 1,66055.10-27kg 1pound = 453,6g Chú ý: 1N/cm = 100N/m Chiều dài 1đvtv = 150.106km = 1năm as 1cm = 10-2m Vận tốc 1mm = 10-3m 18km/h = 5m/s 1 m = 10-6m 36km/h = 10m/s 1nm = 10-9m 54km/h = 15m/s 1pm = 10-12m 72km/h = 20m/s 1A0 = 10-10m Năng lượng điện 1inch = 2,540cm 1mW = 10-3W 1foot = 30,48cm 1KW = 103W 1mile = 1609m 1MW = 106W 1 hải lí = 1852m 1GW = 109W Độ phóng xạ 1mH = 10-3H 1Ci = 3,7.1010B q 1 H = 10-6H
Mức cường độ âm 1 F = 10-6F 1B = 10dB 1mA = 10-3A Năng lượng 1BTU = 1055,05J 1KJ = 103J 1BTU/h = 0,2930W 1J = 24calo 1HP = 746W 1Calo = 0,48J 1CV = 736W
7 ĐƠN VỊ CHUẨN TRONG HỆ SI (Systeme International)
Đơn vị chiều dài: mét (m)
Đơn vị thời gian: giây (s)
Đơn vị khối lượng: kilôgam (kg)
Đơn vị nhiệt độ: kenvin (K)
Đơn vị cường độ dòng điện: ampe (A)
Đơn vị cường độ sáng: canđêla (Cd)
Đơn vị lượng chất: mol (mol)
Chú ý: các bội và ước về đơn vị chuẩn và sử dụng máy tính Casio. ----- --- -
CHƯƠNG I: DAO ĐỘNG ĐIỀU HOÀ
CHUYÊN ĐỀ 1: ĐẠI CƯƠNG VỀ DAO ĐỘNG ĐIỀU HÒA
DẠNG 1: LI ĐỘ, VẬN TỐC, GIA TỐC, HỆ THỨC ĐỘC LẬP
1) Phương trình dao động: x A co s t
2) Phương trình vận tốc: v = - ωAsin(ωt + φ)
3) Phương trình gia tốc: a = - ω2Acos(ωt + φ) = - ω2x thời gian số dao động 2
4) Tần số góc, chu kì, tần số: T = 2 số dao động ; f = thời gian ; f T
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 1
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ
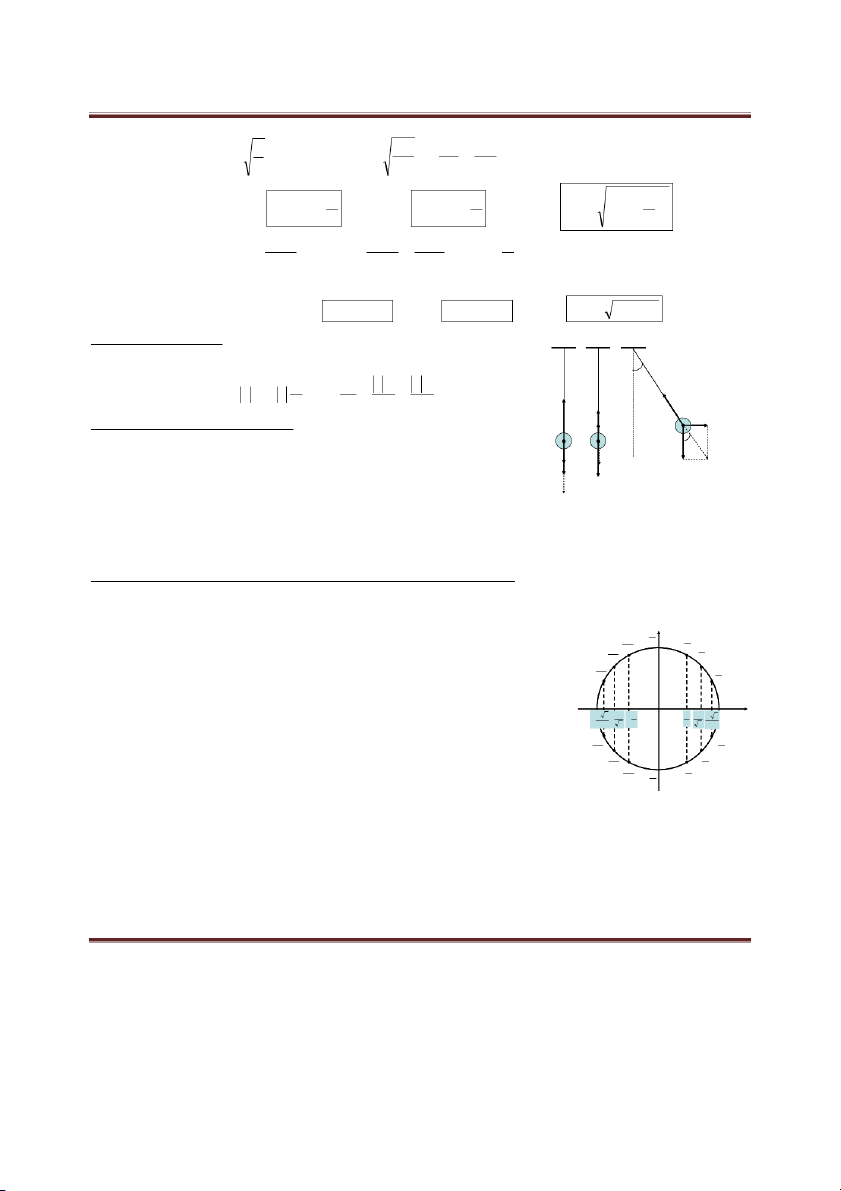
5) Các vị trí đặc biệt: + v v > > 0
Ở VTCB: x = 0; |vmax| = ωA; |amin| = 0 -A a -A O a O A +
Ở biên: x = ±A; |vmin| = 0; |amax | = ω2A vmi m n v v ma m x a mi m n 2 v 2 2 a v ama m x a a a mi m n ma m x a
6) Hệ thức độc lập: 2 2 A x ; 2 A - v v < < 0 2 4 2
Chú ý:x, v, a có thể âm, dương hoặc bằng 0 còn A, ω luôn dương.
DẠNG 2: XÁC ĐỊNH LI ĐỘ, VẬN TỐC, GIA TỐC TẠI THỜI ĐIỂM t CHO TRƯỚC
Thay t vào phương trình của x, v, a để tính.
DẠNG 3: XÁC ĐỊNH THỜI ĐIỂM VẬT QUA LI ĐỘ x0, THỜI ĐIỂM VẬT CÓ VẬN TỐC v0 CHO TRƯỚC Cho x co A s t x
hoặc v = - ωAsin(ωt + φ) = v0 rồi giải phương trình lượng giác sẽ suy ra được các họ nghiệm 0 của t ( k N sao cho t > 0).
Chú ý: Trong trường hợp vật qua li độ x0theo một chiều nhất định thì khi giải phương trình lượng giác, nếu vật qua x0 theo
chiều dương: chọn α là góc âm, nếu vật qua x0 theo chiều âm: chọn α là góc dương.
DẠNG 4: BIẾT LI ĐỘ VÀ CHIỀU CHUYỂN ĐỘNG CỦA VẬT TẠI THỜI ĐIỂM t1 , TÍNH LI ĐỘ CỦA VẬT
TẠI THỜI ĐIỂM SAU ĐÓ ∆t GIÂY x
Tại t1: x Acos(t ) t 1 1 cos( t 1 ) 1
(nếu vật qua x1theo chiều dương: chọn α là góc âm, A
nếu vật qua x1 theo chiều âm: chọn α là góc dương). Có thể bấm máy tính nếu góc không đẹp. Tại t2 = t1 + t : x cA t t A t t A t 2 os ( ) 1 cos( ) 1 cos( ) ?
CHUYÊN ĐỀ 2: NĂNG LƯỢNG TRONG DAO ĐỘNG ĐIỀU HÒA
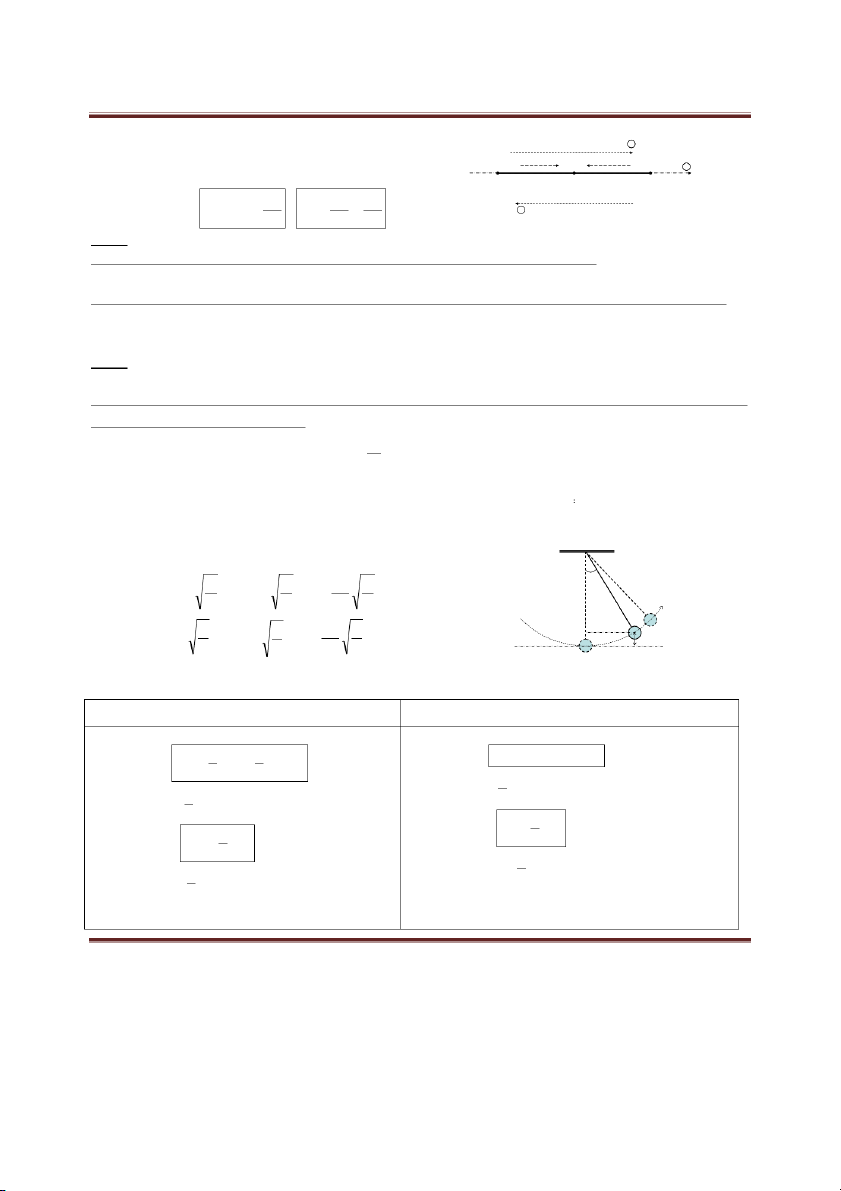
1) Tần số góc, chu kì, tần số của con lắc lò xo, con lắc đơn k m 1 k Con lắc lò xo: ; T 2 ; f m k 2 m l l g l 1 g S0 Con lắc đơn: ; T 2 ; f S l g 2 l O
2) Động năng, thế năng, cơ năng CON LẮC LÒ XO CON LẮC ĐƠN 1 1 W mgl 1 ( cos Thế năng: 2 2 2 W kx m x Thế năng: ) t t 2 2 1 2 2 1 Biểu thức: 2 W m S cos (t ) t 0 Biểu thức: W 2 2 m A cos2 (t ) 2 t 2 1 1 Động năng: 2 W mv đ Động năng: 2 W mv 2 d 2 1 2 2 2 1 Biểu thức: W m S sin (t ) đ 0 Biểu thức: W 2 2 m A sin2 (t ) 2 d 2 Cơ năng: W W W W W t d m t ax m d ax Cơ năng: W W W W W t d m t ax m d ax
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 2
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ 1 1 2 2 2 2 W m A kA mgS 1 0 2 W mgl 2 2 0 2l 2 1 1 A 3) W n x đ Wt W W n t W t W ( n ) 1 W 2 kA t ( 2 n ) 1 kx 2 2 n 1 1 1 A v W n max v t W đ W W n đ W đ W ( n ) 1 2 2 W m A đ ( 2 n ) 1 mv 2 2 n 1 n1 4) Chú ý T
Động năng và thế năng luôn biến thiên tuần hoàn với: ' 2 , T' , f ' f 2 2
Trong một chu kì có 4 lần động năng bằng thế năng. Khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng T A là
. Động năng bằng thế năng tại li độ: x 4 2
CHUYÊN ĐỀ 3: CON LẮC LÒ XO
DẠNG 1: TÍNH CHU KÌ, TẦN SỐ DAO ĐỘNG CỦA CON LẮC LÒ XO. k 2 m 1 1 k 1) Tần số góc: ; chu kì: T 2 ; tần số: f m k T 2 2 m
2) Con lắc lò xo dao động theo phương thẳng đứng: k g
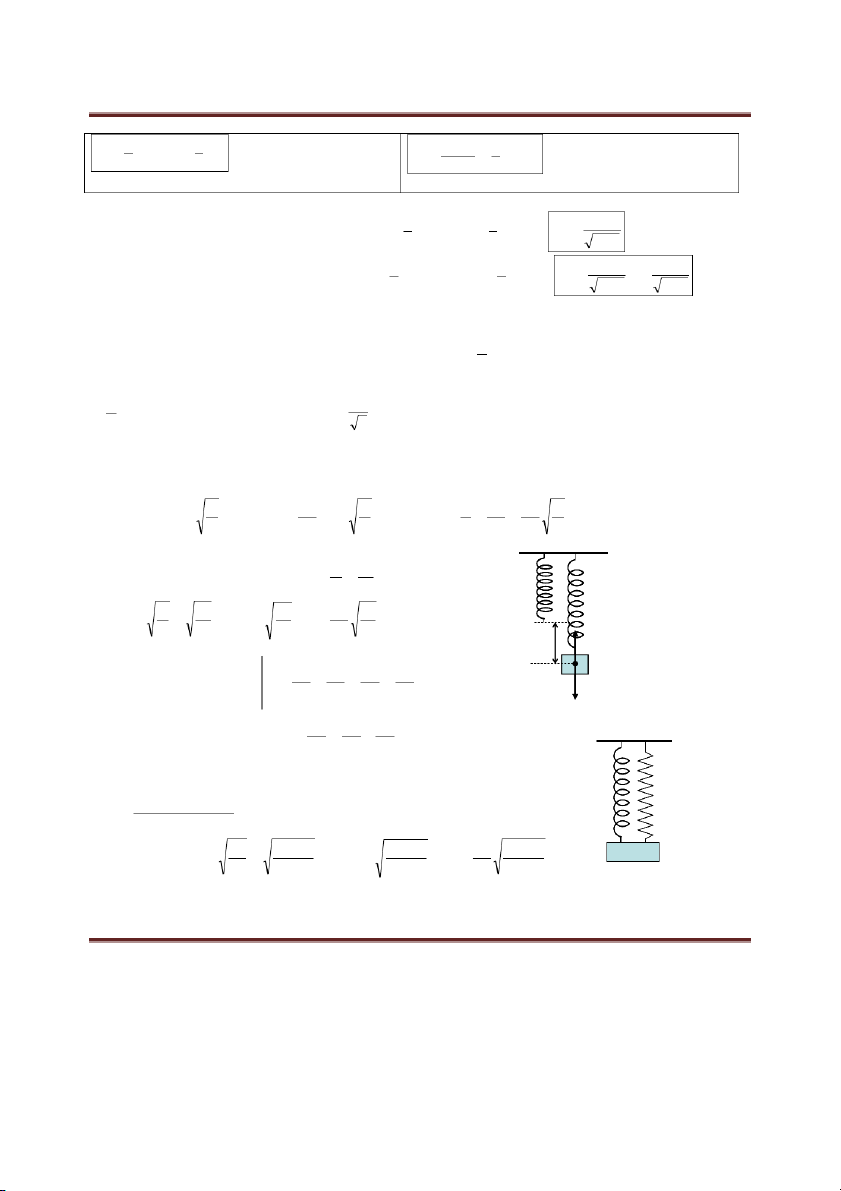
Tại vị trí cân bằng: P = Fđh mg k l m l k k g l 1 g Vậy: ; T 2 ; f m l g 2 l Δl F Δl dh m 3) Vật m 2 2 2 1 → T1, ω1, f1 m T f 1 1 2 2 Vật m P 2 → T2 , ω2 , f2 2 2 2 m T f 2 2 1 1 1 1 1 Vật m = (m 2 2 1 ± m2) → 2 T T T và 1 2 2 2 2 f f f 1 2 4)Cắt, ghép lò xo: a) Ghép song song: k1 k k 1 2
Dấu hiệu nhận biết: hai đầu của hai lò xo nối với tường, hai đầu nối với vật. k m ss k k 1 k k k k k 1 2 ; T 2 ; f 1 2 m ss 1 2 ss m m ss k k ss 2 m 1 2 Lò xo k1 → T1, f1 Lò xo k2 → T2, f2
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 3
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ 1 1 1 k 2 2 1 // k2 → và 2 f f f 2 2 2 T T T ss 1 2 ss 1 2 b) Ghép nối tiếp:
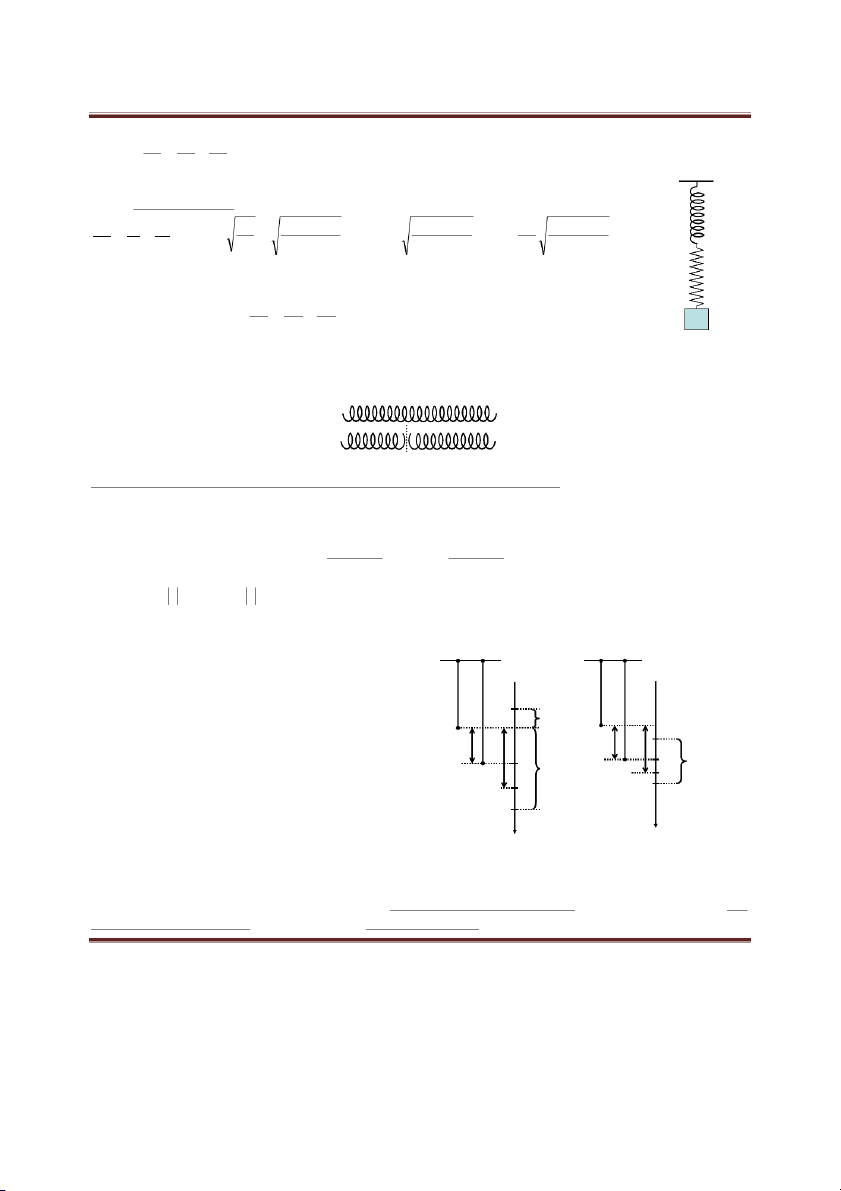
Dấu hiệu nhận biết: đầu lò xo này nối với đuôi lò xo kia. k1 1 1 1 k k k k k m 1 k k 1 2 nt 1 2 ; T 2 ; f 1 2 k k k nt m k k m nt k k nt 2 k k m nt 1 2 1 2 1 2 1 2 Lò xo k1 → T1, f1 k2 Lò xo k2 → T2, f2 1 1 1 k 2 2 1 nt k2 → 2 T T T và nt 1 2 m 2 2 2 f f f nt 1 2 c) Cắt lò xo:
Cắt lò xo có chiều dài l0 thành 2 lò xo có chiều dài l1 và l2 k l k l k l 0 0 1 1 2 2 l , ,k 0 0 l , ,k l , ,k 1 1 2 2
DẠNG 2: CHIỀU DÀI CON LẮC LÒ XO. LỰC ĐÀN HỒI VÀ LỰC HỒI PHỤC
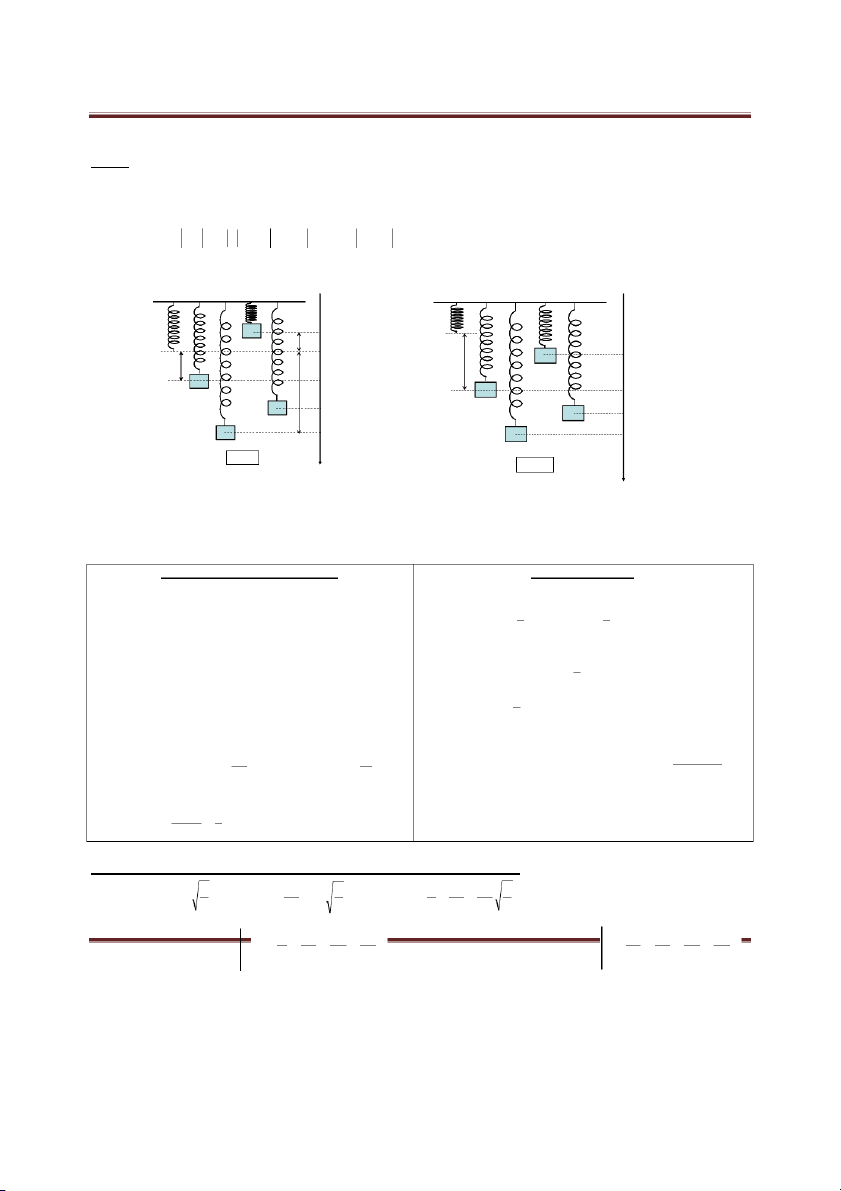
1) CHIỀU DÀI CON LẮC LÒ XO l l l cb 0 l
l A l l A l l l l max cb 0 max min l và max min A l l A l l cb 2 2 min cb 0 A l l x l l
x (dấu + nếu vật ở phía dưới VTCB, dấu – nếu vật ở phía trên VTCB) x cb 0 2) LỰC ĐÀN HỒI F k. d
(Δd: độ biến dạng của lò xo) đh
Lực đàn hồi cực đại: F (k l ) A đ m h ax
Lực đàn hồi cực tiểu: Trước hếtso sánh A với Δl. l l l l 0 cb F ( k l ) A 0 cb nếu A l - A đ m h in nén F
0 (tại x = - Δl) nếu A l - A đ m h in Δl Δl d
Lực nén cực đại: F ( k A )l nếu A l Δ Δd n m énax O O luôn dã d n ã dãn
3) CÁCH VẼ HÌNH ĐỂ GIẢI CÁC BÀI TOÁN TÌM l x x, A, x
Δl, Fđh … KHI KHÔNG CÓ SẴN CÔNG THỨC ĐỂ TÍNH A
Tính Δl (từ mg = k.Δl hoặc Δl = g/ω2) A
Vẽ chiều dài của lò xo khi chưa treo vật (l0).
Vẽ chiều dài của lò xo khi vật ở VTCB (lcb).
Vẽ độ biến dạng tại VTCB (Δl).
Vẽ trục tọa độ, gốc O tại VTCB, chiều dương chọn theo đề bài (nếu đề bài không nói thì chọn hướng xuống).
Vẽ A hoặc x hoặc Δd. (Lưu ý: Độ dãn của lò xo tính từ vị trí lò xo không biến dạng trở xuống, độ nén của lò xo tính
từ vị trí lò xo không biến dạng trở lên. Li độ của vật tính từ vị trí cân bằng trở lên hoặc trở xuống)
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 4
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ
Từ hình vẽ, tìm công thức liên hệ giữa: A, Δl, x, Δd đại lượng cần tìm. Chú ý:
+ Kéo vật xuống hoặc nâng vật lên rồi thả thì chỗ thả chính là biên độ.
+ Lực tác dụng vào điểm treo lò xo chính là lực đàn hồi của lò xo.
4) LỰC HỒI PHỤC (LỰC KÉO VỀ) F x k và F 0 hp F k x F k A hp hp max h m p in lmi m n l l l mi m n l i 0 - A 0 lcb c l nén ma m x a F = 0 - đhmin Δl đhmin Δ đhmin l - A cb c Δl F l Δl đhmi m n i x l O x dãn O l x ma m x a x Fđhma m x a A Fđhmax A đhmax A A ≥ Δl A A < < Δl
CHUYÊN ĐỀ 4: CON LẮC ĐƠN
Con lắc đơn dao động điều hòa:
Con lắc đơn bất kì
Điều kiện để con lắc đơn dao động điều hòa: biên độ góc Thế năng: W W mgl t 1 cos max 0 t mgl 1 cos rất nhỏ ( 0 1 0 ). 0 Động năng: 1 1 2 W mv 2 W mv d d
Phương trình dao động: + Theo li độ dài: max 0 s S cos t 2 2 0 + Theo li độ góc: Cơ năng: cost 0 1
Liên hệ giữa li độ dài và li độ góc: s = α.l (l: độ dài dây 2 W W W m 1 ( gl cos ) m v t d 2 treo) 1 2 Phương trình vận tốc: W W mv mgl 1 cos ma d x ma t x max v S si n t 0 0 2 Phương trình gia tốc: a 2 S c ost s2 Khi: W n W W W nW W n( W ) 1 0 d t t t t 2 n cos Hệ thức độc lập: v 2 2 S s và 2 v2 2 mgl 1 ( cos ) (n ) 1mgl 1 ( cos ) 0 cos 0 0 2 0 gl n1
Năng lượng của con lắc đơn: 2 mgS 1 0 2 W W W mgl t d 0 2l 2
DẠNG 1: CHU KÌ, TẦN SỐ CỦA CON LẮC ĐƠN DAO ĐỘNG ĐIỀU HÒA 1) Tần số góc: g 2 l 1 1 g ; chu kì: T 2 ; tần số: f l g T 2 2 l 2 2 2 l T f 2 2 2 g T f 1 1 2 2 1 2 1 1
“Biển học mênh mông lấy chuyên cần làm bến 2 2 2 l T f 2 2 2 g T f
Mây xanh không lối lấy chí cả dựng nên”2 2 1 1 2 1 2 Page 5 2
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ
2) Chiều dài l1 → T1, ω1, f1 Gia tốc g1 → T1, ω1, f1
Chiều dài l2 → T2, ω2, f2 Gia tốc g2 → T2, ω2, f2 Chiều dài l = (l 1 1 1 2 1 ± l2) → T, ω, f thì 2 2 T T T và 1 2 2 2 2 f f f 1 2
DẠNG 2: VẬN TỐC, LỰC CĂNG DÂY CỦA CON LẮC ĐƠN BẤT KÌ 1) Vận tốc: 1 W W W m g 1 l cos 2
mv mgl1cos v 2gl (cos cos ) t d m t ax 0 2 0
2) Lực căng dây: Theo định luật II Newton: P T a
m . Chiếu lên phương sợi dây, chiều dương hướng vào tâm ta được: v2 v2 gl 2 (cos cos ) Pcos T m a m
T mgcos m mgcos m 0 T mg cos 3 ( c 2 os ) ht l l l 0
Tại biên: v 0; T mg cos ; Tại VTCB: 0 , cos 1 v 2gl 1 ( cos ) ; T mg 3 ( c 2 os ) 0 min min 0 max 0 max 0
3) Chú ý: Tại vị trí cân bằng, lực căng Tmax luôn lớn hơn trọng lực P
DẠNG 3: SỰ NHANH CHẬM CỦA ĐỒNG HỒ
1) Đồng hồ chạy sai và đồng hồ chạy đúng
Một đồng hồ quả lắc chạy đúng có chu kì Tđúng. Vì một số nguyên nhân, đồng hồ chạy sai với chu kì Tsai
Nếu Tsai> Tđúng: đồng hồ chạy chậm. Nếu Tsai< Tđúng: đồng hồ chạy nhanh.
Giả sử khi con lắc thực hiện được 1 chu kì thì kim đồng hồ nhích lên được 1 vạch 1 vạch: đồng hồ chạy đúng mất Tđ T g
(s), đồng hồ chạy sai mất T sai đúng
sai (s) 1 (vạch đúng) = (vạch sai) = (vạch sai) T g đúng sai
2) Các nguyên nhân làm đồng hồ chạy sai(R = 6400km: bán kính trái đất; : hệ số nở dài của dây treo) h
Đưa con lắc từ mặt đất lên độ cao h, mỗi giây đồng hồ chạy chậm: R h
Đưa con lắc từ mặt đất xuống độ sâu h, mỗi giây đồng hồ chạy chậm: 2R 1
Nhiệt độ tăng: mỗi giây đồng hồ chạy chậm; nhiệt độ giảm: mỗi giây đồng hồ chạy nhanh: . t 2 g
g tăng: mỗi giây đồng hồ chạy nhanh; g giảm: mỗi giây đồng hồ chạy chậm: 2g1 l
l tăng: mỗi giây đồng hồ chạy chậm; l giảm: mỗi giây đồng hồ chạy nhanh: 2l1
Đồng hồ vừa chậm vừa nhanh:
Nếu “độ nhanh > độ chậm” thì đồng hồ chạy nhanh một lượng bằng: |độ nhanh – độ chậm|
Nếu “độ chậm > độ nhanh” thì đồng hồ chạy chậm một lượng bằng: |độ chậm – độ nhanh| h 1 2h
Để đồng hồ chạy đúng thì “độ chậm = độ nhanh”: ( t t ) t t R 2 1 2 2 1 R
Chú ý: Để tính độ nhanh (chậm) trong một ngày đêm (là thời gian trái đất tự quay một vòng), ta nhân với 86400.
DẠNG 4: CHU KÌ CON LẮC ĐƠN KHI CÓ THÊM MỘT LỰC KHÔNG ĐỔI TÁC DỤNG 1) Tổng quát
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 6
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ l l T 2 g
Khi chưa có F : T 2 , khi có F : T 2 hd g hd g T2 g hd hd F F 2 F P = P F Nếu F : g g ; Nếu F : g g ; Nếu F : 2 ghd g hd hd m hd m m g P F F
Nếu bài tập có góc α: g ; T P ; ta n hd co s hd co s sin P
2) Các trường hợp của F a) Lực quán tính: F m a F : g g a ; F : g g a ; F : 2 2 g g a qt qt hd qt hd qt hd
Chiều của lực quán tính: F ngược chiều chuyển động nếu chuyển động nhanh dần qt
đều; cùng chiều chuyển động nếu chuyển động chậm dần đều. U F q E qU
b) Lực điện trường: F q E q đ đ d m m md T T T
Các bước xác định chiều của lực điện: Xác định dấu của q Xác định xem hai bản F F
tụ điện được đặt nằm ngang hay thẳng đứng. Bản âm và bản dương, bản nào ở trên, P P P
bản nào ở dưới (nếu đặt nằm ngang) Xác định chiều E : E luôn hướng từ bản Phd P F hd F
dương sang bản âm của tụ điện Xác định chiều của F : F cùng chiều E khi q đ đ Phd
> 0; F ngược chiều E khi q < 0. đ
CHUYÊN ĐỀ 5: DÙNG ĐƯỜNG TRÒN GIẢI CÁC BÀI TOÁN VỀ THỜI GIAN VÀ QUÃNG ĐƯỜNG
DẠNG 1: BIỂU DIỄN DAO ĐỘNG ĐIỀU HÒA TRÊN ĐƯỜNG TRÒN
+ Cho phương trình dao động: x A c o s t
+ Vẽ đường tròn với hai trục tọa độ Ox, Oy. Hai biên dương và âm nằm trên trục Ox.
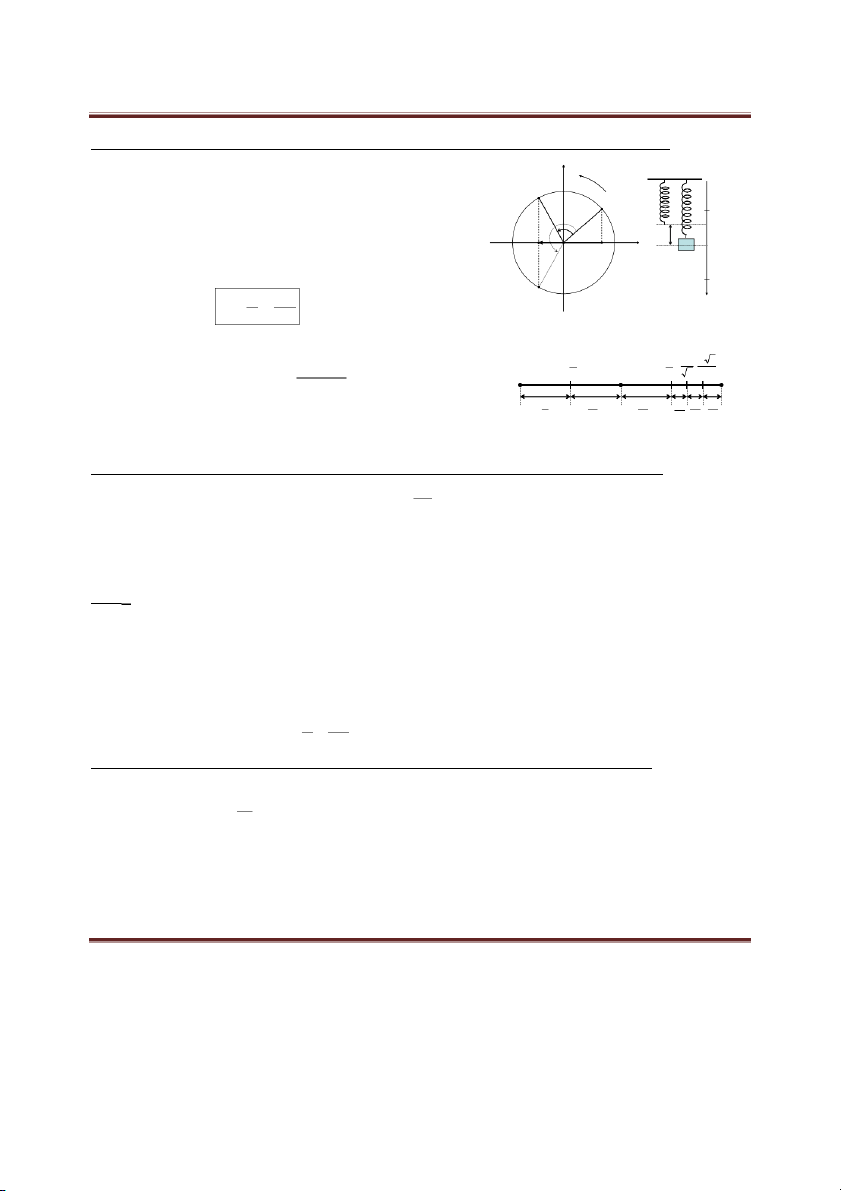
+ Chiều chuyển động của điểm trên đường tròn luôn là chiều ngược chiều kim đồng hồ. 2 2 2
+ Nửa trên đường tròn ứng với v < 0 (vật chuyển động theo chiều âm), nửa dưới đường 3 3 3 3 4 4
tròn ứng với v > 0 (vật chuyển động theo chiều dương). 5 5 6 6
Tại thời điểm ban đầu t = 0:
Vật nằm tại điểm ứng với góc φ trên đường tròn. 0 - A A 3 A A A A A 3 A
Chiếu điểm trên đường tròn xuống trục Ox ta được li độ x của vật. 2 2 2 2 2 2 5 5
Chiều chuyển động của vật tùy theo điểm đang xét là ở nửa trên hay nửa dưới của 6 6 3 đường tròn. 4 2 2 4
Ngược lại, nếu biết trước li độ và chiều chuyển động của vật, ta có thể tìm được vị 3 3 3 2
trí tương ứng trên đường tròn bằng cách: nếu vật chuyển động theo chiều dương thì từ li độ đang xét ta gióng xuống dưới,
nếu vật chuyển động theo chiều âm thì từ li độ đang xét ta gióng lên trên.
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 7
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ
DẠNG 2: TÍNH THỜI GIAN VẬT ĐI TỪ LI ĐỘ X1 ĐẾN LI ĐỘ X2 KHI DAO ĐỘNG ĐIỀU HÒA 1) Phương pháp giải C h
Vẽ đường tròn bán kính A. iều quqauya N N ( - ( ) -
Vị trí M trên đường tròn ứng với tọa độ x1. M - A
Vị trí N trên đường tròn ứng với tọa độ x 2. x x = = - Δl
Thời gian vật đi từ x Δl
1 đến x2 tương ứng với thời gian vật đi trên - A x O 2 O x1 x A
đường tròn từ M đến N với góc quét là .
Tính góc hợp bởi cung MON A T N N ( + ( ) +
Thời gian vật đi là: t 2 2) Chú ý
Vật có thể đi đến li độ x2theo 2 chiều: chiều âm và chiều dương nên có A A A A 3
thể vẽ được nhiều góc quét. Thời gian nhỏ nhất vật đi từ x
1 đến x2 ứng với A 2 O 2 2 2 A
góc quét nhỏ nhất. T T T T T T
Con lắc lò xo treo thẳng đứng, chiều dương hướng xuống, A l thì vị 6 12 1 12 1 24 2 24 2 12 1
trí lò xo không biến dạng là x l
. Lò xo bị dãn trong khoảng từ
x l đến biên dương, bị nén trong khoảng từ x l đến biên âm.
DẠNG 4: TÍNH THỜI GIAN VẬT ĐI HẾT QUÃNG ĐƯỜNG S KỂ TỪ THỜI ĐIỂM BAN ĐẦU S
Trong 1 chu kì, vật đi được quãng đường là 4A. Xét tỉ số: = n. 4 A
Nếu n nguyên S = n.4A (vật đi được n lần 4A) t = n.T
Nếu n không nguyên S = [n].4A + Sdư t = [n].T + tdư
(tdư là thời gian đi hết quãng đường Sdư trong chu kì cuối cùng) x ? Tìm t 1 d :
ư + Xác định điểm đầu, chiều xuất phát từ điểm đầu:
bằng cách thay t= 0 vào biểu thức li độ x và v 0 hayv 0 1 1 biểu thức vận tốc v. + Tính Sdư: Sdư = S – [n].4A
+ Vẽ x1 và cho vật xuất phát từ x1 (theo đúng chiều) thì sau khi đi hết quãng đường Sdư, vật sẽ đến li độ x2 theo một chiều nào đó.
+ Vẽ đường tròn, xác định các điểm trên đường tròn ứng với li độ x1, x2 và tính góc mà bán kính quét được khi chuyển động T
từ điểm đầu đến điểm cuối. Khi đó tdư = 2
DẠNG 5: TÍNH SỐ LẦN VẬT ĐI QUA MỘT VỊ TRÍ CHO TRƯỚC TỪ THỜI ĐIỂM t1 ĐẾN t2
Trước hết phải xem trong 1 chu kì, vật đi qua vị trí đề bài cho mấy lần. Giả sử là k lần. t Đặt t t t . Xét tỉ số: = n 2 1 T Nếu n nguyên t
= nT (vật thực hiện được n chu kì) N = k.n (lần)
Nếu n không nguyên t
= [n].T + tdư N = k.[n] + Ndư (lần)
(Ndư là số lần vật đi qua vị trí đang xét trong phần tdư của chu kì cuối cùng).
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 8
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ x ? Tìm N 1
dư: + Xác định điểm đầu, chiều xuất phát từ điểm đầu:
và điểm cuối, chiều đến điểm cuối: v 0 hayv 0 1 1 x ? 2
bằng cách thay t1, t2 vào biểu thức li độ x và biểu thức vận tốc v. v 0 hayv 0 2 2
+ Vẽ hình, xác định điểm đầu x1, điểm cuối x2 trên hình, khoanh chuyển động từ x1 → x2 theo đúng chiều và xem trong quá
trình chuyển động từ x1 đến x2 vật qua vị trí x đang xét mấy lần Ndư
DẠNG 6: TÍNH THỜI ĐIỂM VẬT QUA MỘT VỊ TRÍ CHO TRƯỚC LẦN THỨ N
Trước hết phải xem trong 1 chu kì, vật đi qua vị trí đề bài cho mấy lần. Giả sử là k lần.
Phân tích: N = k.m + Ndư (lần) t = m.T + tdư
(Ndư là số lần vật đi qua vị trí đang xét trong thời gian tdư cuối cùng: Ndư k. Rất có thể Ndư = k nhưng vì là k lần cuối cùng
nên tdư không được tính là một chu kì)
Tìm tdư: vẽ đường tròn, xác định điểm đầu x1 (x1 là li độ tại t = 0) và điểm đến trên đường tròn (điểm đến trên đường tròn
tương ứng với vị trí đang xét lần cuối cùng) và tính góc mà bán kính quét được khi chuyển động từ điểm đầu đến điểm cuối. T Khi đó tdư = 2
Chú ý: Trong 1 chu kì, vật:
+ qua một vị trí x bất kì 2 lần; qua một vị trí x bất kì theo một chiều nhất định 1 lần.
+ có một vận tốc bất kì 2 lần; có một vận tốc bất kì và đang tiến về (hoặc ra xa) VTCB 1 lần.
+ có một gia tốc bất kì 2 lần; có một gia tốc bất kì và đang tiến về (hoặc ra xa) VTCB 1 lần. A
+ có 4 lần Wđ = nWt và Wđ = nWt tại li độ: x ch c i h ều âm â n 1 - A O A
+ có Wđ = nWt và đang tiến về (hoặc ra xa) VTCB 2 lần. x x
+ đi được quãng đường bằng 4A. 1 2 ch c i h ều dươ d n ươ g n
CHUYÊN ĐỀ 6: TỔNG HỢP DAO ĐỘNG
x A cos(t ) A
Xét 2 dao động cùng phương cùng tần số: 1 1 1 1 x Acos(t ) A.
x A cos(t ) A 2 2 2 2 Khi đó: x = x A A A 1 + x2 hay 1
2 , nghĩa là khi biểu diễn trên giản đồ, véctơ tổng A bằng tổng của hai véctơ thành phần A và A . 1 2
1) Khi giải bài tập, trước hết ta phải tính độ lệch pha Δφ của hai dao động thành phần và nhận xét xem nó có gì đặc biệt
không. Nếu có thì sử dụng ngay kết quả dưới đây, nếu không thì phải dùng công thức tổng quát.
Các trường hợp đặc biệt
Nếu 2 dao động đồng pha ( k 2
) A A A = A1 + A2; 1 2 1 2
Nếu 2 dao động ngược pha ( 2 k 1 ) A A 1 2
A = |A1 - A2 |; φ = pha ban đầu của dao động có biên độ lớn hơn.
Nếu 2 dao động vuông pha ( 2k 1 ) A A 2 2 A A A
; φ tính bằng công thức tổng quát. 2 1 2 1 2
Nếu 2 dao động có biên độ bằng nhau (A1 = A2) thì ta có thể sử dụng ngay công thức lượng giác để tổng hợp dao động: x 1 2 1 = A cos(
t ) A cos(t )= 2A cos cos 2 t 1 1 1 2 1 2 2
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 9
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ
Nếu A , A , A lập thành những hình đặc biệt (VD: khi x1, x2 vừa vuông pha vừa có biên độ bằng nhau thì A , A , A 1 2 1 2
lập thành hình vuông; khi x1, x2 có Δφ = 2π/3 và có biên độ bằng nhau thì A , A , A lập thành tam giác đều) thì ta nên vẽ 1 2
giản đồ véctơ để tính A và φ của dao động tổng hợp.
Công thức tổng quát: Trong mọi trường hợp, ta luôn có:
Biên độ dao động tổng hợp: 2 A 2 A 2 A 2A A co s 1 2 1 2 A sin A sin
Pha ban đầu dao động tổng hợp: 1 1 2 2 t g
với là góc kẹp giữa và A cos A cos 1 2 1 1 2 2 2) Chú ý
Biên độ của dao động tổng hợp luôn có giá trị: A A A A A 1 2 1 2
Nếu đề bài cho trước một dao động thành phần và dao động tổng hợp, bắt tìm phương trình dao động thứ hai, ta làm như sau: x
x x A cos(t ) A cos(t ) Acos( t ) A cos(t ) . 2 1 1 1 1 1
Nghĩa là ta đã biến đổi“hiệu” hai dao động thành “tổng” hai dao động Bài toán trở về một bài tổng hợp dao động bình thường.
Nếu đề bài cho tổng hợp 2 dao động, trong đó 1 dao động viết bằng hàm sin, 1 dao động viết bằng hàm cos thì ta phải
đưa về cùng một hàm rồi tính: sin x cos x ; cos x si n x 2 2
Để lập phương trình dao động tổng hợp của từ 3 dao động trở lên, ta vẽ giản đồ véctơ, tổng hợp 2 dao động thích hợp
nhất trước, sau đó tổng hợp lần lượt với các dao động còn lại. Nếu tất cả các dao động thành phần đề bài cho đều không có
gì đặc biệt, ta dùng cách làm tổng quát sau:
Tính: Ax = A1cosϕ1 + A2cosϕ2 + A3cosϕ3 + …
Ay = A1sinϕ1 + A2sinϕ2 + A3sinϕ3 + … A Khi đó: 2 2 A A A và y ta n x y Ax
Để tính li độ, vận tốc, gia tốc của vật tại một thời điểm t nào đó, ta không nhất thiết phải lập phương trình dao động
tổng hợp mà chỉ cần thay t vào các phương trình li độ, vận tốc, gia tốc của 2 dao động thành phần rồi cộng đại số các giá trị
đó lại với nhau. Tức là: x = x1 + x2; v = v1 + v2; a = a1 + a2.
CHUYÊN ĐỀ 7 : DAO ĐỘNG TẮT DẦN. SỰ CỘNG HƯỞNG
DẠNG 1 : DAO ĐỘNG TẮT DẦN
Con lắc lò xo nằm ngang gồm một lò xo độ cứng k, vật nặng khối lượng m dao động tắt dần với biên độ lúc đầu là A, hệ
số ma sát . Ta công nhận các công thức sau đây : 4mg 4g
Độ giảm biên độ trong mỗi dao động: A không đổi. 2 k Ak A 2
Số dao động vật thực hiện được: N 4 m g 4 g Ak A 2 Hệ số ma sát: 4Nmg 4Ng AkT A
Thời gian vật dao động đến lúc dừng lại: t N T . 4 m g 2 g
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 10
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ kA2
Quãng đường vật đi được đến lúc dừng lại: S 2 m g A
Gọi độ giảm biên độ sau mỗi chu kì là
= a %. Phần trăm năng lượng bị mất đi sau mỗi chu kì là: A 1 1 2 2 kA k ' A 2 2 2 2 2 W W W' 2 2 A ' A ' A A A A 1 1 1 1 2 W W 1 A A A A 2 kA 2 2 2 W' ' A A
Phần trăm năng lượng còn lại sau mỗi chu kì là: 1 W A A
DẠNG 2: SỰ CỘNG HƯỞNG
Hiện tượng cộng hưởng xảy ra khi chu kì bước đi của người (hoặc chu kì dao động của toa xe khi gặp chỗ nối trên đường s
ray) bằng chu kì dao động riêng của hệ dao động: Triêng = Tbước đi = v
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 11
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ
CHƯƠNG II: SÓNG CƠ HỌC
CHUYÊN ĐỀ 1: ĐẠI CƯƠNG VỀ SÓNG CƠ HỌC
DẠNG 1: TÍNH CHU KÌ, TẦN SỐ, BƯỚC SÓNG VÀ VẬN TỐC SÓNG v
Áp dụng công thức liên hệ: v T f
Chú ý:Khoảng cách giữa 2 gợn lồi (gợn lõm) liên tiếp bằng 1 bước sóng tương ứng với 1 chu kì sóng.
Giữa n gợn lồi (gợn lõm) có (n -1) bước sóng.
Nếu sợi dây được kích thích dao động bởi nam châm điện có tần số là f thì tần số của sợi dây là 2f.
DẠNG 2: PHƯƠNG TRÌNH SÓNG TẠI MỘT ĐIỂM Gợn lồi 4 2 Cho: u a co s t (cm) 2 d u a cos t (cm) T O M a
Chú ý:Vận tốc và gia tốc dao động tại chỗ của phần tử tại M là: O 2 d v ' sin (cm/s) M u M a t - a Gợn lõm õ 2 2d a v (cm/s2) M ' M ac os t d
Nếu M ở trước O thì: 2 d u acos (cm) M t O M
Nếu chỉ xét dao động tại chỗ của phần tử M thì bài toán trở về bài toán dao động. Dạng toán hay xét nhất là: cho li độ
tại thời điểm t, tính li độ tại thời điểm sau đó Δt giây.
Nếu đề bài không cho trước dao động tại O, ta phải lập phương trình tại O trước rồi mới lập được phương trình tại M.
DẠNG 3: ĐỘ LỆCH PHA GIỮA HAI ĐIỂM TRÊN PHƯƠNG TRUYỀN SÓNG Cho: u a cos O
t (cm). M, N là hai điểm (sau O) cách O những khoảng lần lượt là dM và dN. d 2 d 2 N M Khi đó: u acos t (cm) và u acos t (cm) N M 2 d d 2 M d
Độ lệch pha giữa hai điểm M, N là: N
M, N dao động cùng pha khi: k 2 , ngược pha khi:
2 k 1 , vuông pha khi: 2k 1 2
Khoảng cách giữa 2 điểm trên phương truyền sóng dao động cùng pha là: d
k ; ngược pha là: d 2 ( k ) 1 ; 2 vuông pha là: d 2 ( k ) 1 4
DẠNG 4: TÍNH VẬN TỐC HOẶC TẦN SỐ SÓNG KHI CHÚNG BỊ KẸP TRONG MỘT KHOẢNG CHO TRƯỚC
Đề bài cho trước độ lệch pha Δφ và khoảng cách Δdgiữa hai điểm M, N. Vận tốc hoặc tần số sóng bị kẹp trong một khoảng
nào đó. Để tìm được chính xác vận tốc hoặc tần số ta làm như sau: 2 d 2 d f Ta có: v
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 12
GV Đỗ Thị Mai THPT Nguyễn Gia Thiều HN kapi291188@gmail.com 0979277623 FB: Kapi Mai Đỗ 2 d f d .f vk .
Trường hợp M, N cùng pha: k 2 2 k v hoặc f v k d . d f d .f . d f d .f Nếu v v v v v k k = ? Thay k vào v = ? min max v min max k v v k max min . vk f . d f vk ma . d x Nếu f f f f f min k k = ? Thay k vào f . f = ? min max min max d v v d
Trường hợp M, N ngược pha:
2 k 1 hoặc M, N vuông pha: 2k 1 , cách làm tương tự. 2
CHUYÊN ĐỀ 2: GIAO THOA SÓNG
DẠNG 1: PHƯƠNG TRÌNH SÓNG TẠI MỘT ĐIỂM M CÁCH HAI NGUỒN CÁC ĐOẠN d1, d2
1. Hai nguồn có độ lệch pha bất kì (tổng quát). Giả sử: u acos(t ) và u c a os(t ) S 1 S 2 1 2 d d d d
Khi đó, phương trình sóng tổng hợp tại M là: u M 2aco s 2 1 1 2co s t 2 1 1 2 2 2
2. Hai nguồn đồng pha. Giả sử: u u a cos t S S 1 2 d d d d 2 1 2 1 d d
Phương trình sóng tổng hợp tại M là: u A M 2aco 2 1 s M 2 a c os c os t 1
Nếu M nằm trên đường cực đại thì: d d k d d k 2 1 2 1
. Nếu M nằm trên đường cực tiểu thì: 2 d d
3. Hai nguồn ngược pha. A M 2 c a o s 2 1 2 1 Cực đại: d d k d d 2 1 ; Cực tiểu: k 2 2 1 1 1
4. Hai nguồn vuông pha. Cực đại: d d k d d k 2 1 2 1 ; Cực tiểu: 4 4
DẠNG 2: XÁC ĐỊNH XEM ĐIỂM M CÁCH HAI NGUỒN (ĐỒNG PHA) CÁC ĐOẠN d1, d2 NẰM TRÊN ĐƯỜNG
CỰC ĐẠI HAY CỰC TIỂU THỨ MẤY
Trong vân cực đại: k bậc
1) Thứ (bậc) của các vân giao thoa
Trong vân cực tiểu: k là thứ (không kết Cực đại: d d k Thứ (bậc) = |k| 2 1 k k = = 0
luận vân bậc mấy) k k = = 1 k k = = - 1 -1 1 Cực tiểu: d d k 2 1 k k = = - 2 - k k = = 2 2
Thứ = k + 1 nếu k ≥ 0; Thứ = |k| nếu k < 0
Chú ý:Nếu M nằm trên đường cực đại (cực tiểu), giữa M và trung trực của S1S2 còn có n 2
đường cực đại (cực tiểu) nữa thì M nằm trên đường cực đại (cực tiểu) thứ (n + 1). d d
2) Điểm M cách hai nguồn các đoạn d 2 1 k k = = - 2 - k k = = 1 1, d2. Xét tỉ số: k k = = - 1 - k k = = 0 d d Nếu 2 1 k
M nằm trên đường cực đại thứ |k| d d 1 Nếu 2
1 k M nằm trên đường cực tiểu thứ (k +1) nếu k ≥ 0; thứ |k| nếu k < 0 2
“Biển học mênh mông lấy chuyên cần làm bến
Mây xanh không lối lấy chí cả dựng nên” Page 13




