
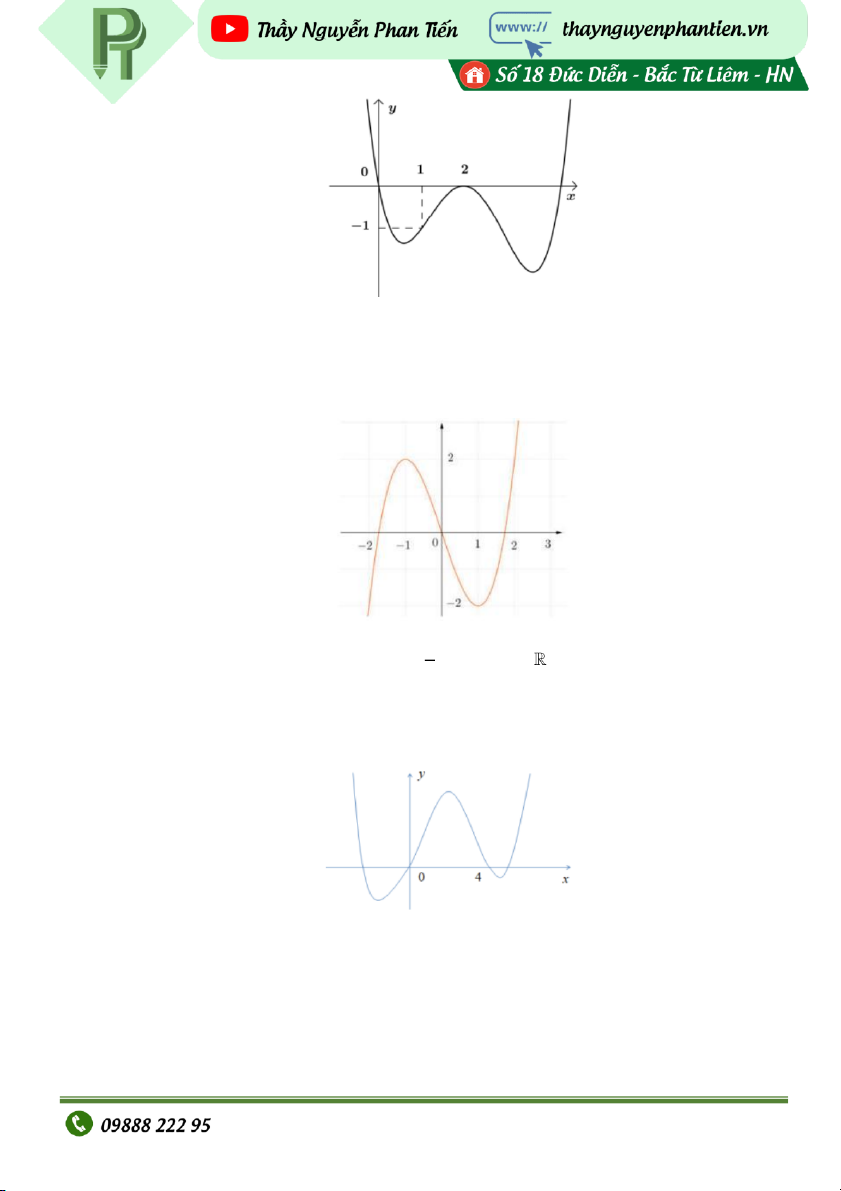


Preview text:
Tổng Ôn : Cực Trị Của Hàm Số
Nội Dung Bài Học :
Dạng 1. Cực Trị của hàm số thông qua BBT, Đồ Thị , Hàm Số
Dạng 2. Cực Trị chứa tham s m ố
Dạng 3. Cực Trị hàm hợp Dạng 4. Bài T p ậ Tổn H g ợp
BÀI TẬP VẬN DỤNG
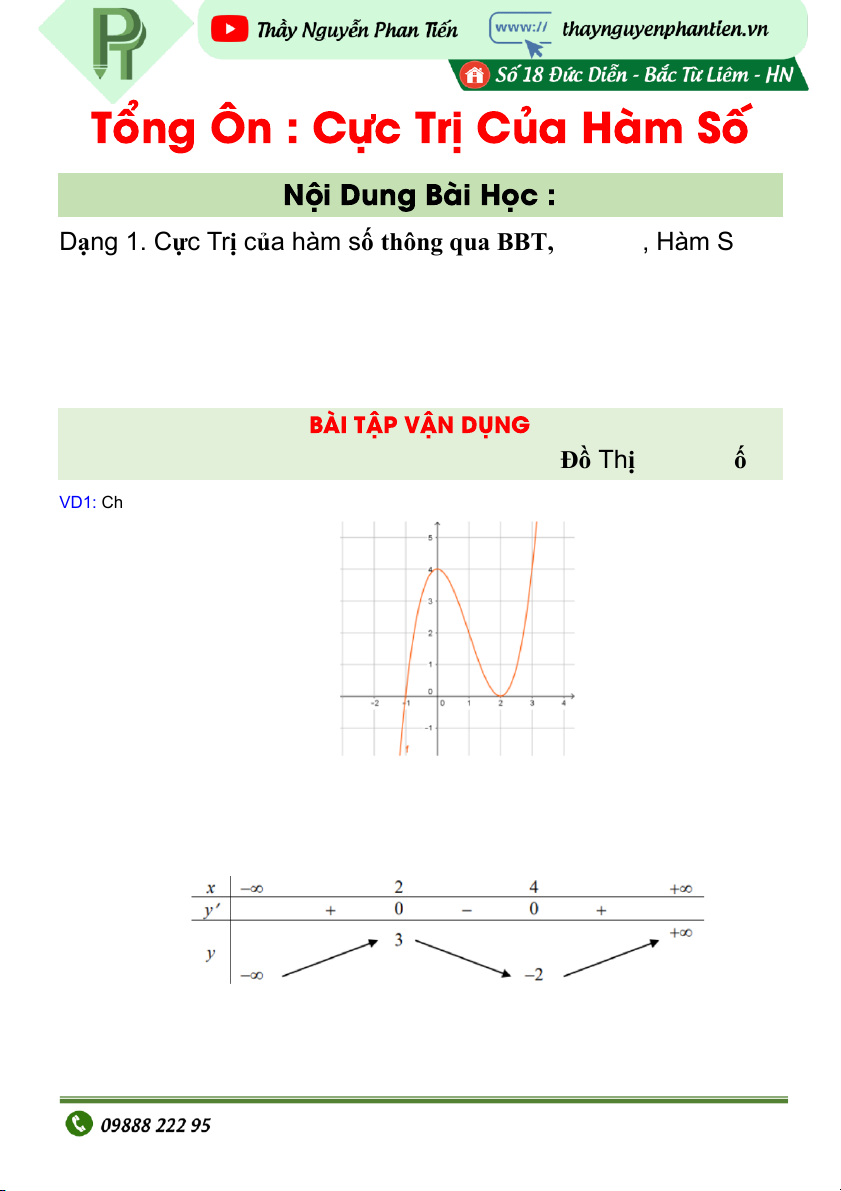
Dạng 1. Cực Trị của hàm số thông qua BBT, Đồ Thị , Hàm Số VD1: Cho hàm s
ốy f x có đồ thị như hình vẽ:
Đồ thị hàm số y f x có mấy điểm c c tr ự ị? A. 2 B. 1 C. 0 D. 3 VD2: Cho hàm s
ốy f x có bảng biến thiên:
Khẳng định nào sau đây là đúng? A. Hàm s ố đạt c i t ực đạ ại x 2 B. Hàm s ố đạt c i t ực đạ ại x 3 C. Hàm s ố đạt c i t ực đạ ại x 4 D. Hàm s ố đạt c i t ực đạ ại x 2 Page | 1 VD3: Cho hàm s
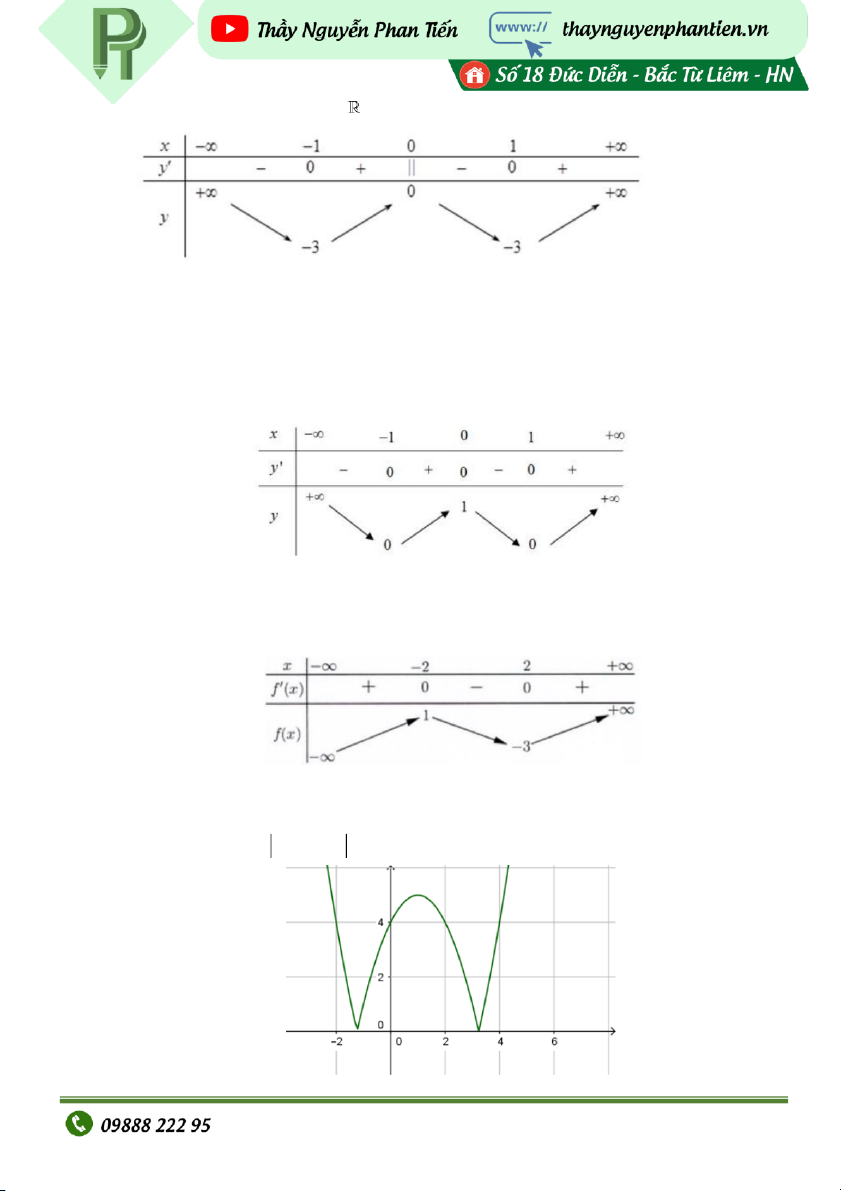
ốy f x liên t c trên ụ
và có bảng biến thiên:
Khẳng định nào sau đây đúng? A. Hàm s ố đạt c i t ực đạ ại x 0 B. Hàm s
ố có đúng hai điểm c c tr ự ị C. Hàm s có giá tr ố
ị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -3 D. Hàm s có giá tr ố ị c c ti ự ểu bằng -1 và 1. VD4: Cho hàm s
ốy f x có bảng bi
ến thiên như hình vẽ dưới đây: Giá trị c i c ực đạ a hàm s ủ ố : đã cho là A. y 1 B. x 0 C. y 0 D. x 1 VD5: Cho hàm s ốf x có bảng bi : ến thiên như sau Điểm cực đạ ủ i c a hàm số : đã cho là A. x 3 B. y 1 C. x 2 D. 2 ; 1 VD6: Cho hàm s ố y f 2 x x 2 x 4
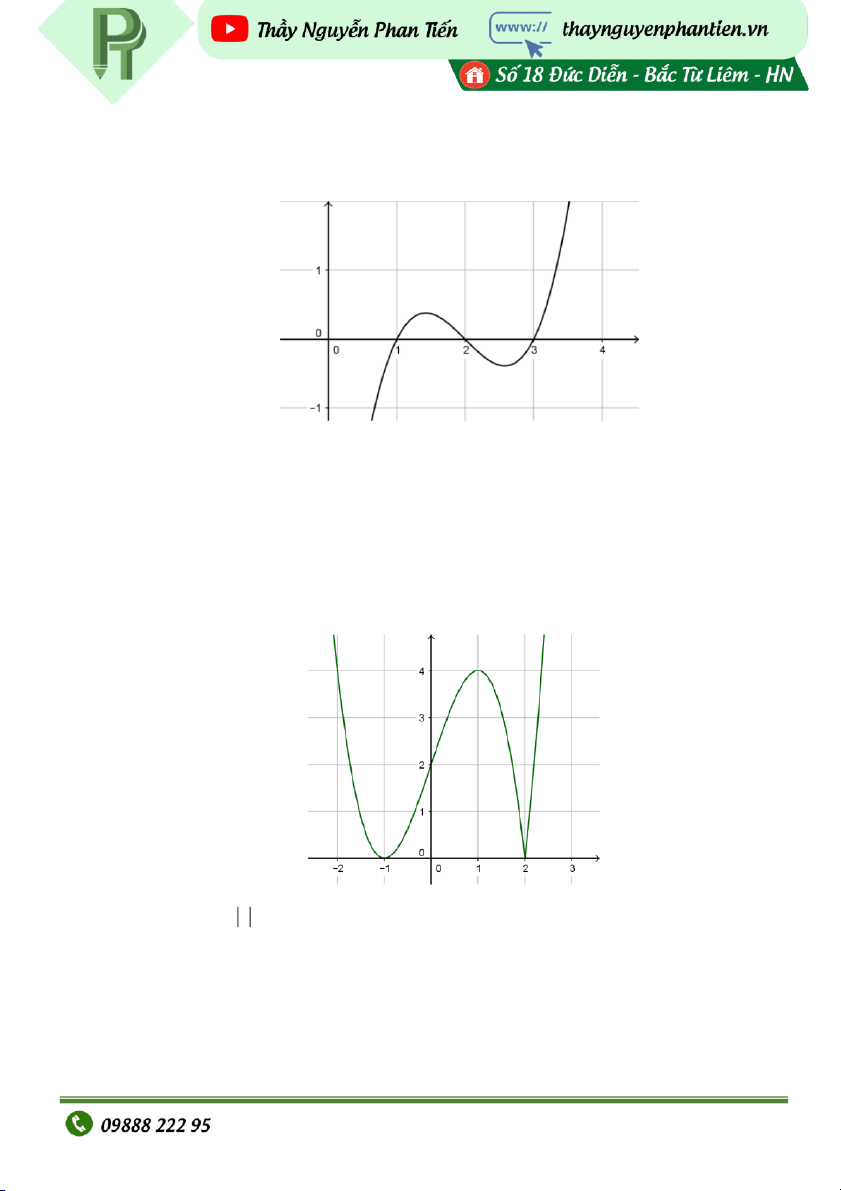
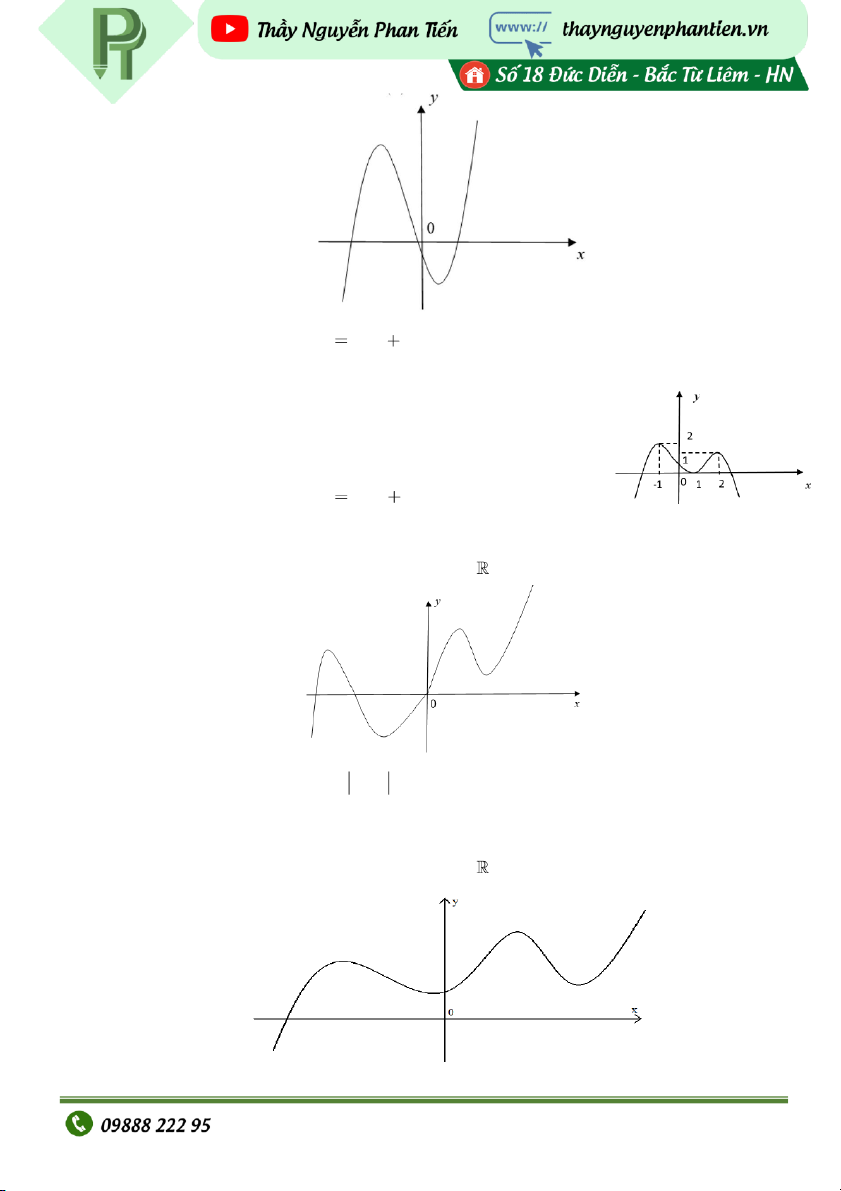
có đồ thị như hình vẽ: Page | 2 Hàm s
ố y f x có mấy cực trị? A. 4 B. 1 C. 3 D. 2 VD7: Cho hàm s
ốy f x . Hàm số y f x có đồ thị : như hình vẽ
Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số y f x cắt trục hoành tại ba điểm phân điểm.
B. Đồ thị hàm số y f x có hai điểm c c tr ự ị.
C. Đồ thị hàm số y f x có ba điểm cực trị.
D. Đồ thị hàm số y f x có một điểm c c tr ự ị. VD8: Cho hàm s
ốy f x có đồ thị : như hình vẽ Hàm s
ố y f x có bao nhiêu điểm cực trị? A. 5 B. 4 C. 3 D. 2 Page | 3 VD9: Cho hàm s
ốy f x có bảng bi : ến thiên như sau
Khi đó hàm số đã cho có:
A. Một điểm cực đại, một điểm cực tiểu.
B. Một điểm cực đại, hai điểm cực tiểu
C. Một điểm cực đại, không có điểm cực tiểu
D. Hai điểm cực đại, một điểm cực tiểu.
VD10: Hàm số y x 2 2 3
2 x đạt cực trị tại điểm có hoành độ là: A. x 1 B. x 0 ; x 1 C. x 0; x 1; x 2 D. Hàm s ố không có điểm cực trị VD11: Cho hàm s ố f x x x 2 x 3 1
1 . Hàm số y f x có bao nhiêu điểm cực trị? A. 2 B. 3 C. 0 D. 1 VD12: Cho hàm s
ố y f x có đạo hàm f x x x 4 2 2 x 8 . Số điểm c c ự trị của hàm s ố y f x là: A. 0 B. 1 C. 2 D. 3 2 VD13: Cho hàm s x 3 x 1 ốy . Tính t ng giá tr ổ
ị cực đại y và giá trị c c ti ự ểu y c a hàm s ủ trên. ố x CĐ CT A. y y 5 . B. y y 1 . C. y y 0 . D. y y 6 . CĐ CT CĐ CT CĐ CT CĐ CT VD14: Giá trị c i c
ực đạ ủa hàm số y s x in 2 trên 0; là: 3 2 3 2 3 3 A. . B. . C. . D. . 6 2 3 2 3 2 3 2 VD15: Hàm số 2 1 x y
x e có bao nhiêu điểm cực trị A. 0 B. 1 C. 2 D. 3 VD16: Cho hàm s ố 2 y x ln 1 2
x. Trong các kết luận sau, t lu đâu là kế ận không đúng? A. Hàm s có hai c ố ực trị 1 B. Hàm s ố đạt c c ti ự ểu tại x 2 1 C. Hàm s có giá tr ố ị c c ti ự ểu bằng ln 2 4 1 D. Hàm s ố ng bi đồ ến trên khoảng ; 2 Page | 4
Dạng 2. Cực Trị chứa tham s m ố
VD17: Tìm tất cả các giá trị th c c ự ủa m để hàm s ố 4 y m x m 2 1 x 2 1 m có 3 điểm cực trị? m 1 A. B. m 1 C. 1 m 0 D. m 1 m 0 2 x mx1
VD18: Tìm các giá trị của m để hàm s ốy
đạt cực đại tại x 2. là: x m A. m 1 . B. m 3 . C. m 1 . D. m 3 . 1
VD19: Tìm các giá trị thực của mđể hàm s ố 3 y x m 2 3 x 4 m 3 3 x m đạt c c ự trị tại x , x 3 1 2 thỏa mãn 1 x x . 1 2 7 m 3 7 A. m 2 B. 3 m 1 C. D. m 3 2 m 1 2
VD20: Tìm các giá trị của tham s ố m để hàm s ố 4 2 4 y x 2 m x 2m m có ba điểm cực trị nh c là ba đỉ ủa một tam giác đều. m 0 A. Không t n t ồ ại m B. C. 3 m 3 D. m 3 3 m 3
VD21: Tìm điều kiện của m để đường cong 4 2 y x 2 mx 4
có ba điểm cực trị đều nằm phía dưới đường thẳng y 5. A. 3 m 3 B. 0 m 3 C. 0 m 4 ,5 D. 1 m 2 ,5 1 VD22: Cho hàm s ốy m 2 1 x m x l
n . Tìm mđể hàm số đạt c i t ực đạ ại x 1 . 2 A. m 2 B. m 1 C. m 2 D. m 1 1
VD23: Đường cong y m 2 3 x 2 m 2 1 x m 3 x 2
có hai điểm cực trị sao cho hoành độ 3 2
điểm này gấp đôi hoành độ điểm kia. ổ Tính t ng S bao g m t ồ ất cả các giá trị m xảy ra. A. S 1 ,5 B. 2 C. S 0 D. S 1
Dạng 3. Cực Trị hàm hợp VD24: Cho hàm s b
ố ậc năm y f x có đồ thị y f x
như hình vẽ dưới đây: Page | 5 Số m c điể ực trị c a hàm s ủ ố g x 2 f x 3 x 4 là: A. 4 B. 6 C. 3 D. 5 VD25: Cho hàm s ốy f x
2 2 có đồ thị như hình bên dưới. 3 Tìm s ố m c điể c tr ự ị c a hàm s ủ g ố 2 x f x 3 x trên . 2 A. 5 B. 4 C. 2 D. 3 VD26: Cho hàm s b
ố ậc 4 y f xcó đồ thị như hình vẽ dưới đây: Số m c điể ực trị c a hàm s ủ ố 2x g x f e 3 là: A. 6 B. 5 C. 4 D. 3 Page | 6 VD27: Cho hàm s
ốy f x . Đồ thị hàm số y f x như hình vẽ dưới đây: Số m c điể ực trị c a hàm s ủ ố 2 g x f x là: A. 1 B. 2 C. 3 D. 4 Dạng 4. Bài T p
ậ Tổng Hợp VD28: Cho hàm s
ốy f xxác định và liên tục trên , có f 2 x x 1. Hàm s ố f 2 x 2 có bao nhiêu điểm cực tiểu? A. 2 B. 5 C. 7 D. 4 VD29: Cho hàm s
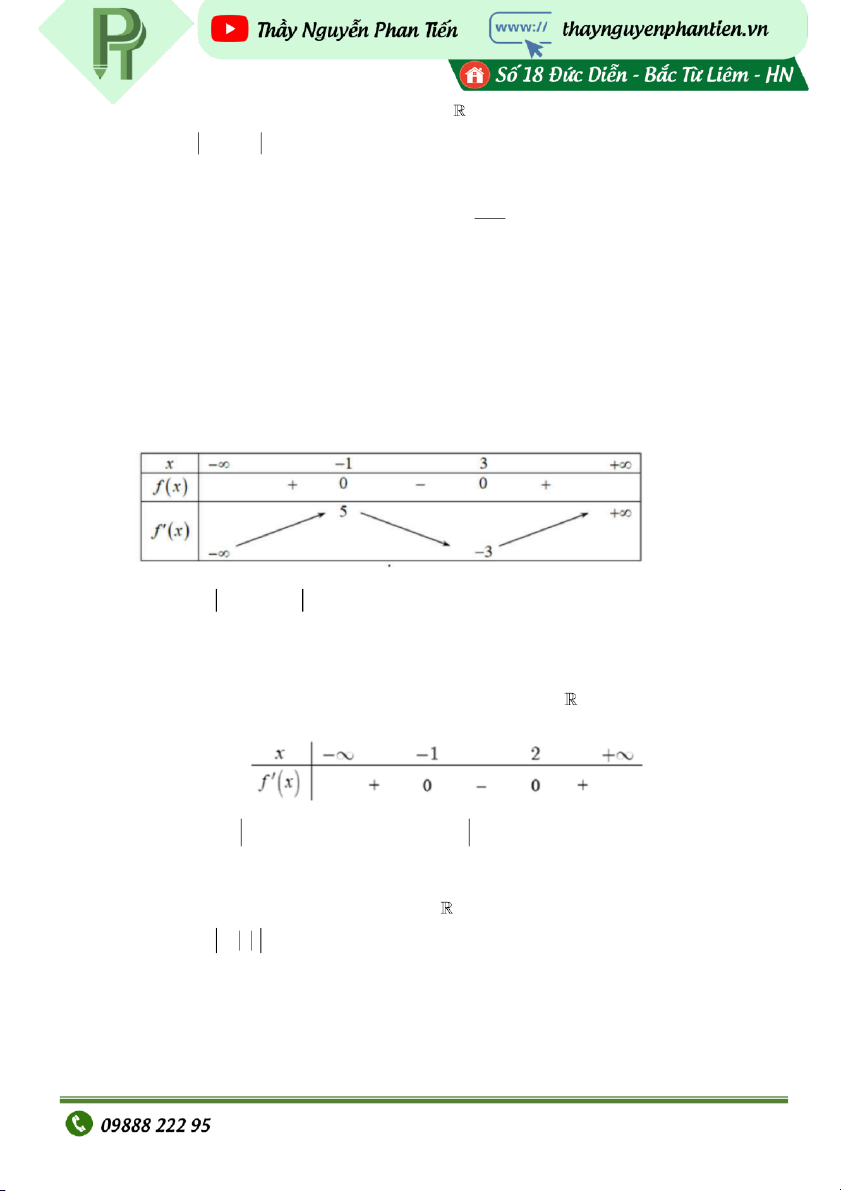
ốy f x có bảng biến thiên: Số m c điể i và c ực đạ ực tiểu c a hàm s ủ ố 2
y f2 x 2 f 2x 1 lần lượt là: A. 2;3 B. 3;2 C. 1;1 D. 2;2 VD30: Cho hàm s
ốy f x có đạo hàm f 3 2 ' x x x 6 x th a ỏ mãn f
0 m. Gọi S là tập hợp các
giá trị nguyên của tham s ố m sao cho hàm số
y f x có 7 điểm cực trị. Tính tổng các phần tử của S. A. 10 B. 28 C. 21 D. 15 Page | 7
BÀI TẬP TỰ LUYỆN Câu 1: Cho hàm s ố
xác định, liên t c trên ụ
và có bảng biến thiên như sau:
Khẳng định nào sau đây là khẳng định đúng? A. Hàm s
ố có đúng một cực trị. B. Hàm s có giá tr ố ị c c ti ự ểu bằng . C. Hàm s có giá tr ố
ị lớn nhất bằng 0 và giá trị nhỏ nhất bằng . D. Hàm s ố đạt c i t ực đạ ại t c và đạ ực tiểu tại . Câu 2: Cho hàm s
ốy f xcó bảng bi bên. M ến thiên như hình vẽ
ệnh đề nào dưới đây đúng? A. y 5 B. y 0 C. min y 4 D. max y 5 CÐ CT Câu 3: Cho hàm s
ốy f x xác định, liên t c trên ụ
và có bảng biến thiên như sau:
Khẳng định nào sau đây là khẳng định đúng? A. Hàm s ố c tr có đúng 1 cự ị B. Hàm s có c ố ực tiểu bằng 1. C. Hàm s có GTLN là 1. ố D. Hàm s
ố đạt CĐ tại x 0 và CT tại x 1 Page | 8 Câu 4: Cho hàm s
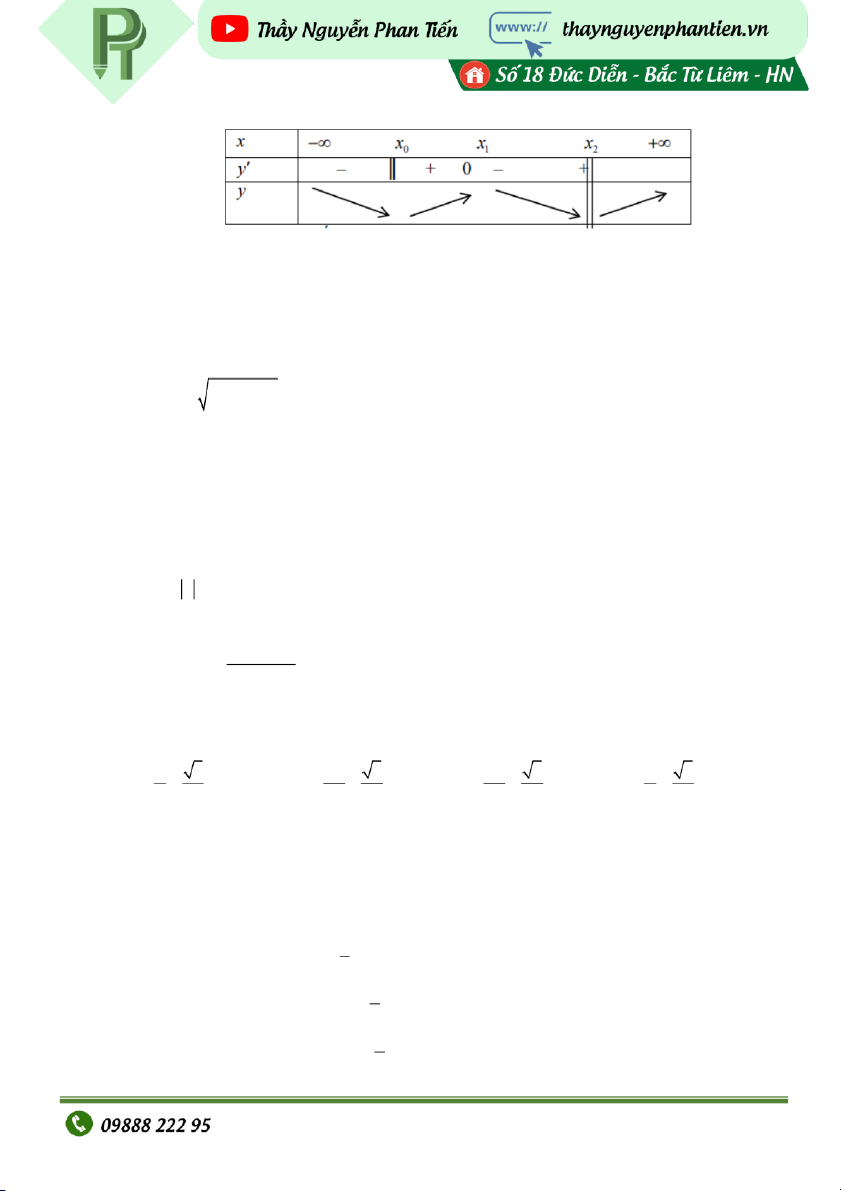
ốy f x có đạo hàm là f x x 2x 4 1 2 x 4. Số m điể c c ự trị c a ủ hàm số y f x là: A. 3 B. 2 C. 4 D. 1 Câu 5: Cho hàm s
ốy f x có đồ thị y f x như sau:
Mệnh đề nào dưới đây đúng? A. Hàm s có giá tr ố ị c c ti ự ểu bằng 2 . B. Hàm s có giá tr ố
ị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -2. C. Hàm s có 2 CT ố và 1 CĐ . D. Hàm s có giá tr ố ị c c ti ự ểu bằng 2
Câu 6: Điểm cực tiểu của đồ thị ố hàm s 3 y x 3 x 5 là: A. Q 3; 1 B. N 1 ; 7 C. P7; 1 D. M 1; 3 Câu 7: Hàm s ố f x o hàm có đạ
f ' x trên khoảng K . Cho đồ thị của hàm số f ' x trên khoảng K như sau: Số m c điể ực trị c a hàm s ủ ốf x trên K là: A. 1 B. 2 C. 3 D. 4 Câu 8: Hàm s ố f x o hàm có đạ
f ' x trên khoảng K . Cho đồ thị của hàm số f ' x trên khoảng K như sau: Page | 9 Số m c điể ực trị c a hàm s ủ ố y trên K là: A. 1 B. 2 C. 3 D. 4 Câu 9: Hàm s
ố f x có đạo hàm f ' x trên khoảng K . Cho đồ thị của hàm số f ' x trên khoảng K : như sau Số m c điể ực trị c a hàm s ủ ố y trên K là: A. 1 B. 2 C. 3 D. 4
Câu 10: Cho hàm số y f x o hàm và liên t có đạ c trên ụ , hàm sy
ố f x đồ thị như hình vẽ: Số m c điể ực trị c a hàm s ủ ố y f x là: A.3. B.4. C.7. D.0. Câu 11: Cho hàm s ốy f x o hàm và liên t có đạ c trên ụ , hàm sy
ố f x đồ thị như hình vẽ: Page | 1 0 Số m c điể ực trị c a hàm s ủ ố y f x là: A.0. B.2. C.4. D.5. 2 Câu 12: Cho hàm số 4 3 2 y x x . x M nào sau ệnh đề đây là đúng? 3 A. Hàm s có giá tr ố ị c c ti ự ểu là 0. 2 5 B. Hàm s có hai giá tr ố ị cực tiểu là và . 3 48 C. Hàm s ố chỉ có m t giá tr ộ ị cực tiểu. 2 5 D. Hàm s có giá tr ố ị c c ti ự ểu là và giá trị c i là ực đạ . 3 48 Câu 13: Tọa độ điểm c i c ực đạ a hàm s ủ ố 3 2 y x 3 x 4 là A. (2; 4). B. (2;0). C. (0; 4) D. (0;4). Câu 14: Cho hàm số 3 y x 3 x có giá trị c i và c ực đạ c ti ự
ểu lần lượt là y, y . Khi đó: 1 2 A. y y 4 B. 2 y y 6 C. 2 y y 6 D. y y 4 . 1 2 1 2 1 2 1 2 2 x 3 Câu 15: Hàm s ốy đạt cực đại tại: x 2 A. x 1 . B. x 2. C. x 3. D. x 0. y
Câu 16: Cho hàm số y f x xác định và liên t c
ụ trên và có đồ thị là đường cong 2 trong hình vẽ bên. H i ỏ m c điể c ti ự
ểu của đồ thị hàm số y f x là điểm nào? x -2 -1 O 1 2 A. x 2 . B. y 2 . C. -2 M 0; 2 D. N 2; 2 2 x 4x1 Câu 17: Cho hàm số y
. Hàm số có hai điểm cực trị x1, x2. Tích x1.x2 bằng x1 A. 4 B. 5 C. 1 D. 2 2 x x Câu 18: Đồ thị ố hàm s : 2 2 y
có 2 điểm cực trị nằm trên đường thẳng y ax ằ 1 a b x b thì b ng A. 2 B. 4 C. 4 D. 2 Câu 19: Cho hàm số y m 3 2 x m
x2 Với giá trị nào của m thì hàm s có c ố ực trị? A. 0 m 2. B. m 1 . C. m 2 m 0 . D. m 1 . 1 Câu 20: Cho hàm số 3 y x m 2 1 x 2 m 2 m x (m là tham s ). ố Tìm tất cả tham s ố thực m để 3 hàm số đạt c c ti ự ểu tại x 2 . A. m 1 . B. m 0. C. m 2 . D. m 3. Page | 1 1
Câu 21: Với giá trị nào c a ủ tham số m thì hàm s ố 2 y2( m 3)si n 2 x s in
m 2 x 3 m đạt cực đại tại x . 3 A. Không t n t ồ ại giá trị m. B. m 1 . C. m 3 D. m 3, m 1 . Câu 22: Cho hàm s ố 3 y x m 2 2 3
1 x 9 x2 m 1 . Tìm giá trị của m để đồ thị hàm s ố (C) có c i, c ực đạ
ực tiểu tại x , x sao cho x x 2 1 2 1 2 m 1 A. m 1 B. m 3 C. D. m m 3 Câu 23: Cho hàm số 3 2 y x (1 2 ) m x (2 )m x 2 m (m là tham s ).G ố ọi x , x 1 2 x 1 x
là hai điểm cực trị của hàm số. Tìm m để 1 2 . A. m 4 B. m 4 C. m 4 D. m 4
Câu 24: Tìm tất cả các giá trị thực của tham số m sao cho đ ồ thị hàm s ố 4 2 4 y x 2 mx 2 m m có ba
điểm cực trị đều thuộc các trục tọa độ. 1 A. m 1 . B. m 2 . C. m . D. m 3 . 2
Câu 25: Tìm các giá trị c a tham ủ s ố m để đồ thị hàm s ố 4 2 2 y x
2 m x 1có ba điểm cực trị là ba đỉnh c a m ủ t tam giác vuông cân. ộ A. m 1 B. m 0 C. m 1 D. m 1
Câu 26: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm s ố 3 y x
3 mx 1có 2 điểm cực trị , A B sao cho tam giác
OAB vuông tại O ( với O là gốc tọa độ ) 3 1 1 A. m B. m C. m 1 D. m 2 2 2
Câu 27: Tìm tất cả các giá trị thực của tham s ố mđể đồ thị tham số 3 2 2 y x
3 mx 3 mcó hai điểm cực
trị Avà B sao cho tam giác
OAB có diện tích bằng 48. A. m 2hoặc m 0 B. m 2 C. m 2 D. m 2 Câu 28: Cho hàm s
ốy f x có đạo hàm f x x x 4 2 2 x
8 . Số điểm cực trị của hàm số y f x là: A. 0 B. 1 C. 2 D. 3 Câu 29: Cho hàm số
y f x có đạo hàm f x 3x 2 3 2 x x 2 . Hàm s
ốy f x có bao nhiêu điểm cực trị? A. 9 B. 8 C. 7 D. 6 Page | 1 2
Câu 30: Cho hàm số y f x xác định và liên t c
ụ trên , có đạo hàm f x x x 2 1 1 x 2
. Hàm số f x x có tối đa bao nhiêu điểm c c tr ự ị? A. 3 B. 5 C. 7 D. 9 x e Câu 31: Phát bi hàm s
ểu nào sau đây đúng khi nói về ốy ? x1 A. Hàm s ngh ố ịch biến trên khoảng ; 0 B. Hàm s ố ng bi đồ ến trên khoảng 0; C. Hàm s ố đạt c i t ực đạ ại x 0 D. Hàm s ố có hai điểm c c tr ự ị Câu 32: Hàm s ố x x y e e có bao nhiêu cực trị? A. 0 B. 1 C. 2 D. 3
Câu 33: Cho hàm số y f x có bảng biến thiên như sau: Hàm s ố y 1 f 3 x 1
có bao nhiêu điểm cực trị? A. 2 B. 3 C. 4 D. 5 Câu 34: Cho hàm s
ốy f x có f
2 0 và đạo hàm liên tục trên và có bảng xét dấu như hình sau: Hàm s ố g x 4 2 f x x 6 2 15 2 2 10 x 30
có bao nhiêu điểm cực trị? A. 2 B. 3 C. 5 D. 7
Câu 35: Cho hàm số y f x xác định, liên t c trên ụ
và có bảng biến thiên sau: Hàm s ố y f
x có nhiều nhất bao nhiêu điểm cực trị. A. 5 B. 7 C. 6 D. 3 --HẾT-- Page | 1 3




