Tổng ôn tập TN THPT 2020 môn Toán: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Tài liệu gồm 82 trang, được tổng hợp và biên soạn bởi thầy giáo Nguyễn Bảo Vương, tuyển chọn các câu hỏi và bài tập trắc nghiệm chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số, có đáp án và lời giải chi tiết, giúp học sinh tổng ôn kiến thức để chuẩn bị cho kỳ thi tốt nghiệp THPT 2020 môn Toán

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

82 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
A. TÌM GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Định lí 1: Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn đó.
Định lí 2
Nếu
( )y f x
đồng biến trên
[ ; ]a b
thì
[ ; ]
min ( ) ( )
a b
f x f a
và
[ ; ]
max ( ) ( ).
a b
f x f b
Nếu
( )y f x
nghịch biến trên
[ ; ]a b
thì
[ ; ]
min ( ) ( )
a b
f x f b
và
[ ; ]
max ( ) ( ).
a b
f x f a
Bài toán 1. Tìm GTLN & GTNN của hàm số
( )y f x
trên đoạn
[ ; ].a b
Bước 1. Hàm số đã cho xác định và liên tục trên đoạn
[ ; ].a b
Tính
( ) 0f x
tìm nghiệm
[ ; ].
i
x a b
Bước 2. Tính
( ), ( ), ( ).
i
f a f b f x
Bước 3. Kết luận:
[ ; ]
max ( ) max ( ); ( ); ( )
i
a b
f x f a f b f x
và
[ ; ]
min ( ) min ( ); ( ); ( ) .
i
a b
f x f a f b f x
Bài toán 2. Tìm GTLN & GTNN của hàm số
( )y f x
trên khoảng
( ; ).a b
Bước 1. Tìm tập xác định. Tính
( ).f x
Cho
( ) 0f x
tìm nghiệm.
Bước 2. Xét dấu biểu thức
( )y f x
và lập bảng biến thiên (có tính giới hạn).
Bước 3. Dựa vào bảng biến thiên để kết luận GTLN (GTNN nếu có).
Lưu ý: Đạo hàm của hàm số mũ và lôgarit
( ) . .ln .
u u
a u a a
( ) . .
u u
e u e
( ) .
x x
e e
(log )
ln
a
u
u
u a
1
(log )
ln
a
x
x a
1
(ln ) ln
u
u x
u x
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 1. Giá trị lớn nhất của hàm số
4 2
( ) 12 1f x x x
trên đoạn
1;2
bằng:
A.
1
. B.
37
. C.
33
. D.
12
.
Câu 2. Giá trị nhỏ nhất của hàm số
4 2
10 2f x x x
trên đoạn
1;2
bằng
A.
2
. B.
23
. C.
22
. D.
7
.
Câu 3. Gọi
M
là giá trị lớn nhất và
m
là giá trị nhỏ nhất của hàm số
4 2
8 5y x x
trên đoạn
3;1
.
Khi đó, giá trị của biểu thức
2M m
bằng
A.
46
. B.
25
. C.
25
. D.
46
.
Câu 4. Cho hàm số
y f x
liên tục trên đoạn
3;3
có đồ thị như hình vẽ.
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y f x
trên
0;3
lần lượt có giá trị là
A.
4;3
4;3
max 4, min 3y y
.
B.
4;3
4;3
max 3,min 3y y
.
C.
0;3
0;3
max 3,min 2y y
.
D.
4;3
4;3
max 4,min 2y y
.
Câu 5. Giá trị nhỏ nhất của hàm số
16
3y x
x
trên đoạn
1;5
là:
A.
5
. B.
20
. C.
5 6
5
. D.
11
.
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT
Vấn đề 4
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 6. Cho hàm số
f x
liên tục trên
3; 5
và có bảng biến thiên như hình vẽ. Gọi
,M m
lần lượt là giá trị
lớn nhất và nhỏ nhất của
f x
trên
[ 3;2]
. Tính
M m
.
A.
6
. B.
4
. C.
5
. D.
3
.
Câu 7. Cho hàm số
( )f x
có đạo hàm
2
' 3 4 ,f x x x x x
. Giá trị lớn nhất của hàm số đã
cho trên đoạn
0;5
bằng
A.
0f
. B.
4f
. C.
3f
. D.
5f
.
Câu 8. Giá trị lớn nhất của hàm số
3
y x 3x 5
trên đoạn
3
0;
2
bằng:
A. 3. B. 5. C. 7. D.
31
8
.
Câu 9. Giá trị lớn nhất của hàm số
3
( ) 6 3f x x x
trên đoạn
0;2
bằng:
A.
3
. B.
3 4 2
. C.
25
. D.
12
.
Câu 10. Giá trị nhỏ nhất của hàm số
8
1 2
f x x
x
trên đoạn
1;2
bằng:
A.
7
2
. B.
18
5
. C.
11
3
. D.
9
2
.
Câu 11. Giá trị nhỏ nhất của hàm số
2
( )
3
x
f x
x
trên đoạn
1;3
bằng:
A.
3
. B.
2
. C.
1
6
. D.
1
4
.
Câu 12. Giá trị nhỏ nhất của hàm số
3 2
( ) 5 6f x x x x
trên đoạn
0;4
bằng:
A.
3
. B.
2
. C.
2
27
. D.
6
.
Câu 13. Giá trị nhỏ nhất của hàm số
3 2
8 16 9 f x x x x
trên đoạn
1;3
bằng:
A.
9
. B.
6
. C.
13
27
. D.
0
.
Câu 14. Cho hàm số
( )y f x
có đồ thị như hình vẽ. Hỏi giá trị nhỏ nhất của hàm số đã cho trên đoạn
[0; 2]
bằng bao nhiêu?
A. 0.
B.
1
.
C.
2
.
D.
1
.
Câu 15. Giá trị lớn nhất của hàm số
4 2
8 16y f x x x
trên đoạn
1;3
bằng:
A.
9
. B.
26
. C.
25
. D.
0
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
+∞ 6
1
5
3
0
0
++
x
∞ 3
1
1
0
0
y'
y
x
y
-1
1
-1
0
1
Câu 16. Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ.
Hỏi giá trị lớn nhất của hàm số đã
cho trên
[-1;3]
bằng bao nhiêu?
A. 3.
B.
3
.
C.
5
.
D.
6
.
Câu 17. Giá trị nhỏ nhất của hàm số
9
y x
x
trên đoạn
2;4
bằng:
A.
6
. B.
13
2
. C.
6
. D.
25
4
.
Câu 18. Cho hàm số
y f x
liên tục trên đoạn
1;1
và có đồ thị như hình vẽ.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và
nhỏ nhất của hàm số đã cho trên đoạn
1;1
.
Giá trị của
M m
bằng
A.
0
. B.
1
.
C.
2
. D.
3
.
Câu 19. Cho hàm số
y f x
liên tục trên đoạn
và có đồ thị như hình vẽ.
Giá trị nhỏ nhất trên tập xác định của hàm số có đồ thị sau là:
A. min 1.y
B. min 1y .
C. min 0y .
D. min 2y .
Câu 20. Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị nhỏ nhất của hàm số có bảng biến thiên sau trên khoảng
2;3
là:
A.
2;3
min 0y
.
B.
2;3
min 3y
.
C.
2;3
min 1y
.
D.
2;3
min 7y
.
Câu 21. Cho đồ thị hàm số
'( )y f x
như hình vẽ.
Hàm số
( )y f x
đạt giá trị lớn nhất trên khoảng
1;3
tại
0
x . Khi đó giá trị của
2
0 0
2 2019x x
bằng bao nhiêu?
A.
2018
. B.
2019
. C.
2021
. D.
2022
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 22. Cho hàm số
y f x
liên tục trên đoạn
1;4
và có đồ thị như hình vẽ bên dưới.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và
nhỏ nhất của hàm số đã cho trên đoạn
1;4
.
Giá trị của
M m
bằng
A.
0
. B.
1
.
C.
2
. D.
5
.
Câu 23. Cho hàm số
y f x
liên tục trên đoạn
3;1
và có đồ thị như hình vẽ bên dưới.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất
của hàm số đã cho trên đoạn
3;1
. Giá trị của
2M m
bằng
A.
0
.
B.
1
.
C.
4
.
D.
5
.
Câu 24. Cho hàm số
y f x
liên tục trên đoạn
2;2
và có đồ thị như hình vẽ bên dưới.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất
của hàm số đã cho trên đoạn
2;2
. Giá trị của
M m
bằng
A.
0
.
B.
1
.
C.
4
.
D.
3
.
Câu 25. Cho hàm số
y f x
liên tục trên đoạn
1;3
và có đồ thị như hình vẽ bên dưới.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất
của hàm số đã cho trên đoạn
1;3
. Giá trị của
2 2
M m
bằng
A.
15
.
B.
11
.
C.
4
.
D.
13
.
Câu 26. Giá trị nhỏ nhất của hàm số
3
6f x x x
trên đoạn
0;2
bằng
A.
4 2
. B.
4
. C.
6 2
. D.
0
.
Câu 27. Cho hàm số
( )y f x
có đạo hàm
2
( ) ( 1)( 2)
f x x x x
với mọi
x
. Giá trị nhỏ nhất của hàm
số
( )y f x
trên đoạn
1;2
là
A.
( 1).f
B.
(0).f
C.
(3).f
D.
(2).f
B. TÌM M ĐỂ GTLN-GTNN THỎA MÃN ĐIỀU KIỆN K
Câu 1. Cho hàm số
1
x m
y
x
(
m
là tham số thực) thỏa mãn
[2;4]
min 3.y
Mệnh đề nào dưới đây đúng?
A.
4m
B.
3 4m
C.
1m
D.
1 3m
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 2. Cho hàm số
1
x m
y
x
(
m
là tham số thực) thoả mãn
1;2
1;2
16
min max
3
y y
. Mệnh đề nào dưới đây
đúng?
A.
m
B.
2 4
m
C.
0
m
D.
0 2
m
Câu 3. Tìm tất cả các giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
3 2
3
y x x m
trên đoạn
1;1
bằng
0
.
A.
2.
m
B.
6.
m
C.
0.
m
D.
4.
m
Câu 4. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x m
y
x
trên đoạn
1;2
bằng
8
(
m
là tham
số thực). Khẳng định nào sau đây là đúng?
A.
10
m
.
B.
8 10
m
.
C.
0 4
m
.
D.
4 8
m
.
Câu 5. Có một giá trị
0
m
của tham số
m
để hàm số
3 2
1 1
y x m x m
đạt giá trị nhỏ nhất bằng
5
trên đoạn
0;1
. Mệnh đề nào sau đây là đúng?
A.
2
0 0
2018 0
m m
. B.
0
2 1 0
m
. C.
2
0 0
6 0
m m
. D.
0
2 1 0
m
.
Câu 6. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
x m
y
x m
trên đoạn
0;4
bằng
1.
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 7. Cho hàm số
2
1
x
y
x m
(m là tham số thực) thỏa mãn
3; 2
1
min
2
y
. Mệnh đề nào dưới đây đúng?
A.
3 4
m
. B.
2 3
m
. C.
m
. D.
2
m
.
Câu 8. Tìm giá trị dương của tham số
m
để giá trị nhỏ nhất của hàm số
2
1
2
m x
y
x
trên đoạn
1;3
bằng
1
.
A.
2
m
. B.
3
m . C.
4
m
. D.
2
m
.
Câu 9. Cho hàm số
2
8
x m
y
x
với
m
là tham số thực. Giả sử
0
m
là giá trị dương của tham số
m
để
hàm số có giá trị nhỏ nhất trên đoạn
0;3
bằng 3. Giá trị
0
m
thuộc khoảng nào trong các khoảng
cho dưới đây?
A.
2;5
. B.
1;4
. C.
6;9
. D.
20;25
.
Câu 10. Tìm giá trị của tham số thực
m
để giá trị nhỏ nhất của hàm số
2
1
x m
y
x
trên đoạn
0;4
bằng
3
.
A.
3
m
. B.
1
m
. C.
m
. D.
5
m
Câu 11. Tìm tất cả các giá trị thực của tham số m để hàm số
3 2
3
y x x m
có giá trị nhỏ nhất trên đoạn
bằng
2
A.
2
m
. B.
2 2
m
. C.
4 2
m
. D.
2 2
4 2
m
m
.
Câu 12. Tìm các giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
2
1
x m m
y
x
trên đoạn
0;1
bằng
2
.
A.
1
2
m
m
. B.
1
2
m
m
. C.
1
2
m
m
. D.
1
2
m
m
.
Câu 13. Có một giá trị
0
m
của tham số
m
để hàm số
3 2
1 1
y x m x m
đạt giá trị nhỏ nhất bằng
5
trên đoạn
0;1
. Mệnh đề nào sau đây là đúng?
A.
2
0 0
2018 0
m m
. B.
0
2 1 0
m
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
C.
2
0 0
6 0
m m
. D.
0
2 1 0
m
.
Câu 14. Nếu hàm số
2
1
y x m x
có giá trị lớn nhất bằng
2 2
thì giá trị của
m
là
A.
2
2
. B.
2
. C.
2
. D.
2
2
.
Câu 15. Cho hàm số
1
x m
y
x
(
m
là tham số thực) thỏa mãn
0;1
min 3y
. Mệnh đề nào dưới đây đúng?
A.
1 3m
B.
6m
C.
1m
D.
3 6m
Câu 16. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x m
y
x
trên
1;2
bằng
8
(
m
là tham số
thực). Khẳng định nào sau đây đúng?
A.
10
m
. B.
8 10
m
. C.
0 4
m
. D.
4 8
m
.
Câu 17. Cho hàm số
3 2
2 3
y x x m
. Trên
hàm số có giá trị nhỏ nhất là
1
. Tính
m
?
A.
6
m
. B.
3
m
. C.
4
m
. D.
5
m
.
Câu 18. Biết
S
là tập giá trị của
m
để tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 2 3 2
2
y x m x x m
trên đoạn
0;1
bằng
16
. Tính tích các phần tử của
S
.
A.
2
. B.
2
. C.
15
. D.
17
.
Câu 19. Gọi
,A B
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
2
1
x m m
y
x
trên đoạn
2;3
.
Tìm tất cả các giá trị thực của tham số
m
để
13
2
A B
.
A.
1; 2
m m
. B.
2
m
. C.
2
m
. D.
1; 2
m m
.
Câu 20. Cho hàm số
2
8
x m
f x
x
với
m
là tham số thực. Giả sử
0
m
là giá trị dương của tham số
m
để
hàm số có giá trị nhỏ nhất trên đoạn
0;3
bằng
3
. Giá trị
0
m
thuộc khoảng nào trong các
khoảng cho dưới đây?
A.
20;25
. B.
. C.
6;9
. D.
2;5
.
Câu 21. Tìm tất cả giá trị thực của tham số
m
để hàm số
2
1x mx
y
x m
liên tục và đạt giá trị nhỏ nhất
trên đoạn
0;2
tại một điểm
0
0;2
x
.
A.
0 1
m
B.
1
m
C.
m
D.
1 1
m
Câu 22. Cho hàm số
1 sin
cos 2
m x
y
x
. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
0;10
để giá
trị nhỏ nhất của hàm số nhỏ hơn
2
?
A.
1
. B.
9
. C.
3
. D.
6
.
Câu 23. Tìm tất cả các giá trị của tham số m để hàm số
2
1
x m
y
x x
có giá trị lớn nhất trên
nhỏ hơn
hoặc bằng 1.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
C. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ CHỨA DẤU GIÁ TRỊ
TUYỆT ĐỐI (chứa tham số)
Dạng 1: Tìm
m
để
;
max 0 .
y f x m a a
Phương pháp:
Cách 1:Trước tiên tìm
;
;
max ; min .f x K f x k K k
Kiểm tra
max , .
2 2 2
m K m k m K m k K k
m K m k
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
TH1:
.
2
K k
a
Để
;
max ;
m k a m a k
y a m a k a K
m K a m a K
.
TH2:
2
K k
a
m
.
Cách 2: Xét trường hợp
TH1:
m K a
Max m K
m K m k
TH2:
m k a
Max m k
m k m K
Dạng 2: Tìm
m
để
;
min 0 .
y f x m a a
Phương pháp:
Trước tiên tìm
;
;
max ; min .f x K f x k K k
Để
;
min .
0 0
m k a m K a m a k m a K
y a
m k m K m k m K
Vậy
1 2
.m S S
Dạng 3: Tìm
m
để
;
max
y f x m
không vượt quá giá trị
M
cho trước.
Phương pháp: Trước tiên tìm
;
;
max ; min .f x K f x k K k
Để
;
max .
m k M
y M M k m M K
m K M
Dạng 4: Tìm
m
để
;
min
y f x m
không vượt quá giá trị
a
cho trước.
Phương pháp: Trước tiên tìm
;
;
max ; min .f x K f x k K k
Để
;
min 0 .
0 0
m k a m K a m a k m a K
y a m K m k K m k
m k m K m k m K
Dang 5: Tìm
m
để
;
max
a b
y f x m
đạt min.
Phương pháp:
Trước tiên tìm
;
;
max ; min .
a b
a b
f x K f x k K k
Đề hỏi tìm
.
2
K k
m m
Đề hỏi tìm min của
;
max
a b
y
giá trị này là
.
2
K k
Dạng 6: Tìm
m
để
;
min
a b
y f x m
đạt min.
Phương pháp: Trước tiên tìm
;
;
max ; min .
a b
a b
f x K f x k K k
Đề hỏi tìm
0
m m K m k K m k
. Đề hỏi tìm min của
;
min
a b
y
giá trị này là
0.
Dạng 7: Cho hàm số
y f x m
.Tìm
m
để
;
;
max .min 0
a b
a b
y h y h
hoặc
max
Min
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương pháp: Trước tiên tìm
;
;
max ; min .
a b
a b
f x K f x k K k
TH1:
1
cung dau
.
K m k m
K m k m
K m h k m m S
TH2:
2
cungdau
.
k m K m
K m k m
k m h K m m S
Vậy
1 2
.m S S
Dạng 8: Cho hàm số
y f x m
.
Phương pháp: Trước tiên tìm
;
;
max ; min .
a b
a b
f x K f x k K k
BT1: Tìm
m
để
;
;
min max
a b
a b
y y m K m k
.
BT2: Tìm
m
để
;
;
min *max *
a b
a b
y y m K m k
.
Câu 1. Gọi
S
là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm
số
3
3f x x x m
trên đoạn
0;3
bằng 16. Tổng tất cả các phần tử của
S
là:
A.
16
. B.
16
. C.
12
.
D.
2
.
Câu 2. Cho hàm số
1
x m
f x
x
(
m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị của
m
sao cho
0;1
0;1
max min 2f x f x
. Số phần tử của
S
là
A.
6
. B.
2
. C.
1
. D.
4
.
Câu 3. Cho hàm số
4 3 2
4 4f x x x x m
(
m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị
của
m
sao cho
0;2
0;2
max min 5f x f x
. Số phần tử của
S
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 4. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
2
2 3y x x m
trên đoạn
1;2
bằng
4
. Tổng tất cả các phần tử của
S
là
A.
6
. B.
8
. C.
9
. D.
12
.
Câu 5. Cho hàm số
3
3f x x x m
(
m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị của
m
sao cho
0;2
0;2
max min 6f x f x
. Tổng tất cả các phần tử của
S
là
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 6. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị nhỏ nhất của hàm số
3
2 6f x x x m
trên đoạn
0;3
bằng 8. Tổng tất cả các phần tử của
S
bằng
A.
8
. B.
16
. C.
32
.
D.
72
.
Câu 7. Có bao nhiêu giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
2
2 4y x x m
trên
đoạn
2;1
đạt giá trị nhỏ nhất?
A. . B. . C. . D. .
Câu 8. Cho hàm số
f x
liên tục trên
, có đồ thị như hình vẽ
Có tất cả bao nhiêu giá trị nguyên của tham số
a
để hàm số
2
8
1
1
x
y f a
x
có giá trị
lớn nhất không vượt quá
20
?
A.
29
. B.
35
. C.
31
. D.
41
.
1
3
4
5
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 9. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm số
2
1
x mx m
f x
x
trên
1;2
bằng
2
. Tổng tất cả các phần tử của
S
là
A.
11
3
. B.
13
6
. C.
11
6
. D.
1
3
.
Câu 10. Cho hàm số
3 2
cos 3sin 3
y x x m
. Gọi
S
là tập hợp các giá trị m sao cho
2max min 9
y y
. Tổng các phần tử của tập hợp
S
bằng:
A.
16
3
. B.
4
. C.
6
. D.
2
.
Câu 11. Cho hàm số
3
3f x x x
. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị
nhỏ nhất của hàm số
2 cos
y f x m
bằng 2. Tổng tất cả các phần tử của
S
bằng
A.
4
. B.
16
. C.
32
. D.
12
.
Câu 12. Cho hàm số
log
log 2
x m
f x
x
(
m
là tham số thực). Gọi
S
là tổng tất cả các giá trị của
m
sao cho
1
1
;1
;1
10
10
max min 2
f x f x
. Tìm
S
.
A.
2
3
. B.
2
. C.
4
3
. D.
10
3
.
Câu 13. Có bao nhiêu giá trị nguyên của tham số
m
để giá trị nhỏ nhất của hàm số
3 2
9 9y x mx x m
trên đoạn
2;2
đạt giá trị nhỏ nhất.
A.
3
. B.
5
. C.
4
. D.
6
.
Câu 14. Có bao nhiêu số nguyên
m
để giá trị nhỏ nhất của hàm số
4 2
8
y f x x x m
trên
đoạn
1; 3
đạt giá trị nhỏ nhất.
A.
23
. B.
24
. C.
25
. D.
26
.
Câu 15. Cho hàm số
2
4 2 3
y x x m
với
m
là tham số thực. Biết rằng giá trị lớn nhất của hàm số
trên đoạn
1;3
đạt giá trị nhỏ nhất bằng
a
khi
m b
. Tính
2
P b a
.
A.
1
2
. B.
13
4
. C.
9
4
. D.
6
.
Câu 16. Cho hàm số
3 2 2
1 27
y x x m x
. Gọi
S
là tập tất cả các giá trị của tham số
m
sao cho
giá trị lớn nhất của hàm số trên đoạn
3; 1
có giá trị nhỏ nhất. Khi đó tích các phần tử của
S
là
A.
4
. B.
4
. C.
8
. D.
8
.
Câu 17. Có bao nhiêu giá trị nguyên của tham số
m
để giá trị lớn nhất của hàm số
4 2
1 19
30
4 2
y x x x m
trên đoạn
0;2
đạt giá trị nhỏ nhất?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 18. Có tất cả bao nhiêu giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
2
2
f x x x m
trên
1;2
bằng 5.
A.
3
. B.
1
. C.
2
. D.
4
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 19. Tính tích tất cả các số thực
m
để hàm số
3 2
4
6 8
3
y x x x m
có giá trị nhỏ nhất trên đoạn
0; 3
bằng
18
là.
A.
432
. B.
216
. C.
432
. D.
288
.
Câu 20. Cho hàm số
4 2
2 1f x x x m
. Gọi
S
là tập hợp tất cả các giá trị của tham số
m
sao cho
giá trị nhỏ nhất của hàm số trên đoạn
0;2
bằng
18
. Tổng tất cả các phần tử của
S
bằng
A.
5
. B.
4
. C.
14
. D.
10
.
Câu 21. Tính tổng tất cả các giá trị nguyên lớn hơn 6 của tham số
m
sao cho giá trị nhỏ nhất của hàm số
2
1y x m x m
trên
2; 1m
nhỏ hơn 2020.
A.
2043210
. B.
2034201
. C.
3421020
D.
3412020
.
Câu 22. Cho hàm số
4 3 2
1
4
y x x x m
. Tính tổng tất cả các số nguyên
m
để
1;2
max 11y
.
A.
19
. B.
37
. C.
30
. D.
11
.
Câu 23. Cho hàm số
2
2 3f x x mx
. Có bao nhiêu giá trị
m
nguyên để giá trị lớn nhất của
f x
trên đoạn
1;2
không lớn hơn
3
?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 24. Cho hàm số
3 2
3 9y x x x m
. Gọi
S
là tập hợp các giá trị nguyên của tham số
m
để
2;3
max 50y
. Tổng các phần tử của
M
là
A.
0
. B.
737
. C. 759. D.
215
.
Câu 25. Cho hàm số
4 3 2
2y x x x a
. Có bao nhiêu giá trị nguyên của tham số
a
để
1; 2
max 100y
.
A.
197
. B.
196
. C.
200
. D.
201
.
Câu 26. Cho hàm số
sin cosy x x m
, có bao nhiêu giá trị nguyên của
m
để hàm số có giá trị lớn
nhất bé hơn
2
.
A.
0
. B.
1
. C.
2
. D.
3
.
D. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT HÀM ẨN, HÀM HỢP
Câu 1. Cho hàm số
y f x
xác định và liên tục trên
, đồ thị của hàm số
y f x
như hình vẽ.
Giá trị lớn nhất của hàm số
y f x
trên đoạn
1;2
là
A.
1f
.
B.
1f
.
C.
2f
.
D.
0f
.
Câu 2. Cho hàm số
y f x
có đạo hàm là hàm
f x
. Đồ thị của hàm số
y f x
được cho như
hình vẽ. Biết rằng
0 3 2 5f f f f
. Giá trị nhỏ nhất, giá trị lớn nhất của
y f x
trên đoạn
0;5
lần lượt là:
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
A.
2f
;
5f
. B.
0f
;
5f
. C.
2f
;
0f
. D.
1f
;
5f
.
Câu 3. Cho hàm số
f x
có đạo hàm là
f x
. Đồ thị của hàm số
y f x
được cho như hình vẽ bên.
Biết rằng
0 1 2 3 5 4f f f f f
. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của
f x
trên đoạn
0;5
.
A.
5 , 3m f M f
B.
5 , 1m f M f
C.
0 , 3
m f M f
D.
1 , 3m f M f
Câu 4. Cho hàm số
y f x
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
2 3 2
1 1
4 3 8
3 3
g x f x x x x x
trên đoạn
1;3
.
A. 15. B.
25
3
. C.
19
3
. D. 12.
Câu 5. Cho hàm số
y f x
liên tục trên
.
Đồ thị của hàm số
y f x
như hình bên. Đặt
2
2 1 .g x f x x
Mệnh đề dưới đây đúng.
A.
3;3
max 3 .g x g
B.
3;3
min 1 .g x g
C.
3;3
max 0 .g x g
D.
3;3
max 1 .g x g
Câu 6. Cho hàm số có đạo hàm cấp hai trên . Biết , và bảng xét
dấu của như sau:
Hàm số đạt giá trị nhỏ nhất tại điểm thuộc khoảng nào sau đây?
A.
; 2017
B.
2017;
C.
0;2
D.
2017;0
y f x
0 3
f
2 2018
f
f x
2017 2018y f x x
0
x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. Cho hàm số
f x
có đạo hàm là
f x
. Đồ thị của hàm số
y f x
được cho như hình vẽ
dưới đây:
Biết rằng
1 0 1 2f f f f
.
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y f x
trên đoạn
1;2
lần lượt là:
A.
1f
;
2f
.
B.
2f
;
0f
.
C.
0f
;
2f
.
D.
1f
;
1f
.
Câu 8. Cho hàm số
y f x
liên tục trên đoạn
7
0;
2
có đồ thị hàm số
'y f x
như hình vẽ.
Hàm số
y f x
đạt giá trị nhỏ nhất trên đoạn
7
0;
2
tại điểm
0
x
nào dưới đây?
A.
0
0x
.
B.
0
7
2
x
.
C.
0
1x
.
D.
0
3x
.
Câu 9. Cho hàm số
y f x
. Đồ thị hàm
y f x
như hình vẽ
Đặt
3
3 3h x f x x x
. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
[ 3; 3]
max ( ) 3 1h x f
. B.
[ 3; 3]
max ( ) 3 3h x f
.
C.
[ 3; 3]
max ( ) 3 3h x f
. D.
[ 3; 3]
max ( ) 3 0h x f
.
Câu 10. Cho hàm số
y f x
có đồ thị
y f x
ở hình vẽ bên. Xét hàm số
3 2
1 3 3
2018,
3 4 2
g x f x x x x
mệnh đề nào dưới đây đúng?
A.
3;1
min 1g x g
. B.
3;1
3 1
min
2
g g
g x
.
C.
3;1
min 3g x g
. D.
3;1
min 1g x g
.
Câu 11. Cho hàm số
f x
. Biết hàm số
y f x
có đồ thị như hình vẽ bên dưới. Trên đoạn
4;3
,
hàm số
2
2 1g x f x x
đạt giá trị nhỏ nhất tại điểm:
A.
0
4x .
B.
0
1x .
C.
0
3x .
D.
0
3x .
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 12. Cho hàm số
y f x
có đạo hàm liên tục trên
R
. Hàm số
'y f x
có đồ thị như hình sau:
Cho bốn mệnh đề sau:
1) Hàm số
y f x
có hai cực trị
2) Hàm số
y f x
đồng biến trên khoảng
1;
3)
1 2 4 .f f f
4) Trên đoạn
1;4
, giá trị lớn nhất của hàm số
y f x
là
1 .f
Số mệnh đề đúng trong bốn mệnh đề trên là:
A.
3.
B.
1.
C.
4.
D.
2.
Câu 13. Cho hàm số
y f x
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
2 3 2
1 1
4 3 8
3 3
g x f x x x x x
trên đoạn
1;3 .
A.
25
.
3
B.
15.
C.
19
.
3
D.
12.
Câu 14. Cho hàm số
y f x
. Hàm số
y f x
có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất
của hàm số
2
2 sing x f x x
trên đoạn
1;1
là
A.
1f
. B.
0f
. C.
2f
. D.
1f
.
Câu 15. Cho hàm số
y f x
liên tục trên
sao cho
1;2
max 3f x
. Xét hàm số
3 1g x f x m
.
Tìm tất cả các giá trị của tham số
m
để
0;1
max 10g x
.
A.
13
. B.
7
. C.
13
. D.
1
.
Câu 16. Cho hàm số
y f x
có đạo hàm cấp 2 trên
, hàm số
y f x
có đồ thị như hình vẽ bên.
Giá trị lớn nhất của hàm số
sin 3cos
2
x x
y f
trên đoạn
5
;
6 6
bằng
A.
3
f
.
B.
0f
.
C.
5
6
f
.
D.
6
f
.
0
0
0
-2
210-1 +
-
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 17. Cho hàm số
y f x
liên tục trên
sao cho
0;10
max 2 4
x
f x f
. Xét hàm số
3 2
2g x f x x x x m
. Giá trị của tham số
m
để
0;2
max 8
x
g x
là
A.
5
. B.
4
. C.
1
. D.
3
.
Câu 18. Cho hai hàm số
y f x
,
y g x
có đạo hàm là
f x
,
g x
. Đồ thị hàm số
y f x
và
g x
được cho như hình vẽ bên dưới.
Biết rằng
0 6 0 6f f g g
. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
h x f x g x
trên đoạn
0;6
lần lượt là:
A.
6h
,
2h
. B.
2h
,
6h
. C.
0h
,
2h
. D.
2h
,
0h
.
E. ỨNG DỤNG GTLN-GTNN GIẢI BÀI TOÁN THỰC TẾ
Câu 1. Ông
A
dự định dùng hết
2
6,5m
kính để làm một bể cá có dạng hình hộp chữ nhật không nắp,
chiều dài gấp đôi chiều rộng (các mối ghép có không đáng kể). Bể cá có dung tích lớn nhất bằng
bao nhiêu (kết quả làm tròn đến hàng phần trăm).
A.
3
2,26 m B.
3
1,61m C.
3
1,33 m D.
3
1,50 m
Câu 2. Một vật chuyển động theo quy luật
3 2
1
6
3
s t t
với
t
(giây) là khoảng thời gian tính từ khi vật
bắt đầu chuyển động và
s
(mét) là quãng đường vật di chuyển được trong khoảng thời gian đó.
Hỏi trong khoảng thời gian
9
giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt
được bằng bao nhiêu?
A.
243
(m/s) B.
27
(m/s) C.
144
(m/s) D.
36
(m/s)
Câu 3. Ông A dự định sử dụng hết
2
5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
A.
3
1,01m
B.
3
0,96 m
C.
3
1,33 m
D.
3
1,51m
Câu 4. Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được
giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể
trong t giờ được cho bởi công thức
2
1
t
c t
t
/mg L
. Sau khi tiêm thuốc bao lâu thì nồng độ
thuốc trong máu của bệnh nhân cao nhất?
A. 4 giờ. B. 1 giờ. C. 3 giờ. D. 2 giờ.
Câu 5. Cho một tấm nhôm hình vuông cạnh
12
cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình
vuông bằng nhau, mỗi hình vuông có cạnh bằng
x
(cm), rồi gập tấm nhôm lại như hình vẽ dưới
đây để được một cái hộp không nắp. Tìm
x
để hộp nhận được có thể tích lớn nhất.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
A.
3x
B.
2x
C.
4x
D.
6x
Câu 6. Đợt xuất khẩu gạo của tỉnh A thường kéo dài trong
2
tháng (
60
ngày). Người ta nhận thấy số
lượng xuất khẩu gạo tính theo ngày thứ
t
được xác định bởi công thức
3 2
2
63 3240 3100
5
S t t t t
với
1 60 t
. Hỏi trong
60
ngày đó thì ngày thứ mấy có số
lượng xuất khẩu gạo cao nhất.
A.
60
B.
45
C.
30
D.
25
Câu 7. Một vật chuyển động theo quy luật
2 3
1
10
3
S t t
, với
t
(giây) là khoảng thời gian tính từ lúc vật
bắt đầu chuyển động và
S m
là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong
khoảng thời gian
15
giây từ lúc vật bắt đầu chuyển động vận tốc
/v m s
của vật đạt giá trị lớn
nhất tại thời điểm
t s
bằng:
A.
8 s
. B.
20 s
C.
10 s
. D.
15 s
.
Câu 8. Một sợi dây có chiều dài
28m
được cắt thành hai đoạn để làm thành một hình vuông và một hình
tròn. Tính chiều dài (theo đơn vị mét) của đoạn dây làm thành hình vuông được cắt ra sao cho
tổng diện tích của hình vuông và hình tròn là nhỏ nhất?
A.
56
4
. B.
112
4
. C.
84
4
. D.
92
4
.
Câu 9. Một xưởng in có
15
máy in được cài đặt tự động và giám sát bởi một kỹ sư, mỗi máy in có thể in
được
30
ấn phẩm trong
1
giờ, chi phí cài đặt và bảo dưỡng cho mỗi máy in cho
1
đợt hàng là
48.000
đồng, chi phí trả cho kỹ sư giám sát là
24.000
đồng/giờ. Đợt hàng này xưởng in nhận
6000
ấn phẩm thì số máy in cần sử dụng để chi phí in ít nhất là
A.
10
máy. B.
11
máy. C.
12
máy. D.
9
máy.
Câu 10. Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật
3 2
4 12s t t t
(m), trong đó t (s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận
tốc của chất điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu?
A. 2 (s). B.
8
3
(s). C. 0 (s). D.
4
3
(s).
Câu 11. Cho một tấm nhôm hình chữ nhật có chiều dài bằng
10cm
và chiều rộng bằng
8cm
. Người ta cắt
bỏ ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
x cm
,
rồi gập tấm nhôm lại (như hình vẽ) để được một cái hộp không nắp. Tìm
x
để hộp nhận được có
thể tích lớn nhất.
A.
8 2 21
3
x
B.
10 2 7
3
x
C.
9 21
9
x
. D.
9 21
3
x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 12. Một đoàn cứu trợ lũ lụt đang ở vị trí
A
của một tỉnh miền trung muốn đến xã
C
để tiếp tế lương
thực và thuốc men. Để đi đến
C
, đoàn cứu trợ phải chèo thuyền từ
A
đến vị trí
D
với vận tốc
4 /km h
, rồi đi bộ đến vị trí
C
với vận tốc
6 /km h
. Biết
A
cách
B
một khoảng
5km
,
B
cách
C
một khoảng
7km
(hình vẽ). Hỏi vị trí điểm
D
cách
A
bao xa để đoàn cứu trợ đi đến xã
C
nhanh nhất?
A.
5 3AD km
. B.
2 5AD km
. C.
5 2AD km
. D.
3 5AD km
.
Câu 13. Một vật chuyển động theo quy luật
2 3
3s t t
. Thời điểm
( )t s
tại đó vận tốc
( / )v m s
của
chuyển động đạt giá trị lớn nhất là
A.
5t
. B.
1t
. C.
2t
. D.
3t
Câu 14. Ông A dự định sử dụng hết
2
5 m
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
A.
3
1,01m
. B.
3
0,96 m
. C.
3
1,33 m
. D.
3
1,51m
.
Câu 15. Một người nông dân có 15.000.000 đồng muốn làm một cái hàng rào hình chữ E dọc theo một con
sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào
song song với bờ sông thì chi phí nguyên vật liệu là 60.000 đồng một mét, còn đối với ba mặt
hàng rào song song nhau thì chi phí nguyên vật liệu là 50.000 đồng một mét. Tìm diện tích lớn
nhất của đất rào thu được
A.
2
3125m . B.
2
50m . C.
2
1250m . D.
2
6250m .
Câu 16. Một người đàn ông muốn trèo thuyền ở vị trí
A
tới điểm
B
về phía hạ lưu bờ đố diện, càng
nhanh càng tốt, trên một bờ sông thẳng rộng 3 km ( như hình vẽ). Anh có thể chèo thuyền của
mình trực tiếp qua sông để đến
C
và sau đó chạy đến
B
, hay có thể chèo trực tiếp đến
B
, hoặc
anh có thể chèo thuyền đến một điểm
D
giữa
C
và
B
và sau đó chạy đến
B
. Biết anh ấy có thể
chèo thuyền 6 km/h, chạy 8 km/h và quãng đường
8 kmBC
. Biết tốc độ của dòng nước là
không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất(
đơn vị: giờ) để người đàn ông đến
B
?
A.
73
6
.
B.
3
2
.
C.
9
.
7
D.
7
1
8
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Câu 17. Ông Khoa muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích
bằng
3
288m
. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây
bể là
500000
đồng/
2
m
. Nếu ông Khoa biết xác định các kích thước của bể hợp lí thì chi phí thuê
nhân công sẽ thấp nhất. Hỏi ông Khoa trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu (Biết
độ dày thành bể và đáy bể không đáng kể)?
A.
90
triệu đồng. B.
168
triệu đồng. C.
54
triệu đồng. D.
108
triệu đồng.
Câu 18. Hình vẽ bên dưới mô tả đoạn đường đi vào GARA ÔTÔ nhà cô Hiền. Đoạn đường đầu tiên có
chiều rộng bằng
x m
, đoạn đường thẳng vào công GARA có chiều rộng
2,6 m
. Biết kích
thước xe ôtô là
5 1,9m m
(chiều dài
chiều rộng). Để tính toán và thiết kế đường đi cho ôtô
người ta coi ôtô như một khối hộp chữ nhật có kích thước chiều dai
5m
, chiều rộng
1,9m
. Hỏi
chiều rộng nhỏ nhất của đoạn đường đầu tiên gần nhất với giá trị nào trong các giá trị bên dưới để
ôtô có thể đi vào GARA được?(giả thiết ôtô không đi ra ngoài đường, không đi nghiêng và ôtô
không bị biến dạng).
A.
3,55x m
. B.
2,6x m
. C.
4,27x m
. D.
3,7 m
.
Câu 19. Một người nông dân có 3 tấm lưới thép B40, mỗi tấm dài
12 m
và muốn rào một mảnh vườn
dọc bờ sông có dạng hình thang cân
ABCD
như hình vẽ (bờ sông là đường thẳng
DC
không
phải rào, mỗi tấm là một cạnh của hình thang). Hỏi ông ta có thể rào được mảnh vườn có diện tích
lớn nhất là bao nhiêu
2
m
?
A. 100 3 . B. 106 3 . C. 108 3 . D. 120 3 .
Câu 20. Cho hình vuông
ABCD
có cạnh bằng 4, chính giữa có một hình vuông đồng tâm với
ABCD
. Biết
rằng bốn tam giác là bốn tam giác cân. Hỏi tổng diện tích của hình vuông ở giữa và bốn tam giác
cân nhỏ nhất bằng bao nhiêu?
A.
19
3
. B.
17
3
. C.
16
3
. D.
14
3
.
C
D
B
A
B
A
D
C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 21. Cho nửa đường tròn đường kính
2AB
và hai điểm
C
,
D
thay đổi trên nửa đường tròn đó sao
cho
ABCD
là hình thang. Diện tích lớn nhất của hình thang
ABCD
bằng
A.
1
2
. B.
3 3
4
. C.
1
. D.
3 3
2
.
Câu 22. Một người đàn ông muốn chèo thuyền ở vị trí
A
tới điểm
B
về phía hạ lưu bờ đối diện, càng
nhanh càng tốt, trên một bờ sông thẳng rộng
3 km
(như hình vẽ). Anh có thể chèo thuyền của
mình trực tiếp qua sông để đến
C
và sau đó chạy đến
B
, hay có thể chèo trực tiếp đến
B
, hoặc
anh ta có thể chèo thuyền đến một điểm
D
giữa
C
và
B
và sau đó chạy đến
B
. Biết anh ấy có
thể chèo thuyền
6 km/ h
, chạy
8 km/ h
và quãng đường
8 kmBC
. Biết tốc độ của dòng nước
là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất
(đơn vị: giờ) để người đàn ông đến
B
.
A.
3
2
. B.
9
7
. C.
73
6
. D.
7
1
8
.
Câu 23. Bác thợ hàn dùng một thanh kim loại dài
250 cm
để uốn thành khung cửa sổ có dạng như hình
vẽ. Gọi
r
là bán kính của nửa đường tròn, tìm
r
để diện tích tạo thành đạt giá trị lớn nhất.
A.
250
cm
4
. B.
125
cm
4
. C.
250
cm
4
. D.
125
cm
4
.
Câu 24. Cho một tấm nhôm hình vuông cạnh
6
cm. Người ta muốn cắt một hình thang như hình vẽ.
Tìm tổng
x y
để diện tích hình thang
EFGH
đạt giá trị nhỏ nhất.
A.
4 2
. B.
7 2
2
. C.
7
. D.
5
.
Câu 25. Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng
3
500
3
m
. Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là
500.000
đồng/m
2
. Hãy xác định kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất
và chi phí đó là:
A.
74
triệu đồng. B.
75
triệu đồng. C.
76
triệu đồng. D.
77
triệu đồng.
x cm
y
cm
3 cm
2 cm
H
G
F
E
D
C
B
A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
A. TÌM GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Định lí 1: Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn đó.
Định lí 2
Nếu
( )y f x
đồng biến trên
[ ; ]a b
thì
[ ; ]
min ( ) ( )
a b
f x f a
và
[ ; ]
max ( ) ( ).
a b
f x f b
Nếu
( )y f x
nghịch biến trên
[ ; ]a b
thì
[ ; ]
min ( ) ( )
a b
f x f b
và
[ ; ]
max ( ) ( ).
a b
f x f a
Bài toán 1. Tìm GTLN & GTNN của hàm số
( )y f x
trên đoạn
[ ; ].a b
Bước 1. Hàm số đã cho xác định và liên tục trên đoạn
[ ; ].a b
Tính
( ) 0f x
tìm nghiệm
[ ; ].
i
x a b
Bước 2. Tính
( ), ( ), ( ).
i
f a f b f x
Bước 3. Kết luận:
[ ; ]
max ( ) max ( ); ( ); ( )
i
a b
f x f a f b f x
và
[ ; ]
min ( ) min ( ); ( ); ( ) .
i
a b
f x f a f b f x
Bài toán 2. Tìm GTLN & GTNN của hàm số
( )y f x
trên khoảng
( ; ).a b
Bước 1. Tìm tập xác định. Tính
( ).f x
Cho
( ) 0f x
tìm nghiệm.
Bước 2. Xét dấu biểu thức
( )y f x
và lập bảng biến thiên (có tính giới hạn).
Bước 3. Dựa vào bảng biến thiên để kết luận GTLN (GTNN nếu có).
Lưu ý: Đạo hàm của hàm số mũ và lôgarit
( ) . .ln .
u u
a u a a
( ) . .
u u
e u e
( ) .
x x
e e
(log )
ln
a
u
u
u a
1
(log )
ln
a
x
x a
1
(ln ) ln
u
u x
u x
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 1. Giá trị lớn nhất của hàm số
4 2
( ) 12 1f x x x= -
trên đoạn
1;2-
bằng:
A.
1
. B.
37
. C.
33
. D.
12
.
Lời giải
Chọn C
4 2
( ) 12 1f x x x= -
liên tục trên
1;2-
và
3 2
0
'( ) 4 24 0 6 ( )
6 ( )
x
f x x x x L
x L
=
= - = Û =
= -
Ta có:
( 1) 12; (2) 33; (0) 1f f f- = = =
Vậy, giá trị lớn nhất của hàm số
4 2
( ) 12 1f x x x= -
trên đoạn
1;2-
bằng 33 tại
2x =
Câu 2. Giá trị nhỏ nhất của hàm số
( )
4 2
10 2f x x x= -
trên đoạn
1;2-
bằng
A.
2
. B.
23-
. C.
22-
. D.
7-
.
Lời giải
Chọn C
Hàm số đã cho liên tục trên đoạn
1;2-
.
Ta có:
( ) ( )
3
0
4 20 , 0
5
x
f x x x f x
x
=
¢ ¢
= - = Û
=
.
Xét hàm số trên đoạn
1;2-
có:
( ) ( ) ( )
1 7; 0 2; 2 22f f f- = - = = -
.
Vậy
( )
1;2
min 22
x
f x
-
= -
.
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT
Vấn đề 4
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 3. Gọi
M
là giá trị lớn nhất và
m
là giá trị nhỏ nhất của hàm số
4 2
8 5y x x= - - trên đoạn
3;1-
. Khi
đó, giá trị của biểu thức
2M m-
bằng
A.
46
. B.
25
. C.
25-
. D.
46-
.
Lời giải
Chọn A
Cách 1:
Ta có:
3
' 4 16y x x= - ;
( )
( )
( )
3
0
' 0 4 16 0 2
2
=
= Û - = Û =
= -
x n
y x x x l
x n
.
Khi đó:
( )
( )
( )
( )
0 5
3 4
2 21
1 12
y
y
y
y
= -
- =
- = -
= -
.
Do đó:
3;1
3;1
max 4; min 21M y m y
-
-
= = = = - .
Vậy
( )
2 4 2. 21 46M m- = - - =
.
Cách 2: Học sinh có thể sử dụng chức năng Table của MTCT để thực hiện cho nhanh.
Câu 4. Cho hàm số
( )
y f x=
liên tục trên đoạn
3;3-
có đồ thị như hình vẽ.
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
( )
y f x=
trên
0;3
lần lượt có giá trị là
A.
4;3
4;3
max 4, min 3y y
-
-
= = -
. B.
4;3
4;3
max 3,min 3y y
-
-
= = -
.
C.
0;3
0;3
max 3,min 2y y= = -
. D.
4;3
4;3
max 4,min 2y y
-
-
= = -
.
Lời giải
Chọn C
Dựa vào đồ thị ta thấy:
Giá trị lớn nhất của hàm số trên
0;3
là
3
và giá trị nhỏ nhất của hàm số trên
0;3
là
2-
.
Câu 5. Giá trị nhỏ nhất của hàm số
16
3y x
x
=
trên đoạn
1;5
là:
A.
5-
. B.
20
. C.
5 6
5
. D.
11
.
Lời giải
Chọn D
Cách 1:
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Ta có:
2
16
1y
x
¢
= -
.
2
4
16
0 1 0
4 ( )
x
y
x l
x
=
¢
= Û - = Û
= -
.
Ta có:
( )
( )
( )
1 20
4 11
56
5
5
y
y
y
=
=
=
.
Vậy
1; 5
min 11y =
khi
4x =
.
Câu 6. Cho hàm số
( )
f x
liên tục trên
3; 5-
và có bảng biến thiên như hình vẽ. Gọi
,M m
lần lượt là giá trị
lớn nhất và nhỏ nhất của
( )
f x
trên
[ 3;2]-
. Tính
M m-
.
A.
6
. B.
4
. C.
5
. D.
3
.
Lời giải
Chọn B
Căn cứ vào bảng biến thiên của hàm số
( )
f x
trên
3; 5-
, ta có
4, 0M m= =
suy ra
4.M m- =
Câu 7. Cho hàm số
( )f x
có đạo hàm
( ) ( ) ( )
2
' 3 4 ,f x x x x x= - - -
. Giá trị lớn nhất của hàm số đã cho
trên đoạn
0;5
bằng
A.
( )
0f
. B.
( )
4f
. C.
( )
3f
. D.
( )
5f
.
Lời giải
Chọn B
Ta có
( ) ( ) ( )
2
' 3 4 0f x x x x= - - - =
( )
0
3
4
x
x k
x
=
Û =
=
.
Bảng biến thiên
Dựa vào BBT ta suy ra
0;5
max ( ) (4)
x
f x f
=
.
Câu 8. Giá trị lớn nhất của hàm số
3
y x 3x 5= -
trên đoạn
3
0;
2
bằng:
A. 3. B. 5. C. 7. D.
31
8
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn B
Ta có:
3 2
3
x 1 0;
2
y x 3x 5 y' 3x 3 0 .
3
x 1 0;
2
=
= - = - = Û
= -
Mà
( ) ( )
3 31
y 0 5, y 1 3, y
2 8
= = =
Nên giá trị nhỏ nhất của hàm số trên đoạn
3
0;
2
là
5
.
Câu 9. Giá trị lớn nhất của hàm số
3
( ) 6 3f x x x= - -
trên đoạn
0;2
bằng:
A.
3-
. B.
3 4 2
- -
. C.
25
. D.
12
.
Lời giải
Chọn A
3
( ) 6 3f x x x= - -
liên tục trên
0;2
và
2
'( ) 3 6
f x x
= -
.
2
'( ) 0
2( )
x
f x
x l
=
= Û
= -
Ta có:
(0) 3; (2) 7; ( 2) 3 4 2
f f f= - = - = - -
Vậy, giá trị lớn nhất của hàm số trên đoạn
1;2
-
bằng -3 tại
0
x
=
.
Câu 10. Giá trị nhỏ nhất của hàm số
( )
8
1 2
f x x
x
=
trên đoạn
1;2
bằng:
A.
7
2
. B.
18
5
. C.
11
3
. D.
9
2
-
.
Lời giải
Chọn A
Hàm số xác định và liên tục trên đoạn
1;2
Ta có
( )
( )
2
16
1
1 2
f x
x
¢
= -
( )
0
f x
¢
=
3
1;2
2
5
1;2
2
x
x
=
Û
= -
.
Khi đó
( )
11
1
3
f
=
;
3 7
2 2
f
=
;
( )
18
2
5
f
=
.
Vậy
( )
1;2
3 7
min
2 2
f x f
= =
.
Câu 11. Giá trị nhỏ nhất của hàm số
2
( )
3
x
f x
x
-
=
trên đoạn
1;3
bằng:
A.
3
. B.
2-
. C.
1
6
-
. D.
1
4
.
Lời giải
Chọn C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
2
( )
3
x
f x
x
-
=
liên tục trên
1;3
và
2
5
'( ) 0; [1;3]
( 3)
f x x
x
-
=
-
.
Vậy, giá trị nhỏ nhất của hàm số trên đoạn
1;3
bằng
1
6
-
tại
3x =
.
Câu 12. Giá trị nhỏ nhất của hàm số
3 2
( ) 5 6f x x x x= -
trên đoạn
0;4
bằng:
A.
3
. B.
2-
. C.
2
27
. D.
6
.
Lời giải
Chọn D
3 2
( ) 5 6f x x x x= -
liên tục trên
0;4
và
2
'( ) 3 2 5f x x x= -
. Phương trình
'( ) 0f x =
vô
nghiệm.
Ta có:
(0) 6; (4) 74f f= =
.
Vậy, giá trị nhỏ nhất của hàm số trên đoạn
0;4
bằng 6 tại
0x =
.
Câu 13. Giá trị nhỏ nhất của hàm số
( )
3 2
8 16 9= - -f x x x x
trên đoạn
1;3
bằng:
A.
9-
. B.
6-
. C.
13
27
. D.
0
.
Lời giải
Chọn B
Ta có
( )
2
3 16 16
¢
= - f x x x
( )
2
0 3 16 16 0
¢
= Û - =f x x x
4 1;3
4
1;3
3
x
x
=
Û
=
.
Có
( )
1 0=f
,
( )
3 6= -f
,
4 13
3 27
=
f
.
Vậy
( )
1;3
min 6f x = -
.
Nên giá trị nhỏ nhất của hàm số trên đoạn
3
0;
2
là
5
.
Câu 14. Cho hàm số
( )y f x=
có đồ thị như hình vẽ. Hỏi giá trị nhỏ nhất của hàm số đã cho trên đoạn
[0; 2]
bằng bao nhiêu?
A. 0. B.
1-
. C.
2
. D.
1
.
Lời giải
Chọn A
Theo đồ thị ta có giá trị nhỏ nhất của hàm số trên đoạn
1;1-
bằng 0 đạt tại
0x =
và
2x =
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 15. Giá trị lớn nhất của hàm số
( )
4 2
8 16y f x x x= = -
trên đoạn
1;3-
bằng:
A.
9
. B.
26
. C.
25
. D.
0
.
Lời giải
Chọn C
Ta có:
4 2 3
8 16 ' 4 16y x x y x x= - = -
Cho
0 1;3
' 0 2 1;3
2 1;3
x
y x
x
= -
= Û = -
= - -
Tính
( ) ( ) ( )
1 9; 2 0; 3 25y y y- = = =
.
Vậy
1;3
max 25y
-
=
.
Câu 16. Cho hàm số
( )y f x=
có bảng biến thiên như hình vẽ.
Hỏi giá trị lớn nhất của hàm số đã cho trên
[-1;3]
bằng bao nhiêu?
A. 3. B.
3-
. C.
5
. D.
6
.
Lời giải
Chọn D
Giá trị lớn nhất của hàm số trên đoạn
[-1;3]
bằng 6, đạt tại
3x =
.
Câu 17. Giá trị nhỏ nhất của hàm số
9
y x
x
=
trên đoạn
2;4
bằng:
A.
6
. B.
13
2
. C.
6-
. D.
25
4
.
Lời giải
Chọn A
Hàm số đã cho liên tục trên đoạn
2;4
.
Ta có:
2
9
1y
x
¢
= -
. Cho
0y
¢
=
ta được
3 2;4
3 2;4
x
x
= -
=
.
Khi đó:
( )
13
2
2
f =
,
( )
3 6f =
,
( )
25
4
4
f =
.
Vậy
2; 4
min 6y = .
Câu 18. Cho hàm số
( )
y f x=
liên tục trên đoạn
1;1-
và có đồ thị như hình vẽ.
+∞ 6
1
5
3
0
0
++
x
∞ 3
1
1
0
0
y'
y
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;1-
. Giá trị của
M m-
bằng
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Từ đồ thị ta thấy
1, 0M m= =
nên
1M m- =
.
Câu 19. Cho hàm số
( )
y f x=
liên tục trên đoạn
và có đồ thị như hình vẽ.
Giá trị nhỏ nhất trên tập xác định của hàm số có đồ thị sau là:
A. min 1.y = - B. min 1y = . C. min 0y = . D. min 2y = - .
Lời giải
Chọn A
Từ đồ thị ta thấy giá trị nhỏ nhất là
1-
.
Câu 20. Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Giá trị nhỏ nhất của hàm số có bảng biến thiên sau trên khoảng
2;3-
là:
A.
2;3
min 0y
-
= . B.
2;3
min 3y
-
= - . C.
2;3
min 1y
-
= . D.
2;3
min 7y
-
= .
Lời giải
Chọn B
Từ bảng biến thiên ta thấy giá trị nhỏ nhất là
3-
.
Câu 21. Cho đồ thị hàm số
'( )y f x=
như hình vẽ.
Hàm số
( )y f x=
đạt giá trị lớn nhất trên khoảng
1;3
tại
0
x . Khi đó giá trị của
2
0 0
2 2019x x-
bằng bao nhiêu?
A.
2018
. B.
2019
. C.
2021
. D.
2022
.
Lời giải
Chọn B
x
y
-1
1
-1
0
1
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào đồ thị của hàm số
'( )y f x=
ta có BBT như sau:
Dựa vào BBT suy ra hàm số
( )y f x=
đạt giá trị lớn nhất trên khoảng
1;3
tại
0
2x = .
Nên
2
0 0
2 2019 2019x x- =
.
Câu 22. Cho hàm số
( )
y f x=
liên tục trên đoạn
1;4-
và có đồ thị như hình vẽ bên dưới.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;4-
. Giá trị của
M m
bằng
A.
0
. B.
1
. C.
2
. D.
5
.
Lời giải
Chọn C
Từ đồ thị ta thấy
3, 1M m= = -
nên
2M m =
.
Câu 23. Cho hàm số
( )
y f x=
liên tục trên đoạn
3;1-
và có đồ thị như hình vẽ bên dưới.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
3;1-
. Giá trị của
2M m-
bằng
A.
0
. B.
1
. C.
4
. D.
5
.
Lời giải
Chọn D
Từ đồ thị ta thấy
1, 3M m= = -
nên
2 5M m- =
.
Câu 24. Cho hàm số
( )
y f x=
liên tục trên đoạn
2;2-
và có đồ thị như hình vẽ bên dưới.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
2;2-
. Giá trị của
M m
bằng
A.
0
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn D
Từ đồ thị ta thấy
3, 0M m= =
nên
3M n =
.
Câu 25. Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3-
và có đồ thị như hình vẽ bên dưới.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3-
. Giá trị của
2 2
M m
bằng
A.
15
. B.
11
. C.
4
. D.
13
.
Lời giải
Chọn D
Từ đồ thị ta thấy
2, 3M m= = -
nên
2 2
13M n =
.
Câu 26. Giá trị nhỏ nhất của hàm số
( )
3
6f x x x= -
trên đoạn
0;2
bằng
A.
4 2-
. B.
4-
. C.
6 2-
. D.
0
.
Lời giải
Chọn A
Hàm số xác định và liên tục trên đoạn
0; 2
.
Ta có
( )
2
3 6f x x
¢
= -
.
Cho
( )
2
2 0;2
0 3 6 0
2 0;2
x
f x x
x
=
¢
= Û - = Û
= -
Ta có
( )
0 0f =
;
( )
2 4 2f = -
;
( )
2 4f = -
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
( )
0;2
min 2 4 2y f= = - .
Câu 27. Cho hàm số
( )=y f x
có đạo hàm
2
( ) ( 1)( 2)
¢
= -f x x x x
với mọi
x
. Giá trị nhỏ nhất của hàm số
( )=y f x
trên đoạn
1;2-
là
A.
( 1).-f
B.
(0).f
C.
(3).f
D.
(2).f
Lời giải
Chọn B
Ta có
2
0
( ) 0 ( 1)( 2) 0 1
2
=
¢
= Û - = Û = -
=
x
f x x x x x
x
Bảng biến thiên
Dựa vào bảng biến thiên của hàm số
( )=y f x
trên đoạn
1;2-
thì giá trị nhỏ nhất của hàm số bằng
(0).f
B. TÌM M ĐỂ GTLN-GTNN THỎA MÃN ĐIỀU KIỆN K
Câu 1. Cho hàm số
=
- 1
x m
y
x
(
m
là tham số thực) thỏa mãn =
[2;4]
min 3.y Mệnh đề nào dưới đây đúng?
A.
4m
B.
3 4m
C.
-1m
D.
1 3m
Lời giải
Chọn A
Ta có
( )
- -
=
-
2
1
'
1
m
y
x
* TH 1.
- - Û -1 0 1m m
suy ra
y
đồng biến trên
2; 4
suy ra
( ) ( )
= = = Û =
2;4
2
min 2 3 1
1
m
f x f m
(loại)
* TH 2.
- - Û -1 0 1m m
suy ra
y
nghịch biến trên
2; 4
suy ra
( ) ( )
= = = Û =
2;4
4
min 4 3 5
3
m
f x f m
suy ra
4m
.
Câu 2. Cho hàm số
1
x m
y
x
=
(
m
là tham số thực) thoả mãn
1;2
1;2
16
min max
3
y y =
. Mệnh đề nào dưới đây
đúng?
A.
4m
B.
2 4m
C.
0m
D.
0 2m
Lời giải
Chọn A
Ta có
( )
2
1
1
m
y
x
-
¢
=
.
Nếu
1 1, 1m y x= = -
. Không thỏa mãn yêu cầu đề bài.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Nếu
1
m
Hàm số đồng biến trên đoạn
1;2
.
Khi đó:
1;2
1;2
16
min max
3
y y
=
( ) ( )
16 1 2 16
1 2 5
3 2 3 3
m m
y y m
Û = Û = Û =
(loại).
Nếu
1
m
Hàm số nghịch biến trên đoạn
1;2
.
Khi đó:
( ) ( )
1;2
1;2
16 16 2 1 16
min max 2 1 5
3 3 3 2 3
m m
y y y y m
= Û = Û = Û =
( t/m)
Câu 3. Tìm tất cả các giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
3 2
3
y x x m= - -
trên đoạn
1;1
-
bằng
0
.
A.
2.
m
=
B.
6.
m
=
C.
0.
m
=
D.
4.
m
=
Lời giải
Chọn D
Xét hàm số
3 2
3
y x x m= - -
trên đoạn
1;1
-
, ta có
2
0 1;1
3 6 ; 0
2 1;1
x
y x x y
x
= -
¢ ¢
= - - = Û
= - -
Mà
( 1) m 2
(0) m
(1) m 4
y
y
y
¢
- = -
¢
=
¢
= -
Do đó
1;1
min 4 0 4.
y m m
-
= - = Û =
Vậy
4
m
=
thỏa yêu cầu bài toán.
Câu 4. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x m
y
x
=
trên đoạn
1;2
bằng
8
(
m
là tham số
thực). Khẳng định nào sau đây là đúng?
A.
10
m
.
B.
8 10
m
.
C.
0 4
m
.
D.
4 8
m
.
Lời giải
Chọn B
Ta có:
( )
2
1
1
m
y
x
-
¢
=
.
- Nếu
1 1m y= =
(loại).
- Nếu
1
m
khi đó
0, 1;2
y x
¢
hoặc
0, 1;2
y x
¢
nên hàm số đạt giá trị lớn nhất và nhỏ
nhất tại
1, 2
x x
= =
.
Theo bài ra:
( ) ( ) ( )
1;2
1;2
1 2 41
max min 8 1 2 8 8;10
2 3 5
m m
y y y y m
= Û = = Û =
.
Câu 5. Có một giá trị
0
m
của tham số
m
để hàm số
3 2
1 1
y x m x m
đạt giá trị nhỏ nhất bằng
5
trên đoạn
0;1
. Mệnh đề nào sau đây là đúng?
A.
2
0 0
2018 0
m m
. B.
0
2 1 0
m
.
C.
2
0 0
6 0
m m
. D.
0
2 1 0
m
.
Lời giải
Chọn A
+ Đặt
3 2
1 1
f x x m x m
.
+ Ta có:
2 2
3 1
y x m
. Dễ thấy rằng
0
y
với mọi
x
,
m
thuộc
nên hàm số đồng biến trên
, suy ra hàm số đồng biến trên
0;1
. Vì thế
0;1
min y
0;1
min
f x
0f
1
m
.
+ Theo bài ra ta có:
1 5
m
, suy ra
4
m
.
+ Như vậy
0
4
m
và mệnh đề đúng là
2
0 0
2018 0
m m
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 6. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2x m
y
x m
trên đoạn
0;4
bằng
1.
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn C
Tập xác định:
\D m
.
2
2
2
0,
m m
y x m
x m
. Do đó hàm số đồng biến trên mỗi khoảng
;m
và
;m 
.
Bảng biến thiên của hàm số:
Từ bảng biến thiên suy ra, hàm số đạt giá trị lớn nhất trên đoạn
0;4
bằng
1
khi
0
4 1
m
f
2
0
2
1
4
m
m
m
2
0
6 0
m
m m
0
2, 3
m
m m
3m
.
Câu 7. Cho hàm số
2
1x
y
x m
=
-
(m là tham số thực) thỏa mãn
3; 2
1
min
2
y
- -
=
. Mệnh đề nào dưới đây đúng?
A.
3 4m
. B.
2 3m-
. C.
4m
. D.
2m -
.
Lời giải
Chọn B
+TXĐ:
2
\ , 3; 2D m D= - -
.
+ Ta có
( )
2
2
2
1
' 0,
m
y x D
x m
- -
=
-
. Nên hàm số nghịch biến trên từng khoảng xác định.
Nên
( )
2
2
3; 2
1 2 1
min 2 2 2 0 2 3
2 2
y y m m m
m
- -
-
= = - = - - = - Û = -
- -
.
Câu 8. Tìm giá trị dương của tham số
m
để giá trị nhỏ nhất của hàm số
2
1
2
m x
y
x
-
=
trên đoạn
1;3
bằng
1
.
A.
2m =
. B. 3m = . C.
4m =
. D.
2m =
.
Lời giải
Chọn A
Tập xác định:
\ 2D = -
.
Ta có:
( )
2
2
2 1
0, 2
2
m
y x
x
¢
= -
.
Hàm số đồng biến trên đoạn
1;3
nên
( )
1;3
max 3y y=
2
3 1
1
5
m -
Û =
2mÛ =
(vì
0m
).
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 9. Cho hàm số
2
8
x m
y
x
với
m
là tham số thực. Giả sử
0
m
là giá trị dương của tham số
m
để hàm số
có giá trị nhỏ nhất trên đoạn
0;3
bằng -3. Giá trị
0
m
thuộc khoảng nào trong các khoảng cho dưới
đây?
A.
2;5
. B.
1;4
. C.
6;9
. D.
20;25
.
Lời giải
Chọn A
+ TXĐ:
\ 8
D
.
+
2
'
2
8
0,
8
m
y x D
x
Vậy hàm số
2
8
x m
y
x
đồng biến trên
0;3
.
2
0;3
min (0)
8
m
y y
Để
2
0;3
min 3 3 2 6.
8
m
y m
0
2 6 2;5
m
. Vậy chọnA.
Câu 10. Tìm giá trị của tham số thực
m
để giá trị nhỏ nhất của hàm số
2
1
x m
y
x
=
trên đoạn
0;4
bằng
3
.
A.
3
m
=
. B.
1
m
=
. C.
m
. D.
5
m
=
Lời giải
Chọn C
Ta có:
( )
2
2
'
1
m
y
x
-
=
.
+ Xét
m
.
Hàm số trở thành:
2
y
=
là hàm số hằng nên không đạt giá trị nhỏ nhất bằng
3
2
m
=
(loại)
+ Xét
m
.
( )
2
2
' 0 ( 1)
1
m
y x
x
-
= -
0;4
8
min (4)
5
m
y y
= =
.
8
3 7
5
m
m
= Û =
(thoả mãn).
+ Xét
2
m
.
( )
2
2
' 0 ( 1)
1
m
y x
x
-
= -
0;4
min (0)
y y m = =
.
3
m
=
(loại).
Vậy
m
.
Câu 11. Tìm tất cả các giá trị thực của tham số m để hàm số
3 2
3
y x x m= -
có giá trị nhỏ nhất trên đoạn
-
bằng
2
A.
2
m
. B.
2 2
m
. C.
4 2
m
. D.
2 2
4 2
m
m
.
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
' 3 6y x x
0
' 0
2
x
y
x
Trên
1;1
-
thì
1 0 1
' 4; ' ; ' 2
y m y m y m
nên
1;1
2 4 2 4 2
Miny m m
Câu 12. Tìm các giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
2
1
x m m
y
x
-
=
trên đoạn
0;1
bằng
2-
.
A.
1
2
m
m
= -
= -
. B.
1
2
m
m
=
=
. C.
1
2
m
m
=
= -
. D.
1
2
m
m
= -
=
.
Lời giải
Chọn D
Tập xác định:
\ 1
D
= -
.
Hàm số đã cho liên tục trên
0;1
.
Ta có:
( )
( ) ( )
2
2
2 2
1
1
0
1 1
m m
m m
y
x x
- -
-
¢
= =
;
x D
.
Hàm số đồng biến trên đoạn
0;1
.
Trên
0;1
hàm số đạt giá trị nhỏ nhất tại
0
x
=
.
Ta có:
( )
2 2
1
0 2 2 2 0
2
m
y m m m m
m
= -
= - Û - = - Û - - = Û
=
.
Câu 13. Có một giá trị
0
m
của tham số
m
để hàm số
3 2
1 1
y x m x m
đạt giá trị nhỏ nhất bằng
5
trên đoạn
0;1
. Mệnh đề nào sau đây là đúng?
A.
2
0 0
2018 0
m m
. B.
0
2 1 0
m
.
C.
2
0 0
6 0
m m
. D.
0
2 1 0
m
.
Lời giải
+ Đặt
3 2
1 1
f x x m x m
.
+ Ta có:
2 2
3 1
y x m
. Dễ thấy rằng
0
y
với mọi
x
,
m
thuộc
nên hàm số đồng biến trên
, suy ra hàm số đồng biến trên
0;1
. Vì thế
0;1
0;1
min
f x
0f
1
m
.
+ Theo bài ra ta có:
1 5
m
, suy ra
4
m
.
+ Như vậy
0
4
m
và mệnh đề đúng là
2
0 0
2018 0
m m
.
Câu 14. Nếu hàm số
2
1
y x m x= -
có giá trị lớn nhất bằng
2 2
thì giá trị của
m
là
A.
2
2
. B.
2
-
. C.
2
. D.
2
2
-
.
Lời giải
Xét hàm số
2
1
y x m x= -
Tập xác định:
1;1
D = -
.
Ta có:
2
1
1
x
y
x
¢
= -
-
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
2
2
1
0
1 0
x x
y
x
- =
¢
= Û
-
2
1 0
1
x
x x
Û
- =
2
1 0
1
1 0
1
2
2 1
2
1
2
x
x
x
x
x
x
=
Û Û Û =
=
= -
.
Ta có:
( ) ( )
1
1 1 , 1 1 , 2
2
y m y m y m
- = - = =
.
Do hàm số
2
1
y x m x= -
liên tục trên
1;1
-
nên
1;1
Max 2
y m
-
=
.
Theo bài ra thì
1;1
Max 2 2
y
-
=
, suy ra
2 2 2 2
m m = Û =
.
Câu 15. Cho hàm số
1
x m
y
x
(
m
là tham số thực) thỏa mãn
0;1
min 3y
. Mệnh đề nào dưới đây đúng?
A.
1 3m
B.
6m
C.
1m
D.
3 6m
Lời giải
Chọn D
Tập xác định:
\ 1
D
.
Với
1m
1y
,
0;1
x
thì
0;1
min 3y
.
Suy ra
1m
. Khi đó
2
1
1
m
y
x
không đổi dấu trên từng khoảng xác định.
TH 1:
0 1y m
thì
0;1
min 0 3
y y m
(loại).
TH 2:
0 1y m
thì
0;1
min 1 5
y y m
( thỏa mãn).
Câu 16. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x m
y
x
trên
1;2
bằng
8
(
m
là tham số
thực). Khẳng định nào sau đây đúng?
A.
10
m
. B.
8 10
m
. C.
0 4
m
. D.
4 8
m
.
Lời giải
Nếu
1
m
=
thì
1
y
(không thỏa mãn tổng của giá trị lớn nhất và nhỏ nhất bằng 8)
Nếu
1
m
thì hàm số đã cho liên tục trên
1;2
và
2
1
'
1
m
y
x
.
Khi đó đạo hàm của hàm số không đổi dấu trên đoạn
1;2
.
Do vậy
( ) ( )
1;2 1;2
1 2 41
1 2 8
2 3 5
x x
m m
Min y Max y y y m
= = = Û =
.
Câu 17. Cho hàm số
3 2
2 3
y x x m= - -
. Trên
1;1
-
hàm số có giá trị nhỏ nhất là
1-
. Tính
m
?
A.
6
m
= -
. B.
3
m
= -
. C.
4
m
= -
. D.
5
m
= -
.
Lời giải
Chọn C
Xét
-
có
2
6 6y x x
¢
= -
.
y
2
6 6 0
x x
Û - =
0 1;1
1 1;1
x
x
= -
Û
= -
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó
( )
1 5
y m- = - -
;
( )
0
y m= -
;
( )
1 1
y m= - -
Ta thấy
5 1
m m m- - - - -
nên
1;1
min 5
y m
-
= - -
.
Theo bài ra ta có
1;1
min 1
y
-
= -
nên
5 1
m
- - = -
4
m
Û = -
.
Câu 18. Biết
S
là tập giá trị của
m
để tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 2 3 2
2
y x m x x m= - - -
trên đoạn
0;1
bằng
16-
. Tính tích các phần tử của
S
.
A.
2
. B.
2-
. C.
15-
. D.
17-
.
Lời giải
TXĐ:
D =
.
Ta có:
3 2 2
4 3 4y x m x x
¢
= - -
( )
3 2 2
2 2 2
0
0 4 3 4 0
4 3 4 0 9 64
x
y x m x x
x m x m
=
¢
= Û - - = Û
- - = =
2 4
2 4
0
3 9 64
1
8
3 9 64
0
8
x
m m
x
m m
x
=
Û =
-
=
Nên hàm số đơn điệu trên
( )
0;1
.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
0;1
bằng
16-
nên
( ) ( )
( )
2 2
0 1 16 1 16 2 15 0
y y m m m m m
= - Û - - - - = - Û - - =
.
Vậy
1 2
. 15
m m
= -
.
Câu 19. Gọi
,A B
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
2
1
x m m
y
x
=
-
trên đoạn
2;3
.
Tìm tất cả các giá trị thực của tham số
m
để
13
2
A B
=
.
A.
1; 2
m m
= = -
. B.
2
m
= -
. C.
2
m
=
. D.
1; 2
m m
= - =
.
Lời giải
Xét hàm số
2
1
x m m
y
x
=
-
trên đoạn
2;3
.
( )
( ) ( )
2 2 2
2
1 3 2
' 0 2;3 3 , 2
2 1
1
m m m m m m
y x A f B f
x
- - -
= = = = =
-
.
2 2
1
13 3 2 13
2
2 2 1 2
m
m m m m
A B
m
=
= Û = Û
= -
.
Câu 20. Cho hàm số
( )
2
8
x m
f x
x
-
=
với
m
là tham số thực. Giả sử
0
m
là giá trị dương của tham số
m
để
hàm số có giá trị nhỏ nhất trên đoạn
0;3
bằng
3-
. Giá trị
0
m
thuộc khoảng nào trong các khoảng
cho dưới đây?
A.
( )
20;25
. B.
. C.
( )
6;9
. D.
( )
2;5
.
Lời giải
Chọn D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Xét hàm số
( )
2
8
x m
f x
x
-
=
trên đoạn
0;3
.
Ta có:
( )
2
2
8
0, 0;3
8
m
y x
x
¢
=
hàm số
( )
2
8
x m
f x
x
-
=
đồng biến trên đoạn
0;3
( ) ( )
2
0;3
min 0 .
8
m
f x f
-
= =
Theo giả thiết, ta có:
( )
2
2
0;3
2 6
min 3 3 24 .
8
2 6
m
m
f x m
m
=
-
= - Û = - Û = Û
= -
Mà
( )
0, 2 6 4,9 2;5m m m = .
Câu 21. Tìm tất cả giá trị thực của tham số
m
để hàm số
2
1x mx
y
x m
=
liên tục và đạt giá trị nhỏ nhất trên
đoạn
0;2
tại một điểm
( )
0
0;2x
.
A.
0 1m
B.
1m
C.
2m
D.
1 1m-
Lời giải
Chọn A
Tập xác định:
\ D m= -
. Hàm số liên tục trên
0;2
0 0
2 2
m m
m m
-
Û Û
- -
Ta có
( )
( )
( )
2
2 2
2 2
1
2 1
x m
x mx m
y
x m x m
-
-
¢
= =
. Cho
1
2
1
0
1
x m
y
x m
= - -
¢
= Û
= -
.
Ta có bảng biến thiên
Hàm số đạt giá trị nhỏ nhất tại
( )
0
0;2x
nên
0 1 2 1 1m m - Û -
So với điều kiện hàm số liên tục trên đoạn
0;2
. Ta có
0 1m
.
CÓ THỂ GIẢI NHƯ SAU:
Điều kiện xác định x m -
Hàm số liên tục trên đoạn
0;2
nên
( )
0 0
0;2 *
2 2
m m
m
m m
-
- Û
- -
( )
( )
( )
2
2 2
2 2
1
2 1
'
x m
x mx m
y
x m x m
-
-
= =
' 0y =
có hai nghiệm là
1
2
1
1
x m
x m
= -
= - -
,
1 2
2x x- =
nên chỉ có nhiều nhất một nghiệm thuộc
( )
0;2
Ta thấy
1 1,m m m- - -
và do đó để hàm số liên tục và đạt giá trị nhỏ nhất trên
0;2
tại một
điểm
( )
0
0;2x
thì
( )
0 1 2 1 1 **m m - Û -
Từ
( ) ( )
* , **
ta có
0 1m
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 22. Cho hàm số
1 sin
cos 2
m x
y
x
-
=
. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
0;10
để giá trị
nhỏ nhất của hàm số nhỏ hơn
2-
?
A.
1
. B.
9
. C.
3
. D.
6
.
Lời giải
Tập xác định:
D =
.
Ta có:
1 sin
cos 2
m x
y
x
-
=
cos sin 1 2y x m x yÛ = -
.
Phương trình có nghiệm khi và chỉ khi:
2 2 2
1 4 4y m y y -
2 2
3 4 1 0y y mÛ - -
2 2
2 1 3 2 1 3
3 3
m m
y
-
Û
.
Theo đề bài, ta có:
2
2 1 3
min 2
3
0;10
x
m
y
m
m
-
= -
2
1 3 8
0;10
m
m
m
Û
2
3 63
0;10
m
m
m
Û
2
21
0;10
m
m
m
Û
5,6,7,8,9,10mÛ
.
Vậy có
6
giá trị nguyên của tham số
m
thỏa yêu cầu bài toán.
Câu 23. Tìm tất cả các giá trị của tham số m để hàm số
2
1
x m
y
x x
=
có giá trị lớn nhất trên
nhỏ hơn hoặc
bằng 1.
A.
1m
. B.
1m
. C.
1m -
. D.
1m -
.
Lời giải
Chọn A
+ TXĐ:
D =
.
+
lim 0
x
y

=
+
( )
2
2
2
2 1
1
x mx m
y
x x
- - -
¢
=
.
2
0 2 1 0 (*)y x mx m
¢
= Û - - - =
2
(*)
1 0,m m m
¢
= -
nên (*) có 2 nghiệm phân biệt
1 2
,x x m
+ BBT:
Vậy hàm số đạt giá trị lón nhất là
( )
2
2
1
2 1
f x
x
=
với
2
2
1x m m m= - -
2
2
1
1 1 2 2 1 1
2 2 1 1
YCBT m m m
m m m
Û Û - -
- -
( vì
( )
2 2
0 2 1 0f x x
)
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
2
2 2
0
0
1 1
1
m
m
m m m m
m m m
Û - Û Û
-
C. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ CHỨA DẤU GIÁ TRỊ
TUYỆT ĐỐI (chứa tham số)
Dạng 1: Tìm
m
để
( ) ( )
;
max 0 .
y f x m a a
= =
Phương pháp:
Cách 1:Trước tiên tìm
( )
( ) ( )
;
;
max ; min .f x K f x k K k
= =
Kiểm tra
max , .
2 2 2
m K m k m K m k K k
m K m k
- - -
=
TH1:
.
2
K k
a
-
Để
;
max ;
m k a m a k
y a m a k a K
m K a m a K
= - = - -
= Û Û - - -
= = -
.
TH2:
2
K k
a
-
m
.
Cách 2: Xét trường hợp
TH1:
m K a
Max m K
m K m k
=
= Û
TH2:
m k a
Max m k
m k m K
=
= Û
Dạng 2: Tìm
m
để
( ) ( )
;
min 0 .
y f x m a a
= =
Phương pháp:
Trước tiên tìm
( )
( ) ( )
;
;
max ; min .f x K f x k K k
= =
Để
;
min .
0 0
m k a m K a m a k m a K
y a
m k m K m k m K
= = - = - = - -
= Û Û
- -
Vậy
1 2
.m S S
Dạng 3: Tìm
m
để
( )
;
max
y f x m
=
không vượt quá giá trị
M
cho trước.
Phương pháp: Trước tiên tìm
( )
( ) ( )
;
;
max ; min .f x K f x k K k
= =
Để
;
max .
m k M
y M M k m M K
m K M
-
Û - - -
Dạng 4: Tìm
m
để
( )
;
min
y f x m
=
không vượt quá giá trị
a
cho trước.
Phương pháp: Trước tiên tìm
( )
( ) ( )
;
;
max ; min .f x K f x k K k
= =
Để
( )( )
;
min 0 .
0 0
m k a m K a m a k m a K
y a m K m k K m k
m k m K m k m K
- - - -
Û Û - -
- -
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dang 5: Tìm
m
để
( )
;
max
a b
y f x m=
đạt min.
Phương pháp:
Trước tiên tìm
( )
( ) ( )
;
;
max ; min .
a b
a b
f x K f x k K k
= =
Đề hỏi tìm
.
2
K k
m m
= -
Đề hỏi tìm min của
;
max
a b
y
giá trị này là
.
2
K k-
Dạng 6: Tìm
m
để
( )
;
min
a b
y f x m=
đạt min.
Phương pháp: Trước tiên tìm
( )
( ) ( )
;
;
max ; min .
a b
a b
f x K f x k K k
= =
Đề hỏi tìm
( )( )
0
m m K m k K m k Û - -
. Đề hỏi tìm min của
;
min
a b
y
giá trị này là
0.
Dạng 7: Cho hàm số
( )
y f x m=
.Tìm
m
để
( )
;
;
max .min 0
a b
a b
y h y h
hoặc
max
Min
=
Phương pháp: Trước tiên tìm
( )
( ) ( )
;
;
max ; min .
a b
a b
f x K f x k K k
= =
TH1:
1
cung dau
.
K m k m
K m k m
K m h k m m S
TH2:
2
cungdau
.
k m K m
K m k m
k m h K m m S
Vậy
1 2
.m S S
Dạng 8: Cho hàm số
( )
y f x m=
.
Phương pháp: Trước tiên tìm
( )
( ) ( )
;
;
max ; min .
a b
a b
f x K f x k K k
= =
BT1: Tìm
m
để
;
;
min max
a b
a b
y y m K m k
= Û =
.
BT2: Tìm
m
để
;
;
min *max *
a b
a b
y y m K m k
= Û =
.
Câu 1. Gọi
S
là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm
số
( )
3
3
f x x x m= -
trên đoạn
0;3
bằng 16. Tổng tất cả các phần tử của
S
là:
A.
16-
. B.
16
. C.
12-
.
D.
2-
.
Lời giải
Chọn A
Xét
3
3
u x x m
trên đoạn
0;3
có
2
0 3 3 0 1 0;3
u x x
.
Khi đó
0;3
0;3
max u max 0 , 1 , 3 max m,m 2,m 18 18
min u min 0 , 1 , 3 min m,m 2,m 18 2
u u u m
u u u m
.
Suy ra
0;3
18 16
18 2
2
ax max 2 , 18 16
14
2 16
2 18
m
m m
m
M f x m m
m
m
m m
.
Do đó tổng tất cả các phần tử của
S
bằng
16
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Câu 2. Cho hàm số
( )
1
x m
f x
x
=
(
m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị của
m
sao cho
( )
( )
0;1
0;1
max min 2f x f x =
. Số phần tử của
S
là
A.
6
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn B
Do hàm số
( )
1
x m
f x
x
=
liên tục trên
0;1
.
Khi
1m =
hàm số là hàm hằng nên
( )
( )
0;1
0;1
max min 1f x f x= =
Khi
1m
hàm số đơn điệu trên đoạn
0;1
nên
+ Khi
( ) ( )
0 ; 1f f
cùng dấu thì
( )
( ) ( ) ( )
0;1
0;1
1
max min 0 1
2
m
f x f x f f m
= =
.
+ Khi
( ) ( )
0 ; 1f f
trái dấu thì
( )
0;1
min 0f x =
,
( ) ( ) ( )
0;1
1
max max 0 ; 1 max ;
2
m
f x f f m
= =
.
TH1:
( ) ( )
1
0 . 1 0 ( 1) 0
0
m
f f m m
m
-
Û Û
.
( )
( )
0;1
0;1
1
1
max min 2 2
5
2
3
m
m
f x f x m
m
=
= Û = Û
= -
(thoả mãn).
TH2:
( ) ( )
0 . 1 0 ( 1) 0 1 0f f m m m Û Û -
( )
( )
0;1
0;1
2
2
max min 2 5
1
2
3
2
m
m
f x f x m
m
m
=
=
= Û = -
=
=
(không thoả mãn).
Số phần tử của
S
là
2
.
Câu 3. Cho hàm số
( )
4 3 2
4 4f x x x x m= -
(
m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị của
m
sao cho
( )
( )
0;2
0;2
max min 5f x f x =
. Số phần tử của
S
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Xét hàm số
( )
4 3 2
4 4f x x x x m= -
.
( )
3 2
4 12 8f x x x x
¢
= -
;
( )
0f x
¢
=
3 2
4 12 8 0x x xÛ - =
0
1
2
x
x
x
=
Û =
=
.
Bảng biến thiên
0
1
m
m
m+1
2
+
f(x)
f'(x)
x
0
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+) Nếu
1m -
thì
( )
0;2
max f x m= -
,
( )
0;2
min 1f x m= - -
Ta có
( )
( )
0;2
0;2
max min 5 1 5 3f x f x m m m = Û - - - = Û = -
(thỏa)
+) Nếu
0m
thì
( )
0;2
max 1f x m=
,
( )
0;2
min f x m=
Ta có
( )
( )
0;2
0;2
max min 5 1 5 2f x f x m m m = Û = Û =
(thỏa)
+) Nếu
1 0m-
thì
( )
0;2
min 0f x =
;
( )
0;2
max max ; 1 1f x m m=
( )
( )
0;2
0;2
max min 5f x f x
(không thỏa điều kiện đề bài)
Vậy
3;2S = -
, có
2
giá trị của
m
thỏa mãn đề bài.
Câu 4. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
2
2 3y x x m= -
trên đoạn
1;2-
bằng
4
. Tổng tất cả các phần tử của
S
là
A.
6-
. B.
8-
. C.
9-
. D.
12-
.
Lời giải
Chọn B
Xét hàm
( )
2
2 3g x x x m= -
. Dễ thấy hàm số
( )
g x
liên tục trên đoạn
1;2-
Ta có
( )
2 2g x x
¢
= -
,
( )
0 1g x x
¢
= Û =
. Do đó
2
1;2
max 2 3 max 2 ; 3 ; 6x x m m m m
-
- =
.
Ta thấy
2 3 6m m m
với mọi
m
.
Suy ra
1;2
max y
-
chỉ có thể là
6m
hoặc
2m
.
Nếu
1;2
max 6y m
-
=
thì
6 4
6 2
m
m m
=
2mÛ = -
.
Nếu
1;2
max 2y m
-
=
thì
2 4
2 6
m
m m
=
6mÛ = -
.
Vậy tổng tất cả các phần tử của
S
bằng
8-
.
Câu 5. Cho hàm số
( )
3
3f x x x m= -
(
m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị của
m
sao
cho
( )
( )
0;2
0;2
max min 6f x f x =
. Tổng tất cả các phần tử của
S
là
A.
3
. B.
0
. C.
1-
. D.
2
.
Lời giải
Chọn B
Xét hàm số
( )
3
3f x x x m= -
.
( )
2
3 3f x x
¢
= -
;
( )
0f x
¢
=
2
3 3 0xÛ - =
1
1
x
x
= -
Û
=
.
Bảng biến thiên
m
m+2
0
x
f'(x)
f(x)
1
+
0
2
m-2
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
+) Nếu
2m -
thì
( )
0;2
max 2f x m= -
,
( )
0;2
min 2f x m= - -
Ta có
( )
( )
0;2
0;2
max min 6 2 2 6 3f x f x m m m = Û - - - = Û = -
(thỏa)
+) Nếu
2m
thì
( )
0;2
max 2f x m=
,
( )
0;2
min 2f x m= -
Ta có
( )
( )
0;2
0;2
max min 6 2 2 6 3f x f x m m m = Û - = Û =
(thỏa)
+) Nếu
2 2m-
thì
( )
0;2
min 0f x =
;
( )
0;2
max max 2 ; 2 4f x m m= -
( )
( )
0;2
0;2
max min 6f x f x
(không thỏa điều kiện đề bài)
Vậy
3;3
S = -
, Tổng các phần tử của
S
là
0
.
Câu 6. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị nhỏ nhất của hàm số
( )
3
2 6f x x x m= -
trên đoạn
0;3
bằng 8. Tổng tất cả các phần tử của
S
bằng
A.
8
. B.
16-
. C.
32-
.
D.
72-
.
Lời giải
Chọn C
Xét
( )
3
2 6u x x x m= -
trên đoạn
0;3
. Dễ thấy hàm số
( )
u x
liên tục trên đoạn
0;3
.
Có
( )
2
0 6 6 0 1 0;3u x x x
¢
= Û - = =
.
Khi đó
( ) ( ) ( )
( ) ( ) ( )
0;3
0;3
max max 0 ; 1 ; 3 max ; 4; 36 36
min min 0 ; 1 ; 3 min ; 4; 36 4
u u u u m m m m
u u u u m m m m
= = - =
= = - = -
.
Theo bài ra
( )
0;3
4 8
4 0
12
min min 4 ; 36 ;0 8
44
36 0
36 8
m
m
m
f x m m
m
m
m
- =
-
=
= - = Û Û
= -
=
.
Do đó
44;12S = -
. Vậy tổng tất cả các phần tử của
S
bằng
32-
.
Câu 7. Có bao nhiêu giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
2
2 4y x x m= -
trên
đoạn
2;1-
đạt giá trị nhỏ nhất?
A. . B. . C. . D. .
Lời giải
Chọn A
Xét hàm
( )
2
2 4g x x x m= -
. Dễ thấy hàm số
( )
g x
liên tục trên đoạn
2;1-
.
Ta có
( )
2 2g x x
¢
=
,
( )
0 1g x x
¢
= Û = -
. Do đó
2
2;1
max 2 4 max 1 ; 4 ; 5x x m m m m
-
- = - - -
.
Ta thấy
5 4 1m m m- - -
với mọi
m
.
Suy ra
2
2;1
max 2 4 max 1 ; 5x x m m m
-
- = - -
.
1 5
1 5
max 1 ; 5 2
2 2
m m
m m
m m
- -
- -
- - = .
Vậy GTNN của
max 1 ; 5m m- -
bằng 2.
1
3
4
5
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đẳng thức xảy ra khi và chỉ khi
1 5m m- = -
3mÛ =
.
Câu 8. Cho hàm số
( )
f x
liên tục trên
, có đồ thị như hình vẽ
Có tất cả bao nhiêu giá trị nguyên của tham số
a
để hàm số
2
8
1
1
x
y f a
x
= -
có giá trị lớn nhất
không vượt quá
20
?
A.
29
. B.
35
. C.
31
. D.
41
.
Lời giải
Chọn C
Đặt
2
8
1
x
t
x
=
. Ta có:
( )
2
2
2
8 8
1
x
t
x
-
¢
=
;
0 1t x
¢
= Û =
.
BBT:
4;4t -
.
Hàm số
2
8
1
1
x
y f a
x
= -
trở thành
( ) ( )
1 , 4;4g t f t a t= - -
.
Đặt
( ) ( )
1, 4;4h t f t a t= - -
, ta có:
( ) ( )
h t f t
¢ ¢
=
.
( ) ( )
0 0h t f t
¢ ¢
= Û =
4 4;4
2 4;4
2 4;4
t
t
t
= - -
Û = - -
= -
.
Ta có:
( )
4 0,8 1 0,2h a a- - = -
;
( )
4 6 1 5h a a= - =
;
( )
2 1,6 1 0,6h a a- - =
;
( )
2 4 1 5h a a= - - = -
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
( )
4;4
Max Max
y h t
-
=
Max 5 ; 5
a a
= -
.
Yêu cầu bài toán
5 20
5 20
a
a
Û
-
20 5 20
20 5 20
a
a
-
Û
- -
25 15
15 25
a
a
-
Û
-
15 15
a
Û -
.
Vậy có tất cả
31
giá trị nguyên của tham số
a
thỏa mãn yêu cầu bài toán.
Câu 9. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm số
( )
2
1
x mx m
f x
x
=
trên
1;2
bằng
2
. Tổng tất cả các phần tử của
S
là
A.
11
3
-
. B.
13
6
. C.
11
6
-
. D.
1
3
.
Lời giải
Chọn C
Xét
( )
2
1
x mx m
u x
x
=
trên đoạn
1;2
. Dễ thấy
( )
u x
liên tục trên đoạn
1;2
.
Ta có
( )
2
2
0 1;2
2
0 0
2 1;2
1
x
x x
u
x
x
=
¢
= Û = Û
= -
.
Khi đó
( ) ( ) ( )
( ) ( ) ( )
1;2
1;2
1 4 4
max max 1 ; 2 max ;
2 3 3
1 4 1
min min 1 ; 2 min ;
2 3 2
u x u u m m m
u x u u m m m
= = =
= = =
.
Suy ra
( )
1;2
1
2
2
1 4
5
2 3
1 4
2
max max ; 2
2
2 3
4
2
3
3
4 1
3 2
m
m m
m
f x m m
m
m
m m
=
= -
= = Û Û
=
=
.
Vậy tổng các phần tử của
S
là
11
6
-
.
Câu 10. Cho hàm số
3 2
cos 3sin 3
y x x m
= -
. Gọi
S
là tập hợp các giá trị m sao cho
2max min 9
y y
=
. Tổng các phần tử của tập hợp
S
bằng:
A.
16
3
-
. B.
4-
. C.
6-
. D.
2-
.
Lời giải
Chọn B
Ta có:
3 2 3 2
cos 3sin 3 cos 3cos .y x x m x x m= - =
Đặt
cos [ 1;1]
t x t
= -
, xét
3 2
( ) 3
g t t t m=
có
2
2
'( ) 3 6 0
0.
t
g t t t
t
= -
= = Û
=
BBT:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ đó:
[ 1;1]
[ 1;1]
min ( ) (0) ;max ( ) (1) 4.g t g m g t g m
-
-
= = = =
+ TH1:
( 4) 0 ( ; 4] [0; ),m m m - -
[ 1;1]
[ 1;1]
2( 4) 9
1
0
3
2max | | min | | 2max | ( ) | min | ( ) | 9
13
2 ( 4) 9
.
3
4
m m
m
m
y y g t g t
m m
m
m
-
-
=
=
= = Û Û
-
- - =
=
-
+ TH2:
( 4) 0 ( 4;0),m m m -
[ 1;1]
min | ( ) | 0,g t
-
=
[ 1;1]
4
9
( )
2 9
2
2max | | min | | 2max | ( ) | 9
1
4
( ).
2
2( 4) 9
m m
m l
m
y y g t
m m
m l
m
-
-
-
=
- =
= = Û Û
-
=
=
Vậy
13 1
,
3 3
S
-
=
Câu 11. Cho hàm số
( )
3
3f x x x= -
. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị
nhỏ nhất của hàm số
( )
2 cosy f x m= -
bằng 2. Tổng tất cả các phần tử của
S
bằng
A.
4
. B.
16-
. C.
32-
. D.
12-
.
Lời giải
Chọn B
Đặt
2 cost x= -
ta có
1;3t
. Khi đó bài toán trở thành tìm m để hàm số
3
3y t t m= -
với
1;3t
đạt giá trị nhỏ nhất bằng 2.
Xét
( )
3
3u t t t m= -
trên đoạn
1;3
. Ta có hàm số
( )
u t
liên tục trên đoạn
1;3
.
( )
2
3 3u t t
¢
= -
;
( )
( )
( )
1 1;3
0
1 1;3
t
u t
t
= -
¢
= Û
=
.
Khi đó:
( ) ( ) ( )
( ) ( ) ( )
1;3
1;3
max max 1 ; 3 max 18; 2 18
min min 1 ; 3 min 18; 2 2
u t u u m m m
u t u u m m m
= = - =
= = - = -
.
Yêu cầu bài tập:
1;3
min 2y = .
Trường hợp 1:
2 0 2m m- Û
1;3
min 2 2y m m = - = -
;
1;3
min 2 2 2 4y m m= Û - = Û =
(thỏa mãn)
Trường hợp 2:
18 0 18m m Û -
( )
1;3
min 18 18y m m = = -
;
( )
1;3
min 2 18 2 20y m m= Û - = Û = -
(thỏa mãn)
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Trường hợp 3:
( )( )
( )
1;3
18 2 0 18 2 min 0 2
m m m f x
- Û - =
(loại)
Vậy tổng tất cả các phần tử của
S
bằng
16-
. Chọn phương án
B
.
Câu 12. Cho hàm số
( )
log
log 2
x m
f x
x
=
(
m
là tham số thực). Gọi
S
là tổng tất cả các giá trị của
m
sao cho
( ) ( )
1
1
;1
;1
10
10
max min 2
f x f x
=
. Tìm
S
.
A.
2
3
-
. B.
2
. C.
4
3
. D.
10
3
.
Lời giải
Chọn C
Đặt
1
log ; ;1 1;0
10
t x x t
= -
Xét hàm số
( )
2
t m
g t
t
=
liên tục trên
1;0
-
Khi đó:
( )
( ) ( )
( )
1
1
1;0
1;0
;1
;1
10
10
max max ;min min
f x g t f x g t
-
-
= =
TH1: Khi
m
hàm số là hàm hằng
( )
1
g t
=
nên
( )
( ) ( ) ( )
( )
( )
1
1
1;0 1;0
1;0 1;0
;1
;1
10
10
max min 1 max min max min 2
g t g t f x f x g t g t
- -
- -
= = = =
nhận
m
TH2: Khi
m
hàm số đơn điệu trên đoạn
1;0
-
nên:
+ TH2.1:
( ) ( ) ( )
0
1 .g 0 0 1 0
1
m
g m m
m
- Û - Û
. Khi đó:
( ) ( )
( )
( )
( ) ( )
( )
( )
1
1
1;0
1;0
;1
;1
10
10
max min 2 max min 2
2
0 1 2 1 2
2
2
3
f x f x g t g t
m L
m
g g m
m N
-
-
= Û =
=
Û - = - = Û
= -
+ TH2.2:
( ) ( ) ( )
1 . 0 0 1 0 0 1
f f m m m
- Û - Û
Khi đó:
( )
( ) ( ) ( )
1;0
1;0
min 0, max max 0 ; 1 max ; 1
2
m
g t g t g g m
-
-
= = - = -
Do đó:
( ) ( )
( )
( )
( )
( )
( )
1
1
1;0
1;0
;1
;1
10
10
max min 2 max min 2
4
2
2
3
1 2
1
f x f x g t g t
m L
m
m L
m
m L
-
-
= Û =
=
=
Û =
- =
= -
Vậy
4
3
S
=
Câu 13. Có bao nhiêu giá trị nguyên của tham số
m
để giá trị nhỏ nhất của hàm số
3 2
9 9y x mx x m
= - -
trên đoạn
2;2
-
đạt giá trị nhỏ nhất.
A.
3
. B.
5
. C.
4
. D.
6
.
Lời giải
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
( )
3 2
9 9f x x mx x m
= - -
. Dễ thấy
( )
2;2
min 0
f x
-
, dấu
" "=
xảy ra khi và chỉ khi phương trình
( )
0
f x
=
có nghiệm
2;2
x -
.
Ta có:
( ) ( ) ( )
( )
( )
2 2
9 9
f x x x m x m x x m
= - - - = - -
.
( )
3
0 3
x
f x x
x m
=
= Û = -
=
.
Do đó điều kiện cần và đủ để
( )
0
f x
=
có nghiệm
2;2
x -
là
2;2
m -
.
Mà
m
nên
2; 1;0;1;2
m - -
.
Vậy có
5
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 14. Có bao nhiêu số nguyên
m
để giá trị nhỏ nhất của hàm số
( )
4 2
8
y f x x x m= = -
trên
đoạn
1; 3
-
đạt giá trị nhỏ nhất.
A.
23
. B.
24
. C.
25
. D.
26
.
Lời giải
Ta có
( )
4 2
8
y f x x x m= = -
=
( )
2
4 2 2
8 4 16
x x m x m- - = - - -
.
Đặt
( )
2
2
4
t x= -
, vì
1; 3
x -
, suy ra
0; 25
t
.
Khi đó
( )
16
y g t t m= = - -
.
Ta có
( )
( )
1;3 0; 25
min min min 9 , 16
f x g t m m
- -
= = -
.
Nếu
9 0 9
m m
- Û
, khi đó
( )
1;3
min
f x
-
=
9 0
m
-
, khi đó
( )
1;3
min min 0
f x
-
=
, khi
m
.
Nếu
16 0 16
m m
Û -
, khi đó
( )
1;3
min
x
f x
-
=
16 0
m
- -
, khi đó
( )
1;3
min min 0
f x
-
=
, khi
16
m
= -
.
Nếu
( )( )
9 16 0 16 9
m m m
- Û -
, khi đó
( )
1;3
min
x
f x
-
=
0
, khi đó
( )
1;3
min min 0
f x
-
=
.
Vậy
( )
1;3
min min 0
f x
-
=
, khi
16 9
m
-
.
Vì
m
, nên có
26
số nguyên
m
thỏa mãn yêu cầu bài toán.
Câu 15. Cho hàm số
2
4 2 3
y x x m
= - -
với
m
là tham số thực. Biết rằng giá trị lớn nhất của hàm số trên
đoạn
1;3
đạt giá trị nhỏ nhất bằng
a
khi
. Tính
2
P b a= -
.
A.
1
2
. B.
13
4
. C.
9
4
-
. D.
6
.
Lời giải
Xét hàm số
( )
2
4 2 3
y f x x x m
= = - -
liên tục trên đoạn
1;3
.
+)
( )
2 4
f x x
¢
= -
;
( )
0 2 1;3
f x x
¢
= Û =
.
+)
( )
1 2 6
f m
= -
,
( )
2 2 7
f m
= -
,
( )
3 2 6
f m
= -
.
Khi đó
( )
1;3
max max 2 6 ; 2 7
f x m m M= - - =
.
Ta có:
2 6
2 2 6 7 2 2 6 7 2 1
2 7 7 2
M m
M m m m m
M m m
-
- - - - =
- = -
1
2
M
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Dấu
" "=
xảy ra
( )( )
1
2 6 2 7
13
2
4
2 6 7 2 0
m m
m
m m
- = - =
Û Û =
- -
.
Do đó
1
2
M a= =
khi
13
4
m b= =
2 6
P b a
= - =
.
Câu 16. Cho hàm số
( )
3 2 2
1 27
y x x m x=
. Gọi
S
là tập tất cả các giá trị của tham số
m
sao cho giá
trị lớn nhất của hàm số trên đoạn
3; 1- -
có giá trị nhỏ nhất. Khi đó tích các phần tử của
S
là
A.
4
. B.
4-
. C.
8
. D.
8-
.
Lời giải
Xét hàm số
( )
( )
3 2 2
1 27
f x x x m x
=
liên tục trên đoạn
3; 1- -
.
Ta có
( )
2 2
3 2 1 0
f x x x m
¢
=
với
3; 1
x
- -
.
Ta có
( )
2
3 6 3f m
- = -
;
( )
2
1 26
f m- = -
.
Khi đó
( )
2 2
3; 1
max max 6 3 ; 26
f x m m M
- -
= - - =
.
Lại có
2 2
2 2
6 3 6 3
4 72 18
26 3 3 78
M m M m
M M
M m M m
- -
Û
- -
.
Dấu bằng xẩy ra khi
( )( )
2 2
2
2 2
6 3 26 18
2 2
8
6 3 3 78 0
2 2
m m
m
m
m m
m
- = - =
=
Û = Û
- -
= -
.
Vậy với
2 2
2 2
m
m
=
= -
thì giá trị lớn nhất của hàm số trên đoạn
3; 1- -
có giá trị nhỏ nhất.
Khi đó tích các giá trị là
( )
2 2. 2 2 8- = -
.
Câu 17. Có bao nhiêu giá trị nguyên của tham số
m
để giá trị lớn nhất của hàm số
4 2
1 19
30
4 2
y x x x m= -
trên đoạn
0;2
đạt giá trị nhỏ nhất?
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Xét hàm số
( )
4 2
1 19
30
4 2
f x x x x m= -
liên tục trên đoạn
0;2
.
Ta có
( )
3
19 30
f x x x
¢
= -
+
( )
5 0;2
0 3 0;2
2 0;2
x
f x x
x
= -
¢
= Û =
=
.
+ Ta có:
( ) ( )
0 ; 2 26
f m f m
= =
.
Khi đó
( )
0;2
max max ; 26
f x m m=
26
m
=
;
( )
0;2
min min ; 26
f x m m=
m=
.
Suy ra
( )
0;2
max max ; 26
f x m m=
M=
.
Ta có
26
M m m
M m
= -
2 26
M m m -
26
2
m m
M
-
Û
26
2
m m-
13=
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dấu bằng xảy ra khi
( )
26 13
26 0
m m
m m
= =
-
13
m
Û = -
.
Do đó giá trị lớn nhất của hàm số
4 2
1 19
30
4 2
y x x x m= -
trên đoạn
0;2
đạt giá trị nhỏ nhất
bằng
13
khi
13
m
= -
.
Vậy có
1
giá trị nguyên của
m
thỏa mãn yêu cầu đề bài.
Câu 18. Có tất cả bao nhiêu giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
( )
2
2
f x x x m= -
trên
1;2
-
bằng 5.
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
+) Đặt
( )
2
2
g x x x m= -
.
+) Ta có:
( )
,
2 2g x x= -
( )
,
0 2 2 0 1g x x x = Û - = Û =
.
+)
( )
( )
( )
1 3
1 1
2
g m
g m
g m
- =
= -
=
.
+) Suy ra
( )
( )
1;2
1;2
min 1
max 3
g x m
g x m
-
-
= -
=
.Vậy
( )
1;2
min min 0; 1 ; 3
g x m m
-
= -
Ta xét các trường hợp sau:
TH1:.
1 5
6
1 3
m
m
m m
- =
Û =
-
.
TH2:.
3 5
8
1 3
m
m
m m
=
Û = -
-
Vậy có hai giá trị của tham số
m
thỏa mãn.
Câu 19. Tính tích tất cả các số thực
m
để hàm số
3 2
4
6 8
3
y x x x m
có giá trị nhỏ nhất trên đoạn
0; 3
bằng
18
là.
A.
432
. B.
216
. C.
432
. D.
288
.
Lời giải
+ Xét hàm số
3 2
4
6 8
3
f x x x x m
liên tục trên đoạn
0; 3
.
+ Ta có
2
4 12 8
f x x x
.
+
2
1 0;3
0 4 12 8 0
2 0;3
x
f x x x
x
.
+
10 8
0 ; 1 ; 2 ; 3 6
3 3
f m f m f m f m
.
Khi đó
0;3
0;3
max max 0 ; 1 ; 2 ; 3 3 6
min min 0 ; 1 ; 2 ; 3 0
f x f f f f f m
f x f f f f f m
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Suy ra
0;3
min min 0; ; 6
y m m
.
TH1.
18
18
6
m
m
m m
.
TH2.
6 18
24
6
m
m
m m
.
Kết luận: tích các số thực
m
thỏa mãn yêu cầu bài toán là:
24.18 432
.
Câu 20. Cho hàm số
( )
4 2
2 1
f x x x m
= - -
. Gọi
S
là tập hợp tất cả các giá trị của tham số
m
sao cho giá
trị nhỏ nhất của hàm số trên đoạn
0;2
bằng
18
. Tổng tất cả các phần tử của
S
bằng
A.
5
. B.
4
. C.
14
. D.
10
.
Lời giải
Xét hàm số
( )
4 2
2 1
g x x x m
= - -
liên tục trên đoạn
0;2
.
( )
3
4 4g x x x
¢
= -
.
( )
0
g x
¢
=
1 0;2
0 0;2
1 0;2
x
x
x
= -
Û =
=
( )
0 1
g m
= -
,
( )
1 2
g m
= -
,
( )
2 7
g m
=
.
( )
0; 2
min 2
x
g x m
= -
,
( )
0;2
max 7
x
g x m
=
.
( )
0;2
min min 0; 2 ; 7
x
f x m m
= -
.
Trường hợp 1:
2 18
20
2 7
m
m
m m
- =
Û =
-
.
Trường hợp 2:.
7 18
25
2 7
m
m
m m
=
Û = -
-
.
Suy ra
20; 25
m -
.
Vậy tổng tất cả các phần tử của
S
bằng
5-
.
Câu 21. Tính tổng tất cả các giá trị nguyên lớn hơn 6 của tham số
m
sao cho giá trị nhỏ nhất của hàm số
( )
2
1
y x m x m= -
trên
2; 1
m
-
nhỏ hơn 2020.
A.
2043210
. B.
2034201
. C.
3421020
D.
3412020
.
Lời giải
+) Xét hàm số
( ) ( )
2
1
f x x m x m= -
liên tục trên
2; 1
m
-
với
m
.
Ta có:
( ) ( ) ( )
1
2 1 ; 0 2; 1
2
m
f x x m f x x m
¢ ¢
= - = Û = -
.
Khi đó:
( )
( )
( )
2
1
1
2 2 ; ; 1 2 .
2 4
m
m
f m f f m m
-
= - = - - = -
+) Vì
( )
2
1
2 0, 6
4
m
m m
-
- -
nên
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
( ) ( ) ( )
[2; 1]
1
max max 2 ; ; 1 2
2
m
m
f x f f f m m
-
= - = -
;
và
( ) ( ) ( )
( )
2
[2;m-1]
1
1
min min 2 ; ; 1
2 4
m
m
f x f f f m
-
= - = -
.
Do đó:
( )
2
[2;m-1]
1
min min 2 ; 2
4
m
y m m
-
= - - = -
+) Theo yêu cầu bài toán:
2 2020 2020 2 2020 2018 2022
m m m- Û - - Û -
+) Vì
m
và
m
nên
7;8;9; ;2021
m
.
+) Vậy tổng tất cả các giá trị nguyên của tham số
m
là:
( )
2021
7
7 2021 2015
2043210
2
n
n
=
= =
.
Câu 22. Cho hàm số
4 3 2
1
4
y x x x m
. Tính tổng tất cả các số nguyên
m
để
1;2
max 11
y
.
A.
19
. B.
37
. C.
30
. D.
11
.
Lời giải
+ Xét hàm số
4 3 2
1
4
f x x x x m
liên tục trên đoạn
1; 2
.
+ Ta có
3 2
3 2f x x x x
.
+
3 2
0 1;2
0 3 2 0 1 1;2
2 1;2
x
f x x x x x
x
.
+
9 1
1 ; 0 ; 1 ; 2
4 4
f m f m f m f m
.
Khi đó
1;2
1;2
9
max max 1 ; 0 ; 1 ; 2 1
4
min min 1 ; 0 ; 1 ; 2 0 2
f x f f f f f m
f x f f f f f f m
.
Vậy
0;3
9
max max ,
4
y m m
theo yêu cầu bài toán
0;3
max 11
y
9
11
4
9
4
11
9
4
m
m m
m
m m
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
53 35
4 4
9 35
9
35
8 4
8
11
9
4
11
11 11
8
9
8
m
m
m
m
m
m
m
.
Vì
m
nguyên nên
11; 10;...;8
m
.
Kết luận: tổng các số nguyên
m
thỏa mãn yêu cầu bài toán là:
11 10 9 ... 8 30
.
Câu 23. Cho hàm số
( )
2
2 3
f x x mx
= -
. Có bao nhiêu giá trị
m
nguyên để giá trị lớn nhất của
( )
f x
trên
đoạn
1;2
không lớn hơn
3
?
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Ta có giá trị lớn nhất của
( )
f x
trên đoạn
1;2
không lớn hơn 3, tức là
( )
1;2
max 3
f x
2
2
2 3 3, 1;2
2 3 3, 1;2
x mx x
x mx x
-
Û
- -
2
2 , 1;2
6
2 , 1;2
m x x
x
m x
x
Û
( ) ( )
( )
1;2
2
1;2
2 max 1
6
2 min 2
m x
x
m
x
Û
.
+)
( )
1 2 2 1.
m m
Û Û
+) Xét hàm
( )
2
6 6
x
g x x
x x
= =
với
1;2
x
có
( )
2
6
1g x
x
¢
= -
.
Suy ra:
( )
0, 1;2
g x x
¢
( ) ( )
1;2
min 2 5
g x g
= =
.
Do đó
( )
5
2
2
m
Û
.
Vậy
5
1
2
m
, mà
m
nên
1;2
m
.
Câu 24. Cho hàm số
3 2
3 9
y x x x m= - -
. Gọi
S
là tập hợp các giá trị nguyên của tham số
m
để
2;3
max 50
y
-
. Tổng các phần tử của
M
là
A.
0
. B.
737
. C. 759. D.
215-
.
Lời giải
Xét hàm số
( )
3 2
3 9
f x x x x m= - -
liên tục trên đoạn
2;3
-
.
Ta có
( )
2
3 6 9f x x x
¢
= - -
.
( )
2
1
0 3 6 9 0
3
x
f x x x
x
= -
¢
= Û - - = Û
=
.
Có
( ) ( ) ( )
2 2; 1 5; 3 27
f m f m f m
- = - - = = -
.
Suy ra
( )
2;3
max 5
f x m
-
=
;
( )
2;3
min 27
f x m
-
= -
.
Do đó
2;3
max max 5 ; 27
M y m m
-
= = -
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
)
( )
( )
5 27
2 22 0
5 50
11;45
50 5 50
50 23;45
2 22 0 23;11
5 27
50 27 50
27 50
m m
m
m
m
m
M m
m m
m m
m
m
-
-
-
Û Û Û Û -
- -
-
- -
-
.
Do đó
22; 21; 20;...; 1;0;1; 2;...;44
S = - - - -
.
Vậy tổng các phần tử của
M
là 737.
Câu 25. Cho hàm số
4 3 2
2
y x x x a= -
. Có bao nhiêu giá trị nguyên của tham số
a
để
1; 2
max 100
y
-
.
A.
197
. B.
196
. C.
200
. D.
201
.
Lời giải
Xét
4 3 2
2
u x x x a= -
liên tục trên đoạn
1; 2
-
.
3 2
' 4 6 2u x x x= -
.
0 1;2
' 0 1 1;2
1
1;2
2
x
u x
x
= -
= Û = -
= -
Suy ra
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )
1; 2
1; 2
1
max max 1 , 0 , , 1 , 2 1 2 4
2
1
min min 1 , 0 , , 1 , 2 0 1
2
M u u u u u u u u a
m u u u u u u u u a
-
-
= = - = - = =
= = - = = =
.
Vậy
1; 2
4 100
100 2
max max 4 , 100
4 100
2 96
a a
a
y a a
a a
a
-
- -
= Û Û
-
.
Vậy
100, 99,..., 96
a - -
có
197
số nguyên thỏa mãn.
Câu 26. Cho hàm số
sin cos
y x x m=
, có bao nhiêu giá trị nguyên của
m
để hàm số có giá trị lớn nhất bé
hơn
2
.
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Xét hàm số
( )
sin cos
f x x x m=
, có tập xác định:
D =
.
Ta có:
2 sin cos 2
m x x m m-
,
x
.
Suy ra
( )
2 2
m f x m-
,
x
.
Vậy:
max 2
D
y m=
hoặc
max 2
D
y m= -
.
Yêu cầu bài toán
2 2
2 2 2 2
2 2
0
2 2 2 2
2 2
0
2 2
m
m
m m
m
m
m
m
m m
- - -
-
Û Û
-
-
-
0 2 2
2 2 2 2
2 2 0
m
m
m
-
Û Û - -
-
.
Do
0
m m
=
. Vậy chỉ có một giá trị nguyên của
m
thỏa yêu cầu bài toán.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
D. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT HÀM ẨN, HÀM HỢP
Câu 1. Cho hàm số
( )
y f x=
xác định và liên tục trên
, đồ thị của hàm số
( )
y f x
¢
=
như hình vẽ.
Giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;2-
là
A.
( )
1f
. B.
( )
1f -
. C.
( )
2f
. D.
( )
0f
.
Lời giải
( )
1
0 1
2
x
f x x
x
= -
¢
= Û =
=
.
Từ đồ thị hàm
y f x
ta có bảng biến thiên
Từ đó suy ra giá trị lớn nhất của hàm số trên
1;2
là
1f
.
Câu 2. Cho hàm số
( )
y f x=
có đạo hàm là hàm
( )
f x
¢
. Đồ thị của hàm số
( )
y f x
¢
=
được cho như hình
vẽ. Biết rằng
( ) ( ) ( ) ( )
0 3 2 5f f f f =
. Giá trị nhỏ nhất, giá trị lớn nhất của
( )
y f x=
trên đoạn
0;5
lần lượt là:
A.
( )
2f
;
( )
5f
. B.
( )
0f
;
( )
5f
. C.
( )
2f
;
( )
0f
. D.
( )
1f
;
( )
5f
.
Lời giải
Dựa vào đồ thị hàm số
( )
f x
¢
ta có bảng biến thiên.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó:
( )
( )
( ) ( )
0;5
min 2
3 2
f x f
f f
=
,
mà
( ) ( ) ( ) ( )
0 3 2 5f f f f =
( ) ( ) ( ) ( )
0 2 2 5f f f f
( ) ( )
0 5f f
.
Vậy giá trị nhỏ nhất, giá trị lớn nhất của
( )
y f x=
trên đoạn
0;5
lần lượt là:
( )
2f
;
( )
5f
.
Câu 3. Cho hàm số
( )
f x
có đạo hàm là
( )
f x
¢
. Đồ thị của hàm số
( )
y f x
¢
=
được cho như hình vẽ bên.
Biết rằng
( ) ( ) ( ) ( ) ( )
0 1 2 3 5 4f f f f f - = -
. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của
( )
f x
trên đoạn
0;5
.
A.
( ) ( )
5 , 3m f M f
= =
B.
( ) ( )
5 , 1m f M f
= =
C.
( ) ( )
0 , 3m f M f= =
D.
( ) ( )
1 , 3m f M f= =
Lời giải
Chọn A
Từ đồ thị ta có bảng biến thiên của
( )
f x
trên đoạn
0;5
( )
3M f =
và
( ) ( ) ( ) ( )
1 3 , 4 3f f f f
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
5 0 1 3 4 3 0 5 0 5
f f f f f f f f m f- = - - =
.
Câu 4. Cho hàm số
( )
y f x=
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
( )
( )
2 3 2
1 1
4 3 8
3 3
g x f x x x x x
= - -
trên đoạn
1;3
.
A. 15. B.
25
3
. C.
19
3
. D. 12.
Lời giải
( ) ( )
( )
2 2
4 2 4 6 8g x x f x x x x
¢ ¢
= - - -
( )
( )
2
2 2 4 4x f x x x
¢
= - - -
.
Với
1;3x
thì
4 0x-
;
2
3 4 4x x -
nên
( )
2
4 0f x x
¢
-
.
Suy ra
( )
2
2 4 4 0f x x x
¢
- -
,
1;3x
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Bảng biến thiên
Suy ra
( ) ( )
1;3
max 2g x g=
( )
4 7 12f= =
.
Câu 5. Cho hàm số
( )
y f x=
liên tục trên
.
Đồ thị của hàm số
( )
y f x
¢
=
như hình bên. Đặt
( ) ( ) ( )
2
2 1 .g x f x x= -
Mệnh đề dưới đây đúng.
A.
( ) ( )
3;3
max 3 .g x g
-
=
B.
( ) ( )
3;3
min 1 .g x g
-
=
C.
( ) ( )
3;3
max 0 .g x g
-
=
D.
( ) ( )
3;3
max 1 .g x g
-
=
Lời giải
Chọn D
( ) ( ) ( ) ( ) ( ) ( )
2
2 1 2 2 1g x f x x g x f x x
¢ ¢
= - = -
Dựa vào đồ thị ta thấy
( ) ( )
3
0 1 1
3
x
g x f x x x
x
= -
¢ ¢
= Û = Û =
=
Và
với
( ) ( ) ( )
; 3 : 1 0x f x x g x
¢ ¢
- -
với
( ) ( ) ( )
3;1 : 1 0x f x x g x
¢ ¢
-
,
với
( ) ( ) ( )
1;3 : 1 0x f x x g x
¢ ¢
với
( ) ( ) ( )
3; : 1 0x f x x g x
¢ ¢

Bảng biến thiên
x
-
3-
1
3
( )
g x
¢
‒ 0
+
0 ‒ 0
+
( )
g x
Dựa vào bảng biến thiên suy ra
( ) ( )
3;3
max 1 .g x g
-
=
Câu 6. Cho hàm số có đạo hàm cấp hai trên . Biết , và bảng xét dấu
của như sau:
( )
y f x
=
( )
0 3
f
¢
=
( )
2 2018
f
¢
= -
( )
f x
¢¢
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số đạt giá trị nhỏ nhất tại điểm thuộc khoảng nào sau đây?
A.
( )
; 2017- -
B.
( )
2017;
C.
( )
0;2
D.
( )
2017;0-
Lời giải
Dựa vào bảng xét dấu của
( )
f x
¢¢
ta có bảng biến thiên của hàm sồ
( )
f x
¢
Đặt
2017t x=
.
Ta có
( ) ( ) ( )
2017 2018 2018 2017.2018y f x x f t t g t= = - =
.
( ) ( )
2018g t f t
¢ ¢
=
.
Dựa vào bảng biến thiên của hàm số
( )
f x
¢
suy ra phương trình
( )
g t
¢
có một nghiệm đơn
( )
;0
-
và một nghiệm kép
2t =
.
Ta có bảng biến thiên
( )
g t
Hàm số
( )
g t
đạt giá trị nhỏ nhất tại
( )
0
;0t
= -
.
Suy ra hàm số đạt giá trị nhỏ nhất tại
0
x mà
( ) ( )
0 0
2017 ;0 ; 2017x x - Û - -
.
Câu 7. Cho hàm số
( )
f x
có đạo hàm là
( )
f x
¢
. Đồ thị của hàm số
( )
y f x
¢
=
được cho như hình vẽ dưới
đây:
Biết rằng
( ) ( ) ( ) ( )
1 0 1 2f f f f-
. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
( )
y f x=
trên
đoạn
1;2-
lần lượt là:
A.
( )
1f
;
( )
2f
. B.
( )
2f
;
( )
0f
. C.
( )
0f
;
( )
2f
. D.
( )
1f
;
( )
1f -
.
Lời giải
( )
2017 2018y f x x
=
0
x
( )
2017 2018y f x x
=
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Từ đồ thị của hàm số
( )
y f x
¢
=
ta có bảng biến thiên của hàm số
( )
y f x=
trên đoạn
1;2-
như
sau
Nhận thấy
( ) ( )
1;2
min 1f x f
-
=
.
 Để tìm
( )
1;2
max f x
-
ta so sánh
( )
1f -
và
( )
2f
.
Theo giả thiết,
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
1 0 1 2 2 1 0 1f f f f f f f f- Û - - -
.
Từ bảng biến thiên, ta có
( ) ( )
0 1 0f f-
. Do đó
( ) ( ) ( ) ( )
2 1 0 2 1f f f f- - Û -
.
Hay
( ) ( )
1;2
max 2f x f
-
=
.
Câu 8. Cho hàm số
( )
y f x=
liên tục trên đoạn
7
0;
2
có đồ thị hàm số
( )
'y f x=
như hình vẽ.
Hàm số
( )
y f x=
đạt giá trị nhỏ nhất trên đoạn
7
0;
2
tại điểm
0
x
nào dưới đây?
A.
0
0x =
. B.
0
7
2
x =
. C.
0
1x =
. D.
0
3x =
.
Lời giải
Chọn D
Dựa vào đồ thị hàm số
( )
'y f x=
ta có bảng biến thiên trên đoạn
7
0;
2
như sau:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó hàm số đạt giá trị nhỏ nhất tại
0
3x =
.
Câu 9. Cho hàm số
( )
y f x=
. Đồ thị hàm
( )
y f x
¢
=
như hình vẽ
Đặt
( ) ( )
3
3 3h x f x x x= -
. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
( )
[ 3; 3]
max ( ) 3 1h x f
-
=
. B.
( )
[ 3; 3]
max ( ) 3 3h x f
-
= -
.
C.
( )
[ 3; 3]
max ( ) 3 3h x f
-
=
. D.
( )
[ 3; 3]
max ( ) 3 0h x f
-
=
.
Lời giải
Chọn B
Ta có:
( ) ( )
2
3 3 3h x f x x
¢ ¢
= -
( ) ( )
( )
2
3 1h x f x x
¢ ¢
Û = - -
.
Đồ thị hàm số
2
1y x= -
là một parabol có toạ độ đỉnh
( )
0; 1C -
, đi qua
( )
3;2A - ,
( )
3;2B .
Từ đồ thị hai hàm số
y f x
và
2
1y x= -
ta có bảng biến thiên của hàm số
( )
y h x=
.
Với
( ) ( )
3 3 3h f- = - ,
( ) ( )
3 3 3h f= .
Vậy
[ 3; 3]
max ( ) 3 3h x f
.
Câu 10. Cho hàm số
( )
y f x=
có đồ thị
( )
y f x
¢
=
ở hình vẽ bên. Xét hàm số
( ) ( )
3 2
1 3 3
2018,
3 4 2
g x f x x x x= - -
mệnh đề nào dưới đây đúng?
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
A.
( ) ( )
3;1
min 1g x g
-
= -
. B.
( )
( ) ( )
3;1
3 1
min
2
g g
g x
-
-
= .
C.
( ) ( )
3;1
min 3g x g
-
= -
. D.
( ) ( )
3;1
min 1g x g
-
=
.
Lời giải
Chọn A
Ta có
( ) ( ) ( )
2 2
3 3 3 3
2 2 2 2
g x f x x x f x x x
¢ ¢ ¢
= - - = - -
.
Vẽ parabol
( )
2
3 3
:
2 2
P y x x= -
. Ta thấy
( )
P
đi qua các điểm có toạ độ
( )
3;3-
,
( )
1;2-
,
( )
1;1
.
 Trên khoảng
( )
3; 1- -
đồ thị hàm số
( )
f x
¢
nằm phía dưới
( )
P
nên
( ) ( )
2
3 3
0
2 2
f x x x g x
¢ ¢
-
.
 Trên khoảng
( )
1;1-
đồ thị hàm số
( )
f x
¢
nằm phía trên
( )
P
nên
( ) ( )
2
3 3
0
2 2
f x x x g x
¢ ¢
-
.
 Trên khoảng
( )
1;

đồ thị hàm số
( )
f x
¢
nằm phía dưới
( )
P
nên
( ) ( )
2
3 3
0
2 2
f x x x g x
¢ ¢
-
.
Bảng biến thiên
Từ bảng biến thiên, ta có
( ) ( )
3;1
min 1g x g
-
= -
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 11. Cho hàm số
( )
f x
. Biết hàm số
( )
y f x
¢
=
có đồ thị như hình vẽ bên dưới. Trên đoạn
4;3-
, hàm
số
( ) ( ) ( )
2
2 1g x f x x= -
đạt giá trị nhỏ nhất tại điểm:
A.
0
4x = - . B.
0
1x = - . C.
0
3x = . D.
0
3x = - .
Lời giải
Chọn B
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
2
2 1 ' 2 ' 2 1 ' 0 ' 1g x f x x g x f x x g x f x x= - = - - = Û = -
Vẽ hai đồ thị
( )
' 1y f x y x= = -
trên cùng một hệ trục
Từ đồ thị ta thấy
( ) ( )
' 0, 4; 1g x - -
và
( ) ( )
' 0, 1;3g x -
Vậy giá trị nhỏ nhất trên đoạn
4;3-
đạt tại điểm
0
1x = - .
Câu 12. Cho hàm số
( )
y f x=
có đạo hàm liên tục trên
R
. Hàm số
( )
'y f x=
có đồ thị như hình sau:
Cho bốn mệnh đề sau:
1) Hàm số
( )
y f x=
có hai cực trị
2) Hàm số
( )
y f x=
đồng biến trên khoảng
( )
1;
3)
( ) ( ) ( )
1 2 4 .f f f
4) Trên đoạn
1;4-
, giá trị lớn nhất của hàm số
( )
y f x=
là
( )
1 .f
Số mệnh đề đúng trong bốn mệnh đề trên là:
A.
3.
B.
1.
C.
4.
D.
2.
Lời giải
Chọn D
Dựa vào đồ thị của hàm số
( )
'y f x=
ta thấy:
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
( )
1
' 0 1
4
x
f x x
x
= -
= Û =
=
( ) ( ) ( )
' 0 ; 1 1;4f x x Û - -
( ) ( ) ( )
' 0 1;1 4;f x x Û - 
Ta có bảng biến thiên của hàm số
( )
y f x=
Dựa vào bảng biến thiên đáp án đúng là mệnh đề số
3
và
4
Câu 13. Cho hàm số
y f x
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
2 3 2
1 1
4 3 8
3 3
g x f x x x x x
trên đoạn
1;3 .
A.
25
.
3
B.
15.
C.
19
.
3
D.
12.
Lời giải
Chọn D
Ta có
2 2 2
4
4 .(4 2 x) x 6 8 2 2 (4 )
2
x
g x f x x x x f x x
Xét thấy
2 2
1;3 3 4 4 (4 ) 0x x x f x x
Mặt khác
4
0
2
x
1;3x
Suy ra
0 2g x x
19 17 17 32
1 (3) (4) 5
3 3 3 3
19 19 19 34
(3) (3) (4) 5
3 3 3 3
(2) 5 7 12.
g f f
g f f
g
1 3 2g g g
Vậy
1;3
max 12g x
tại
2.x
Câu 14. Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
¢
=
có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của
hàm số
( ) ( )
2
2 sing x f x x= -
trên đoạn
1;1-
là
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
( )
1f -
. B.
( )
0f
. C.
( )
2f
. D.
( )
1f
.
Lời giải
Chọn B
Ta có
1;1 2 2;2x x - -
.
Từ bảng biến thiên của
( )
'y f x=
thì bảng biến thiên
( )
y f x=
như sau:
Ta thấy
1;1x -
ta có
( ) ( )
( )
2
2 0
sin 0 sin 0
f x f
x
- =
, do đó
( ) ( ) ( )
0 0g x g f =
.
Dấu “=” xảy ra khi
0x =
.
Câu 15. Cho hàm số
( )
y f x=
liên tục trên
sao cho
( )
1;2
max 3f x
-
=
. Xét hàm số
( ) ( )
3 1g x f x m= -
.
Tìm tất cả các giá trị của tham số
m
để
( )
0;1
max 10g x = -
.
A.
13
. B.
7-
. C.
13-
. D.
1-
.
Lời giải
Chọn C
Đặt
3 1u x= -
( ) ( )
g x f u m =
.
0;1 1;2x u -
.
Do
( )
f x
liên tục trên
nên
( )
( )
( )
( )
0;1 1;2 1;2
max max max 3g x f u m f u m m
- -
= = =
.
Để
( )
0;1
max 10 13g x m= Û = -
.
Câu 16. Cho hàm số
( )
y f x=
có đạo hàm cấp 2 trên
, hàm số
( )
y f x
¢
=
có đồ thị như hình vẽ bên.
Giá trị lớn nhất của hàm số
sin 3cos
2
x x
y f
=
trên đoạn
5
;
6 6
-
bằng
A.
3
f
-
. B.
( )
0f
. C.
5
6
f
-
. D.
6
f
.
0
0
0
-2
210-1 +
-
0 +
0
-+
0-
2
0
-2
+
-
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Lời giải
Chọn A
Đặt
sin 3 cos
sin
2 3
x x
t x
= =
.
Vì
5
; ; 1;1
6 6 3 2 2
x x t
- - -
.
Dựa vào đồ thị của hàm số
( )
f x
¢
, ta có bảng biến thiên
Ta có:
( )
5
1;1
;
6 6
sin 3cos
max max
2
x x
f f t
-
-
=
0 sin 0
3 3
t x x
Û = Û = Û = -
.
Vậy
5
;
6 6
sin 3cos
max
2 3
x x
f f
-
= -
.
Câu 17. Cho hàm số
( )
y f x=
liên tục trên
sao cho
( ) ( )
0;10
max 2 4
x
f x f
= =
. Xét hàm số
( )
( )
3 2
2g x f x x x x m= -
. Giá trị của tham số
m
để
( )
0;2
max 8
x
g x
=
là
A.
5
. B.
4
. C.
1-
. D.
3
.
Lời giải
Chọn D
Đặt
3
t x x=
. Vì
0;2 0;10x t
.
Ta có:
( )
( )
( )
3 2 3 2
0;2 0;2 0;2 0;2
max max 2 max max 2
x x x x
g x f x x x x m f x x x x m
= - -
( )
0;10
max 1
t
f t m
=
(với
3
t x x=
và
2
0;2
max 2 1
x
x x m m
- =
).
( )
0;10
max 1 4 1 5
x
f x m m m
= =
.
Suy ra:
( )
0;2
1
max 5 1
2
x
x
g x m x
t
=
= Û Û =
=
.
Theo giả thiết, ta có:
( )
0;2
max 8 5 8 3
x
g x m m
= Û = Û =
.
Câu 18. Cho hai hàm số
( )
y f x=
,
( )
y g x=
có đạo hàm là
( )
f x
¢
,
( )
g x
¢
. Đồ thị hàm số
( )
y f x
¢
=
và
( )
g x
¢
được cho như hình vẽ bên dưới.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Biết rằng
( ) ( ) ( ) ( )
0 6 0 6f f g g- -
. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( ) ( ) ( )
h x f x g x= -
trên đoạn
0;6
lần lượt là:
A.
( )
6h
,
( )
2h
. B.
( )
2h
,
( )
6h
. C.
( )
0h
,
( )
2h
. D.
( )
2h
,
( )
0h
.
Lời giải
Ta có
( ) ( ) ( )
h x f x g x
¢ ¢ ¢
= -
.
( )
0 2h x x
¢
= Û =
Từ đồ thị ta có bảng biến thiên:
Và
( ) ( ) ( ) ( )
0 6 0 6f f g g- -
( ) ( ) ( ) ( )
0 0 6 6f g f gÛ - -
.
Hay
( ) ( )
0 6h h
.
Vậy
( ) ( )
0;6
max 6h x h=
;
( ) ( )
0;6
min 2h x h=
.
E. ỨNG DỤNG GTLN-GTNN GIẢI BÀI TOÁN THỰC TẾ
Câu 1. Ông
A
dự định dùng hết
2
6,5m kính để làm một bể cá có dạng hình hộp chữ nhật không nắp, chiều
dài gấp đôi chiều rộng (các mối ghép có không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu
(kết quả làm tròn đến hàng phần trăm).
A.
3
2,26 m B.
3
1,61m C.
3
1,33 m D.
3
1,50 m
Lời giải
Chọn D
Giả sử hình hộp chữ nhật có kích thước như hình vẽ. Ta có dung tích của bể cá:
=V abc
c
b
a
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
Mặt khác theo giả thiết ta có:
2 2 6,5
2
=
=
ab bc ac
a b
2
2 6 6,5
2
=
Û
=
b bc
a b
2
6,5 2
6
2
-
=
Û
=
b
c
b
a b
Khi đó
2
2
6,5 2
2 .
6
-
=
b
V b
b
3
6,5 2
3
-
Û =
b b
V
.
Xét hàm số:
( )
3
6,5 2
3
-
=
b b
f b
. Có BBT
Vậy bể cá có dung tích lớn nhất là:
3
39
1,50
6
=
f m
.
Câu 2. Một vật chuyển động theo quy luật
3 2
1
6
3
s t t= -
với
t
(giây) là khoảng thời gian tính từ khi vật bắt
đầu chuyển động và
s
(mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi
trong khoảng thời gian
9
giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng
bao nhiêu?
A.
243
(m/s) B.
27
(m/s) C.
144
(m/s) D.
36
(m/s)
Lời giải
Chọn D
Ta có:
2
12v s t t
¢
= = -
;
2 12v t
¢
= -
;
0 6v t
¢
= Û =
.
BBT
Nhìn bbt ta thấy vận tốc đạt giá trị lớn nhất khi
6t =
. Giá trị lớn nhất là
( )
6 36m/sv =
.
Câu 3. Ông A dự định sử dụng hết
2
5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không
nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích
lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
A.
3
1,01m
B.
3
0,96 m
C.
3
1,33 m
D.
3
1,51 m
Lời giải
Chọn A
Gọi
,x y
lần lượt là chiều rộng và chiều cao của bể cá (điều kiện
, 0x y
).
y
x
2
x
C
D
A
D'
B
C'
B'
A'
t
v
¢
v
0
9
6
0
36
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có thể tích bể cá
2
2V x y= .
Theo đề bài ta có:
2
2 2.2 2 5xy xy x =
2
6 2 5xy xÛ =
2
5 2
6
x
y
x
-
Û =
(Điều kiện kiện
2
0 5 2 0y x Û -
5
0
2
x
)
2 3
2
5 2 5 2
2
6 3
x x x
V x
x
- -
= =
2
5 6
3
x
V
-
¢
=
2
0 5 6 0V x
¢
= Û - =
5
6
xÛ =
3
max
5 30
1,01
27
V m =
.
Câu 4. Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám
sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ
được cho bởi công thức
( )
2
1
t
c t
t
=
( )
/mg L
. Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong
máu của bệnh nhân cao nhất?
A. 4 giờ. B. 1 giờ. C. 3 giờ. D. 2 giờ.
Lời giải
Xét hàm số
( )
2
1
t
c t
t
=
,
( 0)t
.
( )
( )
2
2
2
1
1
t
c t
t
-
¢
=
.
( )
1
0
1
t
c t
t
=
¢
= Û
= -
.
Với
1t =
giờ thì nồng độ thuốc trong máu của bênh nhân cao nhất.
Câu 5. Cho một tấm nhôm hình vuông cạnh
12
cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình
vuông bằng nhau, mỗi hình vuông có cạnh bằng
x
(cm), rồi gập tấm nhôm lại như hình vẽ dưới đây
để được một cái hộp không nắp. Tìm
x
để hộp nhận được có thể tích lớn nhất.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
A.
3x =
B.
2x =
C.
4x =
D.
6x =
Lời giải
Chọn B
Ta có :
( )
h x cm=
là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là:
( )
12 2x cm-
Vậy diện tích đáy hình hộp
( )
( )
2
2
12 2S x cm= -
. Ta có:
( )
0 0
0;6
12 2 0 6
x x
x
x x
Û Û
-
Thể tích của hình hộp là:
( )
2
. 1. 2 2V S xh x= -=
Xét hàm số:
( ) ( )
2
. 12 2 0;6y x x x= -
Ta có :
( ) ( ) ( )( )
2
' 12 2 4 12 2 12 2 12 6y x x x x x= - - - = - -
;
( ) ( )
' 0 12 2 . 12 6 0 2y x x x= Û - - = Û =
hoặc
6x =
(loại).
Suy ra với
2x =
thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là
( )
2 128y =
.
Câu 6. Đợt xuất khẩu gạo của tỉnh A thường kéo dài trong
2
tháng (
60
ngày). Người ta nhận thấy số lượng
xuất khẩu gạo tính theo ngày thứ
t
được xác định bởi công thức
( )
3 2
2
63 3240 3100
5
= - -S t t t t
với
( )
1 60 t
. Hỏi trong
60
ngày đó thì ngày thứ mấy có số lượng xuất khẩu gạo cao nhất.
A.
60
B.
45
C.
30
D.
25
Lời giải
Chọn B
( ) ( )
3 2 2
2 6
63 3240 3100 126 3240
5 5
¢
= - - = - S t t t t S t t t
Ta có:
( )
45
0
60
=
¢
= Û
=
t
S t
t
Câu 7. Một vật chuyển động theo quy luật
2 3
1
10
3
S t t= -
, với
t
(giây) là khoảng thời gian tính từ lúc vật bắt
đầu chuyển động và
( )
S m
là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
thời gian
15
giây từ lúc vật bắt đầu chuyển động vận tốc
( )
/v m s
của vật đạt giá trị lớn nhất tại thời
điểm
( )
t s
bằng:
A.
( )
8 s
. B.
( )
20
s
C.
( )
10 s
. D.
( )
15 s
.
Lời giải
Chọn C.
Ta có:
2 3
1
10
3
S t t
= -
( )
2
20
v t S t t
¢
= = -
.
Xét hàm số
( )
; 0;15
v t t
, ta có:
¢v t
( )
= 20 - 2t = 0 Û t = 10
.
( ) ( ) ( )
0 0; 15 75; 10 100
v v v= = =
. Do đó:
( )
0;15
max 100 10
v t t
= Û =
.
Câu 8. Một sợi dây có chiều dài
28m
được cắt thành hai đoạn để làm thành một hình vuông và một hình
tròn. Tính chiều dài (theo đơn vị mét) của đoạn dây làm thành hình vuông được cắt ra sao cho tổng
diện tích của hình vuông và hình tròn là nhỏ nhất?
A.
56
4
. B.
112
4
. C.
84
4
. D.
92
4
.
Lời giải
Gọi chiều dài của đoạn dây làm thành hình vuông là
x
(
m
) (
0 28
x
)
=> chiều dài của đoạn dây làm thành hình tròn là
28
x-
(
m
)
+) Diện tích hình vuông là:
2
2
4 16
x x
=
+) Bán kính hình tròn là: R =
28
2
x
-
=> Diện tích hình tròn:
2
2
2
28 784 56
.
2 4
x x x
R
- -
= =
+) Tổng diện tích hai hình:
2 2
2
784 56 4 14 196
16 4 16
x x x
x x
-
= -
Xét
2
4 14 196
( )
16
f x x x
= -
. Nhận thấy
( )f x
đạt giá trị nhỏ nhất tại
2
b
x
a
-
= =
( )
14 16 112
.
2 4 4
=
Vậy chiều dài của đoạn dây làm thành hình vuông để tổng diện tích của hai hình đạt giá trị nhỏ nhất
là
112
4
m
Câu 9. Một xưởng in có
15
máy in được cài đặt tự động và giám sát bởi một kỹ sư, mỗi máy in có thể in
được
30
ấn phẩm trong
1
giờ, chi phí cài đặt và bảo dưỡng cho mỗi máy in cho
1
đợt hàng là
48.000
đồng, chi phí trả cho kỹ sư giám sát là
24.000
đồng/giờ. Đợt hàng này xưởng in nhận
6000
ấn phẩm thì số máy in cần sử dụng để chi phí in ít nhất là
A.
10
máy. B.
11
máy. C.
12
máy. D.
9
máy.
Lời giải
Chọn A
Gọi
x
( )
0 15
x
là số máy in cần sử dụng để in lô hàng.
Chi phí cài đặt và bảo dưỡng là
48000x
.
Số giờ in hết số ấn phẩm là
6000
30x
, chi phí giám sát là
6000 48000
.24000
30x x
.
Tổng chi phí in là
( )
4800000
48000P x x
x
=
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
( )
2
4800000
48000P x
x
¢
= -
;
( )
( )
2
10
0 100
10
x
P x x
x L
=
¢
= Û = Û
= -
.
Bảng biến thiên:
Vậy chi phí in nhỏ nhất là
10
máy.
Câu 10. Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật
( )
3 2
4 12s t t t= -
(m), trong đó t (s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc
của chất điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu?
A. 2 (s). B.
8
3
(s). C. 0 (s). D.
4
3
(s).
Lời giải
( ) ( )
2
3 8v t s t t t
¢
= = -
.
( )
6 8v t t
¢
= -
. Có
( )
4
0
3
v t t
¢
= Û =
.
Dựa vào bảng biến thiên ta có
)
0;
4 16
min
3 3
v v
= = -
.
Vậy vận tốc của chất điểm đó đạt giá trị bé nhất khi
4
3
t =
.
Câu 11. Cho một tấm nhôm hình chữ nhật có chiều dài bằng
10cm
và chiều rộng bằng
8cm
. Người ta cắt bỏ
ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
( )
x cm
, rồi
gập tấm nhôm lại (như hình vẽ) để được một cái hộp không nắp. Tìm
x
để hộp nhận được có thể tích
lớn nhất.
A.
8 2 21
3
x
-
=
B.
10 2 7
3
x
-
=
C.
9 21
9
x
=
. D.
9 21
3
x
-
=
Lời giải
x
( )
P x
¢
( )
P x
0
15
10
0
-
( )
10
P
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn D
Ta có :
( )
h x cm=
là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là:
( )
10 2x cm-
và
( )
8 2x cm-
Vậy diện tích đáy hình hộp
( )( )
( )
2
10 2 8 2S x x cm= - -
. Ta có:
( )
0
0
10 2 0 0;4
4
8 2 0
x
x
x x
x
x
- Û Û
-
Thể tích của hình hộp là:
( ) ( )
. 10 2 . 8 2.S xV x xh - -= =
Xét hàm số:
( ) ( ) ( )
. 10 2 . 8 2 0;4y x x x x= - -
Ta có :
2
' 12 72 80y x x= - ;
( )
( )
9 21
4
3
' 0
9 21
3
x l
y
x n
=
= Û
-
=
.
Suy ra với
9 21
3
x
-
=
thì thể tích hộp là lớn nhất và giá trị lớn nhất.
Câu 12. Một đoàn cứu trợ lũ lụt đang ở vị trí
A
của một tỉnh miền trung muốn đến xã
C
để tiếp tế lương
thực và thuốc men. Để đi đến
C
, đoàn cứu trợ phải chèo thuyền từ
A
đến vị trí
D
với vận tốc
( )
4 /km h
, rồi đi bộ đến vị trí
C
với vận tốc
( )
6 /km h
. Biết
A
cách
B
một khoảng
5km
,
B
cách
C
một khoảng
7km
(hình vẽ). Hỏi vị trí điểm
D
cách
A
bao xa để đoàn cứu trợ đi đến xã
C
nhanh
nhất?
A.
5 3AD km=
. B.
2 5AD km=
. C.
5 2AD km=
. D.
3 5AD km=
.
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
Đặt
( )
AD x km=
,
( )
0x
. Ta có
( )
2 2 2
25 5
BD AD AB x x
= - = -
2
7 25CD BC BD x= - = - -
Thời gian đi từ A đến C là:
( )
2
7 25
4 6 4 6
AD DC x x
T x
- -
= =
( )
2
2 2
1 2 3 25 2
4
12 25 12 25
x x x
T x
x x
- - -
¢
= =
- -
.
( )
2
0 3 25 2 3 5T x x x x
¢
= Û - = Û =
Bảng biến thiên
Do đó
)
( )
( )
5;
14 5 5
min 3 5
12
x
T x T

= =
Vậy
( )
3 5AD km=
.
Câu 13. Một vật chuyển động theo quy luật
2 3
3s t t
. Thời điểm
( )t s
tại đó vận tốc
( / )v m s
của chuyển
động đạt giá trị lớn nhất là
A.
5t
. B.
1t
. C.
2t
. D.
3t
Lời giải
Chọn B
Vận tốc của chuyển động là
'v s
tức là
2
( ) 6 3 , 0v t t t t
'( ) 6 6 , ( ) 0' 1v t t v t t
Bảng biến thiên:
Hàm số v(t) đồng biến trên khoảng (0;1) và nghịch biến trên khoảng
1;
Max
3v t
khi
1t
.
Û
t
0
1
+
∞
'( )v t
+
0
–
( )v t
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 14. Ông A dự định sử dụng hết
2
5 m
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không
nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích
lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
A.
3
1,01m
. B.
3
0,96 m
. C.
3
1,33 m
. D.
3
1,51m
.
Lời giải
Chọn A
Gọi
,x y
lần lượt là chiều rộng và chiều cao của bể cá (điều kiện
, 0x y
).
Ta có thể tích bể cá
2
2=V x y
.
Theo đề bài ta có:
2
2 2.2 2 5 =xy xy x
2
6 2 5Û =xy x
2
5 2
6
-
Û =
x
y
x
(Điều kiện kiện
2
0 5 2 0 Û - y x
5
0
2
x
)
2 3
2
5 2 5 2
2
6 3
- -
= =
x x x
V x
x
2
5 6
3
-
¢
=
x
V
2
0 5 6 0
¢
= Û - =V x
5
6
Û =x
x
3
ma
5 30
1,01
27
= mV
.
Câu 15. Một người nông dân có 15.000.000 đồng muốn làm một cái hàng rào hình chữ E dọc theo một con
sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào song
song với bờ sông thì chi phí nguyên vật liệu là 60.000 đồng một mét, còn đối với ba mặt hàng rào
song song nhau thì chi phí nguyên vật liệu là 50.000 đồng một mét. Tìm diện tích lớn nhất của đất
rào thu được
A.
2
3125m . B.
2
50m . C.
2
1250m . D.
2
6250m .
Lời giải
Chọn D
Gọi
x
là chiều dài 1 mặt hàng rào hình chữ E ( trong ba mặt song song,
0x
).
Gọi
y
là chiều dài mặt hàng rào hình chữ E song song với bờ sông (
0y
).
Số tiền phải làm là:
500 5
.3.50000 .60000 15.000.000
2
x
x y y
-
= Û =
.
Diện tích đất:
2
500 5 5
. . 250
2 2
x
S x y x x x
-
= = = -
y
x
2
x
C
D
A
D'
B
C'
B'
A'
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
Ta có:
' 250 5S x= -
.
' 0 250 5 50.S x x= Û - Û =
Bảng biến thiên:
Vậy:
( )
2
0;
max 6250 ( )S m

=
khi
50.x =
Câu 16. Một người đàn ông muốn trèo thuyền ở vị trí
A
tới điểm
B
về phía hạ lưu bờ đố diện, càng nhanh
càng tốt, trên một bờ sông thẳng rộng 3 km ( như hình vẽ). Anh có thể chèo thuyền của mình trực
tiếp qua sông để đến
C
và sau đó chạy đến
B
, hay có thể chèo trực tiếp đến
B
, hoặc anh có thể
chèo thuyền đến một điểm
D
giữa
C
và
B
và sau đó chạy đến
B
. Biết anh ấy có thể chèo thuyền 6
km/h, chạy 8 km/h và quãng đường
8 kmBC =
. Biết tốc độ của dòng nước là không đáng kể so với
tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất( đơn vị: giờ) để người đàn
ông đến
B
?
A.
73
6
. B.
3
2
. C.
9
.
7
D.
7
1
8
.
Lời giải
Chọn D
Đặt
( )
km , 0 8 .DC x x=
Ta có:
2
9 ,AD x=
=8 .DB x-
Thời gian đi từ
A
đến
B
được tính bằng công thức
( )
2
9 8
.
6 8
x x
f x
-
=
( ) ( )
( )
2 2
2 2
0
1 1 9
, 0
16 9 9
8 8
7
6 9 6 9
x
x x
f x f x x
x x
x x
¢ ¢
= - = Û = Û Û =
=
(thỏa mãn điều
kiện
0 8x
).
Mặt khác,
( ) ( )
3 73 9 7
0 , 8 , 1 .
2 6 8
7
f f f
= = =
-
∞
50
0
S'
S
0
x
+
+
∞
0
6250
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 56 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy thời gian ngắn nhất để người đàn ông đi từ
A
đến
B
là
7
1
8
(giờ).
Câu 17. Ông Khoa muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích
bằng
3
288m
. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể
là
500000
đồng/
2
m
. Nếu ông Khoa biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân
công sẽ thấp nhất. Hỏi ông Khoa trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu (Biết độ dày
thành bể và đáy bể không đáng kể)?
A.
90
triệu đồng. B.
168
triệu đồng. C.
54
triệu đồng. D.
108
triệu đồng.
Lời giải
Chọn D
Theo bài ra ta có để chi phí thuê nhân công là thấp nhất thì ta phải xây dựng bể sao cho tổng diện tích
xung quanh và diện tích đáy là nhỏ nhất.
Gọi ba kích thước của bể là
a
,
2a
,
c
( ) ( )
( )
0, 0a m c m
.
Ta có diện tích cách mặt cần xây là
2 2
2 4 2 2 6S a ac ac a ac= =
.
Thể tích bể
2
.2 . 2 288V a a c a c= = =
2
144
c
a
=
.
Suy ra
2 2 2 2
3
2
144 864 432 432 432 432
2 6 . 2 2 3. 2 . . 216S a a a a a
a a a a a a
= = = =
.
Vậy
2
min
216 mS =
, khi đó chi phí thấp nhất là
216.500000 108=
triệu đồng.
Câu 18. Hình vẽ bên dưới mô tả đoạn đường đi vào GARA ÔTÔ nhà cô Hiền. Đoạn đường đầu tiên có chiều
rộng bằng
( )
x m
, đoạn đường thẳng vào công GARA có chiều rộng
( )
2,6 m
. Biết kích thước xe ôtô
là
5 1,9m m
(chiều dài
chiều rộng). Để tính toán và thiết kế đường đi cho ôtô người ta coi ôtô như
một khối hộp chữ nhật có kích thước chiều dai
5m
, chiều rộng
1,9m
. Hỏi chiều rộng nhỏ nhất của
đoạn đường đầu tiên gần nhất với giá trị nào trong các giá trị bên dưới để ôtô có thể đi vào GARA
được?(giả thiết ôtô không đi ra ngoài đường, không đi nghiêng và ôtô không bị biến dạng).
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57
A.
( )
3,55x m=
. B.
( )
2,6x m=
. C.
( )
4,27x m=
. D.
( )
3,7 m
.
Lời giải
Chọn D
Chọn hệ trục tọa độ
Oxy
như hình vẽ.
Khi đó
( )
2,6;M x-
.
Gọi
( )
;0B a-
, suy ra
(
)
2
0; 25A a-
. Phương trình
2
: 1 0
25
x y
AB
a
a
- =
-
-
.
Do
CD
//
AB
nên phương trình
2
: 0
25
x y
CD T
a
a
- =
-
-
.
Mà khoảng cách giữa
AB
và
CD
bằng
1,9
nên
2 2
2
2
1
9,5
1,9 1
25
1 1
25
T
T
a a
a
a
-
= =
-
-
Điều kiện đề ôtô đi qua được là
,M O
nằm khác phía đối với bờ là đường thẳng
CD
.
Suy ra:
2 2
2,6 9,5
1 0
25 25
x
a
a a a
-
- -
-
- -
2
2
9,5 2,6 25
25
a
x a
a a
-
Û - -
đúng với mọi
( )
0;5a
.
( )
( )
0;5
maxx f aÛ
Xét hàm số
( )
2
2
9,5 2,6 25
25
a
f a a
a a
-
= - -
trên
( )
0;5
Ta có:
( )
2
2 2 2
19 65
2
25 25
a
f a
a
a a a
-
¢
= -
- -
( )
3 2
2
2 2 2
65 19 19
0 65 25
2 2
25 25
a
f a a a
a
a a a
¢
= Û = Û = -
- -
( )
3 2 6 3 2
2 65 19 25 4 520 361 7875 0a a a a aÛ - = - Û - =
( )
( )
( )
2
2
3
19 3
2 9 3 *
25 4
a
a
a a
a
=
Û
=
-
Xét phương trình (*). Với mọi
( )
0;5a
ta luôn có:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 58 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
( ) ( )
( )
( )
( )
( )
2
2 2
19 3 19 3
4
25 4
19 3 19 3
1
2 9 3 8 5 15 0
4 4 4
a a
VP
a
a a
VT a a a a
=
-
- = - =
Suy ra phương trình (*) vô nghiệm.
Bảng biến thiên:
Từ bảng biến thiên ta có:
( )
( )
0;5
37
max
10
f a =
. Vậy giá trị nhỏ nhất của
x
là
3,7
.
Câu 19. Một người nông dân có 3 tấm lưới thép B40, mỗi tấm dài
( )
12 m
và muốn rào một mảnh vườn dọc
bờ sông có dạng hình thang cân
ABCD
như hình vẽ (bờ sông là đường thẳng
DC
không phải rào,
mỗi tấm là một cạnh của hình thang). Hỏi ông ta có thể rào được mảnh vườn có diện tích lớn nhất là
bao nhiêu
2
m
?
A.
100 3
. B.
106 3
. C.
108 3
. D.
120 3
.
Lời giải
Chọn C
Kẻ đường cao
BH
, gọi số đo 2 góc ở đáy
CD
của hình thang là
( )
, 0 ;90x x
.
Diện tích mảnh vườn là:
( ) ( ) ( )
2
1 1 1
.sin 2. 2 .cos 2sin sin 2
2 2 2
S BH AB CD BC x AB BC x AB x x= = =
Xét hàm số
( )
2sin sin 2f x x x=
với
( )
0 0
0 ;90x
có
( )
2cos 2cos2f x x x
¢
=
.
Ta có:
( )
2
1
cos
0 2cos 2cos 2 0 2cos cos 1 0
2
cos 1
x
f x x x x x
x
=
¢
= Û = Û - = Û
= -
Do
( )
0 0
0 ;90x
nên ta nhận
0
1
cos 60
2
x x= Û =
. Ta có bảng biến thiên:
C
D
B
A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 59
Từ bảng biến thiên ta thấy:
( )
( )
0 0
0 ;90
3 3
max
2
f x
đạt được tại
0
60x =
.
( )
2
max 108 3S m =
khi góc ở đáy
CD
của hình thang bằng
0
60
( )
0
60C D= =
.
Câu 20. Cho hình vuông
ABCD
có cạnh bằng 4, chính giữa có một hình vuông đồng tâm với
ABCD
. Biết
rằng bốn tam giác là bốn tam giác cân. Hỏi tổng diện tích của hình vuông ở giữa và bốn tam giác cân
nhỏ nhất bằng bao nhiêu?
A.
19
3
. B.
17
3
. C.
16
3
. D.
14
3
.
Lời giải
Chọn C
Đặt
( )
0 4 4 2AM x x ME x= = -
.
( )
2
2
2 2
2 4 2
2(2 )
2(2 )
MQ x
MQ x
MQ x
= -
Û = -
Û = -
Gọi
S
tổng diện tích của hình vuông ở giữa và bốn tam giác cân nhỏ.
2
2 2 2 2 2 2
4. 2 (4 2 ) ( 2) 6 16 16
2
MQ
S PQ MQ MN x x x x= = = - = -
4
' 12 16 0
3
S x x= - = Û =
Bảng biến thiên
B
A
D
C
4
x
4-2x
M
N
E
P
B
A
D
C
Q
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 60 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
min
16
3
S =
Câu 21. Cho nửa đường tròn đường kính
2AB =
và hai điểm
C
,
D
thay đổi trên nửa đường tròn đó sao cho
ABCD
là hình thang. Diện tích lớn nhất của hình thang
ABCD
bằng
A.
1
2
. B.
3 3
4
. C.
1
. D.
3 3
2
.
Lời giải
Chọn B
Gọi
H
là hình chiếu vuông góc của
D
lên
AB
,
I
là trung điểm của đoạn
CD
và
O
là trung điểm
của
AB
. Đặt
DH x=
,
0 1x
. Ta có
2 2 2
2 2 2 2 1DC DI OH OD DH x= = = - = -
.
Diện tích của hình thang
ABCD
là
( )
( )
(
)
2
1 1
2
AB CD DH
S f x x x
= = = - .
Ta có
( )
2 2
2
1 1 2
1
x x
f x
x
- -
¢
=
-
.
( )
2 2
0 1 1 2 0f x x x
¢
= Û - - =
(*)
Đặt
2
1t x= -
, (điều kiện
0t
) khi đó phương trình (*) trở thành
2
1
2 1 0
1
2
t
t t
t
= -
- = Û
=
.
1t = -
loại.
1
2
t =
ta có
2 2
1 3 3
1
2 4 2
x x x- = Û = Û =
.
Bảng biến thiên
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 61
Vậy diện tích lớn nhất của hình thang
ABCD
bằng
3 3
4
.
Câu 22. Một người đàn ông muốn chèo thuyền ở vị trí
A
tới điểm
B
về phía hạ lưu bờ đối diện, càng nhanh
càng tốt, trên một bờ sông thẳng rộng
3 km
(như hình vẽ). Anh có thể chèo thuyền của mình trực
tiếp qua sông để đến
C
và sau đó chạy đến
B
, hay có thể chèo trực tiếp đến
B
, hoặc anh ta có thể
chèo thuyền đến một điểm
D
giữa
C
và
B
và sau đó chạy đến
B
. Biết anh ấy có thể chèo thuyền
6 km/ h
, chạy
8 km/ h
và quãng đường
8 kmBC =
. Biết tốc độ của dòng nước là không đáng kể so
với tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất (đơn vị: giờ) để người
đàn ông đến
B
.
A.
3
2
. B.
9
7
. C.
73
6
. D.
7
1
8
.
Lời giải
Cách 1: Anh chèo thuyền của mình trực tiếp qua sông để đến
C
và sau đó chạy đến
B
Thời gian chèo thuyền trên quãng đường
AC
:
3
0,5
6
=
(giờ)
Thời gian chạy trên quãng đường
CB
:
8
1
8
=
(giờ)
Tổng thời gian di chuyển từ
A
đến
B
là
1,5
(giờ).
Cách 2: chèo trực tiếp trên quãng đường
2 2
3 8 73AB = =
mất
h
73
1 26
6
¢
.
Cách 3:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 62 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
( )
kmx
là độ dài quãng đường
BD
;
( )
8 kmx-
là độ dài quãng đường
CD
.
Thời gian chèo thuyền trên quãng đường
2
9AD x=
là:
2
9
6
x
(giờ)
Thời gian chạy trên quãng đường
DB
là:
8
8
x-
(giờ)
Tổng thời gian di chuyển từ
A
đến
B
là
( )
2
9 8
6 8
x x
f x
-
=
Xét hàm số
( )
2
9 8
6 8
x x
f x
-
=
trên khoảng
( )
0; 8
Ta có
( )
2
1
8
6 9
x
f x
x
¢
= -
;
( )
2
9
0 3 9 4
7
f x x x x
¢
= Û = Û =
Bảng biến thiên
Dựa vào BBT ta thấy thời gian ngắn nhất để di chuyển từ
A
đến
B
là
h
7
1 1 20
8
¢
.
Vậy khoảng thời gian ngắn nhất để người đàn ông đến
B
là
h
7
1 1 20
8
¢
.
Câu 23. Bác thợ hàn dùng một thanh kim loại dài
250 cm
để uốn thành khung cửa sổ có dạng như hình vẽ.
Gọi
r
là bán kính của nửa đường tròn, tìm
r
để diện tích tạo thành đạt giá trị lớn nhất.
A.
250
cm
4
. B.
125
cm
4
. C.
250
cm
4
. D.
125
cm
4
.
Lời giải
* Gọi
1
S ,
2
S lần lượt là diện tích của nửa hình tròn và hình chữ nhật. Khi đó:
2
1
1
2
S r
=
;
2
2S rh= ; với
( )
2 250 2h r r
= -
nên
2 2
2
250 2S r r r
= - -
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 63
* Suy ra diện tích hình cần tìm
2 2 2 2 2
1 1
250 2 2 250
2 2
S r r r r r r r
= - - = - -
. Bài toán trở
thành tìm giá trị lớn nhất của hàm số
( )
2 2
1
2 250
2
S r r r r
= - -
với
0 125r
.
* Ta có
( ) ( )
4 250S r r
¢
= -
;
( )
250
0
4
S r r
¢
= Û =
. Đây là cực trị duy nhất của hàm số đồng
thời
( )
S r
¢
đổi dấu từ dương sang âm khi
r
qua
250
4
nên hàm số đạt giá trị lớn nhất tại điểm này.
Câu 24. Cho một tấm nhôm hình vuông cạnh
6
cm. Người ta muốn cắt một hình thang như hình vẽ.
Tìm tổng
x y
để diện tích hình thang
EFGH
đạt giá trị nhỏ nhất.
A.
4 2
. B.
7 2
2
. C.
7
. D.
5
.
Lời giải
Ta có
( )
EFGH ABCD AHE DHG GCF EBF
S S S S S S= -
.
Để diện tích hình thang
EFGH
đạt giá trị nhỏ nhất thì
AHE DHG GCF
S S S đạt giá trị lớn nhất.
Ta có
1
.
2
AHE
S AE AH=
1
.2.
2
x=
x=
;
1
.
2
DHG
S DH DG=
$SC$;
1
.
2
CGF
S CG CF=
1
3
2
y=
.
Đặt
AHE DHG GCF
S S S S= thì
( )
1
2 3 36 6 6
2
S x y x y xy= - -
( )
1
36 4 3
2
xy x y= - -
(1).
Mặt khác ta lại có
AEH CGF ∽
6
AH AE
xy
CF CG
= =
(2).
Thay (2) vào (1) ta có
1 18
42 4
2
S x
x
= -
.
Ta có
S
lớn nhất khi
18
4x
x
nhỏ nhất
18
4x
x
Û =
3 2
2
xÛ =
.
Khi
3 2
2
x =
thì
2 2y =
. Vậy
7 2
2
x y =
.
Câu 25. Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng
3
500
3
m
.
Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là
500.000
đồng/m
2
. Hãy xác định kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất và chi phí
đó là:
A.
74
triệu đồng. B.
75
triệu đồng. C.
76
triệu đồng. D.
77
triệu đồng.
x
cm
y
cm
3 cm
2 cm
H
G
F
E
D
C
B
A
NG
UYỄN BẢO VƯƠNG - 0946798489
Trang 64 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Giả sử khối hộp chữ nhật là
.ABCD A B C D
¢ ¢ ¢ ¢
và
AB x=
,
2AD x=
và
AA h
¢
=
(
, 0x
h
).
Ta có
.2 .V
x x h=
2
500
2
3
x hÛ =
2
250
3
h
x
Û =
.
Diện tí
ch cần xây là
( )
2
2 2
2S x xh xh=
2
2 6x
xh=
.
Ta cần tìm giá trị nhỏ nhất của
2
500
2S x
x
=
với
0x
.
Ta có
2 2
3
250
250 250 250
2 3 2 . .x x
x x x x
2
250 25
0
2 150x
x x
Û
.
Dấu đẳ
ng thức xảy ra khi
2
250
2x
x
=
5xÛ =
.
S
nhỏ nhất là
150
khi
x = 5
.
Số tiền chi phí là
150.500000 = 75000000
hay
75
triệu đồng.
C'
D'
B'
B
D
A
C
A'
| 1/82
| | Tải xuống

Có thể bạn quan tâm:

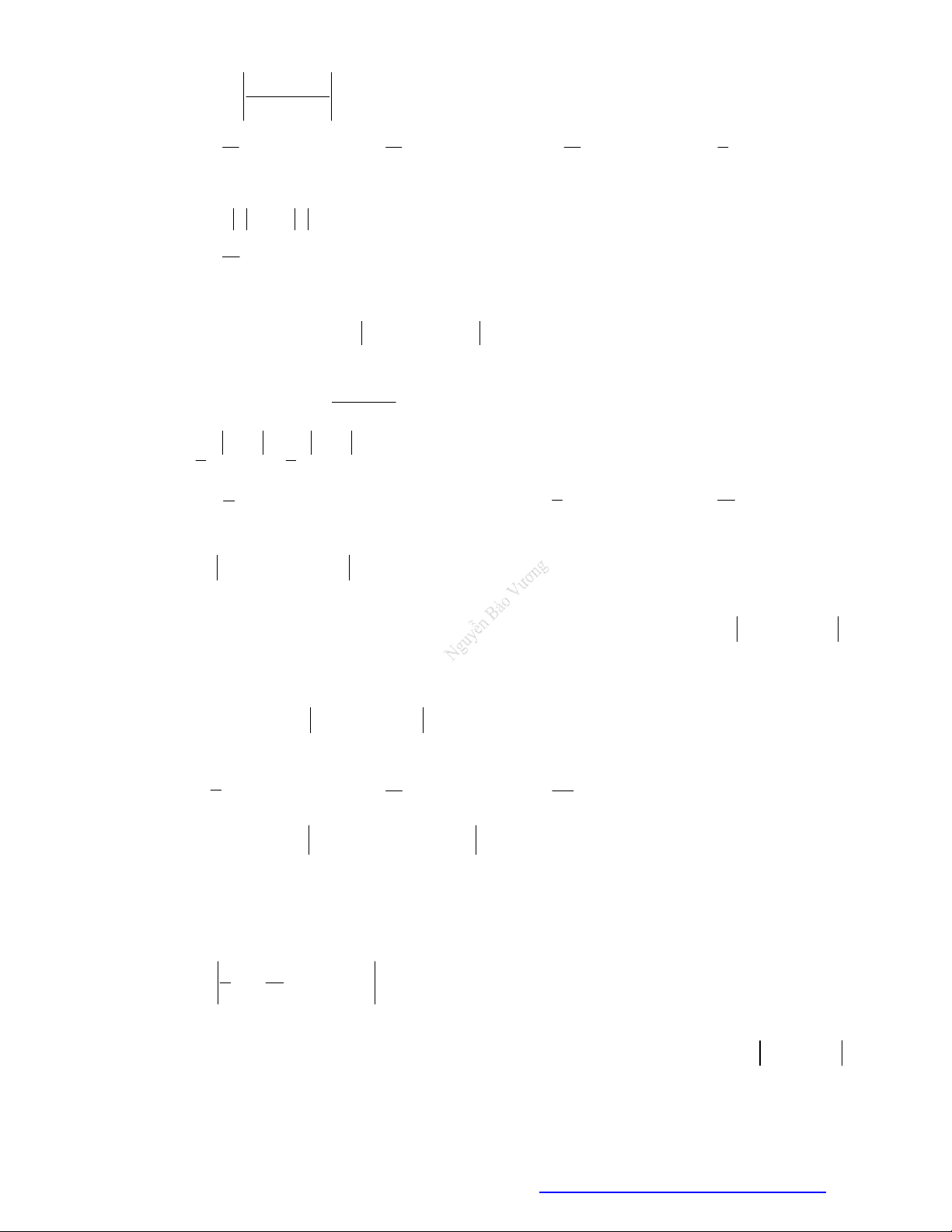
Preview text:


TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 4
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT
A. TÌM GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Định lí 1: Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn đó. Định lí 2
Nếu y f (x) đồng biến trên [a;b] thì min f (x)  f (a) và max f (x)  f (b). [a;b ] [a;b ]
Nếu y f (x) nghịch biến trên [a;b] thì min f (x)  f (b) và max f (x)  f (a). [a;b ] [a;b ]
Bài toán 1. Tìm GTLN & GTNN của hàm số y f (x ) trên đoạn [ ; a b].
Bước 1. Hàm số đã cho xác định và liên tục trên đoạn [ ; a b]. Tính f (
x)  0 tìm nghiệm x  [a;b]. i
Bước 2. Tính f (a), f (b), f (x ). i
Bước 3. Kết luận: max f (x)  max f (a); f (b); f (x
và min f (x)  min f (a); f (b); f (x i  ) . i  ) [a;b ] [a;b ]
Bài toán 2. Tìm GTLN & GTNN của hàm số y f (x ) trên khoảng (a;b).
Bước 1. Tìm tập xác định. Tính f (
x). Cho f (x)  0 tìm nghiệm.
Bước 2. Xét dấu biểu thức y  f (
x) và lập bảng biến thiên (có tính giới hạn).
Bước 3. Dựa vào bảng biến thiên để kết luận GTLN (GTNN nếu có).
Lưu ý: Đạo hàm của hàm số mũ và lôgarit  ( u )  . u a
ua .lna.  ( u )  . u e
ue .  ( x ) x
e   e . u 1 u   (log u) 
 (log x)   u     x  1 (ln ) ln   a u lna a x lna u x
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA Câu 1.
Giá trị lớn nhất của hàm số 4 2
f (x)  x 12x 1 trên đoạn 1; 2bằng: A. 1. B. 37 . C. 33 . D. 12 . Câu 2.
Giá trị nhỏ nhất của hàm số f x 4 2
x 10x  2 trên đoạn  1  ;  2 bằng A. 2 . B. 23  . C. 2  2. D. 7  . Câu 3.
Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số 4 2
y x  8x  5 trên đoạn  3  ;  1 .
Khi đó, giá trị của biểu thức M  2m bằng A. 46 . B. 25 . C. 2  5 . D. 4  6 . Câu 4.
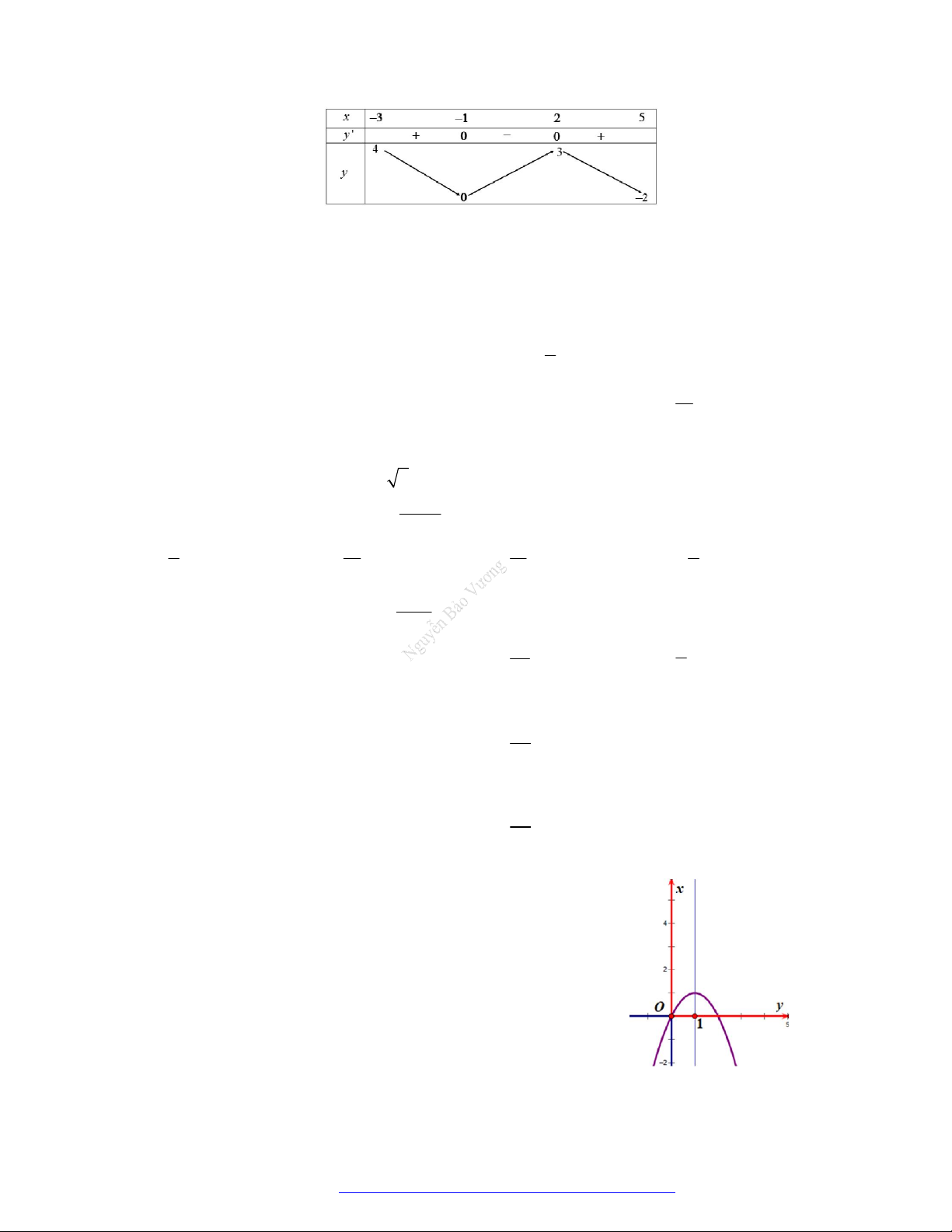
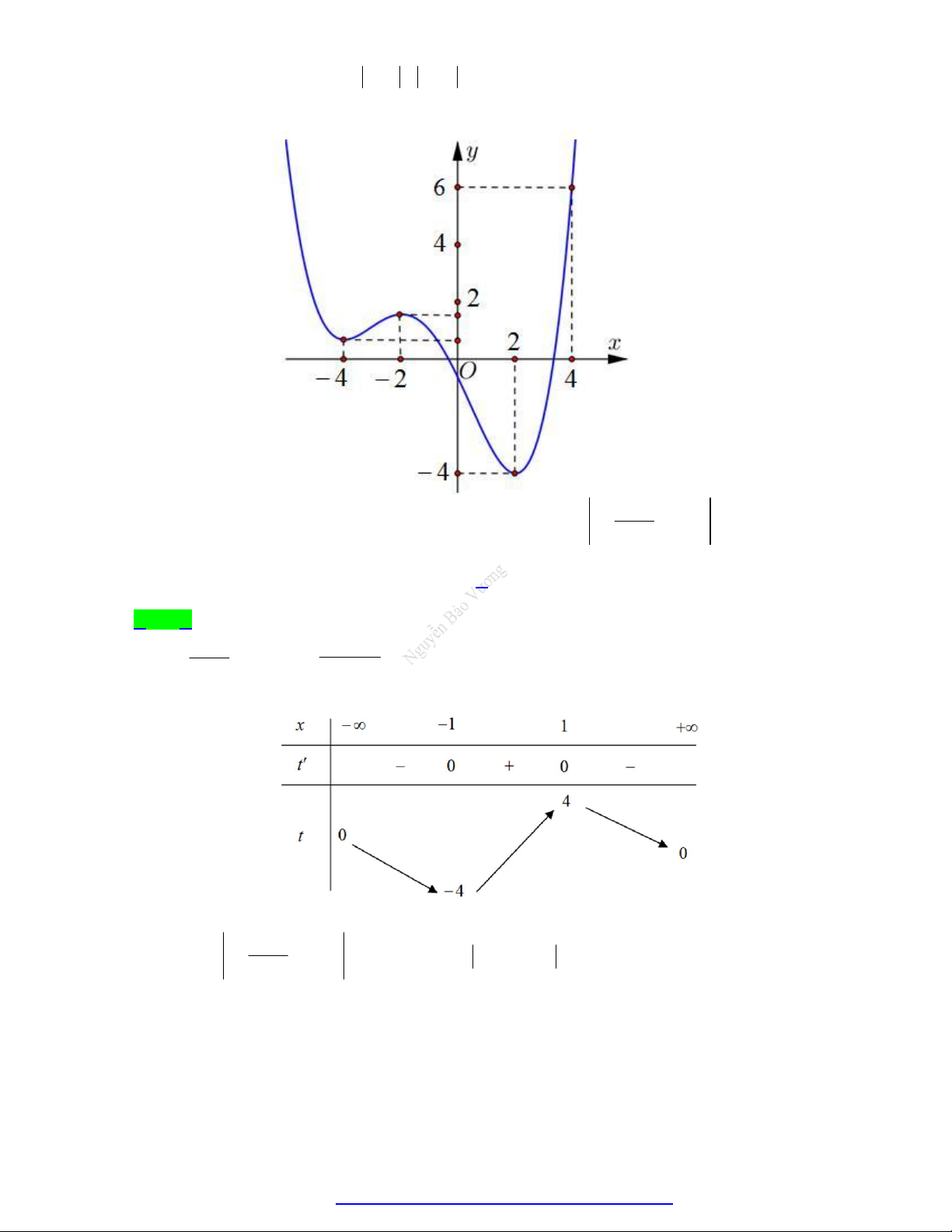
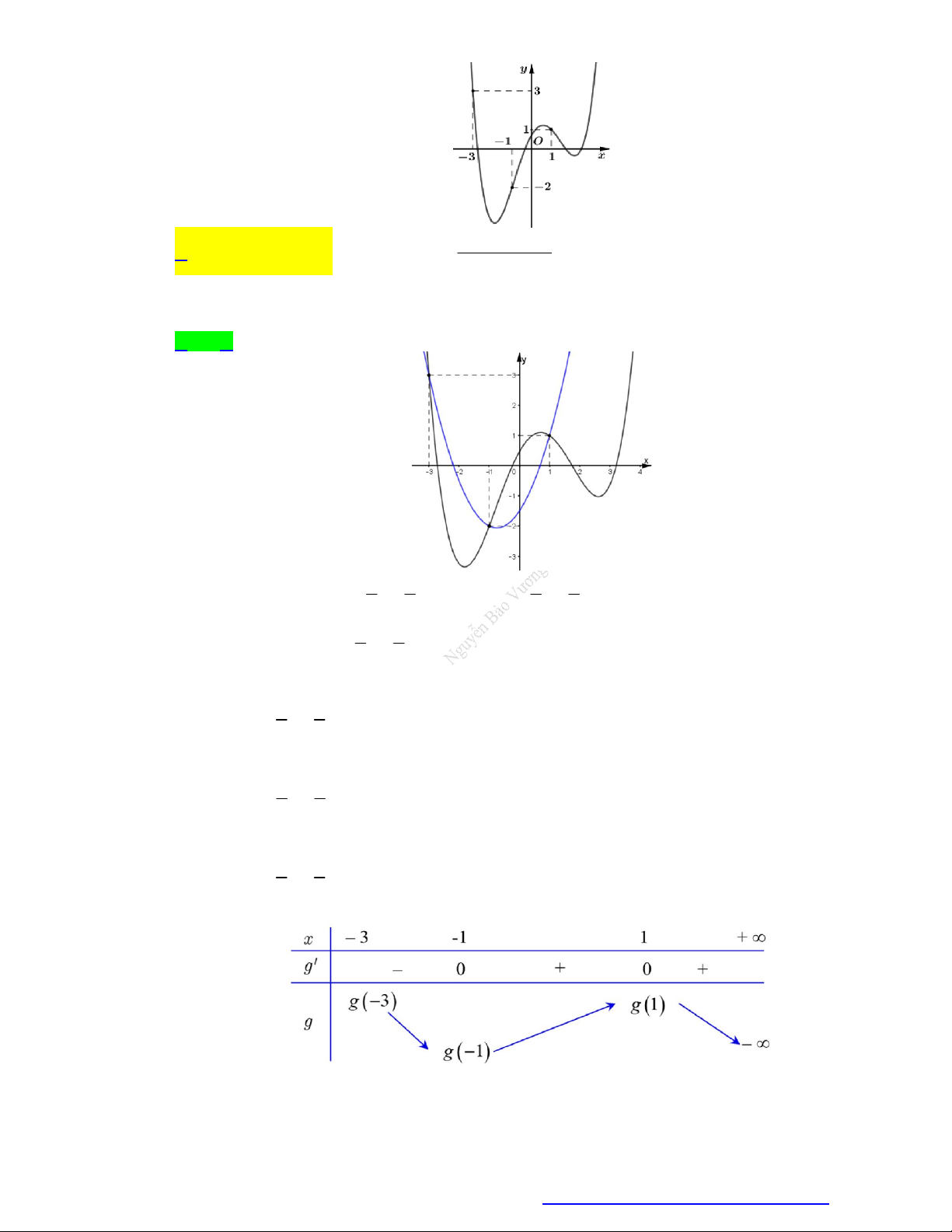
Cho hàm số y f x liên tục trên đoạn  3  ; 
3 có đồ thị như hình vẽ.
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y f x trên 0; 
3 lần lượt có giá trị là
A. max y  4, min y  3 . 4;3 4;3
B. max y  3, min y  3  .  4  ;  3  4  ;  3
C. max y  3, min y  2  . 0  ;3 0;3
D. max y  4, min y  2  .  4  ;  3  4  ;  3 16 Câu 5.
Giá trị nhỏ nhất của hàm số y x
 3 trên đoạn 1;5 là: x 5 6 A. 5  . B. 20 . C. . D. 11. 5
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 6.
Cho hàm số f x liên tục trên  3  ; 
5 và có bảng biến thiên như hình vẽ. Gọi M , m lần lượt là giá trị
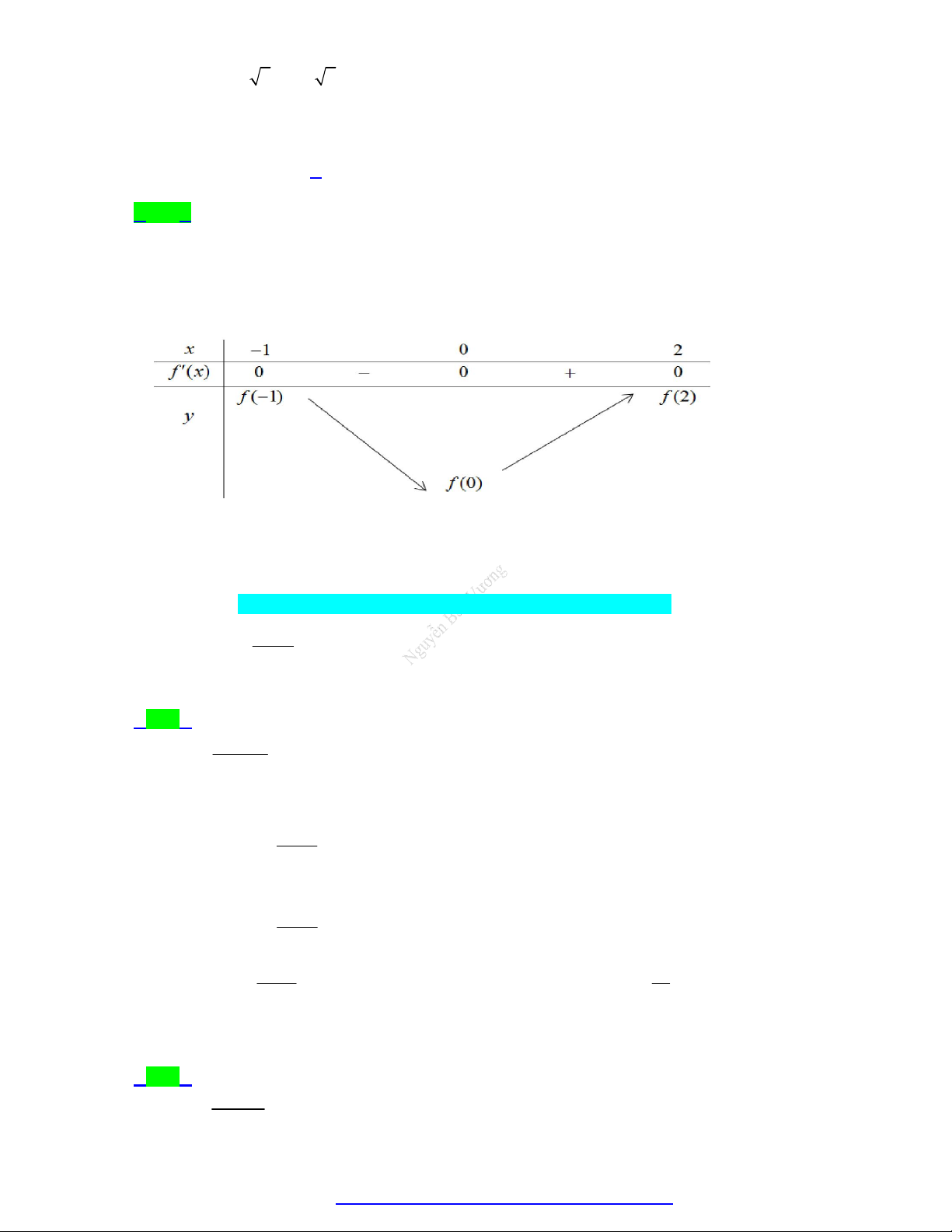
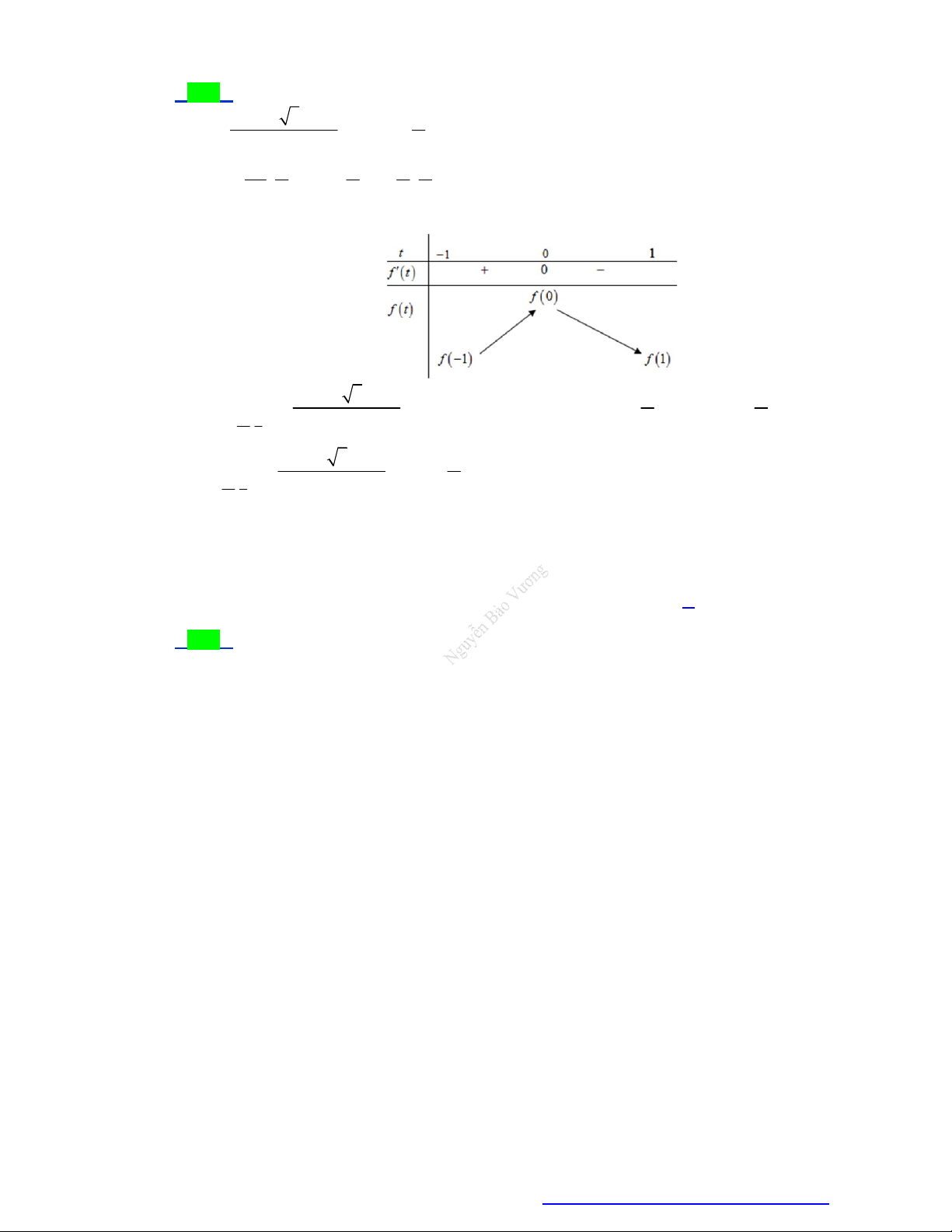
lớn nhất và nhỏ nhất của f x trên [  3; 2] . Tính M m . A. 6 . B. 4 . C. 5 . D. 3. 2 Câu 7. Cho hàm số f ( )
x có đạo hàm f ' x  xx  3  x  4, x
   . Giá trị lớn nhất của hàm số đã cho trên đoạn 0;  5 bằng A. f 0 . B. f 4 . C. f 3 . D. f 5 .  3  Câu 8.
Giá trị lớn nhất của hàm số 3
y  x  3x  5 trên đoạn 0;  bằng: 2    31 A. 3. B. 5. C. 7. D. . 8 Câu 9.
Giá trị lớn nhất của hàm số 3
f (x)  x  6x  3 trên đoạn 0; 2bằng: A. 3  . B. 3   4 2 . C. 25 . D. 12 . 8
Câu 10. Giá trị nhỏ nhất của hàm số f x 
x trên đoạn 1;  2 bằng: 1  2x 7 18 11 9 A. . B. . C. . D.  . 2 5 3 2 2  x
Câu 11. Giá trị nhỏ nhất của hàm số f (x)  trên đoạn 1;  3 bằng: x  3 1 1 A. 3 . B. 2  . C. . D. . 6 4
Câu 12. Giá trị nhỏ nhất của hàm số 3 2
f (x)  x x  5x  6 trên đoạn 0; 4bằng: 2 A. 3 . B. 2  . C. . D. 6 . 27
Câu 13. Giá trị nhỏ nhất của hàm số f x 3 2
x  8x 16x  9 trên đoạn 1;  3 bằng: 13 A. 9  . B. 6  . C. . D. 0 . 27
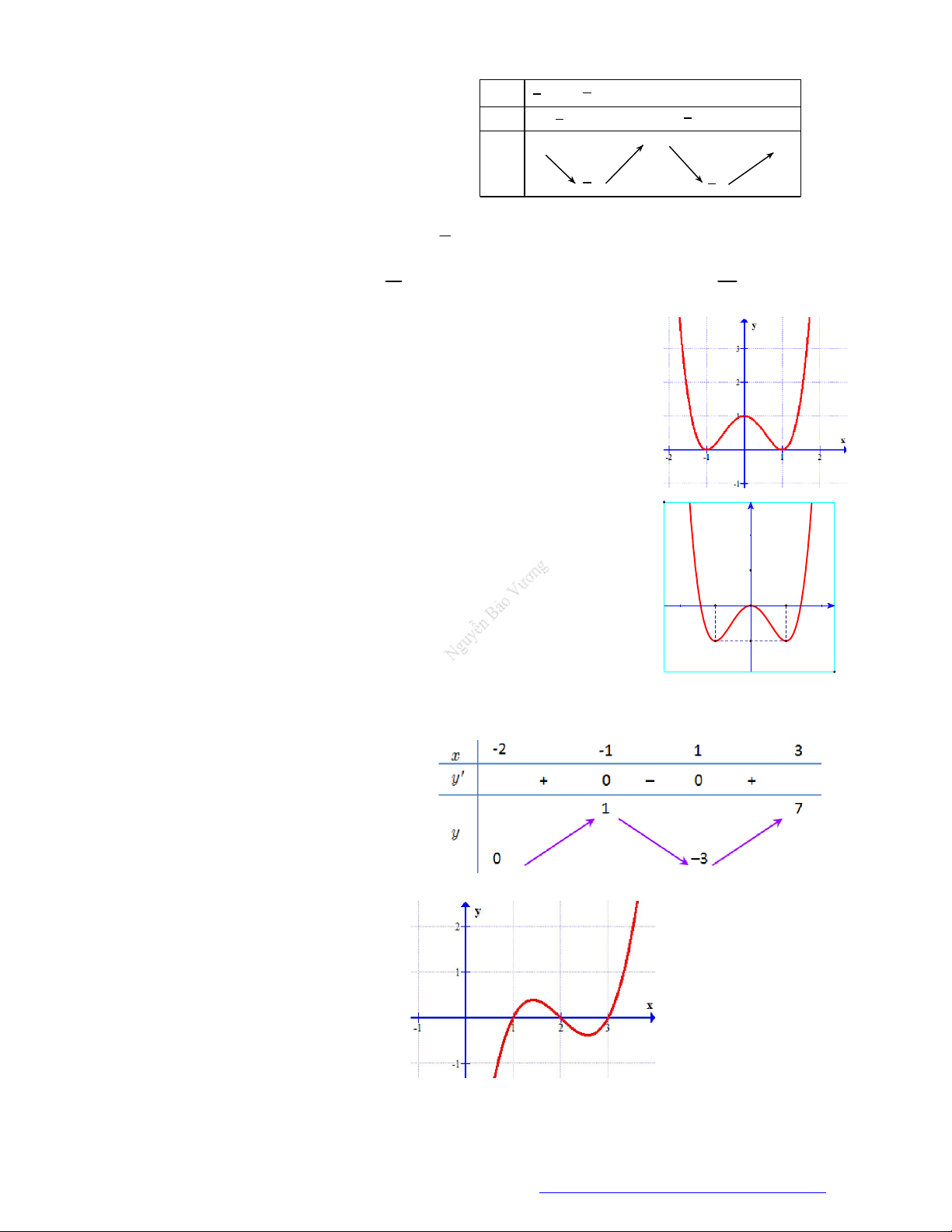
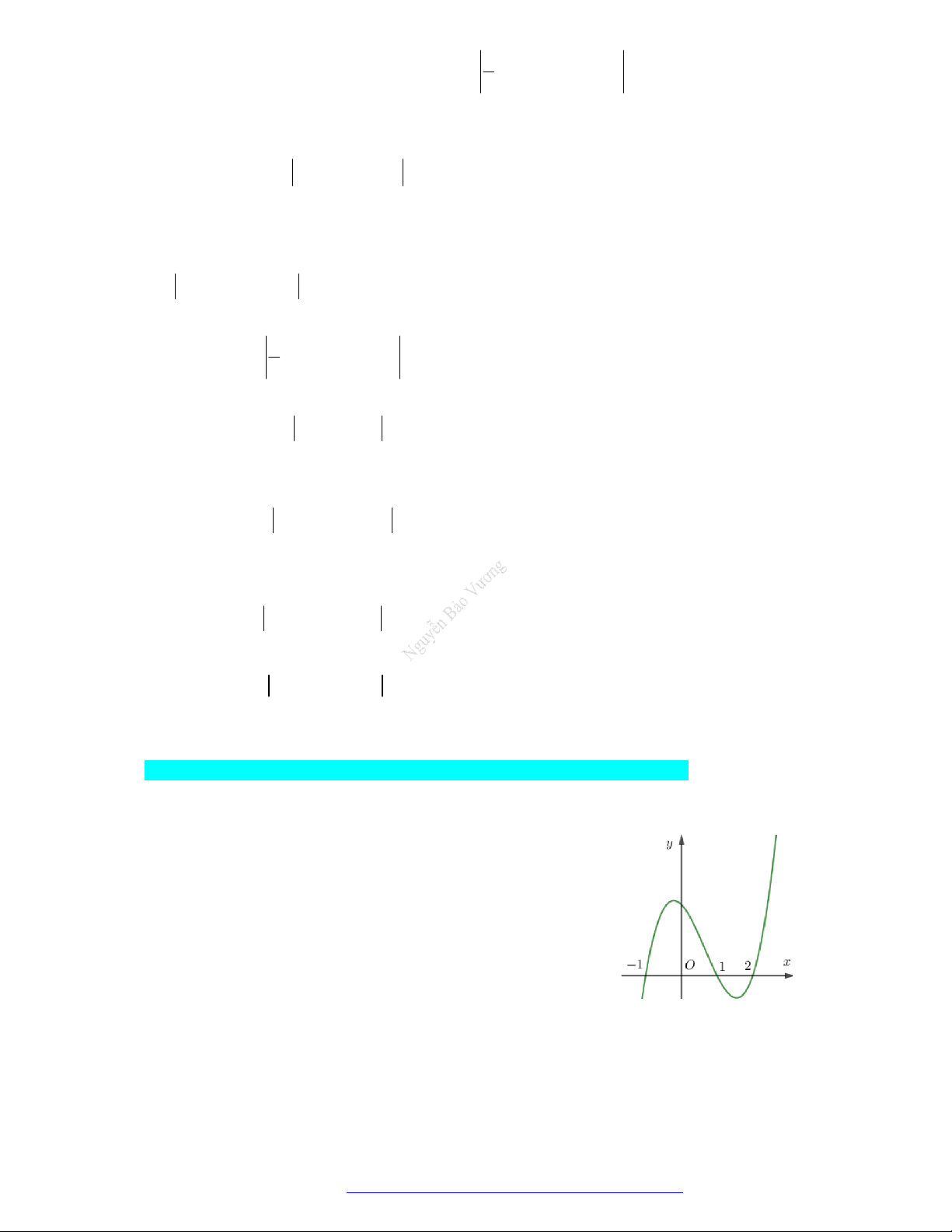
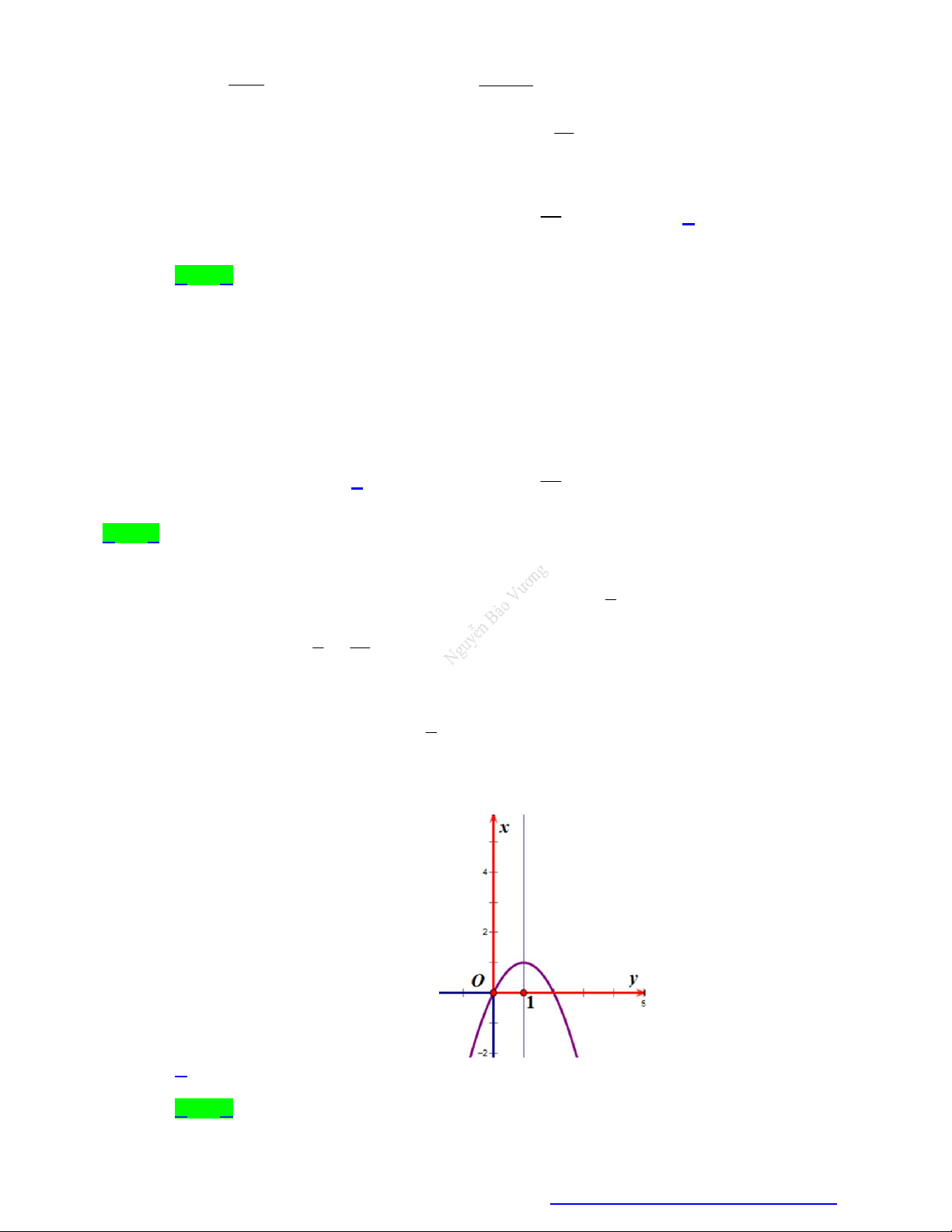
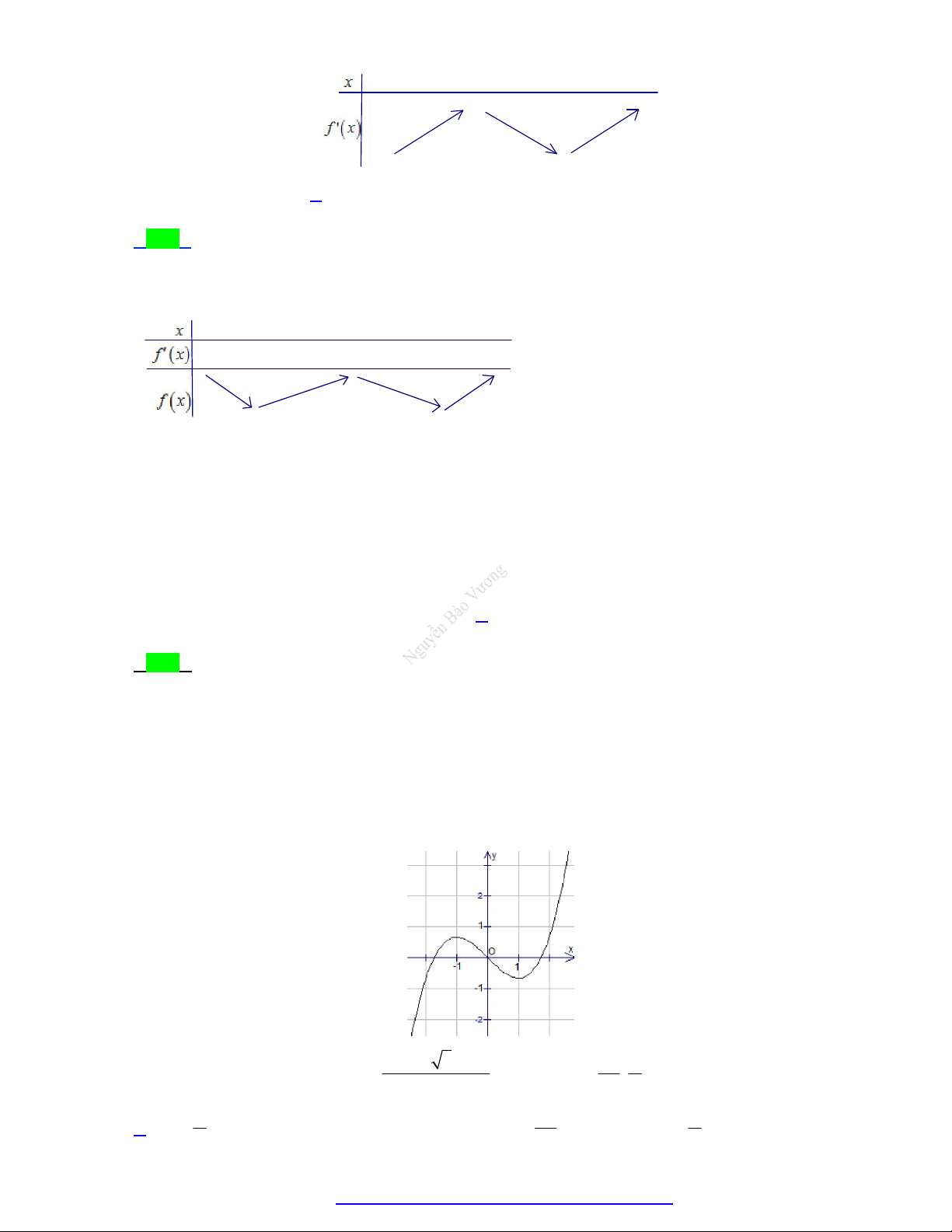
Câu 14. Cho hàm số y f ( x) có đồ thị như hình vẽ. Hỏi giá trị nhỏ nhất của hàm số đã cho trên đoạn [0; 2] bằng bao nhiêu? A. 0. B. 1  . C. 2 . D. 1.
Câu 15. Giá trị lớn nhất của hàm số y f x 4 2
x  8x 16 trên đoạn  1  ;  3 bằng: A. 9 . B. 26 . C. 25 . D. 0 .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
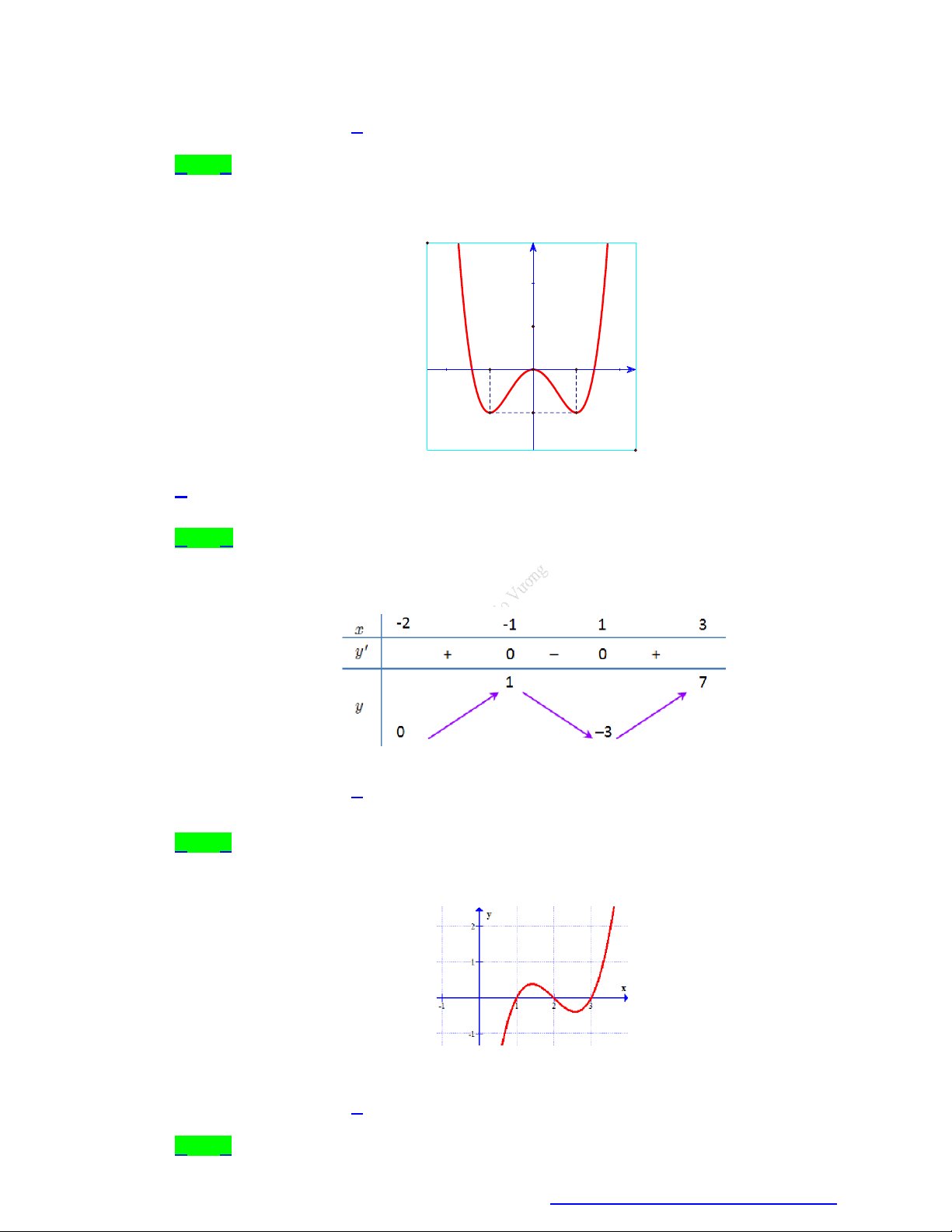
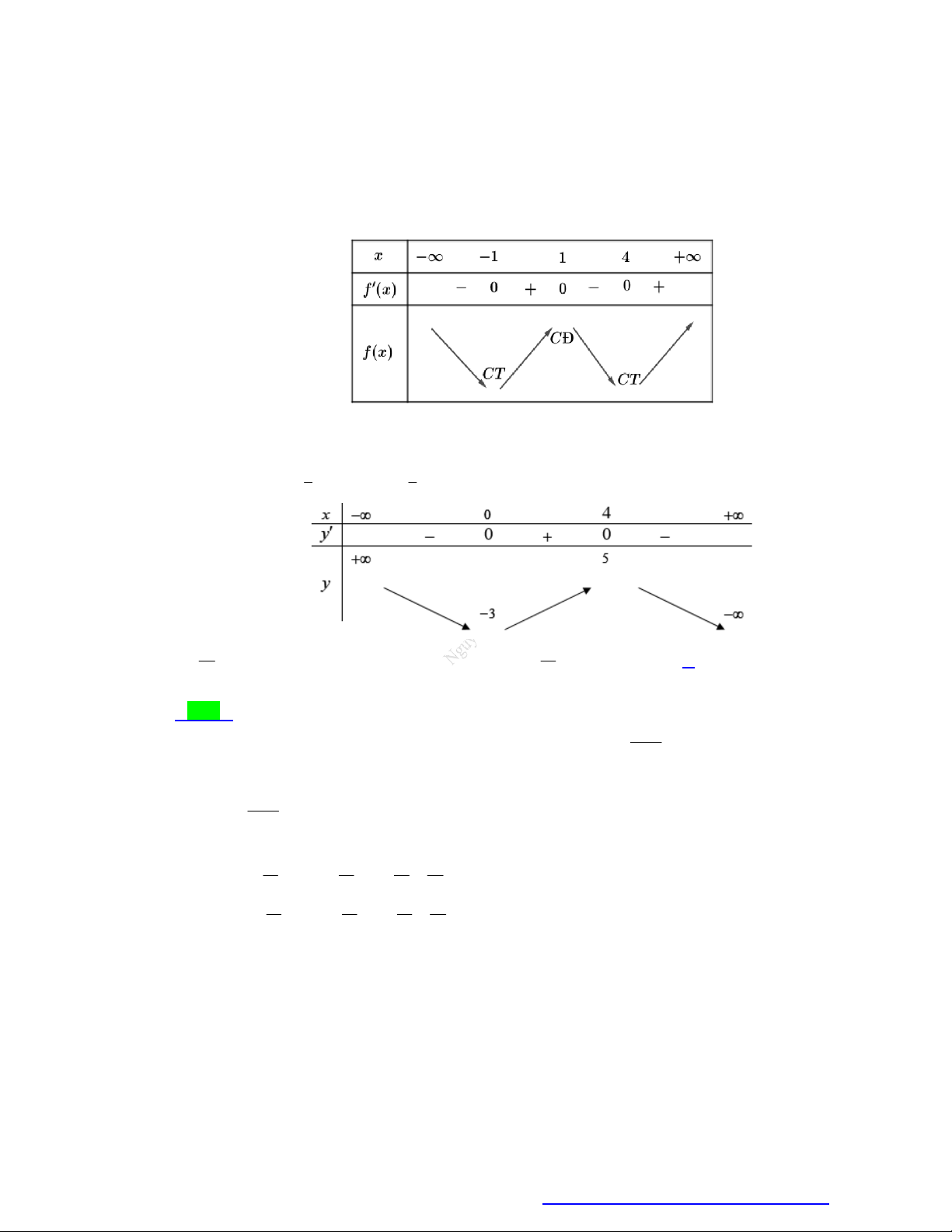
Câu 16. Cho hàm số y f (x) có bảng biến thiên như hình vẽ.
Hỏi giá trị lớn nhất của hàm số đã x ∞ 1 0 1 3
cho trên [-1; 3] bằng bao nhiêu? y' 0 + 0 0 + A. 3. +∞ 5 6 B. 3  . y C. 5 . 3 1 D. 6 . 9
Câu 17. Giá trị nhỏ nhất của hàm số y x  trên đoạn 2;  4 bằng: x 13 25 A. 6 . B. . C. 6  . D. . 2 4
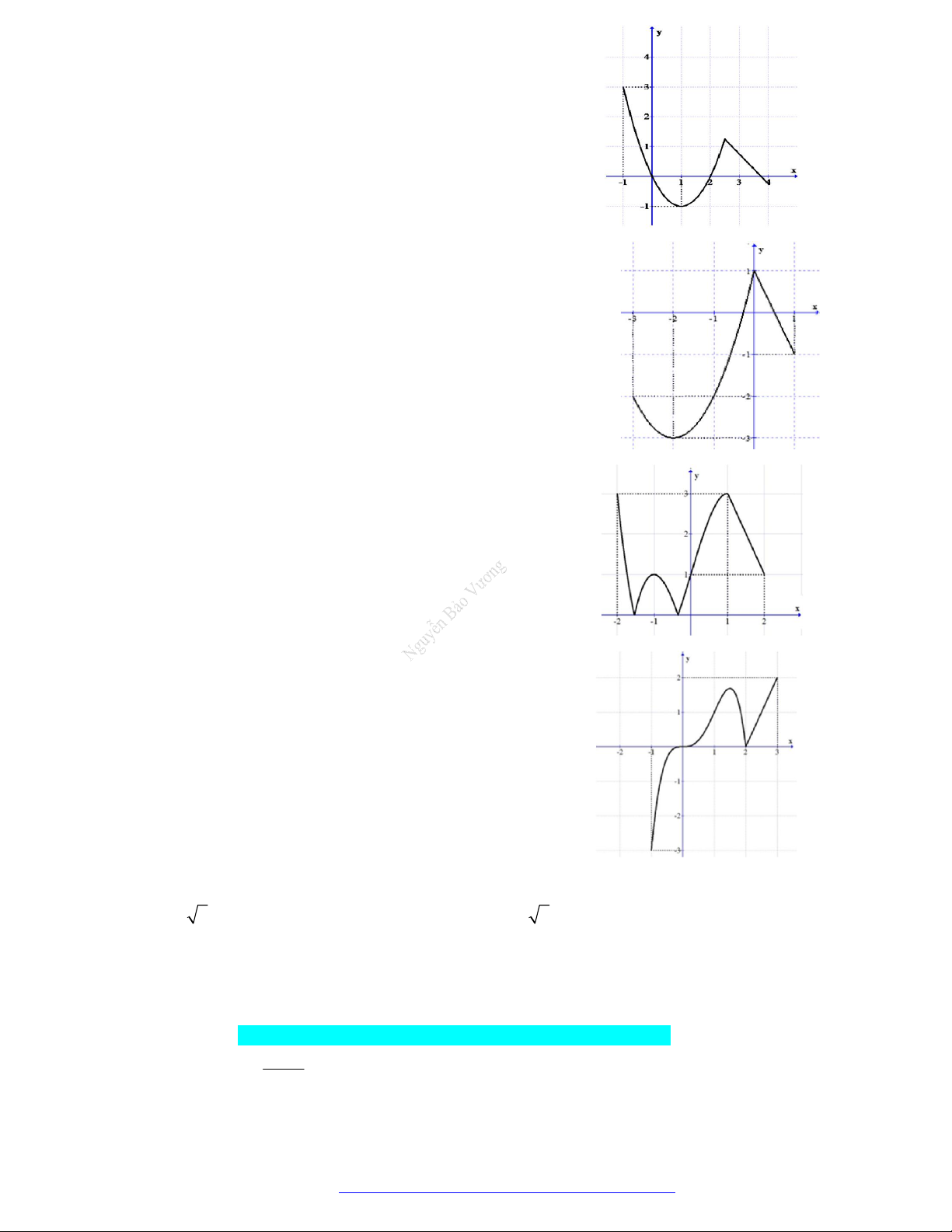
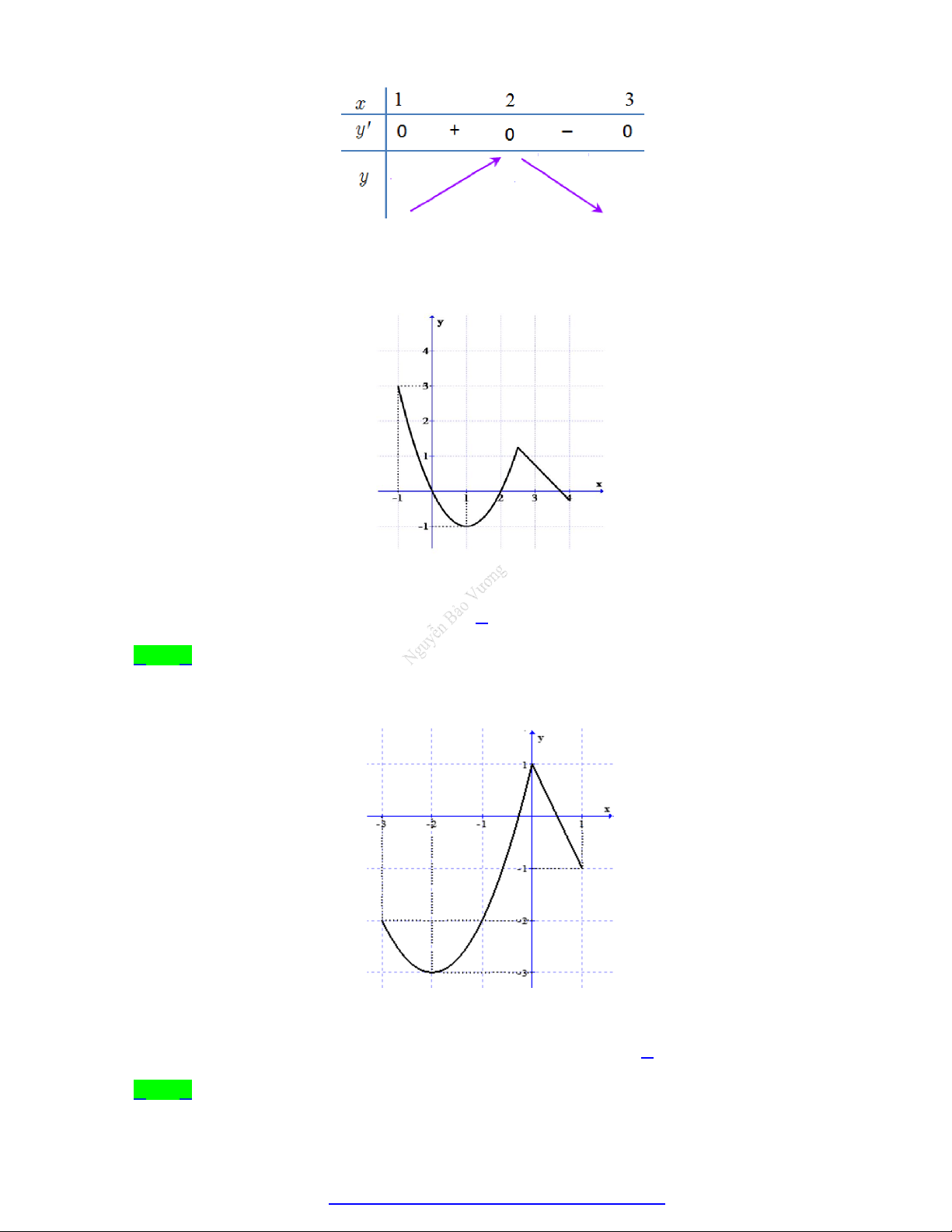
Câu 18. Cho hàm số y f x liên tục trên đoạn  1  
;1 và có đồ thị như hình vẽ.
Gọi M và m lần lượt là giá trị lớn nhất và
nhỏ nhất của hàm số đã cho trên đoạn 1  ;1 .
Giá trị của M m bằng A. 0 . B. 1. C. 2 . D. 3 .
Câu 19. Cho hàm số y f x liên tục trên đoạn  và có đồ thị như hình vẽ. y
Giá trị nhỏ nhất trên tập xác định của hàm số có đồ thị sau là:
A. min y  1. 1
B. min y  1. -1 1 0
C. min y  0 . x D. min y  2  . -1
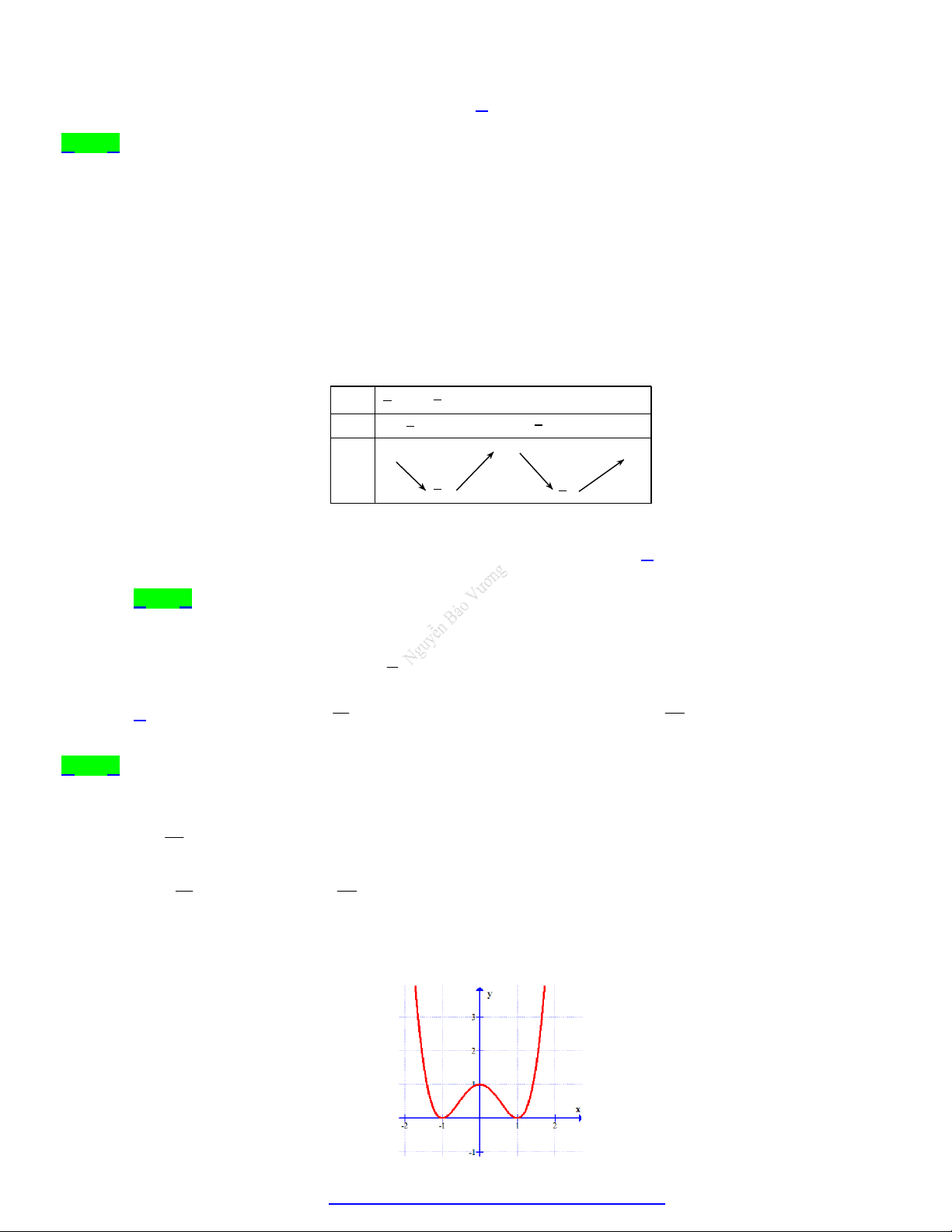
Câu 20. Cho hàm số y f x có bảng biến thiên như sau:
Giá trị nhỏ nhất của hàm số có bảng biến thiên sau trên khoảng  2  ;  3 là:
A. min y  0 .  2   ;3 B. min y  3  . 2  ;3
C. min y  1. 2;  3
D. min y  7 .  2   ;3
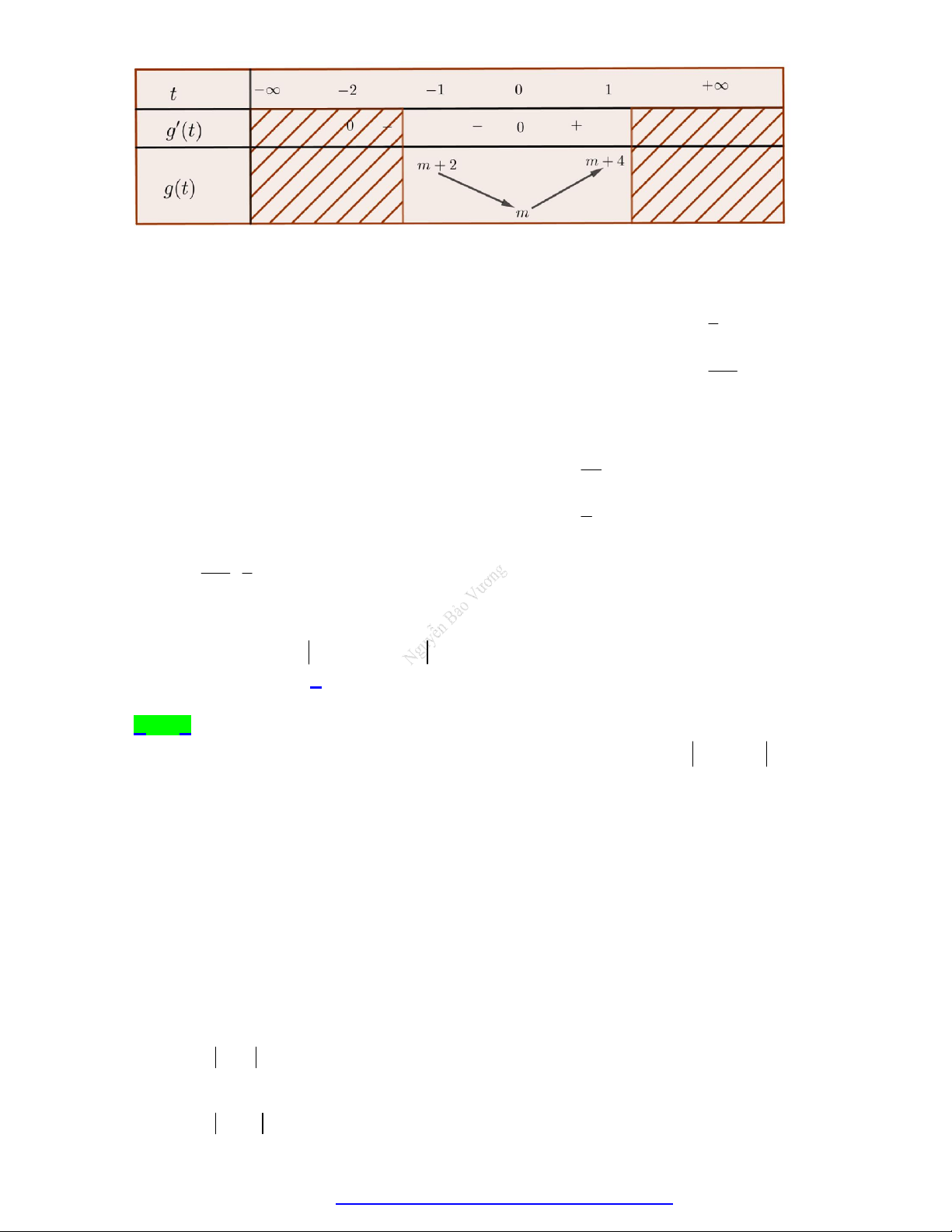
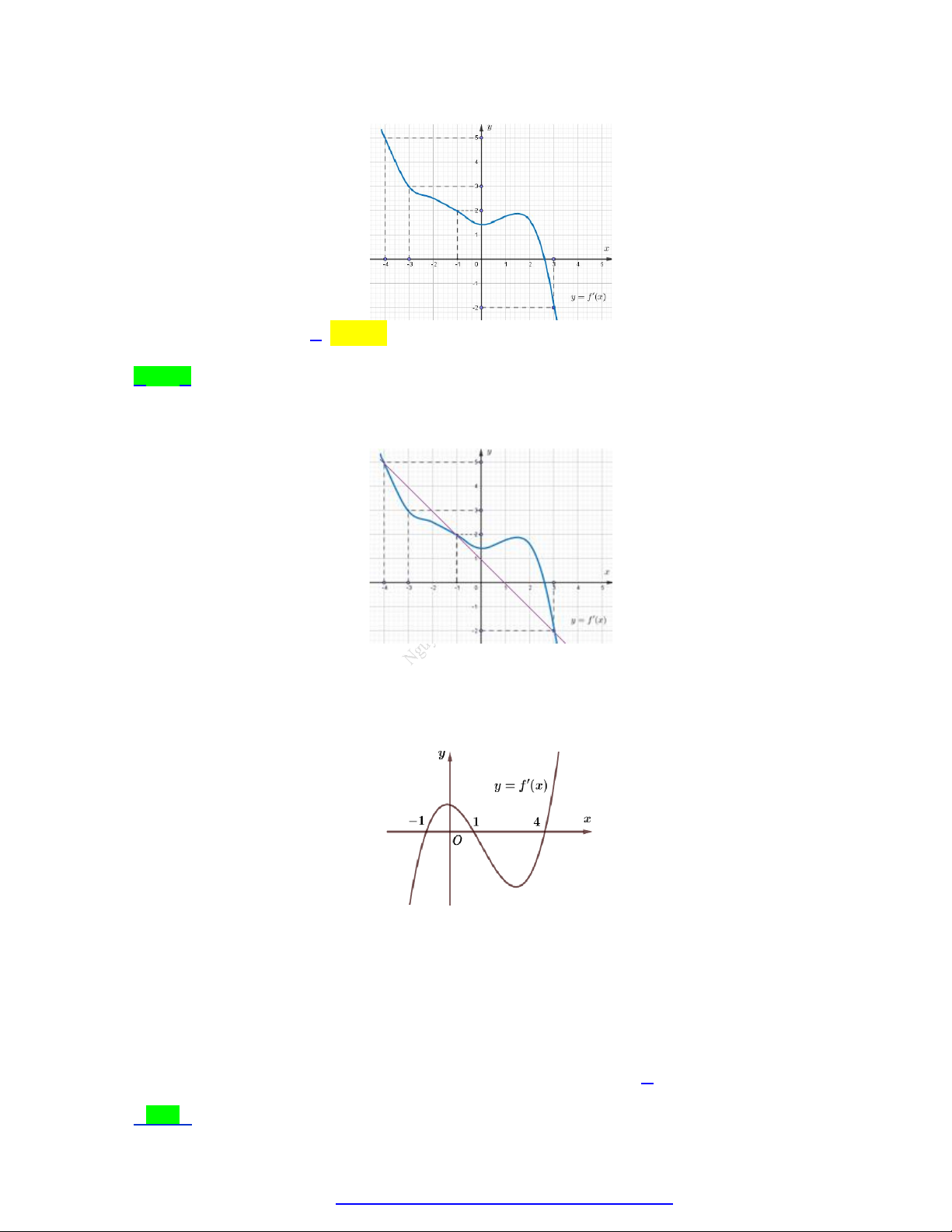
Câu 21. Cho đồ thị hàm số y f '( ) x như hình vẽ.
Hàm số y f ( )
x đạt giá trị lớn nhất trên khoảng 1; 
3 tại x . Khi đó giá trị của 2
x  2x  2019 0 0 0 bằng bao nhiêu? A. 2018 . B. 2019 . C. 2021 . D. 2022 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 22. Cho hàm số y f x liên tục trên đoạn 1
 ; 4và có đồ thị như hình vẽ bên dưới.
Gọi M và m lần lượt là giá trị lớn nhất và
nhỏ nhất của hàm số đã cho trên đoạn  1  ; 4.
Giá trị của M m bằng A. 0 . B. 1. C. 2 . D. 5 .
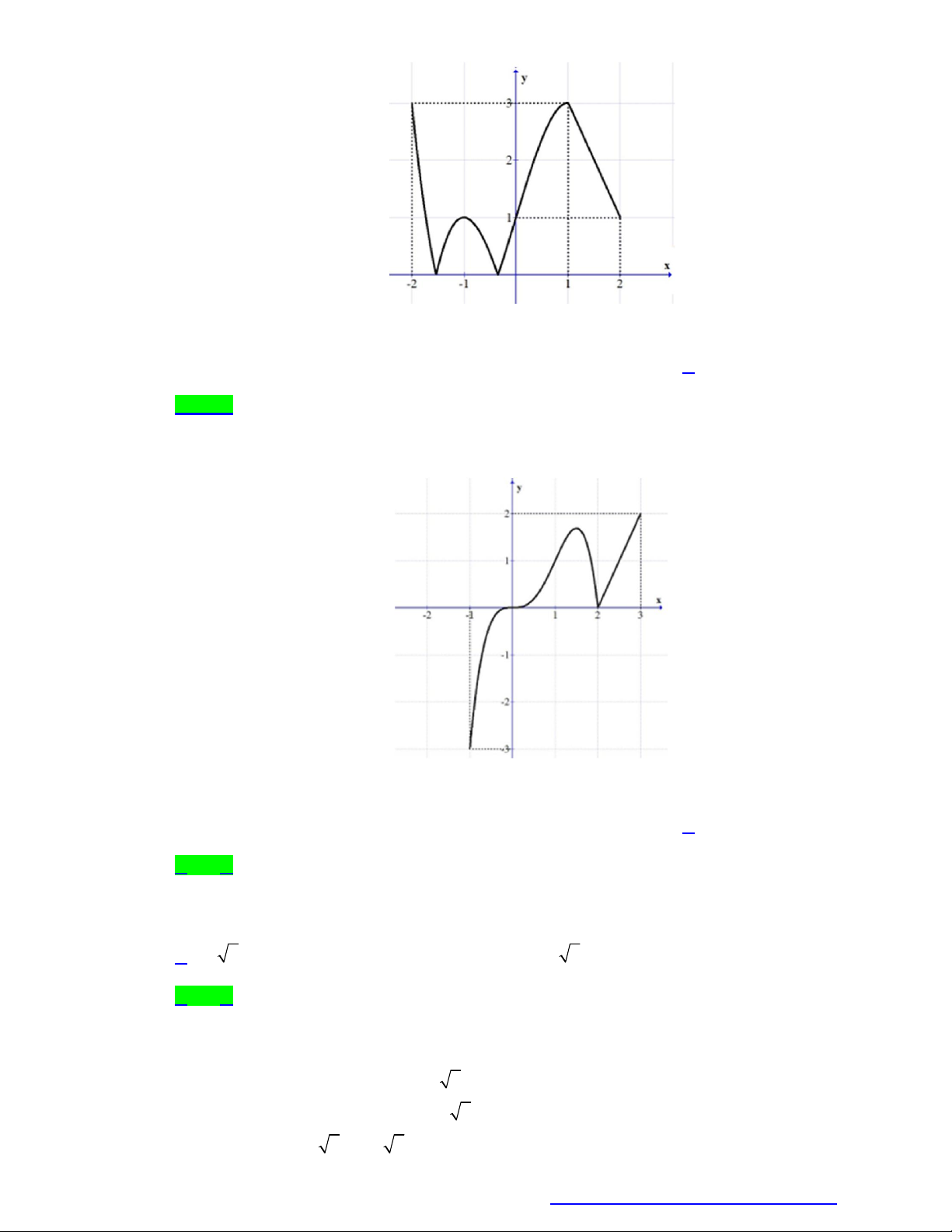
Câu 23. Cho hàm số y f x liên tục trên đoạn 3  ; 
1 và có đồ thị như hình vẽ bên dưới.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất
của hàm số đã cho trên đoạn 3  ; 
1 . Giá trị của 2M m bằng A. 0 . B. 1. C. 4 . D. 5 .
Câu 24. Cho hàm số y f x liên tục trên đoạn 2  ; 
2 và có đồ thị như hình vẽ bên dưới.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất
của hàm số đã cho trên đoạn  2  ; 
2 . Giá trị của M m bằng A. 0 . B. 1. C. 4 . D. 3 .
Câu 25. Cho hàm số y f x liên tục trên đoạn 1  ; 
3 và có đồ thị như hình vẽ bên dưới.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất
của hàm số đã cho trên đoạn 1  ;  3 . Giá trị của 2 2
M m bằng A. 15 . B. 11. C. 4 . D. 13 .
Câu 26. Giá trị nhỏ nhất của hàm số f x 3
x  6x trên đoạn 0; 2 bằng A. 4  2 . B. 4  . C. 6  2 . D. 0 .
Câu 27. Cho hàm số y f (x) có đạo hàm 2 f (  )
x x(x 1)(x  2) với mọi x   . Giá trị nhỏ nhất của hàm
số y f (x) trên đoạn  1  ;  2 là
A. f (1).
B. f (0).
C. f (3). D. f (2).
B. TÌM M ĐỂ GTLN-GTNN THỎA MÃN ĐIỀU KIỆN K x m Câu 1. Cho hàm số y
( m là tham số thực) thỏa mãn min y  3. Mệnh đề nào dưới đây đúng? x  1 [2;4]
A. m  4
B. 3  m  4
C. m  1
D. 1  m  3
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 x m 16 Câu 2. Cho hàm số y
( m là tham số thực) thoả mãn min y  max y
. Mệnh đề nào dưới đây x 1 1;2 1;2 3 đúng? A. m  4
B. 2  m  4
C. m  0
D. 0  m  2 Câu 3.
Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số 3 2
y  x  3x m trên đoạn 1;  1 bằng 0 .
A. m  2.
B. m  6.
C. m  0.
D. m  4. x m Câu 4.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên đoạn 1; 
2 bằng 8 ( m là tham x 1
số thực). Khẳng định nào sau đây là đúng? A. m  10 .
B. 8  m  10 .
C. 0  m  4 .
D. 4  m  8 . Câu 5.
Có một giá trị m của tham số m để hàm số 3 y x  2 m  
1 x m 1 đạt giá trị nhỏ nhất bằng 0 5 trên đoạn 0 
;1 . Mệnh đề nào sau đây là đúng? A. 2
2018m m  0 . B. 2m 1   0 . C. 2
6m m  0 .
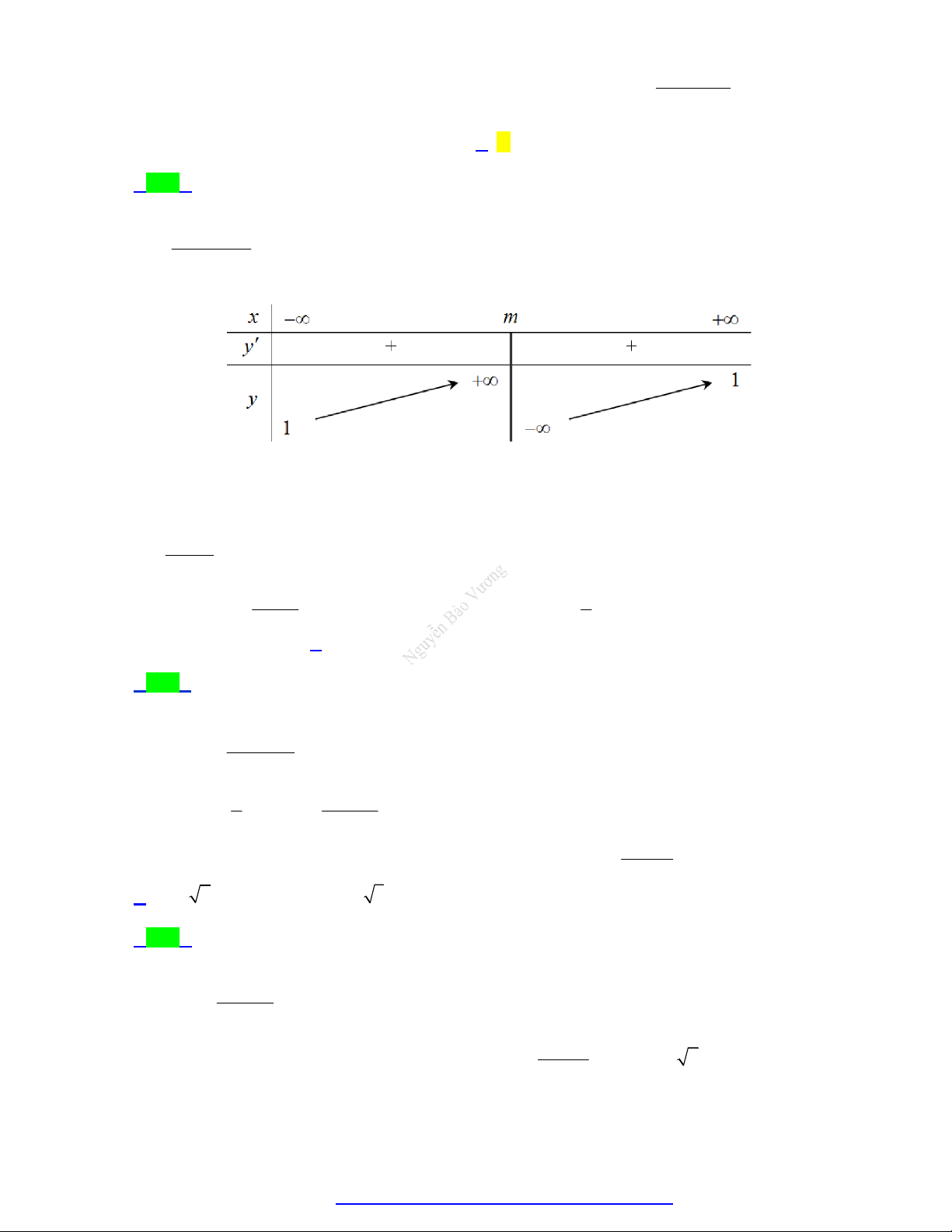
D. 2m 1 0 . 0 0 0 0 0 0 2 x m  2 Câu 6.
Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số y  trên đoạn 0; 4 x m bằng 1  . A. 3 . B. 2 . C. 1. D. 0 . x 1 1 Câu 7. Cho hàm số y
(m là tham số thực) thỏa mãn min y
. Mệnh đề nào dưới đây đúng? 2 x m 3;2 2
A. 3  m  4 . B. 2   m  3 . C. m  4 . D. m  2  . 2 m x 1 Câu 8.
Tìm giá trị dương của tham số m để giá trị nhỏ nhất của hàm số y  trên đoạn 1;3 x  2 bằng 1. A. m  2 . B. m  3 . C. m  4 . D. m  2 . 2 x m Câu 9. Cho hàm số y
với m là tham số thực. Giả sử m là giá trị dương của tham số m để x  8 0
hàm số có giá trị nhỏ nhất trên đoạn 0; 
3 bằng 3. Giá trị m thuộc khoảng nào trong các khoảng 0 cho dưới đây? A. 2;  5 . B. 1; 4 . C. 6;  9 . D. 20; 2  5 . 2x m
Câu 10. Tìm giá trị của tham số thực m để giá trị nhỏ nhất của hàm số y
trên đoạn 0;4 bằng 3 . x 1 A. m  3 .
B. m  1. C. m  7 .
D. m  5
Câu 11. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y x  3x m có giá trị nhỏ nhất trên đoạn  1  ;  1 bằng 2 m  2 2  A. m  2 .
B. m  2  2 .
C. m  4  2 . D.  . m  4 2  2
x m m
Câu 12. Tìm các giá trị của tham số m để giá trị nhỏ nhất của hàm số y  trên đoạn 0;  1 x  1 bằng 2  . m  1   m  1  m  1 m  1 A.  . B.  . C.  . D.  . m  2   m  2  m  2   m  2 
Câu 13. Có một giá trị m của tham số m để hàm số 3 y x  2 m  
1 x m 1 đạt giá trị nhỏ nhất bằng 0 5 trên đoạn 0; 
1 . Mệnh đề nào sau đây là đúng? A. 2
2018m m  0 . B. 2m 1   0 . 0 0 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 C. 2
6m m  0 .
D. 2m 1 0 . 0 0 0
Câu 14. Nếu hàm số 2
y x m  1 x có giá trị lớn nhất bằng 2 2 thì giá trị của m là 2 2 A. . B.  2 . C. 2 . D.  . 2 2 x m
Câu 15. Cho hàm số y
(m là tham số thực) thỏa mãn min y  3 . Mệnh đề nào dưới đây đúng? x  1 0;1  
A. 1  m  3 B. m  6 C. m  1
D. 3  m  6 x m
Câu 16. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
trên 1; 2 bằng 8 ( m là tham số x 1
thực). Khẳng định nào sau đây đúng? A. m  10 .
B. 8  m  10 .
C. 0  m  4 .
D. 4  m  8 . Câu 17. Cho hàm số 3 2
y  2x  3x m . Trên  1  
;1 hàm số có giá trị nhỏ nhất là 1  . Tính m ? A. m  6  . B. m  3  . C. m  4  . D. m  5  .
Câu 18. Biết S là tập giá trị của m để tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 2 3 2
y x m x  2x m trên đoạn 0; 
1 bằng 16 . Tính tích các phần tử của S . A. 2 . B. 2 . C. 15 . D. 17 . 2
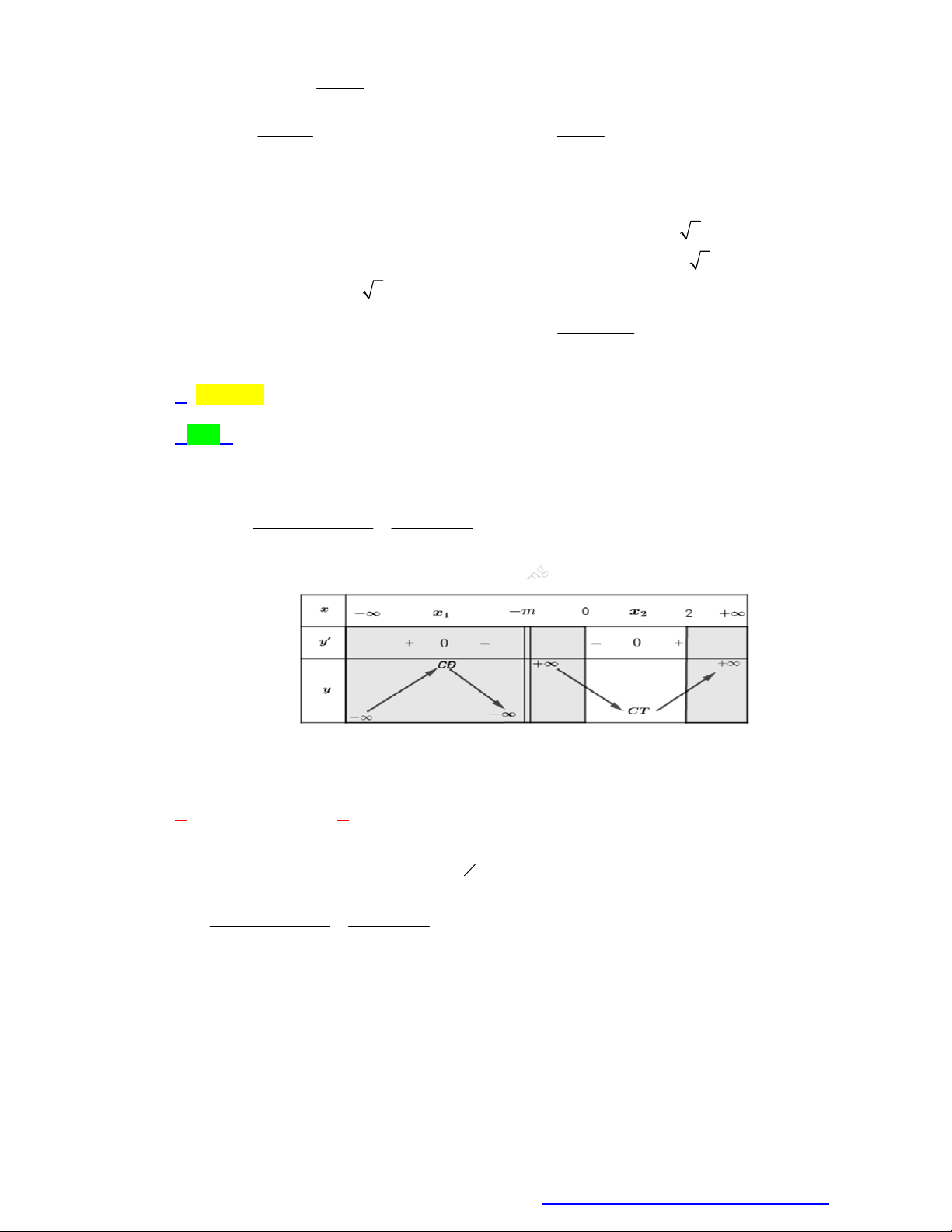
x m m Câu 19. Gọi ,
A B lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số y  trên đoạn 2;3 . x 1 13
Tìm tất cả các giá trị thực của tham số m để A B  . 2
A. m  1; m  2  . B. m  2  . C. m  2  . D. m  1  ; m  2 . 2 x m
Câu 20. Cho hàm số f x 
với m là tham số thực. Giả sử m là giá trị dương của tham số m để x  8 0
hàm số có giá trị nhỏ nhất trên đoạn 0;  3 bằng 3
 . Giá trị m thuộc khoảng nào trong các 0 khoảng cho dưới đây? A. 20;25 . B. 5;6 . C. 6;9 . D. 2;5 . 2 x mx 1
Câu 21. Tìm tất cả giá trị thực của tham số m để hàm số y
liên tục và đạt giá trị nhỏ nhất x m
trên đoạn 0; 2 tại một điểm x  0; 2 . 0  
A. 0  m  1 B. m  1 C. m  2
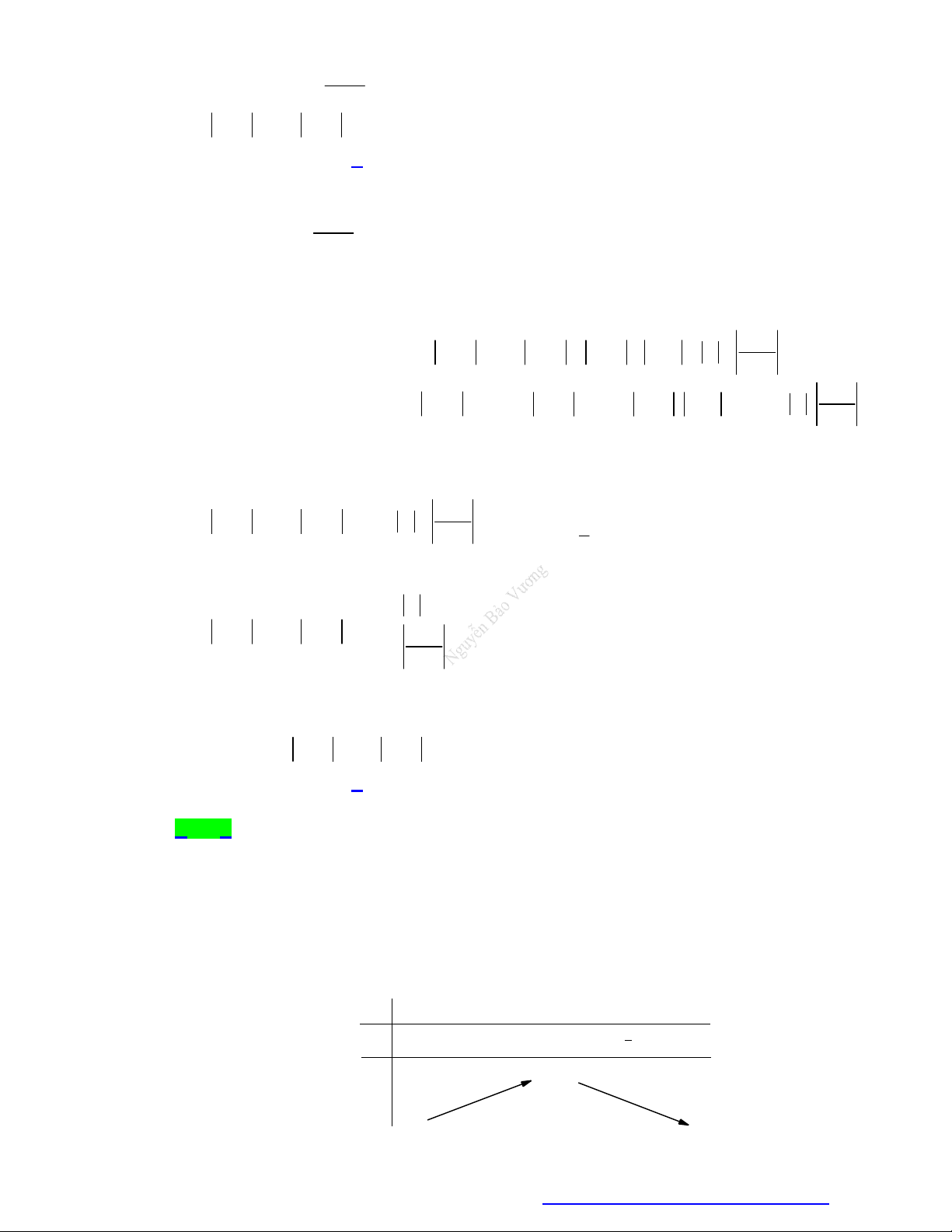
D. 1  m  1 1 m sin x
Câu 22. Cho hàm số y
. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 0;10 để giá cos x  2
trị nhỏ nhất của hàm số nhỏ hơn 2 ? A. 1. B. 9 . C. 3 . D. 6 . x m
Câu 23. Tìm tất cả các giá trị của tham số m để hàm số y
có giá trị lớn nhất trên  nhỏ hơn 2 x x 1 hoặc bằng 1. A. m  1. B. m  1. C. m  1 . D. m  1.
C. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ CHỨA DẤU GIÁ TRỊ
TUYỆT ĐỐI (chứa tham số)
Dạng 1: Tìm m để max y f x  m a a  0.  ;  Phương pháp:
Cách 1:Trước tiên tìm max f x  K;
min f x  k K k . ;  ; 
m K m k
m K m k K k
Kiểm tra max m K , mk     . 2 2 2
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 K k
m k  a
m  a k TH1:  .
a Để max y a    m   
a k;a K . 2  ; 
m K a
m a K   K k TH2:
a m  . 2
Cách 2: Xét trường hợp
m K a
TH1: Max m K  
m K m k  
m k a
TH2: Max m k  
m k m K  
Dạng 2: Tìm m để min y f x  m a a  0.  ;  Phương pháp:
Trước tiên tìm max f x  K;
min f x  k K k . ; ; 
m k a
m K  a
m a k
m  a K
Để min y a        
. Vậy mS S .  1 2  ;  m k  0 m K  0 m  k m  K    
Dạng 3: Tìm m để max y f x  m không vượt quá giá trị M cho trước.  ; 
Phương pháp: Trước tiên tìm max f x  K;
min f x  k K k . ; ; 
m k  M
Để max y M  
 M k m M K.  ; 
m K M
Dạng 4: Tìm m để min y f x  m không vượt quá giá trị a cho trước.  ; 
Phương pháp: Trước tiên tìm max f x  K;
min f x  k K k . ; ; 
m k a
m K  a
m a k
m  a K
Để min y a    
 m K m k   0    
 K m  k.  ;  m k  0 m K  0 m  k m  K    
Dang 5: Tìm m để max y f x  m đạt min. a;bPhương pháp:
Trước tiên tìm max f x  K;
min f x  k K k . a;b a;bK k K k
Đề hỏi tìm m m  
. Đề hỏi tìm min của max y  giá trị này là . 2 a;  b 2
Dạng 6: Tìm m để min y f x  m đạt min. a;  b
Phương pháp: Trước tiên tìm max f x  K;
min f x  k K k . a;b a;b
Đề hỏi tìm m  m K m k   0  K m k
 . Đề hỏi tìm min của min y  giá trị này là 0. a;  b
Dạng 7: Cho hàm số y f x  m .Tìm m để max y  .
h min y h  0 hoặc Min  max  a;b a;b
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
Phương pháp: Trước tiên tìm max f x  K;
min f x  k K k . a;b a;bTH1:
K m k m
K m h k m       m S .
K m cung dau k m 1
k m K m
TH2: k m h K m  m S .
K m cung dau k m 2
Vậy mS S . 1 2
Dạng 8: Cho hàm số y f x  m .
Phương pháp: Trước tiên tìm max f x  K;
min f x  k K k . a;b a;b
BT1: Tìm m để min y  max y    m K m k   . a;b a;b
BT2: Tìm m để min y * max y    m K * m k   . a;b a;bCâu 1.
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số f x 3
x  3x m trên đoạn 0;3 bằng 16. Tổng tất cả các phần tử của S là: A. 16 . B. 16 . C. 12 . D. 2 . x m Câu 2.
Cho hàm số f x 
( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao cho x 1
max f x  min f x  2 . Số phần tử của S là 0;  1 0;  1 A. 6 . B. 2 . C. 1. D. 4 . Câu 3.
Cho hàm số f x 4 3 2
x  4x  4x m ( m là tham số thực). Gọi S là tập hợp tất cả các giá trị
của m sao cho max f x  min f x  5. Số phần tử của S là 0;2 0;2 A. 1. B. 2 . C. 3. D. 4 . Câu 4.
Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị lớn nhất của hàm số 2
y x  2x m  3 trên đoạn  1
 ; 2 bằng 4 . Tổng tất cả các phần tử của S là A. 6  . B. 8  . C. 9  . D. 12  . Câu 5.
Cho hàm số f x 3
x  3x m ( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m
sao cho max f x  min f x  6 . Tổng tất cả các phần tử của S là 0;2 0;2 A. 3. B. 0 . C. 1  . D. 2 . Câu 6.
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số f x 3
 2x  6x m trên đoạn 0; 
3 bằng 8. Tổng tất cả các phần tử của S bằng A. 8 . B. 1  6 . C. 3  2 . D. 7  2 . Câu 7.
Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số 2
y x  2x m  4 trên đoạn  2  
;1 đạt giá trị nhỏ nhất? A. 1. B. 3 . C. 4 . D. 5 . Câu 8.
Cho hàm số f x liên tục trên  , có đồ thị như hình vẽ Có tất cả bao nhi
êu giá trị nguyên của tham số a  8x
để hàm số y fa 1  có giá trị 2   x 1
lớn nhất không vượt quá 20 ? A. 29 . B. 35 . C. 31. D. 41 .
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Câu 9.
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 2
x mx m f x 
trên 1;2 bằng 2 . Tổng tất cả các phần tử của S là x 1 11 13 11 1 A.  . B. . C.  . D. . 3 6 6 3 Câu 10. Cho hàm số 3 2
y  cos x  3sin x m  3 . Gọi S là tập hợp các giá trị m sao cho
2 max y  min y  9 . Tổng các phần tử của tập hợp S bằng: 16 A. . B. 4  . C. 6  . D. 2  . 3
Câu 11. Cho hàm số f x 3
x  3x . Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị
nhỏ nhất của hàm số y f 2  cos x  m bằng 2. Tổng tất cả các phần tử của S bằng A. 4 . B. 1  6 . C. 3  2 . D. 12 . log x m
Câu 12. Cho hàm số f x 
( m là tham số thực). Gọi S là tổng tất cả các giá trị của m sao cho log x  2
max f x  min f x  2 . Tìm S .  1   1  ;1 ;1  10    10  2 4 10 A. . B. 2 . C. . D. . 3 3 3
Câu 13. Có bao nhiêu giá trị nguyên của tham số m để giá trị nhỏ nhất của hàm số 3 2
y x mx  9x  9m trên đoạn  2
 ; 2 đạt giá trị nhỏ nhất. A. 3 . B. 5 . C. 4 . D. 6 .
Câu 14. Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số y f x 4 2
 x  8x m trên đoạn  1  ; 
3 đạt giá trị nhỏ nhất. A. 23. B. 24 . C. 25 . D. 26 . Câu 15. Cho hàm số 2
y x  4x  2m  3 với m là tham số thực. Biết rằng giá trị lớn nhất của hàm số trên đoạn 1; 
3 đạt giá trị nhỏ nhất bằng a khi m b . Tính P  2b a . 1 13 9 A. . B. . C. . D. 6 . 2 4 4 Câu 16. Cho hàm số 3 2
y x x   2 m  
1 x  27 . Gọi S là tập tất cả các giá trị của tham số m sao cho
giá trị lớn nhất của hàm số trên đoạn 3;  
1 có giá trị nhỏ nhất. Khi đó tích các phần tử của S là A. 4 . B. 4 . C. 8 . D. 8 .
Câu 17. Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số 1 19 4 2 y x
x  30x m trên đoạn 0;2 đạt giá trị nhỏ nhất? 4 2 A. 2 . B. 3 . C. 0 . D. 1.
Câu 18. Có tất cả bao nhiêu giá trị của tham số m để giá trị nhỏ nhất của hàm số f x 2
x  2x m trên  1  ; 2 bằng 5. A. 3. B. 1. C. 2 . D. 4 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 4
Câu 19. Tính tích tất cả các số thực m để hàm số 3 2 y
x  6x  8x m có giá trị nhỏ nhất trên đoạn 3 0;  3 bằng 18 là. A. 432 . B. 2  16. C. 4  32. D. 288 .
Câu 20. Cho hàm số f x 4 2
x  2x m 1 . Gọi S là tập hợp tất cả các giá trị của tham số m sao cho
giá trị nhỏ nhất của hàm số trên đoạn 0; 
2 bằng 18 . Tổng tất cả các phần tử của S bằng A. 5  . B. 4 . C. 14 . D. 10  .
Câu 21. Tính tổng tất cả các giá trị nguyên lớn hơn 6 của tham số m sao cho giá trị nhỏ nhất của hàm số 2
y x  m  
1 x m trên 2; m   1 nhỏ hơn 2020. A. 2043210 . B. 2034201. C. 3421020 D. 3412020. 1 Câu 22. Cho hàm số 4 3 2 y
x x x m . Tính tổng tất cả các số nguyên m để max y 11. 4  1  ;  2 A. 1  9. B. 3  7 . C. 3  0. D. 11.
Câu 23. Cho hàm số f x 2
x  2mx  3 . Có bao nhiêu giá trị m nguyên để giá trị lớn nhất của f x
trên đoạn 1;2 không lớn hơn 3? A. 2 . B. 3 . C. 1. D. 4 . Câu 24. Cho hàm số 3 2
y x  3x  9x m . Gọi S là tập hợp các giá trị nguyên của tham số m để
max y  50 . Tổng các phần tử của M là  2;   3 A. 0 . B. 737 . C. 759. D. 2  15. Câu 25. Cho hàm số 4 3 2
y x  2x x a . Có bao nhiêu giá trị nguyên của tham số a để max y  100 .  1  ;  2 A. 197 . B. 196 . C. 200 . D. 201.
Câu 26. Cho hàm số y  sin x  cos x m , có bao nhiêu giá trị nguyên của m để hàm số có giá trị lớn nhất bé hơn 2 . A. 0 . B. 1. C. 2 . D. 3 .
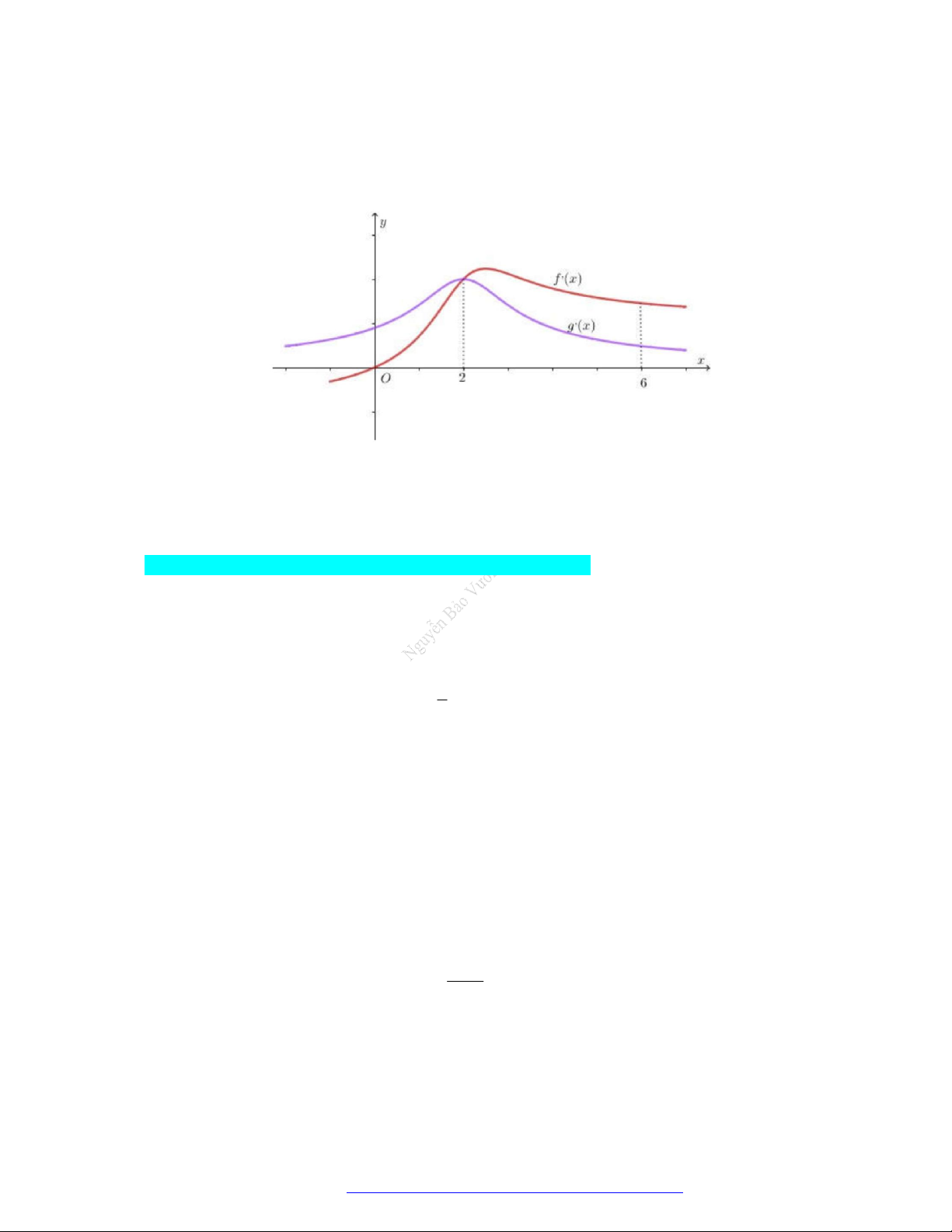
D. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT HÀM ẨN, HÀM HỢP Câu 1.
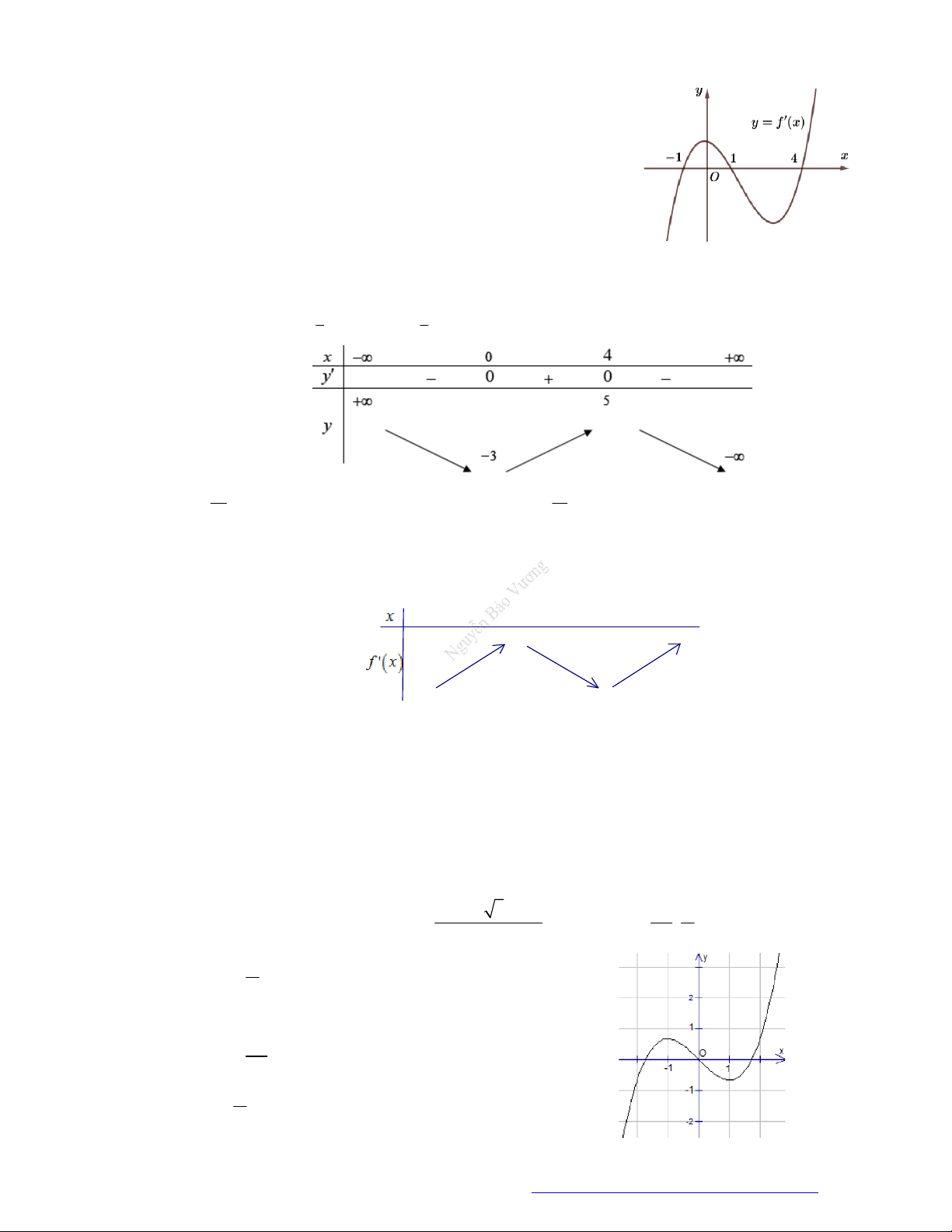
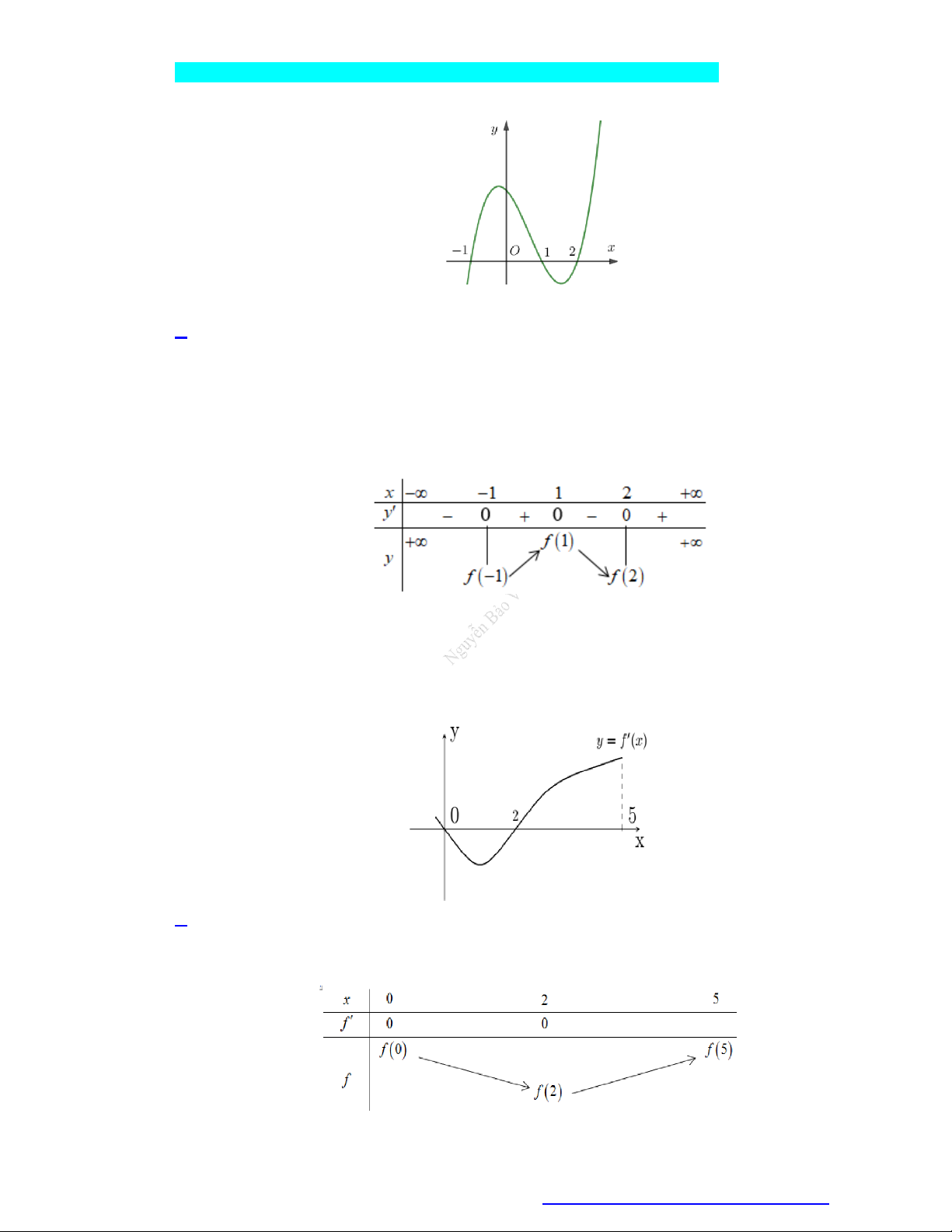
Cho hàm số y f x xác định và liên tục trên  , đồ thị của hàm số y f  x như hình vẽ.
Giá trị lớn nhất của hàm số y f x trên đoạn  1  ;  2 là A. f   1 . B. f   1 . C. f 2 . D. f 0 . Câu 2.
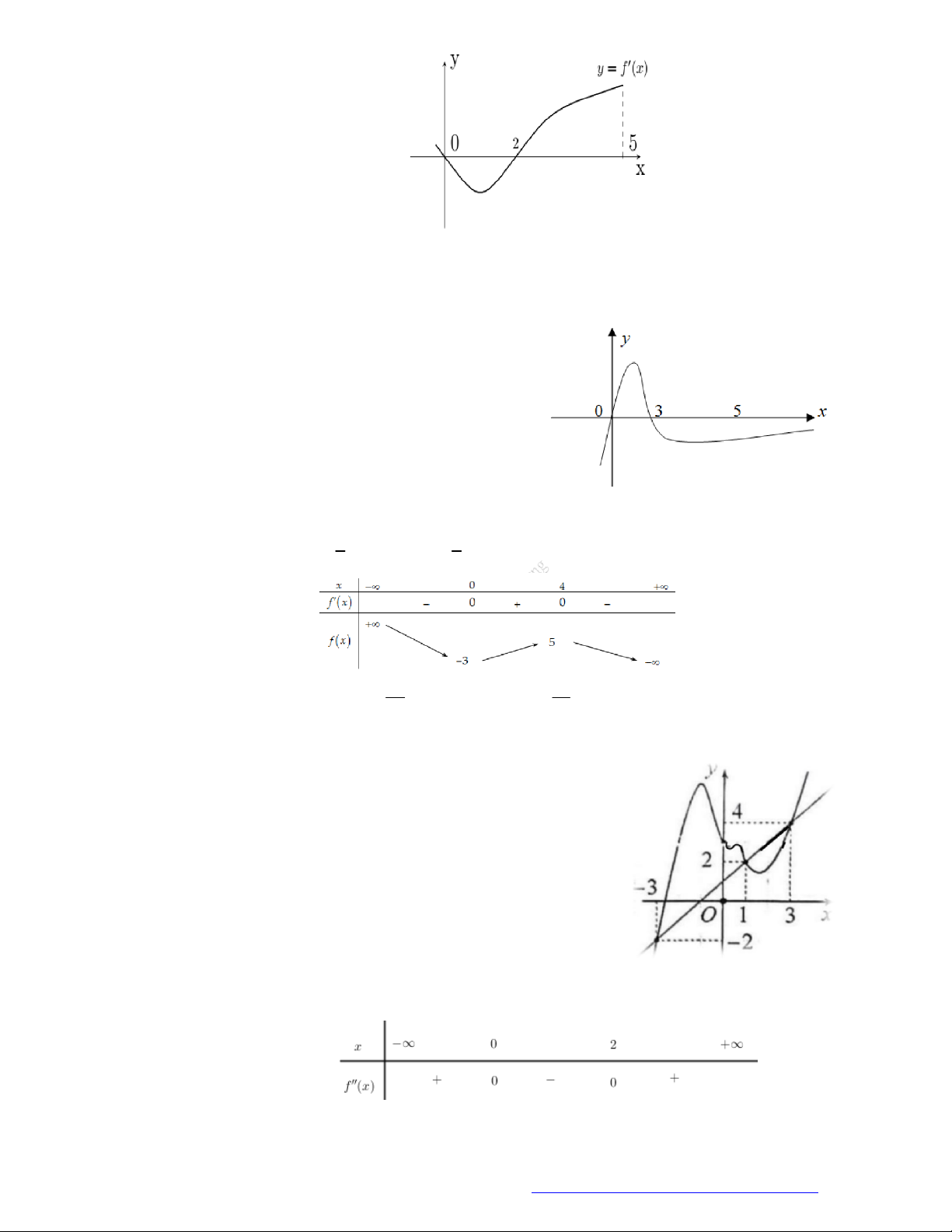
Cho hàm số y f x có đạo hàm là hàm f  x . Đồ thị của hàm số y f  x được cho như
hình vẽ. Biết rằng f 0  f 3  f 2  f 5 . Giá trị nhỏ nhất, giá trị lớn nhất của y f x
trên đoạn 0;5 lần lượt là:
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
A. f 2 ; f 5 .
B. f 0 ; f 5 .
C. f 2 ; f 0 . D. f   1 ; f 5 . Câu 3.
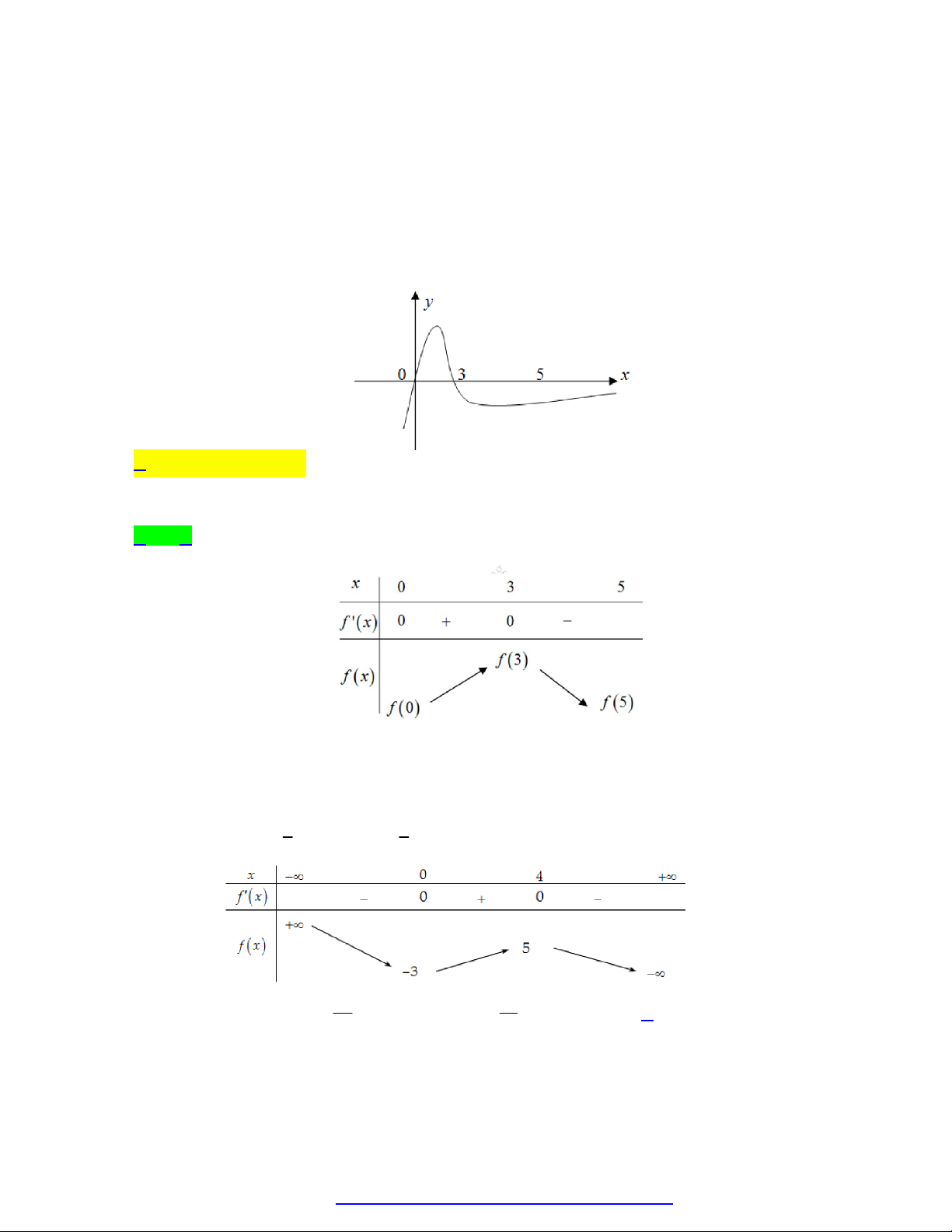
Cho hàm số f x có đạo hàm là f  x . Đồ thị của hàm số y f  x được cho như hình vẽ bên.
Biết rằng f 0  f  
1  2 f 3  f 5  f 4 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của
f x trên đoạn 0;5 .
A. m f 5, M f 3
B. m f 5, M f   1
C. m f 0, M f 3
D. m f  
1 , M f 3 Câu 4.
Cho hàm số y f x có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số 1 1
g x  f  2 4x x  3 2 
x  3x  8x  trên đoạn 1;  3 . 3 3 25 19 A. 15. B. . C. . D. 12. 3 3 Câu 5.
Cho hàm số y f x liên tục trên . Đồ thị của hàm số y f  x như hình bên. Đặt
g x  f x   x  2 2
1 . Mệnh đề dưới đây đúng.
A. max g x  g 3. 3;3
B. min g x  g   1 .   3;3
C. max g x  g 0.  3;   3
D. max g x  g   1 . 3;3 Câu 6.
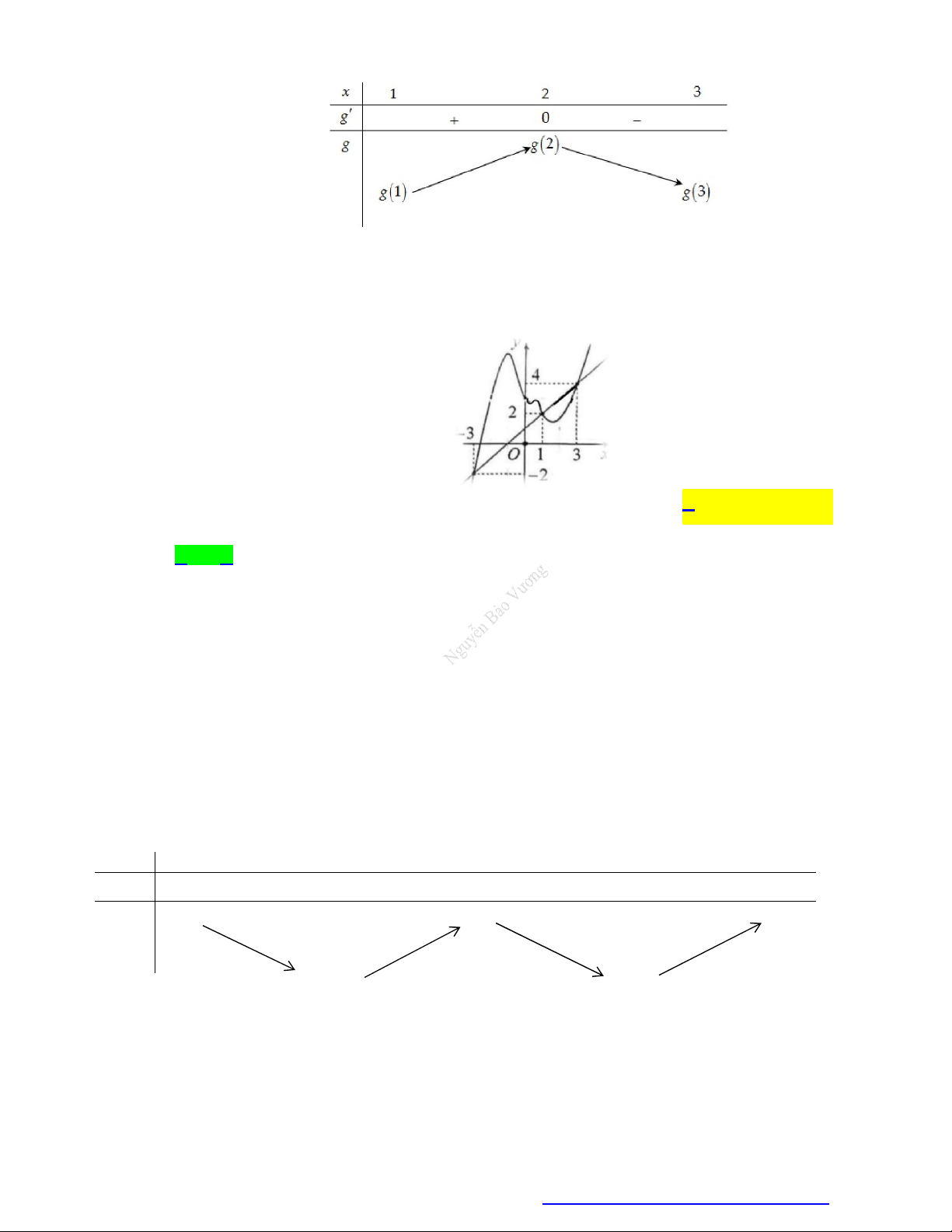
Cho hàm số y f x có đạo hàm cấp hai trên  . Biết f 0  3 , f 2  20  18 và bảng xét
dấu của f  x như sau:
Hàm số y f x  2017  2018x đạt giá trị nhỏ nhất tại điểm x thuộc khoảng nào sau đây? 0
A. ;  2017 B. 2017;  C. 0; 2 D. 2017;0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 7.
Cho hàm số f x có đạo hàm là f  x . Đồ thị của hàm số y f  x được cho như hình vẽ dưới đây:
Biết rằng f  
1  f 0  f   1  f 2 .
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y f x
trên đoạn 1; 2 lần lượt là: A. f   1 ; f 2 .
B. f 2 ; f 0 .
C. f 0 ; f 2 . D. f   1 ; f   1 .  7  Câu 8.
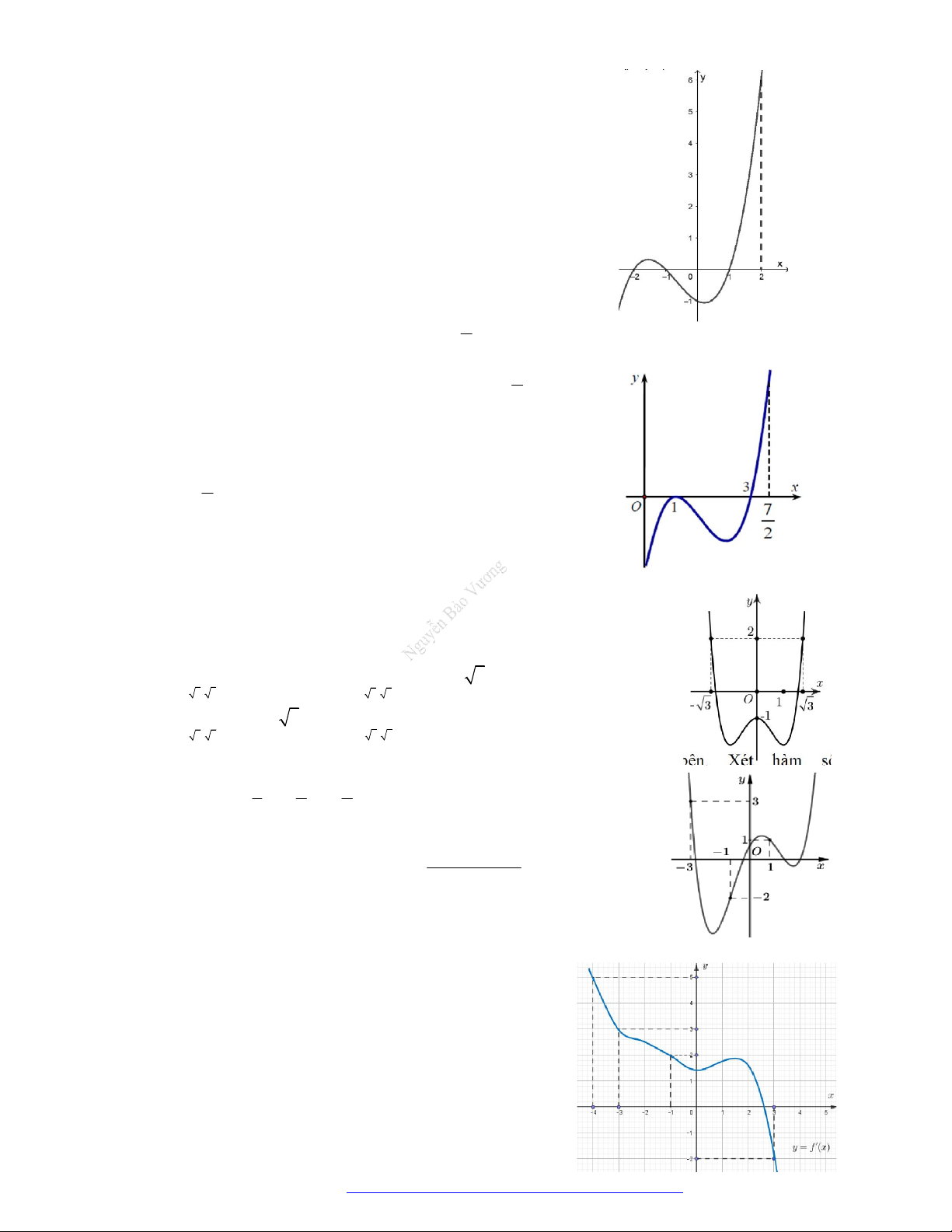
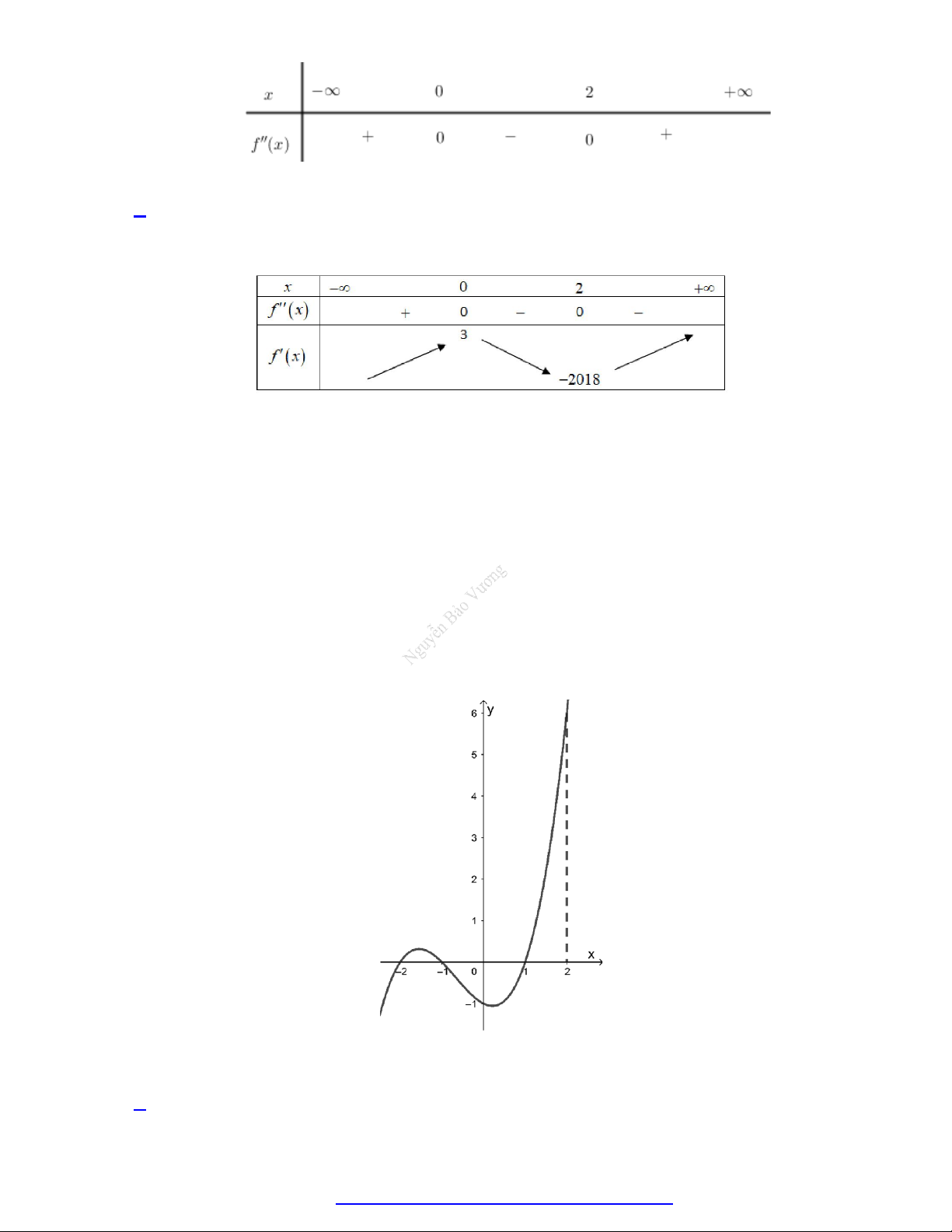
Cho hàm số y f x liên tục trên đoạn 0; 
có đồ thị hàm số y f ' x như hình vẽ. 2     7 
Hàm số y f x đạt giá trị nhỏ nhất trên đoạn 0;  2   
tại điểm x nào dưới đây? 0
A. x  0 . 0 7 B. x  . 0 2
C. x 1. 0
D. x  3. 0 Câu 9.
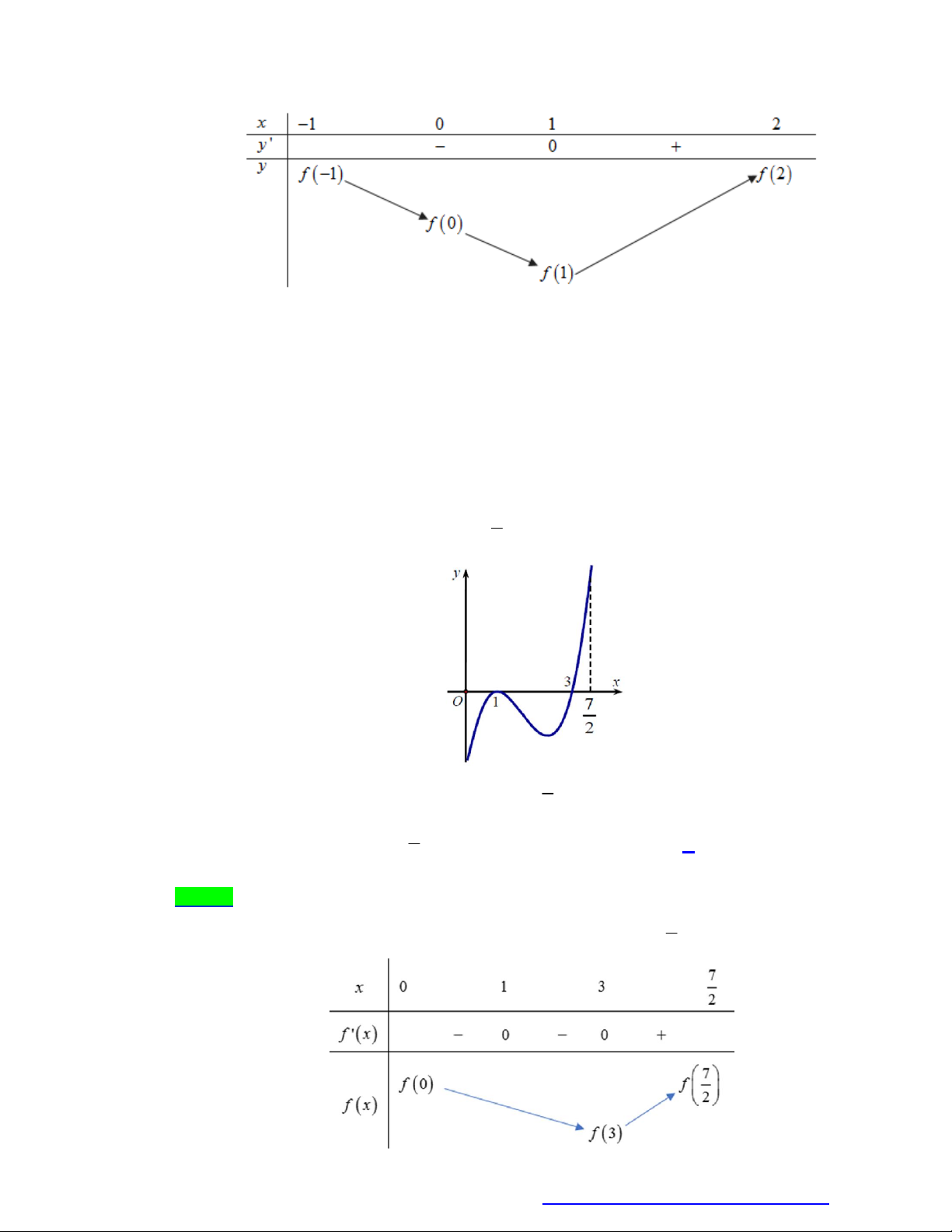
Cho hàm số y f x . Đồ thị hàm y f  x như hình vẽ
Đặt h x  f x 3 3
x  3x . Tìm mệnh đề đúng trong các mệnh đề sau: A. max (
h x)  3 f   1 .
B. max h(x)  3 f  3 . [ 3; 3] [ 3; 3 ]
C. max h(x)  3 f  3 . D. max (
h x)  3 f 0 . [ 3; 3 ] [ 3; 3] Câu 10. Cho hàm số
y f x có đồ thị y f  x ở hình vẽ bên. Xét hàm số 1 3 3
g x  f x 3 2  x x
x  2018, mệnh đề nào dưới đây đúng? 3 4 2 g  3    g   1
A. min g x  g  
1 . B. min g x  . 3;  1  3;   1 2
C. min g x  g 3 . D. min g x  g   1 . 3;  1  3;   1
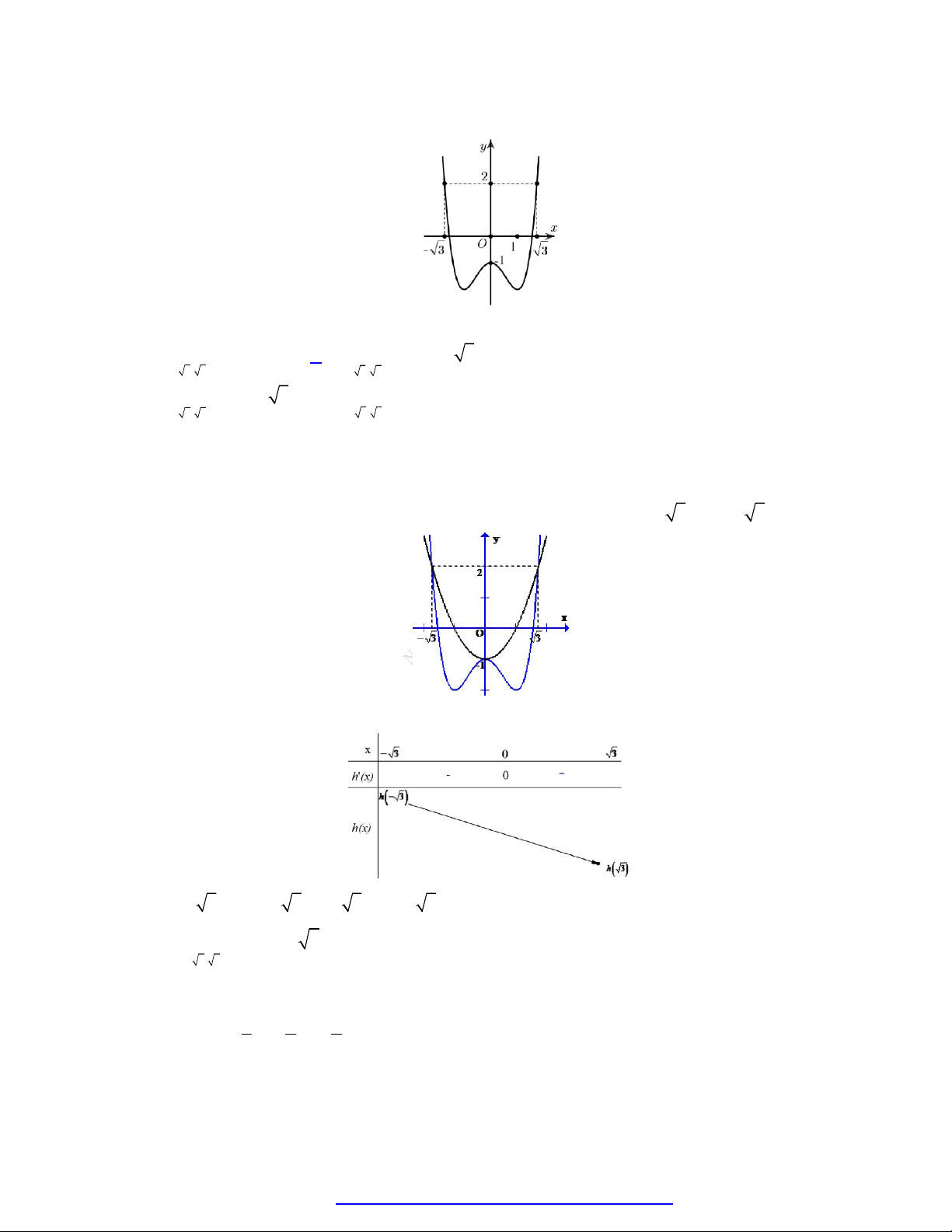
Câu 11. Cho hàm số f x . Biết hàm số y f  x có đồ thị như hình vẽ bên dưới. Trên đoạn  4  ;  3 ,
hàm số g x  f x    x2 2 1
đạt giá trị nhỏ nhất tại điểm: A. x  4  . 0
B. x  1 . 0
C. x  3. 0 D. x  3 . 0
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 12. Cho hàm số y f x có đạo hàm liên tục trên R . Hàm số y f ' x có đồ thị như hình sau: Cho bốn mệnh đề sau:
1) Hàm số y f x có hai cực trị
2) Hàm số y f x đồng biến trên khoảng 1;  3) f  
1  f 2  f 4. 4) Trên đoạn  1  ; 
4 , giá trị lớn nhất của hàm số y f x là f   1 .
Số mệnh đề đúng trong bốn mệnh đề trên là: A. 3. B. 1. C. 4. D. 2.
Câu 13. Cho hàm số y f x có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
g x  f  1 1 2 4x x  3 2
x 3x 8x  trên đoạn 1;  3 . 3 3 25 19 A. . B. 15. C. . D. 12. 3 3
Câu 14. Cho hàm số y f x . Hàm số y f  x có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất
của hàm số g x  f x 2 2
 sin x trên đoạn  1   ;1 là - -2 -1 0 1 2 + 0 0 0 A. f   1 . B. f 0 . C. f 2 . D. f   1 .
Câu 15. Cho hàm số y f x liên tục trên  sao cho max f x  3 . Xét hàm số g x  f 3x   1  m .  1  ;2
Tìm tất cả các giá trị của tham số m để max g x  1  0 . 0;  1 A. 13. B. 7  . C. 1  3 . D. 1  .
Câu 16. Cho hàm số y f x có đạo hàm cấp 2 trên  , hàm số y f  x có đồ thị như hình vẽ bên.
 sin x  3 cos x   5  
Giá trị lớn nhất của hàm số y f   trên đoạn  ; bằng  2       6 6     A. f    .  3  B. f 0 .  5  C. f    .  6     D. f   .  6 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 17. Cho hàm số y f x liên tục trên  sao cho max f x  f 2  4 . Xét hàm số x   0;10
g x  f  3 x x 2
x  2x m . Giá trị của tham số m để max g x  8 là x   0; 2 A. 5 . B. 4 . C. 1  . D. 3 .
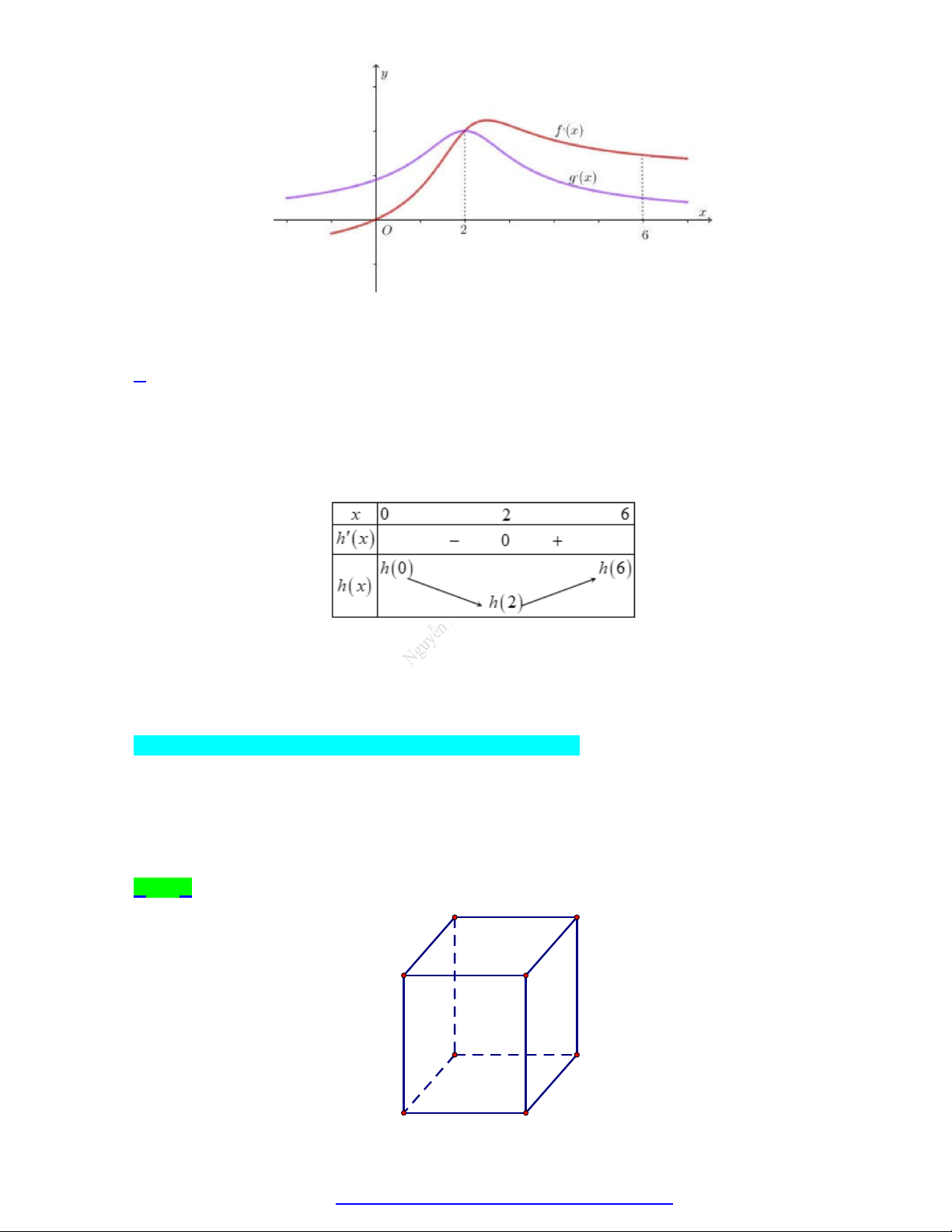
Câu 18. Cho hai hàm số y f x , y g x có đạo hàm là f  x , g x . Đồ thị hàm số y f  x và
g x được cho như hình vẽ bên dưới.
Biết rằng f 0  f 6  g 0  g 6 . Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
h x  f x  g x trên đoạn 0;6 lần lượt là:
A. h 6 , h 2 .
B. h 2 , h 6 .
C. h 0 , h 2 .
D. h 2 , h 0 .
E. ỨNG DỤNG GTLN-GTNN GIẢI BÀI TOÁN THỰC TẾ Câu 1.
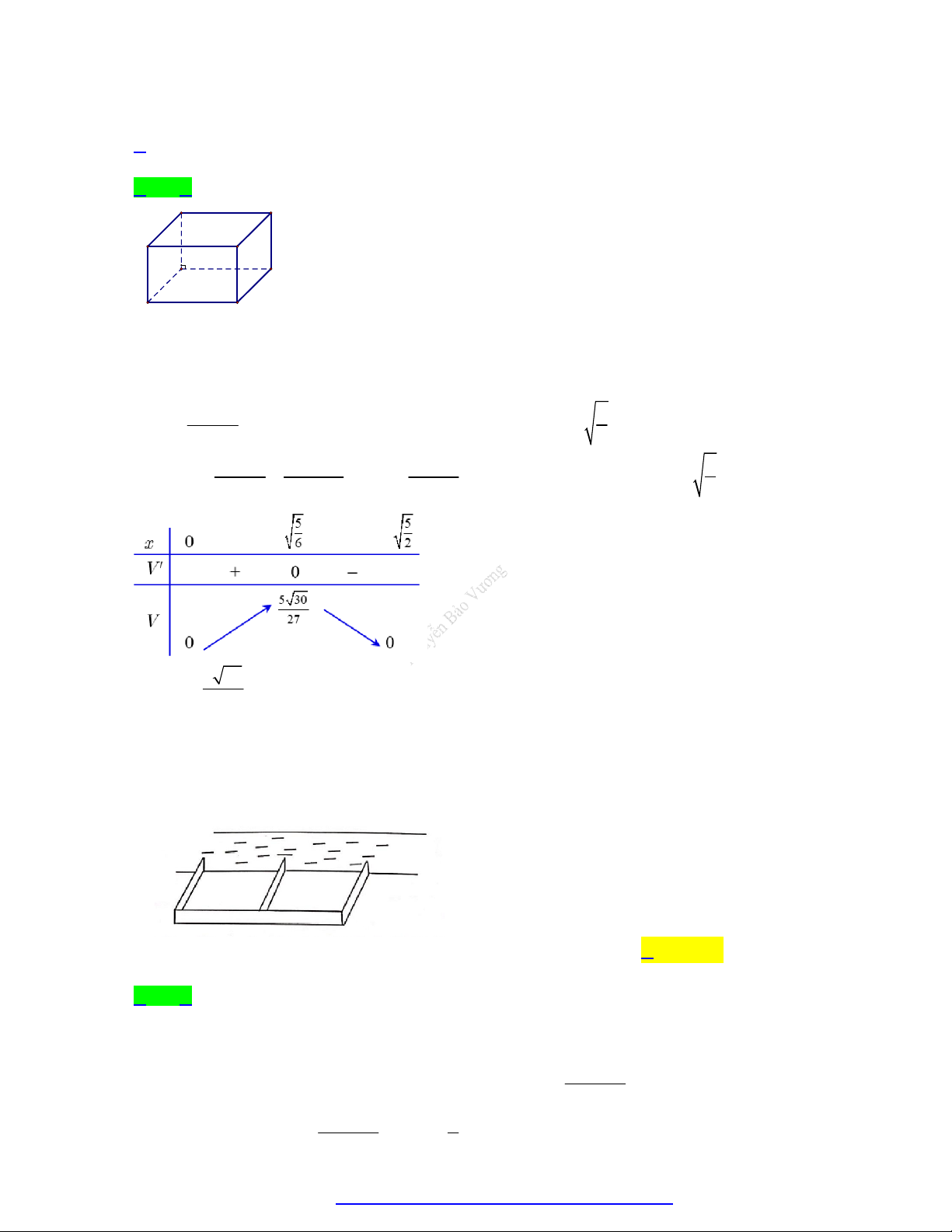
Ông A dự định dùng hết 2
6,5m kính để làm một bể cá có dạng hình hộp chữ nhật không nắp,
chiều dài gấp đôi chiều rộng (các mối ghép có không đáng kể). Bể cá có dung tích lớn nhất bằng
bao nhiêu (kết quả làm tròn đến hàng phần trăm). A. 3 2, 26 m B. 3 1, 61 m C. 3 1,33 m D. 3 1,50 m 1 Câu 2.
Một vật chuyển động theo quy luật 3 2
s   t  6t với t (giây) là khoảng thời gian tính từ khi vật 3
bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó.
Hỏi trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt
được bằng bao nhiêu? A. 243 (m/s) B. 27 (m/s) C. 144 (m/s) D. 36 (m/s) Câu 3.
Ông A dự định sử dụng hết 2
5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? A. 3 1, 01 m B. 3 0, 96 m C. 3 1,33 m D. 3 1,51 m Câu 4.
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được
giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể t
trong t giờ được cho bởi công thức c t  
mg / L . Sau khi tiêm thuốc bao lâu thì nồng độ 2 t 1
thuốc trong máu của bệnh nhân cao nhất? A. 4 giờ. B. 1 giờ. C. 3 giờ. D. 2 giờ. Câu 5.
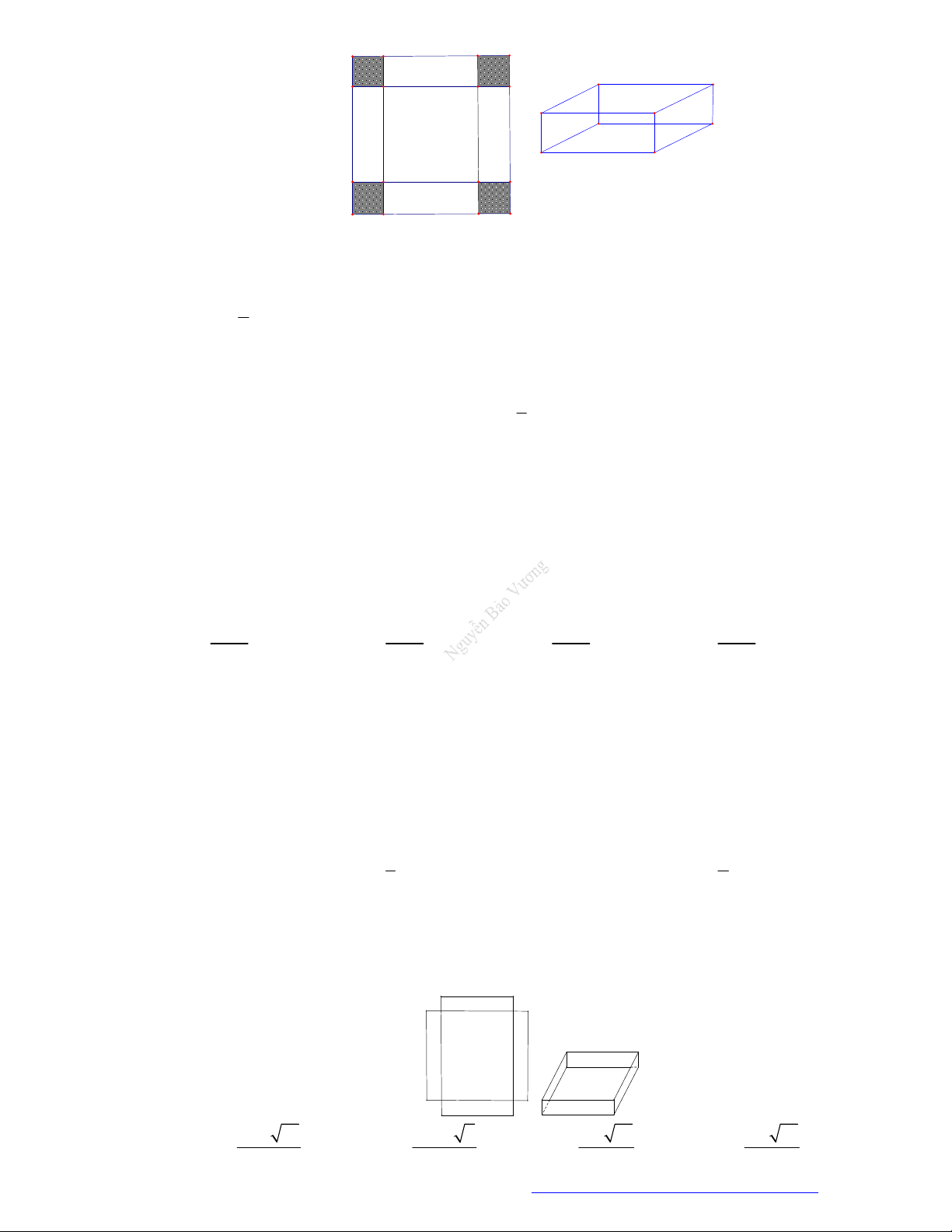
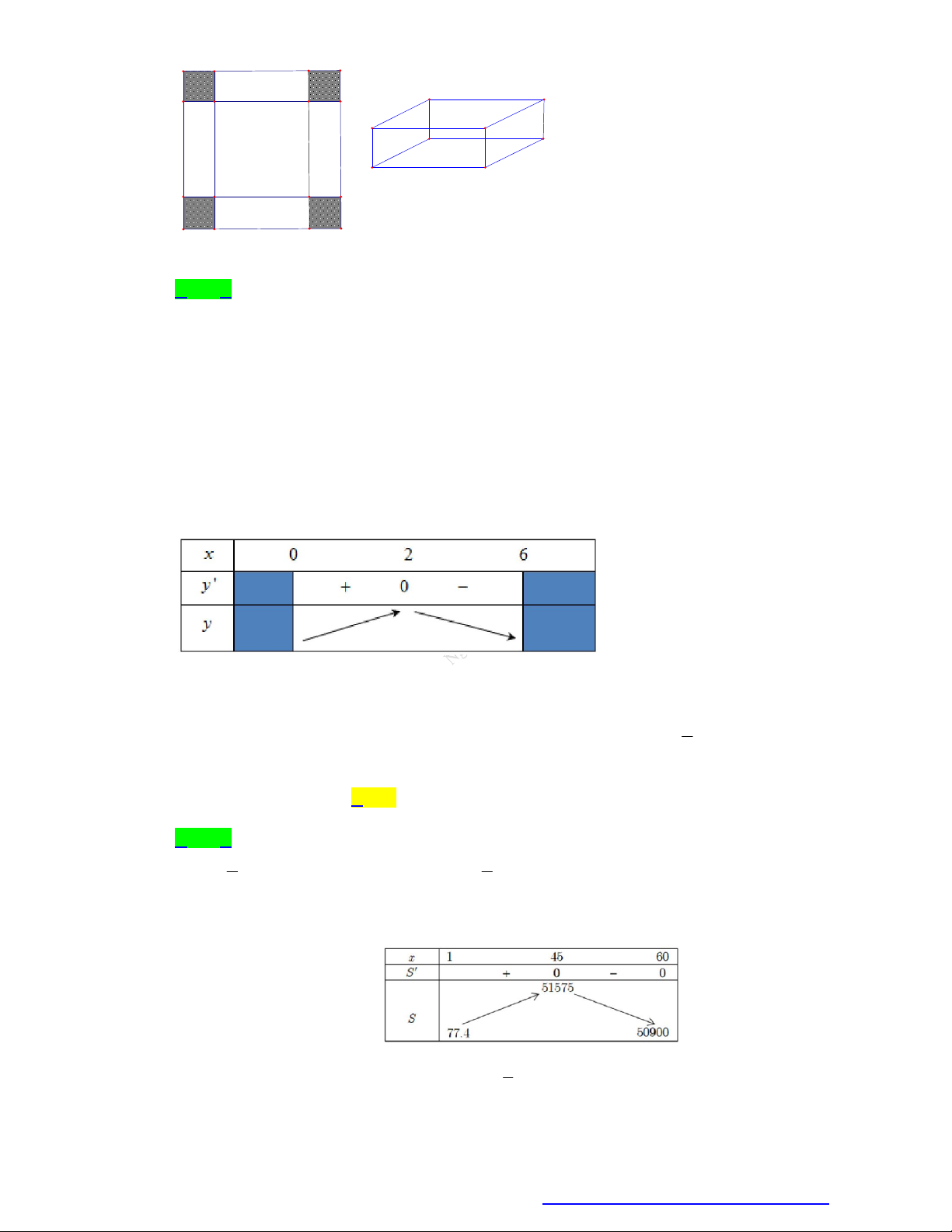
Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình
vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ dưới
đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
A. x  3
B. x  2
C. x  4
D. x  6 Câu 6.
Đợt xuất khẩu gạo của tỉnh A thường kéo dài trong 2 tháng ( 60 ngày). Người ta nhận thấy số
lượng xuất khẩu gạo tính theo ngày thứ
t được xác định bởi công thức 2 S t  3 2 
t  63t  3240t  3100 với 1  t  60 . Hỏi trong 60 ngày đó thì ngày thứ mấy có số 5
lượng xuất khẩu gạo cao nhất. A. 60 B. 45 C. 30 D. 25 1 Câu 7.
Một vật chuyển động theo quy luật 2 3
S  10t t , với t (giây) là khoảng thời gian tính từ lúc vật 3
bắt đầu chuyển động và S m là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong
khoảng thời gian 15 giây từ lúc vật bắt đầu chuyển động vận tốc v m / s của vật đạt giá trị lớn
nhất tại thời điểm t s bằng: A. 8s . B. 20 sC. 10 s . D. 15 s . Câu 8.
Một sợi dây có chiều dài 28m được cắt thành hai đoạn để làm thành một hình vuông và một hình
tròn. Tính chiều dài (theo đơn vị mét) của đoạn dây làm thành hình vuông được cắt ra sao cho
tổng diện tích của hình vuông và hình tròn là nhỏ nhất? 56 112 84 92 A. . B. . C. . D. . 4   4   4   4   Câu 9.
Một xưởng in có 15 máy in được cài đặt tự động và giám sát bởi một kỹ sư, mỗi máy in có thể in
được 30 ấn phẩm trong 1 giờ, chi phí cài đặt và bảo dưỡng cho mỗi máy in cho 1 đợt hàng là
48.000 đồng, chi phí trả cho kỹ sư giám sát là 24.000 đồng/giờ. Đợt hàng này xưởng in nhận
6000 ấn phẩm thì số máy in cần sử dụng để chi phí in ít nhất là A. 10 máy. B. 11 máy. C. 12 máy. D. 9 máy.
Câu 10. Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật s t  3 2
t  4t 12 (m), trong đó t (s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận
tốc của chất điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu? 8 4 A. 2 (s). B. (s). C. 0 (s). D. (s). 3 3
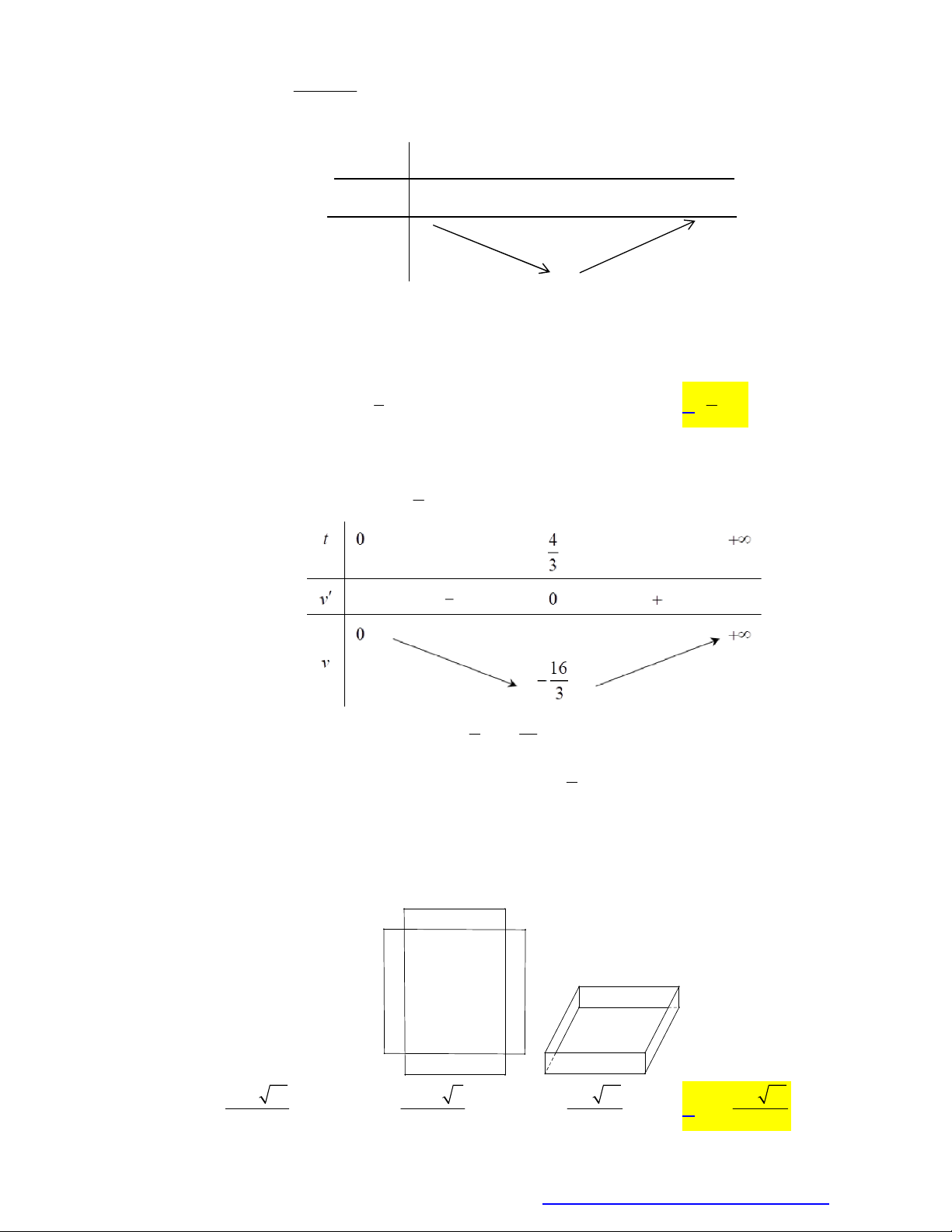
Câu 11. Cho một tấm nhôm hình chữ nhật có chiều dài bằng 10cm và chiều rộng bằng 8cm . Người ta cắt
bỏ ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x cm ,
rồi gập tấm nhôm lại (như hình vẽ) để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. 8  2 21 10  2 7 9  21 9  21 A. x B. x C. x  . D. x  3 3 9 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489
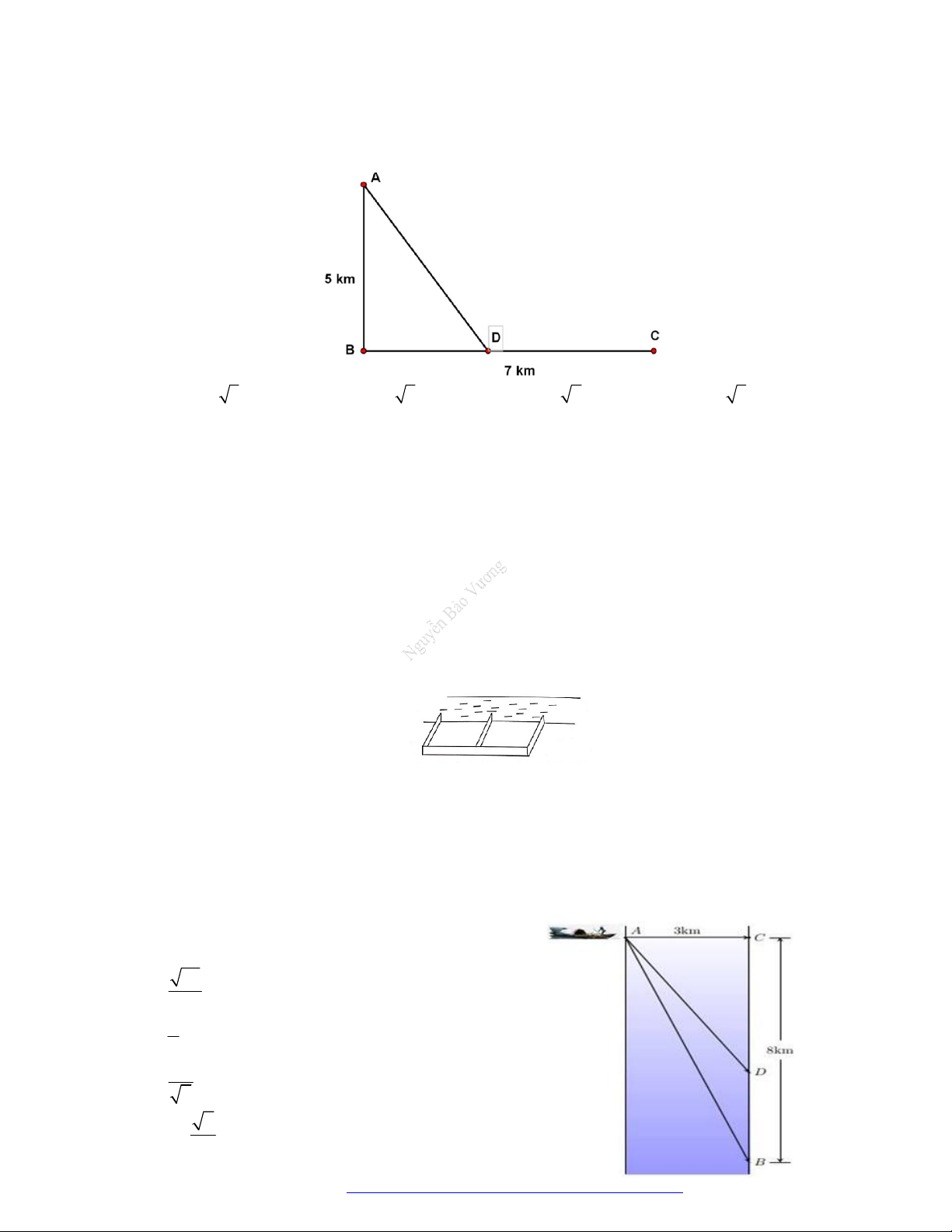
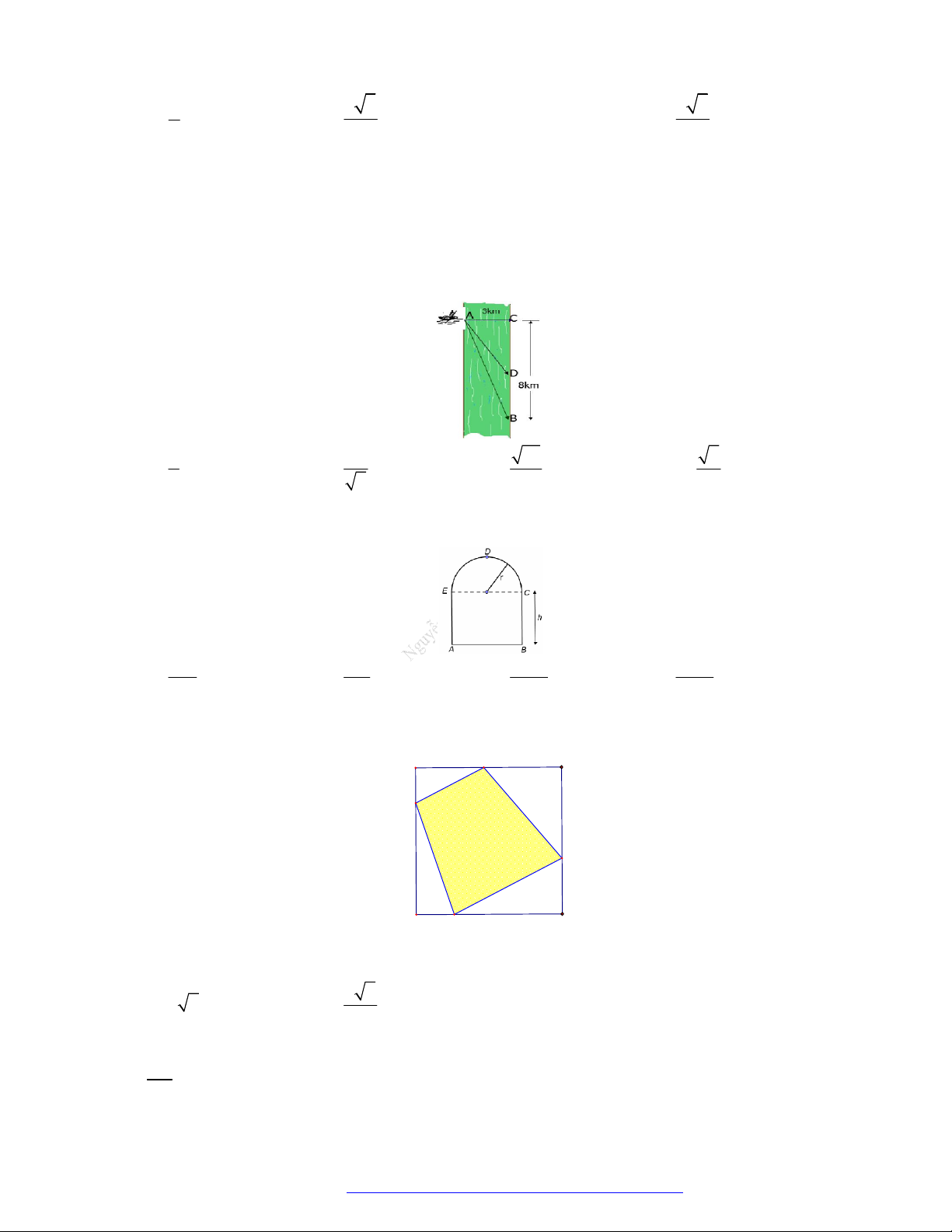
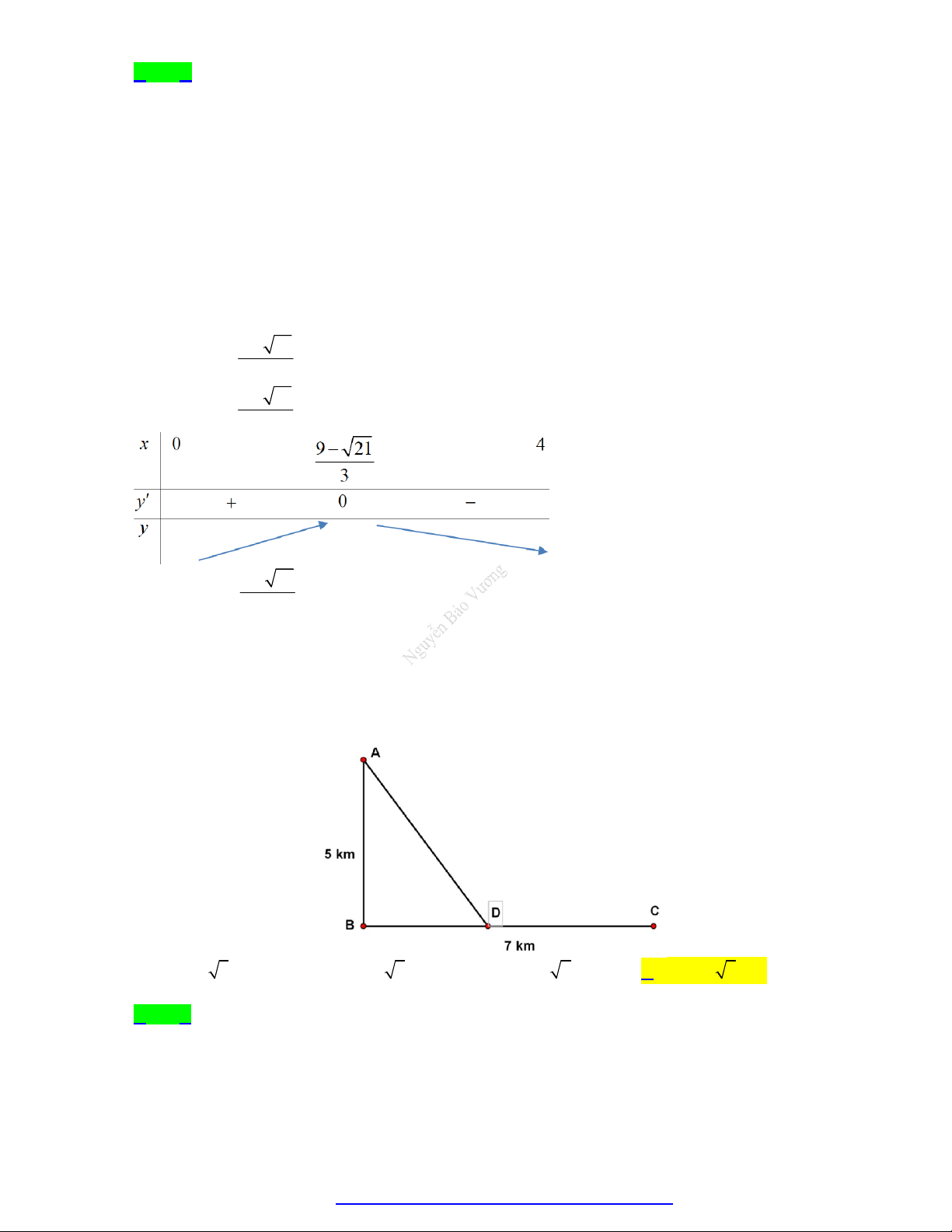
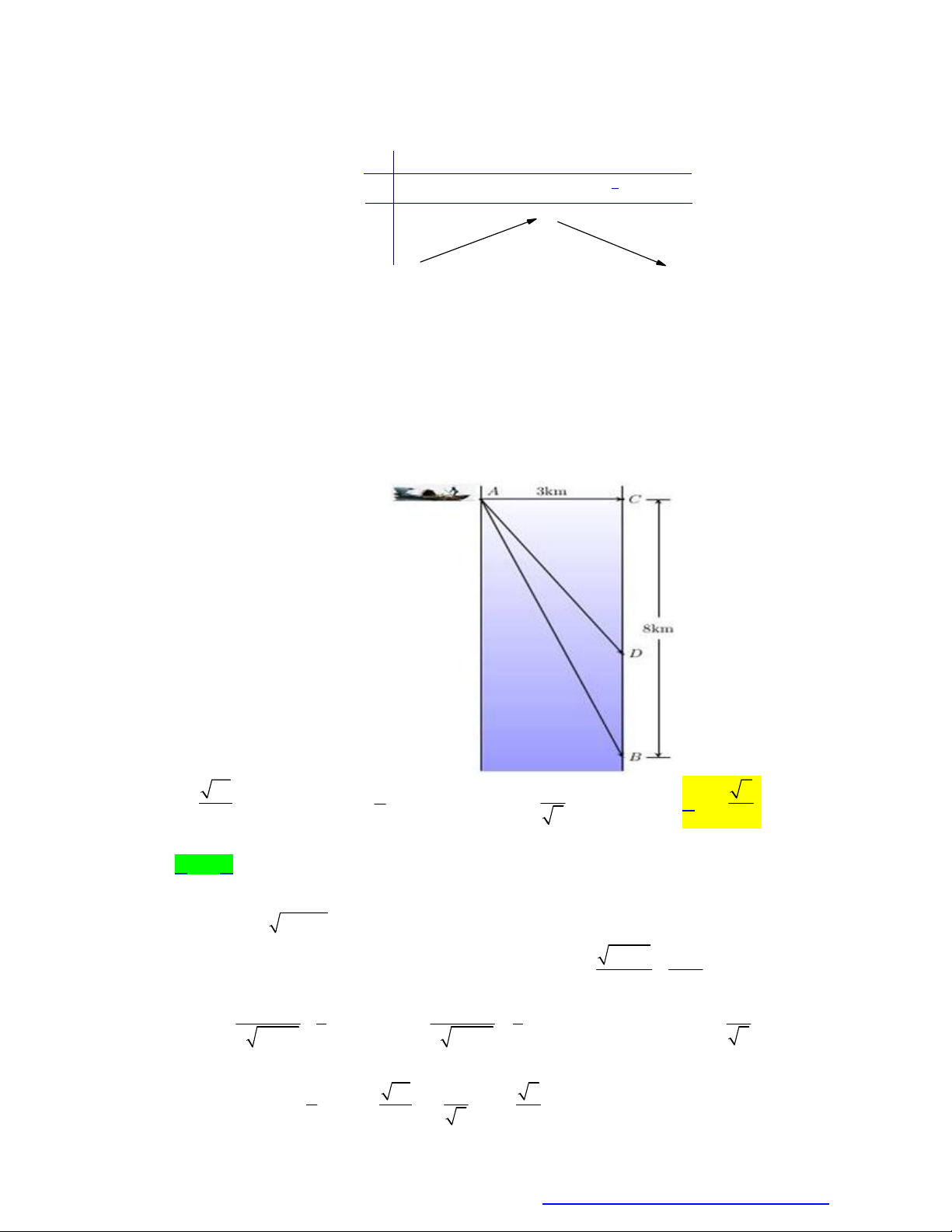
Câu 12. Một đoàn cứu trợ lũ lụt đang ở vị trí A của một tỉnh miền trung muốn đến xã C để tiếp tế lương
thực và thuốc men. Để đi đến C , đoàn cứu trợ phải chèo thuyền từ A đến vị trí D với vận tốc
4 km / h , rồi đi bộ đến vị trí C với vận tốc 6km / h . Biết A cách B một khoảng 5km , B
cách C một khoảng 7km (hình vẽ). Hỏi vị trí điểm D cách A bao xa để đoàn cứu trợ đi đến xã C nhanh nhất?
A. AD  5 3 km .
B. AD  2 5 km .
C. AD  5 2 km .
D. AD  3 5 km .
Câu 13. Một vật chuyển động theo quy luật 2 3
s  3t t . Thời điểm t(s) tại đó vận tốc v(m / s) của
chuyển động đạt giá trị lớn nhất là
A. t  5 .
B. t 1.
C. t  2 .
D. t  3
Câu 14. Ông A dự định sử dụng hết 2
5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? A. 3 1, 01 m . B. 3 0,96 m . C. 3 1,33 m . D. 3 1,51 m .
Câu 15. Một người nông dân có 15.000.000 đồng muốn làm một cái hàng rào hình chữ E dọc theo một con
sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào
song song với bờ sông thì chi phí nguyên vật liệu là 60.000 đồng một mét, còn đối với ba mặt
hàng rào song song nhau thì chi phí nguyên vật liệu là 50.000 đồng một mét. Tìm diện tích lớn
nhất của đất rào thu được A. 2 3125 m . B. 2 50 m . C. 2 1250 m . D. 2 6250 m .
Câu 16. Một người đàn ông muốn trèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đố diện, càng
nhanh càng tốt, trên một bờ sông thẳng rộng 3 km ( như hình vẽ). Anh có thể chèo thuyền của
mình trực tiếp qua sông để đến C và sau đó chạy đến B , hay có thể chèo trực tiếp đến B , hoặc
anh có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B . Biết anh ấy có thể
chèo thuyền 6 km/h, chạy 8 km/h và quãng đường BC  8 km . Biết tốc độ của dòng nước là
không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất(
đơn vị: giờ) để người đàn ông đến B ? 73 A. . 6 3 B. . 2 9 C. . 7 7 D. 1  . 8
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 17. Ông Khoa muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng 3
288m . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây 2
bể là 500000 đồng/ m . Nếu ông Khoa biết xác định các kích thước của bể hợp lí thì chi phí thuê
nhân công sẽ thấp nhất. Hỏi ông Khoa trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu (Biết
độ dày thành bể và đáy bể không đáng kể)? A. 90 triệu đồng.
B. 168 triệu đồng. C. 54 triệu đồng.
D. 108 triệu đồng.
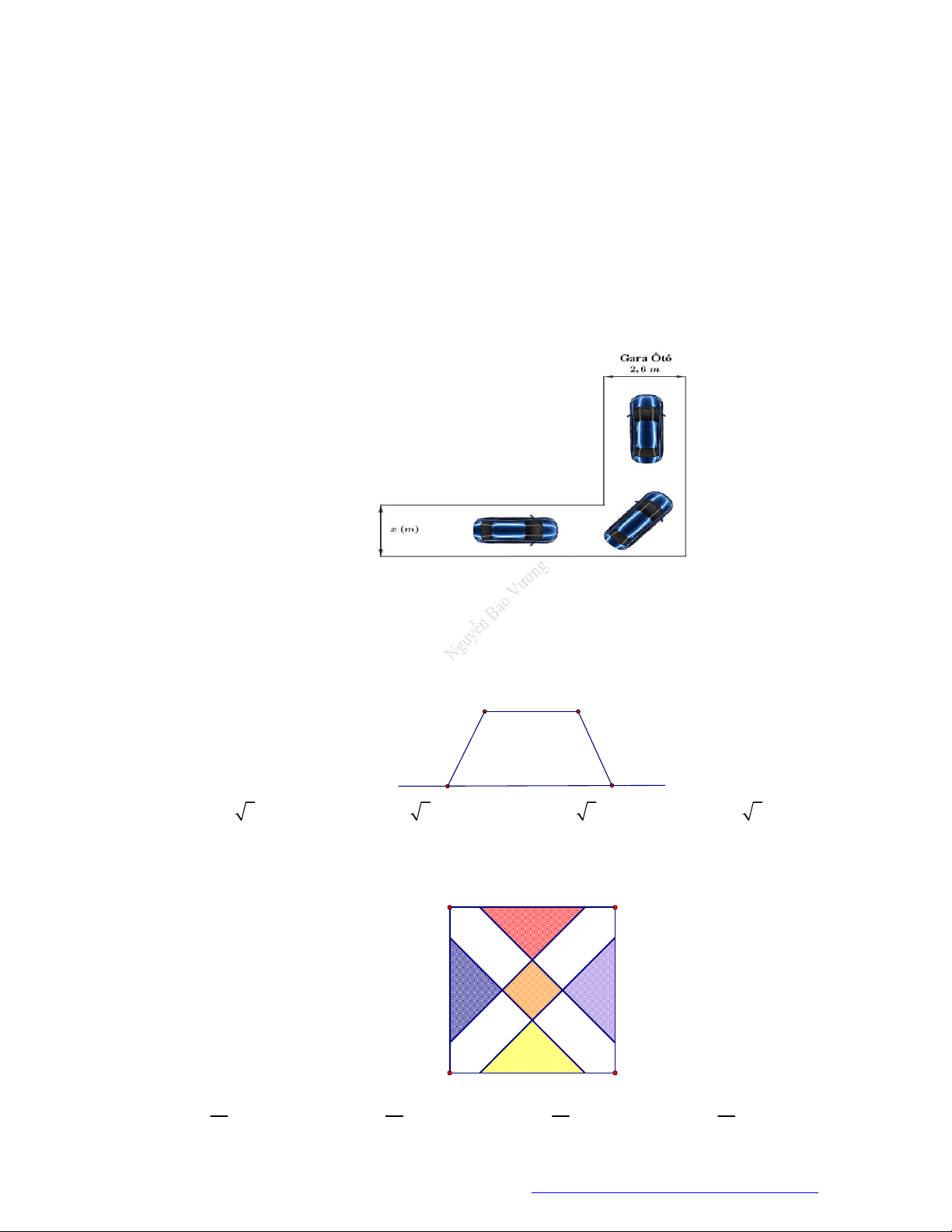
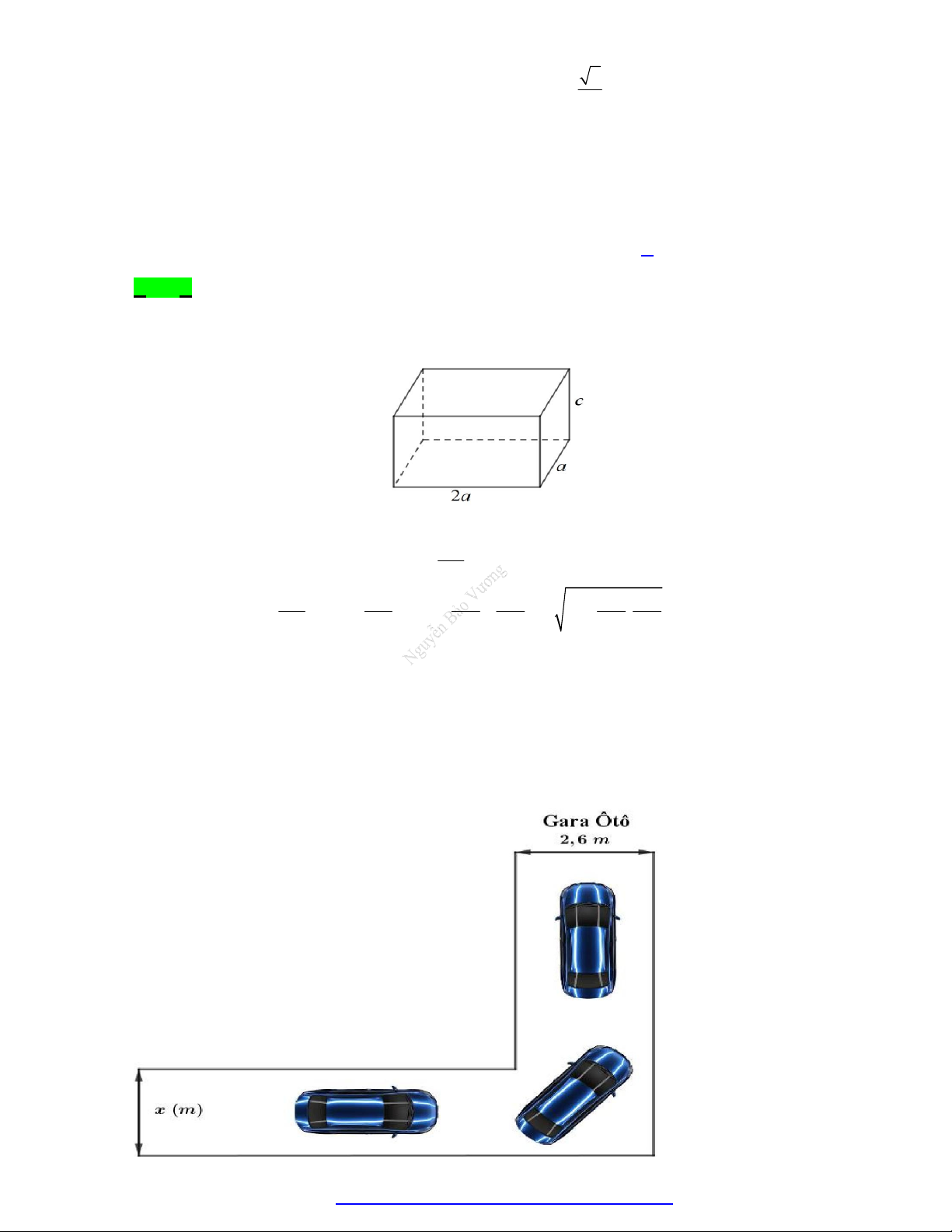
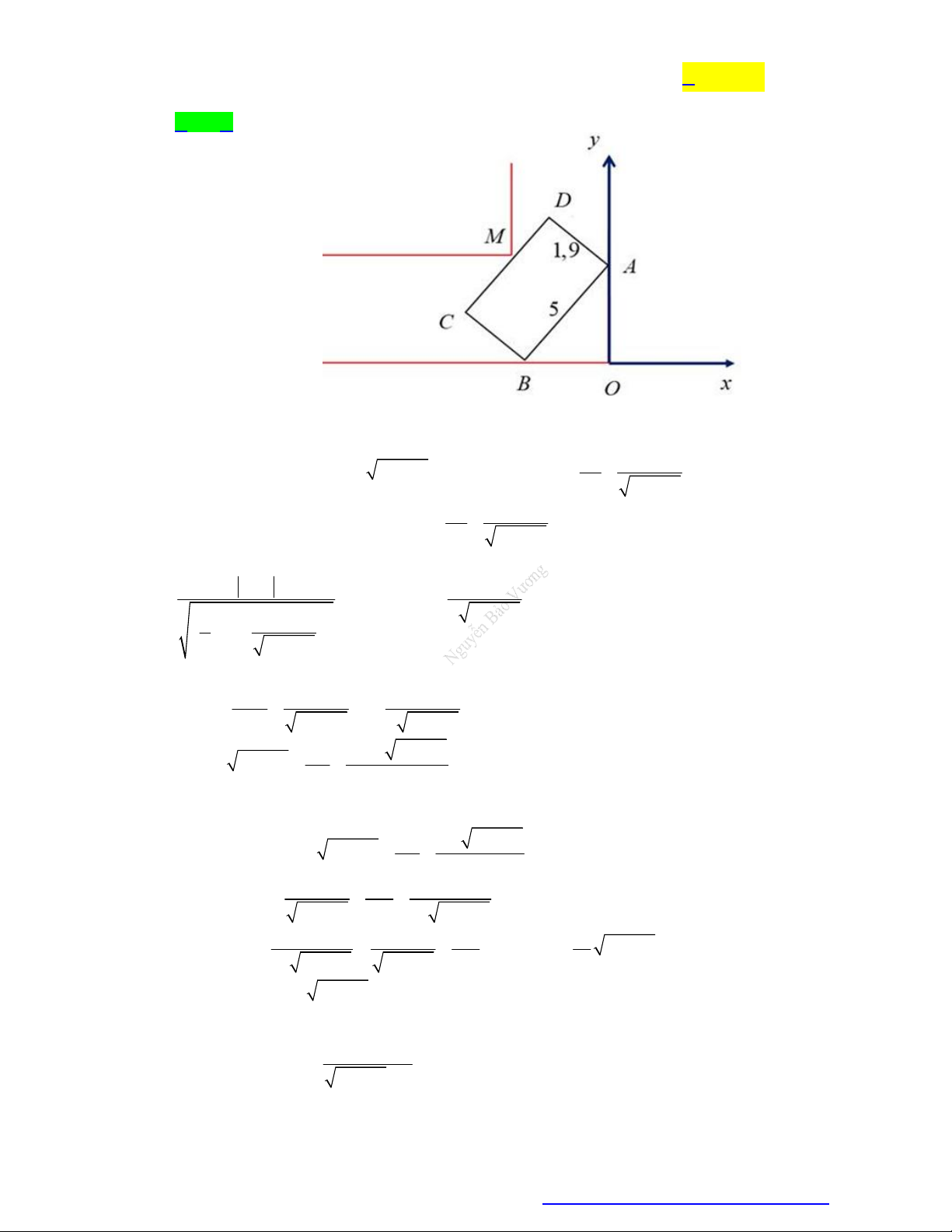
Câu 18. Hình vẽ bên dưới mô tả đoạn đường đi vào GARA ÔTÔ nhà cô Hiền. Đoạn đường đầu tiên có
chiều rộng bằng x m , đoạn đường thẳng vào công GARA có chiều rộng 2, 6m . Biết kích
thước xe ôtô là 5m 1, 9m (chiều dài  chiều rộng). Để tính toán và thiết kế đường đi cho ôtô
người ta coi ôtô như một khối hộp chữ nhật có kích thước chiều dai 5m , chiều rộng 1, 9m . Hỏi
chiều rộng nhỏ nhất của đoạn đường đầu tiên gần nhất với giá trị nào trong các giá trị bên dưới để
ôtô có thể đi vào GARA được?(giả thiết ôtô không đi ra ngoài đường, không đi nghiêng và ôtô không bị biến dạng).
A. x  3,55m .
B. x  2, 6m .
C. x  4, 27m .
D. 3, 7 m .
Câu 19. Một người nông dân có 3 tấm lưới thép B40, mỗi tấm dài 12 m và muốn rào một mảnh vườn
dọc bờ sông có dạng hình thang cân ABCD như hình vẽ (bờ sông là đường thẳng DC không
phải rào, mỗi tấm là một cạnh của hình thang). Hỏi ông ta có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu 2 m ? B A C D A. 100 3 . B. 106 3 . C. 108 3 . D. 120 3 .
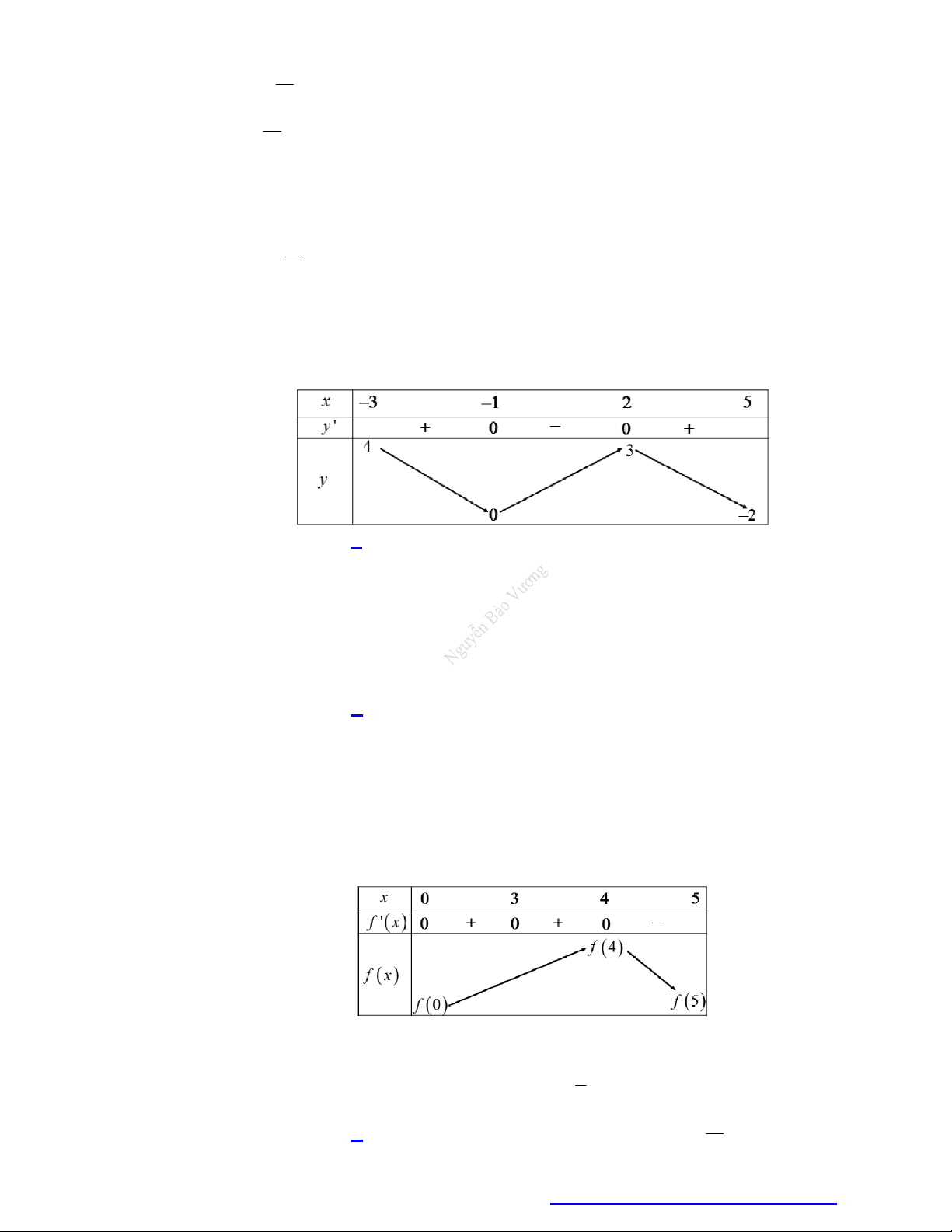
Câu 20. Cho hình vuông ABCD có cạnh bằng 4, chính giữa có một hình vuông đồng tâm với ABCD . Biết
rằng bốn tam giác là bốn tam giác cân. Hỏi tổng diện tích của hình vuông ở giữa và bốn tam giác
cân nhỏ nhất bằng bao nhiêu? A B D C 19 17 16 14 A. . B. . C. . D. . 3 3 3 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489
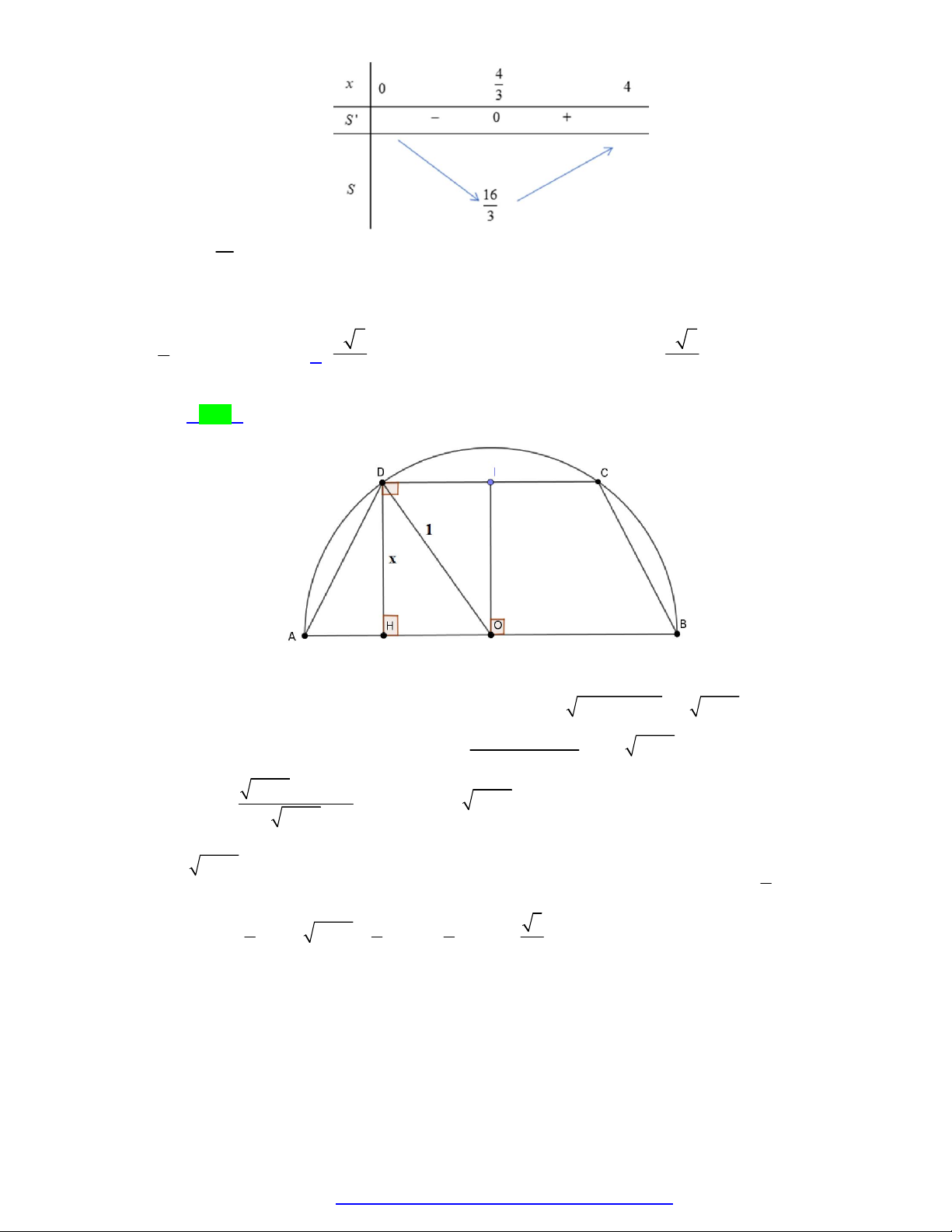
Câu 21. Cho nửa đường tròn đường kính AB  2 và hai điểm C , D thay đổi trên nửa đường tròn đó sao
cho ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng 1 3 3 3 3 A. . B. . C. 1. D. . 2 4 2
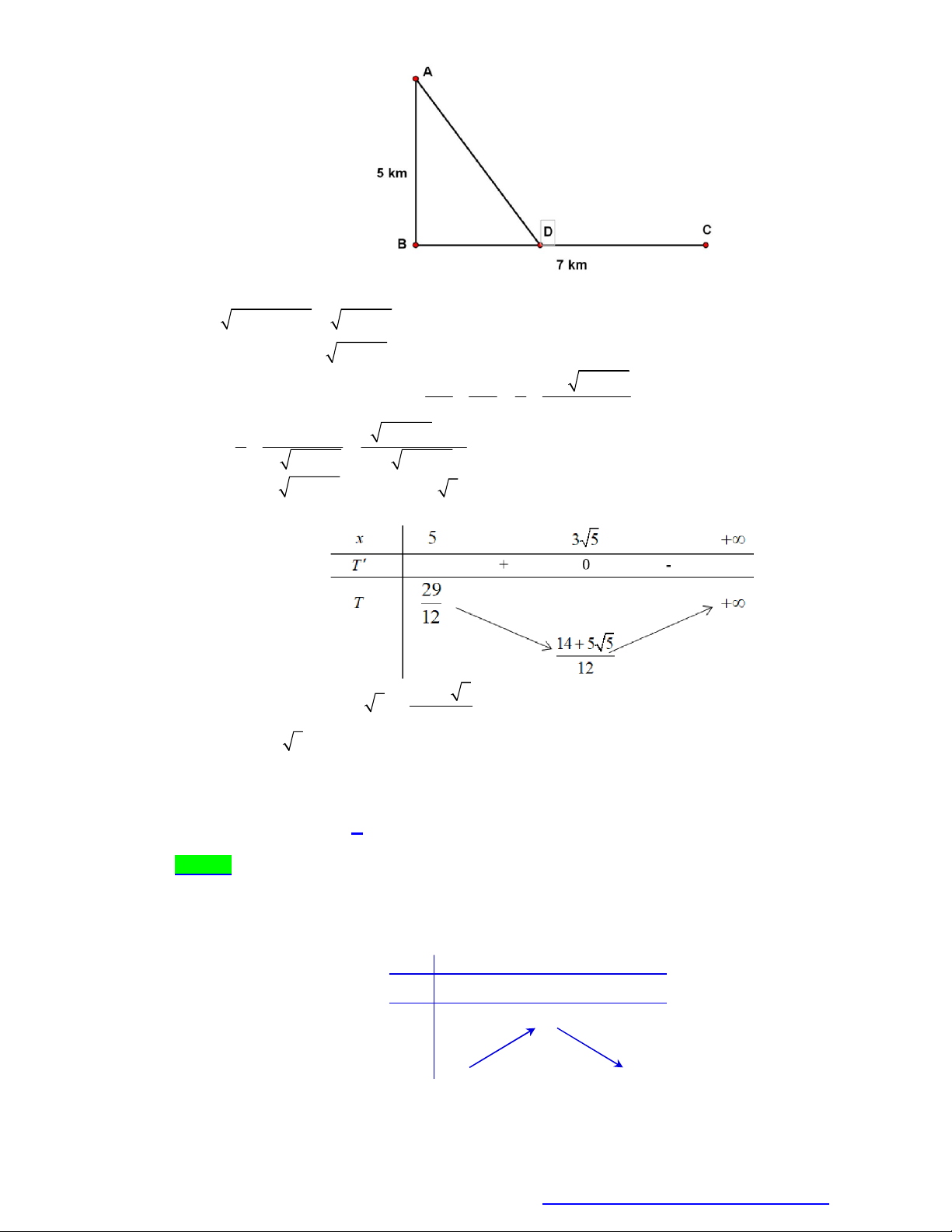
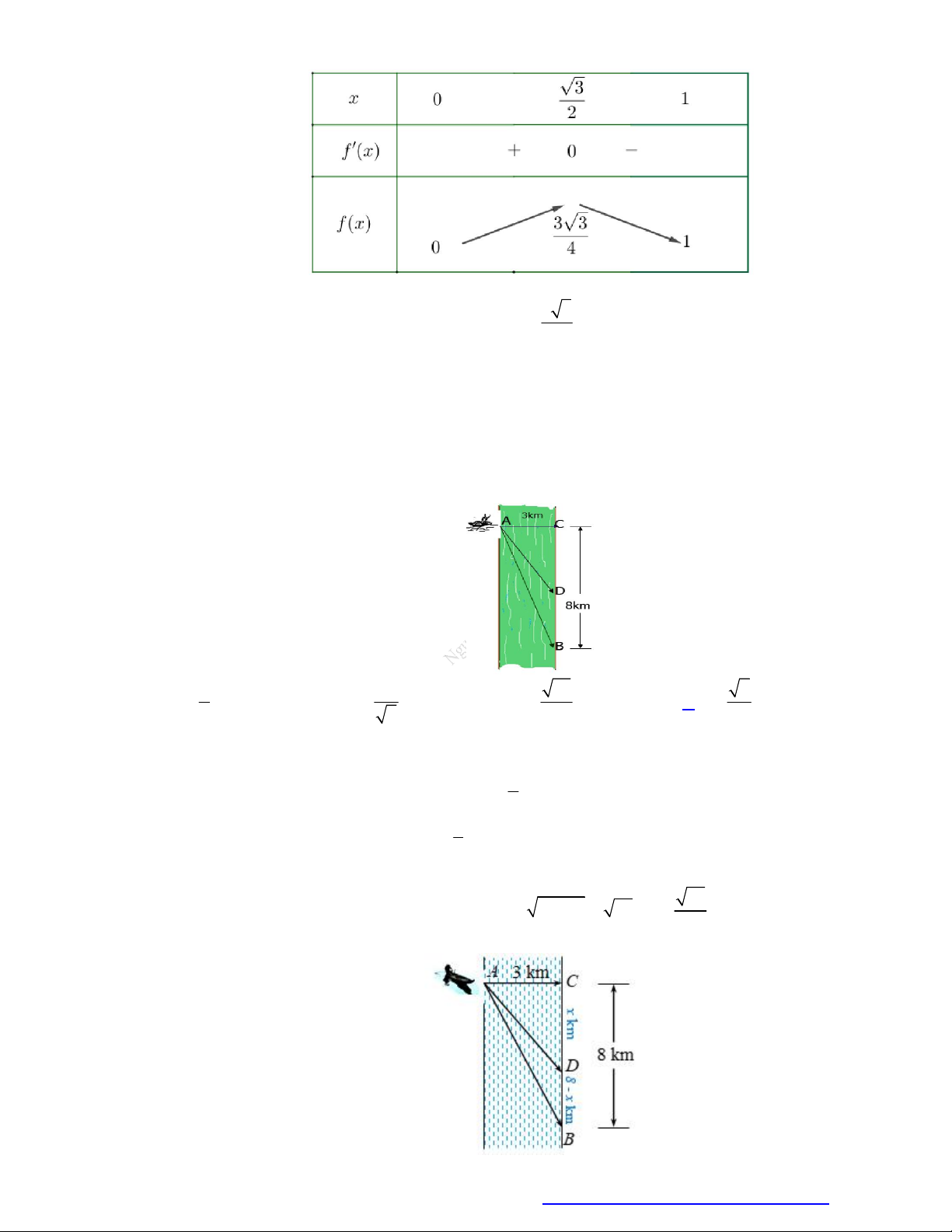
Câu 22. Một người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện, càng
nhanh càng tốt, trên một bờ sông thẳng rộng 3 km (như hình vẽ). Anh có thể chèo thuyền của
mình trực tiếp qua sông để đến C và sau đó chạy đến B , hay có thể chèo trực tiếp đến B , hoặc
anh ta có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B . Biết anh ấy có
thể chèo thuyền 6 km/ h , chạy 8 km/ h và quãng đường BC  8 km . Biết tốc độ của dòng nước
là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất
(đơn vị: giờ) để người đàn ông đến B . 3 9 73 7 A. . B. . C. . D. 1 . 2 7 6 8
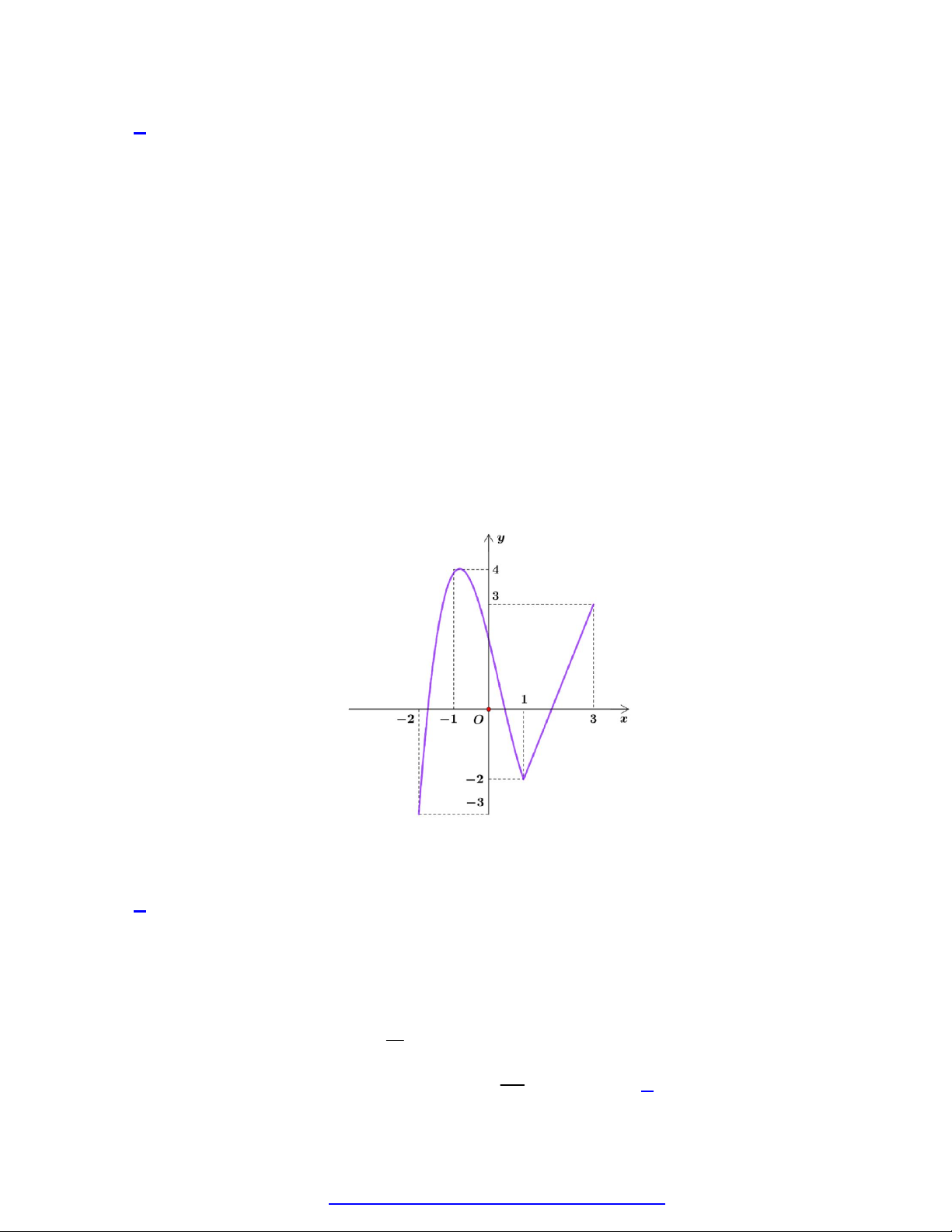
Câu 23. Bác thợ hàn dùng một thanh kim loại dài 250 cm để uốn thành khung cửa sổ có dạng như hình
vẽ. Gọi r là bán kính của nửa đường tròn, tìm r để diện tích tạo thành đạt giá trị lớn nhất. 250 125 250 125 A. cm . B. cm . C. cm . D. cm . 4 4   4 4  
Câu 24. Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. A 2 cm E B x cm H 3 cm F D C G y cm
Tìm tổng x y để diện tích hình thang EFGH đạt giá trị nhỏ nhất. 7 2 A. 4 2 . B. . C. 7 . D. 5 . 2
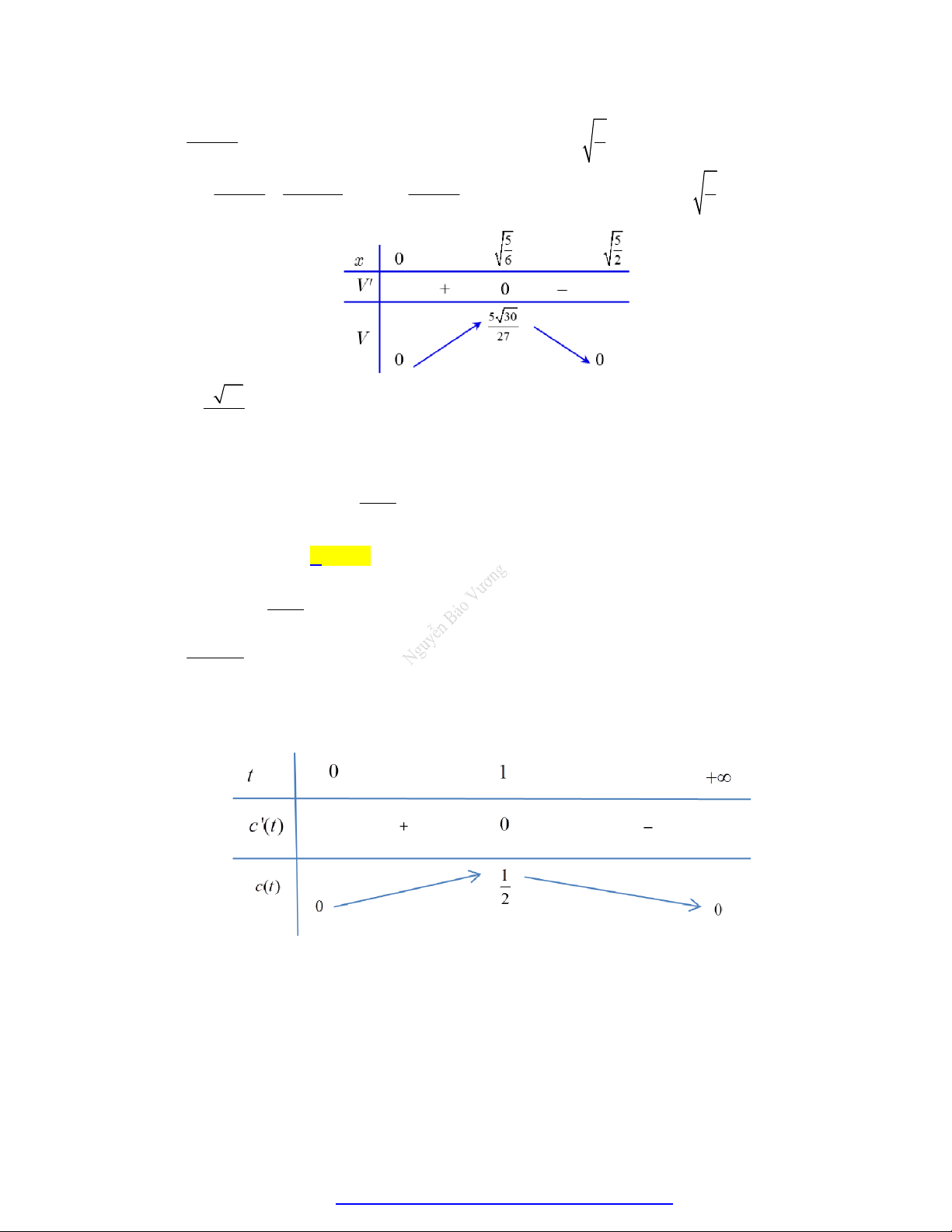
Câu 25. Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng 500 3
m . Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 3
500.000 đồng/m2. Hãy xác định kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất và chi phí đó là:
A. 74 triệu đồng.
B. 75 triệu đồng.
C. 76 triệu đồng.
D. 77 triệu đồng.
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 4
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT
A. TÌM GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Định lí 1: Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn đó. Định lí 2
Nếu y f (x) đồng biến trên [a;b] thì min f (x)  f (a) và max f (x)  f (b). [a;b ] [a;b ]
Nếu y f (x) nghịch biến trên [a;b] thì min f (x)  f (b) và max f (x)  f (a). [a;b ] [a;b ]
Bài toán 1. Tìm GTLN & GTNN của hàm số y f (x ) trên đoạn [ ; a b].
Bước 1. Hàm số đã cho xác định và liên tục trên đoạn [ ; a b]. Tính f (
x)  0 tìm nghiệm x  [a;b]. i
Bước 2. Tính f (a), f (b), f (x ). i
Bước 3. Kết luận: max f (x)  max f (a); f (b); f (x
và min f (x)  min f (a); f (b); f (x i  ) . i  ) [a;b ] [a;b ]
Bài toán 2. Tìm GTLN & GTNN của hàm số y f (x ) trên khoảng (a;b).
Bước 1. Tìm tập xác định. Tính f (
x). Cho f (x)  0 tìm nghiệm.
Bước 2. Xét dấu biểu thức y  f (
x) và lập bảng biến thiên (có tính giới hạn).
Bước 3. Dựa vào bảng biến thiên để kết luận GTLN (GTNN nếu có).
Lưu ý: Đạo hàm của hàm số mũ và lôgarit
 ( u )  . u a
ua .lna.  ( u )  . u e
ue .  ( x ) x
e   e . u 1 u   (log u) 
 (log x)   u     x  1 (ln ) ln   a u lna a x lna u x
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA Câu 1.
Giá trị lớn nhất của hàm số 4 2
f (x) = -x 12x 1 trên đoạn -1; 2bằng: A. 1. B. 37 . C. 33 . D. 12 . Lời giải Chọn C x = 0  4 2
f (x) = -x 12x 1 liên tục trên -1; 2 và 3 2
f '(x) = -4x  24x = 0 Û x = 6 (L)   x = - 6 (L)  Ta có: f ( 1
- ) = 12; f (2) = 33; f (0) = 1
Vậy, giá trị lớn nhất của hàm số 4 2
f (x) = -x 12x 1 trên đoạn -1; 2 bằng 33 tại x = 2 Câu 2.
Giá trị nhỏ nhất của hàm số f ( x) 4 2
= x -10x  2 trên đoạn  1 - ;  2 bằng A. 2 . B. 2 - 3 . C. 2 - 2. D. 7 - . Lời giải Chọn C
Hàm số đã cho liên tục trên đoạn  1 - ; 2.  x = 0 Ta có: f ¢( x) 3 = 4x - 20 ,
x f ¢( x) = 0 Û  . x =  5 
Xét hàm số trên đoạn  1 - ; 2 có: f (- ) 1 = 7
- ; f (0) = 2; f (2) = 2 - 2 .
Vậy min f ( x) = 22 - . x   1 - ;2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 3.
Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số 4 2
y = x - 8x - 5 trên đoạn  3 - ;  1 . Khi
đó, giá trị của biểu thức M - 2m bằng A. 46 . B. 25 . C. 2 - 5 . D. 4 - 6 . Lời giải Chọn A Cách 1: x = 0 (n)  Ta có: 3
y ' = 4x -16x ; 3
y ' = 0 Û 4x -16x = 0 Û x = 2  (l ) . x = 2 - (n)   y (0) = 5 -  y  ( 3 - ) = 4 Khi đó:  . y ( 2 - ) = 21 -   y( ) 1 = 12 - 
Do đó: M = max y = 4; m = min y = 2 - 1 . -3;  1 -3;  1
Vậy M - 2m = 4 - 2.( 2 - ) 1 = 46 .
Cách 2: Học sinh có thể sử dụng chức năng Table của MTCT để thực hiện cho nhanh. Câu 4.
Cho hàm số y = f ( x) liên tục trên đoạn  3 - ; 
3 có đồ thị như hình vẽ.
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f ( x) trên 0; 
3 lần lượt có giá trị là
A. max y = 4, min y = -3 .
B. max y = 3, min y = 3 - . -4;3 -4;3  4 - ;  3  4 - ;  3
C. max y = 3, min y = 2 - .
D. max y = 4, min y = 2 - . 0  ;3 0;3  4 - ;  3  4 - ;  3 Lời giải Chọn C
Dựa vào đồ thị ta thấy:
Giá trị lớn nhất của hàm số trên 0; 
3 là 3 và giá trị nhỏ nhất của hàm số trên 0;  3 là 2 - . 16 Câu 5.
Giá trị nhỏ nhất của hàm số y = x
 3 trên đoạn 1;5 là: x 5 6 A. 5 - . B. 20 . C. . D. 11. 5 Lời giải Chọn D Cách 1:
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 16 Ta có: y¢ = 1- . 2 x 16 x = 4 y¢ = 0 Û 1- = 0 Û . 2  x x = 4 - (l)    y ( ) 1 = 20 
Ta có:  y (4) = 11 .  56  y (5) =  5
Vậy min y = 11 khi x = 4 . 1; 5 Câu 6.
Cho hàm số f ( x) liên tục trên  3 - ; 
5 và có bảng biến thiên như hình vẽ. Gọi M , m lần lượt là giá trị
lớn nhất và nhỏ nhất của f ( x) trên [ - 3; 2] . Tính M - m . A. 6 . B. 4 . C. 5 . D. 3. Lời giải Chọn B
Căn cứ vào bảng biến thiên của hàm số f ( x) trên  3 - ; 
5 , ta có M = 4, m = 0 suy ra M - m = 4. 2 Câu 7. Cho hàm số f ( )
x có đạo hàm f '( x) = -x( x - 3) ( x - 4), x
   . Giá trị lớn nhất của hàm số đã cho trên đoạn 0;  5 bằng A. f (0) . B. f (4) . C. f (3) . D. f (5) . Lời giải Chọn B x = 0 2 
Ta có f '( x) = -x( x - 3) ( x - 4) = 0 Û x = 3(k ) .   x = 4  Bảng biến thiên
Dựa vào BBT ta suy ra max f (x) = f (4) . x   0;5  3  Câu 8.
Giá trị lớn nhất của hàm số 3
y = x - 3x  5 trên đoạn 0;  bằng: 2    31 A. 3. B. 5. C. 7. D. . 8
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn B   3  x = 1 0;   2    Ta có: 3 2 y x 3x 5 y ' 3x 3 0  = -   = - = Û .   3  x = 1 -  0;   2      3  31 Mà y (0) = 5, y ( ) 1 = 3, y =    2  8  3 
Nên giá trị nhỏ nhất của hàm số trên đoạn 0;  là 5 . 2    Câu 9.
Giá trị lớn nhất của hàm số 3
f (x) = x - 6x - 3 trên đoạn 0; 2bằng: A. 3 - . B. 3 - - 4 2 . C. 25 . D. 12 . Lời giải Chọn A x = 2 3
f (x) = x - 6x - 3 liên tục trên 0; 2 và 2
f '(x) = 3x - 6 . f '(x) = 0 Û  x = - 2(l)  Ta có:
f (0) = -3; f (2) = -7; f ( 2) = -3 - 4 2
Vậy, giá trị lớn nhất của hàm số trên đoạn  1
- ; 2bằng -3 tại x = 0 . 8
Câu 10. Giá trị nhỏ nhất của hàm số f ( x) =
x trên đoạn 1;  2 bằng: 1  2x 7 18 11 9 A. . B. . C. . D. - . 2 5 3 2 Lời giải Chọn A
Hàm số xác định và liên tục trên đoạn 1;  2 16
Ta có f ¢( x) = 1- (1 2x)2  3 x = 1; 2  2
f ¢( x) = 0 Û  . 5  x = - 1;2  2 11  3  7 18 Khi đó f ( ) 1 = ; f =   ; f (2) = . 3  2  2 5  3  7
Vậy min f ( x) = f =   . 1;2  2  2 2 - x
Câu 11. Giá trị nhỏ nhất của hàm số f (x) = trên đoạn 1;  3 bằng: x  3 -1 1 A. 3 . B. -2 . C. . D. . 6 4 Lời giải Chọn C
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2 - x -5 f (x) = liên tục trên 1;  3 và f '(x) =  0;x [1;3] . x  3 2 (x - 3) -1
Vậy, giá trị nhỏ nhất của hàm số trên đoạn 1;  3 bằng tại x = 3 . 6
Câu 12. Giá trị nhỏ nhất của hàm số 3 2
f (x) = x - x  5x  6 trên đoạn 0; 4bằng: 2 A. 3 . B. 2 - . C. . D. 6 . 27 Lời giải Chọn D 3 2
f (x) = x - x  5x  6 liên tục trên 0; 4 và 2
f '(x) = 3x - 2x  5 . Phương trình f '(x) = 0 vô nghiệm. Ta có:
f (0) = 6; f (4) = 74 .
Vậy, giá trị nhỏ nhất của hàm số trên đoạn 0; 4bằng 6 tại x = 0 .
Câu 13. Giá trị nhỏ nhất của hàm số f ( x) 3 2
= x - 8x 16x - 9 trên đoạn 1;  3 bằng: 13 A. 9 - . B. 6 - . C. . D. 0 . 27 Lời giải Chọn B x = 4 1;  3 Ta có f ¢( x) 2
= 3x -16x 16  f ¢( x) 2
= 0 Û 3x -16x 16 = 0  Û 4 . x = 1;  3  3  4  13 Có f ( ) 1 = 0 , f (3) = 6 - , f =   .  3  27
Vậy min f ( x) = -6 . 1;3  3 
Nên giá trị nhỏ nhất của hàm số trên đoạn 0;  là 5 . 2   
Câu 14. Cho hàm số y = f (x) có đồ thị như hình vẽ. Hỏi giá trị nhỏ nhất của hàm số đã cho trên đoạn [0; 2] bằng bao nhiêu? A. 0. B. 1 - . C. 2 . D. 1. Lời giải Chọn A
Theo đồ thị ta có giá trị nhỏ nhất của hàm số trên đoạn  1 - 
;1 bằng 0 đạt tại x = 0 và x = 2 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 15. Giá trị lớn nhất của hàm số y = f ( x) 4 2
= x - 8x 16 trên đoạn  1 - ;  3 bằng: A. 9 . B. 26 . C. 25 . D. 0 . Lời giải Chọn C Ta có: 4 2 3
y = x - 8x 16  y ' = 4x -16x x = 0  1 - ;  3 
Cho y ' = 0 Û x = 2    1 - ;  3 x = 2 -  1 - ;  3  Tính y (- )
1 = 9; y (2) = 0; y (3) = 25. Vậy max y = 25 .  1 -  ;3
Câu 16. Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ. x ∞ 1 0 1 3 y' 0 + 0 0 + +∞ 5 6 y 3 1
Hỏi giá trị lớn nhất của hàm số đã cho trên [-1; 3] bằng bao nhiêu? A. 3. B. 3 - . C. 5 . D. 6 . Lời giải Chọn D
Giá trị lớn nhất của hàm số trên đoạn [-1; 3] bằng 6, đạt tại x = 3 . 9
Câu 17. Giá trị nhỏ nhất của hàm số y = x  trên đoạn 2;  4 bằng: x 13 25 A. 6 . B. . C. 6 - . D. . 2 4 Lời giải Chọn A
Hàm số đã cho liên tục trên đoạn 2;  4 . 9 x = -32;4 Ta có: y¢ = 1-
. Cho y¢ = 0 ta được  . 2 xx = 32; 4  13 25 Khi đó: f (2) = , f ( ) 3 = 6 , f (4) = . 2 4
Vậy min y = 6 . 2; 4
Câu 18. Cho hàm số y = f ( x) liên tục trên đoạn  1 - 
;1 và có đồ thị như hình vẽ.
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn -1  ;1 . Giá trị của
M - m bằng A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn B
Từ đồ thị ta thấy M = 1, m = 0 nên M - m = 1.
Câu 19. Cho hàm số y = f ( x) liên tục trên đoạn  và có đồ thị như hình vẽ. y 1 -1 1 0 x -1
Giá trị nhỏ nhất trên tập xác định của hàm số có đồ thị sau là:
A. min y = -1.
B. min y = 1.
C. min y = 0 . D. min y = 2 - . Lời giải Chọn A
Từ đồ thị ta thấy giá trị nhỏ nhất là 1 - .
Câu 20. Cho hàm số y = f ( x) có bảng biến thiên như sau:
Giá trị nhỏ nhất của hàm số có bảng biến thiên sau trên khoảng  2 - ;  3 là:
A. min y = 0 . B. min y = 3 - .
C. min y = 1.
D. min y = 7 .  2 -  ;3  2 -  ;3 -2  ;3  2 -  ;3 Lời giải Chọn B
Từ bảng biến thiên ta thấy giá trị nhỏ nhất là -3 .
Câu 21. Cho đồ thị hàm số y = f '( ) x như hình vẽ.
Hàm số y = f ( )
x đạt giá trị lớn nhất trên khoảng 1; 
3 tại x . Khi đó giá trị của 2 x - 2x  2019 0 0 0 bằng bao nhiêu? A. 2018 . B. 2019 . C. 2021 . D. 2022 . Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
Dựa vào đồ thị của hàm số y = f '(x) ta có BBT như sau:
Dựa vào BBT suy ra hàm số y = f (x) đạt giá trị lớn nhất trên khoảng 1;  3 tại x = 2 . 0 Nên 2
x - 2x  2019 = 2019 . 0 0
Câu 22. Cho hàm số y = f ( x) liên tục trên đoạn 1
- ; 4và có đồ thị như hình vẽ bên dưới.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1 - ; 4. Giá trị của
M m bằng A. 0 . B. 1. C. 2 . D. 5 . Lời giải Chọn C
Từ đồ thị ta thấy M = 3, m = 1
- nên M m = 2 .
Câu 23. Cho hàm số y = f ( x) liên tục trên đoạn 3 - ; 
1 và có đồ thị như hình vẽ bên dưới.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  3 -  ;1 . Giá trị của
2M - m bằng A. 0 . B. 1. C. 4 . D. 5 . Lời giải Chọn D
Từ đồ thị ta thấy M = 1, m = 3
- nên 2M - m = 5 .
Câu 24. Cho hàm số y = f ( x) liên tục trên đoạn 2
- ; 2và có đồ thị như hình vẽ bên dưới.
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  2 - ;  2 . Giá trị của
M m bằng A. 0 . B. 1. C. 4 . D. 3 . Lời giải Chọn D
Từ đồ thị ta thấy M = 3, m = 0 nên M n = 3 .
Câu 25. Cho hàm số y = f ( x) liên tục trên đoạn 1 - ; 
3 và có đồ thị như hình vẽ bên dưới.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1 - ;  3 . Giá trị của 2 2
M m bằng A. 15 . B. 11. C. 4 . D. 13 . Lời giải Chọn D
Từ đồ thị ta thấy M = 2, m = 3 - nên 2 2
M n = 13.
Câu 26. Giá trị nhỏ nhất của hàm số f ( x) 3
= x - 6x trên đoạn 0; 2 bằng A. 4 - 2 . B. 4 - . C. 6 - 2 . D. 0 . Lời giải Chọn A
Hàm số xác định và liên tục trên đoạn 0; 2 . Ta có f ¢( x) 2 = 3x - 6 . x = 2 0;2 Cho f ¢( x) 2
= 0 Û 3x - 6 = 0 Û  x = - 2   0;2
Ta có f (0) = 0; f ( 2) = 4 - 2 ; f (2) = 4 - .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
Vậy min y = f ( 2 ) = 4 - 2 . 0;2
Câu 27. Cho hàm số y = f (x) có đạo hàm 2 f (
¢ x) = x(x 1)(x - 2) với mọi x   . Giá trị nhỏ nhất của hàm số
y = f (x) trên đoạn  1 - ;  2 là A. f ( 1 - ).
B. f (0).
C. f (3).
D. f (2). Lời giải Chọn B x = 0  Ta có 2 f (
¢ x) = 0 Û x(x 1)(x - 2) = 0 Û x = 1 -  x = 2  Bảng biến thiên
Dựa vào bảng biến thiên của hàm số y = f (x) trên đoạn  1 - ; 
2 thì giá trị nhỏ nhất của hàm số bằng f (0).
B. TÌM M ĐỂ GTLN-GTNN THỎA MÃN ĐIỀU KIỆN K x m Câu 1. Cho hàm số y =
( m là tham số thực) thỏa mãn min y = 3. Mệnh đề nào dưới đây đúng? x - 1 [2;4]
A. m  4
B. 3  m  4
C. m  -1
D. 1  m  3 Lời giải Chọn A -1- m Ta có y ' = ( 2 x - ) 1
* TH 1. -1 - m  0 Û m  -1 suy ra y đồng biến trên 2; 4   suy ra m
min f (x) f (2) 2  = = = 3 Û m = 1 (loại) 2;4   1
* TH 2. -1 - m  0 Û m  -1 suy ra y nghịch biến trên 2; 4   suy ra m
min f (x) f (4) 4  = =
= 3 Û m = 5 suy ra m  4 . 2;4   3 x m 16 Câu 2. Cho hàm số y =
( m là tham số thực) thoả mãn min y  max y =
. Mệnh đề nào dưới đây x 1 1;2 1;2 3 đúng? A. m  4
B. 2  m  4
C. m  0
D. 0  m  2 Lời giải Chọn A 1- m Ta có y¢ = . ( x  )2 1
 Nếu m = 1  y = 1, x   1
- . Không thỏa mãn yêu cầu đề bài.
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
 Nếu m  1  Hàm số đồng biến trên đoạn 1;  2 . 16 16 m 1 m  2 16
Khi đó: min y  max y = Û y ( ) 1  y (2) = Û  = Û m = 5 (loại). 1;2 1;2 3 3 2 3 3
 Nếu m  1  Hàm số nghịch biến trên đoạn 1;  2 . 16 16 2  m 1 m 16
Khi đó: min y  max y =
Û y (2)  y ( ) 1 = Û  = Û m = 5 ( t/m) 1;2 1;2 3 3 3 2 3 Câu 3.
Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số 3 2
y = -x - 3x m trên đoạn -1;  1 bằng 0 .
A. m = 2.
B. m = 6.
C. m = 0.
D. m = 4. Lời giải Chọn D x = 0  1 - ;  1 Xét hàm số 3 2
y = -x - 3x m trên đoạn -1;  1 , ta có 2 y¢ = 3 - x - 6 ; x y¢ = 0 Û   x = 2 -  1 -  ;1   y ( ¢ 1 - ) = m- 2  Mà  y ( ¢ 0) = m  y (¢1) = m- 4 
Do đó min y = -4  m = 0 Û m = 4. -1;  1
Vậy m = 4 thỏa yêu cầu bài toán. x m Câu 4.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên đoạn 1; 
2 bằng 8 ( m là tham số x 1
thực). Khẳng định nào sau đây là đúng? A. m  10 .
B. 8  m  10 .
C. 0  m  4 .
D. 4  m  8 . Lời giải Chọn B 1- m Ta có: y¢ = . ( x  )2 1
- Nếu m = 1  y = 1 (loại).
- Nếu m  1khi đó y¢  0, x 1; 2 hoặc y¢  0, x 1; 2 nên hàm số đạt giá trị lớn nhất và nhỏ
nhất tại x =1, x = 2. 1 m 2  m 41
Theo bài ra: max y  min y = 8 Û y ( ) 1  y (2) =  = 8 Û m = (8;10) . 1;  2 1;  2 2 3 5 Câu 5.
Có một giá trị m của tham số m để hàm số 3 y x  2 m  
1 x m 1 đạt giá trị nhỏ nhất bằng 5 0 trên đoạn 0 
;1 . Mệnh đề nào sau đây là đúng? A. 2
2018m m  0 . B. 2m 1   0 . 0 0 0 C. 2
6m m  0 .
D. 2m 1 0 . 0 0 0 Lời giải Chọn A
+ Đặt f x 3  x  2 m  
1 x m 1 . + Ta có: 2 2
y  3x m 1. Dễ thấy rằng y  0 với mọi x , m thuộc  nên hàm số đồng biến trên
 , suy ra hàm số đồng biến trên 0 
;1 . Vì thế min y  min f x  f   0  m 1  . 0;  1 0;  1
+ Theo bài ra ta có: m 1 5 , suy ra m  4 .
+ Như vậy m  4 và mệnh đề đúng là 2
2018m m  0 . 0 0 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 2 x m  2 Câu 6.
Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số y  trên đoạn 0;  4 x m bằng 1  . A. 3 . B. 2 . C. 1. D. 0 . Lời giải Chọn C
Tập xác định: D   \   m . 2 m m  2 y 
 0, x m . Do đó hàm số đồng biến trên mỗi khoảng  ;  m và  ; m    . xm2
Bảng biến thiên của hàm số: m  0 
Từ bảng biến thiên suy ra, hàm số đạt giá trị lớn nhất trên đoạn 0;  4 bằng 1 khi  f 4  1  m  0  m   0  m  0  2  2m        m 3.    1 2    
m  2,m  3   m m 6 0    4m x 1 1 Câu 7. Cho hàm số y =
(m là tham số thực) thỏa mãn min y =
. Mệnh đề nào dưới đây đúng? 2 x - m -3;-2 2
A. 3  m  4 . B. 2 -  m  3 . C. m  4 . D. m  2 - . Lời giải Chọn B +TXĐ: D =   2 \ m , 3 - ; -  2  D . 2 -m -1 + Ta có y ' =  0, x
  D . Nên hàm số nghịch biến trên từng khoảng xác định. (x - m )2 2 1 2 - 1 Nên min y = = y (-2) 2 =  2
- - m = -2 Û m = 0  2 -  m  3 . - -  2 3; 2 2 2 - - m 2 m x -1 Câu 8.
Tìm giá trị dương của tham số m để giá trị nhỏ nhất của hàm số y =
trên đoạn 1;3 bằng 1. x  2 A. m = 2 . B. m = 3 . C. m = 4 . D. m = 2 . Lời giải Chọn A
Tập xác định: D =  \ -  2 . 2 2m 1 Ta có: y¢ =  0, x   -2 . ( x  2)2 2 3m -1
Hàm số đồng biến trên đoạn 1;3 nên max y = y (3) Û = 1 Û m = 2 (vì m  0 ). 1;  3 5
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2 x m Câu 9. Cho hàm số y
với m là tham số thực. Giả sử m là giá trị dương của tham số m để hàm số x  8 0
có giá trị nhỏ nhất trên đoạn 0; 
3 bằng -3. Giá trị m thuộc khoảng nào trong các khoảng cho dưới 0 đây? A. 2;  5 . B. 1; 4 . C. 6;  9 . D. 20; 2  5 . Lời giải Chọn A
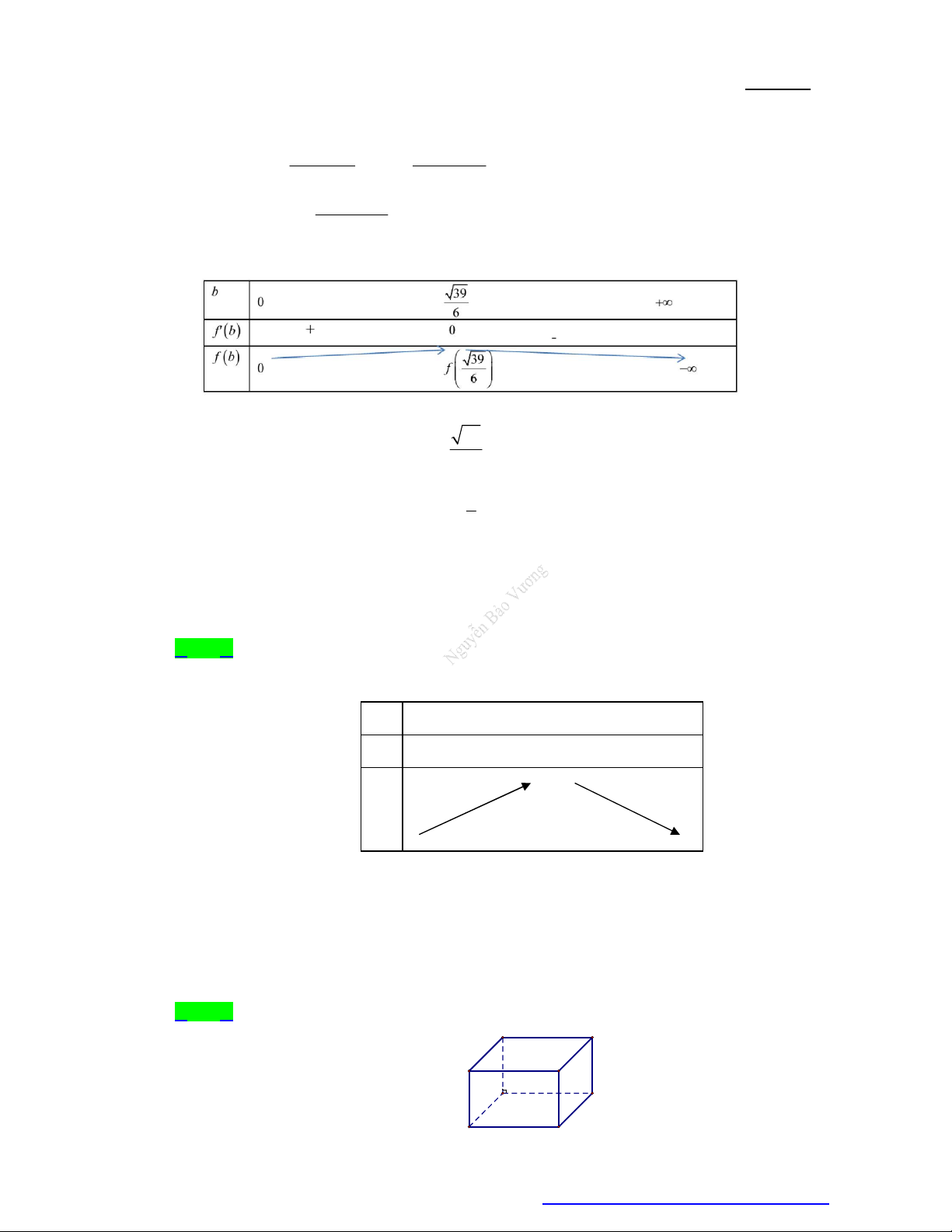
+ TXĐ: D   \   8 . 2 8  m + ' y
 0, x D x  2 8 2 x m Vậy hàm số y
đồng biến trên 0;  3 . x  8 2 m
 min y y(0)  0;  3 8 2 m  Để min y  3    3   m  2  6. 0;3 8
m  2 6  2;5 . Vậy chọnA. 0   2x m
Câu 10. Tìm giá trị của tham số thực m để giá trị nhỏ nhất của hàm số y =
trên đoạn 0;4 bằng 3 . x 1 A. m = 3 .
B. m = 1. C. m = 7 .
D. m = 5 Lời giải Chọn C 2 - m Ta có: y ' = . ( x  )2 1 + Xét m = 2 .
 Hàm số trở thành: y = 2 là hàm số hằng nên không đạt giá trị nhỏ nhất bằng 3  m = 2 (loại) + Xét m  2 . 2 - m 8  my ' =  0 ( x
  -1)  min y = y(4) = . ( x  )2 1 0;4 5 8  m
= 3 Û m = 7 (thoả mãn). 5 + Xét m  2 . 2 - my ' =  0 ( x   1
- )  min y = y(0) = m . ( x  )2 1 0;4  m = 3 (loại). Vậy m = 7 .
Câu 11. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y = x - 3x m có giá trị nhỏ nhất trên đoạn  1 - ;  1 bằng 2 m  2 2  A. m  2 .
B. m  2  2 .
C. m  4  2 . D.  . m  4 2  Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 2
y '  3x 6x x  0 y '  0   x  2  Trên  1 - ;  1 thì y      '  m 4; y ' ; m y ' m 2 1   0   1
nên Miny  2  m  4  2  m  4  2 1;  1 2
x - m m
Câu 12. Tìm các giá trị của tham số m để giá trị nhỏ nhất của hàm số y = trên đoạn 0;  1 bằng x  1 2 - . m = 1 -  m = 1  m = 1 m = -1 A.  . B.  . C.  . D.  . m = 2 -  m = 2  m = 2 -  m = 2  Lời giải Chọn D
Tập xác định: D = \ -  1 .
Hàm số đã cho liên tục trên 0;  1 . 1- ( 2 -m m) 2 m - m 1 Ta có: y¢ = =  0 ; x   D . ( x  )2 1 ( x  )2 1
 Hàm số đồng biến trên đoạn 0;  1 . Trên 0; 
1 hàm số đạt giá trị nhỏ nhất tại x = 0 . m = 1 - Ta có: y (0) 2 2
= -2 Û -m m = -2 Û m - m - 2 = 0 Û  . m = 2 
Câu 13. Có một giá trị m của tham số m để hàm số 3 y x  2 m  
1 x m 1 đạt giá trị nhỏ nhất bằng 5 0 trên đoạn 0; 
1 . Mệnh đề nào sau đây là đúng? A. 2
2018m m  0 . B. 2m 1   0 . 0 0 0 C. 2
6m m  0 .
D. 2m 1 0 . 0 0 0 Lời giải
+ Đặt f x 3  x  2 m  
1 x m 1 . + Ta có: 2 2
y  3x m 1. Dễ thấy rằng y  0 với mọi x , m thuộc  nên hàm số đồng biến trên
 , suy ra hàm số đồng biến trên 0; 
1 . Vì thế min y  min f x  f 0  m 1. 0;  1 0;  1
+ Theo bài ra ta có: m 1  5 , suy ra m  4 .
+ Như vậy m  4 và mệnh đề đúng là 2
2018m m  0 . 0 0 0
Câu 14. Nếu hàm số 2
y = x m  1 - x có giá trị lớn nhất bằng 2 2 thì giá trị của m là 2 2 A. . B. - 2 . C. 2 . D. - . 2 2 Lời giải Xét hàm số 2
y = x m  1 - x
Tập xác định: D =  1 -  ;1 . x Ta có: y¢ = 1- 2 1- x
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1   x  0  1 1   x  0   x = 1 2   1- x = x 1   x  0   Û  Û  2 Û x = y¢ = 0 Û  Û  2 2x = 1  2 . 2   1 2  - x  0   1- x = x   1  x = -    2  1  Ta có: y (- ) 1 = 1 -  , m y ( ) 1 = 1 , m y = 2  m   .  2  Do hàm số 2
y = x m  1 - x liên tục trên  1 - ; 
1 nên Maxy = m  2 . -1;  1
Theo bài ra thì Maxy = 2 2 , suy ra m  2 = 2 2 Û m = 2 .  1 - ;  1 x m
Câu 15. Cho hàm số y
(m là tham số thực) thỏa mãn min y  3 . Mệnh đề nào dưới đây đúng? x  1 0;1  
A. 1  m  3 B. m  6 C. m  1
D. 3  m  6 Lời giải Chọn D
Tập xác định: D   \   1 .
Với m  1  y  1, x 0;1
    thì miny  3 . 0;1   1  m
Suy ra m  1 . Khi đó y  
không đổi dấu trên từng khoảng xác định. x  2 1
TH 1: y  0  m  1 thì min y y  
0  m  3 (loại). 0;1  
TH 2: y  0  m  1 thì min y y  
1  m  5 ( thỏa mãn). 0;1   x m
Câu 16. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
trên 1; 2 bằng 8 ( m là tham số x 1
thực). Khẳng định nào sau đây đúng? A. m  10 .
B. 8  m  10 .
C. 0  m  4 .
D. 4  m  8 . Lời giải
Nếu m = 1 thì y 1 (không thỏa mãn tổng của giá trị lớn nhất và nhỏ nhất bằng 8) 1 m
Nếu m  1 thì hàm số đã cho liên tục trên 1; 2 và y '  . x  2 1
Khi đó đạo hàm của hàm số không đổi dấu trên đoạn 1;2. m 1 m  2 41
Do vậy Min y Max y = y ( ) 1  y (2) =  = 8 Û m = . x   1;2 x   1;2 2 3 5 Câu 17. Cho hàm số 3 2
y = 2x - 3x - m . Trên  1 - 
;1 hàm số có giá trị nhỏ nhất là 1 - . Tính m ? A. m = 6 - . B. m = 3 - . C. m = 4 - . D. m = 5 - . Lời giải Chọn C Xét  1 -  ;1 có 2
y¢ = 6x - 6x . x = 0  1 -  ;1 y¢ = 0 2
Û 6x - 6x = 0 Û  . x = 1 1 -  ;1 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 Khi đó y (- )
1 = -5 - m ; y (0) = -m ; y ( ) 1 = 1 - - m Ta thấy 5 - - m  1
- - m  -m nên min y = 5 - - m . -1;  1
Theo bài ra ta có min y = 1 - nên 5 - - m = 1 - Û m = 4 - . -1;  1
Câu 18. Biết S là tập giá trị của m để tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 2 3 2
y = x - m x - 2x - m trên đoạn 0; 
1 bằng -16 . Tính tích các phần tử của S . A. 2 . B. -2 . C. -15 . D. -17 . Lời giải TXĐ: D =  . Ta có: 3 2 2
y¢ = 4x - 3m x - 4x x = 0 3 2 2
y¢ = 0 Û 4x - 3m x - 4x = 0 Û  2 2
4x - 3m x - 4 = 0  ( 2  = 9m  64)    x = 0  2 4  3m  9m  64 Û x =  1  8  2 4  3m - 9m  64 x =  0   8
Nên hàm số đơn điệu trên (0; ) 1 .
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0;  1 bằng -16 nên
y ( )  y ( ) = - Û -m  ( 2 -m - m - ) 2 0 1 16 1 = 16 -
Û -m - 2m 15 = 0 .
Vậy m .m = -15 . 1 2 2
x m m Câu 19. Gọi ,
A B lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = trên đoạn 2;3 . x -1 13
Tìm tất cả các giá trị thực của tham số m để A B = . 2
A. m = 1; m = 2 - . B. m = -2 . C. m = 2 . D. m = 1 - ; m = 2 . Lời giải 2
x m m Xét hàm số y = trên đoạn 2;3 . x -1 2 2 2 -m - m -1 m m  3 m m  2 y ' =  0 x
  2;3  A = f 3 = , B = f 2 = . 2   ( ) ( ) ( x - ) 1 2 1 2 2 13 m m  3 m m  2 13 m = 1 A B = Û  = Û  . 2 2 1 2 m = -2  2 x - m
Câu 20. Cho hàm số f ( x) =
với m là tham số thực. Giả sử m là giá trị dương của tham số m để x  8 0
hàm số có giá trị nhỏ nhất trên đoạn 0;  3 bằng 3
- . Giá trị m thuộc khoảng nào trong các khoảng 0 cho dưới đây? A. (20;25) . B. (5;6) . C. (6;9) . D. (2;5) . Lời giải Chọn D
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2 x - m
Xét hàm số f ( x) = trên đoạn 0;  3 . x  8 2 8  m 2 x - m Ta có: y¢ =  0, x
  0;3  hàm số f ( x) =
đồng biến trên đoạn 0;  3 2   ( x  8) x  8 2 -m
 min f ( x) = f (0) = . 0;  3 8 2 -mm = 2 6
Theo giả thiết, ta có: min f ( x) 2 = -3 Û = -3 Û m = 24 Û  . 0;  3 8 m = 2 - 6 
Mà m  0, m    m = 2 6  4,9  (2;5) . 2 x mx  1
Câu 21. Tìm tất cả giá trị thực của tham số m để hàm số y =
liên tục và đạt giá trị nhỏ nhất trên x m
đoạn 0; 2 tại một điểm x  0; 2 . 0 ( )
A. 0  m  1 B. m  1 C. m  2
D. -1  m  1 Lời giải Chọn A -m  0 m  0
Tập xác định: D =  \ - 
m . Hàm số liên tục trên 0; 2 Û Û   -m  2 m  2 -  
x  2mx m -1 ( x m)2 2 2 -1  x = -m -1 Ta có y¢ = = . Cho 1 y¢ = 0 Û  . ( x m)2 ( x m)2 x = -m 1  2 Ta có bảng biến thiên
Hàm số đạt giá trị nhỏ nhất tại x  0; 2 nên 0  -m 1  2 Û -1  m  1 0 ( )
So với điều kiện hàm số liên tục trên đoạn 0; 2. Ta có 0  m  1 . CÓ THỂ GIẢI NHƯ SAU:
Điều kiện xác định x  -m -m  0 m  0
Hàm số liên tục trên đoạn 0; 2 nên -m  0; 2  Û   (*) -m  2 m  -2  
x  2mx m -1 ( x m)2 2 2 -1 y ' = = ( x m)2 ( x m)2  x = -m 1
y ' = 0 có hai nghiệm là 1  , x = -m -1  2
x - x = 2 nên chỉ có nhiều nhất một nghiệm thuộc (0; 2) 1 2 Ta thấy m - 1  m - -1, m
 và do đó để hàm số liên tục và đạt giá trị nhỏ nhất trên 0; 2 tại một
điểm x  0; 2 thì 0  -m 1  2 Û -1  m  1 (**) 0 ( )
Từ (*),(**) ta có 0  m  1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 1 - m sin x
Câu 22. Cho hàm số y =
. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 0;10 để giá trị cos x  2
nhỏ nhất của hàm số nhỏ hơn -2 ? A. 1. B. 9 . C. 3 . D. 6 . Lời giải
Tập xác định: D =  . 1 - m sin x Ta có: y =
Û y cos x m sin x = 1- 2 y . cos x  2
Phương trình có nghiệm khi và chỉ khi: 2 2 2
y m  1- 4 y  4 y 2 2
Û 3y - 4 y 1- m  0 2 2 2 - 1 3m 2  1 3m Û  y  . 3 3 2  2 - 1 3m min y =  -2 2  2 2 x 3 1 3m  8 3  m  63 m  21      
Theo đề bài, ta có: m 0;10 Û m 0;10
Û m 0;10 Û m 0;10     m   m   m   m         
Û m 5, 6, 7,8,9,  10 .
Vậy có 6 giá trị nguyên của tham số m thỏa yêu cầu bài toán. x m
Câu 23. Tìm tất cả các giá trị của tham số m để hàm số y =
có giá trị lớn nhất trên  nhỏ hơn hoặc 2 x x 1 bằng 1. A. m  1. B. m  1. C. m  1 - . D. m  -1. Lời giải Chọn A + TXĐ: D =  . + lim y = 0 x 2
-x - 2mx 1- m + y¢ = . (x x  )2 2 1 2
y¢ = 0 Û -x - 2mx 1- m = 0 (*) 2
¢ = m - m 1  0, m
   nên (*) có 2 nghiệm phân biệt x x , m    (*) 1 2 + BBT: 1
Vậy hàm số đạt giá trị lón nhất là f ( x = với 2
x = -m m - m 1 2 ) 2x 1 2 2 1 2 YCBT Û
 1 Û 1- 2m  2 m - m 1  1( vì f ( x  0  2x 1  0 ) 2 ) 2 2 2
- m  2 m - m 1 1
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020m  0 2  Û
m - m 1  m Û m  0 Û m  1   2 2
m - m 1  m 
C. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ CHỨA DẤU GIÁ TRỊ
TUYỆT ĐỐI (chứa tham số)
Dạng 1: Tìm m để max y = f ( x)  m = a (a  0).  ;  Phương pháp:
Cách 1:Trước tiên tìm max f ( x) = K;
min f ( x) = k ( K k ). ; ; 
m K m k
m K - m - k K - k
Kiểm tra max m K , mk    = . 2 2 2 K - k
m k = -a
m = -a - k TH1:  .
a Để max y = a Û Û  m   
-a - k;a - K . 2  ; 
m K = a m = a - K   K - k TH2:
a m  . 2
Cách 2: Xét trường hợp
m K = a
TH1: Max = m K Û 
m K m k  
m k = a
TH2: Max = m k Û 
m k m K  
Dạng 2: Tìm m để min y = f ( x)  m = a (a  0).  ;  Phương pháp:
Trước tiên tìm max f ( x) = K;
min f ( x) = k ( K k ). ; ; 
m k = a
m K = -a
m = a - k
m = -a - K
Để min y = a Û    Û   
. Vậy mS S .  1 2  ;  m k  0 m K  0 m  -k m  -K    
Dạng 3: Tìm m để max y = f ( x)  m không vượt quá giá trị M cho trước.  ; 
Phương pháp: Trước tiên tìm max f ( x) = K;
min f ( x) = k ( K k ). ; ; 
m k  -M
Để max y M  
Û -M - k m M - K.  ; 
m K M
Dạng 4: Tìm m để min y = f ( x)  m không vượt quá giá trị a cho trước.  ; 
Phương pháp: Trước tiên tìm max f ( x) = K;
min f ( x) = k ( K k ). ; ; 
m k a
m K  -a
m a - k
m  -a - K
Để min y a Û   
 (m K )(m k )  0 Û   
 -K m  -k.  ;  m k  0 m K  0 m  -k m  -K    
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489
Dang 5: Tìm m để max y = f ( x)  m đạt min. a;bPhương pháp:
Trước tiên tìm max f ( x) = K;
min f ( x) = k ( K k ). a;b a;bK k K - k
Đề hỏi tìm m m = -
. Đề hỏi tìm min của max y  giá trị này là . 2 a;  b 2
Dạng 6: Tìm m để min y = f ( x)  m đạt min. a;  b
Phương pháp: Trước tiên tìm max f ( x) = K;
min f ( x) = k ( K k ). a;b a;b
Đề hỏi tìm m  (mK )(mk)  0 Û -K m k
- . Đề hỏi tìm min của min y  giá trị này là 0. a;  b
Dạng 7: Cho hàm số y = f ( x)  m .Tìm m để max y  .
h min y (h  0) hoặc Min  max = a;b a;b
Phương pháp: Trước tiên tìm max f ( x) = K;
min f ( x) = k ( K k ). a;b a;bTH1:
K m k m
K m h k m       m S .
K m cung dau k m 1
k m K m
TH2: k m h K m  m S .
K m cung dau k m 2
Vậy mS S . 1 2
Dạng 8: Cho hàm số y = f ( x)  m .
Phương pháp: Trước tiên tìm max f ( x) = K;
min f ( x) = k ( K k ). a;b a;b
BT1: Tìm m để min y  max y =  Û m K m k =  . a;b a;b
BT2: Tìm m để min y *max y =  Û m K * m k =  . a;b a;bCâu 1.
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số f ( x) 3
= x - 3x m trên đoạn 0;3 bằng 16. Tổng tất cả các phần tử của S là: A. -16 . B. 16 . C. -12 . D. 2 - . Lời giải Chọn A Xét 3
u x 3x m trên đoạn 0;3có 2
u  0  3x  3  0  x  1  0;3 . max u  max 
u0,u  1 , u  
3   max m, m 2, m  18  m 18 0  ;3  Khi đó  .
min u  minu0,u  1 , u  
3   min m, m 2, m  18  m  2  0; 3   m18 16 
m18  m2    m  2
Suy ra M ax f x  max  m  2 , m 18  16     . 0;  3    m 2 16 m  14  
m2  m18  
Do đó tổng tất cả các phần tử của S bằng 16 .
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 x m Câu 2.
Cho hàm số f ( x) =
( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao cho x 1
max f ( x)  min f ( x) = 2 . Số phần tử của S là 0;  1 0;  1 A. 6 . B. 2 . C. 1. D. 4 . Lời giải Chọn B x m
Do hàm số f ( x) = liên tục trên 0;  1 x 1 .
Khi m = 1 hàm số là hàm hằng nên max f ( x) = min f ( x) = 1 0;  1 0;  1
Khi m  1 hàm số đơn điệu trên đoạn 0;  1 nên m 1
+ Khi f (0); f ( )
1 cùng dấu thì max f ( x)  min f ( x) = f (0)  f ( ) 1 = m  . 0;  1 0;  1 2  m 1 
+ Khi f (0); f ( )
1 trái dấu thì min f ( x) = 0 , max f ( x) = max f (0) ; f ( ) 1  = max  m ;  . 0;  1 0;  1 2   m  1 -
TH1: f (0). f ( )
1  0 Û m(m 1)  0 Û  . m  0  m = 1 m 1 max f ( x) min f ( x) 2 m 2   = Û  = Û 5 (thoả mãn). 0;  1 0;  1 2 m = -  3
TH2: f (0). f ( )
1  0 Û m(m 1)  0 Û 1 -  m  0  m = 2 m = 2  
max f ( x)  min f ( x) = 2  Û m = -5 m 1 (không thoả mãn). 0;  1 0;  1  2  =  2 m = 3  
Số phần tử của S là 2 . Câu 3.
Cho hàm số f ( x) 4 3 2
= x - 4x  4x m ( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của
m sao cho max f ( x)  min f ( x) = 5 . Số phần tử của S là 0;2 0;2 A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn B
Xét hàm số f ( x) 4 3 2
= x - 4x  4x m . x = 0  f ¢( x) 3 2
= 4x -12x  8x ; f ¢( x) = 0 3 2
Û 4x -12x  8x = 0 Û x = 1 .  x = 2  Bảng biến thiên x 0 1 2 f'(x) + 0 m+1 f(x) m m
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489 +) Nếu m  1
- thì max f ( x) = -m , min f ( x) = -m -1 0;2 0;2
Ta có max f ( x)  min f ( x) = 5 Û -m - m -1 = 5 Û m = 3 - (thỏa) 0;2 0;2
+) Nếu m  0 thì max f ( x) = m 1, min f ( x) = m 0;2 0;2
Ta có max f ( x)  min f ( x) = 5 Û m 1 m = 5 Û m = 2 (thỏa) 0;2 0;2 +) Nếu 1
-  m  0 thì min f ( x) = 0 ; max f ( x) = max m ; m 1 1 0;2 0;2
 max f ( x)  min f ( x)  5 (không thỏa điều kiện đề bài) 0;2 0;2 Vậy S =  3 - ; 
2 , có 2 giá trị của m thỏa mãn đề bài. Câu 4.
Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị lớn nhất của hàm số 2
y = x - 2x m  3 trên đoạn  1
- ; 2 bằng 4 . Tổng tất cả các phần tử của S là A. 6 - . B. 8 - . C. 9 - . D. -12 . Lời giải Chọn B Xét hàm g ( x) 2
= x - 2x m  3 . Dễ thấy hàm số g ( x) liên tục trên đoạn  1 - ; 2
Ta có g¢( x) = 2x - 2 , g¢( x) = 0 Û x = 1. Do đó 2
max x - 2x m  3 = max m  2 ; m  3 ; m  6 .  1 - ;2
Ta thấy m  2  m  3  m  6 với mọi m   .
Suy ra max y chỉ có thể là m  6 hoặc m  2 . -1;2  m  6 = 4 
Nếu max y = m  6 thì  Û m = 2 - . -1;2
m  6  m  2    m  2 = 4 
Nếu max y = m  2 thì  Û m = 6 - .  1 - ;2
m  2  m  6  
Vậy tổng tất cả các phần tử của S bằng 8 - . Câu 5.
Cho hàm số f ( x) 3
= x - 3x m ( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao
cho max f ( x)  min f ( x) = 6 . Tổng tất cả các phần tử của S là 0;2 0;2 A. 3. B. 0 . C. 1 - . D. 2 . Lời giải Chọn B
Xét hàm số f ( x) 3
= x - 3x m . x = 1 - f ¢( x) 2
= 3x - 3 ; f ¢( x) = 0 2 Û 3x - 3 = 0 Û  . x = 1  Bảng biến thiên x 0 1 2 f'(x) 0 + f(x) m m+2 m-2
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 +) Nếu m  2
- thì max f ( x) = -m  2 , min f ( x) = -m - 2 0;2 0;2
Ta có max f ( x)  min f ( x) = 6 Û -m  2 - m - 2 = 6 Û m = 3 - (thỏa) 0;2 0;2
+) Nếu m  2 thì max f ( x) = m  2 , min f ( x) = m - 2 0;2 0;2
Ta có max f ( x)  min f ( x) = 6 Û m  2  m - 2 = 6 Û m = 3 (thỏa) 0;2 0;2 +) Nếu 2
-  m  2 thì min f ( x) = 0 ; max f ( x) = max m  2 ; m - 2  4 0;2 0;2
 max f ( x)  min f ( x)  6 (không thỏa điều kiện đề bài) 0;2 0;2 Vậy S =  3 - ; 
3 , Tổng các phần tử của S là 0 . Câu 6.
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số f ( x) 3
= 2x - 6x m trên đoạn 0; 
3 bằng 8. Tổng tất cả các phần tử của S bằng A. 8 . B. 1 - 6 . C. 3 - 2 . D. 7 - 2 . Lời giải Chọn C Xét u ( x) 3
= 2x - 6x m trên đoạn 0; 
3 . Dễ thấy hàm số u ( x) liên tục trên đoạn 0;  3 . Có u¢( x) 2
= 0 Û 6x - 6 = 0  x = 10;  3 .
max u = maxu (0);u ( ) 1 ;u (3) = max ; m m - 4; m   36 = m  36  0  ;3 Khi đó  . min u = min  u (0);u ( ) 1 ;u (3) = min ; m m - 4; m   36 = m - 4 0  ;3    m - 4 = 8  m - 4  0  m = 12
Theo bài ra min f ( x) = min m - 4 ; m  36 ;  0 = 8 Û Û   . 0  ;3 m  36  0 m = -44     m  36 = 8   Do đó S =  4 - 4;1 
2 . Vậy tổng tất cả các phần tử của S bằng 3 - 2 . Câu 7.
Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số 2
y = x  2x m - 4 trên đoạn  2 - ; 
1 đạt giá trị nhỏ nhất? A. 1. B. 3 . C. 4 . D. 5 . Lời giải Chọn A Xét hàm g ( x) 2
= x  2x m - 4 . Dễ thấy hàm số g ( x) liên tục trên đoạn  2 -  ;1 .
Ta có g¢( x) = 2x  2 , g¢( x) = 0 Û x = 1 - . Do đó 2
max x  2x m - 4 = max m -1 ; m - 4 ; m - 5 .  2 - ;  1
Ta thấy m - 5  m - 4  m -1 với mọi m   . Suy ra 2
max x  2x m - 4 = max m -1 ; m - 5 .  2; -  1 m -1  m - 5  -  - m - m -  m 1 5 m max 1 ; 5   = 2 . 2 2
Vậy GTNN của max  m -1 ; m - 5  bằng 2.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489
Đẳng thức xảy ra khi và chỉ khi m -1 = m - 5 Û m = 3. Câu 8.
Cho hàm số f ( x) liên tục trên  , có đồ thị như hình vẽ  8x
Có tất cả bao nhiêu giá trị nguyên của tham số a để hàm số y = fa -1  có giá trị lớn nhất 2   x 1 không vượt quá 20 ? A. 29 . B. 35 . C. 31. D. 41 . Lời giải Chọn C 8x 2 -8x  8 Đặt t = . Ta có: t¢ =
; t¢ = 0 Û x = 1  . 2 x 1 (x  )2 2 1 BBT:
t - 4; 4 .  8x  Hàm số y = fa -1 
trở thành g (t ) = f (t )  a -1 ,t - 4; 4 . 2   x 1
Đặt h (t ) = f (t )  a -1,t - 4; 
4 , ta có: h¢(t ) = f ¢(t ) .
t = - 4 - 4; 4 
h¢(t ) = 0 Û f ¢(t ) = 0 Û t = - 2   - 4;4 . t = 2-4;4 
Ta có: h (- 4)  0,8  a -1 = a - 0, 2 ; h(4) = 6  a -1 = a  5 ;
h (- 2)  1,6  a -1 = a  0,6 ; h(2) = - 4  a -1 = a - 5.
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Max y = Max h(t) = Max a  5 ; a - 5 .  -4  ;4  a  5  20   2 - 0  a  5  20 - 25  a  15 Yêu cầu bài toán Û  Û  Û  Û -15  a  15 . a - 5  20   2 - 0  a - 5  20  -15  a  25 
Vậy có tất cả 31 giá trị nguyên của tham số a
thỏa mãn yêu cầu bài toán. Câu 9.
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 2
x mx m f ( x) = trên 1; 
2 bằng 2 . Tổng tất cả các phần tử của S là x 1 11 13 11 1 A. - . B. . C. - . D. . 3 6 6 3 Lời giải Chọn C 2
x mx m Xét u ( x) =
trên đoạn 1;2. Dễ thấy u ( x) liên tục trên đoạn 1;2. x 1 2 x = 0 x x   1;2 2  Ta có u¢ = 0 Û = 0 Û  . ( x  )2 1 x = 2 - 1; 2    1 4  4 max u ( x) = max  u ( )
1 ;u (2) = max m  ;m   = m  1;2   2 3  3 Khi đó  .  1 4  1
min u (x) = minu( )
1 ;u (2) = min m  ;m   = m   1;2   2 3  2  1 m  = 2  2   1 4   5  m   m m = - 1 4  2 3     2
Suy ra max f ( x) = max  m  ; m   = 2 Û Û  . 1;2 2 3     4 2   m  = 2 m =   3  3   4 1   m   m    3 2  11
Vậy tổng các phần tử của S là - . 6 Câu 10. Cho hàm số 3 2
y = cos x - 3sin x m  3 . Gọi S là tập hợp các giá trị m sao cho
2 max y  min y = 9 . Tổng các phần tử của tập hợp S bằng: 16 A. - . B. 4 - . C. 6 - . D. 2 - . 3 Lời giải Chọn B Ta có: 3 2 3 2
y = cos x - 3sin x m  3 = cos x  3cos x  . m t = 2 -
Đặt t = cos x t [ -1;1] , xét 3 2
g(t) = t  3t m có 2
g '(t) = 3t  6t = 0 Û  t = 0.  BBT:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489
Từ đó: min g(t) = g(0) = ;
m max g(t) = g(1) = m  4. [ 1 - ;1] [ 1 - ;1]
+ TH1: m(m  4)  0  m  (-; - 4]  [0;  ),
2(m  4)  m = 9  1  m = m  0   3
2 max | y |  min | y |= 2 max | g(t) |  min | g(t) |= 9 Û Û  [-1;1] [-1;1]  2
- m - (m  4) = 9 -13   m = .   m  4  -  3 
+ TH2: m(m  4)  0  m  (-4; 0), min | g(t) |= 0, [ 1 - ;1]
m  4  -m  9 -  m = (l) 2 - m = 9   2
2 max | y |  min | y |= 2 max | g(t) |= 9 Û Û  [ 1 - ;1]
-m m  4 1   m = (l).   2(m  4) = 9  2   13 - 1  Vậy S =  ,   3 3
Câu 11. Cho hàm số f ( x) 3
= x - 3x . Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị
nhỏ nhất của hàm số y = f (2 - cos x)  m bằng 2. Tổng tất cả các phần tử của S bằng A. 4 . B. 1 - 6 . C. 3 - 2 . D. -12 . Lời giải Chọn B
Đặt t = 2 - cos x ta có t 1; 
3 . Khi đó bài toán trở thành tìm m để hàm số 3
y = t - 3t m với t  1; 
3 đạt giá trị nhỏ nhất bằng 2. Xét u (t ) 3
= t - 3t m trên đoạn 1; 
3 . Ta có hàm số u (t ) liên tục trên đoạn 1;  3 . t = 1 -  (1;3) u¢(t ) 2
= 3t - 3 ; u¢(t ) = 0 Û  . t = 1 (1;3) 
max u (t ) = maxu ( )
1 ;u (3) = maxm 18; m -  2 = m 18  1  ;3 Khi đó:  . min u
(t) = minu ( )
1 ;u (3) = minm 18;m -  2 = m - 2 1  ;3 
Yêu cầu bài tập: min y = 2 . 1  ;3
Trường hợp 1: m - 2  0 Û m  2
 min y = m - 2 = m - 2 ; min y = 2 Û m - 2 = 2 Û m = 4 (thỏa mãn) 1  ;3 1  ;3
Trường hợp 2: m 18  0 Û m  1 - 8
 min y = m 18 = - (m 18) ; min y = 2 Û - (m 18) = 2 Û m = -20 (thỏa mãn) 1  ;3 1  ;3
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Trường hợp 3: (m 18)(m - 2)  0 Û -18  m  2  min f ( x) = 0  2 (loại) 1;  3
Vậy tổng tất cả các phần tử của S bằng 1 - 6 . Chọn phương án B . log x m
Câu 12. Cho hàm số f ( x) =
( m là tham số thực). Gọi S là tổng tất cả các giá trị của m sao cho log x  2
max f ( x)  min f ( x) = 2 . Tìm S .  1   1  ;1 ;1  10    10  2 4 10 A. - . B. 2 . C. . D. . 3 3 3 Lời giải Chọn C  1  Đặt t = log ; x x  ;1  t -1;0  10    t m
Xét hàm số g (t ) = liên tục trên  1 - ;  0 t  2
Khi đó: max f ( x) = max g (t ) ;min f ( x) = min g (t )  1  -1;0  1  -1;0 ;1 ;1  10    10 
TH1: Khi m = 2 hàm số là hàm hằng g (t ) = 1nên
max g (t ) = min g (t ) = 1  max f ( x)  min f ( x) = max g (t )  min g (t ) = 2  nhận m = 2 -1;0 -1;0  1   1  -1;0 -1;0 ;1 ;1  10    10 
TH2: Khi m  2 hàm số đơn điệu trên đoạn  1 - ;  0 nên: m  0 + TH2.1: g (- )
1 .g (0)  0 Û m(m - ) 1  0 Û  . Khi đó: m  1 
max f ( x)  min f ( x) = 2 Û max g (t )  min g (t ) = 2  1   1  -1;0 -1;0 ;1 ;1  10    10  m = 2 ( L) m g (0) g ( ) 1 2 m 1 2  Û  - =   - = Û 2 2 m = - ( N )  3 + TH2.2: f (- )
1 . f (0)  0 Û m(m - )
1  0 Û 0  m  1 Khi đó:  m
min g (t ) = 0, max g (t ) = max g (0) ; g (- ) 1  = max  ; m -1   1 - ;0  1 - ;0 2   Do đó:
max f ( x)  min f ( x) = 2 Û max g (t )  min g (t ) = 2  1   1   1 - ;0 -1;0 ;1 ;1  10    10  m = 4  ( L m ) = 2    2 Û m = 3  ( L)  m 1 2   - =  m = -1 ( L)  4 Vậy S = 3
Câu 13. Có bao nhiêu giá trị nguyên của tham số m để giá trị nhỏ nhất của hàm số 3 2
y = x - mx - 9x  9m trên đoạn  2
- ; 2 đạt giá trị nhỏ nhất. A. 3 . B. 5 . C. 4 . D. 6 . Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
NGUYỄN BẢO VƯƠNG - 0946798489 Đặt f ( x) 3 2
= x - mx - 9x  9m . Dễ thấy min f ( x)  0 , dấu " = " xảy ra khi và chỉ khi phương trình  2 - ;2
f ( x) = 0 có nghiệm x  2 - ; 2 . Ta có: f ( x) 2
= x ( x - m) - ( x - m) = ( 2 9
x - 9)( x - m) .  x = 3 
f ( x) = 0 Û x = 3 - .   x = m
Do đó điều kiện cần và đủ để f ( x) = 0 có nghiệm x  2 - ; 2 là m 2 - ; 2 .
Mà m   nên m  2 - ; 1 - ;0;1;  2 .
Vậy có 5 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 14. Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số y = f ( x) 4 2
= -x  8x m trên đoạn  1 - ; 
3 đạt giá trị nhỏ nhất. A. 23. B. 24 . C. 25 . D. 26 . Lời giải
Ta có y = f ( x) 4 2
= -x  8x m = x - x - m = ( x - )2 4 2 2 8 4 -16 - m .
Đặt t = ( x - )2 2 4 , vì x   1 - ; 
3 , suy ra t 0; 2  5 .
Khi đó y = g (t ) = t -16 - m .
Ta có min f ( x) = min g (t ) = min m - 9 , m 16.  1 - ;  3  0 - ; 2  5  
Nếu m - 9  0 Û m  9 , khi đó min f ( x) = m - 9  0 , khi đó min  min f ( x) = 0 , khi m = 9 . -1;3  1 - ;  3    
Nếu m  16  0 Û m  1
- 6 , khi đó min f ( x) = -m -16  0 , khi đó min  min f ( x) = 0 , khi x   -1;3  1 - ;  3   m = 1 - 6 .  
Nếu (m - 9)(m 16)  0 Û 16 -
m  9 , khi đó min f ( x) = 0 , khi đó min  min f ( x) = 0 . x   -1;3  1 - ;  3    
Vậy min  min f ( x) = 0 , khi 1 - 6  m  9 .  1 - ;  3  
Vì m   , nên có 26 số nguyên m thỏa mãn yêu cầu bài toán. Câu 15. Cho hàm số 2
y = x - 4x  2m - 3 với m là tham số thực. Biết rằng giá trị lớn nhất của hàm số trên đoạn 1; 
3 đạt giá trị nhỏ nhất bằng a khi m = b . Tính P = 2b - a . 1 13 -9 A. . B. . C. . D. 6 . 2 4 4 Lời giải
Xét hàm số y = f ( x) 2
= x - 4x  2m - 3 liên tục trên đoạn 1;  3 .
+) f ¢( x) = 2x - 4 ; f ¢( x) = 0 Û x = 21;  3 . +) f ( )
1 = 2m - 6 , f (2) = 2m - 7 , f (3) = 2m - 6 .
Khi đó max f ( x) = max  2m - 6 ; 2m - 7  = M . 1;3 M  2m - 6  1 Ta có: 
 2M  2m - 6  7 - 2m  2m - 6  7 - 2m = 1  M  .
M  2m - 7 = 7 - 2m   2
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020  1
2m - 6 = 2m - 7 =  13 Dấu " = " xảy ra Û  2 Û m = . ( m - )( - m) 4 2 6 7 2  0  1 13 Do đó M = = a khi m =
= b P = 2b - a = 6 . 2 4 Câu 16. Cho hàm số 3 2
y = x x  ( 2 m  )
1 x  27 . Gọi S là tập tất cả các giá trị của tham số m sao cho giá
trị lớn nhất của hàm số trên đoạn -3; - 
1 có giá trị nhỏ nhất. Khi đó tích các phần tử của S là A. 4 . B. -4 . C. 8 . D. -8 . Lời giải
Xét hàm số f ( x) 3 2
= x x  ( 2 m  )
1 x  27 liên tục trên đoạn -3; -  1 . Ta có f ¢( x) 2 2
= 3x  2x m 1  0 với x   3 - ; -  1 . Ta có f (- ) 2
3 = 6 - 3m ; f (- ) 2 1 = 26 - m .
Khi đó max f ( x) = max 2 2
6 - 3m ; 26 - m  = M .  3 - ;-  1 2 2 M  6 - 3mM  6 - 3m   Lại có   
 4M  72 Û M  18 . 2 2 M  26 - m
3M  3m - 78   2 2
 6 - 3m = 26 - m = 18   m = 2 2 Dấu bằng xẩy ra khi 2  Û m = 8 Û  . ( 2 6 - 3m )( 2 3m - 78)  0 m = 2 - 2   m = 2 2 Vậy với 
thì giá trị lớn nhất của hàm số trên đoạn -3; - 
1 có giá trị nhỏ nhất. m = 2 - 2 
Khi đó tích các giá trị là 2 2.(-2 2 ) = -8 .
Câu 17. Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số 1 19 4 2 y = x -
x  30x m trên đoạn 0;2 đạt giá trị nhỏ nhất? 4 2 A. 2 . B. 3 . C. 0 . D. 1. Lời giải 1 19
Xét hàm số f ( x) 4 2 = x -
x  30x m liên tục trên đoạn 0;2 . 4 2 Ta có f ¢( x) 3 = x -19x  30 x = 5 - 0; 2 
+ f ¢( x) = 0 Û x = 3  0;2 . x = 20;2  + Ta có: f (0) = ;
m f (2) = m  26.
Khi đó max f ( x) = max  ; m m  2 
6 = m  26 ; min f ( x) = min ; m m  2  6 = m . 0;2 0;2
Suy ra max f ( x) = max m ; m  26 = M . 0;2
M m = -m  -m m  26 -m m  26 Ta có 
 2M  -m m  26 Û M   = 13. M m  26   2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
NGUYỄN BẢO VƯƠNG - 0946798489
m = m  26 = 13  Dấu bằng xảy ra khi  Û m = 1 - 3. -m  (m  26)  0  1 19
Do đó giá trị lớn nhất của hàm số 4 2 y = x -
x  30x m trên đoạn 0;2 đạt giá trị nhỏ nhất 4 2 bằng 13 khi m = 1 - 3 .
Vậy có 1 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
Câu 18. Có tất cả bao nhiêu giá trị của tham số m để giá trị nhỏ nhất của hàm số f ( x) 2
= x - 2x m trên  1 - ; 2 bằng 5. A. 3. B. 1. C. 2 . D. 4 . Lời giải +) Đặt g ( x) 2
= x - 2x m . +) Ta có: ,
g ( x) = 2x - 2 ,
g ( x) = 0 Û 2x - 2 = 0 Û x = 1. g (- ) 1 = m  3  +) g ( ) 1 = m -1 . g (2) = m
min g ( x) = m -1  1 - ;2 +) Suy ra 
.Vậy min g ( x) = min0; m -1 ; m  3 max g  1 - ;2  ( x) = m  3 -1;2 
Ta xét các trường hợp sau: TH1:.  m -1 = 5   Û m = 6 . m -1  m  3   TH2:.  m  3 = 5   Û m = -8 m -1  m  3  
Vậy có hai giá trị của tham số m thỏa mãn. 4
Câu 19. Tính tích tất cả các số thực m để hàm số 3 2 y
x  6x  8x m có giá trị nhỏ nhất trên đoạn 3 0;  3 bằng 18 là. A. 432 . B. 2  16. C. 4  32. D. 288 . Lời giải 4
+ Xét hàm số f x 3 2
x 6x 8x m liên tục trên đoạn 0;  3 . 3
+ Ta có f x 2  4x 1  2x 8. x 10;  3  + f x 2  0  4x 12
x 8  0   . x  2   0;  3  10 8 + f 0  ; m f   1   ; m f 2   ; m f   3  6  m . 3 3
max f x max   f   0 ; f  
1 ; f 2; f   3   f   3  m  6  0; 3  Khi đó   .
min f x min  f 0; f   1 ; f   2 ; f   3   f   0  m  0  ;3 
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Suy ra min y  min 0; m ; m  6 . 0  ;3 TH1.  m 18   m 18  . m m  6  TH2.  m6 18   m  2  4  . m m  6 
Kết luận: tích các số thực m thỏa mãn yêu cầu bài toán là: 2  4.18  4  32 .
Câu 20. Cho hàm số f ( x) 4 2
= x - 2x m -1 . Gọi S là tập hợp tất cả các giá trị của tham số m sao cho giá
trị nhỏ nhất của hàm số trên đoạn 0; 
2 bằng 18 . Tổng tất cả các phần tử của S bằng A. 5  . B. 4 . C. 14 . D. 10  . Lời giải
Xét hàm số g ( x) 4 2
= x - 2x m -1 liên tục trên đoạn 0;  2 . g¢( x) 3 = 4x - 4x . x = 1 - 0;2 
g¢( x) = 0 Û x = 0  0;2 x =10;2 
g (0) = m -1, g ( )
1 = m - 2 , g (2) = m  7 .
 min g ( x) = m - 2 , max g ( x) = m  7 . x   0; 2 x   0; 2
 min f ( x) = min0; m - 2 ; m  7. x   0;2 Trường hợp 1:  m - 2 = 18   Û m = 20 .
m - 2  m  7   Trường hợp 2:.  m  7 = 18   Û m = 25 - .
m - 2  m  7   Suy ra m 20;-  25 .
Vậy tổng tất cả các phần tử của S bằng 5 - .
Câu 21. Tính tổng tất cả các giá trị nguyên lớn hơn 6 của tham số m sao cho giá trị nhỏ nhất của hàm số 2
y = x - (m  )
1 x m trên 2; m -  1 nhỏ hơn 2020. A. 2043210 . B. 2034201. C. 3421020 D. 3412020. Lời giải
+) Xét hàm số f ( x ) 2
= x - (m  1) x m liên tục trên 2; m -  1 với m  6 . m 1
Ta có: f ¢( x) = 2x - (m  )
1 ; f ¢( x) = 0 Û x = 2;m -  1 . 2  m 1  (m - )2 1 Khi đó: f (2) = 2 - ; m f = - ; f   (m - ) 1 = 2 - . m  2  4 (m - )2 1 +) Vì -
 2 - m  0, m   6 nên 4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
NGUYỄN BẢO VƯƠNG - 0946798489   m 1  
max f ( x) = max  f (2); f ; f   (m - ) 1  = 2 - m ; [2;m 1 - ]   2     m 1  (m - )2 1
và min f ( x) = min  f (2); f ; f   (m - ) 1  = - . [2;m-1]   2  4    (m )2 1  - 
Do đó: min y = min  2 - m ; -  = 2 - m [2;m-1] 4    
+) Theo yêu cầu bài toán: 2 - m  2020 Û 2
- 020  2 - m  2020 Û 2 - 018  m  2022
+) Vì m và m  6 nên m 7;8;9;; 20  21 . 2021 (7  202 ) 1 2015
+) Vậy tổng tất cả các giá trị nguyên của tham số m là: n = = 2043210  . n= 2 7 1 Câu 22. Cho hàm số 4 3 2 y
x x x m . Tính tổng tất cả các số nguyên m để max y 11. 4  1  ;  2 A. 1  9. B. 3  7 . C. 3  0. D. 11. Lời giải 1
+ Xét hàm số f x 4 3 2
x x x m liên tục trên đoạn  1  ; 2. 4
+ Ta có f x 3 2
x 3x  2x . x  0  1  ;2   + f x 3 2
 0  x 3x  2x  0  x 1 1   ; 2 .  x  2  1  ;2  9 1 + f   1   ; m f   0  ; m f   1   ; m f   2  m . 4 4  f x 
f   f   f   f   f   9 max max 1 ; 0 ; 1 ; 2 1  m  1;2 Khi đó 4  .
min f x min   f  
1 ; f 0; f   1 ; f   2   f  
0  f 2  m  1  ;2   9   
Vậy max y  max  m  , m  0;  3  4     9   m 11  4   9 
 m  m 
theo yêu cầu bài toán max y 11   4   0;  3  m 11   9   m m    4  
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020  53 35     m    4 4   9 35   9     m  m   8 4 35    8    11   m   .  9 4   11   m 11   11 m       8  9   m    8
Vì m nguyên nên m   1  1; 10  ;...;  8 .
Kết luận: tổng các số nguyên m thỏa mãn yêu cầu bài toán là: 1  1 1  09...8  3  0 .
Câu 23. Cho hàm số f ( x) 2
= x - 2mx  3 . Có bao nhiêu giá trị m nguyên để giá trị lớn nhất của f ( x) trên
đoạn 1;2 không lớn hơn 3? A. 2 . B. 3 . C. 1. D. 4 . Lời giải
Ta có giá trị lớn nhất của f ( x) trên đoạn 1; 
2 không lớn hơn 3, tức là max f ( x)  3 1;2
2m x, x  1; 2 2
x - 2mx  3  3, x   1;2  Û  2 Û  2 x  6
x - 2mx  3  -3, x     1;2 2m  , x  1; 2  x
2m  max ( x) ( ) 1 1;2   Û 2   . x  6  2m  min   (2) 1;2  x    +) ( )
1 Û 2m  2 Û m  1. 2 x  6 6 6
+) Xét hàm g ( x) = = x
với x 1;2 có g¢( x) =1- . x x 2 x
Suy ra: g¢( x)  0, x  1; 
2  min g ( x) = g (2) = 5 . 1;2 5 Do đó (2) Û m  . 2 5 Vậy 1  m
, mà m nên m 1;  2 . 2 Câu 24. Cho hàm số 3 2
y = x - 3x - 9x m . Gọi S là tập hợp các giá trị nguyên của tham số m để
max y  50 . Tổng các phần tử của M là  2 - ;  3 A. 0 . B. 737 . C. 759. D. 2 - 15. Lời giải
Xét hàm số f ( x ) 3 2
= x - 3x - 9 x m liên tục trên đoạn  2 - ;  3 .
Ta có f ¢ ( x ) 2
= 3x - 6 x - 9 . x = 1 - f ¢( x) 2
= 0 Û 3x - 6x - 9 = 0 Û  . x = 3 
Có f (-2) = m - 2; f (-1) = m  5; f (3) = m - 27 .
Suy ra max f ( x) = m  5 ; min f ( x) = m - 27 . -2;3 -2;3
Do đó M = max y = max m  5 ; m - 27 . -  2;3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
NGUYỄN BẢO VƯƠNG - 0946798489
 m  5  m - 27  2m - 22  0    m  5  50  5 - 0  m  5  50 m    11;45) M  50 Û  Û Û  Û m ( 2 - 3; 45) .
 m  5  m - 27 2m - 22  0 m    ( 2 - 3;1 ) 1    -   5 - 0  m - 27  50 m 27 50   
Do đó S = -22; -21; -20;...; -1;0;1; 2;...; 4  4 .
Vậy tổng các phần tử của M là 737. Câu 25. Cho hàm số 4 3 2
y = x - 2x x a . Có bao nhiêu giá trị nguyên của tham số a để max y  100 .  1 - ;  2 A. 197 . B. 196 . C. 200 . D. 201. Lời giải Xét 4 3 2
u = x - 2x x a liên tục trên đoạn  1 - ; 2. 3 2
u ' = 4x - 6x  2x .  x = 0 1 - ; 2 
u ' = 0 Û x = 1   1 - ; 2  1 x =  1 - ; 2  2    1  
M = max u = max u   (- ) 1 , u (0), u , u   ( )
1 ,u (2) = u (- )
1 = u (2) = a  4  1 - ; 2    2   Suy ra  .    1  
m = min u = min u  (- ) 1 , u (0), u , u   ( )
1 , u (2) = u (0) = u ( ) 1 = a   1 - ; 2    2  
a  4  a  100 -100  a  2 -
Vậy max y = max  a  4 , a   100 Û Û   .  1 - ; 2
a a  4  100 2 -  a  96   Vậy a  1 - 00, - 99,..., 9 
6 có 197 số nguyên thỏa mãn.
Câu 26. Cho hàm số y = sin x  cos x m , có bao nhiêu giá trị nguyên của m để hàm số có giá trị lớn nhất bé hơn 2 . A. 0 . B. 1. C. 2 . D. 3 . Lời giải
Xét hàm số f ( x) = sin x  cos x m , có tập xác định: D =  .
Ta có: - 2  m  sin x  cos x m  2  m , x    .
Suy ra - 2  m f ( x)  2  m , x    .
Vậy: max y = m  2 hoặc max y = m - 2 . D D  m  2  2  
-2 - 2  m  2 - 2   m 2 m 2  -    m  0  Yêu cầu bài toán Û Û     m - 2  2 
-2  2  m  2  2     m  0 
 m  2  m - 2  0  m  2 - 2 Û 
Û -2  2  m  2 - 2 . -2  2  m  0 
Do m  m = 0 . Vậy chỉ có một giá trị nguyên của m thỏa yêu cầu bài toán.
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
D. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT HÀM ẨN, HÀM HỢP Câu 1.
Cho hàm số y = f ( x) xác định và liên tục trên  , đồ thị của hàm số y = f ¢( x) như hình vẽ.
Giá trị lớn nhất của hàm số y = f ( x) trên đoạn  1 - ;  2 là A. f ( ) 1 . B. f (- ) 1 . C. f (2) . D. f (0) . Lời giải x = 1 -  f ¢( x) = 0 Û x = 1 .   x = 2 
Từ đồ thị hàm y f x ta có bảng biến thiên
Từ đó suy ra giá trị lớn nhất của hàm số trên  1  ;  2 là f   1 . Câu 2.
Cho hàm số y = f ( x) có đạo hàm là hàm f ¢( x) . Đồ thị của hàm số y = f ¢( x) được cho như hình
vẽ. Biết rằng f (0)  f (3) = f (2)  f (5) . Giá trị nhỏ nhất, giá trị lớn nhất của y = f ( x) trên đoạn 0;5 lần lượt là:
A. f (2) ; f (5) .
B. f (0) ; f (5) .
C. f (2) ; f (0) . D. f ( ) 1 ; f (5) . Lời giải f ¢( x)
Dựa vào đồ thị hàm số ta có bảng biến thiên.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
NGUYỄN BẢO VƯƠNG - 0946798489
min f ( x) = f (2)  Khi đó: 0;5  ,
f (3)  f (2) 
mà f (0)  f (3) = f (2)  f (5)  f (0)  f (2)  f (2)  f (5)  f (0)  f (5) .
Vậy giá trị nhỏ nhất, giá trị lớn nhất của y = f ( x) trên đoạn 0;5 lần lượt là: f (2) ; f (5) . Câu 3.
Cho hàm số f ( x) có đạo hàm là f ¢( x) . Đồ thị của hàm số y = f ¢( x) được cho như hình vẽ bên.
Biết rằng f (0)  f ( )
1 - 2 f (3) = f (5) - f (4) . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của
f ( x) trên đoạn 0;5 .
A. m = f (5), M = f (3) B. m = f (5), M = f ( ) 1
C. m = f (0), M = f (3) D. m = f ( ) 1 , M = f (3) Lời giải Chọn A
Từ đồ thị ta có bảng biến thiên của f ( x) trên đoạn 0;5
M = f (3) và f ( )
1  f (3), f (4)  f (3)
f (5) - f (0) = f ( )
1 - f (3)  f (4) - f (3)  0  f (5)  f (0)  m = f (5) . Câu 4.
Cho hàm số y = f ( x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số 1 1
g ( x) = f ( 2 4x - x ) 3 2 
x - 3x  8x  trên đoạn 1;  3 . 3 3 25 19 A. 15. B. . C. . D. 12. 3 3 Lời giải
g¢( x) = ( - x) f ¢( 2 x - x ) 2 4 2 4
x - 6x  8 = ( - x)  f ¢( 2 2 2
4x - x )  4 - x   . Với x 1;  3 thì 4 - x  0 ; 2
3  4x - x  4 nên f ¢( 2
4x - x )  0 . Suy ra f ¢( 2 2
4x - x )  4 - x  0 , x  1;  3 .
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Bảng biến thiên
Suy ra max g ( x) = g (2) = f (4)  7 = 12 . 1;  3 Câu 5.
Cho hàm số y = f ( x) liên tục trên . Đồ thị của hàm số y = f ¢( x ) như hình bên. Đặt
g ( x) = f ( x) - ( x  )2 2
1 . Mệnh đề dưới đây đúng.
A. max g ( x) = g (3).
B. min g ( x) = g ( )
1 . C. max g ( x) = g (0). D. max g ( x) = g ( ) 1 . -3;3  3;3 -  -3;  3 -3;3 Lời giải Chọn D
g ( x) = f ( x) - ( x  )2 2
1  g¢( x) = 2 f ¢( x) - 2( x  ) 1
Dựa vào đồ thị ta thấy x = 3 - 
g¢( x) = 0 Û f ¢( x) = x 1 Û x = 1  x = 3  Và
với x  (-; -3) : f ¢( x)  x 1  g¢( x)  0 với x  (-3; )
1 : f ¢ ( x)  x 1  g¢( x)  0 ,
với x  (1;3) : f ¢( x)  x 1  g¢( x)  0
với x  (3; ) : f ¢( x)  x 1  g¢( x)  0 Bảng biến thiên x - -3 1 3  g¢( x) ‒ 0 + 0 ‒ 0 + g ( x)
Dựa vào bảng biến thiên suy ra max g ( x) = g ( ) 1 . -3;  3 Câu 6.
Cho hàm số y = f ( x) có đạo hàm cấp hai trên  . Biết f ¢(0) = 3 , f ¢(2) = 20 - 18 và bảng xét dấu
của f ¢¢( x) như sau:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
NGUYỄN BẢO VƯƠNG - 0946798489
Hàm số y = f ( x  2017)  2018x đạt giá trị nhỏ nhất tại điểm x thuộc khoảng nào sau đây? 0 A. (-; - 2017) B. (2017; ) C. (0; 2) D. (-2017; 0) Lời giải
Dựa vào bảng xét dấu của f ¢ ( x) ta có bảng biến thiên của hàm sồ f ¢( x)
Đặt t = x  2017 .
Ta có y = f ( x  2017)  2018x = f (t )  2018t - 2017.2018 = g (t ) .
g¢(t ) = f ¢(t )  2018 .
Dựa vào bảng biến thiên của hàm số f ¢( x) suy ra phương trình g¢(t ) có một nghiệm đơn
  (-;0) và một nghiệm kép t = 2 .
Ta có bảng biến thiên g (t )
Hàm số g (t ) đạt giá trị nhỏ nhất tại t =   -;0 . 0 ( )
Suy ra hàm số y = f ( x  2017)  2018x đạt giá trị nhỏ nhất tại x mà 0
x  2017  -; 0 Û x  -; -2017 . 0 ( ) 0 ( ) Câu 7.
Cho hàm số f ( x) có đạo hàm là f ¢( x) . Đồ thị của hàm số y = f ¢( x) được cho như hình vẽ dưới đây: Biết rằng f (- )
1  f (0)  f ( )
1  f (2) . Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f ( x) trên
đoạn -1; 2 lần lượt là: A. f ( ) 1 ; f (2) .
B. f (2) ; f (0) .
C. f (0) ; f (2) . D. f ( ) 1 ; f (- ) 1 . Lời giải
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Từ đồ thị của hàm số y = f ¢( x) ta có bảng biến thiên của hàm số y = f ( x) trên đoạn -1; 2 như sau Nhận thấy
min f ( x) = f ( ) 1 -1;2 . f (- ) 1 f (2)
Để tìm max f ( x) ta so sánh và .  1; - 2
Theo giả thiết, f (- )
1  f (0)  f ( )
1  f (2) Û f (2) - f (- )
1  f (0) - f ( ) 1 .
Từ bảng biến thiên, ta có f (0) - f ( )
1  0 . Do đó f (2) - f (- )
1  0 Û f (2)  f (- ) 1 .
Hay max f ( x) = f (2) . -1;2  7  Câu 8.
Cho hàm số y = f ( x) liên tục trên đoạn 0; 
có đồ thị hàm số y = f '( x) như hình vẽ. 2     7 
Hàm số y = f ( x) đạt giá trị nhỏ nhất trên đoạn 0; 
tại điểm x nào dưới đây? 2  0   7
A. x = 0 . B. x = . C. x =1.
D. x = 3. 0 0 2 0 0 Lời giải Chọn D  7 
Dựa vào đồ thị hàm số y = f '( x) ta có bảng biến thiên trên đoạn 0;  như sau: 2   
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
NGUYỄN BẢO VƯƠNG - 0946798489
Do đó hàm số đạt giá trị nhỏ nhất tại x = 3. 0 Câu 9.
Cho hàm số y = f ( x) . Đồ thị hàm y = f ¢( x) như hình vẽ
Đặt h ( x) = f ( x) 3 3
- x  3x . Tìm mệnh đề đúng trong các mệnh đề sau:
A. max h(x) = 3 f ( ) 1 .
B. max h(x) = 3 f (- 3) . [- 3; 3] [- 3; 3 ]
C. max h(x) = 3 f ( 3) . D. max (
h x) = 3 f (0) . [- 3; 3 ] [- 3; 3] Lời giải Chọn B
Ta có: h¢( x) = f ¢( x) 2 3
- 3x  3 Û h¢( x) =  f ¢( x) - ( 2 3 x - ) 1  .   Đồ thị hàm số 2
y = x -1 là một parabol có toạ độ đỉnh C (0; - )
1 , đi qua A(- 3 ;2) , B( 3;2).
Từ đồ thị hai hàm số y f  x  và 2
y = x -1 ta có bảng biến thiên của hàm số y = h( x) .
Với h (- 3) = 3 f (- 3) , h( 3) = 3 f ( 3) .
Vậy max h(x)  3f  3. [ 3; 3 ] Câu 10. Cho hàm số
y = f ( x) có đồ thị
y = f ¢( x) ở hình vẽ bên. Xét hàm số 1 3 3
g ( x) = f ( x) 3 2 - x - x
x  2018, mệnh đề nào dưới đây đúng? 3 4 2
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 g (-3)  g ( ) 1
A. min g ( x) = g (- )
1 . B. min g ( x) = . -3;  1 -3;  1 2
C. min g ( x) = g (-3) . D. min g ( x) = g ( ) 1 . -3;  1 -3;  1 Lời giải Chọn A 3 3  3 3 
Ta có g¢( x) = f ¢( x) 2 - x - x  = f ¢( x) 2 - x x -   . 2 2  2 2  3 3 Vẽ parabol ( P) 2 : y = x x -
. Ta thấy ( P) đi qua các điểm có toạ độ ( 3 - ;3) , ( 1 - ; 2) , ( ) 1;1 . 2 2 Trên khoảng ( 3 - ; - )
1 đồ thị hàm số f ¢( x) nằm phía dưới ( P) nên  3 3  f ¢( x) 2  x x -  g¢   ( x)  0 .  2 2  Trên khoảng ( 1 - ; )
1 đồ thị hàm số f ¢( x) nằm phía trên ( P) nên  3 3  f ¢( x) 2  x x -  g¢   ( x)  0 .  2 2 
Trên khoảng (1; ) đồ thị hàm số f ¢( x) nằm phía dưới ( P) nên  3 3  f ¢( x) 2  x x -  g¢   ( x)  0 .  2 2  Bảng biến thiên
Từ bảng biến thiên, ta có min g ( x) = g (- ) 1 .  3; -  1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 11. Cho hàm số f ( x) . Biết hàm số y = f ¢( x) có đồ thị như hình vẽ bên dưới. Trên đoạn  4 - ;  3 , hàm
số g ( x) = f ( x)  ( - x)2 2 1
đạt giá trị nhỏ nhất tại điểm:
A. x = -4 .
B. x = -1 .
C. x = 3.
D. x = -3 . 0 0 0 0 Lời giải Chọn B
g ( x) = f ( x)  ( - x)2 2 1
g '( x) = 2 f '( x) - 2(1- x)  g '( x) = 0 Û f '( x) = 1 - x
Vẽ hai đồ thị y = f '( x)  y = 1- x trên cùng một hệ trục
Từ đồ thị ta thấy g '( x)  0,  (-4; - )
1 và g '( x)  0,  (-1;3)
Vậy giá trị nhỏ nhất trên đoạn -4;3 đạt tại điểm x = -1. 0
Câu 12. Cho hàm số y = f ( x) có đạo hàm liên tục trên R . Hàm số y = f '( x) có đồ thị như hình sau: Cho bốn mệnh đề sau:
1) Hàm số y = f ( x) có hai cực trị
2) Hàm số y = f ( x) đồng biến trên khoảng (1; ) 3) f ( )
1  f (2)  f (4). 4) Trên đoạn  1 - ; 
4 , giá trị lớn nhất của hàm số y = f ( x) là f ( ) 1 .
Số mệnh đề đúng trong bốn mệnh đề trên là: A. 3. B. 1. C. 4. D. 2. Lời giải Chọn D
Dựa vào đồ thị của hàm số y = f '( x) ta thấy:
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020x = 1 - 
f '( x) = 0 Û x = 1  x = 4 
f '( x)  0 Û x (- ;  - ) 1  (1;4)
f '( x)  0 Û x ( 1 - ; ) 1  (4;)
Ta có bảng biến thiên của hàm số y = f ( x)
Dựa vào bảng biến thiên đáp án đúng là mệnh đề số 3 và 4
Câu 13. Cho hàm số y f x có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
g x  f  1 1 2 4x x  3 2
x 3x 8x  trên đoạn 1;  3 . 3 3 25 19 A. . B. 15. C. . D. 12. 3 3 Lời giải Chọn D  4 x
Ta có g x  f  2 4x x  2
.(4  2 x)  x 6x 8  22 x 2
f (4x x )    2    Xét thấy x    2 2
1;3  3  4x x  4  f (4x x )  0 4  x Mặt khác  0 x  1;  3 2
Suy ra g x  0  x  2 g   19 17 17 32 1  f (3)   f (4)   5   3 3 3 3 19 19 19 34
g (3)  f (3)   f (4)   5   3 3 3 3
g (2)  5  7  12.  g  1  g   3  g   2
Vậy max gx 12 tại x  2. 1  ;3
Câu 14. Cho hàm số y = f ( x) . Hàm số y = f ¢( x) có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của
hàm số g ( x) = f ( x) 2 2
- sin x trên đoạn  1 - ;  1 là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
NGUYỄN BẢO VƯƠNG - 0946798489 - -2 -1 0 1 2 + 0 0 0 A. f (- ) 1 . B. f (0) . C. f (2) . D. f ( ) 1 . Lời giải Chọn B Ta có x  1 - ;  1  2x  2 - ; 2 .
Từ bảng biến thiên của y = f '( x) thì bảng biến thiên y = f ( x) như sau: - -2 02 +- 0 + 0 0 - +
f (2x)  f (0)  Ta thấy x   1 - ;  1 ta có 
, do đó g ( x)  g (0) = f (0) . 2 -sin x  0 = sin  (0) 
Dấu “=” xảy ra khi x = 0 .
Câu 15. Cho hàm số y = f ( x) liên tục trên  sao cho max f ( x) = 3 . Xét hàm số g ( x) = f (3x - ) 1  m .  1 - ;2
Tìm tất cả các giá trị của tham số m để max g ( x) = 1 - 0 . 0;  1 A. 13 . B. 7 - . C. 1 - 3 . D. 1 - . Lời giải Chọn C
Đặt u = 3x -1  g ( x) = f (u)  m . x 0;  1  u  1 - ;  2 .
Do f ( x) liên tục trên  nên max g ( x) = max ( f (u )  m) = max f (u )  m = 3  m . 0;  1  1 - ; 2  1 - ; 2
Để max g ( x) = 10 Û m = -13. 0;  1
Câu 16. Cho hàm số y = f ( x) có đạo hàm cấp 2 trên  , hàm số y = f ¢( x) có đồ thị như hình vẽ bên.
 sin x  3 cos x   5  
Giá trị lớn nhất của hàm số y = f   trên đoạn - ; bằng  2       6 6      5     A. f -   . B. f (0) . C. f -   . D. f   .  3   6   6 
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Lời giải Chọn A
sin x  3 cos x    Đặt t = = sin x    . 2  3   5        Vì x  - ;  x   - ;  t  1; -  1  . 6 6  3  2 2     
Dựa vào đồ thị của hàm số f ¢( x) , ta có bảng biến thiên
 sin x  3 cos x      Ta có: max f
 = max f (t ) Û t = 0 Û sin x  = 0 Û x = -   .  5      1 - ;  1 - ; 2  3  3    6 6   
 sin x  3 cos x     Vậy max f   = f -   .  5     - ; 2  3     6 6   
Câu 17. Cho hàm số y = f ( x) liên tục trên  sao cho max f ( x) = f (2) = 4 . Xét hàm số x   0;10
g ( x) = f ( 3 x x) 2
- x  2x m . Giá trị của tham số m để max g ( x) = 8 là x   0;2 A. 5 . B. 4 . C. 1 - . D. 3 . Lời giải Chọn D Đặt 3
t = x x . Vì x 0; 2  t 0;10 .
Ta có: max g ( x) = max  f ( 3 x x) 2
- x  2x m  max f ( 3 x x) 2
 max -x  2x m     x   0;2 x   0;2 x   0;2 x   0;2
= max f (t ) 1 m (với 3
t = x x và 2
max -x  2x m = 1 m   ). t   0;10 x   0;2
 max f ( x) 1 m = 4 1 m = 5  m . x   0;10 x = 1
Suy ra: max g ( x) = 5  m Û  Û x = 1. x   0;2 t = 2 
Theo giả thiết, ta có: max g ( x) = 8 Û m  5 = 8 Û m = 3 . x   0; 2
Câu 18. Cho hai hàm số y = f ( x) , y = g ( x) có đạo hàm là f ¢( x) , g¢( x) . Đồ thị hàm số y = f ¢( x) và
g¢( x) được cho như hình vẽ bên dưới.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
NGUYỄN BẢO VƯƠNG - 0946798489 Biết rằng
f (0) - f (6)  g (0) - g (6) . Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
h ( x) = f ( x) - g ( x) trên đoạn 0;6 lần lượt là:
A. h (6) , h (2) .
B. h (2) , h (6) .
C. h (0) , h (2) .
D. h (2) , h (0) . Lời giải
Ta có h¢( x) = f ¢( x) - g¢( x) .
h¢( x) = 0 Û x = 2
Từ đồ thị ta có bảng biến thiên:
Và f (0) - f (6)  g (0) - g (6) Û f (0) - g (0)  f (6) - g (6) .
Hay h (0)  h (6) .
Vậy max h ( x) = h(6) ; min h( x) = h (2) . 0;6 0;6
E. ỨNG DỤNG GTLN-GTNN GIẢI BÀI TOÁN THỰC TẾ Câu 1.
Ông A dự định dùng hết 2
6,5m kính để làm một bể cá có dạng hình hộp chữ nhật không nắp, chiều
dài gấp đôi chiều rộng (các mối ghép có không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu
(kết quả làm tròn đến hàng phần trăm). A. 3 2, 26 m B. 3 1, 61 m C. 3 1,33 m D. 3 1,50 m Lời giải Chọn D a b c
Giả sử hình hộp chữ nhật có kích thước như hình vẽ. Ta có dung tích của bể cá: V = abc
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2  6, 5 - 2b
ab  2bc  2ac = 6,5 2
2b  6bc = 6,5 c =
Mặt khác theo giả thiết ta có:  Û  Û  6b a = 2  b a = 2  ba = 2  b 2 6,5 - 2b 3 6,5b - 2b Khi đó 2 V = 2b . Û V = . 6b 3 3 6,5b - 2b
Xét hàm số: f (b) = . Có BBT 3  39 
Vậy bể cá có dung tích lớn nhất là: 3 f   = 1,50 m .  6    1 Câu 2.
Một vật chuyển động theo quy luật 3 2
s = - t  6t với t (giây) là khoảng thời gian tính từ khi vật bắt 3
đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi
trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? A. 243 (m/s) B. 27 (m/s) C. 144 (m/s) D. 36 (m/s) Lời giải Chọn D Ta có: 2
v = s¢ = t - 12t ; v¢ = 2
- t 12 ; v¢ = 0 Û t = 6. BBT t 0 6 9 v¢  0  36 v
Nhìn bbt ta thấy vận tốc đạt giá trị lớn nhất khi t = 6. Giá trị lớn nhất là v (6) = 36m/s . Câu 3.
Ông A dự định sử dụng hết 2
5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không
nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích
lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? A. 3 1, 01 m B. 3 0, 96 m C. 3 1,33 m D. 3 1,51 m Lời giải Chọn A A' D' B' C' y A 2 x D x B C
Gọi x, y lần lượt là chiều rộng và chiều cao của bể cá (điều kiện x, y  0 ).
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
NGUYỄN BẢO VƯƠNG - 0946798489 Ta có thể tích bể cá 2 V = 2x y . Theo đề bài ta có: 2
2xy  2.2xy  2x = 5 2
Û 6xy  2x = 5 2 5 - 2x 5 Û y = (Điều kiện kiện 2
y  0 Û 5 - 2x  0  0  x  ) 6x 2 2 3 5 - 2x 5x - 2x 2 5 - 6x 5 2  V = 2x =  V ¢ = 2
V ¢ = 0 Û 5 - 6x = 0 Û x = 6x 3 3 6 5 30 3  V =  1, 01 m . max 27 Câu 4.
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám
sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ t
được cho bởi công thức c (t ) =
(mg / L) . Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong 2 t 1
máu của bệnh nhân cao nhất? A. 4 giờ. B. 1 giờ. C. 3 giờ. D. 2 giờ. Lời giải t
Xét hàm số c (t ) = , (t  0) . 2 t 1 2 1- t c¢(t ) = . (t  )2 2 1 t = 1
c¢(t ) = 0 Û  . t = -1 
Với t = 1 giờ thì nồng độ thuốc trong máu của bênh nhân cao nhất. Câu 5.
Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình
vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây
để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
A. x = 3
B. x = 2
C. x = 4
D. x = 6 Lời giải Chọn B
Ta có : h = x (cm) là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là: 12 - 2x (cm) 2 x  0 x  0
Vậy diện tích đáy hình hộp S = ( - x) ( 2 12 2 cm ). Ta có:  Û  Û x  (0;6) 12 - 2x  0 x  6  
Thể tích của hình hộp là: V = S.h = x ( 2 - 2x)2 . 1 2 Xét hàm số: y = . x (12 - 2x) x  (0;6) 2
Ta có : y ' = (12 - 2x) - 4x (12 - 2x) = (12 - 2x)(12 - 6x) ;
y ' = 0 Û (12 - 2x).(12 - 6x) = 0 Û x = 2 hoặc x = 6 (loại).
Suy ra với x = 2 thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là y (2) = 128 . Câu 6.
Đợt xuất khẩu gạo của tỉnh A thường kéo dài trong 2 tháng ( 60 ngày). Người ta nhận thấy số lượng 2
xuất khẩu gạo tính theo ngày thứ t được xác định bởi công thức S (t ) 3 2 =
t - 63t  3240t - 3100 với 5
(1 t  60) . Hỏi trong 60 ngày đó thì ngày thứ mấy có số lượng xuất khẩu gạo cao nhất. A. 60 B. 45 C. 30 D. 25 Lời giải Chọn B 2 6 S (t ) 3 2 =
t - 63t  3240t - 3100  S¢(t ) 2 =
t -126t  3240 5 5 t = 45
Ta có: S¢(t ) = 0 Û  t = 60  1 Câu 7.
Một vật chuyển động theo quy luật 2 3
S = 10t - t , với t (giây) là khoảng thời gian tính từ lúc vật bắt 3
đầu chuyển động và S (m) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
NGUYỄN BẢO VƯƠNG - 0946798489
thời gian 15 giây từ lúc vật bắt đầu chuyển động vận tốc v (m / s) của vật đạt giá trị lớn nhất tại thời
điểm t (s) bằng: A. 8(s) . B. 20 (s) C. 10 (s) . D. 15( s) . Lời giải Chọn C. 1 Ta có: 2 3
S = 10t - t v (t ) 2
= S¢ = 20t - t . 3
Xét hàm số v (t );t 0;15 , ta có: v¢(t) = 20 - 2t = 0 Û t = 10.
v (0) = 0; v (15) = 75;v (10) = 100 . Do đó: max v (t ) = 100 Û t = 10 . 0;15 Câu 8.
Một sợi dây có chiều dài 28m được cắt thành hai đoạn để làm thành một hình vuông và một hình
tròn. Tính chiều dài (theo đơn vị mét) của đoạn dây làm thành hình vuông được cắt ra sao cho tổng
diện tích của hình vuông và hình tròn là nhỏ nhất? 56 112 84 92 A. . B. . C. . D. . 4   4   4   4   Lời giải
Gọi chiều dài của đoạn dây làm thành hình vuông là x ( m ) ( 0  x  28 )
=> chiều dài của đoạn dây làm thành hình tròn là 28 - x ( m ) 2 2  x x
+) Diện tích hình vuông là: =    4  16 28 - x
+) Bán kính hình tròn là: R = 2 2 2  28 - x  784 - 56x x
=> Diện tích hình tròn: 2  R =  . =    2  4 2 2 x 784 - 56x x    4  14 196
+) Tổng diện tích hai hình: 2  = x - x    16 4  16       4  14 196 Xét 2 f (x) = x - x   
. Nhận thấy f (x) đạt giá trị nhỏ nhất tại  16    -b 14 16 112 x = = . = 2a  2(  4)   4
Vậy chiều dài của đoạn dây làm thành hình vuông để tổng diện tích của hai hình đạt giá trị nhỏ nhất 112 là m 4   Câu 9.
Một xưởng in có 15 máy in được cài đặt tự động và giám sát bởi một kỹ sư, mỗi máy in có thể in
được 30 ấn phẩm trong 1 giờ, chi phí cài đặt và bảo dưỡng cho mỗi máy in cho 1 đợt hàng là
48.000 đồng, chi phí trả cho kỹ sư giám sát là 24.000 đồng/giờ. Đợt hàng này xưởng in nhận 6000
ấn phẩm thì số máy in cần sử dụng để chi phí in ít nhất là A. 10 máy. B. 11 máy. C. 12 máy. D. 9 máy. Lời giải Chọn A
Gọi x (0  x  15) là số máy in cần sử dụng để in lô hàng.
Chi phí cài đặt và bảo dưỡng là 48000x . 6000 6000 48000
Số giờ in hết số ấn phẩm là , chi phí giám sát là .24000  . 30x 30x x 4800000
Tổng chi phí in là P ( x) = 48000x  . x
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 4800000 x = 10
P¢( x) = 48000 - ; P¢( x) 2 = 0 Û x = 100 Û . 2  x x = -10 ( L)  Bảng biến thiên: x 0 10 15 P¢ ( x) - 0  P ( x) P (10)
Vậy chi phí in nhỏ nhất là 10 máy.
Câu 10. Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật s (t ) 3 2
= t - 4t 12 (m), trong đó t (s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc
của chất điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu? 8 4 A. 2 (s). B. (s). C. 0 (s). D. (s). 3 3 Lời giải
v (t ) = s¢(t ) 2 = 3t - 8t . 4
v¢(t ) = 6t - 8 . Có v¢(t ) = 0 Û t = . 3  4  16
Dựa vào bảng biến thiên ta có min v = v = -   . 0;)  3  3 4
Vậy vận tốc của chất điểm đó đạt giá trị bé nhất khi t = . 3
Câu 11. Cho một tấm nhôm hình chữ nhật có chiều dài bằng 10cm và chiều rộng bằng 8cm . Người ta cắt bỏ
ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm) , rồi
gập tấm nhôm lại (như hình vẽ) để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. 8 - 2 21 10 - 2 7 9  21 9 - 21 A. x = B. x = C. x = . D. x = 3 3 9 3 Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn D
Ta có : h = x (cm) là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là: 10 - 2x (cm) và 8 - 2x (cm ) x  0  x  0
Vậy diện tích đáy hình hộp S = ( - x)( - x)( 2 10 2 8 2 cm ) . Ta có: 10  - 2x  0 Û  Û x  (0; 4) x  4   8 - 2x  0 
Thể tích của hình hộp là: V = S.h = .
x (10 - 2x).(8 - 2x) Xét hàm số: y = .
x (10 - 2x).(8 - 2x)x  (0; 4) Ta có : 2
y ' = 12x - 72x  80 ;  9  21 x =  4  (l) 3 y ' = 0 Û  .  9 - 21 x = (n)  3 9 - 21 Suy ra với x =
thì thể tích hộp là lớn nhất và giá trị lớn nhất. 3
Câu 12. Một đoàn cứu trợ lũ lụt đang ở vị trí A của một tỉnh miền trung muốn đến xã C để tiếp tế lương
thực và thuốc men. Để đi đến C , đoàn cứu trợ phải chèo thuyền từ A đến vị trí D với vận tốc
4 (km / h) , rồi đi bộ đến vị trí C với vận tốc 6(km / h) . Biết A cách B một khoảng 5km , B cách
C một khoảng 7km (hình vẽ). Hỏi vị trí điểm D cách A bao xa để đoàn cứu trợ đi đến xã C nhanh nhất?
A. AD = 5 3 km .
B. AD = 2 5 km .
C. AD = 5 2 km .
D. AD = 3 5 km . Lời giải Chọn B
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Đặt AD = x (km) , ( x  0) . Ta có 2 2 2 BD = AD - AB =
x - 25 ( x  5) 2
CD = BC - BD = 7 - x - 25 2 AD DC x 7 - x - 25
Thời gian đi từ A đến C là: T ( x) =  =  4 6 4 6 2 1 -2x 3 x - 25 - 2x T ¢ ( x) =  = . 2 2 4 12 x - 25 12 x - 25 T ¢( x) 2
= 0 Û 3 x - 25 = 2x Û x = 3 5 Bảng biến thiên 14  5 5
Do đó min T ( x) = T (3 5) = x   5;) 12
Vậy AD = 3 5 (km) .
Câu 13. Một vật chuyển động theo quy luật 2 3
s  3t t . Thời điểm t(s) tại đó vận tốc v(m / s) của chuyển
động đạt giá trị lớn nhất là
A. t  5 .
B. t 1.
C. t  2 .
D. t  3 Lời giải Chọn B
Vận tốc của chuyển động là v s 'tức là 2
v(t)  6t 3t , t  0
v '(t)  6  6t, v (
' t)  0  t  1 Bảng biến thiên: t 0 1 + ∞ v '(t) + 0 – v(t)
Hàm số v(t) đồng biến trên khoảng (0;1) và nghịch biến trên khoảng 1;  
Û Max vt  3 khi t 1.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 14. Ông A dự định sử dụng hết 2
5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không
nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích
lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? A. 3 1, 01 m . B. 3 0,96 m . C. 3 1,33 m . D. 3 1,51 m . Lời giải Chọn A A' D' B' C' y A 2 x D x B C
Gọi x, y lần lượt là chiều rộng và chiều cao của bể cá (điều kiện x, y  0 ). Ta có thể tích bể cá 2 V = 2x y . Theo đề bài ta có: 2
2xy  2.2xy  2x = 5 2
Û 6xy  2x = 5 2 5 - 2x 5 Û y = (Điều kiện kiện 2
y  0 Û 5 - 2x  0  0  x  ) 6x 2 2 3 5 - 2x 5x - 2x 2 5 - 6x 5 2  V = 2x =  V ¢ = 2
V ¢ = 0 Û 5 - 6x = 0 Û x = 6x 3 3 6 5 30 3  V =  1, 01 m . max 27
Câu 15. Một người nông dân có 15.000.000 đồng muốn làm một cái hàng rào hình chữ E dọc theo một con
sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào song
song với bờ sông thì chi phí nguyên vật liệu là 60.000 đồng một mét, còn đối với ba mặt hàng rào
song song nhau thì chi phí nguyên vật liệu là 50.000 đồng một mét. Tìm diện tích lớn nhất của đất rào thu được A. 2 3125 m . B. 2 50 m . C. 2 1250 m . D. 2 6250 m . Lời giải Chọn D
Gọi x là chiều dài 1 mặt hàng rào hình chữ E ( trong ba mặt song song, x  0 ).
Gọi y là chiều dài mặt hàng rào hình chữ E song song với bờ sông ( y  0 ). 500 - 5x
Số tiền phải làm là: .3 x .50000  .
y 60000 = 15.000.000 Û y = . 2 500 - 5x 5 Diện tích đất: 2 S = . x y = . x = 250x - x 2 2
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Ta có: S ' = 250 - 5x .
S ' = 0 Û 250 - 5x Û x = 50. Bảng biến thiên: x 0 50 + ∞ S' + 0 S 6250 0 - ∞ Vậy: 2
max S = 6250 (m ) khi x = 50. (0;)
Câu 16. Một người đàn ông muốn trèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đố diện, càng nhanh
càng tốt, trên một bờ sông thẳng rộng 3 km ( như hình vẽ). Anh có thể chèo thuyền của mình trực
tiếp qua sông để đến C và sau đó chạy đến B , hay có thể chèo trực tiếp đến B , hoặc anh có thể
chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B . Biết anh ấy có thể chèo thuyền 6
km/h, chạy 8 km/h và quãng đường BC = 8 km . Biết tốc độ của dòng nước là không đáng kể so với
tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất( đơn vị: giờ) để người đàn ông đến B ? 73 3 9 7 A. . B. . C. . D. 1  . 6 2 7 8 Lời giải Chọn D
Đặt DC = x km , (0  x  8). Ta có: 2 AD =
9  x , DB=8 - . x 2 9  x 8 - x
Thời gian đi từ A đến B được tính bằng công thức f ( x) =  . 6 8 x  0 x 1 x 1  9 f ¢( x) =
- , f ¢( x) = 0 Û = Û  Û x = (thỏa mãn điều 2 8 8 16x = 9 6 9  6 9   ( 2 2 2 9  x x x ) 7 
kiện 0  x  8 ). 3 73  9  7
Mặt khác, f (0) = , f (8) = , f = 1  .   2 6  7  8
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
NGUYỄN BẢO VƯƠNG - 0946798489 7
Vậy thời gian ngắn nhất để người đàn ông đi từ A đến B là 1 (giờ). 8
Câu 17. Ông Khoa muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng 3
288m . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể 2
là 500000 đồng/ m . Nếu ông Khoa biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân
công sẽ thấp nhất. Hỏi ông Khoa trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu (Biết độ dày
thành bể và đáy bể không đáng kể)? A. 90 triệu đồng.
B. 168 triệu đồng. C. 54 triệu đồng.
D. 108 triệu đồng. Lời giải Chọn D
Theo bài ra ta có để chi phí thuê nhân công là thấp nhất thì ta phải xây dựng bể sao cho tổng diện tích
xung quanh và diện tích đáy là nhỏ nhất.
Gọi ba kích thước của bể là a , 2a , c (a(m)  0,c(m)  0) .
Ta có diện tích cách mặt cần xây là 2 2
S = 2a  4ac  2ac = 2a  6ac . 144 Thể tích bể 2 V = . a 2 .
a c = 2a c = 288  c = . 2 a 144 864 432 432 432 432 Suy ra 2 2 2 2 3 S = 2a  6 . a = 2a  = 2a    3. 2a . . = 216 . 2 a a a a a a Vậy 2 S
= 216 m , khi đó chi phí thấp nhất là 216.500000 = 108 triệu đồng. min
Câu 18. Hình vẽ bên dưới mô tả đoạn đường đi vào GARA ÔTÔ nhà cô Hiền. Đoạn đường đầu tiên có chiều
rộng bằng x (m) , đoạn đường thẳng vào công GARA có chiều rộng 2, 6(m) . Biết kích thước xe ôtô
là 5m 1,9m (chiều dài  chiều rộng). Để tính toán và thiết kế đường đi cho ôtô người ta coi ôtô như
một khối hộp chữ nhật có kích thước chiều dai 5m , chiều rộng 1, 9m . Hỏi chiều rộng nhỏ nhất của
đoạn đường đầu tiên gần nhất với giá trị nào trong các giá trị bên dưới để ôtô có thể đi vào GARA
được?(giả thiết ôtô không đi ra ngoài đường, không đi nghiêng và ôtô không bị biến dạng).
Trang 56 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
A. x = 3,55(m) .
B. x = 2, 6(m) .
C. x = 4, 27(m) .
D. 3, 7 (m) . Lời giải Chọn D
Chọn hệ trục tọa độ Oxy như hình vẽ. Khi đó M ( 2 - , 6; x) . x y Gọi B (- ; a 0) , suy ra A( 2
0; 25 - a ). Phương trình AB :  -1 = 0 . 2 -a 25 - a x y
Do CD // AB nên phương trình CD :  - T = 0 . 2 -a 25 - a
Mà khoảng cách giữa AB và CD bằng 1,9 nên T -1 9, 5 = 1, 9  T = 1 2 2 2 a 25 1  1 - a         2  a   25 - a
Điều kiện đề ôtô đi qua được là M ,O nằm khác phía đối với bờ là đường thẳng CD . 2 - , 6 x 9,5 Suy ra:  -1-  0 2 2 -a 25 - a a 25 - a 2 9, 5 2, 6 25 - a 2
Û x  25 - a  -
đúng với mọi a (0;5) . a a
Û x  max f (a) (0;5) 2 9,5 2, 6 25 - a
Xét hàm số f (a) 2 = 25 - a  - trên (0;5) a a -a 19 65
Ta có: f ¢(a) = -  2 2 2 2 2 25 a - a a 25 - a 65 a 19 19 f ¢(a) 3 2 = 0 Û =  Û 65 = a  25 - a 2 2 2 2 2a 2 a 25 - a 25 - a Û ( 3 - a ) 2 6 3 2 2 65
= 19 25 - a Û 4a - 520a  361a  7875 = 0 a = 3  Û  a  2 ( 19 3 2 9  3a a ) ( ) = (*) 2  25 - a  4
Xét phương trình (*). Với mọi a (0;5) ta luôn có:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57
NGUYỄN BẢO VƯƠNG - 0946798489  19 (3  a) 19 (3  a) VP =   2  4 25 - a  4   19(3  a)  a VT - = 2  ( 19 3 1 2 9  3a a ) ( ) - = ( 2
8a  5a 15)  0  4 4 4
Suy ra phương trình (*) vô nghiệm. Bảng biến thiên: 37
Từ bảng biến thiên ta có: max f (a) =
. Vậy giá trị nhỏ nhất của x là 3, 7 . (0;5) 10
Câu 19. Một người nông dân có 3 tấm lưới thép B40, mỗi tấm dài 12 (m) và muốn rào một mảnh vườn dọc
bờ sông có dạng hình thang cân ABCD như hình vẽ (bờ sông là đường thẳng DC không phải rào,
mỗi tấm là một cạnh của hình thang). Hỏi ông ta có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu 2 m ? B A C D A. 100 3 . B. 106 3 . C. 108 3 . D. 120 3 . Lời giải Chọn C
Kẻ đường cao BH , gọi số đo 2 góc ở đáy CD của hình thang là x, x  (0 ;  90) .
Diện tích mảnh vườn là: 1 1 1 S =
BH ( AB CD) =
BC.sin x (2.AB  2BC.cos x) 2 =
AB (2sin x  sin 2x) 2 2 2
Xét hàm số f ( x) = 2sin x  sin 2x với x ( 0 0
0 ;90 ) có f ¢( x) = 2cos x  2cos 2x .  1 cos x = Ta có: f ( x) 2 0 2 cos x 2 cos 2x 0 2 cos x cos x 1 0  ¢ = Û  = Û  - = Û 2 cos x = -1  1 Do x ( 0 0 0 ;90 ) nên ta nhận 0 cos x =
Û x = 60 . Ta có bảng biến thiên: 2
Trang 58 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 3 3
Từ bảng biến thiên ta thấy: max f ( x)  đạt được tại 0 x = 60 . ( 0 0 0 ;90 ) 2  S = ( 2 max
108 3 m ) khi góc ở đáy CD của hình thang bằng 0 60   ( 0 C = D = 60 ).
Câu 20. Cho hình vuông ABCD có cạnh bằng 4, chính giữa có một hình vuông đồng tâm với ABCD . Biết
rằng bốn tam giác là bốn tam giác cân. Hỏi tổng diện tích của hình vuông ở giữa và bốn tam giác cân
nhỏ nhất bằng bao nhiêu? A B D C 19 17 16 14 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C x M 4-2x E A B N Q P D 4 C
Đặt AM = x (0  x  4)  ME = 4 - 2x . 2MQ = (4 - 2x)2 2 2 2 Û MQ = 2(2 - x) Û MQ = 2(2 - x)
Gọi S tổng diện tích của hình vuông ở giữa và bốn tam giác cân nhỏ. 2 MQ 2 2 2 2 2 2 S = 4.
PQ = 2MQ MN = (4 - 2x)  (x 2) = 6x -16x 16 2 4
S ' = 12x -16 = 0 Û x = 3 Bảng biến thiên
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 59
NGUYỄN BẢO VƯƠNG - 0946798489 16 Vậy S = min 3
Câu 21. Cho nửa đường tròn đường kính AB = 2 và hai điểm C , D thay đổi trên nửa đường tròn đó sao cho
ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng 1 3 3 3 3 A. . B. . C. 1. D. . 2 4 2 Lời giải Chọn B
Gọi H là hình chiếu vuông góc của D lên AB , I là trung điểm của đoạn CD và O là trung điểm
của AB . Đặt DH = x , 0  x  1. Ta có 2 2 2
DC = 2DI = 2OH = 2 OD - DH = 2 1- x .
( AB CD) DH
Diện tích của hình thang ABCD là S = f ( x) = = ( 2 1 1- x ) x . 2 2 2 1- x 1- 2x
Ta có f ¢( x) = . f ¢( x) 2 2
= 0 Û 1- x 1- 2x = 0 (*) 2 1- xt = 1 - Đặt 2
t = 1- x , (điều kiện t  0 ) khi đó phương trình (*) trở thành 2 2t t 1 0   - = Û 1 . t =  2 1 1 3 3 t = 1 - loại. t = ta có 2 2 1- x = Û x = Û x =  . 2 2 4 2 Bảng biến thiên
Trang 60 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 3 3
Vậy diện tích lớn nhất của hình thang ABCD bằng . 4
Câu 22. Một người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện, càng nhanh
càng tốt, trên một bờ sông thẳng rộng 3 km (như hình vẽ). Anh có thể chèo thuyền của mình trực
tiếp qua sông để đến C và sau đó chạy đến B , hay có thể chèo trực tiếp đến B , hoặc anh ta có thể
chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B . Biết anh ấy có thể chèo thuyền
6 km/ h , chạy 8 km/ h và quãng đường BC = 8 km . Biết tốc độ của dòng nước là không đáng kể so
với tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến B . 3 9 73 7 A. . B. . C. . D. 1 . 2 7 6 8 Lời giải
 Cách 1: Anh chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B 3
Thời gian chèo thuyền trên quãng đường AC : = 0, 5 (giờ) 6 8
Thời gian chạy trên quãng đường CB : = 1 (giờ) 8
Tổng thời gian di chuyển từ A đến B là 1,5 (giờ). 73
 Cách 2: chèo trực tiếp trên quãng đường 2 2 AB = 3  8 = 73 mất h  1 26¢ . 6  Cách 3:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 61
NGUYỄN BẢO VƯƠNG - 0946798489
Gọi x (km) là độ dài quãng đường BD ; 8 - x (km) là độ dài quãng đường CD . 2 x  9
Thời gian chèo thuyền trên quãng đường 2 AD = x  9 là: (giờ) 6 8 - x
Thời gian chạy trên quãng đường DB là: (giờ) 8 2 x  9 8 - x
Tổng thời gian di chuyển từ A đến B là f ( x) =  6 8 2 x  9 8 - x
Xét hàm số f ( x) =  trên khoảng (0; 8) 6 8 x 1 9
Ta có f ¢( x) = - ; f ¢( x) 2
= 0 Û 3 x  9 = 4x Û x = 2 8 6 x  9 7 Bảng biến thiên 7
Dựa vào BBT ta thấy thời gian ngắn nhất để di chuyển từ A đến B là h 1  1 20¢ . 8 7
Vậy khoảng thời gian ngắn nhất để người đàn ông đến B là h 1  1 20¢ . 8
Câu 23. Bác thợ hàn dùng một thanh kim loại dài 250 cm để uốn thành khung cửa sổ có dạng như hình vẽ.
Gọi r là bán kính của nửa đường tròn, tìm r để diện tích tạo thành đạt giá trị lớn nhất. 250 125 250 125 A. cm . B. cm . C. cm . D. cm . 4 4   4 4   Lời giải
* Gọi S , S lần lượt là diện tích của nửa hình tròn và hình chữ nhật. Khi đó: 1 2 1 2 S =
r ; S = 2rh ; với 2h = 250 - ( r  2r ) nên 2 2
S = 250r -  r - 2r . 1 2 2 2
Trang 62 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 1
* Suy ra diện tích hình cần tìm 2 2 2 2 2 S =
r  250r -  r - 2r = -  r - 2r  250r . Bài toán trở 2 2 1
thành tìm giá trị lớn nhất của hàm số S (r ) 2 2
= -  r - 2r  250r với 0  r  125 . 2 250
* Ta có S¢(r ) = -(  4) r  250 ; S¢(r ) = 0 Û r =
. Đây là cực trị duy nhất của hàm số đồng   4 250
thời S¢(r ) đổi dấu từ dương sang âm khi r qua
nên hàm số đạt giá trị lớn nhất tại điểm này.   4
Câu 24. Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. A 2 cm E B x cm H 3 cm F D C G y cm
Tìm tổng x y để diện tích hình thang EFGH đạt giá trị nhỏ nhất. 7 2 A. 4 2 . B. . C. 7 . D. 5 . 2 Lời giải Ta có S = S - SSSS . EFGH ABCD ( AHE DHG GCF EBF )
Để diện tích hình thang EFGH đạt giá trị nhỏ nhất thì SSS
đạt giá trị lớn nhất. AHE DHG GCF 1 1 1 1 1 Ta có S = AE.AH =
.2.x = x ; S =
DH.DG $SC$; S = . CG CF = 3y . AHE 2 2 DHG 2 CGF 2 2 1 1 Đặt S = SSS thì S =
(2x  3y  36 - 6x - 6y xy) = (36  xy - 4x - 3y) (1). AHE DHG GCF 2 2 AH AE
Mặt khác ta lại có AEH ∽ CGF  =  xy = 6 (2). CF CG 1   18 
Thay (2) vào (1) ta có S = 42 - 4x     . 2   x  18 18 3 2
Ta có S lớn nhất khi 4x  nhỏ nhất Û 4x = Û x = . x x 2 3 2 7 2 Khi x =
thì y = 2 2 . Vậy x y = . 2 2 500
Câu 25. Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng 3 m . 3
Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500.000
đồng/m2. Hãy xác định kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất và chi phí đó là:
A. 74 triệu đồng.
B. 75 triệu đồng.
C. 76 triệu đồng.
D. 77 triệu đồng.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 63
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải C' B' D' A' C B D A
Giả sử khối hộp chữ nhật là ABC . D A¢B C ¢ D
¢ ¢ và AB = x , AD = 2x và AA¢ = h ( x, h  0 ). 500 250 Ta có V = .2 x . x h 2 Û 2x h = Û h = . 3 2 3x Diện tích cần xây là 2
S = 2x  2 ( xh  2xh) 2 = 2x  6xh . 500
Ta cần tìm giá trị nhỏ nhất của 2 S = 2x  với x  0 . x 250 250 250 250 250 250 Ta có 2 2 2 3 2x    3 2x . . Û 2x    150 . x x x x x x 250
Dấu đẳng thức xảy ra khi 2 2x = Û x = 5 . x
S nhỏ nhất là 150 khi x = 5 .
Số tiền chi phí là 150.500000 = 75000000 hay 75 triệu đồng.
Trang 64 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Document Outline

  • 4. Giá trị lớn nhất - giá trị nhỏ nhất - câu hỏ.pdf
  • 4. Giá trị lớn nhất - giá trị nhỏ nhất - đáp án.pdf