Tổng ôn tập TN THPT 2020 môn Toán: Ứng dụng của tích phân

Tổng ôn tập TN THPT 2020 môn Toán: Ứng dụng của tích phân được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

45 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
A. ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG
Hình phẳng
( )H
giới hạn bởi
1
2
( ) : ( )
( ) : ( )
, ( )
C y f x
C y g x
x a x b a b
thì diện tích là
( ) ( ) d .
b
a
S f x g x x
Hình phẳng
( )H
giới hạn bởi
1
2
( ) : ( )
( ) : : 0
, ( )
C y f x
C Ox y
x a x b a b
thì diện tích là
( ) d .
b
a
S f x x
Hình thức đề thường hay cho
Hình thức 1: Không cho hình vẽ, cho dạng
( ) : { ( ), ( ), , ( )}H y f x y g x x a x b a b
casio
( ) ( ) d
b
a
f x g x x
kết quả, so sánh với bốn đáp án.
Hình thức 2: Không cho hình vẽ, cho dạng
( ) : { ( ), ( )}H y f x y g x
Giải
( ) ( )f x g x
tìm nghiệm
1
,..., ,
i
x x
với
1
x
nhỏ nhất,
i
x
lớn nhất
1
casio
( ) ( ) d .
i
x
x
f x g x x
Hình thức 3: Cho hình vẽ, sẽ giải phương trình tìm tọa độ giao điểm (nếu chưa cho trên hình), chia từng
diện tích nhỏ, xổ hình từ trên xuống, ghi công thức và bấm máy tính.
Hình thức 4: Cho ba hàm trở lên, chẳng hạn
( ), ( ), ( )y f x y g x y h x
ta nên vẽ hình.
Câu 1. Diện tích hình phẳng được gạch chéo trong hình bên bằng
A.
2
2
1
2 2 4 dx x x
. B.
2
2
1
2 2 4 dx x x
.
C.
2
2
1
2 2 4 dx x x
. D.
2
2
1
2 2 4 dx x x
.
Câu 2. Diện tích
S
của hình phẳng giới hạn bởi các đường
2
2y x
,
1y
,
0x
và
1x
được tính
bởi công thức nào sau đây?
A.
1
2
0
2 1 dS x x
. B.
1
2
0
2 1 dS x x
. C.
1
2
2
0
2 1 dS x x
. D.
1
2
0
2 1 dS x x
.
ỨNG DỤNG TÍCH PHÂN
Vấn đề 15
2 2
2 2
( ) : 1
x y
E
a b
elip
.S ab
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 3. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
A.
2
2
1
2 2 4 d
x x x . B.
2
1
2 2 d
x x . C.
2
1
2 2 d
x x . D.
2
2
1
2 2 4 d
x x x .
Câu 4. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
e
x
y
,
0y
,
0x
,
2x
. Mệnh đề nào
dưới đây đúng?
A.
2
2
0
e d
x
S x
.
B.
2
0
e d
x
S x
. C.
2
0
e d
x
S x
. D.
2
2
0
e d
x
S x
.
Câu 5. Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số
y f x
, trục hoành và hai đường
thẳng
x a
,
x b
a b
(phần tô đậm trong hình vẽ) tính theo công thức nào dưới đây ?
A.
d d
c b
a c
S f x x f x x
. B.
d
b
a
S f x x
.
C.
d d
c b
a c
S f x x f x x
. D.
d
b
a
S f x x
.
Câu 6. Cho hàm số
y f x
liên tục trên
và có đồ thì như hình vẽ bên. Hình phẳng được đánh dấu
trong hình vẽ bên có diện tích là
A.
d d
b c
a b
f x x f x x
. B.
d d
b b
a c
f x x f x x
.
C.
d d
b c
a b
f x x f x x
. D.
d d
b c
a b
f x x f x x
.
Câu 7. Diện tích của hình phẳng
( )H
giới hạn bởi đồ thị của hàm số
( )y f x
, trục hoành và hai đường
thẳng
x a
,
( )x b a b
(phần tô đậm trong hình vẽ) tính theo công thức
y
O
2
2 1y x x
2
3
y x
1
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
( )d
b
a
S f x x
. B.
( )d ( )d
c b
a c
S f x x f x x
.
C.
( )
b
a
S f x dx
. D.
( )d ( )d
c b
a c
S f x x f x x
.
Câu 8. Cho hàm số
4 2
5 4y f x x x
có đồ thị như hình vẽ bên. Gọi
S
là diện tích hình phẳng giới
hạn bởi đồ thị hàm số
y f x
và trục hoành (miền phẳng được tô đậm trên hình vẽ). Mệnh đề
nào sau đây sai?
A.
2
2
dS f x x
. B.
2
0
2 dS f x x
.
C.
1 2
0 1
2 d 2 dS f x x f x x
. D.
2
0
2 dS f x x
.
Câu 9. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x x và đồ thị hàm số
2
y x x
A.
37
12
B.
9
4
C.
81
12
D.
13
Câu 10. Cho hàm số
f x
liên tục trên
.
Gọi S là diện tích hình phẳng giới hạn bởi cá đường
,y f x
0, 2 y x
và
3x
(như hình vẽ). Mệnh đề nào dưới đây đúng?
A.
1 3
2 1
d d .
S f x x f x x
B.
1 3
2 1
d d .
S f x x f x x
C.
1 3
2 1
d d .
S f x x f x x
D.
1 3
2 1
d d .
S f x x f x x
x
y
y=f(x)
2
3
O
1
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 11. Cho hàm số
f x
liên tục trên
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
, 0, 1y f x y x
và
4x
(như hình vẽ bên). Mệnh đề nào dưới đây đúng?
A.
1 4
1 1
dx dxS f x f x
. B.
1 4
1 1
dx dxS f x f x
.
C.
1 4
1 1
dx dxS f x f x
. D.
1 4
1 1
dx dxS f x f x
.
Câu 12. Cho hàm số
f x
liên tục trên
. Gọi S là diện tích hình phẳng giới hạn bởi các đường
, 0, 1, 2y f x y x x
(như hình vẽ bên). Mệnh đề nào dưới đây đúng?
A.
1 2
1 1
dx dxS f x f x
. B.
1 2
1 1
dx+ dxS f x f x
.
C.
1 2
1 1
dx dxS f x f x
. D.
1 2
1 1
dx + dxS f x f x
.
Câu 13. Cho hàm số
y f x
liên tục trên
.
Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
, 0, 1y f x y x
và
5x
(như hình vẽ bên).
Mệnh đề nào sau đây đúng?
A.
1 5
1 1
( )d ( )dS f x x f x x
. B.
1 5
1 1
( )d ( )dS f x x f x x
.
C.
1 5
1 1
( )d ( )dS f x x f x x
. D.
1 5
1 1
( )d ( )dS f x x f x x
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 14. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
y x và đường thẳng
y x
là:
A.
1
3
. B.
1
4
. C.
1
2
. D.
1
6
.
Câu 15. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số
2
2 1y x x ,
2
2 4 1y x x là
A.
8
. B.
5
. C.
4
. D.
10
.
Câu 16. Gọi
S
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
1
1
x
y
x
và các trục tọa độ. Khi đó giá
trị của
S
bằng
A.
ln2 1S
. B.
2ln 2 1S
. C.
2ln 2 1S
. D.
ln2 1S
.
Câu 17. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
2
3 4y x x . Gọi
1
S và
2
S lần lượt là diện
tích phần hình
( )H
nằm bên trái và bên phải trục tung. Tính tỷ số
1
2
S
S
.
A.
1
2
208
343
S
S
. B.
1
2
54
343
S
S
. C.
1
2
135
343
S
S
. D.
1
2
135
208
S
S
.
Câu 18. Cho
S
là diện tích của hình phẳng giới hạn bởi đồ thị
C
của hàm số
2
1y x x
, trục hoành,
trục tung và đường thẳng
1x
. Biết
2 , .S a b a b
Tính
.a b
A.
1
6
a b
. B.
1
2
a b
. C.
1
3
a b
. D.
0a b
.
Câu 19. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x
, trục hoành và hai đường thẳng
1, 2x x
biết rằng mỗi đơn vị dài trên các trục tọa độ là
2 cm.
A.
2
15
cm
4
. B.
2
17
cm
4
. C.
2
17 cm
. D.
2
15 cm
.
Câu 20. Cho hàm số
3
2
7 4 0 1
4 1
x khi x
f x
x khi x
. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
f x
và các đường thẳng
0, 3, 0x x y
.
A.
16
.
3
B.
20
.
3
C.
10.
D.
9.
Câu 21. Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số
lny x x
, trục
Ox
và đường thẳng
x e
.
A.
2
3
4
e
S
. B.
2
1
2
e
S
. C.
2
1
2
e
S
. D.
2
1
4
e
S
.
Câu 22. Cho hai hàm số
3 2
1f x ax bx cx
và
2
1
2
g x dx ex
, , , ,a b c d e
. Biết rằng đồ thị
của hàm số
( )y f x
và
( )y g x
cắt nhau tại ba điểm có hoành độ lần lượt
3; 1; 2
(tham khảo
hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
253
12
B.
125
12
C.
253
48
D.
125
48
Câu 23. Cho
H
là hình phẳng giới hạn bởi parabol
2
y 3x
, cung tròn có phương trình
2
y 4 x
(với
0 x 2
) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của
H
bằng
A.
4 3
12
B.
4 3
6
C.
4 2 3 3
6
D.
5 3 2
3
Câu 24. Ông An có một mảnh vườn hình Elip có độ dài trục lớn bằng
16m
và độ dài trục bé bằng
10m
.
Ông muốn trồng hoa trên một dải đất rộng
8m
và nhận trục bé của elip làm trục đối xứng (như
hình vẽ). Biết kinh phí để trồng hoa là
100.000
đồng/
2
1m . Hỏi ông An cần bao nhiêu tiền để
trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn.)
A.
7.862.000
đồng B.
7.653.000
đồng C.
7.128.000
đồng D.
7.826.000
đồng
Câu 25. Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng
10
cm bằng cách
khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết
5cmAB
,
4cmOH
.
Tính diện tích bề mặt hoa văn đó.
A.
2
160
cm
3
. B.
2
140
cm
3
. C.
2
14
cm
3
. D.
2
50 cm
.
Câu 26. Cho hàm số
y f x
là hàm số đa thức bậc 4 và có đồ thị như hình vẽ
Hình phẳng giới hạn bởi đồ thị hàm số
y f x
và
y f x
có diện tích là
A
B
H
O
8m
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A.
127
40
. B.
127
10
. C.
107
5
. D.
13
5
.
Câu 27. Cho parabol
P
có phương trình
2
y x và đường thẳng
d
đi qua điểm
1;3A
. Giả sử khi
đường thẳng
d
có hệ số góc
k
thì diện tích hình phẳng giới hạn bởi parabol
P
và đường thẳng
d
nhỏ nhất. Giá trị thực của
k
thuộc khoảng nào sau đây?
A.
; 3
. B.
3;
. C.
3;0
. D.
0;3
.
Câu 28. Một viên gạch hoa hình vuông cạnh . Người thiết kế đã sử dụng 4 đường parabol có chung
đỉnh tại tâm của viên gạch để tạo ra 4 cánh hoa (được tô màu sẫm như hình vẽ bên). Diện tích mỗi
cánh hoa của viên gạch bằng
A.
2
800
.
3
cm
B.
2
1600
.
3
cm
C.
2
400
.
3
cm
D.
2
250 .cm
Câu 29. Một biển quảng cáo có dạng Elip với bốn đỉnh
1 2 1 2
, , ,A A B B . như hình vẽ. Người ta chia Elip bởi
parapol có đỉnh
1
B ,trục đối xứng
1 2
B B và đi qua các điểm
,M N
.Sau đó sơn phần tô đậm với giá
200.000 đồng/
2
m
và trang trí đèn led phần còn lại với giá 500.000 đồng/
2
m
.Hỏi kinh phí sử dụng
gần nhất với giá trị nào dưới đây? Biết
1 2
4A A m ,
1 2
2 , 2B B m MN m .
A. 2.341.000 đồng. B. 2.057.000 đồng. C. 2.760.000 đồng. D. 1.664.000 đồng.
Câu 30. Cho hai hàm số
3 2
1
( )
2
f x ax bx cx
và
2
( ) 1g x dx ex
( , , , , )a b c d e
. Biết rằng đồ thị
hàm số
( )y f x
và
( )y g x
cắt nhau tại ba điểm có hoành độ lần lượt là
3; 1;1
(tham khảo
hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho (miền tô đậm) có diện tích bằng
A. 8 B. 5 C. 4 D.
9
2
Câu 31. Bạn An cần mua một chiếc gương có đường viền là đường Parabol bậc 2 ( xem hình vẽ). Biết rằng
khoảng cách đoạn
60cmAB
,
30cmOH
. Diện tích của chiếc gương bạn An mua là
80cm
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
900 cm
. B.
2
1000 cm
. C.
2
1200 cm
. D.
2
1400 cm
.
Câu 32. Cho
H
là hình phẳng giới hạn bởi parabol
2
:P y x
, tiếp tuyến với
P
tại điểm
2;4M
và
trục hoành. Tính diện tích của hình phẳng
H
?
A.
2
.
3
B.
8
.
3
C.
1
.
3
D.
4
.
3
Câu 33. Cho hàm số
3 2
f x ax bx cx d
có đồ thị
C
. Đồ thị của hàm số
y f x
được cho bởi
hình vẽ dưới đây
Biết rằng đường thẳng
:d y x
cắt
C
tạo thành hai phần hình phẳng có diện tích bằng nhau.
Tổng
a b c d
bằng
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 34. Một cái cổng có dạng như hình vẽ, với chiều cao 6m và chiều rộng 8m. Mái vòm của cổng có
hình bán elip với chiều rộng là 6m, điểm cao nhất của mái vòm là 5m (tham khảo hình vẽ). Người
ta muốn lát gạch hoa để trang trí cho cổng với chi phí là 250 000 đồng/m
2
. Hỏi số tiền cần chi trả
gần nhất với số nào sau đây?
A.
6.210.000
. B.
6.110.000
. C.
6.100.000
. D.
6.145.000
.
Câu 35. Đợt thi đua 26/3 Đoàn trường THPT Nho Quan A có thực hiện một dự án trưng bày trên một pano
có dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu các lớp gửi hình dự thi và dán lên
khu vực hình chữ nhật
ABCD
, phần còn lại sẽ được trang trí hoa văn cho phù hợp. Chi phí dán
hoa văn là 150.000đ trên
2
1m
bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ
là bao nhiêu( kết quả làm tròn lấy phần nguyên)?
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
A. 575.
034 đồng. B. 676.239 đồng. C. 536.272 đồng. D. 423.215 đồng.
Câu 36. Một khuôn viên có dạng là nửa hình tròn đường kính bằng
4
5 m.
Trên đó, người ta thiết kế một
phần để trồng hoa có dạng của một cách hoa hình parabol có đỉnh trùng với tâm nửa hình tròn, hai
đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô đậm) và cách nhau một khoảng bằng 4 m.
Phần còn lại của khuôn viên (phần không tô đậm) dành để trồng cỏ.
Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ là 100.000 đồng
2
/ m
Số ti
ền cần có để trồng cỏ
là bao nhiêu (số tiền được làm tròn đến hàng nghìn)?
A. 2 388 000 đồng. B. 3 895 000 đồng. C. 1 194 000 đồng. D. 1 948 000 đồng.
Câu 37. Tính diện tích
S
của miền hình phẳng giới hạn bởi đồ thị của hàm số
3
2
,f x ax bx c
các
đường thẳng
1
,x
2x
và
trục hoành (miền gạch chéo cho trong hình vẽ).
A.
51
8
S
. B.
53
8
S
. C.
5
2
8
S
. D.
50
8
S
.
B. ỨNG DỤNG TÍCH PHÂN TÍNH THỂ TÍCH
Thể tích vật thể
Gọi
B
là
phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục
O
x
tại
các điểm
a
v
à
,b
(
)S x
là
diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm
,x
(
).a x b
Giả
sử
(
)S x
là
hàm số liên tục trên đoạn
[
; ].a b
Khi
đó, thể tích của vật thể
B
được
xác
định:
(
)d .
b
a
V
S x x
T
hể tích khối tròn xoay
a) T
hể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
( ),y f x
trục
hoành
và
hai đường thẳng
,
x a x b
quan
h trục
:Ox
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
b) Thể
tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
(
),x g y
trục
hoành
và hai
đường thẳng
,y
c
y
d
quanh
trục
:O
y
c
) Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
(
),y f x
(
)y g x
(cùng
nằm một phía so với
)Ox
và hai
đường thẳng
,x
a
x
b
quanh trục
:O
x
2
2
(
) ( ) d .
b
a
V
f x g x x
Câu
38. Cho hình phẳng
H
giới
hạn bởi các đường
2
3
y
x
,
0
y
,
0
x
,
2
x
.
Gọi
V
l
à thể tích
của khối tròn xoay được tạo thành khi quay
H
xung
quanh trục
Ox
.
Mệnh đề nào dưới đây
đúng?
A.
2
2
2
0
3
V
x dx
B.
2
2
0
3
V
x dx
C
.
2
2
2
0
3
V
x dx
D
.
2
2
0
3
V
x dx
Câu
39. Cho hàm số
y f x
l
iên tục trên đoạn
;a b
.
Gọi
D
là
hình phẳng giới hạn bởi đồ thị hàm số
y
f x
,
trục hoành và hai đường thẳng
,
x
a x b a b
.
Thể tích của khối tròn xoay tạo
thành khi quay
D
qua
nh trục hoành được tính theo công thức:
A.
2
b
a
V
f x dx
B.
2
2
b
a
V
f x dx
C
.
2
2
b
a
V
f x dx
D
.
2
b
a
V
f x dx
Câu 40. Cho hình phẳng
H
giới hạn bởi các đường thẳng
2
2, 0, 1, 2
y x y x x
. Gọi
V
là thể
tích của khối tròn xoay được tạo thành khi quay
H
xung
quanh trục
Ox
.
Mệnh đề nào dưới đây
đúng?
A.
2
2
2
1
2
dV x x
. B.
2
2
2
1
2
dV x x
. C
.
2
2
1
2
dV x x
. D
.
2
2
1
2
dV x x
.
Câu
41. Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo
thành được tính theo công thức nào?
c
y
O
d
x
(
) : ( )
(
) :
C
x g y
Oy x 0
y
c
y d
2
(
)
d
y
c
V
g y dy
(
): ( )
(
):
C
y f x
Ox y 0
x
a
x b
2
( )
b
x
a
V f x dx
a
(
)y f x
y
O
b
x
a
b
x
y
O
(
)f x
( )g x
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
A.
2
( ) ( )
b
a
V f x g x dx
. B.
2
2
( ) ( )
b
a
V f x g x dx
.
C.
2
(
) ( )
b
a
V
f x g x dx
. D.
(
) ( )
b
a
V
f x g x dx
.
Câu 42. Trong không gian với hệ tọa độ
Oxy
z
,
cho vật thể
H
giớ
i hạn bởi hai mặt phẳng có phương
trình
x
a
và
x b
.
Gọi
S
x
là
diện tích thiết diện của
H
bị
cắt bởi mặt phẳng vuông góc
với trục
O
x
tại
điểm có hoành độ là
x
,
với
a
x b
.
Giả sử hàm số
y
S x
liện
tục trên đoạn
;a
b
.
Khi đó, thể tích của vật thể
H
được c
ho bởi công thức :
A.
d
b
a
V
S x x
. B.
2
d
b
a
V
S x x
. C.
2
d
b
a
V
S x x
. D.
d
b
a
V
S x x
.
Câu
43. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng
1x
và
3x
, biết rằng khi cắt vật
thể bởi mặt phẳng vuông góc với trục
Ox
tại
điểm có hoành độ
x
(
1
3x
)
thì được thiết diện
là một hình chữ nhật có độ dài hai cạnh là
3x
và
2
3
2x
.
A.
3
2 2 15V
B.
12
4
3
V
C.
12
4
3
V
D.
(
32 2 15)V
Câu
44. Cho hình phẳng
D
giới hạn bởi đường cong 2 cos ,y x trục hoành và các đường thẳng
0,
2
x x
.
Khối tròn xoay tạo thành khi
D
qua
y quanh trục hoành có thể tích
V
bằn
g bao
nhiêu?
A.
( 1)V
B.
1V
C.
1V
D.
( 1)V
Câu
45. Cho hình phẳng
D
giới
hạn bởi đường cong
2 siny x , trục hoành và các đường thẳng
0x
,
x
. Khối tròn xoay tạo thành khi quay
D
quay quanh trục hoành có thể tích
V
bằng
bao nhiêu?
A.
2
2V
B.
2 1V
C.
2V
D.
2 1V
Câu
46. Cho hình phẳng
D
giới
hạn bởi đường cong
x
y e
,
trục hoành và các đường thẳng
0x
,
1x
.
Khối tròn xoay tạo thành khi quay
D
qua
nh trục hoành có thể tích
V
bằng ba
o nhiêu?
A.
2
1
2
e
V
B.
2
1
2
e
V C.
2
3
e
V D.
2
1
2
e
V
Câu
47. Cho hình phẳng
D
giớ
i hạn với đường cong
2
1y
x , trục hoành và các đường thẳng
0
, 1x x
.
Khối tròn xoay tạo thành khi quay
D
qua
nh trục hoành có thể tích
V
bằ
ng bao
nhiêu?
A.
4
3
V
B.
2V
C.
4
3
V
D.
2V
Câu
48. Cho hình phẳng giới hạn bởi các đường
2y
x
,
0y
và
9x
qua
y xung quanh trục
O
x
.
Tính thể tích khối tròn xoay tạo thành.
A.
5
.
6
V
B.
1
1
.
6
V
C.
7
.
11
V
D.
7
6
V
.
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 49.
T
ính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số
2
3y
x x
và
trục hoành, quanh trục hoành.
A.
8
5
10
(đ
vtt). B.
4
1
7
(đ
vtt). C.
8
1
10
(đ
vtt). D.
8
7
(đ
vtt).
Câu 50. Thể tích của vật thể tròn xoay khi quay hình
H
qu
anh
O
x
với
H
được
giới hạn bởi đồ thị
hàm số
2
4y
x x
và
trục hoành.
A.
31
3
. B.
32
3
. C
.
34
3
. D.
35
3
.
C. ỨNG DỤNG TÍCH PHÂN
VÀO BÀI TOÁN CHUYỂN ĐỘNG
Câu 51. Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động
chậm dần đều với vận tốc
5
10 v t t
(m
/s), trong đó t là khoảng thời gian tính bằng giây, kể
từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu
mét?
A. 0,2m B. 2m C. 10m D. 20m
Câu 52. Một chất điểm
A
xuấ
t phát từ
O
,
chuyển động thẳng với vận tốc biến thiên theo thời gian bởi
quy luật
2
1
13
m/s
100 30
v t t t
,
trong đó
t
(g
iây) là khoảng thời gian tính từ lúc
A
bắ
t đầu
chuyển động. Từ trạng thái nghỉ, một chất điểm
B
cũng
xuất phát từ
O
,
chuyển động thẳng
cùng hướng với
A
nhưng
chậm hơn
10
gi
ây so với
A
và
có gia tốc bằng
2
m
/sa
(
a
là
hằng
số). Sau khi
B
xuấ
t phát được
15
gi
ây thì đuổi kịp
A
.
Vận tốc của
B
tạ
i thời điểm đuổi kịp
A
bằ
ng
A.
1
5 m/s
B.
9
m/s
C
.
4
2 m/s
D.
2
5 m/s
Câu 53. Một chất điểm chuyển động trên đường thẳng nằm ngang với gia tốc phụ thuộc thời gian t (s) là
2
7a t t
(m/s
2
).
Biết vận tốc đầu bằng 10 (m/s), hỏi sau bao lâu thì chất điểm đạt vận tốc 18
(m/s)?
A. 5 (s). B. 7 (s). C. 6 (s). D. 8 (s).
Câu 54. Một ôtô đang chạy với vận tốc
1
9 /m s
thì
người lái hãm phanh, ôtô chuyển động chậm dần đều
với vận tốc
3
8 19 /v t t m s
,
trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt
đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét?
A.
5
m
. B.
4,5 m
. C
.
4,25 m
. D.
4,75 m
.
Câu 55. Tại
một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao
1
62
(mét)
so với mặt đất đã
được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động
theo phương thẳng đứng với vận tốc tuân theo quy luật
2
(
) 10v t t t , trong đó t (phút) là thời
gian tính từ lúc bắt đầu chuyển động,
(
)v t
tính theo đơn vị mét/phút
(
/ )m p
. Nếu như vậy thì khi
bắt đầu tiếp đất vận tốc
v
của khí cầu là:
A.
9
( / ).v m p
B.
5(
/ ).v m p
C
.
7
( / ).v m p
D.
3
( / ).v m p
Câu 56. Một
vật chuyển động trong 3 giờ với vận tốc
( / )v km h
phụ t
huộc vào thời gian
( )t h
c
ó đồ thị vận
tốc như hình bên. Trong thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của
đường parabol có đỉnh
(2; 9)I
v
à trục đối xứng song song với trục tung, khoảng thời gian còn lại
đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường
s
mà vật chuyển động
được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm).
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
A.
1
5, 50( )s km
B.
2
3, 25( )s km
C.
1
3,83( )s km
D.
2
1,58( )s km
Câu
57. Một vật chuyển động trong
3
giờ với
vận tốc
k
m/hv
phụ t
huộc thời gian
ht
có đồ t
hị là một
phần của đường parabol có đỉnh
2
; 9I
và trục đối xứng song song với trục tung như hình bên.
Tính
quãng đường
s
mà
vật di chuyển được trong
3
giờ đó.
A.
26,75 kms
B.
25, 25 kms
C.
24,25 kms
D.
24,75 kms
Câu
58. Một vật chuyển động theo quy luật
3
2
1
6
2
s
t t
với
t
(g
iây) là khoảng thời gian tính từ khi vật
đó bắt đầu chuyển động và
ms
là quãng
đường vật di chuyển được trong khoảng thời gian đó.
Hỏi trong khoảng thời gian
6
giâ
y, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt
được bằng bào nhiêu?
A.
64
m/s
B.
2
4 m/s
C.
18
m/s
D.
108
m/s
Câu
59. Một vật chuyển động trong 4 giờ với vận tốc
v
(k
m/h) phụ thuộc thời gian
t
(
h) có đồ thị của vận
tốc như hình bên. Trong khoảng thời gian
3
giờ kể từ khi
bắt đầu chuyển động, đồ thị đó là một
phần của đường parabol có đỉnh
2
; 9I
với
trục đối xứng song song với trục tung, khoảng thờ
i
gi
an còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường
s
m
à vật di
chuyển được trong
4
giờ đó.
A.
2
6,5s
(km) B.
2
4s
(k
m) C.
28,5s
(km) D.
2
7s
(k
m)
Câu 60. Một vật chuyển động trong
4
giờ với
vận tốc
(
km/ h)v
phụ thuộc
thời gian
(
h)t
c
ó đồ thị là một
phần của đường parabol có đỉnh
(
1;3)I
và trục đối xứng song song với trục tung như hình bên.
Tính quãng đường
s
mà
vật di chuyển được trong
4
giờ kể từ lúc
xuất phát.
A.
50
(
km).
3
s
B.
1
0(km).s
C.
2
0(km).s
D.
64
(
km).
3
s
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 61. Một
chuyển động trong 4 giờ với vận tốc
v
(
km/h) phụ thuộc thời gian
t
(
h ) có đồ thị là một
phần của đường parabol có đỉnh
1
;1I
và
trục đối xứng song song với trục tung như hình bê
n.
T
ính quãng đường
s
mà
vật đi được trong 4 giờ kể từ lúc xuất phát.
A.
40
k
m
3
s
. B.
8
km s
. C
.
46
k
m
3
s
. D.
6
km s
.
------------------------- HẾT -------------------------
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
A. ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG
Hình phẳng
( )H
giới hạn bởi
1
2
( ) : ( )
( ) : ( )
, ( )
C y f x
C y g x
x a x b a b
thì diện tích là
( ) ( ) d .
b
a
S f x g x x
Hình phẳng
( )H
giới hạn bởi
1
2
( ) : ( )
( ) : : 0
, ( )
C y f x
C Ox y
x a x b a b
thì diện tích là
( ) d .
b
a
S f x x
Hình thức đề thường hay cho
Hình thức 1: Không cho hình vẽ, cho dạng
( ) : { ( ), ( ), , ( )}H y f x y g x x a x b a b
casio
( ) ( ) d
b
a
f x g x x
kết quả, so sánh với bốn đáp án.
Hình thức 2: Không cho hình vẽ, cho dạng
( ) : { ( ), ( )}H y f x y g x
Giải
( ) ( )f x g x
tìm nghiệm
1
,..., ,
i
x x
với
1
x
nhỏ nhất,
i
x
lớn nhất
1
casio
( ) ( ) d .
i
x
x
f x g x x
Hình thức 3: Cho hình vẽ, sẽ giải phương trình tìm tọa độ giao điểm (nếu chưa cho trên hình), chia từng
diện tích nhỏ, xổ hình từ trên xuống, ghi công thức và bấm máy tính.
Hình thức 4: Cho ba hàm trở lên, chẳng hạn
( ), ( ), ( )y f x y g x y h x
ta nên vẽ hình.
Câu 1. Diện tích hình phẳng được gạch chéo trong hình bên bằng
A.
2
2
1
2 2 4 dx x x
. B.
2
2
1
2 2 4 dx x x
.
C.
2
2
1
2 2 4 dx x x
. D.
2
2
1
2 2 4 dx x x
.
Lời giải
Chọn A
Dựa và hình vẽ ta có diện tích hình phẳng được gạch chéo trong hình bên là:
ỨNG DỤNG TÍCH PHÂN
Vấn đề 15
2 2
2 2
( ) : 1
x y
E
a b
elip
.S ab
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
2 2 2
1 1
2 2 2 d 2 2 4 d .x x x x x x x
Câu 2. Diện tích
S
của hình phẳng giới hạn bởi các đường
2
2y x
,
1y
,
0x
và
1x
được tính
bởi công thức nào sau đây?
A.
1
2
0
2 1 dS x x
. B.
1
2
0
2 1 dS x x
.
C.
1
2
2
0
2 1 dS x x
. D.
1
2
0
2 1 dS x x
.
Lời giải
Chọn D
Diện tích hình phẳng cần tìm là
1 1
2 2
0 0
2 1 d 2 1 dS x x x x
do
2
2 1 0x
0;1x
.
Câu 3. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
A.
2
2
1
2 2 4 d
x x x . B.
2
1
2 2 d
x x .
C.
2
1
2 2 d
x x . D.
2
2
1
2 2 4 d
x x x .
Lời giải
Chọn D.
Ta thấy:
1; 2 x
:
2 2
3 2 1 x x x
nên
2 2
2 2 2
1 1
3 2 1 d 2 2 4 d
S x x x x x x x .
Câu 4. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
e
x
y
,
0y
,
0x
,
2x
. Mệnh đề
nào dưới đây đúng?
A.
2
2
0
e d
x
S x
.
B.
2
0
e d
x
S x
. C.
2
0
e d
x
S x
. D.
2
2
0
e d
x
S x
.
Lời giải
Diện tích hình phẳng giới hạn bởi các đường
e
x
y
,
0y
,
0x
,
2x
được tính theo công
thức
2 2
0 0
e d e d
x x
S x x
.
Câu 5. Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số
y f x
, trục hoành và hai đường
thẳng
x a
,
x b
a b
(phần tô đậm trong hình vẽ) tính theo công thức nào dưới đây ?
y
O
2
2 1y x x
2
3
y x
1
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
d d
c b
a c
S f x x f x x
. B.
d
b
a
S f x x
.
C.
d d
c b
a c
S f x x f x x
. D.
d
b
a
S f x x
.
Lời giải
Chọn A
Ta có:
d d d d d
b c b c b
a a c a c
S f x x f x x f x x f x x f x x
.
Câu 6. Cho hàm số
y f x
liên tục trên
và có đồ thì như hình vẽ bên. Hình phẳng được đánh dấu
trong hình vẽ bên có diện tích là
A.
d d
b c
a b
f x x f x x
. B.
d d
b b
a c
f x x f x x
.
C.
d d
b c
a b
f x x f x x
. D.
d d
b c
a b
f x x f x x
.
Lời giải
Chọn C
Diện tích hình phẳng:
d d d d d
c b c b c
a a b a b
S f x x f x x f x x f x x f x x
.
Câu 7. Diện tích của hình phẳng
( )H
giới hạn bởi đồ thị của hàm số
( )y f x
, trục hoành và hai
đường thẳng
x a
,
( )x b a b
(phần tô đậm trong hình vẽ) tính theo công thức
A.
( )d
b
a
S f x x
. B.
( )d ( )d
c b
a c
S f x x f x x
.
C.
( )
b
a
S f x dx
. D.
( )d ( )d
c b
a c
S f x x f x x
.
Lời giải
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn D
Ta có:
( )d ( )d ( )d
b c b
a a c
S f x x f x x f x x
.
Dựa vào đồ thị ta thấy trên đoạn
;a c
có
( ) 0f x
; trên
;c b
có
( ) 0f x
.
Suy ra
( )d ( )d
c b
a c
S f x x f x x
.
Câu 8. Cho hàm số
4 2
5 4y f x x x
có đồ thị như hình vẽ bên. Gọi
S
là diện tích hình phẳng
giới hạn bởi đồ thị hàm số
y f x
và trục hoành (miền phẳng được tô đậm trên hình vẽ).
Mệnh đề nào sau đây sai?
A.
2
2
dS f x x
. B.
2
0
2 dS f x x
.
C.
1 2
0 1
2 d 2 dS f x x f x x
. D.
2
0
2 dS f x x
.
Lời giải
Chọn D
Hình phẳng cần tính diện tích nhận trục tung làm trục đối xứng.
Xét PTHĐ giao điểm:
4 2
2
1
5 4 0
1
2
x
x
x x
x
x
Khi đó diện tích hình phẳng cần tìm là:
2 2 1 2
2 0 0 1
d 2 d 2 d 2 dS f x x f x x f x x f x x
Câu 9. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x x và đồ thị hàm số
2
y x x
A.
37
12
B.
9
4
C.
81
12
D.
13
Lời giải
Chọn A
Phương trình hoành độ giao điểm
3 2 3 2
0
2 0 1
2
x
x x x x x x x x
x
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x x và đồ thị hàm số
2
y x x là:
1 0 1
3 2 3 2 3 2
2 2 0
2 2S x x x x dx x x x dx x x x dx
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
0 1
4 3 4 3
2 2
2 0
16 8 1 1 37
4 1
4 3 4 3 4 3 4 3 12
x x x x
x x
.
Câu 10. Cho hàm số
f x
liên tục trên
.
Gọi S là diện tích hình phẳng giới hạn bởi cá đường
,y f x
0, 2 y x
và
3x
(như hình vẽ). Mệnh đề nào dưới đây đúng?
A.
1 3
2 1
d d .
S f x x f x x B.
1 3
2 1
d d .
S f x x f x x
C.
1 3
2 1
d d .
S f x x f x x D.
1 3
2 1
d d .
S f x x f x x
Lời giải
Chọn A
Ta có
3 1 3
2 2 1
d d d .
S f x x S f x x f x x
Do
0f x
với
2;1 x
và
0f x
với
1;3 x
nên
1 3
2 1
d d .
S f x x f x x
Câu 11. Cho hàm số
f x
liên tục trên
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
, 0, 1y f x y x
và
4x
(như hình vẽ bên). Mệnh đề nào dưới đây đúng?
A.
1 4
1 1
dx dxS f x f x
. B.
1 4
1 1
dx dxS f x f x
.
C.
1 4
1 1
dx dxS f x f x
. D.
1 4
1 1
dx dxS f x f x
.
Lời giải
Chọn B
Ta có: hàm số
(x) 0 1;1 ; (x) 0 1;4f x f x
, nên:
4 1 4 1 4
1 1 1 1 1
dx dx dx dx dxS f x f x f x f x f x
. Chọn đáp án B.
x
y
y=f(x)
2
3
O
1
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 12. Cho hàm số
f x
liên tục trên
. Gọi S là diện tích hình phẳng giới hạn bởi các đường
, 0, 1, 2y f x y x x
(như hình vẽ bên). Mệnh đề nào dưới đây đúng?
A.
1 2
1 1
dx dxS f x f x
. B.
1 2
1 1
dx+ dxS f x f x
.
C.
1 2
1 1
dx dxS f x f x
. D.
1 2
1 1
dx + dxS f x f x
.
Lời giải
Chọn C
2 1 2
1 1 1
dx= dx dxS f x f x f x
Nhìn hình ta thấy hàm số
f x
liên tục và nhận giá trị không âm trên đoạn
1;1
nên
1 1
1 1
dx dxf x f x
; hàm số
f x
liên tục và nhận giá trị âm trên đoạn
1;2
nên
2 2
1 1
dx dxf x f x
Vậy
1 2
1 1
dx dxS f x f x
Câu 13. Cho hàm số
y f x
liên tục trên
.
Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
, 0, 1y f x y x
và
5x
(như hình vẽ bên).
Mệnh đề nào sau đây đúng?
A.
1 5
1 1
( )d ( )dS f x x f x x
. B.
1 5
1 1
( )d ( )dS f x x f x x
.
C.
1 5
1 1
( )d ( )dS f x x f x x
. D.
1 5
1 1
( )d ( )dS f x x f x x
.
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Ta có:
1 5 1 5
1 1 1 1
( ) d d d dS f x x f x x f x x f x x
.
Câu 14. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
y x
và đường thẳng
y x
là:
A.
1
3
. B.
1
4
. C.
1
2
. D.
1
6
.
Lời giải
Chọn D
Giao điểm của đồ thị hàm số
2
y x
và đường thẳng
y x
có hoành độ là nghiệm của phương
trình :
2
0
1
x
x x
x
.
Suy ra diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
y x
và đường thẳng
y x
là
1
3 2
1 1
2 2
0 0
0
1
3 2 6
x x
x x dx x x dx
.
Câu 15. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số
2
2 1y x x
,
2
2 4 1y x x
là
A.
8
. B.
5
. C.
4
. D.
10
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm là
2 2 2
2 1 2 4 1 3 6 0
x x x x x x
0
2
x
x
Diện tích hính phẳng là
2
2 2
0
2 4 1 2 1
S x x x x dx
2
2
0
3 6
x x dx
3 2
2
3 4
0
x x
.
Câu 16. Gọi
S
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
1
1
x
y
x
và các trục tọa độ. Khi đó
giá trị của
S
bằng
A.
ln2 1
S
. B.
2ln 2 1
S
. C.
2ln 2 1
S
. D.
ln2 1
S
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm của đồ thị hàm số và trục tung là
1
0 1
1
x
x
x
.
Gọi
S
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
1
1
x
y
x
và các trục tọa độ. Nên ta
có
1 1 1
0 0 0
1
1 1 2
d d 1 d 2ln 1 2ln 2 1
0
1 1 1
x x
S x x x x x
x x x
.
Câu 17. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
2
3 4
y x x
. Gọi
1
S
và
2
S
lần lượt là
diện tích phần hình
( )H
nằm bên trái và bên phải trục tung. Tính tỷ số
1
2
S
S
.
A.
1
2
208
343
S
S
. B.
1
2
54
343
S
S
. C.
1
2
135
343
S
S
. D.
1
2
135
208
S
S
.
Lời giải
Chọn D
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
0
0
2
2 3
1
1
1
5
( 3 4)d ( 4 )
2 2
x
S x x x x x
.
4
4
2
3
4
2 3
2
0
0
104
( 3 4)d ( 4 )
2 27
x
S x x x x x
.
1
2
135
208
S
S
.
Câu 18. Cho
S
là diện tích của hình phẳng giới hạn bởi đồ thị
C
của hàm số
2
1y x x
, trục
hoành, trục tung và đường thẳng
1x
. Biết
2 , .S a b a b
Tính
.a b
A.
1
6
a b
. B.
1
2
a b
. C.
1
3
a b
. D.
0a b
.
Lời giải
Chọn C
Ta có trục tung có phương trình là:
0x
.
Diện tích của hình phẳng giới hạn bởi đồ thị
C
của hàm số
2
1y x x
, trục hoành, trục
tung và đường thẳng
1x
là
1
2
0
1 dS x x x
.
Mặt khác
3
2
1 1
2
2 2 2 2 2
0 0
1
1 1
1 1 1 2 2 1
1 d 1 d 1 1 1
3
0 0
2 2 3 3 3
2
x
S x x x x x x x
Biết
2 ,S a b a b
nên
2
3
a
và
1
3
b
Vậy
1
3
a b
Câu 19. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x
, trục hoành và hai đường thẳng
1, 2x x
biết rằng mỗi đơn vị dài trên các trục tọa độ là
2 cm.
A.
2
15
cm
4
. B.
2
17
cm
4
. C.
2
17 cm
. D.
2
15 cm
.
Lời giải
Chọn C
Mỗi đơn vị diện tích trên mặt phẳng tọa độ là
2
2.2 4 cm .
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Vậy diện tích hình phẳng cần tìm là
2 0 2
3 3 3 2
1 1 0
1
4. d 4. d d 4. 4 17 cm
4
x x x x x x
.
Câu 20. Cho hàm số
3
2
7 4 0 1
4 1
x khi x
f x
x khi x
. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm
số
f x
và các đường thẳng
0, 3, 0
x x y
.
A.
16
.
3
B.
20
.
3
C.
10.
D.
9.
Lời giải
Chọn C
-Vẽ đồ thị hàm số
y f x
.
-Khi đó, diện tích hình phẳng cần tìm là
2 3
1 2 3
3 3
1
3 2 2 4
0
0 1 2
1 2
7 4 4 4 7 4 4 10
3 3
x x
S x dx x dx x dx x x x x
.
Câu 21. Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số
lny x x
, trục
Ox
và đường thẳng
x e
.
A.
2
3
4
e
S
. B.
2
1
2
e
S
. C.
2
1
2
e
S
. D.
2
1
4
e
S
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm của hàm số
lny x x
và trục
Ox
:
ln 0 1x x x
.
Diện tích hình phẳng cần tìm là:
1 1
ln ln
e e
S x x dx x xdx
.
Đặt
2
1
ln
2
du dx
u x
x
dv xdx
x
v
.
2 2 2 2 2 2
1
1 1
1 1
ln
2 2 2 4 2 4 4 4
e e
e
x x e x e e e
S x dx
.
y
O
x
y = f(x)
3
2
1
- 5
3
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 22. Cho hai hàm số
3 2
1f x ax bx cx
và
2
1
2
g x dx ex
, , , ,a b c d e
. Biết rằng đồ
thị của hàm số
( )y f x
và
( )y g x
cắt nhau tại ba điểm có hoành độ lần lượt
3; 1; 2
(tham
khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
A.
253
12
B.
125
12
C.
253
48
D.
125
48
Lời giải
Chọn C
Vì phương trình
( ) ( ) 0f x g x
có 3 nghiệm
3; 1; 2
nên
3 2 1 .f x g x a x x x
So sánh hệ số tự do ta được
3
6
2
a
1
.
4
a
Do đó
2
3
1 253
3 1 2 d
4 48
S x x x x
.
Câu 23. Cho
H
là hình phẳng giới hạn bởi parabol
2
y 3x
, cung tròn có phương trình
2
y 4 x
(với
0 x 2
) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của
H
bằng
A.
4 3
12
B.
4 3
6
C.
4 2 3 3
6
D.
5 3 2
3
Lời giải
Chọn B
Phương trình hoành độ giao điểm giữa parabol và cung tròn ta được
2 2
3 4 1 x x x
với
0 x 2
Ta có diện tích
1
1 2 2 2
2 2 3 2 2
0 1 1 1
0
3 3
3 4 4 4
3 3
S x dx x dx x x dx x dx
Đặt:
2sin 2cos ; 1 ; 2
6 2
 x t dx tdt x t x t
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
2
6
3 1 4 3
2 sin 2
3 2 6
S t t
Câu 24. Ông An có một mảnh vườn hình Elip có độ dài trục lớn bằng
16m
và độ dài trục bé bằng
10m
.
Ông muốn trồng hoa trên một dải đất rộng
8m
và nhận trục bé của elip làm trục đối xứng (như
hình vẽ). Biết kinh phí để trồng hoa là
100.000
đồng/
2
1m . Hỏi ông An cần bao nhiêu tiền để
trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn.)
A.
7.862.000
đồng B.
7.653.000
đồng C.
7.128.000
đồng D.
7.826.000
đồng
Lời giải
Chọn B
Chọn hệ trục tọa độ như hình vẽ
Giả sử elip có phương trình
2 2
2 2
1
x y
a b
.
Từ giả thiết ta có
2 16 8a a
và
2 10 5b b
Vậy phương trình của elip là
2
2 2
1
2
2
5
64 ( )
8
1
5
64 25
64 ( )
8
y x E
x y
y x E
Khi đó diện tích dải vườn được giới hạn bởi các đường
1 2
( ); ( ); 4; 4E E x x và diện tích
của dải vườn là
4 4
2 2
4 0
5 5
2 64 d 64 d
8 2
S x x x x
Tính tích phân này bằng phép đổi biến
8sinx t
, ta được
40
20 3
3
S
Khi đó số tiền là
40
20 3 .100000 7652891,82 7.653.000
3
T
.
8m
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 25. Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng
10
cm bằng
cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết
5cmAB
,
4cmOH
. Tính diện tích bề mặt hoa văn đó.
A.
2
160
cm
3
. B.
2
140
cm
3
. C.
2
14
cm
3
. D.
2
50 cm
.
Lời giải
Chọn B
Đưa parabol
2
:P y ax bx c
0a
vào hệ trục
Oxy
.
Parabol đi qua gốc tọa độ và các điểm
5
;4
2
,
5;0
(do
5cmAB
,
4cmOH
).
Suy ra
0
25 5
4
4 2
25 5 0
c
a b c
a b c
16
25
0
16
5
a
c
b
2
16 16
:
25 5
P y x x
.
Diện tích hình phẳng giới hạn bởi
2
16 16
:
25 5
P y x x
, trục hoành và các đường thẳng
0x
,
5x
là
5
2
0
16 16 40
d
25 5 3
S x x x
.
Tổng diện tích phần bị khoét đi là
2
1
160
4 cm
3
S S
.
Diện tích của hình vuông là
2
100cm
hv
S
.
Vậy diện tích bề mặt hoa văn là
2
2 1
160 140
100 cm
3 3
hv
S S S
.
Câu 26. Cho hàm số
y f x
là hàm số đa thức bậc 4 và có đồ thị như hình vẽ
A
B
H
O
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Hình phẳng giới hạn bởi đồ thị hàm số
y f x
và
y f x
có diện tích là
A.
127
40
. B.
127
10
. C.
107
5
. D.
13
5
.
Lời giải
Chọn C
Vì hàm số
y f x
là hàm số đa thức bậc 4 và có đồ thị như hình vẽ nên hàm số có dạng:
2 2
2 1f x a x x
,
0a
.
Mà
1
1 1
4
f a
. Vậy
2 2
1
2 1
4
f x x x
.
2 2
1 1
2 2 1 2 1 . 2 2 1 2 1
4 2
f x x x x x x x x
.
Xét phương trình
2
1
1
2 1 3 4 0
2
4
x
x
f x f x x x x x
x
x
.
2
1
2 1 3 4
4
f x f x x x x x
.
Vậy diện tích cần tìm là:
4
2
dS f x f x x
1 1 4
2 1 1
d d df x f x x f x f x x f x f x x
107
5
.
Câu 27. Cho parabol
P
có phương trình
2
y x và đường thẳng
d
đi qua điểm
1;3A
. Giả sử khi
đường thẳng
d
có hệ số góc
k
thì diện tích hình phẳng giới hạn bởi parabol
P
và đường
thẳng
d
nhỏ nhất. Giá trị thực của
k
thuộc khoảng nào sau đây?
A.
; 3
. B.
3;
. C.
3;0
. D.
0;3
.
Lời giải
Chọn D
Phương trình của
d
là:
1 3y k x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hoành độ giao điểm của
d
và
P
là nghiệm của phương trình:
2
3 0 1x kx k
.
Do
2
2
4 3 2 8 0,k k k k
nên
1
luôn có hai nghiệm phân biệt
1 2 1 2
,x x x x
.
Theo định lý Vi-ét ta có:
1 2 1 2
, . 3x x k x x k .
Diện tích miền phẳng
D
giới hạn bởi
d
và
P
là:
2
2
1
1
3 2
2
3 3
3 2
x
x
x
x
x x
S x kx k dx k kx x
3 2 3 2
2 2 1 1
2 2 1 1
3 3
3 2 3 2
x x x x
k kx x k kx x
3 3
2 2
1 2
1 2 1 2 1 2
3
3 2
x x k
x x k x x x x
2 2
1 1 2 2
1 2 1 2
3
3 2
x x x x k
x x x x k
2
2
1 2 1 2
1 2
3
3 2
x x x x
k
x x k
2
2
1 2
3
3
3 2
k k
k
x x k
2
2 1
1
4 12
6
x x k k
Suy ra
3
2
2 2
2 2
1 2 1 2
1 1 128
4 . 4 12 2 8
36 36 9
S x x x x k k k
.
8 2
3
S
(do
0S
)
Đẳng thức xảy ra khi và chỉ khi
2k
.
Câu 28. Một viên gạch hoa hình vuông cạnh . Người thiết kế đã sử dụng 4 đường parabol có
chung đỉnh tại tâm của viên gạch để tạo ra 4 cánh hoa (được tô màu sẫm như hình vẽ bên).
Diện tích mỗi cánh hoa của viên gạch bằng
A.
2
800
.
3
cm
B.
2
1600
.
3
cm
C.
2
400
.
3
cm
D.
2
250 .cm
Lời giải
Chọn B
80cm
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Ký hiệu diện tích một cánh hoa, diện tích một hình parabol,diện tích hình vuông lần lượt là
, ,
H P hv
S S S . Ta có:
4
4
P hv
H
S S
S
.
Chọn hệ trục
Oxy
như hình vẽ, sao cho parabol có đỉnh
0;0O
và đi qua điểm
40;40A
Khi đó
2
1
:
40
P y x
.
Diện tích parabol chính là diện tích miền hình phẳng giới hạn bởi các đường
, 40, 40, 40P y x x
.
40
2 2
40
1 6400
40
40 3
P
S x dx cm
. Do đó:
2
6400
4. 80.80
1600
3
4 3
H
S cm
.
Câu 29. Một biển quảng cáo có dạng Elip với bốn đỉnh
1 2 1 2
, , ,A A B B . như hình vẽ. Người ta chia Elip
bởi parapol có đỉnh
1
B ,trục đối xứng
1 2
B B và đi qua các điểm
,M N
.Sau đó sơn phần tô đậm
với giá 200.000 đồng/
2
m
và trang trí đèn led phần còn lại với giá 500.000 đồng/
2
m
.Hỏi kinh
phí sử dụng gần nhất với giá trị nào dưới đây? Biết
1 2
4A A m ,
1 2
2 , 2B B m MN m .
A. 2.341.000 đồng. B. 2.057.000 đồng. C. 2.760.000 đồng. D. 1.664.000 đồng.
Lời giải
Chọn A
Phương trình (E)có dạng:
2 2
1
4 1
x y
.
Diện tích
E
là: 2
E
S ab
.
Vì
2MN m
nên
3
1;
2
M
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vì Parabol có đỉnh
0; 1B
và đi qua
3
1;
2
M
nên
P
có phương
trình:
2
3
1 1.
2
y x
Diện tích phần tô đậm giới hạn bởi
2
3
1 1
2
y x
và
2
1
4
x
y
là:
1
2
2
1
1
3
1 1 1 d
4 2
x
S x x
Vậy kinh phí cần sử dụng là:
1 1
.200000 ( ).500000 2340000
E
P S S S đồng.
Câu 30. Cho hai hàm số
3 2
1
( )
2
f x ax bx cx
và
2
( ) 1g x dx ex
( , , , , )a b c d e
. Biết rằng đồ
thị hàm số
( )y f x
và
( )y g x
cắt nhau tại ba điểm có hoành độ lần lượt là
3; 1;1
(tham
khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho (miền tô đậm) có diện tích bằng
A. 8 B. 5 C. 4 D.
9
2
Lời giải
Chọn C
3 2
3
( ) ( ) ( ) ( )
2
f x g x ax b d x c e x
Do
( ) & ( )y f x y g x
cắt nhau tại 3 điểm có hoành độ lần lượt là
3; 1;1
nên ta có:
3 1
27 9( ) 3( ) 0
2 2
3 3
( ) ( ) 0
2 2
3 1
( ) ( ) 0
2 2
a b d c e a
a b d c e b d
a b d c e c e
3 2
1 3 1 3
( ) ( )
2 2 2 2
f x g x x x x
Khi đó:
1 1
3 1
1 1
3 2 3 2
3 1
( ) ( ) d [g( ) ( )]d
1 1
3 3 d 3 3 d 4
2 2
S f x g x x x f x x
x x x x x x x x
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Câu 31. Bạn An cần mua một chiếc gương có đường viền là đường Parabol bậc 2 ( xem hình vẽ). Biết
rằng khoảng cách đoạn
60cmAB
,
30cmOH
. Diện tích của chiếc gương bạn An mua là
A.
2
900 cm
. B.
2
1000 cm
. C.
2
1200 cm
. D.
2
1400 cm
.
Lời giải
Chọn C
Chọn hệ trục tọa độ như hình vẽ. Đường viền chiếc gương là đường Parabol
2
0y ax bx c a
có đỉnh
0;30H
và đi qua điểm
30; 0B
.
Ta có:
30
30
0 0
2
1
900 30 0
30
c
c
b
b
a
a b c
a
.
Diện tích chiếc gương là diện tích hình phẳng giới hạn bởi Parabol
2
1
30
30
y x
và trục
hoành. Diện tích chiếc gương là:
30
30 30
2 2 3 2
30 0
0
1 1 1
30 d 2 30 d 2 30 1200 cm
30 30 90
S x x x x x x
.
Câu 32. Cho
H
là hình phẳng giới hạn bởi parabol
2
:P y x
, tiếp tuyến với
P
tại điểm
2;4M
và trục hoành. Tính diện tích của hình phẳng
H
?
A.
2
.
3
B.
8
.
3
C.
1
.
3
D.
4
.
3
Lời giải
Chọn A
Ta có
2
2y x x
.
Tiếp tuyến d với
P
tại điểm
2;4M
có phương trình là:
2 2 4 4 2 4 4 4.y f x y x y x
Giao điểm của
và d Ox
là
1; 0A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Trên đoạn
0; 1
hình phẳng được giới hạn bởi đồ thị hàm số
2
y x và trục hoành.
Trên đoạn
1; 2
hình phẳng được giới hạn bởi đồ thị hàm số
2
y x
và tiếp tuyến
d
.
Vậy diện tích của hình phẳng
H
được xác định là:
1 2
2 2
0 1
2
4 4 d .
3
S x dx x x x
Câu 33. Cho hàm số
3 2
f x ax bx cx d
có đồ thị
C
. Đồ thị của hàm số
y f x
được cho
bởi hình vẽ dưới đây
Biết rằng đường thẳng
:d y x
cắt
C
tạo thành hai phần hình phẳng có diện tích bằng nhau. Tổng
a b c d
bằng
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn A
Giả sử
2
0f x mx nx p m
và có đồ thị
P
như hình vẽ đề bài.
1; 3I
là đỉnh của
2 0
1
1 .
2
3
3
n
m n
P
m
m n p
m n p
0;0 0. 2O P p
Từ
1
và
2
, suy ra
2
3, 6 3 6 .m n f x x x
2 3 2
d 3 6 d 3 .f x f x x x x x x x C
6 6f x x
điểm uốn
1; 2 .I C
3.I d C
Thử lại:
3 2
3 3x x x
có 3 nghiệm.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Suy ra
3 2
3 3.f x x x
Vậy
1.a b c d
Câu 34. Một cái cổng có dạng như hình vẽ, với chiều cao 6m và chiều rộng 8m. Mái vòm của cổng có
hình bán elip với chiều rộng là 6m, điểm cao nhất của mái vòm là 5m (tham khảo hình vẽ).
Người ta muốn lát gạch hoa để trang trí cho cổng với chi phí là 250 000 đồng/m
2
. Hỏi số tiền
cần chi trả gần nhất với số nào sau đây?
A.
6.210.000
. B.
6.110.000
. C.
6.100.000
. D.
6.145.000
.
Lời giải
Chọn B
Chọn hệ trục tọa độ
Oxy
như hình vẽ:
• Diện tích hình chữ nhật
ABCD
:
2
1
6.8 48 mS
.
• Bán đường elip có phương trình:
2
5
9
3
y x
Diện tích cổng là diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
5
9
3
y x
và trục
hoành:
3
2 2
2
3
5
9 23,562m
3
S x dx
• Diện tích phần cần lát gạch hoa:
1 2
48 23,562 24,438S S S
.
Số tiền cần chi trả để lát gạch hoa:
24,438 .250000 6.109.500T
đồng.
x
y
8m
6m
D
C
B
A
5
-3 3
O
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 35. Đợt thi đua 26/3 Đoàn trường THPT Nho Quan A có thực hiện một dự án trưng bày trên một
pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu các lớp gửi hình dự thi và
dán lên khu vực hình chữ nhật
ABCD
, phần còn lại sẽ được trang trí hoa văn cho phù hợp. Chi
phí dán hoa văn là 150.000đ trên
2
1m
bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn
trên pano sẽ là bao nhiêu( kết quả làm tròn lấy phần nguyên)?
A. 575.034 đồng. B. 676.239 đồng. C. 536.272 đồng. D. 423.215 đồng.
Lời giải
Chọn B
Gắn hình Parabol đã cho vào hệ trục tọa độ
Oxy
như hình vẽ, dễ thấy phương trình của Parabol
đã cho là
2
y x
.
Đặt tọa độ
2
;A a a
với
0 2a
, ta có
2
; , ; 4 , ; 4B a a C a D a
.
Dễ thấy diện tích phần Parabol phải trang trí nhỏ nhất khi diện tích hình chữ nhật
ABCD
lớn
nhất với
2
. 2 . 4
ABCD
S AB AD a a
2
m
.
Xét
2 2
2 4 8 6f a a a f a a
.
2 3
0
3
f a a
, với điều kiện
0 2a
nên
2 3
3
a
.
Ta có bảng biến thiên
Diên tích phần Parabol trưng bày là:
2
2
2
32
4.4
3
P
S x dx
.
Vậy diện tích cần trang trí ít nhất là:
32 32 3
3 9
.
Chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là:
32 32 3
.150000 676239
3 9
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Câu 36. Một khuôn viên có dạng là nửa hình tròn đường kính bằng
4 5 m.
Trên đó, người ta thiết kế
một phần để trồng hoa có dạng của một cách hoa hình parabol có đỉnh trùng với tâm nửa hình
tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô đậm) và cách nhau một
khoảng bằng 4 m. Phần còn lại của khuôn viên (phần không tô đậm) dành để trồng cỏ.
Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ là 100.000 đồng
2
/ m
Số tiền cần có để trồng
cỏ là bao nhiêu (số tiền được làm tròn đến hàng nghìn)?
A. 2 388 000 đồng. B. 3 895 000 đồng. C. 1 194 000 đồng. D. 1 948 000 đồng.
Lời giải
Chọn D
Chọn hệ trục tọa độ
Oxy
như hình vẽ.
Phương trình nửa đường tròn trên là
2
20y x
Phương trình parabol có đỉnh là gốc tọa độ có dạng
2
y ax
Parabol đi qua điểm
2;4
suy ra. Vậy phương trình parabol là:
2
y x
.
Diện tích phần tô đậm:
2
2 2
1
2
20S x x dx
Diện tích nửa đường tròn:
2
2
1
2 5 10 m
2
S
Diện tích phần trồng cỏ là:
2 1
S S S
.
Khi đó số tiền để trồng cỏ là:
2
100000. S 1948000
đồng.
Câu 37. Tính diện tích
S
của miền hình phẳng giới hạn bởi đồ thị của hàm số
3 2
,f x ax bx c
các
đường thẳng
1,x
2x
và trục hoành (miền gạch chéo cho trong hình vẽ).
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
51
8
S
. B.
53
8
S
. C.
5
2
8
S
. D.
50
8
S
.
Lời giải
Chọn A
Ta
có:
2
3
2y ax bx
0
0
2
3
x
y
b
x
a
Dựa
vào đồ thị, ta thấy đồ thị hàm số đã cho có hai điểm cực trị
0
;3
và
2
;1
.
Khi đó
ta có:
1
3
2
3
2
3
2 3 0
3 2
8 4 2
3
8 4 3 1
a
c
c
b
a b b
a
a b
c
a b
Vậ
y
3
2
1
3
3
2 2
f x x x
.
Khi đó
diện tích phần gạch chéo là:
2
3
2
1
1
3 51
3 .
2 2 8
S x x dx
B. ỨNG DỤNG TÍCH PHÂN TÍNH THỂ TÍCH
T
hể tích vật thể
Gọi
B
là
phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục
Ox
tại
các điểm
a
v
à
,b
(
)S x
l
à
diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục
O
x
tại điểm
,x
(
).a x b
Giả sử
(
)S x
là hàm số liên tục trên đoạn
[
; ].a b
Khi đó, thể tích của vật thể
B
được xác định:
( )d .
b
a
V S x x
T
hể tích khối tròn xoay
a) Thể
tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
(
),y f x
t
r
ục
hoàn
h và hai đường thẳng
, x a x b
quan
h trục
:O
x
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
b) Thể
tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
(
),x g y
t
r
ục
hoành và hai đường thẳng
,y
c
y d
quanh trục
:Oy
c) T
hể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
(
),y f x
(
)y g x
(c
ùng nằm một phía so với
)Ox
v
à hai đường thẳng
,x a
x
b
quanh
trục
:O
x
2
2
(
) ( ) d .
b
a
V
f x g x x
C
âu 38. Cho hình phẳng
H
giới
hạn bởi các đường
2
3
y
x
,
0
y
,
0
x
,
2
x
.
Gọi
V
l
à thể
tích của khối tròn xoay được tạo thành khi quay
H
xung
quanh trục
O
x
.
Mệnh đề nào dưới
đây đúng?
A
.
2
2
2
0
3
V
x dx
B.
2
2
0
3
V
x dx
C.
2
2
2
0
3
V
x dx
D.
2
2
0
3
V
x dx
Lời giải
Chọn A
Thể t
ích của khối tròn xoay được tạo thành khi quay
H
xung
quanh trục
O
x
là:
2
2
2
0
3
V
x dx
.
C
âu 39. Cho hàm số
y
f x
li
ên tục trên đoạn
;a
b
.
Gọi
D
là
hình phẳng giới hạn bởi đồ thị hàm số
y
f x
,
trục hoành và hai đường thẳng
,
x
a x b a b
.
Thể tích của khối tròn xoay tạo
thành khi quay
D
quanh t
rục hoành được tính theo công thức:
A.
2
b
a
V
f x dx
B.
2
2
b
a
V
f x dx
C.
2 2
b
a
V
f x dx
D.
2
b
a
V
f x dx
Lời giải
c
y
O
d
x
( ) : ( )
( ) :
C x g y
Oy x 0
y
c
y d
2
( )
d
y
c
V g y dy
( ): ( )
( ):
C y f x
Ox y 0
x
a
x b
2
(
)
b
x
a
V
f x dx
a
(
)y f x
y
O
b
x
a
b
x
y
O
(
)f x
( )g x
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn A
Câu 40. Cho hình phẳng
H
giới hạn bởi các đường thẳng
2
2
, 0, 1, 2y x y x x
. Gọi
V
là thể
tích của khối tròn xoay được tạo thành khi quay
H
xung
quanh trục
Ox
.
Mệnh đề nào dưới
đây đúng?
A.
2
2
2
1
2 dV x x
. B.
2
2
2
1
2 dV x x
. C.
2
2
1
2 dV x x
. D.
2
2
1
2 dV x x
.
Lời giải
Ta có:
2
2
2
1
2
dV x x
.
Câu
41. Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo
thành được tính theo công thức nào?
A.
2
( ) ( )
b
a
V f x g x dx
. B.
2
2
( ) ( )
b
a
V f x g x dx
.
C.
2
( ) ( )
b
a
V f x g x dx
. D.
( ) ( )
b
a
V f x g x dx
.
Lời
giải
Chọn B
Gọi
1
V l
à thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
(
)y f x
,
trục
Ox
và
hai đường thẳng
;x a x b
khi qua
y quanh trục hoành. Ta có
2
1
(
)
b
a
V
f x dx
.
Gọi
2
V là
thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
(
)y g x
,
t
rục
Ox
và
hai đường thẳng
;x a x b
khi qua
y quanh trục hoành. Ta có
2
2
( )
b
a
V g x dx
.
Do
( ) ( )f x g x
,
;x a b
nê
n thể tích khối tròn xoay tạo thành khi quay hình phẳng (phầ
n
tô đậm) quanh trục hoành
2
2
1 2
(
) ( ) .
b
a
V
V V f x g x dx
Câu 42. Trong không gian với hệ tọa độ
O
xyz
,
cho vật thể
H
giớ
i hạn bởi hai mặt phẳng có phương
trình
x
a
và
x
b
.
Gọi
S
x
là diện tí
ch thiết diện của
H
bị
cắt bởi mặt phẳng vuông góc
với trục
O
x
tại
điểm có hoành độ là
x
,
với
a
x b
.
Giả sử hàm số
y
S x
l
iện tục trên
đoạn
;a
b
. Khi đó, thể tích của vật thể
H
được cho bởi công thức :
A.
d
b
a
V
S x x
. B.
2
d
b
a
V
S x x
.
C.
2
d
b
a
V
S x x
. D.
d
b
a
V
S x x
.
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Lời giải
Chọn
D
Do
S
x
là diện tích thiết diện của
H
bị cắt bởi mặt phẳng vuông góc với trục
O
x
tại điểm
có hoành độ là
x
, vớ
i
a
x b
.
Khi
đó, thể tích của vật thể
H
được tính bởi công thức
d
b
a
V
S x x
.
Câu 43. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng
1x
và
3
x
,
biết rằng khi cắt
vật thể bởi mặt phẳng vuông góc với trục
Ox
tại
điểm có hoành độ
x
(
1
3
x
)
thì được thiết
diện là một hình chữ nhật có độ dài hai cạnh là
3x
và
2
3
2
x
.
A
.
32 2 15
V
B.
124
3
V
C.
124
3
V
D.
(32 2 15)
V
Lời
giải
Chọn
C
Diện tích t
hiết diện là:
2
(
) 3 . 3 2
S
x x x
T
hể tích vật thể là
:
3
2
1
124
3
. 3 2
3
V
x x dx
C
âu 44. Cho hình phẳng
D
giới
hạn bởi đường cong
2
cos ,y x
t
rục hoành và các đường thẳng
0
,
2
x
x
. Khối tròn xoay tạo thành khi
D
quay quanh trục hoành có thể tích
V
bằng bao
nhiêu?
A.
( 1)V
B.
1V
C.
1V
D.
( 1)V
Lời
giải
Chọn A
2
2
2
0
0
2
cos 2 sin ( 1).
V
x dx x x
Câu 45. Cho hình phẳng
D
giới
hạn bởi đường cong
2
siny x
,
trục hoành và các đường thẳng
0x
,
x
.
Khối tròn xoay tạo thành khi quay
D
qua
y quanh trục hoành có thể tích
V
bằng
ba
o nhiêu?
A.
2
2V
B.
2 1
V
C.
2V
D.
2 1
V
Lời
giải
Chọn
B
Ta
có phương trình
2 sin 0
x
vô nghiệm
nên:
2
0
0
2
sin d 2 sin dV x x x x
0
2
cos 2 1
x
x
.
C
âu 46. Cho hình phẳng
D
giới
hạn bởi đường cong
x
y
e
,
trục hoành và các đường thẳng
0x
,
1x
. Khối tròn xoay tạo thành khi quay
D
quanh trục hoành có thể tích
V
bằng bao nhiêu?
A.
2
1
2
e
V
B.
2
1
2
e
V
C.
2
3
e
V
D.
2
1
2
e
V
Lời giải
Chọn
A
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1
2
1
2
2
0
0
1
e
e
d
2 2
x
x
e
V
x
Câu 47. Cho hình phẳng
D
giới hạn với đường cong
2
1
y
x
, trục hoành và các đường thẳng
0
, 1
x
x
.
Khối tròn xoay tạo thành khi quay
D
qua
nh trục hoành có thể tích
V
bằ
ng bao
nhiêu?
A.
4
3
V
B.
2
V
C.
4
3
V
D.
2
V
Lờ
i giải
Chọn
A
Thể t
ích khối tròn xoay được tính theo công thức:
1
1
1
3
2
2 2
0 0
0
4
1
d 1 d
3
3
x
V
x x x x x
C
âu 48. Cho hình phẳng giới hạn bởi các đường
2
y
x
,
0
y
và
9
x
qua
y xung quanh trục
Ox
.
Tính thể tích khối tròn xoay tạo thành.
A.
5
.
6
V
B.
11
.
6
V
C.
7
.
11
V
D.
7
6
V
.
Lờ
i giải
Chọn
B
Hoà
nh độ giao điểm của 2 đồ thị hàm số
2
y
x
và
0
y
là:
0
2
0 4.
2
x
x x
x
Khi
đó:
9
2
4
11
2
dx .
6
V
x
(Dùng MTC
T).
Câu 49.
Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số
2
3
y
x x
và
trục hoành, quanh trục hoành.
A
.
85
1
0
(đvtt
). B
.
4
1
7
(đvtt
). C.
8
1
10
(đvtt). D.
8
7
(đvtt
).
Lờ
i giải
Chọn
C
Xé
t phương trình
2
0
3
0
3
x
x
x
x
.
Tính t
hể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số
2
3
y
x x
và
trục hoành, quanh trục hoành là
3
2
2
0
3 dx
V x x
3
2
3 4
0
9 6 dx
x x x
3
3
4 5
0
3 1 81
3
2
5 10
x
x x
(đvtt).
C
âu 50. Thể tích của vật thể tròn xoay khi quay hình
H
qua
nh
O
x
với
H
được
giới hạn bởi đồ thị
hàm số
2
4
y
x x
và trục hoành.
A.
31
3
. B.
3
2
3
. C.
34
3
. D.
35
3
.
Lờ
i giải
Chọn
B
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
P
hương trình hoành độ giao điểm:
2
0
4 0
4
x
x x
x
.
Thể t
ích của vật thể tròn xoay khi quay hình
H
qua
nh
O
x
là:
2
4
2
0
32
4 d
3
V x x x
.
C. ỨNG DỤN
G TÍCH PHÂN VÀO BÀI TOÁN CHUYỂN ĐỘNG
Câu 51. Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển
động chậm dần đều với vận tốc
5
10
v
t t
(m/
s), trong đó
t
là
khoảng thời gian tính bằng
giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển
bao nhiêu mét?
A. 0,2m B. 2m C. 10m D. 20m
Lời giải
Chọn
C
Xé
t phương trình
5
10 0 2.
t
t
Do
vậy, kể từ lúc người lái đạp phanh thì sau 2s ô tô
dừng hẳn.
Quãng đường ô tô đi được kể từ lúc người lái đạp phanh đến khi ô tô dừng hẳn là
2
2
0
2
5
5 10 10 10 .
0
2
s t dt t t m
Câu 52. Một chất điểm
A
xuấ
t phát từ
O
,
chuyển động thẳng với vận tốc biến thiên theo thời gian bởi
quy luật
2
1 13
m
/s
100 30
v
t t t
,
trong đó
t
(giâ
y) là khoảng thời gian tính từ lúc
A
bắt
đầu
chuyển động. Từ trạng thái nghỉ, một chất điểm
B
cũng
xuất phát từ
O
,
chuyển động thẳng
cùng hướng với
A
nhưng
chậm hơn
10
gi
ây so với
A
và
có gia tốc bằng
2
m
/s
a
(
a
l
à hằn
g
số).
Sau khi
B
xuấ
t phát được
1
5
giây
thì đuổi kịp
A
.
Vận tốc của
B
tại
thời điểm đuổi kịp
A
bằng
A
.
1
5 m/s
B.
9
m/s
C.
4
2 m/s
D.
2
5 m/s
Lời giải
Chọn D
Ta
có
.
dt
B
v
t a at C
,
0 0 0
B
v C
B
v t at
.
Quã
ng đường chất điểm
A
đi được tr
ong
2
5
gi
ây là
25
2
0
1
13
dt
100 30
A
S
t t
25
3
2
0
1
13 375
300 60 2
t
t
.
Quãng đường chất điểm
B
đi được tr
ong
15
gi
ây là
1
5
0
.
dt
B
S
at
2
15
0
225
2
2
at a
.
Ta có
375 225 5
2 2 3
a
a
.
Vận tốc
của
B
tại thời điểm
đuổi kịp
A
là
5
15 .15 25 m/s
3
B
v
.
C
âu 53. Một chất điểm chuyển động trên đường thẳng nằm ngang với gia tốc phụ thuộc thời gian
t
(s
)
là
2 7a t t
(m/s
2
). Biết vận tốc đầu bằng 10 (m/s), hỏi sau bao lâu thì chất điểm đạt vận tốc
18 (m/s)?
A
. 5 (
s). B
. 7 (
s). C. 6 (s). D
. 8 (s).
Lờ
i giải
Chọn
D
Ta
có
2
d
2 7 d 7
v
t a t t t t t t C
, mặt
khác
0
10
v
nê
n
0
10
C
v
.
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
7 10v t t t
.
Để c
hất điểm đạt vận tốc 18 (m/s) thì
2
8
nhËn
18 7 8 0
1 lo¹i
t
v t t t
t
.
Vậy tại thời điểm
8t
(s) thì chất điểm đạt vận tốc 18 (m/s).
Câu 54. Một ôtô đang chạy với vận tốc
1
9 /m s
t
hì người lái hãm phanh, ôtô chuyển động chậm dần
đều với vận tốc
38 19 /v t t m s
,
trong đó t là khoảng thời gian tính bằng giây kể từ
lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu
mét?
A.
5
m
. B.
4
,5 m
. C.
4
,25 m
. D.
4
,75 m
.
Lời
giải
Chọn D
Thờ
i điểm người lái hãm phanh:
0
.t
Thờ
i điểm ôtô dừng hẳn:
1
0
38 19 0
2
v t t t
Ta có:
ds t v t t
.
Từ
lúc hãm phanh đến khi dừng hẳn, ôtô còn di chuyển được:
1 1
2 2
0 0
19
d
38 19 d 4,75 .
4
s v t t t t m
Câu
55. Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao
16
2
(m
ét) so với mặt đất
đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển
động theo phương thẳng đứng với vận tốc tuân theo quy luật
2
(
) 10v t t t , trong đó t (phút) là
thời gian tính từ lúc bắt đầu chuyển động,
( )v t
tí
nh theo đơn vị mét/phút
( / )m p
.
Nếu như vậy
thì khi bắt đầu tiếp đất vận tốc
v
của k
hí cầu là:
A.
9
( / ).v m p
B.
5
( / ).v m p
C.
7
( / ).v m p
D.
3
( / ).v m p
Lời
giải
Chọn A
Gọi
b
(p
hút) là thời gian khí cầu từ độ cao
16
2
(m
ét) chuyển động cho đến khi tiếp đất.
Ta có
2
2 3 3 2
0 0
1 1
( ) 162 (10 ) 162 5 5 162 0 9
3 3
b b
s
v t dt t t dt b b b b b
.
Vậ
y vận tốc của khí cầu tại thời điểm tiếp đất là
2
10.9 9 9( / ).v m p
Câu 56. Một vật chuyển động trong 3 giờ với vận tốc
(
/ )v km h
phụ thuộc
vào thời gian
(
)t h
có
đồ thị
vận tốc như hình bên. Trong thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một
phần của đường parabol có đỉnh
(
2; 9)I
và
trục đối xứng song song với trục tung, khoảng thời
gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường
s
m
à vật
chuyển động được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm).
A.
1
5, 50( )s km
B.
2
3, 25( )s km
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
C.
1
3,83( )s km
D.
2
1,58( )s km
Lời
giải
Chọn D
Gọi phư
ơng trình của parabol
2
v
at bt c
ta
có hệ như sau:
4 5
4 2 9 4
5
2
2 4
c b
a b c c
b
a
a
Với
1t
ta
có
31
4
v
.
Vậy quã
ng đường vật chuyển động được là
3
2
0
1
1
21,
583
5 31 259
5 4
4 4 12
s t t dt dt
Câu
57. Một vật chuyển động trong
3
giờ với
vận tốc
km/hv
phụ t
huộc thời gian
ht
có
đồ thị là
một phần của đường parabol có đỉnh
2; 9I
và trục đối xứng song song với trục tung như hình
bên. Tính quãng đường
s
m
à vật di chuyển được trong
3
giờ đó.
A.
2
6,75 kms
B.
2
5, 25 kms
C.
2
4,25 kms
D.
2
4,75 kms
Lời
giải
Chọn D
Tìm được p
hương trình của vận tốc là
2
3
3 6
4
v t t t
Vậy
3
2
0
3
(
3 6)
4
S t t dt
24,
75
Câu 58. Một vật chuyển động theo quy luật
3
2
1
6
2
s t t
với
t
(giây) là khoảng thời gian tính từ khi
vật đó bắt đầu chuyển động và
ms
là quãng đường vật di chuyển được trong khoảng thời
gian đó. Hỏi trong khoảng thời gian
6
giâ
y, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất
của vật đạt được bằng bào nhiêu?
A.
64
m/s
B.
24
m/s
C.
18
m/s
D.
108
m/s
Lời
giải
Chọn B
Vận tốc
của vật chuyển động là
2
3
1
2
2
v s t t f t
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tìm giá trị lớn nhất của hàm
số
f
t
tr
ên đoạn
0; 6
Ta có
3 12 0 4 0; 6f t t f t t
0 0; 4 24; 6 18f f f
Vậy vận tốc
lớn nhất là
24
m/s
.
Câu
59. Một vật chuyển động trong 4 giờ với vận tốc
v
(km/h)
phụ thuộc thời gian
t
(h
) có đồ thị của
vận tốc như hình bên. Trong khoảng thời gian
3
giờ kể từ khi bắt đầu chuyển động, đồ thị đó là
một phần của đường parabol có đỉnh
2
; 9I
với
trục đối xứng song song với trục tung, khoả
ng
thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường
s
mà
vật di chuyển được trong
4
giờ đó.
A. 26
,5s (km) B.
2
4s
(k
m) C. 28,5s (km) D
.
2
7s
(k
m)
Lời
giải
Chọn C
Gọi
2
:P y ax bx c
.
Vì
P
qua
0
; 0O
và
có đỉnh
2
; 9I
nên
dễ tìm được phương trình là
2
9
9
4
y
x x
.
Ngoà
i ra tại
3x
ta
có
2
7
4
y
Vậy quã
ng đuờng cần tìm là:
3
4
2
0 3
9
27
9 d d 27 ( )
4 4
S x x x x km
.
Câu
60. Một vật chuyển động trong
4
giờ với
vận tốc
(
km/ h)v
phụ thuộc
thời gian
(
h)t
có
đồ thị là
một phần của đường parabol có đỉnh
(
1;3)I
và
trục đối xứng song song với trục tung như hình
bên. Tính quãng đường
s
mà
vật di chuyển được trong
4
giờ kể từ lúc
xuất phát.
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
A.
50
(
km).
3
s
B.
1
0(km).s
C.
2
0(km).s
D.
64
(
km).
3
s
Lời
giải
Chọn
D
Ta
có
2
(
)v t at bt c có dạng parabol đỉnh
(
1;3)I
,
đi qua điểm
(0
;4)A
và
(
4;12)B
.
1
2
3
(0)
4
b
a
a b c
v
1
2
3
0
0 4
b
a
a b c
c
2
1
4
b
a
a b
c
2
( 2 ) 1
4
b a
a a
c
2
1
4
b
a
c
Do
đó
2
(
) 2 4v t t t
.
Quãng đường vật di chuyển được trong
4
giờ kể từ lúc xuất phát được tính như sau
4
4
3 3
2 2 2
0 0
4
4 64
( ) ( 2 4) 4 4 4.4 0
0
3 3 3
t
s v t dt t t dt t t
(k
m).
Câu 61. Một chuyển động trong 4 giờ với vận tốc
v
(
km/h) phụ thuộc thời gian
t
(
h ) có đồ thị là một
phần của đường parabol có đỉnh
1
;1I
và
trục đối xứng song song với trục tung như hình bên.
Tính quãng đường
s
m
à vật đi được trong 4 giờ kể từ lúc xuất phát.
A.
40
k
m
3
s
. B.
8
km s
. C.
46
k
m
3
s
. D.
6
km s
.
Lời
giải
Chọn A
Ta
có phương trình vận tốc
2
v t at bt c P
P
qua
điểm
0
;2
nê
n
2c
.
Mặt
khác
P
có
đỉnh
1
;1
nê
n
2
0 1
1
2
1 2
1
b
a b a
a
a b b
a b c
Nê
n phương trình vận tốc
2
2
2v t t t
Quã
ng đường mà vật đi được trong 4 giờ kể từ lúc xuất phát là:
4
0
2
4
0
2 2
3
km
t
t
dt
.
------------------------- HẾT -------------------------
| 1/45
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 15 ỨNG DỤNG TÍCH PHÂN
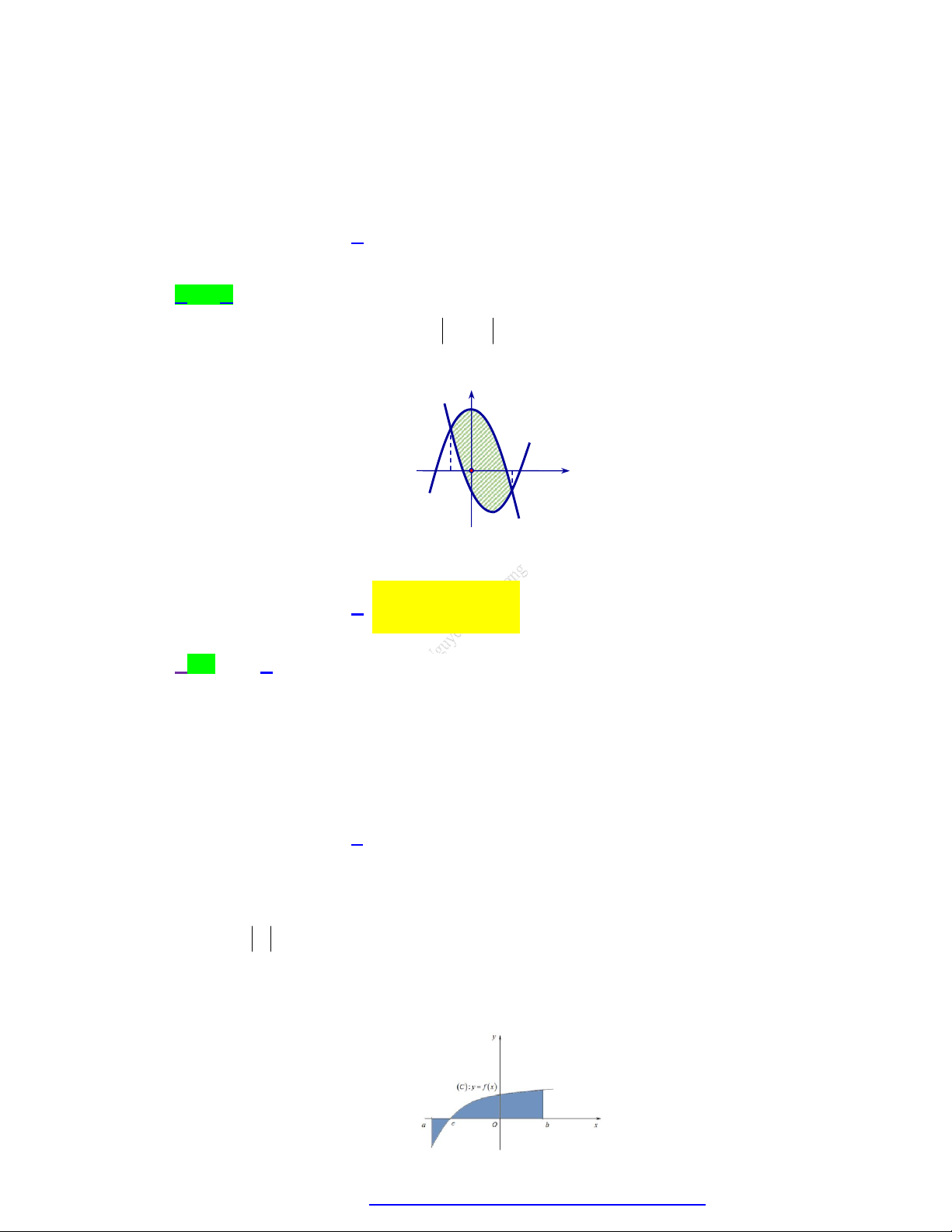
A. ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG (
 C ) : y f (x)  b 1 
Hình phẳng (H ) giới hạn bởi (
 C ) : y g(x)
thì diện tích là S f(x) ( g x) dx .  2
x  a, x b (a b) a  (
 C ) : y f (x)  b 1 
Hình phẳng (H ) giới hạn bởi (
 C ) :Ox : y  0
thì diện tích là S
f (x) dx .  2
x  a, x b (a b) a  Sa . b elip 2 2 x y (E) :   1 2 2 a b
Hình thức đề thường hay cho
Hình thức 1: Không cho hình vẽ, cho dạng (H ) : {y f (x), y g(x), x  ,
a x b (a b)} b casio 
f (x)  g(x) dx  
kết quả, so sánh với bốn đáp án. a
Hình thức 2: Không cho hình vẽ, cho dạng (H ) : {y f (x), y g(x)} xi
Giải f (x)  g(x) tìm nghiệm x ,...,x , với x nhỏ nhất, x lớn nhất casio  
f (x)  g(x) dx. 1 i 1 i x1
Hình thức 3: Cho hình vẽ, sẽ giải phương trình tìm tọa độ giao điểm (nếu chưa cho trên hình), chia từng
diện tích nhỏ, xổ hình từ trên xuống, ghi công thức và bấm máy tính.
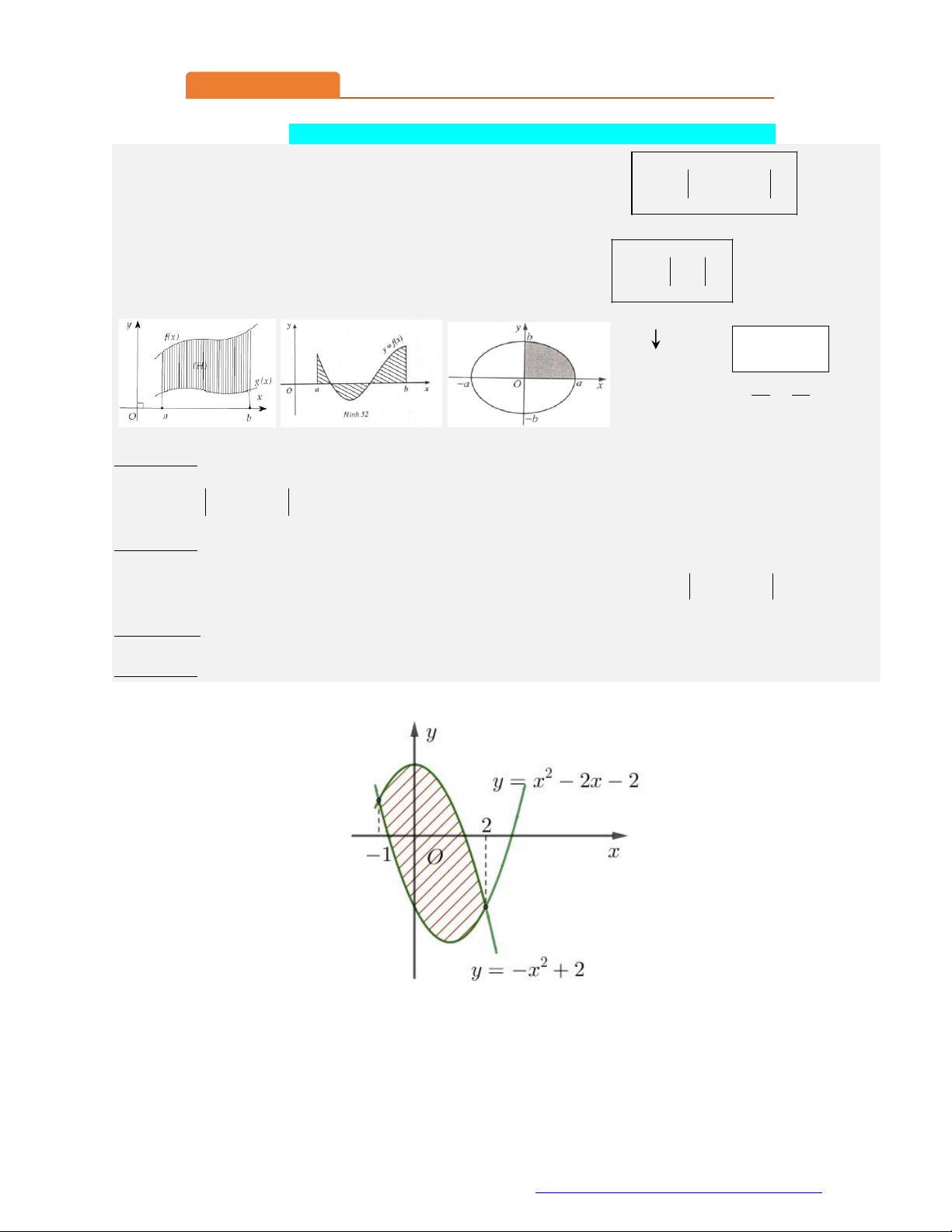
Hình thức 4: Cho ba hàm trở lên, chẳng hạn y f (x), y g(x), y h(x) ta nên vẽ hình. Câu 1.
Diện tích hình phẳng được gạch chéo trong hình bên bằng 2 2 A.   2
2x  2x  4dx . B.   2
2x  2x  4dx . 1 1 2 2 C.   2 2
x  2x  4dx . D.   2
2x  2x  4dx . 1 1 Câu 2.
Diện tích S của hình phẳng giới hạn bởi các đường 2
y  2 x , y  1
 , x  0 và x 1 được tính
bởi công thức nào sau đây? 1 1 1 1 2 A. S    2 2x   
1 dx . B. S   2 2x   
1 dx . C. S   2 2x   
1 dx . D. S   2 2x    1 dx . 0 0 0 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 3.
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? y 2
y x  2x 1 2 1  O x 2
y  x  3 2 2 2 2 A.   2
2x  2x  4 dx . B.  2   2 d  x x . C. 2  2 d  x x . D.   2 2
x  2x  4dx . 1 1 1 1 Câu 4.
Gọi S là diện tích hình phẳng giới hạn bởi các đường ex y
, y  0 , x  0 , x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A. 2   e x S dx  . B.  ex S dx  . C.   ex S dx  . D. 2  e x S dx  . 0 0 0 0 Câu 5.
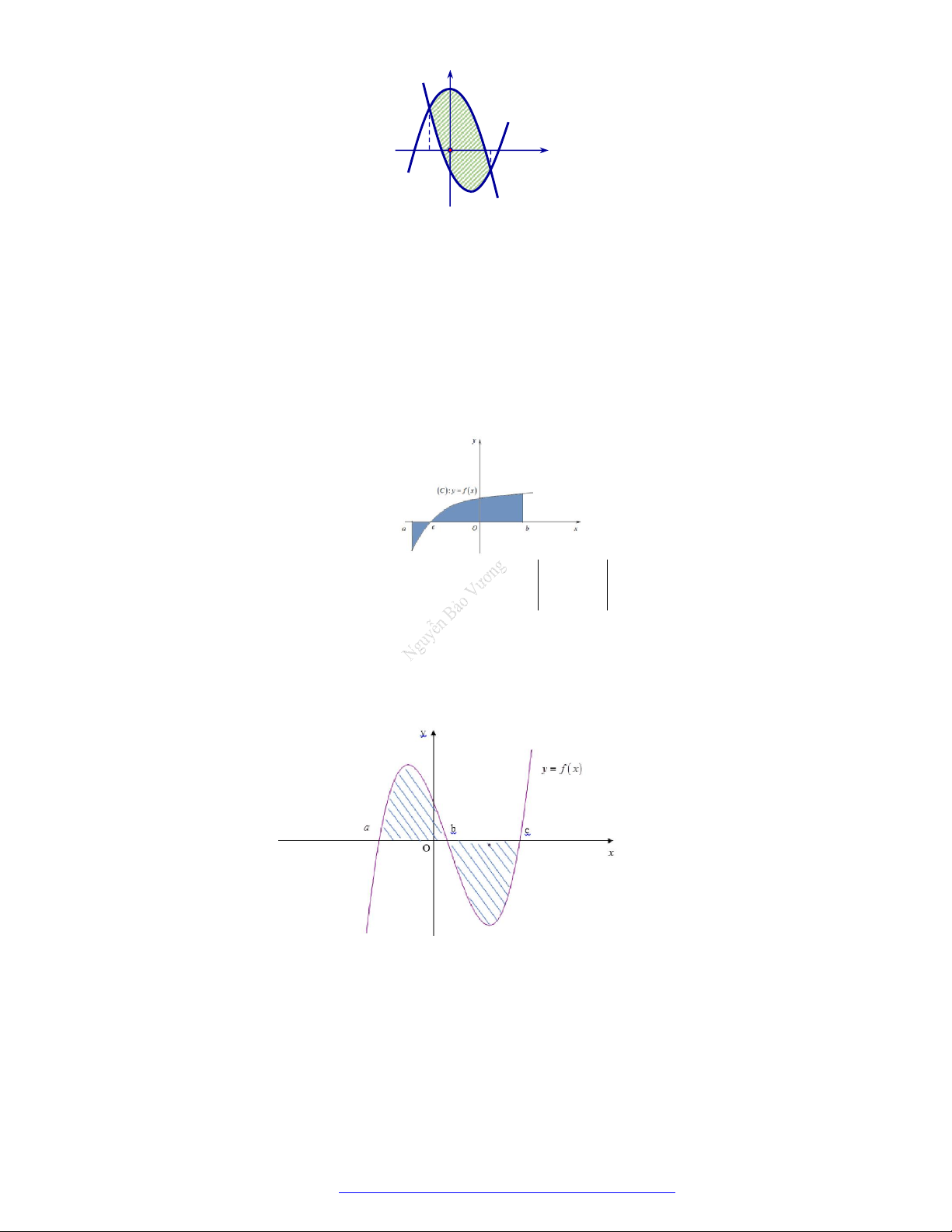
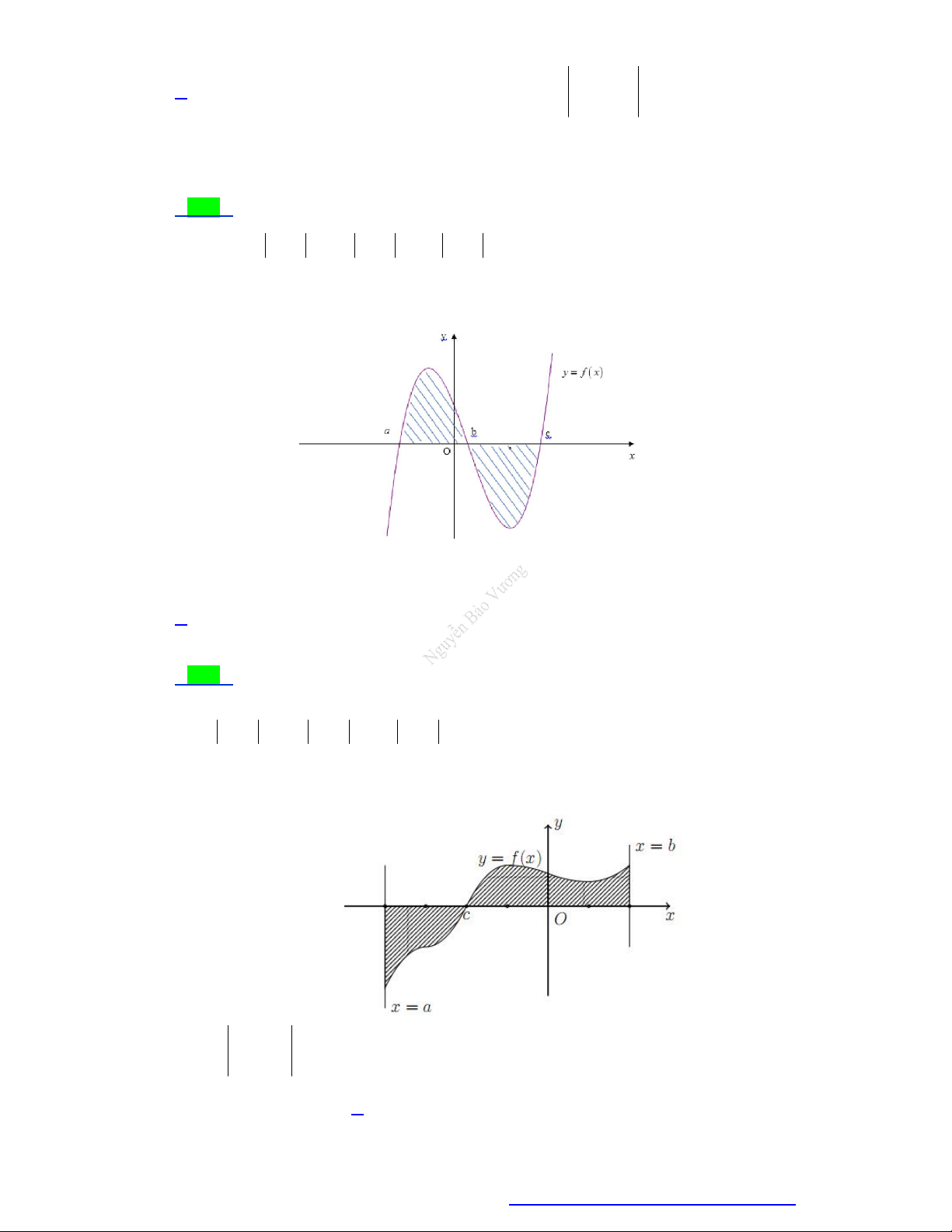
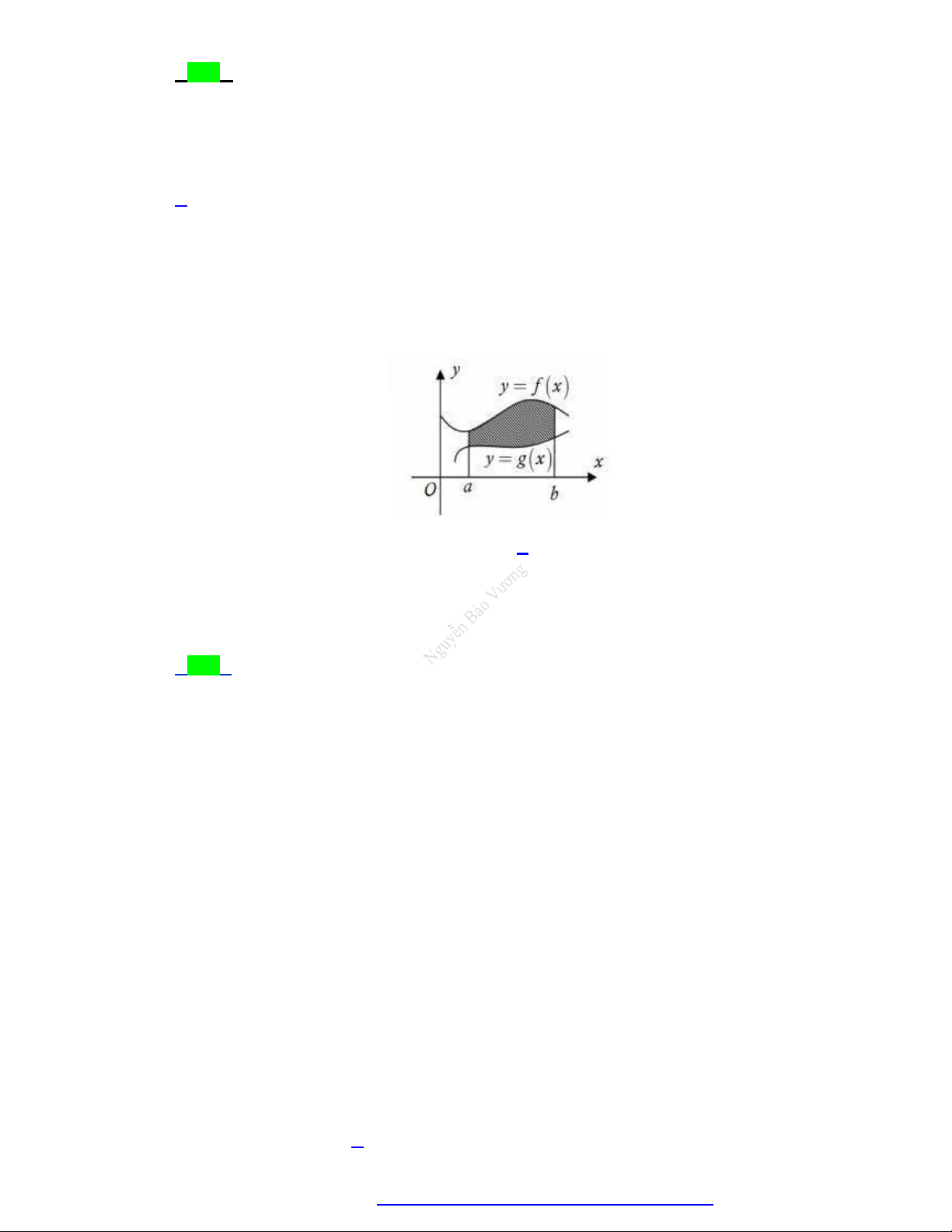
Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số y f x , trục hoành và hai đường
thẳng x a , x b a b (phần tô đậm trong hình vẽ) tính theo công thức nào dưới đây ? c b b
A. S   f x dx f x dx   . B. S
f x dx  . a c a c b b C. S
f x dx f x dx   . D. S
f x dx  . a c a Câu 6.
Cho hàm số y f x liên tục trên  và có đồ thì như hình vẽ bên. Hình phẳng được đánh dấu
trong hình vẽ bên có diện tích là b c b b A.
f x dx f x dx   . B.
f x dx f x dx   . a b a c b c b c C.
f x dx f x dx   .
D. f x dx f x dx   . a b a b Câu 7.
Diện tích của hình phẳng (H ) giới hạn bởi đồ thị của hàm số y f (x) , trục hoành và hai đường
thẳng x a , x b (a b) (phần tô đậm trong hình vẽ) tính theo công thức
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 b c b A. S f (x)dx. B. S
f (x)dx f (x)dx   . a a c b c b C. S f (x)dx.
D. S   f (x)dx f (x)dx   . a a c Câu 8.
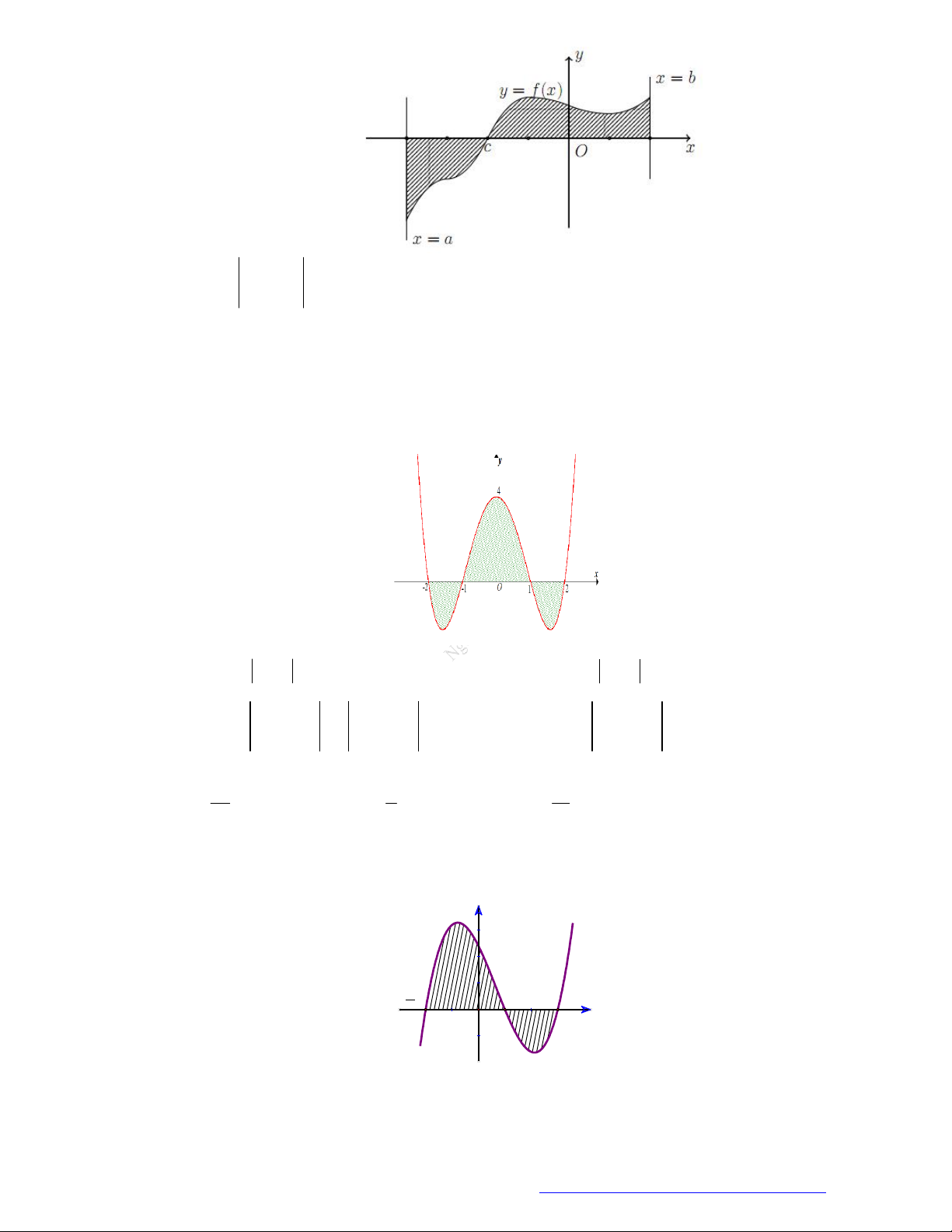
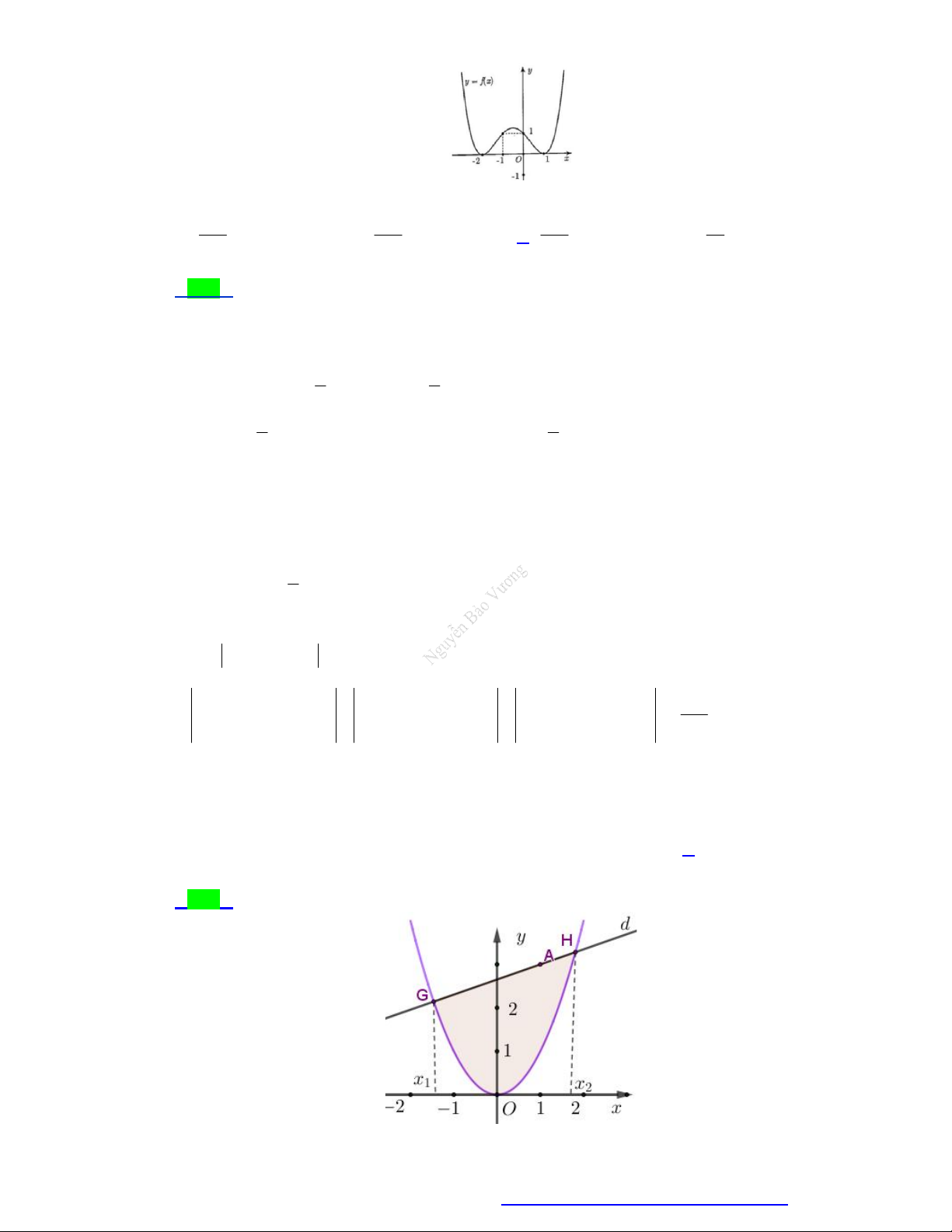
Cho hàm số y f x 4 2
x 5x  4 có đồ thị như hình vẽ bên. Gọi S là diện tích hình phẳng giới
hạn bởi đồ thị hàm số y f x và trục hoành (miền phẳng được tô đậm trên hình vẽ). Mệnh đề nào sau đây sai? 2 2 A. S
f x dx  . B. S  2
f x dx  . 2  0 1 2 2 C. S  2
f x dx  2
f x dx   . D. S  2
f x dx  . 0 1 0 Câu 9.
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x 37 9 81 A. B. C. D. 13 12 4 12
Câu 10. Cho hàm số f x liên tục trên .
 Gọi S là diện tích hình phẳng giới hạn bởi cá đường
y f x, y  0, x  2
 và x  3 (như hình vẽ). Mệnh đề nào dưới đây đúng? y y=f(x) x 2 O 1 3 1 3 1 3 A. S
f x dx f x d .   x B. S  
f x dx f x d .   x 2 1 2 1 1 3 1 3 C. S
f x dx f x d .   x D. S  
f x dx f x d .   x 2 1 2 1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
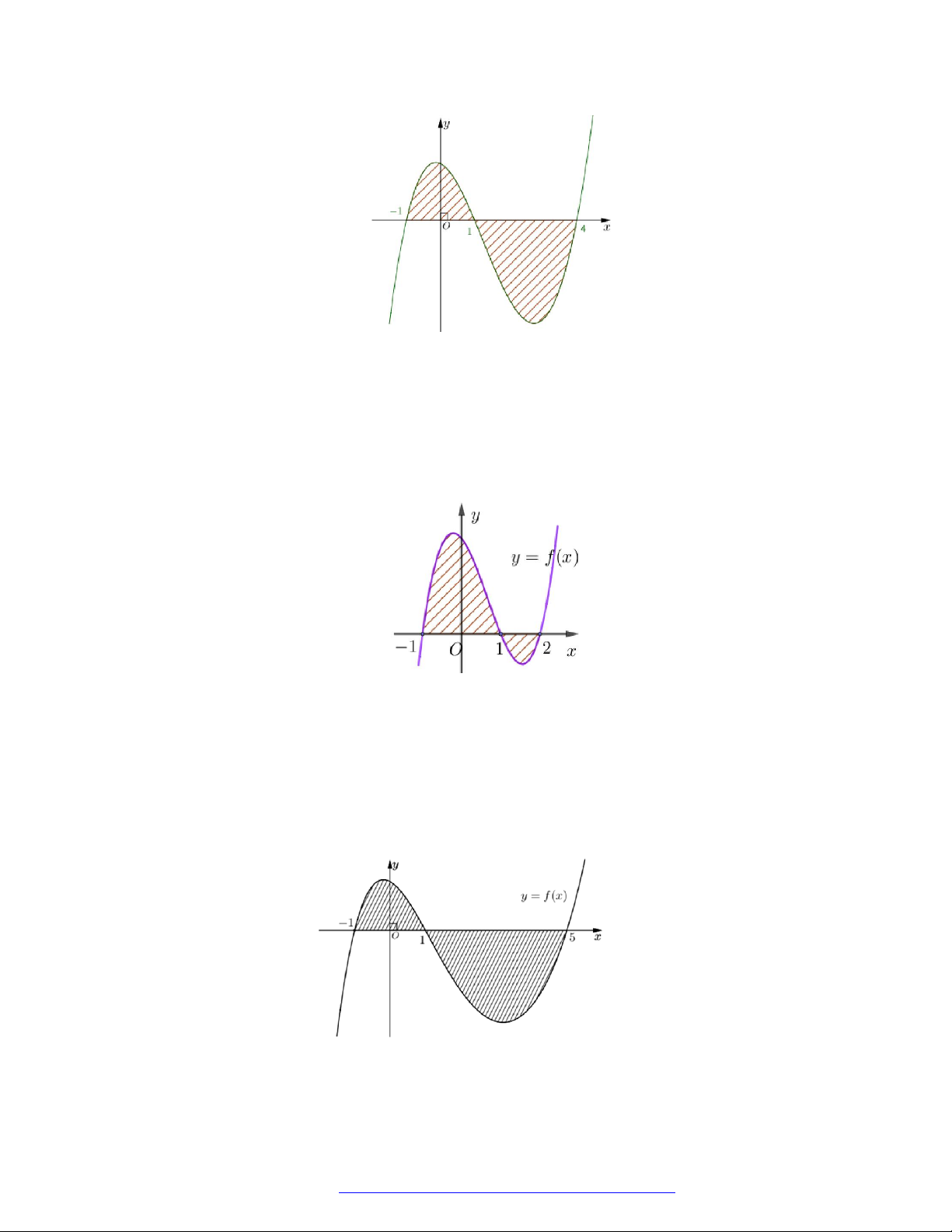
Câu 11. Cho hàm số f x liên tục trên  . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 và x  4 (như hình vẽ bên). Mệnh đề nào dưới đây đúng? 1 4 1 4 A. S  
f x dx  f x dx   . B. S
f x dx  f x dx   . 1  1 1 1 1 4 1 4 C. S
f x dx  f x dx   . D. S  
f x dx  f x dx   . 1  1 1  1
Câu 12. Cho hàm số f x liên tục trên  . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 , x  2 (như hình vẽ bên). Mệnh đề nào dưới đây đúng? 1 2 1 2 A. S  
f x dx  f x dx   . B. S  
f x dx+ f x dx   . 1 1 1 1 1 2 1 2 C. S
f x dx  f x dx   . D. S
f x dx + f x dx   . 1  1 1 1
Câu 13. Cho hàm số y f x liên tục trên .
 Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 và x  5 (như hình vẽ bên).
Mệnh đề nào sau đây đúng? 1 5 1 5 A. S
f (x)dx f (x)dx   . B. S
f (x)dx f (x)dx   . 1 1 1  1 1 5 1 5 C. S  
f (x)dx f (x)dx   . D. S  
f (x)dx f (x)dx   . 1 1 1 1
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
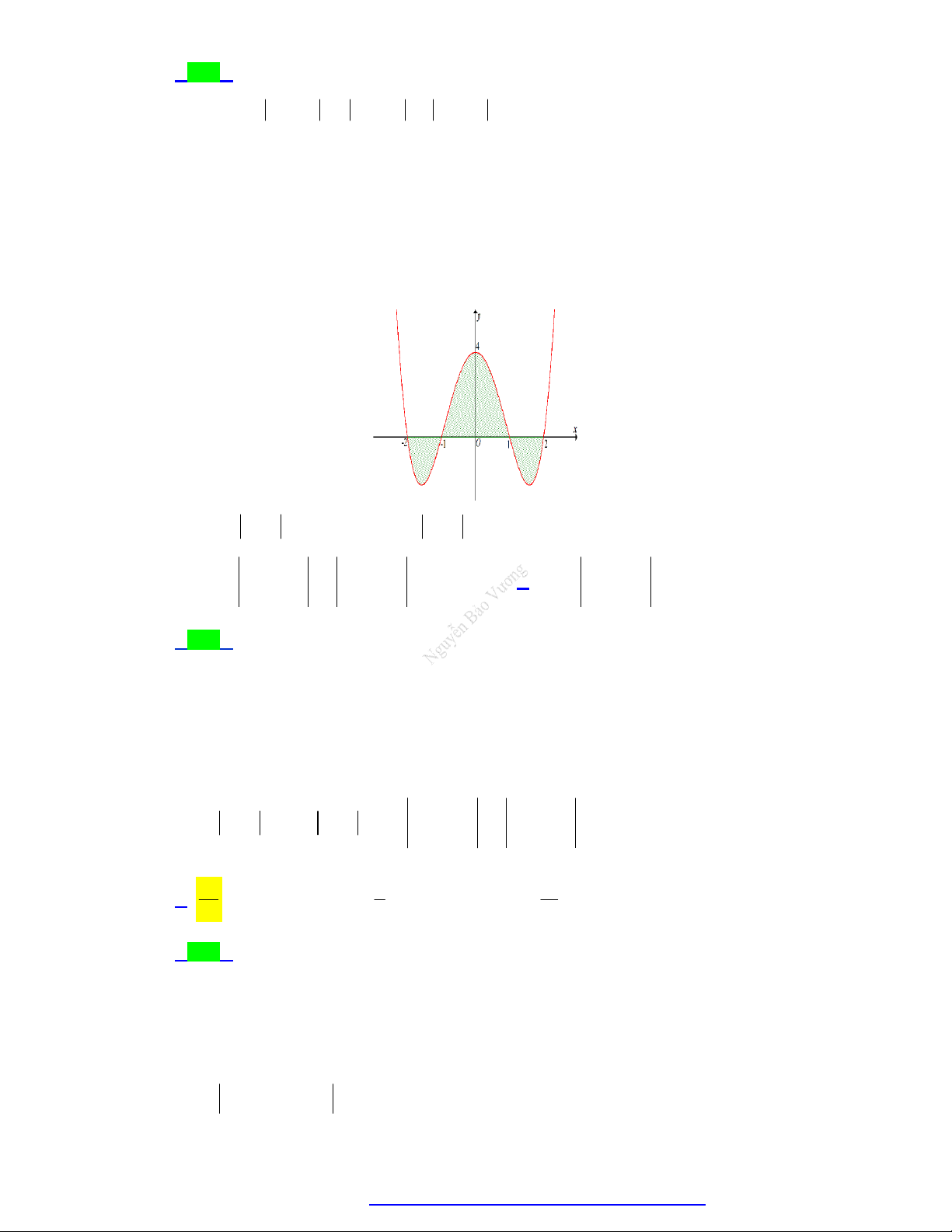
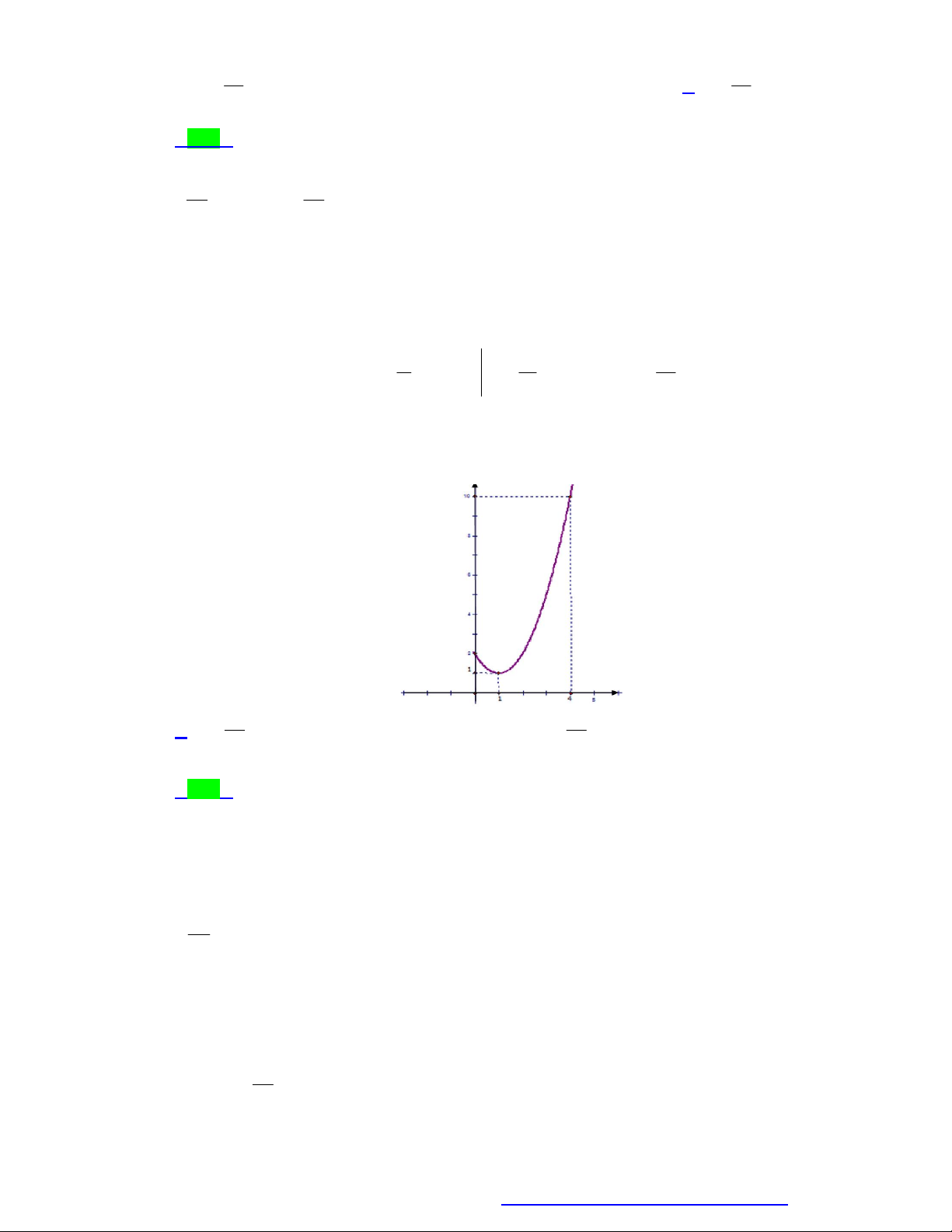
Câu 14. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x và đường thẳng y x là: 1 1 1 1 A. . B. . C. . D. . 3 4 2 6
Câu 15. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2
y  x  2x 1, 2
y  2x  4x 1 là A. 8 . B. 5 . C. 4 . D. 10 . x 1
Câu 16. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y
và các trục tọa độ. Khi đó giá x 1
trị của S bằng
A. S  ln 2 1 .
B. S  2 ln 2 1.
C. S  2 ln 2 1.
D. S  ln 2 1.
Câu 17. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số 2
y  3x x  4 . Gọi S và S lần lượt là diện 1 2 S
tích phần hình (H ) nằm bên trái và bên phải trục tung. Tính tỷ số 1 . S2 S 208 S 54 S 135 S 135 A. 1  . B. 1  . C. 1  . D. 1  . S 343 S 343 S 343 S 208 2 2 2 2
Câu 18. Cho S là diện tích của hình phẳng giới hạn bởi đồ thị C  của hàm số 2
y x 1 x , trục hoành,
trục tung và đường thẳng x  1 . Biết S a 2  b  ,
a b . Tính a  . b 1 1 1
A. a b .
B. a b .
C. a b .
D. a b  0 . 6 2 3
Câu 19. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x , trục hoành và hai đường thẳng x  1
 , x  2 biết rằng mỗi đơn vị dài trên các trục tọa độ là 2 cm. 15 17 A.  2 cm  . B.  2 cm  . C.  2 17 cm  . D.  2 15 cm  . 4 4 3  7  4x
khi 0  x  1
Câu 20. Cho hàm số f x  
. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 4  x khi x  1 
f x và các đường thẳng x  0, x  3, y  0 . 16 20 . . A. 3 B. 3 C. 10. D. 9.
Câu 21. Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số y x ln x , trục Ox và đường thẳng x e . 2 e  3 2 e 1 2 e 1 2 e 1 A. S  . B. S  . C. S  . D. S  . 4 2 2 4 1
Câu 22. Cho hai hàm số f x 3 2
ax bx cx 1 và g x 2
dx ex   , a , b , c d,e 
 . Biết rằng đồ thị 2
của hàm số y f (x) và y g (x) cắt nhau tại ba điểm có hoành độ lần lượt 3; 1; 2 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 253 125 253 125 A. B. C. D. 12 12 48 48
Câu 23. Cho H là hình phẳng giới hạn bởi parabol 2
y  3x , cung tròn có phương trình 2 y  4  x
(với 0  x  2 ) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của H bằng 4  3 4  3 4  2 3  3 5 3  2 A. B. C. D. 12 6 6 3
Câu 24. Ông An có một mảnh vườn hình Elip có độ dài trục lớn bằng 16m và độ dài trục bé bằng10m .
Ông muốn trồng hoa trên một dải đất rộng 8m và nhận trục bé của elip làm trục đối xứng (như
hình vẽ). Biết kinh phí để trồng hoa là 100.000 đồng/ 2
1m . Hỏi ông An cần bao nhiêu tiền để
trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn.) 8m A. 7.862.000 đồng B. 7.653.000 đồng C. 7.128.000 đồng
D. 7.826.000 đồng
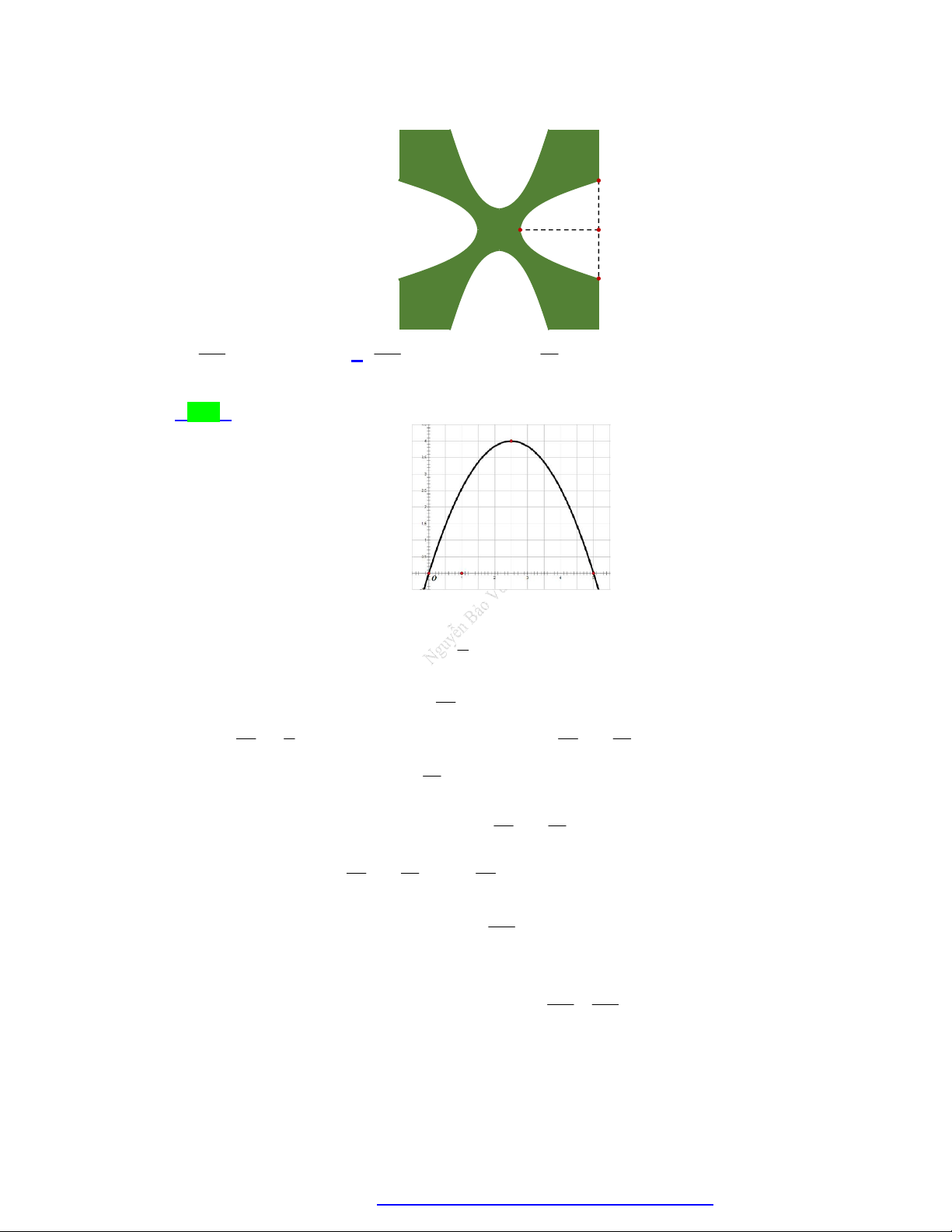
Câu 25. Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng 10 cm bằng cách
khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết AB  5cm , OH  4cm .
Tính diện tích bề mặt hoa văn đó. A O H B 160 140 14 A. 2 cm . B. 2 cm . C. 2 cm . D. 2 50 cm . 3 3 3
Câu 26. Cho hàm số y f x là hàm số đa thức bậc 4 và có đồ thị như hình vẽ
Hình phẳng giới hạn bởi đồ thị hàm số y f x và y f  x có diện tích là
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 127 127 107 13 A. . B. . C. . D. . 40 10 5 5
Câu 27. Cho parabol  P có phương trình 2
y x và đường thẳng d đi qua điểm A1;3 . Giả sử khi
đường thẳng d có hệ số góc k thì diện tích hình phẳng giới hạn bởi parabol  P và đường thẳng
d nhỏ nhất. Giá trị thực của k thuộc khoảng nào sau đây? A.  ;  3 . B. 3;  . C. 3; 0 . D. 0;3 .
Câu 28. Một viên gạch hoa hình vuông cạnh 80cm . Người thiết kế đã sử dụng 4 đường parabol có chung
đỉnh tại tâm của viên gạch để tạo ra 4 cánh hoa (được tô màu sẫm như hình vẽ bên). Diện tích mỗi
cánh hoa của viên gạch bằng 800 1600 400 A.  2 cm . B.  2 cm . C.  2 cm . D.  2 250 cm . 3 3 3
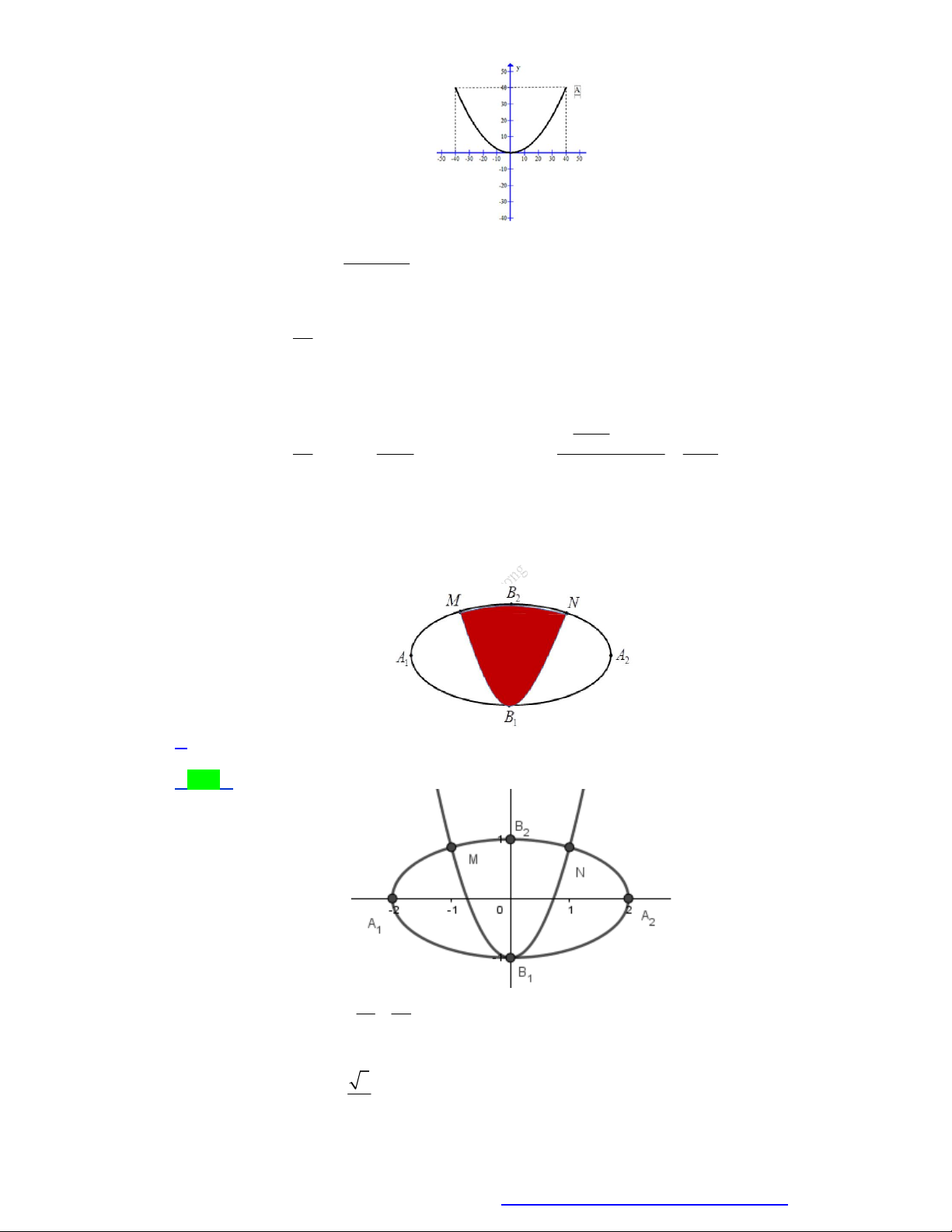
Câu 29. Một biển quảng cáo có dạng Elip với bốn đỉnh A , A , B , B . như hình vẽ. Người ta chia Elip bởi 1 2 1 2
parapol có đỉnh B ,trục đối xứng B B và đi qua các điểm M , N .Sau đó sơn phần tô đậm với giá 1 1 2 200.000 đồng/ 2
m và trang trí đèn led phần còn lại với giá 500.000 đồng/ 2
m .Hỏi kinh phí sử dụng
gần nhất với giá trị nào dưới đây? Biết A A  4m , B B  2 ,
m MN  2m . 1 2 1 2 A. 2.341.000 đồng. B. 2.057.000 đồng. C. 2.760.000 đồng. D. 1.664.000 đồng. 1
Câu 30. Cho hai hàm số 3 2
f (x)  ax bx cx  và 2
g(x)  dx ex 1 (a, b, c, d , e ) . Biết rằng đồ thị 2
hàm số y f (x) và y g (x) cắt nhau tại ba điểm có hoành độ lần lượt là 3; 1;1 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho (miền tô đậm) có diện tích bằng 9 A. 8 B. 5 C. 4 D. 2
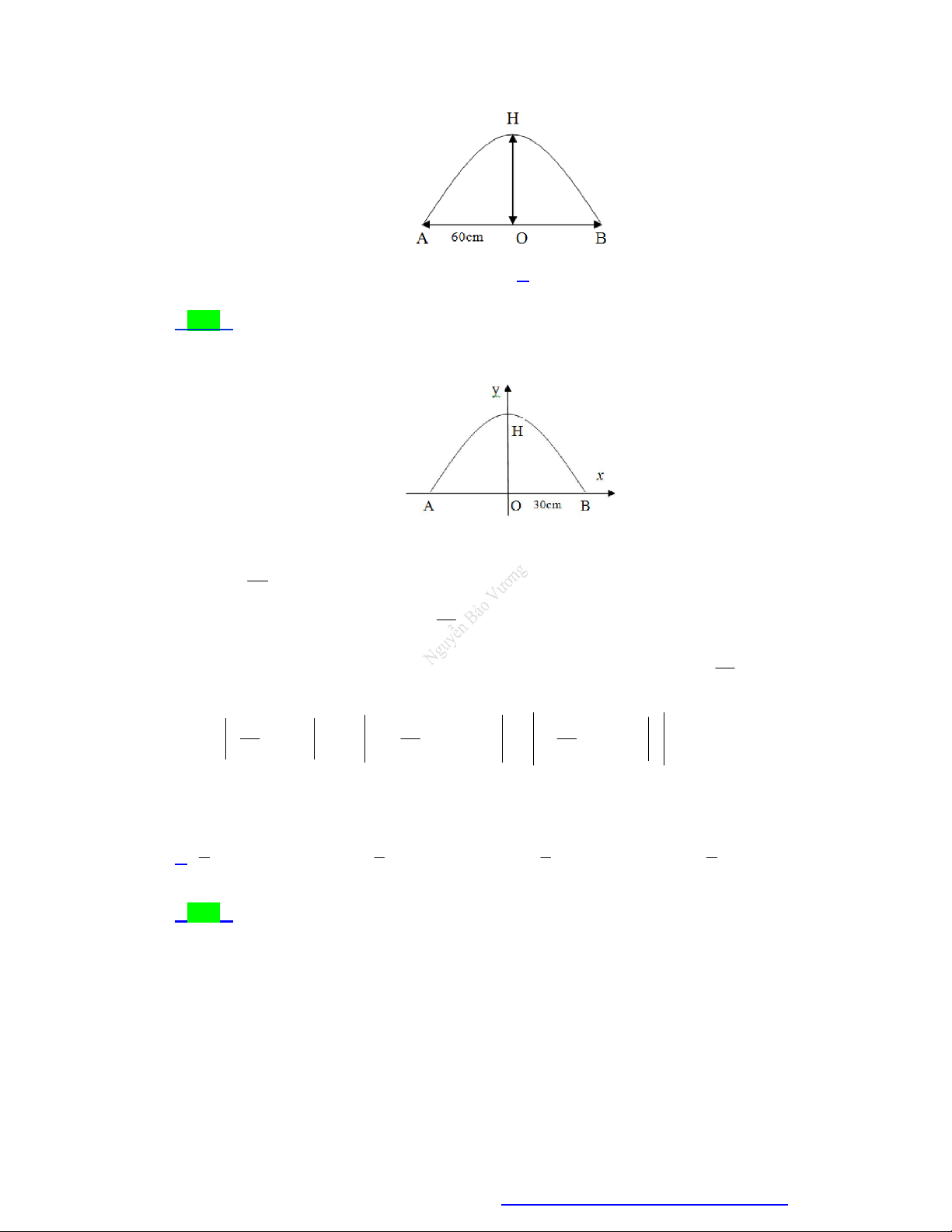
Câu 31. Bạn An cần mua một chiếc gương có đường viền là đường Parabol bậc 2 ( xem hình vẽ). Biết rằng
khoảng cách đoạn AB  60 cm , OH  30 cm . Diện tích của chiếc gương bạn An mua là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 A.  2 900 cm  . B.  2 1000 cm  . C.  2 1200 cm  . D.  2 1400 cm  .
Câu 32. Cho  H  là hình phẳng giới hạn bởi parabol  P 2
: y x , tiếp tuyến với  P tại điểm M 2; 4 và
trục hoành. Tính diện tích của hình phẳng  H  ? 2 8 1 4 A. . B. . C. . D. . 3 3 3 3 Câu 33. Cho hàm số   3 2
f x ax bx cx d có đồ thị C . Đồ thị của hàm số y f  x được cho bởi hình vẽ dưới đây
Biết rằng đường thẳng d : y x cắt C  tạo thành hai phần hình phẳng có diện tích bằng nhau.
Tổng a b c d bằng A. 1. B. 0 . C. 2 . D. 3 .
Câu 34. Một cái cổng có dạng như hình vẽ, với chiều cao 6m và chiều rộng 8m. Mái vòm của cổng có
hình bán elip với chiều rộng là 6m, điểm cao nhất của mái vòm là 5m (tham khảo hình vẽ). Người
ta muốn lát gạch hoa để trang trí cho cổng với chi phí là 250 000 đồng/m2. Hỏi số tiền cần chi trả
gần nhất với số nào sau đây? A. 6.210.000 . B. 6.110.000 . C. 6.100.000 . D. 6.145.000 .
Câu 35. Đợt thi đua 26/3 Đoàn trường THPT Nho Quan A có thực hiện một dự án trưng bày trên một pano
có dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu các lớp gửi hình dự thi và dán lên
khu vực hình chữ nhật ABCD , phần còn lại sẽ được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là 150.000đ trên 2
1m bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ
là bao nhiêu( kết quả làm tròn lấy phần nguyên)?
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A. 575.034 đồng. B. 676.239 đồng. C. 536.272 đồng. D. 423.215 đồng.
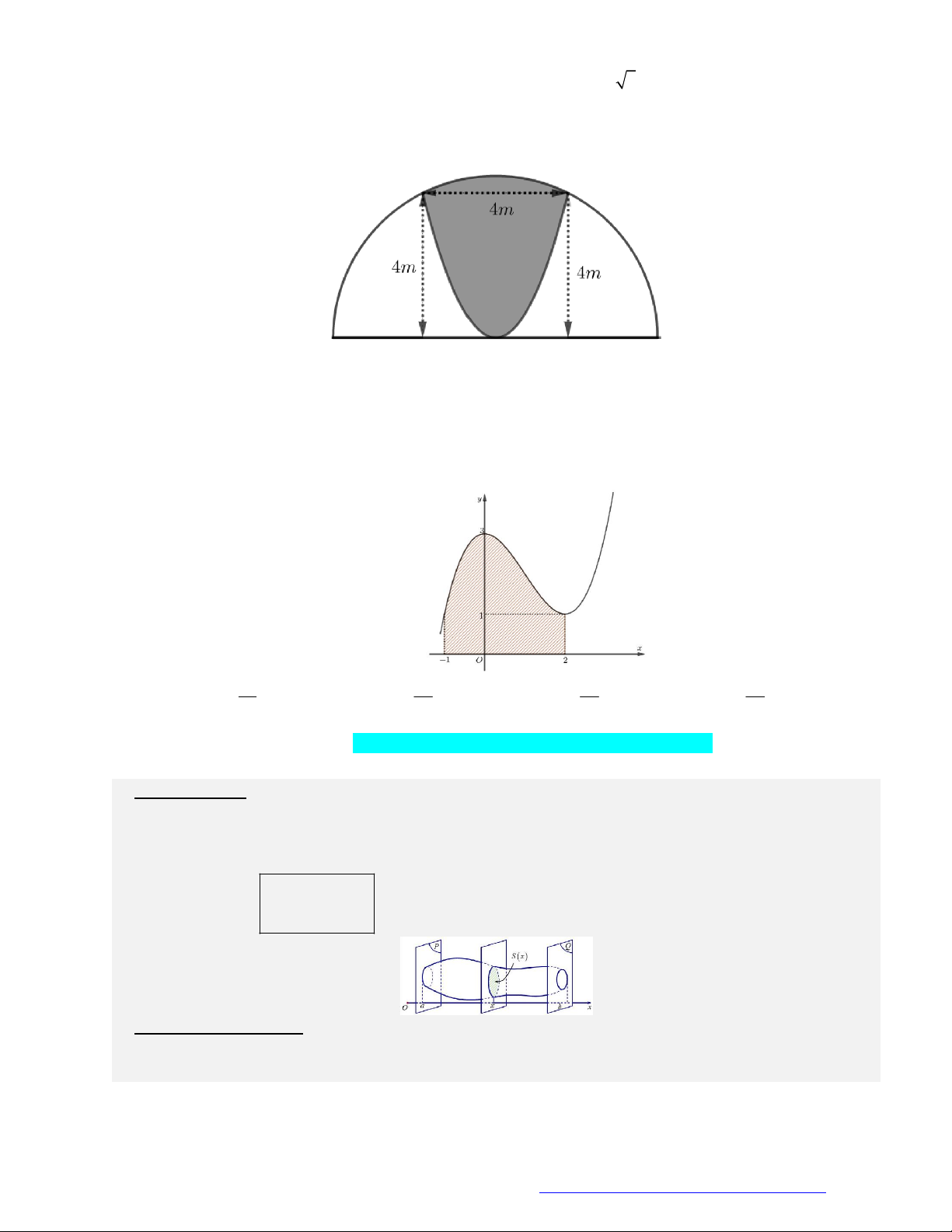
Câu 36. Một khuôn viên có dạng là nửa hình tròn đường kính bằng 4 5 m. Trên đó, người ta thiết kế một
phần để trồng hoa có dạng của một cách hoa hình parabol có đỉnh trùng với tâm nửa hình tròn, hai
đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô đậm) và cách nhau một khoảng bằng 4 m.
Phần còn lại của khuôn viên (phần không tô đậm) dành để trồng cỏ.
Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ là 100.000 đồng 2
/ m Số tiền cần có để trồng cỏ
là bao nhiêu (số tiền được làm tròn đến hàng nghìn)? A. 2 388 000 đồng. B. 3 895 000 đồng. C. 1 194 000 đồng. D. 1 948 000 đồng.
Câu 37. Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số f x 3 2
ax bx  , c các
đường thẳng x  1, x  2 và trục hoành (miền gạch chéo cho trong hình vẽ). 51 53 52 50 A. S  . B. S  . C. S  . D. S  . 8 8 8 8
B. ỨNG DỤNG TÍCH PHÂN TÍNH THỂ TÍCH
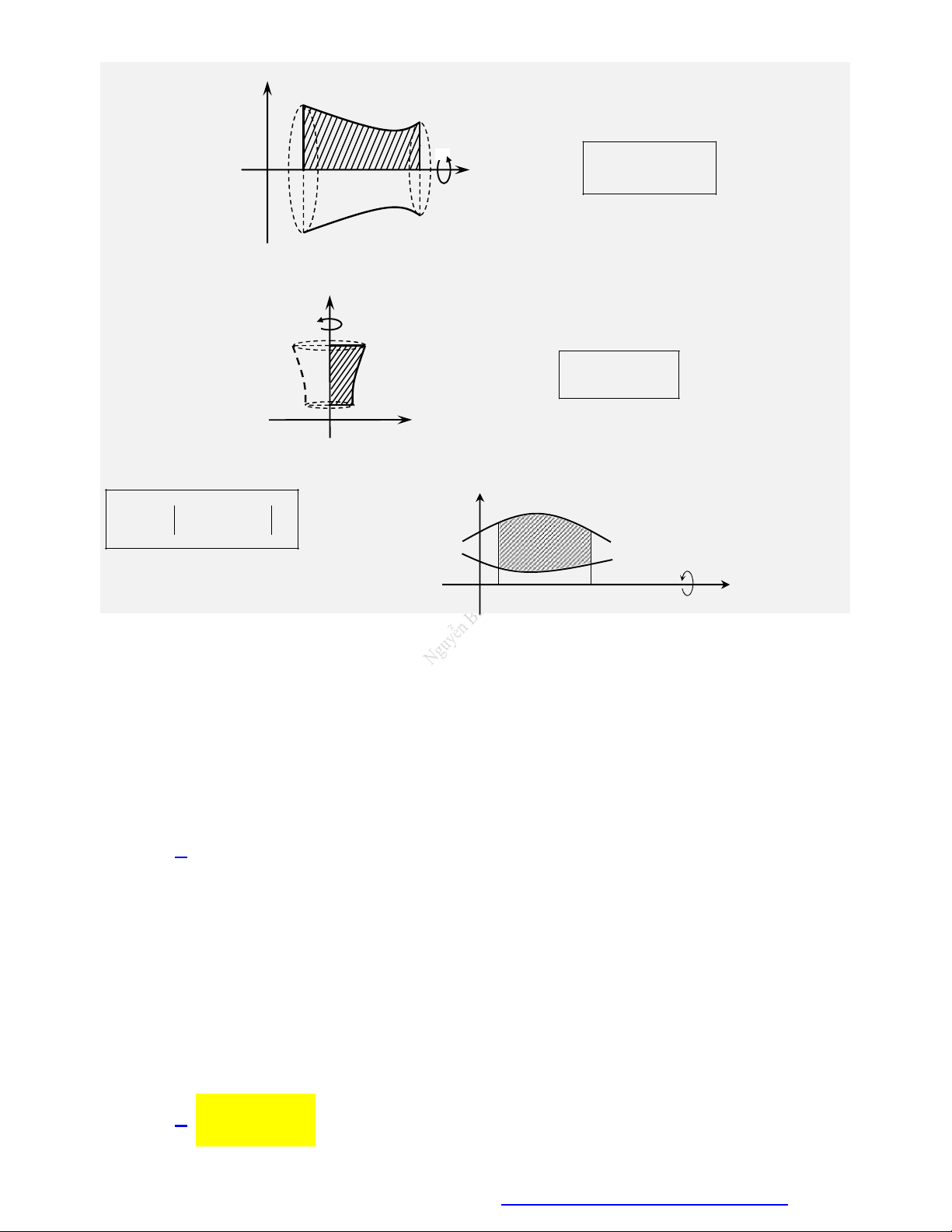
Thể tích vật thể
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và ,
b S(x) là
diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x,
(a x b). Giả sử S(x) là hàm số liên tục trên đoạn [a;b]. Khi đó, thể tích của vật thể B được b xác định: V S(x)dx .  a
Thể tích khối tròn xoay
a) Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y f (x), trục hoành
và hai đường thẳng x  ,
a x b quanh trục Ox :
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 y
y f (x) (
C) : y f (x) (
Ox) : y 0 bV   f x dx x  2 ( ) a O b x x    a ax   b
b) Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x g(y), trục hoành
và hai đường thẳng y c, y d quanh trục Oy : y d
(C ) : x g(y)  d
(Oy) : x 0 2   V
g(y) dy    y y   c c cy   d O x
c) Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y f (x), y g(x)
(cùng nằm một phía so với Ox) và hai đường thẳng x a, x b quanh trục Ox : b y 2 2 V
f (x)  g (x) dx .  f (x) a g(x) a x O b
Câu 38. Cho hình phẳng  H giới hạn bởi các đường 2
y x 3, y  0 , x  0 , x  2 . Gọi V là thể tích
của khối tròn xoay được tạo thành khi quay  H xung quanh trục O x . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2
A. V     2
x  3 dx B. V    2
x  3 dx C. V    2
x  3 dx D. V    2 x  3 dx 0 0 0 0
Câu 39. Cho hàm số y f x liên tục trên đoạn  ; a
b . Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y f x , trục hoành và hai đường thẳng x  ,
a x ba b . Thể tích của khối tròn xoay tạo
thành khi quay D quanh trục hoành được tính theo công thức: b b b b A. 2 V  
f xdxB. 2 V  2
f xdx C. 2 2 V  
f xdx D. 2 V  
f xdxa a a a
Câu 40. Cho hình phẳng  H  giới hạn bởi các đường thẳng 2
y x  2, y  0, x  1, x  2 . Gọi V là thể
tích của khối tròn xoay được tạo thành khi quay  H  xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2
A. V    2
x  2 dx . B. V   2
x  2 dx . C. V    2
x  2dx . D. V   2 x  2dx . 1 1 1 1
Câu 41. Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo
thành được tính theo công thức nào?
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 b b
A. V   f x g x 2 ( ) ( ) dx  . B. 2 2
V    f (x)  g (x) dx    . a a b b
C. V    f x g x 2 ( ) ( ) dx  .
D. V    f (x)  g(x)dx  . a a
Câu 42. Trong không gian với hệ tọa độ Oxyz , cho vật thể  H  giới hạn bởi hai mặt phẳng có phương
trình x a và x b . Gọi S x là diện tích thiết diện của  H  bị cắt bởi mặt phẳng vuông góc
với trục Ox tại điểm có hoành độ là x , với a x b . Giả sử hàm số y S x liện tục trên đoạn
a;b. Khi đó, thể tích của vật thể H  được cho bởi công thức : b b b b
A. V   S x dx  .
B. V   S x 2  dx   
. C. V  S x 2  dx   
. D. V S x dx  . a a a a
Câu 43. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x  1 và x  3, biết rằng khi cắt vật
thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (1  x  3 ) thì được thiết diện
là một hình chữ nhật có độ dài hai cạnh là 3x và 2 3x  2 . 124 124
A. V  32  2 15 B. V C. V
D. V  (32  2 15) 3 3
Câu 44. Cho hình phẳng D giới hạn bởi đường cong y  2  cos x , trục hoành và các đường thẳng  x  0, x
. Khối tròn xoay tạo thành khi D quay quanh trục hoành có thể tích V bằng bao 2 nhiêu?
A. V  (  1)
B. V    1
C. V    1
D. V  (  1)
Câu 45. Cho hình phẳng D giới hạn bởi đường cong y  2  sin x , trục hoành và các đường thẳng
x  0 , x   . Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu? A. V  2 2
B. V  2   1 C. V  2
D. V  2   1
Câu 46. Cho hình phẳng D giới hạn bởi đường cong  x y
e , trục hoành và các đường thẳng x  0 , x  1.
Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?   2 e  1 2 2 e  1  2 e e  1 A. V B. V C. V D. V  2 2 3 2
Câu 47. Cho hình phẳng D giới hạn với đường cong 2 y
x 1 , trục hoành và các đường thẳng
x  0, x  1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 4 4 A. V
B. V  2 C. V D. V  2 3 3
Câu 48. Cho hình phẳng giới hạn bởi các đường y
x  2 , y  0 và x  9 quay xung quanh trục Ox .
Tính thể tích khối tròn xoay tạo thành. 5 11 7 7 A. V  . B. V  . C. V  . D. V  . 6 6 11 6
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 49. Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số 2
y  3x x và trục hoành, quanh trục hoành. 85 41 81 8 A. (đvtt). B. (đvtt). C. (đvtt). D. (đvtt). 10 7 10 7
Câu 50. Thể tích của vật thể tròn xoay khi quay hình  H  quanh Ox với  H  được giới hạn bởi đồ thị hàm số 2 y
4x x và trục hoành. 31 32 34 35 A. . B. . C. . D. . 3 3 3 3
C. ỨNG DỤNG TÍCH PHÂN VÀO BÀI TOÁN CHUYỂN ĐỘNG
Câu 51. Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động
chậm dần đều với vận tốc v t   5
t 10 (m/s), trong đó t là khoảng thời gian tính bằng giây, kể
từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 0,2m B. 2m C. 10m D. 20m
Câu 52. Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi 1 13
quy luật v t  2  t t
 m/s , trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu 100 30
chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng
cùng hướng với A nhưng chậm hơn 10 giây so với A và có gia tốc bằng a  2
 m/s  (a là hằng
số). Sau khi B xuất phát được 15 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng A. 15  m/s B. 9m/s C. 42   m/s D. 25m/s
Câu 53. Một chất điểm chuyển động trên đường thẳng nằm ngang với gia tốc phụ thuộc thời gian t (s) là
a t   2t  7 (m/s2). Biết vận tốc đầu bằng 10 (m/s), hỏi sau bao lâu thì chất điểm đạt vận tốc 18 (m/s)? A. 5 (s). B. 7 (s). C. 6 (s). D. 8 (s).
Câu 54. Một ôtô đang chạy với vận tốc 19 m / s thì người lái hãm phanh, ôtô chuyển động chậm dần đều
với vận tốc v t   3
 8t 19 m / s , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt
đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét? A. 5 m .
B. 4,5 m .
C. 4, 25 m .
D. 4, 75 m .
Câu 55. Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt đất đã
được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động
theo phương thẳng đứng với vận tốc tuân theo quy luật 2
v(t)  10t t , trong đó t (phút) là thời
gian tính từ lúc bắt đầu chuyển động, v(t) tính theo đơn vị mét/phút (m / p) . Nếu như vậy thì khi
bắt đầu tiếp đất vận tốc v của khí cầu là:
A. v  9(m / p).
B. v  5(m / p).
C. v  7(m / p).
D. v  3(m / p).
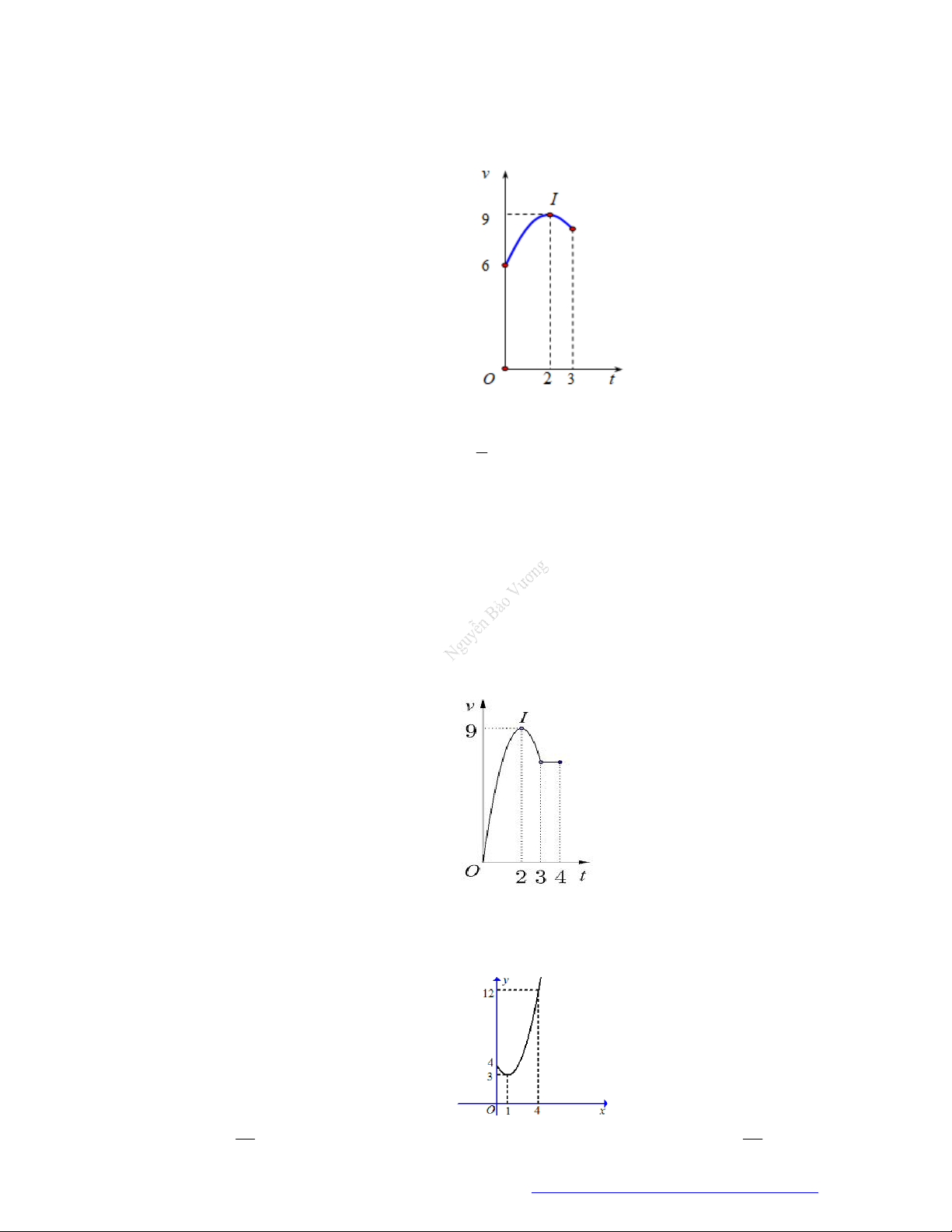
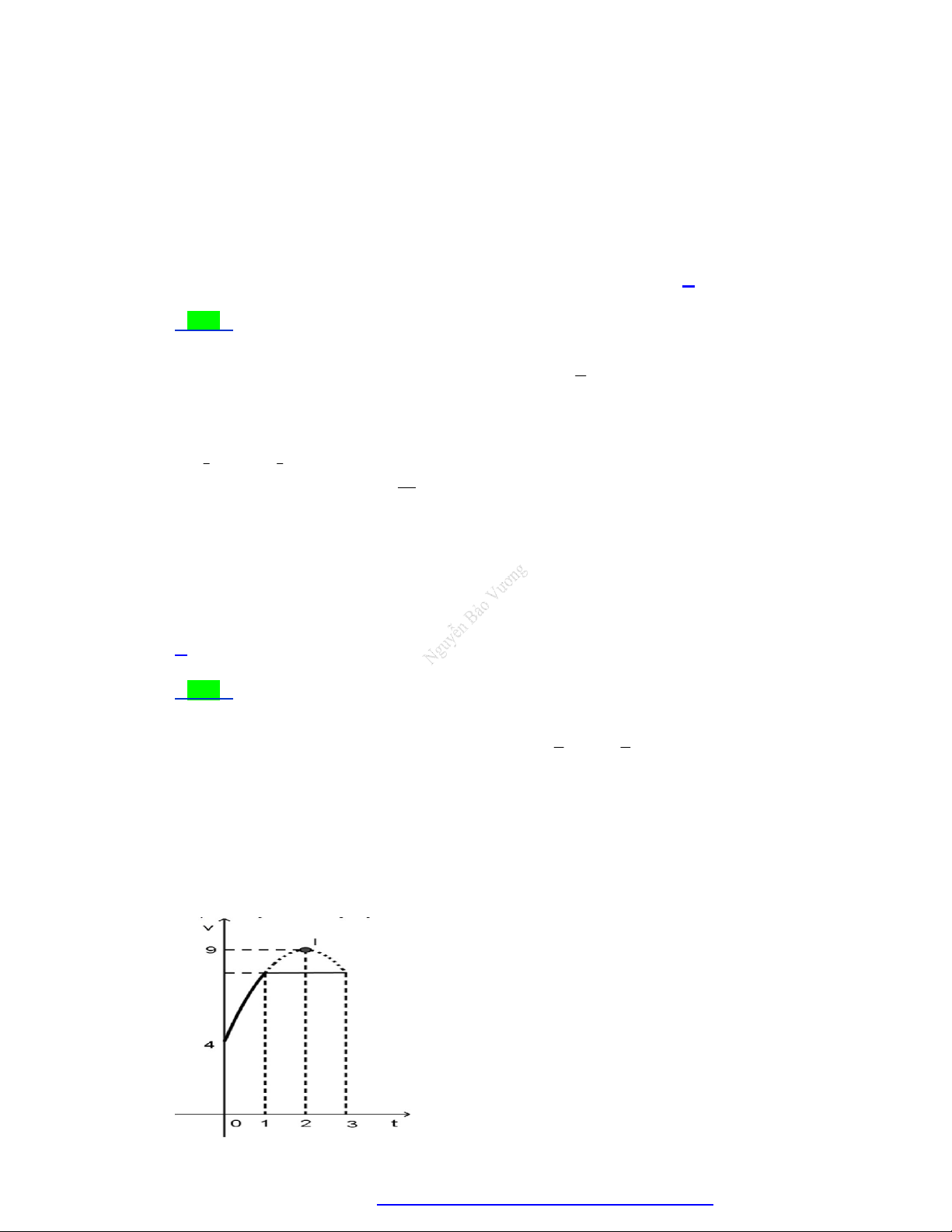
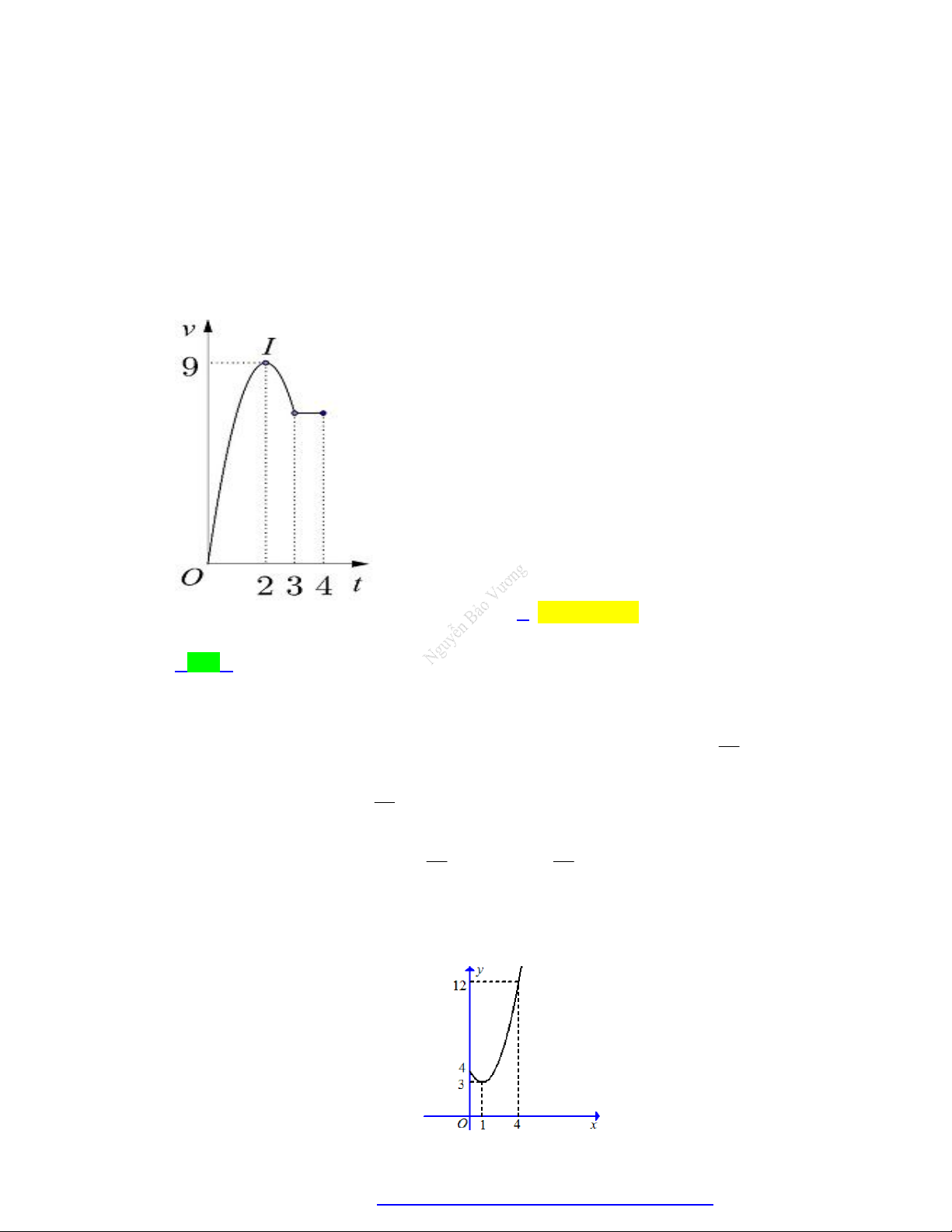
Câu 56. Một vật chuyển động trong 3 giờ với vận tốc v(km / h) phụ thuộc vào thời gian t(h) có đồ thị vận
tốc như hình bên. Trong thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của
đường parabol có đỉnh I(2; 9) và trục đối xứng song song với trục tung, khoảng thời gian còn lại
đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật chuyển động
được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm).
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
A. s  15, 50(km)
B. s  23, 25(km)
C. s  13,83(km)
D. s  21, 58(km)
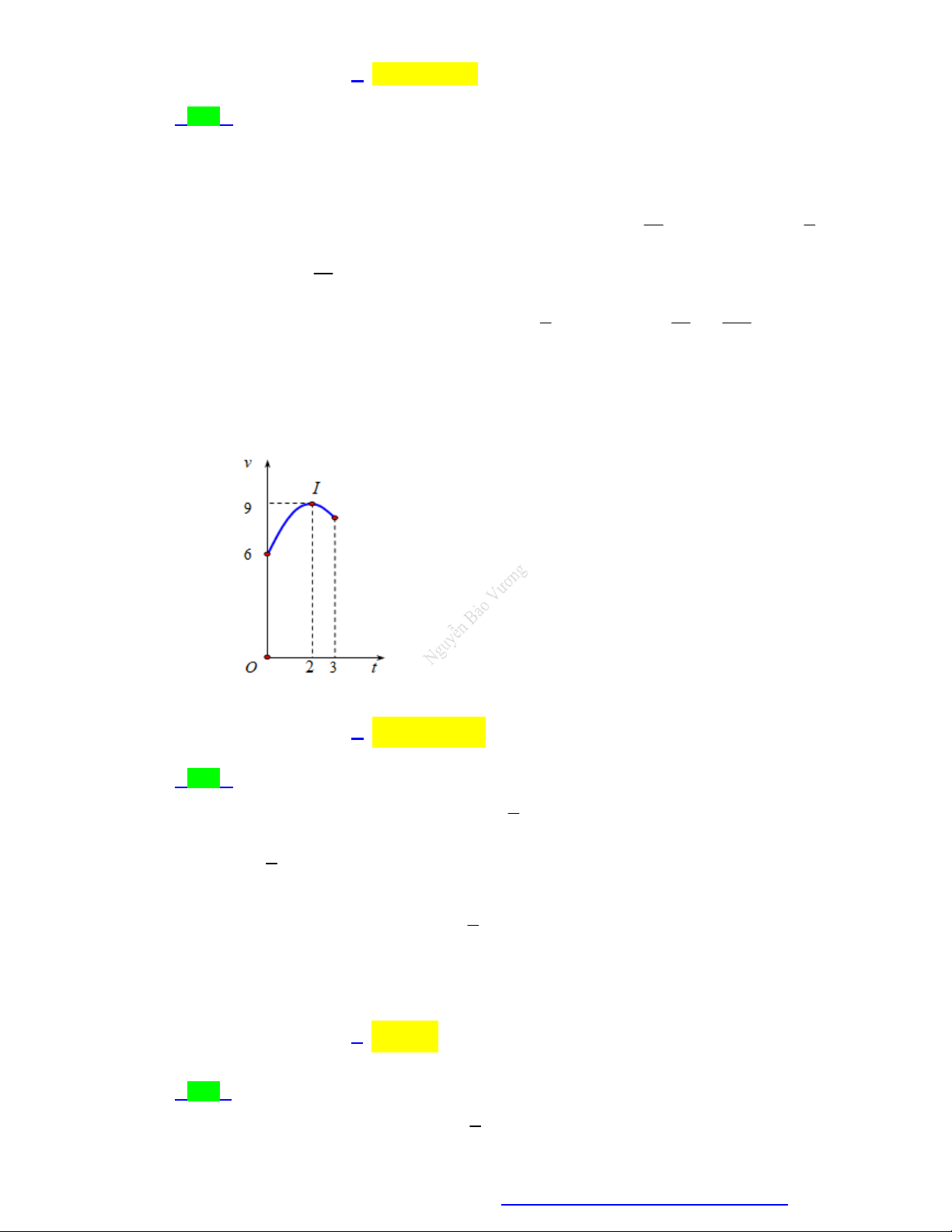
Câu 57. Một vật chuyển động trong 3 giờ với vận tốc v km/h phụ thuộc thời gian t h có đồ thị là một
phần của đường parabol có đỉnh I 2; 9 và trục đối xứng song song với trục tung như hình bên.
Tính quãng đường s mà vật di chuyển được trong 3 giờ đó.
A. s  26,75 km
B. s  25, 25km
C. s  24, 25 km
D. s  24,75 km 1
Câu 58. Một vật chuyển động theo quy luật s   3 t  2
6t với t (giây) là khoảng thời gian tính từ khi vật 2
đó bắt đầu chuyển động và s m là quãng đường vật di chuyển được trong khoảng thời gian đó.
Hỏi trong khoảng thời gian 6 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt
được bằng bào nhiêu? A. 64 m/s B. 24 m/s C. 18 m/s D. 108 m/s
Câu 59. Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị của vận
tốc như hình bên. Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một
phần của đường parabol có đỉnh I 2; 9 với trục đối xứng song song với trục tung, khoảng thời
gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật di
chuyển được trong 4 giờ đó.
A. s  26, 5 (km) B. s  24 (km)
C. s  28, 5 (km) D. s  27 (km)
Câu 60. Một vật chuyển động trong 4 giờ với vận tốc v (km/ h) phụ thuộc thời gian t (h) có đồ thị là một
phần của đường parabol có đỉnh I (1;3) và trục đối xứng song song với trục tung như hình bên.
Tính quãng đường s mà vật di chuyển được trong 4 giờ kể từ lúc xuất phát. 50 64 A. s  (km).
B. s  10 (km).
C. s  20 (km). D. s  (km). 3 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 61. Một chuyển động trong 4 giờ với vận tốc v ( km/h) phụ thuộc thời gian t ( h ) có đồ thị là một
phần của đường parabol có đỉnh I 1; 
1 và trục đối xứng song song với trục tung như hình bên.
Tính quãng đường s mà vật đi được trong 4 giờ kể từ lúc xuất phát. 40 46 A. s   km  .
B. s  8 km  . C. s   km  .
D. s  6  km  . 3 3
------------------------- HẾT -------------------------
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 15 ỨNG DỤNG TÍCH PHÂN
A. ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG (
 C ) : y f (x)  b 1 
Hình phẳng (H ) giới hạn bởi (
 C ) : y g(x)
thì diện tích là S f(x) ( g x) dx .  2
x  a, x b (a b) a  (
 C ) : y f (x)  b 1 
Hình phẳng (H ) giới hạn bởi (
 C ) :Ox : y  0
thì diện tích là S
f (x) dx .  2
x  a, x b (a b) a  Sa . b elip 2 2 x y (E) :   1 2 2 a b
Hình thức đề thường hay cho
Hình thức 1: Không cho hình vẽ, cho dạng (H ) : {y f (x), y g(x), x  ,
a x b (a b)} b casio 
f (x)  g(x) dx  
kết quả, so sánh với bốn đáp án. a
Hình thức 2: Không cho hình vẽ, cho dạng (H ) : {y f (x), y g(x)} xi
Giải f (x)  g(x) tìm nghiệm x ,...,x , với x nhỏ nhất, x lớn nhất casio  
f (x)  g(x) dx. 1 i 1 i x1
Hình thức 3: Cho hình vẽ, sẽ giải phương trình tìm tọa độ giao điểm (nếu chưa cho trên hình), chia từng
diện tích nhỏ, xổ hình từ trên xuống, ghi công thức và bấm máy tính.
Hình thức 4: Cho ba hàm trở lên, chẳng hạn y f (x), y g(x), y h(x) ta nên vẽ hình. Câu 1.
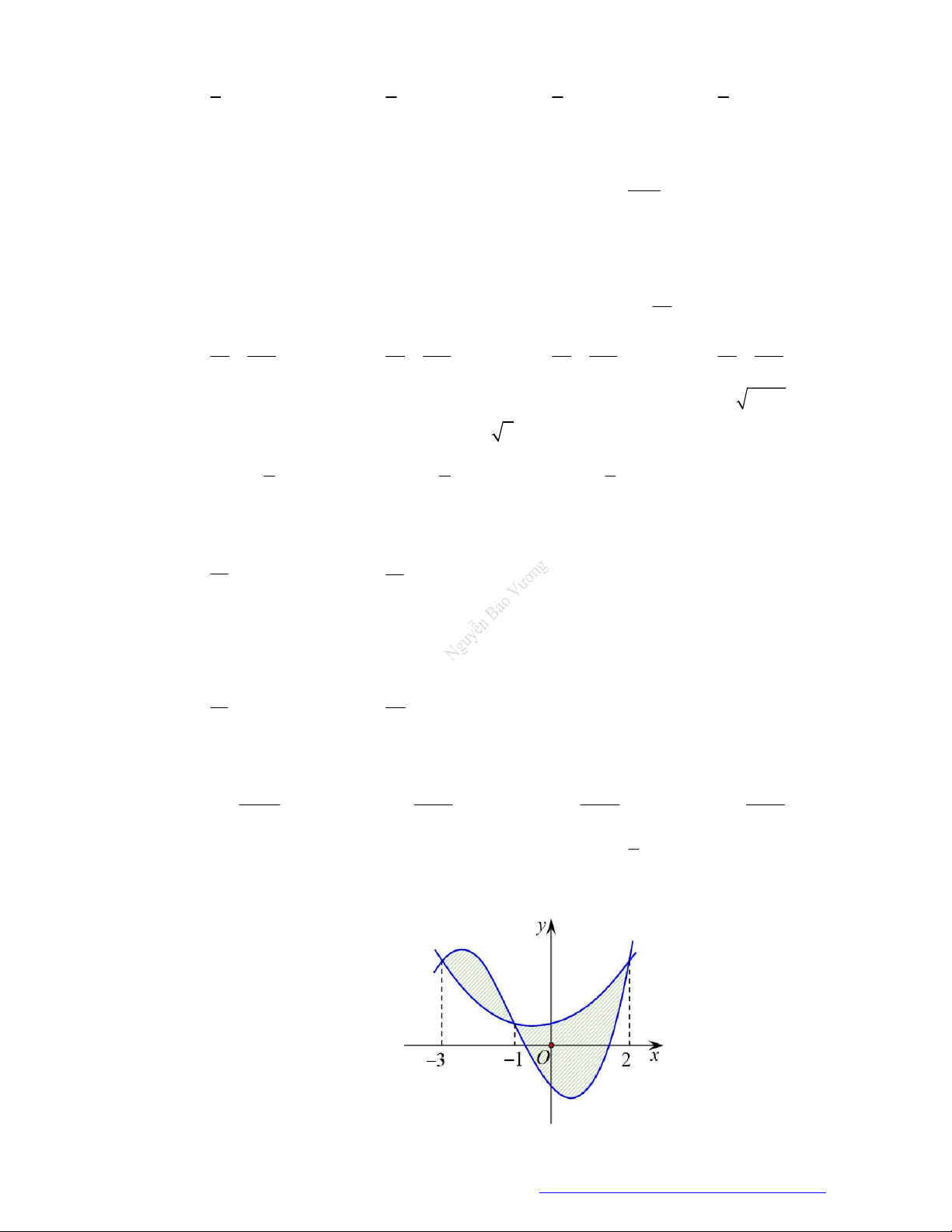
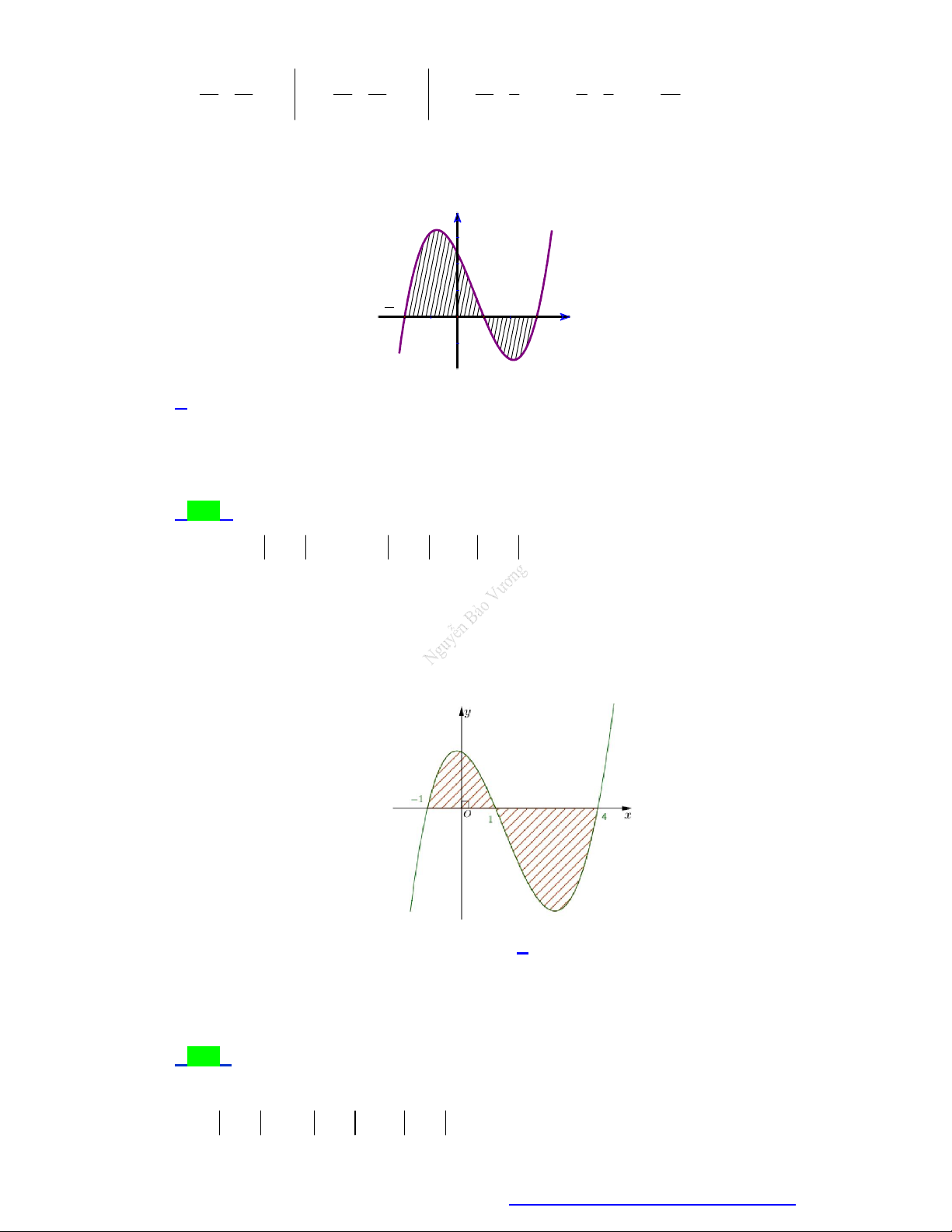
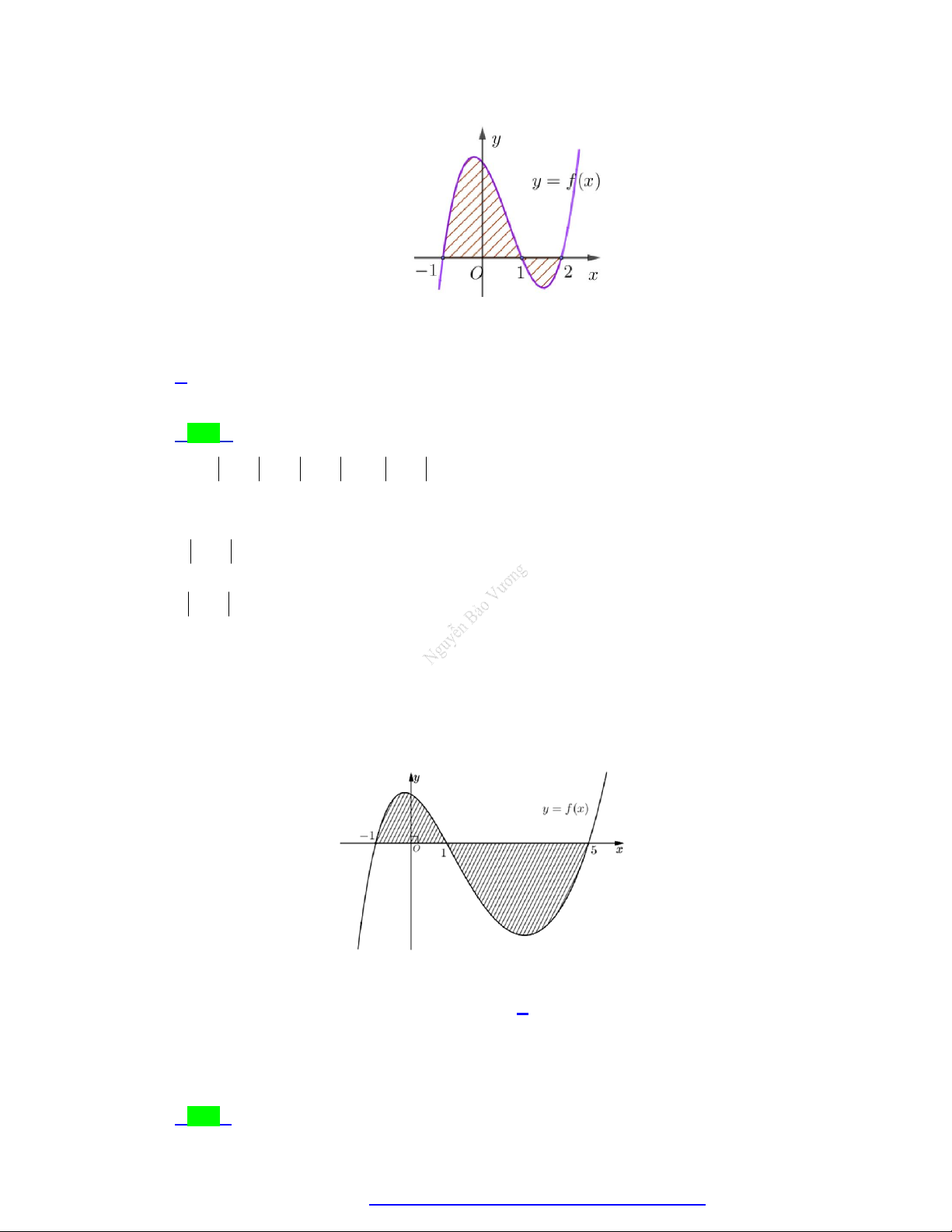
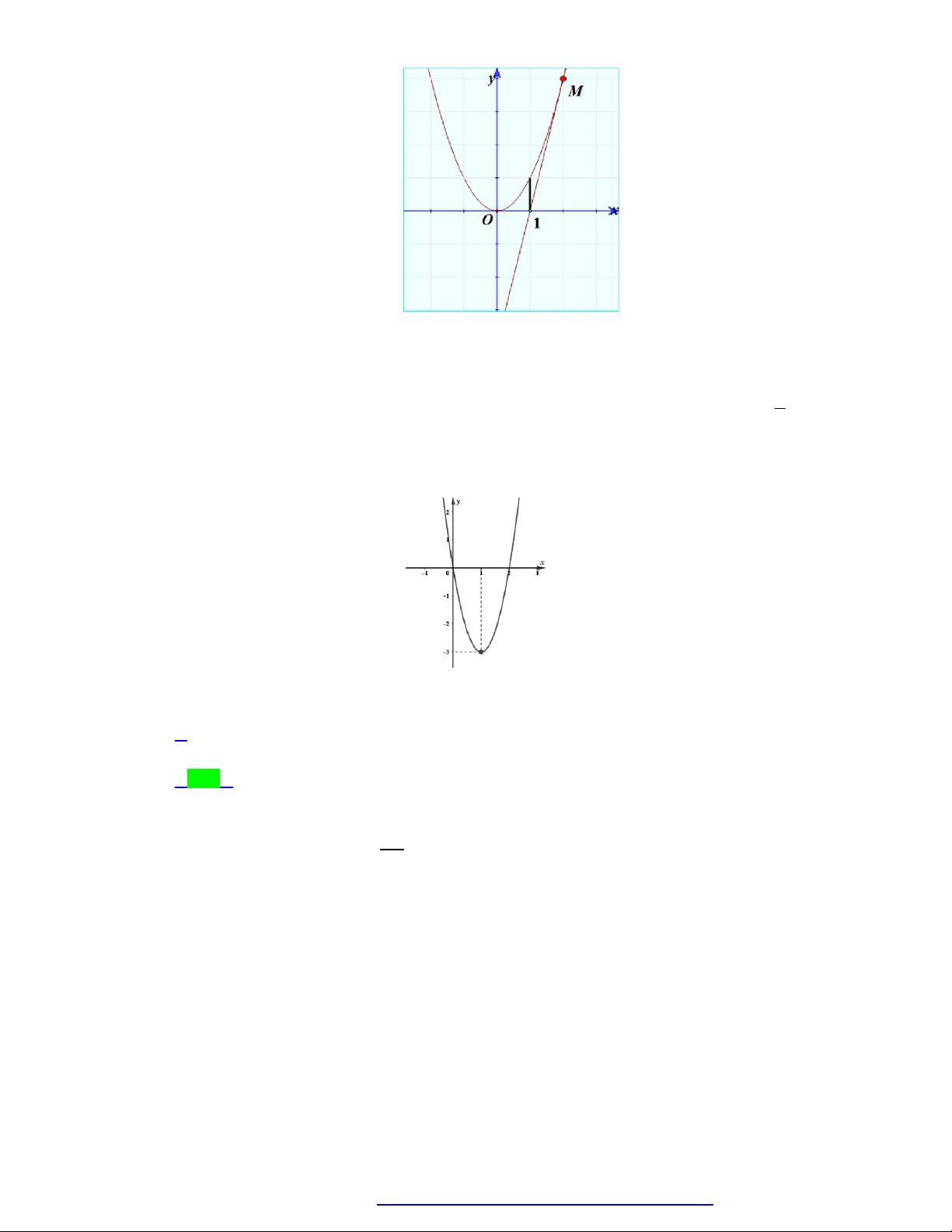
Diện tích hình phẳng được gạch chéo trong hình bên bằng 2 2 A.   2
2x  2x  4 dx . B.   2
2x  2x  4dx . 1  1 2 2 C.   2 2
x  2x  4dx . D.   2
2x  2x  4dx . 1  1  Lời giải Chọn A
Dựa và hình vẽ ta có diện tích hình phẳng được gạch chéo trong hình bên là:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 2 
 x  2  x  2x  2 2 2 2  dx    2 2
x  2x  4d . x 1    1  Câu 2.
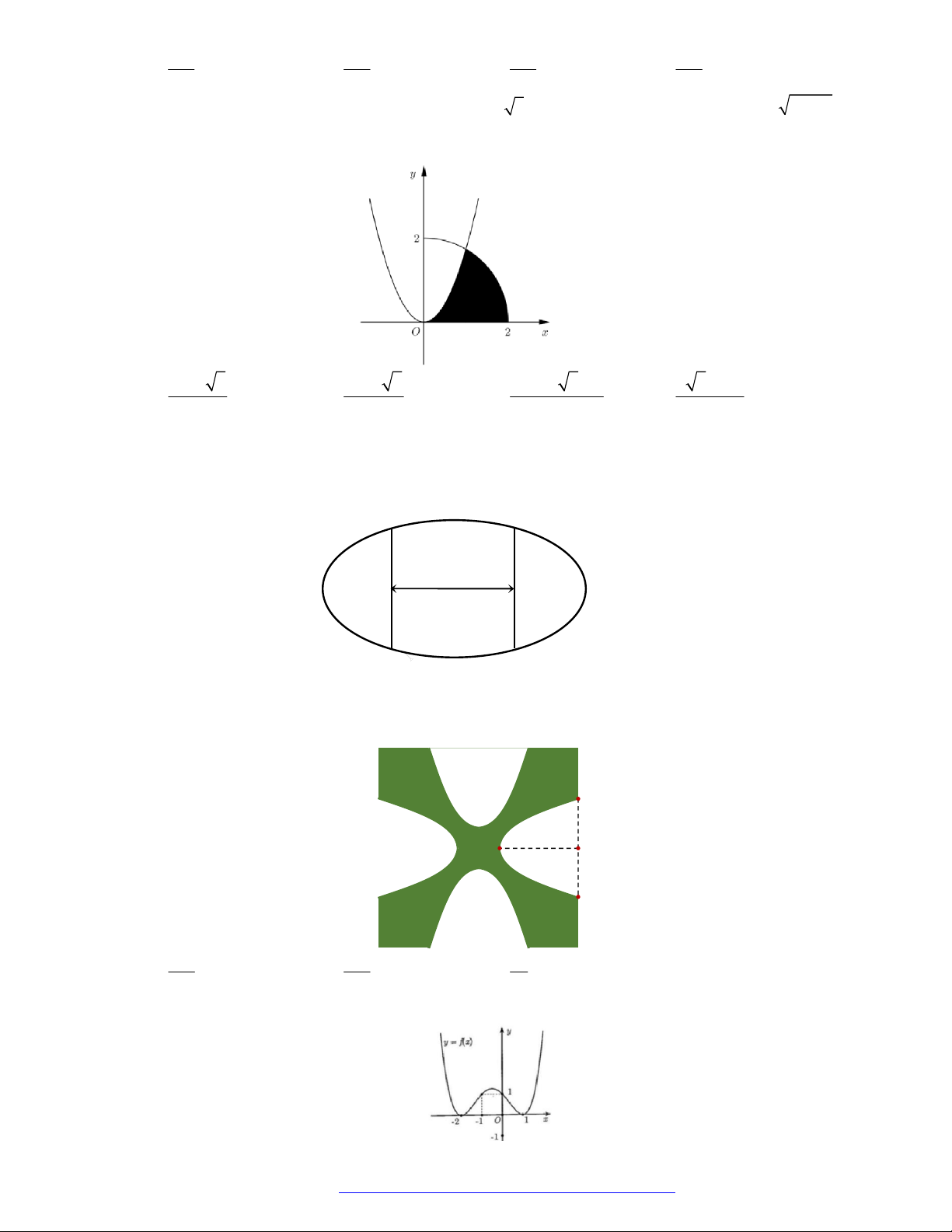
Diện tích S của hình phẳng giới hạn bởi các đường 2
y  2 x , y  1
 , x  0 và x  1 được tính
bởi công thức nào sau đây? 1 1 A. S    2 2x   
1 dx . B. S   2 2x    1 dx . 0 0 1 1 2 C. S   2 2x   
1 dx . D. S   2 2x    1 dx . 0 0 Lời giải Chọn D 1 1
Diện tích hình phẳng cần tìm là 2 S
2x 1 dx   2 2x     1 dx do 2 2x 1  0 x  0;  1 . 0 0 Câu 3.
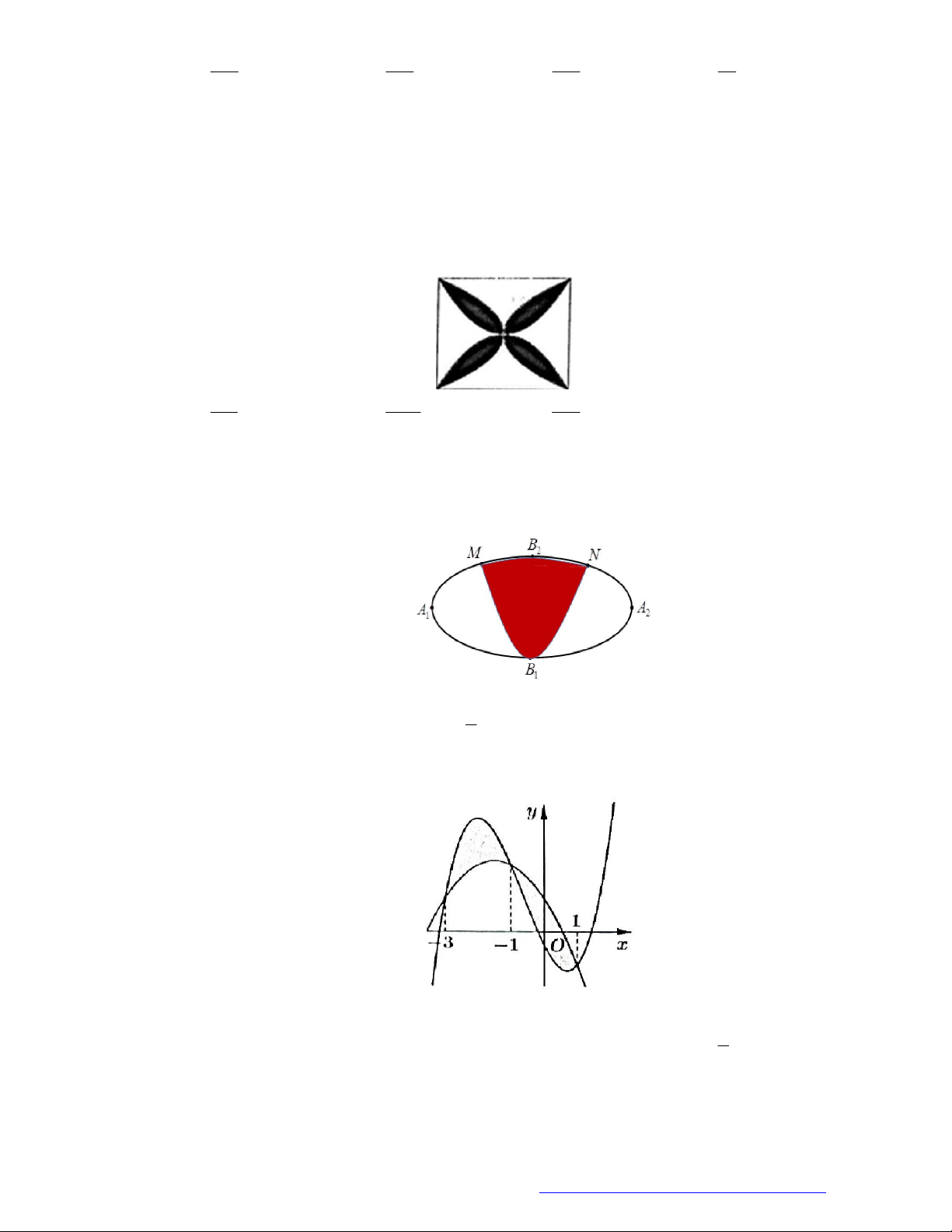
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? y 2
y x  2x 1 2 1  O x 2
y  x  3 2 2 A.   2
2x  2x  4dx . B. 2  2d  x x . 1 1 2 2 C. 2  2 d  x x . D.   2 2
x  2x  4dx . 1  1 Lời giải Chọn D.
Ta thấy: x  1  ; 2: 2 2
x  3  x  2x 1 nên 2 2 S     2 x  3   2 x  2x   1  dx    2 2
x  2x  4dx .   1 1 Câu 4.
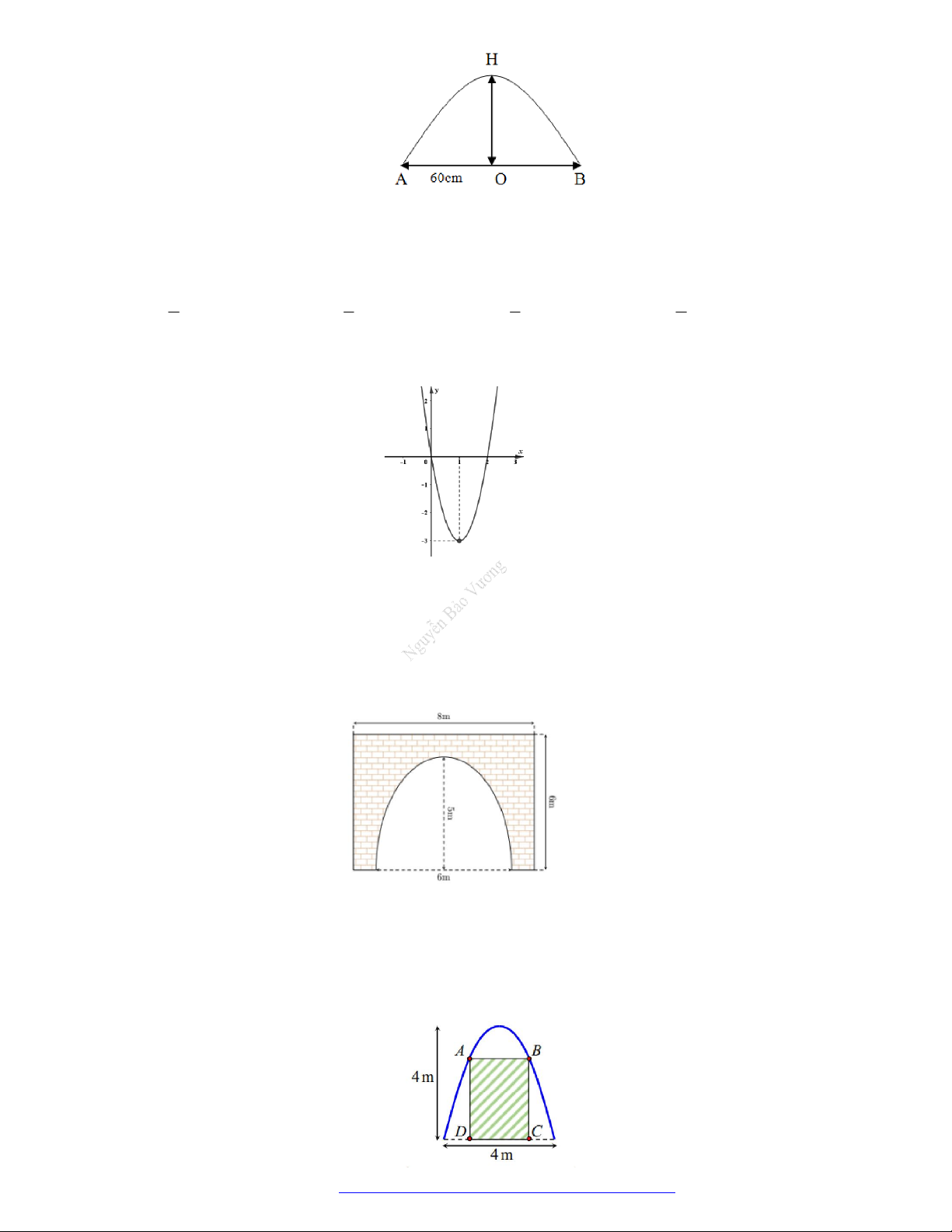
Gọi S là diện tích hình phẳng giới hạn bởi các đường ex y
, y  0 , x  0 , x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A. 2   e x S dx  . B.  ex S dx  . C.   ex S dx  . D. 2  e x S dx  . 0 0 0 0 Lời giải
Diện tích hình phẳng giới hạn bởi các đường ex y
, y  0 , x  0 , x  2 được tính theo công 2 2 thức  ex d  ex S x dx   . 0 0 Câu 5.
Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số y f x , trục hoành và hai đường
thẳng x a , x b a b (phần tô đậm trong hình vẽ) tính theo công thức nào dưới đây ?
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 c b b
A. S   f x dx f x dx   . B. S
f x dx  . a c a c b b C. S
f x dx f x dx   . D. S
f x dx  . a c a Lời giải Chọn A b c b c b Ta có: S
f x dx
f x dx
f x dx   f x dx f x dx      . a a c a c Câu 6.
Cho hàm số y f x liên tục trên  và có đồ thì như hình vẽ bên. Hình phẳng được đánh dấu
trong hình vẽ bên có diện tích là b c b b A.
f x dx f x dx   . B.
f x dx f x dx   . a b a c b c b c C.
f x dx f x dx   .
D. f x dx f x dx   . a b a b Lời giải Chọn C
Diện tích hình phẳng: c b c b c S
f x dx
f x dx
f x dx
f x dx f x dx      . a a b a b Câu 7.
Diện tích của hình phẳng (H ) giới hạn bởi đồ thị của hàm số y f (x) , trục hoành và hai
đường thẳng x a , x b (a b) (phần tô đậm trong hình vẽ) tính theo công thức b c b A. S f (x)dx. B. S
f (x)dx f (x)dx   . a a c b c b C. S f (x)dx.
D. S   f (x)dx f (x)dx   . a a c Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn D b c b Ta có: S
f (x)dx
f (x)dx f (x)dx    . a a c
Dựa vào đồ thị ta thấy trên đoạn  ;
a c có f (x)  0; trên  ;
c b có f (x)  0 . c b
Suy ra S   f (x)dx f (x)dx   . a c Câu 8.
Cho hàm số y f x 4 2
x 5x  4 có đồ thị như hình vẽ bên. Gọi S là diện tích hình phẳng
giới hạn bởi đồ thị hàm số y f x và trục hoành (miền phẳng được tô đậm trên hình vẽ).
Mệnh đề nào sau đây sai? 2 2 A. S
f x dx  . B. S  2
f x dx  . 2  0 1 2 2 C. S  2
f x dx  2
f x dx   . D. S  2
f x dx  . 0 1 0 Lời giải Chọn D
Hình phẳng cần tính diện tích nhận trục tung làm trục đối xứng. x  2    x  1 Xét PTHĐ giao điểm: 4 2
x 5x  4  0   x  1   x  2 
Khi đó diện tích hình phẳng cần tìm là: 2 2 1 2 S
f x dx  2 f x dx  2
f x dx  2
f x dx     2 0 0 1 Câu 9.
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x 37 9 81 A. B. C. D. 13 12 4 12 Lời giải Chọn A x  0 
Phương trình hoành độ giao điểm 3 2 3 2
x x x x x x  2x  0  x  1  x  2  
Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x là: 1 0 1 3 S x x    2
x x dx    3 2
x x  2xdx   3 2
x x  2xdx 2  2  0
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 0 1 4 3 4 3  x x   x x   16 8   1 1  37 2 2    x    x     4   1          . 4 3 4 3      4 3   4 3  12 2  0
Câu 10. Cho hàm số f x liên tục trên .
 Gọi S là diện tích hình phẳng giới hạn bởi cá đường
y f x, y  0, x  2
 và x  3 (như hình vẽ). Mệnh đề nào dưới đây đúng? y y=f(x) x 2 O 1 3 1 3 1 3 A. S
f x dx f x d .   x B. S  
f x dx f x d .   x 2 1 2 1 1 3 1 3 C. S
f x dx f x d .   x D. S  
f x dx f x d .   x 2 1 2 1 Lời giải Chọn A 3 1 3 Ta có S
f x dx S
f x dx f x d .    x 2 2 1 1 3
Do f x  0 với x  2  ; 
1 và f x  0 với x 1;  3 nên S
f x dx f x d .   x 2 1
Câu 11. Cho hàm số f x liên tục trên  . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 và x  4 (như hình vẽ bên). Mệnh đề nào dưới đây đúng? 1 4 1 4 A. S  
f x dx  f x dx   . B. S
f x dx  f x dx   . 1 1 1  1 1 4 1 4 C. S
f xdx  f xdx   . D. S  
f x dx  f xdx   . 1  1 1  1 Lời giải Chọn B
Ta có: hàm số f (x)  0 x   1  
;1 ; f (x)  0 x  1;4 , nên: 4 1 4 1 4 S
f x dx 
f x dx 
f x dx 
f x dx  f x dx      . Chọn đáp án B. 1  1  1 1  1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 12. Cho hàm số f x liên tục trên  . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 , x  2 (như hình vẽ bên). Mệnh đề nào dưới đây đúng? 1 2 1 2 A. S  
f x dx  f x dx   . B. S  
f x dx+ f x dx   . 1  1 1  1 1 2 1 2 C. S
f x dx  f x dx   . D. S
f x dx + f x dx   . 1 1 1  1 Lời giải Chọn C 2 1 2 S f xdx= f xdx  f xdx    1 1  1
Nhìn hình ta thấy hàm số f x liên tục và nhận giá trị không âm trên đoạn  1  ;  1 nên 1 1 f xdx  f xdx  
; hàm số f x liên tục và nhận giá trị âm trên đoạn 1;  2 nên 1 1  2 2
f xdx   f xdx   1 1 1 2 Vậy S
f x dx  f x dx   1 1
Câu 13. Cho hàm số y f x liên tục trên .
 Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 và x  5 (như hình vẽ bên).
Mệnh đề nào sau đây đúng? 1 5 1 5 A. S
f (x)dx f (x)dx   . B. S
f (x)dx f (x)dx   . 1 1 1 1 1 5 1 5 C. S  
f (x)dx f (x)dx   . D. S  
f (x)dx f (x)dx   . 1  1 1  1 Lời giải Chọn B
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 5 1 5 Ta có: S
f (x) dx
f x dx
f x dx f x dx     . 1  1 1 1
Câu 14. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x và đường thẳng y x là: 1 1 1 1 A. . B. . C. . D. . 3 4 2 6 Lời giải Chọn D
Giao điểm của đồ thị hàm số 2
y x và đường thẳng y x có hoành độ là nghiệm của phương x  0 trình : 2 x x   . x  1 
Suy ra diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x và đường thẳng y x là 1 3 2 1 1  x x  1 2 x x dx     2
x xdx      . 0 0 3 2 6   0
Câu 15. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2
y  x  2x 1, 2
y  2x  4x 1 là A. 8 . B. 5 . C. 4 . D. 10 . Lời giải Chọn C
Phương trình hoành độ giao điểm là 2 2 2
x  2x 1  2x  4x 1  3x  6x  0 x  0   x  2  2
Diện tích hính phẳng là S     2
2x  4x   1   2
x  2x   1  dx   0 2 2   2
3x  6xdx   3 2
x  3x   4 . 0 0 x 1
Câu 16. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y
và các trục tọa độ. Khi đó x 1
giá trị của S bằng
A. S  ln 2 1 .
B. S  2 ln 2 1.
C. S  2 ln 2 1.
D. S  ln 2 1. Lời giải Chọn B x 1
Phương trình hoành độ giao điểm của đồ thị hàm số và trục tung là  0  x  1. x 1 x 1
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y
và các trục tọa độ. Nên ta x 1 1 1 1 x 1 x 1  2 1  có S  dx  dx  1 dx     
x  2ln x 1  2ln 2 1. x 1 x 1  x 1 0 0 0 0
Câu 17. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số 2
y  3x x  4 . Gọi S và S lần lượt là 1 2 S
diện tích phần hình (H ) nằm bên trái và bên phải trục tung. Tính tỷ số 1 . S2 S 208 S 54 S 135 S 135 A. 1  . B. 1  . C. 1  . D. 1  . S 343 S 343 S 343 S 208 2 2 2 2 Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 0 0 2 x 5 Ta có: 2 3 S
(3x x  4)dx  (x   4x)  1  . 2 2 1 1 4 4 3 2 4 x 104 2 3 S  ( 3
x x  4)dx  (x   4x)  2  . 2 27 0 0 S 135  1  . S 208 2
Câu 18. Cho S là diện tích của hình phẳng giới hạn bởi đồ thị C  của hàm số 2
y x 1 x , trục
hoành, trục tung và đường thẳng x  1. Biết S a 2  b  ,
a b . Tính a  . b 1 1 1
A. a b .
B. a b .
C. a b .
D. a b  0 . 6 2 3 Lời giải Chọn C
Ta có trục tung có phương trình là: x  0 .
Diện tích của hình phẳng giới hạn bởi đồ thị C  của hàm số 2
y x 1 x , trục hoành, trục 1
tung và đường thẳng x  1 là 2
S x 1 x dx  . 0 Mặt khác 3 1 1 1  x 1 1 1 2 2 1 2  2 1 1 2 2 2
S x 1 x dx
1 x d 1 x       2 1 x  2 1 x      2 2 3 0 3 0 3 3 0 0 2 2 1
Biết S a 2  b  ,
a b  nên a  và b    3 3 1
Vậy a b   3
Câu 19. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x , trục hoành và hai đường thẳng x  1
 , x  2 biết rằng mỗi đơn vị dài trên các trục tọa độ là 2 cm. 15 17 A.  2 cm  . B.  2 cm  . C.  2 17 cm  . D.  2 15 cm  . 4 4 Lời giải Chọn C
Mỗi đơn vị diện tích trên mặt phẳng tọa độ là   2 2.2 4 cm .
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2 0 2    1 
Vậy diện tích hình phẳng cần tìm là 3 3 3
4. x dx  4.  x dx x dx  4.  4  17         2 cm  .  4  1   1 0  3  7  4x
khi 0  x  1
Câu 20. Cho hàm số f x  
. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm 2 4  x khi x  1 
số f x và các đường thẳng x  0, x  3, y  0 . 16 20 . . A. 3 B. 3 C. 10. D. 9. Lời giải Chọn C
y f x -Vẽ đồ thị hàm số . y 3 y = f(x) 2 3 O 1 x - 5
-Khi đó, diện tích hình phẳng cần tìm là 2 3 1 2 3 3 3    x   x S
7  4x dx  4  x dx  4  x dx  7x x 1 3 2 2 4  4x   4x   10     . 0 3 3 0 1 2     1 2
Câu 21. Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số y x ln x , trục Ox và đường thẳng x e . 2 e  3 2 e 1 2 e 1 2 e 1 A. S  . B. S  . C. S  . D. S  . 4 2 2 4 Lời giải Chọn D
Phương trình hoành độ giao điểm của hàm số y x ln x và trục Ox : x ln x  0  x  1 . e e
Diện tích hình phẳng cần tìm là: S
x ln x dx x ln xdx   . 1 1  1 du dx u  ln x    x Đặt    . 2 dv xdxxv    2 e e 2 e 2 2 2 2 2 x x e x ee 1  e 1  S  ln x dx          . 2 2 2 4 2 4 4 4 1 1 1  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 1
Câu 22. Cho hai hàm số f x 3 2
ax bx cx 1 và g x 2
dx ex   , a , b , c d,e   . Biết rằng đồ 2
thị của hàm số y f (x) và y g(x) cắt nhau tại ba điểm có hoành độ lần lượt 3; 1; 2 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 253 125 253 125 A. B. C. D. 12 12 48 48 Lời giải Chọn C
Vì phương trình f ( x)  g ( x)  0 có 3 nghiệm 3; 1; 2 nên
f x  gx  ax   3  x   2  x   1 . 3 1
So sánh hệ số tự do ta được 6a    a  . Do đó 2 4 2 1 253 S
x  3 x  
1  x  2 dx   . 4 48 3
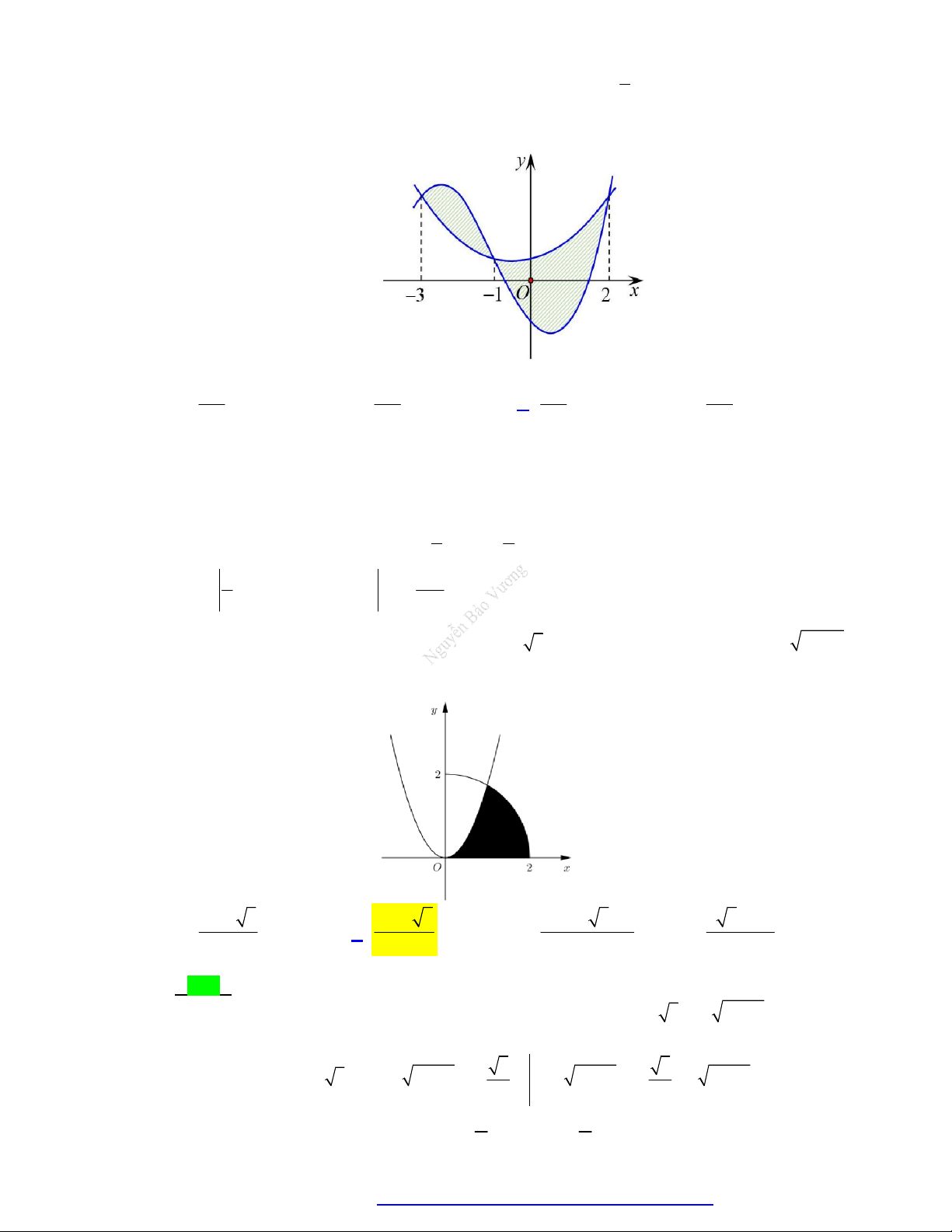
Câu 23. Cho H là hình phẳng giới hạn bởi parabol 2
y  3x , cung tròn có phương trình 2 y  4  x
(với 0  x  2 ) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của H bằng 4  3 4  3 4  2 3  3 5 3  2 A. B. C. D. 12 6 6 3 Lời giải Chọn B
Phương trình hoành độ giao điểm giữa parabol và cung tròn ta được 2 2
3x  4  x x 1 với 0  x  2 1 1 2 2 2 3 3 Ta có diện tích 2 2 3 2 2 S  3x dx  4  x dx x  4  x dx   4      x dx 3 3 0 1 1 1 0  
Đặt: x  2 sin t  dx  2 cos tdt; x  1  t
; x  2  t  6 2
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020  2 3  1  4  3  S   2 t  sin 2t    3  2   6 6
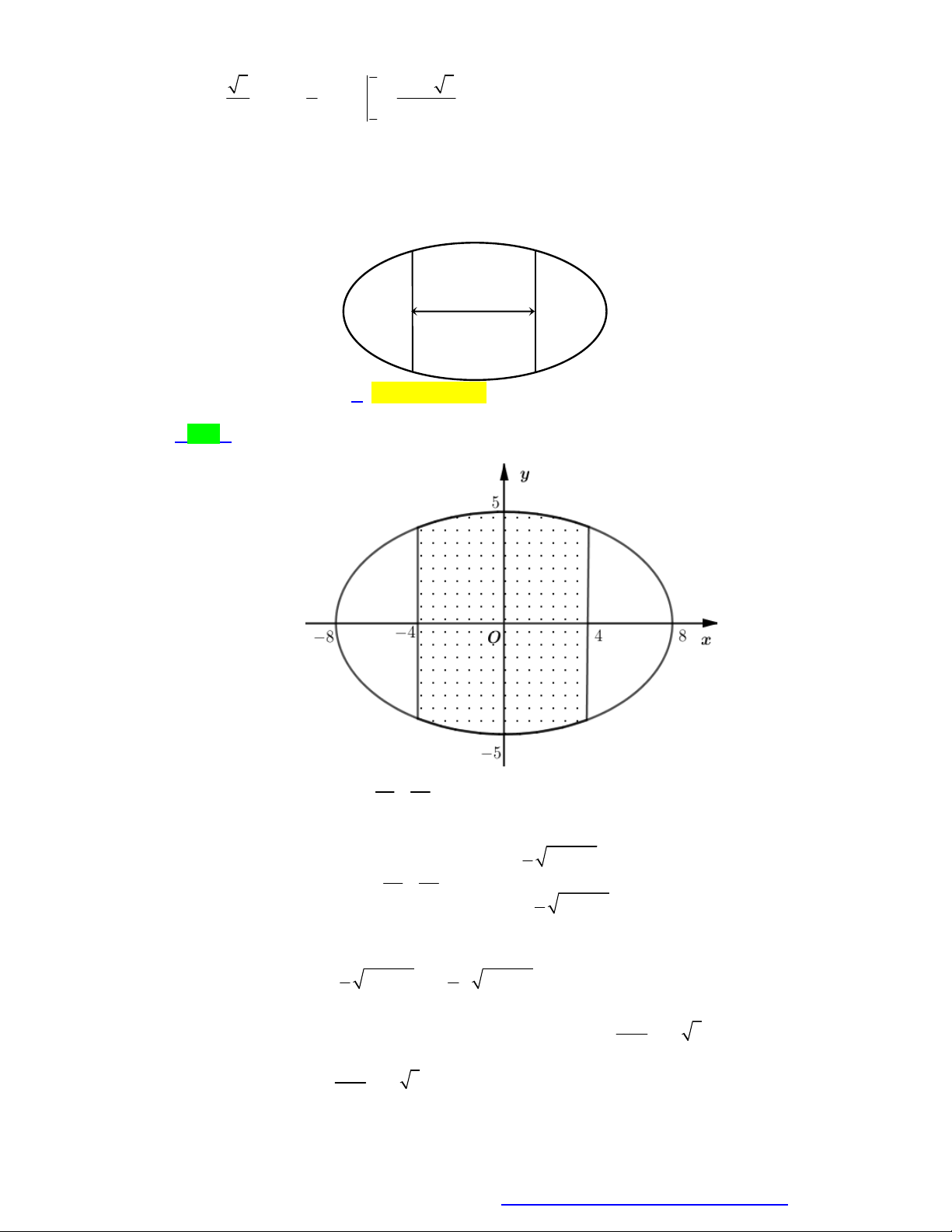
Câu 24. Ông An có một mảnh vườn hình Elip có độ dài trục lớn bằng 16m và độ dài trục bé bằng10m .
Ông muốn trồng hoa trên một dải đất rộng 8m và nhận trục bé của elip làm trục đối xứng (như
hình vẽ). Biết kinh phí để trồng hoa là 100.000 đồng/ 2
1m . Hỏi ông An cần bao nhiêu tiền để
trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn.) 8m A. 7.862.000 đồng B. 7.653.000 đồng C. 7.128.000 đồng
D. 7.826.000 đồng Lời giải Chọn B
Chọn hệ trục tọa độ như hình vẽ 2 2 x y
Giả sử elip có phương trình   1. 2 2 a b
Từ giả thiết ta có 2a 16  a  8 và 2b  10  b  5  5 2 y  64  x (E ) 2 2 1 x y  8
Vậy phương trình của elip là   1   64 25 5  2 y   64  x (E ) 2  8
Khi đó diện tích dải vườn được giới hạn bởi các đường (E ); (E ); x  4
 ; x  4 và diện tích 1 2 4 4 5 5 của dải vườn là 2 2 S  2 64  x dx  64  x dx   8 2 4  0 40
Tính tích phân này bằng phép đổi biến x  8sin t , ta được S   20 3 3  40 
Khi đó số tiền là T
 20 3 .100000  7652891,82  7.653.000   .  3 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 25. Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng 10 cm bằng
cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết AB  5cm ,
OH  4cm . Tính diện tích bề mặt hoa văn đó. A O H B 160 140 14 A. 2 cm . B. 2 cm . C. 2 cm . D. 2 50 cm . 3 3 3 Lời giải Chọn B Đưa parabol  P 2
: y ax bx c a  0 vào hệ trục Oxy .  5 
Parabol đi qua gốc tọa độ và các điểm ; 4 
 , 5;0 (do AB  5cm , OH  4 cm ).  2   16 c  0 a     25  25 5  16 16 Suy ra  a
b c  4  c  0   P 2 : y   x x . 4 2   25 5 16
25a  5b c  0  b    5 16 16
Diện tích hình phẳng giới hạn bởi  P 2 : y   x
x , trục hoành và các đường thẳng 25 5 5  16 16  40
x  0 , x  5 là 2 S   x x dx    .  25 5  3 0 160
Tổng diện tích phần bị khoét đi là 2 S  4S  cm . 1 3
Diện tích của hình vuông là 2 S  100cm . hv 160 140
Vậy diện tích bề mặt hoa văn là 2
S S S  100   cm . 2 hv 1 3 3
Câu 26. Cho hàm số y f x là hàm số đa thức bậc 4 và có đồ thị như hình vẽ
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Hình phẳng giới hạn bởi đồ thị hàm số y f x và y f  x có diện tích là 127 127 107 13 A. . B. . C. . D. . 40 10 5 5 Lời giải Chọn C
Vì hàm số y f x là hàm số đa thức bậc 4 và có đồ thị như hình vẽ nên hàm số có dạng:
f x  a x  2  x  2 2 1 , a  0 . 1 1 2 2 Mà f   1  1  a
. Vậy f x   x  2  x   1 . 4 4 1 1  f x  
2 x  2 x  2 1  2 x   1 . x  22   
x  2 x   1 2x   1 . 4   2  x  1  x  1 
Xét phương trình f x  f  x   x  2 x   1  2
x  3x  4  0   .  x  2   x  4  1
f x  f  x   x  2 x   1  2
x  3x  4 . 4
Vậy diện tích cần tìm là: 4 S
f x  f  x dx  2 1  1 4 107
   f x  f  xdx    f x  f xdx   f x  f xdx  . 5 2  1  1
Câu 27. Cho parabol  P có phương trình 2
y x và đường thẳng d đi qua điểm A1;3 . Giả sử khi
đường thẳng d có hệ số góc k thì diện tích hình phẳng giới hạn bởi parabol  P và đường
thẳng d nhỏ nhất. Giá trị thực của k thuộc khoảng nào sau đây?
A. ; 3 . B. 3;  . C. 3; 0 . D. 0;3 . Lời giải Chọn D
Phương trình của d là: y k x   1  3 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489
Hoành độ giao điểm của d và  P là nghiệm của phương trình: 2
x kx k  3  0   1 .
Do k  k    k  2 2 4 3 2
 8  0, k   nên  
1 luôn có hai nghiệm phân biệt x , x x x . 1 2  1 2 
Theo định lý Vi-ét ta có: x x k, x .x k  3 . 1 2 1 2
Diện tích miền phẳng D giới hạn bởi d và  P là: 2 x x2 3 2   S    x x 2
x kx k  3 dx    kkx  3x   3 2   1 x 1 x 3 2 3 2  x x   x x  2 2 1 1    kkx  3x    kkx  3x  2 2   1 1  3 2 3 2     3 3 x x k 1 2    2 2 x xk x x  3 x x 1 2   1 2   1 2  3 2 2 2
x x x x k
  x x  1 1 2 2  x xk  3 1 2   1 2   3 2     x x x x k    1 2 2 2
  x x  1 2    k  3 1 2 3 2     2
k  k  3 2 k    x x   k  3 1 2    3 2   1 
x x  2 k  4k 12 2 1  6 Suy ra 3 2 1 1 128 S
 x x 2 4x x .k 4k 12 k 22 2 2 8          . 1 2 1 2 36   36   9 8 2  S  (do S  0 ) 3
Đẳng thức xảy ra khi và chỉ khi k  2 .
Câu 28. Một viên gạch hoa hình vuông cạnh 80cm . Người thiết kế đã sử dụng 4 đường parabol có
chung đỉnh tại tâm của viên gạch để tạo ra 4 cánh hoa (được tô màu sẫm như hình vẽ bên).
Diện tích mỗi cánh hoa của viên gạch bằng 800 1600 400 A.  2 cm . B.  2 cm . C.  2 cm . D.  2 250 cm . 3 3 3 Lời giải Chọn B
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Ký hiệu diện tích một cánh hoa, diện tích một hình parabol,diện tích hình vuông lần lượt là 4S S
S , S , S . Ta có: P hv S  . H P hv H 4
Chọn hệ trục Oxy như hình vẽ, sao cho parabol có đỉnh O 0;0 và đi qua điểm A40; 40 1 Khi đó  P 2 : y x . 40
Diện tích parabol chính là diện tích miền hình phẳng giới hạn bởi các đường
P, y  40, x  4  0, x  40 . 6400 40 4.  80.80  1  6400 1600 2  S  40  x dx cm . Do đó: 3 S   cm . H  2  P     2   40  3 4 3 40
Câu 29. Một biển quảng cáo có dạng Elip với bốn đỉnh A , A , B , B . như hình vẽ. Người ta chia Elip 1 2 1 2
bởi parapol có đỉnh B ,trục đối xứng B B và đi qua các điểm M , N .Sau đó sơn phần tô đậm 1 1 2 với giá 200.000 đồng/ 2
m và trang trí đèn led phần còn lại với giá 500.000 đồng/ 2 m .Hỏi kinh
phí sử dụng gần nhất với giá trị nào dưới đây? Biết A A  4m , B B  2 ,
m MN  2m . 1 2 1 2 A. 2.341.000 đồng. B. 2.057.000 đồng. C. 2.760.000 đồng. D. 1.664.000 đồng. Lời giải Chọn A 2 2 x y Phương trình (E)có dạng:   1. 4 1
Diện tích  E là: S   ab  2 . E  3 
Vì MN  2m nên M 1;  .  2   
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489  3 
Vì Parabol có đỉnh B 0;   1 và đi qua M 1;
 nên  P có phương  2     3  trình: 2 y   1 x 1.  2     3  2 x
Diện tích phần tô đậm giới hạn bởi 2 y  
1 x 1 và y  1  2    4 1 2  x   3  là: 2 S   1   
1 x 1 dx 1   4   2  1     
Vậy kinh phí cần sử dụng là: P S .200000  (S S ).500000  2340000 đồng. 1 E 1 1
Câu 30. Cho hai hàm số 3 2
f (x)  ax bx cx  và 2
g(x)  dx ex 1 (a, b, c, d , e ) . Biết rằng đồ 2
thị hàm số y f (x) và y g (x) cắt nhau tại ba điểm có hoành độ lần lượt là 3; 1;1 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho (miền tô đậm) có diện tích bằng 9 A. 8 B. 5 C. 4 D. 2 Lời giải Chọn C 3 3 2
f (x)  g(x)  ax  (b d )x  (c e)x  2
Do y f (x) & y g(x) cắt nhau tại 3 điểm có hoành độ lần lượt là 3; 1;1 nên ta có:  3  1 27 
a  9(b d )  3(c e)   0 a   2  2    3  3
a  (b d )  (c e)   0  b   d  2 2    3  1 
a  (b d )  (c e)   0 c e   2    2 1 3 1 3 3 2
f (x)  g (x)  x x x  2 2 2 2 Khi đó: 1  1 S
f (x)  g(x)dx  [g(x)  f (x)]dx   3  1  1  1 1    1 3 2
x  3x x  3dx    3 2
x  3x x  3dx  4 2 2 3  1 
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 31. Bạn An cần mua một chiếc gương có đường viền là đường Parabol bậc 2 ( xem hình vẽ). Biết
rằng khoảng cách đoạn AB  60 cm , OH  30 cm . Diện tích của chiếc gương bạn An mua là A.  2 900 cm  . B.  2 1000 cm  . C.  2 1200 cm  . D.  2 1400 cm  . Lời giải Chọn C
Chọn hệ trục tọa độ như hình vẽ. Đường viền chiếc gương là đường Parabol 2
y ax bx c a  0 có đỉnh H 0;30 và đi qua điểm B 30 ; 0 .  c   30 c   30   b  Ta có:   0  b   0 . 2a   1 9
 00a  30b c  0 a     30 1
Diện tích chiếc gương là diện tích hình phẳng giới hạn bởi Parabol 2 y   x  30 và trục 30 hoành. Diện tích chiếc gương là: 30 30 30 1  1   1 2 2 3  S  
x  30 dx  2 
x  30 dx  2  x  30 x  1200        2 cm  . 30  30   90  30 0 0
Câu 32. Cho  H  là hình phẳng giới hạn bởi parabol  P 2
: y x , tiếp tuyến với  P tại điểm M 2; 4
và trục hoành. Tính diện tích của hình phẳng  H  ? 2 8 1 4 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn A  Ta có y   2 x   2x .
Tiếp tuyến d với  P tại điểm M 2; 4 có phương trình là:
y f 2 x  2  4  y  4 x  2  4  y  4x  4.
Giao điểm của d và Ox là A1; 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 Trên đoạn 0; 
1 hình phẳng được giới hạn bởi đồ thị hàm số 2
y x và trục hoành.
Trên đoạn 1; 2 hình phẳng được giới hạn bởi đồ thị hàm số 2
y x và tiếp tuyến d . 1 2 2
Vậy diện tích của hình phẳng  H  được xác định là: 2 S x dx    2
x  4x  4 dx  . 3 0 1 Câu 33. Cho hàm số   3 2
f x ax bx cx d có đồ thị C . Đồ thị của hàm số y f  x được cho
bởi hình vẽ dưới đây
Biết rằng đường thẳng d : y x cắt C tạo thành hai phần hình phẳng có diện tích bằng nhau. Tổng
a b c d bằng A. 1. B. 0 . C. 2 . D. 3 . Lời giải Chọn A
Giả sử f  x 2
mx nx pm  0 và có đồ thị  P như hình vẽ đề bài.  n   1
2m n  0 I 1; 
3 là đỉnh của  P  2m     1 .
m n p  3 
m n p  3  
O 0;0  P  p  0. 2 Từ  
1 và 2 , suy ra m n    f  x 2 3, 6  3x  6 . x
f x  f  xx     2 x x 3 2 d 3 6
dx x  3x C.
f  x  6x  6  điểm uốn I 1;C  2.
I d C  3. Thử lại: 3 2
x  3x  3  x có 3 nghiệm.
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Suy ra f x 3 2
x  3x  3.
Vậy a b c d  1.
Câu 34. Một cái cổng có dạng như hình vẽ, với chiều cao 6m và chiều rộng 8m. Mái vòm của cổng có
hình bán elip với chiều rộng là 6m, điểm cao nhất của mái vòm là 5m (tham khảo hình vẽ).
Người ta muốn lát gạch hoa để trang trí cho cổng với chi phí là 250 000 đồng/m2. Hỏi số tiền
cần chi trả gần nhất với số nào sau đây? A. 6.210.000 . B. 6.110.000 . C. 6.100.000 . D. 6.145.000 . Lời giải Chọn B
Chọn hệ trục tọa độ Oxy như hình vẽ: y 8m D C 5 6m x A O B -3 3
• Diện tích hình chữ nhật ABCD : 2 S  6.8  48 m . 1 5
• Bán đường elip có phương trình: 2 y  9  x 3 5
 Diện tích cổng là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 y  9  x và trục 3 hoành: 3 5 2 2 S
9  x dx  23, 562 m 2  3 3 
• Diện tích phần cần lát gạch hoa: S S S  48  23, 562  24, 438 . 1 2
 Số tiền cần chi trả để lát gạch hoa: T  24, 438.250000  6.109.500 đồng.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 35. Đợt thi đua 26/3 Đoàn trường THPT Nho Quan A có thực hiện một dự án trưng bày trên một
pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu các lớp gửi hình dự thi và
dán lên khu vực hình chữ nhật ABCD , phần còn lại sẽ được trang trí hoa văn cho phù hợp. Chi
phí dán hoa văn là 150.000đ trên 2
1m bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn
trên pano sẽ là bao nhiêu( kết quả làm tròn lấy phần nguyên)?
A. 575.034 đồng.
B. 676.239 đồng.
C. 536.272 đồng.
D. 423.215 đồng. Lời giải Chọn B
Gắn hình Parabol đã cho vào hệ trục tọa độ Oxy như hình vẽ, dễ thấy phương trình của Parabol đã cho là 2 y  x . Đặt tọa độ A 2  ;
a a  với 0  a  2 , ta có B  2
a; a ,C a; 4, D a; 4 .
Dễ thấy diện tích phần Parabol phải trang trí nhỏ nhất khi diện tích hình chữ nhật ABCD lớn nhất với S
AB AD a  2 . 2 . 4  a 2 m . ABCD
Xét f a  a  2
a   f a 2 2 4  8  6a . 2 3 2 3
f a  0  a  
, với điều kiện 0  a  2 nên a  . 3 3 Ta có bảng biến thiên 2 32
Diên tích phần Parabol trưng bày là: 2 S  4.4  x dx  P  . 3 2 32 32 3
Vậy diện tích cần trang trí ít nhất là:  . 3 9  32 32 3 
Chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là:  
.150000  676239 .  3 9   
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
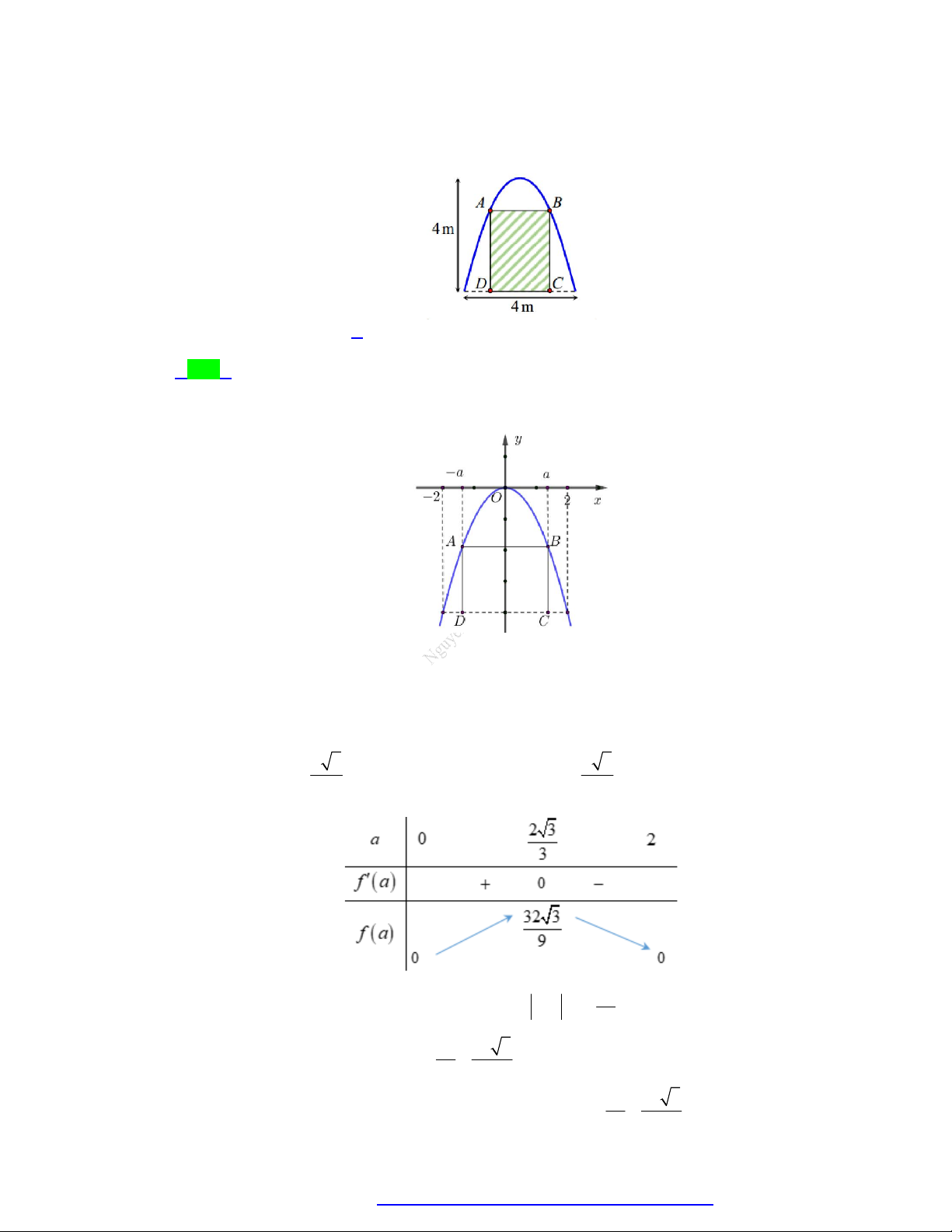
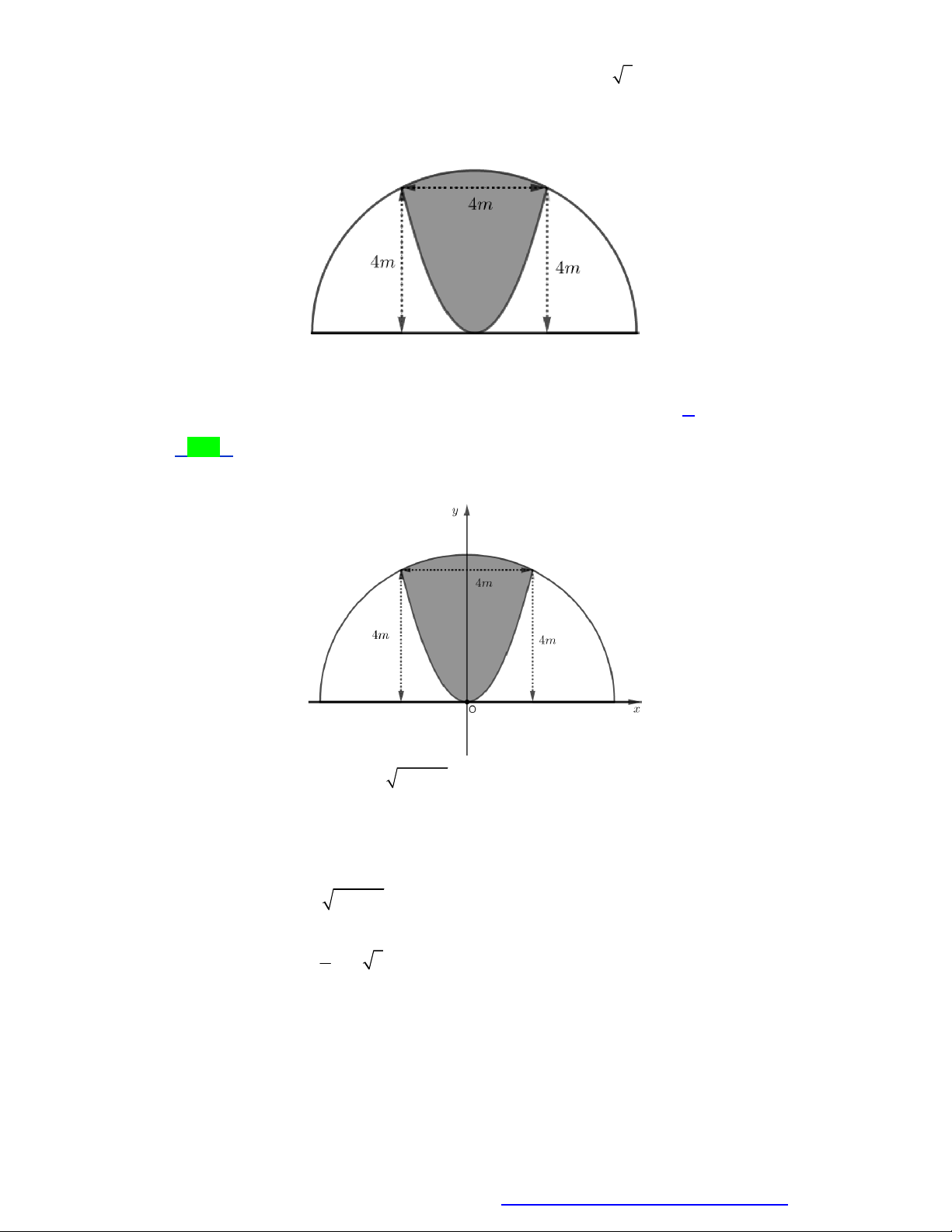
Câu 36. Một khuôn viên có dạng là nửa hình tròn đường kính bằng 4 5 m. Trên đó, người ta thiết kế
một phần để trồng hoa có dạng của một cách hoa hình parabol có đỉnh trùng với tâm nửa hình
tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô đậm) và cách nhau một
khoảng bằng 4 m. Phần còn lại của khuôn viên (phần không tô đậm) dành để trồng cỏ.
Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ là 100.000 đồng 2
/ m Số tiền cần có để trồng
cỏ là bao nhiêu (số tiền được làm tròn đến hàng nghìn)? A. 2 388 000 đồng. B. 3 895 000 đồng. C. 1 194 000 đồng. D. 1 948 000 đồng. Lời giải Chọn D
Chọn hệ trục tọa độ Oxy như hình vẽ.
Phương trình nửa đường tròn trên là 2 y  20  x
Phương trình parabol có đỉnh là gốc tọa độ có dạng 2 y ax
Parabol đi qua điểm 2; 4 suy ra. Vậy phương trình parabol là: 2 y x . 2
Diện tích phần tô đậm: S    2 2
20  x x dx 1  2  2 1
Diện tích nửa đường tròn: S   2 5 10  2 m  2
Diện tích phần trồng cỏ là: S S S . 2 1
Khi đó số tiền để trồng cỏ là: 100000. S 1948000 đồng. 2
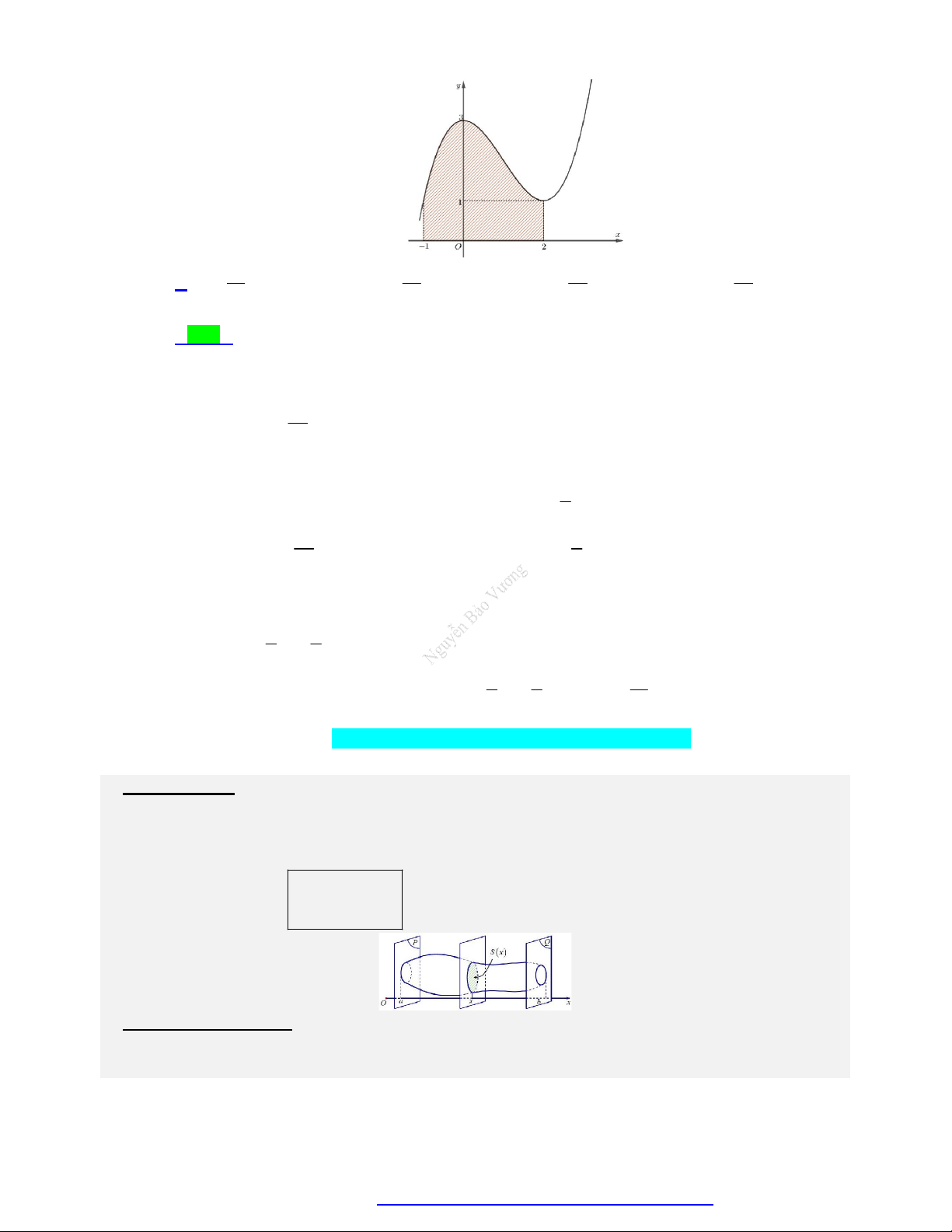
Câu 37. Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số f x 3 2
ax bx c, các
đường thẳng x  1, x  2 và trục hoành (miền gạch chéo cho trong hình vẽ).
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489 51 53 52 50 A. S  . B. S  . C. S  . D. S  . 8 8 8 8 Lời giải Chọn A Ta có: 2
y  3ax  2bxx  0 y 0     2bx    3a
Dựa vào đồ thị, ta thấy đồ thị hàm số đã cho có hai điểm cực trị 0;3 và 2;  1 .  1 a  c  3  2 c  3    2b   3 Khi đó ta có:   2  3
a b  0  b   3a 2  8  a 4b 2     8
a  4b  3  1  c  3    1 3 Vậy f x 3 2  x x  3 . 2 2 2  1 3  51
Khi đó diện tích phần gạch chéo là: 3 2 S x x  3 dx  .    1  2 2  8
B. ỨNG DỤNG TÍCH PHÂN TÍNH THỂ TÍCH
Thể tích vật thể
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và ,
b S(x) là
diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x,
(a x b). Giả sử S(x) là hàm số liên tục trên đoạn [a;b]. Khi đó, thể tích của vật thể B b
được xác định: V S(x)dx .  a
Thể tích khối tròn xoay
a) Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y f (x), trục
hoành và hai đường thẳng x  ,
a x b quanh trục Ox :
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 y
y f (x) (
C) : y f (x) (
Ox) : y 0 bV   f x dx x  2 ( ) a O b x x    a ax   b
b) Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x g(y), trục
hoành và hai đường thẳng y c, y d quanh trục Oy : y d
(C ) : x g(y)  d
(Oy) : x 0 2   V
g(y) dy    y y   c c cy   d O x
c) Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y f (x), y g(x)
(cùng nằm một phía so với Ox) và hai đường thẳng x a, x b quanh trục Ox : b y 2 2 V
f (x)  g (x) dx .  f (x) a g(x) a x O b 2
Câu 38. Cho hình phẳng  H giới hạn bởi các đường y x 3, y  0 , x  0 , x  2 . Gọi V là thể
tích của khối tròn xoay được tạo thành khi quay  H xung quanh trục O x . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2
A. V     2
x  3 dx B. V    2 x  3 dx
C. V    2
x  3 dx D. V    2 x  3 dx 0 0 0 0 Lời giải Chọn A
Thể tích của khối tròn xoay được tạo thành khi quay  H xung quanh trục O x là: 2
V     x  32 2 dx . 0
Câu 39. Cho hàm số y f x liên tục trên đoạn  ; a
b . Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y f x , trục hoành và hai đường thẳng x  ,
a x ba b . Thể tích của khối tròn xoay tạo
thành khi quay D quanh trục hoành được tính theo công thức: b b b b A. 2 V  
f xdxB. 2 V  2
f xdx C. 2 2 V  
f xdx D. 2 V  
f xdxa a a a Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn A
Câu 40. Cho hình phẳng  H  giới hạn bởi các đường thẳng 2
y x  2, y  0, x  1, x  2 . Gọi V là thể
tích của khối tròn xoay được tạo thành khi quay  H  xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2
A. V    2
x  2 dx . B. V   2
x  2 dx . C. V    2
x  2dx . D. V   2 x  2dx . 1 1 1 1 Lời giải 2 2
Ta có: V    2 x  2 dx . 1
Câu 41. Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo
thành được tính theo công thức nào? b b
A. V   f x g x 2 ( ) ( ) dx  . B. 2 2
V    f (x)  g (x) dx    . a a b b
C. V    f x g x 2 ( ) ( ) dx  .
D. V    f (x)  g(x)dx  . a a Lời giải Chọn B
Gọi V là thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số y f (x) , 1 b
trục Ox và hai đường thẳng x  ;
a x b khi quay quanh trục hoành. Ta có 2 V   f (x)dx 1  . a
Gọi V là thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số y g(x) , 2 b
trục Ox và hai đường thẳng x  ;
a x b khi quay quanh trục hoành. Ta có 2
V   g (x)dx 2  . a
Do f (x)  g(x) , x   ;
a b nên thể tích khối tròn xoay tạo thành khi quay hình phẳng (phần b
tô đậm) quanh trục hoành 2 2
V V V    f (x)  g (x) d  . x 1 2    a
Câu 42. Trong không gian với hệ tọa độ Oxyz , cho vật thể  H  giới hạn bởi hai mặt phẳng có phương
trình x a và x b . Gọi S x là diện tích thiết diện của  H  bị cắt bởi mặt phẳng vuông góc
với trục Ox tại điểm có hoành độ là x , với a x b . Giả sử hàm số y S x liện tục trên
đoạn a;b . Khi đó, thể tích của vật thể  H  được cho bởi công thức : b b
A. V   S x dx  .
B. V   S x 2  dx    . a a b b
C. V  S x 2  dx    .
D. V S x dx  . a a
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Lời giải Chọn D
Do S x là diện tích thiết diện của  H  bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm
có hoành độ là x , với a x b . b
Khi đó, thể tích của vật thể  H  được tính bởi công thức V S x dx  . a
Câu 43. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x  1 và x  3 , biết rằng khi cắt
vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (1  x  3 ) thì được thiết
diện là một hình chữ nhật có độ dài hai cạnh là 3x và 2 3x  2 . 124
A. V  32  2 15 B. V  3 124 C. V
D. V  (32  2 15) 3 Lời giải Chọn C
Diện tích thiết diện là: 2 S(x)  3 . x 3x  2 3 124
 Thể tích vật thể là: 2 V  3 .
x 3x  2dx   3 1
Câu 44. Cho hình phẳng D giới hạn bởi đường cong y  2  cos x , trục hoành và các đường thẳng  x  0, x
. Khối tròn xoay tạo thành khi D quay quanh trục hoành có thể tích V bằng bao 2 nhiêu?
A. V  (  1)
B. V    1
C. V    1
D. V  (  1) Lời giải Chọn A  2  2
V    2  cos xdx  2x  sin x 2  (   1). 0 0
Câu 45. Cho hình phẳng D giới hạn bởi đường cong y  2  sin x , trục hoành và các đường thẳng
x  0 , x   . Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu? A. V  2 2
B. V  2   1 C. V  2
D. V  2   1 Lời giải Chọn B
Ta có phương trình 2  sin x  0 vô nghiệm nên:   2 
V    2  sin x  dx   2   
sin xdx  2x  cos x  2   1 . 0 0 0
Câu 46. Cho hình phẳng D giới hạn bởi đường cong  x y
e , trục hoành và các đường thẳng x  0 ,
x  1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?   2 e  1 2 2 e  1  2 e  e  1 A. V B. V C. V D. V  2 2 3 2 Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489 1 xe 1 2 x e  2 1 2  
V   e dx    2 2 0 0
Câu 47. Cho hình phẳng D giới hạn với đường cong 2 y
x 1 , trục hoành và các đường thẳng
x  0, x  1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 4 4 A. V
B. V  2 C. V D. V  2 3 3 Lời giải Chọn A
Thể tích khối tròn xoay được tính theo công thức: 1 1      x   V x 1 1
dx  x   3 2 4 2 2 1 dx   x     3  3 0 0 0
Câu 48. Cho hình phẳng giới hạn bởi các đường y
x  2 , y  0 và x  9 quay xung quanh trục Ox .
Tính thể tích khối tròn xoay tạo thành. 5 11 7 7 A. V  . B. V  . C. V  . D. V  . 6 6 11 6 Lời giải Chọn B
Hoành độ giao điểm của 2 đồ thị hàm số y
x  2 và y  0 là: x  0  x  2  0    x  4.  x  2  9 2 11
Khi đó: V    x  2 dx  .(Dùng MTCT). 6 4
Câu 49. Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số 2
y  3x x và trục hoành, quanh trục hoành. 85 41 81 8 A. (đvtt). B. (đvtt). C. (đvtt). D. (đvtt). 10 7 10 7 Lời giải Chọn C x  0 Xét phương trình 2
3x x  0   . x  3 
Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số 2
y  3x x và trục hoành, quanh trục hoành là 3 3 3  3 1  81
V  3xx 2 2 dx    2 3 4
9x  6x x dx 3 4 5  3
 x x x    2 5  (đvtt). 10 0 0 0
Câu 50. Thể tích của vật thể tròn xoay khi quay hình  H  quanh Ox với  H  được giới hạn bởi đồ thị hàm số 2 y
4 x x và trục hoành. 31 32 34 35 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn B
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020x  0
Phương trình hoành độ giao điểm: 2
4x x  0   . x  4  2 4 32
Thể tích của vật thể tròn xoay khi quay hình  H  quanh Ox là: V    2
4x x  dx   . 3 0
C. ỨNG DỤNG TÍCH PHÂN VÀO BÀI TOÁN CHUYỂN ĐỘNG
Câu 51. Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển
động chậm dần đều với vận tốc v t   5
t 10 (m/s), trong đó t là khoảng thời gian tính bằng
giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 0,2m B. 2m C. 10m D. 20m Lời giải Chọn C
Xét phương trình 5t 10  0  t  2. Do vậy, kể từ lúc người lái đạp phanh thì sau 2s ô tô dừng hẳn.
Quãng đường ô tô đi được kể từ lúc người lái đạp phanh đến khi ô tô dừng hẳn là 2  5 2 s    5  t 10 2
dt   t 10t  10 .    m  2  0 0
Câu 52. Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi 1 13
quy luật v t  2  t t
 m/s , trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu 100 30
chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng
cùng hướng với A nhưng chậm hơn 10 giây so với A và có gia tốc bằng a  2
 m/s  (a là hằng
số). Sau khi B xuất phát được 15 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng A. 15  m/s B. 9m/s C. 42   m/s D. 25  m/s Lời giải Chọn D
Ta có v t   .
a dt  at C v
0  0  C  0  v t at . B   B  , B  
Quãng đường chất điểm A đi được trong 25 giây là 25  1 13 25  1 13  375 2  S   t t dt 3 2  t t   . A       100 30   300 60  0 2 0
Quãng đường chất điểm B đi được trong 15 giây là 15 2 15 at 225a S at.dt   . B  2 0 2 0 375 225a 5 Ta có   a  . 2 2 3 5
Vận tốc của B tại thời điểm đuổi kịp A là v    . B 15  .15 25  m/s 3
Câu 53. Một chất điểm chuyển động trên đường thẳng nằm ngang với gia tốc phụ thuộc thời gian t (s)
là a t   2t  7 (m/s2). Biết vận tốc đầu bằng 10 (m/s), hỏi sau bao lâu thì chất điểm đạt vận tốc 18 (m/s)? A. 5 (s). B. 7 (s). C. 6 (s). D. 8 (s). Lời giải Chọn D
Ta có v t   a t t   t   2 d 2
7 dt t  7t C  
, mặt khác v 0  10 nên C v 0  10 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
NGUYỄN BẢO VƯƠNG - 0946798489v t  2
t  7t 10 . t  8 nhËn
Để chất điểm đạt vận tốc 18 (m/s) thì v t  18  2
t  7t  8  0   .
t  1 lo¹i  
Vậy tại thời điểm t  8 (s) thì chất điểm đạt vận tốc 18 (m/s).
Câu 54. Một ôtô đang chạy với vận tốc 19 m / s thì người lái hãm phanh, ôtô chuyển động chậm dần
đều với vận tốc v t   3
 8t 19 m / s , trong đó t là khoảng thời gian tính bằng giây kể từ
lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét? A. 5 m .
B. 4, 5 m .
C. 4, 25 m .
D. 4, 75 m . Lời giải Chọn D
Thời điểm người lái hãm phanh: t  0. 1
Thời điểm ôtô dừng hẳn: v t   0  38 
t 19  0  t   2
Ta có: s t   v t  dt  .
Từ lúc hãm phanh đến khi dừng hẳn, ôtô còn di chuyển được: 1 1 2 2 19
s v t  dt   38 
t 19 dt   4, 75 m.   4 0 0
Câu 55. Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt đất
đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển
động theo phương thẳng đứng với vận tốc tuân theo quy luật 2
v(t)  10t t , trong đó t (phút) là
thời gian tính từ lúc bắt đầu chuyển động, v(t) tính theo đơn vị mét/phút (m / p) . Nếu như vậy
thì khi bắt đầu tiếp đất vận tốc v của khí cầu là:
A. v  9(m / p).
B. v  5(m / p).
C. v  7(m / p).
D. v  3(m / p). Lời giải Chọn A
Gọi b (phút) là thời gian khí cầu từ độ cao 162 (mét) chuyển động cho đến khi tiếp đất. b b 1 1 Ta có 2 2 3 3 2
s v(t)dt  162  (10t t )dt  162  5b b   b  5b 162  0  b  9   . 3 3 0 0
Vậy vận tốc của khí cầu tại thời điểm tiếp đất là 2
v  10.9  9  9 (m / p).
Câu 56. Một vật chuyển động trong 3 giờ với vận tốc v(km / h) phụ thuộc vào thời gian t(h) có đồ thị
vận tốc như hình bên. Trong thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một
phần của đường parabol có đỉnh I(2; 9) và trục đối xứng song song với trục tung, khoảng thời
gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật
chuyển động được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm).
A. s  15, 50(km)
B. s  23, 25(km)
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
C. s  13,83(km)
D. s  21, 58(km) Lời giải Chọn D   c  4 b  5  
Gọi phương trình của parabol  2 v
at bt c ta có hệ như sau: 4a  2b c  9  c  4   b 5   2 a    2a  4 31
Với t  1 ta có v  . 4 1  5  3 31 259
Vậy quãng đường vật chuyển động được là s   2
t  5t  4 dt dt      21,583 4 4 12 0   1
Câu 57. Một vật chuyển động trong 3 giờ với vận tốc v km/h phụ thuộc thời gian t h có đồ thị là
một phần của đường parabol có đỉnh I 2; 9 và trục đối xứng song song với trục tung như hình
bên. Tính quãng đường s mà vật di chuyển được trong 3 giờ đó.
A. s  26,75 km
B. s  25, 25 km
C. s  24, 25 km
D. s  24,75 km Lời giải Chọn D 3
Tìm được phương trình của vận tốc là v t   2 t  3t  6 4 3 3 Vậy S  ( 2
t  3t  6)dt   24,75 4 0 1
Câu 58. Một vật chuyển động theo quy luật s   3 t  2
6t với t (giây) là khoảng thời gian tính từ khi 2
vật đó bắt đầu chuyển động và s m là quãng đường vật di chuyển được trong khoảng thời
gian đó. Hỏi trong khoảng thời gian 6 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất
của vật đạt được bằng bào nhiêu? A. 64 m/s B. 24 m/s C. 18 m/s D. 108 m/s Lời giải Chọn B 3
Vận tốc của vật chuyển động là v   s   2
t  12t f t 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
NGUYỄN BẢO VƯƠNG - 0946798489
Tìm giá trị lớn nhất của hàm số f t trên đoạn 0; 6  
Ta có f t  3t  12  f t  0  t  4  0; 6  
f 0  0; f 4  24; f 6  18
Vậy vận tốc lớn nhất là 24 m/s .
Câu 59. Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị của
vận tốc như hình bên. Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là
một phần của đường parabol có đỉnh I 2; 9 với trục đối xứng song song với trục tung, khoảng
thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà
vật di chuyển được trong 4 giờ đó.
A. s  26, 5 (km) B. s  24 (km)
C. s  28, 5 (km) D. s  27 (km) Lời giải Chọn C
Gọi Py  2 :
ax bx c . 9
Vì P qua O 0; 0 và có đỉnh I 2; 9 nên dễ tìm được phương trình là y  2 x  9x . 4 27
Ngoài ra tại x  3 ta có y  4 3  9  4 27
Vậy quãng đuờng cần tìm là: S  2
x  9x dx  dx     27 (k ) m . 4 4 0   3
Câu 60. Một vật chuyển động trong 4 giờ với vận tốc v (km/ h) phụ thuộc thời gian t (h) có đồ thị là
một phần của đường parabol có đỉnh I (1;3) và trục đối xứng song song với trục tung như hình
bên. Tính quãng đường s mà vật di chuyển được trong 4 giờ kể từ lúc xuất phát.
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 50 64 A. s  (km).
B. s  10 (km).
C. s  20 (km). D. s  (km). 3 3 Lời giải Chọn D Ta có 2
v(t)  at bt c có dạng parabol đỉnh I (1;3) , đi qua điểm (0
A ; 4) và B(4;12) .  b   b   1   1 2a  2a b   2  a b   2a b   2      
a b c  3  a b c  3  a b  1  a  ( 2
a)  1  a  1 v(0)  4 0  0  c  4 c  4 c  4 c  4        Do đó 2
v(t)  t  2t  4 .
Quãng đường vật di chuyển được trong 4 giờ kể từ lúc xuất phát được tính như sau 4 4 3 3  t  4  4  64 2 2 2
s v(t)dt  (t  2t  4)dt   t  4t   4  4.4  0        (km). 3 0 3 3 0 0    
Câu 61. Một chuyển động trong 4 giờ với vận tốc v ( km/h) phụ thuộc thời gian t ( h ) có đồ thị là một
phần của đường parabol có đỉnh I 1; 
1 và trục đối xứng song song với trục tung như hình bên.
Tính quãng đường s mà vật đi được trong 4 giờ kể từ lúc xuất phát. 40 46 A. s   km  .
B. s  8 km  . C. s   km  .
D. s  6  km  . 3 3 Lời giải Chọn A 2
Ta có phương trình vận tốc v t   at bt cP
P qua điểm 0;2 nên c  2 .
Mặt khác P có đỉnh 1  ;1 nên  b    1
2a b  0 a   1 2a     a b  1  b  2 
a b c 1   
Nên phương trình vận tốc v t  2
t  2t  2
Quãng đường mà vật đi được trong 4 giờ kể từ lúc xuất phát là: 4   2 t t   40 2 2 dt  km . 0 3
------------------------- HẾT -------------------------
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31