Thông tin
Quiz

Tổng ôn tập TN THPT 2021 môn Toán: Nguyên hàm, tích phân và ứng dụng

Tổng ôn tập TN THPT 2021 môn Toán: Nguyên hàm, tích phân và ứng dụng được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề:

Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:

163 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Tổng ôn tập TN THPT 2021 môn Toán: Nguyên hàm, tích phân và ứng dụng

54 27 lượt tải Tải xuống

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1



MỨC ĐỘ NHẬN BIẾT

Câu 1. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho

 

d 10f x x 



và

 

d 7f x x 





thì

 

df x x



bằng:

17

. B.

. C.

. D.

3

.

Câu 2. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Họcácnguyênhàmcủahàmsố

 

4 2

5 6 1f x x x  

là

2 2

x x C   . B.

5 3

2x x x C  

.

5 3

20 12x x x C  

. D.

20 12x x C 

.

Câu 3. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021)





bằng

2ln2

. B.

2ln 2

. C.

2ln 2 1

. D.

ln 2

.

Câu 4. Tínhtíchphân

1 1

I dx

x x

 

 

 

 







 

1I 

I e



Câu 5. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Giảsử

làhàmliêntụctrênkhoảng

và

, ,a b c

làbasốbấtkìtrênkhoảng

.Khẳngđịnhnàosauđâysai?

(x)dx (t)dt

b b

a a

f f

 

. B.

 

(x)dx (x)dx (x)dx, ,

c b b

a c a

f f f c a b  

  

.

(x)dx 1

f 



. D.

(x)dx (x)dx

b a

a b

f f 

 

.

Câu 6. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Nguyênhàmcủahàmsố

   

1 2f x x 

là:

 

1 2x C 

. B.

 

1 2

x C  

. C.

 

1 2

x C  

. D.

 

5 1 2x C 

.

Câu 7. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho

 

d 5f x x







.Tính

 

2sin dI f x x x



 

 

 





 

. B.

7I 

. C.



 

. D.

3I 

.

Câu 8. (Chuyên Lê Hồng Phong - TPHCM - 2021) Biết

 

d 2f x x  



;

 

d 3f x x 



;

 

d 7g x x 



.

Mệnhđềnàosauđâysai?

   

8 4

4 1

d d 8f x x g x x 

 

. B.

   

d 10f x g x x  

 



.

NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG

Chủ đề 3

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

d 5f x x  



. D.

   

4 2 d 2f x g x x   

 



.

Câu 9. (Chuyên Lê Hồng Phong - TPHCM - 2021) Hìnhphẳnggiớihạnbởiđồthịhàmsố

 

y f x

,

trụchoànhvàhaiđườngthẳng

x a

,

x b

tronghìnhdướiđây(phầngạchsọc)códiệntích



bằng



   

d d

c b

a c

f x x f x x

 

. B.

   

d d

c b

a c

f x x f x x

 

.

   

d d

c b

a c

f x x f x x 

 

. D.

   

d d

c b

a c

f x x f x x 

 

.

Câu 10. (Chuyên Lê Hồng Phong - TPHCM - 2021) Họnguyênhàmcủahàmsố

 

f x e

là

e C

. B.

e C

. C.

e C

. D.

e C

.

Câu 11. (Chuyên Lam Sơn - Thanh Hóa - 2021) Chohàmsố

 

f x

có

 

2 2f 

,

 

3 5f 

;hàmsố

 

f x



liêntụctrên

 

2;3

.Khiđó

 

df x x





bằng

. B.

. C.

3

. D.

.

Câu 12. (Chuyên Lam Sơn - Thanh Hóa - 2021) Họtấtcảnguyênhàmcủahàmsố

 

cos2f x x

là

2sin 2x C

. B.

sin 2

x C 

. C.

sin 2

x C

. D.

2sin 2x C 

.

Câu 13. (Chuyên Lam Sơn - Thanh Hóa - 2021) Họtấtcảcácnguyênhàmcủahàmsố

 

4 3

f x







trênkhoảng

 

1;

là

 

2ln 4 3x C 

. B.

 

ln 4 3

x C 

. C.

 

ln 4 3

x C 

. D.

 

4ln 4 3x C 

.

Câu 14. (Chuyên Lam Sơn - Thanh Hóa - 2021) Gọi

làdiệntíchmiềnhìnhphẳngđượcgạchchéo

tronghìnhvẽdướiđây,với

 

y f x

làhàmsốliêntụctrên



.



Côngthứctính

là

 

dS f x x



 



. B.

 

dS f x x







.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

   

1 2

1 1

d dS f x x f x x



 

 

. D.

 

dS f x x







.

Câu 15. (Chuyên KHTN - 2021)

 

2 cos

x x dx





bằng:

2 sin

x x C 

. B.

2 sin

x x C 

. C.

sin

x x C 

. D.

sin

x x C 

.

Câu 16. (Chuyên KHTN - 2021) Cho

 

f x dx

 



và

 

f x dx





.Tínhtíchphân

 

f x dx





 B.

 C.

7.

 D.

10.



Câu 17. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Họ tất cả các nguyên hàm của hàm số

cos

y e x

 

là

sin

e x C  

. B.

sin

e x C 

. C.

sin

e x C 

. D.

sin

e x C  

.

Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Biết

 

f x dx





 và

 

f x dx





. Giá trị

 

f x dx



bằng

1

. B.

. C.

5

. D.

.

Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Gọi

 

làhìnhphẳnggiớihạnbởicácđường

thẳng

, 0, 1, 4

y y x x

   

.Thểtíchvậtthểtrònxoaytạothànhkhiquay

 

quanhtrục



đượctínhtheocôngthứcnàodướiđây?





. B.





. C.



 

 

 



. D.





.

Câu 20. (Chuyên Quốc Học Huế - 2021) Thểtíchcủakhốitrònxoaykhiquayhìnhphẳnggiớihạnbởicác

đường

y x



,trục

vàhaiđườngthẳng

1; 4

x x

 

quanhtrụchoànhđượctínhbởicôngthức

nàodướiđây?

dV x x







. B.

dV x x







. C.

dV x x







. D.

dV x x





.

Câu 21. (Chuyên Quốc Học Huế - 2021) Tìmhọnguyênhàmcủahàmsố

 

5 4

f x





trên

 



 

 



.

 

d ln 5 4

ln5

f x x x C  



. B.

 

d ln 5 4

f x x x C  



.

 

d ln 5 4

f x x x C  



. D.

   

d ln 5 4

f x x x C  



.

Câu 22. (Chuyên Quang Trung - Bình Phước - 2021) Chohaihàmsố

 

f x

,

 

g x

liêntụctrên



.

Trongcácmệnhđềsau,mệnhđềnàosai?

   

d dkf x x k f x x



 

vớimọihằngsố



.

       

d d df x g x x f x x g x x

   

 

  



   

f x x f x C



 



vớimọihàm

 

f x

cóđạohàmtrên



.

       

d d df x g x x f x x g x x

   

 

  



Câu 23. (Chuyên Quang Trung - Bình Phước - 2021) Chohàmsố

( )f x

liêntụcvàxácđịnhtrên

 

,a b

.

Gọi

( )F x

làmộtnguyênhàmcủahàmsố

( )f x

.Chọnphươngánđúngnhất.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

( ) ( ) ( )

f x dx F b F a

 



( ) ( ) ( )

f x dx F a F b

 



( ) ( ) ( )

f x dx F b F a 



2 2

( ) ( ) ( )

f x dx F b F a 



Câu 24. (Chuyên Ngoại Ngữ Hà Nội- 2021) Chohình

 

đượcgiớihạnnhưhìnhvẽ



Diệntíchcủahình

 

đượctínhbởicôngthứcnàodướiđây?

   

g x f x dx 

 



. B.

   

f x g x dx 

 



.

 

f x dx



. D.

 

g x dx



.

Câu 25. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hàm số

 

f x

 thỏa mãn

 

x 1f x d  



 và

 

x 4f x d 



.Giátrịcủa

 

xf x d



bằng

. B.

3

. C.

5

. D.

.

Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021) Chohàmsố

 

f x

liêntụctrênđoạn

 

2;3

.Gọi

 

F x

là

mộtnguyênhàmcủahàmsố

 

f x

trên

 

2;3

và

   

3 2; 2 4F F    

.Tính

 

2I f x dx







.

. B.

. C.

4

. D.

2

Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho

 

d 3I f x x 



.Khiđó

 

4 3 dJ f x x 

 

 





bằng:

A. 6. B. 8. C. 4. D. 2.

Câu 28. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Kếtquả

x dx



bằng

3x C

. B.

x C

. C.

. D.

4x C

.

Câu 29. (Chuyên Hạ Long - Quảng Ninh - 2021) Biết

 

cosF x x

là mộtnguyênhàm củahàmsố

 

f x

trên



.Giátrịcủa

 

3 2 df x x



 

 



bằng

. B.



. C.

2 6





. D.

4

.

Câu 30. (Chuyên Hạ Long - Quảng Ninh - 2021) Biết

 

5f x dx 



 và

 

7g x dx  



. Giá trị của

   

3 2f x g x dx

 

 



bằng

 B.

29

 C.

 D.

31



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Biết

 

I f x dx

 



.Giátrịcủa

 

f x x dx



 

 



bằng

. B.

. C.

. D.

.

Câu 32. (Chuyên ĐH Vinh - Nghệ An - 2021) Họcácnguyênhàmcủahàmsố

 

sin3f x x



là

cos3

x C 

. B.

cos3

x C 

. C.

cos3

x C

. D.

cos3

x C

.

Câu 33. (Chuyên ĐH Vinh - Nghệ An - 2021) Biết

 

f x dx





 và

 

g x dx





 Khi đó

   

 

g x f x dx





bằng

 B.



 C.

1.

 D.



Câu 34. (THPT Quế Võ 1 - Bắc Ninh - 2021) Mệnhđềnàosauđâyđúng.

d ln

x x C

 



. B.

d cot

sin

x x C

 



.

cos d sin

x x x C  



. D.

d tan

cos

x x C

 



.

Câu 35. (THPT Quế Võ 1 - Bắc Ninh - 2021) Khẳngđịnhnàosauđâyđúngvớimọihàm

,f g

liêntục

trên

và

,a b

làcácsốbấtkỳthuộc

?

       

. .

b b b

a a a

f x g x dx f x dx g x dx

 

 

  

.

       

2 2

b b b

a a a

f x g x dx f x dx g x dx

   

 

  

.

 

f x dx

f x

g x

g x dx





.

   

b b

a a

f x dx f x dx

 



 

 

 

.

Câu 36. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hàm số

 

f x

 liên tục trên



 và

có

 

d 2,

f x x





 

d 6

f x x





Tính

 

d .f x x





12I 

. B.



. C.



. D.

4I 

.

Câu 37. (THPT Quốc Oai - Hà Nội - 2021) Cho hai hàmsố

 

y f x



và

 

y g x



liên tục trên



.

Trongcácmệnhđềsau,mệnhđềnàosai?

       

f x g x dx f x dx g x dx

   

 

  

   

kf x dx k f x dx



 

vớimọihằngsố

 

\ 0

k 



       

f x g x dx f x dx g x dx

   

 

  

       

. .

f x g x dx f x dx g x dx



  

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 38. (THPT Quốc Oai - Hà Nội - 2021) Chohàmsố

 

y f x

liêntụctrênđoạn

 

;a b

.Gọi

 

F x

là

mộtnguyênhàmcủahàmsố

 

y f x

.Hãychọnkhẳngđịnhđúngtrongcáckhẳngđịnhsau

     

f x dx F a F b 



. B.

     

2 2

f x dx F b F a 



     

f x dx F b F a 



. D.

     

f x dx F a F b 



.

Câu 39. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho

làmộthằngsố.Trongcácmệnhđềsau,

mệnhđềnàosai?

x x

e dx e C 



. B.

sin cosxdx x C 



2xdx x C 



. D.

 lndx x C

 



.

Câu 40. (THPT Quảng Xương 1-Thanh Hóa - 2021) Nếu

 

d 2f x x 



và

 

d 4f x x  



thì

 

df x x





bằng

. B.

6

. C.

. D.

2

.

Câu 41. (THPT Quảng Xương 1-Thanh Hóa - 2021) Chođồthịhàmsố

 

y f x

.Diệntích

củahình

phẳng(phầntôđậmtronghìnhvẽ)là



   

1 3

0 1

S f x dx f x dx  

 

. B.

   

1 3

0 1

S f x dx f x dx 

 

.

 

S f x dx



. D.

   

1 3

0 1

S f x dx f x dx 

 

.

Câu 42. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Hàmsố

 

3 2

5 4 7 120F x x x x   

lànguyênhàm

củahàmsốnàosauđây?

 

5 4 7f x x x  

. B.

 

15 8 7f x x x  

 

5 4 7f x x x  

. D.

 

2 3 2

5 4 7

4 3 2

x x x

f x   

.

Câu 43. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Mộtnguyênhàmcủahàmsố

2y cos x

là

2sin 2x

. B.

2sin 2x

. C.

sin2

. D.

sin 2

x

.

Câu 44. (THPT Phan Đình Phùng - Quảng Bình - 2021) Tìmnguyênhàmcủahàmsố

 

2021

f x x

trên



.

 

2022

f x x 



. B.

 

2020

d 2021f x x x C 



.

 

2022

f x x C 



. D.

 

2021

f x x C 



.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Câu 45. (THPT Phan Đình Phùng - Quảng Bình - 2021) Nếu

( ) 4

f x dx





và

( ) 3

g x dx





thì

 

2 ( ) 3 ( )f x g x dx





bằng

. B.

. C.

. D.

.

Câu 46. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Chohàmsố

 

f x

liêntụctrênđoạn

 

0;2

.Biết

 

d 5

f x x





và

 

dt 3.

f t





Tính

 

dI f x x





.



. B.

2I 

. C.



. D.

1I 

.

Câu 47. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho

 

F x

 là một nguyên hàm của hàm số

 

3 2

f x





trênkhoảng

;

 



 

 

.Tìm

 

F x

,biết

 

1 5



.

   

ln 3 2 5

F x x

  

. B.

   

3ln 3 2 5

F x x

  

.

 

3 2

F x



 



.D.

   

ln 3 2 5

F x x

  

.

Câu 48. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Chobiết

 

d 2

f x x





và

 

d 3

g x x





.Tính

   

I 4 df x g x x

 

 

 



?

I=3

. B.

I=1

. C.

I=11

. D.

I=5

.

Câu 49. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Biết

 

f x d





 và

 

f t dt





. Tính

 

f u du





. B.



. C.



. D.

.

Câu 50. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình phẳng

 

 được giớihạn bởi các

đường

 

2 1, , 0, 1

f x x Ox x x

   

.Tínhthể tích

củakhốitrònxoaytạothànhkhi quay

 

xungquanhtrục

đượctínhtheocôngthức?

2 1dx

V x



 



. B.

 

2 1 dx

V x 



. C.

 

2 1 dx

V x



 



. D.

2 1dx

V x 



.

Câu 51. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Nếu

 

f x dx





thì

 

f x dx



bằng

18.



Câu 52. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Khẳngđịnhnàosauđâylàđúng

cot

cos

dx x C

  



. B.

.ln

x x

a dx a a C 



e dx C



 



. D.

1 1

dx C

  



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 53. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Tínhtíchphân

 

2 xx d



 



bằng



. B.

. C.

. D.



Câu 54. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Biết

 

dx 4

f x





. Tính tích phân

 

2 dx

I x f x 

 

 



bằng



. B.

12I 

. C.



. D.

4I 

.

Câu 55. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Chohàmsố

( ) 1f x x 

.Trongcáckhẳngđịnh

sau,khẳngđịnhnàođúng?

( ) x

f x d x x C  



. B.

( ) x 2

f x d x x C  



( ) x

f x d x x C  



. D.

( ) x

f x d x C 



Câu 56. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Họcácnguyênhàmcủahàmsố

 

3 1

f x x

 

là.

x x C 

. B.

x C

. C.

x C

. D.

x C 

.

Câu 57. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Biết

 

d 4

f x x





.Giátrịcủa

 

3 df x x



bằng.

. B.

. C.

. D.

.

Câu 58. (THPT Đồng Quan - Hà Nội - 2021) Họnguyênhàmcủahàmsố

 

ln x

f x



là

x C

. B.

x C

. C.

 

ln ln

x C

. D.

ln ln

x x C 

.

Câu 59. (THPT Đồng Quan - Hà Nội - 2021) Họnguyênhàmcủahàmsố

   

2 cos2

f x x x 

là

1 1

sin 2

2 2

x x C  

.B.

sin 2

x x C  

.

1 1

sin 2

2 2

x x C 

. D.

sin 2

x x C 

.

Câu 60. (THPT Đồng Quan - Hà Nội - 2021) Cho

   

  

 

1 0

0 1

3; 2,

f x dx g x dx

khi đó

   

 





f x g x dx

bằngbaonhiêu?

. B.

7

. C.

. D.

1

.

Câu 61. (THPT Lê Lợi - Thanh Hóa - 2021) Nguyênhàmcủahàmsố

y x x 

là

3 2

x x

C 

. B.

2 1

x C 

. C.

x x C 

. D.

x C 

.

Câu 62. (THPT Lê Lợi - Thanh Hóa - 2021) Chohàmsố

( )y f x

cóđồthịnhưhìnhvẽ.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9



Diệntíchhìnhphẳng(phầntôđậm)đượctínhtheocôngthứcnàosauđây?

( ) .S f x dx







. B.

0 3

2 0

( ) ( ) .S f x dx f x dx



 

 

0 3

2 0

( ) ( ) .S f x dx f x dx



  

 

. D.

0 3

2 0

( ) ( ) .S f x dx f x dx



 

 



Câu 63. (THPT Lê Lợi - Thanh Hóa - 2021) Chocáchàmsố

   

,y f x y g x 

liêntụctrên



có

 

dx 1f x



 



;

 

dx 3g x







.Tính

   

2 dxf x g x



 

 



.

. B.

1

. C.

. D.

.

Câu 64. (Sở Vĩnh Phúc - 2021) Tìmhọtấtcảcácnguyênhàmcủahàmsố





.

 

ln 1x x C  

. B.

ln 1x x C  

. C.

 

ln 1x x C  

. D.

ln 1x x C  

.

Câu 65. (Sở Lào Cai - 2021) Khẳngđịnhnàosauđâylàđúng?

 

df x x f x



 



. B.

 

df x x f x







.

 

df x x f x



 



. D.

 

df x x f x







.

Câu 66. (Sở Lào Cai - 2021) Cho

 

1f x x  



d ,khiđó

 

3f x x



d bằng

. B.

1

. C.

4

. D.

3

.

Câu 67. (Sở Lào Cai - 2021) Tíchphân

e d



bằng:

. B.

1e

. C.

e

. D.

e-1

.

Câu 68. (Sở Lào Cai - 2021) Họcácnguyênhàmcủahàmsố

 

sin

f x

 

là:

cot x C

. B.

tan x C 

. C.

cot x C 

. D.

tan x C

.

Câu 69. (Sở Hà Tĩnh - 2021) Biết

 

d 4f x x 



.Giátrịcủa

 

2 3 dx f x x 

 



bằng

. B.

2

. C.

. D.

.

Câu 70. (Sở Hà Tĩnh - 2021)

 

2x x dx 



bằng

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

x C

. B.

4 2

x x C 

. C.

3 2x C 

. D.

4 2

4x x C 

.

Câu 71. (Sở Yên Bái - 2021) Trongcáckhẳngđịnhsau,khẳngđịnhnàosai?

0dx C



(

làhằngsố). B.

dx x C 



(

làhằngsố).

d lnx x C

 



(

làhằngsố). D.

x x C





 





(

làhằngsố).

Câu 72. (Sở Tuyên Quang - 2021) Nguyênhàmcủahàmsố

 

2 1

f x





là

 

ln 2 1F x x C  

.B.

 

2ln 2 1F x x C  

.

 

ln(2 1)

F x x C  

. D.

 

ln 2 1

F x x C  

.

Câu 73. (Sở Tuyên Quang - 2021) Cho

 

2f x dx 



 và

 

5g x dx 



. Khi đó

   

2f x g x dx 

 





bằng:

A. 1 B. -3 C. -8 D. 12

Câu 74. (Sở Tuyên Quang - 2021) Họtấtcảcácnguyênhàmcủahàmsố

 

2 sinf x x x 

là

2 cosx x C 

. B.

2 cosx x C 

. C.

cosx x C 

. D.

cosx x C 

.

Câu 75. (THPT Thanh Chương 1- Nghệ An - 2021) Họnguyênhàmcủahàmsố là?

A. . B. . C. . D. .

Câu 76. (THPT Thanh Chương 1- Nghệ An - 2021) Cho

 

3 2 d 12f x x x  

 



.Khiđó

 

df x x



bằng

A. . B. . C. . D. .

Câu 77. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Chohàmsố

 

y f x

liêntụctrên



vàcóđồthị

 

làđườngcongnhưhìnhvẽbên.



Diệntíchcủahìnhphẳnggiớihạnbởiđồthị

 

,trục

vàhaiđườngthẳng

0, 2x x 

(phần

tôđen)là

   

1 2

0 1

d dS f x x f x x  

 

. B.

 

dS f x x



.

   

1 2

0 1

d dS f x x f x x 

 

. D.

 

dS f x x



.

Câu 78. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Chohàmsố

 

f x

liêntụctrênđoạn

 

;a b

.Khẳng

địnhnàosauđâysai?

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

       

b b b

a a a

f x g x dx f x dx g x dx

   

 

  

. B.

   

a b

b a

f x dx f x

 

 

.

       

. .

b b b

a a a

f x g x dx f x dx g x dx

 

 

  

. D.

   

b b

a a

k f x dx k f x dx



 

.

Câu 79. (THPT Nguyễn Huệ - Phú Yên - 2021) Biết

 

cosF x x



làmộtnguyênhàmcủahàmsố

 

f x



trên



.Giátrịcủa

 

f x dx





bằng

1

. B.

. C.

. D.

.

Câu 80. (THPT Nguyễn Huệ - Phú Yên - 2021) Biết

 

f x dx





.giátrịcủa

 

3f x dx





bằng

. B.

. C.

. D.

.

Câu 81. (THPT Lương Thế Vinh - 2021) Diệntíchhình phẳnggiớihạnbởi cácđường

y x

 

và

4y x 

xácđịnhbởicôngthức

 

x x dx





. B.

 

x x dx





. C.

 

x x dx





. D.

 

x x dx





.

Câu 82. (THPT Lương Thế Vinh - 2021) Họnguyênhàmcủahàmsố

 

f x



là.

3 log3

C

. B.

3 ln3

C

. C.

ln3

C

. D.

log3

C

.

Câu 83. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Chohaihàmsố

 

f x

,

 

g x

liêntụctrênđoạn

 

;a b

vàsốthực

tùyý.Mệnhđềnàodướiđâysai?

       

d d d , ;

b c c

a a b

f x x f x x f x x c a b

   

  

. B.

   

d d

b a

a b

f x x f x x

 

 

.

   

d d

b b

a a

kf x x k f x x



 

. D.

       

d d d

b b b

a a a

f x g x x f x x g x x

   

 

  

.

Câu 84. (THPT Đào Duy Từ - Hà Nội - 2021) Họcácnguyênhàmcủahàmsố

 

2 3f x x x  

là

x x C  

. B.

2 2

x C 

. C.

3 2

x x C 

. D.

3 2

2 3

x x x C  

.

Câu 85. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hàm số

 

y f x



 có đạo hàm trên đoạn

 

1;2

,

 

1 1



và

 

2 2



.Khiđó,

 

dI f x x







bằng

1I 

. B.

1I  

. C.



. D.



.

Câu 86. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Thểtíchcủakhốitrònxoaysinhbởihìnhphẳnggiới

hạnbởihaiđồthịhàmsố

cosy x

,đườngthẳng



,





vàtrục

khiquayquanhtrục

hoànhlà

cos dV x x







. B.

cos dxV x







. C.

cos dV x x







. D.

cos dV x x







.

Câu 87. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Họnguyênhàmcủahàmsố

 

3 2

3f x x x

 

là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

4 3

x x C 

. B.

4 3

x x

C 

. C.

x C 

. D.

3 6

x x C 

.

Câu 88. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho

 

x 2

f x d





và

 

x 3

g x d





. Tích phân

   

2 xf x g x d



 

 





. B.

. C.

1

. D.

.

Câu 89. (THPT Chu Văn An - Thái Nguyên - 2021) Chohàmsố

 

y f x



xácđịnh,liêntụcvàkhông

âm trên

 

;a b

.Thể tích củavật thể tròn xoay sinh bởimiền

 

 giới hạn bởi đồthị hàmsố

 

y f x



,trụchoànhvàhaiđườngthẳng

x a x b 

quayquanh

là

 

V f x x





. B.

 

V f x x





. C.

 

V f x x







. D.

 

V f x x







.

Câu 90. (THPT Chu Văn An - Thái Nguyên - 2021) Nếu

 

d 6

f x x



 



 và

 

d 2

g x x





 thì

 

df x x





bằng

. B.

12

. C.

8

. D.

4

.

Câu 91. (THPT Ba Đình - Thanh Hóa - 2021) Nguyênhàmcủahàmsố

 

f x x

là

x x C 



. B.

x x C 



. C.

x x C 



. D.

3 4

d 4

x x x C 



Câu 92. (THPT Ba Đình - Thanh Hóa - 2021) Biết

 

f x dx





,giátrị

 

f x dx



bằng

. B.

. C.

. D.

.

Câu 93. (THPT Ba Đình - Thanh Hóa - 2021) Cho

2 1dI x x x

 



và

2 1u x 

.Mệnhđềnàodưới

đâysai:

2 2

( 1)d

I x x x

 



. B.

2 2

( 1)d

I u u u

 



.

5 3

2 5 3

u u

 

 

 

 

. D.

2 2

( 1)dI u u u

 



.

Câu 94. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Chohàmsố

 

f x

liêntụctrên





và

làsố

dương.Trongcáckhẳngđịnhsau,khẳngđịnhnàođúng?

 

d 1

f x x 



. B.

 

d 0

f x x





. C.

 

f x x a



. D.

 

d 2

f x x a



.

Câu 95. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Nguyênhàmcủahàmsố

2 1x

y e

 



là

2 1

2 .

e C

 



 B.

2 1

2 .

e C

 

 C.

2 1

e C

 



 D.

2 1

e C

 



Câu 96. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số

 

f x

 thoả mãn

 

2021 ln 2021 cos

f x x



 

và

 

0 2



.Phátbiểunàosauđúng?

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

 

2021

sin 1

ln 2021

f x x  

. B.

 

2021 sin 1

f x x  

.

 

2021 sin 1

f x x  

. D.

 

2021

sin 1

ln 2021

f x x  

.

Câu 97. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Tìmnguyênhàmcủa

x dx



.

x C

. B.

x C

. C.

x C

. D.

x C

.

Câu 98. (Trung Tâm Thanh Tường - 2021) Cho

 

f x

,

 

g x

làcáchàmsốxácđịnhvàliêntụctrên



.

Trongcácmệnhđềsau,mệnhđềnàosai?

       

f x g x dx f x dx g x dx



  

.

   

2 2

f x dx f x dx



 

.

       

f x g x dx f x dx g x dx

 

  

 

  

       

f x g x dx f x dx g x dx

 

  

 

  

.

Câu 99. (Trung Tâm Thanh Tường - 2021) Nếu

2 2

0 0

( ) 5, ( ) 2

f x dx g x dx

 

 

thì

 

( ) 2 ( )f x g x dx





bằng

. B.

. C.

. D.

.

Câu 100. (Trung Tâm Thanh Tường -2021) Họnguyênhàmcủahàmsố

 

f x x e

 

là

xe C

. B.

x e C 

. C.

2 2

x e C 

. D.

2 2 x

x e C 

.

Câu 101. (THPT Triệu Sơn - Thanh Hóa - 2021) Họtấtcảcácnguyênhàmcủahàmsố

 

3 1

f x x

 

là.

x C

. B.

x x C 

. C.

x x C 

. D.

x C

.

Câu 102. (THPT Triệu Sơn - Thanh Hóa - 2021) Biết

 

f x dx

 



khiđó

 

f x dx



bằng

 B.

2.

 C.

8.



Câu 103. (THPT Triệu Sơn - Thanh Hóa - 2021) Chohàmsố

 

y f x



xácđịnhvàliệntụctrênđoạn

 

;a b

.Diệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố

 

y f x



,trụchoànhvàhaiđườngthẳng

;

x a x b 

đượctínhtheocôngthức

 

S f x dx





. B.

 

S f x dx





. C.

 

f x dx



. D.

 

f x dx



.

Câu 104. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho

 

d 6 2sin 2

f x x x x C  



,khiđó

 

f x

bằng

12 4cos2x x

. B.

2 cos2x x



. C.

12 2 2cos x

. D.

6 4 2x cos x

.

Câu 105. (THPT Trần Phú - Đà Nẵng - 2021) Nếu

 

f x dx







và

 

f x dx





thì

 

f x dx





bằng

5.

 B.

 C.

1.

 D.

BẢNG ĐÁP ÁN

1.C

2.B

3.A

4.A

5.C

6.C

7.B

8.A

9.C

10.B

11.A

12.C

13.B

14.C

15.D

16.B

17.C

18.D

19.C

20.C

21.C

22.A

23.A

24.A

25.C

26.B

27.A

28.B

29.C

30.A

31.B

32.A

33.D

34.D

35.B

36.B

37.D

38.C

39.B

40.B

41.B

42.B

43.C

44.C

45.C

46.B

47.D

48.D

49.B

50.C

51.D

52.C

53.B

54.C

55.A

56.A

57.D

58.A

59.D

60.B

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

61.

62.C

63.D

64.B

65.

66.D

67.D

68.A

69.D

70.B

71.D

72.

73.

74.C

75.B

76.A

77.C

78.C

79.A

80.A

81.C

82.C

83.A

84.A

85.A

86.D

87.C

88.D

89.C

90.D

91.

92.C

93.D

94.B

95.

96.B

97.B

98.A

99.B

100.B

101.

102.D

103.D

104.

105.B

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1



MỨC ĐỘ NHẬN BIẾT



Câu 1. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho

 

d 10f x x 



và

 

d 7f x x 





thì

 

df x x



bằng:

17

. B.

. C.

. D.

3

.

Lời giải

Chọn C

     

6 6 4

4 0 0

d d d 10 7 3f x x f x x f x x    

  

.

Câu 2. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Họcácnguyênhàmcủahàmsố

 

4 2

5 6 1f x x x  

là

2 2

x x C   . B.

5 3

2x x x C  

.

5 3

20 12x x x C  

. D.

20 12x x C 

.

Lời giải

Chọn B

Tacó:

 

4 2 5 3

5 6 1 2 .x x dx x x x C     





Câu 3. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021)





bằng

2ln2

. B.

2ln 2

. C.

2ln 2 1

. D.

ln 2

.

Lời giải

Chọn A

Tacó:

   

0 0

3 3

1 1

d d 1 ln 1 ln1 ln 4 2ln 2

1 1

x x x

x x



 

         

 

 

.

Câu 4. Tínhtíchphân

1 1

I dx

x x

 

 

 

 







 

1I 

I e



Lờigiải

ChọnA

1 1 1 1

I dx x

x x x e

   

    

   

   



.

Lời giải

Chọn A

Câu 5. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Giảsử

làhàmliêntụctrênkhoảng

và

, ,a b c

làbasốbấtkìtrênkhoảng

.Khẳngđịnhnàosauđâysai?

(x)dx (t)dt

b b

a a

f f

 

. B.

 

(x)dx (x)dx (x)dx, ,

c b b

a c a

f f f c a b

  

  

.

NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG

Chủ đề 3

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

(x)dx 1





. D.

(x)dx (x) dx

b a

a b

f f 

 

.

Lời giải

Chọn C

Câu 6. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Nguyênhàmcủahàmsố

   

1 2f x x

 

là:

 

1 2

x C 

. B.

 

1 2

x C  

. C.

 

1 2

x C  

. D.

 

5 1 2

x C 

.

Lời giải

Chọn C

Tacó

         

5 5 6

1 1

d 1 2 d 1 2 d 1 2 1 2

2 12

f x x x x x x x C         

  

.

Câu 7. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho

 

d 5

f x x







.Tính

 

2sin dI f x x x



 

 

 





 

. B.



. C.



 

. D.



.

Lời giải

Chọn B

Tacó

   

2 2 2

0 0 0

2sin d d 2sin d 5 2cos 5 2 cos cos0 7

I f x x x I f x x x x x

  



 

          

 

 

 

 

  

.

Câu 8. (Chuyên Lê Hồng Phong - TPHCM - 2021) Biết

 

d 2

f x x

 



;

 

d 3

f x x





;

 

d 7

g x x





.

Mệnhđềnàosauđâysai?

   

8 4

4 1

d d 8

f x x g x x

 

 

. B.

   

d 10

f x g x x

 

 

 



.

 

d 5

f x x

 



. D.

   

4 2 d 2

f x g x x

  

 

 



.

Lời giải

Chọn A

MệnhđềởphươngánAlàsaivì:

         

8 4 8 4 4

4 1 1 1 1

d d d d d 2 3 7 2

f x x g x x f x x f x x g x x

        

    

.

Câu 9. (Chuyên Lê Hồng Phong - TPHCM - 2021) Hìnhphẳnggiớihạnbởiđồthịhàmsố

 

y f x



,

trụchoànhvàhaiđườngthẳng

x a

,

x b

tronghìnhdướiđây(phầngạchsọc)códiệntích



bằng

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3



   

d d

c b

a c

f x x f x x



 

. B.

   

d d

c b

a c

f x x f x x



 

.

   

d d

c b

a c

f x x f x x 

 

. D.

   

d d

c b

a c

f x x f x x 

 

.

Lời giải

Chọn C

 

   

0 d 0 d d d

c b c b

a c a c

S f x x f x x f x x f x x      

   

.

Câu 10. (Chuyên Lê Hồng Phong - TPHCM - 2021) Họnguyênhàmcủahàmsố

 

f x e

là

e C

. B.

e C

. C.

e C

. D.

e C

.

Lời giải

Chọn B

Tacó

2 2

dx=

x x

e e C



.

Câu 11. (Chuyên Lam Sơn - Thanh Hóa - 2021) Chohàmsố

 

f x

có

 

2 2f 

,

 

3 5f 

;hàmsố

 

f x



liêntụctrên

 

2;3

.Khiđó

 

df x x





bằng

. B.

. C.

3

. D.

.

Lời giải

Chọn A

       

d 3 2 5 2 3

f x x f x f f



     



Câu 12. (Chuyên Lam Sơn - Thanh Hóa - 2021) Họtấtcảnguyênhàmcủahàmsố

 

cos2f x x

là

2sin 2x C

. B.

sin 2

x C 

. C.

sin 2

x C

. D.

2sin 2x C 

.

Lời giải

Chọn C

   

1 1

d cos 2 d cos 2 d 2 sin 2

2 2

f x x x x = x x x C  

  

Câu 13. (Chuyên Lam Sơn - Thanh Hóa - 2021) Họtấtcảcácnguyênhàmcủahàmsố

 

4 3

f x







trênkhoảng

 

1;

là

 

2ln 4 3x C 

. B.

 

ln 4 3

x C 

. C.

 

ln 4 3

x C 

. D.

 

4ln 4 3x C 

.

Lời giải

Chọn B

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Tacó

   

2 1 1

d d 2. ln 4 3 ln 4 3

4 3 4 2

f x x x x C x C

      



 

.

Câu 14. (Chuyên Lam Sơn - Thanh Hóa - 2021) Gọi

làdiệntíchmiềnhìnhphẳngđượcgạchchéo

tronghìnhvẽdướiđây,với

 

y f x

làhàmsốliêntụctrên



.



Côngthứctính

là

 

dS f x x



 



. B.

 

dS f x x







.

   

1 2

1 1

d dS f x x f x x



 

 

. D.

 

dS f x x







.

Lời giải

Chọn C

Tacó:

   

1 2

1 1

d dS f x x f x x



 

 

.

Câu 15. (Chuyên KHTN - 2021)

 

2 cosx x dx



bằng:

2 sinx x C 

. B.

2 sinx x C 

. C.

sinx x C 

. D.

sinx x C 

.

Lời giải

Chọn D

Tacó:

 

2 cos sinx x dx x x C   



.

Câu 16. (Chuyên KHTN - 2021) Cho

 

2f x dx  



và

 

5f x dx 



.Tínhtíchphân

 

f x dx





 B.

 C.

7.

 D.

10.



Lời giải

Chọn B

Tacó

     

5 3 5

1 1 3

3.f x dx f x dx f x dx  

  



Câu 17. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Họ tất cả các nguyên hàm của hàm số

cos

y e x  là

sin

e x C  

. B.

sin

e x C 

. C.

sin

e x C 

. D.

sin

e x C  

.

Lời giải

Chọn C

Tacó

 

cos sin

x x

e x dx e x C   





Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Biết

 

2f x dx 



 và

 

3f x dx 



. Giá trị

 

f x dx



bằng

1

. B.

. C.

5

. D.

.

Lời giải

Chọn D

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5



     

4 4 3

3 0 0

3 2 1

f x dx f x dx f x dx

    

  



Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Gọi

 

làhìnhphẳnggiớihạnbởicácđường

thẳng

, 0, 1, 4

y y x x

   

.Thểtíchvậtthểtrònxoaytạothànhkhiquay

 

quanhtrục



đượctínhtheocôngthứcnàodướiđây?





. B.





. C.



 

 

 



. D.





.

Lời giải

Chọn C

Thểtíchvậtthểtrònxoaytạothànhkhiquay

 

quanhtrục

đượctínhtheocôngthức

V x



 



 

 



.

Câu 20. (Chuyên Quốc Học Huế - 2021) Thểtíchcủakhốitrònxoaykhiquayhìnhphẳnggiớihạnbởicác

đường

y x



,trục

vàhaiđườngthẳng

1; 4

x x

 

quanhtrụchoànhđượctínhbởicôngthức

nàodướiđây?

dV x x







. B.

dV x x







. C.

dV x x







. D.

dV x x





.

Lời giải

Chọn C

ÁpdụngcôngthứcSGKtacó

 

4 4

1 1

d dV x x x x

 

 

 

.

Câu 21. (Chuyên Quốc Học Huế - 2021) Tìmhọnguyênhàmcủahàmsố

 

5 4

f x





trên

 



 

 



.

 

d ln 5 4

ln5

f x x x C  



. B.

 

d ln 5 4

f x x x C  



.

 

d ln 5 4

f x x x C  



. D.

   

d ln 5 4

f x x x C  



.

Lời giải

Chọn C

Ápdụngcôngthức

1 1

d ln

x ax b C

ax b a

  





tacó

 

d ln 5 4

f x x x C  



.

Câu 22. (Chuyên Quang Trung - Bình Phước - 2021) Chohaihàmsố

 

f x

,

 

g x

liêntụctrên



.

Trongcácmệnhđềsau,mệnhđềnàosai?

   

d dkf x x k f x x



 

vớimọihằngsố



.

       

d d df x g x x f x x g x x

   

 

  



   

f x x f x C



 



vớimọihàm

 

f x

cóđạohàmtrên



.

       

d d df x g x x f x x g x x

   

 

  



Lời giải

Chọn A

AsaiVì

phảilàhằngsốkhác



Câu 23. (Chuyên Quang Trung - Bình Phước - 2021) Chohàmsố

( )f x

liêntụcvàxácđịnhtrên

 

,a b

.

Gọi

( )F x

làmộtnguyênhàmcủahàmsố

( )f x

.Chọnphươngánđúngnhất.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

( ) ( ) ( )

f x dx F b F a

 



( ) ( ) ( )

f x dx F a F b

 



( ) ( ) ( )

f x dx F b F a 



2 2

( ) ( ) ( )

f x dx F b F a 



Lời giải

Chọn A

Câu 24. (Chuyên Ngoại Ngữ Hà Nội- 2021) Chohình

 

đượcgiớihạnnhưhìnhvẽ



Diệntíchcủahình

 

đượctínhbởicôngthứcnàodướiđây?

   

g x f x dx 

 



. B.

   

f x g x dx 

 



.

 

f x dx



. D.

 

g x dx



.

Lời giải

Chọn A

Diệntíchcủahình

 

là:

   

S g x f x dx  

 



.

Câu 25. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hàm số

 

f x

 thỏa mãn

 

x 1f x d  



 và

 

x 4

f x d





.Giátrịcủa

 

xf x d



bằng

. B.

3

. C.

5

. D.

.

Lời giải

Chọn C

Tacó:

     

2 1 2

0 0 1

f x dx f x dx f x dx 

  

 

1 4 5f x dx     



.

Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021) Chohàmsố

 

f x

liêntụctrênđoạn

 

2;3

.Gọi

 

F x

là

mộtnguyênhàmcủahàmsố

 

f x

trên

 

2;3

và

   

3 2; 2 4F F    

.Tính

 

2I f x dx







.

. B.

. C.

4

. D.

2

Lời giải

Chọn B

Tacó:

       

2 2 3 2 2 2 4 4I f x dx F F



          

   





Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho

 

d 3I f x x 



.Khiđó

 

4 3 dJ f x x  

 





bằng:

A. 6. B. 8. C. 4. D. 2.

Lời giải

Chọn A

Tacó:

 

4 3 dJ f x x 

 

 



 

2 2

0 0

4 d 3df x x x 

 

4.3 3 12 3.2 3.0 6x     

.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Câu 28. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Kếtquả

x dx



bằng

x C

. B.

x C

. C.

. D.

x C

.

Lời giải

Chọn B

Tacó

x dx C 



.

Câu 29. (Chuyên Hạ Long - Quảng Ninh - 2021) Biết

 

cosF x x



 là một nguyênhàm của hàm số

 

f x

trên



.Giátrịcủa

 

3 2 df x x





 

 



bằng

. B.



. C.

2 6





. D.

4

.

Lời giải

Chọn C

Tacó

   

0 0

0 0 0

3 2 d 3 d 2 d 3cos 2 6 2

f x x f x x x x x

  

 



        

 

  

.

Câu 30. (Chuyên Hạ Long - Quảng Ninh - 2021) Biết

 

f x dx





 và

 

g x dx

 



. Giá trị của

   

3 2

f x g x dx



 

 



bằng

 B.

29

 C.

 D.

31



Lời giải

Chọn A

Tacó:

         

3 3 3

1 1 1

3 2 3 2 3.5 2. 7 15 14 29

f x g x dx f x dx g x dx

        

 

 

  

Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Biết

 

I f x dx

 



.Giátrịcủa

 

f x x dx



 

 



bằng

. B.

. C.

. D.

.

Lời giải

Chọn B

Tacó

   

2 2 2

1 1 1

2 2 2 3 5

f x x dx f x dx xdx

     

 

 

  

.

Câu 32. (Chuyên ĐH Vinh - Nghệ An - 2021) Họcácnguyênhàmcủahàmsố

 

sin3f x x



là

cos3

x C 

. B.

cos3

x C 

. C.

cos3

x C

. D.

cos3

x C

.

Lời giải

Chọn A

sin3 cos 3

xdx x C  



.

Câu 33. (Chuyên ĐH Vinh - Nghệ An - 2021) Biết

 

f x dx





 và

 

g x dx





 Khi đó

   

 

g x f x dx





bằng

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 B.



 C.

1.

 D.



Lời giải

Chọn D

Tacó

   

 

   

1 1 1

0 0 0

4 1

3 3

g x f x dx g x dx f x dx

     

  



Câu 34. (THPT Quế Võ 1 - Bắc Ninh - 2021) Mệnhđềnàosauđâyđúng.

d ln

x x C

 



. B.

d cot

sin

x x C

 



.

cos d sin

x x x C  



. D.

d tan

cos

x x C

 



.

Lời giải

Chọn D

Vì

d ln

x x C

 



nênloạiđápán A.

Vì

d cot

sin

x x C

  



nênloạiđápán B.

Vì

cos d sin

x x x C 



nênloạiđápán C.

Câu 35. (THPT Quế Võ 1 - Bắc Ninh - 2021) Khẳngđịnhnàosauđâyđúngvớimọihàm

,f g

liêntục

trên

và

,a b

làcácsốbấtkỳthuộc

?

       

. .

b b b

a a a

f x g x dx f x dx g x dx

 

 

  

.

       

2 2

b b b

a a a

f x g x dx f x dx g x dx

   

 

  

.

 

f x dx

f x

g x

g x dx





.

   

b b

a a

f x dx f x dx

 



 

 

 

.

Lời giải

Chọn B

       

2 2

b b b

a a a

f x g x dx f x dx g x dx

   

 

  

chỉcótínhchấttổngcủa2tíchphân.

Câu 36. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hàm số

 

f x

 liên tục trên



 và

có

 

d 2,

f x x





 

d 6

f x x





Tính

 

d .f x x





12I 

. B.



. C.



. D.

4I 

.

Lời giải

Chọn B

Tacó

     

3 1 3

0 0 1

d d d 2 6 8

f x x f x x f x x

    

  



Câu 37. (THPT Quốc Oai - Hà Nội - 2021) Cho hai hàmsố

 

y f x



và

 

y g x



liên tục trên



.

Trongcácmệnhđềsau,mệnhđềnàosai?

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

       

f x g x dx f x dx g x dx  

 

 

  

   

kf x dx k f x dx



 

vớimọihằngsố

 

\ 0k  

       

f x g x dx f x dx g x dx   

 

  

       

. .f x g x dx f x dx g x dx

  

.

Lời giải

Chọn D

Câu 38. (THPT Quốc Oai - Hà Nội - 2021) Chohàmsố

 

y f x

liêntụctrênđoạn

 

;a b

.Gọi

 

F x

là

mộtnguyênhàmcủahàmsố

 

y f x

.Hãychọnkhẳngđịnhđúngtrongcáckhẳngđịnhsau

     

f x dx F a F b 



. B.

     

2 2

f x dx F b F a 



     

f x dx F b F a 



. D.

     

f x dx F a F b 



.

Lời giải

Chọn C

Câu 39. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho

làmộthằngsố.Trongcácmệnhđềsau,

mệnhđềnàosai?

x x

e dx e C 



. B.

sin cosxdx x C 



2xdx x C 



. D.

 lndx x C

 



.

Lời giải

Chọn B

Tacó:

sin cosxdx x C  



.

Câu 40. (THPT Quảng Xương 1-Thanh Hóa - 2021) Nếu

 

d 2f x x 



và

 

d 4f x x  



thì

 

df x x





bằng

. B.

6

. C.

. D.

2

.

Lời giải

Chọn B

Tacó

           

1 3 3 3 3 1

0 1 0 1 0 0

d d d d d d 4 2 6

f x x f x x f x x f x x f x x f x x

         

     

.

Câu 41. (THPT Quảng Xương 1-Thanh Hóa - 2021) Chođồthịhàmsố

 

y f x

.Diệntích

củahình

phẳng(phầntôđậmtronghìnhvẽ)là



   

1 3

0 1

S f x dx f x dx  

 

. B.

   

1 3

0 1

S f x dx f x dx 

 

.

 

S f x dx



. D.

   

1 3

0 1

S f x dx f x dx 

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn B

     

3 1 3

0 0 1

S f x dx S f x dx f x dx

   

  



Câu 42. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Hàmsố

 

3 2

5 4 7 120

F x x x x   

lànguyênhàm

củahàmsốnàosauđây?

 

5 4 7f x x x  

. B.

 

15 8 7

f x x x

  

 

5 4 7

f x x x

  

. D.

 

2 3 2

5 4 7

4 3 2

x x x

f x   

.

Lời giải

Chọn B

Vì

 

F x

làmộtnguyênhàmcủa

 

f x

nên

   

 

3 2 2

5 4 7 120 15 8 7

f x F x x x x x x



 

       

 

.

Câu 43. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Mộtnguyênhàmcủahàmsố

2y cos x

là

2sin 2x

. B.

2sin 2x

. C.

sin 2

. D.

sin2



.

Lời giải

Chọn C

Tacó

( ) sin( )

cos ax b dx ax b C

   





Câu 44. (THPT Phan Đình Phùng - Quảng Bình - 2021) Tìmnguyênhàmcủahàmsố

 

2021

f x x



trên



.

 

2022

f x x 



. B.

 

2020

d 2021

f x x x C 



.

 

2022

f x x C 



. D.

 

2021

f x x C 



.

Lời giải

Chọn C

Tacó:

 

2022

2021

d d

2022

f x x x x C  

 

.

Câu 45. (THPT Phan Đình Phùng - Quảng Bình - 2021) Nếu

( ) 4

f x dx





và

( ) 3

g x dx





thì

 

2 ( ) 3 ( )f x g x dx





bằng

. B.

. C.

. D.

.

Lời giải

Chọn C

Tacó:

 

1 1 1

0 0 0

2 ( ) 3 ( ) 2 ( ) 3 ( ) 2.4 3.3 17

f x g x dx f x dx g x dx

     

  

.

Câu 46. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Chohàmsố

 

f x

liêntụctrênđoạn

 

0;2

.Biết

 

d 5

f x x





và

 

dt 3.

f t





Tính

 

dI f x x





.



. B.

2I 

. C.



. D.

1I 

.

Lời giải

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Chọn B

Tacó

         

1 2 2 2 2

0 0 1 0 1

d d d d dt 2.

I f x x f x x f x x f x x f t

     

    



Câu 47. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho

 

F x

 là một nguyên hàm của hàm số

 

3 2

f x





trênkhoảng

;

 



 

 

.Tìm

 

F x

,biết

 

1 5



.

   

ln 3 2 5

F x x

  

. B.

   

3ln 3 2 5

F x x

  

.

 

3 2

F x



 



.D.

   

ln 3 2 5

F x x

  

.

Lời giải

Chọn D

Tacó:

 

1 1

d ln 3 2

3 2 3

F x x x C

   





.

Theobài,

 

1 5 5

F C

  

.

Vậy

 

ln 3 2 5

F x x

  

Câu 48. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Chobiết

 

d 2

f x x





và

 

d 3

g x x





.Tính

   

I 4 df x g x x

 

 

 



?

I=3

. B.

I=1

. C.

I=11

. D.

I=5

.

Lời giải

Chọn D

Tacó

       

1 1 1

0 0 0

I 4 d 4 d d 4.2 3 5

f x g x x f x x g x x

      

 

 

  

.

Câu 49. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Biết

 

f x d





 và

 

f t dt





. Tính

 

f u du





. B.



. C.



. D.

.

Lời giải

Chọn B

Tacó

     

4 4 3

3 0 0

f u du f u du f u du



  

  



Câu 50. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình phẳng

 

 được giớihạn bởi các

đường

 

2 1, , 0, 1

f x x Ox x x

   

.Tínhthể tích

củakhốitrònxoaytạothànhkhi quay

 

xungquanhtrục

đượctínhtheocôngthức?

2 1dx

V x



 



. B.

 

2 1 dx

V x 



. C.

 

2 1 dx

V x



 



. D.

2 1dx

V x 



.

Lời giải

Chọn C

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Tacó

 

1 1

0 0

2 1 dx 2 1 dx

V x x

 

   

 

.

Câu 51. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Nếu

 

f x dx





thì

 

f x dx



bằng

18.



Lời giải

Chọn D

Vì

 

f x dx





nên

 

3 3.6 18

f x dx

 



.

Câu 52. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Khẳngđịnhnàosauđâylàđúng

cot

cos

dx x C

  



. B.

.ln

x x

a dx a a C 



e dx C



 



. D.

1 1

dx C

  



.

Lời giải

Chọn C

Tacó:

tan

cos

dx x C

 



a dx C

 



x x

e dx e C C



   



dx x C

 



.

Câu 53. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Tínhtíchphân

 

2 xx d



 



bằng



. B.

. C.

. D.



Lời giải

Chọn B

 

2 x= 2 .

4 4

x d x



 

    

 



 





Câu 54. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Biết

 

dx 4

f x





. Tính tích phân

 

2 dx

I x f x 

 

 



bằng



. B.

12I 

. C.



. D.

4I 

.

Lời giải

Chọn C.

Tacó

     

2 2 2 2

0 0 0 0

2 dx 2xdx dx dx 4 4 8

I x f x f x x f x

        

 

 

   

.

Câu 55. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Chohàmsố

( ) 1f x x 

.Trongcáckhẳngđịnh

sau,khẳngđịnhnàođúng?

( ) x

f x d x x C  



. B.

( ) x 2

f x d x x C  



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

( ) x

f x d x x C  



. D.

( ) x

f x d x C 



Lời giải

Chọn A

Tacó:

( ) x ( 1) x

f x d x d x x C    

 



Dođóchọnphươngán A.

Câu 56. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Họcácnguyênhàmcủahàmsố

 

3 1

f x x

 

là.

x x C 

. B.

x C

. C.

x C

. D.

x C 

.

Lời giải

Chọn A

Tacó

 

2 3

d 3 1 d

f x x x x x x C    

 

.

Câu 57. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Biết

 

d 4

f x x





.Giátrịcủa

 

3 df x x



bằng.

. B.

. C.

. D.

.

Lời giải

Chọn D

Tacó

   

5 5

1 1

3 d 3 d 12

f x x f x x

 

 

.

Câu 58. (THPT Đồng Quan - Hà Nội - 2021) Họnguyênhàmcủahàmsố

 

ln x

f x



là

x C

. B.

x C

. C.

 

ln ln

x C

. D.

ln ln

x x C 

.

Lời giải

Chọn A

Tacó:

 

ln 1

d ln d ln ln

x x x x C

  

 

.

Câu 59. (THPT Đồng Quan - Hà Nội - 2021) Họnguyênhàmcủahàmsố

   

2 cos2

f x x x 

là

1 1

sin 2

2 2

x x C  

.B.

sin 2

x x C  

.

1 1

sin 2

2 2

x x C 

. D.

sin 2

x x C 

.

Lời giải

Chọn D

Tacó

 

2 2

1 1

2 sin 2

2 2

sin 2F x x xx

x C

 

   

 



 





Câu 60. (THPT Đồng Quan - Hà Nội - 2021) Cho

   

  

 

1 0

0 1

3; 2,

f x dx g x dx

khi đó

   

 





f x g x dx

bằngbaonhiêu?

. B.

7

. C.

. D.

1

.

Lời giải

Chọn B

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Tacó

   

 

       

1 1 1 1 0

0 0 0 0 1

2 2 2 3 2.2 7

f x g x dx f x dx g x dx f x dx g x dx

         

    



Câu 61. (THPT Lê Lợi - Thanh Hóa - 2021) Nguyênhàmcủahàmsố

y x x  là

3 2

x x

C 

. B.

2 1x C 

. C.

x x C 

. D.

x C 

.

Lời giải

Chọn C

 

3 2

x x

x x x C   



.

Câu 62. (THPT Lê Lợi - Thanh Hóa - 2021) Chohàmsố

( )y f x

cóđồthịnhưhìnhvẽ.



Diệntíchhìnhphẳng(phầntôđậm)đượctínhtheocôngthứcnàosauđây?

( ) .S f x dx







. B.

0 3

2 0

( ) ( ) .S f x dx f x dx



 

 

0 3

2 0

( ) ( ) .S f x dx f x dx



  

 

. D.

0 3

2 0

( ) ( ) .S f x dx f x dx



 

 



Lời giải

Chọn C

Diệntíchhìnhphẳngcầntính

3 0 3 0 3

2 2 0 2 0

( ) ( ) ( ) ( ) ( ) .S f x dx f x dx f x dx f x dx f x dx

  

     

    



(Do

 

0( ;) 20,f xx   

và

 

3( ) 0, 0;x xf   

)

Câu 63. (THPT Lê Lợi - Thanh Hóa - 2021) Chocáchàmsố

   

,y f x y g x 

liêntụctrên



có

 

dx 1f x



 



;

 

dx 3g x







.Tính

   

2 dxf x g x





 

 



.

. B.

1

. C.

. D.

.

Lời giải

Chọn D

Tacó

       

5 5 5

1 1 1

2 dx dx 2 dx 1 2.3 5f x g x f x g x

  

       

 

  

.

Câu 64. (Sở Vĩnh Phúc - 2021) Tìmhọtấtcảcácnguyênhàmcủahàmsố





.

 

ln 1x x C  

. B.

ln 1x x C  

. C.

 

ln 1x x C  

. D.

ln 1x x C  

.

Lời giải

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Chọn B.

Tacó:





1 d

 





 









 





ln 1

x x C   

.

Câu 65. (Sở Lào Cai - 2021) Khẳngđịnhnàosauđâylàđúng?

 

f x x f x



 



. B.

 

f x x f x







.

 

f x x f x



 



. D.

 

f x x f x







.

Lời giải

Chọn D.

Gọi

 

F x

làmộtnguyênhàmcủa

 

f x

.Tacó

 

f x x F x C f x



  



.

Câu 66. (Sở Lào Cai - 2021) Cho

 

f x x

 



,khiđó

 

f x x



bằng

. B.

1

. C.

4

. D.

3

.

Lời giải

Chọn D

     

2 2

1 1

3 3 3. 1 3

d df x x f x x

    

 

.

Câu 67. (Sở Lào Cai - 2021) Tíchphân

e d



bằng:

. B.

1e

. C.

e

. D.

e-1

.

Lời giải

Chọn D

e d e e 1

x x

  



.

Câu 68. (Sở Lào Cai - 2021) Họcácnguyênhàmcủahàmsố

 

sin

f x

 

là:

cot

x C

. B.

tan

x C 

. C.

cot

x C 

. D.

tan

x C

.

Lời giải

Chọn A.

Tacó

d cot

sin

x x C

  



.

Câu 69. (Sở Hà Tĩnh - 2021) Biết

 

d 4

f x x





.Giátrịcủa

 

2 3 dx f x x



 

 



bằng

. B.

2

. C.

. D.

.

Lời giải

Chọn D

   

5 5 5

2 5

1 1 1

2 3 d = 2 d 3 d | 3.4 24 12 12.

x f x x x x f x x x       

 

  



Câu 70. (Sở Hà Tĩnh - 2021)

 

x x dx

 



bằng

x C

. B.

4 2

x x C 

. C.

3 2

x C 

. D.

4 2

x x C 

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Chọn B

Tacó

 

2 4 4

3 3 2

2 2 2.

2 4 4

x x x

x x dx xdx x dx C x C            

  

.

Câu 71. (Sở Yên Bái - 2021) Trongcáckhẳngđịnhsau,khẳngđịnhnàosai?

x C



(

làhằngsố). B.

x x C 



(

làhằngsố).

d ln

x x C

 



(

làhằngsố). D.

x x C





 





(

làhằngsố).

Lời giải

Chọn D

x x C





 





(

làhằngsố)Saivìthiếuđiềukiện



 

.

Câu 72. (Sở Tuyên Quang - 2021) Nguyênhàmcủahàmsố

 

2 1

f x





là

 

ln 2 1

F x x C  

.B.

 

2ln 2 1

F x x C  

.

 

ln(2 1)

F x x C  

. D.

 

ln 2 1

F x x C  

.

Lời giải

Chọn D

Tacó:

 

1 1

ln 2 1

2 1 2

f x dx dx x C

   



 

.

Câu 73. (Sở Tuyên Quang - 2021) Cho

 

f x dx





 và

 

g x dx





. Khi đó

   

f x g x dx



 

 





bằng:

A. 1 B. -3 C. -8 D. 12

Lời giải

Chọn C

Tacó:

       

1 1 1

0 0 0

2 2 2 2.5 8

f x g x dx f x dx g x dx

      

 

 

  



Câu 74. (Sở Tuyên Quang - 2021) Họtấtcảcácnguyênhàmcủahàmsố

 

2 sinf x x x

 

là

2 cos

x x C 

. B.

2 cos

x x C 

. C.

cos

x x C 

. D.

cos

x x C 

.

Lời giải

Chọn C

Tacó

 

2 sin d = 2 d sin d cos

x x x x x x x x x C    

  

.

Câu 75. (THPT Thanh Chương 1- Nghệ An - 2021) Họnguyênhàmcủahàmsố là?

A. . B. . C. . D. .

Lời giải

Chọn B

Tacó: .

Câu 76. (THPT Thanh Chương 1- Nghệ An - 2021) Cho

 

3 2 d 12

f x x x

 

 

 



.Khiđó

 

df x x



bằng

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

A. . B. . C. . D. .

Lời giải

Chọn A

Tacó

.

Câu 77. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Chohàmsố

 

y f x

liêntụctrên



vàcóđồthị

 

làđườngcongnhưhìnhvẽbên.



Diệntíchcủahìnhphẳnggiớihạnbởiđồthị

 

,trục

vàhaiđườngthẳng

0, 2x x 

(phần

tôđen)là

   

1 2

0 1

d dS f x x f x x  

 

. B.

 

dS f x x



.

   

1 2

0 1

d dS f x x f x x 

 

. D.

 

dS f x x



.

Lời giải

Chọn C

Tacó:

   

1 2

0 1

d dS f x x f x x 

 



Câu 78. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Chohàmsố

 

f x

liêntụctrênđoạn

 

;a b

.Khẳng

địnhnàosauđâysai?

       

b b b

a a a

f x g x dx f x dx g x dx   

 

  

. B.

   

a b

b a

f x dx f x 

 

.

       

. .

b b b

a a a

f x g x dx f x dx g x dx

 

 

  

. D.

   

b b

a a

k f x dx k f x dx



 

.

Lời giải

Chọn C

Câu 79. (THPT Nguyễn Huệ - Phú Yên - 2021) Biết

 

cosF x x

làmộtnguyênhàmcủahàmsố

 

f x



trên



.Giátrịcủa

 

2 f x dx





bằng

1

. B.

. C. 3 . D.

.

Lời giải

Chọn A

Vì

 

cosF x x

làmộtnguyênhàmcủahàmsố

 

f x

nên

 

sinf x x 

.

 

3 3

0 0

2 2 sin 2cos 1f x dx xdx x

 



    

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 80. (THPT Nguyễn Huệ - Phú Yên - 2021) Biết

 

f x dx





.giátrịcủa

 

3f x dx





bằng

. B.

. C.

. D.

.

Lời giải

Chọn A

Tacó

 

3 3 3

2 2 2

3 3 3 3 6

f x dx f x dx dx x

     

  

.

Câu 81. (THPT Lương Thế Vinh - 2021) Diệntíchhìnhphẳnggiớihạnbởicác đường

y x

 

và

4y x 

xácđịnhbởicôngthức

 

x x dx





. B.

 

x x dx





. C.

 

x x dx





. D.

 

x x dx





.

Lời giải

Chọn C

Phươngtrìnhhoànhđộgiaođiểmcủahaiđồthị:

4 4

x x





   







.

Diệntíchcủahìnhphẳnglà:

 

1 1

2 2

0 0

S x x dx x x dx

   

 

.

Câu 82. (THPT Lương Thế Vinh - 2021) Họnguyênhàmcủahàmsố

 

f x



là.

3 log3

C

. B.

3 ln3

C

. C.

ln3

C

. D.

log3

C

.

Lời giải

Chọn C

TheocôngthứcnguyênhàmcơbảnchọnC.

Câu 83. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Chohaihàmsố

 

f x

,

 

g x

liêntụctrênđoạn

 

;a b

vàsốthực

tùyý.Mệnhđềnàodướiđâysai?

       

d d d , ;

b c c

a a b

f x x f x x f x x c a b

   

  

. B.

   

d d

b a

a b

f x x f x x

 

 

.

   

d d

b b

a a

kf x x k f x x



 

. D.

       

d d d

b b b

a a a

f x g x x f x x g x x

   

 

  

.

Lời giải

Chọn A

MệnhđềAsai.Vì:

       

d d d , ;

b c b

a a c

f x x f x x f x x c a b

   

  

.

Câu 84. (THPT Đào Duy Từ - Hà Nội - 2021) Họcácnguyênhàmcủahàmsố

 

2 3f x x x  

là

x x C  

. B.

2 2

x C 

. C.

3 2

x x C 

. D.

3 2

2 3

x x x C  

.

Lời giải

Chọn A

Câu 85. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hàm số

 

y f x



 có đạo hàm trên đoạn

 

1;2

,

 

1 1



và

 

2 2



.Khiđó,

 

dI f x x







bằng

1I 

. B.

1I  

. C.



. D.



.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Lời giải

Chọn A

Tacó:

       

d 2 1 2 1 1

I f x x f x f f



      



.

Câu 86. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Thểtíchcủakhốitrònxoaysinhbởihìnhphẳnggiới

hạnbởihaiđồthịhàmsố

cosy x

,đườngthẳng



,





vàtrục

khiquayquanhtrục

hoànhlà

cos dV x x







. B.

cos dxV x







. C.

cos dV x x







. D.

cos dV x x







.

Lời giải

Chọn D

Dựavàocôngthứctínhthểtíchkhốitrònxoayquayquanhtrục

,tađược

cos dV x x







Câu 87. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Họnguyênhàmcủahàmsố

 

3 2

3f x x x

 

là

4 3

x x C 

. B.

4 3

x x

C 

. C.

x C 

. D.

3 6

x x C 

.

Lời giải

Chọn C

Ápdụngcôngthứcnguyênhàm:

x x C





 





vàcáctínhchấtnguyênhàm.

Tacó:

 

3 2 3

3x d

x x x C   



.

Câu 88. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho

 

x 2

f x d





và

 

x 3

g x d





. Tích phân

   

2 xf x g x d



 

 





. B.

. C.

1

. D.

.

Lời giải

Chọn D

Tacó

       

2 2 2

0 0 0

2 x =2. x- x =2.2-3=1

f x g x d f x d f x d 

 

  

.

Câu 89. (THPT Chu Văn An - Thái Nguyên - 2021) Chohàmsố

 

y f x



xácđịnh,liêntụcvàkhông

âmtrên

 

;a b

.Thể tích của vật thể tròn xoay sinh bởi miền

 

giới hạn bởiđồ thị hàm số

 

y f x



,trụchoànhvàhaiđườngthẳng

x a x b 

quayquanh

là

 

V f x x





. B.

 

V f x x





. C.

 

V f x x







. D.

 

V f x x







.

Lời giải

Chọn C

Câu 90. (THPT Chu Văn An - Thái Nguyên - 2021) Nếu

 

d 6

f x x



 



 và

 

d 2

g x x





 thì

 

df x x





bằng

. B.

12

. C.

8

. D.

4

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Chọn D

Tacó

     

2 0 2

2 2 0

d d d 6 2 4

f x x f x x f x x

 

      

  

.

Câu 91. (THPT Ba Đình - Thanh Hóa - 2021) Nguyênhàmcủahàmsố

 

f x x

là

x x C 



. B.

x x C 



. C.

x x C 



. D.

3 4

d 4

x x x C 



Lời giải

Chọn B

Nguyênhàmcủahàmsố

 

f x x

là

x x C 



.

Câu 92. (THPT Ba Đình - Thanh Hóa - 2021) Biết

 

f x dx





,giátrị

 

f x dx



bằng

. B.

. C.

. D.

.

Lời giải

Chọn C

Tacó:

   

8 8

1 1

5 5 15

f x dx f x dx

 

 

.

Câu 93. (THPT Ba Đình - Thanh Hóa - 2021) Cho

2 1dI x x x

 



và

2 1u x 

.Mệnhđềnàodưới

đâysai:

2 2

( 1)d

I x x x

 



. B.

2 2

( 1)d

I u u u

 



.

5 3

2 5 3

u u

 

 

 

 

. D.

2 2

( 1)dI u u u

 



.

Lời giải

Chọn D

Đặt

2 1 2 1 2dx 2 d dx dx u x u u u u u

         .

Khiđó

4 3 3

2 2

0 1 1

1 1

2 1d . . d ( 1)d

2 2

I x x x u u u u u u



    

  

A,Bđúng.

Đểý

3 3

5 3

2 2 2 2

1 1

1 1 1

( 1)d ( 1)d

2 2 2 5 3

u u

I u u u x x x

 

     

 

 

 

Cđúng.

Dođó

2 2

( 1)dI u u u

 



saiDsai.

Câu 94. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Chohàmsố

 

f x

liêntụctrên





và

làsố

dương.Trongcáckhẳngđịnhsau,khẳngđịnhnàođúng?

 

d 1

f x x 



. B.

 

d 0

f x x





. C.

 

f x x a



. D.

 

d 2

f x x a



.

Lời giải

Chọn B

Tacókhẳngđịnhđúnglà

 

d 0

f x x





.

Câu 95. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Nguyênhàmcủahàmsố

2 1x

y e

 



là

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

2 1

2 .

e C

 



 B.

2 1

2 .

e C

 

 C.

2 1

e C

 



 D.

2 1

e C

 



Lời giải

Chọn D

Tacó

 

2 1 2 1 2 1

1 1

2 1

2 2

x x x

e dx e d x e C

     

      

 

.

Câu 96. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số

 

f x

 thoả mãn

 

2021 ln 2021 cos

f x x



 

và

 

0 2



.Phátbiểunàosauđúng?

 

2021

sin 1

ln 2021

f x x  

. B.

 

2021 sin 1

f x x  

.

 

2021 sin 1

f x x  

. D.

 

2021

sin 1

ln 2021

f x x  

.

Lời giải

Chọn B

   

 

2021 ln 2021 cos 2021 sin

x x

f x f x dx x dx x C



     

 

.

 

2021 sin 02

2 1

0 Cf C 

  

.

Câu 97. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Tìmnguyênhàmcủa

x dx



.

x C

. B.

x C

. C.

x C

. D.

x C

.

Lời giải

Chọn B

Tacó:

6 7

x dx x C 



.

Câu 98. (Trung Tâm Thanh Tường - 2021) Cho

 

f x

,

 

g x

làcáchàmsốxácđịnhvàliêntụctrên



.

Trongcácmệnhđềsau,mệnhđềnàosai?

       

f x g x dx f x dx g x dx



  

.

   

2 2

f x dx f x dx



 

.

       

f x g x dx f x dx g x dx

 

  

 

  

       

f x g x dx f x dx g x dx

 

  

 

  

.

Lời giải

Chọn A.

MệnhđềcâuAsai.

Câu 99. (Trung Tâm Thanh Tường - 2021) Nếu

2 2

0 0

( ) 5, ( ) 2

f x dx g x dx

 

 

thì

 

( ) 2 ( )f x g x dx





bằng

. B.

. C.

. D.

.

Lời giải

Chọn B

Tacó

 

2 2 2

0 0 0

( ) 2 ( ) ( ) 2 ( ) 5 4 9

f x g x dx f x dx g x dx

     

  

.

Câu 100. (Trung Tâm Thanh Tường -2021) Họnguyênhàmcủahàmsố

 

f x x e

 

là

xe C

. B.

x e C 

. C.

2 2

x e C 

. D.

2 2 x

x e C 

.

Lời giải

Chọn B

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Tacó

 

d 2 d 2 d 2

x x

e x x x e x x e C     



 

Câu 101. (THPT Triệu Sơn - Thanh Hóa - 2021) Họtấtcảcácnguyênhàmcủahàmsố

 

x x





l

à.

C

. B.

x C 

. C.

x C 

. D

C

Lời

giải

Chọn C

T

acó

 

3 1 d

x x x x x x C    



Câu

102. (THPT Triệu Sơn - Thanh Hóa - 2021) Biết

 

x dx







khi



đó

 

x dx



bằng

.

Lời giải

Chọn D

acó

   

1 1

2 8

x dx f x dx



 



Câu

103. (THPT Triệu Sơn - Thanh Hóa - 2021) Chohàmsố

 

f x



xá

cđịnhvàliệntụctrênđoạn

 

;a b

.Diệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố

 

y f x



,trụchoànhvàhaiđườngthẳng

;

a x b 

được

tínhtheocôngthức

 

f x dx





. B.

 

f x dx





. C

 

x dx



. D.

 

x dx



.

Lời

giải

Chọn D

Công

thứctổngquáttínhdiệntíchhìnhphẳngbằngtíchphân.

Câu 104. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho

 

d 6 2sin 2

f x x x x C  



,khiđó

 

bằng

12 4cos2x x

. B.

cos2x x



. C

12 2 2cos x

. D

6 4 2x cos x

Lời

giải

Chọn A

acó

 

2sin 2 12 4 2x x C x cos x



   

Câu

105. (THPT Trần Phú - Đà Nẵng - 2021) Nếu

 

x dx







và



 

x dx





thì



 

x dx





bằng

.

Lời

giải

Chọn B

acó

     

3 5

1 1 3

x dx f x dx f x dx





 



 



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1

MỨC ĐỘ THÔNG HIỂU

Câu 1. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Tính

I dx



theo số thực

.25



. B.

(25 1).ln 25



. C.

(25 1)





. D.

(25 1)

ln 25



Câu 2. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Tính tích phân

 

1 dI x x x 



. B.



. C.



. D.

Câu 3. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Họ nguyên hàm của hàm số

 

2 1

f x x e 

là

 

2 1

e x x C  

 

2 1 4

e x x C  

 

2 1

e x x 

 

2 1 4

e x x 

Câu 4. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho

d 1

1 2

x e

a b



 





, với

,a b

là

các số nguyên. Tính

3 3

S a b 

0S 

. B.

2S  

. C.

1S 

. D.

2S 

Câu 5. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Tìm nguyên hàm của hàm số

 

e 1 e

x x

f x



 

 

d e

f x x C 



. B.

 

d e

f x x C



 



 

d e

f x x x C  



. D.

 

d e e

x x

f x x C



  



Câu 6. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Diện tích phần hình phẳng tô đậm

trong hình vẽ bên được tính theo công thức nào dưới đây?

 

2 2 dx x x  



. B.

 

2 2 dx x x  



 

2 2 dx x x 



. D.

 

2 2 dx x x 



NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG

Chủ đề 3

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 7. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho

 

d 1f x x 



. Với

 

e d e

I f x x a

 

   

 



. Khẳng định nào sau đây đúng?



. B.

 

. C.

 

. D.



Câu 8. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Bác thợ xây bơm nước vào bể nước. Gọi

 

h t

là

thể tích nước bơm được sau

giây. Cho

 

h t at bt



 

và ban đầu bể không có nước. Sau

giây thì thể tích nước trong bể là

150m

, sau

giây thì thể tích nước trong bể là

1100m

. Tính

thể tích của nước trong bể sau khi bơm được

giây:

8400m

. B.

600m

. C.

2200m

. D.

4200m

Câu 9. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hàm số

 

f x

thỏa mãn

 

3 5sinf x x



 

và

 

0 10



. Tìm hàm số

 

f x

 

3 5cos 15

f x x x

  

. B.

 

3 5cos 2f x x x  

 

3 5cos 5f x x x  

. D.

 

3 5cos 2

f x x x

  

Câu 10. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình phẳng (H) giới hạn bởi đồ thị hàm số

y x x 

và trục hoành. Tính thể tích V vật thể tròn xoay sinh ra khi cho (H) quay quanh trục

Ox.





. B.



. C.



. D.





Câu 11. (Chuyên KHTN - 2021) Cho hàm số

 

f x

liên tục trên



và thoả mãn

 

d 2

xf x x





. Tích

phân

 

3 dxf x x



bằng

. B.

. C.

. D.

Câu 12. (Chuyên KHTN - 2021) Họ nguyên hàm của hàm số

 

lnf x x



trên khoảng

 

 

là

x x x C 

. B.

C

. C.



. D.

x x x C 

Câu 13. (Chuyên KHTN - 2021) Diện tích hình phẳng giới hạn bởi đồ thị của hàm số

y x x 

và đồ thị

của hàm số

2 2

y x

 

bằng

. B.

. C.

. D.

Câu 14. (Chuyên KHTN - 2021) Họ nguyên hàm

cos dx x x



là

cos sin

x x x C 

. B.

cos sin

x x x C  

cos sin

x x x C 

. D.

cos sin

x x x C  

Câu 15. (Chuyên KHTN - 2021) Diện tích hình phẳng giới hạn bởi đường thẳng

3y x 

và parabol

2 1y x x  

bằng:

. B.

. C.

. D.

Câu 16. (Chuyên KHTN - 2021) Tính nguyên hàm

tan 2

xdx



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

tan 2x x C 

. B.

tan2

x x C 

. C.

tan2

x x C 

. D.

tan 2x x C 

Câu 17. (Chuyên KHTN - 2021) Tìm nguyên hàm

 

2 1 lnx xdx



 

x x x x C    . B.

 

x x x x C    .

 

x x x x C    . D.

 

x x x x C    .

Câu 18. (Chuyên KHTN - 2021) Tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi đường

thẳng

2x 

và đồ thị

y x khi quay xung quanh trục



. B.



. C.



. D.



Câu 19. (Chuyên KHTN - 2021) Tính nguyên hàm

 

2 3

2 1x x dx



 

2 1



 . B.

 

2 1



 . C.

 

2 1



 . D.

 

2 1





Câu 20. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho tích phân

3 1dx x x



, nếu đặt

3 1u x 

thì

3 1dx x x



bằng

u u



. B.

u u



. C.

u u



. D.

u u



Câu 21. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho

 

4 ( ) 2 d 1f x x x 



. Khi đó

( )f x dx



bằng

A. 1. B. -3. C. -1. D. 3.

Câu 22. (Chuyên Quốc Học Huế - 2021) Tính diện tích của hình phẳng (được tô đậm) giới hạn bởi hai

đường

2 2

2 , 4 .y x y x 





. B.





. C.

S 

. D.

S 

Câu 23. (Chuyên Quốc Học Huế - 2021) Cho tích phân

2 cos sinx xdx







. Nếu đặt

2 cost x 

thì kết

quả nào sau đây đúng?

2 .I tdt



.I tdt







.I tdt



.I tdt



Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Nguyên hàm của hàm số

( ) 2 ( 1)(2 1)f x x x x  

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

x x C 

4 3 2

x x x C  

4 3 2

x x x C  

4 3 2

x x x C  

Câu 25. (Chuyên Quang Trung - Bình Phước - 2021) Tìm nguyên hàm

 

F x

của hàm số

( ) .

f x x e



biết

 

1 0



x x

x e e

. B.

. 1

x x

x e e

 

. C.

x e e

. D.

. 1

x e x e  

Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm số thực

để hàm số

   

3 2

3 2 4 3F x mx m x x    

là một nguyên hàm của hàm số

 

3 10 4

f x x x

  



. B.



. C.



. D.

 

Câu 27. (Chuyên Ngoại Ngữ Hà Nội- 2021) Nguyên hàm của hàm số

 

3 1f x x 

là

( ) (3 1) 3 1

f x dx x x C   



. B.

( ) (3 1) 3 1

f x dx x x C   



( ) 3 1

f x dx x C  



. D.

( ) 3 1

f x dx x C  



Câu 28. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho tích phân

 

2 3 2

3 2

x x dx me ne

  



với

, ,

m n



khi

đó

m n

bằng bao nhiêu?

. B.

. C.

. D.

Câu 29. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho

d ln 2 ln5

x a b

x x



 

 



với

,a b

là các số nguyên.

Mệnh đề nào sau đây đúng?

a b

 

. B.

a b

 

. C.

2 11

a b

 

. D.

2 11

a b

 

Câu 30. (Chuyên Ngoại Ngữ Hà Nội- 2021) Thể tích khối tròn xoay sinh ra khi quay quanh

hình

phẳng giới hạn bởi các đường

0, 1, ; 0

x x y xe y

   

là

 





. B.

 



. C.

 



. D.

 





Câu 31. (Chuyên Ngoại Ngữ Hà Nội- 2021) Biết

 

2 d 4xf x x 



. Giá trị của

 

dxf x x



bằng

. B.

. C.

. D.

Câu 32. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Với

,a b

là các tham số thực. Giá trị tích phân

 

3 2 1 d

x ax x

 



bằng

3 2 1b ab 

. B.

3 2

b b a b 

. C.

3 2

b a b b 

. D.

3 2

b ab b 

Câu 33. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Hình vẽ bên biểu diễn trục hoành cắt đồ thị

 

y f x



tại ba điểm có hoành độ

 

0, , 0

a b a b 

. Gọi

là hình phẳng giới hạn bởi đồ thị

 

y f x



và

trục hoành, khẳng định nào sau đây là sai?

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

 

S f x x



. B.

   

S f x dx f x dx  

 

   

S f x dx f x dx 

 

. D.

   

S f x dx f x dx 

 

Câu 34. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình phẳng

giới hạn bởi đường cong

y e ,

trục hoành và các đường thẳng

0, 1x x 

. Khối tròn xoay tạo thành khi quay

quanh trục

hoành có thể tích

bằng bao nhiêu?

 

e 1







. B.





. C.

e 1





. D.

 

e 1







Câu 35. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hàm số

 

y f x

có đạo hàm cấp hai

 

f x



liên

tục trên đoạn

 

0;1

đồng thời thỏa mãn điều kiện

     

0 1 1; 0 2021.f f f



  

Mệnh đề nào sau

đây đúng?

   

1 d 2021x f x x



  



. B.

   

1 d 2021x f x x



 



   

1 d 1x f x x



 



. D.

   

1 d 1x f x x



  



Câu 36. (Chuyên Hạ Long - Quảng Ninh - 2021) Diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

1 5 6y x x x   

và hai trục tọa độ bằng



Câu 37. (Chuyên ĐHSP Hà Nội - 2021) Diện tích hình phẳng thuộc góc phần tư thứ hai, giới hạn bởi

parabol

2y x  , đường thẳng

y x 

và trục

bằng:

. B.

. C.

. D.

Câu 38. (Chuyên ĐHSP Hà Nội - 2021)

 

2 5 dx x



bằng

 

2 5

x C 

. B.

 

18 2 5x C 

. C.

 

9 2 5x C 

. D.

 

2 5

x C 

Câu 39. (Chuyên ĐHSP Hà Nội - 2021) Biết

 

f x

là hàm số liên tục trên

 

0;3

và có

 

3 d 3f x x 



. Giá

trị của biểu thức

 

df x x



bằng:

A. 9. B. 1. C. 3. D.

Câu 40. (Chuyên ĐH Vinh - Nghệ An - 2021) Giả sử

 

f x

là hàm liên tục trên





0;

và diện tích

phần hình phẳng được kẻ dọc ở hình bên bằng

. Tích phân

 

2 df x x



bằng:

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

. B.

. C.

. D.

Câu 41. (Chuyên ĐH Vinh - Nghệ An - 2021) Họ nguyên hàm của hàm số

 

2 1

f x





là

C

. B.

C

. C.

6ln 3

C

. D.

3ln 3

C

Câu 42. (Chuyên ĐH Vinh - Nghệ An - 2021) Một chiếc xe đua

đạt vận tốc lớn nhất là

360 /km h

. Đồ

thị bên hiển thị vận tốc

của xe trong 5 giây đầu tiên kể từ lúc xuất phát. Đồ thị trong 2 giây đầu

là một phần của parabol đỉnh tại gốc tọa đô

, giây tiếp theo là đoạn thẳng và sau đúng ba giây

thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị 1 giây, mỗi đơn vị trục tung

biểu thị

10 /m s

và trong 5 giây đầu xe chuyển động theo đường thẳng. Hỏi trong 5 giây đó sẽ đã

đi được quãng đường là bao nhiêu.

A. 400 (mét). B. 340 (mét). C. 420 (mét). D. 320 (mét).

Câu 43. (THPT Quế Võ 1 - Bắc Ninh - 2021) Gọi

là tiếp tuyến của đồ thị hàm số

lny x

tại giao

điểm của đồ thị đó với trục

. Diện tích của hình tam giác tạo bởi hai trục tọa độ và đường

thẳng

được xác định bởi tích phân



 

1 .x dx



 

1 .x dx



ln .xdx



Câu 44. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hàm số

 

f x

có đạo hàm là

 

f x



. Đồ thị

 

y f x





được cho bởi hình vẽ bên dưới.

Giá trị nhỏ nhất của

 

f x

trên đoạn

 

0;3

là

 

2 .f

B. Không xác định được.

 

0 .f

 

3 .f

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Câu 45. (THPT Quốc Oai - Hà Nội - 2021) Một ô tô đang chạy với vận tốc

10 /m s

thì người lái xe đạp

phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc

   

2 10 /v t t m s

  

, trong

đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Quãng đường ô tô di chuyển

được trong

giây cuối cùng tính đến thời điểm dừng bánh là

16 m

. B.

55m

. C.

25 m

. D.

50 m

Câu 46. (THPT Quốc Oai - Hà Nội - 2021) Cho

 

2 2x

F x ax bx c e

  

là một nguyên hàm của hàm số

 

2 2x

2020 2022 1

f x x x e

  

trên khoảng

 

;

 

. Tính

2 4T a b c  

1004



1018



. C.

1012



. D.

2012

 

Câu 47. (THPT Quốc Oai - Hà Nội - 2021) Nguyên hàm của hàm số

    

2 1 2 1

f x x x x

  

là

4 3 2

x x x C  

. B.

4 3 2

x x x C  

. C.

 

x x C 

. D.

4 3 2

x x x C  

Câu 48. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Tích phân

xe dx



bằng

( 1)



. B.

( 1)



. C.

. D.

2 1e 

Câu 49. (THPT Phan Đình Phùng - Quảng Bình - 2021) Khi đổi biến

3 tanx t

 , tích phân







trở thành tích phân nào?

I dt







. B.

I dt







. C.

I dt







. D.

3I dt







Câu 50. (THPT Phan Đình Phùng - Quảng Bình - 2021) Gọi

là diện tích hình phẳng giới hạn bởi đồ

thị hàm số

 







và các trục tọa độ. Khi đó giá trị của

bằng

ln2 1.

 

2ln 2 1.

 

ln 2 1.

 

2ln 2 1.

 

Câu 51. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hàm số

 

f x

liên tục trên



và thỏa mãn

 

d 20

f x x





. Tính tích phân

 

1 2 dI x f x x x

  





. B.



. C.



. D.



Câu 52. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho biết

d ln 2

x a

x b





, với

,a b 



và

là

phân số tối giản. Tính

a b

. B.

. C.

. D.

Câu 53. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho biết

e d

x x a



 



với

,a b



. Tính

2 2

a b

. B.

. C.

. D.

Câu 54. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Trong mặt phẳng tọa độ

Oxy

cho hình phẳng

 

được giới hạn bởi các đường

sin , 0, 0y x y x  

và





Quay hình phẳng

 

quanh trục

ta được một vật thể tròn xoay có thể tích bằng



. B.



. C.



. D.



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 55. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Trong mặt phẳng tọa độ

Oxy

, cho hình phẳng

 

được giới hạn bởi đồ thị hàm số

1y x 

và hai trục tọa độ

. Tính diện tích

của hình

phẳng

 

S 

. B.

S 

. C.

1S 

. D.

S 

Câu 56. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho tích phân

cosI x xdx







và

, cosu x dv xdx 

. Khẳng định nào sau đây đúng?

sin 2 sinI x x x xdx



 



. B.

sin 2 sinI x x x xdx



 



2 3

sin sin

I x x x xdx



 



. D.

sin sinI x x x xdx



 



Câu 57. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Diện tích

của hình phẳng giới hạn bởi các

đường

2 3

2 3 1, 1y x x y x    

được tính bởi công thức nào dưới đây

   

0 3

2 3 3 2

1 0

2 3 2 3S x x x dx x x x dx



     

 

 

3 2

2 3S x x x dx



  



 

3 2

2 3S x x x dx





  



   

0 3

3 2 2 3

1 0

2 3 2 3S x x x dx x x x dx



     

 

Câu 58. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hàm số

 

f x

liên tục trên đoạn

 

0;9

thỏa

mãn

   

9 7

0 4

8, 3.f x dx f x dx 

 

Khi đó giá trị của

   

4 9

0 7

P f x dx f x dx 

 

là

11P 

. B.

5P 

. C.

20P 

. D.

9P 

Câu 59. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Diện tích phần hình phẳng gạch sọc trong hình vẽ được

tính theo công thức nào dưới đây?

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

2 1y x x  

y x

  

1

 

2 2 4x x dx



  



. B.

 

2 2x dx



 



 

2 2x dx





. D.

 

2 2 4x x dx



 



Câu 60. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho tích phân

ln 2, , .

1 5

I a b a b



   

 



 Khi

đó

E ab

bằng

6.E 

28.E 

8.E 

30.E 

Câu 61. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình

 

giới hạn bởi các đường thẳng

2 ,y x x   trục hoành. Tính thể tích khối tròn xoay sinh bởi hình phẳng

 

quay quanh trục



496



Câu 62. (THPT Đồng Quan - Hà Nội - 2021) Trong mặt phẳng toạ độ

Oxy

, cho hàm số

 

y f x

có đồ

thị là đường cong và hàm số

 

y g x

có đồ thị là đường thẳng. Gọi

S là diện tích miền phẳng

được gạch sọc,

S là diện tích miền phẳng được tô đậm,

1 2

S S (hình vẽ). Tích phân

   

 

f x g x dx





bằng

1 2

S S . B.

1 2

S S  . C.

1 2

S S . D.

2 1

S S .

Câu 63. (THPT Lê Lợi - Thanh Hóa - 2021) Cho

4 1I x x dx 



và

1u x 

. Tìm khẳng định sai

trong các khẳng định sau?

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

I udu





. B.

I udu





. C.

I u u



. D.

I 

Câu 64. (Sở Vĩnh Phúc - 2021) Tìm họ tất cả các nguyên hàm của hàm số

e 2

y x 

x C 

. B.

e 2

C 

. C.

1 2

x C



 



. D.

e 2

x C 

Câu 65. (Sở Vĩnh Phúc - 2021) Cho hình phẳng

giới hạn bởi đồ thị

 

: 2

P y x x 

và trục

. Tính

thể tích của khối tròn xoay tạo thành khi cho

quay quanh trục





. B.





. C.





. D.





Câu 66. (Sở Vĩnh Phúc - 2021) Gọi

là diện tích hình phẳng giới hạn bởi đồ thị hàm số

2021

y x 

trục hoành,

2, 4

x x

  

. Mệnh đề nào sau đây đúng.

2 2

( 2021)S x dx



 



. B.

( 2021)S x dx



 



2021S x dx



 



. D.

2021S x dx



 



Câu 67. (Sở Vĩnh Phúc - 2021) Cho hàm số

 

y f x



liên tục trên



và

 

2021

f x dx





. Tính

 

1010

2 1 .I f x dx

 





Câu 68. (Sở Lào Cai - 2021) Cho

 

f x dx





và

   

2 8

f x g x dx

  

 

 



. Tính tích phân

 

?g x dx



6

. B.

3

. C.

. D.

5

Câu 69. (Sở Hà Tĩnh - 2021) Họ tất cả các nguyên hàm của hàm số

2x 1

( )

( 1)

f x







trên khoảng

 

 

là

2ln( 1)

x C

  



. B.

2ln( 1)

x C

  



2ln( 1)

x C

  



. D.

2ln( 1)

x C

  



Câu 70. (Sở Hà Tĩnh - 2021) Cho hàm số

( )f x

thỏa mãn

(0) 4



và

( ) e ,

f x x x R



   

. Khi đó

 

f x dx



bằng

6 23



. B.

6 17



. C.

6 11



. D.

6 23



Câu 71. (Sở Hà Tĩnh - 2021) Biết

 

F x x

là một nguyên hàm của hàm số

 

f x

trên



. Tính

 

2 dI x f x x

 

 

 





. B.



. C.

117

I 

. D.

I 

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Câu 72. (Sở Tuyên Quang - 2021) Cho

33 4

1 dI x x x

 



. Đặt

t x 

thì

bằng

dt t t





. B.

t t



. C.

dt t



. D.

t t





Câu 73. (Sở Yên Bái - 2021) Tính diện tích hình phẳng giới hạn bởi hai đồ thị

4 6y x x  

và

2 6y x x   

. B.

. C.

. D.

Câu 74. (Sở Yên Bái - 2021) Nếu

( ) 5

f x dx





;

(2 ( ) ( )) 13

f x g x dx

 



thì

( )g x dx



bằng

3

. B.

. C.

23

. D.

Câu 75. (THPT Thanh Chương 1- Nghệ An - 2021)

 

1 sin dx x x





bằng.

A. . B. .

C. . D. .

Câu 76. (THPT Nguyễn Huệ - Phú Yên - 2021) Tính diện tích

hình phẳng giới hạn bởi đồ thị hàm số

6 7y x x  

và đường thẳng

y x 



. B.



. C.





. D.



Câu 77. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho

dx x x



bằng

x x C

. B.

x x C

. C.

x x C

. D.

x x C

Câu 78. (THPT Lương Thế Vinh - 2021) Với biến đổi

lnu x

, tích phân

x x



trở thành



. B.

ln3



. C.



. D.

ln3



Câu 79. (THPT Lương Thế Vinh - 2021) Cho hàm số

 

f x

có đạo hàm trên đoạn

 

1;2

 

2 1



và

 

4 2021

f 

. Giá trị

 

2 dI f x x







bằng

2018

. B.

1010

. C.

1008

. D.

2018

Câu 80. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho tích phân

ln .

I x xdx





Mệnh đề nào dưới

đây đúng?

2 2

ln l

x xd

x x

 



. B.

ln 2 ln

I xx x

xdx

 



2 2

x xd

x x

 



. D.

ln 2 ln

I x x

xdx

 



Câu 81. (THPT Đào Duy Từ - Hà Nội - 2021) Cho tích phân

1 ln

I dx







. Đặt

1 lnu x

  . Khi đó

bằng

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

I u du



. B.

I u du 



. C.

I du



. D.

I u du 



Câu 82. (THPT Đào Duy Từ - Hà Nội - 2021) Gọi

 

là hình phẳng giới hạn bởi đồ thị hàm số

5 4  y x x và trục

. Thể tích của khối tròn xoay sinh ra khi quay hình

 

quanh trục

bằng :

. B.

. C.



. D.



Câu 83. (THPT Đào Duy Từ - Hà Nội - 2021) Biết

 

d 2020f x x 



khi đó

f x

 

 

 



bằng

2020

. B.

1010

. C.

2020

. D.

4040

Câu 84. (THPT Chu Văn An - Thái Nguyên - 2021) Họ nguyên hàm

2 3

x x

 

 

 



 



bằng

2ln 1

x x C    . B.

 

x C

  



2ln 1

x x C    . D.

 

2ln 1x x x C   

Câu 85. (THPT Chu Văn An - Thái Nguyên - 2021) Diện tích hình phẳng giới hạn bởi các đường

2 ,y x y x    bằng:

18.

Câu 86. (THPT Ba Đình - Thanh Hóa - 2021) Diện tích hình phẳng giới hạn bởi các đường

y x

và

2y x 

là

9S 

. B.

S 

. C.

S 

. D.

S 

Câu 87. (Trung Tâm Thanh Tường - 2021) Hình phẳng

gồm hai phần được đánh dấu trong hình vẽ

bên. Diện tích hình

được tính theo công thức nào dưới đây?

   

0 3

2 0

d dS f x x f x x



  

 

. B.

   

0 3

2 0

d dS f x x f x x



  

 

   

0 3

2 0

d dS f x x f x x



 

 

. D.

   

0 3

2 0

d dS f x x f x x



 

 

Câu 88. (Trung Tâm Thanh Tường - 2021) Xét

(1 2 )x dx



, nếu đặt

1 2u x 

thì

(1 2 )x dx



bằng

2 u du





. B.

u du





. C.

u du





. D.

u du





TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Câu 89. (Tr

ung Tâm Thanh Tường -2021) Biết

 

in cosF x a x b x





là

một nguyên hàm của hàm số

 

2sin 8cosf x x x

 

, tí

nh giá trị

T a b 



. B.

4T 

. C.

 

. D.



Câu 90. (THPT Triệu Sơn - Thanh Hóa - 2021) Biết

(

) x 6

x d







, tích phân

(

2 1) xf x d





bằng

A. 3. B. 6. C. 12. D. 2.

Câu 91. (THPT

Trần Phú - Đà Nẵng - 2021) Cho hàm số

 

f x x





. Trong các khẳng định sau,

khẳng định nào đúng?

 

x dx x C

  



. B.

 

x dx C

  



 

x dx C

  



. D.

 

x dx x C

  



Câu 92. (THPT

Trần Phú - Đà Nẵng - 2021) Cho hàm số

( ) tan 2f x x



. Trong các khẳng định sau,

khẳng định nào đúng

( ) d tan 2

x x x C 



. B.

tan 2

(

)d C

f x x







(

)d tan 2

x x x x C  



. D.

(

)d tan 2

x x x x C  



Câu 93. (THPT

Trần Phú - Đà Nẵng - 2021) Cho







. Giá trị của tham số

thuộc khoảng nào

sau đâ

 

1;2

. B.

 

1;0



. C.

;

 

 

 

. D.





 

 

Câu 94. (THPT

Trần Phú - Đà Nẵng - 2021) Biết

 

x x





. Giá t

rị của

 

1 df x x







 



bằng

22

. B.

. C.

. D.

BẢNG ĐÁP

ÁN

1.D

2.D

3.A

4.A

5.C

6.B

7.C

8.A

9.C

10.D

11.C

12.D

13.D

14.C

15.D

16.B

17.

18.C

19.

20.A

21.A

22.D

23.D

24.A

25.A

26.B

27.

28.C

29.

30.A

31.A

32.D

33.C

34.A

35.A

36.A

37.A

38.D

39.A

40.D

41.C

42.D

43.B

44.D

45.D

46.C

47.C

48.

49.

50.D

51.B

52.C

53.B

54.C

55.D

56.

57.

58.B

59.

60.

61.A

62.C

63.A

64.A

65.D

66.

67.B

68.C

69.

70.

71.A

72.B

73.C

74.B

75.

76.C

77.

78.

79.

80.

81.A

82.C

83.D

84.A

85.

86.C

87.

88.B

89.

90.A

91.B

92.C

93.C

94.C

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1

MỨC ĐỘ THÔNG HIỂU

Câu 1. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Tính

I dx



theo số thực

.25



. B.

(25 1).ln 25



. C.

(25 1)





. D.

(25 1)

ln 25



Lời giải

Chọn D

 Có

1 1 1

25 25 | (25 25 ) (25 1).

ln 25 ln 25 ln 25

x x a a a

I dx

     



Câu 2. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Tính tích phân

 

1 dI x x x 



. B.



. C.



. D.

Lời giải

Chọn D

Đặt

1 2 d dx t x x t   

. Đổi cận:

0 1

1 2

x t

  





  



Suy ra

1 32 1 31

2 10 10 10 10

I t t    



Câu 3. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Họ nguyên hàm của hàm số

 

2 1

f x x e 

là

 

2 1

e x x C  

 

2 1 4

e x x C  

 

2 1

e x x 

 

2 1 4

e x x 

Lời giải

Chọn A

 Ta có

 

2 1 d 2 d 2 d 2 d

x x x

x e x xe x x x xe x x    

   

 Xét

 

2 d 2 d 2 . 2 dx 2 . 2 2 1

x x x x x x x

xe x x e x e e x e e e x      

  



 

2 1 d 2 1

x x

x e x e x x C    



Câu 4. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho

d 1

1 2

x e

a b



 





, với

,a b

là

các số nguyên. Tính

3 3

S a b 

0S 

. B.

2S  

. C.

1S 

. D.

2S 

Lời giải

Chọn A

 Ta có

 

1 1 1

0 0 0

d 1

1 d

1 1 1

x x x

x e

x x

e e e



 

   

 

  

 

  

1 ln 1 1 ln



    

 Suy ra

1, 1a b  

. Vậy

3 3

0S a b  

NGUYÊN HÀM - TÍCH PHÂN VÀ ỨNG DỤNG

Chủ đề 3

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 5. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Tìm nguyên hàm của hàm số

 

e 1 e

x x

f x



 

 

d e

f x x C 



. B.

 

d e

f x x C



 



 

d e

f x x x C  



. D.

 

d e e

x x

f x x C



  



Lời giải

Chọn C

Ta có:

 

e 1 e e 1

x x x

f x



   

Suy ra

 

d e 1 d e

x x

f x x x x C    

 

Câu 6. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Diện tích phần hình phẳng tô đậm

trong hình vẽ bên được tính theo công thức nào dưới đây?

 

2 2 dx x x  



. B.

 

2 2 dx x x  



 

2 2 dx x x 



. D.

 

2 2 dx x x 



Lời giải

Chọn B

 Dựa vào hình vẽ ta có:

   

0 1

2 2

1 0

2 d 2 dS x x x x x x



   

       

   

 

 

2 2 dx x x   



Câu 7. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho

 

d 1f x x 



. Với

 

e d e

I f x x a

 

   

 



. Khẳng định nào sau đây đúng?

2a 

. B.

1a  

. C.

2a  

. D.

1a 

Lời giải

Chọn C

Ta có:

   

1 1 1

0 0 0

e d e d d e 1 e 2

x x x

I f x x x f x x

 

       

 

  

Vậy

2a  

Câu 8. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Bác thợ xây bơm nước vào bể nước. Gọi

 

h t

là

thể tích nước bơm được sau

giây. Cho

 

3h t at bt



 

và ban đầu bể không có nước. Sau

giây thì thể tích nước trong bể là

150m

, sau

giây thì thể tích nước trong bể là

1100m

. Tính

thể tích của nước trong bể sau khi bơm được

giây:

8400 m . B.

600m . C.

2200m . D.

4200m .

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Lời giải

Chọn A

Ta có:

 

2 3 2

3 d

h t at bt t at t C    



Từ gt



 

0 0

5 150

10 1100

















125 150

1000 50 1100

a b







 





 

























 

3 2

h t t t 

Vậy thể tích của nước trong bể sau khi bơm được

giây là

 

20 8400h m



Câu 9. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hàm số

 

f x

thỏa mãn

 

3 5sinf x x



 

và

 

0 10



. Tìm hàm số

 

f x

 

3 5cos 15

f x x x

  

. B.

 

3 5cos 2f x x x  

 

3 5cos 5f x x x  

. D.

 

3 5cos 2

f x x x

  

Lời giải

Chọn C

Ta có

     

d 3 5sin d 3 5cos

f x f x x x x x x C



     

 

Mà

 

0 10 3.0 5cos0 10 5

f C C

      

Vậy

 

3 5cos 5f x x x  

Câu 10. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình phẳng (H) giới hạn bởi đồ thị hàm số

y x x 

và trục hoành. Tính thể tích V vật thể tròn xoay sinh ra khi cho (H) quay quanh trục

Ox.





. B.



. C.



. D.





Lời giải

Chọn D

Xét phương trình:

2 0

x x





  







Suy ra:

   

2 2

3 5

2 2 3 4 4

0 0

4 16

2 d 4 4 d

3 5 15

x x

V x x x x x + x x x

   

 

       

 

 

 

Câu 11. (Chuyên KHTN - 2021) Cho hàm số

 

f x

liên tục trên



và thoả mãn

 

d 2

xf x x





. Tích

phân

 

3 dxf x x



bằng

. B.

. C.

. D.

Lời giải

Chọn C

 Đặt:

3 d d

3 3

t x x x t

    

 Đổi cận:

0 0; 1 3x t x t     

 Khi đó:

   

1 3

0 0

1 2

3 d d

9 9

xf x x tf t t

 

 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 12. (Chuyên KHTN - 2021) Họ nguyên hàm của hàm số

 

lnf x x



trên khoảng

 

 

là

x x x C 

. B.

C

. C.



. D.

x x x C 

Lời giải

Chọn D

 Ta tìm

 

d ln dI f x x x x

 

 

 

0;x

 

 Đặt

d d

u x

v x











 











 Khi đó:

ln d ln

I x x x x x x C    



Câu 13. (Chuyên KHTN - 2021) Diện tích hình phẳng giới hạn bởi đồ thị của hàm số

y x x 

và đồ thị

của hàm số

2 2

y x

 

bằng

. B.

. C.

. D.

Lời giải

Chọn D

Phương trình hoành độ giao điểm:

2 2

x x x

  









 



Diện tích hình phẳng cần tính là:

2 d

S x x x



   



Câu 14. (Chuyên KHTN - 2021) Họ nguyên hàm

cos dx x x



là

cos sin

x x x C 

. B.

cos sin

x x x C  

cos sin

x x x C 

. D.

cos sin

x x x C  

Lời giải

Chọn C

 Đặt

d d

cos d sin

u x u x

dv x x v x

 

 



 

 

 

 Ta có:

cos d sin sin d sin cos

I x x x x x x x x x x C     

 

Câu 15. (Chuyên KHTN - 2021) Diện tích hình phẳng giới hạn bởi đường thẳng

3y x 

và parabol

2 1y x x  

bằng:

. B.

. C.

. D.

Lời giải

Chọn D

Phương trình hoành độ giao điểm giữa đường thẳng

3y x 

và parabol

2 1y x x  

là

2 2

3 2 1 2 2 4 0

x x x x x





        



 



Diện tích hình phẳng giới hạn bởi đường thẳng

3y x 

và parabol

2 1y x x  

là

 

2 1 3

S x x x dx



    



2 2 4x x dx



  



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Ta có

 

2 2 4 0, 1;2

x x x     

nên

 

2 2

2 2 2

1 1

2 2 4 2 2 4 4

3 3

S x x dx x x dx x x

 



 

           

 

 

 

Câu 16. (Chuyên KHTN - 2021) Tính nguyên hàm

tan 2

xdx



tan 2

x x C 

. B.

tan2

x x C 

. C.

tan2

x x C 

. D.

tan 2

x x C 

Lời giải

Chọn B

Ta có:

1 1

tan 2 1 tan 2

cos 2 2

xdx dx x x C

 

    

 

 

 

Câu 17. (Chuyên KHTN - 2021) Tìm nguyên hàm

 

2 1 ln

x xdx





 

x x x x C   

. B.

 

x x x x C   

 

x x x x C   

. D.

 

x x x x C   

Lời giải

Chọn D

Đặt

 

2 1

u x

du dx

dv x dx

v x x













 

 





 



 

2 2

2 1 ln ln 1 ln

x xdx x x x x dx x x x x C          

 

Câu 18. (Chuyên KHTN - 2021) Tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi đường

thẳng



và đồ thị

y x

khi quay xung quanh trục



. B.



. C.



. D.



Lời giải

Chọn C

y x

có điểm chung với

tại điểm có hoành độ



5 5

V x x



   



Câu 19. (Chuyên KHTN - 2021) Tính nguyên hàm

 

2 3

2 1

x x dx





 

2 1





. B.

 

2 1





. C.

 

2 1





. D.

 

2 1





Lời giải

Chọn A

Ta có

   

 

   

2 2 2

2 3 2 3 3 3

2 1

2 1 2 1 2 1 2 1

6 6

d x

x x dx x x x d x



     

  

   

3 3

2 1 2 1

6 3 18

x x

C C

 

   

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 20. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho tích phân

3 1dx x x



, nếu đặt

3 1u x 

thì

3 1dx x x



bằng

u u



. B.

u u



. C.

u u



. D.

u u



Lời giải

Chọn A



3 1u x 

d d

3 1

u x

 



 Với

0 1x u  

, với

1 2x u  

Suy ra

1 2

2 2

0 1

3 1d d

x x x u u 

 

Câu 21. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho

 

4 ( ) 2 d 1f x x x 



. Khi đó

( )f x dx



bằng

A. 1. B. -3. C. -1. D. 3.

Lời giải

Chọn A

Ta có:

 

2 2

1 1

4 ( ) 2 d 1 4 ( )dx 2 d 1f x x x f x x x    

  

4 ( )dx 1 ( ) 1

f x x f x dx    

 

Câu 22. (Chuyên Quốc Học Huế - 2021) Tính diện tích của hình phẳng (được tô đậm) giới hạn bởi hai

đường

2 2

2 , 4 .y x y x 





. B.





. C.

S 

. D.

S 

Lời giải

Chọn D

Theo hình vẽ ta có

4 2y x y x  

Xét phương trình hoành độ giao điểm của hai đường

2 , 2y x y x 

0 0

2 2

x x



 



  











Dựa vào đồ thị, diện tích của hình phẳng cần tính là

 

2 3

4 2 2

2 2 d

3 3 3

S x x x x x x

 

    

 

 



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Câu 23. (Chuyên Quốc Học Huế - 2021) Cho tích phân

2 cos sin

x xdx







. Nếu đặt

2 cost x 

thì kết

quả nào sau đây đúng?

2 .I tdt





.I tdt







.I tdt





.I tdt





Lời giải

Chọn D

Đặt

2 cos sin

t x dt xdx    

Đổi cận

0 3, 2

x t x t



     

Khi đó

2 3

3 2

I tdt tdt

  

 

Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Nguyên hàm của hàm số

( ) 2 ( 1)(2 1)

f x x x x

  

 

x x C 

4 3 2

x x x C  

4 3 2

x x x C  

4 3 2

x x x C  

Lời giải

Chọn A

Ta có

   

3 2 4 3 2 2

2 ( 1)(2 1) 4 6 2 2 .x x x dx x x x dx x x x C x x C           

 

Câu 25. (Chuyên Quang Trung - Bình Phước - 2021) Tìm nguyên hàm

 

F x

của hàm số

( ) .

f x x e



biết

 

1 0



x x

x e e

. B.

. 1

x x

x e e

 

. C.

x e e

. D.

. 1

x e x e  

Lời giải

Chọn A

Gọi

 

F x

là một nguyên hàm của hàm số

 

f x

Khi đó

 

F x

có dạng

 

F x 

 

x x x x x x

xe dx xd e xe e dx xe e C     

  

 

1 0



nên



Vậy

 

x x

F x xe e 

Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm số thực

để hàm số

   

3 2

3 2 4 3F x mx m x x    

là một nguyên hàm của hàm số

 

3 10 4

f x x x

  



. B.



. C.



. D.

 

Lời giải

Chọn B

   

3 2

3 2 4 3F x mx m x x    

là một nguyên hàm của hàm số

 

3 10 4

f x x x

  

nên:

   

F x f x



 

 

2 2

3 2 3 2 4 3 10 4 1

mx m x x x m

       

Câu 27. (Chuyên Ngoại Ngữ Hà Nội- 2021) Nguyên hàm của hàm số

 

3 1f x x 

là

( ) (3 1) 3 1

f x dx x x C   



. B.

( ) (3 1) 3 1

f x dx x x C   



( ) 3 1

f x dx x C  



. D.

( ) 3 1

f x dx x C  



Lời giải

Chọn A

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có:

 

3 1

1 1

3 1 3.

3 4

(

3 1 3 1) 1

xx xdx dx C x



     

  

 

Câu 28. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho tích phân

 

2 3 2

3 2

x x dx me ne

  



với

, ,

m n



khi

đó

m n

bằng bao nhiêu?

. B.

. C.

. D.

Lời giải

Chọn C

Ta có

 

2 3 2

3 2

x x dx e e  



Suy ra

1, 1

m n

  

Vậy

m n

 

Câu 29. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho

d ln 2 ln5

x a b

x x



 

 



với

,a b

là các số nguyên.

Mệnh đề nào sau đây đúng?

a b

 

. B.

a b

 

. C.

2 11

a b

 

. D.

2 11

a b

 

Lời giải

Chọn C

Ta có :

 

3 3

2 2

8 3 2

d + d 3ln 1 2ln 2 7ln 2 2ln5.

2 1 2

x x x x

 

 

      

 

   

 

 

Suy ra giá trị là:

7, 2

a b

  

Câu 30. (Chuyên Ngoại Ngữ Hà Nội- 2021) Thể tích khối tròn xoay sinh ra khi quay quanh

hình

phẳng giới hạn bởi các đường

0, 1, ; 0

x x y xe y

   

là

 





. B.

 



. C.

 



. D.

 





Lời giải

Chọn A

Hình phẳng

 

, 0

0, 1

y xe y

x x



 



 



Thể tích khối tròn xoay khi quay

 

quanh

là

   

2 2 2 2 2 2

1 1 1

2 2 1 1

4 4 4 4

x x

V x e dx e x x e e



  

   

         

 

 

   



Câu 31. (Chuyên Ngoại Ngữ Hà Nội- 2021) Biết

 

2 d 4xf x x 



. Giá trị của

 

dxf x x



bằng

. B.

. C.

. D.

Lời giải

Chọn A

 Đặt

2 d 2dt x t x  

Với



thì

0t 

Với



thì

4t 

 Ta có

       

2 4 4 4

0 0 0 0

1 1

4 2 d . . d d d 16

2 2 4

xf x x f t t tf t t tf t t

    

   

. Vậy

 

d 16

xf x x





TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 32. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Với

,a b

là các tham số thực. Giá trị tích phân

 

3 2 1 d

x ax x

 



bằng

3 2 1b ab 

. B.

3 2

b b a b 

. C.

3 2

b a b b 

. D.

3 2

b ab b 

Lời giải

Chọn D

Ta có:

   

2 3 2 3 2

3 2 1 d

x ax x x ax x b b a b       



Câu 33. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Hình vẽ bên biểu diễn trục hoành cắt đồ thị

 

y f x



tại ba điểm có hoành độ

 

0, , 0

a b a b 

. Gọi

là hình phẳng giới hạn bởi đồ thị

 

y f x



và

trục hoành, khẳng định nào sau đây là sai?

 

S f x x





. B.

   

S f x dx f x dx

  

 

   

S f x dx f x dx

 

 

. D.

   

S f x dx f x dx

 

 

Lời giải

Chọn C

Ta có:

 

   

0 0

b b

a a

S f x dx f x dx f x dx f x dx

      

   

Câu 34. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình phẳng

giới hạn bởi đường cong

y e

trục hoành và các đường thẳng

0, 1x x 

. Khối tròn xoay tạo thành khi quay

quanh trục

hoành có thể tích

bằng bao nhiêu?

 

e 1







. B.





. C.

e 1





. D.

 

e 1







Lời giải

Chọn A

Thể tích khối tròn xoay cần tìm là:

 

1 1

2 2

0 0

e 1

e d e d .

2 2

x x x

V x x e



 



   

 

Câu 35. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hàm số

 

y f x



có đạo hàm cấp hai

 

f x



liên

tục trên đoạn

 

0;1

đồng thời thỏa mãn điều kiện

     

0 1 1; 0 2021.

f f f



  

Mệnh đề nào sau

đây đúng?

   

1 d 2021

x f x x



  



. B.

   

1 d 2021

x f x x



 



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

   

1 d 1x f x x



 



. D.

   

1 d 1

x f x x



  



Lời giải

Chọn A

Ta có

       

1 1

0 0

1 d 1 dx f x x x f x

 

  

 

     

1 d

x f x f x x

 

  



     

0 1 0 2021f f f



     

Vậy

   

1 d 2021x f x x



  



Câu 36. (Chuyên Hạ Long - Quảng Ninh - 2021) Diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

1 5 6y x x x   

và hai trục tọa độ bằng



Lời giải

ChọnA

Ta có

 

1 0

1 5 6 0 2.

5 6 0

x x x x

x x





 





      



  









Khi đó diện tích hình phẳng cần tìm bằng

 

     

3 3

2 3 2

0 0

1 2 3

3 2 3 2 3 2

0 1 2

1 2 3

3 2 3 2 3 2

0 1 2

1 2

4 2 4 2 4

3 3

0 1

1 5 6 d 6 11 6 d

6 11 6 d 6 11 6 d 6 11 6 d

11 11

2 6 2 6

4 2 4 2 4

x x x x x x x x

x x x x x x x x x x x x

x x x x x

x x x x

      

           

             

   

           

   

   

 

  

2 6

9 1 1 11

4 4 4 4

x x

 

 

 

 

   

Vậy ta chọn phương án A.

Câu 37. (Chuyên ĐHSP Hà Nội - 2021) Diện tích hình phẳng thuộc góc phần tư thứ hai, giới hạn bởi

parabol

2y x 

, đường thẳng

y x 

và trục

bằng:

. B.

. C.

. D.

Lời giải

Chọn A

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Xét phương trình hoành độ giao điểm

x x





  







Diện tích hình phẳng cần tính là:

 

0 0

1 1

2 d d

S x x x x

 

    

 

Câu 38. (Chuyên ĐHSP Hà Nội - 2021)

 

2 5 dx x



bằng

 

2 5

x C 

. B.

 

18 2 5x C 

. C.

 

9 2 5x C 

. D.

 

2 5

x C 

Lời giải

Chọn D

Ta có:

       

9 9 10

1 1

2 5 d 2 5 d 2 5 2 5

2 20

x x x x x C      

 

Câu 39. (Chuyên ĐHSP Hà Nội - 2021) Biết

 

f x

là hàm số liên tục trên

 

0;3

và có

 

3 d 3f x x 



. Giá

trị của biểu thức

 

df x x



bằng:

A. 9. B. 1. C. 3. D.

Lời giải

Chọn A

Đặt

3 3d d d

x t x t x    

Đổi cận:

   

1 3

0 0

3 d d

1 3

x t

I f x x f t t

x t

  



  



  



 

Mà

     

1 3 3

0 0 0

3 d 3 d 9 d 9f x x f t t f x x    

  

Câu 40. (Chuyên ĐH Vinh - Nghệ An - 2021) Giả sử

 

f x

là hàm liên tục trên





0;

và diện tích

phần hình phẳng được kẻ dọc ở hình bên bằng

. Tích phân

 

2 df x x



bằng:

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

. B.

. C.

. D.

Lời giải

Chọn D

Vì diện tích phần hình phẳng được kẻ dọc ở hình trên bằng

nên ta có:

 

d 3f x x 



Đặt

2 d 2d d

t x t x x    

; Đổi cận

0 0; 1 2x t x t     

Do đó:

       

1 2 2 2

0 0 0 0

d 1 1 3

2 d d d

2 2 2 2

f x x f t f t t f x x   

   

Câu 41. (Chuyên ĐH Vinh - Nghệ An - 2021) Họ nguyên hàm của hàm số

 

2 1

f x





là

C

. B.

C

. C.

6ln 3

C

. D.

3ln 3

C

Lời giải

Chọn C

Ta có

 

2 1

f x



 

Khi đó

 

1 1 9 9

d 9 d .

3 3 ln9 6ln3

x x

f x x x C C    

 

Câu 42. (Chuyên ĐH Vinh - Nghệ An - 2021) Một chiếc xe đua

đạt vận tốc lớn nhất là

360 /km h

. Đồ

thị bên hiển thị vận tốc

của xe trong 5 giây đầu tiên kể từ lúc xuất phát. Đồ thị trong 2 giây đầu

là một phần của parabol đỉnh tại gốc tọa đô

, giây tiếp theo là đoạn thẳng và sau đúng ba giây

thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị 1 giây, mỗi đơn vị trục tung

biểu thị

10 /m s

và trong 5 giây đầu xe chuyển động theo đường thẳng. Hỏi trong 5 giây đó sẽ đã

đi được quãng đường là bao nhiêu.

A. 400 (mét). B. 340 (mét). C. 420 (mét). D. 320 (mét).

Lời giải

Chọn D

Đổi

360 / 100 /km h m s

Quan sát đồ thị hàm số ta thấy điểm

 

2;60A

 

3;100B

thuộc đồ thị hàm số.

Phương trình vận tốc khi xe chuyển động theo Parabol là

15 .y



Phương trình vận tốc khi xe chuyển động theo đường thẳng là

40 20.y x 

Quãng đường xe chuyển động được trong 5 giây đầu là

 

2 5

0 3

40 20 320

15 100

S x dx

x dx dx

  

 



 

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Câu 43. (THPT Quế Võ 1 - Bắc Ninh - 2021) Gọi

là tiếp tuyến của đồ thị hàm số

lny x

tại giao

điểm của đồ thị đó với trục

. Diện tích của hình tam giác tạo bởi hai trục tọa độ và đường

thẳng

được xác định bởi tích phân



 

1 .x dx



 

1 .x dx



ln .xdx



Lời giải

Chọn B

Phương trình hoành độ giao điểm của

lny x

và

là

ln 0 1x x  

Phương trình tiếp tuyến

tại

1x 

là

    

0 0 0

' 1y f x x x f x x    

Diện tích của tam giác tạo bởi hai trục tọa độ và đường thẳng

là

 

S x dx

 



Câu 44. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hàm số

 

f x

có đạo hàm là

 

f x



. Đồ thị

 

y f x





được cho bởi hình vẽ bên dưới.

Giá trị nhỏ nhất của

 

f x

trên đoạn

 

0;3

là

 

2 .f

B. Không xác định được.

 

0 .f

 

3 .f

Lời giải

Chọn D

BBT

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Suy ra giá trị nhỏ nhất của

 

f x

trên đoạn 0; 3

 

 

 

là

 

hoặc

 

Ta có

       

2 2

0 0

3 3

2 2

0 2

3 0

S f x dx f x dx f f

 

    

 

   

 

Dựa theo hình vẽ thì

           

1 2

0 2 3 2 0 3S S f f f f f f      

Vậy giá trị nhỏ nhất của hàm số là

 

Câu 45. (THPT Quốc Oai - Hà Nội - 2021) Một ô tô đang chạy với vận tốc

10 /m s

thì người lái xe đạp

phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc

   

2 10 /v t t m s  

, trong

đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Quãng đường ô tô di chuyển

được trong

giây cuối cùng tính đến thời điểm dừng bánh là

16 m

. B.

55 m

. C.

25 m

. D.

50 m

Lời giải

Chọn D

Khi ô tô dừng bánh, ta có:

0v  2 10 0 5t t     

Do đó, ta có quãng đường xe đi được trong

giây cuối cùng (

giây đi với vận tốc

10 /m s

giây sau khi đạp phanh) là:

 

3.10 2 10S t dt   



 

30 10t t   

30 5 10.5  

 

55 m

Câu 46. (THPT Quốc Oai - Hà Nội - 2021) Cho

 

2 2x

F x ax bx c e  

là một nguyên hàm của hàm số

 

2 2x

2020 2022 1f x x x e  

trên khoảng

 

; 

. Tính

2 4T a b c  

1004T 

1018T 

. C.

1012T 

. D.

2012T  

Lời giải

Chọn C

Ta có

   

'F x f x

. Mà

     

2 2x

' 2 2a 2 2F x ax b x b c e

 

    

 

Do đó:

2a 2020 1010

2a 2 2022 1

2 1 1

b b

b c c

 

 

 

   

 

 

   

 

Vậy

2 4 1012T a b c   

Câu 47. (THPT Quốc Oai - Hà Nội - 2021) Nguyên hàm của hàm số

    

2 1 2 1f x x x x  

là

4 3 2

x x x C  

. B.

4 3 2

2x x x C  

. C.

 

x x C  . D.

4 3 2

x x x C  

Lời giải

Chọn C.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Ta có:

    

2 1 2 1

f x x x x

  

 

2 2 2 1

x x x

  

3 2

4 6 2x x x  

 

3 2

d 4 6 2 df x x x x x x

   

 

4 3 2

x x x C   

 

x x C  

Câu 48. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Tích phân

xe dx



bằng

( 1)



. B.

( 1)



. C.

. D.

2 1e 

Lời giải

Chọn A

Cách 1( Đổi biến): Đặt

t x dt xdx dt xdx

    

Đổi cận:

0 0

1 1

x t

  

. Khi đó

 

1 1

0 0

1 1 1

2 2 2

x t

xe dx e dt e

   

 

Cách 2( Vi phân):

 

2 2

1 1

0 0

1 1 1

2 2 2

x x

xe dx e d x e

   

 

Cách 3: Dùng casio bấm

xe dx



, sau dó đối chiếu với 4 đáp án.

Câu 49. (THPT Phan Đình Phùng - Quảng Bình - 2021) Khi đổi biến

3 tanx t

 , tích phân







trở thành tích phân nào?

I dt







. B.

I dt







. C.

I dt







. D.

3I dt







Lời giải

Chọn C

Ta có :

3 tanx t





 

3 tan 1dx t dt

 

Đổi cận :

0 0x t  

x t



  

Khi đó :

I dt







Câu 50. (THPT Phan Đình Phùng - Quảng Bình - 2021) Gọi

là diện tích hình phẳng giới hạn bởi đồ

thị hàm số

 







và các trục tọa độ. Khi đó giá trị của

bằng

ln2 1.

 

2ln 2 1.

 

ln 2 1.

 

2ln 2 1.

 

Lời giải

Chọn D

Đồ thị hàm số cắt trục

tại

 

1;0

, cắt trục

tại

 

0; 1

. Diện tích hình phẳng cần tìm là

1 1

0 0

1 2

1 1 2ln | 1| 2 ln 2 1

1 1

S dx dx x

x x



 

       

 

 

 

 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 51. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hàm số

 

f x

liên tục trên



và thỏa mãn

 

d 20

f x x





. Tính tích phân

 

1 2 dI x f x x x

  





. B.



. C.



. D.



Lời giải

Chọn B

Đặt

 

2 d 2 1 dx x t t x x

    

Khi



thì



và khi

1x 

thì

3t 

Do đó,

 

1 2 dI x f x x x

  



   

3 3

0 0

1 1 1

d d .20 10

2 2 2

f t t f x x

   

 

Vậy



Câu 52. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho biết

d ln 2

x a

x b





, với

,a b 



và

là

phân số tối giản. Tính

a b

. B.

. C.

. D.

Lời giải

Chọn C

Ta có:

 

4 4

2 3 3

1 1

ln ln ln 4 8

d ln d ln .ln 2

3 3 3

x x

x x x

   

 

Vậy

8, 3 11

a b a b

    

Câu 53. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho biết

e d

x x a



 



với

,a b



. Tính

2 2

a b

. B.

. C.

. D.

Lời giải

Chọn B.

Xét

d du x u x  

d e d

v x





, chọn





Khi đó

 

1 1

1 1 1 0

0 0

e d e e d e e e e e 1

x x x x

      

        

 

Suy ra

1, 2

a b

  

. Vậy

2 2

a b

 

Câu 54. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Trong mặt phẳng tọa độ

Oxy

cho hình phẳng

 

được giới hạn bởi các đường

sin , 0, 0y x y x  

và





Quay hình phẳng

 

quanh trục

ta được một vật thể tròn xoay có thể tích bằng



. B.



. C.



. D.



Lời giải

Chọn C

Khối tròn xoay được sinh ra có thể tích là:

0 0

1 cos 2 sin 2

sin d d .

2 2 2 2

x x

V x x x x



 



 

    

 

 

 

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Câu 55. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Trong mặt phẳng tọa độ

Oxy

, cho hình phẳng

 

được giới hạn bởi đồ thị hàm số

1y x 

và hai trục tọa độ

. Tính diện tích

của hình

phẳng

 

S 

. B.

S 

. C.

1S 

. D.

S 

Lời giải

Chọn D

Ta có

1dS x x



 



Đặt

1; 1 0; 0 1t x x t x t        

;

1 d 2 dx t x t t   

Suy ra

0 1

1 0

2 2

1d .2 d

3 3

S x x t t t t



    

 

Câu 56. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho tích phân

cosI x xdx







và

, cosu x dv xdx 

. Khẳng định nào sau đây đúng?

sin 2 sinI x x x xdx



 



. B.

sin 2 sinI x x x xdx



 



2 3

sin sin

I x x x xdx



 



. D.

sin sinI x x x xdx



 



Lời giải

Chọn A

Đặt

sin

cos

du xdx

u x

v x

dv xdx











 





Do đó

cosI x xdx







sin 2 sinx x x xdx



 



Câu 57. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Diện tích

của hình phẳng giới hạn bởi các

đường

2 3

2 3 1, 1y x x y x    

được tính bởi công thức nào dưới đây

   

0 3

2 3 3 2

1 0

2 3 2 3S x x x dx x x x dx



     

 

 

3 2

2 3S x x x dx



  



 

3 2

2 3S x x x dx





  



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

   

0 3

3 2 2 3

1 0

2 3 2 3S x x x dx x x x dx



     

 

Lời giải

Chọn D

Xét phương trình hoành độ giao điểm:

2 3

2 3 1 1x x x   

3 2

2 3 0x x x   







 







Ta có bảng xét dấu:

Khi đó

0 3

3 2 3 2

1 0

2 3 2 3S x x x dx x x x dx



     

 

   

0 3

3 2 2 3

1 0

2 3 2 3S x x x dx x x x dx



     

 

Câu 58. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hàm số

 

f x

liên tục trên đoạn

 

0;9

thỏa

mãn

   

9 7

0 4

8, 3.f x dx f x dx 

 

Khi đó giá trị của

   

4 9

0 7

P f x dx f x dx 

 

là

11P 

. B.

5P 

. C.

20P 

. D.

9P 

Lời giải

Chọn B

       

4 9 9 7

0 7 0 4

8 3 5.P f x dx f x dx f x dx f x dx      

   

Câu 59. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Diện tích phần hình phẳng gạch sọc trong hình vẽ được

tính theo công thức nào dưới đây?

2 1y x x  

y x

  

1

 

2 2 4x x dx



  



. B.

 

2 2x dx



 



 

2 2x dx





. D.

 

2 2 4x x dx



 



Lời giải

Chọn A

Diện tích hình phẳng là:

   

2 2

2 2 2

1 1

3 2 1 2 2 4S x x x dx x x dx

 

         

 

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Câu 60. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho tích phân

ln 2, , .

1 5

I a b a b



   

 



 Khi

đó

E ab

bằng

6.E 

28.E 

8.E 

30.E 

Lời giải

Chọn C

Đặt

 

5 0x t t   , khi đó

5 d 2 dt x x t t    

Với

4 3; 4 1x t x t      

1 3

3 1

2 1

2 1 d 2.2 2ln 1

1 1

tdt

I t t

t t



 

      

 

 

 

 

4 2ln 2 8I ab    

Câu 61. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình

 

giới hạn bởi các đường thẳng

2 ,y x x   trục hoành. Tính thể tích khối tròn xoay sinh bởi hình phẳng

 

quay quanh trục



496



Lời giải

Chọn A

Hoành độ giao điểm của đường thẳng trên với trục

là

0; 2.x x 

Khi đó thể tích khối tròn xoay sinh bởi hình phẳng

 

quay quanh trục

là

   

2 2

2 4 3 2 5 4 3

0 0

1 4 16

2 d 4 4 d .

5 3 15

V x x x x x x x x x x



  

 

         

 

 

 

Câu 62. (THPT Đồng Quan - Hà Nội - 2021) Trong mặt phẳng toạ độ

Oxy

, cho hàm số

 

y f x

có đồ

thị là đường cong và hàm số

 

y g x

có đồ thị là đường thẳng. Gọi

S là diện tích miền phẳng

được gạch sọc,

S là diện tích miền phẳng được tô đậm,

1 2

S S (hình vẽ). Tích phân

   

 

f x g x dx





bằng

1 2

S S . B.

1 2

S S  . C.

1 2

S S . D.

2 1

S S .

Lời giải

Chọn C.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Phương trình hoành độ giao điểm giữa 2 đồ thị

     

2 4

f x g x x a a



 



     









Ta có

   

 

   

 

   

 

4 4

1 2

2 2

f x g x dx f x g x dx f x g x dx S S

 

      

  

Câu 63. (THPT Lê Lợi - Thanh Hóa - 2021) Cho

4 1I x x dx

 



và

u x

 

. Tìm khẳng định sai

trong các khẳng định sau?

I udu





. B.

I udu





. C.

I u u



. D.

I 

Lời giải

Chọn A

Đặt

1 2

u x du xdx

   

Đổi cận

1 0

x u

  

;

2 3

x u

  

Khi đó

2 3

1 0

4 4

4 1 2 27

3 3

I x x dx udu u u    

 

Câu 64. (Sở Vĩnh Phúc - 2021) Tìm họ tất cả các nguyên hàm của hàm số

e 2

y x 

x C 

. B.

e 2

C 

. C.

1 2

x C



 



. D.

e 2

x C 

Lời giải

Chọn A.

Ta có

 

e 2 d e 2. e

x x x

x x C x C      



Câu 65. (Sở Vĩnh Phúc - 2021) Cho hình phẳng

giới hạn bởi đồ thị

 

: 2

P y x x 

và trục

. Tính

thể tích của khối tròn xoay tạo thành khi cho

quay quanh trục





. B.





. C.





. D.





Lời giải

Chọn D.

Phương trình hoành độ giao điểm:

2 0

x x





  







Do đó

 

2 d

V x x x

 

  



Câu 66. (Sở Vĩnh Phúc - 2021) Gọi

là diện tích hình phẳng giới hạn bởi đồ thị hàm số

2021

y x 

trục hoành,

2, 4

x x

  

. Mệnh đề nào sau đây đúng.

2 2

( 2021)S x dx



 



. B.

( 2021)S x dx



 



2021S x dx



 



. D.

2021S x dx



 



Lời giải

Chọn D

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

là diện tích hình phẳng giới hạn bởi đồ thị hàm số

2021

y x 

, trục hoành,

2, 4

x x

  

thì

diện tích hình phẳng là

2021S x dx



 



Câu 67. (Sở Vĩnh Phúc - 2021) Cho hàm số

 

y f x



liên tục trên



và

 

2021

f x dx





. Tính

 

1010

2 1 .I f x dx

 





Lời giải

Chọn B.

Đặt

2 1t x 

2dt dx 

dx dt

 

Đổi cận

0 1; 1010 2021

x t x t

     

   

1010 2021

0 1

1 1

2 1 .4 2.

2 2

I f x dx f t dt

    

 

Câu 68. (Sở Lào Cai - 2021) Cho

 

f x dx





và

   

2 8

f x g x dx

  

 

 



. Tính tích phân

 

?g x dx



6

. B.

3

. C.

. D.

5

Lời giải

Chọn C

Ta có:

   

2 8

f x g x dx

  

 

 



   

 

1 1

0 0

2 8

2 2 8

f x dx g x dx

g x dx

   

 

 



Câu 69. (Sở Hà Tĩnh - 2021) Họ tất cả các nguyên hàm của hàm số

2x 1

( )

( 1)

f x







trên khoảng

 

 

là

2ln( 1)

x C

  



. B.

2ln( 1)

x C

  



2ln( 1)

x C

  



. D.

2ln( 1)

x C

  



Lời giải

Chọn D

Ta có

2 2 2

2x 1 2x 2 3 2 3 3

( ) ( ) x 2ln( 1)

( 1) ( 1) 1 ( 1) 1

f x f x d x C

x x x x x

  

        

    



Câu 70. (Sở Hà Tĩnh - 2021) Cho hàm số

( )f x

thỏa mãn

(0) 4



và

e' ,( ) x xf

  



. Khi đó

 

f x dx



bằng

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

6 23



. B.

6 17



. C.

6 11



. D.

6 23



Lời giải

Chọn C

Ta có:

 

x x

(

' ) e e

xf x dx

dx C



   



mà

(0) 4 3 ( e)

f C f x   





Khi đó

1 1

2 3

x x

0 0

6 11

( ) e 3 e 3

2 6 6

x x e

f x dx dx x

   



      

   

   

 

Câu 71. (Sở Hà Tĩnh - 2021) Biết

 

F x x

là một nguyên hàm của hàm số

 

f x

trên



. Tính

 

2 dI x f x x

 

 

 





. B.



. C.

117

I 

. D.

I 

Lời giải

Chọn A

Ta có:

   

 

3 3 3

2 3

0 0 0

2 d 2 d d 36

I x f x x x x f x x x x

      

 

 

  

Câu 72. (Sở Tuyên Quang - 2021) Cho

33 4

1 dI x x x

 



. Đặt

t x 

thì

bằng

dt t t





. B.

t t



. C.

dt t



. D.

t t





Lời giải

Chọn B

Với

t x 

3 4

t x  

2 3

3 d 4 dt t x x

  

3 2

d d

x x t t

  

Đổi cận:

0 1x t  

và

1 0x t  

Vậy

0 1

3 3

1 0

3 3

d d

4 4

I t t t t

  

 

Câu 73. (Sở Yên Bái - 2021) Tính diện tích hình phẳng giới hạn bởi hai đồ thị

4 6y x x  

và

2 6y x x   

. B.

. C.

. D.

Lời giải

Chọn C

Xét phương trình:

2 2

4 6 2 6

x x x x

     

2 2 0

x x

  













Diện tích hình phẳng giới hạn bởi hai đồ thị là:

2 2 dS x x x

 



 

2 2 dx x x

 



 

 

 

 

 



Câu 74. (Sở Yên Bái - 2021) Nếu

( ) 5

f x dx





;

(2 ( ) ( )) 13

f x g x dx

 



thì

g( )x dx



bằng

3

. B.

. C.

23

. D.

Lời giải

Chọn B

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

Ta có

2 2 2 2 2

1 1 1 1 1

(2 ( ) ( )) 13 2 ( ) ( ) 13 ( ) 13 2 ( )f x g x dx f x dx g x dx g x dx f x dx       

    

( ) 13 2.5 3g x dx   



Câu 75. (THPT Thanh Chương 1- Nghệ An - 2021) bằng.

A. . B. .

C. . D. .

Lời giải

Chọn C

 Đặt .

 Khi đó .

Câu 76. (THPT Nguyễn Huệ - Phú Yên - 2021) Tính diện tích

hình phẳng giới hạn bởi đồ thị hàm số

6 7y x x   và đường thẳng

3y x 

3S 

. B.

S 

. C.





. D.

60S 

Lời giải

Chọn C

Xét phương trình hoành độ giao điểm:

2 2

6 7 3 5 4 0

x x x x x





        







Diện tích

là:

 

   

4 4

3 2

2 2

1 1

3 6 7 d 5 4 d 5. 4

3 2 2

x x

S x x x x = x x x = x

 

 

           

 

 

 

 

( đvdt).

Câu 77. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho

dx x x



bằng

x x C

. B.

x x C

. C.

x x C

. D.

x x C

Lời giải

Chọn D

Đặt

2x t t x tdt dx    

Ta có

 

2 24 5

d . .2t

2 2

d d

5 5

x x x t t t t t x Ct x x CC      

  

Câu 78. (THPT Lương Thế Vinh - 2021) Với biến đổi

lnu x

, tích phân

x x



trở thành

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/



. B.

ln3



. C.



. D.

ln3



Lời giải

Chọn D

Với

lnu x

ta có

d du x



Đổi cận:

x e u

  

3 ln3

x u

  

Vậy

3 ln3

1 1

d d

x u

x x u



 

Câu 79. (THPT Lương Thế Vinh - 2021) Cho hàm số

 

f x

có đạo hàm trên đoạn

 

1;2

 

2 1



và

 

4 2021

f 

. Giá trị

 

2 dI f x x







bằng

2018

. B.

1010

. C.

1008

. D.

2018

Lời giải

Chọn B

Đặt

2 2d d d d

x t x t x t

    

Khi đó: Với

1 2x t  

; với

2 4

x t

  

Ta có

         

1 1 1 1

d 4 2 2021 1 1010

2 2 2 2

I f t t f t f f



       

 



Câu 80. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho tích phân

ln .

I x xdx





Mệnh đề nào dưới

đây đúng?

2 2

ln l

x xd

x x

 



. B.

ln 2 ln

I xx x

xdx

 



2 2

x xd

x x

 



. D.

ln 2 ln

I x x

xdx

 



Lời giải

Chọn C

Đặt

n2du

dv xdx x















 















2 2

lnln

I x x

x x x

  



Câu 81. (THPT Đào Duy Từ - Hà Nội - 2021) Cho tích phân

1 ln

I dx







. Đặt

1 lnu x

  . Khi đó

bằng

I u du





. B.

I u du

 



. C.

I du





. D.

I u du

 



Lời giải

Chọn A

Đặt

1 ln 1 ln 2 2

dx dx

u x u x udu udu

x x

          

Đổi cận

1 1x u  

x e u

  

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

0 0 1

2 2

1 1 1 0

1 ln

.2 2 2

I dx u udu u du u du



      

   

Câu 82. (THPT Đào Duy Từ - Hà Nội - 2021) Gọi

 

là hình phẳng giới hạn bởi đồ thị hàm số

5 4  

y x x

và trục

. Thể tích của khối tròn xoay sinh ra khi quay hình

 

quanh trục

bằng :

. B.

. C.



. D.



Lời giải

Chọn C

Hoành độ giao điểm của đồ thị hàm số

5 4  

y x x và trục

là nghiệm phương trình :

5 4 0





   







x x

Thể tích của khối tròn xoay sinh ra khi quay hình

 

quanh trục

bằng :

   

4 4

2 2

1 1

5 4 d 5 4 d

 



     

 

x x x x x x

Câu 83. (THPT Đào Duy Từ - Hà Nội - 2021) Biết

 

d 2020

f x x 



khi đó

f x

 

 

 



bằng

2020

. B.

1010

. C.

2020

. D.

4040

Lời giải

Chọn D

Đặt



d d

t x

 

Đổi cận:



 

;



 

Ta có:

f x

 

 

 



 

2. df t t





2.2020

4040

Câu 84. (THPT Chu Văn An - Thái Nguyên - 2021) Họ nguyên hàm

2 3

x x

 

 

 



 



bằng

2ln 1

x x C   

. B.

 

x C

  



2ln 1

x x C   

. D.

 

2ln 1

x x x C   

Lời giải

Chọn A

2 2

2 3 2

1 2ln 1

1 1 2

x x x

dx x dx x x C

x x

 

 

 

       

 

 

 

 

Câu 85. (THPT Chu Văn An - Thái Nguyên - 2021) Diện tích hình phẳng giới hạn bởi các đường

2 ,

y x y x   

bằng:

18.

Lời giải

Chọn B

Xét phương trình hoành độ giao điểm

2 2

2 2 0 .

x x x x

 



       







NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Diện tích hình phẳng giới hạn bởi

2 ,y x y x    là:

 

2 .

S x x dvtt



   



Câu 86. (THPT Ba Đình - Thanh Hóa - 2021) Diện tích hình phẳng giới hạn bởi các đường

y x

và

2y x 

là

9S 

. B.



. C.



. D.



Lời giải

Chọn C

 Phương trình hoành độ giao điểm của đồ thị hàm số

y x

và đường thẳng

2y x 

là

2 2

2 2 0

x x x x

 



      







 Diện tích hình phẳng giới hạn bởi các đường

y x

và

2y x 

là:

 

2 2

3 2

2 2

1 1

2 d 2 d 2

3 2 2

x x

S x x x x x x x

 

 

         

 



 

 

Câu 87. (Trung Tâm Thanh Tường - 2021) Hình phẳng

gồm hai phần được đánh dấu trong hình vẽ

bên. Diện tích hình

được tính theo công thức nào dưới đây?

   

0 3

2 0

d dS f x x f x x



  

 

. B.

   

0 3

2 0

d dS f x x f x x



  

 

   

0 3

2 0

d dS f x x f x x



 

 

. D.

   

0 3

2 0

d dS f x x f x x



 

 

Lời giải

Chọn D.

Ta có

   

0 3

2 0

d dS f x x f x x



 

 

Câu 88. (Trung Tâm Thanh Tường - 2021) Xét

(1 2 )x dx



, nếu đặt

1 2u x 

thì

(1 2 )x dx



bằng

2 u du





. B.

u du





. C.

u du





. D.

u du





Lời giải

Chọn B

Đặt

1 2 2u x du dx    

. Đổi cận

0 1

1 1

x u

  





   



Khi đó

1 1 1

20 20 20

0 1 1

1 1

(1 2 )

2 2

x dx u du u du



   

  

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27

Câu 89. (Trung Tâm Thanh Tường -2021) Biết

 

sin cosF x a x b x

 

là một nguyên hàm của hàm số

 

2sin 8cosf x x x

 

, tính giá trị

T a b 



. B.

4T 

. C.

 

. D.



Lời giải

Chọn A

 

F x

là một nguyên hàm của

 

f x

nên ta có:

   

cos sin 2sin 8cos , 8, 2

F x f x a x b x x x x a b



         

Vậy

a b

 

Câu 90. (THPT Triệu Sơn - Thanh Hóa - 2021) Biết

( ) x 6

f x d







, tích phân

(2 1) xf x d





bằng

A. 3. B. 6. C. 12. D. 2.

Lời giải

Chọn A

Ta có

1 1 1

0 0 1

1 1 1

(2 1) x (2 1) (2x 1) ( ) .6 3

2 2 2

f x d f x d f t dt



      

  

Câu 91. (THPT Trần Phú - Đà Nẵng - 2021) Cho hàm số

 

f x x

 

. Trong các khẳng định sau,

khẳng định nào đúng?

 

f x dx x C

  



. B.

 

f x dx C

  



 

f x dx C

  



. D.

 

f x dx x C

  



Lời giải

Chọn B

Ta có

 

1 1

f x dx x dx C

x x

 

    

 

 

 

Câu 92. (THPT Trần Phú - Đà Nẵng - 2021) Cho hàm số

( ) tan 2f x x



. Trong các khẳng định sau,

khẳng định nào đúng

( ) d tan 2

f x x x C 



. B.

tan 2

( )d C

f x x

 



( )d tan 2

f x x x x C  



. D.

( )d tan 2

f x x x x C  



Lời giải

Chọn C

Ta có

   

2 2

tan 2 d [ tan 2 1 1]d tan 2

x x x x x x C     

 

Câu 93. (THPT Trần Phú - Đà Nẵng - 2021) Cho

d 4

x x







. Giá trị của tham số

thuộc khoảng nào

sau đây?

 

1;2

. B.

 

1;0



. C.

 

 

 

. D.

 

 

 

Lời giải

Chọn C

Ta có:

2 1

1 1

d 4

x x x

 

     





3 1

13 2

 

 

 

 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu

94. (THPT Trần Phú - Đà Nẵng - 2021) Biết

 

x x





. Giá

trị củ

 

1 df x x







 



bằng

2

. B.

. C.

. D

Lời giải

Chọn C

Xét:

   

3 3 3

1 1 1

1 d 5 d 1d 18

x x f x x x



  





 



 

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1



MỨC ĐỘ VẬN DỤNG

Câu 1. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Gọi

làdiệntíchhìnhphẳnggiới

hạnbởiđồthịhàmsố

x x







,đườngthẳng

1y x 

vàcácđườngthẳng

x m

,

2x m



 

1m 

.Giátrịcủa

saocho

ln3S 

là

2m 

. B.

3m 

. C.

5m 

. D.

4m 

.

Câu 2. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Ngườitadùngmáyđàohầm(TBM)

đểđàohaiđườnghầmhìnhtrụtrònxoayđườngkính

12m

,mỗiđườnghàmđềucóchiềudàibằng

20m

,cóhaitrụccắtnhauvàvuônggócvớinhau.Tínhthểtíchkhốiđấtđàođược.

3987.89m

. B.

3619.11m

. C.

4523.89m . D.

3371.89m



Câu 3. (Chuyên Lê Hồng Phong - TPHCM - 2021) Chohàmsố

 

f x

cóđạohàmliêntụctrên



thỏa

mãn

 

3 21f 

,

 

d 9f x x 



.Tínhtíchphân

 

. 3 dI x f x x







.

15I 

. B.

6I 

. C.

12I 

. D.

9I 

.

Câu 4. (Chuyên Lam Sơn - Thanh Hóa - 2021) Chohàmsố

 

f x

liêntụctrên



vàcómộtnguyên

hàmlàhàmsố

 

g x x x  

.Khiđó

 

df x x



bằng:

. B.



. C.

. D.



.

Câu 5. (Chuyên KHTN - 2021) Cho hàm số

3 2

( ) 4f x ax bx cx     và

( )g x mx nx   có đồ thị

tronghìnhbêndưới.



Diệntíchcủahìnhphẳnggiớihạnbởiđồthịcủahaihàmsốtrên(phầngạchchéotronghìnhvẽ)

bằng

NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG

Chủ đề 3

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

. B.

. C.

 D.

.

Câu 6. (Chuyên KHTN - 2021) Biếtrằng

d ln3 ln 2

x a b c

x x



  





với

,

làcácsốhữutỉ.Tính

2 3 4a b c 



19

. B.

. C.

. D.

5

.

Câu 7. (Chuyên KHTN - 2021) Cho hàm số

 

f x

 liên tục trên khoảng

 

0;

 và thỏa mãn

 

2 f x xf x

 

 

 

 

vớimọi

0x 

Tính

 

.f x dx





. B.

. C.

. D.

.

Câu 8. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hai hàm số

 

3 2

f x ax bx cx   

và

 

1g x dx ex  



( , , , , )a b c d e  

.Biếtrằngđồthịhàmsố

 

y f x



và

 

y g x



cắtnhautại

3điểmcóhoànhđộlầnlượtlà

3

;

1

;

(thamkhảohìnhvẽ).Hìnhphẳnggiớihạnbởi2đồthị

đãchocódiệntíchbằng



. B.

. C.

. D.

.

Câu 9. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho

 

d ln 3 ln 2

ln 2

x c

I x a b

x x

   





,

với

, ,a b c 

.Giátrị

2 2 2

a b c 

bằng

A. 11. B. 1. C. 9. D. 3.

Câu 10. (Chuyên Quốc Học Huế - 2021) Cho hàm số

 

f x

 liên tục trên



 và thỏa mãn

   

5 ,f x f x x   

.Biết

 

2f x dx 



.Tính

 

I xf x dx





20I 

. B.

10I 

. C.

15I 

. D.

5I 

.

Câu 11. (Chuyên Quang Trung - Bình Phước - 2021)

 

F x

là một nguyên hàm của hàm số

 

1 2 3y x x x   

.Biết

   

5 5

2 4 1

F F   

và

   

3 5 3 ; ,F F a b a b     .Giá

trị

a b

bằng

. B.

. C.

. D.

Câu 12. (Chuyên Quang Trung - Bình Phước - 2021) Cho

ln ln 2; ,

1 sin

x dx

b a b

x a



   







.Giá

trị

3a b

bằng

. B.

. C.

. D.

.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Câu 13. (Chuyên Ngoại Ngữ Hà Nội- 2021) Chohàmsố

 

y f x

liêntụctrênđoạn

 

5;6

cóđồthị

nhưhìnhvẽ.Giátrịcủa

 

f x dx





bằng.



. B.

. C.

. D.

.

Câu 14. (Chuyên Ngoại Ngữ Hà Nội- 2021) Chohàmsố

( )y f x

cóđạohàmliêntụctrênđoạn

[ 1;1]

,

thỏamãn

( ) 0,f x x  

và

( ) 2 ( ) 0f x f x



 

.Biết

(1) 1f 

.Tính

( 1)f 





. B.



. C.

. D.

.

Câu 15. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho

 

F x  làmộtnguyênhàmcủa

 

f x

.Biết

 

f x

cóđạohàmvàxácđịnhvớimọi

0x 

.Tính

 

f x e x





.

3 6

x x x

x e xe e C  

. B.

6 6

x x x

x e xe e C  

.

3 6 6

x x

x xe e C  

. D.

3 6 6

x x x

x e xe e C  

.

Câu 16. (Chuyên ĐHSP Hà Nội - 2021) Cho

( )F x

 là một nguyên hàm của

( )

2 ( 3)

f x

x x





 trên

 

0;

thỏamãn

(1) ln 3F 

.Giátrịcủa

(2021) (2020)F F

e e

thuộckhoảngnào?

 

 

 

. B.

1 1

;

10 5

 

 

 

. C.

1 1

;

5 3

 

 

 

. D.

1 1

;

3 2

 

 

 

.

Câu 17. (Chuyên ĐH Vinh - Nghệ An - 2021) Giảsử

 

f x

làmộthàmsốcóđạohàmliêntụctrên



.

Biếtrằng

 

G x x

làmộtnguyênhàmcủa

   

g x e f x





trên



.Họtấtcảcácnguyênhàm

của

 

e f x





là

3 2

2 3x x C  

. B.

3 2

3x x C 

. C.

3 2

2 3x x C 

. D.

3 2

3x x C  

.

Câu 18. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho

 

2021

d 2f x x 



. Tính tích phân

 

2021

. ln 1 d

I f x x



 

 

 





.

2I 

. B.

1I 

. C.

5I 

. D.

4I 

.

Câu 19. (THPT Quốc Oai - Hà Nội - 2021) Đườngcong

 

cóphươngtrình

y x

chiahìnhvuông

OABC

cócạnhbằng

thànhhaiphần.Gọi

1 2

,S S lầnlượtlàdiệntíchcủaphầnkhôngtôđậmvà

tôđậmnhưhìnhvẽbêndưới.Tỉsố

bằng

-1

-2

-5

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

. B.

. C.

. D.

.

Câu 20. (THPT Quốc Oai - Hà Nội - 2021) Chohàmsố

 

y f x

liêntụctrên



và

 

d 5f x x 



,

 

2 d 10f x x 



.Tíchphân

 

cos sin dI x f x x







bằng

5I 

. B.

20I 

. C.

15I 

. D.

25I 

.

Câu 21. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho tích

phân

3 2

d ln 2 ln3( , )

x x x

I x a b c a b

 

    







. Chọn khẳng định đúng trong các khẳng

địnhsau.

0b c 

 B.

0c 

 C.

0a 

 D.

0a b c  



Câu 22. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Biếtrằng

  

ln5 ln 2

1 2

I dx a b

x x

  

 



với

,a b

làcácsốhữutỉ.Giátrịcủatổng

a b

là

. B.

1

. C.



. D.

.

Câu 23. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Chohàmsố

 

y f x

xácđịnhvàliêntụctrên



có

 

0f x x  

,

 

1f e

.Biết

 

2 1,

f x

x x

f x



   

.Tìmtấtcảgiátrịcủathamsố

để

phươngtrình

 

f x m

cóhainghiệmthựcphânbiệt.

m e . B.

0 m e  . C.

1 m e  . D.

m e .

Câu 24. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Chohàmsố

( )y f x

cóđồthịnhưhìnhvẽbên.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5



Đặt

1 2 3 4

( ) ; ( ) ; ( ) ; ( ) .

b c d d

a a a c

I f x dx I f x dx I f x dx I f x dx   

   



Phátbiểunàodướiđâyđúng?

1 2 3 4

I I I I  

 B.

2 1 4 3

I I I I  



2 1 3 4

I I I I  

 D.

1 2 4 3

I I I I  



Câu 25. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho

 

f x

và

 

g x

làhaihàmsốcóđạohàmliên

tục trên



 và thỏa mãn

   

0 1, 1 2f f 

;

   

0 2, 1 4g g  

 và

   

d 7f x g x x







. Tính

   

dI f x g x x







.

3I  

. B.

17I 

. C.

3I 

. D.

17I  

.

Câu 26. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Chohàmsố

x m







(với

làthamsốkhác

)cóđồthịlà

 

.Gọilàdiệntíchhìnhphẳnggiớihạnbởiđồthivàhaitrụctọađộ.Cóbao

nhiêugiátrịthựccủa

thỏamãn

1S 

?

. B.

. C.

. D.

.

Câu 27. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hàm số

 

f x

xác định và liên tục trên

 

0; 

thỏamãn

   

f x xf x dx

 



 

0;x  

.Tínhtíchphân

 

f x dx





5 2

e

 B.

3 2 .e

 C.

2 2 .e

 D.

1 2 .e



Câu 28. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho biết

3 1 ln

d ln

3 ln

x b

x a

x x x c



 

 

 



 



 với

, ,a b c

làcácsốnguyêndươngvà

4c 

,tổng

a b c 

bằng

. B.

. C.

. D.

.

Câu 29. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Chohàmsố

4 2

4y x x m   .Tìm

đểđồthị

hàmsốcắttrục

tạibốnđiểmphânbiệtsaochohìnhphẳnggiớihạnbởiđồthịhàmsốvàOx

cóphầnphíatrêntrụchoànhlà

S ,phầndướitrụchoànhxlà

S và

S thỏa

1 2 3

S S S  .Khiđó



(

,a b

làcácsốnguyên,

0b 

,

tốigiản).Giátrịcủabiểuthức

S a b 

là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/



 B.

 C.

 D.

11.

Câu 30. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho

 

. ln

x x e

dx a e b e c

x e





  





 với

, ,a b c



.Tính

P a b c  



2P  

. B.



. C.

1P  

. D.

1P 

.

Câu 31. (THPT Đồng Quan - Hà Nội - 2021) Cho

 

d ln 3 ln 4

x a b c

  





với

, ,a b c

làcácsố

hữutỉ.Giátrịcủa

a b c 

bằng



. B.



. C.

. D.

.

Câu 32. (THPT Đồng Quan - Hà Nội - 2021) Chohàmsố

 

f x

cóđạohàmliêntụctrên



vàthỏamãn

   

. ' 2 4 8; 2 2

x f x dx f

  



.Tính

 

I f x dx







.



. B.



. C.

 

. D.

 

.

Câu 33. (THPT Đồng Quan - Hà Nội - 2021) Chohàmsố

 

f x

liêntụcvàdươngtrên

 



,thỏa

mãn

     

2 2

3 2 , 0

xf x x f x f x x



   

và

 



.Giátrịcủatíchphân

 

f x





. B.

1 5

4 2

. C.

1 5

.ln

2 2

. D.

1 5

.ln

3 2

.

Câu 34. (THPT Lê Lợi - Thanh Hóa - 2021) Biếtrằng tích phân

 

2 3 e d e+

x x a b

 



;

 

,a b

 

.

Tínhgiátrịbiểuthức

P a b 

.

. B.

. C.

. D.

.

Câu 35. (THPT Lê Lợi - Thanh Hóa - 2021) ÔngAncómộtmảnhđấtnhỏhìnhvuôngcạnhbằng

4 m

ở

trướcsân.Ôngmuốntrồnghoavàcỏđểtrangtrímảnhvườncủamìnhnhưsau:Ôngsẽtrồnghoa

trênphầndiệntíchcódạngParabol

 

nhậntrụcđốixứng

củahìnhvuônglàmtrụcđối

xứngcủa

 

vàđỉnhcủa

 

làtrungđiểmcủa

nhưhìnhvẽ,phầncỏsẽtrồngởphầncòn

lại của hình vuông. Biết rằng loại hoa ông muốn trồng có giá

200000

 đồng/

, cỏ có giá

50 000

đồng/

.HỏisốtiềnôngAnbỏrađểlàmmảnhvườnlàbaonhiêu(sốtiềnđượclàm

trònđếnhàngđơnvị)?

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7



1365685,4

đ. B.

2634314,6

đ. C.

138642,5

đ. D. Đápánkhác.

Câu 36. (Sở Vĩnh Phúc - 2021) Cho hàm số

 

y f x

 có đạo hàm liên tục trên



 và thỏa mãn

 

sin .cos ,

f x f x x x x



 

    

 

 



.Biết

 

0 0f 

,tính

 

dI xf x x









.

I  

. B.

I 

. C.





. D.



 

.

Câu 37. (Sở Vĩnh Phúc - 2021) Biếtdiệntíchcủahìnhphẳnggiớihạnbởicácđường

3 , , 0

y y x



  



là

3ln3 6

m n

S  

.Tínhtổng

m n

.

4m n 

. B.

2m n 

. C.

1m n 

. D.

3m n 

.

Câu 38. (Sở Lào Cai - 2021) Cóbaonhiêugiátrịthựccủathamsố

thỏamãn:

3 2 10

x x dx m  



?

. B.

. C.

. D.

.

Câu 39. (Sở Hà Tĩnh - 2021) Chohàmsố

 

y f x

liêntụctrên



vàthỏamãn

   

2021 sin ,f x f x x x x    

.Giátrịcủatíchphân

 

I f x dx









bằng

1010

. B.

2019

. C.

2020

. D.

2022

Câu 40. (Sở Yên Bái - 2021) Biết

d ln 5 ln 3

4 3

x a b

x x



 

 



với

,a b

.Tính

.P a b

.

3P  

. B.

6P  

. C.

6P 

. D.

3P 

.

Câu 41. (Sở Yên Bái - 2021) Biết

, ,a b c

 là các số nguyên dương thỏa mãn

( 1) 1

a b c

x x x x

  

  



.Tínhgiátrịbiểuthức

P a b c  

.

18.P 

 B.

46.P 

 C.

24.P 

 D.

12.P 



Câu 42. (Sở Yên Bái - 2021) Cho hàm số

 

f x

 liên tục và là hàm số chẵn trên



 thỏa mãn

 

d 6.I f x x 



Tínhtíchphân

 

cos . 3sin dJ x f x x









.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

4.J  

 B.

4.J 

 C.

0.J 

 D.

6.J 



Câu 43. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Biết

ln6

ln3

3lna lnb

e 2e 3

x x



 

 



với

,

làcác

sốnguyêndương.Tính

P ab

. B.

10

. C.

. D.

.

Câu 44. (THPT Thanh Chương 1- Nghệ An - 2021) Biếtrằng ,với ;

; làcácsốhữutỷ.Giátrịcủa bằng:

A. . B. . C. . D. .

Câu 45. (THPT Nguyễn Huệ - Phú Yên - 2021) Chohàmsố

 

f x

liêntụctrên

 

0;

vàthỏamãn

 

f x

x x

  

.Biết

 

ln 4f x dx a b 



với

,a b

.Giátrịcủa

2a b

bằng

. B.

. C.

. D.

.

Câu 46. (THPT Lương Thế Vinh - 2021) Chohàmsố

 

y f x

với

1 4x  

cóđồthịcácđoạnthẳng

nhưhìnhbên.

Tíchphân

 

dI f x x







bằng

. B.

. C.

5,5

. D.

2,5

.

Câu 47. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Chohàmsố

( )y f x

liêntụcvàcóđồthịtrên

[ 3;5]

nhưhìnhbên.



Biếtcácmiền

, ,A B C

códiệntíchlầnlượtlà

1377 2673

188, ,

4 4

A B C

S S S  

.Khiđó

 

1f x dx



 

 



bằng

A. 520. B.

2417

. C. -504. D.

2401

.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 48. (THPT Đào Duy Từ - Hà Nội - 2021) Chohàmsố

 

f x

liêntụctrên

 

0;

.Biết

làmột

nguyênhàmcủahàmsố

 

lny f x x

và

 

ln 2

f 

.Khiđó,

 

f x



bằng



. B.

. C.



. D.



Câu 49. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho tích phân

( ) 2.xf x dx 



 Tính tích phân



2 3

( 1)I x f x dx 



?

. B.

. C.

. D.

.

Câu 50. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Chohàmsố

3 2

y x ax bx c    cóđồthị

( )C

.Biết

rằngtiếptuyến

của

( )C



tạiđiểmcóhoànhđộ

1

cắt

( )C

tạiđiểm

cóhoànhđộbằng

(xem

hìnhvẽ).Diệntíchhìnhphẳnggiớihạnbởi

và

( )C

(phầngạchchéotronghình)bằng



. B.

. C.

. D.

.

Câu 51. (THPT Chu Văn An - Thái Nguyên - 2021) ÔngAncómộtmảnhvườnhìnhElipcóđộdàitrục

lớnbằng

16m

vàđộdàitrụcbébằng

10m

.Ôngmuốntrồnghoatrênmộtdảiđấtrộng

vànhận

trụcbécủaeliplàmtrụcđốixứng.Biếtkinhphíđểtrồnghoalà

100.000

đồng/

1m .HỏiôngAn

cầnbaonhiêutiềnđểtrồnghoatrêndảiđấtđó?(Sốtiềnđượclàmtrongđếnhàngnghìn.)

A. 7.826.000đồng. B. 7.862.000đồng. C. 7.128.000đồng. D. 7.653.000đồng.

Câu 52. (THPT Chu Văn An - Thái Nguyên - 2021) Chohàmsố

( )f x



liêntụctrênkhoảng

(0; ).



Biết

(1) 1f 

và

     

ln ; 0;f x xf x x x



    

.Giátrịcủa

( )f e

bằng:

 B.

 C.

 D.

.

Câu 53. (THPT Chu Văn An - Thái Nguyên - 2021) Chohàmsố

 

f x



liêntụctrênđoạn

 

1;4

vàthoả

mãn

 

2 1

f x



 

.Tính

 

I f x dx



?

2ln 2.S 

 B.

ln 2.S 

 C.

2ln 2S 

 D.

3 2ln 2S  

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 54. (THPT Ba Đình - Thanh Hóa - 2021) Cho

cos 4

sin 5sin 6

dx a b

x x c



 

 



, với

, ,a b c   .Tínhtổng

S a b c  

.

1S 

. B.

0S 

. C.

4S 

. D.

3S 

.

Câu 55. (THPT Triệu Sơn - Thanh Hóa - 2021) Chohàmsố

 

y f x

cóđồthịnhưhìnhvẽvàgọi

;

làhaihìnhphẳngđượcgạchtronghìnhbêndướilầnlượtcódiệntíchbằng

và

.



Giátrịcủa

 

3 1 dI f x x



 



bằng:

. B.

. C.

. D.

.

Câu 56. (THPT Triệu Sơn - Thanh Hóa - 2021) Mộtkhuônviêndạngnửahìnhtròn,trênđóngườithiết

kếphầnđểtrồnghoacódạngcủamộtcánhhoahìnhparabolcóđỉnhtrùngvớitâmvàcótrụcđối

xứngvuônggócvớiđườngkínhcủanửahìnhtròn,haiđầumútcủacánhhoanằmtrênnửađường

tròn(phầntômàu)vàcáchnhaumộtkhoảngbằng4m.Phầncònlạicủakhuônviên(phầnkhông

tômàu)dànhđểtrồngcỏNhậtBản.Biếtcáckíchthướcchonhưhìnhvẽ,chiphíđểtrồnghoavà

cỏNhậtBảntươngứnglà

150.000

đồng/

m và

100.000

đồng/

m .Hỏisốtiềncầnđểtrồnghoa

vàtrồngcỏNhậtBảntrongkhuônviênđógầnnhấtvớisốnàosauđây?



3.739.000

(đồng). B.

1.948.000

(đồng). C.

3.926.000

(đồng). D.

4.115.000

(đồng).

Câu 57. (THPT Trần Phú - Đà Nẵng - 2021) Cho

 

làhìnhphẳnggiớihạnbởiđồthịhaihàmsố

1; 1y x y x     vàhaiđườngthẳng

1; 1x x  

.



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Thểt

íchcủakhốitrònxoayđượctạothànhkhiquay

 

quanht

rục

bằ

ng



. B.



. C.



. D.



.

BẢNG ĐÁP

ÁN

1.A

2.D

5.C

8.C

10.D

11.D

12.A

13.D

14.D

15.D

16.A

17.C

18.B

19.C

20.D

21.D

22.C

23.D

24.B

25.

26.B

27.B

28.C

29.

30.A

31.B

32.D

33.C

34.D

35.A

36.

37.

38.

39.

40.A

41.B

42.B

43.D

44.A

45.D

46.D

47.A

48.D

49.D

50.C

51.D

52.B

53.A

54.C

55.D

56.

57.C

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1



MỨC ĐỘ VẬN DỤNG

Câu 1. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Gọi

làdiệntíchhìnhphẳnggiới

hạnbởiđồthịhàmsố

x x







,đườngthẳng

1y x 

vàcácđườngthẳng

x m

,

2x m



 

1m 

.Giátrịcủa

saocho

ln3S 

là

2m 

. B.

3m 

. C.

5m 

. D.

4m 

.

Lời giải

Chọn A

Xétphươngtrìnhhoànhđộgiaođiểmcủahaiđồthịhàmsố:

 

2 2

2 2 1

2 1

x x

x x x x

x x x













     

 



   

  





.

Phươngtrìnhvônghiệm,suyrahaiđồthịhàmsốkhôngcógiaođiểm.

Nhưvậydiệntíchhìnhphẳngcầntínhlà:

 

2 2 2

2 1 1

1 d d d

1 1 1

m m m

x x

S x x x x

x x x

 

    

  

  

.

 

2 2

1 2 1

d 1 ln 1 ln 1 ln

1 1

m m

x x x

x m



 

      

 

 

 



(do

1m 

).

Theođềbài

2 1 2 1

ln3 ln ln3 ln 3

1 1

m m

 

   

    

   

 

   

hoặc

2 1

ln ln 3



 

 

 



 

.

Suyra

 

2 1

2 1 3 1

2 1 1

3 2 1 1

1 3

m m

m KTM

m m











  







 







  















.

Vậy

2m 

.

Câu 2. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Ngườitadùngmáyđàohầm(TBM)

đểđàohaiđườnghầmhìnhtrụtrònxoayđườngkính

12m

,mỗiđườnghàmđềucóchiềudàibằng

20m

,cóhaitrụccắtnhauvàvuônggócvớinhau.Tínhthểtíchkhốiđấtđàođược.

3987.89m

. B.

3619.11m

. C.

4523.89m . D.

3371.89m



Lời giải

Chọn D

NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG

Chủ đề 3

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/



Cắtthiếtdiệncủahaihìnhtrụtheomộtmặtphẳngtheophươngvuônggócvớivớikhốitrụta

đượcmộthìnhvuôngcócạnhbằng

2 36 x



Khiđótacóthểtíchkhốiđấtđucợđàolà

 

2 2

2. 4 36 d 3371.89V R h x x

 



   



.

Câu 3. (Chuyên Lê Hồng Phong - TPHCM - 2021) Chohàmsố

 

f x

cóđạohàmliêntụctrên



thỏa

mãn

 

3 21f 

,

 

d 9f x x 



.Tínhtíchphân

 

. 3 dI x f x x







.

15I 

. B.

6I 

. C.

12I 

. D.

9I 

.

Lời giải

Chọn B

Tacó

       

1 1 3

0 0 0

1 1

. 3 d 3 . 3 d 3 . d

9 9

I x f x x x f x x x f x x

  

  

  

.

Đặt

   

d d

u x u x

v f x x v f x

 

 

 



 



 

 

 

.

Suyra

       

3 3

0 0

. d . d 3 3 9 3.21 9 54x f x x x f x f x x f



      

 

.

Vậy

6I 

.

Câu 4. (Chuyên Lam Sơn - Thanh Hóa - 2021) Chohàmsố

 

f x

liêntụctrên



vàcómộtnguyên

hàmlàhàmsố

 

g x x x  

.Khiđó

 

df x x



bằng:

. B.



. C.

. D.



.

Lời giải

Chọn C

Tacó:

   

1f x g x x



  



   

2 2

1 1

d 1 d

3 3

f x x x x x

 

    

 

 

 

.

Câu 5. (Chuyên KHTN - 2021) Cho hàm số

3 2

( ) 4f x ax bx cx   

 và

( )g x mx nx 

 có đồ thị

tronghìnhbêndưới.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3



Diệntíchcủahìnhphẳnggiớihạnbởiđồthịcủahaihàmsốtrên(phầngạchchéotronghìnhvẽ)

bằng

. B.

. C.

 D.

.

Lời giải

Chọn C

Phươngtrìnhhoànhđộgiaođiểm:

3 2 2 3 2

4 ( ) ( ) 4 0ax bx cx mx nx ax b m x c n x             



Đặt

3 2

( ) ( ) ( ) 4h x ax b m x c n x     



Vì

( ) 0h x 

có

nghiệm

2, 1, 1x x x   

nên

( ) ( 1)( 1)( 2) ( 1)( 2)h x a x x x a x x      



Màtacó

(0) 2 4 2h a a   

.

Suyra

( ) 2( 1)( 2)h x x x  

.

Vậydiệntíchhìnhphẳnglà

2 2

1 1

( ) 2( 1)( 2)

S h x dx x x dx

 

    

 

.

Câu 6. (Chuyên KHTN - 2021) Biếtrằng

d ln 3 ln 2

x a b c

x x



  





với

,

làcácsốhữutỉ.Tính

2 3 4a b c 



19

. B.

. C.

. D.

5

.

Lời giải

Chọn B

Tacó:

2 2

1 1

1 2 1

d 1 d

x x x

x x x x



 

   

 

 

 

 



2ln 1 ln 2ln3 3ln 2

2 2

x x x

 

       

 

 

Suyra:

a 

;

2b 

;

3c  

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vậy

 

2 3 4 2. 3.2 4. 3 19

a b c      

.

Câu 7. (Chuyên KHTN - 2021) Cho hàm số

 

f x

 liên tục trên khoảng

 

0;

 và thỏa mãn

 

2 f x xf x

 

 

 

 

vớimọi

0x 

Tính

 

.f x dx





. B.

. C.

. D.

.

Lời giải

Chọn D

Tacó

   

2 1f x xf x

 

 

 

 



Đặt

1 1

t x

x t

  

khiđóđiềukiệnđềbàichotrởthành

     

1 1 1 1

2 2 . 1 2f f t t f f t

t t t t

   

    

   

   



Từ

 

và

 

tacó:

 

4 2 . 2

1 2

2 . 1

f t t f x

f t

f t t f



 

 

 





  

 





 



 

 



 



.

Lấytíchphâncậntừ

đến

tađược:

 

2 2

1 1

2 2

1 2 3

3 4

f x dx dx



 



 



Câu 8. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hai hàm số

 

3 2

f x ax bx cx   

và

 

1g x dx ex  



( , , , , )a b c d e  

.Biếtrằngđồthịhàmsố

 

y f x



và

 

y g x



cắtnhautại

3điểmcóhoànhđộlầnlượtlà

3

;

1

;

(thamkhảohìnhvẽ).Hìnhphẳnggiớihạnbởi2đồthị

đãchocódiệntíchbằng



. B.

. C.

. D.

.

Lời giải

Chọn C

Phươngtrìnhhoànhđộgiaođiểmcủahaiđồthị

 

y f x

và

 

y g x

là

     

3 2 2 3 2

1 3

1 0. *

2 2

bx cx dx ex ax b d x c ex xa             



Dođồthịhàmsố

 

y f x



và

 

y g x



cắtnhautạibađiểmcóhoànhđộlầnlượtlà

3

;

1

;

nênphươngtrình

 



cóbanghiệm

3x  

;

1x  

;

1x 

.Khiđótacóhệphươngtrình

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

   

27 9 3 0

a b d c e



      



      





     





b d

c e



 



 









 





.

Suyra

   

3 2

1 3 1 3

2 2 2 2

f x g x x x x

    

.

Vậyhìnhphẳnggiớihạnbởihaiđồthịhàmsốđãchocódiệntíchlà:

   

 

   

 

1 1

3 1

d dS f x g x x g x f x x



 

   

 



1 1

3 2 3 2

3 1

1 3 1 3 1 3 1 3

d d

2 2 2 2 2 2 2 2

x x x x x x x x



 

   

       

   

   

 



2 2 4  

.

Câu 9. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho

 

d ln 3 ln 2

ln 2

x c

I x a b

x x

   





,

với

, ,a b c



.Giátrị

2 2 2

a b c 

bằng

A. 11. B. 1. C. 9. D. 3.

Lời giải

Chọn D

Đặt

ln 2

u x

x u







  





 



.

Đổicận:Khi

1 2

x u

  

;Khi

e 3

x u

  

;

Tacó:

2 2

1 2 1

ln ln3 ln 2 1 ln 3 ln 2

 d

d u

I u u

u u u u

   

      





   

  

   



 

.

Suyra



,

 

,

 

.

Vậygiátrị

2 2 2

1 1 1 3

a b c

     

.

Câu 10. (Chuyên Quốc Học Huế - 2021) Cho hàm số

 

f x

 liên tục trên



 và thỏa mãn

   

5 ,f x f x x

   

.Biết

 

f x dx





.Tính

 

I xf x dx









. B.



. C.



. D.



.

Lời giải

Chọn D

Đặt

dt dx

t x

x t

 



  



 



.

Khiđó:

         

3 2 3

2 3 2

5 5 5 5

I xf x dx t f t dt t f t dt

       

  



   

3 3

2 2

5 5 5

f t dt tf t dt

   

 

   

3 3

2 2

f t dt tf t dt

 

 

(Vì

   

5 ,f x f x x

   

).

Khiđó

5.2 2 10 5

I I I I

     

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 11. (Chuyên Quang Trung - Bình Phước - 2021)

 

F x

là một nguyên hàm của hàm số

 

1 2 3y x x x   

.Biết

   

5 5

2 4 1

F F   

và

   

3 5 3 ; ,F F a b a b    

.Giá

trị

a b

bằng

. B.

. C.

. D.

Lời giải

Chọn D

Theođề,

 

F x

códạng

   

 

2 2 2 2

1 1

1 2 3d 2 3 2 3 2 3

2 3

F x x x x x x x d x x x x C            

 



 

5 5 5 5

4 1 1

3 3

F C C     

.

Suyra:

   

3 8 13 1; 5 8 13 1F F     

Dođó:

   

3 5 16 3 2F F    

Đồngnhất

,a b

tađược

16; 2a b 



Vậy

18a b 

.

Câu 12. (Chuyên Quang Trung - Bình Phước - 2021) Cho

ln ln 2; ,

1 sin

x dx

b a b

x a



   







.Giá

trị

3a b

bằng

. B.

. C.

. D.

.

Lời giải

Chọn A

Tacó:

 

4 4 4

2 2

0 0 0

d tan

1 sin cos

x dx x dx

x x

  

  



  

ư

.tan tan d ln cos ln 2 ln 2 ln ln 2

4 4

x x x x x b



  

         





Đồngnhấthệsốtađược

4; 2a b 

.

Vậy

3 4 3.2 10a b   

.

Câu 13. (Chuyên Ngoại Ngữ Hà Nội- 2021) Chohàmsố

 

y f x

liêntụctrênđoạn

 

5;6

cóđồthị

nhưhìnhvẽ.Giátrịcủa

 

f x dx





bằng.



. B.

. C.

. D.

.

Lời giải

-1

-2

-5

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Chọn

Tacó

1 1

. .6.3 9.

2 2

ABC

S BC AB

  



1 1

. .1.2 1.

2 2

DEE

S DF EF  



 

1 1 3

.3.1 .

2 2 2

FEGO

S GO EF DO   



Khiđó

       

0 2 1 0

5 5 2 1

3 13

dx dx dx dx 9 1 .

2 2

ABC DEE FEGO

f x f x f x f x S S S

 

   

         

   



Câu 14. (Chuyên Ngoại Ngữ Hà Nội- 2021) Chohàmsố

( )y f x

cóđạohàmliêntụctrênđoạn

[ 1;1]

,

thỏamãn

( ) 0,f x x  

và

( ) 2 ( ) 0f x f x



 

.Biết

(1) 1f 

.Tính

( 1)f 





. B.



. C.

. D.

.

Lời giải

Chọn D

+Tacó:Vì

( ) 0,f x x   

nên

 

1 1

( ) ( )

( ) 2 ( ) 0 2 2 ln ( ) 2

( ) ( )

f x f x

f x f x dx dx f x x

f x f x



 

 



          

 



(1)

ln 4 ( 1) e

( 1)

     



.

Vậy

( 1) ef   

Câu 15. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho

 

F x  làmộtnguyênhàmcủa

 

f x

.Biết

 

f x

cóđạohàmvàxácđịnhvớimọi

0x 

.Tính

 

f x e x





.

3 6

x x x

x e xe e C  

.B.

6 6

x x x

x e xe e C  

.

3 6 6

x x

x xe e C  

.D.

3 6 6

x x x

x e xe e C  

.

Lời giải

Chọn D

Theobài,

 

   

3 2

d 3

f x f x

F x x F x f x x f x x

x x

 

      



.

Khiđó,

 

2 2 2

d 3 d 3 6 d 3 6 6 d

x x x x x x x

f x e x x e x x e xe x x e xe e x



     

   



3 6 6

x x x

x e xe e C   

.

-1

-2

-5

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vậy

 

d 3 6 6

x x x x

f x e x x e xe e C



   



.

Câu 16. (Chuyên ĐHSP Hà Nội - 2021) Cho

( )F x

 là một nguyên hàm của

( )

2 ( 3)

f x

x x





 trên

 



thỏamãn

(1) ln 3



.Giátrịcủa

(2021) (2020)

F F

e e

thuộckhoảngnào?

 

 

 

. B.

1 1

;

10 5

 

 

 

. C.

1 1

;

5 3

 

 

 

. D.

1 1

;

3 2

 

 

 

.

Lời giải

Chọn A

Tacó

( )

2 ( 3)

F x dx

x x









Đặt

1 3 1

3 .

( 3) 2 ( 3)

x x dt

t x x dt dx dx

x x x x

 

      

 

.

( ) ln 3

F x x x C    

.

Mà

(1) 3 0

F C

  

.Dođó

( ) ln 3

F x x x

   

.

Vậy

(2021) (2020)

2021 2024 2020 2023 0, 0222

F F

e e    



.

Câu 17. (Chuyên ĐH Vinh - Nghệ An - 2021) Giảsử

 

f x

làmộthàmsốcóđạohàmliêntụctrên



.

Biếtrằng

 

G x x

làmộtnguyênhàmcủa

   

g x e f x





trên



.Họtấtcảcácnguyênhàm

của

 

e f x





là

3 2

2 3

x x C  

. B.

3 2

x x C 

. C.

3 2

2 3

x x C 

. D.

3 2

x x C  

.

Lời giải

Chọn C

 

G x x

làmộtnguyênhàmcủa

   

g x e f x





trên



,nên

 

2 2

e f x x





.

Xét

 

I e f x x









.

Đặt

2 2

d 2 d

x x

u e u e x

 

   

và

   

d d

v f x x v f x



  

.

Khiđó:

   

2 2 2 3

2 d 3 2 .

x x

I e f x e f x x x x C

 

    





Vậy

3 2

2 3

I x x C  

.

Câu 18. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho

 

2021

d 2

f x x





. Tính tích phân

 

2021

. ln 1 d

I f x x



 

 

 





.

2I 

. B.

1I 

. C.



. D.

4I 

.

Lời giải

Chọn B

Đặt

 

ln 1 d d

t x t x

   





Với



thì

0t 

và

2021

x e

 

thì

2021



.

Khiđó,

 

   

2021

1 2021 2021

0 0 0

1 1 1

. ln 1 d d d .2 1

1 2 2 2

I f x x f t t f x x



 

     

 



  

.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 19. (THPT Quốc Oai - Hà Nội - 2021) Đườngcong

 

cóphươngtrình

y x

chiahìnhvuông

OABC

cócạnhbằng

thànhhaiphần.Gọi

1 2

,S S lầnlượtlàdiệntíchcủaphầnkhôngtôđậmvà

tôđậmnhưhìnhvẽbêndưới.Tỉsố

bằng

. B.

. C.

. D.

.

Lời giải

Chọn C

Diệntíchhìnhvuông

OABC

:

4.4 16 S



2 3

1 1 16

4 12 3

 

  

 

 



S x dx x



1 2

16 32

3 3

    S S S



Tỉsố

32 16

: 2

3 3

 



Câu 20. (THPT Quốc Oai - Hà Nội - 2021) Chohàmsố

 

y f x

liêntụctrên



và

 

d 5f x x 



,

 

2 d 10f x x 



.Tíchphân

 

cos sin dI x f x x







bằng

5I 

. B.

20I 

. C.

15I 

. D.

25I 

.

Lời giải

Chọn D.

Tacó:

 

2 d 10f x x 





Đặt

2 2d dtx t x  

   

1 1

4 2

2 d d 10

f x x f t t  

 

   

1 1

2 2

d d 20f t t f x x  

 

.

 

d 25f x x 



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

cos sin dI x f x x









Đặt

sin

x t

cos d dx x t 

 

dI f t t

 



 

df x x





25

.

Câu 21. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho tích

phân

3 2

d ln 2 ln3( , )

x x x

I x a b c a b

 

    







. Chọn khẳng định đúng trong các khẳng

địnhsau.

b c

 

 B.



 C.



 D.

a b c

  



Lời giải

Chọn D

Tacó

2 2

3 2 3

2 2

1 1

3 2 6

d 4 6 d 2 6 6ln 1

1 1 3

x x x x

I x x x x x x x

x x

 

 

 

         

 

 

 

 



20 13 7

6ln3 6ln 2 6ln2 6ln3.

3 3 3

   

      

   

   



Theođóthì

; 6; 6 0.

a b c a b c

       



Câu 22. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Biếtrằng

  

ln5 ln 2

1 2

I dx a b

x x

  

 



với

,a b

làcácsốhữutỉ.Giátrịcủatổng

a b

là

. B.

1

. C.



. D.

.

Lời giải

Chọn C

Tacó:

      

1 2

1 2 3 1 3 2

x x x x

 

   

.

      

3 3

2 2

1 2

1 2 3 1 3 2

I dx dx

x x x x

 

  

 

   

 

 



=

3 3

2 2

1 1 2 1 1 2

ln 1 ln 2

3 1 3 2 3 3

dx dx x x

x x

    

 

 



=

   

1 2 2

ln 2 ln1 ln 5 ln 4 ln 5 ln 2

3 3 3

    

.

Suyra

, 1

a b

  

.Vậy

a b

  

.

Câu 23. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Chohàmsố

 

y f x



xácđịnhvàliêntụctrên



có

 

0f x x

  

,

 

f e

.Biết

 

2 1,

f x

x x

f x



    

.Tìmtấtcảgiátrịcủathamsố

để

phươngtrình

 

f x m

cóhainghiệmthựcphânbiệt.

m e

. B.

m e 

. C.

m e 

. D.

m e

.

Lời giải

Chọn D

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Tacó

 

   

2 1, 2 1 ln

f x f x

x x dx x dx f x x x C

f x f x

 

          

 





 

3 3

1 ln 2 1f e e C C     

.Dođó

 

1x x

f x e

 



.

Phươngtrình

 

1 2

1 ln 0 ( 0)

x x

f x m e m x x m m

 

        

.

Đểphươngtrìnhcóhainghiệmphânbiệt

 

1 4 1 ln 0 ln

m m m e          .

Câu 24. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Chohàmsố

( )y f x

cóđồthịnhưhìnhvẽbên.



Đặt

1 2 3 4

( ) ; ( ) ; ( ) ; ( ) .

b c d d

a a a c

I f x dx I f x dx I f x dx I f x dx   

   



Phátbiểunàodướiđâyđúng?

1 2 3 4

I I I I  

 B.

2 1 4 3

I I I I  



2 1 3 4

I I I I  

 D.

1 2 4 3

I I I I  



Lời giải.



Chọn B

Gọi

1 2 3

;S ;SS

làdiệntíchcácphầnđượctômàunhưhìnhvẻtrên.Tacó:

1 1

( )

I f x dx S 



.

2 1 2

 ( ) 

I f x dx S S  



.

3 1 3 2

( )

I f x dx S S S   



.

4 3

 ( )

I f x dx S 



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vậy:

1 2 3 4

( ) ; ( ) ; ( ) ; ( ) .

b c d d

a a a c

I f x dx I f x dx I f x dx I f x dx

   

   



Câu 25. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho

 

f x

và

 

g x

làhaihàmsốcóđạohàmliên

tục trên



 và thỏa mãn

   

0 1, 1 2

f f

 

;

   

0 2, 1 4

g g

  

 và

   

d 7

f x g x x







. Tính

   

dI f x g x x







.

 

. B.



. C.



. D.

 

.

Lời giải

Chọn C

Tacó

               

1 1 1

0 0 0

d d + df x g x x f x g x x f x g x f x g x x

   

 

 

 

  



   

df x g x x





 

 



           

1 1 0 0

f x g x f g f g  

 

2.4 1. 2 10   

.Suyra

   

d 10 7 3

I f x g x x



   



.

Câu 26. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Chohàmsố

x m







(với

làthamsốkhác

)cóđồthịlà

 

.Gọilàdiệntíchhìnhphẳnggiớihạnbởiđồthivàhaitrụctọađộ.Cóbao

nhiêugiátrịthựccủa

thỏamãn



?

. B.

. C.

. D.

.

Lời giải

Chọn B

Tacó

 

C Ox A m 

 

C Oy B m

  

.

Khiđódiệntíchhìnhphẳnggiớihạnbởiđồthivàhaitrụctọađộlà:

2 2 2

0 0 0

1 1 1

m m m

x m x m m

S dx dx dx

x x x

 

  

    

 

  

 

  



 

2 2 2 2

1 ln 1 1 ln 1

m x x m m m       

.

Để



thì

 

2 2 2

1 ln 1 1

m m m

   

 

2 2

ln 1 1 1 1m m e m e         

.

Câu 27. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hàm số

 

f x

xác định và liên tục trên

 



thỏamãn

   

f x xf x dx

 



 

0;x

  

.Tínhtíchphân

 

f x dx





5 2

e

 B.

3 2 .e

 C.

2 2 .e

 D.

1 2 .e



Lời giải

Chọn B

Đặt

 

   

1 1

f x C

C xf x dx

f x x C dx

x x





 



 



 











  















 









 

. 2 2 1 2

2 2

x C

C x C C C C

 







          











 



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

       

1 1

2 2 ln 2 ln 2 ln1 2 3 2 .

e e

f x f x dx dx x x e e e

x x

 







             











 

 



Câu 28. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho biết

3 1 ln

d ln

3 ln

x b

x a

x x x c



 

 

 



 



 với

, ,a b c

làcácsốnguyêndươngvà



,tổng

a b c 

bằng

. B.

. C.

. D.

.

Lời giải

Chọn C

 

2 2 2

1 1 1

3 1 1

d d d 3 ln ln 3 ln

3 ln 3 ln 3 ln

x x x x x x

x x x x x x x



    

  

  

 

ln3

ln 6 ln 2 ln3 ln 2

 

    

 

 

.

2, 3, 2

a b c

   

a b c

   

.

Câu 29. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Chohàmsố

4 2

y x x m  

.Tìm

đểđồthị

hàmsốcắttrục

tạibốnđiểmphânbiệtsaochohìnhphẳnggiớihạnbởiđồthịhàmsốvàOx

cóphầnphíatrêntrụchoànhlà

,phầndướitrụchoànhxlà

và

thỏa

1 2 3

S S S 

.Khiđó



(

,a b

làcácsốnguyên,



,

tốigiản).Giátrịcủabiểuthức

S a b 

là



 B.

 C.

 D.

11.

Lời giải

Chọn D

Gọi

, , , ( 0 )m n p q m n p q   

làhoànhđộcácgiaođiểmcủađồthịvớiOx

DođồthịhàmsốnhậnOy làmtrụcđốixứngnên

   

4 2 4 2

1 2 3 3 2

4 4

p q

S S S S S x x m dx x x m dx

          

 



 

5 3 4 2

4 2

4 4

4 0 0 0

5 3 5 3

q q q q

x x m dx mq m

           



(1)

Mặtkhác

4 2

4 0

q q m

  

(2)

Từ(1)và(2)tacó

m 

.Vậy

20, 9 11

a b a b

    



Câu 30. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho

 

. ln

x x e

dx a e b e c

x e





  





 với

, ,a b c



.Tính

P a b c  



2P  

. B.



. C.

1P  

. D.

1P 

.

Lời giải

Chọn A

Tacó

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

   

 

2 2

1 1 1

0 0 0

. 1 .

. 1

x x

x x e x x e

x e x e

dx dx dx

x e x e



 



 

 



  



Đặt

 

1 1

x x x x

u xe du e xe dx x e dx

      



Khiđó

 

1 1 1

0 1 1

1 1

1 ln ln 1

e e

x x e

dx du du u u e e

u u

x e

 









 

       

 



 

  



Suyra

1, 1, 1 2 1 2 1 2

a b c P a b c

            



Câu 31. (THPT Đồng Quan - Hà Nội - 2021) Cho

 

d ln 3 ln 4

x a b c

  





với

, ,a b c

làcácsố

hữutỉ.Giátrịcủa

a b c 

bằng



. B.



. C.

. D.

.

Lời giải

Chọn B

Tacó

 

1 1

2 2

0 0

3 3

d d

3 3

x x

 



 

 



 

1 3

 

 

 



 



ln 3

 

  

 



 

ln3 ln 4

   



; 1; 1

a b c     

.

Vậy

a b c

   

.

Câu 32. (THPT Đồng Quan - Hà Nội - 2021) Chohàmsố

 

f x

cóđạohàmliêntụctrên



vàthỏamãn

   

. ' 2 4 8; 2 2

x f x dx f

  



.Tính

 

I f x dx







.



. B.



. C.

 

. D.

 

.

Lời giải

Chọn D

Xét

   

. ' 2 4 8 *

x f x dx 





Đặt

 

' 2 4

2 4

du dx

u x

dv f x dx

v f x









 



 

 











     

   

 

1 1

* 2 4 2 4 8

2 2

3 1

2 2 4 8

2 2

2 4 10.

xf x f x dx

f f x dx

f x dx

    

   

   





Đặt

2 2 4

t x dt dx   





TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15



2



Suyra:

 

2 10

f t dt



 



.

Câu 33. (THPT Đồng Quan - Hà Nội - 2021) Chohàmsố

 

f x

liêntụcvàdươngtrên

 



,thỏa

mãn

     

2 2

3 2 , 0

xf x x f x f x x



   

và

 



.Giátrịcủatíchphân

 

f x





. B.

1 5

4 2

. C.

1 5

.ln

2 2

. D.

1 5

.ln

3 2

.

Lời giải

Chọn C

Tacó

     

2 2

3 2 , 0

xf x x f x f x x



   



     

2 3 2

3 2

x f x x f x xf x



  



   

     

2 3

3 3

2 2

x f x x f x

x x

x x x C

f x f x f x



 



      

 

 

.

Thay



tađược

 

2 2 2

1 2 1 1

1 1 1

f x

x x

C C C f x

f x x x

          

 

.

Khiđó

 

2 2

1 1

f x

dx dx

x x





 

.Đặt

1 2

t x dx xdx xdx dt

     

.

Đổicận

 

2 5

1 2

1 1 1 1 5

ln .ln

2 5

2 2 2 2

x t

f x

dx dt t

x t

  



   



  



 

.

Câu 34. (THPT Lê Lợi - Thanh Hóa - 2021) Biết rằng tích phân

 

2 3 e d e+

x x a b

 



;

 

,a b

 

.

Tínhgiátrịbiểuthức

P a b 

.

. B.

. C.

. D.

.

Lời giải

Chọn D

Đặt

2 3

d e d

u x

v x



 













d 2d

u x





















 

2 3 e d

x x

 



 

2 3 e 2e d

x x

  



 

1 1

0 0

2 3 e 2e

x x

x  

3e 1 





















2 7

P a b

   

.

Câu 35. (THPT Lê Lợi - Thanh Hóa - 2021) ÔngAncómộtmảnhđấtnhỏhìnhvuôngcạnhbằng

4 m

ở

trướcsân.Ôngmuốntrồnghoavàcỏđểtrangtrímảnhvườncủamìnhnhưsau:Ôngsẽtrồnghoa

trênphầndiệntíchcódạngParabol

 

nhậntrụcđốixứng

củahìnhvuônglàmtrụcđối

xứngcủa

 

vàđỉnhcủa

 

làtrungđiểmcủa

nhưhìnhvẽ,phầncỏsẽtrồngởphầncòn

lại của hình vuông. Biết rằng loại hoa ông muốn trồng có giá

200000

 đồng/

, cỏ có giá

50000

đồng/

.HỏisốtiềnôngAnbỏrađểlàmmảnhvườnlàbaonhiêu(sốtiềnđượclàm

trònđếnhàngđơnvị)?

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/



1365685,4

đ. B.

2634314,6

đ. C.

138642,5

đ. D. Đápánkhác.

Lời giải

Chọn A



Xéthệtrụctọađộ

Oxy

nhưhìnhvẽ.

Phươngtrìnhcủa

 

là

y x ;phươngtrìnhcủa

là

2y 





Diệntíchphầntrồnghoalà:

 

8 2

2 d 2

3 3

S x x x



 

    

 



 



.

Diệntíchphầntrồngcỏlà:

2 1

8 2 48 8 2

3 3

ABCD

S S S



    

.

VậysốtiềnôngAnbỏrađểlàmmảnhvườnlà:

1 2

200000. 50000. 1365685,4S S  đồng.

Câu 36. (Sở Vĩnh Phúc - 2021) Cho hàm số

 

y f x

 có đạo hàm liên tục trên



 và thỏa mãn

 

sin .cos ,

f x f x x x x



 

    

 

 



.Biết

 

0 0f 

,tính

 

dI xf x x









.

I  

. B.

I 

. C.





. D.



 

.

Lời giải

Chọn A

Do

   

sin .cos 0 0 0

2 2 2

f x f x x x f f f

  

     

       

     

     



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Tacó

 

2 2 2

0 0 0

d d d

2 2 2

I f x x f x x f x x

  

     

      

     

     

  

.

Do

   

2 2

0 0

1 1 1

sin .cos 2 d sin 2 d cos 2

2 2 4 2

f x f x x x f x x x x x

 



 

       

 

 

 



Khiđó

 

f x x







.

Vậy

   

 

   

2 2 2

0 0 0

1 1

d d . d

2 2 4 4

I xf x x x f x x f x f x x f

  



 

 



       

 

 

  

.

Câu 37. (Sở Vĩnh Phúc - 2021) Biếtdiệntíchcủahìnhphẳnggiớihạnbởicácđường

3 , , 0

y y x



  



là

3ln3 6

m n

S  

.Tínhtổng

m n

.

4m n 

. B.

2m n 

. C.

1m n 

. D.

3m n 

.

Lời giải

Chọn D

Xétphươngtrìnhhoànhđộgiaođiểmcủahaihàmsố

3 ,

y y



 



3 3.3 3

x x x

x x

  

     



Nhậnthấy

1x 

là

nghiệm

Với

1 0 1

1 1 0 3 3 3 1 1

x x

x x VT VP

 

          



Với

1 0 1

1 1 0 3 3 3 1 1

x x

x x VP VT

 

          



1x 

lànghiệmduynhất.

 

2 1

3 1 3 1 1 1 1 1 2 1

3 ln3 6 ln3 6 ln3 3ln3 ln3 6 3ln3 6

S dx x

 



 

   

                

 

   

 

   

 





2; 1m n  



3m n  



Câu 38. (Sở Lào Cai - 2021) Cóbaonhiêugiátrịthựccủathamsố

thỏamãn:

3 2 10

x x dx m  



?

. B.

. C.

. D.

.

Lời giải

Chọn A

Đặt

3 2 10

I x x dx m   



;

 

3 2f x x x  .Dấucủa

 

f x

:

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/



Xétcáctrườnghợpsau:

+)Nếu

0m 

:

   

2 3 2 3 2

3 2 10

I x x dx x x m m m       



.

3 2

10 0 2m m m m       

(thỏamãn).

+)Nếu

m 

:

   

2 3 2 3 2

3 2 10

I x x dx x x m m m          



.

3 2

10 0 2,36.m m m m      

(loại).

+)Nếu

m 

:

     

2 2 3 2

3 2 3 2

I x x dx x x dx x x       

 



3 2 3 2

8 278

10 0 2,02.

27 27

m m m m m m m            

(loại).

Vậycó1giátrịthựccủathamsố

thỏamãnbàitoán.

Câu 39. (Sở Hà Tĩnh - 2021) Chohàmsố

 

y f x

liêntụctrên



vàthỏamãn

   

2021 sin ,f x f x x x x    

.Giátrịcủatíchphân

 

I f x dx









bằng

1010

. B.

2019

. C.

2020

. D.

2022

Lời giải

Chọn A

Vì

 

y f x

liêntụctrên



và

     

2021 sin , 1f x f x x x x    

nêntacũngcó

         

2021 sin , 2f x f x x x x      



Từ

   

1 , 2

tacóhệphươngtrình

   

 

2021 sin

sin

2021 sin

2020

f x f x x x

f x x x

f x f x x x

  





 



   







2 2

1 1 1 1

sin cos cos sin

2020 2020 2020 1010

I x xdx x x xdx x

 

 

 

 

     

 

 

 

.

Câu 40. (Sở Yên Bái - 2021) Biết

d ln5 ln 3

4 3

x a b

x x



 

 



với

,a b 

.Tính

.P a b

.

3P  

. B.

6P  

. C.

6P 

. D.

3P 

.

Lời giải

Chọn A

Tacó

   

  

   

2 2 2 2

2 2

0 0

0 0 0 0

2 3 1

5 2 1

d d 2 d d 2ln 1 ln 3

4 3 1 3 1 3

x x

x x x x x x

  



      

     

   



2ln3 ln5 ln3 ln5 3ln3     



Khiđó

1; 3 . 3a b P a b      

.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Câu 41. (Sở Yên Bái - 2021) Biết

, ,a b c

 là các số nguyên dương thỏa mãn

( 1) 1

a b c

x x x x

  

  



.Tínhgiátrịbiểuthức

P a b c  

.

18.



 B.

46.



 C.

24.



 D.

12.





Lời giải

Chọn B

 

2 2 2

1 1 1

1 d 1

d d

( 1) 1

x x x

x x

x x x x

 

 

  

  



Đặt

1 1 1

1 d d 2d d

2 1 2 ( 1)

x x

t x x t x t x

x x x x

 

 

       

 

 

 



Khiđó

2 3

1 2

2 2

d 2 3 4 2 2 32 12 2

I t

t t





 

        

 

 





Dođó

32, 12, 2 32 12 2 46.

a b c P a b c

          



Câu 42. (Sở Yên Bái - 2021) Cho hàm số

 

f x

 liên tục và là hàm số chẵn trên



 thỏa mãn

 

d 6.

I f x x

 



Tínhtíchphân

 

cos . 3sin dJ x f x x









.

 

 B.



 C.



 D.





Lời giải

Chọn B

 

cos . 3sin dJ x f x x









.Đặt

3sin d 3cos dt x t x x  

.

Đổicận:

+

x t





   



+

x t



  

.

 

3 3

3 0

2 2

d ( )d .6 4

3 3 3

f t

J t f t t



   

 

.

Câu 43. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Biết

ln6

ln3

3lna lnb

e 2e 3

x x



 

 



với

,

làcác

sốnguyêndương.Tính

P ab

. B.

10

. C.

. D.

.

Lời giải

Chọn D

Có

 

      

ln6 ln 6 ln 6 ln6

ln3 ln3 ln3 ln3

d e d e d 1 1

e d

e 2e 3

e 2 1 e 2 e 1

e 2 3

x x

x x x x

x x

x x x



 

 

   

 

   

 

 

 

   





     

ln6

ln3

e e e 2 8

d ln ln 3ln 2 ln5 2, 5

e 2 e 1 e 1

x x x

x a b

 



 

       

  

 

 





Vậy

P ab

 



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 44. (THPT Thanh Chương 1- Nghệ An - 2021) Biếtrằng ,với ;

; làcácsốhữutỷ.Giátrịcủa bằng:

A. . B. . C. . D. .

Lời giải

Chọn A

Xét 

Đặt 

Với 



.

Dođó ; ; .Khiđó .

Câu 45. (THPT Nguyễn Huệ - Phú Yên - 2021) Chohàmsố

 

f x

liêntụctrên

 

0;

vàthỏamãn

 

f x

x x

  

.Biết

 

ln 4f x dx a b 



với

,a b

.Giátrịcủa

2a b

bằng

. B.

. C.

. D.

.

Lời giải

Chọn D

Tacó:

 

f x

x x

  

 

2 1 2ln

f x

xf x x

   



 

4 4 4

1 1 1

2 1 2 ln

f x

xf x dx dx xdx

   

  

     

17 2

2 1

2 lnf u du f v dv x x x   

 

 

8ln 4 6f x dx  



.

Vậy

2 8 2.6 20a b   

Câu 46. (THPT Lương Thế Vinh - 2021) Chohàmsố

 

y f x

với

1 4x  

cóđồthịcácđoạnthẳng

nhưhìnhbên.

Tíchphân

 

dI f x x







bằng

. B.

. C.

5,5

. D.

2,5

.

Lời giải

Chọn D

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21



Tacó:

       

4 1 2 4

1 1 1 2

d d d dI f x x f x x f x x f x x

 

   

   

.

Trongđó:

   

d . 1 2 .2 3

ABCD

f x x S



   



.

 

d .1.2 1

BCE

f x x S  



;

   

1 3

d 1 2 .1

2 2

EFGH

f x x S      



.

Vậy

       

4 1 2 4

1 1 1 2

3 5

d d d d 3 1

2 2

I f x x f x x f x x f x x

 

       

   

.

Câu 47. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Chohàmsố

( )y f x

liêntụcvàcóđồthịtrên

[ 3;5]

nhưhìnhbên.



Biếtcácmiền

, ,A B C

códiệntíchlầnlượtlà

1377 2673

188, ,

4 4

A B C

S S S  

.Khiđó

 

1f x dx



 

 



bằng

A. 520. B.

2417

. C. -504. D.

2401

.

Lời giải

Chọn A

         

5 5 5 5

3 3 3 3

1 8 8

a b

A B C

a b

f x dx f x dx dx f x dx f x dx f x dx S S S

   

          

 

 

     

1377 2673

188 8 520

4 4

    



Câu 48. (THPT Đào Duy Từ - Hà Nội - 2021) Chohàmsố

 

f x

liêntụctrên

 

0;

.Biết

làmột

nguyênhàmcủahàmsố

 

lny f x x

và

 

ln 2

f 

.Khiđó,

 

f x



bằng



. B.

. C.



. D.



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn D

Đặt

 

u f x

du f x dx

v x

dv dx

 

 



 











tacó

 

       

2 2

1 1

ln . .ln ln 2. 2 ln1. 1

1 1 7

 ln 2. 1

ln 2 4 4

f x

dx x f x f x xdx f f

x x

    

 

   

 

 

 

Câu 49. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho tích phân

( ) 2.xf x dx 



 Tính tích phân



2 3

( 1)I x f x dx 



?

. B.

. C.

. D.

.

Lời giải

Chọn D

Đặt

3 2 3 2 2

1 1 2 3 .

t x t x tdt x dx x dx dt

        



Đổicận:

0 1; 2 3.x t x t     



Khiđó

3 3

1 1

2 2 4

( ) ( ) .

3 3 3

I f t dt t f t dt  

 



Câu 50. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Chohàmsố

3 2

y x ax bx c    cóđồthị

( )C

.Biết

rằngtiếptuyến

của

( )C



tạiđiểmcóhoànhđộ

1

cắt

( )C

tạiđiểm

cóhoànhđộbằng

(xem

hìnhvẽ).Diệntíchhìnhphẳnggiớihạnbởi

và

( )C

(phầngạchchéotronghình)bằng



. B.

. C.

. D.

.

Lời giải

Chọn C

Giảsử

3 2

( ) : ( )C y f x x ax bx c    



và



: ( )d y g x

.

Khiđóphươngtrìnhhoànhđộgiaođiểmcủa

và

( )C

là:

( ) ( ) ( ) ( ) 0f x g x f x g x   



Dễthấyđathức

( ) ( )f x g x

làđathứcbậcbacóhệsốlũythừalớnnhấtbằng

vàcónghiệm

kép

1x  

vànghiệmđơn

2x 

.Dođó

( ) ( ) ( 1) ( 2).f x g x x x   



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

Diệntíchhìnhphẳnglà

2 2 2

1 1 1

( ) ( ) ( ( ) ( )) ( 1) ( 2)

S f x g x dx g x f x dx x x dx

  

        

  

.

Câu 51. (THPT Chu Văn An - Thái Nguyên - 2021) ÔngAncómộtmảnhvườnhìnhElipcóđộdàitrục

lớnbằng

16m

vàđộdàitrụcbébằng

10m

.Ôngmuốntrồnghoatrênmộtdảiđấtrộng

vànhận

trụcbécủaeliplàmtrụcđốixứng.Biếtkinhphíđểtrồnghoalà

100.000

đồng/

.HỏiôngAn

cầnbaonhiêutiềnđểtrồnghoatrêndảiđấtđó?(Sốtiềnđượclàmtrongđếnhàngnghìn.)

A. 7.826.000đồng. B. 7.862.000đồng. C. 7.128.000đồng. D. 7.653.000đồng.

Lời giải

Chọn D

Giảsửelipcóphươngtrình

2 2

x y

a b

 

với

0, 0

a b

 

.

Theođềbài,tacó

2 16 8

a a

  

và

2 10 5

b b

  

.

Vậyphươngtrìnhcủaelip:

2 2

64 25

x y

 

 

y x E



  







 





.

Khiđódảivườnđượcgiớihạnbởicácđường

   

1 2

E E

4; 4

x x

  

vàdiệntíchcủadảivườnlà

4 4

2 2

4 0

5 5

2 64 d 64 d

8 2

S x x x x



   

 

.

Tính

bằngcáchđổibiến

8sinx t

,tađược

6 4



 

 

 

 



Vậysốtiền

80 .100000 7652891,82.

6 4



 

  

 

 

Vậychọn D.

Câu 52. (THPT Chu Văn An - Thái Nguyên - 2021) Chohàmsố

( )f x



liêntụctrênkhoảng

(0; ).



Biết

(1) 1



và

     

ln ; 0;f x xf x x x



    

.Giátrịcủa

( )f e

bằng:

 B.

 C.

 D.

.

Lời giải

Chọn B

     

ln ; 0;f x xf x x x



    

.

Chia2vếcho



tacó:

 

2 2

( ).

f x x f x

x x







 

f x

x x



 



 

 

 

 

f x



 

 

 

 









Suyra

 

f e

 





.Bấmmáytíchphânvàthay

 

1 1



;tatínhđược

 

f e



.

Vậychọn B.

Câu 53. (THPT Chu Văn An - Thái Nguyên - 2021) Chohàmsố

 

f x



liêntụctrênđoạn

 

1;4

vàthoả

mãn

 

2 1

f x



 

.Tính

 

I f x dx





?

2ln 2.

S 

 B.

ln 2.

S 

 C.

2ln2



 D.

3 2ln 2

S  

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn A

Tacó

     

4 3 4

1 1 3

f x dx f x dx f x dx

 

  



     

4 3 4 3

1 1 1 1

(2 1) lnf x x

I f x dx f x dx dx f x dx

 



     

 

 

   



Đặt 2 1

x t dt

    .

Đổicận

1 1

4 3

x t

  

           

3 3 3 3

2 2

4 4 2

1 1

1 1 1 1

1 1

ln ln 2ln 2

2 2

I f t dt x f x dx f x dx x f x dx      

   

Câu 54. (THPT Ba Đình - Thanh Hóa - 2021) Cho

cos 4

sin 5sin 6

dx a b

x x c



 

 



, với

, ,a b c  

.Tínhtổng

S a b c  

.

1S 

. B.

0S 

. C.

4S 

. D.

3S 

.

Lời giải

Chọn C

Xéttíchphân

cos

sin 5sin 6

I dx

x x





 



.

Đặt

sin cos .t x dt x dx  

.

Đổicận:



Tacó:

1 1

0 0

1 1 1 3 4

ln ln

5 6 3 2 2 3

I dt dt

t t t t t



 

    

 

    

 

 

Vậy

1, 0, 3 4a b c S a b c       

.

Câu 55. (THPT Triệu Sơn - Thanh Hóa - 2021) Chohàmsố

 

y f x

cóđồthịnhưhìnhvẽvàgọi

;

làhaihìnhphẳngđượcgạchtronghìnhbêndướilầnlượtcódiệntíchbằng

và

.



Giátrịcủa

 

3 1 dI f x x



 



bằng:

. B.

. C.

. D.

.

Lời giải

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

Chọn D

Xét

 

3 1 dI f x x



 





Đặt

3 1x t 



d d

x t





Với

1x  



2t  



0x 



1t 





         

1 1 0 1

2 2 2 0

1 1 1 1

d d d d 3

3 3 3 3

A B

I f t t f x x f x x f x x S S

  

 

      

 

 

   

.

Câu 56. (THPT Triệu Sơn - Thanh Hóa - 2021) Mộtkhuônviêndạngnửahìnhtròn,trênđóngườithiết

kếphầnđểtrồnghoacódạngcủamộtcánhhoahìnhparabolcóđỉnhtrùngvớitâmvàcótrụcđối

xứngvuônggócvớiđườngkínhcủanửahìnhtròn,haiđầumútcủacánhhoanằmtrênnửađường

tròn(phầntômàu)vàcáchnhaumộtkhoảngbằng4m.Phầncònlạicủakhuônviên(phầnkhông

tômàu)dànhđểtrồngcỏNhậtBản.Biếtcáckíchthướcchonhưhìnhvẽ,chiphíđểtrồnghoavà

cỏNhậtBảntươngứnglà

150.000

đồng/

m và

100.000

đồng/

m .Hỏisốtiềncầnđểtrồnghoa

vàtrồngcỏNhậtBảntrongkhuônviênđógầnnhấtvớisốnàosauđây?



3.739.000

(đồng). B.

1.948.000

(đồng). C.

3.926.000

(đồng). D.

4.115.000

(đồng).

Lời giải

Chọn A

Kếthợpvàohệtrụctọađộ,tađược:



Gọiparabollà

 

:P y ax

.Do

   

2;4F P

nên

 

:P y x

.

Gọiđườngtròncótâmởgốctọađộlà

 

2 2 2

:C x y R 

.Do

   

2;4F C

nênnửađườngtròn

trênlà

20y x 

.

Đặt

S làdiệntíchphầntôđậm.Khiđó:

 

2 2

5 8

2. 20 d 20arcsin

5 3

S x x x

 

    

 

 



.

Đặt

S làdiệntíchphầnkhôngtôđậm.Khiđó:

2 1

1 5 8

. . 10 20arcsin

2 5 3

S R S

 

 

    

 

 

.

Vậy:SốtiềncầnđểtrồnghoavàcỏNhậtBảnlà:

1 2

150000. 100000. 3738574T S S   (đồng).

NGUYỄN

BẢO VƯƠNG - 0946798489

Câu 57. (THP

T Trần Phú - Đà Nẵng - 2021) Cho

 

là

hìnhphẳnggiớihạnbởiđồthịhaihàmsố

1; 1y x y x     vàhaiđườngthẳng

1x x  

.

Thểtíchcủakhốitrònxoayđượctạothànhkhiquay

 

quanhtr

ục

bằng

176



. B.



. C.



. D.



.

Lời giải

Chọn

Gọi

 

làhìnhphẳ

nggiớihạnbởi

1y x

 ,

1, 0y x x   

.K

hiquay

 

quan

htrục

thìkhốitrònxoayđượctạothànhcóthểtích

 

1 d

V x x





  



Gọi

 

làhìnhphẳngđượcgiớihạnbởi

0; 0, 1.y x y x x     

Khiquay

 

quanh

trục

thì

khốitrònxoayđượctạothànhcóthểtích

 

1 d

x x



 

 



Vậyt

hểtíchcủakhốitrònxoayđượctạothànhkhiquay

 

quanht

rục

là

1 2

V V V



  

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1



MỨC ĐỘ VẬN DỤNG CAO

Câu 1. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Giảsửhàmsố

cóđạohàmđến

cấphaitrên



thỏamãn

 

2 2f





và

   

2 2f x x f x x



  

vớimọi

x

.Giátrịtíchphân

 

dxf x x





bằng:

. B.

. C.

. D.

.

Câu 2. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Sântrườngcómộtbồnhoahìnhtròn

tâm

.Mộtnhómhọcsinhlớp12đượcgiaothiếtkếbồnhoa,nhómnàyđịnhbồnhoathànhbốn

phầnbởi2đườngparabolcócùngđỉnh

vàđốixứngvớinhauquatâm

(nhưhìnhvẽ).



Haiđườngparabolcắtđườngtròntại4điểm

, , ,A B C D

tạothànhmộthìnhvuôngcócạnhbằng

.Phầndiệntích

1 2

,S S dùngđểtrồnghoa,phầndiệntích

3 4

,S S dùngđểtrồngcỏ.Biếtkinh

phítrồnghoalà

150.000

đồng/

,kinhphítrồngcỏlà

100.000

đồng/

.Hỏinhàtrườngcần

baonhiêutiềnđểtrồngbồnhoađó?(sốtiềnlàmtrònđếnhàngchụcnghìn)

3.270.000

đồng B.

5.790.000

đồng. C.

3.000.000

đồng.D

6.060.000

đồng.

Câu 3. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Chohàmsố

 

f x

liêntục,khôngâmtrênđoạn



 

 

 

, thỏa mãn

 

0 3f   và

     

. cos 1 , 0;

f x f x x f x x



 



   

 

 

. Tìm giá trị nhỏ

nhất

vàgiátrịlớnnhất

củahàmsố

 

f x

trênđoạn

;

6 2

 

 

 

 

.

, 3

m M 

. B.

, 3

m M 

3, 2 2m M 

. D.

, 2 2

m M 

Câu 4. (Chuyên Lê Hồng Phong - TPHCM - 2021) Chohàmsố

 

f x

cóđạohàmcấp2liêntụctrên

đoạn

 

0;1

 thỏa mãn

   

1 0; ' 1 1f f 

 và

     

10 5 ' '' 0f x xf x x f x  

với mọi

 

0;1x 

.

Khiđótíchphân

 

f x dx



bằng



. B.



. C.



. D.



.

NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG

Chủ đề 3

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 5. (Chuyên Lam Sơn - Thanh Hóa - 2021) Chohàmsố

( )f x

cóđạohàmliêntụctrên

vàthỏa

mãn

(0) 3



và

( ) (2 ) 2 2

f x f x x x

    

,

x R 

.Tíchphân

. '( )x f x dx



bằng



. B.



. C.



. D.



.

Câu 6. (Chuyên KHTN - 2021) Cho hàm số

 

f x

 liên tục trên



 và thỏa mãn

     

xf x x f x e





  

vớimọi

.Tính

 



.

. B.

1

. C.

. D.

.

Câu 7. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Chohàmsố

( )y f x

cóđạohàmliêntụctrên

đoạn

[1;3]

thỏa mãn

(1) 2



 và

( ) ( 1) ( ) 2 ( ), [1;3]

f x x f x xf x x



    

. Giá trị của

( )f x dx



bằng

1 ln3

. B.

ln 3



. C.

ln 3



. D.

1 ln3

.

Câu 8. (Chuyên Quốc Học Huế - 2021) Cho hàm số

( )f x

có đạo hàm liên tục trên

thỏa mãn:

'( ) ( ) .cos 2021

f x f x e x

 

 và

(0) 0



 Đồ thi hàm số

( )y f x

cắt trục hoành tại bao nhiêu

điểmcóhoànhđộthuộcđoạn

 

1;1



?

1287

4043

Câu 9. (Chuyên Quang Trung - Bình Phước - 2021) Chohàmsố

 

y f x



cóđạohàmliêntụctrên



,

   

e 1, , 1 0

xf x x f



    

.Giátrị

 

dxf x x



bằng



. B.

. C.



. D.

.

Câu 10. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hàm số

( )y f x



liêntục và cóđạohàm trên

 

 

2; 2 \ 0

 ,thỏamãn

(1) 0



và

 

( )

'( ) 2 0

f x

f x x e

   

.Giátrịcủa

 

 

 

bằng

ln7

. B.

ln5

. C.

ln6

. D.

ln3

.

Câu 11. (Chuyên ĐHSP Hà Nội - 2021) Cho hàm số

 

f x

 liên tục trên



 thỏa mãn

   

 

3 3 2

3 sin 2 3 ,

      

f x f x x x x x

.Tíchphân

 





I f x x

thuộckhoảngnào?

 

3; 2 

. B.

 

2; 1 

. C.

 

1;1



. D.

 

1;2

.

Câu 12. (Chuyên ĐH Vinh - Nghệ An - 2021) Giảsử

( )f x

làhàmcóđạohàmliêntụctrên

 



và

 

( )sin ( ) , 0;

f x x x f x cosx x





   

.Biết

( ) 1, ( ) ( ln 2 3)

2 6 12

f f a b c

 



   

,với

, ,a b c

là

cácsốnguyên.Giátrịcủa

a b c 

bằng

1

. B.

. C.

. D.

11

.

Câu 13. (THPT Quế Võ 1 - Bắc Ninh - 2021) Thành phố định xây cây cầu bắc ngang con sông dài

500m

,biếtrằngngườitađịnhxây cầucó10 nhịp cầuhìnhdạngparabol,mỗinhịpcáchnhau

40m

,biết2bênđầucầuvàgiữamốinhịpnốingườitaxây1chântrụrộng

5m

.Bềdàyvàbề

rộngcủanhịpcầukhôngđồilà

20cm

(mặtcắtcủamộtnhịpcầuđượcmôphỏngnhưhìnhvẽ).

Hỏilượngbêtôngđểxâycácnhịpcầulàbaonhiêu(làmtrònđếnhàngđơnvị).

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3



50m

. B.

20m

. C.

100m

. D.

40m

.

Câu 14. (THPT Quốc Oai - Hà Nội - 2021) Chohàmsố

 

y f x

cóđồthị

 

'y f x

nhưhìnhvẽ.Giá

lớnnhấtcủahàmsố

   

3 3g x f x x 

trênđoạn

 

1;1

bằng



 

3 3f  

. B.

 

1 1f 

. C.

 

1 3f  

. D.

 

3 3f 

.

Câu 15. (THPT Quốc Oai - Hà Nội - 2021) Chohàmsố

 

y f x

cóđạohàmliêntụctrên



.Hàmsố

 

y f x





cóđồthịnhưhìnhvẽ

bêndưới.

Sốnghiệmthuộcđoạn

 

2;6

củaphươngtrình

   

0f x f

là

. B.

Câu 16. (THPT Quảng Xương 1-Thanh Hóa - 2021) Chohàmsố

( )f x

liêntụcvàcóđạohàmxácđịnh

trên

 

0;

. Biết rằng

( ) 0f x 

với mọi

 

0;x  

 thỏa mãn

   

( ) ln ( ) 1 '( ) 2 ( ) 0f x f x x f x f x   

và

ln( (2)) ln( (1)) 1f f 

. Giá trị của tích phân

( )xf x dx



nằmtrongkhoảngnàodướiđây:

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

0;6

. B.

 

6;12

. C.

 

12;18

. D.

 

18;24

.

Câu 17. (THPT Phan Đình Phùng - Quảng Bình - 2021) Chohàmsố

 

y f x

cóđạohàmliêntụctrên





thỏamãn

 

sin .cos

f x f x x x



 

  

 

 

với mọi

x 

và

 

0 0f 

.Giá trị của tíchphân

 

. dx f x x







bằng

. B.



. C.



. D.





.

Câu 18. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Chohàmsố

 

f x



liêntụctrên



vàthỏamãn

     

1 1 ;f x f x x x x     

.Tính

 

.I f x dx





 B.

. C.

. D.

.

Câu 19. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Chohàmsố

 

y f x

.Hàmsố

 

y f x





cóđồ

thịnhưhìnhvẽbên



Đặt

 

 

 

 

2;6

max ; minM f x m f x



 

.Tínhgiátrị

S M m 

?

   

0 2S f f 

. B.

   

5 6S f f 

   

5 2S f f  

. D.

   

0 2S f f  

.

Câu 20. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Chohàmsố

 

y f x

cóđạohàmliêntụctrên

 

1;3

,

biết

 

1 1f 

 và

         

. 4 2f x f x x x f x f x

 

    

 với

 

1;3x 

. Biết

 

d 2

f x x c

  



(với

, ,a b c

làcácsốnguyêndương,

làphânsốtốigiản).Khiđó,tổng

a b c 

bằng

. B.

. C.

. D.

.

Câu 21. (THPT Lê Lợi - Thanh Hóa - 2021) Biếtrằng

 

y f x

làhàmsốliêntụcvàkhác

x

vớimọi

 

0;x  

vàthỏamãn

   

1 2; 2 6.f f 

Cótíchphân

   

 

2 2

d ln ;

xf x f x

f x x b











trongđó

,a b

làcácsốnguyêndươngsaochophânsố

tốigiản.Giátrịcủabiểuthức

2 3

a b

bằng

10.

17.

34.

Câu 22. (Sở Lào Cai - 2021) Hàmsốbậcba

 

y f x

cóđồthị

 

điquađiểm

 

1;0A

;hàmsốbậc

hai

 

y g x

cóđồthị

 

điquađiểm

 

1; 4 .B 



   

1 2

,C C

cắtnhautại3điểmphânbiệtcó

hoànhđộlầnlượtlà

1;2;3

.Tínhdiệntíchhìnhphẳnggiớihạnbởihaiđồthị

   

1 2

,C C

?

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

115

. B.

. C.

. D.

112

.

Câu 23. (Sở Tuyên Quang - 2021) Chohàmsố

 

f x

có



 

 

 

 

và

 

4cos2

sin 2

f x





,



 

 

 

 

.

Khiđó

 

df x x





bằng

ln 2





. B.

ln3

. C.



. D.

ln3





.

Câu 24. (Sở Yên Bái - 2021) Chohàmsố

 

f x

cóđạohàmliêntụctrên

 

0;1

vàthỏamãn

 

f 

,

 

f x x



 

 



và

 

180

x f x x 



.Tíchphân

 

df x x



bằng



. B.

. C.

. D.



.

Câu 25. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Chohàmsố

 

f x

cóđạohàmliêntụctrênđoạn

 

0;1

thỏamãn

 

1 1f 

,

 

d 9f x x





 

 





và

 

x f x x 



.Tíchphân

 

dxf x x



bằng

. B.

. C.

. D.

.

Câu 26. (THPT Thanh Chương 1- Nghệ An - 2021) Hướngtớikỉniệm60nămthànhlậptrườngTHPT

ThanhChương1.Khối12K57thiếtkếbồnhoagồmhaiElipbằngnhaucóđộdàitrụclớnbằng

8mvàđộdàitrụcnhỏbằng4mđặtchồnglênnhausaochotrụclớncủaElipnàytrùngvớitrục

nhỏcủaElipkiavàngượclại(nhưhìnhvẽ).



Phầndiệntíchnằmtrongđườngtrònđiqua4giaođiểmcủahaiElipdùngđểtrồngcỏ,phầndiện

tíchbốncánhhoanằmgiữahìnhtrònvàElipdùngđểtrồnghoa.Biếtkinhphíđểtrồnghoalà

300.000đồng ,kinhphíđểtrồngcỏlà200.000đồng .Tổngsốtiềndùngđểtrồnghoavà

trồngcỏchobồnhoagầnvớisốnàonhấttrongcácsốsau:

A. 6.200.000đồng. B. 8.200.000đồng. C. 8.600.000đồng. D. 9.100.000đồng.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 27. (THPT Lương Thế Vinh - 2021) Cho

, ,a b c

làcácsốthựcvà

 

3 2

f x x ax bx c   

thỏamãn

   

5 2f t f t

 

  

với

làhằngsố.Giátrị

 

f x x







bằng

105



. B.

134

. C.



. D.

.

Câu 28. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hàm số

 

f x

 đồng biến, biết

 

 

0, 1;4f x x  

 và có đạo hàm liên tục trên đoạn

 

1;4

, thỏa mãn

 

1 1f 

 và

   

 

f x

f x xf x



 

 

 

vớimọi

 

1;4x 

.Khiđó

 

df x x



bằng

. B.

2ln 2

. C.

2ln 2 2

. D.

2

.

Câu 29. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Chohàmsố

 

y f x

cóđạohàmliêntụctrên

khoảng

 

0; 

thỏamãn

   

ln , 0xf x f x x x x



   

và

 

f 

.Tính

 



2ln 2 1

. B.

4ln 2 1

. C.

2ln 2

 D.

4ln2



Câu 30. (THPT Ba Đình - Thanh Hóa - 2021) Chohàmsố

 

f x

nhậngiátrịdương,cóđạohàmliêntục

trên

 

0;2

. Biết

 

0 1f 

 và

   

2 4

x x

f x f x e



 

 với mọi

 

0;2x 

. Tính tích phân

 

3 2

3x x f x

I dx

f x









.

I  

. B.

I  

. C.

I  

. D.

I  

.

Câu 31. (Trung Tâm Thanh Tường - 2021) Cho

   

,f x g x

lầnlượtlàcáchàmđathứcbậcbavàbậc

nhấtcóđồthịnhưhìnhvẽ.



Biếtdiệntíchhình

(đượctômàu)bằng

250

.Tính

 

f x dx



.

. B.

. C.

. D.

.

Câu 32. (THPT Trần Phú - Đà Nẵng - 2021) Giảsử

 

ln3 ln 2

ln 1 d

3 9

a b c

x x x



  



với

, ,a b c N .

Giátrịcủabiểuthức

b c a 

bằng

2

. B.

. C.

4

. D.

.

Câu 33. Chohàmsố

 

e khi 0

2 3 khi 0

m x

f x

x x x



 







 





liêntụctrên



.Tíchphân

 

dI f x x







bằng

e 2 3 22I   

. B.

e 2 3

I   

. C.

2 3

I e  

. D.

e 2 3

I   

.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Câu 34. Chohàmsốbậcba

 

y f x

cóđồthị

 

làđườngcongtronghìnhbên.Biếthàmsố

 

f x

đạt

cựctrịtạihaiđiểm

1 2

,x x thỏamãn

2 1

2x x  và

1 2

x x

 





 

 

 

.Gọi

làđườngthẳngđiqua

haiđiểmcựctrịcủađồthị

 

.Diệntíchhìnhphẳnggiớihạnbởi

 

và

(phầnđượctôđậm

tronghình)bằng



. B.

. C.

. D.

.

Câu 35. Chohàmsố

 

4 1 , 5

2 6 , 5

x x x

f x

x x



  





 



.Tíchphân

 

ln2

3 1 . d

x x

f e e x



bằng

. B.

. C.

. D.

.

Câu 36. Chohàmsốbậcba

 

3 2

f x ax bx cx d   

vàđườngthẳng

 

:d g x mx n 

cóđồthịnhưhình

vẽ.Gọi

1 2 3

, ,S S S lầnlượtlàdiệntíchcủacácphầngiớihạnnhưhìnhbên.Nếu

4S  thìtỷsố



bằng.



. B.

. C.

. D.

.

Câu 37. Cho hàm số

 

f x

 liên tục trên



 thỏa mãn

 

, 0

x m x

f x

e x

 











 (m là hằng số). Biết

 

f x x a



 



trongđó

,a b

làcácsốhữutỉ.Tính

a b

.

. B.

. C.

. D.

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 38. Chohàmsố

4 2

3y x x m   cóđồthị

 

,với

làthamsốthực.Giảsử

 

cắttrục



tạibốnđiểmphânbiệtnhưhìnhvẽ



Gọi

S ,

S  là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của

 để

1 3 2

S S S  là

. B.



. C.

. D.



.

Câu 39. Chohàmsố

 

1y f x 

,

 

y g x x 

.Giátrị

   

 

min ; dI f x g x x







. B.

. C.

. D.

.

Câu 40. Cho parabol

 

: 4P y x  

 cắt trục hoành tại hai điểm

,

 và đường thẳng

:d y a



 

0 4a 

.Xétparabol

 

điqua

,

vàcóđỉnhthuộcđườngthẳng

y a

.Gọi

S làdiện

tíchhìnhphẳnggiớihạnbởi

 

và

.

S làdiệntíchhìnhphẳnggiớihạnbởi

 

vàtrục

hoành.Biết

1 2

S S (thamkhảohìnhvẽbên).



Tính

3 2

8 48T a a a  

.

99T 

. B.

64T 

. C.

32T 

. D.

72T 

.

Câu 41. Chohàmsố

 

2cos 3 0

x m x

y f x

x x



 



 



 





liêntụctrên



.Giátrị

2cos 1 sin dI f x x x



 





. B.

. C.

. D.



.

Câu 42. Chohàmsốbậcbốn

 

y f x

cóđồthị

 

nhưhìnhvẽbên.Biếthàmsố

 

y f x

đạtcựctrị

tại các điểm

1 2 3

, ,x x x  thỏa mãn

3 1

2x x  ,

     

1 3 2

f x f x f x  

 và

 

 nhận đường

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

thẳng

:d x x làmtrụcđốixứng.Gọi

1 2 3 4

, , ,S S S S làdiệntíchcủacácmiềnhìnhphẳngđược

đánhdấunhưhìnhbên.Tỉsố

1 2

3 4

S S



gầnkếtquảnàonhất

0,60

. B.

0,55

. C.

0,65

. D.

0,70.

Câu 43. Chohàmsố

 

3 2

2 4 khi 4

khi 4

x x

f x

x x x x

 









  





.Tíchphân

 

2sin 3 sin 2 df x x x







bằng

. B.

. C.

341

. D.

341

.

Câu 44. Chohàmsốbậcba

 

y f x

cóđồthịlàđườngcong

 

tronghìnhbên.Hàmsố

 

f x

đạtcực

trị tại hai điểm

1 2

,x x  thỏa

   

1 2

0f x f x 

. Gọi

,A B

 là hai điểm cực trị của đồ thị

 

, ,M N K

làgiaođiểmcủa

 

vớitrụchoành;

làdiệntíchcủahìnhphẳngđượcgạch

tronghình,

S làdiệntíchtamgiác

NBK

.Biếttứgiác

MAKB

nộitiếpđườngtròn,khiđótỉsố

bằng

2 6

. B.

. C.

5 3

. D.

3 3

.

Câu 45. Chohàmsố

 

2 khi 0

3 2 khi 0

x x

f x

x x x



 







  





.Tíchphân

 

3 4cos sin df x x x







bằng

. B.

. C.

. D.

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 46. Chohàmsốbậcbốn

 

y f x

cóđồthị

 

nhưhìnhvẽbên.Biếthàmsố

 

y f x

đạtcựctrị

tại các điểm

1 2 3

, ,x x x

 thỏa mãn

3 1

2x x 

,

     

1 3 2

f x f x f x  

 và

 

 nhận đường

thẳng

:d x x

làmtrụcđốixứng.Gọi

1 2 3 4

, , ,S S S S

làdiệntíchcủacácmiềnhìnhphẳngđược

đánhdấunhưhìnhbên.Tỉsố

1 2

3 4

S S



gầnkếtquảnàonhất

0,60

. B.

0,55

. C.

0,65

. D.

0,70.

Câu 47. Cho hàm số

 

3 2

khi 2

8 10khi 2

x ax b x

f x

x x x x



  







   





 Biết hàm số có đạo hàm tại điểm

2.x 

 Tính

 

I f x dx





. B.

. C.

2

. D.

.

Câu 48. Cho hàm số

ax b

cx d







 có đồ thị

 

. Gọi giao điểm của hai đường tiệm cận là

. Điểm

 

0 0 0

;M x y

diđộngtrên

 

,tiếptuyếntạiđócắthaitiệmcậnlầnlượttại

,A B

và

IAB





.

Tìmgiátrị

saocho

1 2

IAB

S S







(với

1 2

,S S

là2hìnhphẳngminhhọabêndưới)

. B.

. C.

169

. D.

189

.

Câu 49. Chohàmsố

 

2 1 2

5 2

x x khi x

f x

x khi x



  





 



.Tính

 

. ln 1 d .

I f x x



 

 

 







 

2;3

. B.

 

3; 2

. C.

 

2; 1

. D.

 

1;2

.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Câu 50. Chohàmsốbậcba

 

y f x

cóđồthịlàđườngcongởhìnhbêndưới.Gọi

1 2

,x x lầnlượtlàhai

điểmcựctrịthỏamãn

2 1

2x x  và

   

1 2

3 0.f x f x 

Đườngthẳngsongsongvớitrục

và

quađiểmcựctiểucắtđồthịhàmsốtạiđiểmthứhaicóhoànhđộ

x và

1x x  .Tínhtỉsố



(

S và

S lầnlượtlàdiệntíchhaihìnhphẳngđượcgạchởhìnhbêndưới).

. B.

. C.

. D.



Câu 51. Chohàmsố

 

2 2   0

+4 2   0

x khi x

f x

x x khi x

 







 



.Tíchphân

 

sin 2 . cos dI x f x x







bằng

I 

. B.

I  

. C.

I  

. D.

I 

.

Câu 52. Chohàmsốbậcbốntrùngphương

 

y f x

cóđồthịlàđườngcongtronghìnhbên.Biếthàmsố

 

f x

đạtcựctrịtạibađiểm

1 2 3 1 2 3

, , ( )x x x x x x  thỏamãn

1 3

4x x  .Gọi

S và

S làdiện

tíchcủahaihìnhphẳngđượcgạchtronghình.Tỉsố

bằng



 B.

 C.

 D.



BẢNG ĐÁP ÁN

1.C



3.D

4.D

5.A

6.B

7.C

8.C

9.A

10.A

11.C

12.A

13.D

14.A

15.A

16.D

17.C

18.B

19.C

20.B

21.C

22.C

23.B

24.C

25.C

26.C

27.A

28.B

29.D

30.C

31.D

32.B

33.D

34.D

35.B

36.B

37.A

38.A

39.C

40.B

41.A

42.A

43.D

44.D

45.A

46.A

47.D

48.B

49.A

50.A

51.A

52.B



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1



MỨC ĐỘ VẬN DỤNG CAO

Câu 1. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Giảsửhàmsố

cóđạohàmđến

cấphaitrên



thỏamãn

 

2 2f





và

   

2 2f x x f x x



  

vớimọi

x

.Giátrịtíchphân

 

dxf x x





bằng:

. B.

. C.

. D.

.

Lời giải

Chọn C

Tacó:

   

2 2f x x f x x



  



 

2 0f 



Lạicó:

   

2 2 2

2 2

0 0 0

2 d d 2 d 4

f x x x f x x x x x



    

  



Xét

 

2 dI f x x 





Đặt

2 x t 



d dx t 



Với

0x 



2t 



2x 



0t 





     

0 2 2

2 0 0

d d dI f t t f t t f x x   

  



Đặt

 

d d

u f x

v x

















 

d du f x x

v x





















 

       

2 2 2

0 0 0

d 2 d dI xf x xf x x f xf x x xf x x

  

     

  



Xét

 

dI x f x x









Đặt

 

d d

u x

v f x x



















 

d 2 du x x

v f x





















 

       

2 2 2

0 0 0

2 d 4 2 2 d 8 2 dI x f x xf x x f xf x x xf x x

    

     

  



NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG

Chủ đề 3

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vậy

   

2 2

0 0

d 8 2 d 4xf x x xf x x

 

   

 



 

xf x x







.

Câu 2. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Sântrườngcómộtbồnhoahìnhtròn

tâm

.Mộtnhómhọcsinhlớp12đượcgiaothiếtkếbồnhoa,nhómnàyđịnhbồnhoathànhbốn

phầnbởi2đườngparabolcócùngđỉnh

vàđốixứngvớinhauquatâm

(nhưhìnhvẽ).



Haiđườngparabolcắtđườngtròntại4điểm

, , ,A B C D

tạothànhmộthìnhvuôngcócạnhbằng

.Phầndiệntích

1 2

,S S dùngđểtrồnghoa,phầndiệntích

3 4

,S S dùngđểtrồngcỏ.Biếtkinh

phítrồnghoalà

150.000

đồng/

,kinhphítrồngcỏlà

100.000

đồng/

.Hỏinhàtrườngcần

baonhiêutiềnđểtrồngbồnhoađó?(sốtiềnlàmtrònđếnhàngchụcnghìn)

3.270.000

đồng B.

5.790.000

đồng. C.

3.000.000

đồng.D

6.060.000

đồng.

Lời giải

Chọn A

Tacó:vì

ABCD

làhìnhvuôngcạnh

nên

2 4 2; 2 2BD BC OB  

và

( 2;2), (2;2)A B



Phươngtrìnhđườngtròntâm

cóbánkính

2 2OB 

là

2 2 2

( ) : 8 8C x y y x     

Parabolđiquahaiđiểm

( 2;2), (2;2)A B

vàđỉnhngaygốctọađộnênsuyra

( ) :

P y  

Từđồthịtacóđược

S làdiệntíchgiớihạnbởihaiđồthị

8y x  và

( ) :

P y  cùngvới

haiđườngthẳng

2; 2x x  



Từđósuyra

2 2

8 8

2 3

S x dx x dx

 

 

     

 

 

 

;Đặt

2 2sin 2 2 cosx t dx tdt  



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Suyra

4 4 4

2 2

4 4 4

8 8 1 cos2 8 4

8 8sin .2 2.cos . 8cos 8 2

3 3 2 3 3

S t t dt tdt dt

  



  



 

        

 

 

  



Mặtkhác:

1 2 3 4

;

S S S S 

nênsuyra

 

1 2 1

3 4 ( ) 1 2

4 8

2 2 2 4 ( )

3 3

4 8

8 2 2 4 ( )

3 3

S S S m

S S S S S m

 

  



 

     

 



  



 



        

 



 





Vậytổngsốtiềnđểtrồngbồnhoalà:

8 8

4 .150000 4 .100000 3274926

3 3

 

   

   

   

   

đồng.

Câu 3. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Chohàmsố

 

f x

liêntục,khôngâmtrênđoạn



 

 

 

, thỏa mãn

 

0 3

f 

 và

     

. cos 1 , 0;

f x f x x f x x



 



   

 

 

. Tìm giá trị nhỏ

nhất

vàgiátrịlớnnhất

củahàmsố

 

f x

trênđoạn

;

6 2

 

 

 

 

.

, 3

m M 

. B.

, 3

m M

 

3, 2 2

m M 

. D.

, 2 2

m M 

Lời giải

Chọn D

     

   

 

   

 

. cos 1 cos

d cos d sin 1

f x f x

f x f x x f x x

f x

f x f x

x x x x C

f x



   





   



 



Đặt

       

2 2 2

1 1 d . dt f x t f x t t f x f x x



       .

Suyra

   

 

   

2 2

d d 1 2

f x f x

t t

x t t C f x C

f x



      



  



Từ

 

và

 

suyra

 

1 sin

f x x C  

.Thay



vàotacó:

1 3 2

C C

   



Hay

 

1 sin 2f x x  

.

   

 

2 2

sin 2 1 sin 4sin 3

sin 4sin 3

f x x x x

f x x x

      

   



Đặt

sint x

.Với

; ;1

6 2 2

x t

 

   

  

   

   

.

Tađixéthàmsố

 

4 3, ;1

g t t t t

 

   

 

 

.

 

2 1

0, ;1

4 3

g t t

t t



 



   

 

 

 

dođó

 

g t

đồngbiếntrên

 

 

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

   

     

;1 ;

2 6 2

;1 ;

2 6 2

1 21

min min

2 2

max 1 2 2 max

g t g f x m

g t g f x M

 

   

   

   

   

   

   

 

   

 

 

   



Câu 4. (Chuyên Lê Hồng Phong - TPHCM - 2021) Chohàmsố

 

f x

cóđạohàmcấp2liêntụctrên

đoạn

 

0;1

 thỏa mãn

   

1 0; ' 1 1

f f

 

 và

     

10 5 ' '' 0

f x xf x x f x

  

với mọi

 

0;1

x

.

Khiđótíchphân

 

f x dx



bằng



. B.



. C.



. D.



.

Lời giải

Chọn D

Tacó:

     

10 5 ' '' 0

f x xf x x f x

  

vớimọi

 

0;1

x

.

     

1 1 1

0 0 0

10 5 ' '' 0

f x dx xf x dx x f x dx

   

  



Đặt

 

I f x dx





,theophươngpháptíchphântừngphần,tađược:

     

       

 

1 1

0 0

1 1

2 2 1

0 0

' |

'' ' | 2 ' 1 2 1 2

10 5 1 2 0

xf x dx xf x f x dx I

x f x dx x f x xf x dx I I

I I I I



   







      





        

 



Vậy

 

f x dx

 



.

Câu 5. (Chuyên Lam Sơn - Thanh Hóa - 2021) Chohàmsố

( )f x

cóđạohàmliêntụctrên

vàthỏa

mãn

(0) 3



và

( ) (2 ) 2 2

f x f x x x

    

,

x R 

.Tíchphân

. '( )x f x dx



bằng



. B.



. C.



. D.



.

Lời giải

Chọn A

Tacó:

. '( )I x f x dx





,tasửdụngphươngpháptừngphần

Đặt

2 2

0 0

. '( ) 2 (2) ( )

'( ) ( )

u x du dx

I x f x dx f f x dx

dv f x dx v f x

 

 

    

 

 

 

 



( ) (2 ) 2 2

f x f x x x

    

thế



vàotacó:

(0) (2) 2 (2) 1

f f f

    

(1)

Từđótatíchphân2vếtừ0đến2

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

 

2 2 2

0 0 0

( ) (2 ) 2 2

f x dx f x dx x x dx

      

  

.

Mặtkháctalạicó:

2 2

0 0

( ) (2 )f x dx f x dx

 

 



Nênsuyra

2 2 2 2

0 0 0 0

8 4

( ) (2 ) 2 ( ) ( )

3 3

f x dx f x dx f x dx f x dx

     

   

(2)

Từ(1)và(2)suyra

2 2

0 0

4 10

. '( ) 2 (2) ( ) 2

3 3

I x f x dx f f x dx



      

 



Câu 6. (Chuyên KHTN - 2021) Cho hàm số

 

f x

 liên tục trên



 và thỏa mãn

     

xf x x f x e





  

vớimọi

.Tính

 



.

. B.

1

. C.

. D.

.

Lời giải

Chọn B

Tacó:

           

x x

xf x x f x e xf x f x xf x e

 

 

      



     

1 1

x x

xe f x x e f x



   



 

x x

xe f x xe f x



  



 

xe f x



 



 

xe f x dx x C   





 



Với





+)Thayvàobiểuthứcbanđầutacó:

       

0. 0 0 1 0 1 0 1

f f e f





     

.

+)Thayvào

 

,tacó:



.

Khiđó:

   

khi 0

1 khi 0

e x

xe f x x f x







  









Suyra:

 

   

0 0 0

1 1

0 lim lim lim 1

x x

x x x

f x f

e e

x x x

 

  



 



     



.

Câu 7. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Chohàmsố

( )y f x

cóđạohàmliêntụctrên

đoạn

[1;3]

thỏa mãn

(1) 2



 và

( ) ( 1) ( ) 2 ( ), [1;3]

f x x f x xf x x



    

. Giá trị của

( )f x dx



bằng

1 ln3

. B.

ln 3



. C.

ln 3



. D.

1 ln3

.

Lời giải

Chọn C

Xét

( ) 0

f x



:

( ) ( 1) ( ) 2 ( )f x x f x xf x



  

⇔

( ) ( 1) ( )

( )

f x x f x

f x



 



⇔

 

f x



 





 

 



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

⇒

 

2 d

x x

f x







⇔

 

x C

f x



 



(1) 2



⇒



⇒

 

f x





⇔

 

f x







Xét:

( ) 0

f x



⇒

 

thỏamãnđiềukiệnbàitoán.Vậy:

 

f x









   

3 3 3

2 2

1 1 1

1 1 1 1 1 2

d d + d ln ln3 ln1 1 ln 3

3 3

f x x x x x

x x x x



     

         

     

     

  



Câu 8. (Chuyên Quốc Học Huế - 2021) Cho hàm số

( )f x

có đạo hàm liên tục trên

thỏa mãn:

'( ) ( ) .cos 2021

f x f x e x

 

 và

(0) 0



 Đồ thi hàm số

( )y f x

cắt trục hoành tại bao nhiêu

điểmcóhoànhđộthuộcđoạn

 

1;1



?

1287

4043

Lời giải

Chọn C

Tacóphươngtrìnhtrêntươngđươngvới

 

'( ) ( ) .cos 2021 '( ) ( ) .cos 2021

'( ) ( ) cos2021

x x

f x f x e x f x f x e x

e f x e f x x

 

     

   



Đếnđâytanguyênhàmhaivếthuđược:

 

sin 2021

( ) cos2021 ( ) cos2021

2021

x x

e f x x e f x xdx C

 



     





Mà

(0) 0



nên



suyra

sin 2021 .sin 2021

( ) ( )

2021 2021

x e x

e f x f x



  



Phươngtrìnhhoànhđộgiaođiểmcủađồthịhàmsố

( )y f x

vàtrụchoànhlà

 

.sin 2021

( ) 0 0 sin 2021 0 2021 , ,

2021 2021

e x k

f x x x k k Z x k Z



          



Vì

 

1;1

x 

nên

2021 2021

1 1

2021



 



     



Màdo

k Z

nênsuyra

 

643; 642;...;643

k   

nhưvậytakếtluậnđồthihàmsố

( )y f x

cắt

trụchoànhtại1287điểmcóhoànhđộthuộcđoạn

 

1;1





Câu 9. (Chuyên Quang Trung - Bình Phước - 2021) Chohàmsố

 

y f x



cóđạohàmliêntụctrên



,

   

e 1, , 1 0

xf x x f



    

.Giátrị

 

dxf x x



bằng



. B.

. C.



. D.

.

Lời giải

Chọn A

Tính

 

dxf x x



:

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Đặt

 

d d

u f x x

u f x

v x x







 





 











         

 

1 1 1

2 2

0 0 0

1 1 1

d . . d 1 0 .0 1 d

2 2 2 2 2

x x

xf x x f x f x x f f x e x



     

  

.

 

1 1

e 1 d e e

2 2 2

x x x

 

      

 

 





1 1 1

e e e

2 2 4

 

 

      

 

 

 

 

.

Câu 10. (Chuyên Hạ Long - Quảng Ninh - 2021) Chohàm số

( )y f x



liêntụcvà cóđạohàm trên

 

 

2; 2 \ 0



,thỏamãn

(1) 0



và

 

( )

'( ) 2 0

f x

f x x e

   

.Giátrịcủa

 

 

 

bằng

ln7

. B.

ln5

. C.

ln6

. D.

ln3

.

Lời giải

Chọn A

 

   

( ) ( ) ( )

( )

( ) ( )

( )

( ) 2

2 2 ( )

( ) ( )

(1)

'( ) 0 '( ) 2 0

'( )

'( ) 1 0

'( ) 1

,(1)

1 1

Trong (1) cho x=1

f x f x f x

f x

f x f x

f x

f x f x

f x x f x e xe e x

f x e

f x e x e x

d e

f x e x

dx xdx xdx C

e e

C C

       



     



 



 

      



 

    



   

( )

,(2)

1 1 1 1

ln7.

2 8 2

Suy ra

Trong (2) cho x=

f x

 

 

 





 

   

 

 





Câu 11. (Chuyên ĐHSP Hà Nội - 2021) Cho hàm số

 

f x

 liên tục trên



 thỏa mãn

   

 

3 3 2

3 sin 2 3 ,

     

f x f x x x x x

.Tíchphân

 





I f x x

thuộckhoảngnào?

 

3; 2 

. B.

 

2; 1 

. C.

 

1;1



. D.

 

1;2

.

Lời giải

Chọn C

Cách 1. Từgiảthiếttacó

         

3 2

1 3 1 sin 2 1 3 1 1

 

        

 

f x f x x x x



   

 

3 3 2

1 3 1 sin 2 3

       f x f x x x x

 

3 2

sin 2 3

   x x x



       

3 3

1 3 1 3

 

      

 

f x f x f x f x



       

3 3

1 3 1 0

 

      

 

 

f x f x f x f x



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

           

2 2

1 . 1 1 . 3 0

 

        

 

 

f x f x f x f x f x f x



   

1   

f x f x

.

Khiđó

 





I f x x

 

1 d

  



f x x



 



Đặt

1 d d    t x t x

.Đổicận

0 1

1 0

  





  



x t



       

1 0 1 1

0 1 0 0

1 d d d d

      

   

f x x f t t f t t f x x I



 



Từ

 

và

 

suyra

 I I

0 

.Vậy

 

1;1

 I

.

Cách 2.Do

 

3 2

1 sin 2 3 1    

x x x

nên

   

1 3 1   

f x f x

   

4 3 4    

f x f x

.

+Từ

   

3 4  

f x f x

   

3 4 0   

f x f x

     

1 4 0

 

    

 

 

f x f x f x



 

1 0  

f x

 

1  

f x

.

+Từ

   

3 4 

f x f x

   

3 4 0   

f x f x

     

1 4 0

 

    

 

 

f x f x f x



 

1 0  

f x

 

1 

f x

.

Suyra

 

1 1  

f x

   

1 1 1

0 0 0

1 d d 1d

   

  

x f x x x

 

1 d 1   



f x x

.Vậy

 

1;1

 I

.

Câu 12. (Chuyên ĐH Vinh - Nghệ An - 2021) Giảsử

( )f x

làhàmcóđạohàmliêntụctrên

 



và

 

( )sin ( ) , 0;

f x x x f x cosx x





   

.Biết

( ) 1, ( ) ( ln 2 3)

2 6 12

f f a b c

 



   

,với

, ,a b c

là

cácsốnguyên.Giátrịcủa

a b c 

bằng

1

. B.

. C.

. D.

11

.

Lời giải

Chọn A

Tacó:

2 2 2

( )sin ( ) ( )sin ( )

( )sin ( ) ( )

sin sin sin sin

f x x x f x cosx f x x f x cosx x

f x x f x cosx x f x x

x x x x

 

    





 

   

 

 



( )

cot cot cot ln sin

sin sin

f x x

dx x x xdx x x x C

x x

        

 

.

Hay

( )

cot ln sin

sin

f x

x x x C

   

.

1 cot ln sin 1

2 2 2 2

sin

f C C

   



 

       

 

 

.

( )

cot ln sin 1

sin

f x

x x x

    

.

Dođó

 

( )

cot ln sin 1 ( ) 6 6ln 2 3

6 6 6 6 12

sin



   



        

.

6, 6, 1

a b c

     

.

a b c

   

.



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 13. (THPT Quế Võ 1 - Bắc Ninh - 2021) Thành phố định xây cây cầu bắc ngang con sông dài

500m

,biếtrằngngườitađịnhxâycầucó10nhịpcầuhìnhdạngparabol,mỗinhịpcáchnhau

40m

,biết2bênđầucầuvàgiữamốinhịpnốingườitaxây1chântrụrộng

5m

.Bềdàyvàbề

rộngcủanhịpcầukhôngđồilà

20cm

(mặtcắtcủamộtnhịpcầuđượcmôphỏngnhưhìnhvẽ).

Hỏilượngbêtôngđểxâycácnhịpcầulàbaonhiêu(làmtrònđếnhàngđơnvị).



50m

. B.

20m

. C.

100m

. D.

40m

.

Lời giải



Chọn D

Chọnhệtrụctọađộnhưhìnhvẽvớigốc

O(0;0)

làchâncầu(điểmtiếpxúcParaboltrên),

đỉnh

 

25;2I

,điểm

 

50;0A

(điểmtiếpxúcParaboltrênvớichânđế).

GọiParaboltrêncóphươngtrình

 

1 1

:P y ax bx 

(do(P)điqua

).

Phươngtrìnhparaboldưới

 

2 2

20 1

100 5

P y ax bx ax bx     

.

Tacó

 

điqua

 

25;2I

và

 

50;0A



 

2 2

1 1 2

2 4 2 4 1

625 25 625 25 5

P y x x y x x        



Khiđódiệntíchmỗinhịpcầulà

2S S với

S làphầngiớihạnbởi

1 2

;y y trongkhoảng

(0;25)



0,2 25

2 2

0 0,2

2 4 1

2 9,9

625 25 5

S x x dx dx m

 

    

  

 

 

.

Vìbềdàynhịpcầukhôngđổinêncoithểtíchlàtíchdiệntíchvàbềdày

.0,2 9,9.0,2 1,98V S m    sốlượngbêtôngcầnchomỗinhipcầu

2m

.

Vậy10nhịpcầu2bêncần

40m

bêtông.

Câu 14. (THPT Quốc Oai - Hà Nội - 2021) Chohàmsố

 

y f x

cóđồthị

 

'y f x

nhưhìnhvẽ.Giá

lớnnhấtcủahàmsố

   

3 3g x f x x 

trênđoạn

 

1;1

bằng

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/



 

3 3f  

. B.

 

1 1f 

. C.

 

1 3f  

. D.

 

3 3f 

.

Lời giải

Chọn A.

         

' 3 ' 3 3 ' 0 ' 3 1 1g x f x g x f x     



Sốnghiệmcủa

 

làsốgiaođiểmcủađồthịhàmsố

 

' 3y f x

và

1y 



 

3 0

' 3 1

3 1

f x











  









Dựavàođồthịtacóbảngbiếnthiên





  

1 3

   



 

g x



 - 





  0 



 



 

g x

 

 

3 3f  

    

 

1 1f 



Dựavàođồthịtacó

         

     

1 0

' ' 0 1 0

1 3 3 1 1

g x dx g x dx g g g g

g g f g



 

       

 

 

 

       

 

 

 



Giátrịlớnnhấtcủa

 

y g x

trên

 

1;1

là

 

3 3f  

.

Câu 15. (THPT Quốc Oai - Hà Nội - 2021) Chohàmsố

 

y f x

cóđạohàmliêntụctrên



.Hàmsố

 

y f x





cóđồthịnhưhìnhvẽ

bêndưới.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Sốnghiệmthuộcđoạn

 

2;6

củaphươngtrình

   

0f x f

là

. B.

Lời giải

Chọn A

Xét

 

0 2

f x x













  















Tacóbảngbiếnthiêntrênđoạn

 

2;6 :



Gọi làdiệntíchhìnhphẳnggiớihạnbởi

 

; 0; 0; 2.y f x y x x



   



Gọi

S làdiệntíchhìnhphẳnggiớihạnbởi

 

; 0; 2; 5y f x y x x



   

.

Gọi làdiệntíchhìnhphẳnggiớihạnbởi

 

y f x





;

0; 5; 6y x x  

.

Khiđó

     

0 2S f x dx f f



  





     

5 2S f x dx f f



  





     

5 6S f x dx f f



  





Từđồthịtathấy

           

2 1

5 2 0 2 5 0S S f f f f f f      



               

1 3 2

0 2 5 6 5 2 6 0S S S f f f f f f f f         

.

Khiđótacóbảngbiếnthiêntrênđoạn

 

2;6

nhưsau:

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/



Vậyphươngtrình có2nghiệmthuộcđoạn

 

2;6

.

Câu 16. (THPT Quảng Xương 1-Thanh Hóa - 2021) Chohàmsố

( )f x

liêntụcvàcóđạohàmxácđịnh

trên

 

0;

. Biết rằng

( ) 0f x 

với mọi

 

0;x  

 thỏa mãn

   

( ) ln ( ) 1 '( ) 2 ( ) 0f x f x x f x f x   

và

ln( (2)) ln( (1)) 1f f 

. Giá trị của tích phân

( )xf x dx



nằmtrongkhoảngnàodướiđây:

 

0;6

. B.

 

6;12

. C.

 

12;18

. D.

 

18;24

.

Lời giải

Chọn D

Tacó:

   

( ) ln ( ) 1 '( ) 2 ( ) 0f x f x x f x f x   



Do

( ) 0f x 

vớimọi

 

0;x  

nêntachia2vềphươngtrìnhđócho

( )f x



'( ) '( )

ln ( ) 1 . 2 0 ln ( ) . 2 1

( ) ( )

f x f x

f x x x f x x x

f x f x

        



 

ln ( ) 2 1x f x x



  

.Đếnđâytanguyênhàm2vếthìphươngtrìnhtrởthành

ln ( )x f x x x C    (*)

Thế

1x 

vàotathuđược

ln (1) 2f C 



Thế

2x 

vàotathuđược

2ln (2) 6f C 



Lấy2phươngtrìnhtrêntrừnhautathudược:

2ln (2) ln (1) 4f f 



Mảđềcho

ln( (2)) ln( (1)) 1f f 

nêntadễdànggiảihệphươngtrìnhrađượcnghiệmlà:

ln (2) 3 (2)

ln (1) 2

(1)

f f e

f e



 







 







.Thếvàophươngtrình(*)suyrađược

0C 

nêntacóđược

2 1

ln ( ) ln ( ) 1 ( )

x f x x x f x x f x e



       



Nhưvậy

 

2 2 3

1 3

1 1 2

( ) ( 1) 20,085 18;24

x x

xf x dx xe dx x e dx e



     

  



Câu 17. (THPT Phan Đình Phùng - Quảng Bình - 2021) Chohàmsố

 

y f x

cóđạohàmliêntụctrên





thỏamãn

 

sin .cos

f x f x x x



 

  

 

 

với mọi

x

và

 

0 0f 

.Giá trị của tíchphân

 

. dx f x x







bằng

   

0f x f

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

. B.



. C.



. D.





.

Lời giải

Chọn C

Thay





vàođẳngthức

 

sin .cos

f x f x x x



 

  

 

 

 

0 0 0

2 2

f f f

 

   

    

   

   

.

Xét

 

. dI x f x x











Đặt

   

u x du dx

dv f x dx v f x

 

 



 



 

 



     

2 2

0 0

I x f x f x dx f x dx

 



    

 

 



Lạicó:

 

2 2 2

0 0 0

sin .cos

f x dx f x dx x x dx

  



 

  

 

 

  



 

2 2

0 0

2 sin 2

f x dx x dx

 

 

 

   

2 2

0 0

1 1

2 4

f x dx f x dx

 

   

 

.

Vậy

 

.

Câu 18. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Chohàmsố

 

f x



liêntụctrên



vàthỏamãn

     

1 1 ;f x f x x x x

     

.Tính

 

.I f x dx







 B.

. C.

. D.

.

Lời giải

Chọn B

Đặt

1 .    t x dt dx



Đổicận:







Khiđótacó:

           

1 1 1 1 1

0 0 0 0 0

1 1 2. .

       

 

    

f x dx f t dt f x dx f x f x dx f x dx



     

 

1 1

0 0

5 4 3

4 3 2

1 1 d

2 2

5 2 3 30

     

 

 

       

 

 

 

 



f x f x dx x x x

x x x

x x x dx

f x dx



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vậy

 





f x dx



Câu 19. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Chohàmsố

 

y f x

.Hàmsố

 

y f x





cóđồ

thịnhưhìnhvẽbên



Đặt

 

 

 

 

2;6

max ; minM f x m f x



 

.Tínhgiátrị

S M m 

?

   

0 2S f f 

. B.

   

5 6S f f 

   

5 2S f f  

. D.

   

0 2S f f  

.

Lời giải

Chọn C

TacóBBT



Gọi

làdiệntíchhìnhphẳnggiớihạn

 

gồmcácđường:

 

y f x





;

0y 

;

2; 0x x  

.

Gọi

làdiệntíchhìnhphẳnggiớihạn

 

gồmcácđường:

 

y f x





;

0y 

;

0; 2x x 

.

Gọi

làdiệntíchhìnhphẳnggiớihạn

 

gồmcácđường:

 

y f x





;

0y 

;

2; 5x x 

.

Gọi

làdiệntíchhìnhphẳnggiớihạn

 

gồmcácđường:

 

y f x





;

0y 

;

5; 6x x 

.

Tacó:

               

0 2

1 2

2 0

0 2 0 2 2 2S S f x dx f x dx f f f f f f



 

          

 

.

               

2 5

2 3

0 2

0 2 5 2 0 5S S f x dx f x dx f f f f f f

 

         

 



               

5 6

3 4

2 5

5 2 5 6 2 6S S f x dx f x dx f f f f f f

 

         

 



Suyra:

 

   

 

   

2;6

max 5

5 2

min 2

M f x f

T M m f f

m f x f



 



     



  





.

Câu 20. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Chohàmsố

 

y f x

cóđạohàmliêntụctrên

 

1;3

,

biết

 

1 1f 

 và

         

. 4 2f x f x x x f x f x

 

    

 với

 

1;3x 

. Biết

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

 

d 2

f x x c

  



(với

, ,a b c

làcácsốnguyêndương,

làphânsốtốigiản).Khiđó,tổng

a b c 

bằng

. B.

. C.

. D.

.

Lời giải

Chọn B

Tacó:

         

. 4 2

f x f x x x f x f x

 

    



           

d 4 d 2 df x f x x x x x f x f x x

 

     

 

 

  



 

   

4 2

2 2

f x

x x f x C     

.

Theobài,

 

1 1

1 1 4 1 2

2 2

f C C

         

.

Khiđó,

 

         

4 2 2 2 4 2 2

2 2

f x

x x f x f x x x f x x x            

 

 



 

3 3

1 1

4 4

d 2 2 d 2 4 3

3 2 3

f x x x x x x x

 

         

 

 

 

.

Dođó,

4, 3, 12

a b c

  

.

Vậy

4 3 12 19

a b c

     

.

Câu 21. (THPT Lê Lợi - Thanh Hóa - 2021) Biếtrằng

 

y f x



làhàmsốliêntụcvàkhác

x

vớimọi

 

0;x

 

vàthỏamãn

   

1 2; 2 6.

f f

 

Cótíchphân

   

 

2 2

d ln ;

xf x f x

f x x b











trongđó

,a b

làcácsốnguyêndươngsaochophânsố

tốigiản.Giátrịcủabiểuthức

2 3

a b

bằng

10.

17.

34.

Lời giải

Chọn C

Tacó

   

 

2 2

1 1

d d ln

f x

xf x f x f x

f x

f x x x

f x





  

 

 



 

 





 

 

 



1 1 3

ln ln 3; 2

2 2 2

a b

    



Khiđó

2 3

17.

a b

 



Câu 22. (Sở Lào Cai - 2021) Hàmsốbậcba

 

y f x



cóđồthị

 

điquađiểm

 

1;0

;hàmsốbậc

hai

 

y g x



cóđồthị

 

điquađiểm

 

1; 4 .





   

1 2

C C

cắtnhautại3điểmphânbiệtcó

hoànhđộlầnlượtlà

1;2;3

.Tínhdiệntíchhìnhphẳnggiớihạnbởihaiđồthị

   

1 2

C C

?

115

. B.

. C.

. D.

112

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn C

Vì

   

1 2

C C

cắtnhautại3điểmphânbiệtcóhoànhđộlầnlượtlà

1;2;3

nênđathứcbậcba

( ) ( )f x g x

cóbanghiệm

1;2;3

.Dođó,

   

( ) ( ) 1 2 3 ,

f x g x a x x x    

với





Mặtkhácvì

 

điquađiểm

 

1;0

;

 

điquađiểm

 

1; 4



nên

   

1 0, 1 4

f g

  

.Do

đó,

   

1 1 4

f g

 



Suyra

   

1 1 1 2 1 3 4

   

hay



.

Khiđódiệntíchhìnhphẳnggiớihạnbởihaiđồthị

   

1 2

C C

là

       

2 3

1 2

1 2 3 d 1 2 3 d

x x x x x x x x



       

 

(đvdt).

Câu 23. (Sở Tuyên Quang - 2021) Chohàmsố

 

f x

có



 

 

 

 

và

 

4cos2

sin 2

f x





,



 

 

 

 

.

Khiđó

 

df x x





bằng

ln 2





. B.

ln3

. C.



. D.

ln3





.

Lời giải

Chọn B

Tacó

   

4cos 2

d d

sin 2

f x f x x x



 

 

.

Đặt

sin2 2cos2 d dx t x x t  

.

Suyra

 

2d 2 2

sin 2

f x C C C

t t x



 



 

 

        



.

Nhưvậy

   

3 3

6 6

2 2

d d

sin 2 sin 2

f x f x x x I

x x

 

     

 

.

Xét

  

3 3 3 3

2 2

6 6 6 6

2 2sin 2 2sin 2 2sin 2

d d d d

sin 2 sin 2 1 cos 2 1 cos2 1 cos2

x x x

I x x x x

x x x x x

   

   

   

  

   

.

Đặt

cos2 2sin2 d dx a x x a   

.Đổicận:

3 2

6 2

x a





   







  





.

Suyra

  

   

1 1 1 1

2 2 2 2

1 1 1 1

2 2 2 2

d 1 d 1

d 1 1 1 1

1 1 2 1 1 2 1 1

a a

I a

a a a a a a

   

 

 

 

 

    

 

 

     

 

 

 

   

.

1 1

2 2

1 1

2 2

ln 1 ln 1 ln3

a a

 

 

 

     

 

 

.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Phương pháp trắc nghiệm:DùngmáytínhCasiobấmkếtquảcủatíchphân

,sauđóthử4đáp

án,đápánnàotrùngkhớpchínhlàkếtquảcầntính.

Câu 24. (Sở Yên Bái - 2021) Chohàmsố

 

f x

cóđạohàmliêntụctrên

 

0;1

vàthỏamãn

 



,

 

f x x





 

 



và

 

180

x f x x 



.Tíchphân

 

df x x



bằng



. B.

. C.

. D.



.

Lời giải

Chọn C

Đặt

 

u f x

v x

 

 

 



 









,suyra:

     

1 1

3 4

0 0

37 1

d d

180 4 4

x f x x f x x f x x



  

 

   

37 1 1

1 d

180 4 4

f x f x x



  





 

x f x x



  



.

Mặtkháctacó:

8 9

4 4

4 d

9 9

x x x

 



.

Suyra:

   

1 1 1

4 8

0 0 0

4 8 4

d 4 d 4 d 0

9 9 9

f x x x f x x x x

 

     

 

 

  



 

2 d 0

f x x x



 

  

 



   

4 5

f x x f x x C



      

.

Mặtkhác

 



 

3 2 2

1 1

5 5 5

C C f x x

         

.

Vậy

 

1 1

0 0

2 14

d 1 d

5 15

f x x x x

 

   

 

 

 

.



Câu 25. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Chohàmsố

 

f x

cóđạohàmliêntụctrênđoạn

 

0;1

thỏamãn

 

1 1



,

 

d 9

f x x





 

 





và

 

x f x x





.Tíchphân

 

dxf x x



bằng

. B.

. C.

. D.

.

Lời giải

Chọn C

Tacó:

 

d 9

f x x





 

 





 



Tính

 

d .

x f x x







NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Đặt

 

d .d

u f x

v x x

 











 

d d

u f x x



 















 

x f x x 



 

f x

 



 

 

 

. d

x f x x







 

1 1

. d

4 4

x f x x



 





 

. d 1x f x x



  



 

18 . d 18x f x x



  





 



-Lạicó:

9 9

x x  



81 d 9x x 





 



-Cộngvếvớivếcácđẳngthức

 

,

 

và

 

tađược:

   

4 8

18 . 81 d 0f x x f x x x

 

 

   

 



 

9 d 0f x x x



 

  

 



 

. 9 d 0f x x x





 

  

 



ythểtíchkhốitrònxoaysinhbởihìnhphẳnggiớihạnbởiđồthịhàmsố

 

9y f x x



 

,trục

hoành

,cácđườngthẳng

0x 

,

1x 

khiquayquanh

bằng

 

9 0f x x



  

 

9f x x



  

   

.df x f x x



 



x C  

.

Lạido

 

1 1f 

C 

 

9 14

5 5

f x x   



 

dxf x x 



9 14

5 5

x x x

 

 

 

 



9 14

5 5

x x x

 

  

 

 



7 2

9 7 8

35 5 7

x x

 

   

 

 

.

Câu 26. (THPT Thanh Chương 1- Nghệ An - 2021) Hướngtớikỉniệm60nămthànhlậptrườngTHPT

ThanhChương1.Khối12K57thiếtkếbồnhoagồmhaiElipbằngnhaucóđộdàitrụclớnbằng

8mvàđộdàitrụcnhỏbằng4mđặtchồnglênnhausaochotrụclớncủaElipnàytrùngvớitrục

nhỏcủaElipkiavàngượclại(nhưhìnhvẽ).



Phầndiệntíchnằmtrongđườngtrònđiqua4giaođiểmcủahaiElipdùngđểtrồngcỏ,phầndiện

tíchbốncánhhoanằmgiữahìnhtrònvàElipdùngđểtrồnghoa.Biếtkinhphíđểtrồnghoalà

300.000đồng ,kinhphíđểtrồngcỏlà200.000đồng .Tổngsốtiềndùngđểtrồnghoavà

trồngcỏchobồnhoagầnvớisốnàonhấttrongcácsốsau:

A. 6.200.000đồng. B. 8.200.000đồng. C. 8.600.000đồng. D. 9.100.000đồng.

Lời giải

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Chọn C

Tacó:độdàitrụclớnbằng8mvàđộdàitrụcnhỏbằng4m,tacóhìnhvẽnhưtrên:

TiếptheotasẽthiếtlậpphươngtrìnhnửabêntrêntrụchoànhcủacảhaiEliptrên

2phươngtrìnhđólà: .

Gọi làmộttronghaigiaođiểmcủahaiđồthịhàmsố 

Từđó,hoànhđộcủađiểm chínhlànghiệmcủaphươngtrìnhhoànhđộgiaođiểmgiữahaiđồ

thịhàmsố .

.

Suyrabánkínhcủađườngtrònđiqua4giaođiểmcủa2Eliptrênlà .

Phươngtrìnhnửatrêncủađườngtrònlà: .

Diệntíchhìnhtrònđólà: .

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Từđótatínhđượckinhphítrồngcỏlà: đồng.

Tacódiệntíchgiớihạnbởihaiđường , là:

.

Diệntíchphầnhìnhgiớihạnbởihaiđồthị cùngvớitrụchoànhđólà

.

Từđótasuyradiệntíchdùngđểtrồnghoalà: .

Nhưvậygiátiềntrồnghoalà: .

Vậytổnggiátiềndùngđểtrồnghoavàtrồngcỏchobồnhoabằng

(đồng).

Câu 27. (THPT Lương Thế Vinh - 2021) Cho

, ,a b c

làcácsốthựcvà

 

3 2

f x x ax bx c   

thỏamãn

   

5 2

f t f t

 

  

với

làhằngsố.Giátrị

 

f x x







bằng

105



. B.

134

. C.



. D.

.

Lời giải

Chọn A

Tacó

 

3 2

f x x ax b



  

.Vì

   

5 2

f t f t

 

  

nên

và

5t 

làhainghiệmcủaphương

trình

 

2 0 3 2 2 0

f x x ax b



      

.

TheoViettacó

 

2 5

3 5 2

t t

a t

b t t

t t



   

  



 



 



 

  

 







.

Dođó

           

3 2

d 5 5 5 5

I f x x f t f t t t a t t b t t



   



             

 

   





      

5 3 5 5 .5. 2 5 5t t t t t t a t b

 

         

 



 

2 2

125 15 5 2 5 5 3 5 2

t t t t t

 

       

 



   

2 2

15 105

135 30 5 4 20 25

2 2

t t t t       

.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

Câu 28. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hàm số

 

f x

 đồng biến, biết

 

 

0, 1;4

f x x  

 và có đạo hàm liên tục trên đoạn

 

1;4

, thỏa mãn

 

1 1



 và

   

 

f x

f x xf x



  

 

vớimọi

 

1;4

x

.Khiđó

 

df x x



bằng

. B.

2ln 2

. C.

2ln 2 2

. D.

2

.

Lời giải

Chọn B

Tacó

   

 

   

 

2 . ' 2 . '

f x

f x x f x f x x f x

 

    

 



 

. '

1 1

2 2 .

x f x

f x x f x

x x

f x



 

    

 



Suyra

   

2 . 2 . 2

x f x dx dx x f x x C



 

   

 

 

.

Thế

1x 

,tađược

 

2. 1 2 1 0

f C C

   

.

Suyra

     

2 . 2 .x f x x x f x x f x

    

.

Tacó

 

4 4

1 1

ln 2ln 2

f x dx dx x

  

 

.

Câu 29. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hàm số

 

y f x



cóđạohàm liêntụctrên

khoảng

 

 

thỏamãn

   

ln , 0

xf x f x x x x



   

và

 



.Tính

 



2ln2 1

. B.

4ln2 1

. C.

2ln2

 D.

4ln2



Lời giải

Chọn D

   

       

ln ln ln ln

xf x f x f x f x

xf x f x x x x x x x x xdx

x x x



  



       

 

 





Mà

2 2 2 2 2

1 1 1 1 1 1

ln ln . ln . ln

2 2 2 2 4

x xdx x d x x x x dx x x x C

 

     

 

 

  



Suyra

 

3 3

1 1

2 4

f x x x x Cx

  

,mà

 

3 1

1 1

4 4

f C C

    

.

Vậy

 

3 3

1 1

2 4

f x x x x x  

.Khiđó

 

2 4ln 2

f 

Câu 30. (THPT Ba Đình - Thanh Hóa - 2021) Chohàmsố

 

f x

nhậngiátrịdương,cóđạohàmliêntục

trên

 

0;2

. Biết

 

0 1



 và

   

2 4

x x

f x f x e



 

 với mọi

 

0;2

x

. Tính tích phân

 

3 2

3x x f x

I dx

f x









.

 

. B.

 

. C.

 

. D.

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn C

Theogiảthiết,tacó

   

2 4

. 2

x x

f x f x e



 

và

 

f x

nhậngiátrịdươngnên

       

2 4 2

ln . 2 ln ln ln 2 2 4

x x

f x f x e f x f x x x



       

 

.

Mặtkhác,với

0x 

,tacó:

   

0 . 2 1f f 

và

 

0 1f 

nên

 

2 1f 



Xét

 

2 2

x x f x

I x

f x









,tacó

 

2 2

3 d

f x

I x x x

f x



 





Đặt

 

3 2

d 3 6 d

d d

u x x

u x x x

f x

v x

v f x

f x



 



 





 



 



.

Suyra

 

3 2 2

3 ln 3 6 ln dI x x f x x x f x x

 

   

 





 

3 6 ln dx x f x x  



(1).

Đổibiến

2x t dx dt    

.Khi

0 2x t  

và

2 0x t  



Khiđó:

 

  

3 6 ln 2 dI t t f t t   



 

3 6 ln 2 dt t f t t   





 

3 6 ln 2 dx x f x x  



(2).

Từ

 

và

 

tacộngvếtheovế,tađược

 

   

2 3 6 ln ln 2 dI x x f x f x x    

 





Hay

  

2 2

3 6 2 4 d

I x x x x x   



 

4 3 2

6 24 24 d

x x x x   



5 4 3

1 6 16

6 8

2 5 5

x x x

 

   

 

 

Câu 31. (Trung Tâm Thanh Tường - 2021) Cho

   

,f x g x

lầnlượtlàcáchàmđathứcbậcbavàbậc

nhấtcóđồthịnhưhìnhvẽ.



Biếtdiệntíchhình

(đượctômàu)bằng

250

.Tính

 

f x dx



.

. B.

. C.

. D.

.

Lời giải

Chọn D

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

Tacó

 

g x

làhàmsốbậcnhấtđiqua

 

 

 

và

 

3;2

nên

 

3 1

5 5

g x x

 

.

Với

 

3 1

1 1 2 2; 1

5 5

y x x C

           

làgiaođiểmcủa

 

f x

và

 

g x

.

Dođó

       

2 3

f x g x a x x x

 

    

 

 

.

Lạicó

       

4 4

3 3

2 2

250 4 3

d 2 3 d

81 3 20

S f x g x x a x x x x a

 

 

 

        

 

 

 

 

 

 

 

.

Suyra

             

3 4 3 4 3 1

2 3 2 3

20 3 20 3 5 5

f x g x x x x f x x x x x

   

           

   

   

.

Vậy

     

2 2

0 0

3 4 3 1 34

2 3

20 3 5 5 15

f x dx x x x x dx

 

 

      

 

 

 

 

 

.

Câu 32. (THPT Trần Phú - Đà Nẵng - 2021) Giảsử

 

ln3 ln 2

ln 1 d

3 9

a b c

x x x



  



với

, ,

a b c N

 .

Giátrịcủabiểuthức

b c a 

bằng

2

. B.

. C.

4

. D.

.

Lời giải

Chọn B

 

ln 1 dI x x x

 



.

Đặt

 

d d

ln 1

d d

u x

v x x

v x







  

 





 













,suyra

 

5 5

3 3

ln 1

ln 1 d d

3 3 1

x x

I x x x x



   



 



125ln 6 27ln 4 1 1

1 d

3 3 1

x x x



 

    

 



 





3 2

125ln 6 27ln 4 1

ln 1

3 3 3 2

x x

 



     

 

 



126ln 6 28ln 4 80

3 9



 



126

126ln 3 70ln 2 80 ln 3 ln 2

70 24

3 9 3 9

a b c

b b c a





 



         









.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 33. Chohàmsố

 

e khi 0

2 3 khi 0

m x

f x

x x x



 







 





liêntụctrên



.Tíchphân

 

dI f x x







bằng

A. e 2 3 22I    . B.

e 2 3

I   

. C.

2 3

I e  

. D.

e 2 3

I   

.

Lời giải

Chọn D

Tacó

 

0 0

lim lim e 1

x x

f x m m

 

 

    ,

 





0 0

lim lim 2 3 0

x x

f x x x

 

 

  

và

 

0 1f m 

.

Vìhàmsốđãcholiêntụctrên



nênliêntụctại

0x 

.

Suyra

     

0 0

lim lim 0

x x

f x f x f

 

 

 



hay

1 0 1m m    

.

Khiđó

 

     

1 0 1 0 1

2 2 2

1 1 0 1 0

d = 2 3 d e 1 d = 3 d 3 e 1 d

x x

f x x x x x x x x x

  

      

    



   

2 2

2 22

= 3 3 e e 2 3

3 3

x x x



      

.

Câu 34. Chohàmsốbậcba

 

y f x

cóđồthị

 

làđườngcongtronghìnhbên.Biếthàmsố

 

f x

đạt

cựctrịtạihaiđiểm

1 2

,x x thỏamãn

2 1

2x x  và

1 2

x x

 





 

 

 

.Gọi

làđườngthẳngđiqua

haiđiểmcựctrịcủađồthị

 

.Diệntíchhìnhphẳnggiớihạnbởi

 

và

(phầnđượctôđậm

tronghình)bằng



. B.

. C.

. D.

.

Lời giải

Chọn D

Tịnhtiếnđiểmuốnvềgốctọađộ,tađượcđồthịmớinhưhìnhvẽ



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

Vì

 

f x

làhàmbậcba,nhậngốctọađộlàmtâmđốixứngnên

 

 f x ax cx

.

Chọn

1x  

,

1x 

,khiđó

 

3 f x x x

.

Talạicó

 

3 3 2

  f x x x x

,suyra

: 2d y x 

.

Diệntíchhìnhphẳngcầntìmlà

 

1 1

2 3 3 d

3 2

S x x x



  



.

Câu 35. Chohàmsố

 

4 1 , 5

2 6 , 5

x x x

f x

x x



  





 



.Tíchphân

 

ln2

3 1 . d

x x

f e e x



bằng

. B.

. C.

. D.

.

Lời giải

Chọn B

Tacó

     

5 5

lim lim 5 4

x x

f x f x f

 

 

  

nênhàmsốliêntụctại

5x 

.

Vậyhàmsố

 

f x

liêntụctrên



.

Đặt

3 1 d d

x x

t e e x t   



Đổicận:

0x 



4t 

;

ln 2x 



7t 



Khiđó

     

 

7 7 5 7

4 4 4 5

1 1 1 77

d d 2 6 d 4 1 d

3 3 3 9

I f t t f x x x x x x x

 

       

 

 

   

.

Câu 36. Chohàmsốbậcba

 

3 2

f x ax bx cx d   

vàđườngthẳng

 

:d g x mx n 

cóđồthịnhưhình

vẽ.Gọi

1 2 3

, ,S S S lầnlượtlàdiệntíchcủacácphầngiớihạnnhưhìnhbên.Nếu

4S  thìtỷsố



bằng.



. B.

. C.

. D.

.

Lời giải:

Chọn B

Dựavàođồthịnhưhìnhvẽ,tacó:

      

. 2 2f x g x k x x x   

.

 

3g x x 



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

  

1 2

2 2 4S S kx x x dx k



    





   

 

2 3

0 2 .2

3 5 .2

2 2

g g

S S



   



Vì

1 2

4 4S S   

8 4 4S    .Vậy



.

Câu 37. Cho hàm số

 

f x

 liên tục trên



 thỏa mãn

 

, 0

x m x

f x

e x

 











 (m là hằng số). Biết

 

f x x a



 



trongđó

,a b

làcácsốhữutỉ.Tính

a b

.

. B.

. C.

. D.

.

Lời giải

Chọn A

Dohàmsốliêntụctrên



nênhàmsốliêntụctại

     

0 0

0 lim lim 0 1

x x

x f x f x f m

 

 

     



Khiđótacó

       

2 0 2 0 2

1 1 0 1 0

d d d d 1 d

f x x f x x f x x e x x x

  

    

    



2 2 2

1 9 1

2 2 2 2 2 2

e x e



 

       

 

 

.

Dođó

9 1

;

2 2

a b  

.

Vậy

4a b 

.

Câu 38. Chohàmsố

4 2

3y x x m   cóđồthị

 

,với

làthamsốthực.Giảsử

 

cắttrục



tạibốnđiểmphânbiệtnhưhìnhvẽ



Gọi

S ,

S  là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của

 để

1 3 2

S S S  là

. B.



. C.

. D.



.

Lời giải

Chọn A

Gọi

x lànghiệmdươnglớnnhấtcủaphươngtrình

4 2

3 0x x m  

,tacó

4 2

1 1

3m x x  



 

.

Vì

1 3 2

S S S  và

1 3

S S nên

2 3

2S S hay

 

d 0

f x x 



.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27

Mà

 

f x x



 

4 2

3 d

x x m x  



x mx

 

  

 

 

1 1

x mx  

1 1

x x m

 

  

 

 

.

Dođó,

1 1

x x m

 

  

 

 



x m   

 

.

Từ

 

và

 

,tacóphươngtrình

2 4 2

1 1 1

3 0

x x x    

4 2

1 1

4 10 0x x  



x 

.

Vậy

4 2

1 1

3m x x  



.

Câu 39. Chohàmsố

 

1y f x 

,

 

y g x x 

.Giátrị

   

 

min ; dI f x g x x







. B.

. C.

. D.

.

Lời giải

Chọn C

Xétbấtphươngtrình

1x 









 



.

Vậy

 

min 1; 1x 

khi

1 x

hoặc

1x  



 

min 1; x x

khi

1 1x  



Xét

   

 

min ; dI f x g x x







 

min 1; dx x







 

min 1; dx x







 

min 1; dx x





1 2

1 1

d dI x x x



 

 

0 1 2

1 0 1

d d dx x x x x



   

  

0 1

2 2

1 0

2 2

x x



  

=2.

Câu 40. Cho parabol

 

: 4P y x  

 cắt trục hoành tại hai điểm

,

 và đường thẳng

:d y a



 

0 4a 

.Xétparabol

 

điqua

,

vàcóđỉnhthuộcđườngthẳng

y a

.Gọi

S làdiện

tíchhìnhphẳnggiớihạnbởi

 

và

.

S làdiệntíchhìnhphẳnggiớihạnbởi

 

vàtrục

hoành.Biết

1 2

S S (thamkhảohìnhvẽbên).



Tính

3 2

8 48T a a a  

.

99T 

. B.

64T 

. C.

32T 

. D.

72T 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn B

-Gọi

,

làcácgiaođiểmcủa

 

vàtrục

 

2;0

A 

,

 

2;0

 

.

-Gọi

,

làgiaođiểmcủa

 

vàđườngthẳng

 

4 ;M a a

  

,

 

4 ;N a a





2 4

MN a  

.

-Nhậnthấy:

 

làparabolcóphươngtrình

y x a  

.

-Ápdụngcôngthứctínhdiệntíchhìnhphẳngtađược:

2 4 .d

S y y

 



 

 

  

 

 

 

4 4

a a  

.

2 .d

S x a x

 

  

 

 



 

  

 

 



.

-Theogiảthiết:

1 2

S S

 

4 8

4 4

3 3

a a   

 

4 4a a

  

3 2

8 48 64

a a a

   

.

Câu 41. Chohàmsố

 

2cos 3 0

x m x

y f x

x x



 



 



 





liêntụctrên



.Giátrị

2cos 1 sin dI f x x x



 





. B.

. C.

. D.



.

Lời giải

Chọn A

Hàm

 

f x

liêntụctrên



suyra

   

0 0

lim lim

x x

f x f x

 

 



 

0 0

lim lim 2cos 3

x x

x m x

 

 

   

 

Xétbấtphươngtrình

2cos 1 0

 

với



 

.

2cos 1x 

cos

 



  



Vậy

2cos 1 0

 

khi



 

,

2cos 1 0

 

khi

3 2

 

 

.

2cos 1 sin dI f x x x



 



2cos 1 sin d 2cos 1 sin df x x x f x x x



   

 



   

2cos 1 sin d 1 2cos sin dI f x x x f x x x



   

 



Xét

 

2cos 1 sin dI f x x x



 





Xét

2cos 1t x 

d 2sin dt x x  

sin d

x x



 



TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29







t



Suyra

 

2cos 1 sin dI f x x x



 



 

-d

f t



 

f t t



 

f x x





 

1 1

-1 d

2 6 2 3

x x

I x x



   





Xét

 

1 2cos sin dI f x x x



 





Xét

1 2cost x  d 2sin dt x x 

sin d

x x 











t



Suyra

 

2cos 1 sin dI f x x x



 



 

f t



 

f t t



 

f x x





 

1 1

-1 d

2 6 2 3

x x

I x x



   





Suyra

1 2

I I I



  

.

Câu 42. Chohàmsốbậcbốn

 

y f x

cóđồthị

 

nhưhìnhvẽbên.Biếthàmsố

 

y f x

đạtcựctrị

tại các điểm

1 2 3

, ,x x x  thỏa mãn

3 1

2x x  ,

     

1 3 2

f x f x f x  

 và

 

 nhận đường

thẳng

:d x x làmtrụcđốixứng.Gọi

1 2 3 4

, , ,S S S S làdiệntíchcủacácmiềnhìnhphẳngđược

đánhdấunhưhìnhbên.Tỉsố

1 2

3 4

S S



gầnkếtquảnàonhất

0,60

. B.

0,55

. C.

0,65

. D.

0,70.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 30 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn A

Nhậnthấykếtquảbài toánkhông đổikhitatịnh tiếnđồthị

 

sangbêntráisao chođường

thẳng

d x x

trùngvớitrụctungkhiđó

 

làđồthịcủahàmtrùngphương

 

y g x



cóba

điểmcựctrị

1 2 3

1, 0, 1

x x x

   

.Suyra

 

4 2

2 0

y g x k x x c k

    



Lạicó

     

1 3 2

2 2 3

0 2 2 0

3 3 4

f x f x f x k c c c k

         



Suyra:

 

4 2

y g x k x x k

   



Khiđó:

4 2

1 2

3 28 2 17

4 60

S S k x x dx k



    



.

Talạicó:

   

0 1

g g k 

1 2 3 4

S S S S k k     

Suyra

1 2

3 4

28 2 17 77 28 2 28 2 17

0,604

60 60

77 28 2

S S

S S k k k

S S



  

      







Câu 43. Chohàmsố

 

3 2

2 4 khi 4

khi 4

x x

f x

x x x x

 









  





.Tíchphân

 

2sin 3 sin 2 df x x x







bằng

. B.

. C.

341

. D.

341

.

Lời giải

Chọn D

Tacó

       

     

3 2

4 4 4 4

4 4

lim lim 2 4 4; lim lim 4; 4 4

lim lim 4

x x x x

x x

f x x f x x x x f

f x f x f

   

 

   

 

 

       

 

 

  



Nênhàmsốđãcholiêntụctại





Xét

 

2sin 3 sin 2 dI f x x x



 





Đặt

2sin 3x t 



sin 2 d d

x x t





Với





3t 









5t 





     

5 5 4 5

3 2

3 3 3 4

1 1 1 1 1 341

d d d 2 4 d

2 2 2 4 2 96

I f t t f t t t t t t t t

 

       

 

 

   

.

Câu 44. Chohàmsốbậcba

 

y f x



cóđồthịlàđườngcong

 

tronghìnhbên.Hàmsố

 

f x

đạtcực

trị tại hai điểm

1 2

,x x

 thỏa

   

1 2

f x f x

 

. Gọi

,A B

 là hai điểm cực trị của đồ thị

 

, ,M N K

làgiaođiểmcủa

 

vớitrụchoành;

làdiệntíchcủahìnhphẳngđượcgạch

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31

tronghình,

S làdiệntíchtamgiác

NBK

.Biếttứgiác

MAKB

nộitiếpđườngtròn,khiđótỉsố

bằng

2 6

. B.

. C.

5 3

. D.

3 3

.

Lời giải

Chọn D

Kếtquảbàitoánkhôngthayđổikhitatịnhtiếnđồthịđồthị

 

sangtráisaochođiểmuốntrùng

vớigốctọađộ

.(nhưhìnhdưới)



Do

 

f x

làhàmsốbậcba,nhậngốctọađộlàtâmđốixứng

 

O N

.

Đặt

1 2

,x a x a   ,với

0a 



 

2 2

'f x k x a  

với

0k 



 

3 2

f x k x a x

 

  

 

 



3, 3

M K

x a x a   



Có

MAKB

nộitiếpđườngtròntâm

 3OA OM a   

Có

   

2 2 3 3

1 1

1 3 2

2 2

f x OA x f a a k a a a k

 

          

 

 



 

3 2

3 2 1

f x x a x

 

  

 

 



 

4 2 2

3 2 1 9 2

12 2 8

S f x dx x x a



 

   

 

 





NGUYỄN BẢO VƯƠNG - 0946798489

Trang 32 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

1 1 6

. 2. 3

2 2 2

AMO

S S f a MO a a a



    



Vậy

3 3



.

Câu 45. Chohàmsố

 

2 khi 0

3 2 khi 0

x x

f x

x x x



 







  





.Tíchphân

 

3 4cos sin df x x x







bằng

. B.

. C.

. D.

.

Lời giải

Chọn A

Tacó:

 

     

0 0 0 0

0 0

lim lim 2 2; lim lim 3 2 2; 0 2

lim lim 0

x x x x

x x

f x x f x x x f

f x f x f

   

 

   

 

       

  



Nênhàmsốđãcholiêntụctại





Xét

 

3 4cos sin dI f x x x



 





Đặt

3 4 cos

x t 



sin d d

x x t





Với





 









1t 





   

 

1 1 0 1

1 1 1 0

1 1 1 1 37

d d 3 2 d 2 d

4 4 4 4 24

I f t t f t t t t t t t

  

       

   

.

Câu 46. Chohàmsốbậcbốn

 

y f x



cóđồthị

 

nhưhìnhvẽbên.Biếthàmsố

 

y f x



đạtcựctrị

tại các điểm

1 2 3

, ,x x x

 thỏa mãn

3 1

x x

 

,

     

1 3 2

f x f x f x

  

 và

 

 nhận đường

thẳng

d x x

làmtrụcđốixứng.Gọi

1 2 3 4

, , ,S S S S

làdiệntíchcủacácmiềnhìnhphẳngđược

đánhdấunhưhìnhbên.Tỉsố

1 2

3 4

S S



gầnkếtquảnàonhất

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33

0,60

. B.

0,55

. C.

0,65

. D.

0,70.

Lời giải

Chọn A

Nhậnthấykếtquảbàitoánkhôngđổikhitatịnhtiếnđồthị

 

sangbêntráisaochođường

thẳng

:d x x

trùngvớitrụctungkhiđó

 

làđồthịcủahàmtrùngphương

 

y g x

cóba

điểmcựctrị

1 2 3

1, 0, 1x x x   

.Suyra

 

4 2

2 0y g x k x x c k    



Lạicó

     

1 3 2

2 2 3

0 2 2 0

3 3 4

f x f x f x k c c c k         



Suyra:

 

4 2

y g x k x x k   



Khiđó:

4 2

1 2

3 28 2 17

4 60

S S k x x dx k



    



.

Talạicó:

   

0 1g g k 

1 2 3 4

.1S S S S k k     

Suyra

1 2

3 4

28 2 17 77 28 2 28 2 17

0,604

60 60

77 28 2

S S

S S k k k

S S

  

      







Câu 47. Cho hàm số

 

3 2

khi 2

8 10khi 2

x ax b x

f x

x x x x



  







   





 Biết hàm số có đạo hàm tại điểm

2.x 

 Tính

 

I f x dx





. B.

. C.

2

. D.

.

Lời giải

Chọn D

Hàmsốcóđạohàmtại

     

2 2

2 lim lim 4 2 2 2 6.

x x

f f x f x a b a b

 

 

           



 



Có

   

3 2 3 2

2 2 2

8 10 4 2 8 12

lim lim lim

2 2 2

x x x

f x f

x x x a b x x x

x x x

  

  



        

 

  



   

  

2 2

2 3

lim lim 2 3 0;

x x

 

 

 

 

    

 





      

2 2 2

4 2

lim lim lim

2 2 2

x x x

f x f x x a

x ax b a b

x x x

  

  

   

    

 

  

 

lim 2 4.

x a a





    



Hàmsốcóđạohàmtại

2x 

nênhàmsốliêntụctại

2x 



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 34 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

suyra

       

2 2

lim lim 4 0 4.

2 2

x x

f x f f x f

a a

x x

 

 

 

      

 



 



Từ

 

và

 

2 ,

suyra

4a  

và

2.b 



Khiđó

 

3 2

4 2 khi 2

8 10 khi 2

x x x

f x

x x x x



  







   







     

4 2 4

0 0 2

I f x dx f x dx f x dx  

  



   

2 4

3 2 2

0 2

4 3 3

2 2

8 10 4 2

2 4

16 4

4 10 2 2 4

0 2

4 3 3 3 3

x x x dx x x dx

x x x

x x x x

      

   

         

   

   

 



Vậy

4I 

.

Câu 48. Cho hàm số

ax b

cx d







 có đồ thị

 

. Gọi giao điểm của hai đường tiệm cận là

. Điểm

 

0 0 0

;M x y

diđộngtrên

 

,tiếptuyếntạiđócắthaitiệmcậnlầnlượttại

,A B

và

IAB





.

Tìmgiátrị

saocho

1 2

IAB

S S







(với

1 2

,S S

là2hìnhphẳngminhhọabêndưới)

. B.

. C.

169

. D.

189

.

Lời giải

Chọn B

Nhậnthấykếtquảbàitoánkhôngthayđổikhitatịnhtiếnđồthị

 

theo



.Khiđóhaitiệm

cậncủa

 

làhaitrụctọađộ.

Vàhàmsốcủađồthị

 

trởthành:

 

0y y

 





    

.

Gọi

làtiếptuyếntại

   

0 0 0 0

2 2

0 0

; :M x y d y x x x

x x

   

       



Suyra:

 

2 ;0Ox d A x 

và

0;Oy d B



 

 

 

 



. 2 2 2 1

OAB

S OAOB a



 

      



 

0 0 0

1 1 2 2 2

, : , 0; , ;

c y d y x B C

x x x x

   

    

   

   

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35



Và



 

2 0 0

1 1 1 3 1

2 2

S dx x x

x x

 

    

 

 





Theogiảthiết

2 2

1 2

1 2 0 0

2 2

0 0

3 3 5 4

1 1 2

4 5

IAB

S S

S S S x y

x x





           



Vậy

2 2 2

0 0 0

IM x y  

Câu 49. Chohàmsố

 

2 1 2

5 2

x x khi x

f x

x khi x



  





 



.Tính

 

. ln 1 d .

I f x x



 

 

 







 

2;3



. B.

 

3; 2

. C.

 

2; 1

. D.

 

1;2



.

Lời giải

Chọn A

Với



,tacó

 

2 1f x x x  

làhàmđathứcnênliêntụctrên

 



.

Với



,tacó

 

5f x x 

làhàmđathứcnênliêntụctrên

 



.

Tacó

 

2 2

lim lim 2 1 7

x x

f x x x

 

 

   



   

2 2

lim lim 2 7

x x

f x x

 

 

  

;

 

2 7



.

Dođó

     

2 2

lim lim 2

x x

f x f x f

 

 

 

nênhàmsốliêntụctại



.

Khiđóhàmsốđãcholiêntụctrên



.

Đặt

 

2 2

2 d d d

ln 1 d .

1 1 2

x x x x t

t x t

x x

     

 



Đổicận:

Với



tacó

0t 



Với

x e

 

tacó

4t 



Khiđó

   

 

4 4 2 4

0 0 0 2

1 1 1

d d 2 1 5

2 2 2

I f t t f x x x x dx x dx

 

      

 

 

   



3 2

2 4

1 1 14 31

5 16

0 2

2 3 2 2 3 3

x x

x x x

 

   

 

       

 

   

 

 

   

 

.

Câu 50. Chohàmsốbậcba

 

y f x



cóđồthịlàđườngcongởhìnhbêndưới.Gọi

1 2

,x x

lầnlượtlàhai

điểmcựctrịthỏamãn

2 1

x x

 

và

   

1 2

3 0.

f x f x

 

Đườngthẳngsongsongvớitrục

và

quađiểmcựctiểucắtđồthịhàmsốtạiđiểmthứhaicóhoànhđộ

và

x x

 

.Tínhtỉsố



(

và

lầnlượtlàdiệntíchhaihìnhphẳngđượcgạchởhìnhbêndưới).

1 0

0 0

1 2 1 2 1 3 1

2 2

S x dx

x x x x

   

      

   

   



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 36 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

. B.

. C.

. D.



Lời giải

Chọn A

+)Gọi

 

3 2

f x ax bx cx d   

,với

0a 



 

3 2f x ax bx c



   

.

+)Theogiảthiếttacó

           

1 2 1 2 1 1

0 3 3 2f x f x f x a x x x x a x x x x

  

         



     

1 1

3 6f x a x x a x x



    

.

       

3 2

1 1

d 3f x f x x a x x a x x C



      



.

+)Tacó

       

1 2 1 1

3 0 3 2 0f x f x f x f x     



 

3 8 12 0 2 12 0 6C a a C C a C a          

.

Dođó

     

3 2

1 1

3 6f x a x x a x x a    

.

+)

S làdiệntíchhìnhchữnhậtcócạnhbằng3vàvà

 

8 12 6 2f x a a a a   



+)

S  là diện tích hình phẳng giới hạn bởi các đường

0 1 2 1

1, 2x x x x x x      ,

 

2y f x a 

và

     

3 2

1 1

3 6f x a x x a x x a    

nênsuyra

     

1 1

2 2

3 2

1 1 1

1 1

2 d 3 4 d

x x

S f x a x a x x a x x a x

 

 

 

       

 

 



   

4 3

1 1

3 4

4 3 4

a x x x x

a ax





 

 

   

 

 

.

Vậy



.

Câu 51. Chohàmsố

 

2 2   0

+4 2   0

x khi x

f x

x x khi x

 







 



.Tíchphân

 

sin 2 . cos dI x f x x







bằng

I 

. B.

I  

. C.

I  

. D.

I 

.

Lời giải

Chọn A

Do

     

0 0

lim lim 0 2

x x

f x f x f

 

 

   

nênhàmsố

 

f x

liêntụctạiđiểm

0x 

.

Đặt cost x

d sin dt x x  

.

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37

Đổicận:

0 1x t  

;

1x t



   

.

Tacó:

       

1 1

0 0 1 1

sin 2 . cos d 2sin .cos . cos d 2 . d 2 . dx f x x x x f x x t f t t t f t t

 



   

   

   

 

0 1 1 0

1 0 0 1

2 . d 2 . d 2 4 2 d 2 . 2 2 dx f x x x f x x x x x x x x x

 

      

   



4 3 3 2

4 7 10 9

2 4.

4 3 3 2 6 3 2

x x x x



   

       

   

   

.

Câu 52. Chohàmsốbậcbốntrùngphương

 

y f x

cóđồthịlàđườngcongtronghìnhbên.Biếthàmsố

 

f x

đạtcựctrịtạibađiểm

1 2 3 1 2 3

, , ( )x x x x x x  thỏamãn

1 3

4x x  .Gọi

S và

S làdiện

tíchcủahaihìnhphẳngđượcgạchtronghình.Tỉsố

bằng



 B.

 C.

 D.



Lời giải

Chọn B

Rõràngkếtquảbàitoánkhôngđổikhitatịnhtiếnđồthịsangtráisaocho

0x  .



Gọi

4 2

( )g x ax bx c   ,tacóhàmsố

( )g x

làchẵnvàcó3điểmcựctrịtươngứnglà

2;0; 2



làcácnghiệmcủaphươngtrình

4 2 0ax bx 

.

Dựavàođồthị

( )g x

,tacó

(0) 0g 

.Từđósuyra

4 2

( ) ( 8 )g x a x x  với

0a 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 38 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Do

tínhđốixứngcủahàmtrùngphươngnêndiệntíchhìnhchữnhậtbằng

(2) .4 64S S g a



 

acó

l

àdiệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố

(

)g x

trụchoành,đườngthẳng

2, 0

x x

  

.

4 2

2 2

224

(

) d 8 d

g x x a x x x

 



  



.Suyra



24 512

4 2.

5 15

a a

a  

Vậy

4 7

512 16



Bấm Tải xuống để xem toàn bộ.

| 1/163

| | Tải xuống

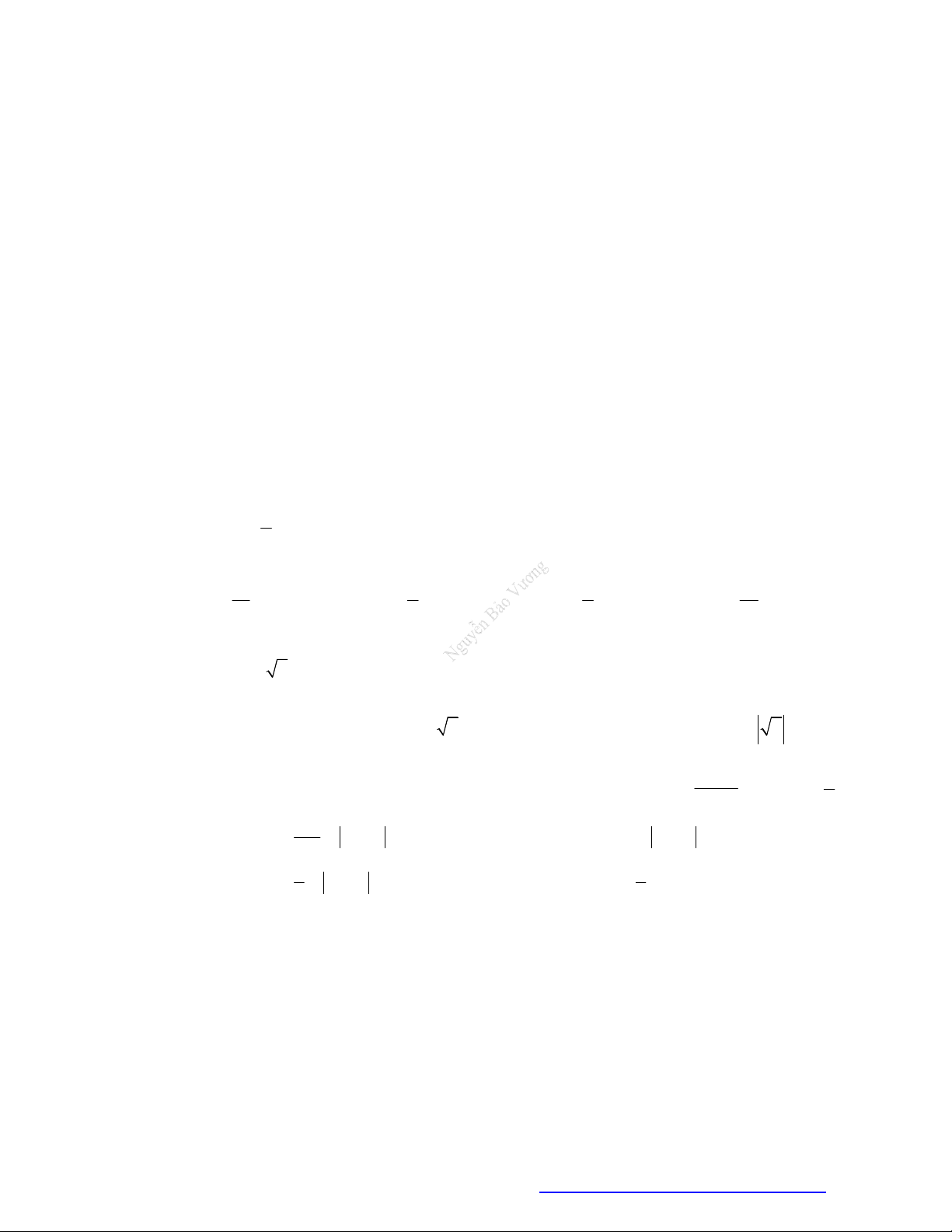
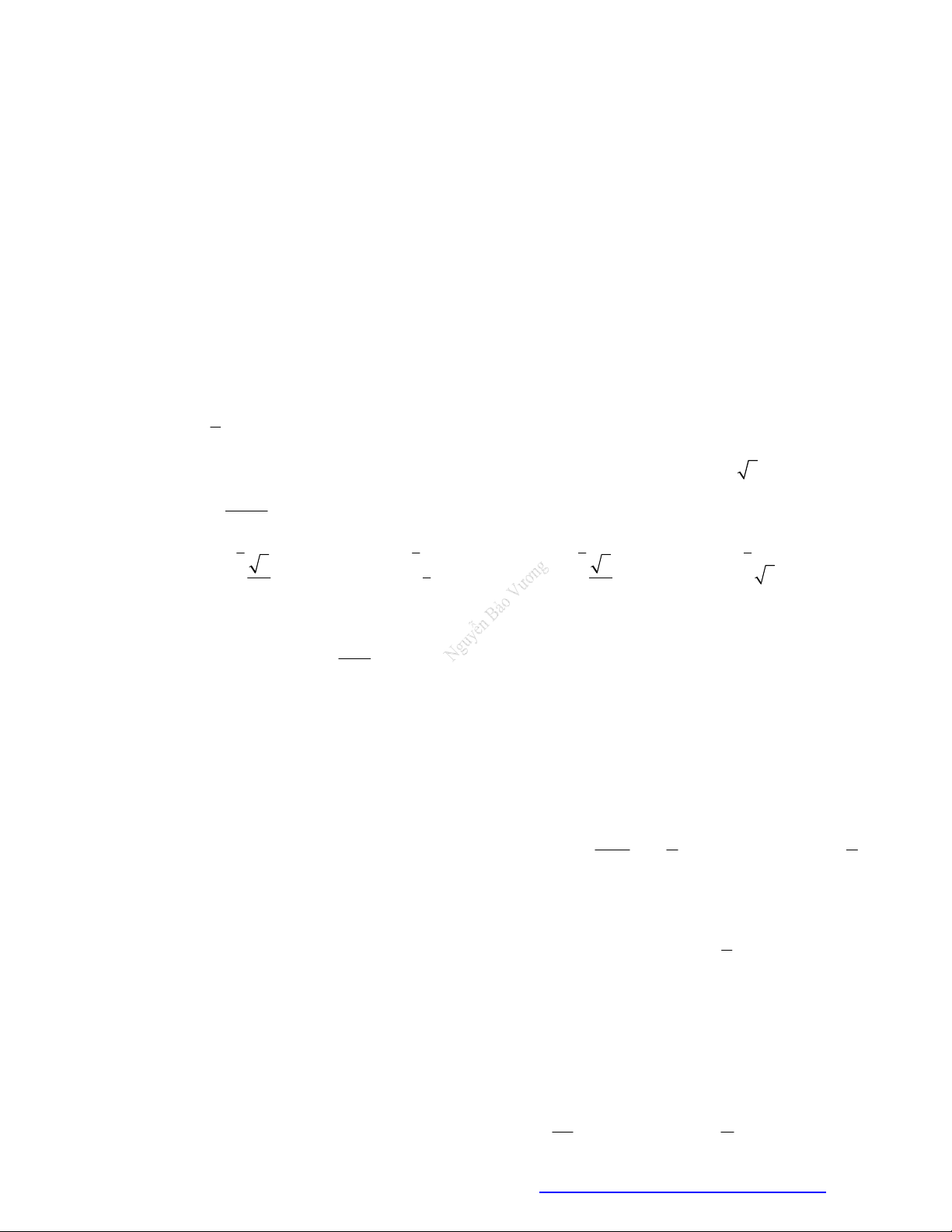
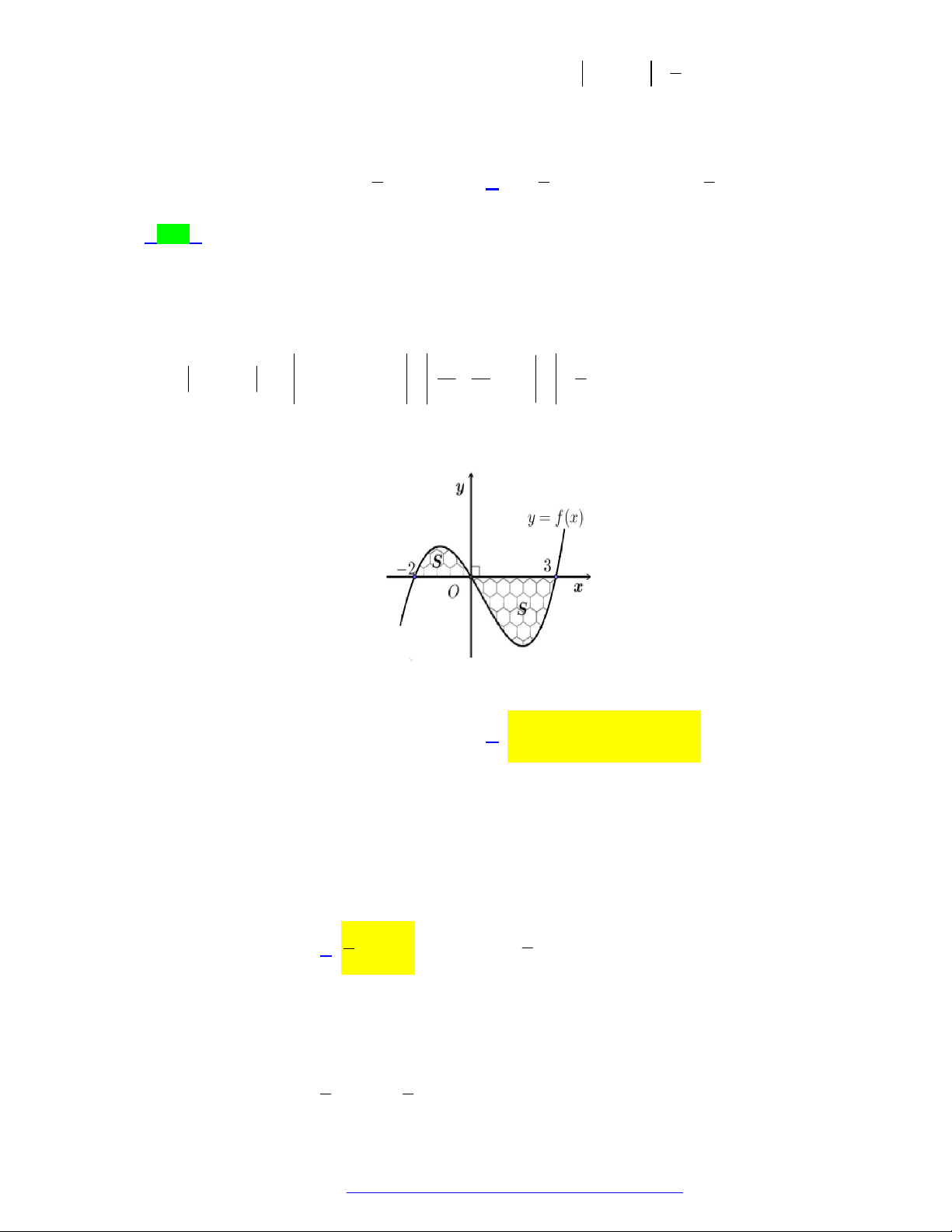
Preview text:

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 3
NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG
MỨC ĐỘ NHẬN BIẾT 6 4 Câu 1.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho
f  x dx  10  và
f  x dx  7  0 0 6 thì
f  x dx  bằng: 4 A. 17  . B. 17 . C. 3 . D. 3  . Câu 2.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Họ các nguyên hàm của hàm số f  x 4 2
 5x  6x 1 là 4 x A. 3
 2x  2x  C . B. 5 3
x  2x  x  C . 4 C. 5 3
20x 12x  x  C . D. 3
20x 12x  C . 0 1 Câu 3.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) dx  bằng 1 x 3  A. 2ln 2 . B. 2  ln 2 . C. 2 ln 2 1 . D. ln 2 . e  1 1  Câu 4. Tính tích phân I   dx  2   x x  1 1 1 A. I  B. I  1
C. I  1
D. I  e e e Câu 5.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Giả sử f là hàm liên tục trên khoảng
K và a, b, c là ba số bất kì trên khoảng K . Khẳng định nào sau đây sai? b b c b b A.
f (x) dx  f (t) dt   . B. f (x) dx
f (x) dx  f (x) dx, c  a,b    . a a a c a b b a C. f (x) dx 1   . D.
f (x) dx   f (x) dx   . a a b Câu 6.
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Nguyên hàm của hàm số f  x    x5 1 2 là: 1 1 A.   6 1 2x  C .
B.  1  2x6  C . C. 
1 2x6  C . D.   6 5 1 2x  C . 2 12   2 2 Câu 7.
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho
f  xdx  5 
. Tính I   f  x  2sin x d  x    0 0  A. I  5  . B. I  7 .
C. I  5   . D. I  3 . 2 8 4 4 Câu 8.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Biết
f  x dx  2   ;
f  x dx  3 
; g  x dx  7  . 1 1 1
Mệnh đề nào sau đây sai? 8 4 4 A.
f  x dx  g  x dx  8   .
B.  f  x  g  x dx  10    . 4 1 1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 8 4 C.
f  x dx  5  .
D. 4 f  x  2g  x dx  2     . 4 1 Câu 9.
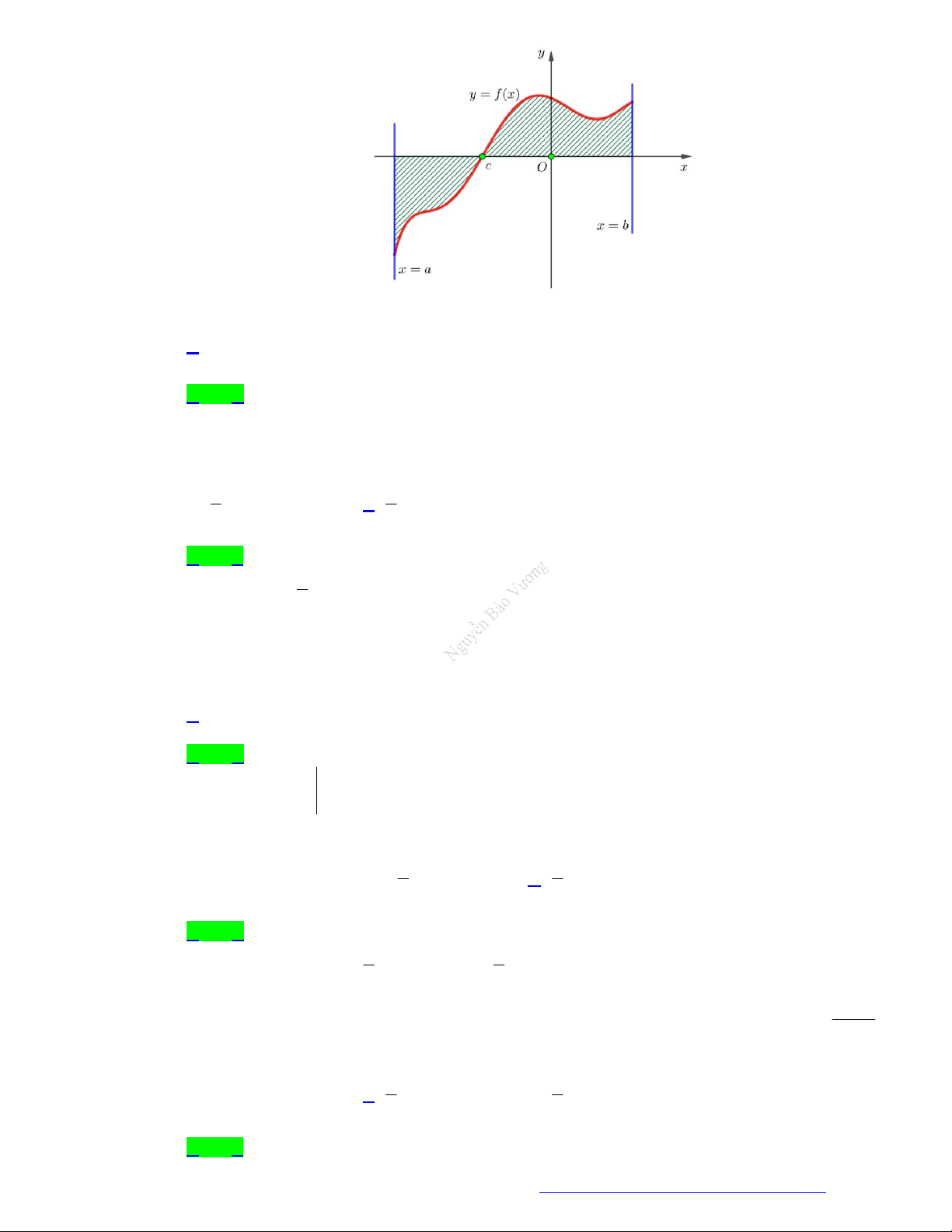
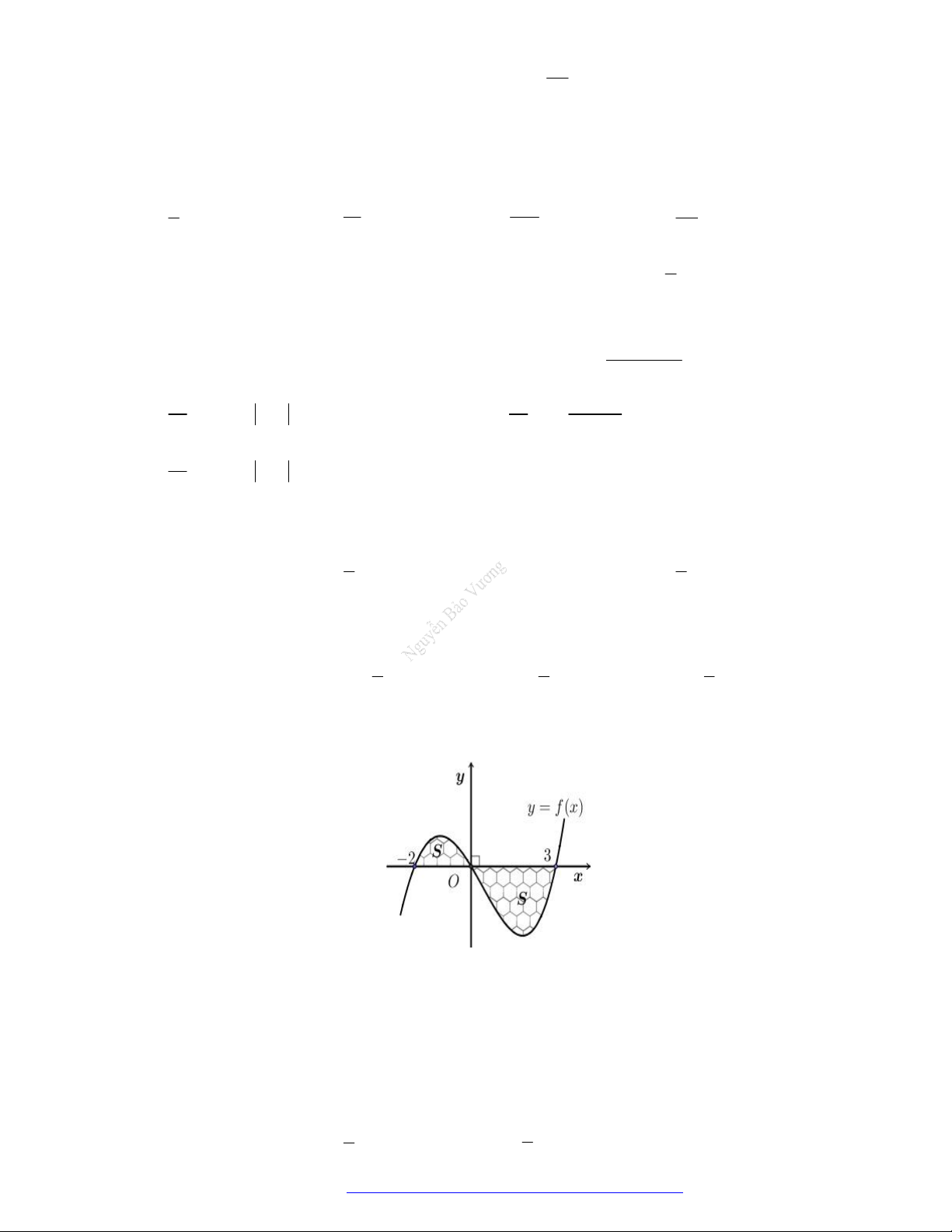
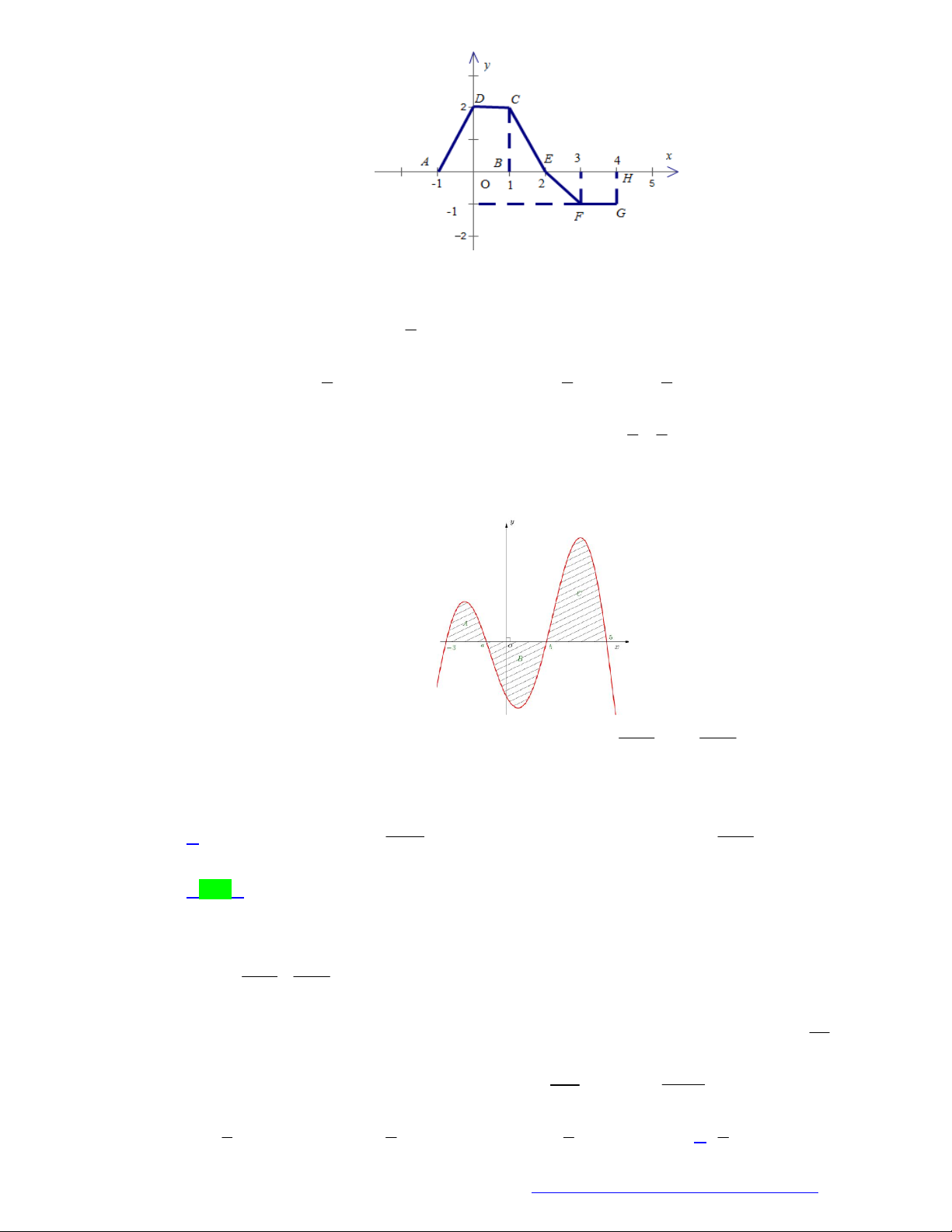
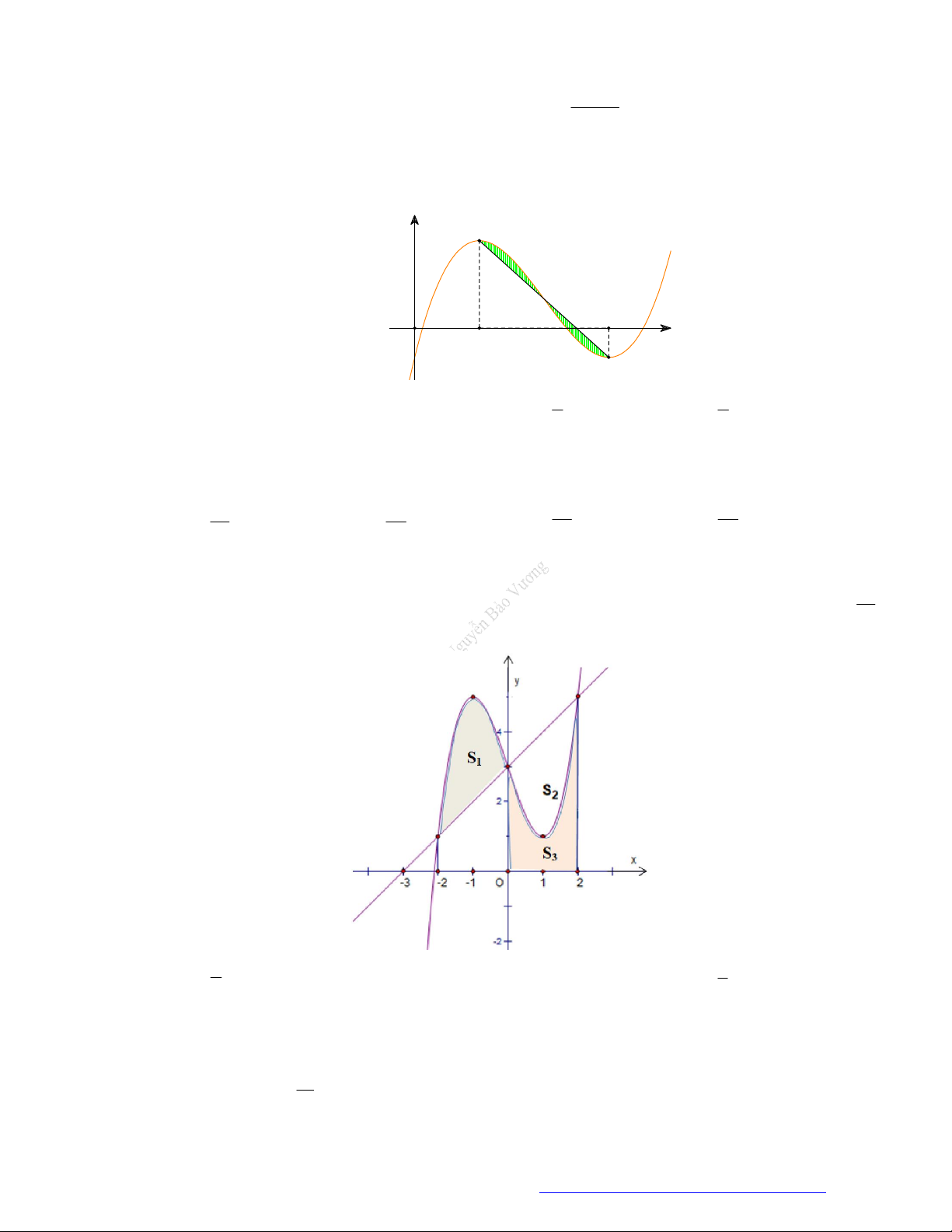
(Chuyên Lê Hồng Phong - TPHCM - 2021) Hình phẳng giới hạn bởi đồ thị hàm số y  f  x ,
trục hoành và hai đường thẳng x  a , x  b trong hình dưới đây (phần gạch sọc) có diện tích S bằng c b c b A.
f  x dx 
f  x dx   . B.
f  x dx 
f  x dx   . a c a c c b c b C. 
f  x dx 
f  x dx   . D. 
f  x dx 
f  x dx   . a c a c
Câu 10. (Chuyên Lê Hồng Phong - TPHCM - 2021) Họ nguyên hàm của hàm số   2 x f x  e là 1 1 A. x e  C . B. 2 x e  C . C. 2 2 x e  C . D. 2 x e  C . 2 2
Câu 11. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hàm số f  x có f 2  2 , f 3  5 ; hàm số 3
f  x liên tục trên 2; 
3 . Khi đó f  x dx  bằng 2 A. 3 . B. 10 . C. 3  . D. 7 .
Câu 12. (Chuyên Lam Sơn - Thanh Hóa - 2021) Họ tất cả nguyên hàm của hàm số f  x  cos 2x là 1 1
A. 2sin 2x  C .
B.  sin 2x  C . C. sin 2x  C . D. 2
 sin 2x  C . 2 2 2
Câu 13. (Chuyên Lam Sơn - Thanh Hóa - 2021) Họ tất cả các nguyên hàm của hàm số f  x  4x  3
trên khoảng 1;  là 1 1
A. 2 ln 4x  3  C . B.
ln 4x  3  C . C. ln 4x  3  C . D. 4ln 4x  3  C . 2 4
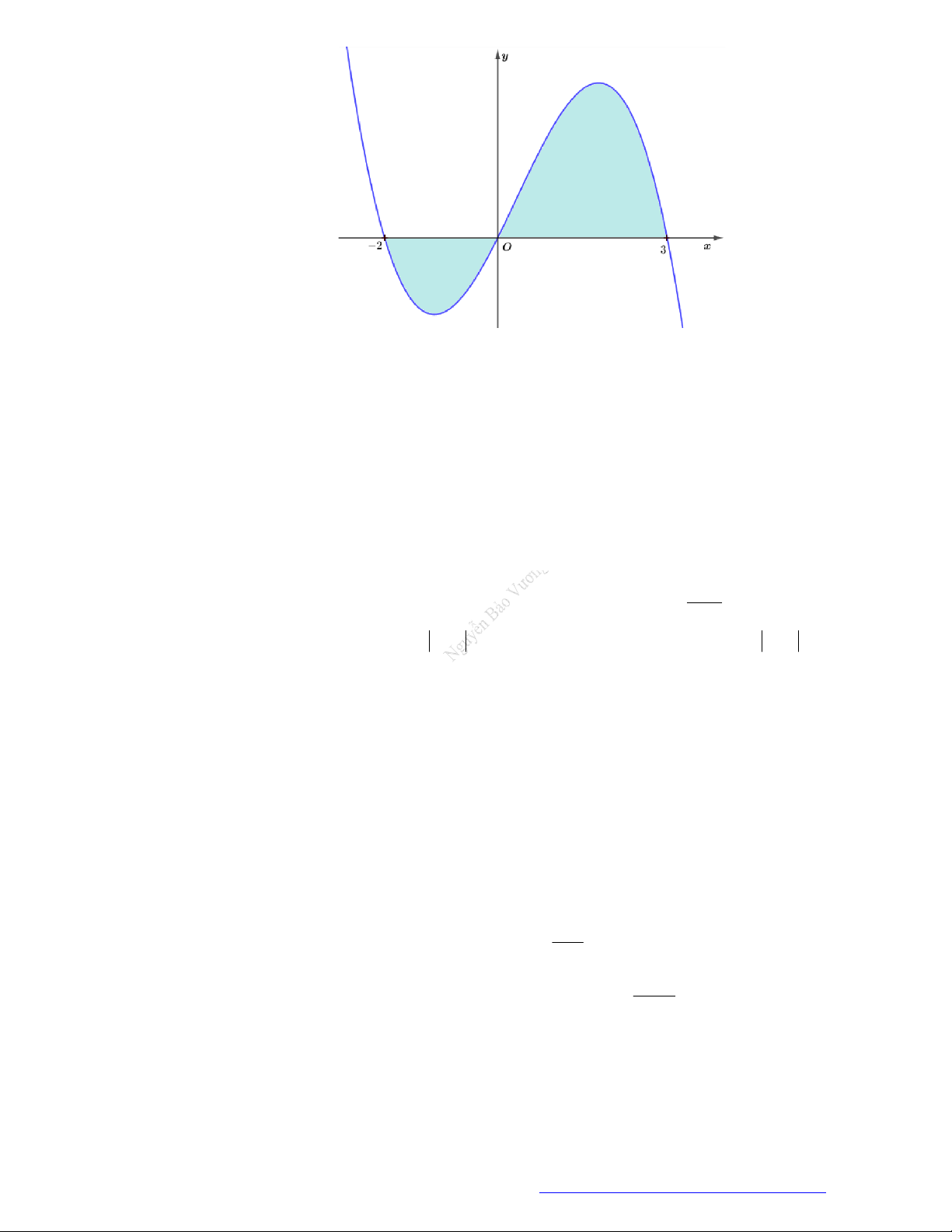
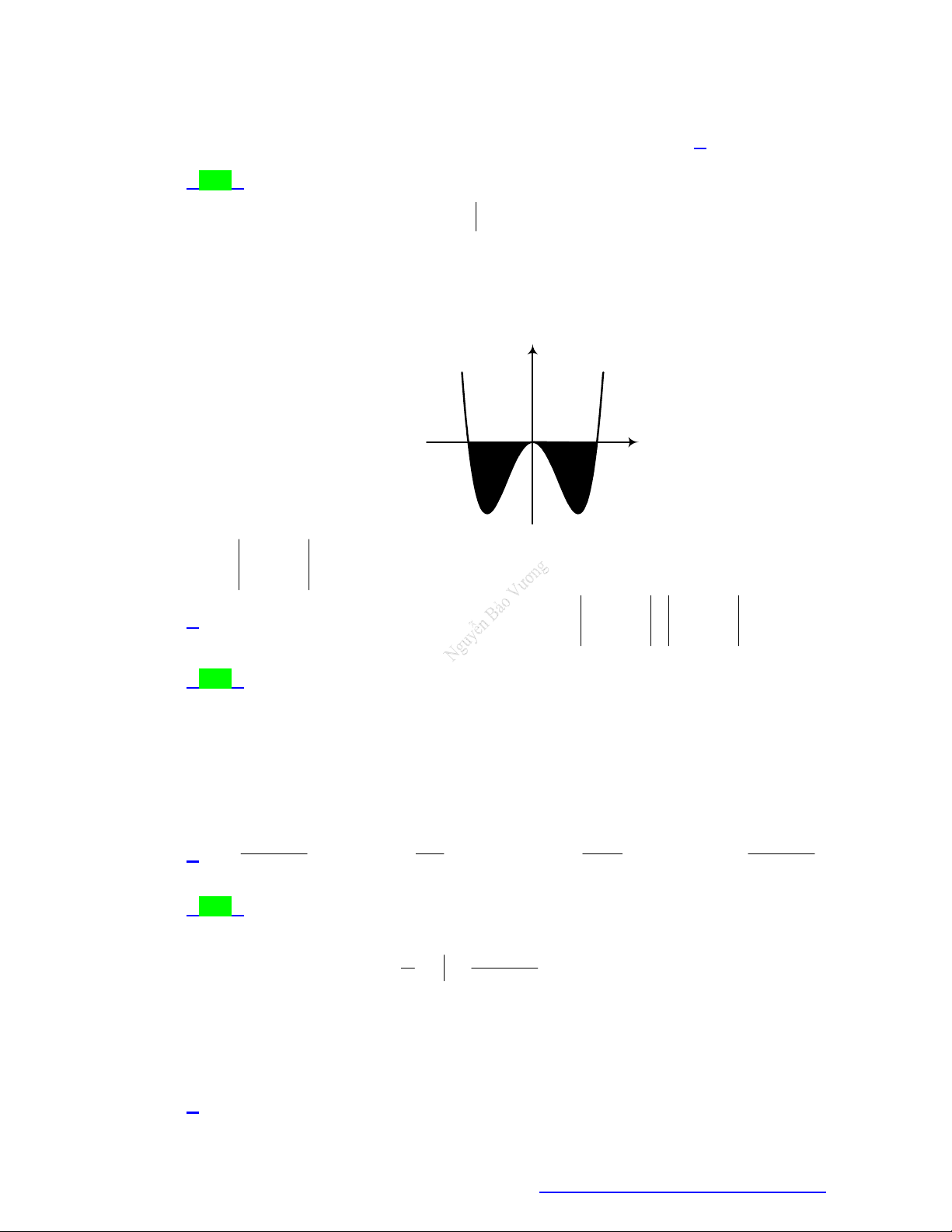
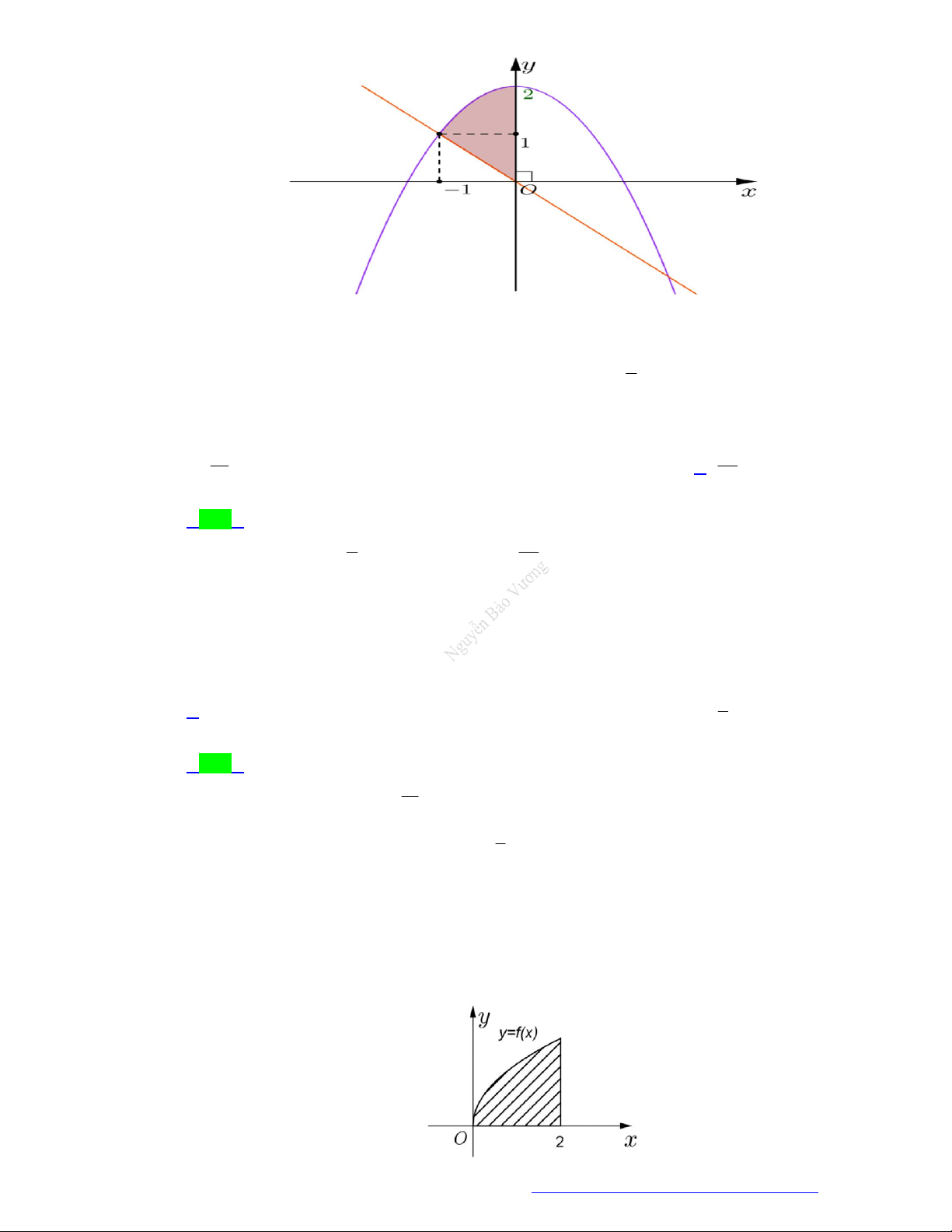
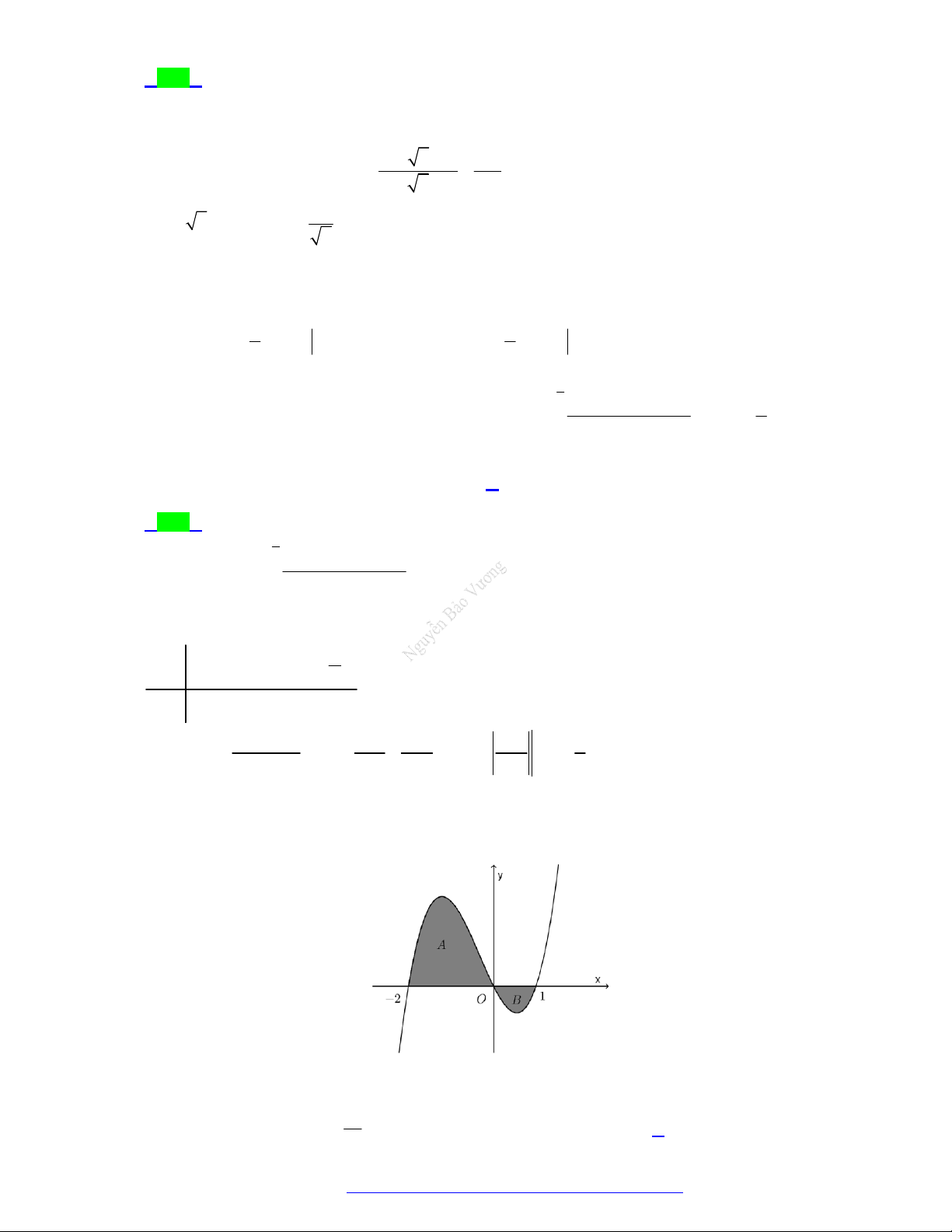
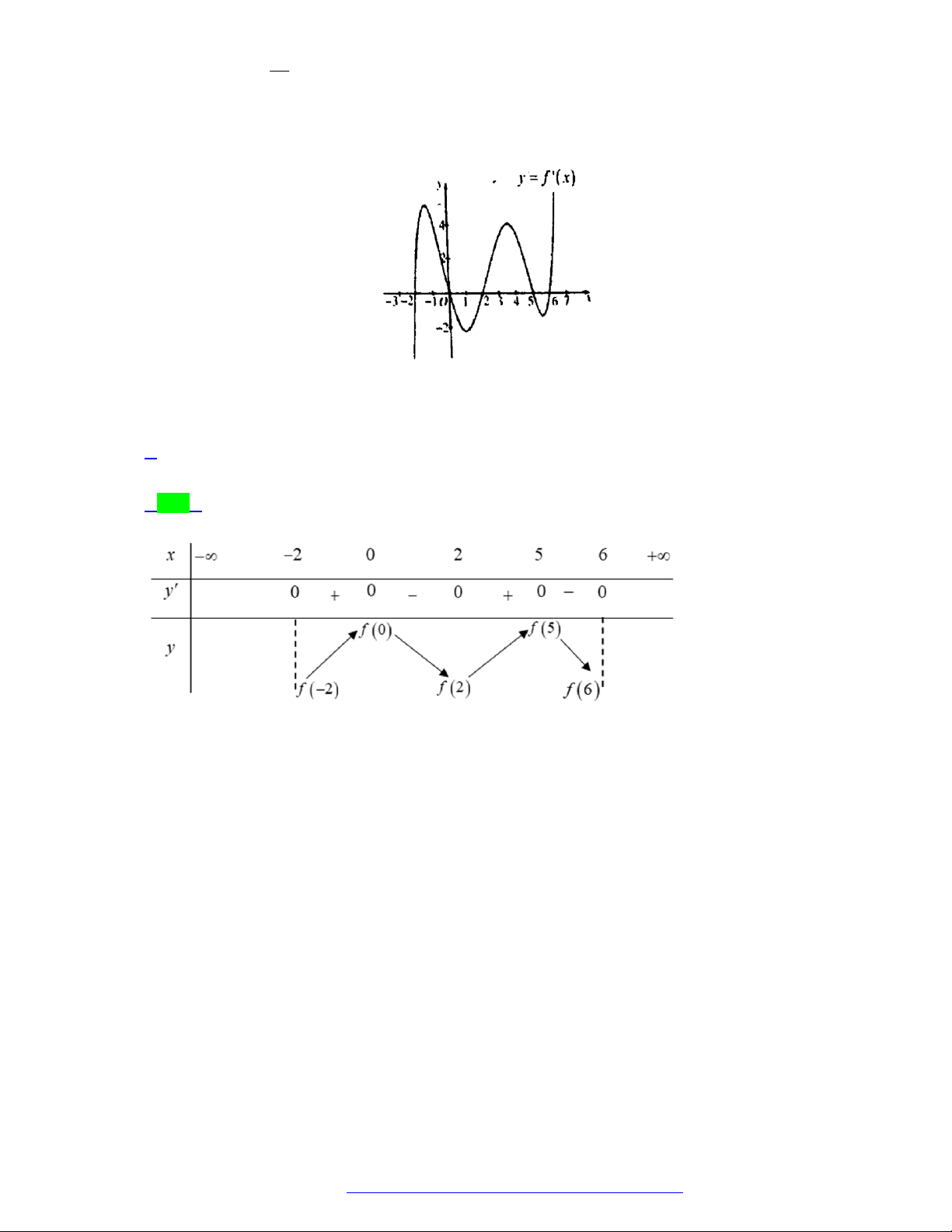
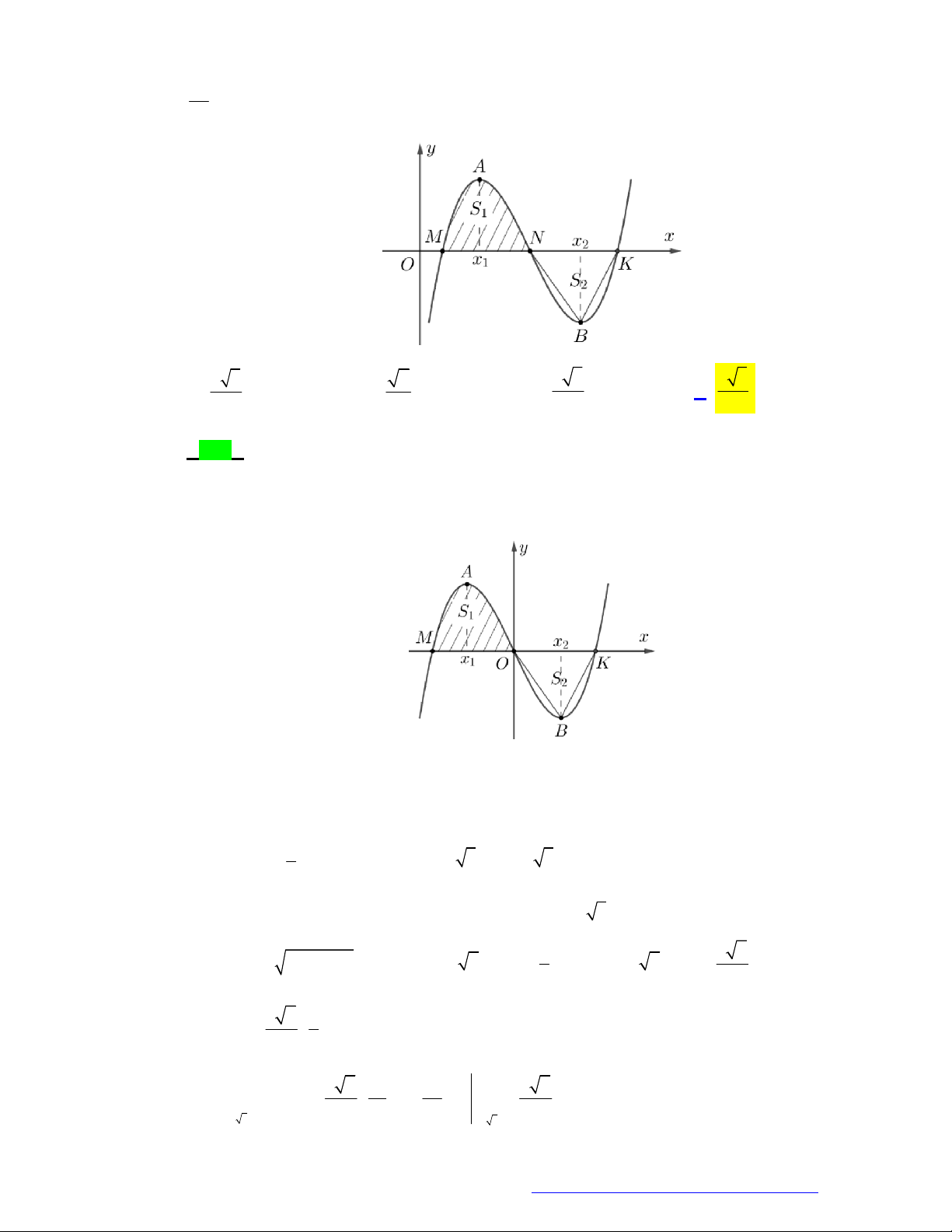
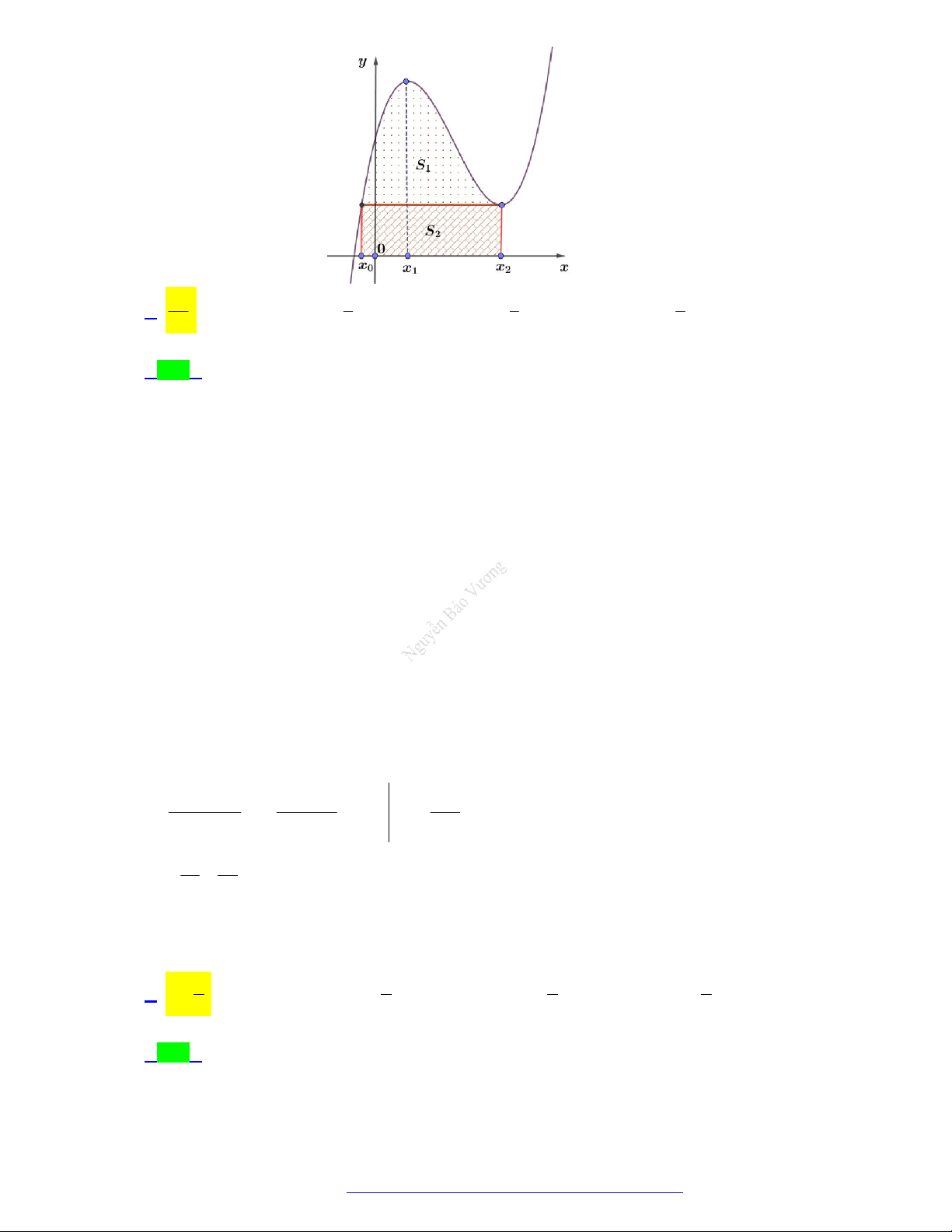
Câu 14. (Chuyên Lam Sơn - Thanh Hóa - 2021) Gọi S là diện tích miền hình phẳng được gạch chéo
trong hình vẽ dưới đây, với y  f  x là hàm số liên tục trên  .
Công thức tính S là 2 2 A. S  
f  x dx  . B. S 
f  x dx  . 1 1 
Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1 2 2 C. S 
f  x dx  f  x dx   . D. S 
f  x dx  . 1 1 1 
Câu 15. (Chuyên KHTN - 2021) 2x  cos xdx  bằng: A. 2
2x  sin x  C . B. 2
2x  sin x  C . C. 2
x  sin x  C . D. 2
x  sin x  C . 3 5 5
Câu 16. (Chuyên KHTN - 2021) Cho
f  x dx  2   và
f  x dx  5  . Tính tích phân
f  x dx  1 3 1 A. 7. B. 3. C. 7  . D. 10.
Câu 17. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Họ tất cả các nguyên hàm của hàm số x
y  e  cos x là A. x
e  sin x  C . B. x
e  sin x  C . C. x
e  sin x  C . D. x
e  sin x  C . 3 4
Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Biết
f  xdx  2  và
f  xdx  3  . Giá trị 0 0 4
f  xdx  bằng 3 A. 1  . B. 5 . C. 5  . D. 1.
Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Gọi  D là hình phẳng giới hạn bởi các đường x thẳng y 
, y  0, x  1, x  4 . Thể tích vật thể tròn xoay tạo thành khi quay  D quanh trục Ox 4
được tính theo công thức nào dưới đây? 4 4 2 x 4 x 4  x  2 x A.  dx  . B.  dx  . C.  dx   . D.  dx  . 16 4  4  4 1 1 1 1
Câu 20. (Chuyên Quốc Học Huế - 2021) Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường y 
x , trục Ox và hai đường thẳng x  1; x  4 quanh trục hoành được tính bởi công thức nào dưới đây? 4 4 4 4 A. 2 V   d x x  . B. V   xdx  . C. V   d x x  . D. V  x dx  . 1 1 1 1 1  4 
Câu 21. (Chuyên Quốc Học Huế - 2021) Tìm họ nguyên hàm của hàm số f  x  trên  \   . 5x  4  5  1 A.
f  x dx 
ln 5x  4  C  . B.
f  x dx  ln 5x  4  C  . ln 5 1 1 C.
f  x dx  ln 5x  4  C  . D.
f  x dx  ln 5x  4  C  . 5 5
Câu 22. (Chuyên Quang Trung - Bình Phước - 2021) Cho hai hàm số f  x , g  x liên tục trên  .
Trong các mệnh đề sau, mệnh đề nào sai?
A. kf  x dx  k f  x dx  
với mọi hằng số k   .
B.  f  x  g  x dx  f  x dx  g  x dx      C.
f  x dx  f  x  C 
với mọi hàm f  x có đạo hàm trên  .
D.  f  x  g  x dx  f  x dx  g  x dx     
Câu 23. (Chuyên Quang Trung - Bình Phước - 2021) Cho hàm số f (x) liên tục và xác định trên  , a b .
Gọi F (x) là một nguyên hàm của hàm số f (x) . Chọn phương án đúng nhất.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 b b A.
f (x)dx  F (b)  F (a)  B.
f (x)dx  F (a)  F (b)  a a b b C.
f (x)dx  F (b)  F (a)  D. 2 2
f (x)dx  F (b)  F (a)  a a
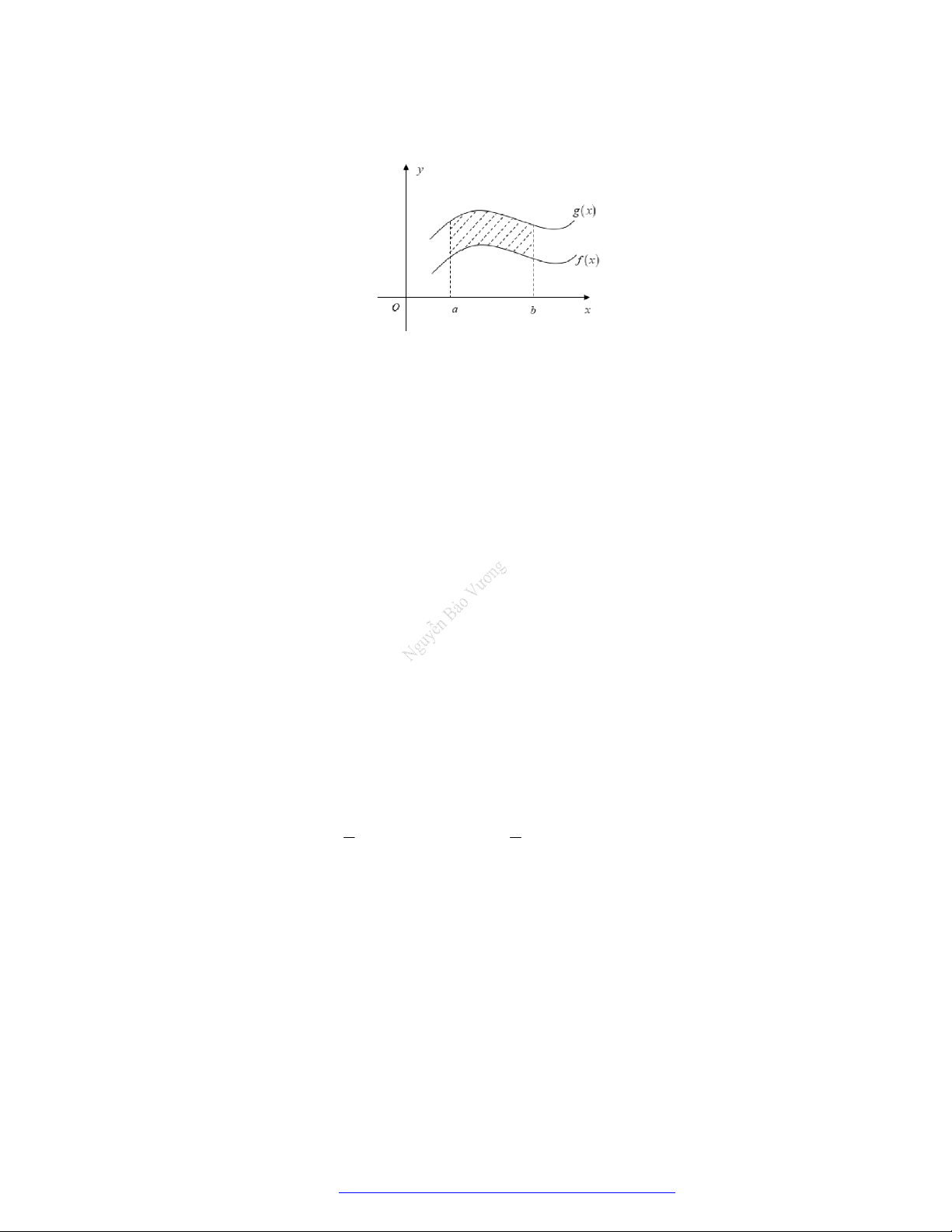
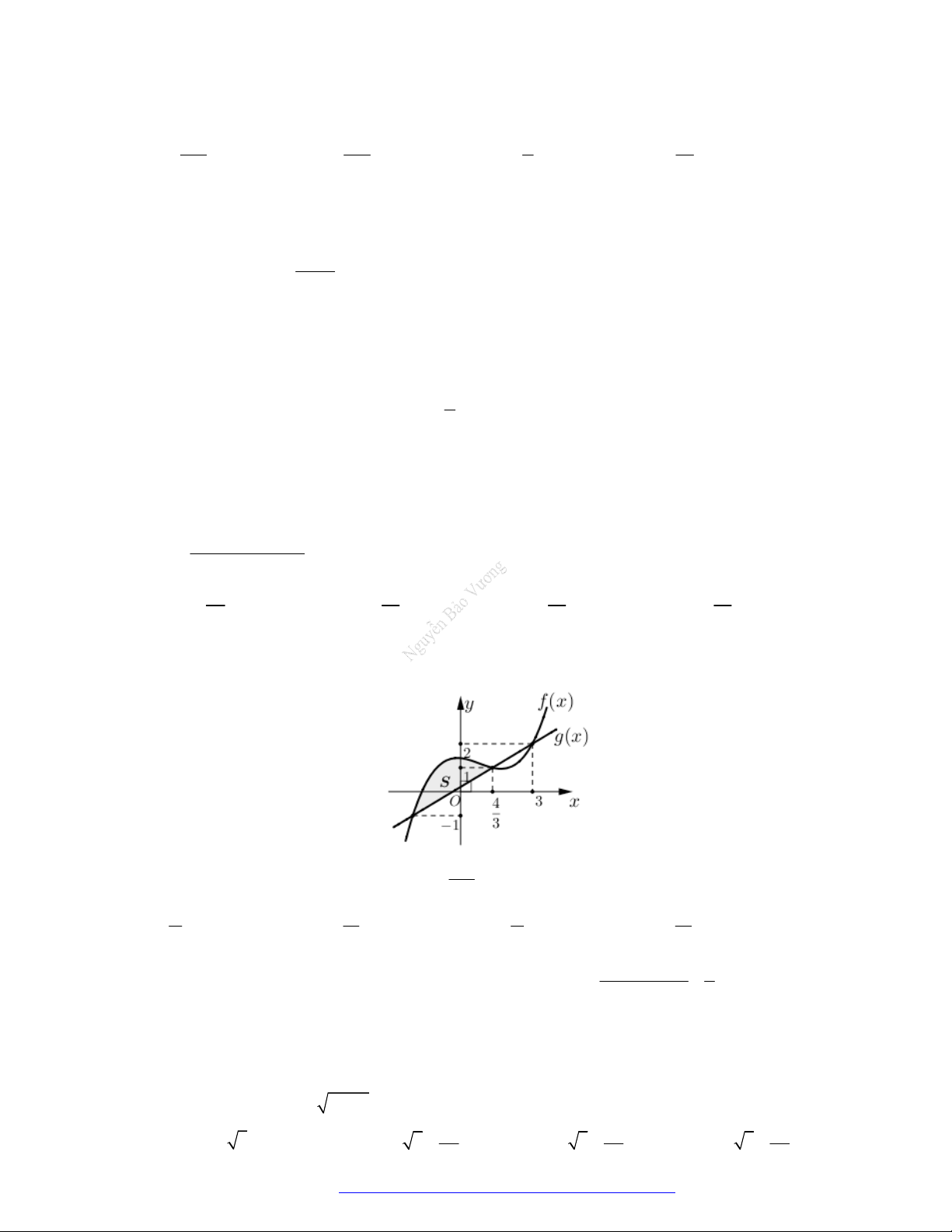
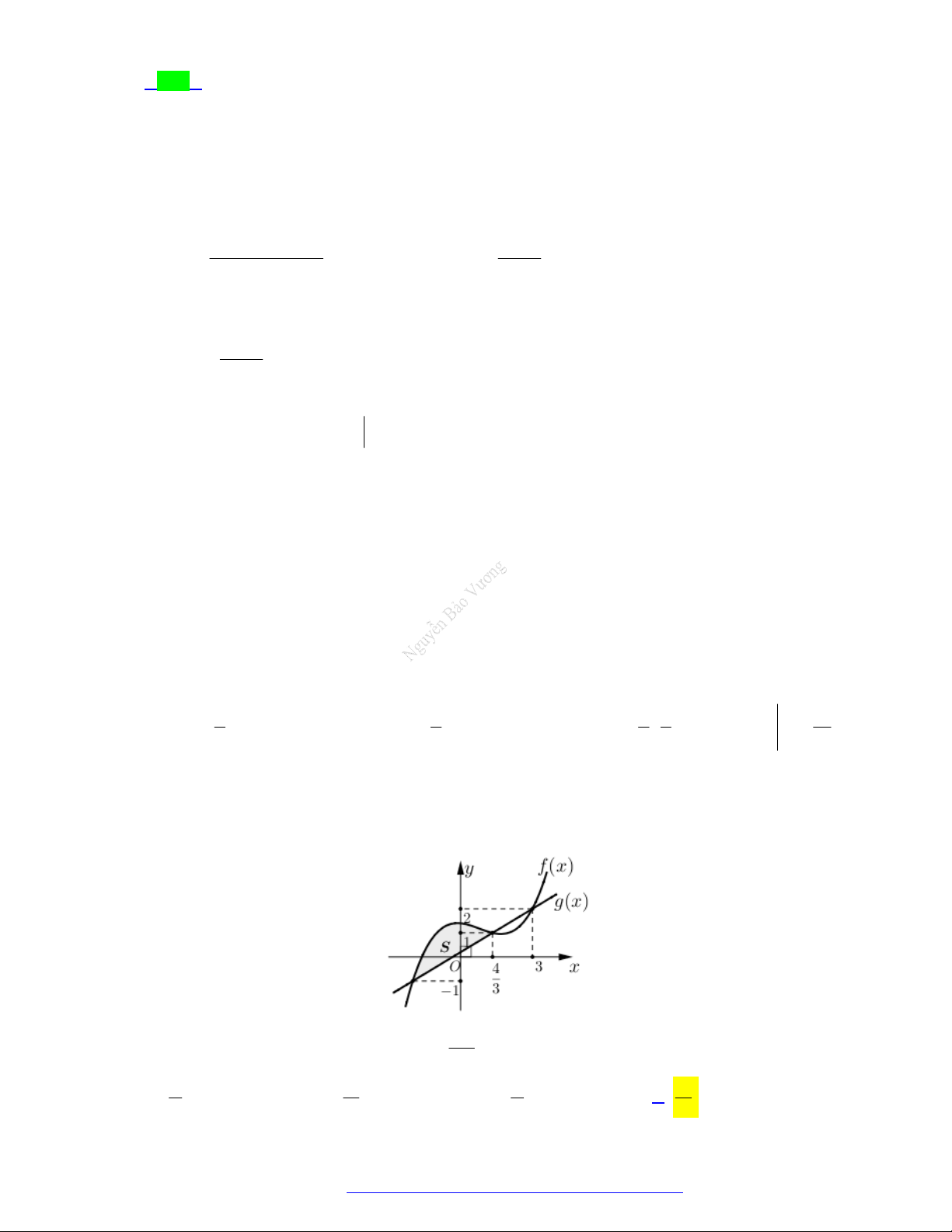
Câu 24. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình  H  được giới hạn như hình vẽ
Diện tích của hình  H  được tính bởi công thức nào dưới đây? b b
A.  g  x  f  x dx    . B.
 f  x  g  x dx    . a a b b C.
f  x dx  . D.
g  x dx  . a a 2
Câu 25. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hàm số f  x thỏa mãn
f  x dx  1  và 0 2 1
f  x dx  4  . Giá trị của
f  x dx  bằng 1 0 A. 5 . B. 3  . C. 5  . D. 3 .
Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hàm số f  x liên tục trên đoạn  2  ; 
3 . Gọi F  x là 3
một nguyên hàm của hàm số f  x trên  2  ;  3 và F 3  2  ; F  2    4  . Tính I  2
f  x dx  . 2  A. 2 . B. 4 . C. 4  . D. 2  2 2
Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho I 
f  x dx  3 
. Khi đó J  4 f  x  3 dx    0 0 bằng: A. 6. B. 8. C. 4. D. 2.
Câu 28. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Kết quả 3 x dx  bằng 1 1 A. 2 3x  C . B. 4 x  C . C. 4 x . D. 4 4x  C . 4 4
Câu 29. (Chuyên Hạ Long - Quảng Ninh - 2021) Biết F  x  cos x là một nguyên hàm của hàm số 
f  x trên  . Giá trị của 3 f  x  2 dx    bằng 0 A. 2 . B. 2 . C. 2  6 . D. 4 . 3 3
Câu 30. (Chuyên Hạ Long - Quảng Ninh - 2021) Biết
f  x dx  5  và
g  x dx  7  . Giá trị của 1 1 3
3 f  x  2g  x dx    bằng 1 A. 29 B. 2  9 C. 1 D. 31 
Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2 2
Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Biết I 
f  x dx  2 
. Giá trị của  f  x  2x dx    bằng 1 1 A. 1. B. 5 . C. 4 . D. 1.
Câu 32. (Chuyên ĐH Vinh - Nghệ An - 2021) Họ các nguyên hàm của hàm số f  x  sin 3x là 1 1
A.  cos 3x  C .
B.  cos 3x  C .
C. cos 3x  C .
D. cos 3x  C . 3 3 1 1 1 4
Câu 33. (Chuyên ĐH Vinh - Nghệ An - 2021) Biết
f  x dx   và
g  x dx  .  Khi đó 3 3 0 0 1
 g x  f  xdx bằng 0 5 5 A. . B.  . C. 1.  D. 1. 3 3
Câu 34. (THPT Quế Võ 1 - Bắc Ninh - 2021) Mệnh đề nào sau đây đúng. 1 1 A.
dx  ln x  C  . B.
dx  cot x  C  . x 2 sin x 1 C. cos d
x x   sin x  C  . D.
dx  tan x  C  . 2 cos x
Câu 35. (THPT Quế Võ 1 - Bắc Ninh - 2021) Khẳng định nào sau đây đúng với mọi hàm f , g liên tục
trên K và a, b là các số bất kỳ thuộc K ? b b b
A.  f  x.g  x dx   f  x .
dx g  xdx      . a a a b b b
B.  f  x  2g  x dx  
f  x dx  2 g  xdx      . a a a b f x dx b    f  x C. a dx   . g  x b a
g  x dx a 2 b b   D. 2
 f  x d  x  f      xdx   . a  a 
Câu 36. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hàm số f  x liên tục trên  và 1 3 3 có
f  x dx  2, 
f  x dx  6  Tính f  x d . x  0 1 0 A. I  12 . B. I  8 . C. I  6 . D. I  4 .
Câu 37. (THPT Quốc Oai - Hà Nội - 2021) Cho hai hàm số y  f  x và y  g  x liên tục trên  .
Trong các mệnh đề sau, mệnh đề nào sai?
A.  f  x  g  x dx  f  x dx  g  x dx      .
B. kf  x dx  k f  x dx  
với mọi hằng số k   \   0 .
C.  f  x  g  x dx  f  x dx  g  x dx      . D.
f  x.g  x dx  f  x .
dx g  x dx    .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 38. (THPT Quốc Oai - Hà Nội - 2021) Cho hàm số y  f  x liên tục trên đoạn a;b . Gọi F  x là
một nguyên hàm của hàm số y  f  x . Hãy chọn khẳng định đúng trong các khẳng định sau b b A.
f  x dx  F a  F b  . B. f  x 2
dx  F b 2  F a  . a a b b C.
f  x dx  F b  F a  . D.
f  x dx  F a  F b  . a a
Câu 39. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho C là một hằng số. Trong các mệnh đề sau, mệnh đề nào sai? A. x x
e dx  e  C  .
B. sin xdx  cos x  C  . 1 C. 2
2xdx  x  C  . D.
dx  ln x  C  . x 1 3 3
Câu 40. (THPT Quảng Xương 1-Thanh Hóa - 2021) Nếu
f  x dx  2  và
f  x dx  4   thì
f  x dx  0 0 1 bằng A. 6 . B. 6 . C. 2 . D. 2 .
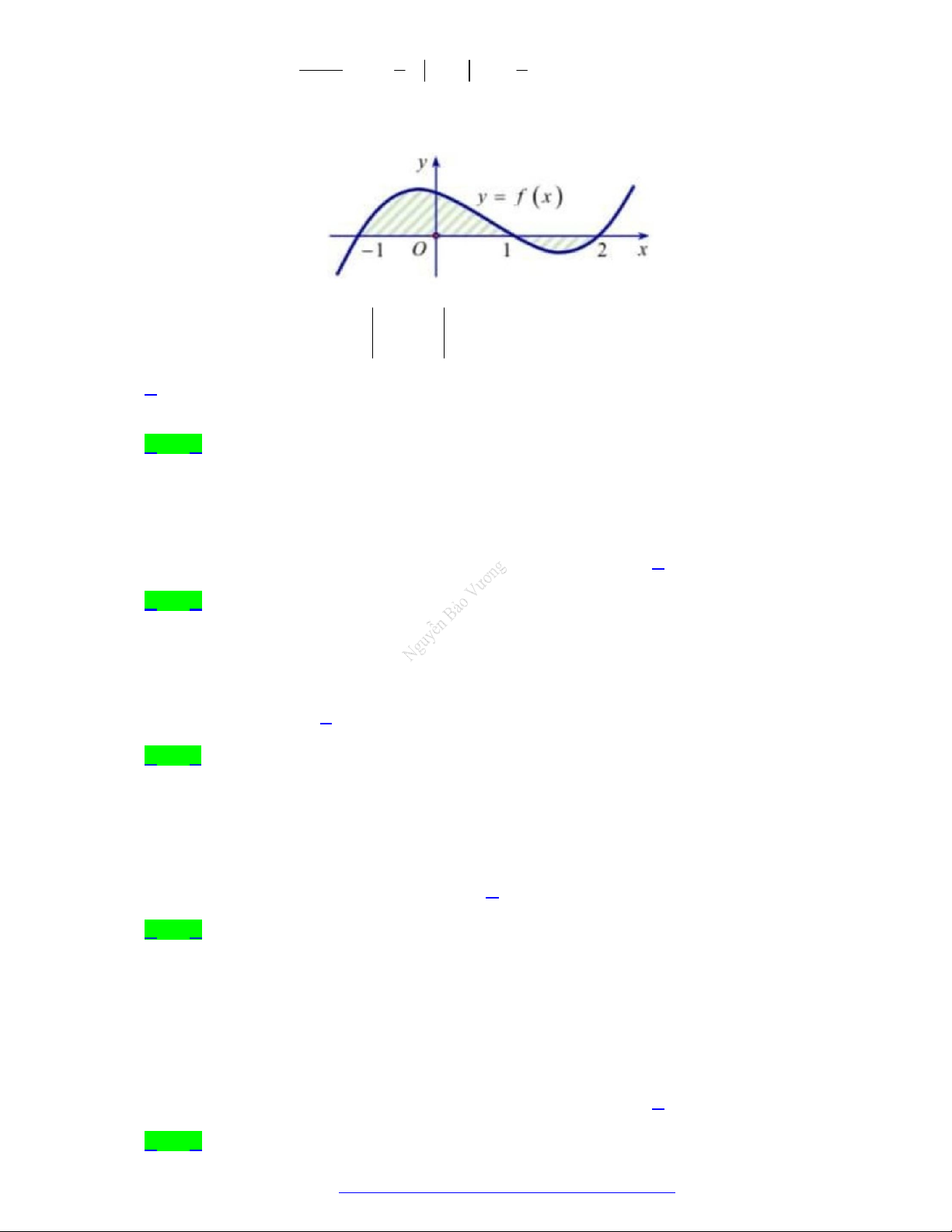
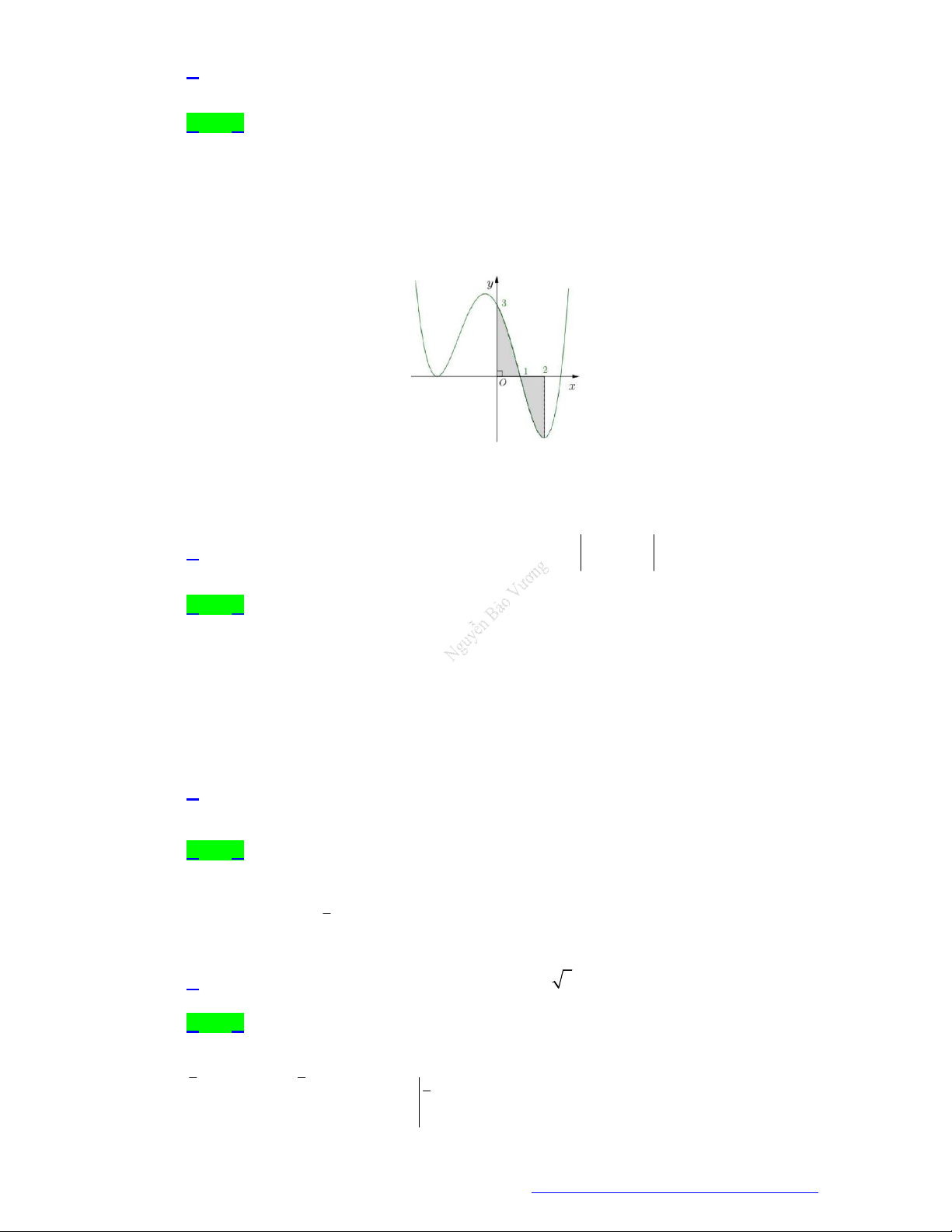
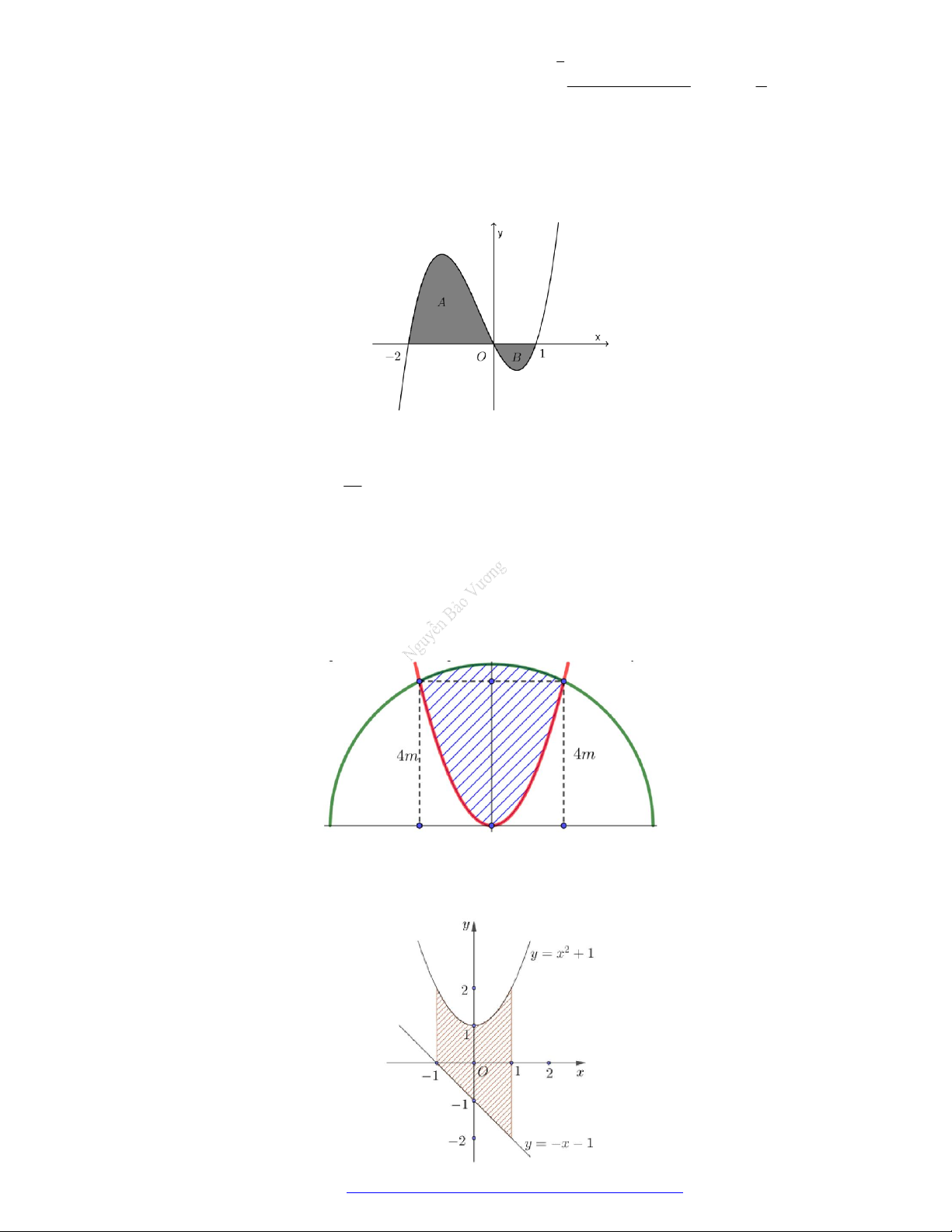
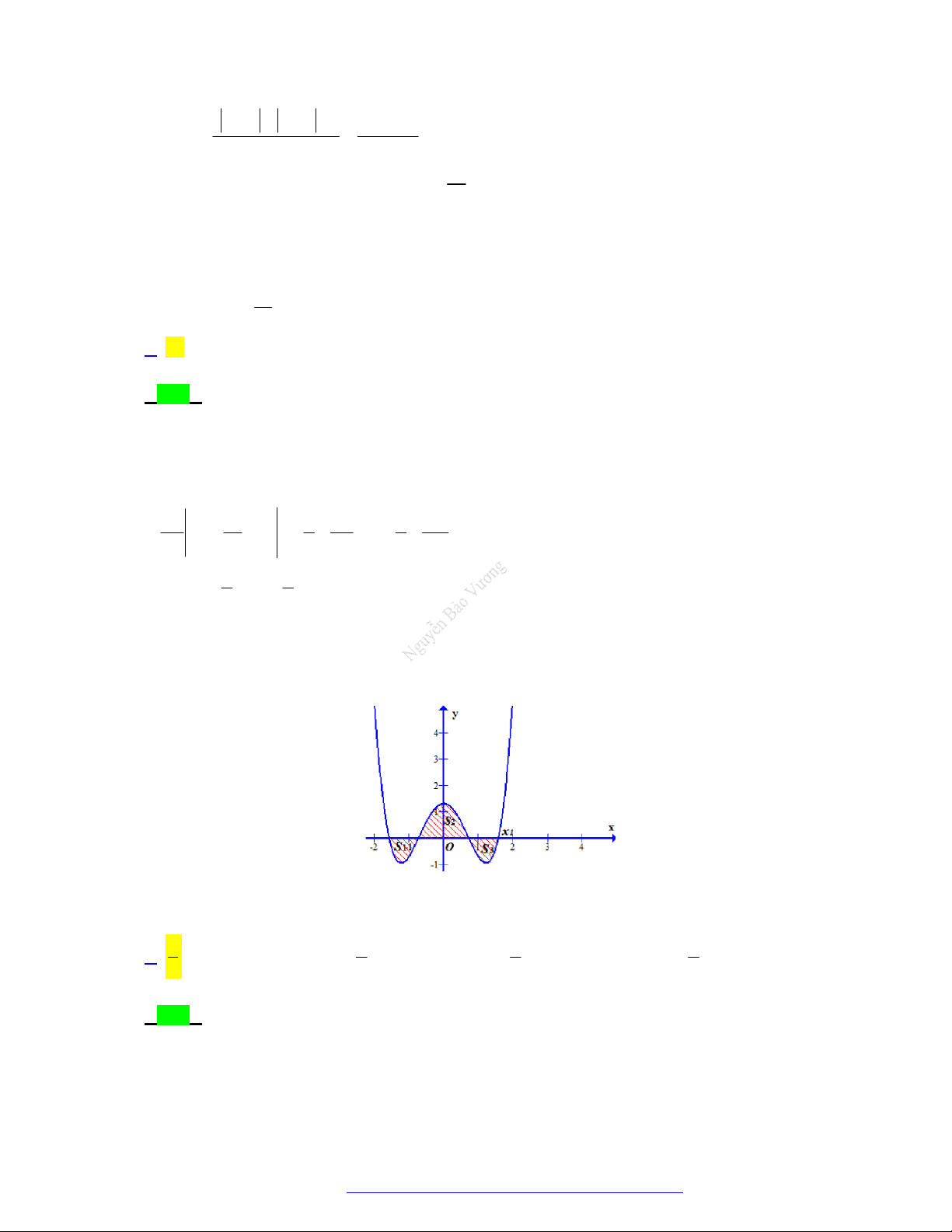
Câu 41. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho đồ thị hàm số y  f  x . Diện tích S của hình
phẳng (phần tô đậm trong hình vẽ) là 1 3 1 3
A. S   f  x dx  f  x dx   . B. S 
f  x dx  f  x dx   . 0 1 0 1 3 1 3 C. S 
f  x dx  . D. S 
f  xdx  f  x dx   . 0 0 1
Câu 42. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Hàm số F  x 3 2
 5x  4x  7x 120 là nguyên hàm
của hàm số nào sau đây?
A. f  x 2
 5x  4x  7 . B. f  x 2
 15x  8x  7 . 2 3 2 5x 4x 7x
C. f  x 2
 5x  4x  7 . D. f  x    . 4 3 2
Câu 43. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Một nguyên hàm của hàm số y  cos2x là 1 1 A. 2sin 2x . B. 2  sin 2x . C. sin 2x . D.  sin 2x . 2 2
Câu 44. (THPT Phan Đình Phùng - Quảng Bình - 2021) Tìm nguyên hàm của hàm số   2021 f x  x trên  . 2022 x A.
f  x dx   . B. f  x 2020 dx  2021x  C  . 2022 2022 x 2021 x C.
f  x dx   C  . D.
f  x dx   C  . 2022 2021
Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1 1
Câu 45. (THPT Phan Đình Phùng - Quảng Bình - 2021) Nếu
f (x)dx  4  và
g(x)dx  3  thì 0 0 1
2 f (x)  3g(x)dx  bằng 0 A. 7 . B. 13 . C. 17 . D. 11.
Câu 46. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hàm số f  x liên tục trên đoạn 0; 2 . Biết 2 2 1
f  xdx  5  và
f t  dt  3.  Tính I 
f  xdx  . 0 1 0 A. I  3 . B. I  2 . C. I  5 . D. I  1.
Câu 47. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho F  x là một nguyên hàm của hàm số 1  2  f  x  trên khoảng ;  
 . Tìm F  x , biết F   1  5 . 3x  2  3 
A. F  x  ln 3x  2  5 .
B. F  x  3ln 3x  2  5 . 3 1
C. F  x 
 8 . D. F  x  ln 3x  2  5 . 3x  22 3 1 1
Câu 48. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho biết
f  x d x  2  và
g  x d x  3  . Tính 0 0 1
I  4 f  x  g  x d x    ? 0 A. I=3 . B. I=1. C. I=11. D. I=5 . 3 5 4 3
Câu 49. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Biết
f  x dx   và
f t  dt   . Tính 3 5 0 0 4
f u du  3 14 16  17 16 A. . B. . C.  . D. . 15 15 15 15
Câu 50. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình phẳng  D được giới hạn bởi các
đường f  x  2x  1,Ox, x  0, x  1 . Tính thể tích V của khối tròn xoay tạo thành khi quay
D xung quanh trục Ox được tính theo công thức? 1 1 1 1 A. V   2x  1dx  .
B. V  2x   1 dx  .
C. V   2x   1 dx  . D. V  2x  1dx  . 0 0 0 0 2 2
Câu 51. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Nếu
f  x dx  6 
thì 3 f  x dx  bằng 0 0 A. 3. B. 6. C. 8. D. 18.
Câu 52. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Khẳng định nào sau đây là đúng 1 A.
dx   cot x  C  . B. x x
a dx  a .ln a  C 2  . cos x x 1 1 1 C. e dx   C  . D. dx    C x  . e 2 x x
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 2
Câu 53. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Tính tích phân   3 x  2 x d bằng 1 9 9 7 7 A.  . B. . C. . D.  . 4 4 4 4 2
Câu 54. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Biết
f  x dx  4  . Tính tích phân 0 2
I  2x  f  x dx    bằng 0 A. I  6 . B. I  12 . C. I  8 . D. I  4 .
Câu 55. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hàm số f (x)  x  1. Trong các khẳng định
sau, khẳng định nào đúng ? 1 A. 2
f (x)dx  x  x  C  . B. 2
f (x)dx  2x  x  C  . 2 C. 2
f (x)dx  x  x  C  . D. 2 f (x) x
d  x  C  .
Câu 56. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Họ các nguyên hàm của hàm số f  x 2  3x 1 là. 3 x A. 3
x  x  C .
B. 6x  C . C. 3 x  C . D.  x  C . 3 5 5
Câu 57. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Biết
f  x dx  4 
. Giá trị của 3 f  x dx  bằng. 1 1 4 A. 7 . B. . C. 64 . D. 12 . 3
Câu 58. (THPT Đồng Quan - Hà Nội - 2021) Họ nguyên hàm của hàm số   ln x f x  là x 1 1 A. 2 ln x  C . B. 2 ln x C .
C. lnln xC . D. 2
ln x  ln x  C . 2 2
Câu 59. (THPT Đồng Quan - Hà Nội - 2021) Họ nguyên hàm của hàm số f  x  2cos 2x  x là 1 1 A. 2  sin 2x 
x  C . B. 2
 sin 2x  x  C . 2 2 1 1 C. 2 sin 2x 
x  C . D. 2
sin 2x  x  C . 2 2 1 0
Câu 60. (THPT Đồng Quan - Hà Nội - 2021) Cho
f  x dx  3; g  x dx    2, khi đó 0 1 1
 f x  2g xdx bằng bao nhiêu? 0 A. 5 . B. 7  . C. 1. D. 1  .
Câu 61. (THPT Lê Lợi - Thanh Hóa - 2021) Nguyên hàm của hàm số 2
y  x  x là 3 2 x x 3 x A.   C .
B. 2x 1  C . C. 2
x  x  C . D.  x  C . 3 2 3
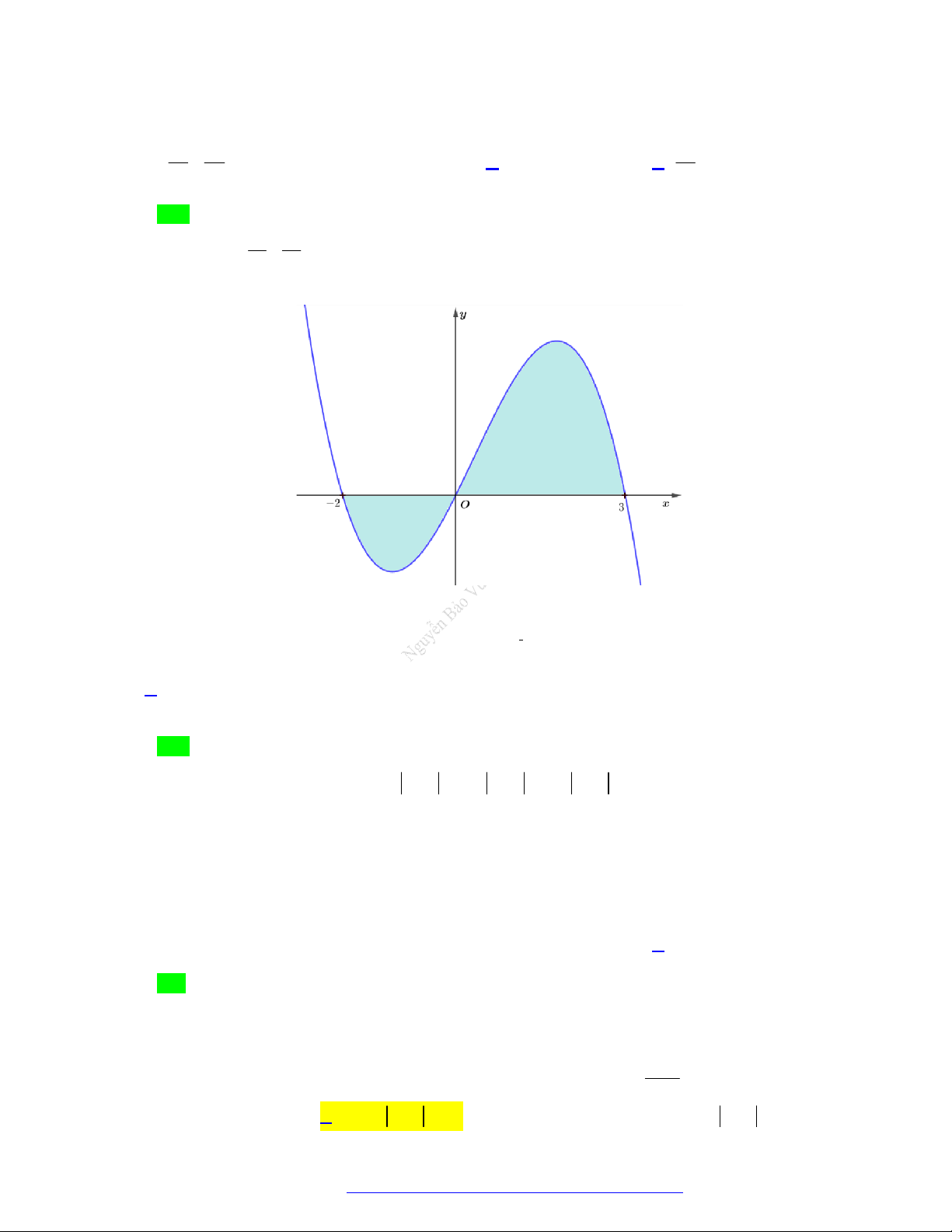
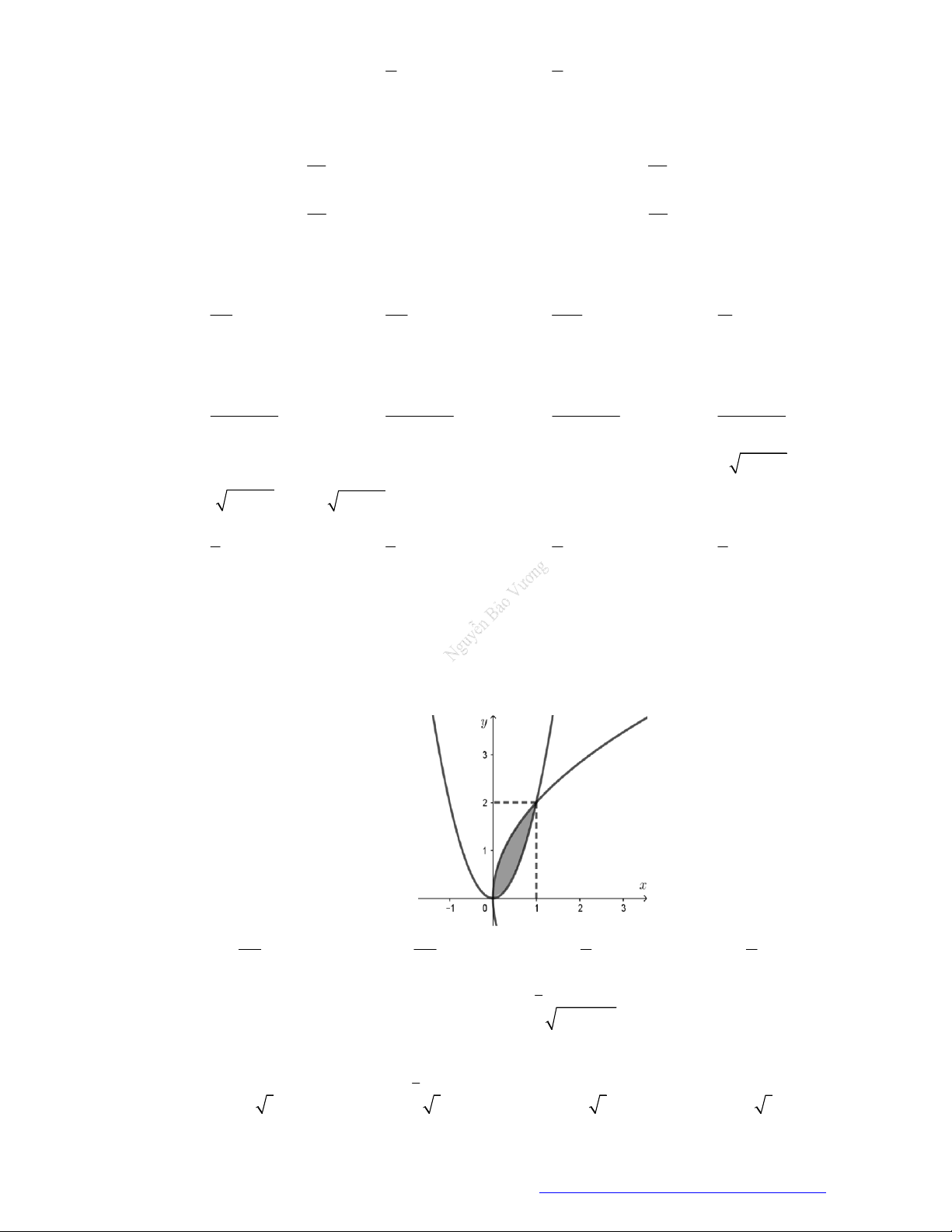
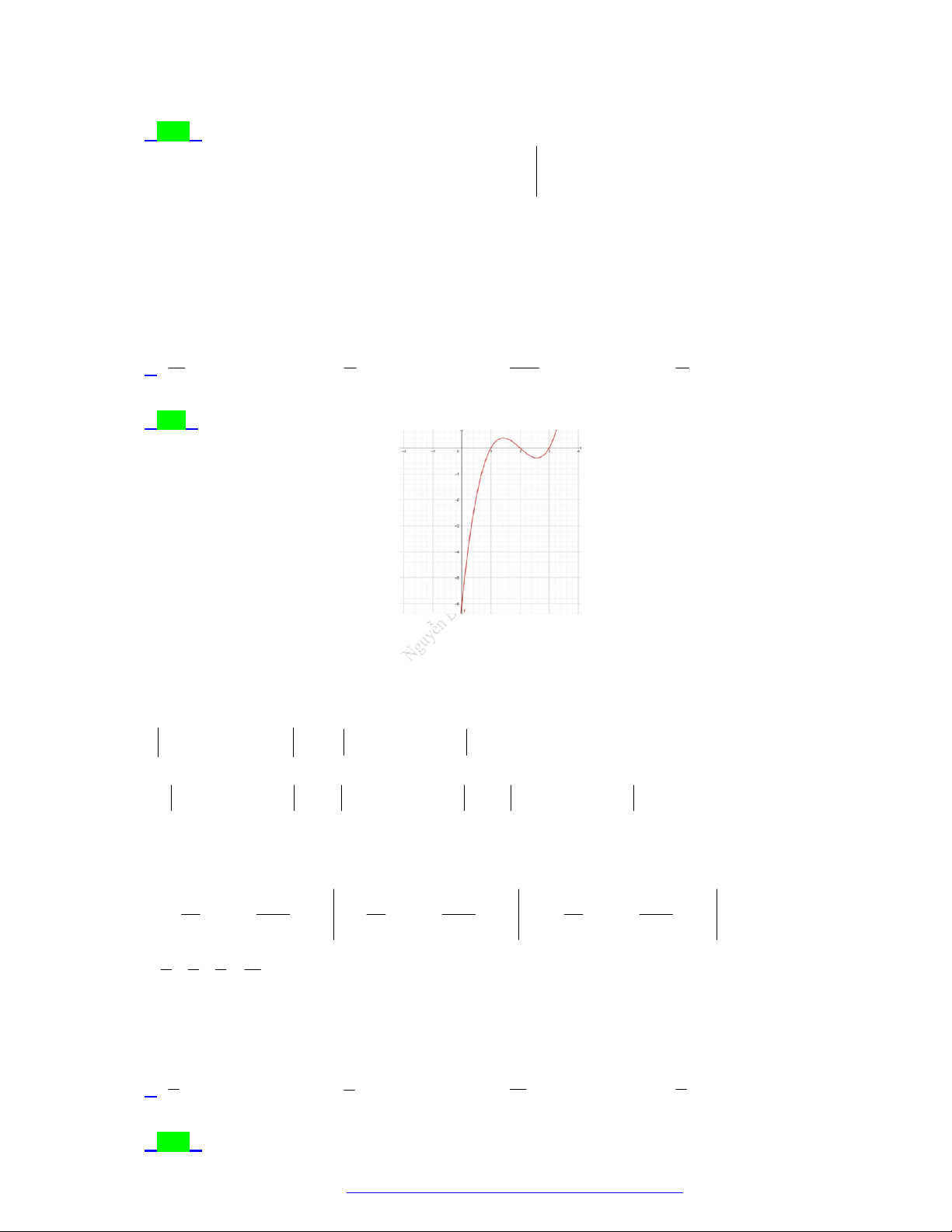
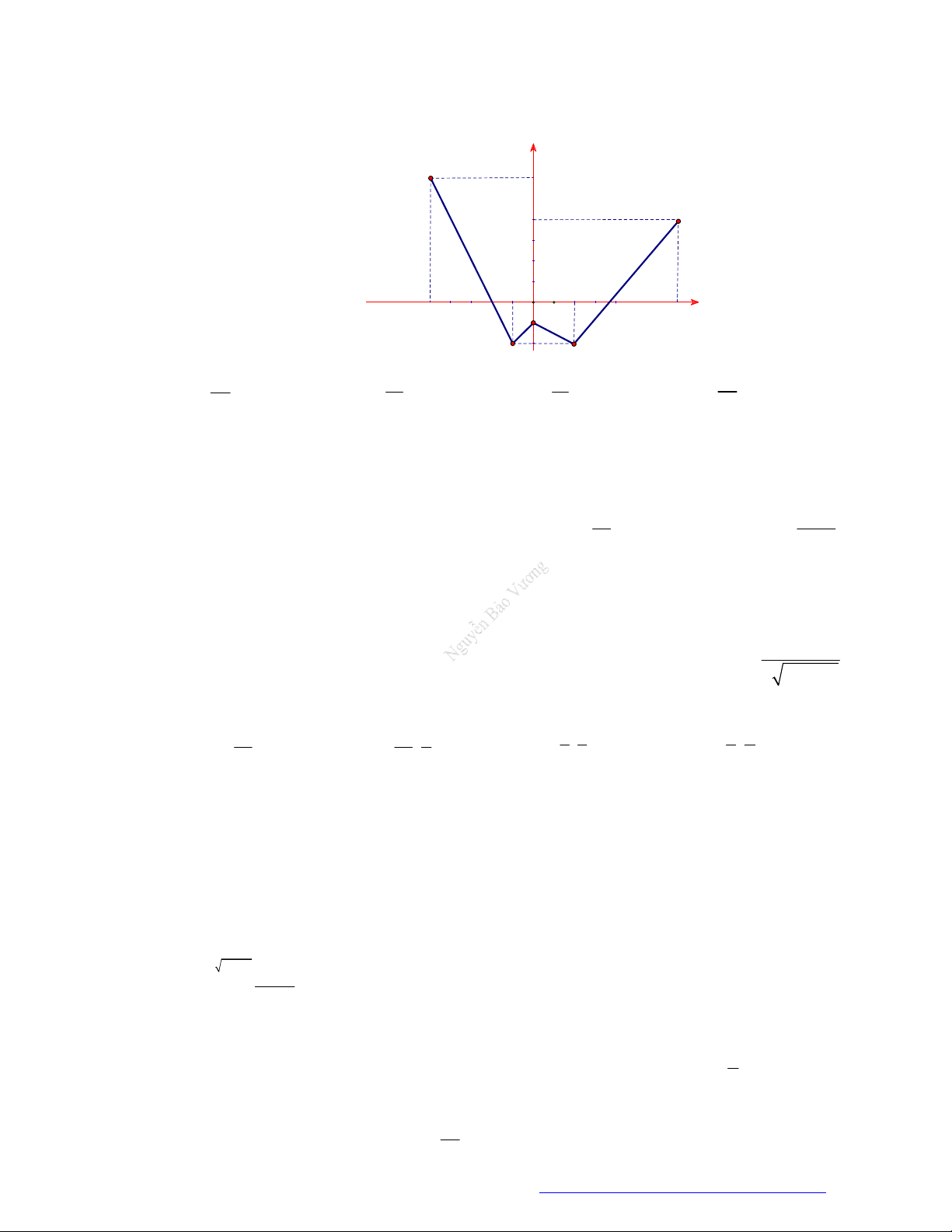
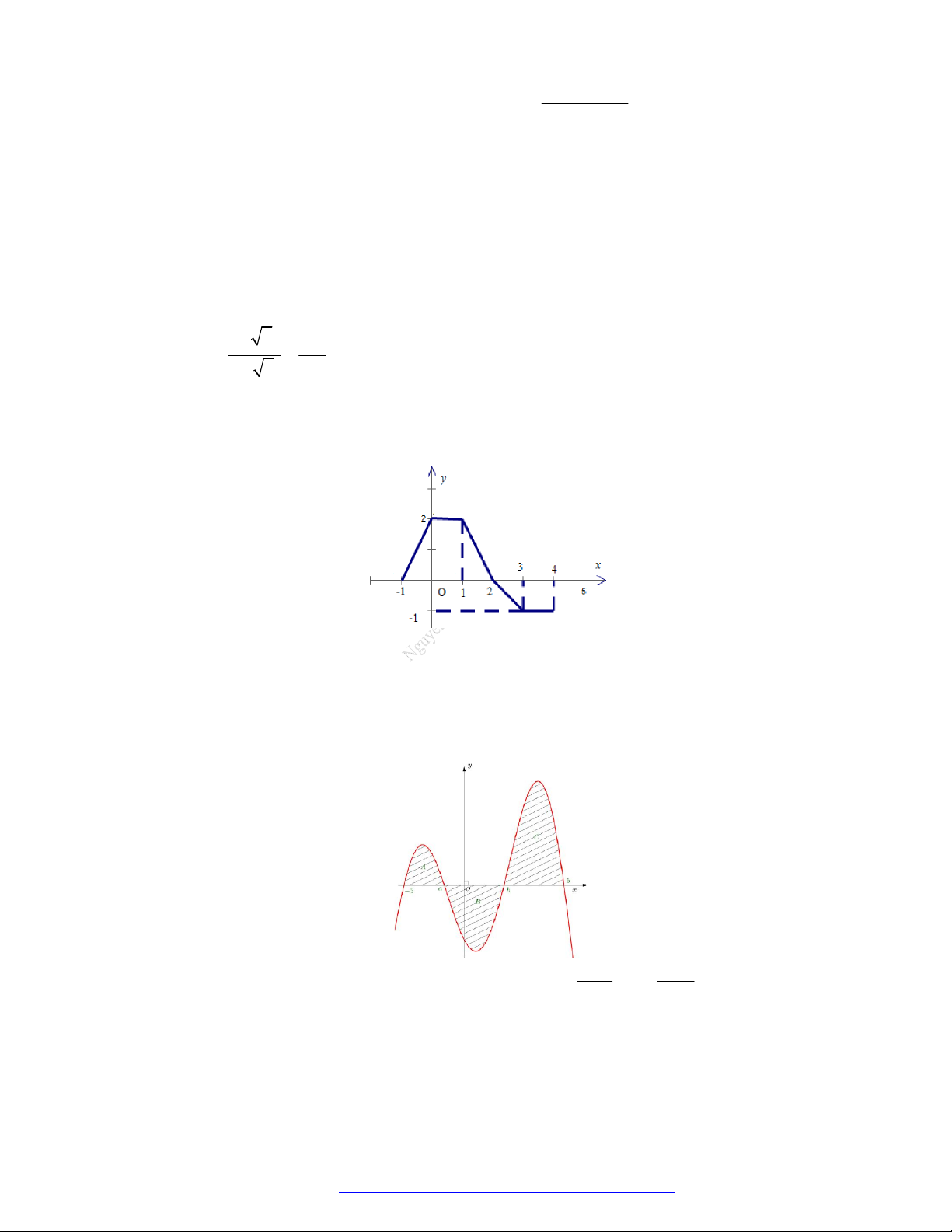
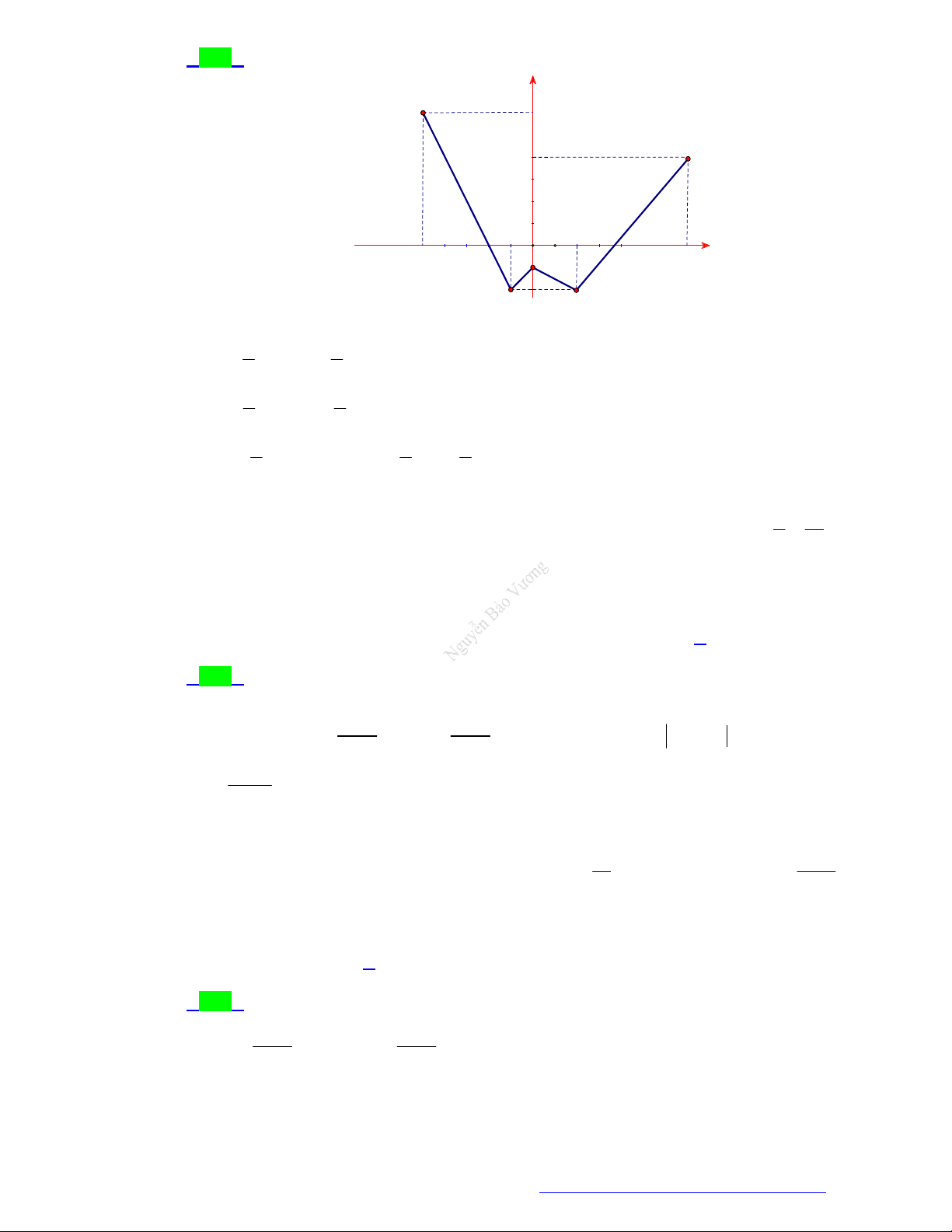
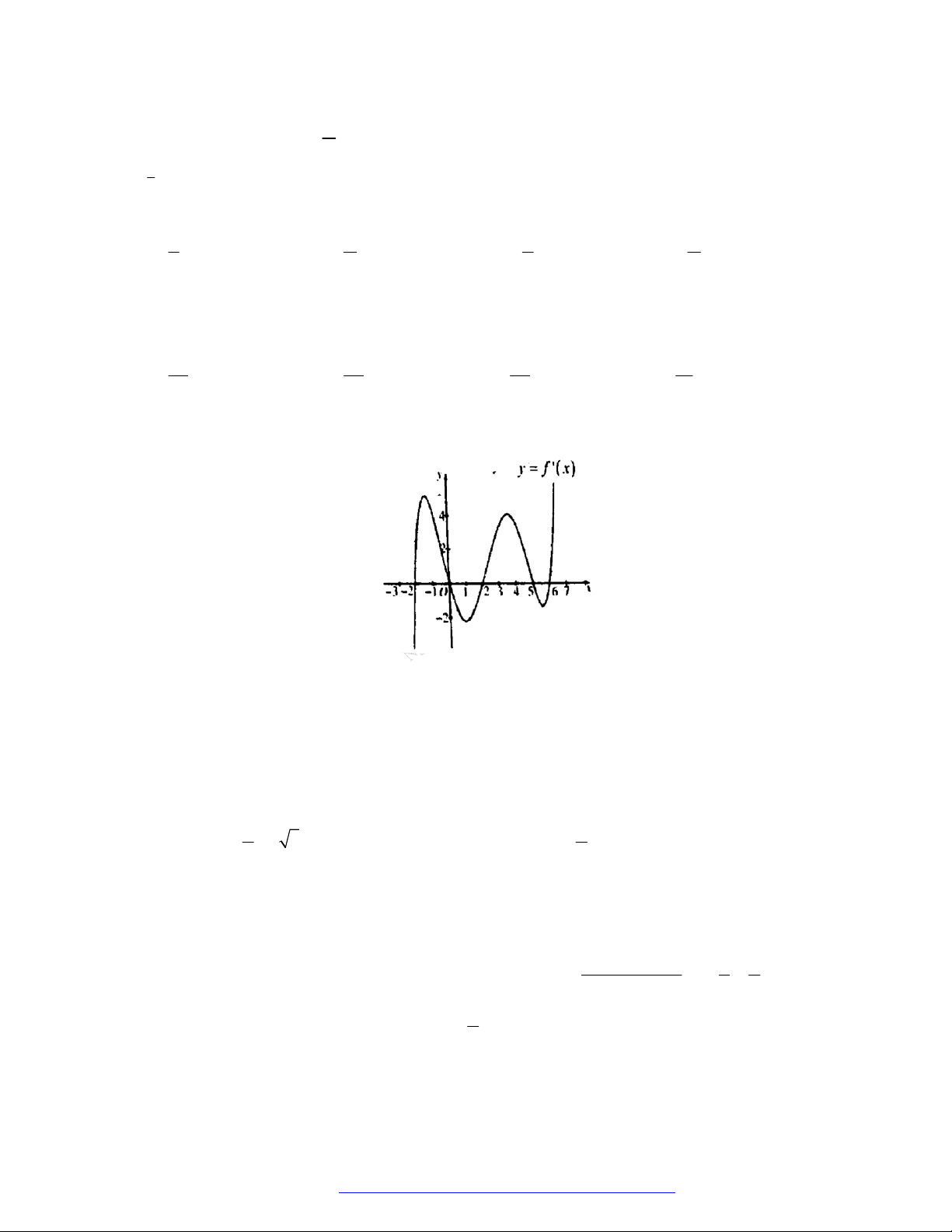
Câu 62. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hàm số y  f (x) có đồ thị như hình vẽ.
Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Diện tích hình phẳng (phần tô đậm) được tính theo công thức nào sau đây? 3 0 3 A. S  f (x) . dx  . B. S 
f (x)dx  f (x)d . x   . 2  2  0 0 3 0 3 C. S  
f (x)dx  f (x)d . x   . D. S 
f (x)dx  f (x) . dx   2  0 2  0
Câu 63. (THPT Lê Lợi - Thanh Hóa - 2021) Cho các hàm số y  f  x, y  g  x liên tục trên  có 5 5 5
f  x dx  1   ;
g  x dx  3 
. Tính  f  x  2g  x dx    . 1 1 1 A. 2 . B. 1. C. 1. D. 5 . x
Câu 64. (Sở Vĩnh Phúc - 2021) Tìm họ tất cả các nguyên hàm của hàm số y  . x 1
A. x  ln x   1  C .
B. x  ln x 1  C .
C. x  ln x  
1  C . D. x  ln x 1  C .
Câu 65. (Sở Lào Cai - 2021) Khẳng định nào sau đây là đúng?  
A.  f  xdx 
   f x .
B.  f  xdx 
  f x .  
C.  f  xdx 
   f x.
D.  f  xdx 
  f x. 2 2
Câu 66. (Sở Lào Cai - 2021) Cho
f  x x  1  d
, khi đó 3 f  x x  d bằng 1 1 A. 2 . B. 1. C. 4 . D. 3 . 1
Câu 67. (Sở Lào Cai - 2021) Tích phân exdx  bằng: 0 e 1 A. e . B. 2 e 1. C. . D. e-1 . 2 1
Câu 68. (Sở Lào Cai - 2021) Họ các nguyên hàm của hàm số f  x   là: 2 sin x
A. cot x  C .
B.  tan x  C .
C.  cot x  C .
D. tan x  C . 5 5
Câu 69. (Sở Hà Tĩnh - 2021) Biết
f  xdx  4 
. Giá trị của 2x  3 f  x d  x    bằng 1 1 A. 13 . B. 2  . C. 6 . D. 12 .
Câu 70. (Sở Hà Tĩnh - 2021)  3 2
 x  x  dx bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 A. 4 x  C . B. 4 2
x  x  C . C. 2
3x  2  C . D. 4 2
4x  x  C . 4 4
Câu 71. (Sở Yên Bái - 2021) Trong các khẳng định sau, khẳng định nào sai?
A. 0dx  C 
( C là hằng số).
B. dx  x  C 
( C là hằng số). 1  1   x C.
dx  ln x  C 
( C là hằng số).
D. x dx   C 
( C là hằng số). x  1 1
Câu 72. (Sở Tuyên Quang - 2021) Nguyên hàm của hàm số f  x  là 2x 1
A. F  x  ln 2x 1  C . B. F  x  2ln 2x 1  C . 1 1
C. F  x  ln(2x 1)  C .
D. F  x  ln 2x 1  C . 2 2 1 1 1
Câu 73. (Sở Tuyên Quang - 2021) Cho
f  x dx  2  và
g  x dx  5  . Khi đó
 f  x  2g  x dx     0 0 0 bằng: A. 1 B. -3 C. -8 D. 12
Câu 74. (Sở Tuyên Quang - 2021) Họ tất cả các nguyên hàm của hàm số f  x  2x  sin x là A. 2
2x  cos x  C . B. 2
2x  cos x  C . C. 2
x  cos x  C . D. 2
x  cos x  C .
Câu 75. (THPT Thanh Chương 1- Nghệ An - 2021) Họ nguyên hàm của hàm số là? A. . B. . C. . D. . 2 2
Câu 76. (THPT Thanh Chương 1- Nghệ An - 2021) Cho 3 f  x  2x dx  12    . Khi đó
f  x dx  bằng 1 1 A. . B. . C. . D. .
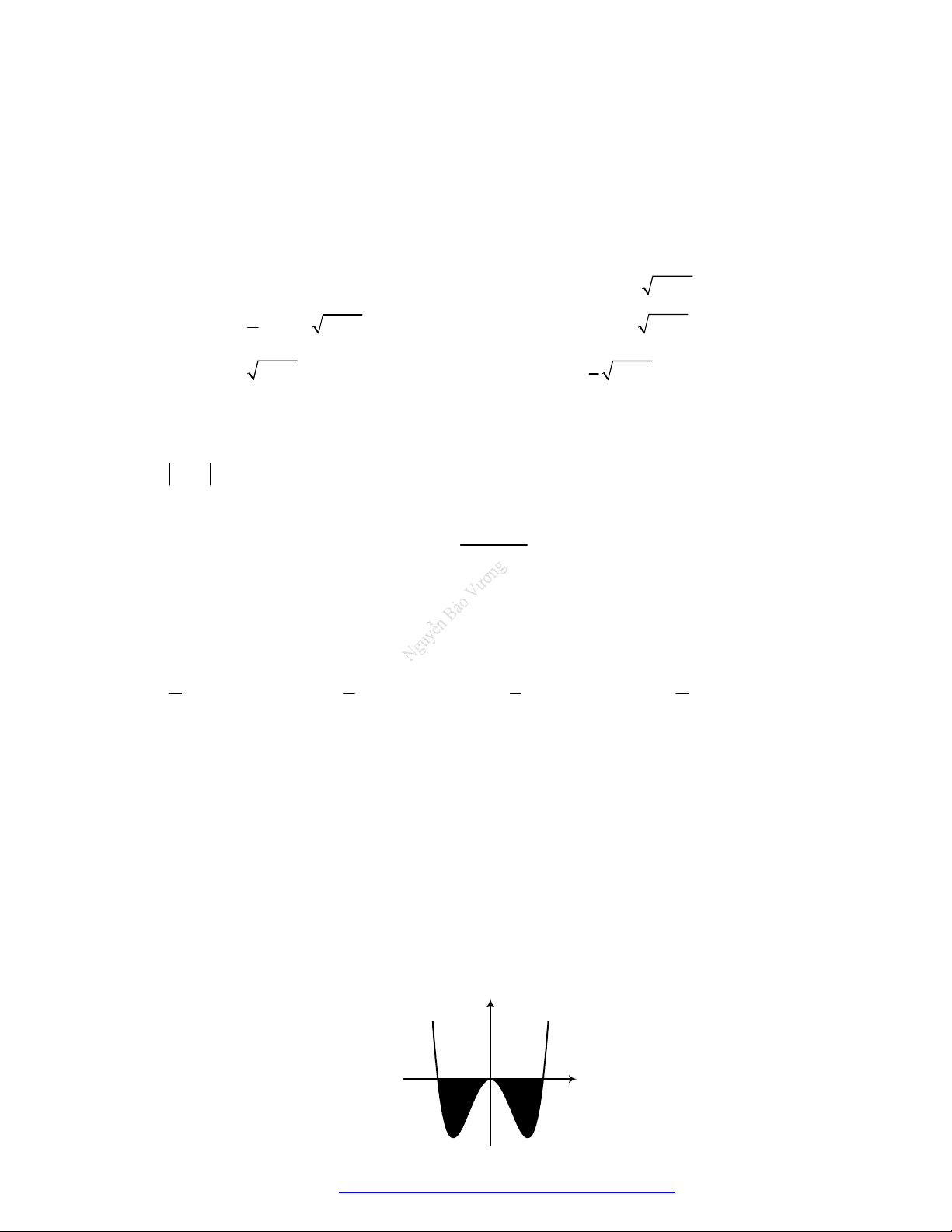
Câu 77. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số y  f  x liên tục trên  và có đồ thị
C là đường cong như hình vẽ bên.
Diện tích của hình phẳng giới hạn bởi đồ thị C  , trục Ox và hai đường thẳng x  0, x  2 (phần tô đen) là 1 2 2 A. S  
f  xdx 
f  xdx   . B. S 
f  xdx  . 0 1 0 1 2 2 C. S 
f  xdx 
f  xdx   . D. S 
f  xdx  . 0 1 0
Câu 78. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số f  x liên tục trên đoạn  ; a b . Khẳng
định nào sau đây sai?
Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 b b b a b
A.  f  x  g  x dx  f  x dx  g  x dx      . B.
f  x dx   f  x   . a a a b a b b b b b
C.  f  x.g  x dx  f  x .
dx g  x dx      .
D. k. f  x dx  k f  x dx   . a a a a a
Câu 79. (THPT Nguyễn Huệ - Phú Yên - 2021) Biết F  x  cos x là một nguyên hàm của hàm số f  x  3
trên  .Giá trị của 2 f  xdx  bằng 0 A. 1  . B. 3 . C. 3 . D. 1. 3 3
Câu 80. (THPT Nguyễn Huệ - Phú Yên - 2021) Biết
f  xdx  3 
.giá trị của  f x  3dx bằng 2 2 A. 6 . B. 3 . C. 9 . D. 5 .
Câu 81. (THPT Lương Thế Vinh - 2021) Diện tích hình phẳng giới hạn bởi các đường 2
y  x  4 và
y  x  4 xác định bởi công thức 2 1 1 2 A.  2
x  x  dx . B.  2
x  x dx . C.  2
x  x  dx . D.  2
x  xdx . 0 0 0 0
Câu 82. (THPT Lương Thế Vinh - 2021) Họ nguyên hàm của hàm số   3x f x  là. 3x 3x
A. 3x log 3  C .
B. 3x ln 3  C . C.  C . D.  C . ln 3 log 3
Câu 83. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hai hàm số f  x , g  x liên tục trên đoạn  ;
a b và số thực k tùy ý. Mệnh đề nào dưới đây sai? b c c b a A.
f  x dx  f  xdx  f  x d , x c   ; a b   
. B. f  x dx   f  x dx   . a a b a b b b b b b
C. kf  x dx  k f  x dx   .
D.  f  x  g  x dx  f  x dx  g  x dx      . a a a a a
Câu 84. (THPT Đào Duy Từ - Hà Nội - 2021) Họ các nguyên hàm của hàm số f  x 2
 x  2x  3 là 3 x A. 2
 x  3x  C .
B. 2x  2  C . C. 3 2
x  x  C . D. 3 2
x  2x  3x  C . 3
Câu 85. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hàm số y  f  x có đạo hàm trên đoạn 1;  2 , 2 f  
1  1 và f 2  2 . Khi đó, I  f  x dx  bằng 1 7 A. I  1. B. I  1  . C. I  . D. I  3 . 2
Câu 86. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Thể tích của khối tròn xoay sinh bởi hình phẳng giới 
hạn bởi hai đồ thị hàm số y  cos x , đường thẳng x  0 , x 
và trục Ox khi quay quanh trục 2 hoành là     A. 2 V  cos d x x  . B. 2 2 V  cos dx x  . C. 2 V   cos d x x  . D. 2 2 V   cos d x x  . 0 0 0 0
Câu 87. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Họ nguyên hàm của hàm số f  x 3 2
 x  3x là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 4 3 x x 4 x A. 4 3
x  x  C . B.   C . C. 3  x  C . D. 2
3x  6x  C . 4 3 4 2 2
Câu 88. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho f  x x d  2  và g  x x d  3  . Tích phân 0 0 2
2 f  x  g  x x d    0 A. 5 . B. 7 . C. 1  . D. 1.
Câu 89. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hàm số y  f  x xác định, liên tục và không âm trên  ;
a b . Thể tích của vật thể tròn xoay sinh bởi miền  D giới hạn bởi đồ thị hàm số
y  f  x , trục hoành và hai đường thẳng x  a, x  b quay quanh Ox là b b b b A. 2 V 
f  x dx  . B. V 
f  x dx  . C. 2 V  
f  x dx  . D. V  
f  x dx  . a a a a 0 2
Câu 90. (THPT Chu Văn An - Thái Nguyên - 2021) Nếu
f  x dx  6  và
g  x dx  2  thì 2 0 2
f  x dx  bằng 2 A. 8 . B. 12  . C. 8 . D. 4 .
Câu 91. (THPT Ba Đình - Thanh Hóa - 2021) Nguyên hàm của hàm số   3 f x  x là 3 4 2 3 x 3 x x
A. x dx   C  .
B. x dx   C  . C. 3 x dx   C  . D. 3 4
x dx  4x  C  . 3 4 2 8 8
Câu 92. (THPT Ba Đình - Thanh Hóa - 2021) Biết
f  x dx  3 
, giá trị 5 f  x dx  bằng 1 1 A. 3 . B. 8 . C. 15 . D. 6 . 4
Câu 93. (THPT Ba Đình - Thanh Hóa - 2021) Cho I  x 2x 1dx 
và u  2x 1 . Mệnh đề nào dưới 0 đây sai: 3 1 3 1 A. 2 2 I 
x (x 1)dx  . B. 2 2 I 
u (u 1)du  . 2 2 1 1 3 5 3 1  u u  3 C. I   2 2   .
D. I  u (u 1)du  . 2 5 3   1 1
Câu 94. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số f  x liên tục trên  và a là số
dương. Trong các khẳng định sau, khẳng định nào đúng? a a a a A.
f  xdx  1  . B.
f  xdx  0  . C. f  x 2 dx  a  . D.
f  xdx  2a  . a a a a
Câu 95. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Nguyên hàm của hàm số 2 x 1 y e   là 1 1 A. 2  x 1 2e   C. B. 2  x 1 2e    C. C. 2  x 1 e   C. D. 2  x 1 e    C. 2 2
Câu 96. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số
f  x thoả mãn    2021x f x
ln 2021 cos x và f 0  2 . Phát biểu nào sau đúng?
Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2021x
A. f  x   sin x 1. B.    2021x f x  sin x 1. ln 2021 2021x C.    2021x f x  sin x 1.
D. f  x   sin x 1. ln 2021
Câu 97. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Tìm nguyên hàm của 6 5x dx  . 5 5 6 A. 7 x  C . B. 7
x  C . C. 7
x  C . D. 7 x  C . 6 7 5
Câu 98. (Trung Tâm Thanh Tường - 2021) Cho f x , g x là các hàm số xác định và liên tục trên  .
Trong các mệnh đề sau, mệnh đề nào sai? A.
f x g xdx  f x . dx
g xdx    . B.
2 f xdx  2
f xdx   . C.
 f x gx dx  f xdx gxdx      D.
 f x gx dx  f xdx  gxdx      . 2 2 2
Câu 99. (Trung Tâm Thanh Tường - 2021) Nếu
f (x)dx  5,
g ( x)dx  2  
thì  f (x)  2g(x)dx  bằng 0 0 0 A. 3 . B. 9 . C. 7 . D. 1.
Câu 100. (Trung Tâm Thanh Tường -2021) Họ nguyên hàm của hàm số    2 x f x x  e  là A. 2 x xe  C . B. 2  2 x x e  C . C. 2 2
x  e  C . D. 2 2 x x  e  C .
Câu 101. (THPT Triệu Sơn - Thanh Hóa - 2021) Họ tất cả các nguyên hàm của hàm số f  x 2  3x 1 là.
A. 6x  C . B. 2
3x  x  C . C. 3
x  x  C . D. 3 x  C . 3 3
Câu 102. (THPT Triệu Sơn - Thanh Hóa - 2021) Biết
f  x dx  4  
khi đó 2 f  x dx  bằng 1 1 A. 2. B. 2  . C. 8. D. 8  .
Câu 103. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hàm số y  f  x xác định và liện tục trên đoạn  ;
a b . Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f  x , trục hoành và hai đường thẳng x  ;
a x  b được tính theo công thức b b a b A. S 
f  x dx  . B. S 
f  x dx  . C.
f  x dx  . D.
f  x dx  . a a b a
Câu 104. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho f  x 2
dx  6x  2sin 2x  C 
, khi đó f  x bằng
A. 12x  4 cos 2x . B. 3 2x  cos 2x .
C. 12  2cos2x .
D. 6x  4cos2x . 3 5 5
Câu 105. (THPT Trần Phú - Đà Nẵng - 2021) Nếu
f  x dx  3  và
f  x dx  2  thì
f  x dx  bằng 1  3 1 A. 5  . B. 5. C. 1  . D. 1. BẢNG ĐÁP ÁN 1.C 2.B 3.A 4.A 5.C 6.C 7.B 8.A 9.C 10.B 11.A 12.C 13.B 14.C 15.D 16.B 17.C 18.D 19.C 20.C 21.C 22.A 23.A 24.A 25.C 26.B 27.A 28.B 29.C 30.A 31.B 32.A 33.D 34.D 35.B 36.B 37.D 38.C 39.B 40.B 41.B 42.B 43.C 44.C 45.C 46.B 47.D 48.D 49.B 50.C 51.D 52.C 53.B 54.C 55.A 56.A 57.D 58.A 59.D 60.B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 61.C 62.C 63.D 64.B 65.D 66.D 67.D 68.A 69.D 70.B 71.D 72.D 73.C 74.C 75.B 76.A 77.C 78.C 79.A 80.A 81.C 82.C 83.A 84.A 85.A 86.D 87.C 88.D 89.C 90.D 91.B 92.C 93.D 94.B 95.D 96.B 97.B 98.A 99.B 100.B 101.C 102.D 103.D 104.A 105.B
Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 3
NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG MỨC ĐỘ NHẬN BIẾT 6 4 Câu 1.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho
f  x dx  10  và
f  x dx  7  0 0 6 thì
f  x dx  bằng: 4 A. 17  . B. 17 . C. 3 . D. 3  . Lời giải Chọn C 6 6 4
f  x dx  f  x dx  f  x dx  10  7  3    . 4 0 0 Câu 2.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Họ các nguyên hàm của hàm số f  x 4 2
 5x  6x 1 là 4 x A. 3
 2x  2x  C . B. 5 3
x  2x  x  C . 4 C. 5 3
20x 12x  x  C . D. 3
20x 12x  C . Lời giải Chọn B Ta có:  4 2 x  x   5 3 5 6
1 dx  x  2x  x  C. 0 1 Câu 3.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) dx  bằng 1 x 3  A. 2ln 2 . B. 2  ln 2 . C. 2 ln 2 1 . D. ln 2 . Lời giải Chọn A 0 0 1 1 0 Ta có: dx  
d 1 x   ln 1 x
  ln1 ln 4  2 ln 2   . 3 1 x 1 x  3  3  e  1 1  Câu 4. Tính tích phân I   dx  2   x x  1 1 1 A. I  B. I  1
C. I  1
D. I  e e e Lời giải Chọn A e e  1 1   1  1 I   dx  ln x    . 2     x x   x  e 1 1 Lời giải Chọn A Câu 5.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Giả sử f là hàm liên tục trên khoảng
K và a, b, c là ba số bất kì trên khoảng K . Khẳng định nào sau đây sai? b b c b b A.
f (x) dx  f (t) dt   . B. f (x) dx
f (x) dx  f (x) dx, c  a,b    . a a a c a
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 b b a C. f (x) dx 1   . D.
f (x) dx   f (x) dx   . a a b Lời giải Chọn C Câu 6.
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Nguyên hàm của hàm số f  x    x5 1 2 là: 1 1 A.   6 1 2x  C .
B.  1  2x6  C . C. 
1 2x6  C . D.   6 5 1 2x  C . 2 12 Lời giải Chọn C 5 1 5 1 6 Ta có
f  xdx  1  2x dx   1  2x d 1  2x  
1 2x  C    . 2 12   2 2 Câu 7.
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho
f  xdx  5 
. Tính I   f  x  2sin x d  x    0 0  A. I  5  . B. I  7 .
C. I  5   . D. I  3 . 2 Lời giải Chọn B Ta có    2 2 2    
I   f  x  2sin x d  x  I  f  x 2 dx  2sin d x x  5  2 cos      | x  5  2 cos  cos 0  7   . 0  2  0 0 0 8 4 4 Câu 8.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Biết
f  x dx  2   ;
f  x dx  3 
; g  x dx  7  . 1 1 1
Mệnh đề nào sau đây sai? 8 4 4 A.
f  x dx  g  x dx  8   .
B.  f  x  g  x dx  10    . 4 1 1 8 4 C.
f  x dx  5   .
D. 4 f  x  2g  x dx  2     . 4 1 Lời giải Chọn A
Mệnh đề ở phương án A là sai vì: 8 4 8 4 4
f  x dx  g  x dx  f  x dx  f  x dx  g  x dx  2  3  7  2      . 4 1 1 1 1 Câu 9.
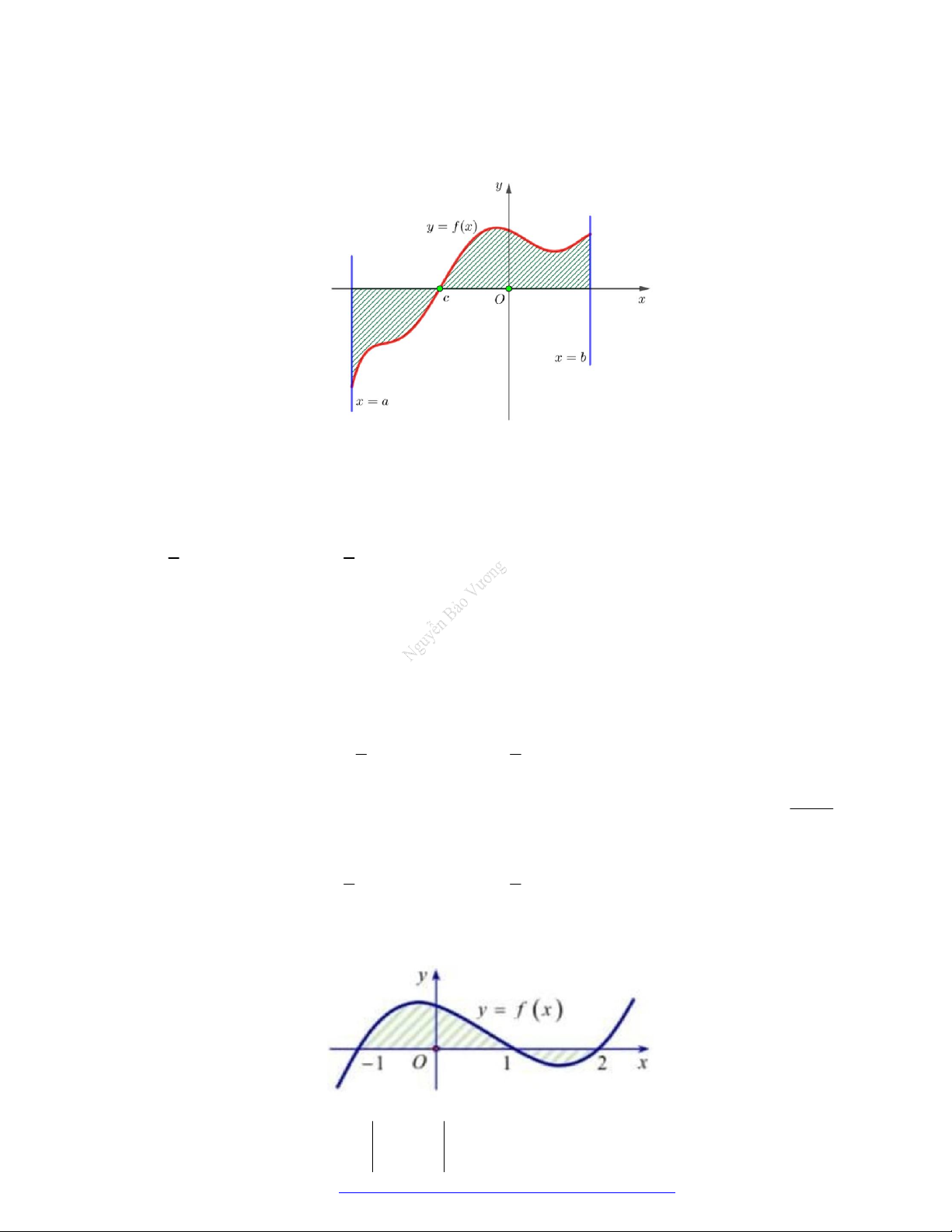
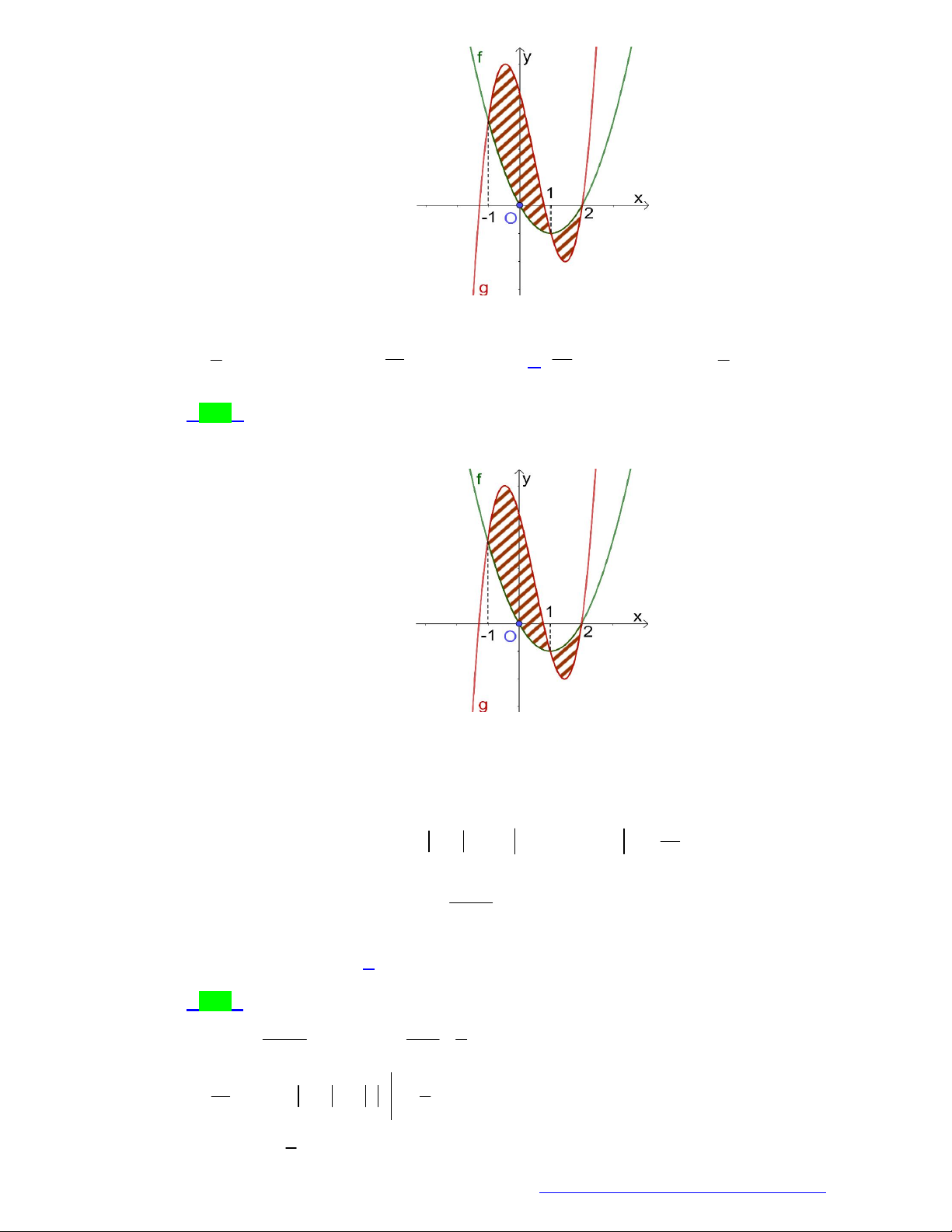
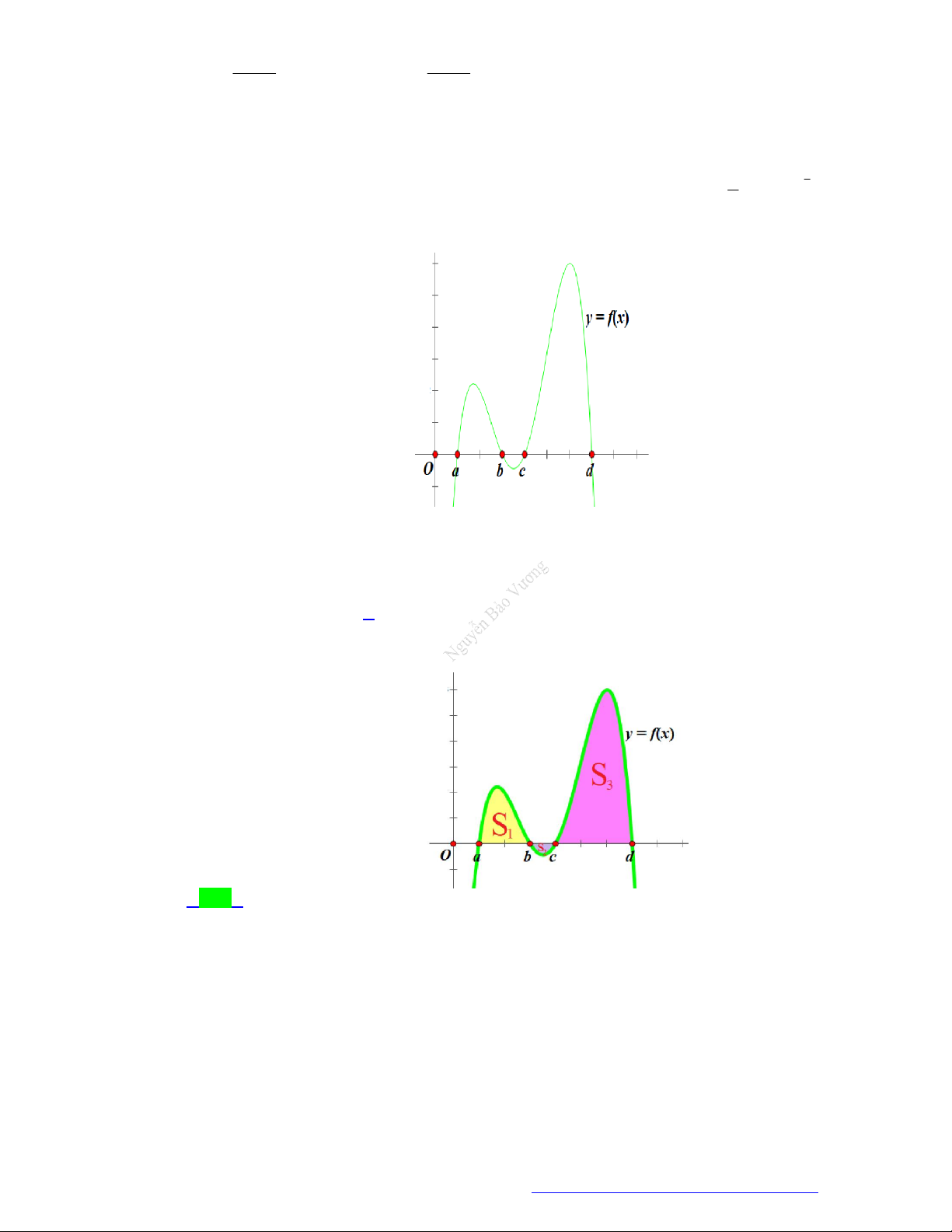
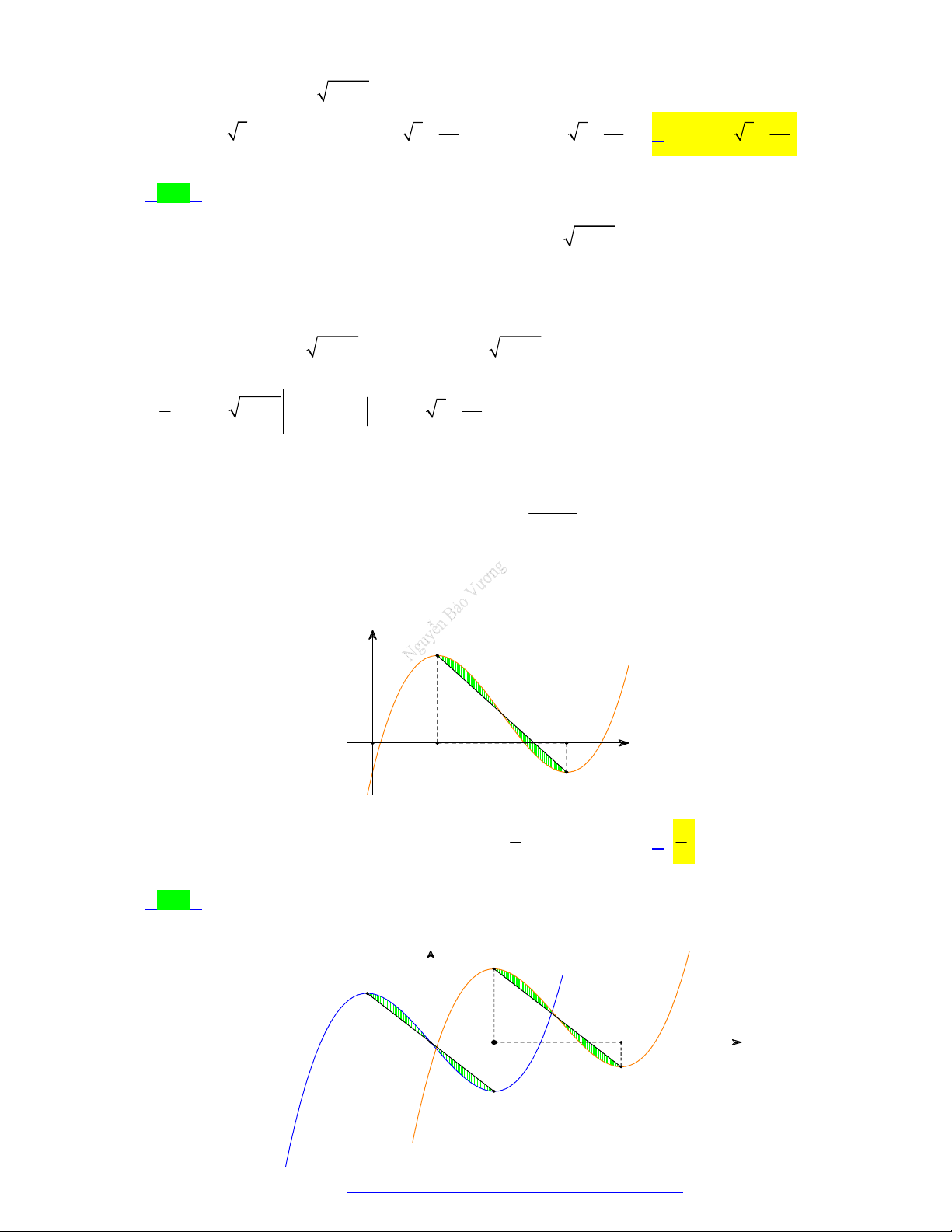
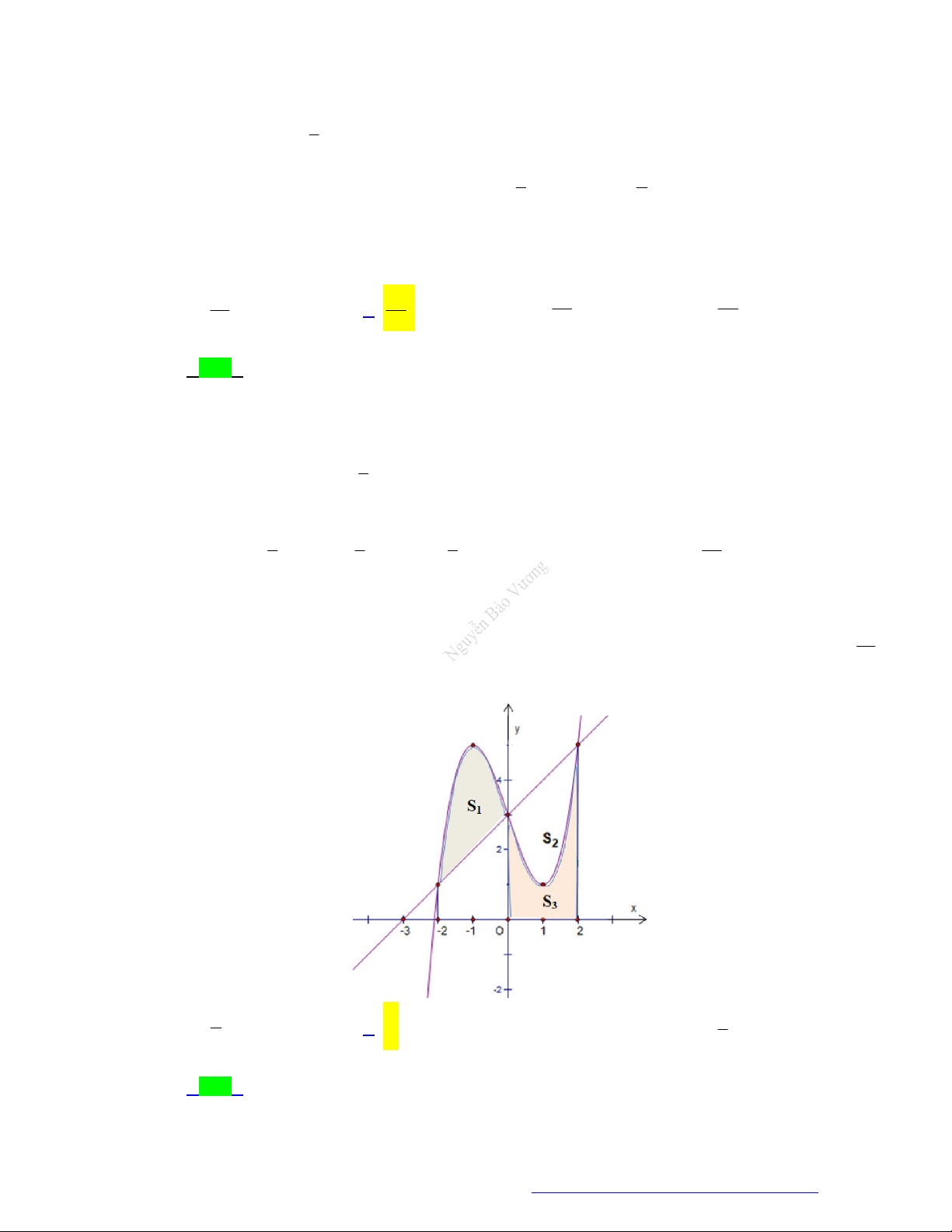
(Chuyên Lê Hồng Phong - TPHCM - 2021) Hình phẳng giới hạn bởi đồ thị hàm số y  f  x ,
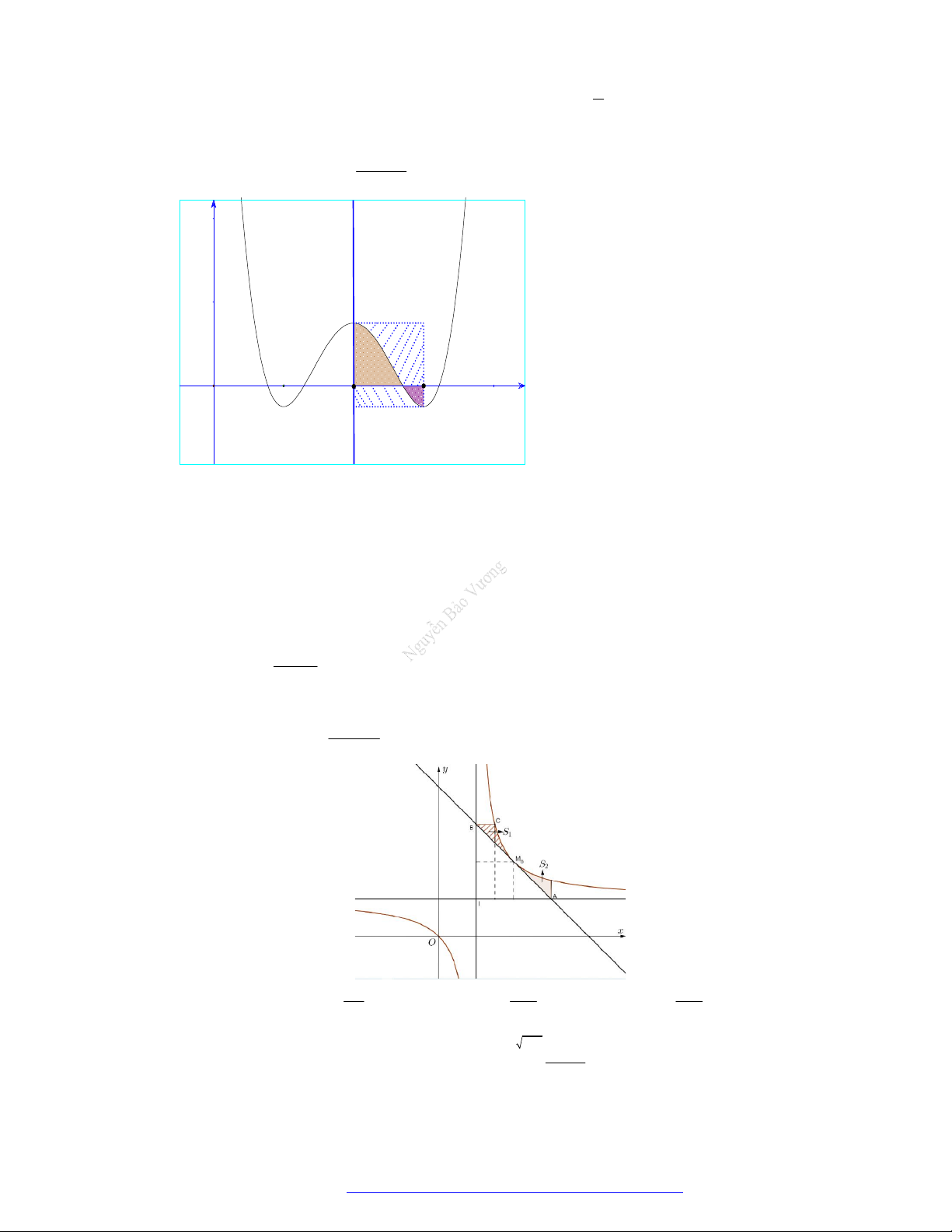
trục hoành và hai đường thẳng x  a , x  b trong hình dưới đây (phần gạch sọc) có diện tích S bằng
Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 c b c b A.
f  x dx 
f  x dx   . B.
f  x dx 
f  x dx   . a c a c c b c b C. 
f  x dx 
f  x dx   . D. 
f  x dx 
f  x dx   . a c a c Lời giải Chọn C c S    b c b
0  f  xdx    f x  0dx   f  xdx  f xdx   . a c a c
Câu 10. (Chuyên Lê Hồng Phong - TPHCM - 2021) Họ nguyên hàm của hàm số   2 x f x  e là 1 1 A. x e  C . B. 2 x e  C . C. 2 2 x e  C . D. 2 x e  C . 2 2 Lời giải Chọn B x 1 Ta có 2 2 dx = x e e  C  . 2
Câu 11. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hàm số f  x có f 2  2 , f 3  5 ; hàm số 3
f  x liên tục trên 2; 
3 . Khi đó f  x dx  bằng 2 A. 3 . B. 10 . C. 3  . D. 7 . Lời giải Chọn A 3 3
f  x dx  f  x  f 3  f 2  5  2  3  . 2 2
Câu 12. (Chuyên Lam Sơn - Thanh Hóa - 2021) Họ tất cả nguyên hàm của hàm số f  x  cos 2x là 1 1
A. 2sin 2x  C .
B.  sin 2x  C . C. sin 2x  C . D. 2
 sin 2x  C . 2 2 Lời giải Chọn C 1 1
f  x dx  cos 2x dx =
cos 2x d 2x  sin 2x  C    2 2 2
Câu 13. (Chuyên Lam Sơn - Thanh Hóa - 2021) Họ tất cả các nguyên hàm của hàm số f  x  4x  3
trên khoảng 1;  là 1 1
A. 2 ln 4x  3  C . B.
ln 4x  3  C . C. ln 4x  3  C . D. 4 ln 4x  3  C . 2 4 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 2 1 1
 Ta có f  x dx 
dx  2. ln 4x  3  C 
ln 4x  3  C   . 4x  3 4 2
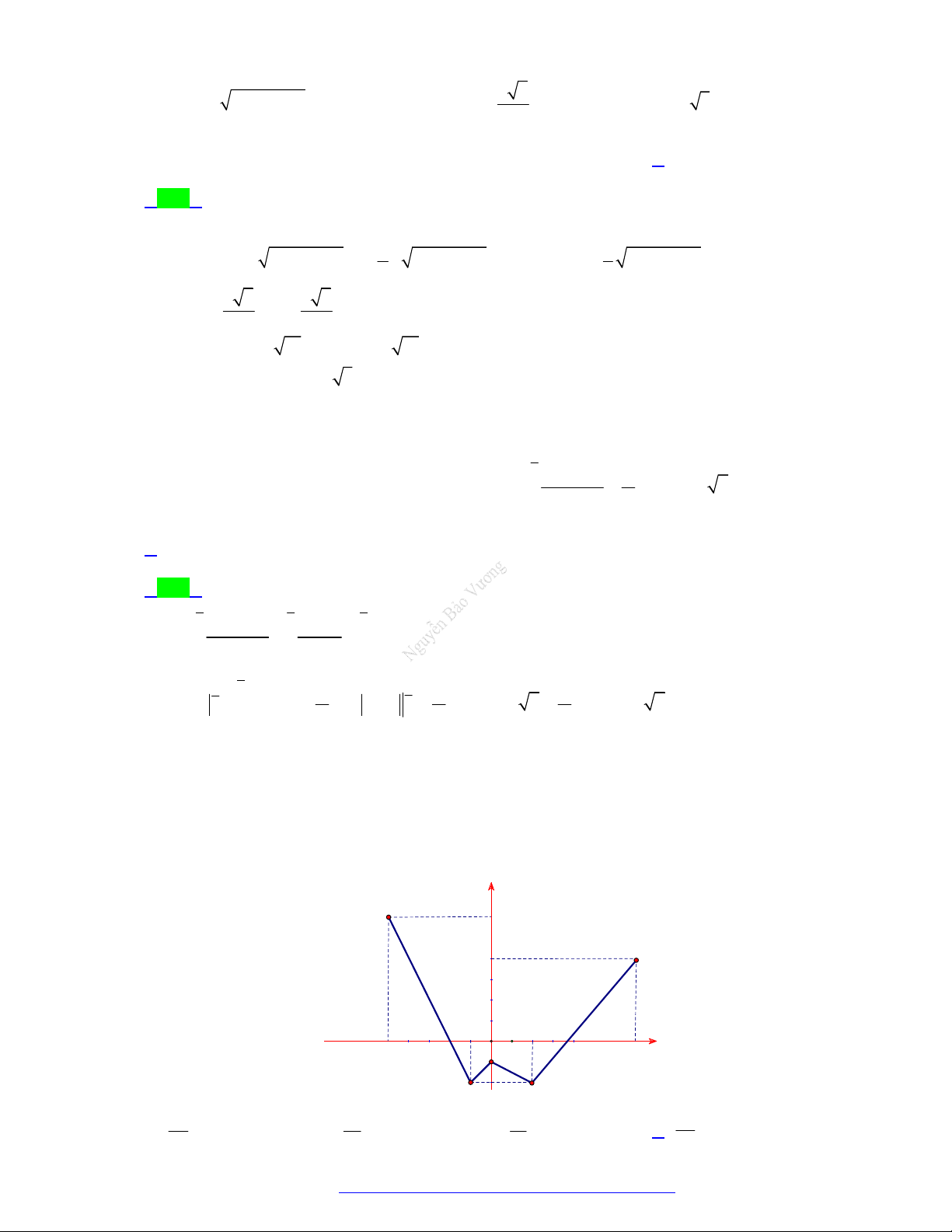
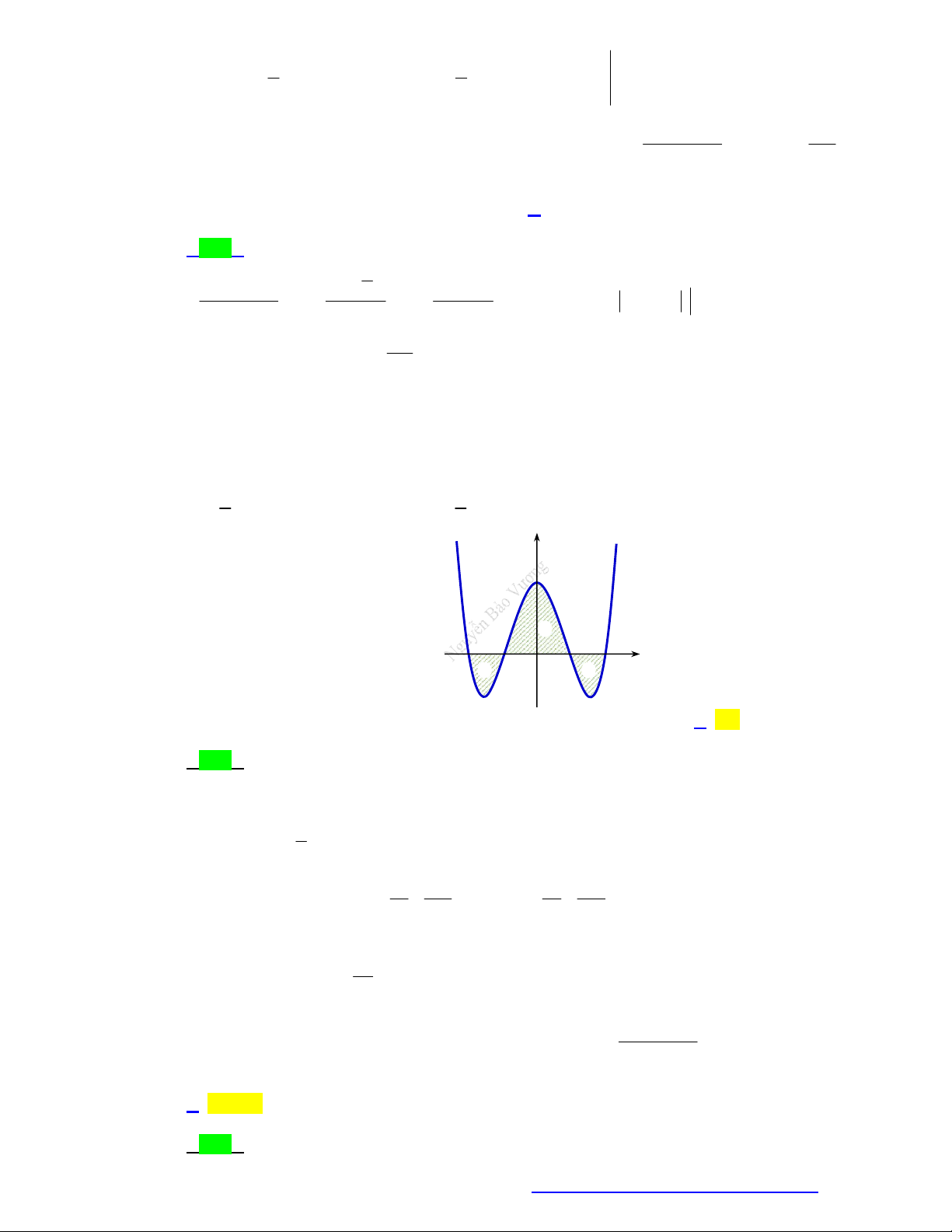
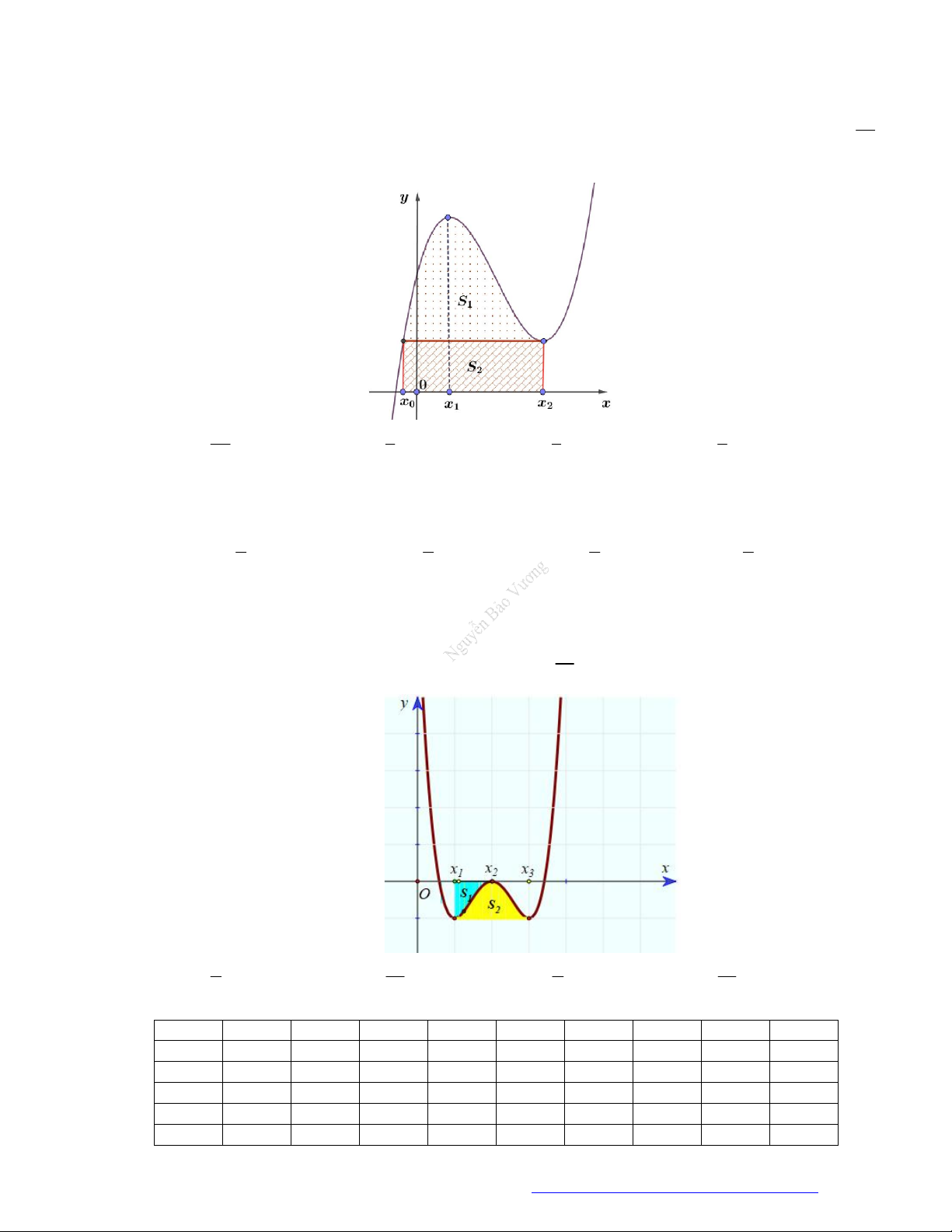
Câu 14. (Chuyên Lam Sơn - Thanh Hóa - 2021) Gọi S là diện tích miền hình phẳng được gạch chéo
trong hình vẽ dưới đây, với y  f  x là hàm số liên tục trên  .
Công thức tính S là 2 2 A. S  
f  x dx  . B. S 
f  x dx  . 1 1  1 2 2 C. S 
f  x dx  f  x dx   . D. S 
f  x dx  . 1  1 1 Lời giải Chọn C 1 2 Ta có: S 
f  x dx  f  x dx   . 1 1
Câu 15. (Chuyên KHTN - 2021) 2x  cos xdx  bằng: A. 2
2x  sin x  C . B. 2
2x  sin x  C . C. 2
x  sin x  C . D. 2
x  sin x  C . Lời giải Chọn D Ta có :  x  x 2 2 cos
dx  x  sin x  C  . 3 5 5
Câu 16. (Chuyên KHTN - 2021) Cho
f  x dx  2   và
f  x dx  5  . Tính tích phân
f  x dx  1 3 1 A. 7. B. 3. C. 7.  D. 10.  Lời giải Chọn B 5 3 5 Ta có
f  x dx  f  x dx  f  x dx  3.    1 1 3
Câu 17. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Họ tất cả các nguyên hàm của hàm số x
y  e  cos x là A. x
e  sin x  C . B. x
e  sin x  C . C. x
e  sin x  C . D. x
e  sin x  C . Lời giải Chọn C
 Ta có  x  cos  x e
x dx  e  sin x  C 3 4
Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Biết
f  xdx  2  và
f  xdx  3  . Giá trị 0 0 4
f  xdx  bằng 3 A. 1  . B. 5 . C. 5  . D. 1. Lời giải Chọn D
Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 4 4 3
 f  xdx  f  xdx  f  xdx  3  2  1    3 0 0
Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Gọi  D là hình phẳng giới hạn bởi các đường x thẳng y 
, y  0, x  1, x  4 . Thể tích vật thể tròn xoay tạo thành khi quay  D quanh trục Ox 4
được tính theo công thức nào dưới đây? 4 4 2 x 4 x 4  x  2 x A.  dx  . B.  dx  . C.  dx   . D.  dx  . 16 4  4  4 1 1 1 1 Lời giải Chọn C
 Thể tích vật thể tròn xoay tạo thành khi quay  D quanh trục Ox được tính theo công thức 4 2  x  V   dx   .  4  1
Câu 20. (Chuyên Quốc Học Huế - 2021) Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường y 
x , trục Ox và hai đường thẳng x  1; x  4 quanh trục hoành được tính bởi công thức nào dưới đây? 4 4 4 4 A. 2 V   d x x  . B. V   xdx  . C. V   d x x  . D. V  x dx  . 1 1 1 1 Lời giải Chọn C 4 4 2
Áp dụng công thức SGK ta có V    x  dx   d x x  . 1 1 1  4 
Câu 21. (Chuyên Quốc Học Huế - 2021) Tìm họ nguyên hàm của hàm số f  x  trên  \   . 5x  4  5  1 A.
f  x dx 
ln 5x  4  C  . B.
f  x dx  ln 5x  4  C  . ln 5 1 1 C.
f  x dx  ln 5x  4  C  . D.
f  x dx  ln 5x  4  C  . 5 5 Lời giải Chọn C 1 1 1 Áp dụng công thức dx 
ln ax  b  C  ta có
f  x dx  ln 5x  4  C  . ax  b a 5
Câu 22. (Chuyên Quang Trung - Bình Phước - 2021) Cho hai hàm số f  x , g  x liên tục trên  .
Trong các mệnh đề sau, mệnh đề nào sai?
A. kf  x dx  k f  x dx  
với mọi hằng số k   .
B.  f  x  g  x dx  f  x dx  g  x dx      C.
f  x dx  f  x  C 
với mọi hàm f  x có đạo hàm trên  .
D.  f  x  g  x dx  f  x dx  g  x dx      Lời giải Chọn A
A sai Vì k phải là hằng số khác 0
Câu 23. (Chuyên Quang Trung - Bình Phước - 2021) Cho hàm số f (x) liên tục và xác định trên  , a b .
Gọi F (x) là một nguyên hàm của hàm số f (x) . Chọn phương án đúng nhất.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 b b A.
f (x)dx  F (b)  F (a)  B.
f (x)dx  F (a)  F (b)  a a b b C.
f (x)dx  F (b)  F (a)  D. 2 2
f (x)dx  F (b)  F (a)  a a Lời giải Chọn A
Câu 24. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình  H  được giới hạn như hình vẽ
Diện tích của hình  H  được tính bởi công thức nào dưới đây? b b
A.  g  x  f  x dx    . B.
 f  x  g  x dx    . a a b b C.
f  x dx  . D.
g  x dx  . a a Lời giải Chọn A b
Diện tích của hình  H  là: S 
g  x  f  x dx    . a 2
Câu 25. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hàm số f  x thỏa mãn
f  x dx  1  và 0 2 1
f  x dx  4  . Giá trị của
f  x dx  bằng 1 0 A. 5 . B. 3  . C. 5  . D. 3 . Lời giải Chọn C 2 1 2 1 Ta có:
f  x dx 
f  x dx 
f  x dx    
f  x dx  1 4  5   . 0 0 1 0
Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hàm số f  x liên tục trên đoạn  2  ; 
3 . Gọi F  x là 3
một nguyên hàm của hàm số f  x trên  2  ;  3 và F 3  2  ; F  2    4  . Tính I  2
f  x dx  . 2  A. 2 . B. 4 . C. 4  . D. 2  Lời giải Chọn B 3
Ta có: I  2 f  x dx  2 F 3  F 2  2 2   4    4      2 2 2
Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho I 
f  x dx  3 
. Khi đó J  4 f  x  3 dx    0 0 bằng: A. 6. B. 8. C. 4. D. 2. Lời giải Chọn A 2 2 2 2
Ta có: J  4 f  x  3 dx   
 4 f  x dx  3dx  
 4.3 3x 12  3.2  3.0  6 . 0 0 0 0
Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 28. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Kết quả 3 x dx  bằng 1 1 A. 2 3x  C . B. 4 x  C . C. 4 x . D. 4 4x  C . 4 4 Lời giải Chọn B 4 x Ta có 3 x dx   C  . 4
Câu 29. (Chuyên Hạ Long - Quảng Ninh - 2021) Biết F  x  cos x là một nguyên hàm của hàm số 
f  x trên  . Giá trị của 3 f  x  2 dx    bằng 0 A. 2 . B. 2 . C. 2  6 . D. 4 . Lời giải Chọn C     
Ta có 3 f  x  2 dx  3 f  x dx  2 dx  3cos x  2x  6   2      . 0 0 0 0 0 3 3
Câu 30. (Chuyên Hạ Long - Quảng Ninh - 2021) Biết
f  x dx  5  và
g  x dx  7  . Giá trị của 1 1 3
3 f  x  2g  x dx    bằng 1 A. 29 B. 2  9 C. 1 D. 3  1 Lời giải Chọn A Ta có: 3 3 3
3 f  x  2g  x dx  3 f  x dx  2 g  x dx  3.5  2.7  15 14  29      . 1 1 1 2 2
Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Biết I 
f  x dx  2 
. Giá trị của  f  x  2x dx    bằng 1 1 A. 1. B. 5 . C. 4 . D. 1. Lời giải Chọn B 2 2 2
Ta có  f  x  2x dx  f  x dx  2xdx  2  3  5      . 1 1 1
Câu 32. (Chuyên ĐH Vinh - Nghệ An - 2021) Họ các nguyên hàm của hàm số f  x  sin 3x là 1 1
A.  cos 3x  C .
B.  cos 3x  C .
C. cos 3x  C .
D. cos 3x  C . 3 3 Lời giải Chọn A 1
sin 3xdx   cos 3x  C  . 3 1 1 1 4
Câu 33. (Chuyên ĐH Vinh - Nghệ An - 2021) Biết
f  x dx   và
g  x dx  .  Khi đó 3 3 0 0 1
 g x  f  xdx bằng 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 5 5 A. . B.  . C. 1  . D. 1. 3 3 Lời giải Chọn D 1 1 1 4 1
Ta có g x  f xdx  g xdx  f xdx   1.   3 3 0 0 0
Câu 34. (THPT Quế Võ 1 - Bắc Ninh - 2021) Mệnh đề nào sau đây đúng. 1 1 A.
dx  ln x  C  . B.
dx  cot x  C  . x 2 sin x 1 C. cos d
x x  sin x  C  . D.
dx  tan x  C  . 2 cos x Lời giải Chọn D 1 Vì
dx  ln x  C  nên loại đáp án A. x 1 Vì
dx   cot x  C  nên loại đáp án B. 2 sin x Vì cos d
x x  sin x  C 
nên loại đáp án C.
Câu 35. (THPT Quế Võ 1 - Bắc Ninh - 2021) Khẳng định nào sau đây đúng với mọi hàm f , g liên tục
trên K và a, b là các số bất kỳ thuộc K ? b b b
A.  f  x.g  x dx   f  x .
dx g  xdx      . a a a b b b
B.  f  x  2g  x dx  
f  x dx  2 g  xdx      . a a a b f x dx b    f  x C. a dx   . g  x b a
g  x dx a 2 b b   D. 2
 f  x d  x  f      xdx   . a  a  Lời giải Chọn B b b b
 f  x  2g  x dx  
f  x dx  2 g  xdx     
chỉ có tính chất tổng của 2 tích phân. a a a
Câu 36. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hàm số f  x liên tục trên  và 1 3 3 có
f  x dx  2, 
f  x dx  6  Tính f  x d . x  0 1 0 A. I  12 . B. I  8 . C. I  6 . D. I  4 . Lời giải Chọn B 3 1 3 Ta có
f  x dx  f  x dx  f  x dx  2  6  8    0 0 1
Câu 37. (THPT Quốc Oai - Hà Nội - 2021) Cho hai hàm số y  f  x và y  g  x liên tục trên  .
Trong các mệnh đề sau, mệnh đề nào sai?
Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
A.  f  x  g  x dx  f  x dx  g  x dx      .
B. kf  x dx  k f  x dx  
với mọi hằng số k   \   0 .
C.  f  x  g  x dx  f  x dx  g  x dx      . D.
f  x.g  x dx  f  x d .
x g  x dx    . Lời giải Chọn D
Câu 38. (THPT Quốc Oai - Hà Nội - 2021) Cho hàm số y  f  x liên tục trên đoạn a;b . Gọi F  x là
một nguyên hàm của hàm số y  f  x . Hãy chọn khẳng định đúng trong các khẳng định sau b b A.
f  x dx  F a  F b  . B. f  x 2
dx  F b 2  F a  . a a b b C.
f  x dx  F b  F a  . D.
f  x dx  F a  F b  . a a Lời giải Chọn C
Câu 39. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho C là một hằng số. Trong các mệnh đề sau, mệnh đề nào sai? A. x x
e dx  e  C  .
B. sin xdx  cos x  C  . 1 C. 2
2xdx  x  C  . D.
dx  ln x  C  . x Lời giải Chọn B
Ta có: sin xdx   cos x  C  . 1 3 3
Câu 40. (THPT Quảng Xương 1-Thanh Hóa - 2021) Nếu
f  x dx  2  và
f  x dx  4   thì
f  x dx  0 0 1 bằng A. 6 . B. 6 . C. 2 . D. 2 . Lời giải Chọn B 1 3 3 3 3 1 Ta có
f  x dx  f  x dx  f  x dx  f  x dx  f  x dx  f  x dx  4   2  6        . 0 1 0 1 0 0
Câu 41. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho đồ thị hàm số y  f  x . Diện tích S của hình
phẳng (phần tô đậm trong hình vẽ) là 1 3 1 3
A. S   f  x dx  f  xdx   . B. S 
f  x dx  f  x dx   . 0 1 0 1 3 1 3 C. S 
f  x dx  . D. S 
f  x dx  f  xdx   . 0 0 1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn B 3 1 3 S 
f  x dx  S  f  x dx  f  x dx    0 0 1
Câu 42. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Hàm số F  x 3 2
 5x  4x  7x 120 là nguyên hàm
của hàm số nào sau đây?
A. f  x 2
 5x  4x  7 . B. f  x 2
 15x  8x  7 . 2 3 2 5x 4x 7x
C. f  x 2
 5x  4x  7 . D. f  x    . 4 3 2 Lời giải Chọn B
Vì F  x là một nguyên hàm của f  x nên  
f  x  F  x     3 2
x  x  x   2 5 4 7 120
 15x  8x  7 .
Câu 43. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Một nguyên hàm của hàm số y  cos2x là 1 1 A. 2sin 2x . B. 2  sin 2x . C. sin 2x . D.  sin 2x . 2 2 Lời giải Chọn C 1
Ta có cos(ax  b)dx 
sin(ax  b)  C  a
Câu 44. (THPT Phan Đình Phùng - Quảng Bình - 2021) Tìm nguyên hàm của hàm số   2021 f x  x trên  . 2022 x A.
f  x dx   . B. f  x 2020 dx  2021x  C  . 2022 2022 x 2021 x C.
f  x dx   C  . D.
f  x dx   C  . 2022 2021 Lời giải Chọn C 2022 x Ta có: f  x 2021 dx  x dx   C   . 2022 1 1
Câu 45. (THPT Phan Đình Phùng - Quảng Bình - 2021) Nếu
f (x)dx  4  và
g(x)dx  3  thì 0 0 1
2 f (x)  3g(x)dx  bằng 0 A. 7 . B. 13 . C. 17 . D. 11. Lời giải Chọn C 1 1 1
Ta có: 2 f (x)  3g(x)dx  2 f (x)dx  3 g(x)dx  2.4  3.3  17    . 0 0 0
Câu 46. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hàm số f  x liên tục trên đoạn 0; 2 . Biết 2 2 1
f  xdx  5  và
f t  dt  3.  Tính I 
f  xdx  . 0 1 0 A. I  3 . B. I  2 . C. I  5 . D. I  1. Lời giải
Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chọn B 1 2 2 2 2 Ta có I 
f  xdx  f  xdx  f  xdx  f  xdx  f t dt  2.      0 0 1 0 1
Câu 47. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho F  x là một nguyên hàm của hàm số 1  2  f  x  trên khoảng ;  
 . Tìm F  x , biết F   1  5 . 3x  2  3 
A. F  x  ln 3x  2  5 .
B. F  x  3ln 3x  2  5 . 3 1
C. F  x 
 8 . D. F  x  ln 3x  2  5 . 3x  22 3 Lời giải Chọn D 1 1
Ta có: F  x  dx 
ln 3x  2  C  . 3x  2 3 Theo bài, F   1  5  C  5 . 1
Vậy F  x  ln 3x  2  5. 3 1 1
Câu 48. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho biết
f  x d x  2  và
g  x d x  3  . Tính 0 0 1
I  4 f  x  g  x d x    ? 0 A. I=3 . B. I=1. C. I=11. D. I=5 . Lời giải Chọn D 1 1 1
Ta có I  4 f  x  g  x d x  4 f  x d x  g  x d x  4.2  3  5      . 0 0 0 3 5 4 3
Câu 49. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Biết
f  x dx   và
f t  dt   . Tính 3 5 0 0 4
f u du  3 14 16  17 16 A. . B. . C.  . D. . 15 15 15 15 Lời giải Chọn B 4 4 3 16  Ta có
f u  du  f u du  f u du  .    15 3 0 0
Câu 50. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình phẳng  D được giới hạn bởi các
đường f  x  2x  1,Ox, x  0, x  1 . Tính thể tích V của khối tròn xoay tạo thành khi quay
D xung quanh trục Ox được tính theo công thức? 1 1 1 1 A. V   2x  1dx  .
B. V  2x   1 dx  .
C. V   2x   1 dx  . D. V  2x  1dx  . 0 0 0 0 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 2
Ta có V    2x 1 dx   2x   1 dx  . 0 0 2 2
Câu 51. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Nếu
f  x dx  6 
thì 3 f  x dx  bằng 0 0 A. 3. B. 6. C. 8. D. 18. Lời giải Chọn D 2 2 Vì
f  x dx  6 
nên 3 f  x dx  3.6  18  . 0 0
Câu 52. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Khẳng định nào sau đây là đúng 1 A.
dx   cot x  C  . B. x x
a dx  a .ln a  C 2  . cos x x 1 1 1 C. e dx   C  . D. dx    C x  . e 2 x x Lời giải Chọn C 1 Ta có:
dx  tan x  C  . 2 cos x x x a a dx   C  . ln a x x 1
e dx  e  C   C  . x e
1 dx  ln x C  . x 2
Câu 53. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Tính tích phân   3 x  2 x d bằng 1 9 9 7 7 A.  . B. . C. . D.  . 4 4 4 4 Lời giải Chọn B 2 4  x  2   9 3 x  2 x d =   2x  .   4 1  4 1    2
Câu 54. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Biết
f  x dx  4  . Tính tích phân 0 2
I  2x  f  x dx    bằng 0 A. I  6 . B. I  12 . C. I  8 . D. I  4 . Lời giải Chọn C. 2 2 2 2 2
Ta có I  2x  f  x dx  2xdx  f  x 2 dx  x 
f  x dx  4  4  8       . 0 0 0 0 0
Câu 55. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hàm số f (x)  x 1. Trong các khẳng định
sau, khẳng định nào đúng ? 1 A. 2
f (x)dx  x  x  C  . B. 2
f (x)dx  2x  x  C  . 2
Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 C. 2
f (x)dx  x  x  C  . D. 2
f (x)dx  x  C  . Lời giải Chọn A 1 Ta có: 2
f (x)dx  (x 1)dx  x  x  C   2 Do đó chọn phương án A.
Câu 56. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Họ các nguyên hàm của hàm số f  x 2  3x 1 là. 3 x A. 3
x  x  C .
B. 6x  C . C. 3 x  C . D.  x  C . 3 Lời giải Chọn A Ta có
f  x x    2 x   3 d 3
1 dx  x  x  C . 5 5
Câu 57. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Biết
f  x dx  4 
. Giá trị của 3 f  x dx  bằng. 1 1 4 A. 7 . B. . C. 64 . D. 12 . 3 Lời giải Chọn D 5 5
Ta có 3 f  x dx  3 f  x dx  12   . 1 1
Câu 58. (THPT Đồng Quan - Hà Nội - 2021) Họ nguyên hàm của hàm số   ln x f x  là x 1 1 A. 2 ln x  C . B. 2 ln x C .
C. lnln xC . D. 2
ln x  ln x  C . 2 2 Lời giải Chọn A ln x 1 Ta có: dx  ln x dln x 2  ln x C   . x 2
Câu 59. (THPT Đồng Quan - Hà Nội - 2021) Họ nguyên hàm của hàm số f  x  2cos 2x  x là 1 1 A. 2  sin 2x 
x  C . B. 2
 sin 2x  x  C . 2 2 1 1 C. 2 sin 2x 
x  C . D. 2
sin 2x  x  C . 2 2 Lời giải Chọn D  1 1 
Ta có F  x 2 2  2 sin 2x  x
 C  sin 2x  x  C    2 2  1 0
Câu 60. (THPT Đồng Quan - Hà Nội - 2021) Cho
f  x dx  3; g  x dx    2, khi đó 0 1 1
 f x  2g xdx bằng bao nhiêu? 0 A. 5 . B. 7  . C. 1. D. 1  . Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 1 1 0
Ta có  f  x  2g  xdx  f  xdx  2 g  xdx  f  xdx  2 g  xdx  3   2.2  7       0 0 0 0 1
Câu 61. (THPT Lê Lợi - Thanh Hóa - 2021) Nguyên hàm của hàm số 2
y  x  x là 3 2 x x 3 x A.   C .
B. 2x 1  C . C. 2
x  x  C . D.  x  C . 3 2 3 Lời giải Chọn C 3 2  x x 2
x  xdx    C . 3 2
Câu 62. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hàm số y  f (x) có đồ thị như hình vẽ.
Diện tích hình phẳng (phần tô đậm) được tính theo công thức nào sau đây? 3 0 3 A. S  f (x)d . x  . B. S 
f (x)dx  f (x) . dx   . 2  2  0 0 3 0 3 C. S  
f (x)dx  f (x)d . x   . D. S 
f (x)dx  f (x)d . x   2  0 2  0 Lời giải Chọn C 3 0 3 0 3
Diện tích hình phẳng cần tính S 
f (x) dx 
f (x) dx 
f (x) dx  
f (x)dx  f (x)d . x      2  2  0 2  0
(Do f (x)  0, x    ;
2 0 và f (x)  0,x 0;  3 )
Câu 63. (THPT Lê Lợi - Thanh Hóa - 2021) Cho các hàm số y  f  x, y  g  x liên tục trên  có 5 5 5
f  x dx  1  
; g  x dx  3 
. Tính  f  x  2g  x dx    . 1  1  1 A. 2 . B. 1. C. 1. D. 5 . Lời giải Chọn D 5 5 5
Ta có  f  x  2g  x dx 
f  x dx  2 g  x dx  1   2.3  5      . 1 1  1  x
Câu 64. (Sở Vĩnh Phúc - 2021) Tìm họ tất cả các nguyên hàm của hàm số y  . x 1
A. x  ln x   1  C .
B. x  ln x 1  C .
C. x  ln x  
1  C . D. x  ln x 1  C . Lời giải
Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chọn B. x   Ta có: dx  1  1     
dx  x ln x 1  C . x 1  x 1
Câu 65. (Sở Lào Cai - 2021) Khẳng định nào sau đây là đúng?  
A.  f  xdx 
   f x .
B.  f  xdx 
  f x .  
C.  f  xdx 
   f x.
D.  f  xdx 
  f x. Lời giải Chọn D. 
Gọi F  x là một nguyên hàm của f  x . Ta có  f  xdx 
 F x C  
 f  x . 2 2
Câu 66. (Sở Lào Cai - 2021) Cho
f  x x  1  d
, khi đó 3 f  x x  d bằng 1 1 A. 2 . B. 1. C. 4 . D. 3 . Lời giải Chọn D 2 2
3 f  x dx  3 f  x dx  3.  1  3    . 1 1 1
Câu 67. (Sở Lào Cai - 2021) Tích phân exdx  bằng: 0 e 1 A. e . B. 2 e 1. C. . D. e-1 . 2 Lời giải Chọn D 1 1 exd ex x   e 1  . 0 0 1
Câu 68. (Sở Lào Cai - 2021) Họ các nguyên hàm của hàm số f  x   là: 2 sin x
A. cot x  C .
B.  tan x  C .
C.  cot x  C .
D. tan x  C . Lời giải Chọn A. 1 Ta có 
dx  cot x  C  . 2 sin x 5 5
Câu 69. (Sở Hà Tĩnh - 2021) Biết
f  xdx  4 
. Giá trị của 2x  3 f  x d  x    bằng 1 1 A. 13 . B. 2 . C. 6 . D. 12 . Lời giải Chọn D 5 5 5
2x  3 f  x d
 x= 2xdx  3 f  x 2 5 dx  x | 3.4   24 12  12.    1   1 1 1
Câu 70. (Sở Hà Tĩnh - 2021)  3 2
 x  x  dx bằng 1 1 A. 4 x  C . B. 4 2
x  x  C . C. 2
3x  2  C . D. 4 2
4x  x  C . 4 4 Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn B 2 4 4 x x x Ta có  3  x  x  3 2 2
dx   2xdx  x dx  2.  
 C  x   C   . 2 4 4
Câu 71. (Sở Yên Bái - 2021) Trong các khẳng định sau, khẳng định nào sai?
A. 0dx  C 
( C là hằng số).
B. dx  x  C 
( C là hằng số). 1  1   x C.
dx  ln x  C 
( C là hằng số).
D. x dx   C 
( C là hằng số). x  1 Lời giải Chọn D  1   x x dx   C 
( C là hằng số) Sai vì thiếu điều kiện   1  .  1 1
Câu 72. (Sở Tuyên Quang - 2021) Nguyên hàm của hàm số f  x  là 2x 1
A. F  x  ln 2x 1  C . B. F  x  2ln 2x 1  C . 1 1
C. F  x  ln(2x 1)  C .
D. F  x  ln 2x 1  C . 2 2 Lời giải Chọn D 1 1 Ta có:
f  x dx  dx  ln 2x 1  C   . 2x 1 2 1 1 1
Câu 73. (Sở Tuyên Quang - 2021) Cho
f  x dx  2  và
g  x dx  5  . Khi đó
 f  x  2g  x dx     0 0 0 bằng: A. 1 B. -3 C. -8 D. 12 Lời giải Chọn C Ta có: 1 1 1
 f  x  2g  x dx  
f  x dx  2 g  x dx  2  2.5  8       0 0 0
Câu 74. (Sở Tuyên Quang - 2021) Họ tất cả các nguyên hàm của hàm số f  x  2x  sin x là A. 2
2x  cos x  C . B. 2
2x  cos x  C . C. 2
x  cos x  C . D. 2
x  cos x  C . Lời giải Chọn C Ta có  x  x 2 2 sin
dx = 2xdx  sin d
x x  x  cos x  C    .
Câu 75. (THPT Thanh Chương 1- Nghệ An - 2021) Họ nguyên hàm của hàm số là? A. . B. . C. . D. . Lời giải Chọn B Ta có: . 2 2
Câu 76. (THPT Thanh Chương 1- Nghệ An - 2021) Cho 3 f  x  2x dx  12    . Khi đó
f  x dx  bằng 1 1
Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A. . B. . C. . D. . Lời giải Chọn A  Ta có .
Câu 77. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số y  f  x liên tục trên  và có đồ thị
C là đường cong như hình vẽ bên.
Diện tích của hình phẳng giới hạn bởi đồ thị C , trục Ox và hai đường thẳng x  0, x  2 (phần tô đen) là 1 2 2 A. S  
f  xdx 
f  xdx   . B. S 
f  xdx  . 0 1 0 1 2 2 C. S 
f  xdx 
f  xdx   . D. S 
f  xdx  . 0 1 0 Lời giải Chọn C 1 2  Ta có: S 
f  xdx 
f  xdx   0 1
Câu 78. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số f  x liên tục trên đoạn  ; a b . Khẳng
định nào sau đây sai? b b b a b
A.  f  x  g  x dx  f  x dx  g  x dx      . B.
f  x dx   f  x   . a a a b a b b b b b
C.  f  x.g  x dx  f  x .
dx g  x dx      .
D. k. f  x dx  k f  x dx   . a a a a a Lời giải Chọn C
Câu 79. (THPT Nguyễn Huệ - Phú Yên - 2021) Biết F  x  cos x là một nguyên hàm của hàm số f  x  3
trên  .Giá trị của 2 f  xdx  bằng 0 A. 1  . B. 3 . C. 3 . D. 1. Lời giải Chọn A
Vì F  x  cos x là một nguyên hàm của hàm số f  x nên f  x  sin x .   3 3  2 f  x 3 dx  2 
sinxdx  2 cos x  1  0   . 0 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 3 3
Câu 80. (THPT Nguyễn Huệ - Phú Yên - 2021) Biết
f  xdx  3 
.giá trị của  f x  3dx bằng 2 2 A. 6 . B. 3 . C. 9 . D. 5 . Lời giải Chọn A 3 3 3
Ta có  f x  3dx  f x 3
dx  3 dx  3  3x  6 2   . 2 2 2
Câu 81. (THPT Lương Thế Vinh - 2021) Diện tích hình phẳng giới hạn bởi các đường 2
y  x  4 và
y  x  4 xác định bởi công thức 2 1 1 2 A.  2
x  x  dx . B.  2
x  xdx . C.  2
x  x  dx . D.  2
x  x dx . 0 0 0 0 Lời giải Chọn C x  0
Phương trình hoành độ giao điểm của hai đồ thị: 2
x  4  x  4   . x  1  1 1
Diện tích của hình phẳng là: 2 S  x  x dx    2
x  x  dx . 0 0
Câu 82. (THPT Lương Thế Vinh - 2021) Họ nguyên hàm của hàm số   3x f x  là. 3x 3x
A. 3x log 3  C .
B. 3x ln 3  C . C.  C . D.  C . ln 3 log 3 Lời giải Chọn C
Theo công thức nguyên hàm cơ bản chọn C.
Câu 83. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hai hàm số f  x , g  x liên tục trên đoạn  ;
a b và số thực k tùy ý. Mệnh đề nào dưới đây sai? b c c b a A.
f  x dx  f  xdx  f  x d , x c   ; a b   
. B. f  x dx   f  x dx   . a a b a b b b b b b
C. kf  x dx  k f  x dx   .
D.  f  x  g  x dx  f  x dx  g  x dx      . a a a a a Lời giải Chọn A b c b
 Mệnh đề A sai. Vì: f  x dx  f  xdx  f  x d , x c   ; a b    . a a c
Câu 84. (THPT Đào Duy Từ - Hà Nội - 2021) Họ các nguyên hàm của hàm số f  x 2
 x  2x  3 là 3 x A. 2
 x  3x  C .
B. 2x  2  C . C. 3 2
x  x  C . D. 3 2
x  2x  3x  C . 3 Lời giải Chọn A
Câu 85. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hàm số y  f  x có đạo hàm trên đoạn 1;  2 , 2 f  
1  1 và f 2  2 . Khi đó, I  f  x dx  bằng 1 7 A. I  1. B. I  1  . C. I  . D. I  3 . 2
Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Lời giải Chọn A 2 2
 Ta có: I  f  xdx  f  x  f 2  f   1  2  1  1  . 1 1
Câu 86. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Thể tích của khối tròn xoay sinh bởi hình phẳng giới 
hạn bởi hai đồ thị hàm số y  cos x , đường thẳng x  0 , x 
và trục Ox khi quay quanh trục 2 hoành là     A. 2 V  cos d x x  . B. 2 2 V  cos dx x  . C. 2 V   cos d x x  . D. 2 2 V   cos d x x  . 0 0 0 0 Lời giải Chọn D 
Dựa vào công thức tính thể tích khối tròn xoay quay quanh trục Ox , ta được 2 2 V   cos xdx  . 0
Câu 87. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Họ nguyên hàm của hàm số f  x 3 2
 x  3x là 4 3 x x 4 x A. 4 3
x  x  C . B.   C . C. 3  x  C . D. 2
3x  6x  C . 4 3 4 Lời giải Chọn C  1   x
 Áp dụng công thức nguyên hàm: x dx   C 
và các tính chất nguyên hàm.  1 4 x  Ta có:  3 2 x   3 3x dx   x  C . 4 2 2
Câu 88. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho f  x x d  2  và g  x x d  3  . Tích phân 0 0 2
2 f  x  g  x x d    0 A. 5 . B. 7 . C. 1  . D. 1. Lời giải Chọn D 2 2 2
Ta có 2 f  x  g  x x
d = 2. f  x x- d f  x x d = 2.2-3=1      . 0 0 0
Câu 89. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hàm số y  f  x xác định, liên tục và không âm trên  ;
a b . Thể tích của vật thể tròn xoay sinh bởi miền  D giới hạn bởi đồ thị hàm số
y  f  x , trục hoành và hai đường thẳng x  a, x  b quay quanh Ox là b b b b A. 2 V 
f  x dx  . B. V 
f  x dx  . C. 2 V  
f  x dx  . D. V  
f  x dx  . a a a a Lời giải Chọn C 0 2
Câu 90. (THPT Chu Văn An - Thái Nguyên - 2021) Nếu
f  x dx  6  và
g  x dx  2  thì 2 0 2
f  x dx  bằng 2 A. 8 . B. 12  . C. 8  . D. 4 . Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn D 2 0 2  Ta có
f  x dx 
f  x dx  f  x dx  6   2  4     . 2  2  0
Câu 91. (THPT Ba Đình - Thanh Hóa - 2021) Nguyên hàm của hàm số   3 f x  x là 3 4 2 3 x 3 x x
A. x dx   C  .
B. x dx   C  . C. 3 x dx   C  . D. 3 4
x dx  4x  C  . 3 4 2 Lời giải Chọn B 4 3 x Nguyên hàm của hàm số   3
f x  x là x dx   C  . 4 8 8
Câu 92. (THPT Ba Đình - Thanh Hóa - 2021) Biết
f  x dx  3 
, giá trị 5 f  x dx  bằng 1 1 A. 3 . B. 8 . C. 15 . D. 6 . Lời giải Chọn C 8 8
Ta có: 5 f  x dx  5 f  x dx  15   . 1 1 4
Câu 93. (THPT Ba Đình - Thanh Hóa - 2021) Cho I  x 2x 1dx 
và u  2x 1 . Mệnh đề nào dưới 0 đây sai: 3 1 3 1 A. 2 2 I 
x (x 1)dx  . B. 2 2 I 
u (u 1)du  . 2 2 1 1 3 5 3 1  u u  3 C. I   2 2   .
D. I  u (u 1)du  . 2 5 3   1 1 Lời giải Chọn D Đặt 2
2x 1  u  2x 1  u  2dx  2 d u u  dx  d u u . 4 3 2 3 u 1 1 Khi đó 2 2
I  x 2x 1 dx  . . u d u u 
u (u 1)du     A,B đúng. 2 2 0 1 1 3 3 3 5 3 1 1 1  u u  Để ý 2 2 2 2 I 
u (u 1)du 
x (x 1)dx        C đúng. 2 2 2 5 3 1 1   1 3 Do đó 2 2
I  u (u 1)du  sai  D sai. 1
Câu 94. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số f  x liên tục trên  và a là số
dương. Trong các khẳng định sau, khẳng định nào đúng? a a a a A.
f  xdx  1  . B.
f  xdx  0  . C. f  x 2 dx  a  . D.
f  xdx  2a  . a a a a Lời giải Chọn B a
 Ta có khẳng định đúng là f  xdx  0  . a
Câu 95. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Nguyên hàm của hàm số 2 x 1 y e   là
Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1 1 A. 2  x 1 2e   C. B. 2  x 1 2e    C. C. 2  x 1 e   C. D. 2  x 1 e    C. 2 2 Lời giải Chọn D  x 1  x 1 Ta có 2 1 2 1 e dx e d  2x  2  x 1 1 e         C   . 2 2
Câu 96. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số
f  x thoả mãn    2021x f x
ln 2021 cos x và f 0  2 . Phát biểu nào sau đúng? 2021x
A. f  x   sin x 1. B.    2021x f x  sin x 1. ln 2021 2021x C.    2021x f x  sin x 1.
D. f  x   sin x 1. ln 2021 Lời giải Chọn B       
2021x ln 2021 cos   2021x f x f x dx x dx
 sin x  C . f 0 0
 2  2021  sin 0  C  2  C  1.
Câu 97. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Tìm nguyên hàm của 6 5x dx  . 5 5 6 A. 7 x  C . B. 7
x  C . C. 7
x  C . D. 7 x  C . 6 7 5 Lời giải Chọn B 5 Ta có: 6 7 5x dx  x  C  . 7
Câu 98. (Trung Tâm Thanh Tường - 2021) Cho f x , g x là các hàm số xác định và liên tục trên  .
Trong các mệnh đề sau, mệnh đề nào sai? A.
f x g xdx  f x . dx
g xdx    . B.
2 f xdx  2
f xdx   . C.
 f x gx dx  f xdx gxdx      D.
 f x gx dx  f xdx  gxdx      . Lời giải Chọn A. Mệnh đề câu A sai. 2 2 2
Câu 99. (Trung Tâm Thanh Tường - 2021) Nếu
f (x)dx  5,
g ( x)dx  2  
thì  f (x)  2g(x)dx  bằng 0 0 0 A. 3 . B. 9 . C. 7 . D. 1. Lời giải Chọn B 2 2 2
Ta có  f (x)  2g(x)dx  f (x)dx  2 g(x)dx  5  4  9    . 0 0 0
Câu 100. (Trung Tâm Thanh Tường -2021) Họ nguyên hàm của hàm số    2 x f x x  e  là A. 2 x xe  C . B. 2  2 x x e  C . C. 2 2
x  e  C . D. 2 2 x x  e  C . Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489 Ta có   x   x 2 2 d  2 d  2 d   2 x x e x x x e x x e  C   .
Câu 101. (THPT Triệu Sơn - Thanh Hóa - 2021) Họ tất cả các nguyên hàm của hàm số f  x 2  3x 1 là.
A. 6x  C . B. 2
3x  x  C . C. 3
x  x  C . D. 3 x  C . Lời giải Chọn C
 Ta có f  x x    2 x   3 d 3
1 dx  x  x  C . 3 3
Câu 102. (THPT Triệu Sơn - Thanh Hóa - 2021) Biết
f  x dx  4   khi đó
2 f  x dx  bằng 1 1 A. 2. B. 2  . C. 8. D. 8  . Lời giải Chọn D 3 3
Ta có 2 f  x dx  2 f  x dx  8    . 1 1
Câu 103. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hàm số y  f  x xác định và liện tục trên đoạn  ;
a b . Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f  x , trục hoành và hai đường thẳng x  ;
a x  b được tính theo công thức b b a b A. S 
f  x dx  . B. S 
f  x dx  . C.
f  x dx  . D.
f  x dx  . a a b a Lời giải Chọn D
Công thức tổng quát tính diện tích hình phẳng bằng tích phân.
Câu 104. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho f  x 2
dx  6x  2sin 2x  C 
, khi đó f  x bằng
A. 12x  4 cos 2x . B. 3 2x  cos 2x .
C. 12  2cos2x .
D. 6x  4cos2x . Lời giải Chọn A  Ta có  2
6x  2 sin 2x  C   12x  4cos2x . 3 5 5
Câu 105. (THPT Trần Phú - Đà Nẵng - 2021) Nếu
f  x dx  3  và
f  x dx  2  thì
f  x dx  bằng 1  3 1 A. 5  . B. 5. C. 1  . D. 1. Lời giải Chọn B 5 3 5 Ta có
f  x dx 
f  x dx  f  x dx  5    1  1  3
Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 3
NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG
MỨC ĐỘ THÔNG HIỂU a Câu 1.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Tính  25x I dx 
theo số thực a . 0 25 1 A. 1 .25a a  .
B. (25a 1).ln 25 . C. (25a 1) . D. (25a 1) . a 1 ln 25 1 4 Câu 2.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Tính tích phân I  x   2 1 x  dx . 0 32 31 30 31 A. . B.  . C.  . D. . 10 10 10 10 Câu 3.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Họ nguyên hàm của hàm số    2  x f x x e   1 là A. x e  x   2 2
1  x  C B. x e  x   2 2 1  4x  C C. x e  x   2 2 1  x D. x e  x   2 2 1  4x 1 dx e 1 Câu 4.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho  a  b ln 
, với a, b là x e 1 2 0 các số nguyên. Tính 3 3
S  a  b . A. S  0 . B. S  2 . C. S  1 . D. S  2 . Câu 5.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Tìm nguyên hàm của hàm số
  ex 1 e x f x    . A.  d  ex f x x  C  . B.  d  ex f x x  C  . C.  d  ex f x x  x  C  . D.
 d  ex  ex f x x  C  . Câu 6.
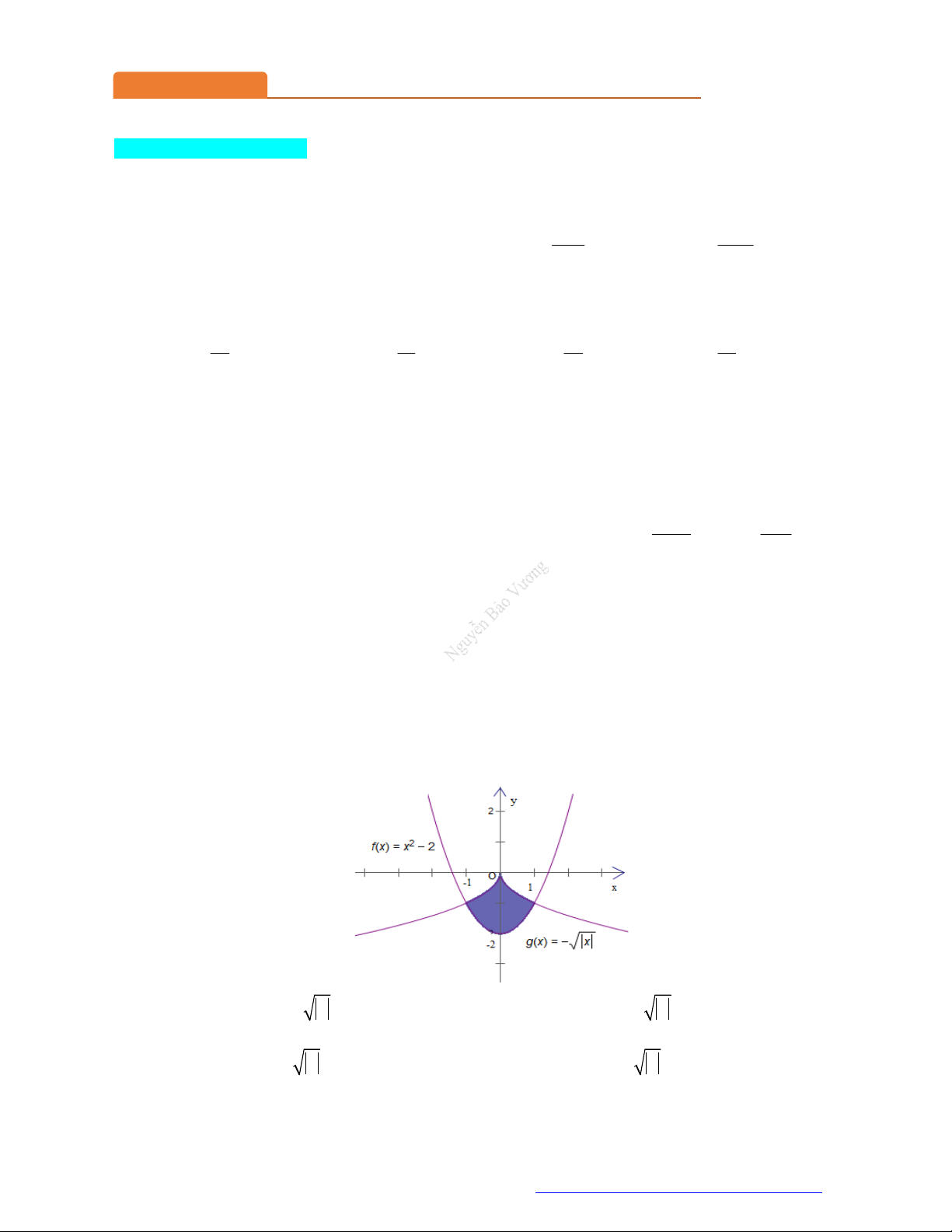
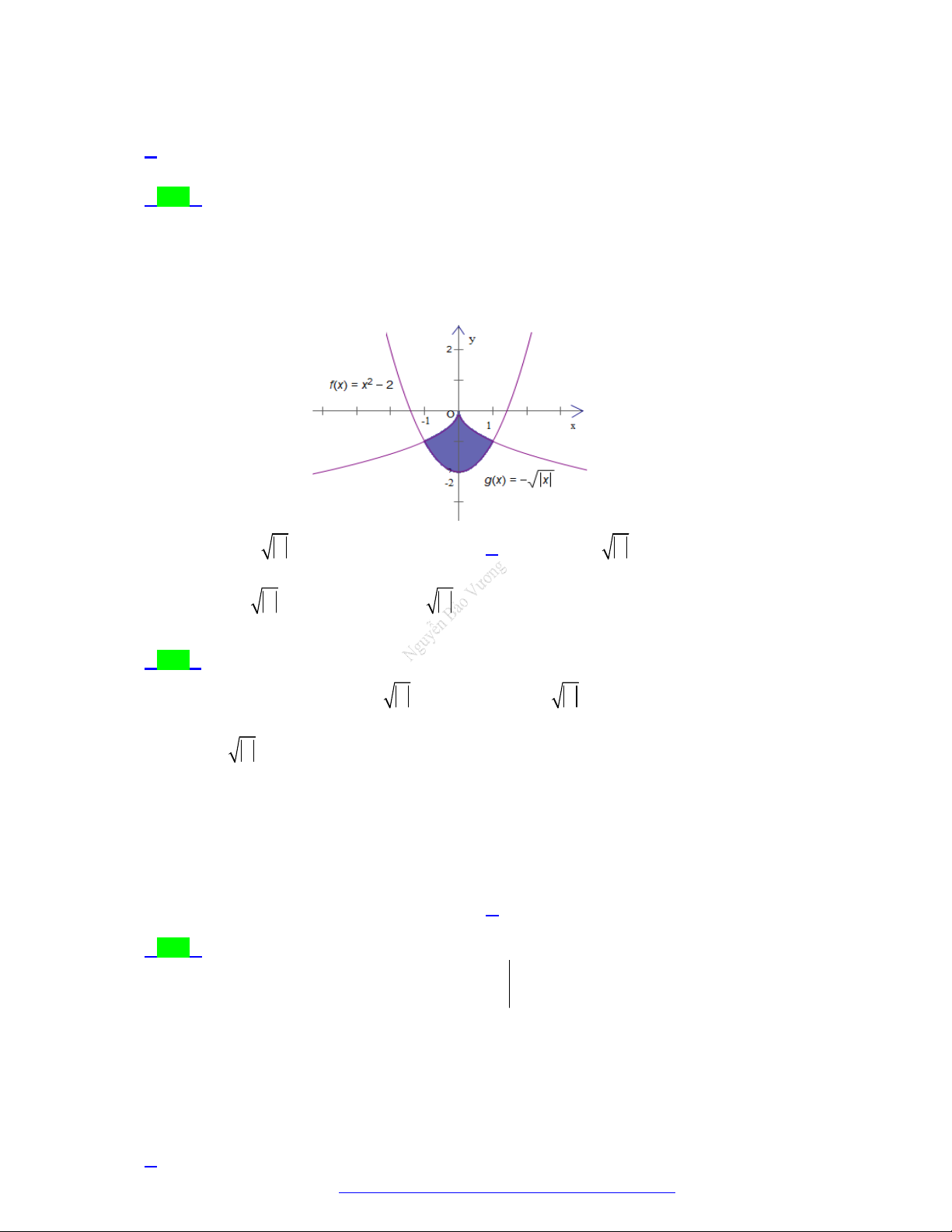
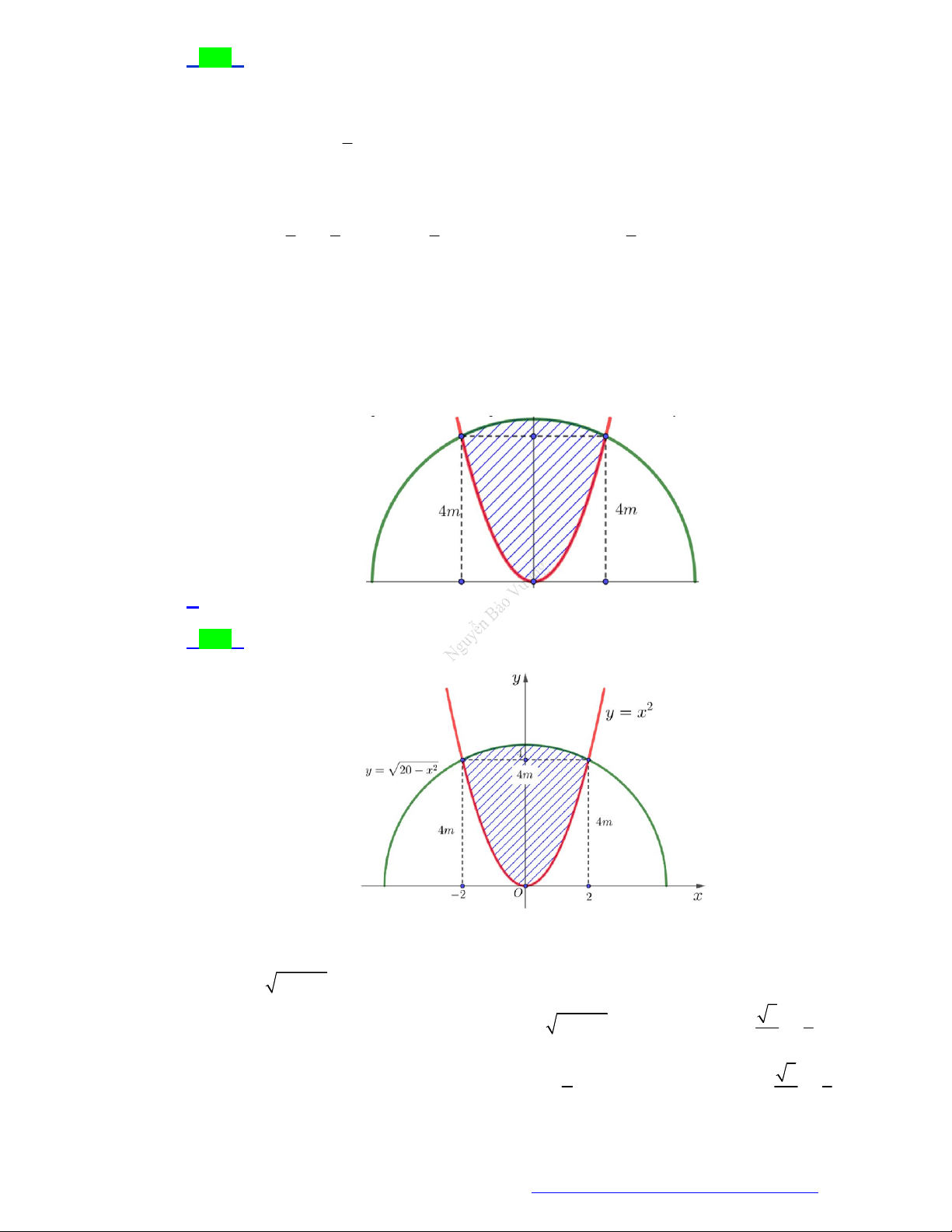
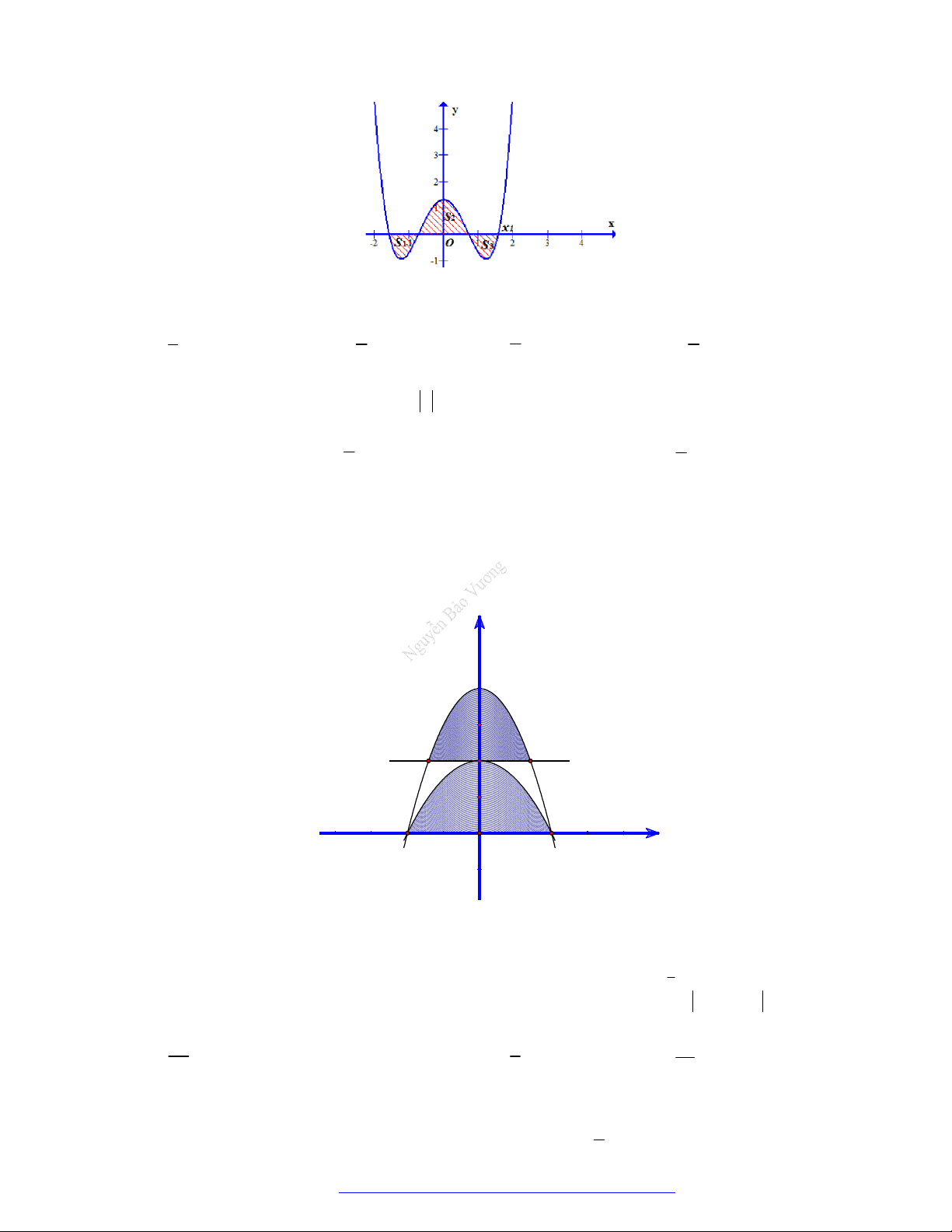
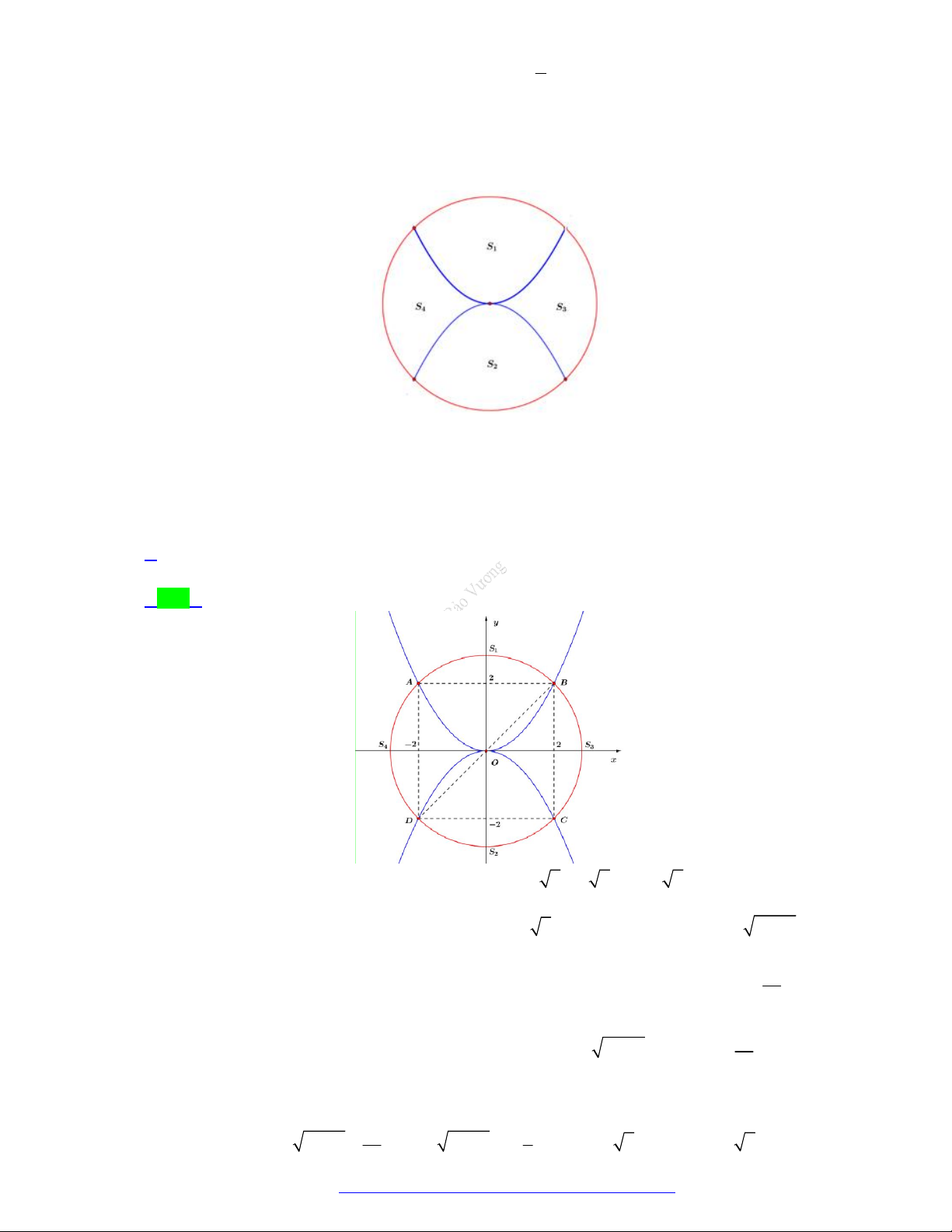
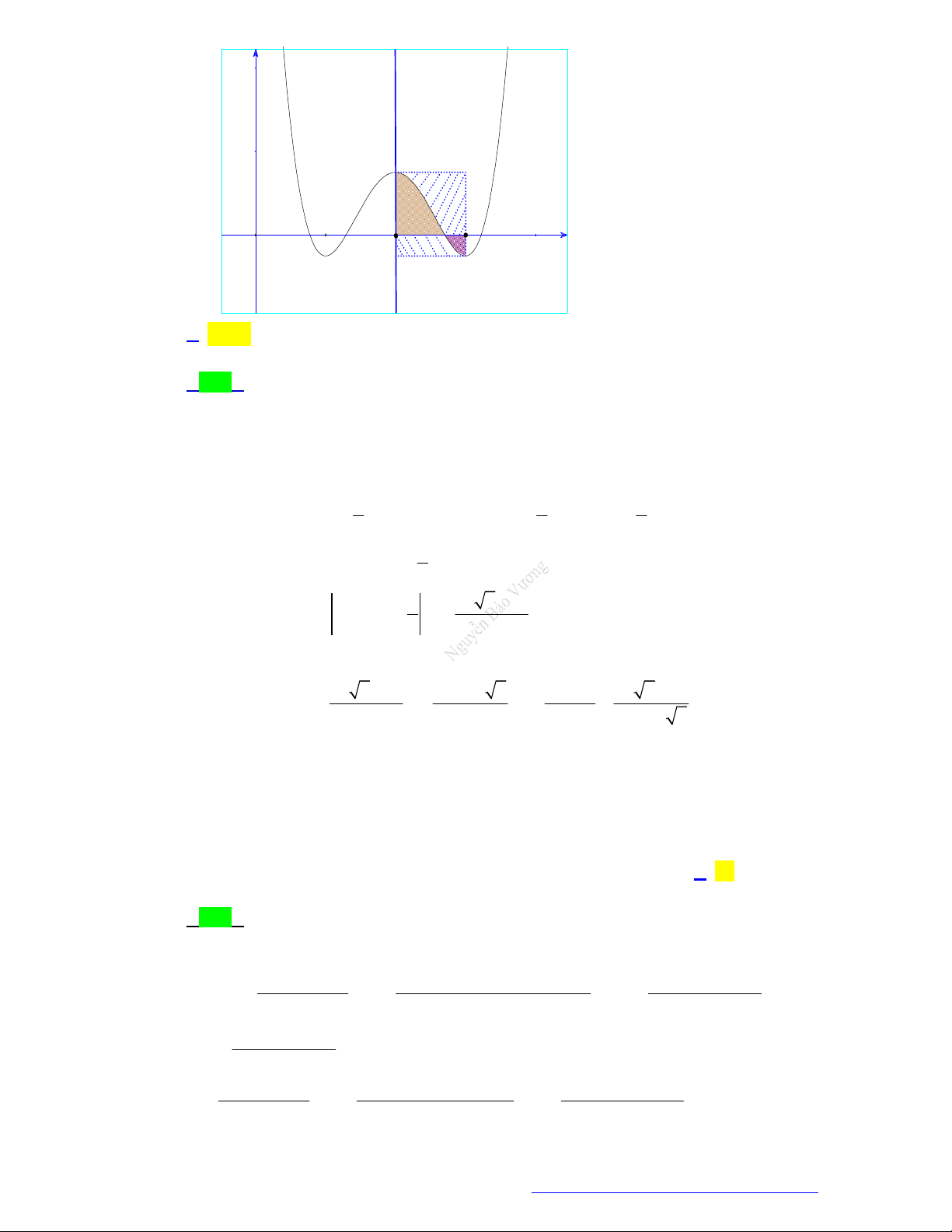
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Diện tích phần hình phẳng tô đậm
trong hình vẽ bên được tính theo công thức nào dưới đây? 1 1 A. 2 2 x  2  x dx . B. 2 2 x  2  x dx . 0 0 1 1 C. 2 2 x  2  x dx . D. 2 2 x  2  x dx . 0 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 1 Câu 7.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho
f  x dx  1  . Với 0 1  ex I
 f  x dx  e  a   
. Khẳng định nào sau đây đúng? 0 A. a  2 . B. a  1  . C. a  2  . D. a  1. Câu 8.
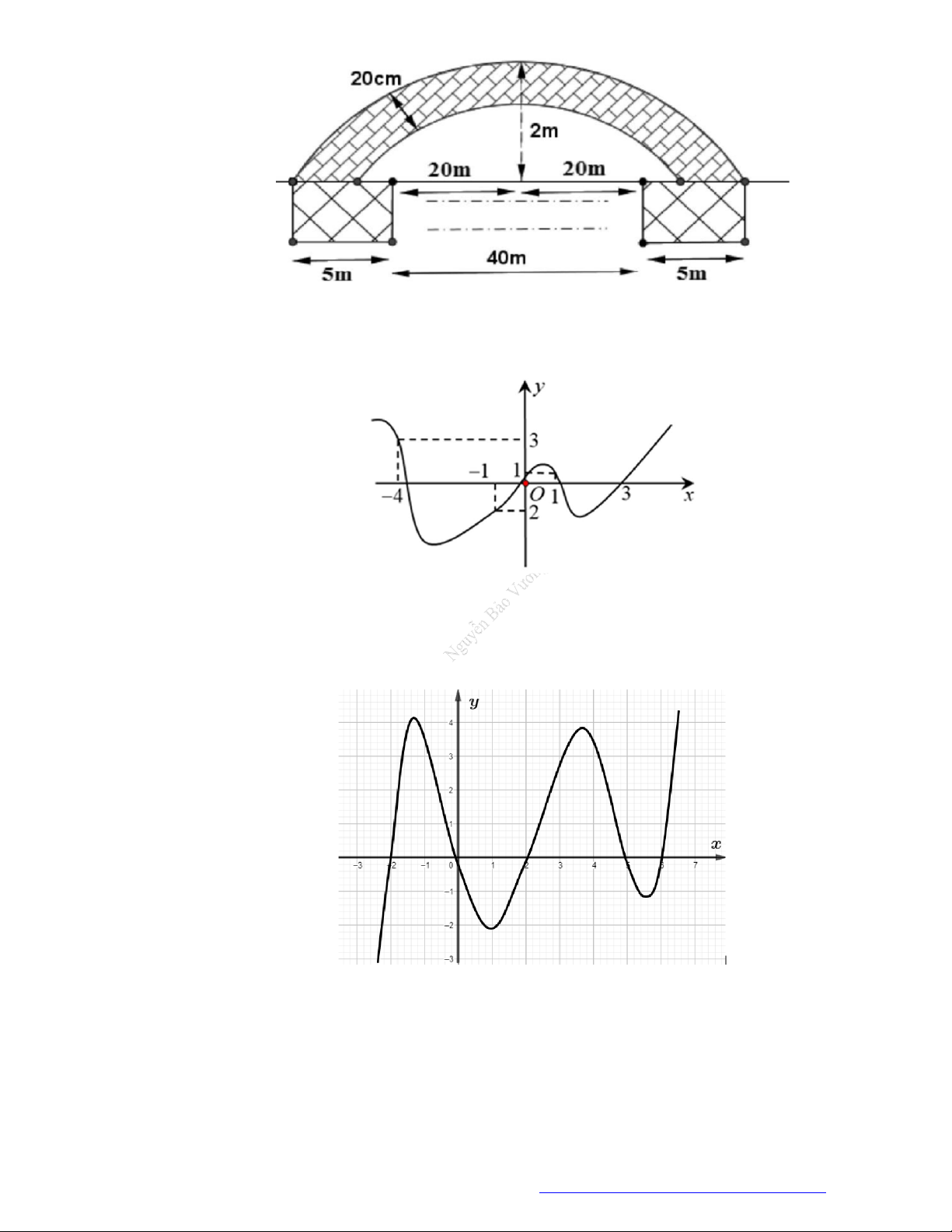
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Bác thợ xây bơm nước vào bể nước. Gọi h t  là
thể tích nước bơm được sau t giây. Cho ht  2
 3at  bt và ban đầu bể không có nước. Sau 5
giây thì thể tích nước trong bể là 3
150 m , sau 10 giây thì thể tích nước trong bể là 3 1100 m . Tính
thể tích của nước trong bể sau khi bơm được 20 giây: A. 3 8400 m . B. 3 600 m . C. 3 2200 m . D. 3 4200 m . Câu 9.
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hàm số f  x thỏa mãn f  x  3  5sin x và
f 0  10 . Tìm hàm số f  x .
A. f  x  3x  5 cos x 15 .
B. f  x  3x  5cos x  2.
C. f  x  3x  5cos x  5 .
D. f  x  3x  5cos x  2 .
Câu 10. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình phẳng (H) giới hạn bởi đồ thị hàm số 2
y  2x  x và trục hoành. Tính thể tích V vật thể tròn xoay sinh ra khi cho (H) quay quanh trục Ox. 4 16 4 16 A. V   . B. V  . C. V  . D. V   . 3 15 3 15 3
Câu 11. (Chuyên KHTN - 2021) Cho hàm số f  x liên tục trên  và thoả mãn xf  xdx  2  . Tích 0 1
phân xf 3x dx  bằng 0 2 2 A. . B. 18 . C. . D. 6 . 3 9
Câu 12. (Chuyên KHTN - 2021) Họ nguyên hàm của hàm số f  x  ln x trên khoảng 0;   là 2 ln x 1
A. x ln x  x  C . B.  C . C.  C .
D. x ln x  x  C . 2 x
Câu 13. (Chuyên KHTN - 2021) Diện tích hình phẳng giới hạn bởi đồ thị của hàm số 2
y  x  x và đồ thị
của hàm số y  2x  2 bằng 1 3 53 9 A. . B. . C. . D. . 6 2 6 2
Câu 14. (Chuyên KHTN - 2021) Họ nguyên hàm x cos xdx  là
A. cos x  x sin x  C .
B.  cos x  x sin x  C .
C. cos x  x sin x  C .
D.  cos x  x sin x  C .
Câu 15. (Chuyên KHTN - 2021) Diện tích hình phẳng giới hạn bởi đường thẳng y  x  3 và parabol 2
y  2x  x 1 bằng: 13 9 13 A. . B. . C. 9 . D. . 6 2 3
Câu 16. (Chuyên KHTN - 2021) Tính nguyên hàm 2 tan 2xdx 
Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1 1
A. tan 2x  x  C . B.
tan 2x  x  C . C.
tan 2x  x  C .
D. tan 2x  x  C . 2 2 2x   1 ln xdx 
Câu 17. (Chuyên KHTN - 2021) Tìm nguyên hàm 2 x 2 x A.  2
x  xln x   x  C . B.  2
x  x ln x   x  C . 2 2 2 x 2 x C.  2
x  xln x   x  C . D.  2
x  xln x   x  C . 2 2
Câu 18. (Chuyên KHTN - 2021) Tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi đường
thẳng x  2 và đồ thị 2
y  x khi quay xung quanh trục Ox . 4 5 32  A. . B. . C. . D. . 5 6 5 6
Câu 19. (Chuyên KHTN - 2021) Tính nguyên hàm x  x   2 2 3 2 1 dx .  x  3 3 2 1  x  3 3 2 1  x  3 3 2 1  x  3 3 2 1 A.  C . B.  C . C.  C . D.  C 18 3 6 9 1
Câu 20. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho tích phân 2
x 3x 1dx  , nếu đặt 0 1 2
u  3x 1 thì 2
x 3x 1dx  bằng 0 2 1 2 1 2 2 1 1 A. 2 u du  . B. d u u  . C. 2 u du  . D. 2 u du  . 1 3 1 3 1 3 0 3 2 2
4 f (x)  2xdx  1  f (x)dx 
Câu 21. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho 1 . Khi đó 1 bằng A. 1. B. -3. C. -1. D. 3.
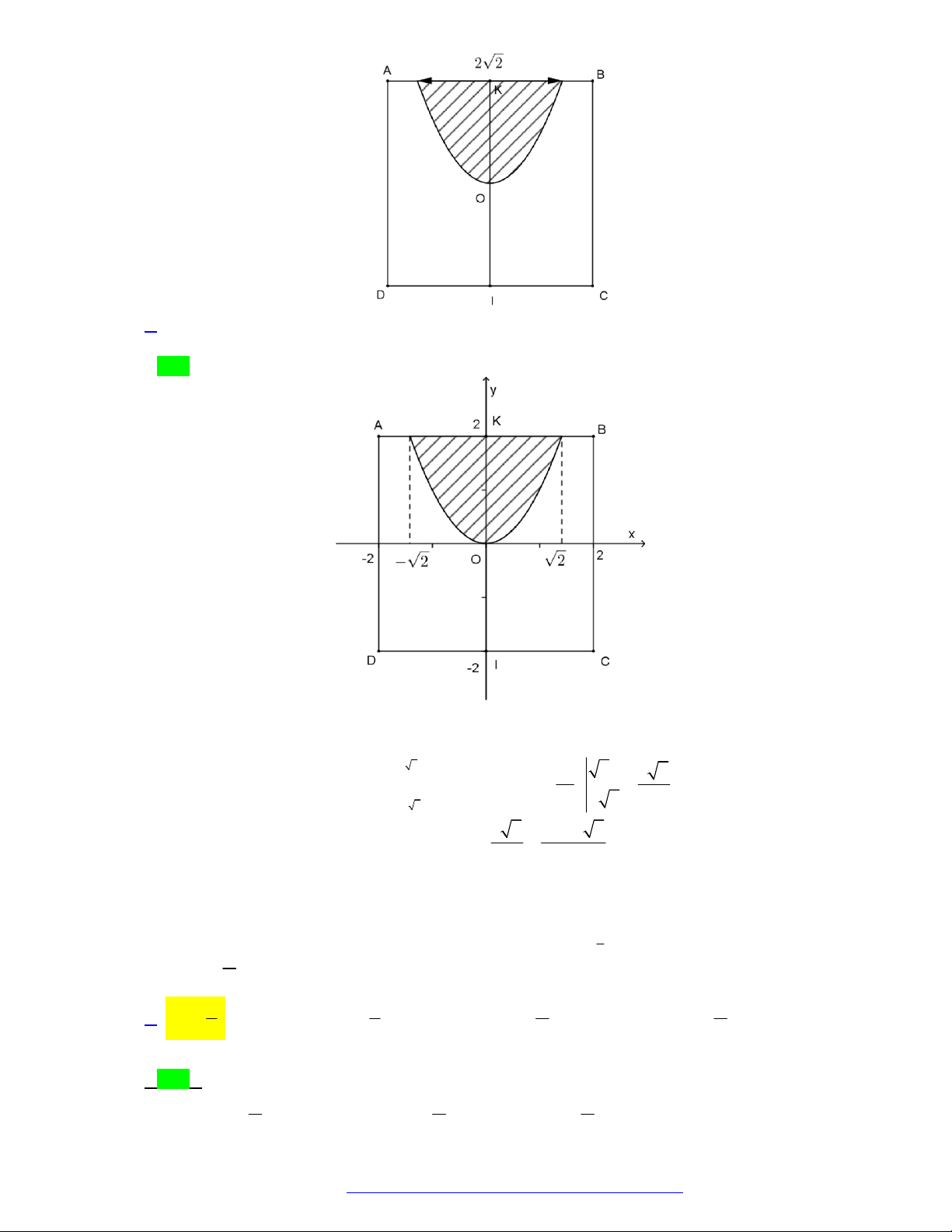
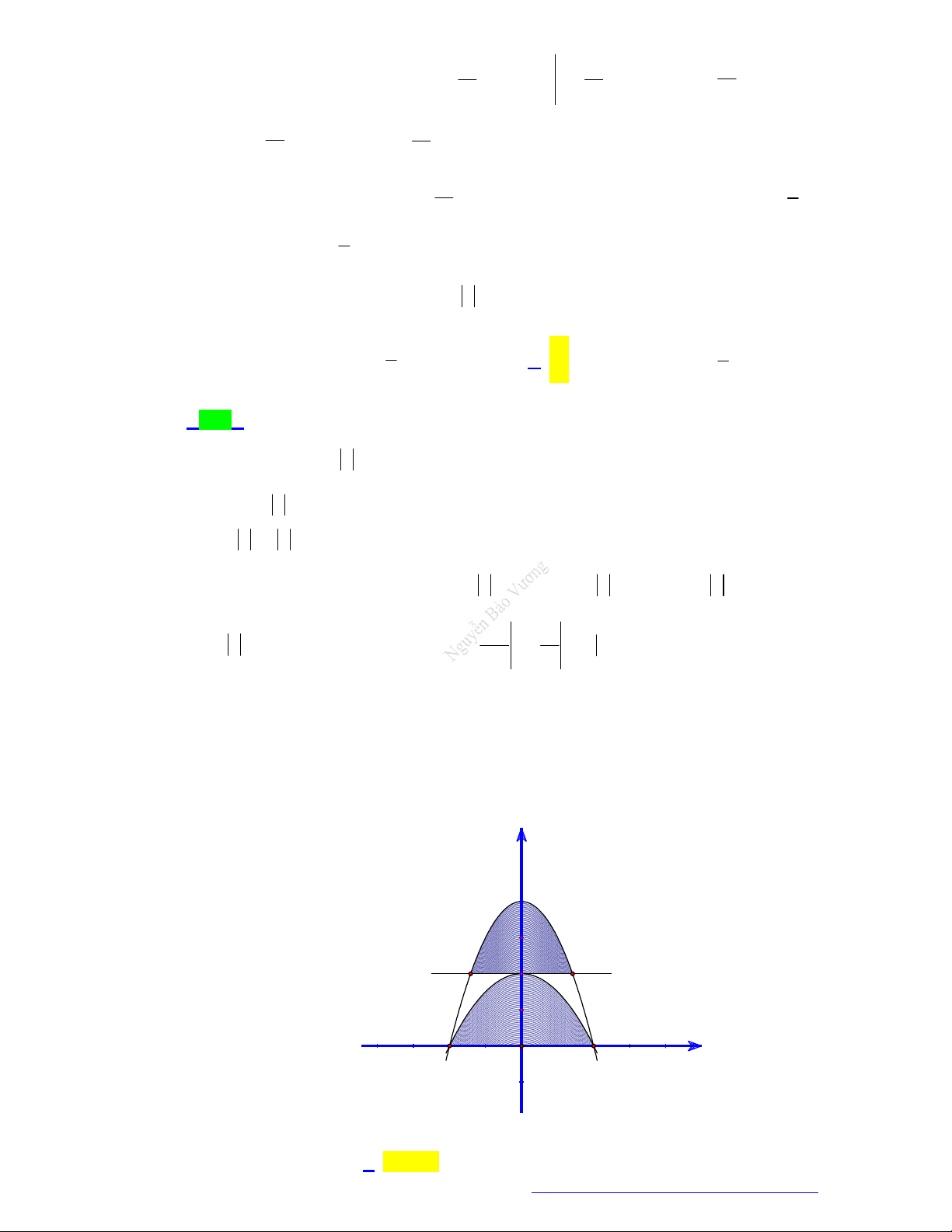
Câu 22. (Chuyên Quốc Học Huế - 2021) Tính diện tích của hình phẳng (được tô đậm) giới hạn bởi hai đường 2 2
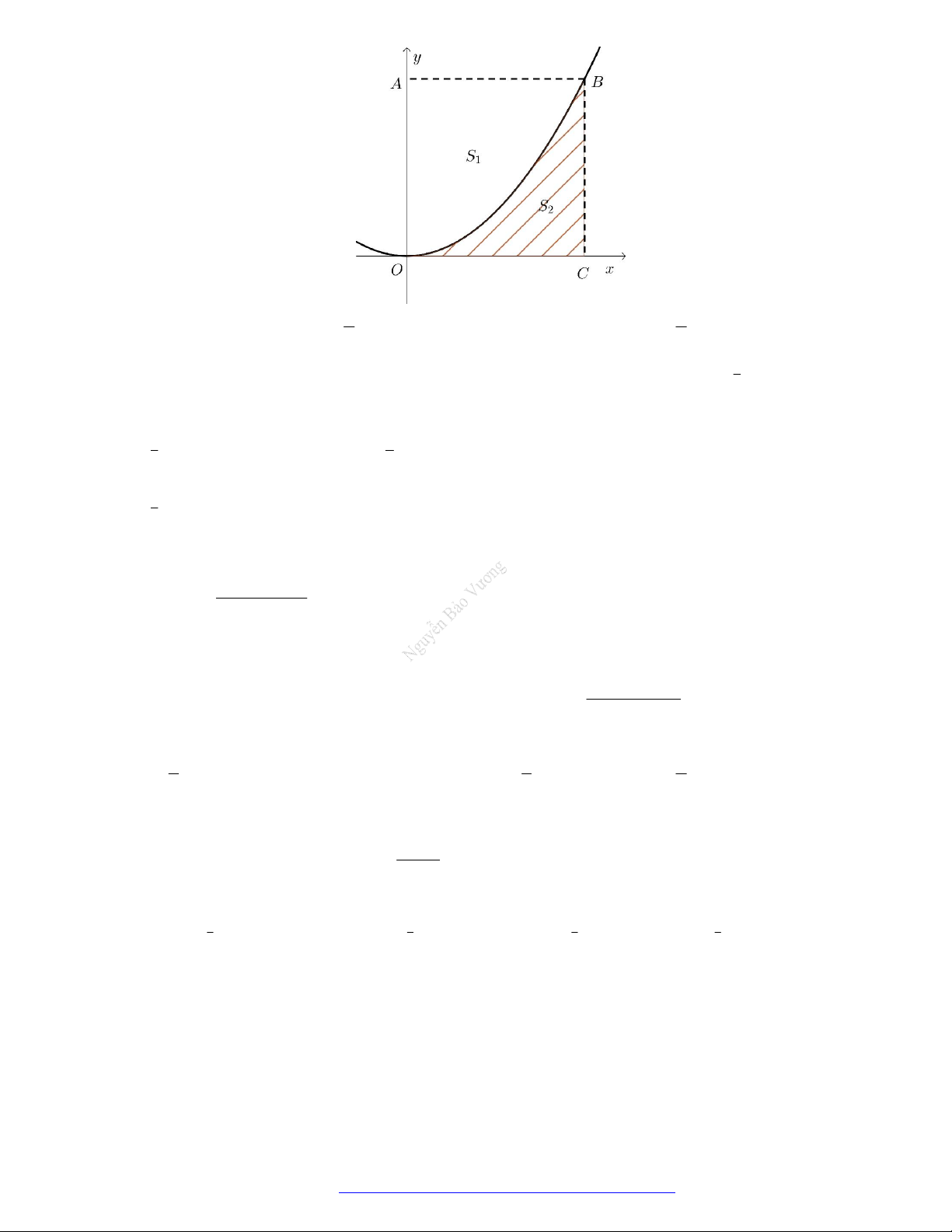
y  2x , y  4 . x 2 4 4 2 A. S  . B. S  . C. S  . D. S  . 3 3 3 3  2
Câu 23. (Chuyên Quốc Học Huế - 2021) Cho tích phân
2  cos x sin xdx 
. Nếu đặt t  2  cos x thì kết 0 quả nào sau đây đúng?  2 2 2 3 A. I  2 tdt.  B. I  tdt.  C. I  tdt.  D. I  tdt.  3 0 3 2
Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Nguyên hàm của hàm số f (x)  2x(x 1)(2x 1) .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 A.   2 2 x x  C B. 4 3 2
x  x  x  C C. 4 3 2
x  x  x  C D. 4 3 2
x  x  2x  C
Câu 25. (Chuyên Quang Trung - Bình Phước - 2021) Tìm nguyên hàm F  x của hàm số ( )  . x f x x e biết F   1  0 . A. . x x x e  e . B. . x x x e  e 1. C. . x x e  e . D. . x
x e  x 1 e .
Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm số thực m để hàm số F  x 3
 mx   m   2 3
2 x  4x  3
là một nguyên hàm của hàm số f  x 2
 3x 10x  4 A. m  2 . B. m  1 . C. m  0 . D. m  1 .
Câu 27. (Chuyên Ngoại Ngữ Hà Nội- 2021) Nguyên hàm của hàm số f  x 3  3x 1 là 1 A. 3
f (x)dx 
(3x 1) 3x 1  C  . B. 3
f (x)dx  (3x 1) 3x 1  C  . 4 1 C. 3
f (x)dx  3x 1  C  . D. 3
f (x)dx  3x 1  C  3 e
Câu 28. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho tích phân  2 3x  2x 3 2
dx  me  ne với m, n  , khi 0
đó m  n bằng bao nhiêu? A. 5 . B. 3 . C. 2 . D. 0 . 3 x  8
Câu 29. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho
dx  a ln 2  b ln 5 
với a, b là các số nguyên. 2 x  x  2 2
Mệnh đề nào sau đây đúng?
A. a  b  3 .
B. a  b  5 .
C. a  2b  11.
D. a  2b  11 .
Câu 30. (Chuyên Ngoại Ngữ Hà Nội- 2021) Thể tích khối tròn xoay sinh ra khi quay quanh Ox hình
phẳng giới hạn bởi các đường  0,  1, x x x
y  xe ; y  0 là  1 1  A.  2 e   1 . B.  2 e   1 . C.  2 e   1 . D.  2 e   1 . 4 4 4 4 2 4
Câu 31. (Chuyên Ngoại Ngữ Hà Nội- 2021) Biết xf 2x dx 4 
. Giá trị của xf  x dx  bằng 0 0 A. 16 . B. 1 . C. 8 . D. 2 .
Câu 32. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Với a,b là các tham số thực. Giá trị tích phân b  2 3x  2ax    1 dx bằng 0 A. 2
3b  2ab 1. B. 3 2
b  b a  b . C. 3 2
b  a b  b . D. 3 2
b  ab  b .
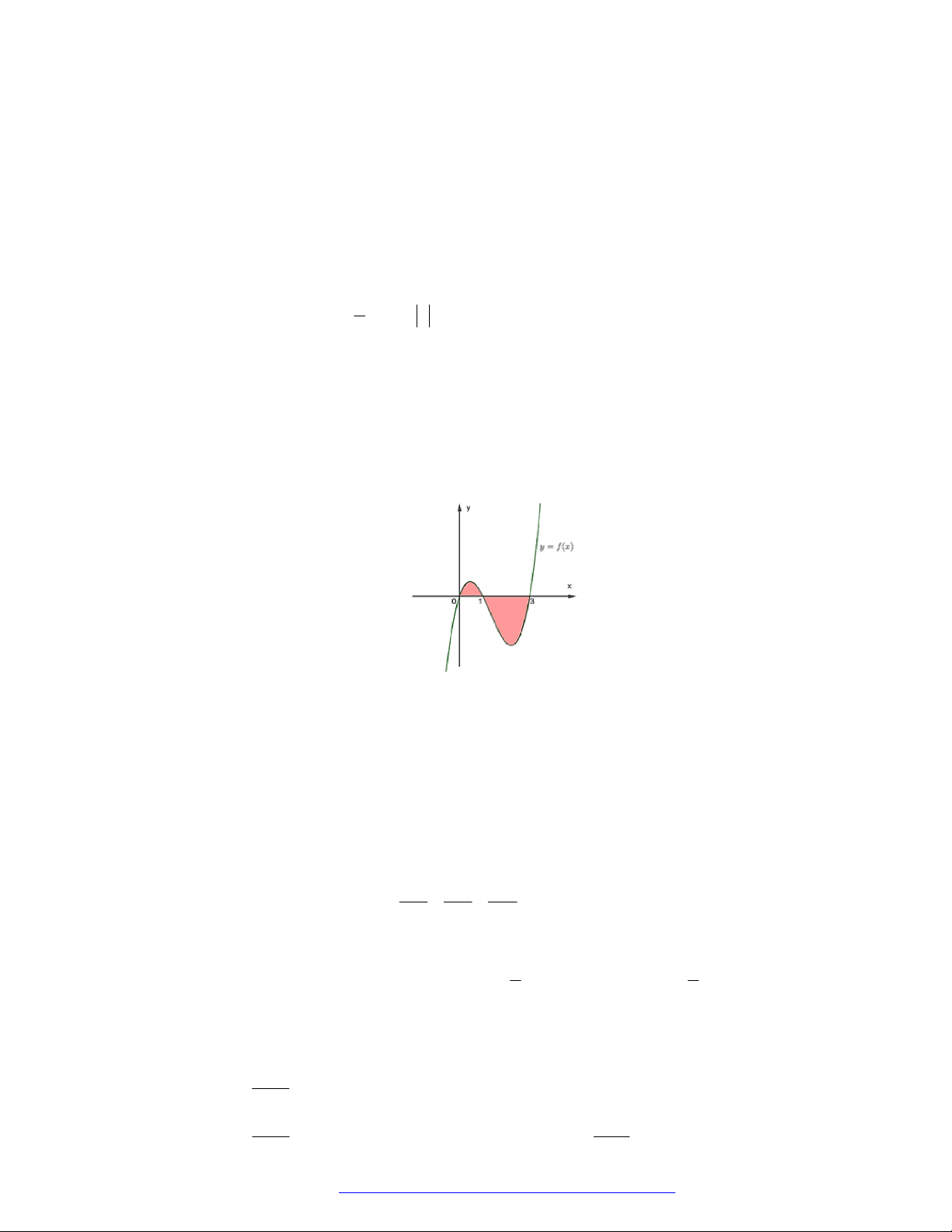
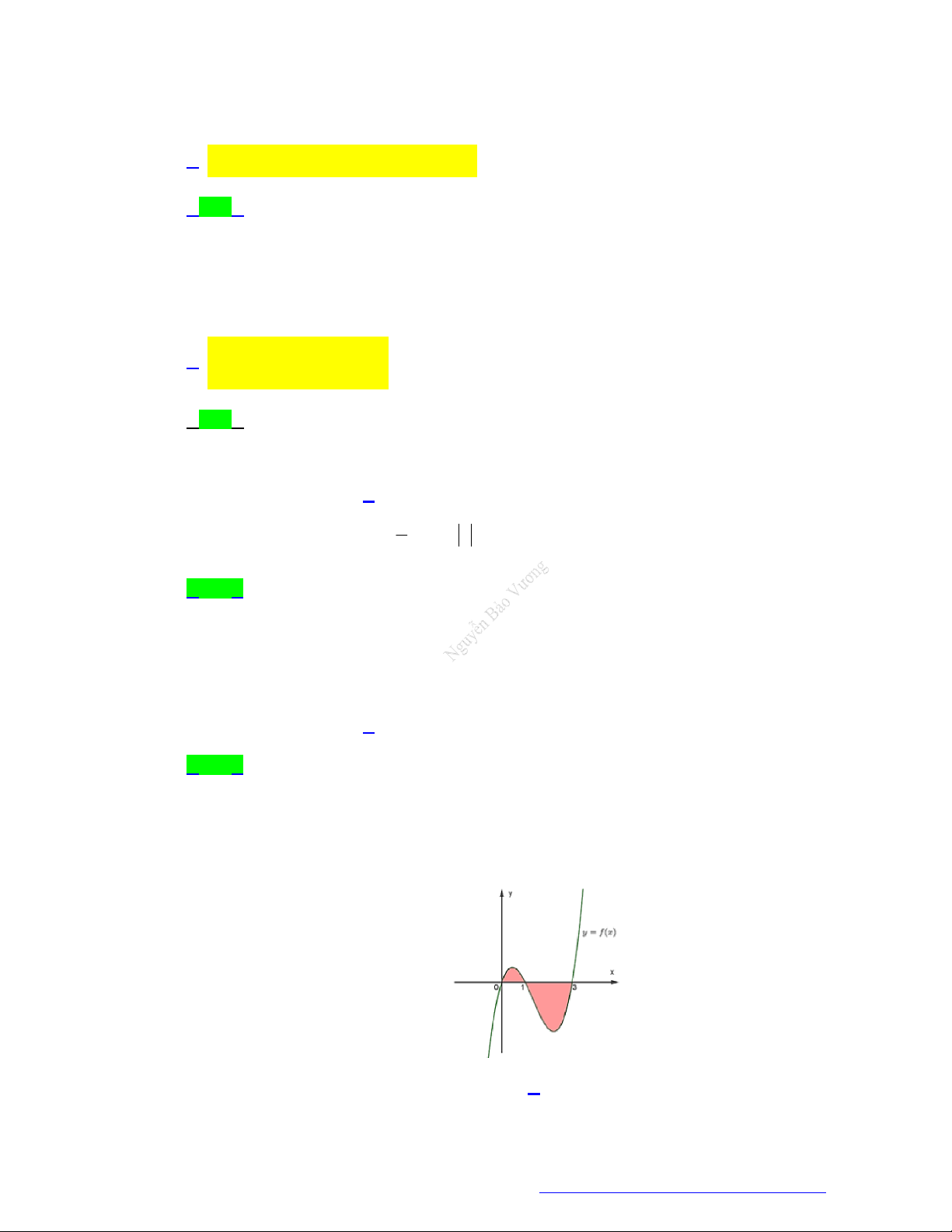
Câu 33. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Hình vẽ bên biểu diễn trục hoành cắt đồ thị y  f  x
tại ba điểm có hoành độ 0 , a , b a  0  b . Gọi S là hình phẳng giới hạn bởi đồ thị y  f  x và
trục hoành, khẳng định nào sau đây là sai? y x O a b
Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 b 0 b A. S 
f  x dx  .
B. S   f  x dx  f  x dx   . a a 0 0 b 0 b C. S 
f  x dx  f  x dx   . D. S 
f  x dx 
f  x dx   . a 0 a 0
Câu 34. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình phẳng D giới hạn bởi đường cong x y  e ,
trục hoành và các đường thẳng x  0, x  1. Khối tròn xoay tạo thành khi quay D quanh trục
hoành có thể tích V bằng bao nhiêu?   2 e   1 2 2  e 2 e 1  e   1 A. V  . B. V  . C. V  . D. V  . 2 2 2 2
Câu 35. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hàm số y  f  x có đạo hàm cấp hai f  x liên tục trên đoạn 0 
;1 đồng thời thỏa mãn điều kiện f 0  f  
1  1; f 0  2021. Mệnh đề nào sau đây đúng? 1 1
A. 1 x f  x dx  2  021  .
B. 1 x f  x dx  2021  . 0 0 1 1
C. 1 x f  x dx  1  .
D. 1 x f  x dx  1   . 0 0
Câu 36. (Chuyên Hạ Long - Quảng Ninh - 2021) Diện tích hình phẳng giới hạn bởi đồ thị hàm số
y   x   2
1 x  5x  6 và hai trục tọa độ bằng 11 1 11  A. . B. . . D. . 4 2 C. 4 2
Câu 37. (Chuyên ĐHSP Hà Nội - 2021) Diện tích hình phẳng thuộc góc phần tư thứ hai, giới hạn bởi parabol 2
y  2  x , đường thẳng y   x và trục Oy bằng: 7 5 11 9 A. . B. . C. . D. . 6 6 6 2
Câu 38. (Chuyên ĐHSP Hà Nội - 2021)  x  9 2 5 dx  bằng 1 1 A.
2x  510  C . B.  x  8 18 2 5  C .
C.  x  8 9 2 5  C . D.
2x  510  C . 10 20 1
Câu 39. (Chuyên ĐHSP Hà Nội - 2021) Biết f  x là hàm số liên tục trên 0;  3 và có
f 3xdx  3  . Giá 0 3 trị của biểu thức
f  xdx  bằng: 0 1 A. 9. B. 1. C. 3. D. . 3
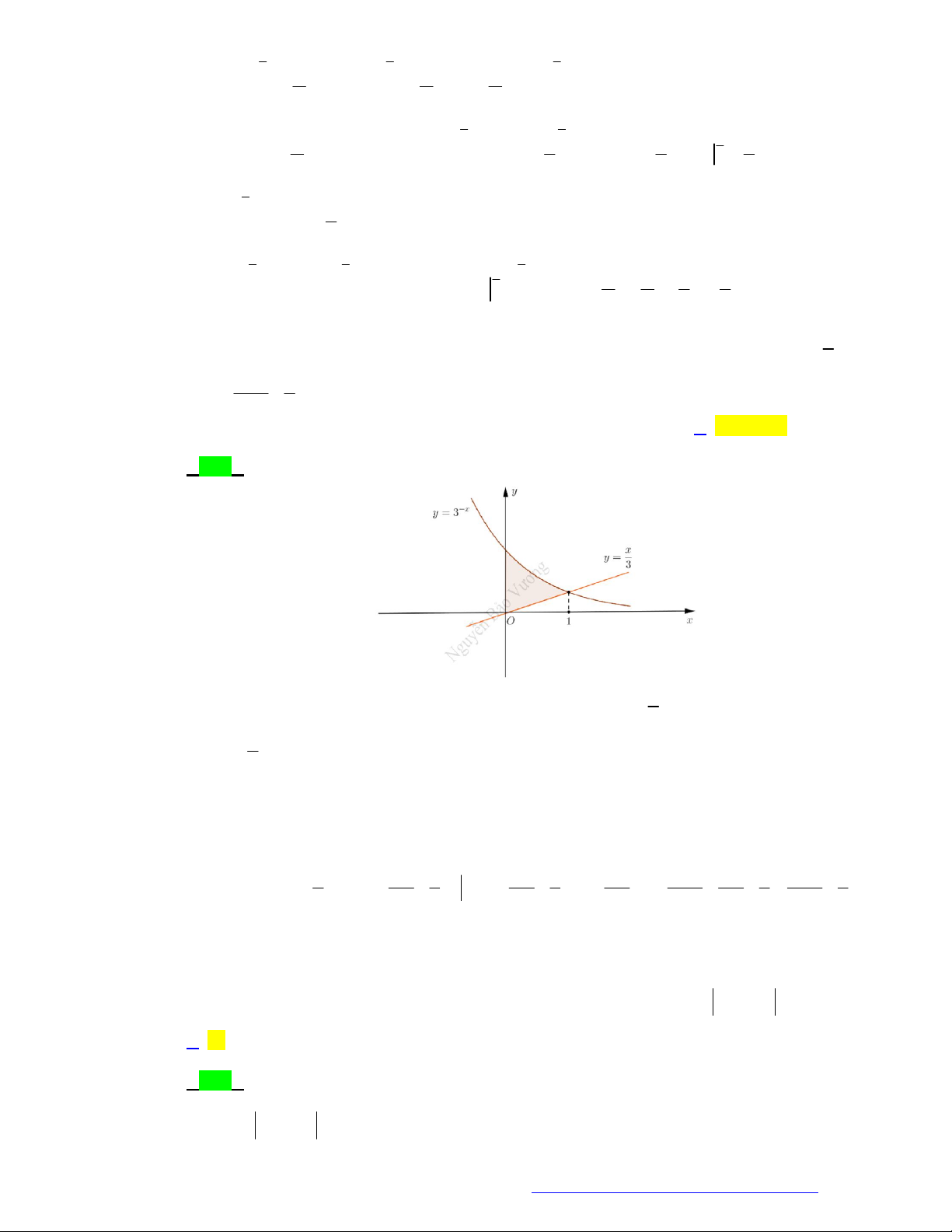
Câu 40. (Chuyên ĐH Vinh - Nghệ An - 2021) Giả sử f  x là hàm liên tục trên 0;  và diện tích 1
phần hình phẳng được kẻ dọc ở hình bên bằng 3 . Tích phân
f 2x dx  bằng: 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 4 3 A. . B. 3 . C. 2 . D. . 3 2
Câu 41. (Chuyên ĐH Vinh - Nghệ An - 2021) Họ nguyên hàm của hàm số   2 1 3 x f x   là 9x 9x 9x 9x A.  C . B.  C . C.  C . D.  C . 3 6 6 ln 3 3ln 3
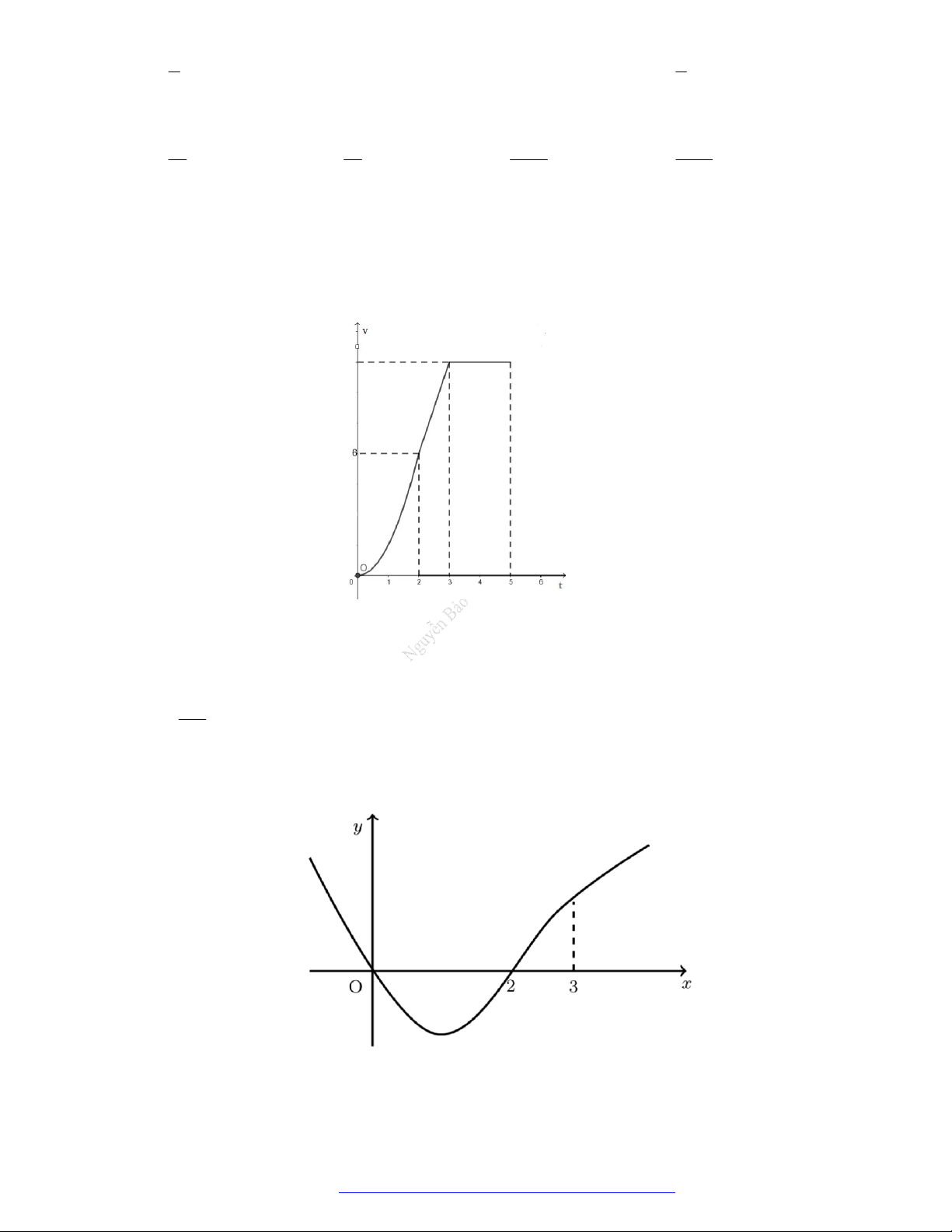
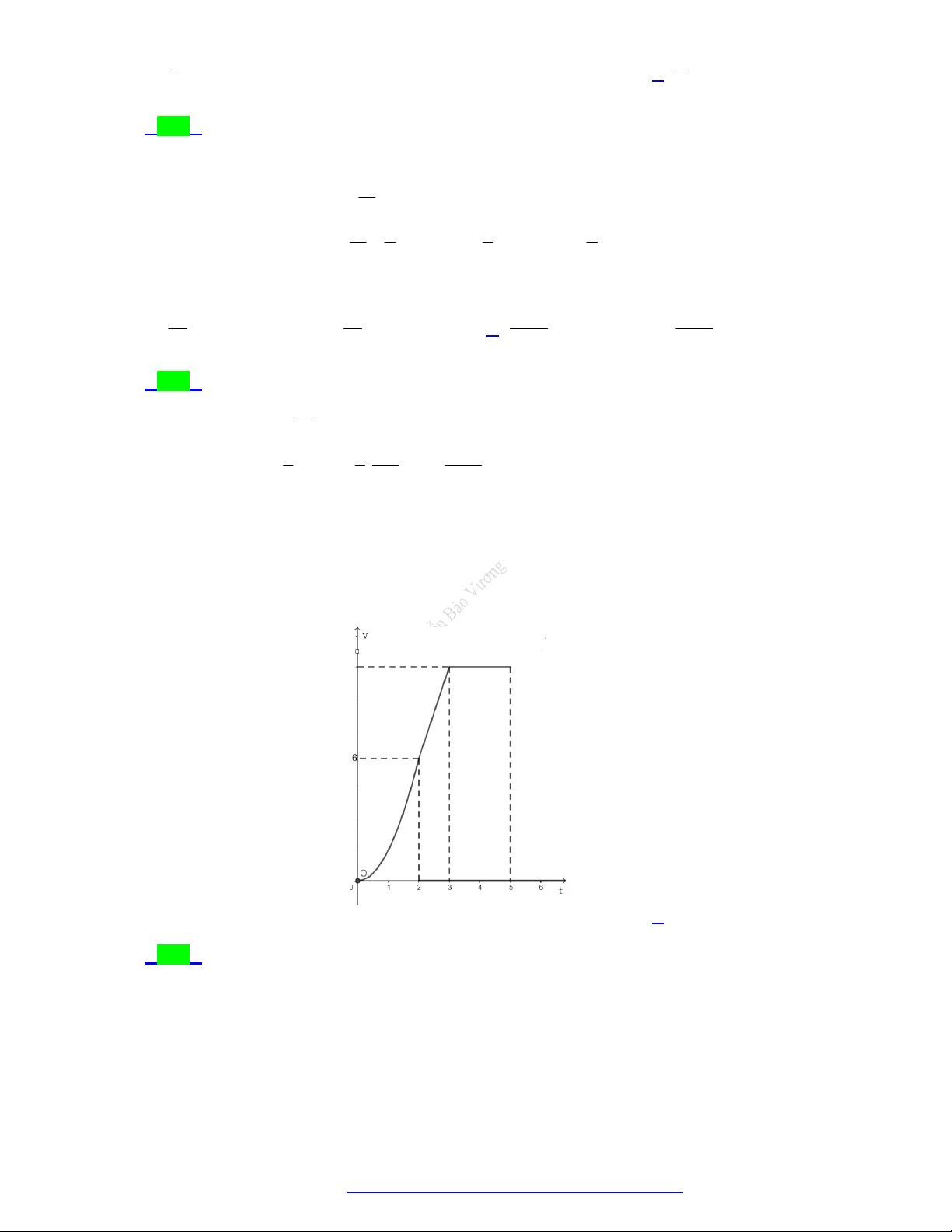
Câu 42. (Chuyên ĐH Vinh - Nghệ An - 2021) Một chiếc xe đua F đạt vận tốc lớn nhất là 360km / h . Đồ 1
thị bên hiển thị vận tốc v của xe trong 5 giây đầu tiên kể từ lúc xuất phát. Đồ thị trong 2 giây đầu
là một phần của parabol đỉnh tại gốc tọa đô O , giây tiếp theo là đoạn thẳng và sau đúng ba giây
thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị 1 giây, mỗi đơn vị trục tung
biểu thị 10m / s và trong 5 giây đầu xe chuyển động theo đường thẳng. Hỏi trong 5 giây đó sẽ đã
đi được quãng đường là bao nhiêu. A. 400 (mét). B. 340 (mét). C. 420 (mét). D. 320 (mét).
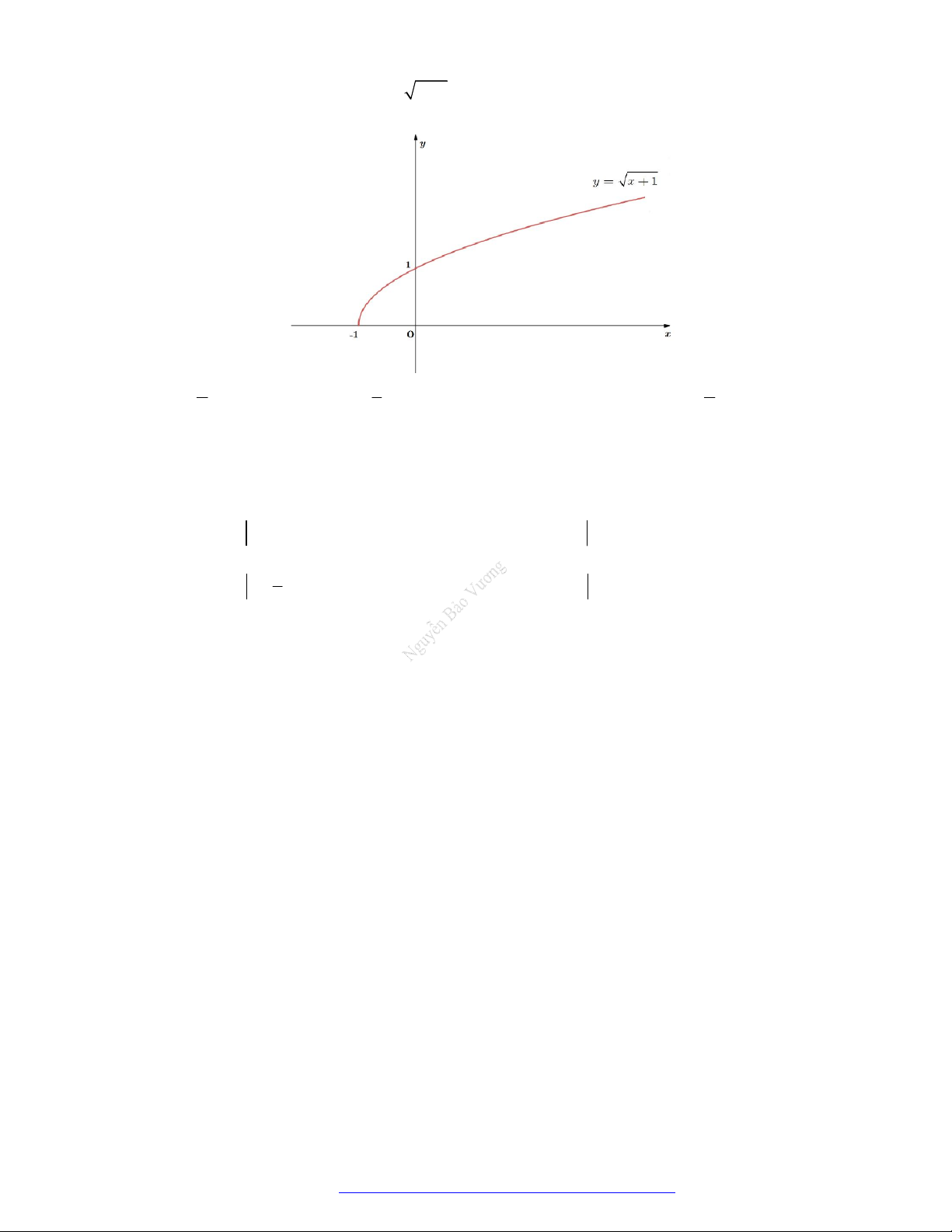
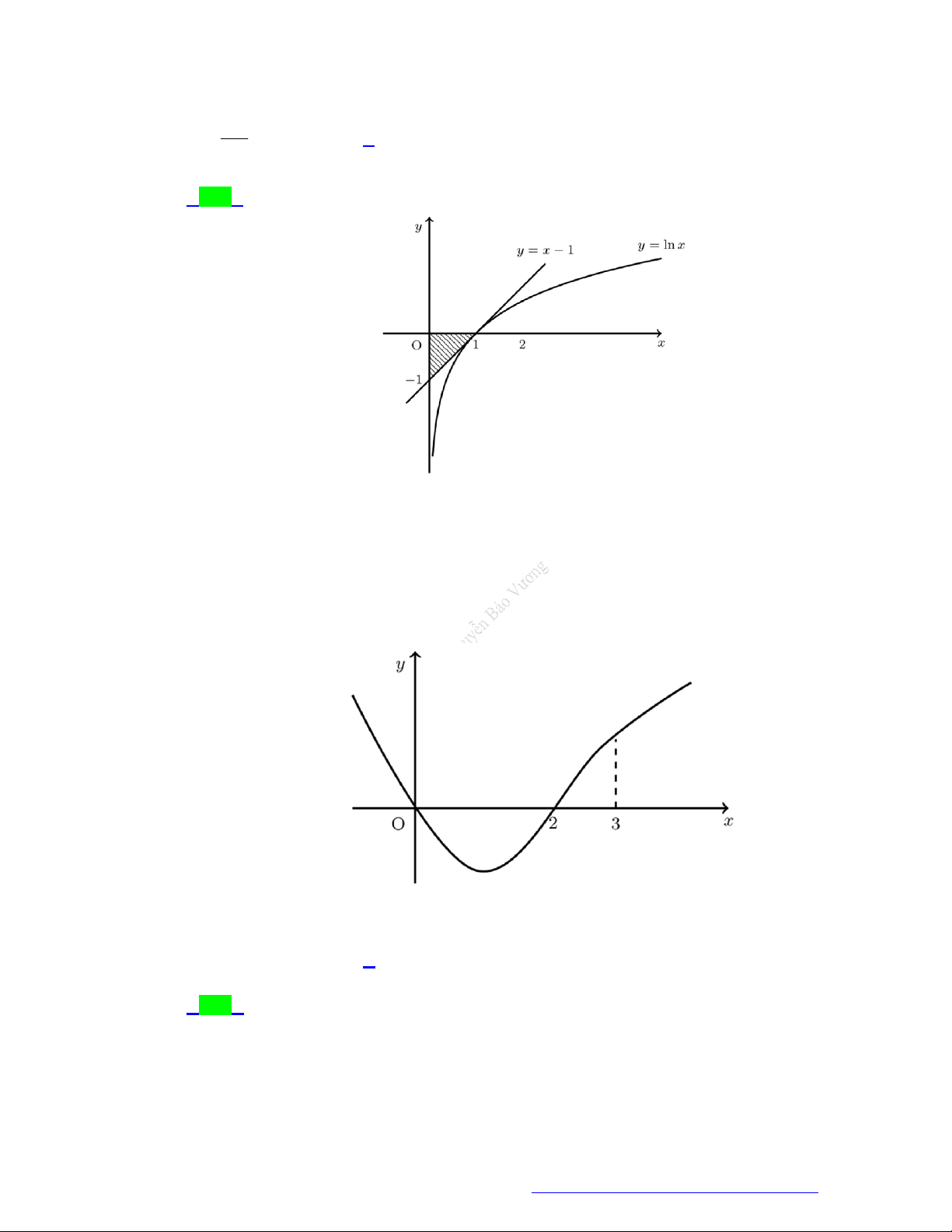
Câu 43. (THPT Quế Võ 1 - Bắc Ninh - 2021) Gọi d là tiếp tuyến của đồ thị hàm số y  ln x tại giao
điểm của đồ thị đó với trục Ox . Diện tích của hình tam giác tạo bởi hai trục tọa độ và đường
thẳng d được xác định bởi tích phân 1 ln x 1 1 1 A. . dx  B. 1 x . dx  C.  x   1 . dx  D. ln x . dx  x 0 0 0 0
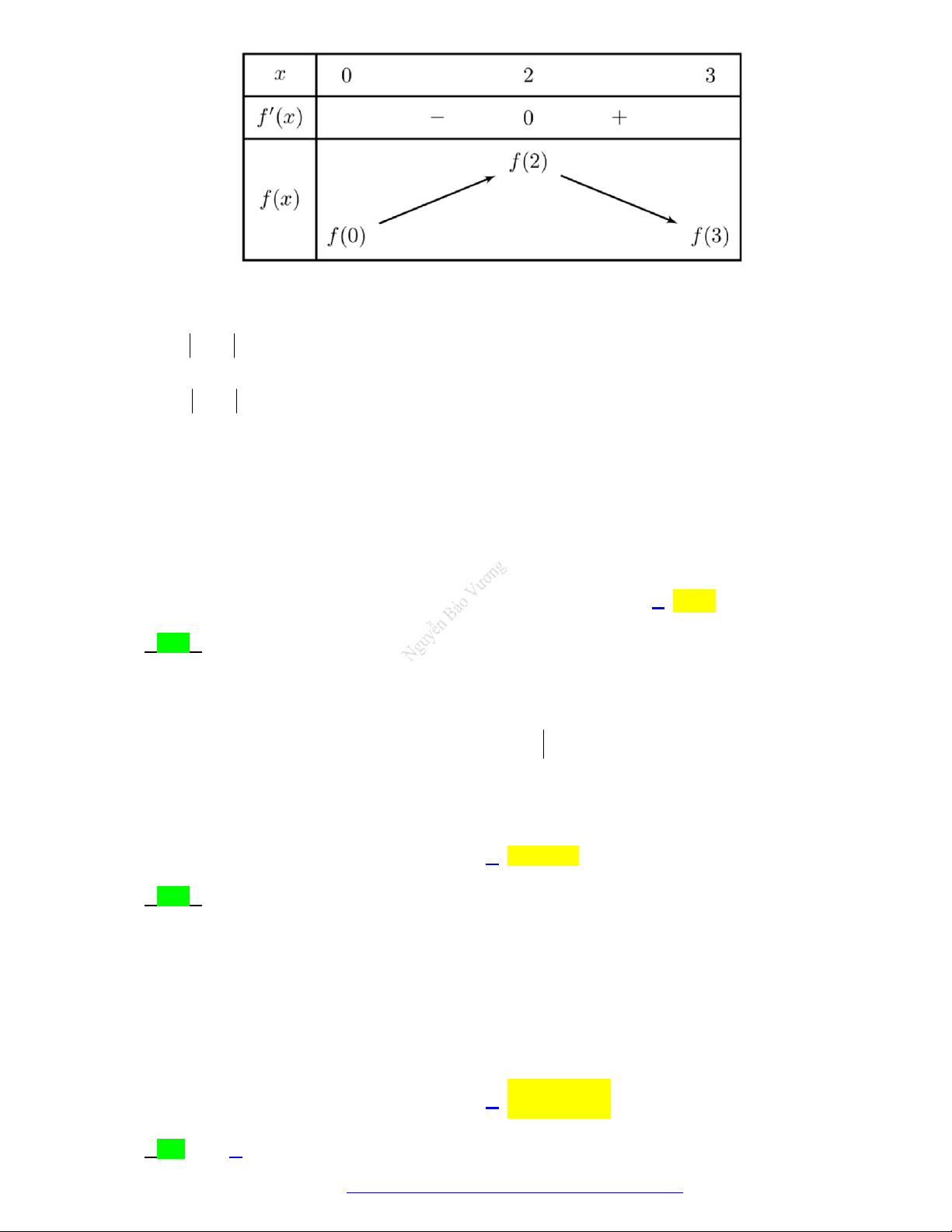
Câu 44. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hàm số f  x có đạo hàm là f  x . Đồ thị y  f  x
được cho bởi hình vẽ bên dưới.
Giá trị nhỏ nhất của f  x trên đoạn 0;3 là A. f 2.
B. Không xác định được.
C. f 0. D. f 3.
Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 45. (THPT Quốc Oai - Hà Nội - 2021) Một ô tô đang chạy với vận tốc 10 m / s thì người lái xe đạp
phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v t   2
 t 10 m / s , trong
đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Quãng đường ô tô di chuyển
được trong 8 giây cuối cùng tính đến thời điểm dừng bánh là A. 16 m .
B. 55 m .
C. 25 m . D. 50 m .
Câu 46. (THPT Quốc Oai - Hà Nội - 2021) Cho
    2    2x F x ax
bx c e là một nguyên hàm của hàm số
f  x   2 x  x   2x 2020 2022
1 e trên khoảng  ;
  . Tính T  a  2b  4c . A. T  1004 B. T  1018 . C. T  1012 .
D. T  2012 .
Câu 47. (THPT Quốc Oai - Hà Nội - 2021) Nguyên hàm của hàm số f x  2xx   1 2x   1 là A. 4 3 2
x  x  x  C . B. 4 3 2
x  x  2x  C . C.   2 2 x x C . D. 4 3 2
x  x  x  C . 1 2
Câu 48. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Tích phân x xe dx  bằng 0 1
A. (e 1) .
B. (e 1) . C. 2e . D. 2e 1. 2
Câu 49. (THPT Phan Đình Phùng - Quảng Bình - 2021) Khi đổi biến x  3 tan t , tích phân 1 dx I  
trở thành tích phân nào? 2 x  3 0     3 3 6 1 6 3 6 A. I  dt  . B. I  dt  . C. I  dt  . D. I  3dt  . 3 t 3 0 0 0 0
Câu 50. (THPT Phan Đình Phùng - Quảng Bình - 2021) Gọi S là diện tích hình phẳng giới hạn bởi đồ x 1
thị hàm số  H  : y 
và các trục tọa độ. Khi đó giá trị của S bằng x 1
A. S  ln 2 1.
B. S  2 ln 2 1.
C. S  ln 2 1.
D. S  2 ln 2 1.
Câu 51. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hàm số f  x liên tục trên  và thỏa mãn 3 1
f  x dx  20 
. Tính tích phân I   x   1 f   2
x  2xdx . 0 0 A. I  20 . B. I  10 . C. I  40 . D. I  30 . 4 2 ln x a a
Câu 52. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho biết 3 dx  ln 2  , với *
a, b   và là x b b 1
phân số tối giản. Tính a  b . A. 4 . B. 5 . C. 11. D. 9 . 1 b
Câu 53. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho biết ex x dx  a  
với a,b   . Tính 0 e 2 2 a  b . A. 7 . B. 5 . C. 3 . D. 4 .
Câu 54. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Trong mặt phẳng tọa độ Oxy cho hình phẳng  H 
được giới hạn bởi các đường y  sin x, y  0, x  0 và x  . Quay hình phẳng  H  quanh trục Ox
ta được một vật thể tròn xoay có thể tích bằng 2   A.  . B. 2  . C. . D. . 2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 55. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Trong mặt phẳng tọa độ Oxy , cho hình phẳng  H 
được giới hạn bởi đồ thị hàm số y 
x 1 và hai trục tọa độ Ox , Oy . Tính diện tích S của hình phẳng  H  . 3 1 2 A. S  . B. S  . C. S  1. D. S  . 2 3 3 
Câu 56. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho tích phân 2
I  x cos xdx  và 0 2
u  x , dv  cos xdx . Khẳng định nào sau đây đúng?     A. 2
I  x sin x  2 x sin xdx  . B. 2
I  x sin x  2 x sin xdx  . 0 0 0 0 1     C. 2 3
I  x sin x  x sin xdx  . D. 2
I  x sin x  x sin xdx  . 0 3 0 0 0
Câu 57. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Diện tích S của hình phẳng giới hạn bởi các đường 2 3
y  2 x  3x 1, y  x 1 được tính bởi công thức nào dưới đây 0 3
A. S    2 3
2x  3x  x dx   3 2
x  2x  3xdx . 1  0 3
B. S    3 2
x  2 x  3 x dx . 1 3 2
C. S     3 2
x  2x  3x dx . 1  0 3 3 2 2 3
D. S   x  2x  3xdx   2x  3x  x dx . 1  0
Câu 58. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hàm số f  x liên tục trên đoạn 0;9 thỏa 9 7 4 9 mãn
f  xdx  8,
f  xdx  3.  
Khi đó giá trị của P 
f  xdx  f  xdx   là 0 4 0 7
A. P  11 .
B. P  5 .
C. P  20 . D. P  9 .
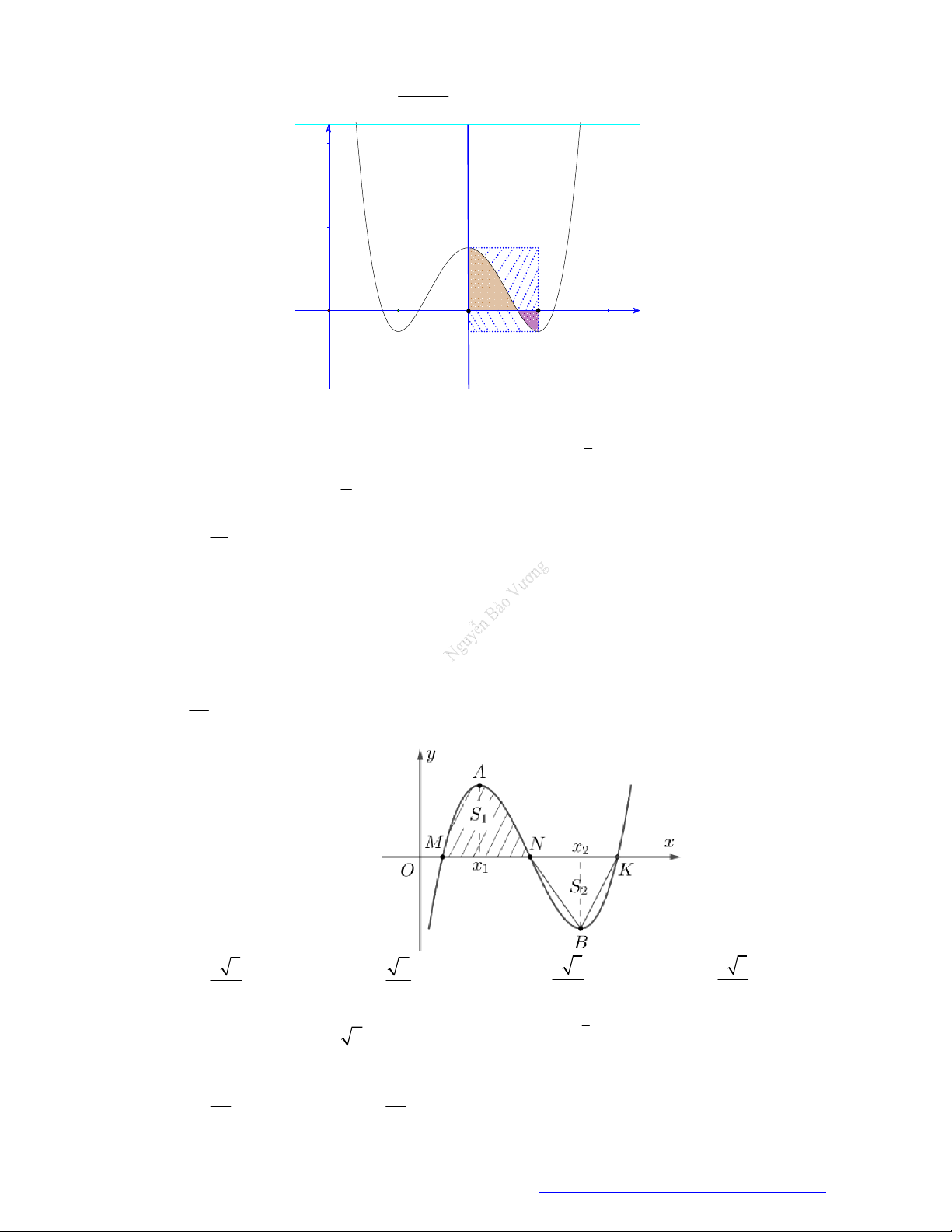
Câu 59. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Diện tích phần hình phẳng gạch sọc trong hình vẽ được
tính theo công thức nào dưới đây?
Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 y 2
y  x  2x 1 x O 2 1  2 y  x  3 2 2 A.   2
2x  2x  4 dx . B.  2
 x  2 dx  . 1 1  2 2
C. 2x  2 dx  . D.   2
2x  2x  4 dx . 1 1  4 dx
Câu 60. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho tích phân I 
 a  b ln 2, a,b  .   Khi 1 5  x 4
đó E  ab bằng A. E  6. B. E  28. C. E  8. D. E  30.
Câu 61. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình  H  giới hạn bởi các đường thẳng 2
y  x  2x, trục hoành. Tính thể tích khối tròn xoay sinh bởi hình phẳng  H  quay quanh trục Ox . 16 4 496 32 A. . B. . C. . D. . 15 3 15 15
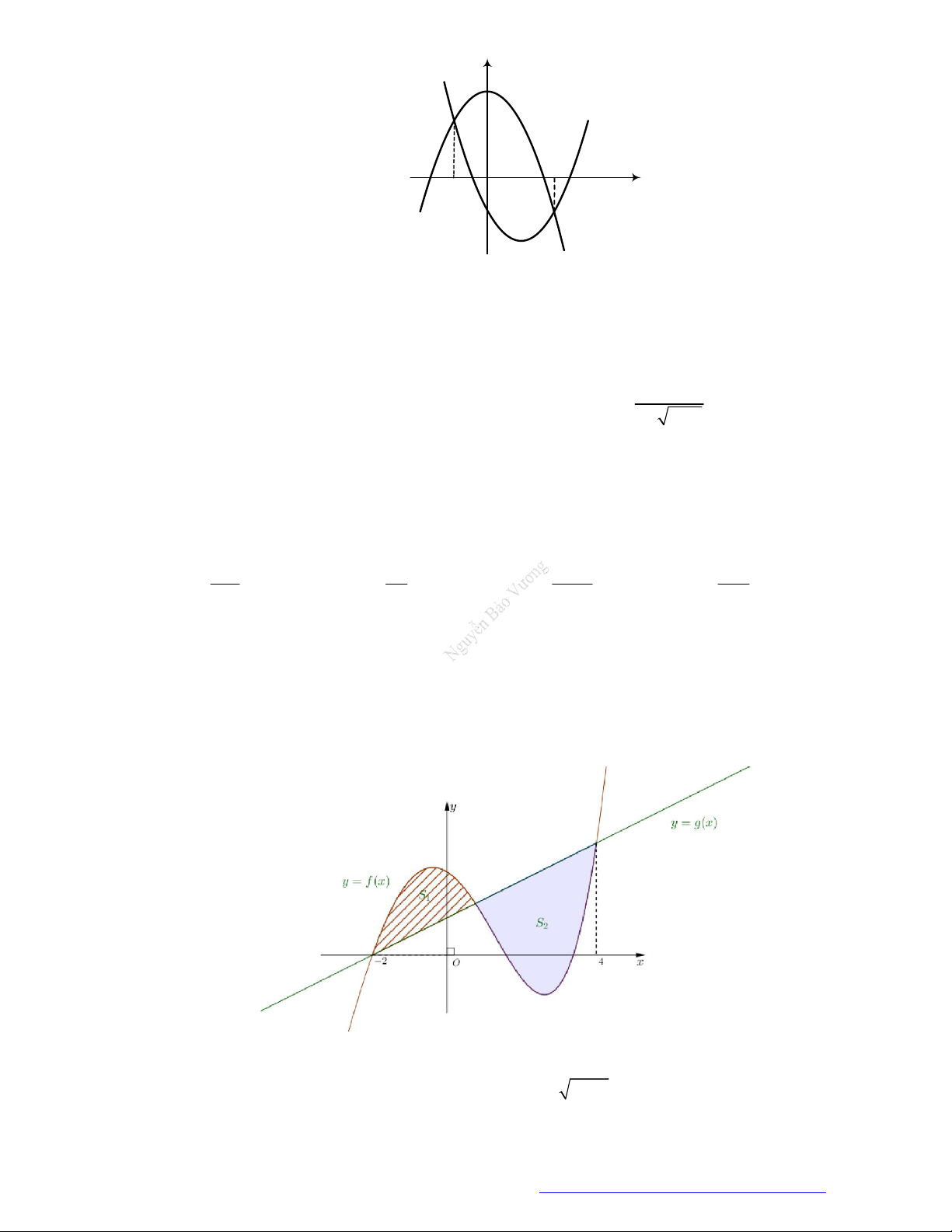
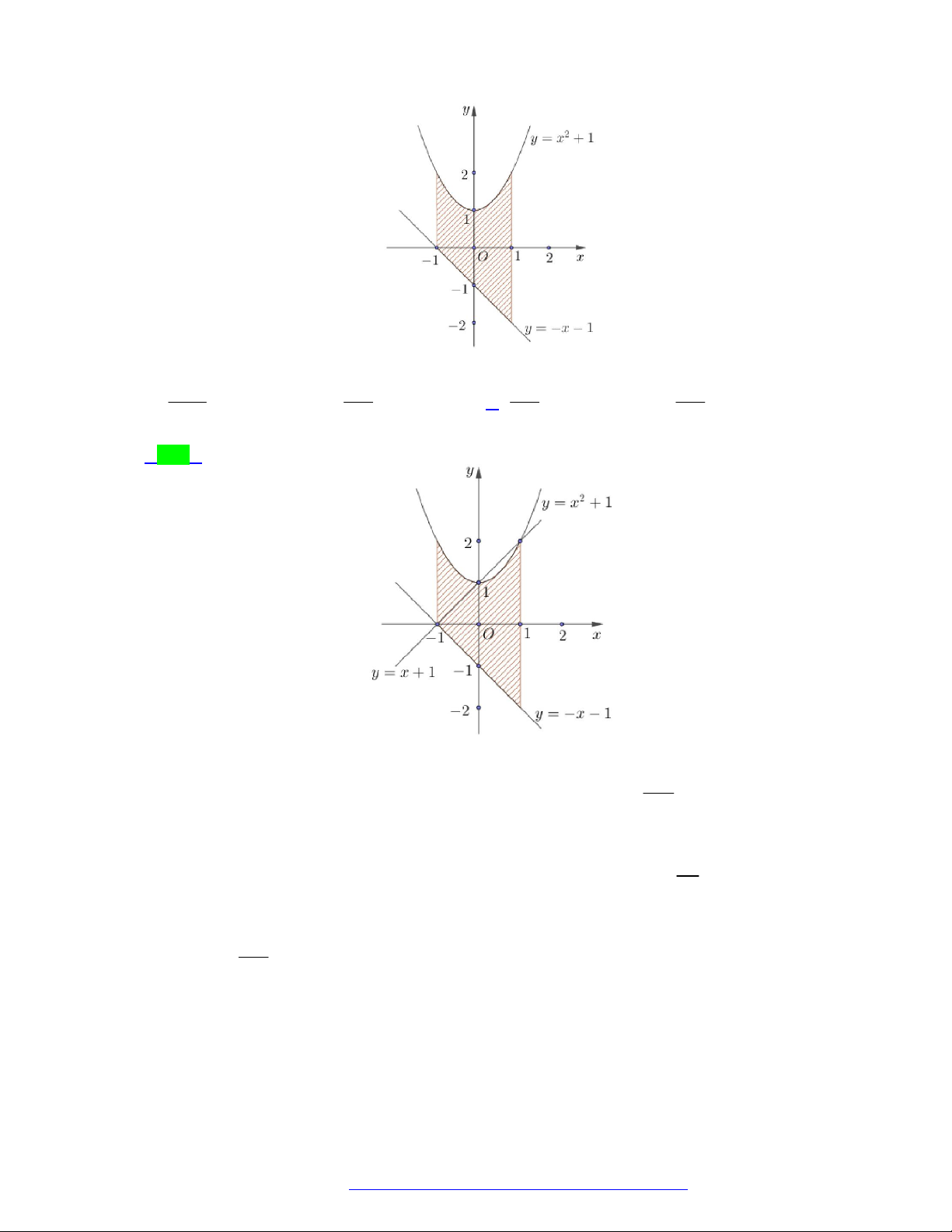
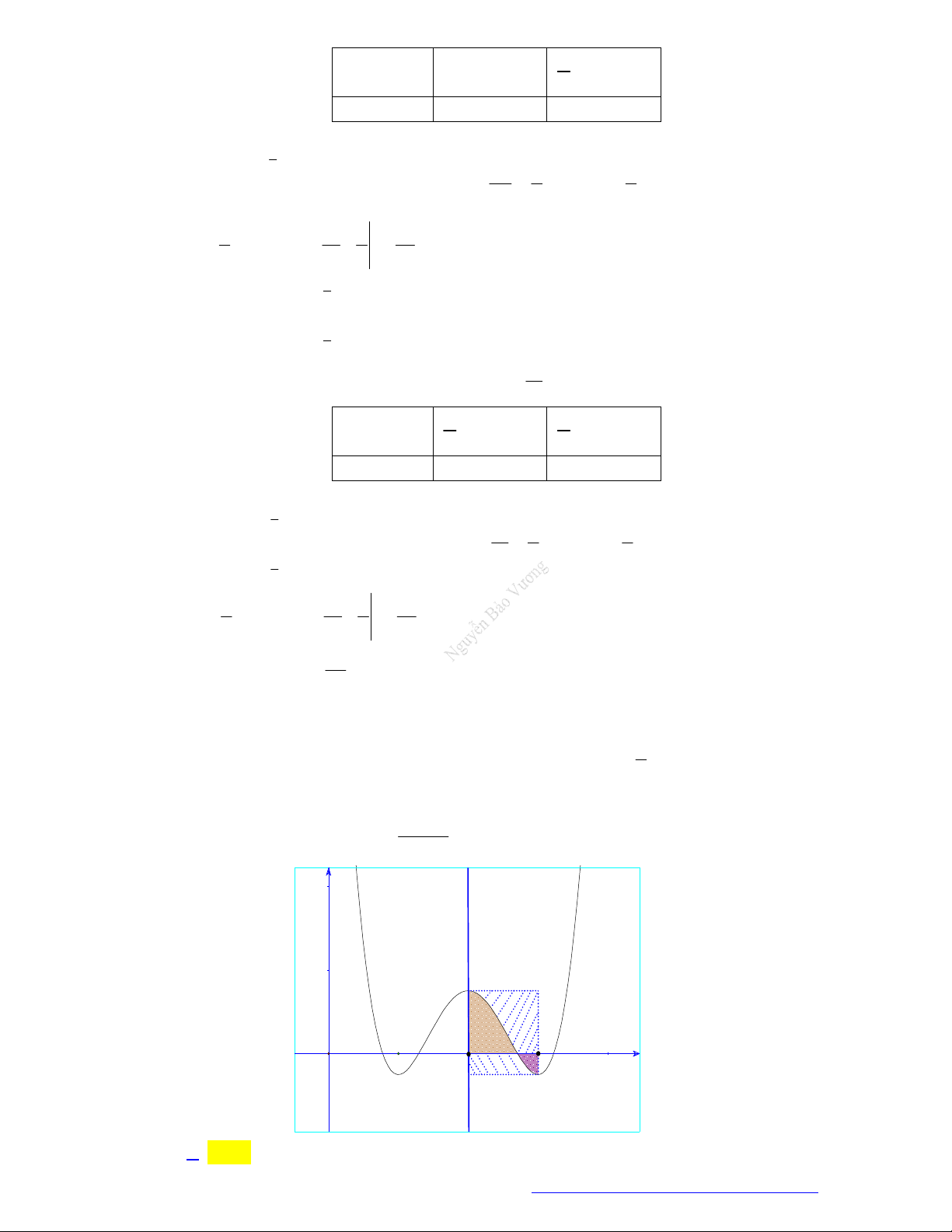
Câu 62. (THPT Đồng Quan - Hà Nội - 2021) Trong mặt phẳng toạ độ Oxy , cho hàm số y  f x có đồ
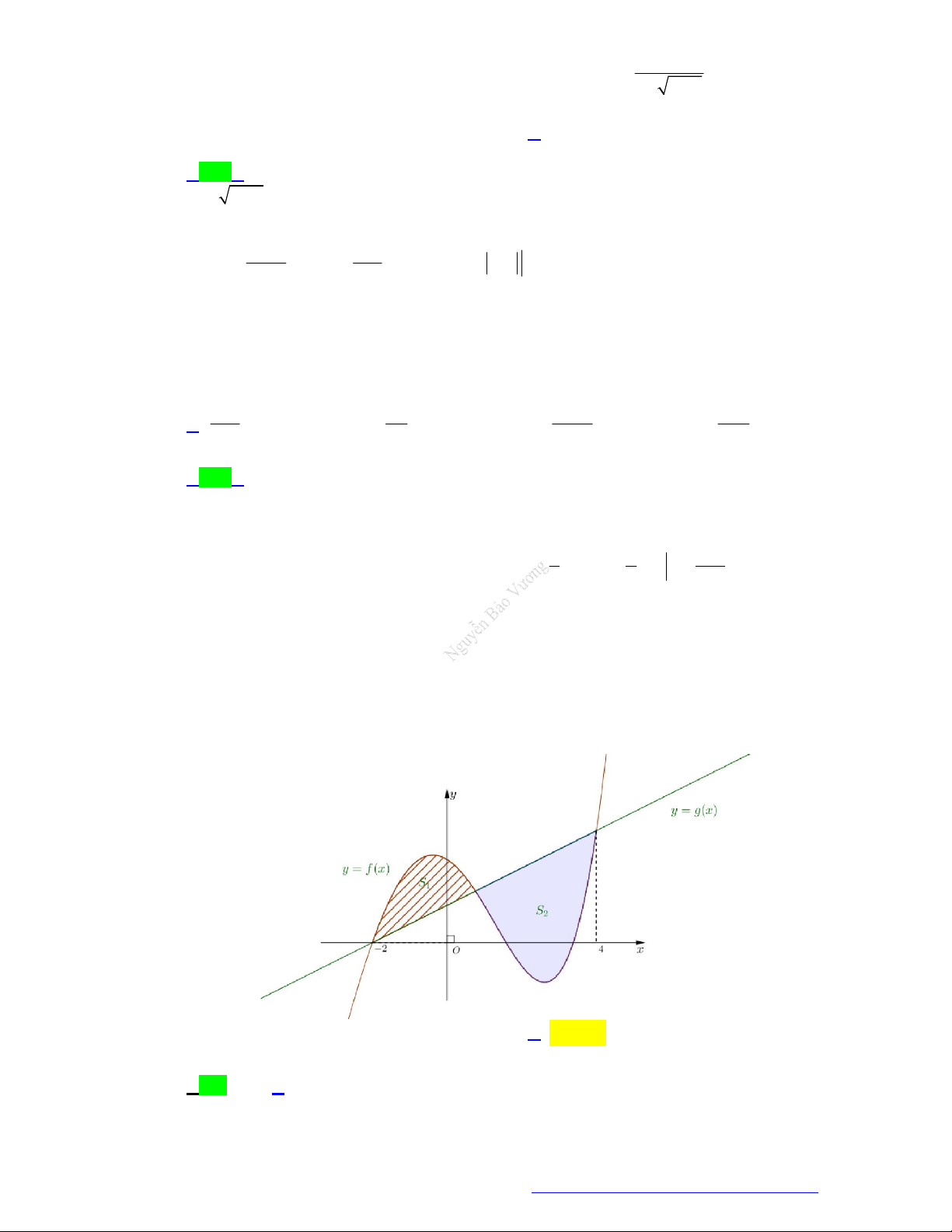
thị là đường cong và hàm số y  g x có đồ thị là đường thẳng. Gọi S là diện tích miền phẳng 1
được gạch sọc, S là diện tích miền phẳng được tô đậm, S  S (hình vẽ). Tích phân 2 1 2 4
  f xgxdx bằng 2 
A. S  S . B. S   S .
C. S  S .
D. S  S . 1 2 1 2 1 2 2 1 2
Câu 63. (THPT Lê Lợi - Thanh Hóa - 2021) Cho 2
I  4x x 1dx  và 2
u  x 1. Tìm khẳng định sai 1
trong các khẳng định sau?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 2 3 3 4 4 A. I  2 udu  . B. I  2 udu  . C. I  u u . D. I  27 . 0 3 3 1 0
Câu 64. (Sở Vĩnh Phúc - 2021) Tìm họ tất cả các nguyên hàm của hàm số  ex y  2x . 1 A. 2
ex  x  C .
B. ex  2  C . C. x 1  2 e
 x  C . D. x 2
e  2x  C . x 1
Câu 65. (Sở Vĩnh Phúc - 2021) Cho hình phẳng D giới hạn bởi đồ thị  P 2
: y  2x  x và trục Ox . Tính
thể tích của khối tròn xoay tạo thành khi cho D quay quanh trục Ox . 19 13 17 16 A. V  . B. V  . C. V  . D. V  . 15 15 15 15
Câu 66. (Sở Vĩnh Phúc - 2021) Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  2021 ,
trục hoành, x  2, x  4 . Mệnh đề nào sau đây đúng. 4 4 A. 2 2 S  (x  2021) dx  . B. 2 S  (x  2021)dx  . 2  2  2  4 C. 2 S  x  2021 dx  . D. 2 S  x  2021 dx  . 4 2  2021
Câu 67. (Sở Vĩnh Phúc - 2021) Cho hàm số y  f  x liên tục trên  và
f  x dx  4  . Tính 1 1010 I  f 2x   1 d . x  0
A. I  8.
B. I  2.
C. I  1.
D. I  4. 1 1 1
Câu 68. (Sở Lào Cai - 2021) Cho
f  x dx  2 
và  f  x  2g  x dx  8    
. Tính tích phân g  x dx ?  0 0 0 A. 6  . B. 3  . C. 5 . D. 5  . 2x 1
Câu 69. (Sở Hà Tĩnh - 2021) Họ tất cả các nguyên hàm của hàm số f (x)  trên khoảng 2 (x 1)  1  ;  là 1 1
A. 2 ln(x 1) 
 C . B. 2 ln(x 1)   C . x 1 x 1 2 3
C. 2 ln(x 1) 
 C . D. 2 ln(x 1)   C . x 1 x 1
Câu 70. (Sở Hà Tĩnh - 2021) Cho hàm số f (x) thỏa mãn f (0)  4 và x f (
 x)  e  x, x   R . Khi đó 1
f  x dx  bằng 0 6e  23 6e 17 6e 11 6e  23 A. . B. . C. . D. . 6 6 6 3
Câu 71. (Sở Hà Tĩnh - 2021) Biết   3
F x  x là một nguyên hàm của hàm số f  x trên  . Tính 3
I  2x  f  x dx    . 0 117 23 A. I  36 . B. I  9 . C. I  . D. I  . 4 4
Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1
Câu 72. (Sở Tuyên Quang - 2021) Cho 3 3 4 I  x 1 x dx  . Đặt 3 4
t  1 x thì I bằng 0 1 1 3 1 1 3 A. 3  t tdt  . B. 3 t dt  . C. 3 t dt  . D. 3  t dt  . 4 4 0 0 0 0
Câu 73. (Sở Yên Bái - 2021) Tính diện tích hình phẳng giới hạn bởi hai đồ thị 2
y  x  4x  6 và 2
y  x  2x  6 . 5 4 1 2 A. . B. . C. . D. . 3 3 3 3 2 2 2
Câu 74. (Sở Yên Bái - 2021) Nếu
f (x)dx  5 
; (2 f (x)  g(x))dx  13 
thì g(x)dx  bằng 1 1 1 A. 3  . B. 3 . C. 2  3 . D. 23 .
Câu 75. (THPT Thanh Chương 1- Nghệ An - 2021)  x   1 sin d x x  bằng. A. . B. . C. . D. .
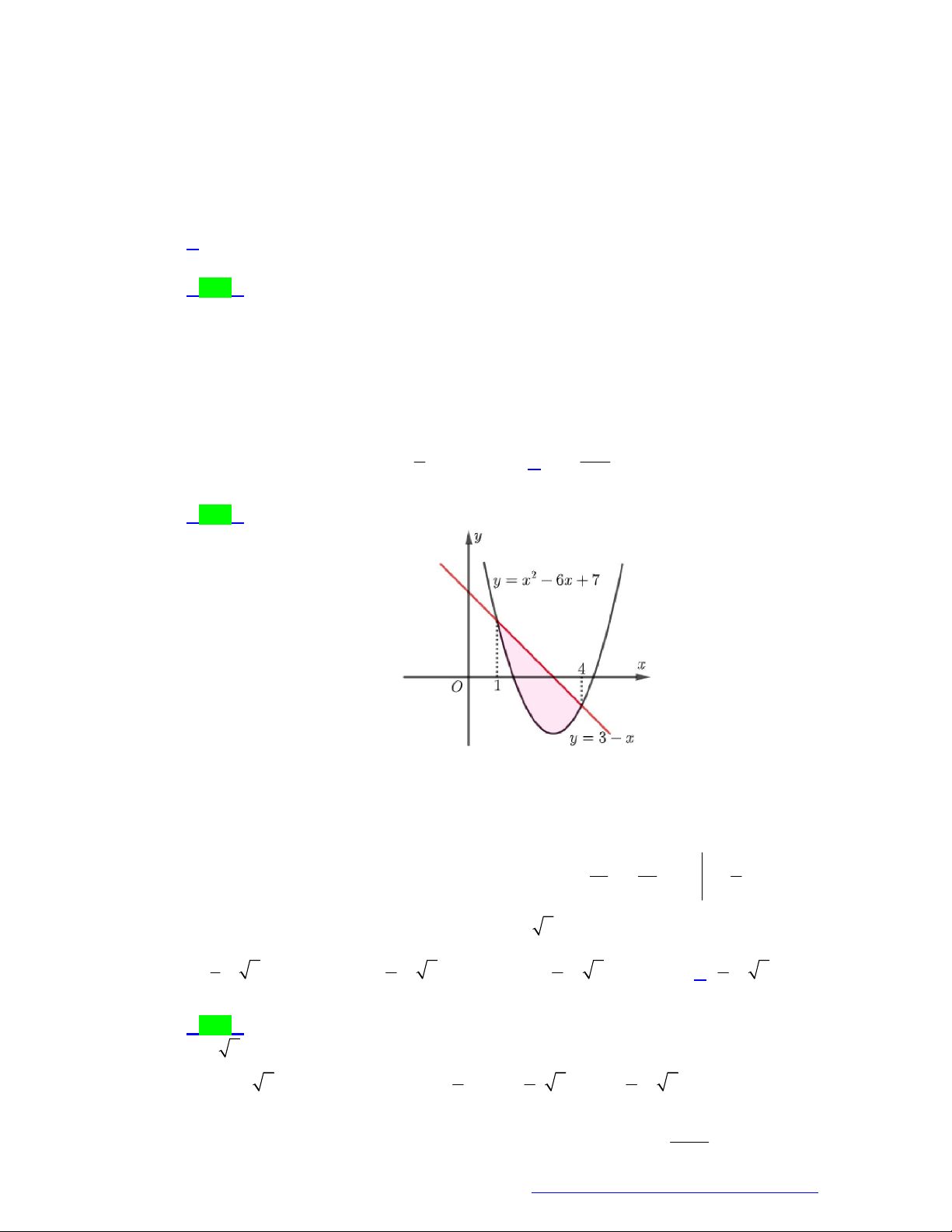
Câu 76. (THPT Nguyễn Huệ - Phú Yên - 2021) Tính diện tích S hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  6x  7 và đường thẳng y  3  x . 9 33 A. S  3. B. S  . C. S  . D. S  60 . 2 5
Câu 77. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho x xdx  bằng 1 1 5 2 A. 3 x x  C . B. 2 x x  C . C. 2 x x  C . D. 2 x x  C . 3 2 2 5 3 1
Câu 78. (THPT Lương Thế Vinh - 2021) Với biến đổi u  ln x , tích phân dx  trở thành x ln x e 3 3 1 ln 3 1 e 1 ln 3 1 A. du  . B. du  . C. du  . D. du  . u u u u e 0 1 1
Câu 79. (THPT Lương Thế Vinh - 2021) Cho hàm số f  x có đạo hàm trên đoạn 1;2, f 2  1 và 2
f 4  2021. Giá trị I  f 2x dx  bằng 1 A. 2  018 . B. 1010 . C. 1  008 . D. 2018 . e
Câu 80. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho tích phân 2 I  x ln . xdx  Mệnh đề nào dưới 1 đây đúng? e 1 e e e A. 2 2 2 I  x ln x  x ln xdx  . B. 2 2
I  x ln x  2 x ln xdx  . 1 2 1 1 1 e 1 e e e C. 2 2 I  x ln x  x ln xdx  . D. 2 2
I  x ln x  2 ln xdx  . 1 2 1 1 1 e 1 ln x
Câu 81. (THPT Đào Duy Từ - Hà Nội - 2021) Cho tích phân I  dx 
. Đặt u  1 ln x . Khi đó x 1 I bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 1 2 0 2 1 2 u 0 A. I  2 2  u du . B. I  2   u du . C. I   du .
D. I    u du . 0 0 2 1 1
Câu 82. (THPT Đào Duy Từ - Hà Nội - 2021) Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  5x  4 và trục Ox . Thể tích của khối tròn xoay sinh ra khi quay hình  H  quanh trục Ox bằng : 9 81 81 9 A. . B. . C. . D. . 2 10 10 2 2 4  x 
Câu 83. (THPT Đào Duy Từ - Hà Nội - 2021) Biết
f  x dx  2020  khi đó f dx    bằng  2  0 0 A. 2020 . B. 1010 . C. 20  20 . D. 4040 . 2
 x  2x  3 
Câu 84. (THPT Chu Văn An - Thái Nguyên - 2021) Họ nguyên hàm dx   bằng x 1   2 x 2 x 1 A.
 x  2 ln x 1  C . B.  x   C . 2 2  x  2 1 2 x C.
 x  2 ln x 1  C . D. 2
x  x  2 ln  x   1  C . 2
Câu 85. (THPT Chu Văn An - Thái Nguyên - 2021) Diện tích hình phẳng giới hạn bởi các đường 2
y  2  x , y  x bằng: 9 9 A. 9. B. . C. 18. D. . 2 4
Câu 86. (THPT Ba Đình - Thanh Hóa - 2021) Diện tích hình phẳng giới hạn bởi các đường 2 y  x và
y  x  2 là 9 9 8 A. S  9 . B. S  . C. S  . D. S  . 4 2 9
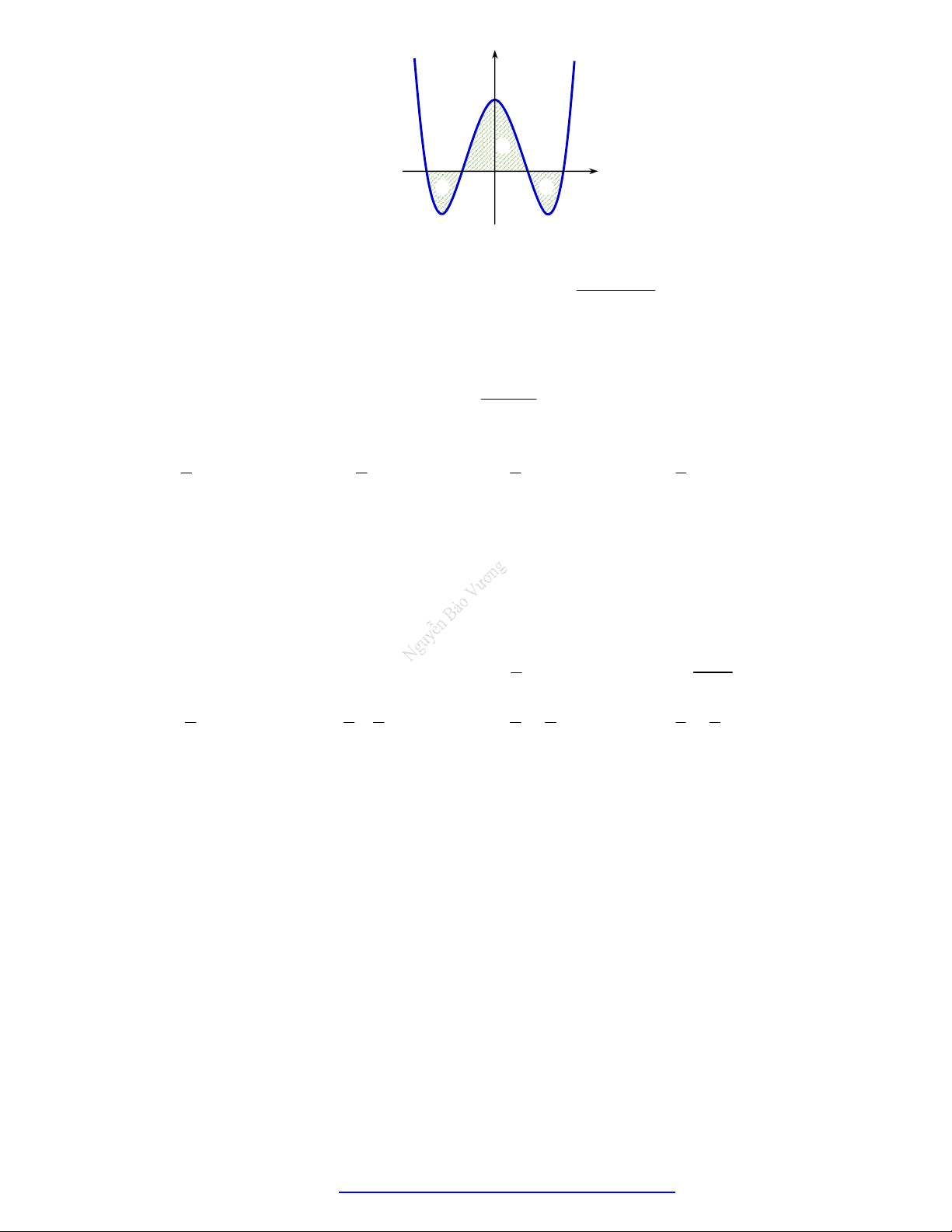
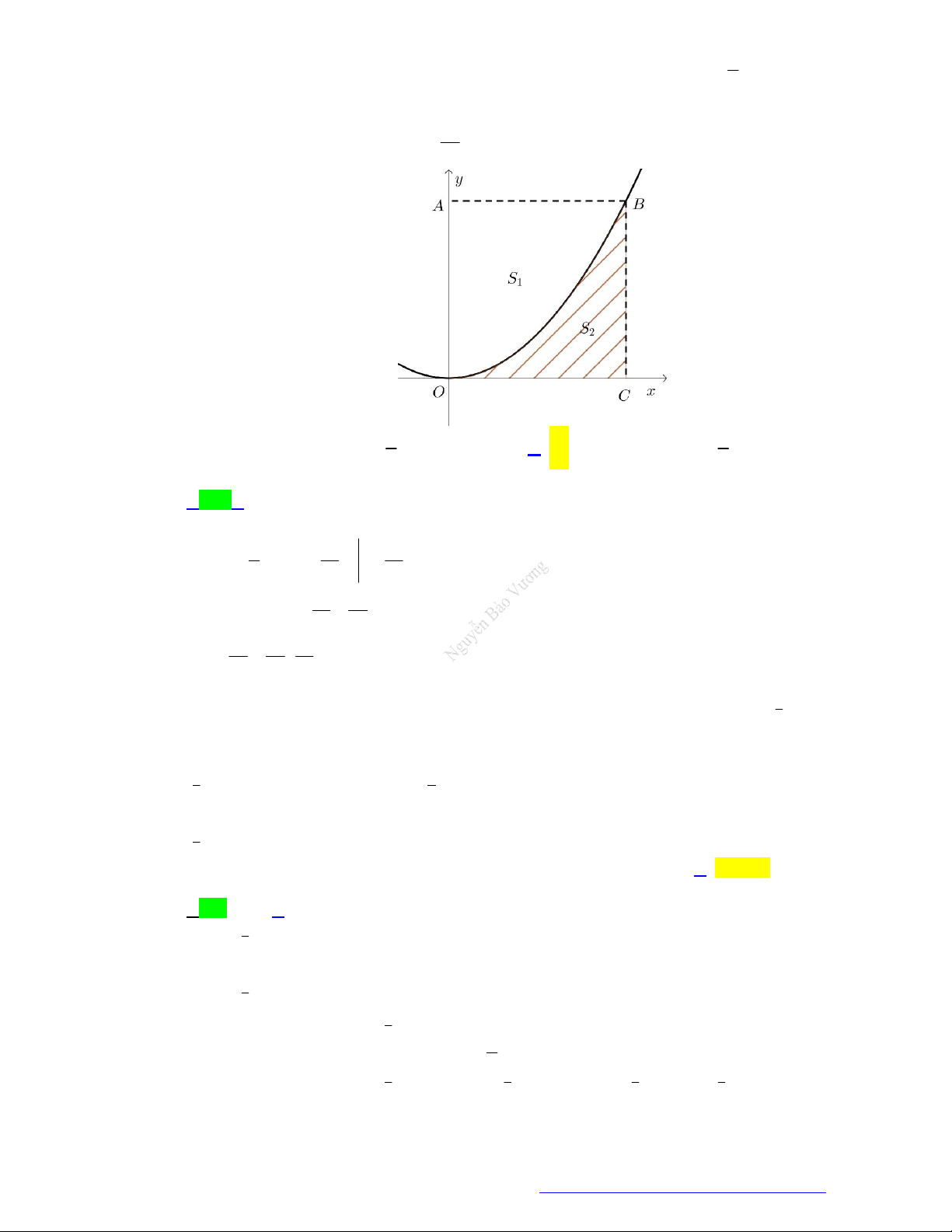
Câu 87. (Trung Tâm Thanh Tường - 2021) Hình phẳng S gồm hai phần được đánh dấu trong hình vẽ
bên. Diện tích hình S được tính theo công thức nào dưới đây? 0 3 0 3 A. S  
f  x dx  f  x dx   . B. S  
f  x dx  f  x dx   . 2  0 2  0 0 3 0 3 C. S 
f  x  dx  f  x dx   . D. S 
f  x  dx  f  x dx   . 2 0 2 0 1 1
Câu 88. (Trung Tâm Thanh Tường - 2021) Xét 20 (1 2x) dx 
, nếu đặt u  1 2x thì 20 (1 2x) dx  bằng 0 0 1 1 1 1 1 1 A. 20 2 u du  . B. 20 u du  . C. 20  u du  . D. 20 u du  . 2 2 1  1  1  1 
Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 89. (Trung Tâm Thanh Tường -2021) Biết F  x  a sin x  b cos x là một nguyên hàm của hàm số
f  x  2sin x  8cos x , tính giá trị T  a  b . A. T  6 . B. T  4 . C. T  6 . D. T  10 . 1 1
Câu 90. (THPT Triệu Sơn - Thanh Hóa - 2021) Biết f (x) x d  6  , tích phân f (2x 1) x d  bằng 1 0 A. 3. B. 6. C. 12. D. 2. 1
Câu 91. (THPT Trần Phú - Đà Nẵng - 2021) Cho hàm số f  x 2  x 
. Trong các khẳng định sau, 2 x khẳng định nào đúng? 1 3 x 1 A.
f  x dx  2x   C  . B.
f  x dx    C  . x 3 x 3 x 1 2 C.
f  x dx    C  . D.
f  x dx  2x   C 3  . 3 x 3 x
Câu 92. (THPT Trần Phú - Đà Nẵng - 2021) Cho hàm số 2
f (x)  tan 2x . Trong các khẳng định sau, khẳng định nào đúng 1 3 tan 2x A.
f (x) dx  tan 2x  C  . B.
f (x) dx   C  . 2 3 1 C.
f (x) dx 
tan 2x  x  C  . D.
f (x) dx  tan 2x  x  C  . 2 3
Câu 93. (THPT Trần Phú - Đà Nẵng - 2021) Cho 2 x dx  4 
. Giá trị của tham số a thuộc khoảng nào a sau đây?  1   1  A. 1;2 . B.  1  ;0 . C. 0;   . D. ;1   .  2   2  3 3
Câu 94. (THPT Trần Phú - Đà Nẵng - 2021) Biết
f  x dx  4  . Giá trị của
5 f  x 1 dx    bằng 1 1 A. 22  . B. 22 . C. 18 . D. 20 . BẢNG ĐÁP ÁN 1.D 2.D 3.A 4.A 5.C 6.B 7.C 8.A 9.C 10.D 11.C 12.D 13.D 14.C 15.D 16.B 17.D 18.C 19.A 20.A 21.A 22.D 23.D 24.A 25.A 26.B 27.A 28.C 29.C 30.A 31.A 32.D 33.C 34.A 35.A 36.A 37.A 38.D 39.A 40.D 41.C 42.D 43.B 44.D 45.D 46.C 47.C 48.A 49.C 50.D 51.B 52.C 53.B 54.C 55.D 56.A 57.D 58.B 59.A 60.C 61.A 62.C 63.A 64.A 65.D 66.D 67.B 68.C 69.D 70.C 71.A 72.B 73.C 74.B 75.C 76.C 77.D 78.D 79.B 80.C 81.A 82.C 83.D 84.A 85.B 86.C 87.D 88.B 89.A 90.A 91.B 92.C 93.C 94.C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 3
NGUYÊN HÀM - TÍCH PHÂN VÀ ỨNG DỤNG
MỨC ĐỘ THÔNG HIỂU a Câu 1.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Tính  25x I dx 
theo số thực a . 0 25 1 A. 1 .25a a  .
B. (25a 1).ln 25 . C. (25a 1) . D. (25a 1) . a 1 ln 25 Lời giải Chọn D a x 1 x a 1 a 1  Có 0  25  25 |  (25  25 )  (25a I dx 1). 0  ln 25 ln 25 ln 25 0 1 4 Câu 2.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Tính tích phân I  x   2 1 x  dx . 0 32 31 30 31 A. . B.  . C.  . D. . 10 10 10 10 Lời giải Chọn D
x  0  t  1 Đặt 2
1 x  t  2 d
x x  dt . Đổi cận:  .
x  1  t  2  2 5 1 t 2 32 1 31 Suy ra 4 I  t dt      . 2 10 1 10 10 10 1 Câu 3.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Họ nguyên hàm của hàm số    2  x f x x e   1 là A. x e  x   2 2
1  x  C B. x e  x   2 2 1  4x  C C. x e  x   2 2 1  x D. x e  x   2 2 1  4x Lời giải Chọn A  Ta có x   x e   x x 2 2
1 dx  2xe dx  2 d
x x  2xe dx  x    .  Xét 2
xd  2 d x 2 . x  2 xdx 2 . x  2 x  2 x xe x x e x e e x e e e  x   1    .    x   x x e
x  e  x   2 2 1 d 2 1  x  C . 1 dx e 1 Câu 4.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho  a  b ln 
, với a, b là x e 1 2 0 các số nguyên. Tính 3 3
S  a  b . A. S  0 . B. S  2 . C. S  1 . D. S  2 . Lời giải Chọn A 1 1 1   d x x e 1 dx e 1    Ta có  1 dx  x   x  x  0  e 1 e 1 x e 1 0 0   0 1 e  x 1
 1  ln e  1  1 ln . 0 2
 Suy ra a  1, b  1 . Vậy 3 3
S  a  b  0 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 5.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Tìm nguyên hàm của hàm số
  ex 1 e x f x    . A.  d  ex f x x  C  . B.  d  ex f x x  C  . C.  d  ex f x x  x  C  . D.
 d  ex  ex f x x  C  . Lời giải Chọn C Ta có:
  ex 1 e x  ex f x     1. Suy ra  d   ex   1 d  ex f x x x  x  C . Câu 6.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Diện tích phần hình phẳng tô đậm
trong hình vẽ bên được tính theo công thức nào dưới đây? 1 1 A. 2 2 x  2  x dx . B. 2 2 x  2  x dx . 0 0 1 1 C. 2 2 x  2 
x dx . D. 2 2 x  2  x dx . 0 0 Lời giải Chọn B 0 1
 Dựa vào hình vẽ ta có: S  x   2 x 2 dx  x   2 x 2         dx .     1  0 1  2 2 x  x  2dx . 0 1 Câu 7.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho
f  x dx  1  . Với 0 1  ex I
 f  x dx  e  a   
. Khẳng định nào sau đây đúng? 0 A. a  2 . B. a  1  . C. a  2  . D. a  1. Lời giải Chọn C 1 1 1 1 Ta có:  ex 
  d  exd    d  ex I f x x x f x x 1  e  2      . 0 0 0 0 Vậy a  2  . Câu 8.
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Bác thợ xây bơm nước vào bể nước. Gọi h t  là
thể tích nước bơm được sau t giây. Cho h t  2
 3at  bt và ban đầu bể không có nước. Sau 5
giây thì thể tích nước trong bể là 3
150 m , sau 10 giây thì thể tích nước trong bể là 3 1100 m . Tính
thể tích của nước trong bể sau khi bơm được 20 giây: A. 3 8400 m . B. 3 600 m . C. 3 2200 m . D. 3 4200 m .
Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Lời giải Chọn A b
Ta có: h t    2 at  bt  3 2 3 dt  at  t  C 2 h 0  0 C   0 a  1    25 
Từ gt  h5  150  12  5a  b  150  b   2  2   h 10  1100 C  0  10 
00a  50b  1100      3 2
h t  t  t
Vậy thể tích của nước trong bể sau khi bơm được 20 giây là h   3 20  8400 m . f  x
f  x  3  5sin x Câu 9.
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hàm số thỏa mãn f 0  10 f  x và . Tìm hàm số .
A. f  x  3x  5 cos x 15 .
B. f  x  3x  5cos x  2.
C. f  x  3x  5cos x  5 .
D. f  x  3x  5cos x  2 . Lời giải Chọn C
Ta có f  x  f  x dx  3  5sin x dx  3x  5cos x  C   .
Mà f 0  10  3.0  5 cos 0  C  10  C  5 .
Vậy f  x  3x  5cos x  5 .
Câu 10. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình phẳng (H) giới hạn bởi đồ thị hàm số 2
y  2x  x và trục hoành. Tính thể tích V vật thể tròn xoay sinh ra khi cho (H) quay quanh trục Ox. 4 16 4 16 A. V   . B. V  . C. V  . D. V   . 3 15 3 15 Lời giải Chọn D  x  0 Xét phương trình: 2
2x  x  0   x  2  2 2 2 3 5 2  4x x  16
Suy ra: V    2
2x  x  dx    2 3 4
4x  4x + x  4 dx   x      . 3 5 15 0 0   0 3
Câu 11. (Chuyên KHTN - 2021) Cho hàm số f  x liên tục trên  và thoả mãn xf  xdx  2  . Tích 0 1
phân xf 3x dx  bằng 0 2 2 A. . B. 18 . C. . D. 6 . 3 9 Lời giải Chọn C t 1
 Đặt: t  3x  x   dx  dt 3 3
 Đổi cận: x  0 t  0; x  1 t  3 . 1 3  1 2
Khi đó: xf 3x dx 
tf t  dt    9 9 0 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 12. (Chuyên KHTN - 2021) Họ nguyên hàm của hàm số f  x  ln x trên khoảng 0;   là 2 ln x 1
A. x ln x  x  C . B.  C . C.  C .
D. x ln x  x  C . 2 x Lời giải Chọn D  Ta tìm I 
f  x dx  ln d x x  
, x 0;  .  1 u   ln x du  dx  Đặt    x . dv  dx  v  x 
 Khi đó: I  x ln x  dx  x ln x  x  C  .
Câu 13. (Chuyên KHTN - 2021) Diện tích hình phẳng giới hạn bởi đồ thị của hàm số 2
y  x  x và đồ thị
của hàm số y  2x  2 bằng 1 3 53 9 A. . B. . C. . D. . 6 2 6 2 Lời giải Chọn D
Phương trình hoành độ giao điểm: x  2 2
x  x  2x  2   . x  1  2 9
Diện tích hình phẳng cần tính là: 2 S 
x  x  2 dx   . 2 1 
Câu 14. (Chuyên KHTN - 2021) Họ nguyên hàm x cos d x x  là
A. cos x  x sin x  C .
B.  cos x  x sin x  C .
C. cos x  x sin x  C .
D.  cos x  x sin x  C . Lời giải Chọn C u   x d  u  dx  Đặt    . dv  cos d x x v  sin x  
 Ta có: I  x cos d
x x  x sin x  sin d
x x  x sin x  cos x  C   .
Câu 15. (Chuyên KHTN - 2021) Diện tích hình phẳng giới hạn bởi đường thẳng y  x  3 và parabol 2
y  2x  x 1 bằng: 13 9 13 A. . B. . C. 9 . D. . 6 2 3 Lời giải Chọn D
Phương trình hoành độ giao điểm giữa đường thẳng y  x  3 và parabol 2
y  2x  x 1 là  x  2 2 2
x  3  2x  x 1  2x  2x  4  0   x  1 
Diện tích hình phẳng giới hạn bởi đường thẳng y  x  3 và parabol 2
y  2x  x 1 là 2 S    2 2x  x  
1   x  3dx 1  2 2 
2x  2x  4 dx  1 
Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Ta có 2
2x  2x  4  0, x   1  ; 2 nên 2 2 2 3  2x  13 2 S 
2x  2x  4 dx      2
2x  2x  4 2 dx    x  4x    . 3 3 1 1    1 2 tan 2xdx 
Câu 16. (Chuyên KHTN - 2021) Tính nguyên hàm 1 1
A. tan 2x  x  C . B.
tan 2x  x  C . C.
tan 2x  x  C .
D. tan 2x  x  C . 2 2 Lời giải Chọn B  1  1 Ta có: 2 tan 2xdx  1 dx 
tan 2x  x  C   . 2   cos 2x  2 2x   1 ln xdx 
Câu 17. (Chuyên KHTN - 2021) Tìm nguyên hàm 2 x 2 x A.  2
x  xln x   x  C . B.  2
x  x ln x   x  C . 2 2 2 x 2 x C.  2
x  xln x   x  C . D.  2
x  xln x   x  C . 2 2 Lời giải Chọn D  1  u  ln x du  dx Đặt    x
dv  2x   1 dx 2 
v  x  x  2 x   x   xdx    2
x  x x   x  dx    2 2 1 ln ln 1
x  xln x   x  C . 2
Câu 18. (Chuyên KHTN - 2021) Tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi đường
thẳng x  2 và đồ thị 2
y  x khi quay xung quanh trục Ox . 4 5 32  A. . B. . C. . D. . 5 6 5 6 Lời giải Chọn C 2
y  x có điểm chung với Ox tại điểm có hoành độ x  0 . 2 5 x 2 32 4 V  
x dx     . 5 0 5 0
Câu 19. (Chuyên KHTN - 2021) Tính nguyên hàm x  x   2 2 3 2 1 dx .  x  3 3 2 1  x  3 3 2 1  x  3 3 2 1  x  3 3 2 1 A.  C . B.  C . C.  C . D.  C 18 3 6 9 Lời giải Chọn A d 2x 1 1 2 3 2 3  3 2 2  2 Ta có x  2x   1 dx  x  2x   1   3 2x   1 d  3 2x 1 2  6x 6  x  3  x  3 3 3 2 1 2 1 1   C   C . 6 3 18
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 1
Câu 20. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho tích phân 2
x 3x 1dx  , nếu đặt 0 1 2
u  3x 1 thì 2
x 3x 1dx  bằng 0 2 1 2 1 2 2 1 1 A. 2 u du  . B. d u u  . C. 2 u du  . D. 2 u du  . 1 3 1 3 1 3 0 3 Lời giải Chọn A 3x  2 u 
3x  1  du  dx . 2 3x 1
 Với x  0  u  1 , với x  1 u  2 . 1 2 1 Suy ra 2 2
x 3x 1dx  u du   . 0 1 3 2 2
4 f (x)  2xdx  1  f (x)dx 
Câu 21. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho 1 . Khi đó 1 bằng A. 1. B. -3. C. -1. D. 3. Lời giải Chọn A 2 2 2 Ta có:
4 f (x)  2xdx 1  4 f (x)dx 2 d x x  1    1 1 1 2 2 2 2 
4 f (x) dx x  1 
f (x)dx  1   1 1 1
Câu 22. (Chuyên Quốc Học Huế - 2021) Tính diện tích của hình phẳng (được tô đậm) giới hạn bởi hai đường 2 2
y  2x , y  4 . x 2 4 4 2 A. S  . B. S  . C. S  . D. S  . 3 3 3 3 Lời giải Chọn D Theo hình vẽ ta có 2
y  4x  y  2 x .
Xét phương trình hoành độ giao điểm của hai đường 2
y  2x , y  2 x  x  0 x  0 2
2x  2 x     . x  1  x  1  
Dựa vào đồ thị, diện tích của hình phẳng cần tính là 1 1   S   4 2 2 2 2 x  2x  3 dx  x x  x    .  3 3  3 0 0
Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021  2
Câu 23. (Chuyên Quốc Học Huế - 2021) Cho tích phân
2  cos x sin xdx 
. Nếu đặt t  2  cos x thì kết 0 quả nào sau đây đúng?  2 2 2 3 A. I  2 tdt.  B. I  tdt.  C. I  tdt.  D. I  tdt.  3 0 3 2 Lời giải Chọn D
Đặt t  2  cos x  dt   sin xdx 
Đổi cận x  0  t  3, x   t  2 2 2 3 Khi đó I   tdt  tdt   . 3 2
Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Nguyên hàm của hàm số f (x)  2x(x 1)(2x 1) . A.   2 2 x x  C B. 4 3 2
x  x  x  C C. 4 3 2
x  x  x  C D. 4 3 2
x  x  2x  C Lời giải Chọn A Ta có x x  x  dx  
 x  x  xdx  x  x  x  C  x  x2 3 2 4 3 2 2 2 ( 1)(2 1) 4 6 2 2  C.
Câu 25. (Chuyên Quang Trung - Bình Phước - 2021) Tìm nguyên hàm F  x của hàm số ( )  . x f x x e biết F   1  0 . A. . x x x e  e . B. . x x x e  e 1. C. . x x e  e . D. . x
x e  x 1 e . Lời giải Chọn A
Gọi F  x là một nguyên hàm của hàm số f  x .
Khi đó F  x có dạng F  x  x     x  x x x x xe dx xd e
 xe  e dx  xe  e  C  Do F   1  0 nên C  0. Vậy   x x
F x  xe  e .
Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm số thực m để hàm số F  x 3
 mx   m   2 3
2 x  4x  3
là một nguyên hàm của hàm số f  x 2
 3x 10x  4 A. m  2 . B. m  1. C. m  0 . D. m  1 . Lời giải Chọn B F  x 3
 mx   m   2 3
2 x  4x  3 là một nguyên hàm của hàm số f  x 2
 3x 10x  4 nên:
F x  f  x  2
mx   m   2 3 2 3
2 x  4  3x 10x  4  m  1.
Câu 27. (Chuyên Ngoại Ngữ Hà Nội- 2021) Nguyên hàm của hàm số f  x 3  3x 1 là 1 A. 3
f (x)dx 
(3x 1) 3x 1  C  . B. 3
f (x)dx  (3x 1) 3x 1  C  . 4 1 C. 3
f (x)dx  3x 1  C  . D. 3
f (x)dx  3x 1  C  3 Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 4 3 1 1 3x 1 1 3   Ta có: I 
3x 1dx  3x  3 3 1 dx  .  C 
(3x 1) 3x 1  C   3 4 4 3 e
Câu 28. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho tích phân  2 3x  2x 3 2
dx  me  ne với m, n  , khi 0
đó m  n bằng bao nhiêu? A. 5 . B. 3 . C. 2 . D. 0 . Lời giải Chọn C e Ta có  2 3x  2x 3 2
dx  e  e 0
Suy ra m  1, n  1
Vậy m  n  2. 3 x  8
Câu 29. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho
dx  a ln 2  b ln 5 
với a, b là các số nguyên. 2 x  x  2 2
Mệnh đề nào sau đây đúng?
A. a  b  3 .
B. a  b  5 .
C. a  2b  11.
D. a  2b  11 . Lời giải Chọn C 3 3 x  8  3 2  Ta có : dx  +
dx  3ln x 1  2 ln x  2  7 ln 2  2 ln 5.  2     32 x  x  2  x 1 x  2  2 2
Suy ra giá trị là: a  7, b  2 .
Câu 30. (Chuyên Ngoại Ngữ Hà Nội- 2021) Thể tích khối tròn xoay sinh ra khi quay quanh Ox hình
phẳng giới hạn bởi các đường  0,  1, x x x
y  xe ; y  0 là  1 1  A.  2 e   1 . B.  2 e   1 . C.  2 e   1 . D.  2 e   1 . 4 4 4 4 Lời giải Chọn A x
 y  xe , y  0
Hình phẳng  H  :  . x  0, x  1 
Thể tích khối tròn xoay khi quay  H  quanh Ox là 1 1      x 1 x 1 1 2 2 2
V   x e dx    e    2
2x  2x   2 1    e     2 e     1 .  4   4 4  4 0 0 2 4
xf 2x dx 4 
xf  x dx 
Câu 31. (Chuyên Ngoại Ngữ Hà Nội- 2021) Biết 0 . Giá trị của 0 bằng A. 16 . B. 1 . C. 8 . D. 2 . Lời giải Chọn A
 Đặt t  2x  dt  2dx .
Với x  0 thì t  0
Với x  2 thì t  4 . 2 4 4 4 t 1 1 4
 Ta có 4  xf 2x dx 
. f t . dt 
tf t  dt  tf t  dt  16    
. Vậy xf  x dx  16  . 2 2 4 0 0 0 0 0
Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 32. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Với a,b là các tham số thực. Giá trị tích phân b  2 3x  2ax    1 dx bằng 0 A. 2
3b  2ab 1. B. 3 2
b  b a  b . C. 3 2
b  a b  b . D. 3 2
b  ab  b . Lời giải Chọn D b b Ta có:  2
3x  2ax   1 dx   3 2
x  ax  x 3 2
 b  b a  b . 0 0
Câu 33. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Hình vẽ bên biểu diễn trục hoành cắt đồ thị y  f  x
tại ba điểm có hoành độ 0 , a , b a  0  b . Gọi S là hình phẳng giới hạn bởi đồ thị y  f  x và
trục hoành, khẳng định nào sau đây là sai? y x O a b b 0 b A. S 
f  x dx  .
B. S   f  x dx  f  x dx   . a a 0 0 b 0 b C. S 
f  x dx  f  x dx   . D. S 
f  x dx 
f  x dx   . a 0 a 0 Lời giải Chọn C 0 b 0 b
Ta có: S   f xdx   f xdx   f xdx  f  xdx   . a 0 a 0
Câu 34. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình phẳng D giới hạn bởi đường cong x y  e ,
trục hoành và các đường thẳng x  0, x  1. Khối tròn xoay tạo thành khi quay D quanh trục
hoành có thể tích V bằng bao nhiêu?   2 e   1 2 2  e 2 e  1  e   1 A. V  . B. V  . C. V  . D. V  . 2 2 2 2 Lời giải Chọn A
Thể tích khối tròn xoay cần tìm là: 2  1  e 1 x 2 x 2 x  2 1 1  V  
e  dx   e dx  .e    . 0 0 0 2 2
Câu 35. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hàm số y  f  x có đạo hàm cấp hai f  x liên tục trên đoạn 0 
;1 đồng thời thỏa mãn điều kiện f 0  f  
1  1; f 0  2021. Mệnh đề nào sau đây đúng? 1 1
A. 1 x f  x dx  202  1  .
B. 1 x f  x dx  2021  . 0 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 1 1
C. 1 x f  x dx  1 
. D. 1 x f  x dx  1   . 0 0 Lời giải Chọn A 1 1 1 1
Ta có 1 x f  x dx  1 x df  x  
 1 x f  x  f  x dx  0 0 0 0
  f 0  f   1  f 0  2  021. 1
Vậy 1 x f  x dx   2021  . 0
Câu 36. (Chuyên Hạ Long - Quảng Ninh - 2021) Diện tích hình phẳng giới hạn bởi đồ thị hàm số
y   x   2
1 x  5x  6 và hai trục tọa độ bằng 11 1 11  A. . B. . . D. . 4 2 C. 4 2 Lời giải ChọnA  x  1 x 1  0 Ta có   x   1  2
x  5x  6  0   x  2.  2 x 5x 6 0       x  3 
Khi đó diện tích hình phẳng cần tìm bằng 3 3  x   1   2
x  5x  6 3 2 dx 
x  6x 11x  6 dx  0 0 1 2 3 3 2 3 2 3 2 
x  6x 11x  6 dx 
x  6x 11x  6 dx 
x  6x 11x  6 dx    0 1 2 1 2 3   3 2
x  6x 11x  6dx   3 2
x  6x 11x  6dx   3 2
x  6x 11x  6dx 0 1 2 1 2 3 4 2 4 2 4  x 11x   x 11x   x 2 11x  3 3    2x   6x   2x   6x    3     2x   6x   4 2 4 2 4     2   0 1 2 9 1 1 11     . 4 4 4 4 Vậy ta chọn phương án A.
Câu 37. (Chuyên ĐHSP Hà Nội - 2021) Diện tích hình phẳng thuộc góc phần tư thứ hai, giới hạn bởi parabol 2
y  2  x , đường thẳng y   x và trục Oy bằng: 7 5 11 9 A. . B. . C. . D. . 6 6 6 2 Lời giải Chọn A
Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 x  1
Xét phương trình hoành độ giao điểm 2
2  x   x   . x  2  0 0 7
Diện tích hình phẳng cần tính là: S   2
2  x dx  x dx    . 6 1  1 
Câu 38. (Chuyên ĐHSP Hà Nội - 2021)  x  9 2 5 dx  bằng 1 1 A.
2x  510  C . B.  x  8 18 2 5  C .
C.  x  8 9 2 5  C . D.
2x  510  C . 10 20 Lời giải Chọn D 9 1 9 1 10
Ta có: 2x  5 dx 
2x  5 d 2x  5 
2x  5  C   . 2 20 1
Câu 39. (Chuyên ĐHSP Hà Nội - 2021) Biết f  x là hàm số liên tục trên 0;  3 và có
f 3xdx  3  . Giá 0 3 trị của biểu thức
f  xdx  bằng: 0 1 A. 9. B. 1. C. 3. D. . 3 Lời giải Chọn A dt
Đặt 3x  t  3dx  dt  dx  3 1 3
x  0  t  0 1 Đổi cận:   I 
f 3x dx 
f t  dt  
x  1  t  3 3  0 0 1 3 3 Mà
f 3x dx  3  f t  dt  9  f  x dx  9    . 0 0 0
Câu 40. (Chuyên ĐH Vinh - Nghệ An - 2021) Giả sử f  x là hàm liên tục trên 0;  và diện tích 1
phần hình phẳng được kẻ dọc ở hình bên bằng 3 . Tích phân
f 2x dx  bằng: 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 4 3 A. . B. 3 . C. 2 . D. . 3 2 Lời giải Chọn D 2
Vì diện tích phần hình phẳng được kẻ dọc ở hình trên bằng 3 nên ta có:
f  x dx  3  . 0 dt
Đặt t  2x  dt  2dx  dx 
; Đổi cận x  0  t  0; x  1  t  2 . 2 1 2 2 2 dt 1 1 3 Do đó:
f 2x dx  f t  
f t  dt 
f  x dx      . 0 0 0 0 2 2 2 2
Câu 41. (Chuyên ĐH Vinh - Nghệ An - 2021) Họ nguyên hàm của hàm số   2 1 3 x f x   là 9x 9x 9x 9x A.  C . B.  C . C.  C . D.  C . 3 6 6 ln 3 3ln 3 Lời giải Chọn C x 9x
Ta có f  x 2 1  3  . 3 1 x 1 9x 9x Khi đó
f  x dx  9 dx  .  C   C   . 3 3 ln 9 6 ln 3
Câu 42. (Chuyên ĐH Vinh - Nghệ An - 2021) Một chiếc xe đua F đạt vận tốc lớn nhất là 360km / h . Đồ 1
thị bên hiển thị vận tốc v của xe trong 5 giây đầu tiên kể từ lúc xuất phát. Đồ thị trong 2 giây đầu
là một phần của parabol đỉnh tại gốc tọa đô O , giây tiếp theo là đoạn thẳng và sau đúng ba giây
thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị 1 giây, mỗi đơn vị trục tung
biểu thị 10m / s và trong 5 giây đầu xe chuyển động theo đường thẳng. Hỏi trong 5 giây đó sẽ đã
đi được quãng đường là bao nhiêu. A. 400 (mét). B. 340 (mét). C. 420 (mét). D. 320 (mét). Lời giải Chọn D
Đổi 360km / h  100m / s
Quan sát đồ thị hàm số ta thấy điểm A2;60 , B 3;100 thuộc đồ thị hàm số.
Phương trình vận tốc khi xe chuyển động theo Parabol là 2 y  15x .
Phương trình vận tốc khi xe chuyển động theo đường thẳng là y  40x  20.
Quãng đường xe chuyển động được trong 5 giây đầu là 2 3 5 2 S  15x dx  
 40x  20dx  100dx  320  . 2 0 3
Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 43. (THPT Quế Võ 1 - Bắc Ninh - 2021) Gọi d là tiếp tuyến của đồ thị hàm số y  ln x tại giao
điểm của đồ thị đó với trục Ox . Diện tích của hình tam giác tạo bởi hai trục tọa độ và đường
thẳng d được xác định bởi tích phân 1 ln x 1 1 1 A. . dx  B. 1 x . dx  C.  x   1 . dx  D. ln xd . x  x 0 0 0 0 Lời giải Chọn B
Phương trình hoành độ giao điểm của y  ln x và Ox là ln x  0  x  1.
Phương trình tiếp tuyến d tại x  1 là y  f ' x x  x  f x  x 1. 0   0   0  1
Diện tích của tam giác tạo bởi hai trục tọa độ và đường thẳng d là S  1 x dx  . 0
Câu 44. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hàm số f  x có đạo hàm là f  x . Đồ thị y  f  x
được cho bởi hình vẽ bên dưới.
Giá trị nhỏ nhất của f  x trên đoạn 0;  3 là A. f 2.
B. Không xác định được.
C. f 0. D. f 3. Lời giải Chọn D BBT
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489
Suy ra giá trị nhỏ nhất của f x  trên đoạn  0; 3 
 là f 0 hoặc f 3 . Ta có 2 2 S 
f  x dx   f  x dx  f 0  f 2 1           0 0 3 3 S  f  x dx 
f  x dx  f 3  f 0 2           2 2
Dựa theo hình vẽ thì S  S  f 0  f 2  f 3  f 2  f 0  f 3 . 1 2            
Vậy giá trị nhỏ nhất của hàm số là f  3 .
Câu 45. (THPT Quốc Oai - Hà Nội - 2021) Một ô tô đang chạy với vận tốc 10 m / s thì người lái xe đạp
phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v t   2
 t 10 m / s , trong
đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Quãng đường ô tô di chuyển
được trong 8 giây cuối cùng tính đến thời điểm dừng bánh là A. 16 m .
B. 55 m .
C. 25 m . D. 50 m . Lời giải Chọn D
Khi ô tô dừng bánh, ta có: v  0  2
 t 10  0  t  5 .
Do đó, ta có quãng đường xe đi được trong 8 giây cuối cùng ( 3 giây đi với vận tốc 10 m / s , 5
giây sau khi đạp phanh) là: 5 S  3.10   2
 t 10 dt   30   t  10t  5 2 2
 30  5  10.5  55 m . 0 0
Câu 46. (THPT Quốc Oai - Hà Nội - 2021) Cho
    2    2x F x ax
bx c e là một nguyên hàm của hàm số
f  x   2 x  x   2x 2020 2022
1 e trên khoảng  ;
  . Tính T  a  2b  4c . A. T  1004 B. T  1018 . C. T  1012 .
D. T  2012 . Lời giải Chọn C
Ta có F ' x  f  x . Mà F  x 2   ax  
 b x  b  c 2x ' 2 2a 2 2  e   2a  2020 a  1010  
Do đó: 2a  2b  2022  b   1 b  2c 1     c  1  
Vậy T  a  2b  4c  1012 .
Câu 47. (THPT Quốc Oai - Hà Nội - 2021) Nguyên hàm của hàm số f x  2xx   1 2x   1 là A. 4 3 2
x  x  x  C . B. 4 3 2
x  x  2x  C . C.   2 2 x x C . D. 4 3 2
x  x  x  C . Lời giải Chọn C.
Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Ta có: f x  2xx   1 2x   1   2
2x  2x2x   1 3 2
 4x 6x  2x . 
f x x     3 2 d
4x  6x  2xdx 4 3 2
 x  2x  x C    2 2 x x C . 1 2
Câu 48. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Tích phân x xe dx  bằng 0 1
A. (e 1) .
B. (e 1) . C. 2e . D. 2e 1. 2 Lời giải Chọn A
Cách 1( Đổi biến): Đặt 2 1
t  x  dt  2xdx  dt  xdx 2
x  0  t  0 1 1 1 2 x 1 t 1 t 1 Đổi cận: . Khi đó xe dx  e dt  e  e     1
x  1  t  1 2 2 0 2 0 0 1 1 1 2 2 2 x 1 x 1 x 1
Cách 2( Vi phân): xe dx  e d  2 x   e  e     1 2 2 2 0 0 0 1 2
Cách 3: Dùng casio bấm x xe dx 
, sau dó đối chiếu với 4 đáp án. 0
Câu 49. (THPT Phan Đình Phùng - Quảng Bình - 2021) Khi đổi biến x  3 tan t , tích phân 1 dx I  
trở thành tích phân nào? 2 x  3 0     3 3 6 1 6 3 6 A. I  dt  . B. I  dt  . C. I  dt  . D. I  3dt  . 3 t 3 0 0 0 0 Lời giải Chọn C
Ta có : x  3 tan t  dx   2 3 tan t   1 dt .
Đổi cận : x  0  t  0 
x  1  t  6  6 3 Khi đó : I  dt  . 3 0
Câu 50. (THPT Phan Đình Phùng - Quảng Bình - 2021) Gọi S là diện tích hình phẳng giới hạn bởi đồ x 1
thị hàm số  H  : y 
và các trục tọa độ. Khi đó giá trị của S bằng x 1
A. S  ln 2 1.
B. S  2 ln 2 1.
C. S  ln 2 1.
D. S  2 ln 2 1. Lời giải Chọn D
Đồ thị hàm số cắt trục Ox tại 1; 0 , cắt trục Oy tại 0;  1 
. Diện tích hình phẳng cần tìm là 1 1 1 x 1  2  S  dx  1 
dx  1  2 ln | x  1|     |  2ln 2 1. 0 x  1  x  1  0 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 51. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hàm số f  x liên tục trên  và thỏa mãn 3 1
f  x dx  20 
. Tính tích phân I   x   1 f   2
x  2xdx . 0 0 A. I  20 . B. I  10 . C. I  40 . D. I  30 . Lời giải Chọn B Đặt 2
x  2x  t  dt  2 x   1 dx .
Khi x  0 thì t  0, và khi x  1 thì t  3 . 1 3 3 1 1 1
Do đó, I   x   1 f   2
x  2xdx 
f t  dt 
f  x dx  .20  10   . 2 2 2 0 0 0 Vậy I  10 . 4 2 ln x a a
Câu 52. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho biết 3 dx  ln 2  , với *
a, b   và là x b b 1
phân số tối giản. Tính a  b . A. 4 . B. 5 . C. 11. D. 9 . Lời giải Chọn C 4 4 2 4 3 3 ln x ln x ln 4 8 Ta có: 2 dx  ln d x ln x    .ln 2   . x 3 3 3 1 1 1
Vậy a  8, b  3  a  b  11. 1 b
Câu 53. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho biết ex x dx  a  
với a,b   . Tính 0 e 2 2 a  b . A. 7 . B. 5 . C. 3 . D. 4 . Lời giải Chọn B.
Xét u  x  du  dx d  ex v dx , chọn e x v   . 1 1 1 1 2 Khi đó  x  x  x 1   x 1 e x dx  e x  e dx  e  e  e     1 0 e  e   1. 0 0 0 0 e Suy ra a  1  ,b  2 . Vậy 2 2 a  b  5 .
Câu 54. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Trong mặt phẳng tọa độ Oxy cho hình phẳng  H 
được giới hạn bởi các đường y  sin x, y  0, x  0 và x  . Quay hình phẳng  H  quanh trục Ox
ta được một vật thể tròn xoay có thể tích bằng 2   A.  . B. 2  . C. . D. . 2 2 Lời giải Chọn C
Khối tròn xoay được sinh ra có thể tích là:    2 1 cos 2x   sin 2x   2 V  sin d x x  dx  x   .     2 2  2  2 0 0 0
Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 55. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Trong mặt phẳng tọa độ Oxy , cho hình phẳng  H 
được giới hạn bởi đồ thị hàm số y 
x 1 và hai trục tọa độ Ox , Oy . Tính diện tích S của hình phẳng  H  . 3 1 2 A. S  . B. S  . C. S  1. D. S  . 2 3 3 Lời giải Chọn D 0 Ta có S  x 1 dx  . 1 Đặt t  x 1; x  1
 t  0; x  0 t  1; 2
x  t 1  dx  2tdt . 0 1 1 2 2 Suy ra 3 S 
x 1 dx  t.2 d t t  t    . 3 3 1 0 0 
Câu 56. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho tích phân 2
I  x cos xdx  và 0 2
u  x , dv  cos xdx . Khẳng định nào sau đây đúng?     A. 2
I  x sin x  2 x sin xdx  . B. 2
I  x sin x  2 x sin xdx  . 0 0 0 0 1     C. 2 3
I  x sin x  x sin xdx  . D. 2
I  x sin x  x sin xdx  . 0 3 0 0 0 Lời giải Chọn A 2 u   x du  2xdx Đặt    . dv  cos xdx v  sin x      Do đó 2
I  x cos xdx  2
 x sin x  2 x sin xdx  . 0 0 0
Câu 57. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Diện tích S của hình phẳng giới hạn bởi các đường 2 3
y  2 x  3x 1, y  x 1 được tính bởi công thức nào dưới đây 0 3
A. S    2 3
2x  3x  x dx   3 2
x  2x  3xdx . 1  0 3
B. S    3 2
x  2 x  3 x dx . 1 3 2
C. S     3 2
x  2x  3x dx . 1 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 0 3 3 2 2 3
D. S   x  2x  3x dx   2x  3x  x dx . 1  0 Lời giải Chọn D
Xét phương trình hoành độ giao điểm: 2 3
2x  3x 1  x 1 3 2
 x 2x 3x  0 x  3   x  1   . x  0  Ta có bảng xét dấu: 0 3 Khi đó 3 2 3 2 S 
x  2x  3x dx 
x  2x  3x dx   1  0 0 3 S    3 2
x  2x  3x dx   2 3
2x  3x  x  dx 1  0
Câu 58. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hàm số f  x liên tục trên đoạn 0;9 thỏa 9 7 4 9 mãn
f  xdx  8,
f  xdx  3.  
Khi đó giá trị của P 
f  xdx  f  xdx   là 0 4 0 7
A. P  11 .
B. P  5 .
C. P  20 . D. P  9 . Lời giải Chọn B 4 9 9 7 P 
f  xdx  f  xdx  f  xdx  f  xdx  8  3  5.     0 7 0 4
Câu 59. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Diện tích phần hình phẳng gạch sọc trong hình vẽ được
tính theo công thức nào dưới đây? y 2
y  x  2x 1 x O 2 1  2
y   x  3 2 2 A.   2 2
 x  2x  4 dx . B.  2
 x  2 dx  . 1 1 2 2
C. 2x  2 dx  . D.   2
2x  2x  4 dx . 1 1 Lời giải Chọn A 2 2
Diện tích hình phẳng là: S    2 2
x  3  x  2x   1 dx    2 2
 x  2x  4 dx . 1  1
Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 4 dx
Câu 60. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho tích phân I 
 a  b ln 2, a,b  .   Khi 1 5  x 4
đó E  ab bằng A. E  6. B. E  28. C. E  8. D. E  30. Lời giải Chọn C
Đặt 5  x  t t  0 , khi đó 2
t  5  x  dx  2  tdt Với x  4
  t  3; x  4  t  1 1 3 2  tdt  1  3  I   2 1
dt  2.2  2 ln 1 t    1 1 t  1 t  3 1
 I  4  2 ln 2  ab  8
Câu 61. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình  H  giới hạn bởi các đường thẳng 2
y  x  2x, trục hoành. Tính thể tích khối tròn xoay sinh bởi hình phẳng  H  quay quanh trục Ox . 16 4 496 32 A. . B. . C. . D. . 15 3 15 15 Lời giải Chọn A
Hoành độ giao điểm của đường thẳng trên với trục Ox là x  0; x  2.
Khi đó thể tích khối tròn xoay sinh bởi hình phẳng  H  quay quanh trục Ox là 2 2   
V   x  2x2 1 4 16 2 dx    4 3 2
x  4x  4x  5 4 3 2 dx   x  x  x  .   0  5 3  15 0 0
Câu 62. (THPT Đồng Quan - Hà Nội - 2021) Trong mặt phẳng toạ độ Oxy , cho hàm số y  f x có đồ
thị là đường cong và hàm số y  g x có đồ thị là đường thẳng. Gọi S là diện tích miền phẳng 1
được gạch sọc, S là diện tích miền phẳng được tô đậm, S  S (hình vẽ). Tích phân 2 1 2 4
  f xgxdx bằng 2 
A. S  S . B. S   S .
C. S  S .
D. S  S . 1 2 1 2 1 2 2 1 Lời giải Chọn C.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489 x  2 
Phương trình hoành độ giao điểm giữa 2 đồ thị f x g x  
 x  a 2  a  4  .  x  4  4 a 4
Ta có   f x gxdx    f x gxdx    f x gxdx  S S . 1 2 2  2 a 2
Câu 63. (THPT Lê Lợi - Thanh Hóa - 2021) Cho 2
I  4x x 1dx  và 2
u  x 1. Tìm khẳng định sai 1
trong các khẳng định sau? 2 3 3 4 4 A. I  2 udu  . B. I  2 udu  . C. I  u u . D. I  27 . 0 3 3 1 0 Lời giải Chọn A Đặt 2
u  x 1  du  2xdx .
Đổi cận x  1 u  0 ; x  2  u  3 2 3 3 4 4 Khi đó 2
I  4x x 1dx  2 udu  u u  27   . 0 3 3 1 0
Câu 64. (Sở Vĩnh Phúc - 2021) Tìm họ tất cả các nguyên hàm của hàm số  ex y  2x . 1 A. 2
ex  x  C .
B. ex  2  C . C. x 1  2 e
 x  C . D. x 2
e  2x  C . x 1 Lời giải Chọn A. 2 x
Ta có  x  x x x 2 e 2 dx  e  2.
 C  e  x  C . 2
Câu 65. (Sở Vĩnh Phúc - 2021) Cho hình phẳng D giới hạn bởi đồ thị  P 2
: y  2x  x và trục Ox . Tính
thể tích của khối tròn xoay tạo thành khi cho D quay quanh trục Ox . 19 13 17 16 A. V  . B. V  . C. V  . D. V  . 15 15 15 15 Lời giải Chọn D. x  0
Phương trình hoành độ giao điểm: 2
2x  x  0   . x  2  2 2 16
Do đó V    2
2x  x  dx   . 15 0
Câu 66. (Sở Vĩnh Phúc - 2021) Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  2021 ,
trục hoành, x  2, x  4 . Mệnh đề nào sau đây đúng. 4 4 A. 2 2 S  (x  2021) dx  . B. 2 S  (x  2021)dx  . 2  2  2  4 C. 2 S  x  2021 dx  . D. 2 S  x  2021 dx  . 4 2  Lời giải Chọn D
Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  2021 , trục hoành, x  2, x  4 thì 4
diện tích hình phẳng là 2 S  x  2021 dx  . 2  2021
Câu 67. (Sở Vĩnh Phúc - 2021) Cho hàm số y  f  x liên tục trên  và
f  x dx  4  . Tính 1 1010 I  f 2x   1 d . x  0
A. I  8.
B. I  2.
C. I  1.
D. I  4. Lời giải Chọn B. 1
Đặt t  2x 1  dt  2dx  dx  dt. 2
Đổi cận x  0  t  1; x  1010  t  2021 1010 2021 1 1 I  f 2x   1 dx 
f t  dt  .4  2.   2 2 0 1 1 1 1
f  x dx  2 
 f  x  2g  x dx  8    
g  x dx ? 
Câu 68. (Sở Lào Cai - 2021) Cho 0 và 0 . Tính tích phân 0 A. 6  . B. 3  . C. 5 . D. 5  . Lời giải Chọn C 1
Ta có:  f  x  2g  x dx  8    0 1 1 
f  x dx  2 g  x dx  8    0 0 1
 2  2 g  x dx  8   0 1
 g  x dx  5. 0 2x 1
Câu 69. (Sở Hà Tĩnh - 2021) Họ tất cả các nguyên hàm của hàm số f (x)  trên khoảng 2 (x 1)  1  ;  là 1 1
A. 2 ln(x 1) 
 C . B. 2 ln(x 1)   C . x 1 x 1 2 3
C. 2 ln(x 1) 
 C . D. 2 ln(x 1)   C . x 1 x 1 Lời giải Chọn D 2x 1 2x  2  3 2 3 3 Ta có f (x)      f (x) x
d  2 ln(x 1)   C 2 2 2  . (x 1) (x 1) x 1 (x 1) x 1 x
Câu 70. (Sở Hà Tĩnh - 2021) Cho hàm số f (x) thỏa mãn f (0)  4 và f '(x)  e  x, x   R . Khi đó 1
f  x dx  bằng 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489 6e  23 6e 17 6e 11 6e  23 A. . B. . C. . D. . 6 6 6 3 Lời giải Chọn C 2 x 2 x Ta có:
f ' x)dx    x e  x x ( dx  e   C mà x
f (0)  4  C  3  f (x)  e   3 2 2 1 1 1 2 3  x   x  6e 11 Khi đó x x
f (x)dx  e   3 dx  e   3x       2 6 6 0 0     0
Câu 71. (Sở Hà Tĩnh - 2021) Biết   3
F x  x là một nguyên hàm của hàm số f  x trên  . Tính 3
I  2x  f  x dx    . 0 117 23 A. I  36 . B. I  9 . C. I  . D. I  . 4 4 Lời giải Chọn A 3 3 3 3
Ta có: I  2x  f  x dx  2 d x x 
f  x dx        2 3
x  x   36 . 0 0 0 0 1
Câu 72. (Sở Tuyên Quang - 2021) Cho 3 3 4 I  x 1 x dx  . Đặt 3 4
t  1 x thì I bằng 0 1 1 3 1 1 3 A. 3  t tdt  . B. 3 t dt  . C. 3 t dt  . D. 3  t dt  . 4 4 0 0 0 0 Lời giải Chọn B 3 Với 3 4 t  1 x 3 4  t  1 x 2 3
 3t dt  4x dx 3 2
 x dx   t dt . 4
Đổi cận: x  0  t  1 và x  1 t  0 . 0 1 3 3 Vậy 3 3 I   t dt  t dt   . 4 4 1 0
Câu 73. (Sở Yên Bái - 2021) Tính diện tích hình phẳng giới hạn bởi hai đồ thị 2
y  x  4x  6 và 2
y  x  2x  6 . 5 4 1 2 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C  x  0 Xét phương trình: 2 2
x  4x  6  x  2x  6 2
 2x  2x  0   . x  1 
Diện tích hình phẳng giới hạn bởi hai đồ thị là: 1 1 1 3  2x  2 1 2 S 
2x  2x dx    2
2x  2xdx 2   x    1  . 3 3 3 0 0   0 2 2 2
f (x)dx  5 
(2 f (x)  g(x))dx  13  g(x)dx 
Câu 74. (Sở Yên Bái - 2021) Nếu 1 ; 1 thì 1 bằng A. 3  . B. 3 . C. 2  3 . D. 23. Lời giải Chọn B
Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2 2 2 2 2
Ta có (2 f (x)  g(x))dx  13  2 f (x)dx  g(x)dx  13  g(x)dx  13  2 f (x)dx      . 1 1 1 1 1 2
 g(x)dx  13  2.5  3  . 1
Câu 75. (THPT Thanh Chương 1- Nghệ An - 2021) bằng. A. . B. . C. . D. . Lời giải Chọn C  Đặt .  Khi đó .
Câu 76. (THPT Nguyễn Huệ - Phú Yên - 2021) Tính diện tích S hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  6x  7 và đường thẳng y  3  x . 9 33 A. S  3. B. S  . C. S  . D. S  60 . 2 5 Lời giải Chọn C  x  1
Xét phương trình hoành độ giao điểm: 2 2
x  6x  7  3  x  x  5x  4  0   . x  4  Diện tích S là: 4 4 3 2  x x  4 9
S  3  x    2
x  6x  7 dx =  2
x  5x  4dx =   5.  4x      ( đvdt). 3 2 1 2 1 1   x xdx
Câu 77. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho  bằng 1 1 5 2 A. 3 x x  C . B. 2 x x  C . C. 2 x x  C . D. 2 x x  C . 3 2 2 5 Lời giải Chọn D Đặt 2
x  t  t  x  2tdt  dx 2 2 2 Ta có 4 5
x xdx  t .t.2tdt  2 t dt  t  C      x5 2 2  C  x x  C . 5 5 5 3 1
Câu 78. (THPT Lương Thế Vinh - 2021) Với biến đổi u  ln x , tích phân dx  trở thành x ln x e
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489 3 3 1 ln 3 1 e 1 ln 3 1 A. du  . B. du  . C. du  . D. du  . u u u u e 0 1 1 Lời giải Chọn D 1
Với u  ln x ta có du  dx . x
Đổi cận: x  e  u  1, x  3  u  ln 3 . 3 ln 3 1 1 Vậy dx  du   . x ln x u e 1 f  x 1;  2 f 2  1
Câu 79. (THPT Lương Thế Vinh - 2021) Cho hàm số
có đạo hàm trên đoạn , và f 4  2021 2 . Giá trị I 
f 2x dx  bằng 1 A. 2  018 . B. 1010 . C. 1  008 . D. 2018 . Lời giải Chọn B 1
Đặt 2x  t  2dx  dt  dx  dt . 2
Khi đó: Với x  1  t  2 ; với x  2  t  4 . 4 4 1 1 1 1 Ta có I 
f t  dt 
f t    f 4  f 2  2021  1  1010  . 2 2 2   2 2 2 e
Câu 80. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho tích phân 2 I  x ln . xdx  Mệnh đề nào dưới 1 đây đúng? e 1 e e e A. 2 2 2 I  x ln x  x ln xdx  . B. 2 2
I  x ln x  2 x ln xdx  . 1 2 1 1 1 e 1 e e e C. 2 2 I  x ln x  x ln xdx  . D. 2 2
I  x ln x  2 ln xdx  . 1 2 1 1 1 Lời giải Chọn C  1
du  2 ln x  dx 2 u ln x     x 1 e e Đặt 2 2     I  x ln x  x ln d x . x  2 dv  xdx x 1  1  2 v    2 e 1 ln x
Câu 81. (THPT Đào Duy Từ - Hà Nội - 2021) Cho tích phân I  dx 
. Đặt u  1 ln x . Khi đó x 1 I bằng 1 0 2 2 1 2 u 0 A. I  2 2  u du . B. I  2   u du . C. I   du .
D. I    u du . 0 0 2 1 1 Lời giải Chọn A dx dx Đặt 2
u  1 ln x  u  1 ln x  2udu     2  udu . x x
Đổi cận x  1  u  1
x  e  u  0 .
Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 e 0 0 1 1 ln x 2 2  I  dx   .
u 2udu   2u du  2 u du     . x 1 1 1 0
Câu 82. (THPT Đào Duy Từ - Hà Nội - 2021) Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  5x  4 và trục Ox . Thể tích của khối tròn xoay sinh ra khi quay hình  H  quanh trục Ox bằng : 9 81 81 9 A. . B. . C. . D. . 2 10 10 2 Lời giải Chọn C
Hoành độ giao điểm của đồ thị hàm số 2
y  x  5x  4 và trục Ox là nghiệm phương trình : x  1 2
x  5x  4  0   . x  4 
Thể tích của khối tròn xoay sinh ra khi quay hình  H  quanh trục Ox bằng : 4 4 
  x  5x  42dx    x  5x  42 81 2 2 dx    . 10 1 1 2 4  x 
f  x dx  2020  f dx     2
Câu 83. (THPT Đào Duy Từ - Hà Nội - 2021) Biết  0 khi đó 0 bằng A. 2020 . B. 1010 . C. 2  020 . D. 4040 . Lời giải Chọn D  x 1 Đặt t   dt  dx . 2 2
Đổi cận: x  0  t  0 ; x  4  t  2 . 4 2  x   Ta có: f dx
    2. f t dt   2.2020  4040.  2  0 0 2
 x  2x  3 
Câu 84. (THPT Chu Văn An - Thái Nguyên - 2021) Họ nguyên hàm dx   bằng x 1   2 x 2 x 1 A.
 x  2 ln x 1  C . B.  x   C . 2 2  x  2 1 2 x C.
 x  2 ln x 1  C . D. 2
x  x  2 ln  x   1  C . 2 Lời giải Chọn A 2 2
 x  2x  3   2  x dx  x 1 dx 
 x  2 ln x 1  C     x 1    x 1 2
Câu 85. (THPT Chu Văn An - Thái Nguyên - 2021) Diện tích hình phẳng giới hạn bởi các đường 2
y  2  x , y  x bằng: 9 9 A. 9. B. . C. 18. D. . 2 4 Lời giải Chọn B x  1 
Xét phương trình hoành độ giao điểm 2 2
2  x  x  x  x  2  0  .  x  2 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489 2 9
Diện tích hình phẳng giới hạn bởi 2
y  2  x , y  x là: 2 S 
x  x  2  dvtt.  2 1 
Câu 86. (THPT Ba Đình - Thanh Hóa - 2021) Diện tích hình phẳng giới hạn bởi các đường 2 y  x và
y  x  2 là 9 9 8 A. S  9 . B. S  . C. S  . D. S  . 4 2 9 Lời giải Chọn C
 Phương trình hoành độ giao điểm của đồ thị hàm số 2
y  x và đường thẳng y  x  2 là x  1 2 2
x  x  2  x  x  2  0   . x  2 
 Diện tích hình phẳng giới hạn bởi các đường 2
y  x và y  x  2 là: 2 2 3 2  x x  2 9 2 S 
x  x  2 dx     2
x  x  2 dx    2x    . 3 2 1  2 1  1   
Câu 87. (Trung Tâm Thanh Tường - 2021) Hình phẳng S gồm hai phần được đánh dấu trong hình vẽ
bên. Diện tích hình S được tính theo công thức nào dưới đây? 0 3 0 3 A. S  
f  x dx  f  x dx   . B. S  
f  x dx  f  x dx   . 2  0 2  0 0 3 0 3 C. S 
f  x  dx 
f  x dx   . D. S 
f  x  dx  f  x dx   . 2 0 2 0 Lời giải Chọn D. 0 3 Ta có S 
f  x dx  f  x  dx   . 2 0 1 1 20 (1 2x) dx  20 (1 2x) dx 
Câu 88. (Trung Tâm Thanh Tường - 2021) Xét 0
, nếu đặt u  1 2x thì 0 bằng 1 1 1 1 1 1 A. 20 2 u du  . B. 20 u du  . C. 20  u du  . D. 20 u du  . 2 2 1  1  1  1  Lời giải Chọn B
x  0  u  1
Đặt u  1 2x  du  2dx . Đổi cận  .
x  1  u  1   1 1  1 1 1 Khi đó 20 20 20
(1 2x) dx   u du  u du    . 2 2 0 1 1 
Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 89. (Trung Tâm Thanh Tường -2021) Biết F  x  a sin x  b cos x là một nguyên hàm của hàm số
f  x  2sin x  8cos x , tính giá trị T  a  b .
A. T  6 .
B. T  4 .
C. T  6 . D. T  10 . Lời giải Chọn A
Do F  x là một nguyên hàm của f  x nên ta có:
F x  f  x  a cos x  bsin x  2sin x  8cos x , x
  a  8,b  2  .
Vậy a  b  6 . 1 1
Câu 90. (THPT Triệu Sơn - Thanh Hóa - 2021) Biết
f (x)dx  6  , tích phân f (2x 1) x d  bằng 1 0 A. 3. B. 6. C. 12. D. 2. Lời giải Chọn A 1 1 1 1 1 1 Ta có f (2x 1) x d 
f (2x 1)d (2x 1) 
f (t)dt  .6  3    . 2 2 2 0 0 1 1
Câu 91. (THPT Trần Phú - Đà Nẵng - 2021) Cho hàm số f  x 2  x 
. Trong các khẳng định sau, 2 x khẳng định nào đúng? 1 3 x 1 A.
f  x dx  2x   C  . B.
f  x dx    C  . x 3 x 3 x 1 2 C.
f  x dx    C  . D.
f  x dx  2x   C 3  . 3 x 3 x Lời giải Chọn B 3  1  x 1 Ta có f  x 2 dx  x  dx    C   . 2   x  3 x
Câu 92. (THPT Trần Phú - Đà Nẵng - 2021) Cho hàm số 2
f (x)  tan 2x . Trong các khẳng định sau, khẳng định nào đúng 1 3 tan 2x A.
f (x) dx  tan 2x  C  . B.
f (x) dx   C  . 2 3 1 C.
f (x) dx 
tan 2x  x  C  . D.
f (x) dx  tan 2x  x  C  . 2 Lời giải Chọn C 1 Ta có  2
tan 2x dx  [   2 tan 2x   1 1]dx 
tan 2x  x  C . 2 3
Câu 93. (THPT Trần Phú - Đà Nẵng - 2021) Cho 2 x dx  4 
. Giá trị của tham số a thuộc khoảng nào a sau đây?  1   1  A. 1;2 . B.  1  ;0 . C. 0;   . D. ;1   .  2   2  Lời giải Chọn C 3 3   1 1 3  1  Ta có: 2 1
x dx  x     4   a   0;   . a 3 a 13  2  a
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
NGUYỄN BẢO VƯƠNG - 0946798489 3 3
Câu 94. (THPT Trần Phú - Đà Nẵng - 2021) Biết
f  x dx  4  . Giá trị của
5 f  x 1 dx    bằng 1 1 A. 2  2 . B. 22 . C. 18 . D. 20 . Lời giải Chọn C 3 3 3 Xét:
5 f  x 1 dx  5
f  x dx  1dx  18      . 1 1 1
Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 3
NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG
MỨC ĐỘ VẬN DỤNG Câu 1.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Gọi S là diện tích hình phẳng giới 2 x  2x
hạn bởi đồ thị hàm số y 
, đường thẳng y  x 1 và các đường thẳng x  m , x  2m x 1 m  
1 . Giá trị của m sao cho S  ln 3 là A. m  2 . B. m  3 . C. m  5 . D. m  4 . Câu 2.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Người ta dùng máy đào hầm (TBM)
để đào hai đường hầm hình trụ tròn xoay đường kính 12 m , mỗi đường hàm đều có chiều dài bằng
20 m , có hai trục cắt nhau và vuông góc với nhau. Tính thể tích khối đất đào được. A. 3 3987.89m . B. 3 3619.11m . C. 3 4523.89 m . D. 3 3371.89m Câu 3.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hàm số f  x có đạo hàm liên tục trên  thỏa 3 1
mãn f 3  21, f  x dx  9 
. Tính tích phân I  .
x f 3x dx  . 0 0 A. I  15 . B. I  6 . C. I  12 . D. I  9 . Câu 4.
(Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hàm số f  x liên tục trên  và có một nguyên 1 2
hàm là hàm số g  x 2 
x  x 1. Khi đó f  2 x dx  bằng: 2 1 2 4 4 2 A. . B.  . C. . D.  . 3 3 3 3 Câu 5.
(Chuyên KHTN - 2021) Cho hàm số 3 2
f (x)  ax  bx  cx  4 và 2
g(x)  mx  nx có đồ thị trong hình bên dưới.
Diện tích của hình phẳng giới hạn bởi đồ thị của hai hàm số trên (phần gạch chéo trong hình vẽ) bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 9 37 37 9 A. . B. . C. D. . 4 12 6 2 2 3 x 1 Câu 6.
(Chuyên KHTN - 2021) Biết rằng
dx  a  b ln 3  c ln 2 
với a , b , c là các số hữu tỉ. Tính 2 x  x 1
2a  3b  4c A. 19 . B. 19 . C. 5 . D. 5  . Câu 7.
(Chuyên KHTN - 2021) Cho hàm số f  x liên tục trên khoảng 0; và thỏa mãn 2  1 
2 f  x  xf  x  
với mọi x  0 Tính f  x . dx   x  1 2 7 7 9 3 A. . B. . C. . D. . 12 4 4 4 1 Câu 8.
(Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hai hàm số f  x 3 2
 ax  bx  cx  và 2 g  x 2
 dx  ex 1 (a, b, c, d , e  ) . Biết rằng đồ thị hàm số y  f  x và y  g  x cắt nhau tại
3 điểm có hoành độ lần lượt là 3
 ; 1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị
đã cho có diện tích bằng 9 A. 5 . B. . C. 4 . D. 8 . 2 e ln x c Câu 9.
(Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho I 
dx  a ln 3  b ln 2   ,
x ln x  22 3 1 với a, ,
b c   . Giá trị 2 2 2
a  b  c bằng A. 11. B. 1. C. 9. D. 3.
Câu 10. (Chuyên Quốc Học Huế - 2021) Cho hàm số f  x liên tục trên  và thỏa mãn 3 3
f  x  f 5  x, x
   . Biết f  x dx  2 
. Tính I  xf  x dx  2 2 A. I  20 . B. I  10 . C. I  15 . D. I  5 .
Câu 11. (Chuyên Quang Trung - Bình Phước - 2021) F  x là một nguyên hàm của hàm số 5 5
y   x   2 1
x  2x  3 . Biết F  2
   F 4 1  và F  3
   F 5  a 3  ;
b a,b   . Giá 3
trị a  b bằng A. 17 . B. 9 . C. 12 . D. 18 .  4 x dx 
Câu 12. (Chuyên Quang Trung - Bình Phước - 2021) Cho * 
 ln b  ln 2; a,b    . Giá 2 1 sin x a 0
trị a  3b bằng A. 10 . B. 8 . C. 12 . D. 4 .
Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 13. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hàm số y  f  x liên tục trên đoạn  5  ;6có đồ thị 0
như hình vẽ. Giá trị của
f  x dx  bằng. 5  y 6 4 -1 O 1 2 -5 -2 6 x -1 -2 25 19 11 13 A. . B. . C. . D. . 2 2 2 2
Câu 14. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hàm số y  f (x) có đạo hàm liên tục trên đoạn [ 1;1] ,
thỏa mãn f (x)  0, x    và f (
 x)  2 f (x)  0 . Biết f (1)  1. Tính f ( 1  ) A. 2 e . B. 4 e . C. 2 e . D. 4 e . 3 x f  x
Câu 15. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho F  x  là một nguyên hàm của . Biết 3 x
f  x có đạo hàm và xác định với mọi x  0 . Tính   x f x e dx  . A. 2 3 x  6 x x x e
xe  e  C . B. 2 x  6 x  6 x x e xe e  C . C. 2 3  6 x  6 x x xe e  C . D. 2 3
x  6 x  6 x x e xe e  C . 1
Câu 16. (Chuyên ĐHSP Hà Nội - 2021) Cho F (x) là một nguyên hàm của f (x)  trên 2 x(x  3)
0; thỏa mãn F (1)  ln 3 . Giá trị của F(2021) F ( 2020) e  e
thuộc khoảng nào?  1   1 1   1 1  1 1  A. 0;   . B. ;   . C. ;   . D. ;   .  10   10 5   5 3  3 2 
Câu 17. (Chuyên ĐH Vinh - Nghệ An - 2021) Giả sử f  x là một hàm số có đạo hàm liên tục trên  . Biết rằng   3
G x  x là một nguyên hàm của   2  x g x  e
f  x trên  . Họ tất cả các nguyên hàm của 2  x e
f  x là A. 3 2
2x  3x  C . B. 3 2
x  3x  C . C. 3 2
2x  3x  C . D. 3 2
 x  3x  C . 2021
Câu 18. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho
f  x dx  2  . Tính tích phân 0 2021 e 1  x I  . f ln   2 x 1  dx . 2  x 1    0 A. I  2 . B. I  1. C. I  5 . D. I  4 . 1
Câu 19. (THPT Quốc Oai - Hà Nội - 2021) Đường cong C có phương trình 2 y  x chia hình vuông 4
OABC có cạnh bằng 4 thành hai phần. Gọi S , S lần lượt là diện tích của phần không tô đậm và 1 2 S
tô đậm như hình vẽ bên dưới. Tỉ số 1 bằng S2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 1 3 A. 3 . B. . C. 2 . D. . 2 2 1 2
Câu 20. (THPT Quốc Oai - Hà Nội - 2021) Cho hàm số y  f x liên tục trên  và
f xdx  5  , 0 1  2 2
f 2xdx 10  . Tích phân I 
cos x f sin xdx  bằng 1 0 4 A. I  5 . B. I  20 . C. I  15 . D. I  25 . Câu 21. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho tích 2 3 2
x  3x  2x phân I 
dx  a  b ln 2  c ln 3 (a,b  ) 
 . Chọn khẳng định đúng trong các khẳng x 1 1 định sau.
A. b  c  0 B. c  0 C. a  0
D. a  b  c  0 3 x
Câu 22. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Biết rằng I 
dx  a ln 5  b ln 2  với x 1 x  2 2   
a, b là các số hữu tỉ. Giá trị của tổng a  b là 1 1 2 A. . B. 1. C.  . D. . 3 3 3
Câu 23. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho hàm số y  f  x xác định và liên tục trên  có f  x
f  x  0 x    , f   3 1  e . Biết  2x 1, x
   . Tìm tất cả giá trị của tham số m để f  x
phương trình f  x  m có hai nghiệm thực phân biệt. 3 3 3 3 A. 4
m  e . B. 4
0  m  e . C. 4
1  m  e . D. 4 m  e .
Câu 24. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hàm số y  f (x) có đồ thị như hình vẽ bên.
Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 b c d d Đặt I  f (x) ; dx I  f (x) ; dx I  f (x) ; dx I  f (x) . dx 1 2 3 4     a a a c
Phát biểu nào dưới đây đúng?
A. I  I  I  I
B. I  I  I  I 1 2 3 4 2 1 4 3
C. I  I  I  I
D. I  I  I  I 2 1 3 4 1 2 4 3
Câu 25. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho f  x và g  x là hai hàm số có đạo hàm liên 1
tục trên  và thỏa mãn f 0  1, f  
1  2 ; g 0  2  , g   1  4 và
f  x g  x dx  7  . Tính 0 1 I 
f  x g x dx  . 0 A. I  3  . B. I  17 . C. I  3. D. I  1  7 . 2 x  m
Câu 26. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hàm số y 
( với m là tham số khác x 1
0 ) có đồ thị là C  . Gọi là diện tích hình phẳng giới hạn bởi đồ thi và hai trục tọa độ. Có bao
nhiêu giá trị thực của m thỏa mãn S  1? A. 4 . B. 2 . C. 1. D. 0 .
Câu 27. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hàm số f x xác định và liên tục trên 2 e  1
0; thỏa mãn f x   xf
 xdx ,x  0;. Tính tích phân f  xdx. x 1 1 5  2e A. . B. 3  2e. C. 2  2 . e D. 1  2e. 3 2 3x 1  ln b 
Câu 28. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho biết dx  ln a   với 2  
3x  x ln x  c  1
a, b, c là các số nguyên dương và c  4 , tổng a  b  c bằng A. 5. B. 6 . C. 7 . D. 9.
Câu 29. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hàm số 4 2
y  x  4x  m . Tìm m để đồ thị
hàm số cắt trục Ox tại bốn điểm phân biệt sao cho hình phẳng giới hạn bởi đồ thị hàm số và Ox
có phần phía trên trục hoành là S , phần dưới trục hoành x là S và S thỏa S  S  S . Khi đó 1 2 3 1 2 3 a a m 
( a, b là các số nguyên, b  0 ,
tối giản). Giá trị của biểu thức S  a  b là b b
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 y S3 O x S S 1 2 A. 2. B. 7. C. 9. D. 11.  2 1
x  x  x e
Câu 30. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho
dx  a.e  b ln 
e  c với x x  e 0 a, ,
b c   . Tính P  a  2b  c A. P  2  .
B. P  0 . C. P  1  . D. P  1. 1 x
Câu 31. (THPT Đồng Quan - Hà Nội - 2021) Cho
dx  a  b ln 3  c ln 4 
với a, b, c là các số  x  32 0
hữu tỉ. Giá trị của a  b  c bằng 1 1 4 1 A.  . B.  . C. . D. . 2 4 5 5
Câu 32. (THPT Đồng Quan - Hà Nội - 2021) Cho hàm số f  x có đạo hàm liên tục trên  và thỏa mãn 3 1 .
x f '2x  4 dx  8; f 2  2  . Tính I 
f 2x dx  . 0 2
A. I  5 .
B. I  10 .
C. I  5 .
D. I  10 .
Câu 33. (THPT Đồng Quan - Hà Nội - 2021) Cho hàm số f  x liên tục và dương trên 0;  , thỏa 1 2 f  x mãn xf  x 2
 x f  x 2 3
 2 f  x, x   0 và f   1 
. Giá trị của tích phân dx  2 2 x 1 5 1 5 1 5 1 5 A. ln . B. ln . C. .ln . D. .ln . 2 4 2 2 2 3 2 1
Câu 34. (THPT Lê Lợi - Thanh Hóa - 2021) Biết rằng tích phân 2   3 ex x
d x  ae+b 
; a,b . 0
Tính giá trị biểu thức P  2a  b . A. 5 . B. 2 . C. 3 . D. 7 .
Câu 35. (THPT Lê Lợi - Thanh Hóa - 2021) Ông An có một mảnh đất nhỏ hình vuông cạnh bằng 4 m ở
trước sân. Ông muốn trồng hoa và cỏ để trang trí mảnh vườn của mình như sau: Ông sẽ trồng hoa
trên phần diện tích có dạng Parabol  P nhận trục đối xứng KI của hình vuông làm trục đối
xứng của  P và đỉnh của  P là trung điểm của KI như hình vẽ, phần cỏ sẽ trồng ở phần còn
lại của hình vuông. Biết rằng loại hoa ông muốn trồng có giá 200 000 đồng/ 2 1m , cỏ có giá 50 000 đồng/ 2
1m . Hỏi số tiền ông An bỏ ra để làm mảnh vườn là bao nhiêu (số tiền được làm
tròn đến hàng đơn vị)?
Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A. 1365685, 4 đ. B. 2634314, 6 đ. C. 138642, 5 đ. D. Đáp án khác.
Câu 36. (Sở Vĩnh Phúc - 2021) Cho hàm số y  f  x có đạo hàm liên tục trên  và thỏa mãn     2
f  x  f  x  sin . x cos , x x    
 . Biết f 0  0, tính I  xf  xdx  .  2  0 1 1   A. I   . B. I  . C. I  . D. I   . 4 4 4 4  x
Câu 37. (Sở Vĩnh Phúc - 2021) Biết diện tích của hình phẳng giới hạn bởi các đường y  3 x , y  , x  0 3 m n là S  
. Tính tổng m  n . 3ln 3 6
A. m  n  4 .
B. m  n  2 .
C. m  n  1.
D. m  n  3 . m
Câu 38. (Sở Lào Cai - 2021) Có bao nhiêu giá trị thực của tham số m thỏa mãn: 2
3x  2x dx  m 10  ? 0 A. 1 . B. 2 . C. 4 . D. 3 .
Câu 39. (Sở Hà Tĩnh - 2021) Cho hàm số y  f  x liên tục trên  và thỏa mãn  2
2021 f  x  f x  x sin , x x
   . Giá trị của tích phân I 
f  x dx  bằng   2 1 2 1 3 A. . B. . C. . D. . 1010 2019 2020 2022 2 x  5
Câu 40. (Sở Yên Bái - 2021) Biết
dx  a ln 5  b ln 3 
với a,b   . Tính P  . a b . 2 x  4x  3 0 A. P  3 . B. P  6 . C. P  6 . D. P  3 . Câu 41. (Sở Yên Bái - 2021) Biết a, b, c là các số nguyên dương thỏa mãn 2 dx 
a  b  c 
. Tính giá trị biểu thức P  a  b  c .
(x 1) x  x x 1 1 A. P  18. B. P  46. C. P  24. D. P  12.
Câu 42. (Sở Yên Bái - 2021) Cho hàm số f  x liên tục và là hàm số chẵn trên  thỏa mãn  3 2 I 
f  xdx  6. 
Tính tích phân J  cos .
x f 3sin x dx  . 0   2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 A. J  4  . B. J  4. C. J  0. D. J  6. ln 6 dx
Câu 43. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Biết  3lna lnb 
với a , b là các
ex  2ex  3 ln 3
số nguyên dương. Tính P  ab . A. 20 . B. 1  0 . C. 15 . D. 10 .
Câu 44. (THPT Thanh Chương 1- Nghệ An - 2021) Biết rằng , với ;
; là các số hữu tỷ. Giá trị của bằng: A. . B. . C. . D. .
Câu 45. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hàm số f  x liên tục trên 0;   và thỏa mãn f x ln x 17 2   f  x   1   . Biết
f  xdx  a ln 4  b 
với a,b   . Giá trị của a  2b bằng 4x x x 1 A. 16 . B. 12 . C. 8 . D. 20 .
Câu 46. (THPT Lương Thế Vinh - 2021) Cho hàm số y  f  x với 1
  x  4 có đồ thị các đoạn thẳng như hình bên. 4 Tích phân I 
f  x dx  bằng 1 A. 4 . B. 1. C. 5,5 . D. 2,5.
Câu 47. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hàm số y  f (x) liên tục và có đồ thị trên [3; 5] như hình bên. 1377 2673 Biết các miền ,
A B, C có diện tích lần lượt là S  188, S  , S  . Khi đó A B 4 C 4 5
 f  x 1 dx     bằng 3  2417 2401 A. 520. B. . C. -504. D. . 2 2
Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1
Câu 48. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hàm số f  x liên tục trên 0;   . Biết là một 2 x 1 2 f  x nguyên hàm của hàm số '
y  f  xln x và f 2  . Khi đó, dx  bằng ln 2 x 1 7 1 1 7 A.  . B. . C.  . D. . 4 2 2 4 3
Câu 49. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho tích phân
xf (x)dx  2.  Tính tích phân 1 2 2 3
I  x f ( x 1)dx  ? 0 2 4 A. 3 . B. . C. 1. D. . 3 3
Câu 50. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hàm số 3 2
y  x  ax  bx  c có đồ thị (C) . Biết
rằng tiếp tuyến d của (C) tại điểm có hoành độ 1
 cắt (C) tại điểm B có hoành độ bằng 2 (xem
hình vẽ). Diện tích hình phẳng giới hạn bởi d và (C) (phần gạch chéo trong hình) bằng 25 13 27 11 A. . B. . C. . D. . 4 2 4 2
Câu 51. (THPT Chu Văn An - Thái Nguyên - 2021) Ông An có một mảnh vườn hình Elip có độ dài trục
lớn bằng 16m và độ dài trục bé bằng 10m . Ông muốn trồng hoa trên một dải đất rộng 8m và nhận
trục bé của elip làm trục đối xứng.Biết kinh phí để trồng hoa là 100.000 đồng/ 2 1m . Hỏi ông An
cần bao nhiêu tiền để trồng hoa trên dải đất đó? (Số tiền được làm trong đến hàng nghìn.) A. 7.826.000 đồng. B. 7.862.000 đồng. C. 7.128.000 đồng. D. 7.653.000 đồng.
Câu 52. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hàm số f (x) liên tục trên khoảng (0;).
Biết f (1)  1 và f  x  xf  x  ln ; x x
 0;  . Giá trị của f ( ) e bằng: 1 A. 1. B. 2. C. . e D. . e
Câu 53. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hàm số f  x liên tục trên đoạn 1;  4 và thoả f 2 x   1 ln x
mãn f  x   . Tính x x 4 I 
f  x dx  ? 3 A. 2 S  2 ln 2. B. 2 S  ln 2. C. S  2 ln 2 D. 2 S  3  2 ln 2 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489  2 cos x 4
Câu 54. (THPT Ba Đình - Thanh Hóa - 2021) Cho dx  a ln  b  , với 2
sin x  5sin x  6 c 0 *
a,b  , c   . Tính tổng S  a  b  c . A. S  1. B. S  0 . C. S  4 . D. S  3.
Câu 55. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hàm số y  f  x có đồ thị như hình vẽ và gọi A ;
B là hai hình phẳng được gạch trong hình bên dưới lần lượt có diện tích bằng 14 và 5 . 0 Giá trị của I  f 3x   1 dx  bằng: 1  19 A. 9 . B. . C. 27 . D. 3 . 3
Câu 56. (THPT Triệu Sơn - Thanh Hóa - 2021) Một khuôn viên dạng nửa hình tròn, trên đó người thiết
kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối
xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường
tròn (phần tô màu) và cách nhau một khoảng bằng 4m. Phần còn lại của khuôn viên (phần không
tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ, chi phí để trồng hoa và
cỏ Nhật Bản tương ứng là 150.000 đồng/ 2 m và 100.000 đồng/ 2
m . Hỏi số tiền cần để trồng hoa
và trồng cỏ Nhật Bản trong khuôn viên đó gần nhất với số nào sau đây?
A. 3.739.000 (đồng).
B. 1.948.000 (đồng). C. 3.926.000 (đồng). D. 4.115.000 (đồng).
Câu 57. (THPT Trần Phú - Đà Nẵng - 2021) Cho  H  là hình phẳng giới hạn bởi đồ thị hai hàm số 2
y  x 1; y  x 1 và hai đường thẳng x  1  ; x  1 .
Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Thể tích của khối tròn xoay được tạo thành khi quay  H  quanh trục Ox bằng 176 14 21 16 A. . B. . C. . D. . 15 3 5 15 BẢNG ĐÁP ÁN 1.A 2.D 3.B 4.C 5.C 6.B 7.D 8.C 9.D 10.D 11.D 12.A 13.D 14.D 15.D 16.A 17.C 18.B 19.C 20.D 21.D 22.C 23.D 24.B 25.C 26.B 27.B 28.C 29.D 30.A 31.B 32.D 33.C 34.D 35.A 36.A 37.D 38.A 39.A 40.A 41.B 42.B 43.D 44.A 45.D 46.D 47.A 48.D 49.D 50.C 51.D 52.B 53.A 54.C 55.D 56.A 57.C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 3
NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG
MỨC ĐỘ VẬN DỤNG Câu 1.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Gọi S là diện tích hình phẳng giới 2 x  2x
hạn bởi đồ thị hàm số y 
, đường thẳng y  x 1 và các đường thẳng x  m , x  2m x 1 m  
1 . Giá trị của m sao cho S  ln 3 là A. m  2 . B. m  3 . C. m  5 . D. m  4 . Lời giải Chọn A
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số: 2 x  1 x  2x  x  1  x 1      x   . 2 x 1
x  2x   x   2 2 2 1
x  2x  x  2x 1  
Phương trình vô nghiệm, suy ra hai đồ thị hàm số không có giao điểm.
Như vậy diện tích hình phẳng cần tính là: 2m 2 2m 2 x  2x 1 m  1 S    x   1 dx  dx  dx    . x 1 x 1 x 1 m m m 2m 1 2m 2m  2m 1  d  x   1  ln x 1  ln x 1  ln    (do m  1). x 1 m m  m 1  m  2m 1   2m 1   2m 1 
Theo đề bài S  ln 3  ln  ln 3  ln  3     hoặc ln   ln 3   .  m 1   m 1   m 1   2m 1  3 m  
2m 1  3m   2 1 m 1 Suy ra      2 . 2m 1 1  32m   1  m 1 m  KTM     5  m 1 3 . Vậy m  2 . Câu 2.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Người ta dùng máy đào hầm (TBM)
để đào hai đường hầm hình trụ tròn xoay đường kính 12 m , mỗi đường hàm đều có chiều dài bằng
20 m , có hai trục cắt nhau và vuông góc với nhau. Tính thể tích khối đất đào được. A. 3 3987.89m . B. 3 3619.11m . C. 3 4523.89 m . D. 3 3371.89m Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
Cắt thiết diện của hai hình trụ theo một mặt phẳng theo phương vuông góc với với khối trụ ta
được một hình vuông có cạnh bằng 2 2 36  x 6
Khi đó ta có thể tích khối đất đucợ đào là 2
V  2. R h   4   2
36  x dx  3371.89 . 6  Câu 3.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hàm số f  x có đạo hàm liên tục trên  thỏa 3 1
mãn f 3  21, f  x dx  9 
. Tính tích phân I  .
x f 3x dx  . 0 0 A. I  15 . B. I  6 . C. I  12 . D. I  9 . Lời giải Chọn B 1 1 3 1 1 Ta có I  .
x f 3x dx  3 .
x f 3x d 3x  .
x f  x dx    . 9 9 0 0 0 u   x  du  dx  Đặt    . dv  f    x dx v  f    x  3 3 3 Suy ra .
x f  x dx  .
x f  x  f  x dx  3 f 3  9  3.21 9  54   . 0 0 0 Vậy I  6 . Câu 4.
(Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hàm số f  x liên tục trên  và có một nguyên 1 2
hàm là hàm số g  x 2 
x  x 1. Khi đó f  2 x dx  bằng: 2 1 2 4 4 2 A. . B.  . C. . D.  . 3 3 3 3 Lời giải Chọn C 2 2 3  x  2 4
Ta có: f  x  g x  x 1  f   2
x dx   2 x   1 dx   x    . 3 1 3 1 1   Câu 5.
(Chuyên KHTN - 2021) Cho hàm số 3 2
f (x)  ax  bx  cx  4 và 2
g(x)  mx  nx có đồ thị trong hình bên dưới.
Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Diện tích của hình phẳng giới hạn bởi đồ thị của hai hàm số trên (phần gạch chéo trong hình vẽ) bằng 9 37 37 9 A. . B. . C. D. . 4 12 6 2 Lời giải Chọn C
Phương trình hoành độ giao điểm: 3 2 2 3 2
 ax  bx  cx  4  mx  nx  ax  (b  m)x  (c  n)x  4  0 Đặt 3 2
h(x)  ax  (b  m)x  (c  n)x  4
Vì h(x)  0 có 3 nghiệm x  2, x  1, x  1 nên 2
h(x)  a(x  1)(x 1)(x  2)  a(x 1)(x  2)
Mà ta có h(0)  2a  4  a  2 . Suy ra 2
h(x)  2(x 1)(x  2) . 2 2 37
Vậy diện tích hình phẳng là 2 S 
h(x) dx 
2(x  1)(x  2) dx    . 6 1 1 2 3 x 1 Câu 6.
(Chuyên KHTN - 2021) Biết rằng
dx  a  b ln 3  c ln 2 
với a , b , c là các số hữu tỉ. Tính 2 x  x 1
2a  3b  4c A. 19 . B. 19 . C. 5 . D. 5  . Lời giải Chọn B 2 3 2 x 1  2 1   Ta có: dx  x 1  dx  2   x  x  x 1 x  1 1 2  x  2 1 
 x  2 ln x 1  ln x   2 ln 3  3ln 2   . 2 1 2   1  Suy ra: a 
; b  2 ; c  3  . 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 1
 Vậy 2a  3b  4c  2.  3.2  4. 3    19 . 2 Câu 7.
(Chuyên KHTN - 2021) Cho hàm số f  x liên tục trên khoảng 0; và thỏa mãn 2  1 
2 f  x  xf  x  
với mọi x  0 Tính f  x . dx   x  1 2 7 7 9 3 A. . B. . C. . D. . 12 4 4 4 Lời giải Chọn D  1 
 Ta có 2 f  x  xf  x     1  x  1 1  Đặt
 t  x  khi đó điều kiện đề bài cho trở thành x t  1  1 1  1  2 f  f  
t   2t. f  f   t 1 2  t  t t  t    1 
4 f t   2t. f  2x      t  1 2t  Từ   1 và 2 ta có: 
 f t   .  1  3
 f t  2t. f  1      t  1 2 2 1 2x 3
 Lấy tích phân cận từ đến 2 ta được:
f  x dx  dx  .   2 3 4 1 1 2 2 1 Câu 8.
(Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hai hàm số f  x 3 2
 ax  bx  cx  và 2 g  x 2
 dx  ex 1 (a, b, c, d , e  ) . Biết rằng đồ thị hàm số y  f  x và y  g  x cắt nhau tại
3 điểm có hoành độ lần lượt là 3
 ; 1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị
đã cho có diện tích bằng 9 A. 5 . B. . C. 4 . D. 8 . 2 Lời giải Chọn C
 Phương trình hoành độ giao điểm của hai đồ thị y  f  x và y  g  x là 1 3 3 2 2 3 x a
 bx  cx 
 dx  ex 1  ax  b  d  2
x  c  e x   0.  * 2 2
 Do đồ thị hàm số y  f  x và y  g x cắt nhau tại ba điểm có hoành độ lần lượt là 3  ;
1; 1 nên phương trình * có ba nghiệm x  3  ; x  1
 ; x  1. Khi đó ta có hệ phương trình
Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021  3  3 27 
a  9b  d   3c  e   0  b  d  2  2    3  1
a  b  d   c  e   0  a  . 2  2   3  1
a  b  d   c  e   0  c  e    2  2 1 3 1 3
Suy ra f  x  g  x 3 2  x  x  x  . 2 2 2 2
 Vậy hình phẳng giới hạn bởi hai đồ thị hàm số đã cho có diện tích là: 1  1
S    f  x  g xdx   g x  f xdx 3  1  1  1  1 3 1 3   1 3 1 3 3 2 3 2   x  x  x  dx  x  x  x  dx        2 2 2 2   2 2 2 2  3 1  2  2  4 . e ln x c Câu 9.
(Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho I 
dx  a ln 3  b ln 2   ,
x ln x  22 3 1 với a, ,
b c   . Giá trị 2 2 2
a  b  c bằng A. 11. B. 1. C. 9. D. 3. Lời giải Chọn D  dx d  u 
 Đặt u  ln x  2   x . ln  x  u  2 
 Đổi cận: Khi x  1  u  2 ; Khi x  e  u  3; 3 3 3 u  2  1 2   2  2 1  Ta có: I  du   du  ln u   ln 3 
 ln 2 1  ln 3  ln 2   . 2  2    u  u u   u  3 3 2 2 2
 Suy ra a  1 , b  1, c  1.  Vậy giá trị 2 2 2
a  b  c  111  3 .
Câu 10. (Chuyên Quốc Học Huế - 2021) Cho hàm số f  x liên tục trên  và thỏa mãn 3 3
f  x  f 5  x, x
   . Biết f  x dx  2 
. Tính I  xf  x dx  2 2 A. I  20 . B. I  10 . C. I  15 . D. I  5 . Lời giải Chọn D dt  dx
Đặt t  5  x   . x  5  t  Khi đó : 3 2 3
I  xf  x dx   5  t  f 5  t  dt  5  t  f 5  t  dt    2 3 2 3 3 3 3
 5 f 5  t  dt  tf 5  t  dt  
 5 f t  dt  tf t  dt  
( Vì f  x  f 5  x, x    ). 2 2 2 2
Khi đó I  5.2  I  2I  10  I  5 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 11. (Chuyên Quang Trung - Bình Phước - 2021) F  x là một nguyên hàm của hàm số 5 5
y   x   2 1
x  2x  3 . Biết F  2
   F 4 1  và F  3
   F 5  a 3  ;
b a,b   . Giá 3
trị a  b bằng A. 17 . B. 9 . C. 12 . D. 18 . Lời giải Chọn D
Theo đề, F  x có dạng 3 1 1
F  x   x   2 2 1
x  2x  3dx 
x  2x  3d    2
x  2x  3 2 
x  2x  3  C 2 3 5 5 5 5 F 4 1   C   C  1. 3 3
Suy ra: F 3  8 13 1; F 5  8 13 1 Do đó: F  3
   F 5  16 3  2
Đồng nhất a, b ta được a  16;b  2
Vậy a  b  18 .  4 x dx 
Câu 12. (Chuyên Quang Trung - Bình Phước - 2021) Cho * 
 ln b  ln 2; a,b    . Giá 2 1 sin x a 0
trị a  3b bằng A. 10 . B. 8 . C. 12 . D. 4 . Lời giải Chọn A    4 4 4 x dx x dx Ta có:   d
x tan x   2  2  ư 1 sin x cos x 0 0 0   4     4 4  . x tan x  tan d x x   ln cos x   ln 2  ln 2   ln b  ln 2 0  0 4 4 a 0
Đồng nhất hệ số ta được a  4;b  2 .
Vậy a  3b  4  3.2  10 .
Câu 13. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hàm số y  f  x liên tục trên đoạn  5  ;6có đồ thị 0
như hình vẽ. Giá trị của
f  x dx  bằng. 5  y 6 4 -1 O 1 2 -5 -2 6 x -1 -2 25 19 11 13 A. . B. . C. . D. . 2 2 2 2 Lời giải
Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chọn D y A 6 4 B C -1 D O 1 2 F x -5 -2 -1 6 G E -2 Ta có 1 1 S  BC.AB  .6.3  9. ABC 2 2 1 1 S  DF.EF  .1.2  1. DEE 2 2 1 1 3 S  GO  EF DO   FEGO   .3.1 . 2 2 2 Khi đó 0 2  1  0 3 13 f  xdx  f  xdx  f  xdx 
f  xdx  S S  S  9 1   . ABC DEE FEGO     2 2 5  5  2  1 
Câu 14. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hàm số y  f (x) có đạo hàm liên tục trên đoạn [ 1;1] , 
thỏa mãn f (x)  0, x
   và f (x)  2 f (x)  0 . Biết f (1) 1. Tính f ( 1  ) A. 2 e . B. 4 e . C. 2 e . D. 4 e . Lời giải Chọn D
+ Ta có :Vì f (x)  0, x    nên 1 1 f (  x) f (  x) f (
 x)  2 f (x)  0   2  dx  2 
dx  ln  f (x) 1 1  2x   1 1 f (x) f (x)  1  1 f (1) 4  ln  4   f ( 1  )  e . f (1) Vậy 4 f ( 1  )  e 3 x f  x
Câu 15. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho F  x  là một nguyên hàm của . Biết 3 x
f  x có đạo hàm và xác định với mọi x  0 . Tính   x f x e dx  . A. 2 3 x  6 x x x e
xe  e  C . B. 2 x  6 x  6 x x e xe e  C . C. 2 3  6 x  6 x x xe
e  C . D. 2 3
x  6 x  6 x x e xe e  C . Lời giải Chọn D f  x f  x
Theo bài, F  x 
x  F x   f  x 3
 x  f  x 2 d  3x  . x x Khi đó,   x 2 x 2 x x 2 d  3 d  3  6 d  3 x  6 x  6 x f x e x x e x x e xe x x e xe e dx     2  3
x  6 x  6 x x e xe e  C .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 Vậy   x 2 d  3
x  6 x  6 x f x e x x e xe e  C  . 1
Câu 16. (Chuyên ĐHSP Hà Nội - 2021) Cho F (x) là một nguyên hàm của f (x)  trên 2 x(x  3)
0; thỏa mãn F (1)  ln 3. Giá trị của F(2021) F ( 2020) e  e
thuộc khoảng nào?  1   1 1   1 1  1 1  A. 0;   . B. ;   . C. ;   . D. ;   .  10   10 5   5 3  3 2  Lời giải Chọn A 1 Ta có F (x)  dx  2 x(x  3) 1 x  x  3 dt 1 Đặt t 
x  x  3  dt  . dx   dx . 2 x(x  3) t 2 x(x  3)  F (x)  ln
x  x  3  C .
Mà F (1)  3  C  0 . Do đó  F (x)  ln x  x  3 . Vậy F (2021) F ( 2020) e  e 
2021  2024  2020  2023  0, 0222 .
Câu 17. (Chuyên ĐH Vinh - Nghệ An - 2021) Giả sử f  x là một hàm số có đạo hàm liên tục trên  . Biết rằng   3
G x  x là một nguyên hàm của   2  x g x  e
f  x trên  . Họ tất cả các nguyên hàm của 2  x e
f  x là A. 3 2
2x  3x  C . B. 3 2
x  3x  C . C. 3 2
2x  3x  C . D. 3 2
 x  3x  C . Lời giải Chọn C   3
G x  x là một nguyên hàm của   2  x g x  e
f  x trên  , nên 2  x e f  x 2  3x . Xét 2  x I  e
f  xdx  . Đặt 2 x 2   d  2 x u e u e
dx và dv  f  x dx  v  f  x . Khi đó: 2 x    2  x I e f x  e f  x 2 3 2
dx  3x  2x  C.  Vậy 3 2
I  2x  3x  C . 2021
Câu 18. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho
f  x dx  2  . Tính tích phân 0 2021 e 1  x I  . f ln   2 x 1  dx . 2  x 1    0 A. I  2 . B. I  1. C. I  5 . D. I  4 . Lời giải Chọn B 2x Đặt t  ln  2 x   1  dt  dx 2 x 1
Với x  0 thì t  0 và 2021 x  e 1 thì t  2021. 2021 e 1  2021 2021 x 1 1 1 Khi đó, I  . f ln   2
x 1  dx  f t dt 
f x dx  .2  1 2        . x 1    2 2 2 0 0 0
Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1
Câu 19. (THPT Quốc Oai - Hà Nội - 2021) Đường cong C có phương trình 2 y  x chia hình vuông 4
OABC có cạnh bằng 4 thành hai phần. Gọi S , S lần lượt là diện tích của phần không tô đậm và 1 2 S
tô đậm như hình vẽ bên dưới. Tỉ số 1 bằng S2 1 3 A. 3 . B. . C. 2 . D. . 2 2 Lời giải Chọn C
Diện tích hình vuông OABC : S  4.4  16 4 4  1  1 16 2 3 S  x dx  x  2    0  4  12 3 0 16 32
S  S  S  16   1 2 3 3 S 32 16 Tỉ số 1  :  2 S 3 3 2 1 2
Câu 20. (THPT Quốc Oai - Hà Nội - 2021) Cho hàm số y  f x liên tục trên  và
f xdx  5  , 0 1  2 2
f 2xdx 10  . Tích phân I 
cos x f sin xdx  bằng 1 0 4 A. I  5 . B. I  20 . C. I  15 . D. I  25 . Lời giải Chọn D. 1 2 Ta có:
f 2xdx  10  1 4 1 2 1 1 1 1
Đặt 2x  t  2d x  d t 
f 2xd x 
f tdt  10   
f tdt 
f xdx  20   . 2 1 1 1 1 4 2 2 2 1 
f xdx  25  . 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489  2 I 
cos x f sin xdx  0 1 1
Đặt sin x  t  cos x dx  d t  I 
f tdt  
f xdx   25 . 0 0 Câu 21. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho tích 2 3 2
x  3x  2x phân I 
dx  a  b ln 2  c ln 3 (a,b  ) 
 . Chọn khẳng định đúng trong các khẳng x 1 1 định sau.
A. b  c  0 B. c  0 C. a  0
D. a  b  c  0 Lời giải Chọn D 2 2 3 2 2 3
x  3x  2x  6   x  Ta có 2 2 I  dx 
x  4x  6  dx 
 2x  6x  6 ln x  1      x 1  x 1  3 1 1   1  20   13  7   6ln 3   6ln 2   6ln 2  6ln 3.      3   3  3 7 Theo đó thì a 
;b  6;c  6  a  b  c  0. 3 3 x
Câu 22. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Biết rằng I 
dx  a ln 5  b ln 2  với x 1 x  2 2   
a, b là các số hữu tỉ. Giá trị của tổng a  b là 1 1 2 A. . B. 1. C.  . D. . 3 3 3 Lời giải Chọn C x 1 2 Ta có:   .  x   1  x  2 3 x   1 3 x  2 3 3 x  1 2  I  dx     dx   x 1 x 2  3 x 1 3 x 2      2    2       3 3 3 3 1 1 2 1 1 2 = dx  dx  ln x 1  ln x  2   3 x 1 3 x  2 3 3 2 2 2 2 1 2 2 = ln 2  ln  1 
ln 5  ln 4  ln 5  ln 2 . 3 3 3 2 1 Suy ra a 
, b  1 . Vậy a  b   . 3 3
Câu 23. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho hàm số y  f  x xác định và liên tục trên  có f  x
f  x  0 x    , f   3 1  e . Biết  2x 1, x
   . Tìm tất cả giá trị của tham số m để f  x
phương trình f  x  m có hai nghiệm thực phân biệt. 3 3 3 3 A. 4
m  e . B. 4
0  m  e . C. 4
1  m  e . D. 4 m  e . Lời giải Chọn D
Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 f  x f  x Ta có  x  x    
dx   x   dx  f  x 2 2 1, 2 1 ln
 x  x  C   f  x f  x f   3 3
1  e  ln e  2  C  C  1 . Do đó f  x 2 x x 1 e    .
Phương trình f  x 2 x  x 1  2  m  e
 m  x  x 1 ln m  0 (m  0) . 3 3
Để phương trình có hai nghiệm phân biệt    1 4 1 ln m 4  0  ln m   m  e . 4
Câu 24. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hàm số y  f (x) có đồ thị như hình vẽ bên. b c d d Đặt I  f (x) ; dx I  f (x) ; dx I  f (x) ; dx I  f (x) . dx 1 2 3 4     a a a c
Phát biểu nào dưới đây đúng?
A. I  I  I  I
B. I  I  I  I 1 2 3 4 2 1 4 3
C. I  I  I  I
D. I  I  I  I 2 1 3 4 1 2 4 3 Lời giải. Chọn B
Gọi S ; S ; S là diện tích các phần được tô màu như hình vẻ trên. Ta có: 1 2 3 b I 
f (x)dx  S 1 1  . a c I 
f (x)dx  S  S 2 1 2  . a d I 
f (x)dx  S  S  S 3 1 3 2  . a d I 
f (x)dx  S 4 3  . c
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 b c d d Vậy: I 
f (x)dx; I 
f (x)dx; I 
f (x)dx; I  f (x) . dx 1 2 3 4     a a a c
Câu 25. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho f  x và g  x là hai hàm số có đạo hàm liên 1
tục trên  và thỏa mãn f 0  1, f  
1  2 ; g 0  2  , g   1  4 và
f  x g  x dx  7  . Tính 0 1 I 
f  x g x dx  . 0 A. I  3  . B. I  17 . C. I  3 . D. I  1  7 . Lời giải Chọn C 1 1 1 Ta có
f  x g  x dx  f  x g x dx   f  x g  x +f  x g x dx      0 0 0 1 1
f  x g  x     dx   
 f  x g  x  f   1 g  
1  f 0 g 0  2.4 1. 2    10 . Suy ra 0 0 1 I 
f  x g x dx  10  7  3  . 0 2 x  m
Câu 26. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hàm số y 
( với m là tham số khác x 1
0 ) có đồ thị là C  . Gọi là diện tích hình phẳng giới hạn bởi đồ thi và hai trục tọa độ. Có bao
nhiêu giá trị thực của m thỏa mãn S 1? A. 4 . B. 2 . C. 1. D. 0 . Lời giải Chọn B
Ta có C   Ox  A 2
m ; 0 , C   Oy  B  2 0; m  .
Khi đó diện tích hình phẳng giới hạn bởi đồ thi và hai trục tọa độ là: 2 2 2 m 2 m 2 m 2 x  m x  m  m 1  S  dx   dx  1 dx      x 1 x 1 x 1 0 0 0       1 ln 1   2 2 m m x x |   2 m   2 2
1 ln m 1  m . 0
Để S  1 thì  2 m   2 2
1 ln m  1  m  1   2 m   2 ln
1  1  m 1  e  m   e 1 .
Câu 27. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hàm số f x xác định và liên tục trên 2 e  1
0;  thỏa mãn f x   xf
 xdx , x  0;. Tính tích phân f  xdx. x 1 1 5  2e A. . B. 3  2e. C. 2  2 . e D. 1  2e. 3 Lời giải Chọn B  1    2 f x C  x Đặt C  xf
 xdx   2 1 1      1 f  x  
x  C dx       * x x   1 2 x 2  C 
 C  x C.
 C  2  2C  1  
    C  2 2 1  2 
Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 e e    1      f  x 1 e f x 2 dx     2 dx
  lnx  2x    
lne 2eln1  2  3  2 . e x x  1 1 1 2 3x 1  ln b 
Câu 28. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho biết dx  ln a   với 2  
3x  x ln x  c  1
a, b, c là các số nguyên dương và c  4 , tổng a  b  c bằng A. 5. B. 6 . C. 7 . D. 9. Lời giải Chọn C 1 2 2 2 3  2 3x 1 1 d x x  dx 
d 3x  ln x  ln 3x  ln x  2    
3x  x ln x 3x  ln x 3x  ln x 1 1 1 1  ln 3 
 ln 6  ln 2  ln 3  ln 2    .  2 
 a  2, b  3, c  2  a  b  c  7 .
Câu 29. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hàm số 4 2
y  x  4x  m . Tìm m để đồ thị
hàm số cắt trục Ox tại bốn điểm phân biệt sao cho hình phẳng giới hạn bởi đồ thị hàm số và Ox
có phần phía trên trục hoành là S , phần dưới trục hoành x là S và S thỏa S  S  S . Khi đó 1 2 3 1 2 3 a a m 
( a, b là các số nguyên, b  0 ,
tối giản). Giá trị của biểu thức S  a  b là b b y S3 O x S S 1 2 A. 2. B. 7. C. 9. D. 11. Lời giải Chọn D
Gọi m, n, p, q (m  n  0  p  q) là hoành độ các giao điểm của đồ thị với Ox
Do đồ thị hàm số nhận Oy làm trục đối xứng nên 1 p q
S  S  S 
S  S   4 2
x  4x  mdx     4 2
x  4x  m dx 1 2 3 3 2  2 0 p q 5 3 4 2   q 4q q 4q 4 2
x  4x  mdx  0    mq  0    m  0 (1) 5 3 5 3 0 Mặt khác 4 2
q  4q  m  0 (2) 20
Từ (1) và (2) ta có m 
. Vậy a  20, b  9  a  b  11 9  2 1
x  x  x e
Câu 30. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho
dx  a.e  b ln e  c  với x x  e 0
a, b, c   . Tính P  a  2b  c A. P  2  .
B. P  0 . C. P  1  . D. P  1. Lời giải Chọn A Ta có
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489  2
x  x x e  2 1 1
x  x  x 1 e x. x e  x   1 x e . dx  dx  dx   x  1  x  e x. x e  1 0 0 x  0 x e Đặt x   1    x x      1 x u xe du e xe dx x e dx Khi đó  2 1
x  x  x e 1  e 1 e u  1   1  dx  du  1  du    
u  ln u  e 1  1
 e  ln e     1  x x  e u  u  0 1 1
Suy ra a  1, b  1, c  1  P  a  2b  c  1  2  1  2 1 x
Câu 31. (THPT Đồng Quan - Hà Nội - 2021) Cho
dx  a  b ln 3  c ln 4 
với a, b, c là các số  x  32 0
hữu tỉ. Giá trị của a  b  c bằng 1 1 4 1 A.  . B.  . C. . D. . 2 4 5 5 Lời giải Chọn B 1 1 x  x  3  3 Ta có dx  dx    x  32  x  32 0 0 1  1 3   3  1 1     dx   ln x  3     ln 3  ln 4    x  3  x  32   x  3  0 4 0   1
 a   ;b  1  ; c  1 . 4 1
Vậy a  b  c   . 4
Câu 32. (THPT Đồng Quan - Hà Nội - 2021) Cho hàm số f  x có đạo hàm liên tục trên  và thỏa mãn 3 1 .
x f '2x  4 dx  8; f 2  2  . Tính I 
f 2x dx  . 0 2
A. I  5 .
B. I  10 .
C. I  5 .
D. I  10 . Lời giải Chọn D 3 Xét .
x f '2x  4 dx  8 *  0 du  dx u   x   Đặt    dv  f   x   1 ' 2 4 dx v  f   2x  4  2 3 3 1 1
*  xf 2x  4 
f 2x  4 dx  8  2 2 0 0 3 3 1  f 2 
f 2x  4 dx  8  2 2 0 3 
f 2x  4 dx  10  . 0
Đặt 2t  2x  4  dt  dx x 0 3
Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 t 2 1 1 Suy ra:
f 2t  dt  10   . 2 
Câu 33. (THPT Đồng Quan - Hà Nội - 2021) Cho hàm số f  x liên tục và dương trên 0;  , thỏa 1 2 f  x mãn xf  x 2
 x f  x 2 3
 2 f  x, x   0 và f   1 
. Giá trị của tích phân dx  2 2 x 1 5 1 5 1 5 1 5 A. ln . B. ln . C. .ln . D. .ln . 2 4 2 2 2 3 2 Lời giải Chọn C
Ta có xf  x 2
 x f  x 2 3
 2 f  x, x   0 2  x f  x 3
 x f  x 2 3
 2xf  x 2  3x f  x 3
 x f  x 3 3  x  x 2   2x     2x   x  C . 2 f  x
 f x  f  x   3 1 x f  x x
Thay x  0 ta được
 1 C  2  1 C  C  1  f  x    . f   2 2 2 1 x 1 x x 1 2 f  x 2 x 1 Khi đó dx  dx 
t  x 1  dx  2xdx  xdx  dt . 2  . Đặt 2 2 x x 1 2 1 1 2
x  1  t  2 f  x 5 5 1 1 1 1 5 Đổi cận   dx  dt  ln t  .ln  . 2    2
x  2  t  5 x 2 t 2 2 2  1 2 1
Câu 34. (THPT Lê Lợi - Thanh Hóa - 2021) Biết rằng tích phân 2   3 ex x
d x  ae+b 
; a,b . 0
Tính giá trị biểu thức P  2a  b . A. 5 . B. 2 . C. 3 . D. 7 . Lời giải Chọn D u   2x 3  d  u  2dx  Đặt    d  v   exdx  v    ex  1 1   1 2   3 ex x dx   2   3 ex  2ex x dx  2   1 1 3 ex 2ex x  3e 1 0 0 0 0 0 a  3   
 P  2a  b  7 . b  1 
Câu 35. (THPT Lê Lợi - Thanh Hóa - 2021) Ông An có một mảnh đất nhỏ hình vuông cạnh bằng 4 m ở
trước sân. Ông muốn trồng hoa và cỏ để trang trí mảnh vườn của mình như sau: Ông sẽ trồng hoa
trên phần diện tích có dạng Parabol  P nhận trục đối xứng KI của hình vuông làm trục đối
xứng của  P và đỉnh của  P là trung điểm của KI như hình vẽ, phần cỏ sẽ trồng ở phần còn
lại của hình vuông. Biết rằng loại hoa ông muốn trồng có giá 200 000 đồng/ 2 1m , cỏ có giá 50 000 đồng/ 2
1m . Hỏi số tiền ông An bỏ ra để làm mảnh vườn là bao nhiêu (số tiền được làm
tròn đến hàng đơn vị)?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 A. 1365685, 4 đ. B. 2634314, 6 đ. C. 138642, 5 đ. D. Đáp án khác. Lời giải Chọn A
Xét hệ trục tọa độ Oxy như hình vẽ.
Phương trình của  P là 2
y  x ; phương trình của AB là y  2 2 3  x  2 8 2
 Diện tích phần trồng hoa là: S    2 2  x dx  2x   . 1    3 3  2    2 8 2 48  8 2
Diện tích phần trồng cỏ là: 2 S  S  S  4   . 2 ABCD 1 3 3
Vậy số tiền ông An bỏ ra để làm mảnh vườn là: 200 000.S  50 000.S  1365685, 4 đồng. 1 2
Câu 36. (Sở Vĩnh Phúc - 2021) Cho hàm số y  f  x có đạo hàm liên tục trên  và thỏa mãn     2
f  x  f  x  sin .
x cos x, x    
 . Biết f 0  0, tính I  xf  xdx  .  2  0 1 1   A. I   . B. I  . C. I  . D. I   . 4 4 4 4 Lời giải Chọn A         
Do f  x  f  x  sin .
x cos x  f  f     0  0  f  0    2   2   2 
Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021    2 2 2          Ta có I  f
 x dx   f  x d  x  f          xdx  .  2   2   2  0 0 0   2 2   1 1   1
Do f  x  f  x  sin .
x cos x  2 f  x 2 dx  sin 2 d
x x   cos 2x      0  2  2 4 2 0 0  2 1 Khi đó
f  x dx   . 4 0    2 2  2     1 1
Vậy I  xf  x dx  d x 
  f x  .x f x 2  f  xdx  f       . 0 2  2  4 4 0 0 0  x
Câu 37. (Sở Vĩnh Phúc - 2021) Biết diện tích của hình phẳng giới hạn bởi các đường y  3 x , y  , x  0 3 m n là S  
. Tính tổng m  n . 3ln 3 6
A. m  n  4 .
B. m  n  2 .
C. m  n  1.
D. m  n  3 . Lời giải Chọn D  x
Xét phương trình hoành độ giao điểm của hai hàm số y  3 x , y  3  x x  x 1  3   3.3
 x  3 x  x 3
Nhận thấy x  1là 1 nghiệm Với 1 x 0 1  1  1  0  3  3  3 x x x
 1  VT  1  VP Với 1 x 0 1  1  1  0  3  3  3 x x x
 1  VP  1  VT
 x  1là nghiệm duy nhất. 1  x 1           x    S 3 x  3 1 3 1 1 1 1 1 2 1 2 1  dx    x               0       3  ln 3 6 ln 3 6     ln 3  3ln 3 ln 3 6 3ln 3 6 0
 m  2; n  1
 m  n  3 m
Câu 38. (Sở Lào Cai - 2021) Có bao nhiêu giá trị thực của tham số m thỏa mãn: 2
3x  2x dx  m 10  ? 0 A. 1 . B. 2 . C. 4 . D. 3 . Lời giải Chọn A m Đặt 2 I 
3x  2x dx  m 10  ; f  x 2
 3x  2x . Dấu của f  x : 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489
Xét các trường hợp sau: m m
+) Nếu m  0 : I   2
3x  2xdx   3 2 x  x  3 2
 m  m  m 10 . 0 0 3 2
 m  m  m 10  0  m  2  ( thỏa mãn). m 2 m +) Nếu 0  m  : I   2
3x  2x dx   3 2 x  x  3 2
 m  m  m 10 . 3 0 0 3 2
 m  m  m 10  0  m  2, 36. ( loại). 2 m m 2 3 4 +) Nếu m  : I   2
3x  2xdx  2
3x  2xdx    3 2 x  x  2 3 27 0 2 3 3 3 2 8 3 2 278  m  m 
 m 10  m  m  m   0  m  2  , 02. ( loại). 27 27
Vậy có 1 giá trị thực của tham số m thỏa mãn bài toán.
Câu 39. (Sở Hà Tĩnh - 2021) Cho hàm số y  f  x liên tục trên  và thỏa mãn  2
2021 f  x  f x  xsin x, x
   . Giá trị của tích phân I 
f  x dx  bằng   2 1 2 1 3 A. . B. . C. . D. . 1010 2019 2020 2022 Lời giải Chọn A
Vì y  f  x liên tục trên  và 2021 f  x  f x  x sin x, x      1 nên ta cũng có
2021 f x  f  x  xsin x, x    2 
 2021 f  x  f x  x sin x 1 Từ  
1 , 2 ta có hệ phương trình 
 f  x  x sin x  f 
 x  2021f x  xsin x 2020      2  2 1 1   1  1 2 2 I  x sin xdx  x cos x  cos xdx  sin x    . 2020 2020     2020   1010  2  2     2  2  2 x  5
Câu 40. (Sở Yên Bái - 2021) Biết
dx  a ln 5  b ln 3 
với a, b   . Tính P  . a b . 2 x  4x  3 0 A. P  3  . B. P  6 . C. P  6 . D. P  3 . Lời giải Chọn A 2 2 x  5
2  x  3   x   2 2 1 2 1 2 2 Ta có dx  dx  2 dx 
dx  2 ln x 1  ln x  3  2        x  4x  3  x   1  x  3 0 0 x 1 x  3 0 0 0 0
 2ln 3  ln 5  ln 3   ln 5  3ln 3 Khi đó a  1
 ;b  3  P  . a b  3  .
Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Câu 41. (Sở Yên Bái - 2021) Biết a, b, c là các số nguyên dương thỏa mãn 2 dx 
a  b  c 
. Tính giá trị biểu thức P  a  b  c .
(x 1) x  x x 1 1 A. P  18. B. P  46. C. P  24. D. P  12. Lời giải Chọn B 2 2 2 1 dx x  x 1 dx   dx   
(x 1) x  x x 1
x(x 1)  x 1  x 
x(x 1)  x  x 12 1 1 1  1 1  x 1  x Đặt t  x 1  x  dt   dx  2dt  dx    2 x 1 2 x  x(x 1) 2  3 2  3 2  2   Khi đó I  dt 
 2 3  4 2  2  32  12  2  2   t  t  1 2 1 2
Do đó a  32, b  12, c  2  P  a  b  c  32  12  2  46.
Câu 42. (Sở Yên Bái - 2021) Cho hàm số f  x liên tục và là hàm số chẵn trên  thỏa mãn  3 2 I 
f  xdx  6. 
Tính tích phân J  cos .
x f 3sin x dx  . 0   2 A. J  4  . B. J  4. C. J  0. D. J  6. Lời giải Chọn B  2 J  cos .
x f 3sin x dx 
. Đặt t  3sin x  dt  3cos d x x .   2 Đổi cận:   + x   t  3 2  + x   t  3 . 2 3 f t  3 2 2 J  dt 
f (t)dt  .6  4   . 3 3 3 3 0 ln 6 dx
Câu 43. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Biết  3lna lnb 
với a , b là các
ex  2ex  3 ln 3
số nguyên dương. Tính P  ab . A. 20 . B. 10  . C. 15 . D. 10 . Lời giải Chọn D ln 6 ln 6 x ln 6 x ln 6 dx e dx e dx   x 1 1 Có    e   d  x    
ex  2ex  3  x x x x ex 2 x e  2 e 1    e  2 e 1 ln 3 ln 3 2 3e ln 3    ln3       ln 6 ln 6  ex ex  ex  2 8    d  x  ln  ln
 3ln 2  ln 5  a  2,b  5   ex  2 ex 1  ex 1 5 ln 3         ln 3
Vậy P  ab  10
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 44. (THPT Thanh Chương 1- Nghệ An - 2021) Biết rằng , với ;
; là các số hữu tỷ. Giá trị của bằng: A. . B. . C. . D. . Lời giải Chọn A Xét Đặt Với . Do đó ; ; . Khi đó .
Câu 45. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hàm số f  x liên tục trên 0;   và thỏa mãn f x ln x 17 2   f  x   1   . Biết
f  xdx  a ln 4  b 
với a,b   . Giá trị của a  2b bằng 4x x x 1 A. 16 . B. 12 . C. 8 . D. 20 . Lời giải Chọn D f x ln x f x 2   2  
Ta có: f  x   1  
 2xf  x   1   2 ln x 4x x x 2 x 4 4 f x 17 2 2   4 4  2xf  x   1 dx  dx  2 ln xdx   
f udu  f vdv  2 x ln x  x   2 x 1 1 1 1 2 1 17 
f  xdx  8ln 4  6  . 1
Vậy a  2b  8  2.6  20 .
Câu 46. (THPT Lương Thế Vinh - 2021) Cho hàm số y  f  x với 1
  x  4 có đồ thị các đoạn thẳng như hình bên. 4 Tích phân I 
f  x dx  bằng 1 A. 4 . B. 1. C. 5,5 . D. 2,5. Lời giải Chọn D
Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 4 1 2 4 Ta có: I 
f  x dx 
f  x dx  f  x dx  f  x dx     . 1 1 1 2 1 1 Trong đó:
f  x dx  S  .   ABCD 1 2.2 3  . 2 1  2 1 4 1 3
f  x dx  S  .1.2  1
f x dx  S   1 2 .1   BCE  ;   EFGH    . 2 2 2 1 2 4 1 2 4 3 5 Vậy I 
f  x dx 
f  x dx  f  x dx  f  x dx  3 1      . 2 2 1  1 1 2
Câu 47. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hàm số y  f (x) liên tục và có đồ thị trên [3; 5] như hình bên. 1377 2673 Biết các miền ,
A B, C có diện tích lần lượt là S  188, S  , S  . Khi đó A B 4 C 4 5
 f  x 1 dx     bằng 3  2417 2401 A. 520. B. . C. -504. D. . 2 2 Lời giải Chọn A 5 5 5 a b 5
 f  x 1 dx  
f  x dx  dx  f  x dx  f  x dx  f  x dx  8 S 
 S  S  8    A B C      3  3  3  3  a b 1377 2673  188    8  520 4 4 1
Câu 48. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hàm số f  x liên tục trên 0;   . Biết là một 2 x 1 2 f  x nguyên hàm của hàm số '
y  f  xln x và f 2  . Khi đó, dx  bằng ln 2 x 1 7 1 1 7 A.  . B. . C.  . D. . 4 2 2 4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn D u
  f  x  
du  f ' x dx Đặt  1   ta có dv  dx v  ln x    x 2 f  x 2 2 1 dx  ln . x f  x 2 ' 
f  x.ln xdx  ln 2. f 2  ln1. f   1    2 1 x x 1 1 1 1  1  7  ln 2.  1    ln 2  4  4 3
Câu 49. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho tích phân
xf (x)dx  2.  Tính tích phân 1 2 2 3
I  x f ( x 1)dx  ? 0 2 4 A. 3 . B. . C. 1. D. . 3 3 Lời giải Chọn D 2t  Đặt 3 2 3 2 2 t 
x 1  t  x 1  2tdt  3x dx  x dx  dt. 3
Đổi cận: x  0  t  1; x  2  t  3. 3 3 2t 2 4  Khi đó I 
f (t)dt 
t f (t)dt  .   3 3 3 1 1
Câu 50. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hàm số 3 2
y  x  ax  bx  c có đồ thị (C) . Biết
rằng tiếp tuyến d của (C) tại điểm có hoành độ 1
 cắt (C) tại điểm B có hoành độ bằng 2 (xem
hình vẽ). Diện tích hình phẳng giới hạn bởi d và (C) (phần gạch chéo trong hình) bằng 25 13 27 11 A. . B. . C. . D. . 4 2 4 2 Lời giải Chọn C  Giả sử 3 2
(C) : y  f (x)  x  ax  bx  c và d : y  g(x) .
Khi đó phương trình hoành độ giao điểm của d và (C) là: f (x)  g(x)  f (x)  g(x)  0
 Dễ thấy đa thức f (x)  g(x) là đa thức bậc ba có hệ số lũy thừa lớn nhất bằng 1 và có nghiệm 2 kép x  1
 và nghiệm đơn x  2 . Do đó f (x)  g(x)  (x 1) (x  2).
Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2 2 2 27
 Diện tích hình phẳng là 2 S 
f (x)  g(x) dx 
(g(x)  f (x))dx 
(x 1) (x  2)dx     . 4 1 1 1 
Câu 51. (THPT Chu Văn An - Thái Nguyên - 2021) Ông An có một mảnh vườn hình Elip có độ dài trục
lớn bằng 16m và độ dài trục bé bằng 10m . Ông muốn trồng hoa trên một dải đất rộng 8m và nhận
trục bé của elip làm trục đối xứng.Biết kinh phí để trồng hoa là 100.000 đồng/ 2 1m . Hỏi ông An
cần bao nhiêu tiền để trồng hoa trên dải đất đó? (Số tiền được làm trong đến hàng nghìn.) A. 7.826.000 đồng. B. 7.862.000 đồng. C. 7.128.000 đồng. D. 7.653.000 đồng. Lời giải Chọn D 2 2 x y
Giả sử elip có phương trình 
 1 với a  0, b  0 . 2 2 a b
Theo đề bài, ta có 2a  16  a  8 và 2b  10  b  5 .  5 2 y  
64  x  E1  2 2 x y  8
Vậy phương trình của elip:   1   . 64 25 5  2 y 
64  x  E2   8
Khi đó dải vườn được giới hạn bởi các đường  E , E , x  4; x  4
 và diện tích của dải vườn là 1   2  4 4 5 5 2 2 S  2 64  x dx  64  x dx   . 8 2 4 0   3 
Tính S bằng cách đổi biến x  8sin t ,ta được S  80     6 4      3 
Vậy số tiền T  80 
.100000  7652891,82. Vậy chọn D.  6 4   
Câu 52. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hàm số f (x) liên tục trên khoảng (0;).
Biết f (1)  1 và f  x  xf  x  ln ; x x
 0;  . Giá trị của f (e) bằng: 1 A. 1. B. 2. C. . e D. . e Lời giải Chọn B
f  x  xf  x  ln ; x x  0;  . 1 Chia 2 vế cho  ta có: 2 x f (
 x).x  f  x    ln x
 f  x   ln x
e  f  x  e ln x     dx   dx 2 2      x x 2 x x 2   x x 1   1 f e e ln x Suy ra  f   1   dx 
. Bấm máy tích phân và thay f  
1  1; ta tính được f e  2 . e 2 x 1 Vậy chọn B.
Câu 53. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hàm số f  x liên tục trên đoạn 1;  4 và thoả f 2 x   1 ln x
mãn f  x   . Tính x x 4 I 
f  x dx  ? 3 A. 2 S  2 ln 2. B. 2 S  ln 2. C. S  2 ln 2 D. 2 S  3  2 ln 2 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn A 4 3 4 Ta có
f  x dx  f  x dx  f  x dx    1 1 3 4 3 4 3  f (2   x 1) ln x  I 
f  x dx  f  x dx    dx  
f  x dx     x x  1 1 1   1 dx
Đặt 2 x 1  t  dt  . x Đổi cận
x  1  t  1
x  4  t  3 3 3 3 3 1 1 I 
f t  dt  ln x2  f  x dx  f  x dx  ln x2 4 4  f  x 2 dx  2 ln 2 1 1     . 2 2 1 1 1 1  2 cos x 4
Câu 54. (THPT Ba Đình - Thanh Hóa - 2021) Cho dx  a ln  b  , với 2
sin x  5sin x  6 c 0 *
a,b  , c   . Tính tổng S  a  b  c . A. S  1. B. S  0 . C. S  4 . D. S  3. Lời giải Chọn C  2 cos x Xét tích phân I  dx  . 2
sin x  5sin x  6 0
Đặt t  sin x  dt  cos . x dx . Đổi cận:  x 0 2 t 0 1 1 1 1 1  1 1  t  3 4 Ta có: I  dt   dt  ln  ln  . 2   t  5t  6  t  3 t  2  t  2 3 0 0 0
Vậy a  1, b  0, c  3  S  a  b  c  4 .
Câu 55. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hàm số y  f  x có đồ thị như hình vẽ và gọi A ;
B là hai hình phẳng được gạch trong hình bên dưới lần lượt có diện tích bằng 14 và 5 . 0 Giá trị của I  f 3x   1 dx  bằng: 1  19 A. 9 . B. . C. 27 . D. 3 . 3 Lời giải
Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chọn D 0 Xét I  f 3x   1 dx  1 1
Đặt 3x 1  t  dx  dt 3 Với x  1   t  2 
x  0  t  1 1 1 0 1 1 1 1   1  I 
f t  dt 
f  x dx  f   
 xdx  f  xdx    
S  S   3 . 3 3 3 3 A B 2  2   2  0 
Câu 56. (THPT Triệu Sơn - Thanh Hóa - 2021) Một khuôn viên dạng nửa hình tròn, trên đó người thiết
kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối
xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường
tròn (phần tô màu) và cách nhau một khoảng bằng 4m. Phần còn lại của khuôn viên (phần không
tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ, chi phí để trồng hoa và
cỏ Nhật Bản tương ứng là 150.000 đồng/ 2 m và 100.000 đồng/ 2
m . Hỏi số tiền cần để trồng hoa
và trồng cỏ Nhật Bản trong khuôn viên đó gần nhất với số nào sau đây?
A. 3.739.000 (đồng).
B. 1.948.000 (đồng). C. 3.926.000 (đồng). D. 4.115.000 (đồng). Lời giải Chọn A
Kết hợp vào hệ trục tọa độ, ta được:
Gọi parabol là  P 2
: y  ax . Do F 2; 4  P nên  P 2 : y  x .
Gọi đường tròn có tâm ở gốc tọa độ là C  2 2 2
: x  y  R . Do F 2; 4 C nên nửa đường tròn trên là 2
y  20  x . 2  5  8
Đặt S là diện tích phần tô đậm. Khi đó: S  2.  2 2 20  x  x dx  20 arcsin    . 1 0  1  5  3   1  5  8
Đặt S là diện tích phần không tô đậm. Khi đó: 2 S 
. .R  S  10  20 arcsin    . 2 2 1 2  5  3  
Vậy: Số tiền cần để trồng hoa và cỏ Nhật Bản là: T  150000.S 100000.S  3738574 (đồng). 1 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 57. (THPT Trần Phú - Đà Nẵng - 2021) Cho  H  là hình phẳng giới hạn bởi đồ thị hai hàm số 2
y  x 1; y  x 1 và hai đường thẳng x  1  ; x  1 .
Thể tích của khối tròn xoay được tạo thành khi quay  H  quanh trục Ox bằng 176 14 21 16 A. . B. . C. . D. . 15 3 5 15 Lời giải Chọn C
Gọi  H là hình phẳng giới hạn bởi 2
y  x 1, y  0; x  1
 , x  0 . Khi quay  H quanh trục 1  1  0 2 28
Ox thì khối tròn xoay được tạo thành có thể tích V     2 x 1 dx  . 1  15 1
Gọi  H là hình phẳng được giới hạn bởi y  x 1, y  0; x  0, x  1. Khi quay  H quanh 2  2  1 2 7
trục Ox thì khối tròn xoay được tạo thành có thể tích V   x 1 dx  2    . 3 0
Vậy thể tích của khối tròn xoay được tạo thành khi quay  H  quanh trục Ox là 21
V  V V  . 1 2 5
Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 3
NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG
MỨC ĐỘ VẬN DỤNG CAO Câu 1.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Giả sử hàm số f có đạo hàm đến
cấp hai trên  thỏa mãn f 2  2 và f   x 2 2
 x f  x  2x với mọi x  . Giá trị tích phân 2
xf  x dx  bằng: 0 1 4 A. 0 . B. . C. . D. 1. 3 3 Câu 2.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Sân trường có một bồn hoa hình tròn
tâm O . Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này định bồn hoa thành bốn
phần bởi 2 đường parabol có cùng đỉnh O và đối xứng với nhau qua tâm O (như hình vẽ).
Hai đường parabol cắt đường tròn tại 4 điểm ,
A B,C, D tạo thành một hình vuông có cạnh bằng
4m . Phần diện tích S , S dùng để trồng hoa, phần diện tích S , S dùng để trồng cỏ. Biết kinh 1 2 3 4
phí trồng hoa là 150.000 đồng/ 2
m , kinh phí trồng cỏ là 100.000 đồng/ 2
m . Hỏi nhà trường cần
bao nhiêu tiền để trồng bồn hoa đó? (số tiền làm tròn đến hàng chục nghìn) A. 3.270.000 đồng B. 5.790.000 đồng.
C. 3.000.000 đồng. D 6.060.000 đồng. Câu 3.
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hàm số f  x  liên tục, không âm trên đoạn       0; 2  
, thỏa mãn f 0  3 và f  x. f  x  cos x 1 f  x , x   0; . Tìm giá trị nhỏ 2       2    
nhất m và giá trị lớn nhất M của hàm số f  x trên đoạn ;  . 6 2    5 5 A. m  , M  3 . B. m  , M  3. 2 2 21
C. m  3, M  2 2 . D. m  , M  2 2 . 2 Câu 4.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hàm số f  x có đạo hàm cấp 2 liên tục trên đoạn 0;  1 thỏa mãn f   1  0; f '  1  1 và
f  x  xf  x 2 10 5 '
 x f '  x  0 với mọi x 0;  1 . 1 Khi đó tích phân
f  x dx  bằng 0 1 2 1 1 A.  . B.  . C.  . D.  . 15 5 10 17
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 5.
(Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hàm số f (x) có đạo hàm liên tục trên R và thỏa 2 mãn f (0)  3 và 2
f (x)  f (2  x)  x  2x  2 , x
  R . Tích phân .
x f '(x)dx  bằng 0 10  5  11 7  A. . B. . C. . D. . 3 3 3 3 Câu 6.
(Chuyên KHTN - 2021) Cho hàm số
f  x liên tục trên  và thỏa mãn     1   x xf x x f x e    
với mọi x . Tính f 0 . 1 A. 1. B. 1  . C. e . D. . e Câu 7.
(Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hàm số y  f (x) có đạo hàm liên tục trên đoạn [1;3] thỏa mãn f (1)  2 và 2
f (x)  (x 1) f (
 x)  2xf (x), x
 [1;3] . Giá trị của 3 f (x)dx  bằng 1 2 2 A. 1 ln 3. B.  ln 3. C.  ln 3 . D. 1 ln 3. 3 3 Câu 8.
(Chuyên Quốc Học Huế - 2021) Cho hàm số f (x) có đạo hàm liên tục trên R thỏa mãn: '( )  ( ) x f x
f x  e .cos 2021x và f (0)  0 Đồ thi hàm số y  f (x) cắt trục hoành tại bao nhiêu
điểm có hoành độ thuộc đoạn  1  ;  1 ? A. 3 B. 1 C. 1287 D. 4043 Câu 9.
(Chuyên Quang Trung - Bình Phước - 2021) Cho hàm số y  f  x có đạo hàm liên tục trên 1  ,    ex xf x 1, x   ,  f  
1  0 . Giá trị xf  x dx  bằng 0 1 1 1 1 A.  . B. . C.  . D. . 4 4 2 2
Câu 10. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hàm số y  f (x) liên tục và có đạo hàm trên  x  1   2; 2  \ 
0 , thỏa mãn f (1)  0 và f '(x)  x  f (x) e  2 
 0 . Giá trị của f bằng f (x)   e  2  A. ln 7 . B. ln 5 . C. ln 6 . D. ln 3 .
Câu 11. (Chuyên ĐHSP Hà Nội - 2021) Cho hàm số
f  x liên tục trên  thỏa mãn 1 3
f  x  f  x   3 2 3
sin 2x  3x  x,x   . Tích phân I  f  xd 
x thuộc khoảng nào? 0 A.  3  ; 2   . B.  2  ;  1 . C.  1  ;  1 . D. 1;2 .
Câu 12. (Chuyên ĐH Vinh - Nghệ An - 2021) Giả sử f (x) là hàm có đạo hàm liên tục trên 0;  và   1 f (
 x)sin x  x  f (x)cosx, x
 0;  . Biết f ( )  1, f ( ) 
(a  b ln 2  c 3) , với a, b, c là 2 6 12
các số nguyên. Giá trị của a  b  c bằng A. 1  . B. 1. C. 11. D. 11.
Câu 13. (THPT Quế Võ 1 - Bắc Ninh - 2021) Thành phố định xây cây cầu bắc ngang con sông dài
500 m , biết rằng người ta định xây cầu có 10 nhịp cầu hình dạng parabol,mỗi nhịp cách nhau
40 m , biết 2 bên đầu cầu và giữa mối nhịp nối người ta xây 1 chân trụ rộng 5 m . Bề dày và bề
rộng của nhịp cầu không đồi là 20 cm (mặt cắt của một nhịp cầu được mô phỏng như hình vẽ).
Hỏi lượng bê tông để xây các nhịp cầu là bao nhiêu (làm tròn đến hàng đơn vị).
Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A. 3 50m . B. 3 20m . C. 3 100m . D. 3 40m .
Câu 14. (THPT Quốc Oai - Hà Nội - 2021) Cho hàm số y  f  x có đồ thị y  f ' x như hình vẽ.Giá
lớn nhất của hàm số g  x  f 3x  3x trên đoạn  1  ;  1 bằng A. f  3    3 . B. f   1 1. C. f   1  3.
D. f 3  3 .
Câu 15. (THPT Quốc Oai - Hà Nội - 2021) Cho hàm số y  f x có đạo hàm liên tục trên  . Hàm số
y  f x có đồ thị như hình vẽ bên dưới.
Số nghiệm thuộc đoạn 2;6 của phương trình f x  f   0 là A. 2 . B. 3. C. 4. D. 5.
Câu 16. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hàm số f (x) liên tục và có đạo hàm xác định trên 0; . Biết rằng
f (x)  0 với mọi x  0;  thỏa mãn
f (x) ln f (x)  
1  x  f '(x)  2 f (x)  0 và ln( f (2))  ln( f (1))  1. Giá trị của tích phân 2 xf (x)dx 
nằm trong khoảng nào dưới đây: 1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 A. 0;6 . B. 6;12 . C. 12;18 . D. 18;24 .
Câu 17. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hàm số y  f  x có đạo hàm liên tục trên    
thỏa mãn f  x  f  x  sin . x cos x  
với mọi x   và f 0  0. Giá trị của tích phân  2   2 .
x f   x dx  bằng 0 1  1  A. . B. . C.  . D.  . 4 4 4 4
Câu 18. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hàm số f  x liên tục trên  và thỏa mãn 1
f  x  f   x  x   x2 2 1 1
; x  . Tính I 
f  x d . x  0 1 1 1 1 A. . B. . C. . D. . 30 60 45 15
Câu 19. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình vẽ bên
Đặt M  max f  x ; m  min f  x . Tính giá trị S  M  m ?  2  ;6  2   ;6
A. S  f 0  f 2 .
B. S  f 5  f 6 .
C. S  f 5  f 2 .
D. S  f 0  f  2   .
Câu 20. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hàm số y  f  x có đạo hàm liên tục trên 1;  3 , biết f   1  1 và
f  x. f  x  x  4   x  2 f  x  f  x với x  1;  3 . Biết 3 a a
f  x dx    2 c 
(với a, b, c là các số nguyên dương,
là phân số tối giản). Khi đó, tổng b b 1
a  b  c bằng A. 10 . B. 19 . C. 17 . D. 53 .
Câu 21. (THPT Lê Lợi - Thanh Hóa - 2021) Biết rằng y  f  x là hàm số liên tục và khác x với mọi
2 xf  x  f  x 1 a
x 0; và thỏa mãn f  
1  2; f 2  6. Có tích phân dx  ln ;  trong đó 2 f  x 2  x 2 b 1 a
a,b là các số nguyên dương sao cho phân số
tối giản. Giá trị của biểu thức 2 3 a  b bằng b A. 5. B. 10. C. 17. D. 34.
Câu 22. (Sở Lào Cai - 2021) Hàm số bậc ba y  f  x có đồ thị C đi qua điểm A1;0 ; hàm số bậc 1 
hai y  g  x có đồ thị C đi qua điểm B 1;4. C , C cắt nhau tại 3 điểm phân biệt có 1   2  2 
hoành độ lần lượt là 1;2;3. Tính diện tích hình phẳng giới hạn bởi hai đồ thị C , C ? 1   2 
Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 115 32 71 112 A. . B. . C. . D. . 3 3 6 3    4 cos 2x   
Câu 23. (Sở Tuyên Quang - 2021) Cho hàm số f  x có f  2   
và f  x  , x   0; . 2    4  sin 2x  2   3 Khi đó
f  xdx  bằng  6    A.  ln 2 . B. ln 3 . C. . D.  ln 3 . 3 6 2 3
Câu 24. (Sở Yên Bái - 2021) Cho hàm số f  x có đạo hàm liên tục trên 0 
;1 và thỏa mãn f   1  , 5 1 4 1 37 1
 f  x 2  dx   3  
và x f  x dx   . Tích phân
f  x dx  bằng 9 180 0 0 0 14 1 14 1 A.  . B. . C. . D.  . 15 15 15 15
Câu 25. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số f  x có đạo hàm liên tục trên đoạn 1  2 0;  1 thỏa mãn f  
1  1,  f  x dx  9    0 1 1 1 và 3
x f  x dx  
. Tích phân xf  x dx  bằng 2 0 0 6 2 8 5 A. . B. . C. . D. . 5 3 7 2
Câu 26. (THPT Thanh Chương 1- Nghệ An - 2021) Hướng tới kỉ niệm 60 năm thành lập trường THPT
Thanh Chương 1. Khối 12K57 thiết kế bồn hoa gồm hai Elip bằng nhau có độ dài trục lớn bằng
8m và độ dài trục nhỏ bằng 4m đặt chồng lên nhau sao cho trục lớn của Elip này trùng với trục
nhỏ của Elip kia và ngược lại (như hình vẽ).
Phần diện tích nằm trong đường tròn đi qua 4 giao điểm của hai Elip dùng để trồng cỏ, phần diện
tích bốn cánh hoa nằm giữa hình tròn và Elip dùng để trồng hoa. Biết kinh phí để trồng hoa là 300.000 đồng
, kinh phí để trồng cỏ là 200.000 đồng
. Tổng số tiền dùng để trồng hoa và
trồng cỏ cho bồn hoa gần với số nào nhất trong các số sau: A. 6.200.000 đồng. B. 8.200.000 đồng. C. 8.600.000 đồng. D. 9.100.000 đồng.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 27. (THPT Lương Thế Vinh - 2021) Cho a, ,
b c là các số thực và   3 2
f x  x  ax  bx  c thỏa mãn t 5
f t   f t  5  2 với t là hằng số. Giá trị
f  x dx  bằng t 105 134 1 19 A.  . B. . C.  . D. . 2 3 2 4
Câu 28. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hàm số f  x đồng biến, biết
f  x  0, x
 1; 4 và có đạo hàm liên tục trên đoạn 1;4 , thỏa mãn f   1  1 và 4 2 f  x
2 f  x  xf  x   
với mọi x 1; 4. Khi đó f  xdx  bằng x 1 A. 1. B. 2 ln 2 . C. 2 ln 2  2 . D. 2  .
Câu 29. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hàm số y  f  x có đạo hàm liên tục trên
khoảng 0;  thỏa mãn 3
xf  x  f  x 3  x ln x, x   0 và f   1  . Tính f 2 4 A. 2 ln 2 1. B. 4 ln 2 1. C. 2 ln 2 D. 4ln 2
Câu 30. (THPT Ba Đình - Thanh Hóa - 2021) Cho hàm số f  x nhận giá trị dương, có đạo hàm liên tục trên 0; 
2 . Biết f 0  1 và     2 2 4 2 x x f x f x e   
với mọi x 0; 2 . Tính tích phân  3 2 2
x  3x  f  x I  dx  . 0 f  x 32 16 16 14 A. I   . B. I   . C. I   . D. I   . 5 3 5 3
Câu 31. (Trung Tâm Thanh Tường - 2021) Cho f  x, g  x lần lượt là các hàm đa thức bậc ba và bậc
nhất có đồ thị như hình vẽ. 2 250
Biết diện tích hình S (được tô màu) bằng . Tính
f  x  dx  . 81 0 7 38 8 34 A. . B. . C. . D. . 3 15 3 15 5
a ln 3  b ln 2 c
Câu 32. (THPT Trần Phú - Đà Nẵng - 2021) Giả sử 2
x ln  x   1 dx    với * a, , b c  N . 3 9 3
Giá trị của biểu thức b  c  a bằng A. 2  . B. 24 . C. 4  . D. 4 .
ex  m khi x  0 1 
Câu 33. Cho hàm số f  x  
liên tục trên  . Tích phân I 
f  xdx  bằng 2
2x 3  x khi x  0  1 22 22 22
A. I  e  2 3  22 .
B. I  e  2 3 
. C. I  e  2 3  .
D. I  e  2 3  . 3 3 3
Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 34. Cho hàm số bậc ba y  f  x có đồ thị C là đường cong trong hình bên. Biết hàm số f  x đạt  x  x 
cực trị tại hai điểm x , x thỏa mãn x  x  2 và 1 2 f    3
 . Gọi d là đường thẳng đi qua 1 2 2 1 2  
hai điểm cực trị của đồ thị C . Diện tích hình phẳng giới hạn bởi C và d ( phần được tô đậm trong hình) bằng y x2 x O x1 1 1 A. 1. B. 2 . C. . D. . 4 2 2
x  4x 1 , x  5 ln 2
Câu 35. Cho hàm số f  x  x x  . Tích phân f 3e    1 .e dx bằng 2x  6 , x  5  0 77 77 68 77 A. . B. . C. . D. . 3 9 3 6
Câu 36. Cho hàm số bậc ba   3 2
f x  ax  bx  cx  d và đường thẳng d : g  x  mx  n có đồ thị như hình S
vẽ. Gọi S , S , S lần lượt là diện tích của các phần giới hạn như hình bên. Nếu S  4 thì tỷ số 2 1 2 3 1 S3 bằng. 3 1 A. . B. 1. C. 2 . D. . 2 2
x  m , x  0
Câu 37. Cho hàm số f  x liên tục trên  thỏa mãn f  x  
(m là hằng số). Biết 2 x e , x  0  2 b
f  xdx  a  
trong đó a, b là các số hữu tỉ. Tính a  b . 2 e 1 A. 4 . B. 3 . C. 0 . D. 1.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 38. Cho hàm số 4 2
y  x  3x  m có đồ thị C
, với m là tham số thực. Giả sử C cắt trục Ox m  m 
tại bốn điểm phân biệt như hình vẽ
Gọi S , S , S là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để 1 2 3
S  S  S là 1 3 2 5 5 5 5 A. . B.  . C. . D.  . 4 4 2 2 2
Câu 39. Cho hàm số y  f  x  1, y  g  x  x . Giá trị I  min 
 f x; g xdx 1  3 5 A. 1. B. . C. 2 . D. . 2 2
Câu 40. Cho parabol  P  2
: y  x  4 cắt trục hoành tại hai điểm A , B và đường thẳng d : y  a 1
0  a  4 . Xét parabol P đi qua A , B và có đỉnh thuộc đường thẳng y  a . Gọi S là diện 2  1
tích hình phẳng giới hạn bởi  P và d . S là diện tích hình phẳng giới hạn bởi  P và trục 2  1  2
hoành. Biết S  S (tham khảo hình vẽ bên). 1 2 y M N
y = a A B O x Tính 3 2
T  a  8a  48a . A. T  99 . B. T  64 . C. T  32 . D. T  72 .  2 x  m   x  0 2
Câu 41. Cho hàm số y  f  x  
liên tục trên  . Giá trị I 
f 2 cos x 1 sin d x x  2 cos x  3   x  0  0 2  1 1  A. . B. 0 . C. . D. . 3 3 3
Câu 42. Cho hàm số bậc bốn y  f  x có đồ thị C  như hình vẽ bên. Biết hàm số y  f  x đạt cực trị 2
tại các điểm x , x , x thỏa mãn x  x  2 , f  x  f x  f x
 0 và C  nhận đường 1   3   2  1 2 3 3 1 3
Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
thẳng d : x  x làm trục đối xứng. Gọi S , S , S , S là diện tích của các miền hình phẳng được 2 1 2 3 4 S  S
đánh dấu như hình bên. Tỉ số 1
2 gần kết quả nào nhất S  S 3 4 y d S3 S1 x1 x3 O x2 S2 x S4 A. 0, 60 . B. 0,55 . C. 0, 65 . D. 0, 70.  2x  4 khi x  4  2
Câu 43. Cho hàm số f  x  2 1 . Tích phân f
 2sin x  3sin 2 d x x bằng 3 2
x  x  x khi x  4   4 0 28 341 341 A. . B. 8 . C. . D. . 3 48 96
Câu 44. Cho hàm số bậc ba y  f  x có đồ thị là đường cong C trong hình bên. Hàm số f  x đạt cực
trị tại hai điểm x , x thỏa f  x  f x  0 . Gọi ,
A B là hai điểm cực trị của đồ thị 1   2  1 2
C; M , N, K là giao điểm của C với trục hoành; S là diện tích của hình phẳng được gạch
trong hình, S là diện tích tam giác NBK . Biết tứ giác MAKB nội tiếp đường tròn, khi đó tỉ số 2 S1 bằng S2 2 6 6 5 3 3 3 A. . B. . C. . D. . 3 2 6 4    x  2 khi x  0 3
Câu 45. Cho hàm số f  x   . Tích phân
f 3  4cos xsin d x x  bằng 2 3
 x  x  2 khi x  0  0 37 37 A. . B. . C. 6 . D. 12 . 24 6
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 46. Cho hàm số bậc bốn y  f  x có đồ thị C  như hình vẽ bên. Biết hàm số y  f  x đạt cực trị 2
tại các điểm x , x , x thỏa mãn x  x  2 , f  x  f x  f x
 0 và C  nhận đường 1   3   2  1 2 3 3 1 3
thẳng d : x  x làm trục đối xứng. Gọi S , S , S , S là diện tích của các miền hình phẳng được 2 1 2 3 4 S  S
đánh dấu như hình bên. Tỉ số 1
2 gần kết quả nào nhất S  S 3 4 y d S3 S1 x1 x3 O x2 S2 x S4 A. 0, 60 . B. 0,55 . C. 0, 65 . D. 0, 70. 2 
x  ax  b khi x  2
Câu 47. Cho hàm số f  x  
. Biết hàm số có đạo hàm tại điểm x  2. Tính 3 2
x  x  8x 10khi x  2  4 I 
f  xdx  0 A. 3 . B. 0 . C. 2  . D. 4 . ax  b
Câu 48. Cho hàm số y 
có đồ thị C  . Gọi giao điểm của hai đường tiệm cận là I . Điểm cx  d M S  0  0 x ; 0
y  di động trên C  , tiếp tuyến tại đó cắt hai tiệm cận lần lượt tại A, B và 2 IAB . S  S Tìm giá trị 2 IM sao cho 1 2
(với S , S là 2 hình phẳng minh họa bên dưới) 0  1 1 2 SIAB 41 169 189 A. 2 . B. . C. . D. . 20 60 60 2  4
x  2x 1 khi x  2 e 1  x
Câu 49. Cho hàm số f  x   . Tính I  . f ln   2 x 1  d . x 2 
x  5 khi x  2    x 1 0 A.  2  ;3 . B. 3; 2   . C. 2;  1  . D.  1  ; 2 .
Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 50. Cho hàm số bậc ba y  f  x có đồ thị là đường cong ở hình bên dưới. Gọi x , x lần lượt là hai 1 2
điểm cực trị thỏa mãn x  x  2 và f  x  3 f x  0. Đường thẳng song song với trục Ox và 1   2  2 1 S
qua điểm cực tiểu cắt đồ thị hàm số tại điểm thứ hai có hoành độ x và x  x 1. Tính tỉ số 1 0 1 0 S2
( S và S lần lượt là diện tích hai hình phẳng được gạch ở hình bên dưới). 1 2 27 5 3 3 A. . B. . C. . D. . 8 8 8 5
2x  2 khi x  0 
Câu 51. Cho hàm số f  x  
. Tích phân I  sin 2 .
x f cosx dx 2  bằng
x +4x  2 khi x  0  0 9 9 7 7 A. I  . B. I   . C. I   . D. I  . 2 2 6 6
Câu 52. Cho hàm số bậc bốn trùng phương y  f  x có đồ thị là đường cong trong hình bên. Biết hàm số
f  x đạt cực trị tại ba điểm x , x , x (x  x  x ) thỏa mãn x  x  4 . Gọi S và S là diện 1 2 3 1 2 3 1 3 1 2 S
tích của hai hình phẳng được gạch trong hình. Tỉ số 1 bằng S2 2 7 1 7 A. . B. . C. . D. . 5 16 2 15 BẢNG ĐÁP ÁN 1.C 2.A 3.D 4.D 5.A 6.B 7.C 8.C 9.A 10.A 11.C 12.A 13.D 14.A 15.A 16.D 17.C 18.B 19.C 20.B 21.C 22.C 23.B 24.C 25.C 26.C 27.A 28.B 29.D 30.C 31.D 32.B 33.D 34.D 35.B 36.B 37.A 38.A 39.C 40.B 41.A 42.A 43.D 44.D 45.A 46.A 47.D 48.B 49.A 50.A 51.A 52.B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 3
NGUYÊN HÀM - TÍCH PHÂN & ỨNG DỤNG
MỨC ĐỘ VẬN DỤNG CAO Câu 1.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Giả sử hàm số f có đạo hàm đến
cấp hai trên  thỏa mãn f 2  2 và f   x 2 2
 x f  x  2x với mọi x  . Giá trị tích phân 2
xf  x dx  bằng: 0 1 4 A. 0 . B. . C. . D. 1. 3 3 Lời giải Chọn C
Ta có: f   x 2 2
 x f  x  2x  f 2  0 2 2 2 2 Lại có: f 2  x 2
dx  x f  x 2 dx  2 d x x  x  4    0 0 0 0 2 Xét I 
f 2  x dx 1    0
Đặt 2  x  t  dx  d  t
Với x  0  t  2
x  2  t  0 0 2 2
 I   f t dt  f t dt  f x dx 1          2 0 0 
u  f  x 
du  f  x dx Đặt    dv  dx  v  x  2 2 2 2  I  xf x
 xf  x dx  f 2  xf  x dx   xf  x dx 1               0 0 0 0 2 Xét 2
I  x f  x dx 2    0 2  u  x du  2 d x x  Đặt    dv  f    xdx    v f   x  2 2 2 2  I   2 x f  x
 2xf  x dx  4 f  2  2 xf  x dx  8  2 xf  x dx 2              0 0 0 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 2 2 2 4
Vậy  xf  x dx  8  2 xf  x dx  4  
 xf  x dx   . 3 0 0 0 Câu 2.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Sân trường có một bồn hoa hình tròn
tâm O . Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này định bồn hoa thành bốn
phần bởi 2 đường parabol có cùng đỉnh O và đối xứng với nhau qua tâm O (như hình vẽ).
Hai đường parabol cắt đường tròn tại 4 điểm ,
A B,C, D tạo thành một hình vuông có cạnh bằng
4m . Phần diện tích S , S dùng để trồng hoa, phần diện tích S , S dùng để trồng cỏ. Biết kinh 1 2 3 4
phí trồng hoa là 150.000 đồng/ 2
m , kinh phí trồng cỏ là 100.000 đồng/ 2
m . Hỏi nhà trường cần
bao nhiêu tiền để trồng bồn hoa đó? (số tiền làm tròn đến hàng chục nghìn) A. 3.270.000 đồng B. 5.790.000 đồng.
C. 3.000.000 đồng. D 6.060.000 đồng. Lời giải Chọn A
 Ta có: vì ABCD là hình vuông cạnh 4 nên BD  BC 2  4 2;OB 2 2 và (
A 2; 2), B(2; 2)
 Phương trình đường tròn tâm O có bán kính OB  2 2 là 2 2 2
(C) : x  y  8  y  8  x 2 x
 Parabol đi qua hai điểm (
A 2; 2), B(2; 2) và đỉnh ngay gốc tọa độ nên suy ra (P) : y  2 2 x
Từ đồ thị ta có được S là diện tích giới hạn bởi hai đồ thị 2
y  8  x và (P) : y  cùng với 1 2
hai đường thẳng x  2; x  2 2 2 2  x  8 Từ đó suy ra 2 2 S  8  x  dx  8  x dx  x  t  dx  tdt 1     ; Đặt 2 2 sin 2 2 cos 2 3 2   2
Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021    4 4 4 8 8  1  cos 2t  8 4 Suy ra 2 2 S 
8  8sin t .2 2.cost.dt   8cos tdt   8 dt   2  1      3 3  2  3 3       4 4 4   4  8 2
S  S  2S  2 2   4  (m )  1 2 1     3  3
Mặt khác: S  S ; S  S nên suy ra 1 2 3 4   4  8
S  S  S  S  S         m C   2 8 2 2 4 ( ) 3 4 ( ) 1 2      3  3  8   8 
Vậy tổng số tiền để trồng bồn hoa là: 4  .150000  4  .100000  3274926     đồng.  3   3  Câu 3.
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hàm số f  x liên tục, không âm trên đoạn       0; 2  
, thỏa mãn f 0  3 và f  x. f  x  cos x 1 f  x , x   0; . Tìm giá trị nhỏ 2       2    
nhất m và giá trị lớn nhất M của hàm số f  x trên đoạn ;  . 6 2    5 5 A. m  , M  3 . B. m  , M  3. 2 2 21
C. m  3, M  2 2 . D. m  , M  2 2 . 2 Lời giải Chọn D
f x . f  x 2    
f  x. f  x  cos x 1 f  x   cos x 2 1 f  x
f  x. f  x  dx  cos d
x x  sin x  C 1 1     2 1 f  x Đặt 2 t   f  x 2 2 1
 t  1 f  x  tdt  f  x. f  x dx .
f  x. f  x d t t Suy ra 2 dx 
 dt  t  C  1 f x  C 2 2   2      2 1   t f x Từ   1 và 2 suy ra 2
1 f  x  sin x  C . Thay x  0 vào ta có: 1 3  C  C  2 Hay 2
1 f  x  sin x  2 .
 f  x  sin x  22 2 2
1  sin x  4 sin x  3  f  x 2
 sin x  4 sin x  3     1 
Đặt t  sin x . Với x  ;  t  ;1  . 6 2   2       1 
Ta đi xét hàm số g t  2
 t  4t  3, t  ;1  . 2    t  2  1   1  gt    0, t  
;1 do đó g t  đồng biến trên ;1 . 2       2  t 4t 3   2 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489  1  21
min g t   g   min f    x  m  1     ;1  2  2 ;  2   6 2     
max g t   g  
1  2 2  max f  x  M  1     ;1 ;  2   6 2      Câu 4.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hàm số f  x có đạo hàm cấp 2 liên tục trên đoạn 0;  1 thỏa mãn f   1  0; f '  1  1 và
f  x  xf  x 2 10 5 '
 x f '  x  0 với mọi x 0  ;1 . 1 Khi đó tích phân
f  x dx  bằng 0 1 2 1 1 A.  . B.  . C.  . D.  . 15 5 10 17 Lời giải Chọn D Ta có:
f  x  xf  x 2 10 5 '
 x f '  x  0 với mọi x 0;  1 . 1 1 1
 10 f  x dx  5xf ' x 2
dx  x f '  x dx  0    0 0 0 1 Đặt I 
f  x dx 
, theo phương pháp tích phân từng phần, ta được: 0 1 1  xf ' 
 xdx  xf  x 1|  f x dx  I 0      0 0  1 1  2 x f '  x 2
dx  x f ' x 1| 2 xf ' x dx  1 2 I  1 2I 0        0 0 1
 10I  5I  1 2I  0  I   17 1 1 Vậy
f  x dx    . 17 0 Câu 5.
(Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hàm số f (x) có đạo hàm liên tục trên R và thỏa 2 mãn f (0)  3 và 2
f (x)  f (2  x)  x  2x  2 , x
  R . Tích phân .
x f '(x)dx  bằng 0 10  5  1  1 7  A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn A 2  Ta có: I  .
x f '(x)dx 
, ta sử dụng phương pháp từng phần 0 2 2 u   x du  dx Đặt     I  .
x f '(x)dx  2 f (2)  f (x)dx  
dv  f '(x)dx
v  f (x)   0 0 2
f (x)  f (2  x)  x  2x  2 thế x  0 vào ta có: f (0)  f (2)  2  f (2)  1  (1)
 Từ đó ta tích phân 2 vế từ 0 đến 2
Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2 2 2 
f (x)dx 
f (2  x)dx   8 2
x  2x  2 dx     . 3 0 0 0 2 2
 Mặt khác ta lại có: f (x)dx 
f (2  x)dx   0 0 2 2 2 2 8 4 Nên suy ra
f (x)dx 
f (2  x)dx  2 f (x)dx  
f (x)dx      (2) 3 3 0 0 0 0 2 2 4 10 
 Từ (1) và (2) suy ra I  .
x f '(x)dx  2 f (2) 
f (x)dx  2      3 3 0 0 Câu 6.
(Chuyên KHTN - 2021) Cho hàm số
f  x liên tục trên  và thỏa mãn     1   x xf x x f x e    
với mọi x . Tính f 0 . 1 A. 1. B. 1  . C. e . D. . e Lời giải Chọn B Ta có:       1    x            x xf x x f x e xf x f x xf x  e x        1 x xe f x x
e f  x  1 x 
    x  xe f x
xe  f  x  1  x 
 xe f  x 1 x
 xe f  x  dx  x  C  * Với x  0
+) Thay vào biểu thức ban đầu ta có: f     f   0 0. 0 0 1 0 e    
 1  f 0  1.
+) Thay vào * , ta có: C  0 .  x e  khi x  0 Khi đó: x
xe f  x  x  f  x   1 khi x  0 
f  x  f 0  x e 1  x e 1
Suy ra: f 0  lim  lim   lim  1  . x0 x0 x0 x x x Câu 7.
(Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hàm số y  f (x) có đạo hàm liên tục trên đoạn [1;3] thỏa mãn f (1)  2 và 2
f (x)  (x 1) f (
 x)  2xf (x), x
 [1;3] . Giá trị của 3 f (x)dx  bằng 1 2 2 A. 1 ln 3. B.  ln 3 . C.  ln 3 . D. 1 ln 3. 3 3 Lời giải Chọn C 
f (x)  (x 1) f (  x)  x 1 
 Xét f (x)  0 : 2
f (x)  (x 1) f (
 x)  2xf (x) ⇔  2x ⇔    2x 2 f (x) f  x  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 x 1 x 1 ⇒  2 d x x  ⇔ 2  x  C f  x f  x x 1 x 1
f (1)  2 ⇒ C  0 ⇒ 2
 x ⇔ f  x  f  x 2 x x 1
Xét: f (x)  0 ⇒ x  1
 thỏa mãn điều kiện bài toán. Vậy: f  x  2 x 3 3 3 3 x 1  1 1   1   1  2
 f  x dx  dx  + dx  ln x   ln 3   ln11  ln 3    2  2        x  x x   x   3  3 1 1 1 1 Câu 8.
(Chuyên Quốc Học Huế - 2021) Cho hàm số f (x) có đạo hàm liên tục trên R thỏa mãn: '( )  ( ) x f x
f x  e .cos 2021x và f (0)  0 Đồ thi hàm số y  f (x) cắt trục hoành tại bao nhiêu
điểm có hoành độ thuộc đoạn  1  ;  1 ? A. 3 B. 1 C. 1287 D. 4043 Lời giải Chọn C
Ta có phương trình trên tương đương với
 f '(x)  f (x) x
 e .cos 2021x  f '(x)  f (x) x
 e .cos 2021x  x  e
f '(x)   x
e  f (x)  cos 2021x
Đến đây ta nguyên hàm hai vế thu được:      x x e f x  x sin 2021
( )  cos 2021x  e
f (x)  cos 2021xdx   C  2021  sin 2021 x x e x x .sin 2021
Mà f (0)  0 nên C  0 suy ra e f (x)   f (x)  2021 2021
Phương trình hoành độ giao điểm của đồ thị hàm số y  f (x) và trục hoành là x e .sin 2021x k f (x)  0 
 0  sin 2021x  0  2021x  k , k  Z  x  ,k  Z  2021 2021 k 2021 2021 Vì x  1   ;1 nên 1   1   k  2021  
Mà do k  Z nên suy ra k  6  43; 6  42;...; 64 
3 như vậy ta kết luận đồ thi hàm số y  f (x) cắt
trục hoành tại 1287 điểm có hoành độ thuộc đoạn  1  ;  1 Câu 9.
(Chuyên Quang Trung - Bình Phước - 2021) Cho hàm số y  f  x có đạo hàm liên tục trên 1  ,    ex xf x 1, x   ,  f  
1  0 . Giá trị xf  x dx  bằng 0 1 1 1 1 A.  . B. . C.  . D. . 4 4 2 2 Lời giải Chọn A 1
 Tính xf  x dx  : 0
Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
du  f  x dx u
  f  x  Đặt 2    x dv  d x x  v    2 1 2 1 2 1 x 1 x 1 1 1
xf  x dx  . f  x 
. f  x dx  f   1  f 0.0  x  x e      1 dx . 2 0 2 2 2 2 0 0 0 1 2 1  x  x 1 1   x  e   1 dx   ex x  ex    2 2 2 0 0   1  1   1 0   e  e   e      . 2  2  4 
Câu 10. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hàm số y  f (x) liên tục và có đạo hàm trên  x  1   2; 2  \ 
0 , thỏa mãn f (1)  0 và f '(x)  x  f (x) e  2 
 0 . Giá trị của f bằng f (x)   e  2  A. ln 7 . B. ln 5 . C. ln 6 . D. ln 3 . Lời giải Chọn A x f ( x) f ( x)
f '(x)  x 
 0  f '(x)e  xe e   x  f x  f (x) 2 0 ( )  e f ( x) f x   x e  x  f x e  2 ( ) ( ) f '(x)e f '( ) 1  0   x  f x e  2 ( ) 1 f ( x) f ( x) d e  2
 f '(x)e   1 x  dx  xdx   xdx    C, (1)     e  2 f x f x 1  f x e  2 ( ) ( ) ( ) e 1 2 1 1 1 2 1 x Trong (1) cho x=1  
 C  C  0. Suy ra  , (2) f (1) e 1 2 f ( x) e 1 2 1 1 1  1  Trong (2) cho x=    f  ln 7.    1 2  f 8  2     2 e  1
Câu 11. (Chuyên ĐHSP Hà Nội - 2021) Cho hàm số
f  x liên tục trên  thỏa mãn 1 3
f  x  f  x   3 2 3
sin 2x  3x  x,x   . Tích phân I  f  xd 
x thuộc khoảng nào? 0 A.  3  ; 2   . B.  2  ;  1 . C.  1  ;  1 . D. 1;2 . Lời giải Chọn C 3 2
Cách 1. Từ giả thiết ta có 3
f 1 x 3 f 1 x sin 21 x 31 x 1 x            3
 f   x  f   x   3 2 1 3 1
sin 2x  3x  x    3 2
sin 2x  3x  x 3
 f   x  f   x 3 1 3 1
   f  x  3 f  x   3
  f   x 3 1
 f  x  3  f 1 x  f  x  0    
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
  f   x  f  x 2
  f   x  f   x f  x 2 1 . 1 1 .
 f  x  3  0    
 f 1 x   f  x . 1 1 Khi đó I  f  xd  x   1 d  f x x   1 0 0
x  0  t  1
Đặt t  1 x  dt  d
 x . Đổi cận 
x  1  t  0  1 0 1 1 
f 1 xdx   f t dt  f t dt  f  xdx      I 2 0 1 0 0 Từ  
1 và 2 suy ra I  I  I  0 . Vậy I  1  ;  1 . Cách 2. Do    3 2 1
sin 2x  3x  x  1 nên 3 1
  f  x  3 f  x  1 3  4
  f  x  3 f  x  4 . + Từ 3
f  x  3 f  x  4  3
 f  x  3 f  x  4  0   f  x 2
 1  f  x  f  x  4  0    
 f  x 1  0  f  x  1  . + Từ 3
f  x  3 f  x  4 3
 f  x  3 f  x  4  0   f  x 2
1  f  x  f  x  4  0    
 f  x 1 0  f  x  1. 1 1 1 1 Suy ra 1
  f  x  1    1 dx 
f  xdx  1d    x  1    d 1  f x x . Vậy I   1  ;  1 . 0 0 0 0
Câu 12. (Chuyên ĐH Vinh - Nghệ An - 2021) Giả sử f (x) là hàm có đạo hàm liên tục trên 0;  và   1 f (
 x)sin x  x  f (x)cosx, x
 0;  . Biết f ( )  1, f ( ) 
(a  b ln 2  c 3) , với a, b, c là 2 6 12
các số nguyên. Giá trị của a  b  c bằng A. 1  . B. 1. C. 11. D. 11. Lời giải Chọn A f (
 x) sin x  x  f (x)cosx  f (
 x) sin x  f (x)cosx  x Ta có:
f (x) sin x f (x)cosx x f (x)      x     2 2   2 sin x sin x  sin x  sin x f (x) x  
dx  x cot x  cot xdx  x cot x  ln sin x  C  2  . sin x sin x f (x) Hay
 x cot x  ln sin x  C . sin x    1    f  1    cot  ln sin
 C  C  1   .  2   2 2 2 sin 2 f (x) 
 x cot x  ln sin x 1. sin x  f ( )     1 Do đó 6    cot  ln sin 1  f ( )  66ln 2 3.  6 6 6 6 12 sin 6
 a  6, b  6
 , c  1. a  b  c  1.
Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 13. (THPT Quế Võ 1 - Bắc Ninh - 2021) Thành phố định xây cây cầu bắc ngang con sông dài
500 m , biết rằng người ta định xây cầu có 10 nhịp cầu hình dạng parabol,mỗi nhịp cách nhau
40 m , biết 2 bên đầu cầu và giữa mối nhịp nối người ta xây 1 chân trụ rộng 5 m . Bề dày và bề
rộng của nhịp cầu không đồi là 20 cm (mặt cắt của một nhịp cầu được mô phỏng như hình vẽ).
Hỏi lượng bê tông để xây các nhịp cầu là bao nhiêu (làm tròn đến hàng đơn vị). A. 3 50m . B. 3 20m . C. 3 100m . D. 3 40m . Lời giải Chọn D
Chọn hệ trục tọa độ như hình vẽ với gốc O(0; 0) là chân cầu (điểm tiếp xúc Parabol trên),
đỉnh I 25;2 , điểm A50;0 (điểm tiếp xúc Parabol trên với chân đế).
Gọi Parabol trên có phương trình  P  2
: y  ax  bx (do (P) đi qua O ). 1 1 20 1
 Phương trình parabol dưới  P  2 2
: y  ax  bx 
 ax  bx  . 2 2 100 5 2 4 2 4 1
Ta có  P đi qua I 25;2 và A50;0   P : y   x  x  y   x  x  1  2 2 1  1 2 625 25 625 25 5
Khi đó diện tích mỗi nhịp cầu là S  2S với S là phần giới hạn bởi y ; y trong khoảng (0; 25) 1 1 1 2 0,2 25   2 4  1  2 2 S  2  x  x dx  dx  9,9m       . 0 0,2   625 25  5 
Vì bề dày nhịp cầu không đổi nên coi thể tích là tích diện tích và bề dày 3
V  S.0, 2  9, 9.0, 2  1,98m  số lượng bê tông cần cho mỗi nhip cầu 3  2m .
Vậy 10 nhịp cầu 2 bên cần 3  40m bê tông.
Câu 14. (THPT Quốc Oai - Hà Nội - 2021) Cho hàm số y  f  x có đồ thị y  f ' x như hình vẽ.Giá
lớn nhất của hàm số g  x  f 3x  3x trên đoạn  1  ;  1 bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 A. f  3    3 . B. f   1 1. C. f   1  3.
D. f 3  3 . Lời giải Chọn A.
g ' x  3 f '3x  3  g ' x  0  f '3x  1  1 Số nghiệm của  
1 là số giao điểm của đồ thị hàm số y  f '3x và y  1  x  0 3x  0 f '3x 1      1 3x  1  x    3
Dựa vào đồ thị ta có bảng biến thiên x 1  0 1 3 1 g ' x - 0  0  0
g  x f  3    3 f   1 1 Dựa vào đồ thị ta có 1 0 3  1 
g ' xdx  g ' xdx  g 0  g   1  g  g     0  3  1  0  1   g   1  g  f  
3  3  g   1 1  3 
Giá trị lớn nhất của y  g  x trên  1   ;1 là f  3    3 .
Câu 15. (THPT Quốc Oai - Hà Nội - 2021) Cho hàm số y  f x có đạo hàm liên tục trên  . Hàm số
y  f x có đồ thị như hình vẽ bên dưới.
Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Số nghiệm thuộc đoạn 2;6 của phương trình f x  f   0 là A. 2 . B. 3. C. 4. D. 5. Lời giải Chọn A x  2   x  0 
Xét f x  0   x  2  x  5   x  6 
Ta có bảng biến thiên trên đoạn 2;6:
Gọi S là diện tích hình phẳng giới hạn bởi y  f  1
x; y  0;x  0;x  2.
Gọi S là diện tích hình phẳng giới hạn bởi y  f x; y  0; x  2; x  5 . 2
Gọi S là diện tích hình phẳng giới hạn bởi y  f  3
x; y  0;x  5;x  6. 2 Khi đó S  
f xdx  f   0  f   2  1 0 5 S 
f  x dx  f 5  f 2  2       2 6 S  
f  x dx  f 5  f 6  3       5
Từ đồ thị ta thấy S  S  f 5  f 2  f 0  f 2  f 5  f 0 2 1            
S  S  S  f 0  f 2  f 5  f 6  f 5  f 2  f 6  f 0 . 1 3 2                
Khi đó ta có bảng biến thiên trên đoạn 2;6 như sau:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489
Vậy phương trình f x  f  
0 có 2 nghiệm thuộc đoạn 2;6.
Câu 16. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hàm số f (x) liên tục và có đạo hàm xác định trên 0; . Biết rằng
f (x)  0 với mọi x  0; thỏa mãn
f (x) ln f (x)  
1  x  f '(x)  2 f (x)  0 và ln( f (2))  ln( f (1))  1. Giá trị của tích phân 2 xf (x)dx 
nằm trong khoảng nào dưới đây: 1 A. 0;6 . B. 6;12 . C. 12;18 . D. 18;24 . Lời giải Chọn D
Ta có: f ( x) ln f (x)  
1  x  f '(x)  2 f (x)  0
Do f (x)  0 với mọi x  0; nên ta chia 2 về phương trình đó cho f (x) f '(x) f '(x)
 ln f (x) 1  . x
 2x  0  ln f (x)  . x  2x  1 f (x) f (x)
 xln f (x) 
 2x  1. Đến đây ta nguyên hàm 2 vế thì phương trình trở thành 2
 x ln f (x)  x  x  C (*)
Thế x  1 vào ta thu được ln f (1)  2  C
Thế x  2 vào ta thu được 2ln f (2)  6  C
Lấy 2 phương trình trên trừ nhau ta thu dược: 2ln f (2)  ln f (1)  4
Mả đề cho ln( f (2))  ln( f (1))  1 nên ta dễ dàng giải hệ phương trình ra được nghiệm là: 3 l  n f (2)  3   f (2)  e   
. Thế vào phương trình (*) suy ra được C  0 nên ta có được 2 ln f (1)  2   f (1)  e  2 1 ln ( ) ln ( ) 1 ( ) x x f x x x f x x f x e          2 2 3 Như vậy x 1  x 3
xf (x)dx  xe
dx  (x 1)e dx  e  20,085 18;24    1 1 2
Câu 17. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hàm số y  f  x có đạo hàm liên tục trên    
thỏa mãn f  x  f  x  sin . x cos x  
với mọi x   và f 0  0. Giá trị của tích phân  2   2 .
x f   x dx  bằng 0
Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1  1  A. . B. . C.  . D.  . 4 4 4 4 Lời giải Chọn C           Thay x 
vào đẳng thức f  x  f  x  sin . x cos x    f  f   0  0  f  0   . 2  2   2   2   2 Xét I  .
x f   x dx  0 u   x du  dx Đặt   
dv  f  x dx
v  f  x      2 2  I  .
x f  x 2  f  x dx   f  x dx     1 0 0 0    2 2 2    Lại có:
f  x dx  f  x dx  sin . x cos x dx       2  0 0 0     2 2 1 2 2 1 1
 2 f  x dx  sin 2x dx  
 2 f  x dx  
f  x dx    . 2 2 4 0 0 0 0 1 Vậy I   . 4 f  x
Câu 18. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hàm số
liên tục trên  và thỏa mãn 1
f  x  f   x  x   x2 2 1 1 ; x  I 
f  x d . x  . Tính 0 1 1 1 1 A. . B. . C. . D. . 30 60 45 15 Lời giải Chọn B
Đặt t  1  x  dt  d . x Đổi cận: x 0 1 t 1 0 1 1 1 1 1 Khi đó ta có:
f 1  x dx 
f t  dt 
f  x dx 
 f  x  f 1  x dx  2. f  x .        dx 0 0 0 0 0 1 1 
 f  x  f 1  x dx  x 1  x2 2 d     x 0 0 1 5 4 3 1 1  x x x  1  2
f  x dx     4 3 2
x  2x  x  dx       0 0 5 2 3 30   0 1 1 
f  x dx  . 0 60
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 Vậy    .  f x dx 0 60
Câu 19. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hàm số y  f  x . Hàm số y  f  x có đồ thị như hình vẽ bên
Đặt M  max f  x ; m  min f  x . Tính giá trị S  M  m ?  2  ;6  2   ;6
A. S  f 0  f 2 .
B. S  f 5  f 6 .
C. S  f 5  f 2 .
D. S  f 0  f  2   . Lời giải Chọn C Ta có BBT Gọi gồm các đường:   ; ; . 1
S là diện tích hình phẳng giới hạn  1 H  y
f  x y  0 x  2  ; x  0 Gọi   ; ; . 2
S là diện tích hình phẳng giới hạn H gồm các đường: 2  y
f  x y  0 x  0; x  2 Gọi   ; ; . 3
S là diện tích hình phẳng giới hạn  H gồm các đường: 3  y
f  x y  0 x  2; x  5 Gọi   ; ; . 4
S là diện tích hình phẳng giới hạn H gồm các đường: 4  y
f  x y  0 x  5; x  6 0 2 Ta có:      . 1 S S2 f   x dx f
  x dx  f 0  f  2
   f 0  f 2  f  2    f 2 2  0 2 5 S       2 3 S f   x dx f
  x dx  f 0  f 2  f 5  f 2  f 0  f 5 0 2 5 6       3 S S4 f   x dx f 
 x dx  f 5  f 2  f 5  f 6  f 2  f 6 2 5
M  max f  x   f 5  2;6 Suy ra: 
 T  M  m  f 5  f 2 . m  min f 
 x  f 2 2;6 
Câu 20. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hàm số y  f  x có đạo hàm liên tục trên 1;  3 , biết f   1  1 và
f  x. f  x  x  4   x  2 f  x  f  x với x  1;  3 . Biết
Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 3 a a
f  x dx    2 c 
(với a, b, c là các số nguyên dương,
là phân số tối giản). Khi đó, tổng b b 1
a  b  c bằng A. 10 . B. 19 . C. 17 . D. 53 . Lời giải Chọn B
Ta có: f  x. f  x  x  4   x  2 f  x  f  x 
f  x f  x dx   x  4 dx   x  2 f  x  f  x dx      2 f  x 2 x  
 4x   x  2 f  x  C . 2 2 1 1 Theo bài, f   1  1  
 4  1 C  C  2  . 2 2 2 f  x 2 x 2 Khi đó, 
 4x   x  2 f  x  2   f  x   x  2  4x  f  x  2 x  x  2 2 2   3 3 3 2  4 x  4 
f  x dx  
2 x  x  2 3 dx  x   2x    4 3   . 3 2 3 1 1   1
Do đó, a  4, b  3, c  12 .
Vậy a  b  c  4  3 12  19 .
Câu 21. (THPT Lê Lợi - Thanh Hóa - 2021) Biết rằng y  f  x là hàm số liên tục và khác x với mọi
2 xf  x  f  x 1 a
x 0; và thỏa mãn f  
1  2; f 2  6. Có tích phân dx  ln ;  trong đó 2 f  x 2  x 2 b 1 a ,
a b là các số nguyên dương sao cho phân số
tối giản. Giá trị của biểu thức 2 3 a  b bằng b A. 5. B. 10. C. 17. D. 34. Lời giải Chọn C 2 f  x
2 xf  x  f  x 2  f  x 1 1  1 Ta có d  d  ln x x  2    f  x 2  x x 2 f x 1
1  f  x  2      1 1   x x 1   1 a 1 3  ln  ln
 a  3;b  2 2 b 2 2 Khi đó 2 3 a  b 17.
Câu 22. (Sở Lào Cai - 2021) Hàm số bậc ba y  f  x có đồ thị C đi qua điểm A1;0 ; hàm số bậc 1 
hai y  g  x có đồ thị C đi qua điểm B 1; 4
 . C , C cắt nhau tại 3 điểm phân biệt có 1   2  2 
hoành độ lần lượt là 1;2;3. Tính diện tích hình phẳng giới hạn bởi hai đồ thị C , C ? 1   2  115 32 71 112 A. . B. . C. . D. . 3 3 6 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn C
Vì C , C cắt nhau tại 3 điểm phân biệt có hoành độ lần lượt là 1;2;3 nên đa thức bậc ba 1   2 
f (x)  g(x) có ba nghiệm 1
 ; 2;3. Do đó, f (x)  g(x)  a  x  
1  x  2 x  3, với a  0.
Mặt khác vì C đi qua điểm A1;0 ; C đi qua điểm B 1;4 nên f   1  0, g   1  4 . Do 2  1  đó, f   1  g   1  4 Suy ra a 1 
1 1 21 3  4 hay a  1.
Khi đó diện tích hình phẳng giới hạn bởi hai đồ thị C , C là 1   2  2 3 71  x  
1  x  2  x  3 dx   x  
1  x  2 x  3 dx    (đvdt). 6 1 2    4 cos 2x   
Câu 23. (Sở Tuyên Quang - 2021) Cho hàm số f  x có f  2  
và f  x  , x   0; . 2    4  sin 2x  2   3 Khi đó
f  xdx  bằng  6    A.  ln 2 . B. ln 3 . C. . D.  ln 3 . 3 6 2 Lời giải Chọn B 4 cos 2x
Ta có f  x  f  xdx  dx   . 2 sin 2x
Đặt sin 2x  t  2cos 2 d x x  dt .    f  2 2dt 2 2   
Suy ra f  x  4 C C          C  0  . 2 t t sin 2x   3 3 2 2
Như vậy f  x   
f  xdx   dx  I   . sin 2x sin 2x   6 6     3 3 3 3 2  2  sin 2x 2  sin 2x 2sin 2x Xét I  dx  dx  dx  dx   2  2  . sin 2x sin 2x 1  cos 2x       1
cos 2x1 cos 2x 6 6 6 6   1 x   a     3 2
Đặt cos 2x  a  2  sin 2 d
x x  da . Đổi cận:  .  1 x   a    6 2 1 1 1 1      2 2 2 da 1  1 1  1  d a   2 1 d a   1  Suy ra I    da         . 1 a 1 a 2  a 1 a 1  2  a 1 a 1        1    1 1 1   2 2  2 2   1 1    1   2 2   ln a  1  ln a 1    ln 3 . 2 1 1      2 2 
Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Phương pháp trắc nghiệm: Dùng máy tính Casio bấm kết quả của tích phân I , sau đó thử 4 đáp
án, đáp án nào trùng khớp chính là kết quả cần tính. 3
Câu 24. (Sở Yên Bái - 2021) Cho hàm số f  x có đạo hàm liên tục trên 0; 
1 và thỏa mãn f   1  , 5 1 4 1 37 1
 f  x 2  dx   3  
và x f  x dx   . Tích phân
f  x dx  bằng 9 180 0 0 0 14 1 14 1 A.  . B. . C. . D.  . 15 15 15 15 Lời giải Chọn C     u   f   x u f  x  Đặt 4    , suy ra: 3 x v  x  v   4 1 1 4 1 37 x 1 1 37 1 1 3
 x f  x dx  f  x 4 
x f  x dx     f   4 1 
x f  xdx  180 4 4 180 4 4 0 0 0 0 1 2 4
 x f  x dx    . 9 0 1 1 4 4 Mặt khác ta có: 8 9 4x dx  x   . 9 9 0 0 1 1 1 2 4 8 4
Suy ra:  f  x 4
 dx  4 x f  x 8
dx  4x dx     0      9 9 9 0 0 0 1 2 2
  f  x 4
 2x  dx  0  4 5  
 f  x  2x  f  x   x  C . 5 0 3 3 2 2 Mặt khác f   1    
 C  C  1  f  x 5   x 1. 5 5 5 5 1 1  2  14 Vậy f  x 5 dx   x 1 dx     .  5  15 0 0
Câu 25. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hàm số f  x có đạo hàm liên tục trên đoạn 1  2 0;  1 thỏa mãn f  
1  1,  f  x dx  9    0 1 1 1 và 3
x f  x dx  
. Tích phân xf  x dx  bằng 2 0 0 6 2 8 5 A. . B. . C. . D. . 5 3 7 2 Lời giải Chọn C 1 2
Ta có:  f  x dx  9      1 0 1 1 Tính 3
x f  x dx  .  2 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489
du  f  x dx u   f   x  Đặt  4   3 x
dv  x .dx  v   4 1 1 1 4  x  1 1 1 1 1 3 
 x f  x dx   . f 4 4   x 
x . f  x dx   
x . f  x dx  2 4 4 4 4 0   0 0 0 1 1 4
 x . f  x dx  1   4
 18 x . f  x dx  18   2 0 0 1 1 9 x 1 1 - Lại có: 8 x dx    8
 81 x dx  9  3 9 9 0 0 0
- Cộng vế với vế các đẳng thức  
1 , 2 và 3 ta được: 1 1 1  2 2  f  x 2 4
 18x . f  x 8  81x    dx  0  4 4  
  f  x  9x  dx  0   .  f  x  9x  dx  0 Ha         0 0 0
y thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi đồ thị hàm số y  f  x 4  9x , trục
hoành Ox , các đường thẳng x  0 , x  1 khi quay quanh Ox bằng 9
0  f  x 4
 9x  0  f  x 4  9
 x  f  x  f  x.dx  5   x  C . 5 14 9 14 Lại do f   1  1  C   f  x 5   x  5 5 5 1 1 1 1  9 14   9 14   9 7  8
 xf  x dx   5 x  x  dx  6 7 2     x  x dx     x  x    .  5 5   5 5   35 5  7 0 0 0 0
Câu 26. (THPT Thanh Chương 1- Nghệ An - 2021) Hướng tới kỉ niệm 60 năm thành lập trường THPT
Thanh Chương 1. Khối 12K57 thiết kế bồn hoa gồm hai Elip bằng nhau có độ dài trục lớn bằng
8m và độ dài trục nhỏ bằng 4m đặt chồng lên nhau sao cho trục lớn của Elip này trùng với trục
nhỏ của Elip kia và ngược lại (như hình vẽ).
Phần diện tích nằm trong đường tròn đi qua 4 giao điểm của hai Elip dùng để trồng cỏ, phần diện
tích bốn cánh hoa nằm giữa hình tròn và Elip dùng để trồng hoa. Biết kinh phí để trồng hoa là 300.000 đồng
, kinh phí để trồng cỏ là 200.000 đồng
. Tổng số tiền dùng để trồng hoa và
trồng cỏ cho bồn hoa gần với số nào nhất trong các số sau: A. 6.200.000 đồng. B. 8.200.000 đồng. C. 8.600.000 đồng. D. 9.100.000 đồng. Lời giải
Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chọn C
 Ta có: độ dài trục lớn bằng 8m và độ dài trục nhỏ bằng 4m, ta có hình vẽ như trên:
 Tiếp theo ta sẽ thiết lập phương trình nửa bên trên trục hoành của cả hai Elip trên 2 phương trình đó là: . Gọi
là một trong hai giao điểm của hai đồ thị hàm số
Từ đó, hoành độ của điểm
chính là nghiệm của phương trình hoành độ giao điểm giữa hai đồ thị hàm số . . .
Suy ra bán kính của đường tròn đi qua 4 giao điểm của 2 Elip trên là .
Phương trình nửa trên của đường tròn là: .
Diện tích hình tròn đó là: .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489
Từ đó ta tính được kinh phí trồng cỏ là: đồng.
Ta có diện tích giới hạn bởi hai đường , là: .
Diện tích phần hình giới hạn bởi hai đồ thị
cùng với trục hoành đó là .
Từ đó ta suy ra diện tích dùng để trồng hoa là: .
Như vậy giá tiền trồng hoa là: .
Vậy tổng giá tiền dùng để trồng hoa và trồng cỏ cho bồn hoa bằng (đồng).
Câu 27. (THPT Lương Thế Vinh - 2021) Cho a, ,
b c là các số thực và   3 2
f x  x  ax  bx  c thỏa mãn t 5
f t   f t  5  2 với t là hằng số. Giá trị
f  x dx  bằng t 105 134 1 19 A.  . B. . C.  . D. . 2 3 2 4 Lời giải Chọn A
Ta có f  x 2
 3x  2ax  b . Vì f t   f t  5  2 nên t và t  5 là hai nghiệm của phương
trình f  x 2
 2  0  3x  2ax  b  2  0 .  2a      3 t t 5 
a   2t  5  3  Theo Viet ta có   2  . b  2 t  t  5  b
  3 2t  5t  2 3    Do đó t 5 I 
f  x x  f t    f t  
 t  3  t   a t  2 3 2 d 5 5 5
 t   b t  5  t        t t t 3 5
3t t 5t 5 t          .5
a .2t  5  5b     t  t 15 125 15 5  2t  52 2  5 3 2
t  5t   2 2    135  30 15 105 2 t  5t    2
4t  20t  25   . 2 2
Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 28. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hàm số f  x đồng biến, biết
f  x  0, x
 1; 4 và có đạo hàm liên tục trên đoạn 1; 4 , thỏa mãn f   1  1 và 4 2 f  x
2 f  x  xf  x   
với mọi x 1; 
4 . Khi đó f  xdx  bằng x 1 A. 1. B. 2 ln 2 . C. 2 ln 2  2 . D. 2  . Lời giải Chọn B 2 f  x f  x
 Ta có 2 f  x  .
x f ' x 
 2 f  x  .
x f ' x    x x . x f ' x 1  1 2 f  x 2 . x f  x       f  x x   x  1  Suy ra 2 . x
f  x  dx  dx  2 . x
f  x  2 x  C     . x
 Thế x  1, ta được 2. f  
1  2 1  C  C  0 . 1 Suy ra 2 . x f  x 2
 2 x  x . f  x  x  f  x  . x 4 4 4 1
 Ta có f  x dx  dx  ln x  2 ln 2   . 1 x 1 1
Câu 29. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hàm số y  f  x có đạo hàm liên tục trên
khoảng 0;   thỏa mãn 3
xf  x  f  x 3  x ln x, x   0 và f   1  . Tính f 2 4 A. 2 ln 2 1. B. 4 ln 2 1. C. 2ln 2 D. 4ln 2 Lời giải Chọn D xf x f x f x      f x 3        
xf  x  f  x  x ln x   x ln x   x ln x   x ln xdx 2    x x x    1  1 1 1 1 1 Mà 2 2 2 2 2
x ln xdx  ln . x d x  x ln x  x . dx  x ln x  x  C       2  2 2 x 2 4 1 1 3 1
Suy ra f  x 3 3  x ln x 
x  Cx , mà f   1   C   C  1. 2 4 4 4 1 1 Vậy f  x 3 3  x ln x 
x  x . Khi đó f 2  4ln 2 . 2 4
Câu 30. (THPT Ba Đình - Thanh Hóa - 2021) Cho hàm số f  x nhận giá trị dương, có đạo hàm liên tục
trên 0;2 . Biết f 0  1 và     2 2 4 2 x x f x f x e   
với mọi x 0;2 . Tính tích phân  3 2 2
x  3x  f  x I  dx  . 0 f  x 32 16 16 14 A. I   . B. I   . C. I   . D. I   . 5 3 5 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn C Theo giả thiết, ta có     2 2 4 . 2 x x f x f x e   
và f  x nhận giá trị dương nên       2 2 x 4 x f x f x   e  f  x  f   x 2 ln . 2 ln ln ln 2  2x  4x   .
Mặt khác, với x  0 , ta có: f 0. f 2  1 và f 0  1 nên f 2  1  2 2 2
x  3x  f  x 2 f  x Xét I  dx  , ta có I   2 2 x  3x    dx f x f x 0   0   3 2 u   x  3x du     2
3x  6xdx Đặt  f  x   . dv  dx    f  x v ln f  x   2 2 2 Suy ra I   3 2
x  3x ln f  x   2
3x  6xln f  xdx 2  
3x  6x ln f x dx (1).        0 0 0
Đổi biến x  2  t  dx  dt . Khi x  0  t  2 và x  2  t  0 Khi đó: 0 2 2 I    2
3t  6t ln f 2  t dt    2
3t  6t ln f 2  t dt    2
3x  6xln f 2  xdx (2). 2 0 0 2 Từ  
1 và 2 ta cộng vế theo vế, ta được 2I    2
3x  6x ln f  x  ln f 2  x dx   0 2 2 1 2 1 1  6  16 Hay I    2
3x  6x 2
2x  4xdx    4 3 2
6x  24x  24x dx 5 4 3  
x  6x 8x     2 2 2  5  5 0 0 0 .
Câu 31. (Trung Tâm Thanh Tường - 2021) Cho f  x, g  x lần lượt là các hàm đa thức bậc ba và bậc
nhất có đồ thị như hình vẽ. 2 250
Biết diện tích hình S (được tô màu) bằng . Tính
f  x  dx  . 81 0 7 38 8 34 A. . B. . C. . D. . 3 15 3 15 Lời giải Chọn D
Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021  4  3 1
Ta có g  x là hàm số bậc nhất đi qua A ;1 
 và B 3; 2 nên g  x  x  .  3  5 5 3 1 Với y  1  x 
 1  x  2  C 2;  
1 là giao điểm của f  x và g  x . 5 5  4 
Do đó f  x  g  x  a  x  2 x     x  3 .  3  4 4 3 3 250   4   3 Lại có S 
 f  x  g  x dx  
a  x  2 x       
  x  3 dx  a   . 81   3  20 2 2  3  4  3  4  3 1
Suy ra f  x  g  x 
 x  2 x 
 x  3  f  x 
 x  2 x 
 x  3  x      . 20  3  20  3  5 5 2 2  3  4  3 1  34 Vậy
f  x dx  
   x  2 x 
 x  3  x  dx     . 20   3  5 5 15 0 0  5
a ln 3  b ln 2 c
Câu 32. (THPT Trần Phú - Đà Nẵng - 2021) Giả sử 2
x ln  x   1 dx    với *
a,b, c  N . 3 9 3
Giá trị của biểu thức b  c  a bằng A. 2 . B. 24 . C. 4 . D. 4 . Lời giải Chọn B 5 2
I  x ln  x   1 dx  . 3  1     x    du dx u ln 1   x 1 Đặt    , suy ra 2
dv  x dx 1 3  v  x   3 5 5 3
x ln  x   5 3 1 1 x 2
I  x ln  x   1 dx   dx   3 3 x 1 3 3 3 5 125ln 6  27 ln 4 1  1 2    x  x 1 dx   3 3  x 1  3 5 3 2 125ln 6  27 ln 4 1  x x    
 x  ln x 1   3 3 3 2   3 126 ln 6  28ln 4 80   3 9 a  126 126 ln 3  70 ln 2 80
a ln 3  b ln 2 c       b
  70  b  c  a  24 . 3 9 3 9 c  80 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489
ex  m khi x  0 1 
Câu 33. Cho hàm số f  x  
liên tục trên  . Tích phân I 
f  xdx  bằng 2
2x 3  x khi x  0  1 22 22 22
A. I  e  2 3  22 .
B. I  e  2 3 
. C. I  e  2 3  .
D. I  e  2 3  . 3 3 3 Lời giải Chọn D
Ta có lim f  x  lim  
 , lim f  x  lim x  x 
và f 0  m 1.  x     2 2 3 0 x 0 0     e x m m 1 x0 x0
Vì hàm số đã cho liên tục trên  nên liên tục tại x  0 .
Suy ra lim f  x  lim f  x  f 0 hay m 1  0  m  1  . x 0 x 0   1 0 1 0 1 Khi đó   2 d = 2 3  d  ex   2 1 d = 3  d  2 3    ex f x x x x x x x x        1 dx 1  1  0 1  0 0 2 = 3   3  ex x x  x 1 22 2 2  e  2 3  . 0 3 3 1 
Câu 34. Cho hàm số bậc ba y  f  x có đồ thị C là đường cong trong hình bên. Biết hàm số f  x đạt  x  x 
cực trị tại hai điểm x , x thỏa mãn x  x  2 và 1 2 f    3
 . Gọi d là đường thẳng đi qua 1 2 2 1 2  
hai điểm cực trị của đồ thị C . Diện tích hình phẳng giới hạn bởi C và d ( phần được tô đậm trong hình) bằng y x2 x O x1 1 1 A. 1. B. 2 . C. . D. . 4 2 Lời giải Chọn D
Tịnh tiến điểm uốn về gốc tọa độ, ta được đồ thị mới như hình vẽ y x2 x O x1
Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Vì f  x là hàm bậc ba, nhận gốc tọa độ làm tâm đối xứng nên f  x 3  ax  cx .
Chọn x  1 , x  1 , khi đó f  x 3  x  3x . 1 2 1
Ta lại có f  x  x  2
3x  3  2x , suy ra d : y  2  x . 3 0 1 1
Diện tích hình phẳng cần tìm là S  2 x  2
3x  3dx   . 3 2 1  2
x  4x 1 , x  5 ln 2
Câu 35. Cho hàm số f  x  x x  . Tích phân f 3e    1 .e dx bằng 2x  6 , x  5  0 77 77 68 77 A. . B. . C. . D. . 3 9 3 6 Lời giải Chọn B
Ta có lim f  x  lim f  x  f 5  4 nên hàm số liên tục tại x  5 . x 5 x 5  
Vậy hàm số f  x liên tục trên  . x x 1
Đặt t  3e 1  e dx  dt 3
Đổi cận: x  0  t  4 ; x  ln 2  t  7 7 7 5 7 1 1 1   77 Khi đó I 
f t dt 
f  xdx   2x  6dx      2 x  4x   1 dx   . 3 3 3 9 4 4  4 5 
Câu 36. Cho hàm số bậc ba   3 2
f x  ax  bx  cx  d và đường thẳng d : g  x  mx  n có đồ thị như hình S
vẽ. Gọi S , S , S lần lượt là diện tích của các phần giới hạn như hình bên. Nếu S  4 thì tỷ số 2 1 2 3 1 S3 bằng. 3 1 A. . B. 1. C. 2 . D. . 2 2 Lời giải: Chọn B
 Dựa vào đồ thị như hình vẽ, ta có: f  x  g  x  k.x  x  2 x  2 .
g  x  x  3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489 0 S  S  kx x  2
x  2 dx  4k 1 2     2 
 g 0  g 2 .2 35.2 S  S    8 2 3 2 2 S
Vì S  4  S  4  S  8  4  4 . Vậy 2  1 . 1 2 3 S3
x  m , x  0
Câu 37. Cho hàm số f  x liên tục trên  thỏa mãn f  x  
(m là hằng số). Biết 2 x e , x  0  2 b
f  xdx  a  
trong đó a, b là các số hữu tỉ. Tính a  b . 2 e 1  A. 4 . B. 3 . C. 0 . D. 1. Lời giải Chọn A
Do hàm số liên tục trên  nên hàm số liên tục tại x  0  lim f  x  lim f  x  f 0  m  1 x 0 x 0   2 0 2 0 2 Khi đó ta có  d   d    2 d x f x x f x x f x x 
e dx   x   1 dx      1  1 0 1 0 0 2 2 x 2 2 e  x  1 e 9 1    x    4     . 2 2 2 2 2 2 2e 1    0 9 1 Do đó a  ; b   . 2 2
Vậy a  b  4 . Câu 38. Cho hàm số 4 2
y  x  3x  m có đồ thị C
, với m là tham số thực. Giả sử C cắt trục Ox m  m 
tại bốn điểm phân biệt như hình vẽ
Gọi S , S , S là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để 1 2 3
S  S  S là 1 3 2 5 5 5 5 A. . B.  . C. . D.  . 4 4 2 2 Lời giải Chọn A
Gọi x là nghiệm dương lớn nhất của phương trình 4 2
x  3x  m  0 , ta có 4 2
m  x  3x   1 . 1 1 1 x1
Vì S  S  S và S  S nên S  2S hay
f  x dx  0 1 3 2 1 3 2 3  . 0
Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 x 1 x 1 x 1 5  x  5 x 4  x  Mà
f  x dx    4 2
x  3x  mdx 3   x  mx 1 3 1 2   
 x  mx  x  x  m . 1  1  5 1 1 5 5 0 0     0 4  x  4 x Do đó, 1 2 x
 x  m  0  1 2
 x  m  0 2 . 1  1  5 1   5 4 x 5 Từ  
1 và 2 , ta có phương trình 1 2 4 2
 x  x  3x  0  4 2 4
 x 10x  0  2 x  . 1 1 1 5 1 1 1 2 5 Vậy 4 2
m  x  3x  . 1 1 4 2
y  f  x  1 y  g  x  x Câu 39. Cho hàm số , . Giá trị I  min 
 f  x; g  xdx 1  3 5 A. 1. B. . C. 2 . D. . 2 2 Lời giải Chọn C x  1
Xét bất phương trình x  1   . x  1  
Vậy min 1; x   1 khi 1  x hoặc x  1 
min 1; x   x khi 1   x 1 2 2 1 2 Xét I  min 
 f  x; g  xdx  min 
1; x dx  min 
1; x dx  min  1; xdx 1  1  1  1 1 2 0 1 2 0 1 2 2 x x I 
x dx  dx 2     d x x  d x x  dx       x =2. 1 2 2 1  1 1  0 1 1 0
Câu 40. Cho parabol  P  2
: y  x  4 cắt trục hoành tại hai điểm A , B và đường thẳng d : y  a 1
0  a  4 . Xét parabol P đi qua A , B và có đỉnh thuộc đường thẳng y  a . Gọi S là diện 2  1
tích hình phẳng giới hạn bởi  P và d . S là diện tích hình phẳng giới hạn bởi  P và trục 2  1  2
hoành. Biết S  S (tham khảo hình vẽ bên). 1 2 y M N
y = a A B O x Tính 3 2
T  a  8a  48a . A. T  99 . B. T  64 . C. T  32 . D. T  72 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn B
- Gọi A , B là các giao điểm của  P và trục Ox  A 2
 ; 0 , B 2;0  AB  4 . 1 
- Gọi M , N là giao điểm của  P và đường thẳng d  M  4  a;a, N  4  a;a 1 
 MN  2 4  a . a
- Nhận thấy:  P là parabol có phương trình 2 y   x  a . 2  4
- Áp dụng công thức tính diện tích hình phẳng ta được: 4 4 3 4   4 S  2 4  y.dy 2   4  y 
4  a 4  a . 1      3   3 a a 2 2  a 3  ax  8a 2  S  2 
x  a .dx  2   ax  . 2      4  12 3 0   0 4 8a
- Theo giả thiết: S  S 
4  a 4  a     a3 2 4  4a 3 2
 a  8a  48a  64 . 1 2 3 3  2 x  m   x  0 2
Câu 41. Cho hàm số y  f  x  
liên tục trên  . Giá trị I 
f 2 cos x 1 sin d x x  2 cos x  3   x  0  0 2  1 1  A. . B. 0 . C. . D. . 3 3 3 Lời giải Chọn A
Hàm f  x liên tục trên  suy ra
lim f  x  lim f  x  lim     m  1   2 x
m lim 2cos x 3 x 0 x 0   x 0 x 0   
Xét bất phương trình 2cos x 1  0 với 0  x  . 2 1 
 2cos x  1  cos x   0  x  2 3 
Vậy 2 cos x 1  0 khi 0  x  , 3   2 cos x 1  0 khi  x  . 3 2    2 3 2 I 
f 2 cos x 1 sin d x x  
f 2 cos x 1 sin d x x 
f 2 cos x 1 sin d x x   0 0  3   3 2 I 
f 2 cos x   1 sin d x x 
f 1 2 cos xsin d x x   0  3  3 Xét I 
f 2 cos x 1 sin d x x 1    0 dt
Xét t  2 cos x 1  dt  2  sin d x x   sin d x x 2
Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 x 0  3 t 1 0  3 0 -dt 1 1 1 1 Suy ra I 
f 2 cos x 1 sin d x x  f t  f t dt  f x dx 1             2 2 2 0 1 0 0 1 1 3 1  I   x x 1 2 x -1 dx    1  2 6 2 3 0 0  2 Xét I 
f 1 2 cos x sin d x x 2     3 dt
Xét t  1 2 cos x  dt  2sin d x x   sin d x x 2 x   3 2 t 0 1  2 1 dt 1 1 1 1 Suy ra I 
f 2 cos x 1 sin d x x  f t  f t dt  f x dx 2             2 2 2  0 0 0 3 1 1 3 1  I    x x 1 2 x -1 dx    2  2 6 2 3 0 0 2
Suy ra I  I  I  . 1 2 3
Câu 42. Cho hàm số bậc bốn y  f  x có đồ thị C  như hình vẽ bên. Biết hàm số y  f  x đạt cực trị 2
tại các điểm x , x , x thỏa mãn x  x  2 , f  x  f x  f x
 0 và C  nhận đường 1   3   2  1 2 3 3 1 3
thẳng d : x  x làm trục đối xứng. Gọi S , S , S , S là diện tích của các miền hình phẳng được 2 1 2 3 4 S  S
đánh dấu như hình bên. Tỉ số 1
2 gần kết quả nào nhất S  S 3 4 y d S3 S1 x1 x3 O x2 S2 x S4 A. 0, 60 . B. 0, 55 . C. 0, 65 . D. 0, 70.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn A
Nhận thấy kết quả bài toán không đổi khi ta tịnh tiến đồ thị C sang bên trái sao cho đường
thẳng d : x  x trùng với trục tung khi đó C  là đồ thị của hàm trùng phương y  g  x có ba 2
điểm cực trị x  1
 , x  0, x  1 . Suy ra y  g  x  k  4 2
x  2x   c k  0 1 2 3 2 2 3
Lại có f  x  f x  f x
 0  2k  2c 
c  0  c  k 1   3   2  3 3 4 3
Suy ra: y  g  x  k  4 2
x  2x   k 4 1 3 28 2 17 Khi đó: 4 2
S  S  k x  2x  dx  k 1 2  . 4 60 0
Ta lại có: g 0  g  
1  k  S  S  S  S  k.1  k . 1 2 3 4 28 2 17 77  28 2 S  S 28 2 17 Suy ra 1 2
S  S  k  k  k    0, 604 3 4 60 60 S  S 77  28 2 3 4  2x  4 khi x  4  2
Câu 43. Cho hàm số f  x  2  1 . Tích phân f
 2sin x  3sin 2 d x x bằng 3 2
x  x  x khi x  4   4 0 28 341 341 A. . B. 8 . C. . D. . 3 48 96 Lời giải Chọn D Ta có  1 
lim f  x  lim 2x  4  4; lim f  x 3 2  lim
x  x  x  4; f   4  4 x4 x4 x4 x4  4 
 lim f  x  lim f  x  f 4 x4 x4
Nên hàm số đã cho liên tục tại x  4  2 Xét I  f   2 2sin x  3sin 2 d x x 0 1 Đặt 2
2 sin x  3  t  sin 2 d x x  dt 2
Với x  0  t  3  x   t  5 2 5 5 4 5 1 1 1  1  1 341  I 
f t  dt  f t  3 2 dt 
t  t  t dt 
2t  4dt       . 2 2 2  4  2 96 3 3 3 4
Câu 44. Cho hàm số bậc ba y  f  x có đồ thị là đường cong C trong hình bên. Hàm số f  x đạt cực
trị tại hai điểm x , x thỏa f  x  f x  0 . Gọi ,
A B là hai điểm cực trị của đồ thị 1   2  1 2
C; M , N, K là giao điểm của C với trục hoành; S là diện tích của hình phẳng được gạch
Trang 30 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
trong hình, S là diện tích tam giác NBK . Biết tứ giác MAKB nội tiếp đường tròn, khi đó tỉ số 2 S1 bằng S2 2 6 6 5 3 3 3 A. . B. . C. . D. . 3 2 6 4 Lời giải Chọn D
Kết quả bài toán không thay đổi khi ta tịnh tiến đồ thị đồ thị C sang trái sao cho điểm uốn trùng
với gốc tọa độ O . (như hình dưới)
Do f  x là hàm số bậc ba, nhận gốc tọa độ là tâm đối xứng O  N  .
Đặt x  a, x  a , với a  0  f  x  k  2 2 '
x  a  với k  0 1 2  1   f  x 3 2  k x  a x    x  a  3, x  a 3 M K  3 
Có MAKB nội tiếp đường tròn tâm O  OA  OM  a 3  1  3 2 Có f  x  2 2  OA  x  f a 3 3
 a 2  k  a  a
 a 2  k  1 1   2  3  2a 3 2  1   f  x 3 2  x  a x 2   2a  3  0 0 2 3 2  1 a  9 2 S  f  x 4 2 2 dx  x  x  a 1  2   2a 12 2 8  a 3   a 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 6 S  S  f a MO  a a  a AMO   2 . 2. 3 2 2 2 2 S 3 3 Vậy 1  . S 4 2    x  2 khi x  0 3
Câu 45. Cho hàm số f  x   . Tích phân
f 3  4cos xsin d x x  bằng 2 3
 x  x  2 khi x  0  0 37 37 A. . B. . C. 6 . D. 12 . 24 6 Lời giải Chọn A Ta có:
lim f  x  lim           x
2 2; lim f  x lim    3 3x
x 2 2; f 0 2 x0 x0 x0 x0
 lim f  x  lim f  x  f 0 x0 x0
Nên hàm số đã cho liên tục tại x  0  3 Xét I 
f 3  4cos xsin d x x  0 1
Đặt 3  4 cos x  t  sin d x x  dt 4
Với x  0  t  1  x   t  1 3 1 1 0 1 1 1 1 1 37  I 
f t dt 
f t dt   2
3t  t  2dt 
 t  2dt      . 4 4 4 4 24 1  1  1  0
Câu 46. Cho hàm số bậc bốn y  f  x có đồ thị C  như hình vẽ bên. Biết hàm số y  f  x đạt cực trị 2
tại các điểm x , x , x thỏa mãn x  x  2 , f  x  f x  f x
 0 và C  nhận đường 1   3   2  1 2 3 3 1 3
thẳng d : x  x làm trục đối xứng. Gọi S , S , S , S là diện tích của các miền hình phẳng được 2 1 2 3 4 S  S
đánh dấu như hình bên. Tỉ số 1
2 gần kết quả nào nhất S  S 3 4
Trang 32 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 y d S3 S1 x1 x3 O x2 S2 x S4 A. 0, 60 . B. 0, 55 . C. 0, 65 . D. 0, 70. Lời giải Chọn A
Nhận thấy kết quả bài toán không đổi khi ta tịnh tiến đồ thị C  sang bên trái sao cho đường
thẳng d : x  x trùng với trục tung khi đó C  là đồ thị của hàm trùng phương y  g  x có ba 2
điểm cực trị x  1
 , x  0, x  1 . Suy ra y  g  x  k  4 2
x  2x   c k  0 1 2 3 2 2 3
Lại có f  x  f x  f x
 0  2k  2c 
c  0  c  k 1   3   2  3 3 4 3
Suy ra: y  g  x  k  4 2
x  2x   k 4 1 3 28 2 17 Khi đó: 4 2
S  S  k x  2x  dx  k 1 2  . 4 60 0
Ta lại có: g 0  g  
1  k  S  S  S  S  k.1  k . 1 2 3 4 28 2 17 77  28 2 S  S 28 2 17 Suy ra 1 2
S  S  k  k  k    0, 604 3 4 60 60 S  S 77  28 2 3 4 2 
x  ax  b khi x  2
Câu 47. Cho hàm số f  x  
. Biết hàm số có đạo hàm tại điểm x  2. Tính 3 2
x  x  8x 10khi x  2  4 I 
f  xdx  0 A. 3 . B. 0 . C. 2  . D. 4 . Lời giải Chọn D
 Hàm số có đạo hàm tại  f 2  lim f  x  lim f  x  4  2a  b  2
  2a  b  6  .   1 x 2 x 2  
f  x  f 2 3 2 3 2
x  x  8x 10  4  2a  b
x  x  8x 12  Có lim  lim  lim x 2 x 2 x 2 x  2 x  2     x  2
 x  22  x  3  lim
 lim  x  2 x  3  0;   x 2 x 2 x  2   
f  x  f 2 2
x  ax  b  4  2a  b
 x  2 x  2  a lim  lim  lim
 lim  x  a  2  a  4. x 2 x 2 x 2 x  2 x  2     x  2 x 2 
Hàm số có đạo hàm tại x  2 nên hàm số liên tục tại x  2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
NGUYỄN BẢO VƯƠNG - 0946798489
f  x  f 2
f  x  f 2 suy ra lim  lim
 a  4  0  a  4.  2 x 2 x 2 x  2    x  2 Từ  
1 và 2, suy ra a  4 và b  2. 2 
x  4x  2 khi x  2
Khi đó f  x   . 3 2
x  x  8x 10 khi x  2  4 2 4 I 
f  xdx  f  xdx  f  xdx    0 0 2 2 4   3 2
x  x  8x 10dx   2
x  4x  2dx 0 2 4 3 3  x x  2  x  4 16 4 2 2    4x 10x   2x  2x    4     4 3 0 3 2 3 3     Vậy I  4 . ax  b
Câu 48. Cho hàm số y 
có đồ thị C  . Gọi giao điểm của hai đường tiệm cận là I . Điểm cx  d M S  0  0 x ; 0
y  di động trên C  , tiếp tuyến tại đó cắt hai tiệm cận lần lượt tại A, B và 2 IAB . S  S Tìm giá trị 2 IM sao cho 1 2
(với S , S là 2 hình phẳng minh họa bên dưới) 0  1 1 2 SIAB 41 169 189 A. 2 . B. . C. . D. . 20 60 60 Lời giải Chọn B 
Nhận thấy kết quả bài toán không thay đổi khi ta tịnh tiến đồ thị C theo IO . Khi đó hai tiệm
cận của C là hai trục tọa độ.  
Và hàm số của đồ thị C  trở thành: y 
  0  y   . 2 x x    2
Gọi d là tiếp tuyến tại M 0  0
x ; y0   d : y    x  0 x     x  2 2 x x x x 0 0 0 0  2 
Suy ra: Ox d  A2 0
x ;0 và Oy d  B 0;    0 x  1  S  O .
AOB  2  2a  2  1 O  AB 2 1 1 2  2   x 2   c 0 y  , d : y   x  , B 0; , C ; 2     x x x x 2 x 0 0  0   0 
Trang 34 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Và x0 1  2 1   2 1  3 1  1 S  0 x    dx        2 2  o x 0 x  x  0 x x  x 2 0 0 2 2x0  1  1 1 3 1 S 2  dx   2 0 x  0 x      2  x  2 x x x 0 4 2 0 0 S  S 3 3 5 4 Theo giả thiết 1 2 2 2  1  1
S  S2  S    1  2 IAB  x0   y0  2 2 SIAB x 4 x 4 5 0 0 41 Vậy 2 2 2 IM0  0 x  0 y  . 20 2  4
x  2x 1 khi x  2 e 1  x
Câu 49. Cho hàm số f  x   . Tính I  . f ln   2 x 1  d . x 2 
x  5 khi x  2    x  1 0 A.  2  ;3 . B. 3; 2   . C. 2;  1  . D.  1  ; 2 . Lời giải Chọn A
Với x  2 , ta có f  x 2
 x  2x 1 là hàm đa thức nên liên tục trên  ;  2 .
Với x  2 , ta có f  x  x  5 là hàm đa thức nên liên tục trên 2;  .
Ta có lim f  x  lim  2 x  2x      1 7 x2 x2
lim f  x  lim  x  2  7 ; f 2  7 . x 2 x 2  
Do đó lim f  x  lim f  x  f 2 nên hàm số liên tục tại x  2 . x 2 x 2  
Khi đó hàm số đã cho liên tục trên  . 2 d x x d x x dt Đặt t  ln  2 x   1  dt    . 2 2 x 1 x 1 2 Đổi cận:
Với x  0 ta có t  0 Với 4
x  e 1 ta có t  4 4 4 2 4 1 1 1   Khi đó I 
f t  dt 
f  x dx      2 x  2x  
1 dx   x  5 dx   2 2 2 0 0  0 2  3 2 1  x  2  x  4 1  14  31 2   x  x   5x  16         . 2 3 0 2 2 2      3  3 
Câu 50. Cho hàm số bậc ba y  f  x có đồ thị là đường cong ở hình bên dưới. Gọi x , x lần lượt là hai 1 2
điểm cực trị thỏa mãn x  x  2 và f  x  3 f x  0. Đường thẳng song song với trục Ox và 1   2  2 1 S
qua điểm cực tiểu cắt đồ thị hàm số tại điểm thứ hai có hoành độ x và x  x 1. Tính tỉ số 1 0 1 0 S2
( S và S lần lượt là diện tích hai hình phẳng được gạch ở hình bên dưới). 1 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
NGUYỄN BẢO VƯƠNG - 0946798489 27 5 3 3 A. . B. . C. . D. . 8 8 8 5 Lời giải Chọn A +) Gọi   3 2
f x  ax  bx  cx  d , với a  0  f  x 2
 3ax  2bx  c .
+) Theo giả thiết ta có f  x  f  x  0  f  x  3a x  x x  x  3a x  x x  x  2 1   2     1   2   1   1 
 f  x  3a  x  x 2  6a x  x . 1  1 
 f  x  f  x dx  a  x  x 3  3a  x  x 2  C 1 1  .
+) Ta có f  x  3 f x  0  f x  3 f x  2  0 1   2   1  1 
 C  38a 12a  C   0  2
 C 12a  0  C  6a . 3 2
Do đó f  x  a  x  x  3a x  x  6a . 1   1 
+) S là diện tích hình chữ nhật có cạnh bằng 3 và và f  x  8a 12a  6a  2a 2  2
+) S là diện tích hình phẳng giới hạn bởi các đường x  x  x 1, x  x  x  2 , 1 0 1 2 1
y  f  x  2a 3 2
và f  x  a  x  x  3a x  x  6a nên suy ra 1   1  2  1 x 2 1 x 2 S
 f  x 2a dx
a  x x 3 3a  x x 2 4a        dx 1    1 1    x 1  x 1  1 1 x 2 1
 a x x 4  x x 3    27a 1 1    3a  4ax  . 4 3 4     x 1  1 S 27 Vậy 1  . S 8 2
2x  2 khi x  0 
Câu 51. Cho hàm số f  x  
. Tích phân I  sin 2 .
x f cosx dx 2  bằng
x +4x  2 khi x  0  0 9 9 7 7 A. I  . B. I   . C. I   . D. I  . 2 2 6 6 Lời giải Chọn A
Do lim f  x  lim f  x  f 0  2
 nên hàm số f  x liên tục tại điểm x  0 . x 0 x 0  
Đặt t  cos x  dt   sin d x x .
Trang 36 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Đổi cận: x  0  t  1; x    t  1  . Ta có:   1  1 sin 2 .
x f cosx dx  2sin . x cos .
x f cosx dx   2t. f t  dt  2 t. f t  dt     0 0 1 1 0 1 1 0  2 .
x f  x dx  2 .
x f  x dx  2 x     2
x  4x  2 dx  2 .
x 2x  2 dx  1  0 0 1  0 4 3 3 2  x 4x  1  x x  7 10 9 2  2   x  4.         . 4 3 0 3 2 6 3 2     1 
Câu 52. Cho hàm số bậc bốn trùng phương y  f  x có đồ thị là đường cong trong hình bên. Biết hàm số
f  x đạt cực trị tại ba điểm x , x , x (x  x  x ) thỏa mãn x  x  4 . Gọi S và S là diện 1 2 3 1 2 3 1 3 1 2 S
tích của hai hình phẳng được gạch trong hình. Tỉ số 1 bằng S2 2 7 1 7 A. . B. . C. . D. . 5 16 2 15 Lời giải Chọn B
Rõ ràng kết quả bài toán không đổi khi ta tịnh tiến đồ thị sang trái sao cho x  0 . 2 Gọi 4 2
g(x)  ax  bx  c , ta có hàm số g( )
x là chẵn và có 3 điểm cực trị tương ứng là 2  ;0; 2
là các nghiệm của phương trình 3
4ax  2bx  0 .
Dựa vào đồ thị g( )
x , ta có g(0)  0 . Từ đó suy ra 4 2
g(x)  a(x  8x ) với a  0 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
NGUYỄN BẢO VƯƠNG - 0946798489
Do tính đối xứng của hàm trùng phương nên diện tích hình chữ nhật bằng
2S  S  g (2) .4  64a 1 2
Ta có S là diện tích hình phẳng giới hạn bởi đồ thị hàm số g( )
x , trục hoành, đường thẳng 1 0 0 224a 224a 512a x  2  , x  0 . 4 2 S 
g(x) dx  a
x  8x dx  S  64a  2.  . 1   . Suy ra 15 2 15 15 2 2  S 224 7 Vậy 1   . S 512 16 2
Trang 38 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
Document Outline

[NBV]-Chủ đề 3-Tích phân-Mức độ nhận biết-câu hỏi
[NBV]-Chủ đề 3-Tích phân-Mức độ nhận biết-đáp án
[NBV]-Chủ đề 3-Tích phân-Mức độ thông hiểu-câu hỏi
[NBV]-Chủ đề 3-Tích phân-Mức độ thông hiểu-đáp án
[NBV]-Chủ đề 3-Tích phân-Mức độ vận dụng-câu hỏi
[NBV]-Chủ đề 3-Tích phân-Mức độ vận dụng-đáp án
[NBV]-Chủ đề 3-Tích phân-Mức độ VDC-câu hỏi
[NBV]-Chủ đề 3-Tích phân-Mức độ VDC-đáp án