








































































































Preview text:
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 11 Đề ôn tập: SỐ 1 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 001
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN 2 8n 3n 1 Câu 1. Tính lim . 2 4 5n 2n 1 1 A. . B. 2 . C. . D. 4 . 4 2 3 2x 2x khi x 1
Câu 2. Cho hàm số f x
. Khi đó lim f x bằng 3 x 3x khi x 1 x 1 A. 3 . B. 2 . C. 2 . D. 4 .
Câu 3. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a . Số đo góc giữa hai đường thẳng BC , SA bằng A. 90 . B. 60 . C. 45 . D. 120 .
Câu 4. Mệnh đề nào sau đây là đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
23n2 n 4
Câu 5. Tính I lim . n 3 1 A. I 9 . B. I 9 . C. I 3 . D. I 3 .
Câu 6. Cho lim f x , kết quả của lim 3
. f x bằng xa xa A. . B. . C. 0 . D. 3 .
Câu 7. Giá trị đúng của lim 3n 5n là: A. . B. . C. 2 . D. 2 .
Câu 8. Cho hàm số y f x có đồ thị như hình bên.
Kết quả của lim f x là x Trang 1/4 - Mã đề 001 A. 1. B. 3 . C. 1 . D. 3 .
Câu 9. Hình chiếu song song của hai đường thẳng chéo nhau không thể có vị trí nào trong các vị trí tương đối sau? A. Trùng nhau. B. Chéo nhau. C. Cắt nhau. D. Song song.
Câu 10. Chọn mệnh đề đúng trong các mệnh đề sau:
A. Nếu lim u thì lim u .
B. Nếu lim u thì lim u . n n n n
C. Nếu lim u 0 thì lim u 0 .
D. Nếu lim u a thì lim u a . n n n n 2 3
2x x 1 2x 3
Câu 11. Tìm giới hạn C lim . 2 x 1 3x 2 A. 3 2 5 . B. 3 3 9 . C. . D. . 4 2 2x 1 Câu 12. lim bằng.
x 3 x A. 2 2 . B. . C. 1. D. 2 . 3
Câu 13. Cho hàm số y f x liên tục trên ;
a b . Điều kiện cần và đủ để hàm số liên tục trên ; a b là
A. lim f x f a và lim f x f b .
B. lim f x f a và lim f x f b . x a x b x a x b
C. lim f x f a và lim f x f b .
D. lim f x f a và lim f x f b . x a x b x a x b
Câu 14. Cho k là một số nguyên dương. Chọn mệnh đề sai. A. 2 lim k x . B. lim k x 8 . C. lim 0 . D. lim k 8x . x x k x x x
Câu 15. Cho hình hộp ABC .
D A' B 'C ' D ' . Đẳng thức nào sau đây là đẳng thức đúng?
A. BA BC BB ' BD .
B. BA BC BB ' BA' .
C. BA BC BB ' BC ' .
D. BA BC BB ' BD ' . x 2 khi x 4 Câu 16. Cho hàm số x 4 f (x)
. Khẳng định nào sau đây đúng nhất ? 1 khi x 4 4
A. Hàm số liên tục tại x 4 .
B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại x 4 .
C. Hàm số không liên tục tại x 4 .
D. Tất cả đều sai. 3
x 2 khi x 1
Câu 17. Cho hàm số f x
. Chọn khẳng định đúng trong các khẳng định sau: 2
x 4 khi x 1
A. Hàm số liên tục tại x 1.
B. Hàm số liên tục trên ; 1 .
C. Hàm số liên tục trên 1; .
D. Hàm số liên tục trên . Trang 2/4 - Mã đề 001 2 x 1 f x , khi x 1 x 1 2 Câu 18. Cho hàm số m 2, khi x 1.
Có bao nhiêu giá trị m để hàm số f x liên tục tại x 1? A. 0 . B. 1. C. 2 . D. 3 .
Câu 19. Tính: I 2 lim
n 3n 12 n . 5 A. I . B. I 3 0 . C. I .
D. I . 3 2
Câu 20. Cho hình tứ diện ABCD có trọng tâm G . Mệnh đề nào sau đây là sai?
1
A. AG AB AC AD.
B. GA GB GC GD 0 4
1
2
C. OG OA OB OC OD
D. AG AB AC AD 4 3
Câu 21. Trong các hàm số sau đây, hàm số nào liên tục tại x 1 ? x 1 x 2
A. y x 1 . B. y . C. 2
y x 2x 1 . D. y . x 1 2 x 1
Câu 22. Giá trị của 2
A lim( n 2n 3 n) bằng A. 0. B. 1 C. . D. .
Câu 23. Cho hình hộp ABC . D AB C D
có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào có thể sai?
A. AB DC .
B. BC AD .
C. AC BD .
D. BB BD . 2 x 1 Câu 24. Giá trị lim bằng x 1 x 1 A. 2 . B. 1. C. 0 . D. 2 .
Câu 25. Cho hình chóp S.ABC có SA SB SC và ASB BSC
CSA . Hãy xác định góc giữa cặp vectơ SB và AC ? A. 90 . B. 120 . C. 45 . D. 60 . 2 3 7n 2n 1
Câu 26. Tìm I lim . 3 2 3n 2n 1 7 2 A. 0 . B. 1. C. . D. . 3 3 Câu 27. Biết
x x x a b a, b
S 5a b x 2 lim 5 2 5 5 với . Tính . A. S 5. B. S 5 . C. S 1 . D. S 1. 2 n
Câu 28. Tính I lim 3 n . 4 n 5
A. I . B. I 1. C. I 1 . D. I 0 .
Câu 29. Giá trị của A 2
lim n 2n 2 n bằng: A. 2 . B. 1 . C. . D. .
Câu 30. Cho hình lập phương ABC . D AB C D
cạnh a . Tính A . B AD . A. 2 2a . B. 0 . C. 2 a . D. 2 4a . 2 2x 3x 2 Câu 31. lim bằng 2 x 2 x 4 Trang 3/4 - Mã đề 001 5 5 A. 2 . B. 1 . C. . D. . 4 4 4
Câu 32. Cho hình hộp ABC .
D A B C D . Trong các khẳng định sau, khẳng định nào sai? 1 1 1 1
A. AC A C AA .
B. CA AC CC . 1 1 1 1 1
C. AC A C 2AC .
D. AC CA 2C C 0 . 1 1 1 1 1 2
a 2x 3 2017 1
Câu 33. Cho số thực a thỏa mãn lim
. Khi đó giá trị của a là x 2x 2018 2 1 A. a 1 . B. a 2 . C. a 2 . D. a . 2 2 2 2
Câu 34. Cho hình chóp S.ABCD có SA a , SB 2a , SC 3a , ASB BSC 60 ,
CSA 90 . Gọi là
góc giữa hai đường thẳng SA và BC . Tính cos . 7 A. cos 7 .
B. cos . C. cos 2 0 . D. cos . 7 7 3 2 x 16 khi x 4
Câu 35. Tìm m để hàm số f x x 4
liên tục tại điểm x 4 . mx 1 khi x 4 7 A. m 8 . B. m 7 . C. m . D. m 8 . 4 4 PHẦN II: TỰ LUẬN u 1 1
Câu 36. Cho dãy số u 22u lim u n
n được xác định bởi 1 . Tính . u ;n n n * 1 u 3 n 1 3
Câu 37. Tìm giới hạn : lim 3 x 1
1 x 1 x
Câu 38. Chứng minh rằng phương trình 2 m 5 1
x 3x 1 0 luôn có nghiệm.
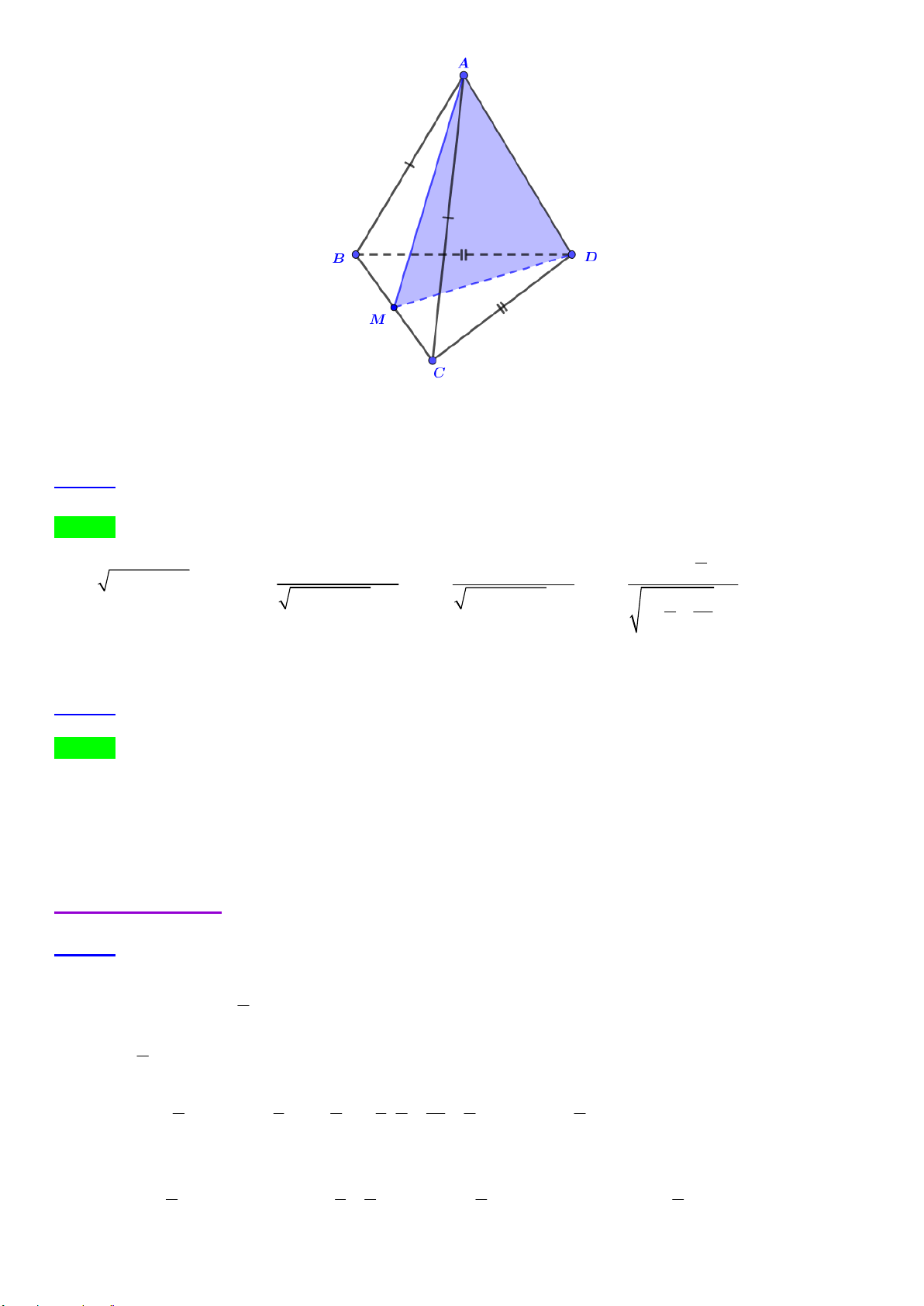
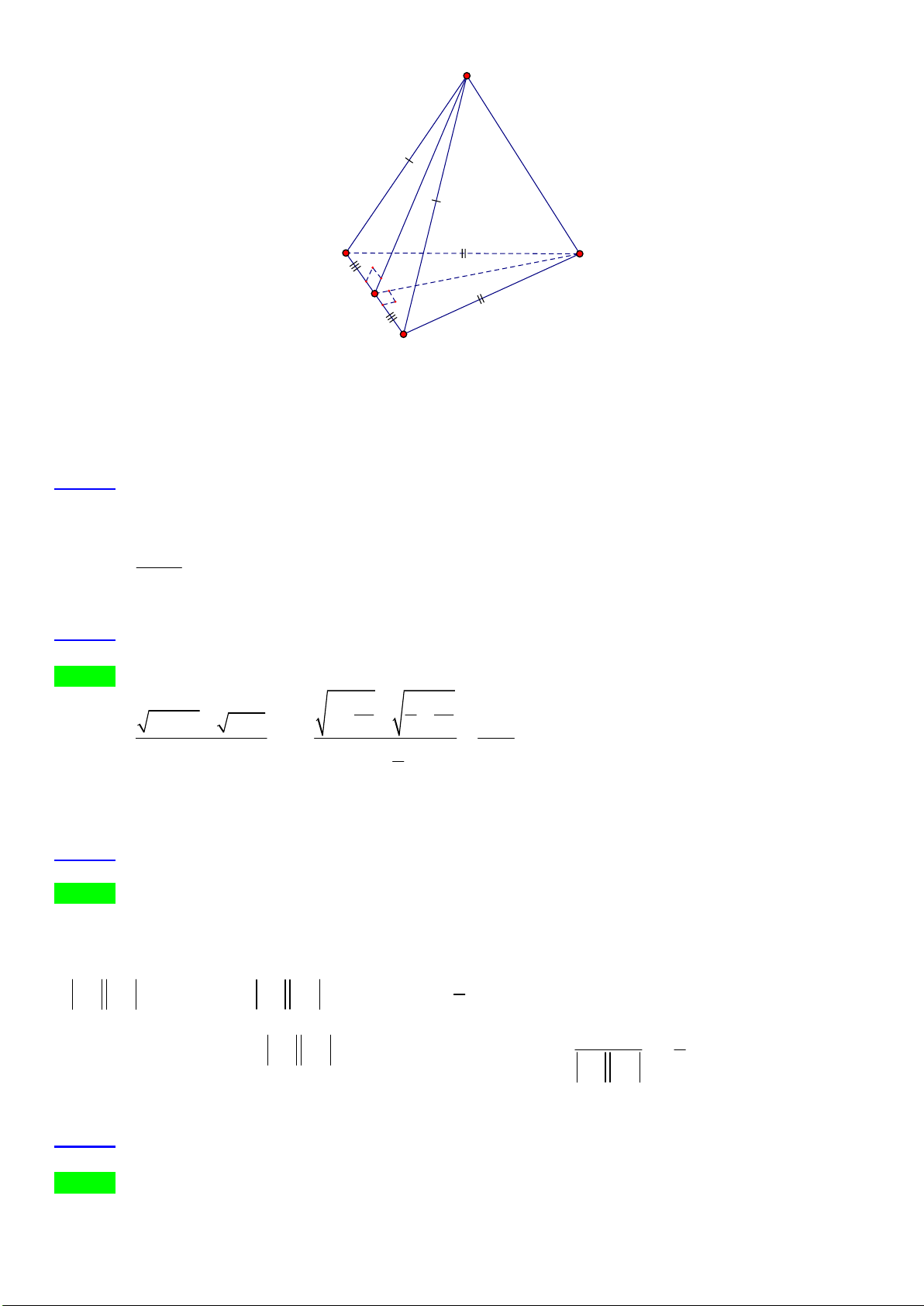
Câu 39. Cho tứ diện ABCD có AC a, BD 3a . Gọi M và N lần lượt là trung điểm của AD và BC . Biết
AC vuông góc với BD . Tính MN .
------------- HẾT ------------- Trang 4/4 - Mã đề 001
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 11 Đề ôn tập: SỐ 2 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 002
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho hai dãy số u , v n
n . Chọn mệnh đề sai.
A. Nếu lim u , lim v thì lim u v n n 0 . n n
B. Nếu lim u 2017, lim v thì lim u .v n n . n n u
C. Nếu lim u 2017, lim v thì lim n . n n v n
D. Nếu u v , n
và limv 0 thì limu 0 . n n n n
Câu 2. Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau? A. Hình chữ nhật B. Hình thoi C. Hình thang D. Hình bình hành
Câu 3. Trong các giới hạn sau giới hạn nào bằng 1 ? 2 2n 3 2 2n 3 A. lim . B. lim . 3 2 n 4 2 2 n 1 2 2n 3 3 2n 3 C. lim . D. lim . 3 2 2 n 2n 2 2 n 1
Câu 4. Cho hình hộp ABC . D AB C D
. Gọi I, J lần lượt là trung điểm của AB và CD . Khẳng định nào dưới đây là đúng?
A. AI CJ . B. D A IJ .
C. BI D J .
D. AI JC . 2x 1 Câu 5. lim bằng
x x 1 A. 2 . B. 1 . C. 1. D. 2 .
Câu 6. Tìm khẳng điịnh đúng?
A. lim x x . B. lim x
q 0q 1 . 0 x 0 x x C. 4 lim x . D. 3 lim x . x x
Câu 7. Khẳng định nào sau đây là đúng?
A. Ta nói dãy số u n u n có giới hạn khi
nếu có thể nhỏ hơn một số dương bất kì, kể từ một n
số hạng nào đó trở đi.
B. Ta nói dãy số u n u n có giới hạn khi
nếu có thể lớn hơn một số dương bất kì, kể từ một n
số hạng nào đó trở đi.
C. Ta nói dãy số u a u a n
lim u a n 0
n có giới hạn là số (hay dần tới ) khi , nếu . n n
D. Ta nói dãy số u 0 n u
n có giới hạn là
khi dần tới vô cực, nếu
có thể lớn hơn một số dương tùy ý, n
kể từ một số hạng nào đó trở đi. 2
2 x 1 5 x 3 Câu 8. lim bằng. x 2 2x 3 1 1 A. 3 . B. . C. 7 . D. . 7 3
Câu 9. Cho một hàm số f x . Khẳng định nào sau đây là đúng?
A. Cả ba khẳng định trên đều sai.
B. Nếu hàm số liên tục trên ;
a b thì f a. f b 0 . Trang 1/4 - Mã đề 002
C. Nếu f a. f b 0 thì hàm số liên tục trên ; a b .
D. Nếu hàm số liên tục trên ;
a b và f a. f b 0 thì phương trình f x 0 có nghiệm.
Câu 10. Hàm số nào sau đây gián đoạn tại x 2 ? x A. y 3 4 tan x . B. y .
C. y sin x . D. 4 2
y x 2x 1 x 2
Câu 11. Trong không gian, cho các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì vuông góc với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
Câu 12. Mệnh đề nào dưới đây đúng? A. 2
lim 2019n n . B. 2
lim 2019n n . C. 2
lim 2019n n . D. 2
lim 2019n n 2018.
Câu 13. Cho hình lập phương ABC . D AB C D
. Tính góc giữa hai đường thẳng B D
và AA . A. 30 . B. 45 . C. 60 . D. 90 . 1 Câu 14. Tính lim . x 3 x 3 A. 1 . B. . C. . D. 0 . 6 1 2n Câu 15. Tính lim . 3n 1 2 A. 5 . B. 7 . C. 1 . D. . 3 3
Câu 16. Trong các giới hạn sau, giới hạn nào bằng ? A. 3 5
lim 2x x 7 . B. 3 2 lim 4
x 2x 3 . x x C. 2 lim 4
x 7x 1 . D. 3 4
lim 1 x x . x x
Câu 17. Trong các giới hạn sau đây, giới hạn nào bằng 0 ? 2 3 n 2n n 4 3 n 6n 2 3n n 1 A. lim . B. lim . C. lim . D. lim . 3 5n 7 2 3n 5 2 4n 9 4 2 n 2n 2
a 2x 3 2017 1
Câu 18. Cho số thực a thỏa mãn lim
. Khi đó giá trị của a là x 2x 2018 2 1 A. a 2 . B. a 2 . C. a 1 . D. a . 2 2 2 2
Câu 19. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a . Gọi I và J lần lượt là trung điểm của SC
và BC . Số đo của góc IJ,CD bằng A. 60 . B. 90 . C. 30 . D. 45 . x 3 2 x 1
Câu 20. Cho hàm số f x x 1
. Để hàm số liên tục tại x 1 thì a nhận giá trị là ax2 x 1 1 7 A. . B. 1. C. D. 0 . 2 4
Câu 21. Cho hình tứ diện ABCD có trọng tâm G . Mệnh đề nào sau đây sai.
1
A. OG OA OB OC OD.
B. GA GB GC GD 0 . 4 Trang 2/4 - Mã đề 002
2
1
C. AG AB AC AD.
D. AG AB AC AD. 3 4
Câu 22. Tính giới hạn 2
lim ( x x 1 x) . x A. 1 . B. . C. . D. 0. 2
Câu 23. Tìm khẳng định đúng trong các khẳng định sau:
I . f x 5 2
x – x 1 liên tục trên . 1
II . f x
liên tục trên khoảng –1; 1 . 2 x 1
III . f x x 2 liên tục trên đoạn 2; .
A. Chỉ I và II .
B. Chỉ II và III .
C. Chỉ I và III .
D. Chỉ I đúng. 3 3n 2n 1
Câu 24. Giới hạn lim bằng 4 4n 2n 1 2 A. 0 . B. . C. 3 . D. . 7 4
Câu 25. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, SA SB 2a , AB a . Gọi là góc
giữa hai véc tơ CD và AS . Tính cos ? 7 A. cos 1 B. cos 7
C. cos 1
D. cos 8 4 8 4 3 x 1 khi x 1 Câu 26. Cho hàm số x 1 f (x)
. Khẳng định nào sau đây đúng nhất ? 1 khi x 1 3
A. Tất cả đều sai.
B. Hàm số liên tục tại x 1.
C. Hàm số liên tục tại mọi điểm.
D. Hàm số không liên tục tại tại x 1. Câu 27. n 2 2 lim n 2 n 1 bằng 3 A. . B. 1, 499 . C. 0 . D. . 2 Câu 28. Cho hàm số 2
f (x) 2x x . Mệnh đề nào sau đây là đúng?
A. Hàm số liên tục trên 0;2 .
B. Hàm số liên tục trên ; 0.
C. Hàm số liên tục trên 2;.
D. Hàm số liên tục trên 2 ;2. a a Câu 29. Biết: 2
lim 3n 3 9n 8n với a,b là các số nguyên dương và là phân số tối giản. Khi đó b b 2a 7b bằng A. 1. B. 5 . C. 26 . D. 10 . 2 2018 x 4 Câu 30. lim bằng 2018 2018 x2 x 2 A. 2018 2 . B. 2 . C. 2019 2 . D. .
Câu 31. Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng ABC và tam giác ABC vuông
tại B . Kẻ đường cao AH của tam giác SAB . Khẳng định nào sau đây sai?
A. AH AC .
B. AH BC .
C. SA BC .
D. AH SC .
Câu 32. Cho hình lập phương ABC .
D EFGH có cạnh bằng a . Ta có A . B EG bằng? Trang 3/4 - Mã đề 002 2 a 2 A. 2 a 2 . B. 2 a . C. 2 a 3 . D. . 2
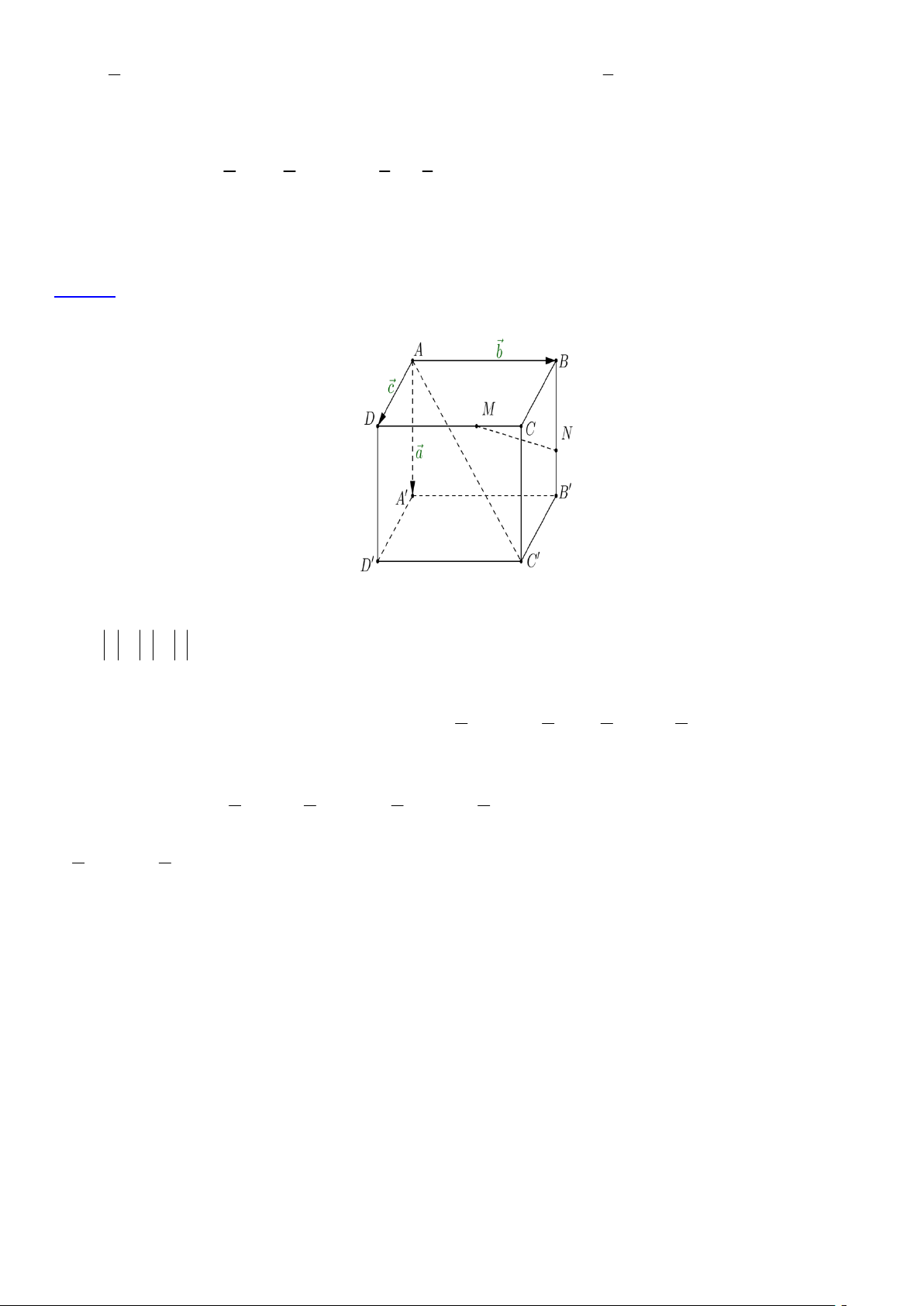
Câu 33. Cho hình chóp S.ABCD . Gọi M , N, P,Q, R,T lần lượt là trung điểm của AC, BD, BC, CD, S ,
A SD Bốn điểm nào sau đây đồng phẳng?
A. M , N, R,T .
B. P,Q, R,T .
C. M , P, R,T .
D. M ,Q,T , R . x 4 2
Câu 34. Tìm giới hạn hàm số lim bằng định nghĩa. x0 2x 1 A. 1. B. . C. . D. 2 . 8
1 5 4n 3
Câu 35. Giới hạn lim bằng 2n 1 A. 0 . B. 1. C. 2 . D. . 2 PHẦN II: TỰ LUẬN 2
n n 1 3n
Câu 36. Tính giới hạn lim . 2n 1 1 1
Câu 37. Tìm giới hạn : lim 2
x2 x 2 x 4
Câu 38. Cho 3 số a, ,
b c thỏa mãn 12a 15b 20c 0 . Chứng minh phương trình 2
ax bx c 0 luôn có 4 nghiệm thuộc 0; . 5
Câu 39. Cho tứ diện ABCD có các cạnh đối bằng nhau từng đôi một, AC BD a, AB CD 2a,
AD BC a 6 . Tính góc giữa hai đường thẳng AD và BC .
------------- HẾT ------------- Trang 4/4 - Mã đề 002
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 11 Đề ôn tập: SỐ 3 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 003
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN 4n 2018
Câu 1. Tính giới hạn lim . 2n 1 1 A. 4 . B. 2 . C. 2018 . D. . 2 1
Câu 2. Tính giới hạn lim là x x A. 0 . B. 1. C. . D. . Câu 3. Tính 3 2 lim 2
x 4x 5 x A. . B. . C. 3 . D. 2 . 2
x x 1 2x 1
Câu 4. Tìm giới hạn D lim . x 3 3
2x x 1 x A. . B. 4 . C. . D. 0. 3
Câu 5. Mệnh đề nào sau đây là đúng?
A. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c khi b song song hoặc trùng với c .
B. Góc giữa hai đường thẳng bằng góc giữa hai véctơ chỉ phương của hai đường thẳng đó.
C. Góc giữa hai đường thẳng là góc nhọn.
D. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c thì b song song với c . 4x 3 Câu 6. lim có kết quả là x 3 x 3 A. . B. . C. 9 . D. 0 . 2 x 3
Câu 7. Giới hạn lim bằng 3 x 1 x 2 3 A. . B. 2 . C. 1. D. 2 . 2
Câu 8. Cho f x 4 2
x x 1; g x cos x . Tìm khẳng định sai? f x
A. Hàm số f x g x liên tục trên . B. Hàm số liên tục trên . g x
C. Hàm số f x g x liên tục trên .
D. Hàm số f x.g x liên tục trên .
Câu 9. Chọn mệnh đề đúng trong các mệnh đề sau:
A. Nếu lim u , thì lim u .
B. Nếu lim u 0 , thì lim u 0 . n n n n
C. Nếu lim u a , thì lim u a .
D. Nếu lim u , thì lim u . n n n n 3n 2
Câu 10. Tìm I lim . n 1 A. I 2 B. I 0 C. I 2 D. I 3
Câu 11. Trong các mệnh đề sau mệnh đề nào đúng? Trang 1/4 - Mã đề 003
A. Ba vectơ a, ,
b c đồng phẳng nếu có một trong ba vectơ đó bằng vectơ 0 .
B. Ba vectơ a, ,
b c đồng phẳng khi và chỉ khi ba vectơ đó cùng có giá thuộc một mặt phẳng.
C. Cho hai vectơ không cùng phương a và b và một vectơ c trong không gian. Khi đó a, , b c đồng phẳng
khi và chỉ khi có cặp số m, n duy nhất sao cho c ma nb .
D. Ba vectơ a, ,
b c đồng phẳng nếu có hai trong ba vectơ đó cùng phương. 3x 1
Câu 12. Cho bốn hàm số f x 2x 3x 1 f x
f x cos x 3 f x log x 4 3 2 1 3 , , và . Hỏi có x 2 3
bao nhiêu hàm số liên tục trên tập ? A. 3 . B. 4 . C. 2 . D. 1.
Câu 13. Phát biểu nào trong các phát biểu sau là sai? 1 1 A. lim 0 k 1 . B. lim 0 . k n n C. lim n
q 0 | q | 1 .
D. lim u c ( u c là hằng số). n n
Câu 14. Khẳng định nào sau đây sai?
A. Phép chiếu song song có thể biến đường tròn thành đường elip.
B. Phép chiếu song song có thể biến đường tròn thành một điểm.
C. Phép chiếu song song có thể biến đường tròn thành đường tròn.
D. Phép chiếu song song có thể biến đường tròn thành đoạn thẳng.
Câu 15. Trong các mệnh đề dưới đây mệnh đề đúng là?
A. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
B. Trong không gian , hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.
D. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng vuông
góc với đường thẳng thứ hai. Câu 16. Giới hạn 3 2
lim n 4n 1 bằng A. 0 . B. . C. 1. D. .
Câu 17. Cho tứ diện đều ABCD . Gọi M , N lần lượt là trung điểm của AB và CD . Mệnh đề nào sau đây sai?
A. MN AB .
B. AB CD .
C. MN CD .
D. MN AD . 2 4 3n 2n 3n 2
Câu 18. Giá trị của lim là 2 4n 3n 2 A. 3 2 . B. . 4 3 C. Không tồn tại. D. . a 2 Câu 19. Biết lim 2 2
4n 5n 2020 4n 3n 2019 a . Giá trị biểu thức 0 T bằng 0 a 1 0 5 A. T . B. T 4 2 . C. T 3 . D. T . 3 3 2 2
x 3x 2 khi x 1
Câu 20. Giá trị của tham số m để hàm số f x x 1
liên tục tại x 1là 0 m khi x 1 A. 2 . B. 1. C. 1 . D. 2 .
Câu 21. Cho tứ diện đều ABCD cạnh a , M là trung điểm cạnh BC . Khi đó, cos
AB,DM bằng Trang 2/4 - Mã đề 003 1 3 3 2 A. . B. . C. . D. . 2 2 6 2 sin 5x x 0
Câu 22. Cho hàm số f x 5x
. Tìm a để f x liên tục tại x 0. a 2 x 0 A. 1. B. 1 . C. 2 . D. 2.
Câu 23. Cho hình lăng trụ tam giác đều ABC.
A BC có cạnh đáy bằng a , cạnh bên bằng 2a . Tính AB .BC . 1 1 A. 2
AB .BC a . B. 2
AB .BC a . C. 2
AB .BC a . D. 2
AB .BC a . 2 2
Câu 24. Tìm khẳng định đúng trong các khẳng định sau: 1
I f x liên tục trên . 2 x 1
II sin x f x
có giới hạn khi x 0. x
III f x 2
9 x liên tục trên đoạn 3 ; 3 .
A. Chỉ I và II .
B. Chỉ II và III .
C. Chỉ II .
D. Chỉ III . 3 2 n n 1
Câu 25. Cho dãy số u u lim u n có . Khi đó bằng n 2 3n 1 n A. . B. 0 . C. 1 . D. . 3 x x
Câu 26. Cho hàm số f x 2 4 2 2
. Tìm khẳng định đúng trong các khẳng định sau:. 1 x 2
I f xkhông xác định tại x 3.
II f xliên tục tại x 2 .
III lim f x 2 x2
A. Cả I ; II ; III đều sai.
B. Chỉ I .
C. Chỉ I và II .
D. Chỉ I và III .
Câu 27. Cho hình hộp ABC .
D A B C D . Tìm giá trị của k thích hợp điền vào đẳng thức vectơ: 1 1 1 1
AB B C DD k AC 1 1 1 1 A. k 1. B. k 0 . C. k 2 . D. k 4 . 2 x 2x 1
Câu 28. Chọn kết quả đúng trong các kết quả sau của lim là? x 1 2x 2 1 A. . B. 0 . C. . D. . 2
Câu 29. Tìm m để A 4 với A lim 2 2
2x x m 3 . x 1
A. m 2, m 2 . B. m 2 . m 2
C. 2 m 2 . D. . m 2 Trang 3/4 - Mã đề 003 Câu 30. lim x 1 x 3 x bằng A. . B. . C. 0. D. 2.
Câu 31. Cho dãy số u *
u n 2018 n 2017, n n thỏa mãn
. Khẳng định nào sau đây sai? n
A. Dãy số u lim u 0 n là dãy tăng. B. . n n 1 u C. * 0 u , n . D. n 1 lim 1 . n 2 2018 n un
Câu 32. Cho tứ diện ABCD có AB a, BD 3a . Gọi M và N lần lượt là trung điểm của AD và BC . Biết
AC vuông góc với BD . Tính MN . 3a 2 a a a A. MN 2 3 . B. MN 10 . C. MN 6 . D. MN . 2 3 2 3
Câu 33. Cho hai điểm phân biệt ,
A B và một điểm O bất kỳ không thuộc đường thẳng AB . Mệnh đề nào sau đây là đúng?
A. Điểm M thuộc đường thẳng AB khi và chỉ khi OM kOA 1 k OB .
B. Điểm M thuộc đường thẳng AB khi và chỉ khi OM OB k OB OA .
C. Điểm M thuộc đường thẳng AB khi và chỉ khi OM OA OB .
D. Điểm M thuộc đường thẳng AB khi và chỉ khi OM OB k BA .
Câu 34. Tính giới hạn n 1 n n 1 lim 16 4 16 3n T 1 A. T B. T 1 0 C. T 1 D. T 16 4 8 x +3 -2 a Câu 35. lim
= . Khẳng định nào sau đây là đúng? x 1 ® 2x -1-1 b
A. a +b = -5
B. a +b = 2
C. a +b =1
D. a +b = 5 PHẦN II: TỰ LUẬN
Câu 36. Tính giới hạn 3 lim 2n n 2n 2 .
Câu 37. Tìm giới hạn sau: 2 3 3 lim x 1 x 1 x x x
Câu 38. Cho hàm số f x 3 5 khi 2 . Với giá trị nào của f x a thì hàm số liên tục tại
ax 1 khi x 2 x 2 ?
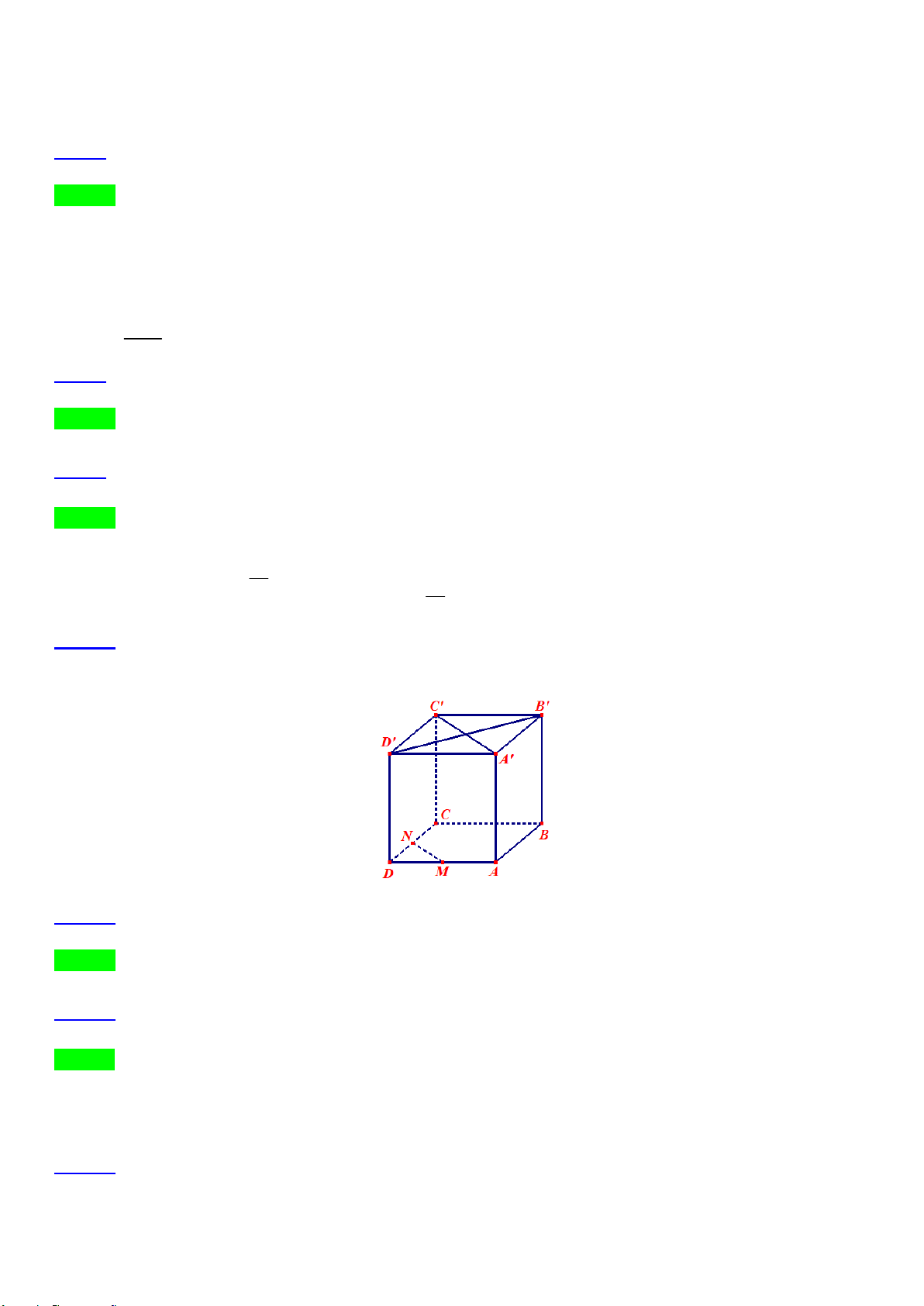
Câu 39. Cho hình lập phương ABC . D AB C D
có cạnh bằng a . Trên các cạnh DC và BB ta lần lượt lấy
các điểm M và N sao cho DM BN x với 0 x a . Chứng minh rằng AC vuông góc với MN .
------------- HẾT ------------- Trang 4/4 - Mã đề 003
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 11 Đề ôn tập: SỐ 4 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 004
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho hình lập phương ABC . D AB C D
(hình vẽ bên dưới). Góc giữa hai đường thẳng AC và AD bằng A. 30 . B. 60 . C. 90 . D. 45 . 3 x 1
Câu 2. Giới hạn lim bằng x 1 x 1 A. 2 . B. 2 . C. . D. .
Câu 3. Mệnh đề nào sau đây sai? 1 u A. lim
0 với k là số nguyên dương.
B. Nếu lim u a và lim v thì lim n 0 . k n n n vn u a
C. Nếu q 1 thì lim n q 0 .
D. Nếu lim u a và lim v b thì lim n . n n v b n Câu 4. 4 2 lim n 2n 3 bằng A. 4 . B. . C. . D. 1.
Câu 5. Qua phép chiếu song song, tính chất nào không được bảo toàn? A. thẳng hàng. B. Chéo nhau. C. đồng qui. D. Song song. 2 x 1
Câu 6. Cho hàm số f (x)
.Khi đó hàm số y f x liên tục trên các khoảng nào sau đây? 2 x 5x 6 A. 2;3. B. 3 ;2. C. 2 ; . D. ; 3 . x 1
Câu 7. Giới hạn lim bằng
x x 22 2 A. 0 . B. . C. 3 . D. . 16
Câu 8. Mệnh đề nào sau đây là đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
B. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.
Câu 9. Tính giới hạn lim 2
2x 3x 5 . x0 Trang 1/4 - Mã đề 004 A. 3 . B. 2 . C. 5 . D. 0 .
Câu 10. Phát biểu nào trong các phát biểu sau là sai? 1 1 A. lim 0 k 1 . B. lim 0 . k n n C. lim n
q 0 | q | 1 .
D. lim u c ( u c là hằng số). n n 1
Câu 11. Giá trị của C lim bằng: 2 n 2 n 7 A. 1 . B. . C. . D. 0 .
Câu 12. Giả sử ta có lim f x a và lim g x b . Trong các mệnh đề sau, mệnh đề nào sai? x x
f x a A. lim . B. lim f
x g x a b .
x g x b x C. lim f
x.g x . a b .
D. lim f x g x a b . x x 2 n
Câu 13. Giá trị của lim bằng n 1 A. 0 . B. 1. C. 2 . D. 1 . 2x 1
Câu 14. Tính giới hạn lim .
x x 1 A. 2 . B. 1 1 . C. . D. 1. 2
Câu 15. Cho hàm số y f x xác định trên khoảng a;b và x a;b
y f x 0 . Hàm số được gọi là
liên tục tại x nếu 0
A. lim f (x) a .
B. lim f (x) b . x 0 x x 0 x
C. lim f (x) f (x ) .
D. lim f (x) x . 0 0 x 0 x x 0 x
Câu 16. Cho hình hộp ABC . D AB C D
. Thực hiện phép toán u AD AB AA .
A. u BD .
B. u AC .
C. u BC .
D. u BA .
Câu 17. Cho hình lăng trụ đều ABC.AB C
có cạnh đáy bằng 1, cạnh bên bằng 2 . Gọi C là trung điểm của 1
CC . Tính côsin của góc giữa hai đường thẳng BC và AB . 1 2 2 2 2 A. . B. . C. . D. . 4 3 8 6
Câu 18. Cho hình chóp S.ABC, gọi G là trọng tâm tam giác ABC . Ta có
A. SA SB SC 3SG .
B. SA SB SC 4SG .
C. SA SB SC SG .
D. SA SB SC 2SG . Câu 19. Giới hạn 2 2 lim
n 2n n 2n bằng A. 1. B. 2 . C. 4 . D. . 2 x 1
Câu 20. Cho hàm số f x và f 2
2 m 2 với x 2 . Giá trị của m để f x liên tục tại x 2 là: x 1 A. 3 B. 3 . C. 3 . D. 3 . x 2 Câu 21. Tìm lim . Kết quả là x 2 3x 10 x Trang 2/4 - Mã đề 004 4 7 A. . B. 4 . C. 7 . D. . 7 4 a a Câu 22. Biết 2
lim n 1 n n với a,b là các số nguyên dương và là phân số tối giản. Khi đó a b b b bằng A. 1. B. 5 . C. 2 . D. 3 .
Câu 23. Giá trị của B 3 3 n 2 lim
9n n bằng: A. . B. . C. 0 . D. 3 . 3 2 2n n 1
Câu 24. Kết quả của lim bằng n 1 2 2n 1 A. 2 . B. 3 . C. 1. D. 0 .
Câu 25. Cho tứ diện đều ABCD . Tích vô hướng A . B CD bằng? 2 a 2 a A. B. 0 C. D. 2 a 2 2
Câu 26. Cho hàm số f x 2x+1
, hàm số đã cho liên tục trên khoảng nào dưới đây? x 1 A. ; 1 2 . B. ; . 2 1 C. 1; . D. ; 2 . 2 3 n 2n
Câu 27. Kết quả của lim bằng 3 2n 1 A. 3 B. 0 C. 1 1 D. 2
Câu 28. Cho tứ diện ABCD có G là trọng tâm tam giá BCD Khẳng định nào sau đây đúng?
1
2
A. AG AB AC AD .
B. AG AB AC AD . 3 3
1
2
C. AG AB AC AD .
D. AG AB AC AD. 3 3
Câu 29. Cho tứ diện ABCD có AB AC AD và BAC 0 BAD 0
60 , CAD 90 . Gọi I và J lần lượt là
trung điểm của AB và C .
D Hãy xác định góc giữa cặp vectơ IJ và CD ? A. 45 . B. 90 . C. 60 . D. 120 . 1 x
Câu 30. Tính gới hạn L lim . x 1 2 x 1 A. L 2 . B. L 2 . C. L 6 . D. L 4 . 3 1 x khi x 1
Câu 31. Cho hàm số f (x) x 1
. Với giá trị nào của m thì hàm số liên tục tại x 1
2mx 1 khi x 1 A. 2 B. 1 C. 1 D. 2 ìï 1+2x -1 ï khi x ï > 0
Câu 32. Cho hàm số f (x) = í x
. Mệnh đề nào sau đây đúng? ï1ïï+3x khi x £ 0 ïî
A. Hàm số gián đoạn tại x 1 .
B. Hàm số liên tục trên .
C. Hàm số gián đoạn tại x 3 .
D. Hàm số gián đoạn tại x 0 . Trang 3/4 - Mã đề 004
Câu 33. Cho tứ diện ABCD có AB AC và DB DC . Khẳng định nào sau đây đúng?
A. CD AB .
B. AC BD .
C. BC AD .
D. BC CD . Câu 34. Tính 2 lim x 4x 2 x x A. 4 . B. 2 . C. 4 . D. 2 . 2
x ax 1 khi x 2
Câu 35. Tìm a để hàm số f x
có giới hạn khi x 2 . 2
2x x 3a khi x 2 1 1 A. . B. . C. 1. D. 1 . 2 2 PHẦN II: TỰ LUẬN n n 9 3.4
Câu 36. Tính giới hạn lim . n n 6.7 8 1 x
Câu 37. Tìm giới hạn : lim x . x 1 2 1 x 1 x 3
6x 5 4x 3 khi x 1
Câu 38. Tìm các giá trị của tham số m để hàm số f x 2 (x 1)
liên tục tại x 1 ?
2019m khi x 1
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SAB , SAD là các tam giác vuông tại A .
Gọi AE , AF lần lượt là các đường cao của tam giác SAB và SAD . Chứng minh EF vuông góc với SC .
------------- HẾT ------------- Trang 4/4 - Mã đề 004
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 11 Đề ôn tập: SỐ 5 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 005
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Tìm 3 2
lim n 4n 3 . A. 0. B. 1. C. . D. .
Câu 2. Cho hàm số f x xác định trên a;b . Tìm mệnh đề đúng.
A. Nếu hàm số f x liên tục, tăng trên a;b và f a f b 0 thì phương trình f x 0 không có nghiệm trong khoảng ; a b .
B. Nếu phương trình f x 0 có nghiệm trong khoảng ;
a b thì hàm số f x phải liên tục trên ; a b .
C. Nếu hàm số f x liên tục trên a;b và f a f b 0 thì phương trình f x 0 không có nghiệm trong khoảng ; a b .
D. Nếu f a f b 0 thì phương trình f x 0 có ít nhất một nghiệm trong khoảng ; a b .
Câu 3. Biết limu 5 ; limv a ; lim u 3v a n n 2019 , khi đó bằng n n 2024 2018 2014 A. 671 . B. . C. . D. . 3 3 3 x 1
Câu 4. Tìm giới hạn A lim . 2 x 2
x x 4 A. 1 . B. . C. 1. D. . 6
Câu 5. Hàm số nào trong các hàm số dưới đây không liên tục trên ? x x
A. y x . B. y .
C. y sin x . D. y . x 1 x 1
Câu 6. Cho hình lăng trụ tam giác ABCAB C
. Đặt AA a, AB ,
b AC c, BC d . Trong các biểu thức
véctơ sau đây, biểu thức nào đúng.
A. a b c d .
B. a b c .
C. a b c d 0 .
D. b c d 0 . 1
Câu 7. Giới hạn lim bằng x a x a A. 0 . B. . C. 1 . D. . 2a
Câu 8. Giả sử ta có lim f x a và lim g x b . Trong các mệnh đề sau, mệnh đề nào sai? x x A. lim f
x g x a b . x B. lim f
x.g x . a b . x C. lim f
x g x a b . x
f x a D. lim .
x g x b Trang 1/4 - Mã đề 005 Câu 9. 3 lim x 5 bằng x A. . B. 1. C. . D. 5 .
Câu 10. Cho hình lập phương ABC . D AB C D
có cạnh bằng a . Gọi M , N lần lượt là trung điểm của
AD,CD . Góc giữa hai đường thẳng MN và B D là A. o 90 . B. o 45 . C. o 60 . D. o 30 .
Câu 11. Trong không gian cho các đường thẳng a, ,
b c và mặt phẳng P . Mệnh đề nào sau đây sai?
A. Nếu a P và b //P thì a b . B. Nếu a ,
b c b và a cắt c thì b vuông góc với mặt phẳng chứa a và c .
C. Nếu a // b và b c thì c a .
D. Nếu a b và b c thì a // c .
Câu 12. Chọn mệnh đề đúng trong các mệnh đề sau đây?
A. Trong không gian hình biểu diễn của một góc thì phải là một góc bằng nó.
B. Trong không gian hai đường thẳng chéo nhau thì không có điểm chung.
C. Trong không gian hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
D. Nếu mặt phẳng P chứa hai đường thẳng cùng song song với mặt phẳng Q thì P và Q song song với nhau. 2 2x 1 Câu 13. lim bằng: 2
x 3 x 1 A. 2 . B. 2 . C. 1 . D. . 3 3 5 3 8n 2n 1 Câu 14. Tìm lim . 5 2 4n 2n 1 A. 4 . B. 8 . C. 1. D. 2 . 3n 2 Câu 15. lim bằng. n 3 A. 3 . B. 2 2 . C. . D. 1. 3
Câu 16. Cho q là số thực thỏa q 1, kết quả của lim n q bằng A. . B. q . C. 0 . D. .
Câu 17. Giá trị của. F lim n1 n bằng: A. 1 . B. . C. 0 . D. . 2
n 2n 2n
Câu 18. Tính giới hạn lim . 3n 2 2 1 A. . B. 1. C. . D. . 3 3
2n 14 n29 2
Câu 19. Giá trị của C lim bằng: 17 n 1 A. 1 . B. . C. . D. 16 .
Câu 20. Cho hình chóp S.ABCD . Gọi O là giao điểm của AC và BD . Trong các khẳng định sau, khẳng định nào sai?
A. Nếu ABCD là hình bình hành thì SA SB SC SD 4SO .
B. Nếu ABCD là hình thang thì SA SB 2SC 2SD 6SO .
C. Nếu SA SB SC SD 4SO thì ABCD là hình bình hành. Trang 2/4 - Mã đề 005
D. Nếu SA SB 2SC 2SD 6SO thì ABCD là hình thang. 2 x x 2
2x khi x 2
Câu 21. Cho hàm số f (x) x 2
. Khẳng định nào sau đây đúng nhất ? 2
x x 3 khi x 2
A. Hàm số không liên tục tại x 2 .
B. Tất cả đều sai. 0
C. Hàm số liên tục tại x 2 .
D. Hàm số liên tục tại mọi điểm. 0 2 9 x Câu 22. Tìm lim . Kết quả là 2
x3 x 4x 3 A. 3 . B. 3 . C. 4 . D. 4 .
Câu 23. Cho tứ diện ABCD . Tìm giá trị của k thích hợp thỏa mãn: A .
B CD AC.DB A . D BC k A. k 4 . B. k 1. C. k 2 . D. k 0 .
Câu 24. Cho hình lăng trụ đứng tam giác ABCAB C
có đáy ABC là tam giác cân AB AC a ,
BAC 120 , cạnh bên AA a 2 . Tính góc giữa hai đường thẳng AB và BC . A. 45 . B. 60 . C. 90 . D. 30 .
Câu 25. Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ . Chọn đẳng thức đúng:
A. BD BA BC BB .
B. AC AC AB AD .
C. DB DA DD DC .
D. AB AB AA AD . n2 2 5
Câu 26. Kết quả đúng của lim là: 3n 2.5n 1 25 A. 5 . B. . C. 5 . D. . 50 2 2 2
Câu 27. Cho hình lập phương ABC .
D EFGH , góc giữa hai vectơ AC, BG là A. 0 45 . B. 0 30 . C. 0 60 . D. 0 120 .
Câu 28. Cho hình chóp S.ABCD có đáy là hình thoi tâm O và SA SC , SB SD . Trong các mệnh đề sau mệnh đề nào sai?
A. BD SA .
B. AC SA.
C. AC SD .
D. BD AC . 2 x 5x 6 Câu 29. Tìm lim . x2 4x 1 3 3 2 A. . B. 3 . C. 1 . D. . 2 3 2 2
cos 3x cos 4x
Câu 30. Tìm giới hạn A lim .
x0 cos 5x cos 6x Trang 3/4 - Mã đề 005 A. . B. 7 . C. . D. 0. 11
Câu 31. Giá trị của. M 3 2 n 3 lim 1
8n 2n bằng: 1 A. . B. . C. 0 . D. 1 . 12 2 x 2x
Câu 32. Cho hàm số f x
chưa xác định tại x 0 . Để f x liên tục tại x 0 , cần phải gán cho x
f 0 giá trị là bao nhiêu? A. 0 . B. 1 . C. 2 . D. 3 .
Câu 33. Trong các khẳng định dưới đây, khẳng định nào sai?
A. Hàm số y sin x liên tục trên tập .
B. Hàm số y x 3 liên tục tại điểm x 3 . x 1
C. Hàm số y
gián đoạn tại điểm x 0 . x D. Hàm số 4 2
y x 3x 2 liên tục trên tập .
2x m khi x 0
Câu 34. Cho hàm số f x
. Tìm tất cả các giá trị của m để tồn tại giới hạn 1 4x 1 khi x 0 x lim f x. x0 A. m 1. B. m 1 . C. m 3 . D. m 2 . 2
x 5x 6 khi x 2
Câu 35. Cho hàm số y 2x 4
. Tìm a để hàm số liên tục tại x 2 . 2a 3 khi x 2 7 A. a 7 . B. a 7 . C. a 7 . D. a . 4 2 4 2 PHẦN II: TỰ LUẬN u 1 1
Câu 36. Cho dãy số u 1 lim u 2 n
n được xác định bởi: . Tính * u u ;n n n n 1 2 2
Câu 37. Tìm giới hạn : 2x 5x 2 lim 3 x2 x 8
Câu 38. Chứng minh rằng phương trình: 2 m m 4
1 x 2x 2 0 luôn có nghiệm.
Câu 39. Cho 4 điểm ,
A B,C, D trong không gian. Chứng minh rằng: A .
B CD BC.AD C . A BD 0 . Từ đó
suy ra: “Trong một tứ diện nếu có hai cặp cạnh đối vuông góc thì cặp cạnh còn lại cũng vuông góc.”
------------- HẾT ------------- Trang 4/4 - Mã đề 005
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 11 Đề ôn tập: SỐ 6 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 006
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Với k là số nguyên âm, kết quả của giới hạn lim k n là A. 1 . B. . C. 0 . D. .
Câu 2. Cho tứ diện ABCD . Gọi G là trọng tâm tam giác ABD . Khi đó
A. CA CB CD CG .
B. CA CB CD 3CG .
C. CA CB CD 3GC .
D. CA CB CD 2CG .
Câu 3. Giá trị đúng của 2 2 lim
n 1 3n 2 là: A. . B. . C. 0 . D. 1.
Câu 4. Trong không gian cho đường thẳng và điểm O . Qua O có mấy đường thẳng vuông góc với ? A. Vô số. B. 2 . C. 1. D. 3 .
Câu 5. Tìm giới hạn A 2 3 3 lim x x 1 2x x 1 x . A. 4 . B. . C. 0. D. . 3
Câu 6. Trong các mệnh đề mệnh đề sau, mệnh đề nào sai?
A. Hàm số y 2x 1 liên tục trên .
B. Hàm số y cos x liên tục trên .
C. Hàm số y sin x liên tục trên .
D. Hàm số y tan x liên tục trên .
Câu 7. Tìm giới hạn lim 3 x 1 . x2 A. 1. B. . C. . D. 9. 5 x khi x 0
Câu 8. Cho hàm số f x
. Mệnh đề nào sau đây đúng? 2
x 1 khi x 0
A. Hàm số liên tục trên .
B. Hàm số liên tục tại x 0 .
C. Hàm số gián đoạn tại x 1.
D. Hàm số gián đoạn tại x 0 . x 15
Câu 9. Kết quả của giới hạn lim là x 2 x 2 A. . B. 1. C. . D. 0 .
Câu 10. Biết limu và lim v . Khẳng định nào sau đây sai ? n n 1 A. lim 0. B. lim( 3 v ) . u n n
C. lim(u v ) 0 .
D. lim(u v ) . n n n n
Câu 11. Cho lim f x ;
L lim g x M , với L, M . Chọn khẳng định sai. x 0 x x 0 x A. lim f
x g x L M .
B. lim f x .g x . L M . x 0 x x 0 x f x L C. lim . D. lim f
x g x L M . x 0 x g x M x 0 x Trang 1/4 - Mã đề 006
Câu 12. Cho tam giác ABC ở trong mp và phương l . Biết hình chiếu (theo phương l ) của tam giác
ABC lên mp P là một đoạn thẳng. Khẳng định nào sau đây đúng ?
A. P
B. / /l hoặc l C. ; A ; B C đều sai.
D. / / P n 2 Câu 13. Tính lim . Kết quả là 2 n 3n 1 2 A. 2 . B. 0 . C. 1. D. . 3
Câu 14. Cho hai đường thẳng a,b lần lượt có véctơ chỉ phương là u,v . Giả sử u,v 125 . Tính góc giữa
hai đường thẳng a,b . A. 55 . B. 125 . C. 5 5 . D. 1 25 . 3 2x
Câu 15. Tính giới hạn lim . x 2 x 2 A. . B. 3 . C. . D. 2 . 2 2 3 n 3n
Câu 16. Giới hạn lim bằng 3 2n 5n 2 3 1 3 A. 0 . B. . C. . D. . 2 2 2
Câu 17. Cho tam giác ABC có diện tích S . Tìm giá trị của k thích hợp thỏa mãn: 1 2 2 S
AB .AC 2k A . B AC 2 . 2 1 A. k 1 . B. k = 0. C. k . D. k 1. 4 2
Câu 18. Cho hàm số f x 3 2
x –1000x 0,01. Phương trình f x 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây? I. 1 ;0 . II. 0; 1 . III. 1;2 . A. Chỉ II. B. Chỉ III. C. Chỉ I. D. Chỉ I và II.
Câu 19. Hàm số nào sau đây không liên tục trên ? x 1 x
A. f x .
B. f x 1 . 2 x 1 x 1
C. f x sin x .
D. f x 3 2
x 2x x 7 . 5
Câu 20. Cho tứ diện ABCD có G là trọng tâm tam giác BCD . Đặt x AB ; y AC ; z AD . Khẳng định nào sau đây đúng? 2 2
A. AG x y z .
B. AG x y z . 3 3 1 1
C. AG x y z .
D. AG x y z . 3 3 2 x 12x 35 Câu 21. lim bằng x5 25 5x 2 A. . B. 2 . C. . D. . 5 5 Trang 2/4 - Mã đề 006 3 x 1 khi x 1 Câu 22. Cho hàm số x 1 f (x)
. Khẳng định nào sau đây đúng nhất ? 3
1 x 2 khi x 1 x 2
A. Hàm số gián đoạn tại các điểm x 1 .
B. Hàm số liên tục trên .
C. Hàm số không liên tục trên .
D. Hàm số không liên tục trên 1: .
Câu 23. Hình lập phương ABC . D AB C D
cạnh a . Tính độ dài vectơ x AA AC theo a . a 6 A. . B. a 2 .
C. 1 3a . D. a 6 . 2
Câu 24. Cho tứ diện ABCD có AB AC 2, DB DC 3. Khẳng định nào sau đây đúng?
A. DC ABC .
B. BC AD .
C. AC BD .
D. AB BCD . sin 5x x 0
Câu 25. Cho hàm số f x 5x
. Tìm a để f x liên tục tại x 0.
a 2 x 0 A. 1. B. 1 . C. 2 . D. 2. 2
4n 1 n 2 Câu 26. lim bằng 2n 3 3 A. . B. 2. C. 1. D. . 2
Câu 27. Cho tứ diện ABCD có DA DB DC AC AB a ,
ABC 45 . Tính góc giữa hai đường thẳng AB và DC . A. 90 . B. 30 . C. 60 . D. 120 . 2 x 1
Câu 28. Biết rằng lim
ax b 5
. Tính tổng a b .
x x 2 A. 5 . B. 7 . C. 8 . D. 6 . Câu 29. Giới hạn 2 lim
n n n bằng 1 A. . B. 0 . C. . D. . 2
Câu 30. Trong các dãy số sau, dãy số nào là dãy có giới hạn 0 ? 2 n 2n 1 2 3 n A. u . B. u . n 2 3 n n n 2 n 1 3 n n 2 2n 1 C. u . D. u . n 2 n 2 n 2 n 2n 3
1 3 5 .... 2n 1
Câu 31. Tính giới hạn lim . 2 3n 4 1 2 A. . B. . C. 1. D. 0 . 3 3
Câu 32. Trong không gian cho hai tam giác đều ABC và ABC ' có chung cạnh AB và nằm trong hai mặt
phẳng khác nhau. Gọi M , N, P, Q lần lượt là trung điểm của các cạnh AC, CB, BC ' và C ' A . Hãy xác
định góc giữa cặp vectơ AB và CC ' ? A. 0 90 . B. 0 120 . C. 0 60 . D. 0 45 . cos x
Câu 33. Tìm giới hạn L lim . x 2 x 2 Trang 3/4 - Mã đề 006 A. L 0 B. L C. L 1 D. L 1 2 5x 3 3 m
Câu 34. Giới hạn lim ( , m ,
n k Z ) . Tính m n k ? x0 x n k A. 8 . B. 0 C. 6 . D. 4 .
Câu 35. Giới hạn lim n n 4 n 3 bằng 7 A. 1 . B. . C. . D. 0 . 2 2 PHẦN II: TỰ LUẬN 1 1 1 1 1 1
Câu 36. Tính tổng S ... .... 2 3 4 9 2n 3n 2
x a 3 x 2 a 1
Câu 37. Tính giới hạn của hàm số f x
khi x 2 theo a . 2 x 4 2x a khi x 1
Câu 38. Tìm a để hàm số liên tục trên với f x 3 2 .
x x 2x 2 khi x 1 x 1
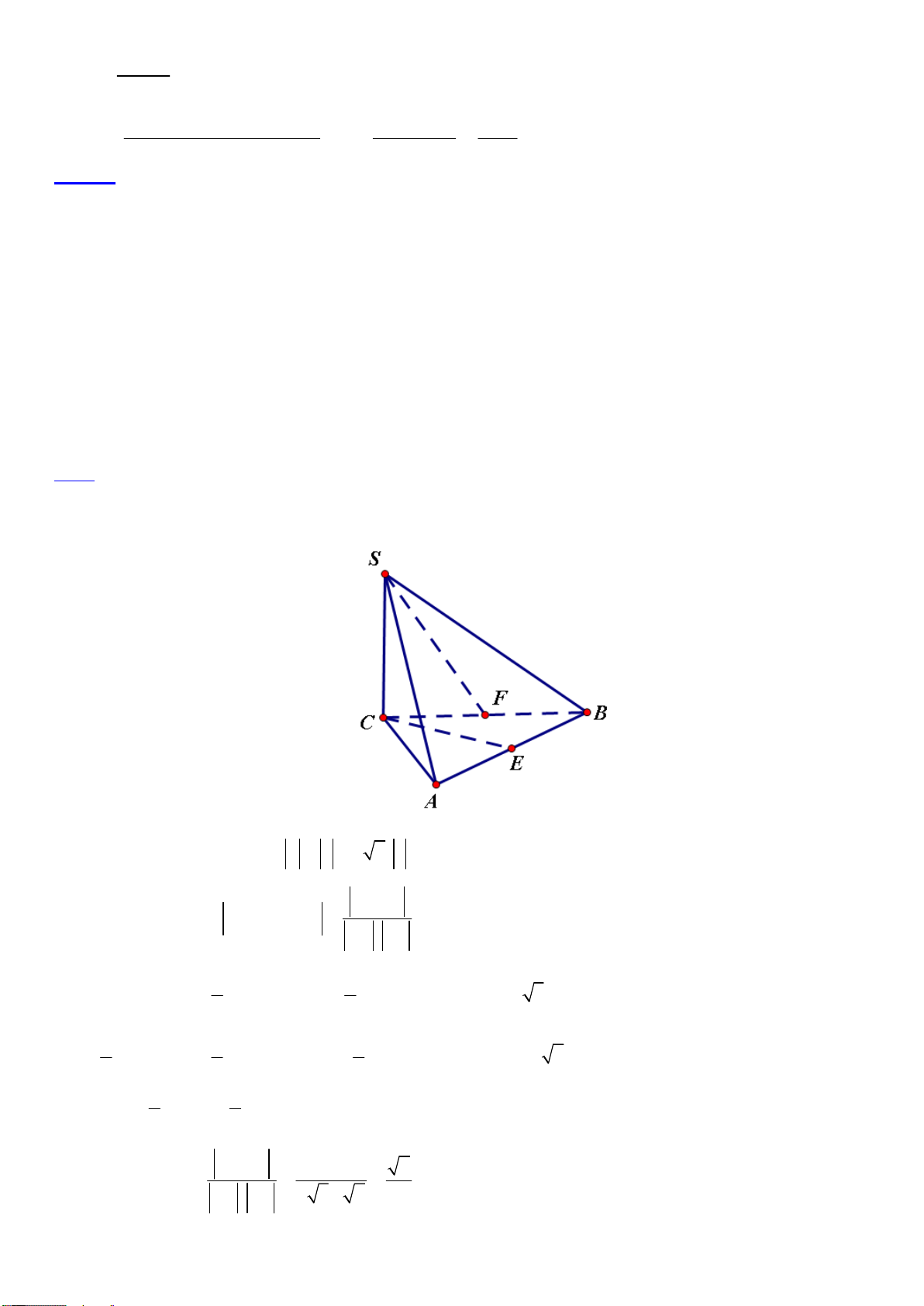
Câu 39. Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 4 2 , SC vuông góc với CA và CB ,
SC 2 . Gọi E, F lần lượt là trung điểm cạnh AB, BC . Tính góc giữa hai đường thẳng CE và SF .
------------- HẾT ------------- Trang 4/4 - Mã đề 006
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 11 Đề ôn tập: SỐ 7 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 007
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Tính giới hạn L 2
lim 3n 5n 3. A. L . B. L . C. L 5. D. L 3.
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD 2a, SA a và SA ABCD.
Gọi M , N lần lượt là trung điểm của AB và CD . Tính khoảng cách giữa đường thẳng MD và mặt phẳng SBN . a a
A. d MD SBN 4 , .
B. d MD SBN 2 , . 33 33 a a
C. d MD SBN 3 , .
D. d MD,SBN . 33 33 3 2 3x x 1 Câu 3. lim bằng x 1 x 2 5 5 A. 5. B. 1. C. . D. . 3 3
Câu 4. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Trong không gian, nếu hai đường thẳng cùng vuông góc với một đường thẳng thì hai đường thẳng đó song song.
B. Trong không gian, nếu hai đường thẳng cùng vuông góc với một đường thẳng thì hai đường thẳng đó vuông góc với nhau.
C. Trong không gian, nếu một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau
thì đường thẳng đó song song với đường thẳng còn lại
D. Trong không gian, nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì
vuông góc với đường thẳng còn lại.
Câu 5. Nếu limu L thì lim u 9 bằng n n A. L 9 . B. L 3. C. L 3. D. L 9 .
Câu 6. Tìm dạng hữu tỷ của số thập phân vô hạn tuần hoàn P = 2,13131313. ., 211 A. P = 211 . B. P = 212 . C. P = 213 D. P = . 100 99 99 100 x 2
Câu 7. Tính giới hạn lim ta được kết quả x2 x 1 A. 3 . B. 1. C. 2 . D. 4 . 1 2n Câu 8. lim bằng 3n 1 2 2 A. 1 . B. . C. 1. D. . 3 3 3 2 3 n 3n Câu 9. lim bằng: 3 2n 5n 2 Trang 1/4 - Mã đề 007 3 1 A. 1 . B. . C. . D. 0 . 2 5 2
Câu 10. Cho hình chóp S.ABCD có đáy là hình thoi tâm O và SA SC , SB SD . Trong các mệnh đề sau mệnh đề nào sai?
A. BD SA .
B. AC SA.
C. AC SD .
D. BD AC . 3 ìï 4x -2 ïï khi x ï ¹ 2
Câu 11. Cho hàm số f (x)= í x-2
. Xác định a để hàm số liên tục trên R : ïïïax ï +3 khi x = 2 î 4 A. a = 4 . B. a = - . C. a = - 1 1 . D. a = . 3 3 6
Câu 12. Cho hình lập phương ABC .
D A' B 'C ' D ' . Chọn khẳng định sai?
A. Góc giữa AD và B 'C bằng 0 45 .
B. Góc giữa BD và A'C ' bằng 0 90 .
C. Góc giữa AC và B ' D ' bằng 0 90 .
D. Góc giữa B ' D ' và AA' bằng 0 60 .
Câu 13. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AB và C .
D Tìm giá trị thực của k thỏa
mãn đẳng thức vectơ MN k AC BD. A. k 1 2. B. k 1 . C. k . D. k 3. 2 3 2
x ax 1 khi x 2
Câu 14. Tìm a để hàm số f x
có giới hạn tại x 2 2
2x x 1 khi x 2 A. 2 B. 1 C. 1 D. 2
Câu 15. Cho hình hộp ABC .
D A B C D . Khẳng định nào dưới đây là đúng? 1 1 1 1
A. BD, BD , BC đồng phẳng.
B. CD , AD, A B đồng phẳng. 1 1 1 1 1
C. CD , AD, A C đồng phẳng.
D. AB, AD, C A đồng phẳng. 1 1 1
Câu 16. Cho hình hộp ABC . D AB C D
. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ
AC BA' k DB C 'D 0. A. k 4. B. k 2. C. k 0. D. k 1. x
Câu 17. Cho lim (x 2) . Tính giới hạn đó. 2 x2 x 4 A. . B. 1. C. 0 . D. . sin x sin x khi x 1
Câu 18. Biết rằng lim
1. Tìm giá trị thực của tham số m để hàm số f x x 1 liên x0 x m khi x 1 tục tại x 1. A. m 1 . B. m 1.
C. m .
D. m .
Câu 19. Trong các giới hạn sau giới hạn nào bằng 1 ? 2 2x x 1 3 2 x x 3 2 x 1 2x 3 A. lim B. lim C. lim D. lim 2 x 3x x 2 3
x 5x x
x x 1 2
x x 5x
Câu 20. Cho hình hộp ABC . D AB C D
có AB a, AC b, AA c . Gọi I là trung điểm của B C , K là
giao điểm của AI và B D
. Mệnh đều nào sau đây đúng? 1
A. DK 4a 2b 3c.
B. DK 4a 2b 3c. 3 1
C. DK 4a 2b c.
D. DK 4a 2b c. 3 Trang 2/4 - Mã đề 007
Câu 21. Tìm m để hàm số y f x 2
x 2 x 2 khi x 2 liên tục trên ? 2 5
x 5m m khi x 2
A. m 2; m 3 B. m 2 ;m 3
C. m 1; m 6 D. m 1 ;m 6 2 2x 6 Câu 22. Tính lim
a b ( a , b nguyên). Khi đó giá trị của P a b bằng x 3 x 3 A. 6 . B. 10 . C. 5 . D. 7 .
Câu 23. Giới hạn lim n n 4 n 3 bằng 1 A. 7 . B. . C. . D. 0 . 2 2
2x khi x 0
Câu 24. Số điểm gián đoạn của hàm số h x 2
x 1 khi 0 x 2 là: 3
x 1 khi x 2 A. 0. B. 1. C. 2. D. 3. 2018 2 x 4x 1
Câu 25. Tìm giới hạn: lim x 2x 2019 1 1 1 1 A. . B. . C. . D. 0. 2018 2 2019 2 2017 2 2 x
Câu 26. Kết quả của giới hạn lim là: 2
x2 2x 5x 2 1 A. . B. . C. . 1 D. . 3 3
Câu 27. Cho tứ diện đều ABC .
D Số đo góc giữa hai đường thẳng AB và CD bằng: A. 0 60 . B. 0 30 . C. 0 90 . D. 0 45 .
Câu 28. Cho tứ diện ABCD và điểm G thỏa mãn GA GB GC GD 0 ( G là trọng tâm của tứ diện).
Gọi G là giao điểm của GA và mặt phẳng BCD. Khẳng định nào dưới đây là đúng? 0
A. GA 2G . G
B. GA 4G . G
C. GA 3G . G
D. GA 2G . G 0 0 0 0 2
x 3x ax
Câu 29. Cho a , b là các số thực khác 0 . Để giới hạn lim 3 thì x bx 1 a 1 a a a A. 1 3. B. 1 3 . C. 1 3. D. 3. b b b b 1 1 1
Câu 30. Giá trị của giới hạn lim ... là: 1.2 2.3 nn 1 A. . 1 B. . C. 1. D. 0. 2 x 1 1 khi x 0
Câu 31. Tìm tất cả các giá trị thực của m để hàm số f (x) x liên tục trên . 2
x 1 m khi x 0 1 3 1 A. m . B. m . C. m . D. m 2 . 2 2 2 2 2 3 2
1 2 3 ... n Câu 32. Tính lim
2nn 76n 5 Trang 3/4 - Mã đề 007 1 1 1 A. . B. . C. . D. . 6 2 6 2
Câu 33. Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau và OA OB OC . Gọi M là
trung điểm của BC . Góc giữa hai đường thẳng OM và AB bằng A. 0 45 B. 0 90 C. 0 30 D. 0 60 1 1 1
Câu 34. Cho dãy số u u = + +...+ . limu . n với Tính n 1.3 3.5 (2n- )1 (.2n+ )1 n 1 1 A. . B. 0. C. 1. D. . 2 4 Câu 35. Thu gọn 2 3
S 1 tan tan tan với 0 . 4 tan A. S . B. 2 S tan . 1 tan 1 cos C. S . D. S . 1 tan 2 sin 4 PHẦN II: TỰ LUẬN
Câu 36. Có bao nhiêu giá trị nguyên của tham số a thuộc khoảng 1 0;10 để L
n 2a 3 lim 5 3 2 n . a b b a
Câu 37. Biết rằng a b 4 và lim
hữu hạn. Tính giới hạn L lim . 3 x 1
1 x 1 x 3 x 1 1 x 1 x
x x 2 khi x 2 2 x 4
Câu 38. Cho hàm số f x 2
x ax 3b khi x 2 liên tục tại x 2. Tính I a b .
2a b 6 khi x 2
Câu 39. Gọi M , N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABC .
D Gọi I là trung
điểm của đoạn MN và P là một điểm bất kỳ trong không gian. Tìm giá trị thực của k thỏa mãn đẳng thức
vectơ PI k PA PB PC PD.
------------- HẾT ------------- Trang 4/4 - Mã đề 007
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 11 Đề ôn tập: SỐ 8 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 008
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN u
Câu 1. Cho các dãy số u , v
lim u a, lim v lim n n n và thì bằng n n vn A. 1. B. 0 . C. . D. .
Câu 2. Cho hàm số f x xác định trên a;b . Tìm mệnh đề đúng.
A. Nếu phương trình f x 0 có nghiệm trong khoảng ;
a b thì hàm số f x phải liên tục trên ; a b .
B. Nếu hàm số f x liên tục trên a;b và f a f b 0 thì phương trình f x 0 không có nghiệm trong khoảng ; a b .
C. Nếu f a f b 0 thì phương trình f x 0 có ít nhất một nghiệm trong khoảng ; a b .
D. Nếu hàm số f x liên tục, tăng trên ;
a b và f a f b 0 thì phương trình f x 0 không có nghiệm trong khoảng ; a b .
Câu 3. Xét trong không gian, mệnh đề nào dưới đây là đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì vuông góc với nhau.
C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại. 3 3n 2n 1
Câu 4. Tìm I lim . 4 4n 2n 1 A. I . B. I 7 0. C. I 3 . D. I . 2 4 2 x 2x 3
Câu 5. Giới hạn lim bằng? x 1 x 1 A. 2 . B. 1. C. 0 . D. 3 . u
Câu 6. Cho các dãy số u , v
lim u a, lim v lim n n n và thì bằng n n vn A. . B. 1. C. 0 . D. .
Câu 7. Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại. Câu 8. 3
lim 2n 3n là: A. 2 . B. 3 . C. . D. . Trang 1/4 - Mã đề 008 3 2n 3n
Câu 9. Kết quả của giới hạn lim là: 2 4n 2n 1 5 3 A. 0 B. . C. . D. . 7 4
Câu 10. Giá trị của lim 2
3x 2x 1 bằng: x 1 A. 3 . B. . C. 2 . D. 1.
Câu 11. Giá trị của giới hạn 3 3 3 3 lim
n 1 n 2 bằng: A. 1. B. 3. C. 2. D. 0. 2 21 x 7 21 1 2x
Câu 12. Giá trị của giới hạn lim là: x0 x 21 2 21 2 21 2 21 1 2 A. . B. . C. . D. . 7 5 5 7 2
x 3x 2 khi x 1
Câu 13. Để hàm số y
liên tục tại điểm x 1
thì giá trị của a là 4x a khi x 1 A. 1 . B. 4 . C. 4. D. 1.
Câu 14. Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a .
Gọi M và N lần lượt là trung điểm của AD và SD . Số đo của góc MN, SC bằng A. 90 . B. 60 . C. 45 . D. 30 .
Câu 15. Cho tứ diện ABC .
D Gọi M , N lần lượt là trung điểm của AD, BC. Khẳng định nào dưới đây là
khẳng định sai?
A. Ba vectơ AB, DC, MN đồng phẳng.
B. Ba vectơ AB, AC, MN không đồng phẳng.
C. Ba vectơ AN, CM , MN đồng phẳng.
D. Ba vectơ BD, AC, MN đồng phẳng.
Câu 16. Cho hình lập phương ABC . D AB C D có cạnh bằng .
a Gọi G là trọng tâm của tam giác AB C .
Khẳng định nào dưới đây là đúng?
A. AC 4 A . G
B. BD 4 B . G
C. BD 3 B . G
D. AC 3 A . G x m x
Câu 17. Tìm tất cả các giá trị của tham số thực m sao cho hàm số f x 2 khi 0 liên tục trên mx 2 khi x 0 . A. m 2 . B. m 0 . C. m 2 . D. m 2 . 2
x x x
Câu 18. Giá trị của giới hạn lim là: 2 x0 x A. . B. 1. C. . D. 0. 2
x 3x 2 khi x 1
Câu 19. Có bao nhiêu số tự nhiên m để hàm số f x x 1
liên tục tại điểm x 1? 2 m m 1 khi x 1 A. 0. B. 3 . C. 2 . D. 1. Câu 20. Tính 2 lim x 4x 2 x x A. 2 . B. 4 . C. 2 . D. 4 . 2 x 13x 30
Câu 21. Kết quả của giới hạn lim là: x 3
x 3 2x 5 Trang 2/4 - Mã đề 008 2 A. 0. B. . C. 2 . D. 2. 15
Câu 22. Cho tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây là sai?
2
A. GA GB GC GD 0.
B. AG AB AC AD. 3
1
1
C. AG AB AC AD.
D. OG OA OB OC OD. 4 4 x 3 2 Câu 23. lim bằng x 1 x 1 1 A. . B. 1 . C. . D. 1. 4 2 x 3 Câu 24. lim bằng 2
x x 2 A. 2 3 . B. . C. 1. D. 0 . 2
Câu 25. Cho tứ diện ABCD có AB CD . Gọi I, J , E, F lần lượt là trung điểm của AC, BC, BD, AD . Góc
IE, JF bằng A. 60 . B. 90 . C. 30 . D. 45 .
Câu 26. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AB, CD và G là trung điểm của MN.
Khẳng định nào dưới đây là sai?
A. GA GB GC GD 0.
B. GM GN 0.
C. MA MB MC MD 4M . G
D. GA GB GC G .
D
Câu 27. Cho hình lăng trụ ABC.AB C
. Gọi M là trung điểm của BB . Đặt CA a, CB b, AA c. Khẳng
định nào dưới đây là đúng? 1 1 1 1
A. AM b c a.
B. AM b a c.
C. AM a c . b
D. AM a c . b 2 2 2 2 2 x 16 khi x 4
Câu 28. Tìm m để hàm số f x x 4
liên tục tại điểm x 4 .
mx 1 khi x 4 7 7 A. m . B. m 8 . C. m . D. m 8 . 4 4 Câu 29. Rút gọn 2 4 6 2 1 cos cos cos c s o n S x x x
x với cos x 1 . 1 1 A. S . B. 2 S sin . x C. 2 S cos . x D. S . 2 cos x 2 sin x
Câu 30. Tứ diện đều có góc tạo bởi hai cạnh đối diện bằng A. 45 . B. 90 . C. 60 . D. 30 . 1 1 1 Câu 31. lim 1 ... bằng: 1.2 2.3 n(n 1) A. 3 . B. 2 . C. 1. D. 0 . 2 x 1 khi x 1
Câu 32. Cho hàm số f x x 1
. Tìm m để hàm số f x liên tục trên .
m2 khi x 1 A. m 1. B. m 2 . C. m 4 . D. m 4 . Trang 3/4 - Mã đề 008 1 1 1
Câu 33. Cho dãy số (u u = + +...+ lim u n ) với . Ta có bằng: n 1.3 3.5 (2n- )1(2n+ )1 n 1 1 A. . B. . C. 1. D. 2 . 2 4 1 u n 2
Câu 34. Cho dãy số có giới hạn u . limu .
n xác định bởi Tính 1 n u , n 1 n 1 2 u n A. lim u 1. B. lim u 1 0. C. lim u . D. lim u 1 . n n n 2 n 2
x 3x 1 Câu 35. Cho lim +ax
b 1.Khi đó giá trị của biểu thức T a b bằng x x 1 A. 2 . B. 2 . C. 0 . D. 1. PHẦN II: TỰ LUẬN 2 an 1 1
Câu 36. Có bao nhiêu giá trị nguyên của a thuộc 0;20 sao cho lim 3 là một số nguyên. 2 3 n 2n Câu 37. Biết rằng
x x x a b S 5a . b x 2 lim 5 2 5 5 . Tính 4x 1 1 khi x 0
Câu 38. Tìm a để hàm số f x 2
ax 2a 1 x
liên tục tại x 0 . 3 khi x 0
Câu 39. Cho hình hộp ABC . D AB C D
. Gọi P và Q là hai điểm lần lượt trên hai cạnh AB và AD sao cho 2 3 AP AB, AQ
AD , gọi I và J là hai điểm nằm trên hai đoạn B Q
và AP sao cho IJ song song với AC . 3 4 IB Hãy tính tỉ số . QB
------------- HẾT ------------- Trang 4/4 - Mã đề 008
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 11 Đề ôn tập: SỐ 9 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 009
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN 3 n 2n
Câu 1. Kết quả của giới hạn lim là: 2 1 3n 1 A. . 2 B. . C. . D. . 3 3 1
Nếu lim u = L thì lim bằng bao nhiêu? n 3 u +8 n 1 1 1 1 A. . B. C. . D. 3 L +8 L + 8 3 L + 2 L +8
Câu 3. Giá trị của giới hạn 2 lim x 4 là: x 3 A. 1. B. 2. C. 3. D. 0.
Câu 4. Phát biểu nào trong các phát biểu sau là đúng?
A. Nếu hàm số y f x có đạo hàm phải tại x0 thì nó liên tục tại điểm đó.
B. Nếu hàm số y f x có đạo hàm tại x0 thì nó liên tục tại điểm đó.
C. Nếu hàm số y f x có đạo hàm tại x x
0 thì nó liên tục tại điểm . 0
D. Nếu hàm số y f x có đạo hàm trái tại x0 thì nó liên tục tại điểm đó. 2 n n 5
Câu 5. Tính giới hạn L lim . 2 2n 1 3 A. L 1 . B. L . C. L 2. D. L 1. 2 2
Câu 6. Khẳng định nào sau đây là đúng?
A. Ta nói dãy số u n u n có giới hạn khi
nếu có thể nhỏ hơn một số dương bất kì, kể từ một n
số hạng nào đó trở đi.
B. Ta nói dãy số u n u n có giới hạn khi
nếu có thể lớn hơn một số dương bất kì, kể từ một n
số hạng nào đó trở đi.
C. Ta nói dãy số u a u a n
lim u a n 0
n có giới hạn là số (hay dần tới ) khi , nếu . n n
D. Ta nói dãy số u 0 n u
n có giới hạn là
khi dần tới vô cực, nếu
có thể lớn hơn một số dương tùy ý, n
kể từ một số hạng nào đó trở đi.
Câu 7. Trong không gian cho đường thẳng và điểm O . Qua O có bao nhiêu đường thẳng vuông góc với ? A. 1 . B. 3 . C. 2 . D. Vô số.
Câu 8. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau. Trang 1/4 - Mã đề 009
C. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
D. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau. Câu 9. 2 lim x 4 bằng x 3 A. 5 . B. 1. C. 5 . D. 1 . 3
Câu 10. Giá trị của giới hạn lim là: 2 4n 2n 1 3 A. . B. . C. 0. D. 1 . 4 2016 x x 2 khi x 1
Câu 11. Cho hàm số f x 2018x 1 x 2018
. Tìm k để hàm số f x liên tục tại x 1. k khi x 1 2017. 2018
A. k 2 2019 . B. k . 2 C. k 20016 1. D. k 2019 . 2017 x 1 Câu 12. lim bằng x 1 x 1 A. 0 B. . C. . D. 1.
Câu 13. Cho hình hộp ABC .
D A B C D . Gọi M là trung điểm của A .
D Khẳng định nào dưới đây là đúng? 1 1 1 1
1 1
A. C M C C C D C B .
B. BB B A B C 2B . D 1 1 1 1 1 1 2 2 1 1 1 1 1 1
1
C. B M B B B A B C .
D. C M C C C D C B . 1 1 1 1 1 1 1 1 1 1 1 1 2
Câu 14. Cho tứ diện ABC .
D Đặt AB a, AC b, AD c . Gọi M là trung điểm của đoạn thẳng BC. Đẳng
thức nào dưới đây là đúng? 1 1
A. DM a 2b c.
B. DM a b 2c. 2 2 1 1
C. DM 2a b c.
D. DM a 2b c. 2 2
Câu 15. Cho hình hộp ABC . D AB C D tâm .
O Gọi I là tâm của hình hình hành ABC . D Đặt
AC u, CA v, BD x, DB . y Khi đó 1 1
A. 2OI u v x y.
B. 2OI u v x y. 4 2 1 1
C. 2OI u v x y.
D. 2OI u v x y. 2 4
Câu 16. Cho tứ diện ABCD có AB AC AD và BAC BAD 60 ,
CAD 90 . Gọi I và J lần lượt là
trung điểm của AB và CD . Hãy xác định góc giữa cặp vectơ AB và IJ ? A. 120 . B. 90 . C. 60 . D. 45 .
Câu 17. Cho hình lập phương ABC . D AB C D
. Gọi M , N, P lần lượt là trung điểm của AB, BC,C D . Xác
định góc giữa MN và AP . A. 60 . B. 30 . C. 90 . D. 45 1
Câu 18. Kết quả của giới hạn. 2
lim x sin x . là: 2 x0 x Trang 2/4 - Mã đề 009 A. . p B. + . ¥ C. 0 . D. -1 . 2 x 3
Câu 19. Giá trị của lim là. x x 3 A. 1 B. . C. 1 . D. .
Câu 20. Cho tam giác đều ABC cạnh a 2 . Hỏi mệnh đề nào sau đây sai?
A. BC.CA 2 .
B. BC AC.BA 2.
C. AB BC.AC 4 .
D. AB.AC.BC 2BC . Câu 21. Tính I n 2 2 lim n 2 n 1 . A. I 0 . B. I 3 . C. I .
D. I 1, 499 . 2 2
x 2x 3 ví i x 3
Câu 22. Cho hàm số f x 1
ví i x 3. Khẳng định nào dưới đây sai? 2 3 2x ví i x 3
A. lim f x 1 5.
B. lim f x 6. x 3 x 3
C. Không tồn tại lim f x.
D. lim f x 6. x3 x 3
Câu 23. Cho hình hộp ABC .
D EFGH. Gọi I là tâm của hình bình hành ABEF và K là tâm của hình bình
hành BCGF. Khẳng định nào dưới đây là đúng?
A. BD, EK, GF đồng phẳng.
B. BD, IK, GC đồng phẳng.
C. BD, AK, GF đồng phẳng.
D. BD, IK, GF đồng phẳng.
Câu 24. Tìm tất cả các giá trị của tham số m để hàm số
liên tục tại x = 2 .
A. Không tồn tại m B. m 2 C. m 2 D. m 3
Câu 25. Hàm số nào trong các hàm số sau đây liên tục tại điểm x 1? 2x 1
A. f x .
B. f x 1 2x . 2 x 1 x x x x
C. f x 1 khi 1 .
D. f x 1 khi 1 . 3
x 1 khi x 1 3
x 1 khi x 1 3
x 1 khi x 1
Câu 26. Cho hàm số y
, m là tham số. Tìm m để hàm số liên tục trên .
x m khi x 1 A. m 1 . B. m 3 . C. m 3 . D. m 5 . 2 4x x 1
Câu 27. Kết quả của giới hạn lim là: x x 1 A. 2 . B. 1 . C. 2 . D. . 3 x 1
Câu 28. Giá trị của giới hạn lim là: x 1 3 4x 4 2 A. 1. B. . C. 1 . D. 0.
Câu 29. Số thập phân vô hạn tuần hoàn 0,5111 a
được biểu diễn bởi phân số tối giản . Tính tổng b T a . b Trang 3/4 - Mã đề 009 A. 137. B. 17. C. 68. D. 133.
2 a x 3 Câu 30. Biết rằng
có giới hạn là khi x (với a là tham số). Tính giá trị nhỏ nhất của 2 x 1 x 2
P a 2a 4. A. P 5. B. P 1. C. P 3. D. P 4. min min min min 2 an 1 1
Câu 31. Có bao nhiêu giá trị nguyên của a thuộc 0;20 sao cho lim 3 là một số nguyên. 2 3 n 2n A. 1. B. 3. C. 2. D. 4.
3x a 1, khi x 0
Câu 32. Cho hàm số f x
. Tìm tất cả giá trị của a để hàm số đã cho liên tục tại 1 2x 1 , khi x 0 x điểm x 0 . A. a 4 . B. a 1. C. a 3. D. a 2 . n n 1 4 2 1
Câu 33. Tìm tất cả giá trị nguyên của a thuộc 0;2018 để 4 lim .
3n 4na 0 1 4 2 A. 2007. B. 2008. C. 2017. D. 2016. 2 n
Câu 34. Cho dãy số u u 2 n 2 ... 2 . n với
Mệnh đề nào sau đây đúng ?
A. lim u .
B. Không tồn tại lim u . n n
C. lim u . 2 D. lim u . n n 1 2
Câu 35. Cho tứ diện ABCD trong đó AB 6, CD 3, góc giữa AB và CD là 60 và điểm M trên BC
sao cho BM 2MC . Mặt phẳng P qua M song song với AB và CD cắt BD, AD, AC lần lượt tại
N, P,Q . Diện tích MNPQ bằng: 3 A. 2 3. B. . C. 2 2. D. 3. 2 PHẦN II: TỰ LUẬN n 5 n 1 2 1 2 2n 3 a 5
Câu 36. Biết rằng lim
c với a, , b c .
Tính giá trị của biểu thức n n 1 2 n 1 5.2 5 3 b 2 2 2
S a b c .
Câu 37. Giá trị của giới hạn 2 3 3 2 lim x x x x x là:
1 x 1 x khi x 0
Câu 38. Tìm tất cả các giá trị của m để hàm số x f x
liên tục tại x 0 . 1 x m khi x 0 1 x
Câu 39. Cho tứ diện ABCD có AB CD a . Gọi M , N lần lượt là trung điểm của AD và BC . Xác định
độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng 30 .
------------- HẾT ------------- Trang 4/4 - Mã đề 009
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 11 Đề ôn tập: SỐ 10 Mã đề thi
Họ và tên :………………………………………...Lớp:………….......……..……… 010
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. L 3
lim 5n n là: A. -4 . B. -¥ . C. +¥ . D. -6 .
Câu 2. Trong không gian cho đường thẳng và điểm O . Qua O có mấy đường thẳng vuông góc với ? A. 3 . B. Vô số. C. 2 . D. 1. x 1
Câu 3. Giá trị của giới hạn lim là: 4 x 1
x x 3 3 3 2 A. 2 . B. . C. . D. . 2 3 2 3
Câu 4. Cho hình lập phương ABC . D AB C D
. Đường thẳng nào sau đây vuông góc với đường thẳng BC? A. AD . B. AC . C. BB .
D. AD .
Câu 5. Cho các mệnh đề:
1) Hàm số y f x có đạo hàm tại điểm x thì nó liên tục tại điểm x . 0 0
2) Hàm số y f x liên tục tại điểm x thì nó có đạo hàm tại điểm x . 0 0
3) Hàm số y f x liên tục trên đoạn a;b và f a. f b 0 thì phương trình f x 0 có ít nhất một
nghiệm trên khoảng a;b .
4) Hàm số y f x xác định trên đoạn a;b thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó. Số mệnh đề đúng là: A. 3 . B. 1. C. 2 . D. 4 .
Câu 6. Phát biểu nào trong các phát biểu sau là sai? A. lim n
q 0 | q | 1 .
B. lim u c ( u c là hằng số). n n 1 1 C. lim 0 k 1 . D. lim 0 . k n n
Câu 7. Dãy số nào sau đây có giới hạn bằng 0 ? 2 n 6 n 3 n 3n A. 2
u n 4n . B. u . C. u . D. u . n n n 3 5 n n 1
Câu 8. Phát biểu nào sau đây là sai?
A. limu = c (u = c là hằng số ). B. lim n q = 0 q > . ( )1 n n 1 1 C. lim = 0 . D. lim = 0 k > . ( )1 n k n 3 2
3x 4 3x 2
Câu 9. Giá trị của giới hạn lim là: x2 x 1 A. . 3 B. 2 . C. . D. 0. 2 3 Trang 1/4 - Mã đề 010 1 Câu 10. lim bằng 2n 7 1 A. 0 . B. 1 . C. . D. . 2 7 x 1 khi x 1
Câu 11. Cho hàm số f x x 1
. Tìm a để hàm số liên tục tại x 1. 0 a khi x 1 A. a 1 0 . B. a 1 . C. a . D. a 1. 2 2
Câu 12. Cho hình lăng trụ tam giác ABC.AB C
. Đặt AA a, AB b, AC c, BC d . Khẳng định nào dưới đây là đúng?
A. a b c d.
B. a b c.
C. a b c d 0.
D. b c d 0. 2 x x 2 3
Câu 13. Số nào trong các số sau là bằng lim ? x3 x 3 7 3 7 3 3 A. . B. 3 . C. . D. . 12 12 12 12
Câu 14. Cho tứ diện ABC .
D Đặt AB a, AC b, AD c . Gọi G là trọng tâm của tam giác BCD. Trong
các đẳng thức sau, đẳng thức nào sau đây đúng? 1 1
A. AG a b c.
B. AG a b c. 2 4 1
C. AG a b c.
D. AG a b c. 3 2 2
x x 4x 1
Câu 15. Giá trị giới hạn lim bằng: x 2x 3 A. 1 . B. 1 . C. . D. 0 . 2 2
Câu 16. Cho tứ diện đều ABCD có độ dài cạnh bằng a . Tính tích vô hướng của hai vectơ AB và CD . 2
a A. A . B CD 0 . B. 2 A . B CD a . C. A . B CD . D. 2 A . B CD a . 2
Câu 17. Cho hình hộp ABC . D AB C D
. Gọi I, K lần lượt là tâm của hình bình hành ABB A và BCC B .
Khẳng định nào dưới đây là sai? A. k 0. B. k 2. C. k 4. D. k 1.
Câu 18. Tính giới hạn n 1 n n 1 lim 16 4 16 3n T 1 A. T 1 . B. T . C. T 1 0 . D. T . 8 16 4 2
4x 3x 1
Câu 19. Cho hai số thực a và b thỏa mãn lim
ax b 0. Khi đó a b bằng x x 2 A. 7 . B. 7 . C. 4 . D. 4 . 2
x 4x 3 khi x 1
Câu 20. Tìm m để hàm số f (x) x 1
liên tục tại điểm x 1 . mx 2 khi x 1 A. m 0 . B. m 4 . C. m 4 . D. m 2 . Trang 2/4 - Mã đề 010 3 3x 2 2 khi x 2
Câu 21. Tìm giá trị lớn nhất của a để hàm số f x x 2
liên tục tại x 2. 1 2 a x khi x 2 4 A. a 2. B. a 3. C. a 0. D. a 1. max max max max
Câu 22. Cho hình lập phương ABC . D AB C D
. Tính góc giữa hai đường thẳng AB và AD A. 0 45 . B. 0 30 C. 0 90 . D. 0 60 . 2 x 16 khi x 4
Câu 23. Tìm m để hàm số f x x 4
liên tục tại điểm x 4 . mx 1 khi x 4 7 A. m 7 . B. m . C. m 8 . D. m 8 . 4 4 2 x 3 khi x 1
Câu 24. Cho hàm số y f x 2 x 1
. Tính lim f x . 1 x 1 khi x 1 8 1 A. 1 . B. . C. . D. 0 . 8 8
Câu 25. Cho hình lăng trụ ABC.A¢B C
¢ .¢ Đặt AB = a, AA¢ = b, AC = c. Khẳng định nào sau đây đúng? A. B C ¢ = a - +b -c . B. B C ¢ = a - -b +c . C. B C ¢ = a - +b +c D. B C
¢ = a +b -c .
Câu 26. Cho hình chóp S.ABC có SA SB SC và ASB BSC
CSA . Hãy xác định góc giữa cặp vectơ SC và AB ? A. 90 . B. 45 . C. 60 . D. 120 . 10 2x Câu 27. lim là 2
x5 x 6x 5 1 1 A. . B. . C. . D. 0 . 2 2 x 2 2
Câu 28. Giới hạn lim x bằng 2 x 2 1 1 A. 1. B. . C. . D. 0 . 2 4 2 n n 1
Câu 29. Biết rằng lim a sin . b Tính 3 3
S a b . 2 n n 2 4 A. S 1 . B. S 1. C. S 8. D. S 0.
Câu 30. Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos AB, DM bằng 3 1 3 2 A. . B. . C. . D. . 2 2 6 2 2
n 2n 1 n
Câu 31. Kết quả của giới hạn lim bằng: 3n 1 3n 2 1 A. . B. 1 1 . C. . D. . 3 3 3 Trang 3/4 - Mã đề 010
Câu 32. Số thập phân vô hạn tuần hoàn 0,17232323 a
được biểu diễn bởi phân số tối giản . Khẳng định b nào dưới đây đúng? A. 15 a b 2 . B. 14 a b 2 . C. 13 a b 2 . D. 12 a b 2 .
Câu 33. Tìm tất cả các giá trị của tham số m để hàm số sau liên tục trên x 1 f x khi x 1 ln x x 1 2 . m e 1 2mx khi x 1 1 A. m . B. m 0 . C. m 1. D. m 1 . 2 2 a x 1 2017 1 Câu 34. Cho lim ;
x bx x
P 4a b x 2 lim 1 2. Tính . x x 2018 2 A. P 2 . B. P 1 . C. P 3 . D. P 1 .
Câu 35. Cho hai dãy số u , v n
n đều tồn tại giới hạn hữu hạn. Biết rằng hai dãy số đồng thời thỏa mãn các hệ thức u 4v 2, v
u 1 với mọi n
. Giá trị của giới hạn lim u 2v n n bằng n 1 n n 1 n n 3 A. 1 1 . B. . C. 0. D. . 2 2 PHẦN II: TỰ LUẬN
Câu 36. Trong các dãy số u 1
n cho dưới đây, dãy số nào có giới hạn khác ? Câu 37. Cho
x ax x a x 2 lim 5
5 thì giá trị của là một nghiệm của phương trình nào trong các phương trình sau? 4x 1 1 khi x 0
Câu 38. Tìm a để hàm số f x 2
ax 2a 1 x
liên tục tại x 0 . 3 khi x 0
Câu 39. Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng a và ABCD là hình vuông.
Gọi M là trung điểm của CD . Tính giá trị MS.CB .
------------- HẾT ------------- Trang 4/4 - Mã đề 010
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 001 Mã đề [001] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 D B B D A B B A B C A A A B D A C B 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 C D C B D A A D D C C B D C C A C
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn D 3 1 2 8 2 8n 3n 1 Ta có lim lim n n 4 . 2 4 5n 2n 4 5 2 2 n n Câu 2. Lời giải Chọn B
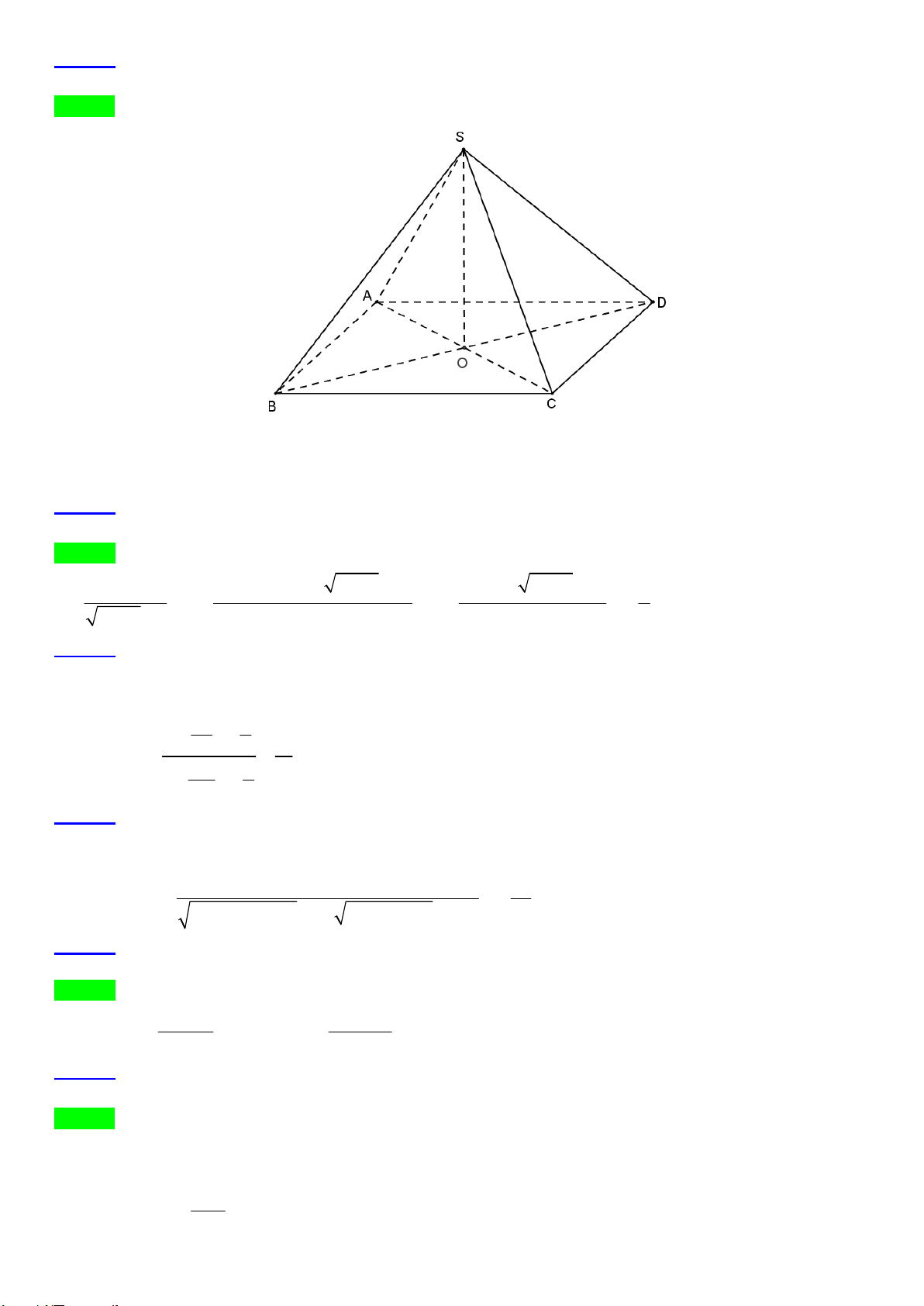
lim f x lim x x 3 3 1 3 2 . x 1 x 1 Câu 3. Lời giải Chọn B S B C O A D
Vì AD//BC nên góc giữa BC và SA là góc giữa AD và SA .
Hình chóp có tất cả các cạnh đều bằng a nên S
AD đều, suy ra AD,SA 60 . Câu 4. Câu 5. Lời giải Chọn A 2 2 4 3 1
2 3n2 n 4 n n I lim lim 9 . n 3 1 3 1 1 n Câu 6. Lời giải Chọn B Ta có lim 3
. f x 3
.lim f x . xa xa Câu 7. Lời giải Chọn B n n n 3 n lim 3 5 lim 5 1 . 5 n 3 n Vì lim5 ; lim 1 1 . 5 Câu 8. Lời giải Chọn A
Ta có lim f x 1. x Câu 9. Lời giải Chọn B
Do hình chiếu của hai đường thẳng ban đầu nằm trên cùng một mặt phẳng nên chúng không thể chéo nhau. Câu 10. Lời giải Chọn C Câu 11. Lời giải Chọn A 3 C 2 5 . Câu 12. Lời giải Chọn A 1 2x 1 2 Ta có: lim lim x 2 .
x 3 x x 3 1 x Câu 13. Lời giải Chọn A
Theo định nghĩa hàm số liên tục trên đoạn a;b . Câu 14. Lời giải Chọn B
Khi k là số chẵn tức là k có dạng k 2m thì k 2 lim x lim m x . x x Câu 15. Lời giải Chọn D
Áp dụng quy tắc hình bình hành ta có: BA BC BD .
Suy ra BA BC BB ' BD BB ' BD ' . Câu 16. Lời giải Chọn A x 2 1 1
Ta có : lim f (x) lim lim f (4) x4 x4 x4 x 4 x 2 4
Hàm số liên tục tại điểm x 4 . Câu 17. Lời giải Chọn C
Hàm số đã cho xác định trên .
Ta có: lim f x lim 2 x 4 5 f 1 . x 1 x 1
và lim f x lim 3x 2 1 f 1 x 1 x 1
Với mọi x 1;
lim f x lim 2 x 4 2
x 4 f x 0 0 0 ta có : . x 0 x x 0 x
Vậy hàm số liên tục trên 1; . Câu 18. Lời giải Chọn B
Hàm số liên tục tại x 1 f
1 lim f x x1 2 2 x 1 m 2 lim lim x 1 2 2
m 0 m 0 . x1 x1 x 1
Vậy có một giá trị của tham số m thỏa ycbt. Câu 19. Lời giải Chọn C 12 3 3 n 12 3
Ta có lim 2 3 12 lim lim n I n n n . 2
n 3n 12 n 3 12 2 1 1 2 n n Câu 20. Lời giải Chọn D
G là trọng tâm tứ diện ABCD
1
GA GB GC GD 0 4GA AB AC AD 0 AG AB AC AD . 4 Câu 21. Lời giải Chọn C
Các hàm số trong câu A, B, C không xác định tại x 1
do đó không liên tục tại x 1 .
Xét hàm số y f x 2
x 2x 1 ta có:
+ f x xác định trên và 1 + lim f x 2
lim x 2x 1 4 f 1 x 1 x 1
Suy ra f x liên tục tại x 1 .
Vậy hàm số trong câu D liên tục tại x 1 . Câu 22. Lời giải Chọn B
2n 2n3n 2n 2n3n A 2 lim
n 2n 3 n lim 2
n 2n 3 n 3 2 2
n 2n 3 n 2 2n 3 lim lim lim n 1. 2
n 2n 3 n 2
n 2n 3 n 2 3 1 1 2 n n Câu 23. Lời giải Chọn D A' D' B' C' A D B C
Chú ý: Hình hộp có tất cả các cạnh bằng nhau còn gọi là hình hộp thoi. A đúng vì:
AC B D
AC BD . B D // BD B sai vì:
AB AB C đúng vì:
AB DC . AB // DC BC B C D đúng vì:
BC AD . B C // A D Câu 24. Lời giải Chọn A 2 x 1
x 1x 1 Ta có: lim lim lim x 1 2 . x 1 x 1 x 1 x 1 x 1 Câu 25. Lời giải. Chọn A S A C G B Ta có: S AB S BC S
CA c g c AB BC CA.
Do đó tam giác ABC đều. Gọi G là trọng tâm của tam giác ABC .
Vì hình chóp S.ABC có SA SB SC
nên hình chiếu của S trùng với G
Hay SG ABC . AC BG Ta có:
AC SBG AC SG
Suy ra AC SB .
Vậy góc giữa cặp vectơ SB và AC bằng 0 90 . Câu 26. Lời giải Chọn D 7 1 2 3 2 3 7n 2n 1 2 Ta có lim lim n n I . 3 2 3n 2n 1 2 1 3 3 3 n n Câu 27. Lời giải Chọn D 2x 2 1 2 lim
5x 2x x 5 lim lim 5 . x x 2
5x 2x x 5 x 2 5 5 5 x 1
Suy ra: a , b 0 . Vậy S 1 . 5 Câu 28. Lời giải Chọn C 2 4 n 3 n 3 1
Ta có I lim 3 n lim 1 lim 1 1 . 4 4 n 5 n n 5 n 5 1 4n Câu 29. Lời giải Chọn C 2 2
Ta có A lim n 1 1 2 n n 2 2
Do lim n ; lim 1 1 2 . 2 n n Câu 30. Lời giải Chọn B A B D C A B D C
Ta có AB AB và AB AAD D
nên AB, AD AB , AD 90 .
Do đó AB, AD 90 nên A . B AD 0 . Câu 31. Lời giải Chọn D 2 2x 3x 2 2x 1 x 2 2x 1 5 Ta có lim lim lim . 2 x 2 x 4 x 2
x 2 x 2 x 2 x 2 4 Câu 32. Lời giải Chọn C
+ Gọi O là tâm của hình hộp ABC . D A B C D . 1 1 1 1
+ Vận dụng công thức trung điểm để kiểm tra. D C A B C â u 3 O 3 . D1 C1 A1 B1 Lời giải Chọn C 3 2017 2 a 2
a 2x 3 2017 1 2 x x 1 a 2 1 Ta có: lim lim 2 a . x 2x 2018 2 x 2018 2 2 2 2 2 x Câu 34. Lời giải Chọn A
S . A BC S .
A (SC SB) S . A SC S . A SB S .
A SC.cos 90 S . A S . B cos 60 7
cos cos(S , A BC) . S . A BC S . A BC S . A BC 2 2 .
a 4a 9a 2.2 . a 3 . a cos 60 7 Câu 35. Lời giải Chọn C 2 x 16
Ta có: lim f x lim
lim x 4 8 . x 4 x 4 x 4 x 4
Và: lim f x lim mx
1 4m 1 f 4. x 4 x 4
Hàm số f x liên tục tại điểm x 4 nếu lim f x lim f x f 4 . x 4 x 4 7
4m 1 8 m . 4 PHẦN II: TỰ LUẬN Câu 36. Lời giải
Từ công thức xác định dãy u u 0, n * n suy ra . n
Ta chứng minh un là dãy số bị chặn trên bởi 2 bằng phương quy nạp 22u u n 1 Thật vậy ta có 2 4
u 1 2 . Giả sử u 2 thì u 2 2 n 0 u 2 nên 1 n n 1 n 1 u 3 u 3 n n u 2,n n *
Ta chứng minh dãy ( u ) tăng. n 22u n 2 1 u u 2 Thật vậy n n u u u 0, n
* V×0 u 2 n 1 n n n u 3 u 3 n n
Dãy (u ) là dãy tăng và bị chặn trên nên có giới hạn. n 22L 1
Đặt lim u L 0 L 2 , giải phương trình L
ta được nghiệm dương L 2 n L 3 Vậy lim u 2 . n Câu 37. Lời giải Ta có: 1 3 2
1 x x 3
x 1x 2 x 2 lim lim lim lim 1 . 3 x 1
1 x 1 x 3 x 1 1 x
x 1 x 2 1 1 x x 2 x 1 1 x x Câu 38. Lời giải
Đặt f x 2 m 5 1 x 3x 1.
+ Hàm số f x 2 m 5 1
x 3x 1 liên tục trên nên hàm số liên tục trên 1 ;0.
+Ta có: f 0 1 f 2
1 m 1 0, m
nên f 0. f 1 0 Vậy phương trình 2 m 5 1
x 3x 1 0 có ít nhất 1 nghiệm trong khoảng 1
;0 nên phương trình luôn có nghiệm. Câu 39. Lời giải
Ta có MN MA AC CN; MN MB BD DN
1
2MN AC BD MN (AC BD) 2
2 1 1 a 10 Khi đó 2
MN (AC BD) 2 2
a 9a MN 4 4 2
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 002 Mã đề [002] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 A C B D D A C A D B D B D C C B B B 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 A C C A C A D B A A B C A B D C D
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn A
Ví dụ lấy dãy u ; v 3
u n ,v n lim u ; lim v n n với thỏa mãn điều kiện nhưng n n n n
lim u v n n . Câu 2. Lời giải Chọn C
Do phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau,
nên không thể có đáp án A. Câu 3. Lời giải Chọn B 3 2 2 2 2n 3 2 lim lim n 1 2 2 n 1 1 2 2 2 n Câu 4. Lời giải Chọn D Câu 5. Lời giải Chọn D 1 2 2x 1 lim lim x 2 .
x x 1 x 1 1 x Câu 6. Lời giải Chọn A Câu 7. Lời giải Chọn C Câu 8. Lời giải Chọn A Lời giải 2
2 x 1 5 x 3 2 5 Ta có lim 3 . x 2 2x 3 1 Câu 9. Lời giải Chọn A Câu 10. Lời giải Chọn B 3x 4 Ta có: y
có tập xác định: D \
2 , do đó gián đoạn tại x 2 . x 2 Câu 11. Lời giải Chọn D
Dựa vào định nghĩa hai đường thẳng vuông góc trong không gian ta suy ra đáp án C đúng. Câu 12. Lời giải Chọn B 2019 Ta có: lim 2 2019n n 2 lim n 1 . n Câu 13. Lời giải Chọn D B C A D B' C' A' D' Ta có ABC . D AB C D
là hình lập phương nên cạnh AA AB C D và B D
AB C D
Nên AA B D
A , A B D 90 . Câu 14. Lời giải Chọn C
Ta có lim x 3 0, x 3 0, x 3 . x 3 Câu 15. Lời giải Chọn C 1 2 1 2n 2 lim lim n . 3n 1 1 3 3 n Câu 16. Lời giải Chọn B Ta có. Dễ thấy 3 2 lim 4
x 2x 3 . Chọn đáp án . D . x Câu 17. Lời giải Chọn B 1 4 n 4 2 0 0 lim lim n n 0 . 2 3n 5 5 3 3 0 2 n Câu 18. Lời giải Chọn B 3 2017 2 a 2
a 2x 3 2017 1 2 x x 1 a 2 1 Ta có: lim lim 2 a . x 2x 2018 2 x 2018 2 2 2 2 2 x Câu 19. Lời giải Chọn A S I A B O J D C
Gọi O là tâm của hình vuông ABCD O là tâm đường tròn ngoại tiếp của hình vuông ABCD (1).
Ta có: SA SB SC SD S nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2).
Từ (1) và (2) SO ABCD .
Từ giả thiết ta có: IJ // SB (do IJ là đường trung bình của S
AB ). IJ,CD SB, AB .
Mặt khác, ta lại có S
AB đều, do đó
SBA 60 SB, AB 60 IJ,CD 60 . Câu 20. Lời giải Chọn C f 1 a 2 .
lim f x lim ax 2 a 2 . x 1 x 1 x 1 1 1 f x x 3 2 lim lim lim lim . x 1 x 1 x 1 x 1
x32x 1 x 1 x32 4
Hàm số liên tục tại x 1 f
1 lim f x 1
lim f x a 2 7 a . x 1 x 1 4 4 Câu 21. Lời giải Chọn C
1
Theo giả thuyết trên thì với O là một điểm bất kỳ ta luôn có: OG OA OB OC OD. 4
Ta thay điểm O bởi điểm A thì ta có:
1
AG AA AB AC AD 1
AG AB AC AD 4 4
2
Do vậy AG AB AC AD là sai. 3 Câu 22. Lời giải: Chọn A 2
lim ( x x 1 x) = 2
lim (x( x x 1 1)) . x x Câu 23. Lời giải Chọn C
Ta có I đúng vì f x 5 2
x x 1 là hàm đa thức nên liên tục trên .
Ta có III đúng vì f x x 2 liên tục trên 2; và lim f x f 2 0 nên hàm số liên tục trên x 2 2; . Câu 24. Lời giải Chọn A 3 2 1 n 3 2 1 3 3 3n 2n 1 2 3 n n 2 3 lim lim lim n n 0 4 4n 2n 1 4 2 1 2 1 n 4 n 4 3 4 n n 3 4 n n Câu 25. Lời giải Chọn D Ta có 2 2 SB AS AB 2 2 2
SB AS 2AS.AB AB
2 2 2 2
SB SA AB a
AS.CD AS.BA AS.AB . 2 2 a 2 C . D AS
Vậy cos cosCD, AS 2 1 . C . D AS . a 2a 4 Câu 26. Lời giải Chọn B 3 x 1 1 1
Ta có : lim f (x) lim lim f (1) x 1 x4 x4 3 2 3 x 1 x x 1 3
Hàm số liên tục tại điểm x 1. Câu 27. Lời giải Chọn A 3n 3 3 Ta có: n lim lim 2 2 lim n 2 n 1 2 2
n 2 n 1 2 1 2 1 1 2 2 n n Câu 28. Lời giải Chọn A
Hàm số xác định khi : 2
2x x 0 x 0;2
Hàm số liên tục trên từng khoảng xác định của nó, do đó ta chọn đáp án Câu 29. Lời giải Chọn B Ta có:
3n 32 2 9n 8n 26n 9 2
lim 3n 3 9n 8n lim lim 2
3n 3 9n 8n 2
3n 3 9n 8n 9 26 13 lim n
a 13,b 3 2a 7b 5 . 3 8 3 3 9 n n Câu 30. Lời giải Chọn C 2 2018 x 4 2018 x 2 2018 x 2 Ta có lim lim 2018 lim x 2 2018 2018 2019 2 2 2 2018 . 2018 2018 x2 x 2 2018 2018 x2 x 2 x2 Câu 31. Lời giải Chọn A
Ta có SA ABC SA BC , suy ra C đúng.
Lại có BC AB , BC SA BC SAB AH BC AH , suy ra B đúng.
Mặt khác AH SB , AH BC AH SBC SC AH SC , suy ra A đúng. Vậy Chọn A Câu 32. Lời giải Chọn B B A D C F E H G
2 A . B EG A .
B EF EH A . B EF A .
B EH AB A .
B AD (EH AD) 2
a (Vì AB AD ). Câu 33. Lời giải Chọn D Xét tam giác C
AD ta có MQ là đường trung bình nên suy ra MQ / / AD 1 .
Xét tam giác SAD ta có RT là đường trung bình nên suy ra RT / / AD 2 . Từ
1 ;2 MQ / /RT . Suy ra 4 điểm M ,Q, R,T đồng phẳng. Câu 34. Lời giải Chọn C
Với mọi dãy x x n : lim 0 ta có: n x 4 2 x 4 2 x 1 1 lim lim n lim n lim . x0 2x 2x 2 x 4 2 8 n 2x x n n 4 2 n Câu 35. Lời giải Chọn D 1
1 5 4n 3 n2n 1 2 lim lim 2 lim n . 2n 1 2n 1 1 2 2 n PHẦN II: TỰ LUẬN Câu 36. Lời giải Đặt *
u v 3 n
, thì v u 3 2 . n n 1 1 1 3 1 3 1 Khi đó u
u v 3
v 3 v v ; n * vn n 1 n n 1 n nên dãy
là một cấp số nhân với n 1 2 2 2 2 2 n 1 n 1 n2 n2 1 1 1 v 2
;q , suy ra v 2 . u 3 lim u 3 1 2 n 2 2 n 2 n n Câu 37. Lời giải x 3x 2 x 1 2 3 2
x 2x 2 2 2 Ta có: x 2x 2 1 2.1 2 3 lim lim lim . 2 x 1 x 1 x 4x 3 x 1 x 3 x 1 x 3 1 3 2 Câu 38. Lời giải Xét hàm số 2
f x ax bx c . + Hàm số 2
f x ax bx c liên tục trên . 4 16 4 75 4 75 + Ta có f
a b c nên f
12a 15b c . 5 25 5 4 5 4
f 0 c nên 5 f 5 0 c . 4 4 75 4 5 Do đó f f
0 12a 15b 20c 0. 4 5 4 4
Suy ra f , f 0 trái dấu hoặc cả hai đều bằng 0. 5 4 Vậy phương trình 2
ax bx c 0 luôn có nghiệm thuộc 0; . 5 Câu 39. Lời giải
A . D BC A .
D AC AB A . D AC A . D AB A . D AC.cos CAD A . D A . B cos BAD 2 2 2 2 2 2
AC AD CD
AB AD BD A . D AC. A . D A . B 2.AC.AD 2.A . B AD
a a 62 2a
2a a 62 2 2 2 a2 a 6. . a a 6.2 . a 2 3 a 2. . a a 6 2.2 . a a 6 2 A . D BC 3 a 1
Suy ra cos AD, BC
AD,BC 120. A . D BC a 6.a 6 2
Vậy góc giữa hai đường thẳng AD và BC là 60 .
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 003 Mã đề [003] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 B A A A A B D B B D C C C B D D D A 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 C C C B B B A C A B D C A C A D D
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn C 2018 4 4n 2018 Ta có lim lim n 2 . 2n 1 1 2 n Câu 2. Lời giải Chọn A Câu 3. Lời giải Chọn A 4 5 Ta có: lim 3 2 2
x 4x 5 3 lim x 2 . 3 x x x x Câu 4. Lời giải Chọn A 2 1 2 1 x 1 2 2 x x x Ta có: D lim . x 2 2 1 1 1 3 x 3 5 6 x x x x Câu 5. Lời giải Chọn A
Phương án A: chỉ đúng trong cùng một mặt phẳng nhưng thiếu trường hợp b trùng với c không đúng trong không gian.
Phương án B: góc giữa hai đường thẳng bằng góc giữa hai véc tơ chỉ phương của hai đường thẳng đó khi góc
giữa hai véc tơ chỉ phương là góc nhọn, nếu góc giữa véc tơ chỉ phương của hai đường thẳng đó là góc tù thì sai.
Phương án C: góc giữa hai đường thẳng có thể là góc vuông... Câu 6. Lời giải Chọn B 4x 3
lim 4x 3 9 0 , lim x 3 0 và x 3 0 với mọi x 3 nên lim . x 3 x 3 x 3 x 3 Câu 7. Lời giải Chọn D x 3 2 2 1 3 lim 2 . 3 x 1 x 2 3 1 2 Câu 8. Lời giải Chọn B f x Ta thấy hàm số
liên tục trên những khoảng thỏa mãn cos x 0 . g x Câu 9. Lời giải Chọn B Theo nội dung định lý. Câu 10. Lời giải Chọn D 2 n 3 2 3 3n 2 n I lim lim lim n 3 . n 1 1 1 n 1 1 n n Câu 11. Lời giải Chọn C
Theo định lý về tính đồng phẳng của ba vectơ chọn D Câu 12. Lời giải Chọn C 3x 1
* Ta có hai hàm số f x f x log x 4 2 và
có tập xác định không phải là tập nên không thỏa yêu cầu. x 2 3
* Cả hai hàm số f x 2x 3x 1
f x cos x 3 3 1 3 và
đều có tập xác định là đồng thời liên tục trên . Câu 13. Lời giải: Chọn C A sai vì lim n
q 0 khi q 1 . Câu 14. Lời giải Chọn B
Phương chiếu vuông góc với mặt phẳng chứa đường tròn biến đường tròn thành đường tròn.
Phương chiếu nằm trong mặt phẳng chứa đường tròn biến đường tròn thành đoạn thẳng.
Phương chiếu cắt (không vuông góc) với mặt phẳng chứa đường tròn biến đường tròn thành đường elip. Câu 15. Lời giải Chọn D Theo lý thuyết. Câu 16. Lời giải Chọn D 4 1 lim 4 1 3 2 n 4n 3 1 lim n 1 . (Vì 3
lim n và lim 1 1 0 ). 3 n n 3 n n Câu 17. Lời giải Chọn D
1 1
Ta có MN.AD AD BC.AD AD AC AB.AD 2 2 1
1 2
AD AC.AD A . B AD 2
AD 0 . Do đó mệnh đề MN AD sai. 2 2 Câu 18. Lời giải Chọn A 2 3 2 3 2 n 3 2 3 2 3 4 3 4 2 4 3n 2n 3n 2 n n n n lim lim limn 2 4n 3n 2 2 2 n 4 3 4 3 2 2 n n 3 2 3 2 3 4 n n 3 2 Vì lim n ; lim 0 . 2 4 3 4 3 2 n Câu 19. Lời giải Chọn C 2 2
4n 5n 2020 4n 3n 2019 2 2
4n 5n 2020 4n 3n 2019 a lim 0 2 2 Ta có
4n 5n 2020 4n 3n 2019 2
4n 5n 2020 2
4n 3n 2019 8n 4039 lim lim 2 2 2 2
4n 5n 2020 4n 3n 2019
4n 5n 2020 4n 3n 2019 4039 8 n 2 . 5 2020 3 2019 4 4 2 2 n n n n a 2 4 0 T Do đó a 1 3 0 . Câu 20. Lời giải Chọn C
Hàm số đã cho liên tục tại x 1khi và chỉ khi 0 2
f x f x 3x 2 lim 1 lim
m limx 2 m m 1 . x 1 x 1 x 1 x 1 Câu 21. Lời giải Chọn C A N B D M C
Gọi N là trung điểm của AC MN / / AB
DM,AB DM,MN. a a Ta có MN 3 , DM DN . 2 2 a 2 2 2
MN MD DN cos DMN 1 2 3 . 2MN.MD a 3 2 3 6 2. 2 Câu 22. Lời giải Chọn B sin 5x Ta có: lim
1; f 0 a 2 . x0 5x
Vậy để hàm số liên tục tại x 0 thì a 2 1 a 1 . Câu 23. Lời giải Chọn B
Ta có: AB .BC AB BB.BC .
A .
B BC BB .BC . A .
B BC (vì BB BC nên BB .BC 0 ). B . A BC . 1 1 A .
B BC.cos 60 . a . a 2 a . 2 2 Câu 24. Lời giải Chọn B
Dễ thấy kđ (I) sai, Kđ (II) là lí thuyết.
Hàm số: f x 2
9 x liên tục trên khoảng 3
;3 . Liên tục phải tại 3 và liên tục trái tại 3 . Nên f x 2
9 x liên tục trên đoạn 3 ; 3 . Câu 25. Lời giải Chọn A 3 2 1 2 1 n 1 3 2 3 1 3 n n 1 n n lim lim lim lim . n n u n n 2 3n 1 1 1 2 n 3 3 2 2 n n lim n 2 1 1 vì 1 3 0.. lim n n 3 1 3 2 n Câu 26. Lời giải Chọn C D 2 ; 2
f x không xác định tại x 3. 2
lim 4 x 0 ; f 2
0 . Vậy hàm số liên tục tại x 2 . x 2 lim f x 2
lim 4 x 0 ; lim f x 1. Vậy không tồn tại giới hạn của hàm số khi x 2.. x 2 x 2 x 2 Câu 27. Lời giải Chọn A D C A B D1 C1 A1 B1
Vì B C BC; DD CC nên ta có: AB B C DD AB BC CC AC . 1 1 1 1 1 1 1 1 1 Vậy k 1. Câu 28. Lời giải Chọn B x 2x 1 x 2 2 1 x 1 lim lim lim 0 . x 1 x 1 2x 2
2 x x 1 1 2 Câu 29. Lời giải Chọn D
Ta có: A lim 2 2
2x x m 3 2 2
2 1 m 3 m 6. x 1 m 2 Suy rA. 2 2
A 4 m 6 4 m 2 0 . m 2 Câu 30. Lời giải Chọn C x x 4 lim 1 3 lim lim 0 x 1 x 3 x . x
x 1 x 3 x
x 1 x 3 Câu 31. Lời giải Chọn A 1
Ta có: u n 2018 n 2017 . n
n 2018 n 2017 u
n 2018 n 2017 Suy rA. n 1 1với mọi * n . u n n n 2019 2018
Do đó, dãy số un giảm. Vậy Chọn A Chú ý: 1 + lim u lim 0 . n n n
n 2018 n 2017 u
n 2018 n 2017 + n 1 lim lim 1. n n u n n n 2019 2018 1 1 1 + 0 u . n
n 2018 n 2017 2 n 2017 2 2018 Câu 32. Lời giải Chọn C
Gọi E, F lần lượt là trung điểm của AB và CD . Khi đó, ta có: NE / /MF / / AC Ta có:
nên MENF là hình bình hành. ME / /NF / / BD NE / / AC Mặt khác: góc giữa AC và BD là 0 E NF 90 . NF / / B D
Suy ra: MENF là hình chữ nhật.
Hình như đề cho dữ kiện sai: AC a thay vì AB a .
Nếu AB a thì không giải được.
Nếu AC a thì ta giải như sau: Xét M
NE vuông tại E. Theo định lí Pitago, ta có: 2 2 3a a a 10 2 2
MN ME NE . 2 2 2 Câu 33. Lời giải
Chọn A
A. Sai vì OA OB 2OI ( I là trung điểm AB ) OM 2OI O, M , I thẳng hàng.
B. Sai vì OM OB M B và OB k BA O, B, A thẳng hàng: vô lý
C. OM kOA 1 k OB OM OB k OAOB BM kBA B, , A M thẳng hàng.
D. Sai vì OB OA AB OB k OB OA k AB O, B, A thẳng hàng: vô lý. Câu 34. Lời giải Chọn D 4n 3n Ta có T n 1 n n 1 lim 16 4 16 3 lim n 1 n n 1 16 4 16 3n 3 n 1 4n 3n 4 1 1 lim lim .
16.16n 4n 16.16n 3n 1 n 3 n 4 4 8 16 16 4 4 Câu 35. Lời giải Chọn D x
( x+3- )2( x+3+ )2( 2x-1+ + - )1 3 2 Ta có: lim = lim . x 1 ® x 1 2x -1-1
® ( 2x-1- )1( x+3+ )2( 2x-1+ )1 (x- )1( 2x-1+ )1 ( 2x-1+ )1 1 = lim = lim = . x 1
® (2x-2)( x+3+ ) x 1 2 ® 2( x+3+ )2 4
Do đó: a =1; b = 4 . Vậy a +b = 5 . PHẦN II: TỰ LUẬN Câu 36. Lời giải 1 1 1
Ta có u 1;u ; u ; u 1
. Từ đó dự đoán u (*) 1 2 3 4 2 3 4 n n
Chứng minh (*) luôn đúng bằng phương pháp quy nạp:
Với n 1 u 1 (đúng ). 1
Gỉa sử (*) đúng với n k (k 1 1) nghĩa là u k k 1
Ta chứng minh (*) đúng khi n k 1.Nghĩa là ta phải chứng mính: u k 1 k 1 u 1 k 1
Thật vậy theo bài ra và giả thiết quy nap ta có k u . đúng, k 1
u 1 k k 1 k 1 k
nghĩa là (*) cũng đúng với n k 1. 1 Vậy u với n 1
1. Ta có limu lim 0. Vậy limu 0. n n n n n Câu 37. Lời giải 2 x 4
x 2x 2 Ta có: lim lim
lim x 2 2 2 4 . x2 x2 x2 x 2 x 2 Câu 38. Lời giải
Đặt f x 5 3
x 5x 4x 1.
+ Hàm số f x 5 3
x x x x 2 x 2 5 4 1
1 x 4 1 liên tục trên . + Ta có f 2 1 3 105 73 0 , f 1 0 , f 1 1 1 45 13 0 , f 1 0 , f 1 1 0 , 2 32 32 2 32 32 f 3 119 0. 3 Vì f 3 2 . f 0
nên phương trình có ít nhất 1 nghiệm thuộc khoảng 2 ; . 2 2 3 3 Vì f . f
1 0 nên phương trình có ít nhất 1 nghiệm thuộc khoảng ; 1 . 2 2 1 Vì f 1 1 . f 0
nên phương trình có ít nhất 1 nghiệm thuộc khoảng 1 ; . 2 2 1 1 Vì f . f
1 0 nên phương trình có ít nhất 1 nghiệm thuộc khoảng ;1 . 2 2 Vì f
1 . f 3 0 nên phương trình có ít nhất 1 nghiệm thuộc khoảng 1;3 3 3 1 1 Do các khoảng 2 ; ; ; 1 ; 1 ; ; ;1
; 1;3 không giao nhau nên phương trình có ít nhất 5 2 2 2 2 nghiệm.
Mà phương trình đã cho là phương trình bậc 5 có không quá 5 nghiệm.
Vậy phương trình đã cho có đúng 5 nghiệm. Câu 39. Lời giải
Đặt AA a , AB b , AD c .
Ta có a b c a và . a b . a c . b c 0 .
AC AA AB AD a b c .
x x x x
MN AN AM AB BN AD DM b a c b a 1 b c . a a a a Do đó
AC MN a b c x x x 2 x 2 2 . a 1
b c .a 1 b c a a a a x x 2 2 2 .a 1 .a a 0 . a a
Vậy AC MN .
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 004 Mã đề [004] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 B A D B B C C C C C D A D A C B A A 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B D A B D A B C D C B A A B C D D
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn B
Ta có: AC, AD
AC , AD
DAC 60 .
Vì AD AC C D . Câu 2. Lời giải Chọn A 3 x 1 3 .11 Ta có: lim 2 . x 1 x 1 11 Câu 3. Lời giải Chọn D
Vì chỉ đúng với b 0 . Câu 4. Lời giải Chọn B lim 2 3 4 2 n 2n 3 4 lim n 1 2 4 n n 2 3 Vì 4 lim n ; lim 1 1. 2 4 n n Câu 5. Lời giải Chọn B
Qua phép chiếu song song, tính chất chéo nhau không được bảo toàn. Câu 6. Lời giải Chọn C x 3 Hàm số có nghĩa khi 2
x 5x 6 0 . x 2 2 x 1
Vậy theo định lí ta có hàm số f x
liên tục trên khoảng ; 3 ; 3 ; 2 và 2 ; . 2 x 5x 6 Câu 7. Lời giải Chọn C x 1 1 Ta có: lim lim . x 1 2 2 . x 2 x 2 x 2 x 2 1 Do lim
và lim x 1 1 0 .
x x 22 2 x 2 Câu 8. Câu 9. Lời giải Chọn C Ta có lim 2
2x 3x 5 5 . x0 Câu 10. Lời giải: Chọn C A sai vì lim n
q 0 khi q 1 . Câu 11. Lời giải Chọn D C 0 . Câu 12. Lời giải Chọn A
Vì có thể b 0 . Câu 13. Lời giải Chọn D 2 1 2 n 0 1 Ta có: lim lim n 1 . n 1 1 1 1 0 n Câu 14. Lời giải Chọn A 1 2 2x 1 lim lim x 2.
x x 1 x 1 1 x Câu 15. Lời giải Chọn C
Dựa vào ĐỊNH NGHĨA 1 SGK Đại số và Giải tích 11 (trang 136):
“Cho hàm số y f x xác định trên khoảng K và x K . Hàm số y f x được gọi là liên tục tại x nếu 0 0
lim f (x) f (x ) ”. 0 x 0 x
Ta thay khoảng K bởi khoảng a;b sẽ được mệnh đề đúng. Câu 16. A' D' B' C' D A B C Lời giải Chọn B
Ta có u AD AB AA AC AA AC . Câu 17. Lời giải Chọn A A C B C1 A C B
Ta có AB // AB
BC ,AB BC ,AB ABC 1 1 .1 2 2 2
AB BC AC
Tam giác ABC có AB 1; AC BC 2 và 1 1 cos B 2 cos B . 1 1 1 2A . B BC 4 1 Câu 18. Lời giải Chọn A
Ta có G là trọng tâm tam giác ABC nên GA GB GC 0
Suy ra SA SB SC SG GA SG GB SG GC 3SG (GA GB GC) 3SG . Câu 19. Lời giải Chọn D n lim 4 4 2 2
n 2n n 2n lim lim 2 2 2 .
n 2n n 2n 2 2 1 1 n n Câu 20. Lời giải Chọn D
Hàm số liên tục tại x 2 lim f x f 2 . x2 2 x 1 Ta có lim limx 1 1. x2 x2 x 1 m 3 Vậy 2 m 2 1 . m 3 Câu 21. Lời giải Chọn A
x 2 3x10 x 3x10 2 x x 4 lim lim lim . 2 x 2 x 2 x 2 3x 10 x 3x 10 x 5 x 7 Câu 22. Lời giải Chọn B 1 n 2 1 2 n n 3n 1 3 3 Ta có: 2
lim n 1 n n lim lim lim n . 2
n 1 n n 2
n 1 n n 1 1 2 1 1 n n
a 3,b 2 a b 5. Câu 23. Lời giải Chọn D Ta có: B 3 3 2
lim n 9n n 2 9 lim n 3 3 2 n 9n 2 3 3 2 2
n n 9n n 9 lim 3. 2 9 9 3 1 1 1 n n Câu 24. Lời giải Chọn A 3 1 1 1 1 n . 2 3 2 3 2 3 2n n 1 n n Ta có lim lim lim n n 2 . n 1 2 2n 1 1 2 1 1 1 n 1 .n 2 1 2 2 2 n n n n Câu 25. Lời giải Chọn B D A C B
A .
B CD CB CA.CD C . B CD C . A CD 0 0 C . B C . D cos 60 C . A C . D cos 60 0 . Câu 26. Lời giải Chọn C
Hàm phân thức liên tục trên mỗi khoảng xác định của nó. Tại điểm x 1 hàm số không xác định, do đó hàm
số không liên tục tại những khoảng chứa x 1. Câu 27. Lời giải Chọn D 2 3 n 2n 1 2 1 Ta có lim lim n . 3 2n 1 1 2 2 3 n Câu 28. Lời giải Chọn C
Vì G là trọng tâm tam giác BCD nên GB GC GD 0 .
AB AC AD AG GB AG GC AG GD 3A . G Câu 29. Lời giải Chọn B
Ta có BAC và BAD là 2 tam giác đều, I là trung điểm của AB nên CI DI (2 đường trung tuyến của 2
tam giác đều chung cạnh AB ) nên CID là tam giác cân ở I . Do đó IJ C . D Câu 30. Lời giải Chọn A
1 x 2 x x 1 1 L lim lim
lim 2 x 1 2 x 1 x 1 x 1 . 2 x 1 x 1 Câu 31. Lời giải Chọn A Ta có: f 1 2m 1. 1 x x 1 2 3 x x lim f x 1 lim lim lim 2 x x 1 3 . x 1 x 1 x 1 x 1 x 1 x 1
Để hàm số liên tục tại x 1 thì lim f x f 1 2m 1 3 m 2 . x 1 Câu 32. Lời giải Chọn B
Hàm số y f x xác định trên R .
Với x 0 ta có hàm số 1 2x 1 f x
liên tục trên khoảng 0; . x
Với x 0 ta có f x 1 3x liên tục trên khoảng ; 0.
Với x 0 ta có: f 0 1
lim f x lim(1 3x) 1. x 0 x 0 f x 1 2x 1 2x 2 lim lim lim lim 1. x 0 x 0 x 0 x x 1 2x x 0 1 1 2x 1
Vì lim f x lim f x f (0) , nên hàm số liên tục tại x 0 . Vậy hàm số liên tục trên . x 0 x 0 Câu 33. Lời giải Chọn C
Gọi M là trung điểm BC . Do tam giác ABC cân tại A và tam giác DBC cân tại D nên, có: BC DM BC AD . BC AM Câu 34. Lời giải Chọn D 2 2 2
x 4x 2 x 4 4 x 2 2 lim
x 4x 2 x lim lim lim x 2 . x
x 2x4x2x x 2x4x2x x 4 2 1 1 2 x x Câu 35. Lời giải Chọn D
Ta có lim f x lim x
a lim f x lim x x a a 2 2 3 6 3 2 ax 1 5 2 , . x2 x2 x2 x2
Hàm số có giới hạn khi x 2 khi và chỉ khi lim f x lim f x 5 2a 6 3a a 1 . x 2 x 2 Vậy a 1 PHẦN II: TỰ LUẬN Câu 36. Lời giải 1
Ta chứng minh 0 u ; n
*(1) bằng quy nạp. n 2 1
Ta có u nên (1) đúng. 1 2 1 2 1 1 1 1 5 1 1 Giả sử 0 u 2
0 u u 0 u n 2 n n n 1 3 2 3 2 12 2 2
Vậy (1) đúng với mọi số nguyên dương n . n 1 1 1 5 5 5
Ta có 0 u ; n *
0 u 0 u u ; n * 0 u u n n n 1 n n 1 2 3 6 6 6 n 1 5 Vì lim
u 0 nên theo nguyên lý giới hạn kẹp suy ra lim u 0 1 6 n Câu 37. Lời giải 2 x 4x 3
x 1x 3 x 3 lim lim lim 2. 2 x 1 x 1 x 3x 2 x
1 x 2 x 1 x 2 Câu 38. Lời giải Xét hàm số 2
f x ax bx c . + Hàm số 2
f x ax bx c liên tục trên . a b
+ Ta có f 0 c , f 2 4a 2b 1 c , f c 2 4 2 1
Do đó f 0 4 f f
2 5a 4b6c 0 2
Suy ra tồn tại hai giá trị p , q sao cho f p. f q 0 . Vậy phương trình 2
ax bx c 0 luôn có nghiệm. Câu 39. Lời giải S F E A D B C Ta có S AB S
AD BE DF EF // BD EF k BD,k 0 .
Do đó EF.SC k B .
D SA AC kB .
D SA k AD AB.SA 0 .
Suy ra EF SC hay EF SC .
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 005 Mã đề [005] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 C A B B B D C D C A D B B D A A D C 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 D B A B D B A A C B C C A C B B A
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn C 4 3 Ta có. lim 3 2
n 4n 3 3 lim n 1 . 3 n n Câu 2. Lời giải Chọn A
Vì f a f b 0 nên f a và f b cùng dương hoặc cùng âm. Mà f x liên tục, tăng trên ;
a b nên đồ
thị hàm f x nằm trên hoặc nằm dưới trục hoành trên ;
a b hay phương trình f x 0 không có nghiệm
trong khoảng a;b . Câu 3. Lời giải Chọn B
Ta có: lim u 3v 2019 n n
limu 3lim v 2019 n n 5 3a 2019 2024 a . 3 Câu 4. Lời giải Chọn B 1 A . 6 Câu 5. Lời giải Chọn B x
Tập xác định của hàm số y là \ 1 . x 1
Hàm số liên tục trên từng khoảng ;
1 và 1; nên hàm số không liên tục trên . Câu 6. Lời giải Chọn D
Ta có: b c d AB AC BC CB BC 0 . Câu 7. Lời giải Chọn C lim 1 1 0 xa
Ta có: lim 1 a 0 . xa
x a 0 khi x a 1 Vậy lim . x a x a Câu 8. Lời giải Chọn D
Vì có thể b 0 . Câu 9. Lời giải Chọn C 3 lim x x lim 5 3 x 5 3 lim x 1 vì . 3 5 x x x lim 1 1 0 3 x x Câu 10. Lời giải Chọn A
Ta có MN / / AC mà AC B D
MN B D . Câu 11. Lời giải Chọn D
Sai vì a và c có có thể không đồng phẳng. Câu 12. Lời giải Chọn B
Mệnh đề đúng là “Trong không gian hai đường thẳng chéo nhau thì không có điểm chung.” Câu 13. Lời giải Chọn B 1 2 2 2x 1 2 Cách 1: lim lim x 2 . 2
x 3 x x 3 1 2 x 2 2x 1
Cách 2: Bấm máy tính như sau: + CACL + 9
x 10 và so đáp án. 2 3 x 2 2x 1
Cách 3: Dùng chức lim của máy VNCALL 570ES Plus: lim và so đáp án. 2 3 x 9 x 10 Câu 14. Lời giải Chọn D 5 2 1 n 8 2 1 5 3 8n 2n 1 2 5 8 n n 2 5 8 Ta có lim lim = lim n n 2 . 5 2 4n 2n 1 2 1 5 2 1 4 n 4 4 3 5 n n 3 5 n n Câu 15. Lời giải Chọn A 2 3 3n 2 Ta có: lim lim n 3. n 3 3 1 n Câu 16. Lời giải Chọn A Câu 17. Lời giải Chọn D F . Câu 18. Lời giải Chọn C
2n 2n2n 2n 2n2n 2
n 2n 2n 2 2n 3n lim lim lim 3n 2
3n 2 2n 2n 2n
3n 2 2n 2n 2n n2 3n n 1 1 lim lim lim .
3n 2 2n 2n 2n 2
n 2n 2n 2 3 1 2 n Câu 19. Lời giải Chọn D 8 1 4 9 2 9 1 4 2 9
n (2 ) .n (1 ) (2 ) .(1 ) 2 2 Ta có: C lim n n lim n n 17 1 1 n (1 ) 1 17 17 n n Suy ra C 16 . Câu 20. Lời giải Chọn B S A D O B C
A. Đúng vì SA SB 2SC 2SD 6SO SC BIH . Vì O, ,
A C và BIH thẳng hàng nên đặt OA kOC;OB mOD k
1 OC m 1 OD 0 . OA OB
Mà OC,OD không cùng phương nên k 2 và m 2
2 AB / /C . D OC OD
B. Đúng. Hs tự biến đổi bằng cách chêm điểm O vào vế trái.
C. Sai. Vì nếu ABCD là hình thang cân có 2 đáy là AD, BC thì sẽ sai.
D. Đúng. Tương tự đáp án A với k 1 , m 1
O là trung điểm 2 đường chéo. Câu 21. Lời giải Chọn A
(x 1)(x 2)
Ta có : lim f (x) lim 2x 4 x 2 x 2 x 2
lim f (x) lim 2
x x 3 5 lim f(x) x 2 x 2 x 2
Hàm số không liên tục tại x 2 . 0 Câu 22. Lời giải Chọn B 2 9 x
x 3x 3 x 3 Ta có: lim lim lim 3 . 2
x3 x 4x 3
x3 x 3 x 1 x3 x 1 Câu 23. Lời giải Chọn D
A .
B CD AC.DB A .
D BC AC CB.CD AC.DB A . D CB
AC CD DB CBCD AD AC.CB C . B AC 0. Câu 24. Lời giải Chọn D
Trong ABC : kẻ AD sao cho ACBD là hình bình hành.
Ta có: BC // AD Nên AB ; BC AB ; AD B A D .
Ta có AD BC a 3 , 2 2
AB AB AB a 3 , 2 2
DB BB AC a 3 . Vậy tam giác B A D đều nên B A D 60 . Câu 25. Lời giải Chọn A
Lý thuyết quy tắc hình hộp, bắt đầu từ đỉnh B . Câu 26. Lời giải Chọn A 2 1 1 n2 0 2 5 n 1 5 25 25 lim lim . 3n 2.5n 3 n 0 2 50 2. 5 Câu 27. Lời giải Chọn C B C A D F G E H
Gọi cạnh hình lập phương bằng a .
2
Ta có BG BF BC AC.BF AC BF BC 2
AC.BF AC.BC . a a 2. a 2 1 Lại có 2
AC.BG 2a cos AC, BG cos AC, BG AC, BG 0 60 . 2 Câu 28. Lời giải Chọn B
Ta có tam giác SAC cân tại S và SO là đường trung tuyến cũng đồng thời là đường cao.
Do đó SO AC .
Trong tam giác vuông SOA thì AC và SA không thể vuông tại A . Câu 29. Lời giải Chọn C 2 x x
x 2x 3 4x 13
x 3 4x 13 5 6 3 lim lim lim . x2 x2 4x 1 3 4 x 2 x2 4 2 Câu 30. Lời giải Chọn C 7x x sin sin 7 Ta có: 2 2 A lim . x0 11x x 11 sin sin 2 2 Câu 31. Lời giải Chọn A 2 1 n 1 Ta có: M lim . 3 2 3 2 3 2 3 2
(1 n 8n ) 2n 1 n 8n 4n 12 Câu 32. Lời giải Chọn A 2 x 2x x x 2 YCBT lim f 0 lim
f 0 limx 2 f 0 f 0 2 . x0 x x0 x x0 Câu 33. Lời giải Chọn B
Ta có khẳng định A đúng vì hàm số y sin x là hàm sơ cấp.
Ta có khẳng định B sai vì tại x 3
hàm số không xác định. x 1 Ta có hàm số y
gián đoạn tại điểm x 0 vì hàm số không xác định tại x 0 . x Hàm số 4 2
y x 3x 2 là hàm sơ cấp liên tục trên . Vậy khẳng định B sai. Câu 34. Lời giải Chọn C
Ta có lim f x lim 2x m m x 0 x 0 f x 1 4x 1 4 lim lim lim 2 x 0 x 0 x 0 x 1 4x 1
Tồn tại giới hạn lim f x khi và chỉ khi lim f x lim f x m 2 . x0 x 0 x 0 Câu 35. Lời giải Chọn A 2 x 5x 6
Hàm số liên tục tại x 2 khi và chỉ khi lim f x f 2 lim f 2 x2 x2 2x 4
x 2x 3 x 3 lim f 2 lim 2a 1 3 2a 7 3 a . x 2 x 2 2 x2 2 2 4 PHẦN II: TỰ LUẬN Câu 36. Lời giải n 1 n2 1 1 1
Ta có : u u u u u
u u u n ... ... 1 n n 1
n 1 n2 2 1 . 1 2 2 2 n 1 n2 1 1 1 1 Dãy ,
,..., ,1 là một cấp số nhân có n số hạng với số hạng đầu u 1 và công bội q nên 2 2 2 1 2 1 n 1 n 1 2 1 n 1 1 u 2
.Vậy lim u 2 n lim 0. n 1 2 1 2 2 Câu 37. Lời giải 2 2x 5x 2 2x 1 x 2 Ta có: 2x 1 2.2 1 1 lim lim lim . 3 x x 8
x x 2 2 2 2
x 2x 4 2 2
x2 x 2x 4 2 2.2 4 4 Câu 38. Lời giải
Đặt f x 2
m m 4
1 x 2x 2 .
+ Hàm số f x 2
m m 4
1 x 2x 2 liên tục trên nên hàm số liên tục trên 0; 1 . + Ta có f 0 2 2 f 1 3 2
1 m m 1 m 0, m 2 4
Nên f 0. f 1 0 Vậy phương trình 2 m m 4
1 x 2x 2 0 có ít nhất một nghiệm trong khoảng 0; 1 nên phương trình luôn có nghiệm. Câu 39. Lời giải:
Ta có: A .
B CD BC.AD C . A BD A .
B CD BC. AC CD C .
A BC CD
AB BC CA.CD BC AC CA 0.CD BC.0 0 (đpcm)
Giả sử trong tứ diện ABCD có AB CD, AC BD thì ta có: AB CD A . B CD 0
AC BD C . A BD 0
Theo CM trên ta có A .
B CD BC.AD C .
A BD 0 BC.AD 0 BC AD (đpcm)
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 006
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn C k 1 Ta có: lim n lim 0 . k n Câu 2. Lời giải Chọn B
G là trọng tâm tam giác ABD nên GA GB GD 0 CA CB CD 3CG 0
CA CB CD 3CG . Câu 3. Lời giải Chọn B 1 2 2 2 lim
n 1 3n 2 lim n 1 3 . 2 2 n n 1 2 Vì lim n ; lim 1 3 1 3 0 . 2 2 n n Câu 4. Lời giải Chọn A
Trong không gian có vô số đường thẳng qua O và vuông góc với . Câu 5. Lời giải Chọn A 1 1 1 1 Ta có: 3
A lim x 1 x 2 2 2 3 x x x x x 1 1 1 1 3 lim x 1 2 . 2 2 3 x x x x x Câu 6. Lời giải Chọn D
Hàm số y tan x xác định khi x
k nên không liên tục trên . Chỉ liên tục trên tập xác định của nó. 2 Câu 7. Lời giải Chọn D lim 3 x 1 9 . x2 Câu 8. Lời giải Chọn D f 0 0.
lim f x lim 2
x f 0 1 1 . x0 x0
Vậy hàm số gián đoạn tại x 0 . Câu 9. Lời giải Chọn A
lim x 15 1 3 0 Ta có x2 . lim x 2 0 x2 Vì x 2
nên x 2 . Do đó x 2 0 . x 15 Vậy lim . x 2 x 2 Câu 10. Lời giải Chọn C Câu 11. Lời giải Chọn C
Khẳng định D chỉ đúng khi M 0 . Câu 12. Lời giải Chọn B
Khi phương chiếu l thỏa mãn / /l hoặc l thì các đoạn thẳng AB , BC ,CA có hình chiếu lên P
nằm trên giao tuyến của và P . Câu 13. Lời giải Chọn B 1 2 2 n 2 Ta có: lim lim n n 0 . 2 n 3n 1 3 1 1 2 n n Câu 14. Lời giải Chọn A
Hai đường thẳng a,b lần lượt có véc tơ chỉ phương là u,v và u,v 125 thì góc giữa hai đường thẳng a,b
bằng 180 125 55 . Câu 15. Lời giải Chọn B 3 2x lim
vì lim (3 2x) 1
0; lim (x 2) 0 và x 2 0 khi x 2 . x 2 x 2 x 2 x 2 Câu 16. Lời giải Chọn D 1 2 3 3 n 3n 3 Ta có lim lim n . 3 2n 5n 2 5 2 2 2 2 3 n n Câu 17. Lời giải Chọn C 1 1 1 2 2 2 2 2 S A . B AC.sin C
AB .AC sin C AB .AC 2 1 cos C 2 2 2 1 2 2
AB .AC A . B AC 2 . 2 Câu 18. Lời giải Chọn D TXĐ: D .
Hàm số f x 3 2
x 1000x 0,01 liên tục trên nên liên tục trên 1 ;0, 0; 1 và 1;2, 1 . Ta có f 1 1
000,99 ; f 0 0,01 suy ra f
1 . f 0 0, 2 . Từ
1 và 2 suy ra phương trình f x 0 có ít nhất một nghiệm trên khoảng 1 ;0 .
Ta có f 0 0,01; f 1 9
99,99 suy ra f 0. f 1 0 , 3 . Từ
1 và 3 suy ra phương trình f x 0 có ít nhất một nghiệm trên khoảng 0; 1 . Ta có f 1 9
99,99 ; f 2 3
9991,99 suy ra f
1 . f 2 0 , 4 . Từ
1 và 4 ta chưa thể kết luận về nghiệm của phương trình f x 0 trên khoảng 1;2 . Câu 19. Lời giải Chọn B A x
Hàm số f x 1
có tập xác định \ 1 nên hàm số không liên tục trên . x 1 x z Câu 20. y B D Lời giải Chọn C G M
Gọi M là trung điểm CD . C Ta phân tích:
2 2
AG AB BG AB BM AB AM AB 3 3
2 1
AB AC AD 1 AB
AB AC AD 1
x y z . 3 2 3 3 Câu 21. Lời giải Chọn A 2 x 12x 35
x 7x 5 x 7 2 Ta có lim lim lim . x5 x5 25 5x 5 x 5 x5 5 5 Câu 22. Lời giải Chọn B
Hàm số xác định với mọi x thuộc 1 x 2
Với x 1 f (x) hàm số liên tục x 2 3 x 1
Với x 1 f (x) hàm số liên tục x 1 2
Tại x 1 ta có : f (1) 3 3 x 1
(x 1)( x 1) 2
lim f (x) lim lim ; x 1 x 1 x 1 3 2 3 x 1
(x 1)( x x 1) 3 1 x 2 2
lim f (x) lim
lim f (x) f (1) x1 x1 x x 2 3 1
Hàm số liên tục tại x 1.
Vậy hàm số liên tục trên . Câu 23. Lời giải Chọn D
Gọi AC B D {O }
, ta có: AA AC 2AO .
Lại có AAO vuông tại A nên: 2 a a 3 2 2 a 3
AO AA AO 2 a
AA AO 2 AO 2. a 6 . 2 2 2 Câu 24. Lời giải Chọn B A B D H C
Theo đề bài ta có: A BC, D
BC lần lượt cân tại ,
A D . Gọi H là trung điểm của BC . AH BC AD ADH BC AD . DH BC BC ADH Câu 25. Lời giải Chọn B sin 5x Ta có: lim
1; f 0 a 2 . x0 5x
Vậy để hàm số liên tục tại x 0 thì a 2 1 a 1 . Câu 26. Lời giải Chọn C 1 1 2 2 4
4n 1 n 2 2 2 2 0 Ta có: lim lim n n n 1. 2n 3 3 2 2 n Câu 27. Lời giải Chọn C
Ta có tam giác ABC vuông cân tại A , tam giác BDC vuông cân tại D .
Ta có A .
B CD DB DACD D . B CD D . A CD
DB CD cosDB,CD DA CD cosD , A CD 1 2 a . 2
AB CD
Mặt khác ta lại có AB CD AB CD
ABCD AB CD . 1 . cos . cos ,
AB CD 2
AB,DC 120 AB,CD 60. Câu 28. Lời giải Chọn D 2 x 1 a 2
1 x 2a b x 2b 1 Ta có lim
ax b lim 5
x x 2 x x 2 a 1 0 a 1
a b 6.
2a b 5 b 7 Câu 29. Lời giải Chọn C n 1 1 2 lim
n n n lim lim . 2
n n n 1 2 1 1 n Câu 30. Lời giải Chọn A
Trắc nghiệm: Dãy số có giới hạn 0 khi bậc tử bé hơn bậc mẫu nên chọn 1 2 1 2 2 3 n 2n 1 Tự luận: lim lim n n n 0. 2 3 n n 1 1 n Câu 31. Lời giải Chọn A 1 n 2 1 1 3 5 .... 2 1 n n 1 Ta có: lim lim lim n . 2 2 3n 4 3n 4 4 3 3 2 n Câu 32. Lời giải Chọn A I C C' M Q A N P B
Gọi I là trung điểm CC C
AC cân tại A CC AI (1) C
BC cân tại B CC BI (2) (1),(2)
CC AIB CC AB CC AB
Kết luận: góc giữa CC và AB là 90 . Câu 33. Lời giải Chọn D
Đặt: t x . 2 cos t 2 sin t Khi x
thì t 0 . Vậy L lim lim 1 . 2 t0 t0 t t Câu 34. Lời giải Chọn C 5x 3 3 5x 5 Có lim lim
m 5;n 2;k 3 . x0 x0 x
x( 5x 3 3) 2 3 Câu 35. Lời giải n 1 1
lim n n 4 n 3 lim lim .
n 4 n 3 4 3 2 1 1 n n PHẦN II: TỰ LUẬN Câu 36. Lời giải 1 1
Đặt u v , n
* thì v u 1 n n 4 1 1 4 1 1
Khi đó n 22 u n u n 1 n 2 v n v n 1 n 1 n 2 2 2 n 1 4 n 4 2 n n 22 2 v
n v v v ; n * n 1 n n 1 n 2 n 2 2 2 2 2 2
n 1 n 2 1 2 2 2 1 Suy ra v v v u n 1 1
n 1 n 3
(n 1)n
(n 1)n n
(n 1)n 4 1 Vậy lim u n 4 Câu 37. Lời giải 0 x 2 .P x
Phương pháp: Giới hạn trên có dạng nên ta đưa hàm số về dạng f x . 0
x 2.Qx
Cách 1: Phương trình 2
x a 3 x 2a
1 0 có một nghiệm là x 2 mà tổng hai nghiệm là S a 3
nên nghiệm thứ hai của phương trình là x a 1. Do đó 2
x a 3 x 2a
1 x 2 x a 1 . 2
x a 3 x 2a 1
x 2x a 1
x a 1 1 a Vậy lim lim lim . 2 x2 x2 x 4
x 2x 2 x2 x 2 4
Cách 2: Sử dụng quy tắc L’Hôpital f x f ' x lim lim . x 0 x g x x 0 x g ' x
Trong đó f x , g x xác định trên khoảng ;
a b và x ; a b 0 .
lim f x lim g x 0 hoặc lim f x lim g x . x 0 x x 0 x x 0 x x 0 x f ' x Và lim tồn tại. x 0 x g ' x 2
x a 3 x 2a 1
2x a 3 1 a Vậy lim lim . 2 x2 x2 x 4 2x 4 Câu 38. Lời giải
Đặt f x 4 2
4x 2x x 3 .
+ Hàm số f x 4 2
4x 2x x 3 liên tục trên nên liên tục trên 1 ;0, 0; 1. + Ta có f
1 4 , f 0 3 , f 1 2 Vì f
1 . f 0 0 nên phương trình có ít nhất 1 nghiệm thuộc khoảng 1 ;0.
Vì f 0. f
1 0 nên phương trình có ít nhất 1 nghiệm thuộc khoảng 0; 1 . Mà 1 ;0và 0;
1 là hai khoảng phân biệt. Vậy phương trình 4 2
4x 2x x 3 0 có ít nhất hai nghiệm trong khoảng 1 ; 1. Câu 39. Lời giải
Đặt CA a,CB ,
b CS c thì a b 4 2, c 2 và . a c . b c 0, . a b 16 . CE SF Ta có, CE SF CE SF . cos , cos ,
. CE . SF 2
1 1 Mà 2
SF CF CS b c SF b c 12 SF 2 3 . 2 2
1
CE CA CB 1 a b 1
CE a b2 2 24 CE 2 6. 2 2 4
1
CE SF a b 1 . . b c 12. 2 2 CE.SF 12 2
Vậy cos CE, SF
hay góc giữa hai đường thẳng CE, SF bằng 0 45 CE . SF 2 3.2 6 2
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 007
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn A 2 lim n L lim 5 3 2
3n 5n 3 2 lim n 2 vì 5 3 . 2 n n lim 2 2 0 2 n n Giải nhanh : 2 2
3n 5n 3 3n . Câu 2. Lời giải Chọn B S H A D M N I B C
Ta có: MD// SBN nên d MD,SBN d M ,SBN .
d M , SBN MB 1 1
Mà MA SBN B
. Vậy d M ,SBN d ,
A SBN . d , A SBN AB 2 2
Kẻ AI BN, AH SI thì AH SBN d ,
A SBN AH. AI AB MN AB a a a Ta có A BI . 2 . 4 N
BM g.g AI . MN NB NB a 17 17 2 1 1 1 1 17 33 4a Lại có AH . 2 2 2 2 2 2 AH SA AI a 16a 16a 33 a a
Vậy d MD SBN 1 4 2 , . . 2 33 33 Câu 3. Lời giải Chọn C 3. x x 3 1 2 3 2 1 1 3 1 5 lim . x 1 x 2 1 2 3 Câu 4. Lời giải: Chọn D
Nếu a ^ c thì a c =
; khi a / /b ta có b c = a c = vậy ( ) 0 ; 90 ( ) ( ) 0 ; ; 90 b ^ c Câu 5. Câu 6. Lời giải Chọn B
Lấy máy tính bấm từng phương án thì phần D ra kết quả đề bài Câu 7. Lời giải Chọn D x 2 2 2 Dễ thấy lim 4 x2 x 1 2 1 Câu 8. Lời giải: Chọn A. 1 2 1 2n 2 Ta có lim lim n . 3n 1 1 3 3 n Câu 9. Câu 10. Lời giải Chọn B
Ta có tam giác SAC cân tại S và SO là đường trung tuyến cũng đồng thời là đường cao.
Do đó SO AC .
Trong tam giác vuông SOA thì AC và SA không thể vuông tại A . Câu 11. Lời giải Chọn B 3 3 4x -2 4x -2
Vơi mọi x ¹ 2 ta có: lim f (x) 0 = lim = = f (x x
0 ) , suy ra hàm số liên tục tại . 0 x® 0 0 x x® 0 x x -2 x -2 0
Xét tại x = 2 , ta có: 3 4x -2 4x -8
+) lim f (x)= lim = lim x®2 x®2 x®2 x -2 (x-2) 3 (4x) ( 2 3 +2 4x +4) 4 4 1 = lim = = x®2 3 ( x) ( 2+ x+ ) 3( ) ( 2 3 3 + + ) 3 4 2 4 4 8 2 8 4 +) f (2)= 2a +3 1 4
Để hàm số liên tục trên R thì phải liên tục tại x = 2 Û lim f (x)= f (2) Û 2a +3 = Û a = - x®2 3 3 Câu 12. Lời giải Chọn D D' C' A' B' D C A B
Ta có AA', B ' D ' BB ' B ' D ' 0 ,
BB 'C 90 . Khẳng định B sai. Câu 13. Lời giải Chọn B A M B D N C
Ta có N là trung điểm của CD MC MD 2 MN 1.
Và M là trung điểm của AB suy ra MA MB 0 2.
1 1 1 Từ
1 ,2 suy ra MN MC MD MA AC MB BD AC BD. 2 2 2
Kết hợp giả thiết MN k AC BD 1 k . 2 Câu 14. Lời giải Chọn B Ta có:
+ lim f x lim 2 x ax 1 2a 5 x2 x2
+ lim f x lim 2 2x x 1 7 x2 x2 2
x ax 1 khi x 2
+ Hàm số f x
có giới hạn tại x 2 2
2x x 1 khi x 2
2a 5 7 a 1. Câu 15. Lời giải Chọn C A1 B1 D1 C1 A B D C
Ta có AD A D A C CD suy ra CD , AD, A C đồng phẳng. 1 1 1 1 1 1 Câu 16. Lời giải Chọn D B C A D C' B' A' D'
Ta có AC BA AC CD AD và DB C D
DB DC C B D . A
Suy ra AC BA' k DB C 'D AD k D A
0 k 1 D A 0 k 1. Câu 17. Lời giải Chọn C x 2 x(x 2) (x 2)x lim (x 2) = lim lim 0 . 2 x2 x 4 2 x 2 x 2 x 4 x 2 Câu 18. Lời giải Chọn C
Tập xác định D .
Điều kiện bài toán tương đương với f x sin x m f 1 lim lim x 1 x 1 x 1
sin x
sin x 1
sin x 1 lim lim lim . * . x 1 x 1 x 1 x 1 x 1 x 1
Đặt t x
1 thì t 0 khi x 1. Do đó (*) trở thành: sin t m lim . . t0 t Câu 19. Lời giải Chọn B 2 3 2 2x 3
Giới hạn ở phương án A là: lim lim x x 0 . 2
x x 5 x x 5 1 x 1 1 2 2 2 2x x 1
Giới hạn ở phương án B là: lim lim x x 2 . 2 x 3 x x x 3 1 x 1 3 3 2 1 2 3 x x 3
Giới hạn ở phương án C là: lim lim x x 1 . 2 3 x 5 x x x 5 1 x 2 x 1
Giới hạn ở phương án D là: lim lim x 1 .
x x 1 x Câu 20. Lời giải Chọn B A' B' K I D' C' A B D C
Vì I là trung điểm của B C
AB AC 2 AI.
Và K là giao điểm của AI, B D
nên theo định lí Talet 2
AK AI. 3
2 1 1 1
Ta có AK AA AK AA AI AA AB AC a b c . 3 3 3 3
Khi đó DK DA AK CB AK AB AC AK .
1 1 4 2
a b a b c a b c . 3 3 3 3 Câu 21. Lời giải Chọn A
Xét hàm số y f x 2
x 2 x 2 khi x 2 2 5
x 5m m khi x 2 +/ TXĐ: D
+/ Dễ thấy hàm số liên tục trên từng khoảng ; 2 và 2;
Nên hàm số liên tục trên hàm số liên tục tại x 2 lim f (x) f (2) 1 x2 Ta có:
lim f (x) lim
lim f (x) lim f 2 4 2 5x 5m m 2 m 5m 10 2 x 2 x 2 4; ; x2 x2 x2 x2 f x
f x f 2 2 m 2 1 lim ( ) lim ( )
2 m 5m 10 4 m 5m 6 0 x 2 x 2 m 3 Câu 22. Lời giải Chọn D. 2x 6 2 2 2 x 3 Ta có lim lim
lim 2x 3 4 3 . x 3 x 3 x 3 x 3 x 3
Suy ra a 4 , b 3 . Vậy P a b 7 . Câu 23. Lời giải Chọn C
n n n 1 1 1 lim 4 3 lim n lim .
n 4 n 3 4 3 2 1 1 n n Câu 24. Lời giải Chọn B
Hàm số y h x có TXĐ: D .
Dễ thấy hàm số y h x liên tục trên mỗi khoảng ;
0,0;2 và 2; . h0 1 Ta có
f x không liên tục tại x 0 . lim h x lim 2x 0 x 0 x 0 h2 5
Ta có lim h x lim x 2 2 x 1 5
f x liên tục tại . x2 x2
lim h x lim 3x 1 5 x2 x2 Câu 25. Lời giải Chọn A Ta có: 2018 1 x .x. 4 2018 2 2018 2 x 4x 1 x 4x 2 1 x lim lim lim 2x 2019 2019 1 1 2019 1 2019 x x x x 2 x 2 x x 1 4 2 x 4 lim 0 2 1 1 2019 202019 2019 2018 x 2 2 2 x Câu 26. Lời giải Chọn D 2 x 2 x 1 1 Ta có lim lim lim . 2 x 2 x 2 2x 5x 2
2 x1 2x x 2 1 2x 3 Câu 27. Lời giải Chọn C A C B M D
Gọi M là trung điểm của CD .
Ta có C .
D AM 0 và C . D MB 0 .
Do đó C . D AB C .
D AM MB C . D AM C .
D MB 0 nên số đo góc giữa hai đường thẳng AB và CD bằng 0 90 . Câu 28. Lời giải Chọn C A G B D G0 M C
Vì G là giao điểm của đường thẳng AG với mặt phẳng BCD. 0
Suy ra G là trọng tâm của tam giác BCD G B G C G D 0. 0 0 0 0
Theo bài ra, ta có GA GB GC GD GA 3GG G B G C G D 0 0 0 0 0 0
GA 3GG 0 GA 3G G. 0 0 Câu 29. Lời giải Chọn A 2 2
x 3x ax
x 3x ax2 2
x 1 a x 3 Ta có lim lim lim x bx 1
x bx
1 2x 3x ax x bx 1 2x 3x ax 2 a 3 1 2 1 a a 1 lim x 3 . x 1 3 b 1 a b b
1 a x x Câu 30. Lời giải Chọn C Ta có 1 1 1 1 1 1 1 1 1 lim ... n n lim 1 lim 1 1. 1.2 2.3 1 2 2 3 n n 1 n 1 Câu 31. Lời giải Chọn C x Khi x 1 1
0 ta có: f (x)
liên tục trên khoảng 0; . x Khi x 0 ta có: 2
f (x) x 1 m liên tục trên khoảng ; 0.
Hàm số liên tục trên khi và chỉ khi hàm số liên tục tại x 0 . x 1 1 1 1
Ta có: lim f (x) lim lim . x 0 x 0 x 0 x x 1 1 2
lim f (x) lim
x m m f x 2 1 1 0 x 0 0 .
Do đó hàm số liên tục tại x 1 1
0 khi và chỉ khi 1 m m . 2 2 Câu 32. Lời giải ChọnA. n n 1 2n 1 2 2 2 2
Ta có: 1 2 3 ... n . 6 1 1 1 2 2 2 3 2
1 2 3 ... n nn 1 2n 1 n n 1 Khi đó: lim lim lim .
2nn 76n 5
12nn 76n 5 7 5 6 12 1 6 n n Câu 33. Lời giải Chọn D
Đặt OA a suy ra OB OC a và AB BC AC a 2 a 2
Gọi N là trung điểm AC ta có MN / / AB và MN 2 Suy ra góc OM AB OM MN , , . Xét OMN a 2
Trong tam giác OMN có ON OM MN
nên OMN là tam giác đều 2 Suy ra 0
OMN 60 . Vậy OM AB OM MN 0 , , 60 Câu 34. Lời giải Chọn A 1 1 1 1 1 æ 1 1 1 1 1 ö Ta có : u = + +...+ = çç - + - + + - ÷ n ( ÷ n- ) ( n+ ) ... 1.3 3.5 2 1 . 2 1 2 1 çè 3 3 5 2n-1 2n +1÷ø 1 1 æ 1 ö n = çç - ÷÷= 2 1
çè 2n+1÷ø 2n+1 n 1 Suy ra : limu lim . n 2n 1 2 Câu 35. Lời giải Chọn D
Ta có tan 0; 1 với mọi 0; , do đó 4 1 cos cos 2 3
S 1 tan tan tan .
1 tan sin cos CSN lv : h 1 u 1,q tan 2 sin 4 PHẦN II: TỰ LUẬN Câu 36. Lời giải 5
Ta có lim 5n 3 2 a 2 3 n 3 lim n 3 2 a 2 2 n 5 lim 3 2a 2 2
a 2 0 2 a 2 a 1 ; 0; 1. 2 a ,a 10;10 n Câu 37. Lời giải 2 2 a b
a ax ax b
a ax ax b Ta có lim lim lim . 3 3 x 1 x 1 x x 1 x x 1 x 2 1 1 1 1 x x a b Khi đó lim hữu hạn 2 1 . a 1 .
a 1 b 0 2a b 1 . 3 x 1
1 x 1 x a b 4 a 1 a b Vậy ta có L lim 3 x 1
2a b 1 b 3
1 x 1 x 2 x x 2 x 2 lim lim 1.
x 1 x 2 1 1 x x 2 x 1 1 x x Câu 38. Lời giải
Ta có: lim f x 4 2a 3b x 2 x x 2 x 1 3
và lim f x lim lim 2 x2 x2 x 4 x 2
x 2x x 2 16 3
4 2a 3b 179 16 a
Hàm số liên tục tại x 2 lim f x lim f x f 2 32 x 2 x 2 3
2a b 6 b 5 16 179 19
Vậy I a b 5 . 32 32 Câu 39. Lời giải A M P I C D N B
IA IC 2 IM
Vì M , N lần lượt là trung điểm của AC, BD .
IB ID 2 IN
Mặt khác IM IN 0 ( I là trung điểm của MN ) IA IB IC ID 0.
Khi đó PA PB PC PD 4 PI IA IB IC ID 4 PI
1
Mà PI k PA PB PC PD nên suy ra 4k 1 k . 4
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 008
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn B u
Dùng tính chất giới hạn: cho dãy số u , v
lim u a, lim v a lim n 0 n n và trong đó hữu hạn thì . n n vn Câu 2. Lời giải Chọn D
Vì f a f b 0 nên f a và f b cùng dương hoặc cùng âm. Mà f x liên tục, tăng trên ;
a b nên đồ
thị hàm f x nằm trên hoặc nằm dưới trục hoành trên a;b hay phương trình f x 0 không có nghiệm trong khoảng ; a b . Câu 3. Lời giải Chọn D Câu 4. Lời giải Chọn B 3 2 1 3 3 4 3n 2n 1 0 Ta có: lim lim n n n I 0. 4 4n 2n 1 2 1 4 4 3 4 n n Câu 5. Lời giải Chọn B 2 2
x 2x 3 1 2.1 3 Ta có: lim 1. x 1 x 1 11 Câu 6. Lời giải Chọn C u
Dùng tính chất giới hạn: cho dãy số u , v
lim u a, lim v a lim n 0 n n và trong đó hữu hạn thì . n n vn Câu 7. Lời giải Câu 8. 2 4n n 2 Cho dãy số u u u 2 a n n với . Để
có giới hạn bằng , giá trị của là: n 2 an 5 A. 4 . B. 3 . C. 4 . D. 2 . Câu 9. Lời giải Chọn D 3 2 2 n 3 3 2 3 2 2n 3n n lim lim lim . n n .Ta có 2 4n 2n 1 2 1 2 1 2 n 4 4 2 2 n n n n lim n 2 2 3 3 2 2n 3 3 n n 2 3 im lim . n . n 2 lim 0 4n 2n 1 2 1 2 1 4 4 2 4 n n 2 n n 3 3 2n 3n 3n 3 Giải nhanh : .n . 2 2
4n 2n 1 4n 4 Câu 10. Lời giải. Chọn C lim 2
3x 2x 2 1 3.1 2.11 2. x 1 Câu 11. Lời giải Chọn D 3 3 3 3 3 3 3 3
n 1 n 2 n n 0
nhân lượng liên hợp : 1 3 3 3 3 lim
n 1 n 2 lim 0. 3n 2 3 3 3 3
1 n 1. n 2 3 3 3 n 2 Câu 12. Lời giải Chọn A 2 21 x 7 21 1 2x 2 21
x 7 1 2x 1 21 2 Ta có lim lim lim x . x0 x0 x0 x x 7 Câu 13. Lời giải Chọn C
Hàm số liên tục tại x 1
khi và chỉ khi lim y lim y y 1 x 1 x 1
lim 4x a lim
a 4 0 a 4 2 x 3x 2 y 1 . x 1 x 1 Câu 14. Lời giải Chọn A S N B C A M D
Do ABCD là hình vuông cạnh a AC a 2 . 2 2 2 2
AC 2a SA SC S
AC vuông tại S .
Từ giả thiết ta có MN là đường trung bình của D 1
SA NM SA 2
1
Khi đó NM .SC S .
A SC 0 MN SC MN, SC 90 . 2 Câu 15. Lời giải Chọn C A M B D N C
Vì M , N lần lượt là trung điểm của AD, BC suy ra:
1
1
MN AB DC và MN BD AC. 2 2
Khi đó, dựa vào đáp án, ta thấy rằng:
1
A đúng, vì MN AB DC AB, DC, MN đồng phẳng. 2
B đúng, vì MN không nằm trong mặt phẳng ABC.
C sai, tương tự ta thấy AN không nằm trong mặt phẳng MNC.
1
D đúng, vì MN BD AC BD, AC, MN đồng phẳng. 2 Câu 16. Lời giải Chọn C C B I D A G C' B' D' A'
Cách 1. Gọi I là tâm của hình vuông ABCD I là trung điểm của B . D BG BI 1 BG 1 Ta có B IG D B G
BD 3 B . G D G D B 2 BD 3
Cách 2. Theo quy tắc hình hộp, ta có BA BC BB BD.
Do G là trọng tâm của tam giác AB C
suy ra BA BC BB 3BG BD 3B . G Câu 17. Lời giải Chọn A
Trên khoảng 0; hàm số f x 2 x m là hàm số liên tục. Trên khoảng ;
0 hàm số f x mx 2 là hàm số liên tục.
Ta có lim f x lim
x m m f
lim f x lim mx 2 2 2 0 và . x0 x0 x 0 x 0
Hàm số f x liên tục trên khi và chỉ khi
lim f x lim f x f 0 m 2 m 2 . x 0 x 0 Câu 18. Lời giải Chọn C
x x x 2 2
x x x 1 Ta có lim lim lim 2 x 0 x 0 2 x
x 2x x x x 0 2
x x x vì 1 0 ; lim 2
x x x 0 x 0. 2x x x 0 x 0 và với mọi Câu 19. Lời giải Chọn D 2 x 3x 2
x 1x 2 lim lim
limx 2 1 . x 1 x 1 x 1 x 1 x 1
Để hàm số f x liên tục tại điểm x 1 cần: lim f x f 1 x 1 2
m m 1 1 m 0 (TM) 2
m m 0 . m 1 (L) Câu 20. Lời giải Chọn C 2 2 2 4 x 4x 2 x 4x 2 lim lim lim x 2 2 lim x 4x 2 x x . x 2
x 4x 2 x x 2
x 4x 2 x x 4 2 1 1 2 x x Câu 21. Lời giải Chọn A
Ta có x 3 0 với mọi x 3 , nên: 2 x 13x 30
x 3x 10
x 3. x 10 3 3 3 7 lim lim lim 0 . x 3
x 3 2x 5 x 3 x 3 2x 5 x 3 2 x 5 3 2 5 Câu 22. Lời giải Chọn B A G B D C
Vì G là trọng tâm của tứ diện ABCD suy ra GA GB GC GD 0.
1 1
Khi đó OG .4OG OA AG OB BG OC CG OD DG 4 4
1
OAOB OC OD 1
AO OG AO OAOB OC OD. 4 4
1
AO OA AB AC AD 1
AO OA AB AC AD 1 4
AB AC AD. 4 4 4
1
2
Vậy AG AB AC AD nên mệnh đề AG AB AC AD sai. 4 3 Câu 23. Hướng dẫn giải Chọn A. x 3 2 x 3 4 1 1 Ta có: lim lim lim . x 1 x 1 x 1 x
1 x 3 2 x 1 x 3 2 4 Câu 24. Lời giải Chọn D 1 3 x 3 2 0 Ta có lim lim x x 0 . 2
x x 2 x 2 1 1 2 x Câu 25. Lời giải Chọn B A F I B D E J C IF CD
Ta có IF là đường trung bình của A CD 1 . IF CD 2 JE CD
Lại có JE là đường trung bình của B CD 1 . JE CD 2 IF JE
Tứ giác IJEF là hình bình hành. IF JE 1 IJ AB Mặt khác: 2
. Mà AB CD IJ E J . 1 JE CD 2
Do đó IJEF là hình thoi. Suy ra IE, JF 90. Câu 26. Lời giải Chọn D A M G B D N C G
AGB 2GM
Vì M , N lần lượt là trung điểm của AB, CD suy ra . G
C GD 2GN
Mà G là trung điểm của MN GM GN 0 GA GB GC GD 0.
Khi đó MA MB MC MD 4 MG GA GB GC GD 4M . G Câu 27. Lời giải Chọn B A C B M A' C' B' 1
Vì M là trung điểm của BB BM BB. 2
1
1 1
Ta có AM AB BM BA BB CA CB BB a b c. 2 2 2 Câu 28. Lời giải Chọn A 2 x 16
Ta có lim f x f 4 4m 1; lim f x lim
lim x 4 8. x 4 x 4 x 4 x 4 x 4
Hàm số liên tục tại điểm x 4 lim f x lim f x f 4 4m 1 7 8 m . x 4 x 4 4 Câu 29. Lời giải Chọn D Ta có n 1 1 2 4 6 2
S 1 cos x cos x cos x cos x .
2 2 1 cos x sin x 2 CSN lv : h 1
u 1, q cos x Câu 30. Lời giải Chọn B A B D H I C
Giả sử tứ diện đều ABCD có I là trung điểm của CD , H là tâm của tam giác BCD suy ra AH BCD . CD BH Khi đó ta có: CD AB . C D AH
Vậy góc giữa CD và AB là 90 . Câu 31. Câu 32. Lời giải Chọn C 2 x 1
Do lim f x lim limx
1 2 nên hàm số liên tục tại x 1 khi x 1 x 1 x 1 x 1
lim f x f
1 m 2 2 m 4 . Khi đó hàm số liên tục trên . x 1 Câu 33. Câu 34. Lời giải Chọn A
Giả sử lim u a thì ta có n 1 1 a 2 a 2 a lim u lim a 1. n 1 2 u 2 a a a
a a n 2 2 1 2 1 0 Câu 35. Lời giải Chọn B 2
x 3x 1 a 2
1 x a b 3 x b 1 lim +ax
b 1 lim 1 x x 1 x x 1
a x a b b 1 1 3 lim x 1 x 1 1 x a 1 0 a 1
a b 3 1
T a b 2 . b 1 b 1 0 PHẦN II: TỰ LUẬN Câu 36. Lời giải 1 2 a 2 an 1 lim lim n a 2 2 3 n 3 an 1 1 Ta có 1 2 lim 3 3 a. n 2 3 n 2n 1 1 n lim lim 0 2n 2 a
0;20, a Ta có a 1;6;1 3 . a 3 Câu 37. Lời giải 2x Ta cóTa có lim
x x x x 2 5 2 5 lim x 2
5x 2x x 5 1 2 2 1 1 a lim 5 5 S 1 . x 2 2 5 5 5 5 5 b 0 x 2 2 x
5x 2x x 5 5x x 5 5x x 5 0 Giải nhanh: 2 x
5x 2x x 5 2x 2x 2x 1 . 2 2
5x 2x x 5 5x x 5 2 5x 5 Câu 38. Lời giải f 0 3 x x lim f x 4 1 1 4 1 1 lim lim 2 x0
x0 ax 2a x0 1 x
x ax 2a 1 4x 1 1 4 4 lim
x0 ax 2a 1 4x 1 1 22a 1 4 1
Hàm số liên tục tại x 0 khi f 0 lim f x 3 a . x0 22a 1 6 Câu 39. Lời giải.
Ta thấy rằng IJ , AP, AB nằm trong 3 mặt phẳng song song với nhau nên. IB JA k QB PA
IJ IB B A JA .
k QB PA B A
kQP k 1 AB
kQP k 1 AB
2 3 5
3
Mà QP AP AQ AB AD . Nên IJ
k 1 AB k AD . 3 4 3 4
5 3 12
Mà AC AB AD . Vậy nên IJ //AC . Nếu k 1 k k . 3 4 29
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 009
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn A 3 2 2 n 1 3 2 1 2 n 2n n lim lim lim . n n . Ta có 2 1 3n 1 1 2 n 3 3 2 2 n n lim n 2 2 3 1 2 n 2 1 n n 2 1 im lim . n n 2 lim 0 1 3n 1 1 3 3 2 3 n 2 n 3 3 n 2n n 1 Giải nhanh : n . 2 2 1 3n 3 n 3 Câu 2. Câu 3. Lời giải Chọn A
lim x 4 32 2 4 1 x 3 Câu 4. Lời giải Chọn B
Đáp án D đúng vì nó là một định lý trong SGK Đại số và Giải tích lớp 11. Câu 5. Lời giải Chọn B 1 5 2 1 2 n n 5 1 Ta có lim lim n n L 2 2n 1 1 2 2 2 n 2 2 n n 5 n 1 Giải nhanh: . 2 2 2n 1 2n 2 Câu 6. Lời giải Chọn C Câu 7. Lời giải Chọn D
Cho đường thẳng thì qua O có duy nhất một mặt phẳng P vuông góc với , nên qua O có vô số đường
thẳng thuộc P vuông góc với . Câu 8. Lời giải Chọn C Câu 9. Lời giải Chọn B 2
lim x 4 3 4 1 x 3 Câu 10. Lời giải Chọn C 3 2 3 0 Ta có lim lim n 0. 2 4n 2n 1 2 1 4 4 2 n n
Giải nhanh : Dạng « bậc tử » « bậc mẫu » nên kết quả bằng 0. Câu 11. Lời giải Chọn A x x 2016 2016 x 1 x
1 2018x 1 x 2018 2 Ta có: lim lim x 1 x 1
2018x 1 x 2018 2017x 2017 x 1 2015 2014 x x
... x 1
1 2018x 1 x 2018 lim 2 2019 x 1 2017 x 1
Để hàm số liên tục tại x 1 lim f x f 1 k 2 2019 . x 1 Câu 12. Lời giải Chọn B
Đặt f x x 1; g x x 1. Ta có lim f x 2; lim g x 0; g x 0khix 1 x 1 x 1 x 1 Vậy lim . x 1 x 1 Câu 13. Lời giải Chọn D A B M D C A1 B1 D C 1 1
Dựa vào đáp án, ta thấy rằng:
1 1
A sai, vì B M B B BM BB
BA BD BB B A B D . 1 1 1 1 1 1 1 1 2 2
1 1 BB
B A B A B C BB B A B C . 1 1 1 1 1 1 1 1 1 1 1 1 2 2
1 1
B đúng, vì C M C C CM C C
CA CD C C C A C D . 1 1 1 1 1 1 1 1 2 2
1 1 C C
C B C D C D C C C D C B . 1 1 1 1 1 1 1 1 1 1 1 1 2 2
1 1
C sai, vì C M C C C D C B (từ đáp án B). 1 1 1 1 1 1 2 2
D sai, vì BB B A B C BA BC BA A D BD . 1 1 1 1 1 1 1 1 1 1 Câu 14. Lời giải Chọn B A B D M C 1
Vì M là trung điểm của BC suy ra BM BC. 2
1 1
Ta có DM DA AB BM AB AD BC AB AD BA AC. 2 2
1 1 1 1 1
AB AC AD a b c a b 2c. 2 2 2 2 2 Câu 15. Lời giải Chọn A D N C I A B M O D' C' A' B'
Gọi M , N lần lượt là trung điểm của AB, C . D
Vì I là trung điểm của MN suy ra OM ON 2OI . O
AOB 2OM
1
Kết hợp với
2OI OAOB OC OD. O
C OD 2ON 2
1 1 1 1 1 1
AC CA BD DB
u v x y. 2 2 2 2 2 4 Câu 16. Lời giải Chọn B A I B D J C
1
Xét tam giác ICD có J là trung điểm đoạn CD IJ IC ID. 2
Tam giác ABC có AB AC và 0 BAC 60 A
BC đều CI AB . Tương tự, ta có A
BD đều nên DI AB .
1 1 1
Ta có IJ.AB IC ID.AB IC.AB I . D AB 0 2 2 2
IJ AB AB,IJ 90 . Câu 17. Lời giải Chọn D
Ta có MN song song AC (Đường trung bình)
MN, AP AC, AP
Giả sử hình lập phương ABC . D AB C D
có độ dài các cạnh bằng 1
Xét tam giác APC có: 2 1 5 2 1 3 2 PC 1 ; 2 2 AC 1 1 2 ; 2 2
AP 1 1 . 2 2 2 2 9 5 2 1
Theo định ý hàm cos trong tam giác APC ta có: 4 4 cosPAC PAC 45 . 3 2 2 2. 2 Câu 18. Lời giải Chọn D 1 Ta có 2
lim x sin x lim
2x sinx1 1 . 2 x0 x0 x Câu 19. Lờigiải Chọn C 3 3 2 x 1 1 x 3 Ta có: lim lim x lim x 1 x x 3 x 3 x 3 x(1 ) (1 ) x x . Câu 20. Lời giải Chọn B A B C 1
BC.CA BC.C . A cos120 2.2. 2 . 2
BC AC .BA BC CA.BA 2
AB 4 nên B sai.
AB BC .AC .AC.AC 2 AC 4 .
AB.AC .BC AB.AC.cos60
.BC 2BC . Do đó ta chọn đáp án A. Câu 21. Lời giải Chọn C 3n 3 3 Ta có: I n lim lim 2 2 lim n 2 n 1 2 2
n 2 n 1 2 1 2 1 1 2 2 n n Câu 22. Lời giải Chọn D
lim f x lim 2 x 2x 3 6 Ta có x3 x3
. Do lim f x lim f x nên không tồn tại giới hạn khi x 3.
lim f x lim x 3 x 3 2 3 2x 15 x3 x3
Vậy chỉ có khẳng định C sai. Câu 23. Lời giải Chọn D D C B A K I H G E F
Vì I, K lần lượt là trung điểm của AF và CF.
Suy ra IK là đường trung bình của tam giác AFC IK // AC IK // ABCD.
Mà GF // ABCD và BD ABCD suy ra ba vectơ BD, IK, GF đồng phẳng. Câu 24. Lời giải Chọn D 2 x 2x x x 2
Ta có lim f x lim lim lim x 2 . x 2 x 2 x 2 x 2 x 2 x 2
lim f x lim mx 4 2m 4 x 2 x 2
Hàm số liên tục tại x 2 khi lim f x lim f x 2m 4 2 m 3. x 2 x 2 Câu 25. Lời giải Chọn C.
Hàm số ở câu C và D không xác định tại điểm x 1 nên không liên tục tại điểm x 1. Xét câu A:
lim f x lim 3x
1 2 , lim f x lim x 1 2 , f 1 2 x 1 x 1 x 1 x 1
Suy ra lim f x lim f x f 1 2 x 1 x 1
Vậy hàm số liên tục tại điểm x 1. Xét câu B:
lim f x lim 3x
1 4 , lim f x lim x 1 2 x 1 x 1 x 1 x 1
Suy ra lim f x lim f x x 1 x 1
Vậy hàm số không liên tục tại điểm x 1. Câu 26. Hướng dẫn giải Chọn A
Ta có hàm số liên tục trên các khoảng ; 1 và 1 ; .
Xét tính liên tục của hàm số tại x 1 . Có y 1 2
lim y và lim y 1 m . x 1 x 1
Để hàm số liên tục trên thì y
1 lim y lim y 2 1
m m 1 . x 1 x 1 Câu 27. Lời giải Chọn C 1 1 2 4 2 4x x 1 x x 4 Ta có lim lim 2 . x x 1 x 1 1 1 x 2 2 4x x 1 4x 2 x
Giải nhanh: khi x 2 . x 1 x x Câu 28. Lời giải Chọn A (x 1) x 3 3 4x 42 3 2 4x 4 4 1 Ta có lim lim x 1 3 x 1 4x 4 2
4x 483 2 3 x x 1 34x42 3
2 4x 4 4 12 lim 1. x 1 3 2 3 x x 12 4 1 Câu 29. Lời giải Chọn C Ta có 2 3
0,5111 0,5 10 10 10n Dãy số 2 3
10 ;10 ;...;10n;... là một cấp số nhân lùi vô hạn có số hạng đầu bằng 2 u 10 , công bội bằng 1 2 1 u 10 1 q 10 nên 1 S . 1 1 q 110 90 46 23 a 23
Vậy 0,5111... 0,5 S
T a b 68. 90 45 b 45 Câu 30. Lời giải Chọn C
2 a x 3 3 1 Ta có lim
lim 2 a x 3 x x x a x x 2 1 2 lim 2 1 1 . 2 2 x 1 x x x x 2 lim x x
2 a x 3 Vì lim 1 x 2 lim 1 1 4 0 x 1 x 2 x x 3 lim 2 a
2 a 0 a 2 . x x 2x 3
Giải nhanh : ta có x 2 x 1 x
a x 2x x a x 2 2 3 1 2 .
x x 22 a x a 2 . Khi đó 2
P a 2a 4 a 2
1 3 3, P 3 a 1 2 P 3. i m n Câu 31. Lời giải Chọn B 1 2 a 2 an 1 lim lim n a 2 2 3 n 3 an 1 1 Ta có 1 2 lim 3 3 a. n 2 3 n 2n 1 1 n lim lim 0 2n 2 a
0;20, a Ta có a 1;6;1 3 . a 3 Câu 32. Hướng dẫn giải Chọn D Ta có:
f 0 lim f x lim 3x a 1 a 1. x 0 x 0 2x 2 f x 1 2x 1 lim lim lim lim 1. x 0 x 0 x x 0
x 1 2x 1 x 0 1 2x 1
Hàm số liên tục tại x 0 f 0 lim f x lim f x a 1 1 a 2 . x 0 x 0 Câu 33. Lời giải Chọn B n n 1 4 2 4n 1 1 Giải nhanh: a 10 4 4
2 1024 2 a 1 . 0 n n2 3 4 4na 2a 1024
Mà a 0;2018 và a nên a 10;201 7 có 2008 giá trị . a 1 n 1 2. n n 1 4 2 2 1 1 1 Cụ thể : 4 lim lim . n na 4 3 4 3 n 4a a 2a a 2 2 4 4 Câu 34. Lời giải Chọn A 2 n
Vì 2, 2 , , 2 lập thành cấp số nhân có u 2 q nên 1 n 1 2 n
a 2 2 0 u 2. u . n 2 2 2 1 lim vì 1 2 n q 2 1 Câu 35. Lời giải Chọn A A 6 P Q B D N 3 M C MNPQ //AB Ta có MQ//A . B MNPQ ABC MQ
Tương tự ta có MN //CD, NP//AB, QP//CD .
Do đó tứ giác MNPQ là hình bình hành Ta có AB CD QM MP 0 ; ; 60 . Suy ra 0 S
QM.QN.sin 60 . MNPQ CM MQ 1 Ta có C MQ ∽ C BA MQ 2. CB AB 3 AQ QN 2 A QN ∽ A CD QN 2. AC CD 3 3 Vậy 0 S
QM.QN.sin 60 2.2. 2 3. MNPQ 2 PHẦN II: TỰ LUẬN Câu 36. Lời giải Giải nhanh : n n n 1 a 1 5 2 1 2 n 5 2 3 2 2n 1 5 b n n 5.2n 5 2 2 5. 1 2 n 1 3 5 1 2n 5 5 c 2 Vậy 2 2 2
S 1 5 2 30. n n n 5 2 1 3 n 1 1 2. 2 1 2 2 2 2n 3 Cụ thể : 5 5 lim n n n n 5.2n 5 lim 1 2 n 1 1 3 2 1 1 5. 5 . 2 5 5 n 1 5 2 2. 5 5 Câu 37. Lời giải Ta có 2 3 3 2 x x x x 2 3 3 2 lim lim x x x x x x x x 2 x x 1 1 5 lim . x 2 2 3
x 1 x x x x 1 3 2 3 6 3 x 2 3 1 Giải nhanh: 2 3 3 2
2 3 3 2 x x x x x x x
x x x 2 2 x x x x 2 2 3 x 1 x 1 3 3 2 2 2 3 3 6 6 3 1 x x
x x x x x x x x 1 1 5
x . 2 3 6 Câu 38. Lời giải
Ta có: f 0 m 1. f x 1 x lim lim m m 1. x 0 x 0 1 x f x 1 x 1 x 2x 2 lim lim lim lim 1 . x 0 x 0 x 0 x
1 x 1 x x 0 x
1 x 1 x
f x liên tục tại x 0 lim f x lim f x f 0 m 1 1 m 2 . x 0 x 0 Câu 39. Lời giải A M I B D N C Đặt MN .
x Gọi I là trung điểm của AC 1 a
NI //AB, NI AB ; 2 2 1 a
MI //CD, NI CD . 2 2
IM IN 0 MNI 90 MN AB MN NI MNI 0 , , MNI 30 2 2 a 2 a
NI NM MI x x a Có 2 2 2 cos MNI 0 4 4 cos30 3 3 x . 2MN.NI a 2. .x 2 a 2 2
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 010
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Câu 2. Lời giải Chọn B
Trong không gian có vô số đường thẳng qua O và vuông góc với . Câu 3. Lời giải Chọn D x 1 1 1 2 Ta có lim . 4 x 1
x x 3 11 3 3 Câu 4. Lời giải Chọn D
Ta có: AD / /B C , B C
BC AD BC Câu 5. Lời giải Chọn C
Mệnh đề 1 và 3 là đúng.
Mệnh đề 2 sai. Ví dụ hàm số y x liên tục tại x 0 nhưng không có đạo hàm tại x 0 . 0 0 Câu 6. Lời giải: Chọn A. A sai vì lim n
q 0 khi q 1 . Câu 7. Lời giải: Chọn B. 2 n 2 2 lim u lim 0 (Vì 1). n n n 3 3 3 Câu 8. Lời giải Chọn B
Theo định nghĩa giới hạn hữu hạn của dãy số (SGK ĐS11-Chương 4) thì lim n q = 0 q < . ( )1 Câu 9. Lời giải Chọn D 3 2 3
3x 4 3x 2 12 4 6 2 0 Ta có: lim 0 . x2 x 1 3 3 Câu 10. Lời giải Chọn A 1 1 Ta có: lim lim n 0 . 2n 7 7 2 n Câu 11. Lời giải Chọn C x 1 x 1 1 1
Ta có lim f x lim lim lim . x 1 x 1 x 1 x 1 x 1 x 1 x 1 x 1 2
Để hàm số liên tục tại x 1 khi lim f x 1 f 1 a . 0 x 1 2 Câu 12. Lời giải Chọn D A C B A' C' B'
Ta có BC AC AB d c b b c d 0. Câu 13. Lời giải Chọn A 2 x x 2 3 2 x x 12 Ta có lim lim x3 x 3
x3 x 3 2x x 2 3
x 3x 4 x 4 3 4 7 lim lim 7 3 .
x3 x 3 2x x 2 3 x3 2x x 2 3 2 3 3 2 3 4 3 12 Câu 14. Lời giải Chọn D A B D G M C 2
Gọi M là trung điểm của CD suy ra BG BM . 3
2 2 1 1
Ta có AG AB BG AB BM AB . BC BD AB BC BD. 3 3 2 3
1
AB AC AB AD AB 1
AB AC AD 1
a b c. 3 3 3 Câu 15. Lời giải Chọn C 1 1 1 1 x 1 4 x 1 4 2 2 2 2
x x 4x 1 x x x x 1 Ta có: lim lim lim . x 2x 3 x 3 x 3 2 x 2 x 2 x x Câu 16. Lời giải Chọn A
Gọi M là trung điểm của DC .
Do ABCD là tứ diện đều nên ta có: DC AM
DC AMB DC AB A . B CD 0. DC BM Câu 17. Lời giải Chọn D B A C D K I A' B' C' D'
Dựa vào đáp án, ta thấy rằng:
A đúng, vì IK, AC cùng thuộc mặt phẳng B A C.
1 1
B đúng, vì IK IB B K
AC AC . 2 2
C sai, vì IK IB B ' K
Ta có AB B C DD AB BC CC AC CC AC k 1. 1 1 1 1 1 1 Câu 18. Lời giải Chọn A 4n 3n Ta có T n 1 n n 1 lim 16 4 16 3 lim n 1 n n 1 16 4 16 3n 3 n 1 4n 3n 4 1 1 lim lim .
16.16n 4n 16.16n 3n 1 n 3 n 4 4 8 16 16 4 4 Câu 19. Lời giải Chọn B 2
4x 3x 1 4 a 0 a 4 lim
ax b 0 a 23 lim 4 x b 11 0 x x 2 x x 2 1 1 b 0 b 1 1
a b 7 . Câu 20. Hướng dẫn giải Chọn B. 2 x 4x 3 x 1 x 3
Ta có: lim f x lim lim
lim x 3 2 . x 1 x 1 x 1 x 1 x 1 x 1
lim f x lim mx 2 m 2 . x 1 x 1 f 1 m 2 .
Để hàm số đã cho liên tục tại điểm x 1
thì lim f x lim f x f
1 2 m 2 m 0 . x 1 x 1 Câu 21. Lời giải Chọn D 3 3x 2 2 khi x 2
Hàm số f x x 2
liên tục tại x 2 khi lim f x lim f x f 2. * 1 x 2 x 2 2 a x khi x 2 4 f 2 7 2 2a 4 3 3x 2 2 1
Ta có lim f x lim * a 1 a 1. max x2 x2 x 2 4 lim f x 1 7 2 2 lim a x 2a x2 x2 4 4 Câu 22. S A C M B Lời giải. Chọn A (SAB) ^ (ABC) üïïï
Vì (SAC ) (ABC ) ï ^ ý Þ SA ^ (ABC) ï (SAB) (SAC) SAï Ç = ïïþ
Gọi M là trung điểm của BC. Khi đó ta có AM ^ BC (vì tam giác ABC đều)
Mà SA ^ BC Þ BC ^ (SAM) Þ BC ^ SM
(SBC)Ç(ABC)= BCüï Có ï
ý Þ SMA là góc giữa hai mặt phẳng (SBC) và (ABC)
AM ^ BC,SM ^ BC ïïþ a 3 SA Có AM = Þ tanSMA = = 1. 2 AM 0 Þ SMA = 45 Câu 23. Lời giải Chọn B 2 x 16
Ta có: lim f x lim
lim x 4 8 . x 4 x 4 x 4 x 4
Và: lim f x lim mx
1 4m 1 f 4. x 4 x 4
Hàm số f x liên tục tại điểm x 4 nếu lim f x lim f x f 4 . x 4 x 4 7
4m 1 8 m . 4 Câu 24. Lời giải Chọn C 2 x 3 4 x 3 1
Ta có lim f x lim lim lim 2 x 1 x 1 x 1 x 1 x 1 x
1 2 x 3 x 1 x 1 2 x 3 Câu 25. A' C' B' A C B Lời giải Chọn B
Ta có B 'C B ' B BC
BB ' BA AC BB ' AB AC b a c B C
a b c hay B C
a b c . Câu 26. Lời giải Chọn A S A C B
Ta có SC.AB SC.SB SA SC.SB SC.SA
SC . SB .cosSC.SB SC . SA .cosSC.SA SC.S . B cos
BSC SC.S . A cos
ASC.
Mà SA SB SC và BSC
ASC SC.AB 0 .
Do đó SC, AB 90. Câu 27. Lời giải Chọn B 10 2x 2x 10 2 1 lim lim lim 2 2 x 5 x 5 x 5 x 6x 5 x 6x 5 x 1 2 Câu 28. Lời giải Chọn C x 2 2 x 2 1 1 lim lim lim . x2 x 2
x2 x 2 x 2 2 x2 x 2 2 4 Câu 29. Lời giải Chọn C 1 2 1 1 2 n n 1 n 1 1 Ta có lim lim 2 2 sin 2 n n 2 1 2 1 4 1 n n a 2 2 S 8 b 0 Câu 30. Lời giải Chọn C. A N B D M C
Gọi N là trung điểm của AC và a là độ dài cạnh tứ diện đều.
Ta có MN // AB AB, DM MN, DM DMN . a 3 a
DM MN DN
Tam giác DMN có DM DN 1
, MN AB và 2 2 2 cos DMN . 2 2 2 2.DM .MN 2 2 2
a 3 a a 3 2 2 2 3 cos DMN . a 3 a 6 2. . 2 2 Vậy AB DM 3 cos , . 6 Câu 31. Lời giải Chọn C 2
n 2n n 2 1 n 2n 1 n Ta có lim lim lim . Ta có 3n 1 3n 3n 1 3n 2 2 1 n 2n n 1 lim lim 3n 1 1 2 3 n 3
n 2n 1 1 lim . n 3n 1 3n 3 1 n 1 n 1n 0 0 lim 0 3n 3 3n Câu 32. Lời giải Chọn D Ta có 1 1 1 0,17232323 0,17 23 4 6 8 10 10 10 1 17 17 23 1706 853 10000 23. . 100 1 100 100.99 9900 4950 1 100 a 853 12 13
2 T 4097 2 . b 4950 Câu 33. Hướng dẫn giải Chọn D.
Tập xác định D , f 1 1 m .
Ta thấy hàm số f x liên tục trên các khoảng ; 1 và 1; . x x 1 lim f lim
1, lim f x lim x 1 2 . m e 1 2mx 1 m . x 1 x 1 ln x x 1 x 1
Hàm số f x liên tục trên khi và chỉ khi hàm số f x liên tục tại x 1 lim f x lim f x f 1 . x 1 x 1
1 m 1 m 0 . Câu 34. Lời giải Chọn A 1 2017 x a 1 1 2017 2 a 1 a x 1 2017 2 x x 2 Ta có: lim lim lim x x a . x x 2018 x 2018 x 2018 x 1 1 x x 1 Nên a 1 a . 2 2
2x bx1x 2x bx1x Ta có: lim 2 lim x bx 1 x x x 2
x bx 1 x 1 x b 1 bx 1 b x b lim lim lim x . x b 1 x b 1 x b 1 2 x 1 1 x 1 1 1 1 2 x x 2 2 x x x x b
Nên 2 b 4 . 2 1 Vậy P 4 4 2 . 2 Câu 35. Lời giải Chọn C 2 a lim u a lim u lim 4v 2 n 1 n a 4b 2 Giả sử n 3 , ta có . lim v b lim v lim u 1 b a 1 1 n 1 n n b 3
Vậy lim u 2v a 2 1 b 2. 0 n n 2 . n 3 3 PHẦN II: TỰ LUẬN Câu 36. Lời giải Ta có: 2017 2017 2018 2018 2018 nn 2017 n 1 1 2018 n n +) lim lim lim 1. n 20172018 2018 2018 2018 2017 2017 n 1 1 n n n 2020 2017 +) lim n 2 2
n 2020 4n 2017 lim 1 4 1 2 2 n n n 1 1 1 +) Ta có: A .... . 1.3 3.5
2n 12n 3 2 2 2 2A .... . 1.3 3.5
2n 12n 3 1 1 1 1 1 1 1
2A 1 ... . 3 3 5 5 7 2n 1 2n 3 1 2n 2 n 1 2A 1 A . 2n 3 2n 3 2n 3 1 1 1 1 1 n 1 1 Nên lim .... n 1.3 3.5
2n 12n 3 lim lim . 2n 3 3 2 2 n u 2018 1 2019 2021 2025 2033 +) Dãy 1
có u 2018; u ; u ; u ; u ;... u u 1 , n 1 1 2 3 4 5 2 4 8 16 n 1 n 2 n 1 2 2017 Dự đoán u với * n n n 1 2
Dễ dàng chứng minh dự đoán trên bằng phương pháp quy nạp. n 1 n 1 2 2017 1 Từ đó lim u lim lim 1 2017. 1. n n 1 2 2 Câu 37. Lời giải 2 2
x ax 5 x ax 5 Ta có:
x ax x lim 5 lim 5 x 2 lim 5 5 x 2
x ax 5 x x 2
x ax 5 x 5 a a lim x 5 5 a 10. x a 5 2 1 1 2 x x
Vì vậy giá trị của a là một nghiệm của phương trình 2
x 9x 10 0 . Câu 38. Lời giải f 0 3 x x lim f x 4 1 1 4 1 1 lim lim 2 x0
x0 ax 2a x0 1 x
x ax 2a 1 4x 1 1 4 4 lim
x0 ax 2a 1 4x 1 1 22a 1 4 1
Hàm số liên tục tại x 0 khi f 0 lim f x 3 a . x0 22a 1 6 Câu 39. Lời giải S A D O M B C
Cách 1: Trong ABCD , gọi O AC BD, ta có: SO ABCD . 1 3 OM MC ; a 2 2
SM SC MC a . 2 2
Ta có OM BC MS,CB SM . O OM 3
Ta có SOM vuông tại O nên cos SMO . SM 3 3 3 2
Vậy MS.CB MS.C .
B cos MS,CB a . . a a . 2 3 2
Cách 2: Trong ABCD , gọi O AC BD, ta có: SO ABCD .
MS.CB MO SOCB M . O CB S . O CB M .
O CB do SO CB M . O C . B cos M ; O CB 2 0 a . . a cos 0 a . 2 2
Document Outline
- 10 DE ON TAP LOP 11 GIUA KY 2 - 2021
- BTPRO [CD] GIUA KY 2 - LOP 11 - HDG




