

































Preview text:
ĐỀ 1
ĐỀ ÔN THI HỌC SINH GIỎI MÔN: TOÁN 11
Bài 1/ Cho số thực 0 £ a £ 1 và dãy số (xn) được xác định bởi điều kiện n≥ 1 ÏÔ a x Ô = Ô , 1 Ô 2 Ì 2 Ô Ô a xn- 1 x Ô = - ," n > 1. n Ô Ô Ó 2 2
Chứng minh rằng dãy số (xn) có giới hạn hữu hạn. Tìm giới hạn đó. n≥ 1
Bài 2/ Tìm tất cả hàm số f : R Æ R thỏa mãn đồng thời hai điều kiện sau:
i) f (x + 1) ≥ f ( )
x + 1 với mọi x ŒR ;
ii) f (xy) ≥ f (x). f (y) với mọi x,y ŒR .
Bài 3/ Tìm tất cả các số nguyên dương k thỏa điều kiện: tồn tại các số nguyên m ≥ 2,n ≥ 2 để 3k + 5k m = n .
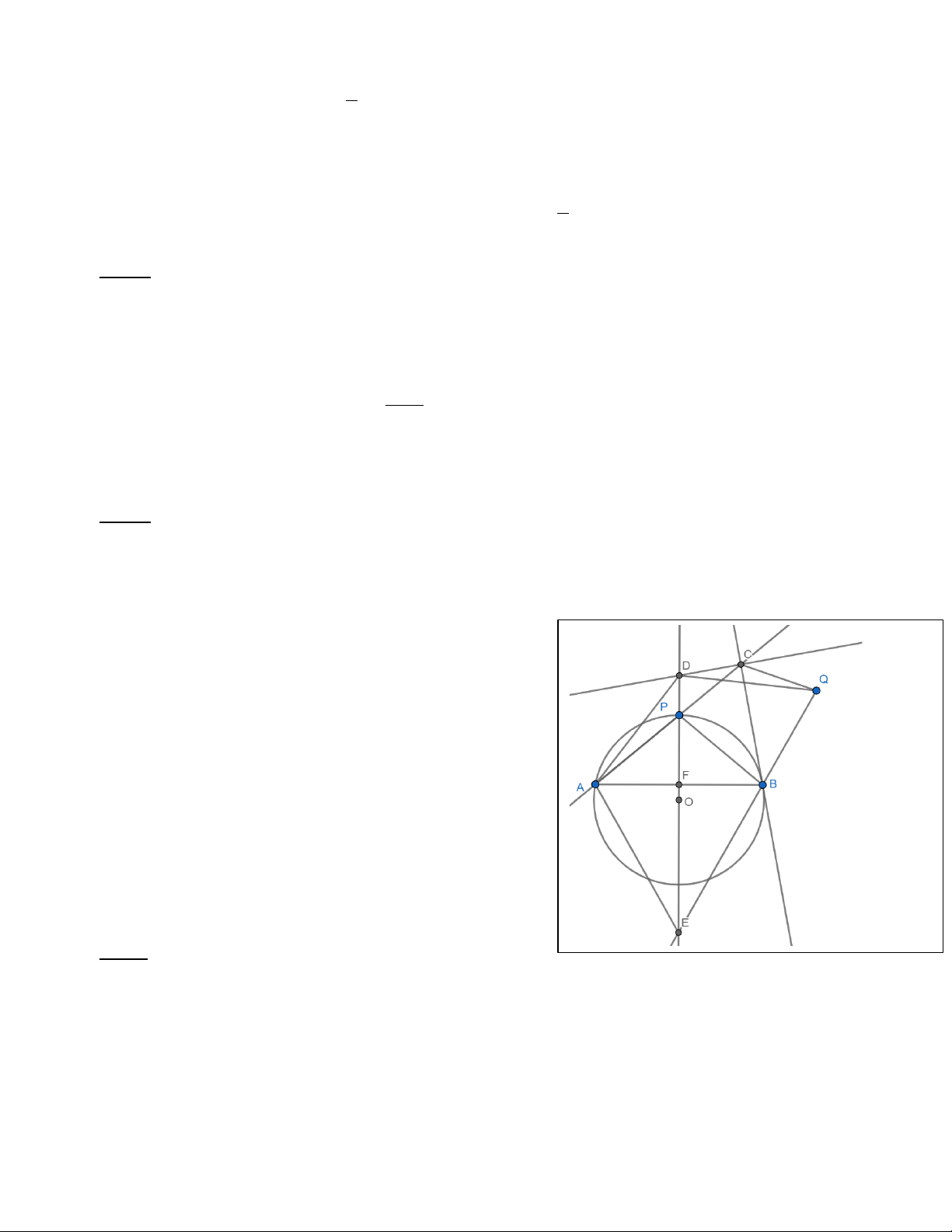
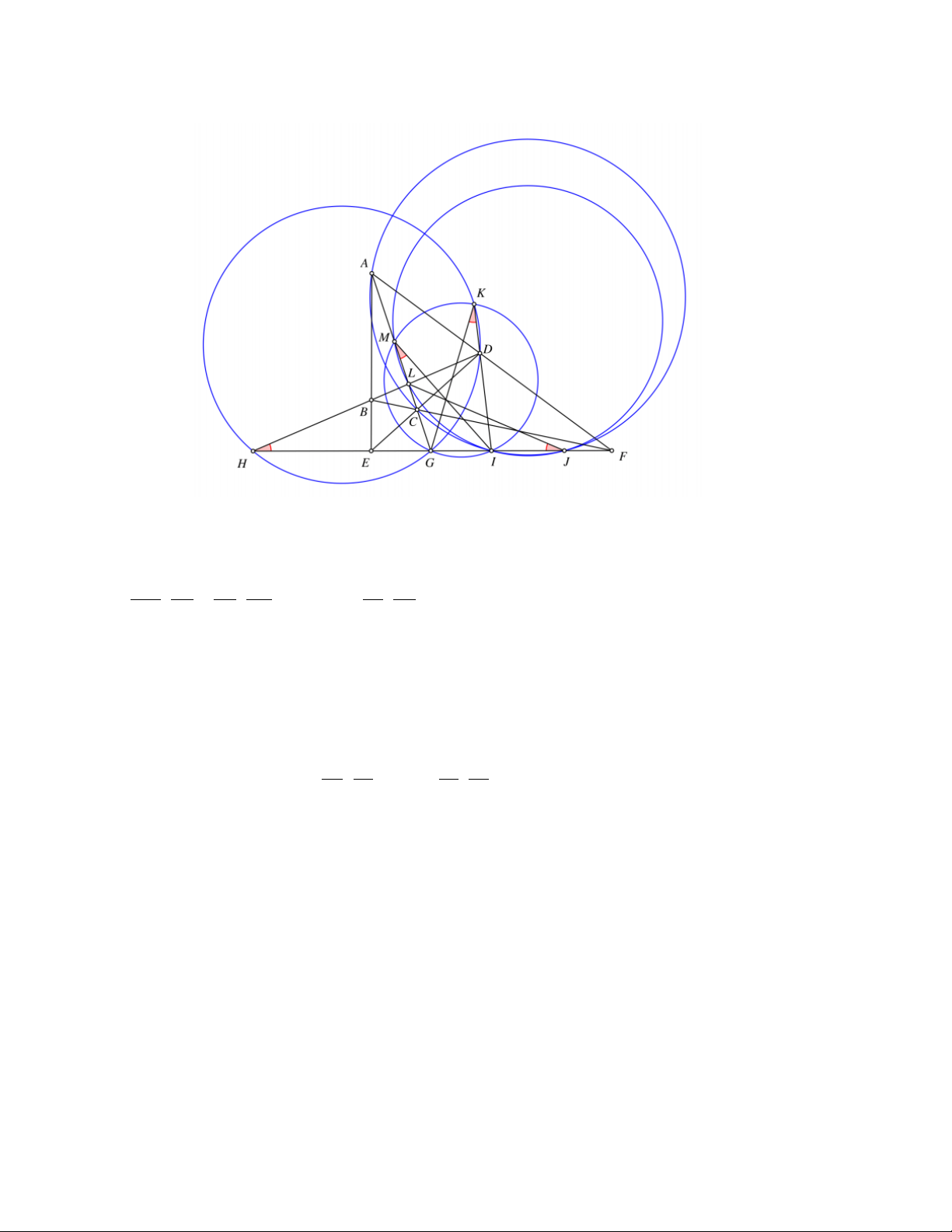
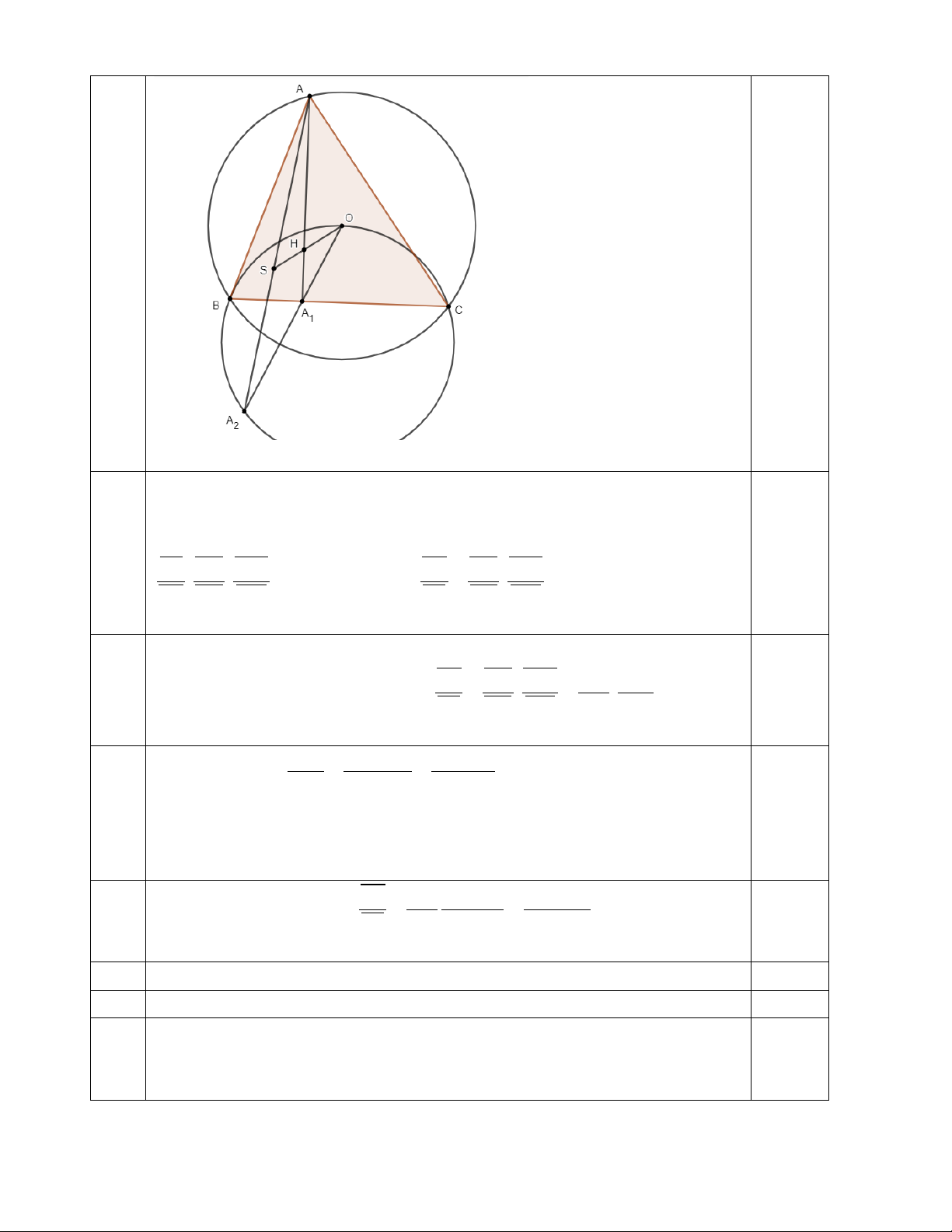
Bài 4. Cho tam giác ABC cân tại A , nội tiếp đường tròn (O .
) Lấy các điểm D,E lần lượt thuộc các cạnh ,
CA AB sao cho DE không song song với BC. Các tia BD,CE lần lượt cắt đường tròn (O
) tại M,N ( M π ,
B N π C). Đường tròn tâm M , bán kính MC cắt đoạn thẳng
BD tại P. Đường tròn tâm N , bán kính NB cắt đoạn thẳng CE tại Q.
a. Gọi T là trung điểm cung BC không chứa điểm A của đường tròn (O . C ) hứng minh rằng TP = TQ.
b. Chứng minh rằng các đường thẳng , DE P , Q BC đồng quy.
Bài 5/ Theo dọc trên đường tròn, người ta ghi sẵn 299 số gồm số 0 và một số 1.
Ở mỗi bước đi sau đó của trò chơi, người chơi được phép thực hiện một trong hai động tác sau:
1/ Thay mỗi số đang có bởi hiệu giữa nó và tổng của hai số nằm kề với nó (lúc chưa thay) trên đường tròn;
2/ Chọn tùy ý hai số mà giữa chúng (trên đường tròn) có đúng hai số, rồi trừ mỗi số được
chọn cho 1 hoặc cộng mỗi số được chọn cho 1.
Hỏi sau hữu hạn bước ta có thể thu được
a/ 298 số 0 và hai số 1 nằm kề nhau trên đường tròn?
b/ 297 số 0 ba số 1 nằm kề liên tiếp nhau trên đường tròn?
…………………………..HẾT……………………………. Trang 1 LỜI GIẢI
Bài 1/ Cho số thực 0 £ a £ 1 và dãy số (xn) được xác định bởi điều kiện n≥ 1 ÏÔ a x Ô = Ô , 1 Ô 2 Ì 2 Ô Ô a xn- 1 x Ô = - ," n > 1. n Ô Ô Ó 2 2
Chứng minh rằng dãy số (xn) có giới hạn hữu hạn. Tìm giới hạn đó. n≥ 1 Giải a
1/ Bằng quy nạp ta chứng minh được 0 £ x £ . (1) n 2 È a ˘
2/ Giới hạn x = lim x , nếu có, sẽ là nghiệm của trong đoạn 0; Í ˙ của phương trình n Í 2˙ Î ˚ 2 a x 2 x = -
€ x + 2x- a = 0 € c = : x = - 1+ 1+ a 2 2 2 a c a
Vì a ≥ 0 nên 0 £ c = - £ . (1') 2 2 2
3/ Từ công thức truy hồi của dãy nên ta có 2 2 2 2 a Ê x ˆ Ê ˆ - Á - ˜ a c Á ˜ c x n 1 n- 1 x - c = Á - ˜ - Á ˜ Á - ˜ = n 2 Á Ë 2 ˜¯ 2 Á Ë 2 ˜˜¯ 2 Ê 1ˆ Á ˜ = - Á ˜(x + - Á ˜ - c x - c n 1 )( n 1 ) Ë 2˜¯ = ... n- 1 n- 1 Ê 1ˆ Á ˜ = - Á ˜
’ (x + c x - c Á ˜ i )( . . (2) 1 ) Ë 2˜¯ i=1
Từ (1) và (1’) suy ra 0 x c a 1, i + £ + £ £ " ŒZ nên i n- 1
0 £ ’ (x + c £ i ) 1 i= 1 1
Từ đó và (2) kéo theo 0 £ x - c £
x - c ," n> 1. n n- 1 1 2
Vì thế limx = - 1+ 1+ a. n
Bài 2/ Tìm tất cả hàm số f : R Æ R thỏa mãn đồng thời hai điều kiện sau:
i) f (x + 1) ≥ f ( )
x + 1 với mọi x ŒR ;
ii) f (xy) ≥ f (x). f (y) với mọi x,y ŒR . Giải. Trang 2
Giả sử f là một nghiệm hàm. Ta quy ước ( )n f x viết thay ( ( ) ) n f x . Từ ii) ta có f ( )
x ≥ f ( x)2 ≥ 0, "x ≥ 0.(1) Ï f
Ô (1) = f (0 + 1) ≥ f (0) + 1≥ 1 Do đó Ô Ì suy ra f (1) =
1 và do đó f (0) = 0. (2) 2 f Ô (1) = f (1.1) ≥ Ô f (1) Ó
Theo i) và quy nạp ta được f (x + )
n ≥ f(x)+ n," x ŒR,nŒN. (3)
Theo ii) và quy nạp ta được ( n) ( )n f x
f x , x 0,n + ≥ " ≥ ŒZ . (4)
Với x ≥ 0 suy ra x È ˘ŒN,{ } x ≥ 0 thì Î ˚ f( ) x = f { ( } x + x È Î ) ˘ ≥ f { ˚ ( }
x )+ xÈ˘≥ xÈ˘> x- 1. Î ˚ Î ˚
Vì vậy, nếu x 1,n + > ŒZ thì Ï f Ô ( n x ) n > x - 1> Ô 0 Ô Ô n Ì Ê Ô 1 ˆ Á ˜ 1 Ê ˆ f Ô Á ˜ ≥ f Á ˜ Á ˜ ≥ 0 n (theo (1),(4 ) ) Ô Ô x Á ˜ Ë ¯ x Á ˜ Ë ¯ Ó n Ê ˆ Ê ˆ Ê ˆ fi = f ( ) n 1 = f x Á ˜ Á ˜ ≥ f Á ˜ ( n x ) 1 f Á ˜ Á ˜ ≥ ˜ Ë ¯ Á ˜ ( n x - f Á ˜ Á ˜ n n ) 1 (2) 1 1 1 x x ˜ Ë ¯ x Á ˜ Ë ¯ Hay 1 n Ê ˆ 1 1 Ê ˆ Á ˜ Á ˜ 1 1 f Á ˜ £ fi f Á ˜ £ = Á ˜ n x˜ Ë ¯ x - 1 Á ˜ n n x Ë ¯ x - 1 1 n x 1- n x 1 Ê ˆ Á ˜ 1
Cho n Æ • , từ bất đẳng thức này ta nhận được f Á ˜ £ với mọi x>1. Nói cách khác x Á ˜ Ë ¯ x f( ) x £ x, " x Œ 0 È;1 .˘ (5) Î ˚
Ta có thể viết (3) dưới dạng f (x- ) n £ f( )
x - n,"x ŒR,nŒN . (3’)
Từ (3’) và (5) ta thấy nếu x £ 0 thì - x È˘ŒN,1> { } x ≥ 0 khi đó Î ˚ f( ) x = f { ( }
x - (- xÈÎ )˘˚ £ f { ( }
x )- (- xÈÎ )˘£ { } x - ˚
(- xÈÎ )˘= .x ˚
Vậy (5) đã nới thành f (x) £ x, " x £ 1. (5’)
Với mọi - 1£ x £ 0, dùng ii) và (5’) ta còn thấy ( )2 £ ( 2) 2 f x
f x £ x suy ra f( )
x ≥ - x = x fi f( ) x = x. (*)
Ta sẽ chứng minh (*) cũng đúng khi x<-1. Ê 1ˆ 1 Ê ˆ Á ˜ Á ˜ 1
Ta có 1 = f (1) = f Á .
x ˜ ≥ f (x). f Á ˜ = f(x). fi f(x) ≥ x và theo (5’) ta suy ra (*). Á Ë x˜¯ x Á ˜ Ë ¯ x Trang 3
Bây giờ ta chứng minh (*) cho trường hợp x>0. Ta có { }
x - 1< 0, x + 1 + È˘ Œ nên từ (3) ta có Î ˚ Z f( ) x = f { ( } x - 1+ x È ˘+ Î ˚ ) 1 ≥ f { ( } x - ) 1 + x È ˘+ 1= { } x - 1+ x È ˘+ 1= x> 0 (6) Î ˚ Î ˚ 1 1 Ê ˆ Á ˜ 1
Thay x bởi ta có f Á ˜ ≥ > 0 (6’). x x Á ˜ Ë ¯ x Ê 1ˆ 1 Ê ˆ Á ˜ Á ˜ 1
Nhưng 1 = f (1) = f Á .
x ˜ ≥ f (x)f Á ˜ ≥ . x = 1. Á Ë x˜¯ x Á ˜ Ë ¯ x
Dấu “=” xảy ra nên nó xảy ra ở (6) và (6’).
Tóm lại f (x) = x," x ŒR. Thử lại ta thấy hàm số đã tìm thỏa yêu cầu đề.
Bài 3/ Tìm tất cả các số nguyên dương k thỏa điều kiện: tồn tại các số nguyên m ≥ 2,n ≥ 2 để 3k + 5k m = n . Giải
1/ Với k = 1 thỏa điều kiện của đề bài 1 1 3 3 + 5 = 2 .
2/ Ta sẽ chứng minh k > 1 không thỏa yêu cầu đề. Ï 3k Ô = 9l ∫ Ô ( 1 mod4)
Với k = 2l , khi đó Ô Ì suy ra 3k 5k + ∫ 2(mod4 ) nên 3k 5k v + = 1, 2 ( ) 5k Ô = 25l ∫ Ô ( 1 mod4) Ô Ó Trong khi đó m v n m M m v n > 1. 3k + 5k m π n . 2 ( ) 2 ( ) nên Suy ra
Với k = 2l + 1 khi đó 3k + 5k = (3+ ) 5 ( 2l 2l- 1 2l- 1 2 3 - 3 .5+ L - 3.5 + 5 l ) 2l = 8. (- )i 2
1 .3 l- i.5i i= 0 Hay 3k 5k v + = 3. k 2 ( )
Từ đó, nếu thỏa mãn yêu cầu ở đề thì 2 £ | m = 3k + 5k m v n v = 3 fi m = 3 2 ( ) 2( ) Mà 3 n ∫ - 1;0; ( 1 mod )
9 . Nên ta xét đồng dư của 3k 5k + theo mod9.
Ta có, k lẻ nên 3k ∫ 0(mod ) 9 ,k ∫ 1;3;5(mod ) 6 . p Nếu k = 6p + 1 thì k 6p+ 1 = = ( 6 5 5
5. 5 ) ∫ 5(mod9 )mâu thuẫn. p
Nếu k = 6p + 5 thì k 6p+ 5 5 = = ( 6 5 5
5 . 5 ) ∫ 2(mod9 )mâu thuẫn.
Như vậy chỉ còn trường hợp k = 6p + 3 p p Ta lại thấy 3 n ∫ - 1;0; ( 1 mod7). Mà k k + = ( 6) 3 + ( 6) 3 3 5 3 .3
5 .5 ∫ - 2(mod7). Như vậy
không tồn tại m,n thỏa yêu cầu bài. Trang 4 Bài 4.
Cho tam giác ABC cân tại A , nội tiếp đường tròn (O . L
) ấy các điểm D,E lần lượt thuộc các cạnh ,
CA AB sao cho DE không song song với BC. Các tia BD,CE lần lượt cắt đường tròn
(O )tại M,N ( M π ,
B N π C). Đường tròn tâm M , bán kính MC cắt đoạn thẳng BD tại P.
Đường tròn tâm N , bán kính NB cắt đoạn thẳng CE tại Q.
a. Gọi T là trung điểm cung BC không chứa điểm A của đường tròn (O . C ) hứng minh rằng TP = TQ.
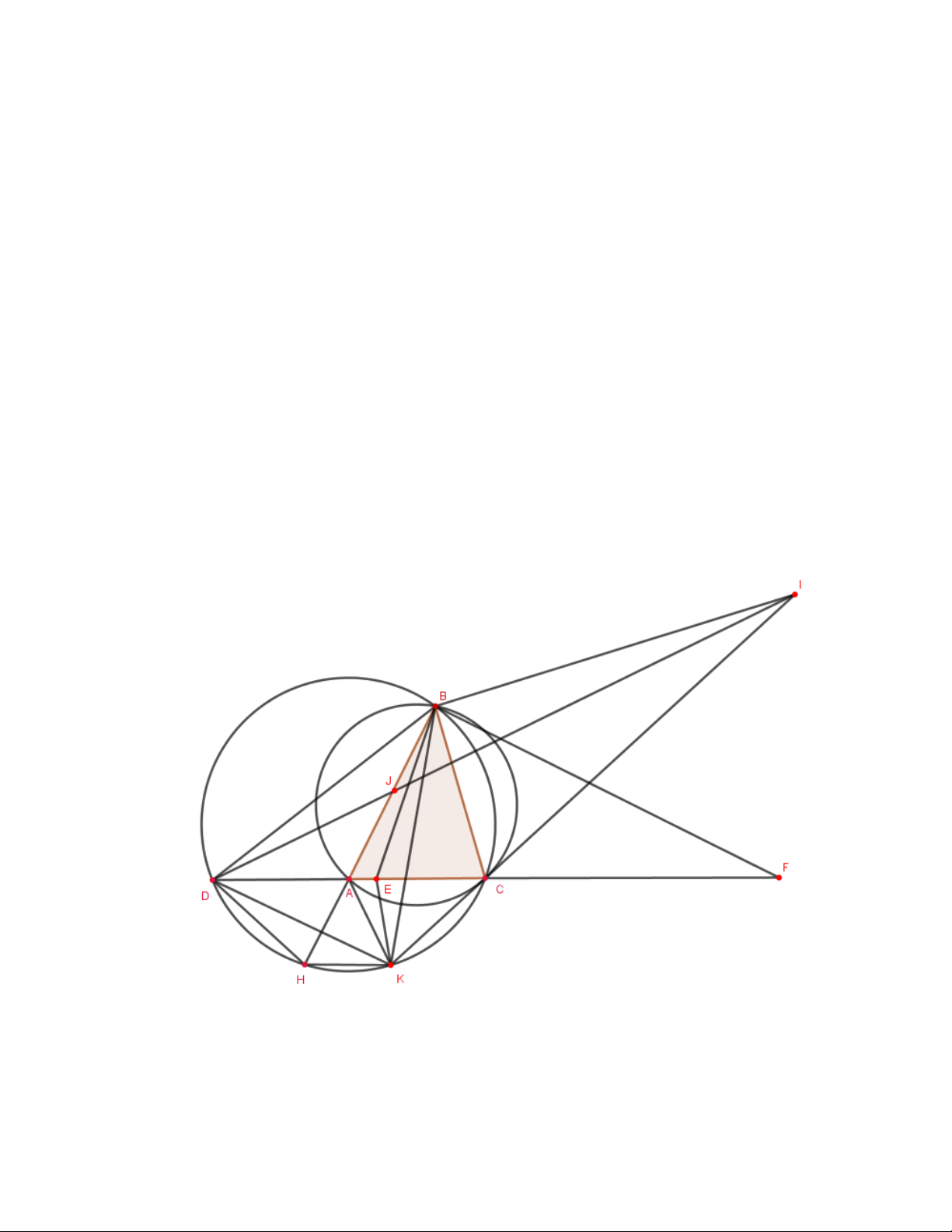
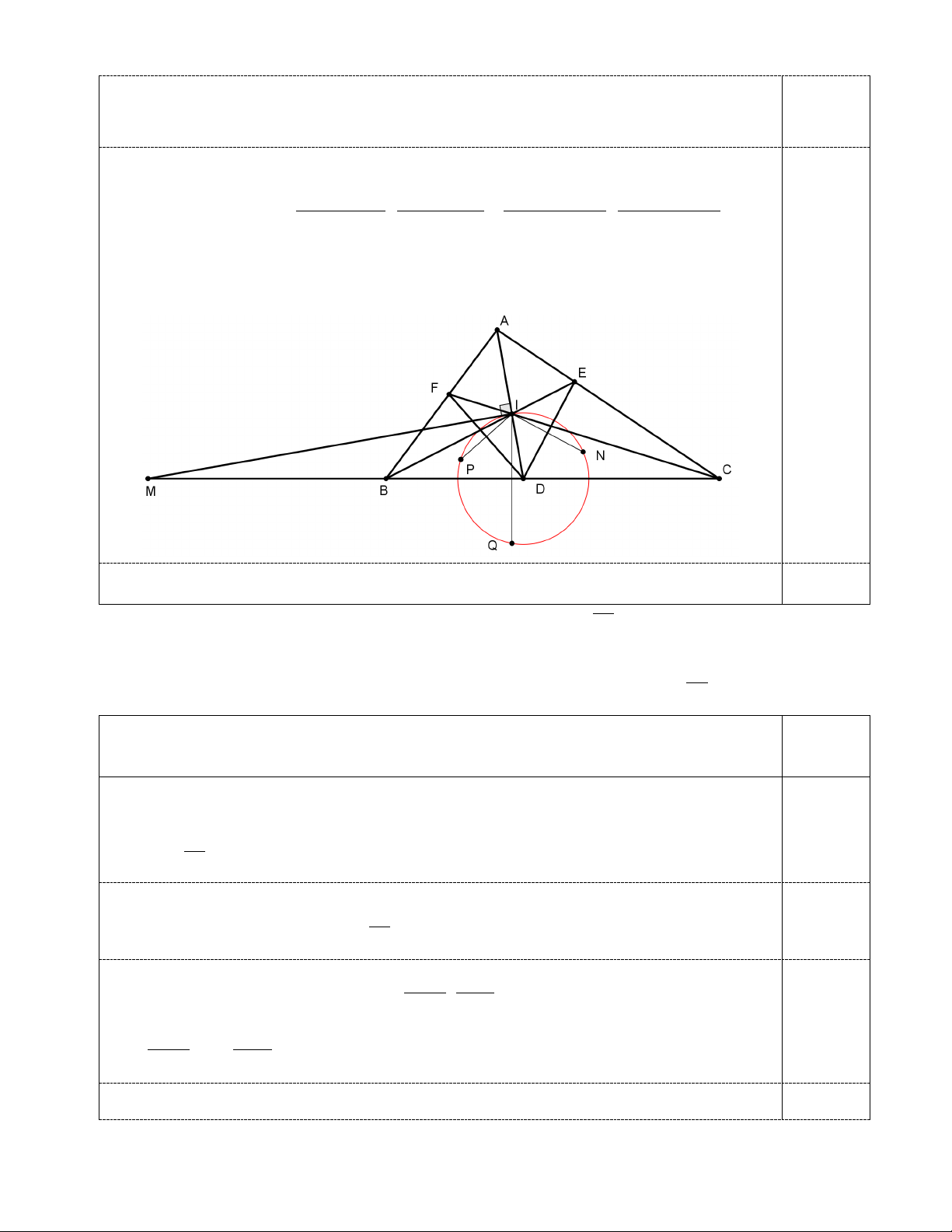
b. Chứng minh rằng các đường thẳng , DE P , Q BC đồng quy. A M D H O N E P Q K C B T a)
Các tam giác cân ABC,MCP,NBQ có góc ở đỉnh bằng nhau nên đồng dạng. Suy ra ∑ ∑
BPC = BQC, do đó bốn điểm ,
B C,P,Q cùng thuộc một đường tròn w. ∑ BAC Hơn nữa ∑ ∑ BPC = BQC = 90 +
nên nếu gọi I là tâm đường tròn nội tiếp tam giác ABC 2 ∑ BAC
thì điểm I cũng thuộc w (vì ∑ BIC = 90 + ). 2
Bằng biến đổi góc, cũng dễ dàng kiểm tra được TB = TI = TC nên T là tâm đường tròn ngoại
tiếp tam giác BIC (tức là đường tròn w).
Do đó TP = TQ. b) Dễ thấy ,
AB AC là các tiếp tuyến của đường tròn w.
Gọi K là giao điểm của các đường thẳng BP,CQ; H là giao điểm của các đường thẳng BQ,CP. Trang 5
Ta có biến đổi tỷ số kép (xét trên đường tròn w)
(BA,BK,BH,BC)= (BB,BP,BQ,BC)= (CB,CP,CQ,CC)
= (CB,CH,CK, )
CA = (CA,CK,CH, ) CB
Do đó, A,K,H thẳng hàng.
Hai tam giác BEQ và CDP có BE« CD = ,
A BQ« CP = H,BP« CQ = K mà A,K,H thẳng
hàng nên theo định lý Desargues, ta có , DE P , Q BC đồng quy.
Bài 5/ Theo dọc trên đường tròn, người ta ghi sẵn 299 số gồm số 0 và một số 1.
Ở mỗi bước đi sau đó của trò chơi, người chơi được phép thực hiện một trong hai động tác sau:
1/ Thay mỗi số đang có bởi hiệu giữa nó và tổng của hai số nằm kề với nó (lúc chưa thay) trên đường tròn;
2/ Chọn tùy ý hai số mà giữa chúng (trên đường tròn) có đúng hai số, rồi trừ mỗi số được
chọn cho 1 hoặc cộng mỗi số được chọn cho 1.
Hỏi sau hữu hạn bước ta có thể thu được
a/ 298 số 0 và hai số 1 nằm kề nhau trên đường tròn?
b/ 297 số 0 ba số 1 nằm kề liên tiếp nhau trên đường tròn? Giải
Trên đường tròn ta đánh dấu (x) tại vị trí mà người ta đã ghi sẵn số 1 (và giữ nguyên dấu (x) đó suốt trò chơi).
Giả sử a ,a ,K ,a là các số đang có mặt trên đường tròn, kể theo thứ tự liên tiếp ngược chiều 1 2 300
kim đồng hồ. Trong đó, a là số nằm tại vị trí có dấu (x). 1 300 300 100
Đặt S := Â a ; A : - = Â - a T = Â a k ( )k 1 1 ; : . k 3k k= 1 k= 1 k= 1
Ta hãy tìm xem sau mỗi bước đi các tổng này có thể thay đổi thế nào.
Nếu bước đi được thực hiện bởi động tác 1, thì
a với 1£ k £ 300 được thay bởi ,a := a - a -
a = a ;a = a - a (quy ước ). k k k k 1 k+ 1 301 1 0 300 300
Từ động tác 1 đưa tổng S thành ,
S' = Â a = - S. k k= 1 300
Nếu bước đi được thực hiện bởi động tác 2, thì dễ thấy ,
S' = Â a = S± 2. k k= 1
a/ Từ các phân tích trên ta thấy S giữ nguyên tính chẵn lẻ qua mỗi bước đi. Khi chưa thực hiện
bước đi nào thì S=1, nên không thể thực hiện được yêu cầu của câu a. 300
b/ Nếu mỗi bước đi được thực hiện bởi động tác 1, thì A' = Â (- )k- 1 , 1 a = 3A k k= 1
Dễ thấy nếu thực hiện bởi động tác 2, thì A không thay đổi.
Khi chưa thực hiện bước đi nào thì A = 1, trong khi ở trạng thái 297 số 0 và ba số 1 nằm kề
nhau thì A = ± 1. Như vậy theo phân tích trên về cách thay đổi của A thì điều kiện cần và đủ để
thu được trạng thái 297 số 0 và ba số 1 nằm liền kề sau hữu hạn bước là không bao giờ thực
hiện bước đi bởi động tác 1 và ba số 1 phải nằm ở vị trí sao cho tổng A=1. Trang 6
Tuy nhiên, ở chiều ngược lại với cách thực hiện các bước đi như thế (không thực hiện động tác
1) thì hoặc là các số a ,a ,K ,a đều được giữ nguyên hoặc là có đúng hai trong 100 số này 3 6 300 100
thay đổi, theo cách cùng tăng 1 hoặc cùng giảm 1. Vì thế ,
T' = Â a = T ± 2. Vậy, tính chẵn le 3k k= 1 của T là không đổi.
Khi chưa thực hiện bước đi nào, tổng T=0, là một số chẵn, trong khi ở trạng thái 297 số 0 và ba
số 1 nằm liền kề thì T=1. Như vậy không thể thực hiện được. ĐỀ 2
ĐỀ ÔN THI HỌC SINH GIỎI MÔN: TOÁN 11 ìx = 4 1 ï
Bài 1. Cho dãy số (x ) được xác định í n 25n + 26 3 2 x
= x - 5x + 3x + -1,n ³1. ï n 1+ n n n î n +1
Chứng minh rằng dãy số (x ) có giới hạn hữu hạn. Tìm lim x . n n
Bài 2. Tìm tất cả đa thức P(x)Î ![x] thỏa mãn: 2 P x = P( 2 ( ) 7 x -15)+ 2023, x " Î! (1)
Bài 3. Tìm tất cả các số nguyên tố , m n sao cho 2 ( 1) | (13n m + +1) và 2 ( 1) | (13m n + +1).
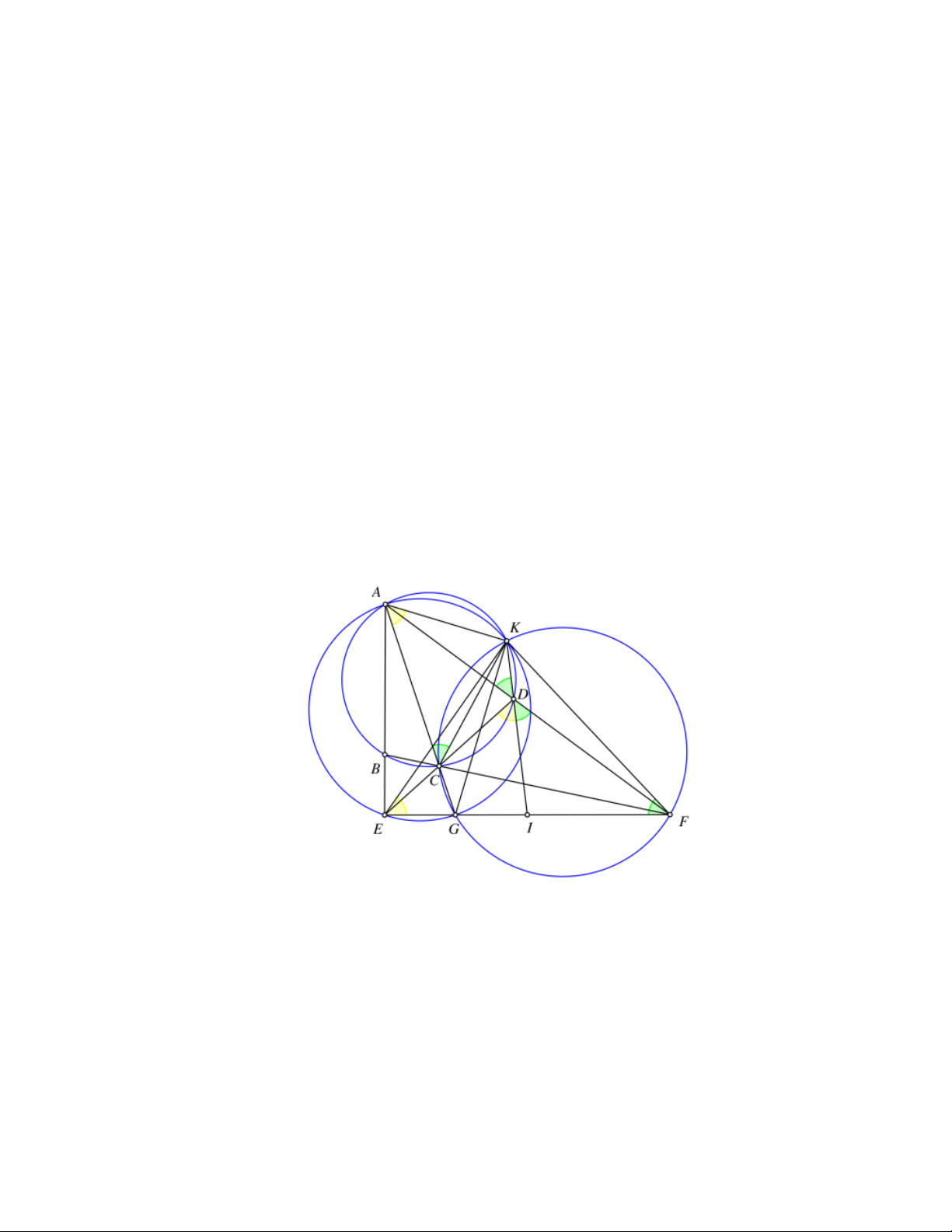
Bài 4. Cho tứ giác ABCD nội tiếp trong đường tròn (O) sao cho AB cắt CD tại E và AD cắt BC tại F, gọi
G là giao điểm của AC và BD. Các đường tròn (ADE) và (CDF) cắt nhau tại D và H. Phân giác trong góc ∑
AHB cắt AB, AD lần lượt tại I, J và phân giác trong góc ∑
DHC cắt CB, CD lần lượt tại K, L. Gọi
M, M’ là giao điểm của BH với AD, CD tương ứng, N, N’ là giao điểm của DH với BC, BA tương ứng.
Chứng minh IL, KJ, MN và M’N’ đồng quy tại G.
Bài 5. Cho tập hợp X là một tập hợp con của tập các số nguyên dương sao cho trong 2023 số tự nhiên
liên tiếp bất kì luôn có một số thuộc tập X. Chứng minh rằng tồn tại hai số trong X sao cho số này chia hết cho số kia. LỜI GIẢI ìx = 4 1 ï
Bài 1. Cho dãy số (x ) được xác định í n 25n + 26 3 2 x
= x - 5x + 3x + -1,n ³1. ï n 1+ n n n î n +1
Chứng minh rằng dãy số (x ) có giới hạn hữu hạn. Tìm lim x . n n Giải:
Trước hết, ta chứng minh * x > 3, n
" Î • (1) bằng phương pháp quy nạp. n
* Hiển nhiên x = 4 > 3. 1
* Với n ³ 2 ,ta có Trang 7 1 2 x
= (x +1)(x -3) +16 + -1> 16 -1= 3 n 1 + n n n +1
Do đó x > 3 với mọi số nguyên dương . n n
Tiếp theo, ta chứng minh dãy số (x ) là dãy giảm hay * x < x , n
" Î • (2)bằng phương pháp quy nạp. n n 1 + n
* Với n =1, x = 18 -1< 4 = x . 2 1
* Giả sử 3 < x < x < ... < x = 4 n n 1 - 1 Khi đó xét hiệu æ 25n + 26 ö æ 25(n -1) + 26 2 2 3 2 3 2 ö H = (x
+1) - (x +1) = x - 5x + 3x +
- x - 5x + 3x + n 1 + n ç n n n ÷ ç n 1- n 1 - n 1 ÷ è n +1 - ø è n ø = (x - x
x + x x + x - x - x + + - n n- ) ( 1 1 2 2 . 5 5 3 1 n n n 1 - n 1 - n n 1 - ) n +1 n é 5 5 25ù 1 1 2 2
= (x - x ) (x - ) + (x - ) + x .x + 3- + - < 0, n " ³ 2. n n 1 - ê n n 1 - n n 1 ë 2 2 - 2 úû n +1 n Vì x - x
< 0 (gt quy nạp) và x > 3, x > 3nên n n 1 - n n 1 - 2 2 é 5 5 25ù æ 5 ö æ 5 ö 25 2 2 2 2 (x - ) + (x - ) + x .x + 3 - > 3 - + 3 - + 3.3 + 3 - = 0; - < 0, n " ³ 2.Từ n n 1 ê - n n 1 ú ç ÷ ç ÷ ë 2 2 - 2 û è 2 ø è 2 ø 2 n +1 n
đó suy ra dãy số (x ) giảm và bị chặn dưới nên theo nguyên lý Weierstrat dãy số có giới hạn hữu n hạn.Đặt lim x = ,
a 3 £ a < 4 . n
Từ hệ thức truy hồi cho n dần đến dương vô cực ta có phương trình
a = a - 5a + 3a + 25 -1 Û (a + )2 3 2 3 2
1 = a - 5a + 3a + 25 2
Û (a - 3)(a - 3a - 8) = 0 é êa = 3 ê ê 3 - 41 Û a = ê 2 ê ê 3 + 41 a = êë 2
Kết hợp với điều kiện của a ta có a = 3 Vậy lim x = 3 n
Bài 2. Tìm tất cả đa thức P(x)Î ![x] thỏa mãn: 2 P x = P( 2 ( ) 7 x -15)+ 2023, x " Î! (1)
Lời giải: Trước hết chúng ta cần tìm số thực a là nghiệm của phương trình; é 1- 61 êx = 2 2 2
x = x -15 Û x - x -15 = 0 Û ê ê 1+ 61 êx = ë 2 ìï - + ü Với 1 61 1 61 ï a Î í ; thì a thỏa 2 a = a - 5 hay 2 a - a - 5 = 0. ý ï 2 2 î ïþ Trang 8
Giả sử đa thức P(x) thỏa mãn yêu cầu bài toán.
Trong (1) thay x = a ta có: 2
P (a) = P( 2 a - ) 2 7
15 + 2023 Û P (a) -7P(a) - 2023 = 0 é - êP (a) 7 8141 = 2 Û ê ê + êP (a) 7 8141 = ë 2 ìï - + ü Giả sử ï
P(x) là đa thức khác hằng, khi đó P(x) ¹ b với 7 8141 7 8141 bÎí ; và b thỏa ý ï 2 2 î ïþ 2
b - 7b - 2023 = 0
Do P(a) = b nên ta viết P(x) dưới dạng ( ) = ( - )n P x
x a ×Q(x) + b với Q(a) ¹ 0. Thay vào (1) ta được ( )2 (é 2 )n n x a Q x b x a Q( 2 ( ) ( ) 7 15 x 15) bù - + = - - × - + + 2023. êë úû Hay 2 2 2 - × + - × + = ( 2 - - )n n n x a Q x b x a Q x b x a Q( 2 ( ) ( ) 2 ( ) ( ) 7 15
x -15)+ 7b + 2023 (2) Vì 2 b = 7b + 2023, 2
a = a +15 nên (2) được viết thành 2n 2 n
(x - a) ×Q (x) + 2b(x - a)n ×Q(x) = 7( 2 2
x - a ) Q( 2 x -15) n 2
hay (x - a) ×Q (x) + 2b ×Q(x) = 7(x + a)n ×Q ( 2 x -15) (3)
Trong (3) thay x=a ta có: n b ×Q a = a ×Q ( 2 2 ( ) 7(2 ) a -15)
Û 2bQ(a) = 7(2a)n ×Q(a) vì 2 a -15 = a )
Û 2b = 7×(2a)n Hay 7 8141 7(1 61)n ± = ±
điều này không xảy ra với mọi số nguyên dương n
Do đó P(x) º b
Thử lại P(x) º b thỏa mãn yêu cầu bài toán 7 - 8141 + Vậy P(x) º 7 8141 hoặc P(x) º 2 2
Bài 3. Tìm tất cả các số nguyên tố , m n sao cho 2 ( 1) | (13n m + +1) và 2 ( 1) | (13m n + +1).
Lời giải:Vì vai trò của ,
m n như nhau nên không mất tính tổng quát, giả sử m £ n .
● Nếu m = 2 , ta có: 5 |13n +1 (1) và 2 2 (n +1) |13 + 1 (2).
Từ (1) suy ra n là số chẵn nên có n = 2 .Thử lại ( , m )
n = (2, 2) là cặp số thỏa mãn.
● Nếu m > 2 , vì m lẻ nên 2
m +1 º 2 (mod 4)do đó 2
m +1 có ít nhất một ước là số lẻ. Gọi r là một ước nguyên tố lẻ của 2
m +1(*). Từ giả thiết suy ra 13n º 1 - (mod r ) 2 13 n Þ º 1 (mod r ). Trang 9
Đặt d = ord (13), khi đó d | 2n. Mà ta có 13n º 1
- (mod r ) nên d ¹ n. Từ đó suy ra d | 2 hoặc d = 2n. r - TH1: d | 2 khi đó 2 3
r |13 -1 =168 = 2 ×3×7. Vì r lẻ nên r = 3 hoặc r = 7 .
+) Xét r = 3, vì 13 º 1 (mod 3) nên 13n 1 (mod3) 13n º Þ
+1 º 2 (mod3) (điều này mâu thuẫn với (*))
+) Xét r = 7 , theo định lí Fermat nhỏ 6 2 4 2
m º1 (mod 7) Þ (m -1)(m + m +1) º 0 (mod 7) . Nếu 2
m -1 º 0 (mod 7) thì 2
m +1 º 2 (mod 7) (mâu thuẫn (*)). Nếu 4 2
m + m +1 º 0 (mod 7) thì 2 4
m +1 º -m º 0 (mod 7), suy ra m º 0 (mod 7) (vô lí vì m là số nguyên tố).
- TH2: d = 2n , theo định lí Fermat nhỏ ta có r 1 13 - º1 (mod r) ,
suy ra d = 2n | (r -1) , do đó n | (r -1). Điều này nghĩa là các ước nguyên tố lẻ của 2 m + 1 đều chia cho n dư 1 và hơn nữa 2
m +1 º 2 (mod 4) , từ đây suy ra 2 m +1 º 2 (mod ) n .
Suy ra (m -1)(m +1) º 0 (mod n) hay n | (m +1) hoặc n | (m -1). Vì m £ n nên n = m +1. Do đó m = 2 ,
n = 3 nhưng điều này mâu thuẫn với m > 2 . Vậy ( , m )
n = (2, 2) là cặp số duy nhất thỏa mãn.
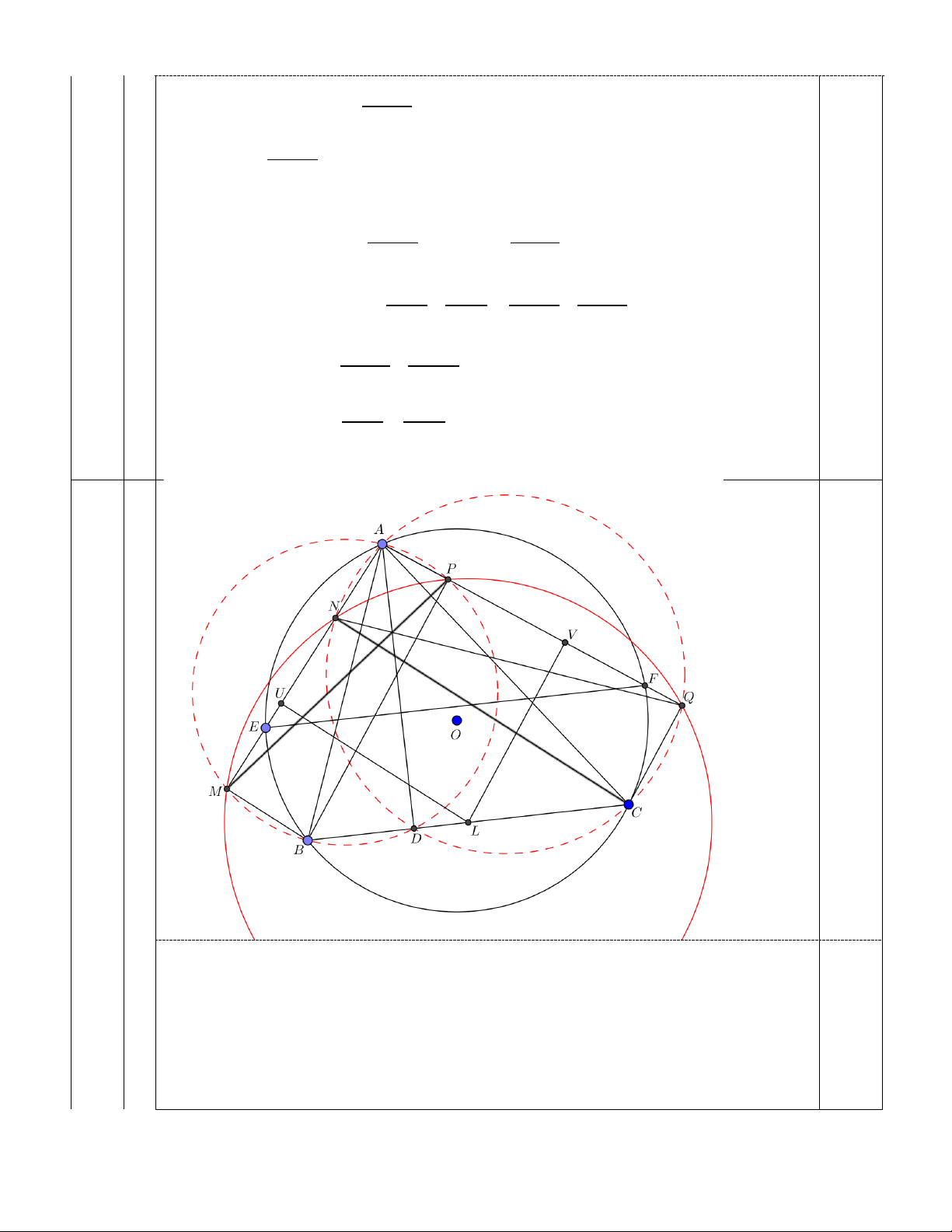
Bài 4. Cho tứ giác ABCD nội tiếp trong đường tròn (O) sao cho AB cắt CD tại E và AD cắt BC tại F, gọi
G là giao điểm của AC và BD. Các đường tròn (ADE) và (CDF) cắt nhau tại D và H. Phân giác trong góc ∑
AHB cắt AB, AD lần lượt tại I, J và phân giác trong góc ∑
DHC cắt CB, CD lần lượt tại K, L. Gọi
M, M’ là giao điểm của BH với AD, CD tương ứng, N, N’ là giao điểm của DH với BC, BA tương ứng.
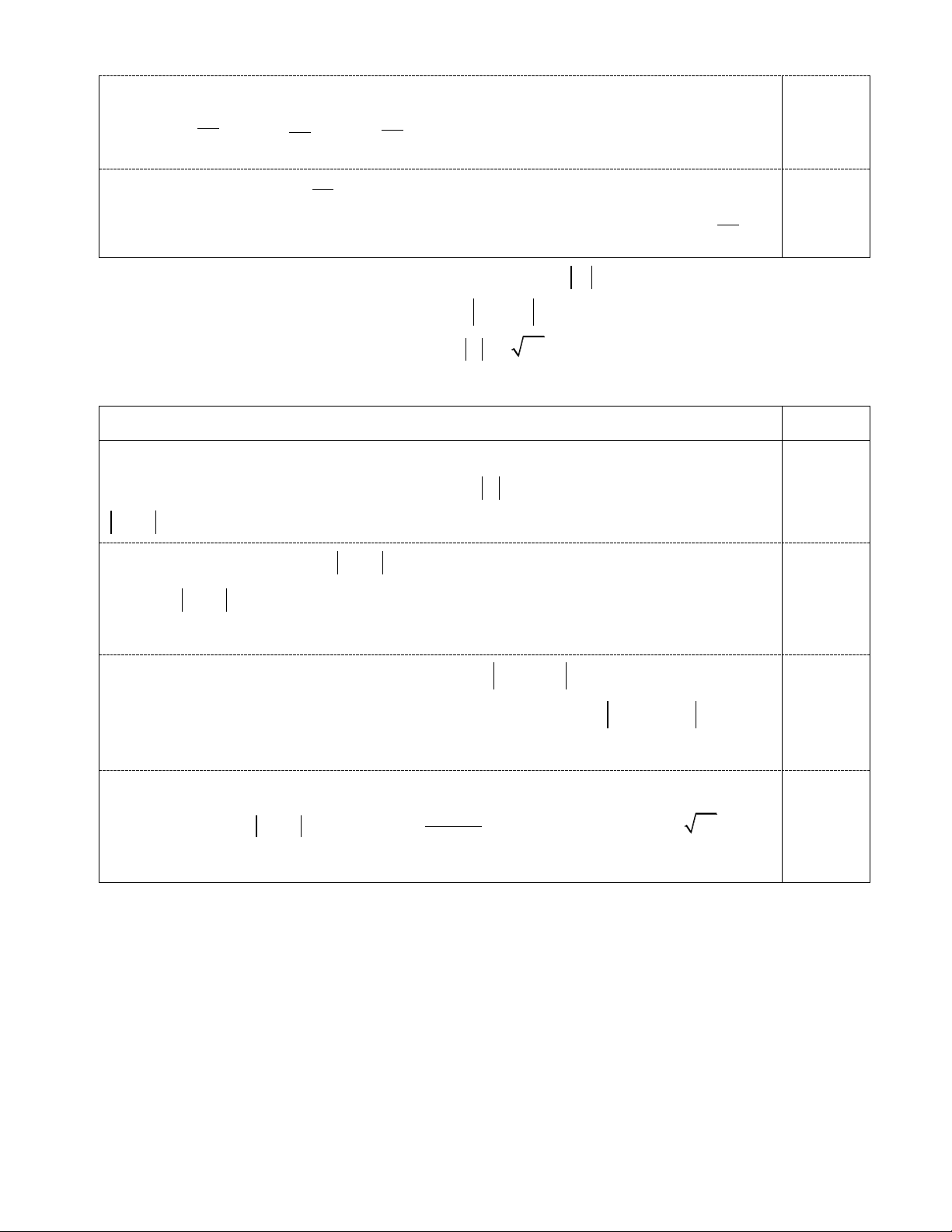
Chứng minh IL, KJ, MN và M’N’ đồng quy tại G. Lời giải : Trang 10 E A I J M H D G L B N K C F
Lời giải. Trước hết ta chứng minh H, E, F thẳng hàng. Thật vậy, do các tứ giác ABCD, AEHD, CFHD nội tiếp nên ta có ( , HD HE) º ( A , D AE) º ( A , D AB) º (C , D CB) º (C , D CF ) º ( , HD HF )( d mo p )
Suy ra H, E, F thẳng hàng.
Xét hai tam giác HCB và HAD, ta có ( , HA HD) º (E , A ED) º (E , B EC) º ( , HB HC)(modp )
(Để ý H là điểm Miquel của tứ giác toàn phần ABCDEFG) ( , CB CH ) º ( , CB CD) + ( , CD CH ) º ( A , B AD) + (F , D FH )
º ( AE, AD) + ( , AD EH ) º ( , EA EH ) º (D , A DH ) (modp )
Suy ra hai tam giác HCB và HDA đồng dạng. Do đó HB HA HC CB = , = (1) HC HD HD DA GC GB BC Dễ thấy G D BC ! G D AD nên = = (2) GD GA AD
Theo giả thiết thì HL, HI lần lượt là phân giác trong của ∑ ∑
CHD, AHB nên ta lại có LC HC IA HA = , = (3) LD HD IB HB GC LC
Từ (1), (2), (3) ta được = GA IA và =
. Suy ra GI, GL tương ứng là phân giác trong các góc GD LD GB IB ∑ CGD và ∑
AGB. Mà hai góc nay là hai góc đối đỉnh nên G, I, L thẳng hàng. Trang 11
Tiếp theo ta cần chứng minh KJ và MN, M’N’ cũng qua G. Xét hai tam giác AIJ và CKL ta có CK cắt AJ
tại F, IJ cắt KL tại H, IA cắt LC tại E. Mà H, F, E thẳng hàng nên theo định lý Desargues thì AC, JK, IL đồng quy tại G.
Lại xét hai tam giác FAC và HBD có FH, AB, CD đồng quy. Mà FA cắt HB tại M, AC cắt BD tại G, FC
cắt HD tại N nên theo định lý Desargues thì M, N, G thẳng hàng.
Tương tự thì M’N’ cũng qua G. Vậy các đường thẳng MN, M’N’, IL, KJ đồng quy tại G.
Bài 5. Cho tập hợp X là một tập hợp con của tập các số nguyên dương sao cho trong 2023 số tự nhiên
liên tiếp bất kì luôn có một số thuộc tập X. Chứng minh rằng tồn tại hai số trong X sao cho số này chia hết cho số kia. Lời giải :
Xét một bảng gồm 2023 cột và 2024 hàng
Ta điền các số vào trong bảng theo quy tắc sau :
Trong hàng đầu tiên ta điền từ trái qua phải các số 1,2, … ,2023.
Giả sử trong hàng thứ i được điền các số ( từ trái sang phải) là k +1, k + 2,..., k + 2023
Đặt A = (k +1)(k + 2)...(k + 2023) Ta điền các số ( từ trái sang phải) vào hàng thứ i +1 các số
A + k +1, A + k + 2,..., A + k + 2023
Như vậy ta được một bảng gồm 2023 cột và 2024 hàng thỏa mãn hai tính chất sau :
1)Mỗi hàng đều chứa 2023 số nguyên dương liên tiếp
2)Trong mỗi cột, số ở hàng j+1 chia hết cho hàng thứ j với mọi j =1, 2,..., 2023
Theo giả thiết,, trong mỗi hàng luôn chứa một phần tử của tập hợp X. Do 2024>2023 nên theo nguyên lí
Dirichlet tồn tại 2 phần tử của X nằm cùng một cột. Từ tính chất 2) của bảng đang xét ta có đpcm. ĐỀ 3
ĐỀ ÔN THI HỌC SINH GIỎI MÔN: TOÁN 11
Câu 1 (4 điểm). Cho a ¹ 0 và dãy số (xn ) định bởi 1 2(n +1)
x = a > 0 ; x = x + n >1 1 n 1 + n ( ). 2 nxn
Chứng minh rằng dãy số (xn ) có giới hạn hữu hạn và tìm giới hạn đó.
Câu 2 (4 điểm). Tìm tất cả các cặp đa thức hệ số nguyên P(x) , ( Q x) thỏa mãn
Q(0) = 0 và P(Q(x)) = (x - )
1 (x - 2)...(x -15)
Câu 3 (4 điểm). Tìm tất cả các số tự nhiên n sao cho Trang 12 n + f ( )
n + f ( f ( )
n ) + f ( f ( f (n))) +... = 2023,
trong đó f (k) là ước nguyên dương lớn nhất của số tự nhiên k và khác k và biết
f (0) = f (1) = 0 .
Câu 4 (4 điểm). Cho tam giác nhọn ABC nội tiếp đường tròn (O), ∑ 0 ABC < 45 . Một
đường thẳng đi qua B và vuông góc với BC cắt tiếp tuyến tại C của đường tròn (O) tại
điểm I. Gọi D là điểm đối xứng với C qua A. Đường tròn ngoại tiếp tam giác BCD cắt
AB và CI lần lượt tại H và K
a/ Chứng minh : DB.DH = CH .CB.
b/ Gọi J là giao điểm của AB và DI . Chứng minh rằng bốn điểm B, I, K, J nằm trên
đường tròn có tâm thuộc đường thẳng CD.
Câu 5 (4 điểm). Bạn Bình và An mỗi bạn có một hộp bi Trong mỗi hộp đều có chứa bi
trắng và có chứa bi đen tổng số bi trong hai hộp là 25 ( các bi giống nhau về kích thước và trọng lượng)
a/ Biết hộp của Bình có 3bi trắng 10 bi đen , còn hộp của An 10 bi trắng và 2 bi đen
. Mỗi bạn lấy ngẫu nhiên từ hộp của mình ra 2 viên Tính xác suất để bốn viên cùng màu.
b/ Biết hộp của Bình chứa nhiều bi hơn hộp của An và số bi đen trong hộp của Bình
nhiều hơn số bi đen trong hộp của An .Từ mỗi hộp của mình mỗi bạn lấy ngẫu nhiên ra
một viên .Tính xác suất để hai viên được lấy ra khác màu và biết rằng xác suất lấy ra
được hai viên cùng đen là 0,42.
-------------- HẾT -------------- HƯỚNG DẪN CHẤM Câu 1 (4 điểm).
Nhận xét được x > 0, n " ³1. n Trang 13 Theo BĐT Cô si, 1 2(n +1) n +1 n x = x + ³ 2 ³ > " ³ + , suy ra x 2 2, n 2. (1 điểm) n 1 2 n nx n n n -1 n 1 2(n +1) x = x + = f (x ) n 1 + 2 n n nxn Ta có: + f ( x) 1 2(n 1) 1 = x + . 2 n x 0< +
f ( x) 1 2(n 1) 1 1 ' = - . < (do (*)) (1 điểm) 2 2 n x 2
Với mọi x,y Î[2,+¥) , theo định lí Lagrang- có cÎ(x,y) hay cÎ(y,x) sao cho:
f ( x) - f ( y) |
= f '(c) || x - y | (1 điểm)
Þ f (x) - f ( y) 1 £ | x - y | 2
Do vậy f là ánh xạ co suy ra dãy ( xn ) có giới hạn L
Trong phương trình xác định dãy cho n dần tới vô cùng ta được 1 2
L = L + Û L = 2 . 2 L
Do đó kết luận Limx = 2 (1 điểm) n Câu 2 (4 điểm).
Trường hợp 1 : Deg P = 0,degQ = 0 không thỏa
Trường hợp 2 : DegP = p ³1, DegQ = q ³1
Nhận xét : Đa thức DegP(Q) =15 và có hệ số cao nhất là 1
Nên hệ số cao nhất của P(x),Q(x) đều bằng 1
Đa thức Q(x) có hế số tự do bằng 0 (vì Q(0) = 0 ) Trang 14
Đa thức P(Q(x)) có tập nghiệm là S = {1,2,3,...,1 } 5
Mặt khác Deg (P(Q)) = . p q ( 0,5 điểm)
ì q =1 ìq =15 ìq = 3 ìq = 5 Cân bằng bậc ta có . p q =15 Þ í , í ,í , í 0,5 điểm) î p =15 p =1 î
î p = 5 î p = 3 ì q =1 ì Q(x) = x +Khi í Thì ta có í là nghiệm î p =15 P(x) = î
(x - )1(x - 2)...(x -15) ìq =15 +Khi í
Thì P(x) = x + C Þ P(Q(x)) = Q(x) + C = (x - )
1 .(x - 2)...(x -15) + C î p =1
Do Q(0) = 0 Þ C = 1 - 5 ! ì
P(x) = x +15! ï
Vậy ta có cặp nghiệm là 15 í (1 điểm)
Q(x) = Õ(x -i) -15! ïî i 1 = ìq = 3 +Khi í î p = 5
Thì P(x) = (x - x x - x x - x x - x x - x 1 )( 2 )( 3 )( 4 )( 5 ) 3 2
Q(x) = x - ax + bx ( Do Q(0) = 0 )
T a có P(Q(x)) = (Q(x) - x Q(x) - x Q(x) - x Q(x) - x Q(x) - x 1 )( 2 )( 3 )( 4 )( 5 ) Suy ra ( Q x) = x i =1,5 i Mỗi phương trình ( Q )
x = x ,i =1,5 có ba nghiệm a ,b ,c i i i i
Theo Định lý Viet ta có a + b + c = -a i " Î
a b + b c + c a = b i i i {1,2,3,4, } 5 , i i i i i i Trang 15 5
Cũng theo Viets ta có å(a + b + c = + + + Þ a = i i i ) (1 2 ... 15) 24 i 1 =
Ta lại có (a + b + c = a + b + c + a b + bc + c a Þ a + b + c = a - b i i i )2 2 2 2 i i i ( i i i i i i ) 2 2 2 2 2 2 i i i 5 Suy ra å( 2 2 2 a + b + c = + + + Þ a - b = i i i ) ( 2 2 2 1 2 ... 15 ) 2 2 2 248 i 1 =
Do P(Q(x)) có nghiệm là 1 nên trong 5 phương trình Q(x) = x có bộ nghiệm là i
( b c Þb +c = º j j ) 2 2 1, , 247 3mod4 j j Mà 2
n º 0,1mod4 nên vô lý (1 điểm) ì p = 3 + Khi í
Þ P(x) = (x - x x - x x - x ,Q(x) = x + ax + bx + cx + dx 1 )( 2 )( 2 ) 5 4 3 2 îq = 5 Ta có ( P ( Q ) x = 0 Û ( Q )
x = x ,i =1,3 i
Mỗi phương trình Q(x) = x có 5 nghiệm a ,b ,c ,d ,e i i i i i i
Ta đặt A = {a ,b ,d ,e ,,,a ,b ,c ,d ,e Þ A = S i 1 1 1 1 3 3 3 3 3} 3 ! i i 1 = 1 1240 Ta có 2 2 2 2 2 2 2 2
a + b + c + d + e = (1 + 2 + ... +15 ) = Vô lý (1 điểm) i i i i i 3 3 Thử lại và kết luận
Câu 3 (4 điểm).
Giả sử n là số tự nhiên thỏa yêu cầu của đề bài
Cứ mỗi n tồn tại N sao cho n = p .p .p ...p 1 2 3 N
Trong đó p là số nguyên tố với mọi i =1, N và p £ p £ ... £ p ) i 1 2 N Trang 16
Từ giả thiết ta có : p .p p ...p + p p ...p + ... + p .p + p = 2022 (*) (1điểm) 1 2 3 N 2 3 N N 1 - N N
Suy ra p | 2022 Þ p Î N N {2,3,33 } 7
Nếu p = 337 đem thay vào (*) thu gọn ta có : N
p .p p ...p + p p ...p
+ ... + p . = 5 Þ p
= 5 Þ n = 5.337 =1685 (1 điểm) 1 2 3 N 1 - 2 3 N 1 - N 1 - N 1 -
Khi p = 2 Thì (*) thành N N 1 - N 1 2 2 ... 2 1 2 + + + + + =
-1= 2022( vô lý ) (1 điểm) N
Khi p = 3 Thì (*) thành p .p p ...3 + p p ...3 + ... + p .3 + 3 = 2022 N 1 2 3 2 3 N 1 -
p .p p ...p + p p ...p + ... + p = 673 Þ p | 673 (vô lý vì p = 2 ) 1 2 3 n 1 - 2 3 n 1 - N 1 - N 1 - N 1 -
Thử lại và kết luận n =1685 (1 điểm) Câu 4 (4 điểm).
a/ Ta có: ∠DCK = ∠ACK = ∠ABC = ∠HBC = ∠HDC.
Xét tứ giác nội tiếp CDHK có
∠C = ∠D và ∠D + ∠K = 1800 nên ∠C + ∠K = 1800 suy ra CD // HK
suy ra tứ giác CDHK là hình thang cân. (1 điểm) Trang 17
nên DH = CK ⇒ ∠DBH = ∠KBC
⇒ BK là đường đối trung của góc B ⇒ tứ giác BDKC là tứ giác điều hòa ⇒ BD KD = ⇒ .
BD KC = BC.KD BC KC
Kết hợp với CDHK là hình thang cân suy ra DB.DH = CH .CB (1 điểm)
b/ Vì tứ giác BDKC là tứ giác điều hòa nên BD KD = BC KC
⇒ 2 đường phân giác trong của ∠DBC và ∠DKC cắt nhau tại điểm E thuộc CD ; 2 đường
phân giác ngoài của ∠DBC và ∠DKC cắt nhau tại điểm F thuộc CD
⇒ B và K thuộc đường tròn Apollonius của tam giác DBC và DKC dựng trên đoạn CD
có đường kính EF. + Ta lại có: ∑ 1 0 ∑ ∑ ∑ 0 0 ∑ ∑ ∑ 0 ∑
BEK = 360 - BCK - (EBC + EKC) = 360 - (90 + BIC) - (DBC + DKC) =180 - BIC . 2
Suy ra tứ giác BEKI nội tiếp. (1 điểm)
+ Từ trên suy ra I cũng thuộc đường tròn Apollonius của tam giác DBC dựng trên đoạn
CD nên IE là phân giác của góc DIC suy ra ID ED KD = = hay ID IC =
nên DC là phân giác của góc IDK IC EC KC KD KC
Lại có ∠CAK = ∠DAH = ∠CAB
Do đó phép đối xứng trục CD biến DI thành DK, biến AB thành AK nên biến điểm J
thành điểm K. Phép đối xứng trục CD biến đường tròn Apollonius của tam giác DBC
dựng trên đoạn CD thành chính nó, mà K thuộc đường tròn Apollonius nên J cũng nằm trên đường tròn đó.
Vậy bốn điểm B, I, K, J nằm trên đường tròn Apollonius của tam giác DBC dựng trên
đoạn CD có tâm là trung điểm EF thuộc đường thẳng CD. (1 điểm) Câu 5 (4 điểm).
a/ ( 2 điểm) Tính xác suất để An và Bình lấy ra được bốn viên cùng màu
Ta gọi A , A lần lượt là biến cố An lấy ra được hai bi trắng , 2 bi đen t d Trang 18
Gọi B , B lần lượt là biến cố Bình lấy ra được hai bi trắng , hai bi đen t d
Trường hợp cả hai đều lấy ra hai bi đen 2 C
P(A B ) = P(A ).P B = = = d d d ( d ) 1 1 1 10 . ( 1 điểm) 2 2 2 C C C 78 10 13 13
Trường hợp cả hai đều lấy ra được hai bi trắng 2 2 ( C C
P A B = P A P B = = t t ) ( t ). ( t ) 15 10 3 . 2 2 C C 572 12 13
Qui tắc cộng ta có P(C) 15 1 67 = + = ( 1điểm) 572 78 1726 b/ ( 2 điểm)
Ta ký hiệu 2D , 2T , 1T1D lần lượt là các biến cố lấy được 2 bi trắng , 2 bi đen , 1 bi
trắng và 1 bi đen và các biến cố ấy là xung khắc
Gọi n ,n lần lượt là số bi trong hộp của An và Bình . Ta có n < n và n + n = 25 A B A B A B
Và gọi d ,d lần lượt là số bi đen trong hộp của An và Bình . Ta có d <d A B A B ì n < n
ì25 = n + n < 2n ì n ³13 Từ A B A B B B í Þ í Þ í ( 1 điểm) n + n = 25 n + n = 25 n + n = 25 î A B î A B î A B k k 21 Đề cho P(2D) A = . B = 0,42 =
Û 50.k .k = 21.n .n Þ n .n !5 và n + n = 25 n n 50 A B A B A B A B A B
Nên có hai trường hợp xảy ra
Trường hợp 1 : n = 5Þ n = 20 Þ d .d = 42 Þ d = 3,d =14 A B . A B A B
Và do đó số bi trắng trong hộp của An và Bình lần lượt là 2 và 6 Trang 19 2 6 Vậy P(2T ) = .
= 0,12 Þ P(1T1D) =1- 0,42 - 0,2 = 0,46 5 20
Trường hợp 2 : n =10Þ n =15 Þ d .d = 63 Þ d = 5,d = 9 A B . A B A B
Do đó số bi trắng trong hộp của An và Bình lần lượt là 3 và 6 3 6 Vậy P(2T ) = .
= 0,12 Þ P(1T1D) =1- 0,42 - 0,2 = 0,46 (1 điểm) 10 15 Kết luận : 0,46 ĐỀ 4
ĐỀ ÔN THI HỌC SINH GIỎI MÔN: TOÁN 11
Bài 1 (4 điểm). Với mỗi số nguyên dương n , xét phương trình x n e + x = 3 (1).
a) Chứng minh rằng với mọi n phương trình (1) có duy nhất một nghiệm dương.
b) Kí hiệu nghiệm dương của phương trình (1) là x . Chứng minh rằng các dãy số (x n(x - n )1 n ) và có n
giới hạn hữu hạn và tính các giới hạn đó.
Bài 2 (4 điểm). Cho ba số thực x, y, z thỏa mãn 1 £ x, y, z £ 6 và x + y + z = 12 . Tìm giá trị lớn nhất và
giá trị nhỏ nhất của biểu thức 2 2 2
P = x + y + z .
Bài 3 (4 điểm). Cho tam giác nhọn ABC có các đường cao ,
AD BE,CF . Đường tròn (O) ngoại tiếp
tam giác ABC cắt đường thẳng EF tại M và N (các điểm M , F, E, N lần lượt nằm theo thứ tự). Giả
sử BM cắt DF tại I , CN cắt DE tại K . Chứng minh rằng tam giác AIK là tam giác cân.
Bài 4 (4 điểm). Cho dãy số (a 2 a = 9;a = 2a -1 n " ³1.
n ) xác định như sau 1 n 1 + n
a) Xác định công thức tổng quát của dãy a . n
b) Cho m là một số nguyên dương tùy ý và p là một ước số nguyên tố của 2
m - 5. Chứng minh rằng
nếu a chia hết cho p thì 2
2n+ là ước số của p - 1. n Trang 20
Bài 5 (4 điểm). Cho số nguyên dương n và kí hiệu X = {1;2;3;...;4n -1;4 }
n . Với mỗi hoán vị { 4n
a ;a ;...;a X
S = å 3a - k
{a ;a ;...;a X 1 2 4n} 1 2 4n} của ; đặt
. Hỏi có bao nhiêu hoán vị của thỏa mãn k k 1 = 4n
biểu thức S = å 3a - k đạt giá trị lớn nhất. k k 1 = ----- HẾT ----- ĐÁP ÁN Bài Nội dung Điểm
a) Với mỗi số nguyên dương n , xét hàm số f x = e + x - n ( ) x n 3. Có f = - < lim (x) = +¥ f x n ( ) n (0) 2 0; và
là hàm liên tục, đơn điệu tăng trên khoảng 1,5 x®+¥
(0;+¥) nên PT (1) có duy nhất một nghiệm dương xn. b) f
= e - > = f x Þ x < n ( ) 1 2 0 n ( n ) . 1 n
Lại có f x = e + x - = < e + x - - = f x Þ x > x n ( n ) x n x n 1 n 3 0 n 3 n n n 1 - ( n ) . . n n 1 - 1
Þ $lim x = A hữu hạn và x < A £1 n " . 1,5 (4 n n
điểm) Suy ra f x = < f A =e + A - n ( n ) 0 n ( ) A n 3. Cho A ® +¥ Þ
+ lim n - 3 ³ 0 Þ lim n ³ 3 A n e A A
- e > 0 Þ A ³1Þ A = . 1 Có + x - n n x
x = - e Þ n x = - e Þ n x - x = - e n n ( n x ) ( n ) 1 ( n )1 3 .ln ln 3 1 .ln ln n (3 nx ) 1,0 x -1 n
Cho n ® +¥ Þ limn( x - ) 1 = ln(3 - e n ). Bài Nội dung Điểm 2
+Áp dụng BĐT Bunhiacôpxki: 1,0 Trang 21 (4
(x + y + z )≥ (x + y + z)2 2 2 2 3 = 144 2 2 2
fi x + y + z ≥ 48. điểm)
Vậy min P = 48. Đẳng thức xảy ra khi và chỉ khi a = b = c = 4.
Giả sử x £ y £ z fi x £ 4 . Ta có 2 2 2
x + y + z = 144 - 2xy - 2yz - 2zx = 144 - 2x (12 - x)- 2yz
Mà yz - 6y - 6z + 36 = (y - ) 6 (z - )
6 ≥ 0 fi yz ≥ 6(y + z)- 36 = 36 - 6x 3,0 2 2 2
fi x + y + z £
- x ( - x)- ( - x) 2 144 2 12
2 36 6 = 72 + 2x - 12x 2 2 2
Þ x + y + z £ 62 + 2(x - ) 1 (x -5) £ 62
Vậy max P = 62. Đẳng thức xảy ra khi và chỉ khi (x;y;z)= (1;5;6 )và các hoán vị. Bài Nội dung Điểm I K A N P E F H M O 3 B C D (4 2,0 điểm)
Gọi H là trực tâm tam giác ABC , P là giao điểm của AO và EF . 0 ∑ 180 - AOC Ta có ∑ ∑ ∑ 0 ∑ ∑ 0 PAE + AEP =
+ AEP = 90 - ABC + AEP = 90 (vì 2 ∑ ∑ ABC = AEP) ∑ 0
Þ APE = 90 Þ OA ^ MN . Mà OM = ON Þ OA là trung trực đoạn Trang 22
MN Þ AM = AN (1). ∑ ∑ Þ ABM = ABN (2).
Lại có hai tứ giác ACDF và BCEF nội tiếp suy ra ∑ ∑ ∑ ∑
AFD = BFE Þ BFI = BFE (3).
Từ (2) và (3) suy ra BFI D = BFN D (g. .
c g) Þ BI = BN, FI = FN Þ BF là trung 2,0 trực đoạn IN .
Dẫn đến AI = AN . Hoàn toàn tương tự c/m AK = AM .
Kết hợp (1) suy ra 4 đoạn thẳng AI, AK, AM, AN bằng nhau Þ đpcm. Bài Nội dung Điểm 2n 2n ( 5+2) +( 5-2)
Bằng phương pháp chứng minh quy nạp ta có a = n 2 1,5 2n 2n m + 2 + m - 2 Do 2 m º 5(mod p) ( ) ( ) Þ a º p n (mod ). 2 4 ( n n
m + 2)2 + (m - 2)2 a ! p Û ! p Þ m + + m - ! p n ( n n 2)2 ( 2)2 (4 Vì vậy (1) . 2 điểm) Hơn nữa 2
m º 5(mod p) Þ (m + 2)(m - 2) º ( 1 mod p). 2,5 n+
Vì vậy ( ) Û (m + ) 1 2 1 2 +1! p ìï( + m + ) n 1 2 2 -1! p
Ta có a ! 2 Þ p! 2 Þ n+2 í Þ 2 = ord m + 2 n+2 p ( ). n ( ï m + 2 î )2 -1! p
Mà (m + )p 1- º ( p) n+2 2 1 mod Þ p -1!2 , đpcm. Trang 23 Bài Nội dung Điểm
Với mỗi k Î{1;2;3;...;4 }
n , kí hiệu b = max{3a ;k};c = min{3a ;k k k k k }. 4n 4n 4n 4n
Khi đó å 3a - k =å b - c = åb - åc k ( k k ) . k k k 1 = k 1 = k 1 = k 1 = Chú ý 4n 2 2,0
+ åb £ 3é n + + n + + + nù + é n + + n + + + nù = n + n k ë(
)1 ( 2) ... 4 û ë(3 )1 (3 2) ... 4 26 5 û k 1 = 5 4n (4
+ åc ³ 3 + + + n + + + + n = n + n k (1 2 ... ) (1 2 ... 3 ) 2 6 3 k 1 = điểm) 4n 2
Suy ra å 3a - k £ 20n + 2n k k 1 =
Đẳng thức xảy ra khi và chỉ khi 2 điều kiện sau được thỏa mãn:
+ Với mọi k Î{1;2;3;...;3 }
n thì a Î{n +1;n + 2;n +3;...;4n k } 2,0
+ Với mọi k Î{3n +1;3n + 2;3n +3;...;4 }
n thì a Î{1;2;3;...;n k }
Vậy có tất cả n!.(3n)! hoán vị thỏa mãn. ĐỀ 5
ĐỀ ÔN THI HỌC SINH GIỎI MÔN: TOÁN 11
Câu 1 (4 điểm) Cho dãy số (u ) được xác định bởi * u = 3,u
= u + 2n + 2, n " Î • n 1 n 1 + n æ u ö
a) Chứng minh rằng dãy số n
có giới hạn hữu hạn và tính giới hạn đó. ç 2 ÷ è n ø v v ...v
b) Với mỗi số nguyên dương n , đặt 2 v = u +1 và 1 3 2n 1 w - =
. Tìm tất cả các số thực a sao cho n n n v v ...v 2 4 2n
dãy số (na w ) có giới hạn hữu hạn khác 0 . n Trang 24
Câu 2 (4 điểm) Tìm hàm số thỏa mãn f : + +
! ® ! thỏa mãn xf (x + y)( yf (x) + ) 2023 = 2023
Câu 3 (4 điểm) Cho đường tròn (O) và dây AB, P là điểm chính giữa cung nhỏ AB ( ! 0 sd AB > 60 ).
Tiếp tuyến tại B của (O) cắt AP tại C. Gọi Q là điểm đối xứng với P qua BC. Đường OP cắt đường
thẳng qua C vuông BC tại D. Chứng minh 4 điểm A, D, C, Q cùng thuộc một đường tròn.
Câu 4 (4 điểm) Cho a,b là các số nguyên dương thỏa mãn với số nguyên dương n nào đó mà 2
na + na +1 là lập phương đúng của một số nguyên dương thì nb +1 cũng là lập phương đúng của một
số nguyên dương. Chứng minh rằng 4b +1 là một số chính phương.
Câu 5 (4 điểm) Cho số thực x lớn hơn 2 thỏa mãn với mọi số nguyên dương n thì n
x là số vô tỉ. Với
mọi số tự nhiên t , xét các quân bài gồm các loại có giá trị bằng t
x . Hỏi có xảy ra trường hợp với mọi số
nguyên dương m thì đều có thể chọn ra được một số quân bài có tổng giá trị bằng m và mỗi loại bài
được chọn đều không quá 6 quân hay không?
………………………. HẾT ……………………. ĐÁP ÁN
Câu 1 Cho dãy số (u ) được xác định bởi * u = 3,u
= u + 2n + 2, n " Î • n 1 n 1 + n æ u ö
a) Chứng minh rằng dãy số n
có giới hạn hữu hạn và tính giới hạn đó. ç 2 ÷ è n ø v v ...v
b) Với mỗi số nguyên dương n , đặt 2 v = u +1 và 1 3 2n 1 w - =
. Tìm tất cả các số thực a sao cho n n n v v ...v 2 4 2n
dãy số (na w ) có giới hạn hữu hạn khác 0 . n Lời giải
a) Với mỗi số nguyên dương n , đặt 2
t = u - n - n , ta có * v
= v = ... = v = 1, n " Î • . n n n 1 + n 1 2 u n + n +1
Lúc này ta sẽ có được 2 *
u = n + n +1, n
" Î • . Vì vậy lim n = lim =1. n 2 2 n n b) Ta có 2 2 2 2 *
v = (n + n +1) +1 = (n +1)[(n +1) +1], n " Î • nên n 2 2 2 2 2 2 v v ...v
(1 +1)(2 +1)(3 +1)(4 +1)...[(2n -1) +1][(2 ) n +1] 2 1 1 3 2n 1 - * w = = = = , n " Î • n 2 2 2 2 2 2 2 2 v v ...v
(2 +1)(3 +1)(4 +1)(5 +1)...[(2n) +1][(2n +1) +1] (2n +1) +1 2n + 2n +1 2 4 2n Trang 25 1
Vì vậy ta sẽ có được 2 lim n w = . n 2
Nếu a > 2 thì rõ ràng lim na w = +¥ , còn nếu a < 2 thì lim na w = 0. n n 1
Vì vậy tất cả các số thực a cần tìm là a = 2 , và 2 lim n w = . n 2
Câu 2. Tìm hàm số thỏa mãn f : + +
! ® ! thỏa mãn xf (x + y)( yf (x) + ) 2023 = 2023
HD: Đổi chỗ x và y ta được yf (x + y)(xf ( y) + )
2023 = 2023 = xf (x + y)( yf (x)+ ) 2023
Mà f(x+y)>0 nên y(xf ( y) + )
2023 = x( yf (x)+ )
2023 suy ra xyf ( y) + 2023y = xyf (x) + 2023x
Thay y=1 và biến đổi ta được ( ) 2023 f x =
+ C với C = f ( ) 1 - 2023 x
Biện luận ta được không tồn tại C. Vậy không tồn tại hàm thỏa mãn đề. Câu 3.
Cho đường tròn (O) và dây AB, P là điểm chính giữa cung nhỏ AB có sđ>60 độ. Tiếp tuyến tại B của
(O) cắt AP tại C. Gọi Q là điểm đối xứng với P qua BC. Đường OP cắt đường thẳng qua C vuông BC tại
D. Chứng minh 4 điểm A, D, C, Q cùng thuộc một đường tròn.
HD:+ OP cắt QB, AB lần lượt tại E, F.
+ Cm tg QCDE, QDAE nội tiếp
Câu 4 Cho a,b là các số nguyên dương thỏa mãn với số nguyên dương n nào đó mà 2 na + na +1 là
lập phương đúng của một số nguyên dương thì nb +1 cũng là lập phương đúng của một số nguyên dương.
a) Chứng minh rằng tồn tại vô số số nguyên dương n để 2
na + na +1 là lập phương đúng của một số nguyên dương.
b) Chứng minh rằng 4b +1 là một số chính phương. Trang 26 Lời giải a) Đặt 3 2 2 2 2 *
n = k (a + a) + 3(a + a)k + 3k, k " Î • , khi đó 2 2 3
n a + n a +1 = [k(a + a) +1] là lập phương k k k
đúng của một số nguyên dương.
Vì thế tồn tại vô số số nguyên dương n để 2
na + na +1 là lập phương đúng của một số nguyên dương.
b) Đầu tiên, ta có bổ đề sau:
Bổ đề: Cho đa thức P(x) hệ số nguyên có bậc bằng 3 thỏa mãn với mọi số nguyên dương n thì ta đều
có P(n) là lập phương đúng. Khi đó sẽ tồn tại đa thức hệ số nguyên Q(x) sao cho 3
P(x) = Q(x) .
Chứng minh bổ đề: Viết 3 2
P(x) = ax + bx + cx + d với a, , b ,
c d là các số nguyên, a ¹ 0 .
Với mỗi số nguyên dương n , tồn tại số nguyên x để 3
x = P(n) . n n
Ta có với mọi số nguyên dương n thì 2
a(3n + 3n +1) + b(2n +1) + c 3 3 2 3 3 2 x
- x = a(n +1) + b(n +1) + c(n +1) + d - ax + bx + cx + d = n 1 + n 3 2 3 3 2
P(n +1) + P(n)P(n +1) + P(n) 3 1 2 1 c a(3 + + ) + b( + ) + 2 2 2 n n n n n = 2 2 P(n +1)
P(n)P(n +1) P(n) 3 3 3 + + 6 3 3 6 n n .n n Vì vậy 3
lim(x - x ) = a , ta lại có giới hạn của một dãy số nguyên là một số nguyên nên 3 a là số n 1 + n
nguyên và tồn tại n để 3
x - x = a, n
" ³ n . Khi đó sẽ tồn tại số nguyên A để 3 A = a và 0 n 1 + n 0 x - x = , A n " ³ n . n 1 + n 0 Ta có x = . A n + x = (
A n + n ) + x - . A n , n
" ³ n nên x = . A n + , B n
" ³ n , ở đây B = x - . A n . + 0 n n 0 n 0 0 n 0 0 n 0 0 n 0 Vì vậy 3 3 ( .
A n + B) = x = P(n), n " ³ n nên 3 P(x) = ( .
A x + B) , lúc này ta chọn Q(x) = .
A x + B là bổ đề n 0 được chứng minh.
Trở lại bài toán:
Với n đã chọn ở phía trên, ta có n b +1 cũng là lập phương đúng. k k Trang 27 Xét đa thức 2 2 3 2 2 P(x) = (
b a + a) .x + 3 (
b a + a)x + 3bx +1, ta có n b +1 là lập phương đúng nên P(k) là k
lập phương đúng với mọi số nguyên dương k .
Áp dụng bổ đề thì sẽ tồn tại các só nguyên , A B để 3
P(x) = (Ax + B) .
Vì vậy sau khi đồng nhất hệ số ta sẽ có được B = 1,b = A nên 2
b = a + a .
Lúc này ta sẽ có được 2
4b +1 = (2a +1) là số chính phương, từ đó ta có điều phải chứng minh.
Câu 5 Cho số thực x lớn hơn 2 thỏa mãn với mọi số nguyên dương n thì n
x là số vô tỉ. Với mọi số tự
nhiên t , xét các quân bài gồm các loại có giá trị bằng t
x . Hỏi có xảy ra trường hợp với mọi số nguyên
dương m thì đều có thể chọn ra được một số quân bài có tổng giá trị bằng m và mỗi loại bài được chọn
đều không quá 6 quân hay không? Lời giải
Câu trả lời là có thể xảy ra trường hợp đấy.
Giả sử tồn tại số thực x thỏa mãn yêu cầu đề bài, khi đó ta có thể chọn ra một số quân bài có tổng bằng
7 và mỗi loại bài đều không quá 6 quân.
Trong các quân bài được chọn, không có quân nào có dạng t
x với t ³ 3 , bởi vì nếu có thì t x > 8, vô lý,
ta cũng có nhận xét rằng không thể có 2 quân bài 2 x .
Rõ ràng phải có ít nhất một quân bài 2
x , vì nếu không thì x sẽ không phải là số vô tỉ. Vì vậy 2
r + x + kx = 7 , với r, k Î{0,1, 2,...,6}. Vì x > 2 nên ta có thể chọn x là số thực thỏa mãn 2 x + x = 7 . 29 -1 Lúc này, chọn x =
, ta sẽ chứng minh với mọi số nguyên dương m thì đều có thể chọn ra được 2
một số quân bài có tổng giá trị bằng m và mỗi loại bài được chọn đều không quá 6 quân.
Thật vậy, ta sẽ chứng minh với mọi số nguyên dương m sẽ đều tồn tại các số thực a , a ,..., a để 0 1 s 2
P(t) = (t + t - 7)( s
a t + ...+ a ) + m có các hệ số đều thuộc {0,1, 2,...,6 . } s 0
Nếu có điều này thì rõ ràng P(x) = m và sẽ thỏa mãn yêu cầu đề bài. Ta có các hệ số 0 1 2 , ,..., s t t
t + của P(t) lần lượt là
m - 7a ,a - 7a , a + a - 7a ,..., a
+ a - 7a ,a + a ,a 0 0 1 0 1 2 s-2 s 1 - s s 1 - s s Trang 28 émù éa ù éa + a ù éa + a ù
Lúc này ta chỉ cần chọn 0 0 1 1 2 a = , a = , a = , a =
,... là ta sẽ có được các hệ số 0 ê ú 1 ê ú 2 ê ú 3 ë 7 û ë 7 û ë 7 ê û ë 7 úû
của P(t) đều thuộc {0,1, 2,...,6}.
Từ đó ta có được khẳng định cho bài toán là có thể. ĐỀ 6
ĐỀ ÔN THI HỌC SINH GIỎI MÔN: TOÁN 11
Câu 1. (2 điểm) Cho dãy số {a 2 2a - 2a + a = 0 a {an} n } xác định bởi . Tìm điều kiện của để dãy có giới hạn hũu n 1 + n n 0
han. Trong trường hợp này, tìm lim (nan ) . n®+¥
Câu 2. (2 điểm)
Tìm tất cả các hàm f : ! ® ! thỏa mãn [
x f (x + y) - f (x - y)] = 4yf (x) " ; x y Î !
Câu 3. (2 điểm)
Cho tứ giác lồi ABCD nội tiếp (O) . Giả sử tia AB cắt DC tại E , tia BC cắt AD tại F , đường
thẳng AC cắt đường thẳng EF tại G . Giả sử đường tròn ngoại tiếp tam giác AEG cắt lại (O) tại K khác . A
a) Chứng minh rằng KD đi qua trung điểm I của EF .
b) Giả sử EF lần lượt cắt BD , đường tròn ngoại tiếp tam giác IAC tại H; J (J ¹ I) .
Chứng minh rằng OH = OJ .
Câu 4. (2 điểm)
Chứng minh rằng không tồn tại các số nguyên dương x, y > 2 phân biệt sao cho : 2021 2021 x + y!= y + x !
Câu 5. (2 điểm)
Cho đa giác lồi n đỉnh. Ta nối tất cả các đường chéo. Biết rằng không có 3 đường chéo nào đồng quy
bên trong của đa giác đã cho. Tính số miền đa giác được tạo thành bên trong của đa giác lồi đó (ta chỉ
tính các đa giác mà bên trong nó không có điểm nào thuộc đường chéo của đa giác ban đầu) -Hết- Trang 29 HƯỚNG DẪN CHẤM Câu 1:
Ta có 2(a - a = -a ³ 0 {a {a A n } n } n 1 + n ) 2 , suy ra dãy
đơn điệu giảm. Giả sử
có giới hạn hữu hạn là , từ n 2 2a
- 2a + a = 0 ta có 2
2A - 2A + A = 0 hay A = 0 . n 1 + n n
Nếu a < 0 thì {a {an}
n } không thể có giới hạn bằng 0 do đơn điệu giảm. 0
Nếu a > 2 thì a < 0 do đó {a {an}
n } không thể có giới hạn bằng 0 do đơn điệu giảm. 0 1
Nếu 0 £ a £ 2 thì 0 £ a £ 2, n
" , do đó {an} có giới hạn bằng 0 . 0 n
Tiếp theo chúng ta tính lim (nan ) . n®+¥
Nếu a = 0 hoặc a = 2 thì lim (na = n ) 0. 0 0 n®+¥
Nếu 0 < a < 2 ta có 0 1 2 1 1 = = + 2 a 2a - a 2 - a a n 1 + n 1 + n n n Suy ra n 1 1 1 - 1 - =
theo Định lý trung bình công Stolz-Cesàro, ta có å a a = - a n i 2 0 0 i n 1 1 - 1 1 1 lim å = lim
= .Vậy từ đẳng thức trước đó, ta có ngay lim (na = n ) 2 . n®+¥ n n ®+¥ - - n®+¥ i=0 2 a 2 a 2 i n 1 - Câu 2:
Cho a = f (0) . Thay x = y vào (*) ta có
f (2x) = a + 4 f (x) với mọi x ¹ 0 .
Thay x, y bởi 2x, 2y vào (*) và dùng tính chất bên trên (ta chọn x, y sao cho x + y, x - y, x ¹ 0 ), ta có 2 [
x 4 f (x + y) - 4 f (x - y)] = 8 [
y a + 4 f (x)], hay ay 4y
f (x + y) - f (x - y) = + f (x). (1) x x Trang 30
Kết hợp (2) và (*), ta có a = 0 hay f (0) = 0; từ đó f (2x) = 4 f (x) với mọi x .
Thay y = -x ở (*) ta có f ( 2
- x) = 4 f (x) = f (2x) với mọi x ¹ 0 . Do f (0) = 0, ta suy ra f là hàm chẵn.
Thay x bởi -x ở (1) ta có: [
x f (-x - y) - f (y - x)] = 4yf (-x), hay [
x f (y + x) - f (y - x)] = 4yf (x). Điều này dẫn đến 2 [
xy f (y + x) - f (y - x)] = 4y f (x). Từ (*) ta có [
y f (y + x) - f (y - x)] = 4xf (y) . Kết hợp với phương trình bên trên ta có 2 2
x f (y) = y f (x)với mọi x, y. Điều này dẫn đến 2
f (x) = cx Câu 3: a)
Giả sử KD Ç EF tại I , ta chứng minh I là trung điểm EF +) IE Ð K = G
Ð AK(K Î(AEG)) = ID
Ð E(K Î(O)) nên !IEK ~!IDE Dẫn tới 2 IE = . ID IK
+) Ta có K là điểm Miquel của tứ giác toàn phần EBCGAF do K thuộc (ABC),(AEG) nên
K Î(FCG). Từ đó, ta được IF Ð K = A Ð CK = A
Ð DK(K Î(O)) = ID
Ð F nên !IFK ~ ID D F, dần tối 2 2 IF = .
ID IK = IE hay IE = IF Trang 31 b)
Gọi L là giao điểm của AC; D
B . theo định lý Brocard, OL ^ EF º HJ nên yêu cầu bài toán tương
đương chứng minh LH = LJ. Gọi M là trung điểm A C. Do (AC, LG) = - 1 nên
GM ×GL = GA×GC = P
= GI ×GJ nên tứ giác MLIJ nội tiếp. Suy ra LJ Ð H = G Ð MI G\(IAC)
- Do K là giao điểm của (GAE),(GCF) nên tồn tai phép vị tự quay S tâm K sao cho
S : A ® E,C ® F mà M;I là trung diểm AC; EF nên S : M ® I dẫn tới K Î(GMI ). Suy ra GM Ð I = GK Ð . D
- Do (HG, EF) = - 1 nên 2
IH × IG = IE = ID× IK nên tứ giác KDGH nội tiếp. Suy ra LH Ð J = G Ð KD = G Ð MI = LJ
Ð H hay !LHJ cân tai L Câu 4:
Ta sẽ chứng minh : "với mỗi số nguyên dưong n ³ 2 , nếu 2m n ¹ -1 thì hàm số *
f : • ® ! được xác định bởi ( ) = ! n f x
x - x là đơn ánh".
a) Trước hết, ta chứng minh f (x) là hàm tăng với x ³ 2n . Ta có x 2 x 2
(x!) = Õi(x +1-i) n
³ x ³ x .Suy ra ! n x ³ x hay *
f (x) ³ 0, x
" Ε , x ³ 2n. i 1 = Trang 32 Hơn nũa n 2 æ 1 ö æ 1 n ö 1+ £ 1+
£ e .Khi đó với x ³ 2n ta có ç ÷ ç ÷ è x ø è 2n ø æ ö n æ 1 n ö + = + - + = + ç ÷ ( n æ ö f x x x x - x ) 1 n ( 1) ( 1)! ( 1) 1 ! + ç x +1- 1+ ç
÷ ÷ x!³ f (x) + (x +1- )
e x! > f (x). x ç x ÷ è ø è ø è ø
Do đó f (x) là hàm tăng với mọi x ³ 2n .
b) Bây giờ ta sẽ chứng minh f là đơn ánh.
Giả sử tồn tại hai số nguyên dương x < y sao cho f (x) = f (y) . Dễ thấy x < 2n . Gọi p là một ước
nguyên tố của x . Khi đó ∣ ! n - = ! n - = !( +1) ( … -1) n p x x y y x x y
y - y .Suy ra p∣ y . Mặt khác, ta có
y!- x!= x!((x +1)…(y -1)y -1).Suy ra
v (x!) = v (y!- x!) = v ( n n
y - x ³ n p p p ) . Hơn thế nữa +¥ x +¥ x x 2n v (x!) = å £ å = < . p i i - - i 1 = p i 1 = p p 1 p 1
Từ (1) và (2) suy ra ( p -1)n £ ( p -1)v (x!) < 2n . Điều này dẫn đến p = 2 hay x chỉ nhận 2 làm ước p nguyên tố tức là 2m x =
với mọi số nguyên m ³ 2 . Khi đó: +¥ 2m n n
v y - x = v (x!) = å = 2m -1 2 ( ) . 2 i i 1 = 2 Đặt k y = z ( * 2
z Ε ,gcd(z,2) = ) 1 .
Xét các trường hợp sau đây:
- Nếu k ¹ n thì n n - = 2kn n - 2mn v y x v z = n×min{k, } m . ∣2m n -1
2m = x < 2n 2m n = -1 2 ( ) 2( ) Suy ra . Do nên (vô lý).
- Nếu k = n thì Trang 33 n n - = 2mn n -1 n v y x v z
= mn + v z -1 ³ m . n
2m = x < 2n 1 2m n - > 2 ( ) 2 ( ( ) 2 ( ) Do nên . Vì thế 2m 1 n n 2.2m 2m v y x mn - - = - ³ > = (vô lý). f x ³ 2 2 ( ) 1
Vậy là đơn ánh với mọi . Câu 5:
Gọi a ;a ;...;a lần lượt là số miền tam giác; tứ giác; ngũ giác;…; m- giác được tạo thành. 3 4 m
Ta cần tính S = a + a +...+ a 1 2 m
+) Trước hết; ta đếm tổng tất cả các đỉnh của các miền đa giác.
Ta thấy ngay tổng này bằng A = 3a + 4a +...+ . m a . 3 4 m
Hơn nữa; nếu đếm như vậy thì mỗi giao điểm của 2 đường chéo sẽ được tính 4 lần (do giao điểm đó
thuộc 4 miền). Mỗi đỉnh của đa giác ban đầu sẽ được đếm n - 2 lần (do thuộc n - 2 miền) Như vậy, 4
A = 3a + 4a + ...+ .
m a = 4.C + n(n - 2) (1) 3 4 m n
+) Tiếp theo, ta đếm tổng tất cả các góc trong các miền của đa giác. Ta có tổng này bằng 0 0 0 0
B = 180 .a +180 .2.a +180 .3.a + ...+180 .(m - 2)a 3 4 5 m
Mặt khác, tổng các góc trên chính là tổng các góc của đa giác ban đầu ( 0
180 .(n - 2)) cộng với 0 360
nhân tổng các giao điểm của các đường chéo. Như vậy, 0 0 0 0 0 0 4
B = 180 .a +180 .2.a +180 .3.a + ...+180 .(m - 2)a = 180 (n - 2) + 360 .C 3 4 5 m n Suy ra 4
a + 2a + ...+ (m - 2).a = 2.C + (n - 2) (2) 3 4 m n 1 Từ (1);(2) suy ra 4
S = 1+ C + n(n - 3) . n 2 thuvienhoclieu.com
ĐỀ ÔN THI HỌC SINH GIỎI Trang 34 ĐỀ 7 MÔN: TOÁN 11
Bài 1 (5,0 điểm) 1
Cho 0 < a < và hàm số f (x) = ax + ln(x + 2). 2
a) Chứng minh dãy số (xn ) xác định bởi n 1 ³ x > 0, x
= f x ,n =1,2,... 1 n 1 + ( n)
có giới hạn hữu hạn. 100
b) Tồn tại hay không các số thực a , a ,..., a thỏa åa = 0 đồng thời dãy số ( yn ) xác định bởi 1 2 100 i n 1 ³ i 1 = æ f (n + ) 1 f (n + 2) f (n +100) ö y = n ça + a +...+ a ÷,n =1,2,... n 1 2 100 n + 2 n + 3 n +101 è ø
có giới hạn là số khác 0?
Bài 2 (4,0 điểm)
Tìm tất cả các hàm số f : ! ® ! thỏa mãn
f (x) f ( y + x) = xf ( f ( y)) 2 + f (x)," , x y Î!
Bài 3 (5,0 điểm)
Cho tam giác ABC nhọn không cân, nội tiếp đường tròn (O) và có đường cao .
AD Gọi E là điểm di
động trên cung nhỏ AB ( E khác ,
A B ). Đường thẳng qua E và song song với BC và cắt đường tròn
(O) tại điểm thứ hai là F. Đường tròn đường kính AB cắt AE, AF lần lượt tại M, N. Đường tròn
đường kính AC cắt AE, AF lần lượt tại N, .
Q Chứng minh tiếp tuyến chung ngoài của các đường tròn
ngoại tiếp các tam giác DMQ và DNP luôn đi qua một điểm cố định.
Bài 4 (3,0 điểm)
Cho dãy số (un ) xác định bởi n 1 ³ 2(2n + 3) u = 0, u =
u - 3 n +1 , n " ³1 1 n 1 + n ( ) n + 2
a) Chứng minh u là số nguyên với mọi số nguyên dương . n n
b) Chứng minh tồn tại vô hạn số nguyên tố p sao cho u - p chia hết cho 3 p . p 1 -
Bài 5 (3,0 điểm)
Cho số nguyên tố p > 3, có bao nhiêu bộ ( , a , b c) với , a ,
b cÎ{0,1,2,..., p - } 1 thỏa mãn 2 2 2
a + b + c º ab + bc + ca(mod p) ? --Hết--
HƯỚNG DẪN ĐÁP ÁN Trang 35 Bài Ý Nội dung Điểm 1 a 1,0
Xét g (x) = x - f (x) với x > 0 . Ta có g (x) = ( - a) 1 1 ' 1 -
> - a > 0 với mọi x + 2 2 x > 0
Do lim g (x) = +¥, lim g (x) = -ln 2 < 0và g liên tục trên (0;+¥) nên phương trình x®+¥ x 0+ ®
g (x) = 0 có nghiệm x > 0 duy nhất. 0 1,0
Nhận xét x > 0với mọi n và f (x) 1 1 ' = a +
< a + với mọi x > 0 nên với mọi n x + 2 2
n > 1, áp dụng định lí Lagrange cho hàm số f . Ta có n 1 æ 1 ö æ 1 - ö
x - x = f x - f x £ a + x
- x £ ... £ a + x - x n 0 ( n 1-) ( 0 ) ç ÷ n 1- 0 ç ÷ 1 0 è 2 ø è 2 ø 1 n 1 1 - æ ö
Vì 0 < a + < 1 nên lim a +
= 0 , do đó lim x = x . 2 ç ÷ è 2 ø n 0 b n 1 1,0
Bổ đề: Cho dãy số (t t = å , n ³ 1. limt = + . ¥ n ) xác định bởi Khi đó n 1 ³ n n j 1 = j
Chứng minh. Xét hàm số h(x) = x với x > 0 Khi đó, h (x) 1 ' =
liên tục trên (0;+¥) nên với mọi số nguyên dương j , áp dụng 2 x
định lý Lagrange trên các đoạn [ j; j + ]
1 thì tồn tại c Î( j; j + ) 1 để
h( j + ) - h( j) = h (c) 1 1 1 ' = < 2 c 2 j
Đánh giá trên đúng với mọi j = 1, 2,..., n nên h(n + ) 1 - h( ) 1 = (h(n + )
1 - h(n)) + (h(n) - h(n - ) 1 ) +... n
+ (h( ) - h( )) 1 1 2 1 < å 2 i 1= i hay t > 2 n + - n
( 1 )1, từ đó bổ đề được chứng minh. 100 æ + ö 1,0 f (n i)
Trở lại bài toán, giả sử y = n çåa
có giới hạn bằng l > 0 n i ÷ + + è i 1= n i 1 ø 100 f (n + i) Đặt z = åa , n =1, 2,... n i + + i 1 = n i 1 l l
Tồn tại số nguyên dương N sao cho y > , n
" > N hay z > , n " > N . Vậy với n 2 n 2 n n n l 1
mọi n > N thì å z > å . j j=N 1 +
2 j=N 1+ j n
Theo bổ đề, suy ra limåz = +¥ j j 1 =
Mặt khác, đặt A = max a đồng thời chú ý rằng 1,0 i i 1 = ,100 Trang 36 f (x) x ln (x + 2) 100 = a + < a +1, x " > 0 và åa = 0, x +1 x +1 x +1 i i 1 =
Với mọi n > N +100 thì n n 100
f ( j + i) 100
f ( N + i + ) 100 1 f (n + i) å z = å åa = åa +...+ åa j i i i + + + + + + j=N 1 + j=N 1 + i 1 = j i 1 i 1 = N i 2 i 1 = n i 1 f ( N + 2) f N + 3 f N +100 = a + a + a + ...+ a + ..+ a 1 ( 1 2 ) ( ) ( 1 99 ) ( ) N + 3 N + 4 N +101 + ( f n + 2 f n +100 a + ...+ a +...+ a 2 100 ) ( ) ( ) 100 n + 3 n +101
< 2( A + 2A +...+ 99A)(a + )
1 = 99.100A(a + ) 1
Điều này dẫn đến mâu thuẫn.
Trong trường hợp lim y = l ' < 0 thì ta cũng tìm được mâu thuẫn bằng cách thay f n
bởi - f . Vậy không tồn tại các số thực a , a ,..., a thỏa yêu cầu bài toán. 1 2 100 2
Ký hiệu f (x) f ( y + x) = xf ( f ( y)) 2 + f (x)," , x y Î! ( ) 1 1,0
TH1. f là hàm hằng thì f (x) = 0, x " Î!.
TH2. f không phải hàm hằng
Thay x = 0 được f ( ) f ( y) 2 0
= f (0), vì f không phải hàm hằng nên f (0) = 0.
Giả sử tồn tại u để f (u) = 0 thì thay x = u vào ( )
1 ta được u f ( f ( y)) = 0
Nếu u ¹ 0 thì f ( f ( y)) = 0 với mọi .y Khi đó ( ) ( + ) 2
f x f y x = f (x)
Cho y = -x vào phương trình trên suy ra f (x) = 0, x " : mâu thuẫn
Vậy u = 0 hay f (x) = 0 Û x = 0.
+Chứng minh f đơn ánh. Giả sử tồn tại các số thực a,b sao cho f (a) = f (b) 1,0
Nếu f (a) = f (b) = 0 thì a = b = 0.
Nếu f (a) = f (b) ¹ 0 thì lần lượt thay x = a, y = b và x = , b y = a suy ra ( ( )) 2 + ( ) = ( ( )) 2 af f b f a
bf f a + f (b)
Vậy a = b hay f đơn ánh.
+Chứng minh f lẻ . Thay y = -x suy ra 2
f (x) = -xf ( f (-x)) hay 1,0 2
f (-x) = xf ( f (x))
Thay y = x thì f (x) f ( x) = xf ( f (x)) 2 + f (x) 2 = f (-x) 2 2
+ f (x), x " (2)
Do đó f (x). f (2x) là hàm chẵn. Thay y = 2 - x ta được
f (x) f (-x) = xf ( f (- x)) 2 2 + f (x)
Thay x bởi 2x và y = 2
- x được = xf ( f (- x)) 2 0 2 2 + f (2x) Hay 2 f (2x) = 2 - xf ( f ( 2
- x)) = 2 f (x)( f (x)- f (-x)) Suy ra 2 f ( x) 2 f (x) 3 2
= 2 f (x)( f (x)- f (-x)) Vậy 2 f ( x) 2 f (x) 3 2
= 2 f (-x)( f (-x)- f (x)), suy ra f lẻ Trang 37 2 f x 1,0
Từ (2), suy ra f ( f (x)) ( ) = , x " ¹ 0, nên từ ( ) 1 ta có x 2 f (x + y) f ( y) = . x + f x , x " , y ¹ 0 yf (x) ( )
Hoán đổi vai trò x, y : 2 f ( y) 2 f x . x + = +
yf ( x) f ( x) ( ) .
y xf (y) f (y)
æ f (x) f ( y) 2 öæ f ( y) 2 f ( x) ö Û ç - ÷ç + ÷ = 0 x y y x è øè ø 2 f ( x) 2 f ( y)
Vì vậy với x, y > 0 thì + > 0 nên x y f (x) f ( y) =
Þ f (x) = f ( ) 1 , x x " > 0 x y
Vì f lẻ nên f (x) = f ( ) 1 , x x
" . KL f (x) = a ,x x " (aÎ! ). 3 Gọi ,
L U,V theo thứ tự là trung điểm BC, MN, . PQ 1,0 Ta có các bộ điểm ( , A , B M , P), ( ,
A C, N,Q) cùng thuộc một đường tròn và các tam
giác ABM , ACQ đồng dạng ngược hướng. Do đó
(PM,PQ) º (PM,PA) º (BM,BA) º (C , A CQ) º ( ,
NA NQ) º (NM , NQ)(modp ).
Vậy các điểm M , N, ,
P Qthuộc một đường tròn. Trang 38 LB UM
Vì BM / /CN và = 1 - =
nên theo định lí Thales đảo LU / /BM / /CN. Do LC UN
đó LU vuông góc MN. Vậy LU là trung trực MN.
Tương tự LV là trung trực của PQ. Vậy L là tâm đường tròn qua các điểm
M , N, P, . Q
Gọi W ,W '; R, R ' theo thứ tự là tâm và bán kính các đường tròn (DMQ);(DNP); 1,0
K, K ' là các giao điểm OL và (O); H là trực tâm tam giác ABC ; G là giao điểm
của AH và (O);S,S ' theo thứ tự là giao điểm của HK, HK ' và WW ' ; Z là tâm đường tròn (DPQ) . Ta có ( , DL DM ) º ( , DB DM ) º ( A ,
B AM ) º -( AC, AQ)
º -(DC, DQ)(modp )
nên kết hợp với LM = LQ, suy ra L thuộc đường tròn (DMQ). Vậy WW ' là trung trực DL (1)
Do đó S, S ' theo thứ tự là trung điểm HK, HK '. Kết hợp D là trung điểm HG (kết 1,0
quả quen thuộc) suy ra DS / /GK; DS '/ /GK '.
Kết hợp GK ^ GK ' suy ra DS ^ DS '. Trang 39
Gọi X ,Y theo thứ tự là trung điểm của AB, AC (2).
Từ (1) và (2) suy ra tâm đường tròn Euler của tam giác ABC nằm trên WW ' và
WW ' là trung trực XY (3)
Ta có DP là dây cung chung của các đường tròn ( X ) và (Z ); DQ là dây cung 1,0
chung của các đường tròn (Y ) và (Z ) nên DP ^ ZX , DQ ^ ZY . Suy ra
(ZX,ZY ) º (D , P DQ) º (D , P AP) + ( A , P DQ) º ( ,
DB AB) + ( AC, DC) º ( AC, AB) º (LX , LY )(modp )
Vậy Z thuộc đường tròn (DLXYSS ') (đường tròn Euler của tam giác ABC ) (4)
Từ (3), (4) suy ra (SS 'WW ') = Z (SS 'WW ') = Z (SS ' XY ) = 1 - 1,0
Kết hợp DS ^ DS ' suy ra DS, DS ' là phân giác của góc tạo bởi DW , DW '
Theo tính chất đường phân giác SW DW R S 'W DW R = - = - ; = = SW ' DW '
R ' S 'W ' DW ' R'
Suy ra S, S ' theo thứ tự là tâm vị tự trong và tâm vị tự ngoài của các đường tròn
(DMQ),(DNP) nên cố định. Nói riêng tiếp tuyến chung ngoài của các đường tròn
(DMQ) và (DNP) luôn đi qua điểm cố định. 4
a Đặt u = n + -v n " ³ n ( 2) , 1 thì 1,0 n ( + + n + ) 2(2n 3) 2 2n 3 3 - v =
n + 2 - v - 3 n +1 Þ v = v n 1 + ( n ) ( ) ( ) n 1 n + 2 + n + 2 n
Khi đó v = 3 và chứng minh quy nạp được n v = C với mọi . n 1 n 2n 1 + Vậy u = n + -C u . n n
( 2) n nên là số nguyên với mọi số nguyên dương 2n 1 + n
b Nhận xét. Với mọi số nguyên tố p ³ 5 thì p C º p p- ( 3 1 mod 2 1 ) 1,0 p + p + p - p ( )1( 2)...(2 ) 1 Chứng minh C = 2 p 1 - ( p - )1!
Ta chứng minh ( p + )( p + ) ( p - ) -( p - ) 3 1 2 ... 2 1 1 !! p p 1 - p 1 - p 1 - æ ö æ æ öö æ ö Ta có ( p - ) 1 å = ç ÷ ( p - ) 1 1 çå + ç ÷÷ = p( p - ) 1 2 1 ! 1 ! 1 !åç ÷ ç ÷ è ø è è - ø - i 1 = i i 1 = i p i ø i 1 = è ( p i)i ø Hệ {1;2;...; p - }
1 thu gọn theo modunlo p nên p 1 - p 1 - p 1 - ( æ ö p - ) 1 1 2 1 !åç
÷ º - p -1 !å º - p -1 !åi ç ÷ - i 1 = è ( p i) ( ) 2 ( ) i i 1 = i i 1 = ø ( - -
º - p - ) p( p ) 1 (2 p ) 1 1 ! (mod p) 6 p 1 - p 1 - ( æ ö æ ö Þ p - ) 1 1 2 1 !åç
÷ º 0 mod p Þ p -1 ! å º 0 mod p ç ÷ ç ÷ - i 1 = è ( p i) ( ) ( ) ( ) i ø è i 1= i ø Ta cũng có 1,0 Trang 40 2 æ ö æ p 1- p 1 - ö ( æ ö p - ) 1 ç å ÷ = ( p - ) 1 1 2 1 ! 1 !ç å - å ÷ ç ÷ 2 ç ÷
è1£i< j£p 1- ij ø è i 1= i ø i 1 = i è ø p 1 - p 1 - º -( p - ) 1
1 !å º - p -1 !åi 2 ( ) 2 i 1 = i i 1 = º -( - ) ( p - ) 1 (2 p - ) 1 p p 1 ! º 0(mod p) 6 æ 1 ö Nên ( p - ) 1 !ç å ÷ º 0(mod p).
è1£i< j£p 1- ij ø Do đó,
( p + )1( p + 2)...(2p - )1-( p - ) 1 ! æ ö æ ö 3 2
= Ap + p ( p - ) 1 ç å ÷ + p ( p - ) 1 1 ! 1 !ç å ÷
è1£i< j£p 1- ij ø
è1£i< j£p 1- i ø º 0( 3 mod p )
Vậy nhận xét được chứng minh
Do đó với mọi số nguyên tố p ³ 5 thì p 1 u - p =1-C - º 0 p p- p- ( 3 mod . 1 2 1 ) 5
Biến đổi (a -b)2 +(b -c)2 +(c -a)2 º 0(mod p) 1,0
Đặt a - b = x và b - c = y thì 2 2
x + y + xy º 0(mod p) (1),
TH1. Nếu p º 2(mod3) thì từ ( )
1 , ta có ( x + y)2 2 2 º 3 - y (mod p) p 1 - p 1 -
Nếu ( y, p) =1 thì ( ) 3 . p y
º (2x + y)p 1 1 - - - 2 (mod p) Þ(- ) 3 2 º ( 1 mod p) æ 3 - ö Vậy =1Þ p º1 ç ÷
(mod6), mâu thuẫn vì p º 2(mod3) è p ø
Do vậy y º x º 0(mod p). Khi đó a º b º c(mod p), tức có p bộ thỏa. TH2. Nếu p º ( 1 mod3) thì 3
- là thặng dư bình phương modunlo p nên phương 1,0 trình 2
z + z +1º 0(mod p) có hai nghiệm z và 1 z- theo modunlo . p 0 0 Khi đó (x z y)( 1 x z- - - y º 0 mod p
x º z y mod p 0 ( ) 0 0 ) ( ), suy ra hoặc 1 x z- º y mod p 0 ( )
Nếu x º z y mod p
a º (z +1 b - z c mod p 2 p 0 ) 0 ( ) 0 ( ) thì , nên có bộ thỏa. Nếu 1 x z- º y mod p a ( 1 z- ) 1 1 b z- º + - c mod p 2 p 0 0 ( ) 0 ( ) thì , nên có bộ thỏa
Giả sử tồn tại bộ ( , a ,
b c) thỏa đồng thời a º (z +1 b - z c mod p 0 ) 0 ( ) và 1,0 a ( 1 z- ) 1 1 b z- º + - c mod p ( 1 z z- -
b - c º 0 mod p 0 0 )( ) ( ) 0 0 ( ) thì Do 1 z- º 1 - - z mod p 1 z- - z º 1
- - 2z º 0 mod p
b º c(mod p) 0 0 0 ( ) 0 0 ( ) nên , do đó ,
tức có p bộ như thế. Vậy trường hợp này có 2
2 p - p bộ thỏa. Trang 41 ĐỀ 8
ĐỀ ÔN THI HỌC SINH GIỎI MÔN: TOÁN 11 u ì =1 1 ï
Câu 1. Cho dãy số xác định bởi í 2022
* Tìm tất cả các giá trị sao u = u + u + , n " Ε a . n 1 + n n ï 2023 u î n ua æ ö cho dãy số n ç
÷ có giới hạn hữu hạn. n è ø
Câu 2. Tìm tất cả các hàm số liên tục f , g, h :! ® ! thỏa mãn
f (x + y) + g(xy) = h(x) + h( y)," , x y Î ! .
Câu 3. Cho tam giác nhọn ABC nội tiếp (O), các đường cao AA ; BB ;CC đồng quy tại H. 1 1 1
Đường thẳng OA cắt lại (OBC) tại A , OB cắt lại (OC )
A tại B , OC cắt lại (OAB) tại C . 1 2 1 2 1 2
Chứng minh rằng AA ; BB ;CC đồng quy. 2 2 2
Câu 4. Cho X Ì • , X ¹ Æ thỏa mãn đồng thời hai điều kiện sau:
1. Nếu a,b Î X thì a + b Î X .
2. Với mọi a Î • , a > 1 luôn tồn tại b Î X sao cho b không chia hết cho . a
Chứng minh rằng • \ X là tập có hữu hạn phần tử.
Câu 5. Xét bảng 7´ 7 ô vuông có bốn ô ở bốn góc bị xóa .Ta tô màu n ô trong bảng còn các ô
còn lại không tô màu .Tìm số n nhỏ nhất sao cho với mọi cách tô màu thỏa mãn yêu cầu bài
toán đều không tồn tại một hình chữ thập nào mà 5 ô của hình này đều không màu Đáp Án Câu Đáp Án Điểm 1
Chứng minh được limu = +¥ 0.5 n Xét với 1 a = . Ta có 1.0 2 2022 u + n 2023 2022 un 1 u
- u = u + u + - u = ® . n 1 + n n n n 2023 u 2022 2 n u + u + + u n n n 2023 un Trang 42 1 2 u 1 Suy ra lim n = . n 2 1 1.0 a 1 2 u u a - Với 1 a > , ta có n n 2 lim = lim .u = + . ¥ 2 n n n 1 1.0 a 1 2 u u a - Với 1 a < , ta có n n 2 lim = lim .u = 0. 2 n n n ua æ ö 0.5 Vậy, 1 dãy số n
có giới hạn hữu hạn khi và chỉ khi a £ . ç ÷ n è ø 2 2
f (x + y) + g(xy) = h(x) + h( y)," , x y Î ! . (*)
Từ (*) cho y = 0 ta có f (x) + g(0) = h(x) + h(0), suy ra 0.5
h(x + y) - h(x) - h(y) = p(xy) (1), trong đó p(x) = -g(x) - g(0) + h(0).
Trong (1) thay y bởi y + z ta có 1.0
h(x + y + z) = h(x) + h( y + z) + p(xy + xz)
= h(x) + h(y) + h(z) + p(yz) + p(xy + xz), (2)
Trong (2) thay đổi vị trí x và z ta có
p(xy) + p( yz + zx) = p( yz) + p(xy + zx)," x, y, z Î ! . (3) 1.0 ac ab bc Với a, ,
b c > 0 bất kỳ , chọn x = ; y = ; z = thế vào (3) ta có b c a
p(a) + p(b + c) = p(b) + p(a + c), cho a 0+ ® ta có
p(0) + p(b + c) = p(b) + p(c). ac ab bc
Với a,c > 0;b < 0 bất kỳ chọn x = - ; y = ; z = thế vào (3) ta có b c a
p(a) + p(b + c) = p(b) + p(a + c), cho b 0+ ® ta có
p(0) + p(a + c) = p(a) + p(c). Cho a 0-
® ta có p(0) + p(b + c) = p(b) + b(c).
Như vậy p(a + b) = p(a) + p(b) - p(0), a
" ,b ¹ 0, kết hợp với p liên tục ta có 0.5
p(x) = ax + . b a 2 1.0
Đặt k(x) = h(x) - x , khi đó k(x) liên tục trên ! , kết hợp (1) ta có 2
k(x + y) = k(x) + k(y) + , b x
" , y Î!., suy ra k(x) = cx - b. Do đó a 2
h(x) = x + cx - . b Thử lại ta có 2 a a 2 2
g(x) = -a ;
x h(x) = x + cx - ;
b f (x) = x + cx - . b 2 2 Trang 43 3
Gọi S, S ' lần lượt là giao điểm của AA , BB với OH . 1.0 2 2
Áp dụng định lý Menelaus cho tam giác HOA với các điểm , A A , S 1 2 thẳng hàng ta có SO AH A A SH AH A A 2 1 . . =1, từ đây suy ra 2 1 = . (1) SH AA A O SO AA A O 1 2 1 2
Vì tam giác ABC nhọn nên H nằm giữa A và A ; A nằm trong (OBC) 1.0 1 1 nên nó nằm giữa SH AH A A AH A A
A và O . Do đó 2 1 2 1 = . = . (1) 2 SO AA A O AA A O 1 2 1 2 A A A A .OA A . B A C 2 1 1 2 1 1 1 1.0 Mặt khác lại có = = (2) A O OA .OA OA .OA 2 1 2 1 2 Lai có OA D B ! OB D A nên 2 2
OA .OA = OB = R (3) 1 2 1 2
Tam giác ABA ! CHA nên A . B AC = A . A A H (4) 1 1 1 1 1 1 SH AH A . B AC AH.A H 1.0
Từ (1), (2), (3), (4) ta có 1 1 1 = = . 2 2 SO AA R R 1 4
Từ 2 điều kiên trên ta suy ra tồn tại x ¹ 0, x Î X . Khi đó *
kx ΠX , k " Ε . 0.5
Nếu x = 1 thì • \ X Ì {0} là tập hữu hạn 0.5 k 1.0 Nếu x > 1 thì i
x = Õ pa , trong đó pi là các số nguyên tố khác nhau. Từ i i 1 =
điều kiện 2 suy ra tồn tại x Î X không chia hết cho pi . i Trang 44 æ ö Đặt x y = åç .x ÷ i i pa è i ø
Dễ thấy y Î X . Ta sẽ chứng minh mọi số nguyên n > xy đếu thuộc X. 1.0 Thật vậy Vì ( ,
x y) =1 nên {n - ,
x n - 2x,..., n - y }
x là một hệ đầy đủ modul y . Do 1.0 đó tồn tại *
l Î • sao cho n -lx! .
y Suy ra n = lx + ky Î X .
Vậy • \ X là tập có hữu hạn phần tử. 5
+Gọi (i, j)là ô vuông nằm ở hàng i cột j. Để ý rằng một hình chữ 1.0
thập được xác định một cách duy nhất bởi ô ở chính giữa. Ta ký
hiệu C là hình chữ thập có tâm là ô (i, j)trong đó i, j Î{2,3,4,5, } 6 . ij
Do đó tổng số hình chữ thập trong bảng là 25, chia các ô trong bảng thành bốn loại.
Loại 1 : các ô thuộc đúng một hình chữ thập là các ô
(1, j),(i,1),(7, j),(i,7)với (i, j)Î{2,3,4,5, } 6
Loại 2 : Các ô trong bảng thuộc đúng ba hình chữ thập gồm các ô (2, 2),(2,6),(6, 2),(6,6)
Loại 3 : Các ô trong bảng thuộc đúng bốn hình chữ thập gồm các ô
(2,i),(i, 2),(6,i),(i,6)với i Î{3,4, } 5
Loại 4 : Các ô trong bảng thuộc đúng năm hình chữ thập bao gồm
các ô (i, j) 3 £ i, j £ 5
Nếu không thấy được 5 ô không màu của hình C thì trong các ô 1.0 22
(2, 2),(2,1),(1, 2),(2,3),(3, 2)có ít nhất một ô được tô màu.
Nếu hình C được tô màu thì trong các ô (6,2), (6,1), (6,3), (7,2), 62
(5,2) có ít nhất 1 ô được tô màu
Nếu hình C được tô màu thì trong các ô (2,6), (2,5), (2,7), (1,6), 26
(3,6) có ít nhất 1 ô được tô màu.
Nếu hình C được tô màu thì trong các ô (6,6), (6,5), (6,7), (5,6), 66
(7,6) có ít nhất một ô được tô màu
Theo cách phân loại trên các ô kể trên thuộc không quá 4 hình chữ 1.0 thập.
Gọi x là số ô được tô màu trong loại 4, số hình chữ thập được tô màu £ 5x + 4.4
Nếu với mọi hình chữ thập đều được tô màu thì 5x +16 ³ 25 (1) 1.0 Û x ³ 2
Nếu các ô được tô màu là 6 tương ứng x = 2 và do vậy theo (1) có
không quá 1 hình chữ thập chứa nhiều hơn 1 ô được tô màu. Nếu
có 2 ô có 1 cạnh chung và có 1 đỉnh chung được tô màu thì sẽ có 2 Trang 45
hình chữ thập mà mỗi hình có ít nhất 2 ô được tô màu đo được.
Suy ra (4,4), (3,3), (3,5), (5,3), (5,5) không màu.
Không gian tổng quát : giả sử (4,3), (4,5) được tô màu Þ C ,C 34 54
không màu. Vậy n = 6 không thỏa mãn n ³ 7
Với n = 7 cách tô trên thỏa mãn. Vậy min n = 7 ĐỀ 9
ĐỀ ÔN THI HỌC SINH GIỎI MÔN: TOÁN 11
Câu 1 (4 điểm). Cho dãy số (𝑢!) thỏa mãn 𝑢" = #$#% , 𝑢 với 𝑛 ≥ 1. #$## !&" = 𝑢! + 2*𝑢! + !! '" a) Tính .*𝑢#$#%/.
b) Chứng minh rằng dãy 𝑎! = " + # + ⋯ + ! không có giới hạn hữu hạn. '# '! '"
Câu 2 (4 điểm). Cho tam giác ABC nội tiếp đường tròn (O) có M là trung điểm BC. Tiếp tuyến tại B,C
của O cắt nhau tại T. (BOC) lần lượt cắt lại AC,AB tại điểm thứ hai là E,F. Gọi S là hình chiếu của O
trên AT, H là trực tâm của tam giác BOC.
a) Kẻ đường cao AD của tam giác ABC, gọi L là điểm Lemoine của tam giác ABC. Chứng minh
rằng khi A di động trên (O) sao cho ABC là tam giác nhọn, DL luôn đi qua một điểm cố định.
b) Chứng minh rằng hai đường tròn (AEF) và (HST) trực giao.
Câu 3 (4 điểm). Tìm tất cả các hàm số 𝑓: 𝑅 → 𝑅 thỏa mãn:
𝑓7𝑥𝑦 + 𝑥𝑓(𝑦)< = 𝑥𝑦 + 𝑦𝑓(𝑥), ∀𝑥, 𝑦 ∈ 𝑅.
Câu 4 (4 điểm). Cho a là số nguyên dương thỏa mãn gcd(an+1,2n+1) = 1 với mọi số nguyên n.
a) Chứng minh rằng gcd(a-2,2n+1) = 1 với mọi số nguyên n.
b) Tìm tất cả số nguyên a thỏa mãn.
Câu 5 (4 điểm). Cho một bảng kích thước 2024 × 2024 được điền các số tự nhiên từ 1 đến
2024 theo quy tắc sau: Hàng thứ nhất ta điền các số từ 1 đến 2024 từ trái qua phải, ở
hàng thứ hai ta đánh các số từ 2025 đến 4048 từ phải qua trái, các hàng tiếp theo được
đánh theo kiểu zích zắc tương tự như trên. Hãy tìm các phủ kín bẳng trên bởi 1012 × 2024
quân cơ Domino 1x2 sao cho tổng của tích các số trên mỗi quân cờ Domino lớn nhất. ------ Hết ------
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM THI Trang 46
Câu 1 (4 điểm). Cho dãy số (𝑢!) thỏa mãn 𝑢" = #$#% , 𝑢 với 𝑛 ≥ 1. #$## !&" = 𝑢! + 2*𝑢! + !! '" a) Tính .*𝑢#$#%/.
b) Chứng minh rằng dãy 𝑎! = " + # + ⋯ + ! không có giới hạn hữu hạn. '# '! '" Nội dung Điểm
a) Ta sẽ chứng minh bằng quy nạp: 𝑛# < 𝑢! < (𝑛 + 1)#. 0,5
Thật vậy: Xét 𝑛 = 1 đúng, giả sử khẳng định đúng tới 𝑛 = 𝑘 ≥ 1, ta sẽ chứng minh khẳng
định vẫn đúng với 𝑛 = 𝑘 + 1 Ta có: 𝑢 0,5
(&" = 𝑢( + 2*𝑢( + (! > 𝑘# + 2𝑘 + 1 = (𝑘 + 1)# '$
𝑢(&" = 𝑢( + 2*𝑢( + (! < (𝑘 + 1)# + 2(𝑘 + 1) + 1 = (𝑘 + 2)# '$
Vậy theo nguyên lý quy nạp toán học, ta có 𝑛# < 𝑢! < (𝑛 + 1)#. 0,5 → .*𝑢#$#%/ = 2023. 0,5
b) Rõ ràng (𝑎!) là dãy tăng, hơn nữa: 0,5 1 2 𝑛 1 2 𝑛 𝑎! = + + ⋯ + > + + ⋯ + 𝑢" 𝑢# 𝑢! 2# 3# (𝑛 + 1)#
Ta sẽ chứng minh: lim B " + # + ⋯ + ! C = +∞. Thật vậy: 0,5 #! %! (!&")! Gọi (𝑠 !
!) là dãy thỏa mãn: 𝑠! = ∑ ( (+" . Xét dãy con (𝑠 ((&")! #$,"), ta có: 2( 2( + 1 2(&" − 1
2( + 2( + 1 + ⋯ + 2(&" − 1 + + ⋯ + > (2( + 1)# (2( + 1)# (2( + 1)# 2#( 2((2( + 2(&" − 1) 2( + 2(&" − 1 2(&" 1 0,5 = = > = 2#(&% 2#( 2(&% 4 𝑘 0,5
→ 𝑠#$," > , ∀𝑘 ∈ 𝑁∗ 4 Mà lim ( = +∞ nên lim𝑠 (→&/ 0
#$," = +∞ → lim𝑠! = +∞.
Câu 2 (4 điểm). Cho tam giác ABC nội tiếp đường tròn (O) có M là trung điểm BC. Tiếp tuyến tại B,C
của O cắt nhau tại T. (BOC) lần lượt cắt lại AC,AB tại điểm thứ hai là E,F. Gọi S là hình chiếu của O
trên AT, H là trực tâm của tam giác BOC. Trang 47
a) Kẻ đường cao AD của tam giác ABC, gọi L là điểm Lemoine của tam giác ABC. Chứng minh
rằng khi A di động trên (O) sao cho ABC là tam giác nhọn, DL luôn đi qua một điểm cố định.
b) Chứng minh rằng hai đường tròn (AEF) và (HST) trực giao. Nội dung Điểm A H E S O L B C D M F T
a) Gọi M là trung điểm BC, ta có chùm điều hòa cơ bản D(AM,ST)=-1 (1). 0,5
Mặt khác, do H là trực tâm của tam giác BOC nên 𝑀𝑂 OOOOO. 𝑀𝐻 OOOOO = −𝑀𝐵 OOOOO. 𝑀𝐶 OOOOO = −𝑀𝑇 OOOOO. 𝑀𝑂 OOOOO → 1,0 𝑀𝐻 OOOOO = −𝑀𝑇
OOOOO hay M là trung điểm HT.
Lại có 𝐷𝐴//𝐻𝑇 nên D(AM,HT)=-1 (2). Từ (1) và (2) suy ra D,L,H thẳng hàng. Rõ ràng khi A 0,5
di động thì H là điểm cố định nên ta có điều phải chứng minh.
b) Xét phép nghịch đảo f cực A, phương tích 𝐴𝐵 OOOO. 𝐴𝐹 OOOO, ta có: 0,5
f: 𝐵 ↔ 𝐹, 𝐶 ↔ 𝐸, 𝑆 ↔ 𝑇, (𝐴𝐸𝐹) ↔ 𝐵𝐶, (𝐻𝑆𝑇) ↔ (𝐻𝑆𝑇) . 0,5
Mặt khác, theo ý a ta có H,T đối xứng nhau qua BC nên tâm của (HST) thuộc BC. 0,5
Do phép nghịch đảo có tính bảo toàn góc nên (AEF) trực giao với (HST), ta có điều phải 0,5 chứng minh. Trang 48
Câu 3 (4 điểm). Tìm tất cả các hàm số 𝑓: 𝑅 → 𝑅 thỏa mãn:
𝑓7𝑥𝑦 + 𝑥𝑓(𝑦)< = 𝑥𝑦 + 𝑦𝑓(𝑥), ∀𝑥, 𝑦 ∈ 𝑅. Nội dung Điểm Gọi P( ;
x y) là phép thế chỉ khẳng định 0,5
f (xy + xf (y)) = xy + yf (x). (1)
P(0;0) : f (0) = 0. (1
P ; x) : f (x + f (x)) = x + xf (1), x " Î!. (2) Giả sử a
$ ¹ 0sao cho f (a) = 0. P( ;
x a) : f (ax) = ax + af (x), x " Î! . (3) ( P ;
a x) : f (ax + af (x)) = a , x x " Î! .
Từ (3) Þ a(x + f (x)) + af (x + f (x)) = a , x x " Î!. 0,5
Þ ax + af (x) + a(x + xf (1)) = , ax x " Î!.
Þ f (x) + x + xf (1) = 0, x " Î!.
Þ f (x) = -( f (1) + ) 1 , x x " Î!. (4) 1 -
Trong (4) thay x = 1 : f (1) = - f (1) -1Þ f (1) = . 2 1 Þ f (x) = - , x x
" Î! . Thử lại thấy không thỏa mãn. 2
Suy ra f (x) = 0 Û x = 0. Xét 2 trường hợp sau: 1,0 Trường hợp 1: b
$ ¹ 0 : f (b) = - . b P( ;
b x) : f (bx + bf (x)) = 0, x " Î!.
Þ bx + bf (x) = 0, x " Î!. Þ f (x) = - , x x
" ¹ 0. Thử lại thấy thỏa mãn. Trang 49
Trường hợp 2: f (x) ¹ -x, x " ¹ 0.
ìïx + x = f x + x ¹ 0 0 1 ( 1) Giả sử x
$ , x ¹ 0 : f x = f x = x Þ x ¹ 0 1 í . 1 2 ( 1) ( 2) và 0 0
ïx + x = f x + x ¹ 0 î 0 1 ( 1) 1 P( ; x x : f . x x + . x x = .
x x + x . f (x), x " Î!. 1 ) ( 1 0 ) (5) 1 1 P( ; x x : f . x x + . x x = .
x x + x . f (x), x " Î!. 1 ) ( 2 0 ) (6) 2 2 Từ (5), (6) suy ra 0,5
f ((x + x x
x x + f (x) 1 0 ) ) 1( ) = , x " ¹ 0.
f ((x + x x
x x + f (x) 2 0 ) ) 2 ( )
Þ f ((x + x ) x) x1 = f x + x x , x " ¹ 0. 1 0 (( 2 0) ) (7) x2 x æ x + x ö x
Trong (7) thay x bởi 1 0 1 : f ç × x÷ = f (x), x " ¹ 0. (8) x + x x + x x 2 0 è 2 0 ø 2 æ x + x ö æ x + x ö x + x æ x + x ö 1 0 1 0 Pç × ; x y ÷ : f ç
(xy + xf (y)) 1 0 1 0 ÷ = × xy + yf ç × x÷, x " ¹ 0; y Î!. x + x x + x x + x x + x è 2 0 ø è 2 0 ø 2 0 è 2 0 ø x x + x x 0,5
Từ (8) suy ra 1 f ( xy + xf (y)) 1 0 1 = × xy + yf (x), x " ¹ 0; y Î ! . x x + x x 2 2 0 2 x x x
Cũng từ (1) : 1 f ( xy + xf (y)) 1 1 = × xy + yf (x), x " , y Î ! . x x x 2 2 2 Suy ra x + x x 1 0 1 × xy = × xy, x " ¹ 0; y Î ! . x + x x 2 0 2 x + x x 1 0 1 Þ =
Þ x x + x x = x x + x x Þ x = x . 1 2 0 2 1 2 1 0 1 2 x + x x 2 0 2
Kết hợp với f (x) = 0 Û x = 0suy ra f đơn ánh trên ! . Viết lại (1) thành
f (x( y + f (y))) = y(x + f (x)), " , x y Î!. (9)
Trong (9) thay y ® y + f (y) ta được Trang 50
f (x( y + f (y) + f ( y + f (y))) = ( y + f (y))(x + f (x)), x " , y Î!.
Đổi vai trò x, y suy ra 0,5
f (x( y + f (y) + f ( y + f (y))) = f ( y(x + f (x) + f (x + f (x))) , x " , y Î !.
Þ x( y + f (y) + f ( y + f (y))) = y(x + f (x) + f (x + f (x))), x " , y Î! .
Thay x =1 : x(1+ f (1) + f (1+ f (1))) = x + f (x) + f (x + f (x)), " , x y Î!.
Từ (2) Þ x(1+ f (1) +1+ f (1)) = x + f (x) + x + xf (1), x " Î!.
Þ f (x) = xf (1), x " Î! .
Thử lại ta được f (x) = , x x " Î ! . 0,5
Vậy tất cả các hàm thỏa mãn là f (x) = x, x
" Î! ; f (x) = -x, x " Î ! .
Câu 4 (4 điểm). Cho a là số nguyên dương thỏa mãn gcd(an+1,2n+1) = 1 với mọi số nguyên n.
c) Chứng minh rằng gcd(a-2,2n+1) = 1 với mọi số nguyên n.
d) Tìm tất cả số nguyên a thỏa mãn. Nội dung Điểm
a) Ta có an + 1 = 2n + 1 + (a-2)n nên (an+1,2n+1) = (2n+1,(a-2)n)=1 1,0 Suy ra (2n+1,a-2) = 1
b) TH1 : a chẵn , đặt a=2k ( k nguyên dương) 1,0
Theo ý a ta có (2n+1,2k-2) = (2n+1,a-2) = 1 với mọi n nguyên
Hay (2n+1, k-1) = 1 với mọi n nguyên
Suy ra k-1 = 2x nên a = 2x+1 +2 với x là số nguyên không âm TH2 : a lẻ 1,0
Nếu a = 1 hoặc a = 3 thì thỏa mãn
Nếu a = 1 hoặc a = 3 thì thỏa mãn 1,0
Xét a ≥ 5 , đặt a = 2k+1 với k ≥ 2
Khi đó với n = 3k – 2 thì gcd (an+1,2n+1) = 2k-1 > 1 Trang 51
Vậy a = 1, a = 3 hoặc a = 2m + 2, m ≥ 1 thì thỏa mãn
Câu 5 (4 điểm). Cho một bảng kích thước 2024 × 2024 được điền các số tự nhiên từ 1 đến
2024 theo quy tắc sau: Hàng thứ nhất ta điền các số từ 1 đến 2024 từ trái qua phải, ở
hàng thứ hai ta đánh các số từ 2025 đến 4048 từ phải qua trái, các hàng tiếp theo được
đánh theo kiểu zích zắc tương tự như trên. Hãy tìm các phủ kín bẳng trên bởi 1012 × 2024
quân cơ Domino 1x2 sao cho tổng của tích các số trên mỗi quân cờ Domino lớn nhất. Nội dung Điểm
Đặt A = { 1,2,…,20242 }. Gọi 𝑎1 , 𝑏1 là hai số được ghi trên quân cờ Domino thứ I với 𝑎1 , 𝑏1 ∈ 0,5
{ 1,2,…, 20242 } ; i = 1,…, 1006 x 2012 và S = ∑! 𝑎
1+" 1. 𝑏1 với n = 1012 x 2024. Ta cần tìm giá trị nhỏ nhất của S.
Vì xy = 2! & 4! - (2 , 4)! 1,0 # # Nên ta có:
S = " ∑! 7𝑎 # + 𝑏 #< - " ∑! (𝑎 # 1+" 1 1 # 1+" 1 − 𝑏1)#
Mặt khác 𝑎1 , 𝑏1 là các số tự nhiên khác nhau thuộc tập A nên 1,0 ∑! 7𝑎 # # #! 1+" 1 + 𝑏1 < = ∑ 𝑖# 1+" và (𝑎1 − 𝑏1)# ≥ 1
Suy ra S ≤ " ∑#! (𝑖# − 𝑛) # 1+" 0,5
Đẳng thức xảy ra khi và chỉ khi 𝑎1 , 𝑏1 là hai số tự nhiên liên tiếp 1,0
Vậy để S lớn nhất ta phủ các quân cờ Domino sao cho mỗi quân cờ chứa hai số tự nhiên liên tiếp. ĐỀ 10
ĐỀ ÔN THI HỌC SINH GIỎI MÔN: TOÁN 11 ìx = a
Câu 1 (4,0 điểm). Cho dãy ï
(x ) xác định bởi 1 í , với a Î ! . n 2 *
ïx = 2 - x , n " Î î • n 1 + n
Tìm tất cả các giá trị của a sao cho dãy (x ) có giới hạn hữu hạn. n Trang 52
Câu 2 (4,0 điểm). Chứng minh rằng với mọi hàm số f : + +
! ® ! , luôn tồn tại x, y > 0 sao cho
f (x + y) < yf ( f (x)).
Câu 3 (4,0 điểm). Cho tam giác ABC và điểm I thuộc miền trong tam giác ABC D
; AI, BI,CI lần lượt cắt BC,C ,
A AB tại D, E, F. Đường thẳng qua I và vuông góc với
AI cắt BC tại M; N, P lần lượt là các điểm đối xứng với I qua DE, DF. Chứng minh
rằng M , P, N thẳng hàng.
Câu 4 (4,0 điểm). Cho 1 r 2 n = p . r p ... kr p k ³ r Î • i " = k n k ( * 2; , 1, 1 2 i
) là phân tích của thành tích
các thừa số nguyên tố.
Chứng minh rằng nếu phương trình 2023 x
º a (mod n) có nghiệm nguyên với mọi a Î!
thì r = r = ... = r =
1 và gcd( p -1,2023) = 1, i " =1,k. 1 2 k i
Câu 5 (4,0 điểm). Cho X là một tập hữu hạn với X = n và cho A , A ,..., A (m ³ 2) là 1 2 m
các tập con có ba phần tử của X sao cho A Ç A £1 với mọi i ¹ .j i j
Chứng minh rằng tồn tại một tập A là tập con của X sao cho A ³ é 2nù và không ë û A
chứa tập nào trong các tập A , A ,..., A . 1 2 m -----Hết-----
Ghi chú: - Thí sinh không được sử dụng tài liệu và máy tính cầm tay trong khi làm bài.
- Cán bộ coi thi không giải thích gì thêm. HƯỚNG DẪN CHẤM ----- ìx = a
Câu 1 (4,0 điểm). Cho dãy ï
(x ) xác định bởi 1 í
, với a Î ! . Tìm tất n 2 *
ïx = 2 - x , n " Î î • n 1 + n
cả các giá trị của a sao cho dãy (x ) có giới hạn hữu hạn. n Hướng dẫn chấm 4,0 điểm
Với a < 2 chỉ ra được dãy không có giới hạn hữu hạn. Ta xét trường hợp 1,0 a £ 2. Trang 53
Đặt x = a = 2c - osa, a Î 0;p . x - = - a n " Ε a n ( n 1 ) * 2cos 2 , . 1 [ ] Ta có Giả sử là số
mà tồn tại lim x . Khi đó 2
L = 2 - L Þ LÎ{ 2 - ; } 1 . n Đặt 2 *
f (x) = 2 - x , nΕ . Khi đó f (L) = . L Ta có Lagrange
x - L = f (x ) - f (L) =
f (¢c ) x - L = 2c x - L , n 1 + n n n n n với c x . L
n là một số nào đó nằm giữa n và Do 3 lim x = LÎ - *
n Î • : x > , n " ³ n . n { 2; } 1 nên tồn tại Suy ra 0 n 0 4 1,0 3 c > , n " ³ n . n 0 4 k Khi đó 3 æ 3 ö x - L > x - L , n " ³ n . Do vậy * x - L > x - L , k " Î • . n 1 + n 0 ç ÷ 2 + 0 n k 0 è 2 n ø (*)
Nếu x - L ¹ 0 thì trong (*) cho k ® +¥ ta suy ra điều vô lý. Vậy x = . L n 0 n 0
Trường hợp 1: L = 2. - Xét phương trình 0,5 p - - - m 2c - os( n n n .2 0 1 2 a ) = 2 - Û cos( 0 1 2 a ) 0 1 =1 Û 2 a = . m 2p Û a = , m " Î . ! - 0 n 1 2
Trường hợp 2: L =1. Xét phương trình - ± + m p 2c - os( n - n - 1 1 3 .2 1 2 a ) =1Û cos( 1 2 a ) ( ) 0 0 = Û a = , m " Î . ! - 0 n 1 2 3.2 0,5 Kết hợp lại ta được .2 p p a = , p Î , ! q Î • . 3.2q Thử lại, xét .2 p p a = , p Î , ! q Î • .Ta có 3.2q æ p p - p ö æ - - p n .2 n q .2 1 1 ö * x = 2c - os 2 × = 2c - os 2 × , n " Î • . n ç ÷ ç ÷ è 3.2q ø è 3 ø
Với n ³ q +1, thì
+) Nếu p º 0(mod3) thì x - - = - × p¢ p = - n " ³ q + n ( n 1 2cos 2 q .2 ) 2, 1 . p +) Nếu æ n- -q 2 ö p º 1(mod 3) thì 1 x = 2c - os 2 × , n " ³ q +1.Ta thấy 1,0 n ç ÷ è 3 ø p n 1 æ ö 2 - -q º 1 ± 2 (mod3) nên x = 2c - os ± =1, n
" ³ q +1, p º1(mod3). n ç ÷ è 3 ø p +) Nếu æ n- -q 4 ö p º 2(mod 3) thì 1 x = 2c - os 2 × , n " ³ q +1.Ta thấy n ç ÷ è 3 ø p n 1 æ ö 2 - -q º 1 ± 4 (mod3) nên x = 2c - os ± =1, n
" ³ q +1, p º 2(mod3). n ç ÷ è 3 ø Trang 54 p Tóm lại, với æ .2 p ö x = a = 2c - os , p Î ,
! q Î • thì dãy hội tụ. 1 ç ÷ è 3.2q ø
Câu 2 (4,0 điểm). Chứng minh rằng với mọi hàm số f : + +
! ® ! , luôn tồn tại x, y > 0 sao cho
f (x + y) < yf ( f (x)). Hướng dẫn chấm 4,0 điểm
Giả thiết phản chứng f (x + y) ³ yf ( f (x)); " ,x y > 0. Lấy a >1 và đặt
t = f ( f (a)) > 0. 1,0 Xét æ 1 1 ö b = a 1+ + > . a ç 2 ÷ è t t ø Ta có æ ö
f b = f ( b - a + a) ³ b - a f ( f a ) 1 ( ) ( ) ( )
( ) = (b - a)t = a 1+ > a (1) ç ÷ è t ø a 1,0
và f ( f (b)) = f (a +( f (b) - a)) = ( f (b) - a) f ( f (a)) ³ ×t = .a t (2) Ta có f ( )
x = f (b +(x -b)) = (x -b) f ( f ( )
b ) > (x -b) , a x " > . b (3) Xét ab
f (x) > (x -b)a > x Þ x > . Khi đó 1,0 a -1 f ( f ( )
x ) = f (x +( f (x) - x)) ³ ( f (x) - x) f ( f (x)) Þ1³ f (x) - x Þ f (x) £ x +1. (4) Trong (3), ta chọn +
x sao cho (x -b) ab 1
a > x +1 Û x >
thì f (x) > x +1. (5) a -1 Tóm lại, với ab +1 x >
thì ta có đồng thời (4) và (5). Đây là điều vô lý hay 1,0 a -1
giả thiết phản chứng là sai.
Câu 3 (4,0 điểm). Cho tam giác ABC và điểm I thuộc miền trong tam giác ABC D
; AI, BI,CI lần lượt cắt BC,C ,
A AB tại D, E, F. Đường thẳng qua I và vuông góc với
AI cắt BC tại M; N, P lần lượt là các điểm đối xứng với I qua DE, DF. Chứng minh
rằng M , P, N thẳng hàng. Hướng dẫn chấm 4,0 điểm
Gọi Q là điểm đối xứng với I qua BC. Ta có DN = DI = DP = DQ nên bốn 1,0 điểm N, I, ,
P Q cùng nằm trên đường tròn tâm . D Mặt khác, vì ∑ 0
DIM = 90 nên IM tiếp xúc với (D) tại I. Vì I , Q đối xứng với 1,0
nhau qua BC nên MQ tiếp xúc với (D) tại . Q Trang 55
Đặt X , Y là các giao điểm của EF với BC, . AD Khi đó (XYEF) = 1 - Þ D(XYEF) = 1
- hoặc có thể viết D(M, I, E, F) = 1 - . !!" !!" !!" !!" !!!" !!!!" !!!" !!!!" Lại có IN IQ IP IQ DE DM DF DM
I (Q, M , N, P) sin( , ) sin( , ) sin( ; ) sin( , ) = !!" !!!" : !!" !!!" = !!!" !!!" : !!!" !!!"
sin(IN, IM ) sin(IP, IM ) sin(DE, DI) sin(DF, DI)
= D(M,I,E,F) = - . 1 (vì ,
IQ IM , IN, IP theo thứ tự vuông góc với DM , DI, DE, DF ). 1,5 Suy ra I (I, , Q N, P) = -
1 hay tứ giác IPQN điều hòa. Vậy M , P, N thẳng hàng. 0,5
Câu 4 (4,0 điểm). Cho 1 r 2 n = p . r p ... kr p k ³ r Î • i " = k n k ( * 2; , 1, 1 2 i
) là phân tích của thành tích
các thừa số nguyên tố. Chứng minh rằng: Nếu phương trình 2023 x
º a (mod n) có nghiệm
nguyên với mọi a Î! thì r = r = ... = r =
1 và gcd( p -1,2023) = 1, i " =1,k. 1 2 k i Hướng dẫn chấm 4,0 điểm
Giả sử phương trình 2023 x
º a (mod n) có nghiệm nguyên với mọi a Î . ! Khi đó các phương trình 2023 x º a (mod ir
pi ) cũng có nghiệm nguyên với mọi 0,5
a Î !, i = 1, k.
Nếu tồn tại i sao cho r >1 thì chọn a = p . Từ 2023 x º p (mod ir p r > 1 i i ) và suy i i i 0,5 ra 2
p ! p , vô lí. Vậy r =1, i " =1,k. i i i æ - ö Giả sử p 1 2023
gcd( p -1,2023) = d Þ gcd i , = 1. Suy ra tồn tại * s Î • sao i i ç ÷ d d è i i ø 1,0 cho p -1 2023 i = 1+ . . s d d i i Với a Î ,
! gcd(a, p ) =1, gọi x là nghiệm nguyên của phương trình 1,0 i Trang 56 2023 x
º a (mod n) thì gcd( , x p ) =1. Suy ra i p 1 - i p - d p - i a º ( i 2023 x
) 1d º ( ix )2023 (Fermat) 1 di i º 1 (mod p ); a " Î ,
! gcd(a, p) = 1. i p 1 - i
Do đó đa thức P(t) di = t
-1 có p -1 nghiệm t º1,2,..., p -1(mod p ). Theo i i i 1,0
Định lí Lagrage thì deg P(t) = p -1Þ d =1. Vậy gcd( p -1,2023) =1, i " =1,k. i i i
Câu 5 (4,0 điểm). Cho X là một tập hữu hạn với X = n và cho A , A ,..., A (m ³ 2) là 1 2 m
các tập con có ba phần tử của X sao cho A Ç A £1 với mọi i ¹ .j Chứng minh rằng tồn i j
tại một tập A là tập con của X sao cho A ³ é 2nù và không chứa tập nào trong các ë û A
tập A , A ,..., A . 1 2 m Hướng dẫn chấm 4,0 điểm
Gọi B là tập hợp con của X có số phần tử lớn nhất sao cho B không chứa
tập nào trong các tập A , A ,..., A . Giả sử B = k. Khi đó số phần tử của tập 1 2 m 1,0
X \ A = n - k.
Ta sẽ đếm số phần tử của X \ A theo các cách khác như sau:
Nếu xÎ X \ A thì AÈ{ }
x không thỏa mãn yêu cầu của bài toán nên tồn tại 1,0
i(x)Î{1, 2,..., }
m sao cho A Ì AÈ x . x Î A A \ x Ì . A i(x) { } i(x) { } Suy ra và i( x)
Mặt khác tập A có số phần tử bằng 3 nên A \ x = 2. i(x) { } i( x) Ta thấy với , x y Î X \ ,
A x ¹ y, nếu A \ x = A \ y A È A = 2. i(x)
{ } i(y) { } thì Đây 1,0 i(x) i( y)
là điều vô lý, suy ra A \ x ¹ A \ y . i(x) { } i(y) { }
Do vậy, mỗi phần tử của tập X \ A tương ứng với một tập con có hai phần tử của A nên ta có k(k -1) 2 2
X \ A £ C Û n - k £
Û k + k - 2n ³ 0 Û k ³ é 2n ù .Đây k 1,0 2 ë û
là điều phải chứng minh. Trang 57




