TOP 10 đề thi học kỳ 1 toán 11 (có đáp án)

TOP 10 đề thi học kỳ 1 toán 11 có đáp án chi tiết. Các đề thi được tổng hợp từ các trường THPT trong cả nước và được viết dưới dạng file PDF gồm 51 trang. Các bạn xem và tải về ở dưới.

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 11

Môn: Toán 11

Thông tin:

51 trang 6 tháng trước

Tác giả:

Profile Thùy Dương (H)
! Trang!1!
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT CÂY DƯƠNG
( Đề có 3 trang )
ĐỀ THI HỌC KỲ I - NĂM HỌC 2017 - 2018
MÔN TOAN – 11
Thời gian làm bài: 90 Phút
ĐIỂM
Họ tên :...................................................... Số báo danh : ...............Lớp 11B..
I. PHẦN TRẮC NGHIỆM: Gồm 30 câu. (6 điểm)
Câu 1: Trong một hộp phấn màu có 2 viên phấn xanh, 3 viên phấn đỏ và 5 viên phấn vàng. Hỏi có bao
nhiêu cách chọn một viên phấn từ hộp đó.
A. 9. B. 11. C. 30. D. 10.
Câu 2: Tìm khẳng định sai trong các khẳng định sau.
A. Hàm số tuần hoàn với chu kì .
B. Hàm số tuần hoàn với chu kì .
C. Hàm số tuần hoàn với chu kì .
D. Hàm số tuần hoàn với chu kì .
Câu 3: Tìm tất cả các tham số thực m để phương trình có nghiệm.
A.
. B. . C.
. D.
.
Câu 4: Trong mặt phẳng Oxy, cho điểm là ảnh của điểm N qua phép quay tâm O góc .
Tìm tọa độ điểm N.
A. B. C. D.
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của BC. Mặt phẳng (α) đi
qua M và song song với các đường thẳng BD, SC. Gọi là thiết diện tạo bởi mp(α) và hình chóp
S.ABCD. Tìm mệnh đề đúng?
A. là một lục giác. B. là một hình bình hành.
C. là một tam giác. D. là một ngũ giác.
Câu 6: Trong mặt phẳng Oxy, cho đường tròn . Viết phương trình đường tròn là
ảnh của đường tròn qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số
và phép tịnh tiến theo vectơ .
A. B. C. D.
Câu 7: Tìm tập nghiệm của phương trình .
A. . B. . C. . D.
.
Câu 8: Trong mặt phẳng Oxy, cho đường thẳng . Viết phương trình đường thẳng là ảnh
của đường thẳng d qua phép vị tự tâm O tỉ số .
A. B. C. D.
Câu 9: Từ 6 điểm phân biệt , có thể thành lập được bao nhiêu vectơ khác vectơ ?
A. 21. B. 30. C. 120. D. .720.
Câu 10: Cho hình chóp S.ABCD có O là giao điểm của AC và BD, M là trung điểm của SC. Xác định giao
cotyx=
p
tanyx=
cosyx=
sinyx=
5 sin 2 cos 1xxm+=-
42mm³Ú £-
02m££
24m-£ £
31mm=Ú =-
( )
4; 2M -
0
90
( )
2; 4--
( )
2; 4
( )
2; 4-
( )
2; 4-
( )
H
( )
H
( )
H
( )
H
( )
H
( ) ( ) ( )
22
:1 25Cx y++- =
( )
C
3-
( )
5; 2v =-
!
( ) ( )
22
4 2 45xy+++=
( ) ( )
22
2 4 45xy+++=
( ) ( )
22
2 4 15xy-+-=
( ) ( )
22
8 8 15xy-++=
2
cos 2 cos 2 6 0xx+-=
Æ
{ }
3; 2-
,
6
kk
p
p
ìü
±+ Î
íý
îþ
!
2,
4
kk
p
p
ìü
±+ Î
íý
îþ
!
:3 2 0dxy+-=
1
2
k =-
310xy+-=
310xy+-=
310xy++=
310xy++=
,,, ,,ABCDEF
0
!
Mã đề 989
! Trang!2!
điểm I của đường thẳng AM và mp(SBD).
A. . B. . C. . D. .
Câu 11: Tìm tập xác định của hàm số .
A. . B. . C. . D.
.
Câu 12: Dãy số được cho bởi công thức nào dưới đây là dãy số không tăng, không giảm ?
A. . B. . C. . D. .
Câu 13: Cho dãy số , biết (với ). Tìm số hạng thứ 5 của dãy số.
A. . B. . C. . D. .
Câu 14: Cho cấp số nhân có số hạng đầu và công bội q. Tìm mệnh đề sai.
A. . B. . C. . D. .
Câu 15: Tìm hàm số chẵn trong các hàm số sau.
A. . B. . C. . D. .
Câu 16: Gieo một đồng tiền xu cân đối và đồng chất 3 lần. Tìm số phần tử của không gian mẫu.
A. 3. B. 16. C. 8. D. 6.
Câu 17: Ba số x, y, z theo thứ tự đó lập thành một cấp số nhân có công bội khác 1. Đồng thời chúng lần
lượt là số hạng đầu, số hạng thứ hai và số hạng thứ năm của một cấp số cộng. Hãy tìm tích của ba số đó, biết
rằng tổng của chúng là 26.
A. . B. . C. . D. .
Câu 18: Tìm số hạng đầu và công sai d của cấp số cộng , biết: .
A. . B. . C. . D. .
Câu 19: Tìm mệnh đề sai ?
A. Hai đường thẳng được gọi là song song nếu chúng không có điểm chung.
B. Một đường thẳng và một mặt phẳng được gọi là song song nếu chúng không có điểm chung.
C. Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung.
D. Hai đường thẳng được gọi chéo nhau nếu chúng không đồng phẳng.
Câu 20: Trong mặt phẳng Oxy, cho điểm là ảnh của điểm qua phép tịnh tiến theo
vectơ . Tìm mệnh đề đúng ?
A. B. C. D.
Câu 21: Giải phương trình .
A. . B. . C. . D.
.
Câu 22: Cho lăng trụ tam giác ABC.A’B’C’ . Tìm giao tuyến của hai mặt phẳng (ACC’) và (A’BC).
I AM BD=Ç
I AM SB=Ç
I AM SO=Ç
I AM SD=Ç
cot
3
yx
p
æö
=+
ç÷
èø
\,
3
kk
p
p
ìü
-+ Î
íý
îþ
!!
\,
3
kk
p
p
ìü
-+ Î
íý
îþ
!"
\2,
3
kk
p
p
ìü
-+ Î
íý
îþ
!"
\,
3
kk
p
p
ìü
+Î
íý
îþ
!"
1
n
n
u
n
=
+
1
2
n
n
n
u
+
=
( ) ( )
1.4 3
n
n
un=- +
2
2
n
un=-
( )
n
u
1
1
4
32
nn
u
uu
+
=
ì
í
=-
î
*
n Î •
5
730u =
5
82u =
5
2188u =
5
244u =
( )
n
u
1
u
1
.
n
n
uuq=
1
1
.
n
n
uuq
-
=
11
.
n
n
uuq
+
=
1
.
nn
uuq
+
=
sinyx=
cosyx=
cotyx=
tanyx=
. . 248xyz=
. . 264xyz=
. . 216xyz=
. . 224xyz=
1
u
( )
n
u
25
5, 7uu=- =
1
2
12
u
d
=-
ì
í
=
î
1
9
4
u
d
=-
ì
í
=
î
1
17
3
2
3
u
d
ì
=-
ï
ï
í
ï
=
ï
î
1
12
4
u
d
=-
ì
í
=
î
( )
'';'Mxy
( )
;Mxy
( )
;vab=
!
'
'
xxa
yyb
=+
ì
í
=+
î
'
'
xxa
yyb
=-
ì
í
=-
î
'
'
xxb
yya
=+
ì
í
=+
î
'
'
xax
yby
=-
ì
í
=-
î
3 sin cos 1xx-=-
2
,
3
2
xk
k
xk
p
p
pp
é
=- +
ê
Î
ê
=+
ë
!
,
4
3
xk
k
xk
p
p
p
=
é
ê
Î
ê
=+
ë
!
2
,
4
2
3
xk
k
xk
p
p
p
=
é
ê
Î
ê
=+
ë
!
2
,
2
xk
k
xk
p
pp
=
é
Î
ê
=+
ë
!
! Trang!3!
A. A’B. B. AB’. C. A’C. D. AC’.
Câu 23: Cho cấp số nhân có số hạng đầu và công bội . Tính tổng của 11 số hạng đầu.
A. . B. . C. . D. .
Câu 24: Từ một hộp có 7 cây viết tím, 4 cây viết xanh và 3 cây viết đỏ, lấy ngẫu nhiên 3 cây viết. Tính xác
suất sao cho lấy được 1 cây viết tím, 1 cây viết xanh và 1 cây viết đỏ.
A. . B. . C. . D. .
Câu 25: Có bao nhiêu số tự nhiên gồm 6 chữ số khác nhau lấy từ tập các chữ số ?
A. 24 B. 33 C. 120. D. 720.
Câu 26: Cho cấp số cộng gồm 5 số hạng: . Tìm công sai d của cấp số cộng.
A. . B. . C. . D. .
Câu 27: Tìm mệnh đề sai ?
A. . B. .
C. . D. .
Câu 28: Tìm mệnh đề đúng ?
A. Tồn tại duy nhất một mặt phẳng đi qua 3 điểm không thẳng hàng.
B. Tồn tại vô số mặt phẳng phân biệt đi qua 3 điểm không thẳng hàng.
C. Tồn tại duy nhất một mặt phẳng đi qua 1 điểm và một đường thẳng.
D. Tồn tại vô số mặt phẳng phân biệt cùng chứa hai đường thẳng cắt nhau.
Câu 29: Dãy số nào dưới đây là một cấp số cộng.
A. . B. . C. . D. .
Câu 30: Hai xạ thủ A và B cùng bắn vào bia. Xác suất để xạ thủ A bắn trúng bia là 0,6 và xác suất để xạ thủ
B bắn trúng bia là 0,8. Tính xác suất để có đúng một xạ thủ bắn trúng bia.
A. B. C. D.
II. PHẦN TỰ LUẬN: Gồm 4 bài (4 điểm)
Bài 1. Giải các phương trình sau:
a/ . (0,4 điểm) b/ . (0,6 điểm)
Bài 2. Viết khai triển biểu thức sau theo công thức nhị thức Niu – tơn: . (1 điểm)
Bài 3. Dùng phương pháp quy nạp, chứng minh rằng với mọi thì “ chia hết cho
6”. (1 điểm)
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD là đáy lớn.
a/ Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD). (0,5 điểm)
b/ Gọi M là trung điểm của SA. Tìm giao điểm N của SD và mp(MBC). (0,5 điểm)
------ HẾT ------
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT CÂY DƯƠNG
THI HỌC KỲ I - ĐÁP ÁN NĂM HỌC 2017 - 2018
MÔN TOAN – 11
( )
n
u
1
6u =
2q =-
11
4098S =
11
4089S =
11
6147S =-
11
6147S =
1
156
1
6
1
26
{ }
3,4,5, 6 , 7,8
5 11
1; ; 4; ; 7
22
5
2
d =
2
5
d =
3
2
d =
2
3
d =
( ) ( )
vv
ATB BT A
-
=Û=
!!
( ) ( )
,,
22
OO
AQ B BQ A
pp
æö æ ö
-
ç÷ ç ÷
èø è ø
=Û=
( )
( ) ( )
,1
,
Ok
O
k
AV B BV A
æö
ç÷
èø
=Û=
( )
( )
( )
( )
,,Ok O k
AV B BV A
-
=Û=
1111
1; ; ; ;
2345
12345
; ; ; ;
23456
17; 14; 11; 8; 5
1; 2; 4; 8; 16
0, 48.
0, 2.
1,4.
0, 44.
( )
0
tan 15 3x -=
2 sin 4 1 0x -=
( )
4
2x +
*n Î •
2
73 31
n
n
Ann=+ --
! Trang!4!
()
Thời gian làm bài : 90 Phút
Phần đáp án câu trắc nghiệm:
989
1
D
2
B
3
C
4
B
5
D
6
B
7
A
8
C
9
B
10
C
11
B
12
C
13
D
14
A
15
B
16
C
17
C
18
B
19
A
20
A
21
C
22
C
23
A
24
D
25
D
26
C
27
D
28
A
29
C
30
D
SỞ GD&ĐT TUYÊN QUANG
TRƯỜNG THPT SƠN DƯƠNG
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2018 - 2019
Môn: TOÁN 11
! Trang!5!
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Họ và tên:.............................................................Lớp:11B…
A.Phần trắc nghiệm: (Học sinh lựa chọn phương án trả lời rồi điền các chữ A, B, C, D vào bảng sau).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Câu 1: Nghiệm của phương trình cosx = 1 là:
A. B. C. D.
Câu 2: Điều kiện xác định của hàm số là:
A. B. C. D.
Câu 3: Nghiệm của phương trình là:
A. B. C. D.
Câu 4: Tìm tập xác định của hàm số
A. B. C. D.
Câu 5: Nghiệm dương nhỏ nhất của pt là:
A. B. C. D.
Câu 6: Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên Tính
giá trị
A. B. C. D.
Câu 7: Tính tổng .
A. B. C. D.
Câu 8: Với mệnh đề nào dưới đây sai ?
A. B.
C. D.
Câu 9: Cho 5 chữ số Từ 5 chữ số này ta lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau?
A. B. C. D.
Câu 10: Xét phép thử “Xếp 3 bạn nam và 3 bạn nữ theo đội hình hàng ngang sao cho nam nữ xen kẽ nhau”.
Khi đó không gian mẫu là:
A. 6. B. 6! C. (3!)
2
D. 2 (3!)
2
Câu 11: Cho dãy số với .Khẳng định nào sau đây là đúng?
A. Năm số hạng đầu của dãy là : . C. Là dãy số tăng.
B. 5 số số hạng đầu của dãy là : . D. Bị chặn dưới bởi 1.
Câu 12: Khẳng định nào sau đây là sai?
A. Dãy số là một cấp số cộng: .
xk
p
=
,.k Î ¢
2
2
xk
p
p
=+
,.k Î ¢
2xk
p
=
,.k Î ¢
2
xk
p
p
=+
,.k Î ¢
y cotx=
2
xk
p
p
¹+
,.k Î ¢
4
xk
p
p
¹+
,.k Î ¢
,.
82
xkk
pp
π+ Œ¢
xk
p
¹
,.k Î ¢
cos 3 cosxx=
2xk
p
=
,.k Î ¢
2
,.
2
2
xk
k
xk
p
p
p
=
é
ê
Î
ê
=+
ë
¢
2xk
p
=
,.k Î ¢
2
xk
p
=
,.k Î ¢
2
cot
.
sin 1
x
y
x
=
-
\2,.
2
DR k kZ
p
p
ìü
=+Î
íý
îþ
!"
\.
2
DR k
p
ìü
=
íý
îþ
!
\.
22
DR k
pp
ìü
=+
íý
îþ
!
\2;.
2
DR k k
p
pp
ìü
=+
íý
îþ
!
2 sin sin 22 0xx+=
3
4
x
p
=
4
x
p
=
3
x
p
=
x
p
=
, Mm
44
sin cosyxx=+
.!
..Mn
1
.
2
3
.
2
6.
2.
012
...
n
nnn n
SC C C C=++++
2 1.
n
S =-
2.
n
S =
1
2.
n
S
-
=
2 1.
n
S =+
*
nNÎ
!.
n
Pn=
!
(1 ).
()!
k
n
n
Akn
nk
=££
-
!
(0 ).
!( )!
k
n
n
Ckn
kn k
=££
-
!(0 ).
kk
nn
CkA kn=££
1, 2,3, 4,5.
120
60
30
40
( )
Un
1
n
Un
n
-
=
+
12355
;;;;
23456
-----
12345
;;;;
23456
-----
113
;0; ;1; ;...
222
-
1
11
,
22
ud=- =
! Trang!6!
B. Dãy số là một cấp số cộng: .
C. Dãy số : … là cấp số cộng .
D. Dãy số: không phải là một cấp số cộng.
Câu 13: Cho một cấp số cộng có . Tìm ?
A. B. C. D.
Câu 14: Xác định x để 3 số: 1–x; x
2
; 1+x lập thành một cấp số cộng?
A. B. C. D.
Câu 15: Trong mặt phẳng cho vectơ . Phép biến hình biến mỗi điểm M thành điểm được gọi là phép
tịnh tiến theo vectơ nếu thỏa mãn:
A. B. C. D.
Câu 16: Cho phép vị tự . Mệnh đề nào sau đây sai?
A. là phép đồng nhất. B. biến tâm I thành chính nó.
C. biến gốc tọa độ O thành chính nó. D. là phép đối xứng tâm I.
Câu 17: Ảnh của đường thẳng qua phép vị tự tâm O tỉ số là
A. B.
C. D.
Câu 18: Ảnh của đường tròn qua phép vị tự tâm O tỉ số là
A. B.
C. D.
Câu 19: Trong không gian, cho 4 điểm không đồng phẳng. Hình tạo bởi 4 điểm trên là hình có bao nhiêu
mặt?
A. 6 B. 4 C. 3 D. 2
Câu 20: Cho đường thẳng và mặt phẳng trong không gian. Có bao nhiêu vị trí tương đối của và
?
A. 2 B. 3 C. 1 D. 4
B. Phần tự luận.
Câu 21(1,5 điểm). Giải các phương trình
a) b) c)
Câu 22(2,0 điểm).
a) Một bình đựng quả cầu xanh và quả cầu đỏ và quả cầu vàng. Chọn ngẫu nhiên quả cầu. Tính
xác suất để được quả cầu khác màu nhau.
b) Tìm hệ số chứa x
5
trong khai khai triển nhị thức biết n thoả mãn
c) Chứng minh rằng với mọi thì chia hết cho 3
Câu 23 (1,5 điểm).
a) Trong mặt phẳng tọa độ , cho đường thẳng có phương trình
và . Viết
phương trình đường thẳng là ảnh của qua phép tịnh tiến .
b) Cho hình chóp đáy là hình bình hành. Gọi lần lượt là trọng tâm của các tam giác
, , là trung điểm của . Xác định thiết diện của chóp với mặt phẳng
Đáp án và thang điểm
I. Trắc nghiệm
23
11 1
; ; ;...
22 2
1
11
,
22
ud==
–2; –2; –2; –2;
1
2, 0ud=- =
0,1;0,01;0,001;0, 0001
16
3; 27uu=- =
d
5d =
7d =
6d =
8d =
3x =±
2x =±
1x =±
0x =
v
!
'M
v
!
'MM v=-
!!!!!" "
'MM v=
!!!!!!" "
'MM kv=
!!!!!" "
'MM v=
!!!!!" "
( )
;Ik
V
( )
;1I
V
( )
;Ik
V
( )
;Ik
V
( )
;1I
V
-
:2 5 3 0dx y-+=
3k =-
2590xy-+ +=
2590xy-- +=
2390xy-+=
2390xy-+ +=
( ) ( ) ( )
22
:4 11Cx y-++=
2k =
( ) ( ) ( )
22
': 8 2 4Cx y++- =
( ) ( ) ( )
22
': 8 2 4Cx y-++ =
( ) ( ) ( )
22
': 8 2 4Cx y+++=
( ) ( ) ( )
22
': 8 2 4Cx y-+- =
a
( )
P
a
( )
P
33 0tanx+=
2
sin – sin 2xx=+
2
sin sin .cos 13xxx+=
5
4
3
3
3
2
3
3
n
x
x
æö
-
ç÷
èø
65
10
nn
AA=
*nNÎ
3
2nn+
Oxy
d
2350xy-+=
( )
1; 3v =-
!
'd
d
v
T
!
.,S ABCD
ABCD
,IJ
SAB
SAD
M
CD
( )
.IJ M
! Trang!7!
1C
2D
3D
4D
5A
6A
7B
8D
9A
10D
11B
12B
13C
14C
15D
16C
17A
18B
19B
20B
II. Tự luận
Câu
ý
Nội dung đáp án
Điểm
21
(1,5đ)
a)
a)
b)
Đặt
c)
0,25
0,25
0,25
0,25
0,25
0,25
22
a
0,5
a) Một bình đựng quả cầu xanh và quả cầu đỏ và quả cầu vàng. Chọn ngẫu
nhiên quả cầu. Tính xác suất để được quả cầu khác màu nhau.
Gọi là biến cố lấy ra 3 quả cầu khác màu nhau.
0,25
0,25
b
1,0
b) Tìm hệ số chứa x
5
trong khai khai triển nhị thức biết n thoả
mãn
Ta có :
Xét số hạng thứ trong khai triển của nhị thức là :
Với số hạng chứa ta có: hệ số của là:
0,25
0,25
0,25
0,25
c
0,5
c) Chứng minh rằng với mọi thì chia hết cho 3.
33 0tanx+=
3
tan
3
;
6
x
xkk
p
p
€=-
€=-+ Œ¢
2
sin – sin 2xx=+
2
sin sin 2 0xx€+-=
( )
2
1
sin ; 1 2 0
2
u
uxu uu
u loai
È
=
Í
=£fi+-=€
Í
=-
Î
12;k
2
uxk
p
p€=€=+ Œ¢
22
33
;
;
2
2
1
tan
;
36
cos 0
sin sin .cos 1 sin .cos cos 0
3 sin cos 0
x
xxx xxx
xx
x
x
kk
kk
x
xkk
p
p
p
p
p
p
=
é
+Î
+Î
+=Û-=Û
ê
+
=
=+
=
ë
é
é
=
=
ê
ê
ê
ÛÛ
ê
ê
ê
ê
ê
Î
ë
ë
!
!
!
5
4
3
3
3
A
( ) ( )
( )
111 3
543 12
.. 60;n 220
60 3
220 11
nA CC C C
PA
fi= =W==
fi==
2
3
3
n
x
x
æö
-
ç÷
èø
65
10
nn
AA=
( ) ( )
( ) ( )( )
65
! 10 !
10
6! 5!
1 10 10
1 5 10 15
6! 5 6! 5
nn
nn
AA
nn
nn
nnn n
=Û =
--
Û= Û=Û-=Û=
--- -
1k +
2
3
3
n
x
x
æö
-
ç÷
èø
( )
( )
15
2305
15 15
3
3
3
k
k
k
kkk
Cx Cx
x
-
-
ʈ
-
˜
Á
=-
˜
Á
˜
Á
˯
5
x
30 5 5 5kk-=€=fi
5
x
55
15
3729729C-=
*nNÎ
3
2nn+
! Trang!8!
Xét dãy số
Với
Với giả sử ta cần chứng minh
Thật vậy theo giả thiết quy nạp ta có:
Vậy:
0,25
0,25
23
a
a) Trong mặt phẳng tọa độ , cho đường thẳng có phương trình
và . Viết phương trình đường thẳng là ảnh của qua
phép tịnh tiến .
Ta có : gọi
Và
có vectơ pháp tuyến là:
có phương trình:
Vậy
0,5
0,5
b
b) Cho hình chóp đáy là hình bình hành. Gọi lần lượt là
trọng tâm của các tam giác , , là trung điểm của . Xác định thiết
diện của chóp với mặt phẳng
Gọi là trung điểm , là trung điểm của .
Gọi
. Gọi lần lượt là trung điểm của
Gọi
Vậy thiết diện là hình ngũ giác
0,25
0,25
3
2
n
Un n=+
1
1: U 3 3n ==M
nk=
3
23
k
Uk k=+M
( ) ( )
3
1
12 13
k
Uk k
+
=+ + +M
( ) ( )
3
1
12 1
k
Uk k
+
=+ + +=
( ) ( )
32 3 2
33122 23 33kkk k kk kk=+ ++++= + + ++M
3
23
n
Un n=+M
Oxy
d
2350xy-+=
( )
1; 3v =-
!
'd
d
v
T
!
( )
1;1Md-Œ
( )
( )
;
v
Mxy TM M d
¢¢¢ ¢ ¢
=fiŒ
r
( )
( )
( )
1 1;1 3 0; 2M
¢
=- + +- = -
//ddd
¢¢
fi
( )
2; 3n -
r
d
¢
fi
( ) ( )
203202360xy xy-- +=€ - -=
:2 3 6 0dxy
¢
--=
.,S ABCD
ABCD
,IJ
SAB
SAD
M
CD
( )
.IJ M
P
K
H
F
G
L
M
J
O
I
N
B
D
C
A
S
O
AB
N
AD
( )
,,L AM ON G SL IJ F MG SA MF IJM=« =« =«fi Ã
,HFISDKFJSB=« = «
,ON
,AB AD
( )
2
// //
3
SI SJ
IJ ON ON IJM
SN SO
fi==fi fi
( )
//P CD IJM MP ON=« fi
MPKFH
! Trang!9!
SỞ GD&ĐT TUYÊN QUANG
TRƯỜNG THPT SƠN DƯƠNG
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2018 - 2019
Môn: TOÁN 11
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Họ và tên:.............................................................Lớp:11B…
A.Phần trắc nghiệm: (Học sinh lựa chọn phương án trả lời rồi điền các chữ A, B, C, D vào bảng sau).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Câu 1: Nghiệm của phương trình là:
A. B. C. D.
Câu 2: Điều kiện xác định của hàm số là:
A. B. C. D.
Câu 3: Nghiệm của phương trình là:
A. B. C. D.
Câu 4: Tìm tập xác định của hàm số
A. B.
C. D.
Câu 5: Nghiệm âm lớn nhất của phương trình là:
A. . B. . C. . D. .
Câu 6: Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên Tính
giá trị
A. B. C. D.
Câu 7: Tính tổng .
A. B. C. D.
Câu 8: Với mệnh đề nào dưới đây sai ?
A. B.
C. D.
Câu 9: Có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số khác nhau từ các chữ số
A. B. C. D.
Câu 10: Xét phép thử “Xếp 5 bạn nam và 5 bạn nữ theo đội hình hàng ngang sao cho nam nữ xen kẽ nhau”.
Khi đó số phần tử của không gian mẫu là:
A. 10!. B. 86400. C.14400.
.
D. 28800
Câu 11: Cho dãy số với . Khẳng định nào sau đây là sai?
sin 0x =
xk
p
=
,.k Î ¢
2
2
xk
p
p
=+
,.k Î ¢
2xk
p
=
,.k Î ¢
2
xk
p
p
=+
,.k Î ¢
1 sin
co s x
y
x+
=
4
xk
p
p
¹+
,.k Î ¢
2
xk
p
p
¹+
,.k Î ¢
82
xk
pp
¹+
,.k Î ¢
xk
p
¹
,.k Î ¢
sin 2 sinxx=
2xk
p
=
,.k Î ¢
2
,.
2
33
¢
xk
k
xk
p
pp
=
é
ê
Î
ê
=+
ë
xk
p
=
,.k Î ¢
2
,.
2
3
xk
k
xk
p
p
=
é
ê
Î
ê
=
ë
¢
=
-
cot
.
co s 1
x
y
x
p
p
ìü
=+Î
íý
îþ
°¢\2,.
2
Dkk
p
ìü
=Î
íý
îþ
°¢\, .
4
Dkk
{ }
p
=롢\2; .Dkk
{ }
p
=Î\, .Dkk°¢
cos sin 2 0xx+=
12
=-x
p
6
=-x
p
3
x
p
=-
x
p
=-
,Mm
=+
66
sin cosyxx
.!
.Mn+
1
.
4
5
.
4
1
.
2
3
.
2
0123
... ( 1) C ... ( 1)
kk nn
nnnn n n
SC C C C C=-+-++- +-
2 1.
n
S =-
2.
n
S =
1
2.
n
S
-
=
0.S =
*
nNÎ
( 1.)!
n
Pnn=³
!
(1 ).
()!
k
n
n
Akn
nk
=££
-
k!
(0 ).
n!( )!
k
n
Ckn
nk
=££
-
!C (0 ).
kk
nn
Ak kn=££
0,1, 2, 3, 4, 5?
46656.
600.
720.
( )
Un
1
2
Un
n
=
--
! Trang!10!
A. Năm số hạng đầu của dãy là : C. Là dãy số tăng.
B. Là dãy số bị chặn. D. Là dãy số giảm.
Câu 12: Khẳng định nào sau đây là sai?
A. Dãy số là một cấp số cộng:
B. Dãy số là một cấp số cộng:
C. Dãy số là cấp số cộng
D. Dãy số ( ) với không phải là một cấp số cộng.
Câu 13: Cho một cấp số cộng có . Tìm d ?
A. B. C. D.
Câu 14: Xác định x để 3 số: lập thành một cấp số cộng?
A. B. C. D.
Câu 15: Trong mặt phẳng, phép tịnh tiến ( với ). Khi đó mệnh đề nào sau
đây là sai ?
A. . B. . C. . D. .
Câu 16: Cho phép vị tự . Mệnh đề nào sau đây đúng?
A. là phép đối xứng tâm I. B. biến tâm I thành chính nó.
C. là phép đồng dạng tỉ số đồng dạng là k. D. là phép quay tâm I góc quay 360
Câu 17: Ảnh của đường thẳng qua phép vị tự tâm O tỉ số là:
A. B.
C. D.
Câu 18: Ảnh của đường tròn qua phép vị tự tâm O tỉ số là
A. B.
C. D.
Câu 19: Cho biết mệnh đề nào sau đây là sai?
A. Qua ba điểm không thẳng hàng xác định duy nhất một mặt phẳng.
B. Qua một đường thẳng và một điểm không thuộc nó xác định duy nhất một mặt phẳng.
C. Qua hai đường thẳng bất kỳ xác định duy nhất một mặt phẳng.
D. Qua hai đường thẳng cắt nhau xác định duy nhất một mặt phẳng.
Câu 20: Cho hình chóp S.ABCDE. Số mặt bên của hình chóp là:
A. 3. B. 4. C. 5. D. 6.
B. Phần tự luận.
Câu 21(1,5 điểm). Giải các phương trình:
a) b) c)
Câu 22(2,0 điểm).
a) Một bình đựng 7 quả cầu xanh và 6 quả cầu đỏ và 5 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Tính xác
suất để được 3 quả cầu khác màu nhau.
11111
;;;;.
34567
-----
2, 1, 0,1, 2,...--
1
2, 1.ud=- =
23
2, 2 , 2 ,...
1
2, 2.ud==
2, 2, 2, 2,…
1
2, 0.ud==
n
u
23
n
n
un=+
17
5; 13uu==-
3.d =-
3.d =
6.d =
6.d =-
2
2– ;;2xx x+
2.x =±
2.x =±
1.x =±
0.x =
( ) ( )
'à '
vv
TM MvTN N==
!!
0v ¹
!!
''MM NN=
!!!!!" !!!!"
''MN M N=
!!! !" !!!!!!"
''MN NM=
!!!! " !!!! !"
''MM NN=
( )
;Ik
V
( )
;1I
V
( )
;Ik
V
( )
;Ik
V
( )
;1I
V
-
0
.
:210dx y-+=
2k =-
2 2 0.xy-+ + =
2 2 0.xy-++=
2 2 0.xy-+=
2 2 0.xy-+-=
( ) ( ) ( )
22
:3 24Cx y++- =
2k =-
( ) ( ) ( )
22
' : 6 4 4.Cx y-++=
( ) ( ) ( )
22
' : 6 4 16.Cx y++-=
( ) ( ) ( )
22
' : 6 4 4.Cx y++-=
( ) ( ) ( )
22
' : 6 4 16.Cx y-++=
cot3 1 0;x+ =
2
sin 2sin 3;xx-=
2
sin 22 si n3 2.x x- =
! Trang!11!
b) Tìm hệ số chứa trong khai khai triển nhị thức biết n thoả mãn:
.
c) Chứng minh rằng với mọi n Î thì chia hết cho 6.
Câu 23 (1,5 điểm).
a) Trong mặt phẳng tọa độ , cho đường thẳng có phương trình
và . Viết
phương trình đường thẳng là ảnh của qua phép tịnh tiến .
b) Cho hình chóp đáy là hình bình hành. Gọi lần lượt là trọng tâm của các
tam giác và là trung điểm của Xác định thiết diện của chóp với mặt phẳng
Đáp án đề 2
I. Trắc nghiệm
1A
2B
3B
4D
5B
6B
7D
8C
9C
10D
11D
12B
13A
14B
15C
16B
17A
18D
19C
20C
II. Tự luận
Câu
ý
Nội dung đáp án
Điểm
21
(1,5đ)
a)
aCâu 21(1,5 điểm). Giải các phương trình:
a)
điều kiện:
b)
Đặt
Ta có phương trình:
c)
0,25
0,25
0,25
0,25
0,25
0,25
a
0,5
a) Một bình đựng 7 quả cầu xanh và 6 quả cầu đỏ và 5 quả cầu vàng. Chọn ngẫu
nhiên 3 quả cầu. Tính xác suất để được 3 quả cầu khác màu nhau.
Gọi là biến cố lấy được 3 quả cầu cùng màu.
Ta có
0,25
8
x
2
2
n
x
x
æö
-
ç÷
èø
34
11
nn
AA=
*
N•
32
23nnn-+
Oxy
d
230xy+-=
( )
1; 2v =-
!
'd
d
v
T
!
.,S ABCD
ABCD
,MN
SBC
,SCD
K
.AD
( )
.KMN
cot3 1 0;x+ =
;xkkpπŒ¢
1
cot 0 co1 txk;k;3
3
3
xx
p
p
=Û =- Û =- + Î+ !
2
sin 2sin 3;xx-=
sin ; 1txt=£
22
1
23 230
3
t
tt tt
t
È
=-
Í
-=€--=€
Í
=
Î
[
sin 1xfi=-€
sin 1 2 ;
2
xx kkZ
p
pfi=-€=-+ Œ
2
si2 si n2 .n3 2x x- =
( )
222 2
2 sin 3.2 sin cos 2 sin cos 2 3 s in cos 2 cosxxxxx xxx€- =+€- =
( )
cos 0
2 cos 3 sin cos 0
3 sin cos 0
cos 0
2
;
1
tan
3
6
x
xxx
xx
x
xk
kZ
x
xk
p
p
p
p
È
=
Í
€+=€
Í
+=
Î
È
È
=
Í
=+
Í
Í
Í
€€ Œ
Í
Í
=-
Í
Í
=+
Í
Î
Í
Î
A
! Trang!12!
22
0,25
b
1,0
b) Tìm hệ số chứa trong khai khai triển nhị thức biết n thoả mãn:
.
Ta có :
Xét số hạng thứ trong khai triển của nhị thức là :
Với số hạng chứa ta có: hệ số của là:
0,25
0,25
0,25
0,25
c
0,5
c) Chứng minh rằng với mọi n Î thì chia hết cho 6.
Xét dãy số
Với
Với giả sử ta cần chứng minh
Thật vậy theo giả thiết quy nạp ta có:
Vậy:
0,25
0,25
23
a
Câu 23 (1,5 điểm).
Đường thẳng đi qua điểm . Gọi
Gọi
có vectơ pháp tuyến là: có phương trình:
0,5
0,5
b
b) Cho hình chóp đáy là hình bình hành. Gọi lần
lượt là trọng tâm của các tam giác và là trung điểm của
Xác định thiết diện của chóp với mặt phẳng
( ) ( )
( )
( )
( )
111 3
765 18
.. 210. 816
210 35
816 136
nA CCC n C
nA
PA
n
==W==
fi===
W
8
x
2
2
n
x
x
æö
-
ç÷
èø
34
11
nn
AA=
( ) ( )
( ) ( )( )
34
! 11 !
11
4! 3!
1 11 11
1 3 11 14
4! 3 4! 3
nn
nn
AA
nn
nn
nnn n
=Û =
--
Û= Û=Û-=Û=
--- -
1k +
2
2
n
x
x
æö
-
ç÷
èø
( )
14 14 3
14 14
2
2
2
k
k
kk k k
Cx Cx
x
--
ʈ
-
˜
Á
=-
˜
Á
˜
Á
˯
8
x
14 3 8 2kk-=€=fi
8
x
( )
2
2
14
2364C-=
*
N•
32
23nnn-+
32
23
n
Unnn=- +
1
1: U 0 6n ==M
nk=
32
23 6
k
Ukkk=- +M
( ) ( ) ( )
32
1
2131 16
k
Uk k k
+
=+-+++M
( ) ( ) ( )
( ) ( )
( )
32
32 2
1
32 2
2 1 3 1 1 2 2.3. 2 3 2 1 1
23 66.
k
Uk k k k kk kkk
kkkk
+
=+-+++=+ ++- ++++
=-++M
32
23 6
n
Unnn=- +M
d
( )
1;1A
( )
( )
( )
110
;
12 3
v
x
TA Axy
y
Ï
¢
=+- =
Ô
Ô
¢¢¢
=fi
Ì
Ô
¢
=+ =
Ô
Ó
r
( )
0;3A
¢
fi
( )
//
v
dd
Td d
Ad
Ï
¢
Ô
Ô
¢
=fi
Ì
Ô
¢¢
Œ
Ô
Ó
r
d
¢
( )
1; 2nd
¢
fi
r
( ) ( )
02 30 2 60xy xy-+ -=€+-=
.,S ABCD
ABCD
,MN
SBC
,SCD
K
.AD
( )
.KMN
! Trang!13!
Gọi là trung điểm , là trung điểm của .
Gọi
. Gọi lần lượt là trung điểm của
Gọi
Vậy thiết diện là hình ngũ giác
0,25
0,25
SỞ GD&ĐT HẢI DƯƠNG
TTGDNN-GDTX NAM SÁCH
ĐỀ THI HỌC KÌ 1 – Năm học 2018-2019
Môn TOÁN Lớp 11
Thời gian làm bài 90 phút
Đề số 1
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . .lớp………………. .
I.Trắc nghiệm :
Câu 1: Tập xác định của hàm số là
A. B. C. D.
Câu 2: Giá trị đặc biệt nào sau đây là đúng
A. B.
C. D.
Câu 3: Gieo một con súc sắc 2 lần. Số phần tử của không gian mẫu là?
A. 36 B. 12 C. 6 D. 18
Câu 4: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu
nhiên 3 quyển sách. Tính xác suất để 3 quyển được lấy ra đều là môn toán.
A. B. C. D.
Câu 5: Gieo một đồng tiền liên tiếp 3 lần. Tính xác suất của biến cố A: " kết qủa của 3 lần
gieo là như nhau"
P
J
H
F
G
L
K
M
O
N
I
B
D
A
C
S
O
BC
I
CD
( )
,,L CK OI G SL MN F KG SC KF KMN=« =« =«fi Ã
,HFNSDJFMSB=« = «
,OI
,BC CD
( )
2
// //
3
SN SM
MN OI ON KMN
SI SO
fi==fi fi
( )
//P AB KMN KP OI=« fi
FHKPJ
1 3 cos
sin
x
y
x
-
=
2
xk
p
p
¹+
2xk
p
¹
2
k
x
p
¹
xk
p
¹
cos 1
2
xxk
p
p
¹Û ¹ +
cos 0
2
xxk
p
p
¹Û¹ +
cos 1 2
2
xxk
p
p
¹- Û ¹- +
cos 0 2
2
xxk
p
p
¹Û¹ +
1
21
37
42
2
7
5
42
! Trang!14!
A. B. C. D.
Câu 6:Cho hình bình hành ABCD. Phép tịnh tiến biến:
A. B thành C. B. C thành A. C. C thành B. D. A thành D.
Câu 7: Cho các giả thiết sau, giả thiết nào sau đây kết luận đường thẳng d1 // (P)
A. d1 // d2 và d2 // (P) B.
C. d1 // d2 và d2 (P) D. d1 // (Q) và (Q) // (P)
Câu 8: Trong các mệnh đề sau, mệnh đề nào đúng:
A. Hai đường thẳng không cắt nhau và không song song thì chéo nhau.
B. Hai đường thẳng không song song thì chéo nhau.
C. Hai đường thẳng không có điểm chung thì chéo nhau.
D. Hai đường thẳng chéo nhau thì không có điểm chung.
II. Tự luận :
Bài 1: (1 đ). Giải các phương trình sau:
a) b)
Bài 2: (2 đ). Trong một hộp đựng 5 viên bi xanh và 4 viên bi đỏ. Lấy ngẫu nhiên đồng thời 3
viên bi. Tính xác suất để trong 3 viên bi lấy ra:
a) Có 2 viên bi màu xanh b) Có ít nhất một viên bi màu xanh.
Bài 3: (0,5 đ). Trong mặt phẳng Oxy cho điểm , . Tìm tọa độ ảnh của điểm
M qua phép tịnh tiến .
Bài 4: (2 đ). Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn là AD
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
b) Gọi M, N và P lần lượt là trung điểm của AB, SA và SD.
Chứng minh rằng: NP// (SBC)
Bài 5: (0.5đ) Khai triển nhị thức Newton .
--------------------Hết-------------------
SỞ GD&ĐT HẢI DƯƠNG
TTGDNN-GDTX NAM SÁCH
ĐÁP ÁN ĐỀ THI HỌC KÌ 1 năm 2018-2019
Môn TOÁN Lớp 11
Thời gian làm bài 90 phút
Đề số 1
I.Trắc nghiệm : ( mỗi câu trả lời đúng : 0,5 điểm ).
1 D
2 B
3 A
4 A
5 A
6 C
7 B
8 D
II. Tự luận :
Bài
Ý
Nội dung
Điểm
1
1.0
a)
0,5
1
()
4
PA=
7
()
8
PA=
3
()
8
PA=
1
()
2
PA=
( )
1dPÇ =Æ
Ì
2
5sin cos 1 0xx+-=
x2sin 3 1 0
4
p
æö
+-=
ç÷
èø
)2;5(-M
( )
1;1-=
®
v
®
v
( )
5
2xy+
22
2
5sin cos 1 0 5(1 cos ) cos 1 0
cos 1
2
5cos cos 4 0 ,( )
4
arccos 2
cos
5
p
p
+-=Û- +-=
=
é
=
é
ê
Û- + + = Û Û Î
ê
ê
=± +
=-
ë
ë
xx x x
x
xk
xx kZ
xxk
x
! Trang!15!
b)
0,5
2
2.0
a)
Vì lấy ngẫu nhiên 3 viên bi trong túi có 9 viên bi nên số ptử của không
gian mẫu là:
Kí hiệu: A: “3 viên lấy ra có hai viên bi màu xanh”
Ta có:
Vậy xác suất của biến cố A là:
0,25
0,5
0,25
b)
Kí hiệu: B: “3 viên lấy ra có ít nhất 1 viên bi màu xanh”
Ta có: : “Cả 3 viên bi lấy ra đều màu đỏ”
Vậy xác suất của biến cố B là:
0,5
0,5
3
Gọi là ảnh của điểm M(x; y) qua phép tịnh tiến
Theo BTTĐ, ta có: Vậy
0,5
4
2,0
a)
a) + (SAB) và (SCD) có điểm chung thứ nhất là S
+ Kéo dài AB và CD cắt nhau tại E ta có E là điểm chung thứ hai của 2
mp trên.
Vậy giao tuyến cần tìm là đường thẳng SE.
0,25
0,75
ax
xk
xk
xk
k
x
k
k
x
) 2 sin(3 ) 1 0 (1)
4
32
1
46
(1) sin(3 ) ( )
42
32
46
2
36 3
()
72
36 3
p
pp
p
p
pp
pp
pp
pp
+-=
é
+=+
ê
Û+=Û Î
ê
ê
+=-+
ë
é
=- +
ê
ÛÎ
ê
ê
=+
ë
!
!
( )
nC
3
9
84
W
==
( )
nA C C
21
54
. 40==
( )
( )
( )
nA
PA
n
40 10
84 21
W
===
B
( )
nB C
3
4
=
( )
( )
( )
nA
PB
n
1
21
W
Þ= =
( )
( )
PB PB
1 20
11
21 21
=- =- =
)';'(' yxM
®
v
î
í
ì
+=
+=
byy
axx
'
'
Û
î
í
ì
+=
--=
12'
15'
y
x
î
í
ì
=
-=
Û
3'
6'
y
x
)3;6(' -M
A
E
D
S
B
C
M
N
P
! Trang!16!
b)
Ta có NP//AD
mà AD//BC nên NP//BC (2)
Mà BC (SBC)
Do đó NP//(SBC)
1,0
5
0.5
SỞ GD&ĐT HẢI DƯƠNG
TTGDNN-GDTX NAM SÁCH
ĐỀ THI HỌC KÌ 1 – Năm học 2018-2019
Môn TOÁN Lớp 11
Thời gian làm bài 90 phút
Đề số 2
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . .lớp………………. .
I.Trắc nghiệm :
Câu 1: Tập xác định của hàm số là
A. B. C. D.
Câu 2: Giá trị đặc biệt nào sau đây là đúng
A. B.
C. D.
Câu 3: Gieo một đồng tiền liên tiếp 2 lần. Số phần tử của không gian mẫu là?
A. 2 B. 8 C. 4 D. 1
Câu 4: Một lớp học có 40 học sinh gồm 25 nam và 15 nữ. Chọn 3 học sinh tham gia vệ sinh
công cộng toàn trường, hỏi có bao nhiêu cách chọn 3 học sinh trong lớp?
A. 455 B. 9880 C. 2300 D. 59280
Câu 5: Gieo một đồng tiền liên tiếp 3 lần. Tính xác suất của biến cố A: " có đúng 2 lần xuất
hiện mặt sấp"
A. B. C. D.
Câu 6:Cho hình bình hành ABCD. Phép tịnh tiến biến:
A. B thành C. B. C thành A. C. A thành D. D. C thành B.
Câu 7: Xét các mệnh đề sau :
1. Hai đường thẳng không có điểm chung thì chéo nhau.
2. Hai đường thẳng không cắt nhau và không song song thì chéo nhau.
3. Hai đường thẳng chéo nhau thì không có điểm chung
Mệnh đề nào đúng ?
A. 1 và 2 đúng B. 1 và 3 đúng
C. Chỉ 3 đúng D. Cả 1, 2 và 3 đều đúng
Câu 8:Cho hai mặt phẳng (P) và (Q) song song với nhau. Mệnh đề nào sau đây sai:
A. Nếu đường thẳng a Ì (Q) thì a // (P)
Ì
( ) ( )
( ) ( ) ( )
52
05 14 23
55 5
345
32 4 5
555
2 .2 2
222
+=+ +
+++
xy CxCxyCxy
Cx y Cx y C y
54 32 23 4 5
10 40 80 80 32xxyxy xyxy y=+ + + + +
1 sin
cos
x
y
x
-
=
2
2
xk
p
p
¹+
2
xk
p
p
¹+
2
2
xk
p
p
¹- +
xk
p
¹
cos 1
2
xxk
p
p
¹Û ¹ +
cos 1 2
2
xxk
p
p
¹- Û ¹- +
cos 0
2
xxk
p
p
¹Û¹ +
cos 0 2
2
xxk
p
p
¹Û¹ +
7
()
8
PA=
1
()
2
PA=
1
()
4
PA=
3
()
8
PA=
! Trang!17!
B. Mọi đường thẳng đi qua điểm A Î (P) và song song với (Q) đều nằm trong (P).
C. d Ì (P) và d' Ì (Q) thì d //d'.
D. Nếu đường thẳng D cắt (P) thì D cũng cắt (Q).
II. Tự luận :
Bài 1: (1 đ). Giải các phương trình sau:
a) 2sin
2
x – 3sinx + 1 = 0 b)
Bài 2: (2,0 đ) Có 5 bông hoa hồng nhung, 7 bông hoa cúc vàng và 4 bông hoa hồng bạch.
Chọn ngẫu nhiên 3 bông hoa. Tính xác suất để 3 bông hoa được chọn là:
a) Cùng một loại
b) Ít nhất có một bông hoa hồng nhung.
Bài 3 : (0,5đ). Trong mặt phẳng Oxy cho điểm , . Tìm tọa độ ảnh của điểm
M qua phép tịnh tiến .
Bài 4 : (2 đ). Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn là AD
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
b) Gọi M, N và P lần lượt là trung điểm của AB, SA và SD.
Chứng minh rằng: NP// (SBC)
Bài 5: (0,5đ) Khai triển nhị thức Newton
--------------------Hết-------------------
SỞ GD&ĐT HẢI DƯƠNG
TTGDNN-GDTX NAM SÁCH
ĐÁP ÁN ĐỀ THI HỌC KÌ 1 –Năm 2018-2019
Môn TOÁN Lớp 11
Thời gian làm bài 90 phút
Đề số 2
I.Trắc nghiệm : ( mỗi câu trả lời đúng : 0,5 điểm ).
1 B
2 C
3 C
4 A
5 D
6 D
7 C
8 C
II. Tự luận :
Bài
Ý
Nội dung
Điểm
1
1,0
x2sin 3 1 0
4
p
æö
+-=
ç÷
èø
)2;5(-M
( )
1;1-=
®
v
®
v
( )
5
2xy+
! Trang!18!
a)
Đặt t = sinx, đk
PTTT: 2t
2
– 3t + 1 = 0
*) Với t = 1
*) Với t =
Vậy, PT trên có nghiệm : ; và
.
0,5
b)
0,5
2
2.0
a)
Chọn ngẫu nhiên ba bông hoa từ 5 bông hoa hồng nhung, 7 bông hoa
cúc vàng và 4 bông hoa hồng bạch là một tổ hợp chập 3 của 16 bông
hoa các loại. Khi đó không gian mẫu là: n( ) =
Gọi A là biến cố ba bông hoa cùng một loại. Khi đó số khả năng thuận
lợi cho biến cố A là:
Vậy
0,25
0,5
0,25
b)
Gọi B là biến cố có ít nhất một bông hoa hồng nhung. Khi đó số khả
năng thuận lợi cho biến cố B là:
Vậy
0,5
0,5
3
0,5
a)
Gọi là ảnh của điểm M(x; y) qua phép tịnh tiến
Theo BTTĐ, ta có: Vậy
0,5
4
2,0
t11-££
tN
tN
1( )
1
()
2
é
=
ê
Û
=
ê
ë
x x k ksin 1 2 ,
2
p
p
Û=Û=+ Î
!
xkk
x
xkk
2,
11
6
sin
5
22
2,
6
p
p
p
p
é
=+ Î
ê
Û=Û
ê
ê
=+ Î
ë
!
!
kk
2
2,
p
p
+Î
!
kk2,
6
p
p
+Î
!
kk
5
2,
6
p
p
+Î
!
ax
xk
xk
xk
k
x
k
k
x
) 2 sin(3 ) 1 0 (1)
4
32
1
46
(1) sin(3 ) ( )
42
32
46
2
36 3
()
72
36 3
p
pp
p
p
pp
pp
pp
pp
+-=
é
+=+
ê
Û+=Û Î
ê
ê
+=-+
ë
é
=- +
ê
ÛÎ
ê
ê
=+
ë
!
!
W
C
3
16
560=
nA C C C
333
574
( ) 49=++=
nA
PA
n
( ) 49 7
()
( ) 560 80
W
===
nB C C C CC
321 12
5 5 11 5 11
( ) 395=+ + =
nB
PB
n
( ) 395 79
()
( ) 560 112
W
===
)';'(' yxM
®
v
î
í
ì
+=
+=
byy
axx
'
'
Û
î
í
ì
+=
--=
12'
15'
y
x
î
í
ì
=
-=
Û
3'
6'
y
x
)3;6(' -M
! Trang!19!
a)
a) + (SAB) và (SCD) có điểm chung thứ nhất là S
+ Kéo dài AB và CD cắt nhau tại E ta có E là điểm chung thứ hai của 2
mp trên.
Vậy giao tuyến cần tìm là đường thẳng SE.
0,25
0,75
b)
Ta có NP//AD
mà AD//BC nên NP//BC (2)
Mà BC (SBC)
Do đó NP//(SBC)
1,0
5
0.5
0,25
0,25
TRƯỜNG THPT NGUYỄN HUỆ
Tổ: Toán – Tin
(Đề thi gồm có 3 trang)
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KÌ 1
Năm học 2018 – 2019
Môn thi: Toán 11
Thời gian: 90 phút ( không kể thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (5.0 điểm): Chọn phương án đúng cho mỗi câu sau đây.
Câu 1. Tập xác định của hàm số là:
A. B. C. D.
Câu 2. Giả sử cần chọn hoặc là một học sinh nam khối 12 hoặc là một học sinh nữ khối 11 để làm
đại biểu trong hội đồng của một trường THPT. Hỏi có bao nhiêu cách chọn vị đại biểu này nếu
khối 12 có 81 học sinh nam và khối 11 có 72 học sinh nữ.
A. 153 B. 81 C. 72 D. 5832
câu 3. Tọa độ điểm ảnh của điểm M( 1; 2) qua phép tịnh tiến theo véctơ là:
A. M’(3; -3) B. M’(1; -3) C. M’(3; 1) D. M’( -3; 1)
Câu 4. Tất cả các nghiệm của phương trình là:
A
E
D
S
B
C
M
N
P
Ì
( ) ( )
( ) ( ) ( )
52
05 14 23
55 5
345
32 4 5
555
2 .2 2
222
+=+ +
+++
xy CxCxyCxy
Cx y Cx y C y
54 32 23 4 5
10 40 80 80 32xxyxy xyxy y=+ + + + +
tanyx=
!
\,
2
kk
p
p
ìü
+Î
íý
îþ
! Z
{ }
\,kk
p
Î! Z
\,
4
kk
p
p
ìü
+Î
íý
îþ
! Z
'M
( )
2; 1v -
!
sin 1x =
Mã đề 1101
! Trang!20!
A. B. C. D.
Câu 5. Công thức nào dưới đây đúng?
A. B. C. D.
Câu 6. Cho hình chóp S.ABCD và O là giao điểm của hai đường chéo AC với BD. Giao tuyến của
hai mặt phẳng (SAC) và (SBD) là:
A. SO B. SA C. SB D. SC
Câu 7. Số các hạng tử trong khai triển của nhị thức niu tơn là:
A. 7 B. 8 C. 9 D. 10
Câu 8. Tất cả các nghiệm của phương trình là:
A. B. C. D.
Câu 9. Có bao nhiêu vị trí tương đối giữa hai đường thẳng a và b trong không gian.
A. 2 B. 3 C. 4 D. 5
Câu 10. Gieo một đồng tiền cân đối và đồng chất 4 lần. Số phần tử không gian mẫu của phép thử
là:
A. 4 B. 8 C. 16 D. 32
Câu 11. Tất cả các nghiệm của phương trình là:
A. B. C. D. Vô
nghiệm
Câu 12. Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điển các cạch SA, SB. Đường thẳng MN
song song với đường thẳng nào dưới đây:
A. AC B. SC C. BC D. AB.
Câu 13. Tất cả các nghiệm của phương trình là:
A. B. C. D. Vô nghiệm
Câu 14. Gieo một con súc sắc cân đối đồng chất một lần. Xác suất để mặt 4 chấm xuất hiện là:
A. B. C. D.
Câu 15. Trong các dãy số dưới đây, dãy số nào là dãy số hữa hạn:
A. 2, 4, 6, 8, 10. B. 3, 5, 7, 9, 11,... C. -5, -2, 1, 4, 7, 10,… D. 2, 4, 8, 16, 32,…
Câu 16. Cho tập số có 3 chữ số khác nhau được hình thành từ tập A là:
A. 35 B. 5040 C. 210 D. 180
2,
2
xkk
p
p
=+ ÎZ
,xkk
p
=ÎZ
,
2
xkk
p
p
=+ ÎZ
2,
2
xkk
p
p
=- + ÎZ
n
Pn=
n
nn
pC=
n
nn
PA=
( )
1
2
n
nn
P
+
=
( )
7
23x +
1
cos
2
x =
2,
6
xkk
p
p
=± + Î!
2,
4
xkk
p
p
=± + Î!
2,
3
xkk
p
p
=± + Î!
2
2,
3
xkk
p
=± + Î!
3
sin
2
x =
2
3
,
2
2
3
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
3
arcsin 2
2
,
3
arcsin 2
2
xk
k
xk
p
pp
é
=+
ê
Î
ê
ê
=- +
ê
ë
!
2
6
,
5
2
6
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
sin cos 2xx+=
2,
4
xkk
p
p
=+ Î!
3
2,
4
xkk
p
p
=+ Î!
2,
4
xkk
p
p
=- + Î!
1
2
1
4
1
3
1
6
{ }
1, 2, 3, 4, 5, 6, 7A =
! Trang!21!
Câu 17. Tập xác định của hàm số là:
A. B. C. D.
Câu 18. Cho dãy số có số hạng tổng quát . Năm số hạng đầu của dãy số
là:
A. B. C. D.
Câu 19. Ảnh của đường thẳng qua phép tịnh tiến theo véctơ là đường
thẳng có phương trình là:
A. B. C. D.
Câu 20. Tập tất cả các nghiệm của phương trình là:
A. B.
C. D.
Câu 21. Tất cả các nghiệm của phương trình là;
A. B. C. D.
Câu 22. Một tổ có 6 bạn nam và 7 bạn nữ. Có bao nhiêu cách chọn 4 bạn trong tổ để phân công
trực nhật?
A. 50 B. 525 C. 715 D. 17160
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Lấy M, N lần lượt thuộc các đoạn
thẳng SA, SB sao cho . Khẳng định nào sau đây đúng:
A. B. C. D.
Câu 24. Gọi M là tập hợp tất cả các số có 3 chữ số khác nhau được lập từ các số 1, 2, 3, 4, 5, 6.
Lấy ngẫu nhiên 3 số từ tập M. Xác suất để 3 số được lấy là 3 số chẵn:
A. B. C. D.
Câu 25. Tập tất cả các nghiệm của phương trình là:
A. B. C. D.
II. PHẦN TỰ LUẬN ( 5.0 điểm).
Câu 26 (2.0 điểm). Giải các phương trình lượng giác sau.
a) b) c)
Câu 27 (1.5 điểm)
1 cos
1 sin
x
y
x
+
=
-
!
{ }
\,kk
p
Î!"
\,
2
kk
p
p
ìü
+Î
íý
îþ
!"
\2,
2
kk
p
p
ìü
+Î
íý
îþ
!"
( )
n
u
*
223,
n
n
unn=-+ Ε
( )
n
u
3, 3, 6,9,12
3, 3, 6,10,15
3, 3, 6,11, 25
3, 3, 6,12, 27
:2 3 0xyD-+=
( )
2; 1v -
!
'D
220xy--=
230xy++=
280xy-+=
260xy++=
1
cos
2
x =-
2,
3
xkk
p
p
=± + Î!
2,
6
xkk
p
p
=± + Î!
2
2,
3
xkk
p
p
=± + Î!
5
2,
6
xkk
p
p
=± + Î!
2
cos 3 cos 2 0xx-+=
2,xk k
p
=Î!
2
,
arccos 2 2
xk
k
xk
p
p
=
é
Î
ê
=± +
ë
!
,xkk
p
=Î!
,
arccos 2 2
xk
k
xk
p
p
=
é
Î
ê
=+
ë
!
2
3
SM SN
SA SB
==
MN CD!
( )
MN SAD!
MN AD!
( )
MN SBC!
1
2
29
1428
29
238
87
119
22
3
sin 2 2 cos 0
4
xx-+=
2,
6
xkk
p
p
=± + Î!
,
6
xkk
p
p
=± + Î!
2,
3
xkk
p
p
=± + Î!
,
3
xkk
p
p
=± + Î!
3
cos
2
x =
2
2sin 3sin 1 0xx-+=
5 cos 2
2 cos
32tan
x
x
x
+
=
+
! Trang!22!
a) Một hộp đựng 6 viên bi trắng và 8 viên bi vàng. Lấy ngẫu nhiên cùng lúc 5 viên bi từ hộp. Tính
xác suất để 5 viên bi được lấy có đủ cả 2 màu.
b) Tìm hệ số của số hạng chứa trong khai triển nhị thức .
Câu 28 (1.5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Gọi M là điểm nằm
trong mặt phẳng (SCD).
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (ABM).
………………Hết……………
Họ và tên thí sinh:……………………………………………………. SBD:…………………
Chữ kí giám thị 1:………………………………….. Chữ kí giám thị 2:…………………………….
TRƯỜNG THPT NGUYỄN HUỆ
Tổ: Toán – Tin
( Đề thi gồm có 3 trang)
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KÌ 1
Năm học 2018 – 2019
Môn thi: Toán 11
Thời gian: 90 phút ( không kể thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (5.0 điểm): Chọn phương án đúng cho mỗi câu sau đây.
Câu 1. Trong các dãy số dưới đây, dãy số nào là dãy số vô hạn.
A. 2, 4, 6, 8, 10. B. 3, 5, 7, 9, 11. C. -5, -2, 1, 4, 7, 10,… D. 2, 4, 8, 16, 32.
Câu 2. Gieo một đồng tiền cân đối và đồng chất 2 lần. Xác suất để số mặt xuất hiện trong 2 lần
gieo như nhau là:
A. B. C. D.
Câu 3. Tất cả các nghiệm của phương trình là:
A. B. C. D. Vô nghiệm
Câu 4. Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điển các cạch SA, SC. Đường thẳng MN
song song với đường thẳng nào dưới đây:
A. AC B. SC C. BC D. AB.
Câu 5. Tập xác định của hàm số là:
A. B. C. D.
Câu 6. Giả sử cần chọn hoặc là một học sinh nam khối 12 hoặc là một học sinh nữ khối 11 để làm
đại biểu trong hội đồng của một trường THPT. Hỏi có bao nhiêu cách chọn vị đại biểu này nếu
khối 12 có 61 học sinh nam và khối 11 có 72 học sinh nữ.
A. 153 B. 4392 C. 72 D. 133
Câu 7. Tọa độ điểm M’ là ảnh của điểm M( 1; -2) qua phép tịnh tiến theo véctơ là:
A. M’(3; -3) B. M’(1; -3) C. M’(3; 1) D. M’( -3; 1)
Câu 8. Tất cả các nghiệm của phương trình là:
6
x
6
2
1
2x
x
æö
-
ç÷
èø
1
2
1
4
1
3
3
4
sin cos 2xx-=
2,
4
xkk
p
p
=+ Î!
3
2,
4
xkk
p
p
=+ Î!
3
2,
4
xkk
p
p
=- + Î!
cotyx=
!
\,
2
kk
p
p
ìü
+Î
íý
îþ
! Z
{ }
\,kk
p
Î! Z
{ }
\2,kk
p
Î! Z
( )
2; 1v -
!
cos 1x =
Mã đề 1102
! Trang!23!
A. B. C. D.
Câu 9. Cho n là số nguyên dương. P, A, C kí hiệu là hoán vị, chỉnh hợp, tổ hợp. Công thức nào
dưới đây đúng?
A. B. C. D.
Câu 10. Cho hình chóp S.ABCD và O là giao điểm của hai đường chéo AC với BD, I là giao điểm
của AD và BC. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là:
A. SO B. SA C. SI D. SC
Câu 11. Số các hạng tử trong khai triển của nhị thức niu tơn là:
A. 7 B. 8 C. 9 D. 10
Câu 12. Tất cả các nghiệm của phương trình là:
A. B. C. D.
Câu 13. Có bao nhiêu vị trí tương đối giữa hai mặt phẳng và trong không gian.
A. 2 B. 3 C. 4 D. 5
Câu 14. Gieo một con súc sắc cân đối và đồng chất 3 lần. Số phần tử không gian mẫu của phép thử
là:
A. 6 B. 18 C. 36 D. 216
Câu 15. Tất cả các nghiệm của phương trình là:
A. B. C. D. Vô
nghiệm
Câu 16. Tập tất cả các nghiệm của phương trình là;
A. B. C. D. Vô
nghiệm
Câu 17. Một tổ gồm có 8 bạn nam và 7 bạn nữ. Có bao nhiêu cách chọn 4 bạn trong tổ để phân
công trực nhật?
A. 105 B. 1365 C. 2450 D. 32760
Câu 18. Ảnh của đường thẳng qua phép tịnh tiến theo véctơ là đường thẳng
có phương trình là:
A. B. C. D.
Câu 19. Tập tất cả các nghiệm của phương trình là:
2,
2
xkk
p
p
=+ ÎZ
2,xkk
pp
=+ ÎZ
2,xk k
p
=ÎZ
,
2
xkk
p
p
=+ ÎZ
!
k
k
n
n
A
C
k
=
n
nn
pC=
k
k
n
n
A
C
k
=
( )
1
2
n
nn
P
+
=
( )
9
23x -
3
cos
2
x =-
5
2,
6
xkk
p
p
=± + Î!
2,
6
xkk
p
p
=± + Î!
2,
3
xkk
p
p
=± + Î!
2
2,
3
xkk
p
=± + Î!
( )
a
( )
b
3
cos
2
x =
2
3
,
2
3
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=- +
ê
ë
!
3
arccos 2
2
,
3
arccos 2
2
xk
k
xk
p
p
é
=+
ê
Î
ê
ê
=- +
ê
ë
!
2
6
,
2
6
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=- +
ê
ë
!
2
sin 3sin 2 0xx-+=
,
2
xkk
p
p
=+ Î!
2
arcsin 2 2 ,
arcsin 2 2
xk
xkk
xk
p
p
pp
=
é
ê
=+ Î
ê
ê
=- +
ë
!
2,
2
xkk
p
p
=+ Î!
:2 3 0xyD-+=
( )
2;1v
!
'D
260xy-+=
20xy+=
20xy-=
260xy++=
1
sin
2
x =
! Trang!24!
A. B.
C. D.
Câu 20. Cho tập có bao nhiêu số có 3 chữ số khác nhau được hình thành từ
tập A ?
A. 336 B. 56 C. 210 D. 180
Câu 21. Tập xác định của hàm số là:
A. B. C. D.
Câu 22. Cho dãy số có số hạng tổng quát . Năm số hạng đầu của dãy số
là:
A. B. C. D.
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Lấy M, N lần lượt thuộc các đoạn
thẳng SA, SB sao cho . Khẳng định nào sau đây đúng:
A. B. C. D.
Câu 24. Gọi M là tập hợp tất cả các số có 3 chữ số khác nhau được lập từ các số 1, 2, 3, 4, 5, 6, 7.
Lấy ngẫu nhiên 3 số từ tập M. Xác suất để 3 số lấy ra là 3 số lẻ:
A. B. C. D.
Câu 25. Tập tất cả các nghiệm của phương trình là:
A. B. C. D.
II. PHẦN TỰ LUẬN ( 5.0 điểm).
Câu 26 (2.0 điểm). Giải các phương trình lượng giác sau.
a) b) c)
Câu 27 (1.5 điểm)
a) Một tổ gồm có 7 bạn nam và 8 bạn nữ. Lấy ngẫu nhiên cùng lúc 4 bạn. Tính xác suất để 4 bạn
được lấy có cả nam và nữ.
b) Tìm hệ số của số hạng chứa trong khai triển nhị thức .
Câu 28 (1.5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm nằm
trong mặt phẳng (SCD).
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (ABM).
……………………………Hết……………………
2
3
,
2
2
3
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
2
6
,
5
2
6
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
2,
3
xkk
p
p
=± + Î!
2,
6
xkk
p
p
=± + Î!
{ }
1, 2, 3, 4, 5, 6, 7, 8A =
1 sin
1 cos
x
y
x
+
=
+
D = !
{ }
\2,kk
p
Î!"
\,
2
kk
p
p
ìü
+Î
íý
îþ
!"
{ }
\2,kk
pp
+Î!"
( )
n
u
*
35 3,
n
n
unn=-+ Ε
( )
n
u
1, 2,15, 64, 215
1, 2,15, 64, 221
1, 2,15, 64, 245
1, 2,15, 64, 231
2
3
SM SN
SA SB
==
MN BC!
( )
MN SCD!
MN AD!
( )
MN SAD!
1003
5434
4
7
29
238
895
4563
22
3
sin 2 2 sin 0
4
xx-+=
2,
6
xkk
p
p
=± + Î!
,
6
xkk
p
p
=± + Î!
2,
3
xkk
p
p
=± + Î!
,
3
xkk
p
p
=± + Î!
2
sin
2
x =
2
2 cos 3cos 1 0xx-+=
5 cos 2
2sin
3 2 cot
x
x
x
-
=
+
6
x
9
2
2
x
x
æö
-
ç÷
èø
! Trang!25!
ĐÁP ÁN VÀ THANG ĐIỂM
Mã đề 1101
I. TRẮC NGHIỆM
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
Đ.án
B
A
C
A
C
A
B
C
C
C
D
D
A
Câu
14
15
16
17
18
19
20
21
22
23
24
25
Đ.án
D
A
C
D
C
A
C
A
C
A
C
B
II. TỰ LUẬN
Câu
Đáp án
Thang
điểm
1
a
0.25
0.25
b
0.25
0.25
c
Đk
Pt
Đối chiếu ĐK suy ra tập nghiệm pt là
Số phần tử của không gian mẫu là
0.25
3
cos cos cos
26
xx
p
=Û =
2,
6
xkk
p
p
=± + Î!
2
sin 1
2sin 3sin 1 0
1
sin
2
x
xx
x
=
é
ê
-+=Û
ê
=
ë
2
2
2,
6
5
2
6
xk
xkk
xk
p
p
p
p
p
p
é
=+
ê
ê
ê
Û=+ Î
ê
ê
ê
=+
ê
ë
!
cos 0
2
,
3
32tan 0
tan
2
xk
x
k
x
x acr k
p
p
p
ì
¹+
ï
¹
ì
ï
ÛÎ
íí
+¹
æö
î
ï
¹-+
ç÷
ï
èø
î
!
( )
22 22
5 cos sin 2 cos 3 2 tan 5 cos sin 6 cos 4 sinxx x x xx x xÛ+ - = + Û+ - = +
( ) ( )
22
22
cos 6 cos 9 sin 4 sin 4 cos 3 sin 2xx xx x xÛ- +=++Û-=+
cos sin 5
cos sin 1
xx
xx
-=
é
Û
ê
+=
ë
2
2
2 cos 1 cos ,
2
442
2
xk
xx k
xk
p
p
pp
p
é
=+
æö æö
ê
Û-=Û-=Û Î
ç÷ ç÷
ê
èø èø
=
ë
!
2,xk k
p
=Î!
( )
5
14
2002CW= =
! Trang!26!
2.
a
Gọi A là biến cố lấy ra 5 viên bi có đủ cả 2 màu, khi đó biến cố lấy ra 5 viên bi
cùng màu nên
0.25
Xác suất cần tìm là
0.25
Áp dụng công thức tổng quát ta có
0.25
Theo bài ra
0.25
Vậy hệ số của số hạng chứa là
0.25
3.
S
N
M
A D
O
B C
a
Ta có (1)
0.25
Gọi suy ra (2)
0.25
Từ (1) và (2) suy ra
0.25
b
Chọn mp(SCD) chứa đường thẳng SD. Ta có (1)
0.25
Do suy ra giao tuyến của hai mặt phẳng (ABM) và (SCD) là đường thẳng
d đi qua M song song với CD trong mp(SCD)
0.25
Gọi suy ra
0.25
A
( )
55
86
62nA C C=+=
( )
( )
62 970
11
2002 1001
PA PA=- =- =
( )
( )
6
2 6 12 3
66
1
22.1.
k
k
k
kkkk
Cx C x
x
-
--
-
æö
=-
ç÷
èø
12 3 6 2kk-=Û=
6
x
( )
2
24
6
.2 . 1 240C -=
( ) ( )
S SAC SBDÎÇ
O AC BD=Ç
( )
( )
( ) ( )
O AC SAC
O SAC SBD
O BD SBD
ì
ÎÌ
ï
ÞÎ Ç
í
ÎÌ
ï
î
( ) ( )
SO SAC SBD=Ç
( ) ( )
M ABM SCDÎÇ
AB CD!
N d SD=Ç
( )
N SD ABM=Ç
! Trang!27!
Mã đề 1102
I. TRẮC NGHIỆM
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
Đ.án
C
A
B
A
C
D
A
C
A
C
D
A
B
Câu
14
15
16
17
18
19
20
21
22
23
24
25
Đ.án
D
D
C
B
C
B
A
D
B
B
A
D
II. TỰ LUẬN
Câu
Đáp án
Thang
điểm
1
a
0.25
0.25
b
0.25
0.25
c
Đk
Pt
0.25
0.25
0.25
Đối chiếu ĐK suy ra tập nghiệm pt là
o.25
a
Số phần tử của không gian mẫu là
0.25
Gọi A là biến cố lấy ra 4 bạn có cả nam và nữ, khi đó biến cố lấy ra 4 bạn cùng
giới nên
0.25
2
sin sin sin
24
xx
p
=Û =
2
4
,
3
2
4
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
2
cos 1
2 co s 3 cos 1 0
1
cos
2
x
xx
x
=
é
ê
-+=Û
ê
=
ë
2
,
2
3
xk
k
xk
p
p
p
=
é
ê
ÛÎ
ê
=± +
ë
!
sin 0
,
3
cot
3 2 cot 0
2
xk
x
k
x acr k
x
p
p
¹
ì
¹
ì
ï
ÛÎ
íí
æö
¹-+
+¹
î
ç÷
ï
èø
î
!
( )
( )
( )
22 22
5 cos sin 2 cos 3 2 tan 5 cos sin 2 sin 3 2 cotxx x x xx x xÛ+ - = + Û- - = +
22
5 cos sin 6 sin 4 cosxx x x-+= +
( ) ( )
22
22
sin 6 sin 9 cos 4 cos 4 sin 3 cos 2xx x x x xÛ- += + +Û-=+
sin cos 5
sin cos 1
xx
xx
-=
é
Û
ê
+=
ë
2
2
2 cos 1 cos ,
2
442
2
xk
xx k
xk
p
p
pp
p
é
=+
æö æö
ê
Û-=Û-=Û Î
ç÷ ç÷
ê
èø èø
=
ë
!
2,
2
xkk
p
p
=+ Î!
( )
4
15
1365CW= =
A
( )
44
87
105nA C C=+=
! Trang!28!
2.
Xác suất cần tìm là
0.25
b
Áp dụng công thức tổng quát ta có
0.25
Theo bài ra
0.25
Vậy hệ số của số hạng chứa là
0.25
3.
S
N
M
A D
O
B C
a
Ta có (1)
0.25
Gọi suy ra (2)
0.25
Từ (1) và (2) suy ra
0.25
b
Chọn mp(SCD) chứa đường thẳng SD. Ta có (1)
0.25
Do suy ra giao tuyến của hai mặt phẳng (ABM) và (SCD) là đường thẳng
d đi qua M song song với CD trong mp(SCD)
0.25
Gọi suy ra
0.25
Các đồng chí chấm theo thang điểm đáp án. Học sinh ko vẽ đề ko chấm bài hình.
Học sinh làm phương pháp khác đúng cho điểm tối đa.
Xem lại đáp án có sai sót nữa ko. Trước khi chấm.
( )
( )
105 12
11
1365 13
PA PA=- =- =
( )
( )
9
2 18 3
99
2
.2.
k
k
k
kkk
Cx C x
x
-
-
-
æö
=-
ç÷
èø
18 3 6 4kk-=Û=
6
x
( )
4
4
9
. 2 2016C -=
( ) ( )
S SAC SBDÎÇ
O AC BD=Ç
( )
( )
( ) ( )
O AC SAC
O SAC SBD
O BD SBD
ì
ÎÌ
ï
ÞÎ Ç
í
ÎÌ
ï
î
( ) ( )
SO SAC SBD=Ç
( ) ( )
M ABM SCDÎÇ
AB CD!
N d SD=Ç
( )
N SD ABM=Ç
! Trang!29!
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT QUANG TRUNG - ĐỐNG ĐA
___________________________________________________
KIỂM TRA HỌC KỲ I NĂM HỌC 2018 - 2019
MÔN: TOÁN – LỚP 11
(Thời gian làm bài 90 phút)
________________________________
Họ và tên .............................................................................................................................................
Phòng thi ..................................................................
MÃ ĐỀ 001
Lớp ...................................................................................................................................................................
Số thứ tự .........................................................................
I. PHẦN TRẮC NGHIỆM (7 điểm)
(Thời gian làm bài 63 phút)
ĐIỂM
(Số câu đúng ....................... / ......................)
BÀI LÀM
Số thứ tự câu trả lời trong bảng dưới đây ứng với số thứ tự câu trắc nghiệm trong đề.
Đối với mỗi câu trắc nghiệm, học sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng.
1. ; / = ~
6. ; / = ~
11. ; / ~
16. ; / = ~
21. ; / = ~
26. ; / = ~
31. ; / = ~
2. ; / = ~
7. ; / = ~
12. ; / = ~
17. ; / = ~
22. ; / = ~
27. ; / = ~
32. ; / = ~
3. ; / = ~
8. ; / = ~
13. ; / = ~
18. ; / = ~
23. ; / = ~
28. ; / = ~
33. ; / = ~
4. ; / = ~
9. ; / = ~
14. ; / = ~
19. ; / = ~
24. ; / = ~
29. ; / = ~
34. ; / = ~
5. ; / = ~
10. ; / = ~
15. ; / = ~
20. ; / = ~
25. ; / = ~
30. ; / = ~
35. ; / = ~
CÂU HỎI TRẮC NGHIỆM
Câu 1:
Trong mặt phẳng tọa độ , cho 2 điểm . Gọi lần lượt là ảnh của qua phép tịnh tiến
theo vectơ . Khẳng định nào trong các khẳng định sau đúng?
A.
là hình thoi
B.
là hình bình hành
C.
là hình chữ nhật
D.
thẳng hàng
Câu 2:
Một đa giác đều có số đường chéo gấp đôi số cạnh. Hỏi đa giác đó có bao nhiêu cạnh?
A.
6
B.
7
C.
5
D.
8
Câu 3:
Có tất cả 120 cách chọn 3 học sinh từ một nhóm có học sinh. Số là nghiệm của phương trình nào sau đây?
A.
B.
C.
D.
Câu 4:
Số hạng không phụ thuộc vào trong khai triển là:
A.
B.
C.
D.
Câu 5:
Cho hình chóp , có đáy là hình bình hành. Gọi là trung điểm của và là điểm thuộc miền
trong của tam giác . Thiết diện của hình chóp khi cắt bởi mặt phẳng là:
A.
Tam giác
B.
Hình thang
C.
Ngũ giác
D.
Hình bình hành
Câu 6:
Cho hình lăng trụ tam giác . Gọi là trung điểm của và đường thẳng là giao tuyến của hai
mặt phẳng và . Khẳng định nào sau đây sai?
A.
B.
C.
D.
Câu 7:
Hệ số của số hạng chứa trong khai triển là:
A.
B.
C.
D.
Câu 8:
Cho tam giác đều tâm . Có bao nhiêu phép quay tâm góc , biến thành chính nó?
A.
2
B.
3
C.
4
D.
1
Câu 9:
Có 5 cuốn sách Văn khác nhau và 7 cuốn sách Toán khác nhau. Có bao nhiêu cách xếp các cuốn sách lên một kệ dài
của giá sách sao cho các cuốn sách Văn phải xếp cạnh nhau?
A.
B.
C.
D.
Câu 10:
Trong mặt phẳng tọa độ , cho đường thẳng . Phép dời hình có được bằng cách thực hiện liên
tiếp phép đối xứng tâm và phép tịnh tiến theo vectơ biến đường thẳng thành đường thẳng nào cho
dưới đây?
A.
B.
C.
D.
Câu 11:
Có 40 thí sinh, trong đó có A và B, được xếp vào một phòng thi có 20 bàn, mỗi bàn có đủ chỗ cho hai thí sinh.
Tính xác suất để hai thí sinh A và B cùng ngồi trên cùng một bàn.
A.
B.
C.
D.
Oxy
( ) ( )
1; 6 , 1; 4AB--
,CD
,AB
( )
5;1v
!
ABDC
ABCD
ABDC
,,,ABC D
n
n
( )( )
12240nn n--=
( )( )
12360nn n--=
( )( )
12120nn n--=
( )( )
12720nn n--=
x
(
)
18
2
2
x
x
-
13 13
18
2 C-
12 12
18
2 C-
12 6
18
2 C
13 13
18
2 C
.SABCD
ABCD
M
BC
I
SADD
.SABCD
( )
IMC
.' ' 'ABC A B C
M
''AB
d
( )
'CMC
( )
''ABB A
( )
'dCCMÌ
'BC dÇ
( )
'// 'BC AMC
( )
// 'dACC
7
x
(
)
10
3
2
4
x -
3
10
54C
3
10
27C-
2
10
144C-
7
10
54C-
ABCD
O
O
a
02
ap
<£
ABCD
7.5!.7!
12!
2.5!.7!
5!.8!
Oxy
:20dx y+-=
O
( )
3; 2v
!
d
20xy++=
30xy+-=
3320xy+-=
70xy--=
323
390
323
780
1
78
1
39
! Trang!30!
Câu 12:
Gieo một súc sắc cân đối và đồng chất liên tiếp hai lần. Xác suất để hiệu số chấm xuất hiện trong hai lần gieo là số chia
hết cho 3 là:
A.
B.
C.
D.
Câu 13:
Trong măt phẳng tọa độ , cho đường thẳng và số thực . Phép vị tự tâm tỉ số
biến thành đường thẳng nào cho dưới đây?
A.
B.
C.
D.
Câu 14:
Phương trình nào cho dưới đây tương đương với phương trình ?
A.
B.
C.
D.
Câu 15:
Nghiệm của phương trình trên khoảng là:
A.
B.
C.
Đáp án khác
D.
Câu 16:
Cho bốn điểm không cùng nằm trên một mặt phẳng. Gọi lần lượt là trung điểm của , trên
cạnh lấy điểm sao cho . Gọi là giao điểm của với mp . Khẳng định nào sau đây
đúng?
A.
song song với
B.
C.
song song với
D.
Câu 17:
Một hộp có 90 bóng đèn loại I và 10 bóng loại II. Chọn ngẫu nhiên 2 bóng trong hộp để kiểm tra chất lượng. Xác
suất để chọn được ít nhất 1 bóng loại I là:
A.
B.
C.
D.
Đáp án khác
Câu 18:
Trong mặt phẳng tọa độ , phép vị tự tâm tỉ số biến điểm thành có tọa độ là:
A.
B.
C.
D.
Câu
19:
Phương trình có tập nghiệm , với . Khi đó bằng:
A.
B.
C.
D.
Câu 20:
Cho . Giá trị của là:
A.
B.
C.
D.
Câu 21:
Tìm tổng các nghiệm của phương trình trên khoảng là:
A.
B.
C.
D.
Câu 22:
Số nghiệm của phương trình trên đoạn là:
A.
0
B.
2
C.
3
D.
1
Câu 23:
Xét hàm số trên đoạn . Khẳng định nào sau đây đúng về hàm số đã cho?
A.
Hàm số đồng biến trên các khoảng và
B.
Hàm số đồng biến trên khoảng và nghịch biến trên khoảng
C.
Hàm số nghịch biến trên khoảng và đồng biến trên khoảng
D.
Hàm số nghịch biến trên các khoảng và
Câu 24:
Có 5 học sinh nam và 4 học sinh nữ. Hỏi có bao nhiêu cách chọn 4 bạn sao cho trong đó luôn có học sinh nam và học
sinh nữ?
A.
80
B.
126
C.
60
D.
120
Câu 25:
Một hộp chứa 10 quả cầu đỏ được đánh số từ 1 đến 10 và 20 quả cầu đen được đánh số từ 1 đến 20. Lấy ngẫu
nhiên 1 quả cầu từ trong hộp. Xác suất để chọn được quả cầu mầu đen hoặc ghi số chẵn là:
A.
B.
C.
D.
Đáp án khác
Câu 26:
Cho hàm số . Phát biểu nào sau đây là đúng về hàm số đã cho?
A.
Hàm số đã cho có tập xác định là
B.
Đồ thị hàm số đã cho có tâm đối xứng
C.
Đồ thị hàm số đã cho có trục xứng
D.
Hàm số có tập giá trị là
1
4
11
36
5
18
1
3
Oxy
:2 3 0dxy+-=
1k ¹
( )
4; 5I -
k
d
240xy++=
230xy--=
250xy+-=
230xy+-=
22
sin cos 1 0xx--=
cos 2 1x =
cos 2 1x =-
2
2cos 1 0x -=
2
(sin cos ) 1xx-=
(
)
3tan 1 0
3
x
p
+-=
( )
0;
p
6
x
p
=-
6
x
p
=
5
6
x
p
=
,,,ABCD
,MN
,AD AC
BC
K
3KB CK=
I
BD
( )
MNK
KI
AM
2MN IK=
KN
2DI BI=
821
990
89
110
109
110
Oxy
( )
2; 3I
3k =-
( )
3; 2M -
'M
( )
13; 0-
( )
17; 6
( )
17; 0
( )
13; 6-
sin 3 cos 1xx+=
{ }
2, 2;kkk
apbp
++Î!
( )
,;
ab pp
Î-
.
ab
2
6
p
2
18
p
-
2
2
p
-
2
12
p
-
23 20192019
2019 2019 2019
48...2SC C C=-+-
S
4040-
2017
4036
4038
3cos sin 2 0xx-=
[ ]
0;
p
p
3
2
p
2
p
0
(
)
2sin 1 0
4
x
p
++=
[ ]
0;
p
sinyx=
[ ]
;0
p
-
(
)
;
2
p
p
--
(
)
;0
2
p
-
(
)
;
2
p
p
--
(
)
;0
2
p
-
(
)
;
2
p
p
--
(
)
;0
2
p
-
(
)
;
2
p
p
--
(
)
;0
2
p
-
1
6
5
6
2
3
.sin 2yx x=
{ }
\0!
[ ]
1; 1-
! Trang!31!
Câu 27:
Gọi giá trị nhỏ nhất của hàm số . Khi đó:
A.
B.
C.
D.
Câu 28:
Hai đường thẳng nằm trong mp . Hai đường thẳng nằm trong mp . Khẳng định nào sau đây
đúng?
A.
Nếu // thì // và //
B.
Nếu và // , // thì //
C.
Nếu // và // thì //
D.
Nếu // và // thì //
Câu 29:
Tập xác định của hàm số là:
A.
B.
C.
D.
Câu 30:
Có bao nhiêu giá trị nguyên của tham số để phương trình có nghiệm?
A.
5
B.
11
C.
Vô số
D.
7
Câu 31:
Cho hai đường thẳng chéo nhau và . Trên đường thẳng lấy hai điểm và trên đường thẳng lấy hai
điểm . Khẳng định nào sau đây đúng khi nói về hai đường thẳng và ?
A.
Song song
B.
Chéo nhau
C.
Song song hoặc cắt nhau
D.
Cắt nhau
Câu 32:
Một hộp đựng 9 thẻ được đánh số từ 1 đến 9. Rút ngẫu nhiên hai thẻ từ trong hộp và nhân hai số ghi trên hai thẻ
với nhau. Xác suất để tích của hai số ghi trên hai thẻ là một số lẻ là:
A.
B.
C.
D.
Câu 33:
Trong mặt phẳng , cho điểm . Phép quay tâm góc quay biến điểm thành điểm có
tọa độ là:
A.
B.
C.
D.
Câu 34:
Trong mặt phẳng tọa độ , cho 3 điểm và số thực . Phép vị tự tâm tỷ số
biến điểm thành . Khi đó giá trị của là:
A.
B.
C.
D.
Câu 35:
Cho các số 0, 1, 2, 3, 4, 5, 6. Số các số tự nhiên gồm 5 chữ số lấy từ 7 chữ số trên sao cho chữ số đầu tiên bằng 3
là:
A.
B.
C.
D.
----- Hết -----
m
32cos 2sinyxx=- +
5m =-
32m =-
1m =
32m =+
,ab
( )
a
', 'ab
( )
a
a
'a
b
'b
abÇ
a
'a
b
'b
( )
a
a
b
'a
'b
( )
a
a
'a
b
'b
( )
a
cot
1sin
x
y
x
=
-
{ }
\,;
2
kkk
p
pp
+Î!"
{ }
\2;
2
kk
p
p
+Î!"
{ }
\2,;
2
kkk
p
pp
+Î!"
{ }
\;
2
kk
p
Î!"
m
( )
6sin cos cos 2 2 0xxm x-+=
a
b
a
,AB
b
,CD
AD
BC
3
18
1
9
5
18
7
18
Oxy
( )
2018; 2019A -
O
0
90
A
'A
( )
2019;2018
( )
2018; 2019-
( )
2019; 2018--
( )
2019; 2018-
Oxy
( ) ( ) ( )
4; 2 , 3; 5 , 7; 5IAB-- -
1k ¹
I
k
A
B
k
3
7
k =
7
3
k =-
3
7
k =-
7
3
k =
4
6
A
7
4
4
7
4
P
! Trang!32!
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT QUANG TRUNG - ĐỐNG ĐA
___________________________________________________
KIỂM TRA HỌC KỲ I NĂM HỌC 2018 - 2019
MÔN: TOÁN – LỚP 11
(Thời gian làm bài 90 phút)
________________________________
Họ và tên .............................................................................................................................................
Phòng thi ..................................................................
MÃ ĐỀ 001
Lớp ...................................................................................................................................................................
Số thứ tự .........................................................................
I. PHẦN TRẮC NGHIỆM (7 điểm)
(Thời gian làm bài 63 phút)
ĐIỂM
(Số câu đúng ....................... / ......................)
BÀI LÀM
Số thứ tự câu trả lời trong bảng dưới đây ứng với số thứ tự câu trắc nghiệm trong đề.
Đối với mỗi câu trắc nghiệm, học sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng.
1. ; / = ~
6. ; / = ~
11. ; / = ~
16. ; / = ~
21. / = ~
26. ; / = ~
31. ; / = ~
2. ; / = ~
7. ; / = ~
12. ; / = ~
17. ; / = ~
22. ; / = ~
27. ; / = ~
32. ; / = ~
3. ; / = ~
8. ; / = ~
13. ; / = ~
18. ; / = ~
23. ; / = ~
28. ; / = ~
33. ; / = ~
4. ; / = ~
9. ; / = ~
14. ; / = ~
19. ; / = ~
24. ; / = ~
29. ; / = ~
34. ; / = ~
5. ; / = ~
10. ; / = ~
15. ; / = ~
20. ; / = ~
25. ; / = ~
30. ; / = ~
35. ; / = ~
CÂU HỎI TRẮC NGHIỆM
Câu 1:
Trong mặt phẳng tọa độ , cho 2 điểm . Gọi lần lượt là ảnh của qua phép tịnh tiến
theo vectơ . Khẳng định nào trong các khẳng định sau đúng?
A.
là hình thoi
B.
là hình bình hành
C.
là hình chữ nhật
D.
thẳng hàng
Câu 2:
Một đa giác đều có số đường chéo gấp đôi số cạnh. Hỏi đa giác đó có bao nhiêu cạnh?
A.
6
B.
7
C.
5
D.
8
Câu 3:
Có tất cả 120 cách chọn 3 học sinh từ một nhóm có học sinh. Số là nghiệm của phương trình nào sau đây?
A.
B.
C.
D.
Câu 4:
Số hạng không phụ thuộc vào trong khai triển là:
A.
B.
C.
D.
Câu 5:
Cho hình chóp , có đáy là hình bình hành. Gọi là trung điểm của và là điểm thuộc miền
trong của tam giác . Thiết diện của hình chóp khi cắt bởi mặt phẳng là:
A.
Tam giác
B.
Hình thang
C.
Ngũ giác
D.
Hình bình hành
Câu 6:
Cho hình lăng trụ tam giác . Gọi là trung điểm của và đường thẳng là giao tuyến của hai
mặt phẳng và . Khẳng định nào sau đây sai?
A.
B.
C.
D.
Câu 7:
Hệ số của số hạng chứa trong khai triển là:
A.
B.
C.
D.
Câu 8:
Cho tam giác đều tâm . Có bao nhiêu phép quay tâm góc , biến thành chính nó?
A.
2
B.
3
C.
4
D.
1
Câu 9:
Có 5 cuốn sách Văn khác nhau và 7 cuốn sách Toán khác nhau. Có bao nhiêu cách xếp các cuốn sách lên một kệ dài
của giá sách sao cho các cuốn sách Văn phải xếp cạnh nhau?
A.
B.
C.
D.
Câu 10:
Trong mặt phẳng tọa độ , cho đường thẳng . Phép dời hình có được bằng cách thực hiện liên
tiếp phép đối xứng tâm và phép tịnh tiến theo vectơ biến đường thẳng thành đường thẳng nào cho
dưới đây?
A.
B.
C.
D.
Câu 11:
Có 40 thí sinh, trong đó có A và B, được xếp vào một phòng thi có 20 bàn, mỗi bàn có đủ chỗ cho hai thí sinh.
Tính xác suất để hai thí sinh A và B cùng ngồi trên cùng một bàn.
A.
B.
C.
D.
Oxy
( ) ( )
1; 6 , 1; 4AB--
,CD
,AB
( )
5;1v
!
ABDC
ABCD
ABDC
,,,ABC D
n
n
( )( )
12240nn n--=
( )( )
12360nn n--=
( )( )
12120nn n--=
( )( )
12720nn n--=
x
(
)
18
2
2
x
x
-
13 13
18
2 C-
12 12
18
2 C-
12 6
18
2 C
13 13
18
2 C
.SABCD
ABCD
M
BC
I
SADD
.SABCD
( )
IMC
.' ' 'ABC A B C
M
''AB
d
( )
'CMC
( )
''ABB A
( )
'dCCMÌ
'BC dÇ
( )
'// 'BC AMC
( )
// 'dACC
7
x
(
)
10
3
2
4
x -
3
10
54C
3
10
27C-
2
10
144C-
7
10
54C-
ABCD
O
O
a
02
ap
<£
ABCD
7.5!.7!
12!
2.5!.7!
5!.8!
Oxy
:20dx y+-=
O
( )
3; 2v
!
d
20xy++=
30xy+-=
3320xy+-=
70xy--=
323
390
323
780
1
78
1
39
! Trang!33!
Câu 12:
Gieo một súc sắc cân đối và đồng chất liên tiếp hai lần. Xác suất để hiệu số chấm xuất hiện trong hai lần gieo là số chia
hết cho 3 là:
A.
B.
C.
D.
Câu 13:
Trong măt phẳng tọa độ , cho đường thẳng và số thực . Phép vị tự tâm tỉ số
biến thành đường thẳng nào cho dưới đây?
A.
B.
C.
D.
Câu 14:
Phương trình nào cho dưới đây tương đương với phương trình ?
A.
B.
C.
D.
Câu 15:
Nghiệm của phương trình trên khoảng là:
A.
B.
C.
Đáp án khác
D.
Câu 16:
Cho bốn điểm không cùng nằm trên một mặt phẳng. Gọi lần lượt là trung điểm của , trên
cạnh lấy điểm sao cho . Gọi là giao điểm của với mp . Khẳng định nào sau đây
đúng?
A.
song song với
B.
C.
song song với
D.
Câu 17:
Một hộp có 90 bóng đèn loại I và 10 bóng loại II. Chọn ngẫu nhiên 2 bóng trong hộp để kiểm tra chất lượng. Xác
suất để chọn được ít nhất 1 bóng loại I là:
A.
B.
C.
D.
Đáp án khác
Câu 18:
Trong mặt phẳng tọa độ , phép vị tự tâm tỉ số biến điểm thành có tọa độ là:
A.
B.
C.
D.
Câu
19:
Phương trình có tập nghiệm , với . Khi đó bằng:
A.
B.
C.
D.
Câu 20:
Cho . Giá trị của là:
A.
B.
C.
D.
Câu 21:
Tìm tổng các nghiệm của phương trình trên khoảng là:
A.
B.
C.
D.
Câu 22:
Số nghiệm của phương trình trên đoạn là:
A.
0
B.
2
C.
3
D.
1
Câu 23:
Xét hàm số trên đoạn . Khẳng định nào sau đây đúng về hàm số đã cho?
A.
Hàm số đồng biến trên các khoảng và
B.
Hàm số đồng biến trên khoảng và nghịch biến trên khoảng
C.
Hàm số nghịch biến trên khoảng và đồng biến trên khoảng
D.
Hàm số nghịch biến trên các khoảng và
Câu 24:
Có 5 học sinh nam và 4 học sinh nữ. Hỏi có bao nhiêu cách chọn 4 bạn sao cho trong đó luôn có học sinh nam và học
sinh nữ?
A.
80
B.
126
C.
60
D.
120
Câu 25:
Một hộp chứa 10 quả cầu đỏ được đánh số từ 1 đến 10 và 20 quả cầu đen được đánh số từ 1 đến 20. Lấy ngẫu
nhiên 1 quả cầu từ trong hộp. Xác suất để chọn được quả cầu mầu đen hoặc ghi số chẵn là:
A.
B.
C.
D.
Đáp án khác
Câu 26:
Cho hàm số . Phát biểu nào sau đây là đúng về hàm số đã cho?
A.
Hàm số đã cho có tập xác định là
B.
Đồ thị hàm số đã cho có tâm đối xứng
C.
Đồ thị hàm số đã cho có trục xứng
D.
Hàm số có tập giá trị là
1
4
11
36
5
18
1
3
Oxy
:2 3 0dxy+-=
1k ¹
( )
4; 5I -
k
d
240xy++=
230xy--=
250xy+-=
230xy+-=
22
sin cos 1 0xx--=
cos 2 1x =
cos 2 1x =-
2
2cos 1 0x -=
2
(sin cos ) 1xx-=
(
)
3tan 1 0
3
x
p
+-=
( )
0;
p
6
x
p
=-
6
x
p
=
5
6
x
p
=
,,,ABCD
,MN
,AD AC
BC
K
3KB CK=
I
BD
( )
MNK
KI
AM
2MN IK=
KN
2DI BI=
821
990
89
110
109
110
Oxy
( )
2; 3I
3k =-
( )
3; 2M -
'M
( )
13; 0-
( )
17; 6
( )
17; 0
( )
13; 6-
sin 3 cos 1xx+=
{ }
2, 2;kkk
apbp
++Î!
( )
,;
ab pp
Î-
.
ab
2
6
p
2
18
p
-
2
2
p
-
2
12
p
-
23 20192019
2019 2019 2019
48...2SC C C=-+-
S
4040-
2017
4036
4038
3cos sin 2 0xx-=
[ ]
0;
p
p
3
2
p
2
p
0
(
)
2sin 1 0
4
x
p
++=
[ ]
0;
p
sinyx=
[ ]
;0
p
-
(
)
;
2
p
p
--
(
)
;0
2
p
-
(
)
;
2
p
p
--
(
)
;0
2
p
-
(
)
;
2
p
p
--
(
)
;0
2
p
-
(
)
;
2
p
p
--
(
)
;0
2
p
-
1
6
5
6
2
3
.sin 2yx x=
{ }
\0!
[ ]
1; 1-
! Trang!34!
Câu 27:
Gọi giá trị nhỏ nhất của hàm số . Khi đó:
A.
B.
C.
D.
Câu 28:
Hai đường thẳng nằm trong mp . Hai đường thẳng nằm trong mp . Khẳng định nào sau đây
đúng?
A.
Nếu // thì // và //
B.
Nếu và // , // thì //
C.
Nếu // và // thì //
D.
Nếu // và // thì //
Câu 29:
Tập xác định của hàm số là:
A.
B.
C.
D.
Câu 30:
Có bao nhiêu giá trị nguyên của tham số để phương trình có nghiệm?
A.
5
B.
11
C.
Vô số
D.
7
Câu 31:
Cho hai đường thẳng chéo nhau và . Trên đường thẳng lấy hai điểm và trên đường thẳng lấy hai
điểm . Khẳng định nào sau đây đúng khi nói về hai đường thẳng và ?
A.
Song song
B.
Chéo nhau
C.
Song song hoặc cắt nhau
D.
Cắt nhau
Câu 32:
Một hộp đựng 9 thẻ được đánh số từ 1 đến 9. Rút ngẫu nhiên hai thẻ từ trong hộp và nhân hai số ghi trên hai thẻ
với nhau. Xác suất để tích của hai số ghi trên hai thẻ là một số lẻ là:
A.
B.
C.
D.
Câu 33:
Trong mặt phẳng , cho điểm . Phép quay tâm góc quay biến điểm thành điểm có
tọa độ là:
A.
B.
C.
D.
Câu 34:
Trong mặt phẳng tọa độ , cho 3 điểm và số thực . Phép vị tự tâm tỷ số
biến điểm thành . Khi đó giá trị của là:
A.
B.
C.
D.
Câu 35:
Cho các số 0, 1, 2, 3, 4, 5, 6. Số các số tự nhiên gồm 5 chữ số lấy từ 7 chữ số trên sao cho chữ số đầu tiên bằng 3
là:
A.
B.
C.
D.
II. PHẦN TỰ LUẬN (3 điểm)
(Thời gian làm bài 27 phút)
Câu 1: Giải phương trình lượng giác .
Câu 2: Tìm số hạng chứa trong khai triển , .
Câu 3: Cho hình chóp , có đáy là hình bình hành tâm . Trên cạnh lấy điểm sao
cho , gọi là trọng tâm của tam giác .
a) Chứng minh đường thẳng song song với mặt phẳng .
b) Dựng thiết diện của hình chóp với mặt đi qua và song song với .
----- Hết -----
ĐÁP ÁN.
Câu 1: Giải phương trình lượng giác . ĐS:
Câu 2: Tìm số hạng chứa trong khai triển , . ĐS:
m
32cos 2sinyxx=- +
5m =-
32m =-
1m =
32m =+
,ab
( )
a
', 'ab
( )
a
a
'a
b
'b
abÇ
a
'a
b
'b
( )
a
a
b
'a
'b
( )
a
a
'a
b
'b
( )
a
cot
1sin
x
y
x
=
-
{ }
\,;
2
kkk
p
pp
+Î!"
{ }
\2;
2
kk
p
p
+Î!"
{ }
\2,;
2
kkk
p
pp
+Î!"
{ }
\;
2
kk
p
Î!"
m
( )
6sin cos cos 2 2 0xxm x-+=
a
b
a
,AB
b
,CD
AD
BC
3
18
1
9
5
18
7
18
Oxy
( )
2018; 2019A -
O
0
90
A
'A
( )
2019;2018
( )
2018; 2019-
( )
2019; 2018--
( )
2019; 2018-
Oxy
( ) ( ) ( )
4; 2 , 3; 5 , 7; 5IAB-- -
1k ¹
I
k
A
B
k
3
7
k =
7
3
k =-
3
7
k =-
7
3
k =
4
6
A
7
4
4
7
4
P
sin 2 1 3 cos 2xx+=
15
x
(
)
40
3
2
1
2
4
x
x
-
( )
0x ¹
.SABCD
ABCD
O
SA
I
3SA AI=
G
ACDD
IG
( )
SBC
G
,AC S D
sin 2 1 3 cos 2xx+=
12
3
4
xk
xk
p
p
p
p
é
=+
ê
ê
=+
ê
ë
15
x
(
)
40
3
2
1
2
4
x
x
-
( )
0x ¹
21 23 15
40
.2 .Cx
-
-
! Trang!35!
KIỂM TRA HỌC KỲ I LỚP 11
Môn thi: MÔN TOÁN
Câu 1: Giá trị lớn nhất của hàm số là:
A. 4
B.
C. –2
D.
Câu 2: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số lần lượt là:
A.
B.
C.
D.
Câu 3: GTLN của hàm số y = 2cosx -3 là:
A. 2
B. 1
C. –1
D. –3
Câu 4: Cho hàm số: . GTNN của hàm số là:
A. 5
B. –2
C. 3
D. 1
Câu 5: Tìm tập xác định của hàm số .
A. D =
B. D =
C. D =
D. D =
Câu 6: Cho hàm số: , TXĐ của hàm số là:
A.
B.
C. D = R
D.
Câu 7: Với giá trị nào của m thì phương trình có nghiệm?
A.
B.
C.
D.
Câu 8: Phương trình vô nghiệm khi và chỉ khi:
A.
B.
C.
D.
Câu 9: Số nghiệm của phương trình: với là:
A. 3
B. 0
C. 2
D. 1
Câu 10: Giải phương trình . Kết quả thu được là:
A.
B.
C.
D.
Câu 11: Giải phương trình .
A.
B.
C.
D.
Câu 12: Giải phương trình lượng giác : có nghiệm là
A.
B.
C.
D.
Câu 13: Phương trình nào sau đây vô nghiệm:
3cos 1
2
yx
p
æö
=-+
ç÷
èø
5
3
4 sin 3 1yx=+-
42 à8v
42 1à7v-
2à4v
2à2v
3cos2 += xy
D
1 4 sin
cos
x
y
x
-
=
1sin2
cos3
-
=
x
x
y
þ
ý
ü
î
í
ì
=
2
1
\RD
þ
ý
ü
î
í
ì
ZÎ++= kkkRD ,2
6
;2
6
5
\
p
p
p
p
þ
ý
ü
î
í
ì
ZÎ+= kkRD ,2
6
\
p
p
sin 1xm-=
01m££
0m £
20m-£ £
1m ³
cos 0xm-=
1m >
1m <-
11m-£ £
1
1
m
m
<-
é
ê
>
ë
sin 1
4
x
p
æö
+=
ç÷
èø
5x
pp
££
( )
0
tan 2 tan 80x =
00
40 180xk=+
00
40 90xk=+
00
40 45xk=+
00
80 180xk=+
2
2 si n 3sin 2 0xx--=
4
2; 2
33
xkxk
pp
pp
=- + = +
5
2; 2
66
xkx k
pp
pp
=+ = +
7
2; 2
66
xkxk
pp
pp
=- + = +
2
2; 2
33
xkx k
pp
pp
=+ = +
2 cos 3 0
2
x
+=
5
2
3
xk
p
p
=± +
5
2
6
xk
p
p
=± +
5
4
6
xk
p
p
=± +
5
4
3
xk
p
p
=± +
! Trang!36!
A. sin x + 3 = 0
B.
C. tan x + 3 = 0
D. 3sin x – 2 = 0
Câu 14: Phương trình có nghiệm là:
A.
B.
C.
D.
Câu 15: Cho phương trình . Tìm tất cả các giá trị của để phương trình đã cho
có nghiệm.
A.
B.
C.
D.
Câu 16: Nghiệm của phương trình là:
A. .
B. .
C. .
D. .
Câu 17: Cho phương trình . Nghiệm của phương trình là
A.
B.
C.
D.
Câu 18: Từ các chữ số 0, 1, 2, 3, 4, 5. Có thể lập được bao nhiêu số tự nhiên chẵn có 4 chữ số khác
nhau?
A. 1080
B. 156
C. 300
D. 144
Câu 19: Khối 11 trường ta có 35 học sinh nam và 36 học sinh nữ. Đoàn trường cần chọn một học
sinh tham gia giải chạy việt dã cấp tỉnh. Hỏi có bao nhiêu cách chọn?
A. 36
B. 35
C. 71
D. 1260
Câu 20: Khối 11 trường ta có 32 học sinh nam và 39 học sinh nữ. Nhà trường cần chọn hai học sinh
trong đó có một nam và một nữ đi dự trại hè của tỉnh đoàn. Hỏi nhà trường có bao nhiêu cách chọn?
A. 39
B. 32
C. 71
D. 1248
Câu 21: Một đội công nhân cầu đường có 10 nam và 9 nữ, chọn ra một nhóm 5 người trong đó có ít
nhất 1 nữ làm việc ca đêm. Hỏi có bao nhiêu cách chọn?
A. 11376
B. 19
C. 90
D. 4320
Câu 22: Từ các chữ số 0, 1, 2, 3, 4, 5. Có thể lập được bao nhiêu số tự nhiên lẻ có 3 chữ số khác
nhau?
A. 180
B. 48
C. 100
D. 52
Câu 23: Cho A={1, 2, 3, 4, 5, 6, 7}. Từ tập A có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số
khác nhau?
A. 28
B. 480
C. 840
D. 5040
Câu 24: Một đội công nhân cầu đường có 8 nam và 12 nữ, chọn ra một nhóm 5 người gồm 2 nam và
3 nữ làm việc ca đêm. Hỏi có bao nhiêu cách chọn?
A. 20
B. 5664
C. 96
D. 6160
Câu 25: Từ một hộp đựng 5 viên bi màu xanh, 7 viên bi màu vàng, lấy ra 6 viên bi. Tính số phần tử
của biến cố A: “ 6 viên lấy ra có 4 viên bi màu xanh, 2 viên bi màu vàng”. Kết quả thu được là bao
nhiêu?
A. 105
B. 210
C. 720
D. 120
Câu 26: Có bao nhiêu cách xếp 5 học sinh nam và 4 học sinh nữ vào một hàng dọc?
A. 20
B. 362880
C. 2880
D. 9
Câu 27: Cho nhị thức . Số hạng chứa x
3
trong khai triển là kết quả nào sau đây?
2
2 cos cos 1 0xx--=
1 2 cos 2 0x+=
3
k
p
p
±
3
k
p
p
±+
3
k
p
p
+
2
3
k
p
p
±+
2 cos 4 sin4xxm-=
m
33m-££
3; 3mm£- ³
55m-££
5; 5mm£- ³
sin – 3 cos 0 xx=
2
6
xk
p
p
=+
2
3
xk
p
p
=+
6
xk
p
p
=+
3
xk
p
p
=+
2
3cos 2 cos 5 0xx+-=
2k
p
2
k
p
p
-+
2
2
k
p
p
+
9
2
1
x
x
æö
-
ç÷
èø
! Trang!37!
A. 84 x
3
B. – 36x
3
C. 36x
3
D. – 84x
3
Câu 28: Lớp 11 trường A có 7 nam và 28 nữ. Chọn 2 học sinh tham gia vệ sinh công cộng toàn
trường. Hỏi có bao nhiêu cách chọn?
A. 70
B. 196
C. 35
D. 595
Câu 29: Một tổ học sinh có 6 nam và 4 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người
được chọn đều là nữ.
A.
B.
C.
D.
Câu 30:
Một đa giác đều có 20 đường chéo. Số cạnh của đa giác đó là bao nhiêu?
A. 7 cạnh
B. 8 cạnh
C. 9 cạnh
D. 10 cạnh
Câu 31: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3
quyển sách. Tính xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán.
A.
B.
C.
D.
Câu 32: Gieo một đồng tiền liên tiếp 3 lần. Tính xác suất của biến cố A: “ kết quả của 3 lần gieo là
như nhau”.
A.
B.
C.
D.
Câu 33: Hệ số của số hạng chứa x
2
trong khai triển nhị thức Niu tơn (1+2x)
6
là bao nhiêu?
A. 60
B. 40
C. 80
D. 20
Câu 34:
Có bao nhiêu cách xếp 6 học sinh ngồi vào 6 chiếc ghế xếp quanh một bàn tròn?
A. 6
B. 120
C. 36
D. 720
Câu 35: Trong mp(Oxy) cho . Tìm tọa độ của điểm M’ ảnh của điểm M qua phép vị tự tâm
O tỉ số ?
A. M’(4; 8)
B. M’(–8; 4)
C. M’(–4; 8)
D. M’(4; –8)
Câu 36: Trong mặt phẳng Oxy nếu phép tịnh tiến biến điểm A (3; 2) thành điểm A’(2; 3) thì nó biến
điểm
B (2, 5) thành điểm nào sau đây?
A. B’(5; 5)
B. B’(5; 2)
C. B’(1; 1)
D. B’(1; 6)
Câu 37: Trong các phép tịnh tiến theo các vectơ sau, phép tịnh tiến theo vectơ nào biến đường thẳng
d: 9x –7y+10=0 thành chính nó:
A. = (7; 9)
B. (–9; 7)
C. = (7; –9)
D. = (9; –7)
Câu 38: Phép vị tự tỉ số k biến hình vuông thành:
A. Hình thoi
B. Hình vuông
C. Hình bình hành
D. Hình chữ nhật
Câu 39: Cho hình bình hành ABCD, phép tịnh tiến theo véc tơ biến điểm B thành điểm nào sau
đây?
A. Điểm B
B. Điểm A
C. Điểm C
D. Điểm D
Câu 40: Trong mặt phẳng Oxy cho điểm A(–3;0). Phép quay biến điểm A thành điểm:
A. A’(–3; 0)
B. A’(0; –3)
C. A’(3; 0)
D. A’(0; 3)
Câu 41: Trong mặt phẳng toạ độ Oxy, phép tịnh tiến theo vectơ
biến điểm M(–3; 2) thành điểm
M’(–5; 3). Véctơ có toạ độ là:
2
7
1
21
37
42
5
42
1
()
2
PA=
3
()
8
PA=
7
()
8
PA=
1
()
4
PA=
( 2;4)M -
2k =
( ; 90 )
0
O
Q
-
! Trang!38!
A. (–2; 1)
B. (2; – 1)
C. (–8; 5)
D. (8; – 5)
Câu 42: Trong mặt phẳng Oxy , ảnh của đường tròn (C) : qua phép tịnh tiến theo
véctơ là đường tròn có phương trình là:
A.
B.
C.
D.
Câu 43: Phép vị tự tâm I(–1;2) tỉ số 3 biến điểm A(4; 1) thành điểm có toạ độ :
A. (14; 1)
B. (6; 5)
C. (14; –1)
D. (16; 1)
Câu 44: Trong mặt phẳng Oxy, phép tịnh tiến theo vectơ biến đường thẳng
thành đường thẳng có phương trình là:
A.
B.
C.
D.
Câu 45: Cho d: 2x + y – 3 = 0. Phép vị tự tâm O tỉ số 2 biến đường thẳng d thành:
A. 2x + y – 6=0
B. 2x + y + 3 =0
C. 4x + 2y – 3 = 0
D. 4x + 2y – 5 = 0
Câu 46: Trong mặt phẳng Oxy, cho điểm M(2; 0) và điểm N(0; 2). Phép quay tâm O biến điểm M
thành điểm N, khi đó góc quay của nó là:
A.
B.
C.
D.
Câu 47: Trong mặt phẳng Oxy cho A(5; –3) . Hỏi A là ảnh của điểm nào trong các điểm sau qua
phép tịnh tiến theo vectơ là:
A. (4; 10)
B. (–10; 0)
C. (0; –10)
D. (10; 4)
Câu 48: Trong mặt phẳng Oxy, phép quay tâm O (0;0) góc quay 90 biến đường thẳng
thành đường thẳng có phương trình là:
A.
B.
C.
D.
Câu 49: Trong mặt phẳng Oxy , cho điểm M(4; 6) và I(2; 3) . Hỏi phép vị tự tâm I tỉ số k=2 biến M
thành điểm M’ có tọa độ là:
A. (6; 9)
B. (2; 4)
C. (3; 2)
D. (6; 4)
Câu 50: Trong mặt phẳng cho tam giác ABC . Gọi M,N,P lần lượt là trung điểm của AB, BC, CA.
Khi đó phép tịnh tiến theo vectơ biến:
A. M thành B
B. M thành N
C. M thành P
D. M thành A
Trường THPT Nguyễn Du
Tổ: Toán - Tin
ĐỀ THI HỌC KỲ I MÔN TOÁN LỚP 11, NĂM HỌC 2018 - 2019
Thời gian: 90 phút ( Không kể thời gian phát đề)
---------------------------------------------------------------------------------------------------------------------------
Họ tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .SBD………….
I. Trắc nghiệm ( 6 điểm)
Mã đề: 143
Câu 1.
Hàm số nào sau đây là hàm số chẵn:
A.
B.
C.
D.
Câu 2.
Phương trình có nghiệm là:
22
( 2) ( 3) 9xy++-=
22
( 6) ( 6) 9xy++-=
22
( 2) 9xy-+=
22
( 2) ( 6) 9xy-+-=
22
( 2) ( 3) 9xy++-=
:3 5 8 0dx y+-=
3580xy+-=
35 0xy+=
3590xy+-=
3 5 26 0xy+-=
6
p
j
=
2
p
j
=
2
p
j
=-
6
p
j
=-
:10dx y-+=
30xy+-=
30xy-+=
10xy-+=
10xy++=
sinyx=
sin
3
yx
p
æö
=+
ç÷
èø
osycx=
s
3
ycox
p
æö
=-
ç÷
èø
sin 2 2 cos sin 1
0
tan 3
xxx
x
+--
=
+
! Trang!39!
A.
B.
C.
D.
Câu 3.
Nghiệm của phương trình là:
A.
B.
C.
D.
Câu 4.
Năm 2009, Hệ thống mạng viễn thông quân đội Viettel tiến hành ra đầu số thuê bao di động mới gồm dãy 10 số có dạng
097.XXXXXXX, trong đó X là một chữ số được chọn ngẫu nhiên từ các số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Một số di động được gọi là
"số phong thủy lộc phát" nếu hai chữ số cuối của số di động đó là 68. Tính xác suất để trong lần ra đầu số mới này của Viettlel
chọn được số di động là "số phong thủy lộc phát"?
A.
B.
C.
D.
Câu 5.
Trong mặt phẳng Oxy, cho đường tròn (C) có phương trình . Tìm phương trình
đường tròn ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số
A.
B.
C.
D.
Câu 6.
Số hạng thứ trong khai triển nhị thức là
A.
B.
C.
D.
Câu 7.
Tính tổng tất cả các nghiệm của phương trình trên đoạn
A.
B.
C.
D.
Câu 8.
Tìm n biết
A.
B.
C.
D.
Câu 9.
Có bao nhiêu số tự nhiên có 9 chữ số trong đó có 4 chữ số 1 xếp kề nhau và 5 chữ số 2,3,4,5,6
A.
24
B.
362880
C.
120
D.
720
Câu 10.
Trong mặt phẳng Oxy cho A(9;1). Phép tịnh tiến theo vectơ biến điểm A thành điểm nào
trong các điểm sau:
A.
E(8;14)
B.
B(4;-6)
C.
D(13;7)
D.
C(14;8)
Câu 11.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Khi đó, giao tuyến của 2 mặt
phẳng (SAC) và (SAB) là:
A.
SA
B.
SC
C.
SO
D.
SB
Câu 12.
Tập giá trị của hàm số là:
A.
B.
C.
D.
Câu 13.
Khai triển của nhị thức có bao nhiêu số hạng?
A.
B.
C.
D.
Câu 14.
Nghiệm âm lớn nhất của phương trình là:
A.
B.
C.
D.
Câu 15.
Giá trị nhỏ nhất của hàm số là
A.
B.
C.
D.
2; 2,
23
xkxkk
pp
pp
=- + = + Î!
2; ,
23
xkxkk
pp
pp
=- + = + Î!
2; ,
232
xkxkk
ppp
p
=- + = + Î!
2; 2,
23
xkxkk
pp
pp
=- + =- + Î!
tan 3x =
2
,
33
k
xk
pp
=+ ΢
,
3
xkk
p
p
=- + ΢
,
3
xkk
p
p
=+ ΢
2,
3
xkk
p
p
=- + ΢
5
7
5
10
5
7
10
10
7
10
10
10
( ) ( )
22
844xy-+- =
= 3.k
( ) ( )
22
24 12 12xy-+-=
( ) ( )
22
24 12 36xy+++=
( ) ( )
22
24 12 36xy-+-=
( ) ( )
22
12 24 12xy+++ =
1k +
( )
+2
n
x
-
2
knk k
n
Cx
+--+111knkk
n
Ca b
-
2
knk n
n
Cx
2
knk
n
Cx
T
2
2 sin 3 cos 0
44
xx
-=
[ ]
0;8 .p
4T
p
=
0T =
16T
p
=
8T
p
=
-=-
22
3155.
nn
AC n
5, 6nn==
6, 1 2nn==
5, 7nn==
5, 12nn==
(5;7)v
!
s inx osycx=+
2; 2
éù
-
ëû
°
[ ]
0;1
[ ]
1;1-
26
2
1
2x
x
æö
-
ç÷
èø
25
27
26
52
1
sin cos 1 sin 2
2
xx x+=-
2
p
-
3
2
p
-
2
p
-
p
-
2
sin sin
3
yx x
p
ʈ
Á˜
=++
Á˜
˯
3
2
1-
2-
3
2
-
! Trang!40!
Câu 16.
Cho đường tròn (O), đoạn thẳng AB cố định không cắt (O) và C là điểm di động trên (O). Tập hợp
điểm D sao cho tứ giác ABCD là hình bình hành là:
A.
Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo
B.
Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo
C.
Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo
D.
Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo
Câu 17.
Trong các điều kiện sau điều kiện nào để xác định một mặt phẳng
A.
Ba điểm phân biệt.
B.
Hai đường thẳng không song song.
C.
Hai đường thẳng cắt nhau.
D.
Một đường thẳng và một điểm bất kì.
Câu 18.
Với giá trị nào của m thì phương trình có nghiệm
A.
B.
C.
D.
Câu 19.
Phương trình có nghiệm là:
A.
B.
C.
D.
Câu 20.
Tập xác định của hàm số là:
A.
B.
C.
D.
Câu 21.
Tổng có kết quả bằng :
A.
B.
C.
D.
Câu 22.
Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất 2 lần. Xác suất để tổng số chấm trên mặt xuất
hiện trong 2 lần gieo bằng 8 là
A.
B.
C.
D.
Câu 23.
Trong một hội nghị học sinh giỏi, có 12 bạn nam và 10 bạn nữ. Hỏi có bao nhiêu cách chọn một bạn
lên phát biểu ?
A.
120
B.
22
C.
12
D.
10
Câu 24.
Trong mặt phẳng, cho trước điểm O cố định và góc lượng giác Phép biến hình F biến O thành
chính nó, biến mỗi điểm M khác O thành điểm M' sao cho OM' = OM và . F là phép biến
hình nào đã học?
A.
Phép vị tự.
B.
Phép quay tâm O, góc quay
C.
Phép tịnh tiến
D.
Phép quay tâm O, góc quay
Câu 25.
Số nghiệm của phương trình trên ?
A.
B.
C.
D.
Câu 26.
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi E, F lần lượt là trung điểm của cạnh
SB, SC. Chọn mệnh đề đúng:
A.
(OEF)//(SBC)
B.
(OEF)//(SAD)
C.
(OEF)//(SAB)
D.
(OEF)//(ABCD)
Câu 27.
Phương trình có nghiệm là
A.
, .
B.
, .
C.
, .
D.
, .
Câu 28.
Cho tứ diện ABCD. Gọi I, J, K lần lượt là các điểm nằm trên các cạnh AC, AD và BC sao cho IJ
không song song với CD. Khi đó, giao điểm của CD với mặt phẳng (IJK) là:
A.
Giao điểm của CD với IJ
B.
Giao điểm của CD với JK
C.
Trung điểm của BD
D.
Giao điểm của CD với IK
Câu 29.
Các thành phố A, B, C, D được nối với nhau bởi các con đường như vẽ dưới đây. Hỏi có bao nhiêu
cách đi từ A đến D mà qua B và C chỉ một lần
AB
uu ur
2BA
uu r
1
2
BA
uu r
2
sin 4 1 0xm+-=
0 16m££
13m££
04m££
01m££
2 cos x 1 0+=
4
xk,k
3
p
=± + p Î!
xk,k
3
p
=± + p Î!
2
xk2,k
3
p
=± + p Î!
xk2,k
6
p
=± + p Î!
cotyx=
\,
4
Dkk
p
p
ìü
=+Î
íý
îþ
°¢
\,k
2
Dk
p
p
ìü
=+Î
íý
îþ
°¢
D = °
{ }
\,Dkk
p
=롢
02018 120172 220163 20172018
2017 2017 2017 2017
32 32 32 ... 3.2SC C C C=+ + ++
2017
5
2018
5
2017
6.5
2018
6.5
1
6
1
3
5
36
13
36
.
a
( )
∑
;'OM OM
a
=
2.
a
.
a
22
cos 3 s in cos 2 sin 0xxx x-+=
( )
2;2pp-
6
8
4
2
sin 3 cos 1xx+=
2, 2
62
xkxk
pp
pp
=- + = +
k ΢
2, 2
62
xkx k
pp
pp
=+ =-+
k ΢
2, 2
62
xkxk
pp
pp
=+ =+
k ΢
2
2, 2
3
xk x k
p
pp
==+
k ΢
! Trang!41!
A.
9
B.
76
C.
24
D.
20
Câu 30.
Phương trình có nghiệm là:
A.
B.
C.
D.
II. Tự luận (4 điểm)
Câu 1. Một tổ có 5 nam và 7 nữ. Chọn ngẫu nhiên 6 học sinh. Tính xác suất để 6 học sinh được chọn có 3
học sinh nữ.
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm
của AB, AD và SO.
a. Chứng minh rằng MN song song với mặt phẳng (SBD).
b. Xác định thiết diện của hình chóp với mặt phẳng (MNP).
Câu 3. Giải phương trình:
--------------o0o--------------
2
2 sin sin 3 0xx--=
2,
6
xkk
p
p
=- + Î!
,
2
xkk
p
p
=- + Î!
2,
3
xkk
p
p
=- + Î!
2,
2
xkk
p
p
=- + Î!
( )
3
cos2 cos6 4 3sin 4 si n 1 0.xx x x-+ - +=
! Trang!42!
Trường THPT Nguyễn Du
Tổ: Toán - Tin
ĐỀ THI HỌC KỲ I MÔN TOÁN LỚP 11, NĂM HỌC 2018- 2019
Thời gian: 90 phút ( Không kể thời gian phát đề)
---------------------------------------------------------------------------------------------------------------------------
Họ tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .SBD………….
I. Trắc nghiệm ( 6 điểm)
Mã đề: 177
Câu 1.
Phương trình có nghiệm là:
A.
B.
C.
D.
Câu 2.
Nghiệm của phương trình là:
A.
B.
C.
D.
Câu 3.
Hàm số nào sau đây là hàm số chẵn:
A.
B.
C.
D.
Câu 4.
Cho đường tròn (O), đoạn thẳng AB cố định không cắt (O) và C là điểm di động trên (O). Tập hợp
điểm D sao cho tứ giác ABCD là hình bình hành là:
A.
Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo
B.
Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo
C.
Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo
D.
Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo
Câu 5.
Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất 2 lần. Xác suất để tổng số chấm trên mặt xuất
hiện trong 2 lần gieo bằng 8 là
A.
B.
C.
D.
Câu 6.
Cho tứ diện ABCD. Gọi I, J, K lần lượt là các điểm nằm trên các cạnh AC, AD và BC sao cho IJ
không song song với CD. Khi đó, giao điểm của CD với mặt phẳng (IJK) là:
A.
Giao điểm của CD với IJ
B.
Giao điểm của CD với IK
C.
Trung điểm của BD
D.
Giao điểm của CD với JK
Câu 7.
Trong mặt phẳng Oxy, cho đường tròn (C) có phương trình . Tìm phương trình
đường tròn ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số
A.
B.
C.
D.
Câu 8.
Trong mặt phẳng, cho trước điểm O cố định và góc lượng giác Phép biến hình F biến O thành
chính nó, biến mỗi điểm M khác O thành điểm M' sao cho OM' = OM và . F là phép biến
hình nào đã học?
A.
Phép vị tự.
B.
Phép quay tâm O, góc quay
C.
Phép tịnh tiến
D.
Phép quay tâm O, góc quay
Câu 9.
Trong các điều kiện sau điều kiện nào để xác định một mặt phẳng
A.
Hai đường thẳng cắt nhau.
B.
Hai đường thẳng không song song.
C.
Ba điểm phân biệt.
D.
Một đường thẳng và một điểm bất kì.
Câu 10.
Trong mặt phẳng Oxy cho A(9;1). Phép tịnh tiến theo vectơ biến điểm A thành điểm nào
trong các điểm sau:
A.
D(13;7)
B.
C(14;8)
C.
E(8;14)
D.
B(4;-6)
2
2 sin sin 3 0xx--=
2,
3
xkk
p
p
=- + Î!
2,
6
xkk
p
p
=- + Î!
,
2
xkk
p
p
=- + Î!
2,
2
xkk
p
p
=- + Î!
tan 3x =
2,
3
xkk
p
p
=- + ΢
,
3
xkk
p
p
=+ ΢
2
,
33
k
xk
pp
=+ ΢
,
3
xkk
p
p
=- + ΢
sinyx=
osycx=
sin
3
yx
p
æö
=+
ç÷
èø
s
3
ycox
p
æö
=-
ç÷
èø
1
2
BA
uu r
2BA
uu r
AB
uu ur
1
6
1
3
13
36
5
36
( ) ( )
22
844xy-+- =
= 3.k
( ) ( )
22
24 12 12xy-+-=
( ) ( )
22
12 24 12xy+++ =
( ) ( )
22
24 12 36xy+++=
( ) ( )
22
24 12 36xy-+-=
.
a
( )
∑
;'OM OM
a
=
2.
a
.
a
(5;7)v
!
! Trang!43!
Câu 11.
Giá trị nhỏ nhất của hàm số là
A.
B.
C.
D.
Câu 12.
Tìm n biết
A.
B.
C.
D.
Câu 13.
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi E, F lần lượt là trung điểm của cạnh
SB, SC. Chọn mệnh đề đúng:
A.
(OEF)//(ABCD)
B.
(OEF)//(SAD)
C.
(OEF)//(SBC)
D.
(OEF)//(SAB)
Câu 14.
Có bao nhiêu số tự nhiên có 9 chữ số trong đó có 4 chữ số 1 xếp kề nhau và 5 chữ số 2,3,4,5,6
A.
24
B.
362880
C.
120
D.
720
Câu 15.
Tính tổng tất cả các nghiệm của phương trình trên đoạn
A.
B.
C.
D.
Câu 16.
Với giá trị nào của m thì phương trình có nghiệm
A.
B.
C.
D.
Câu 17.
Tập xác định của hàm số là:
A.
B.
C.
D.
Câu 18.
Nghiệm âm lớn nhất của phương trình là:
A.
B.
C.
D.
Câu 19.
Số nghiệm của phương trình trên ?
A.
B.
C.
D.
Câu 20.
Phương trình có nghiệm là
A.
, .
B.
, .
C.
, .
D.
, .
Câu 21.
Khai triển của nhị thức có bao nhiêu số hạng?
A.
B.
C.
D.
Câu 22.
Trong một hội nghị học sinh giỏi, có 12 bạn nam và 10 bạn nữ. Hỏi có bao nhiêu cách chọn một bạn
lên phát biểu ?
A.
22
B.
120
C.
10
D.
12
Câu 23.
Năm 2009, Hệ thống mạng viễn thông quân đội Viettel tiến hành ra đầu số thuê bao di động mới gồm dãy 10 số có
dạng 097.XXXXXXX, trong đó X là một chữ số được chọn ngẫu nhiên từ các số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Một số di động được
gọi là "số phong thủy lộc phát" nếu hai chữ số cuối của số di động đó là 68. Tính xác suất để trong lần ra đầu số mới này của
Viettlel chọn được số di động là "số phong thủy lộc phát"?
A.
B.
C.
D.
Câu 24.
Tập giá trị của hàm số là:
A.
B.
C.
D.
Câu 25.
Phương trình có nghiệm là:
2
sin sin
3
yx x
p
ʈ
Á˜
=++
Á˜
˯
2-
1-
3
2
3
2
-
-=-
22
3155.
nn
AC n
6, 1 2nn==
5, 12nn==
5, 6nn==
5, 7nn==
T
2
2 sin 3 cos 0
44
xx
-=
[ ]
0;8 .p
8T
p
=
0T =
16T
p
=
4T
p
=
2
sin 4 1 0xm+-=
01m££
04m££
13m££
0 16m££
cotyx=
D = °
{ }
\,Dkk
p
=롢
\,k
2
Dk
p
p
ìü
=+Î
íý
îþ
°¢
\,
4
Dkk
p
p
ìü
=+Î
íý
îþ
°¢
1
sin cos 1 sin 2
2
xx x+=-
2
p
-
p
-
2
p
-
3
2
p
-
22
cos 3 s in cos 2 sin 0xxx x-+=
( )
2;2pp-
4
6
8
2
sin 3 cos 1xx+=
2, 2
62
xkxk
pp
pp
=+ =+
k ΢
2
2, 2
3
xk x k
p
pp
==+
k ΢
2, 2
62
xkxk
pp
pp
=- + = +
k ΢
2, 2
62
xkx k
pp
pp
=+ =-+
k ΢
26
2
1
2x
x
æö
-
ç÷
èø
25
26
27
52
7
10
10
10
5
7
5
10
5
7
10
10
s inx osycx=+
[ ]
0;1
°
[ ]
1;1-
2; 2
éù
-
ëû
sin 2 2 cos sin 1
0
tan 3
xxx
x
+--
=
+
! Trang!44!
A.
B.
C.
D.
Câu 26.
Các thành phố A, B, C, D được nối với nhau bởi các con đường như vẽ dưới đây. Hỏi có bao nhiêu
cách đi từ A đến D mà qua B và C chỉ một lần
A.
9
B.
24
C.
76
D.
20
Câu 27.
Phương trình có nghiệm là:
A.
B.
C.
D.
Câu 28.
Tổng có kết quả bằng :
A.
B.
C.
D.
Câu 29.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Khi đó, giao tuyến của 2 mặt
phẳng (SAC) và (SAB) là:
A.
SB
B.
SC
C.
SA
D.
SO
Câu 30.
Số hạng thứ trong khai triển nhị thức là
A.
B.
C.
D.
II. Tự luận (4 điểm)
Câu 1. Một tổ có 5 nam và 7 nữ. Chọn ngẫu nhiên 6 học sinh. Tính xác suất để 6 học sinh được chọn có 3
học sinh nữ.
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm
của AB, AD và SO.
c. Chứng minh rằng MN song song với mặt phẳng (SBD).
d. Xác định thiết diện của hình chóp với mặt phẳng (MNP).
Câu 3. Giải phương trình:
--------------o0o--------------
2; ,
23
xkxkk
pp
pp
=- + = + Î!
2; ,
232
xkxkk
ppp
p
=- + = + Î!
2; 2,
23
xkxkk
pp
pp
=- + = + Î!
2; 2,
23
xkxkk
pp
pp
=- + =- + Î!
2 cos x 1 0+=
xk2,k
6
p
=± + p Î!
2
xk2,k
3
p
=± + p Î!
4
xk,k
3
p
=± + p Î!
xk,k
3
p
=± + p Î!
02018 120172 220163 20172018
2017 2017 2017 2017
32 32 32 ... 3.2SC C C C=+ + ++
2017
6.5
2017
5
2018
5
2018
6.5
1k +
( )
+2
n
x
-
2
knk k
n
Cx
2
knk
n
Cx
+--+111knkk
n
Ca b
-
2
knk n
n
Cx
( )
3
cos2 cos6 4 3sin 4 si n 1 0.xx x x-+ - +=
! Trang!45!
Đáp án mã đề: 143
01. C; 02. A; 03. C; 04. B; 05. C; 06. A; 07. D; 08. A; 09. D; 10. D; 11. A; 12. A; 13. B; 14. B; 15. B;
16. B; 17. C; 18. D; 19. C; 20. D; 21. C; 22. C; 23. B; 24. D; 25. B; 26. B; 27. A; 28. A; 29. C; 30. D;
Đáp án mã đề: 177
01. D; 02. B; 03. B; 04. C; 05. D; 06. A; 07. D; 08. D; 09. A; 10. B; 11. B; 12. C; 13. B; 14. D; 15. A;
16. A; 17. B; 18. D; 19. C; 20. C; 21. C; 22. A; 23. C; 24. D; 25. C; 26. B; 27. B; 28. A; 29. C; 30. A;
ĐÁP ÁN VÀ BIỂU ĐIỂM PHẦN TỰ LUẬN
CÂU
Ý
NỘI DUNG
ĐIỂM
1
(1đ)
Không gian mẫu: “ chọn ngẫu nhiên 6 học sinh từ 12 học sinh”
Gọi A là biến cố “ chọn 6 học sinh có 3 học sinh nữ”
Vậy
0,25
0,25
0,5
2
a.
b.
Hình vẽ đúng
Ta có:
0,25
0,25
0,25
0,25
0,25
( )
6
12
924nCW= =
( )
33
57
. 350nA CC==
( )
( )
( )
350 25
924 66
nA
PA
n
===
W
X
P
R
B
O
M
A
N
E
D
C
Q
S
( )
// ( )
/ /( )
MN SBD
MN BD SBD
MN SBD
Ë
ì
í
Ì
î
Þ
! Trang!46!
Ta có:
Trong mp(SBD), gọi và
Trong mặt phẳng (ABCD) gọi
Trong mp(SCD), gọi
Khi đó:
Vậy thiết diện là ngũ giác MNRQX
0,25
0,25
0,25
3
0,25
0,25
0,25
0,25
SỞ GD & ĐT TỈNH HƯNG YÊN
TRƯỜNG THPT YÊN MỸ
(Đề có 3 trang)
ĐỀ THI HỌC KÌ I – NĂM HỌC 2017 - 2018
MÔN: TOÁN 11
Thời gian làm bài : 90 Phút.
Họ tên :............................................................... Số báo danh : ...................
I – TRẮC NGHIỆM (7.5 điểm)
Câu 1: Với mọi , so sánh cos(sinx) với cos1 thì
A. không so sánh được. B. cos(sinx) < cos1.
C. cos(sinx) > cos1. D. cos(sinx) ≥ cos1.
Câu 2: Xét các phương trình lượng giác
(I) sinx + cosx = 2 (II) tanx + cotx = 2 (III)
//
()
()
()()
MN BD
MN MNP
BD SBD
P MNP SBD
ì
ï
Ì
ï
í
Ì
ï
ï
ÎÇ
î
( ) ( )
// //MNP SBD Px MN BDÞÇ=
X Px SB=Ç
R Px SD=Ç
EMNCD=Ç
( ) ( )
=ERMNP SCDÞÇ
ERQ SC=Ç
( ) ( )
( )
()
()()
()()
()()
MNP ABCD MN
MNP SAD NR
MNP SCD RQ
MNP SBC QX
MNP SAB XM
Ç=
Ç=
Ç=
Ç=
Ç=
( )
( ) ( )
( )
3
22
2
2
cos2 cos6 4 3sin 4 sin 1 0
1 cos2 1 cos6 4sin 3 2 0
2cos 2 sin 3 4sin 3 2 0
cos sin 3 1 0
cos 0
sin 3 1
2
2
2
2
63
xx x x
xxx
xxx
xx
x
x
xk
xl
xk
p
p
p
p
pp
-+ - +=
Û+ +- + +=
Û+ + +=
Û+ +=
=
ì
Û
í
=-
î
ì
=+
ï
ï
ÛÛ=+
í
ï
=- +
ï
î
0;
2
x
p
æö
Î
ç÷
èø
Mã đề 162
! Trang!47!
Trong các phương trình trên, phương trình nào có nghiệm:
A. (II) và (III) B. (II) C. (I) D. (III)
Câu 3: Cho B = {1, 2, 3, 4, 5, 6}. Từ tập B có thể lập được bao nhiêu số chẵn có 6 chữ số đôi một
khác nhau ?
A. 46656. B. 360. C. 720. D. 2160.
Câu 4: Cho tam giác ABC. Số mặt phẳng chứa tất cả các đỉnh của tam giác ABC?
A. 3. B. 2. C. 4. D. 1.
Câu 5: Cho có: . Số hạng thứ 7 của cấp số cộng này là
A. 1,6. B. 0,5. C. 6. D. 0,6.
Câu 6: Phương trình có tập nghiệm trùng với tập nghiệm của phương trình
A. . B. . C. . D. .
Câu 7: Hàm số tuần hoàn với chu kỳ
A. . B. C. D.
Câu 8: Cho hàm số , GTNN và GTLN của hàm số là
A. . B. – 5 ; 5. C. . D. – 7 ; 7.
Câu 9:
Số
nghiệm
của
phương
trình
sin2x – sin x
=
0
trên [–2p;2p]
là
A. 2. B. 9. C. 8. D. 4.
Câu 10: Cho ngũ giác đều ABCDE tâm O, biết OA = a . Phép quay biến A thành A’, biến B
thành B’. Độ dài đoạn A’B’ bằng
A. . B. . C. . D. .
Câu 11: Phép tịnh tiến T theo vectơ , biến đường thẳng d thành đường thẳng d’. Nếu d’ trùng
với d thì giá của vectơ
A. không song song với d. B. trùng với d.
C. song song với d. D. song song hoặc trùng với d.
Câu 12: Trong mặt phẳng Oxy, cho vectơ và M’(-2 ; 8). Biết . Khi đó toạ độ
của M là
A. M(-5 ; 13) B. M(13 ; - 5) C. M(-1 ; -3) D. M(1 ; 3)
Câu 13: Tìm hệ số của trong khai triển thành đa thức của , biết n là số nguyên dương
thỏa mãn : .
A. 2099529. B. . C. . D. .
Câu 14: Tổng bằng
A. 5
n
. B. 7
n
. C. 6
n
. D. 4
n
.
Câu 15: Một hộp đựng 10 viên bi xanh và 5 viên bi vàng. Có bao nhiêu cách lấy ngẫu nhiên 4 viên
bi trong đó có ít nhất 2 viên bi màu xanh?
A. 1260. B. 1050. C. 105. D. 1200.
Câu 16: Gieo một đồng tiền và một con súc sắc. Số phần tử của không gian mẫu là
A. . B. . C. . D. .
Câu 17: Trong mp(Oxy) cho đường thẳng . Phép vị tự tâm O tỉ số k = −2 biến d
thành đường thẳng có phương trình
A. B.
( )
n
CS C u
1
u0,1;d0,1=- =
+=sin 3 sin 2 sinxxx
=sin 0x
é=
ê
ê
=
ê
ë
sin 0
1
cos
2
x
x
=-
1
cos
2
x
=-cos 1x
cot x=y
T
p
=
2T
p
=
2
T
p
=
4
T
p
=
5sin 2 6 cos=+yx x
26;26-
526;526-- +
( )
,C
Q
p
sin 72
o
a
2 cos 36
o
a
cos 72
o
a
2 sin 36
o
a
u0¹
!!
u
!
(3;5)v =-
!
() '
v
TM M=
!
7
x
2
(2 3 )-
n
x
135 21
21 21 21 21
... 1024
+
+++ +
++++ =
n
nnn n
CCC C
2099529-
2099520-
2099520
0122
5 5 ... 5
nn
nn n n
AC C C C=+ + ++
8
24
6
12
dx y:ñ20+=
4 0.xy++=
2 2 ñ 4 0.xy+=
! Trang!48!
C. D.
Câu 18: Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (m) của con
kênh tính theo thời gian t (giờ) trong một ngày được cho bởi công thức: . Thời
điểm mực nước của kênh cao nhất là
A. t = 14. B. t = 13. C. t = 15. D. t= 16.
Câu 19: Nghiệm của phương trình 2cosx + 1 = 0 là
A. . B. . C. . D. .
Câu 20: Tìm giá trị của x, y sao cho dãy số theo thứ tự lập thành một cấp số cộng?
A. B. C. D.
Câu 21: Cho dãy số có các số hạng đầu là 8, 15, 22, 29, 36, … .Số hạng tổng quát của dãy số này là
A. . B. C. D.
Câu 22: Cho tam giác ABC có trọng tâm G. Gọi M, N, P theo thứ tự là trung điểm các cạnh BC,
CA, AB. Phép vị tự tâm G tỉ số biến tam giác ABC thành tam giác
A. BCA. B. CAB. C. MNP. D. MNC.
Câu 23: Công thức tính số chỉnh hợp là
A. . B. . C. . D.
.
Câu 24: Từ 6 số 0, 1, 2, 3, 4, 5 có thể tạo thành bao nhiêu số tự nhiên có 3 chữ số?
A. 100. B. 125. C. 180. D. 216.
Câu 25: Cho hình lập phương ABCD.A’B’C’D’.
Số đường thẳng chứa cạnh của hình lập phương
chéo nhau với đường thẳng AB là
A. 3. B. 1.
C. 2. D. 4.
Câu 26: Một hộp đựng 6 viên bi đỏ và 4 viên bi xanh. Lấy lần lượt 2 viên bi từ hộp đó. Xác suất để
viên bi được lấy lần thứ 2 màu xanh là
A. . B. . C. . D. .
Câu 27: Phép quay tâm O góc quay 90
0
biến đường thẳng d thành d’. Khi đó
A. d // d’. B.
C.
.
D. d // d’ hoặc
Câu 28: Nghiệm của phương trình sinx = –1 là
A. . B. . C. . D. .
Câu 29: Tập xác định của hàm số là
A. . B.
.
2 2 0.xy+=
ñ 4 0.xy+=
1
cos 3
284
t
h
pp
æö
=++
ç÷
èø
2
3
xk
p
p
=± +
2
6
xk
p
p
=± +
6
xk
p
p
=± +
2
2
3
xk
p
p
=± +
2, , 4,- xy
2, 8.==xy
1, 7.==xy
2, 10.==xy
6, 2.=- =xy
n
u7n=+
n
u7n1=+
n
u7n=
n
u7n7=+
1
2
k =-
!
()!
k
n
n
A
nk
=
-
!
()!
k
n
n
C
nk
=
-
!
()!!
k
n
n
C
nkk
=
-
!
()!!
k
n
n
A
nkk
=
-
D'
C'
B'
A'
D
C
B
A
4
5
1
5
2
5
3
5
.
¢
^dd
'.ºdd
'.ºdd
xk
p
=
3
2
xk
p
p
=+
2
2
xk
p
p
=- +
2
xk
p
p
=- +
2017
1 s inx
=
+
y
\2
2
ìü
=-+
íý
îþ
DR k
p
p
\2
4
DR k
p
p
ìü
=+
íý
îþ
! Trang!49!
C. . D.
.
Câu 30: Cho dãy số với . Số hạng đầu tiên của dãy là
A. 2018. B. 2018
2
. C. 1. D. 2017.
II – TỰ LUẬN (2.5 điểm)
Câu 1:Cho hình chóp S.ABCD đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, CD.
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Chứng minh MN song song với (SBC).
Câu 2: Giải phương trình: a) b)
Câu 3: Một bình đựng quả cầu xanh, quả cầu đỏ và quả cầu vàng . Các quả cầu khác nhau về
kích thước. Chọn ngẫu nhiên quả cầu. Tính xác suất để được quả cầu lấy ra đủ màu ?
------ HẾT ------
Phần đáp án câu trắc nghiệm:
162
1
C
2
B
3
B
4
D
5
B
6
B
7
A
8
D
9
B
10
D
11
D
12
D
13
C
14
C
15
A
16
D
17
A
18
A
19
D
\2
4
ìü
=-+
íý
îþ
DR k
p
p
\
2
DR k
p
p
ìü
=+
íý
îþ
( )
n
u
( )
n
n
u2017n=+
sin 3 cos 2+=xx
3
os
42
æö
+=
ç÷
èø
cx
p
5
4
3
3
3
! Trang!50!
20
B
21
B
22
C
23
A
24
C
25
D
26
C
27
B
28
C
29
A
30
A
! Trang!51!
ĐÁP ÁN PHẦN TỰ LUẬN
Bài 1.
a/ .
(0,2 điểm)
(0,2 điểm)
b/ .
(0,2 điểm)
(0,2 điểm)
(0,2 điểm)
Bài 2. Viết khai triển biểu thức sau theo công thức nhị thức Niu – tơn:.
(0,2 + 0,2 + 0,2 + 0,2 + 0,2) điểm
Bài 3. “ chia hết cho 6”. (*)
• chia hết cho 6. (0,2 điểm)
• Giả sử (*) đúng với số tự nhiên bất kỳ n = k với , nghĩa là: chia hết cho 6.
(0,2 điểm)
• Ta cần chứng minh (*) cũng đúng với số tự nhiên n = k +1.
Nghĩa là: chia hết cho 6. (0,2 điểm)
• Thật vậy, ta có:
(0,2 điểm)
(0,2 điểm)
Vậy, chứng tỏ (*) đúng với mọi số nguyên dương n.
Bài 4. a/ Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
• S là điểm chung thứ nhất. (0,1 điểm)
• Gọi E là giao điểm của AB và CD thì E là điểm chung
thứ 2. (0,2 điểm)
• Vậy, SE là giao tuyến của (SAB) và (SCD). (0,2 điểm)
b/ Gọi M là trung điểm của SA. Tìm giao điểm N của SD và
mp(MBC).
• M là điểm chung của mp(SAD) và (MBC). (0,1 điểm)
• Hai mặt phẳng (SAD) và (SCD) lần lượt chứa hai đường
thẳng song song là AD và BC. Do đó, giao tuyến của
chúng là đường thẳng Mx, với Mx song song với AD. (0,2 điểm)
• Vậy, . (0,2 điểm)
Lưu ý: Bài giải của bài 4 phải có hình kèm theo đúng và đủ mới được tính điểm.
( )
0
tan 15 3x -=
00 0
15 60 180xk-= +
00
75 180 , xkk=+ Î!
2 si n 4 1 0x -=
1
sin 4
2
xÛ=
42
6
5
42
6
xk
xk
p
p
p
p
ì
=+
ï
ï
Û
í
ï
=+
ï
î
24 2
,
5
24 2
xk
k
xk
pp
pp
ì
=+
ï
ï
ÛÎ
í
ï
=+
ï
î
!
( )
4
43 2
2 8 24 32 16xxxxx+=++ + +
2
73 31
n
n
Ann=+ --
1
6A =
1k ³
2
73 31
k
k
Akk=+ --
1k
A
+
( ) ( )
2
1
1
731311
k
k
Akk
+
+
=++-+-
( ) ( )
22
1
77 3 3 1 63 4 1
k
k
Akkkk
+
=+--- --
( )
2
1
7. 6 3 4 1
kk
AAkk
+
=- --
N Mx SD=Ç
E
N
M
A
D
B
S
C
| 1/51
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT KIÊN GIANG
ĐỀ THI HỌC KỲ I - NĂM HỌC 2017 - 2018 ĐIỂM TRƯỜNG THPT CÂY DƯƠNG
MÔN TOAN – 11
Thời gian làm bài: 90 Phút ( Đề có 3 trang )
Họ tên :...................................................... Số báo danh : ...............Lớp 11B.. Mã đề 989
I. PHẦN TRẮC NGHIỆM: Gồm 30 câu. (6 điểm)
Câu 1: Trong một hộp phấn màu có 2 viên phấn xanh, 3 viên phấn đỏ và 5 viên phấn vàng. Hỏi có bao
nhiêu cách chọn một viên phấn từ hộp đó. A. 9. B. 11. C. 30. D. 10.
Câu 2: Tìm khẳng định sai trong các khẳng định sau.
A. Hàm số y = cot x tuần hoàn với chu kì p .
B. Hàm số y = tan x tuần hoàn với chu kì 2p .
C. Hàm số y = cos x tuần hoàn với chu kì 2p .
D. Hàm số y = sin x tuần hoàn với chu kì 2p .
Câu 3: Tìm tất cả các tham số thực m để phương trình 5 sin x + 2cos x = 1- m có nghiệm.
A. m ³ 4 Ú m £ -2 .
B. 0 £ m £ 2 . C. 2 - £ m £ 4 .
D. m = 3Ú m = 1 - .
Câu 4: Trong mặt phẳng Oxy, cho điểm M ( 4;
- 2) là ảnh của điểm N qua phép quay tâm O góc 0 90 .
Tìm tọa độ điểm N. A. ( 2; - 4 - ) B. (2;4) C. ( 2; - 4) D. (2; 4 - )
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của BC. Mặt phẳng (α) đi
qua M và song song với các đường thẳng BD, SC. Gọi (H ) là thiết diện tạo bởi mp(α) và hình chóp
S.ABCD. Tìm mệnh đề đúng?
A. (H ) là một lục giác.
B. (H ) là một hình bình hành.
C. (H ) là một tam giác.
D. (H ) là một ngũ giác.
Câu 6: Trong mặt phẳng Oxy, cho đường tròn (C) ( x + )2 + ( y - )2 : 1
2 = 5 . Viết phương trình đường tròn là
ảnh của đường tròn (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số ! 3
- và phép tịnh tiến theo vectơ v = ( 5; - 2).
A. ( x + )2 + ( y + )2 4
2 = 45 B. ( x + )2 + ( y + )2 2
4 = 45 C. ( x - )2 + ( y - )2 2 4 = 15 D.
(x - )2 +( y + )2 8 8 = 15
Câu 7: Tìm tập nghiệm của phương trình 2
cos 2x + cos 2x - 6 = 0 . ì p ü A. Æ . B. { 3; - } 2 .
C. í± + kp ,k Î!ý . D. î 6 þ ì p ü
í± + k2p , k Î!ý . î 4 þ
Câu 8: Trong mặt phẳng Oxy, cho đường thẳng d : 3x + y - 2 = 0 . Viết phương trình đường thẳng là ảnh 1
của đường thẳng d qua phép vị tự tâm O tỉ số k = - . 2
A. x + 3y -1 = 0
B. 3x + y -1 = 0
C. 3x + y +1 = 0
D. x + 3y +1 = 0 !
Câu 9: Từ 6 điểm phân biệt A, B,C, D, E, F , có thể thành lập được bao nhiêu vectơ khác vectơ 0 ? A. 21. B. 30. C. 120. D. .720.
Câu 10: Cho hình chóp S.ABCD có O là giao điểm của AC và BD, M là trung điểm của SC. Xác định giao Trang 1
điểm I của đường thẳng AM và mp(SBD).
A. I = AM Ç BD .
B. I = AM Ç SB .
C. I = AM Ç SO .
D. I = AM Ç SD . æ p ö
Câu 11: Tìm tập xác định của hàm số y = cot x + . ç ÷ è 3 ø ì p ü ì p ü ì p ü
A. ! \ í- + kp ,k Î ! ý. B. ! \ í- + kp ,k Î"ý. C. ! \ í- + k2p ,k Î"ý . D. î 3 þ î 3 þ î 3 þ ìp ü
! \ í + kp ,k Î"ý . î 3 þ
Câu 12: Dãy số được cho bởi công thức nào dưới đây là dãy số không tăng, không giảm ? n 1+ n A. u = . B. u = . C. u = - n + 2 u = n - 2 n
( )1n .(4 3) . D. . n n +1 n 2n n u ì = 4
Câu 13: Cho dãy số (u 1 í * n Î • n ) , biết (với
). Tìm số hạng thứ 5 của dãy số. u = 3u - 2 î n 1+ n A. u = 730 . B. u = 82 . C. u = 2188 . D. u = 244 . 5 5 5 5
Câu 14: Cho cấp số nhân (u u
n ) có số hạng đầu
và công bội q. Tìm mệnh đề sai. 1
A. u = u . n q . B. 1 u u . n q - = . C. u = u . n q . D. u = u .q . n 1 n 1 n 1 + 1 n 1 + n
Câu 15: Tìm hàm số chẵn trong các hàm số sau.
A. y = sin x .
B. y = cos x .
C. y = cot x .
D. y = tan x .
Câu 16: Gieo một đồng tiền xu cân đối và đồng chất 3 lần. Tìm số phần tử của không gian mẫu. A. 3. B. 16. C. 8. D. 6.
Câu 17: Ba số x, y, z theo thứ tự đó lập thành một cấp số nhân có công bội khác 1. Đồng thời chúng lần
lượt là số hạng đầu, số hạng thứ hai và số hạng thứ năm của một cấp số cộng. Hãy tìm tích của ba số đó, biết
rằng tổng của chúng là 26. A. . x . y z = 248 . B. . x . y z = 264 . C. . x . y z = 216 . D. . x . y z = 224 .
Câu 18: Tìm số hạng đầu u và công sai d của cấp số cộng (u u = 5, - u = 7 n ) , biết: . 1 2 5 ì 17 = - u ì = 2 - u ì = 9 - u ï 1 ï 3 u ì = 12 - A. 1 í . B. 1 í . C. í . D. 1 í . îd =12 îd = 4 2 ï îd = 4 d = ïî 3
Câu 19: Tìm mệnh đề sai ?
A. Hai đường thẳng được gọi là song song nếu chúng không có điểm chung.
B. Một đường thẳng và một mặt phẳng được gọi là song song nếu chúng không có điểm chung.
C. Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung.
D. Hai đường thẳng được gọi chéo nhau nếu chúng không đồng phẳng.
Câu 20: Trong mặt phẳng Oxy, cho điểm M '( x '; y ') là ảnh của điểm M ( ;
x y) qua phép tịnh tiến theo !
vectơ v = (a;b) . Tìm mệnh đề đúng ?
ìx ' = x + a
ìx ' = x - a
ìx ' = x + b
ìx ' = a - x A. í B. í C. í D. í
îy ' = y + b
îy ' = y - b
îy ' = y + a
îy ' = b - y
Câu 21: Giải phương trình 3 sin x - cos x = 1 - . é p éx = kp éx = k2p x = - + k2p A. ê 3
, k Î ! . B. ê 4p
, k Î ! . C. ê 4p , k Î ! . D. ê êx = + kp êx = + k2p ëx = p + k2p ë 3 ë 3 éx = k2p , k Î ! . ê ëx = p + k2p
Câu 22: Cho lăng trụ tam giác ABC.A’B’C’ . Tìm giao tuyến của hai mặt phẳng (ACC’) và (A’BC). Trang 2 A. A’B. B. AB’. C. A’C. D. AC’.
Câu 23: Cho cấp số nhân (u u = 6 q = 2 -
n ) có số hạng đầu và công bội
. Tính tổng của 11 số hạng đầu. 1 A. S = 4098 . B. S = 4089 . C. S = 6147 - . D. S = 6147 . 11 11 11 11
Câu 24: Từ một hộp có 7 cây viết tím, 4 cây viết xanh và 3 cây viết đỏ, lấy ngẫu nhiên 3 cây viết. Tính xác
suất sao cho lấy được 1 cây viết tím, 1 cây viết xanh và 1 cây viết đỏ. 1 1 1 3 A. . B. . C. . D. . 156 6 26 13
Câu 25: Có bao nhiêu số tự nhiên gồm 6 chữ số khác nhau lấy từ tập các chữ số {3,4,5,6,7, } 8 ? A. 24 B. 33 C. 120. D. 720. 5 11
Câu 26: Cho cấp số cộng gồm 5 số hạng: 1; ; 4;
; 7 . Tìm công sai d của cấp số cộng. 2 2 5 A. d = 2 . B. d = 3 . C. d = 2 . D. d = . 2 5 2 3
Câu 27: Tìm mệnh đề sai ?
A. A = T! (B) Û B = T ! ( A A = Q Û = æ ö ( B ) B Qæ ö ( A p p ) - ). B. . v v O, O,- ç ÷ ç ÷ è 2 ø è 2 ø
C. A = V
B Û B = V A A = V
B Û B = V A O,k ( ) O,-k ( ) O,k ( ) æ 1 ö ( ) . D. . ( ) ( ) ( ) O, ç ÷ è k ø
Câu 28: Tìm mệnh đề đúng ?
A. Tồn tại duy nhất một mặt phẳng đi qua 3 điểm không thẳng hàng.
B. Tồn tại vô số mặt phẳng phân biệt đi qua 3 điểm không thẳng hàng.
C. Tồn tại duy nhất một mặt phẳng đi qua 1 điểm và một đường thẳng.
D. Tồn tại vô số mặt phẳng phân biệt cùng chứa hai đường thẳng cắt nhau.
Câu 29: Dãy số nào dưới đây là một cấp số cộng. 1 1 1 1 1 2 3 4 5 A. 1; ; ; ; . B. ; ; ; ; . C. 17; 14; 11; 8; 5 . D. 1; 2; 4; 8; 16 . 2 3 4 5 2 3 4 5 6
Câu 30: Hai xạ thủ A và B cùng bắn vào bia. Xác suất để xạ thủ A bắn trúng bia là 0,6 và xác suất để xạ thủ
B bắn trúng bia là 0,8. Tính xác suất để có đúng một xạ thủ bắn trúng bia. A. 0,48. B. 0,2. C. 1,4. D. 0,44.
II. PHẦN TỰ LUẬN: Gồm 4 bài (4 điểm)
Bài 1. Giải các phương trình sau: a/ ( 0 tan x -15 ) = 3 . (0,4 điểm)
b/ 2sin 4x -1 = 0 . (0,6 điểm)
Bài 2. Viết khai triển biểu thức sau theo công thức nhị thức Niu – tơn: ( x + )4 2 . (1 điểm)
Bài 3. Dùng phương pháp quy nạp, chứng minh rằng với mọi n Î • * thì “ n 2
A = 7 + 3n - 3n -1 chia hết cho n 6”. (1 điểm)
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD là đáy lớn.
a/ Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD). (0,5 điểm)
b/ Gọi M là trung điểm của SA. Tìm giao điểm N của SD và mp(MBC). (0,5 điểm)
------ HẾT ------
SỞ GD&ĐT KIÊN GIANG
THI HỌC KỲ I - ĐÁP ÁN NĂM HỌC 2017 - 2018 TRƯỜNG THPT CÂY DƯƠNG
MÔN TOAN – 11 Trang 3
Thời gian làm bài : 90 Phút ()
Phần đáp án câu trắc nghiệm: 989 1 D 2 B 3 C 4 B 5 D 6 B 7 A 8 C 9 B 10 C 11 B 12 C 13 D 14 A 15 B 16 C 17 C 18 B 19 A 20 A 21 C 22 C 23 A 24 D 25 D 26 C 27 D 28 A 29 C 30 D
SỞ GD&ĐT TUYÊN QUANG
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2018 - 2019
TRƯỜNG THPT SƠN DƯƠNG Môn: TOÁN 11 Trang 4
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Họ và tên:.............................................................Lớp:11B…
A.Phần trắc nghiệm: (Học sinh lựa chọn phương án trả lời rồi điền các chữ A, B, C, D vào bảng sau). 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Câu 1: Nghiệm của phương trình cosx = 1 là: p p
A. x = kp , k ΢ . B. x =
+ k2p , k ΢ . C. x = k2p , k ΢ . D. x = + kp , k ΢ . 2 2
Câu 2: Điều kiện xác định của hàm số y = cotx là: p p A. x ¹
+ kp , k ΢ . B. x ¹ + kp , k ΢ . C. p p x π
+ k ,k Œ¢ . D. x ¹ kp , k Î ¢ . 2 4 8 2
Câu 3: Nghiệm của phương trình cos3x = cos x là: éx = k2p p
A. x = k2p , k ΢ . B. ê p
, k Î ¢ . C. x = k2p , k ΢ . D. x = k , k Î ¢ . ê x = + k2p 2 ë 2 2 cot x
Câu 4: Tìm tập xác định của hàm số y = . sin x -1 ìp ü ì p ü ìp p ü ìp ü
A. D = R \! í + k2p ,k Î Z"ý. B. D = R \! ík ý. C. D = R! \ í + k ý. D. D = R! \ í + k2p;kp ý. î 2 þ î 2 þ î 2 2 þ î 2 þ
Câu 5: Nghiệm dương nhỏ nhất của pt 2sin x + 2 sin 2x = 0 là: 3p p p A. x = B. x = C. x = D. x = p 4 4 3
Câu 6: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 4
y = sin x + cos x trên ! . Tính giá trị M . . n 1 3 A. . B. . C. 6. D. 2. 2 2 Câu 7: Tính tổng 0 1 2
S = C + C + C + ... n + C . n n n n A. 2n S = -1. B. 2 .n S = C. n 1 S 2 - = . D. 2n S = +1. Câu 8: Với *
n Î N mệnh đề nào dưới đây sai ? n A. P = k ! n!. B. A = (1 £ k £ n). n n (n - k)! n k ! C. C =
(0 £ k £ n). D. k C = k ! k A (0 £ k £ n). n
k !(n - k)! n n
Câu 9: Cho 5 chữ số 1, 2,3, 4,5. Từ 5 chữ số này ta lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau?
A. 120 B. 60 C. 30 D. 40
Câu 10: Xét phép thử “Xếp 3 bạn nam và 3 bạn nữ theo đội hình hàng ngang sao cho nam nữ xen kẽ nhau”.
Khi đó không gian mẫu là: A. 6. B. 6! C. (3!)2 D. 2 (3!)2 -n
Câu 11: Cho dãy số (Un) với Un =
.Khẳng định nào sau đây là đúng? n +1 1 - 2 - 3 - 5 - 5 -
A. Năm số hạng đầu của dãy là : ; ; ; ;
. C. Là dãy số tăng. 2 3 4 5 6 1 - 2 - 3 - 4 - 5 -
B. 5 số số hạng đầu của dãy là : ; ; ; ;
. D. Bị chặn dưới bởi 1. 2 3 4 5 6
Câu 12: Khẳng định nào sau đây là sai? 1 - 1 3 1 1 A. Dãy số
;0; ;1; ;... là một cấp số cộng: u = - , d = . 2 2 2 1 2 2 Trang 5 1 1 1 1 1 B. Dãy số ; ;
;... là một cấp số cộng: u = , d = . 2 3 2 2 2 1 2 2
C. Dãy số : –2; –2; –2; –2; … là cấp số cộng u = 2, - d = 0. 1
D. Dãy số: 0,1;0,01;0,001;0,0001 không phải là một cấp số cộng.
Câu 13: Cho một cấp số cộng có u = 3
- ;u = 27 . Tìm d ? 1 6 A. d = 5 B. d = 7 C. d = 6 D. d = 8
Câu 14: Xác định x để 3 số: 1–x; x2; 1+x lập thành một cấp số cộng? A. x = 3 ± B. x = 2 ± C. x = 1 ± D. x = 0 !
Câu 15: Trong mặt phẳng cho vectơ v . Phép biến hình biến mỗi điểm M thành điểm M ' được gọi là phép !
tịnh tiến theo vectơ v nếu thỏa mãn: !!!!!" " !!!!!!" " !!!!!" " !!!!!" "
A. MM ' = -v
B. M ' M = v
C. MM ' = kv D. MM ' = v
Câu 16: Cho phép vị tự V
. Mệnh đề nào sau đây sai? (I;k) A. V là phép đồng nhất. B. V
biến tâm I thành chính nó. (I ) ;1 (I;k) C. V
biến gốc tọa độ O thành chính nó. D. V
là phép đối xứng tâm I. (I;k) (I;- )1
Câu 17: Ảnh của đường thẳng d : 2x - 5y + 3 = 0 qua phép vị tự tâm O tỉ số k = 3 - là A. 2
- x + 5y + 9 = 0 B. 2
- x - 5y + 9 = 0
C. 2x - 3y + 9 = 0 D. 2
- x + 3y + 9 = 0
Câu 18: Ảnh của đường tròn (C) ( x - )2 + ( y + )2 : 4
1 = 1 qua phép vị tự tâm O tỉ số k = 2 là
A. (C ) ( x + )2 + ( y - )2 ' : 8 2 = 4
B. (C ) ( x - )2 + ( y + )2 ' : 8 2 = 4
C. (C ) ( x + )2 + ( y + )2 ' : 8 2 = 4
D. (C ) ( x - )2 + ( y - )2 ' : 8 2 = 4
Câu 19: Trong không gian, cho 4 điểm không đồng phẳng. Hình tạo bởi 4 điểm trên là hình có bao nhiêu mặt? A. 6 B. 4 C. 3 D. 2
Câu 20: Cho đường thẳng a và mặt phẳng (P) trong không gian. Có bao nhiêu vị trí tương đối của a và (P)? A. 2 B. 3 C. 1 D. 4 B. Phần tự luận.
Câu 21(1,5 điểm). Giải các phương trình a) 3 + 3tanx = 0 b) 2
sin x = – sin x + 2 c) 2 sin x + 3 sin . x cos x = 1 Câu 22(2,0 điểm).
a) Một bình đựng 5 quả cầu xanh và 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Tính
xác suất để được 3 quả cầu khác màu nhau. æ 3 n ö
b) Tìm hệ số chứa x5 trong khai khai triển nhị thức 2 x - biết n thoả mãn 6 5 A = 10A ç 3 ÷ è x ø n n
c) Chứng minh rằng với mọi n Î N * thì 3
n + 2n chia hết cho 3 Câu 23 (1,5 điểm). !
a) Trong mặt phẳng tọa độ Oxy , cho đường thẳng d có phương trình 2x - 3y + 5 = 0 và v = (1; 3 - ) . Viết
phương trình đường thẳng d ' là ảnh của d qua phép tịnh tiếnT! . v
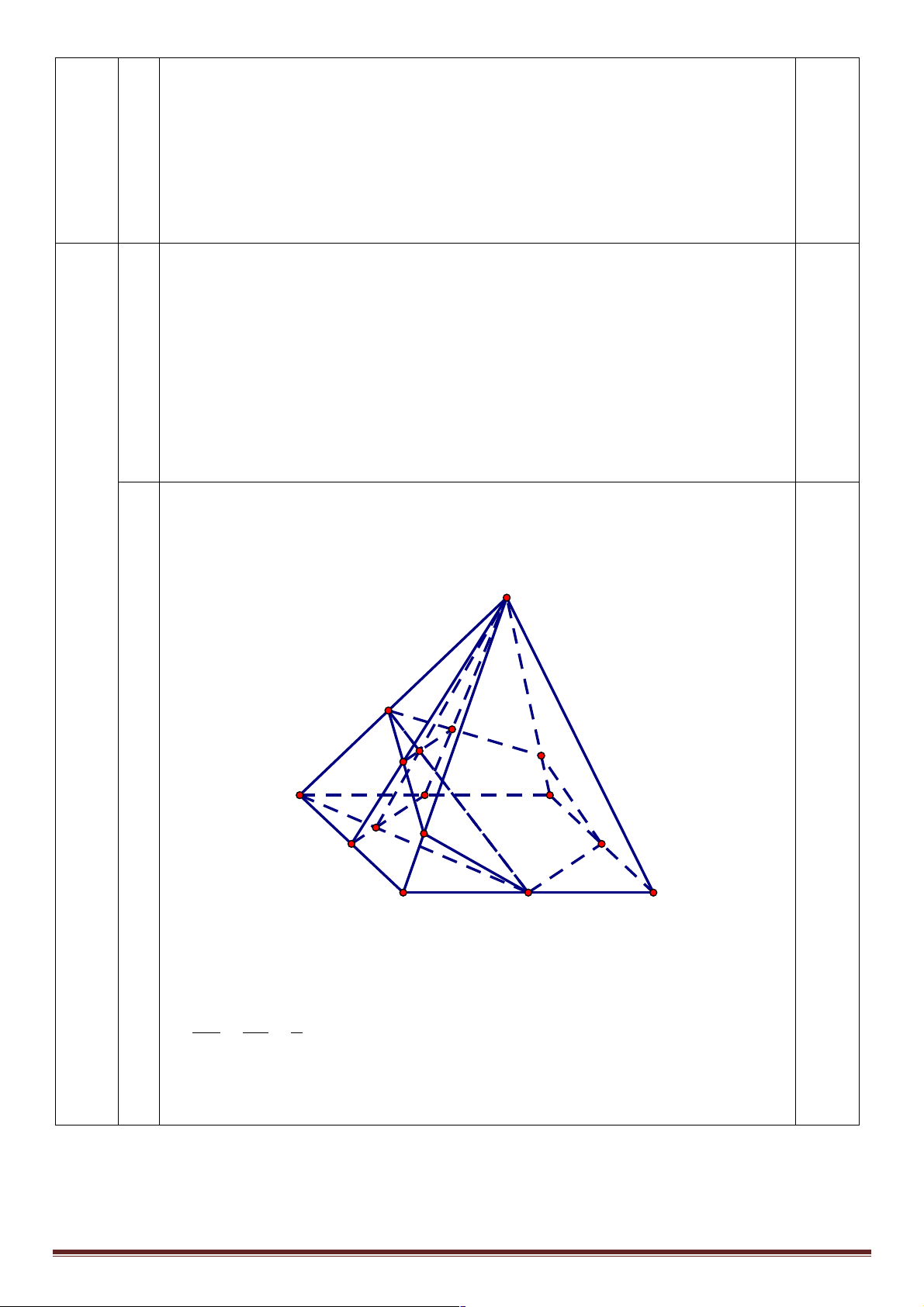
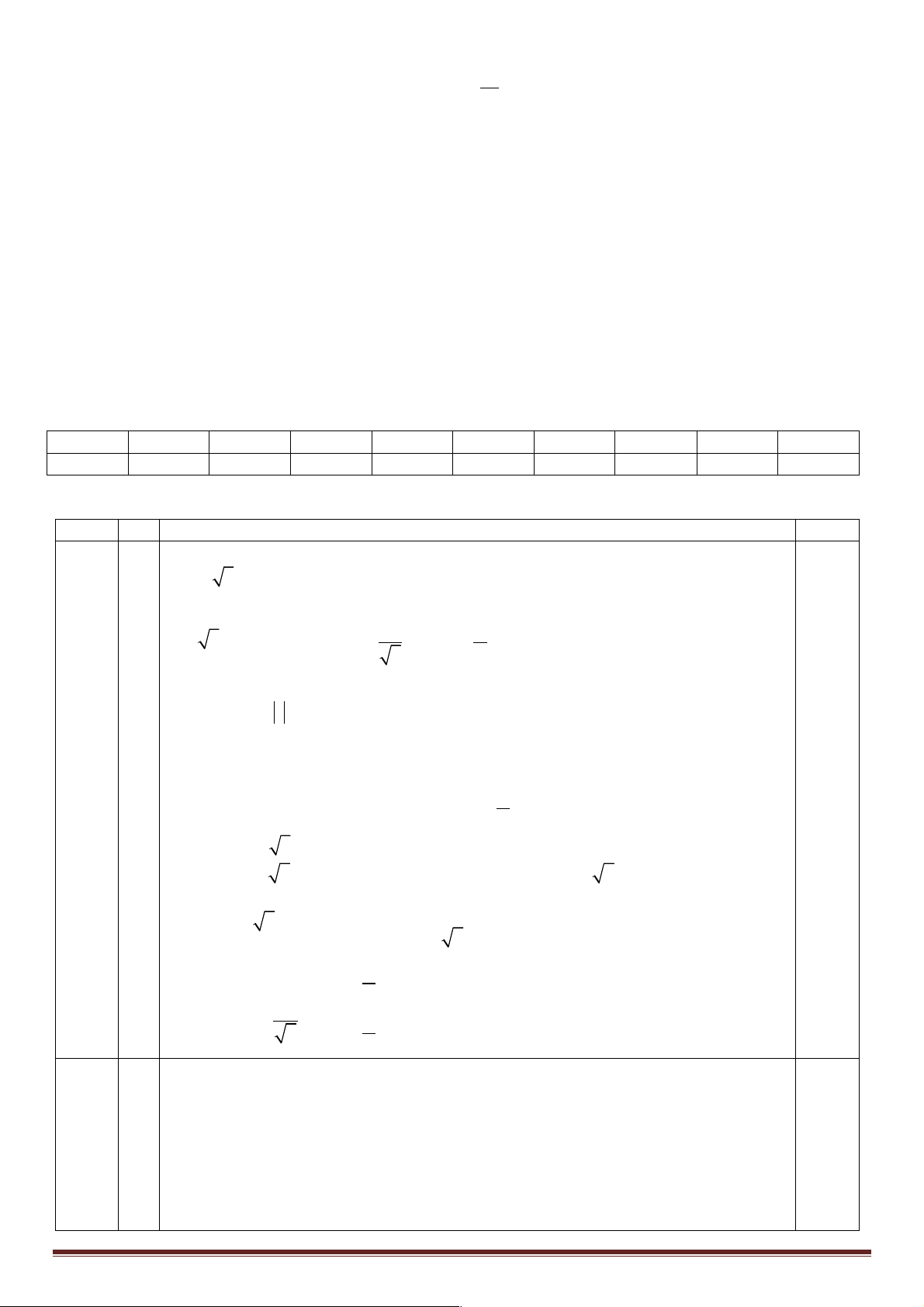
b) Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm của các tam giác
SAB , SAD , M là trung điểm của CD . Xác định thiết diện của chóp với mặt phẳng (IJM ).
Đáp án và thang điểm I. Trắc nghiệm Trang 6 1C 2D 3D 4D 5A 6A 7B 8D 9A 10D 11B 12B 13C 14C 15D 16C 17A 18B 19B 20B II. Tự luận Câu ý Nội dung đáp án Điểm
a) a) 3 + 3tanx = 0 3 € tan x = - 0,25 3 21 p (1,5đ) € x = - + kp;k Œ¢ 0,25 6 2
b) sin x = – sin x + 2 2
€ sin x + sin x - 2 = 0 u È = 1 Đặt 2 u sin x; u 1 u u 2 0 Í = £ fi + - = € 0,25 u Í = - 2(loai) Î p
€ u = 1 € x = + k2p;k Œ¢ 2 0,25 écos x = 0 2 2 sin x + 3 sin .
x cos x = 1 Û 3 sin .
x cos x - cos x = 0 Û ê
ë 3 sin x + cos x = 0 0,25 c) é p é p x = + kp;k Î! x = + kp;k Î ê ê ! 2 2 Û ê Û ê 1 ê p tan x =
êx = + kp;k ! êë 3 ê Î ë 6 0,25
a) Một bình đựng 5 quả cầu xanh và 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu
nhiên 3 quả cầu. Tính xác suất để được 3 quả cầu khác màu nhau.
Gọi A là biến cố lấy ra 3 quả cầu khác màu nhau. a 1 1 1 3
fi n(A)= C .C .C = 60;n W = C = 220 5 4 3 ( ) 0,5 12 0,25 fi P (A) 60 3 = = 220 11 0,25 æ 3 n ö
b) Tìm hệ số chứa x5 trong khai khai triển nhị thức 2 x - biết n thoả ç 3 ÷ è x ø 22 mãn 6 5 A = 10A n n b 1,0 Ta có : 0,25 n! 10n! 6 5 A = 10A Û = n n (n -6)! (n -5)! 1 10 10 0,25 Û = Û 1 =
Û n - 5 = 10 Û n = 15
(n -6)! (n -5)(n -6)! n - 5 æ 3 n ö
Xét số hạng thứ k + 1 trong khai triển của nhị thức 2 x - là : ç 3 ÷ è x ø 0,25 - Ê- 3 k k ˆ Á ˜ Á ˜ = - 3 k k k - k C x C x 15 ( )15 2 ( ) 30 5 3 15 Ëx Á ˜¯ Với số hạng chứa 5
x ta có: 30 - 5k = 5 € k = 5 fi hệ số của 5 x là: 5 5 - 3 C = 729729 15 0,25
c c) Chứng minh rằng với mọi nÎ N * thì 3
n + 2n chia hết cho 3. 0,5 Trang 7 Xét dãy số 3
U = n + 2n n Với n = 1: U = 3 3 M 1 3 3 0,25
Với n = k giả sử U = k + 2k 3
M ta cần chứng minh U
= k + 1 + 2 k + 1 3 M k+ 1 ( ) ( ) k
Thật vậy theo giả thiết quy nạp ta có: U = + + + = + (k )3 1 2 k 1 k 1 ( ) 3 2
= k + k + k + + k + = ( 3 k + k)+ ( 2 3 3 1 2 2 2 3 k + k)+ 3 3 M 3 0,25
Vậy: U = n + 2n 3 M n
a) Trong mặt phẳng tọa độ Oxy , cho đường thẳng d có phương trình ! 2x - 3y + 5 = 0 v = (1; 3 - ) d ' d và
. Viết phương trình đường thẳng là ảnh của qua
a phép tịnh tiếnT! . v Ta có : M (- 1 ) ;1 d Œ gọi M ( ¢ x ;¢ y )
¢ = Tr (M )fi M ¢ d Œ ¢ 23 v 0,5
Và M ¢= (- 1+ 1;1+ (- ) 3 )= (0;- 2) r d // ¢ d fi d c
¢ ó vectơ pháp tuyến là: n(2;- ) 3 fi d
¢ có phương trình: 2(x - 0)- 3(y + 2)= 0 € 2x - 3y - 6 = 0 0,5 Vậy d :
¢ 2x - 3y - 6 = 0
b) Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi I, J lần lượt là
trọng tâm của các tam giác SAB , SAD , M là trung điểm của CD . Xác định thiết
diện của chóp với mặt phẳng (IJM ). b S F J K G I O A B H P L N D C M
Gọi O là trung điểm AB , N là trung điểm của AD .
Gọi L = AM « ON ,G = SL « IJ , F = MG « SA fi MF Ã (IJM )
H = FI « SD, K = FJ « SB . Gọi O, N lần lượt là trung điểm của AB, AD 0,25 SI SJ 2 fi = =
fi IJ //ON fi ON //(IJM ) SN SO 3
Gọi P = CD « (IJM )fi MP //ON
Vậy thiết diện là hình ngũ giác MPKFH 0,25 Trang 8
SỞ GD&ĐT TUYÊN QUANG
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2018 - 2019
TRƯỜNG THPT SƠN DƯƠNG Môn: TOÁN 11
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Họ và tên:.............................................................Lớp:11B…
A.Phần trắc nghiệm: (Học sinh lựa chọn phương án trả lời rồi điền các chữ A, B, C, D vào bảng sau). 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Câu 1: Nghiệm của phương trình sin x = 0 là: p p
A. x = kp , k ΢ . B. x =
+ k2p , k ΢ . C. x = k2p , k ΢ . D. x = + kp , k ΢ . 2 2 1+ sin x
Câu 2: Điều kiện xác định của hàm số y = là: cos x p p p p A. x ¹
+ kp , k ΢ . B. x ¹ + kp , k ΢ . C. x ¹ + k , k Î ¢ .
D. x ¹ kp , k ΢ . 4 2 8 2
Câu 3: Nghiệm của phương trình sin 2x = sin x là: é x = k2p é x = k2p
A. x = k2p , k Î ¢ . B. ê p
2p , k Î ¢ . C. x = kp , k ΢ . D. ê 2p , k ΢ . êx = + k êx = k ë 3 3 ë 3 cot x
Câu 4: Tìm tập xác định của hàm số y = . cos x - 1 ìp ü ì ü
A. D = ° \í + k p 2 ,k p
Î ¢ ý. B. D = ° \ík ,k ΢ ý. î 2 þ î 4 þ C. D = ° { \ k p
2 ; k ΢ }. D. D = ° { \ p
k ,k ΢ }.
Câu 5: Nghiệm âm lớn nhất của phương trình cos x + sin 2x = 0 là: p p p A. x = - . B. x = - . C. x = - . D. x = p - . 12 6 3
Câu 6: Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 6 x + 6 sin cos x trên ! . Tính giá trị M + . n 1 5 1 3 A. . B. . C. . D. . 4 4 2 2 Câu 7: Tính tổng 0 1 2 3
S = C - C + C - C + ...+ (-1)k Ck ...+ ( 1 - )n n C . n n n n n n A. 2n S = -1. B. 2 .n S = C. n 1 S 2 - =
. D. S = 0. Câu 8: Với *
n Î N mệnh đề nào dưới đây sai ? n
A. P = n ( ! n ³ k ! 1 .
) B. A = (1 £ k £ n). n n (n - k)! k k! C. C = (0 £ k £ n). D. k
A = k !Ck (0 £ k £ n). n n!(n - k)! n n
Câu 9: Có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số khác nhau từ các chữ số 0,1, 2,3, 4,5? A. 36.
B. 46656. C. 600. D. 720.
Câu 10: Xét phép thử “Xếp 5 bạn nam và 5 bạn nữ theo đội hình hàng ngang sao cho nam nữ xen kẽ nhau”.
Khi đó số phần tử của không gian mẫu là: A. 10!. B. 86400.
C.14400.. D. 28800 1
Câu 11: Cho dãy số (Un) với Un =
. Khẳng định nào sau đây là sai? -n - 2 Trang 9 1 1 1 1 1
A. Năm số hạng đầu của dãy là : - ; - ; - ; - ; - . C. Là dãy số tăng. 3 4 5 6 7
B. Là dãy số bị chặn. D. Là dãy số giảm.
Câu 12: Khẳng định nào sau đây là sai? A. Dãy số 2 - , 1
- ,0,1, 2,... là một cấp số cộng: u = 2 - , d = 1. 1 B. Dãy số 2 3
2, 2 , 2 ,... là một cấp số cộng: u = 2, d = 2. 1
C. Dãy số 2, 2, 2, 2,… là cấp số cộng u = 2, d = 0. 1
D. Dãy số ( u ) với u = 2n + 3n không phải là một cấp số cộng. n n
Câu 13: Cho một cấp số cộng có u = 5;u = 13 - . Tìm d ? 1 7 A. d = 3. - B. d = 3. C. d = 6. D. d = 6. -
Câu 14: Xác định x để 3 số: 2 2 – ;
x x ; 2 + x lập thành một cấp số cộng? A. x = 2.
± B. x = ± 2. C. x = 1. ± D. x = 0. ! !
Câu 15: Trong mặt phẳng, phép tịnh tiến T! (M ) = M ' à
v T! ( N ) = N ' ( với v ¹ 0 ). Khi đó mệnh đề nào sau v v đây là sai ? !!!!!" !!!!" !!!!" !!!!!!" !!!!" !!!!!"
A. MM ' = NN ' . B. MN = M ' N '. C. MN ' = NM '. D. MM ' = NN '.
Câu 16: Cho phép vị tự V
. Mệnh đề nào sau đây đúng? (I;k) A. V
là phép đối xứng tâm I. B. V
biến tâm I thành chính nó. (I ) ;1 (I;k) C. V
là phép đồng dạng tỉ số đồng dạng là k. D. V
là phép quay tâm I góc quay 360 0. (I;k) (I;- )1
Câu 17: Ảnh của đường thẳng d : x - 2y +1 = 0 qua phép vị tự tâm O tỉ số k = 2 - là:
A. -x + 2y + 2 = 0. B. 2
- x + y + 2 = 0.
C. x - 2y + 2 = 0. D. 2
- x + y - 2 = 0.
Câu 18: Ảnh của đường tròn (C) ( x + )2 + ( y - )2 : 3
2 = 4 qua phép vị tự tâm O tỉ số k = 2 - là
A. (C ) ( x - )2 + ( y + )2 ' : 6 4 = 4.
B. (C ) ( x + )2 + ( y - )2 ' : 6 4 = 16.
C. (C ) ( x + )2 + ( y - )2 ' : 6 4 = 4.
D. (C ) ( x - )2 + ( y + )2 ' : 6 4 = 16.
Câu 19: Cho biết mệnh đề nào sau đây là sai?
A. Qua ba điểm không thẳng hàng xác định duy nhất một mặt phẳng.
B. Qua một đường thẳng và một điểm không thuộc nó xác định duy nhất một mặt phẳng.
C. Qua hai đường thẳng bất kỳ xác định duy nhất một mặt phẳng.
D. Qua hai đường thẳng cắt nhau xác định duy nhất một mặt phẳng.
Câu 20: Cho hình chóp S.ABCDE. Số mặt bên của hình chóp là: A. 3.
B. 4. C. 5. D. 6. B. Phần tự luận.
Câu 21(1,5 điểm). Giải các phương trình: a) 1+ 3 cot x = 0 ; b) 2
sin x - 2sin x = 3; c) 2
2sin x - 3 sin 2x = 2. Câu 22(2,0 điểm).
a) Một bình đựng 7 quả cầu xanh và 6 quả cầu đỏ và 5 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Tính xác
suất để được 3 quả cầu khác màu nhau. Trang 10 æ 2 n ö b) Tìm hệ số chứa 8
x trong khai khai triển nhị thức x - biết n thoả mãn: ç 3 4 11A = A 2 ÷ n n . è x ø
c) Chứng minh rằng với mọi n Î * N • thì 3 2
2n - 3n + n chia hết cho 6. Câu 23 (1,5 điểm). !
a) Trong mặt phẳng tọa độ Oxy , cho đường thẳng d có phương trình x + 2y - 3 = 0 và v = ( 1; - 2). Viết
phương trình đường thẳng d ' là ảnh của d qua phép tịnh tiếnT! . v
b) Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi M , N lần lượt là trọng tâm của các
tam giác SBC và SCD, K là trung điểm của AD. Xác định thiết diện của chóp với mặt phẳng (KMN ). Đáp án đề 2 I. Trắc nghiệm 1A 2B 3B 4D 5B 6B 7D 8C 9C 10D 11D 12B 13A 14B 15C 16B 17A 18D 19C 20C II. Tự luận Câu ý Nội dung đáp án Điểm
a) aCâu 21(1,5 điểm). Giải các phương trình: a) 1+ 3 cot x = 0 ; điều kiện: 0,25
x π kp;k Œ¢ 21 p (1,5đ) 1
1+ 3 cot x = 0 Û cot x = - Û x = - + kp;k Î ; ! 0,25 3 3 b) 2
sin x - 2sin x = 3;
Đặt t = sin x; t £ 1 tÈ = - 1 Ta có phương trình: 2 2
t - 2t = 3 € t - 2t - 3 = 0 € Í 0,25 tÍ = 3 Î p
fi sin x = - 1 € [ fi sin x = - 1 € x = - + 2kp;k Z Œ 0,25 2 c) 2
2sin x - 3 sin 2x = . 2 2 € x - x x = ( 2 2 x + x) 2 2 sin 3.2 sin cos 2 sin cos
€ - 2 3 sin x cos x = 2 cos x 0,25 È x = Í € x ( x + x) cos 0 2 cos 3 sin cos
= 0 € Í 3sin x + cosx = 0 Î È p È cos x = 0 x Í = + kp Í Í 2 € Í 1 € Í ; Œ 0,25 k Z ta Í n x = - Í p ÍÎ 3 x Í = + kp ÍÎ 6
a) Một bình đựng 7 quả cầu xanh và 6 quả cầu đỏ và 5 quả cầu vàng. Chọn ngẫu
nhiên 3 quả cầu. Tính xác suất để được 3 quả cầu khác màu nhau.
a Gọi A là biến cố lấy được 3 quả cầu cùng màu. 0,5 Ta có 0,25 Trang 11 1 1 1 3
n(A)= C .C .C = 210.n W = C = 816 7 6 5 ( ) 18 0,25 22 n(A) 210 35 fi P (A)= = = n( ) W 816 136 æ 2 n ö b) Tìm hệ số chứa 8
x trong khai khai triển nhị thức x - biết n thoả mãn: ç 2 ÷ è x ø 3 4 11A = A n n . b 1,0 Ta có : n! 11n! 3 4 11A = A Û = n n (n - 4)! (n -3)! 0,25 1 11 11 Û = Û 1 =
Û n - 3 = 11 Û n = 14
(n - 4)! (n -3)(n - 4)! n - 3 0,25 æ 2 n ö
Xét số hạng thứ k + 1 trong khai triển của nhị thức x - là : ç 2 ÷ è x ø Ê- ˆ - 2 k 14 Á ˜ Á ˜ = (- 2)k k k k 14- 3k C x C x 14 2 14 Ëx Á ˜¯ 0,25 Với số hạng chứa 8
x ta có: 14 - 3k = 8 € k = 2 fi hệ số của 8 x là: (- 2)2 2 C = 364 14 0,25
c c) Chứng minh rằng với mọi n Î * N • thì 3 2
2n - 3n + n chia hết cho 6. 0,5 Xét dãy số 3 2
U = 2n - 3n + n n Với n = 1: U = 0 6 M 1 3 2
Với n = k giả sử U = 2k - 3k + k 6 M ta cần chứng minh k 0,25 U = 2 + - + + + M + (k )3 1 3(k )2 1 k 1 6 k 1 ( )
Thật vậy theo giả thiết quy nạp ta có: 3 2 3 2 2 U
= 2 k + 1 - 3 k + 1 + k + 1 = 2k + 2.3. k + k + 2 - 3 k + 2k + 1 + k + 1 k+ 1 ( ) ( ) ( ) ( ) ( ) = ( 3 2
2k - 3k + k) 2 + 6k 6 M. 0,25 Vậy: 3 2
U = 2n - 3n + n 6 M n Câu 23 (1,5 điểm). Ï x Ô ¢= 1+ (- ) 1 = 0
Đường thẳng d đi qua điểm A(1;1 . G
) ọi Tr (A)= A (x ; y ) Ô ¢ ¢ ¢ fi Ì a v Ô y¢ Ô = 1+ 2 = 3 Ó 23 fi A ( ¢ 0;3 ) 0,5 Ï d Ô // ¢ d
Gọi Tr (d )= d Ô ¢fi Ì v A Ô ¢ d Œ ¢ Ô Ó r d
¢ có vectơ pháp tuyến là: n(1;2)fi d c ¢ ó phương trình: (x - 0)+ 2(y - )
3 = 0 € x + 2y - 6 = 0 0,5
b) Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi M , N lần
lượt là trọng tâm của các tam giác SBC và SCD, K là trung điểm của AD.
b Xác định thiết diện của chóp với mặt phẳng (KMN ). Trang 12 S F M J G N O C B H P L I D A K
Gọi O là trung điểm BC , I là trung điểm của CD . 0,25
Gọi L = CK « OI ,G = SL « MN , F = KG « SC fi KF Ã (KMN )
H = FN « SD, J = FM « SB . Gọi O, I lần lượt là trung điểm của BC,CD SN SM 2 fi = =
fi MN //OI fi ON //(KMN ) 0,25 SI SO 3
Gọi P = AB « (KMN )fi KP //OI
Vậy thiết diện là hình ngũ giác FHKPJ
SỞ GD&ĐT HẢI DƯƠNG
ĐỀ THI HỌC KÌ 1 – Năm học 2018-2019
TTGDNN-GDTX NAM SÁCH Môn TOÁN Lớp 11
Thời gian làm bài 90 phút Đề số 1
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . .lớp………………. . I.Trắc nghiệm :
Câu 1: Tập xác định của hàm số 1- 3cos x y = là sin x A. p
B. x ¹ k2p C. kp
D. x ¹ kp x ¹ + kp x ¹ 2 2
Câu 2: Giá trị đặc biệt nào sau đây là đúng p p
A. cos x ¹ 1 Û x ¹ + kp
B. cos x ¹ 0 Û x ¹ + kp 2 2 p p C. cos x ¹ 1
- Û x ¹ - + k2p
D. cos x ¹ 0 Û x ¹ + k2p 2 2
Câu 3: Gieo một con súc sắc 2 lần. Số phần tử của không gian mẫu là? A. 36 B. 12 C. 6 D. 18
Câu 4: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu
nhiên 3 quyển sách. Tính xác suất để 3 quyển được lấy ra đều là môn toán. 1 37 2 5 A. B. C. D. 21 42 7 42
Câu 5: Gieo một đồng tiền liên tiếp 3 lần. Tính xác suất của biến cố A: " kết qủa của 3 lần gieo là như nhau" Trang 13 1 A. P( ) A = 7 B. P( ) A = 3 C. P( ) A = 1 D. P( ) A = 4 8 8 2
Câu 6:Cho hình bình hành ABCD. Phép tịnh tiến T!!!" biến: DA A. B thành C. B. C thành A. C. C thành B. D. A thành D.
Câu 7: Cho các giả thiết sau, giả thiết nào sau đây kết luận đường thẳng d1 // (P)
A. d1 // d2 và d2 // (P) B. d1Ç(P) = Æ
C. d1 // d2 và d2Ì (P) D. d1 // (Q) và (Q) // (P)
Câu 8: Trong các mệnh đề sau, mệnh đề nào đúng:
A. Hai đường thẳng không cắt nhau và không song song thì chéo nhau.
B. Hai đường thẳng không song song thì chéo nhau.
C. Hai đường thẳng không có điểm chung thì chéo nhau.
D. Hai đường thẳng chéo nhau thì không có điểm chung. II. Tự luận :
Bài 1: (1 đ). Giải các phương trình sau: æ p ö a) 2
5sin x + cos x -1 = 0
b) 2sinç3x + ÷ -1 = 0 è 4 ø
Bài 2: (2 đ). Trong một hộp đựng 5 viên bi xanh và 4 viên bi đỏ. Lấy ngẫu nhiên đồng thời 3
viên bi. Tính xác suất để trong 3 viên bi lấy ra: a) Có 2 viên bi màu xanh
b) Có ít nhất một viên bi màu xanh. ®
Bài 3: (0,5 đ). Trong mặt phẳng Oxy cho điểm M (- ; 5 ) 2 , v = (- ) 1 ;
1 . Tìm tọa độ ảnh của điểm ®
M qua phép tịnh tiến v .
Bài 4: (2 đ). Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn là AD
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
b) Gọi M, N và P lần lượt là trung điểm của AB, SA và SD.
Chứng minh rằng: NP// (SBC)
Bài 5: (0.5đ) Khai triển nhị thức Newton ( x + y)5 2 .
--------------------Hết-------------------
SỞ GD&ĐT HẢI DƯƠNG
ĐÁP ÁN ĐỀ THI HỌC KÌ 1 năm 2018-2019
TTGDNN-GDTX NAM SÁCH Môn TOÁN Lớp 11
Thời gian làm bài 90 phút Đề số 1
I.Trắc nghiệm : ( mỗi câu trả lời đúng : 0,5 điểm ). 1 D 2 B 3 A 4 A 5 A 6 C 7 B 8 D II. Tự luận : Bài Ý Nội dung Điểm 1 1.0 a) 2 2
5sin x + cos x -1 = 0 Û 5(1- cos x) + cos x -1 = 0 écos x =1 0,5 éx = k2p 2 5cos x cos x 4 0 ê Û - + + = Û 4 Û ,(k Î Z ) cos ê ê x = -
ëx = ± arccos x + k2p ë 5 Trang 14 b) p
a) 2sin(3x + ) -1 = 0 (1) 4 0,5 é p p 3x + = + k2 1 p p ê Û x 4 6 (1) sin(3 + ) = Û ê (k Î ! ) 4 2 p p
ê3x + = p - + k2p ë 4 6 é p k2p x = - + ê 36 3 Û ê (k Î ! ) 7p k2p êx = + ë 36 3 2 2.0
a) Vì lấy ngẫu nhiên 3 viên bi trong túi có 9 viên bi nên số ptử của không
gian mẫu là: n(W ) = C3 = 84 0,25 9
Kí hiệu: A: “3 viên lấy ra có hai viên bi màu xanh”
Ta có: n(A) = C2 C1 . = 40 5 4 0,5 n A
Vậy xác suất của biến cố A là: 40 10 P ( A) ( ) = = = n(W ) 84 21 0,25
b) Kí hiệu: B: “3 viên lấy ra có ít nhất 1 viên bi màu xanh”
Ta có: B : “Cả 3 viên bi lấy ra đều màu đỏ” n A 1
n(B) = C3 Þ P(B) ( ) = = 4 W 21 0,5 n( )
Vậy xác suất của biến cố B là: 1 20
P (B) =1- P(B) =1- = 0,5 21 21 3 ®
Gọi M '(x'; y') là ảnh của điểm M(x; y) qua phép tịnh tiến v 0,5
ìx'= x + a ìx'= -5 -1 ìx'= -6 Theo BTTĐ, ta có: í Û í Û í Vậy M '(- ) 3 ; 6
îy'= y + b î y'= 2 +1 î y'= 3 4 2,0 a) S 0,25 N P A D M B C E
a) + (SAB) và (SCD) có điểm chung thứ nhất là S
+ Kéo dài AB và CD cắt nhau tại E ta có E là điểm chung thứ hai của 2 0,75 mp trên.
Vậy giao tuyến cần tìm là đường thẳng SE. Trang 15 b) Ta có NP//AD mà AD//BC nên NP//BC (2) Mà BC Ì (SBC) 1,0 Do đó NP//(SBC) 5 0.5
(x + 2y)5 = C x +C x .2y +C x 2y 5 5 5 ( )2 0 5 1 4 2 3 3 4 5 3 2 +C x (2y) 4 + C x (2y) 5 + C 2y 5 5 5 ( ) 5 4 3 2 2 3 4 5
= x +10x y + 40x y + 80x y + 80xy + 32y
SỞ GD&ĐT HẢI DƯƠNG
ĐỀ THI HỌC KÌ 1 – Năm học 2018-2019
TTGDNN-GDTX NAM SÁCH Môn TOÁN Lớp 11
Thời gian làm bài 90 phút Đề số 2
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . .lớp………………. .
I.Trắc nghiệm :
Câu 1: Tập xác định của hàm số 1- sin x y = là cos x p p p
A. x ¹ + k2p
B. x ¹ + kp
C. x ¹ - + k2p
D. x ¹ kp 2 2 2
Câu 2: Giá trị đặc biệt nào sau đây là đúng p p
A. cos x ¹ 1 Û x ¹ + kp B. cos x ¹ 1
- Û x ¹ - + k2p 2 2 p p
C. cos x ¹ 0 Û x ¹ + kp
D. cos x ¹ 0 Û x ¹ + k2p 2 2
Câu 3: Gieo một đồng tiền liên tiếp 2 lần. Số phần tử của không gian mẫu là? A. 2 B. 8 C. 4 D. 1
Câu 4: Một lớp học có 40 học sinh gồm 25 nam và 15 nữ. Chọn 3 học sinh tham gia vệ sinh
công cộng toàn trường, hỏi có bao nhiêu cách chọn 3 học sinh trong lớp? A. 455 B. 9880 C. 2300 D. 59280
Câu 5: Gieo một đồng tiền liên tiếp 3 lần. Tính xác suất của biến cố A: " có đúng 2 lần xuất hiện mặt sấp" 7 3 A. P( ) A = 1 B. P( ) A = 1 C. P( ) A = D. P( ) A = 8 2 4 8
Câu 6:Cho hình bình hành ABCD. Phép tịnh tiến T!!!" biến: DA A. B thành C. B. C thành A. C. A thành D. D. C thành B.
Câu 7: Xét các mệnh đề sau :
1. Hai đường thẳng không có điểm chung thì chéo nhau.
2. Hai đường thẳng không cắt nhau và không song song thì chéo nhau.
3. Hai đường thẳng chéo nhau thì không có điểm chung Mệnh đề nào đúng ? A. 1 và 2 đúng B. 1 và 3 đúng C. Chỉ 3 đúng
D. Cả 1, 2 và 3 đều đúng
Câu 8:Cho hai mặt phẳng (P) và (Q) song song với nhau. Mệnh đề nào sau đây sai:
A. Nếu đường thẳng a Ì (Q) thì a // (P) Trang 16
B. Mọi đường thẳng đi qua điểm A Î (P) và song song với (Q) đều nằm trong (P).
C. d Ì (P) và d' Ì (Q) thì d //d'.
D. Nếu đường thẳng D cắt (P) thì D cũng cắt (Q). II. Tự luận :
Bài 1: (1 đ). Giải các phương trình sau: æ p ö
a) 2sin2x – 3sinx + 1 = 0
b) 2sinç3x + ÷ -1 = 0 è 4 ø
Bài 2: (2,0 đ) Có 5 bông hoa hồng nhung, 7 bông hoa cúc vàng và 4 bông hoa hồng bạch.
Chọn ngẫu nhiên 3 bông hoa. Tính xác suất để 3 bông hoa được chọn là: a) Cùng một loại
b) Ít nhất có một bông hoa hồng nhung. ®
Bài 3 : (0,5đ). Trong mặt phẳng Oxy cho điểm M (- ; 5 ) 2 , v = (- ) 1 ;
1 . Tìm tọa độ ảnh của điểm ®
M qua phép tịnh tiến v .
Bài 4 : (2 đ). Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn là AD
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
b) Gọi M, N và P lần lượt là trung điểm của AB, SA và SD.
Chứng minh rằng: NP// (SBC)
Bài 5: (0,5đ) Khai triển nhị thức Newton ( x + y)5 2
--------------------Hết-------------------
SỞ GD&ĐT HẢI DƯƠNG
ĐÁP ÁN ĐỀ THI HỌC KÌ 1 –Năm 2018-2019
TTGDNN-GDTX NAM SÁCH Môn TOÁN Lớp 11
Thời gian làm bài 90 phút Đề số 2
I.Trắc nghiệm : ( mỗi câu trả lời đúng : 0,5 điểm ). 1 B 2 C 3 C 4 A 5 D 6 D 7 C 8 C II. Tự luận : Bài Ý Nội dung Điểm 1 1,0 Trang 17 a) Đặt t = sinx, đk 1 - £ t £ 1 ét = 1 (N) 0,5 PTTT: 2t2 – 3t + 1 = 0 Û ê 1 êt = (N) ë 2 p
*) Với t = 1 Û sin x =1Û x = + k2p ,k Î! 2 é p
x = + k2p ,kÎ ê ! *) Với t = 1 1 Û x 6 sin = Û ê 2 2 5p êx = + k2p ,kÎ! ë 6 p p
Vậy, PT trên có nghiệm : + k2p ,k Î! ; + k2p ,kÎ! và 2 6 5p + k2p,kÎ! . 6 b) p
a) 2sin(3x + ) -1 = 0 (1) 4 0,5 é p p 3x + = + k2 1 p p ê Û x 4 6 (1) sin(3 + ) = Û ê (k Î ! ) 4 2 p p
ê3x + = p - + k2p ë 4 6 é p k2p x = - + ê 36 3 Û ê (k Î ! ) 7p k2p êx = + ë 36 3 2 2.0
a) Chọn ngẫu nhiên ba bông hoa từ 5 bông hoa hồng nhung, 7 bông hoa
cúc vàng và 4 bông hoa hồng bạch là một tổ hợp chập 3 của 16 bông 0,25
hoa các loại. Khi đó không gian mẫu là: n( W ) = C3 = 560 16
Gọi A là biến cố ba bông hoa cùng một loại. Khi đó số khả năng thuận 0,5
lợi cho biến cố A là: n(A) = C3 + C3 + C3 = 49 5 7 4 Vậy n(A) 49 7 P(A) = = = 0,25 n(W ) 560 80
b) Gọi B là biến cố có ít nhất một bông hoa hồng nhung. Khi đó số khả
năng thuận lợi cho biến cố B là: n(B) = C3 + C2C1 + C C 1 2 = 395 0,5 5 5 11 5 11 Vậy n(B) 395 79 P(B) = = = 0,5 n(W ) 560 112 3 0,5 a) ®
Gọi M '(x'; y') là ảnh của điểm M(x; y) qua phép tịnh tiến v 0,5
ìx'= x + a ìx'= -5 -1 ìx'= -6 Theo BTTĐ, ta có: í Û í Û í Vậy M '(- ) 3 ; 6
îy'= y + b î y'= 2 +1 î y'= 3 4 2,0 Trang 18 a) S 0,25 N P 0,75 A D M B C E
a) + (SAB) và (SCD) có điểm chung thứ nhất là S
+ Kéo dài AB và CD cắt nhau tại E ta có E là điểm chung thứ hai của 2 mp trên.
Vậy giao tuyến cần tìm là đường thẳng SE. b) Ta có NP//AD mà AD//BC nên NP//BC (2) Mà BC Ì (SBC) 1,0 Do đó NP//(SBC) 5 0.5
(x + 2y)5 = C x +C x .2y +C x 2y 5 5 5 ( )2 0 5 1 4 2 3 3 4 5 3 2 4 5 0,25
+C x 2y + C x 2y + C 2y 5 ( ) 5 ( ) 5 ( ) 5 4 3 2 2 3 4 5
= x +10x y + 40x y + 80x y + 80xy + 32y 0,25 TRƯỜNG THPT NGUYỄN HUỆ
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KÌ 1 Tổ: Toán – Tin
Năm học 2018 – 2019
(Đề thi gồm có 3 trang) Môn thi: Toán 11
Thời gian: 90 phút ( không kể thời gian phát đề) Mã đề 1101
I. PHẦN TRẮC NGHIỆM (5.0 điểm): Chọn phương án đúng cho mỗi câu sau đây.
Câu 1. Tập xác định của hàm số y = tan x là: ìp ìp A. ü ü !
B. ! \ í + kp ,k ÎZ ý C. ! \{kp ,k ÎZ}
D. ! \ í + kp ,k ÎZ ý î 2 þ î 4 þ
Câu 2. Giả sử cần chọn hoặc là một học sinh nam khối 12 hoặc là một học sinh nữ khối 11 để làm
đại biểu trong hội đồng của một trường THPT. Hỏi có bao nhiêu cách chọn vị đại biểu này nếu
khối 12 có 81 học sinh nam và khối 11 có 72 học sinh nữ. A. 153 B. 81 C. 72 D. 5832 !
câu 3. Tọa độ điểm M ' ảnh của điểm M( 1; 2) qua phép tịnh tiến theo véctơ v(2;- ) 1 là: A. M’(3; -3) B. M’(1; -3) C. M’(3; 1)
D. M’( -3; 1)
Câu 4. Tất cả các nghiệm của phương trình sin x = 1 là: Trang 19 p p A. x =
+ k2p ,k ÎZ
B. x = kp ,k ÎZ C. x =
+ kp ,k ÎZ D. 2 2 p
x = - + k2p , k Î Z 2
Câu 5. Công thức nào dưới đây đúng? n(n + ) 1
A. P = n B. n p = C C. n P = A D. P = n n n n n n 2
Câu 6. Cho hình chóp S.ABCD và O là giao điểm của hai đường chéo AC với BD. Giao tuyến của
hai mặt phẳng (SAC) và (SBD) là: A. SO B. SA C. SB D. SC
Câu 7. Số các hạng tử trong khai triển của nhị thức niu tơn ( x + )7 2 3 là: A. 7 B. 8 C. 9 D. 10
Câu 8. Tất cả các nghiệm của phương trình 1 cos x = là: 2 p p p
A. x = ± + k2p ,k Î !
B. x = ± + k2p ,k Î ! C. x = ± + k2p ,k Î! D. 6 4 3 2p x = ± + k2,k Î ! 3
Câu 9. Có bao nhiêu vị trí tương đối giữa hai đường thẳng a và b trong không gian. A. 2 B. 3 C. 4 D. 5
Câu 10. Gieo một đồng tiền cân đối và đồng chất 4 lần. Số phần tử không gian mẫu của phép thử là: A. 4 B. 8 C. 16 D. 32
Câu 11. Tất cả các nghiệm của phương trình 3 sin x = là: 2 é p é 3 é p x = + k2p ê x = arcsin + k2p ê x = + k2p ê A. 3 ê , k Î ! B. 2 ê , k Î ! C. 6 ê , k Î ! D. Vô 2p ê 3 5p x = + k2p ê = p - + p ê = + p ê x arcsin k2 x k2 ë 3 êë 2 êë 6 nghiệm
Câu 12. Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điển các cạch SA, SB. Đường thẳng MN
song song với đường thẳng nào dưới đây: A. AC B. SC C. BC D. AB.
Câu 13. Tất cả các nghiệm của phương trình sin x + cos x = 2 là: p 3p p A. x = + k2p ,k Î! B. x =
+ k2p ,k Î! C. x = - + k2p ,k Î! D. Vô nghiệm 4 4 4
Câu 14. Gieo một con súc sắc cân đối đồng chất một lần. Xác suất để mặt 4 chấm xuất hiện là: A. 1 B. 1 C. 1 D. 1 2 4 3 6
Câu 15. Trong các dãy số dưới đây, dãy số nào là dãy số hữa hạn: A. 2, 4, 6, 8, 10.
B. 3, 5, 7, 9, 11,... C. -5, -2, 1, 4, 7, 10,… D. 2, 4, 8, 16, 32,…
Câu 16. Cho tập A = {1,2,3,4,5,6, }
7 số có 3 chữ số khác nhau được hình thành từ tập A là: A. 35 B. 5040 C. 210 D. 180 Trang 20 1+ cos x
Câu 17. Tập xác định của hàm số y = là: 1- sin x ìp ìp A. ü ü !
B. ! \ {kp ,k Î }
" C. ! \ í + kp ,k Î"ý
D. ! \ í + k2p ,k Î"ý î 2 þ î 2 þ
Câu 18. Cho dãy số (u n *
u = 2 - 2n + 3, n Î •
n ) có số hạng tổng quát
. Năm số hạng đầu của dãy số n (un) là: A. 3,3,6,9,12 B. 3,3,6,10,15 C. 3,3,6,11,25 D. 3,3,6,12,27 !
Câu 19. Ảnh của đường thẳng D : 2x - y + 3 = 0 qua phép tịnh tiến theo véctơ v(2;- ) 1 là đường
thẳng D ' có phương trình là:
A. 2x - y - 2 = 0
B. x + 2y + 3 = 0
C. 2x - y + 8 = 0
D. 2x + y + 6 = 0
Câu 20. Tập tất cả các nghiệm của phương trình 1 cos x = - là: 2 p p
A. x = ± + k2p ,k Î !
B. x = ± + k2p ,k Î ! 3 6 2p 5p C. x = ± + k2p ,k Î! D. x = ± + k2p ,k Î ! 3 6
Câu 21. Tất cả các nghiệm của phương trình 2
cos x - 3cos x + 2 = 0 là; éx = k2p
A. x = k2p ,k Î! B.
, k Î ! C. x = kp ,k Î! D. ê
ëx = ± arccos 2 + k2p éx = kp , k Î ! ê
ëx = arccos 2 + k2p
Câu 22. Một tổ có 6 bạn nam và 7 bạn nữ. Có bao nhiêu cách chọn 4 bạn trong tổ để phân công trực nhật? A. 50 B. 525 C. 715 D. 17160
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Lấy M, N lần lượt thuộc các đoạn SM SN 2 thẳng SA, SB sao cho =
= . Khẳng định nào sau đây đúng: SA SB 3
A. MN ! CD
B. MN ! (SAD)
C. MN ! AD D. MN ! (SBC)
Câu 24. Gọi M là tập hợp tất cả các số có 3 chữ số khác nhau được lập từ các số 1, 2, 3, 4, 5, 6.
Lấy ngẫu nhiên 3 số từ tập M. Xác suất để 3 số được lấy là 3 số chẵn: 1 29 29 87 A. B. C. D. 2 1428 238 119
Câu 25. Tập tất cả các nghiệm của phương trình 2 2 3
sin 2x - 2cos x + = 0 là: 4 p p p p
A. x = ± + k2p ,k Î !
B. x = ± + kp ,k Î ! C. x = ± + k2p ,k Î! D. x = ± + kp ,k Î! 6 6 3 3
II. PHẦN TỰ LUẬN ( 5.0 điểm).
Câu 26 (2.0 điểm). Giải các phương trình lượng giác sau. + a) 3 x cos x = b) 2
2sin x - 3sin x +1 = 5 cos 2 0 c) = 2cos x 2 3 + 2 tan x
Câu 27 (1.5 điểm) Trang 21
a) Một hộp đựng 6 viên bi trắng và 8 viên bi vàng. Lấy ngẫu nhiên cùng lúc 5 viên bi từ hộp. Tính
xác suất để 5 viên bi được lấy có đủ cả 2 màu. 6
b) Tìm hệ số của số hạng chứa 6 æ ö
x trong khai triển nhị thức 2 1 2x - . ç ÷ è x ø
Câu 28 (1.5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Gọi M là điểm nằm
trong mặt phẳng (SCD).
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (ABM).
………………Hết……………
Họ và tên thí sinh:……………………………………………………. SBD:…………………
Chữ kí giám thị 1:………………………………….. Chữ kí giám thị 2:…………………………….
TRƯỜNG THPT NGUYỄN HUỆ
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KÌ 1 Tổ: Toán – Tin
Năm học 2018 – 2019
( Đề thi gồm có 3 trang) Môn thi: Toán 11
Thời gian: 90 phút ( không kể thời gian phát đề) Mã đề 1102
I. PHẦN TRẮC NGHIỆM (5.0 điểm): Chọn phương án đúng cho mỗi câu sau đây.
Câu 1. Trong các dãy số dưới đây, dãy số nào là dãy số vô hạn. A. 2, 4, 6, 8, 10. B. 3, 5, 7, 9, 11.
C. -5, -2, 1, 4, 7, 10,… D. 2, 4, 8, 16, 32.
Câu 2. Gieo một đồng tiền cân đối và đồng chất 2 lần. Xác suất để số mặt xuất hiện trong 2 lần gieo như nhau là: 1 1 1 3 A. B. C. D. 2 4 3 4
Câu 3. Tất cả các nghiệm của phương trình sin x - cos x = 2 là: p 3p 3p A. x = + k2p ,k Î! B. x =
+ k2p ,k Î! C. x = -
+ k2p ,k Î! D. Vô nghiệm 4 4 4
Câu 4. Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điển các cạch SA, SC. Đường thẳng MN
song song với đường thẳng nào dưới đây: A. AC B. SC C. BC D. AB.
Câu 5. Tập xác định của hàm số y = cot x là: ìp A. ü !
B. ! \ í + kp ,k ÎZ ý C. ! \{kp ,k ÎZ}
D. ! \ {k2p ,k ÎZ} î 2 þ
Câu 6. Giả sử cần chọn hoặc là một học sinh nam khối 12 hoặc là một học sinh nữ khối 11 để làm
đại biểu trong hội đồng của một trường THPT. Hỏi có bao nhiêu cách chọn vị đại biểu này nếu
khối 12 có 61 học sinh nam và khối 11 có 72 học sinh nữ. A. 153 B. 4392 C. 72 D. 133 !
Câu 7. Tọa độ điểm M’ là ảnh của điểm M( 1; -2) qua phép tịnh tiến theo véctơ v(2;- ) 1 là: A. M’(3; -3) B. M’(1; -3) C. M’(3; 1)
D. M’( -3; 1)
Câu 8. Tất cả các nghiệm của phương trình cos x = 1 là: Trang 22 p p A. x =
+ k2p ,k ÎZ
B. x = p + k2p ,k Î Z C. x = k2p ,k ÎZ D. x =
+ kp ,k ÎZ 2 2
Câu 9. Cho n là số nguyên dương. P, A, C kí hiệu là hoán vị, chỉnh hợp, tổ hợp. Công thức nào dưới đây đúng? k A k A n(n + ) 1 A. k n C = B. n p = C C. k n C = D. P = n k ! n n n k n 2
Câu 10. Cho hình chóp S.ABCD và O là giao điểm của hai đường chéo AC với BD, I là giao điểm
của AD và BC. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là: A. SO B. SA C. SI D. SC
Câu 11. Số các hạng tử trong khai triển của nhị thức niu tơn ( x - )9 2 3 là: A. 7 B. 8 C. 9 D. 10 3
Câu 12. Tất cả các nghiệm của phương trình cos x = - là: 2 p p p A. 5 x = ±
+ k2p ,k Î ! B. x = ± + k2p ,k Î! C. x = ± + k2p ,k Î! D. 6 6 3 2p x = ± + k2,k Î ! 3
Câu 13. Có bao nhiêu vị trí tương đối giữa hai mặt phẳng (a ) và (b ) trong không gian. A. 2 B. 3 C. 4 D. 5
Câu 14. Gieo một con súc sắc cân đối và đồng chất 3 lần. Số phần tử không gian mẫu của phép thử là: A. 6 B. 18 C. 36 D. 216
Câu 15. Tất cả các nghiệm của phương trình 3 cos x = là: 2 é p é 3 é p x = + k2p ê x = arccos + k2p ê x = + k2p ê A. 3 ê , k Î ! B. 2 ê , k Î ! C. 6 ê , k Î ! D. Vô p ê 3 p x = - + k2p ê = - + p ê = - + p ê x arccos k2 x k2 ë 3 êë 2 êë 6 nghiệm
Câu 16. Tập tất cả các nghiệm của phương trình 2
sin x - 3sin x + 2 = 0 là; éx = k2p p p A. x = + kp ,k Î!
B. êx = arcsin 2 + k2p
, k Î ! C. x =
+ k2p ,k Î! D. Vô 2 ê 2
êx = p - arcsin 2 + k2p ë nghiệm
Câu 17. Một tổ gồm có 8 bạn nam và 7 bạn nữ. Có bao nhiêu cách chọn 4 bạn trong tổ để phân công trực nhật? A. 105 B. 1365 C. 2450 D. 32760 !
Câu 18. Ảnh của đường thẳng D : 2x - y + 3 = 0 qua phép tịnh tiến theo véctơ v(2 ) ;1 là đường thẳng D ' có phương trình là:
A. 2x - y + 6 = 0
B. x + 2y = 0
C. 2x - y = 0
D. 2x + y + 6 = 0
Câu 19. Tập tất cả các nghiệm của phương trình 1 sin x = là: 2 Trang 23 é p é p x = + k2p ê x = + k2p ê A. 3 ê , k Î ! B. 6 ê , k Î ! 2p ê 5p x = + k2p ê = + p ê x k2 ë 3 êë 6 p p
C. x = ± + k2p ,k Î !
D. x = ± + k2p ,k Î ! 3 6
Câu 20. Cho tập A = {1,2,3,4,5,6,7, }
8 có bao nhiêu số có 3 chữ số khác nhau được hình thành từ tập A ? A. 336 B. 56 C. 210 D. 180 1+ sin x
Câu 21. Tập xác định của hàm số y = là: 1+ cos x ìp A. ü
D = ! B. ! \ {k2p ,k Î }
" C. ! \ í + kp ,k Î"ý D. ! \{p + k2p ,k Î } " î 2 þ
Câu 22. Cho dãy số (u n *
u = 3 - 5n + 3, n Î •
n ) có số hạng tổng quát
. Năm số hạng đầu của dãy số n (un) là: A. 1,2,15,64,215 B. 1,2,15,64,221 C. 1,2,15,64,245
D. 1,2,15,64,231
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Lấy M, N lần lượt thuộc các đoạn
thẳng SA, SB sao cho SM SN 2 =
= . Khẳng định nào sau đây đúng: SA SB 3
A. MN ! BC
B. MN ! (SCD)
C. MN ! AD D. MN ! (SAD)
Câu 24. Gọi M là tập hợp tất cả các số có 3 chữ số khác nhau được lập từ các số 1, 2, 3, 4, 5, 6, 7.
Lấy ngẫu nhiên 3 số từ tập M. Xác suất để 3 số lấy ra là 3 số lẻ: 1003 4 29 895 A. B. C. D. 5434 7 238 4563
Câu 25. Tập tất cả các nghiệm của phương trình 2 2 3
sin 2x - 2sin x + = 0 là: 4 p p p p
A. x = ± + k2p ,k Î !
B. x = ± + kp ,k Î ! C. x = ± + k2p ,k Î! D. x = ± + kp ,k Î! 6 6 3 3
II. PHẦN TỰ LUẬN ( 5.0 điểm).
Câu 26 (2.0 điểm). Giải các phương trình lượng giác sau. 2 - x a) sin x = b) 2
2cos x - 3cos x +1 = 5 cos 2 0 c) = 2sin x 2 3 + 2cot x Câu 27 (1.5 điểm)
a) Một tổ gồm có 7 bạn nam và 8 bạn nữ. Lấy ngẫu nhiên cùng lúc 4 bạn. Tính xác suất để 4 bạn
được lấy có cả nam và nữ. 9
b) Tìm hệ số của số hạng chứa 6 æ ö
x trong khai triển nhị thức 2 2 x - . ç ÷ è x ø
Câu 28 (1.5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm nằm
trong mặt phẳng (SCD).
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (ABM).
……………………………Hết…………………… Trang 24
ĐÁP ÁN VÀ THANG ĐIỂM Mã đề 1101 I. TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 Đ.án B A C A C A B C C C D D A Câu 14 15 16 17 18 19 20 21 22 23 24 25 Đ.án D A C D C A C A C A C B II. TỰ LUẬN Câu Đáp án Thang điểm 3 p 0.25 cos x = Û cos x = cos a 2 6 p x = ± + k2p ,k Î! 0.25 6 ésin x = 1 0.25 2
2sin x 3sin x 1 0 ê - + = Û 1 êsin x = ë 2 b é p x = + k2p ê 2 ê p ê 0.25
Û x = + k2p ,k Î! ê 6 ê 5p ê x = + k2p êë 6 1 ì p x ¹ + kp ìcos x 0 ï ¹ ï 2 Đk í Û í , k Î ! 3 î + 2 tan x ¹ 0 æ 3 ö ïx ¹ acr tan - + kp ç ÷ ïî è 2 ø Pt 2 2 Û + x - x = x ( + x) 2 2 5 cos sin 2cos 3 2 tan
Û 5 + cos x - sin x = 6cos x + 4sin x c 2 2
écos x - sin x = 5 2 2
Û cos x - 6cos x + 9 = sin x + 4sin x + 4 Û (cos x - 3) = (sin x + 2) Û ê
ëcos x + sin x = 1 é p æ p ö æ p ö 2 x = + k2p 2 cos x 1 cos x ê Û - = Û - = Û 2 , k Î ç ÷ ç ÷ ! è 4 ø è 4 ø 2 ê ëx = k2p
Đối chiếu ĐK suy ra tập nghiệm pt là x = k2p ,k Î!
Số phần tử của không gian mẫu là (W) 5 = C = 2002 0.25 14 Trang 25
Gọi A là biến cố lấy ra 5 viên bi có đủ cả 2 màu, khi đó biến cố A lấy ra 5 viên bi 0.25 a
cùng màu nên n( A) 5 5 = C + C = 62 8 6
Xác suất cần tìm là P( A) = - P( A) 62 970 1 = 1- = 0.25 2. 2002 1001 k 6-k 0.25 æ 1 -
Áp dụng công thức tổng quát ta có ö 2 = 2 - . 1 k k k k - . - k C x C x 6 ( 2 ) 6 ç ÷ 6 ( ) 12 3 è x ø
Theo bài ra 12 - 3k = 6 Û k = 2 0.25
Vậy hệ số của số hạng chứa 6 x là C .2 . 1 - = 240 6 ( )2 2 4 0.25 S N M A D O B C
Ta có S Î(SAC) Ç (SBD) (1) 0.25 O ì Î AC Ì ï (SAC) 0.25 a
Gọi O = AC Ç BD suy ra í
Þ O Î(SAC) Ç (SBD) (2) 3. O ï Î BD Ì î (SBD)
Từ (1) và (2) suy ra SO = (SAC) Ç (SBD) 0.25
Chọn mp(SCD) chứa đường thẳng SD. Ta có M Î( ABM ) Ç (SCD) (1) 0.25
Do AB ! CD suy ra giao tuyến của hai mặt phẳng (ABM) và (SCD) là đường thẳng 0.25 b
d đi qua M song song với CD trong mp(SCD)
Gọi N = d Ç SD suy ra N = SD Ç ( ABM ) 0.25 Trang 26 Mã đề 1102 I. TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 Đ.án C A B A C D A C A C D A B Câu 14 15 16 17 18 19 20 21 22 23 24 25 Đ.án D D C B C B A D B B A D II. TỰ LUẬN Câu Đáp án Thang điểm 2 p 0.25 sin x = Û sin x = sin a 2 4 é p x = + k2p ê 4 ê , k Î ! 0.25 3p êx = + k2p êë 4 écos x = 1 0.25 2
2cos x 3cos x 1 0 ê - + = Û 1 êcos x = ë 2 b éx = k2p ê Û p , k Î ! êx = ± + k2p ë 3 0.25 1 ìx ¹ kp sin ì x ¹ 0 ï Đk í Û í æ 3 ö , k Î ! 3 î + 2cot x ¹ 0 x ¹ acr cot - + kp ï ç ÷ î è 2 ø 0.25 Pt 2 2 Û + x - x = x ( + x) Û - ( 2 2 5 cos sin 2cos 3 2 tan 5
cos x - sin x) = 2sin x(3 + 2cot x) 2 2 c
5 - cos x + sin x = 6sin x + 4cos x 2 2
ésin x - cos x = 5 2 2
Û sin x - 6sin x + 9 = cos x + 4cos x + 4 Û (sin x - 3) = (cos x + 2) Û ê
ësin x + cos x = 1 0.25 é p æ p ö æ p ö 2 x = + k2p 2 cos x 1 cos x ê Û - = Û - = Û ç ÷ ç ÷ 2 , k Î ! 0.25 è 4 ø è 4 ø 2 ê ëx = k2p p
Đối chiếu ĐK suy ra tập nghiệm pt là x = + k2p ,k Î! o.25 2
Số phần tử của không gian mẫu là (W) 4 = C = 1365 0.25 15
Gọi A là biến cố lấy ra 4 bạn có cả nam và nữ, khi đó biến cố A lấy ra 4 bạn cùng 0.25
a giới nên n(A) 4 4 = C + C = 105 8 7 Trang 27
Xác suất cần tìm là P( A) = - P( A) 105 12 1 = 1- = 0.25 1365 13 2. k 9-k 0.25 æ 2 - ö = . 2 k k k - . - k C x C x 9 ( 2 ) ç ÷ 9 ( ) 18 3
b Áp dụng công thức tổng quát ta có è x ø
Theo bài ra 18 - 3k = 6 Û k = 4 0.25
Vậy hệ số của số hạng chứa 6 x là C . 2 - = 2016 9 ( )4 4 0.25 S N M A D O B C
Ta có S Î(SAC) Ç (SBD) (1) 0.25 O ì Î AC Ì ï (SAC) 0.25
a Gọi O = AC Ç BD suy ra í
Þ O Î(SAC) Ç (SBD) (2) 3. O ï Î BD Ì î (SBD)
Từ (1) và (2) suy ra SO = (SAC) Ç (SBD) 0.25
Chọn mp(SCD) chứa đường thẳng SD. Ta có M Î( ABM ) Ç (SCD) (1) 0.25
Do AB ! CD suy ra giao tuyến của hai mặt phẳng (ABM) và (SCD) là đường thẳng 0.25
b d đi qua M song song với CD trong mp(SCD)
Gọi N = d Ç SD suy ra N = SD Ç ( ABM ) 0.25
Các đồng chí chấm theo thang điểm đáp án. Học sinh ko vẽ đề ko chấm bài hình.
Học sinh làm phương pháp khác đúng cho điểm tối đa.
Xem lại đáp án có sai sót nữa ko. Trước khi chấm. Trang 28
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KIỂM TRA HỌC KỲ I NĂM HỌC 2018 - 2019
TRƯỜNG THPT QUANG TRUNG - ĐỐNG ĐA
MÔN: TOÁN – LỚP 11
___________________________________________________
(Thời gian làm bài 90 phút)
________________________________
Họ và tên ............................................................................................................................................. Phòng thi .................................................................. MÃ ĐỀ 001
Lớp ................................................................................................................................................................... Số thứ tự ........................................................................
I. PHẦN TRẮC NGHIỆM (7 điểm)
(Thời gian làm bài 63 phút) ĐIỂM BÀI LÀM
(Số câu đúng ....................... / ......................)
Số thứ tự câu trả lời trong bảng dưới đây ứng với số thứ tự câu trắc nghiệm trong đề.
Đối với mỗi câu trắc nghiệm, học sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng. 1. ; / = ~ 6. ; / = ~ 11. ; / ~ 16. ; / = ~ 21. ; / = ~ 26. ; / = ~ 31. ; / = ~ 2. ; / = ~ 7. ; / = ~ 12. ; / = ~ 17. ; / = ~ 22. ; / = ~ 27. ; / = ~ 32. ; / = ~ 3. ; / = ~ 8. ; / = ~ 13. ; / = ~ 18. ; / = ~ 23. ; / = ~ 28. ; / = ~ 33. ; / = ~ 4. ; / = ~ 9. ; / = ~ 14. ; / = ~ 19. ; / = ~ 24. ; / = ~ 29. ; / = ~ 34. ; / = ~ 5. ; / = ~ 10. ; / = ~ 15. ; / = ~ 20. ; / = ~ 25. ; / = ~ 30. ; / = ~ 35. ; / = ~
CÂU HỎI TRẮC NGHIỆM
Câu 1: Trong mặt phẳng tọa độ Oxy , cho 2 điểm A(1;- ) 6 , B (-1; )
4 . Gọi C, D lần lượt là ảnh của ,
A B qua phép tịnh tiến ! theo vectơ v(5; )
1 . Khẳng định nào trong các khẳng định sau đúng?
A. ABDC là hình thoi
B. ABCD là hình bình hành C. ABDC là hình chữ nhật D. , A ,
B C, D thẳng hàng
Câu 2: Một đa giác đều có số đường chéo gấp đôi số cạnh. Hỏi đa giác đó có bao nhiêu cạnh? A. 6 B. 7 C. 5 D. 8
Câu 3: Có tất cả 120 cách chọn 3 học sinh từ một nhóm có n học sinh. Số n là nghiệm của phương trình nào sau đây?
A. n(n - ) 1 (n - ) 2 = 240
B. n(n - ) 1 (n - ) 2 = 360
C. n(n - ) 1 (n - ) 2 = 120
D. n(n - ) 1 (n - ) 2 = 720
Câu 4: Số hạng không phụ thuộc vào x trong khai triển ( - x)18 2 2 x là: A. 13 13 -2 C 12 12 -2 C 12 6 2 C 13 13 2 C 18 B. 18 C. 18 D. 18
Câu 5: Cho hình chóp .
S ABCD , có đáy ABCD là hình bình hành. Gọi M là trung điểm của BC và I là điểm thuộc miền
trong của tam giác DSAD . Thiết diện của hình chóp .
S ABCD khi cắt bởi mặt phẳng (IMC) là: A. Tam giác B. Hình thang C. Ngũ giác D. Hình bình hành
Câu 6: Cho hình lăng trụ tam giác .
ABC A' B 'C ' . Gọi M là trung điểm của A' B ' và đường thẳng d là giao tuyến của hai
mặt phẳng (CMC )' và (ABB ' A )' . Khẳng định nào sau đây sai?
A. d Ì (CC 'M )
B. B 'C Ç d
C. B 'C / / (AMC )'
D. d / / (ACC )'
Câu 7: Hệ số của số hạng chứa 7
x trong khai triển ( x - )10 3 2 là: 4 A. 3 54C 3 -27C 2 -144C 7 -54C 10 B. 10 C. 10 D. 10
Câu 8: Cho tam giác DABC đều tâm O . Có bao nhiêu phép quay tâm O góc a , 0 < a £ 2p biến DABC thành chính nó? A. 2 B. 3 C. 4 D. 1
Câu 9: Có 5 cuốn sách Văn khác nhau và 7 cuốn sách Toán khác nhau. Có bao nhiêu cách xếp các cuốn sách lên một kệ dài
của giá sách sao cho các cuốn sách Văn phải xếp cạnh nhau? A. 7.5!.7! B. 12! C. 2.5!.7! D. 5!.8!
Câu 10: Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : x + y - 2 = 0 . Phép dời hình có được bằng cách thực hiện liên !
tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ v(3; )
2 biến đường thẳng d thành đường thẳng nào cho dưới đây?
A. x + y + 2 = 0
B. x + y - 3 = 0
C. 3x + 3y - 2 = 0
D. x - y - 7 = 0
Câu 11: Có 40 thí sinh, trong đó có A và B, được xếp vào một phòng thi có 20 bàn, mỗi bàn có đủ chỗ cho hai thí sinh.
Tính xác suất để hai thí sinh A và B cùng ngồi trên cùng một bàn. A. 323 B. 323 C. 1 D. 1 390 780 78 39 Trang 29
Câu 12: Gieo một súc sắc cân đối và đồng chất liên tiếp hai lần. Xác suất để hiệu số chấm xuất hiện trong hai lần gieo là số chia hết cho 3 là: A. 1 B. 11 C. 5 D. 1 4 36 18 3
Câu 13: Trong măt phẳng tọa độ Oxy , cho đường thẳng d : 2x + y - 3 = 0 và số thực k ¹ 1. Phép vị tự tâm I (4;- ) 5 tỉ số k
biến d thành đường thẳng nào cho dưới đây?
A. 2x + y + 4 = 0
B. 2x - y - 3 = 0
C. 2x + y - 5 = 0
D. 2x + y - 3 = 0
Câu 14: Phương trình nào cho dưới đây tương đương với phương trình 2 2
sin x - cos x -1 = 0 ? A. cos 2x =1 B. cos 2x = -1 C. 2 2cos x -1 = 0 D. 2 (sin x - cos ) x = 1
Câu 15: Nghiệm của phương trình 3tan (x p + - = (0;p) 3) 1 0 trên khoảng là: A. x p = - B. x p = C. Đáp án khác D. 5 x p = 6 6 6
Câu 16: Cho bốn điểm , A ,
B C, D không cùng nằm trên một mặt phẳng. Gọi M, N lần lượt là trung điểm của , AD AC , trên
cạnh BC lấy điểm K sao cho 3KB = CK . Gọi I là giao điểm của BD với mp(MNK) . Khẳng định nào sau đây đúng?
A. KI song song với AM B. MN = 2IK
C. MI song song với KN D. DI = 2BI
Câu 17: Một hộp có 90 bóng đèn loại I và 10 bóng loại II. Chọn ngẫu nhiên 2 bóng trong hộp để kiểm tra chất lượng. Xác
suất để chọn được ít nhất 1 bóng loại I là: A. 821 B. 89 C. 109 D. Đáp án khác 990 110 110
Câu 18: Trong mặt phẳng tọa độ Oxy , phép vị tự tâm I (2; )
3 tỉ số k = -3 biến điểm M (-3; )
2 thành M ' có tọa độ là: A. (-13; ) 0 B. (17; ) 6 C. (17; ) 0 D. (-13; ) 6
Câu Phương trình sin x + 3cos x =1 có tập nghiệm {a + k2p, b + k2p; k Î } ! , với a, b Î( p - ;p ) . Khi đó a.b bằng: 19: 2 2 2 A. p 2 B. p - C. p - D. p - 6 18 2 12 Câu 20: Cho 2 3 2019 2019 S = 4C - 8C + ... - 2 C
. Giá trị của S là: 2019 2019 2019 A. -4040 B. 2017 C. 4036 D. 4038
Câu 21: Tìm tổng các nghiệm của phương trình 3cos x - sin 2x = 0 trên khoảng [0;p] là: A. p B. 3p C. p D. 0 2 2
Câu 22: Số nghiệm của phương trình 2sin (x p + + = [0;p] 4) 1 0 trên đoạn là: A. 0 B. 2 C. 3 D. 1
Câu 23: Xét hàm số y = sin x trên đoạn [ p - ]
;0 . Khẳng định nào sau đây đúng về hàm số đã cho? p p
A. Hàm số đồng biến trên các khoảng ( p - ;- (-2 );0 2) và p p
B. Hàm số đồng biến trên khoảng ( p - ;- (-2 );0
2) và nghịch biến trên khoảng p p
C. Hàm số nghịch biến trên khoảng ( p - ;- (-2 );0
2) và đồng biến trên khoảng p p
D. Hàm số nghịch biến trên các khoảng ( p - ;- (-2 );0 2) và
Câu 24: Có 5 học sinh nam và 4 học sinh nữ. Hỏi có bao nhiêu cách chọn 4 bạn sao cho trong đó luôn có học sinh nam và học sinh nữ? A. 80 B. 126 C. 60 D. 120
Câu 25: Một hộp chứa 10 quả cầu đỏ được đánh số từ 1 đến 10 và 20 quả cầu đen được đánh số từ 1 đến 20. Lấy ngẫu
nhiên 1 quả cầu từ trong hộp. Xác suất để chọn được quả cầu mầu đen hoặc ghi số chẵn là: A. 1 B. 5 C. 2 D. Đáp án khác 6 6 3
Câu 26: Cho hàm số y = x .sin 2x . Phát biểu nào sau đây là đúng về hàm số đã cho?
A. Hàm số đã cho có tập xác định là ! \ { } 0
B. Đồ thị hàm số đã cho có tâm đối xứng
C. Đồ thị hàm số đã cho có trục xứng
D. Hàm số có tập giá trị là [-1; ] 1 Trang 30
Câu 27: Gọi m giá trị nhỏ nhất của hàm số y = 3 - 2cos x + 2sin x . Khi đó: A. m = -5 B. m = 3 - 2 C. m =1 D. m = 3 + 2
Câu 28: Hai đường thẳng ,
a b nằm trong mp (a) . Hai đường thẳng a ', b' nằm trong mp (b) . Khẳng định nào sau đây đúng?
A. Nếu (a) // (b) thì a // a ' và b // b'
B. Nếu a Ç b và a // a ', b // b' thì (a)// (b)
C. Nếu a // b và a '// b' thì (a)// (b)
D. Nếu a // a ' và b // b' thì (a)// (b)
Câu 29: Tập xác định của hàm số cot x y = là: 1- sin x
A. ! \ {p + kp, kp; k Î"
! \ {p + k2p; k Î"
! \ {p + k2p, kp; k Î" ! \ {kp ; k Î" 2 } 2 } 2 } 2 } B. C. D.
Câu 30: Có bao nhiêu giá trị nguyên của tham số m để phương trình 6sin xcos x - m(cos2x + ) 2 = 0 có nghiệm? A. 5 B. 11 C. Vô số D. 7
Câu 31: Cho hai đường thẳng chéo nhau a và b . Trên đường thẳng a lấy hai điểm ,
A B và trên đường thẳng b lấy hai
điểm C, D . Khẳng định nào sau đây đúng khi nói về hai đường thẳng AD và BC ? A. Song song B. Chéo nhau
C. Song song hoặc cắt nhau D. Cắt nhau
Câu 32: Một hộp đựng 9 thẻ được đánh số từ 1 đến 9. Rút ngẫu nhiên hai thẻ từ trong hộp và nhân hai số ghi trên hai thẻ
với nhau. Xác suất để tích của hai số ghi trên hai thẻ là một số lẻ là: A. 3 B. 1 C. 5 D. 7 18 9 18 18
Câu 33: Trong mặt phẳng Oxy , cho điểm A(-2018; )
2019 . Phép quay tâm O góc quay 0
90 biến điểm A thành điểm A' có tọa độ là: A. (2019; ) 2018 B. (-2018; ) 2019 C. (-2019;- ) 2018 D. (2019;- ) 2018
Câu 34: Trong mặt phẳng tọa độ Oxy , cho 3 điểm I (4;- ) 2 , A(-3; ) 5 , B (7;- )
5 và số thực k ¹ 1. Phép vị tự tâm I tỷ số k
biến điểm A thành B . Khi đó giá trị của k là: A. 3 k = B. 7 k = - C. 3 k = - D. 7 k = 7 3 7 3
Câu 35: Cho các số 0, 1, 2, 3, 4, 5, 6. Số các số tự nhiên gồm 5 chữ số lấy từ 7 chữ số trên sao cho chữ số đầu tiên bằng 3 là: A. 4 A 7 4 P 6 B. 4 C. 7 D. 4 ----- Hết ----- Trang 31
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KIỂM TRA HỌC KỲ I NĂM HỌC 2018 - 2019
TRƯỜNG THPT QUANG TRUNG - ĐỐNG ĐA
MÔN: TOÁN – LỚP 11
___________________________________________________
(Thời gian làm bài 90 phút)
________________________________
Họ và tên ............................................................................................................................................. Phòng thi .................................................................. MÃ ĐỀ 001
Lớp ................................................................................................................................................................... Số thứ tự .........................................................................
I. PHẦN TRẮC NGHIỆM (7 điểm)
(Thời gian làm bài 63 phút) ĐIỂM BÀI LÀM
(Số câu đúng ....................... / ......................)
Số thứ tự câu trả lời trong bảng dưới đây ứng với số thứ tự câu trắc nghiệm trong đề.
Đối với mỗi câu trắc nghiệm, học sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng. 1. ; / = ~ 6. ; / = ~ 11. ; / = ~ 16. ; / = ~ 21. / = ~ 26. ; / = ~ 31. ; / = ~ 2. ; / = ~ 7. ; / = ~ 12. ; / = ~ 17. ; / = ~ 22. ; / = ~ 27. ; / = ~ 32. ; / = ~ 3. ; / = ~ 8. ; / = ~ 13. ; / = ~ 18. ; / = ~ 23. ; / = ~ 28. ; / = ~ 33. ; / = ~ 4. ; / = ~ 9. ; / = ~ 14. ; / = ~ 19. ; / = ~ 24. ; / = ~ 29. ; / = ~ 34. ; / = ~ 5. ; / = ~ 10. ; / = ~ 15. ; / = ~ 20. ; / = ~ 25. ; / = ~ 30. ; / = ~ 35. ; / = ~
CÂU HỎI TRẮC NGHIỆM
Câu 1: Trong mặt phẳng tọa độ Oxy , cho 2 điểm A(1;- ) 6 , B (-1; )
4 . Gọi C, D lần lượt là ảnh của ,
A B qua phép tịnh tiến ! theo vectơ v(5; )
1 . Khẳng định nào trong các khẳng định sau đúng?
A. ABDC là hình thoi
B. ABCD là hình bình hành C. ABDC là hình chữ nhật D. , A ,
B C, D thẳng hàng
Câu 2: Một đa giác đều có số đường chéo gấp đôi số cạnh. Hỏi đa giác đó có bao nhiêu cạnh? A. 6 B. 7 C. 5 D. 8
Câu 3: Có tất cả 120 cách chọn 3 học sinh từ một nhóm có n học sinh. Số n là nghiệm của phương trình nào sau đây?
A. n(n - ) 1 (n - ) 2 = 240
B. n(n - ) 1 (n - ) 2 = 360
C. n(n - ) 1 (n - ) 2 = 120
D. n(n - ) 1 (n - ) 2 = 720
Câu 4: Số hạng không phụ thuộc vào x trong khai triển ( - x)18 2 2 x là: A. 13 13 -2 C 12 12 -2 C 12 6 2 C 13 13 2 C 18 B. 18 C. 18 D. 18
Câu 5: Cho hình chóp .
S ABCD , có đáy ABCD là hình bình hành. Gọi M là trung điểm của BC và I là điểm thuộc miền
trong của tam giác DSAD . Thiết diện của hình chóp .
S ABCD khi cắt bởi mặt phẳng (IMC) là: A. Tam giác B. Hình thang C. Ngũ giác D. Hình bình hành
Câu 6: Cho hình lăng trụ tam giác .
ABC A' B 'C ' . Gọi M là trung điểm của A' B ' và đường thẳng d là giao tuyến của hai
mặt phẳng (CMC )' và (ABB ' A )' . Khẳng định nào sau đây sai?
A. d Ì (CC 'M )
B. B 'C Ç d
C. B 'C / / (AMC )'
D. d / / (ACC )'
Câu 7: Hệ số của số hạng chứa 7
x trong khai triển ( x - )10 3 2 là: 4 A. 3 54C 3 -27C 2 -144C 7 -54C 10 B. 10 C. 10 D. 10
Câu 8: Cho tam giác DABC đều tâm O . Có bao nhiêu phép quay tâm O góc a , 0 < a £ 2p biến DABC thành chính nó? A. 2 B. 3 C. 4 D. 1
Câu 9: Có 5 cuốn sách Văn khác nhau và 7 cuốn sách Toán khác nhau. Có bao nhiêu cách xếp các cuốn sách lên một kệ dài
của giá sách sao cho các cuốn sách Văn phải xếp cạnh nhau? A. 7.5!.7! B. 12! C. 2.5!.7! D. 5!.8!
Câu 10: Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : x + y - 2 = 0 . Phép dời hình có được bằng cách thực hiện liên !
tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ v(3; )
2 biến đường thẳng d thành đường thẳng nào cho dưới đây?
A. x + y + 2 = 0
B. x + y - 3 = 0
C. 3x + 3y - 2 = 0
D. x - y - 7 = 0
Câu 11: Có 40 thí sinh, trong đó có A và B, được xếp vào một phòng thi có 20 bàn, mỗi bàn có đủ chỗ cho hai thí sinh.
Tính xác suất để hai thí sinh A và B cùng ngồi trên cùng một bàn. A. 323 B. 323 C. 1 D. 1 390 780 78 39 Trang 32
Câu 12: Gieo một súc sắc cân đối và đồng chất liên tiếp hai lần. Xác suất để hiệu số chấm xuất hiện trong hai lần gieo là số chia hết cho 3 là: A. 1 B. 11 C. 5 D. 1 4 36 18 3
Câu 13: Trong măt phẳng tọa độ Oxy , cho đường thẳng d : 2x + y - 3 = 0 và số thực k ¹ 1. Phép vị tự tâm I (4;- ) 5 tỉ số k
biến d thành đường thẳng nào cho dưới đây?
A. 2x + y + 4 = 0
B. 2x - y - 3 = 0
C. 2x + y - 5 = 0
D. 2x + y - 3 = 0
Câu 14: Phương trình nào cho dưới đây tương đương với phương trình 2 2
sin x - cos x -1 = 0 ? A. cos 2x =1 B. cos 2x = -1 C. 2 2cos x -1 = 0 D. 2 (sin x - cos ) x = 1
Câu 15: Nghiệm của phương trình 3tan (x p + - = (0;p) 3) 1 0 trên khoảng là: A. x p = - B. x p = C. Đáp án khác D. 5 x p = 6 6 6
Câu 16: Cho bốn điểm , A ,
B C, D không cùng nằm trên một mặt phẳng. Gọi M, N lần lượt là trung điểm của , AD AC , trên
cạnh BC lấy điểm K sao cho 3KB = CK . Gọi I là giao điểm của BD với mp(MNK) . Khẳng định nào sau đây đúng?
A. KI song song với AM B. MN = 2IK
C. MI song song với KN D. DI = 2BI
Câu 17: Một hộp có 90 bóng đèn loại I và 10 bóng loại II. Chọn ngẫu nhiên 2 bóng trong hộp để kiểm tra chất lượng. Xác
suất để chọn được ít nhất 1 bóng loại I là: A. 821 B. 89 C. 109 D. Đáp án khác 990 110 110
Câu 18: Trong mặt phẳng tọa độ Oxy , phép vị tự tâm I (2; )
3 tỉ số k = -3 biến điểm M (-3; )
2 thành M ' có tọa độ là: A. (-13; ) 0 B. (17; ) 6 C. (17; ) 0 D. (-13; ) 6
Câu Phương trình sin x + 3cos x =1 có tập nghiệm {a + k2p, b + k2p; k Î } ! , với a, b Î( p - ;p ) . Khi đó a.b bằng: 19: 2 2 2 A. p 2 B. p - C. p - D. p - 6 18 2 12 Câu 20: Cho 2 3 2019 2019 S = 4C - 8C + ... - 2 C
. Giá trị của S là: 2019 2019 2019 A. -4040 B. 2017 C. 4036 D. 4038
Câu 21: Tìm tổng các nghiệm của phương trình 3cos x - sin 2x = 0 trên khoảng [0;p] là: A. p B. 3p C. p D. 0 2 2
Câu 22: Số nghiệm của phương trình 2sin (x p + + = [0;p] 4) 1 0 trên đoạn là: A. 0 B. 2 C. 3 D. 1
Câu 23: Xét hàm số y = sin x trên đoạn [ p - ]
;0 . Khẳng định nào sau đây đúng về hàm số đã cho? p p
A. Hàm số đồng biến trên các khoảng ( p - ;- (-2 );0 2) và p p
B. Hàm số đồng biến trên khoảng ( p - ;- (-2 );0
2) và nghịch biến trên khoảng p p
C. Hàm số nghịch biến trên khoảng ( p - ;- (-2 );0
2) và đồng biến trên khoảng p p
D. Hàm số nghịch biến trên các khoảng ( p - ;- (-2 );0 2) và
Câu 24: Có 5 học sinh nam và 4 học sinh nữ. Hỏi có bao nhiêu cách chọn 4 bạn sao cho trong đó luôn có học sinh nam và học sinh nữ? A. 80 B. 126 C. 60 D. 120
Câu 25: Một hộp chứa 10 quả cầu đỏ được đánh số từ 1 đến 10 và 20 quả cầu đen được đánh số từ 1 đến 20. Lấy ngẫu
nhiên 1 quả cầu từ trong hộp. Xác suất để chọn được quả cầu mầu đen hoặc ghi số chẵn là: A. 1 B. 5 C. 2 D. Đáp án khác 6 6 3
Câu 26: Cho hàm số y = x .sin 2x . Phát biểu nào sau đây là đúng về hàm số đã cho?
A. Hàm số đã cho có tập xác định là ! \ { } 0
B. Đồ thị hàm số đã cho có tâm đối xứng
C. Đồ thị hàm số đã cho có trục xứng
D. Hàm số có tập giá trị là [-1; ] 1 Trang 33
Câu 27: Gọi m giá trị nhỏ nhất của hàm số y = 3 - 2cos x + 2sin x . Khi đó: A. m = -5 B. m = 3 - 2 C. m =1 D. m = 3 + 2
Câu 28: Hai đường thẳng ,
a b nằm trong mp (a) . Hai đường thẳng a ', b' nằm trong mp (b) . Khẳng định nào sau đây đúng?
A. Nếu (a) // (b) thì a // a ' và b // b'
B. Nếu a Ç b và a // a ', b // b' thì (a)// (b)
C. Nếu a // b và a '// b' thì (a)// (b)
D. Nếu a // a ' và b // b' thì (a)// (b)
Câu 29: Tập xác định của hàm số cot x y = là: 1- sin x
A. ! \ {p + kp, kp; k Î"
! \ {p + k2p; k Î"
! \ {p + k2p, kp; k Î" ! \ {kp ; k Î" 2 } 2 } 2 } 2 } B. C. D.
Câu 30: Có bao nhiêu giá trị nguyên của tham số m để phương trình 6sin xcos x - m(cos2x + ) 2 = 0 có nghiệm? A. 5 B. 11 C. Vô số D. 7
Câu 31: Cho hai đường thẳng chéo nhau a và b . Trên đường thẳng a lấy hai điểm ,
A B và trên đường thẳng b lấy hai
điểm C, D . Khẳng định nào sau đây đúng khi nói về hai đường thẳng AD và BC ? A. Song song B. Chéo nhau
C. Song song hoặc cắt nhau D. Cắt nhau
Câu 32: Một hộp đựng 9 thẻ được đánh số từ 1 đến 9. Rút ngẫu nhiên hai thẻ từ trong hộp và nhân hai số ghi trên hai thẻ
với nhau. Xác suất để tích của hai số ghi trên hai thẻ là một số lẻ là: A. 3 B. 1 C. 5 D. 7 18 9 18 18
Câu 33: Trong mặt phẳng Oxy , cho điểm A(-2018; )
2019 . Phép quay tâm O góc quay 0
90 biến điểm A thành điểm A' có tọa độ là: A. (2019; ) 2018 B. (-2018; ) 2019 C. (-2019;- ) 2018 D. (2019;- ) 2018
Câu 34: Trong mặt phẳng tọa độ Oxy , cho 3 điểm I (4;- ) 2 , A(-3; ) 5 , B (7;- )
5 và số thực k ¹ 1. Phép vị tự tâm I tỷ số k
biến điểm A thành B . Khi đó giá trị của k là: A. 3 k = B. 7 k = - C. 3 k = - D. 7 k = 7 3 7 3
Câu 35: Cho các số 0, 1, 2, 3, 4, 5, 6. Số các số tự nhiên gồm 5 chữ số lấy từ 7 chữ số trên sao cho chữ số đầu tiên bằng 3 là: A. 4 A 7 4 P 6 B. 4 C. 7 D. 4
II. PHẦN TỰ LUẬN (3 điểm)
(Thời gian làm bài 27 phút)
Câu 1: Giải phương trình lượng giác sin 2x +1 = 3cos 2x .
Câu 2: Tìm số hạng chứa 15 x trong khai triển ( 1 2x - (x ¹ ) 0 2 4x )40 3 , .
Câu 3: Cho hình chóp .
S ABCD , có đáy ABCD là hình bình hành tâm O . Trên cạnh SA lấy điểm I sao
cho SA = 3AI , gọi G là trọng tâm của tam giác DACD .
a) Chứng minh đường thẳng IG song song với mặt phẳng (SBC) .
b) Dựng thiết diện của hình chóp với mặt (P) đi qua G và song song với AC, SD . ----- Hết ----- ĐÁP ÁN. éx p = + kp
Câu 1: Giải phương trình lượng giác sin 2x +1 = 3cos 2x . ĐS: ê 12 ê 3 x p = + kp êë 4
Câu 2: Tìm số hạng chứa 15 x trong khai triển ( 1 2x - (x ¹ ) 0 21 -23 15 C - .2 .x 2 4x )40 3 , . ĐS: 40 Trang 34
KIỂM TRA HỌC KỲ I LỚP 11 Môn thi: MÔN TOÁN æ p ö
Câu 1: Giá trị lớn nhất của hàm số y = 3cos x - +1 ç ÷ là: è 2 ø A. 4 B. 5 C. –2 D. 3
Câu 2: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 4 sin x + 3 -1 lần lượt là: A. 4 2 à v 8 B. 4 2 -1 à v 7 C. 2 à v 4 D. 2 à v 2
Câu 3: GTLN của hàm số y = 2cosx -3 là: A. 2 B. 1 C. –1 D. –3
Câu 4: Cho hàm số: y = 2cos x + 3. GTNN của hàm số là: A. 5 B. –2 C. 3 D. 1 1- 4sin x
Câu 5: Tìm tập xác định D của hàm số y = . cos x A. D = B. D = C. D = D. D = 3cos x
Câu 6: Cho hàm số: y = , TXĐ của hàm số là: 2sin x -1 ì1ü ì5p p ü
A. D = R \ í ý
B. D = R \ í
+ k2p; + k2p ,k Î Zý î2þ î 6 6 þ ìp ü C. D = R
D. D = R \ í + k2p ,k Î Zý î 6 þ
Câu 7: Với giá trị nào của m thì phương trình sin x - m = 1 có nghiệm? A. 0 £ m £ 1 B. m £ 0 C. 2 - £ m £ 0 D. m ³ 1
Câu 8: Phương trình cos x - m = 0 vô nghiệm khi và chỉ khi: ém < 1 - A. m > 1 B. m < 1 - C. 1 - £ m £ 1 D. ê ëm > 1 æ p ö
Câu 9: Số nghiệm của phương trình: sin x + =1 ç ÷
với p £ x £ 5p là: è 4 ø A. 3 B. 0 C. 2 D. 1
Câu 10: Giải phương trình ( x) 0 tan 2
= tan 80 . Kết quả thu được là: A. 0 0 x = 40 + 180 k B. 0 0 x = 40 + k90 C. 0 0 x = 40 + k45 D. 0 0 x = 80 + 180 k
Câu 11: Giải phương trình 2
2sin x - 3sin x - 2 = 0 . p 4p p p
A. x = - + k2p ; x = + 5 k2p B. x = + k2p; x = + k2p 3 3 6 6 p 7p p p
C. x = - + k2p ; x = + 2 k2p D. x = + k2p; x = + k2p 6 6 3 3 x
Câu 12: Giải phương trình lượng giác : 2cos + 3 = 0 có nghiệm là 2 5p p p p A. x = ± + 5 k2p B. x = ± + 5 k2p C. x = ± + 5 k4p D. x = ± + k4p 3 6 6 3
Câu 13: Phương trình nào sau đây vô nghiệm: Trang 35 A. sin x + 3 = 0 B. 2
2cos x - cos x -1 = 0 C. tan x + 3 = 0 D. 3sin x – 2 = 0
Câu 14: Phương trình 1+ 2 cos 2x = 0 có nghiệm là: p p p p A. ± kp B. ± + kp C. + kp D. ± + k2p 3 3 3 3
Câu 15: Cho phương trình 2cos 4x - sin4x = m . Tìm tất cả các giá trị của m để phương trình đã cho có nghiệm.
A. - 3 £ m £ 3
B. m £ - 3; m ³ 3
C. - 5 £ m £ 5
D. m £ - 5; m ³ 5
Câu 16: Nghiệm của phương trình sin x – 3 cos x = 0 là: p p p p A. x = + k2p . B. x = + k2p . C. x = + kp . D. x = + kp . 6 3 6 3
Câu 17: Cho phương trình 2
3cos x + 2cos x - 5 = 0 . Nghiệm của phương trình là p p A. k2p B. - + kp C. + k2p D. kp 2 2
Câu 18: Từ các chữ số 0, 1, 2, 3, 4, 5. Có thể lập được bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau? A. 1080 B. 156 C. 300 D. 144
Câu 19: Khối 11 trường ta có 35 học sinh nam và 36 học sinh nữ. Đoàn trường cần chọn một học
sinh tham gia giải chạy việt dã cấp tỉnh. Hỏi có bao nhiêu cách chọn? A. 36 B. 35 C. 71 D. 1260
Câu 20: Khối 11 trường ta có 32 học sinh nam và 39 học sinh nữ. Nhà trường cần chọn hai học sinh
trong đó có một nam và một nữ đi dự trại hè của tỉnh đoàn. Hỏi nhà trường có bao nhiêu cách chọn? A. 39 B. 32 C. 71 D. 1248
Câu 21: Một đội công nhân cầu đường có 10 nam và 9 nữ, chọn ra một nhóm 5 người trong đó có ít
nhất 1 nữ làm việc ca đêm. Hỏi có bao nhiêu cách chọn? A. 11376 B. 19 C. 90 D. 4320
Câu 22: Từ các chữ số 0, 1, 2, 3, 4, 5. Có thể lập được bao nhiêu số tự nhiên lẻ có 3 chữ số khác nhau? A. 180 B. 48 C. 100 D. 52
Câu 23: Cho A={1, 2, 3, 4, 5, 6, 7}. Từ tập A có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau? A. 28 B. 480 C. 840 D. 5040
Câu 24: Một đội công nhân cầu đường có 8 nam và 12 nữ, chọn ra một nhóm 5 người gồm 2 nam và
3 nữ làm việc ca đêm. Hỏi có bao nhiêu cách chọn? A. 20 B. 5664 C. 96 D. 6160
Câu 25: Từ một hộp đựng 5 viên bi màu xanh, 7 viên bi màu vàng, lấy ra 6 viên bi. Tính số phần tử
của biến cố A: “ 6 viên lấy ra có 4 viên bi màu xanh, 2 viên bi màu vàng”. Kết quả thu được là bao nhiêu? A. 105 B. 210 C. 720 D. 120
Câu 26: Có bao nhiêu cách xếp 5 học sinh nam và 4 học sinh nữ vào một hàng dọc? A. 20 B. 362880 C. 2880 D. 9 9 æ 1 ö
Câu 27: Cho nhị thức x -
. Số hạng chứa x3 trong khai triển là kết quả nào sau đây? ç 2 ÷ è x ø Trang 36 A. 84 x3 B. – 36x3 C. 36x3 D. – 84x3
Câu 28: Lớp 11 trường A có 7 nam và 28 nữ. Chọn 2 học sinh tham gia vệ sinh công cộng toàn
trường. Hỏi có bao nhiêu cách chọn? A. 70 B. 196 C. 35 D. 595
Câu 29: Một tổ học sinh có 6 nam và 4 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người
được chọn đều là nữ. A. B. C. D. Câu 30:
Một đa giác đều có 20 đường chéo. Số cạnh của đa giác đó là bao nhiêu? A. 7 cạnh B. 8 cạnh C. 9 cạnh D. 10 cạnh
Câu 31: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3
quyển sách. Tính xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán. 2 1 37 5 A. B. C. D. 7 21 42 42
Câu 32: Gieo một đồng tiền liên tiếp 3 lần. Tính xác suất của biến cố A: “ kết quả của 3 lần gieo là như nhau”. 1 A. P( ) A = 3 B. P( ) A = 7 C. P( ) A = 1 D. P( ) A = 2 8 8 4
Câu 33: Hệ số của số hạng chứa x2 trong khai triển nhị thức Niu tơn (1+2x)6 là bao nhiêu? A. 60 B. 40 C. 80 D. 20 Câu 34:
Có bao nhiêu cách xếp 6 học sinh ngồi vào 6 chiếc ghế xếp quanh một bàn tròn? A. 6 B. 120 C. 36 D. 720
Câu 35: Trong mp(Oxy) cho M ( 2
- ;4) . Tìm tọa độ của điểm M’ ảnh của điểm M qua phép vị tự tâm
O tỉ số k = 2 ? A. M’(4; 8) B. M’(–8; 4) C. M’(–4; 8) D. M’(4; –8)
Câu 36: Trong mặt phẳng Oxy nếu phép tịnh tiến biến điểm A (3; 2) thành điểm A’(2; 3) thì nó biến điểm
B (2, 5) thành điểm nào sau đây? A. B’(5; 5) B. B’(5; 2) C. B’(1; 1) D. B’(1; 6)
Câu 37: Trong các phép tịnh tiến theo các vectơ sau, phép tịnh tiến theo vectơ nào biến đường thẳng
d: 9x –7y+10=0 thành chính nó: A. = (7; 9) B. (–9; 7) C. = (7; –9) D. = (9; –7)
Câu 38: Phép vị tự tỉ số k biến hình vuông thành: A. Hình thoi B. Hình vuông C. Hình bình hành D. Hình chữ nhật
Câu 39: Cho hình bình hành ABCD, phép tịnh tiến theo véc tơ
biến điểm B thành điểm nào sau đây? A. Điểm B B. Điểm A C. Điểm C D. Điểm D
Câu 40: Trong mặt phẳng Oxy cho điểm A(–3;0). Phép quay Q
biến điểm A thành điểm: ( ; 900 O - ) A. A’(–3; 0) B. A’(0; –3) C. A’(3; 0) D. A’(0; 3)
Câu 41: Trong mặt phẳng toạ độ Oxy, phép tịnh tiến theo vectơ biến điểm M(–3; 2) thành điểm
M’(–5; 3). Véctơ có toạ độ là: Trang 37 A. (–2; 1) B. (2; – 1) C. (–8; 5) D. (8; – 5)
Câu 42: Trong mặt phẳng Oxy , ảnh của đường tròn (C) : 2 2
(x + 2) + ( y - 3) = 9 qua phép tịnh tiến theo véctơ
là đường tròn có phương trình là: A. 2 2
(x + 6) + ( y - 6) = 9 B. 2 2 (x - 2) + y = 9 C. 2 2
(x - 2) + ( y - 6) = 9 D. 2 2
(x + 2) + ( y - 3) = 9
Câu 43: Phép vị tự tâm I(–1;2) tỉ số 3 biến điểm A(4; 1) thành điểm có toạ độ : A. (14; 1) B. (6; 5) C. (14; –1) D. (16; 1)
Câu 44: Trong mặt phẳng Oxy, phép tịnh tiến theo vectơ biến đường thẳng
d : 3x + 5y - 8 = 0 thành đường thẳng có phương trình là:
A. 3x + 5y - 8 = 0
B. 3x + 5y = 0
C. 3x + 5y - 9 = 0
D. 3x + 5y - 26 = 0
Câu 45: Cho d: 2x + y – 3 = 0. Phép vị tự tâm O tỉ số 2 biến đường thẳng d thành: A. 2x + y – 6=0 B. 2x + y + 3 =0 C. 4x + 2y – 3 = 0 D. 4x + 2y – 5 = 0
Câu 46: Trong mặt phẳng Oxy, cho điểm M(2; 0) và điểm N(0; 2). Phép quay tâm O biến điểm M
thành điểm N, khi đó góc quay của nó là: p p p p A. j = B. j = C. j = - D. j = - 6 2 2 6
Câu 47: Trong mặt phẳng Oxy cho A(5; –3) . Hỏi A là ảnh của điểm nào trong các điểm sau qua
phép tịnh tiến theo vectơ là: A. (4; 10) B. (–10; 0) C. (0; –10) D. (10; 4)
Câu 48: Trong mặt phẳng Oxy, phép quay tâm O (0;0) góc quay 90 biến đường thẳng
d : x - y +1 = 0 thành đường thẳng có phương trình là:
A. x + y - 3 = 0
B. x - y + 3 = 0
C. x - y +1 = 0
D. x + y +1 = 0
Câu 49: Trong mặt phẳng Oxy , cho điểm M(4; 6) và I(2; 3) . Hỏi phép vị tự tâm I tỉ số k=2 biến M
thành điểm M’ có tọa độ là: A. (6; 9) B. (2; 4) C. (3; 2) D. (6; 4)
Câu 50: Trong mặt phẳng cho tam giác ABC . Gọi M,N,P lần lượt là trung điểm của AB, BC, CA.
Khi đó phép tịnh tiến theo vectơ biến: A. M thành B B. M thành N C. M thành P D. M thành A
Trường THPT Nguyễn Du Tổ: Toán - Tin
ĐỀ THI HỌC KỲ I MÔN TOÁN LỚP 11, NĂM HỌC 2018 - 2019
Thời gian: 90 phút ( Không kể thời gian phát đề)
---------------------------------------------------------------------------------------------------------------------------
Họ tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .SBD………….
I. Trắc nghiệm ( 6 điểm) Mã đề: 143
Câu 1. Hàm số nào sau đây là hàm số chẵn: æ p ö æ p ö
A. y = sinx
B. y = sin x + ç ÷
C. y = cosx
D. y = cos x - ç ÷ è 3 ø è 3 ø
sin 2x + 2cos x - sin x -1
Câu 2. Phương trình = 0 có nghiệm là: tan x + 3 Trang 38 p p p p A. x = -
+ k2p; x = + k2p , k Î! B. x = -
+ k2p; x = + kp ,k Î! 2 3 2 3 p p p p p
C. x = - + k2p ; x = + k , k Î! D. x = -
+ k2p; x = - + k2p , k Î! 2 3 2 2 3
Câu 3. Nghiệm của phương trình tan x = 3 là: p k2p p p p A. x = + , k Î ¢ B. x = -
+ kp ,k ΢ C. x = + kp ,k ΢ D. x = - + k2p ,k ΢ 3 3 3 3 3
Câu 4. Năm 2009, Hệ thống mạng viễn thông quân đội Viettel tiến hành ra đầu số thuê bao di động mới gồm dãy 10 số có dạng
097.XXXXXXX, trong đó X là một chữ số được chọn ngẫu nhiên từ các số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Một số di động được gọi là
"số phong thủy lộc phát" nếu hai chữ số cuối của số di động đó là 68. Tính xác suất để trong lần ra đầu số mới này của Viettlel
chọn được số di động là "số phong thủy lộc phát"? 5 5 5 10 7 10 A. B. C. D. 5 10 7 10 7 10 10 10
Câu 5. Trong mặt phẳng Oxy, cho đường tròn (C) có phương trình ( x - )2 + ( y - )2 8 4 = 4 . Tìm phương trình
đường tròn ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số k = 3. 2 2 2 2
A. ( x - 24) + ( y -12) = 12
B. ( x + 24) + ( y +12) = 36 2 2 2 2
C. ( x - 24) + ( y -12) = 36
D. ( x +12) + ( y + 24) = 12 n
Câu 6. Số hạng thứ k + 1 trong khai triển nhị thức (2 + x) là A. k n- C 2 k k
x B. k+1 n-k-1 k+1 C a b k n-
C. C 2 k n
x D. k n k n n n C 2 x n x x
Câu 7. Tính tổng T tất cả các nghiệm của phương trình 2 2 sin
- 3cos = 0 trên đoạn [0;8p ]. 4 4 A.T = 4p B.T = 0 C.T = 16p D.T = 8p
Câu 8. Tìm n biết 2 A - 2 3C = 15 - 5 . n n n
A. n = 5, n = 6
B. n = 6, n = 12
C. n = 5, n = 7
D. n = 5, n = 12
Câu 9. Có bao nhiêu số tự nhiên có 9 chữ số trong đó có 4 chữ số 1 xếp kề nhau và 5 chữ số 2,3,4,5,6 A.24 B.362880 C.120 D.720 !
Câu 10. Trong mặt phẳng Oxy cho A(9;1). Phép tịnh tiến theo vectơ v(5;7) biến điểm A thành điểm nào trong các điểm sau: A.E(8;14) B.B(4;-6) C.D(13;7) D.C(14;8)
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Khi đó, giao tuyến của 2 mặt phẳng (SAC) và (SAB) là: A.SA B.SC C.SO D.SB
Câu 12. Tập giá trị của hàm số y = sinx + cosx là: A. é- 2; 2 ù B. C. 0;1 D.[-1; ] 1 ë û ° [ ] 26 æ 1 ö
Câu 13. Khai triển của nhị thức 2x - có bao nhiêu số hạng? ç 2 ÷ è x ø A. 25 B. 27 C. 26 D. 52 1
Câu 14. Nghiệm âm lớn nhất của phương trình sin x + cos x = 1- sin 2x là: 2 3p p A. 2 - p B. - C. - D. p - 2 2 Ê 2p ˆ
Câu 15. Giá trị nhỏ nhất của hàm số y = sin x Á + ˜ +sin x Á ˜ là Ë 3 ¯ 3 A. B. 1 - C. 2 - 3 D. - 2 2 Trang 39
Câu 16. Cho đường tròn (O), đoạn thẳng AB cố định không cắt (O) và C là điểm di động trên (O). Tập hợp
điểm D sao cho tứ giác ABCD là hình bình hành là: uuur
A. Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo AB uur
B. Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo BA uur
C. Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo 2BA 1 uur
D. Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo BA 2
Câu 17. Trong các điều kiện sau điều kiện nào để xác định một mặt phẳng
A.Ba điểm phân biệt.
B.Hai đường thẳng không song song.
C.Hai đường thẳng cắt nhau.
D.Một đường thẳng và một điểm bất kì.
Câu 18. Với giá trị nào của m thì phương trình 2
sin 4x + m -1 = 0 có nghiệm A. 0 £ m £ 16 B.1 £ m £ 3 C. 0 £ m £ 4 D. 0 £ m £ 1
Câu 19. Phương trình 2cos x +1 = 0 có nghiệm là: 4p p 2p p A. x = ± + k , p k Î! B. x = ± + k , p k Î! C. x = ± + k 2 ,
p k Î! D. x = ± + k 2 , p k Î! 3 3 3 6
Câu 20. Tập xác định của hàm số y = cot x là: ìp ü ìp ü
A. D = ° \ í + kp , k Î ¢ ý
B. D = ° \ í + kp , k Î ¢ ý î 4 þ î 2 þ C. D = °
D. D = ° \ {kp , k ΢ } Câu 21. Tổng 0 2018 1 2017 2 2 2016 3 2017 2018 S = C 3 2 + C 3 2 + C 3 2 + ... + C 3.2 có kết quả bằng : 2017 2017 2017 2017 A. 2017 5 B. 2018 5 C. 2017 6.5 D. 2018 6.5
Câu 22. Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất 2 lần. Xác suất để tổng số chấm trên mặt xuất
hiện trong 2 lần gieo bằng 8 là 1 1 5 13 A. B. C. D. 6 3 36 36
Câu 23. Trong một hội nghị học sinh giỏi, có 12 bạn nam và 10 bạn nữ. Hỏi có bao nhiêu cách chọn một bạn lên phát biểu ? A.120 B.22 C.12 D.10
Câu 24. Trong mặt phẳng, cho trước điểm O cố định và góc lượng giác a. Phép biến hình F biến O thành
chính nó, biến mỗi điểm M khác O thành điểm M' sao cho OM' = OM và (∑
OM ;OM ') = a . F là phép biến hình nào đã học? A.Phép vị tự.
B.Phép quay tâm O, góc quay 2a. C.Phép tịnh tiến
D.Phép quay tâm O, góc quaya.
Câu 25. Số nghiệm của phương trình 2 2
cos x - 3sin x cos x + 2 sin x = 0 trên (- 2p;2p)? A. 6 B.8 C. 4 D. 2
Câu 26. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi E, F lần lượt là trung điểm của cạnh
SB, SC. Chọn mệnh đề đúng: A. (OEF)//(SBC) B. (OEF)//(SAD) C. (OEF)//(SAB) D. (OEF)//(ABCD)
Câu 27. Phương trình sin x + 3 cos x = 1 có nghiệm là p p p p A. x = -
+ k2p , x = + k2p , k ΢ . B. x =
+ k2p , x = - + k2p , k ΢ . 6 2 6 2 p p 2p C. x =
+ k2p , x = + k2p , k ΢ .
D. x = k 2p , x =
+ k2p , k ΢ . 6 2 3
Câu 28. Cho tứ diện ABCD. Gọi I, J, K lần lượt là các điểm nằm trên các cạnh AC, AD và BC sao cho IJ
không song song với CD. Khi đó, giao điểm của CD với mặt phẳng (IJK) là:
A. Giao điểm của CD với IJ
B. Giao điểm của CD với JK
C. Trung điểm của BD
D. Giao điểm của CD với IK
Câu 29. Các thành phố A, B, C, D được nối với nhau bởi các con đường như vẽ dưới đây. Hỏi có bao nhiêu
cách đi từ A đến D mà qua B và C chỉ một lần Trang 40 A.9
B.76 C.24 D. 20
Câu 30. Phương trình 2
2sin x - sin x - 3 = 0 có nghiệm là: p p p p A. x = -
+ k2p ,k Î! B. x = - + kp ,k Î! C. x = - + k2p ,k Î! D. x = - + k2p ,k Î! 6 2 3 2
II. Tự luận (4 điểm)
Câu 1. Một tổ có 5 nam và 7 nữ. Chọn ngẫu nhiên 6 học sinh. Tính xác suất để 6 học sinh được chọn có 3 học sinh nữ.
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của AB, AD và SO.
a. Chứng minh rằng MN song song với mặt phẳng (SBD).
b. Xác định thiết diện của hình chóp với mặt phẳng (MNP).
Câu 3. Giải phương trình: x - x + ( 3 cos2 cos6
4 3sin x - 4sin x + ) 1 = 0.
--------------o0o-------------- Trang 41
Trường THPT Nguyễn Du Tổ: Toán - Tin
ĐỀ THI HỌC KỲ I MÔN TOÁN LỚP 11, NĂM HỌC 2018- 2019
Thời gian: 90 phút ( Không kể thời gian phát đề)
---------------------------------------------------------------------------------------------------------------------------
Họ tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .SBD………….
I. Trắc nghiệm ( 6 điểm) Mã đề: 177
Câu 1. Phương trình 2
2sin x - sin x - 3 = 0 có nghiệm là: p p p p A. x = -
+ k2p ,k Î! B. x = - + k2p ,k Î! C. x = - + kp ,k Î! D. x = - + k2p ,k Î! 3 6 2 2
Câu 2. Nghiệm của phương trình tan x = 3 là: p p p k2p p A. x = -
+ k2p ,k ΢ B. x = + kp ,k ΢ C. x = +
, k Î ¢ D. x = - + kp , k Î ¢ 3 3 3 3 3
Câu 3. Hàm số nào sau đây là hàm số chẵn: æ p ö æ p ö
A. y = sinx
B. y = cosx
C. y = sin x + ç ÷
D. y = cos x - ç ÷ è 3 ø è 3 ø
Câu 4. Cho đường tròn (O), đoạn thẳng AB cố định không cắt (O) và C là điểm di động trên (O). Tập hợp
điểm D sao cho tứ giác ABCD là hình bình hành là: 1 uur
A. Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo BA 2uur
B. Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo 2BA uur
C. Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo BA uuur
D. Đường tròn (O') là ảnh của (O) qua phép tịnh tiến theo AB
Câu 5. Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất 2 lần. Xác suất để tổng số chấm trên mặt xuất
hiện trong 2 lần gieo bằng 8 là 1 1 13 5 A. B. C. D. 6 3 36 36
Câu 6. Cho tứ diện ABCD. Gọi I, J, K lần lượt là các điểm nằm trên các cạnh AC, AD và BC sao cho IJ
không song song với CD. Khi đó, giao điểm của CD với mặt phẳng (IJK) là:
A. Giao điểm của CD với IJ
B. Giao điểm của CD với IK
C. Trung điểm của BD
D. Giao điểm của CD với JK
Câu 7. Trong mặt phẳng Oxy, cho đường tròn (C) có phương trình ( x - )2 + ( y - )2 8 4 = 4 . Tìm phương trình
đường tròn ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số k = 3. 2 2 2 2
A. ( x - 24) + ( y -12) = 12
B. ( x +12) + ( y + 24) = 12 2 2 2 2
C. ( x + 24) + ( y +12) = 36
D. ( x - 24) + ( y -12) = 36
Câu 8. Trong mặt phẳng, cho trước điểm O cố định và góc lượng giác a. Phép biến hình F biến O thành
chính nó, biến mỗi điểm M khác O thành điểm M' sao cho OM' = OM và (∑
OM ;OM ') = a . F là phép biến hình nào đã học? A.Phép vị tự.
B.Phép quay tâm O, góc quay 2a. C.Phép tịnh tiến
D.Phép quay tâm O, góc quaya.
Câu 9. Trong các điều kiện sau điều kiện nào để xác định một mặt phẳng
A.Hai đường thẳng cắt nhau.
B.Hai đường thẳng không song song.
C.Ba điểm phân biệt.
D.Một đường thẳng và một điểm bất kì. !
Câu 10. Trong mặt phẳng Oxy cho A(9;1). Phép tịnh tiến theo vectơ v(5;7) biến điểm A thành điểm nào trong các điểm sau: A.D(13;7) B.C(14;8) C.E(8;14) D.B(4;-6) Trang 42 Ê 2p ˆ
Câu 11. Giá trị nhỏ nhất của hàm số y = sin x Á + ˜ +sin x Á ˜ là Ë 3 ¯ 3 3 A. 2 - B. 1 - C. D. - 2 2
Câu 12. Tìm n biết 2 A - 2 3C = 15 - 5 . n n n
A. n = 6, n = 12
B. n = 5, n = 12
C. n = 5, n = 6
D. n = 5, n = 7
Câu 13. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi E, F lần lượt là trung điểm của cạnh
SB, SC. Chọn mệnh đề đúng: A. (OEF)//(ABCD) B. (OEF)//(SAD) C. (OEF)//(SBC) D. (OEF)//(SAB)
Câu 14. Có bao nhiêu số tự nhiên có 9 chữ số trong đó có 4 chữ số 1 xếp kề nhau và 5 chữ số 2,3,4,5,6 A.24 B.362880 C.120 D.720 x x
Câu 15. Tính tổng T tất cả các nghiệm của phương trình 2 2 sin
- 3cos = 0 trên đoạn [0;8p ]. 4 4 A.T = 8p B.T = 0 C.T = 16p D.T = 4p
Câu 16. Với giá trị nào của m thì phương trình 2
sin 4x + m -1 = 0 có nghiệm A. 0 £ m £ 1 B. 0 £ m £ 4 C.1 £ m £ 3 D. 0 £ m £ 16
Câu 17. Tập xác định của hàm số y = cot x là: ìp ü A. D = °
B. D = ° \ {kp , k ΢ } C. D = ° \ í + kp , k Î ¢ ý î 2 þ ìp ü
D. D = ° \ í + kp , k Î ¢ ý î 4 þ 1
Câu 18. Nghiệm âm lớn nhất của phương trình sin x + cos x = 1- sin 2x là: 2 p p A. 2 - p B. p - C. - 3 D. - 2 2
Câu 19. Số nghiệm của phương trình 2 2
cos x - 3sin x cos x + 2 sin x = 0 trên (- 2p;2p)? A. 4 B. 6 C.8 D. 2
Câu 20. Phương trình sin x + 3 cos x = 1 có nghiệm là p p 2p A. x =
+ k2p , x = + k2p , k ΢ .
B. x = k 2p , x = + k2p , k ΢ . 6 2 3 p p p p C. x = -
+ k2p , x = + k2p , k ΢ . D. x =
+ k2p , x = - + k2p , k Œ¢ . 6 2 6 2 26 æ 1 ö
Câu 21. Khai triển của nhị thức 2x - có bao nhiêu số hạng? ç 2 ÷ è x ø A. 25 B. 26 C. 27 D. 52
Câu 22. Trong một hội nghị học sinh giỏi, có 12 bạn nam và 10 bạn nữ. Hỏi có bao nhiêu cách chọn một bạn lên phát biểu ?
A.22 B.120 C.10 D.12
Câu 23. Năm 2009, Hệ thống mạng viễn thông quân đội Viettel tiến hành ra đầu số thuê bao di động mới gồm dãy 10 số có
dạng 097.XXXXXXX, trong đó X là một chữ số được chọn ngẫu nhiên từ các số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Một số di động được
gọi là "số phong thủy lộc phát" nếu hai chữ số cuối của số di động đó là 68. Tính xác suất để trong lần ra đầu số mới này của
Viettlel chọn được số di động là "số phong thủy lộc phát"? 7 10 5 5 5 10 A. B. C. D. 5 10 10 10 7 10 7 10
Câu 24. Tập giá trị của hàm số y = sinx + cosx là: A.[0; ] 1 B. ° C.[-1; ] 1 D. é- 2; 2 ù ë û
sin 2x + 2cos x - sin x -1
Câu 25. Phương trình = 0 có nghiệm là: tan x + 3 Trang 43 p p p p p A. x = -
+ k2p; x = + kp ,k Î! B. x = -
+ k2p; x = + k ,k Î! 2 3 2 3 2 p p p p C. x = -
+ k2p; x = + k2p , k Î! D. x = - + k2p; x = - + k2p ,k Î! 2 3 2 3
Câu 26. Các thành phố A, B, C, D được nối với nhau bởi các con đường như vẽ dưới đây. Hỏi có bao nhiêu
cách đi từ A đến D mà qua B và C chỉ một lần A.9
B.24 C.76 D. 20
Câu 27. Phương trình 2cos x +1 = 0 có nghiệm là: p 2p A. x = ± + k 2 , p k Î! B. x = ± + k 2 , p k Î! 6 3 4p p C. x = ± + k , p k Î! D. x = ± + k , p k Î! 3 3 Câu 28. Tổng 0 2018 1 2017 2 2 2016 3 2017 2018 S = C 3 2 + C 3 2 + C 3 2 + ... + C 3.2 có kết quả bằng : 2017 2017 2017 2017 A. 2017 6.5 B. 2017 5 C. 2018 5 D. 2018 6.5
Câu 29. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Khi đó, giao tuyến của 2 mặt phẳng (SAC) và (SAB) là: A.SB B.SC C.SA D.SO n
Câu 30. Số hạng thứ k + 1 trong khai triển nhị thức (2 + x) là A. k n- C 2 k k x B.
k+1 n-k-1 k+1 k n k n k n k C. C a b - D. C 2 x n C 2 x n n n II. Tự luận (4 điểm)
Câu 1. Một tổ có 5 nam và 7 nữ. Chọn ngẫu nhiên 6 học sinh. Tính xác suất để 6 học sinh được chọn có 3 học sinh nữ.
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của AB, AD và SO.
c. Chứng minh rằng MN song song với mặt phẳng (SBD).
d. Xác định thiết diện của hình chóp với mặt phẳng (MNP).
Câu 3. Giải phương trình: x - x + ( 3 cos2 cos6
4 3sin x - 4sin x + ) 1 = 0.
--------------o0o-------------- Trang 44
Đáp án mã đề: 143
01. C; 02. A; 03. C; 04. B; 05. C; 06. A; 07. D; 08. A; 09. D; 10. D; 11. A; 12. A; 13. B; 14. B; 15. B;
16. B; 17. C; 18. D; 19. C; 20. D; 21. C; 22. C; 23. B; 24. D; 25. B; 26. B; 27. A; 28. A; 29. C; 30. D;
Đáp án mã đề: 177
01. D; 02. B; 03. B; 04. C; 05. D; 06. A; 07. D; 08. D; 09. A; 10. B; 11. B; 12. C; 13. B; 14. D; 15. A;
16. A; 17. B; 18. D; 19. C; 20. C; 21. C; 22. A; 23. C; 24. D; 25. C; 26. B; 27. B; 28. A; 29. C; 30. A;
ĐÁP ÁN VÀ BIỂU ĐIỂM PHẦN TỰ LUẬN CÂU Ý NỘI DUNG ĐIỂM
Không gian mẫu: “ chọn ngẫu nhiên 6 học sinh từ 12 học sinh” 0,25 n(W) 6 = C = 924 12
Gọi A là biến cố “ chọn 6 học sinh có 3 học sinh nữ” 1 n( A) 3 3 = C .C = 350 (1đ) 5 7 0,25 n A 350 25 Vậy P ( A) ( ) = = = 0,5 n(W) 924 66 Hình vẽ đúng 0,25 S Q X P R B C M 2 O D A N a. E 0,25 0,25 Ta có: ìMN Ë (SBD) b. í
îMN / /BD Ì (SBD) 0,25 Þ MN / /(SBD) 0,25 Trang 45 ìMN / /BD ï ïMN Ì (MNP) Ta có: í BD Ì (SBD) ï
ïîPÎ(MNP) Ç(SBD) 0,25
Þ (MNP) Ç (SBD) = Px / /MN / /BD 0,25
Trong mp(SBD), gọi X = Px Ç SB và R = Px Ç SD
Trong mặt phẳng (ABCD) gọi E = MN Ç CD
Þ (MNP) Ç (SCD)=ER
Trong mp(SCD), gọi Q = ER Ç SC 0,25 Khi đó:
(MNP) Ç(ABCD) = MN
(MNP) Ç(SAD) = NR
(MNP) Ç (SCD) = RQ
(MNP) Ç (SBC) = QX
(MNP) Ç (SAB) = XM
Vậy thiết diện là ngũ giác MNRQX 3 - + - + =
cos2x cos6x 4(3sin x 4sin x ) 1 0
Û (1+ cos2x) + (1- cos6x) + 4sin 3x + 2 = 0 2 2
Û 2cos x + 2sin 3x + 4sin 3x + 2 = 0 0,25 2 2
Û cos x + (sin 3x + ) 1 = 0 3 ìcosx = 0 Û í 0,25 si î n 3x = 1 - ì p 0,25 x = + kp ïï p 2 Û í Û x = + l2p p 2p 2 ïx = - + k 0,25 ïî 6 3
SỞ GD & ĐT TỈNH HƯNG YÊN
ĐỀ THI HỌC KÌ I – NĂM HỌC 2017 - 2018 TRƯỜNG THPT YÊN MỸ MÔN: TOÁN 11
Thời gian làm bài : 90 Phút. (Đề có 3 trang)
Họ tên :............................................................... Số báo danh : ................... Mã đề 162
I – TRẮC NGHIỆM (7.5 điểm) æ p Câu 1: Với mọi ö x Î 0;
, so sánh cos(sinx) với cos1 thì ç ÷ è 2 ø
A. không so sánh được.
B. cos(sinx) < cos1.
C. cos(sinx) > cos1.
D. cos(sinx) ≥ cos1.
Câu 2: Xét các phương trình lượng giác
(I) sinx + cosx = 2 (II) tanx + cotx = 2 (III) Trang 46
Trong các phương trình trên, phương trình nào có nghiệm: A. (II) và (III) B. (II) C. (I) D. (III)
Câu 3: Cho B = {1, 2, 3, 4, 5, 6}. Từ tập B có thể lập được bao nhiêu số chẵn có 6 chữ số đôi một khác nhau ? A. 46656. B. 360. C. 720. D. 2160.
Câu 4: Cho tam giác ABC. Số mặt phẳng chứa tất cả các đỉnh của tam giác ABC? A. 3. B. 2. C. 4. D. 1. Câu 5: Cho CSC(u u = -0,1; d = 0,1 n ) có:
. Số hạng thứ 7 của cấp số cộng này là 1 A. 1,6. B. 0,5. C. 6. D. 0,6.
Câu 6: Phương trình sin 3x + sin 2x = sin x có tập nghiệm trùng với tập nghiệm của phương trình ésin x = 0 1
A. sin x = 0 . B. ê . C. cos x = - .
D. cos x = -1 . ê 1 cos x = 2 êë 2
Câu 7: Hàm số y = cot x tuần hoàn với chu kỳ p p A. T = p . B. T = 2p C. T = D. T = 2 4
Câu 8: Cho hàm số y = 5sin x + 2 6 cos x , GTNN và GTLN của hàm số là A. 2 - 6; 2 6 . B. – 5 ; 5. C. 5 - - 2 6; 5 + 2 6 . D. – 7 ; 7.
Câu 9: Số nghiệm của phương trình sin2x – sin x = 0 trên [–2p;2p] là A. 2. B. 9. C. 8. D. 4.
Câu 10: Cho ngũ giác đều ABCDE tâm O, biết OA = a . Phép quay Q
biến A thành A’, biến B (C,p )
thành B’. Độ dài đoạn A’B’ bằng A. sin 72o a . B. 2 cos36o a . C. cos 72o a . D. 2 sin 36o a . ! !
Câu 11: Phép tịnh tiến T theo vectơ u ¹ 0 , biến đường thẳng d thành đường thẳng d’. Nếu d’ trùng !
với d thì giá của vectơ u
A. không song song với d. B. trùng với d.
C. song song với d.
D. song song hoặc trùng với d. !
Câu 12: Trong mặt phẳng Oxy, cho vectơ v = ( 3
- ; 5) và M’(-2 ; 8). Biết T! (M ) = M '. Khi đó toạ độ v của M là A. M(-5 ; 13) B. M(13 ; - 5) C. M(-1 ; -3) D. M(1 ; 3)
Câu 13: Tìm hệ số của 7
x trong khai triển thành đa thức của 2 (2 - 3 ) n x
, biết n là số nguyên dương thỏa mãn : 1 3 5 2n 1 C + C + C + ... + + C = 1024 . 2n 1 + 2n 1 + 2n 1 + 2n 1 + A. 2099529. B. 2099529 - . C. 2099520 - . D. 2099520 . Câu 14: Tổng 0 1 2 2
A = C + 5C + 5 C + ...+ 5n n C bằng n n n n A. 5n. B. 7n. C. 6n. D. 4n.
Câu 15: Một hộp đựng 10 viên bi xanh và 5 viên bi vàng. Có bao nhiêu cách lấy ngẫu nhiên 4 viên
bi trong đó có ít nhất 2 viên bi màu xanh? A. 1260. B. 1050. C. 105. D. 1200.
Câu 16: Gieo một đồng tiền và một con súc sắc. Số phần tử của không gian mẫu là A. 8 . B. 24 . C. 6 . D. 12 .
Câu 17: Trong mp(Oxy) cho đường thẳngd : x + y ñ 2 = 0 . Phép vị tự tâm O tỉ số k = −2 biến d
thành đường thẳng có phương trình
A. x + y + 4 = 0.
B. 2x + 2y ñ 4 = 0. Trang 47
C. 2x + 2y = 0.
D. x + y ñ 4 = 0.
Câu 18: Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (m) của con 1 æ pt p
kênh tính theo thời gian t (giờ) trong một ngày được cho bởi công thức: ö h = cos + + 3. Thời ç ÷ 2 è 8 4 ø
điểm mực nước của kênh cao nhất là A. t = 14. B. t = 13. C. t = 15. D. t= 16.
Câu 19: Nghiệm của phương trình 2cosx + 1 = 0 là p p p p
A. x = ± + k2p .
B. x = ± + k2p . C. x = ± + 2 kp . D. x = ± + k2p . 3 6 6 3
Câu 20: Tìm giá trị của x, y sao cho dãy số 2,
- x, 4, y theo thứ tự lập thành một cấp số cộng?
A. x = 2, y = 8.
B. x = 1, y = 7.
C. x = 2, y = 10. D. x = 6 - , y = 2.
Câu 21: Cho dãy số có các số hạng đầu là 8, 15, 22, 29, 36, … .Số hạng tổng quát của dãy số này là
A. u = 7 + n . B. u = 7n + 1 C. u = 7n D. u = 7n + 7 n n n n
Câu 22: Cho tam giác ABC có trọng tâm G. Gọi M, N, P theo thứ tự là trung điểm các cạnh BC, 1
CA, AB. Phép vị tự tâm G tỉ số k = - biến tam giác ABC thành tam giác 2 A. BCA. B. CAB. C. MNP. D. MNC.
Câu 23: Công thức tính số chỉnh hợp là k n ! k n ! k n ! k n ! A. A = . B. C = . C. C = . D. A = . n (n - k) ! n (n - k) ! n
(n - k) !k ! n
(n - k) !k !
Câu 24: Từ 6 số 0, 1, 2, 3, 4, 5 có thể tạo thành bao nhiêu số tự nhiên có 3 chữ số? A. 100. B. 125. C. 180. D. 216.
Câu 25: Cho hình lập phương ABCD.A’B’C’D’. B
Số đường thẳng chứa cạnh của hình lập phương C
chéo nhau với đường thẳng AB là A D A. 3. B. 1. B' C' C. 2. D. 4. A' D'
Câu 26: Một hộp đựng 6 viên bi đỏ và 4 viên bi xanh. Lấy lần lượt 2 viên bi từ hộp đó. Xác suất để
viên bi được lấy lần thứ 2 màu xanh là 4 1 2 3 A. . B. . C. . D. . 5 5 5 5
Câu 27: Phép quay tâm O góc quay 900 biến đường thẳng d thành d’. Khi đó A. d // d’.
B. d¢ ^ d.
C. d º d '..
D. d // d’ hoặc d º d '.
Câu 28: Nghiệm của phương trình sinx = –1 là p p p A. x = 3 kp . B. x = + kp .
C. x = - + k2p .
D. x = - + kp . 2 2 2 2017
Câu 29: Tập xác định của hàm số y = là 1+ sinx ì p ü ìp ü
A. D = R \ í- + k2p ý.
B. D = R \ í + k2p ý . î 2 þ î 4 þ Trang 48 ì p ü ìp ü
C. D = R \ í- + k2p ý.
D. D = R \ í + kp ý. î 4 þ î 2 þ
Câu 30: Cho dãy số (u u = 2017 + n n ( )n n ) với
. Số hạng đầu tiên của dãy là A. 2018. B. 20182. C. 1. D. 2017.
II – TỰ LUẬN (2.5 điểm)
Câu 1:Cho hình chóp S.ABCD đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, CD.
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Chứng minh MN song song với (SBC). æ p ö 3
Câu 2: Giải phương trình: a) sin x + 3 cos x = 2 b) os c x + = ç ÷ è 4 ø 2
Câu 3: Một bình đựng 5 quả cầu xanh, 4 quả cầu đỏ và 3 quả cầu vàng . Các quả cầu khác nhau về
kích thước. Chọn ngẫu nhiên 3 quả cầu. Tính xác suất để được 3quả cầu lấy ra đủ màu ?
------ HẾT ------
Phần đáp án câu trắc nghiệm: 162 1 C 2 B 3 B 4 D 5 B 6 B 7 A 8 D 9 B 10 D 11 D 12 D 13 C 14 C 15 A 16 D 17 A 18 A 19 D Trang 49 20 B 21 B 22 C 23 A 24 C 25 D 26 C 27 B 28 C 29 A 30 A Trang 50
ĐÁP ÁN PHẦN TỰ LUẬN Bài 1. a/ ( 0 tan x -15 ) = 3 . 0 0 0 x -15 = 60 + 180 k (0,2 điểm) 0 0 x = 75 + 180 k , k Î ! (0,2 điểm)
b/ 2sin 4x -1 = 0 . 1 Û sin 4x =
(0,2 điểm) 2 ì p 4x = + k2p ïï 6 Û í
(0,2 điểm) 5p ï4x = + k2p ïî 6 ì p p x = + k ïï 24 2 Û í , k Î ! (0,2 điểm) 5p p ïx = + k ïî 24 2
Bài 2. Viết khai triển biểu thức sau theo công thức nhị thức Niu – tơn:. (x + )4 4 3 2
2 = x + 8x + 24x + 32x +16
(0,2 + 0,2 + 0,2 + 0,2 + 0,2) điểm Bài 3. “ n 2
A = 7 + 3n - 3n -1 chia hết cho 6”. (*) n
• A = 6 chia hết cho 6. (0,2 điểm) 1
• Giả sử (*) đúng với số tự nhiên bất kỳ n = k với k ³1, nghĩa là: k 2
A = 7 + 3k - 3k -1 chia hết cho 6. k
(0,2 điểm)
• Ta cần chứng minh (*) cũng đúng với số tự nhiên n = k +1.
Nghĩa là: A chia hết cho 6. (0,2 điểm) k 1 +
• Thật vậy, ta có: A = 7k+ + 3 k + - k + - k + ( )2 1 1 3 1 1 1 ( ) A = 7 + k - k - - k - k - k + ( k 2 7 3 3 )1 6( 2 3 4 1 1 )
(0,2 điểm) A
= 7.A - 6 k - k - + k ( 2 3 4 1 k 1 )
(0,2 điểm)
Vậy, chứng tỏ (*) đúng với mọi số nguyên dương n.
Bài 4. a/ Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD). S
• S là điểm chung thứ nhất. (0,1 điểm)
• Gọi E là giao điểm của AB và CD thì E là điểm chung thứ 2.
(0,2 điểm) M
• Vậy, SE là giao tuyến của (SAB) và (SCD). (0,2 điểm) N B E
b/ Gọi M là trung điểm của SA. Tìm giao điểm N của SD và A mp(MBC). • C
M là điểm chung của mp(SAD) và (MBC). (0,1 điểm)
• Hai mặt phẳng (SAD) và (SCD) lần lượt chứa hai đường D
thẳng song song là AD và BC. Do đó, giao tuyến của
chúng là đường thẳng Mx, với Mx song song với AD.
(0,2 điểm)
• Vậy, N = Mx Ç SD . (0,2 điểm)
Lưu ý: Bài giải của bài 4 phải có hình kèm theo đúng và đủ mới được tính điểm. Trang 51