Top 15 đề ôn tập học kỳ 1 Toán 11 năm học 2020 – 2021 – Đặng Việt Đông

Tài liệu gồm 361 trang, được biên soạn bởi thầy giáo Đặng Việt Đông, tuyển chọn 15 đề ôn tập học kỳ 1 Toán 11 năm học 2020 – 2021, các đề được biên soạn theo dạng trắc nghiệm với 50 câu hỏi và bài toán, thời gian làm bài 90 phút, có đáp án và lời giải chi tiết.

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 11

Môn: Toán 11

Thông tin:

151 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
BỘ ĐỀ ÔN TẬP CUỐI KÌ 1
MÔN TOÁN – KHỐI 11
CHINH PHỤC CUỐI KÌ I
Admin:
HOÀNG TUYÊN – LÊ MINH TÂM
Sưu tầm và Tổng hợp:
TÀI LIỆU LƯU HÀNH NỘI BỘ
NĂM HỌC: 2020 – 2021
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 2 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
MỤC LỤC
(Dựa trên các đề của Sở và các trường THPT biên soạn, bổ sung theo cấu trúc:
25 câu trắc nghiệm và 5 câu tự luận)
A. PHẦN ĐỀ.
1. ĐỀ SỞ NAM ĐỊNH KHỐI 11.............................................................................................. Trang 03
2. ĐỀ SỞ HÀ NỘI – THPT AMSTERDAM KHỐI 11 ......................................................... Trang 07
3. ĐỀ SỞ BẠC LIÊU KHỐI 11 ................................................................................................. Trang 11
4. ĐỀ SỞ HƯNG YÊN KHỐI 11 .............................................................................................. Trang 15
5. ĐỀ SỞ HUẾ KHỐI 11 ............................................................................................................ Trang 18
6. ĐỀ SỞ HUẾ – THPT CHUYÊN QUỐC HỌC HUẾ KHỐI 11 ........................................ Trang 21
7. ĐỀ SỞ HUẾ – THPT ĐẶNG TRẦN CÔN KHỐI 11 ....................................................... Trang 25
8. ĐỀ SỞ HUẾ – THPT GIA HỘI KHỐI 11 .......................................................................... Trang 29
9. ĐỀ SỞ HUẾ – THPT CHI LĂNG KHỐI 11 ....................................................................... Trang 33
10. ĐỀ SỞ ĐẮK LẮK KHỐI 11 ............................................................................................... Trang 37
B. PHẦN ĐÁP ÁN & HƯỚNG DẪN GIẢI.
11. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ SỞ NAM ĐỊNH ................................... Trang 40
12. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ THPT AMSTERDAM ........................ Trang 51
13. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ SỞ BẠC LIÊU ....................................... Trang 64
14. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ SỞ HƯNG YÊN ................................... Trang 76
15. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ SỞ HUẾ ................................................. Trang 87
16. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ CHUYÊN QUỐC HỌC HUẾ ............. Trang 96
17. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ THPT ĐẶNG TRẦN CÔN .............. Trang 108
18. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ THPT GIA HỘI ................................. Trang 118
19. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ THPT CHI LĂNG ............................. Trang 128
20. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ SỞ ĐẮK LẮK ..................................... Trang 138
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 3
SỞ GIÁO DỤC & ĐÀO TẠO
NAM ĐỊNH
---------------------------
KHỐI 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1
NĂM HỌC: 2019 - 2020
Thời gian: 90 phút
Họ tên: .............................................................................................. Lớp: ...................................................
A. TRẮC NGHIỆM
Câu 1: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
3
siny x
. B.
2
siny x
. C. tany x x
. D. coty x
.
Câu 2: Phương trình
sin 2 0x m
có nghiệm khi và chỉ khi
A.
1m
. B.
1m
. C.
2 2m
. D.
1 1m
.
Câu 3: Từ các chữ số
1;2;3; 4;5
có thể lập được bao nhiêu số tự nhiên gồm
5
chữ số đôi một
khác nhau
A.
5
. B.
15
. C.
5
5
. D.
120
.
Câu 4: Một câu lạc bộ cờ vua có
15
người. hỏi có bao nhiêu cách bầu ra ba người vào ba vị trí
gồm Chủ tịch, Phó chủ tịch và Thư kí, biết trằng ai cũng có khả năng làm được các vị
trí trên.
A.
455
. B.
2730
. C.
6
. D.
45
.
Câu 5: Một lớp học có 20 học sinh nam và 21 học sinh nữ. Số cách chọn ngẫu nhiên 10 học
sinh trong lớp là
A.
41
10
C
. B.
10
41
A
. C.
10!
. D.
10
41
C
.
Câu 6: Số tập con có 3 phần tử của một tập hợp có 2009 phần tử là
A.
3
2009
C
. B.
3
2009
A
. C.
2009!
3!
. D.
2009
.
Câu 7: Cho tập
1;2;3;4;5A
. Chọn ngẫu nhiên 3 số từ tập
A
. Tính xác suất để 3 số được
chọn có tổng bằng 10.
A.
1
10
. B.
1
5
. C.
2
5
D.
3
10
.
Câu 8: Hệ số của số hạng chứa
8
x
trong khai triển nhị thức Niuton
10
2
1
x
là
A.
210
. B.
8
200x
. C.
200
D.
8
210x
.
Câu 9: Trong mặt phẳng với hệ tọa độ
Oxy
, cho vectơ
2; 1
v
và điểm
3;2M
. Tìm tọa
độ ảnh
M
của điểm
M
qua phép tịnh tiến theo vec tơ
v
.
A.
' 5; 3M
. B.
' 1; 1M
. C.
' 1;1M
. D.
' 5;3M
.
Câu 10: Chọn khẳng định sai?
A. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
B. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung
khác nữa.
C. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
D. Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt.
Câu 11: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng không cắt nhau và không song song thì chéo nhau.
B. Hai đường thẳng phân biệt không song song thì chéo nhau.
C. Hai đường thẳng chéo nhau thì không có điểm chung.
D. Hai đường thẳng không có điểm chung thì song song.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 4 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 12: Cho hàm số
2
cos 2 2cos
f x x x m
. Với
2; 2
m
, tìm giá trị nhỏ nhất của
hàm số trên đoạn
0;
.
A.
3
. B.
3
2
. C.
1
. D.
0
.
Câu 13: Hàm số
cos
y x
nghịch biến trên khoảng:
A.
;
2 2
. B.
0;
2
. C.
;0
. D.
;
.
Câu 14: Trên giá sách có
5
quyển sách Toán khác nhau,
6
quyển sách Anh khác nhau và
8
quyển
sách Văn khác nhau. Số cách chọn ra ba quyển sách có đủ ba môn là:
A.
19
. B.
118
. C.
20
. D.
240
.
Câu 15: Cho dãy số
n
u
với
1
2 5
n
n
u
n
. Số hạng thứ mười một của dãy số bằng
A.
1
27
. B.
1
27
. C.
1
25
. D.
1
7
.
Câu 16: Cho cấp số cộng
n
u
với
1
2
u
và công sai
3
d
. Tổng
10
số hạng đầu tiên
10
S
của
n
u
là
A.
155
. B.
115
. C.
145
. D.
165
.
Câu 17: Trong mặt phẳng toạ độ
Oxy
, cho điểm
2;0
A . Ảnh của
A
qua phép quay
;90
O
Q
có toạ
độ là
A.
0;2
M
. B.
0; 2
N
. C.
2;0
P
. D.
1;1
Q
.
Câu 18: Trong không gian, có bao nhiêu vị trí tương đối giữa hai đường thẳng phân biệt
a
và
b
?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 19: Tập nghiệm của phương trình
sin 3 cot 1 0
x x
là
A.
, ,
6
k k k
. B.
,
6
k k
.
C.
,
3
k k
. D.
, ,
3
k k k
.
Câu 20: Tổng các hệ số trong khai triển
2
1
n
x
x
là
4096
. Hệ số của số hạng không chứa
x
trong
khai triển là
A.
495
. B.
133
. C.
334
. D.
775
.
Câu 21: Từ một hộp chứa
16
cái thẻ đánh số từ
1
đến
16
. Chọn ngẫu nhiên
3
thẻ. Xác suất để
được
3
thẻ đều là số lẻ là
A.
1
10
. B.
1
2
. C.
56
506
. D.
3
16
.
Câu 22: Cho hình chóp .
S ABCD
có đáy là hình bình hành tâm
O
,
M
là trung điểm cạnh
SA
. Gọi
P
là mặt phẳng đi qua
M
đồng thời song song với
SC
và
AD
. Thiết diện của hình
chóp
.
S ABCD
cắt bởi
P
là một
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 5
A. hình thang. B. hình bình hành. C. tứ giác. D. ngũ giác.
Câu 23: Trong mặt phẳng
Oxy
cho đường thẳng
a
. Gọi
b
là ảnh của
a
qua phép đồng dạng có
được bằng cách thực hiện liên tiếp phép vị tự tâm
O
tỉ số
2
k
và phép đối xứng trục
Oy
. Biết đường thẳng
b
có phương trình là
2 16 0
x y
, khi đó phương trình đường
thẳng
a
là
A.
2 8 0
x y
. B.
2 32 0
x y
. C.
2 32 0
x y
. D.
2 8 0
x y
.
Câu 24: Cho dãy số
n
u
xác định bởi
1
1
u
và
2
1
2
n n
u u
,
*
n
. Tổng
2 2 2 2
1 2 3 1001
...
S u u u u
bằng
A.
1002001
. B.
1001001
. C.
1001002
. D.
1002002
.
Câu 25: Ngân hàng đề thi học kỳ I môn Văn của trường Y có
50
câu hỏi. Mỗi đề gồm bốn câu hỏi được
lấy ngẫu nhiên từ ngân hàng đề thi. Thí sinh
A
đã học thuộc
25
câu trong ngân hàng đề thi.
Tính xác suất để khi thí sinh
A
nhận đề thì có ít nhất ba câu đã học thuộc.
A.
135
458
. B.
1403
4606
. C.
13
19
. D.
7
19
.
B. TỰ LUẬN.
Câu 1: Giải phương trình sau:
1)
sin 2 cos 0
x x
.
2)
tan 30 3 0
x
.
Câu 2: Tìm số nguyên dương
n
thỏa mãn điều kiện:
2
9
n
C n
.
Câu 3: Tìm số hạng chứa
11
x
trong khai triển nhị thức Niutơn của biểu thức
2
2
n
x
x
, biết
n
là số nguyên dương thỏa mãn
0 2 1 4 2 2 5
3 3 ... 3 100
n n
n n n n
C C C C
.
Câu 4: Cho một đa giác đều
n
cạnh. Chọn ngẫu nhiên
3
đỉnh của đa giác đều đó. Gọi
P
là
xác xuất sao cho
3
đỉnh đó tạo thành một tam giác tù. Tính
n
, biết
n
là số lẻ,
3
n
và
45
.
62
P
Câu 5: Cho hình chóp .
S ABCD
có đáy
ABCD
là hình thang với
//
AB CD
, 2 3
AB CD
. Gọi
M
là điểm thuộc đoạn
SB
sao cho
2
5
SM
SB
,
O
lả giao điểm của hai đường chéo
AC
và
BD
.
1) Xác định giao tuyến của hai mặt phẳng
SAB
và
SCD
.
2) Chứng minh rằng:
//
SD MAC
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 6 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
3) Gọi
N
là giao điểm của đường thẳng
AM
và mặt phẳng
SDC
. Gọi
OMNC
S là diện
tích của tứ giác
OMNC
,
OMC
S là diện tích của tam giác
OMC
. Tính tỉ số
OMC
OMNC
S
S
.
----------HẾT----------
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 7
SỞ GIÁO DỤC & ĐÀO TẠO
HÀ NỘI
---------------------------
THPT AMSTERDAM
KHỐI 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1
NĂM HỌC: 2019 - 2020
Thời gian: 90 phút
Họ tên: .............................................................................................. Lớp: ...................................................
A. TRẮC NGHIỆM
Câu 1: Tập xác định của hàm số là
A. . B. .
C. . D. .
Câu 2: Trong các phép biến hình sau, phép biến hình nào không là một phép dời hình?
A. Thực hiện liên tiếp hai phép quay.
B. Thực hiện liên tiếp hai phép đối xứng trục.
C. Thực hiện liên tiếp hai phép vị tự có cùng tâm và tỷ số vị tự là 2 số đối nhau.
D. Thực hiện liên tiếp hai phép vị tự có cùng tâm và tỷ số vị tự là 2 số nghịch đảo của
nhau.
Câu 3: Một lớp 11 có 30 học sinh, gồm 15 nam và 15 nữ. Có bao nhiêu cách xếp các học sinh
thành hai hàng, một hàng nam và một hàng nữ trong lúc tập thể dục giữa giờ?
A. . B. . C. . D. .
Câu 4: Trong mặt phẳng tọa độ , gọi là ảnh của qua phép vị tự tâm , tỷ số
. Tọa độ điểm là
A. . B. . C. . D. .
Câu 5: Cho điểm phân biệt trong đó có điểm thẳng hàng
ngoài ra không có 3 điểm nào thẳng hàng, Hỏi có bao nhiêu tam giác có 3 đỉnh trong
19 điểm trên?
A. . B. . C. . D. .
Câu 6: Trong khai triển nhị thức Newton của biểu thức (với ), hệ số của số
hạng chứa là :
A. . B. . C. . D. .
Câu 7: Nghiệm của phương trình là:
A. . B. . C. D. vô nghiệm.
Câu 8: Từ các chữ số lập được tất cả bao nhiêu số tự nhiên có chữ số đôi một
khác nhau và chia hết cho ?
A. số. B. số. C. số. D. số.
Câu 9: Mệnh đề nào trong các mệnh đề sau là sai?
A. . B. .
C. . D. .
1
sin 2
y
x
\ ,
2
k
k
\ ,
4 2
k
k
\ ,
2
k k
\ ,k k
30!
15
30
A
2
2 15!
15
30
C
Oxy
A
1 ; 3
A
O
2
k
A
2 ; 6
2 ; 6
2 ; 6
2 ; 6
19
1 2 3 19
, , ,...
A A A A
5
1 2 3 4 5
, , , ,
A A A A A
959
969
364
374
11
2
3
x
x
0
x
7
x
7
11
C
7 7
11
3
C
5
11
C
5 5
11
3
C
2 1
1
5
x
x x
A C
5
x
3
x
4
x
0;1;2;3;4;5;6;7
3
5
112
78
42
84
0 1 2
0 1
n
n
n n n n
C C C C
0 1 2
2
n n
n n n n
C C C C
0 1 2
1 2 4 2
n
n
n n n n
C C C C
0 1 2
3 2 4 2
n n n
n n n n
C C C C
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 8 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 10: Cho là hai biến cố độc lập của phép thử . Xác suất xảy ra biến cố là và
xác suất xảy ra biến cố là . Xác suất để xảy ra biến cố và là
A. . B. . C. . D. .
Câu 11: Khẳng định nào trong các khẳng định sau là đúng?
A. Nếu hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.
B. Hai đường thẳng chéo nhau khi chúng không có điểm chung.
C. Hai đường thẳng song song khi chúng ở trên cùng một mặt phẳng.
D. Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo
nhau.
Câu 12: Cho chóp .
S ABCD
có đáy
ABCD
là hình thang có
AB
//
CD
. Gọi
,
M N
và
P
lần lượt
là
trung điểm
,
SA BC
và
AD
. Giao tuyến của hai mặt phẳng
SAB
và
MNP
là
A. Đường thẳng qua
S
và song song với
AB
.
B. Đường thẳng qua
N
và song song với
SC
.
C. Đường thẳng qua
M
và song song với
AB
.
D. Đường thẳng
MN
.
Câu 13: Cho 100 tấm thẻ được đánh số từ
1
đến
100
, chọn ngẫu nhiên đồng thời 3 tấm thẻ. Xác
suất để
chọn được 3 tấm thẻ có tổng các số ghi trên thẻ là số chia hết cho 2 là:
A.
5
6
. B.
1
2
. C.
3
4
. D.
49
198
.
Câu 14: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật tâm
O
, điểm
M
nằm trên
cạnh
SB
sao cho 4
SB BM
. Giao điểm của đường thẳng
SD
và mặt phẳng
ACM
nằm trên
đường
thẳng nào sau đây:
A.
OM
. B.
AM
. C.
CM
. D.
AC
.
Câu 15: Cho hình chóp có các cạnh bên bằng nhau, đáy là hình vuông,
. Gọi là điểm nằm trên cạnh SA sao cho . Gọi là mặt phẳng
đi qua M, song song với hai đường thẳng AB và
AC
. Mặt phẳng cắt hình chóp
theo thiết diện là một hình tứ giác có diện tích bằng:
A. . B. . C. . D. .
Câu 16: Phương trình có đúng 6 nghiệm thuộc khi và chỉ
khi . Khi đó tổng là số nào?
A. . B. . C. . D. .
Câu 17: Tập xác định của
1 sin
y x
là
A.
1;

. B.
; 1

. C.
. D.
\ 2 ,k k
.
Câu 18: Người ta trồng
1275
cây theo hình tam giác như sau: Hàng thứ nhất có
1
cây, hàng thứ
2
có
2
cây, hàng thứ
3
có
3
cây
, ,
hàng thứ
k
có
k
cây
1
k
. Hỏi có bao nhiêu hàng?
,
A B
T
A
0,5
B
0,25
A
B
0,25
0,125
0,75
0,375
.
S ABCD
ABCD
20
AB cm
M
2
3
SM
SA
P
P
.
S ABCD
2
80
9
cm
2
400
9
cm
2
800
9
cm
2
1600
9
cm
2
cos 1 sin sin 0
x x x m
0;2
;
m a b
a b
0, 5
0, 25
0, 25
0,5
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 9
A.
51
. B.
52
. C.
53
. D.
50
.
Câu 19: Nghiệm của phương trình
2 1
3
x x
A A
là:
A.
1
x
. B.
3
x
. C.
1
x
và
3
x
. D.
1
x
.
Câu 20: Cô giáo chia
4
quả táo,
3
quả cam và
2
quả chuối cho
9
cháu (mỗi cháu
1
quả). Hỏi có bao
nhiêu cách chia khác nhau
A.
120
. B.
1260
. C.
9
. D.
24
.
Câu 21: Một chiếc máy có
2
động cơ I và II hoạt động độc lập với nhau.Xác suất để động cơ I chạy tốt
và động cơ II chạy tốt lần lượt là
0,8
và
0,7
. Tính xác suất để có ít nhất
1
động cơ chạy tốt là
A.
0,56
. B.
0,06
. C.
0,83
. D.
0,94
.
Câu 22: Cho .
S ABCD
có đáy là hình bình hành. Mệnh đề nào sau đây sai?
A.
SAD SBC
là đường thẳng qua
S
và song song với
AC
.
B.
SAB SAD SA
.
C.
//
SBC AD
.
D.
SA
và
CD
chéo nhau.
Câu 23: Tổng
1 2 3 2017
2017 2017 2017 2017
...C C C C
bằng
A.
2017
2 1
. B.
2017
2 1
. C.
2017
2
. D.
2017
4
.
Câu 24: Trong mặt phẳng
Oxy
cho đường tròn
C
có phương trình
2 2
2 2 4
x y
Hỏi phép
đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm
O
tỉ số
1
2
k
và phép quay
tâm
O
góc quay
90
sẽ biến
C
thành các đường tròn nào trong các đường tròn sau
A.
2 2
1 1 1
x y
. B.
2 2
1 1 1
x y
.
C.
2 2
2 1 1
x y
. D.
2 2
2 2 1
x y
.
Câu 25: Cho tứ diện
ABCD
đều cạnh
a
. Gọi
G
là trọng tâm tam giác
ABC
, mặt phẳng
CGD
cắt tứ
diện theo một thiết diện có diện tích là.
A.
2
2
6
a
. B.
2
3
4
a
. C.
2
2
4
a
. D.
2
3
2
a
.
B. TỰ LUẬN
Bài 1. Giải phương trình:
2 2
3 cos sin 2 3 sin 1
x x x
.
Bài 2.
a) Cho
2
0 1 2
( 2)
n n
n
x a a x a x a x
. Tìm n để
5 6
: 12:7
a a
.
b) Trong một hộp có 10 viên bi màu xanh và 8 viên bi màu đỏ. Bạn Bình lấy ngẫu
nhiên 1 viên bi
(lấy xong không trả lại vào hộp), sau đó bạn An lấy tiếp 1 viên bi nữa. Tính xác suất để
hai bạn lấy được bi cùng màu.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 10 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Bài 3.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm các
cạnh AB,
CD
.
a) Chứng minh rằng: MN song song với mặt phẳng (SBC), (SAD).
b) Gọi P là trung điểm
SA
. Chứng minh rằng: SB, SC song song với mặt phẳng (MNP).
c) Gọi
1 2
;
G G
lần lượt là trọng tâm tam giác ABC,
SBC
. Chứng minh rằng: đường
thẳng G1G2 song song với mặt phẳng (SAC).
d) Dựng thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng
2
PNG
.
Bài 4. Cho cấp số cộng
n
u
có số hạng đầu
1
3
u
và công sai
5
d
. Tính
2
u
,
7
u
và
8
S
(tổng
của
8
số hạng đầu tiên trong cấp số cộng
n
u
).
Bài 5. Cho dãy số
n
u
với
2 1
cos
3
n
n
u
.
a) Chứng minh rằng
3
n n
u u
với mọi
1
n
.
b) Hãy tính tổng của
17
số hạng đầu tiên của dãy số đã cho.
----------HẾT----------
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 11
SỞ GIÁO DỤC & ĐÀO TẠO
BẠC LIÊU
---------------------------
KHỐI 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1
NĂM HỌC: 2019 - 2020
Thời gian: 90 phút
Họ tên: .............................................................................................. Lớp: ...................................................
A. TRẮC NGHIỆM
Câu 1: Nghiệm của phương trình
2cos 3 0x
là
A.
2
6
2
6
x k
k
x k
. C.
2
3
2
2
3
x k
k
x k
.
B.
2
3
x k k
. D.
2
6
x k k
.
Câu 2: Cho hình bình hành
ABCD
. Khẳng định nào sau đây là đúng
A.
BC
T A D
. B.
BC
T D A
. C.
BC
T A B
. D.
BC
T C B
.
Câu 3: Phương trình
cos sin 3 2 cos sin sin 4x x x x x
có tổng tất cả các nghiệm
0;x
là
A.
2
. B.
6
. C.
11
8
. D.
5
8
.
Câu 4: Trong mặt phẳng tọa độ
Oxy
, tìm phương trình đường thẳng
'
là ảnh của đường
thẳng
: 2 1 0x y
qua phép tịnh tiến theo vecto
1; 1v
A.
': 2 2 0x y
. B.
': 2 0x y
. C.
': 2 3 0x y
. D.
': 2 1 0x y
.
Câu 5: Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá của mét khoan đầu tiên là
10.000
đồng và kể từ mét khoan thứ hai, giá mỗi mét khoan sau tăng thêm
3000
đồng
so với giá mét khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan
giếng này để khoan một giếng sâu
100
mét lấy nước dùng cho sinh hoạt gia đình. Hỏi
sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan
giếng số tiền bằng bao nhiêu
A.
15.580.000
đồng. B.
18.500.000
đồng. C.
15.850.000
đồng. D.
15.050.000
đồng.
Câu 6: Cho dãy số
n
u
có số hạng tổng quát
*
2
n
n
n
u n
. Số hạng thứ tư của dãy số
n
u
là
A.
1
2
. B.
1
16
. C.
1
4
. D.
1
8
.
Câu 7: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
, ,M N P
lần lượt là
trung điểm của
, ,AB AD SC
. Gọi
Q
là giao điểm của
SD
với
( )MNP
. Tính
SQ
SD
.
A.
1
4
. B.
3
4
. C.
2
3
. D.
1
3
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 12 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 8: Từ
20
học sinh ưu tú gồm
10
nam và
10
nữ, người ta muốn lập một đoàn đại biểu
gồm
6
người để tham dự một buổi hội thảo, trong đó có
1
trưởng đoàn là nam và
2
phó đoàn là nữ. Hỏi có bao nhiêu cách thành lập một đoàn đại biểu như vậy?
A.
27907 200
. B.
306000
. C.
38760
. D.
513000
.
Câu 9: Cho tứ diện
ABCD
,
G
là trọng tâm tam giác
ABD
,
M
là điểm trên cạnh
BC
sao cho
2
MB MC
. Khẳng định nào sau đây đúng?
A.
//
MG ACD
. B.
//
MG ABC
. C.
//
MG ABD
. D.
//
MG BCD
.
Câu 10: Từ các chữ số của tập
1; 2;3;4;5;6;8
A
có thể lập được bao nhiêu số tự nhiên có ba
chữ số đôi một khác nhau ?
A.
3
8
. B.
3
7
C
. C.
3
7
A
. D.
8
3
.
Câu 11: Hệ số của
10
x
trong khai triển
10
2
3 1
x bằng
A.
0 0
10
3
C
. B.
5 10
10
3
C
. C.
10 10
10
3
C
. D.
5 5
10
3
C
.
Câu 12: Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành,
O
là giao điểm
AC
và
BD
.
Gọi
,
M N
lần lượt là trung điểm
,
SA SB
. Giao tuyến của hai mặt phẳng
SAC
và
SBD
là
A.
SO
. B.
SM
. C.
SN
. D.
SD
.
Câu 13: Trong mặt phẳng
Oxy
, cho hai đường thẳng
: 2 2 0
x y
,
' : 2 2 0
x y
và
vectơ
(2;0)
v
. Khẳng định nào sau đây đúng?
A.
(0;3)
( ) '
V
. B.
0
(0;90 )
( ) '
Q
. C.
( ) '
v
T
. D.
0
(0;180 )
( ) '
Q
.
Câu 14: Trong mặt phẳng
Oxy
, tìm ảnh đường tròn
( ')
C
của đường tròn
2 2
( ) : 2 4 0
C x y x y
qua phép vị tự tâm
0
tỉ số
2
k
A.
2 2
( ) : ( 2) ( 4) 10
C x y
. B.
2 2
( ) : ( 2) ( 4) 20
C x y
.
C.
2 2
( ) : ( 2) ( 4) 20
C x y
. D.
2 2
( ) : ( 2) ( 4) 10
C x y
.
Câu 15: Có bao nhiêu số hạng là số nguyên trong biểu thức
30
3
2 3
?
A.
6
. B.
8
. C.
7
. D.
5
.
Câu 16: Phương trình
sin 2 3 cos2 1
x x
tương đương với phương trình
A.
sin 2 sin
3 3
x
. B.
sin 2 sin
3 3
x
.
C.
sin 2 sin
3 6
x
. D.
sin 2 sin
3 6
x
.
Câu 17: Trong mặt phẳng
Oxy
, cho điểm
1; 2
I
. Gọi
I
là ảnh của
I
qua phép vị tự
; 2
O
V
.
Khi đó,
I
có tọa độ là
A.
2; 4
. B.
4;2
. C.
4; 2
. D.
2;4
.
Câu 18: Điều kiện để hàm số
tan 1
4
y x
xác định là
A.
4
x k k
. B.
4
x k k
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 13
C.
2
x k k
. D.
4
x k k
.
Câu 19: Trong một cuộc thi, Ban tổ chức dùng
7
cuốn sách môn Toán,
6
cuốn sách môn Vật
lý và
5
cuốn sách môn Hóa học để làm phần thưởng cho
9
học sinh có kết quả cao
nhất. Các cuốn sách cùng thể loại Toán, Vật lý, Hóa học đều giống nhau. Mỗi học sinh
nhận thưởng sẽ được hai cuốn sách khác nhau, trong đó có An. Tính xác suất để An
nhận thưởng có sách Toán.
A.
7
18
. B.
11
18
. C.
7
9
. D.
9
18
.
Câu 20: Số nghiệm của phương trình
3
sin
2
x
là
A.
4
. B.
2
. C.
0
. D.
1
.
Câu 21: Long và Hưng cùng
8
bạn rủ nhau đi xem bóng đá. Số cách xếp nhóm bạn trên vào
10
chỗ ngồi sắp hàng ngang sao cho Long và Hưng ngồi cạnh nhau là:
A.
9.8!
. B.
18.8!
. C.
8!
. D.
9!
.
Câu 22: Định
m
để phương trình có nghiệm:
6 6 2
sin cos cos 2
x x x m
với
0
8
x
.
A.
0 1
m
. B.
0 2
m
. C. 0
3
8
m
. D. 0
1
8
m
.
Câu 23: Tại một buổi lễ có
13
cặp vợ chồng tham dự, mỗi ông bắt tay với một người trừ vợ
mình, các bà không ai bắt tay nhau. Hỏi có bao nhiêu cái bắt tay?
A.
234
. B.
312
. C.
78
. D.
185
.
Câu 24: Cho cấp số cộng
n
u
biết
3
6
u
,
8
16
u
. Tính công sai
d
và tổng của
10
số hạng đầu
tiên.
A.
2
d
;
10
100
S
. B.
1
d
;
10
80
S
. C.
2
d
;
10
120
S
. D.
2
d
;
10
110
S
.
Câu 25: Trong mặt phẳng
Oxy
cho đường thẳng
d
có phương trình
2 1 0
x y
để phép tịnh
tiến theo véctơ
v
biến
d
thành chính nó thì
v
phải là véctơ nào trong các véctơ sau :
A.
2;1
v
. B.
2; 1
v
. C.
1;2
v
. D.
1;2
v
.
B. TỰ LUẬN
Câu 1: Giải phương trình
2cos 1 0
x
Câu 2:
a) Từ một hộp chứa
7
quả cầu màu đỏ và
5
quả cầu màu vàng, Hùng lấy ngẫu nhiên
đồng thời
3
quả cầu. Tính xác suất để Hùng lấy được
3
quả cầu trong đó có hai quả
cầu màu đỏ.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 14 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
b) Tìm số hạng không chứa
x
trong khai triển của
2
n
x
x
, biết
n
là số tự nhiên thỏa
mãn
1 2 3 2 496
4 1 4 1 4 1 4 1
... 2 1
n
n n n n
C C C C
Câu 3: Cho hình chóp .
S ABCD
có đáy
ABCD
là hình thang, với đáy lớn
AD
và 2
AD BC
.
a) (1,0 điểm) Tìm giao điểm của đường thẳng
CD
và mặt phẳng
SAB
.
b) (0,5 điểm) Gọi
I
là điểm nằm trên cạnh
SC
sao cho
2 3
SC SI
. Chứng minh đường
thẳng
SA
song song với mặt phẳng
BID
.
Câu 4: Tìm hệ số của
31
x
trong khai triển
40
2
1
, 0
x x
x
Câu 5: Rút gọn tổng
2 2 2 2
1 1 1 .1! 2 2 1 2! 3 3 1 .3! ... 1 . !
S n n n
.
----------HẾT----------
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 15
SỞ GIÁO DỤC & ĐÀO TẠO
HƯNG YÊN
---------------------------
KHỐI 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1
NĂM HỌC: 2019 - 2020
Thời gian: 90 phút
Họ tên: .............................................................................................. Lớp: ...................................................
A. TRẮC NGHIỆM
Câu 1. Tính tổng
S
tất cả các hệ số trong khai triển
11
3 4x
:
A.
1S
. B.
1S
. C.
0S
. D.
8192S
.
Câu 2. Làng Duyên Yên, xã Ngọc Thanh, huyện Kim Động, tỉnh Hưng Yên nổi tiếng với trò
chơi dân gian đánh đu. Trong trò chơi này, khi người chơi nhún đều thì cây đu sẽ đưa
người chơi dao động qua lại ở vị trí cân bằng. Nghiên cứu trò chơi này, người ta thấy
rằng khoảng cách
h
(tính bằng mét) từ người chơi đu đến vị trí cân bằng được biểu
diễn qua thời gian
t
(
0t
và được tính bằng giây) bởi hệ thức
h d
với
3cos 2 1
3
d t
trong đó quy ước rằng
0d
khi vị trí cân bằng ở phía sau lưng
người chơi đu và
0d
trong trường hợp trái lại. Tìm thời điểm đầu tiên sau
10
giây
mà người chơi đu ở xa vị trí cân bằng nhất.
A. Giây thứ
13
. B. Giây thứ
12,5
. C. Giây thứ
10,5
. D. Giây thứ
11
.
Câu 3. Bạn An muốn mua một chiếc áo sơ mi cỡ
39
hoặc
40
. Biết áo cỡ
39
có
3
màu khác
nhau, áo cỡ
40
có
5
màu khác nhau. Hỏi bạn An có bao nhiêu lựa chọn để mua một
chiếc áo ?
A.
8
. B.
3
. C.
5
. D.
15
.
Câu 4. Số đường chéo của đa giác
10
cạnh là
A.
35
. B.
7
. C.
45
. D.
10
.
Câu 5. Từ các chữ số của tập hợp
1; 2; 3; 4; 5; 6A
có thể lập được bao nhiêu số tự nhiên có
3
chữ số mà các chữ số đôi một khác nhau?
A.
125
. B.
120
.
C.
6
. D.
10
.
Câu 6. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
B. Hai đường thẳng phân biệt không chéo nhau thì hoặc cắt nhau hoặc song song.
C. Hai đường thẳng không có điểm chung thì chéo nhau.
D. Hai đường thẳng chéo nhau thì không có điểm chung.
Câu 7. Mệnh đề nào sau đây là đúng?
A.
0 1 1 1 2 2
2 2 2 2 2 2
... ...
n n n n
n n n n n n
C C C C C C
.
B.
0 1 2 1 2 2
2 2 2 2 2 2
... ...
n n n n
n n n n n n
C C C C C C
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 16 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
C.
0 1 1 1 2 2
2 2 2 2 2 2
... ...
n n n n
n n n n n n
C C C C C C
.
D.
0 1 1 2 2
2 2 2 2 2 2
... ...
n n n n
n n n n n n
C C C C C C
.
Câu 8. Chọn ngẫu nhiên một hộp chứa 16 thẻ được đánh số từ 1 đến 16. Tính xác suất để
nhận được thẻ đánh số lẻ.
A.
9
16
. B.
1
2
. C.
3
8
. D.
7
16
.
Câu 9. Từ một cỗ bài tú lơ khơ 52 quân, rút ngẫu nhiên cùng một lúc 4 quân bài. Tính xác
suất sao cho cả 4 quân đều là K?
A.
1
6497400
. B.
4
6497400
. C.
1
270725
. D.
4
270725
.
Câu 10: Phương trình
5
cos 1
6
x
có nghiệm là
A.
3
x k
. B.
2
3
x k
. C.
5
6
x k
. D.
5
2
6
x k
.
Câu 11: Một hộp chứa
6
quả cầu đỏ khác nhau và
4
quả cầu xanh khác nhau. Chọn ngẫu
nhiên cùng một lúc
2
quả cầu từ hộp. Tính xác suất của biến cố “Lấy được hai quả
cùng màu”.
A.
7
15
. B.
4
9
. C.
8
15
. D.
7
45
.
Câu 12: Lớp 11A có
35
học sinh nam và
10
học sinh nữ. Hỏi có bao nhiêu cách chọn ngẫu
nhiên một bạn trong lớp ?
A.
20
. B.
50
. C.
45
. D.
25
.
Câu 13. Gọi
M
là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos2 cos 2
y x x
. Tính
M m
A.
25
8
. B.
4
. C.
21
8
. D.
2
Câu 14. Có bao nhiêu số tự nhiên có 8 chữ số đôi một khác nhau được lập từ tập
1,2,3,4,5,6,7,8
A sao cho số đó chia hết cho
1111
?
A.
384
. B.
345
. C.
3840
. D.
1920
.
Câu 15. Trong mặt phẳng tọa độ
Oxy
, ảnh của đường thẳng
: 2 3 0
d x y
qua phép đối
xứng tâm
(4;3)
I
là:
A.
2 17 0
x y
B.
2 7 0
x y
. C.
2 17 0
x y
. D.
2 15 0
x y
.
Câu 16: Điều kiện cần và đủ để phương trình
sin cos
a x b x c
có nghiệm là
A.
2 2
a b c
. B.
2 2 2
a b c
. C.
2 2
a b c
. D.
2 2 2
a b c
.
Câu 17: Hàm số nào sau đây có đồ thị nhận gốc tọa độ
O
làm tâm đối xứng?
A.
2
sin
y x
. B.
cos
y x
. C.
tan
y x
. D.
2
cot
y x
.
Câu 18: Có bao nhiêu cách lấy ngẫu nhiên cùng lúc
3
ba quả cầu từ một hộp chứa
10
quả cầu
khác nhau
A.
2
P
. B.
3
10
C
. C.
10
P
. D.
2
10
A
.
Câu 19: Tính tổng
0 1 2 2
2 2 2 2
...
n
n n n n
S C C C C
.
A.
2
2
n
S
. B.
2
2 1
n
S
. C.
2
n
S
. D.
2
2 1
n
S
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 17
Câu 20: Cô dâu và chú rể mời
6
người ra chụp ảnh kỉ niệm, người thợ chụp hình có bao nhiêu
cách sắp xếp sao cho cô dâu, chú rể đứng cạnh nhau.
A.
6.7!
. B.
2.7!
. C.
8! 7!
. D.
2! 6!
.
Câu 21: Cho hình vuông
ABCD
tâm
I
. Gọi
,
M N
lần lượt là trung điểm của
,
AD DC
. Phép
tịnh tiến theo véc tơ nào sau đây biến
AMI
thành
MDN
?
A.
AC
. B.
AM

. C.
NI
. D.
MN
.
Câu 22: Cho hai đường thẳng cắt nhau
d
và
d
. Có bao nhiêu phép đối xứng trục biến đường
thẳng này thành đường thẳng kia?
A. Vô số. B. Hai. C. Không có. D. Một
Câu 23: Tìm hệ số của
5
x
trong khai triển
11
1
x
.
A.
55440
. B.
462
. C.
246
. D.
252
Câu 24: Cho ba mặt phẳng phân biệt
, ,
có
1
d
;
2
d
;
3
d
. Khi đó ba đường thẳng
1 2 3
, ,
d d d
:
A. Đôi một song song. B. Đồng quy.
C. Đôi một cắt nhau. D. Đôi một song song hoặc đồng quy
Câu 25: Hãy mô tả không gian mẫu của phép thử: “Gieo một đồng xu cân đối và đồng chất hai
lần liên tiếp”.
A.
,
SS NN
. B.
,
S N
.
C.
, , ,
SS SN NS NN
. D.
,
SN NS
.
B. TỰ LUẬN
Câu 1. Giải các phương trình sau đây
a)
2
cos 3cos 2 0
x x
. b)
2cos 1 2sin cos sin 2 sin
x x x x x
Câu 2. Một lớp học có 15 nữ và 20 nam. Có bao nhiêu cách chọn ra từ lớp đó 10 bạn sao cho có ít nhất 1 bạn
nam ?
Câu 3. Tìm số hạng không chứa
x
trong khai triển thành đa thức của biểu thức
12
3
1
3x
x
.
Câu 4. Tìm tất cả các giá trị thực của tham số
m
sao cho phương trình lượng giác sau đây có nghiệm:
sin 2 12 cos 2 13
m x x
.
Câu 5. Cho hình chóp
.
S ABCD
, có đáy
ABCD
là hình thang có đáy lớn
AD
. Gọi
,
E F
lần
lượt là trung điểm của
,
SA SD
.
a) Tìm giao tuyến của các cặp mặt phẳng:
SAC
và
SBD
,
SAD
và
SBC
.
b) Chứng minh
//
EF ABCD
và
//
EF SBC
.
c) Gọi
K
là giao điểm của
AB
và
CD
. Tìm
,
M N
lần lượt là giao điểm của
SB
và
CDE
;
SC
và
EFM
. Từ đó, tìm thiết diện của hình chóp cắt bởi mặt phẳng
KEF
.
d) Cho
2
AD BC
. Tính tỉ số diện tích của tam giác
KMN
và tam giác
KEF
.
----------HẾT----------
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 18 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
SỞ GIÁO DỤC & ĐÀO TẠO
HUẾ
---------------------------
KHỐI 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1
NĂM HỌC: 2019 - 2020
Thời gian: 90 phút
Họ tên: .............................................................................................. Lớp: ...................................................
A. TRẮC NGHIỆM
Câu 1. Tìm hệ số của
3 3
x y
trong khai triển biểu thức
6
x y
A.
20.
B.
6.
C.
15.
D.
1.
Câu 2. Hàm số nào sau đây là hàm số chẵn?
A.
tan .y x
B.
cot .y x
C.
cos .y x
D.
sin .y x
Câu 3.
Tập xác định của hàm số
sin 2 ?y x
A.
;2 .D 
B.
.D
C.
\ 2 .D
D.
2; .D 
Câu 4.
Một nhóm công nhân có
15
người trong đó có
10
nam và
5
nữ. Có bao nhiêu cách
chọn
6
người đi dự đại hội công ty?
A.
4785.
B.
3603600.
C.
720.
D.
5005.
Câu 5. Trong mặt phẳng
Oxy
, cho điểm
1; 0A
. Tìm ảnh của
A
qua phép dời hình có được
bằng cách thực hiện liên tiếp phép quay tâm
O
góc quay
90
và phép tịnh tiến theo
véctơ
2 ; 0v
.
A.
2 ; 1A
. B.
2 ;1A
. C.
2 ;1A
. D.
1; 2A
.
Câu 6. Cho dãy số
n
u
là cấp số cộng có
1 6
3 , 27u u
. Tìm công sai
d
?
A.
5d
. B.
4d
. C.
6d
. D.
24
5
d
.
Câu 7. Cho
3 2
3 5
n
P n n n
với
n
. Khẳng định nào sau đây đúng?
A.
n
P
chia hết cho
2
. B.
n
P
chia hết cho
5
. C.
n
P
chia hết cho
6
. D.
n
P
chia hết cho
3
.
Câu 8. Có
5
học sinh gồm
2
nữ và
3
nam được xếp vào dãy ghế được đánh số
1,2,3, 4,5
. Hỏi
có bao nhiêu cách sắp xếp chổ ngồi cho
5
học sinh nói trên, biết rằng vị trí số
1
phải
dành cho một học sinh nữ?
A.
52.
B.
48.
C.
50.
D.
42.
Câu 9. Tính chất nào sau đây không phải là tính chất của phép đồng dạng.
A. Biến đường tròn thành đường tròn có cùng bán kính.
B. Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và bảo toàn thứ tự của 3 điểm đó.
C. Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.
D. Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn
thẳng.
Câu 10. Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi
O
là giao điểm của
AC
và
BD
.
Xác định giao tuyến của hai mặt phẳng
SAD
và
SBC
.
A. Đường thẳng qua
S
và song song với
AC
.
B. Đường thẳng qua
S
và song song với
AD
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 19
C. Đường thẳng qua
S
và song song với
AB
.
D. Đường thẳng
SO
.
Câu 11. Cho
A
và
B
là hai biến cố liên quan đến một phép thử. Khẳng định nào sau đây sai?
A. nếu
A
thì
A
là biến cố chắc chắn.
B. Nếu A B
thì
A
và
B
là hai biến cố xung khắc.
C. Nếu
A B
thì
A
và
B
là hai biến cố đối nhau.
D. Nếu A
thì
A
là biến cố không.
Câu 12. Trong mặt phẳng
Oxy
, phép tịnh tiến theo vec tơ
1; 3
v
biến đường tròn
2 2
: 1 2 6
C x y
thành đường tròn có phương trình nào sau đây?
A.
2
2
1 6
x y
. B.
2 2
2 5 6
x y
.
C.
2
2
1 6
x y
. D.
2 2
2 5 6
x y
.
Câu 13. Trong mặt phẳng
Oxy
, phép quay tâm
O
góc quay
90
o
biến điểm
M
thành
'(3; 1)
M
Tìm tọa độ điểm
M
.
A.
( 3;1).
M
B.
(1;3).
M C.
(1; 3).
M
D.
(3; 1).
M
Câu 14. Tìm tất cả các nghiệm của phương trình
1
sin
2
x
thỏa mãn
2 2
x
A.
2 .
3
x k
B.
.
3
x
C.
5
2 .
6
x k
D.
.
6
x
Câu 15. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
O
là giao điểm của
AC
và
.
BD
Gọi
,
I J
lần lượt là trung điểm của
SA
và
.
SB
Khẳng định nào sau đây sai?
A.
IJ//(ABCD)
và
IJ//(SCD)
B.
IJCD
là hình thang.
C.
IJ
và
SO
chéo nhau
D.
(IJ )
C
cắt hình chóp
.
S ABCD
theo thiết diện là tam giá
IJ .
C
Câu 16. Từ một đội học sinh giỏi Toán có 3 nam và 5 nữ, chọn ngẫu nhiên 2 em đi thi học sinh
giỏi Toán. Tính xác suất để chọn được 1 nam và 1 nữ.
A.
15
.
56
B.
25
.
28
C.
15
.
28
D.
8
.
56
Câu 17.
Trong không gian có bao nhiêu vị trí tương đối giữa hai đường thẳng.
A.
3.
B.
4.
C.
5.
D.
2.
Câu 18.
Các hình sau đây biểu diễn một hình chóp tứ giác trong không gian. Hình nào sai?
A. Hình 2. B. Hình 3. C. Hình 4. D. Hình 1.
Hình 4
Hình 3
Hình 2
Hình 1
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 20 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 19. Tìm nghiệm của phương trình:
2
sin sinx 0
x
thỏa mãn
2 2
x
.
A.
4
x
. B.
2
x
. C.
2
x
. D.
0.
x
Câu 20. Cho dãy số
n
u
với
2
1
n
n
u
n
. Tìm
5
.
u
A.
5
5
.
26
u
B.
5
5
6
u
. C.
5
5
26
u . D.
5
5.
u
Câu 21. Từ các chữ số 2,3,4,6,7,9 lập được bao nhiêu số chẵn có ba chữ số?
A.
108.
B.
36.
C.
20.
D.
40.
Câu 22. Trong mặt phẳng
Oxy
, cho
(2; 1)
v
và điểm
( 3;2).
M
Tìm điểm
'
M
là ảnh của điểm
M
qua phép tịnh tiến theo vectơ
.
v
A.
'( 1;1).
M
B.
'(1; 1).
M
C.
'( 1;0).
M
D.
'(1;1).
M
Câu 23. Trong mặt phẳng
Oxy
, cho đường thẳng
: 2 3 3 0
d x y
. Tìm phương trình đường
thẳng
d
là ảnh của
d
qua phép vị tự tâm
O
tỉ số
2
k
.
A.
4 2 3 0
x y
. B.
4 2 5 0
x y
. C.
2 3 0
x y
. D.
2 3 6 0
x y
.
Câu 24. Cho dãy số
n
u
là cấp số cộng có số hạng đầu
1
u
, công sai
d
,
n
S
là tổng của
n
số
hạng đầu tiên. Với
2
n
, đẳng thức nào sau đây sai?
A.
1
1
n
u u n d
. B.
1 1
2
n n
n
u u
u
.
C.
1n n
u u d
. D.
1
1
2
n
n
S u n d
.
Câu 25. Tìm tập giá trị
T
của hàm số
3 2sin
y x
.
A.
2;4 .
T B.
1;5 .
T C.
1;1 .
T D.
0;3 .
T
B. TỰ LUẬN
Câu 1. Giải phương trình:
sin 3cos 1
x x
.
Câu 2. Trong khoảng
(0;3 ),
phương trình
3
sin 2
2
x
có bao nhiêu nghiệm?
Câu 3. Một hộp chứa 10 quả cầu được đánh số từ 1 đến 10. Lấy ngẫu nhiên một quả. Tính xác
suất của biến cố A: “Nhận được quả cầu ghi số chẵn”.
Câu 4. Tìm số hạng không chứa
x
trong khai triển
6
2
, 0
x x
x
.
Câu 5. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Trên cạnh CD lấy
điểm P sao cho 2
PD PC
.
a) Tìm giao điểm của đường thẳng BD và mặt phẳng
MNP
.
b) Tìm giao tuyến của mặt phẳng
MNP
và
ABD
.
----------HẾT----------
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 21
SỞ GIÁO DỤC & ĐÀO TẠO
HUẾ
---------------------------
THPT CHUYÊN QUỐC HỌC
KHỐI 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1
NĂM HỌC: 2019 - 2020
Thời gian: 90 phút
Họ tên: .............................................................................................. Lớp: ...................................................
A. TRẮC NGHIỆM
Câu 1: Tìm tập xác định của hàm số
1
sin
y
x
.
A.
\ ,D k k
. B.
\ ,
2
D k k
.
C.
\ 0D
. D.
D
.
Câu 2: Cho hình chóp
.S ABCD
có đáy là một tứ giác lồi. Hình nào sau đây không thể là thiết
diện của nó.
A. Lục giác. B. Tam giác. C. Tứ giác. D. Ngũ giác.
Câu 3: Có
10
cây bút khác nhau và
9
quyển sách khác nhau. Tìm số cách chọn
1
cây bút và
1
quyển sách.
A.
80
. B.
70
. C.
19
. D.
90
.
Câu 4: Một hộp chứa
6
quả bóng đỏ (được đánh số từ
1
đến
6),
5
quả bóng vàng (đươc
đánh số từ
1
đến
5),
4 quả bóng xanh (được đánh số từ
1
đến
4).
Lấy ngẫu nhiên
4
quả bóng. Tính xác suất để
4
quả bóng lấy ra có đủ ba màu và không có hai quả bóng
nào có số thứ tự trùng nhau.
A.
43
.
91
B.
74
.
455
C.
381
.
455
D.
48
.
91
Câu 5: Tìm số cách xếp
5
bạn nam và
4
ban nữ thành một hàng ngang sao cho
4
bạn nữ
luôn đứng cạnh nhau.
A.
17280.
B.
362880.
C.
5760.
D.
2880.
Câu 6: Cho tập hợp
0;2;4;5;6 ,A
tìm số chỉnh hợp chập
3
của
.A
A.
60.
B.
96.
C.
20.
D.
10.
Câu 7: Gieo đồng thời 2 con súc sắc cân đối, đồng chất, một con màu đỏ và một con màu đen.
Tính xác suất của biến cố: “Số chấm trên con đen lớn hơn số chấm trên con đỏ 2 đơn
vị.”
A.
5
.
36
B.
9
.
36
C.
32
.
36
D.
1
.
9
Câu 8: Gọi M là tổng các nghiệm thuộc
;5
của phương trình
1 sin
1,
cos
x
x
tìm M.
A.
13 .M
B.
15
.
2
M
C.
23
.
2
M
D.
27
.
2
M
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 22 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 9: Cho
ABC
vuông tại B và
60
A
(các đỉnh của tam giác ghi theo thứ tự ngược
chiều kim đồng hồ). Về phía ngoài tam giác, vẽ tam giác đều ACD. Tìm ảnh của cạnh
BC qua phép quay tâm A, góc quay
60 .
A. AI với I là trung điểm của CD. B. DK với K là trung điểm của AC.
C. AD. D. CJ với J là trung điểm của AD.
Câu 10: Tìm số điểm biểu diễn các họ nghiệm của phương trình
2
2sin 3sin 5 0
x x
trên
đường tròn lượng giác là.
A.
2.
B.
3.
C.
1.
D.
4.
Câu 11: Tìm điều kiện của tham số thực
m
để phương trình
sin 3cos 5
m x x
có nghiệm.
A.
4.
m
B.
34.
m C.
4
.
4
m
m
D.
4 4.
m
Câu 12: Cho cấp số cộng có số hạng đầu
1
1
u
và công sai
2.
d
Tổng
n
số hạng đầu tiên
của cấp số cộng này là
9800,
n
S
tìm
.
n
A.
101.
B.
100.
C.
98.
D.
99.
Câu 13: Tìm số các nghiệm thuộc
0;2019
của phương trình
3 cot 3 0
x
.
A.
2018.
B.
2019.
C.
4038.
D.
4039.
Câu 14: Tìm mệnh đề sai trong các mệnh đề sau đây.
A. Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với
nó.
B. Phép đồng dạng bảo toàn độ lớn góc.
C. Phép dời hình là phép đồng dạng tỉ số
1
k
.
D. Phép vị tự tỉ số
k
là phép đồng dạng tỉ số
k
.
Câu 15: Tìm phương trình tương đương với phương trình
2 2
3sin cos
x x
.
A.
2
3
sin .
4
x
B.
1
sin .
2
x
C.
3
cos .
2
x
D.
2
cot 3.
x
Câu 16: Một lớp học có
30
học sinh gồm có cả nam và nữ. Chọn ngẫu nhiên
3
học sinh để
tham gia hoạt động của Đoàn trường. Biết xác suất chọn được
2
nam và
1
nữ là
12
,
29
gọi
n
là số học sinh nữ của lớp, tìm mệnh đề đúng?
A.
20;23 .
n B.
15;19 .
n C.
12;15 .
n D.
8;12 .
n
Câu 17: Tìm chu kỳ tuần hoàn
T
của hàm số
sin
2
x
y
với
0 .
x
A.
.
2
T
B.
2 .
T
C.
4 .
T
D.
.
T
Câu 18: Gieo
3
đồng xu một lúc, gọi
A
là biến cố “có đúng một đồng xu xuất hiện mặt ngửa”.
Tìm xác suất của biến cố
.
A
A.
1
.
2
B.
1
.
4
C.
3
.
8
D.
1
.
8
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 23
Câu 19: Trong mặt phẳng
Oxy
cho
2;0 , 2;2 , 4;2 , 4;0
A B C D . Chọn ngẫu nhiên một
điểm có tọa độ
;
x y
(với
,
x y
là các số nguyên) nằm trong hình chữ nhật
ABCD
(kể
cả các điểm nằm trên cạnh). Gọi
A
là biến cố: “
,
x y
đều chia hết cho 2”, tính xác suất
của biến cố
A
.
A.
13
21
. B.
7
21
. C.
1
. D.
8
21
.
Câu 20: Tìm số các giá trị nguyên của hàm số
5 4cos 2 sin 2
y x x
.
A. 5. B. 6. C. 3. D. 4.
Câu 21: Tìm số các số tự nhiên có 5 chữ số đôi một phân biệt, được lập từ các chữ số 1,2,3,4,5,6,
biết rằng trong các số đó phải có các chữ số 1 và 5.
A. 735. B. 1200. C. 600. D. 480.
Câu 22: Một lô hàng gồm
30
sản phẩm tốt và
10
sản phẩm xấu. Lấy ngẫu nhiên
3
sản phẩm.
Tính xác suất để
3
sản phẩm lấy ra có ít nhất một sản phẩm tốt.
A.
244
.
247
B.
15
.
26
C.
135
.
988
D.
3
.
247
Câu 23: Cho cấp số cộng
( )
n
u
có
4 14
12; 18.
u u
Tìm số hạng đầu tiên
1
u
và công sai
d
của
cấp số cộng.
A.
1
22; 3.
u d
B.
1
21; 3.
u d
C.
1
20; 3.
u d
D.
1
21; 3.
u d
Câu 24: Trong mặt phẳng
,
Oxy
cho hai đường thẳng
,
a b
lần lượt có phương trình là
2 3 0
x y
và
2 5 0.
x y
Nếu có phép quay với góc quay
0
(0 180 )
biến
đường thẳng này thành đường thẳng kia thì số đo của
là:
A.
0
45 .
B.
0
90 .
C.
0
60 .
D.
0
120 .
Câu 25: Tìm số hạng tổng quát
n
u
trong các trường hợp dưới đây để dãy số
n
u
giảm.
A.
1
.
2
n
n
u
B.
2
.
n
u n
C.
3 1
.
1
n
n
u
n
D.
2.
n
u n
B. TỰ LUẬN
Câu 1: Cho hình chóp
.
S ABCD
, có đáy
ABCD
là hình thang với đáy lớn
AB
và đáy nhỏ
CD
.
Gọi
,
M N
lần lượt là trung điểm của
SA
và
SB
; gọi
E
là giao điểm của
AD
và
BC
.
a) Tìm giao tuyến của
SBC
và
ADM
. Xác đinh giao điểm
P
của đường thẳng
SC
và
mặt phẳng
ADM
.
b) Gọi
I
là giao điểm của
DP
và
AM
. Chứng minh
SI
song song với
AB
.
c) Xác định thiết diện của hình chóp với mặt phẳng
α
biết
α
qua
MN
và song song
với
SC
.
Câu 2: Trong mặt phẳng
,
Oxy
tìm phương trình đường thẳng
là ảnh của đường thẳng
: 2 1 0
x y
qua phép tịnh tiến theo vectơ
1; 1 .
v
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 24 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 3: Cho hàm số
4sin 3 cos
y x m x
với
m
là tham số thực. Tìm giá trị của tham số m để giá
trị lớn nhất của hàm số bằng
3 2
.
Câu 4: Tìm hệ số chứa
30
x
trong khai triển nhị thức
15
3
2
2
x
x
với
0 .
x
Câu 5: Cho dãy số
n
u
cho bởi
1
1
1
2
2
n n
u
u u
, tìm công thức số hạng tổng quát của dãy số đó.
----------HẾT----------
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 25
SỞ GIÁO DỤC & ĐÀO TẠO
HUẾ
---------------------------
THPT ĐẶNG TRẦN CÔN
KHỐI 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1
NĂM HỌC: 2019 - 2020
Thời gian: 90 phút
Họ tên: .............................................................................................. Lớp: ...................................................
A. TRẮC NGHIỆM
Câu 1: Trên giá sách có
5
quyển sách toán khác nhau và
4
quyển sách tiếng Anh khác nhau.
Hỏi có tất cả mấy cách chọn một quyển sách?
A.
20.
B.
5.
C.
4.
D.
9.
Câu 2: Mệnh đề nào sau đây sai?
A. Hai đường thẳng phân biệt có một điểm chung thì cắt nhau.
B. Hai đường thẳng không đồng phẳng thì chéo nhau.
C. Hai đường thẳng song song thì đồng phẳng.
D. Hai đường thẳng không có điểm chung thì song song.
Câu 3: Tìm tất cả các giá trị của tham số
m
để hàm số
sinxy m
xác định trên đoạn
3
;
4 4
?
A.
2
2
m
.
B.
1m
. C.
0m
.
D.
2
.
2
m
Câu 4: Trong trường A, tỉ lệ học sinh giỏi môn Văn là 12%, học sinh giỏi Toán là 9% và học
sinh giỏi cả hai môn là 7%. Chọn ngẫu nhiên một học sinh của trường A. Tính xác suất
p để học sinh đó không học giỏi văn và không học giỏi Toán.
A.
0,72.p
B.
0,86.
C.
0,79.
D.
0,93.p
Câu 5: Cho cấp số cộng
n
u
có công sai
d
. Công thức nào sau đây đúng?
A.
1 1
1
n
u u n d
. B.
1 1
2
n
u u nd
.
C.
1 1
1
n
u u n d
. D.
1 1n
u u nd
.
Câu 6: Tất cả các nghiệm của phương trình
cot 3 0x
là:
A.
,
6
x k k
. B.
,
6
x k k
.
C.
,
3
x k k
. D.
,
3
x k k
.
Câu 7: Phương trình
2 2
2 1 cos 2sin cos 2 1 sin 0x x x x
tương đương với phương
trình nào sau đây?
A.
cos 2 1.
4
x
B.
2
cos 2 .
4 2
x
C.
3
cos 2 .
4 2
x
D.
1
cos 2 .
4 2
x
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 26 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 8: Cho hình chóp S.ABCD có đáy là hình thoi. Gọi O là giao điểm của AC và BD ; E và F
lần lượt là trung điểm của OA và OC ; điểm I thay đổi trên đoạn
;
AC I A I O
. Gọi
(P) là mặt phẳng qua I và song song với BD và SA. Biết (P) cắt S.ABCD theo thiết diện
là đa giác (H). Hãy xác định tất cả các vị trí của I để (H) có số cạnh nhiều nhất.
A. I thuộc đoạn
; .
OA I O I A
B. I thuộc đoạn
; .
EA I E I A
C. I thuộc đoạn
; .
FC I C I F
D. I thuộc đoạn
; .
OC I C I O
Câu 9: Mệnh đề nào sau đây sai?
A.
2
cos cos
2
x k
x
x k
,k
. B.
2
sin sin
2
x k
x
x k
,k
.
C.
tan tan ,x x k k
. D.
cot cot ,x m x acr m k k
.
Câu 10: Cho dãy số
n
u
với
2
n
n
u n
. Số hạng thứ 6 của dãy bằng:
A. -58. B. 70. C. -27. D. 38.
Câu 11: Cho cấp số nhân
n
u
có công bội
1
q
. Tổng của n số hạng đầu tiên bằng.
A.
1
1
1
n
u q
q
. B.
1
1
n
u q
q
. C.
1
1
1
n
u q
q
. D.
1
1
n
u q
q
.
Câu 12: Có tất cả mấy cách xếp ba bạn nam và hai bạn nữ ngồi vào một bàn gồm năm chỗ?
A.
150.
B.
3125.
C.
25.
D.
120.
Câu 13: Mệnh đề nào sau đây sai?
A.
s 0 2 , .
inx x k k
B.
3
s 1 2 , .
2
inx x k k
C.
s 1 2 , .
co x x k k
D.
s 1 2 , .
co x x k k
Câu 14: Cho cấp số cộng
n
u
có công sai
3
d
và
1
1
.
2
u
Số hạng thứ chín của cấp số đã
cho bằng
A.
53
.
2
B.
41
.
2
C.
35
.
2
D.
47
.
2
Câu 15: Hệ số của số hạng chứa
5
x
trong khai triển và rút gọn của biểu thức
5 10
2
1 2 1 3
x x x x
bằng:
A. 61204. B. 3320. C. 61268. D. 3160.
Câu 16: Số cạnh của một hình tứ diện đều là:
A.
6
. B.
4
. C.
3
. D.
5
.
Câu 17: Gọi
n
là số tự nhiên thỏa mãn
0 1 2
4 1
n n n
C C C
. Hãy chọn mệnh đề đúng trong các
mệnh đề sau:
A.
15
n
. B.
5;8
n . C.
8;12
n . D.
12;15
n .
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 27
Câu 18: Cho tứ diện đều
ABCD
có các cạnh đều bằng
a
. Gọi
G
là trọng tâm tam giác
ABC
,
M
là trung điểm của cạnh
CD
. Diện tích thiết diện của tứ diện
ABCD
khi cắt bởi mặt
phẳng
AMG
(tính theo
a
) bằng:
A.
2
11
16
a
. B.
2
11
8
a
. C.
2
11
2
a
. D.
2
11
32
a
.
Câu 19: Cho tứ diện
ABCD
. Gọi
,
M N
và
P
lần lượt là trung điểm của các cạnh
,
AB BC
và
DA
Mệnh đề nào sau đây sai?
A.
DC MNP
. B.
MP BCD
. C.
MN ACD
. D.
BD MNP
Câu 20: Biết đoạn
;
a b
là tập hợp tất cả các giá trị của tham số
m
để phương trình
sin 1 2
x m
có nghiệm. Gía trị của biểu thức
3
a b
bằng:
A. 2. B. 3. C. 4. D. 1
Câu 21: Trong mặt phẳng tọa độ
Oxy
, cho vectơ
3;2
a
và đường tròn
C
có phương trình
2 2
1 3 4
x y
. Phép tịnh tiến
a
T
biến đường tròn
C
thành đường tròn có
phương trình:
A.
2 2
2 5 4.
x y
B.
2 2
1 3 4.
x y
C.
2 2
2 5 4.
x y
D.
2 2
4 1 4.
x y
Câu 22: Điều kiện xác định của hàm số
sin cos
sin cos
x x
y
x x
là:
A.
2 , .
4
x k k
B.
, .
4
x k k
C.
2 , .
4
x k k
D.
, .
4
x k k
Câu 23: Cho cấp số cộng
n
u
có
1
3
u
và công sai
2.
d
Tổng
10
số hạng đầu của cấp số cộng
đã cho bằng
A.
105.
B.
115.
C.
130.
D.
120.
Câu 24: Tất cả các nghiệm của phương trình
2cos3 2 0
x
là
A.
2 ; .
4
x k k
B.
3 2
; .
4 3
x k k
C.
2
; .
4 3
x k k
D.
3
2 ; .
4
x k k
Câu 25: Cho cấp số nhân
( )
n
u
biết
1 3
2; 486
u u
.Tổng của 8 số hạng đầu tiên bằng?
A.
5765
. B.
4376
. C.
6792
. D.
7210.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 28 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
B. TỰ LUẬN
Câu 1. Giải phương trình:
3
sin3
2
x
.
Câu 2. Từ một bình chứa 7 quả cầu đỏ và 4 quả cầu xanh. Lấy ra ngẫu nhiên đồng thời 3 quả.
Tính xác suất để lấy được 3 quả cùng màu.
Câu 3. Cho cấp số nhân
n
u
có
1
1024
u
và công bội
1
2
q
. Tính
15
u
.
Câu 4. Cho cấp số cộng có số hạng thứ ba bằng
5
và công sai bằng
1
3
. Tính tổng
100
số hạng
đầu tiên của cấp số cộng đã cho.
Câu 5. Cho hình chóp .
S ABC
. Gọi
, ,
M N P
lần lượt là trọng tâm của các tam giác
,
SAB SAC
và
ABC
a) Chứng minh
.
MN SBC
b) Xác định giao điểm của đường thẳng
SP
và
.
AMN
----------HẾT----------
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 29
SỞ GIÁO DỤC & ĐÀO TẠO
HUẾ
---------------------------
THPT GIA HỘI
KHỐI 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1
NĂM HỌC: 2019 - 2020
Thời gian: 90 phút
Họ tên: .............................................................................................. Lớp: ...................................................
A. TRẮC NGHIỆM
Câu 1. Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 1 2 9C x y
. Tìm phương trình
đường tròn
C
là ảnh của
C
qua phép tịnh tiến theo vectơ
2;3v
.
A.
2 2
: 1 1 9.C x y
B.
2 2
: 3 5 9.C x y
C.
2 2
: 3 5 9.C x y
D.
2 2
: 1 1 9.C x y
Câu 2. Tìm hệ số của số hạng chứa
5
x
trong khai triển
12
1 3x
A.
192456.
B.
729.
C.
192456.
D.
729.
Câu 3. Tìm giá trị lớn nhất (
max y
), giá trị nhỏ nhất (
min y
) của hàm số
4 4
sin cosy x x
.
A.
1
min
.
2
max 1
y
y
B.
1
min
.
2
max 1
y
y
C.
min 1
.
1
max
2
y
y
D.
min 1
.
1
max
2
y
y
Câu 4. Trong mặt phẳng
Oxy
, cho vectơ
3; 5v
và điểm
1;1M
. Tìm tọa độ điểm
'M
là
ảnh của điểm
M
qua phép tịnh tiến theo vectơ
v
.
A.
' 4; 6 .M
B.
' 2; 4 .M
C.
' 4; 4 .M
D.
' 2; 6 .M
Câu 5. Đẳng thức nào sau đây là sai?
A.
1 ! ! 2 . !n n n n
. B.
2 . 1 ! 2 !n n n
.
C.
0! 1! 2!
. D.
1 . ! 1 !n n n
.
Câu 6.
20
đường thẳng phân biệt có tối đa bao nhiêu giao điểm?
A.
200
. B.
190
. C.
380
. D.
20
.
Câu 7. Tìm tất cả các nghiệm của phương trình
4 4
cos sin 0.x x
A.
, .
2
x k k Z
B.
, .
4 2
x k k Z
C.
2 , .x k k Z
D.
, .x k k Z
Câu 8. Tìm tất cả các nghiệm của phương trình
1
sin .
2
x
A.
2
2 2 , .
3 3
x k x k k Z
B.
7
2 2 , .
6 6
x k x k k Z
C.
5
2 2 , .
6 6
x k x k k Z
D.
5
2 2 , .
6 6
x k x k k Z
Câu 9. Tìm tập xác định
D
của hàm số
1
1 sin 2
y
x
.
A.
\ 2 ,
2
D k k
. B.
\ ,
4
D k k
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 30 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
C.
\ 2 ,
4
D k k
. D.
\ ,
4
D k k
.
Câu 10. Các hàm số sau được xét trên tập xác định của chúng. Trong các mệnh đề sau, mệnh
đề nào sai?
A. Hàm số
cos
y x
là hàm số chẵn.
B. Hàm số
cos .sin
y x x
là hàm số không chẵn cũng không lẻ.
C. Hàm số
3 3
sin .cos
y x x
là hàm số lẻ.
D. Hàm số
sin , tan , cot
y x y x y x
đều là các hàm số lẻ.
Câu 11. Gieo đồng thời một con súc sắc và một đồng xu. Tính xác suất để xuất hiện đồng xu có
mặt ngửa và con súc sắc có số chấm không vượt quá 4.
A.
1
.
2
B.
1
.
6
C.
1
.
4
D.
1
.
3
Câu 12. Tìm tập nghiệm của phương trình
2 cos sin 3 0.
x x
A.
.
B.
, .
2
k k
C.
, .
2
k k
D.
.
Câu 13. Biết
4
126
n
C
. Tính
4
.
n
A
A.
3024.
B.
24.
C.
504.
D.
756.
Câu 14. Tìm điều kiện xác định của phương trình
tan 2 3.
3
x
A.
5
, .
12 2
x k k
B.
, .
2
x k k
C.
5
, .
12
x k k
D.
, .
6 2
x k k
Câu 15. Tính số tập hợp con của tập hợp
; ; ; ; ; ; .
A a b c d e f g
A.
127.
B.
15.
C.
128.
D.
14.
Câu 16. Trong các mệnh đề sau, tìm mệnh đề đúng ?
A. Trên khoảng
0;
2
hàm số
sin
y x
và hàm số
cos
y x
cùng nghịch biến.
B. Trên khoảng
0;
2
hàm số
sin
y x
nghịch biến và hàm số
cos
y x
đồng biến.
C. Trên khoảng
0;
2
hàm số
sin
y x
đồng biến và hàm số
cos
y x
nghịch biến.
D. Trên khoảng
0;
2
hàm số
sin
y x
và hàm số
cos
y x
cùng đồng biến.
Câu 17. Tìm tất cả các nghiệm của phương trình
cos 3 sin 0
x x
.
A.
2 ,
3
x k k
B.
,
2
x k k
C.
,
6
x k k
. D.
, .
6
x k k
Câu 18. Trong mặt phẳng
Oxy
cho điểm
1;7
M và vectơ
2; 5
v
. Tìm
M
là ảnh của
M
qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ
v
và phép vị tự tâm
O
tỉ số
2
k
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 31
A.
1
;6
2
M
. B.
3
;1
2
M
. C.
2;24
M
. D.
6;4 .
M
Câu 19. Tìm số nghiệm của phương trình
cos3 sin 2 0
x x
trên đoạn
0; .
A.
3
. B.
4
. C.
2
. D.
1
Câu 20. Tính tổng
0 1 2
3 9 ... 3 .
n n
n n n n
S C C C C
A.
4
n
. B.
3
n
. C.
2
n
. D.
1
3
n
Câu 21. Phương trình
2
sin 1
x
tương đương với phương trình sau đây?
A.
sin 0
x
. B.
sin 1
x
. C.
sin 1
x
. D.
sin 1
x
.
Câu 22. Cho E là tập hợp các số tự nhiên gồm 2 chữ số khác nhau được lập từ các chữ số 1, 2, 3,
4, 5, 6. Lấy ngẫu nhiên một phần tử của E, tính xác suất để được một số chia hết cho 4
hoặc chia hết cho 7?
A.
7
10
. B.
11
30
. C.
4
5
. D.
13
30
.
Câu 23. Tìm tập nghiệm của phương trình
cos 2 1
4
x
.
A.
,
8
k k
. B.
1
2 ,
2 8
k k
.
C.
,
8
k k
. D.
2 ,
4
k k
.
Câu 24. Tìm tập xác định
D
của hàm số
1
2 sin 7 2017
y
x
.
A.
\ ,
2
D k k
. B.
2019
\
7
D
.
C.
2019
\ 2 ,
7
D k k
. D.
D
.
Câu 25. Cho hàm số
sin cos ,
y x x
tìm khẳng định đúng?
A.
y 2 y 2.
B.
0 y 2.
C.
2 y 2.
D.
2 y 0.
B. TỰ LUẬN
Câu 1. Tìm tập nghiệm của phương trình
2cos 3 0.
2
x
Câu 2. Trong mặt phẳng
O
xy
, cho đường thẳng
: 3 4 12 0.
d x y
Tìm phương trình đường
thẳng
d
là ảnh của
d
qua phép tịnh tiến vectơ
2;1 .
v
Câu 3. Đội văn nghệ của lớp có 5 bạn nam và 7 bạn nữ. Chọn ngẫu nhiên 5 bạn tham gia biểu
diễn. Tính xác suất để trong 5 bạn được chọn có cả nam và nữ, đồng thời số bạn nữ
nhiều hơn số bạn nam.
Câu 4. Tìm tất cả các giá trị của tham số
m
để phương trình
2 2
3
cos x m
có nghiệm?
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 32 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 5. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
a
. Hai mặt bên
SAB
và
SCD
là các tam giác đều. Gọi
G
là trọng tâm tam giác
SAB
,
E
là điểm di động trên đoạn
thẳng
BG
(
E
khác
B
). Cho mặt phẳng
qua
E
, song song với
SA
và
BC
.
a) Chứng minh đường thẳng
AD
song song với mặt phẳng
. Tìm giao điểm
, , ,
M N P Q
của mặt phẳng
với các cạnh
, , ,
SB SD DC BA
.
b) Gọi
I
là giao điểm của
QM
và
PN
. Chứng minh
I
nằm trên một đường thẳng cố
định khi điểm
E
di động trên đoạn
BG
.
c) Chứng minh tam giác
IPQ
là tam giác đều. Tính diện tích tam giác
IPQ
theo
a
.
----------HẾT----------
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 33
SỞ GIÁO DỤC & ĐÀO TẠO
HUẾ
---------------------------
THPT CHI LĂNG
KHỐI 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1
NĂM HỌC: 2019 - 2020
Thời gian: 90 phút
Họ tên: .............................................................................................. Lớp: ...................................................
A. TRẮC NGHIỆM
Câu 1. Trong mặt phẳng
Oxy
cho
3;6B
và
5; 4 .v
Tìm tọa độ điểm
C
sao cho
v
T C B
A.
8; 10 .C
B.
2; 2 .C
C.
2;2 .C
D.
8;10 .C
Câu 2. Tìm tập xác định của hàm số
sin 1
sin
x
y
x
A.
\ 2 ; .
2
D k k
B.
\ ; .D k k
C.
\ ; .
2
D k k
D.
\ 2 ; .D k k
Câu 3. Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình vẽ. Hỏi có
bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?
A.
24.
B.
18.
C.
10.
D.
9.
Câu 4. Tìm tất cả cá nghiệm của phương trình
2cos 2 0.x
A.
3
2
4
.
2
4
x k
x k
B.
5
2
4
.
5
2
4
x k
x k
C.
2
4
.
3
2
4
x k
x k
D.
2
4
.
2
4
x k
x k
Câu 5. Trong mặt phẳng tọa độ
Oxy
cho đường tròn
C
có phương trình
2 2
2 2 4.x y
Phép đồng dạng có được bằng việc thực hiện liên tiếp các phép vị
tự tâm
O
tỉ số
1
2
k
và phép quay tâm
O
góc quay
0
90
sẽ biến đường tròn
C
thành
đường tròn nào trong các đường tròn sau đây?
A.
2 2
2 2 1.x y
B.
2 2
1 1 1.x y
C.
2 2
1 1 1.x y
D.
2 2
2 1 1.x y
Câu 6. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng không có điểm chung thì chéo nhau.
B. Hai đường thẳng chéo nhau thì không có điểm chung.
C. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
D. Hai đường thẳng phân biệt không chéo nhau thì hoặc song song hoặc cắt nhau.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 34 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 7. Cho hình chóp
.
S ABCD
có đáy là hình thang cân đáy lớn
AD
,
,
M N
lần lượt là là
trung điểm của
AB
và
CD
,
P
là mặt phẳng qua
MN
và cắt mặt bên
SBC
theo một
giao tuyến. Thiết diện của
P
và hình chóp là hình gì?
A. Hình bình hành. B. Hình thang. C. Hình chữ nhật. D. Hình vuông.
Câu 8. Một đề thi có 20 câu hỏi trắc nghiệm khách quan, mỗi câu có 4 phương án lựa chọn,
trong đó chỉ có một phương án trả lời đúng. Khi thi, một học sinh đã chọn ngẫu nhiên
một phương án trả lời với mỗi câu của đề thi đó. Trong trường hợp đó xác suất để học
sinh đó trả lời không đúng cả 20 câu là bao nhiêu?
A.
1
4
. B.
3
4
. C.
1
20
. D.
20
3
4
.
Câu 9. Hiếu có 8 người bạn. Hiếu muốn mời 4 trong 8 người bạn đó về quê chơi vào cuối
tuần. Nhưng trong 8 người bạn đó có 2 bạn là Khoa và Tuấn không thích đi chơi với
nhau. Như vậy số cách chọn nhóm 4 người để về quê của Hiếu là bao nhiêu?
A.
4
8
C
. B.
4 3
6 6
2
C C
. C.
4 3
6 6
C C
. D.
4 3
6 7
C C
.
Câu 10. Một họp có 10 viên bi màu trắng, 20 viên bi màu xanh, 30 viên bi màu đỏ, mỗi viên bi
chỉ có một màu. Có bao nhiêu cách để chọn ngẫu nhiên 8 trong số các viên bi thuộc
hộp đó để được 8 viên bi cùng màu trắng?
A.
4
20
C
. B.
8
10
C
. C.
8
60
C
. D.
4
30
C
.
Câu 11. Cho tập hợp
2;3;4;5;6;7
A
. Có thể lập được tất cả bao nhiêu số tự nhiên gồm 3 chữ
số khác nhau được thành lập từ các chữ số thuộc
A
?
A.
120.
B.
216.
C.
256.
D.
180.
Câu 12. Trong khai triển
10
2 1
x
. Tìm hệ số của số hạng chứa
8
x
.
A.
256.
B.
45.
C.
11520.
D.
11520.
Câu 13. Hãy viết ba số hạng tiếp theo hai số hạng đầu của dãy số
n
u
có
1 2 2 1
1, 1,
n n n
u u u u u
.
A.
2;3;5.
B.
3;4;7.
C.
2;5;7.
D.
3;5;8.
Câu 14. Xét phép thử là gieo một con xúc xắc hai lần. Gọi
N
là biến cố” lần đầu xuất hiện mặt
5
chấm”, gọi
M
là biến cố” lần hai xuất hiện mặt
5
chấm” thì
A.
5;1 , 5;2 , 5;3 , 5;4 , 5;5 , 5;6 , 1;5 , 2;5 , 3;5 , 4;5 ,
5;5 , 6;5 .
M N
B.
1;5 , 2;5 , 3;5 , 4;5 , 5;5 , 6;5 .
M N
C.
5;1 , 5;2 , 5;3 , 5;4 , 5;5 , 5;6 .
M N
D.
5;5 .
M N
Câu 15. Tìm giá trị lớn nhất và giá trị bé nhất của hàm số
1 3sin 2
4
y x
A.
max 3 ; min 2
y y
. B.
max 2 ; min 3
y y
.
C.
max 4 ; min 2
y y
. D.
max 4 ; min 2
y y
.
Câu 16. Tìm tất cả các nghiệm
0 ;
2
x
của phương trình
2
2sin 3sin 1 0
x x
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 35
A.
12
x
. B.
5
6
x
. C.
6
x
. D.
2
x
.
Câu 17. Có bao nhiêu cách sắp xếp bốn bạn Văn, Bình, Nhi, Thi ngồi vào một bàn dài gồm 4
chỗ ?
A.
1.
B.
8.
C.
4.
D.
24.
Câu 18. Trong không gian, cho
4
điểm không đồng phẳng. Có bao nhiêu tam giác từ
4
điểm
đã cho ?
A.
6.
B.
4.
C.
3.
D.
2.
Câu 19.
Trong mặt
Oxy
cho điểm
3;6
B . Tìm tọa độ điểm
E
sao cho
B
là ảnh của
E
qua
phép quay tâm
O
, góc quay
90
.
A.
6;3
E . B.
3;6
E . C.
6; 3
E
. D.
3; 6
E
.
Câu 20. Tìm số tự nhiên
n
, biết hệ số của số hạng thứ 3 theo số mũ giảm dần của
x
trong khai
triển
1
3
n
x
bằng
4
.
A.
8
. B.
4
. C.
9
. D.
17
.
Câu 21. Phép vị tự
;
I k
V
biến điểm
M
thành điểm
'
M
là phép đồng nhất khi nào?
A.
1.
k
B.
0.
k
C.
1.
k
D.
1.
k
Câu 22. Cho hình tứ diện
ABCD
có
,
M N
lần lượt là trung điểm của
, .
AB BD
Các điểm
,
G H
lần lượt trên cạnh
,
AC CD
sao cho
NH
cắt
MG
tại
.
I
Khẳng định nào sau đây là
khẳng định đúng?
A.
, ,
B G H
thẳng hàng. B.
, ,
B C I
thẳng hàng.
C.
, ,
N G H
thẳng hàng. D.
, ,
A C I
thẳng hàng.
Câu 23. Cho cấp số cộng có các số hạng lần lượt là
5;9;13;17;...
Khi đó
n
u
có thể được tính theo
biểu thức nào dưới đây.
A.
5 1.
n
u n
B.
4 1.
n
u n
C.
5 1.
n
u n
D.
4 1.
n
u n
Câu 24. Trong mặt phẳng
Oxy
, cho điểm
2; 1
A
. Tìm ảnh của
A
qua phép dời hình có được
bằng cách thực hiện liên tiếp phép tịnh tiến theo
3;1
u
và phép quay tâm
O
góc
quay
90 .
A.
5;0 .
B.
0;5 .
C.
5;0 .
D.
0; 5 .
Câu 25. Gía trị của biểu thức
1 2 2 3 3 2020 2020
2020 2020 2020 2020
1 2 2 2 ... 2P C C C C là:
A.
2020
3
P . B.
1
P
. C.
2020
3
P . D.
1
P
.
B. TỰ LUẬN.
Câu 1. Giải các phương trình sau:
a)
3tan 2 3
x
. b)
2
2sin cos 2 0
x x
.
Câu 2. Ngân hàng đề thi gồm
100
câu hỏi, mỗi đề thi có
5
câu. Một học sinh học thuộc
80
câu. Tính xác suất để học sinh đó rút ngẫu nhiên được một đề thi có
4
câu học thuộc.
Câu 3. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành tâm
,
O
gọi
,
M N
lần lượt là
trung điểm của
, .
SA SD
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 36 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
a) Tìm giao tuyến của hai mặt phẳng
SAC
và
.
SBD
b) Tìm thiết diện của hình chóp .
S ABCD
cắt bởi mặt phẳng
.
OMN
Thiết diện đó là
hình gì?
Câu 4. Hệ số của
5
x
trong khai triển
7
2
2 4 3
x x
là ?
Câu 5. Tồng các nghiệm của phương trình
sin 3 cos 2
x x
trện đoạn
0;4
là ?
----------HẾT----------
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 37
SỞ GIÁO DỤC & ĐÀO TẠO
ĐẮK LẮK
---------------------------
THPT
CHUYÊN NGUYỄN DU
KHỐI 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1
NĂM HỌC: 2019 - 2020
Thời gian: 90 phút
Họ tên: .............................................................................................. Lớp: ...................................................
A. TRẮC NGHIỆM
Câu 1. Trong các phương trình sau phương trình nào có nghiệm:
A.
2
cot cot 3 0x x
. B.
3 sin 2x
.
C.
1 1
cos 4
4 2
x
. D.
2sin 3cos 4x x
.
Câu 2. Tập xác định của hàm số
cos 1y x
là:
A.
2
2
k k
. B.
. C.
2k k
. D.
k k
.
Câu 3. Trong các hàm số sau, hàm số nào là hàm số chẵn:
A.
2019cos 2020siny x x
. B.
tan 2019 cot 2020y x x
.
C.
cot 2019 2020siny x x
. D.
sin 2019 cos 2020y x x
.
Câu 4. Gieo hai con súc sắc. Xác suất để số chấm xuất hiện trên hai con súc sắc như nhau là
A.
1
3
. B.
1
12
. C.
1
6
. D.
1
36
.
Câu 5. Gọi
G
là trọng tâm tứ diện
ABCD
. Gọi
A
là trọng tâm tam giác
BCD
. Tỉ số
GA
GA
bằng
A.
3
. B.
3
4
. C.
2
. D.
1
3
.
Câu 6. Phép quay
;O
Q
biến điểm
M
thành điểm
M
. Khi đó
A.
OM OM

và
MOM
. B.
OM OM
và
,OM OM
.
C.
OM OM
và
,OM OM
. D.
OM OM
và
MOM
.
Câu 7. Cho tứ diện
ABCD
. Gọi
, , , , ,M N P Q R S
lần lượt là trung điểm các cạnh
, , , , ,AC BD AB CD AD BC
. Bốn điểm nào sau đây không đồng phẳng?
A.
, , ,M P S N
. B.
, , ,M N R S
. C.
, , ,P Q R S
. D.
, , ,M N P Q
.
Câu 8. Trong các mệnh đề sau đây mệnh đề nào sai?
A. Phép dời hình là phép đồng dạng tỉ số
1k
.
B. Phép vị tự tỉ số
k
là phép đồng dạng tỉ số .
C. Phép đồng dạng biến đường thẳng thành đường thẳng // hoặc trùng với nó.
D. Phép đồng dạng bảo toàn độ lớn góc.
Câu 9. Hàm số nào sau đây là hàm số tuần hoàn với chu kì
T
?
A.
2cosy x
. B.
cosy x
. C.
cos2y x
. D.
cos 2y x
.
Câu 10. Hàm số
tany x
đồng biến trên mỗi khoảng
k
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 38 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
A.
; ,k k k
. B.
3
; ,
4 4
k k k
.
C.
2 ; 2 ,k k k
. D.
; ,
2 2
k k k
.
Câu 11. Cho phép thử có không gian mẫu
1,2,3,4,5,6
. Các cặp biến cố không đối nhau
là:
A.
1
A
và
2, 3, 4,5,6
B
. B.
và
.
C.
1, 4, 6
E
và
2,3
F
. D.
1,4,5
C
và
2,3,6
D
.
Câu 12. Số tập hợp con khác rỗng của tập hợp gồm 15 phần tử là
A.
32768
. B.
32767
. C.
15!
. D.
2
15
.
Câu 13. Cho tứ diện
ABCD
. Gọi
M
,
N
lần lượt là trung điểm của
AB
và
AC
. Đường thẳng
MN
song song với mặt phẳng:
A.
ACD
. B.
ABD
. C.
BCD
. D.
ABC
.
Câu 14. Cho
2;0
I
. Phép đồng dạng hợp thành của phép
1
;
2
o
V
và phép
OI
T
(
O
là gốc tọa độ).
Biến đường tròn
2 2
: 4
C x y
thành
C
có phương trình
A.
2 2
4 3 0
x y x
. B.
2 2
4 1 0
x y x
. C.
2 2
4 0
x y x
. D.
2 2
4 3 0
x y x
.
Câu 15. Trong hệ trục
Oxy
, cho đường thẳng
:2 1 0
d x y
, phép tịnh tiến theo vectơ
v
biến
d
thành chính nó thì
v
phải là vectơ nào trong các vectơ sau?
A.
2; 4
v
. B.
4; 2
v
. C.
2; 1
v
. D.
1;2
v
.
Câu 16. Một đa giác lồi có 27 đường chéo. Số đỉnh của đa giác đó là:
A. 9. B. 8. C. 11. D. 10.
Câu 17. Cho hình chóp tứ giác .
S ABCD
đáy không phải là hình thang và
M
tùy ý nằm trong
SCD
. Gọi
d MAB SCD
. Chọn câu đúng:
A.
, ,
CD d BC
đồng quy. B.
, ,
AB d AC
đồng quy.
C.
, ,
AB CD d
đồng quy. D.
, ,
d AD CD
đồng quy.
Câu 18. Xác suất bắn trúng mục tiêu của một vận động viên khi bắn một viên đạn là
0,6
.
Người đó bắn hai viên một cách độc lập. Xác suất để một viên bắn trúng và một viên
trượt mục tiêu là:
A.
0,24
. B.
0,4
. C.
0,48
. D.
0,45
.
Câu 19. Cho tứ diện
ABCD
. Gọi
, ,
M N P
lần lượt là các điểm trên các cạnh
AB
,
AC
và
BD
sao
cho
MN
không song song với
BC
,
MP
không song song với
AD
. Mặt phẳng
( )
MNP
cắt các đường thẳng
, ,
BC CD AD
lần lượt tại
, ,
K I J
. Ba điểm nào sau đây thẳng
hàng:
A.
, ,
M I J
. B.
, ,
N K J
. C.
, ,
K I J
. D.
, ,
N I J
.
Câu 20. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
sin 2 2 sin cos 2
y x x x
là
A.
min 1 2 2; max 1 2 2
y y
. B.
min 2; max 2
y y
C.
min 1 2 2; max 4
y y
D.
min 1 2 2; max 3
y y
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 39
Câu 21. Hệ số của
8
x
trong khai triển
5 6 10
1 1 ... 1
x x x
là:
A.
55
. B.
37
. C.
147
. D.
147
.
Câu 22. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho điểm
1;5 , 3;2
A B
. Biết các điểm
,
A B
theo thứ tự là ảnh của các điểm
,
M N
qua phép vị tự tâm
O
, tỉ số
2
k
. Độ dài
đoạn thẳng
MN
là:
A.
50
. B.
12,5
. C.
10
. D.
2,5
.
Câu 23. Số nghiệm của phương trình
2sin 2 1
3
x
thuộc khoảng
;
là:
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 24. Cho tập
0;1; 2;3;4;5;6;7;8;9
A
. Số các số tự nhiên có 5 chữ số đôi một khác nhau lấy
ra từ tập
A
là:
A.
27162
. B.
30240
. C.
30420
. D.
27216
.
Câu 25. Tìm
m
để phương trình
2
1
(1 2 ) tan 2 3 0
cos
m x m
x
có nghiệm thuộc khoảng
0;
4
.
A.
3
2
m
. B.
1
m
. C.
3
1
2
m
. D.
1
m
hoặc
3
2
m
.
B. TỰ LUẬN
Bài 1. 1. Giải phương trình
3
sin 3 sin 2sin 2
2
x x x
.
2. Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn không
vượt quá
2019
, đồng thời nó chia hết cho
5
.
Bài 2 . Cho hình chóp .
S ABC
,
G
là trọng tâm tam giác
ABC
. Đường thẳng qua
G
song song
với
SA
cắt mặt phẳng
SBC
tại
A
. Nêu cách xác định điểm
A
và thiết diện của hình
chóp khi cắt bởi mặt phẳng qua
A
, song song với
SG
và
BC
.
Bài 3. 1. Giải hệ phương trình sau:
2019 2019 1 2018 2 2017 2017 2
2019 2019 2019
3 2
2020 2.
3 6 .
x x y C y C y C y y
y x x
2.
Cho tập hợp
0;1; 2;3;...;2019
A
. Một tập hợp con
X
của
A
được gọi là tập cân
nếu trong tập hợp
X
số các số chẵn và số các số lẻ bằng nhau. ( Tập rỗng là một tập
cân). Chứng minh rằng số tập cân của tập hợp
A
là
1010
2020
C
.
Bài 4. Cho hình chóp .
S ABCD
có đáy là hình bình hành,
M
là một điểm di động trên cạnh
SC
. Mặt phẳng
P
chứa
AM
và song song với
BD
. Mặt phẳng
P
cắt
,
SB SD
lần
lượt tại các điểm
N
và
E
. Chứng minh rằng:
2 . . .
SB SM SN SM SC SN
.
Bài 5. Cho phương trình
sin2 3 2cos 3 sinx
x m x m . Để phương trình có nhiều hơn một
nghiệm trong
0;
thì giá trị của
m
thỏa
----------HẾT----------
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 40 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
PHẦN ĐÁP ÁN & HƯỚNG DẪN GIẢI
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 1 – SỞ NAM ĐỊNH
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
B
D
D
B
D
A
B
A
C
D
C
D
B
D
A
16
17
18
19
20
21
22
23
24
25
B A C C A A A D A B
Câu 1. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
3
sin
y x
. B.
2
sin
y x
. C.
tan
y x x
. D.
cot
y x
.
Lời giải
Chọn B
Xét hàm số
2
sin
y x
có tập xác định
D
nên
x D
x D
.
Mặt khác:
2
2 2
sin sin sin
x x x
.
Do đó hàm số
2
sin
y x
là hàm số chẵn.
Câu 2. Phương trình
sin 2 0
x m
có nghiệm khi và chỉ khi
A.
1
m
. B.
1
m
. C.
2 2
m
. D.
1 1
m
.
Lời giải
Chọn D
Ta có: sin 2 0 sin 2
x m x m
.
Phương trình đã cho có nghiệm
1 1
m
.
Câu 3. Từ các chữ số
1;2;3; 4;5
có thể lập được bao nhiêu số tự nhiên gồm
5
chữ số đôi một
khác nhau
A.
5
. B.
15
. C.
5
5
. D.
120
.
Lời giải
Chọn D
Số các số tự nhiên có
5
chữ số đôi một khác nhau được lập từ các chữ số
1;2;3;4;5
là
5! 120
.
Câu 4. Một câu lạc bộ cờ vua có
15
người. hỏi có bao nhiêu cách bầu ra ba người vào ba vị trí
gồm Chủ tịch, Phó chủ tịch và Thư kí, biết trằng ai cũng có khả năng làm được các vị
trí trên.
A.
455
. B.
2730
. C.
6
. D.
45
.
Lời giải
Chọn B
Số cách chọn ra ba người vào ba vị trí gồm Chủ tịch, Phó chủ tịch và Thư kí là
5
15
2730
A .
Câu 5. Một lớp học có 20 học sinh nam và 21 học sinh nữ. Số cách chọn ngẫu nhiên 10 học
sinh trong lớp là
A.
41
10
C
. B.
10
41
A
. C.
10!
. D.
10
41
C
.
Lời giải
Chọn D
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 41
Ta có: chọn ngẫu nhiên 10 học sinh trong lớp là một tổ hợp chập 10 của 41 phần tử
Số cách chọn là
10
41
C
.
Câu 6. Số tập con có 3 phần tử của một tập hợp có 2009 phần tử là
A.
3
2009
C
. B.
3
2009
A
.
C.
2009!
3!
. D.
2009
.
Lời giải
Chọn A
Số tập con có 3 phần tử của một tập hợp có 2009 phần tử là số tổ hợp chập 3 của 2009
phần tử.
Số tập hợp con có 3 phần tử là
3
2019
C
.
Câu 7. Cho tập
1;2;3;4;5
A . Chọn ngẫu nhiên 3 số từ tập
A
. Tính xác suất để 3 số được
chọn có tổng bằng 10.
A.
1
10
. B.
1
5
. C.
2
5
D.
3
10
.
Lời giải
Chọn B
Ta có:
3
5
10
n C
.
Gọi
B
là biến cố “ từ tập
A
chọn được 3 số có tổng bằng 10”.
Ta có:
2
n B
Xác suất của biến cố
B
là
2 1
10 5
n B
P B
n
.
Vậy xác suất cần tìm là
1
5
P B
.
Câu 8. Hệ số của số hạng chứa
8
x
trong khai triển nhị thức Niuton
10
2
1
x
là
A.
210
. B.
8
200
x
. C.
200
D.
8
210
x
.
Lời giải
Chọn A
Số hạng
1
k
T
trong khai triển
10
2
1
x
.
20 2 20 2
1 10 10
. .1 . , ,0 10
k k k k k
k
T C x C x k k
.
Hệ số của số hạng chứa
8
x
khi
6
k
.
Vậy hệ số cần tìm là
6
10
210
C
.
Câu 9. Trong mặt phẳng với hệ tọa độ
Oxy
, cho vectơ
2; 1
v
và điểm
3;2
M . Tìm tọa
độ ảnh
M
của điểm
M
qua phép tịnh tiến theo vec tơ
v
.
A.
' 5; 3
M
. B.
' 1; 1
M
. C.
' 1;1
M . D.
' 5;3
M .
Lời giải
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 42 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Chọn C
Do
M
là ảnh của điểm
M
qua phép tịnh tiến theo vec tơ
v
nên ta có:
2 1
1 1
M M
M M
x x
y y
.
Vậy
' 1;1
M .
Câu 10. Chọn khẳng định sai?
A. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
B. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung
khác nữa.
C. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
D. Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt.
Lời giải
Chọn D
Đáp án D sai do: có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho
trước.
Câu 11. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng không cắt nhau và không song song thì chéo nhau.
B. Hai đường thẳng phân biệt không song song thì chéo nhau.
C. Hai đường thẳng chéo nhau thì không có điểm chung.
D. Hai đường thẳng không có điểm chung thì song song.
Lời giải
Chọn C
Mệnh đề đúng là: Hai đường thẳng chéo nhau thì không có điểm chung.
Câu 12. Cho hàm số
2
cos 2 2cos
f x x x m
. Với
2; 2
m
, tìm giá trị nhỏ nhất của
hàm số trên đoạn
0;
.
A.
3
. B.
3
2
. C.
1
. D.
0
.
Lời giải
Chọn D
Ta có:
2 2 2
cos 2 2cos 2cos 2cos 1
f x x x m x x m
.
Đặt
cos
t x
, với
0; 1;1
x t
. Ta có hàm số:
2 2
2 2 1
g t t t m
, với
1;1
t .
Xét parabol
2 2
2 2 1
h t t t m
có đỉnh
2
1 3
;
2 2
I m
.
Ta có bảng biến thiên của
h t
trên đoạn
1;1
:
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 43
Do
2; 2m
nên:
2 2 2
3
1 0 3
2
m m m
.
Từ đó:
0g t h t
.
Suy giá trị nhỏ nhất của hàm số
g t h t
trên đoạn
1;1
bằng
0
khi
0
1
1;
2
t t
.
Vậy giá trị nhỏ nhất của hàm số
y f x
trên đoạn
0;
bằng
0
.
Câu 13. Hàm số
cosy x
nghịch biến trên khoảng:
A.
;
2 2
. B.
0;
2
. C.
;0
. D.
;
.
Lời giải
Chọn B.
Phát họa đồ thị hàm số
cosy x
trên khoảng
;
, ta thấy đồ thị hàm số đi xuống
trên khoảng
0;
2
.
Do đó hàm số nghịch biến trên khoảng
0;
2
.
Câu 14. Trên giá sách có
5
quyển sách Toán khác nhau,
6
quyển sách Anh khác nhau và
8
quyển sách Văn khác nhau. Số cách chọn ra ba quyển sách có đủ ba môn là:
A.
19
. B.
118
. C.
20
. D.
240
.
Lời giải
Chọn D.
Chọn ra ba quyển sách có đủ ba môn tức là mỗi môn
1
quyển.
Vậy có
1 1 1
5 6 8
. . 240C C C
(cách).
Câu 15. Cho dãy số
n
u
với
1
2 5
n
n
u
n
. Số hạng thứ mười một của dãy số bằng
A.
1
27
. B.
1
27
. C.
1
25
. D.
1
7
.
O
x
y
1
2
2
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 44 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Lời giải
Chọn A.
Số hạng thứ mười một của dãy số là
11
11
1
1
2.11 5 27
u
.
Câu 16. Cho cấp số cộng
n
u
với
1
2
u
và công sai
3
d
. Tổng
10
số hạng đầu tiên
10
S
của
n
u
là
A.
155
. B.
115
. C.
145
. D.
165
.
Lời giải
Chọn B.
Tổng
10
số hạng đầu tiên
10 1
10 45 115
S u d
.
Câu 17. Trong mặt phẳng toạ độ
Oxy
, cho điểm
2;0
A
. Ảnh của
A
qua phép quay
;90
O
Q
có
toạ độ là
A.
0;2
M . B.
0; 2
N
. C.
2;0
P . D.
1;1
Q .
Lời giải
Chọn A.
Qua phép quay
;90
O
Q
, ảnh của
2;0
A là
0;2
M .
Câu 18. Trong không gian, có bao nhiêu vị trí tương đối giữa hai đường thẳng phân biệt
a
và
b
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C.
Trong không gian,
4
vị trí tương đối giữa hai đường thẳng phân biệt
a
và
b
là song
song, chéo nhau, cắt nhau.
Câu 19. Tập nghiệm của phương trình
sin 3 cot 1 0
x x
là
A.
, ,
6
k k k
. B.
,
6
k k
.
C.
,
3
k k
. D.
, ,
3
k k k
.
Lời giải
Chọn C.
Điều kiện:
sin 0
x
x k
k
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 45
Với điều kiện trên:
sin 3 cot 1 0
x x
3
cot
3
x
3
x k
k
.
Câu 20. Tổng các hệ số trong khai triển
2
1
n
x
x
là
4096
. Hệ số của số hạng không chứa
x
trong khai triển là
A.
495
. B.
133
. C.
334
. D.
775
.
Lời giải
Chọn A.
Ta có:
2 2
0
1 1
n k
n
n k
k
n
k
x C x
x x
2 3
0
n
k n k
n
k
C x
.
Tổng hệ số của khai triển là
0 1 2
0
....
n
k n
n n n n n
k
C C C C C
1 1
n
2
n
4096
12
2
.
Do đó:
12
n
nên ta có khai triển
12
2
1
x
x
12
24 3
12
0
k k
k
C x
.
Số hạng không chứa
x
trong khai triển ứng với:
24 3 0
k
8
k
.
Vậy hệ số của số hạng không chứa
x
trong khai triển là
8
12
495
C
.
Câu 21. Từ một hộp chứa
16
cái thẻ đánh số từ
1
đến
16
. Chọn ngẫu nhiên
3
thẻ. Xác suất để
được
3
thẻ đều là số lẻ là
A.
1
10
. B.
1
2
. C.
56
506
. D.
3
16
.
Lời giải
Chọn A.
Số phần tử không gian mẫu là
3
16
560
C .
Gọi
A
là biến cố 3 thẻ được rút đều mang số lẻ. Khi đó số phần tử của biến cố
A
là
3
8
56
A C
.
Vậy xác suất để 3 thẻ được chọn đều mang số lẻ là
56 1
560 10
P A .
Câu 22. Cho hình chóp .
S ABCD
có đáy là hình bình hành tâm
O
,
M
là trung điểm cạnh
SA
.
Gọi
P
là mặt phẳng đi qua
M
đồng thời song song với
SC
và
AD
. Thiết diện của
hình chóp .
S ABCD
cắt bởi
P
là một
A. hình thang. B. hình bình hành. C. tứ giác. D. ngũ giác.
Lời giải
Chọn A.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 46 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Vì
//
P AD
nên giao tuyến của
P
với
SAD
là đường thẳng qua
M
song song với
AD
cắt
SD
tại
E
là trung điểm
SD
.
Vì
//
P SC
nên giao tuyến của
P
với
SCD
là đường thẳng qua
E
song song với
SC
cắt
CD
tại
F
là trung điểm
CD
.
Vì
//
P AD
nên giao tuyến của
P
với
ABCD
là đường thẳng qua
F
song song với
AD
cắt
AB
tại
N
là trung điểm
AB
. Dễ thấy
MN P SAB
.
Vì
ME
và
NF
cùng song song với
AD
nên chúng song song với nhau.
Vậy thiết diện là hình thang
MEFN
.
Câu 23. Trong mặt phẳng
Oxy
cho đường thẳng
a
. Gọi
b
là ảnh của
a
qua phép đồng dạng
có được bằng cách thực hiện liên tiếp phép vị tự tâm
O
tỉ số
2
k
và phép đối xứng
trục
Oy
. Biết đường thẳng
b
có phương trình là
2 16 0
x y
, khi đó phương trình
đường thẳng
a
là
A.
2 8 0
x y
. B.
2 32 0
x y
. C.
2 32 0
x y
. D.
2 8 0
x y
.
Lời giải
Chọn D.
Giả sử
;
M x y
là một điểm bất kì thuộc đường thẳng
a
,
; 2
;
O
M x y V M
.
Ta có
2
2 1
2
x x
OM OM
y y
.
Gọi
;
Oy
M x y D M
. Khi đó ta có
2
x x
y y
.
Từ
1
,
2
suy ra
2
x x
và
2
y y
, mà
M b
nên
2 16 0
x y
4 2 16 0 2 8 0
x y x y
*
Vì
;
M x y
là một điểm bất kì thuộc đường thẳng
a
và tọa độ điểm
M
thỏa mãn
phương trình
*
nên
*
chính là phương trình đường thẳng
a
.
Câu 24. Cho dãy số
n
u
xác định bởi
1
1
u
và
2
1
2
n n
u u
,
*
n
. Tổng
2 2 2 2
1 2 3 1001
...
S u u u u
bằng
A.
1002001
. B.
1001001
. C.
1001002
. D.
1002002
.
N
F
E
M
O
D
B
C
A
S
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 47
Lời giải
Chọn A.
Từ giả thiết
2
1
2
n n
u u
ta có
2 2
1
2
n n
u u
.
Xét dãy số
2
n n
v u
với
*
n
ta có
1
2
1
n
n
v u
2
2
n
u
hay
1
2
n n
v v
dãy số
n
v
là
một cấp số cộng với số hạng đầu
2
1 1
1
v u
và công sai
2
d
.
Do đó
2 2 2 2
1 2 3 1001
...
S u u u u
1 2 3 1001
...
v v v v
1001 2.1 1001 1 2
2
10002001
.
Câu 25. Ngân hàng đề thi học kỳ I môn Văn của trường Y có
50
câu hỏi. Mỗi đề gồm bốn câu
hỏi được lấy ngẫu nhiên từ ngân hàng đề thi. Thí sinh
A
đã học thuộc
25
câu trong
ngân hàng đề thi. Tính xác suất để khi thí sinh
A
nhận đề thì có ít nhất ba câu đã học
thuộc.
A.
135
458
. B.
1403
4606
. C.
13
19
. D.
7
19
.
Lời giải
Chọn B .
Số đề thi có thể tạo được từ ngân hàng đề thi là
4
50
C
.
Số đề thi có ít nhất ba câu mà thí sinh
A
đã học thuộc là
3 1 4
25 25 25
C C C
.
Vậy xác suất để khi thí sinh
A
nhận đề thì có ít nhất ba câu đã học thuộc là
3 1 4
25 25 25
4
50
1403
4606
C C C
P
C
.
PHẦN II. TỰ LUẬN.
Câu 1. Giải phương trình sau:
1)
sin 2 cos 0
x x
.
2)
tan 30 3 0
x
.
Lời giải
1) Phương trình
sin 2 cos 0 2sin .cos cos 0
x x x x x
cos 2sin 1 0
x x
cos 0
1
sin
2
x
x
.
cos 0
x
2
x k
.
sin 0
x
2
6
5
2
6
x k
x k
.
Vậy phương trình đã cho có 3 họ nghiệm
2
x k
,
2
6
x k
,
5
2 ,
6
x k k
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 48 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
2) Phương trình
tan 30 3 0
x
tan 30 3 tan 60
x
30 60 .180
x k
90 .180
x k
. Vậy phương trình có 1 họ nghiệm là
90 .180 ,x k k
.
Câu 2. Tìm số nguyên dương
n
thỏa mãn điều kiện:
2
9
n
C n
.
Lời giải
Điều kiện:
2
n
.
Phương trình
2
!
9 9
2! 2 !
n
n
C n n
n
1 2 18
n n n
2
3 18 0
n n
6
3
n
n l
.
Vậy
6
n
là giá trị cần tìm.
Câu 3. Tìm số hạng chứa
11
x
trong khai triển nhị thức Niutơn của biểu thức
2
2
n
x
x
, biết
n
là số nguyên dương thỏa mãn
0 2 1 4 2 2 5
3 3 ... 3 100
n n
n n n n
C C C C .
Lời giải
Khai triển
2 0 1 2 2 4 2
1 ...
n
n n
n n n n
x C C x C x C x
.
Cho
3
x
ta được
0 2 1 4 2 2
10 3 3 ... 3
n n n
n n n n
C C C C
.
Từ giả thiết ta có
5 10
10 100 10 10 10
n n
n
.
Với
10
n
, khai triển
10
2
2
x
x
có số hạng tổng quát là:
10
2 20 3
10 10
2
.2 .
k
k
k k k k
C x C x
x
.
Số hạng chứa
11
x
nên
20 3 11 3
k k
. Vậy số hạng cần tìm là
3 3 11 11
10
.2 . 960
C x x
.
Câu 4. (1 điểm) Cho một đa giác đều
n
cạnh. Chọn ngẫu nhiên
3
đỉnh của đa giác đều đó.
Gọi
P
là xác xuất sao cho
3
đỉnh đó tạo thành một tam giác tù. Tính
n
, biết
n
là số lẻ,
3
n
và
45
.
62
P
Lời giải
Số phần tử của không gian mẫu:
3
n
n C
.
Chọn
1
đỉnh của đa giác (ký hiệu là
A
) có
n
cách chọn.
Gọi
O
là tâm đường tròn ngoại tiếp đa giác. Khi đó, đường thẳng
OA
chia đa giác
thành
2
phần đối xứng nhau qua
OA
.
Để tạo thành tam giác tù, chỉ cần lấy 2 đỉnh còn lại trong
1
2
n
điểm về 1 phía của
OA
.
Do đó, số tam giác tù tạo thành là
2
1
2
.
n
n C
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 49
Theo bài ra, ta có
2
1
3 2
2
1
3
2
.
45
45. 62 .
62
n
n n
n
n C
P C n C
C
1
!
!
2
45. 62
1
3! 3 !
2! 2 !
2
n
n
n
n
n
1 1
15 1 2 62 . . 1
2 2
n n
n n n n
30 1 2 31 1 3
n n n n n
30 60 31 93 33
n n n
.
Vậy
33
n
là giá trị cần tìm.
Câu 5. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang với
//
AB CD
,
2 3
AB CD
. Gọi
M
là điểm thuộc đoạn
SB
sao cho
2
5
SM
SB
,
O
lả giao điểm của hai đường chéo
AC
và
BD
.
1) Xác định giao tuyến của hai mặt phẳng
SAB
và
SCD
.
2) Chứng minh rằng:
//
SD MAC
.
3) Gọi
N
là giao điểm của đường thẳng
AM
và mặt phẳng
SDC
. Gọi
OMNC
S là diện
tích của tứ giác
OMNC
,
OMC
S
là diện tích của tam giác
OMC
. Tính tỉ số
OMC
OMNC
S
S
.
Lời giải
1) Ta có
//
AB CD
,
AB SAB
,
CD SCD
,
S SAB SCD
Suy ra
SAB SCD d
, với
d
là đường thẳng đi qua
S
và song song với
AB
và
CD
.
2) Vì
//
AB CD
suy ra
3 3
2 5
OB AB BO
OD CD BD
1
Mà
2 3
5 5
SM BM
SB BS
2
Trong tam giác
SBD
, từ
1
và
2
ta suy ra
//
SD OM
.
Ta có
SD MAC
,
OM MAC
,
//
SD OM
suy ra
//
SD MAC
.
d
O
D
C
S
A
B
M
N
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 50 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
3) Trong mặt phẳng
SAB
có
AM d N N AM SCD
.
Vì
//
SN AB
nên ta có
3 3 3
2 5 5
AM BM AM AM AO
NM SM AN AN AC
.
Suy ra
//
OM CN
, suy ra
9
25
AOM
ACN
S
S
.
Suy ra
16
25
OMNC
ACN
S
S
,
16
25
OMNC ACN
S S
. Mà
2
3
OMC AMO
S S
, suy ra
3
8
OMC
OMNC
S
S
.
---- HẾT -----
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 51
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 2 – SỞ HÀ NỘI
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
A C C B A D A B C B D C B A D
16
17
18
19
20
21
22
23
24
25
B C D B B D A A B C
Câu 1. Tập xác định của hàm số
1
sin 2
y
x
là
A.
\ ,
2
k
k
. B.
\ ,
4 2
k
k
.
C.
\ ,
2
k k
. D.
\ ,k k
.
Lời giải
Chọn A
Điều kiện xác định:
sin 2 0 2 ,
2
k
x x k x k
.
Vậy tập xác định của hàm số là
\ ,
2
k
D k
.
Câu 2. Trong các phép biến hình sau, phép biến hình nào không là một phép dời hình?
A. Thực hiện liên tiếp hai phép quay.
B. Thực hiện liên tiếp hai phép đối xứng trục.
C. Thực hiện liên tiếp hai phép vị tự có cùng tâm và tỷ số vị tự là 2 số đối nhau.
D. Thực hiện liên tiếp hai phép vị tự có cùng tâm và tỷ số vị tự là 2 số nghịch đảo của
nhau.
Lời giải
Chọn C
Giả sử
1
;
1
;
O k
O k
V M M
V M M
1
1
OM kOM
OM kOM


2
.
OM k kOM k OM

.
Vậy thực hiện thực hiện liên tiếp hai phép vị tự có cùng tâm và tỷ số vị tự là 2 số đối
nhau thì thu được một phép vị tự với tỷ số là tích của 2 tỷ số đã cho (không phải phép
dời hình).
Câu 3. Một lớp 11 có 30 học sinh, gồm 15 nam và 15 nữ. Có bao nhiêu cách xếp các học sinh
thành hai hàng, một hàng nam và một hàng nữ trong lúc tập thể dục giữa giờ?
A.
30!
. B.
15
30
A
. C.
2
2 15!
. D.
15
30
C
.
Lời giải
Chọn C
Chọn vị trí cho hai hàng nam và nữ xếp cạnh nhau có
2!
cách
Xếp 15 bạn nam thành một hàng có
15!
cách
Tương tự, xếp 15 bạn nữ thành một hàng có
15!
cách
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 52 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Theo quy tắc nhân, có tất cả:
2
2!.15!.15! 2 15!
cách xếp thỏa mãn đề bài.
Câu 4. Trong mặt phẳng tọa độ
Oxy
, gọi
A
là ảnh của
1 ; 3
A qua phép vị tự tâm
O
, tỷ số
2
k
. Tọa độ điểm
A
là
A.
2 ; 6
. B.
2 ; 6
. C.
2 ; 6
. D.
2 ; 6
.
Lời giải
Chọn B
; 2O
V A A
2
OA OA
. Mà
1 ; 3
A nên tọa độ điểm
2 ; 6
A
.
Câu 5. Cho
19
điểm phân biệt
1 2 3 19
, , ,...
A A A A
trong đó có
5
điểm
1 2 3 4 5
, , , ,
A A A A A
thẳng hàng
ngoài ra không có 3 điểm nào thẳng hàng, Hỏi có bao nhiêu tam giác có 3 đỉnh trong
19 điểm trên?
A.
959
. B.
969
. C.
364
. D.
374
.
Lời giải
Chọn A
Để tạo ra một tam giác có 3 đỉnh trong số 19 điểm trên ta thực hiện theo 3 phương án
sau:
+Phương án 1: lấy 2 đỉnh từ
6 7 19
, ,...,
A A A
và 1 đỉnh từ
1 2 3 4 5
, , , ,
A A A A A
.
Số tam giác được tạo thành là
2 1
14 5
.
C C
.
+Phương án 2: lấy 1 đỉnh từ
6 7 19
, ,...,
A A A
và 2 đỉnh từ
1 2 3 4 5
, , , ,
A A A A A
.
Số tam giác được tạo thành là
1 2
14 5
.
C C
.
+Phương án 3: lấy 3 đỉnh từ
6 7 19
, ,...,
A A A
.
Số tam giác được tạo thành là
3
14
C
.
Vậy số tam giác được tạo thành là
2 1 1 2 3
14 5 14 5 14
. . 959.
C C C C C
Câu 6. Trong khai triển nhị thức Newton của biểu thức
11
2
3
x
x
(với
0
x
), hệ số của số
hạng chứa
7
x
là :
A.
7
11
C
. B.
7 7
11
3
C
. C.
5
11
C
. D.
5 5
11
3
C
.
Lời giải
Chọn D
Ta có
11
11 11
11
2 2 22 3
11 11
0 0
3 3
. 3 .
k
k
k k k k
k k
x C x C x
x x
Xác định hệ số của số hạng chứa
7
x
ta giải phương trình
22 3 7 5
k k
Vậy hệ số của số hạng chứa
7
x
là
5 5
11
3
C
Câu 7. Nghiệm của phương trình
2 1
1
5
x
x x
A C
là:
A.
5
x
. B.
3
x
. C.
4
x
D. vô nghiệm.
Lời giải
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 53
Chọn A
TXĐ:
2;x x
.
Ta có
2 1
1
5
x
x x
A C
1 !
!
5
2 ! 1 !.2!
x
x
x x
1
1 5
2
x x
x x
2 1 1 10
x x x x
2
2 (L)
3 10 0
5 (TM)
x
x x
x
Câu 8. Từ các chữ số
0;1;2;3;4;5;6;7
lập được tất cả bao nhiêu số tự nhiên có
3
chữ số đôi một
khác nhau và chia hết cho
5
?
A.
112
số. B.
78
số. C.
42
số. D.
84
số.
Lời giải
Chọn B
Gọi số cần lập là
abc
.
Để lập được số thỏa mãn bài toán, xét các trường hợp
Trường hợp 1:
0
c
: Chọn
,
a b
có
2
7
A
cách.
Trường hợp 2:
5
c
: Chọn
0
a
có
6
cách, chọn
b
có
6
cách.
Vậy số cách lập số thỏa mãn là
2
7
6 6 78
A
cách.
Câu 9. Mệnh đề nào trong các mệnh đề sau là sai?
A.
0 1 2
0 1
n
n
n n n n
C C C C
. B.
0 1 2
2
n n
n n n n
C C C C
.
C.
0 1 2
1 2 4 2
n
n
n n n n
C C C C
. D.
0 1 2
3 2 4 2
n n n
n n n n
C C C C
.
Lời giải
Chọn C
Xét khai triển
0 1 1 2 2 2 3 3 3 1 1
n
n n n n n n n n
n n n n n n
a b C a C a b C a b C a b C ab C b
.
Với
1, 1
a b
ta có
0 1 2
0 1
n
n
n n n n
C C C C
.
Với
1
a b
ta có
0 1 2
2
n n
n n n n
C C C C
.
Với
1, 2
a b
ta có
0 1 2
3 2 4 2
n n n
n n n n
C C C C
.
Với
1, 2
a b
ta có
0 1 2
1 2 4 2
n n
n
n n n n
C C C C
.
Câu 10. Cho
,
A B
là hai biến cố độc lập của phép thử
T
. Xác suất xảy ra biến cố
A
là
0,5
và
xác suất xảy ra biến cố
B
là
0,25
. Xác suất để xảy ra biến cố
A
và
B
là
A.
0,25
. B.
0,125
. C.
0,75
. D.
0,375
.
Lời giải
Chọn B
Vì
A
và
B
là hai biến cố độc lập nên
0,5 0,25 0,125
P A B P A P B .
Câu 11. Khẳng định nào trong các khẳng định sau là đúng?
A. Nếu hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.
B. Hai đường thẳng chéo nhau khi chúng không có điểm chung.
C. Hai đường thẳng song song khi chúng ở trên cùng một mặt phẳng.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 54 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
D. Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo
nhau.
Lời giải
Chọn D
Đáp án A sai vì nếu hai đường thẳng ở trên hai mặt phẳng chúng có thể song song, cắt
nhau và chéo nhau hoặc trùng nhau.
Đáp án B sai vì hai đường thẳng chéo nhau khi chúng không cùng nằm trong 1 mặt
phẳng và
không có điểm chung.
Đáp án C sai vì hai đường thẳng song song khi chúng cùng thuộc 1 mặt phẳng và
không có điểm chung.
Do đó đáp án D đúng.
Câu 12. Cho chóp .
S ABCD
có đáy
ABCD
là hình thang có
AB
//
CD
. Gọi
,
M N
và
P
lần lượt
là
trung điểm
,
SA BC
và
AD
. Giao tuyến của hai mặt phẳng
SAB
và
MNP
là
A. Đường thẳng qua
S
và song song với
AB
.
B. Đường thẳng qua
N
và song song với
SC
.
C. Đường thẳng qua
M
và song song với
AB
.
D. Đường thẳng
MN
.
Lời giải
Chọn C
Ta có
M
là điểm chung của 2 mặt phẳng
SAB
và
MNP
.
/ / NP
AB
( do N, P là trung điểm BC và AD)
,
AB SAB NP MNP
Do đó
SAB MNP
với
thỏa mãn:
; / /
M AB
.
Câu 13. Cho 100 tấm thẻ được đánh số từ
1
đến
100
, chọn ngẫu nhiên đồng thời 3 tấm thẻ. Xác
suất để
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 55
chọn được 3 tấm thẻ có tổng các số ghi trên thẻ là số chia hết cho 2 là:
A.
5
6
. B.
1
2
. C.
3
4
. D.
49
198
.
Lời giải
Chọn B
Không gian mẫu: “ lấy ngẫu nhiên đồng thời 3 tấm thẻ từ
100
tấm thẻ”
3
100
C
.
Biến cố
:
A
“ chọn được 3 tấm thẻ có tổng các số ghi trên thẻ là số chia hết cho 2”
Từ 1 đến 100 có 50 thẻ lẻ và 50 thẻ chẵn.
Trường hợp 1: Chọn được 2 thẻ lẻ và 1 thẻ chẵn:
2 1
50 50
.
C C
.
Trường hợp 2: Chọn được 3 thẻ chẵn:
3
50
C
2 1 3
50 50 50
.
A C C C
Do đó xác suất của biến cố
A
là
1
2
A
A
P
.
Câu 14. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình chữ nhật tâm
O
, điểm
M
nằm trên
cạnh
SB
sao cho 4
SB BM
. Giao điểm của đường thẳng
SD
và mặt phẳng
ACM
nằm trên
đường
thẳng nào sau đây:
A.
OM
. B.
AM
. C.
CM
. D.
AC
.
Lời giải
Chọn A
Ta có:
SDB ACM MO
.
Trong mặt phẳng
SBD
:
Q SD
MO SD Q
Q MO ACM
.
Do đó:
SD ACM Q
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 56 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Vậy giao điểm của
SD
và mặt phẳng
ACM
thuộc đường thẳng
MO
.
Câu 15. Cho hình chóp .
S ABCD
có các cạnh bên bằng nhau, đáy
ABCD
là hình vuông,
20
AB cm
. Gọi
M
là điểm nằm trên cạnh SA sao cho
2
3
SM
SA
. Gọi
P
là mặt phẳng
đi qua M, song song với hai đường thẳng AB và
AC
. Mặt phẳng
P
cắt hình chóp
.
S ABCD
theo thiết diện là một hình tứ giác có diện tích bằng:
A.
2
80
9
cm
. B.
2
400
9
cm
. C.
2
800
9
cm
. D.
2
1600
9
cm
.
Lời giải
Chọn D
Gọi
1 1
d P SAC M d
Ta có:
/ /
AC SAC
AC P
1
/ /
d AC
, gọi H là giao điểm của
1
d
với SC
Gọi
2 2
d P SAB M d
Ta có:
/ /
AB SAB
AB P
2
/ /
d AB
, Gọi N là giao điểm của
2
( )
d
với SB ( ) ( )
P SAB MN
(1)
Gọi
3 3
d P SCD H d
Ta có:
/ /
CD SAD
CD P
3
/ /
d CD
.
(
P
)
K
H
N
M
D
B
A
C
S
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 57
Gọi F là giao điểm của
3
d
với SD
P SCD HK
P SAD MK
P SBC NH
(2)
Từ (1) và (2) suy ra thiết diện của (P) với hình chóp .
S ABCD
là tứ giác MNHK
Ta có:
/ / ; / / ; / / ; / /
EF AD EH AB HK BC KF CD
;
2
3
SM MN NH HK KM
SA AB BC CD AD
Tứ giác ABCD là hình vuông nên tứ giác MNHK là hình vuông có cạnh là
40
3
cm
Suy ra diện tích thiết diện là:
2
1600
9
cm
Câu 16. Phương trình
2
cos 1 sin sin 0
x x x m
có đúng 6 nghiệm thuộc
0;2
khi và chỉ
khi
;
m a b
. Khi đó tổng
a b
là số nào?
A.
0,5
. B.
0, 25
. C.
0, 25
. D.
0,5
.
Lời giải
Chọn B
Ta có:
2
cos 1 sin sin 0
x x x m
2 2
cos 1 0 cos 1
sin sin 0 sin sin 0
x x
x x m x x m
(1)
(2)
(1) cos 1 2 ,x x k k
với
0; 2 0; 2
x x
Xét (2) Đặt
sin
t x
;
1;1
t
phương trình (2) được viết lại như sau:
2 2
0
t t m t t m
(*)
Để phương trình đã cho có đúng 6 nghiệm thuộc
0;2
thì phương trình (2) có đúng
4 nghiệm thuộc
0;2
(*)
có 2 nghiệm phân biệt
1 2
; t 1;1 \ 0
t
Ta có phương trình
(*)
là phương trình hoành độ giao điểm của 2 đồ thị hàm số
d
và
P
với
2
( ) ; 1;1
y f t t t t
y m
P
d
Để phương trình
(*)
có 2 nghiệm phân biệt
1 2
; t 1;1 \ 0
t
thì
d
cắt
P
tại 2 điểm
phân biệt có hoành độ
1 2
; t 1;1 \ 0
t
Xét
2
( ) ; 1;1
y f t t t t
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 58 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Ta có
P
là Parabol có tọa độ đỉnh là
1 1
;
2 4
I
Bảng biến thiên:
Dựa vào bảng biến thiên
d
cắt
P
tại 2 điểm phân biệt có hoành độ
1 2
; t 1;1 \ 0
t
1 1
0 0
4 4
m m
1
0;
4
m
. Vậy
0,25
a b
.
Câu 17. Tập xác định của
1 sin
y x
là
A.
1;

. B.
; 1

. C.
. D.
\ 2 ,k k
.
Lời giải
Chọn C.
Ta có
1 sin 1 1 sin 0
x x
, x
.
Câu 18. Người ta trồng
1275
cây theo hình tam giác như sau: Hàng thứ nhất có
1
cây, hàng
thứ
2
có
2
cây, hàng thứ
3
có
3
cây
, ,
hàng thứ
k
có
k
cây
1
k
. Hỏi có bao
nhiêu hàng?
A.
51
. B.
52
. C.
53
. D.
50
.
Lời giải
Chọn D.
Việc trồng các cây trên theo quy luật của một cấp số cộng nên ta có
1
S 1 2 ... 1275
2
k
k k
k
50
51 0
k
k
.
Câu 19. Nghiệm của phương trình
2 1
3
x x
A A
là:
A.
1
x
. B.
3
x
. C.
1
x
và
3
x
. D.
1
x
.
Lời giải
Chọn B.
Điều kiện
2
x
,
*
x
.
Ta có
2 1
3
x x
A A
!
3
2 !
x
x
x
1 3
x x x
2
2 3 0
x x
3
x
vì
2
x
,
*
x
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 59
Câu 20. Cô giáo chia
4
quả táo,
3
quả cam và
2
quả chuối cho
9
cháu (mỗi cháu
1
quả). Hỏi
có bao nhiêu cách chia khác nhau
A.
120
. B.
1260
. C.
9
. D.
24
.
Lời giải
Chọn D.
Số cách chia
4
quả táo có
4
cách
Số cách chia
3
quả cam có
3
cách
Số cách chia
2
quả chuối có
2
cách
Vậy số cách chia cho
9
cháu là
4.3.2 24
(cách).
Câu 21. Một chiếc máy có
2
động cơ I và II hoạt động độc lập với nhau.Xác suất để động cơ I
chạy tốt và động cơ II chạy tốt lần lượt là
0,8
và
0,7
. Tính xác suất để có ít nhất
1
động cơ chạy tốt là
A.
0,56
. B.
0,06
. C.
0,83
. D.
0,94
.
Lời giải
Chọn D.
Gọi
A
là biến cố “Động cơ I chạy tốt”,
B
là biến cố “Động cơ II chạy tốt”
Gọi
D
là biến cố “Cả hai động cơ đều chạy không tốt”. Ta thấy
.
D A B
. Hai biến cố
A
và
B
độc lập với nhau nên
P D P A P B
1 1 0,2.0,3 0,06
P A P B
Gọi
K
là biến cố “Có ít nhất một động cơ đều chạy tốt” khi đó
1 1 0,06 0,94
P K P D .
Câu 22. Cho .
S ABCD
có đáy là hình bình hành. Mệnh đề nào sau đây sai?
A.
SAD SBC
là đường thẳng qua
S
và song song với
AC
.
B.
SAB SAD SA
.
C.
//
SBC AD
.
D.
SA
và
CD
chéo nhau.
Lời giải
Chọn A.
Đáp án A sai vì
SAD SBC
là đường thẳng qua
S
và song song với
AD
hoặc
BC
.
Đáp án B, C, D đúng.
D
A
B
C
S
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 60 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 23. Tổng
1 2 3 2017
2017 2017 2017 2017
...C C C C
bằng
A.
2017
2 1
. B.
2017
2 1
. C.
2017
2
. D.
2017
4
.
Lời giải
Chọn A.
Xét khai triển
2017
0 2 2 2 2017 2017
2017 2017 2017 2017
1
x C C x C x C x
.
Cho
1
x
ta được:
2017 0 1 2 3 2017
2017 2017 2017 2017 2017
2 C C C C C
.
Vậy
1 2 3 2017 2017
2017 2017 2017 2017
... 2 1
C C C C
.
Câu 24. Trong mặt phẳng
Oxy
cho đường tròn
C
có phương trình
2 2
2 2 4
x y
Hỏi
phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm
O
tỉ số
1
2
k
và
phép quay tâm
O
góc quay
90
sẽ biến
C
thành các đường tròn nào trong các
đường tròn sau
A.
2 2
1 1 1
x y
. B.
2 2
1 1 1
x y
.
C.
2 2
2 1 1
x y
. D.
2 2
2 2 1
x y
.
Lời giải
Chọn C.
C
có tâm
2;2
I , bán kính
2
R
.
Gọi
1 1 1
1
;
2
1
1;1
2
O
I V I OI OI I

.
Gọi
1
1
;
2
O
C V C
1
C
có tâm
1
1;1
I , bán kính
1
1
1
2
R R
.
1
;90O
C Q C C
có tâm
1;1
I
, bán kính
1
1
R R
.
Vậy phương trình đường tròn
C
là ảnh của
C
qua phép đồng dạng trên là:
2 2
1 1 1
x y
.
Câu 25. Cho tứ diện
ABCD
đều cạnh
a
. Gọi
G
là trọng tâm tam giác
ABC
, mặt phẳng
CGD
cắt tứ diện theo một thiết diện có diện tích là.
A.
2
2
6
a
. B.
2
3
4
a
. C.
2
2
4
a
. D.
2
3
2
a
.
Lời giải
Chọn C.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 61
Trong mặt phẳng
ABC
:
I CG AB
I
là trung điểm của
AB
.
Ta có:
CGD ABC CI
;
CGD ABD ID
;
CGD ACD CD
.
Suy ra: thiết diện của tứ diện tạo bởi mặt phẳng
CGD
là tam giác
ICD
.
Vì
ABCD
là tứ diện đều cạnh
a
nên:
3
2
a
IC ID ICD
cân tại
I
.
Gọi
M
là trung điểm của
CD
2 2
2 2
3
4 4
2
a a a
IM IC CM
.
Vậy diện tích thiết diện là:
2
1 1
. .
2 2
2 2 2
ICD
a a
S IM CD a .
PHẦN II. TỰ LUẬN (6 ĐIỂM)
Bài 1. Giải phương trình:
2 2
3 cos sin 2 3sin 1
x x x
.
Lời giải
2 2
3 cos sin 2 3 sin 1
x x x
2 2
3 sin 2sin cos 3 cos 1 0
x x x x
(1)
+ Dễ thấy các giá trị của x mà cos x = 0 không là nghiệm của phương trình (1)
+ Chia hai vế của (1) cho cos
2
x, ta được phương trình tương đương:
2 2
3 tan 2 tan 3 1 tan 0
x x x
2
( 3 1) tan 2 tan (1 3) 0
x x
tan 1
4
( )
tan 3 2
12
x k
x
k
x
x k
Bài 2.
a) Cho
2
0 1 2
( 2)
n n
n
x a a x a x a x
. Tìm n để
5 6
: 12:7
a a
.
Lời giải
Hệ số của số hạng chứa x
k
của khai triển là
2
k n k
k n
a C
với 0
k n
và
, ; 6
k n n
O
G
I
M
D
C
B
A
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 62 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Vì
5 5
5 5 6 6
5
6 6
6
2
12 12 12
2 2
7 2 7 7
n
n n
n
n n
n
n
a C
C C
a C
5 6
! 12 !
2 2
5!( 5)! 7 6! ( 6)!
n n
n n
n n
2 12
12
5 7.6
n
n
( thỏa mãn điều kiện). Vậy
12
n
.
b) Trong một hộp có 10 viên bi màu xanh và 8 viên bi màu đỏ. Bạn Bình lấy ngẫu
nhiên 1 viên bi (lấy xong không trả lại vào hộp), sau đó bạn An lấy tiếp 1 viên bi nữa.
Tính xác suất để hai bạn lấy được bi cùng màu.
Lời giải
Xét phép thử T: Bình lấy 1 viên bi trong hộp có 10 bi xanh và 8 bi đỏ, sau đó đến lượt
An
lấy tiếp 1 viên bi.
Số phần tử của không gian mẫu là:
2
18
( ) 18.17
n A
Gọi A là biến cố: “ Hai bạn lấy được bi cùng màu”
Số cách để hai bạn lấy được bi cùng màu xanh là:
Số cách để hai bạn lấy được bi cùng màu đỏ là:
Nên số cách để hai bạn lấy được bi cùng màu là:
( ) 10.9 8.7 146
n A
Xác suất để hai bạn lấy được bi cùng màu là:
( ) 146 73
( )
( ) 18.17 153
n A
P A
n
Bài 3.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm các
cạnh AB,
CD
.
a) Chứng minh rằng: MN song song với mặt phẳng (SBC), (SAD).
b) Gọi P là trung điểm
SA
. Chứng minh rằng: SB, SC song song với mặt phẳng (MNP).
c) Gọi
1 2
;
G G
lần lượt là trọng tâm tam giác ABC,
SBC
. Chứng minh rằng: đường
thẳng G1G2
song song với mặt phẳng (SAC).
d) Dựng thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (PNG2).
Lời giải
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 63
a) Do MN // BC và MN (SBC) MN // (SBC).
Tương tự MN // (SAD).
b) Ta có: MP // SB nên MP // (SBC).
Theo câu a, ta có: MN // (SBC) nên (MNP) // (SBC) SB // (MNP), SC // (MNP).
c) Gọi E là trung điểm của BC A,
1
G
, E không thẳng hàng và S,
2
G
, E không thẳng
hàng. Ta có
1 2
1 2
1
//
3
EG EG
G G SA
EA ES
mà SA (SAC) nên
1 2
G G
// (SAC).
d) Gọi Q là trung điểm của SB C,
2
G
, Q không thẳng hàng.
Ta có PQ // AB nên PQ // CD C, D, P, Q cùng thuộc một mặt phẳng
Mp (PN
2
G
) cắt S.ABCD theo thiết diện là tứ giác CDPQ.
Bài 4. Cho cấp số cộng
n
u
có số hạng đầu
1
3
u
và công sai
5
d
. Tính
2
u
,
7
u
và
8
S
(tổng
của
8
số hạng đầu tiên trong cấp số cộng
n
u
).
Lời giải
Ta có
2 1
3 5 8
u u d
,
7 1
6 3 6.5 33
u u d
và
8
8. 2.3 7.5
164
2
S
.
Bài 5. Cho dãy số
n
u
với
2 1
cos
3
n
n
u
.
a) Chứng minh rằng
3
n n
u u
với mọi
1
n
.
b) Hãy tính tổng của
17
số hạng đầu tiên của dãy số đã cho.
Lời giải
a) Ta có
3
2 5
cos
3
n
n
u
2 1
cos 2
3
n
2 1
cos
3
n
n
u
.
b) Đặt
1 2
...
n n
S u u u
. Vì
3
n n
u u
nên
17 3 2
5
S S S
.
Ta có
1
1
cos
3 2
u
,
2
cos 1
u
,
3
5 1
cos
3 2
u
3
0
S
và
2
1
2
S
.
Vậy
17
1
2
S
.
---- HẾT -----
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 64 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 3 – SỞ BẠC LIÊU
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
D
A
C
B
C
C
B
B
A
C
D
A
D
C
A
16
17
18
19
20
21
22
23
24
25
26
D D B C C B D A D C A
Câu 1. Nghiệm của phương trình
2cos 3 0
x
là
A.
2
6
2
6
x k
k
x k
. C.
2
3
2
2
3
x k
k
x k
.
B.
2
3
x k k
. D.
2
6
x k k
.
Lời giải
Chọn D
Ta có:
3
2cos 3 0 cos cos cos 2
2 6 6
x x x x k k
Vậy nghiệm của phương trình là
2
6
x k k
Câu 2. Cho hình bình hành
ABCD
. Khẳng định nào sau đây là đúng
A.
BC
T A D
. B.
BC
T D A
. C.
BC
T A B
. D.
BC
T C B
.
Lời giải
Chọn A
Ta thấy ngay
BC
T A D
vì
BC AD
.
Câu 3. Phương trình
cos sin 3 2 cos sin sin 4
x x x x x
có tổng tất cả các nghiệm
0;
x
là
A.
2
. B.
6
. C.
11
8
. D.
5
8
.
Lời giải
Chọn C
Ta có:
cos sin 3 2 cos sin sin 4
x x x x x
cos sin 3 2cos sin 4
4
x x x x
cos sin 3 sin 3 sin 5
4 4
x x x x
cos cos 5 sin 3 sin 3
4 4
x x x x
A
B
C
D
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 65
3
sin 2 sin 3 sin 3 sin
8 8 8 8
x x x
24 3
sin 3 0
8
4
3
sin 2 sin
3
8 8
8
k
x
x
x k k
x
x k
sin 2 sin 3 sin 3 cos
8 8 8 8
x x x
Các nghiệm của phương trình trên khoảng
0;
là
3 17
; ; ;
24 8 24 4
x x x x
Vậy tổng cần tìm
11
8
.
Câu 4. Trong mặt phẳng tọa độ
Oxy
, tìm phương trình đường thẳng
'
là ảnh của đường
thẳng
: 2 1 0
x y
qua phép tịnh tiến theo vecto
1; 1
v
A.
': 2 2 0
x y
. B.
': 2 0
x y
. C.
': 2 3 0
x y
. D.
': 2 1 0
x y
.
Lời giải
Chọn B
Lấy
1;0 : 2 1 0
M x y
Gọi
' '; '
M x y
là ảnh của
;
M x y
qua phép tịnh tiến theo vecto
1; 1
v
Suy ra
' 2; 1 '
M
Đường thẳng
'
là ảnh của đường thẳng
: 2 1 0
x y
qua phép tịnh tiến theo vecto
1; 1
v
và đi qua
' 2; 1
M
có phương trình
': 2 0
x y
Vậy
': 2 0
x y
.
Câu 5. Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá của mét khoan đầu tiên là
10.000
đồng và kể từ mét khoan thứ hai, giá mỗi mét khoan sau tăng thêm
3000
đồng
so với giá mét khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan
giếng này để khoan một giếng sâu
100
mét lấy nước dùng cho sinh hoạt gia đình. Hỏi
sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan
giếng số tiền bằng bao nhiêu
A.
15.580.000
đồng. B.
18.500.000
đồng. C.
15.850.000
đồng. D.
15.050.000
đồng.
Lời giải
Chọn C
Ta kí hiệu giá mét khoan thứ
n
là
*
n
u n
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 66 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Theo đề bài ta có
1
10.000
u
,
2 1
3000
u u
, …,
1
3000 2
n n
u u n
. Như vậy ta có
một cấp số cộng có
100
số hạng với
1
10.000
u
, công sai
3000
d
Suy ra
100 1 100 1
... 50 2 99 15.850.000
S u u u d
Vậy số tiền cần phải trả là
15.850.000
đồng
Câu 6. Cho dãy số
n
u
có số hạng tổng quát
*
2
n
n
n
u n
. Số hạng thứ tư của dãy số
n
u
là
A.
1
2
. B.
1
16
. C.
1
4
. D.
1
8
.
Lời giải
Chọn C
Ta có số hạng thứ tư của dãy số là
4
4
4 1
(4)
2 4
u u
Câu 7. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
, ,
M N P
lần lượt là
trung điểm của
, ,
AB AD SC
. Gọi
Q
là giao điểm của
SD
với
( )
MNP
. Tính
SQ
SD
.
A.
1
4
. B.
3
4
. C.
2
3
. D.
1
3
.
Lời giải
Chọn D
Gọi
,
O AC BD I MN AC
,
K SO IP
Ta có
/ /
( ) ( ) ( )
( )
MN BD
MN MNP MNP SBD Kx
BD SBD
sao cho
/ /
Kx BD
,
Kx SD Q
vậy
Q SD
với
/ /
QK DB
H
Q
K
O
I
P
M
N
C
A
D
S
B
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 67
Kẻ
/ / ( )
AE IP E SC
, ta có
3
4
IP CP
AE CE
mà
P
là trung điểm
SC
suy ra
2
3
SE SF
SP SK
lại có
K
là trung điểm của
OF
do đó
3
4
SK
SO
mà
3
/ /
4
SQ SK
KQ BD
SD SO
Vậy
3
4
SQ
SD
.
Câu 8. Từ
20
học sinh ưu tú gồm
10
nam và
10
nữ, người ta muốn lập một đoàn đại biểu
gồm
6
người để tham dự một buổi hội thảo, trong đó có
1
trưởng đoàn là nam và
2
phó đoàn là nữ. Hỏi có bao nhiêu cách thành lập một đoàn đại biểu như vậy?
A.
27907 200
. B.
306000
. C.
38760
. D.
513000
.
Lời giải
Chọn B
Chọn
1
nam làm trưởng đoàn có
10
cách
Chọn
2
nữ phó đoàn có
2
10
C
cách
Chọn
3
người còn lại trong 17 người có
3
17
C
cách.
Vậy có tất cả
2 3
10 17
10. . 306000
C C
cách.
Câu 9. Cho tứ diện
ABCD
,
G
là trọng tâm tam giác
ABD
,
M
là điểm trên cạnh
BC
sao cho
2
MB MC
. Khẳng định nào sau đây đúng?
A.
//
MG ACD
. B.
//
MG ABC
. C.
//
MG ABD
. D.
//
MG BCD
.
Lời giải
Chọn A
Gọi
N
là trung điểm
AD
.
F
K
E
I
P
O
S
A
C
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 68 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Trong tam giác
BCN
ta có:
2
3
BG BM
BN BC
suy ra
//
MG CN
.
// //
MG ACD
MG CN MG ACD
CN ACD
.
Câu 10. Từ các chữ số của tập
1; 2;3; 4;5;6;8
A
có thể lập được bao nhiêu số tự nhiên có ba
chữ số đôi một khác nhau ?
A.
3
8
. B.
3
7
C
. C.
3
7
A
. D.
8
3
.
Lời giải
Chọn C
Mỗi số có ba chữ số đôi một khác nhau lập được từ các chữ số trong
1; 2;3; 4;5;6;8
A
là một chỉnh hợp chập 3 của 7 phần tử.
Vậy số các số lập được là :
3
7
A
.
Câu 11. Hệ số của
10
x
trong khai triển
10
2
3 1
x bằng
A.
0 0
10
3
C
. B.
5 10
10
3
C
. C.
10 10
10
3
C
. D.
5 5
10
3
C
.
Lời giải
Chọn D
Số hạng tổng quát của khai triển là:
10
2 10 20 2
10 10
3 3 .
k
k k k k
C x C x
với
,0 10
k k
.
Số hạng chứa
10
x
ứng với
20 2 10 2 10 5
k k k
.
Hệ số của
10
x
trong khai triển
10
2
3 1
x bằng:
5 5
10
3
C
.
Câu 12. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành,
O
là giao điểm
AC
và
BD
.
Gọi
,
M N
lần lượt là trung điểm
,
SA SB
. Giao tuyến của hai mặt phẳng
SAC
và
SBD
là
A.
SO
. B.
SM
. C.
SN
. D.
SD
.
Lời giải
Chọn A
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 69
Ta có:
O AC SAC
O SAC SBD
O BD SBD
.
Vậy
SO
là giao tuyến của hai mặt phẳng
SAC
và
SBD
.
Câu 13. Trong mặt phẳng
Oxy
, cho hai đường thẳng
: 2 2 0
x y
,
' : 2 2 0
x y
và
vectơ
(2;0)
v
. Khẳng định nào sau đây đúng?
A.
(0;3)
( ) '
V
. B.
0
(0;90 )
( ) '
Q
. C.
( ) '
v
T
. D.
0
(0;180 )
( ) '
Q
.
Lời giải.
Chọn D
Gọi
( ; )
M x y
bất kỳ,
M
. Gọi
0
(0;180 )
'
'( '; ') ( ) ( '; ')
' y
x x
M x y Q M M x y
y
2 ' y' 2 0 2 ' ' 2 0
M x x y
. Suy ra
' ' : 2 2 0
M x y
.
Vậy
0
(0;180 )
( ) '
Q
.
Câu 14. Trong mặt phẳng
Oxy
, tìm ảnh đường tròn
( ')
C
của đường tròn
2 2
( ) : 2 4 0
C x y x y
qua phép vị tự tâm
0
tỉ số
2
k
A.
2 2
( ) : ( 2) ( 4) 10
C x y
. B.
2 2
( ) :( 2) ( 4) 20
C x y
.
C.
2 2
( ) : ( 2) ( 4) 20
C x y
. D.
2 2
( ) : ( 2) ( 4) 10
C x y
.
Lời giải.
Chọn C
Đường tròn
( )
C
có tâm
(1; 2)
I
, bán kính
5
R
. Suy ra
( ')
C
có tâm
'(2; 4)
I
, bán
kính
' 2 2 5
R R
. Vậy
2 2
( ') : ( 2) ( 4) 20
C x y
.
Câu 15. Có bao nhiêu số hạng là số nguyên trong biểu thức
30
3
2 3
?
A.
6
. B.
8
. C.
7
. D.
5
.
Lời giải.
Chọn A
Số hạng tổng quát trong khai triển là
10
3
2
10
.2 .3
k
k
k
T C
với
0 30,k k
.
T
là số nguyên
k
chia hết cho 2 và 3
k
chia hết cho 6 6 ,k h h
Vì
0 30 0 6 30 0 5
k h h
vì
0,1,2,3,4,5
h h
. Vậy có 6 số nguyên
trong biểu thức trên.
Câu 16. Phương trình
sin 2 3cos2 1
x x
tương đương với phương trình
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 70 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
A.
sin 2 sin
3 3
x
. B.
sin 2 sin
3 3
x
.
C.
sin 2 sin
3 6
x
. D.
sin 2 sin
3 6
x
.
Lời giải.
Chọn D
Ta có
1 3 1
sin 2 3 cos 2 1 sin 2 cos 2 sin 2 sin
2 2 2 3 6
x x x x x
.
Câu 17. Trong mặt phẳng
Oxy
, cho điểm
1; 2
I
. Gọi
I
là ảnh của
I
qua phép vị tự
; 2
O
V
.
Khi đó,
I
có tọa độ là
A.
2; 4
. B.
4;2
. C.
4; 2
. D.
2;4
.
Lời giải
Chọn D
Ta có:
, 2
2
O
V I I OI OI
2.1 2
2;4
2 2 4
I
I
x
I
y
.
Câu 18. Điều kiện để hàm số
tan 1
4
y x
xác định là
A.
4
x k k
. B.
4
x k k
.
C.
2
x k k
. D.
4
x k k
.
Lời giải
Chọn B
Hàm số
tan 1
4
y x
xác định
cos 0
4
x
4 2 4
x k x k k
.
Câu 19. Trong một cuộc thi, Ban tổ chức dùng
7
cuốn sách môn Toán,
6
cuốn sách môn Vật
lý và
5
cuốn sách môn Hóa học để làm phần thưởng cho
9
học sinh có kết quả cao
nhất. Các cuốn sách cùng thể loại Toán, Vật lý, Hóa học đều giống nhau. Mỗi học sinh
nhận thưởng sẽ được hai cuốn sách khác nhau, trong đó có An. Tính xác suất để An
nhận thưởng có sách Toán.
A.
7
18
. B.
11
18
. C.
7
9
. D.
9
18
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 71
Lời giải
Chọn C
Gọi
x
là số phần quà gồm 1 cuốn sách Toán và 1 cuốn sách Vật lý.
Gọi
y
là số phần quà gồm 1 cuốn sách Vật lý và 1 cuốn sách Hóa học.
Gọi
z
là số phần quà gồm 1 cuốn sách Hóa học và 1 cuốn sách Toán.
Ta có
7 4
6 2
5 3
x z x
x y y
y z z
.
Như vậy có:
4
phần quà gồm 1 cuốn sách Toán và 1 cuốn sách Vật lý.
2
phần quà gồm 1 cuốn sách Vật lý và 1 cuốn sách Hóa học.
3
phần quà gồm 1 cuốn sách Hóa học và 1 cuốn sách Toán.
Có tổng cộng
9
phần quà trong đó có
7
phần quà có sách toán.
Vậy xác suất để An nhận thưởng có sách Toán là
7
9
.
Câu 20. Số nghiệm của phương trình
3
sin
2
x
là
A.
4
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn C
Ta có
3
1
2
nên phương trình
3
sin
2
x
vô nghiệm.
Câu 21. Long và Hưng cùng
8
bạn rủ nhau đi xem bóng đá. Số cách xếp nhóm bạn trên vào
10
chỗ ngồi sắp hàng ngang sao cho Long và Hưng ngồi cạnh nhau là:
A.
9.8!
. B.
18.8!
. C.
8!
. D.
9!
.
Lời giải
Chọn B.
Có
2!
cách sắp xếp Long và Hưng ngồi cạnh nhau.
Mỗi cách sắp xếp Long và Hưng cạnh nhau xem là phần tử
X
.
Có
9!
cách sắp xếp
X
và
8
bạn còn lại vào dãy ghế hàng ngang.
Vậy, có:
2!.9! 18.8!
.
Câu 22. Định
m
để phương trình có nghiệm:
6 6 2
sin cos cos 2
x x x m
với
0
8
x
.
A.
0 1
m
. B.
0 2
m
. C. 0
3
8
m
. D. 0
1
8
m
.
Lời giải
Chọn D.
Ta có:
6 6 2 2 2 2
sin cos cos 2 1 3sin .cos cos 2
x x x m x x x m
2 2 2
3 1 cos 4
sin 2 sin 2 sin 2 4 4 1 8 cos 4
4 2
x
x x m x m m m x
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 72 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Với
0
8
x
thì
0 cos4 1
x
. Suy ra để phương trình ban đầu có nghiệm
0
8
x
khi và chỉ khi
1
0 1 8 1 1 8 0 0
8
m m m
.
Câu 23. Tại một buổi lễ có
13
cặp vợ chồng tham dự, mỗi ông bắt tay với một người trừ vợ
mình, các bà không ai bắt tay nhau. Hỏi có bao nhiêu cái bắt tay?
A.
234
. B.
312
. C.
78
. D.
185
.
Lời giải
Chọn B.
TH1) Có
13
cách chọn một người đàn ông. Mỗi cách chọn một người đàn ông có
12
cách bắt tay với một phụ nữ mà người đó không là vợ. Suy ra có:
13.12 156
(cái bắt
tay).
TH2) Mỗi cách chọn
2
nam từ
13
nam có một cái bắt tay. Suy ra có:
2
13
78
C
(cái bắt
tay).
Vậy có:
156 78 234
(cái bắt tay).
Câu 24. Cho cấp số cộng
n
u
biết
3
6
u
,
8
16
u
. Tính công sai
d
và tổng của
10
số hạng đầu
tiên.
A.
2
d
;
10
100
S
. B.
1
d
;
10
80
S
. C.
2
d
;
10
120
S
. D.
2
d
;
10
110
S
.
Lời giải
Chọn D.
Ta có:
1
1
1
2 6
2
7 16
2
u d
u
u d
d
. Vậy
10
10.9
10.2 .2 110
2
S
.
Câu 25. Trong mặt phẳng
Oxy
cho đường thẳng
d
có phương trình
2 1 0
x y
để phép tịnh
tiến theo véctơ
v
biến
d
thành chính nó thì
v
phải là véctơ nào trong các véctơ sau :
A.
2;1
v
. B.
2; 1
v
. C.
1;2
v
. D.
1;2
v
.
Lời giải
Chọn C.
Phép tịnh tiến theo một vectơ khác vectơ
0
biến một đường thẳng
d
thành chính nó
khi và chỉ khi vectơ tịnh tiến có giá song song hoặc trùng với đường thẳng
d
. Ta chọn
1;2
v
vì nó là vectơ chỉ phương của đường thẳng
d
.
B. TỰ LUẬN
Câu 1. Giải phương trình
2cos 1 0
x
Lời giải
2cos 1 0
x
1
cos cos
2 3
x
2
3
,
2
3
x k
k
x k
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 73
Vậy phương trình đã cho có nghiệm là
2
3
,
2
3
x k
k
x k
.
Câu 2.
a) Từ một hộp chứa
7
quả cầu màu đỏ và
5
quả cầu màu vàng, Hùng lấy ngẫu nhiên
đồng thời
3
quả cầu. Tính xác suất để Hùng lấy được
3
quả cầu trong đó có hai quả
cầu màu đỏ.
b) Tìm số hạng không chứa
x
trong khai triển của
2
n
x
x
, biết
n
là số tự nhiên thỏa
mãn
1 2 3 2 496
4 1 4 1 4 1 4 1
... 2 1
n
n n n n
C C C C
Lời giải
a) Ta có:
3
12
220
n C .
Gọi biến cố
A
: “Trong
3
quả cầu trong đó có hai quả cầu màu đỏ” ,
Suy ra
2 1
7 5
. 105
n A C C
Vậy xác suất của biến cố A cần tìm là
105 21
220 44
n A
P A
n
.
b) Xét khai triển:
4 1
0 1 2 2 2 2 4 1 4 1
4 1 4 1 4 1 4 1 4 1
1 ...
n
n n
n n n n n
x C C x C x C x C x
Ta chọn
1
x
, khi đó ta có:
4 1 0 1 2 3 4 1
4 1 4 1 4 1 4 1 4 1
2 ...
n n
n n n n n
C C C C C
4 1 0 1 2 3 2
4 1 4 1 4 1 4 1 4 1
2 2 ...
n n
n n n n n
C C C C C
4 0 1 2 3 2
4 1 4 1 4 1 4 1 4 1
2 ...
n n
n n n n n
C C C C C
1 2 3 2 4
4 1 4 1 4 1 4 1
... 2 1
n n
n n n n
C C C C
Khi đó ta có
4 496
2 1 2 1 4 496 124
n
n n .
Với
124
n
ta xét khai triển:
124
124
2 2
x x
x x
Số hạng tổng quát thứ
1
k
trong khai triển trên là:
124 124 2
124 124
2
. . . 2 .
k
k
k k k k
k
T C x C x
x
Số hạng không chứa
x
trong khai triển trên tương ứng với
124 2 0 62
k k
.
Vậy số hạng không chứa
x
trong khai triển trên là
62
62
124
. 2
C
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 74 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 3. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang, với đáy lớn
AD
và
2
AD BC
.
a) (1,0 điểm) Tìm giao điểm của đường thẳng
CD
và mặt phẳng
SAB
.
b) (0,5 điểm) Gọi
I
là điểm nằm trên cạnh
SC
sao cho
2 3
SC SI
. Chứng minh đường
thẳng
SA
song song với mặt phẳng
BID
.
Lời giải
a) Gọi
E CD AB
.
Ta có:
E CD
;
E AB SAB
nên
E SAB
Vậy
CD SAB E
b) Ta có:
2 3
SC SI
1
3
CI
CS
1
.
Gọi
O AC BD
Tam giác
OCB
đồng dạng tam giác
OAD
nên
1
2
OC BC
OA AD
1
3
CO
CA
2
.
Từ
1
và
2
ta có:
1
3
CO CI
CA CS
//
OI SA
.
Mà
OI BDI
nên
//
SA BDI
Câu 4. Tìm hệ số của
31
x
trong khai triển
40
2
1
, 0
x x
x
Lời giải
Ta có
40
40 40
40 40 3
40 40
2 2
0 0
1 1
. .
k
k k k k
k k
x C x C x
x x
Theo đề bài:
40 3 31 3
k k
Vậy hệ số của
31
x
là
3
40
9880
C
Câu 5. Rút gọn tổng
2 2 2 2
1 1 1 .1! 2 2 1 2! 3 3 1 .3! ... 1 . !
S n n n
.
Lời giải
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 75
2 2 2 2
1 1 1 .1! 2 2 1 2! 3 3 1 .3! ... 1 . !
S n n n
Ta có
2 2
1 . ! 2 1 . !
k k k k k k k
2
1 . ! . !
k k k k
1 . 1 ! . !
k k k k
2 ! 1 ! 1 ! !
k k k k
2 ! 2 1 ! !
k k k
+Vậy
2
2
2
2
2
2
1 1 1 .1! 3! 2.2! 1!
2 2 1 .2! 4! 2.3! 2!
3 3 1 .3! 5! 2.4! 3!
4 4 1 .4! 6! 2.5! 4!
1 1 1 . 1 ! 1 ! 2. ! 1 !
1 . ! 2 ! 2 1 ! !
n n n n n n
n n n n n n
Cộng
n
đẳng thức này lại thì được
1! 2! 1 ! 2 ! 2 ! 1 ! 1 1 1 ! 1
S n n n n n n
---- HẾT -----
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 76 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
BẢNG ĐÁP ÁN & HƯỚNG DẪ GIẢI ĐỀ 4 – SỞ HƯNG YÊN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
B D C A B C A B C D A C A A A
16
17
18
19
20
21
22
23
24
25
C C B A B B B B D C
Câu 1. Tính tổng
S
tất cả các hệ số trong khai triển
11
3 4
x :
A.
1
S
. B.
1
S
. C.
0
S
. D.
8192
S
.
Lời giải
Chọn B
11
11
11 11
11
0
3 4 .3 .4 . 1 .
k
k k k k
k
x C x
.
Khi đó, tổng các hệ số trong khai triên là:
11
11
11
0
.3 .4 . 1 1
k
k k k
k
S C
.
Câu 2. Làng Duyên Yên, xã Ngọc Thanh, huyện Kim Động, tỉnh Hưng Yên nổi tiếng với trò
chơi dân gian đánh đu. Trong trò chơi này, khi người chơi nhún đều thì cây đu sẽ đưa
người chơi dao động qua lại ở vị trí cân bằng. Nghiên cứu trò chơi này, người ta thấy
rằng khoảng cách
h
(tính bằng mét) từ người chơi đu đến vị trí cân bằng được biểu
diễn qua thời gian
t
(
0
t
và được tính bằng giây) bởi hệ thức
h d
với
3cos 2 1
3
d t
trong đó quy ước rằng
0
d
khi vị trí cân bằng ở phía sau lưng
người chơi đu và
0
d
trong trường hợp trái lại. Tìm thời điểm đầu tiên sau
10
giây
mà người chơi đu ở xa vị trí cân bằng nhất.
A. Giây thứ
13
. B. Giây thứ
12,5
. C. Giây thứ
10,5
. D. Giây thứ
11
.
Lời giải
Chọn D
Ta có
1 cos 2 1 1 3 3cos 2 1 3
3 3
t t
.
Để người chơi đu ở xa vị trí cân bằng nhất thì
3cos 2 1 3 cos 2 1 1
3 3
t t
.
1 3
sin 2 1 0 2 1
3 3 2
k
t t k t
.
Thời điểm đầu tiên sau
10
giây mà người chơi đu ở xa vị trí cân bằng nhất:
1 3 19
10 10
2 3
k
t k
mà k
nên
7
k
.
Với
7 11
k t
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 77
Câu 3. Bạn An muốn mua một chiếc áo sơ mi cỡ
39
hoặc
40
. Biết áo cỡ
39
có
3
màu khác
nhau, áo cỡ
40
có
5
màu khác nhau. Hỏi bạn An có bao nhiêu lựa chọn để mua một
chiếc áo ?
A.
8
. B.
3
. C.
5
. D.
15
.
Lời giải
Chọn C
Trường hợp 1: Áo cỡ 39 có: 3 cách chọn.
Trường hợp 2: Áo cỡ 40 có: 5 cách chọn.
Vậy có
3 5 8
cách chọn.
Câu 4. Số đường chéo của đa giác
10
cạnh là
A.
35
. B.
7
. C.
45
. D.
10
.
Lời giải
Chọn A
Ta có số đường chéo của đa giác
10
cạnh là :
2
10
10 35
C
.
Câu 5. Từ các chữ số của tập hợp
1; 2; 3; 4; 5; 6
A
có thể lập được bao nhiêu số tự nhiên có
3
chữ số mà các chữ số đôi một khác nhau?
A.
125
. B.
120
.
C.
6
. D.
10
.
Lời giải
Chọn B
Mỗi số tự nhiên có
3
chữ số mà các chữ số đôi một khác nhau lập được từ các chữ số
của tập hợp
1; 2; 3; 4; 5; 6
A
là một chỉnh hợp chập 3 của 6 phần tử nên ta có tất cả
3
6
120
A
số.
Câu 6. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
B. Hai đường thẳng phân biệt không chéo nhau thì hoặc cắt nhau hoặc song song.
C. Hai đường thẳng không có điểm chung thì chéo nhau.
D. Hai đường thẳng chéo nhau thì không có điểm chung.
Lời giải
Chọn C
Hai đường thẳng không có điểm chung thì chúng có thể song song.
Câu 7. Mệnh đề nào sau đây là đúng?
A.
0 1 1 1 2 2
2 2 2 2 2 2
... ...
n n n n
n n n n n n
C C C C C C
.
B.
0 1 2 1 2 2
2 2 2 2 2 2
... ...
n n n n
n n n n n n
C C C C C C
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 78 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
C.
0 1 1 1 2 2
2 2 2 2 2 2
... ...
n n n n
n n n n n n
C C C C C C
.
D.
0 1 1 2 2
2 2 2 2 2 2
... ...
n n n n
n n n n n n
C C C C C C
.
Lời giải
Chọn A.
Ta có:
0 2
2 2
n
n n
C C
;
1 2 1
2 2
n
n n
C C
;…;
1 1
2 2
n n
n n
C C
.
Vậy
0 1 1 1 2 2
2 2 2 2 2 2
... ...
n n n n
n n n n n n
C C C C C C
.
Câu 8. Chọn ngẫu nhiên một hộp chứa 16 thẻ được đánh số từ 1 đến 16. Tính xác suất để
nhận được thẻ đánh số lẻ.
A.
9
16
. B.
1
2
. C.
3
8
. D.
7
16
.
Lời giải
Chọn B.
Từ 1 đến 16 có 8 số lẻ nên nếu chọn 1 trong 16 thẻ được đánh số từ 1 đến 16 thì xác
suất để nhận được thẻ đánh số lẻ là
8 1
16 2
.
Câu 9. Từ một cỗ bài tú lơ khơ 52 quân, rút ngẫu nhiên cùng một lúc 4 quân bài. Tính xác
suất sao cho cả 4 quân đều là K?
A.
1
6497400
. B.
4
6497400
. C.
1
270725
. D.
4
270725
.
Lời giải
Chọn C.
Xác suất để 4 quân bài được rút ngẫu nhiên từ cỗ bài 52 quân đều là K là:
4
52
1 1
270725
C
.
Câu 10. Phương trình
5
cos 1
6
x
có nghiệm là
A.
3
x k
. B.
2
3
x k
. C.
5
6
x k
. D.
5
2
6
x k
.
Lời giải
Chọn D
Ta có
5
cos 1
6
x
5
2
6
x k
5
2
6
x k
.
Câu 11. Một hộp chứa
6
quả cầu đỏ khác nhau và
4
quả cầu xanh khác nhau. Chọn ngẫu
nhiên cùng một lúc
2
quả cầu từ hộp. Tính xác suất của biến cố “Lấy được hai quả
cùng màu”.
A.
7
15
. B.
4
9
. C.
8
15
. D.
7
45
.
Lời giải
Chọn A
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 79
: “Chọn ngẫu nhiên cùng một lúc
2
quả cầu từ hộp”
2
10
45
n C
.
A
: “Lấy được hai quả cùng màu”
2 2
6 4
21
n A C C
.
Ta có
n A
P A
n
21 7
45 15
.
Câu 12. Lớp 11A có
35
học sinh nam và
10
học sinh nữ. Hỏi có bao nhiêu cách chọn ngẫu
nhiên một bạn trong lớp ?
A.
20
. B.
50
. C.
45
. D.
25
.
Lời giải
Chọn C
Số cách chọn ngẫu nhiên một bạn trong lớp là
35 10 45
.
Câu 13. Gọi
M
là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos 2 cos 2
y x x
. Tính
M m
A.
25
8
. B.
4
. C.
21
8
. D.
2
Lời giải
Chọn A
2
2
1 25
cos 2 cos 2 2 cos cos 3 2 cos
4 8
y x x x x x
.
Ta có:
2 2
3 1 5 1 25 25 1 25
1 cos 1 cos 0 2 cos 2 cos 0
4 4 4 4 8 8 4 8
x x x x
Vậy
25
8
M m .
Câu 14. Có bao nhiêu số tự nhiên có 8 chữ số đôi một khác nhau được lập từ tập
1,2,3,4,5,6,7,8
A sao cho số đó chia hết cho
1111
?
A.
384
. B.
345
. C.
3840
. D.
1920
.
Lời giải
Chọn A
Gọi số cần tìm
n
1 2 3 4 5 6 7 8
a a a a a a a a
chia hết cho 1111.
Vì tổng các chữ số:
1 2 3 4 5 6 7 8
36 9
a a a a a a a a
nên
9
n
Mà
1111
n
đồng thời 9 và 1111 là 2 số nguyên tố cùng nhau
Nên
9999
n
.
Ta có
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
.10000
a a a a a a a a a a a a a a a a
1 2 3 4 1 2 3 4 5 6 7 8
.9999
a a a a a a a a a a a a
Để
1 2 3 4 5 6 7 8
a a a a a a a a
9999 thì
1 2 3 4 5 6 7 8
a a a a a a a a
9999.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 80 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Mà
1 2 3 4 5 6 7 8 1 5 2 6 3 7 4 8
1000 100 10
a a a a a a a a a a a a a a a a
Nên suy ra
1 5 2 7 3 6 4 5
9
a a a a a a a a
Từ các chữ số của
A
ta có các cặp có tổng bằng 9 là:
1;8 , 2;7 , 3;6 , 4;5
.
Chọn
1
a
có 8 cách, chọn
5
a
có 1 cách.
Chọn
2
a
có 6 cách, chọn
6
a
có 1 cách.
Chọn
3
a
có 4 cách, chọn
7
a
có 1 cách.
Chọn
4
a
có 2 cách, chọn
8
a
có 1 cách.
Vậy có
8.6.4.2 384
số thỏa mãn.
Câu 15. Trong mặt phẳng tọa độ
Oxy
, ảnh của đường thẳng
: 2 3 0
d x y
qua phép đối
xứng tâm
(4;3)
I
là:
A.
2 17 0
x y
B.
2 7 0
x y
. C.
2 17 0
x y
. D.
2 15 0
x y
.
Lời giải
Chọn A
Đường thẳng
: 2 0
d x y c
.
Lấy
(3;0)
M d
.
Gọi
M
là ảnh của
M
qua phép đối xứng tâm
I
suy ra
I
là trung điểm của
MM
.
2 5
2 6
M I M
M I M
x x x
y y y
(5;6)
M
.
(5;6) 17
M d c
.
Vậy
: 2 17 0
d x y
.
Câu 16. Điều kiện cần và đủ để phương trình
sin cos
a x b x c
có nghiệm là
A.
2 2
a b c
. B.
2 2 2
a b c
. C.
2 2
a b c
. D.
2 2 2
a b c
.
Lời giải
Chọn C
Câu 17. Hàm số nào sau đây có đồ thị nhận gốc tọa độ
O
làm tâm đối xứng?
A.
2
sin
y x
. B.
cos
y x
.
C.
tan
y x
. D.
2
cot
y x
.
Lời giải
Chọn C
Hàm số lẻ có đồ thị nhận gốc tọa độ làm tâm đối xứng.
Câu 18. Có bao nhiêu cách lấy ngẫu nhiên cùng lúc
3
ba quả cầu từ một hộp chứa
10
quả cầu
khác nhau
A.
2
P
. B.
3
10
C
. C.
10
P
. D.
2
10
A
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 81
Lời giải
Chọn B
Số cách lấy ba quả cầu ngẫu nhiên đồng thời từ một hộp chứa mười quả cầu bằng số
tổ hợp chập ba của mười phần tử.
Câu 19. Tính tổng
0 1 2 2
2 2 2 2
...
n
n n n n
S C C C C
.
A.
2
2
n
S
. B.
2
2 1
n
S
. C.
2
n
S
. D.
2
2 1
n
S
.
Lời giải
Chọn A
Xét khai triển:
2
0 1 2 2 2 2
2 2 2 2
1 ...
n
n n
n n n n
x C C x C x C x
Cho
1
x
ta được
2 0 1 2 2
2 2 2 2
2 ...
n n
n n n n
C C C C
.
Vậy
2
2
n
S
.
Câu 20. Cô dâu và chú rể mời
6
người ra chụp ảnh kỉ niệm, người thợ chụp hình có bao nhiêu
cách sắp xếp sao cho cô dâu, chú rể đứng cạnh nhau.
A.
6.7!
. B.
2.7!
. C.
8! 7!
. D.
2! 6!
.
Lời giải
Chọn B
Số cách xếp cô dâu, chú rể đứng cạnh nhau là:
2!.7
cách.
Số cách xếp
6
người khách là:
6!
cách.
Vậy số cách xếp thoả mãn yêu cầu bài toán là:
2!.7.6! 2!.7! 2.7!
cách.
Câu 21. Cho hình vuông
ABCD
tâm
I
. Gọi
,
M N
lần lượt là trung điểm của
,
AD DC
. Phép
tịnh tiến theo véc tơ nào sau đây biến
AMI
thành
MDN
?
A.
AC
. B.
AM

. C.
NI
. D.
MN
.
Lời giải
Chọn B
I
N
M
D
C
B
A
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 82 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Ta có:
AM
AM AM
AM
AM AM T A M
AM MD T M D T AMI MDN
AM IN T I N
Câu 22. Cho hai đường thẳng cắt nhau
d
và
d
. Có bao nhiêu phép đối xứng trục biến đường
thẳng này thành đường thẳng kia?
A. Vô số. B. Hai. C. Không có. D. Một
Lời giải
Chọn B.
Hai đường phân giác của góc tạo bởi hai đường thẳng
d
và
’
d
là các trục đối xứng
trục biến đường thẳng
d
thành đường thẳng
’
d
.
Câu 23. Tìm hệ số của
5
x
trong khai triển
11
1
x
.
A.
55440
. B.
462
. C.
246
. D.
252
Lời giải
Chọn B.
Ta có:
11
11
11
0
1 .
k k
k
x C x
nên hệ số
5
x
ứng với
5
k là
5
11
462
C
.
Câu 24. Cho ba mặt phẳng phân biệt
, ,
có
1
d
;
2
d
;
3
d
. Khi đó ba đường thẳng
1 2 3
, ,
d d d
:
A. Đôi một song song. B. Đồng quy.
C. Đôi một cắt nhau. D. Đôi một song song hoặc đồng quy
Lời giải
Chọn D.
Ta có ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến thì ba giao tuyến này hoặc
song song, hoặc đồng quy.
Câu 25. Hãy mô tả không gian mẫu của phép thử: “Gieo một đồng xu cân đối và đồng chất hai
lần liên tiếp”.
A.
,
SS NN
. B.
,
S N
.
C.
, , ,
SS SN NS NN
. D.
,
SN NS
.
d
1
d
3
d
2
d
2
d
3
d
1
A
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 83
Lời giải
Chọn C.
Không gian mẫu là
, , ,
SS SN NS NN
.
B. TỰ LUẬN
Câu 1. Giải các phương trình sau đây
a)
2
cos 3cos 2 0
x x
.
b)
2cos 1 2sin cos sin 2 sin
x x x x x
Lời giải
a)
2
cos 3cos 2 0
x x
cos 1
cos 2
x
x
.
cos 1 2
x x k
với k
.
cos 2
x
(vô nghiệm).
b)
2cos 1 2sin cos sin 2 sin
x x x x x
2cos 1 2sin cos sin 2cos 1
x x x x x
2cos 1 sin cos 0
x x x
2cos 1 0
sin cos 0
x
x x
.
1
2cos 1 0 cos cos
2 3
x x
2 ,
3
x k k
.
sin cos 0 2 sin 0
4
x x x
,
4
x k k
.
Câu 2. Một lớp học có 15 nữ và 20 nam. Có bao nhiêu cách chọn ra từ lớp đó 10 bạn sao cho có ít
nhất 1 bạn nam ?
Lời giải
Chọn 10 học sinh bất kỳ từ 35 học sinh. Có
10
35
C
cách chọn.
Chọn 10 học sinh nữ từ 15 học sinh nữ. Có
10
15
C
cách chọn.
Số cách chọn thỏa bài toán là
10 10
35 15
C C
cách chọn.
Câu 3. Tìm số hạng không chứa
x
trong khai triển thành đa thức của biểu thức
12
3
1
3x
x
.
Lời giải
Số hạng thứ
1 0 12
k k
:
12
12 12 4
1 12 12
3
1
3 3
k
k
k k k k
k
T C x C x
x
.
Khi đó:
1
k
T
không chứa
12 4 0 3
x k k
.
Vậy số hạng không chứa
x
là
9 3
4 12
3
T C
.
Câu 4. Tìm tất cả các giá trị thực của tham số
m
sao cho phương trình lượng giác sau đây có
nghiệm:
sin 2 12 cos 2 13
m x x
.
Lời giải
Phương trình có nghiệm
2
2 2
12 13
m
2
25
m
5
m
hoặc
5
m
.
Vậy với
; 5 5;m
thì phương trình đã cho có nghiệm.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 84 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 5. Cho hình chóp
.
S ABCD
, có đáy
ABCD
là hình thang có đáy lớn
AD
. Gọi
,
E F
lần
lượt là trung điểm của
,
SA SD
.
a) Tìm giao tuyến của các cặp mặt phẳng:
SAC
và
SBD
,
SAD
và
SBC
.
b) Chứng minh
//
EF ABCD
và
//
EF SBC
.
c) Gọi
K
là giao điểm của
AB
và
CD
. Tìm
,
M N
lần lượt là giao điểm của
SB
và
CDE
;
SC
và
EFM
. Từ đó, tìm thiết diện của hình chóp cắt bởi mặt phẳng
KEF
.
d) Cho
2
AD BC
. Tính tỉ số diện tích của tam giác
KMN
và tam giác
KEF
.
Lời giải
a)
+) giao tuyến của các cặp mặt phẳng:
SAC
và
SBD
S
là điểm chung thứ nhất của
SAC
và
SBD
.
O
là giao điểm của
AC
và
BD
nên
,
O AC O BD
do đó
O
là điểm chung thứ hai của
SAC
và
SBD
. Vậy giao tuyến của hai mặt phẳng
SAC
và
SBD
là
SO
.
+) giao tuyến của các cặp mặt phẳng:
SAD
và
SBC
,
/ /
S SAD SBC
AD SAD BC SBC
AD BC
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 85
SAD SBC d
với
d
là đường thẳng đi qua
S
và
d
song song với
,
AD BC
.
b)
//
// .
,
ABCD EF AB
EF AD
EF A
D
BCD
AD C
Ta có
//
//
//
EF AD
EF BC
AD BC
Do đó
//
/ .
,
/
SBC EF S
EF BC
EF
C
SBC
BC B
c)
● Chọn mặt phẳng phụ
SAB
chứa
SB
.
● Tìm giao tuyến của hai mặt phẳng
SAB
và
ECD
.
Ta có
E SA SAB
E ECD
E
là điểm chung thứ nhất của
SBD
và
ABM
.
K AB SAB
K CD ECD
K
là điểm chung thứ hai của
SBD
và
ABM
Do đó
SAB ECD EK
.
Trong
SAK
lấy
M EK ECD
M EK SB
M SB
thì
M SB ECD
.
● Chọn mặt phẳng phụ
SBC
chứa
SC
.
● Tìm giao tuyến của hai mặt phẳng
SBC
và
EFM
.
Ta có
M SB SBC
M EFM
M
là điểm chung thứ nhất của
SBC
và
EFM
.
,
/ /
M SBC EFM
BC SBC EF EFM
EF BC
SBC EFM d
với
d
là đường thẳng đi qua
M
và
d
song song với
,
EF BC
.
Trong
SBC
lấy
N d EFM
N d SC
N SC
thì
M SC EFM
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 86 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Ta có
KEF SAD EF
KEF SAB EM
KEF SBC MN
KEF SCD NF
suy ra thiết diện của hình chóp cắt bởi mặt phẳng
KEF
là tứ giác
EMNF
d) Vì
2
AD BC
nên
,
M N
là trọng tâm tam giác
SAK
và
SDK
, do đó
2
3
KM KN
KE KF
suy ra phép vị tự tâm
K
, tỉ số
3
2
biến tam giác
KMN
thành tam giác
KEF
. Vậy tỉ số
diện tích của tam giác
KMN
và tam giác
KEF
là
4
9
.
--- HẾT ---
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 87
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 5 – SỞ HUẾ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
A
C
B
D
C
C
D
B
A
B
C
D
B
D
D
16
17
18
19
20
21
22
23
24
25
C
B
A
D
A
A
A
D
C
B
Câu 1. Tìm hệ số của
3 3
x y
trong khai triển biểu thức
6
x y
A.
20.
B.
6.
C.
15.
D.
1.
Lời giải
Chọn A
Số hạng thứ
1
k
trong khai triển là:
6
1 6
k k k
k
T C x y
Ta có:
6 3
3
3
k
k
k
Vậy hệ số của
3 3
x y
trong khai triển là:
3
6
20.
C
Câu 2. Hàm số nào sau đây là hàm số chẵn?
A.
tan .
y x
B.
cot .
y x
C.
cos .
y x
D.
sin .
y x
Lời giải
Chọn C
Hàm số
( ) cos
y f x x
TXĐ:
D
+
; .
x x
+
, ( ) cos( ) cos ( ).
x f x x x f x
Vậy hàm số
cos
y x
là hàm số chẵn.
Câu 3.
Tập xác định của hàm số
sin 2 ?
y x
A.
;2 .
D 
B.
.
D
C.
\ 2 .
D
D.
2; .
D

Lời giải
Chọn B
Hàm số
sin 2
y x
xác định với
.
x
Câu 4.
Một nhóm công nhân có
15
người trong đó có
10
nam và
5
nữ. Có bao nhiêu cách
chọn
6
người đi dự đại hội công ty?
A.
4785.
B.
3603600.
C.
720.
D.
5005.
Lời giải
Chọn D
Chọn 6 người trong 15 người đi dự đại hộ công ty:
6
15
5005.
C
Câu 5. Trong mặt phẳng
Oxy
, cho điểm
1; 0
A . Tìm ảnh của
A
qua phép dời hình có được
bằng cách thực hiện liên tiếp phép quay tâm
O
góc quay
90
và phép tịnh tiến theo
véctơ
2 ; 0
v
.
A.
2 ; 1
A
. B.
2 ;1
A
. C.
2 ;1
A
. D.
1; 2
A
.
Lời giải
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 88 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Chọn C
Giả sử
1
1
1 1
; 90
0 ;1 .
A A
O
A A
x y
Q A A A
y x
1
1
1
2
2 ;1 .
0
A A
v
A A
x x
T A A A
y y
Vậy ảnh của
A
qua phép dời hình trên là
2 ;1 .
A
Câu 6. Cho dãy số
n
u
là cấp số cộng có
1 6
3 , 27
u u
. Tìm công sai
d
?
A.
5
d
. B.
4
d
. C.
6
d
. D.
24
5
d .
Lời giải
Chọn C
Ta có:
6 1 6 1
1 1
5 27 3 6.
5 5
u u d d u u
Câu 7. Cho
3 2
3 5
n
P n n n
với n
. Khẳng định nào sau đây đúng?
A.
n
P
chia hết cho
2
. B.
n
P
chia hết cho
5
. C.
n
P
chia hết cho
6
. D.
n
P
chia hết cho
3
.
Lời giải
Chọn D
Với
1
1 1 3 5 9
n P
chia hết cho
3
, không chia hết cho
2
,
không chia hết cho
5
và
không chia hết cho
6
.
Câu 8. Có
5
học sinh gồm
2
nữ và
3
nam được xếp vào dãy ghế được đánh số
1,2,3, 4,5
. Hỏi
có bao nhiêu cách sắp xếp chổ ngồi cho
5
học sinh nói trên, biết rằng vị trí số
1
phải
dành cho một học sinh nữ?
A.
52.
B.
48.
C.
50.
D.
42.
Lời giải
Chọn B
+ Vị trí ghế số
1
: có
2
cách.
+ Ghế
2,3,4,5
sắp xếp
4
người còn lại là
4
24
P
cách.
Vậy số cách sắp xếp là:
2.24 48
.
Câu 9. Tính chất nào sau đây không phải là tính chất của phép đồng dạng.
A. Biến đường tròn thành đường tròn có cùng bán kính.
B. Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và bảo toàn thứ tự của 3 điểm đó.
C. Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.
D. Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn
thẳng.
Lời giải
Chọn A
Phép đồng dạng biến đường tròn có bán kính
R
thành đường tròn có bán kính
kR
với
0
k
là tỉ số đồng dạng.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 89
Câu 10. Cho hình chóp
.
S ABCD
có đáy là hình bình hành. Gọi
O
là giao điểm của
AC
và
BD
.
Xác định giao tuyến của hai mặt phẳng
SAD
và
SBC
.
A. Đường thẳng qua
S
và song song với
AC
.
B. Đường thẳng qua
S
và song song với
AD
.
C. Đường thẳng qua
S
và song song với
AB
.
D. Đường thẳng
SO
.
Lời giải
Chọn B
Ta có:
S SAD SBC
.
Vì
//
AD BC
nên đường thẳng
d
là giao tuyến của
SAD
và
SBC
là đường thẳng qua
S
và song song với
AD
và
BC
.
Câu 11. Cho
A
và
B
là hai biến cố liên quan đến một phép thử. Khẳng định nào sau đây sai?
A. nếu
A
thì
A
là biến cố chắc chắn.
B. Nếu A B
thì
A
và
B
là hai biến cố xung khắc.
C. Nếu
A B
thì
A
và
B
là hai biến cố đối nhau.
D. Nếu A
thì
A
là biến cố không.
Lời giải
Chọn C
Câu 12. Trong mặt phẳng
Oxy
, phép tịnh tiến theo vec tơ
1; 3
v
biến đường tròn
2 2
: 1 2 6
C x y
thành đường tròn có phương trình nào sau đây?
A.
2
2
1 6
x y
. B.
2 2
2 5 6
x y
.
C.
2
2
1 6
x y
. D.
2 2
2 5 6
x y
.
Lời giải
Chọn C
Đường tròn
C
có tâm
1; 2
I
, bán kính
6
R
.
v
T C C
Đường tròn
C
và
C
có cùng bán kính
6
R
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 90 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
2; 5
v
T I I I
.
Phương trình đường tròn
:
C
2 2
2 5 6
x y
.
Câu 13. Trong mặt phẳng
Oxy
, phép quay tâm
O
góc quay
90
o
biến điểm
M
thành
'(3; 1)
M
Tìm tọa độ điểm
M
.
A.
( 3;1).
M
B.
(1;3).
M
C.
(1; 3).
M
D.
(3; 1).
M
Bài giải
Chọn B
Phép quay tâm
O
góc quay
90
o
biến điểm
M
thành
'(3; 1)
M
0 0
0 0
' cos( 90 ) sin( 90 )
' sin( 90 ) cos( 90 )
M M
M M
x x y
y x y
Khi đó
0 0
0 0
3 cos( 90 ) sin( 90 ) 3.
1 sin( 90 ) cos( 90 ) 1.
(1;3).
M M M M
M M M M
x y y y
x y x x
M
Câu 14. Tìm tất cả các nghiệm của phương trình
1
2
sinx
thỏa mãn
2 2
x
A.
2 .
3
x k
B.
.
3
x
C.
5
2 .
6
x k
D.
.
6
x
Bài giải
Chọn D
1
2 .
2
6
sinx x k
Vì
2 2
x
Vậy
.
6
x
Câu 15. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
O
là giao điểm của
AC
và
.
BD
Gọi
,
I J
lần lượt là trung điểm của
SA
và
.
SB
Khẳng định nào sau đây sai?
A.
IJ//(ABCD)
và
IJ//(SCD)
B.
IJCD
là hình thang.
C.
IJ
và
SO
chéo nhau
D.
(IJ )
C
cắt hình chóp
.
S ABCD
theo thiết diện là tam giá
IJ .
C
Lời giải
Chọn D
J
I
O
D
C
B
A
S
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 91
IJ
là đường trung bình tam giác
SAB
nên
IJ//AB,
mà
AB//CD
(vì
ABCD
là hình bình
hành) nên
IJ//CD.
Từ đó suy ra
IJ//(ABCD)
,
IJ//(SCD)
và
IJCD
là hình thang.
Do đó, các khẳng định ở đáp án A, B đúng.
IJ, SO
phân biệt. Giả sử
IJ, SO
không chéo nhau thì
IJ//SO
hoặc
IJ
cắt
SO.
Từ đó suy ra
( ) ( ),
SAC SAB
điều này vô lý. Vậy
IJ
và
SO
chéo nhau. Do đó, khẳng định ở đáp án C
đúng.
(IJC)
cắt hình chóp .
S ABCD
theo thiết diện là tứ giác
.
IJCD
Do đó, khẳng định ở đáp án
D sai.
Chọp đáp án D.
Câu 16. Từ một đội học sinh giỏi Toán có 3 nam và 5 nữ, chọn ngẫu nhiên 2 em đi thi học sinh
giỏi Toán. Tính xác suất để chọn được 1 nam và 1 nữ.
A.
15
.
56
B.
25
.
28
C.
15
.
28
D.
8
.
56
Lời giải
Chọn C
Chon ngẫu nhiên 2 học sinh từ đội học sinh có 8 em thì số phần tử không gian mẫu là
2
8
( ) 28.
n C
Gọi A là biến cố: “2 học sinh được chọn có 1 nam và 1 nữ” thì ta có
( ) 3.5 15.
n A
Vậy
( ) 15
( ) .
( ) 28
n A
P A
n
Chọn đáp án C.
Câu 17.
Trong không gian có bao nhiêu vị trí tương đối giữa hai đường thẳng.
A.
3.
B.
4.
C.
5.
D.
2.
Lời giải:
Chọn B
Trong không gian có 4 vị trí tương đối của
2
đường thẳng:
2 đường thẳng song song.
2 đường thẳng trùng nhau.
2 đường thẳng cắt nhau.
2 đường thẳng chéo nhau.
Câu 18.
Các hình sau đây biểu diễn một hình chóp tứ giác trong không gian. Hình nào sai?
A. Hình 2. B. Hình 3. C. Hình 4. D. Hình 1.
Lời giải:
Chọn A
Hình 4
Hình 3
Hình 2
Hình 1
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 92 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Hình 2 sai vì không có hướng nào nhìn thỏa mãn.
Hình 1 và Hình 4 nhìn từ đỉnh xuống vẫn thỏa mãn.
Câu 19. Tìm nghiệm của phương trình:
2
sin sinx 0
x
thỏa mãn
2 2
x
.
A.
4
x
. B.
2
x
. C.
2
x
. D.
0.
x
Lời giải
Chọn D
2
sin 0
sin sinx 0 sin sin 1 0 .
sin 1
2
2
x k
x
x x x k
x
x k
Với
0 0
k x
thỏa mãn
2 2
x
.
Câu 20. Cho dãy số
n
u
với
2
1
n
n
u
n
. Tìm
5
.
u
A.
5
5
.
26
u
B.
5
5
6
u
. C.
5
5
26
u
. D.
5
5.
u
Lời giải
Chọn A
Thay
5
n
ta có
5
2
5 5
26
5 1
u
.
Câu 21. Từ các chữ số 2,3,4,6,7,9 lập được bao nhiêu số chẵn có ba chữ số?
A.
108.
B.
36.
C.
20.
D.
40.
Lời giải
Chọn A
Gọi số tự nhiên có 3 chữ số cần tìm là:
.
abc
Vì cần lập ra số chẵn có 3 chữ số nên c có 3 cách chọn là
2;c 4
c
hoặc
6.
c
Hai chữ số a và b đều có 6 cách chọn.
Do đó, số số tự nhiên thỏa mãn là:
6.6.3 108
(số)
Câu 22. Trong mặt phẳng
Oxy
, cho
(2; 1)
v
và điểm
( 3;2).
M
Tìm điểm
'
M
là ảnh của điểm
M
qua phép tịnh tiến theo vectơ
.
v
A.
'( 1;1).
M
B.
'(1; 1).
M
C.
'( 1;0).
M
D.
'(1;1).
M
Lời giải
Chọn A
Gọi
'( ; )
M x y
là ảnh của điểm
M
qua phép tịnh tiến theo vectơ
.
v
Ta có:
' ( 3; 2) (2; 1)
MM v x y

3 2 1
.
2 1 1
x x
y y
Vậy
'( 1;1).
M
Câu 23. Trong mặt phẳng
Oxy
, cho đường thẳng
: 2 3 3 0
d x y
. Tìm phương trình đường
thẳng
d
là ảnh của
d
qua phép vị tự tâm
O
tỉ số
2
k
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 93
A.
4 2 3 0
x y
. B.
4 2 5 0
x y
. C.
2 3 0
x y
. D.
2 3 6 0
x y
.
Lời giải
Chọn D
;2O
d V d d
cùng phương với
d
, do đó
d
có phương trình dạng
2 3 0
x y m
.
Lấy
0;1
M d
, gọi
;2
;
O
M x y V M
ta có
2 0;2
OM OM M

.
Mà
M d
nên
2.3 0 6
m m
.
Vậy phương trình
: 2 3 6 0
d x y
.
Câu 24. Cho dãy số
n
u
là cấp số cộng có số hạng đầu
1
u
, công sai
d
,
n
S
là tổng của
n
số
hạng đầu tiên. Với
2
n
, đẳng thức nào sau đây sai?
A.
1
1
n
u u n d
. B.
1 1
2
n n
n
u u
u
.
C.
1n n
u u d
. D.
1
1
2
n
n
S u n d
.
Lời giải
Chọn C
Công thức đúng là
1 1
.
n
u u n d
.
Câu 25. Tìm tập giá trị
T
của hàm số
3 2sin
y x
.
A.
2;4 .
T B.
1;5 .
T C.
1;1 .
T D.
0;3 .
T
Lời giải
Chọn B
Ta có
1 sin 1, .
x x
Suy ra
2 2sin 2, 1 3 2sin 5, .
x x x x
Vậy tập giá trị
T
của hàm số
3 2sin
y x
là
1;5 .
T
B. TỰ LUẬN
Câu 1. Giải phương trình:
sin 3cos 1
x x
.
Lời giải
Phương trình:
sin 3 cos 1 2 sin .cos cos .sin 1
3 3
x x x x
2.sin 1
3
x
1
sin
3 2
x
2
3 6
,
5
2
3 6
x k
k
x k
2
2
,
7
2
6
x k
k
x k
.
Câu 2. Trong khoảng
(0;3 ),
phương trình
3
sin 2
2
x
có bao nhiêu nghiệm?
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 94 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Lời giải
Ta có:
3
sin 2
2
x
sin 2 sin
3
2 2
3
,
2
2 2
3
6
,
3
x
x k
k Z
x k
x k
k Z
x k
Vì nghiệm của phương trình chỉ xét trên khoảng
(0;3 )
nên ta có các trường hợp sau:
TH1:
1 17
0 3 0;1;2.
6 6 6
k k k
Suy ra các nghiệm là:
7 13
; ; .
6 6 6
TH2:
1 8
0 3 0;1;2.
3 3 3
k k k
Suy ra các nghiệm là:
4 7
; ; .
3 3 3
Vậy phương trình đã cho có 6 nghiệm trong khoảng
(0;3 ).
Câu 3. Một hộp chứa 10 quả cầu được đánh số từ 1 đến 10. Lấy ngẫu nhiên một quả. Tính xác
suất của biến cố A: “Nhận được quả cầu ghi số chẵn”.
Lời giải
Lấy ngẫu nhiên một quả cầu trong 10 quả cầu, suy ra số phần tử của không gian mẫu là
( ) 10.
n
Trong 10 số từ 1 đến 10, có 5 số là số chẵn nên
( ) 5.
n A
Vậy xác suất của biến cố A là:
5 1
( ) .
10 2
P A
Câu 4. Tìm số hạng không chứa
x
trong khai triển
6
2
, 0
x x
x
.
Lời giải
Ta có:
6
6 6
6 6 2
6 6
0 0
2 2
2 .
k
k k k k k
k k
x C x C x
x x
Số hạng không chứa
x
trong khai triển tương ứng với
k
thỏa mãn:
6 2 0 3
k k
.
Số hạng không chứa
x
trong khai triển
6
2
, 0
x x
x
là:
3 3
6
.2 160
C
.
Câu 5. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Trên cạnh CD lấy điểm P
sao cho
2
PD PC
.
a) Tìm giao điểm của đường thẳng BD và mặt phẳng
MNP
.
b) Tìm giao tuyến của mặt phẳng
MNP
và
ABD
.
Lời giải
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 95
a) Trong
BCD
gọi
I BD NP
,
I BD
I NP NP MNP I MNP
Vậy:
I BD MNP
b) Ta có:
,
,
I BD BD ABD I ABD
I NP NP MNP I MNP
Do đó:
1
I ABD MNP
Mặt khác:
,AB
M MNP
M AB ABD M ABD
Suy ra:
2
M ABD MNP
Từ (1) và (2) ta có:
.
IM ABD MNP
--- HẾT ---
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 96 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 6 – CHUYÊN QUỐC HỌC HUẾ
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
A
A
D
B
A
A
D
A
B
C
C
B
B
A
D
16 17 18 19 20 21 22 23 24 25
C C C D A D A D D A
Câu 1. Tìm tập xác định của hàm số
1
sin
y
x
.
A.
\ ,D k k
. B.
\ ,
2
D k k
.
C.
\ 0D
. D.
D
.
Lời giải
Chọn A
Hàm số
1
sin
y
x
xác định
sin 0x x k k
.
Câu 2. Cho hình chóp
.S ABCD
có đáy là một tứ giác lồi. Hình nào sau đây không thể là thiết
diện của nó.
A. Lục giác. B. Tam giác. C. Tứ giác. D. Ngũ giác.
Lời giải
Chọn A
Vì hình chóp tứ giác có
5
mặt (gồm
4
mặt bên và
1
mặt đáy) nên thiết diện của nó có
tối đa
5
cạnh. Vậy thiết diện không thể là lục giác.
Câu 3. Có
10
cây bút khác nhau và
9
quyển sách khác nhau. Tìm số cách chọn
1
cây bút và
1
quyển sách.
A.
80
. B.
70
. C.
19
. D.
90
.
Lời giải
Chọn D
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 97
Vì có
10
cây bút khác nhau và
9
quyển sách khác nhau nên số cách chọn
1
cây bút và
1
quyển sách là
10.9 90
(cách)
Câu 4. Một hộp chứa
6
quả bóng đỏ (được đánh số từ
1
đến
6),
5
quả bóng vàng (đươc
đánh số từ
1
đến
5),
4 quả bóng xanh (được đánh số từ
1
đến
4).
Lấy ngẫu nhiên
4
quả bóng. Tính xác suất để
4
quả bóng lấy ra có đủ ba màu và không có hai quả bóng
nào có số thứ tự trùng nhau.
A.
43
.
91
B.
74
.
455
C.
381
.
455
D.
48
.
91
Lời giải
Chọn B
Số phần tử của không gian mẫu bằng
4
15
C
.
Lấy được 4 quả bóng có đủ cả ba màu mà không có hai quả bóng nào có số thứ tự
trùng nhau có các trường hợp sau:
 TH1: Lấy được 1 quả bóng xanh, 2 quả bóng vàng và 1 quả bóng đỏ
Lấy 1 quả bóng xanh có
1
4
C
cách.
Lấy 2 quả bóng vàng có số thứ tự không trùng với số thứ tự của bóng xanh đã lấy có
2
4
C
cách.
Lấy 1 quả bóng đỏ có số thứ tự không trùng với số thứ tự của bóng xanh và bóng vàng
đã lấy có
1
3
C
cách.
Vậy TH1 có
1 2 1
4 4 3
. .
C C C
cách lấy.
 TH2: Lấy được 2 quả bóng xanh, 1 quả bóng vàng và 1 quả bóng đỏ
Lấy 2 quả bóng xanh có
2
4
C
cách.
Lấy 1 quả bóng vàng có số thứ tự không trùng với số thứ tự của bóng xanh đã lấy có
1
3
C
cách.
Lấy 1 quả bóng đỏ có số thứ tự không trùng với số thứ tự của bóng xanh và bóng vàng
đã lấy có
1
3
C
cách.
Vậy TH2 có
2 1 1
4 3 3
. .
C C C
cách lấy.
 TH3: Lấy được 1 quả bóng xanh, 1 quả bóng vàng và 2 quả bóng đỏ
Lấy 1 quả bóng xanh có
1
4
C
cách.
Lấy 1 quả bóng vàng có số thứ tự không trùng với số thứ tự của bóng xanh đã lấy có
1
4
C
cách.
Lấy 2 quả bóng đỏ có số thứ tự không trùng với số thứ tự của bóng xanh và bóng vàng
đã lấy có
2
4
C
cách.
Vậy TH3 có
1 1 2
4 4 4
. .
C C C
cách lấy.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 98 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Như vậy xác xuất lấy được 4 quả bóng có đủ cả ba màu mà không có hai quả bóng nào
có số thứ tự trùng nhau là
1 2 1 2 1 1 1 1 2
4 4 3 4 3 3 4 4 4
4
15
. . . . . .
74
.
455
C C C C C C C C C
C
Câu 5. Tìm số cách xếp
5
bạn nam và
4
ban nữ thành một hàng ngang sao cho
4
bạn nữ
luôn đứng cạnh nhau.
A.
17280.
B.
362880.
C.
5760.
D.
2880.
Lời giải
Chọn A
Có
6
cách chọn
4
vị trí từ
9
vị trí trên một hàng ngang để
4
bạn nữ đứng cạnh nhau.
Xếp
4
bạn nữ vào
4
vị trí đã chọn có
4!
cách.
Xếp
5
bạn nam vào
5
vị trí còn lại có
5!
cách.
Vậy có
6.4!.5! 17280
cách xếp.
Câu 6. Cho tập hợp
0;2;4;5;6 ,
A tìm số chỉnh hợp chập
3
của
.
A
A.
60.
B.
96.
C.
20.
D.
10.
Lời giải
Chọn A
Số chỉnh hợp chập
3
của
5
phần tử là
3
5
60.
A
Câu 7. Gieo đồng thời 2 con súc sắc cân đối, đồng chất, một con màu đỏ và một con màu đen.
Tính xác suất của biến cố: “Số chấm trên con đen lớn hơn số chấm trên con đỏ 2 đơn
vị.”
A.
5
.
36
B.
9
.
36
C.
32
.
36
D.
1
.
9
Lời giải
Chọn D
Không gian mẫu:
; | 1 , 6
a b a b
, trong đó a và b lần lượt là số chấm trên con
đỏ và con đen. Do đó,
6.6 36.
n
Gọi A: “Số chấm trên con đen lớn hơn số chấm trên con đỏ 2 đơn vị.”
Ta có:
6; 4 ; 5; 3 ; 4;2 ; 3;1
A
.
Do đó,
( ) 4 1
( ) .
36 9
n A
P A
n
Câu 8. Gọi M là tổng các nghiệm thuộc
;5
của phương trình
1 sin
1,
cos
x
x
tìm M.
A.
6 .
M
B.
15
.
2
M
C.
23
.
2
M
D.
27
.
2
M
Lời giải
Chọn A
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 99
Điều kiện:
sin 1
, .
cos 0
2
x
x k k
x
Ta có:
2
2
1 sin
1 1 sin cos
cos
cos 0
1 sin cos
cos 0
1 sin 1 sin
x
x x
x
x
x x
x
x x
cos 0
sin 0
sin 1
x
x
x
cos 0
,
2 ,
2
x
x m m
x n n

Đối chiếu với điều kiện, tập các nghiệm thuộc
;5
của phương trình trên là
0;2 ;4
S
Câu 9. Cho
ABC
vuông tại B và
60
A
(các đỉnh của tam giác ghi theo thứ tự ngược
chiều kim đồng hồ). Về phía ngoài tam giác, vẽ tam giác đều ACD. Tìm ảnh của cạnh
BC qua phép quay tâm A, góc quay
60 .
A. AI với I là trung điểm của CD. B. DK với K là trung điểm của AC.
C. AD. D. CJ với J là trung điểm của AD.
Lời giải
Chọn B
Gọi K là trung điểm của AC.
Vì
ABC
vuông tại B và
60
A
nên
1
.
2
AB AC AK
Do đó,
( ;60 )
o
A
Q B K
và
( ;60 )
.
o
A
Q C D
(Vì tam giác ACD đều).
Vậy ảnh của cạnh BC qua phép quay tâm A, góc quay
60
là DK.
D
C
K
A
B
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 100 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 10. Tìm số điểm biểu diễn các họ nghiệm của phương trình
2
2sin 3sin 5 0
x x
trên
đường tròn lượng giác là.
A.
2.
B.
3.
C.
1.
D.
4.
Lời giải
Chọn C
Phương trình tương đương
sin 1
2
5
2
sin
2
x
x k
x
Do đó có 1 điểm biểu diễn. Ta chọn C
Câu 11. Tìm điều kiện của tham số thực
m
để phương trình
sin 3cos 5
m x x
có nghiệm.
A.
4.
m
B.
34.
m
C.
4
.
4
m
m
D.
4 4.
m
Lời giải
Chọn C
Phương trình có nghiệm khi
2
2 2 2
4
3 5 16 .
4
m
m m
m
Ta chọn đáp án C
Câu 12. Cho cấp số cộng có số hạng đầu
1
1
u
và công sai
2.
d
Tổng
n
số hạng đầu tiên
của cấp số cộng này là
9800,
n
S
tìm
.
n
A.
101.
B.
100.
C.
98.
D.
99.
Lời giải
Chọn B
Ta có
2
1
100
2 1 2 9800 2 9800 0
98
2
n
n
n
S u n d n n n n
n
Do
n
là số tự nhiên nên
100
n
. Ta chọn B
Câu 13. Tìm số các nghiệm thuộc
0;2019
của phương trình
3 cot 3 0
x
.
A.
2018.
B.
2019.
C.
4038.
D.
4039.
Lời giải
Chọn B
3 cot 3 0 cot 3
6
x x x k k
Vì
0;2019
x
nên
1 12113
0 2019 2019
6 6 6 6 6
k k k
Do
k
nên
0 2018
k
.
Số các nghiệm thuộc
0;2019
của phương trình là
2019.
Câu 14. Tìm mệnh đề sai trong các mệnh đề sau đây.
A. Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với
nó.
B. Phép đồng dạng bảo toàn độ lớn góc.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 101
C. Phép dời hình là phép đồng dạng tỉ số
1
k
.
D. Phép vị tự tỉ số
k
là phép đồng dạng tỉ số
k
.
Lời giải
Chọn A
Câu 15. Tìm phương trình tương đương với phương trình
2 2
3sin cos
x x
.
A.
2
3
sin .
4
x
B.
1
sin .
2
x
C.
3
cos .
2
x
D.
2
cot 3.
x
Lời giải
Chọn D
Nhận xét:
2
sin 0 cos 1
x x
. Khi đó phương trình trở thành:
0 1
( vô lý ).
Vậy
cos 0
x
. Chia hai vế cho
2
sin
x
, ta có:
2 2 2
3sin cos cot 3
x x x
.
Câu 16. Một lớp học có
30
học sinh gồm có cả nam và nữ. Chọn ngẫu nhiên
3
học sinh để
tham gia hoạt động của Đoàn trường. Biết xác suất chọn được
2
nam và
1
nữ là
12
,
29
gọi
n
là số học sinh nữ của lớp, tìm mệnh đề đúng.
A.
20;23 .
n B.
15;19 .
n C.
12;15 .
n D.
8;12 .
n
Lời giải
Chọn C
Chọn
3
học sinh trong số
30
học sinh nên không gian mẫu có số phần tử là
3
30
.
n C
Gọi
A
là biến cố “chọn được
2
nam và
1
nữ”.
Lúc đó:
3 2
2 1
30
30 !.n 30 29 .n
59 870
. .
2! 30 2 ! 2 2
n n
n n n
n n n
n A C C
n
Ta có xác suất của biến cố
A
là
3 2
3 2
12 59 870 12
59 870 3360 14.
29 2.4060 29
n n n
P A n n n n
Vậy
12;15 .
n
Câu 17. Tìm chu kỳ tuần hoàn
T
của hàm số
sin
2
x
y
với
0 .
x
A.
.
2
T
B.
2 .
T
C.
4 .
T
D.
.
T
Lời giải
Chọn C
Hàm số
sin
2
x
y
là hàm số tuần hoàn với chu kỳ
2
4 .
1
2
T
Câu 18. Gieo
3
đồng xu một lúc, gọi
A
là biến cố “có đúng một đồng xu xuất hiện mặt ngửa”.
Tìm xác suất của biến cố
.
A
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 102 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
A.
1
.
2
B.
1
.
4
C.
3
.
8
D.
1
.
8
Lời giải
Chọn C
Gieo
3
đồng xu một lúc nên không gian mẫu là
; ; ; ; ; ; ; .
SSS SSN SNS NSS SNN NSN NNS NNN
Ta có
8; 3.
n n A
Vậy xác suất của biến cố
A
là
3
.
8
n A
P A
n
Câu 19. Trong mặt phẳng
Oxy
cho
2;0 , 2;2 , 4;2 , 4;0
A B C D . Chọn ngẫu nhiên một
điểm có tọa độ
;
x y
(với
,
x y
là các số nguyên) nằm trong hình chữ nhật
ABCD
(kể
cả các điểm nằm trên cạnh). Gọi
A
là biến cố: “
,
x y
đều chia hết cho 2”, tính xác suất
của biến cố
A
.
A.
13
21
. B.
7
21
. C.
1
. D.
8
21
.
Lời giải
Chọn D
Gọi
;
M x y
là tọa độ cần tìm.
Để
;
M x y
nằm trong hình chữ nhật có tọa độ nguyên thì
2; 1;0;1; 2;3;4
0;1;2
x
y
số
các điểm
;
M x y
có tọa độ nguyên là: 7.3=21.
Theo giả thiết
,
x y
đều chia hết cho 2 nên ta có:
2;;0;; 2;; 4
0;;2
x
y
có 4.2=8 điểm.
Vậy xác suất cần tìm là
8
21
.
Câu 20. Tìm số các giá trị nguyên của hàm số
5 4cos 2 sin 2
y x x
.
A. 5. B. 6. C. 3. D. 4.
Lời giải
Chọn A
Ta có
5 4sin 2 cos 2 5 2sin 4
y x x x
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 103
Với
x
ta có:
1 sin 4 1 2 2sin 4 2 3 5 2sin 4 7
x x x
hay
3 7
y
mà
y
nên
3;4;5;6;7
y .
Vậy
y
có 5 giá trị nguyên.
Câu 21. Tìm số các số tự nhiên có 5 chữ số đôi một phân biệt, được lập từ các chữ số 1,2,3,4,5,6,
biết rằng trong các số đó phải có các chữ số 1 và 5.
A. 735. B. 1200. C. 600. D. 480.
Lời giải
Chọn D
Gọi số cần tìm là
n abcde
.
Xếp 2 chữ số 1 và 5 vào 2 vị trí trong 5 vị trí nên có
2
5
A
cách.
Chọn 3 chữ số khác nhau trong 4 chữ số
2;3;4;6
và xếp vào 3 vị trí còn lại nên có
3
4
A
cách.
Theo quy tắc nhân có:
2
5
A
.
3
4
A
=480 ( cách).
Câu 22. Một lô hàng gồm
30
sản phẩm tốt và
10
sản phẩm xấu. Lấy ngẫu nhiên
3
sản phẩm.
Tính xác suất để
3
sản phẩm lấy ra có ít nhất một sản phẩm tốt.
A.
244
.
247
B.
15
.
26
C.
135
.
988
D.
3
.
247
Lời giải
Chọn A
3
40
( ) .
n C
Gọi
:
A
“
3
sản phẩm lấy ra có ít nhất một sản phẩm tốt”.
:
A
“
3
sản phẩm lấy ra không có sản phẩm tốt”.
3
10
( ) .
n A C
3
10
3
40
244
( ) 1 ( ) 1 .
247
C
P A P A
C
Câu 23. Cho cấp số cộng
( )
n
u
có
4 14
12; 18.
u u
Tìm số hạng đầu tiên
1
u
và công sai
d
của
cấp số cộng.
A.
1
22; 3.
u d
B.
1
21; 3.
u d
C.
1
20; 3.
u d
D.
1
21; 3.
u d
Lời giải
Chọn D
Ta có
4 1
1
14 1
12 3 12
21
18 13 18
3
u u d
u
u u d
d
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 104 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 24. Trong mặt phẳng
,
Oxy
cho hai đường thẳng
,
a b
lần lượt có phương trình là
2 3 0
x y
và
2 5 0.
x y
Nếu có phép quay với góc quay
0
(0 180 )
biến
đường thẳng này thành đường thẳng kia thì số đo của
là:
A.
0
45 .
B.
0
90 .
C.
0
60 .
D.
0
120 .
Lời giải
Chọn B
Đường thẳng
a
có vecto pháp tuyến
(1; 2).
n
Đường thẳng
b
có vecto pháp tuyến
'(2; 1).
n
Vì
. ' 0
n n
nên
'
n n
hay
a b
Do vậy
0 0
90 180 , .
k k Z
Mặt khác
0
0 180
nên trong 4 đáp án chỉ có đáp án B thỏa mãn.
Câu 25. Tìm số hạng tổng quát
n
u
trong các trường hợp dưới đây để dãy số
n
u
giảm.
A.
1
.
2
n
n
u
B.
2
.
n
u n
C.
3 1
.
1
n
n
u
n
D.
2.
n
u n
Lời giải
Chọn A
Xét dãy số
1
2
n
n
u
ta có
1
1 1
1 1 1
0, *
2 2 2
n n
n n n
u u n
dãy số
n
u
giảm.
Đáp án A đúng.
II. PHẦN TỰ LUẬN
Câu 1. Cho hình chóp
.
S ABCD
, có đáy
ABCD
là hình thang với đáy lớn
AB
và đáy nhỏ
CD
.
Gọi
,
M N
lần lượt là trung điểm của
SA
và
SB
; gọi
E
là giao điểm của
AD
và
BC
.
a) Tìm giao tuyến của
SBC
và
ADM
. Xác đinh giao điểm
P
của đường thẳng
SC
và mặt phẳng
ADM
.
b) Gọi
I
là giao điểm của
DP
và
AM
. Chứng minh
SI
song song với
AB
.
c) Xác định thiết diện của hình chóp với mặt phẳng
α
biết
α
qua
MN
và song song
với
SC
.
Lời giải
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 105
a) * Tìm giao tuyến của
SBC
và
ADM
.
Ta có:
+
M SB SBC
M AM ABM
M
là điểm chung thứ nhất
+
E BC SBC
E AD ADM
E
là điểm chung thứ hai
SBC ADM ME
* Xác đinh giao điểm
P
của đường thẳng
SC
và mặt phẳng
ADM
.
Ta có:
SC SBC
SBC ADM ME
Gọi
P SC ME
P SC ADM
b) Ta có:
S SAB SDC
I AM SAB
I SAB SDC
I DP SDC
SAB SDC SI
Mà
/ /
AB SAB
CD SCD
AB CD
/ / / /
SI AB CD
c) Ta có:
α SAB MN
Trong mặt phẳng
SAB
dựng
/ /
MF SC
cắt
BC
tại
F
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 106 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
α SAB MF
Trong mặt phẳng
SAC
dựng
/ /
NG SC
cặt
AC
tại
G
Gọi
H GF AD
α ABCD FH
α SAD NH
Vậy thiết diện của hình chóp cắt bởi mặt phẳng
α
là tứ giác
MNHF
Câu 2. Trong mặt phẳng
,
Oxy
tìm phương trình đường thẳng
là ảnh của đường thẳng
: 2 1 0
x y
qua phép tịnh tiến theo vectơ
1; 1 .
v
Lời giải
Gọi
; .
M x y
v
T M M
. Tọa độ điểm
;
M x y
thỏa mãn
1 1
1 1
x x x x
y y y y
;M x y
nên:
1 2 1 1 0 2 0
x y x y
Vậy
: 2 0.
x y
Câu 3. Cho hàm số
4sin 3 cos
y x m x
với
m
là tham số thực. Tìm giá trị của tham số m để
giá trị lớn nhất của hàm số bằng
3 2
.
Lời giải
Điều kiện xác định:
0.
m
4 3
4sin 3 cos 16 9 sin cos
16 9 16 9
16 9 cos .sin sin .cos 16 9 .sin
m
y x m x m x x
m m
m x x m x
(với
3 4
sin ; cos
16 9 16 9
m
m m
)
Ta có:
1 sin 1 16 9 16 9
x m y m
Suy ra giá trị lớn nhất của hàm số là
16 9 .
m
Giá trị lớn nhất của hàm số bằng
3 2
khi và chỉ khi
2
16 9 3 2 16 9 18 .
9
m m m
Câu 4. Tìm hệ số chứa
30
x
trong khai triển nhị thức
15
3
2
2
x
x
với
0 .
x
Lời giải
Ta có số hạng tổng quát trong khai triển
15
3 15 30 5
1
2
2
. . .2 . 1 .
k
k
k
k k k k
k n n
T C x C x
x
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 107
Theo đề
30 5 30 12
k k
Hệ số chứa
30
x
trong khai triển nhị thức
15
3
2
2
x
x
là
12
12 3
15
.2 1 3640.
C
Câu 5. Cho dãy số
n
u
cho bởi
1
1
1
2
2
n n
u
u u
, tìm công thức số hạng tổng quát của dãy số đó.
Lời giải
Ta có
1 2 1 3 2 4 3
1 1 3 7 11
; 2 2 ; 2 ; 2 ;.....
2 2 2 2 2
u u u u u u u
Từ đó ta phân tích được:
1
2
3
4
1 5
2.1
2 2
3 5
2.2
2 2
7 5
2.3
2 2
11 5
2.4
2 2
.....
5
2.
2
n
u
u
u
u
u n
--- HẾT ---
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 108 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 7 – TRƯỜNG ĐẶNG TRẦN CÔN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
D D B B D A A A A B A D A D B
16
17
18
19
20
21
22
23
24
25
B C A A D A B A C C
Câu 1. Trên giá sách có
5
quyển sách toán khác nhau và
4
quyển sách tiếng Anh khác nhau.
Hỏi có tất cả mấy cách chọn một quyển sách?
A.
20.
B.
5.
C.
4.
D.
9.
Lời giải
Chọn D
Chọn sách Toán có
5
cách.
Chọn sách tiếng Anh có
4
cách.
Vậy có 9 cách chọn một quyển sách.
Câu 2. Mệnh đề nào sau đây sai?
A. Hai đường thẳng phân biệt có một điểm chung thì cắt nhau.
B. Hai đường thẳng không đồng phẳng thì chéo nhau.
C. Hai đường thẳng song song thì đồng phẳng.
D. Hai đường thẳng không có điểm chung thì song song.
Lời giải
Chọn D
Mệnh đề D sai vì hai đường thẳng không có điểm chung thì có thể song song hoặc
chéo nhau.
Câu 3. Tìm tất cả các giá trị của tham số
m
để hàm số
s
inx
y m
xác định trên đoạn
3
;
4 4
?
A.
2
2
m
.
B.
1
m
. C.
0
m
.
D.
2
.
2
m
Lời giải
Chọn B
Điều kiện:
3
inx; [ ; ]
s
4 4
m x
Đặt
3
inx; [) s
4
(
; ]
4
xf x
3
[ ; ]
4 4
max ( ) ( ) sin( ) 1
2 2
f x f
Vậy
1
m
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 109
Câu 4. Trong trường A, tỉ lệ học sinh giỏi môn Văn là 12%, học sinh giỏi Toán là 9% và học
sinh giỏi cả hai môn là 7%. Chọn ngẫu nhiên một học sinh của trường A. Tính xác
suất p để học sinh đó không học giỏi văn và không học giỏi Toán.
A.
0,72.
p
B.
0,86.
C.
0,79.
D.
0,93.
p
Lời giải
Chọn B
Gọi
1
B
là biến cố: “Học sinh được chọn giỏi Văn”.
2
B
là biến cố: “Học sinh được chọn giỏi Toán”.
Suy ra
1 2
B B B
là biến cố: “Học sinh được chọn giỏi Văn hoặc giỏi Toán”.
Ta có công thức:
1 2 1 2 1 2
( ) ( ) ( ) ( ) ( ) 0,12 0,9 0,7 0,14.
P B P B B P B P B P B B
Gọi
B
là biến cố: “Học sinh được chọn không học giỏi văn và không học giỏi Toán”.
Ta có:
( ) 1 ( ) 1 0,14 0,86.
P B P B
Câu 5. Cho cấp số cộng
n
u
có công sai
d
. Công thức nào sau đây đúng?
A.
1 1
1
n
u u n d
. B.
1 1
2
n
u u nd
.
C.
1 1
1
n
u u n d
. D.
1 1n
u u nd
.
Lời giải
Chọn D
Theo công thức số hạng tổng quát của cấp số cộng:
1
1
n
u u n d
suy ra
1 1
n
u u nd
.
Câu 6. Tất cả các nghiệm của phương trình
cot 3 0
x
là:
A. ,
6
x k k
. B. ,
6
x k k
.
C. ,
3
x k k
. D. ,
3
x k k
.
Lời giải
Chọn A
Ta có: cot 3 0 cot 3 ,
6
x x x x k k
.
Câu 7. Phương trình
2 2
2 1 cos 2sin cos 2 1 sin 0
x x x x
tương đương với phương
trình nào sau đây?
A.
cos 2 1.
4
x
B.
2
cos 2 .
4 2
x
C.
3
cos 2 .
4 2
x
D.
1
cos 2 .
4 2
x
Lời giải
Chọn A
Ta có:
2 2
( 2 1) cos 2sin cos ( 2 1)sin 0
x x x x
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 110 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
1 cos 2 1 cos 2
( 2 1) sin 2 ( 2 1) 0
2 2
( 2 1) 1 cos 2 2sin 2 ( 2 1) 1 cos 2 0
2 2 2cos 2 2sin 2 0
cos 2 sin 2 2
2 cos 2 2
4
cos 2 1.
4
x x
x
x x x
x x
x x
x
x
Câu 8. Cho hình chóp S.ABCD có đáy là hình thoi. Gọi O là giao điểm của AC và BD ; E và F
lần lượt là trung điểm của OA và OC ; điểm I thay đổi trên đoạn
;
AC I A I O
. Gọi
(P) là mặt phẳng qua I và song song với BD và SA. Biết (P) cắt S.ABCD theo thiết diện
là đa giác (H). Hãy xác định tất cả các vị trí của I để (H) có số cạnh nhiều nhất.
A. I thuộc đoạn
; .
OA I O I A
B. I thuộc đoạn
; .
EA I E I A
C. I thuộc đoạn
; .
FC I C I F
D. I thuộc đoạn
; .
OC I C I O
Lời giải
Chọn A
+ Mặt phẳng (P) qua I song song với BD cắt AD tại L, AB tại M, BC tại K.
+ Mặt phẳng (P) qua I song song với SA cắt SC tại N.
+ Mặt phẳng (P) qua L song song SA cắt SD tại P.
+ Gọi Q là giao điểm của SB và NK.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 111
Ta có:
P ABCD ML
P SAD LP
P SCD PN
P SBC NQ
P SAB QM
Vậy thiết diện cần tìm là ngũ giác MLPNQ (như hình vẽ).
Câu 9. Mệnh đề nào sau đây sai?
A.
2
cos cos
2
x k
x
x k
,k
. B.
2
sin sin
2
x k
x
x k
,k
.
C. tan tan ,x x k k
. D. cot cot ,x m x acr m k k
.
Lời giải
Chọn A
2
cos cos ,
2
x k
x k
x k
.
Câu 10. Cho dãy số
n
u
với
2
n
n
u n
. Số hạng thứ 6 của dãy bằng:
A. -58. B. 70. C. -27. D. 38.
Lời giải
Chọn B
6
6
2 6 70
u
.
Câu 11. Cho cấp số nhân
n
u
có công bội
1
q
. Tổng của n số hạng đầu tiên bằng.
A.
1
1
1
n
u q
q
. B.
1
1
n
u q
q
. C.
1
1
1
n
u q
q
. D.
1
1
n
u q
q
.
Lời giải
Chọn A
Câu 12. Có tất cả mấy cách xếp ba bạn nam và hai bạn nữ ngồi vào một bàn gồm năm chỗ?
A.
150.
B.
3125.
C.
25.
D.
120.
Lời giải
Chọn D
Số cách xếp ba bạn nam và hai bạn nữ ngồi vào một bàn gồm năm chỗ:
5! 120
.
Câu 13. Mệnh đề nào sau đây sai?
A.
s 0 2 , .
inx x k k
B.
3
s 1 2 , .
2
inx x k k
C.
s 1 2 , .
co x x k k
D.
s 1 2 , .
co x x k k
Lời giải
Chọn A
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 112 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Ta có
s 0 ,inx x k k
nên mệnh đề ở đáp án A sai.
Câu 14. Cho cấp số cộng
n
u
có công sai
3
d
và
1
1
.
2
u
Số hạng thứ chín của cấp số đã
cho bằng
A.
53
.
2
B.
41
.
2
C.
35
.
2
D.
47
.
2
Lời giải
Chọn D
Vì
n
u
là cấp số cộng có công sai
3
d
và
1
1
2
u
nên
9 1
1 47
8 8. 3 .
2 2
u u d
Vậy chọn đáp án D
Câu 15. Hệ số của số hạng chứa
5
x
trong khai triển và rút gọn của biểu thức
5 10
2
1 2 1 3
x x x x
bằng:
A. 61204. B. 3320. C. 61268. D. 3160.
Lời giải
Chọn B
+
5
1 2
x x
Số hạng tổng quát của
5
1 2
x
là:
5
5 5 5
1 2 2 2
k k k
k k k k k
C x C x C x
Số hạng chứa
5
x
trong khai triển
5
1 2
x x
là:
5
. 2
k
k k
x C x
Do đó: k = 4
Suy ra: hệ số của số hạng chứa
5
x
trong khai triển
5
1 2
x x
là:
4
4
5
2 80.
C
+
10
2
1 3
x x
Số hạng tổng quát của
10
1 3
x
là:
10
10 10 10
1 3 3 3
k k
k k k k k k
C x C x C x
Số hạng chứa
5
x
trong khai triển
10
2
1 3
x x
là:
10
3
k k
C
Do đó: k = 3
Suy ra: hệ số của số hạng chứa
5
x
trong khai triển
10
2
1 3
x x
là:
3 3
10
3 3240
C
.
Vậy: Hệ số của số hạng chứa
5
x
trong khai triển và rút gọn của biểu thức
5 10
2
1 2 1 3
x x x x
bằng:
80 + 3240 = 3320.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 113
Câu 16. Số cạnh của một hình tứ diện đều là:
A.
6
. B.
4
. C.
3
. D.
5
.
Lời giải
Chọn B
Câu 17. Gọi
n
là số tự nhiên thỏa mãn
0 1 2
4 1
n n n
C C C
. Hãy chọn mệnh đề đúng trong các
mệnh đề sau:
A.
15
n
. B.
5;8
n . C.
8;12
n . D.
12;15
n .
Lời giải
Chọn C
Điều kiện:
2,n n
.
Phương trình cho
1
1 4 1
2
n n
n
2
0
9 0
9
n L
n n
n
.
Câu 18. Cho tứ diện đều
ABCD
có các cạnh đều bằng
a
. Gọi
G
là trọng tâm tam giác
ABC
,
M
là trung điểm của cạnh
CD
. Diện tích thiết diện của tứ diện
ABCD
khi cắt bởi mặt
phẳng
AMG
(tính theo
a
) bằng:
A.
2
11
16
a
. B.
2
11
8
a
. C.
2
11
2
a
. D.
2
11
32
a
.
Lời giải
Chọn A
A
B
C
D
M
G
I
H
Gọi
I
là trung điểm của
BC
. Khi đó, thiết diện của
AMG
và tứ diện
ABCD
là tam
giác
AMI
.
Ta có:
3
;
2 2
a a
AM AI MI
AMI
cân tại
A
.
Gọi
H
là trung điểm của
MI
. Ta có:
2
2
2 2
3 11
4 4 4
a a a
AH AM MH
.
Vậy:
2
1 1 11 11
. . .
2 2 4 2 16
AMI
a a a
S AH MI
.
Câu 19. Cho tứ diện
ABCD
. Gọi
,
M N
và
P
lần lượt là trung điểm của các cạnh
,
AB BC
và
DA
Mệnh đề nào sau đây sai?
A.
DC MNP
. B.
MP BCD
. C.
MN ACD
. D.
BD MNP
Lời giải
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 114 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Chọn A
MP BD MP BCD
,
MN AC MN ACD
BD MP BD MNP
.
Câu 20. Biết đoạn
;
a b
là tập hợp tất cả các giá trị của tham số
m
để phương trình
sin 1 2
x m
có nghiệm. Gía trị của biểu thức
3
a b
bằng:
A. 2. B. 3. C. 4. D. 1
Lời giải
Chọn D
sin 1 2 sin 2 1
x m x m
phương trình có nghiệm khi và chỉ khi
1 2 1 1 0 1
m m
Suy ra
3 1
a b
Câu 21. Trong mặt phẳng tọa độ
Oxy
, cho vectơ
3;2
a
và đường tròn
C
có phương trình
2 2
1 3 4
x y
. Phép tịnh tiến
a
T
biến đường tròn
C
thành đường tròn có
phương trình:
A.
2 2
2 5 4.
x y
B.
2 2
1 3 4.
x y
C.
2 2
2 5 4.
x y
D.
2 2
4 1 4.
x y
Lời giải
Chọn A
C
có tâm là
1;3
I , bán kính
2
R
.
Gọi
;
I x y
, ta có
1; 3 3;2
1 3 2
3 2 5
a
T I I II a x y
x x
y y
Vậy
2;5
I
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 115
Phép tịnh tiến
a
T
biến đường tròn
C
thành đường tròn có tâm
2;5
I
, bán kính
2
R
nên có phương trình là:
2 2
2 5 4.
x y
Câu 22. Điều kiện xác định của hàm số
sin cos
sin cos
x x
y
x x
là:
A.
2 , .
4
x k k
B.
, .
4
x k k
C.
2 , .
4
x k k
D.
, .
4
x k k
Lời giải
Chọn B
Điều kiện
sin cos 0 sin cos tan 1 , .
4
x x x x x x k k
Câu 23. Cho cấp số cộng
n
u
có
1
3
u
và công sai
2.
d
Tổng
10
số hạng đầu của cấp số cộng
đã cho bằng
A.
105.
B.
115.
C.
130.
D.
120.
Lời giải
Chọn A
Áp dụng công thức tổng
n
số hạng đầu của cấp số cộng
1
1
2
n
n u n d
S
.
Ta có
10
10 3 9.2
105.
2
S
Câu 24. Tất cả các nghiệm của phương trình
2cos3 2 0
x
là
A.
2 ; .
4
x k k
B.
3 2
; .
4 3
x k k
C.
2
; .
4 3
x k k
D.
3
2 ; .
4
x k k
Lời giải
Chọn C
Ta có
2
3
3 2
2
4 3
4
2cos3 2 0 cos3 ; .
3 2
2
3 2
4 4 3
x k
x k
x x k
x k x k
Câu 25. Cho cấp số nhân
( )
n
u
biết
1 3
2; 486
u u
.Tổng của 8 số hạng đầu tiên bằng?
A.
5765
. B.
4376
. C.
6792
. D.
7210.
Lời giải
Chọn C
Ta có:
3 1
3 1 8 1
2 242 7 2 7.242 1696.
2
u u
u u d d u u d
1 8
8
( ).8
(2 1696).8
6792.
2 2
u u
S
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 116 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
B. TỰ LUẬN.
Câu 1. Giải phương trình:
3
sin3
2
x .
Lời giải:
Ta có:
2
3 2
3
3 9 3
sin 3 sin 3 sin
2 2 2
2 3
3 2
3 9 3
k
x k x
x x
k
x k x
.
Câu 2. Từ một bình chứa 7 quả cầu đỏ và 4 quả cầu xanh. Lấy ra ngẫu nhiên đồng thời 3 quả.
Tính xác suất để lấy được 3 quả cùng màu.
Lời giải:
Số cách lấy ra 3 quả từ bình là:
3
11
165
n C
Số cách lấy ra 3 quả cùng màu là:
3 3
7 4
39
C C
.
Suy ra xác suất lấy được 3 quả cùng màu là:
39 13
165 55
.
Câu 3. Cho cấp số nhân
n
u
có
1
1024
u
và công bội
1
2
q
. Tính
15
u
.
Lời giải:
Ta có:
14
14
15 1
1 1
. 1024. .
2 16
u u q
Câu 4. Cho cấp số cộng có số hạng thứ ba bằng
5
và công sai bằng
1
3
. Tính tổng
100
số hạng
đầu tiên của cấp số cộng đã cho.
Lời giải
Theo giả thiết;
3 1 1 1
2 13
5 2 .
3 3
u u d u u
Vậy
100 1 2 100 1
100 6250
... . 2 99 .
2 3
S u u u u d
Câu 5. Cho hình chóp .
S ABC
. Gọi
, ,
M N P
lần lượt là trọng tâm của các tam giác
,
SAB SAC
và
ABC
a) Chứng minh
.
MN SBC
b) Xác định giao điểm của đường thẳng
SP
và
.
AMN
Lời giải
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 117
a) Chứng minh
.
MN SBC
Gọi
, , , ,
I J K E F
lần lượt là trung điểm của
, , , ,
SA AB AC SB SC
.
Vì
2
3
SM SN
SJ SK
(Tính chất trọng tâm), nên
.
MN JK
,
MN ABC
MN ABC
MN JK JK ABC
(đpcm).
b) Xác định giao điểm của đường thẳng
SP
và
.
AMN
.
AMN AEF
;
.
Trong ;
SBK SP SBK AEF EN
SP AEF O
SBK EN SP O
Vậy
.
SP AMN O
--- HẾT ---
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 118 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 8 – TRƯỜNG GIA HỘI
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
A A B C D B B B B B D D A A C
16
17
18
19
20
21
22
23
24
25
C D D A A C D C D C
A. TRẮC NGHIỆM.
Câu 1. Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 1 2 9
C x y
. Tìm phương trình
đường tròn
C
là ảnh của
C
qua phép tịnh tiến theo vectơ
2;3
v
.
A.
2 2
: 1 1 9.
C x y
B.
2 2
: 3 5 9.
C x y
C.
2 2
: 3 5 9.
C x y
D.
2 2
: 1 1 9.
C x y
Lời giải
Chọn A
Đường tròn
C
có bán kính
3
R
và tâm
1; 2
I
.
Đường tròn
C
là ảnh của
C
qua phép tịnh tiến theo vectơ
2;3
v
nên đường
tròn
C
có bán kính
3
R
và tâm
;
I x y
.
Ta có:
1 2 1
1;1
2 3 1
x x
II v I
y y
.
Vậy phương trình đường tròn
C
là
2 2
: 1 1 9.
C x y
Câu 2. Tìm hệ số của số hạng chứa
5
x
trong khai triển
12
1 3
x
A.
192456.
B.
729.
C.
192456.
D.
729.
Lời giải
Chọn A
Ta có:
12 12
12
12 12
0 0
1 3 3 3 .
k k
k k k
k k
x C x C x
Số hạng chứa
5
x
trong khai triển
12
1 3
x
5
k
.
Vậy hệ số của số hạng chứa
5
x
trong khai triển
12
1 3
x
là
5
5
12
3 192456.
C
Câu 3. Tìm giá trị lớn nhất (
max
y
), giá trị nhỏ nhất (
min
y
) của hàm số
4 4
sin cos
y x x
.
A.
1
min
.
2
max 1
y
y
B.
1
min
.
2
max 1
y
y
C.
min 1
.
1
max
2
y
y
D.
min 1
.
1
max
2
y
y
Lời giải
Chọn B
Ta có:
4 4 2 2 2 2 2
1
sin cos sin cos 2sin cos 1 sin 2
2
y x x x x x x x
.
Ta có:
2 2 2
1 1 1 1
0 sin 2 1 sin 2 0 1 sin 2 1
2 2 2 2
x x x
hay
1
1
2
y
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 119
Vậy
max 1
y
và
1
min
2
y
.
Câu 4. Trong mặt phẳng
Oxy
, cho vectơ
3; 5
v
và điểm
1;1
M . Tìm tọa độ điểm
'
M
là
ảnh của điểm
M
qua phép tịnh tiến theo vectơ
v
.
A.
' 4; 6 .
M
B.
' 2; 4 .
M
C.
' 4; 4 .
M
D.
' 2; 6 .
M
Lời giải
Chọn C
Tọa độ điểm
'
M
là ảnh của điểm
M
qua phép tịnh tiến theo vectơ
v
là:
'
'
1 3 4
' 4; 4
1 5 4
M
M
x
M
y
.
Câu 5. Đẳng thức nào sau đây là sai?
A.
1 ! ! 2 . !
n n n n
. B.
2 . 1 ! 2 !
n n n
.
C.
0! 1! 2!
. D.
1 . ! 1 !
n n n
.
Lời giải
Chọn D
Câu 6.
20
đường thẳng phân biệt có tối đa bao nhiêu giao điểm?
A.
200
. B.
190
. C.
380
. D.
20
.
Lời giải
Chọn B
Hai đường thẳng phân biệt có tối đa một giao điểm nên
20
đường thẳng có tối đa
2
20
190
C
giao điểm.
Câu 7. Tìm tất cả các nghiệm của phương trình
4 4
cos sin 0.
x x
A.
, .
2
x k k Z
B.
, .
4 2
x k k Z
C.
2 , .
x k k Z
D.
, .
x k k Z
Lời giải
Chọn B
Ta có:
4 4
cos sin 0
x x
2 2 2 2
(cos sin ).(cos sin ) 0
cos 2 0
2 ,
2
, .
4 2
x x x x
x
x k k Z
x k k Z
Vậy tập nghiệm của phương trình là:
, .
4 2
x k k Z
Câu 8. Tìm tất cả các nghiệm của phương trình
1
sin .
2
x
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 120 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
A.
2
2 2 , .
3 3
x k x k k Z
B.
7
2 2 , .
6 6
x k x k k Z
C.
5
2 2 , .
6 6
x k x k k Z
D.
5
2 2 , .
6 6
x k x k k Z
Lời giải
Chọn B
Ta có:
1
sin
2
x
sin sin
6
2
6
( )
2
6
2
6
( ).
7
2
6
x
x k
k Z
x k
x k
k Z
x k
Vậy tập nghiệm của phương trình là:
7
2 2 , .
6 6
x k x k k Z
Câu 9. Tìm tập xác định
D
của hàm số
1
1 sin 2
y
x
.
A.
\ 2 ,
2
D k k
. B.
\ ,
4
D k k
.
C.
\ 2 ,
4
D k k
. D.
\ ,
4
D k k
.
Lời giải
Chọn B
Hàm số
1
1 sin 2
y
x
xác định khi
1 sin 2 0 2 2 , ,
2 4
x x k k x k k
Tập xác định
D
của hàm số là
\ ,
4
D k k
.
Câu 10. Các hàm số sau được xét trên tập xác định của chúng. Trong các mệnh đề sau, mệnh
đề nào sai?
A. Hàm số
cos
y x
là hàm số chẵn.
B. Hàm số
cos .sin
y x x
là hàm số không chẵn cũng không lẻ.
C. Hàm số
3 3
sin .cos
y x x
là hàm số lẻ.
D. Hàm số
sin , tan , cot
y x y x y x
đều là các hàm số lẻ.
Lời giải
Chọn B
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 121
+ Hàm số
cos
y x
có tập xác định
D
và
cos( ) cos
x x
nên hàm số
cos
y x
là
hàm số chẵn.
+ Hàm số
cos .sin
y x x
có tập xác định
D
và
cos .sin sin .cos
x x x x
nên
hàm số
cos .sin
y x x
là hàm số lẻ.
+ Hàm số
3 3
sin .cos
y x x
có tập xác định
D
và
3 3 3 3
cos .sin sin .cos
x x x x
nên hàm số
3 3
sin .cos
y x x
là hàm số lẻ.
+ Hàm số
sin
y x
có tập xác định
D
và
sin( ) sin
x x
nên hàm số
sin
y x
là
hàm số lẻ.
+ Hàm số
tan
y x
có tập xác định
\ ,
2
D k k
và
tan( ) tan
x x
nên hàm
số
tan
y x
là hàm số lẻ.
+ Hàm số
cot
y x
có tập xác định
\ ,D k k
và
cot( ) cot
x x
nên hàm số
cot
y x
là hàm số lẻ
Câu 11. Gieo đồng thời một con súc sắc và một đồng xu. Tính xác suất để xuất hiện đồng xu có
mặt ngửa và con súc sắc có số chấm không vượt quá 4.
A.
1
.
2
B.
1
.
6
C.
1
.
4
D.
1
.
3
Lời giải
Chọn D
* Không gian mẫu:
1; 2; 3; 4; 5; 6; 1; 2; 3; 4; 5; 6
N N N N N N S S S S S S
12
n
* Gọi A là biến cố: Đồng xu có mặt ngửa và con súc sắc có số chấm không vượt quá 4.
1; 2; 3; 4
A N N N N
4
n A
Vậy :
4 1
.
12 3
n A
P A
n
Câu 12. Tìm tập nghiệm của phương trình
2 cos sin 3 0.
x x
A.
.
B.
, .
2
k k
C.
, .
2
k k
D.
.
Lời giải
Chọn D
Ta có:
3
2 cos sin 3 0 2 2 cos 3 0 cos
4 4
2 2
x x x x
Vì
3 3
1
2 2 2 2
nên phương trình
2 cos sin 3 0
x x
vô nghiệm.
Vậy tập nghiệm của phương trình là:
.
S
Câu 13. Biết
4
126
n
C
. Tính
4
.
n
A
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 122 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
A.
3024.
B.
24.
C.
504.
D.
756.
Lời giải
Chọn A
Điều kiện:
4.
n
Ta có
4 4
! !
126 126 3024 3024.
4! 4 ! 4 !
n n
n n
C A
n n
Câu 14. Tìm điều kiện xác định của phương trình
tan 2 3.
3
x
A.
5
, .
12 2
x k k
B.
, .
2
x k k
C.
5
, .
12
x k k
D.
, .
6 2
x k k
Lời giải
Chọn A
Điều kiện
cos 2 0 2
3 3 2
x x k
5
, .
12 2
x k k
Câu 15. Tính số tập hợp con của tập hợp
; ; ; ; ; ; .
A a b c d e f g
A.
127.
B.
15.
C.
128.
D.
14.
Lời giải
Chọn C
Tập hợp
A
có
7
phần tử
số tập hợp con của
A
là
7
2 128.
Câu 16. Trong các mệnh đề sau, tìm mệnh đề đúng ?
A. Trên khoảng
0;
2
hàm số
sin
y x
và hàm số
cos
y x
cùng nghịch biến.
B. Trên khoảng
0;
2
hàm số
sin
y x
nghịch biến và hàm số
cos
y x
đồng biến.
C. Trên khoảng
0;
2
hàm số
sin
y x
đồng biến và hàm số
cos
y x
nghịch biến.
D. Trên khoảng
0;
2
hàm số
sin
y x
và hàm số
cos
y x
cùng đồng biến.
Lời giải
Chọn C
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 123
Vẽ đồ thị hàm
sin
y x
( đường nét đứt ) và đồ thị hàm
cos
y x
( đường nét liền ) trên
cùng một hệ trục tọa độ ta thấy : trên khoảng
0;
2
hàm số
sin
y x
đồng biến và
hàm số
cos
y x
nghịch biến.
Câu 17. Tìm tất cả các nghiệm của phương trình
cos 3 sin 0
x x
.
A. 2 ,
3
x k k
B. ,
2
x k k
C. ,
6
x k k
. D.
, .
6
x k k
Lời giải
Chọn D
Ta có: cos 3 sin 0 cos 3 sin cot 3
6
x x x x x x k
Câu 18. Trong mặt phẳng
Oxy
cho điểm
1;7
M và vectơ
2; 5
v
. Tìm
M
là ảnh của
M
qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ
v
và phép vị tự tâm
O
tỉ số
2
k
.
A.
1
;6
2
M
. B.
3
;1
2
M
. C.
2;24
M
. D.
6;4 .
M
Lời giải
Chọn D
Gọi
1
M
là ảnh của
M
qua
v
T
khi đó:
1
1
1
2 3
3;2
5 2
M M
M M
x x
M
y y
.
Vì
1
M
là ảnh của
M
qua
;2
O
V nên:
1
6
2
4
M
M
x
OM OM
y
.
Vậy
6;4
M
Câu 19. Tìm số nghiệm của phương trình
cos3 sin 2 0
x x
trên đoạn
0; .
A.
3
. B.
4
. C.
2
. D.
1
Lời giải
Chọn A
Xét phương trình
2
10 5
cos3 sin 2 sin 3 sin 2
2
2
2
k
x
x x x x
x k
Với
2
10 5
k
x
, do
2
0; 0 0.25 2,25
10 5
k
x k
Mà
0; 1; 2
k Z k k k
Với
2
2
x k
, do
0; 0 2 0.75 0.25
2
x k k
Mà
k Z k
.Ứng với mỗi giá trị của
k
tương ứng với một nghiệm của phương
trình
cos3 sin 2 0
x x
trên đoạn
0; .
Vậy có phương trình có 3 nghiệm.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 124 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 20. Tính tổng
0 1 2
3 9 ... 3 .
n n
n n n n
S C C C C
A.
4
n
. B.
3
n
. C.
2
n
. D.
1
3
n
Lời giải
Chọn A
Xét
0 1 2 2
1 ... .
n
n n
n n n n
x S C C x C x C x
3
x
ta có
0 1 2
4 3 9 ... 3 .
n n n
n n n n
C C C C
Câu 21. ThaPhương trình
2
sin 1
x
tương đương với phương trình sau đây?
A.
sin 0
x
. B.
sin 1
x
. C.
sin 1
x
. D.
sin 1
x
.
Lời giải
Chọn C
Ta có
2
2 2
sin 1 sin 1 sin 1
x x x
.
Câu 22. Cho E là tập hợp các số tự nhiên gồm 2 chữ số khác nhau được lập từ các chữ số 1, 2, 3,
4, 5, 6. Lấy ngẫu nhiên một phần tử của E, tính xác suất để được một số chia hết cho 4
hoặc chia hết cho 7?
A.
7
10
. B.
11
30
. C.
4
5
. D.
13
30
.
Lời giải
Chọn D
Không gian mẫu
5 6 30
n
.
Các số chia hết cho 4: 12, 16, 24, 32, 36, 52, 56, 64.
Các số chia hết cho 7: 14, 21, 35, 42, 56, 63.
Xác suất để được một số chia hết cho 4 hoặc chia hết cho 7 là
13
30
.
Câu 23. Tìm tập nghiệm của phương trình
cos 2 1
4
x
.
A.
,
8
k k
. B.
1
2 ,
2 8
k k
.
C.
,
8
k k
. D.
2 ,
4
k k
.
Lời giải
Chọn C
Ta có:
cos 2 1 2 2
4 4 8
x x k k x k k
Câu 24. Tìm tập xác định
D
của hàm số
1
2 sin 7 2017
y
x
.
A.
\ ,
2
D k k
. B.
2019
\
7
D
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 125
C.
2019
\ 2 ,
7
D k k
. D.
D
.
Lời giải
Chọn D
Hàm số
1
2 sin 7 2017
y
x
xác định
2 sin 7 2017 0
x
sin 7 2017 2
x
(luôn đúng x
).
Vậy
D
.
Câu 25. Cho hàm số
sin cos ,
y x x
tìm khẳng định đúng?
A.
y 2 y 2.
B.
0 y 2.
C.
2 y 2.
D.
2 y 0.
Lời giải
Chọn C
Ta có
sin cos 2 sin 2 2
4
y x x x y
.
B. TỰ LUẬN.
Câu 1. Tìm tập nghiệm của phương trình
2cos 3 0.
2
x
Lời giải
Ta có
3 5 5
2cos 3 0 cos 2 , 4 ,
2 2 2 2 6 3
x x x
k k x k k
Câu 2. Trong mặt phẳng
O
xy
, cho đường thẳng
: 3 4 12 0.
d x y
Tìm phương trình đường
thẳng
d
là ảnh của
d
qua phép tịnh tiến vectơ
2;1 .
v
Lời giải
Gọi
; , ;
M x y d M x y d
Ta có
2 2
1 1
v v
x x x x
T d d T M M
y y y y
Thay
;
M x y
vào
:3 4 12 0
d x y
ta được
3 2 4 1 12 0 3 4 14 0
x y x y
Vậy
:3 4 14 0.
d x y
Câu 3. Đội văn nghệ của lớp có 5 bạn nam và 7 bạn nữ. Chọn ngẫu nhiên 5 bạn tham gia biểu
diễn. Tính xác suất để trong 5 bạn được chọn có cả nam và nữ, đồng thời số bạn nữ
nhiều hơn số bạn nam.
Lời giải
TH 1: Có 3 nữ, 2 nam:
3 2
7 5
350
C C
cách.
TH 2: Có 4 nữ, 1 nam:
4 1
7 5
175
C C
cách.
Suy ra xác suất cần tính bằng:
5
12
350 175 175
264
C
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 126 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 4. Tìm tất cả các giá trị của tham số
m
để phương trình
2 2
3
cos x m
có nghiệm?
Lời giải
Phương trình
2 2
3
cos x m
có nghiệm
1 2 1 2 1 0 2 1
m m m
2 3.
m
Câu 5. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
a
. Hai mặt bên
SAB
và
SCD
là các tam giác đều. Gọi
G
là trọng tâm tam giác
SAB
,
E
là điểm di động trên đoạn
thẳng
BG
(
E
khác
B
). Cho mặt phẳng
qua
E
, song song với
SA
và
BC
.
a) Chứng minh đường thẳng
AD
song song với mặt phẳng
. Tìm giao điểm
, , ,
M N P Q
của mặt phẳng
với các cạnh
, , ,
SB SD DC BA
.
b) Gọi
I
là giao điểm của
QM
và
PN
. Chứng minh
I
nằm trên một đường thẳng cố
định khi điểm
E
di động trên đoạn
BG
.
c) Chứng minh tam giác
IPQ
là tam giác đều. Tính diện tích tam giác
IPQ
theo
a
.
Lời giải
a)Ta có:
//
// //
AD BC
BC AD
AD
.
Trong mặt phẳng
SAB
, kẻ đường thẳng qua
E
và song song với
SA
, cắt
SB
tại
M
,
cắt
AB
tại
Q
.
Trong
ABCD
, kẻ đường thẳng qua
Q
và song song với
BC
, cắt
CD
tại
P
.
Trong
SBC
, kẻ đường thẳng qua
M
và song song với
BC
, cắt
SC
tại
N
.
Vậy
, , ,
M N P Q
là giao điểm của mặt phẳng
với các cạnh
, , ,
SB SD DC BA
.
I
Q
P
N
M
E
G
D
C
B
A
S
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 127
b) Ta có:
I QM PN
I QM SAB
I PN SCD
.
Xét hai mặt phẳng
SAB
và
SCD
có
//
,
S SAB SCD
AB CD
AB SAB CD SCD
SAB SCD d
,
d
qua
S
và
// , //
d AB d CD
d
cố định.
Do đó
I d
.
c)Do các tứ giác
ISAQ
và
ISDP
là các hính bình hành nên
IQ SA
IP SD
.
Mà
SA AB AD SD a
nên
IPQ
là tam giác đều cạnh
a
.
Vậy diện tích tam giác
IPQ
là
2
3
4
a
S
.
--- HẾT---
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 128 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 9 – TRƯỜNG CHI LĂNG
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
D B A B C A B D B B A D A D C
16
17
18
19
20
21
22
23
24
25
C D B C C A B D D D
Câu 1. Trong mặt phẳng
Oxy
cho
3;6
B và
5; 4 .
v
Tìm tọa độ điểm
C
sao cho
v
T C B
A.
8; 10 .
C B.
2; 2 .
C
C.
2;2 .
C D.
8;10 .
C
Lời giải
Chọn D
Gọi tọa độ
;
C a b
Do
v
T C B
nên
8
8;10
10
v b
v b
x a x
a
C
y b y b
Câu 2. Tìm tập xác định của hàm số
sin 1
sin
x
y
x
A.
\ 2 ; .
2
D k k
B.
\ ; .
D k k
C.
\ ; .
2
D k k
D.
\ 2 ; .
D k k
Lời giải
Chọn B
ĐKXĐ sin 0 ;x x k k
Vậy TXĐ của hàm số là
\ ; .
D k k
Câu 3. Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình vẽ. Hỏi có
bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần ?
A.
24.
B.
18.
C.
10.
D.
9.
Lời giải
Chọn A
Từ A đến B có
4
cách.
Từ B đến C có
2
cách.
Từ C đến D
3
cách.
Do đó, từ A đến D có
4.2.3 24
cách mà qua B và C chỉ một lần.
Câu 4. Tìm tất cả cá nghiệm của phương trình
2cos 2 0.
x
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 129
A.
3
2
4
.
2
4
x k
x k
B.
5
2
4
.
5
2
4
x k
x k
C.
2
4
.
3
2
4
x k
x k
D.
2
4
.
2
4
x k
x k
Lời giải
Chọn B
Ta có:
3 5
2 2
2
4 4
2cos 2 0 cos ; .
3 5
2
2 2
4 4
x k x k
x x k
x k x k
Câu 5. Trong mặt phẳng tọa độ
Oxy
cho đường tròn
C
có phương trình
2 2
2 2 4.
x y
Phép đồng dạng có được bằng việc thực hiện liên tiếp các phép vị
tự tâm
O
tỉ số
1
2
k
và phép quay tâm
O
góc quay
0
90
sẽ biến đường tròn
C
thành
đường tròn nào trong các đường tròn sau đây?
A.
2 2
2 2 1.
x y
B.
2 2
1 1 1.
x y
C.
2 2
1 1 1.
x y
D.
2 2
2 1 1.
x y
Lời giải
Chọn A
Đường tròn
C
có tâm
2;2 ; 2
I R
Gọi đường tròn
C
có tâm
I
bán kính
R
là ảnh của đường tròn
C
có tâm
2;2 ; 2
I R
qua phép vị tự tâm
O
tỉ số
1
2
k
suy ra
1
,
2
1;1
1
1
.
2
O
I V I
I
R
R R
Gọi đường tròn
C
có tâm
I
bán kính
R
là ảnh của đường tròn
C
có tâm
1;1 ; 1
I R
phép quay tâm
O
góc quay
0
90
suy ra
0
,90
1;1
1
O
I Q I
I
R
R R
Vậy ảnh của đường tròn
C
qua phép đồng dạng có được bằng việc thực hiện liên
tiếp các phép vị tự tâm
O
tỉ số
1
2
k
và phép quay tâm
O
góc quay
0
90
là đường tròn
2 2
: 1 1 1.
C x y

Câu 6. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng không có điểm chung thì chéo nhau.
B. Hai đường thẳng chéo nhau thì không có điểm chung.
C. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
D. Hai đường thẳng phân biệt không chéo nhau thì hoặc song song hoặc cắt nhau.
Lời giải
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 130 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Chọn A
Hai đường thẳng không có điểm chung thì có thể song song với nhau
Câu 7. Cho hình chóp
.S ABCD
có đáy là hình thang cân đáy lớn
AD
,
,M N
lần lượt là là
trung điểm của
AB
và
CD
,
P
là mặt phẳng qua
MN
và cắt mặt bên
SBC
theo một
giao tuyến. Thiết diện của
P
và hình chóp là hình gì?
A. Hình bình hành. B. Hình thang. C. Hình chữ nhật. D. Hình vuông.
Lời giải
Chọn B
Gọi
P SBC PQ
với
, P SB Q SC
.
Ta thấy
P
chứa
MN
,
SBC
chứa
BC
và
BC MN
. Suy ra
.PQ MN
Vậy thiết diện là hình thang
MNQP
.
Câu 8. Một đề thi có 20 câu hỏi trắc nghiệm khách quan, mỗi câu có 4 phương án lựa chọn,
trong đó chỉ có một phương án trả lời đúng. Khi thi, một học sinh đã chọn ngẫu nhiên
một phương án trả lời với mỗi câu của đề thi đó. Trong trường hợp đó xác suất để học
sinh đó trả lời không đúng cả 20 câu là bao nhiêu?
A.
1
4
. B.
3
4
. C.
1
20
. D.
20
3
4
.
Lời giải
Chọn D
Một câu sai có xác suất là
3
4
.
Xác suất để học sinh đó trả lời không đúng cả 20 câu là
20
3
4
.
Câu 9. Hiếu có 8 người bạn. Hiếu muốn mời 4 trong 8 người bạn đó về quê chơi vào cuối
tuần. Nhưng trong 8 người bạn đó có 2 bạn là Khoa và Tuấn không thích đi chơi với
nhau. Như vậy số cách chọn nhóm 4 người để về quê của Hiếu là bao nhiêu?
A.
4
8
C
. B.
4 3
6 6
2C C
. C.
4 3
6 6
C C
. D.
4 3
6 7
C C
.
Lời giải
Chọn B
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 131
+ TH1: Chọn 4 bạn nhưng không có 2 bạn Khoa và Tuấn có:
4
6
C
(cách).
+ TH2: Chọn 4 bạn trong đó có Khoa hoặc Tuấn có:
3
6
2.
C
(cách).
Vậy theo quy tắt cộng có tất cả:
4 3
6 6
2
C C
(cách).
Câu 10. Một họp có 10 viên bi màu trắng, 20 viên bi màu xanh, 30 viên bi màu đỏ, mỗi viên bi
chỉ có một màu. Có bao nhiêu cách để chọn ngẫu nhiên 8 trong số các viên bi thuộc
hộp đó để được 8 viên bi cùng màu trắng?
A.
4
20
C
. B.
8
10
C
. C.
8
60
C
. D.
4
30
C
.
Lời giải
Chọn B
Chọn 8 viên bi màu trắng từ 10 viên bi màu trắng có:
8
10
C
(cách)
Câu 11. Cho tập hợp
2;3;4;5;6;7
A . Có thể lập được tất cả bao nhiêu số tự nhiên gồm 3 chữ
số khác nhau được thành lập từ các chữ số thuộc
A
?
A.
120.
B.
216.
C.
256.
D.
180.
Lời giải
Chọn A
Gọi
abc
là số cần tìm, trong đó
0
a
,
a b c
và
, ,
a b c A
.
Số cách chọn ra
3
số trong
6
số của tập
A
để xếp vào
3
vị trí
abc
là
3
6
120
A
(số).
Câu 12. Trong khai triển
10
2 1
x
. Tìm hệ số của số hạng chứa
8
x
.
A.
256.
B.
45.
C.
11520.
D.
11520.
Lời giải
Chọn D
Xét khai triển:
10
10
2 1 2 1x x
Số hạng tổng quát thứ
1
k
trong khai triển trên là:
10
1 10
2 1
k k
k
k
T C x
10 10
10
1 2
k
k k k
C x
Số hạng chứa
8
x
tương ứng với
10 8
k
2
k
.
Vậy hệ số của số hạng chứa
8
x
trong khai triển trên là
2
2 10 2
10
1 2 11520
C
.
Câu 13. Hãy viết ba số hạng tiếp theo hai số hạng đầu của dãy số
n
u
có
1 2 2 1
1, 1,
n n n
u u u u u
.
A.
2;3;5.
B.
3;4;7.
C.
2;5;7.
D.
3;5;8.
Lời giải
Chọn A
Ta có
3 2 1
2
u u u
,
4 3 2
2 1 3
u u u
,
5 4 3
3 2 5.
u u u
Câu 14. Xét phép thử là gieo một con xúc xắc hai lần. Gọi
N
là biến cố” lần đầu xuất hiện mặt
5
chấm”, gọi
M
là biến cố” lần hai xuất hiện mặt
5
chấm” thì
A.
5;1 , 5;2 , 5;3 , 5;4 , 5;5 , 5;6 , 1;5 , 2;5 , 3;5 , 4;5 ,
5;5 , 6;5 .
M N
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 132 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
B.
1;5 , 2;5 , 3;5 , 4;5 , 5;5 , 6;5 .
M N
C.
5;1 , 5;2 , 5;3 , 5;4 , 5;5 , 5;6 .
M N
D.
5;5 .
M N
Lời giải
Chọn D
Ta có
5;1 , 5;2 , 5;3 , 5;4 , 5;5 , 5;6 .
N
1;5 , 2;5 , 3;5 , 4;5 , 5;5 , 6;5 .
M
Khi đó
5;5 .
M N
Câu 15. Tìm giá trị lớn nhất và giá trị bé nhất của hàm số
1 3sin 2
4
y x
A.
max 3 ; min 2
y y
. B.
max 2 ; min 3
y y
.
C.
max 4 ; min 2
y y
. D.
max 4 ; min 2
y y
.
Lời giải
Chọn C
Ta có:
1 sin 2 1 3 3sin 2 3
4 4
x x
.
2 1 3sin 2 4
4
x
hay
2 4
y
.
2 sin 2 1 ; .
4 8
3
4 sin 2 1 ; .
4 8
y x x k k
y x x k k
Vậy
max 4 ; min 2
y y
.
Câu 16. Tìm tất cả các nghiệm
0 ;
2
x
của phương trình
2
2sin 3sin 1 0
x x
A.
12
x
. B.
5
6
x
. C.
6
x
. D.
2
x
.
Lời giải
Chọn C
2
2
2
sinx 1
2sin 3sin 1 0 2 .
1
6
sinx
2
5
2
6
x k
x x x k
x k
0 ; .
2 6
x x
Câu 17. Có bao nhiêu cách sắp xếp bốn bạn Văn, Bình, Nhi, Thi ngồi vào một bàn dài gồm 4
chỗ ?
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 133
A.
1.
B.
8.
C.
4.
D.
24.
Lời giải
Chọn D
Xếp
4
bạn vào một bàn dài gồm
4
chỗ có
4! 24
cách.
Câu 18. Trong không gian , cho
4
điểm không đồng phẳng. Có bao nhiêu tam giác từ
4
điểm
đã cho ?
A.
6.
B.
4.
C.
3.
D.
2.
Lời giải
Chọn B
Một bộ
3
điểm bất kỳ từ
4
điểm ta xác định được
1
tam giác. Vậy có
3
4
4
C
tam giác.
Câu 19.
Trong mặt
Oxy
cho điểm
3;6
B . Tìm tọa độ điểm
E
sao cho
B
là ảnh của
E
qua
phép quay tâm
O
, góc quay
90
.
A.
6;3
E . B.
3;6
E . C.
6; 3
E
. D.
3; 6
E
.
Lời giải
Chọn C
Vì
B
là ảnh của
E
qua phép quay tâm
O
, góc quay
90
nên ( ;90 ) :
Q O B E
Suy ra
6; 3
E
.
Câu 20. Tìm số tự nhiên
n
, biết hệ số của số hạng thứ 3 theo số mũ giảm dần của
x
trong khai
triển
1
3
n
x
bằng
4
.
A.
8
. B.
4
. C.
9
. D.
17
.
Lời giải
Chọn C
Ta có
2 3
0 1 1 2 2 3 3
1 1 1 1 1
...
3 3 3 3 3
n n
n n n n n
n n n n n
x C x C x C x C x C
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 134 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Suy ra hệ số của số hạng thứ 3 theo số mũ giảm dần của
x
trong khai triển đã cho là
2
2
1
3
n
C
Do đó
2
2
1 ! 1
4 4
3 2!( 2)! 9
n
n
C
n
2
9
( 1) 72 72 0
8
n
n n n n
n
Vì
n
là số tự nhiên và
2
n
nên
9
n
.
Câu 21. Phép vị tự
;
I k
V
biến điểm
M
thành điểm
'
M
là phép đồng nhất khi nào?
A.
1.
k
B.
0.
k
C.
1.
k
D.
1.
k
Lời giải
Chọn A
Câu 22. Cho hình tứ diện
ABCD
có
,
M N
lần lượt là trung điểm của
, .
AB BD
Các điểm
,
G H
lần lượt trên cạnh
,
AC CD
sao cho
NH
cắt
MG
tại
.
I
Khẳng định nào sau đây là
khẳng định đúng?
A.
, ,
B G H
thẳng hàng. B.
, ,
B C I
thẳng hàng.
C.
, ,
N G H
thẳng hàng. D.
, ,
A C I
thẳng hàng.
Lời giải
Chọn B
Ta có:
ABC DBC BC
Mà
I MG ABC I ABC
và
I NH DBC I DBC
Do đó,
.
I ABC DBC
Suy ra
.
I BC
Vậy
, ,
B C I
thẳng hàng.
Câu 23. Cho cấp số cộng có các số hạng lần lượt là
5;9;13;17;...
Khi đó
n
u
có thể được tính theo
biểu thức nào dưới đây.
A.
5 1.
n
u n
B.
4 1.
n
u n
C.
5 1.
n
u n
D.
4 1.
n
u n
Lời giải
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 135
Chọn D
Gọi cấp số cộng cần tìm là
1
1
n
u u d n
với
d
là công sai; n
.
Ta có
9 5 4
d
1 1
4 1 4 4
n
u u n n u
loại A, C.
+ Thử đáp án B:
3
4 1 5
2
n n
(loại).
+ Thử đáp án D:
4 1 5 1
n n
(thỏa).
Câu 24. Trong mặt phẳng
Oxy
, cho điểm
2; 1
A
. Tìm ảnh của
A
qua phép dời hình có được
bằng cách thực hiện liên tiếp phép tịnh tiến theo
3;1
u
và phép quay tâm
O
góc
quay
90 .
A.
5;0 .
B.
0;5 .
C.
5;0 .
D.
0; 5 .
Lời giải
Chọn D
Gọi
B
là ảnh của
A
qua phép tịnh tiến theo
3;1 .
u
Khi đó:
5
.
0
B u A
B
B u A B
x x x
x
y y y y
Phép quay tâm
O
góc quay
90
biến điểm
5;0
B thành điểm
;
C C
C x y
.
Khi đó
0
.
5
C B
C B
x y
y x
Vậy ảnh của điểm
A
là
0; 5 .
C
Câu 25. Gía trị của biểu thức
1 2 2 3 3 2020 2020
2020 2020 2020 2020
1 2 2 2 ... 2P C C C C là:
A.
2020
3
P
. B.
1
P
. C.
2020
3
P
. D.
1
P
.
Lời giải
Chọn D
Dễ thấy
2020
1 2 2 3 3 2020 2020 2020
2020 2020 2020 2020
1 2 2 2 ... 2 1 2 1 1
P C C C C
B. TỰ LUẬN.
Câu 1. Giải phương trình:
a.
3tan 2 3
x
b.
2
2sin cos 2 0
x x
Lời giải
a) Ta có:
3
3tan 2 3 tan 2 tan 2 tan
3 6
x x x
2
6 12 2
k
x k x k
♥ Vậy phương trình (1) có họ nghiệm là
12 2
k
x k
.
b) Ta có:
2
1 cos 2 1
2sin cos 2 0 2. cos2 0 cos 2
2 2
x
x x x x
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 136 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
cos2 cos 2 2
3 3 6
x x k x k
♥ Vậy phương trình (1) có các họ nghiệm là
6
x k k
Câu 2. Ngân hàng đề thi gồm
100
câu hỏi, mỗi đề thi có
5
câu. Một học sinh học thuộc
80
câu. Tính xác suất để học sinh đó rút ngẫu nhiên được một đề thi có
4
câu học thuộc.
Lời giải
♥ Số phần tử của không gian mẫu là:
5
100
C
♥ Gọi A là biến cố: “học sinh rút ngẫu nhiên được một đề thi có
4
câu học thuộc”
Số kết quả thuận lợi cho biến cố A là:
4 1
A 80 20
.
C C
♥ Vậy xác suất cần tính là
4 1
A
80 20
5
100
.
5135
A .
12222
C C
P
C
Câu 3. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành tâm
,
O
gọi
,
M N
lần lượt là
trung điểm của
, .
SA SD
a) Tìm giao tuyến của hai mặt phẳng
SAC
và
.
SBD
b) Tìm thiết diện của hình chóp
.
S ABCD
cắt bởi mặt phẳng
.
OMN
Thiết diện đó là
hình gì?
Lời giải
a) Tìm giao tuyến của hai mặt phẳng
SAC
và
.
SBD
♥ Ta có:
S SAC SBD
(1)
♥ Do
O SAC
O AC
AC BD O O SAC SBD
O BD
O SBD
(2)
♥ Từ (1) và (2) suy ra
.
SAC SBD SO
b) Tìm thiết diện của hình chóp
.
S ABCD
cắt bởi mặt phẳng
.
OMN
Thiết diện đó là
hình gì?
♥ Do
,
M N
lần lượt là trung điểm của
, / /
SA SD MN AD
P
Q
N
M
O
D
A
B
C
S
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 137
♥ Mặt phẳng
OMN
và mặt phẳng
ABCD
có điểm chung
O
và lần lượt chứa hai
đường thẳng
MN
và
AD
song song với nhau nên chúng cắt nhau theo giao tuyến
PQ
thỏa
/ / / /
O PQ
PQ MN AD
với
, .
P CD Q AB
♥ Suy ra tứ giác
MNPQ
là thiết diện của hình chóp .
S ABCD
cắt bởi mặt phẳng
.
OMN
♥ Do
/ /
MN PQ
nên tứ giác
MNPQ
là hình thang với hai đáy là
, .
MN PQ
Câu 4. Hệ số của
5
x
trong khai triển
7
2
2 4 3
x x
là
Lời giải
Số hạng tổng quát của
7
2
2 4 3
x x
là
2 7 7 2
1 7 7
2 4 3 2 4 . 3
k k
k k k k k
k
T x C x C x
5
x
ứng với
2
k
x
hay
2 5 3
k k
.
Hệ số của
5
x
là
3
3 4
7
2 4 . 3 483840
C
.
Câu 5. Tổng các nghiệm của phương trình
sin 3 cos 2
x x
trện đoạn
0;4
là:
Lời giải
Ta có
1 3
sin 3 cos 2 sin cos 1 sin 1
2 2 3
x x x x x
2 2
3 2 6
x k x k
.
Do
0;4
x
nên
6
x
và
13
6
x
, do đó tổng các nghiệm trên đoạn
0;4
của
phương trình là
7
3
.
--- HẾT ---
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 138 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 10 – TRƯỜNG CHUYÊN NGUYỄN DU
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
A C D C A C A C C D C B C A A
16
17
18
19
20
21
22
23
24
25
A C C D C A D A D C
Câu 1. Trong các phương trình sau phương trình nào có nghiệm:
A.
2
cot cot 3 0
x x
. B.
3 sin 2
x
.
C.
1 1
cos 4
4 2
x
. D.
2sin 3cos 4
x x
.
Lời giải
Chọn A
Xét phương trình:
2
cot cot 3 0
x x
1
.
Đặt
cot
t x
phương trình
1
trở thành:
2
3 0
t t
2
. Dễ thấy phương trình
2
luôn có hai nghiệm phân biệt nên phương trình
1
luôn có nghiệm. Do đó đáp án A là
đáp án đúng.
Câu 2. Tập xác định của hàm số
cos 1
y x
là:
A.
2
2
k k
. B.
. C.
2k k
. D.
k k
.
Lời giải
Chọn C
Điều kiện
cos 1 0 cos 1 1
x x
.
Vì cos 1,x x
nên
1 cos 1
x
2 ,x k k
. Do đó tập xác định của hàm số
đã cho là
2k
.
Câu 3. Trong các hàm số sau, hàm số nào là hàm số chẵn:
A.
2019cos 2020sin
y x x
. B.
tan 2019 cot 2020
y x x
.
C.
cot 2019 2020sin
y x x
. D.
sin 2019 cos 2020
y x x
.
Lời giải
Chọn D
Dễ thấy các hàm số
sin , tan 2019
y x y x
,
cot 2020 , cot 2019
y x y x
là các hàm số lẻ
và các hàm số
cos , cos2020 ,
y x y x
sin 2019
y x
là các hàm số chẵn. Do đó ta dự
đoán các hàm số trong 4 đáp án
, ,
A B
,
C D
có hàm số ở đáp án
D
là hàm số chẵn.
Thật vậy, hàm số
sin 2019 cos 2020
y x x
có tập xác định là
.
+)
.
x x
+)
x
:
sin 2019 cos 2020
y x x x
sin 2019 cos 2020
x x y x
.
Suy ra
sin 2019 cos 2020
y x x
là hàm số chẵn. Vậy D là đáp án đúng.
Câu 4. Gieo hai con súc sắc. Xác suất để số chấm xuất hiện trên hai con súc sắc như nhau là
A.
1
3
. B.
1
12
. C.
1
6
. D.
1
36
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 139
Lời giải
Chọn C
+) Số phần tử của không gian mẫu là:
6.6 36
n
.
+) Gọi
A
là biến cố “ số chấm xuất hiện trên hai con súc sắc giống nhau”.
Khi đó,
1;1 , 2;2 , 3;3 , 4;4 , 5;5 , 6;6
A
6
n A
.
Xác suất của biến cố
A
là:
6 1
36 6
n A
P A
n
.
Câu 5. Gọi
G
là trọng tâm tứ diện
ABCD
. Gọi
A
là trọng tâm tam giác
BCD
. Tỉ số
GA
GA
bằng
A.
3
. B.
3
4
. C.
2
. D.
1
3
.
Lời giải
Chọn A
Vì
G
là trọng tâm tứ diện
ABCD
nên:
0
GA GB GC GD
0
A A A G A B A G A C A G A D A G
   
4 0
A A A G A B A C A D
 
4
A A A G
3
AG GA

.
Vậy
3
GA
GA
.
Câu 6. Phép quay
;
O
Q
biến điểm
M
thành điểm
M
. Khi đó
A.
OM OM

và
MOM
. B.
OM OM

và
,OM OM
.
C.
OM OM
và
,OM OM
. D.
OM OM
và
MOM
.
Lời giải
Chọn C
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 140 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 7. Cho tứ diện
ABCD
. Gọi
, , , , ,
M N P Q R S
lần lượt là trung điểm các cạnh
, , , , ,
AC BD AB CD AD BC
. Bốn điểm nào sau đây không đồng phẳng?
A.
, , ,
M P S N
. B.
, , ,
M N R S
. C.
, , ,
P Q R S
. D.
, , ,
M N P Q
.
Lời giải
Chọn A
+)
//
MR NS
(vì cùng song song với
CD
) nên 4 điểm
, , ,
M N R S
đồng phẳng. Đáp án B
sai.
+)
//
PR SQ
(vì cùng song song với
BD
) nên 4 điểm
, , ,
P Q R S
đồng phẳng. Đáp án C sai.
+)
//
MP NQ
(vì cùng song song với
BC
) nên 4 điểm
, , ,
M N P Q
đồng phẳng. Đáp án D
sai.
Câu 8. Trong các mệnh đề sau đây mệnh đề nào sai?
A. Phép dời hình là phép đồng dạng tỉ số
1
k
.
B. Phép vị tự tỉ số
k
là phép đồng dạng tỉ số .
C. Phép đồng dạng biến đường thẳng thành đường thẳng // hoặc trùng với nó.
D. Phép đồng dạng bảo toàn độ lớn góc.
Lời giải
Chọn C
Câu 9. Hàm số nào sau đây là hàm số tuần hoàn với chu kì T
?
A.
2cos
y x
. B.
cos
y x
. C.
cos2
y x
. D.
cos 2
y x
.
Lời giải
Chọn C
Hàm số
2cos
y x
,
cos 2
y x
và
cos
y x
tuần hoàn với chu kì
1
2
T
.
Hàm số
cos2
y x
tuần hoàn với chu kì
2
2
2
T
.
S
Q
N
R
P
M
B
D
C
A
k
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 141
Câu 10. Hàm số
tan
y x
đồng biến trên mỗi khoảng
A.
; ,k k k
. B.
3
; ,
4 4
k k k
.
C.
2 ; 2 ,k k k
. D.
; ,
2 2
k k k
.
Lời giải
Chọn D
Theo Sgk Đại số và Giải tích 11 cơ bản, hàm số
tan
y x
đồng biến trên mỗi khoảng
; ,
2 2
k k k
.
Câu 11. Cho phép thử có không gian mẫu
1,2,3,4,5,6
. Các cặp biến cố không đối nhau
là:
A.
1
A
và
2, 3, 4,5,6
B
. B.
và
.
C.
1, 4, 6
E
và
2,3
F
. D.
1,4,5
C
và
2,3,6
D
.
Lời giải
Chọn C
Vì
\
A B
nên
A
và
B
đối nhau.
Vì
\
nên
và
đối nhau.
Vì
\ 2;3;5; 6
E
, tập này không bằng tập
F
nên
E
và
F
là cặp biến cố không đối
nhau.
Vì
\
C D
nên
C
và
D
đối nhau.
Câu 12. Số tập hợp con khác rỗng của tập hợp gồm 15 phần tử là
A.
32768
. B.
32767
. C.
15!
. D.
2
15
.
Lời giải
Chọn B
Số tập hợp con của tập hợp gồm 15 phần tử là
15
2 32768
.
Suy ra số tập hợp con khác rỗng của tập hợp gồm 15 phần tử là
32768 1 32767
.
Câu 13. Cho tứ diện
ABCD
. Gọi
M
,
N
lần lượt là trung điểm của
AB
và
AC
. Đường thẳng
MN
song song với mặt phẳng:
A.
ACD
. B.
ABD
. C.
BCD
. D.
ABC
.
Lời giải
Chọn C
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 142 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Ta có
M
,
N
lần lượt là trung điểm của
AB
,
AC
MN
là đường trung bình của tam
giác
ABC
//
MN BC
.
Ta có
// ,
//
MN BC BC BCD
MN BCD
MN BCD
.
Câu 14. Cho
2;0
I
. Phép đồng dạng hợp thành của phép
1
;
2
o
V
và phép
OI
T
(
O
là gốc tọa độ).
Biến đường tròn
2 2
: 4
C x y
thành
C
có phương trình
A.
2 2
4 3 0
x y x
. B.
2 2
4 1 0
x y x
. C.
2 2
4 0
x y x
. D.
2 2
4 3 0
x y x
.
Lời giải
Chọn A
Đường tròn
2 2
: 4
C x y
có tâm
0;0
O
, bán kính
2
R
.
+) Gọi
1
C
là ảnh của đường tròn
C
qua phép
1
;
2
O
V
.
Ta có: phép vị tự tâm
O
, tỉ số
1
2
biến điểm
O
thành chính nó, biến đường tròn
C
bán kính
2
R
thành đường tròn
1
C
bán kính
1
1 1
. .2 1
2 2
R R
.
+) Vì
C
là ảnh của
C
qua phép hợp thành của
1
;
2
O
V
và phép
OI
T
nên
C
là ảnh
của
1
C
qua phép
OI
T
.
Gọi
OI
O T O
OO OI
 
2;0
I O O
.
Phương trình đường tròn
C
có tâm
2;0
O
và bán kính
1
1
R R
là
2
2
2 1
x y
hay
2 2
4 3 0
x y x
.
Câu 15. Trong hệ trục
Oxy
, cho đường thẳng
:2 1 0
d x y
, phép tịnh tiến theo vectơ
v
biến
d
thành chính nó thì
v
phải là vectơ nào trong các vectơ sau?
A.
2; 4
v
. B.
4; 2
v
. C.
2; 1
v
. D.
1;2
v
.
Lời giải
Chọn A
+)
: 2 1 0
d x y
một vectơ pháp tuyến của
d
là
2; 1
d
n
và một vectơ chỉ phương
của
d
là
1;2
d
u
.
N
M
B
D
C
A
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 143
+) Phép tịnh tiến theo vectơ
v
biến
d
thành chính nó khi và chỉ khi vectơ
v
có giá
song song hoặc trùng với
d
v
cùng phương với
1;2
d
u
.
Mà
2;4 2 1;2 2
d
v u
.
Chọn đáp án A.
Câu 16. Một đa giác lồi có 27 đường chéo. Số đỉnh của đa giác đó là:
A. 9. B. 8. C. 11. D. 10.
Lời giải
Chọn A
+) Giả sử số đỉnh của đa giác lồi là
, 3
n n n
. Khi đó đa giác cũng có
n
cạnh.
+) Nối hai đỉnh bất kì của đa giác này ta được
2
n
C
đoạn thẳng bao gồm các cạnh của đa
giác và các đường chéo của đa giác, trong đó đoạn thẳng nối hai đỉnh kề nhau tạo
thành 1 cạnh của đa giác, mà đa giác có
n
cạnh nên số đường chéo của đa giác đó là:
2
n
C n
.
Theo đề bài ta có:
2
!
27 27
2 !.2!
n
n
C n n
n
2
1
27 3 54 0
2
n n
n n n
9
6 ¹
n nhËn
n lo i
.
Vậy số đỉnh của đa giác là 9.
Câu 17. Cho hình chóp tứ giác .
S ABCD
đáy không phải là hình thang và
M
tùy ý nằm trong
SCD
. Gọi
d MAB SCD
. Chọn câu đúng:
A.
, ,
CD d BC
đồng quy. B.
, ,
AB d AC
đồng quy.
C.
, ,
AB CD d
đồng quy. D.
, ,
d AD CD
đồng quy.
Lời giải
Chọn C
+ Ta thấy
M
là 1 điểm chung của 2 mặt phẳng
MAB
và
SCD
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 144 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
+ Do tứ giác
ABCD
không phải là hình thang nên hai đường thẳng
AB
và
CD
cắt nhau
tại
N
.
Suy ra
MAB SCD MN
nên
d
chính là đường thẳng đi qua 2 điểm
M
và
N
.
Vậy
, ,AB CD d
đồng quy tại
N
.
Câu 18. Xác suất bắn trúng mục tiêu của một vận động viên khi bắn một viên đạn là
0,6
.
Người đó bắn hai viên một cách độc lập. Xác suất để một viên bắn trúng và một viên
trượt mục tiêu là:
A.
0,24
. B.
0,4
. C.
0,48
. D.
0,45
.
Lời giải
Chọn C
Gọi
i
A
là biến cố: “Vận động viên bắn viên đạn thứ
i
trúng mục tiêu” với
1, 2i
.
i
A
là biến cố: “Vận động viên bắn viên đạn thứ
i
không trúng mục tiêu” với
1, 2i
.
Ta có:
0,6
i
P A
1 1 0,6 0,4
i i
P A P A
.
Xác suất vận động viên bắn một viên trúng và một viên không trúng mục tiêu là
1 2 1 2
. .P P A P A P A P A
0,6. 0,4 0, 4. 0,6 0, 48
.
Câu 19. Cho tứ diện
ABCD
. Gọi
, , M N P
lần lượt là các điểm trên các cạnh
AB
,
AC
và
BD
sao cho
MN
không song song với
BC
,
MP
không song song với
AD
. Mặt phẳng
( )MNP
cắt các đường thẳng
, , BC CD AD
lần lượt tại
, , K I J
. Ba điểm nào sau đây
thẳng hàng:
A.
, , M I J
. B.
, , N K J
. C.
, , K I J
. D.
, , N I J
.
Lời giải
Chọn D
Ta có
( )N MNP
và
N AC
( ) ( )N MNP ACD
Ta có
( )I MNP CD ( ) ( )I MNP ACD
Ta có
( )J MNP AD ( ) ( )J MNP ACD
Ba điểm
, , N I J
cùng thuộc hai mặt phẳng phân biệt
( )MNP
và
( )ACD
, suy ra ba
điểm
, , N I J
thẳng hàng.
Câu 20. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
sin 2 2 sin cos 2y x x x
là
A.
min 1 2 2; max 1 2 2y y
. B.
min 2; max 2y y
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Trang 145
C.
min 1 2 2; max 4y y
D.
min 1 2 2; max 3y y
.
Lời giải
Chọn C
Đặt
sin cos , 2; 2t x x t
.
2 2 2
sin cos 2sin .cost x x x x
1 sin 2x
2
sin 2 1x t
.
Khi đó hàm số trở thành
2
1 2 2y t t
2
2 3t t
.
Xét hàm số
2
2 3f t t t
,
2; 2t
ta có bảng biến thiên sau:
Dựa vào bảng biến thiên ta có
2; 2
4max f t
khi
1t
2; 2
; 1 2 2min f t
khi
2t
.
Vậy
min 1 2 2 ; max 4y y
.
Câu 21.
Hệ số của
8
x
trong khai triển
5 6 10
1 1 ... 1x x x
là:
A.
55
. B.
37
. C.
147
. D.
147
.
Lời giải
Chọn A
Hệ số của
8
x
trong khai triển
5 6 10
1 1 ... 1x x x
chỉ xuất hiện trong khai triển
của
8 9 10
1 ; 1 ; 1x x x
.
+)
8
8
8
0
1 1
k
k k
k
x C x
do hệ số chứa
8
x
nên
8k
hệ số là :
8
8
C
.
+)
9
9
9
0
1 1
k
k k
k
x C x
do hệ số chứa
8
x
nên
8k
hệ số là :
8
9
C
+)
10
10
10
0
1 1
k
k k
k
x C x
do hệ số chứa
8
x
nên
8k
hệ số là :
8
10
C
Vậy hệ số của
8
x
trong khai triển là
8 8 8
8 9 10
1 9 45 55C C C
.
Câu 22. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho điểm
1;5 , 3;2A B
. Biết các điểm
,A B
theo thứ tự là ảnh của các điểm
,M N
qua phép vị tự tâm
O
, tỉ số
2k
. Độ dài
đoạn thẳng
MN
là:
A.
50
. B.
12,5
. C.
10
. D.
2,5
.
Lời giải
Chọn D
+) Ta có
2 2
4; 3 3 4 5AB AB
.
+)
, 2
, 2
O
O
V M A
V N B
2 2AB MN MN
5
2,5
2
MN
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 146 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Câu 23. Số nghiệm của phương trình
2sin 2 1
3
x
thuộc khoảng
;
là:
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn A
+) Ta có
2sin 2 1
3
x
1
sin 2
3 2
x
sin 2 sin
3 6
x
2 2
3 6
5
2 2
3 6
x k
x k
k
12
4
x k
x k
k
.
+)
12
x k
11 13
12 12
k
11
0;1 ;
12 12
k k x
.
+)
4
x k
5 3
4 4
k
3
1;0 ;
4 4
k k x
.
Vậy có
4
nghiệm thuộc khoảng
;
.
Câu 24. Cho tập
0;1;2;3; 4;5;6;7;8;9
A
. Số các số tự nhiên có 5 chữ số đôi một khác nhau lấy
ra từ tập
A
là:
A.
27162
. B.
30240
. C.
30420
. D.
27216
.
Lời giải
Chọn D
Lập
abcde
có các chữ số đôi một khác nhau gồm các bước:
+) Chọn
a
:
9
cách
\ 0
a A
.
+) Chọn bộ thứ tự
, , ,
b c d e
: lấy ra
4
số từ
9
số thuộc tập
\
A a
và sắp xếp có
4
9
A
cách.
Vậy có
4
9
9.A 27216
số.
Câu 25. Tìm
m
để phương trình
2
1
(1 2 ) tan 2 3 0
cos
m x m
x
có nghiệm thuộc khoảng
0;
4
.
A.
3
2
m
. B.
1
m
. C.
3
1
2
m
. D.
1
m
hoặc
3
2
m
.
Lời giải
Chọn C
Phương trình luôn xác định
0;
4
x
.
Khi đó ta có:
2
tan 1
tan (1 2 ) tan 2 2 0
tan 2 2
x
x m x m
x m
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 147
Vì phương trình
tan 1
x
không có nghiệm thuộc khoảng
0;
4
và hàm số
tan
y x
đồng biến trên khoảng
0;
4
nên phương trình đã cho có nghiệm thuộc khoảng
0;
4
khi và chỉ khi
tan 0 2 2 tan 0 2 2 1
4
m m
3
1
2
m
.
B. TỰ LUẬN.
Bài 1. 1) Giải phương trình
3
sin 3 sin 2sin 2
2
x x x
.
Lời giải
Ta có :
3
sin 3 sin 2sin 2
2
x x x
sin 3 cos 2sin 2
x x x
1 3
sin cos sin 2
2 2
x x x
sin sin 2
3
x x
2 2
3
2 2
3
x x k
x x k
2
3
, k .
2 2
9 3
x k
k
x
Vậy,
2 2
2 ; , k .
3 9 3
k
S k
2) Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn không
vượt quá
2019
, đồng thời nó chia hết cho
5
.
Lời giải
Số các số tự nhiên có 4 chữ số là
9.10.10.10 9000
(số). Suy ra số phần tử của không
gian mẫu là
9000
n
.
Gọi
A
là biến cố “ Số được chọn không vượt quá
2019
và chia hết cho
5
”.
Số có bốn chữ số nhỏ nhất có bốn chữ số chia hết cho
5
là
1000
, số có bốn chữ số lớn
nhất không vượt quá
2019
chia hết cho
5
là
2015
.
Suy ra số phần tử của biến cố
A
là
2015 1000 : 5 1 204
n A
.
Xác suất của biến cố
A
là
204 17
9000 750
n A
P A
n
.
Bài 2. Cho hình chóp .
S ABC
,
G
là trọng tâm tam giác
ABC
. Đường thẳng qua
G
song song
với
SA
cắt mặt phẳng
SBC
tại
A
. Nêu cách xác định điểm
A
và thiết diện của hình
chóp khi cắt bởi mặt phẳng qua
A
, song song với
SG
và
BC
.
Lời giải
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 148 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
*
Cách dựng điểm
A
Gọi
I
là trung điểm của
BC
,
là đường thẳng qua
G
và song song với
SA
.
+ Chọn mặt phẳng
SAI
chứa
.
+ Ta có
SI
là giao tuyến của hai mặt phẳng
SAI
và
SBC
.
+ Trong mặt phẳng
SAI
,
SI A
Suy ra
A
là điểm cần dựng.
*
Xác định thiết diện của hình chóp cắt bởi mặt phẳng
P
qua
A
, song song với
SG
và
BC
.
+
//
A P SBC
P BC P SBC A x
BC SBC
, với
A x
là đường thẳng đi qua
A
, song song
với
BC
. Giả sử
A x
cắt
SB
tại
M
và cắt
SC
tại
N
. Suy ra
P SBC MN
.
+
//
A P SAI
P SG P SAI A E
SG SAI
, với
A E
là đường thẳng đi qua
A
, song song
với
SG
, cắt
AI
tại
E
.
+
//
E P ABC
P BC P ABC Ey
BC ABC
, với
Ey
là đường thẳng đi qua
E
, song song
với
BC
. Giả sử
Ey
cắt
AC
tại
P
và cắt
AB
tại
Q
. Suy ra
P ABC PQ
.
Vậy thiết diện là tứ giác
MNPQ
.
Bài 3. 1. Giải hệ phương trình sau:
2019 2019 1 2018 2 2017 2017 2
2019 2019 2019
3 2
2020 2.
3 6 .
x x y C y C y C y y
y x x
I
A
C
B
S
G
A'
M
E
Q
P
N
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 149
Lời giải
Giải hệ:
2019 2019 1 2018 2 2017 2017 2
2019 2019 2019
3 2
... 2020 2 1
3 6 2
x x y C y C y C y y
y x x
Ta có
2019
2019
1 1 1
x x y y
*
Xét hàm số
2019
f t t t
, có
2018
2019 1 0,f t t t
.
Suy ra
f t
là hàm số đồng biến trên
. Khi đó
* 1
f x f y
1
x y
.
Với
1 1
x y y x
thay vào
2
ta được:
3
2
1 3 6
x x x
3
3 1 0
x x
3
.
Xét hàm
3
3 1
g x x x
có:
2 3
2 . 1 3 0
1 1
1 . 0 1 0
0 1
0 . 2 1 0
2 1
g
g g
g
g g
g
g g
g
.
Suy ra
3
có ít nhất
3
nghiệm thuộc khoảng
2;2
.
Mặt khác
3
là phương trình bậc ba nên có nhiều nhất 3 nghiệm thực.
Suy ra
3
có đúng 3 nghiệm thuộc khoảng
2;2
.
Đặt
2cos
x t
với
0;2
t
. Thay vào
3
ta được:
3
2cos 3 2cos 1 0
t t
3
8cos 6cos 1 0
t t
1
cos3
2
t
9
5
9
7
9
t
t
t
.
+) Với
9
t
2 cos
9
x
2cos 1
9
y
.
+) Với
5
9
t
5
2 cos
9
x
5
2cos 1
9
y
.
+) Với
7
9
t
7
2cos
9
x
7
2cos 1
9
y
.
Vậy hệ phương trình có tập nghiệm là:
5 5 7 7
2cos ;2cos 1 , 2cos ;2cos 1 , 2cos ;2cos 1
9 9 9 9 9 9
S
2. Cho tập hợp
0;1; 2;3;...;2019
A
. Một tập hợp con
X
của
A
được gọi là tập cân
nếu trong tập hợp
X
số các số chẵn và số các số lẻ bằng nhau. ( Tập rỗng là một tập
cân). Chứng minh rằng số tập cân của tập hợp
A
là
1010
2020
C
.
Lời giải
Gọi
1
0;2;4; ;2018
A
,
2
1;3;5; ;2019
A
.
Ta có: Số phần tử tập cân của
A
là số tự nhiên chẵn, không vượt quá 2020 và nếu
X
là
tập cân có
2
k
phần tử thì
1 2
=
X X X
,
1 1 2 2
,
X A X A
,
1 2
=
X X k
,
0 1010
k
.
Số cách chọn
1
X
là
1010
C
k
.
Số cách chọn
2
X
là
1010
C
k
.
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 150 TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
Do đó số tập cân của
A
là
2
1010
1010
0
C
k
k
.
Ta có
2020
2020
2020
0
C 1
i i
i
x x
1010 1010
1 1x x
1010 1010
1010
1010 1010
0 0
C C
i i i i
i i
x x
.
Đồng nhất hệ số
1010
x
ta có
2
1010
1010
1010 2020
0
C C
k
k
.
Vậy số tập cân của tập hợp
A
là
1010
2020
C
.
Bài 4. Cho hình chóp .
S ABCD
có đáy là hình bình hành,
M
là một điểm di động trên cạnh
SC
. Mặt phẳng
P
chứa
AM
và song song với
BD
. Mặt phẳng
P
cắt
,
SB SD
lần lượt tại
các điểm
N
và
E
. Chứng minh rằng:
2 . . .
SB SM SN SM SC SN
.
Lời giải
Gọi
O
là tâm của hình bình hành
ABCD
,
I
là trung điểm
MC
.
Gọi
K
là giao điểm của
AM
với
SO
.
Trong mặt phẳng
SBD
kẻ đường thẳng qua
K
và song song với
BD
cắt
SB
,
SD
lần
lượt tại
,
N E
. Khi đó mặt phẳng
P
chính là mặt phẳng
ANME
.
Ta có ( ) ( )
P SBD NE
.
Vì
//
NE BD
và
//
OI AM
nên
SB SO SI
SN SK SM
.
Suy ra
2 ( )
2 2 1
SB SC SI SC SI SI IC SI MI
SN SM SM SM SM SM
.
Do đó:
2 1 . . 2 .
SB SC
SC SN SM SN SB SM
SN SM
Bài 5. Cho phương trình
sin2 3 2cos 3 sinx
x m x m
. Để phương trình có nhiều hơn một
nghiệm trong
0;
thì giá trị của
m
thỏa ?
Lời giải
Ta có
sin 2 3 2 cos 3 s inx sin 2 3 2 cos 3 s inx = 0 1
x m x m x m x m
sinx 1 0
2cos sinx 1 3 sinx 1 0 sinx 1 2cos 3 0
2cos 3 0
x m x m
x m
2
sinx = 1
2
2cos 3 0 3
cos
2
x k
x m m
x
.
NHÓM WORD 🙲 BIÊN SOẠN TOÁN BỘ ĐỀ KIỂM TRA HỌC KÌ 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 151
Xét trong khoảng
0;
ta được
2
3
cos 2
2
x
m
x
.
Trong khoảng
0;
phương trình
1
có hơn một nghiệm
2
có một nghiệm khác
2
3
1
2 3
2
3
3
0
cos
2 2
m
m
m
m
.Vậy
2 3
0
3
m
.
| 1/151
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHINH PHỤC CUỐI KÌ I
BỘ ĐỀ ÔN TẬP CUỐI KÌ 1 MÔN TOÁN – KHỐI 11 Sưu tầm và Tổng hợp:
Admin: HOÀNG TUYÊN – LÊ MINH TÂM
TÀI LIỆU LƯU HÀNH NỘI BỘ NĂM HỌC: 2020 – 2021
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT MỤC LỤC
(Dựa trên các đề của Sở và các trường THPT biên soạn, bổ sung theo cấu trúc:
25 câu trắc nghiệm và 5 câu tự luận) A. PHẦN ĐỀ.
1. ĐỀ SỞ NAM ĐỊNH KHỐI 11. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 03
2. ĐỀ SỞ HÀ NỘI – THPT AMSTERDAM KHỐI 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 07
3. ĐỀ SỞ BẠC LIÊU KHỐI 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 11
4. ĐỀ SỞ HƯNG YÊN KHỐI 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 15
5. ĐỀ SỞ HUẾ KHỐI 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 18
6. ĐỀ SỞ HUẾ – THPT CHUYÊN QUỐC HỌC HUẾ KHỐI 11 . . . . . . . . . . . . . . . . . . . . Trang 21
7. ĐỀ SỞ HUẾ – THPT ĐẶNG TRẦN CÔN KHỐI 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 25
8. ĐỀ SỞ HUẾ – THPT GIA HỘI KHỐI 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 29
9. ĐỀ SỞ HUẾ – THPT CHI LĂNG KHỐI 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 33
10. ĐỀ SỞ ĐẮK LẮK KHỐI 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 37
B. PHẦN ĐÁP ÁN & HƯỚNG DẪN GIẢI.
11. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ SỞ NAM ĐỊNH . . . . . . . . . . . . . . . . . . Trang 40
12. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ THPT AMSTERDAM . . . . . . . . . . . . Trang 51
13. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ SỞ BẠC LIÊU . . . . . . . . . . . . . . . . . . . . Trang 64
14. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ SỞ HƯNG YÊN . . . . . . . . . . . . . . . . . . Trang 76
15. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ SỞ HUẾ . . . . . . . . . . . . . . . . . . . . . . . . . Trang 87
16. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ CHUYÊN QUỐC HỌC HUẾ . . . . . . . Trang 96
17. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ THPT ĐẶNG TRẦN CÔN . . . . . . . Trang 108
18. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ THPT GIA HỘI . . . . . . . . . . . . . . . . . Trang 118
19. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ THPT CHI LĂNG . . . . . . . . . . . . . . . Trang 128
20. BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ SỞ ĐẮK LẮK . . . . . . . . . . . . . . . . . . . Trang 138 Trang 2
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1 NAM ĐỊNH NĂM HỌC: 2019 - 2020 --------------------------- Thời gian: 90 phút KHỐI 11
Họ tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . A. TRẮC NGHIỆM
Câu 1: Trong các hàm số sau, hàm số nào là hàm số chẵn? A. 3 y  sin x . B. 2 y  sin x . C. y  x  tan x . D. y  cot x .
Câu 2: Phương trình sin 2xm  0 có nghiệm khi và chỉ khi A. m 1. B. m 1. C. 2  m  2 . D. 1   m 1.
Câu 3: Từ các chữ số 1;2;3;4;5 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau A. 5. B. 15. C. 5 5 . D. 120.
Câu 4: Một câu lạc bộ cờ vua có 15 người. hỏi có bao nhiêu cách bầu ra ba người vào ba vị trí
gồm Chủ tịch, Phó chủ tịch và Thư kí, biết trằng ai cũng có khả năng làm được các vị trí trên. A. 455 . B. 2730 . C. 6 . D. 45 .
Câu 5: Một lớp học có 20 học sinh nam và 21 học sinh nữ. Số cách chọn ngẫu nhiên 10 học sinh trong lớp là A. 41 C . B. 10 A . C. 10!. D. 10 C . 10 41 41
Câu 6: Số tập con có 3 phần tử của một tập hợp có 2009 phần tử là A. 3 C . B. 3 A . C. 2009! . D. 2009 . 2009 2009 3!
Câu 7: Cho tập A  1;2;3;4; 
5 . Chọn ngẫu nhiên 3 số từ tập A . Tính xác suất để 3 số được chọn có tổng bằng 10. A. 1 . B. 1 . C. 2 D. 3 . 10 5 5 10
Câu 8: Hệ số của số hạng chứa 8
x trong khai triển nhị thức Niuton x  10 2 1 là A. 210 . B. 8 200x . C. 200 D. 8 210x . 
Câu 9: Trong mặt phẳng với hệ tọa độ Oxy , cho vectơ v  2;  1 và điểm M  3  ;2 . Tìm tọa 
độ ảnh M  của điểm M qua phép tịnh tiến theo vec tơ v . A. M '5; 3   . B. M '1;  1 . C. M ' 1  ;  1 . D. M ' 5  ;3 .
Câu 10: Chọn khẳng định sai?
A. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
B. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.
C. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
D. Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt.
Câu 11: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng không cắt nhau và không song song thì chéo nhau.
B. Hai đường thẳng phân biệt không song song thì chéo nhau.
C. Hai đường thẳng chéo nhau thì không có điểm chung.
D. Hai đường thẳng không có điểm chung thì song song.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 3
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 12: Cho hàm số f x 2
 cos 2x  2cos x  m . Với m  2; 2 
 , tìm giá trị nhỏ nhất của
hàm số trên đoạn 0; . A. 3. B. 3 . C. 1. D. 0 . 2
Câu 13: Hàm số y  cos x nghịch biến trên khoảng: A.         ;   . B. 0;   . C.    ;0 . D.    ;  .  2 2   2 
Câu 14: Trên giá sách có 5 quyển sách Toán khác nhau, 6 quyển sách Anh khác nhau và 8 quyển
sách Văn khác nhau. Số cách chọn ra ba quyển sách có đủ ba môn là: A. 19. B. 118. C. 20 . D. 240 .   1 n
Câu 15: Cho dãy số u với u 
. Số hạng thứ mười một của dãy số bằng n  n 2n  5 A. 1  . B. 1 . C. 1 . D. 1  . 27 27 25 7
Câu 16: Cho cấp số cộng u với u  2
 và công sai d  3. Tổng 10 số hạng đầu tiên S của n  1 10 u là n  A. 155. B. 115. C. 145. D. 165.
Câu 17: Trong mặt phẳng toạ độ Oxy , cho điểm A2;0 . Ảnh của A qua phép quay  Q có toạ O;90 độ là A. M 0;2 . B. N 0; 2 . C. P 2;0 . D. Q1;  1 .
Câu 18: Trong không gian, có bao nhiêu vị trí tương đối giữa hai đường thẳng phân biệt a và b ? A. 1. B. 2 . C. 3. D. 4 .
Câu 19: Tập nghiệm của phương trình sin x 3cot x   1  0 là A.      
k ,  k , k   .
B.   k ,k  .  6   6      C.     k , k   .
D. k ,  k ,k  .  3   3  Câu 20:  1 n 
Tổng các hệ số trong khai triển 2 x  
 là 4096 . Hệ số của số hạng không chứa x trong  x  khai triển là A. 495 . B. 133 . C. 334. D. 775.
Câu 21: Từ một hộp chứa 16 cái thẻ đánh số từ 1 đến 16. Chọn ngẫu nhiên 3 thẻ. Xác suất để
được 3 thẻ đều là số lẻ là 1 1 56 3 A. . B. . C. . D. . 10 2 506 16
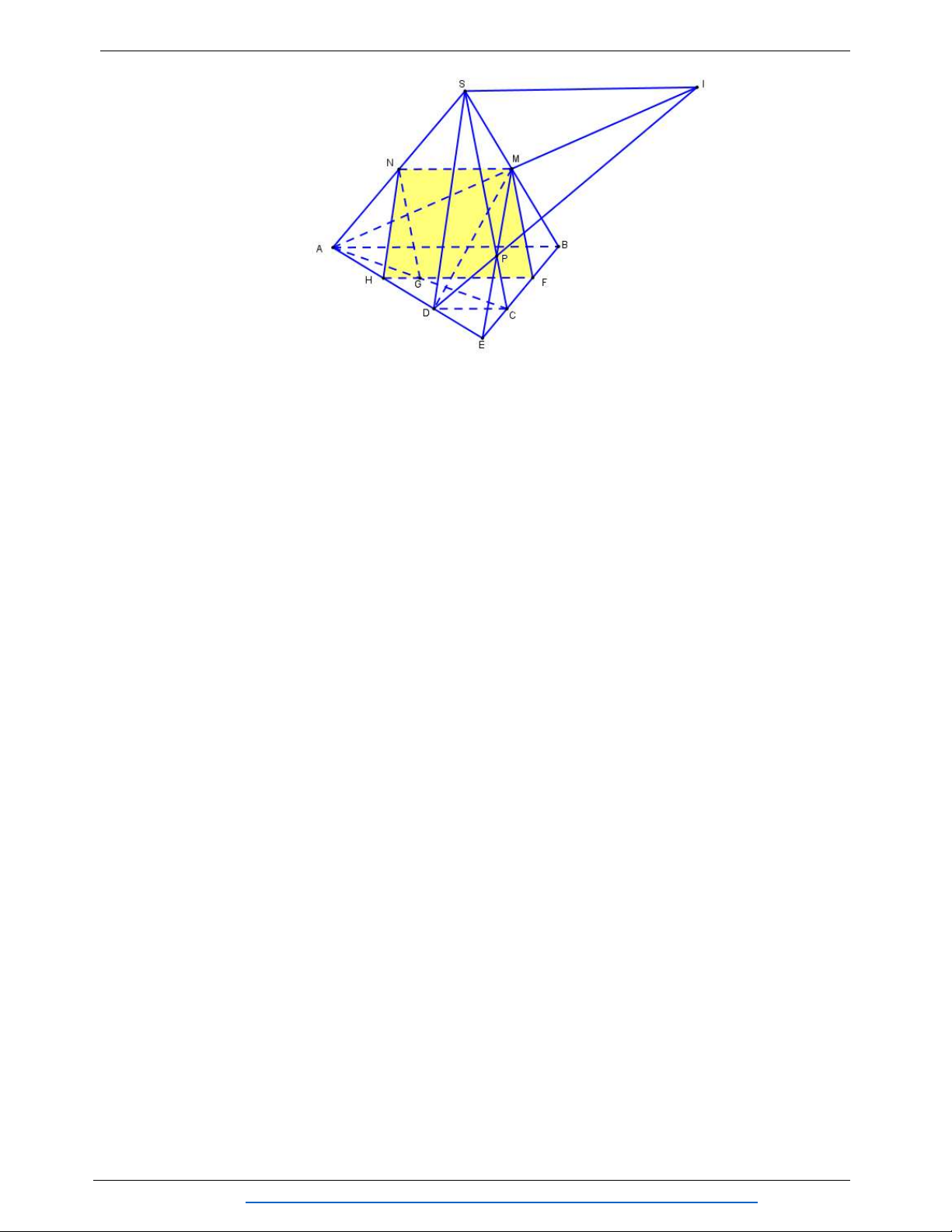
Câu 22: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, M là trung điểm cạnh SA . Gọi
P là mặt phẳng đi qua M đồng thời song song với SC và AD . Thiết diện của hình
chóp S.ABCD cắt bởi P là một Trang 4
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 A. hình thang. B. hình bình hành. C. tứ giác. D. ngũ giác.
Câu 23: Trong mặt phẳng Oxy cho đường thẳng a . Gọi b là ảnh của a qua phép đồng dạng có
được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k  2
 và phép đối xứng trục
Oy . Biết đường thẳng b có phương trình là 2x  y 16  0 , khi đó phương trình đường thẳng a là A. 2x  y  8  0 . B. 2x  y  32  0. C. 2x  y  32  0 . D. 2x  y  8  0 .
Câu 24: Cho dãy số u xác định bởi u 1 và 2 u  u  2 , * n    . Tổng n  1 n 1  n 2 2 2 2
S  u  u  u  ...  u bằng 1 2 3 1001 A. 1002001. B. 1001001. C. 1001002 . D. 1002002 .
Câu 25: Ngân hàng đề thi học kỳ I môn Văn của trường Y có 50 câu hỏi. Mỗi đề gồm bốn câu hỏi được
lấy ngẫu nhiên từ ngân hàng đề thi. Thí sinh A đã học thuộc 25 câu trong ngân hàng đề thi.
Tính xác suất để khi thí sinh A nhận đề thì có ít nhất ba câu đã học thuộc. 135 1403 13 7 A. . B. . C. . D. . 458 4606 19 19 B. TỰ LUẬN.
Câu 1: Giải phương trình sau: 1) sin 2x  cos x  0 .
2) tan x 30  3  0.
Câu 2: Tìm số nguyên dương n thỏa mãn điều kiện: 2 C  n  9 . n Câu 3:   Tìm số hạng chứa 11
x trong khai triển nhị thức Niutơn của biểu thức 2 2 n x    , biết n  x 
là số nguyên dương thỏa mãn 0 2 1 4 2 2n n 5
C  3 C  3 C  ... 3 C  100 . n n n n
Câu 4: Cho một đa giác đều n cạnh. Chọn ngẫu nhiên 3 đỉnh của đa giác đều đó. Gọi P là
xác xuất sao cho 3 đỉnh đó tạo thành một tam giác tù. Tính n , biết n là số lẻ, n  3 và 45 P  . 62
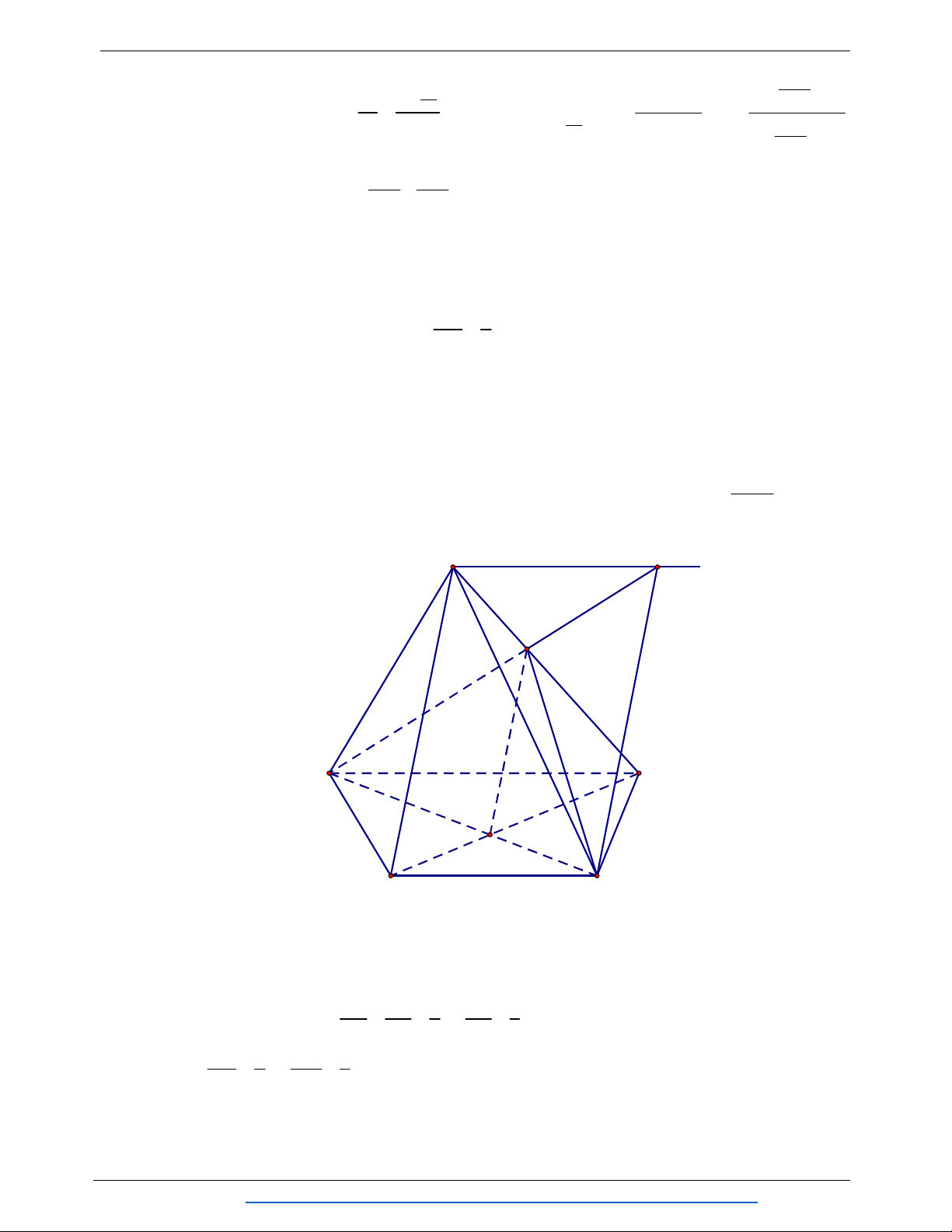
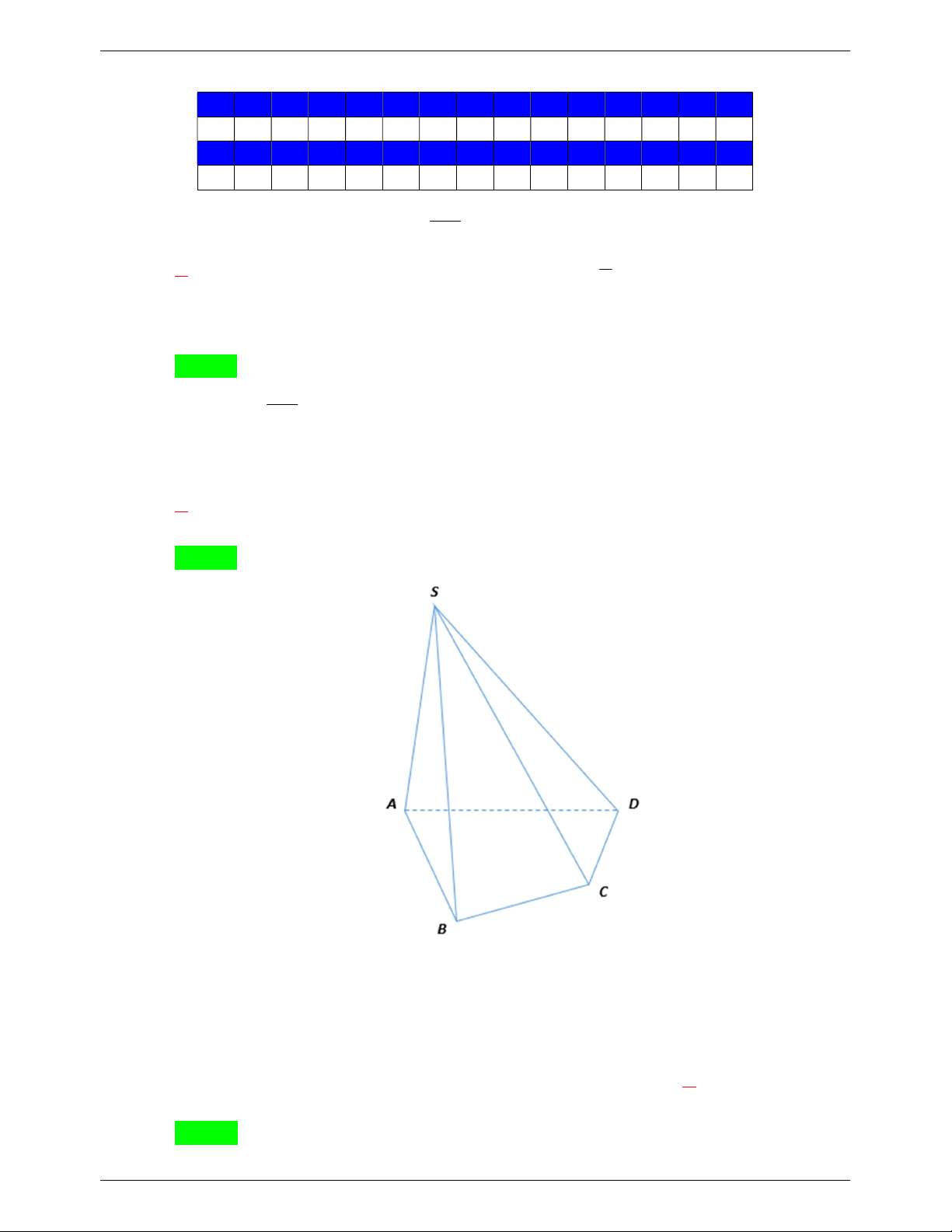
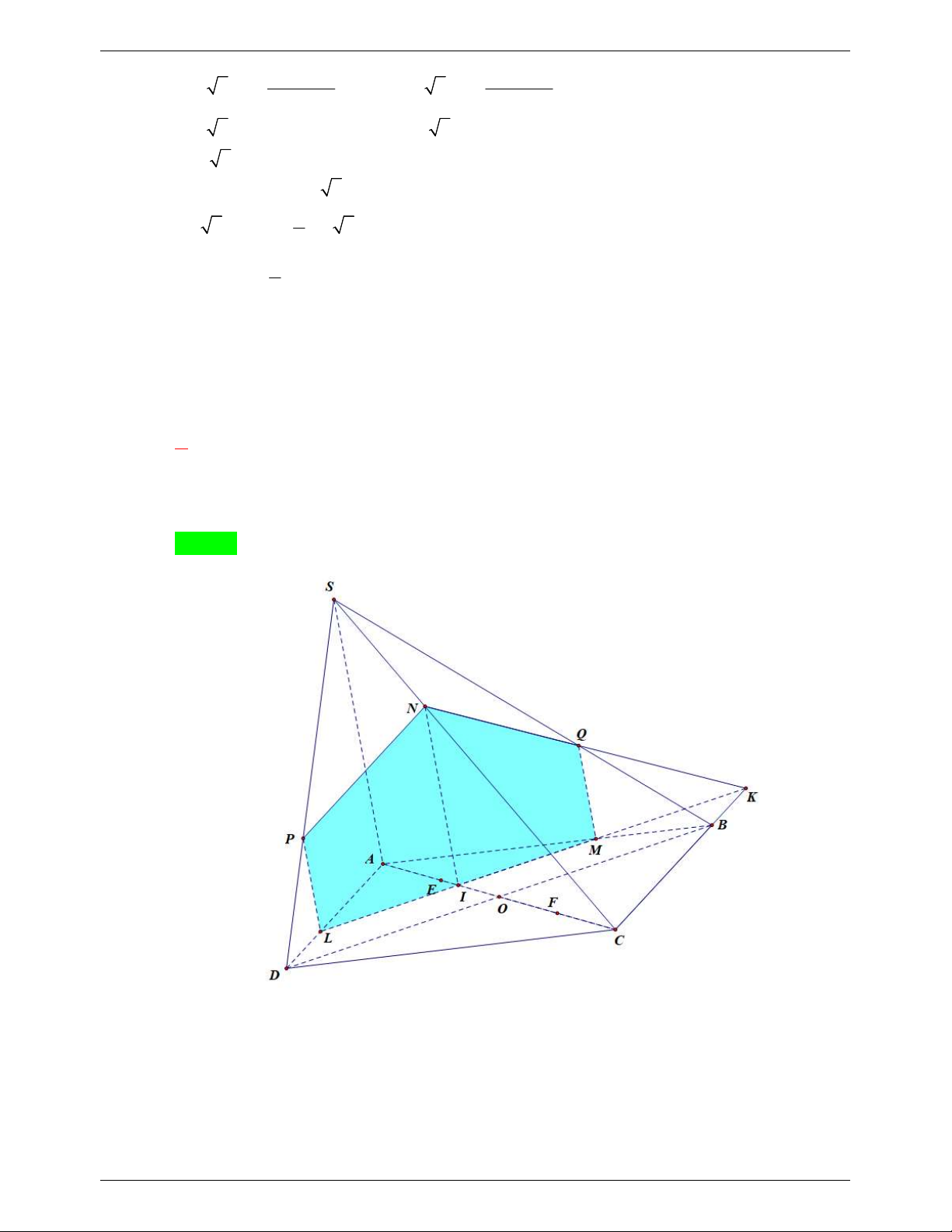
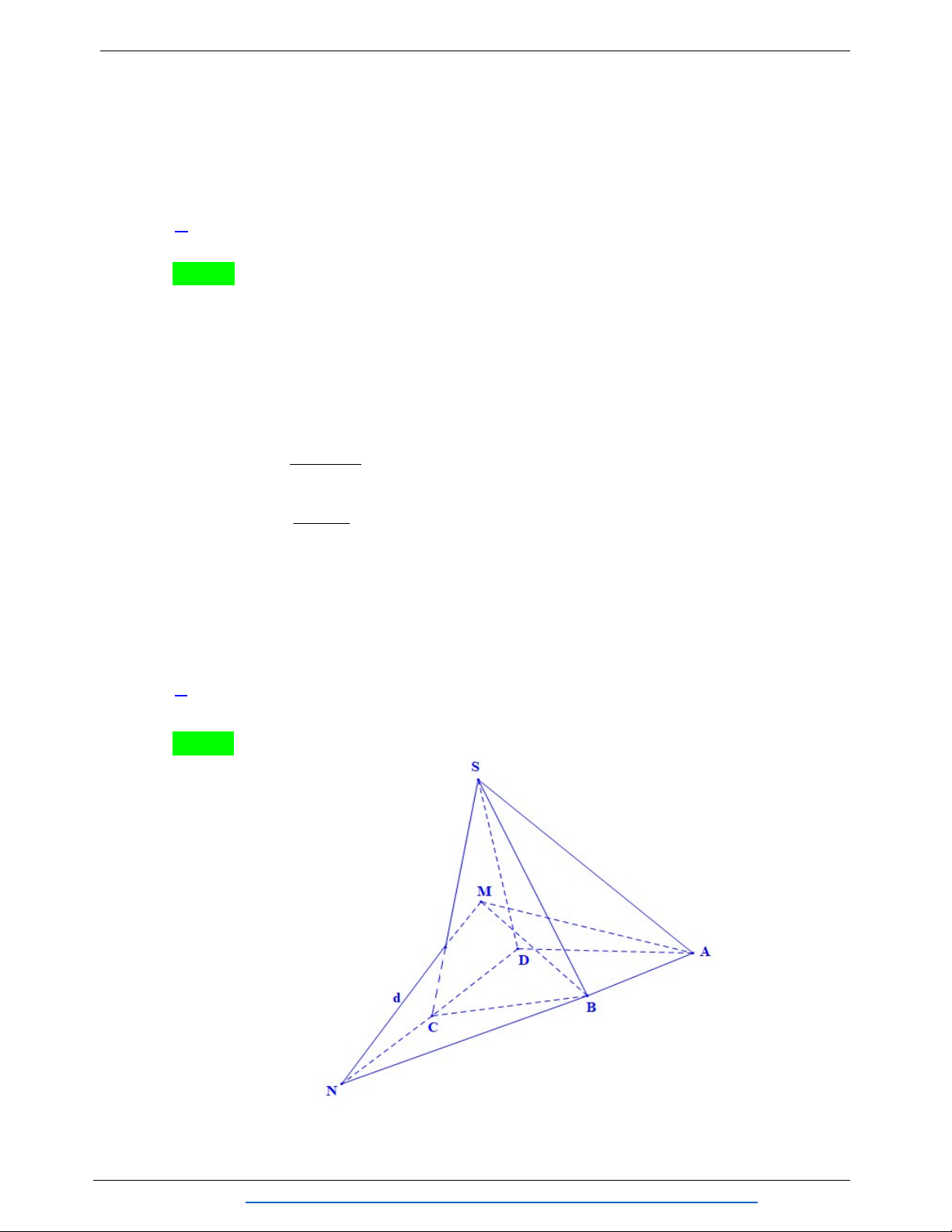
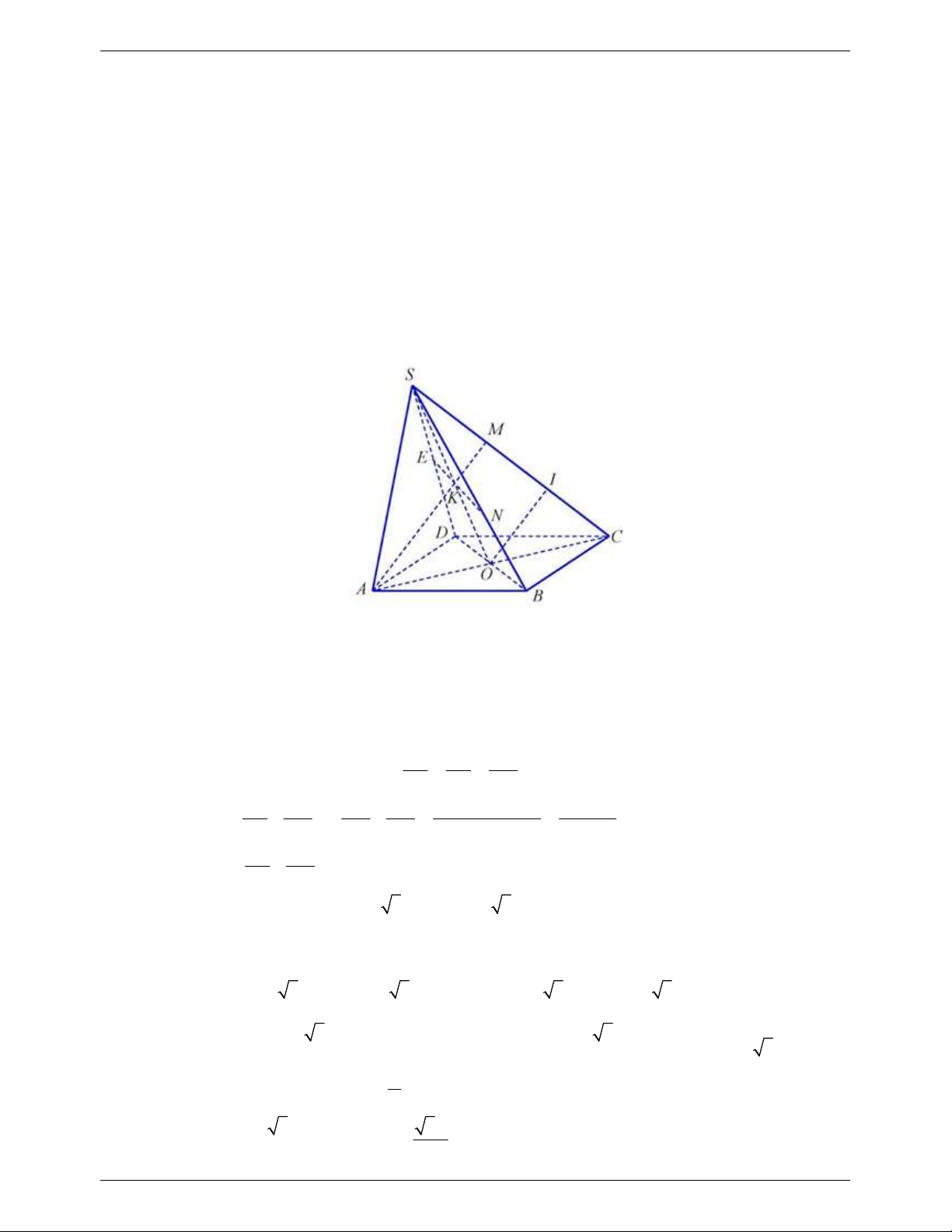
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB//CD , 2AB  3CD . Gọi M là điểm thuộc đoạn SM SB sao cho 2
 , O lả giao điểm của hai đường chéo AC và SB 5 BD .
1) Xác định giao tuyến của hai mặt phẳng SAB và SCD .
2) Chứng minh rằng: SD// MAC .
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 5
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
3) Gọi N là giao điểm của đường thẳng AM và mặt phẳng SDC . Gọi S là diện OMNC tích của tứ giác S OMNC , S
là diện tích của tam giác OMC . Tính tỉ số OMC . OMC SOMNC ----------HẾT---------- Trang 6
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1 HÀ NỘI NĂM HỌC: 2019 - 2020 --------------------------- Thời gian: 90 phút THPT AMSTERDAM KHỐI 11
Họ tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . A. TRẮC NGHIỆM Câu 1: 1
Tập xác định của hàm số y  là sin 2x A.  k    k  \  , k   . B.  \   , k   .  2   4 2  C.  
 \   k , k  . D.  \k , k    .  2 
Câu 2: Trong các phép biến hình sau, phép biến hình nào không là một phép dời hình?
A. Thực hiện liên tiếp hai phép quay.
B. Thực hiện liên tiếp hai phép đối xứng trục.
C. Thực hiện liên tiếp hai phép vị tự có cùng tâm và tỷ số vị tự là 2 số đối nhau.
D. Thực hiện liên tiếp hai phép vị tự có cùng tâm và tỷ số vị tự là 2 số nghịch đảo của nhau.
Câu 3: Một lớp 11 có 30 học sinh, gồm 15 nam và 15 nữ. Có bao nhiêu cách xếp các học sinh
thành hai hàng, một hàng nam và một hàng nữ trong lúc tập thể dục giữa giờ? A. 30!. B. 15 A  2 2 15! 15 C 30 . C. . D. 30 .
Câu 4: Trong mặt phẳng tọa độ Oxy , gọi A là ảnh của A1 ; 3 qua phép vị tự tâm O , tỷ số k  2
 . Tọa độ điểm A là A. 2 ; 6 . B. 2 ;  6 . C.  2  ; 6 . D. 2 ;  6.
Câu 5: Cho 19 điểm phân biệt A , A , A ,...A 5 A , A , A , A , A 1 2 3 19 trong đó có
điểm 1 2 3 4 5thẳng hàng
ngoài ra không có 3 điểm nào thẳng hàng, Hỏi có bao nhiêu tam giác có 3 đỉnh trong 19 điểm trên? A. 959 . B. 969. C. 364. D. 374. 11   Câu 6: 3
Trong khai triển nhị thức Newton của biểu thức 2 x
   (với x  0 ), hệ số của số  x hạng chứa 7 x là : A. 7 C 7 7 3 C 5 C 5 5 3 C 11 . B. 11 . C. 11 . D. 11 .
Câu 7: Nghiệm của phương trình 2 x 1 A  C   5 x x 1  là: A. x  5. B. x  3. C. x  4 D. vô nghiệm.
Câu 8: Từ các chữ số 0;1;2;3;4;5;6;7 lập được tất cả bao nhiêu số tự nhiên có 3 chữ số đôi một
khác nhau và chia hết cho 5 ? A. 112 số. B. 78 số. C. 42 số. D. 84 số.
Câu 9: Mệnh đề nào trong các mệnh đề sau là sai? A. 0 1 2
0  C  C  C     1 n n C 0 1 2       n n n n . B. 2n n C C C C n n n n . C. 0 1 2
1  C  2C  4C   2n n C n 0 1 2 n n      n n n n . D. 3 C 2C 4C 2 C n n n n .
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 7
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Câu 10: Cho ,
A B là hai biến cố độc lập của phép thử T . Xác suất xảy ra biến cố A là 0,5 và
xác suất xảy ra biến cố B là 0,25. Xác suất để xảy ra biến cố A và B là A. 0,25 . B. 0,125. C. 0,75 . D. 0,375.
Câu 11: Khẳng định nào trong các khẳng định sau là đúng?
A. Nếu hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.
B. Hai đường thẳng chéo nhau khi chúng không có điểm chung.
C. Hai đường thẳng song song khi chúng ở trên cùng một mặt phẳng.
D. Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
Câu 12: Cho chóp S.ABCD có đáy ABCD là hình thang có AB // CD . Gọi M , N và P lần lượt là trung điểm S ,
A BC và AD . Giao tuyến của hai mặt phẳng SAB và MNP là
A. Đường thẳng qua S và song song với AB .
B. Đường thẳng qua N và song song với SC .
C. Đường thẳng qua M và song song với AB . D. Đường thẳng MN .
Câu 13: Cho 100 tấm thẻ được đánh số từ 1 đến 100, chọn ngẫu nhiên đồng thời 3 tấm thẻ. Xác suất để
chọn được 3 tấm thẻ có tổng các số ghi trên thẻ là số chia hết cho 2 là: A. 5 . B. 1 . C. 3 . D. 49 . 6 2 4 198
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, điểm M nằm trên cạnh SB
sao cho SB  4BM . Giao điểm của đường thẳng SD và mặt phẳng  ACM  nằm trên đường thẳng nào sau đây: A. OM . B. AM . C. CM . D. AC .
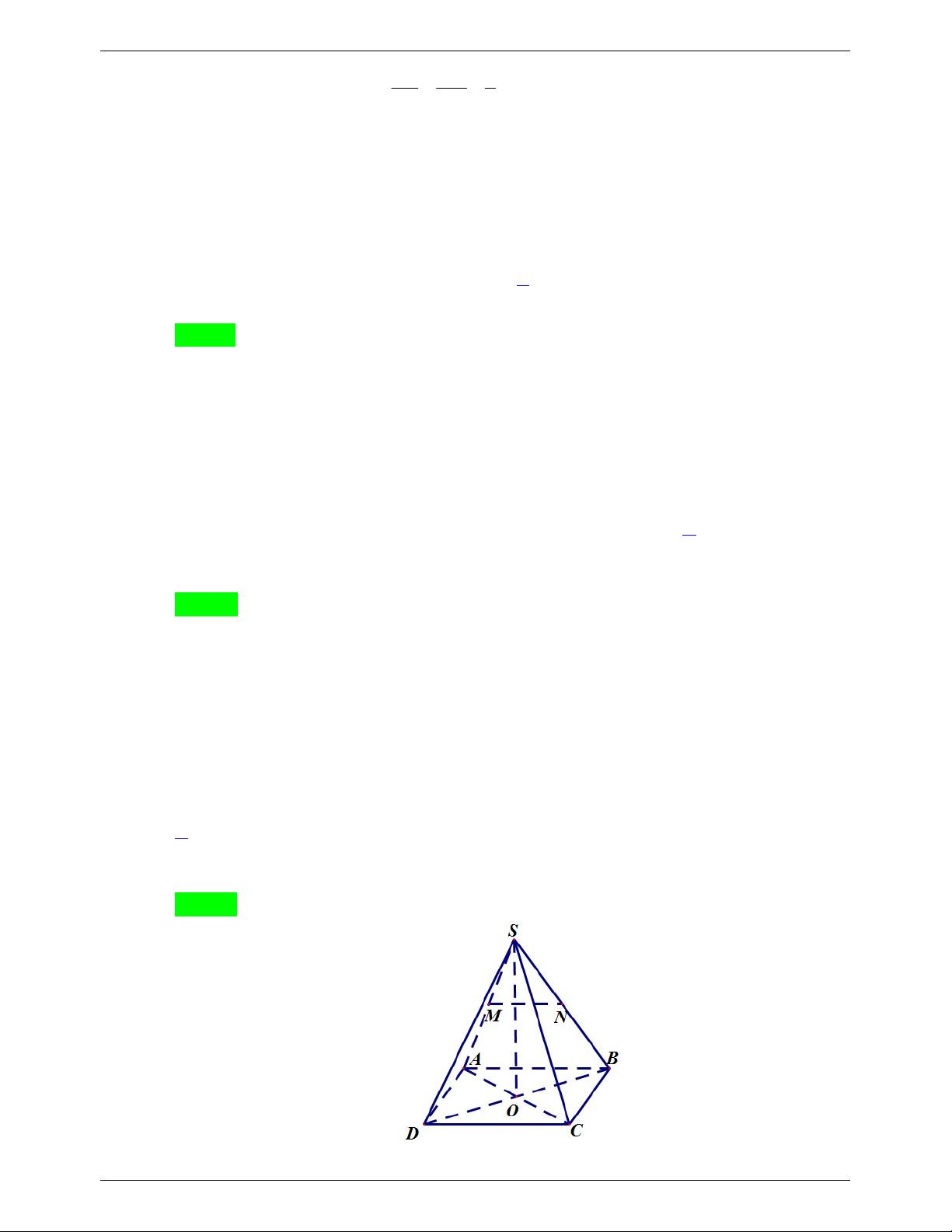
Câu 15: Cho hình chóp S.ABCD có các cạnh bên bằng nhau, đáy ABCD là hình vuông, SM 2
AB  20cm . Gọi M là điểm nằm trên cạnh SA sao cho
 . Gọi P là mặt phẳng SA 3
đi qua M, song song với hai đường thẳng AB và AC . Mặt phẳng P cắt hình chóp
S.ABCD theo thiết diện là một hình tứ giác có diện tích bằng: 80 400 800 1600 A. 2 cm . B. 2 cm . C. 2 cm . D. 2 cm . 9 9 9 9 Câu 16: Phương trình  x   2 cos
1 sin x  sin x  m   0 có đúng 6 nghiệm thuộc 0;2  khi và chỉ
khi m a;b . Khi đó tổng a  b là số nào? A. 0,5 . B. 0, 25 . C. 0, 25 . D. 0,5 .
Câu 17: Tập xác định của y  1 sin x là A.  1  ; . B.  ;    1 . C.  . D.  \k2 ,k    .
Câu 18: Người ta trồng 1275 cây theo hình tam giác như sau: Hàng thứ nhất có 1 cây, hàng thứ 2 có
2 cây, hàng thứ 3 có 3 cây ,, hàng thứ k có k cây k  
1 . Hỏi có bao nhiêu hàng? Trang 8
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 A. 51. B. 52. C. 53 . D. 50 .
Câu 19: Nghiệm của phương trình 2 1 A  A  3 là: x x A. x  1  . B. x  3. C. x  1  và x  3. D. x 1.
Câu 20: Cô giáo chia 4 quả táo, 3 quả cam và 2 quả chuối cho 9 cháu (mỗi cháu 1 quả). Hỏi có bao nhiêu cách chia khác nhau A. 120 . B. 1260 . C. 9 . D. 24 .
Câu 21: Một chiếc máy có 2 động cơ I và II hoạt động độc lập với nhau.Xác suất để động cơ I chạy tốt
và động cơ II chạy tốt lần lượt là 0,8 và 0,7 . Tính xác suất để có ít nhất 1 động cơ chạy tốt là A. 0,56 . B. 0,06 . C. 0,83 . D. 0,94 .
Câu 22: Cho S.ABCD có đáy là hình bình hành. Mệnh đề nào sau đây sai?
A. SAD SBC là đường thẳng qua S và song song với AC .
B. SAB SAD  SA . C. SBC // AD . D. SA và CD chéo nhau. Câu 23: Tổng 1 2 3 2017 C  C  C  ...  C bằng 2017 2017 2017 2017 A. 2017 2 1. B. 2017 2 1. C. 2017 2 . D. 2017 4 .
Câu 24: Trong mặt phẳng Oxy cho đường tròn C có phương trình  x  2   y  2 2 2  4 Hỏi phép 1
đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k  và phép quay 2
tâm O góc quay 90 sẽ biến C  thành các đường tròn nào trong các đường tròn sau
A.  x  2   y  2 1 1  1.
B.  x  2   y  2 1 1  1 .
C.  x  2   y  2 2 1  1.
D.  x  2   y  2 2 2  1.
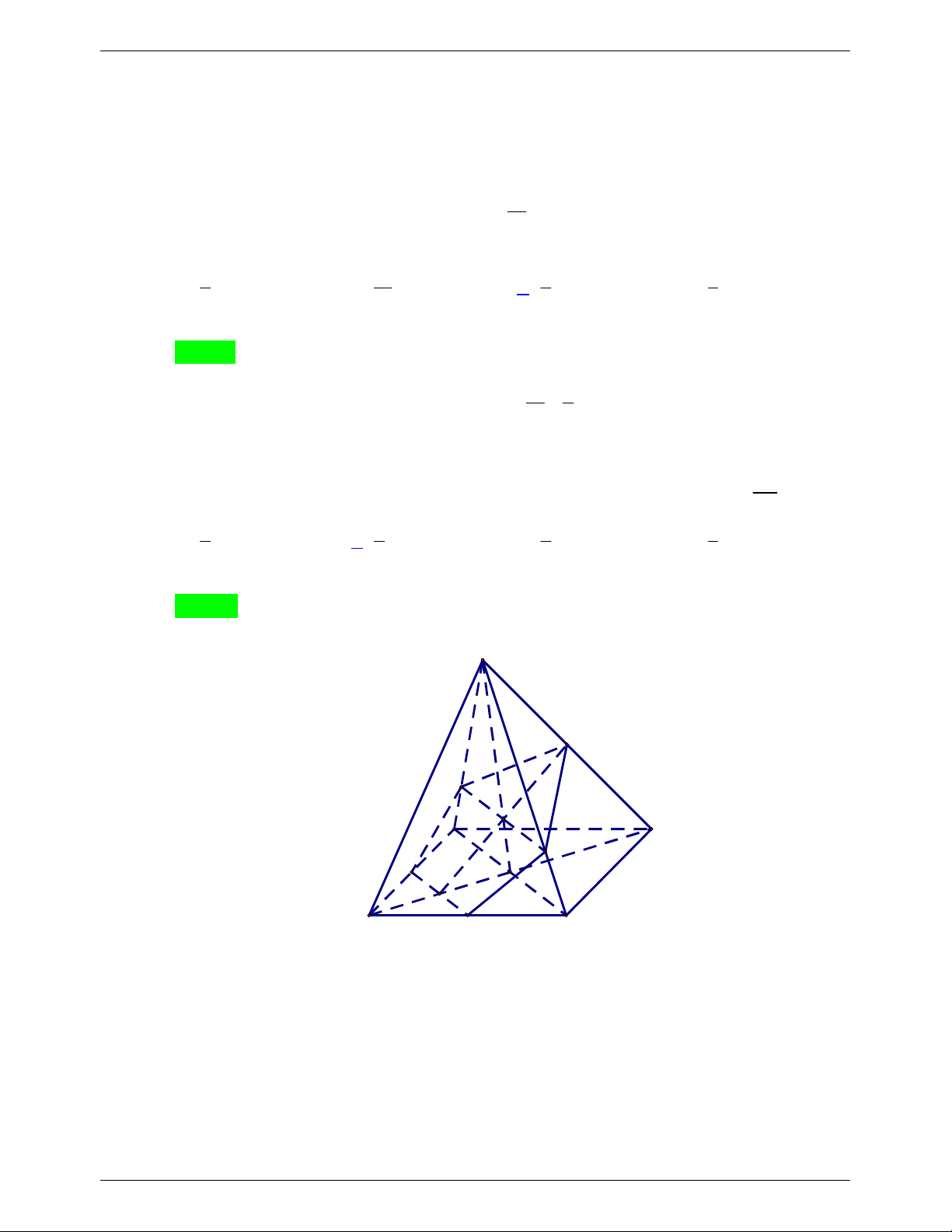
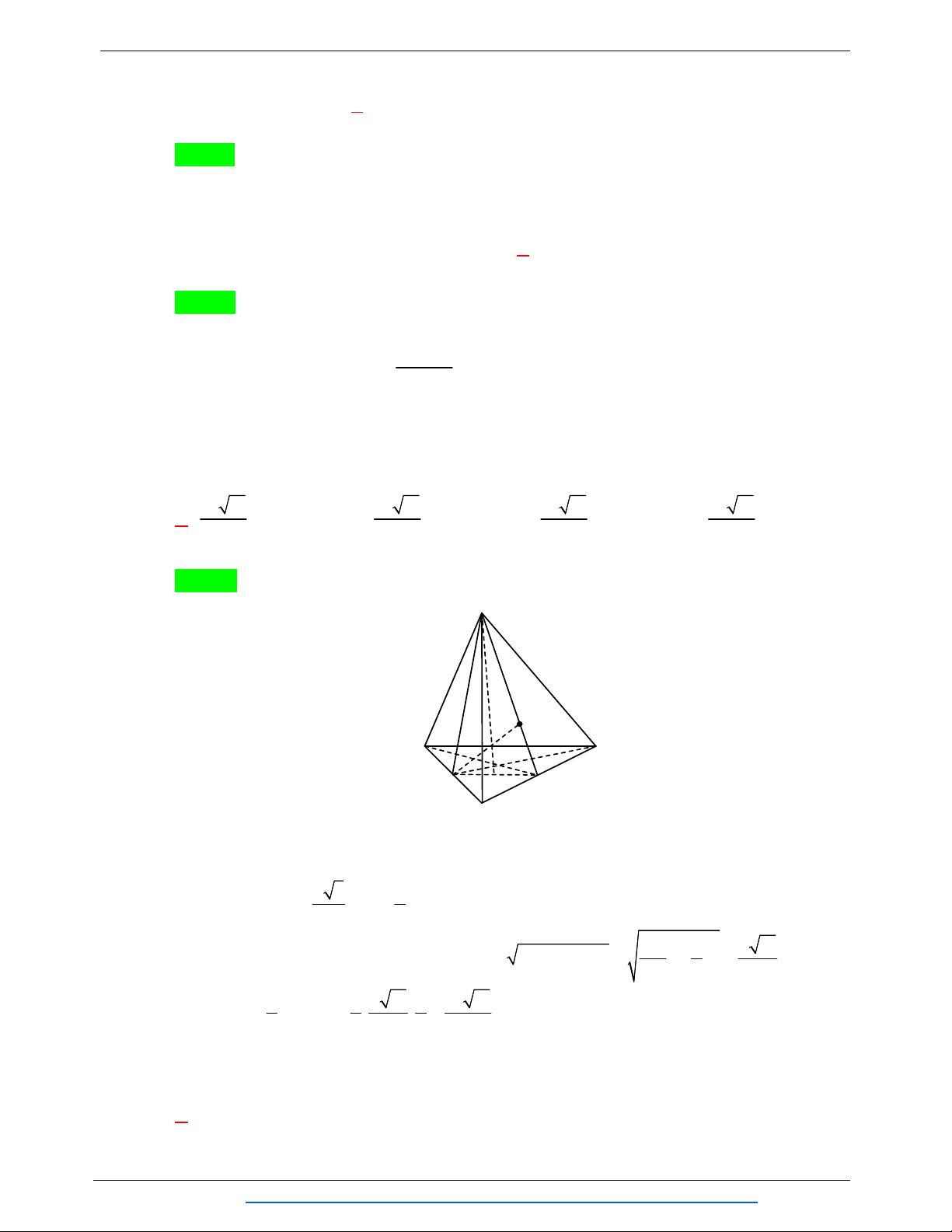
Câu 25: Cho tứ diện ABCD đều cạnh a . Gọi G là trọng tâm tam giác ABC , mặt phẳng CGD cắt tứ
diện theo một thiết diện có diện tích là. 2 a 2 2 a 3 2 a 2 2 a 3 A. . B. . C. . D. . 6 4 4 2 B. TỰ LUẬN Bài 1. Giải phương trình: 2 2
3 cos x  sin 2x  3 sin x  1. Bài 2. a) Cho 2 (x  2)n n
 a  a x  a x  a x . Tìm n để a : a 12 : 7 . 0 1 2 n 5 6
b) Trong một hộp có 10 viên bi màu xanh và 8 viên bi màu đỏ. Bạn Bình lấy ngẫu nhiên 1 viên bi
(lấy xong không trả lại vào hộp), sau đó bạn An lấy tiếp 1 viên bi nữa. Tính xác suất để
hai bạn lấy được bi cùng màu.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 9
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Bài 3.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm các cạnh AB, CD .
a) Chứng minh rằng: MN song song với mặt phẳng (SBC), (SAD).
b) Gọi P là trung điểm SA . Chứng minh rằng: SB, SC song song với mặt phẳng (MNP).
c) Gọi G ;G lần lượt là trọng tâm tam giác ABC, SBC . Chứng minh rằng: đường 1 2
thẳng G1G2 song song với mặt phẳng (SAC).
d) Dựng thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng PNG . 2  Bài 4.
Cho cấp số cộng u có số hạng đầu u  3 và công sai d  5. Tính u , u và S (tổng n  1 2 7 8
của 8 số hạng đầu tiên trong cấp số cộng u ). n  2n   Bài 5. Cho dãy số  1 u với u  cos . n  n 3
a) Chứng minh rằng u  u với mọi n 1. n n3
b) Hãy tính tổng của 17 số hạng đầu tiên của dãy số đã cho. ----------HẾT---------- Trang 10
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1 BẠC LIÊU NĂM HỌC: 2019 - 2020 --------------------------- Thời gian: 90 phút KHỐI 11
Họ tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . A. TRẮC NGHIỆM
Câu 1: Nghiệm của phương trình 2cos x  3  0 là     x   k2  x   k2  A. 6  k . C. 3  k .   2 x   k2   x   k2  6  3 B.  
x    k 2 k  .
D. x    k2 k  . 3 6
Câu 2: Cho hình bình hành ABCD . Khẳng định nào sau đây là đúng
A. T  A  D .
B. T D  A .
C. T  A  B .
D. T C  B . BC BC BC BC
Câu 3: Phương trình cos x  sin 3x  2 cos x  sin xsin 4x có tổng tất cả các nghiệm x0;  là   A. 2. B. 6. C. 11 . D. 5 . 8 8
Câu 4: Trong mặt phẳng tọa độ Oxy , tìm phương trình đường thẳng  ' là ảnh của đường 
thẳng  : x  2y 1  0 qua phép tịnh tiến theo vecto v  1;  1
A.  ': x  2y  2  0 . B.  ': x  2y  0.
C.  ': x  2y  3  0 . D.  ': x  2y 1  0 .
Câu 5: Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá của mét khoan đầu tiên là
10.000 đồng và kể từ mét khoan thứ hai, giá mỗi mét khoan sau tăng thêm 3000 đồng
so với giá mét khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan
giếng này để khoan một giếng sâu 100mét lấy nước dùng cho sinh hoạt gia đình. Hỏi
sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan
giếng số tiền bằng bao nhiêu A. 15.580.000 đồng.
B. 18.500.000đồng. C. 15.850.000đồng. D. 15.050.000đồng. Câu 6: n
Cho dãy số u có số hạng tổng quát u 
n   . Số hạng thứ tư của dãy số u n  n n  *  n  2 là A. 1 . B. 1 . C. 1 . D. 1 . 2 16 4 8
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N, P lần lượt là
trung điểm của AB, AD, SC . Gọi Q là giao điểm của SD với (MNP) . Tính SQ . SD A. 1 . B. 3 . C. 2 . D. 1 . 4 4 3 3
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 11
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 8: Từ 20 học sinh ưu tú gồm 10 nam và 10 nữ, người ta muốn lập một đoàn đại biểu
gồm 6 người để tham dự một buổi hội thảo, trong đó có 1 trưởng đoàn là nam và 2
phó đoàn là nữ. Hỏi có bao nhiêu cách thành lập một đoàn đại biểu như vậy? A. 27907 200 . B. 306000 . C. 38760. D. 513000.
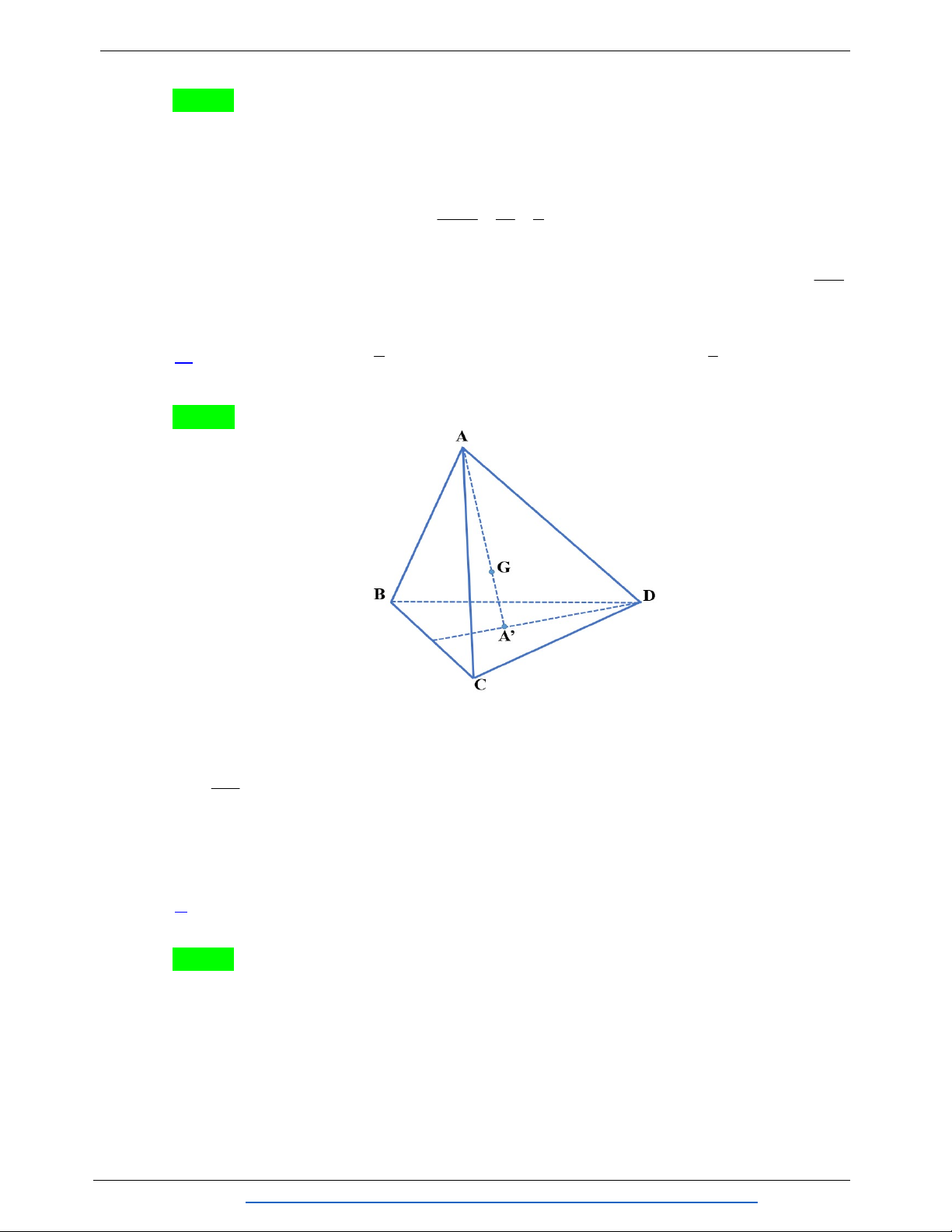
Câu 9: Cho tứ diện ABCD , G là trọng tâm tam giác ABD , M là điểm trên cạnh BC sao cho
MB  2MC . Khẳng định nào sau đây đúng? A. MG //  ACD . B. MG //  ABC . C. MG //  ABD. D. MG // BCD.
Câu 10: Từ các chữ số của tập A  1;2;3;4;5;6; 
8 có thể lập được bao nhiêu số tự nhiên có ba
chữ số đôi một khác nhau ? A. 3 8 . B. 3 C . C. 3 A . D. 8 3 . 7 7 Câu 11: Hệ số của 10
x trong khai triển  x  10 2 3 1 bằng A. 0 0 3 C . B. 5 10 3 C . C. 10 10 3 C . D. 5 5 3 C . 10 10 10 10
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, O là giao điểm AC và BD .
Gọi M , N lần lượt là trung điểm SA, SB . Giao tuyến của hai mặt phẳng SAC và SBD là A. SO . B. SM . C. SN . D. SD .
Câu 13: Trong mặt phẳng Oxy , cho hai đường thẳng  : 2x  y  2  0 ,  ' : 2x  y  2  0 và 
vectơ v  (2;0) . Khẳng định nào sau đây đúng? A. V ()   '. B. Q ()   ' . C. T ()   ' . D. Q ()   '. (0;3) 0 (0;90 ) v 0 (0;180 )
Câu 14: Trong mặt phẳng Oxy , tìm ảnh đường tròn (C ') của đường tròn 2 2
(C) : x  y  2x  4y  0 qua phép vị tự tâm 0 tỉ số k  2 A. 2 2 (C )
 : (x  2)  (y  4) 10 . B. 2 2 (C )
 : (x  2)  (y  4)  20 . C. 2 2 (C )
 : (x  2)  (y  4)  20 . D. 2 2 (C )
 : (x  2)  ( y  4) 10 .
Câu 15: Có bao nhiêu số hạng là số nguyên trong biểu thức   30 3 2 3 ? A. 6 . B. 8 . C. 7 . D. 5.
Câu 16: Phương trình sin 2x  3 cos2x  1
 tương đương với phương trình     A.       sin 2x   sin   . B. sin 2x   sin  .  3  3      3   3      C.      sin 2x   sin    . D. sin 2x   sin  .  3  6      3   6 
Câu 17: Trong mặt phẳng Oxy , cho điểm I 1; 2
  . Gọi I là ảnh của I qua phép vị tự V . O;2
Khi đó, I có tọa độ là A. 2;4 . B. 4;2 . C. 4;2 . D. 2;4 . Câu 18:   
Điều kiện để hàm số y  tan x  1   xác định là  4   
A. x    k k .
B. x   k k  . 4 4 Trang 12
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1  
C. x   k k  .
D. x    k k  . 2 4
Câu 19: Trong một cuộc thi, Ban tổ chức dùng 7 cuốn sách môn Toán, 6 cuốn sách môn Vật
lý và 5 cuốn sách môn Hóa học để làm phần thưởng cho 9 học sinh có kết quả cao
nhất. Các cuốn sách cùng thể loại Toán, Vật lý, Hóa học đều giống nhau. Mỗi học sinh
nhận thưởng sẽ được hai cuốn sách khác nhau, trong đó có An. Tính xác suất để An
nhận thưởng có sách Toán. A. 7 . B. 11 . C. 7 . D. 9 . 18 18 9 18
Câu 20: Số nghiệm của phương trình 3 sin x  là 2 A. 4 . B. 2 . C. 0 . D. 1.
Câu 21: Long và Hưng cùng 8 bạn rủ nhau đi xem bóng đá. Số cách xếp nhóm bạn trên vào
10 chỗ ngồi sắp hàng ngang sao cho Long và Hưng ngồi cạnh nhau là: A. 9.8!. B. 18.8!. C. 8!. D. 9!. Câu 22:   
Định m để phương trình có nghiệm: 6 6 2
sin x  cos x  cos 2x  m với 0  x    .  8  A. 3 1 0  m  1. B. 0  m  2 . C. 0  m  . D. 0  m  . 8 8
Câu 23: Tại một buổi lễ có 13 cặp vợ chồng tham dự, mỗi ông bắt tay với một người trừ vợ
mình, các bà không ai bắt tay nhau. Hỏi có bao nhiêu cái bắt tay? A. 234 . B. 312. C. 78. D. 185.
Câu 24: Cho cấp số cộng u biết u  6 , u 16 . Tính công sai d và tổng của 10 số hạng đầu n  3 8 tiên. A. d  2 ; S 100 . B. d 1; S  80 .
C. d  2 ; S 120 . D. d  2 ; S 110 . 10 10 10 10
Câu 25: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x  y 1  0 để phép tịnh tiến theo véctơ  
v biến d thành chính nó thì v phải là véctơ nào trong các véctơ sau : A.     v  2;  1 . B. v  2;  1 . C. v  1;2 . D. v   1  ;2. B. TỰ LUẬN
Câu 1: Giải phương trình 2cos x 1 0 Câu 2:
a) Từ một hộp chứa 7 quả cầu màu đỏ và 5quả cầu màu vàng, Hùng lấy ngẫu nhiên
đồng thời 3quả cầu. Tính xác suất để Hùng lấy được 3 quả cầu trong đó có hai quả cầu màu đỏ.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 13
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
b) Tìm số hạng không chứa   x trong khai triển của 2 n x  
 , biết n là số tự nhiên thỏa  x  mãn 1 2 3 2n 496 C  C  C ... C  2 1 4n 1  4n 1  4n 1  4n 1 
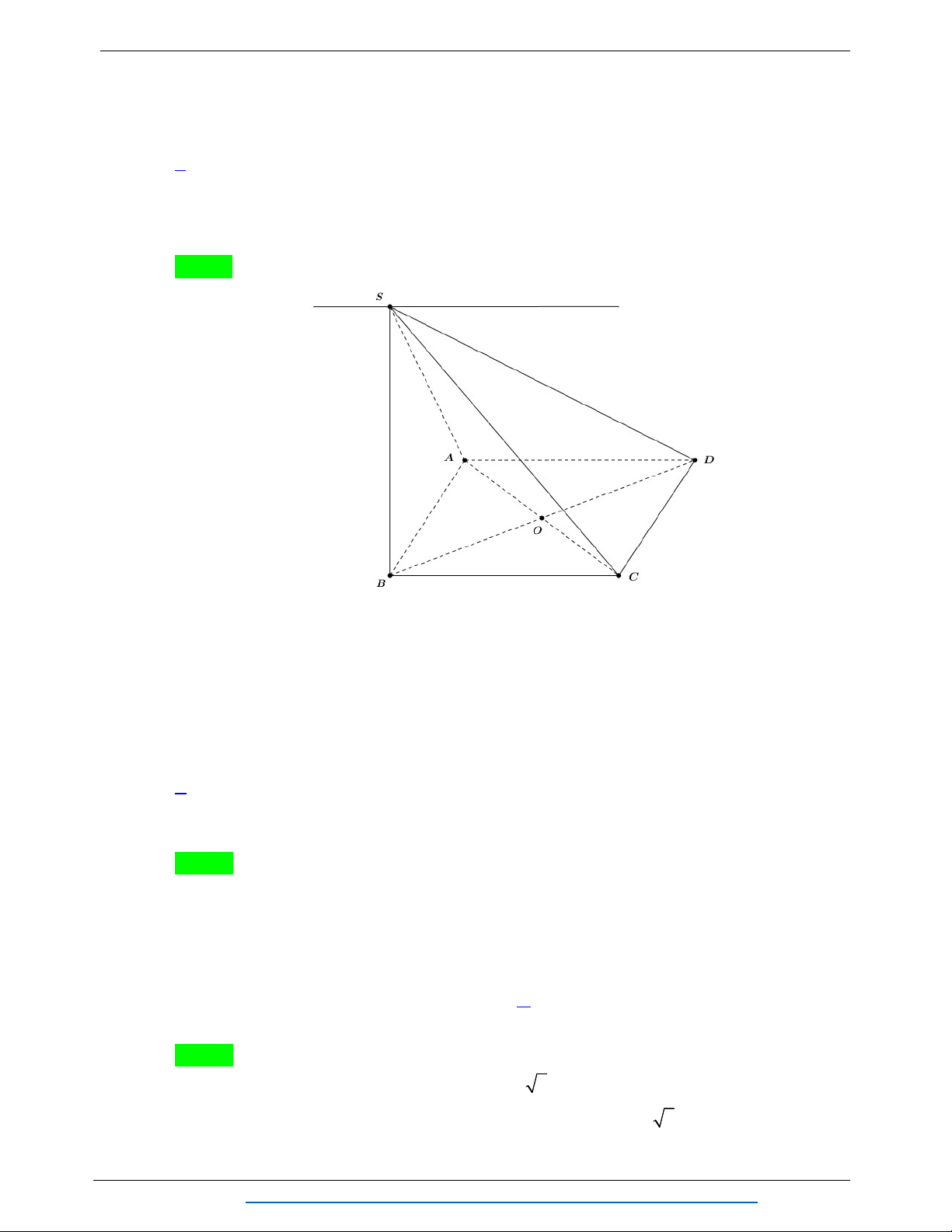
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình thang, với đáy lớn AD và AD  2BC .
a) (1,0 điểm) Tìm giao điểm của đường thẳng CD và mặt phẳng SAB .
b) (0,5 điểm) Gọi I là điểm nằm trên cạnh SC sao cho 2SC  3SI . Chứng minh đường
thẳng SA song song với mặt phẳng BID . 40 Câu 4:  1  Tìm hệ số của 31 x trong khai triển x  , x  0  2   x 
Câu 5: Rút gọn tổng S   2      2      2       2 1 1 1 .1! 2 2 1 2! 3 3 1 .3! ... n  n   1 .n! . ----------HẾT---------- Trang 14
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1 HƯNG YÊN NĂM HỌC: 2019 - 2020 --------------------------- Thời gian: 90 phút KHỐI 11
Họ tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . A. TRẮC NGHIỆM
Câu 1. Tính tổng S tất cả các hệ số trong khai triển  x  11 3 4 : A. S  1 . B. S  1 . C. S  0 . D. S  8192 .
Câu 2. Làng Duyên Yên, xã Ngọc Thanh, huyện Kim Động, tỉnh Hưng Yên nổi tiếng với trò
chơi dân gian đánh đu. Trong trò chơi này, khi người chơi nhún đều thì cây đu sẽ đưa
người chơi dao động qua lại ở vị trí cân bằng. Nghiên cứu trò chơi này, người ta thấy
rằng khoảng cách h (tính bằng mét) từ người chơi đu đến vị trí cân bằng được biểu
diễn qua thời gian t (t  0 và được tính bằng giây) bởi hệ thức h  d với   d  3cos 2t   1 
trong đó quy ước rằng d  0 khi vị trí cân bằng ở phía sau lưng 3   
người chơi đu và d  0 trong trường hợp trái lại. Tìm thời điểm đầu tiên sau 10 giây
mà người chơi đu ở xa vị trí cân bằng nhất. A. Giây thứ 13 . B. Giây thứ 12,5 . C. Giây thứ 10,5 . D. Giây thứ 11.
Câu 3. Bạn An muốn mua một chiếc áo sơ mi cỡ 39 hoặc 40 . Biết áo cỡ 39 có 3 màu khác
nhau, áo cỡ 40 có 5 màu khác nhau. Hỏi bạn An có bao nhiêu lựa chọn để mua một chiếc áo ? A. 8 . B. 3 . C. 5 . D. 15 .
Câu 4. Số đường chéo của đa giác 10 cạnh là A.35. B.7 . C. 45. D. 10.
Câu 5. Từ các chữ số của tập hợp A  1; 2; 3; 4; 5; 
6 có thể lập được bao nhiêu số tự nhiên có
3 chữ số mà các chữ số đôi một khác nhau? A.125. B.120. C. 6 . D. 10.
Câu 6. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
B. Hai đường thẳng phân biệt không chéo nhau thì hoặc cắt nhau hoặc song song.
C. Hai đường thẳng không có điểm chung thì chéo nhau.
D. Hai đường thẳng chéo nhau thì không có điểm chung.
Câu 7. Mệnh đề nào sau đây là đúng? A. 0 1 n 1  n 1  n2 2 C  C  ...  C  C  C  ...  n C . 2n 2n 2n 2n 2n 2n B. 0 1 n2 n 1  n2 2 C  C  ...  C  C  C  ... n C . 2n 2n 2n 2n 2n 2n
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 15
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT C. 0 1 n 1  n 1  n2 2 C  C  ...  C  C  C  ... n C . 2n 2n 2n 2n 2n 2n D. 0 1 n n 1  n2 2 C  C  ...  C  C  C  ... n C . 2n 2n 2n 2n 2n 2n
Câu 8. Chọn ngẫu nhiên một hộp chứa 16 thẻ được đánh số từ 1 đến 16. Tính xác suất để
nhận được thẻ đánh số lẻ. A. 9 . B. 1 . C. 3 . D. 7 . 16 2 8 16
Câu 9. Từ một cỗ bài tú lơ khơ 52 quân, rút ngẫu nhiên cùng một lúc 4 quân bài. Tính xác
suất sao cho cả 4 quân đều là K? A. 1 . B. 4 . C. 1 . D. 4 . 6497400 6497400 270725 270725 Câu 10: Phương trình  5  cos x   1   có nghiệm là  6  A.     x   k . B. x   k2 . C. 5 x   k . D. 5 x   k2 . 3 3 6 6
Câu 11: Một hộp chứa 6 quả cầu đỏ khác nhau và 4 quả cầu xanh khác nhau. Chọn ngẫu
nhiên cùng một lúc 2 quả cầu từ hộp. Tính xác suất của biến cố “Lấy được hai quả cùng màu”. A. 7 . B. 4 . C. 8 . D. 7 . 15 9 15 45
Câu 12: Lớp 11A có 35 học sinh nam và 10 học sinh nữ. Hỏi có bao nhiêu cách chọn ngẫu
nhiên một bạn trong lớp ? A. 20 . B. 50. C. 45 . D. 25 .
Câu 13. Gọi M là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos2x  cos x  2 . Tính M  m A. 25 . B. 4 . C. 21 . D. 2 8 8
Câu 14. Có bao nhiêu số tự nhiên có 8 chữ số đôi một khác nhau được lập từ tập A  1,2,3, 4,5,6,7, 
8 sao cho số đó chia hết cho 1111? A. 384. B. 345. C. 3840. D. 1920 .
Câu 15. Trong mặt phẳng tọa độ Oxy , ảnh của đường thẳng d : x  2y  3  0 qua phép đối xứng tâm I(4;3) là: A. x  2y 17  0 B. x  2y  7  0.
C. x  2y 17  0. D. x  2y 15  0 .
Câu 16: Điều kiện cần và đủ để phương trình asin x  bcos x  c có nghiệm là A. 2 2 a  b  c . B. 2 2 2 a  b  c . C. 2 2 a  b  c . D. 2 2 2 a  b  c .
Câu 17: Hàm số nào sau đây có đồ thị nhận gốc tọa độ O làm tâm đối xứng? A. 2 y  sin x . B. y  cos x . C. y  tan x . D. 2 y  cot x .
Câu 18: Có bao nhiêu cách lấy ngẫu nhiên cùng lúc 3 ba quả cầu từ một hộp chứa 10 quả cầu khác nhau A. P . B. 3 C . C. P . D. 2 A . 2 10 10 10 Câu 19: Tính tổng 0 1 2 2 S  C  C  C  ... n  C . 2n 2n 2 n 2n A. 2 2 n S  . B. 2 2 n S  1. C. 2n S  . D. 2 2 n S  1 . Trang 16
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Câu 20: Cô dâu và chú rể mời 6 người ra chụp ảnh kỉ niệm, người thợ chụp hình có bao nhiêu
cách sắp xếp sao cho cô dâu, chú rể đứng cạnh nhau. A. 6.7!. B. 2.7!. C. 8! 7!. D. 2! 6!.
Câu 21: Cho hình vuông ABCD tâm I . Gọi M , N lần lượt là trung điểm của AD, DC . Phép
tịnh tiến theo véc tơ nào sau đây biến AMI thành M  DN ?     A. AC . B. AM . C. NI . D. MN .
Câu 22: Cho hai đường thẳng cắt nhau d và d . Có bao nhiêu phép đối xứng trục biến đường
thẳng này thành đường thẳng kia? A. Vô số. B. Hai. C. Không có. D. Một
Câu 23: Tìm hệ số của 5 x trong khai triển  11 1 x . A. 55440. B. 462 . C. 246 . D. 252
Câu 24: Cho ba mặt phẳng phân biệt  ,  ,   có       d ;      d ; 1 2
     d . Khi đó ba đường thẳng d , d , d : 3 1 2 3 A. Đôi một song song. B. Đồng quy. C. Đôi một cắt nhau.
D. Đôi một song song hoặc đồng quy
Câu 25: Hãy mô tả không gian mẫu của phép thử: “Gieo một đồng xu cân đối và đồng chất hai lần liên tiếp”. A.   SS, NN. B.   S, N .
C.   SS, SN, NS, NN. D.   SN, NS. B. TỰ LUẬN
Câu 1. Giải các phương trình sau đây a) 2
cos x  3cos x  2  0 . b) 2cos x  
1 2sin x  cos x  sin 2x  sin x
Câu 2. Một lớp học có 15 nữ và 20 nam. Có bao nhiêu cách chọn ra từ lớp đó 10 bạn sao cho có ít nhất 1 bạn nam ? 12 Câu 3.  1 
Tìm số hạng không chứa x trong khai triển thành đa thức của biểu thức 3x   . 3   x 
Câu 4. Tìm tất cả các giá trị thực của tham số m sao cho phương trình lượng giác sau đây có nghiệm:
m sin 2x 12 cos 2x  13 .
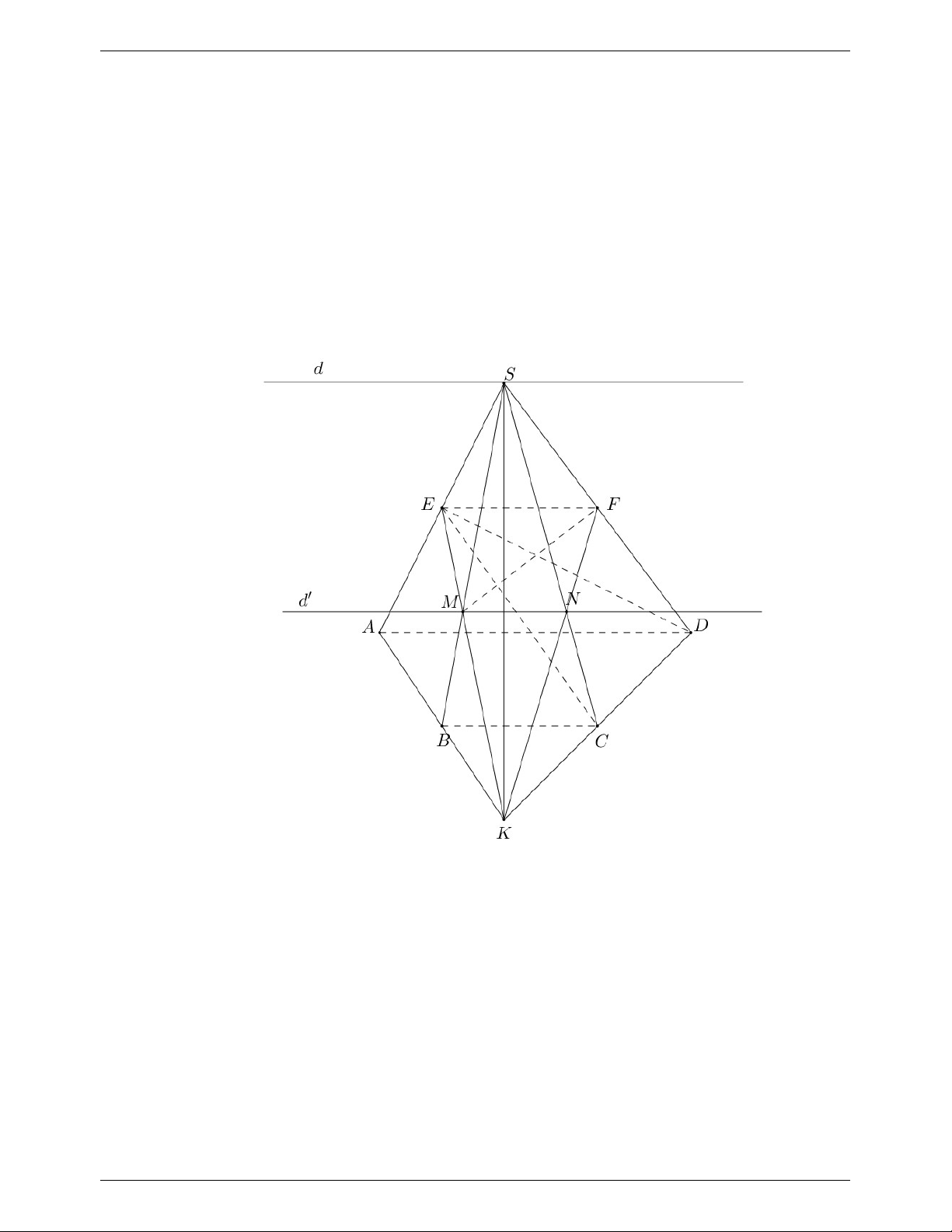
Câu 5. Cho hình chóp S.ABCD , có đáy ABCD là hình thang có đáy lớn AD . Gọi E,F lần
lượt là trung điểm của S , A SD .
a) Tìm giao tuyến của các cặp mặt phẳng: SAC và SBD , SAD và SBC.
b) Chứng minh EF// ABCD và EF //SBC.
c) Gọi K là giao điểm của AB và CD . Tìm M , N lần lượt là giao điểm của SB và
CDE; SC và EFM  . Từ đó, tìm thiết diện của hình chóp cắt bởi mặt phẳng KEF.
d) Cho AD  2BC . Tính tỉ số diện tích của tam giác KMN và tam giác KEF . ----------HẾT----------
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 17
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1 HUẾ NĂM HỌC: 2019 - 2020 --------------------------- Thời gian: 90 phút KHỐI 11
Họ tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . A. TRẮC NGHIỆM
Câu 1. Tìm hệ số của 3 3
x y trong khai triển biểu thức   6 x y A. 20. B. 6. C. 15. D. 1.
Câu 2. Hàm số nào sau đây là hàm số chẵn? A. y  tan . x B. y  cot . x C. y  cos . x D. y  sin . x
Câu 3. Tập xác định của hàm số y  sin 2x? A. D   ;  2. B. D  .  C. D   \  2 . D. D  2;.
Câu 4. Một nhóm công nhân có 15 người trong đó có 10 nam và 5 nữ. Có bao nhiêu cách
chọn 6 người đi dự đại hội công ty? A. 4785. B. 3603600. C. 720. D. 5005.
Câu 5. Trong mặt phẳng Oxy , cho điểm A1; 0 . Tìm ảnh của A qua phép dời hình có được
bằng cách thực hiện liên tiếp phép quay tâmO góc quay 90 và phép tịnh tiến theo  véctơ v  2 ; 0 . A. A2 ;   1 . B. A 2  ;  1 . C. A2 ;  1 . D. A1; 2 .
Câu 6. Cho dãy số u là cấp số cộng có u  3
 , u  27 . Tìm công sai d ? n  1 6 A. d  5. B. d  4 . C. d  6 . D. 24 d  . 5 Câu 7. Cho 3 2 P  n  3n  5n với n 
 . Khẳng định nào sau đây đúng? n
A. P chia hết cho 2 . B. P chia hết cho 5 . C. P chia hết cho 6 . D. P chia hết cho 3 . n n n n
Câu 8. Có 5 học sinh gồm 2 nữ và 3 nam được xếp vào dãy ghế được đánh số 1,2,3,4,5. Hỏi
có bao nhiêu cách sắp xếp chổ ngồi cho 5 học sinh nói trên, biết rằng vị trí số 1 phải
dành cho một học sinh nữ? A. 52. B. 48. C. 50. D. 42.
Câu 9. Tính chất nào sau đây không phải là tính chất của phép đồng dạng.
A. Biến đường tròn thành đường tròn có cùng bán kính.
B. Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và bảo toàn thứ tự của 3 điểm đó.
C. Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.
D. Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.
Câu 10. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi O là giao điểm của AC và BD .
Xác định giao tuyến của hai mặt phẳng SAD và SBC.
A. Đường thẳng qua S và song song với AC .
B. Đường thẳng qua S và song song với AD . Trang 18
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
C. Đường thẳng qua S và song song với AB . D. Đường thẳng SO .
Câu 11. Cho A và B là hai biến cố liên quan đến một phép thử. Khẳng định nào sau đây sai?
A. nếu A   thì A là biến cố chắc chắn.
B. Nếu A B   thì A và B là hai biến cố xung khắc.
C. Nếu A  B   thì A và B là hai biến cố đối nhau.
D. Nếu A   thì A là biến cố không. 
Câu 12. Trong mặt phẳng Oxy , phép tịnh tiến theo vec tơ v  1;3 biến đường tròn
C x  2   y  2 : 1
2  6 thành đường tròn có phương trình nào sau đây? A. x   y  2 2 1  6 .
B.  x  2   y  2 2 5  6 . C. x   y  2 2 1  6 .
D.  x  2   y  2 2 5  6 .
Câu 13. Trong mặt phẳng Oxy , phép quay tâm Ogóc quay 90o 
biến điểm M thành M '(3; 1  ) Tìm tọa độ điểm M . A. M (3;1). B. M (1;3). C. M (1; 3  ). D. M (3;1). Câu 14.  
Tìm tất cả các nghiệm của phương trình 1 sinx  thỏa mãn  x  2 2 2     A. x   k2. B. x  . C. 5 x   k2. D. x  . 3 3 6 6
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC
và BD. Gọi I, J lần lượt là trung điểm của SA và S .
B Khẳng định nào sau đây sai? A. IJ//(ABCD) và IJ//(SCD) B. IJCD là hình thang. C. IJ và SO chéo nhau
D. (IJC) cắt hình chóp S.ABCD theo thiết diện là tam giá IJC.
Câu 16. Từ một đội học sinh giỏi Toán có 3 nam và 5 nữ, chọn ngẫu nhiên 2 em đi thi học sinh
giỏi Toán. Tính xác suất để chọn được 1 nam và 1 nữ. A. 15 . B. 25 . C. 15 . D. 8 . 56 28 28 56
Câu 17. Trong không gian có bao nhiêu vị trí tương đối giữa hai đường thẳng. A. 3. B. 4. C. 5. D. 2.
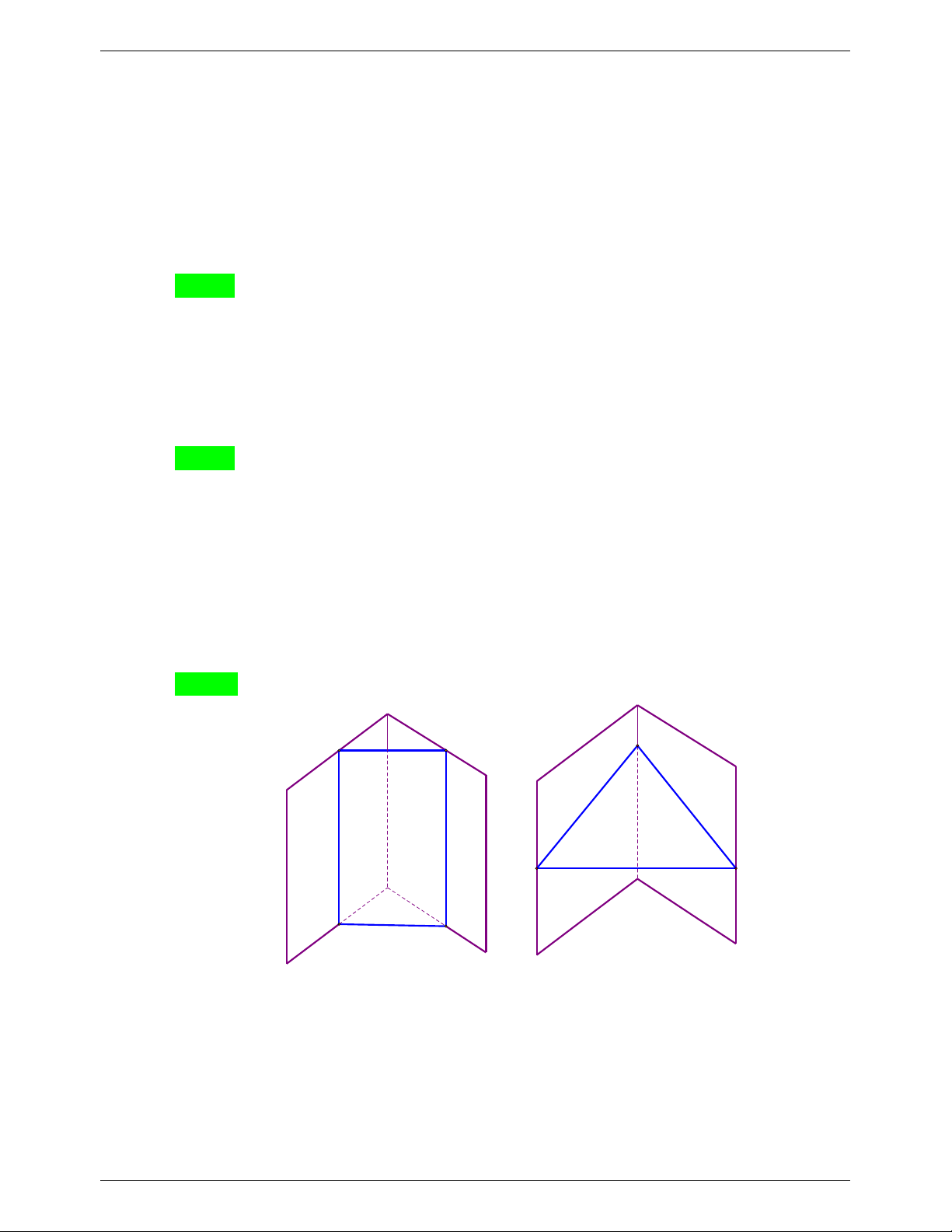
Câu 18. Các hình sau đây biểu diễn một hình chóp tứ giác trong không gian. Hình nào sai? Hình 4 Hình 1 Hình 2 Hình 3 A. Hình 2. B. Hình 3. C. Hình 4. D. Hình 1.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 19
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Câu 19.   
Tìm nghiệm của phương trình: 2
sin x  sinx  0 thỏa mãn  x  . 2 2     A. x  . B. x  . C. x  . D. x  0. 4 2 2 Câu 20. n
Cho dãy số u với u  . Tìm u . n  n 2 5 n 1 A. 5 5 5 u  . B. u  . C. u  . D. u  5. 5 26 5 5 5 6 26
Câu 21. Từ các chữ số 2,3,4,6,7,9 lập được bao nhiêu số chẵn có ba chữ số? A. 108. B. 36. C. 20. D. 40. 
Câu 22. Trong mặt phẳng Oxy , cho v  (2;1) và điểm M ( 3
 ;2). Tìm điểm M ' là ảnh của điểm 
M qua phép tịnh tiến theo vectơ . v A. M '( 1  ;1). B. M '(1; 1  ). C. M '(1;0). D. M '(1;1).
Câu 23. Trong mặt phẳng Oxy , cho đường thẳng d : 2x  3y  3  0 . Tìm phương trình đường
thẳng d là ảnh của d qua phép vị tự tâm O tỉ số k  2. A. 4x  2y  3  0 . B. 4x  2y  5  0 . C. 2x  y  3  0. D. 2x  3y  6  0 .
Câu 24. Cho dãy số u là cấp số cộng có số hạng đầu u , công sai d , S là tổng của n số n  1 n
hạng đầu tiên. Với n  2 , đẳng thức nào sau đây sai?  A. u u u  u  n 1 d . B. n 1 n 1 u    . n 1   n 2 C. n u  u  d . D. S  u  n 1 d  n  1   n 1  n 2  .
Câu 25. Tìm tập giá trị T của hàm số y  3 2sin x . A. T  2;4. B. T  1;  5 . C. T   1  ;  1 . D. T  0;  3 . B. TỰ LUẬN
Câu 1. Giải phương trình: sin x  3cos x 1.
Câu 2. Trong khoảng (0;3 ), phương trình 3 sin 2x  có bao nhiêu nghiệm? 2
Câu 3. Một hộp chứa 10 quả cầu được đánh số từ 1 đến 10. Lấy ngẫu nhiên một quả. Tính xác
suất của biến cố A: “Nhận được quả cầu ghi số chẵn”. 6 Câu 4.  2 
Tìm số hạng không chứa x trong khai triển x  , x  0   .  x 
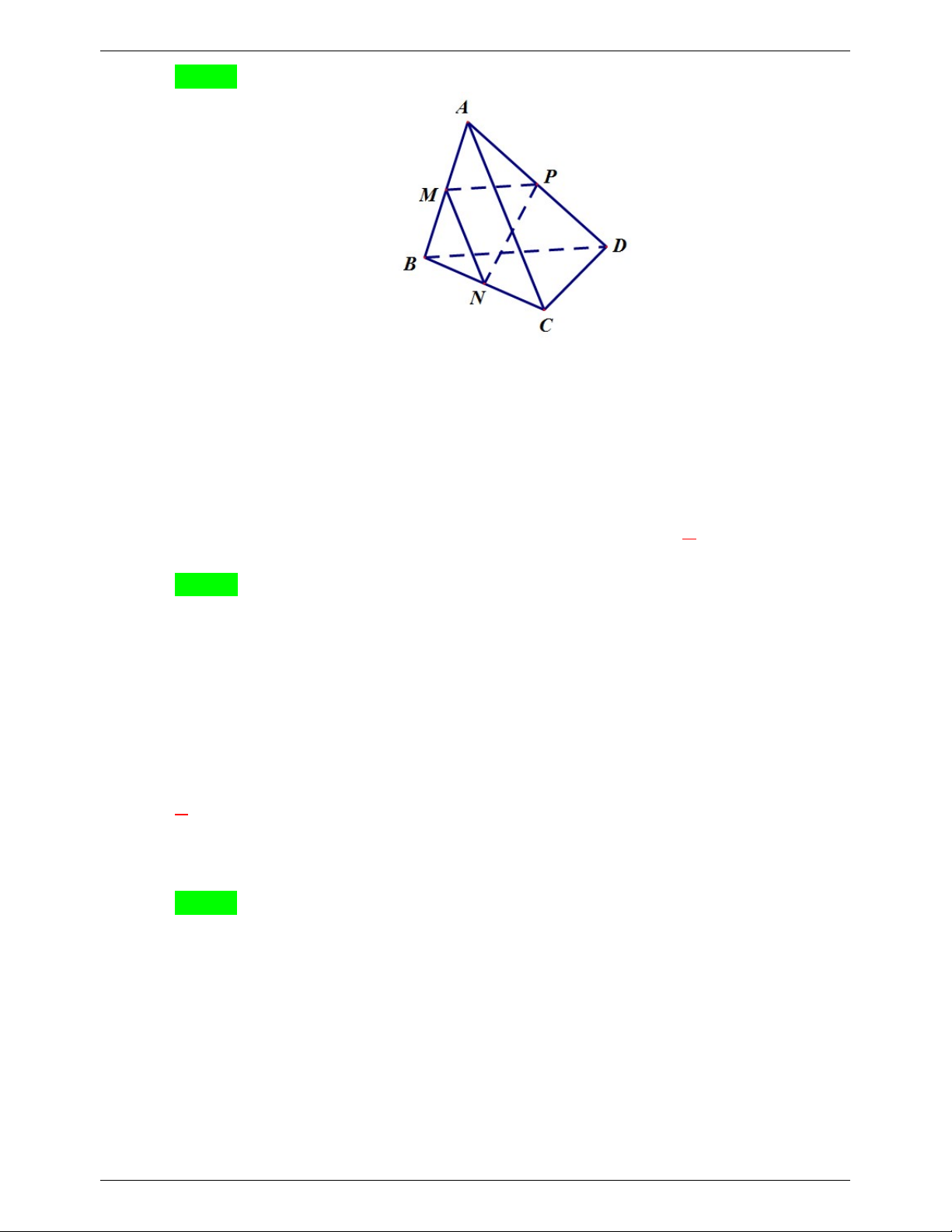
Câu 5. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Trên cạnh CD lấy
điểm P sao cho PD  2PC .
a) Tìm giao điểm của đường thẳng BD và mặt phẳng MNP .
b) Tìm giao tuyến của mặt phẳng MNP và  ABD. ----------HẾT---------- Trang 20
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1 HUẾ NĂM HỌC: 2019 - 2020 --------------------------- Thời gian: 90 phút THPT CHUYÊN QUỐC HỌC KHỐI 11
Họ tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . A. TRẮC NGHIỆM
Câu 1: Tìm tập xác định của hàm số 1 y  . sin x A.   D   \k ,k    .
B. D   \   k,k  .  2  C. D   \  0 . D. D   .
Câu 2: Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Hình nào sau đây không thể là thiết diện của nó. A. Lục giác. B. Tam giác. C. Tứ giác. D. Ngũ giác.
Câu 3: Có 10 cây bút khác nhau và 9 quyển sách khác nhau. Tìm số cách chọn 1 cây bút và 1 quyển sách. A. 80 . B. 70 . C. 19 . D. 90 .
Câu 4: Một hộp chứa 6 quả bóng đỏ (được đánh số từ 1 đến 6), 5 quả bóng vàng (đươc
đánh số từ 1 đến 5), 4 quả bóng xanh (được đánh số từ 1 đến 4). Lấy ngẫu nhiên 4
quả bóng. Tính xác suất để 4 quả bóng lấy ra có đủ ba màu và không có hai quả bóng
nào có số thứ tự trùng nhau. A. 43. B. 74 . C. 381. D. 48. 91 455 455 91
Câu 5: Tìm số cách xếp 5 bạn nam và 4 ban nữ thành một hàng ngang sao cho 4 bạn nữ luôn đứng cạnh nhau. A. 17280. B. 362880. C. 5760. D. 2880.
Câu 6: Cho tập hợp A  0;2;4;5; 
6 , tìm số chỉnh hợp chập 3 của . A A. 60. B. 96. C. 20. D. 10.
Câu 7: Gieo đồng thời 2 con súc sắc cân đối, đồng chất, một con màu đỏ và một con màu đen.
Tính xác suất của biến cố: “Số chấm trên con đen lớn hơn số chấm trên con đỏ 2 đơn vị.” 5 9 32 1 A. . . . . 36 B. 36 C. 36 D. 9 1 sinx
Câu 8: Gọi M là tổng các nghiệm thuộc  ;5 của phương trình  1, tìm M. cosx 15 23 27 A. M  13 .  B. M   . C. M   . D. M   . 2 2 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 21
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Câu 9: Cho A
 BC vuông tại B và A  60 (các đỉnh của tam giác ghi theo thứ tự ngược
chiều kim đồng hồ). Về phía ngoài tam giác, vẽ tam giác đều ACD. Tìm ảnh của cạnh
BC qua phép quay tâm A, góc quay 60 .
A. AI với I là trung điểm của CD.
B. DK với K là trung điểm của AC. C. AD.
D. CJ với J là trung điểm của AD.
Câu 10: Tìm số điểm biểu diễn các họ nghiệm của phương trình 2
2sin x  3sin x  5  0 trên
đường tròn lượng giác là. A. 2. B. 3. C. 1. D. 4.
Câu 11: Tìm điều kiện của tham số thực m để phương trình msin x  3cos x  5 có nghiệm. m  4 A. m  4. B. m  34. C. .  D. 4   m  4. m  4
Câu 12: Cho cấp số cộng có số hạng đầu u  1 và công sai d  2
 . Tổng n số hạng đầu tiên 1
của cấp số cộng này là S  9  800, tìm . n n A. 101. B. 100. C. 98. D. 99.
Câu 13: Tìm số các nghiệm thuộc 0;2019  của phương trình 3 cot x 3  0 . A. 2018. B. 2019. C. 4038. D. 4039.
Câu 14: Tìm mệnh đề sai trong các mệnh đề sau đây.
A. Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
B. Phép đồng dạng bảo toàn độ lớn góc.
C. Phép dời hình là phép đồng dạng tỉ số k 1.
D. Phép vị tự tỉ số k là phép đồng dạng tỉ số k .
Câu 15: Tìm phương trình tương đương với phương trình 2 2 3sin x  cos x . A. 2 3 sin x  . B. 1 sin x  . C. 3 cos x  . D. 2 cot x  3. 4 2 2
Câu 16: Một lớp học có 30 học sinh gồm có cả nam và nữ. Chọn ngẫu nhiên 3 học sinh để
tham gia hoạt động của Đoàn trường. Biết xác suất chọn được 2 nam và 1 nữ là 12 , 29
gọi n là số học sinh nữ của lớp, tìm mệnh đề đúng? A. n20;23. B. n 15;19. C. n 12;15. D. n8;12. Câu 17:  x 
Tìm chu kỳ tuần hoàn T của hàm số y  sin    với  x  0.  2   A. T  . B. T  2. C. T  4. D. T . 2
Câu 18: Gieo 3 đồng xu một lúc, gọi A là biến cố “có đúng một đồng xu xuất hiện mặt ngửa”.
Tìm xác suất của biến cố . A A. 1 . B. 1 . C. 3. D. 1. 2 4 8 8 Trang 22
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Câu 19: Trong mặt phẳng Oxy cho A 2
 ;0, B2;2,C 4;2, D4;0 . Chọn ngẫu nhiên một điểm có tọa độ  ;
x y (với x, y là các số nguyên) nằm trong hình chữ nhật ABCD (kể
cả các điểm nằm trên cạnh). Gọi A là biến cố: “ x, y đều chia hết cho 2”, tính xác suất của biến cố A . A. 13 . B. 7 . C. 1. D. 8 . 21 21 21
Câu 20: Tìm số các giá trị nguyên của hàm số y  5  4cos 2xsin 2x . A. 5. B. 6. C. 3. D. 4.
Câu 21: Tìm số các số tự nhiên có 5 chữ số đôi một phân biệt, được lập từ các chữ số 1,2,3,4,5,6,
biết rằng trong các số đó phải có các chữ số 1 và 5. A. 735. B. 1200. C. 600. D. 480.
Câu 22: Một lô hàng gồm 30 sản phẩm tốt và 10 sản phẩm xấu. Lấy ngẫu nhiên 3 sản phẩm.
Tính xác suất để 3 sản phẩm lấy ra có ít nhất một sản phẩm tốt. A. 244 . B. 15 . C. 135 . D. 3 . 247 26 988 247
Câu 23: Cho cấp số cộng (u ) có u  1
 2;u 18. Tìm số hạng đầu tiên u và công sai d của n 4 14 1 cấp số cộng. A. u  2  2;d  3. B. u  2  1;d  3  . C. u  20;d  3  . D. u  2  1;d  3. 1 1 1 1
Câu 24: Trong mặt phẳng Oxy, cho hai đường thẳng a,b lần lượt có phương trình là
x  2 y  3  0 và 2x  y  5  0. Nếu có phép quay với góc quay 0
 (0   180 ) biến
đường thẳng này thành đường thẳng kia thì số đo của  là: A. 0   45 . B. 0   90 . C. 0   60 . D. 0  120 .
Câu 25: Tìm số hạng tổng quát u trong các trường hợp dưới đây để dãy số u giảm. n  n A. 1 n  u  . u  n C. 3 1 u  . D. u  n  2. n 2n B. 2 . n n n 1 n B. TỰ LUẬN Câu 1: Cho hình chóp .
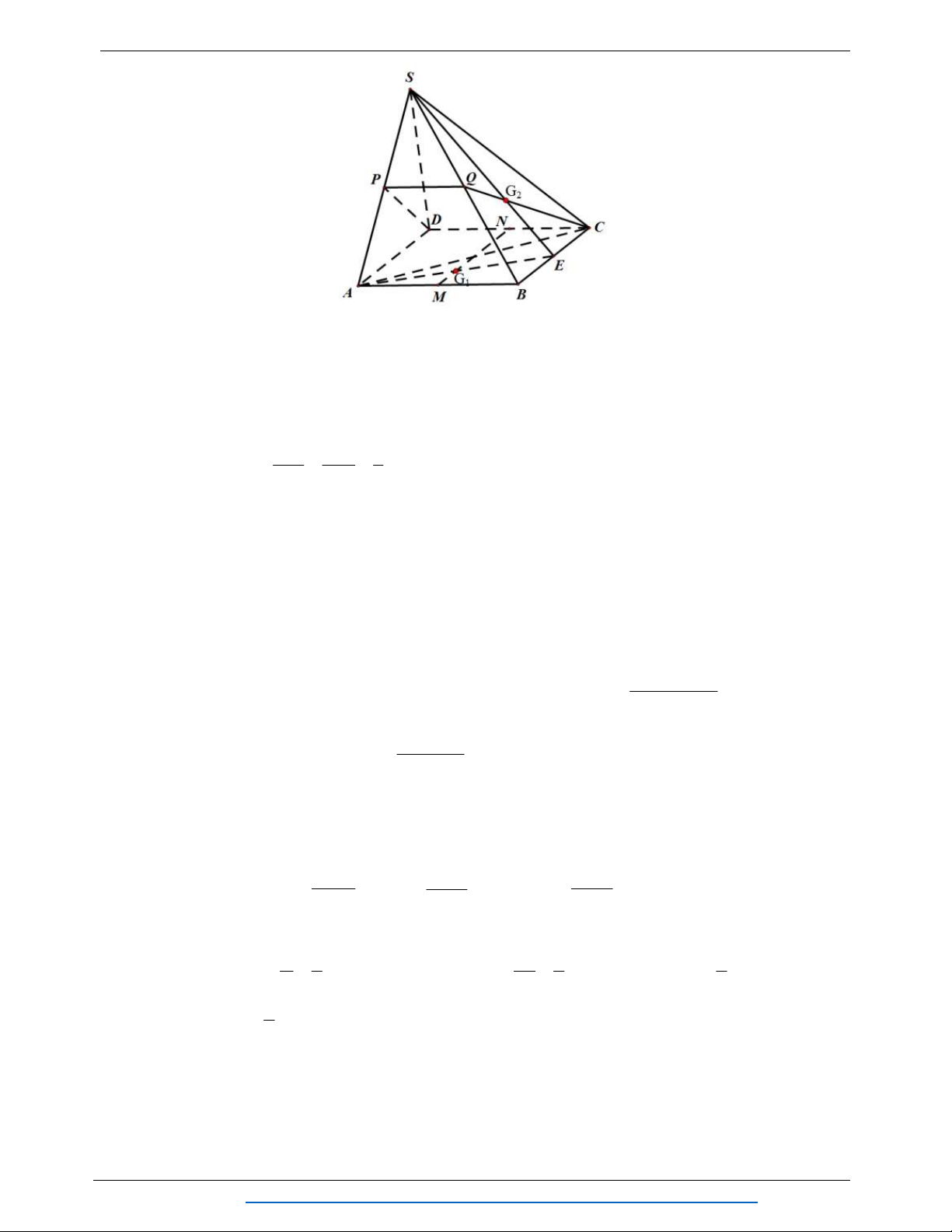
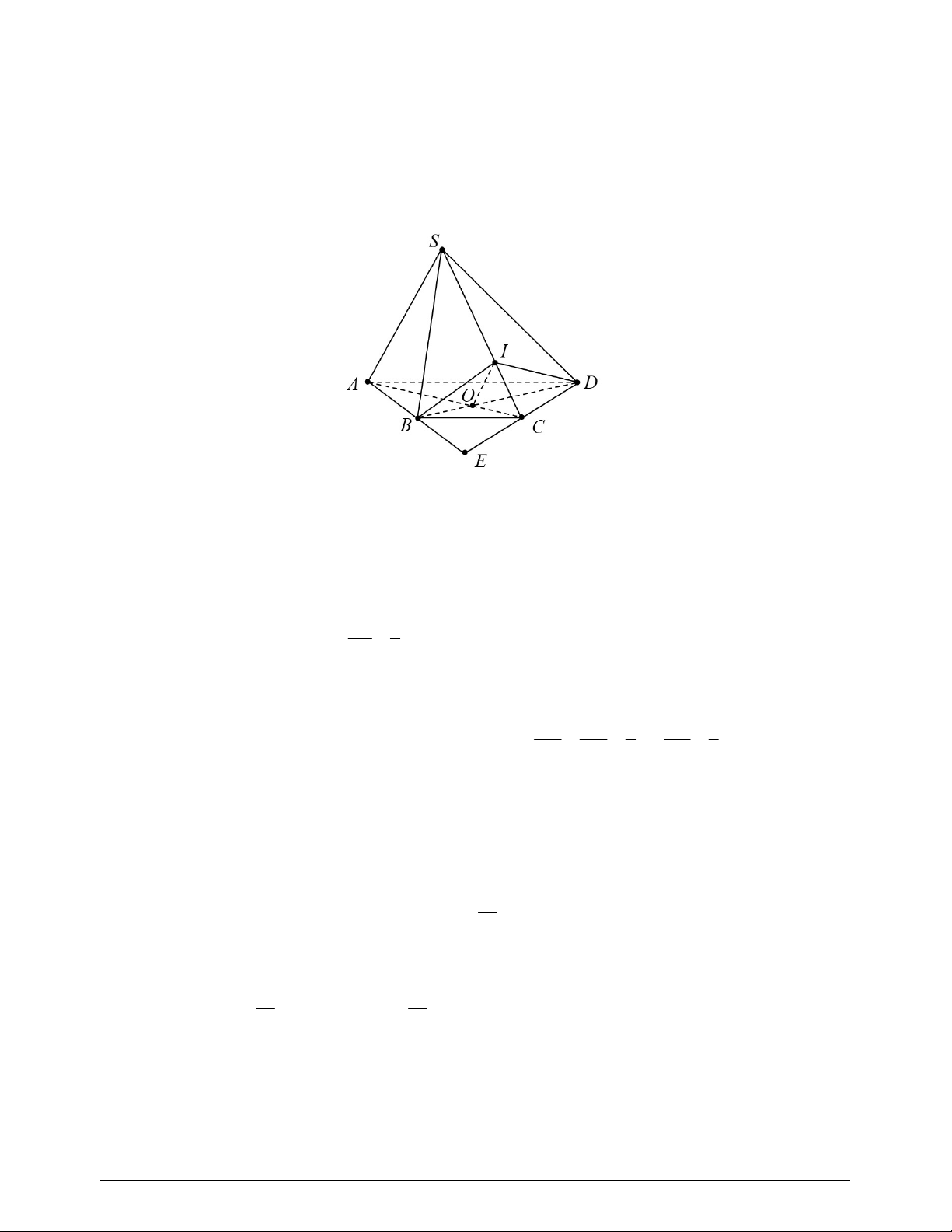
S ABCD , có đáy ABCD là hình thang với đáy lớn AB và đáy nhỏ CD .
Gọi M,N lần lượt là trung điểm của SA và SB ; gọi E là giao điểm của AD và BC .
a) Tìm giao tuyến của SBC và ADM. Xác đinh giao điểm P của đường thẳng SC và mặt phẳng ADM.
b) Gọi I là giao điểm của DP và AM . Chứng minh SI song song với AB.
c) Xác định thiết diện của hình chóp với mặt phẳng   α biết   α qua MN và song song với SC .
Câu 2: Trong mặt phẳng Oxy, tìm phương trình đường thẳng  là ảnh của đường thẳng 
 : x  2y 1  0 qua phép tịnh tiến theo vectơ v  1;  1 .
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 23
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 3: Cho hàm số y  4sin x  3 m cos x với m là tham số thực. Tìm giá trị của tham số m để giá
trị lớn nhất của hàm số bằng 3 2 . 15 Câu 4:  2  Tìm hệ số chứa 30
x trong khai triển nhị thức 3  x  với x  0. 2   x   1   Câu 5: u
Cho dãy số u cho bởi 1
, tìm công thức số hạng tổng quát của dãy số đó. n   2 u   u  2  n 1 n ----------HẾT---------- Trang 24
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1 HUẾ NĂM HỌC: 2019 - 2020 --------------------------- Thời gian: 90 phút THPT ĐẶNG TRẦN CÔN KHỐI 11
Họ tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . A. TRẮC NGHIỆM
Câu 1: Trên giá sách có 5 quyển sách toán khác nhau và 4 quyển sách tiếng Anh khác nhau.
Hỏi có tất cả mấy cách chọn một quyển sách? A. 20. B. 5. C. 4. D. 9.
Câu 2: Mệnh đề nào sau đây sai?
A. Hai đường thẳng phân biệt có một điểm chung thì cắt nhau.
B. Hai đường thẳng không đồng phẳng thì chéo nhau.
C. Hai đường thẳng song song thì đồng phẳng.
D. Hai đường thẳng không có điểm chung thì song song.
Câu 3: Tìm tất cả các giá trị của tham số m để hàm số y  m  sinx xác định trên đoạn   3  ;  ? 4 4    A. 2 m  . B. m 1. C. m  0 . D. 2 m   . 2 2
Câu 4: Trong trường A, tỉ lệ học sinh giỏi môn Văn là 12%, học sinh giỏi Toán là 9% và học
sinh giỏi cả hai môn là 7%. Chọn ngẫu nhiên một học sinh của trường A. Tính xác suất
p để học sinh đó không học giỏi văn và không học giỏi Toán. A. p  0,72. B. 0,86. C. 0,79. D. p  0,93.
Câu 5: Cho cấp số cộng u có công sai d . Công thức nào sau đây đúng? n  A. u  u  n 1 d . B. u  2u  nd . n 1  1   n 1  1 C. u  u  n 1 d . D. u  u  nd . n 1  1   n 1  1
Câu 6: Tất cả các nghiệm của phương trình cotx  3  0 là: A.   x   k , k  .
B. x    k , k  . 6 6 C.  
x    k , k   .
D. x   k , k  . 3 3
Câu 7: Phương trình    2 x  x x     2 2 1 cos 2sin cos
2 1 sin x  0 tương đương với phương trình nào sau đây? A.       cos 2x   1.   B. 2 cos 2x   .    4   4  2 C.    3    cos 2x   .   D. 1 cos 2x   .    4  2  4  2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 25
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 8: Cho hình chóp S.ABCD có đáy là hình thoi. Gọi O là giao điểm của AC và BD ; E và F
lần lượt là trung điểm của OA và OC ; điểm I thay đổi trên đoạn AC I  ; A I  O . Gọi
(P) là mặt phẳng qua I và song song với BD và SA. Biết (P) cắt S.ABCD theo thiết diện
là đa giác (H). Hãy xác định tất cả các vị trí của I để (H) có số cạnh nhiều nhất.
A. I thuộc đoạn OAI  O; I  A.
B. I thuộc đoạn EAI  E; I  A.
C. I thuộc đoạn FC I  C; I  F .
D. I thuộc đoạn OC I  C; I  O.
Câu 9: Mệnh đề nào sau đây sai? x    k2 x    k2 A. cos x  cos  
, k  . B. sin x  sin   , k  . x     k2 x     k2
C. tan x  tan  x    k, k  .
D. cot x  m  x  acr cot m  k ,k  .
Câu 10: Cho dãy số u với u  
 n . Số hạng thứ 6 của dãy bằng: n  2n n  A. -58. B. 70. C. -27. D. 38.
Câu 11: Cho cấp số nhân u có công bội q  1. Tổng của n số hạng đầu tiên bằng. n  1 n u  q n 1 n u  q n 1   1   A. . B. u  q u  q 1 . C. . D. 1 . 1 q 1 q 1 q 1 q
Câu 12: Có tất cả mấy cách xếp ba bạn nam và hai bạn nữ ngồi vào một bàn gồm năm chỗ? A. 150. B. 3125. C. 25. D. 120.
Câu 13: Mệnh đề nào sau đây sai? 3 A. sinx  0  x  k2 ,  k  .  B. sinx  1  x    k2 ,  k  .  2
C. cos x  1  x    k2 ,  k  . 
D. cos x  1  x  k2,k  .  1
Câu 14: Cho cấp số cộng u có công sai d  3
 và u  . Số hạng thứ chín của cấp số đã n  1 2 cho bằng 53 41 35 47 A.  . B.  . C.  . D.  . 2 2 2 2
Câu 15: Hệ số của số hạng chứa 5
x trong khai triển và rút gọn của biểu thức x   x5 2 1 2  x 1 3x10 bằng: A. 61204. B. 3320. C. 61268. D. 3160.
Câu 16: Số cạnh của một hình tứ diện đều là: A. 6 . B. 4 . C. 3 . D. 5 .
Câu 17: Gọi n là số tự nhiên thỏa mãn 0 1 2
C  4C  C  1. Hãy chọn mệnh đề đúng trong các n n n mệnh đề sau: A. n  15. B. n5;8 . C. n8;12 . D. n12;15. Trang 26
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
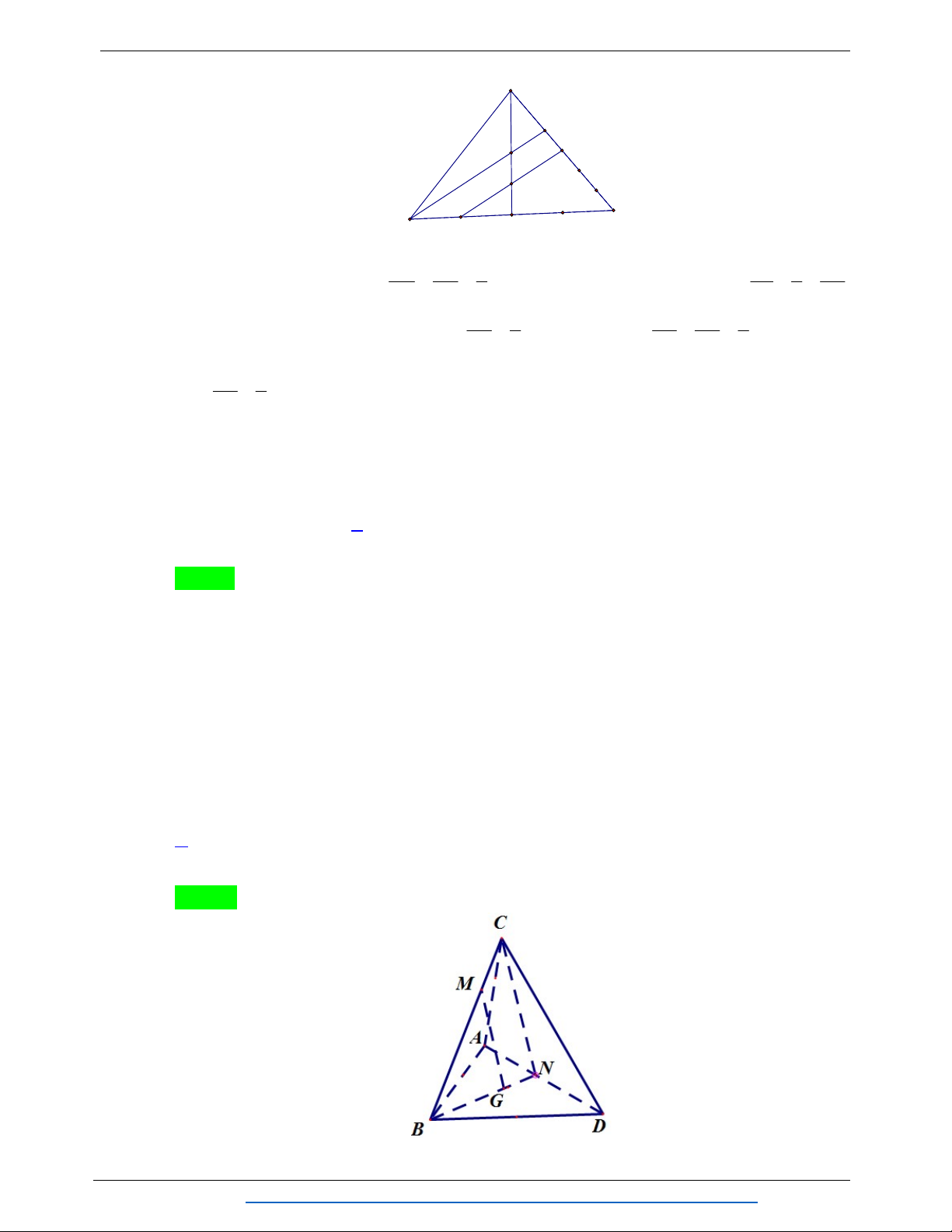
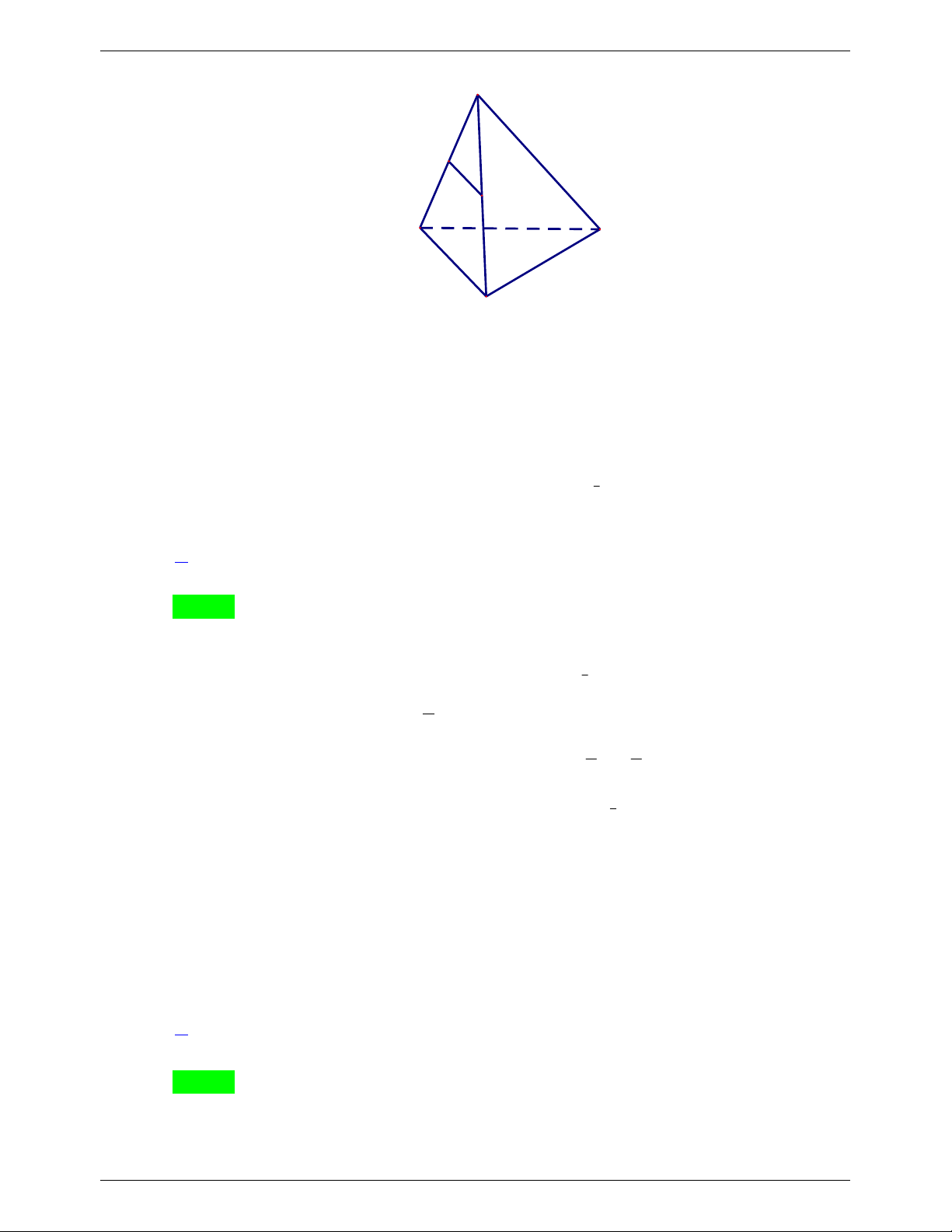
Câu 18: Cho tứ diện đều ABCD có các cạnh đều bằng a . Gọi G là trọng tâm tam giác ABC ,
M là trung điểm của cạnh CD . Diện tích thiết diện của tứ diện ABCD khi cắt bởi mặt
phẳng  AMG (tính theo a ) bằng: 2 2 2 2 A. a 11 . B. a 11 . C. a 11 . D. a 11 . 16 8 2 32
Câu 19: Cho tứ diện ABCD . Gọi M , N và P lần lượt là trung điểm của các cạnh A , B BC và
DA Mệnh đề nào sau đây sai? A. DC  MNP . B. MP  BCD . C. MN   ACD. D. BD  MNP Câu 20: Biết đoạn  ;
a b là tập hợp tất cả các giá trị của tham số m để phương trình
sin x 1  2m có nghiệm. Gía trị của biểu thức 3a  b bằng: A. 2. B. 3. C. 4. D. 1 Câu 21: 
Trong mặt phẳng tọa độ Oxy , cho vectơ a  3;2 và đường tròn C có phương trình
x  2  y  2 1
3  4 . Phép tịnh tiến T biến đường tròn C thành đường tròn có a phương trình:
A. x  2   y  2 2 5  4.
B. x  2   y  2 1 3  4.
C. x  2   y  2 2 5  4.
D. x  2   y  2 4 1  4. Câu 22: x  x
Điều kiện xác định của hàm số sin cos y  là: sin x  cos x A.   x   k2 ,  k  .  B. x   k ,  k  .  4 4 C.   x    k2 ,  k  .  D. x    k ,  k  .  4 4
Câu 23: Cho cấp số cộng u có u  3 và công sai d  2. Tổng 10 số hạng đầu của cấp số cộng n  1 đã cho bằng A. 105. B. 115. C. 130. D. 120.
Câu 24: Tất cả các nghiệm của phương trình 2cos3x  2  0 là A.    x    k2; k  .  B. 3 2 x    k ; k  .  4 4 3 C.  2  x    k ; k  .  D. 3 x    k2 ;k  .  4 3 4
Câu 25: Cho cấp số nhân (u ) biết u  2;u  486 .Tổng của 8 số hạng đầu tiên bằng? n 1 3 A. 5765. B. 4376 . C. 6792 . D. 7210.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 27
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT B. TỰ LUẬN
Câu 1. Giải phương trình: 3 sin 3x  . 2
Câu 2. Từ một bình chứa 7 quả cầu đỏ và 4 quả cầu xanh. Lấy ra ngẫu nhiên đồng thời 3 quả.
Tính xác suất để lấy được 3 quả cùng màu.
Câu 3. Cho cấp số nhân u có u 1024 và công bội 1 q  . Tính u . n  1 2 15
Câu 4. Cho cấp số cộng có số hạng thứ ba bằng 5 và công sai bằng 1 . Tính tổng 100 số hạng 3
đầu tiên của cấp số cộng đã cho.
Câu 5. Cho hình chóp S.ABC . Gọi M , N, P lần lượt là trọng tâm của các tam giác SAB, SAC và ABC
a) Chứng minh MN  SBC.
b) Xác định giao điểm của đường thẳng SP và  AMN . ----------HẾT---------- Trang 28
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1 HUẾ NĂM HỌC: 2019 - 2020 --------------------------- Thời gian: 90 phút THPT GIA HỘI KHỐI 11
Họ tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . A. TRẮC NGHIỆM
Câu 1. Trong mặt phẳng Oxy , cho đường tròn C x  2   y  2 : 1
2  9 . Tìm phương trình 
đường tròn C là ảnh của C qua phép tịnh tiến theo vectơ v  2;3 .
A. C x  2   y  2 : 1 1  9.
B. C  x  2   y  2 : 3 5  9.
C. C x  2   y  2 : 3 5  9.
D. C x  2   y  2 : 1 1  9.
Câu 2. Tìm hệ số của số hạng chứa 5
x trong khai triển   12 1 3x A. 1  92456. B. 7  29. C. 192456. D. 729.
Câu 3. Tìm giá trị lớn nhất ( max y ), giá trị nhỏ nhất ( min y ) của hàm số 4 4 y  sin x  cos x .  1  1 min y 1 min y  1 min y   min y  A.    2 . B.  2 . C.  1 . D.  1 .  max y  max y  max y 1 max y 1  2  2 
Câu 4. Trong mặt phẳng Oxy , cho vectơ v  3;5 và điểm M 1; 
1 . Tìm tọa độ điểm M ' là 
ảnh của điểm M qua phép tịnh tiến theo vectơ v . A. M '4; 6  . B. M ' 2  ; 4  . C. M '4; 4  . D. M ' 2  ; 6  .
Câu 5. Đẳng thức nào sau đây là sai? A. n  
1 ! n!  n  2.n!. B. n  2.n   1 !  n  2!. C. 0!1! 2!. D. n   1 .n!  n   1 !.
Câu 6. 20 đường thẳng phân biệt có tối đa bao nhiêu giao điểm? A. 200 . B. 190. C. 380. D. 20 .
Câu 7. Tìm tất cả các nghiệm của phương trình 4 4 cos x  sin x  0. A.    x 
 k , k  Z. B. x   k ,k  Z. C. x    k2, k  Z. D. x  k ,k  Z. 2 4 2
Câu 8. Tìm tất cả các nghiệm của phương trình 1 sin x   . 2 A.  2   x   k2  x   k2 , k  Z. B. 7 x    k 2  x   k2 ,k  Z. 3 3 6 6 C.  5   x   k2  x   k2 , k  Z. D. 5 x    k 2  x   k2 ,k  Z. 6 6 6 6
Câu 9. Tìm tập xác định D của hàm số 1 y  . 1 sin 2x A.     
D   \   k2 , k   .
B. D   \   k,k  .  2   4 
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 29
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT C.     
D   \   k2 , k .
D. D   \   k ,k  .  4   4 
Câu 10. Các hàm số sau được xét trên tập xác định của chúng. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số y  cos x là hàm số chẵn.
B. Hàm số y  cos .xsin x là hàm số không chẵn cũng không lẻ. C. Hàm số 3 3 y  sin . x cos x là hàm số lẻ.
D. Hàm số y  sin x, y  tan x, y  cot x đều là các hàm số lẻ.
Câu 11. Gieo đồng thời một con súc sắc và một đồng xu. Tính xác suất để xuất hiện đồng xu có
mặt ngửa và con súc sắc có số chấm không vượt quá 4. A. 1 . B. 1 . C. 1 . D. 1 . 2 6 4 3
Câu 12. Tìm tập nghiệm của phương trình 2cos x  sin x  3  0. A.    .  B.   k , k  .
C.   k ,k . D. .   2   2  Câu 13. Biết 4 C  126 . Tính 4 A . n n A. 3024. B. 24. C. 504. D. 756. Câu 14.   
Tìm điều kiện xác định của phương trình tan 2x   3.    3  A. 5   x   k , k  .  B. x   k , k  .  12 2 2 C. 5   x   k , k  .  D. x   k , k  .  12 6 2
Câu 15. Tính số tập hợp con của tập hợp A   ; a ; b ; c d; ; e f ; g. A. 127. B. 15. C. 128. D. 14.
Câu 16. Trong các mệnh đề sau, tìm mệnh đề đúng ? A. Trên khoảng    0; 
 hàm số y  sin x và hàm số y  cos x cùng nghịch biến.  2  B. Trên khoảng    0; 
 hàm số y  sin x nghịch biến và hàm số y  cos x đồng biến.  2  C. Trên khoảng    0; 
 hàm số y  sin x đồng biến và hàm số y  cos x nghịch biến.  2  D. Trên khoảng    0; 
 hàm số y  sin x và hàm số y  cos x cùng đồng biến.  2 
Câu 17. Tìm tất cả các nghiệm của phương trình cos x  3sin x  0. A.     x 
 k2 , k  B. x   k,k  C. x    k ,k  . D. x   k,k  .  3 2 6 6 
Câu 18. Trong mặt phẳng Oxy cho điểm M 1;7 và vectơ v  2;5 . Tìm M  là ảnh của M 
qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ v
và phép vị tự tâm O tỉ số k  2 . Trang 30
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 A.  1    M   ; 6   . B. 3 M  ;1   . C. M  2  ;24 . D. M6;4.  2   2 
Câu 19. Tìm số nghiệm của phương trình cos3x sin 2x  0 trên đoạn 0; . A. 3. B. 4 . C. 2 . D. 1 Câu 20. Tính tổng 0 1 2
S  C  3C  9C  ...  3n n C . n n n n A. 4n . B. 3n . C. 2n . D. 1 3n Câu 21. Phương trình 2
sin x  1 tương đương với phương trình sau đây? A. sin x  0. B. sin x  1  . C. sin x  1  . D. sin x 1.
Câu 22. Cho E là tập hợp các số tự nhiên gồm 2 chữ số khác nhau được lập từ các chữ số 1, 2, 3,
4, 5, 6. Lấy ngẫu nhiên một phần tử của E, tính xác suất để được một số chia hết cho 4 hoặc chia hết cho 7? A. 7 . B. 11 . C. 4 . D. 13 . 10 30 5 30 Câu 23.   
Tìm tập nghiệm của phương trình cos 2x   1   .  4  A.      
  k , k   . B. 1
   k2 , k   .  8  2 8  C.       k , k   .
D.   k2,k  .  8   4  Câu 24. 1
Tìm tập xác định D của hàm số y  . 2  sin 7x  2017 A.       D   \   k , k   . B. 2019 D   \   .  2   7  C. 2019  D   \   k2 , k  . D. D   .  7 
Câu 25. Cho hàm số y  sin x  cos x, tìm khẳng định đúng?
A. y   2  y  2. B. 0  y  2. C.  2  y  2. D. 2   y  0. B. TỰ LUẬN Câu 1. x
Tìm tập nghiệm của phương trình 2cos  3  0. 2
Câu 2. Trong mặt phẳng Oxy , cho đường thẳng d : 3x  4y 12  0. Tìm phương trình đường 
thẳng d là ảnh của d qua phép tịnh tiến vectơ v  2;  1 .
Câu 3. Đội văn nghệ của lớp có 5 bạn nam và 7 bạn nữ. Chọn ngẫu nhiên 5 bạn tham gia biểu
diễn. Tính xác suất để trong 5 bạn được chọn có cả nam và nữ, đồng thời số bạn nữ nhiều hơn số bạn nam. Câu 4.   
Tìm tất cả các giá trị của tham số m để phương trình cos  2x  m  2   có nghiệm?  3 
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 31
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a . Hai mặt bên SAB và SCD
là các tam giác đều. Gọi G là trọng tâm tam giác SAB , E là điểm di động trên đoạn
thẳng BG ( E khác B ). Cho mặt phẳng   qua E , song song với SA và BC .
a) Chứng minh đường thẳng AD song song với mặt phẳng   . Tìm giao điểm
M , N, P, Q của mặt phẳng   với các cạnh SB, SD, DC, BA .
b) Gọi I là giao điểm của QM và PN . Chứng minh I nằm trên một đường thẳng cố
định khi điểm E di động trên đoạn BG .
c) Chứng minh tam giác IPQ là tam giác đều. Tính diện tích tam giác IPQ theo a . ----------HẾT---------- Trang 32
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1 HUẾ NĂM HỌC: 2019 - 2020 --------------------------- Thời gian: 90 phút THPT CHI LĂNG KHỐI 11
Họ tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . A. TRẮC NGHIỆM 
Câu 1. Trong mặt phẳng Oxy cho B3;6 và v5; 4
 . Tìm tọa độ điểm C sao cho T C  B v A. C 8; 1  0. B. C  2  ; 2  . C. C 2;2. D. C 8;10. Câu 2. x 
Tìm tập xác định của hàm số sin 1 y  sin x  A.  D   \   k2 ;  k . B. D   \   k ;  k    . 2   C.  D   \   k ;  k . D. D   \k2 ;  k    . 2 
Câu 3. Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình vẽ. Hỏi có
bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần? A. 24. B. 18. C. 10. D. 9.
Câu 4. Tìm tất cả cá nghiệm của phương trình 2cos x  2  0.  3  5     x   k2   x   k2  x   k2  x   k2  A. 4  . B. 4  . C. 4  . D. 4  .   5   3   x   k2              x k2 x k2 x k2  4  4  4  4
Câu 5. Trong mặt phẳng tọa độ Oxy cho đường tròn C có phương trình
x  2   y  2 2
2  4. Phép đồng dạng có được bằng việc thực hiện liên tiếp các phép vị tự tâm O tỉ số 1
k  và phép quay tâm O góc quay 0
90 sẽ biến đường tròn C thành 2
đường tròn nào trong các đường tròn sau đây?
A. x  2   y  2 2 2  1.
B. x  2   y  2 1 1  1.
C. x  2   y  2 1 1  1.
D. x  2   y  2 2 1  1.
Câu 6. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng không có điểm chung thì chéo nhau.
B. Hai đường thẳng chéo nhau thì không có điểm chung.
C. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
D. Hai đường thẳng phân biệt không chéo nhau thì hoặc song song hoặc cắt nhau.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 33
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
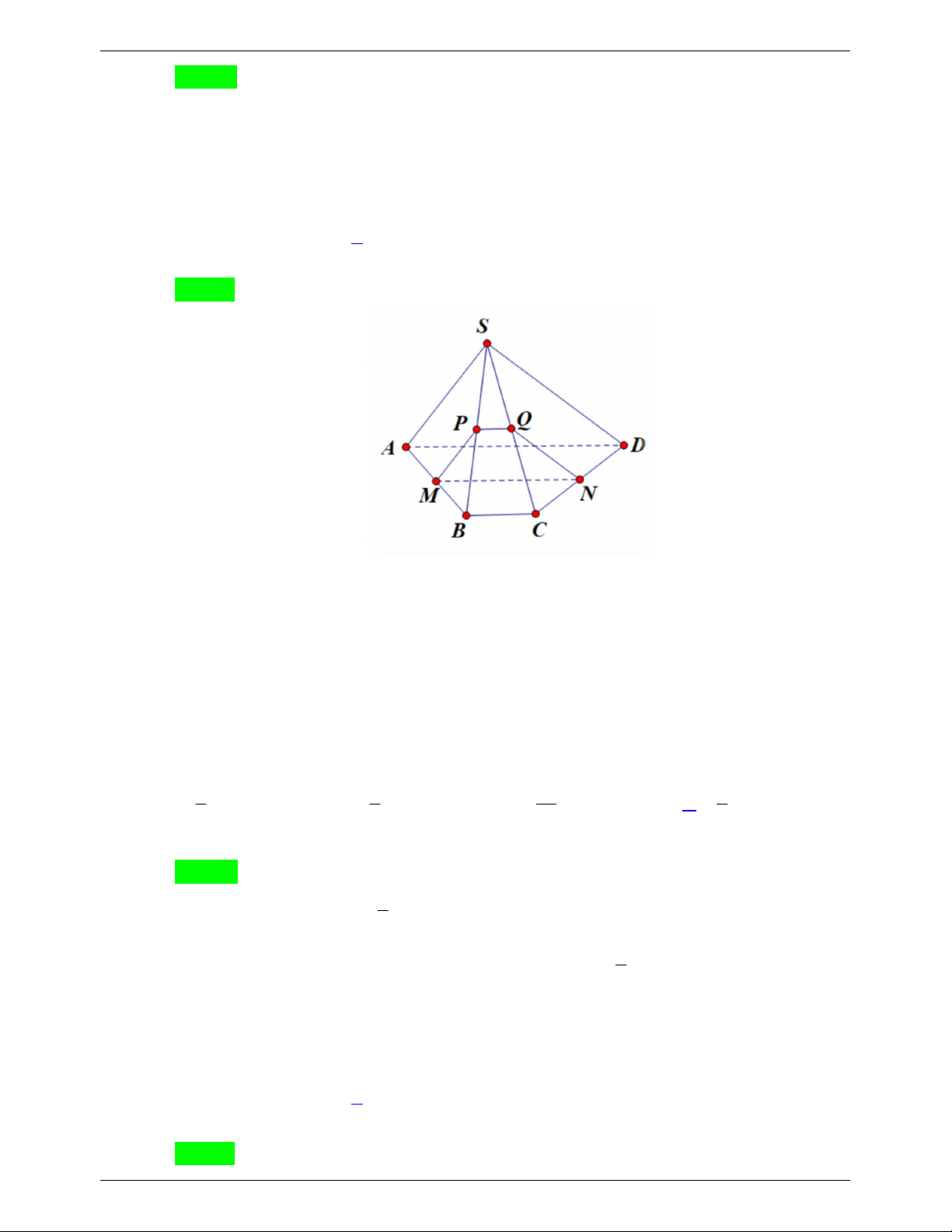
Câu 7. Cho hình chóp S.ABCD có đáy là hình thang cân đáy lớn AD , M , N lần lượt là là
trung điểm của AB và CD , P là mặt phẳng qua MN và cắt mặt bên SBC theo một
giao tuyến. Thiết diện của P và hình chóp là hình gì?
A. Hình bình hành. B. Hình thang.
C. Hình chữ nhật. D. Hình vuông.
Câu 8. Một đề thi có 20 câu hỏi trắc nghiệm khách quan, mỗi câu có 4 phương án lựa chọn,
trong đó chỉ có một phương án trả lời đúng. Khi thi, một học sinh đã chọn ngẫu nhiên
một phương án trả lời với mỗi câu của đề thi đó. Trong trường hợp đó xác suất để học
sinh đó trả lời không đúng cả 20 câu là bao nhiêu? 20 A. 1 . B. 3 . C. 1 . D.  3    . 4 4 20  4 
Câu 9. Hiếu có 8 người bạn. Hiếu muốn mời 4 trong 8 người bạn đó về quê chơi vào cuối
tuần. Nhưng trong 8 người bạn đó có 2 bạn là Khoa và Tuấn không thích đi chơi với
nhau. Như vậy số cách chọn nhóm 4 người để về quê của Hiếu là bao nhiêu? A. 4 C . B. 4 3 C  2C . C. 4 3 C  C . D. 4 3 C  C . 8 6 6 6 6 6 7
Câu 10. Một họp có 10 viên bi màu trắng, 20 viên bi màu xanh, 30 viên bi màu đỏ, mỗi viên bi
chỉ có một màu. Có bao nhiêu cách để chọn ngẫu nhiên 8 trong số các viên bi thuộc
hộp đó để được 8 viên bi cùng màu trắng? A. 4 C . B. 8 C . C. 8 C . D. 4 C . 20 10 60 30
Câu 11. Cho tập hợp A  2;3;4;5;6; 
7 . Có thể lập được tất cả bao nhiêu số tự nhiên gồm 3 chữ
số khác nhau được thành lập từ các chữ số thuộc A ? A. 120. B. 216. C. 256. D. 180.
Câu 12. Trong khai triển  x  10 2
1 . Tìm hệ số của số hạng chứa 8 x . A. 256. B. 45. C. 1  1520. D. 11520.
Câu 13. Hãy viết ba số hạng tiếp theo hai số hạng đầu của dãy số u có n  u 1,u 1,u  u  u . 1 2 n2 n 1  n A. 2;3;5. B. 3;4;7. C. 2;5;7. D. 3;5;8.
Câu 14. Xét phép thử là gieo một con xúc xắc hai lần. Gọi N là biến cố” lần đầu xuất hiện mặt
5 chấm”, gọi M là biến cố” lần hai xuất hiện mặt 5 chấm” thì A. M  N  
 5; 1,5;2,5;3,5;4,5;5,5;6,1;5,2;5,3;5,4;5,5;5,6;5. B. M  N  
 1;5,2;5,3;5,4;5,5;5,6;5. C. M  N  
 5; 1,5;2,5;3,5;4,5;5,5;6. D. M  N  5;  5 . Câu 15.   
Tìm giá trị lớn nhất và giá trị bé nhất của hàm số y  1 3sin 2x     4  A. max y  3 ; min y  2  . B. max y  2  ; min y  3. C. max y  4 ; min y  2  .
D. max y  4 ; min y  2 . Câu 16.   
Tìm tất cả các nghiệm x  0 ;   của phương trình 2 2sin x  3sin x 1  0  2  Trang 34
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 A.     x  . B. 5 x  . C. x  . D. x  . 12 6 6 2
Câu 17. Có bao nhiêu cách sắp xếp bốn bạn Văn, Bình, Nhi, Thi ngồi vào một bàn dài gồm 4 chỗ ? A. 1. B. 8. C. 4. D. 24.
Câu 18. Trong không gian, cho 4 điểm không đồng phẳng. Có bao nhiêu tam giác từ 4 điểm đã cho ? A. 6. B. 4. C. 3. D. 2.
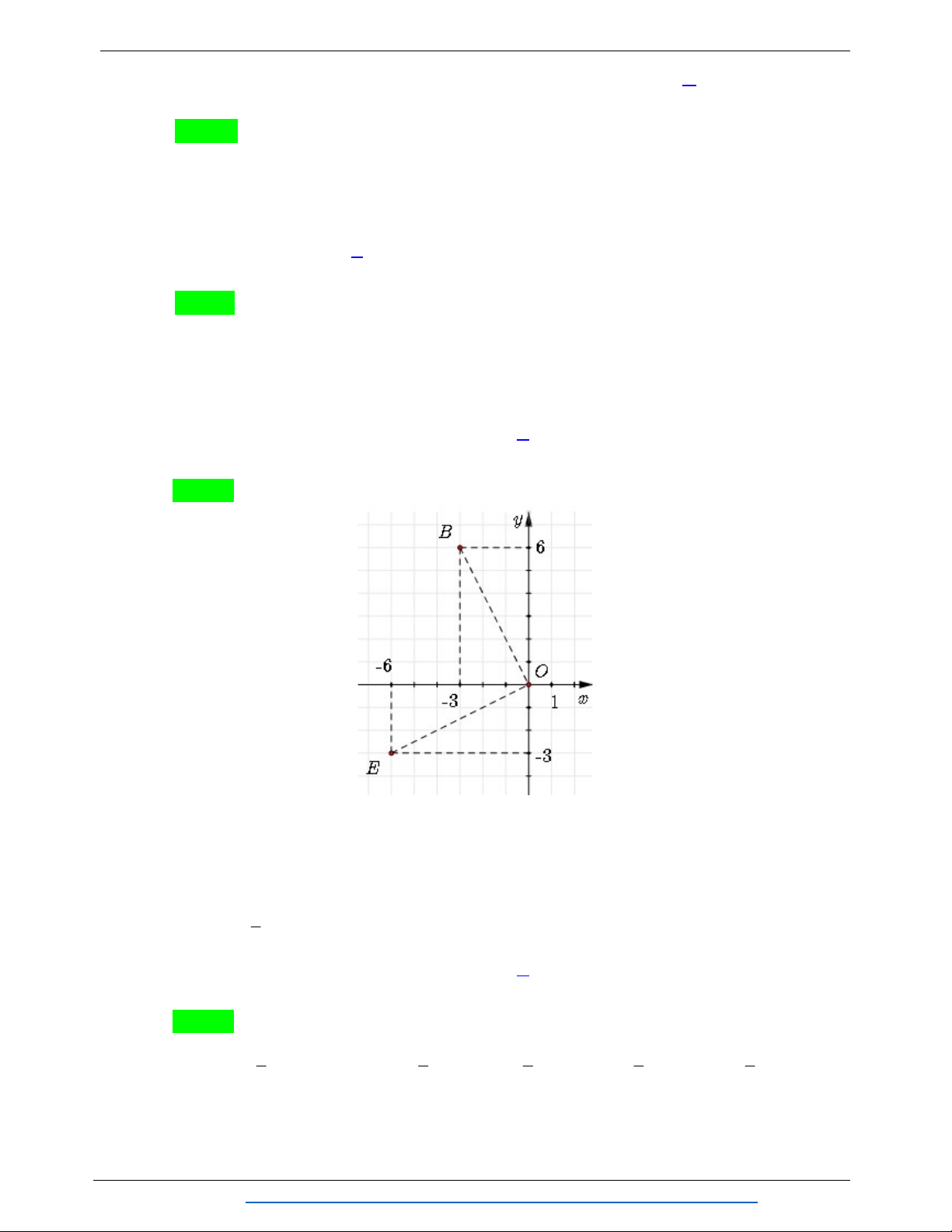
Câu 19. Trong mặt Oxy cho điểm B 3
 ;6 . Tìm tọa độ điểm E sao cho B là ảnh của E qua
phép quay tâm O, góc quay 90 . A. E 6;3 . B. E 3;6. C. E  6  ;3 . D. E  3  ;6 .
Câu 20. Tìm số tự nhiên n , biết hệ số của số hạng thứ 3 theo số mũ giảm dần của x trong khai n triển  1  x    bằng 4 .  3  A. 8 . B. 4 . C. 9. D. 17 .
Câu 21. Phép vị tự V biến điểm M thành điểm M ' là phép đồng nhất khi nào? I ;k  A. k 1. B. k  0. C. k  1  . D. k  1  .
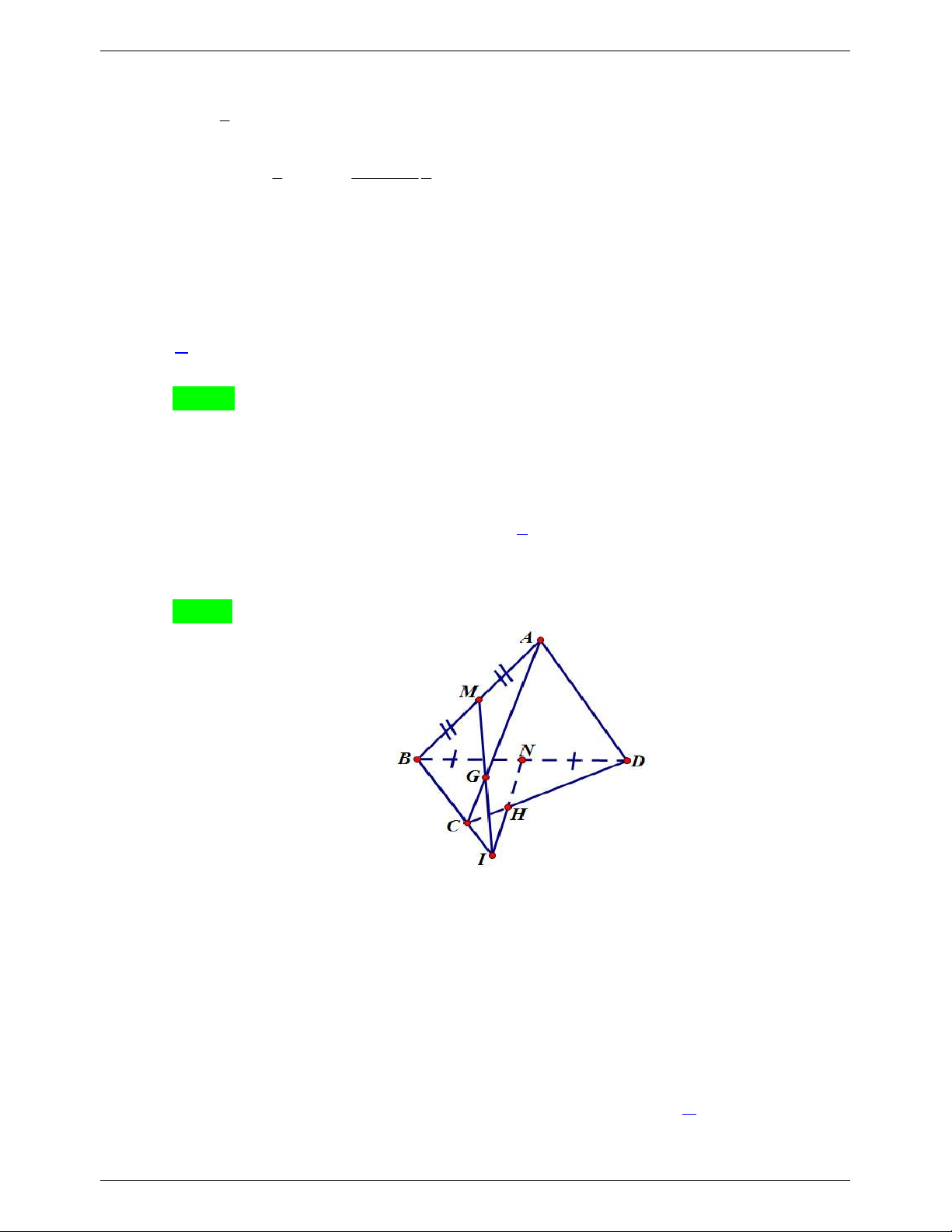
Câu 22. Cho hình tứ diện ABCD có M , N lần lượt là trung điểm của AB, B . D Các điểm G, H
lần lượt trên cạnh AC,CD sao cho NH cắt MG tại I. Khẳng định nào sau đây là khẳng định đúng? A. B,G, H thẳng hàng. B. B,C, I thẳng hàng. C. N,G, H thẳng hàng. D. , A C, I thẳng hàng.
Câu 23. Cho cấp số cộng có các số hạng lần lượt là 5;9;13;17;... Khi đó u có thể được tính theo n
biểu thức nào dưới đây. A. u  5n 1. B. u  4n 1. C. u  5n 1. D. u  4n 1. n n n n
Câu 24. Trong mặt phẳng Oxy , cho điểm A2; 
1 . Tìm ảnh của A qua phép dời hình có được 
bằng cách thực hiện liên tiếp phép tịnh tiến theo u  3;  1 và phép quay tâm O góc quay 9  0 . A.  5  ;0. B. 0;5. C. 5;0. D. 0; 5  .
Câu 25. Gía trị của biểu thức 1 2 2 3 3 2020 2020 P  1 2C  2 C  2 C ... 2 C là: 2020 2020 2020 2020 A. 2020 P  3  . B. P  1  . C. 2020 P  3 . D. P 1. B. TỰ LUẬN.
Câu 1. Giải các phương trình sau: a) 3tan 2x  3 . b) 2 2sin x  cos 2x  0 .
Câu 2. Ngân hàng đề thi gồm 100 câu hỏi, mỗi đề thi có 5 câu. Một học sinh học thuộc 80
câu. Tính xác suất để học sinh đó rút ngẫu nhiên được một đề thi có 4 câu học thuộc.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, gọi M , N lần lượt là trung điểm của S , A S . D
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 35
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
a) Tìm giao tuyến của hai mặt phẳng SAC và SBD.
b) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng OMN . Thiết diện đó là hình gì? Câu 4. Hệ số của 5
x trong khai triển x   x7 2 2 4 3 là ?
Câu 5. Tồng các nghiệm của phương trình sin x  3 cos x  2 trện đoạn 0;4  là ? ----------HẾT---------- Trang 36
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ ÔN TẬP KIỂM TRA CUỐI KÌ 1 ĐẮK LẮK NĂM HỌC: 2019 - 2020 --------------------------- Thời gian: 90 phút THPT CHUYÊN NGUYỄN DU KHỐI 11
Họ tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . A. TRẮC NGHIỆM
Câu 1. Trong các phương trình sau phương trình nào có nghiệm: A. 2 cot x  cot x  3  0 . B. 3 sin x  2 . C. 1 1 cos 4x  . D. 2sin x  3cos x  4. 4 2
Câu 2. Tập xác định của hàm số y  cos x 1 là: A.  
  k2 k   . B.  . C. k2 k    . D.k k    .  2 
Câu 3. Trong các hàm số sau, hàm số nào là hàm số chẵn:
A. y  2019cos x  2020sin x .
B. y  tan 2019x  cot 2020x .
C. y  cot 2019x  2020sin x .
D. y  sin 2019x  cos 2020x .
Câu 4. Gieo hai con súc sắc. Xác suất để số chấm xuất hiện trên hai con súc sắc như nhau là A. 1 . B. 1 . C. 1 . D. 1 . 3 12 6 36
Câu 5. Gọi G là trọng tâm tứ diện ABCD . Gọi A là trọng tâm tam giác BCD. Tỉ số GA bằng GA A. 3. B. 3 . C. 2 . D. 1 . 4 3 Câu 6. Phép quay biến điểm  Q
M thành điểm M . Khi đó O; 
 
  A. OM  OM  và  MOM    .
B. OM  OM  và OM ,OM    .
C. OM  OM  và OM ,OM    . D. OM  OM  và  MOM    .
Câu 7. Cho tứ diện ABCD . Gọi M , N, P,Q, R, S lần lượt là trung điểm các cạnh
AC, BD, AB,CD, AD, BC . Bốn điểm nào sau đây không đồng phẳng? A. M , P, S, N . B. M , N, R, S . C. , P , Q , R S . D. M , N, P,Q .
Câu 8. Trong các mệnh đề sau đây mệnh đề nào sai?
A. Phép dời hình là phép đồng dạng tỉ số k 1.
B. Phép vị tự tỉ số k là phép đồng dạng tỉ số k .
C. Phép đồng dạng biến đường thẳng thành đường thẳng // hoặc trùng với nó.
D. Phép đồng dạng bảo toàn độ lớn góc.
Câu 9. Hàm số nào sau đây là hàm số tuần hoàn với chu kì T   ? A. y  2cos x . B. y  cos x . C. y  cos 2x. D. y  cos x  2 .
Câu 10. Hàm số y tan x đồng biến trên mỗi khoảng
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 37
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT A.      
k;  k,k   . B. 3
 k; k,k   4 4   . C.     
k2;  k2,k  .
D.  k; k,k   2 2   .
Câu 11. Cho phép thử có không gian mẫu   1,2,3,4,5, 
6 . Các cặp biến cố không đối nhau là: A. A    1 và B  2,3, 4,5,  6 . B.  và  . C. E  1, 4,  6 và F  2,  3 . D. C  1,4,  5 và D  2,3,  6 .
Câu 12. Số tập hợp con khác rỗng của tập hợp gồm 15 phần tử là A.32768. B. 32767 . C. 15!. D. 2 15 .
Câu 13. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AB và AC . Đường thẳng
MN song song với mặt phẳng: A.  ACD. B.  ABD. C. BCD . D.  ABC .
Câu 14. Cho I 2;0. Phép đồng dạng hợp thành của phép V
và phép T (O là gốc tọa độ).  1  o; OI    2 
Biến đường tròn C  2 2
: x  y  4 thành C có phương trình A. 2 2
x  y  4x  3  0 . B. 2 2
x  y  4x  1  0 . C. 2 2 x  y  4x  0 . D. 2 2 x  y  4x  3  0 . 
Câu 15. Trong hệ trục Oxy , cho đường thẳng d : 2x  y 1 0, phép tịnh tiến theo vectơ v biến 
d thành chính nó thì v phải là vectơ nào trong các vectơ sau?     A. v2;4. B. v4;2. C. v2;  1 . D. v1;2 .
Câu 16. Một đa giác lồi có 27 đường chéo. Số đỉnh của đa giác đó là: A. 9. B. 8. C. 11. D. 10.
Câu 17. Cho hình chóp tứ giác S.ABCD đáy không phải là hình thang và M tùy ý nằm trong S
 CD . Gọi d  MAB  SCD . Chọn câu đúng: A. C , D d, BC đồng quy. B. A , B d, AC đồng quy. C. AB,C , D d đồng quy. D. d, A , D CD đồng quy.
Câu 18. Xác suất bắn trúng mục tiêu của một vận động viên khi bắn một viên đạn là 0,6 .
Người đó bắn hai viên một cách độc lập. Xác suất để một viên bắn trúng và một viên trượt mục tiêu là: A. 0,24 . B. 0,4 . C. 0,48 . D. 0,45 .
Câu 19. Cho tứ diện ABCD . Gọi M, N, P lần lượt là các điểm trên các cạnh AB , AC và BD sao
cho MN không song song với BC , MP không song song với AD. Mặt phẳng (MNP)
cắt các đường thẳng BC, C ,
D AD lần lượt tại K, I, J . Ba điểm nào sau đây thẳng hàng: A. M, I, J . B. N, K, J . C. K, I, J . D. N, I, J .
Câu 20. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  sin 2x  2sin x  cos x  2 là
A. min y  1 2 2; max y  1 2 2 .
B. min y   2; max y  2
C. min y  1 2 2; max y  4
D. min y  1 2 2; max y  3 . Trang 38
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Câu 21. Hệ số của 8x trong khai triển   x5   x6    x10 1 1 ... 1 là: A. 55 . B. 37 . C. 147 . D. 147 .
Câu 22. Trong mặt phẳng với hệ trục tọa độ Oxy , cho điểm A1;5, B3;2 . Biết các điểm ,
A B theo thứ tự là ảnh của các điểm M , N qua phép vị tự tâm O , tỉ số k  2 . Độ dài đoạn thẳng MN là: A. 50. B. 12,5 . C. 10. D. 2,5.
Câu 23. Số nghiệm của phương trình    2 sin 2x   1   thuộc khoảng    ;  là:  3  A. 4 . B. 1. C. 2 . D. 3 .
Câu 24. Cho tập A  0;1;2;3;4;5;6;7;8; 
9 . Số các số tự nhiên có 5 chữ số đôi một khác nhau lấy ra từ tập A là: A. 27162 . B. 30240 . C. 30420 . D. 27216 . Câu 25. Tìm 1 m để phương trình
 (1 2m) tan x  2m  3  0 có nghiệm thuộc khoảng 2 cos x    0;   .  4  A. 3 m  . B. m 1. C. 3 1  m  . D. m  1hoặc 3 m  . 2 2 2 B. TỰ LUẬN Bài 1. 1. Giải phương trình  3  sin x  3 sin  x  2sin 2x   .  2 
2. Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn không
vượt quá 2019 , đồng thời nó chia hết cho 5 .
Bài 2 . Cho hình chóp S.ABC , G là trọng tâm tam giác ABC . Đường thẳng qua G song song
với SA cắt mặt phẳng SBC tại A. Nêu cách xác định điểm A và thiết diện của hình
chóp khi cắt bởi mặt phẳng qua A, song song với SG và BC .
Bài 3. 1. Giải hệ phương trình sau: 2019 2019 1 2018 2 2017 2017 2 x  x  y  C y  C y C y  2020y  2. 2019 2019 2019  3 2 y 3x  6 .x
2. Cho tập hợp A 0;1;2;3;...;201 9. Một tập hợp con X của A được gọi là tập cân
nếu trong tập hợp X số các số chẵn và số các số lẻ bằng nhau. ( Tập rỗng là một tập
cân). Chứng minh rằng số tập cân của tập hợp A là 1010 C . 2020 Bài 4.
Cho hình chóp S.ABCD có đáy là hình bình hành, M là một điểm di động trên cạnh
SC . Mặt phẳng P chứa AM và song song với BD . Mặt phẳng P cắt SB, SD lần
lượt tại các điểm N và E . Chứng minh rằng: 2S . B SM  SN.SM  SC.SN .
Bài 5. Cho phương trình sin 2x  3m  2cos x  3msinx . Để phương trình có nhiều hơn một
nghiệm trong 0;  thì giá trị của m thỏa ----------HẾT----------
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 39
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
PHẦN ĐÁP ÁN & HƯỚNG DẪN GIẢI
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 1 – SỞ NAM ĐỊNH
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 B D D B D A B A C D C D B D A 16 17 18 19 20 21 22 23 24 25 B A C C A A A D A B
Câu 1. Trong các hàm số sau, hàm số nào là hàm số chẵn? A. 3 y  sin x . B. 2 y  sin x . C. y  x  tan x . D. y  cot x . Lời giải Chọn B Xét hàm số 2
y  sin x có tập xác định D   nên x  D  x  D . Mặt khác: x x2 2 2 sin sin  sin x . Do đó hàm số 2
y  sin x là hàm số chẵn.
Câu 2. Phương trình sin 2xm  0 có nghiệm khi và chỉ khi A. m 1. B. m 1. C. 2  m  2 . D. 1 m 1. Lời giải Chọn D
Ta có: sin 2xm  0  sin 2x  m .
Phương trình đã cho có nghiệm  1 m 1.
Câu 3. Từ các chữ số 1;2;3;4;5 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau A. 5. B. 15. C. 5 5 . D. 120. Lời giải Chọn D
Số các số tự nhiên có 5 chữ số đôi một khác nhau được lập từ các chữ số 1;2;3;4;5 là 5!  120 .
Câu 4. Một câu lạc bộ cờ vua có 15 người. hỏi có bao nhiêu cách bầu ra ba người vào ba vị trí
gồm Chủ tịch, Phó chủ tịch và Thư kí, biết trằng ai cũng có khả năng làm được các vị trí trên. A. 455 . B. 2730 . C. 6 . D. 45 . Lời giải Chọn B
Số cách chọn ra ba người vào ba vị trí gồm Chủ tịch, Phó chủ tịch và Thư kí là 5 A  2730 . 15
Câu 5. Một lớp học có 20 học sinh nam và 21 học sinh nữ. Số cách chọn ngẫu nhiên 10 học sinh trong lớp là A. 41 C . B. 10 A . C. 10!. D. 10 C . 10 41 41 Lời giải Chọn D Trang 40
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Ta có: chọn ngẫu nhiên 10 học sinh trong lớp là một tổ hợp chập 10 của 41 phần tử Số cách chọn là 10 C . 41
Câu 6. Số tập con có 3 phần tử của một tập hợp có 2009 phần tử là A. 3 C . B. 3 A . 2009 2009 C. 2009! . D. 2009 . 3! Lời giải Chọn A
Số tập con có 3 phần tử của một tập hợp có 2009 phần tử là số tổ hợp chập 3 của 2009 phần tử.
Số tập hợp con có 3 phần tử là 3 C . 2019
Câu 7. Cho tập A  1;2;3;4; 
5 . Chọn ngẫu nhiên 3 số từ tập A . Tính xác suất để 3 số được chọn có tổng bằng 10. A. 1 . B. 1 . C. 2 D. 3 . 10 5 5 10 Lời giải Chọn B Ta có: n 3  C 10 . 5
Gọi B là biến cố “ từ tập A chọn được 3 số có tổng bằng 10”. Ta có: nB  2 Xác suất của biến cố n B 2 1 B là P B      . n  10 5
Vậy xác suất cần tìm là PB 1  . 5
Câu 8. Hệ số của số hạng chứa 8
x trong khai triển nhị thức Niuton x  10 2 1 là A. 210 . B. 8 200x . C. 200 D. 8 210x . Lời giải Chọn A
Số hạng T trong khai triển x  10 2 1 . k 1  k 202k k k 202 T  C .x .1  C . k x , k  ,0  k 10 . k 1  10 10  
Hệ số của số hạng chứa 8 x khi k  6 .
Vậy hệ số cần tìm là 6 C  210 . 10 
Câu 9. Trong mặt phẳng với hệ tọa độ Oxy , cho vectơ v  2;  1 và điểm M  3  ;2 . Tìm tọa 
độ ảnh M  của điểm M qua phép tịnh tiến theo vec tơ v . A. M '5; 3   . B. M '1;  1 . C. M ' 1  ;  1 . D. M ' 5  ;3 . Lời giải
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 41
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Chọn C 
Do M  là ảnh của điểm M qua phép tịnh tiến theo vec tơ v nên ta có: x       x 2 1 M M  .  y       y M M   1 1 Vậy M ' 1  ;  1 .
Câu 10. Chọn khẳng định sai?
A. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
B. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.
C. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
D. Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt. Lời giải Chọn D
Đáp án D sai do: có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
Câu 11. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng không cắt nhau và không song song thì chéo nhau.
B. Hai đường thẳng phân biệt không song song thì chéo nhau.
C. Hai đường thẳng chéo nhau thì không có điểm chung.
D. Hai đường thẳng không có điểm chung thì song song. Lời giải Chọn C
Mệnh đề đúng là: Hai đường thẳng chéo nhau thì không có điểm chung.
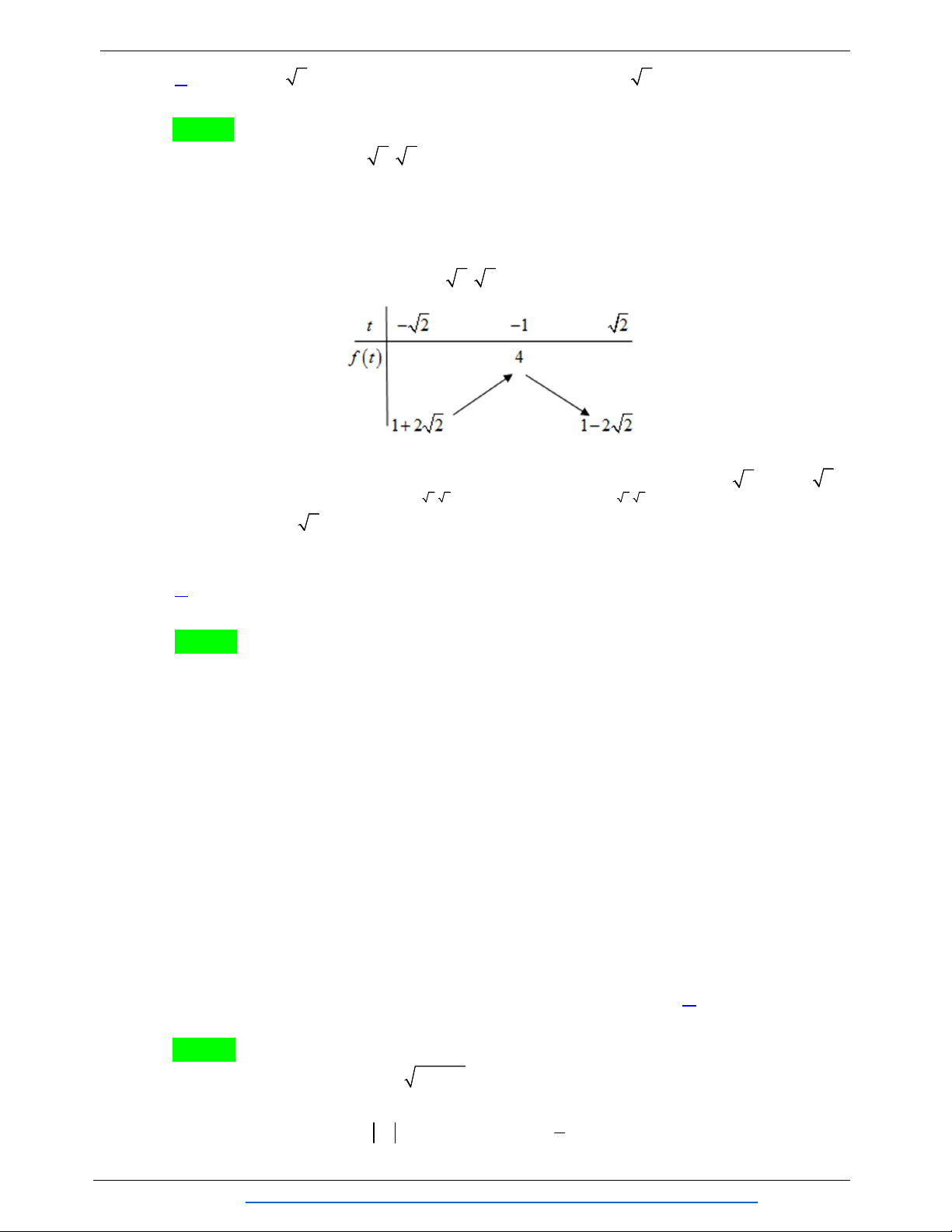
Câu 12. Cho hàm số f x 2
 cos 2x  2cos x  m . Với m  2; 2 
 , tìm giá trị nhỏ nhất của
hàm số trên đoạn 0; . A. 3. B. 3 . C. 1. D. 0 . 2 Lời giải Chọn D Ta có: f x 2 2 2
 cos 2x  2cos x  m  2cos x  2cos x  m 1 .
Đặt t  cos x , với x0;   t  1  ; 
1 . Ta có hàm số: g t  2 2
 2t  2t  m 1 , với t 1;  1 . Xét parabol  1 3 h t 2 2
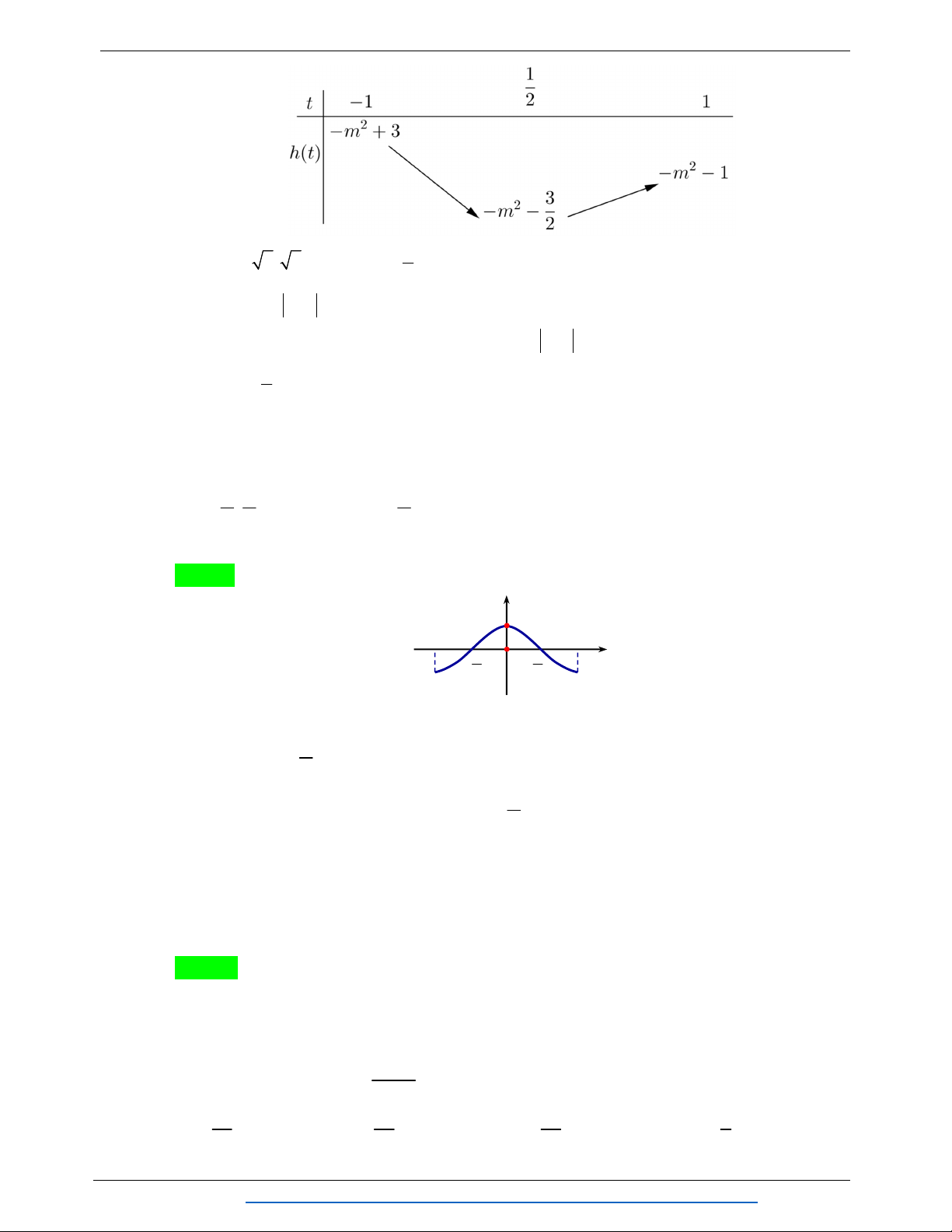
 2t  2t  m 1 có đỉnh 2  I ; m    .  2 2 
Ta có bảng biến thiên của ht trên đoạn 1;  1 : Trang 42
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Do 3 m  2; 2   nên: 2 2 2
m   m 1 0  m  3. 2
Từ đó: g t  ht  0 .
Suy giá trị nhỏ nhất của hàm số g t  ht trên đoạn 1;  1 bằng 0 khi  1  t  t  1  ; . 0    2 
Vậy giá trị nhỏ nhất của hàm số y  f  x trên đoạn 0;  bằng 0 .
Câu 13. Hàm số y  cos x nghịch biến trên khoảng: A.         ;   . B. 0;   . C.    ;0 . D.    ;  .  2 2   2  Lời giải Chọn B. y 1      O  x 2 2
Phát họa đồ thị hàm số y  cos x trên khoảng  
 ;  , ta thấy đồ thị hàm số đi xuống trên khoảng    0;   .  2 
Do đó hàm số nghịch biến trên khoảng    0;   .  2 
Câu 14. Trên giá sách có 5 quyển sách Toán khác nhau, 6 quyển sách Anh khác nhau và 8
quyển sách Văn khác nhau. Số cách chọn ra ba quyển sách có đủ ba môn là: A. 19. B. 118. C. 20 . D. 240 . Lời giải Chọn D.
Chọn ra ba quyển sách có đủ ba môn tức là mỗi môn 1 quyển. Vậy có 1 1 1 C .C .C  240 (cách). 5 6 8  1n
Câu 15. Cho dãy số u với u 
. Số hạng thứ mười một của dãy số bằng n  n 2n  5 A. 1  . B. 1 . C. 1 . D. 1  . 27 27 25 7
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 43
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Lời giải Chọn A.  11
Số hạng thứ mười một của dãy số là 1 1 u    . 11 2.11 5 27
Câu 16. Cho cấp số cộng u với u  2
 và công sai d  3. Tổng 10 số hạng đầu tiên S của n  1 10 u là n  A. 155. B. 115. C. 145. D. 165. Lời giải Chọn B.
Tổng 10 số hạng đầu tiên S 10u  45d 115 . 10 1
Câu 17. Trong mặt phẳng toạ độ Oxy , cho điểm A2;0 . Ảnh của A qua phép quay  Q có O;90 toạ độ là A. M 0;2 . B. N 0; 2 . C. P 2  ;0 . D. Q1;  1 . Lời giải Chọn A. Qua phép quay  Q
, ảnh của A2;0 là M 0;2 . O;90
Câu 18. Trong không gian, có bao nhiêu vị trí tương đối giữa hai đường thẳng phân biệt a và b ? A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn C.
Trong không gian, 4 vị trí tương đối giữa hai đường thẳng phân biệt a và b là song song, chéo nhau, cắt nhau.
Câu 19. Tập nghiệm của phương trình sin x 3cot x  1  0 là A.      
k ,  k , k   .
B.   k ,k  .  6   6  C.         k , k   .
D. k,  k ,k  .  3   3  Lời giải Chọn C.
Điều kiện: sin x  0  x  k k  . Trang 44
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Với điều kiện trên:  sin x  3 cot x   1  3 0  cot x 
 x   k k  . 3 3 Câu 20.  1 n 
Tổng các hệ số trong khai triển 2 x  
 là 4096 . Hệ số của số hạng không chứa x  x  trong khai triển là A. 495 . B. 133. C. 334. D. 775. Lời giải Chọn A. n k n n Ta có:  1 nk  k  1 2  x   C x   k 2n 3k  C x  . n  2     x  n k 0  x  k 0 n
Tổng hệ số của khai triển là k 0 1 2 C  C C C .... n  C 1  1 n   2n   4096 12  2 . n n n n n k 0 12 12 Do đó:  1 
n  12 nên ta có khai triển 2 x    k 24 3k  C x  .  x  12 k 0
Số hạng không chứa x trong khai triển ứng với: 24  3k  0  k  8 .
Vậy hệ số của số hạng không chứa x trong khai triển là 8 C  495 . 12
Câu 21. Từ một hộp chứa 16 cái thẻ đánh số từ 1 đến 16. Chọn ngẫu nhiên 3 thẻ. Xác suất để
được 3 thẻ đều là số lẻ là A. 1 . B. 1 . C. 56 . D. 3 . 10 2 506 16 Lời giải Chọn A.
Số phần tử không gian mẫu là 3   C  560 . 16
Gọi A là biến cố 3 thẻ được rút đều mang số lẻ. Khi đó số phần tử của biến cố A là 3 A  C  56. 8
Vậy xác suất để 3 thẻ được chọn đều mang số lẻ là P A 56 1   . 560 10
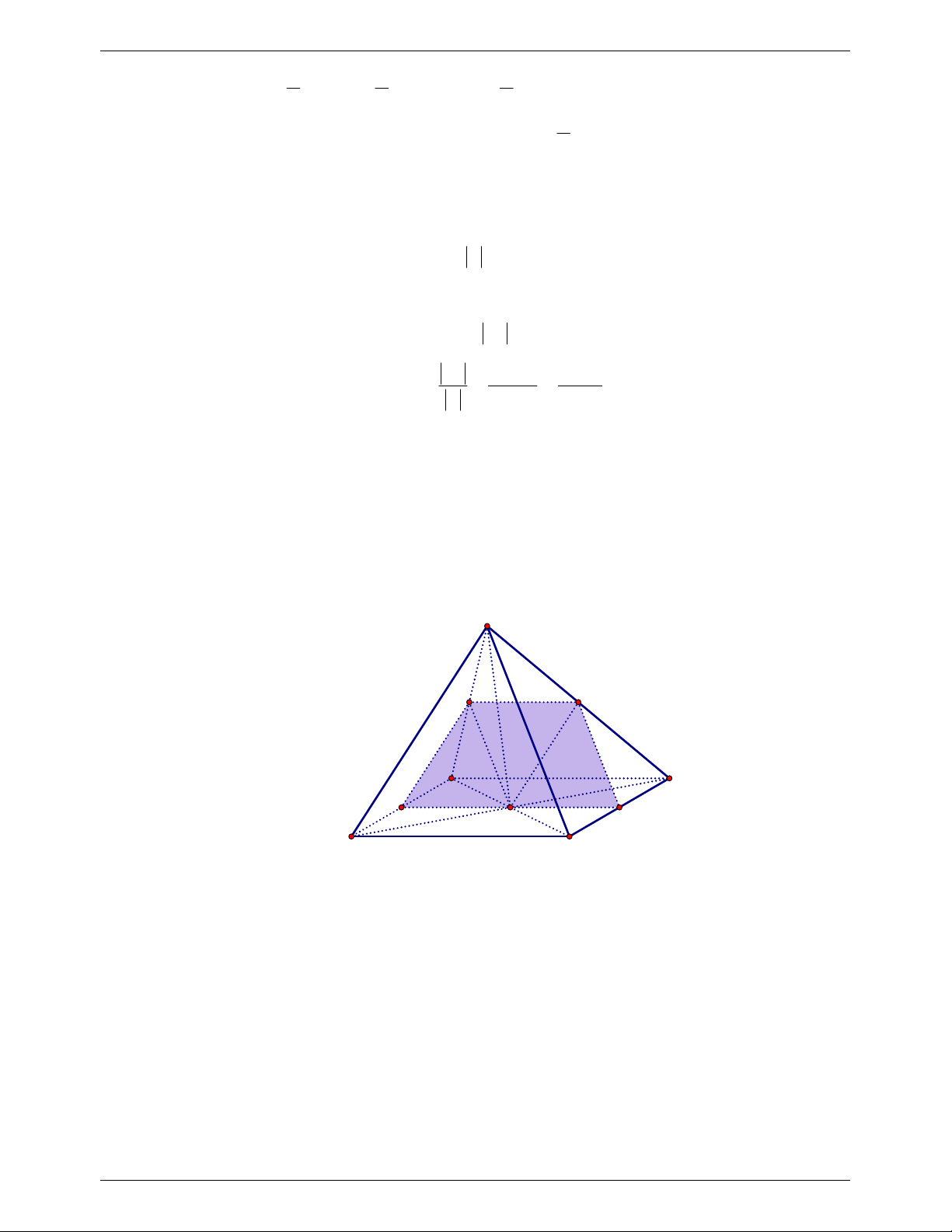
Câu 22. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, M là trung điểm cạnh SA .
Gọi P là mặt phẳng đi qua M đồng thời song song với SC và AD . Thiết diện của
hình chóp S.ABCD cắt bởi P là một A. hình thang.
B. hình bình hành. C. tứ giác. D. ngũ giác. Lời giải Chọn A.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 45
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
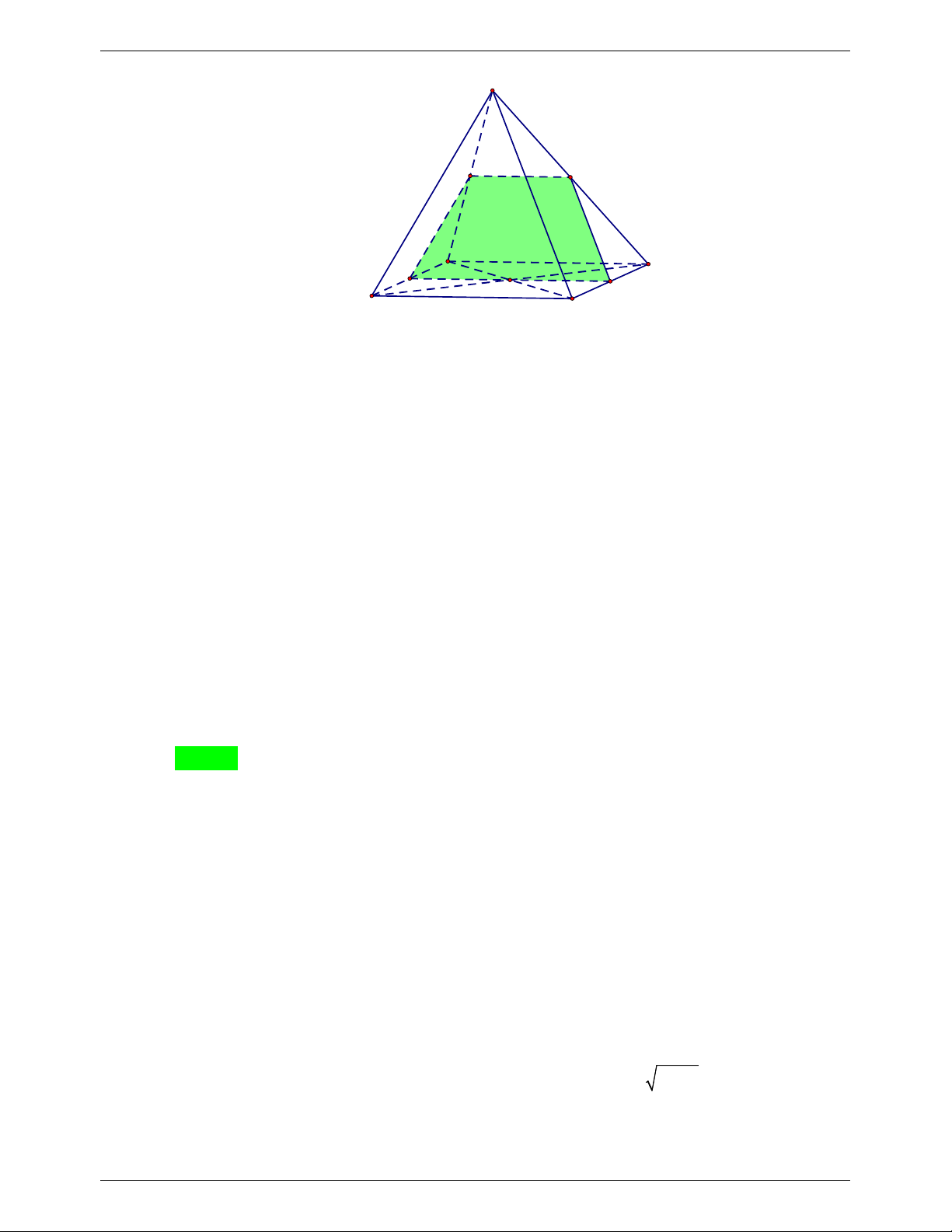
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT S M E N D A O F B C
Vì P // AD nên giao tuyến của P với SAD là đường thẳng qua M song song với
AD cắt SD tại E là trung điểm SD .
Vì P // SC nên giao tuyến của P với SCD là đường thẳng qua E song song với
SC cắt CD tại F là trung điểm CD .
Vì P // AD nên giao tuyến của P với  ABCD là đường thẳng qua F song song với
AD cắt AB tại N là trung điểm AB . Dễ thấy MN  P SAB .
Vì ME và NF cùng song song với AD nên chúng song song với nhau.
Vậy thiết diện là hình thang MEFN .
Câu 23. Trong mặt phẳng Oxy cho đường thẳng a . Gọi b là ảnh của a qua phép đồng dạng
có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k  2  và phép đối xứng
trục Oy . Biết đường thẳng b có phương trình là 2x  y 16  0 , khi đó phương trình đường thẳng a là A. 2x  y 8  0 . B. 2x  y  32  0. C. 2x  y  32  0 . D. 2x  y  8  0 . Lời giải Chọn D.
Giả sử M x; y là một điểm bất kì thuộc đường thẳng a , M x; y  V M . O;2       x  2  x
Ta có OM   2OM     1 .  y  2  y x  x
Gọi M  x ; y   D M . Khi đó ta có  2. Oy    y  y Từ  
1 , 2 suy ra x  2x và y  2y , mà M  b nên 2x  y 16  0
 4x  2y 16  0  2x  y  8  0 *
Vì M x; y là một điểm bất kì thuộc đường thẳng a và tọa độ điểm M thỏa mãn
phương trình * nên * chính là phương trình đường thẳng a .
Câu 24. Cho dãy số u xác định bởi u 1 và 2 u  u  2 , * n    . Tổng n  1 n 1  n 2 2 2 2
S  u  u  u  ...  u bằng 1 2 3 1001 A. 1002001. B. 1001001. C. 1001002. D. 1002002. Trang 46
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Lời giải Chọn A. Từ giả thiết 2 u  u  2 ta có 2 2 u  u  2 . n 1  n n 1  n Xét dãy số 2 v  u với * n    ta có 2 v  u 2
 u  2 hay v  v  2  dãy số v là n  n n n 1   n 1  n n 1 n
một cấp số cộng với số hạng đầu 2
v  u  1 và công sai d  2 . 1 1 Do đó 10012.1  1001 12 2 2 2 2 
S  u  u  u  ...  u  v  v  v ... v  10002001. 1 2 3 1001 1 2 3 1001 2
Câu 25. Ngân hàng đề thi học kỳ I môn Văn của trường Y có 50 câu hỏi. Mỗi đề gồm bốn câu
hỏi được lấy ngẫu nhiên từ ngân hàng đề thi. Thí sinh A đã học thuộc 25 câu trong
ngân hàng đề thi. Tính xác suất để khi thí sinh A nhận đề thì có ít nhất ba câu đã học thuộc. A. 135 . B. 1403 . C. 13 . D. 7 . 458 4606 19 19 Lời giải Chọn B .
Số đề thi có thể tạo được từ ngân hàng đề thi là 4 C . 50
Số đề thi có ít nhất ba câu mà thí sinh A đã học thuộc là 3 1 4 C C  C . 25 25 25
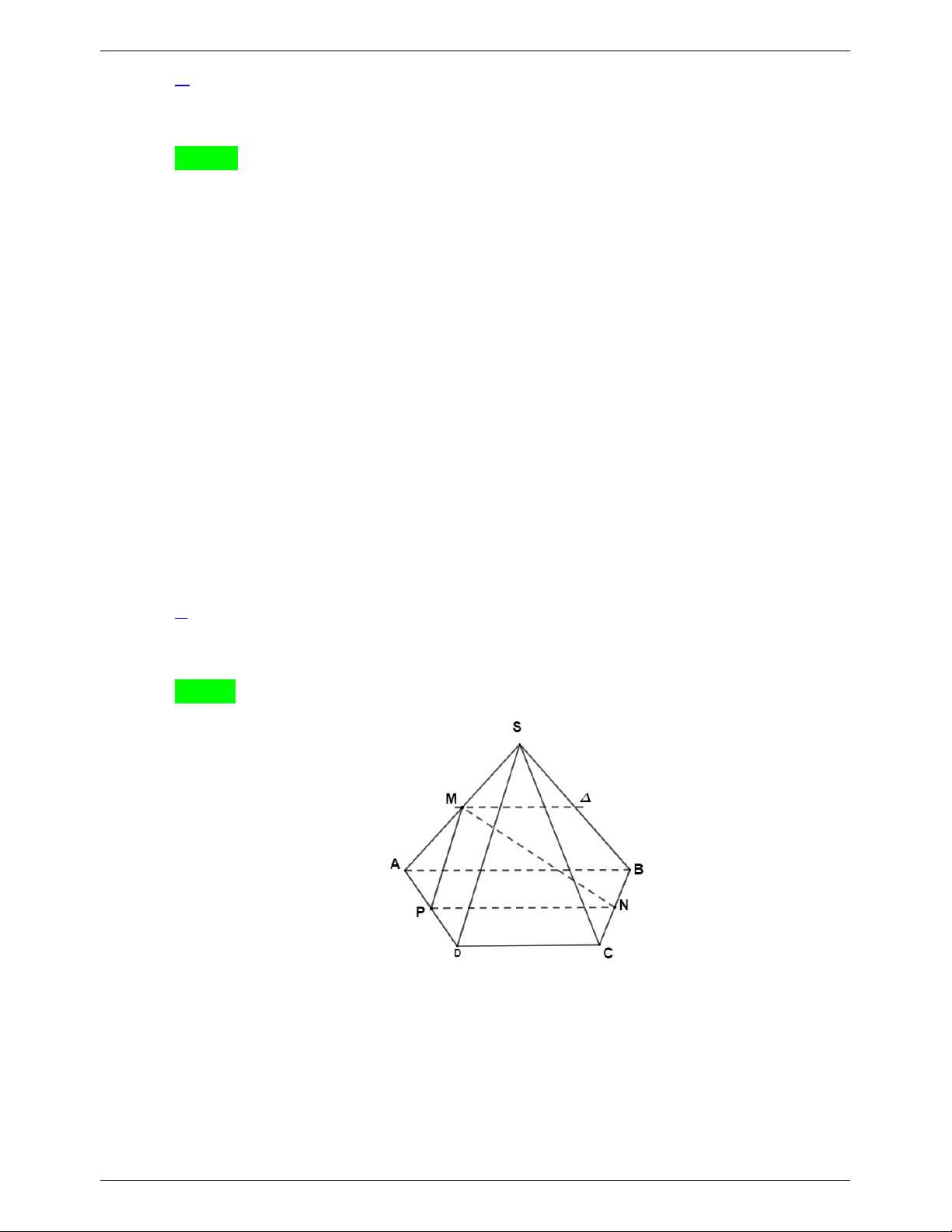
Vậy xác suất để khi thí sinh A nhận đề thì có ít nhất ba câu đã học thuộc là 3 1 4 C C  C 1403 25 25 25 P   . 4 C 4606 50 PHẦN II. TỰ LUẬN.
Câu 1. Giải phương trình sau: 1) sin 2x  cos x  0 .
2) tan x 30  3  0. Lời giải 1) Phương trình
sin 2x  cos x  0  2sin .
x cos x  cos x  0  cos x2sin x   1  0 cos x  0   1 . sin x   2 
 cos x  0  x   k . 2   x   k2   sin x  0 6   . 5   x   k2  6   
Vậy phương trình đã cho có 3 họ nghiệm x   k , x   k2 , 5 x   k2 ,k . 2 6 6
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 47
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT 2) Phương trình
tan  x  30  3  0  tan  x  30  3  tan 60
 x  30  60  k.180  x  90  k.180 . Vậy phương trình có 1 họ nghiệm là x  90  k.180 ,  k   .
Câu 2. Tìm số nguyên dương n thỏa mãn điều kiện: 2 C  n  9 . n Lời giải Điều kiện: n  2 . Phương trình 2 n! C  n  9   n   nn   1  2n  18 n n   9 2! 2 ! n  6 2
 n  3n 18  0   . n  3   l
Vậy n  6 là giá trị cần tìm. Câu 3.   Tìm số hạng chứa 11
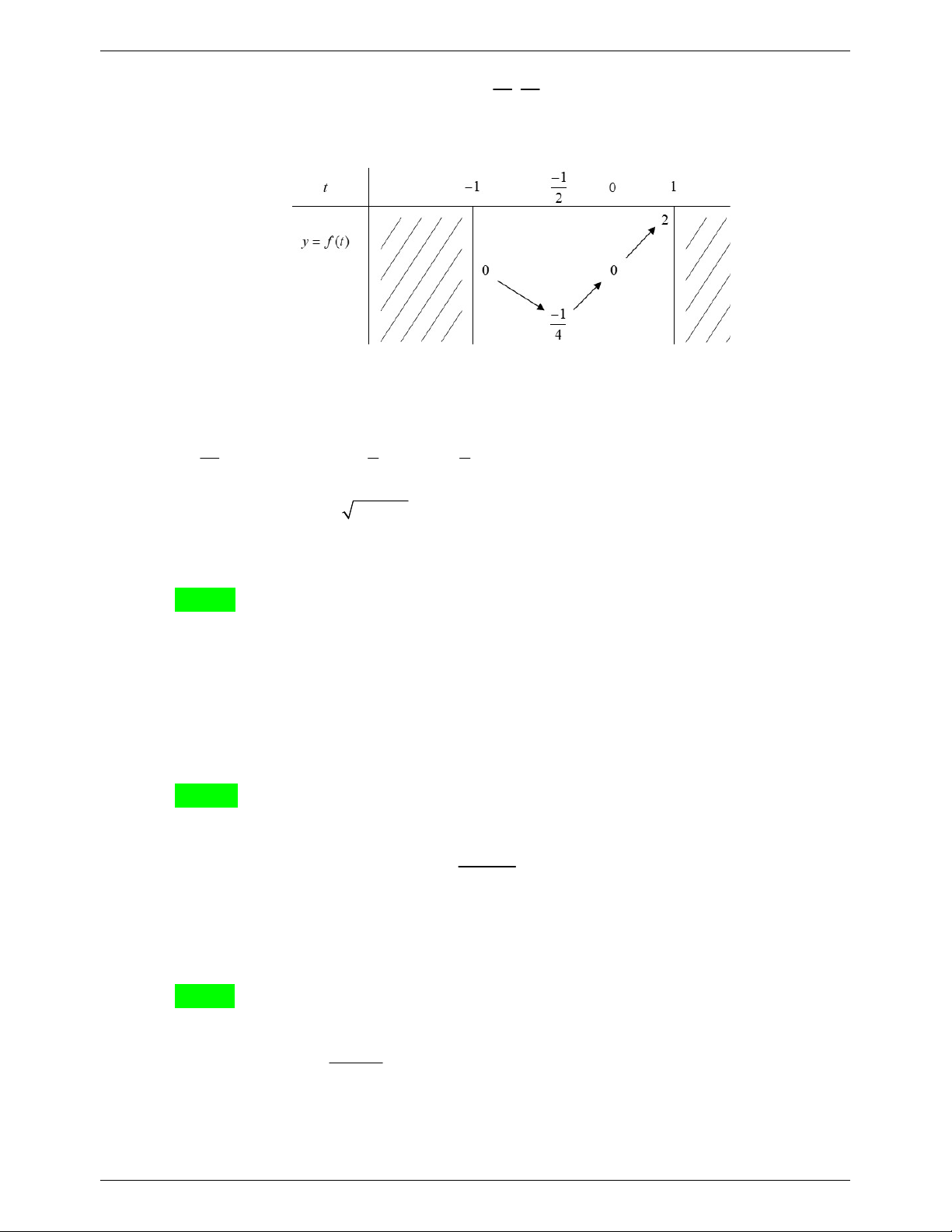
x trong khai triển nhị thức Niutơn của biểu thức 2 2 n x    , biết n  x 
là số nguyên dương thỏa mãn 0 2 1 4 2 2n n 5
C  3 C  3 C  ... 3 C  100 . n n n n Lời giải Khai triển  2  x n 0 1 2 2 4 n 2 1  C  C x  C x  ... n  C x . n n n n Cho x  3 ta được n 0 2 1 4 2 2
10  C  3 C  3 C ... 3 n n C . n n n n Từ giả thiết ta có n 5 n 10
10  100  10  10  n  10 . 10 k Với   k k  2  n  10 , khai triển 2 2 x  
 có số hạng tổng quát là: k  .2k.  k C x C x . 10  10 2 20 3    x  10  x  Số hạng chứa 11
x nên 20  3k 11  k  3 . Vậy số hạng cần tìm là 3 3 11 11 C .2 .x  960x . 10
Câu 4. (1 điểm) Cho một đa giác đều n cạnh. Chọn ngẫu nhiên 3 đỉnh của đa giác đều đó.
Gọi P là xác xuất sao cho 3 đỉnh đó tạo thành một tam giác tù. Tính n , biết n là số lẻ, n  3 và 45 P  . 62 Lời giải
Số phần tử của không gian mẫu: n 3  C . n
Chọn 1 đỉnh của đa giác (ký hiệu là A) có n cách chọn.
Gọi O là tâm đường tròn ngoại tiếp đa giác. Khi đó, đường thẳng OA chia đa giác
thành 2 phần đối xứng nhau qua OA.
Để tạo thành tam giác tù, chỉ cần lấy 2 đỉnh còn lại trong n 1 điểm về 1 phía của OA. 2
Do đó, số tam giác tù tạo thành là 2 . n C . n 1  2 Trang 48
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 2 . n C  n 1 n 1  !   Theo bài ra, ta có 45 n! 2 3 2 P    45.C  62 . n C  2 45. 62n    3 n n 1 62 C  3  ! n  3!  n 1  n 2 2!  2 !    2       nn  n   n 1 n 1 15 1 2  62 . n . 1    30nn  
1 n  2  31n   1 n  3 2  2 
 30n  60  31n 93  n  33.
Vậy n  33 là giá trị cần tìm.
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB//CD , 2AB  3CD . Gọi M là điểm thuộc đoạn SM SB sao cho 2
 , O lả giao điểm của hai đường chéo AC và SB 5 BD .
1) Xác định giao tuyến của hai mặt phẳng SAB và SCD .
2) Chứng minh rằng: SD// MAC .
3) Gọi N là giao điểm của đường thẳng AM và mặt phẳng SDC . Gọi S là diện OMNC tích của tứ giác S OMNC , S
là diện tích của tam giác OMC . Tính tỉ số OMC . OMC SOMNC Lời giải S N d M B A O D C
1) Ta có AB//CD , AB  SAB , CD  SCD , S SAB SCD
Suy ra SAB SCD  d , với d là đường thẳng đi qua S và song song với AB và CD . 2) Vì OB AB BO AB//CD suy ra 3 3       1 OD CD 2 BD 5 Mà SM 2 BM 3    2 SB 5 BS 5
Trong tam giác SBD , từ  
1 và 2 ta suy ra SD//OM .
Ta có SD  MAC , OM  MAC , SD//OM suy ra SD// MAC .
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 49
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
3) Trong mặt phẳng SAB có  AM  d  N  N  AM SCD. Vì AM BM AM AM AO SN//AB nên ta có 3 3 3        . NM SM 2 AN 5 AN AC 5 Suy ra S OM //CN , suy ra 9 AOM  . S 25 ACN Suy ra S 16 S OMNC  , 16 S  S . Mà 2 S  S , suy ra 3 OMC  . S 25 OMNC 25 ACN OMC 3 AMO S 8 ACN OMNC ---- HẾT ----- Trang 50
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 2 – SỞ HÀ NỘI
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A C C B A D A B C B D C B A D 16 17 18 19 20 21 22 23 24 25 B C D B B D A A B C
Câu 1. Tập xác định của hàm số 1 y  là sin 2x A.  k    k  \  , k  . B.  \   , k   .  2   4 2  C.  
 \   k , k  . D.  \k , k    .  2  Lời giải Chọn A  Điều kiện xác định: k
sin 2x  0  2x  k  x  , k  . 2
Vậy tập xác định của hàm số là  k  D   \  , k   .  2 
Câu 2. Trong các phép biến hình sau, phép biến hình nào không là một phép dời hình?
A. Thực hiện liên tiếp hai phép quay.
B. Thực hiện liên tiếp hai phép đối xứng trục.
C. Thực hiện liên tiếp hai phép vị tự có cùng tâm và tỷ số vị tự là 2 số đối nhau.
D. Thực hiện liên tiếp hai phép vị tự có cùng tâm và tỷ số vị tự là 2 số nghịch đảo của nhau. Lời giải Chọn C V  M  M    O ; k   O  M  kOM    Giả sử   1  1  
  OM  k  2 .kOM  k OM . V M  M       O ; k  1     OM kOM  1
Vậy thực hiện thực hiện liên tiếp hai phép vị tự có cùng tâm và tỷ số vị tự là 2 số đối
nhau thì thu được một phép vị tự với tỷ số là tích của 2 tỷ số đã cho (không phải phép dời hình).
Câu 3. Một lớp 11 có 30 học sinh, gồm 15 nam và 15 nữ. Có bao nhiêu cách xếp các học sinh
thành hai hàng, một hàng nam và một hàng nữ trong lúc tập thể dục giữa giờ? A. 30!. B. 15 A . C.  2 2 15! . D. 15 C . 30 30 Lời giải Chọn C
Chọn vị trí cho hai hàng nam và nữ xếp cạnh nhau có 2! cách
Xếp 15 bạn nam thành một hàng có 15! cách
Tương tự, xếp 15 bạn nữ thành một hàng có 15! cách
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 51
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Theo quy tắc nhân, có tất cả:   2
2!.15!.15! 2 15! cách xếp thỏa mãn đề bài.
Câu 4. Trong mặt phẳng tọa độ Oxy , gọi A là ảnh của A1 ; 3 qua phép vị tự tâm O, tỷ số k  2
 . Tọa độ điểm A là A. 2 ; 6 . B.  2  ;  6 . C.  2  ; 6. D. 2 ;  6. Lời giải Chọn B   V A  A  OA  2
 OA. Mà A1 ; 3 nên tọa độ điểm A 2  ;  6 . O ; 2    
Câu 5. Cho 19 điểm phân biệt A , A , A ,...A trong đó có 5điểm A , A , A , A , A thẳng hàng 1 2 3 19 1 2 3 4 5
ngoài ra không có 3 điểm nào thẳng hàng, Hỏi có bao nhiêu tam giác có 3 đỉnh trong 19 điểm trên? A. 959 . B. 969. C. 364. D. 374. Lời giải Chọn A
Để tạo ra một tam giác có 3 đỉnh trong số 19 điểm trên ta thực hiện theo 3 phương án sau:
+Phương án 1: lấy 2 đỉnh từ A , A ,..., A và 1 đỉnh từ A , A , A , A , A . 6 7 19 1 2 3 4 5
Số tam giác được tạo thành là 2 1 C .C . 14 5
+Phương án 2: lấy 1 đỉnh từ A , A ,..., A và 2 đỉnh từ A , A , A , A , A . 6 7 19 1 2 3 4 5
Số tam giác được tạo thành là 1 2 C .C . 14 5
+Phương án 3: lấy 3 đỉnh từ A , A ,..., A . 6 7 19
Số tam giác được tạo thành là 3 C . 14
Vậy số tam giác được tạo thành là 2 1 1 2 3 C .C  C .C  C  959. 14 5 14 5 14 11 Câu 6.  3
Trong khai triển nhị thức Newton của biểu thức 2 x    
(với x  0 ), hệ số của số  x hạng chứa 7 x là : A. 7 C . B. 7 7 3 C . C. 5 C . D. 5 5 3 C . 11 11 11 11 Lời giải Chọn D 11 11 k 11 Ta có  3    x     C    x 11 k k 3 2 2 k k 22 3 .     C 3  k x .  11 11 x x k0 k0
Xác định hệ số của số hạng chứa 7
x ta giải phương trình 223k  7  k  5
Vậy hệ số của số hạng chứa 7 x là 5 5 3 C11
Câu 7. Nghiệm của phương trình 2 x 1 A  C   5 là: x x 1  A. x  5. B. x  3. C. x  4 D. vô nghiệm. Lời giải Trang 52
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Chọn A TXĐ: x  2; x   . x! x  1!  Ta có x x 2 x 1 A  C   5    5  x x     1 1   5 x x 1 
x  2! x  1!.2! 2 x  2 (L)  2x x   1   x   1 x  10 2
 x  3x 10  0   x  5 (TM)
Câu 8. Từ các chữ số 0;1;2;3;4;5;6;7 lập được tất cả bao nhiêu số tự nhiên có 3 chữ số đôi một
khác nhau và chia hết cho 5 ? A. 112 số. B. 78 số. C. 42 số. D. 84 số. Lời giải Chọn B
Gọi số cần lập là abc.
Để lập được số thỏa mãn bài toán, xét các trường hợp
Trường hợp 1: c  0: Chọn a,b có 2 A cách. 7
Trường hợp 2: c  5 : Chọn a  0 có 6 cách, chọn b có 6 cách.
Vậy số cách lập số thỏa mãn là 2 A  6  6  78 cách. 7
Câu 9. Mệnh đề nào trong các mệnh đề sau là sai? A. 0 1 2
0  C  C  C     1 n n C . B. 0 1 2 2n n
 C  C  C    C . n n n n n n n n C. 0 1 2
1  C  2C  4C   2n n C . D. n 0 1 2
3  C  2C  4C    2n n C . n n n n n n n n Lời giải Chọn C
Xét khai triển a  bn 0 n 1 n 1  2 n2 2 3 n3 3 n 1  n 1  n n
 C a  C a b  C a b  C a b  C ab  C b . n n n n n n
Với a  1,b  1 ta có 0 1 2
0  C  C  C     1 n n C . n n n n Với a  b  1 ta có 0 1 2 2n n
 C  C  C    C . n n n n Với a  1,b  2 ta có n 0 1 2
3  C  2C  4C    2n n C . n n n n Với a  1,b  2  ta có  n 0 1 2
1  C  2C  4C   2n n C . n n n n Câu 10. Cho ,
A B là hai biến cố độc lập của phép thử T . Xác suất xảy ra biến cố A là 0,5 và
xác suất xảy ra biến cố B là 0,25. Xác suất để xảy ra biến cố A và B là A. 0,25. B. 0,125. C. 0,75. D. 0,375. Lời giải Chọn B
Vì A và B là hai biến cố độc lập nên P A B  P A PB  0,50,25  0,125 .
Câu 11. Khẳng định nào trong các khẳng định sau là đúng?
A. Nếu hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.
B. Hai đường thẳng chéo nhau khi chúng không có điểm chung.
C. Hai đường thẳng song song khi chúng ở trên cùng một mặt phẳng.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 53
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
D. Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau. Lời giải Chọn D
Đáp án A sai vì nếu hai đường thẳng ở trên hai mặt phẳng chúng có thể song song, cắt
nhau và chéo nhau hoặc trùng nhau.
Đáp án B sai vì hai đường thẳng chéo nhau khi chúng không cùng nằm trong 1 mặt phẳng và không có điểm chung.
Đáp án C sai vì hai đường thẳng song song khi chúng cùng thuộc 1 mặt phẳng và không có điểm chung. Do đó đáp án D đúng.
Câu 12. Cho chóp S.ABCD có đáy ABCD là hình thang có AB // CD . Gọi M , N và P lần lượt là trung điểm S ,
A BC và AD . Giao tuyến của hai mặt phẳng SAB và MNP là
A. Đường thẳng qua S và song song với AB .
B. Đường thẳng qua N và song song với SC .
C. Đường thẳng qua M và song song với AB . D. Đường thẳng MN . Lời giải Chọn C
Ta có M là điểm chung của 2 mặt phẳng SAB và MNP .
AB / / NP ( do N, P là trung điểm BC và AD)
AB  SAB, NP  MNP
Do đó SABMNP   với  thỏa mãn: M ; / / AB .
Câu 13. Cho 100 tấm thẻ được đánh số từ 1 đến 100, chọn ngẫu nhiên đồng thời 3 tấm thẻ. Xác suất để Trang 54
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
chọn được 3 tấm thẻ có tổng các số ghi trên thẻ là số chia hết cho 2 là: A. 5 . B. 1 . C. 3 . D. 49 . 6 2 4 198 Lời giải Chọn B
Không gian mẫu: “ lấy ngẫu nhiên đồng thời 3 tấm thẻ từ 100 tấm thẻ” 3    C . 100
Biến cố A: “ chọn được 3 tấm thẻ có tổng các số ghi trên thẻ là số chia hết cho 2”
Từ 1 đến 100 có 50 thẻ lẻ và 50 thẻ chẵn.
Trường hợp 1: Chọn được 2 thẻ lẻ và 1 thẻ chẵn: 2 1 C .C . 50 50
Trường hợp 2: Chọn được 3 thẻ chẵn: 3 C 50 2 1 3  A  C .C  C 50 50 50 A
Do đó xác suất của biến cố A là 1 P   . A  2
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, điểm M nằm trên cạnh SB
sao cho SB  4BM . Giao điểm của đường thẳng SD và mặt phẳng  ACM  nằm trên đường thẳng nào sau đây: A. OM . B. AM . C. CM . D. AC . Lời giải Chọn A
Ta có: SDB ACM   MO . Q   SD Trong mặt phẳng   SBD : MO  SD    Q   . Q   MO    ACM 
Do đó: SD  ACM     Q .
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 55
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Vậy giao điểm của SD và mặt phẳng  ACM  thuộc đường thẳng MO .
Câu 15. Cho hình chóp S.ABCD có các cạnh bên bằng nhau, đáy ABCD là hình vuông, SM
AB  20cm . Gọi M là điểm nằm trên cạnh SA sao cho 2
 . Gọi P là mặt phẳng SA 3
đi qua M, song song với hai đường thẳng AB và AC . Mặt phẳng P cắt hình chóp
S.ABCD theo thiết diện là một hình tứ giác có diện tích bằng: 80 400 800 1600 A. 2 cm . B. 2 cm . C. 2 cm . D. 2 cm . 9 9 9 9 Lời giải Chọn D S M K (P) H N A D B C
Gọi d  P  SAC  M  d 1       1 AC   SAC Ta có:  AC / /  P
 d / / AC , gọi H là giao điểm của d với SC 1  1 
Gọi d  P  SAB  M  d 2       2 AB   SAB Ta có:  AB / /  P
 d / / AB , Gọi N là giao điểm của (d ) với SB  (P)  (SAB)  MN (1) 2  2
Gọi d  P  SCD  H  d 3       3 CD   SAD Ta có:  CD / /  P  d / /CD . 3  Trang 56
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1   P SCD  HK 
Gọi F là giao điểm của d với SD  
 P  SAD  MK (2) 3    P    SBC   NH
Từ (1) và (2) suy ra thiết diện của (P) với hình chóp S.ABCD là tứ giác MNHK Ta có: SM MN NH HK KM EF / / A ;
D EH / / AB; HK / /BC; KF / /CD ; 2      SA AB BC CD AD 3
Tứ giác ABCD là hình vuông nên tứ giác MNHK là hình vuông có cạnh là 40 cm 3
Suy ra diện tích thiết diện là: 1600 2 cm 9 Câu 16. Phương trình  x   2 cos
1 sin x  sin x  m   0 có đúng 6 nghiệm thuộc 0;2  khi và chỉ
khi m  a;b . Khi đó tổng a  b là số nào? A. 0,5 . B. 0, 25 . C. 0, 25 . D. 0,5 . Lời giải Chọn B Ta có:  x   2 cos
1 sin x  sin x  m  0 cos x 1  0 cos x  1 (1)    2 2 sin x  sin x  m  0
sin x  sin x  m  0 (2)
(1)  cos x  1  x  k 2 , k   với x  0; 2   x  0; 2 
Xét (2) Đặt t  sin x ; t 1; 
1 phương trình (2) được viết lại như sau: 2 2
t  t  m  0  t  t  m (*)
Để phương trình đã cho có đúng 6 nghiệm thuộc 0;2  thì phương trình (2) có đúng
4 nghiệm thuộc 0;2   (*) có 2 nghiệm phân biệt t ; t  1;1 \ 0 1 2    
Ta có phương trình (*) là phương trình hoành độ giao điểm của 2 đồ thị hàm số d  và P với 2
 y  f (t)  t  t; t 1;  1  P    y  m d 
Để phương trình (*) có 2 nghiệm phân biệt t ; t  1;1 \ 0 thì d  cắt P tại 2 điểm 1 2    
phân biệt có hoành độ t ; t  1;1 \ 0 1 2     Xét 2
y  f (t)  t  t; t  1;  1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 57
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Ta có     
P là Parabol có tọa độ đỉnh là 1 1 I ;    2 4  Bảng biến thiên:
Dựa vào bảng biến thiên d  cắt P tại 2 điểm phân biệt có hoành độ t ; t  1;1 \ 0 1 2     1 1      m  0  0  m  1  m  0; 
 . Vậy a  b  0, 25 . 4 4  4 
Câu 17. Tập xác định của y  1 sin x là A.  1  ; . B.  ;    1 . C.  . D.  \k2,k    . Lời giải Chọn C. Ta có 1
  sin x 11 sin x  0 , x    .
Câu 18. Người ta trồng 1275 cây theo hình tam giác như sau: Hàng thứ nhất có 1 cây, hàng
thứ 2 có 2 cây, hàng thứ 3 có 3 cây,, hàng thứ k có k cây k   1 . Hỏi có bao nhiêu hàng? A. 51. B. 52. C. 53. D. 50. Lời giải Chọn D.
Việc trồng các cây trên theo quy luật của một cấp số cộng nên ta có k k   1 k  50 S  1 2  ...  k   1275  . k  2 k  51   0
Câu 19. Nghiệm của phương trình 2 1 A  A  3 là: x x A. x  1  . B. x  3. C. x  1  và x  3. D. x 1. Lời giải Chọn B. Điều kiện x  2 , * x   . Ta có x! 2 1 A  A  3   x  3  xx   1  x  3 x x x  2! 2
 x  2x  3  0  x  3 vì x  2 , * x   . Trang 58
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Câu 20. Cô giáo chia 4 quả táo, 3 quả cam và 2 quả chuối cho 9 cháu (mỗi cháu 1 quả). Hỏi
có bao nhiêu cách chia khác nhau A. 120. B. 1260. C. 9. D. 24 . Lời giải Chọn D.
Số cách chia 4 quả táo có 4 cách
Số cách chia 3 quả cam có 3 cách
Số cách chia 2 quả chuối có 2 cách
Vậy số cách chia cho 9 cháu là 4.3.2  24 (cách).
Câu 21. Một chiếc máy có 2 động cơ I và II hoạt động độc lập với nhau.Xác suất để động cơ I
chạy tốt và động cơ II chạy tốt lần lượt là 0,8 và 0,7 . Tính xác suất để có ít nhất 1 động cơ chạy tốt là A. 0,56. B. 0,06 . C. 0,83 . D. 0,94. Lời giải Chọn D.
Gọi A là biến cố “Động cơ I chạy tốt”, B là biến cố “Động cơ II chạy tốt”
Gọi D là biến cố “Cả hai động cơ đều chạy không tốt”. Ta thấy D  . A B . Hai biến cố
A và B độc lập với nhau nên
P D  P  A PB  1   P  A 1   P  
B  0,2.0,3  0,06 
Gọi K là biến cố “Có ít nhất một động cơ đều chạy tốt” khi đó
P K  1 P D 1 0,06  0,94 .
Câu 22. Cho S.ABCD có đáy là hình bình hành. Mệnh đề nào sau đây sai?
A. SADSBC là đường thẳng qua S và song song với AC .
B. SABSAD  SA . C. SBC // AD . D. SA và CD chéo nhau. Lời giải Chọn A. S A D B C
Đáp án A sai vì SAD SBC là đường thẳng qua S và song song với AD hoặc BC . Đáp án B, C, D đúng.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 59
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Câu 23. Tổng 1 2 3 2017 C  C  C  ...  C bằng 2017 2017 2017 2017 A. 2017 2 1. B. 2017 2 1. C. 2017 2 . D. 2017 4 . Lời giải Chọn A.
Xét khai triển 1 x2017 0 2 2 2 2017 2017  C  C x  C x  C x . 2017 2017 2017 2017 Cho x 1 ta được: 2017 0 1 2 3 2017 2  C  C  C  C   C . 2017 2017 2017 2017 2017 Vậy 1 2 3 2017 2017 C  C  C  ... C  2 1. 2017 2017 2017 2017
Câu 24. Trong mặt phẳng Oxy cho đường tròn C có phương trình x  2   y  2 2 2  4 Hỏi
phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 1 k  và 2
phép quay tâm O góc quay 90 sẽ biến C thành các đường tròn nào trong các đường tròn sau
A. x  2   y  2 1 1  1.
B. x  2   y  2 1 1  1 .
C. x  2   y  2 2 1  1.
D. x  2   y  2 2 2  1. Lời giải Chọn C.
C có tâm I 2;2 , bán kính R  2 .   Gọi 1 I  V I  OI  OI  I 1;1 . 1  1    1 1   O;   2  2  Gọi  1 C  V
C  C có tâm I 1;1 , bán kính R  R  1. 1   1  1   1    1 O;   2  2  C  Q C  C có tâm I 1  ; 
1 , bán kính R  R  1. O;90  1      1
Vậy phương trình đường tròn C là ảnh của C qua phép đồng dạng trên là:
x  2   y  2 1 1  1.
Câu 25. Cho tứ diện ABCD đều cạnh a . Gọi G là trọng tâm tam giác ABC , mặt phẳng CGD
cắt tứ diện theo một thiết diện có diện tích là. 2 2 2 2 A. a 2 . B. a 3 . C. a 2 . D. a 3 . 6 4 4 2 Lời giải Chọn C. Trang 60
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 A I G B D O M C
Trong mặt phẳng  ABC: I  CG  AB  I là trung điểm của AB .
Ta có: CGD ABC  CI ; CGD ABD  ID ; CGD ACD  CD .
Suy ra: thiết diện của tứ diện tạo bởi mặt phẳng CGD là tam giác ICD . Vì a
ABCD là tứ diện đều cạnh a nên: 3 IC  ID   ICD cân tại I . 2 2 2 Gọi 3a a a M là trung điểm của CD 2 2  IM  IC  CM    . 4 4 2 2
Vậy diện tích thiết diện là: 1 1 a a S  IM .CD  .a  . ICD 2 2 2 2 2
PHẦN II. TỰ LUẬN (6 ĐIỂM) Bài 1. Giải phương trình: 2 2
3 cos x  sin 2x  3 sin x 1. Lời giải 2 2
3 cos x  sin 2x  3 sin x  1 2 2
 3 sin x  2sin x cos x  3 cos x 1  0 (1)
+ Dễ thấy các giá trị của x mà cos x = 0 không là nghiệm của phương trình (1)
+ Chia hai vế của (1) cho cos2 x, ta được phương trình tương đương: 2 2
3 tan x  2 tan x  3 1 tan x  0 2
 ( 3 1) tan x  2 tan x  (1 3)  0    tan 1 x   k x   4     (k  ) tan x  3  2  x    k     12 Bài 2. a) Cho 2 (x  2)n n
 a  a x  a x  a x . Tìm n để a : a 12 : 7 . 0 1 2 n 5 6 Lời giải
Hệ số của số hạng chứa xk của khai triển là k
a  C  2nk với 0  k  n và k, n  ;  n  6 k n
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 61
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT 5 n5  Vì a 12 C 2 12 n n 12 5 5 5 6 n6     n!  n n 12 ! C  2  C 2 5 n6   2    2 6 n6 a 7 C  2 7 n 7 n 5!(n  5)! 7 6!(n  6)! 6 n 2 12  
 n 12 ( thỏa mãn điều kiện). Vậy n 12 . n  5 7.6
b) Trong một hộp có 10 viên bi màu xanh và 8 viên bi màu đỏ. Bạn Bình lấy ngẫu
nhiên 1 viên bi (lấy xong không trả lại vào hộp), sau đó bạn An lấy tiếp 1 viên bi nữa.
Tính xác suất để hai bạn lấy được bi cùng màu. Lời giải
Xét phép thử T: Bình lấy 1 viên bi trong hộp có 10 bi xanh và 8 bi đỏ, sau đó đến lượt An lấy tiếp 1 viên bi.
Số phần tử của không gian mẫu là: 2 n()  A  18.17 18
Gọi A là biến cố: “ Hai bạn lấy được bi cùng màu”
Số cách để hai bạn lấy được bi cùng màu xanh là:
Số cách để hai bạn lấy được bi cùng màu đỏ là:
Nên số cách để hai bạn lấy được bi cùng màu là: n( ) A  10.9  8.7  146
Xác suất để hai bạn lấy được bi cùng màu là: n( ) A 146 73 P( ) A    n() 18.17 153 Bài 3.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm các cạnh AB, CD .
a) Chứng minh rằng: MN song song với mặt phẳng (SBC), (SAD).
b) Gọi P là trung điểm SA . Chứng minh rằng: SB, SC song song với mặt phẳng (MNP).
c) Gọi G ;G lần lượt là trọng tâm tam giác ABC, SBC . Chứng minh rằng: đường 1 2 thẳng G1G2
song song với mặt phẳng (SAC).
d) Dựng thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (PNG2). Lời giải Trang 62
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
a) Do MN // BC và MN  (SBC)  MN // (SBC). Tương tự MN // (SAD).
b) Ta có: MP // SB nên MP // (SBC).
Theo câu a, ta có: MN // (SBC) nên (MNP) // (SBC)  SB // (MNP), SC // (MNP).
c) Gọi E là trung điểm của BC  A, G , E không thẳng hàng và S, G , E không thẳng 1 2 hàng. Ta có EG EG 1 1 2 
  G G // SA mà SA  (SAC) nên G G // (SAC). 1 2 EA ES 3 1 2
d) Gọi Q là trung điểm của SB  C, G , Q không thẳng hàng. 2
Ta có PQ // AB nên PQ // CD  C, D, P, Q cùng thuộc một mặt phẳng
 Mp (PNG ) cắt S.ABCD theo thiết diện là tứ giác CDPQ. 2 Bài 4.
Cho cấp số cộng u có số hạng đầu u  3 và công sai d  5. Tính u , u và S (tổng n  1 2 7 8
của 8 số hạng đầu tiên trong cấp số cộng u ). n  Lời giải 8.2.3  7.5
Ta có u  u  d  3 5  8, u  u  6d  3 6.5  33 và S   164 . 2 1 7 1 8 2 2n   Bài 5. Cho dãy số  1 u với u  cos . n  n 3
a) Chứng minh rằng u  u với mọi n 1. n n3
b) Hãy tính tổng của 17 số hạng đầu tiên của dãy số đã cho. Lời giải a) Ta có 2n  5  n   2n 1 u  cos  2 1  cos   2  cos   u . n3 3    3  3 n
b) Đặt S  u  u ... u . Vì u  u nên S  5S  S . n 1 2 n n n3 17 3 2 Ta có  1 5 1 1 u  cos  , u  cos  1  , u  cos
  S  0 và S   . 1 3 2 2 3 3 2 3 2 2 Vậy 1 S   . 17 2 ---- HẾT -----
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 63
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 3 – SỞ BẠC LIÊU 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 D A C B C C B B A C D A D C A
16 17 18 19 20 21 22 23 24 25 26 D D B C C B D A D C A
Câu 1. Nghiệm của phương trình 2cos x  3  0 là     x   k2  x   k2  A. 6  k . C. 3  k .   2 x   k2   x   k2  6  3 B.  
x    k2 k  .
D. x    k2 k . 3 6 Lời giải Chọn D Ta có: 3  
2 cos x  3  0  cos x 
 cos x  cos  x    k2 k  2 6 6
Vậy nghiệm của phương trình là  x    k2 k  6
Câu 2. Cho hình bình hành ABCD . Khẳng định nào sau đây là đúng
A. T  A  D .
B. T D  A .
C. T  A  B .
D. T C  B . BC BC BC BC Lời giải Chọn A A B D C  
Ta thấy ngayT  A  D vì BC  AD. BC
Câu 3. Phương trình cos x  sin 3x  2 cos x  sin xsin 4x có tổng tất cả các nghiệm x0;  là   A. 2. B. 6. C. 11 . D. 5 . 8 8 Lời giải Chọn C Ta có:   
cos x  sin 3x  2 cos x  sin xsin 4x  cos x  sin 3x  2cos x  sin 4x    4              
cos x  sin 3x  sin 3x   sin 5x       cos x  cos  5x  sin 3x   sin 3x      4   4   4   4  Trang 64
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1           3   sin 2x  sin 3x   sin 3x  sin          8   8   8   8    k x        24 3 sin 3x   0      8     
 x   k k       3   4 sin 2x   sin         8   8 3  x   k  8               sin 2x  sin 3x   sin 3x  cos          8   8   8   8     
Các nghiệm của phương trình trên khoảng 0;  là 3 17 x  ; x  ; x  ; x  24 8 24 4  Vậy tổng cần tìm 11 . 8
Câu 4. Trong mặt phẳng tọa độ Oxy , tìm phương trình đường thẳng  ' là ảnh của đường 
thẳng  : x  2y 1  0 qua phép tịnh tiến theo vecto v  1;  1
A.  ': x  2y  2  0 . B.  ': x  2y  0.
C.  ': x  2y 3  0 . D.  ': x  2y 1  0 . Lời giải Chọn B
Lấy M 1;0 : x  2y 1 0 
Gọi M 'x '; y ' là ảnh của M  ;
x y qua phép tịnh tiến theo vecto v  1;  1 Suy ra M '2;  1   '
Đường thẳng  ' là ảnh của đường thẳng  : x  2y 1  0 qua phép tịnh tiến theo vecto
v 1; 1 và đi qua M '2; 1 có phương trình ':x2y 0 Vậy  ': x  2y  0.
Câu 5. Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá của mét khoan đầu tiên là
10.000 đồng và kể từ mét khoan thứ hai, giá mỗi mét khoan sau tăng thêm 3000đồng
so với giá mét khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan
giếng này để khoan một giếng sâu 100mét lấy nước dùng cho sinh hoạt gia đình. Hỏi
sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan
giếng số tiền bằng bao nhiêu A. 15.580.000 đồng.
B. 18.500.000đồng. C. 15.850.000đồng. D. 15.050.000đồng. Lời giải Chọn C
Ta kí hiệu giá mét khoan thứ n là u  * n   n 
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 65
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Theo đề bài ta có u 10.000 , u  u 3000 , …, u  u  3000 n  2 . Như vậy ta có n n 1    1 2 1
một cấp số cộng có 100 số hạng với u 10.000 , công sai d  3000 1
Suy ra S  u  ... u  50 2u  99d  15.850.000 100 1 100  1 
Vậy số tiền cần phải trả là 15.850.000đồng Câu 6. n
Cho dãy số u có số hạng tổng quát u 
n   . Số hạng thứ tư của dãy số u n  n n  *  n  2 là A. 1 . B. 1 . C. 1 . D. 1 . 2 16 4 8 Lời giải Chọn C
Ta có số hạng thứ tư của dãy số là 4 1 u  u(4)   4 4 2 4
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N, P lần lượt là
trung điểm của AB, AD, SC . Gọi Q là giao điểm của SD với (MNP) . Tính SQ . SD A. 1 . B. 3 . C. 2 . D. 1 . 4 4 3 3 Lời giải Chọn D S P Q K D H C O N I A M B
Gọi O  AC  BD, I  MN  AC , K  SO  IP MN / /BD  Ta có 
MN  (MNP)  (MNP)  (SBD)  Kx sao cho Kx / /BD , Kx  SD  Q vậy BD (SBD)   
Q  SD   với QK / /DB Trang 66
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 S E P F K C A I O Kẻ IP CP SE SF AE / /IP (E  SC) , ta có 3 
 mà P là trung điểm SC suy ra 2   AE CE 4 SP 3 SK lại có SK SQ SK
K là trung điểm của OF do đó 3  mà 3 KQ / /BD    SO 4 SD SO 4 Vậy SQ 3  . SD 4
Câu 8. Từ 20 học sinh ưu tú gồm 10 nam và 10 nữ, người ta muốn lập một đoàn đại biểu
gồm 6 người để tham dự một buổi hội thảo, trong đó có 1 trưởng đoàn là nam và 2
phó đoàn là nữ. Hỏi có bao nhiêu cách thành lập một đoàn đại biểu như vậy? A. 27907 200 . B. 306000 . C. 38760. D. 513000. Lời giải Chọn B
Chọn 1 nam làm trưởng đoàn có 10 cách
Chọn 2 nữ phó đoàn có 2 C cách 10
Chọn 3 người còn lại trong 17 người có 3 C cách. 17 Vậy có tất cả 2 3 10.C .C  306000 cách. 10 17
Câu 9. Cho tứ diện ABCD , G là trọng tâm tam giác ABD , M là điểm trên cạnh BC sao cho
MB  2MC . Khẳng định nào sau đây đúng? A. MG //  ACD . B. MG //  ABC . C. MG //  ABD. D. MG // BCD. Lời giải Chọn A
Gọi N là trung điểm AD .
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 67
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Trong tam giác BG BM BCN ta có: 2   suy ra MG // CN . BN BC 3 MG   ACD  MG // CN  MG //  ACD . C  N    ACD
Câu 10. Từ các chữ số của tập A  1;2;3;4;5;6; 
8 có thể lập được bao nhiêu số tự nhiên có ba
chữ số đôi một khác nhau ? A. 3 8 . B. 3 C . C. 3 A . D. 8 3 . 7 7 Lời giải Chọn C
Mỗi số có ba chữ số đôi một khác nhau lập được từ các chữ số trong A  1;2;3;4;5;6; 
8 là một chỉnh hợp chập 3 của 7 phần tử.
Vậy số các số lập được là : 3 A . 7 Câu 11. Hệ số của 10
x trong khai triển  x  10 2 3 1 bằng A. 0 0 3 C . B. 5 10 3 C . C. 10 10 3 C . D. 5 5 3 C . 10 10 10 10 Lời giải Chọn D
Số hạng tổng quát của khai triển là:  k k 3 10 2 10k k 202  3 . k C x C x
với k  ,0  k 10 . 10 10 Số hạng chứa 10
x ứng với 20  2k 10  2k 10  k  5 . Hệ số của 10
x trong khai triển  x  10 2 3 1 bằng: 5 5 3 C . 10
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, O là giao điểm AC và BD .
Gọi M , N lần lượt là trung điểm SA, SB . Giao tuyến của hai mặt phẳng SAC và SBD là A. SO . B. SM . C. SN . D. SD . Lời giải Chọn A Trang 68
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 O   AC   SAC Ta có: 
 O SAC SBD. O   BD   SBD
Vậy SO là giao tuyến của hai mặt phẳng SACvà SBD.
Câu 13. Trong mặt phẳng Oxy , cho hai đường thẳng  : 2x  y  2  0 ,  ' : 2x  y  2  0 và 
vectơ v  (2;0) . Khẳng định nào sau đây đúng? A. V ()   '. B. Q ()   ' . C. T ()   ' . D. Q ()   '. (0;3) 0 (0;90 ) v 0 (0;180 ) Lời giải. Chọn D x '  x Gọi M ( ;
x y) bất kỳ, M   . Gọi M '(x '; y ')  Q (M )    M (x ';  y ') 0 (0;180 )  y '   y M    2
 x ' y' 2  0  2x ' y ' 2  0 . Suy ra M ' ' : 2x  y  2  0 . Vậy Q ()   '. 0 (0;180 )
Câu 14. Trong mặt phẳng Oxy , tìm ảnh đường tròn (C ') của đường tròn 2 2
(C) : x  y  2x  4y  0 qua phép vị tự tâm 0 tỉ số k  2  A. 2 2 (C )
 : (x  2)  (y  4) 10 . B. 2 2 (C )
 : (x  2)  (y  4)  20 . C. 2 2 (C )
 : (x  2)  (y  4)  20 . D. 2 2 (C )
 : (x  2)  (y  4) 10 . Lời giải. Chọn C
Đường tròn (C) có tâm I(1;2) , bán kính R  5 . Suy ra (C ') có tâm I '(2; 4  ) , bán
kính R'  2R  2 5 . Vậy 2 2
(C ') : (x  2)  ( y  4)  20 .
Câu 15. Có bao nhiêu số hạng là số nguyên trong biểu thức   30 3 2 3 ? A. 6 . B. 8 . C. 7 . D. 5. Lời giải. Chọn A 10k k
Số hạng tổng quát trong khai triển là k 2 3 T  C .2
.3 với 0  k  30, k   . 10
T là số nguyên  k chia hết cho 2 và 3  k chia hết cho 6  k  6h,h  
Vì 0  k  30  0  6h  30  0  h  5 vì h    h 0,1,2,3,4,  5 . Vậy có 6 số nguyên trong biểu thức trên.
Câu 16. Phương trình sin 2x  3 cos2x  1
 tương đương với phương trình
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 69
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT     A. sin 2x   sin   . B.  3  3       sin 2x   sin      .  3   3      C. sin 2x   sin   . D.  3  6       sin 2x   sin      .  3   6  Lời giải. Chọn D Ta có 1 3 1        sin 2x  3 cos 2x  1   sin 2x  cos 2x   sin 2x   sin      . 2 2 2  3   6 
Câu 17. Trong mặt phẳng Oxy , cho điểm I 1; 2
  . Gọi I là ảnh của I qua phép vị tự V . O;2
Khi đó, I có tọa độ là A. 2;4 . B. 4;2 . C. 4;2 . D. 2;4 . Lời giải Chọn D   x       2.1 2 Ta có: V I  I  OI  2  OI I    I 2; 4 . O, 2       y       2 I  2   4 Câu 18.   
Điều kiện để hàm số y  tan x  1   xác định là  4   
A. x    k k .
B. x   k k  . 4 4  
C. x   k k  .
D. x    k k  . 2 4 Lời giải Chọn B Hàm số       y  tan x  1   xác định  cos x   0    4   4    
 x    k  x   k k  . 4 2 4
Câu 19. Trong một cuộc thi, Ban tổ chức dùng 7 cuốn sách môn Toán, 6 cuốn sách môn Vật
lý và 5 cuốn sách môn Hóa học để làm phần thưởng cho 9 học sinh có kết quả cao
nhất. Các cuốn sách cùng thể loại Toán, Vật lý, Hóa học đều giống nhau. Mỗi học sinh
nhận thưởng sẽ được hai cuốn sách khác nhau, trong đó có An. Tính xác suất để An
nhận thưởng có sách Toán. A. 7 . B. 11 . C. 7 . D. 9 . 18 18 9 18 Trang 70
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Lời giải Chọn C
Gọi x là số phần quà gồm 1 cuốn sách Toán và 1 cuốn sách Vật lý.
Gọi y là số phần quà gồm 1 cuốn sách Vật lý và 1 cuốn sách Hóa học.
Gọi z là số phần quà gồm 1 cuốn sách Hóa học và 1 cuốn sách Toán. x  z  7 x  4 Ta có  
x  y  6   y  2 . y z 5    z  3   Như vậy có:
4 phần quà gồm 1 cuốn sách Toán và 1 cuốn sách Vật lý.
2 phần quà gồm 1 cuốn sách Vật lý và 1 cuốn sách Hóa học.
3 phần quà gồm 1 cuốn sách Hóa học và 1 cuốn sách Toán.
Có tổng cộng 9 phần quà trong đó có 7 phần quà có sách toán.
Vậy xác suất để An nhận thưởng có sách Toán là 7 . 9
Câu 20. Số nghiệm của phương trình 3 sin x  là 2 A. 4 . B. 2 . C. 0 . D. 1. Lời giải Chọn C
Ta có 3 1 nên phương trình 3 sin x  vô nghiệm. 2 2
Câu 21. Long và Hưng cùng 8 bạn rủ nhau đi xem bóng đá. Số cách xếp nhóm bạn trên vào
10 chỗ ngồi sắp hàng ngang sao cho Long và Hưng ngồi cạnh nhau là: A. 9.8!. B. 18.8!. C. 8!. D. 9!. Lời giải Chọn B.
Có 2! cách sắp xếp Long và Hưng ngồi cạnh nhau.
Mỗi cách sắp xếp Long và Hưng cạnh nhau xem là phần tử X .
Có 9! cách sắp xếp X và 8 bạn còn lại vào dãy ghế hàng ngang. Vậy, có: 2!.9!18.8!. Câu 22.   
Định m để phương trình có nghiệm: 6 6 2
sin x  cos x  cos 2x  m với 0  x    .  8  A. 3 1 0  m  1. B. 0  m  2 . C. 0  m  . D. 0  m  . 8 8 Lời giải Chọn D. Ta có: 6 6 2 2 2 2
sin x  cos x  cos 2x  m  1 3sin . x cos x  cos 2x  m 3 1 cos 4x 2 2 2
 sin 2x  sin 2x  m  sin 2x  4m 
 4m  1 8m  cos 4x . 4 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 71
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Với    0  x  
 thì 0  cos 4x 1. Suy ra để phương trình ban đầu có nghiệm  8     0  x    khi và chỉ khi 1 0  1 8m  1  1   8  m  0  0  m  .  8  8
Câu 23. Tại một buổi lễ có 13 cặp vợ chồng tham dự, mỗi ông bắt tay với một người trừ vợ
mình, các bà không ai bắt tay nhau. Hỏi có bao nhiêu cái bắt tay? A. 234 . B. 312. C. 78. D. 185. Lời giải Chọn B.
TH1) Có 13 cách chọn một người đàn ông. Mỗi cách chọn một người đàn ông có 12
cách bắt tay với một phụ nữ mà người đó không là vợ. Suy ra có: 13.12 156 (cái bắt tay).
TH2) Mỗi cách chọn 2 nam từ 13nam có một cái bắt tay. Suy ra có: 2 C  78 (cái bắt 13 tay).
Vậy có: 156  78  234 (cái bắt tay).
Câu 24. Cho cấp số cộng u biết u  6 , u 16 . Tính công sai d và tổng của 10 số hạng đầu n  3 8 tiên. A. d  2 ; S 100 . B. d 1; S  80.
C. d  2 ; S 120 . D. d  2 ; S 110 . 10 10 10 10 Lời giải Chọn D. u   2d  6 u   2 Ta có: 1 1 10.9    . Vậy S 10.2  .2  110 . u  7d  16  d  2 10 2 1
Câu 25. Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x  y 1  0 để phép tịnh tiến theo véctơ  
v biến d thành chính nó thì v phải là véctơ nào trong các véctơ sau : A.     v  2;  1 . B. v  2;  1 . C. v  1;2 . D. v   1  ;2. Lời giải Chọn C. 
Phép tịnh tiến theo một vectơ khác vectơ 0 biến một đường thẳng d thành chính nó
khi và chỉ khi vectơ tịnh tiến có giá song song hoặc trùng với đường thẳng d . Ta chọn
v  1;2 vì nó là vectơ chỉ phương của đường thẳng d . B. TỰ LUẬN
Câu 1. Giải phương trình 2cos x 1 0 Lời giải       x k2  2cos x 1  1 0  cos x   cos 3   ,k  . 2 3   x    k2  3 Trang 72
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1   x   k2 
Vậy phương trình đã cho có nghiệm là 3  ,k  .   x    k2  3 Câu 2.
a) Từ một hộp chứa 7 quả cầu màu đỏ và 5quả cầu màu vàng, Hùng lấy ngẫu nhiên
đồng thời 3quả cầu. Tính xác suất để Hùng lấy được 3 quả cầu trong đó có hai quả cầu màu đỏ.
b) Tìm số hạng không chứa   x trong khai triển của 2 n x  
 , biết n là số tự nhiên thỏa  x  mãn 1 2 3 2n 496 C  C  C ... C  2 1 4n 1  4n 1  4n 1  4n 1  Lời giải a) Ta có: n 3  C  220 . 12
Gọi biến cố A : “Trong 3 quả cầu trong đó có hai quả cầu màu đỏ” , Suy ra n A 2 1  C .C 105 7 5
Vậy xác suất của biến cố A cần tìm là P A n A 105 21    . n 220 44
b) Xét khai triển: 1 x4n 1 0 1 2 2 2 2 4n 1  4n 1  C  C x  C x  C x  ...  C x  4n 1  4n 1  4n 1  4n 1  4n 1 
Ta chọn x 1, khi đó ta có: 4n 1  0 1 2 3 4n 1 2  C  C  C  C ... C  4n 1  4n 1  4n 1  4n 1  4n 1  4n 1  2   2 0 1 2 3 2 C  C  C  C  ... n  C 4n 1  4n 1  4n 1  4n 1  4n 1   4n 0 1 2 3 2  2  C  C  C  C ... n  C 4n 1  4n 1  4n 1  4n 1  4n 1  1 2 3 2n 4  C  C  C ... C  2 n 1 4n 1  4n 1  4n 1  4n 1  Khi đó ta có 4n 496 2 1  2
1  4n  496  n 124 . 124 124 Với  2    2 
n  124 ta xét khai triển: x   x        x  x     
Số hạng tổng quát thứ k 1 trong khai triển trên là:   2 k 124  T  C .x .   C . 2    k k k k 1242 . k x k 124 124  x 
Số hạng không chứa x trong khai triển trên tương ứng với 124  2k  0  k  62 .
Vậy số hạng không chứa x trong khai triển trên là C .262 62 . 124
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 73
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình thang, với đáy lớn AD và AD  2BC .
a) (1,0 điểm) Tìm giao điểm của đường thẳng CD và mặt phẳng SAB .
b) (0,5 điểm) Gọi I là điểm nằm trên cạnh SC sao cho 2SC  3SI . Chứng minh đường
thẳng SA song song với mặt phẳng BID . Lời giải a) Gọi E  CD  AB .
Ta có: E CD; E  AB  SAB nên E SAB Vậy CD SAB  E b) Ta có: CI 2SC  1 3SI     1 . CS 3 Gọi O  AC  BD Tam giác OC BC CO
OCB đồng dạng tam giác OAD nên 1   1   2 . OA AD 2 CA 3 Từ   CO CI 1 và 2 ta có: 1    OI //SA . CA CS 3 Mà OI  BDI  nên S / A / BDI  40 Câu 4.  1  Tìm hệ số của 31 x trong khai triển x  , x  0  2   x  Lời giải 40 40 k 40 Ta có  1  k k  1 40  k 403 x   C .x . k  C x  2  40  2  40  x  k 0  x  k 0
Theo đề bài: 40  3k  31 k  3 Vậy hệ số của 31 x là 3 C  9880 40
Câu 5. Rút gọn tổng S   2      2      2       2 1 1 1 .1! 2 2 1 2! 3 3 1 .3! ... n  n   1 .n!. Lời giải Trang 74
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
S   2      2      2       2 1 1 1 .1! 2 2 1 2! 3 3 1 .3! ... n  n   1 .n! Ta có  2 k  k   k   2 1 . ! k  2k 1 k .k!  k  2 1 .k ! k.k !  k   1 .k   1 ! k.k !
 k  2! k   1 !  k   1 ! k !    
 k  2! 2k   1 ! k !
 21 1 1.1! 3!2.2!1!
 22 2 1.2! 4!2.3!2!
 23 3 1.3! 5!2.4!3! +Vậy  2 4  4   1 .4!  6! 2.5! 4! n  2 1  n   1 1 .n   1 !  n   1 ! 2.n! n   1 !  
 2n n 1.n! n2!2n 1!n!
Cộng n đẳng thức này lại thì được S  1! 2! n  
1 ! n  2! n  2! n   1 !1  n   1 n   1 !1 ---- HẾT -----
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 75
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
BẢNG ĐÁP ÁN & HƯỚNG DẪ GIẢI ĐỀ 4 – SỞ HƯNG YÊN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 B D C A B C A B C D A C A A A 16 17 18 19 20 21 22 23 24 25 C C B A B B B B D C
Câu 1. Tính tổng S tất cả các hệ số trong khai triển  x  11 3 4 : A. S  1 . B. S  1 . C. S  0 . D. S  8192 . Lời giải Chọn B 3x  4 11 11 11
 C .3  .4 . k k k k 11 1 . k x . 11 k 0 11
Khi đó, tổng các hệ số trong khai triên là: 11 S  C .3  .4 . 1 k k k k  1. 11   k 0
Câu 2. Làng Duyên Yên, xã Ngọc Thanh, huyện Kim Động, tỉnh Hưng Yên nổi tiếng với trò
chơi dân gian đánh đu. Trong trò chơi này, khi người chơi nhún đều thì cây đu sẽ đưa
người chơi dao động qua lại ở vị trí cân bằng. Nghiên cứu trò chơi này, người ta thấy
rằng khoảng cách h (tính bằng mét) từ người chơi đu đến vị trí cân bằng được biểu
diễn qua thời gian t (t  0 và được tính bằng giây) bởi hệ thức h  d với   d  3cos 2t   1 
trong đó quy ước rằng d  0 khi vị trí cân bằng ở phía sau lưng 3   
người chơi đu và d  0 trong trường hợp trái lại. Tìm thời điểm đầu tiên sau 10 giây
mà người chơi đu ở xa vị trí cân bằng nhất. A. Giây thứ 13 . B. Giây thứ 12,5 . C. Giây thứ 10,5 . D. Giây thứ 11. Lời giải Chọn D Ta có     1  cos 2t   1  1  3  3cos 2t   1  3  . 3   3     
Để người chơi đu ở xa vị trí cân bằng nhất thì     3cos 2t   1  3  cos 2t   1  1  . 3   3          
t      t   1 3k sin 2 1 0 2 1  k   t   . 3    3 2
Thời điểm đầu tiên sau 10 giây mà người chơi đu ở xa vị trí cân bằng nhất: 1 3k 19 t  10   10  k  mà k  nên k  7. 2 3 Với k  7  t 11. Trang 76
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Câu 3. Bạn An muốn mua một chiếc áo sơ mi cỡ 39 hoặc 40 . Biết áo cỡ 39 có 3 màu khác
nhau, áo cỡ 40 có 5 màu khác nhau. Hỏi bạn An có bao nhiêu lựa chọn để mua một chiếc áo ? A. 8 . B. 3 . C. 5 . D. 15 . Lời giải Chọn C
Trường hợp 1: Áo cỡ 39 có: 3 cách chọn.
Trường hợp 2: Áo cỡ 40 có: 5 cách chọn.
Vậy có 3 5  8 cách chọn.
Câu 4. Số đường chéo của đa giác 10 cạnh là A.35. B. 7 . C. 45. D. 10. Lời giải Chọn A
Ta có số đường chéo của đa giác 10 cạnh là : 2 C 10  . 35 10
Câu 5. Từ các chữ số của tập hợp A  1; 2; 3; 4; 5; 
6 có thể lập được bao nhiêu số tự nhiên có
3 chữ số mà các chữ số đôi một khác nhau? A.125. B.120. C. 6 . D. 10. Lời giải Chọn B
Mỗi số tự nhiên có 3 chữ số mà các chữ số đôi một khác nhau lập được từ các chữ số
của tập hợp A  1; 2; 3; 4; 5; 
6 là một chỉnh hợp chập 3 của 6 phần tử nên ta có tất cả 3 A  120 số. 6
Câu 6. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
B. Hai đường thẳng phân biệt không chéo nhau thì hoặc cắt nhau hoặc song song.
C. Hai đường thẳng không có điểm chung thì chéo nhau.
D. Hai đường thẳng chéo nhau thì không có điểm chung. Lời giải Chọn C
Hai đường thẳng không có điểm chung thì chúng có thể song song.
Câu 7. Mệnh đề nào sau đây là đúng? A. 0 1 n 1  n 1  n2 2 C  C  ...  C  C  C  ...  n C . 2n 2n 2n 2n 2n 2n B. 0 1 n2 n 1  n2 2 C  C  ... C  C  C  ...  n C . 2n 2n 2n 2n 2n 2n
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 77
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT C. 0 1 n 1  n 1  n2 2 C  C  ...  C  C  C  ... n C . 2n 2n 2n 2n 2n 2n D. 0 1 n n 1  n2 2 C  C  ...  C  C  C  ... n C . 2n 2n 2n 2n 2n 2n Lời giải Chọn A. Ta có: 0 2 C  n C ; 1 2 1  C  n C ;…; n 1 n 1  C  C . 2n 2n 2n 2n 2n 2n Vậy 0 1 n 1  n 1  n2 2 C  C  ...  C  C  C  ... n C . 2n 2n 2n 2n 2n 2n Câu 8.
Chọn ngẫu nhiên một hộp chứa 16 thẻ được đánh số từ 1 đến 16. Tính xác suất để
nhận được thẻ đánh số lẻ. A. 9 . B. 1 . C. 3 . D. 7 . 16 2 8 16 Lời giải Chọn B.
Từ 1 đến 16 có 8 số lẻ nên nếu chọn 1 trong 16 thẻ được đánh số từ 1 đến 16 thì xác
suất để nhận được thẻ đánh số lẻ là 8 1  . 16 2 Câu 9.
Từ một cỗ bài tú lơ khơ 52 quân, rút ngẫu nhiên cùng một lúc 4 quân bài. Tính xác
suất sao cho cả 4 quân đều là K? A. 1 . B. 4 . C. 1 . D. 4 . 6497400 6497400 270725 270725 Lời giải Chọn C.
Xác suất để 4 quân bài được rút ngẫu nhiên từ cỗ bài 52 quân đều là K là: 1 1  . 4 C 270725 52 Câu 10.    Phương trình 5 cos x   1   có nghiệm là  6  A.     x   k . B. x   k2 . C. 5 x   k . D. 5 x   k2 . 3 3 6 6 Lời giải Chọn D Ta có  5  5  cos x   1    x   5 k2  x   k2 .  6  6 6
Câu 11. Một hộp chứa 6 quả cầu đỏ khác nhau và 4 quả cầu xanh khác nhau. Chọn ngẫu
nhiên cùng một lúc 2 quả cầu từ hộp. Tính xác suất của biến cố “Lấy được hai quả cùng màu”. A. 7 . B. 4 . C. 8 . D. 7 . 15 9 15 45 Lời giải Chọn A Trang 78
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
 : “Chọn ngẫu nhiên cùng một lúc 2 quả cầu từ hộp” n 2  C  45 . 10
A : “Lấy được hai quả cùng màu” n A 2 2  C  C  21. 6 4 Ta có P A n A  21 7   . n 45 15
Câu 12. Lớp 11A có 35 học sinh nam và 10 học sinh nữ. Hỏi có bao nhiêu cách chọn ngẫu
nhiên một bạn trong lớp ? A. 20 . B. 50. C. 45 . D. 25 . Lời giải Chọn C
Số cách chọn ngẫu nhiên một bạn trong lớp là 3510  45.
Câu 13. Gọi M là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos 2x  cos x  2 . Tính M  m A. 25 . B. 4 . C. 21 . D. 2 8 8 Lời giải Chọn A 2  1  25 2
y  cos 2x  cos x  2  2 cos x  cos x  3  2 cos x     .  4  8 Ta có: 2 2 3 1 5  1  25 25  1  25
1  cos x  1    cos x    0  2 cos x      2 cos x    0     4 4 4  4  8 8  4  8 Vậy 25 M  m  . 8
Câu 14. Có bao nhiêu số tự nhiên có 8 chữ số đôi một khác nhau được lập từ tập A  1,2,3, 4,5,6,7, 
8 sao cho số đó chia hết cho 1111? A. 384. B. 345. C. 3840. D. 1920. Lời giải Chọn A
Gọi số cần tìm n  a a a a a a a a chia hết cho 1111. 1 2 3 4 5 6 7 8
Vì tổng các chữ số: a  a  a  a  a  a  a  a  369 nên n9 1 2 3 4 5 6 7 8 Mà n 1
 111 đồng thời 9 và 1111 là 2 số nguyên tố cùng nhau Nên n9999 .
Ta có a a a a a a a a  a a a a .10000  a a a a  a a a a .9999  a a a a  a a a a 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 1 2 3 4 1 2 3 4 5 6 7 8
Để a a a a a a a a  9999 thì a a a a  a a a a  9999. 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 79
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Mà a a a a  a a a a 1000 a  a 100 a  a 10 a  a  a  a 1 2 3 4 5 6 7 8  1 5  2 6   3 7   4 8
Nên suy ra a  a  a  a  a  a  a  a  9 1 5 2 7 3 6 4 5
Từ các chữ số của A ta có các cặp có tổng bằng 9 là: 1;8,2;7,3;6,4;5 .
Chọn a có 8 cách, chọn a có 1 cách. 1 5
Chọn a có 6 cách, chọn a có 1 cách. 2 6
Chọn a có 4 cách, chọn a có 1 cách. 3 7
Chọn a có 2 cách, chọn a có 1 cách. 4 8
Vậy có 8.6.4.2  384 số thỏa mãn.
Câu 15. Trong mặt phẳng tọa độ Oxy , ảnh của đường thẳng d : x  2y  3  0 qua phép đối xứng tâm I(4;3) là: A. x  2y 17  0 B. x  2y  7  0.
C. x  2y 17  0. D. x  2y 15  0 . Lời giải Chọn A
Đường thẳng d : x  2y  c  0 . Lấy M (3;0)  d .
Gọi M  là ảnh của M qua phép đối xứng tâm I suy ra I là trung điểm của MM. x  2x  x  5 M I M   M (5;6) . y      2y y 6 M I M M (  5;6) d  c  1  7 .
Vậy d: x  2y 17  0.
Câu 16. Điều kiện cần và đủ để phương trình asin x  bcos x  c có nghiệm là A. 2 2 a  b  c . B. 2 2 2 a  b  c . C. 2 2 a  b  c . D. 2 2 2 a  b  c . Lời giải Chọn C
Câu 17. Hàm số nào sau đây có đồ thị nhận gốc tọa độ O làm tâm đối xứng? A. 2 y  sin x . B. y  cos x. C. y  tan x . D. 2 y  cot x . Lời giải Chọn C
Hàm số lẻ có đồ thị nhận gốc tọa độ làm tâm đối xứng.
Câu 18. Có bao nhiêu cách lấy ngẫu nhiên cùng lúc 3 ba quả cầu từ một hộp chứa 10 quả cầu khác nhau A. P . B. 3 C . C. P . D. 2 A . 2 10 10 10 Trang 80
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Lời giải Chọn B
Số cách lấy ba quả cầu ngẫu nhiên đồng thời từ một hộp chứa mười quả cầu bằng số
tổ hợp chập ba của mười phần tử. Câu 19. Tính tổng 0 1 2 2 S  C  C  C  ... n  C . 2n 2n 2 n 2n A. 2 2 n S  . B. 2 2 n S  1. C. 2n S  . D. 2 2 n S  1 . Lời giải Chọn A
Xét khai triển: 1 x2n 0 1 2 2 2n 2  C  C x  C x  ... n  C x 2n 2n 2n 2n Cho x 1 ta được 2n 0 1 2 2 2  C  C  C  ... n  C . 2n 2n 2n 2n Vậy 2 2 n S  .
Câu 20. Cô dâu và chú rể mời 6 người ra chụp ảnh kỉ niệm, người thợ chụp hình có bao nhiêu
cách sắp xếp sao cho cô dâu, chú rể đứng cạnh nhau. A. 6.7!. B. 2.7!. C. 8! 7!. D. 2! 6!. Lời giải Chọn B
Số cách xếp cô dâu, chú rể đứng cạnh nhau là: 2!.7 cách.
Số cách xếp 6 người khách là: 6! cách.
Vậy số cách xếp thoả mãn yêu cầu bài toán là: 2!.7.6! 2!.7! 2.7! cách.
Câu 21. Cho hình vuông ABCD tâm I . Gọi M , N lần lượt là trung điểm của AD, DC . Phép
tịnh tiến theo véc tơ nào sau đây biến AMI thành M  DN ?     A. AC . B. AM . C. NI . D. MN . Lời giải Chọn B A M D N I B C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 81
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
 
AM  AM  T  A  M AM
 
Ta có: AM  MD  T M   D  T  A  MI   M  DN AM AM   AM 
 IN  T I   N  AM
Câu 22. Cho hai đường thẳng cắt nhau d và d . Có bao nhiêu phép đối xứng trục biến đường
thẳng này thành đường thẳng kia? A. Vô số. B. Hai. C. Không có. D. Một Lời giải Chọn B.
Hai đường phân giác của góc tạo bởi hai đường thẳng d và d’ là các trục đối xứng
trục biến đường thẳng d thành đường thẳng d’ .
Câu 23. Tìm hệ số của 5 x trong khai triển  11 1 x . A. 55440. B. 462 . C. 246 . D. 252 Lời giải Chọn B. Ta có: 1 x 11 11   k C . k x nên hệ số 5 x ứng với k  5 là 5 C  462 . 11 11 k 0
Câu 24. Cho ba mặt phẳng phân biệt  ,  ,   có       d ;      d ; 1 2
     d . Khi đó ba đường thẳng d , d , d : 3 1 2 3
A. Đôi một song song. B. Đồng quy.
C. Đôi một cắt nhau. D. Đôi một song song hoặc đồng quy Lời giải Chọn D. A d3 d3 d1 d d 1 d 2 2
Ta có ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến thì ba giao tuyến này hoặc
song song, hoặc đồng quy.
Câu 25. Hãy mô tả không gian mẫu của phép thử: “Gieo một đồng xu cân đối và đồng chất hai lần liên tiếp”. A.   SS, NN. B.   S, N .
C.   SS, SN, NS, NN. D.   SN, NS. Trang 82
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Lời giải Chọn C.
Không gian mẫu là   SS, SN, NS, NN . B. TỰ LUẬN
Câu 1. Giải các phương trình sau đây a) 2
cos x  3cos x  2  0 . b) 2cos x  
1 2sin x  cos x  sin 2x sin x Lời giải cos x 1 a) 2
cos x  3cos x  2  0   . cos x  2
 cos x 1  x  k2 với k  .
 cos x  2 (vô nghiệm). b) 2cos x  
1 2sin x  cos x  sin 2x sin x  2cos x  
1 2sin x  cos x  sin x2cos x   1 2cos x 1  0  2cos x  
1 sin x  cos x  0   . sin x  cos x  0    1
2cos x 1  0  cos x   cos  x    k2 ,  k  . 2 3 3     
sin x  cos x  0  2 sin x   0    x    k ,  k  .  4  4
Câu 2. Một lớp học có 15 nữ và 20 nam. Có bao nhiêu cách chọn ra từ lớp đó 10 bạn sao cho có ít nhất 1 bạn nam ? Lời giải
Chọn 10 học sinh bất kỳ từ 35 học sinh. Có 10 C cách chọn. 35
Chọn 10 học sinh nữ từ 15 học sinh nữ. Có 10 C cách chọn. 15
Số cách chọn thỏa bài toán là 10 10 C  C cách chọn. 35 15 12 Câu 3.  1 
Tìm số hạng không chứa x trong khai triển thành đa thức của biểu thức 3x   . 3   x  Lời giải k Số hạng thứ k k  1 
k 1 0  k  12 : T  C  .  3x12 k 12k 124 C 3 k x k 1 12  3  12  x 
Khi đó: T không chứa x  12  4k  0  k  3. k 1 
Vậy số hạng không chứa x là 9 3 T  3 C . 4 12
Câu 4. Tìm tất cả các giá trị thực của tham số m sao cho phương trình lượng giác sau đây có
nghiệm: m sin 2x 12 cos 2x  13 . Lời giải
Phương trình có nghiệm  m   2 2 2 12 13 2
 m  25  m  5 hoặc m  5 .
Vậy với m  ; 5 5;  thì phương trình đã cho có nghiệm.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 83
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 5. Cho hình chóp S.ABCD , có đáy ABCD là hình thang có đáy lớn AD . Gọi E,F lần
lượt là trung điểm của S , A SD .
a) Tìm giao tuyến của các cặp mặt phẳng: SAC và SBD , SAD và SBC.
b) Chứng minh EF// ABCD và EF //SBC.
c) Gọi K là giao điểm của AB và CD . Tìm M , N lần lượt là giao điểm của SB và
CDE; SC và EFM  . Từ đó, tìm thiết diện của hình chóp cắt bởi mặt phẳng KEF.
d) Cho AD  2BC . Tính tỉ số diện tích của tam giác KMN và tam giác KEF . Lời giải a)
+) giao tuyến của các cặp mặt phẳng: SAC và SBD
S là điểm chung thứ nhất của SAC và SBD .
O là giao điểm của AC và BD nên O AC,OBD do đó O là điểm chung thứ hai của
SAC và SBD . Vậy giao tuyến của hai mặt phẳng SAC và SBD là SO.
+) giao tuyến của các cặp mặt phẳng: SAD và SBC
S SAD  SBC 
AD  SAD,BC  SBC  AD / /BC  Trang 84
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
 SAD  SBC  d với d là đường thẳng đi qua S và d song song với A , D BC . b) EF //AD  EF // ABCD . AD   ABCD ,EF  AB D C     EF //AD Ta có   EF //BC AD//BC Do đó EF //BC  EF // SBC . BC   SBC ,EF  S C B     c)
● Chọn mặt phẳng phụ SAB chứa SB .
● Tìm giao tuyến của hai mặt phẳng SAB và ECD . E  SA   SAB Ta có 
 E là điểm chung thứ nhất của SBD và  ABM . E   ECD K  AB   SAB 
 K là điểm chung thứ hai của SBD và  ABM  K CD   ECD
Do đó SAB  ECD  EK . M  EK  ECD
Trong SAK  lấy M  EK  SB  
thì M  SB  ECD . M SB
● Chọn mặt phẳng phụ SBC chứa SC .
● Tìm giao tuyến của hai mặt phẳng SBC và EFM  . M  SB   SBC Ta có 
 M là điểm chung thứ nhất của SBC và EFM  . M   EFM 
M SBC  EFM  
BC  SBC, EF  EFM  EF / /BC 
 SBC  EFM   d với d là đường thẳng đi qua M và d song song với EF,BC . N d  EFM 
Trong SBC lấy N  d SC  
thì M  SC  EFM . N  SC
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 85
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
KEF   SAD  EF 
KEF   SAB  EM Ta có 
suy ra thiết diện của hình chóp cắt bởi mặt phẳng KEF 
KEF   SBC  MN 
KEF   SCD  NF là tứ giác EMNF d) Vì KM KN
AD  2BC nên M , N là trọng tâm tam giác SAK và SDK , do đó 2   KE KF 3
suy ra phép vị tự tâm K , tỉ số 3 biến tam giác KMN thành tam giác KEF . Vậy tỉ số 2
diện tích của tam giác KMN và tam giác KEF là 4 . 9 --- HẾT --- Trang 86
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 5 – SỞ HUẾ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A C B D C C D B A B C D B D D 16 17 18 19 20 21 22 23 24 25 C B A D A A A D C B
Câu 1. Tìm hệ số của 3 3
x y trong khai triển biểu thức   6 x y A. 20. B. 6. C. 15. D. 1. Lời giải Chọn A
Số hạng thứ k 1trong khai triển là: k 6k k T  C x y k 1  6 6  k  3 Ta có:   k  3  k  3 Vậy hệ số của 3 3 x y trong khai triển là: 3 C  20. 6
Câu 2. Hàm số nào sau đây là hàm số chẵn? A. y  tan . x B. y  cot . x C. y  cos . x D. y  sin . x Lời giải Chọn C
Hàm số y  f (x)  cos x TXĐ: D   + x   ;  x  .  + x
  , f (x)  cos(x)  cos x  f (x).
Vậy hàm số y  cos x là hàm số chẵn.
Câu 3. Tập xác định của hàm số y  sin 2x? A. D   ;  2. B. D  .  C. D   \  2 . D. D  2;. Lời giải Chọn B
Hàm số y  sin 2x xác định với x   . 
Câu 4. Một nhóm công nhân có 15 người trong đó có 10 nam và 5 nữ. Có bao nhiêu cách
chọn 6 người đi dự đại hội công ty? A. 4785. B. 3603600. C. 720. D. 5005. Lời giải Chọn D
Chọn 6 người trong 15 người đi dự đại hộ công ty: 6 C  5005. 15
Câu 5. Trong mặt phẳng Oxy , cho điểm A1; 0 . Tìm ảnh của A qua phép dời hình có được
bằng cách thực hiện liên tiếp phép quay tâm O góc quay 90 và phép tịnh tiến theo  véctơ v  2 ; 0 . A. A2 ;   1 . B. A 2  ;  1 . C. A2 ;  1 . D. A1; 2 . Lời giải
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 87
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Chọn C x   y Giả sử  A A Q A  A    A 0 ;1 . O ; 90   1 1 1     y  x  1A A x     x 2 T  A A A  A    A 2 ;1 . v 1  1   y     y 0 A  1 A
Vậy ảnh của A qua phép dời hình trên là A2 ;  1 .
Câu 6. Cho dãy số u là cấp số cộng có u  3
 , u  27 . Tìm công sai d ? n  1 6 A. d  5. B. d  4 . C. d  6 . D. 24 d  . 5 Lời giải Chọn C Ta có: 1 1 u  u  5d  d  u  u  27  3  6. 6 1  6 1   5 5 Câu 7. Cho 3 2 P  n  3n  5n với n 
 . Khẳng định nào sau đây đúng? n
A. P chia hết cho 2 . B. P chia hết cho 5. C. P chia hết cho 6 . D. P chia hết cho 3. n n n n Lời giải Chọn D
Với n 1 P 1 3 5  9 chia hết cho 3, không chia hết cho 2 1 , không chia hết cho 5 và không chia hết cho 6 .
Câu 8. Có 5 học sinh gồm 2 nữ và 3 nam được xếp vào dãy ghế được đánh số 1,2,3,4,5. Hỏi
có bao nhiêu cách sắp xếp chổ ngồi cho 5 học sinh nói trên, biết rằng vị trí số 1 phải
dành cho một học sinh nữ? A. 52. B. 48. C. 50. D. 42. Lời giải Chọn B
+ Vị trí ghế số 1: có 2 cách.
+ Ghế 2,3, 4,5 sắp xếp 4 người còn lại là P  24 cách. 4
Vậy số cách sắp xếp là: 2.24  48 .
Câu 9. Tính chất nào sau đây không phải là tính chất của phép đồng dạng.
A. Biến đường tròn thành đường tròn có cùng bán kính.
B. Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và bảo toàn thứ tự của 3 điểm đó.
C. Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.
D. Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng. Lời giải Chọn A
Phép đồng dạng biến đường tròn có bán kính R thành đường tròn có bán kính kR với
k  0 là tỉ số đồng dạng. Trang 88
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Câu 10. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi O là giao điểm của AC và BD .
Xác định giao tuyến của hai mặt phẳng SAD và SBC.
A. Đường thẳng qua S và song song với AC .
B. Đường thẳng qua S và song song với AD .
C. Đường thẳng qua S và song song với AB . D. Đường thẳng SO . Lời giải Chọn B
Ta có: S SADSBC.
Vì AD//BC nên đường thẳng d là giao tuyến của SAD và SBC là đường thẳng qua
S và song song với AD và BC .
Câu 11. Cho A và B là hai biến cố liên quan đến một phép thử. Khẳng định nào sau đây sai?
A. nếu A   thì A là biến cố chắc chắn.
B. Nếu A B   thì A và B là hai biến cố xung khắc.
C. Nếu A  B   thì A và B là hai biến cố đối nhau.
D. Nếu A   thì A là biến cố không. Lời giải Chọn C 
Câu 12. Trong mặt phẳng Oxy , phép tịnh tiến theo vec tơ v  1;3 biến đường tròn
C x  2   y  2 : 1
2  6 thành đường tròn có phương trình nào sau đây? A. x   y  2 2 1  6 .
B.  x  2   y  2 2 5  6 . C. x   y  2 2 1  6 .
D.  x  2   y  2 2 5  6 . Lời giải Chọn C
Đường tròn C có tâm I 1; 2
  , bán kính R  6 .
T C  C  Đường tròn C và C có cùng bán kính R  6 . v
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 89
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
T I   I  I2;5 . v
Phương trình đường tròn C:  x  2   y  2 2 5  6 .
Câu 13. Trong mặt phẳng Oxy , phép quay tâm Ogóc quay 90o 
biến điểm M thành M '(3; 1  ) Tìm tọa độ điểm M . A. M (3;1). B. M (1;3). C. M (1; 3  ). D. M (3;1). Bài giải Chọn B Phép quay tâm Ogóc quay 90o 
biến điểm M thành M '(3; 1  ) 0 0 x '  x cos( 9  0 )  y sin( 9  0 ) M M 0 0
y '  x sin(90 )  y cos( 9  0 ) M M Khi đó 0 0
3  x cos(90 )  y sin( 9  0 )  y  y  3. M M M M 0 0 1  x sin( 9
 0 )  y cos(90 )  x  x  1. M M M M  M (1;3). Câu 14.   
Tìm tất cả các nghiệm của phương trình 1 sinx  thỏa mãn  x  2 2 2     A. x   k2. B. x  . C. 5 x   k2. D. x  . 3 3 6 6 Bài giải Chọn D 1     sinx   x   k2. Vì  x  2 6 2 2  Vậy x  . 6
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và B .
D Gọi I, J lần lượt là trung điểm của SA và S .
B Khẳng định nào sau đây sai? A. IJ//(ABCD) và IJ//(SCD) B. IJCD là hình thang. C. IJ và SO chéo nhau
D. (IJC) cắt hình chóp S.ABCD theo thiết diện là tam giá IJC. Lời giải Chọn D S J I A B O D C Trang 90
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
IJ là đường trung bình tam giác SAB nên IJ//AB, mà AB//CD (vì ABCD là hình bình
hành) nên IJ//CD.Từ đó suy ra IJ//(ABCD) , IJ//(SCD) và IJCD là hình thang.
Do đó, các khẳng định ở đáp án A, B đúng.
IJ, SO phân biệt. Giả sử IJ, SO không chéo nhau thì IJ//SO hoặc IJ cắt SO. Từ đó suy ra
(SAC)  (SAB), điều này vô lý. Vậy IJ và SO chéo nhau. Do đó, khẳng định ở đáp án C đúng.
(IJC) cắt hình chóp S.ABCD theo thiết diện là tứ giác IJC .
D Do đó, khẳng định ở đáp án D sai. Chọp đáp án D.
Câu 16. Từ một đội học sinh giỏi Toán có 3 nam và 5 nữ, chọn ngẫu nhiên 2 em đi thi học sinh
giỏi Toán. Tính xác suất để chọn được 1 nam và 1 nữ. A. 15 . B. 25. C. 15 . D. 8 . 56 28 28 56 Lời giải Chọn C
Chon ngẫu nhiên 2 học sinh từ đội học sinh có 8 em thì số phần tử không gian mẫu là 2 n()  C  28. 8
Gọi A là biến cố: “2 học sinh được chọn có 1 nam và 1 nữ” thì ta có n( ) A  3.5  15. Vậy n( ) A 15 P( ) A   . n() 28 Chọn đáp án C.
Câu 17. Trong không gian có bao nhiêu vị trí tương đối giữa hai đường thẳng. A. 3. B. 4. C. 5. D. 2. Lời giải: Chọn B
Trong không gian có 4 vị trí tương đối của 2 đường thẳng:
2 đường thẳng song song.
2 đường thẳng trùng nhau.
2 đường thẳng cắt nhau.
2 đường thẳng chéo nhau.
Câu 18. Các hình sau đây biểu diễn một hình chóp tứ giác trong không gian. Hình nào sai? Hình 4 Hình 1 Hình 2 Hình 3 A. Hình 2. B. Hình 3. C. Hình 4. D. Hình 1. Lời giải: Chọn A
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 91
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Hình 2 sai vì không có hướng nào nhìn thỏa mãn.
Hình 1 và Hình 4 nhìn từ đỉnh xuống vẫn thỏa mãn. Câu 19.   
Tìm nghiệm của phương trình: 2
sin x  sinx  0 thỏa mãn  x  . 2 2     A. x  . B. x  . C. x  . D. x  0. 4 2 2 Lời giải Chọn D x  k sin x  0 2 sin x sinx 0 sin xsin x  1 0            k . sin x  1 x   k2  2   
Với k  0  x  0 thỏa mãn  x  . 2 2 Câu 20. n
Cho dãy số u với u  . Tìm u . n  n 2 5 n 1 A. 5 5 5 u  . B. u  . C. u  . D. u  5. 5 26 5 5 5 6 26 Lời giải Chọn A Thay 5 5 n  5 ta có u   . 5 2 5 1 26
Câu 21. Từ các chữ số 2,3,4,6,7,9 lập được bao nhiêu số chẵn có ba chữ số? A. 108. B. 36. C. 20. D. 40. Lời giải Chọn A
Gọi số tự nhiên có 3 chữ số cần tìm là: ab . c
Vì cần lập ra số chẵn có 3 chữ số nên c có 3 cách chọn là c  2;c  4 hoặc c  6.
Hai chữ số a và b đều có 6 cách chọn.
Do đó, số số tự nhiên thỏa mãn là: 6.6.3 108 (số) 
Câu 22. Trong mặt phẳng Oxy , cho v  (2;1) và điểm M ( 3
 ;2). Tìm điểm M ' là ảnh của điểm 
M qua phép tịnh tiến theo vectơ . v A. M '( 1  ;1). B. M '(1; 1  ). C. M '(1;0). D. M '(1;1). Lời giải Chọn A  Gọi M '( ;
x y) là ảnh của điểm M qua phép tịnh tiến theo vectơ . v  
Ta có: MM '  v  (x  3; y  2)  (2; 1) x  3  2 x  1      . y  2  1  y  1 Vậy M '(1;1).
Câu 23. Trong mặt phẳng Oxy , cho đường thẳng d : 2x  3y  3  0 . Tìm phương trình đường
thẳng d là ảnh của d qua phép vị tự tâm O tỉ số k  2. Trang 92
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 A. 4x  2y  3  0 . B. 4x  2y  5  0 . C. 2x  y  3  0. D. 2x  3y  6  0 . Lời giải Chọn D d  V
d  d cùng phương với d , do đó d có phương trình dạng 2x  3y  m  0. O;2       Lấy M 0; 
1  d , gọi M  x ; y  V
M ta có OM   2OM  M 0;2 . O;2    
Mà Md nên 2.3 m  0  m  6.
Vậy phương trình d : 2x  3y  6  0 .
Câu 24. Cho dãy số u là cấp số cộng có số hạng đầu u , công sai d , S là tổng của n số n  1 n
hạng đầu tiên. Với n  2 , đẳng thức nào sau đây sai?  A. u u u  u  n 1 d . B. n 1 n 1 u    . n 1   n 2 C. n u  u  d . D. S  u  n 1 d  n  1   n 1  n 2  . Lời giải Chọn C
Công thức đúng là u  u  . n d . n 1  1
Câu 25. Tìm tập giá trị T của hàm số y  3 2sin x . A. T  2;4. B. T  1;  5 . C. T   1  ;  1 . D. T  0;  3 . Lời giải Chọn B Ta có 1   sin x  1, x   .  Suy ra 2   2sin x  2, x
   1 3 2sin x  5, x   . 
Vậy tập giá trị T của hàm số y  3  2sin x là T  1;  5 . B. TỰ LUẬN
Câu 1. Giải phương trình: sin x  3 cos x 1. Lời giải Phương trình:    
sin x  3 cos x  1  2 sin . x cos  cos . x sin  1    3 3         2.sin x   1   1  sin x      3   3  2    x    k2  3 6   ,k    5 x    k2  3 6   x   k2  2   ,k  . 7 x   k2  6
Câu 2. Trong khoảng (0;3 ), phương trình 3 sin 2x  có bao nhiêu nghiệm? 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 93
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Lời giải Ta có: 3 sin 2x  2   sin 2x  sin 3   2x   k2  3   , k  Z 2   2x   k2  3   x   k  6   , k  Z   x   k  3
Vì nghiệm của phương trình chỉ xét trên khoảng (0;3 ) nên ta có các trường hợp sau:     TH1: 1 17 0 k 3       k 
 k  0;1; 2. Suy ra các nghiệm là: 7 13 ; ; . 6 6 6 6 6 6     TH2: 1 8 0 k 3     
 k   k  0;1; 2. Suy ra các nghiệm là: 4 7 ; ; . 3 3 3 3 3 3
Vậy phương trình đã cho có 6 nghiệm trong khoảng (0;3 ).
Câu 3. Một hộp chứa 10 quả cầu được đánh số từ 1 đến 10. Lấy ngẫu nhiên một quả. Tính xác
suất của biến cố A: “Nhận được quả cầu ghi số chẵn”. Lời giải
Lấy ngẫu nhiên một quả cầu trong 10 quả cầu, suy ra số phần tử của không gian mẫu là
n()  10. Trong 10 số từ 1 đến 10, có 5 số là số chẵn nên n( ) A  5.
Vậy xác suất của biến cố A là: 5 1 P( ) A   . 10 2 6 Câu 4.  2 
Tìm số hạng không chứa x trong khai triển x  , x  0   .  x  Lời giải 6 6 k 6 Ta có:  2  k k  2 6  k k 62 x   C x  C 2 . k x   6   6  x  k 0  x  k 0
 Số hạng không chứa x trong khai triển tương ứng với k thỏa mãn: 6  2k  0  k  3. 6  Số hạng không chứa  2  x trong khai triển x  , x  0   là: 3 3 C .2  160 .  x  6
Câu 5. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Trên cạnh CD lấy điểm P sao cho PD  2PC .
a) Tìm giao điểm của đường thẳng BD và mặt phẳng MNP .
b) Tìm giao tuyến của mặt phẳng MNP và  ABD. Lời giải Trang 94
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
a) Trong BCD gọi I  BD  NP I  BD
I  NP, NP  MNP  I MNP Vậy: I  BD MNP b) Ta có:
I  BD, BD   ABD  I  ABD
I  NP, NP  MNP  I MNP
Do đó: I  ABDMNP   1 Mặt khác: M MNP
M  AB, AB   ABD  M  ABD
Suy ra: M  ABD MNP 2
Từ (1) và (2) ta có: IM   ABD MNP. --- HẾT ---
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 95
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 6 – CHUYÊN QUỐC HỌC HUẾ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A A D B A A D A B C C B B A D 16 17 18 19 20 21 22 23 24 25 C C C D A D A D D A
Câu 1. Tìm tập xác định của hàm số 1 y  . sin x A.   D   \k ,k    .
B. D   \   k,k  .  2  C. D   \  0 . D. D   . Lời giải Chọn A Hàm số 1 y 
xác định  sin x  0  x  k k  . sin x
Câu 2. Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Hình nào sau đây không thể là thiết diện của nó. A. Lục giác. B. Tam giác. C. Tứ giác. D. Ngũ giác. Lời giải Chọn A
Vì hình chóp tứ giác có 5 mặt (gồm 4 mặt bên và 1 mặt đáy) nên thiết diện của nó có
tối đa 5 cạnh. Vậy thiết diện không thể là lục giác.
Câu 3. Có 10 cây bút khác nhau và 9 quyển sách khác nhau. Tìm số cách chọn 1 cây bút và 1 quyển sách. A. 80 . B. 70 . C. 19 . D. 90 . Lời giải Chọn D Trang 96
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Vì có 10 cây bút khác nhau và 9 quyển sách khác nhau nên số cách chọn 1 cây bút và 1
quyển sách là 10.9  90 (cách)
Câu 4. Một hộp chứa 6 quả bóng đỏ (được đánh số từ 1 đến 6), 5 quả bóng vàng (đươc
đánh số từ 1 đến 5), 4 quả bóng xanh (được đánh số từ 1 đến 4). Lấy ngẫu nhiên 4
quả bóng. Tính xác suất để 4 quả bóng lấy ra có đủ ba màu và không có hai quả bóng
nào có số thứ tự trùng nhau. A. 43. B. 74 . C. 381. D. 48. 91 455 455 91 Lời giải Chọn B
Số phần tử của không gian mẫu bằng 4 C . 15
Lấy được 4 quả bóng có đủ cả ba màu mà không có hai quả bóng nào có số thứ tự
trùng nhau có các trường hợp sau:
 TH1: Lấy được 1 quả bóng xanh, 2 quả bóng vàng và 1 quả bóng đỏ Lấy 1 quả bóng xanh có 1 C cách. 4
Lấy 2 quả bóng vàng có số thứ tự không trùng với số thứ tự của bóng xanh đã lấy có 2 C cách. 4
Lấy 1 quả bóng đỏ có số thứ tự không trùng với số thứ tự của bóng xanh và bóng vàng đã lấy có 1 C cách. 3 Vậy TH1 có 1 2 1 C .C .C cách lấy. 4 4 3
 TH2: Lấy được 2 quả bóng xanh, 1 quả bóng vàng và 1 quả bóng đỏ Lấy 2 quả bóng xanh có 2 C cách. 4
Lấy 1 quả bóng vàng có số thứ tự không trùng với số thứ tự của bóng xanh đã lấy có 1 C cách. 3
Lấy 1 quả bóng đỏ có số thứ tự không trùng với số thứ tự của bóng xanh và bóng vàng đã lấy có 1 C cách. 3 Vậy TH2 có 2 1 1 C .C .C cách lấy. 4 3 3
 TH3: Lấy được 1 quả bóng xanh, 1 quả bóng vàng và 2 quả bóng đỏ Lấy 1 quả bóng xanh có 1 C cách. 4
Lấy 1 quả bóng vàng có số thứ tự không trùng với số thứ tự của bóng xanh đã lấy có 1 C cách. 4
Lấy 2 quả bóng đỏ có số thứ tự không trùng với số thứ tự của bóng xanh và bóng vàng đã lấy có 2 C cách. 4 Vậy TH3 có 1 1 2 C .C .C cách lấy. 4 4 4
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 97
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Như vậy xác xuất lấy được 4 quả bóng có đủ cả ba màu mà không có hai quả bóng nào 1 2 1 2 1 1 1 1 2
có số thứ tự trùng nhau là C .C .C  C .C .C  C .C .C 74 4 4 3 4 3 3 4 4 4  . 4 C 455 15
Câu 5. Tìm số cách xếp 5 bạn nam và 4 ban nữ thành một hàng ngang sao cho 4 bạn nữ luôn đứng cạnh nhau. A. 17280. B. 362880. C. 5760. D. 2880. Lời giải Chọn A
Có 6 cách chọn 4 vị trí từ 9 vị trí trên một hàng ngang để 4 bạn nữ đứng cạnh nhau.
Xếp 4 bạn nữ vào 4 vị trí đã chọn có 4! cách.
Xếp 5 bạn nam vào 5 vị trí còn lại có 5! cách.
Vậy có 6.4!.5!17280 cách xếp.
Câu 6. Cho tập hợp A  0;2;4;5; 
6 , tìm số chỉnh hợp chập 3 của . A A. 60. B. 96. C. 20. D. 10. Lời giải Chọn A
Số chỉnh hợp chập 3 của 5 phần tử là 3 A  60. 5
Câu 7. Gieo đồng thời 2 con súc sắc cân đối, đồng chất, một con màu đỏ và một con màu đen.
Tính xác suất của biến cố: “Số chấm trên con đen lớn hơn số chấm trên con đỏ 2 đơn vị.” 5 9 32 1 A. . B. . C. . D. . 36 36 36 9 Lời giải Chọn D
Không gian mẫu:   a;b|1  a,b  6, trong đó a và b lần lượt là số chấm trên con
đỏ và con đen. Do đó, n   6.6  36.
Gọi A: “Số chấm trên con đen lớn hơn số chấm trên con đỏ 2 đơn vị.”
Ta có: A  6;4;5;3;4;2;3; 1. Do đó, n( ) A 4 1 P( ) A    n  . 36 9 1sinx
Câu 8. Gọi M là tổng các nghiệm thuộc  ;5 của phương trình  1, tìm M. cosx 15 23 27 A. M  6 .  B. M   . C. M   . D. M   . 2 2 2 Lời giải Chọn A Trang 98
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 s  inx 1   Điều kiện:   x  k ,  k  . c  osx  0  2  Ta có:
1 sinx 1  1sinx  cosx cosx c  osx  0    2 1  sinx  cos x cosx 0    2 1  sinx  1sin x  c  osx  0 c  osx  0      
  sinx  0  x  m ,  m         sinx  1      x   n2 ,  n     2
Đối chiếu với điều kiện, tập các nghiệm thuộc  ;5 của phương trình trên là S  0;2 ;4   Câu 9. Cho A
 BC vuông tại B và A  60 (các đỉnh của tam giác ghi theo thứ tự ngược
chiều kim đồng hồ). Về phía ngoài tam giác, vẽ tam giác đều ACD. Tìm ảnh của cạnh
BC qua phép quay tâm A, góc quay 60 .
A. AI với I là trung điểm của CD.
B. DK với K là trung điểm của AC. C. AD.
D. CJ với J là trung điểm của AD. Lời giải Chọn B D A K C B
Gọi K là trung điểm của AC. Vì A
 BC vuông tại B và A  60 nên 1 AB  AC  AK. 2 Do đó, Q B  K và Q
C  D (Vì tam giác ACD đều). o . ( ; A 60 )   ( ;60o A )  
Vậy ảnh của cạnh BC qua phép quay tâm A, góc quay 60 là DK.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 99
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 10. Tìm số điểm biểu diễn các họ nghiệm của phương trình 2
2sin x  3sin x  5  0 trên
đường tròn lượng giác là. A. 2. B. 3. C. 1. D. 4. Lời giải Chọn C sin x  1  
Phương trình tương đương   5  x   k2 sin x  2  2
Do đó có 1 điểm biểu diễn. Ta chọn C
Câu 11. Tìm điều kiện của tham số thực m để phương trình msin x  3cos x  5 có nghiệm. m  4 A. m  4. B. m  34. C. .  D. 4   m  4. m  4 Lời giải Chọn C m  4
Phương trình có nghiệm khi m   3  2 2 2 2  5  m  16  .  m  4 Ta chọn đáp án C
Câu 12. Cho cấp số cộng có số hạng đầu u  1 và công sai d  2. Tổng n số hạng đầu tiên 1
của cấp số cộng này là S  9  800, tìm . n n A. 101. B. 100. C. 98. D. 99. Lời giải Chọn B n n  100 Ta có S  u  n  d  n n     n  n    n 2   1   2 2 9800 2 9800 0 1 2  n  98
Do n là số tự nhiên nên n  100. Ta chọn B
Câu 13. Tìm số các nghiệm thuộc 0;2019  của phương trình 3 cot x 3  0 . A. 2018. B. 2019. C. 4038. D. 4039. Lời giải Chọn B 
3 cot x  3  0  cot x  3  x   k k  6 Vì      1 12113
x 0;2019  nên 0   k  2019   k   2019   k  6 6 6 6 6
Do k  nên 0  k  2018.
Số các nghiệm thuộc 0;2019  của phương trình là 2019.
Câu 14. Tìm mệnh đề sai trong các mệnh đề sau đây.
A. Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
B. Phép đồng dạng bảo toàn độ lớn góc. Trang 100
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
C. Phép dời hình là phép đồng dạng tỉ số k 1.
D. Phép vị tự tỉ số k là phép đồng dạng tỉ số k . Lời giải Chọn A
Câu 15. Tìm phương trình tương đương với phương trình 2 2 3sin x  cos x . A. 2 3 sin x  . B. 1 sin x  . C. 3 cos x  . D. 2 cot x  3. 4 2 2 Lời giải Chọn D Nhận xét: 2
sin x  0  cos x  1. Khi đó phương trình trở thành: 0  1( vô lý ).
Vậy cos x  0. Chia hai vế cho 2 sin x , ta có: 2 2 2
3sin x  cos x  cot x  3.
Câu 16. Một lớp học có 30 học sinh gồm có cả nam và nữ. Chọn ngẫu nhiên 3 học sinh để
tham gia hoạt động của Đoàn trường. Biết xác suất chọn được 2 nam và 1 nữ là 12 , 29
gọi n là số học sinh nữ của lớp, tìm mệnh đề đúng. A. n20;23. B. n 15;19. C. n 12;15. D. n8;12. Lời giải Chọn C
Chọn 3 học sinh trong số 30 học sinh nên không gian mẫu có số phần tử là n 3  C . 30
Gọi A là biến cố “chọn được 2 nam và 1 nữ”. 30  n !.n 30  n 29  n .n n  59n  870n 2 1    3 2 Lúc đó: n A    C .C    . 30n n 2  ! 30  n  2! 2 2 Ta có xác suất của biến cố A là 3 2   P  A 12 n 59n 870n 12 3 2   
 n  59n  870n  3360  n  14. 29 2.4060 29 Vậy n 12;15.
Câu 17. Tìm chu kỳ tuần hoàn  x 
T của hàm số y  sin    với  x  0.  2   A. T  . B. T  2. C. T  4. D. T . 2 Lời giải Chọn C Hàm số  x   y  sin  
 là hàm số tuần hoàn với chu kỳ 2 T   4.  2  1  2
Câu 18. Gieo 3 đồng xu một lúc, gọi A là biến cố “có đúng một đồng xu xuất hiện mặt ngửa”.
Tìm xác suất của biến cố . A
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 101
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT A. 1 . B. 1 . C. 3. D. 1. 2 4 8 8 Lời giải Chọn C
Gieo 3 đồng xu một lúc nên không gian mẫu là
  SSS;SSN;SNS; NSS;SNN;NSN; NNS;NNN.
Ta có n  8;n A  3.
Vậy xác suất của biến cố n A 3 A là P  A     n . 8
Câu 19. Trong mặt phẳng Oxy cho A 2
 ;0, B2;2,C 4;2, D4;0 . Chọn ngẫu nhiên một điểm có tọa độ  ;
x y (với x, y là các số nguyên) nằm trong hình chữ nhật ABCD (kể
cả các điểm nằm trên cạnh). Gọi A là biến cố: “ x, y đều chia hết cho 2”, tính xác suất của biến cố A . A. 13 . B. 7 . C. 1. D. 8 . 21 21 21 Lời giải Chọn D
Gọi M x; y là tọa độ cần tìm.
x 2;1;0;1;2;3;  Để 4
M x; y nằm trong hình chữ nhật có tọa độ nguyên thì   số  y   0;1;  2
các điểm M x; y có tọa độ nguyên là: 7.3=21. x 2;;0;;2;;  Theo giả thiết 4
x, y đều chia hết cho 2 nên ta có:   có 4.2=8 điểm.  y   0;;  2
Vậy xác suất cần tìm là 8 . 21
Câu 20. Tìm số các giá trị nguyên của hàm số y  5  4cos 2xsin 2x . A. 5. B. 6. C. 3. D. 4. Lời giải Chọn A
Ta có y  5  4sin 2x cos 2x  5  2sin 4x Trang 102
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Với x ta có: 1   sin 4x 1  2
  2sin 4x  2  3  5  2sin 4x  7 hay 3  y  7 mà
y   nên y 3;4;5;6;  7 .
Vậy y có 5 giá trị nguyên.
Câu 21. Tìm số các số tự nhiên có 5 chữ số đôi một phân biệt, được lập từ các chữ số 1,2,3,4,5,6,
biết rằng trong các số đó phải có các chữ số 1 và 5. A. 735. B. 1200. C. 600. D. 480. Lời giải Chọn D
Gọi số cần tìm là n  abcde .
Xếp 2 chữ số 1 và 5 vào 2 vị trí trong 5 vị trí nên có 2 A cách. 5
Chọn 3 chữ số khác nhau trong 4 chữ số 2;3;4; 
6 và xếp vào 3 vị trí còn lại nên có 3 A 4 cách. Theo quy tắc nhân có: 2 A . 3 A =480 ( cách). 5 4
Câu 22. Một lô hàng gồm 30 sản phẩm tốt và 10 sản phẩm xấu. Lấy ngẫu nhiên 3 sản phẩm.
Tính xác suất để 3 sản phẩm lấy ra có ít nhất một sản phẩm tốt. A. 244 . B. 15 . 247 26 C. 135 . D. 3 . 988 247 Lời giải Chọn A 3 n()  C . 40
Gọi A: “3 sản phẩm lấy ra có ít nhất một sản phẩm tốt”.
A: “ 3 sản phẩm lấy ra không có sản phẩm tốt”. 3 n( ) A  C . 10 3 C 244 10 P( ) A  1 P( ) A  1  . 3 C 247 40
Câu 23. Cho cấp số cộng (u ) có u  1
 2;u 18. Tìm số hạng đầu tiên u và công sai d của n 4 14 1 cấp số cộng. A. u  2  2;d  3. B. u  2  1;d  3  . 1 1 C. u  20;d  3  . D. u  2  1;d  3. 1 1 Lời giải Chọn D u   1  2 u   3d  1  2 u   2  1 Ta có 4 1 1      u  18 u 13d  18 d     3 14 1
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 103
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 24. Trong mặt phẳng Oxy, cho hai đường thẳng a,b lần lượt có phương trình là
x  2 y  3  0 và 2x  y  5  0. Nếu có phép quay với góc quay 0
 (0   180 ) biến
đường thẳng này thành đường thẳng kia thì số đo của  là: A. 0   45 . B. 0   90 . C. 0   60 . D. 0  120 . Lời giải Chọn B 
Đường thẳng a có vecto pháp tuyến n(1;2). 
Đường thẳng b có vecto pháp tuyến n '(2;1).     Vì .
n n '  0 nên n  n' hay a  b Do vậy 0 0   90  1 k 80 , k  Z. Mặt khác 0
0    180 nên trong 4 đáp án chỉ có đáp án B thỏa mãn.
Câu 25. Tìm số hạng tổng quát u trong các trường hợp dưới đây để dãy số u giảm. n  n A. 1 n  u  . u  n C. 3 1 u  . D. u  n  2. n 2n B. 2 . n n n 1 n Lời giải Chọn A Xét dãy số 1 1 1 1 u  ta có u u      0, n *
  dãy số u giảm. n  n 2n n 1  n n 1  n n 1 2 2 2  Đáp án A đúng. II. PHẦN TỰ LUẬN Câu 1. Cho hình chóp .
S ABCD , có đáy ABCD là hình thang với đáy lớn AB và đáy nhỏ CD .
Gọi M,N lần lượt là trung điểm của SA và SB ; gọi E là giao điểm của AD và BC .
a) Tìm giao tuyến của SBC và ADM. Xác đinh giao điểm P của đường thẳng SC và mặt phẳng ADM.
b) Gọi I là giao điểm của DP và AM . Chứng minh SI song song với AB.
c) Xác định thiết diện của hình chóp với mặt phẳng   α biết   α qua MN và song song với SC . Lời giải Trang 104
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
a) * Tìm giao tuyến của SBC và ADM. Ta có: M  SB SBC +   
M là điểm chung thứ nhất M   AM ABM   E  BC SBC +   
E là điểm chung thứ hai E   AD ADM  
SBCADM ME
* Xác đinh giao điểm P của đường thẳng SC và mặt phẳng ADM. Ta có: SC SBC SBCADM ME Gọi P  SC  ME
 P SC ADM b) Ta có:
SSABSDC I  AM SAB     I
  DP SDC I SAB SDC  SABSDCSI AB  SA  B  Mà CD SCD AB//CD  SI / /AB / /CD c) Ta có: αSAB MN Trong mặt phẳng SA 
B dựng MF / /SC cắt BC tại F
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 105
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT  αSA  B  MF
Trong mặt phẳng SAC dựng NG / /SC cặt AC tại G
Gọi H GF  AD αABCD FH αSAD NH
Vậy thiết diện của hình chóp cắt bởi mặt phẳng   α là tứ giác MNHF
Câu 2. Trong mặt phẳng Oxy, tìm phương trình đường thẳng  là ảnh của đường thẳng 
 : x  2y 1  0 qua phép tịnh tiến theo vectơ v  1;  1 . Lời giải Gọi M x; y. x  x 1 x  x 1
T M   M  . Tọa độ điểm M x ; y thỏa mãn    v  y  y 1  y  y 1
M x; y  nên:  x   1  2 y  
1 1  0  x  2y  0
Vậy  : x  2y  0.
Câu 3. Cho hàm số y  4sin x  3 m cos x với m là tham số thực. Tìm giá trị của tham số m để
giá trị lớn nhất của hàm số bằng 3 2 . Lời giải
Điều kiện xác định: m  0.  4 3 m 
y  4sin x  3 m cos x  16  9m  sin x  cos x   16 9m 16 9m     
 16  9m cos.sin x  sin.cos x  16  9m.sin x   (với 3 m 4 sin  ; cos  ) 16  9m 16  9m Ta có: 1
  sinx   1  169m  y  16 9m
Suy ra giá trị lớn nhất của hàm số là 16  9m.
Giá trị lớn nhất của hàm số bằng 3 2 khi và chỉ khi 2
16  9m  3 2  16  9m  18  m  . 9 15 Câu 4. Tìm hệ số chứa  2 30 
x trong khai triển nhị thức 3  x  với x  0. 2   x  Lời giải 15k
Ta có số hạng tổng quát trong khai triển  2 k  T  C . . x  C   x   n    3 15 .2 . n  k k k k 30 5 1 . k k 1 2  x  Trang 106
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Theo đề 3
 0  5k  30  k  12 15 Hệ số chứa 30  2 
x trong khai triển nhị thức 3  x  là C .2 1  3640. 15  12 12 3 2   x   1   Câu 5. Cho dãy số  u u cho bởi 1
, tìm công thức số hạng tổng quát của dãy số đó. n   2 u   u  2  n 1 n Lời giải Ta có 1 1 3 7 11
u  ;u  u  2   2   ;u  u  2   ;u  u  2   ;..... 1 2 1 3 2 4 3 2 2 2 2 2
Từ đó ta phân tích được: 1 5 u    2.1 1 2 2 3 5 u     2.2 2 2 2 7 5 u     2.3 3 2 2 11 5 u     2.4 4 2 2 ..... 5 u   2.n n 2 --- HẾT ---
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 107
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 7 – TRƯỜNG ĐẶNG TRẦN CÔN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 D D B B D A A A A B A D A D B 16 17 18 19 20 21 22 23 24 25 B C A A D A B A C C
Câu 1. Trên giá sách có 5quyển sách toán khác nhau và 4 quyển sách tiếng Anh khác nhau.
Hỏi có tất cả mấy cách chọn một quyển sách? A. 20. B. 5. C. 4. D. 9. Lời giải Chọn D
Chọn sách Toán có 5cách.
Chọn sách tiếng Anh có 4 cách.
Vậy có 9 cách chọn một quyển sách.
Câu 2. Mệnh đề nào sau đây sai?
A. Hai đường thẳng phân biệt có một điểm chung thì cắt nhau.
B. Hai đường thẳng không đồng phẳng thì chéo nhau.
C. Hai đường thẳng song song thì đồng phẳng.
D. Hai đường thẳng không có điểm chung thì song song. Lời giải Chọn D
Mệnh đề D sai vì hai đường thẳng không có điểm chung thì có thể song song hoặc chéo nhau.
Câu 3. Tìm tất cả các giá trị của tham số m để hàm số y  m  sinx xác định trên đoạn  3  ;  ? 4 4    A. 2 m  . B. m 1. C. m  0 . D. 2 m   . 2 2 Lời giải Chọn B Điều kiện:  3 m  s inx; x  [  ; ] 4 4 Đặt   3 f (x)  s inx;x [ ; ] 4 4  
max f (x)  f ( )  sin( )  1  3 2 2 [ ; ] 4 4 Vậy m 1. Trang 108
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Câu 4. Trong trường A, tỉ lệ học sinh giỏi môn Văn là 12%, học sinh giỏi Toán là 9% và học
sinh giỏi cả hai môn là 7%. Chọn ngẫu nhiên một học sinh của trường A. Tính xác
suất p để học sinh đó không học giỏi văn và không học giỏi Toán. A. p  0,72. B. 0,86. C. 0,79. D. p  0,93. Lời giải Chọn B Gọi 1
B là biến cố: “Học sinh được chọn giỏi Văn”. 2
B là biến cố: “Học sinh được chọn giỏi Toán”. Suy ra B  B  1 2
B là biến cố: “Học sinh được chọn giỏi Văn hoặc giỏi Toán”.
Ta có công thức: P(B)  P(B  B  P B  P B  P B  B     1 2 ) ( 1) ( 2 ) ( 1 2 ) 0,12 0,9 0, 7 0,14.
Gọi B là biến cố: “Học sinh được chọn không học giỏi văn và không học giỏi Toán”.
Ta có: P(B)  1 P(B)  1 0,14  0,86.
Câu 5. Cho cấp số cộng u có công sai d . Công thức nào sau đây đúng? n 
A. u  u  n 1 d . B. u  2u  nd . n 1  1   n 1  1
C. u  u  n 1 d . D. u  u  nd . n 1  1   n 1  1 Lời giải Chọn D
Theo công thức số hạng tổng quát của cấp số cộng: u  u  n 1 d suy ra n 1   u  u  nd . n 1  1
Câu 6. Tất cả các nghiệm của phương trình cotx  3  0 là: A.   x 
 k , k  . B. x    k , k  . 6 6 C.  
x    k , k   . D. x   k , k  . 3 3 Lời giải Chọn A Ta có: 
cotx  3  0  cotx  3  x  x   k , k  . 6
Câu 7. Phương trình    2 x  x x     2 2 1 cos 2sin cos
2 1 sin x  0 tương đương với phương trình nào sau đây? A.       cos 2x   1.   B. 2 cos 2x   .    4   4  2 C.    3    cos 2x   .   D. 1 cos 2x   .    4  2  4  2 Lời giải Chọn A Ta có: 2 2
( 2 1) cos x  2 sin x cos x  ( 2  1) sin x  0
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 109
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT  1  cos 2x   1  cos 2x   ( 2 1)  sin 2x  ( 2  1)  0      2   2 
 ( 2 1) 1 cos 2x  2sin 2x  ( 2 1)1 cos 2x  0
 2 2  2 cos 2x  2sin 2x  0  cos 2x  sin 2x  2     2 cos 2x   2    4      cos 2x   1.    4 
Câu 8. Cho hình chóp S.ABCD có đáy là hình thoi. Gọi O là giao điểm của AC và BD ; E và F
lần lượt là trung điểm của OA và OC ; điểm I thay đổi trên đoạn AC I  ; A I  O . Gọi
(P) là mặt phẳng qua I và song song với BD và SA. Biết (P) cắt S.ABCD theo thiết diện
là đa giác (H). Hãy xác định tất cả các vị trí của I để (H) có số cạnh nhiều nhất.
A. I thuộc đoạn OAI  O; I  A.
B. I thuộc đoạn EAI  E; I  A.
C. I thuộc đoạn FC I  C; I  F .
D. I thuộc đoạn OC I  C; I  O. Lời giải Chọn A
+ Mặt phẳng (P) qua I song song với BD cắt AD tại L, AB tại M, BC tại K.
+ Mặt phẳng (P) qua I song song với SA cắt SC tại N.
+ Mặt phẳng (P) qua L song song SA cắt SD tại P.
+ Gọi Q là giao điểm của SB và NK. Trang 110
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Ta có: P  ABCD  ML P SAD  LP P SCD  PN P SBC   NQ P SAB  QM
Vậy thiết diện cần tìm là ngũ giác MLPNQ (như hình vẽ).
Câu 9. Mệnh đề nào sau đây sai? x    k2 x    k2 A. cos x  cos  
, k  . B. sin x  sin   , k  . x     k2 x     k2
C. tan x  tan  x    k, k  .
D. cot x  m  x  acr cot m  k ,k  . Lời giải Chọn A x    k2 cos x  cos  , k    . x     k2
Câu 10. Cho dãy số u với u  
 n . Số hạng thứ 6 của dãy bằng: n  2n n  A. -58. B. 70. C. -27. D. 38. Lời giải Chọn B
u  26  6  70 . 6
Câu 11. Cho cấp số nhân u có công bội q  1. Tổng của n số hạng đầu tiên bằng. n  1 n u  q n 1 n u  q n 1   1   A. . B. u  q u  q 1 . C. . D. 1 . 1 q 1 q 1 q 1 q Lời giải Chọn A
Câu 12. Có tất cả mấy cách xếp ba bạn nam và hai bạn nữ ngồi vào một bàn gồm năm chỗ? A. 150. B. 3125. C. 25. D. 120. Lời giải Chọn D
Số cách xếp ba bạn nam và hai bạn nữ ngồi vào một bàn gồm năm chỗ: 5!120 .
Câu 13. Mệnh đề nào sau đây sai? 3 A. sinx  0  x  k2 ,  k  .  B. sinx  1  x    k2 ,  k  .  2
C. cos x  1  x    k2 ,  k  . 
D. cos x  1  x  k2,k  .  Lời giải Chọn A
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 111
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Ta có sinx  0  x  k,k   nên mệnh đề ở đáp án A sai. 1
Câu 14. Cho cấp số cộng u có công sai d  3
 và u  . Số hạng thứ chín của cấp số đã n  1 2 cho bằng 53 41 35 47 A.  . B.  . C.  . D.  . 2 2 2 2 Lời giải Chọn D 1
Vì u là cấp số cộng có công sai d  3  và u  nên n  1 2 1 47
u  u  8d   8. 3   . 9 1   2 2 Vậy chọn đáp án D
Câu 15. Hệ số của số hạng chứa 5
x trong khai triển và rút gọn của biểu thức x   x5 2 1 2  x 1 3x10 bằng: A. 61204. B. 3320. C. 61268. D. 3160. Lời giải Chọn B + x   x5 1 2
Số hạng tổng quát của   5 1 2x là: k 5k k k k k k k C      5 1
 2x C5  2x C5  2 x Số hạng chứa 5
x trong khai triển x   x5 1 2 là: . k k k x C  5  2 x Do đó: k = 4
Suy ra: hệ số của số hạng chứa 5
x trong khai triển x   x5 1 2 là: 4 C   5  2 4 80. + 2 x 1 3x10
Số hạng tổng quát của   10 1 3x là: k 10k k k k k k k   1 C 01 3x 1 C 0 3x 1 C 03 x Số hạng chứa 5 x trong khai triển 2 x 1 3x10 là: k k 1 C 0 3 Do đó: k = 3
Suy ra: hệ số của số hạng chứa 5 x trong khai triển 2 x 1 3x10 là: 3 3 1 C  . 0 3 3240
Vậy: Hệ số của số hạng chứa 5
x trong khai triển và rút gọn của biểu thức x   x5 2 1 2  x 1 3x10 bằng: 80 + 3240 = 3320. Trang 112
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Câu 16. Số cạnh của một hình tứ diện đều là: A. 6 . B. 4 . C. 3 . D. 5 . Lời giải Chọn B
Câu 17. Gọi n là số tự nhiên thỏa mãn 0 1 2
C  4C  C  1. Hãy chọn mệnh đề đúng trong các n n n mệnh đề sau: A. n  15. B. n5;8 . C. n8;12 . D. n12;15. Lời giải Chọn C
Điều kiện: n  2, n  . n n   n  0 L 2   Phương trình cho 1  1 4n 
 1  n  9n  0   . 2  n  9
Câu 18. Cho tứ diện đều ABCD có các cạnh đều bằng a . Gọi G là trọng tâm tam giác ABC ,
M là trung điểm của cạnh CD . Diện tích thiết diện của tứ diện ABCD khi cắt bởi mặt
phẳng  AMG (tính theo a ) bằng: 2 2 2 2 A. a 11 . B. a 11 . C. a 11 . D. a 11 . 16 8 2 32 Lời giải Chọn A A G B D M H I C
Gọi I là trung điểm của BC . Khi đó, thiết diện của  AMG và tứ diện ABCD là tam giác AMI . Ta có: a 3 a AM  AI 
; MI   AMI cân tại A . 2 2 2 2 Gọi 3a  a  a 11
H là trung điểm của MI . Ta có: 2 2 AH  AM  MH      . 4  4  4 2 Vậy: 1 1 a 11 a a 11 S  AH.MI  . .  . AMI 2 2 4 2 16
Câu 19. Cho tứ diện ABCD . Gọi M , N và P lần lượt là trung điểm của các cạnh A , B BC và
DA Mệnh đề nào sau đây sai? A. DC  MNP . B. MP  BCD . C. MN   ACD. D. BD  MNP Lời giải
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 113
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Chọn A
MP  BD  MP  BCD ,
MN  AC  MN   ACD . BD  MP  BD  MNP Câu 20. Biết đoạn  ;
a b là tập hợp tất cả các giá trị của tham số m để phương trình
sin x 1  2m có nghiệm. Gía trị của biểu thức 3a  b bằng: A. 2. B. 3. C. 4. D. 1 Lời giải Chọn D
sin x 1  2m  sin x  2m 1 phương trình có nghiệm khi và chỉ khi 1
  2m 11  0  m  1 Suy ra 3a  b 1
Câu 21. Trong mặt phẳng tọa độ 
Oxy , cho vectơ a  3;2 và đường tròn C có phương trình
x  2  y  2 1
3  4 . Phép tịnh tiến T biến đường tròn C thành đường tròn có a phương trình:
A. x  2   y  2 2 5  4.
B. x  2   y  2 1 3  4.
C. x  2   y  2 2 5  4.
D. x  2   y  2 4 1  4. Lời giải Chọn A
C có tâm là I 1;3 , bán kính R  2 . Gọi Ix; y , ta có  
T I   I  II  a   x 1; y  3  3;2 a x 1  3 x  2      y  3  2  y  5 Vậy I2;5 Trang 114
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Phép tịnh tiến T biến đường tròn C thành đường tròn có tâm I2;5 , bán kính a
R  2 nên có phương trình là:  x  2   y  2 2 5  4.
Câu 22. Điều kiện xác định của hàm số sin x  cos x y  là: sin x  cos x A.   x   k2 ,  k  .  B. x   k ,  k  .  4 4 C.   x    k2 ,  k  .  D. x    k ,  k  .  4 4 Lời giải Chọn B Điều kiện 
sin x  cos x  0  sin x  cos x  tan x  1  x   k ,  k  .  4
Câu 23. Cho cấp số cộng u có u  3 và công sai d  2. Tổng 10 số hạng đầu của cấp số cộng n  1 đã cho bằng A. 105. B. 115. C. 130. D. 120. Lời giải Chọn A n u  n 1 d   1  
Áp dụng công thức tổng n số hạng đầu của cấp số cộng S   . n 2 103  9.2 Ta có S   105. 10 2
Câu 24. Tất cả các nghiệm của phương trình 2cos3x  2  0 là A.    x    k2; k  .  B. 3 2 x    k ; k  .  4 4 3 C.  2  x    k ; k  .  D. 3 x    k2;k  .  4 3 4 Lời giải Chọn C  3   2 3x   k2 x   k    Ta có 2 4 4 3
2 cos 3x  2  0  cos3x      ; k  .  2 3    2 3x    k2 x    k  4  4 3
Câu 25. Cho cấp số nhân (u ) biết u  2;u  486 .Tổng của 8 số hạng đầu tiên bằng? n 1 3 A. 5765. B. 4376 . C. 6792 . D. 7210. Lời giải Chọn C Ta có: u  u 3 1 u  u  2d  d 
 242  u  u  7d  2  7.242  1696. 3 1 8 1 2 (u  u ).8 (2 1696).8 1 8 S    6792. 8 2 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 115
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT B. TỰ LUẬN.
Câu 1. Giải phương trình: 3 sin 3x  . 2 Lời giải:     k2 3x   k2 x      Ta có: 3 3 9 3 sin 3x   sin 3x  sin     . 2 3 2   2   k2 3x   k2 x    3  9 3
Câu 2. Từ một bình chứa 7 quả cầu đỏ và 4 quả cầu xanh. Lấy ra ngẫu nhiên đồng thời 3 quả.
Tính xác suất để lấy được 3 quả cùng màu. Lời giải:
Số cách lấy ra 3 quả từ bình là: n 3  C  165 11
Số cách lấy ra 3 quả cùng màu là: 3 3 C  C  39 . 7 4
Suy ra xác suất lấy được 3 quả cùng màu là: 39 13  . 165 55
Câu 3. Cho cấp số nhân u có u 1024 và công bội 1 q  . Tính u . n  1 2 15 Lời giải: 14 Ta có:  1  1 14 u  u .q  1024.  . 15 1    2  16
Câu 4. Cho cấp số cộng có số hạng thứ ba bằng 5 và công sai bằng 1 . Tính tổng 100 số hạng 3
đầu tiên của cấp số cộng đã cho. Lời giải  Theo giả thiết; 2 13
5  u  u  2d  u   u  . 3 1 1 1 3 3  Vậy 100 6250 S  u  u  ... u  . 2u  99d  . 100 1 2 100  1  2 3
Câu 5. Cho hình chóp S.ABC . Gọi M , N, P lần lượt là trọng tâm của các tam giác SAB, SAC và ABC
a) Chứng minh MN  SBC.
b) Xác định giao điểm của đường thẳng SP và  AMN . Lời giải Trang 116
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
a) Chứng minh MN  SBC.
 Gọi I, J, K, E, F lần lượt là trung điểm của S , A AB, AC, SB, SC .  Vì SM SN 2 
 (Tính chất trọng tâm), nên MN  JK. SJ SK 3 MN   ABC  
 MN   ABC (đpcm). MN  JK, JK    ABC
b) Xác định giao điểm của đường thẳng SP và  AMN .
  AMN    AEF .   SBK 
  SP; SBK  AEF   EN    SP   AEF     SBK  . O Trong ; EN  SP  O
 Vậy SP  AMN   . O --- HẾT ---
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 117
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 8 – TRƯỜNG GIA HỘI 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A A B C D B B B B B D D A A C 16 17 18 19 20 21 22 23 24 25 C D D A A C D C D C A. TRẮC NGHIỆM.
Câu 1. Trong mặt phẳng Oxy , cho đường tròn C x  2   y  2 : 1
2  9 . Tìm phương trình 
đường tròn C là ảnh của C qua phép tịnh tiến theo vectơ v  2;3 .
A. C x  2   y  2 : 1 1  9.
B. C x  2   y  2 : 3 5  9.
C. C x  2   y  2 : 3 5  9.
D. C x  2   y  2 : 1 1  9. Lời giải Chọn A
Đường tròn C có bán kính R  3 và tâm I 1; 2   . 
Đường tròn C là ảnh của C qua phép tịnh tiến theo vectơ v  2;3 nên đường
tròn C có bán kính R  3 và tâm Ix ; y .   x 1  2  x  1 Ta có: II  v      I 1  ;  1 .  y  2  3 y  1
Vậy phương trình đường tròn C là C x  2   y  2 : 1 1  9.
Câu 2. Tìm hệ số của số hạng chứa 5
x trong khai triển   12 1 3x A. 1  92456. B. 7  29. C. 192456. D. 729. Lời giải Chọn A 12 12
Ta có: 1 3x12  C 3 k  x  C 3 k k k k x . 12   12   k 0 k 0 Số hạng chứa 5
x trong khai triển   12 1 3x  k  5 .
Vậy hệ số của số hạng chứa 5
x trong khai triển   12 1 3x là C 35 5  192456. 12 4 4
Câu 3. Tìm giá trị lớn nhất ( max y ), giá trị nhỏ nhất ( min y ) của hàm số y  sin x  cos x .  1  1 min y 1 min y  1 min y   min y  A.    2 . B.  2 . C.  1 . D.  1 .  max y  max y  max y 1 max y 1  2  2 Lời giải Chọn B Ta có: 1 4 4
y  sin x  cos x   2 2 sin x  cos x 2 2 2
 2sin xcos x 1 sin 2x . 2 Ta có: 1 1 1 1 2 2 2
0  sin 2x  1     sin 2x  0 
 1 sin 2x 1 hay 1  y 1. 2 2 2 2 2 Trang 118
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Vậy max y 1 và 1 min y  . 2 
Câu 4. Trong mặt phẳng Oxy , cho vectơ v  3; 5
  và điểm M 1; 
1 . Tìm tọa độ điểm M ' là 
ảnh của điểm M qua phép tịnh tiến theo vectơ v . A. M '4;6. B. M '2;4. C. M '4;4. D. M '2;6. Lời giải Chọn C 
Tọa độ điểm M ' là ảnh của điểm M qua phép tịnh tiến theo vectơ v là: x  1 3  4 M '   M '4; 4   . y  1 5  4   M '
Câu 5. Đẳng thức nào sau đây là sai? A. n  
1 ! n!  n  2.n!. B. n  2.n   1 !  n  2!. C. 0!1! 2!. D. n   1 .n!  n   1 !. Lời giải Chọn D
Câu 6. 20 đường thẳng phân biệt có tối đa bao nhiêu giao điểm? A. 200 . B. 190. C. 380. D. 20 . Lời giải Chọn B
Hai đường thẳng phân biệt có tối đa một giao điểm nên 20 đường thẳng có tối đa 2 C  190 giao điểm. 20
Câu 7. Tìm tất cả các nghiệm của phương trình 4 4 cos x  sin x  0. A.    x 
 k , k  Z. B. x   k , k  Z. C. x    k2 , k  Z. D. x  k ,k  Z. 2 4 2 Lời giải Chọn B Ta có: 4 4 cos x  sin x  0 2 2 2 2
 (cos x  sin x).(cos x  sin x)  0  cos 2x  0   2x   k ,k  Z 2    x   k , k  Z. 4 2  
Vậy tập nghiệm của phương trình là: x   k ,k  Z. 4 2
Câu 8. Tìm tất cả các nghiệm của phương trình 1 sin x   . 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 119
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT A.  2   x   k2  x   k2 , k  Z. B. 7 x    k2  x   k2 ,k  Z. 3 3 6 6 C.  5   x   k2  x   k2 ,k  Z. D. 5 x    k 2  x   k2 , k  Z. 6 6 6 6 Lời giải Chọn B Ta có: 1 sin x   2      sin x  sin    6     x   k2  6   (k  Z )      x     k2     6     x   k2  6   (k  Z ). 7 x   k2  6  7
Vậy tập nghiệm của phương trình là: x    k2  x   k2 ,k  Z. 6 6
Câu 9. Tìm tập xác định D của hàm số 1 y  . 1 sin 2x A.     
D   \   k2 , k  .
B. D   \   k,k  .  2   4  C.     
D   \   k2 , k .
D. D   \   k ,k  .  4   4  Lời giải Chọn B Hàm số 1 y  xác định khi 1 sin 2x  
1 sin 2x  0  2x  
 k2 ,k    x    k ,k  2 4    Tập xác định 
D của hàm số là D   \   k , k   .  4 
Câu 10. Các hàm số sau được xét trên tập xác định của chúng. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số y  cos x là hàm số chẵn.
B. Hàm số y  cos .xsin x là hàm số không chẵn cũng không lẻ. C. Hàm số 3 3 y  sin . x cos x là hàm số lẻ.
D. Hàm số y  sin x, y  tan x, y  cot x đều là các hàm số lẻ. Lời giải Chọn B Trang 120
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
+ Hàm số y  cos x có tập xác định D   và cos(x)  cos x nên hàm số y  cos x là hàm số chẵn.
+ Hàm số y  cos .xsin x có tập xác định D   và cosx.sinx  sin .xcos x nên
hàm số y  cos .xsin x là hàm số lẻ. + Hàm số 3 3 y  sin .
x cos x có tập xác định D   và 3 x 3 x 3 3 cos .sin  sin . x cos x nên hàm số 3 3 y  sin . x cos x là hàm số lẻ.
+ Hàm số y  sin x có tập xác định D   và sin(x)  sin x nên hàm số y  sin x là hàm số lẻ. + Hàm số  
y  tan x có tập xác định D   \   k , k  và tan(x)   tan x nên hàm  2 
số y  tan x là hàm số lẻ.
+ Hàm số y  cot x có tập xác định D   \k,k  
 và cot(x)  cot x nên hàm số
y  cot x là hàm số lẻ
Câu 11. Gieo đồng thời một con súc sắc và một đồng xu. Tính xác suất để xuất hiện đồng xu có
mặt ngửa và con súc sắc có số chấm không vượt quá 4. A. 1 . B. 1 . C. 1 . D. 1 . 2 6 4 3 Lời giải Chọn D
* Không gian mẫu:   N1; N2; N3; N4; N5; N6; 1 S ; S2; S3; S 4; S5; S  6 n 12
* Gọi A là biến cố: Đồng xu có mặt ngửa và con súc sắc có số chấm không vượt quá 4. A  N1; N 2; N3; N  4 n  A  4
Vậy : P A n A 4 1    n  . 12 3
Câu 12. Tìm tập nghiệm của phương trình 2cos x  sin x  3  0. A.    .  B.   k , k  .
C.   k ,k . D. .   2   2  Lời giải Chọn D Ta có:         x  x 3 2 cos sin  3  0  2 2 c os x   3  0  cos x        4   4  2 2 Vì 3  3 
 1 nên phương trình 2cos x  sin x  3  0vô nghiệm. 2 2 2 2
Vậy tập nghiệm của phương trình là: S  .  4 4 Câu 13. Biết C 126 A . n . Tính n
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 121
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT A. 3024. B. 24. C. 504. D. 756. Lời giải Chọn A Điều kiện: n  4. Ta có n! n! 4 4 C  126      A  n
n   126 n   3024 3024. 4! 4 ! 4 ! n Câu 14.   
Tìm điều kiện xác định của phương trình tan 2x   3.    3  A. 5   x   k , k  .
 B. x   k , k  .  12 2 2 C. 5   x   k , k  .  D. x   k , k  .  12 6 2 Lời giải Chọn A Điều kiện      5  cos 2x   0  2x    k    x   k , k  .   3  3 2 12 2
Câu 15. Tính số tập hợp con của tập hợp A   ; a ; b ; c d; ; e f ; g. A. 127. B. 15. C. 128. D. 14. Lời giải Chọn C
Tập hợp A có 7phần tử  số tập hợp con của A là 7 2  128.
Câu 16. Trong các mệnh đề sau, tìm mệnh đề đúng ? A. Trên khoảng    0; 
 hàm số y  sin x và hàm số y  cos x cùng nghịch biến.  2  B. Trên khoảng    0; 
 hàm số y  sin x nghịch biến và hàm số y  cos x đồng biến.  2  C. Trên khoảng    0; 
 hàm số y  sin x đồng biến và hàm số y  cos x nghịch biến.  2  D. Trên khoảng    0; 
 hàm số y  sin x và hàm số y  cos x cùng đồng biến.  2  Lời giải Chọn C Trang 122
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Vẽ đồ thị hàm y  sin x ( đường nét đứt ) và đồ thị hàm y  cos x ( đường nét liền ) trên
cùng một hệ trục tọa độ ta thấy : trên khoảng    0; 
 hàm số y  sin x đồng biến và  2 
hàm số y  cos x nghịch biến.
Câu 17. Tìm tất cả các nghiệm của phương trình cos x  3sin x  0. A.     x 
 k2 , k  B. x   k,k  C. x    k ,k  . D. x   k,k  .  3 2 6 6 Lời giải Chọn D Ta có: 
cos x  3 sin x  0  cos x  3 sin x  cot x  3  x   k 6 
Câu 18. Trong mặt phẳng Oxy cho điểm M 1;7 và vectơ v  2;5 . Tìm M  là ảnh của M 
qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ v
và phép vị tự tâm O tỉ số k  2 . A.  1    M   ; 6   . B. 3 M  ;1   . C. M  2  ;24 . D. M6;4.  2   2  Lời giải Chọn D x  x  2  3 Gọi  M là ảnh của M qua T M M  khi đó: 1   M 3;2 . 1   1 v y  y  5  2  M  1 M   x  6 Vì M là ảnh của M qua V nên: OM   2 M OM   . 1   O;2 1 y    4 M Vậy M 6;4
Câu 19. Tìm số nghiệm của phương trình cos3x sin 2x  0 trên đoạn 0; . A. 3. B. 4 . C. 2 . D. 1 Lời giải Chọn A   k2 x    Xét phương trình    10 5 cos 3x  sin 2x  sin  3x  sin 2x      2   x    k2  2 Với  k 2  k  x   , do x   2 0;  0      0  .25  k  2,25 10 5 10 5
Mà k  Z  k  0;k  1;k  2 Với   x  
 k2 , do x 0;   0    k2    0  .75  k  0  .25 2 2
Mà k Z  k  .Ứng với mỗi giá trị của k tương ứng với một nghiệm của phương trình
cos3x  sin 2x  0 trên đoạn 0; . Vậy có phương trình có 3 nghiệm.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 123
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT 0 1 2 n n
Câu 20. Tính tổng S  C  3C  9C  ... 3 C . n n n n A. 4n . B. 3n . C. 2n . D. 1 3n Lời giải Chọn A Xét   xn 0 1 2 2 1
 S  C  C x  C x  ... n n  C x . n n n n x  3 ta có n 0 1 2
4  C  3C  9C  ...  3n n C . n n n n Câu 21. ThaPhương trình 2
sin x  1 tương đương với phương trình sau đây? A. sin x  0. B. sin x  1  . C. sin x  1  . D. sin x 1. Lời giải Chọn C Ta có x   x   2 2 2 sin 1 sin 1  sin x  1.
Câu 22. Cho E là tập hợp các số tự nhiên gồm 2 chữ số khác nhau được lập từ các chữ số 1, 2, 3,
4, 5, 6. Lấy ngẫu nhiên một phần tử của E, tính xác suất để được một số chia hết cho 4 hoặc chia hết cho 7? A. 7 . B. 11 . C. 4 . D. 13 . 10 30 5 30 Lời giải Chọn D
Không gian mẫu n  56  30.
Các số chia hết cho 4: 12, 16, 24, 32, 36, 52, 56, 64.
Các số chia hết cho 7: 14, 21, 35, 42, 56, 63.
Xác suất để được một số chia hết cho 4 hoặc chia hết cho 7 là 13 . 30 Câu 23.   
Tìm tập nghiệm của phương trình cos 2x   1   .  4  A.      
  k , k   . B. 1
   k2 , k   .  8  2 8  C.       k , k   .
D.   k2 ,k  .  8   4  Lời giải Chọn C Ta có:      cos 2x 
 1  2x   k2 k   x   k k      4  4 8 Câu 24. 1
Tìm tập xác định D của hàm số y  . 2  sin 7x  2017 A.       D   \   k , k   . B. 2019 D   \   .  2   7  Trang 124
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 C. 2019  D   \   k2 ,k . D. D   .  7  Lời giải Chọn D Hàm số 1 y 
xác định  2  sin 7x  2017  0 2  sin 7x  2017
 sin 7x  2017  2  (luôn đúng x    ). Vậy D   .
Câu 25. Cho hàm số y  sin x  cos x, tìm khẳng định đúng?
A. y   2  y  2. B. 0  y  2. C.  2  y  2. D. 2   y  0. Lời giải Chọn C Ta có   
y  sin x  cos x  2 sin x    2  y  2   .  4  B. TỰ LUẬN. Câu 1. x
Tìm tập nghiệm của phương trình 2cos  3  0. 2 Lời giải Ta có x x 3 x 5 5
2 cos  3  0  cos     
 k2 , k    x    k4 , k   2 2 2 2 6 3
Câu 2. Trong mặt phẳng Oxy , cho đường thẳng d : 3x  4y 12  0. Tìm phương trình đường 
thẳng d là ảnh của d qua phép tịnh tiến vectơ v  2;  1 . Lời giải Gọi M  ;
x yd, M  x ; yd x  x  x  x 
Ta có T d   d  T M  2 2  M      v v  y  y 1  y  y 1
Thay M x; y vào d :3x  4y 12  0 ta được
3 x  2  4 y  
1 12  0  3x  4 y 14  0
Vậy d:3x  4y 14  0.
Câu 3. Đội văn nghệ của lớp có 5 bạn nam và 7 bạn nữ. Chọn ngẫu nhiên 5 bạn tham gia biểu
diễn. Tính xác suất để trong 5 bạn được chọn có cả nam và nữ, đồng thời số bạn nữ nhiều hơn số bạn nam. Lời giải TH 1: Có 3 nữ, 2 nam: 3 2 C C  350 cách. 7 5 TH 2: Có 4 nữ, 1 nam: 4 1 C C  175 cách. 7 5
Suy ra xác suất cần tính bằng: 350 175 175  . 5 C 264 12
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 125
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Câu 4.   
Tìm tất cả các giá trị của tham số m để phương trình cos  2x  m  2   có nghiệm?  3  Lời giải Phương trình    cos  2x  m  2   có nghiệm  3   1
  m  2 1  m  2 1  0  m  2 1  2  m  3.
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a . Hai mặt bên SAB và SCD
là các tam giác đều. Gọi G là trọng tâm tam giác SAB , E là điểm di động trên đoạn
thẳng BG ( E khác B ). Cho mặt phẳng   qua E , song song với SA và BC .
a) Chứng minh đường thẳng AD song song với mặt phẳng   . Tìm giao điểm
M , N, P, Q của mặt phẳng   với các cạnh SB, SD, DC, BA .
b) Gọi I là giao điểm của QM và PN . Chứng minh I nằm trên một đường thẳng cố
định khi điểm E di động trên đoạn BG .
c) Chứng minh tam giác IPQ là tam giác đều. Tính diện tích tam giác IPQ theo a . Lời giải S I G N M A D E P Q B C AD // BC  
   // BC  AD //   AD     a)Ta có: .
Trong mặt phẳng SAB , kẻ đường thẳng qua E và song song với SA , cắt SB tại M , cắt AB tại Q .
Trong  ABCD , kẻ đường thẳng qua Q và song song với BC , cắt CD tại P .
Trong SBC, kẻ đường thẳng qua M và song song với BC , cắt SC tại N .
Vậy M , N, P, Q là giao điểm của mặt phẳng   với các cạnh SB, SD, DC, BA . Trang 126
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 I QM   SAB b) Ta có: I  QM  PN  . I  PN   SCD S SABSCD 
Xét hai mặt phẳng SAB và SCD có AB // CD AB  SAB,CD   SCD
 SAB SCD  d , d qua S và d // AB,d // CD  d cố định. Do đó I  d . IQ  SA
c)Do các tứ giác ISAQ và ISDP là các hính bình hành nên  . IP  SD
Mà SA  AB  AD  SD  a nên IPQ là tam giác đều cạnh a . 2 Vậy diện tích tam giác a 3 IPQ là S  . 4 --- HẾT---
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 127
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 9 – TRƯỜNG CHI LĂNG 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 D B A B C A B D B B A D A D C 16 17 18 19 20 21 22 23 24 25 C D B C C A B D D D 
Câu 1. Trong mặt phẳng Oxy cho B3;6 và v5;4. Tìm tọa độ điểm C sao cho T C  B v A. C 8; 1  0. B. C  2  ; 2  . C. C 2;2. D. C 8;10. Lời giải Chọn D Gọi tọa độ C  ; a b x  a  x a  8  Do T C  B nên v b     C  8  ;10 v y  b  y b    10 v b Câu 2. x 
Tìm tập xác định của hàm số sin 1 y  sin x  A.  D   \   k2 ;  k . B. D   \   k ;  k    . 2   C.  D   \   k ;  k  . D. D   \k2 ;  k    . 2  Lời giải Chọn B
ĐKXĐ sin x  0  x    k;k  
Vậy TXĐ của hàm số là D   \   k ;  k    .
Câu 3. Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình vẽ. Hỏi có
bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần ? A. 24. B. 18. C. 10. D. 9. Lời giải Chọn A Từ A đến B có 4 cách. Từ B đến C có 2 cách. Từ C đến D 3 cách.
Do đó, từ A đến D có 4.2.3  24 cách mà qua B và C chỉ một lần.
Câu 4. Tìm tất cả cá nghiệm của phương trình 2cos x  2  0. Trang 128
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1  3  5     x   k2   x   k2  x   k2  x   k2  A. 4  . B. 4  . C. 4  . D. 4  .   5   3   x   k2              x k2 x k2 x k2  4  4  4  4 Lời giải Chọn B  3  5 x   k2 x   k2    Ta có: 2 4 4
2cos x  2  0  cos x      ;k  .  2 3   5 x k2    x   k2  4  4
Câu 5. Trong mặt phẳng tọa độ Oxy cho đường tròn C có phương trình
x  2   y  2 2
2  4. Phép đồng dạng có được bằng việc thực hiện liên tiếp các phép vị tự tâm O tỉ số 1
k  và phép quay tâm O góc quay 0
90 sẽ biến đường tròn C  thành 2
đường tròn nào trong các đường tròn sau đây?
A. x  2   y  2 2 2  1.
B. x  2   y  2 1 1  1.
C. x  2   y  2 1 1  1.
D. x  2   y  2 2 1  1. Lời giải Chọn A
Đường tròn C có tâm I 2;2; R  2
Gọi đường tròn C có tâm I bán kính R là ảnh của đường tròn C có tâm I  V I  1    O,        2  I 1;  1
I 2;2; R  2 qua phép vị tự tâm O tỉ số 1 k  suy ra    2 1    R 1 R  .R  2
Gọi đường tròn C  có tâm I bán kính R là ảnh của đường tròn C có tâm I  Q I    0 I 1  ;1 I1; 
1 ; R  1 phép quay tâm O góc quay 0 90 suy ra O,90              R 1 R R
Vậy ảnh của đường tròn Cqua phép đồng dạng có được bằng việc thực hiện liên
tiếp các phép vị tự tâm O tỉ số 1
k  và phép quay tâm O góc quay 0 90 là đường tròn 2
C  x  2   y  2 : 1 1  1.
Câu 6. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng không có điểm chung thì chéo nhau.
B. Hai đường thẳng chéo nhau thì không có điểm chung.
C. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
D. Hai đường thẳng phân biệt không chéo nhau thì hoặc song song hoặc cắt nhau. Lời giải
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 129
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Chọn A
Hai đường thẳng không có điểm chung thì có thể song song với nhau
Câu 7. Cho hình chóp S.ABCD có đáy là hình thang cân đáy lớn AD , M , N lần lượt là là
trung điểm của AB và CD , P là mặt phẳng qua MN và cắt mặt bên SBC theo một
giao tuyến. Thiết diện của P và hình chóp là hình gì?
A. Hình bình hành. B. Hình thang.
C. Hình chữ nhật. D. Hình vuông. Lời giải Chọn B
Gọi P SBC  PQ với P  SB, Q  SC .
Ta thấy P chứa MN , SBC chứa BC và BC  MN . Suy ra PQ  MN.
Vậy thiết diện là hình thang MNQP .
Câu 8. Một đề thi có 20 câu hỏi trắc nghiệm khách quan, mỗi câu có 4 phương án lựa chọn,
trong đó chỉ có một phương án trả lời đúng. Khi thi, một học sinh đã chọn ngẫu nhiên
một phương án trả lời với mỗi câu của đề thi đó. Trong trường hợp đó xác suất để học
sinh đó trả lời không đúng cả 20 câu là bao nhiêu? 20 A. 1 . B. 3 . C. 1 . D.  3    . 4 4 20  4  Lời giải Chọn D
Một câu sai có xác suất là 3 . 4 20
Xác suất để học sinh đó trả lời không đúng cả 20 câu là  3    .  4 
Câu 9. Hiếu có 8 người bạn. Hiếu muốn mời 4 trong 8 người bạn đó về quê chơi vào cuối
tuần. Nhưng trong 8 người bạn đó có 2 bạn là Khoa và Tuấn không thích đi chơi với
nhau. Như vậy số cách chọn nhóm 4 người để về quê của Hiếu là bao nhiêu? A. 4 C . B. 4 3 C  2C . C. 4 3 C  C . D. 4 3 C  C . 8 6 6 6 6 6 7 Lời giải Chọn B Trang 130
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
+ TH1: Chọn 4 bạn nhưng không có 2 bạn Khoa và Tuấn có: 4 C (cách). 6
+ TH2: Chọn 4 bạn trong đó có Khoa hoặc Tuấn có: 3 2.C (cách). 6
Vậy theo quy tắt cộng có tất cả: 4 3 C  2C (cách). 6 6
Câu 10. Một họp có 10 viên bi màu trắng, 20 viên bi màu xanh, 30 viên bi màu đỏ, mỗi viên bi
chỉ có một màu. Có bao nhiêu cách để chọn ngẫu nhiên 8 trong số các viên bi thuộc
hộp đó để được 8 viên bi cùng màu trắng? A. 4 C . B. 8 C . C. 8 C . D. 4 C . 20 10 60 30 Lời giải Chọn B
Chọn 8 viên bi màu trắng từ 10 viên bi màu trắng có: 8 C (cách) 10
Câu 11. Cho tập hợp A  2;3;4;5;6; 
7 . Có thể lập được tất cả bao nhiêu số tự nhiên gồm 3 chữ
số khác nhau được thành lập từ các chữ số thuộc A ? A. 120. B. 216. C. 256. D. 180. Lời giải Chọn A
Gọi abc là số cần tìm, trong đó a  0, a  b  c và a,b,c A.
Số cách chọn ra 3 số trong 6 số của tập A để xếp vào 3 vị trí abc là 3 A  120 (số). 6
Câu 12. Trong khai triển  x  10 2
1 . Tìm hệ số của số hạng chứa 8 x . A. 256. B. 45. C. 1  1520. D. 11520. Lời giải Chọn D
Xét khai triển:  x  10 2 1  2x    10 1   
Số hạng tổng quát thứ k 1 trong khai triển trên là: T  C   1 k k 2 k k C x 10   10 10  2x10k 1 k k k 1 10   Số hạng chứa 8
x tương ứng với 10  k  8  k  2 .
Vậy hệ số của số hạng chứa 8
x trong khai triển trên là  C  2 2 102 1 2  11520 . 10
Câu 13. Hãy viết ba số hạng tiếp theo hai số hạng đầu của dãy số u có n  u 1,u 1,u  u  u . 1 2 n2 n 1  n A. 2;3;5. B. 3;4;7. C. 2;5;7. D. 3;5;8. Lời giải Chọn A
Ta có u  u  u  2, u  u  u  2 1  3, u  u  u  3 2  5. 3 2 1 4 3 2 5 4 3
Câu 14. Xét phép thử là gieo một con xúc xắc hai lần. Gọi N là biến cố” lần đầu xuất hiện mặt
5 chấm”, gọi M là biến cố” lần hai xuất hiện mặt 5 chấm” thì A. M  N  
 5; 1,5;2,5;3,5;4,5;5,5;6,1;5,2;5,3;5,4;5,5;5,6;5.
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 131
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT B. M  N  
 1;5,2;5,3;5,4;5,5;5,6;5. C. M  N  
 5; 1,5;2,5;3,5;4,5;5,5;6. D. M  N  5;  5 . Lời giải Chọn D Ta có N  
 5; 1,5;2,5;3,5;4,5;5,5;6. M  
 1;5,2;5,3;5,4;5,5;5,6;5. Khi đó M  N  5;  5 . Câu 15.   
Tìm giá trị lớn nhất và giá trị bé nhất của hàm số y  1 3sin 2x     4  A. max y  3 ; min y  2  . B. max y  2  ; min y  3. C. max y  4 ; min y  2  .
D. max y  4 ; min y  2 . Lời giải Chọn C Ta có:       1  sin 2x   1  3  3sin 2x   3     .  4   4      2  1 3sin 2x   4   hay 2  y  4 .  4       y  2  sin 2x   1  x   k ; k  .     4  8    3 y  4  sin 2x   1  x   k ; k  .     4  8
Vậy max y  4 ; min y  2  . Câu 16.   
Tìm tất cả các nghiệm x  0 ;   của phương trình 2 2sin x  3sin x 1  0  2  A.     x  . B. 5 x  . C. x  . D. x  . 12 6 6 2 Lời giải Chọn C   x   k2  2 sinx 1   2 2sin x  3sin x 1  0    1  x   k2 .  s inx   6  2  5 x   k2  6     x  0 ;  x  .    2  6
Câu 17. Có bao nhiêu cách sắp xếp bốn bạn Văn, Bình, Nhi, Thi ngồi vào một bàn dài gồm 4 chỗ ? Trang 132
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 A.1. B. 8. C. 4. D. 24. Lời giải Chọn D
Xếp 4 bạn vào một bàn dài gồm 4 chỗ có 4! 24 cách.
Câu 18. Trong không gian , cho 4 điểm không đồng phẳng. Có bao nhiêu tam giác từ 4 điểm đã cho ? A. 6. B. 4. C. 3. D. 2. Lời giải Chọn B
Một bộ 3 điểm bất kỳ từ 4 điểm ta xác định được 1 tam giác. Vậy có 3 C  4 tam giác. 4
Câu 19. Trong mặt Oxy cho điểm B3;6 . Tìm tọa độ điểm E sao cho B là ảnh của E qua
phép quay tâm O, góc quay 90 . A. E 6;3 . B. E 3;6. C. E  6  ;3 . D. E  3  ;6 . Lời giải Chọn C Vì B  
là ảnh của E qua phép quay tâm O, góc quay 90 nên Q( ; O 90 ) : B  E Suy ra E  6  ;3 .
Câu 20. Tìm số tự nhiên n , biết hệ số của số hạng thứ 3 theo số mũ giảm dần của x trong khai n triển  1  x    bằng 4 .  3  A. 8 . B. 4 . C. 9. D.17 . Lời giải Chọn C n 2 3 n Ta có  1  n n  1  n  1  n  1  n  1 0 1 1 2 2 3 3  x   C x  C x   C x   C x   ... C             3 n n   3 n   3 n   3 n   3 
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 133
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Suy ra hệ số của số hạng thứ 3 theo số mũ giảm dần của x trong khai triển đã cho là 2  1 2  C  n    3  2 Do đó  1  n! 1 2 C   4   4 n    3  2!(n  2)! 9 n  9  2
(n 1)n  72  n  n  72  0   n  8
Vì n là số tự nhiên và n  2 nên n  9.
Câu 21. Phép vị tự V biến điểm M thành điểm M ' là phép đồng nhất khi nào? I ;k  A. k 1. B. k  0. C. k  1  . D. k  1  . Lời giải Chọn A
Câu 22. Cho hình tứ diện ABCD có M , N lần lượt là trung điểm của AB, B . D Các điểm G,H
lần lượt trên cạnh AC,CD sao cho NH cắt MG tại I. Khẳng định nào sau đây là khẳng định đúng? A. B,G, H thẳng hàng. B. B,C, I thẳng hàng. C. N,G, H thẳng hàng. D. , A C, I thẳng hàng. Lời giải Chọn B
Ta có:  ABC DBC  BC
Mà I  MG   ABC  I  ABC và I NH  DBC I DBC
Do đó, I  ABC DBC. Suy ra I  BC. Vậy B,C, I thẳng hàng.
Câu 23. Cho cấp số cộng có các số hạng lần lượt là 5;9;13;17;... Khi đó u có thể được tính theo n
biểu thức nào dưới đây. A. u  5n 1. B. u  4n 1. C. u  5n 1. D. u  4n 1. n n n n Lời giải Trang 134
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Chọn D
Gọi cấp số cộng cần tìm là u  u  d n 1 với d là công sai; n . n 1  
Ta có d  9 5  4  u  u  4 n 1  4n  u  4  loại A, C. n 1   1 + Thử đáp án B: 3
4n 1  5  n  (loại). 2
+ Thử đáp án D: 4n 1 5  n 1 (thỏa).
Câu 24. Trong mặt phẳng Oxy , cho điểm A2; 
1 . Tìm ảnh của A qua phép dời hình có được 
bằng cách thực hiện liên tiếp phép tịnh tiến theo u  3;  1 và phép quay tâm O góc quay 9  0 . A.  5  ;0. B. 0;5. C. 5;0. D. 0; 5  . Lời giải Chọn D 
Gọi B là ảnh của A qua phép tịnh tiến theo u  3;  1 . x  x  x x  5 Khi đó: B u A B    . y  y  y y  0  B u A  B
Phép quay tâm O góc quay 90 biến điểm B5;0 thành điểm C x ; y . C C  x  y  0 Khi đó C B  . y  x  5   C B
Vậy ảnh của điểm A là C 0; 5  .
Câu 25. Gía trị của biểu thức 1 2 2 3 3 2020 2020 P  1 2C  2 C  2 C ... 2 C là: 2020 2020 2020 2020 A. 2020 P  3  . B. P  1  . C. 2020 P  3 . D. P 1. Lời giải Chọn D Dễ thấy P 1 2C  2 C  2 C ... 2 C  1 22020 1 2 2 3 3 2020 2020 2020 1 1 2020 2020 2020 2020 B. TỰ LUẬN.
Câu 1. Giải phương trình: a. 3tan 2x  3 b. 2 2sin x  cos 2x  0 Lời giải a) Ta có: 3  3 tan 2x  3  tan 2x   tan 2x  tan 3 6   k  2x   k  x   k  6 12 2  k
♥ Vậy phương trình (1) có họ nghiệm là x   k  . 12 2 b) Ta có: 1 cos 2x 1 2 2sin x  cos 2x  0  2.
 cos 2x  0  cos 2x  2 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 135
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT   
 cos 2x  cos  2x    k2  x    k 3 3 6 
♥ Vậy phương trình (1) có các họ nghiệm là x    k k  6
Câu 2. Ngân hàng đề thi gồm 100 câu hỏi, mỗi đề thi có 5 câu. Một học sinh học thuộc 80
câu. Tính xác suất để học sinh đó rút ngẫu nhiên được một đề thi có 4 câu học thuộc. Lời giải
♥ Số phần tử của không gian mẫu là: 5   C 100
♥ Gọi A là biến cố: “học sinh rút ngẫu nhiên được một đề thi có 4 câu học thuộc”
Số kết quả thuận lợi cho biến cố A là: 4 1   C .C A 80 20 4 1  C .C 5135
♥ Vậy xác suất cần tính là PA A 80 20    . 5  C 12222 100
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, gọi M , N lần lượt là trung điểm của S , A S . D
a) Tìm giao tuyến của hai mặt phẳng SAC và SBD.
b) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng OMN . Thiết diện đó là hình gì? Lời giải S N M A D P Q O B C
a) Tìm giao tuyến của hai mặt phẳng SAC và SBD.
♥ Ta có: S SAC  SBD (1) O   AC O    SAC ♥ Do AC  BD    O    
 O SAC SBD (2) O   BD O    SBD
♥ Từ (1) và (2) suy ra SAC SBD  S . O
b) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng OMN . Thiết diện đó là hình gì?
♥ Do M , N lần lượt là trung điểm của S , A SD  MN / / AD Trang 136
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
♥ Mặt phẳng OMN  và mặt phẳng  ABCD có điểm chung O và lần lượt chứa hai
đường thẳng MN và AD song song với nhau nên chúng cắt nhau theo giao tuyến PQ O   PQ thỏa  với P CD,Q  A . B PQ / /MN / / AD
♥ Suy ra tứ giác MNPQ là thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng OMN .
♥ Do MN / /PQ nên tứ giác MNPQ là hình thang với hai đáy là MN, P . Q Câu 4. Hệ số của 5
x trong khai triển x   x7 2 2 4 3 là Lời giải
Số hạng tổng quát của x   x7 2 2 4 3 là 2 7 T  2x C 4   x  C   x  k   3 k 7 2 4 . 3k k k k k k 2 1 7 7 5 x ứng với k 2
x  hay k  2  5  k  3 . Hệ số của 5 x là 2C 4 . 3  3 3 4  483840. 7
Câu 5. Tổng các nghiệm của phương trình sin x  3 cos x  2 trện đoạn 0;4  là: Lời giải Ta có 1 3   
sin x  3 cos x  2  sin x  cos x 1 sin x  1   2 2  3    
 x    k2  x   k2 . 3 2 6 Do   x   0;4  nên x  và 13 x 
, do đó tổng các nghiệm trên đoạn 0;4  của 6 6 phương trình là 7 . 3 --- HẾT ---
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 137
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
BẢNG ĐÁP ÁN & HƯỚNG DẪN GIẢI ĐỀ 10 – TRƯỜNG CHUYÊN NGUYỄN DU 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A C D C A C A C C D C B C A A 16 17 18 19 20 21 22 23 24 25 A C C D C A D A D C
Câu 1. Trong các phương trình sau phương trình nào có nghiệm: A. 2 cot x  cot x  3  0 . B. 3 sin x  2 . C. 1 1 cos 4x  . D. 2sin x  3cos x  4. 4 2 Lời giải Chọn A Xét phương trình: 2
cot x  cot x  3  0 1 .
Đặt t  cot x phương trình 1 trở thành: 2t  t  3  0 2 . Dễ thấy phương trình 2
luôn có hai nghiệm phân biệt nên phương trình 1 luôn có nghiệm. Do đó đáp án A là đáp án đúng.
Câu 2. Tập xác định của hàm số y  cos x 1 là: A.  
  k2 k   . B.  . C. k2 k    . D.k k    .  2  Lời giải Chọn C
Điều kiện cos x 1  0  cos x  1  1 . Vì cos x 1, x    nên  
1  cos x  1  x  k 2 , k   . Do đó tập xác định của hàm số đã cho là k2    .
Câu 3. Trong các hàm số sau, hàm số nào là hàm số chẵn:
A. y  2019cos x  2020sin x .
B. y  tan 2019x  cot 2020x .
C. y  cot 2019x  2020sin x .
D. y  sin 2019x  cos 2020x . Lời giải Chọn D
Dễ thấy các hàm số y  sin x, y  tan 2019x , y  cot 2020x, y  cot 2019x là các hàm số lẻ
và các hàm số y  cos x, y  cos2020x, y  sin 2019x là các hàm số chẵn. Do đó ta dự
đoán các hàm số trong 4 đáp án ,
A B, C, D có hàm số ở đáp án D là hàm số chẵn.
Thật vậy, hàm số y  sin 2019x  cos 2020x có tập xác định là  . +) x     x .  +) x
   : y x  sin 2019x  cos2020x  sin 2019x  cos 2020x  y x.
Suy ra y  sin 2019x  cos 2020x là hàm số chẵn. Vậy D là đáp án đúng.
Câu 4. Gieo hai con súc sắc. Xác suất để số chấm xuất hiện trên hai con súc sắc như nhau là A. 1 . B. 1 . C. 1 . D. 1 . 3 12 6 36 Trang 138
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Lời giải Chọn C
+) Số phần tử của không gian mẫu là: n   6.6  36 .
+) Gọi A là biến cố “ số chấm xuất hiện trên hai con súc sắc giống nhau”. Khi đó, A  
 1; 1,2;2,3;3,4;4,5;5,6;6  nA  6 . n A Xác suất của biến cố 6 1 A là: P  A      . n 36 6
Câu 5. Gọi G là trọng tâm tứ diện ABCD . Gọi A là trọng tâm tam giác BCD. Tỉ số GA GA bằng A. 3. B. 3 . C. 2 . D. 1 . 4 3 Lời giải Chọn A
Vì G là trọng tâm tứ diện ABCD nên:
    
        
GA  GB  GC  GD  0  AA  AG  AB  AG  AC  AG  AD  AG  0 
        
 AA  4AG  AB  AC  AD  0  AA  4AG  AG  3GA . Vậy GA  3 . GA Câu 6. Phép quay
biến điểm M thành điểm M . Khi đó  Q O;
 
  A. OM  OM  và  MOM    .
B. OM  OM  và OM ,OM    .
C. OM  OM  và OM ,OM    . D. OM  OM  và  MOM    . Lời giải Chọn C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 139
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 7. Cho tứ diện ABCD . Gọi M, N, , P , Q ,
R S lần lượt là trung điểm các cạnh AC, B , D A , B C , D A ,
D BC . Bốn điểm nào sau đây không đồng phẳng? A. M, , P S, N . B. M, N, , R S . C. , P , Q , R S . D. M, N, , P Q. Lời giải Chọn A A P R M N B D S Q C
+) MR//NS (vì cùng song song với CD) nên 4 điểm M, N, ,
R S đồng phẳng. Đáp án B sai.
+) PR//SQ (vì cùng song song với BD) nên 4 điểm , P , Q ,
R S đồng phẳng. Đáp án C sai.
+) MP //NQ (vì cùng song song với BC ) nên 4 điểm M, N, ,
P Q đồng phẳng. Đáp án D sai.
Câu 8. Trong các mệnh đề sau đây mệnh đề nào sai?
A. Phép dời hình là phép đồng dạng tỉ số k 1.
B. Phép vị tự tỉ số k là phép đồng dạng tỉ số k .
C. Phép đồng dạng biến đường thẳng thành đường thẳng // hoặc trùng với nó.
D. Phép đồng dạng bảo toàn độ lớn góc. Lời giải Chọn C Câu 9.
Hàm số nào sau đây là hàm số tuần hoàn với chu kì T   ? A. y  2cos x . B. y  cos x . C. y  cos2x. D. y  cos x  2 . Lời giải Chọn C
Hàm số y  2cos x , y  cos x  2 và y  cos x tuần hoàn với chu kì T  2 . 1 Hàm số 2
y  cos 2x tuần hoàn với chu kì T    . 2 2 Trang 140
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
Câu 10. Hàm số y  tan x đồng biến trên mỗi khoảng A.      
k;  k,k   . B. 3
 k; k,k   4 4   . C.     
k2;  k2,k  .
D.  k; k,k   2 2   . Lời giải Chọn D
Theo Sgk Đại số và Giải tích 11 cơ bản, hàm số y tan x đồng biến trên mỗi khoảng       k ;  k ,k     .  2 2 
Câu 11. Cho phép thử có không gian mẫu   1,2,3,4,5, 
6 . Các cặp biến cố không đối nhau là: A. A    1 và B  2,3, 4,5,  6 . B.  và  . C. E  1, 4,  6 và F  2,  3 . D. C  1,4,  5 và D  2,3,  6 . Lời giải Chọn C
Vì  \ A  B nên A và B đối nhau.
Vì  \    nên  và  đối nhau. Vì  \ E  2;3;5; 
6 , tập này không bằng tập F nên E và F là cặp biến cố không đối nhau.
Vì  \ C  D nên C và D đối nhau.
Câu 12. Số tập hợp con khác rỗng của tập hợp gồm 15 phần tử là A.32768. B. 32767 . C. 15!. D. 2 15 . Lời giải Chọn B
Số tập hợp con của tập hợp gồm 15 phần tử là 15 2  32768 .
Suy ra số tập hợp con khác rỗng của tập hợp gồm 15 phần tử là 327681 32767.
Câu 13. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AB và AC . Đường thẳng
MN song song với mặt phẳng: A.  ACD. B.  ABD. C. BCD . D.  ABC . Lời giải Chọn C
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 141
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT A M N B D C
Ta có M , N lần lượt là trung điểm của AB , AC  MN là đường trung bình của tam giác ABC  MN // BC . MN // BC, BC   BCD Ta có   MN //BCD . MN   BCD
Câu 14. Cho I 2;0. Phép đồng dạng hợp thành của phép T V
và phép OI (O là gốc tọa độ).  1  o;    2 
Biến đường tròn C  2 2
: x  y  4 thành C có phương trình A. 2 2
x  y  4x  3  0 . B. 2 2
x  y  4x  1  0 . C. 2 2 x  y  4x  0 . D. 2 2 x  y  4x  3  0 . Lời giải Chọn A Đường tròn C  2 2
: x  y  4 có tâm O 0;0 , bán kính R  2 .
+) Gọi C là ảnh của đường tròn C  qua phép V . 1   1  O;    2 
Ta có: phép vị tự tâm O , tỉ số 1 biến điểm O thành chính nó, biến đường tròn C  2 bán kính 1 1
R  2 thành đường tròn C bán kính R  .R  .2 1. 1  1 2 2
+) Vì C là ảnh của C  qua phép hợp thành của V
và phépT nên C là ảnh  1  O; OI    2 
của C qua phép T . 1  OI  
Gọi O  T O  OO  OI  I  O  O2;0 . OI
Phương trình đường tròn C có tâm O2;0 và bán kính R  R 1 là 1 x  2 2 2  y  1 hay 2 2 x  y  4x  3  0 . 
Câu 15. Trong hệ trục Oxy , cho đường thẳng d : 2x  y 1 0, phép tịnh tiến theo vectơ v biến 
d thành chính nó thì v phải là vectơ nào trong các vectơ sau?     A. v2;4. B. v4;2 . C. v2;  1 . D. v1;2 . Lời giải Chọn A 
+) d : 2x  y 1 0 một vectơ pháp tuyến của d là n 2; 
1 và một vectơ chỉ phương d  của d là u 1;2 . d  Trang 142
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1  
+) Phép tịnh tiến theo vectơ v biến d thành chính nó khi và chỉ khi vectơ v có giá  
song song hoặc trùng với d  v cùng phương với u 1;2 . d   
Mà v  2;4  21;2  2u . d Chọn đáp án A.
Câu 16. Một đa giác lồi có 27 đường chéo. Số đỉnh của đa giác đó là: A. 9. B. 8. C. 11. D. 10. Lời giải Chọn A
+) Giả sử số đỉnh của đa giác lồi là n n ,n  3. Khi đó đa giác cũng có n cạnh.
+) Nối hai đỉnh bất kì của đa giác này ta được 2
C đoạn thẳng bao gồm các cạnh của đa n
giác và các đường chéo của đa giác, trong đó đoạn thẳng nối hai đỉnh kề nhau tạo
thành 1 cạnh của đa giác, mà đa giác có n cạnh nên số đường chéo của đa giác đó là: 2 C  n . n Theo đề bài ta có: n! 2 C  n  27   n  n n   27 2 !.2! nn   n  9 nhËn 1 2 
 n  27  n  3n  54  0   . 2 n    6 lo¹i
Vậy số đỉnh của đa giác là 9.
Câu 17. Cho hình chóp tứ giác S.ABCD đáy không phải là hình thang và M tùy ý nằm trong S
 CD . Gọi d  MAB  SCD . Chọn câu đúng: A. C , D d, BC đồng quy. B. A , B d, AC đồng quy. C. AB,C , D d đồng quy. D. d, A , D CD đồng quy. Lời giải Chọn C
+ Ta thấy M là 1 điểm chung của 2 mặt phẳng MAB và SCD .
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 143
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
+ Do tứ giác ABCD không phải là hình thang nên hai đường thẳng AB và CD cắt nhau tại N .
Suy ra MAB SCD  MN nên d chính là đường thẳng đi qua 2 điểm M và N .
Vậy AB,CD,d đồng quy tại N .
Câu 18. Xác suất bắn trúng mục tiêu của một vận động viên khi bắn một viên đạn là 0,6 .
Người đó bắn hai viên một cách độc lập. Xác suất để một viên bắn trúng và một viên trượt mục tiêu là: A. 0,24 . B. 0,4 . C. 0,48 . D. 0,45 . Lời giải Chọn C
Gọi A là biến cố: “Vận động viên bắn viên đạn thứ i trúng mục tiêu” với i 1,  2 . i
 A là biến cố: “Vận động viên bắn viên đạn thứ i không trúng mục tiêu” với i i 1,  2 .
Ta có: P  A   0,6  P A   P A    . i  1  i  1 0,6 0,4 i
Xác suất vận động viên bắn một viên trúng và một viên không trúng mục tiêu là
P  P  A .P A  P A .P A  0,6.0,4  0,4.0,6  0, 48 . 1   2  1  2
Câu 19. Cho tứ diện ABCD . Gọi M, N, P lần lượt là các điểm trên các cạnh AB , AC và BD
sao cho MN không song song với BC , MP không song song với AD. Mặt phẳng
(MNP) cắt các đường thẳng BC, C ,
D AD lần lượt tại K, I, J . Ba điểm nào sau đây thẳng hàng: A. M, I, J . B. N, K, J . C. K, I, J . D. N, I, J . Lời giải Chọn D
Ta có N (MNP) và N  AC  N (MNP)(AC ) D
Ta có I  (MNP)CD  I (MN ) P (AC ) D
Ta có J  (MNP) AD  J (MNP)(ACD)
Ba điểm N, I, J cùng thuộc hai mặt phẳng phân biệt (MNP) và (ACD), suy ra ba
điểm N, I, J thẳng hàng.
Câu 20. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  sin 2x  2sin x  cos x  2 là
A. min y  1 2 2; max y  1 2 2 .
B. min y   2; max y  2 Trang 144
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
C. min y  1 2 2; max y  4
D. min y  1 2 2; max y  3 . Lời giải Chọn C
Đặt t  sin x  cos x, t   2; 2   . 2 2 2
 t  sin x  cos x  2sin . x cos x 1 sin 2x 2  sin 2x  1 t .
Khi đó hàm số trở thành 2 y  1 t  2t  2 2  t  2t  3. Xét hàm số f t 2
 t  2t  3 , t   2; 2 
 ta có bảng biến thiên sau:
Dựa vào bảng biến thiên ta có max f t  4 khi t  1 ; min f t 1 2 2 khi t  2 .  2; 2    2; 2  
Vậy min y  1 2 2 ; max y  4 . Câu 21.
Hệ số của 8x trong khai triển   x5   x6    x10 1 1 ... 1 là: A. 55 . B. 37 . C. 147 . D. 147 . Lời giải Chọn A
Hệ số của 8x trong khai triển   x5   x6    x10 1 1 ... 1
chỉ xuất hiện trong khai triển của
  x8   x9   x10 1 ; 1 ; 1 . +) 8 1x8  C  1 k k k x do hệ số chứa 8
x nên k  8  hệ số là : 8 C . 8   8 k0 +) 9 1x9  C 1 k k k
  x do hệ số chứa 8x nên k  8  hệ số là : 8 C 9   9 k0 +) 10 1x10  C 1 k k k  x do hệ số chứa 8
x nên k  8  hệ số là : 8 C 10    10 k0 Vậy hệ số của 8 x trong khai triển là 8 8 8
C  C  C  1  9  45  55 . 8 9 10 Câu 22.
Trong mặt phẳng với hệ trục tọa độ Oxy , cho điểm A1;5, B3;2 . Biết các điểm ,
A B theo thứ tự là ảnh của các điểm M , N qua phép vị tự tâm O , tỉ số k  2 . Độ dài đoạn thẳng MN là: A. 50. B. 12,5 . C. 10. D. 2,5. Lời giải Chọn D 
+) Ta có AB     2 2
4; 3  AB  3  4  5 . V  M  A  O,2   +)     AB  2 MN  5 2MN  MN   2,5 . V N  B  2 O,2     
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 145
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Câu 23.   
Số nghiệm của phương trình 2sin 2x   1   thuộc khoảng    ;  là:  3  A. 4 . B. 1. C. 2 . D. 3 . Lời giải Chọn A +) Ta có       1     2 sin 2x   1    sin 2x    sin 2x   sin  3       3  2  3  6      2x    k2  x    k  3 6    12 k     k  .   5  2x    k2   x   k  3 6  4 +)        11 13  x         k      k   k  k  11 0;1  x   ;  . 12 12 12  12 12  +)        5 3  x      
 k      k   k  k  3 1;0  x   ;  . 4 4 4  4 4 
Vậy có 4 nghiệm thuộc khoảng    ;  .
Câu 24. Cho tập A  0;1;2;3;4;5;6;7;8; 
9 . Số các số tự nhiên có 5 chữ số đôi một khác nhau lấy ra từ tập A là: A. 27162 . B. 30240 . C. 30420 . D. 27216 . Lời giải Chọn D
Lập abcde có các chữ số đôi một khác nhau gồm các bước:
+) Chọn a : 9 cách a  A \  0  .
+) Chọn bộ thứ tự b,c,d ,e: lấy ra 4 số từ 9 số thuộc tập A \  a và sắp xếp có 4 A 9 cách. Vậy có 4 9.A  27216 số. 9 Câu 25. 1 Tìm m để phương trình
 (1 2m) tan x  2m  3  0 có nghiệm thuộc khoảng 2 cos x    0;   .  4  A. 3 m  . B. m  1. C. 3 1  m  . D. m  1hoặc 3 m  . 2 2 2 Lời giải Chọn C
Phương trình luôn xác định    x  0;   .  4  tan x 1 Khi đó ta có: 2
tan x  (1 2m) tan x  2m  2  0   tan x  2m  2 Trang 146
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Vì phương trình   
tan x  1 không có nghiệm thuộc khoảng 0;   và hàm số y  tan x  4 
đồng biến trên khoảng    0; 
 nên phương trình đã cho có nghiệm thuộc khoảng  4      0; 
 khi và chỉ khi tan 0  2m  2  tan  0  2m  2  1 3  1  m  .  4  4 2 B. TỰ LUẬN. Bài 1. 1) Giải phương trình  3  sin x  3 sin  x  2sin 2x   .  2  Lời giải Ta có :  3  sin x  3 sin  x  2sin 2x    2 
 sinx  3 cos x  2sin 2x 1 3  sinx  cos x  sin 2x 2 2     s in x   sin 2x    3      x   2x  k2  x   k2  3   3   , k  .    2   k2 x     2x  k2  x    3  9 3 Vậy,  2 k 2  S    k2 ;  , k  .  3 9 3 
2) Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn không
vượt quá 2019 , đồng thời nó chia hết cho 5 . Lời giải
Số các số tự nhiên có 4 chữ số là 9.10.10.10  9000 (số). Suy ra số phần tử của không
gian mẫu là n   9000 .
Gọi A là biến cố “ Số được chọn không vượt quá 2019 và chia hết cho 5 ”.
Số có bốn chữ số nhỏ nhất có bốn chữ số chia hết cho 5 là 1000 , số có bốn chữ số lớn
nhất không vượt quá 2019 chia hết cho 5 là 2015 .
Suy ra số phần tử của biến cố A là nA20151000:51 204. Xác suất của biến cố n A A là PA   204 17    . n 9000 750
Bài 2. Cho hình chóp S.ABC , G là trọng tâm tam giác ABC . Đường thẳng qua G song song
với SA cắt mặt phẳng SBC tại A. Nêu cách xác định điểm A và thiết diện của hình
chóp khi cắt bởi mặt phẳng qua A, song song với SG và BC . Lời giải
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 147
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT S N A' M P A C G E I Q B * Cách dựng điểm A
Gọi I là trung điểm của BC ,  là đường thẳng qua G và song song với SA.
+ Chọn mặt phẳng SAI  chứa  .
+ Ta có SI là giao tuyến của hai mặt phẳng SAI  và SBC.
+ Trong mặt phẳng SAI  ,   SI  A
Suy ra A là điểm cần dựng.
* Xác định thiết diện của hình chóp cắt bởi mặt phẳng P qua A, song song với SG và BC . AP SBC  +   P // BC
 P SBC  Ax , với A x
 là đường thẳng đi qua A, song song BC   SBC với BC . Giả sử A x
 cắt SB tại M và cắt SC tại N . Suy ra P SBC   MN . APSAI   + P// SG
 P SAI   AE , với AE là đường thẳng đi qua A, song song SG   SAI  với SG , cắt AI tại E . E P  ABC  +   P// BC
 P  ABC  Ey , với Ey là đường thẳng đi qua E , song song BC   ABC
với BC . Giả sử Ey cắt AC tại P và cắt AB tại Q . Suy ra P  ABC   PQ .
Vậy thiết diện là tứ giác MNPQ .
Bài 3. 1. Giải hệ phương trình sau: 2019 2019 1 2018 2 2017 2017 2 x  x  y  C y  C y C y  2020y  2. 2019 2019 2019  3 2 y 3x  6 .x Trang 148
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1 Lời giải 2019 2019 1 2018 2 2017 2017 2 x  x  y  C y  C y ... C y  2020y  2 1  2019 2019 2019   Giải hệ:  3 2 y  3x  6x  2 Ta có    x  x   y  2019 2019 1 1   y   1 * Xét hàm số   2019 f t  t  t , có f t 2018  2019t 1  0,t   .
Suy ra f t là hàm số đồng biến trên  . Khi đó *  f x  f  y 1  x  y 1.
Với x  y 1  y  x 1 thay vào 2 ta được: x  3 2 1  3x  6x 3
 x  3x 1  0 3 . Xét hàm g x 3  x  3x 1 có: g  2    3  
g 2.g      g   1 3 0 1  1    g   1 .g 0    . g   1 0 0  1  
g0.g2      g    1 0 2  1
Suy ra 3 có ít nhất 3 nghiệm thuộc khoảng 2;2 .
Mặt khác 3 là phương trình bậc ba nên có nhiều nhất 3 nghiệm thực.
Suy ra 3 có đúng 3 nghiệm thuộc khoảng 2;2 .
Đặt x  2cost với t 0;2  . Thay vào 3 ta được:   t   9   5   t3 2cos 32cost 1 0 3  1
8cos t  6 cost 1  0  cos3t   t  . 2  9  7 t   9 +) Với    t 
 x  2 cos  y  2cos 1. 9 9 9 +) Với 5   t  5  x  2 cos 5  y  2cos 1. 9 9 9 +) Với 7   t  7  x  2cos 7  y  2 cos 1. 9 9 9
Vậy hệ phương trình có tập nghiệm là:      5 5   7 7 
S   2cos ;2cos 1 , 2cos ; 2cos 1 , 2cos ; 2cos 1         9 9   9 9   9 9 
2. Cho tập hợp A  0;1;2;3;...;201 
9 . Một tập hợp con X của A được gọi là tập cân
nếu trong tập hợp X số các số chẵn và số các số lẻ bằng nhau. ( Tập rỗng là một tập
cân). Chứng minh rằng số tập cân của tập hợp A là 1010 C . 2020 Lời giải
Gọi A  0;2;4;;2018 , A  1;3;5;;2019 . 2   1  
Ta có: Số phần tử tập cân của A là số tự nhiên chẵn, không vượt quá 2020 và nếu X là
tập cân có 2k phần tử thì X =X  X , X  A , X  A , X = X  k , 0  k 1010. 1 2 1 1 2 2 1 2 Số cách chọn X là Ck . 1 1010 Số cách chọn X là Ck . 2 1010
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 149
BỘ ĐỀ KIỂM TRA HỌC KÌ 1
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Do đó số tập cân của A là Ck 2 1010 . 1010 k 0 2020 1010 1010 Ta có     Ci i
x  1 x2020    x1010  x  1010 1 1 i i i 1010  C x C i x  . 2020  1010  1010  i0  i0  i0  Đồng nhất hệ số 1010 x ta có Ck 2 1010 1010  C . 1010 2020 k 0
Vậy số tập cân của tập hợp A là 1010 C . 2020
Bài 4. Cho hình chóp S.ABCD có đáy là hình bình hành, M là một điểm di động trên cạnh SC
. Mặt phẳng P chứa AM và song song với BD . Mặt phẳng P cắt SB, SD lần lượt tại
các điểm N và E . Chứng minh rằng: 2S . B SM  SN.SM  SC.SN . Lời giải
Gọi O là tâm của hình bình hành ABCD , I là trung điểm MC .
Gọi K là giao điểm của AM với SO .
Trong mặt phẳng SBD kẻ đường thẳng qua K và song song với BD cắt SB , SD lần
lượt tại N, E . Khi đó mặt phẳng P chính là mặt phẳng  ANME. Ta có (P)  (SBD)  NE .
Vì NE // BD và OI // AM nên SB SO SI   . SN SK SM Suy ra SB SC SI SC 2SI  (SI  IC) SI  MI 2   2     1 . SN SM SM SM SM SM Do đó: SB SC 2 
 1  SC.SN  SM .SN  2SB.SM SN SM
Bài 5. Cho phương trình sin 2x  3m  2cos x  3msinx . Để phương trình có nhiều hơn một
nghiệm trong 0;  thì giá trị của m thỏa ? Lời giải
Ta có sin 2x  3m  2cos x  3msinx  sin 2x  3m  2cos x  3m sinx = 01    x     m        x  m s inx 1 0 2 cos s inx 1 3 s inx 1 0 s inx 1 2 cos 3  0   2cos x  3m  0   x   k2 sinx = 1  2     . 2cos x  3m  0  3m cos x   2 Trang 150
TỔNG HỢP: HOÀNG TUYÊN – LÊ MINH TÂM
NHÓM WORD 🙲 BIÊN SOẠN TOÁN
BỘ ĐỀ KIỂM TRA HỌC KÌ 1   x   Xét trong khoảng  2 0;  ta được  .  3m cos x   2  2
Trong khoảng 0;  phương trình  
1 có hơn một nghiệm  2 có một nghiệm khác  2  3m   1  2 3  2  m      3 .Vậy 2 3 0  m  .   3m  3   m  0 cos  2 2
THAM GIA NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Trang 151