Top 5 đề ôn thi giữa kỳ 2 Toán 11 có đáp án và lời giải – Nguyễn Bảo Vương

Tài liệu gồm 82 trang, được biên soạn bởi thầy giáo Nguyễn Bảo Vương, tuyển chọn 5 đề ôn thi giữa học kỳ 2 môn Toán lớp 11 có đáp án và lời giải chi tiết, các đề được biên soạn theo hình thức đề trắc nghiệm khách quan kết hợp với tự luận, trong đó phần trắc nghiệm gồm 35 câu

49 25 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 11

Môn: Toán 11

Thông tin:

82 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Phần 1. Trắc nghiệm
Câu 1. Dãy số nào sau đây có giới hạn khác
0
.
A.
1
n
. B.
1
n
. C.
2 1n
n
. D.
cosn
n
.
Câu 2. Dãy số nào sau đây không có giới hạn ?
A.
0,99
n
. B.
1
n
. C.
0,99
n
. D.
0,89
n
.
Câu 3. Gọi
1
lim
4
n
L
n
. Khi đó
L
bằng
A.
1
5
. B.
1
4
. C.
1
D.
0
.
Câu 4. Tính giới hạn
2 2017
lim
3 2018
n
I
n
.
A.
2
3
I
. B.
3
2
I
. C.
2017
2018
I
. D.
1I
.
Câu 5. Phát biểu nào sau đây là sai?
A.
lim
n
u c
(
n
u c
là hằng số ). B.
lim 0
n
q
1q
.
C.
1
lim 0
n
. D.
1
lim 0
k
n
1k
.
Câu 6.
2 2
1
lim
2 4n n
bằng
A.
0
. B.

. C.

. D.
1
.
Câu 7. Giới hạn
lim 1 n n
có kết quả bằng:
A. Không có giới hạn. B.
0
C.
1
. D.

Câu 8. Giới hạn
2
lim
2 3
n
n
có kết quả là:
A.
2
. B.
0
. C.

. D.
4
.
Câu 9. Tính
2 2 2 2
1 2 3 ...
lim
2 7 6 5
n
n n n
A.
1
6
. B.
1
2 6
. C.
1
2
. D.

.
Câu 10. Giới hạn
3 2
lim
4
n n
n
có kết quả là:
A.
0
B.
5
4
. C.
3
4
D.

Đề ôn thi giữa kỳ 1 - Lớp 11
Đề 1
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 11. Tính
2
1
1
lim
1
x
x
x
A.
1
2
. B.
2
. C.
1
2
. D.
1
.
Câu 12. Giới hạn
2
3
2 15
lim
3
x
x x
x
có kết quả là:
A.
B.
2
. C.
1
8
D.
8
Câu 13. Tìm giới hạn
3 2
2
1
3 2
lim
4 3
x
x x
A
x x
:
A.

. B.
. C.
3
2
. D.
1
.
Câu 14. Tính
2
2
2
lim
2
x
x
x

.
A.
2
. B.
1
. C.
1
2 2
. D.
2
.
Câu 15. Tìm giới hạn
1
4 3
lim
1
x
x
x
A.

. B.
2
. C.
. D.
2
.
Câu 16. Tìm giới hạn
1
4 2
lim
1
x
x
x
A.

. B.
2
. C.
. D.
2
.
Câu 17. Chọn kết quả đúng trong các kết quả sau của
4
3 2
2
8
lim
2 2
x
x x
x x x

là:
A.
21
5
. B.
21
5
. C.
24
5
. D.
24
5
.
Câu 18. Giới hạn nào dưới đây có kết quả là
1
2
?
A.
2
lim 1
2
x
x
x x

. B.
2
lim 1
x
x x x

.
C.
2
lim 1
2
x
x
x x

. D.
2
lim 1
x
x x x

.
Câu 19. Cho hàm số
y f x
có đồ thị như hình bên.
Các khẳng định sau:
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
(I)
1
lim
x
f x

(II)
2
lim
x
f x

(III)
lim
x
f x


(IV)
2
lim
x
f x

Khẳng định đúng là:
A. 4. B. 3. C. 2. D. 1
Câu 20. Cho hàm số
y f x
liên tục trên khoảng
; a b
. Điều kiện cần và đủ để hàm số liên tục trên
đoạn
; a b
là?
A.
lim
x a
f x f a
và
lim
x b
f x f b
. B.
lim
x a
f x f a
và
lim
x b
f x f b
.
C.
lim
x a
f x f a
và
lim
x b
f x f b
. D.
lim
x a
f x f a
và
lim
x b
f x f b
.
Câu 21. Hàm số
2
2
1
5 6
x
f x
x x
liên tục trên khoảng nào sau đây?
A.
;3
. B.
2;3
. C.
3;2
. D.
3; 
.
Câu 22. Cho hàm số . Tìm tất cả các giá trị của tham số thực để
hàm số liên tục trên .
A. . B. . C. . D. .
Câu 23. Cho hàm số
2 2
2
khi 2,
2 khi 2
a x x a
f x
a x x
. Giá trị của
a
để
f x
liên tục trên
là:
A.
1
và
2
. B.
1
và
–1
. C.
–1
và
2
. D.
1
và
–2
.
Câu 24. Cho hàm số
3 2
4 3
khi 1
1
5
khi 1
2
x x
x
x
f x
ax x
. Xác định
a
để hàm số liên tục trên
.
A.
5
2
a
. B.
5
2
a
. C.
15
2
a
. D.
15
2
a
.
Câu 25. Tìm tất cả các giá trị của tham số thực
m
sao cho hàm số
2 khi 0
2 khi 0
x m x
f x
mx x
liên tục
trên
.
A.
2m
. B.
2 m
. C.
2 m
. D.
0m
.
Câu 26. Qua phép chiếu song song, tính chất nào không được bảo toàn?
A. Chéo nhau. B. Đồng qui.
C. Song song. D. Thẳng hàng.
Câu 27. Cho
1 1 1 1
.ABCD A B C D
là hình hộp, với K là trung điểm CC
1
. Tìm khẳng định đúng trong các khẳng
định sau:
A.
1
1
2
AK AB AD AA
B.
1
AK AB BC AA
 
C.
1
AK AB AD AA
D.
1
1 1
2 2
AK AB AD AA
2
2 4 3 khi 2
1
khi 2
2 3 2
x x
f x
x
x
x mx m
m
3
m
4
m
5
m
6
m
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 28. Cho hình hộp
1 1 1 1
.
ABCD A B C D
với
1 1
M CD C D
. Khi đó:
A.
1
1 1 1
2 2 2
AM AB AD AA

B.
1
1 1
2 2
AM AB AD AA

C.
1
D.
1
1 1
2 2
AM AB AD AA
Câu 29. Cho tứ diện
ABCD
. Trên các cạnh
, AC BD
lần lượt lấy
, M N
sao cho
3 ; 3
AM MD BN NC
. Gọi P,Q lần lượt là trung điểm của
, AD BC
. Trong các khẳng định
sau, khẳng định nào sai?
A. Các vec tơ
, ,
BD AC MN
 
không đồng phẳng
B. Các vec tơ
, ,MN DC PQ
đồng phẳng
C. Các vec tơ
, ,AB DC PQ
  
đồng phẳng
D. Các vec tơ
, ,
AC DC MN
đồng phẳng
Câu 30. Cho tứ diện
ABCD
. Gọi M, Nlaafn lượt là trung điểm của
, AD BC
. Trong ccs khẳng định sau,
khẳng định nào sai?
A. Các vec tơ
, ,
AB DC MN
 
đồng phẳng
B. Các vec tơ
, ,MN AB AC

không đồng phẳng
C. Các vec tơ
, ,
AN CM MN

đồng phẳng
D. Các vec tơ
, ,
AC BD MN
  
đồng phẳng
Câu 31. Trong các mệnh đề dưới đây mệnh đề đúng là?
A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì
cũng vuông góc với đường thẳng thứ hai.
B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song
song với nhau.
C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Câu 32. Cho đường thẳng d có vectơ chỉ phương
a
. Vectơ nào sau đây không là vec tơ chỉ phương của d?
A.
2a
B.
1
2
a
C.
0
D.
ka
( 0)
k
Câu 33. Cho hình hộp
.
ABCD A B C D
có độ dài tất cả các cạnh bằng
a
và các góc
,
BAD DAA
,
A AB
đều bằng
60
. Gọi
M
,
N
lần lượt là trung điểm của
,AA CD
. Gọi
là góc tạo bởi hai đường
thẳng
MN
và
B C
, giá trị của
cos
bằng:
A.
2
5
. B.
1
5
. C.
3
5
. D.
3 5
10
.
Câu 34. Cho hình lập phương
.
ABCD EFGH
. Hãy xác định góc giữa cặp vectơ
AB

và
DH
?
.A.
0
45 .
B.
0
90 .
C.
0
120 .
D.
0
60 .
Câu 35. Cho tứ diện đều
ABCD
,
M
là trung điểm của cạnh
BC
. Khi đó
cos ,
AB DM
bằng
A.
6
3
. B.
2
2
. C.
2
3
. D.
2
1
.
Phần 2. Tự luận
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 36. Biết rằng
2 2
lim 2 1
a
n n n
b
trong đó
a
b
là phân số tối giản,
*
,
a b
. Tính giá
trị của biểu thức
2 2
5
P a b
Câu 37. Cho hàm số
y f x
xác định trên
thỏa mãn
2
16
lim 12
2
x
f x
x
.Tính giới hạn
3
2
2
5 16 4
lim
2 8
x
f x
x x
.
Câu 38. Chứng minh phương trình:
sin 2 2016 sin cos 0
m x x x
(
m
là tham số) có nghiệm với mọi
m
thuộc
.
Câu 39. Cho hình lập phương
.
ABCD A B C D
, biết:
4 2
AN AB k AA AD
k
;
2 3
AM AB AA AD
. Tìm
k
để
AN AM
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
BẢNG ĐÁP ÁN
1.C 2.B 3.D 4.A 5.B 6.C 7.B 8.B 9.A 10.A
11.C 12.D 13.C 14.C 15.A 16.C 17.C 18.D 19.B 20.A
21.B 22.C 23.D 24.D 25.C 26.A 27.A 28.B 29.A 30.C
31.A 32.C 33.D 34.B 35.A
Phần 1. Trắc nghiệm
Câu 1. Dãy số nào sau đây có giới hạn khác
0
.
A.
1
n
. B.
1
n
. C.
2 1n
n
. D.
cosn
n
.
Lời giải
Chọn C
Ta có
2 1
lim 2
n
n
.
Câu 2. Dãy số nào sau đây không có giới hạn ?
A.
0,99
n
. B.
1
n
. C.
0,99
n
. D.
0,89
n
.
Lời giải
Chọn B
Vì
lim 1 1
n
nếu
n
lẻ hoặc
lim 1 1
n
nếu
n
chẳn nên dãy số
1
n
n
u
không có giới
hạn.
Câu 3. Gọi
1
lim
4
n
L
n
. Khi đó
L
bằng
A.
1
5
. B.
1
4
. C.
1
D.
0
.
Lời giải
Chọn D
Ta có:
1
1
4 4
n
n n
và
1
lim 0
4n
nên
1
lim 0
4
n
L
n
.
Câu 4. Tính giới hạn
2 2017
lim
3 2018
n
I
n
.
A.
2
3
I
. B.
3
2
I
. C.
2017
2018
I
. D.
1I
.
Lời giải
Ta có
2 2017
lim
3 2018
n
I
n
2017
2
lim
2018
3
n
n
2
3
.
Câu 5. Phát biểu nào sau đây là sai?
A.
lim
n
u c
(
n
u c
là hằng số ). B.
lim 0
n
q
1
q
.
C.
1
lim 0
n
. D.
1
lim 0
k
n
1
k
.
Lời giải
Theo định nghĩa giới hạn hữu hạn của dãy số (SGK ĐS11-Chương 4) thì
lim 0
n
q
1
q
.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 6.
2 2
1
lim
2 4
n n
bằng
A.
0
. B.

. C.

. D.
1
.
Lời giải
Chọn C
Ta có:
2 2
2 2
2 2
2 2
2 2
2 4
1 1
1 2 4
lim lim lim
2
2 4
2 4
n
n n
n n
n n
n n

.
Câu 7. Giới hạn
lim 1
n n
có kết quả bằng:
A. Không có giới hạn. B.
0
C.
1
. D.

Lời giải
Chọn B
1 1
lim 1 lim
1
n n n n
n n
n n
1
lim
1
n n
1
lim
1
1 1n
n
0
Câu 8. Giới hạn
2
lim
2 3
n
n
có kết quả là:
A.
2
. B.
0
. C.

. D.
4
.
Lời giải
Chọn B
3
2
2
1
0
lim lim 0.
3
2 3 2 0
2
n
n
n
n
Câu 9. Tính
2 2 2 2
1 2 3 ...
lim
2 7 6 5
n
n n n
A.
1
6
. B.
1
2 6
. C.
1
2
. D.

.
Lời giải
Chọn A
Ta có:
2 2 2 2
1 2 1
1 2 3 ...
6
n n n
n
.
Khi đó:
2 2 3 2
1 2 1
1 2 3 ...
lim lim
2 7 6 5 12 7 6 5
n n n
n
n n n n n n
1 1
1 2
lim
7 5
12 1 6
n n
n n
1
6
.
Câu 10. Giới hạn
3 2
lim
4
n n
n
có kết quả là:
A.
0
B.
5
4
. C.
3
4
D.

Lời giải
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn A
Ta có
3 2
3 2
4 4
lim lim 0
4 1
n n
n n
n
Câu 11. Tính
2
x 1
x 1
lim
x 1
A.
1
2
. B.
2
. C.
1
2
. D.
1
.
Lời giải
Chọn C
2
x 1 x 1
x 1 1 1
lim lim
x 1 x 1 2
.
Câu 12. Giới hạn
2
3
2 15
lim
3
x
x x
x
có kết quả là:
A.

B.
2
. C.
1
8
D.
8
Lời giải
Chọn D
2
x 3 x 3 x 3
x 3 x 5
x 2x 15
lim lim lim x 5 8
x 3 x 3
.
Câu 13. Tìm giới hạn
3 2
2
1
3 2
lim
4 3
x
x x
A
x x
:
A.

. B.
. C.
3
2
. D.
1
.
Lời giải
Chọn C
Ta có:
3 2 2
2
1 1
3 2 ( 1)( 2 2)
lim lim
4 3 ( 1)( 3)
x x
x x x x x
A
x x x x
2
1
2 2 3
lim
3 2
x
x x
x
.
Câu 14. Tính
2
x 2
x 2
lim
x 2

.
A.
2
. B.
1
. C.
1
2 2
. D.
2
.
Lời giải
Chọn C
2
x 2 x 2
x 2 1 1
lim lim
x 2
x 2 2 2
.
Câu 15. Tìm giới hạn
1
4 3
lim
1
x
x
x
A.

. B.
2
. C.

. D.
2
.
Lời giải
Chọn A
Ta có
1
4 3
lim
1
x
x
x

vì
1
lim 4 3 1
x
x
,
1
lim 1 0
x
x
,
1 0
x
khi
1
x
.
Câu 16. Tìm giới hạn
1
4 2
lim
1
x
x
x
A.

. B.
2
. C.

. D.
2
.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Lời giải
Chọn C
Ta có
1
4 2
lim
1
x
x
x

vì
1
lim 4 2 6
x
x
,
1
lim 1 0
x
x
,
1 0x
khi
1x
.
Câu 17. Chọn kết quả đúng trong các kết quả sau của
4
3 2
2
8
lim
2 2
x
x x
x x x

là:
A.
21
5
. B.
21
5
. C.
24
5
. D.
24
5
.
Lời giải
Chọn C
2 2
4
3 2
2 2
2 2 2
2 2 4 2 4
8 24
lim lim lim .
2 2 5
2 1 1
x x x
x x x x x x x
x x
x x x
x x x

Câu 18. Giới hạn nào dưới đây có kết quả là
1
2
?
A.
2
lim 1
2
x
x
x x

. B.
2
lim 1
x
x x x

.
C.
2
lim 1
2
x
x
x x

. D.
2
lim 1
x
x x x

.
Lời giải
Chọn D
Xét:
2
2
2 2
lim 1 lim lim lim
1 1
1
1 1
x x x x
x x x
x x x
x x
x x x x
x x
   
.
2
1 1
lim
2
1
1 1
x
x

.
Câu 19. Cho hàm số
y f x
có đồ thị như hình bên.
Các khẳng định sau:
(I)
1
lim
x
f x

(II)
2
lim
x
f x

(III)
lim
x
f x


(IV)
2
lim
x
f x

Khẳng định đúng là:
A. 4. B. 3. C. 2. D. 1
Lời giải
Đáp án B
Chỉ có khẳng định (III) sai các khẳng định còn lại đúng.
Câu 20. Cho hàm số
y f x
liên tục trên khoảng
; a b
. Điều kiện cần và đủ để hàm số liên tục trên
đoạn
; a b
là?
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
lim
x a
f x f a
và
lim
x b
f x f b
. B.
lim
x a
f x f a
và
lim
x b
f x f b
.
C.
lim
x a
f x f a
và
lim
x b
f x f b
. D.
lim
x a
f x f a
và
lim
x b
f x f b
.
Lời giải
Chọn A
Hàm số
f
xác định trên đoạn
; a b
được gọi là liên tục trên đoạn
; a b
nếu nó liên tục trên
khoảng
; ,a b
đồng thời
lim
x a
f x f a
và
lim
x b
f x f b
.
Câu 21. Hàm số
2
2
1
5 6
x
f x
x x
liên tục trên khoảng nào sau đây?
A.
;3
. B.
2;3
. C.
3;2
. D.
3; 
.
Lời giải
Chọn B
Tập xd
\ 2; 3D
Câu 22. Cho hàm số . Tìm tất cả các giá trị của tham số thực để
hàm số liên tục trên .
A. . B. . C. . D. .
Lời giải
Chọn C
Cách 1: Hàm số xác định trên , liên tục trên khoảng .
Ta có .
Nếu thì nên hàm số không liên tục tại .
Nếu thì ta có .
Để hàm số liên tục tại thì .
Với thì khi , liên tục trên .
Tóm lại với thì hàm số đã cho liên tục trên .
Cách 2: Hàm số xác định trên , liên tục trên khoảng .
Ta có .
Thử lần lượt các giá trị từ A dến C thấy thỏa mãn . Do đó chọn đáp án. C.
Câu 23. Cho hàm số
2 2
2
khi 2,
2 khi 2
a x x a
f x
a x x
. Giá trị của
a
để
f x
liên tục trên
là:
A.
1
và
2
. B.
1
và
–1
. C.
–1
và
2
. D.
1
và
–2
.
Lời giải
Chọn D.
TXĐ:
D
.
Với
2x
ta có hàm số
2 2
f x a x
liên tục trên khoảng
2; .
Với
2x
ta có hàm số
2
2 f x a x
liên tục trên khoảng
; 2 .
2
2 4 3 khi 2
1
khi 2
2 3 2
x x
f x
x
x
x mx m
m
3
m
4
m
5
m
6
m
2;
2 2
2 3; lim lim 2 4 3 3
x x
f f x x
6
m
2
2 2
1
lim lim
12 20
x x
x
f x
x x
2
x
6
m
2
2 2
1 3
lim lim
2 3 2 6
x x
x
f x
x mx m m
2
x
3
3 6 1 5
6
m m
m
5
m
2
x
2
1
10 17
x
f x
x x
;2

5
m
2;
2 2
2 3; lim lim 2 4 3 3
x x
f f x x
5
m
2
lim 3
x
f x
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Với
2
x
ta có
2
2 2
f a
.
2
2 2
lim lim 2 2 2
x x
f x a x a
;
2 2 2
2 2
lim lim 2
x x
f x a x a
.
Để hàm số liên tục tại
2
x
2 2
lim lim 2
x x
f x f x f
2
2 2 2
a a
2
2 0
a a
1
2
a
a
.
Vậy
1
a
hoặc
2
a
thì hàm số liên tục trên
.
Câu 24. Cho hàm số
3 2
4 3
khi 1
1
5
khi 1
2
x x
x
x
f x
ax x
. Xác định
a
để hàm số liên tục trên
.
A.
5
2
a
. B.
5
2
a
. C.
15
2
a
. D.
15
2
a
.
Lời giải
Chọn D
Với
1x
, ta có
3 2
4 3
1
x x
f x
x
liên tục trên tập xác định.
2
3 2
1 1
3 3 1
4 3
lim lim 5
1 1
x x
x x x
x x
x x
.
5
1
2
f a
.
Để hàm số liên tục trên
thì hàm số phải liên tục tại
1x
. Điều này xảy ra khi
1
lim 1
x
f x f
5
5
2
a
15
2
a
.
Câu 25. Tìm tất cả các giá trị của tham số thực
m
sao cho hàm số
2 khi 0
2 khi 0
x m x
f x
mx x
liên tục
trên
.
A.
2
m
. B.
2
m
. C.
2
m
. D.
0
m
.
Lời giải
Chọn C
Trên khoảng
0;
hàm số
2
f x x m
là hàm số liên tục.
Trên khoảng
;0
hàm số
2
f x mx
là hàm số liên tục.
Ta có
0 0
lim lim 2 0
x x
f x x m m f
và
0 0
lim lim 2 2
x x
f x mx
.
Hàm số
f x
liên tục trên
khi và chỉ khi
0 0
lim lim 0
x x
f x f x f
2 2
m m
.
Câu 26. Qua phép chiếu song song, tính chất nào không được bảo toàn?
A. Chéo nhau. B. Đồng qui.
C. Song song. D. Thẳng hàng.
Lời giải
Chọn A.
Do hai đường thẳng qua phép chiếu song song ảnh của chúng sẽ cùng thuộc một mặt phẳng.
Suy ra tính chất chéo nhau không được bảo toàn.
Câu 27. Cho
1 1 1 1
.
ABCD A B C D
là hình hộp, với K là trung điểm CC
1
. Tìm khẳng định đúng trong các khẳng
định sau:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
1
2
AK AB AD AA

B.
1
AK AB BC AA
 
C.
1
AK AB AD AA

D.
1
1 1
2 2
AK AB AD AA
Lời giải
Chọn A
Có
1 1
1 1
( )
2 2
AK AC CK AB AD AA AB AD AA
 
Câu 28. Cho hình hộp
1 1 1 1
.ABCD A B C D
với
1 1
M CD C D
. Khi đó:
A.
1
1 1 1
2 2 2
AM AB AD AA

B.
1
1 1
2 2
AM AB AD AA
 
C.
1
1
2
AM AB AD AA

D.
1
1 1
2 2
AM AB AD AA
Lời giải
Chọn B
( hính vẽ câu 1)
Ta có:
1 1 1
1 1 1
( DD )
2 2 2
AM AD DM AD DC AD DC AD AB AA
 
Câu 29. Cho tứ diện
ABCD
. Trên các cạnh
, AC BD
lần lượt lấy
, M N
sao cho
3 ; 3AM MD BN NC
. Gọi P,Q lần lượt là trung điểm của
, AD BC
. Trong các khẳng định
sau, khẳng định nào sai?
A. Các vec tơ
, ,
BD AC MN
không đồng phẳng
B. Các vec tơ
, ,MN DC PQ
 
đồng phẳng
C. Các vec tơ
, ,AB DC PQ
 
đồng phẳng
D. Các vec tơ
, ,AC DC MN

đồng phẳng
Lời giải
Chon A
B1
D1
A1
C1
A
B
D
C
K
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Lấy điểm E trên cạnh AC sao cho AE=3EC, lấy F trên BD sao cho BF=3FD
1
/ / ,
3
/ / , / /
1
/ / ,
3
NE AB NE AB
NE MF NE MF
MF AB MF AB
NEMF là hình bình hành và 3 vec tơ
, ,
BA DC MN
có giá song song hoặc nằm trên mặt phẳng
(MFNE)
, ,BA DC MN
đồng phẳng
, ,
BD AC MN
 
không đồng phẳng.
Câu 30. Cho tứ diện
ABCD
. Gọi M, Nlaafn lượt là trung điểm của
, AD BC
. Trong ccs khẳng định sau,
khẳng định nào sai?
A. Các vec tơ
, ,AB DC MN

đồng phẳng
B. Các vec tơ
, ,MN AB AC
  
không đồng phẳng
C. Các vec tơ
, ,AN CM MN
 
đồng phẳng
D. Các vec tơ
, ,
AC BD MN
  
đồng phẳng
Lời giải
Chọn C
Gọi P, Q lần lượt là trung điểm AC, BD
Ba vec tơ
, ,
AB DC MN


có giá song song hoặc nằm trên mặt phẳng (MNPQ) nên 3 véc tơ này
đồng phẳng A đúng
Ba vec tơ
, ,
AB AC MN


không đồng phẳng B đúng
Ba vec tơ
, ,AN CM MN

có giá không thể song song với mặt phẳng nào C sai
B
C
D
A
Q
P
N
F
M
E
C
D
A
B
P
N
Q
M
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 31. Trong các mệnh đề dưới đây mệnh đề đúng là?
A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì
cũng vuông góc với đường thẳng thứ hai.
B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song
song với nhau.
C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Lời giải
Chọn A
Theo lý thuyết.
Câu 32. Cho đường thẳng d có vectơ chỉ phương
a
. Vectơ nào sau đây không là vec tơ chỉ phương của d?
A.
2a
B.
1
2
a
C.
0
D.
ka
( 0)k
Lời giải
Chọn C
Theo định nghĩa
a
là vectơ chỉ phương của d thì
, 0ka k
cũng là vectơ chỉ phương của d.
Câu 33. Cho hình hộp
.ABCD A B C D
có độ dài tất cả các cạnh bằng
a
và các góc
,BAD DAA
,
A AB
đều bằng
60
. Gọi
M
,
N
lần lượt là trung điểm của
,AA CD
. Gọi
là góc tạo bởi hai đường
thẳng
MN
và
B C
, giá trị của
cos
bằng:
A.
2
5
. B.
1
5
. C.
3
5
. D.
3 5
10
.
Lời giải
Chọn D
Ta có
/ /
/ /
AD B C
MN A P
với P là trung điểm của
DC
.
Suy ra
, ,MN B C A P A D DA P
.
Vì
' ' 60BAD DAA A AB
và các cạnh của hình hộp bằng a. Do đó
, 3A D a C D C A a
.
Suy ra
2 2 2
5
2 4 2
A D A C DC a
A P A P
.
Áp dụng định lý cos cho tam giác
A DP
, ta có
2 2 2
3 5
cos
2 . 10
A D A P DP
A D A P
.
Câu 34. Cho hình lập phương
.ABCD EFGH
. Hãy xác định góc giữa cặp vectơ
AB

và
DH
?
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
.A.
0
45 .
B.
0
90 .
C.
0
120 .
D.
0
60 .
Lời giải
Chọn B
Vì
DH AE
 
(
ADHE
là hình vuông) nên
0
, , 90AB DH AB AE BAE
(
ABFE
là hình
vuông).
Câu 35. Cho tứ diện đều
ABCD
,
M
là trung điểm của cạnh
BC
. Khi đó
cos ,AB DM
bằng
A.
6
3
. B.
2
2
. C.
2
3
. D.
2
1
.
Lời giải
Chọn A.
Không mất tính tổng quát, giả sử tứ diện
ABCD
có cạnh bằng
a
.
Gọi
H
là tâm đường tròn ngoại tiếp
BCD AH BCD
.
Gọi
E
là trung điểm
AC
// , ,ME AB AB DM ME MD
Ta có:
cos , cos , cos , cosAB DM ME MD ME MD EMD
.
Do các mặt của tứ diện đều là tam giác đều, từ đó ta dễ dàng tính được độ dài các cạnh của
MED
:
ME a
,
3
2
a
ED MD
.
Xét
MED
, ta có:
2 2
2
2 2 2
3 3
2 2 2
3
cos
2 . 6
3
2. .
2 2
a a a
ME MD ED
EMD
ME MD
a a
.
Từ đó:
3 3
cos ,
6 6
AB DM
.
Phần 2. Tự luận
Câu 36. Biết rằng
2 2
lim 2 1
a
n n n
b
trong đó
a
b
là phân số tối giản,
*
, a b . Tính giá
trị của biểu thức
2 2
5P a b
Lời giải
Ta có:
2 2
lim 2 1 n n n
2 2
2 2
2 1
lim
2 1
n n n
n n n
2 2
1
lim
1 2 1
1 1
n
n n
n n n
A
B
C
D
F
H
G
E
E
H
M
B
D
C
A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
1
1
1
lim
2
1 2 1
1 1
n
n n n
Suy ra :
1
2
a
b
Vậy
2 2
5 1
P a b
.
Câu 37. Cho hàm số
y f x
xác định trên
thỏa mãn
2
16
lim 12
2
x
f x
x
.Tính giới hạn
3
2
2
5 16 4
lim
2 8
x
f x
x x
.
Lời giải
Theo giả thiết có
2 2 2
lim 16 0 lim 16 0 lim 16
x x x
f x f x f x
.
Ta có:
3
2
2
5 16 4
lim
2 8
x
f x
x x
2
2
2
3 3
5 16 64
lim
2 4 5 16 4 5 16 4
x
f x
x x f x f x
2
2
2
3 3
5 16
lim
2 4 5 16 4 5 16 4
x
f x
x x f x f x
2
2
2
3 3
16
5
lim .
2
4 5 16 4 5 16 4
x
f x
x
x f x f x
2
3 3
5 5
12. .
24
6 5.16 16 4 5.16 16 16
Câu 38. Chứng minh phương trình:
sin 2 2016 sin cos 0
m x x x
(
m
là tham số) có nghiệm với mọi
m
thuộc
.
Lời giải
Đặt
sin 2 2016 sin cosf x m x x x
Vì
f x
liên tục trên
nên
f x
liên tục trên
0;
2
Ta có:
2
0 2016
0 . 2016 0
2
2016
2
f
f f
f
.
phương trình
0
f x
có ít nhất 1 nghiệm trong
0;
2
với mọi
m
.
Vậy phương trình đã cho luôn có nghiệm với mọi
m
thuộc
(đpcm).
Câu 39. Cho hình lập phương
.
ABCD A B C D
, biết:
4 2
AN AB k AA AD
k
;
2 3
AM AB AA AD
. Tìm
k
để
AN AM
Lời giải
ĐỀ
ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Vì
.A
BCD A B C D
là
hình lập phương nên:
+
A
B AA AD
;
+ Các vectơ
AB
,
AA
,
AD
đôi một vuông góc với nhau. Do đó:
.
0AB AA
,
.
0AB AD
,
. 0AA AD
.
Để
A
N AM

thì
.
0AN AM
4
2 . 2 3 0AB k AA AD AB AA AD

8
. 4 . 12 . . 2 3 2 . 2 3 0AB AB AB AA AB AD k AA AB AA AD AD AB AA AD
 
2
8
0 0 2 . . 3 . 4 . 2 . 6 . 0AB k AA AB k AA AA k AA AD AD AB AD AA AD AD
       
2
2 2
8
0 0 0 0 0 0 6 0AB k AA AD

2
2 2
8
6 0AB kAA AD
(M
à
A
B AA AD
)
2
2 2
8
6 0AB kAB AB
2
8
6 0k AB
8
6 0k 2 0 2k k
.
Vậy giá trị
k
thích
hợp để
A
N AM

là
2k
.
D'
A
'
B'
C'
D
A
B
C
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Phần 1. Trắc nghiệm
Câu 1. Dãy số nào sau đây có giới hạn bằng 0?
A.
5
3
n
. B.
1
3
n
. C.
5
3
n
. D.
4
3
n
.
Câu 2. Giới hạn của dãy số sau đây bằng bao nhiêu.
3
lim
2n
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 3. Giá trị của
2
lim
1
n
n
bằng
A.
1
. B.
2
. C.
1
. D.
0
.
Câu 4.
2
6 5
2 3
lim
5
n
n n
bằng:
A.
2
. B.
0
. C.
3
5
. D.
3
.
Câu 5. Dãy số nào sau đây có giới hạn khác
0
?
A.
1
n
. B.
1
n
. C.
1n
n
. D.
sin n
n
.
Câu 6. Kết quả
lim 10n n là
A.
10
. B.

. C.
0
. D.
10
.
Câu 7. Tổng
2
1 1 1
... ...
3
3 3
n
S
có giá trị là:
A.
1
3
. B.
1
2
. C.
1
9
. D.
1
4
.
Câu 8. Tổng các cấp số nhân vô hạn:
1
1
1
1 1 1
1, , , ,...., ,...
2 4 8
2
n
n
là
A.
3
2
. B.
2
3
. C.
2
3
. D.
2
.
Câu 9. Số thập phân vô hạn tuần hoàn
0,233333...
biểu diễn dưới dạng số là:
A.
1
23
. B.
2333
10000
. C.
5
23333
10
. D.
7
30
.
Câu 10.
lim 5 1n n bằng:
A.
0
. B.
1
. C.
5
. D.
3
.
Câu 11. Tìm giới hạn hàm số
2
1
2 3
lim
1
x
x x
x
bằng định nghĩa.
A.

. B.
5
. C.
2
. D.
1
.
Câu 12. Giới hạn
3
2
8
lim
2
x
x
x
có kết quả là:
A.
12
B.
12
. C.
8
D.
5
Đề ôn thi giữa kỳ 1 - Lớp 11
Đề 2
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 13. Giới hạn
2
lim 2

x
x x x
bằng:
A.
0
B.

C.
1
D.
2
Câu 14. Trong các giới hạn sau, giới hạn nào có kết quả là 0?
A.
3
1
1
lim
1
x
x
x
B.
2
2 5
lim
10
x
x
x
.
C.
2
2
1
1
lim
3 2
x
x
x x
D.
2
lim 1

x
x x
Câu 15.
lim 1 3
x
x x

bằng
A.
0
. B.
2
. C.
. D.

.
Câu 16. Giới hạn của hàm số
2 2
4
2 1 2
2 1
x x x
f x
x x x
khi x tiến đến + có kết quả là:
A.
4
B.

. C.
0
D.
1
4
Câu 17. Tính
2
0
1 1
lim
x
x x x
x
.
A.
0
. B.
1
. C.
. D.
2
.
Câu 18. Tìm giới hạn
4 2
3
2
5 4
lim
8
x
x x
B
x
:
A.

. B.
. C.
1
6
. D.
1
.
Câu 19. Trong các mệnh đề sau mệnh đề nào sai
A.
2
3
lim 1 2
2
x
x x x

. B.
2
lim 1 2
x
x x x


.
C.
1
3 2
lim
1
x
x
x


. D.
1
3 2
lim
1
x
x
x

.
Câu 20. Cho hàm số
2
2 3 1
khi 1
1
1 khi 1
x x
x
f x
x
x
. Mệnh đề nào sau đây sai?
A. Hàm số gián đoạn tại
1x
. B. Hàm số liên tục tại
1x
.
C. Hàm số liên tục tại
3x
. D. Hàm số liên tục tại
5x
.
Câu 21. Cho hàm số
2
2
2
1 , 1
3 , 1
, 1
x x
f x x x
k x
. Tìm
k
để
f x
gián đoạn tại
1x
.
A.
2 k
. B.
2k
. C.
2 k
. D.
1 k
.
Câu 22. Biết rằng hàm số
2
5 6
khi 2
2
khi 2
x x
x
f x
x
mx n x
liên tục trên
và
n
là một số thực tùy ý.
Giá trị của
m
(tính theo
n
) bằng
A.
2
n
. B.
1
2
n
. C.
1
2
n
. D.
1
.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 23. Cho hàm số
2
2 6
khi 3
3 27
1
khi 3
9
x
x
x
f x
x
. Mệnh đề nào sau đây là đúng?
A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc khoảng
3;3
.
B. Hàm số liên tục tại mọi điểm trừ điểm
3
x
.
C. Hàm số liên tục tại mọi điểm trừ điểm
3
x
.
D. Hàm số liên tục trên
.
Câu 24. Cho hàm số
sin cos 0
1 cos cos 0
x x
f x
x x
neáu
neáu
. Hỏi hàm số
f
có tất cả bao nhiêu điểm gián
đoạn trên khoảng
0;2018
?
A.
2018
. B.
1009
. C.
542
. D.
321
.
Câu 25. Cho hàm số
3 1 khi 0
1 2 1
khi 0
x a x
f x
x
x
x
. Tìm tất cả giá trị của
a
để hàm số đã cho liên tục
trên
.
A.
1
a
. B.
3
a
. C.
2
a
. D.
4
a
.
Câu 26. Trong các mệnh đề sau mệnh đề nào sai?
A. Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng
thảnh đoạn thẳng.
B. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.
C. Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không thay đổi
thứ tự của ba điểm đó.
D. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường
thẳng song song hoặc cùng nằm trên một đường thẳng.
Câu 27. Trong các khẳng định sau đây, khẳng định nào sai?
A. Nếu giá của ba vectơ cắt nhau từng đôi một thì 3 vectơ đồng phẳng
B. Nếu ba vectơ
, ,a b c
có một vec tơ
0
thì ba vectơ đồng phẳng
C. Nếu giá của ba vectơ
, ,a b c
cùng song song với một mật phẳng thì ba vec tơ đó đồng phẳng
D. Nếu trong ba vectơ
, ,a b c
có ha vec tơ cùng phương thì ba vectơ đó đồng phẳng
Câu 28. Cho hình hộp
' ' ' '
.
ABCD A B C D
Gọi
, I K
lần lượt là tâm của các hình bình hành
' '
ABB A
và
' '
BCC B
. Khẳng định nào sau đây là sai?
A. Bốn điểm
, , , I K C A
đồng phẳng
B.
' '
1 1
2 2
IK AC A C

C. Ba vec tơ
, , ' 'BD IK B C
 
không đồng phẳng
D.
2 2
BD IK BC
Câu 29. Cho hình lập phương
.
ABCD A B C D
, góc giữa hai đường thẳng
A B
và
B C
là
A.
90
. B.
60
. C.
30
. D.
45
.
Câu 30. Cho tứ diện đều
ABCD
cạnh
a
. Tính cosin góc giữa hai đường thẳng
AB
và
CI
, với
I
là trung
điểm của
AD
.
A.
3
6
. B.
1
2
. C.
3
4
. D.
3
2
.
Câu 31. Cho ba đường thẳng a, b, c. Mệnh đề nào sau đây sai?
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. Nếu a//b thì
, , .a c c b
B. Nếu c//b thì
, , .a b a c
C. Nếu a//c thì
0
, 0 .
a c
D. Nếu
a b
thì
, , .a c c b
Câu 32. Cho ba đường thẳng a, b, c. Khẳng định nào sau đây đúng?
A. Nếu
a c
và
b c
thì a//b. B. Nếu
a b
và
b c
thì
.a c
C. Nếu
a c
và
b c
thì
a b
. D. Nếu a//b và
c b
thì
c a
.
Câu 33. Cho hình chóp
.
S ABCD
có đáy là hình vuông
ABCD
cạnh bằng
a
và các cạnh bên đều bằng
a
.
Gọi
M
và
N
lần lượt là trung điểm của
AD
và
SD
. Số đo của góc
,
MN SC
bằng
A.
30
. B.
45
. C.
60
. D.
90
.
Câu 34. Cho hình hộp
' ' ' '
.A BAB CD
D
C
. Giả sử tam giác
'AB C
và
' 'A DC
đều có ba góc nhọn. Góc
giữa hai đường thẳng
AC
và
'A D
là góc nào sau đây?
A.
'AB C
. B.
' 'DA C
. C.
'BB D
. D.
'BDB
.
Câu 35. Cho tứ diện đều ABCD có cạnh bằng a, M là trung điểm của cạnh BC. Gọi
là góc giữa hai
đường thẳng
AB
và DM, khi đó
cos
bằng
A.
3
6
B.
2
2
C.
3
2
D.
1
2
Phần 2. Tự luận
Câu 36. Cho dãy số
n
u
xác định bởi:
1
1
2020
1
1 , 1
2
n n
u
u u n
. Tìm
lim
n
u
.
Câu 37. Tính các giới hạn sau:
3
2
3 1
lim .
4
x
x x
x x

Câu 38. Tìm giá trị của
m
để hàm số
f x
liên tục tại
0
2
x
.
2
3 5
khi 2
2
2 3 khi 2
x
x
f x
x
m x
Câu 39. Cho tứ diện đều
ABCD
,
M
là trung điểm của cạnh
BC
. Tính
cos ,
AB DM
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
BẢNG ĐÁP ÁN
1.B
2.C
3.C
4.B
5.C
6.C
7.B
8.B
9.D
10.A
11.B
12.A
13.C
14.D
15.A
16.C
17.A
18.D
19.C
20.A
21.A
22.C
23.C
24.D
25.C
26.B
27.A
28.C
29.B
30.A
31.D
32.D
33.D
34.B
35.A
Phần 1. Trắc nghiệm
Câu 1. Dãy số nào sau đây có giới hạn bằng 0?
A.
5
3
n
. B.
1
3
n
. C.
5
3
n
. D.
4
3
n
.
Lời giải
Chọn B
1
3
n
n
u
Vì
1
1
3
.
Áp dụng công thức
lim 0
n
q
, với
1
q
. Nên
1
lim 0
3
n
.
Câu 2. Giới hạn của dãy số sau đây bằng bao nhiêu.
3
lim
2n
A.
3
. B.
1
. C.
0
. D.
2
.
Lời giải
Chọn A
Câu 3. Giá trị của
2
lim
1
n
n
bằng
A.
1
. B.
2
. C.
1
. D.
0
.
Lời giải
Ta có:
2
lim
1
n
n
2
1
lim
1
1
n
n
0 1
1 0
1
.
Câu 4.
2
6 5
2 3
lim
5
n
n n
bằng:
A.
2
. B.
0
. C.
3
5
. D.
3
.
Lời giải
Ta có
2
6 5
2 3
lim
5
n
n n
4 6
2 3
lim
5
1
n n
n
0
.
Câu 5. Dãy số nào sau đây có giới hạn khác
0
?
A.
1
n
. B.
1
n
. C.
1n
n
. D.
sin n
n
.
Lời giải
Chọn C
Có
1 1
lim lim1 lim 1
n
n n
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 6. Kết quả
lim 10
n n
là
A.
10
. B.

. C.
0
. D.
10
.
Lời giải
Chọn C
10 10
lim 10 lim lim 0
10 10
n n
n n
n n n n
.
Câu 7. Tổng
2
1 1 1
... ...
3
3 3
n
S
có giá trị là:
A.
1
3
. B.
1
2
. C.
1
9
. D.
1
4
.
Lời giải
Chọn B
Ta có
2
1 1 1
... ...
3
3 3
n
S
1
1 1
3 1 ... ...
3
3
n
S
1 1
2 lim 1 1
2
3
n
S S
.
Câu 8. Tổng các cấp số nhân vô hạn:
1
1
1
1 1 1
1, , , ,...., ,...
2 4 8
2
n
n
là
A.
3
2
. B.
2
3
. C.
2
3
. D.
2
.
Lời giải
Chọn B
Ta có:
1
1
1
1 1 1
1 ... ...
2 4 8
2
n
n
S
1
1
1 1
2 2 1 ... ...
2 4
2
n
n
S
1 1
1 1
3 2 ... lim 1 2
2 2
n n
n n
S
2
3
S
.
Câu 9. Số thập phân vô hạn tuần hoàn
0,233333...
biểu diễn dưới dạng số là:
A.
1
23
. B.
2333
10000
. C.
5
23333
10
. D.
7
30
.
Lời giải
Chọn D
Câu 10.
lim 5 1
n n
bằng:
A.
0
. B.
1
. C.
5
. D.
3
.
Lời giải
Chọn A.
5 1 5 1
4
lim 5 1 lim lim 0.
5 1 5 1
n n n n
n n
n n n n
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 11. Tìm giới hạn hàm số
2
1
2 3
lim
1
x
x x
x
bằng định nghĩa.
A.

. B.
5
. C.
2
. D.
1
.
Lời giải
Chọn B
Với mọi dãy ( ) : lim 1
n n
x x ta có:
2
2
1
2 3
2 3
lim lim lim 2 3 5
1 1
n n
n
x
n
x x
x x
x
x x
.
Câu 12. Giới hạn
3
2
8
lim
2
x
x
x
có kết quả là:
A.
12
B.
12
. C.
8
D.
5
Lời giải
Chọn A
2
3
x 2 x 2
x 2 x 2x 4
x 8
lim lim 12
2 x 2 x
.
Câu 13. Giới hạn
2
lim 2

x
x x x
bằng:
A.
0
B.

C.
1
D.
2
Lời giải
Chọn C
  
2
2
x x x
2x 2
lim x 2x x lim lim 1
2
x 2x x
1 1
x
.
Câu 14. Trong các giới hạn sau, giới hạn nào có kết quả là 0?
A.
3
1
1
lim
1
x
x
x
B.
2
2 5
lim
10
x
x
x
.
C.
2
2
1
1
lim
3 2
x
x
x x
D.
2
lim 1

x
x x
Lời giải
Chọn D
  
2
2
x x x
2
1
1
x
lim x 1 x lim lim 0
1
x 1 x
1 1
x
.
Câu 15.
lim 1 3
x
x x

bằng
A.
0
. B.
2
. C.

. D.

.
Lời giải
Chọn A
lim 1 3
x
x x

1 3
lim
1 3
x
x x
x x

4
lim
1 3
x
x x

0
.
Câu 16. Giới hạn của hàm số
2 2
4
2 1 2
2 1
x x x
f x
x x x
khi x tiến đến + có kết quả là:
A.
4
B.

. C.
0
D.
1
4
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
2
4
3
1 1
2 2
2 1 2
1
lim lim lim . 0
1 1
2 1
2 1
x x x
x x x
x x
f x
x
x x x
x x
  
Câu 17. Tính
2
x 0
x 1 x x 1
lim
x
.
A.
0
. B.
1
. C.
. D.
2
.
Lời giải
Chọn A
2 2
2
x 0 x 0
2
x 1 x x 1 x 1 x x 1
x 1 x x 1
lim lim
x
x x 1 x x 1
2
x 0
2
x
lim
x x 1 x x 1
x 0
2
x
lim 0
x 1 x x 1
Câu 18. Tìm giới hạn
4 2
3
2
5 4
lim
8
x
x x
B
x
:
A.

. B.
. C.
1
6
. D.
1
.
Lời giải
Chọn D
Ta có:
4 2 2 2
3 3 3
2 2
5 4 ( 1)( 4)
lim lim
8 2
x x
x x x x
B
x x
2
2
2
( 1)( 2)( 2)
lim
( 2)( 2 4)
x
x x x
x x x
2
2
2
( 1)( 2)
lim 1
2 4
x
x x
x x
.
Câu 19. Trong các mệnh đề sau mệnh đề nào sai
A.
2
3
lim 1 2
2
x
x x x

. B.
2
lim 1 2
x
x x x


.
C.
1
3 2
lim
1
x
x
x

. D.
1
3 2
lim
1
x
x
x

.
Hướng dẫn giải
Chọn C
+ Với đáp án A ta có:
2 2
2
2
1 4 4
lim 1 2 lim
1 2
x x
x x x x
x x x
x x x
 
2
2
3
3
3 3 3
lim lim
2
1 1 2
1 2
1 1
x x
x
x
x
x x x
x
x x x
 
A đúng.
+ Với đáp án B ta có:
2 2
2
2
1 4 4
lim 1 2 lim
1 2
x x
x x x x
x x x
x x x
 
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
2
2
3
3
3 3
lim lim
1 1 2
1 2
1 1
x x
x
x
x
x x x
x
x x x
 
3
lim
0
x

B đúng.
+ Với đáp án C ta có
1
lim 1 0
x
x
,
1 0
x
với mọi
1
x
và
1
lim 3 2 1 0
x
x
.
Vậy
1
3 2
lim
1
x
x
x

C sai.
+ Với đáp án D ta có
1
lim 1 0
x
x
,
1 0
x
với mọi
1
x
và
1
lim 3 2 1 0
x
x
.
Vậy
1
3 2
lim
1
x
x
x

D đúng.
Câu 20. Cho hàm số
2
2 3 1
khi 1
1
1 khi 1
x x
x
f x
x
x
. Mệnh đề nào sau đây sai?
A. Hàm số gián đoạn tại
1x
. B. Hàm số liên tục tại
1x
.
C. Hàm số liên tục tại
3
x
. D. Hàm số liên tục tại
5
x
.
Lời giải
Chọn A
+) Hàm số đã cho có tập xác định
D
.
+) Với
1x
thì
2
2 3 1
1
x x
f x
x
liên tục trên từng khoảng
;1
và
1;

. Do đó hàm số
liên tục tại các điểm
5
x
và
3
x
.Suy ra mệnh đề C và D đúng.
+) Mặt khác
2
1 1 1 1
2 1 1
2 3 1
lim lim lim lim 2 1 1 1
1 1
x x x x
x x
x x
f x x f
x x
Do đó hàm số liên tục tại
1x
. Suy ra mệnh đề B đúng.
Vậy mệnh đề A sai.
Câu 21. Cho hàm số
2
2
2
1 , 1
3 , 1
, 1
x x
f x x x
k x
. Tìm
k
để
f x
gián đoạn tại
1x
.
A.
2
k
. B.
2
k
. C.
2
k
. D.
1
k
.
Lời giải
Chọn A
TXĐ:
D
.
Với
1x
ta có:
2
1
f k
Với
1x
ta có:
2
1 1
lim lim 3 4
x x
f x x ;
2
1 1
lim lim 1 4
x x
f x x
suy ra
1
lim 4
x
f x
.
Vậy để hàm số gián đoạn tại
1x
khi
2
1
lim
x
f x k
2
4
k
2
k
.
Câu 22.
Biết rằng hàm số
2
5 6
khi 2
2
khi 2
x x
x
f x
x
mx n x
liên tục trên
và
n
là một số thực tùy
ý. Giá trị của
m
(tính theo
n
) bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
n
.
B.
1
2
n
.
C.
1
2
n
.
D.
1
.
Lời giải
Chọn C
Ta có
2
2 2
5 6
lim lim
2
x x
x x
f x
x
2
lim 3
x
x
1
.
2 2
lim lim
x x
f x mx n
2
m n
.
2 2
f m n
.
Để hàm số liên tục tại
2
x
thì
2 2
lim lim 2
x x
f x f x f
2 1m n
1
2
n
m
.
Câu 23. Cho hàm số
2
2 6
khi 3
3 27
1
khi 3
9
x
x
x
f x
x
. Mệnh đề nào sau đây là đúng?
A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc khoảng
3;3
.
B. Hàm số liên tục tại mọi điểm trừ điểm
3
x
.
C. Hàm số liên tục tại mọi điểm trừ điểm
3
x
.
D. Hàm số liên tục trên
.
Lời giải.
Chọn C
Ta có
2
3 3
2 6
lim lim
3 27
x x
x
f x
x
, vì
3
lim 2 6 12 0
x
x
và
2
3
lim 3 27 0
x
x
nên hàm số không
có giới hạn tại
3
x
. Ta loại hai phương án A và. D.
Ta tiếp tục tính giới hạn
2
3 3 3 3
2 3
2 6 2 1
lim lim lim lim
3 27 3 3 3 3 3 9
x x x x
x
x
f x
x x x x
.
Vì
3
1
lim 3
9
x
f x f
nên hàm số liên tục tại
3
x
.
Câu 24. Cho hàm số
sin cos 0
1 cos cos 0
x x
f x
x x
neáu
neáu
. Hỏi hàm số
f
có tất cả bao nhiêu điểm gián
đoạn trên khoảng
0;2018
?
A.
2018
. B.
1009
. C.
542
. D.
321
.
Lời giải
Chọn D
Xét hàm số
f x
trên đoạn
0;2
, khi đó:
3
sin 0; ;2
2 2
3
1 cos ;
2 2
x x
f x
x x
neáu
neáu
Ta có
0
lim 0 0
x
f x f
;
2
lim 0 2
x
f x f
.
Hàm số rõ ràng liên tục trên các khoảng
0;
2
;
3
;
2 2
và
3
;2
2
.
Ta xét tại
2
x
:
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
2 2
lim lim 1 cos 1
x x
f x x
;
2 2
lim lim sin 1
x x
f x x
;
1
2
f
;
 Như vậy
2 2
lim lim
2
x x
f x f x f
nên hàm số
f x
liên tục tại điểm
2
x
.
Ta xét tại
3
2
x
:
3 3
2 2
lim lim sin 1
x x
f x x
;
3 3
2 2
lim lim 1 cos 1
x x
f x x
;
 Vì
3 3
2 2
lim lim
x x
f x f x
nên hàm số
f x
gián đoạn tại điểm
3
2
x
.
Do đó, trên đoạn
0;2
hàm số chỉ gián đoạn tại điểm
3
2
x
.
Do tính chất tuần hoàn của hàm số
cosy x
và
siny x
suy ra hàm số gián đoạn tại các điểm
3
2 ,
2
x k k
.
Ta có
0;2018
x
3
0 2 2018
2
k
3 1009 3
320,42
4 4
k
.
Vì
k
nên
0,1,2,....,320
k
.
Vậy, hàm số
f
có
321
điểm gián đoạn trên khoảng
0;2018
.
Câu 25. Cho hàm số
3 1 khi 0
1 2 1
khi 0
x a x
f x
x
x
x
. Tìm tất cả giá trị của
a
để hàm số đã cho liên tục
trên
.
A.
1
a
. B.
3
a
. C.
2
a
. D.
4
a
.
Lời giải
Chọn C
Tập xác định
D
.
Ta có: Hàm số liên tục trên các khoảng
;0
và
0;
.
0 0
lim lim 3 1 1.
x x
f x x a a
0 0 0
1 2 1 2
lim lim lim 1.
1 2 1
x x x
x
f x
x
x
0 1.
f a
Hàm số liên tục trên
Hàm số liên tục tại điểm
0 1 1 2.
x a a
Câu 26. Trong các mệnh đề sau mệnh đề nào sai?
A. Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng
thảnh đoạn thẳng.
B. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.
C. Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không thay đổi
thứ tự của ba điểm đó.
D. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường
thẳng song song hoặc cùng nằm trên một đường thẳng.
Lời giải
Chọn B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tính chất của phép chiếu song song.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc
trùng nhau. Suy ra B sai: Chúng có thể trùng nhau.
Câu 27. Trong các khẳng định sau đây, khẳng định nào sai?
A. Nếu giá của ba vectơ cắt nhau từng đôi một thì 3 vectơ đồng phẳng
B. Nếu ba vectơ
, ,a b c
có một vec tơ
0
thì ba vectơ đồng phẳng
C. Nếu giá của ba vectơ
, ,a b c
cùng song song với một mật phẳng thì ba vec tơ đó đồng phẳng
D. Nếu trong ba vectơ
, ,a b c
có ha vec tơ cùng phương thì ba vectơ đó đồng phẳng
Lời giải
Chọn A
Câu 28. Cho hình hộp
' ' ' '
.ABCD A B C D
Gọi
, I K
lần lượt là tâm của các hình bình hành
' '
ABB A
và
' '
BCC B
. Khẳng định nào sau đây là sai?
A. Bốn điểm
, , , I K C A
đồng phẳng
B.
' '
1 1
2 2
IK AC A C
C. Ba vec tơ
, , ' 'BD IK B C
 
không đồng phẳng
D.
2 2BD IK BC
Lời giải
Chọn C
Câu 29. Cho hình lập phương
.ABCD A B C D
, góc giữa hai đường thẳng
A B
và
B C
là
A.
90
. B.
60
. C.
30
. D.
45
.
Lời giải
Chọn B
Ta có
//B C A D
; ;A B B C A B A D
DA B
.
Xét
DA B
có
A D A B
BD
nên
DA B
là tam giác đều.
Vậy
DA B
60
.
Câu 30. Cho tứ diện đều
ABCD
cạnh
a
. Tính cosin góc giữa hai đường thẳng
AB
và
CI
, với
I
là trung
điểm của
AD
.
A.
3
6
. B.
1
2
. C.
3
4
. D.
3
2
.
Lời giải
Chọn A
D
D'
A
A'
C
C'
B
B'
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Gọi
M
là trung điểm của
BD
.
Ta có:
//IM AB
.
,AB IC
,IM IC
.
cos ,AB IC
cos ,IM IC
cos ,IM IC
cos MIC
.
Mà:
cos MIC
2 2 2
2. .
MI IC MC
MI IC
2 2
2
3 3
2 2 2
3
2. .
2 2
a a a
a a
3
6
.
cos ,AB IC
cos MIC
3
6
.
Câu 31. Cho ba đường thẳng a, b, c. Mệnh đề nào sau đây sai?
A. Nếu a//b thì
, , .a c c b
B. Nếu c//b thì
, , .a b a c
C. Nếu a//c thì
0
, 0 .a c
D. Nếu
a b
thì
, , .a c c b
Lời giải
Chọn D.
Câu 32. Cho ba đường thẳng a, b, c. Khẳng định nào sau đây đúng?
A. Nếu
a c
và
b c
thì a//b. B. Nếu
a b
và
b c
thì
.a c
C. Nếu
a c
và
b c
thì
a b
. D. Nếu a//b và
c b
thì
c a
.
Lời giải
Chọn D
Câu 33. Cho hình chóp
.S ABCD
có đáy là hình vuông
ABCD
cạnh bằng
a
và các cạnh bên đều bằng
a
.
Gọi
M
và
N
lần lượt là trung điểm của
AD
và
SD
. Số đo của góc
,MN SC
bằng
A.
30
. B.
45
. C.
60
. D.
90
.
Lời giải
Chọn D.
Gọi
O
là tâm của hình vuông
ABCD
O
là tâm đường tròn ngoại tiếp của hình vuông
ABCD
(1).
Ta có:
SA SB SC SD S
nằm trên trục của đường tròn ngoại tiếp hình vuông
ABCD
(2).
Từ (1) và (2)
SO ABCD
.
Từ giả thiết ta có:
// MN SA
(do
MN
là đường trung bình của
SAD
).
, ,MN SC SA SC
.
Xét
SAC
, ta có:
2 2 2 2 2
2 2
2
2 2
SA SC a a a
SAC
AC AD a
vuông tại
S
SA SC
.
M
I
B
C
D
A
N
M
O
D
A
B
C
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
, , 90SA SC MN SC
.
Câu 34. Cho hình hộp
' ' ' '.A BAB CD DC
. Giả sử tam giác
'AB C
và
' 'A DC
đều có ba góc nhọn. Góc
giữa hai đường thẳng
AC
và
'A D
là góc nào sau đây?
A.
'AB C . B.
' 'DA C . C.
'BB D
. D.
'BDB
.
Lời giải
Chọn B
Ta có
' 'AC A C
(
' 'A B CD
là hình bình hành) mà
' 'DA C nhọn nên
, ,' ' ' ' ' '.AC A D A C A DAD C
.
Câu 35. Cho tứ diện đều ABCD có cạnh bằng a, M là trung điểm của cạnh BC. Gọi
là góc giữa hai
đường thẳng
AB
và DM, khi đó
cos
bằng
A.
3
6
B.
2
2
C.
3
2
D.
1
2
Lời giải:
Gọi N là trung điểm của AC
MN
là đường trung bình của
ABC
/ /
1
2
MN AB
MN AB
Vì
BCD
và
ACD
là các tam giác đều cạnh bằng a
3
2
a
MD ND
.
Vì
/ / , ,MN AB AB DM MN DM
Xét
MND
, ta có:
2 2 2
cos
2 .
MN MD ND
NMD
MN MD
D'
C'
B'
A'
D
C
B
A
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
2 2
2
3 3
2 2 2
1 3
0
6
3 2 3
2. .
2 2
a a a
a a
90 ,
NMD MN DM NMD
Vậy
3
cos cos
6
NMD
.
Chọn đáp án A
Phần 2. Tự luận
Câu 36. Cho dãy số
n
u
xác định bởi:
1
1
2020
1
1 , 1
2
n n
u
u u n
. Tìm
lim
n
u
.
Lời giải
Ta có
1 1
1 1
1 1 1
2 2
n n n n
u u u u
.
Đặt
1
n n
v u
, ta có
1
1
2019
1
1
.
2
n n
v
n
v v
.
Suy ra dãy
n
v
là một cấp số nhân có số hạng đầu bằng
2019
, công bội bằng
1
2
nên
1
1
2019.
2
n
n
v
1
n
.
Suy ra
1
1
2019. 1
2
n
n
u
1
n
, do đó
lim 1
n
u
.
Câu 37. Tính các giới hạn sau:
3
2
3 1
lim .
4
x
x x
x x

Lời giải
Ta có
3
3
2 3 2 3
2
2
3 1 3 1
1 1
3 1
.
4
4
4
1
1
x
x x
x x x x
x
x x
x
x
x
Vì
lim
x
x


và
2 3
3 1
1
lim 1 0
4
1
x
x x
x

. Nên
2 3
3 1
1
lim
4
1
x
x x
x
x


.
Vậy
3
2 3
2
3 1
1
3 1
lim lim .
4
4
1
x x
x x
x x
x
x x
x
 

Câu 38. Tìm giá trị của
m
để hàm số
f x
liên tục tại
0
2
x
.
NGUYỄN
BẢO VƯƠNG - 0946798489
2
3 5
khi 2
2
2 3
khi 2
x
x
f x
x
m
x
Lời giải
Tập xác định:
D
,
0
2x D
và
2 2
3f m
.
2 2
2
2 2 2 2
2
2
3 5 4 2
l
im lim lim lim
2 3
3 5
2 3 5
x x x x
x
x x
f
x
x
x
x x
.
Hàm số
f x
liên tục tại
0
2x khi
2
2 11
lim 2 2 3
3 6
x
f x
f m m
.
Câu 39. Cho tứ diện đều
ABC
D
,
M
là
trung điểm của cạnh
BC
.
Tính
co
s ,AB DM
Lời giải
Giả sử cạnh của tứ diện là
a
.
Ta
m giác
BC
D
đều
3
2
a
DM
.
Ta
m giác
AB
C
đều
3
2
a
AM
.
Ta
có:
. .
c
os ,
3
.
.
2
AB DM AB DM
AB DM
a
AB DM
a
Mặt khác:
. . .AB DM AB AM AD AB AM AB AD
2 2
2
. .
cos . . .cos .
. .cos30 . .cos60
3 3 1 3
. . . .
2 2 2 4 2 4
AB AM AB AM AB AD AB AD
AB AM AB AD
a a a a
a a a

3 3
0 ,c
os ,
6
os
6
, c
,AB DM AB DM AB DMAB DM
.
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
M
B
D
C
A
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
Phần 1. Trắc nghiệm
Câu 1. Dãysốnàosauđâycógiớihạnkhác
0
.
A.
1
2n
. B.
1
n
. C.
4
3
n
. D.
1
n
n
.
Câu 2. Giớihạn
4
lim 50 11 n n
cókếtquảlà:
A.
1
B.
0
C.
2
D.

Câu 3. Tínhgiớihạn
4 2018
lim
2 1
n
n
.
A.
1
2
. B.
4
. C.
2
. D.
2018
.
Câu 4. Giớihạncủadãysố
2
sin
2 1
n
n
n
n
u
bằng
A.
1
. B.
2
. C.
0
D.
4
.
Câu 5.
2
lim 1n n n
bằng
A.
. B.
1
. C.
0
. D.
1
2
.
Câu 6. Giớihạncủadãysố
2
2
1 cos 1
lim
n
n
n
bằng
A.
1
3
. B.
2
. C.
0
. D.
3
.
Câu 7.
2
1
lim
n n n
bằng
A.
0
. B.

. C.
2
. D.
2
.
Câu 8. Giớihạn
2
lim n n n
cókếtquảbằng:
A.
0
B.

. C.

D.
1
2
Câu 9. Gọi
1
1
1 1
... .
3 9
3
n
n
S
lim S
bằng:
A.
3
4
. B.
1
4
. C.
1
2
. D.
1
.
Câu 10. Chocấpsốnhân
1 2
, ,...u u
vớicôngbội
q
thỏađiềukiện
1q
.Lúcđó,tanóicấpsốnhânđãcho
làlùivôhạn.Tổngcủacấpsốnhânđãcholà
1 2 3
... ...
n
S u u u u
bằng:
A.
1
1
u
q
. B.
1
1
1
n
u q
q
. C.
1
1
u
q
. D.
1
1
u
q
.
Câu 11. Tính
2
3
2 15
lim
3
x
x x
x
.
Đề ôn thi giữa kỳ 1 - Lớp 11
Đề 3
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
. B.
2
. C.
1
8
. D.
8
.
Câu 12. Giớihạncủahàmsốnàodướiđâycókếtquảbằng1?
A.
2
1
3 2
lim
1

x
x x
x
B.
2
2
3 2
lim
2

x
x x
x
.
C.
2
1
3 2
lim
1

x
x x
x
D.
2
1
4 3
lim
1
x
x x
x
Câu 13. Trongcácmệnhđềsaumệnhđềnàosai
A.
2
3
lim 1 2
2
x
x x x

. B.
1
3 2
lim
1
x
x
x


.
C.
2
lim 1 2
x
x x x


. D.
1
3 2
lim
1
x
x
x


.
Câu 14. Trongcácmệnhđềsau,mệnhđềnàosai?
A.
0
1
lim
x
x

. B.
0
1
lim
x
x

. C.
5
0
1
lim
x
x

. D.
0
1
lim
x
x

.
Câu 15. Chohàmsố
2
2 3
khi 1
1
1
khi 1
8
x
x
x
y f x
x
.Tính
1
lim
x
f x
.
A.
1
8
. B.

. C.
0
. D.
1
8
.
Câu 16. Xácđịnh
2
0
lim
x
x
x
.
A.
0
. B.
. C. Khôngtồntại. D.

.
Câu 17. Giớihạn
2
0
1 1
lim
x
x x x
x
cókếtquảbằng:
A.
0
B.
1
. C.

D.
2
Câu 18. Tính
2
lim 4 3 1 2 ?
x
I x x x

A.
1
2
I
. B.
I 
. C.
0I
. D.
3
4
I
.
Câu 19. Chođồthịhàmsốy=f(x)nhưhìnhvẽ.
Xétcácmệnhđềsau
x
I . lim f x 2

x
II . lim f x

x 1
III . lim f x 2
x 1
IV . lim f x

ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Cóbaonhiêumệnhđềđúng?
A. 4. B. 3. C. 1. D. 2.
Câu 20. Chohàmsố
2
3
khi 1
2
1
khi 1
x
x
f x
x
x
.Khẳngđịnhnàodướiđâylàsai?
A. Hàmsố
f x
liêntụctại
1x
.
B. Hàmsố
f x
cóđạohàmtại
1x
.
C. Hàmsố
f x
liêntụctại
1x
vàhàmsố
f x
cũngcóđạohàmtại
1x
.
D. Hàmsố
f x
khôngcóđạohàmtại
1x
.
Câu 21. Chohàmsố
3
7 3 1
, 1
( )
1
, 1
x x
x
f x
x
ax x
.Tìm
a
đểhàmsốliêntụctại
0
1
x .
A. -3. B. 2. C.
3
.
2
. D. -2.
Câu 22. Chohàmsố
2
2
khi 1
1
3 khi 1
x x
x
f x
x
m x
.Tìmtấtcảcácgiátrịthựccủathamsốmđểhàmsố
giánđoạntại
1.
x
A.
2.
m
B.
1.
m
C.
2.
m
D.
3.
m
Câu 23. Chohàmsố
2
2
4
khi 2
2
3 khi 2
x
x
f x
x
m m x
.Tìm
m
đểhàmsốliêntụctại
0
2
x
.
A.
0
m
hoặc
1
m
. B.
1
m
hoặc
4
m
.
C.
4
m
hoặc
1
m
.D.
0
m
hoặc
4
m
.
Câu 24. Tìm
a
đểhàmsố
2 1 5
khi 4
4
2
khi 4
4
x x
x
x
f x
a x
x
liêntụctrêntậpxácđịnh.
A.
3
a
. B.
5
2
a
. C.
2
a
. D.
11
6
a
.
Câu 25. Chohàmsố
2
2 4 3 khi 2
1
khi 2
2 x 3 2
x x
f x
x
x
x m m
.Tìmtấtcảcácgiátrịcủathamsốthực
m
để
hàmsốliêntụctrên
.
A.
3
m
. B.
4
m
. C.
5
m
. D.
6
m
.
Câu 26. Qua phép chiếusong song lên mặt phẳng
( )P
,haiđường thẳng
a
và
b
có hình chiếulà hai
đườngthẳngsongsong
a
và
'b
.Khiđó:
A.
a
và
b
phảisongsongvớinhau
B.
a
và
b
phảicắtnhau
C.
a
và
b
cóthểchéonhauhoặcsongsongvớinhau
D.
a
và
b
khôngthểsongsong.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 27. Chobavectơ
, ,a b c
khôngđồngphẳngxétcácvectơ
2 ; 4 2 ; 3 2x a b y a b z a c
Chọn
mênhđềđúngtrongcácmệnhđềsau:
A. Haivectơ
,y z
cùngphương
B. Haivectơ
,x y
cùngphương
C. Haivectơ
,x z
cùngphương
D. Haivectơ
, ,x y z
đồngphẳng
Câu 28. Trongcáckhẳngđịnhsauđây,khẳngđịnhnàosai?
A. Nếugiácủabavectơcắtnhautừngđôimộtthì3vectơđồngphẳng
B. Nếubavectơ
, ,a b c
cómộtvectơ
0
thìbavectơđồngphẳng
C. Nếugiácủabavectơ
, ,a b c
cùngsongsongvớimộtmậtphẳngthìbavectơđóđồngphẳng
D. Nếutrongbavectơ
, ,a b c
cóhavectơcùngphươngthìbavectơđóđồngphẳng
Câu 29. Chohìnhlậpphương
1 1 1 1
.ABCD A B C D
.GọiMlàtrungđiểmcủa
AD
.Chọnkhẳngđịnhđúng:
A.
1 1 1 1 1 1
B M B B B A B C

B.
1 1 1 1 1 1
1
2
C M C C C D C B

C.
1 1 1 1 1 1
1 1
2 2
C M C C C D C B

D.
1 1 1 1 1 1
2BB B A B C B D
 
Câu 30. Chohìnhlậpphương
.ABCD A B C D
.Bộbavectơnàosauđâyđồngphẳng?
A.
, ,
BC AD A B

. B.
, ,D C D D AC

. C.
, ,
CB CD CC
. D.
, ,
AB AD AA
  
.
Câu 31. Trongkhônggian,mệnhđềnàosauđâylàmệnhđềđúng?
A. Códuynhấtmộtđườngthẳngđiquamộtđiểmchotrướcvàvuônggócvớimộtmặtphẳngcho
trước.
B. Códuynhấtmộtđườngthẳngđiquamộtđiểmchotrướcvàvuônggócvớimộtđườngthẳng
chotrước.
C. Códuynhấtmộtmặtphẳngđiquamộtđiểmchotrướcvàvuônggócvớimộtmặtphẳngcho
trước.
D. Códuynhấtmộtmặtphẳngđiquamộtđườngthẳngchotrướcvàvuônggócvớimộtđường
thẳngchotrước.
Câu 32. Chohìnhlậpphương
.ABCD EFGH
.Hãyxácđịnhgócgiữacặpvectơ
AB

và
EG
?
A.
90
. B.
60
. C.
45
. D.
120
.
Câu 33. Chohìnhchóp
.S ABCD
cótấtcảcáccạnhđềubằng
a
.Gọi
I
và
J
lầnlượtlàtrungđiểmcủa
SC
và
BC
.Sốđocủagóc
,IJ CD
bằng:
A.
o
30
. B.
o
45
. C.
o
60
. D.
o
90
.
Câu 34. ChohìnhchópS.ABCD,cóđáyABCDlàhìnhvuôngtâmO,cạnhbằnga;SAvuônggócvớiđáy
và 3SA a .Khiđó,cosingócgiữaSBvàACbằng
A.
2
2
B.
2
4
C.
3
2
D.
3
4
Câu 35. Tứdiện
OABC
cócáccạnh
, ,OA OB OC
đôimộtvuônggócvàđều
cóđộdàilà
1
.Gọi
M
làtrungđiểmcạnh
AB
.Gócgiữahaivectơ
BC
và
OM
bằng
A.
0
0
. B.
0
45
.
C.
0
90
. D.
0
120
.
M
C
O
A
B
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Phần 2. Tự luận
Câu 1. Giớihạn
2
5 3 3
lim
2 3 2
n n a
n b
(với
,a b
làcácsốnguyêndươngvà
a
b
làphânsốtốigiản).Tính
T a b
.
Câu 2. Chohàmsố
( )f x
xácđịnhvớimọi
0
x
thỏamãn
1
( ) 2 3 , 0
f x f x x
x
.Tính
2
( )
lim
2
x
f x
x
Câu 3. Chứngminhrằngphươngtrìnhsauluôncóhainghiệmtráidấuvớimọi
giátrịthựccủathamsố
m
:
3 2
2 1 2 2 0
x m x m x m
Câu 4. Chotứdiện
ABCD
có
AC a
,
3BD a
.Gọi
M
và
N
lầnlượtlàtrungđiểmcủa
AD
và
BC
.
Biết
AC
vuônggócvới
BD
.Tính
MN
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
BẢNG ĐÁP ÁN
1.C
2.D
3.C
4.C
5.D
6.C
7.D
8.D
9.B
10.D
11.D
12.A
13.B
14
15.B
16.C
17.A
18.D
19.D
20.D
21.C
22.B
23.B
24.D
25
26.C
27.B
28.A
29.B
30.A
31.A
32.C
33.C
34.B
35.D
Phần 1. Trắc nghiệm
Câu 1. Dãysốnàosauđâycógiớihạnkhác
0
.
A.
1
2n
. B.
1
n
. C.
4
3
n
. D.
1
n
n
.
Lờigiải
ChọnB
Câu 2. Giớihạn
4
lim 50 11
n n
cókếtquảlà:
A.
1
B.
0
C.
2
D.

Lờigiải
ChọnD
Tacó
lim limn n n
n n

4 4
2
50 11
50 11 1
Câu 3. Tínhgiớihạn
4 2018
lim
2 1
n
n
.
A.
1
2
. B.
4
. C.
2
. D.
2018
.
Lờigiải
Tacó
2018
4
4 2018
lim lim 2
1
2 1
2
n
n
n
n
.
Câu 4. Giớihạncủadãysố
2
sin
2 1
n
n
n
n
u
bằng
A.
1
. B.
2
. C.
0
D.
4
.
Lờigiải
ChọnC
Tacó:
2 2 2
2
sin sin sin
sin
2 1 2 1 2 2
n n n
n
n n n
n n n
n
Vì
2
sin
1
2
n
(do
2
0 sin 1n
)nên
2
sin
lim 0
2
n
n
.Suyra:
lim 0
n
u
.
Vậy
lim 0
n
u
.
Câu 5.
2
lim 1
n n n
bằng
A.
. B.
1
. C.
0
. D.
1
2
.
Lờigiải
ChọnC
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Tacó:
2 2
2
2
1 1
lim 1 lim
1
n n n n n n
n n n
n n n
2
1 1
lim
2
1 1
1
n
n n
n n
Câu 6. Giớihạncủadãysố
2
2
1 cos 1
lim
n
n
n
bằng
A.
1
3
. B.
2
. C.
0
. D.
3
.
Lờigiải
ChọnC
Tacos:
2
1 1 cos 1 1
n
n
2
2 2 2
1 cos 1
1 1
n
n
n n n
Mà
2
1
lim 0
n
,
2
1
lim 0
n
nên
2
2
1 cos 1
lim 0
n
n
n
.
Câu 7.
2
1
lim
n n n
bằng
A.
0
. B.

. C.
2
. D.
2
.
Lờigiải
ChọnD
Tacó:
2
2
2 2
1
lim lim
n n n
n n n
n n n n n n
1
1
1
lim lim 1 1 2
n n
n
n n
Câu 8. Giớihạn
2
lim
n n n
cókếtquảbằng:
A.
0
B.

. C.

D.
1
2
Lờigiải
ChọnD
2 2
2
2
lim lim
n n n n n n
n n n
n n n
2 2
2
lim
n n n
n n n
2
lim
n
n n n
1 1
lim
2
1
1 1
n
Câu 9. Gọi
1
1
1 1
... .
3 9
3
n
n
S
lim S
bằng:
A.
3
4
. B.
1
4
. C.
1
2
. D.
1
.
Lờigiải
ChọnB
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tacó:
1
1
1 1
... .
3 9
3
n
n
S
1
1
1
1 1 1
3 1 ...
3 9 27
3
n
n
S
1 1
1 1
1 1
4 1 .
4 4 3
3
n n
n
n
S S
Câu 10. Chocấpsốnhân
1 2
, ,...
u u
vớicôngbội
q
thỏađiềukiện
1
q
.Lúcđó,tanóicấpsốnhânđãcho
làlùivôhạn.Tổngcủacấpsốnhânđãcholà
1 2 3
... ...
n
S u u u u
bằng:
A.
1
1
u
q
. B.
1
1
1
n
u q
q
. C.
1
1
u
q
. D.
1
1
u
q
.
Lờigiải
ChọnD
Theođịnhnghĩacấpsốnhânlùivôhạntachứngminhđược
1 2 1
1
1 2 3 1 1 1 1
... ... u ... ...
1
n
n
u
S u u u u u q u q u q
q
.
Câu 11. Tính
2
x 3
x 2x 15
lim
x 3
.
A.
. B.
2
. C.
1
8
. D.
8
.
Lờigiải
ChọnD
2
x 3 x 3 x 3
x 3 x 5
x 2x 15
lim lim lim x 5 8
x 3 x 3
Câu 12. Giớihạncủahàmsốnàodướiđâycókếtquảbằng1?
A.
2
1
3 2
lim
1
x
x x
x
B.
2
2
3 2
lim
2

x
x x
x
.
C.
2
1
3 2
lim
1
x
x x
x
D.
2
1
4 3
lim
1

x
x x
x
Lờigiải
ChọnB
2
1 1 1
1 2
3 2
lim lim lim 2 1
1 1

x x x
x x
x x
x
x x
Câu 13. Trongcácmệnhđềsaumệnhđềnàosai
A.
2
3
lim 1 2
2
x
x x x

. B.
1
3 2
lim
1
x
x
x

.
C.
2
lim 1 2
x
x x x


. D.
1
3 2
lim
1
x
x
x

.
Hướngdẫngiải
ChọnB
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Tacó:
2
lim 1 2
x
x x x

2
2
2
1 2
lim
1 2
x
x x x
x x x

2
3 3
lim
1 2
x
x
x x x

2
3
3
lim
1 1 2
1 1
x
x
x x x

3
2
đápánAđúng.
2
2
1 1 2
lim 1 2 lim 1 1
x x
x x x x
x x x
 
.
Do
lim
x
x


và
2
1 1 2
lim 1 1 2 0
x
x x x

nên
2
1 1 2
lim 1 1
x
x
x x x


đápánCđúng.
Do
1
lim 3 2 1 0
x
x
và
1 0
x
với
1
x
nên
1
3 2
lim
1
x
x
x

đápánBsai.
Do
1
lim 3 2 1 0
x
x
và
1 0
x
với
1
x
nên
1
3 2
lim
1
x
x
x

đápánDđúng.
Câu 14. Trongcácmệnhđềsau,mệnhđềnàosai?
A.
0
1
lim
x
x

. B.
0
1
lim
x
x

. C.
5
0
1
lim
x
x

. D.
0
1
lim
x
x

.
Lờigiải
ChọnB
Tacó:
0
1
lim
x
x

do
0
lim 0
x
x
và
0
x
.VậyđápánAđúng.
SuyrađápánBsai.
CácđápánCvàDđúng.Giảithíchtươngtựđápán A.
Câu 15. Chohàmsố
2
2 3
khi 1
1
1
khi 1
8
x
x
x
y f x
x
.Tính
1
lim
x
f x
.
A.
1
8
. B.

. C.
0
. D.
1
8
.
Lờigiải
ChọnB
Tacó
2
1 1 1 1
2 3 4 3 1
lim lim lim lim
1
1 1 2 3 1 2 3
x x x x
x x
f x
x
x x x x x

Câu 16. Xácđịnh
2
0
lim
x
x
x
.
A.
0
. B.

. C. Khôngtồntại. D.

.
Lờigiải
ChọnC
Tacó
2 2
0 0 0
1
lim lim lim

x x x
x
x
x x x
.
2 2
0 0 0
1
lim lim lim

x x x
x
x
x x x
.
Vậykhôngtồntại
2
0
lim
x
x
x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 17. Giớihạn
2
0
1 1
lim
x
x x x
x
cókếtquảbằng:
A.
0
B.
1
. C.

D.
2
Lờigiải
ChọnA
2
2 2
0 0 0
2 2
1 1
1 1
lim lim lim
1 1 1 1
x x x
x x x
x x x x
x
x x x x x x x x
0
2
lim 0
1 1
x
x
x x x
Câu 18. Tính
2
lim 4 3 1 2 ?

x
I x x x
A.
1
2
I
. B.
I 
. C.
0I
. D.
3
4
I
.
Lờigiải
ChọnD
Phươngpháp:Khửdạngvôđịnh:
-Trụccănthức
2
2
3 1
4 3 1 2
4 3 1 2
x
f x x x x
x x x
-Chiacảtửvàmẫucủa
f x
cho
x
rồicho x
Cáchgiải:
2 2
2
2
4 3 1 2 4 3 1 2
lim 4 3 1 2 lim
4 3 1 2
 
x x
x x x x x x
x x x
x x x
2 2
2 2
2
1
3
4 3 1 2 3 1 3 3
lim lim lim
4
3 1 4 2
4 3 1 2 4 3 1 2
4 2
  
x x x
x x x x
x
x x x x x x
x x
.
Câu 19. Chođồthịhàmsốy=f(x)nhưhìnhvẽ.
Xétcácmệnhđềsau
x
I . lim f x 2

x
II . lim f x

x 1
III . lim f x 2
x 1
IV . lim f x

Cóbaonhiêumệnhđềđúng?
A. 4. B. 3. C. 1. D. 2.
Lờigiải
ĐápánD
Mệnhđề
x
lim f x 2
đúng.Mệnhđề
x
lim f x

sai
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Mệnhđề
x 1
lim f x 2
sai.Mệnhđề
x 1
lim f x

đúng
Vậycó2mênhđềđúng.
Câu 20. Chohàmsố
2
3
khi 1
2
1
khi 1
x
x
f x
x
x
.Khẳngđịnhnàodướiđâylàsai?
A. Hàmsố
f x
liêntụctại
1x
.
B. Hàmsố
f x
cóđạohàmtại
1x
.
C. Hàmsố
f x
liêntụctại
1x
vàhàmsố
f x
cũngcóđạohàmtại
1x
.
D. Hàmsố
f x
khôngcóđạohàmtại
1x
.
Lờigiải
ChọnD
+)
2
1 1
3
lim lim 1
2
x x
x
f x
và
1 1
1
lim lim 1
x x
f x
x
.Dođó,hàmsố
f x
liêntụctại
1x
.
Vậy A. đúng
+)
2
1 1 1
1
1 1
lim lim lim 1
1 2 1 2
x x x
f x f
x x
x x
và
1 1 1
1
1 1
lim lim lim 1
1 1
x x x
f x f
x
x x x x
.Dođó,hàmsố
f x
cóđạohàmtại
1x
.
VậyBđúng
TừđóthấyCđúngvà Dsai
Câu 21. Chohàmsố
3
7 3 1
, 1
( )
1
, 1
x x
x
f x
x
ax x
.Tìm
a
đểhàmsốliêntụctại
0
1
x
.
A. -3. B. 2. C.
3
.
2
. D. -2.
Lờigiải
ChọnC
3 3
1 1 1
7 3 1 7 2 2 3 1
lim lim lim
1 1 1
x x x
x x x x
f x
x x x
2
1
3 3
3 1
1
lim
1 2 3 1
1 7 2. 7 4
x
x
x
x x
x x x
2
1
3 3
1 3 3
lim .
2
2 3 1
7 2. 7 4
x
x
x x
Hàmsốliêntụctại
0
1
3
1 lim 1
2
x
x f x f a
.
Câu 22. Chohàmsố
2
2
khi 1
1
3 khi 1
x x
x
f x
x
m x
.Tìmtấtcảcácgiátrịthựccủathamsốmđểhàmsố
giánđoạntại
1.
x
A.
2.
m
B.
1.
m
C.
2.
m
D.
3.
m
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lờigiải
ChọnB
Tậpxácđịnhcủahàmsốlà
.
Hàmsốgiánđoạntại
1x
khi
2
1 1
2
lim 1 lim 3
1
x x
x x
f x f m
x
1 1
1 2
lim 3 lim 2 3 3 3 1.
1
x x
x x
m x m m m
x
Câu 23. Chohàmsố
2
2
4
khi 2
2
3 khi 2
x
x
f x
x
m m x
.Tìm
m
đểhàmsốliêntụctại
0
2
x
.
A.
0
m
hoặc
1
m
. B.
1
m
hoặc
4
m
.
C.
4
m
hoặc
1
m
.D.
0
m
hoặc
4
m
.
Lờigiải
ChọnB
Tậpxácđịnh
D
.
Tacó
2
lim
x
f x
2
2
4
lim
2
x
x
x
2
lim 2
x
x
2 2 4
.
Hàmsốđãcholiêntụctại
0
2
x
khivàchỉkhi
2
lim 2
x
f x f
2
4 3m m
2
3 4 0
m m
1
4
m
m
.
Câu 24. Tìm
a
đểhàmsố
2 1 5
khi 4
4
2
khi 4
4
x x
x
x
f x
a x
x
liêntụctrêntậpxácđịnh.
A.
3
a
. B.
5
2
a
. C.
2
a
. D.
11
6
a
.
Lờigiải
ChọnD
*TXĐ:
D
.
NX:Hàmsố
f x
liêntụctrêncáckhoảng
;4
và
4;
Dođó,đểhàmsốliêntụctrên
tacầntìm
a
đểhàmsốliêntụctại
4
x
ĐK:
4 4
lim lim 4
x x
f x f x f
4 4 4
2 1 5 2 1 5
1 1
lim lim lim
6
2 1 5
4 2 1 5
x x x
x x x x
f x
x x
x x x
4
lim
x
f x
4
2
lim
4
x
a x
2
a
4
f
Cầncó:
1 11
2
6 6
a a
.
Câu 25. Chohàmsố
2
2 4 3 khi 2
1
khi 2
2 x 3 2
x x
f x
x
x
x m m
.Tìmtấtcảcácgiátrịcủathamsốthực
m
để
hàmsốliêntụctrên
.
A.
3
m
. B.
4
m
. C.
5
m
. D.
6
m
.
Lờigiải
Chọn C.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Cách1:Hàmsốxácđịnhtrên
,liêntụctrênkhoảng
2;

.
Tacó.
2 2
2 3; lim lim 2 4 3 3
x x
f f x x
Nếu
6
m
thì
2
2 2
1
lim lim
12x 20
x x
x
f x
x

nênhàmsốkhôngliêntụctại
2
x
.
Nếu
6
m
thìtacó
2
2 2
1 3
lim lim
2 x 3 2 6
x x
x
f x
x m m m
.
Đểhàmsốliêntụctại
2
x
thì
3
3 6 1 5
6
m m
m
.
Với
5
m
thìkhi
2
x
2
1
10x 17
x
f x
x
liêntụctrên
;2

.
Tómlạivới
5
m
thìhàmsốđãcholiêntụctrên
.
Câu 26. Qua phép chiếusong song lên mặt phẳng
( )P
,haiđường thẳng
a
và
b
có hình chiếulà hai
đườngthẳngsongsong
a
và
'b
.Khiđó:
A.
a
và
b
phảisongsongvớinhau
B.
a
và
b
phảicắtnhau
C.
a
và
b
cóthểchéonhauhoặcsongsongvớinhau
D.
a
và
b
khôngthểsongsong.
Lờigiải
ChọnC
Nếu
a
//b’
mặtphẳng(
a
,
a
)//mặtphẳng(
b
,
'b
)
Khiđó
a
và
b
cóthểsongsonghoặcchéonhau.
Câu 27. Chobavectơ
, ,a b c
khôngđồngphẳngxétcácvectơ
2 ; 4 2 ; 3 2x a b y a b z a c
Chọn
mênhđềđúngtrongcácmệnhđềsau:
A. Haivectơ
,y z
cùngphương
B. Haivectơ
,x y
cùngphương
C. Haivectơ
,x z
cùngphương
D. Haivectơ
, ,x y z
đồngphẳng
Lờigiải
ChọnB
Tathấy
2y x
nên
,x y
cùngphương.
Câu 28. Trongcáckhẳngđịnhsauđây,khẳngđịnhnàosai?
A. Nếugiácủabavectơcắtnhautừngđôimộtthì3vectơđồngphẳng
B. Nếubavectơ
, ,a b c
cómộtvectơ
0
thìbavectơđồngphẳng
C. Nếugiácủabavectơ
, ,a b c
cùngsongsongvớimộtmậtphẳngthìbavectơđóđồngphẳng
D. Nếutrongbavectơ
, ,a b c
cóhavectơcùngphươngthìbavectơđóđồngphẳng
Lờigiải
ChọnA
Câu 29. Chohìnhlậpphương
1 1 1 1
.
ABCD A B C D
.GọiMlàtrungđiểmcủa
AD
.Chọnkhẳngđịnhđúng:
A.
1 1 1 1 1 1
B M B B B A B C

B.
1 1 1 1 1 1
1
2
C M C C C D C B
  
C.
1 1 1 1 1 1
1 1
2 2
C M C C C D C B
   
D.
1 1 1 1 1 1
2
BB B A B C B D
Lờigiải
ChọnB
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tacó
1 1 1 1 1 1 1 1 1
1
D D
2
C M C D DM C D C C C B
 
Câu 30. Chohìnhlậpphương
.ABCD A B C D
.Bộbavectơnàosauđâyđồngphẳng?
A.
, ,BC AD A B

. B.
, ,D C D D AC

. C.
, ,CB CD CC
. D.
, ,AB AD AA
  
.
Hướngdẫngiải
ChọnA
Từhìnhvẽbên tathấy
A B
//
ABCD
và
,BC AD ABCD
nên
, ,BC AD A B
đồngphẳng.
, ,//AC ABCD D C ABCD DD ABCD
, ,D C D D AC
khôngđồngphẳng.
, ,CB CD ABCD CC ABCD
, ,CB CD CC
khôngđồngphẳng.
, ,AB AD ABCD AA ABCD
, ,
AB AD AA

khôngđồngphẳng.
Câu 31. Trongkhônggian,mệnhđềnàosauđâylàmệnhđềđúng?
A. Códuynhấtmộtđườngthẳngđiquamộtđiểmchotrướcvàvuônggócvớimộtmặtphẳngcho
trước.
B. Códuynhấtmộtđườngthẳngđiquamộtđiểmchotrướcvàvuônggócvớimộtđườngthẳng
chotrước.
C. Códuynhấtmộtmặtphẳngđiquamộtđiểmchotrướcvàvuônggócvớimộtmặtphẳngcho
trước.
D. Códuynhấtmộtmặtphẳngđiquamộtđườngthẳngchotrướcvàvuônggócvớimộtđường
thẳngchotrước.
Câu 32. Chohìnhlậpphương
.ABCD EFGH
.Hãyxácđịnhgócgiữacặpvectơ
AB

và
EG
?
A.
90
. B.
60
. C.
45
. D.
120
.
Lờigiải
ChọnC
A1
D1
B1
C1
A
D
B
C
a
a
M
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Tacó:
//EG AC
(do
ACGE
làhìnhchữnhật)
, , 45AB EG AB AC BAC
.
Câu 33. Chohìnhchóp
.S ABCD
cótấtcảcáccạnhđềubằng
a
.Gọi
I
và
J
lầnlượtlàtrungđiểmcủa
SC
và
BC
.Sốđocủagóc
,IJ CD
bằng:
A.
o
30
. B.
o
45
. C.
o
60
. D.
o
90
.
Lờigiải
ChọnC
Vì
/ /IJ SB
nên
o
, , 60IJ SC SB SC
(do
SBC
đều).
Câu 34. ChohìnhchópS.ABCD,cóđáyABCDlàhìnhvuôngtâmO,cạnhbằnga;SAvuônggócvớiđáy
và 3SA a .Khiđó,cosingócgiữaSBvàACbằng
A.
2
2
B.
2
4
C.
3
2
D.
3
4
Lời giải
GọiIlàtrungđiểmcủaSD
OI
làđườngtrungbìnhcủa
SBD
E
F
A
G
H
B
C
D
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2 2 2
/ /
3
2 2 2
OI SB
SB SA AB a a
OI a
Vì
/ / , ,OI SB SB AC OI AC AOI
Tacó:
2 2 2 2
3
2 2 2
SD SA AD a a
AI a
AI OI AOI
cântạiI.
GọiHlàtrungđiểmcủa
OA IH OA
Và
2
2 4 4
OA AC a
OH
Xét
OHI
,tacó:
2
2
4
cos
4
a
OH
HOI
OI a
Vậy
2
cos , cos
4
SB AC HOI
.
Chọn đáp án B
Câu 35. Tứdiện
OABC
cócáccạnh
, ,OA OB OC
đôimộtvuônggócvàđều
cóđộdàilà
1
.Gọi
M
làtrungđiểmcạnh
AB
.Gócgiữahaivectơ
BC
và
OM
bằng
A.
0
0
. B.
0
45
.
C.
0
90
. D.
0
120
.
Lờigiải
ChọnD
LoạiphươngánAvìhaivéctơOM

và BC

khôngcùngphương;
LoạiphươngánBvìgócgiữahaivéctơOM

và BC

khôngthểnhọn.
LoạiđápánCvìhaivéctơOM

và BC

khôngvuônggócvớinhau.
VậyphươngánDđúngvì:
.
cos , .
2
. 2
2
OM BC
OM BC OM BC
 
   
Mà:

1 1
. .
2 2
OM BC OA OB OC OB
    
Suyra:
0
, 120OM BC
 
.
Phần 2. Tự luận
Câu 1. Giớihạn
2
5 3 3
lim
2 3 2
n n a
n b
(với
,a b
làcácsốnguyêndươngvà
a
b
làphânsốtốigiản).Tính
T a b
.
Lờigiải
2
5 3
lim
2 3 2
n n
n
1
5 3
lim
4
6
n
n
n
n
5 3
6
5
6
a
b
M
C
O
A
B
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Khiđó
11T a b
.
Câu 2. Chohàmsố
( )f x
xácđịnhvớimọi
0x
thỏamãn
1
( ) 2 3 , 0f x f x x
x
.Tính
2
( )
lim
2
x
f x
x
Lờigiải
Tacó
1
( ) 2 3 , 0 1f x f x x
x
1 3
2 ( ) , 0 2f f x x
x x
1 1
( ) 2 3 ( ) 2 3
2
1 , 2 ( )
1 3 1 6
2 ( ) 2 4 ( )
f x f x f x f x
x x
f x x
x
f f x f f x
x x x x
Dođó
2 2 2 2
2
( ) ( 2)( 2) ( 2)
lim lim lim lim 2
2 2 ( 2)
x x x x
x
f x x x x
x
x
x x x x
.
Câu 3. Chứngminhrằngphươngtrìnhsauluôncóhainghiệmtráidấuvớimọi
giátrịthựccủathamsố
m
:
3 2
2 1 2 2 0x m x m x m
Lờigiải
Đặt
3 2
2 1 2 2f x x m x m x m
.
Với
0m
thì
3 2
2f x x x x
3 2
0 2 0f x x x x
0
1
2
x
x
x
.
Khinày,phươngtrìnhluôncóhainghiệmtráidấulà
1, 2x x
với
0m
1
.
Với
0m
,tathấy
0 2f m
;
1f m
;
2 4f m
.
Nhậnthấy
2
1 . 0 2 0f f m
vớimọi
0m
và
2
0 . 2 8 0f f m
vớimọi
0m
.
Mà
f x
làhàmđathứcbậcbanên
f x
liêntụctrên
.Suyra
f x
liêntụctrêncácđoạn
1;0
và
0;2
.
Khiđóluôntồntại
1
1;0x
và
2
0;2x
saocho
1 2
0, 0f x f x
.Hayphươngtrình
0f x
luôncóhainghiệmtráidấuvớimọi
0m
2
.
Từ
1
và
2
suyraphươngtrình
0f x
luôncóhainghiệmtráidấuvớimọisốthực
m
.
Suyrađiềuphảichứngminh.
Câu 4. Chotứdiện
ABCD
có
AC a
,
3BD a
.Gọi
M
và
N
lầnlượtlàtrungđiểmcủa
AD
và
BC
.
Biết
AC
vuônggócvới
BD
.Tính
MN
.
Lờigiải
Gọi
E
,
F
lầnlượtlàtrungđiểmcủa
AB
và
CD
.
Tacó:
//
, , 90
//
EN AC
AC BD NE NF NE NF
NF BD
(1).
M
F
N
E
C
D
B
A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Mà:
1
2
1
2
NE
FM AC
NF ME BD
(2).
Từ(1),(2)
M
ENF
làhì
nhchữnhật.
Từđótacó:
2
2 2 2
2 2
3 10
2 2 2 2 2
AC BD a a a
MN NE NF
.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Phần 1. Trắc nghiệm
Câu 1. Dãy số nào sau đây có giới hạn bằng
0
.
A.
0,909
n
. B.
1,012
n
. C.
1,013
n
. D.
1,901
n
.
Câu 2. Giới hạn của dãy số sau đây bằng bao nhiêu.
2
3
2 1
lim
3 3
n
n n
A.
1
3
. B.
2
. C.
0
D.
1
.
Câu 3. Tính giới hạn
1 1 1 1
lim ...
1.2 2.3 3.4 1n n
.
A.
0
. B.
2
. C.
1
. D.
3
2
.
Câu 4.
2
lim 2 1n n n
bằng
A.
. B.
1
. C.
0
. D.
1
2
.
Câu 5. Số thập phân vô hạn tuần hoàn
0,511111...
được biểu diễn bởi phân số
A.
47
90
. B.
46
90
. C.
6
11
. D.
43
90
.
Câu 6. Tổng của cấp số nhân lùi vô hạn
1
1
1 1 1
, , ,...., ,....
3 9 27 3
n
n
là?
A.
4
. B.
1
2
. C.
3
4
. D.
1
4
.
Câu 7.
2 2
lim 1 2n n n
bằng:
A.
1
2
. B.
1
2
. C.
3
2
. D.
1
.
Câu 8. Giới hạn
2 2
lim 2 28 4 5 n n n n
có kết quả bằng:
A.
0
B.

C.
3
D.

Câu 9.
2 2
lim 2 2n n n n
có kết quả là
A.
4
. B.
2
. C.
1
. D.

.
Câu 10. Tính
3
1 1 1
9 3 1 ... ...
3 9
3
n
S
Kết quả là:
A.
27
2
. B.
14
. C.
16
. D.
15
.
Câu 11. Giới hạn
2 3
1
1 1
lim
x
x x
x x
có kết quả là:
A.
1
B.
1
C.
2
D.
2
Đề ôn thi giữa kỳ 1 - Lớp 11
Đề 4
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 12. Giới hạn
2
1
3 2
lim
1
x
x x
x
có kết quả là:
A.
1
B.

. C.

D.
1
Câu 13. Trong các mệnh đề sau, mệnh đề nào sai?
A.
0
1
lim
x
x

. B.
0
1
lim
x
x

. C.
5
0
1
lim
x
x

. D.
0
1
lim
x
x

.
Câu 14. Tính giới hạn
2
4 1
lim
1
x
x
K
x

.
A.
0
K
. B.
1K
. C.
2K
. D.
4K
.
Câu 15. Tính
2018
1
lim
1
x
x
x

.
A.
1
. B.
1
. C.
2
. D.
0
.
Câu 16. Trong các mệnh đề sau mệnh đề nào sai
A.
2
3
lim 1 2
2
x
x x x

. B.
2
lim 1 2
x
x x x


.
C.
1
3 2
lim
1
x
x
x

. D.
1
3 2
lim
1
x
x
x

.
Câu 17. Cho hàm số
2 khi 0
1 4 1
khi 0
x m x
f x
x
x
x
. Tìm tất cả các giá trị của
m
để tồn tại giới hạn
0
lim
x
f x
.
A.
2
m
. B.
1
m
. C.
3
m
. D.
1
m
.
Câu 18. Tìm
2
2
4 4
lim
2
x
x x
x
.
A. Không tồn tại. B.
1
. C.
1
. D.
1
.
Câu 19. Tìm giới hạn
2 3
lim
1 3
x
x
x

:
A.
2
3
. B.
2
3
. C.
3
2
. D.
2
.
Câu 20. Hàm số nào dưới đây liên tục trên khoảng
;

?
A.
1
1
y
x
. B.
2
1
1
y
x
. C.
1y x
. D.
2
1
y x
x
.
Câu 21. Tìm tất cả các giá trị của tham số
m
để hàm số
2
2
khi 2
2
4 khi 2
x x
x
f x
x
mx x
liên tục tại
2.
x
A.
1
m
. B. Không tồn tại
m
. C.
3
m
. D.
2
m
.
Câu 22. Hàm số
2
1 khi 1
khi 1
x x
f x
x m x
liên tục tại điểm
0
1
x
khi
m
nhận giá trị
A.
1
m
. B.
2
m
. C.
m
bất kỳ. D.
1
m
.
Câu 23. Để hàm số
2
3 2 khi 1
4 khi 1
x x x
y
x a x
liên tục tại điểm
1
x
thì giá trị của
a
là
A.
4
. B.
1
. C.
1
. D.
4
.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 24. Hàm số
1, 0
( )
cos sin , 0
ax b khi x
f x
a x b x khi x
liên tục trên
khi và chỉ khi
A.
1a b
. B.
1
a b
. C.
1a b
D.
1a b
Câu 25. Cho
a
,
b
là hai số thực sao cho hàm số
2
khi 1
1
2 1 khi 1
x ax b
x
f x
x
ax x
liên tục trên
. Tính
a b
.
A.
0
. B.
1
. C.
5
. D.
7
.
Câu 26. Qua phép chiếu song song lên mặt phẳng
( )P
, hai đường thẳng chéo nhau
a
và
b
có hình chiếu
là 2 đường thẳng
a
và
'b
. Mệnh đề nào sau đây đúng:
A.
a
và
'b
luôn cắt nhau
B.
a
và
'b
có thể trùng nhau
C.
a
và
'b
không thể song song
D.
a
và
'b
có thể cắt nhau hoặc song song với nhau.
Câu 27. Trong các mệnh đề sau đây mệnh đề nào sai?
A. Nếu
0
AB BC CD DA
thì bốn điểm
, , ,A B C D
đồng phẳng
B. Tam giác
ABC
có
I
là trung điểm cạnh
BC
thì ta có đẳng thức:
2
AI AB AC
C. Vì
0
BA BC
nên suy ra
B
là trung điểm của
AC
D. Vì
2 3
AB AC AD
nên 4 điểm
, , ,A B C D
đồng phẳng.
Câu 28. Cho tứ diện
ABCD
có
AB
,
AC
,
AD
đôi một vuông góc với nhau, biết
1
AB AC AD
. Số
đo góc giữa hai đường thẳng
AB
và
CD
bằng
A.
45
. B.
60
. C.
30
. D.
90
.
Câu 29. Cho hình lập phương
1 1 1 1
.
ABCD A B C D
, đặt
1 1 1 1 1
( , ); ( ,BB ); ( , )AC DC DA AA C C
  
Khi
đó: là
:
A. 360
0
B. 375
0
C. 315
0
D. 275
0
Câu 30. Cho hình lăng trụ tam giác
1 1 1
.
ABC A B C
. Đặt
1 1
AA ; AB ;AC ;
a b c BC d

trong các đẳng
thức sau đẳng thức nào đúng.
A.
0
a b c d
B.
a b c d
C.
0
b c d
D.
a b c
Câu 31. Mệnh đề nào sau đây là đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song
với đường thẳng còn lại.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với
đường thẳng còn lại.
Câu 32. Cho hình lập phương
1 1 1 1
.
ABCD A B C D
. Góc giữa
AC
và
1
DA
là
A.
45
. B.
90
. C.
60
. D.
120
.
Câu 33. Cho hình lập phương
.
ABCD EFGH
. Hãy xác định góc giữa cặp vectơ
AB

và
EG
?
A.
0
90 .
B.
0
60 .
C.
0
45 .
D.
0
120 .
Câu 34. Cho tứ diện
ABCD
có
AB CD a
,
3
2
IJ
a
(
I
,
J
lần lượt là trung điểm của
BC
và
AD
).
Số đo góc giữa hai đường thẳng
AB
và
CD
là
A.
30
. B.
45
. C.
60
. D.
90
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 35. Cho tứ diện đều
ABCD
(Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa hai đường thẳng
AB
và
CD
bằng
A.
30
. B.
45
. C.
60
. D.
90
.
Phần 2. Tự luận
Câu 1. Biết
2 2
2
4 4 1 6 3
lim
2
3 1
n n n a
b
n n
, trong đó
a
b
là phân số tối giản,
a
và
b
là các số
nguyên dương. Tính
.a b
Câu 2.
Tính giới hạn sau:
0
lim
1 1
x
x
x x
Câu 3. Cho hàm số
3 2
5 1 h 1
1
khi
1
k i
(
1
)
x x
x
f
x a a
x
x
x
x
. Tìm
a
để hàm số liên tục tại
1
x
Câu 4. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
,
SA a
.
SA
vuông góc với mặt
đáy. Gọi
,M N
lần lượt là trung điểm của các cạnh
,AB BC
. Tính côsin của góc giữa hai đường
thẳng
,
SM DN
.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
BẢNG ĐÁP ÁN
1.A
2.C
3.C
4.B
5.B
6.D
7.C
8.C
9.B
10.A
11.B
12.A
13.B
14.C
15.D
16.C
17.A
18.A
19.B
20.B
21.C
22.D
23.A
24.A
25.D
26.D
27.A
28.D
29.B
30.C
31.D
32.C
33.C
34.C
35.D
Phần 1. Trắc nghiệm
Câu 1. Dãy số nào sau đây có giới hạn bằng
0
.
A.
0,909
n
. B.
1,012
n
. C.
1,013
n
. D.
1,901
n
.
Lời giải
Chọn A
Áp dụng công thức
lim 0
n
q
, với
1
q
.
Câu 2. Giới hạn của dãy số sau đây bằng bao nhiêu.
2
3
2 1
lim
3 3
n
n n
A.
1
3
. B.
2
. C.
0
D.
1
.
Lời giải
Chọn C
2
3
2 1
lim
3 3
n
n n
2
3
3
3
2 1
lim
3 3
n
n
n n
n
3
2 3
2 1
lim
3 3
1
n n
n n
3
2 3
2 1
lim
0
0
3 3
1
lim 1
n n
n n
.
Câu 3. Tính giới hạn
1 1 1 1
lim ...
1.2 2.3 3.4 1
n n
.
A.
0
. B.
2
. C.
1
. D.
3
2
.
Lời giải
Ta có:
1 1 1 1
...
1.2 2.3 3.4 1
n n
1 1 1 1 1 1 1 1
1 2 2 3 1 1n n n n
1
1
1n
.
Vậy
1 1 1 1
lim ...
1.2 2.3 3.4 1
n n
1
lim 1 1
1n
.
Câu 4.
2
lim 2 1
n n n
bằng
A.
. B.
1
. C.
0
. D.
1
2
.
Lời giải
Chọn C
Ta có:
2 2
2
2
2 1 2 1
lim 2 1 lim
2 1
n n n n n n
n n n
n n n
2
2 1
lim 1
2 1
1 1
n
n n
Câu 5. Số thập phân vô hạn tuần hoàn
0,511111...
được biểu diễn bởi phân số
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
47
90
. B.
46
90
. C.
6
11
. D.
43
90
.
Lời giải
Chọn D
Ta có
2
0,51111... 0,5 0,01 0,001 0,0001 ...
1 1 1 1 1 1 1 1 1 1 23 46
... 1 ... .
1
2 100 1000 2 100 10 10 2 100 45 90
1
10
.
Câu 6. Tổng của cấp số nhân lùi vô hạn
1
1
1 1 1
, , ,...., ,....
3 9 27 3
n
n
là?
A.
4
. B.
1
2
. C.
3
4
. D.
1
4
.
Lời giải
Chọn D
Cấp số nhân có
1
1 1
,
3 3
u q
. Do đó tổng cần tìm là
1
1
1 3 1
3
.
1
1 3 4 4
1
3
u
S
q
.
Câu 7.
2 2
lim 1 2
n n n
bằng:
A.
1
2
. B.
1
2
. C.
3
2
. D.
1
.
Lời giải
Chọn C.
2 2 2 2
2 2
2 2
2 2 2 2
1 2 . 1 2
1 2
lim 1 2 lim lim
1 2 1 2
n n n n
n n
n n n n n
n n n n
2 2 2 2
2 2 2 2 2 2 2 2
3 3 3
lim lim
2
1 2 1 2
n
n n n n
n n
n n n n n n n n
.
Câu 8. Giới hạn
2 2
lim 2 28 4 5
n n n n
có kết quả bằng:
A.
0
B.

C.
3
D.

Lời giải
Chọn C
2 2
2 2
6 23
lim 2 28 4 5 lim
2 28 4 5
n
n n n n
n n n n
2
23
6
lim
2 4 5
1 28 1
n
n n n
3
Câu 9.
2 2
lim 2 2n n n n
có kết quả là
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A.
4
. B.
2
. C.
1
. D.

.
Lời giải
Chọn B
Ta có
2 2
lim 2 2n n n n
2 2
4
lim
2 2
n
n n n n
4
lim 2
2 2
1 1
n n
.
Câu 10. Tính
3
1 1 1
9 3 1 ... ...
3 9
3
n
S
Kết quả là:
A.
27
2
. B.
14
. C.
16
. D.
15
.
Lời giải
Chọn A
Ta có
3
1 1 1
9 3 1 ... ...
3 9
3
n
S
2
1 1
3 27 9 3 1 ... ...
3
3
n
S
2
1 27
2 lim 27 27
2
3
n
S S
.
Câu 11. Giới hạn
2 3
1
1 1
lim
x
x x
x x
có kết quả là:
A.
1
B.
1
C.
2
D.
2
Lời giải
Chọn D
2 3 2 3 2
1 1 1
1 1 1 1 1 1
lim lim lim 1
x x x
x x x x x
x x x x x
Câu 12. Giới hạn
2
1
3 2
lim
1
x
x x
x
có kết quả là:
A.
1
B.

. C.

D.
1
Lời giải
Chọn D
2
1 1 1
1 2 2
3 2
lim lim lim 1
1 1 1
x x x
x x x
x x
x x
( vì
x 1 0
)
Câu 13. Trong các mệnh đề sau, mệnh đề nào sai?
A.
0
1
lim
x
x

. B.
0
1
lim
x
x

. C.
5
0
1
lim
x
x

. D.
0
1
lim
x
x

.
Lời giải
Chọn B
Ta có:
0
1
lim
x
x

do
0
lim 0
x
x
và
0
x
. Vậy đáp án A đúng.
Suy ra đáp án B sai.
Các đáp án C và D đúng. Giải thích tương tự đáp án A
Câu 14. Tính giới hạn
2
4 1
lim
1
x
x
K
x

.
A.
0
K
. B.
1K
. C.
2K
. D.
4K
.
Lời giải
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
2
2 2
1 1
4 4
4 1
lim lim lim 2
1
1 1
1
x x x
x
x
x x
K
x x
x
  
.
Câu 15. Tính
2018
1
lim
1
x
x
x

.
A.
1
. B.
1
. C.
2
. D.
0
.
Lời giải
2
2018 2017
2017
1 1
1 1
lim lim . 0
1
1
1
x x
x
x x
x x
x
 
.
Câu 16. Trong các mệnh đề sau mệnh đề nào sai
A.
2
3
lim 1 2
2
x
x x x

. B.
2
lim 1 2
x
x x x


.
C.
1
3 2
lim
1
x
x
x

. D.
1
3 2
lim
1
x
x
x

.
Hướng dẫn giải
Chọn C
+ Với đáp án A ta có:
2 2
2
2
1 4 4
lim 1 2 lim
1 2
x x
x x x x
x x x
x x x
 
2
2
3
3
3 3 3
lim lim
2
1 1 2
1 2
1 1
x x
x
x
x
x x x
x
x x x
 
A đúng.
+ Với đáp án B ta có:
2 2
2
2
1 4 4
lim 1 2 lim
1 2
x x
x x x x
x x x
x x x
 
2
2
3
3
3 3
lim lim
1 1 2
1 2
1 1
x x
x
x
x
x x x
x
x x x
 
3
lim
0
x

B đúng.
+ Với đáp án C ta có
1
lim 1 0
x
x
,
1 0
x
với mọi
1
x
và
1
lim 3 2 1 0
x
x
.
Vậy
1
3 2
lim
1
x
x
x

C sai.
+ Với đáp án D ta có
1
lim 1 0
x
x
,
1 0
x
với mọi
1
x
và
1
lim 3 2 1 0
x
x
.
Vậy
1
3 2
lim
1
x
x
x

D đúng.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 17. Cho hàm số
2 khi 0
1 4 1
khi 0
x m x
f x
x
x
x
. Tìm tất cả các giá trị của
m
để tồn tại giới hạn
0
lim
x
f x
.
A.
2
m
. B.
1
m
. C.
3
m
. D.
1
m
.
Lời giải
Chọn A
Ta có
0 0
lim lim 2
x x
f x x m m
0 0 0
1 4 1 4
lim lim lim 2
1 4 1
x x x
x
f x
x
x
Tồn tại giới hạn
0
lim
x
f x
khi và chỉ khi
0 0
lim lim 2
x x
f x f x m
.
Câu 18. Tìm
2
2
4 4
lim
2
x
x x
x
.
A. Không tồn tại. B.
1
. C.
1
. D.
1
.
Lời giải
Chọn A
2
2
4 4
lim
2
x
x x
x
2
2
2
lim
2
x
x
x
2
2
lim
2
x
x
x
.
Xét:
2
2
lim
2
x
x
x
2
2
lim
2
x
x
x
1
.
2
2
lim
2
x
x
x
2
2
lim
2
x
x
x
1
.
Ta có:
2 2
2 2
lim lim
2 2
x x
x x
x x
nên không tồn tại
2
2
lim
2
x
x
x
.
Câu 19. Tìm giới hạn
2 3
lim
1 3
x
x
x

:
A.
2
3
. B.
2
3
. C.
3
2
. D.
2
.
Lời giải
Chọn B
Ta có:
2 3
lim
1 3
x
x
x

3
2
2
lim
1
3
3
x
x
x

.
Câu 20. Hàm số nào dưới đây liên tục trên khoảng
;

?
A.
1
1
y
x
. B.
2
1
1
y
x
. C.
1y x
. D.
2
1
y x
x
.
Lời giải
Chọn B
Câu 21. Tìm tất cả các giá trị của tham số
m
để hàm số
2
2
khi 2
2
4 khi 2
x x
x
f x
x
mx x
liên tục tại
2.
x
A.
1
m
. B. Không tồn tại
m
. C.
3
m
. D.
2
m
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn C
Ta có:
2 2 4
f m
;
2
lim 4 2 4
x
mx m
;
2
2 2
2
lim lim 2
2
x x
x x
x
x
.
Để hàm số liên tục tại
2
x
2 2
lim lim 2
x x
f x f x f
2 4 2 3
m m
.
Câu 22. Hàm số
2
1 khi 1
khi 1
x x
f x
x m x
liên tục tại điểm
0
1
x
khi
m
nhận giá trị
A.
1
m
. B.
2
m
. C.
m
bất kỳ. D.
1
m
.
Lời giải
Chọn D
Ta có
2
1 1
lim lim 1 0
x x
f x x
;
1 0
f
;
1 1
lim lim 1
x x
f x x m m
Hàm số liên tục tại
0
1
x
1 1
lim lim 1
x x
f x f x f
1 0 1
m m
.
Câu 23. Để hàm số
2
3 2 khi 1
4 khi 1
x x x
y
x a x
liên tục tại điểm
1
x
thì giá trị của
a
là
A.
4
. B.
1
. C.
1
. D.
4
.
Lời giải
Chọn A
Hàm số xác định trên
.
Ta có
1 0
f
.
2
1 1
lim lim 3 2 0
x x
f x x x
và
1 1
lim lim 4 4
x x
f x x a a
.
Hàm số đã cho liên tục tại
1
x
khi và chỉ khi
1 1
lim lim 1
x x
f x f x f
4 0 4
a a
.
Câu 24. Hàm số
1, 0
( )
cos sin , 0
ax b khi x
f x
a x b x khi x
liên tục trên
khi và chỉ khi
A.
1a b
. B.
1
a b
. C.
1a b
D.
1a b
Lời giải
Chọn A
Khi
0
x
thì
cos sinf x a x b x
liên tục với
0
x
.
Khi
0
x
thì
1f x ax b
liên tục với mọi
0
x
.
Tại
0
x
ta có
0
f a
.
0
lim
x
f x
0
lim 1
x
ax b
1b
.
0
lim
x
f x
0
lim cos sin
x
a x b x
a
.
Để hàm số liên tục tại
0
x
thì
0
lim
x
f x
0
lim
x
f x
0
f
1a b
1
a b
.
Câu 25. Cho
a
,
b
là hai số thực sao cho hàm số
2
khi 1
1
2 1 khi 1
x ax b
x
f x
x
ax x
liên tục trên
. Tính
a b
.
A.
0
. B.
1
. C.
5
. D.
7
.
Lời giải
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Chọn D
Ta có
1 2 1f a
.
Để hàm số liên tục trên
thì phải tồn tại
2
1 1
lim lim
1
x x
x ax b
f x
x
và
1
lim 1
x
f x f
.
Để tồn tại
2
1
lim
1
x
x ax b
x
thì
2
1 1 0 1x ax b x a b b a
.
Khi đó
2
1 1 1 1
1 1
lim lim lim lim 1 2
1 1
x x x x
x x a
x ax b
f x x a a
x x
.
Do đó để hàm số liên tục trên
thì
1
lim 1
x
f x f
2 1 2 3
a a a
. Suy ra
4
b
.
Vậy
7
a b
.
Câu 26. Qua phép chiếu song song lên mặt phẳng
( )P
, hai đường thẳng chéo nhau
a
và
b
có hình chiếu
là 2 đường thẳng
a
và
'b
. Mệnh đề nào sau đây đúng:
A.
a
và
'b
luôn cắt nhau
B.
a
và
'b
có thể trùng nhau
C.
a
và
'b
không thể song song
D.
a
và
'b
có thể cắt nhau hoặc song song với nhau.
Lời giải
Chọn D
+ Gọi
d
là phương chiếu,
( )a P
,
( )b Q
và
d
//
( )P
,
d
//
( )Q
.
+ Nếu
( )P
( )Q
a
và
'b
cắt nhau
+ Nếu
( )P
//
( )Q
a
//
'b
Câu 27. Trong các mệnh đề sau đây mệnh đề nào sai?
A. Nếu
0
AB BC CD DA
thì bốn điểm
, , ,A B C D
đồng phẳng
B. Tam giác
ABC
có
I
là trung điểm cạnh
BC
thì ta có đẳng thức:
2
AI AB AC
C. Vì
0
BA BC
nên suy ra
B
là trung điểm của
AC
D. Vì
2 3
AB AC AD
nên 4 điểm
, , ,A B C D
đồng phẳng.
Lời giải
Chọn A
Bằng quy tắc 3 điểm ta nhận thấy rằng
0
AB BC CD DA
đúng với mọi điểm
, , ,A B C D
nằm trong không gian chứ không phải chỉ riêng 4 điểm đồng phẳng.
Câu 28. Cho tứ diện
ABCD
có
AB
,
AC
,
AD
đôi một vuông góc với nhau, biết
1
AB AC AD
. Số
đo góc giữa hai đường thẳng
AB
và
CD
bằng
A.
45
. B.
60
. C.
30
. D.
90
.
Lời giải
Chọn D
CÁCH 1. Vì
AB AC
AB ACD AB CD
AB AD
.
Câu 29. Cho hình lập phương
1 1 1 1
.
ABCD A B C D
, đặt
1 1 1 1 1
( , ); ( ,BB ); ( , )AC DC DA AA C C
  
Khi
đó: là
:
A. 360
0
B. 375
0
C. 315
0
D. 275
0
Lời giải
Chọn B
( hình câu 3)
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
0
1 1
( , ) ( , ) 60
AC DC AC AB
0
1 1 1 1
( , BB ) ( , A ) 135DA DA A
0
1 1 1 1
( , ) ( , ) 180AA C C AA A A

0 0 0 0
60 135 180 375
Câu 30. Cho hình lăng trụ tam giác
1 1 1
.ABC A B C
. Đặt
1 1
AA ; AB ;AC ;a b c BC d
trong các đẳng
thức sau đẳng thức nào đúng.
A.
0a b c d
B.
a b c d
C.
0b c d
D.
a b c
Lời giải
Chọn C
Ta có:
0
b c d AB AC BC CB BC
 
Câu 31. Mệnh đề nào sau đây là đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song
với đường thẳng còn lại.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với
đường thẳng còn lại.
Lời giải
Chọn D
Câu 32. Cho hình lập phương
1 1 1 1
.ABCD A B C D . Góc giữa
AC
và
1
DA là
A.
45
. B.
90
. C.
60
. D.
120
.
Lời giải
Chọn C
A1
B1
C1
A
C
B
B
1
C
1
C
D
1
A
1
A
D
B
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Vì
' '//A C AC
nên góc giữa
AC
và
1
DA là
1 1
DAC
.
Vì tam giác
1 1
DA C đều nên
0
1 1
60DAC
.
Câu 33. Cho hình lập phương
.ABCD EFGH
. Hãy xác định góc giữa cặp vectơ
AB
và
EG
?
A.
0
90 .
B.
0
60 .
C.
0
45 .
D.
0
120 .
Lời giải
Chọn C
Vì
EG AC
(
AEGC
là hình chữ nhật) nên
0
, , 45AB EG AB AC BAC

(
ABCD
là hình
vuông).
Câu 34. Cho tứ diện
ABCD
có
AB CD a
,
3
2
IJ
a
(
I
,
J
lần lượt là trung điểm của
BC
và
AD
).
Số đo góc giữa hai đường thẳng
AB
và
CD
là
A.
30
. B.
45
. C.
60
. D.
90
.
Lời giải
Chọn C.
Gọi
M
,
N
lần lượt là trung điểm
AC
,
BC
.
Ta có:
1 1
2 2 2
// // //
a
MI NI AB CD
MINJ
MI AB CD NI
là hình thoi.
Gọi
O
là giao điểm của
MN
và
IJ
.
Ta có:
2MIN MIO .
Xét
MIO
vuông tại
O
, ta có:
3
3
4
cos 30 60
2
2
a
IO
MIO MIO MIN
a
MI
.
Mà:
, , 60
AB CD IM IN MIN
.
Câu 35. Cho tứ diện đều
ABCD
(Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa hai đường thẳng
AB
và
CD
bằng
A.
30
. B.
45
. C.
60
. D.
90
.
Lời giải
Chọn D.
Gọi
H
là tâm đường tròn ngoại tiếp
BCD AH BCD
.
Gọi
E
là trung điểm
CD
BE CD
(do
BCD
đều).
Do
AH BCD AH CD
.
Ta có:
, 90
CD BE
CD ABE CD AB AB CD
CD AH
.
Phần 2. Tự luận
E
G
H
F
D
C
B
A
O
J
M
I
N
B
D
C
A
H
E
B
D
C
A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 1. Biết
2 2
2
4 4 1 6 3
lim
2
3 1
n n n a
b
n n
, trong đó
a
b
là phân số tối giản,
a
và
b
là các số
nguyên dương. Tính
.a b
Lời giải
2 2
2
2
2
4 1
1 4
4 4 1 1 3 6 3 7
lim lim
2 2 2
1
3 1
3 1
n n n
n n
n n
n
.
Suy ra
7
7; 2 . 14
2
a
a b a b
b
.
Câu 2.
Tính giới hạn sau:
0
lim
1 1
x
x
x x
Lời giải
Ta có
0
lim
1 1
x
x
x x
0
1 1
lim
1 1
x
x x x
x x
0
1 1
lim
2
x
x x x
x
0
1 1
lim
2
x
x x
1 1
1
2
.
Câu 3. Cho hàm số
3 2
5 1 h 1
1
khi
1
k i
(
1
)
x x
x
f
x a a
x
x
x
x
. Tìm
a
để hàm số liên tục tại
1x
Lời giải
Ta có
1 1
lim ( ) lim 5 1 1 1
x x
f x x f

.
3 2
1 1
1
lim ( ) lim
1
x x
x ax ax
f x
x

2
1
1 1 1
lim
1
x
x x a x
x

2
1
lim 1 1 3
x
x a x a
.
Hàm số
( )f x
liên tục tại
1x
1 1
lim ( ) lim ( ) (1)
x x
f x f x f

3 1 2a a
.
Câu 4. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
,
SA a
.
SA
vuông góc với mặt
đáy. Gọi
,M N
lần lượt là trung điểm của các cạnh
,AB BC
. Tính côsin của góc giữa hai đường
thẳng
,SM DN
.
Lời giải
Gọi
E
là trung điểm
AD
,
F
là trung điểm
AE
.
Ta có
// // MF BE ND
góc giữa
SM
và
ND
bằng góc giữa
SM
và
MF
.
Ta có
2 2 2 2 2 2
2SM SA AM a a a
2SM a
.
2SF SM a
.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
2
2
5
5
2
2
BE a
BE AB AE a MF
.
Áp dụng định
lí côsin trong
S
MF
:
2 2 2
2
. cos
SF
SM MF SM MF SMF
2
2 2
c
os
2.
.
SM MF SF
SM
F
SM
MF
2
2
2
5
2
2
10
4
8
5
2
. 2.
2
a
a
a
a
a
.
Vậ
y cosin của góc giữa
S
M
và
N
D
bằ
ng
10
8
.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
Phần 1. Trắc nghiệm
Câu 1. Tính
2 1
lim
1
n
n
đượckếtquảlà
A.
2
. B.
0
. C.
1
2
. D.
1
.
Câu 2. Dãysốnàosauđâycógiớihạnkhác
0
?
A.
1
n
. B.
1
n
. C.
1n
n
. D.
sin n
n
.
Câu 3. Đểtìmgiớihạn
2 2
lim 4 6 4 .n n n
Mộthọcsinhlậpluậnbabướcsau:
Bước1:Tacó
2 2
4 6 4n n n
2 2
2 2
4 6 4
1 1n n
n
n n
2 2
4 6 4
1 1n
n
n n
Bước2:Dođó
2 2
2 2
4 6 4
lim 4 6 4 lim 1 1n n n n
n
n n
Bước3:Do
lim
n
u
và
2 2
4 6 4
lim 1 1 0
n
n n
nên
lim 0
n
u
Hỏilậpluậntrênđúnghaysai?Nếusaithìsaibắtđầutừbướcnào?
A. Saitừbước1. B. Saitừbước3. C. Lậpluậnđúng. D. Saitừbước2.
Câu 4. Giớihạn
2
lim 2 3 n n n
cókếtquảbằng:
A.
1
B.
0
. C.

D.

Câu 5. Sốthậpphânvôhạntuầnhoàn0,212121.biểudiễndướidạngphânsốlà:
A.
4
2121
10
. B.
1
21
. C.
7
33
. D.
6
212121
10
.
Câu 6. Tổngcủacấpsốnhânvôhạn
1
2
,
1
4
,
1
8
,…,
1
1
2
n
n
,…là
A.
2
3
. B.
1
. C.
1
3
. D.
1
3
.
Câu 7. Tổngcủacấpsốnhânlùivôhạn
1
1
1
1 1 1
, , ,...., ,....
2 6 18 2.3
n
n
là?
A.
3
4
. B.
8
3
. C.
2
3
. D.
3
8
.
Câu 8. Tìm
1 1 1
lim ...
1 1 2 1 2 ...
L
n
A.
5
2
L
. B.
L 
. C.
2L
. D.
3
2
L
.
Câu 9.
lim 1n n n
bằng
Đề ôn thi giữa kỳ 1 - Lớp 11
Đề 5
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
0
. B.
1
2
. C.
1
3
. D.
1
4
.
Câu 10. Gọi
2 4 2
1 ... ...
3 9
3
n
n
S
.Giátrịcủa
S
bằng
A.
3
. B.
5
. C.
6
. D.
4
.
Câu 11.
1
lim
2 5
x
x

bằng:
A.
0
. B.
. C.
. D.
1
2
.
Câu 12.
1
lim
3 2
x
x
x

bằng:
A.
1
3
. B.
1
2
. C.
1
3
. D.
1
2
.
Câu 13.
3 1
lim
5
x
x
x

bằng:
A.
3
. B.
3
. C.
1
5
. D.
5
.
Câu 14. Giátrịcủa
2
2 1
lim
1 1
x
x
x

bằng
A.
0
. B.
2
. C.
. D.
2
.
Câu 15.
3 4
lim
5 2
x
x
x
bằng
A.
5
4
. B.
5
4
. C.
4
5
. D.
4
5
.
Câu 16. Tínhgiớihạn
2
2
5 2 3
lim
1
x
x x
x

.
A.
5
. B.
4
. C.
3
. D.
2
.
Câu 17. Giớihạncủahàmsố
2
4
1 1
2 1
x x
f x
x x x
khixtiếnđến- cókếtquảlà:
A.
0
B.
1
2
. C.
2
D.
Câu 18. Giớihạn
4 2
3
2
lim
1 3 1

x
x x
x x
cókếtquảlà:
A.
3
B.
3
. C.
3
3
D.
3
3
Câu 19. Trongcácmệnhđềsau,mệnhđềnàođúng?
A.
4
lim
1 2
x
x x
x


. B.
4
lim 1
1 2
x
x x
x

. C.
4
lim
1 2
x
x x
x


.D.
4
lim 0
1 2
x
x x
x

.
Câu 20. Có baonhiêugiátrị nguyêncủa thamsố
m
thỏamãn hàm số
2
2 9y x mx
liêntụctrên
khoảng
; 
.
A.
6
. B.
7
. C.
5
. D. Vôsố.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 21. Giátrịcủa
a
đểhàmsố
2
1 1
khi 2
3 2
2 1
khi 2
6
x
x
x x
f x
a
x
liêntụctại
2x
.
A.
2
. B.
1
2
. C.
3
. D.
1
.
Câu 22. Chohàmsố
f x
liêntụctrênđoạn
2;3
saocho
2 5f
;
3 1f
.Hỏi
phươngtrình
3f x
cóbaonhiêunghiệmtrênđoạn
2;3
?
A. Vônghiệm. B. Cóítnhấtmộtnghiệm.
C. Cóítnhấthainghiệm. D. Cóítnhấtbanghiệm.
Câu 23. Chohàmsố
2
2 7 6
khi 2
2
1
khi 2
2
x x
x
x
y f x
x
a x
x
.Biết
a
làgiátrịđểhàmsố
f x
liêntụctại
0
2x ,tìmsốnghiệmnguyêncủabấtphươngtrình
2
7
0
4
x ax
.
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 24. Nếuhàmsố
2
khi 5
17 khi 5 10
10 khi 10
x ax b x
f x x x
ax b x
liêntụctrên
thì
a b
bằng
A.
1
. B.
0
. C.
1
. D.
2
.
Câu 25. Tìmthamsốthực
m
đểhàmsố
y f x
2
12
khi 4
4
1khi 4
x x
x
x
mx x
liêntụctạiđiểm
0
4x .
A.
4m
. B.
3m
. C.
2m
. D.
5m
.
Câu 26. Phépchiếusongsongtheophương
l
khôngsongsongvới
a
hoặc
b
,mặtphẳngchiếulà
P
,
haiđườngthẳng
a
và
b
biếnthành
'a
và
'b
.Quanhệnàogiữa
a
và
b
khôngđượcbảotoàn
trongphépchiếusongsong?
A. Cắtnhau. B. Trùngnhau. C. Songsong. D. Chéonhau.
Câu 27. Cho
1 1 1 1
.ABCD A B C D
làhìnhhộp,trongcáckhẳngđịnhsaukhẳngđịnhsai:
A.
1 1
2AC A C AC
 
B.
1 1 1
2 0AC CA CC
C.
1 1 1
AC A C AA
D.
1 1
CA AC CC

Câu 28. Chobavectơ
, ,a b c
khôngđồngphẳngxétcácvectơ
2 ; 4 2 ; 3 2x a b y a b z a c
Chọn
mênhđềđúngtrongcácmệnhđềsau:
A. Haivectơ
,y z
cùngphương
B. Haivectơ
,x y
cùngphương
C. Haivectơ
,x z
cùngphương
D. Haivectơ
, ,x y z
đồngphẳng
Câu 29. Hãychọnmệnhđềsaitrongcácmệnhđềsauđây:
A. Bavéctơ
, ,a b c
đồngphẳngnếucóhaitrongbavéctơđócùngphương.
B. Bavéctơ
, ,a b c
đồngphẳngnếucómộttrongbavéctơđóbằngvéctơ
0
.
C. véctơ luônluônđồngphẳngvớihaivéctơ
a
và
b
.
x a b c
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
D. Chohìnhhộp
. ’ ’ ’ ’ABCD A B C D
bavéctơ
, ,
AB C A DA

đồngphẳng
Câu 30. Cho hình hộp
.
ABCD A B C D
có tâm
O
. Đặt
AB a
;
BC b
.
M
là điểm xác định bởi
1
2
OM a b

.Khẳngđịnhnàosauđâyđúng?
A.
M
làtâmhìnhbìnhhành
ABB A
. B.
M
làtâmhìnhbìnhhành
BCC B
.
C.
M
làtrungđiểm
BB
. D.
M
làtrungđiểm
CC
.
Câu 31. Trongkhônggianchobađườngthẳngphânbiệt
a
,
b
,
c
.Khẳngđịnhnàosauđâyđúng?
A. Nếu
a
và
b
cùngvuônggócvới
c
thì
//a b
.
B. Nếu
//a b
và
c a
thì
c b
.
C. Nếugócgiữa
a
và
c
bằnggócgiữa
b
và
c
thì
//a b
.
D. Nếu
a
và
b
cùngnằmtrongmp
// c
thìgócgiữa
a
và
c
bằnggócgiữa
b
và
c
.
Câu 32. Chohìnhlậpphương
ABCDEFGH
,gócgiữahaiđườngthẳng
EG
và
BC
là:
A.
0
. B.
45
. C.
90
. D.
30
Câu 33. Chohìnhlậpphương
. ' ' ' 'ABCD A B C D
.Gócgiữa
AC
và
'DA
là:
A.
0
45 .
B.
0
90 .
C.
0
60 .
D.
0
120 .
Câu 34. Chotứdiện
ABCD
có
AB CD
.Gọi
, , ,I J E F
lầnlượtlàtrungđiểmcủa
, , ,
AC BC BD AD
.
Góc
,
IE JF
bằng
A.
30
. B.
45
. C.
60
. D.
90
.
Câu 35. Chotứdiện
ABCD
có
AB AC AD
và
60
BAC BAD
,
90
CAD
.Gọi
I
và
J
lầnlượt
làtrungđiểmcủa
AB
và
CD
.Hãyxácđịnhgócgiữacặpvectơ
AB
và
IJ
?
A.
120
. B.
90
. C.
60
. D.
45
.
Phần 2. Tự luận
Câu 36. Cho
,a b
làcácsốthựcthỏamãn
3 2
2
2 4
lim 1.
1
an bn n
n
Tính
2a b
Câu 37. Tínhgiớihạn
2
4 3 13 2 1
lim
7
x
x x x
x

.
Câu 38. Chứngminhrằngphươngtrìnhsauluôncónghiệmvớimọigiátrịcủathamsố
m
:
cos cos 2 0
x m x
Câu 39. Cho tứ diện
ABCD
với
3
,
2
AC AD
0
60 ,
CAB DAB
CD AD
.Gọi
là gócgiữa
AB
và
CD
.Tính
cos

ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
BẢNG ĐÁP ÁN
1.A
2.C
3.B
4.A
5.C
6.D
7.D
8.C
9.B
10.A
11.A
12.C
13.A
14.B
15.C
16.A
17.A
18.D
19.A
20.B
21.D
22.B
23.D
24.A
25.C
26.D
27.C
28.B
29.C
30.C
31.B
32.B
33.C
34.D
35.B
Phần 1. Trắc nghiệm
Câu 1. Tính
2 1
lim
1
n
n
đượckếtquảlà
A.
2
. B.
0
. C.
1
2
. D.
1
.
Lờigiải
Tacó
1
1
2
2
2 1 2 0
lim lim lim 2
1
1
1 0 1
1
1
n
n
n
n
n
n
n
n
.
Câu 2. Dãysốnàosauđâycógiớihạnkhác
0
?
A.
1
n
. B.
1
n
. C.
1n
n
. D.
sin n
n
.
Lờigiải
ChọnC
Có
1 1
lim lim1 lim 1
n
n n
.
Câu 3. Đểtìmgiớihạn
2 2
lim 4 6 4 .
n n n
Mộthọcsinhlậpluậnbabướcsau:
Bước 1: Ta có
2 2
4 6 4
n n n
2 2
2 2
4 6 4
1 1n n
n
n n
2 2
4 6 4
1 1n
n
n n
Bước2:Dođó
2 2
2 2
4 6 4
lim 4 6 4 lim 1 1n n n n
n
n n
Bước3:Do
lim
n
u
và
2 2
4 6 4
lim 1 1 0
n
n n
nên
lim 0
n
u
Hỏilậpluậntrênđúnghaysai?Nếusaithìsaibắtđầutừbướcnào?
A.Saitừbước1. B.Saitừbước3. C.Lậpluậnđúng. D.Saitừbước2.
Lờigiải
ChọnB
Bạnsaitừbước3,tacóthểlàmtiếpnhưsau:
2 2
2 2
4 6 4
lim 4 6 4 lim 1 1n n n n
n
n n
2 2
2 2 2 2
4 6 4
2
1 1
4
lim lim 2
4 6 4 4 6 4
1 1 1 1
n
n
n n
n
n n
n n n n
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 4. Giớihạn
2
lim 2 3
n n n
cókếtquảbằng:
A.
1
B.
0
. C.

D.

Lờigiải
ChọnA
2 2
2
2
2 3 2 3
lim 2 3 lim
2 3
n n n n n n
n n n
n n n
2 2
2
2 3
lim
2 3
n n n
n n n
2
2 3
lim
2 3
n
n n n
2
1
lim 1
2 3
1 1
n n
Câu 5. Sốthậpphânvôhạntuầnhoàn0,212121.biểudiễndướidạngphânsốlà:
A.
4
2121
10
. B.
1
21
. C.
7
33
. D.
6
212121
10
.
Lờigiải
ChọnC
2 1 2 1 2 1
0,212121... ...
10 100 1000 10000 100000 1000000
2 3 4 5
2 1 2 1 2
...
10 10 10 10 10
3 5 7 2 4 6 8
1 1 1 1 1 1 1 1
2 .. ..
10 10 10 10 10 10 10 10
.
2
2 2
1 1
20 1 7
10 10
2
1 1
99 99 33
1 1
10 10
Câu 6. Tổngcủacấpsốnhânvôhạn
1
2
,
1
4
,
1
8
,…,
1
1
2
n
n
,…là
A.
2
3
. B.
1
. C.
1
3
. D.
1
3
.
Lờigiải
ChọnD
Tacó
1
1
1 1 1 1 1 1
... ... .
1
2 4 8 2 2 3
1
2
n
n
S
.
Câu 7. Tổngcủacấpsốnhânlùivôhạn
1
1
1
1 1 1
, , ,...., ,....
2 6 18 2.3
n
n
là?
A.
3
4
. B.
8
3
. C.
2
3
. D.
3
8
.
Lờigiải
ChọnD
Cấpsốnhâncó
1
1 1
,
2 3
u q
.Dođótổngcầntìmlà
1
1
1 3 3
2
.
1
1 2 4 8
1
3
u
S
q
.
Câu 8. Tìm
1 1 1
lim ...
1 1 2 1 2 ...
L
n
A.
5
2
L
. B.
L
. C.
2L
. D.
3
2
L
.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Lờigiải
ChọnC
Tacó
1 2 3 ... k
làtổngcủacấpsốcộngcó
1
1
u
,
1
d
nên
1
1 2 3 ...
2
k k
k
1 2
1 2 ... 1
k k k
2 2
1k k
,
*
k
.
2 2 2 2 2 2 2 2
lim ...
1 2 2 3 3 4 1
L
n n
2 2
lim
1 1
n
2
.
Câu 9.
lim 1
n n n
bằng
A.
0
. B.
1
2
. C.
1
3
. D.
1
4
.
Lờigiải
ChọnB
Tacó
lim 1
n n n
2 2
lim
n n n
2 2
lim
n
n n n
1
lim
1
1 1
n
1
2
.
Câu 10. Gọi
2 4 2
1 ... ...
3 9
3
n
n
S
.Giátrịcủa
S
bằng
A.
3
. B.
5
. C.
6
. D.
4
.
Lờigiải
ChọnA
Tacó:
2 4 2
1 ... ...
3 9
3
n
n
S
1
1
3 3 2 2
1 ... ...
2 2 3
3
n
n
S
1 3 2 3 2 3
... lim
2 2 2 2
3 3
n n
n n
S
3
S
.
Câu 11.
1
lim
2 5
x
x

bằng:
A.
0
. B.

. C.
. D.
1
2
.
Lờigiải
ChọnA
Ápdụngquytắctìmgiớihạn,tacó:
1 1
lim lim 0
5
2 5
2
x x
x
x
x
 
.
Câu 12.
1
lim
3 2
x
x
x

bằng:
A.
1
3
. B.
1
2
. C.
1
3
. D.
1
2
.
Lờigiải
ChọnC
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tacó
1
1
1 1
lim lim
2
3 2 3
3
x x
x
x
x
x
 
.
Câu 13.
3 1
lim
5
x
x
x

bằng:
A.
3
. B.
3
. C.
1
5
. D.
5
.
Lờigiải
ChọnA
Tacó
3 1
lim
5
x
x
x

1
3
lim 3
5
1
x
x
x

.
Câu 14. Giátrịcủa
2
2 1
lim
1 1
x
x
x

bằng
A.
0
. B.
2
. C.
. D.
2
.
Lờigiải
ChọnB
Tacó:
2
2 1
lim
1 1
x
x
x

2
2 1
lim
1
1 1
x
x
x
x

2
1
2
lim
1 1
1
x
x
x x

2
.
Câu 15.
3 4
lim
5 2
x
x
x

bằng
A.
5
4
. B.
5
4
. C.
4
5
. D.
4
5
.
Lờigiải
3 4
lim
5 2
x
x
x

3
4
lim
2
5
x
x
x
x
x
3
4
lim
2
5
x
x
x
4
5
.
Câu 16. Tínhgiớihạn
2
2
5 2 3
lim
1
x
x x
x

.
A.
5
. B.
4
. C.
3
. D.
2
.
Lờigiải
Tacó:
2
2
5 2 3
lim
1
x
x x
x

2
2
2 3
5
lim
1
1
x
x x
x

5
.
Câu 17. Giớihạncủahàmsố
2
4
1 1
2 1
x x
f x
x x x
khixtiếnđến- cókếtquảlà:
A.
0
B.
1
2
. C.
2
D.
Lờigiải
ChọnA
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
2
2
2
4
3
1 1
1 1
1 1
1
lim lim lim . 0
1 1
2 1
2 1
x x x
x x
x x
f x
x
x x x
x x
  
Câu 18. Giớihạn
4 2
3
2
lim
1 3 1

x
x x
x x
cókếtquảlà:
A.
3
B.
3
. C.
3
3
D.
3
3
Lờigiải
ChọnD
4 2
2 4
3
3
1 2
1
2 3
lim lim
1 1
3
1 3 1
1 3
x x
x x
x x
x x
x x
 
Câu 19. Trongcácmệnhđềsau,mệnhđềnàođúng?
A.
4
lim
1 2
x
x x
x


. B.
4
lim 1
1 2
x
x x
x

. C.
4
lim
1 2
x
x x
x


.D.
4
lim 0
1 2
x
x x
x

.
Lờigiải
ChọnA
Vì
2 2
4
1 1
.
lim lim lim
1
1
1 2
2
2
x x x
x x x
x x
x x
x
x
x x
x
x
  

.VậyAđúng.
.
Câu 20. Có baonhiêu giá trị nguyêncủa tham số
m
thỏa mãn hàmsố
2
2 9
y x mx
liêntục trên
khoảng
;

.
A.
6
. B.
7
. C.
5
. D.Vôsố.
Lờigiải
ChọnB
Hàmsốđãcholiêntụctrênkhoảng
;

khivàchỉkhi
2 2
2 9 0, 9 0 3 3
x mx x m m
.
Vậycó7giátrịnguyên
m
thỏamãnyêucầubàitoán.
Câu 21. Giátrịcủa
a
đểhàmsố
2
1 1
khi 2
3 2
2 1
khi 2
6
x
x
x x
f x
a
x
liêntụctại
2
x
.
A.
2
. B.
1
2
. C.
3
. D.
1
.
Lờigiải
ChọnD
Tacó:
2 1
2
6
a
f
.
2
2 2
1 1 2 1
lim lim
3 2 2
2 1 1 1
x x
x x
x x
x x x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàmsốliêntụctại
2
x
2
2 1 1
lim 2 1
6 2
x
a
f x f a
.
Câu 22. Chohàmsố
f x
liêntụctrênđoạn
2;3
saocho
2 5
f
;
3 1
f
.Hỏi
phươngtrình
3
f x
cóbaonhiêunghiệmtrênđoạn
2;3
?
A.Vônghiệm. B.Cóítnhấtmộtnghiệm.
C.Cóítnhấthainghiệm. D.Cóítnhấtbanghiệm.
Lờigiải
ChọnB
Tacó
3
f x
3 0
f x
.Đặt
3
g x f x
.
Khiđó
2 2 3 2
2 . 3 2 .2 4 0
3 3 3 2
g f
g g
g f
Vì
( )f x
liêntụctrênđoạn
2;3
nên
( )g x
liêntụctrên
2;3
.
Dođóphươngtrình
0
g x
cóítnhấtmộtnghiệmthuộckhoảng
2;3
.
Vậyphươngtrình
3
f x
cóítnhấtmộtnghiệmthuộckhoảng
2;3
.
Câu 23. Chohàmsố
2
2 7 6
khi 2
2
1
khi 2
2
x x
x
x
y f x
x
a x
x
.Biết
a
làgiátrịđểhàmsố
f x
liêntụctại
0
2
x
,tìmsốnghiệmnguyêncủabấtphươngtrình
2
7
0
4
x ax
.
A.
1
. B.
4
. C.
3
. D.
2
.
Lờigiải
ChọnD
Tại
0
2
x
,tacó:
1
2
4
f a
2 2
1 1
lim lim
2 4
x x
x
f x a a
x
.
2
lim
x
f x
2
2
2 7 6
lim
2
x
x x
x
2
2 2 3
lim
2
x
x x
x
2
2 2 3
lim
2
x
x x
x
2
lim 2 3 1
x
x
.
Đểhàmsốliêntụctại
0
2
x
thì
2 2
2 lim lim
x x
f f x f x
1
1
4
a
3
4
a
.
Với
3
4
a
,xétbấtphươngtrình
2
3 7
0
4 4
x x
7
1
4
x
Mà
x
nên
1;0
x
.
Vậybấtphươngtrìnhđãchocó
2
nghiệmnguyên.
Câu 24. Nếuhàmsố
2
khi 5
17 khi 5 10
10 khi 10
x ax b x
f x x x
ax b x
liêntụctrên
thì
a b
bằng
A.
1
. B.
0
. C.
1
. D.
2
.
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Lờigiải
ChọnA
Với
5
x
tacó
2
f x x ax b
,làhàmđathứcnênliêntụctrên
; 5
.
Với
5 10
x
tacó
7
f x x
,làhàmđathứcnênliêntụctrên
5;10
.
Với
10
x
tacó
10
f x ax b
,làhàmđathứcnênliêntụctrên
10;
.
Đểhàmsốliêntụctrên
thìhàmsốphảiliêntụctại
5
x
và
10
x
.
Tacó:
5 12
f
;
10 17
f
.
5
lim
x
f x

2
5
lim
x
x ax b
5 25
a b
.
5 5
lim lim 17 12
x x
f x x
 
.
10 10
lim lim 17 27
x x
f x x
.
10 10
lim lim 10 10 10
x x
f x ax b a b
.
Hàmsốliêntụctại
5
x
và
10
x
khi
5 25 12
10 10 27
a b
a b
5 13
10 17
a b
a b
2
3
a
b
1
a b
Câu 25. Tìmthamsốthực
m
đểhàmsố
y f x
2
12
khi 4
4
1khi 4
x x
x
x
mx x
liêntụctạiđiểm
0
4
x
.
A.
4
m
. B.
3
m
. C.
2
m
. D.
5
m
.
Lờigiải
ChọnC
Tậpxácđịnh:
D
.
Tacó:
+
2
4 4
12
lim lim
4
x x
x x
f x
x

4
3 4
lim
4
x
x x
x

4
lim 3
x
x

7
.
+
4 4 1
f m
.
Hàmsố
f x
liêntụctạiđiểm
0
4
x
khivàchỉkhi
4
lim 4
x
f x f

4 1 7
m
2
m
.
Câu 26. Phépchiếusongsongtheophương
l
khôngsongsongvới
a
hoặc
b
,mặtphẳngchiếulà
P
,
haiđườngthẳng
a
và
b
biếnthành
'a
và
'b
.Quanhệnàogiữa
a
và
b
khôngđượcbảotoàn
trongphépchiếusongsong?
A.Cắtnhau. B.Trùngnhau. C.Songsong. D.Chéonhau.
Lờigiải
Chọn D.
Do
a
và
b
cùngđượcchứatrongmặtphẳngchiếu
P
.Suyratínhchấtchéonhaukhôngđược
bảotoàn.
Câu 27. Cho
1 1 1 1
.
ABCD A B C D
làhìnhhộp,trongcáckhẳngđịnhsaukhẳngđịnhsai:
A.
1 1
2
AC A C AC
  
B.
1 1 1
2 0
AC CA CC
C.
1 1 1
AC A C AA
D.
1 1
CA AC CC
 
Lờigiải
ChọnC
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tacó:
1 1 1
AA
AC A C

1 1 1 1 1 1
AA
AC AC A C C A
  
Câu 28. Chobavectơ
, ,a b c
khôngđồngphẳngxétcácvectơ
2 ; 4 2 ; 3 2x a b y a b z a c
Chọn
mênhđềđúngtrongcácmệnhđềsau:
A.Haivectơ
,y z
cùngphương
B.Haivectơ
,x y
cùngphương
C.Haivectơ
,x z
cùngphương
D.Haivectơ
, ,x y z
đồngphẳng
Lờigiải
ChọnB
Tathấy
2y x
nên
,x y
cùngphương.
Câu 29. Hãychọnmệnhđềsaitrongcácmệnhđềsauđây:
A.Bavéctơ
, ,a b c
đồngphẳngnếucóhaitrongbavéctơđócùngphương.
B.Bavéctơ
, ,a b c
đồngphẳngnếucómộttrongbavéctơđóbằngvéctơ
0
.
C.véctơ luônluônđồngphẳngvớihaivéctơ
a
và
b
.
D.Chohìnhhộp
. ’ ’ ’ ’ABCD A B C D
bavéctơ
, ,
AB C A DA
đồngphẳng
Lờigiải
ChọnC
A.Đúngvìtheođịnhnghĩađồngphẳng.
B.Đúngvìtheođịnhnghĩađồngphẳng.
C.Sai
D.Đúngvì
DA AA AD a c
AB a b AB DA CA
C A CA b c
3vectơ
, ,AB C A DA

đồngphẳng.
A1
D1
B1
C1
A
D
B
C
x a b c
b
c
a
D'
C'
B'
A'
D
C
B
A
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 30. Cho hình hộp
.ABCD A B C D
có tâm
O
. Đặt
AB a
;
BC b
.
M
là điểm xác định bởi
1
2
OM a b

.Khẳngđịnhnàosauđâyđúng?
A.
M
làtâmhìnhbìnhhành
ABB A
. B.
M
làtâmhìnhbìnhhành
BCC B
.
C.
M
làtrungđiểm
BB
. D.
M
làtrungđiểm
CC
.
Lờigiải
Chọn C.
Taphântích:
1 1 1 1
2 2 2 2
OM a b AB BC AB AD DB
 
.
M
làtrungđiểmcủa
BB
.
Câu 31. Trongkhônggianchobađườngthẳngphânbiệt
a
,
b
,
c
.Khẳngđịnhnàosauđâyđúng?
A.Nếu
a
và
b
cùngvuônggócvới
c
thì
//a b
.
B.Nếu
//a b
và
c a
thì
c b
.
C.Nếugócgiữa
a
và
c
bằnggócgiữa
b
và
c
thì
//a b
.
D.Nếu
a
và
b
cùngnằmtrongmp
//c
thìgócgiữa
a
và
c
bằnggócgiữa
b
và
c
.
Lờigiải
Chọn B.
Nếu
a
và
b
cùngvuônggócvới
c
thì
a
và
b
hoặcsongsonghoặcchéonhau.
Csaido:
Giảsửhaiđườngthẳng
a
và
b
chéonhau,tadựngđườngthẳng
c
làđườngvuônggócchungcủa
a
và
b
.Khiđógócgiữa
a
và
c
bằngvớigócgiữa
b
và
c
vàcùngbằng
90
,nhưnghiểnnhiên
haiđườngthẳng
a
và
b
khôngsongsong.
Dsaido:giảsử
a
vuônggócvới
c
,
b
songsongvới
c
,khiđógócgiữa
a
và
c
bằng
90
,còn
gócgiữa
b
và
c
bằng
0
.
DođóBđúng.
Câu 32. Chohìnhlậpphương
ABCDEFGH
,gócgiữahaiđườngthẳng
EG
và
BC
là:
A.
0
. B.
45
. C.
90
. D.
30
Lờigiải
ChọnB
ABCDEFGH
làhìnhlậpphương
/ /BC EG
gócgiữahaiđườngthẳng
EG
và
BC
là
45EGF
Vậygócgiữa
AC
và
1
DA bằng
0
60
.
Câu 33. Chohìnhlậpphương
. ' ' ' 'ABCD A B C D
.Gócgiữa
AC
và
'DA
là:
A.
0
45 .
B.
0
90 .
C.
0
60 .
D.
0
120 .
Lờigiải
ChọnC
O
D'
B'
C'
B
A
D
C
A'
a
b
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
a
làđộdàicạnhhìnhlậpphương.Khiđó,tamgiác
'AB C
đều(
' 2' B CAB CA a
)do
đó
0
' 60B CA .
Lạicó,
'DA
songsong
'CB
nên
0
, ' , ' ' .60AC DA AC CB ACB
.
Câu 34. Chotứdiện
ABCD
có
AB CD
.Gọi
, , ,I J E F
lầnlượtlàtrungđiểmcủa
, , ,AC BC BD AD
.
Góc
,IE JF
bằng
A.
30
. B.
45
. C.
60
. D.
90
.
Lờigiải
ChọnD
Tacó
IF
làđườngtrungbìnhcủa
ACD
1
2
IF CD
IF CD
.
Lạicó
JE
làđườngtrungbìnhcủa
BCD
1
2
JE CD
JE CD
.
IF JE
IF JE
Tứgiác
IJEF
làhìnhbìnhhành.
Mặtkhác:
1
2
1
2
IJ AB
JE CD
.Mà
JB EA CD IJ
.
Dođó
IJEF
làhìnhthoi.Suyra
90,IE JF
.
Câu 35. Chotứdiện
ABCD
có
AB AC AD
và
60BAC BAD
,
90CAD
.Gọi
I
và
J
lầnlượt
làtrungđiểmcủa
AB
và
CD
.Hãyxácđịnhgócgiữacặpvectơ
AB
và
IJ
?
A.
120
. B.
90
. C.
60
. D.
45
.
Lờigiải
ChọnB
A
B
C
D
B'
D'
C'
A'
J
E
I
F
B
D
C
A
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Xéttamgiác
ICD
có
J
làtrungđiểmđoạn
CD
1
.
2
IJ IC ID
Tamgiác
ABC
có
AB AC
và
0
60BAC
ABC
đều
CI AB
.
Tươngtự,tacó
ABD
đềunên
DI AB
.
Tacó
1 1 1
. . . . 0
2 2 2
IJ AB IC ID AB IC AB ID AB

, 90IJ AB AB IJ

.
Phần 2. Tự luận
Câu 36. Cho
,a b
làcácsốthựcthỏamãn
3 2
2
2 4
lim 1.
1
an bn n
n
Tính
2a b
Lờigiải
Do
3 2
2
2 4
lim 1 0
1
an bn n
a
n
(vìnếu
0a
thìbậccaonhấtcủatửlớnhơnbậccao
nhấtcủamẫuthìgiớihạnlàvôcực).
Lúcđó:
3 2 2
2
2 2
2
2 4
2 4 2 4
lim lim lim 1.
1
1 1
1
b
an bn n bn n
n n
b
n n
n
Vậy
2 1.a b
Câu 37. Tínhgiớihạn
2
4 3 13 2 1
lim
7
x
x x x
x

.
Lờigiải
2
2
3 13
| |. 4 2 1
4 3 13 2 1
lim lim
7 7
x x
x x
x x x
x x
x x
 
2
3 13
. 4 2 1
lim
7
x
x x
x x
x

2
3 13 1
4 2
lim
7
x
x x x

4
7
.
J
I
B
D
C
A
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 38. Chứngmi
nhrằngphươngtrìnhsauluôncónghiệmvớimọigiátrịcủathamsố
m
:
co
s cos 2 0x m x
Lờ
igiải
Đặt
c
os cos2f x x m x
Tậ
pxácđịnh
D
T
acóhàmsố
y
f x
l
iêntụctrên
H
àmsố
y
f x
liên
tụctrênđoạn
3
;
4
4
1
2
2
c
os cos
4 4 4 2
f m
2
3
3 6
cos cos
4 4 4 2
f m
.
3
.
0,
4 4
f f m
2
Từ
1
và
2
s
uyraphươngtrình
0f
x
luôn
cóítnhấtmộtnghiệmtrongkhoảng
3
;
4
4
hayphươngtrình
cos cos2 0x m x
luôncónghiệmvớimọigiátrịcủathamsố
m
.
Câu 39. Chotứdiện
ABCD
với
3
,
2
A
C AD
0
6
0 ,CAB DAB
CD AD
.
Gọi
là
gócgiữa
A
B
v
à
C
D
. Tính
c
os
Lờigiải
Tacó:
.
.
cos ,
.
.
AB CD AB CD
AB CD
AB
AB CD
CD
Mặtkhác:
. . .AB CD AB AD AC AB AD AB AC

0
0
. .cos60 . .cos60AB AD AB AC
1
3 1 1 1
. . . . . . .
2 2 2 4 4
AB AD AB AD AB AD AB CD
D
ođó:
1
.
1
4
cos ,
4.
AB CD
AB CD
AB CD
cos
1
4
.
| 1/82
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 Đề 1
Đề ôn thi giữa kỳ 1 - Lớp 11
Phần 1. Trắc nghiệm Câu 1.
Dãy số nào sau đây có giới hạn khác 0 . 1 1 2n 1 cosn A. . B. . C. . D. . n n n n Câu 2.
Dãy số nào sau đây không có giới hạn ? n n n n A. 0,99 . B.   1 . C.  0  , 99 . D.  0  ,89 .  n 1 Câu 3. Gọi L  lim . Khi đó L bằng n  4 1 1 A.  . B.  . C. 1 D. 0 . 5 4 2n  2017 Câu 4.
Tính giới hạn I  lim . 3n  2018 2 3 2017 A. I  . B. I  . C. I  . D. I  1. 3 2 2018 Câu 5.
Phát biểu nào sau đây là sai?
A. limu c ( u c là hằng số ). B. lim n
q  0  q   1 . n n 1 1 C. lim  0 . D. lim  0 k   1 . n k n 1 Câu 6. lim bằng 2 2
n  2  n  4 A. 0 . B.  . C.  . D. 1. Câu 7.
Giới hạn lim n n 1 có kết quả bằng:
A. Không có giới hạn. B. 0 C. 1. D.  n Câu 8. Giới hạn lim có kết quả là: 2 2n  3 A. 2 . B. 0 . C.  . D. 4 . 2 2 2 2
1  2  3  ...  n Câu 9. Tính lim
2n n  76n  5 1 1 1 A. . B. . C. . D.  . 6 2 6 2 3n  2n
Câu 10. Giới hạn lim có kết quả là: 4n 5 3 A. 0 B. . C. D.  4 4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 x 1 Câu 11. Tính lim 2 x 1  x 1 1 1 A.  . B. 2 . C. . D. 1. 2 2 2 x  2x 15
Câu 12. Giới hạn lim có kết quả là: x 3  x  3 1 A.  B. 2 . C. D. 8 8 3 2 x  3x  2
Câu 13. Tìm giới hạn A  lim : 2 x 1  x  4x  3 3 A.  . B.  . C. . D. 1. 2 x  2 Câu 14. Tính lim . 2
x 2 x  2 1 A. 2 . B. 1. C.  . D. 2 . 2 2 4x  3
Câu 15. Tìm giới hạn lim x 1  x 1 A.  . B. 2 . C.  . D. 2 . 4x  2
Câu 16. Tìm giới hạn lim x 1  x 1 A.  . B. 2 . C.  . D. 2 . 4 x  8x
Câu 17. Chọn kết quả đúng trong các kết quả sau của lim là: 3 2 x 2 
x  2x x  2 21 21 24 24 A.  . B. . C.  . D. . 5 5 5 5 1
Câu 18. Giới hạn nào dưới đây có kết quả là ? 2 x A.
x   x . B. x   .   2 lim x 1 x xx  2 lim 1  2 x C.
x   x . D. x   .   2 lim x 1 x xx  2 lim 1  2
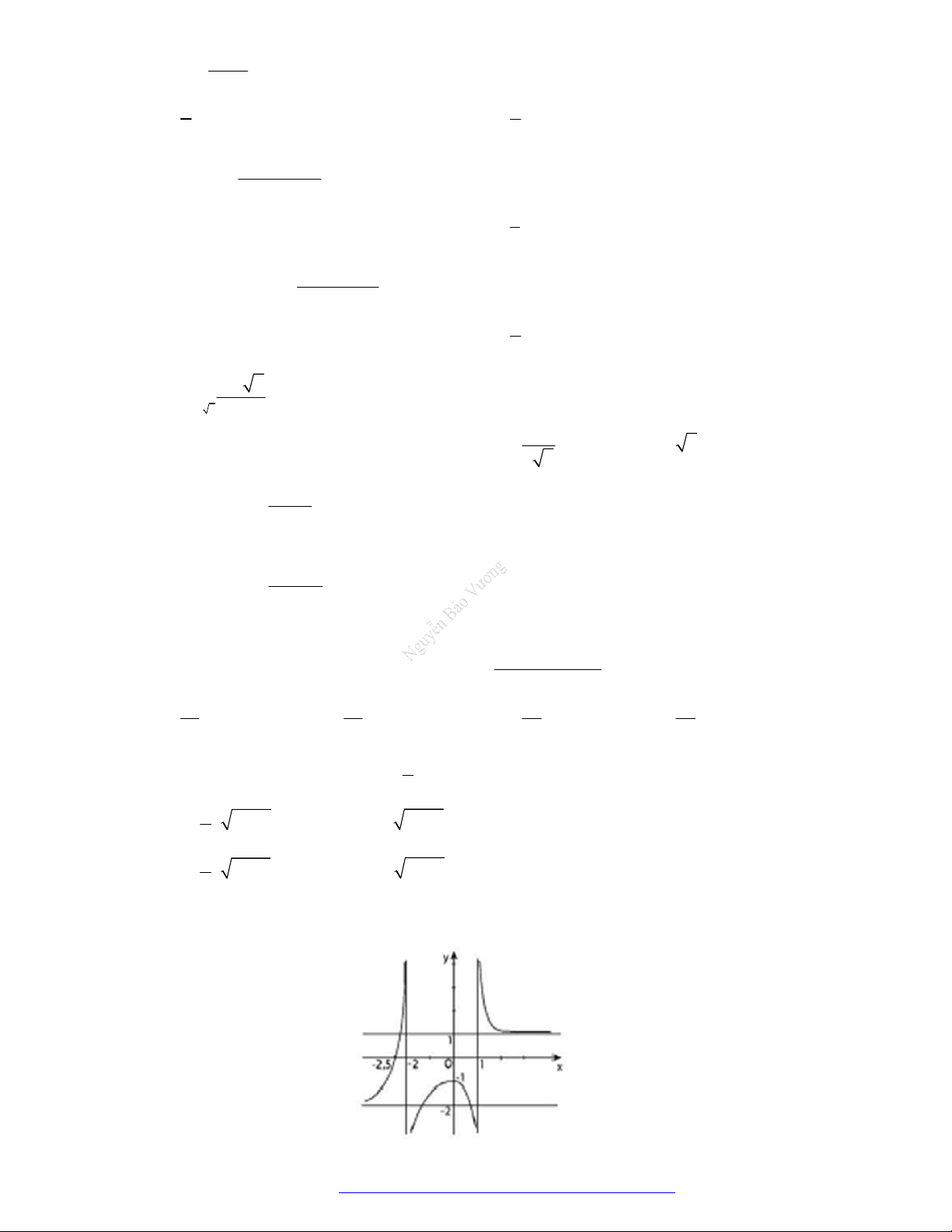
Câu 19. Cho hàm số y f x có đồ thị như hình bên. Các khẳng định sau:
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
(I) lim f x   (II) lim f x   x 1  x 2 
(III) lim f x   (IV) lim f x   x x 2  Khẳng định đúng là: A. 4. B. 3. C. 2. D. 1
Câu 20. Cho hàm số y f x liên tục trên khoảng  ;
a b . Điều kiện cần và đủ để hàm số liên tục trên đoạn  ; a b là?
A. lim f x  f a và lim f x  f b .
B. lim f x  f a và lim f x  f b . x a  x b  x a  x b 
C. lim f x  f a và lim f x  f b .
D. lim f x  f a và lim f x  f b . x a  x b  x a  x b  2 x 1
Câu 21. Hàm số f x 
liên tục trên khoảng nào sau đây? 2 x  5x  6 A.  ;  3 . B. 2;3 . C.  3  ; 2 . D.  3  ;  .  2x  4  3 khi x  2 
Câu 22. Cho hàm số f x  
. Tìm tất cả các giá trị của tham số thực m để x 1 khi x  2  2
x  2mx  3m  2
hàm số liên tục trên  . A. m  3 . B. m  4 . C. m  5 . D. m  6 . 2 2
a x khi x  2, a   
Câu 23. Cho hàm số f x  
. Giá trị của a để f x liên tục trên  là: 2   a 2 x khi x  2  A. 1 và 2 . B. 1 và –1. C. –1 và 2 . D. 1 và –2 . 3 2
x  4x  3 khi x  1  
Câu 24. Cho hàm số f xx 1  
. Xác định a để hàm số liên tục trên  . 5 ax  khi x  1   2 5 5 15 15 A. a   . B. a  . C. a  . D. a   . 2 2 2 2 
2 x m khi x  0
Câu 25. Tìm tất cả các giá trị của tham số thực m sao cho hàm số f x   liên tục mx  2 khi x  0  trên  . A. m  2 . B. m  2  . C. m  2  . D. m  0 .
Câu 26. Qua phép chiếu song song, tính chất nào không được bảo toàn? A. Chéo nhau. B. Đồng qui. C. Song song. D. Thẳng hàng.
Câu 27. Cho ABC .
D A B C D là hình hộp, với K là trung điểm CC 1 1 1 1
1. Tìm khẳng định đúng trong các khẳng định sau: 
  1  
  
A. AK AB AD AA
B. AK AB BC AA 1 2 1 
   
 1  1 
C. AK AB AD AA
D. AK AB AD AA 1 1 2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 28. Cho hình hộp AB .
CD A B C D với M CD C D . Khi đó: 1 1 1 1 1 1  1  1  1   1   1  A. AM AB AD AA B. AM AB AD AA 1 2 2 2 1 2 2
   1   1  1  
C. AM AB AD AA D. AM AB AD AA 1 2 1 2 2
Câu 29. Cho tứ diện
ABCD . Trên các cạnh
AC, BD lần lượt lấy M , N sao cho
AM  3MD; BN  3NC . Gọi P,Q lần lượt là trung điểm của AD, BC . Trong các khẳng định
sau, khẳng định nào sai?
  
A. Các vec tơ BD, AC, MN không đồng phẳng
  
B. Các vec tơ MN , DC, PQ đồng phẳng
  
C. Các vec tơ AB, DC, PQ đồng phẳng
  
D. Các vec tơ AC, DC, MN đồng phẳng
Câu 30. Cho tứ diện ABCD . Gọi M, Nlaafn lượt là trung điểm của AD, BC . Trong ccs khẳng định sau, khẳng định nào sai?
  
A. Các vec tơ AB, DC, MN đồng phẳng
  
B. Các vec tơ MN , AB, AC không đồng phẳng
  
C. Các vec tơ AN , CM , MN đồng phẳng
  
D. Các vec tơ AC, BD, MN đồng phẳng
Câu 31. Trong các mệnh đề dưới đây mệnh đề đúng là?
A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì
cũng vuông góc với đường thẳng thứ hai.
B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau. 
Câu 32. Cho đường thẳng d có vectơ chỉ phương a . Vectơ nào sau đây không là vec tơ chỉ phương của d?  1    A. 2a B. a C. 0
D. k a (k  0) 2
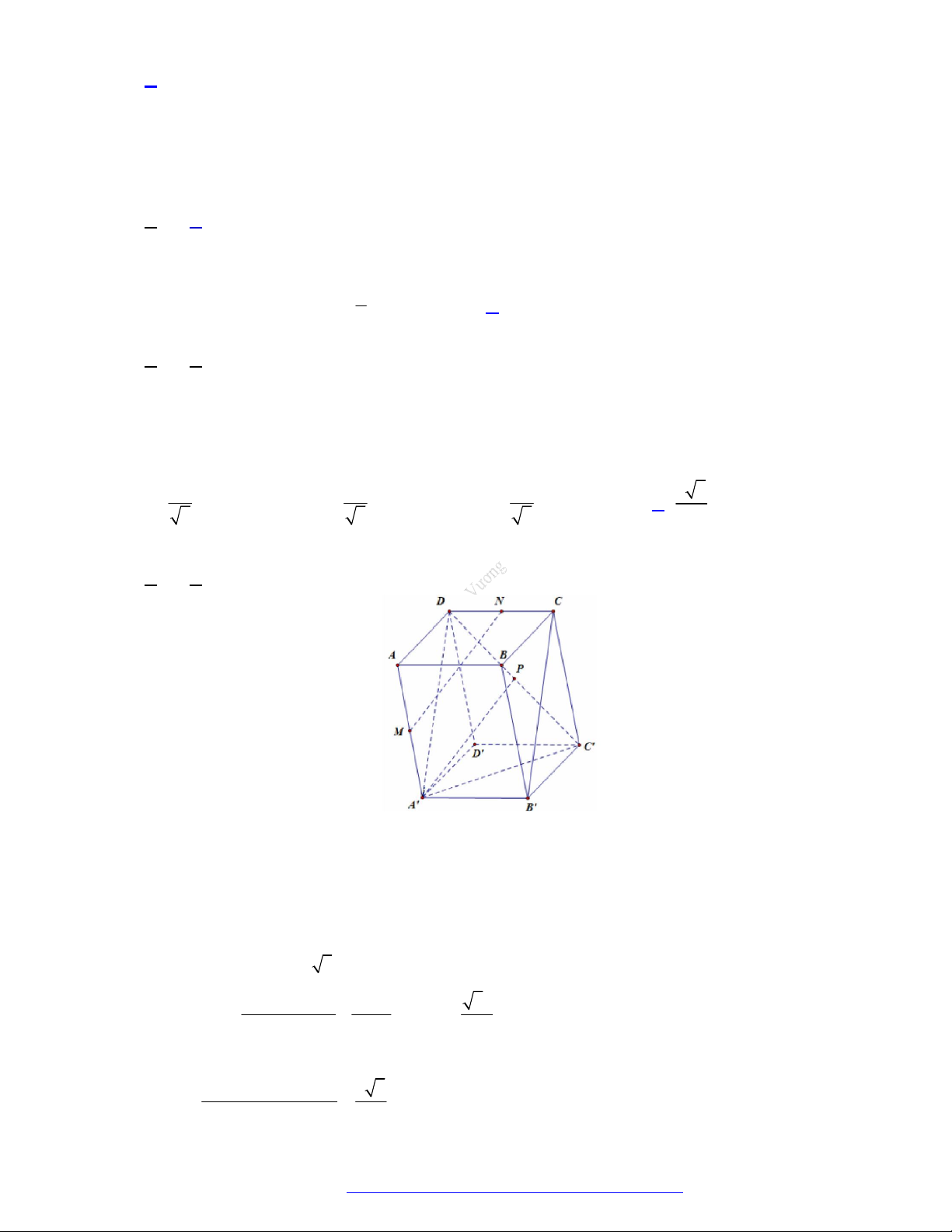
Câu 33. Cho hình hộp AB . CD A BCD
  có độ dài tất cả các cạnh bằng a và các góc BAD, DAA , AAB
đều bằng 60 . Gọi M , N lần lượt là trung điểm của AA ,
CD . Gọi  là góc tạo bởi hai đường
thẳng MN và B C
 , giá trị của cos bằng: 2 1 3 3 5 A. . B. . C. . D. . 5 5 5 10  
Câu 34. Cho hình lập phương AB .
CD EFGH . Hãy xác định góc giữa cặp vectơ AB và DH ? .A. 0 45 . B. 0 90 . C. 0 120 . D. 0 60 .
Câu 35. Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos  AB, DM  bằng 3 2 3 1 A. . B. . C. . D. . 6 2 2 2 Phần 2. Tự luận
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 a a Câu 36. Biết rằng  2 2 lim
n n  2  n 1  trong đó là phân số tối giản, *
a  ,b   . Tính giá b b trị của biểu thức 2 2
P  5a b f x 16
Câu 37. Cho hàm số y f x xác định trên  thỏa mãn lim  12 .Tính giới hạn x2 x  2
3 5 f x 16  4 lim . 2 x2 x  2x  8
Câu 38. Chứng minh phương trình: m sin 2x  2016sin x  cos x  0 ( m là tham số) có nghiệm với mọi m thuộc  .     Câu 39. Cho hình lập phương ABC . D AB CD   , biết:
AN  4AB k AA  2 AD k   ;      
AM  2 AB AA  3AD . Tìm k để AN AM
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 BẢNG ĐÁP ÁN 1.C 2.B 3.D 4.A 5.B 6.C 7.B 8.B 9.A 10.A 11.C 12.D 13.C 14.C 15.A 16.C 17.C 18.D 19.B 20.A 21.B 22.C 23.D 24.D 25.C 26.A 27.A 28.B 29.A 30.C 31.A 32.C 33.D 34.B 35.A
Phần 1. Trắc nghiệm Câu 1.
Dãy số nào sau đây có giới hạn khác 0 . 1 1 2n 1 cosn A. . B. . C. . D. . n n n n Lời giải Chọn C  2n 1 Ta có lim  2   . nCâu 2.
Dãy số nào sau đây không có giới hạn ? n n n n A. 0,99 . B.   1 . C.  0  , 99 . D.  0  ,89 . Lời giải Chọn B n n n Vì lim   1  1
 nếu n lẻ hoặc lim   1
 1 nếu n chẳn nên dãy số u   không có giới n   1 hạn.  n 1 Câu 3. Gọi L  lim . Khi đó L bằng n  4 1 1 A.  . B.  . C. 1 D. 0 . 5 4 Lời giải Chọn D n  n 1 1 1   1 Ta có:  và lim  0 nên L  lim  0 . n  4 n  4 n  4 n  4 2n  2017 Câu 4.
Tính giới hạn I  lim . 3n  2018 2 3 2017 A. I  . B. I  . C. I  . D. I  1. 3 2 2018 Lời giải 2017 2  2n  2017 n 2 Ta có I  lim  lim  . 3n  2018 2018 3  3 n
Câu 5. Phát biểu nào sau đây là sai?
A. limu c ( u c là hằng số ). B. lim n
q  0  q   1 . n n 1 1 C. lim  0 . D. lim  0 k   1 . n k n Lời giải
Theo định nghĩa giới hạn hữu hạn của dãy số (SGK ĐS11-Chương 4) thì lim n
q  0  q   1 .
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 1 lim 2 2 Câu 6.
n  2  n  4 bằng A. 0 . B.  . C.  . D. 1. Lời giải Chọn C  2 4  n  1  1 2 2  2 2 1
n  2  n  4 n n Ta có: lim lim lim       . n n     
n  2   n  2 2 2 2 2 2 2 4 2 4 Câu 7.
Giới hạn lim  n n 1 có kết quả bằng:
A. Không có giới hạn. B. 0 C. 1. D.  Lời giải Chọn B
n n 1 n n 1 1  1 
lim  n n 1  lim  lim  lim
n n 1
n n1  1  n  1  1  n    0 n Câu 8. Giới hạn lim có kết quả là: 2 2n  3 A. 2 . B. 0 . C.  . D. 4 . Lời giải Chọn B 1 3 n n 0 lim  lim   0. 2 2n  3 3 2  0 2  2 n 2 2 2 2
1  2  3  ...  n Câu 9. Tính lim
2n n  76n  5 1 1 1 A. . B. . C. . D.  . 6 2 6 2 Lời giải Chọn A n n 1 2n 1 2 2 2 2   
Ta có: 1  2  3  ...  n  . 6  1   1  1 2  2 2 3 2
1  2  3  ...  n n n   1 2n   1      n   n 1 Khi đó: lim  lim   lim  .
2n n  76n  5
12n n  76n  5  7   5  6 12 1 6       n   n  3n  2n
Câu 10. Giới hạn lim có kết quả là: 4n 5 3 A. 0 B. . C. D.  4 4 Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn A n n  3   2   3n 2n       4   4 Ta có lim lim    0 4n 1 x 1 lim 2 Câu 11. Tính x 1  x 1 1 1 A.  . B. 2 . C. . D. 1. 2 2 Lời giải Chọn C x 1 1 1 lim  lim  . 2 x 1  x 1 x 1  x 1 2 2 x  2x 15
Câu 12. Giới hạn lim có kết quả là: x3 x  3 1 A.  B. 2 . C. D. 8 8 Lời giải Chọn D 2 x  2x 15 x  3x  5 lim  lim
 lim  x  5  8 . x 3 x 3 x 3 x  3 x  3 3 2 x  3x  2
Câu 13. Tìm giới hạn A  lim : 2 x 1  x  4x  3 3 A.  . B.  . C. . D. 1. 2 Lời giải Chọn C 3 2 2 x  3x  2
(x 1)(x  2x  2) 2 x  2x  2 3 Ta có: A  lim  lim  lim  . 2 x 1  x 1 x  4x  3 
(x 1)(x  3) x 1  x  3 2 x  2 lim 2
Câu 14. Tính x 2 x  2 . 1 A. 2 . B. 1. C.  . D. 2 . 2 2 Lời giải Chọn C x  2 1 1 lim  lim   . 2 x 2 x  2 x  2 x  2 2 2 4x  3
Câu 15. Tìm giới hạn lim x 1  x 1 A.  . B. 2 . C.  . D. 2 . Lời giải Chọn A 4x  3 Ta có lim
  vì lim 4x  3  1 , lim  x  
1  0 , x 1  0 khi x 1  . x 1  x 1 x 1  x 1  4x  2
Câu 16. Tìm giới hạn lim x 1  x 1 A.  . B. 2 . C.  . D. 2  .
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 Lời giải Chọn C 4  x  2 Ta có lim   vì lim  4  x  2  6  , lim  x  
1  0 , x 1  0 khi x 1  . x 1  x 1 x 1  x 1  4 x  8x
Câu 17. Chọn kết quả đúng trong các kết quả sau của lim là: 3 2 x 2 
x  2x x  2 21 21 24 24 A.  . B. . C.  . D. . 5 5 5 5 Lời giải Chọn C x x xx  2 2
x  2x  4 x  2 4 x  2x  4 8  24 lim  lim  lim   . 3 2 x
x  2x x  2 x  x  2 2 x   1 x  2 2 2 2 x   1 5 1
Câu 18. Giới hạn nào dưới đây có kết quả là ? 2 x A.
x   x . B. x   .   2 lim x 1 x xx  2 lim 1  2 x C.
x   x . D. x   .   2 lim x 1 x xx  2 lim 1  2 Lời giải Chọn D x x x Xét: lim x x   x    . x  2 1  lim lim lim x 2 x 1 xx  1 x 1 x 1  x x 1  x 2 2 x x 1 1  lim  . x 1 2 1 1 2 x
Câu 19. Cho hàm số y f x có đồ thị như hình bên. Các khẳng định sau:
(I) lim f x   (II) lim f x   x 1  x 2 
(III) lim f x   (IV) lim f x   x x 2  Khẳng định đúng là: A. 4. B. 3. C. 2. D. 1 Lời giải Đáp án B
Chỉ có khẳng định (III) sai các khẳng định còn lại đúng.
Câu 20. Cho hàm số y f x liên tục trên khoảng  ;
a b . Điều kiện cần và đủ để hàm số liên tục trên đoạn  ; a b là?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
A. lim f x  f a và lim f x  f b .
B. lim f x  f a và lim f x  f b . x a  x b  x a  x b 
C. lim f x  f a và lim f x  f b .
D. lim f x  f a và lim f x  f b . x a  x b  x a  x b  Lời giải Chọn A
Hàm số f xác định trên đoạn  ; a
b được gọi là liên tục trên đoạn  ;
a b nếu nó liên tục trên khoảng  ;
a b, đồng thời lim f x  f a và lim f x  f b . x a  x b  2 x 1
Câu 21. Hàm số f x 
liên tục trên khoảng nào sau đây? 2 x  5x  6 A.  ;  3 . B. 2;3 . C.  3  ; 2 . D.  3  ;  . Lời giải Chọn B
Tập xd D   \  2  ;   3  2x  4  3 khi x  2 
Câu 22. Cho hàm số f x  
. Tìm tất cả các giá trị của tham số thực m để x 1 khi x  2  2
x  2mx  3m  2
hàm số liên tục trên  . A. m  3 . B. m  4 . C. m  5 . D. m  6 . Lời giải Chọn C
Cách 1: Hàm số xác định trên  , liên tục trên khoảng 2;   .
Ta có f 2  3; lim f x  lim       2x 4 3 3 . x2 x2 x 1
Nếu m  6 thì lim f x  lim
  nên hàm số không liên tục tại x  2 .   2 x2 x2 x 12x  20 x 1 3
Nếu m  6 thì ta có lim f x  lim  .   2 x2 x2
x  2mx  3m  2 6  m 3
Để hàm số liên tục tại x  2 thì
 3  6  m  1  m  5 . 6  m x 1
Với m  5 thì khi x  2 , f x  liên tục trên  ;  2 . 2 x 10x 17
Tóm lại với m  5 thì hàm số đã cho liên tục trên  .
Cách 2: Hàm số xác định trên  , liên tục trên khoảng 2;   .
Ta có f 2  3; lim f x  lim       2x 4 3 3 . x2 x2
Thử lần lượt các giá trị từ A dến C thấy m  5 thỏa mãn lim f x  3. Do đó chọn đáp án. C. x 2  2 2
a x khi x  2, a   
Câu 23. Cho hàm số f x  
. Giá trị của a để f x liên tục trên  là: 2  a 2 x khi x  2  A. 1 và 2 . B. 1 và –1. C. –1 và 2 . D. 1 và –2 . Lời giải Chọn D. TXĐ: D   .
Với x  2 ta có hàm số f x 2 2
a x liên tục trên khoảng  2; .
Với x  2 ta có hàm số f x    a 2 2
x liên tục trên khoảng  ;  2  .
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Với x  2 ta có f   2 2  2a .
lim f x  lim 2  a 2
x  22  a ; lim f x 2 2 2
 lim a x  2a .     x 2 x 2 x 2 x 2
Để hàm số liên tục tại x  2 a  1
 lim f x  lim f x  f  2 2
 2a  22  a 2
a a  2  0   .    x 2 x 2 a  2  
Vậy a  1 hoặc a  2 thì hàm số liên tục trên  . 3 2
x  4x  3 khi x  1  
Câu 24. Cho hàm số f xx 1  
. Xác định a để hàm số liên tục trên  . 5 ax  khi x  1   2 5 5 15 15 A. a   . B. a  . C. a  . D. a   . 2 2 2 2 Lời giải Chọn D 3 2 x  4x  3
Với x  1 , ta có f x 
liên tục trên tập xác định. x 1 x x  2 3 2
x  3x  3 x     1 4 3 lim  lim  5  . x 1  x 1 x 1  x 1 5 f   1  a  . 2
Để hàm số liên tục trên  thì hàm số phải liên tục tại x  1 . Điều này xảy ra khi 5 15
lim f x  f   1  a   5  a   . x 1  2 2 
2 x m khi x  0
Câu 25. Tìm tất cả các giá trị của tham số thực m sao cho hàm số f x   liên tục mx  2 khi x  0  trên  . A. m  2 . B. m  2  . C. m  2  . D. m  0 . Lời giải Chọn C
Trên khoảng 0; hàm số f x  2 x m là hàm số liên tục. Trên khoảng  ;
 0 hàm số f x  mx  2 là hàm số liên tục.
Ta có lim f x  lim
x m  m f
và lim f x  lim mx  2  2 .    2  0 x0 x0 x 0 x 0  
Hàm số f x liên tục trên  khi và chỉ khi
lim f x  lim f x  f 0  m  2  m  2 . x 0 x 0  
Câu 26. Qua phép chiếu song song, tính chất nào không được bảo toàn? A. Chéo nhau. B. Đồng qui. C. Song song. D. Thẳng hàng. Lời giải Chọn A.
Do hai đường thẳng qua phép chiếu song song ảnh của chúng sẽ cùng thuộc một mặt phẳng.
Suy ra tính chất chéo nhau không được bảo toàn.
Câu 27. Cho ABC .
D A B C D là hình hộp, với K là trung điểm CC 1 1 1 1
1. Tìm khẳng định đúng trong các khẳng định sau:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 
  1  
  
A. AK AB AD AA
B. AK AB BC AA 1 2 1 
   
 1  1 
C. AK AB AD AA
D. AK AB AD AA 1 1 2 2 Lời giải Chọn A      1 
  1 
Có AK AC CK  ( AB AD) 
AA AB AD AA 1 1 2 2 A B D C K B1 A1 D1 C1 ABC . D A B C D
M CD C D
Câu 28. Cho hình hộp 1 1 1 1 với 1 1 . Khi đó:  1  1  1   1   1  AM AB AD AA AM AB AD AA 1 1 A. 2 2 2 B. 2 2 
  1   1  1  
AM AB AD AA AM AB AD AA 1 1 C. 2 D. 2 2 Lời giải Chọn B ( hính vẽ câu 1)      1  
 1  1 
Ta có: AM AD DM AD DC AD
(DC  DD )  AD AB AA 1 1 1 2 2 2
Câu 29. Cho tứ diện
ABCD . Trên các cạnh
AC, BD lần lượt lấy M , N sao cho
AM  3MD; BN  3NC . Gọi P,Q lần lượt là trung điểm của AD, BC . Trong các khẳng định
sau, khẳng định nào sai?
  
A. Các vec tơ BD, AC, MN không đồng phẳng
  
B. Các vec tơ MN , DC, PQ đồng phẳng
  
C. Các vec tơ AB, DC, PQ đồng phẳng
  
D. Các vec tơ AC, DC, MN đồng phẳng Lời giải Chon A
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 A P M E B F D Q C N
Lấy điểm E trên cạnh AC sao cho AE=3EC, lấy F trên BD sao cho BF=3FD  1
NE / / AB, NE AB   3 
NE / /MF, NE / /MF 1
MF / / AB, MF AB   3
  
 NEMF là hình bình hành và 3 vec tơ B ,
A DC, MN có giá song song hoặc nằm trên mặt phẳng
   (MFNE)  B ,
A DC, MN đồng phẳng
  
BD, AC, MN không đồng phẳng.
Câu 30. Cho tứ diện ABCD . Gọi M, Nlaafn lượt là trung điểm của AD, BC . Trong ccs khẳng định sau, khẳng định nào sai?
  
A. Các vec tơ AB, DC, MN đồng phẳng
  
B. Các vec tơ MN , AB, AC không đồng phẳng
  
C. Các vec tơ AN , CM , MN đồng phẳng
  
D. Các vec tơ AC, BD, MN đồng phẳng Lời giải Chọn C A M P B Q D N C
Gọi P, Q lần lượt là trung điểm AC, BD
    Ba vec tơ AB
, DC, MN có giá song song hoặc nằm trên mặt phẳng (MNPQ) nên 3 véc tơ này đồng phẳng  A đúng
   Ba vec tơ AB
, AC, MN không đồng phẳng  B đúng
   Ba vec tơ AN
,CM , MN có giá không thể song song với mặt phẳng nào  C sai
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 31. Trong các mệnh đề dưới đây mệnh đề đúng là?
A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì
cũng vuông góc với đường thẳng thứ hai.
B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau. Lời giải Chọn A Theo lý thuyết. 
Câu 32. Cho đường thẳng d có vectơ chỉ phương a . Vectơ nào sau đây không là vec tơ chỉ phương của d?  1    A. 2a B.a C. 0
D. k a (k  0) 2 Lời giải Chọn C  
Theo định nghĩa a là vectơ chỉ phương của d thì k a,k  0 cũng là vectơ chỉ phương của d.
Câu 33. Cho hình hộp ABC . D AB CD
  có độ dài tất cả các cạnh bằng a và các góc BAD, DAA , AAB
đều bằng 60 . Gọi M , N lần lượt là trung điểm của AA ,
CD . Gọi  là góc tạo bởi hai đường
thẳng MN và B C
 , giá trị của cos bằng: 2 1 3 3 5 A. . B. . C. . D. . 5 5 5 10 Lời giải Chọn D
AD / / B C  Ta có 
với P là trung điểm của DC . MN / / A P   Suy ra MN B C  
   AP AD   , ,  DA P  .   
Vì BAD DAA'  A' AB  60 và các cạnh của hình hộp bằng a. Do đó
AD a, C D   C A    a 3 . 2 2 2 A D   ACDC 5a Suy ra A P     AP  . 2 4 2
Áp dụng định lý cos cho tam giác ADP , ta có 2 2 2 A D
AP DP 3 5 cos   . 2A . D A P  10  
Câu 34. Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AB và DH ?
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 .A. 0 45 . B. 0 90 . C. 0 120 . D. 0 60 . Lời giải Chọn B H G E F D C A B      
Vì DH AE ( ADHE là hình vuông) nên  AB DH    AB AE  0 , ,
BAE  90 ( ABFE là hình vuông).
Câu 35. Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos  AB, DM  bằng 3 2 3 1 A. . B. . C. . D. . 6 2 2 2 A Lời giải Chọn A.
Không mất tính tổng quát, giả sử tứ diện ABCD có cạnh bằng a . E
Gọi H là tâm đường tròn ngoại tiếp B
CD AH   BCD . B D H
Gọi E là trung điểm AC ME // AB   ,
AB DM    ME, MDM   C Ta có:  AB DM   ME MD  ME MD  cos , cos , cos ,  cos EMD .
Do các mặt của tứ diện đều là tam giác đều, từ đó ta dễ dàng tính được độ dài các cạnh của a 3
MED : ME a , ED MD  . 2 2 2 2 aa 3   a 3            2 2 2
ME MD ED  2  2 2 3 Xét     MED , ta có:  cos EMD    . 2ME.MD a a 3 6 2. . 2 2 3 3
Từ đó: cos  AB, DM    . 6 6 Phần 2. Tự luận a a Câu 36. Biết rằng  2 2 lim
n n  2  n 1  trong đó là phân số tối giản, *
a  ,b   . Tính giá b b trị của biểu thức 2 2
P  5a b Lời giải Ta có:  2 2 lim
n n  2  n  1 2
n n  2   2 n   1  lim 2 2
n n  2  n  1 n  1  lim 1 2 1 n 1    n 1  2 2 n n n
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 1 1  1  lim n  1 2 1 2 1    1  2 2 n n na  1 Suy ra :  b  2  Vậy 2 2
P  5a b  1. f x 16
Câu 37. Cho hàm số y f x xác định trên  thỏa mãn lim  12 .Tính giới hạn x2 x  2
3 5 f x 16  4 lim . 2 x2 x  2x  8 Lời giải
Theo giả thiết có lim  f x 16  0  lim f x 16  0  lim f x  16 . x2 x2 x2
3 5 f x 16  4
5 f x 16  64 Ta có: lim  lim 2 x2 x  2x  8 2 x2   
x  2 x  4  5 f x 16  4 5 f x 2 3 3 16  4   
5 f x 16  lim 2 x2   
x  2 x  4  5 f x 16  4 5 f x 2 3 3 16  4     
f x 16 5    lim  .  2 x2 x  2     x
4  5 f x 16  4 5 f x 2 3 3 16 4             5 5  12.  .    2 3 3  24 6 5.16 16  4 5.16 16 16  
Câu 38. Chứng minh phương trình: m sin 2x  2016sin x  cos x  0 ( m là tham số) có nghiệm với mọi m thuộc  . Lời giải
Đặt f x  msin 2x  2016sin x  cos x   
Vì f x liên tục trên  nên f x liên tục trên 0;  2    Ta có: f 0  20  16         f  0 2 . f  20  16  0   . f  2016  2      2     
 phương trình f x  0 có ít nhất 1 nghiệm trong 0;   với mọi m .  2 
Vậy phương trình đã cho luôn có nghiệm với mọi m thuộc  (đpcm).     Câu 39. Cho hình lập
phương ABCD.AB CD   , biết: AN  4
AB k AA  2 AD k   ;      
AM  2 AB AA  3AD . Tìm k để AN AM Lời giải
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 D C A B D' C' A' B'
Vì ABCD.AB CD
  là hình lập phương nên:
+ AB AA  AD ;
      
+ Các vectơ AB , AA , AD đôi một vuông góc với nhau. Do đó: A .
B AA  0 , A . B AD  0 ,  
AA .AD  0 .          
Để AN AM thì AN.AM  0   4
AB k AA  2 AD.2AB AA  3AD  0                8A . B AB  4 A .
B AA 12 A .
B AD k AA .2AB AA  3AD  2A .
D 2AB AA  3AD  0                 AB2 8
 0  0  2k AA .AB k AA .AA  3k AA .AD  4 AD.AB  2 AD.AA  6 AD.AD  0   
   AB2     k AA2      AD2 8 0 0 0 0 0 0 6  0 2 2 2  8
AB kAA  6AD  0 (Mà AB AA  AD ) 2 2 2  8
AB kAB  6AB  0    k   2 8
6 AB  0  8  k  6  0  k  2  0  k  2 .  
Vậy giá trị k thích hợp để AN AM là k  2 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 Đề 2
Đề ôn thi giữa kỳ 1 - Lớp 11
Phần 1. Trắc nghiệm Câu 1.
Dãy số nào sau đây có giới hạn bằng 0? n n n n  5   1   5   4  A.   . B.   . C.    . D.    .  3   3   3   3  3 Câu 2.
Giới hạn của dãy số sau đây bằng bao nhiêu. lim n  2 A. 3 . B. 1. C. 0 . D. 2  . 2  n Câu 3. Giá trị của lim bằng n 1 A. 1. B. 2 . C. 1. D. 0 . 2 2n  3 Câu 4. lim bằng: 6 5 n  5n 3 A. 2 . B. 0 . C. . D. 3  . 5 Câu 5.
Dãy số nào sau đây có giới hạn khác 0 ? 1 1 n 1 sin n A. . B. . C. . D. . n n n n Câu 6.
Kết quả lim  n 10  n  là A. 10 . B.  . C. 0 . D. 1  0 . 1 1 1 Câu 7. Tổng S    ...   ... có giá trị là: 2 3 3 3n 1 1 1 1 A. . B. . C. . D. . 3 2 9 4 n 1 1 1   1 1 Câu 8.
Tổng các cấp số nhân vô hạn: 1,  , ,  ,...., ,... là n 1 2 4 8 2  3 2 2 A. . B. . C. . D. 2 . 2 3 3 Câu 9.
Số thập phân vô hạn tuần hoàn 0, 233333... biểu diễn dưới dạng số là: 1 2333 23333 7 A. . B. . C. . D. . 23 10000 5 10 30
Câu 10. lim  n  5  n 1 bằng: A. 0 . B. 1. C. 5 . D. 3 . 2 2x x  3
Câu 11. Tìm giới hạn hàm số lim
bằng định nghĩa. x 1  x 1 A.  . B. 5 . C. 2 . D. 1. 3 x  8
Câu 12. Giới hạn lim có kết quả là: x2 2  x A. 12 B. 12. C. 8 D. 5
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 13. Giới hạn  2 lim
x  2x x bằng: x  A. 0 B.  C. 1 D. 2
Câu 14. Trong các giới hạn sau, giới hạn nào có kết quả là 0? x 1 2x  5 A. lim B. lim . 3 x 1  x 1
x2 x  10 2 x 1 C. lim D.  2 lim
x 1  x x  2 x 1  x  3x  2
Câu 15. lim  x 1  x  3 bằng x A. 0 . B. 2 . C.  . D.  .  2 2x   1  2 2x x
Câu 16. Giới hạn của hàm số f x 
khi x tiến đến +  có kết quả là:  4
2x x x   1 1 A. 4 B.  . C. 0 D. 4 2
x 1  x x 1 Câu 17. Tính lim . x0 x A. 0 . B. 1. C.  . D. 2 . 4 2 x  5x  4
Câu 18. Tìm giới hạn B  lim : 3 x2 x  8 1 A.  . B.  . C.  . D. 1. 6
Câu 19. Trong các mệnh đề sau mệnh đề nào sai 3 A. lim
x x   x   . B.       .   2 lim x x 1 x 2 xx  2 1 2 2 3x  2 3x  2 C. lim   . D. lim   . x 1  x 1 x 1  x 1 2
 2x  3x 1  khi x  1
Câu 20. Cho hàm số f x   x 1
. Mệnh đề nào sau đây sai? 1  khi x  1 
A. Hàm số gián đoạn tại x  1.
B. Hàm số liên tục tại x 1.
C. Hàm số liên tục tại x  3 .
D. Hàm số liên tục tại x  5  .   x  2 1 , x  1  
Câu 21. Cho hàm số f x 2
 x  3 , x  1 . Tìm k để f x gián đoạn tại x  1 .  2 k , x  1  
A. k  2 .
B. k  2 .
C. k  2 . D. k  1  . 2
x  5x  6  khi x  2 
Câu 22. Biết rằng hàm số f x   x  2
liên tục trên  và n là một số thực tùy ý.  mx n khi x  2 
Giá trị của m (tính theo n ) bằng n n 1 n 1 A. . B. . C. . D. 1. 2 2 2
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021  2x  6 khi x  3   2 3x  27
Câu 23. Cho hàm số f x  
. Mệnh đề nào sau đây là đúng? 1  khi x  3   9
A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc khoảng  3  ;  3 .
B. Hàm số liên tục tại mọi điểm trừ điểm x  3  .
C. Hàm số liên tục tại mọi điểm trừ điểm x  3 .
D. Hàm số liên tục trên  . sin  x neáu cos x  0
Câu 24. Cho hàm số f x  
. Hỏi hàm số f có tất cả bao nhiêu điểm gián 1 cos x neáu cos x  0 
đoạn trên khoảng 0;2018 ? A. 2018 . B. 1009 . C. 542 . D. 321. 3x a 1 khi x  0 
Câu 25. Cho hàm số f x   1 2x 1
. Tìm tất cả giá trị của a để hàm số đã cho liên tục khi x  0   x trên  . A. a  1 . B. a  3 . C. a  2 . D. a  4 .
Câu 26. Trong các mệnh đề sau mệnh đề nào sai?
A. Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thảnh đoạn thẳng.
B. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.
C. Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không thay đổi
thứ tự của ba điểm đó.
D. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường
thẳng song song hoặc cùng nằm trên một đường thẳng.
Câu 27. Trong các khẳng định sau đây, khẳng định nào sai?
A. Nếu giá của ba vectơ cắt nhau từng đôi một thì 3 vectơ đồng phẳng    
B. Nếu ba vectơ a, b, c có một vec tơ 0 thì ba vectơ đồng phẳng   
C. Nếu giá của ba vectơ a, b, c cùng song song với một mật phẳng thì ba vec tơ đó đồng phẳng   
D. Nếu trong ba vectơ a, b, c có ha vec tơ cùng phương thì ba vectơ đó đồng phẳng
Câu 28. Cho hình hộp ' ' ' ' ABC .
D A B C D Gọi I , K lần lượt là tâm của các hình bình hành ' ' ABB A và ' '
BCC B . Khẳng định nào sau đây là sai?
A. Bốn điểm I , K , C, A đồng phẳng    1 1 B. ' ' IK AC A C 2 2
  
C. Ba vec tơ BD, IK , B 'C ' không đồng phẳng   
D. BD  2IK  2BC
Câu 29. Cho hình lập phương AB . CD AB CD
  , góc giữa hai đường thẳng A B  và B C  là A. 90 . B. 60 . C. 30 . D. 45 .
Câu 30. Cho tứ diện đều ABCD cạnh a . Tính cosin góc giữa hai đường thẳng AB và CI , với I là trung điểm của AD . 3 1 3 3 A. . B. . C. . D. . 6 2 4 2
Câu 31. Cho ba đường thẳng a, b, c. Mệnh đề nào sau đây sai?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489  
A. Nếu a//b thì a,c   c,b.
B. Nếu c//b thì a,b   a,c.  
C. Nếu a//c thì a c 0 ,  0 .
D. Nếu a b thì a,c 
 c,b.
Câu 32. Cho ba đường thẳng a, b, c. Khẳng định nào sau đây đúng?
A. Nếu a c và b c thì a//b.
B. Nếu a b và b c thì a  . c
C. Nếu a c và b c thì a b .
D. Nếu a//b và c b thì c a .
Câu 33. Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a .
Gọi M và N lần lượt là trung điểm của AD và SD . Số đo của góc MN , SC  bằng A. 30 . B. 45 . C. 60 . D. 90 .
Câu 34. Cho hình hộp ABC .
D A' B 'C ' D ' . Giả sử tam giác AB 'C và A' DC ' đều có ba góc nhọn. Góc
giữa hai đường thẳng AC và A ' D là góc nào sau đây?    
A. AB 'C .
B. DA 'C ' .
C. BB ' D .
D. BDB ' .
Câu 35. Cho tứ diện đều ABCD có cạnh bằng a, M là trung điểm của cạnh BC. Gọi  là góc giữa hai
đường thẳng AB và DM, khi đó cos bằng 3 2 3 1 A. B. C. D. 6 2 2 2 Phần 2. Tự luận u  2020 1 
Câu 36. Cho dãy số u xác định bởi: . Tìm lim u . n   1 n uu 1 , n  1  n 1   n   2 3 x  3 x 1
Câu 37. Tính các giới hạn sau: lim . 2 x x  4x
Câu 38. Tìm giá trị của m để hàm số f x liên tục tại x  2 . 0 2 3  x  5   f x khi x 2   x  2  2m  3 khi x  2 
Câu 39. Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Tính cos  AB, DM
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 BẢNG ĐÁP ÁN 1.B 2.C 3.C 4.B 5.C 6.C 7.B 8.B 9.D 10.A 11.B 12.A 13.C 14.D 15.A 16.C 17.A 18.D 19.C 20.A 21.A 22.C 23.C 24.D 25.C 26.B 27.A 28.C 29.B 30.A 31.D 32.D 33.D 34.B 35.A
Phần 1. Trắc nghiệm Câu 1.
Dãy số nào sau đây có giới hạn bằng 0? n n n n  5   1   5   4  A.   . B.   . C.    . D.    .  3   3   3   3  Lời giải Chọn B n  1  1 u  Vì  1. n    3  3 n  1 
Áp dụng công thức lim n
q  0 , với q  1 . Nên lim  0   .  3  3 Câu 2.
Giới hạn của dãy số sau đây bằng bao nhiêu. lim n  2 A. 3 . B. 1. C. 0 . D. 2 . Lời giải Chọn A 2  n Câu 3. Giá trị của lim bằng n 1 A. 1. B. 2 . C. 1. D. 0 . Lời giải 2 1 2  n n 0 1 Ta có: lim  lim   1 . n 1 1 1 1 0 n 2 2n  3 Câu 4. lim bằng: 6 5 n  5n 3 A. 2 . B. 0 . C. . D. 3  . 5 Lời giải 2 3  2 2n  3 4 6 n n Ta có lim  lim  0 . 6 5 n  5n 5 1 n Câu 5.
Dãy số nào sau đây có giới hạn khác 0 ? 1 1 n 1 sin n A. . B. . C. . D. . n n n n Lời giải Chọn C n 1 1 Có lim  lim1  lim  1 . n n
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
lim  n 10  n Câu 6. Kết quả là A. 10 . B.  . C. 0 . D. 1  0 . Lời giải Chọn C    n   n n 10 n 10 lim 10  lim  lim  0 . n 10  n n 10  n 1 1 1 Câu 7. Tổng S    ...   ... có giá trị là: 2 3 3 3n 1 1 1 1 A. . B. . C. . D. . 3 2 9 4 Lời giải Chọn B 1 1 1 Ta có S    ...   ... 2 3 3 3n 1 1  3S  1  ...   ... 1 3 3n  1  1  2S  lim 1  1  S    .  3n  2 n 1 1 1   1 1 Câu 8.
Tổng các cấp số nhân vô hạn: 1,  , ,  ,...., ,... là n 1 2 4 8 2  3 2 2 A. . B. . C.. D. 2 . 2 3 3 Lời giải Chọn B n 1 1 1   1 1 Ta có: S  1    ...   ... n 1 2 4 8 2  n 1 1   1 1  2S  2 1   ...   ... 2 4 2n  n 1    n 1  1 1     3S  2   ...  lim 1   2 2n  2n    2  S  . 3 Câu 9.
Số thập phân vô hạn tuần hoàn 0, 233333... biểu diễn dưới dạng số là: 1 2333 23333 7 A. . B. . C. . D. . 23 10000 5 10 30 Lời giải Chọn D
lim  n  5  n 1 Câu 10. bằng: A. 0 . B. 1. C. 5 . D. 3 . Lời giải Chọn A.
n5  n1 n5  n1  4 lim
n  5  n 1  lim  lim  0.
n5  n1
n5  n1
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 2 2x x  3
Câu 11. Tìm giới hạn hàm số lim
bằng định nghĩa. x 1  x 1 A.  . B. 5 . C. 2 . D. 1. Lời giải Chọn B 2 2 2x x  3 2x x  3
Với mọi dãy (x ) : lim x  1 ta có: lim  lim n n
 lim 2x  3  . n  5 n n x 1  x 1 x 1 n 3 x  8
Câu 12. Giới hạn lim có kết quả là: x2 2  x A. 12 B. 12. C. 8 D. 5 Lời giải Chọn A  x  2 2 3 x  2x  4 x 8  lim  lim  12 . x2 x2 2  x 2  x Câu 13. Giới hạn  2 lim
x  2x x bằng: x  A. 0 B.  C. 1 D. 2 Lời giải Chọn C  2  2x 2
lim  x  2x  x  lim  lim  1 . x   x 2 x   2 x 2x x 1   1 x
Câu 14. Trong các giới hạn sau, giới hạn nào có kết quả là 0? x 1 2x  5 A. lim B. lim . 3 x 1  x 1
x2 x  10 2 x 1 C. lim D.  2 lim
x 1  x x  2 x 1  x  3x  2 Lời giải Chọn D 1  2  1 x
lim  x  1  x   lim  lim  0 . x   x 2 x   1 x 1 x 1   1 2 x Câu 15.
lim  x 1  x  3 bằng x A. 0 . B. 2 . C.  . D.  . Lời giải Chọn A
x 1 x  3 4
lim  x 1  x  3  lim  lim  0 . x x
x 1  x  3 x
x 1  x  3  2 2x   1  2 2x x
Câu 16. Giới hạn của hàm số f x 
khi x tiến đến +  có kết quả là:  4
2x x x   1 1 A. 4 B.  . C. 0 D. 4 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489  1  1   2   2x  1  2 2x x 2 2  2      1  x  x
lim f x  lim  lim .  0 x x  4
2x x x   1 x x  1  1  2  1  3     x  x  2 x 1  x  x 1 lim Câu 17. Tính x0 x . A. 0 . B. 1. C. . D. 2 . Lời giải Chọn A      2 x 1  x  x 1 2 2 x 1  x  x 1 x 1 x x 1  lim  lim x0 x0 x x  2 x 1  x  x 1 2 x  lim x 0 x  2 x 1  x  x 1 x  lim  0 x0  2 x 1  x  x 1 4 2 x  5x  4
Câu 18. Tìm giới hạn B  lim : 3 x2 x  8 1 A.  . B.  . C.  . D. 1. 6 Lời giải Chọn D Ta có: 4 2 2 2 x  5x  4
(x 1)(x  4) 2
(x 1)(x  2)(x  2) 2
(x 1)(x  2) B  lim  lim  lim  lim  1. 3 3 3 x2 x2 x  8 x  2 2
x2 (x  2)(x  2x  4) 2 x2 x  2x  4
Câu 19. Trong các mệnh đề sau mệnh đề nào sai 3  A. lim
x x   x   . B.       .   2 lim x x 1 x 2 xx  2 1 2 2 3x  2 3x  2 C. lim   . D. lim   . x 1  x 1 x 1  x 1
Hướng dẫn giải Chọn C 2 2
x x 1 x  4x  4 
+ Với đáp án A ta có: lim
x x   x     x  2 1 2 lim x 2 
x x 1  x  2   3     x 3      3x  3    x   3  lim    lim   A đúng. x 2   
x x 1  x  2 x   1 1 2  2  x  1  1  2   x x x      2 2
x x 1 x  4x  4 
+ Với đáp án B ta có: lim
x x   x     x  2 1 2 lim x 2 
x x 1  x  2 
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021  3     x 3      3x  3    x    3   lim    lim  lim      B đúng. x 2   
x x 1  x  2 x   1 1 2  x  0   x  1  1   2  x x x     
+ Với đáp án C ta có lim  x  
1  0 , x  1  0 với mọi x  1và lim 3x  2  1  0 . x 1  x 1  3x  2 Vậy lim    C sai. x 1  x 1
+ Với đáp án D ta có lim  x  
1  0 , x  1  0 với mọi x  1 và lim 3x  2  1  0 . x 1  x 1  3x  2 Vậy lim    D đúng. x 1  x 1 2
 2x  3x 1  khi x  1
Câu 20. Cho hàm số f x   x 1
. Mệnh đề nào sau đây sai? 1  khi x  1 
A. Hàm số gián đoạn tại x  1.
B. Hàm số liên tục tại x  1.
C. Hàm số liên tục tại x  3 .
D. Hàm số liên tục tại x  5  . Lời giải Chọn A
+) Hàm số đã cho có tập xác định D   . 2 2x  3x 1
+) Với x  1 thì f x 
liên tục trên từng khoảng ; 
1 và 1;  . Do đó hàm số x 1
liên tục tại các điểm x  5
 và x  3 .Suy ra mệnh đề C và D đúng. +) Mặt khác 2 2x  3x 1 2x   1  x   1
lim f x  lim  lim  lim 2x   1  1  f   1 x 1  x 1  x 1  x 1 x 1 x 1 
Do đó hàm số liên tục tại x  1. Suy ra mệnh đề B đúng.
Vậy mệnh đề A sai.   x  2 1 , x  1  
Câu 21. Cho hàm số f x 2
 x  3 , x  1 . Tìm k để f x gián đoạn tại x  1 .  2 k , x  1  
A. k  2 .
B. k  2 .
C. k  2 .
D. k  1. Lời giải Chọn A TXĐ: D   .
Với x  1 ta có: f   2 1  k Với x  1 ta có:
lim f x  lim x
 ; lim f x  lim  x  2 1
 4 suy ra lim f x  4.    2 3 4 x 1  x 1  x 1 x 1   x 1 
Vậy để hàm số gián đoạn tại x  1 khi lim f x 2  k 2
k  4  k  2 . x 1  2
x  5x  6  khi x  2 
Câu 22. Biết rằng hàm số f x   x  2
liên tục trên  và n là một số thực tùy  mx n khi x  2  
ý. Giá trị của m (tính theo n ) bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 n n 1 n 1 A. . B. . C. . D. 1. 2 2 2 Lời giải Chọn C 2 x  5x  6
Ta có lim f x  lim
 lim  x  3  1  .    x2 x 2   x  2 x2
lim f x  lim mx n  2m n .   x   2   x   2   f  2    2  m n .
Để hàm số liên tục tại x  2  thì n 1
lim f x  lim f x  f  2
   2m n  1  m  .   x2 x2 2  2x  6 khi x  3   2 3x  27
Câu 23. Cho hàm số f x  
. Mệnh đề nào sau đây là đúng? 1  khi x  3    9
A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc khoảng  3  ;3 .
B. Hàm số liên tục tại mọi điểm trừ điểm x  3  .
C. Hàm số liên tục tại mọi điểm trừ điểm x  3 .
D. Hàm số liên tục trên  . Lời giải. Chọn C 2x  6
Ta có lim f x  lim
, vì lim2x  6 12  0 và lim  2
3x  27  0 nên hàm số không 2 x3 x3 3x  27 x 3  x3
có giới hạn tại x  3 . Ta loại hai phương án A và. D.
Ta tiếp tục tính giới hạn 2x  6 2  x  3 2 1
lim f x  lim  lim  lim  . 2 x 3  x3 x3 3x  27
3 x  3 x  3 x 3  3 x  3 9 1
Vì lim f x  f  3
    nên hàm số liên tục tại x  3  . x3 9 s  in x neáu cos x  0
Câu 24. Cho hàm số f x  
. Hỏi hàm số f có tất cả bao nhiêu điểm gián 1 cos x neáu cos x  0 
đoạn trên khoảng 0;2018 ? A. 2018 . B. 1009 . C. 542 . D. 321. Lời giải Chọn D
Xét hàm số f x trên đoạn 0; 2 , khi đó:      3  sin x neáu x  0;  ; 2   2   2      
f x     3  1
  cos x neáu x  ;      2 2 
Ta có lim f x  0  f 0 ; lim f x  0  f 2  . x 0  x 2        3   3 
Hàm số rõ ràng liên tục trên các khoảng 0;   ; ;   và ; 2   .  2   2 2   2   Ta xét tại x  : 2
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
lim f x  lim 1 cos x  1; lim f x  lim sin x 1;                 xx     xx      2   2   2   2     f  1   ;  2     
Như vậy lim f x  lim f x  f   nên hàm số f x liên tục tại điểm x  .          2  2 xx      2   2  3 Ta xét tại x  : 2 lim
f x  lim sin x  1
 ; lim f x  lim 1 cos x 1;      3   3   3   3  xx     xx      2   2   2   2  3 Vì lim
f x  lim f x nên hàm số f x gián đoạn tại điểm x  .    3   3  2 xx      2   2  3
Do đó, trên đoạn 0; 2  hàm số chỉ gián đoạn tại điểm x  . 2
Do tính chất tuần hoàn của hàm số y  cos x và y  sin x suy ra hàm số gián đoạn tại các điểm 3 x
k 2 , k   . 2 3 3 1009 3
Ta có x 0;201  8  0 
k 2  2018    k    320, 42 . 2 4  4
Vì k   nên k 0,1, 2,....,32  0 .
Vậy, hàm số f có 321 điểm gián đoạn trên khoảng 0;2018 . 3x a 1 khi x  0 
Câu 25. Cho hàm số f x   1 2x 1
. Tìm tất cả giá trị của a để hàm số đã cho liên tục khi x  0   x trên  . A. a  1 . B. a  3 . C. a  2 . D. a  4 . Lời giải Chọn C
Tập xác định D   .
Ta có: Hàm số liên tục trên các khoảng  ;  0 và 0; .
lim f x  lim 3x a   1  a 1. x 0 x 0   1 2x 1 2
lim f x  lim  lim  1. x 0 x 0 x 0 x     1 2x 1
f 0  a 1.
Hàm số liên tục trên   Hàm số liên tục tại điểm x  0  a 1  1  a  2.
Câu 26. Trong các mệnh đề sau mệnh đề nào sai?
A. Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thảnh đoạn thẳng.
B. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.
C. Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không thay đổi
thứ tự của ba điểm đó.
D. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường
thẳng song song hoặc cùng nằm trên một đường thẳng. Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489
Tính chất của phép chiếu song song.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc
trùng nhau. Suy ra B sai: Chúng có thể trùng nhau.
Câu 27. Trong các khẳng định sau đây, khẳng định nào sai?
A. Nếu giá của ba vectơ cắt nhau từng đôi một thì 3 vectơ đồng phẳng    
B. Nếu ba vectơ a, b, c có một vec tơ 0 thì ba vectơ đồng phẳng   
C. Nếu giá của ba vectơ a, b, c cùng song song với một mật phẳng thì ba vec tơ đó đồng phẳng   
D. Nếu trong ba vectơ a, b, c có ha vec tơ cùng phương thì ba vectơ đó đồng phẳng Lời giải Chọn A
Câu 28. Cho hình hộp ' ' ' ' ABC .
D A B C D Gọi I , K lần lượt là tâm của các hình bình hành ' ' ABB A và ' '
BCC B . Khẳng định nào sau đây là sai?
A. Bốn điểm I , K , C, A đồng phẳng    1 1 B. ' ' IK AC A C 2 2
  
C. Ba vec tơ BD, IK , B 'C ' không đồng phẳng   
D. BD  2IK  2BC Lời giải Chọn C
Câu 29. Cho hình lập phương . ABCD A BCD
  , góc giữa hai đường thẳng A B  và B C  là A. 90 . B. 60 . C. 30 . D. 45 . Lời giải Chọn B C B D A C' B' D' A'  Ta có B C  // A D
  AB B C     A BAD  ; ;  DA B  . Xét DA B  có A D   A B
  BD nên DA B  là tam giác đều. 
Vậy DAB  60 .
Câu 30. Cho tứ diện đều ABCD cạnh a . Tính cosin góc giữa hai đường thẳng AB và CI , với I là trung điểm của AD . 3 1 3 3 A. . B. . C. . D. . 6 2 4 2 Lời giải Chọn A
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 A I M D B C
Gọi M là trung điểm của BD .
Ta có: IM // AB .
  AB, IC    IM , IC  .   
 cos  AB, IC   cos IM , IC   cos IM , IC  cos MIC . 2 2 2 aa 3   a 3            2 2 2
MI IC MC  2  2 2 3 Mà:  cos MIC        . 2.MI.IC a a 3 6 2. . 2 2  3
 cos  AB, IC   cos MIC  . 6
Câu 31. Cho ba đường thẳng a, b, c. Mệnh đề nào sau đây sai?  
A. Nếu a//b thì a,c    , c b.
B. Nếu c//b thì a,b   a,c.  
C. Nếu a//c thì a c 0 ,  0 .
D. Nếu a b thì a,c 
 c,b. Lời giải Chọn D.
Câu 32. Cho ba đường thẳng a, b, c. Khẳng định nào sau đây đúng?
A. Nếu a c và b c thì a//b.
B. Nếu a b và b c thì a  . c
C. Nếu a c và b c thì a b .
D. Nếu a//b và c b thì c a . Lời giải Chọn D
Câu 33. Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a .
Gọi M và N lần lượt là trung điểm của AD và SD . Số đo của góc MN, SC  bằng A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn D.
Gọi O là tâm của hình vuông ABCD O là tâm đường tròn ngoại tiếp của h
S ình vuông ABCD (1).
Ta có: SA SB SC SD S nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2).
Từ (1) và (2)  SO   ABCD . N
Từ giả thiết ta có: MN // SA (do MN là đường trung bình của S
AD ).  MN, SC   S , A SC  . A B 2 2 2 2 2 
SA SC a a  2a Xét SAC , ta có: 
 SAC vuông tại S M SA S OC . 2 2
AC  2 AD  2aD C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489  S ,
A SC    MN, SC   90 .
Câu 34. Cho hình hộp ABC .
D A' B 'C ' D ' . Giả sử tam giác AB 'C và A' DC ' đều có ba góc nhọn. Góc
giữa hai đường thẳng AC và A ' D là góc nào sau đây?    
A. AB 'C .
B. DA 'C ' .
C. BB ' D .
D. BDB ' . Lời giải Chọn B B' C' A' D' B C A D
Ta có AC A 'C ' ( A' B 'CD là hình bình hành) mà DA'C ' nhọn nên
AC A' D   A'C ' A' D  , ,  DA 'C '. .
Câu 35. Cho tứ diện đều ABCD có cạnh bằng a, M là trung điểm của cạnh BC. Gọi  là góc giữa hai
đường thẳng AB và DM, khi đó cos bằng 3 2 3 1 A. B. C. D. 6 2 2 2
Lời giải:
Gọi N là trung điểm của AC
MN là đường trung bình của ABC MN / / AB    1 MN AB   2 Vì BCD và ACD
là các tam giác đều cạnh bằng a a 3
MD ND  . 2 Vì MN
AB     AB DM    MN DM   / / , , Xét MND , ta có:  2 2 2
MN MD ND cos NMD  2MN.MD
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 2 2 2 aa 3   a 3             2  2 2 1 3         0 a a 3 2 3 6 2. . 2 2   NMD    MN DM    90 ,  NMD Vậy  3 cos  cos NMD  . 6
Chọn đáp án A Phần 2. Tự luận u   2020 1 
Câu 36. Cho dãy số u xác định bởi: . Tìm lim u . n   1 n uu 1 , n  1  n 1   n   2 Lời giải 1 1 Ta có uu 1  u 1  u 1 . n 1   nn 1   n  2 2 v  2019 1 
Đặt v u 1 , ta có  1 n   1 . n n v  .vn 1   2 n 1
Suy ra dãy v là một cấp số nhân có số hạng đầu bằng 2019 , công bội bằng nên n  2 n 1   1  v  2019. n   1 . n    2  n 1   1  Suy ra u  2019. 1 n  
1 , do đó lim u  1 . n   n  2  3 x  3 x 1
Câu 37. Tính các giới hạn sau: lim . 2 x x  4x Lời giải  3 1   3 1 3  x 1  1  3  2 3   2 3  x  3 x 1  x x   x x  Ta có   x . 2 x  4x  4  4 2 x 1 1    x x   3 1   3 1  1   1  2 3   2 3   x x   x x
Vì lim x   và lim
 1  0 . Nên lim x   . x x 4 x 4 1 1 x x  3 1  1  3  2 3 x 3 x 1     x x  Vậy lim  lim x   .  2 x x  4 x x  4 1 x
Câu 38. Tìm giá trị của m để hàm số f x liên tục tại x  2 . 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 2 3  x  5   f x khi x 2   x  2  2m  3 khi x  2  Lời giải
Tập xác định: D   , x  2  D và f 2  2m  3 . 0 2 2 3  x  5 4  x   x  2 2
lim f x  lim  lim  lim   . x2 x2 x2 x  2  x  2 2 3 
x  5  x2 2 3 3  x  5 2 11
Hàm số f x liên tục tại x  2 khi lim f x  f 2  2m  3    m   . 0 x2 3 6
Câu 39. Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Tính cos  , AB DM Lời giải A B D M C
Giả sử cạnh của tứ diện là a . a 3
Tam giác BCD đều  DM  . 2 a 3
Tam giác ABC đều  AM  . 2       AB DM AB DM Ta có:  AB DM  . . cos ,
    AB . DM a 3 . a 2
    
    Mặt khác: A .
B DM AB AM AD  . AB AM  . AB AD        
AB . AM .cos  A .
B AM   AB . AD .cos A . B AD    
AB . AM .cos 30  AB . AD .cos 60 2 2 2 a 3 3 1 3a a a  . a .  . a . a    2 2 2 4 2 4    
 cos  AB, DM  3 
   AB, DM  3 0
  AB, DM   os c
AB, DM   . 6 6
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 Đề 3
Đề ôn thi giữa kỳ 1 - Lớp 11
Phần 1. Trắc nghiệm Câu 1.
Dãy số nào sau đây có giới hạn khác 0 . n n 1 1  4    1 A. . B. . C.   . D. . 2n n  3  n Câu 2. Giới hạn  4
lim n  50n 1  1 có kết quả là: A. 1 B. 0 C. 2 D.  4n  2018 Câu 3. Tính giới hạn lim . 2n 1 1 A. . B. 4 . C. 2 . D. 2018 . 2  n 2 sin nCâu 4.
Giới hạn của dãy số u   bằng n 2n 1 A. 1. B. 2 . C. 0 D. 4 . Câu 5.  2 lim
n n 1  n bằng 1 A.  . B. 1. C. 0 . D.  . 2  n 2 1 cos n   1 Câu 6.
Giới hạn của dãy số lim bằng 2 n 1 A. . B. 2 . C. 0 . D. 3 . 3 1 Câu 7. lim bằng 2
n n n A. 0 . B.  . C. 2 . D. 2 . Câu 8. Giới hạn  2 lim
n n n có kết quả bằng: 1 A. 0 B.  . C.  D. 2 n 1 1   1 1 Câu 9. Gọi S    ...  . lim S bằng: 3 9 3n 3 1 1 A. . B. . C. . D. 1. 4 4 2
Câu 10. Cho cấp số nhân u ,u ,... với công bội q thỏa điều kiện q  1 . Lúc đó, ta nói cấp số nhân đã cho 1 2
là lùi vô hạn. Tổng của cấp số nhân đã cho là S u u u ...  u ... bằng: 1 2 3 n n u u q 1 1   u u A. 1 . B. . C. 1 . D. 1 . q 1 q 1 1 q 1 q 2 x  2x 15 Câu 11. Tính lim . x 3  x  3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 1 A.  . B. 2 . C. . D. 8 . 8
Câu 12. Giới hạn của hàm số nào dưới đây có kết quả bằng 1? 2 x  3x  2 2 x  3x  2 A. lim B. lim . x 1  x 1 x 2  x  2 2 x  3x  2 2 x  4x  3 C. lim D. lim x 1  1 x x 1  x 1
Câu 13. Trong các mệnh đề sau mệnh đề nào sai 3 3x  2 A. lim
x x   x    . B. lim   . x  2 1 2 2 x 1  x 1 3x  2 C.       . D. lim   .   2 lim x x 1 x 2 xx 1  x 1
Câu 14. Trong các mệnh đề sau, mệnh đề nào sai? 1 1 1 1 A. lim   . B. lim   . C. lim   . D. lim   .  5 x 0  x x 0  x x0 x x 0  x  2  x  3  khi x  1 2 
Câu 15. Cho hàm số y f xx 1  
. Tính lim f x . 1   x 1  khi x  1  8 1 1 A. . B.  . C. 0 . D.  . 8 8 x
Câu 16. Xác định lim . 2 x0 x A. 0 . B.  . C. Không tồn tại. D.  . 2
x 1  x x 1
Câu 17. Giới hạn lim có kết quả bằng: x0 x A. 0 B. 1. C.  D. 2
Câu 18. Tính I   2 lim
4x  3x 1  2x  ? x 1 3 A. I  .
B. I   . C. I  0 . D. I  . 2 4
Câu 19. Cho đồ thị hàm số y = f (x) như hình vẽ. Xét các mệnh đề sau I. lim f x  2 x
II. lim f x    x 
III. lim f x  2 x 1 
IV. lim f x   x 1 
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Có bao nhiêu mệnh đề đúng? A. 4. B. 3. C. 1. D. 2. 2 3  x khi x  1   2
Câu 20. Cho hàm số f x  
. Khẳng định nào dưới đây là sai? 1  khi x  1   x
A. Hàm số f x liên tục tại x  1 .
B. Hàm số f x có đạo hàm tại x  1 .
C. Hàm số f x liên tục tại x  1 và hàm số f x cũng có đạo hàm tại x  1 .
D. Hàm số f x không có đạo hàm tại x  1. 3
x  7  3x 1  , x  1
Câu 21. Cho hàm số f (x)   x 1
. Tìm a để hàm số liên tục tại x  1. 0 ax, x  1  3 A. -3. B. 2. C. . . D. -2. 2 2
x x  2  khi x  1
Câu 22. Cho hàm số f x   x 1
. Tìm tất cả các giá trị thực của tham số m để hàm số 3
m khi x  1 
gián đoạn tại x  1. A. m  2. B. m  1. C. m  2. D. m  3. 2  x  4  khi x  2
Câu 23. Cho hàm số f x   x  2
. Tìm m để hàm số liên tục tại x  2 . 0 2
m  3m khi x  2 
A. m  0 hoặc m  1.
B. m  1 hoặc m  4  . C. m  4
 hoặc m  1. D. m  0 hoặc m  4  .
 2x 1  x  5  khi x  4  x  4
Câu 24. Tìm a để hàm số f x  
liên tục trên tập xác định.
a  2 x khi x  4   4 5 11
A. a  3 . B. a  . C. a  2 . D. a   . 2 6
 2x  4  3 khi x  2 
Câu 25. Cho hàm số f x   x 1
. Tìm tất cả các giá trị của tham số thực m để khi x  2  2  x  2 x m  3m  2
hàm số liên tục trên  . A. m  3 . B. m  4 . C. m  5 . D. m  6 .
Câu 26. Qua phép chiếu song song lên mặt phẳng (P) , hai đường thẳng a và b có hình chiếu là hai
đường thẳng song song a và b ' . Khi đó:
A. a và b phải song song với nhau
B. a và b phải cắt nhau
C. a và b có thể chéo nhau hoặc song song với nhau
D. a và b không thể song song.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489            
Câu 27. Cho ba vectơ a, b, c không đồng phẳng xét các vectơ x  2a  ;
b y  4a  2 ;
b z  3a  2c Chọn
mênh đề đúng trong các mệnh đề sau:  
A. Hai vec tơ y, z cùng phương   B. Hai vec tơ , x y cùng phương  
C. Hai vec tơ x, z cùng phương   
D. Hai vec tơ x, y, z đồng phẳng
Câu 28. Trong các khẳng định sau đây, khẳng định nào sai?
A. Nếu giá của ba vectơ cắt nhau từng đôi một thì 3 vectơ đồng phẳng    
B. Nếu ba vectơ a, b, c có một vec tơ 0 thì ba vectơ đồng phẳng   
C. Nếu giá của ba vectơ a, b, c cùng song song với một mật phẳng thì ba vec tơ đó đồng phẳng   
D. Nếu trong ba vectơ a, b, c có ha vec tơ cùng phương thì ba vectơ đó đồng phẳng
Câu 29. Cho hình lập phương ABC .
D A B C D . Gọi M là trung điểm của AD . Chọn khẳng định đúng: 1 1 1 1 
   
  1 
A. B M B B B A B C
B. C M C C C D C B 1 1 1 1 1 1 1 1 1 1 1 1 2 
 1  1 
   
C. C M C C C D C B
D. BB B A B C  2B D 1 1 1 1 1 1 2 2 1 1 1 1 1 1
Câu 30. Cho hình lập phương ABC . D AB CD
  . Bộ ba vectơ nào sau đây đồng phẳng?
  
  
  
  
A. BC, AD, AB . B. D C  ,  D D  , AC .
C. CB, CD, CC .
D. AB, AD, AA .
Câu 31. Trong không gian, mệnh đề nào sau đây là mệnh đề đúng?
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
B. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
D. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một đường thẳng cho trước.  
Câu 32. Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AB và EG ? A. 90 . B. 60 . C. 45 . D. 120 .
Câu 33. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a . Gọi I và J lần lượt là trung điểm của
SC và BC . Số đo của góc  IJ ,CD bằng: A. o 30 . B. o 45 . C. o 60 . D. o 90 .
Câu 34. Cho hình chóp S.ABCD, có đáy ABCD là hình vuông tâm O, cạnh bằng a; SA vuông góc với đáy
và SA a 3 . Khi đó, cosin góc giữa SB và AC bằng 2 2 3 3 A. B. C. D. 2 4 2 4
Câu 35. Tứ diện OABC có các cạnh ,
OA OB, OC đôi một vuông góc và đều C
có độ dài là 1. Gọi M là trung điểm cạnh AB . Góc giữa hai vec tơ  
BC và OM bằng A. 0 0 . B. 0 45 . C. 0 90 . D. 0 120 . O B M A
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 Phần 2. Tự luận 2 5 3n n a 3 a Câu 1. Giới hạn lim 
(với a, b là các số nguyên dương và
là phân số tối giản). Tính 23n  2 b b
T a b .  1  Câu 2.
Cho hàm số f (x) xác định với mọi x  0 thỏa mãn f (x)  2 f  3x, x  0   . Tính  x f (x) lim x 2 x  2 Câu 3.
Chứng minh rằng phương trình sau luôn có hai nghiệm trái dấu với mọi
giá trị thực của tham số m : 3
x   m   2 2
1 x  m  2 x  2m  0 Câu 4.
Cho tứ diện ABCD có AC a , BD  3a . Gọi M và N lần lượt là trung điểm của AD và BC .
Biết AC vuông góc với BD . Tính MN .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 BẢNG ĐÁP ÁN 1.C 2.D 3.C 4.C 5.D 6.C 7.D 8.D 9.B 10.D 11.D 12.A 13.B 14 15.B 16.C 17.A 18.D 19.D 20.D 21.C 22.B 23.B 24.D 25 26.C 27.B 28.A 29.B 30.A 31.A 32.C 33.C 34.B 35.D
Phần 1. Trắc nghiệm Câu 1.
Dãy số nào sau đây có giới hạn khác 0 . n n 1 1  4    1 A. . B. . C.   . D. . 2n n  3  n Lời giải Chọn B Câu 2. Giới hạn  4
lim n  50n 1  1 có kết quả là: A. 1 B. 0 C. 2 D.  Lời giải Chọn D 4 4  50 11 
Ta có lim n  50n  11  lim n 1      2   n n  4n  2018 Câu 3. Tính giới hạn lim . 2n 1 1 A. . B. 4 . C. 2 . D. 2018 . 2 Lời giải 2018 4  4n  2018 n Ta có lim  lim  2 . 2n 1 1 2  nn 2 sin nCâu 4.
Giới hạn của dãy số u   bằng n 2n 1 A. 1. B. 2 . C. 0 D. 4 . Lời giải Chọn C n n n 2 n  2 n  2 nn 2 sin sin sin  sin n  Ta có:       2n 1 2n 1 2n 2   n 2 sin n 2  sin n  Vì  1 (do 2
0  sin n  1 ) nên lim  0  
. Suy ra: lim u  0 . 2 2 n   Vậy lim u  0 . n  2 lim
n n 1  nCâu 5. bằng 1 A.  . B. 1. C. 0 . D.  . 2 Lời giải Chọn C
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
 2n n 1 n 2n n 1  n 2 
Ta có: lim  n n 1  n  lim 2
n n  1  nn  1 1  lim   1 1 2 n 1    n 2 n n  n 2 1 cos n   1 Câu 6.
Giới hạn của dãy số lim bằng 2 n 1 A. . B. 2 . C. 0 . D. 3 . 3 Lời giải Chọn C n 2 n 1   1 cos n   1 1 Ta cos :     2 1 1 cos n   1  1    2 2 2 n n n n 1 1   2 1 cos n   1 Mà lim  0 , lim  0 nên lim  0 . 2 n 2 n 2 n 1 lim 2 Câu 7.
n n n bằng A. 0 . B.  . C. 2 . D. 2 . Lời giải Chọn D 2 1
n n n Ta có: lim  lim 2
n n n
 2n n n 2n n n 1 n 1   n n  1   lim  lim 1   1  2   n n   Câu 8. Giới hạn  2 lim
n n n có kết quả bằng: 1 A. 0 B.  . C.  D. 2 Lời giải Chọn D
 2n n n 2n n n 2 2 2 
n n n n
lim  n n n  lim  lim  lim
 2n n n
 2n n n 2
n n n 1 1  lim  1 2 1 1 n n 1 1   1 1 Câu 9. Gọi S    ...  . lim S bằng: 3 9 3n 3 1 1 A. . B. . C. . D. 1. 4 4 2 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 n 1 1   1 1 Ta có: S    ...  . 3 9 3n n 1 1 1   1 1  3S  1    ...  n 1  3 9 27 3  n 1  nn 1   1 1 1  1   4S  1  S   .  3n 4 4  3 
Câu 10. Cho cấp số nhân u ,u ,... với công bội q thỏa điều kiện q  1 . Lúc đó, ta nói cấp số nhân đã cho 1 2
là lùi vô hạn. Tổng của cấp số nhân đã cho là S u u u ... u ... bằng: 1 2 3 n n u u q 1 1   u u A. 1 . B. . C. 1 . D. 1 . q 1 q 1 1  q 1  q Lời giải Chọn D
Theo định nghĩa cấp số nhân lùi vô hạn ta chứng minh được  u 1 2 n 1 1
S u u u  ...  u  ...  u  u q u q  ...  u q  ...  . 1 2 3 n 1 1 1 1 1 q 2 x  2x 15 lim Câu 11. Tính x3 x  3 . 1 A.  . B. 2 . C. . D. 8 . 8 Lời giải Chọn D 2 x  2x 15 x  3x  5 lim  lim  lim  x  5  8 x 3 x 3 x3 x  3 x  3
Câu 12. Giới hạn của hàm số nào dưới đây có kết quả bằng 1? 2 x  3x  2 2 x  3x  2 A. lim B. lim . x 1  x 1 x 2  x  2 2 x  3x  2 2 x  4x  3 C. lim D. lim x 1  1 x x1 x 1 Lời giải Chọn B 2 x  3x  2  x   1  x  2 lim  lim
 lim  x  2  1 x 1  x 1  x 1 x 1 x 1 
Câu 13. Trong các mệnh đề sau mệnh đề nào sai 3 3x  2 A. lim
x x   x    . B. lim   . x  2 1 2 2 x 1  x 1 3x  2 C.       . D. lim   .   2 lim x x 1 x 2 xx 1  x 1
Hướng dẫn giải Chọn B
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 Ta có:
x x 1  x  22 2 3x  3      lim  lim   2 lim x x 1 x 2 x
x 2x x1x2 x 2x x1x2 3 3  3  lim x  
 đáp án A đúng. x 1 1 2 2  1  1 2 x x x   lim
x x   x   x       . x  1 1 2 2 1 2 lim 1 1 2 x  x x x     1 1 2   1 1 2 
Do lim x   và lim  1  1
  2  0 nên lim x  1  1     x 2 x  x x x  2     x x x x   đáp án C đúng. 3x  2
Do lim 3x  2  1  0 và x 1  0 với x  1 nên lim
   đáp án B sai. x 1  x 1  x 1 3x  2
Do lim 3x  2  1
  0 và x  1  0 với x  1 nên lim
   đáp án D đúng. x 1  x 1  x 1
Câu 14. Trong các mệnh đề sau, mệnh đề nào sai? 1 1 1 1 A. lim   . B. lim   . C. lim   . D. lim   .  5 x 0  x x 0  x x0 x x 0  x Lời giải Chọn B 1 Ta có: lim
  do lim x  0 và x  0 . Vậy đáp án A đúng. x 0  x x 0  Suy ra đáp án B sai.
Các đáp án C và D đúng. Giải thích tương tự đáp án A.
 2  x  3 khi x 1  2 
Câu 15. Cho hàm số y f xx 1  
. Tính lim f x . 1   x 1  khi x  1  8 1 1 A. . B.  . C. 0 . D.  . 8 8 Lời giải Chọn B 2  x  3 4  x  3 1 
Ta có lim f x  lim  lim  lim     2 x 1 x 1 x 1 x 1   x   1  x  
1 2  x  3 x 1      x   1 2  x  3 x lim 2
Câu 16. Xác định x0 x . A. 0 . B.  . C. Không tồn tại. D.  . Lời giải Chọn C x x 1 Ta có lim  lim  lim   .  2  2 x 0 x 0 x 0    x x x xx 1  lim  lim  lim   .  2  2 x 0 x 0 x 0    x x x x Vậy không tồn tại lim . 2 x0 x
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 2
x 1  x x 1
Câu 17. Giới hạn lim có kết quả bằng: x0 x A. 0 B. 1. C.  D. 2 Lời giải Chọn A x x x  2 2
x 1 x x       2 1 1 1 x lim  lim  lim x0 x0 x x  2
x 1  x x 1 x0 x 2
x 1  x x 1 x  lim  0 x0  2 x 1  x x 1 I
x x   x x  2 lim 4 3 1 2 ? Câu 18. Tính 1 3 A. I  .
B. I   . C. I  0 . D. I  . 2 4 Lời giải Chọn D
Phương pháp: Khử dạng vô định:  3x 1
- Trục căn thức f x 2 
4x  3x 1  2x  2
4x  3x 1  2x
- Chia cả tử và mẫu của f x cho x rồi cho x   Cách giải: 2 2
4x  3x 1  2x 4x  3x 1  2x 2 lim
4x  3x 1  2x  lim x x 2
4x  3x 1  2x 1 2 2 3 
4x  3x 1 2x 3x 1 3 3 lim  lim  lim x   . x 2 x 2
4x  3x 1  2x
4x  3x 1  2 x x 3 1 4  2 4 4    2 2 x x
Câu 19. Cho đồ thị hàm số y = f (x) như hình vẽ. Xét các mệnh đề sau I. lim f x  2 x
II. lim f x    x 
III. lim f x  2 x 1 
IV. lim f x   x 1 
Có bao nhiêu mệnh đề đúng? A. 4. B. 3. C. 1. D. 2. Lời giải Đáp án D
Mệnh đề lim f  x   2 đúng. Mệnh đề lim f x    sai x x
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Mệnh đề lim f x   2 sai. Mệnh đề lim f x    đúng x 1  x1
Vậy có 2 mênh đề đúng. 2 3  x khi x  1   2
Câu 20. Cho hàm số f x  
. Khẳng định nào dưới đây là sai? 1  khi x  1   x
A. Hàm số f x liên tục tại x  1 .
B. Hàm số f x có đạo hàm tại x  1 .
C. Hàm số f x liên tục tại x  1 và hàm số f x cũng có đạo hàm tại x  1 .
D. Hàm số f x không có đạo hàm tại x  1. Lời giải Chọn D 2 3  x 1
+) lim f x  lim
 1 và lim f x  lim
 1. Do đó, hàm số f x liên tục tại x  1 . x 1 x 1   2 x 1 x 1   x Vậy A. đúng
f x  f   2 1 1 x 1 x +) lim  lim  lim  1  và x 1 x 1 x 1  2  x   x 1 1     2
f x  f   1 1 x 1 lim  lim  lim
 1. Do đó, hàm số f x có đạo hàm tại x  1 . x 1 x 1 x 1
x x   x 1 1     x Vậy B đúng
Từ đó thấy C đúng và D sai 3
x  7  3x 1  , x  1
Câu 21. Cho hàm số f (x)   x 1
. Tìm a để hàm số liên tục tại x  1. 0 ax, x  1  3 A. -3. B. 2. C. . . D. -2. 2 Lời giải Chọn C 3 3
x  7  3x 1  x  7  2 2  3x 1 
lim f x  lim  lim    x 1  x 1  x 1 x 1   x 1 x 1          x 1 3 x   1   lim    2 x 1   x x
  x    3 x   3   x      1 2  3 1 1 7 2. 7 4            1 3  3  lim    . x     x  7 2 1 3 3 2  3x 1 2  2. x  7  4    3
Hàm số liên tục tại x  1  lim f x f 1  a   . 0     x 1  2 2
x x  2  khi x  1
Câu 22. Cho hàm số f x   x 1
. Tìm tất cả các giá trị thực của tham số m để hàm số 3
m khi x  1 
gián đoạn tại x  1. A. m  2. B. m  1. C. m  2. D. m  3.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn B
Tập xác định của hàm số là  . 2 x x  2
Hàm số gián đoạn tại x  1 khi lim f x  f   1  lim  3m x 1  x 1  x 1  x   1  x  2  lim
 3m  lim  x  2  3m  3  3m m  1. x 1  x 1 x 1  2  x  4  khi x  2
Câu 23. Cho hàm số f x   x  2
. Tìm m để hàm số liên tục tại x  2 . 0 2
m  3m khi x  2 
A. m  0 hoặc m  1.
B. m  1 hoặc m  4  . C. m  4
 hoặc m  1. D. m  0 hoặc m  4  . Lời giải Chọn B
Tập xác định D   . 2 x  4
Ta có lim f x  lim
 lim x  2  2  2  4 . x2 x2 x  2 x 2 
Hàm số đã cho liên tục tại x  2 khi và chỉ khi lim f x  f 2 0 x2 m  1 2
 4  m  3m 2
m  3m  4  0   . m  4 
 2x 1  x  5 khi x  4   x  4
Câu 24. Tìm a để hàm số f x  
liên tục trên tập xác định.
a  2 x khi x  4   4 5 11
A. a  3 . B. a  . C. a  2 . D. a   . 2 6 Lời giải Chọn D * TXĐ: D   .
NX: Hàm số f x liên tục trên các khoảng  ;  4 và 4; 
Do đó, để hàm số liên tục trên  ta cần tìm a để hàm số liên tục tại x  4
ĐK: lim f x  lim f x  f 4 x 4 x 4  
 2x 1 x 5 2x 1 x 5 1 1
lim f x  lim  lim  x 4 x 4
x  4 2x 1  x  5 x 4    2x 1  x  5 6 a  2 x
lim f x  lim
a  2  f 4 x 4  x 4  4 1 11 Cần có: a  2   a   . 6 6
 2x  4  3 khi x  2 
Câu 25. Cho hàm số f x   x 1
. Tìm tất cả các giá trị của tham số thực m để khi x  2  2
x  2mx  3m  2
hàm số liên tục trên  . A. m  3 . B. m  4 . C. m  5 . D. m  6 . Lời giải Chọn C.
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Cách 1: Hàm số xác định trên  , liên tục trên khoảng 2;  .
Ta có. f 2  3; lim f x  lim       2x 4 3 3 x2 x2 x 1
Nếu m  6 thì lim f x  lim
  nên hàm số không liên tục tại x  2 .   2 x2 x2 x 12x  20 x 1 3
Nếu m  6 thì ta có lim f x  lim  .   2 x2 x2 x  2 x m  3m  2 6  m 3
Để hàm số liên tục tại x  2 thì
 3  6  m  1  m  5 . 6  m x 1
Với m  5 thì khi x  2 f x   ;  2 . 2 liên tục trên   x 10x 17
Tóm lại với m  5 thì hàm số đã cho liên tục trên  .
Câu 26. Qua phép chiếu song song lên mặt phẳng (P) , hai đường thẳng a và b có hình chiếu là hai
đường thẳng song song a và b ' . Khi đó:
A. a và b phải song song với nhau
B. a và b phải cắt nhau
C. a và b có thể chéo nhau hoặc song song với nhau
D. a và b không thể song song. Lời giải Chọn C
Nếu a // b’  mặt phẳng ( a , a ) // mặt phẳng ( b , b ' )
Khi đó a và b có thể song song hoặc chéo nhau.            
Câu 27. Cho ba vectơ a, b, c không đồng phẳng xét các vectơ x  2a b; y  4a  2 ;
b z  3a  2c Chọn
mênh đề đúng trong các mệnh đề sau:  
A. Hai vec tơ y, z cùng phương   B. Hai vec tơ , x y cùng phương  
C. Hai vec tơ x, z cùng phương   
D. Hai vec tơ x, y, z đồng phẳng Lời giải Chọn B     Ta thấy y  2  x nên , x y cùng phương.
Câu 28. Trong các khẳng định sau đây, khẳng định nào sai?
A. Nếu giá của ba vectơ cắt nhau từng đôi một thì 3 vectơ đồng phẳng    
B. Nếu ba vectơ a, b, c có một vec tơ 0 thì ba vectơ đồng phẳng   
C. Nếu giá của ba vectơ a, b, c cùng song song với một mật phẳng thì ba vec tơ đó đồng phẳng   
D. Nếu trong ba vectơ a, b, c có ha vec tơ cùng phương thì ba vectơ đó đồng phẳng Lời giải Chọn A
Câu 29. Cho hình lập phương ABC .
D A B C D . Gọi M là trung điểm của AD . Chọn khẳng định đúng: 1 1 1 1 
   
  1 
A. B M B B B A B C
B. C M C C C D C B 1 1 1 1 1 1 1 1 1 1 1 1 2 
 1  1 
   
C. C M C C C D C B
D. BB B A B C  2B D 1 1 1 1 1 1 2 2 1 1 1 1 1 1 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 A a B a M D C A1 B1 D1 C1 
  
  1 
Ta có C M C D  D D  DM C D C C C B 1 1 1 1 1 1 1 1 1 2
Câu 30. Cho hình lập phương ABC . D AB CD
  . Bộ ba vectơ nào sau đây đồng phẳng?
  
  
  
  
A. BC, AD, AB . B. D C  ,  D D  , AC .
C. CB, CD, CC .
D. AB, AD, AA .
Hướng dẫn giải Chọn A Từ hình vẽ bên
ta thấy   
AB //  ABCD và BC, AD   ABCD nên BC, AD, AB đồng phẳng.
  
AC   ABCD , D C
 //  ABCD , DD   ABCD  D C  , D D
 , AC không đồng phẳng.
  
CB,CD   ABCD ,CC   ABCD  CB, CD, CC không đồng phẳng.
  
AB, AD   ABCD , AA   ABCD  AB, AD, AA không đồng phẳng.
Câu 31. Trong không gian, mệnh đề nào sau đây là mệnh đề đúng?
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
B. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
D. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một đường thẳng cho trước.  
Câu 32. Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AB và EG ? A. 90 . B. 60 . C. 45 . D. 120 . Lời giải Chọn C
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 E H F G A D B C
Ta có: EG//AC (do ACGE là hình chữ nhật)    
  AB EG   AB AC  , ,  BAC  45 .
Câu 33. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a . Gọi I và J lần lượt là trung điểm của
SC và BC . Số đo của góc  IJ ,CD bằng: A. o 30 . B. o 45 . C. o 60 . D. o 90 . Lời giải Chọn C
Vì IJ / /SB nên  IJ SC    SB SC  o , ,  60 (do SBC đều).
Câu 34. Cho hình chóp S.ABCD, có đáy ABCD là hình vuông tâm O, cạnh bằng a; SA vuông góc với đáy
và SA a 3 . Khi đó, cosin góc giữa SB và AC bằng 2 2 3 3 A. B. C. D. 2 4 2 4
Lời giải
Gọi I là trung điểm của SD
OI là đường trung bình của SBD
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 OI / /SB  2 2 2 2   SB SA AB 3a a OI     a  2 2 2 Vì OI
SB  SB AC   OI AC   / / , ,  AOI 2 2 2 2 SD SA AD 3a a Ta có: AI     a 2 2 2
AI OI A
OI cân tại I.
Gọi H là trung điểm của OA IH OA OA AC a 2 Và OH    2 4 4 a 2  OH 2 Xét OHI , ta có: 4 cos HOI    OI a 4 Vậy SB AC    2 cos ,  cos HOI  . 4
Chọn đáp án B
Câu 35. Tứ diện OABC có các cạnh ,
OA OB, OC đôi một vuông góc và đều C
có độ dài là 1. Gọi M là trung điểm cạnh AB . Góc giữa hai vec tơ  
BC và OM bằng A. 0 0 . B. 0 45 . C. 0 90 . D. 0 120 . Lời giải O Chọn D B  
Loại phương án A vì hai véc tơ OM và BC không cùng phương; M  
Loại phương án B vì góc giữa hai véc tơ OM và BC không thể nhọn.   A
Loại đáp án C vì hai véc tơ OM và BC không vuông góc với nhau.     OM BC  
Vậy phương án D đúng vì: OM BC . cos ,   OM .BC 2 . 2 2   1     1
Mà: OM .BC  OAOBOC OB  . 2 2   Suy ra: OM BC 0 , 120 . Phần 2. Tự luận 2 5 3n n a 3 a Câu 1. Giới hạn lim 
(với a, b là các số nguyên dương và
là phân số tối giản). Tính 2 3n  2 b b
T a b . Lời giải  1  n 5 3   2 5 3n n n   5 3 a  5 lim  lim    2 3n  2  4  6 b  6 n 6      n
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Khi đó T a b  11.  1  Câu 2.
Cho hàm số f (x) xác định với mọi x  0 thỏa mãn f (x)  2 f  3x, x  0   . Tính  x f (x) lim x 2 x  2 Lời giải  1 
Ta có f (x)  2 f  3x, x  0     1  x   1  3  f  2 f (x)  , x  0   2  x x   1    1 
f (x)  2 f  3x
f (x)  2 f  3x         x    x  2   1 , 2    
f (x)  x   1  3  1  6 xf 2 f (x)    2 f  4 f (x)       x x       x x 2 x f (x)
(x  2)(x  2) (x  2) Do đó lim  lim x  lim  lim  2 . x 2 x 2 x 2 x 2 x  2 x  2 x(x  2) x Câu 3.
Chứng minh rằng phương trình sau luôn có hai nghiệm trái dấu với mọi
giá trị thực của tham số m : 3
x   m   2 2
1 x  m  2 x  2m  0 Lời giải
Đặt f x 3
x   m   2 2
1 x  m  2 x  2m . x  0 
Với m  0 thì f x 3 2
x x  2x f x 3 2
 0  x x  2x  0  x  1.  x  2 
Khi này, phương trình luôn có hai nghiệm trái dấu là x  1, x  2 với m  0   1 .
Với m  0 , ta thấy f 0  2
m ; f  
1  m ; f 2  4m .
Nhận thấy f   f   2 1 . 0  2
m  0 với mọi m  0 và f   f   2 0 . 2  8
m  0 với mọi m  0 .
Mà f x là hàm đa thức bậc ba nên f x liên tục trên  . Suy ra f x liên tục trên các đoạn  1  ;0 và 0; 2 .
Khi đó luôn tồn tại x  1
 ;0 và x  0; 2 sao cho f x  0, f x  0 . Hay phương trình 1   2  2   1  
f x  0 luôn có hai nghiệm trái dấu với mọi m  0 2 . Từ  
1 và 2 suy ra phương trình f x  0 luôn có hai nghiệm trái dấu với mọi số thực m .
Suy ra điều phải chứng minh. Câu 4.
Cho tứ diện ABCD có AC a , BD  3a . Gọi M và N lần lượt là trung điểm của AD và BC .
Biết AC vuông góc với BD . Tính MN . Lời giải
Gọi E , F lần lượt là trung điểm của AB và CD . EN // AC Ta có: A
  AC, BD   NE, NF   90  NE NF (1). NF // BDM E C D F
Facebook Nguyễn Vương https://www.facebook.com/ph N ong.baovuongTrang 17 B
NGUYỄN BẢO VƯƠNG - 0946798489  1 NE FM AC   2 Mà:  (2). 1
NF ME BD   2
Từ (1), (2)  MENF là hình chữ nhật. 2 2 2 2  AC   BD   a   3a a 10 Từ đó ta có: 2 2 MN NE NF              .  2   2   2   2  2
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 Đề 4
Đề ôn thi giữa kỳ 1 - Lớp 11
Phần 1. Trắc nghiệm Câu 1.
Dãy số nào sau đây có giới hạn bằng 0 . n n n n A. 0,909 . B.  1  , 012 . C. 1, 013 . D.  1  ,90  1 . 2 2n 1 Câu 2.
Giới hạn của dãy số sau đây bằng bao nhiêu. lim 3 n  3n  3 1 A. . B. 2 . C. 0 D. 1  . 3  1 1 1 1  Câu 3. Tính giới hạn lim     ...   . 1.2 2.3 3.4 n n   1   3 A. 0 . B. 2 . C. 1. D. . 2 Câu 4.  2 lim
n  2n 1  n bằng 1 A.  . B. 1. C. 0 . D.  . 2 Câu 5.
Số thập phân vô hạn tuần hoàn 0, 511111... được biểu diễn bởi phân số 47 46 6 43 A. . B. . C. . D. . 90 90 11 90 n 1 1 1   1 1 Câu 6.
Tổng của cấp số nhân lùi vô hạn ,  , ,...., ,.... là? 3 9 27 3n 1 3 1 A. 4 . B. . C. . D. . 2 4 4 Câu 7. n  2 2 lim
n 1  n  2  bằng: 1 1 3 A.  . B. . C. . D. 1. 2 2 2 Câu 8. Giới hạn  2 2 lim
n  2n  28  n  4n  5  có kết quả bằng: A. 0 B.  C. 3 D.  Câu 9.  2 2 lim
n  2n n  2n  có kết quả là A. 4 . B. 2 . C. 1. D.  . 1 1 1
Câu 10. Tính S  9  3 1   ...   ... Kết quả là: 3 3 9 3n 27 A. . B. 14. C. 16 . D. 15 . 2
1 x x 1
Câu 11. Giới hạn lim có kết quả là: x 1  2 3 x x A. 1 B. 1 C. 2 D. 2 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 2 x  3x  2
Câu 12. Giới hạn lim có kết quả là: x    1 x 1 A. 1 B.  . C.  D. 1
Câu 13. Trong các mệnh đề sau, mệnh đề nào sai? 1 1 1 1 A. lim   . B. lim   . C. lim   . D. lim   .  5  x 0  x x 0  x x0 x x0 x 2 4x 1
Câu 14. Tính giới hạn K  lim . x x 1 A. K  0 . B. K 1. C. K  2  . D. K  4 . x 1 Câu 15. Tính lim . 2018 x x 1 A. 1. B. 1. C. 2 . D. 0 .
Câu 16. Trong các mệnh đề sau mệnh đề nào sai 3  A. lim
x x   x   . B.       .   2 lim x x 1 x 2 xx  2 1 2 2 3x  2 3x  2 C. lim   . D. lim   . x 1  x 1 x 1  x 1
2x m khi x  0 
Câu 17. Cho hàm số f x   1 4x 1
. Tìm tất cả các giá trị của m để tồn tại giới hạn khi x  0   x
lim f x . x0 A. m  2 . B. m  1. C. m  3 . D. m  1. 2 x  4x  4 Câu 18. Tìm lim . x2 x  2 A. Không tồn tại. B. 1. C. 1. D. 1. 2x  3
Câu 19. Tìm giới hạn lim :
x 1  3x 2 2 3 A. . B.  . C.  . D. 2 . 3 3 2
Câu 20. Hàm số nào dưới đây liên tục trên khoảng  ;   ? 1 1 1 A. y  . B. y  . C. y x 1 . D. 2 y   x . x 1 2 x 1 x 2  x  2x  khi x  2
Câu 21. Tìm tất cả các giá trị của tham số m để hàm số f x   x  2
liên tục tại x  2. mx  4 khi x  2  A. m  1.
B. Không tồn tại m . C. m  3 . D. m  2  . 2
x 1 khi x  1
Câu 22. Hàm số f x  
liên tục tại điểm x  1 khi m nhận giá trị 0
x m khi x  1  A. m  1. B. m  2 .
C. m bất kỳ. D. m  1. 2
x  3x  2 khi x  1 
Câu 23. Để hàm số y  
liên tục tại điểm x  1
 thì giá trị của a là 4x a khi x  1  A. 4 . B. 1. C. 1  . D. 4  .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
ax b 1, khi x  0
Câu 24. Hàm số f (x)  
liên tục trên  khi và chỉ khi
a cos x b sin x, khi x  0 
A. a b  1.
B. a b  1.
C. a b  1
D. a b  1 2
x ax b  khi x  1
Câu 25. Cho a , b là hai số thực sao cho hàm số f x   x 1
liên tục trên  . Tính 2ax 1 khi x  1  a b . A. 0 . B. 1  . C. 5 . D. 7 .
Câu 26. Qua phép chiếu song song lên mặt phẳng (P) , hai đường thẳng chéo nhau a và b có hình chiếu
là 2 đường thẳng a và b ' . Mệnh đề nào sau đây đúng:
A. a và b ' luôn cắt nhau
B. a và b ' có thể trùng nhau
C. a và b ' không thể song song
D. a và b ' có thể cắt nhau hoặc song song với nhau.
Câu 27. Trong các mệnh đề sau đây mệnh đề nào sai?
    
A. Nếu AB BC CD DA  0 thì bốn điểm ,
A B, C, D đồng phẳng   
B. Tam giác ABC có I là trung điểm cạnh BC thì ta có đẳng thức: 2AI AB AC   
C. Vì BA BC  0 nên suy ra B là trung điểm của AC    D. Vì AB  2
AC  3AD nên 4 điểm ,
A B, C, D đồng phẳng.
Câu 28. Cho tứ diện ABCD có AB , AC , AD đôi một vuông góc với nhau, biết AB AC AD  1 . Số
đo góc giữa hai đường thẳng AB và CD bằng A. 45 . B. 60 . C. 30 . D. 90 .  
   
Câu 29. Cho hình lập phương AB .
CD A B C D , đặt   ( AC, DC );   (DA , BB );   ( AA , C C) Khi 1 1 1 1 1 1 1 1 1
đó: là     : A. 3600 B. 3750 C. 3150 D. 2750    
Câu 30. Cho hình lăng trụ tam giác AB .
C A B C . Đặt AA  a; AB  ; b AC  ;
c BC d trong các đẳng 1 1 1 1 1
thức sau đẳng thức nào đúng.         
A. a b c d  0
B. a b c d       
C. b c d  0
D. a b c
Câu 31. Mệnh đề nào sau đây là đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song
với đường thẳng còn lại.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
Câu 32. Cho hình lập phương ABC .
D A B C D . Góc giữa AC và DA là 1 1 1 1 1 A. 45 . B. 90 . C. 60 . D. 120 .  
Câu 33. Cho hình lập phương AB .
CD EFGH . Hãy xác định góc giữa cặp vectơ AB và EG ? A. 0 90 . B. 0 60 . C. 0 45 . D. 0 120 . a 3
Câu 34. Cho tứ diện ABCD có AB CD a , IJ
( I , J lần lượt là trung điểm của BC và AD ). 2
Số đo góc giữa hai đường thẳng AB và CD là A. 30 . B. 45 . C. 60 . D. 90 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 35. Cho tứ diện đều ABCD (Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa hai đường thẳng
AB và CD bằng A. 30 . B. 45 . C. 60 . D. 90 . Phần 2. Tự luận 2 2
n  4n  4n 1 6  3 a a Câu 1. Biết lim   , trong đó
là phân số tối giản, a và b là các số 2 2 3 1 b nn b nguyên dương. Tính . a b Tính giới hạn sau: x lim Câu 2. x0 1 x  1 xx  5 1 h k i x  1  Câu 3. Cho hàm số 3 2
f ( x)   x x aax 1
. Tìm a để hàm số liên tục tại x  1  khi x  1    x 1 Câu 4.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , SA a . SA vuông góc với mặt
đáy. Gọi M , N lần lượt là trung điểm của các cạnh AB, BC . Tính côsin của góc giữa hai đường
thẳng SM , DN .
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 BẢNG ĐÁP ÁN 1.A 2.C 3.C 4.B 5.B 6.D 7.C 8.C 9.B 10.A 11.B 12.A 13.B 14.C 15.D 16.C 17.A 18.A 19.B 20.B 21.C 22.D 23.A 24.A 25.D 26.D 27.A 28.D 29.B 30.C 31.D 32.C 33.C 34.C 35.D
Phần 1. Trắc nghiệm Câu 1.
Dãy số nào sau đây có giới hạn bằng 0 . n n n n A. 0,909 . B.  1  , 012 . C. 1, 013 . D.  1  ,90  1 . Lời giải Chọn A
Áp dụng công thức lim n
q  0 , với q  1 . 2 2n 1 Câu 2.
Giới hạn của dãy số sau đây bằng bao nhiêu. lim 3 n  3n  3 1 A. . B. 2 . C. 0 D. 1  . 3 Lời giải Chọn C 2 2n 1 2 1  2 1  lim  2  2n 1   3 3 3  n n  0 lim  lim n  lim n n    0 . 3 n  3n  3 3 n  3n  3 3 3  3 3  1 1  lim 1  3 2 3   n n n 2 3  n n   1 1 1 1  Câu 3. Tính giới hạn lim     ...   . 1.2 2.3 3.4 n n   1   3 A. 0 . B. 2 . C. 1. D. . 2 Lời giải 1 1 1 1 1 1 1 1 1 1 1 1 Ta có:    ...       1      1 . 1.2 2.3 3.4 n n   1 1 2 2 3 n 1 n n n 1 n 1  1 1 1 1   1  Vậy lim     ...    lim 1  1   . 1.2 2.3 3.4 n n   1    n 1   2 lim
n  2n 1  nCâu 4. bằng 1 A.  . B. 1. C. 0 . D.  . 2 Lời giải Chọn C
 2n 2n1n 2n 2n1 n 2 
Ta có: lim  n  2n 1  n  lim 2
n  2n 1  n 2n 1  lim  1 2 1 1   1 2 n n Câu 5.
Số thập phân vô hạn tuần hoàn 0, 511111... được biểu diễn bởi phân số
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 47 46 6 43 A. . B. . C. . D. . 90 90 11 90 Lời giải Chọn D Ta có
0, 51111...  0, 5  0, 01 0, 001 0, 0001 ... 1 1 1 1 1  1 1  1 1 1 23 46     ...   1   ...   .    . 2  2 100 1000 2 100  10 10  2 100 1 45 90 1 10 n 1 1 1   1 1 Câu 6.
Tổng của cấp số nhân lùi vô hạn ,  , ,...., ,.... là? 3 9 27 3n 1 3 1 A. 4 . B. . C. . D. . 2 4 4 Lời giải Chọn D 1 1
Cấp số nhân có u  , q   1
. Do đó tổng cần tìm là 3 3 1 u 1 3 1 1 3 S    .  . 1 q 1 3 4 4 1 3 n  2 2 lim
n 1  n  2  Câu 7. bằng: 1 1 3 A.  . B. . C. . D. 1. 2 2 2 Lời giải Chọn C. n 1 n 2 . n 1 n 2 n 1 n 2 2 2
 2   2    2   2   2 2
lim n n 1  n  2       lim n  lim n
 2n 1 2n 2
 2n 1 2n 2 3n 3 3  lim  lim  . 2 2 2 2 2 n 1 n 2 n 1 n 2 n   n     2 2 2 2 2 2 2 2 n n n n n n n n Câu 8. Giới hạn  2 2 lim
n  2n  28  n  4n  5 có kết quả bằng: A. 0 B.  C. 3 D.  Lời giải Chọn C n  lim  6 23 2 2
n  2n  28  n  4n  5   lim  2 2
n  2n  28  n  4n  5  23 6   lim n  3 2 4 5 1  28  1  2 n n n  2 2 lim
n  2n n  2n Câu 9. có kết quả là
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 A. 4 . B. 2 . C. 1. D.  . Lời giải Chọn B 4n 4 Ta có  2 2 lim
n  2n n  2n   lim  lim  2 . 2 2
n  2n n  2n 2 2 1   1  n n 1 1 1
Câu 10. Tính S  9  3 1   ...   ... Kết quả là: 3 3 9 3n 27 A. . B. 14. C. 16 . D. 15 . 2 Lời giải Chọn A 1 1 1
Ta có S  9  3 1   ...   ... 3 3 9 3n 1 1
 3S  27  9  3 1  ...   ... 2 3 3n  1  27  2S  lim 27   27  S   . 2   3n  2
1 x x 1
Câu 11. Giới hạn lim có kết quả là:  2 3 x 1  x x A. 1 B. 1 C. 2 D. 2  Lời giải Chọn D
1 x x 1
1 x x 1 1  1 x lim  lim  lim  1  2 3  2 3  2 x 1  x 1  x 1 x x x xx 2 x  3x  2
Câu 12. Giới hạn lim có kết quả là: x    1 x 1 A. 1 B.  . C.  D. 1 Lời giải Chọn D 2 x  3x  2  x   1  x  2  x  2 lim  lim  lim  1  ( vì x  1  0 )    x  1 x 1 x  1 x 1 x  1 1
Câu 13. Trong các mệnh đề sau, mệnh đề nào sai? 1 1 1 1 A. lim   . B. lim   . C. lim   . D. lim   .  5  x 0  x x 0  x x0 x x0 x Lời giải Chọn B 1 Ta có: lim
  do lim x  0 và . Vậy đáp án A đúng.  x  0 x 0  x x0 Suy ra đáp án B sai.
Các đáp án C và D đúng. Giải thích tương tự đáp án A 2 4x 1
Câu 14. Tính giới hạn K  lim . x x 1 A. K  0 . B. K 1. C. K  2  . D. K  4 . Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 x 2 4   4  2 2 4x 1 Ta có: x x K  lim  lim  lim  2  . x x 1 x x 1 x 1 1 x x 1 lim 2018
Câu 15. Tính x x 1 . A. 1. B. 1. C. 2 . D. 0 . Lời giải 1 1  2 x 1 1 lim  lim . x x  0 . 2018 2017 x x 1 x x 1 1 2017 x
Câu 16. Trong các mệnh đề sau mệnh đề nào sai 3  A. lim
x x   x   . B.       .   2 lim x x 1 x 2 xx  2 1 2 2 3x  2 3x  2 C. lim   . D. lim   . x 1  x 1 x 1  x 1
Hướng dẫn giải Chọn C 2 2
x x 1 x  4x  4 
+ Với đáp án A ta có: lim
x x   x     x  2 1 2 lim x 2 
x x 1  x  2   3     x 3      3x  3    x   3  lim    lim   A đúng. x 2   
x x 1  x  2 x   1 1 2  2  x  1  1  2   x x x      2 2
x x 1 x  4x  4 
+ Với đáp án B ta có: lim
x x   x     x  2 1 2 lim x 2 
x x 1  x  2   3     x 3      3x  3    x    3   lim    lim  lim      B đúng. x 2   
x x 1  x  2 x   1 1 2  x  0   x  1  1  2   x x x     
+ Với đáp án C ta có lim  x  
1  0 , x  1  0 với mọi x  1và lim 3x  2  1  0 . x 1  x 1  3x  2 Vậy lim    C sai. x 1  x 1
+ Với đáp án D ta có lim  x  
1  0 , x  1  0 với mọi x  1 và lim 3x  2  1  0 . x 1  x 1  3x  2 Vậy lim    D đúng. x 1  x 1
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
2x m khi x  0 
Câu 17. Cho hàm số f x   1 4x 1
. Tìm tất cả các giá trị của m để tồn tại giới hạn khi x  0   x
lim f x . x0 A. m  2 . B. m  1. C. m  3 . D. m  1. Lời giải Chọn A
Ta có lim f x  lim 2x m  m x 0 x 0   1 4x 1 4
lim f x  lim  lim  2 x 0 x 0 x 0    x 1 4x 1
Tồn tại giới hạn lim f x khi và chỉ khi lim f x  lim f x  m  2 . x0 x 0 x 0   2 x  4x  4 lim
Câu 18. Tìm x2 x  2 . A. Không tồn tại. B. 1. C. 1. D. 1. Lời giải Chọn A 2 x  4x  4  x  22 x  2 lim  lim  lim . x2 x  2 x2 x  2 x2 x  2 Xét: x  2 x  2  lim  lim  1. x 2  x  2 x 2  x  2 x  2   x  2  lim  lim  1 . x 2  x  2 x 2  x  2 x  2 x  2 x  2 Ta có: lim  lim nên không tồn tại lim . x 2 x 2 x  2    x  2 x2 x  2 2x  3
Câu 19. Tìm giới hạn lim :
x 1  3x 2 2 3 A. . B.  . C.  . D. 2 . 3 3 2 Lời giải Chọn B 3 2  2x  3 2 Ta có: lim  lim x   .
x 1  3x x 1 3  3 x
Câu 20. Hàm số nào dưới đây liên tục trên khoảng  ;   ? 1 1 1 A. y  . B. y  . C. y x 1 . D. 2 y   x . x 1 2 x 1 x Lời giải Chọn B 2  x  2x  khi x  2
Câu 21. Tìm tất cả các giá trị của tham số m để hàm số f x   x  2
liên tục tại x  2. mx  4 khi x  2  A. m  1.
B. Không tồn tại m . C. m  3 . D. m  2  .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn C 2 x  2x
Ta có: f 2  2m  4; lim mx  4  2m  4 ; lim  lim x  2 . x 2  x 2 x 2 x  2   
Để hàm số liên tục tại x  2  lim f x  lim f x  f 2  2m  4  2  m  3 . x 2 x 2   2
x 1 khi x  1
Câu 22. Hàm số f x  
liên tục tại điểm x  1 khi m nhận giá trị 0
x m khi x  1  A. m  1. B. m  2 .
C. m bất kỳ. D. m  1. Lời giải Chọn D
Ta có lim f x  lim  2 x   ; f  
1  0; lim f x  lim  x m  m 1    1 0 x 1  x 1  x 1 x 1  
Hàm số liên tục tại x  1  lim f x  lim f x  f  
1  m 1  0  m  1. 0 x 1 x 1   2
x  3x  2 khi x  1 
Câu 23. Để hàm số y  
liên tục tại điểm x  1
 thì giá trị của a là 4x a khi x  1  A. 4 . B. 1. C. 1  . D. 4  . Lời giải Chọn A
Hàm số xác định trên  . Ta có f   1  0 .
lim f x  lim  
 và lim f x  lim 4x a  a  4 .    2 x 3x 2 0   x     1 x     1 x     1 x  1
Hàm số đã cho liên tục tại x  1
 khi và chỉ khi lim f x  lim f x  f   1   x     1 x     1
a  4  0  a  4 .
ax b 1, khi x  0
Câu 24. Hàm số f (x)  
liên tục trên  khi và chỉ khi
a cos x b sin x, khi x  0 
A. a b  1.
B. a b  1 .
C. a b  1
D. a b  1 Lời giải Chọn A
Khi x  0 thì f x  a cos x bsin x liên tục với x  0 .
Khi x  0 thì f x  ax b 1 liên tục với mọi x  0 .
Tại x  0 ta có f 0  a .
lim f x  limax b   1  b 1. x 0  x 0 
lim f x  lima cos x bsin x  a . x 0  x 0 
Để hàm số liên tục tại x  0 thì lim f x  lim f x  f 0  a b 1  a b  1 . x 0  x 0  2
x ax b  khi x  1
Câu 25. Cho a , b là hai số thực sao cho hàm số f x   x 1
liên tục trên  . Tính 2ax 1 khi x  1  a b . A. 0 . B. 1  . C. 5 . D. 7 . Lời giải
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 Chọn D Ta có f   1  2a 1. 2
x ax b
Để hàm số liên tục trên  thì phải tồn tại lim f x  lim
và lim f x  f   1 . x 1  x 1  x 1 x 1  2
x ax b Để tồn tại lim thì  2
x ax b x  
1  1  a b  0  b  a 1 . x 1  x 1 2
x ax bx  
1  x a   1
Khi đó lim f x  lim  lim
 lim  x a   1  a  2 . x 1  x 1  x 1  x 1 x 1 x 1 
Do đó để hàm số liên tục trên  thì lim f x  f   1 x 1 
 2a 1  a  2  a  3 . Suy ra b  4  .
Vậy a b  7 .
Câu 26. Qua phép chiếu song song lên mặt phẳng (P) , hai đường thẳng chéo nhau a và b có hình chiếu
là 2 đường thẳng a và b ' . Mệnh đề nào sau đây đúng:
A. a và b ' luôn cắt nhau
B. a và b ' có thể trùng nhau
C. a và b ' không thể song song
D. a và b ' có thể cắt nhau hoặc song song với nhau. Lời giải Chọn D
+ Gọi d là phương chiếu, a  (P) , b  (Q) và d // (P) , d // (Q) .
+ Nếu (P)  (Q)  a và b ' cắt nhau
+ Nếu (P) // (Q)  a // b '
Câu 27. Trong các mệnh đề sau đây mệnh đề nào sai?
    
A. Nếu AB BC CD DA  0 thì bốn điểm ,
A B, C, D đồng phẳng   
B. Tam giác ABC có I là trung điểm cạnh BC thì ta có đẳng thức: 2AI AB AC   
C. Vì BA BC  0 nên suy ra B là trung điểm của AC    D. Vì AB  2
AC  3AD nên 4 điểm ,
A B, C, D đồng phẳng. Lời giải Chọn A
    
Bằng quy tắc 3 điểm ta nhận thấy rằng AB BC CD DA  0 đúng với mọi điểm ,
A B, C, D
nằm trong không gian chứ không phải chỉ riêng 4 điểm đồng phẳng.
Câu 28. Cho tứ diện ABCD có AB , AC , AD đôi một vuông góc với nhau, biết AB AC AD  1 . Số
đo góc giữa hai đường thẳng AB và CD bằng A. 45 . B. 60 . C. 30 . D. 90 . Lời giải Chọn D AB AC  CÁCH 1. Vì
  AB   ACD  AB CD . AB AD  
   
Câu 29. Cho hình lập phương AB .
CD A B C D , đặt   ( AC, DC );   (DA , BB );   ( AA , C C) Khi 1 1 1 1 1 1 1 1 1
đó: là     : A. 3600 B. 3750 C. 3150 D. 2750 Lời giải Chọn B ( hình câu 3)
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489     0
  ( AC, DC )  ( AC, AB )  60 1 1
 
  0
  (DA , BB )  (DA , A ) A  135 1 1 1 1     0
  ( AA , C C)  ( AA , A ) A  180 1 1 1 1 0 0 0 0
       60 135 180  375    
Câu 30. Cho hình lăng trụ tam giác AB .
C A B C . Đặt AA  a; AB  ; b AC  ;
c BC d trong các đẳng 1 1 1 1 1
thức sau đẳng thức nào đúng.         
A. a b c d  0
B. a b c d       
C. b c d  0
D. a b c Lời giải Chọn C A C B C1 A1   
   B  1   
Ta có: b c d AB AC BC CB BC  0
Câu 31. Mệnh đề nào sau đây là đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song
với đường thẳng còn lại.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại. Lời giải Chọn D
Câu 32. Cho hình lập phương ABC .
D A B C D . Góc giữa AC và DA là 1 1 1 1 1 A. 45 . B. 90 . C. 60 . D. 120 . Lời giải Chọn C B C A D B C1 1 A1 D1
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021
Vì A 'C ' //AC nên góc giữa AC và DA là DA C . 1 1 1 
Vì tam giác DA C đều nên 0 DA C  60 . 1 1 1 1  
Câu 33. Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AB và EG ? A. 0 90 . B. 0 60 . C. 0 45 . D. 0 120 . Lời giải Chọn C H G E F D C A B      
Vì EG AC ( AEGC là hình chữ nhật) nên  AB EG   AB AC  0 , ,
BAC  45 ( ABCD là hình vuông). a 3
Câu 34. Cho tứ diện ABCD có AB CD a , IJ
( I , J lần lượt là trung điểm của BC và AD ). 2
Số đo góc giữa hai đường thẳng AB và CD là A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn C. A
Gọi M , N lần lượt là trung điểm AC , BC . Ta có: J  1 1 aMI NI AB CD M  2 2
2  MINJ là hình thoi. O
MI // AB // CD // NIB D N
Gọi O là giao điểm của MN và IJ . I  
Ta có: MIN  2MIO . C a 3  IO 3 4   Xét M
IO vuông tại O , ta có: cos MIO   
MIO  30  MIN  60 . MI a 2 2
Mà:  AB CD   IM IN   , ,  MIN  60 .
Câu 35. Cho tứ diện đều ABCD (Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa hai đường thẳng
AB và CD bằng A. 30 . B. 45 . C. 60 . D. 90 . Lời giải A Chọn D.
Gọi H là tâm đường tròn ngoại tiếp B
CD AH   BCD .
Gọi E là trung điểm CD BE CD (do BCD  đều).
Do AH   BCD  AH CD . B D CD BE Ta có: H
CD   ABE  CD AB   AB CD  ,  90 . E CD AHC Phần 2. Tự luận
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 2 2
n  4n  4n 1 6  3 a a Câu 1. Biết lim   , trong đó
là phân số tối giản, a và b là các số 2 2 3 1 b nn b nguyên dương. Tính . a b Lời giải 4 1 2 2 1  4  2
n  4n  4n 1 n n 1   3 6  3 7 lim  lim    . 2 3n 1  n 1 2 2 2 3  1 2 n a 7 Suy ra 
a  7;b  2  . a b  14 . b 2 Tính giới hạn sau: lim x Câu 2. x0 1 x  1 x Lời giải
x  1 x  1 x
x  1 x  1 x  Ta có lim x  lim  lim x0 1 x  1 x x0
1 x  1 xx0 2 x 1 x  1 x 11  lim   1. x0 2 2  x  5 1 h k i x  1  Câu 3. Cho hàm số 3 2
f ( x)   x ax ax 1
. Tìm a để hàm số liên tục tại x  1  khi x  1   x 1 Lời giải
Ta có lim f ( x)  lim      .    x 5 1 1 f  1 x 1  x 1  2      3 2  x  1 x  a  1 x 1
x ax ax 1  
lim f ( x)  lim  lim    x 1  x 1  x 1 x 1  x 1 2
 lim x  a  
1 x 1  3  a .    x 1 
Hàm số f ( x) liên tục tại x  1
  lim f ( x)  lim f ( x)  f (1)  3  a  1  a  2 .   x 1  x 1  Câu 4.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , SA a . SA vuông góc với mặt
đáy. Gọi M , N lần lượt là trung điểm của các cạnh A ,
B BC . Tính côsin của góc giữa hai đường
thẳng SM , DN . Lời giải
Gọi E là trung điểm AD , F là trung điểm AE .
Ta có MF // BE // ND  góc giữa SM và ND bằng góc giữa SM và MF . Ta có 2 2 2 2 2 2
SM SA AM a a  2a SM a 2 .
SF SM a 2 .
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 BE a 5 2 2 BE
AB AE a 5  MF   . 2 2
Áp dụng định lí côsin trong SMF : 2 2 2 
SF SM MF  2SM .MF cos SMF 2 5a 2 2 2a   2a  2 2 2
SM MF SF 10  4 cos SMF    . 2.SM .MF a 5 8 2.a 2. 2 10
Vậy cosin của góc giữa SM và ND bằng . 8
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 Đề 5
Đề ôn thi giữa kỳ 1 - Lớp 11
Phần 1. Trắc nghiệm 2n 1 Câu 1. Tính lim được kết quả là 1  n 1 A. 2 . B. 0 . C. . D. 1. 2 Câu 2.
Dãy số nào sau đây có giới hạn khác 0 ? 1 1 n 1 sin n A. . B. . C. . D. . n n n n Câu 3. Để tìm giới hạn  2 2 lim
n  4n  6  n  4 . Một học sinh lập luận ba bước sau: Bước 1: Ta có   2 2  4 6   4  4 6 4
n  4n  6  n  4 2 2  n 1   n 1   n  1   1 2   2    n n   n   2 2 n n n     4 6 4  Bước 2: Do đó lim  2 2
n  4n  6  n  4   lim n 1   1   2 2 n n n     4 6 4 
Bước 3: Do limu   u n và lim  1   1   0 nên lim 0  2 2 n n n n   
Hỏi lập luận trên đúng hay sai? Nếu sai thì sai bắt đầu từ bước nào? A. Sai từ bước 1. B. Sai từ bước 3.
C. Lập luận đúng. D. Sai từ bước 2. Câu 4. Giới hạn  2 lim
n  2n  3  n có kết quả bằng: A. 1 B. 0 . C.  D.  Câu 5.
Số thập phân vô hạn tuần hoàn 0,212121. biểu diễn dưới dạng phân số là: 2121 1 7 212121 A. . B. . C. . D. . 4 10 21 33 6 10 n 1 1 1   1 1 Câu 6.
Tổng của cấp số nhân vô hạn ,  , ,…, ,…là 2 4 8 2n 2 1 1 A.  . B. 1. C.  . D. . 3 3 3 n 1 1 1   1 1 Câu 7.
Tổng của cấp số nhân lùi vô hạn ,  , ,...., ,.... là? n 1 2 6 18 2.3  3 8 2 3 A. . B. . C. . D. . 4 3 3 8  1 1 1  Câu 8. Tìm L  lim   ...     1 1 2
1 2  ...  n  5 3 A. L  .
B. L   .
C. L  2 . D. L  . 2 2 Câu 9.
lim n n 1  n  bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 1 A. 0 . B. . C. . D. . 2 3 4 2 4 2n
Câu 10. Gọi S  1   ... 
 ... .Giá trị của S bằng 3 9 3n A. 3 . B. 5 . C. 6 . D. 4 . 1  Câu 11. lim bằng:
x 2x  5 1 A. 0 . B.  . C.  . D.  . 2 1 x Câu 12. lim bằng:
x 3x  2 1 1 1 1 A. . B. . C.  . D.  . 3 2 3 2 3x 1 Câu 13. lim bằng:
x x  5 1 A. 3. B. 3  . C.  . D. 5. 5 2x 1
Câu 14. Giá trị của lim bằng x 2 x 1 1 A. 0 . B. 2  . C.  . D. 2 . 3  4x Câu 15. lim bằng
x 5x  2 5 5 4 4 A. . B.  . C.  . D. . 4 4 5 5 2 5x  2x  3
Câu 16. Tính giới hạn lim . 2 x x 1 A. 5. B. 4 . C. 3. D. 2.  2 x   1  x   1
Câu 17. Giới hạn của hàm số f x 
khi x tiến đến -  có kết quả là:  4
2x x x   1 1 A. 0 B. . C. 2 D.  2 4 2 x x  2
Câu 18. Giới hạn lim có kết quả là: x  3 x   1 3x   1 3 3 A.  3 B. 3 . C. D. 3 3
Câu 19. Trong các mệnh đề sau, mệnh đề nào đúng? 4 x x 4 x x 4 x x 4 x x A. lim   . B. lim  1. C. lim   . D. lim  0 . x 1 2x x 1 2x x 1 2x x 1 2x
Câu 20. Có bao nhiêu giá trị nguyên của tham số m thỏa mãn hàm số 2 y
x  2mx  9 liên tục trên khoảng  ;   . A. 6 . B. 7 . C. 5 . D. Vô số.
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 x 1 1  khi x  2 2 
Câu 21. Giá trị của a để hàm số f xx  3x  2  
liên tục tại x  2 . 2a 1  khi x  2   6 1 A. 2 . B. . C. 3 . D. 1. 2
Câu 22. Cho hàm số f x liên tục trên đoạn  2  ;  3 sao cho f  2    5
 ; f 3  1. Hỏi
phương trình f x  3
 có bao nhiêu nghiệm trên đoạn  2  ;  3 ?
A. Vô nghiệm.
B. Có ít nhất một nghiệm.
C. Có ít nhất hai nghiệm.
D. Có ít nhất ba nghiệm. 2
 2x  7x  6  khi x  2 
Câu 23. Cho hàm số y f xx  2  
. Biết a là giá trị để hàm số f x liên tục tại  1 x a  khi x  2   2  x 7
x  2 , tìm số nghiệm nguyên của bất phương trình 2 x ax   0 . 0 4 A. 1. B. 4 . C. 3 . D. 2 . 2
x ax b khi x  5  
Câu 24. Nếu hàm số f x  x 17
khi  5  x  10 liên tục trên thì a b bằng
ax b 10 khi x 10  A. 1. B. 0 . C. 1. D. 2 . 2
x x 12  khi x  4
Câu 25. Tìm tham số thực m để hàm số y f x   x  4
liên tục tại điểm x  4  . 0
mx 1 khi x  4   A. m  4 . B. m  3 . C. m  2 . D. m  5 .
Câu 26. Phép chiếu song song theo phương l không song song với a hoặc b , mặt phẳng chiếu là  P ,
hai đường thẳng a và b biến thành a ' và b ' . Quan hệ nào giữa a và b không được bảo toàn
trong phép chiếu song song? A. Cắt nhau. B. Trùng nhau. C. Song song. D. Chéo nhau.
Câu 27. Cho ABC .
D A B C D là hình hộp, trong các khẳng định sau khẳng định sai: 1 1 1 1
      
A. AC A C  2 AC
B. AC CA  2CC  0 1 1 1 1 1
     
C. AC A C AA
D. CA AC CC 1 1 1 1 1            
Câu 28. Cho ba vectơ a, b, c không đồng phẳng xét các vectơ x  2a  ;
b y  4a  2 ;
b z  3a  2c Chọn
mênh đề đúng trong các mệnh đề sau:  
A. Hai vec tơ y, z cùng phương  
B. Hai vec tơ x, y cùng phương  
C. Hai vec tơ x, z cùng phương   
D. Hai vec tơ x, y, z đồng phẳng
Câu 29. Hãy chọn mệnh đề sai trong các mệnh đề sau đây:   
A. Ba véctơ a, b, c đồng phẳng nếu có hai trong ba véctơ đó cùng phương.    
B. Ba véctơ a, b, c đồng phẳng nếu có một trong ba véctơ đó bằng véctơ 0 .      
C. véctơ x a b c luôn luôn đồng phẳng với hai véctơ a và b .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
  
D. Cho hình hộp AB . CD ’ A ’ B C’ ’
D ba véctơ AB , C A
 , DA đồng phẳng    
Câu 30. Cho hình hộp ABC . D AB CD
  có tâm O . Đặt AB a ; BC b . M là điểm xác định bởi  1   OM
a b . Khẳng định nào sau đây đúng? 2
A. M là tâm hình bình hành ABB A   .
B. M là tâm hình bình hành BCC B   .
C. M là trung điểm BB .
D. M là trung điểm CC .
Câu 31. Trong không gian cho ba đường thẳng phân biệt a , b , c . Khẳng định nào sau đây đúng?
A. Nếu a và b cùng vuông góc với c thì a // b .
B. Nếu a // b và c a thì c b .
C. Nếu góc giữa a và c bằng góc giữa b và c thì a // b .
D. Nếu a và b cùng nằm trong mp   // c thì góc giữa a và c bằng góc giữa b và c .
Câu 32. Cho hình lập phương ABCDEFGH , góc giữa hai đường thẳng EG và BC là: A. 0 . B. 45 . C. 90 . D. 30
Câu 33. Cho hình lập phương AB .
CD A' B 'C ' D ' . Góc giữa AC và DA ' là: A. 0 45 . B. 0 90 . C. 0 60 . D. 0 120 .
Câu 34. Cho tứ diện ABCD có AB CD . Gọi I , J , E, F lần lượt là trung điểm của AC, BC, BD, AD .
Góc  IE, JF  bằng A. 30 . B. 45 . C. 60 . D. 90 .
Câu 35. Cho tứ diện ABCD có AB AC AD và  
BAC BAD  60 , 
CAD  90 . Gọi I và J lần lượt  
là trung điểm của AB và CD . Hãy xác định góc giữa cặp vectơ AB và IJ ? A. 120 . B. 90 . C. 60 . D. 45 . Phần 2. Tự luận 3 2
an bn  2n  4
Câu 36. Cho a, b là các số thực thỏa mãn lim
 1.Tính 2a b 2 n 1 2
4x  3x 13  2x 1
Câu 37. Tính giới hạn lim . x 7x
Câu 38. Chứng minh rằng phương trình sau luôn có nghiệm với mọi giá trị của tham số m :
cos x m cos 2 x  0 3  
Câu 39. Cho tứ diện ABCD với AC A , D 0
CAB DAB  60 , CD AD . Gọi  là góc giữa AB và 2 CD . Tính cos 
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 BẢNG ĐÁP ÁN 1.A 2.C 3.B 4.A 5.C 6.D 7.D 8.C 9.B 10.A 11.A 12.C 13.A 14.B 15.C 16.A 17.A 18.D 19.A 20.B 21.D 22.B 23.D 24.A 25.C 26.D 27.C 28.B 29.C 30.C 31.B 32.B 33.C 34.D 35.B
Phần 1. Trắc nghiệm 2n 1 Câu 1. Tính lim được kết quả là 1  n 1 A. 2 . B. 0 . C. . D. 1. 2 Lời giải  1  1 n 2    2  2n 1  n  2  0 n Ta có lim  lim  lim   2 . 1 n  1  1 0 1 n 1 1    n nCâu 2.
Dãy số nào sau đây có giới hạn khác 0 ? 1 1 n 1 sin n A. . B. . C. . D. . n n n n Lời giải Chọn C n 1 1 Có lim  lim1  lim  1 . n n Câu 3. Để tìm giới hạn  2 2 lim
n  4n  6  n  4 . Một học sinh lập luận ba bước sau: Bước 1: Ta có   2 2  4 6   4  4 6 4
n  4n  6  n  4 2 2  n 1   n 1   n  1   1 2   2    n n   n   2 2 n n n     4 6 4  Bước 2: Do đó lim  2 2
n  4n  6  n  4   lim n 1   1   2 2 n n n     4 6 4 
Bước 3: Do limu   u n và lim  1   1   0 nên lim 0  2 2 n n n n   
Hỏi lập luận trên đúng hay sai? Nếu sai thì sai bắt đầu từ bước nào? A. Sai từ bước 1. B. Sai từ bước 3.
C. Lập luận đúng. D. Sai từ bước 2. Lời giải Chọn B
Bạn sai từ bước 3, ta có thể làm tiếp như sau:    2 2 n n   n   4 6 4 lim 4 6
4  lim n  1   1   2 2 n n n     4 6 4  2 n 1  1  2 2  4    n n n lim   lim n  2  4 6 4 4 6 4 1   1 1   1 . 2 2 2 2 n n n n n n
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 4. Giới hạn  2 lim
n  2n  3  n có kết quả bằng: A. 1 B. 0 . C.  D.  Lời giải Chọn A
 2n 2n3 n 2n 2n3 n 2 2 2 
n  2n  3  n
lim  n  2n  3  n  lim  lim
 2n 2n3 n
 2n  2n3 n 2n  3 1  lim  lim  1 2
n  2n  3  n 2 3 1  1 2 n n Câu 5.
Số thập phân vô hạn tuần hoàn 0,212121. biểu diễn dưới dạng phân số là: 2121 1 7 212121 A. . B. . C. . D. . 4 10 21 33 6 10 Lời giải Chọn C 2 1 2 1 2 1 2 1 2 1 2 0, 212121...        ...       ... 10 100 1000 10000 100000 1000000 2 3 4 5 10 10 10 10 10 1 1  1 1 1 1   1 1 1 1  2 20 1 7  2     ..      .. 10 10   . 2     3 5 7   2 4 6 8   10 10 10 10   10 10 10 10  1 1 99 99 33 1  1  2 2 10 10 n 1 1 1   1 1  n Câu 6.
Tổng của cấp số nhân vô hạn 2 , 4 , 8 ,…, 2 ,…là 2 1 1 A.  . B. 1. C.  . D. . 3 3 3 Lời giải Chọn D n 1 1 1   1 1 1 1 1 Ta có S     ...   ...  .  . 2 4 8 2n 2 1 3 1 2 n 1 1 1   1 1 Câu 7.
Tổng của cấp số nhân lùi vô hạn ,  , ,...., ,.... là? n 1 2 6 18 2.3  3 8 2 3 A. . B. . C. . D. . 4 3 3 8 Lời giải Chọn D 1 1
Cấp số nhân có u  , q   1
. Do đó tổng cần tìm là 2 3 1 u 1 3 3 1 2 S    .  . 1 q 1 2 4 8 1 3  1 1 1  Câu 8. Tìm L  lim   ...     1 1 2
1 2  ...  n  5 3 A. L  .
B. L   .
C. L  2 . D. L  . 2 2
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 Lời giải Chọn C 1 k k
Ta có 1  2  3  ...  k là tổng của cấp số cộng có u  1, d  1 nên 1 2  3  ...  k  1 2 1 2 2 2     , * k    . 1 2  ...  k k k   1 k k 1  2 2 2 2 2 2 2 2   2 2  L  lim       ...      lim     2 .  1 2 2 3 3 4 n n 1   1 n 1 
lim n n 1  n Câu 9. bằng 1 1 1 A. 0 . B. . C. . D. . 2 3 4 Lời giải Chọn B n 1 1
Ta có lim n n 1  n    2 2 lim
n n n   lim  lim  . 2 2
n n n 1 2 1   1 n 2 4 2n
Câu 10. Gọi S  1   ... 
 ... .Giá trị của S bằng 3 9 3n A. 3 . B. 5 . C. 6 . D. 4 . Lời giải Chọn A 2 4 2n Ta có: S  1   ...   ... 3 9 3n n 1 3 3 2 2   S  1  ...   ... n 1 2 2 3 3  1 3 2n  3 2n  3  S    ...  lim     2 2 3n 2 3n 2    S  3 . 1  Câu 11. lim bằng:
x 2x  5 1 A. 0 . B.  . C.  . D.  . 2 Lời giải Chọn A 1  1  lim  lim  0
Áp dụng quy tắc tìm giới hạn, ta có: x 2  5 x x   5  . x 2     x  1 x Câu 12. lim bằng:
x 3x  2 1 1 1 1 A. . B. . C.  . D.  . 3 2 3 2 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 1 x 1 Ta có lim  lim x   .
x 3x  2 x 2 3 3  x 3x 1 Câu 13. lim bằng:
x x  5 1 A. 3. B. 3  . C.  . D. 5. 5 Lời giải Chọn A 1 3  3x 1 Ta có lim  lim x  3 .
x x  5 x 5 1 x 2x 1
Câu 14. Giá trị của lim bằng x 2 x 1 1 A. 0 . B. 2  . C.  . D. 2 . Lời giải Chọn B 1 2x 1 2  2x 1  lim x Ta có: lim x 1  lim  2 . x 2 x 1 1 x 1 1 x 1 1 2 x  1  2 x x 3  4x Câu 15. lim bằng
x  5x  2 5 5 4 4 A. . B.  . C.  . D. . 4 4 5 5 Lời giải  3   3  x  4    4   3  4xx   x  4  lim  lim  lim  .
x  5x  2 x   2  x   2  5 x 5    5     x   x  2 5x  2x  3
Câu 16. Tính giới hạn lim . 2 x x 1 A. 5. B. 4 . C. 3. D. 2. Lời giải 2 3 5   2 5x  2x  3 2 Ta có: x x lim  lim  5 . 2 x x 1 x 1 1 2 x  2 x   1  x   1
Câu 17. Giới hạn của hàm số f x 
khi x tiến đến -  có kết quả là:  4
2x x x   1 1 A. 0 B. . C. 2 D.  2 Lời giải Chọn A
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021  1  1   2   x  1  x  1 1  2 1      1  x  x
lim f x  lim  lim .  0 x x  4
2x x x   2 1 x x  1   1  2  1  3     x   x  4 2 x x  2
Câu 18. Giới hạn lim có kết quả là: x  3 x   1 3x   1 3 3 A.  3 B. 3 . C. D. 3 3 Lời giải Chọn D 1 2 4 2 1  2 4 x x  2 3 lim  lim x xx  3 x   1 3x   1 x  1   1  3 1 3   3     x   x
Câu 19. Trong các mệnh đề sau, mệnh đề nào đúng? 4 x x 4 x x 4 x x 4 x x A. lim   . B. lim  1. C. lim   . D. lim  0 . x 1 2x x 1 2x x 1 2x x 1 2x Lời giải Chọn A 1 1 2 2 x x x 4 .  x x x x Vì lim  lim  lim   . Vậy A đúng. x 1 2 x x   1 x  1 x  2x  2x    x x  .
Câu 20. Có bao nhiêu giá trị nguyên của tham số m thỏa mãn hàm số 2 y
x  2mx  9 liên tục trên khoảng  ;   . A. 6 . B. 7 . C. 5 . D. Vô số. Lời giải Chọn B
Hàm số đã cho liên tục trên khoảng  ;
  khi và chỉ khi 2 2
x  2mx  9  0, x
    m  9  0  3   m  3.
Vậy có 7 giá trị nguyên m thỏa mãn yêu cầu bài toán.  x 1 1 khi x  2  2 
Câu 21. Giá trị của a để hàm số f xx  3x  2  
liên tục tại x  2 . 2a 1  khi x  2   6 1 A. 2 . B. . C. 3 . D. 1. 2 Lời giải Chọn D 2a 1 Ta có: f 2  . 6 x 1 1 x  2 1 lim  lim  . 2 x2 x2 x  3x  2
x  2 x   1  x 1   1 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 2a 1 1
Hàm số liên tục tại x  2  lim f x  f 2    a  1. x2 6 2 f x  2  ;  3 f  2    5  f 3  1  Câu 22. Cho hàm số liên tục trên đoạn sao cho ; . Hỏi
phương trình f x  3
 có bao nhiêu nghiệm trên đoạn  2  ;  3 ?
A. Vô nghiệm.
B. Có ít nhất một nghiệm.
C. Có ít nhất hai nghiệm.
D. Có ít nhất ba nghiệm. Lời giải Chọn B
Ta có f x  3
  f x  3  0 . Đặt g x  f x  3. g   2
   f 2  3  2  Khi đó   g  2
 .g 3   2  .2  4   0 g
 3  f 3  3  2 
Vì f (x) liên tục trên đoạn  2  ; 
3 nên g(x) liên tục trên  2  ;  3 .
Do đó phương trình g x  0 có ít nhất một nghiệm thuộc khoảng  2  ;3 .
Vậy phương trình f x  3
 có ít nhất một nghiệm thuộc khoảng  2  ;3 . 2
 2x  7x  6  khi x  2 
Câu 23. Cho hàm số y f xx  2  
. Biết a là giá trị để hàm số f x liên tục tại  1 x a  khi x  2   2  x 7
x  2 , tìm số nghiệm nguyên của bất phương trình 2 x ax   0 . 0 4 A. 1. B. 4 . C. 3 . D. 2 . Lời giải Chọn D
Tại x  2 , ta có: 0 1
f 2  a  4  1  x  1
 lim f x  lim a   a    . x 2 x 2    2  x  4 2 2x  7x  6
x  22x  3
 lim f x  lim  lim x 2  x 2  x  2 x 2  x  2
  x  22x  3  lim
  lim 2x 3  1  . x 2  x  2 x 2 
Để hàm số liên tục tại x  2 thì f 2  lim f x  lim f x 0 x 2 x 2   1 3  a   1   a   . 4 4 3 3 7 7 Với a   , xét bất phương trình 2 x x   0    x  1 4 4 4 4
Mà x   nên x  1  ;  0 .
Vậy bất phương trình đã cho có 2 nghiệm nguyên. 2
x ax b khi x  5  
Câu 24. Nếu hàm số f x  x 17
khi  5  x  10 liên tục trên thì a b bằng
ax b 10 khi x 10  A. 1. B. 0 . C. 1. D. 2 .
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 Lời giải Chọn A
Với x  5 ta có   2
f x x ax b , là hàm đa thức nên liên tục trên  ;  5   .
Với 5  x  10 ta có f x  x  7 , là hàm đa thức nên liên tục trên  5  ;10 .
Với x  10 ta có f x  ax b 10 , là hàm đa thức nên liên tục trên 10; .
Để hàm số liên tục trên thì hàm số phải liên tục tại x  5 và x  10 . Ta có: f  5
  12 ; f 10 17.
lim f x  lim  2
x ax b  5a b  25 .   x 5  x5
lim f x  lim  x 17  12. x 5 x 5  
lim f x  lim  x 17  27 . x 10 x 10  
lim f x  lim ax b 10 10a b 10. x 10 x 10  
Hàm số liên tục tại x  5 và x  10 khi
5a b  25  12
5a b  13  a  2     
a b  1
10a b  10  27  10a b  17  b  3   2
x x 12  khi x  4
Câu 25. Tìm tham số thực m để hàm số y f x   x  4
liên tục tại điểm x  4 . 0
mx 1 khi x  4   A. m  4 . B. m  3 . C. m  2 . D. m  5 . Lời giải Chọn C
Tập xác định: D   . Ta có: 2 x x 12
x  3 x  4
+ lim f x  lim  lim  lim  x   3  7 . x 4  x 4  x  4 x 4  x  4 x 4  + f  4    4  m 1.
Hàm số f x liên tục tại điểm x  4 khi và chỉ khi lim f x  f  4
   4m 1  7 0 x 4   m  2 .
Câu 26. Phép chiếu song song theo phương l không song song với a hoặc b , mặt phẳng chiếu là  P ,
hai đường thẳng a và b biến thành a ' và b ' . Quan hệ nào giữa a và b không được bảo toàn
trong phép chiếu song song? A. Cắt nhau. B. Trùng nhau. C. Song song. D. Chéo nhau. Lời giải Chọn D.
Do a và b cùng được chứa trong mặt phẳng chiếu  P . Suy ra tính chất chéo nhau không được bảo toàn.
Câu 27. Cho ABC .
D A B C D là hình hộp, trong các khẳng định sau khẳng định sai: 1 1 1 1
      
A. AC A C  2 AC
B. AC CA  2CC  0 1 1 1 1 1
     
C. AC A C AA
D. CA AC CC 1 1 1 1 1 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 A B D C A1 B1 D1 C1
 
 
   
Ta có: AC A C  AA AC  AA  AC A C C A 1 1 1 1 1 1 1 1 1            
Câu 28. Cho ba vectơ a, b, c không đồng phẳng xét các vectơ x  2a  ;
b y  4a  2 ;
b z  3a  2c Chọn
mênh đề đúng trong các mệnh đề sau:  
A. Hai vec tơ y, z cùng phương   B. Hai vec tơ , x y cùng phương  
C. Hai vec tơ x, z cùng phương   
D. Hai vec tơ x, y, z đồng phẳng Lời giải Chọn B    
Ta thấy y  2x nên ,
x y cùng phương.
Câu 29. Hãy chọn mệnh đề sai trong các mệnh đề sau đây:   
A. Ba véctơ a, b, c đồng phẳng nếu có hai trong ba véctơ đó cùng phương.    
B. Ba véctơ a, b, c đồng phẳng nếu có một trong ba véctơ đó bằng véctơ 0 .      
C. véctơ x a b c luôn luôn đồng phẳng với hai véctơ a và b .
  
D. Cho hình hộp ABC . D ’ A ’ B C’ ’
D ba véctơ AB , C A
 , DA đồng phẳng Lời giải Chọn C B' C' A' D' C B a b A c D
A. Đúng vì theo định nghĩa đồng phẳng.
B. Đúng vì theo định nghĩa đồng phẳng. C. Sai
    
DA  AA  AD a c    
  
D. Đúng vì AB  a b
AB  DA  CA     C A
   CA b   c  
    3 vectơ AB ,  C A
 , DA đồng phẳng.
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021    
Câu 30. Cho hình hộp AB . CD AB CD
  có tâm O . Đặt AB a ; BC b . M là điểm xác định bởi  1   OM
a b . Khẳng định nào sau đây đúng? 2
A. M là tâm hình bình hành ABB A   .
B. M là tâm hình bình hành BCC B   .
C. M là trung điểm BB .
D. M là trung điểm CC . Lời giải A' D' Chọn C. Ta phân tích: B' C'  1        OM  a b 1 
AB BC 1 
AB AD 1  DB . O  2 2 2 2 A D a
M là trung điểm của BB .  B C
Câu 31. Trong không gian cho ba đường thẳng phân biệt a , b , c . Khẳng định nào sau b đây đúng?
A. Nếu a và b cùng vuông góc với c thì a // b .
B. Nếu a // b và c a thì c b .
C. Nếu góc giữa a và c bằng góc giữa b và c thì a // b .
D. Nếu a và b cùng nằm trong mp   // c thì góc giữa a và c bằng góc giữa b và c . Lời giải Chọn B.
Nếu a và b cùng vuông góc với c thì a và b hoặc song song hoặc chéo nhau. C sai do:
Giả sử hai đường thẳng a và b chéo nhau, ta dựng đường thẳng c là đường vuông góc chung của
a và b . Khi đó góc giữa a và c bằng với góc giữa b và c và cùng bằng 90 , nhưng hiển nhiên
hai đường thẳng a và b không song song.
D sai do: giả sử a vuông góc với c , b song song với c , khi đó góc giữa a và c bằng 90 , còn
góc giữa b và c bằng 0 . Do đó B đúng.
Câu 32. Cho hình lập phương ABCDEFGH , góc giữa hai đường thẳng EG và BC là: A. 0 . B. 45 . C. 90 . D. 30 Lời giải Chọn B
ABCDEFGH là hình lập phương  BC / /EG  góc giữa hai đường thẳng EG và BC là  EGF  45
Vậy góc giữa AC và DA bằng 0 60 . 1
Câu 33. Cho hình lập phương ABC .
D A' B 'C ' D ' . Góc giữa AC và DA ' là: A. 0 45 . B. 0 90 . C. 0 60 . D. 0 120 . Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 D' C' A' B' D C A B
Gọi a là độ dài cạnh hình lập phương. Khi đó, tam giác AB 'C đều ( AB '  B 'C CA a 2 ) do  đó 0 B 'CA  60 .
Lại có, DA ' song song CB ' nên  AC DA    AC CB   0 , ' , '  ACB '  60 . .
Câu 34. Cho tứ diện ABCD có AB CD . Gọi I , J , E, F lần lượt là trung điểm của AC, BC, BD, AD .
Góc  IE, JF  bằng A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn D A F I B D E J C IF CD
Ta có IF là đường trung bình của ACD    1 . IF CD   2 JE CD
Lại có JE là đường trung bình của BCD    1 . JE CD   2 IF JE  
 Tứ giác IJEF là hình bình hành. IF JE    1 IJ AB   2 Mặt khác:  . Mà B
A CD IJ JE . 1 JE CD   2
Do đó IJEF là hình thoi. Suy ra  IE, JF   90 .   
Câu 35. Cho tứ diện ABCD có AB AC AD và BAC BAD  60 , CAD  90 . Gọi I và J lần lượt  
là trung điểm của AB và CD . Hãy xác định góc giữa cặp vectơ AB và IJ ? A. 120 . B. 90 . C. 60 . D. 45 . Lời giải Chọn B
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ĐỀ ÔN THI GIỮA KỲ 2- LỚP 11- NĂM HỌC 2021 A I B D J C  1  
Xét tam giác ICD có J là trung điểm đoạn CD I J
IC ID. 2
Tam giác ABC có AB AC và  0 BAC  60  A
BC đều  CI AB .
Tương tự, ta có ABD đều nên DI AB .   1    1   1  
Ta có IJ .AB
IC ID.AB IC.AB  . ID AB  0 2 2 2    
I J AB   AB, IJ   90 . Phần 2. Tự luận 3 2
an bn  2n  4
Câu 36. Cho a, b là các số thực thỏa mãn lim
 1.Tính 2a b 2 n 1 Lời giải 3 2
an bn  2n  4 Do lim
 1  a  0 ( vì nếu a  0 thì bậc cao nhất của tử lớn hơn bậc cao 2 n 1
nhất của mẫu thì giới hạn là vô cực). 2 4 3 2 2 b   2
an bn  2n  4 bn  2n  4 Lúc đó: lim  lim  lim n n b 1. 2 2 n 1 n 1 1 1 2 n
Vậy 2a b  1. 2
4x  3x 13  2x 1
Câu 37. Tính giới hạn lim . x 7x Lời giải 3 13 2 | x | . 4    2x 1 2
4x  3x 13  2x 1 x x lim  lim x 7 x x  7x 3 13  . x 4    2x 1 2 x x  lim x 7x 3 13 1  4    2  2 x x x  lim x 7 4   . 7
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 38. Chứng minh rằng phương trình sau luôn có nghiệm với mọi giá trị của tham số m :
cos x m cos 2 x  0 Lời giải
Đặt f x  cos x m cos 2 x
Tập xác định D  
Ta có hàm số y f x liên tục trên    
 Hàm số y f x liên tục trên đoạn 3 ;    1  4 4     f     m  2 cos cos  4 4 4  2 2    f  3  3   m  6 cos cos   . 4 4 4  2 2  3  f  . f   0, m  2 4 4  3 Từ  
1 và 2 suy ra phương trình f x  0 luôn có ít nhất một nghiệm trong khoảng  ; 4 4 
hay phương trình cos x m cos 2 x  0 luôn có nghiệm với mọi giá trị của tham số m . 3  
Câu 39. Cho tứ diện ABCD với AC A , D 0
CAB DAB  60 , CD AD . Gọi  là góc giữa AB và 2 CD . Tính cos  Lời giải       AB CD AB CD Ta có :  AB CD . . cos ,
    AB . CD A . B CD Mặt khác :
    
    A .
B CD AB AD AC  A . B AD A . B AC 0 0  A . B A . D cos 60  A . B A . C cos 60 1 3 1 1 1  A . B A . DA . B A . D   A . B AD   A . B C . D 2 2 2 4 4 1  A . B CD   1 1 Do đó : AB CD 4 cos ,     cos  . A . B CD 4 4
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Document Outline

  • Đề số 1
  • Đề sô 2
  • Đề số 3
  • Đề số 4
  • Đề số 5