TOP 747 bài tập trắc nghiệm cực trị hàm số – Nguyễn Bảo Vương Toán 12

747 bài tập trắc nghiệm cực trị hàm số – Nguyễn Bảo Vương Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

68 34 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

105 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
NGUYỄN BẢO VƯƠNG
747 BÀI TẬP TRẮC
NGHIỆM CỰC TRỊ HÀM SỐ
BIÊN SOẠN VÀ SƯU TẦM
SDT: 0946798489
Bờ Ngoong – Chư Sê – Gia Lai
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 1
Thầy Phan Ngọc Chiến
Câu 1: Giá trị cực đại của hàm số
3
34y x x
là
A. 2 B. 1 C.
6
D.
1
Câu 2: Điểm cực đại của đồ thị hàm số
32
2 3 2y x x
là:
A.
0; 2
B.
2;2
C.
1; 3
D.
Câu 3 : Điểmcựcđạicủađồthịhàmsố
32
32y x x x
là:
A.
1;0
B.
3 2 3
1;
39




C.
0;1
D.
3 2 3
1;
29





.
Câu 4: Hàm số
2
33
2
xx
y
x

đạt cực đại tại:
A.
1x
B.
2x
C.
3x
D.
0x
Câu 5: Hàm số:
3
34y x x
đạt cực tiểu tại x bằng
A. -1 B. 1 C. - 3 D. 3
Câu 6: Hàm số:
42
1
23
2
y x x
đạt cực đại tại x bằng
A. 0 B.
2
C.
2
D.
2
Câu 7: Hàm số
32
3 3 4y x x x
có bao nhiêu cực trị?
A. 1 B. 2 C.0 D. 3
Câu 8: Cho hàm số
3
2
2
23
33
x
y x x
. Toạ độ điểm cực đại của đồ thị hàm số là
SDT: 0946798489 2
A. (-1;2) B. (1;2) C.
3;
2
3



D. (1;-2)
Câu 9: Hàm số
42
4 3 1y x x
có
A.Một cự đại và hai cực tiểu B. Một cực tiểu và hai cực đại
C. Một cực đại duy nhất D. Một cực tiểu duy nhất
Câu 10: Giá trị cực đại của hàm số
32
3 3 2y x x x
bằng
A.
3 4 2
B.
3 4 2
C.
3 4 2
D.
3 4 2
Câu 11: Tìm m để hàm số
32
3 12 2y mx x x
đạt cực đại tại
2x
A.
2m 
B.
3m 
C.
0m
D.
1m 
Câu 12: Cho hàm số
4
3
41
4
x
y x x
. Gọi
12
, xx
là hai nghiệm của phương trình
'0y
. Khi đó,
12
xx
bằng:
A.
1
B. 2 C. 0 D. 1
Câu 13: Tìm m để hàm số
42
2 1 3y x m x
có ba cực trị
A.
0m
B.
1m 
C.
1m
D.
0m
Câu 14: Tìm m để hàm số
3 2 2
1
12
3
y x m x m m x
có cực đại và cực tiểu
A.
2m 
B.
1
3
m 
C.
2
3
m 
D.
1m 
Câu 15: Gọi
12
, yy
lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số
42
10 9y x x
. Khi đó,
12
yy
bằng:
A.
7
B. 9 C.
25
D.
25
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 3
Câu 16:Hàm số
32
3y x x mx
đạt cực tiểu tại x = 2 khi:
A.
0m
B.
0m
C.
0m
D.
0m
VD1
Câu 17: Cho hàm số
32
1
2 1 1
3
y x m x m x
. Mệnh đề nào sau đây là sai?
A.
1m
thì hàm số có cực đại và cực tiểu;
B.
1m
thì hàm số có hai điểm cực trị;
C.
1m
thì hàm số có cực trị;
D. Hàm số luôn có cực đại và cực tiểu.
Câu 18: Cho hàmsố y=x
3
-3x
2
+1. Tích các giá trị cực đại và cực tiểu của đồ thị hàm số bằng
A. -6 B. -3 C. 0 D. 3
Câu 19:Hàmsố
3
1y x mx
có 2 cựctrị khi :
A.
0m
B.
0m
C.
0m
D.
0m
VD1
Câu 20:Khẳng định nào sau đây là đúng về đồ thị hàm số
2
25
1
xx
y
x
:
A.
0
CD CT
yy
B.
4
CT
y 
C.
1
CD
x 
D.
3
CD CT
xx
Thầy Nguyễn Việt Dũng
Câu 21. Số điểm cực trị của hàm số
3
7
3
x
yx
là:
A.1 B. 0 C. 2 D. 3
Câu 22. Hàm số
32
3 9 2y x x x
có điểm cực tiểu tại:
A.
1x
B.
3x
C.
1x
D.
3x
SDT: 0946798489 4
Câu 23. Số điểm cực trị của hàm số
43
3 4 5y x x
là:
A.1 B.0 C.3 D.2
Câu 24. Hàm số
1
yx
x
có
y
cực đại là:
A.-2 B. 2 C. 1 D. -1
Câu 25. Hàm số
3
3y x x
có
y
cực tiểu là:
A.-2 B. 2 C. 1 D. -1
Câu 26. Hàm số nào sau đây không có cực trị:
A.
3
3y x x
B.
42
21y x x
C.
1
yx
x
D.
2
21
x
y
x
Câu 27. Cho hàm số
43
3 4 .y x x
Khẳng định nào sau đây đúng?
A. Hàm số không có cực trị B. Điểm
(1; 1)A
là điểm cực tiểu
C. Hàm số đạt cực đại tại gốc tọa độ D. Hàm số đạt cực tiểu tại gốc tọa độ
Câu 28. Cho hàm số
3
3 2.y x x
Khẳng định nào sau đây sai?
A. Hàm số đạt cực đại tại
1.x
B. Hàm số đạt cực tiểu tại
1.x
C. Hàm số không có cực trị D. Hàm số có 2 điểm cực trị.
Câu 29. Hàm số nào sau đây chỉ có cực đại mà không có cực tiểu?
A.
32
32y x x
B.
1
2
x
y
x
C.
4
2
1
2
x
yx
D.
2
1
x
y
x
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 5
Câu 30. Cho hàm số
4 3 2
1 4 7
2 1.
4 3 2
y x x x x
Khẳng định nào sau đây đúng?
A. Hàm số không có cực trị B. Hàm số chỉ có 1 cực tiểu và không có cực đại
C. Hàm số có 1 cực đại và 2 cực tiểu D. Hàm số có 1 cực tiểu và 2 cực đại
Câu 31. Hàm số
23
32y x x
đạt cực trị tại
A.
1; 0
CD CT
xx
B.
1; 0
CD CT
xx
C.
0; 1
CD CT
xx
D.
0; 1
CD CT
xx
Câu 32. Cho hàm số
32
2 3 2.y x x
Câu nào sau đây sai?
A.Hàm số đạt cực tiểu trên khoảng
11
;
22
B. Hàm số đạt cực đại trên khoảng
1
;2
2



C. Hàm số có 2 cực trị trên khoảng
1
;2
2
D. Hàm số có 2 cực trị trên khoảng
1
;3
3
Câu 33. Hàm số
4
2
21
4
x
yx
đạt cực đại taị
A.
2x
B.
2x
C.
0x
D.
2x
Câu 34. Hàm số
3
2
2 3 5
3
x
y x x
đạt cực tiểu tại
A.
1x
B.
3x
C.
1x
D.
3x
Câu 35. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
3
2
2 3 5
3
x
y x x
A.Song song với đường thẳng
1x
B.Song song với trục hoành
C.Có hệ số góc dương D.Có hệ số góc bằng -1
SDT: 0946798489 6
Câu 36. Tìm
m
để hàm số
3 2 2
33y x mx m
có 2 điểm cực trị.
A.
0m
B.
0m
C.
0m
D.
0m
Câu 37. Tìm
m
để hàm số
32
32y x mx x
đạt cực tiểu tại
2.x
A.
15
4
m
B.
4
15
m
C.
4
15
m
D.
15
4
m
Câu 38. Với giá trị nào của
m
thì hàm số
32
3 2 1y x mx x m
có cực đại và cực tiểu?
A.
3;3m
B.
; 3 3;m
C.
3;3m
D.
; 3 3;m
Câu 39. Tìm
m
để hàm số
32
31y x x mx
có 2 điểm cực trị
12
,xx
thỏa
22
12
3xx
.
A.
1m
B.
2
3
m
C.
3
2
m
D.
1m
Câu 40. Với giá trị nào của
m
thì hàm số
2
2( 1)y x m x m
có cực trị trên khoảng
(0;1)?
A.
10m
B.
01m
C.
21m
D.
20m
Thầy Nguyễn Viết Thông
Câu 41. Số điểm cực trị của đồ thị hàm số
42
21y x x
là:
A. 0 B. 1 C. 2 D. 3
Câu 42. Cho hàm số
32
2 3 5y x x
. Tổng các giá trị cực trị của hàm số là:
A. -9 B. 1 C. -1 D. -5
Câu 43. Số các điểm cực trị của hàm số
53
21y x x
là:
A. 1 B. 3 C. 5 D. 7
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 7
Câu 44. Cho hàm số
2
32y x x
. Trong các điểm sau, điểm nào có tọa độ sau đây là điểm cực trị của
hàm số đã cho
A.
1;2
B.
3;0
C.
1;0
D.
2; 3
Câu 45. Điểm cực trị của đồ thị hàm số
2
32y x x
có tọa độ là:
A.
1;2
B.
0; 3
C.
1;0
D.
3;0
Câu 46 .Giá trị của m để hàm số
3
23y m x mx
không có cực trị là:
A.
0
2
m
m
B.
2m
C.
0
2
m
m
D.
02m
Câu 47. Hàm số
6
2 4 7y x x
có số điểm cực trị là:
A. 0 B. 1 C. 2 D. 3
Câu 48. Hàm số
3 2 2 2
3 3 2 1y x mx m m x m
có hai điểm cực trị khi:
A.
0m
B.
0m
C.
1m
D. m tùy ý
Câu 49. Hàm số
2
2 2 1
21
x mx m
y
x
có hai điểm cực trị khi:
A.
1m 
B.
1m 
C.
1m 
D. m tùy ý
Câu 50. Đồ thị hàm số
1
1
1
yx
x
có hai điểm cực trị nằm trên đường thẳng
y ax b
thì tích
.ab
bằng:
A. 0 B. 2 C. 4 D. -2
Câu 51. Cho hàm số
2
21
1
xx
y
x

. Khoảng cách giữa hai điểm cực trị là:
SDT: 0946798489 8
A.
45
B. 4 C. 8 D.
52
Câu 52. Cho hàm số
2 1 4 1y x x
. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Giá trị cực đại bằng
1
2
B. Điểm cực tiểu có tọa độ là
1
;1
2



C. Điểm cực tiểu là
11
;
42



D. Hàm số không có cực trị.
Câu 53. Trong các đường thẳng sau, đường thẳng nào đi qua hai điểm cực trị của hàm số
32
3 4 2y x x x
A.
23yx
B.
11
33
yx
C.
2 10yx
D.
2 3 10 0xy
Câu 54. Hàm số
3
11y x m x
đạt cực tiểu tại điểm
2x
khi:
A.
13m
B.
13m
C.
1m
D.
m
Câu 55. Điều kiện của m để hàm số
32
3 3 2y x x mx m
có cực trị là:
A.
1m
B.
1m
C.
1m
D.
1m
Câu 56. Hàm số
3 2 2
1
11
3
y x mx m m x
đạt cực đại tại điểm
1x
khi:
A.
1m
hoặc
2m
B.
1m
C.
2m
D. m tùy ý
Câu 57. Hàm số
42
2 2 3y x m x m
đạt cực đại tại điểm
1x
thì:
A.
3m
B.
5m
C.
3m
D.
5m
Câu 58. Số cực trị của hàm số
2
41y x x
A. 1 B. 2 C. 3 D. 4
Câu 59. Với m bằng bao nhiêu thì đồ thị hàm số
32
2y x mx m
có hai cực trị thẳng hàng với gốc tọa độ
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 9
A.
0m
B.
3m
C.
1
3
m
D.
3m
Câu 60. Cho hàm số
cos2 1yx
,
;0x

thì khẳng định nào sau đây sai:
A. Hàm số đạt cực tiểu tại điểm
7
12
x

B. Hàm số đạt cực đại tại điểm
11
12
x

C. Tại
2
x

hàm số không đạt cực đại D. Tại
12
x

hàm số không đạt cực tiểu
Không biết của ai thành ra của mình :D
Câu 61. Điểm cực đại của hàm số
3
y x 3x 3
có hoành độ là:
A. -3 B. -2 C. -1 D. 1
Câu 62. Hàm số:
3
34y x x
đạt cực tiểu tại:
A. -1 B. 1 C. – 3 D. 3
Câu 63. Cho hàm số
32
3 9 2y x x x
. Hàm số này:
A. Đạt cực tiểu tại x = 3 B. Đạt cực tiểu tại x = 1.
C. Đạt cực đại tại x = -1 D. Đạt cực đại tại x = 3.
Câu 64. Hoành độ điểm cực đại của đồ thị hàm số:
42
1
23
2
y x x
là:
A.
2
B.
2
C.
2
D. 0
Câu 65. Cho hàm số
4
2
( ) 2 6
4
x
f x x
. Hàm số đạt cực đại tại
A.
2x 
B.
2x
C.
0x
D.
1x
Câu 66. Các điểm cực tiểu của hàm số
42
32y x x
là:
SDT: 0946798489 10
A.
1x 
B.
5x
C.
0x
D.
1, 2xx
Câu 67. Số điểm cực trị hàm số
42
23y x x
A. 0 B. 1 C. 3 D. 2
Câu 68. Cho hàm số
3
2
2
23
33
x
y x x
.Toạ độ điểm cực đại của hàm số là
A. (-1;2) B. (3;
2
3
) C. (1;-2) D. (1;2)
Câu 69. Đồ thi hàm số
3
31y x x
có điểm cực tiểu là:
A. ( 1 ; 3 ) B. ( -1 ; -1 ) C. ( -1 ; 3 ) D. ( -1 ; 1 )
Câu 70: Điểm cực đại của đồ thị hàm số
32
69y x x x
là:
A.
1;4
B.
3;0
C.
0;3
D.
4;1
.
Câu 71. Điểm cực tiểu của đồ thị hàm số
32
69y x x x
là:
A.
1;4
B.
3;0
C.
0;3
D.
4;1
.
Câu 72. Điểm cực đại của đồ thị hàm số
32
2y x x
là:
A.
2;0
B.
2 50
;
3 27



C.
0;2
D.
50 3
;
27 2



.
Câu 73. Điểm cực tiểu của đồ thị hàm số
32
2y x x
là:
A.
2;0
B.
2 50
;
3 27



C.
0;2
D.
50 3
;
27 2



.
Câu 74. Điểm cực đại của đồ thị hàm số
3
34y x x
là:
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 11
A.
1
;1
2



B.
1
;1
2



C.
1
;1
2




D.
1
;1
2



.
Câu 75. Điểm cực tiểu của đồ thị hàm số
3
34y x x
là:
A.
1
;1
2



B.
1
;1
2



C.
1
;1
2




D.
1
;1
2



.
Câu 76. Điểm cực đại của đồ thị hàm số
3
12 12y x x
là:
A.
B.
2; 4
C.
4;28
D.
2;2
.
Câu 17. Điểm cực tiểu của đồ thị hàm số
3
12 12y x x
là:
A.
B.
2; 4
C.
4;28
D.
2;2
.
Câu 78. Điểm cực đại của đồ thị hàm số
32
5 7 3y x x x
là:
A.
1;0
B.
0;1
C.
7 32
;
3 27



D.
7 32
;
3 27



.
Câu 79. Điểm cực tiểu của đồ thị hàm số
32
5 7 3y x x x
là:
A.
1;0
B.
0;1
C.
7 32
;
3 27



D.
7 32
;
3 27



.
Câu 80. Điểm cực đại của đồ thị hàm số
32
32y x x x
là:
A.
1;0
B.
3 2 3
1;
29




C.
0;1
D.
3 2 3
1;
29





.
Câu 81. Điểm cực tiểu của đồ thị hàm số
32
32y x x x
là:
SDT: 0946798489 12
A.
1;0
B.
3 2 3
1;
29




C.
0;1
D.
3 2 3
1;
29





.
Câu 82. Đồ thị hàm số
3
31y x x
có điểm cực tiểu là:
A. (-1; -1) B. (-1; 3) C. (-1; 1) D. (1; 3)
Câu 83. Cho hàm số
42
2 2016y x x
. Hàm số có mấy cực trị.
A. 1 B. 2 C. 3 D.4
Câu 84.
Số điểm cực trị của hàm số
3
1
7
3
y x x
là :
A. 1 B. 0 C. 3 D. 2
Câu 85.
Số điểm cực đại của hàm số
4
100yx
là :
A. 0 B. 1 C. 2 D. 3
Câu 86. Số cực trị của hàm số
42
33y x x
là:
A. 1 B. 3 C. 2 D. 4
Câu 87. Số điểm cự trị của y = x
4
– 2x
2
- 3
A. 0 B. 1 C. 3 D. 2
Câu 88. Cho hàm số
42
1
21
4
y x x
. Hàm số có
A. Một cực đại và hai cực tiểu B. Một cực tiểu và hai cực đại
C. Một cực đại và không có cực tiểu D. Một cực tiểu và một cực đại
Câu 89. Cho hàm số y = x
3
- 3x
2
+ 1. Tích các giá trị cực đại và cực tiểu của hàm số bằng
A. 6 B. -3 C. 0 D. 3
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 13
Câu 90. Đồ thị hàm số nào sau đây có 3 điểm cực trị:
A.
42
21y x x
B.
42
21y x x
C.
42
2 4 1y x x
D.
42
2 4 1y x x
Câu 91. Khẳng định nào sau đây là đúng về hàm số
42
42y x x
:
A. Đạt cực tiểu tại x = 0 B. Có cực đại và cực tiểu
C. Có cực đại và không có cực tiểu D. Không có cực trị.
Câu 92. Trong các khẳng định sau về hàm số
42
11
3
42
y x x
, khẳng định nào là đúng?
A. Hàm số đạt cực tiểu tại x = 0; B. Hàm số đạt cực đại tại x = 1;
C. Hàm số đạt cực đại tại x = -1; D. Cả 3 câu trên đều đúng.
Câu 93. hàm số:
32
1
2 5 17
3
y x x x
có tích hoành độ các điểm cực trị bằng:
A. 5 B. 8 C. -5 D. -8
Câu 94. Đồ thi hàm số nào sau đây có 3 điểm cực trị :
A.
42
2 4 1y x x
B.
42
21y x x
C.
42
21y x x
D.
42
21y x x
Câu 95. Cho hàm số
42
1
21
4
y x x
.Hàm số có
A. một cực tiểu và một cực đại B. một cực đại và không có cực tiểu
C. một cực tiểu và hai cực đại D. một cực đại và hai cực tiểu
Câu 96.Cho hàm số
4
2
( ) 2 6
4
x
f x x
. Giá trị cực đại của hàm số là
A.
6
CÐ
f
B.
2
CÐ
f
C.
20
CÐ
f
D.
6
CÐ
f 
SDT: 0946798489 14
Câu 97. Hàm số
43
86y x x
có bao nhiêu cực trị ?
A. 3 B. không có cực trị C. 2 D. 1
Câu 98. Hàm số y = x
3
– 3x
2
+ 3x:
A. có hai cực trị. B. có một cực trị. C. không có cực trị. D. có ba cực trị.
Câu 99. Hàm số y =
4
2
5
3
22
x
x
có bao nhiêu cực trị ?
A. 3 cực trị B. Không có cực trị C. 2 cực trị D. 1 cực trị
Câu 100. Hàm số y = x
4
+ 2x
2
+ 3:
A. có 3 cực trị B. có 1 cực trị C. có 2 cực trị D. không có cực trị
Câu 101. Hàm số nào sau đây nhận x = 1 làm hoành độ độ điểm cực đại:
A. y = x
3
+ 3x - 3 B. y = x
3
-3x – 3 C. y = -x
3
+ 3x – 3 D. y = -x
3
– 3x –
3
Câu 102. Cho hàm số y = –x
3
+ 3x
2
– 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số luôn nghịch biến; B. Hàm số luôn đồng biến;
C. Hàm số đạt cực đại tại x = 1; D. Hàm số đạt cực tiểu tại x = 1.
Câu 103. Trong các khẳng định sau về hàm số
24
1
x
y
x
, hãy tìm khẳng định đúng?
A. Hàm số có một điểm cực trị;
B. Hàm số có một điểm cực đại và một điểm cực tiểu;
C. Hàm số đồng biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên từng khoảng xác định.
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 15
Câu 104. Trong các hàm số sau hàm số nào có cực đại, cực tiểu và
CT CD
xx
?
A.
32
2 8 2y x x x
B.
3
32y x x
C.
32
9 3 5y x x x
D.
32
9 3 2y x x x
Câu 105. Hàm số
42
10 9y x x
đạt cực đại, cực tiểu lần lượt tại
12
,xx
. Khi đó, ta có
12
xx
bằng:
A.
5
B.
4
C.
25
D.
5
Câu 106. Trong các hàm số sau, hàm số nào chỉ có 1 cực đại mà không có cực tiểu?
A.
2
45
2
xx
y
x

B.
32
3 6 1y x x x
C.
21x
y
x
D.
42
5y x x
Câu 107. Trong các khẳng định sau về hàm số
42
11
3
42
y x x
, khẳng định nào là đúng?
A. Hàm số có điểm cực tiểu là x = 0; B. Hàm số có hai điểm cực đại là x = 1;
C. Cả A và B đều đúng; D. Chỉ có A là đúng.
Câu 108. Cho hàm số y = x
3
- 3x
2
+ 1. Tích các giá trị cực đại và cực tiểu của đồ thị hàm số bằng
A. -6 B. -3 C. 0 D. 3
Câu 109. Cho hàm số
2
41
1
xx
y
x

.Hàm số có hai điểm cực trị x
1
, x
2
.Tích x
1
.x
2
bằng
A. -4 B. -5 C. -1 D. -2
Câu 110. Số điểm cực trị của hàm số
11
2
x
y
x
là:
A. 1 B. 3 C. 2 D. 0
Câu 111. Số điểm cực trị của hàm số
2
1yxx 
là:
SDT: 0946798489 16
A. 1 B. 3 C. 2 D. 4
Câu 112. Đồ thị hàm số nào sau đây có 3 điểm cực trị:
A.
42
21y x x
B.
42
21y x x
C.
42
31y x x
D.
42
21y x x
Câu 113. Hàm
32
3 21 1y x x x
có 2 điểm cực trị
12
;xx
thì tích
12
.xx
bằng:
A. 7 B. -7 C. 2 D. -2
Câu 114. Hàm số
42
23y x x
có
A. 3 cực trị và 1 cực đại B. 3 cực trị và 1 cực tiểu
C. 2 cực trị và 1 cực đại D. 2 cực trị và 1 cực tiểu.
Câu 115. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
32
1
2 3 5
3
y x x x
A. song song với đường thẳng
1x
B. song song với trục hoành
C. Có hệ số góc dương D. Có hệ số góc bằng -1
Câu 116. Hàm số
32
( ) 3 9 11f x x x x
A. Nhận điểm
1x 
làm điểm cực tiểu B. Nhận điểm
3x
làm điểm cực đại
C. Nhận điểm
1x
làm điểm cực đại D. Nhận điểm
3x
làm điểm cực tiểu
Câu 117. Hàm số
43
45y x x
A. Nhận điểm
3x
làm điểm cực tiểu B. Nhận điểm
0x
làm điểm cực đại
C. Nhận điểm
3x
làm điểm cực đại D. Nhận điểm
0x
làm điểm cực tiểu
Câu 118. Số điểm cực trị hàm số
2
36
1
xx
y
x

A. 0 B. 2 C. 1 D. 3
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 17
Câu 119. Hàm số f có đạo hàm là
22
'( ) ( 1) (2 1)f x x x x
. Số điểm cực trị của hàm số là
A. 1 B. 2 C. 0 D. 3
Câu 120. Hàm số
sin2 3y x x
A. Nhận điểm
6
x

làm điểm cực tiểu B. Nhận điểm
2
x
làm điểm cực đại
C. Nhận điểm
6
x

làm điểm cực đại D. Nhận điểm
2
x

làm điểm cực tiểu
Câu 121. Cho hàm số y = –x
3
+ 3x
2
– 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số luôn nghịch biến; B. Hàm số luôn đồng biến;
C. Hàm số đạt cực đại tại x = 1; D. Hàm số đạt cực tiểu tại x = 1.
Câu 122. Trong các khẳng định sau về hàm số
24
1
x
y
x
, hãy tìm khẳng định đúng?
Câu 123. Trong các khẳng định sau về hàm số
42
11
3
42
y x x
, khẳng định nào là đúng?
A. Hàm số đạt cực tiểu tại x = 0; B. Hàm số đạt cực đại tại x = 1;
C. Hàm số đạt cực đại tại x = -1; D. Cả 3 câu trên đều đúng.
Câu 124. Khẳng định nào sau đây là đúng về hàm số
42
42y x x
:
A. Đạt cực tiểu tại x = 0 B. Có cực đại và cực tiểu
A. Hàm số có một điểm cực trị;
B. Hàm số có một điểm cực đại và một điểm cực tiểu;
C. Hàm số đồng biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên từng khoảng xác định.
SDT: 0946798489 18
C. Có cực đại và không có cực tiểu D. Không có cực trị.
Câu 125. Khẳng định nào sau đây là đúng về đồ thị hàm số
2
25
1
xx
y
x
:
A.
0
CD CT
yy
B.
4
CT
y 
C.
1
CD
x 
D.
3
CD CT
xx
Câu 126. hàm số:
32
1
2 5 17
3
y x x x
có tích hoành độ các điểm cực trị bằng
A. 5 B. 8 C. -5 D. -8
Câu 127. Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số
32
34y x x
là:
A.
25
B.
45
C.
65
D.
85
Câu 128. Hàm số nào sau đây không có cực trị :
A. y = x
3
+ 2 B. y =
22
1
x
x
C. y =
2
3
2
xx
x

D. Cả 3 đều đúng
Câu 129. Hàm số nào sau đây không có cực trị ?
A. y = 2x
2
– 6 x + 1 B. y = 2x
3
+ x
2
– x + 5 C.
2
x + x - 2
y=
x + 1
D. y =
1
4
x
4
– 2x
2
Câu 130. Tại điểm x = e, hàm số y =
ln
x
x
:
A. đạt cực tiểu B. đạt cực đại C. không đạt cực trị D. không xác định
Câu 131: Hàm số y = x – e
x
tại điểm x = 0 thì :
A. đạt cực tiểu B. đạt cực đại C. không xác định D. không đạt cực trị.
Câu 132. Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số
32
34y x x
là:
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 19
A.
25
B.
45
C.
65
D.
85
Câu 133. Phương trình đường thẳng đi qua các điểm cực trị của đồ thị hàm số
32
31y x x x
là:
A. Một kết quả khác B.
2
76
9
yx
C.
1
20 6
9
yx
D.
1
31
9
yx
Câu 134. Hàm số
sin2 3y x x
:
A. nhận điểm
6
x

làm điểm cực đại. B. Nhận điểm
2
x
làm điểm cực tiểu
C. Nhận điểm
6
x

làm điểm cực tiểu. D. Nhận điểm
2
x

làm điểm cực đại.
Câu 135. Trong các mệnh đề sau, hãy tìm mệnh đề sai:
A. Hàm số
1
21
2
yx
x
không có cực trị; B. Hàm số
1
1
1
yx
x
có hai cực trị.
C. Hàm số y = –x
3
+ 3x
2
– 3 có cực đại và cực tiểu; D. Hàm số y = x
3
+ 3x + 1 có cực trị;
Câu 136. Đồ thị hàm số:
2
22
1
xx
y
x

có 2 điểm cực trị nằm trên đường thẳng y = ax + b với: a + b =
A. 2 B. 4 C. - 4 D. - 2
Câu 137. Cho đồ thị hàm số
2
2
1
yx
x
. Khi đó
CD CT
yy
A. 6 B. -2 C. -1 / 2 D.
3 2 2
Câu 138. Cho hàm số
y x x
42
21
(C). Tiếp tuyến của (C) tại điểm cực đại có phương trình là:
A.
x 0
B.
y 0
C.
y 1
D.
y 2
SDT: 0946798489 20
Câu 139. Hàm số
yx
4
5
có bao nhiêu điểm cực đại?
A. 1 B. 3 C. 0 D. 2
Câu 140. hàm số
2
xx
ee
y
có bao nhiêu điểm cực trị ?
A. 0 B. 1 C. 2 D. 3
Câu 141. Hàm số
2
3y x ax b
đạt cực trị bằng 2 tại x = 2 khi và chỉ khi:
A.
12, 6ab
B.
12, 10ab
C.
4, 2ab
D.
10, 12ab
Câu 142. cho hàm số f(x) =
3 2 2
3 3( 1)x mx m x
. Tìm m để f đạt giá trị cực đại tại x
0
=1.
A. m=2 B. m = 0 C. m = 0 hay m = 2 D. m
0 và m
2
Câu 143. Hàm số
32
3y x x mx
đạt cực tiểu tại x = 2 khi :
A.
0m
B.
0m
C.
0m
D.
0m
Câu 144. Hàm số
3
1y x mx
có 2 cực trị khi
A.
0m
B.
0m
C.
0m
D.
0m
Câu 145. Với giá trị nào của m thì hàm số
32
( 1) 2 1y x m x m
đạt cực đại tại
2x
?
A. m=0 B. m=1 C. m=2 D. m=3
Câu 146. Hàm số
3 2
2
7
3
y x xmxm



có cực trị tại x = 1 khi:
A.
7
9
m
B.
2
1
m
m

C.
12m
D. Không có giá trị m thỏa mãn
Câu 147. Hàm số
3 22
(1
3
2
1
)m m m xy x x
có cực đại tại x = 1 khi:
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 21
A.
1m
B. m = 2 C.
2m
và
1m
D. Không có giá trị m thỏa mãn
Câu 148. Hàm số
3 22
(1
3
2
1
)m m m xy x x
có cực tiểu tại x = 1 khi:
A.
1m
B. m = 2 C.
2m
và
1m
D. Không có giá trị m thỏa mãn
Câu 149. Hàm số
2
1xxm
m
y
x

có cực đại tại x = 2 khi:
A.
1m 
B.
3m 
C.
3m 
và
1m 
D. Không có giá trị m thỏa mãn
Câu 150. Cho hàm số
32
2
5
3
y x mx m x



. Tìm m để hàm số đạt cực tiểu tại
1x
A.
2
5
m
B
7
.
3
m
C.
3
7
m
D.
0m
Câu 151. Hàm số
32
1
1 2 2
3
y x mx m x m
có cực đại cực tiểu khi và chỉ khi:
A.
1m 
B. mọi m C.
1m 
D. không có giá trị nào của
Câu 152. Giá trị của m để hàm số y = x
3
+ 3x
2
+ (m + 4)x - 2 có cực đại, cực tiểu là:
A.
m1
B.
m2
C.
m0
D. m =2
Câu 153. Cho hàm số y = (m + 2)x
3
+ 3x
2
+ mx – 5. Tất cả các giá trị của tham số m để hàm số có cực trị
là:
A. –3 < m < 1 B. –3 < m < 1 và m –2 C. –3 m 1 D. –3 m 1 và m –2
Câu 154. Hàm số
3
1y x mx
có 2 cực trị khi :
A.
0m
B.
0m
C.
0m
D.
0m
Câu 155. Hàm số
32
1
( 6) (2 1)
3
y x mx m x m
có cực trị khi:
SDT: 0946798489 22
A.
3
2
m
m

B.
3
2
m
m

C.
2
3
m
m

D.
23m
Câu 156. Hàm số
32
1
( 6) (2 1)
3
y m x mx x m
có 2 cực trị khi:
A.
3
2
m
m

B.
3
2
m
m

C.
3
2
m
m

và
6m 
D.
23m
Câu 157. Hàm số
2
2
4
xxm
y
x

có cực đại và cực tiểu khi:
A.
8m 
B.
8m 
C.
8m 
và
2m
D.
8m
Câu 158. Hàm số y =
2
2
1
x mx
x

có cực trị khi:
A. m = -3 B. m < -2 C. m > -3 D. – 3 < m < -2
Câu 159. Có hai giá trị m để hàm số
32
( 2) (1 ) 3 1y x m x m x m
đạt cực trị tại x
1
, x
2
mà
12
2xx
. Tổng hai số đó là:
A. -7 B. -5 C. -3 D. 1
Câu 160. Biết đồ thị hàm số
42
2y x px q
có một điểm cực trị là (1;2), thế thì khoảng cách giữa
điểm cực tiểu và điểm cực đại là
A.
26
B.
5
C.
2
D. 2
Câu 161. Có bao nhiêu giá trị nguyên của m để hàm số
2
ln( 2)y m x x x
có hai điểm cực trị trái
dấu
A. 3 B. 2 C. 1 D. 0
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 23
Câu 162. Xác định m để hàm số
3 2 3
31
22
y x mx m
có các điểm cực đại , cực tiểu đối xứng nhau qua
đường thẳng y = x:
A.
2m
B.
2m
C.
2m
D.
3m
Câu 163. Khoảng cách giữa 2 điểm cực trị của đồ thi hàm số
2
1
x mx m
y
x

bằng :
A.
25
B.
52
C.
45
D.
5
Câu 164. Giả sử đồ thị hàm số
32
3 3( 6) 1y x mx m x
có hai cực trị. Khi đó đường thẳng qua hai
điểm cực trị có phương trình là:
A.
2
2 6 1y x m m
B.
22
2( 6) 6 1y m m x m m
C.
2
2 6 1y x m m
D. Tất cả đều sai
Câu 165. Hàm số
32
1
( 6) (2 1)
3
y x mx m x m
không có cực trị khi:
A.
3
2
m
m


B.
23m
C.
2
3
m
m
D.
23m
Câu 166. Hàm số
4 2 2
2( 1)y x m x m
có 3 điểm cực trị khi:
A. m > -1 B. m < -1 C. m -1 D. m > 1
Câu 167. Hàm số
4 2 2
2(3 ) 1y x m m x m
có 3 điểm cực trị khi:
A.
03m
B.
3
0
m
m

C.
0
3
m
m

D.
03m
Câu 168. Hàm số
4 2 2
2(3 ) 1y x m m x m
có 1 điểm cực trị khi:
SDT: 0946798489 24
A.
03m
B.
3
0
m
m

C.
3
0
m
m

D.
03m
Câu 169. Hàm
32
31y x x mx
có 2 điểm cực trị
12
;xx
:
22
12
3xx
khi:
A.
1m
B.
3
2
m
C.
2
3
m
D.
3
2
m 
Câu 170. Hàm
32
( 1) 5 1
3
()
1
y x xm m x
có 2 điểm cực trị trái dấu nhau khi:
A.
5m
B.
5m
C.
5m
D.
5m
Câu 171. Hàm
32
( 1) 5 1
3
()
1
y x xm m x
có 2 điểm cực trị cùng dương khi:
A.
5m
B.
5m
C.
5m
D.
5m
Câu 172. Hàm số
32
3 3 2 3y x mx x m
không có cực đại, cực tiểu với m
A.
1m
B.
1m
C.
11m
D.
11mm
Câu 173. Hàm số
42
3 2 1y mx m x m
chỉ có cực đại mà không có cực tiểu với m:
A.
3m
B
0m
C.
30m
D.
03mm
Câu 174. Hàm số
32
3 1 1y x mx m x
đạt cực đại tại x = 1 với m bằng :
A. m = - 1 B.
3m 
C.
3m 
D. m = - 6
Câu 175. Hàm số y= x
3
-3x
2
+mx-1=0 có 2 điểm cực trị x
1
,x
2
thoả mãn
3
2
2
2
1
xx
khi:
A. m = 3 B. m =
3
2
C. m =
2
3
D. m = -
2
3
Câu 176. Hàm số y= x
3
- 3x
2
+ mx - 1 có 2 điểm cực trị x
1
,x
2
thoả mãn
3
2
2
2
1
xx
khi:
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 25
A.m < 3 B. m >
2
3
C. m <
2
3
D.
2
3
< m < 3
Câu 177. Hàm số y= x
3
- 3x
2
+ mx - 1 có 2 điểm cực trị x
1
,x
2
thoả mãn
3
2
2
2
1
xx
khi:
A. m < 3 B. m >
2
3
C. m <
2
3
D.
2
3
< m < 3
Câu 178. Đồ thị hàm số y = x
3
- 3mx
2
+ 1 có 2 điểm trị A,B thoả mãn: AB = 2
5
khi:
A. m = 1 B. m = -1 C.m =
1
D. kết quả khác
Câu 179. Đồ thị hàm số y=x
3
-3mx
2
+1 có 2 điểm trị A,B thoả mãn : AB>2
5
khi:
A. -1< m < 1 B. m
);1(1; 
C. m < 1 D. m
0\)1,1(
Câu 180. Đồ thị hàm số y = x
3
- 3mx
2
+ 1 có 2 điểm trị A, B thoả mãn trung điểm I của AB thuộc Ox khi:
A. m=1 B. m=0 C. m=
3
2
1
D. Không có m thoả
mãn
Câu 181. Đồ thị hàm số y = x
3
- 3mx + 1 có 2 điểm cực trị B, C thoả mãn tam giác ABC cân tại
A(2; 3) nếu:
A. m = 0 hoặc m =
2
1
B. m =
2
1
C. m = 0 D. đáp án khác
Câu 182. Đồ thị hàm số y = x
3
- 3mx + 1 có 2 điểm cực trị B,C thoả mãn tam giác ABC vuông tại
A(2; 2) nếu
A.m = 0 B. m = 1 C. m = -1 D. đáp án khác
SDT: 0946798489 26
Câu 183. Đồ thị hàm số y = x
4
- 4mx
2
+ 3m - 2 có 3 điểm cực trị thoả mãn:Khoảng cách từ điểm cực đại
tới đường thẳng qua 2 điểm cực tiểu bằng 8 khi:
A. m =
2
B. m =
2
C. m = -
2
D. đáp án khác
Câu 184. Đồ thị hàm số y = x
4
- 4mx
2
+ 3m - 2 có 3 điểm cực trị lập thành tam giác vuông khi:
A. m = 1 B. m = 0 hoặc m =
2
1
C. m =
2
1
D. đáp án khác
Câu 185. Đồ thị hàm số y = x
4
- 4mx
2
+ 3m - 2 có 3 điểm cực trị lập thành tam giác nhận G(0;
3
5
) làm
trọng tâm khi:
A. m = 1 B. m = 1 hoặc m =
8
1
C. m =
8
1
D. đáp án khác
Câu 186. Hàm số y = x
3
- (m - 1)x
2
+ (m - 4)x + 4 có 2 điểm cực trị cùng dương khi:
A. m > 1 B. m > 4 C. m < 4 D. m < 1
Câu 187. Hàm số y = x
3
- (m - 1)x
2
+ (m - 4)x + 4 có 2 điểm cực trị cùng âm khi:
A. m < 1 B. m > 1 C. m < 4 D. Không có m
Câu 188. Hàm số y = x
3
- (m - 1)x
2
+ (m - 4)x + 4 có 2 điểm cực trị trái dấu khi:
A. m > 1 B. m > 4 C. m < 4 D. m < 1
Câu 189. Đồ thị hàm số y = x
3
- (m - 1)x
2
+ (m - 4)x + 4 có 2 điểm cực trị nằm bên phải Oy khi:
A. m > 1 B. m > 4 C. m < 4 D. m < 1
Câu 190. Đồ thị hàm số y = x
3
- (m - 1)x
2
+ (m - 4)x + 4 có 2 điểm cực trị nằm bên trái Oy khi:
A. m<1 B. m>1 C. m<4 D. Không có m
Câu 191. Hàm số y = x
3
- (m - 1)x
2
+ (m - 4)x + 4 có 2 điểm cực trị nằm 2 phía 0y khi:
A. m > 1 B. m > 4 C. m < 4 D. m < 1
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 27
Câu 192. Hàm số y =
3
2
)13(2
3
2
223
xmmxx
có 2 điểm cực trị x
1
;x
2
thoả: x
1
.x
2
+ 2(x
1
+ x
2
) = 1 khi
A. m = 0 hoặc m =
3
2
B. m =
3
2
C. m =
2
3
D. Không có m
Câu 193. Hàm số y =
3
2
)13(2
3
2
223
xmmxx
có 2 điểm cực trị x
1
;x
2
thoả: x
1
.x
2
+ 2(x
1
+ x
2
)
1 khi
A. m
]
3
2
,
13
132
[
B. m
]
3
2
,0[
C.
3
2
;
13
132
m
D. d,m
 ;
3
2
0;
Câu 194. Hàm số y=
3
2
)13(2
3
2
223
xmmxx
có 2 điểm cực trị x
1
;x
2
thoả mãn: x
1
.x
2
+2(x
1
+x
2
)
1 khi
A. m
 ;
3
2
0;
B. m
]
3
2
,0[
C.
3
2
;
13
132
m
D. m

;
3
2
13
132
;
Câu 195. Với giá trị nào của m thì đồ thị hsố
4 2 2
21y x m x
có ba cực trị tạo thành tam giác vuông
cân
A.
0m
B.
1m
C.
1m 
D.
2m 
Câu 196. Với giá trị nào của m thì đồ thị hàm số
32
2 3( 1) 6( 2) 1y x m x m x
có cực đại, cực tiểu
thỏa mãn |x
CĐ
+x
CT
|=2:
A.
1m
B.
2m
C.
1m 
D.
2m 
Câu 197. Hàm số
3
1y x mx
có 2 cực trị khi :
A.
0m
B.
0m
C.
0m
D.
0m
Câu 198. Hàm số
32
3 3 2 3y x mx x m
không có cực đại, cực tiểu với m
SDT: 0946798489 28
A.
1m
B.
1m
C.
11m
D.
11mm
Câu 199. Hàm số
42
3 2 1y mx m x m
chỉ có cực đại mà không có cực tiểu với m:
A.
3m
B
0m
C.
30m
D.
03mm
Câu 200. Hàm số
32
3 1 1y x mx m x
đạt cực đại tại x = 1 với m bằng :
A. m = - 1 B.
3m 
C.
3m 
D. m = - 6
Câu 201. Hàm số y= x
3
-3x
2
+mx-1=0 có 2 điểm cực trị x
1
,x
2
thoả mãn
3
2
2
2
1
xx
khi:
A. m=3 B. m=
3
2
C. m=
2
3
D. m=-
2
3
Câu 202. Hàm số y= x
3
-3x
2
+mx-1=0 có 2 điểm cực trị x
1
,x
2
thoả mãn
3
2
2
2
1
xx
khi:
A. m < 3 B. m >
2
3
C. m<
2
3
D.
2
3
<m<3
Câu 203. Hàm số y= x
3
-3x
2
+mx-1=0 có 2 điểm cực trị x
1
,x
2
thoả mãn
3
2
2
2
1
xx
khi:
A. m<3 B. m >
2
3
C. m<
2
3
D.
2
3
<m<3
Câu 204. Đồ thị hàm số y=x
3
-3mx
2
+1 có 2 điểm trị A,B thoả mãn : AB=2
5
khi:
A. m=1 B. m=-1 C. m=
1
D. kết quả khác
Câu 205. Đồ thị hàm số y = x
3
- 3mx
2
+ 1 có 2 điểm trị A,B thoả mãn AB > 2
5
khi:
A. -1<m<1 B. m
);1(1; 
C. m<1 D. m
0\)1,1(
Câu 206. Đồ thị hàm số y = x
3
- 3mx
2
+ 1 có 2 điểm trị A, B và trung điểm I của AB thuộc Ox khi:
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 29
A. m = 1 B. m = 0 C. m =
3
2
1
D. Không có m thoả mãn
Câu 207. Đồ thị hàm số y=x
3
-3mx+1 có 2 điểm cực trị B,C thoả mãn tam giác ABC cân tại A(2,3) nếu:
A. m=0 hoặc m=
2
1
B. m=
2
1
C. m=0 D. đáp án khác
Câu 208. Đồ thị hàm số y = x
3
- 3mx + 1 có 2 điểm cực trị B,C thoả mãn ABC vuông tại A(2,2) nếu
A. m=0 B. m=1 C. m=-1 D. đáp án khác
Câu 209. Đồ thị hàm số y = x
4
- 4mx
2
+ 3m - 2 có 3 điểm cực trị thoả mãn khoảng cách từ điểm cực đại
tới đường thẳng qua 2 điểm cực tiểu bằng 8 khi
A. m=
2
B. m=
2
C. m=-
2
D. đáp án khác
Câu 210. Đồ thị hàm số y = x
4
- 4mx
2
+ 3m - 2 có 3 điểm cực trị lập thành tam giác vuông khi:
A. m = 1 B. m = 0 hoặc m =
2
1
C. m =
2
1
D. đáp án khác
Câu 211. Đồ thị hàm số y = x
4
- 4mx
2
+ 3m - 2 có 3 điểm cực trị lập thành tam giác nhận G(0;
3
5
) làm
trọng tâm khi:
A. m=1 B. m=1 hoặc m=
8
1
C. m=
8
1
D. đáp án khác
Câu 212. Hàm số y = x
3
- (m - 1)x
2
+ (m - 4)x + 4 có 2 điểm cực trị cùng dương khi:
A.m>1 B. m>4 C. m<4 D. m<1
Câu 213. Hàm số y=x
3
-(m-1)x
2
+(m-4)x+4 có 2 điểm cực trị cùng âm khi:
A.m<1 B. m>1 C. m<4 D. Không có m
Câu 214. Hàm số y = x
3
- (m - 1)x
2
+ (m - 4)x + 4 có 2 điểm cực trị trái dấu khi:
SDT: 0946798489 30
A. m>1 B. m>4 C. m<4 C. m<1
Câu 215. Đồ thị hàm số y = x
3
- (m - 1)x
2
+ (m - 4)x + 4 có 2 điểm cực trị nằm bên phải Oy khi:
A. m>1 B. m>4 C. m<4 D. m<1
Câu 216. Đồ thị hàm số y = x
3
- (m - 1)x
2
+ (m - 4)x + 4 có 2 điểm cực trị nằm bên trái Oy khi:
A. m<1 B. m>1 C. m<4 D. Không có m
Câu 217. Hàm số y = x
3
- (m - 1)x
2
+ (m - 4)x + 4 có 2 điểm cực trị nằm 2 phía 0y khi:
A. m>1 B. m>4 C. m<4 D. m<1
Câu 218. Hàm số y=
3
2
)13(2
3
2
223
xmmxx
có 2 điểm cực trị x
1
;x
2
thoả mãn: x
1
.x
2
+2(x
1
+x
2
)
1 khi
A, m
 ;
3
2
0;
B. m
]
3
2
,0[
C.
3
2
;
13
132
m
D.

;
3
2
13
132
;
Câu 219. Với giá trị nào của m thì đồ thị hàm số
4 2 2
21y x m x
có ba cực trị tạo thành tam giác
vuông cân
A.
0m
B.
1m
C.
1m 
D.
2m 
Câu 220.Với giá trị nào của m thì đồ thị hàm số
32
2 3( 1) 6( 2) 1y x m x m x
có cực đại, cực tiểu
thỏa mãn |x
CĐ
+x
CT
|=2
A. m = 1 B. m = 2 C. m = -1 D. m = -2
Câu 221. Cho hàm số
32
1
(2 1) 1
3
y x mx m x
. Mệnh đề nào sau đây là sai?
A.
1m
thì hàm số có cực đại và cực tiểu; B.
1m
thì hàm số có hai điểm cực trị;
C.
1m
thì hàm số có cực trị; D. Hàm số luôn có cực đại và cực tiểu.
Nhóm Toán – thầy Nguyễn Phú Khánh
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 31
Câu 222
:
Trong các hàm số
, , ,A B C D
dưới đây, hàm số nào có cực đại, cực tiểu và
CT CD
xx
A.
32
9 3 2y x x x
B.
32
9 3 5y x x x
C.
32
2 8 5y x x x
D.
3
52y x x
Câu 223
:
Số điểm cực trị của hàm số
2017
2016
2
1 3 2y x x x
là:
A.
2
B.
3
C.
1
D.
0
Câu 224
:
Gọi
M
và
N
lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số
3
3y x x
. Lúc đó, tổng
23MN
bằng:
A.
-2
B.
-4
C.
4
D.
2
Câu 225
:
Hàm số
43
( ) 8 32y f x x x
có bao nhiêu điểm cực trị?
A.
3 điểm
B.
2 điểm
C.
1 điểm
D.
Không có cực trị
Câu 226
:
Số các điểm cực tri của hàm số :
4
2
26
4
x
yx
là:
A.
1
B.
2
C.
3
D.
4
Câu 227
:
Cho đồ thị hàm số
y f x
hình bên. Khẳng định nào là sai
A.
Hàm số
y f x
có một điểm cực đại.
B.
Hàm số
y f x
luôn đồng biến trên
0;
C.
Hàm số
y f x
có một điểm cực tiểu
0x
D.
Hàm số
y f x
có một điểm cực trị.
O
x
y
SDT: 0946798489 32
Câu 228
:
Xét hàm số
fx
xác định, liên tục trên và có bảng biến thiên:
Mệnh đề nào sau đây là sai.
A.
Hàm số
fx
nghịch biến trên khoảng
1,2
B.
Hàm số
fx
đạt cực tiểu tại
1x
C.
Hàm số
fx
đạt cực đại tại
0x
D.
Hàm số
fx
đồng biến trên khoảng
1,
Câu 229
:
Tổng các giá trị cực trị của hàm số là bao nhiêu ?
A.
5
B.
0
C.
6
D.
7
Câu 230
:
Hàm số
()fx
xác định, liên tục trên và có đạo hàm
22
'( ) ( 1) 4f x x x
. Số điểm cực trị của
hàm số là:
A.
0
B.
2
C.
3
D.
1
Câu 231
:
Hàm số
42
23f x x x
có giá trị cực đại bằng a và giá trị cực tiểu bằng b. Khi đó giá trị của
2ab
bằng:
A.
4
B.
-5
C.
2
D.
5
Câu 232
:
Khẳng định nào đúng về hàm số
42
11
3
42
y x x
?
A.
Hàm số chỉ có một điểm cực trị
0x
B.
Hàm số có không có cực trị
C.
Hàm số đạt cực tiểu tại 2 điểm
1x
và
1x
D.
Hàm số đạt cực đại tại 2 điểm
1x
và
1x
Câu 233
:
Hệ thức liên hệ giữa giá trị cực đại (
CD
y
) và giá trị cực tiểu (
CT
y
) của hàm số
2
1
24
xx
y
x
là:
A.
CD CT
yy
B.
23
CT CD
yy
C.
5
CD CT
yy
D.
0
CD CT
yy
x
–∞
- 1
0
1
+∞
y
–
0
+
0
–
0
+
y
+∞
1
2
1
+∞
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 33
Câu 234
:
Hàm số
2
65y x x
có mấy cực trị ?
A.
2
B.
3
C.
1
D.
4
Câu 235
:
Cho hàm số
y f x
là hàm liên tục trên , có đạo hàm
2 2016
11f x x x x
. Đồ thị hàm số
có số điểm cực trị là :
A.
3
B.
0
C.
2
D.
1
Câu 236
:
Hàm số
32
2 9 12 3y x x x
có giá trị cực đại là
A.
1
B.
8
C.
-1
D.
3
Câu 237
:
Số cực trị của hàm số
42
32xyx
là :
A.
0
B.
1
C.
2
D.
3
Câu 238
:
Đồ thị hàm số
3
2
32y x x
có số điểm cực trị là:
A.
3
B.
2
C.
0
D.
1
Câu 239
:
Khẳng định nào đúng về hàm số
34
41f x x x
?
A.
Nhận điểm
3x
làm điểm cực đại
B.
Nhận điểm
0x
làm điểm cực đại
C.
Nhận điểm
0x
làm điểm cực tiểu
D.
Nhận điểm
3x
làm điểm cực tiểu
Câu 240
:
Cho hàm số có đạo hàm
23
'( ) ( 1) ( 2) (2 1)f x x x x
. Số cực trị của hàm số là:
A.
0
B.
3
C.
1
D.
2
Câu 241
:
Hàm số
3y x x
đạt cực đại tại:
A.
4x
B.
2x
C.
3x
D.
1x
SDT: 0946798489 34
Câu 242
:
Trong các hàm số
, , ,A B C D
dưới đây, hàm số nào có 3 điểm cực trị ?
A.
4
12yx
B.
42
2 5 12y x x
C.
42
2 12y x x
D.
32
21y x x x
Câu 243
:
Khẳng định nào đúng về hàm số
42
1
21
4
y x x
?
A.
Một cực đại và hai cực tiểu
B.
Một cực tiểu và hai cực đại
C.
Một cực đại và không có cực tiểu
D.
Một cực tiểu và một cực đại
Câu 244
:
Điểm cực tiểu của hàm số
32
37y x x
là:
A.
3
B.
0
C.
2
D.
7
Câu 245
:
Đồ thị hàm số
42
21y x x
có bao nhiêu điểm cực trị?
A.
3
B.
5
C.
4
D.
6
Câu 246
:
Khẳng định nào sai về hàm số
42
25y x x
?
A.
Hàm số đã cho đồng biến trên khoảng
1;0
B.
Hàm số đã cho có 2 cực tiểu
C.
Hàm số đã cho nghịch biến trên khoảng
1;
D.
Hàm số đạt cực đại tại
0x
Câu 247
:
Toạ độ điểm cực đại của đồ thị hàm số
32
69y x x x
là:
A.
3,0
B.
1,2
C.
0,0
D.
2,1
Câu 248
:
Hàm số
42
21y f x x x
có giá trị cực tiểu là:
A.
-4
B.
0
C.
1
D.
4/3
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 35
Câu 249
:
Khẳng định nào đúng về hàm số
2
1 2x 3yx
?
A.
Không có cực trị
B.
Có 1 cực trị
C.
Có 2 cực trị
D.
Có 3 cực trị
Câu 250
:
Giá trị cực đại của hàm số
3
32y x x
là:
A.
0
cd
y
B.
1
cd
y
C.
2
cd
y
D.
3
cd
y
Câu 251
:
Trong các hàm số
, , ,A B C D
dưới đây, hàm số nào có hai cực trị thỏa mãn giá trị cực tiểu lớn hơn giá
trị cực đại?.
A.
21
2
x
y
x
B.
3
32y x x
C.
42
23y x x
D.
2
1
2
x
y
x
Câu 252
:
Cho A.hàm số
42
21y x x
. Số giao điểm của đồ thị hàm số với trục hoành là:
A.
4
B.
1
C.
3
D.
2
Câu 253
:
Hàm số
42
6 8 1y x x x
nghịch biến trên khoảng nào sau đây ?
A.
(1; )
B.
( 2; )
C.
( ; 2)
D.
( 2;1)
Câu 254
:
Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
42
1y x x
B.
41
2
x
y
x
C.
3
1y x x
D.
2
1yx
Câu 255
:
Lựa chọn mệnh đề sai
A.
Hàm số
y f x
là đồng biến trên (a;b) nếu có
'0fx
;x a b
B.
Nếu hàm
y f x
có
'0fx
;x a b
và
'0fx
tại một số điểm hữu hạn thì là hàm nghịch
biến trên (a; b)
SDT: 0946798489 36
C.
Nếu hàm
y f x
có
'0fx
;x a b
thì là hàm nghịch biến trên
;ab
D.
Hàm số
y f x
là đồng biến trên (a;b) nếu có
'0fx
;x a b
Câu 256
:
Cho hàm số
4
f x x
x
. Kết luận nào sau đây đúng?
A.
Hàm số
fx
nghịch biến trên
B.
Hàm số
fx
đồng biến trên các khoảng
;0
và
0;
C.
Hàm số
fx
đồng biến trên
D.
Hàm số
fx
nghịch biến trên các khoảng
;0
và
0;
Câu 257
:
Hàm số
32
3
18 5
2
y x x x
đồng biến trên :
A.
2;3
B.
;2
và
3;
C.
;3
và
2;
D.
3;3
Câu 258
:
Hàm số nào sau đây nghịch biến trên khoảng
1;3
?
A.
2
1
23
2
y x x
B.
25
1
x
y
x
C.
2
1
1
xx
y
x
D.
32
2
4 6 10
3
y x x x
Câu 259
:
Cho hàm số
3
3y x x
. Hàm số đồng biến trên:
A.
( ;0)
B.
(0; )
C.
(0;2)
D.
(2;3)
Câu 260
:
Trong các hàm số sau đây, hàm số nào đồng biến trên toàn miền xác định của nó?
A.
3
1yx
B.
sinyx
C.
21
1
x
y
x
D.
2
2
1x
y
x
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 37
Câu
261:
Cho hàm số
2
cosy x x
. Trong các khẳng định sua, khẳng định nào đúng:
A.
' 1 sin 2yx
B.
0;D
C.
Hàm số luôn đồng biến trên
D.
Hàm số có 1 cực trị.
Câu 262
:
Hàm số
11
2
y
xx
nghịch biến trên:
A.
0;1
B.
;0
C.
;0
và
0;1
D.
0;
Câu 263
:
Hàm số nào sau đây đồng biến trên tập xác định của nó
A.
2
2
x
y
x
B.
2
2
x
y
x
C.
2
2
x
y
x
D.
2
2
x
y
x
Câu
264:
Hàm số
42
2 4 1y x x
nghịch biến trên khoảng nào sau đây?
A.
31
;
43
B.
1;1
C.
0;2
D.
1
0;
2
Câu 265
:
Cho hàm số
4
2
yx
x
.Phát biểu nào sau đây đúng ?
A.
Hàm số đồng biến trên
R
B.
Hàm số đồng biến trên từng khoảng
,2
,
2,
C.
Hàm số đồng biến trên
\2R
D.
Hàm số nghịch biến trên
,2
,đồng biến
trên
2,
Câu 266
:
Trong các hàm số sau hàm số nào nghịch biến trên
2;
A.
32
13
21
32
y x x x
B.
32
13
21
32
y x x x
C.
32
6 9 2y x x x
D.
2
52y x x
SDT: 0946798489 38
Câu 267
:
Cho hàm số
32
3 9 12y x x x
trong các mệnh đề sau, mệnh đề nào sai?
A.
Hàm số tăng trên khoảng
;2
B.
Hàm số giảm trên khoảng
1;2
C.
Hàm số tăng trên khoảng
5;
D.
Hàm số giảm trên khoảng
2;5
Câu 268
:
Khẳng định dưới đây khẳng định nào sai?
A.
Hàm số
2
8y x x
nghịch biến trên
B.
Hàm số
2
8y x x
nghịch biến trên
C.
Hàm số
2
osy x c x
đồng biến trên
D.
Hàm số
7 6 5
7
9 7 12
5
y x x x
đồng biến trên
Câu 269
:
Cho hàm số
32
2 3 2y x x
. Khẳng định nào sau đây là đúng về tính đơn điệu của hàm số?
A.
Hàm số nghịch biến trên khoảng
( ;0)
và
(1; )
B.
Hàm số nghịch biến trên khoảng
( ; 1)
và
(0; )
C.
Hàm số nghịch biến trên khoảng
(0;1)
D.
Hàm số đồng biến trên khoảng
( ;0)
Câu 270
:
Hàm số
32
1
32
3
y x x x
đồng biến trên khoảng nào?
A.
3;
B.
3;1
C.
5; 2
D.
4;2
Câu
271:
Khoảng nghịch biến của hàm số
43
1
41
4
y x x x
là:
A.
( 1; )
B.
( ; 1)
C.
( 2; 1)
D.
( ;2)
Câu
272:
Cho hàm số (1):
32
11
2
32
y x x x
. Phát biểu nào sau đây đúng ?
A.
Hàm số (1) đồng biến trên khoảng
;1
B.
Hàm số (1) nghịch biến trên khoảng
2;
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 39
C.
Hàm số (1) nghịch biến trên
D.
Hàm số (1) đồng biến trên khoảng
1;2
Câu
273:
Hàm số
4
21yx
đồng biến trên khoảng:
A.
( ,0)
B.
(1, )
C.
( , )
D.
(0, )
Câu
274:
Cho hàm số
32
31y x x
nghịch biến trên khoảng:
A.
;0
B.
1;
C.
;
D.
0;1
Câu
275:
Tìm tất cả giá trị thực
m
để đồ thị hàm số
3
31y x x
có 2 điểm cực trị A,B đồng thời A,B,
2
( 2; 3 2)C m m
thẳng hàng ?
A.
1m
B.
1m
C.
2m
D.
1m
Câu 276
:
Tìm tất cả các giá trị thực của tham số
m
để hàm số
4
2 1 1y mx m x
có
3
cực trị?
A.
0m
B.
0
1
m
m
C.
01m
D.
2m
Câu 277
:
Tìm tất cả các giá trị của tham số thực
m
để hàm số
42
2 1 3y x m x
có 3 cực trị?.
A.
0m
B.
1m
C.
0m
D.
1m
Câu 278
:
Biết rằng đồ thị hàm số
4 2 2
21y x m x m
có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác
vuông khi giá trị của tham số
m
là:
A.
3
B.
0
C.
1
D.
2
Câu 279
:
Tìm tất cả giá trị thực
m
để hàm số
3
2
2017
3
mx
y x x
có hai điểm cực trị?
A.
1
0
m
m
B.
1m
C.
1
0
m
m
D.
1m
SDT: 0946798489 40
Câu 280
:
Tìm tất cả giá trị thực
m
để hàm số
4
32
2
1
4 3 2
xm
y mx x m
có đúng 1 cực trị?
A.
01m
B.
01m
C.
01m
D.
01m
Câu 281
:
Biết rằng đồ thị hàm số
32
3 3 3 4x mxy xm
có điểm cực trị, thì tất cả giá trị thực
m
nào thích
hợp?
A.
1m
B.
1m
C.
1m
D.
1m
Câu 282
:
Tìm tất cả giá trị thực của tham số
m
để đồ thị hàm số
3 2 2 3 2
3 3 1y x mx m x m m
có hai
điểm cực trị và đường thẳng đi qua hai điểm cực trị này đi qua gốc tọa độ ?
A.
2m
B.
0m
hoặc
1m
C.
0m
D.
1m
Câu
283:
Tìm tất cả các giá trị của tham số thực
m
để đồ thị hàm số
42
21y x mx
có 3 điểm cực trị tạo
thành một tam giác có tâm đường tròn ngoại tiếp trùng với gốc tọa độ
O
?
A.
1m
hoặc
15
2
m
B.
1m
hoặc
15
2
m
C.
15
2
m
hoặc
15
2
m
D.
0m
hoặc
1m
Câu 284
:
Biết rằng hàm số
3 2 2 2
3 3 1 3 1y x x m x m
có hai cực trị
1
x
và
2
x
đồng thời
12
2xx
.
Giá trị thực
m
thích hợp có thể là:
A.
2m
B.
1m
C.
4m
D.
3m
Câu 285
:
Tìm tất cả giá trị thực của tham số
m
để hàm số
4 2 2
2y x mx m m
có 3 cực trị đồng thời
khoảng cách hai điểm cực tiểu bằng
22
A.
1
B.
2
C.
22
D.
3
Câu 286
:
Biết rằng hàm số
3 2 2
2
1 4 3
3
y x m x m m x
có cực trị
12
,.xx
Giá trị lớn nhất của biểu thức
1 2 1 2
2A x x x x
bằng :
A.
9
2
A
B.
9
2
A
C.
1A
D.
3A
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 41
Câu 287
:
Tìm tất cả giá trị thực của tham số
m
để hàm số
32
3 3(2 1) 1y x mx m x
có cực đại, cực tiểu ?
A.
B.
C.
1m
D.
Câu
288:
Tìm tất cả giá trị thực
m
để hàm số
3 2 2
1
( 1) 2
3
y x mx m x
đạt cực tiểu tại
1x
?
A.
2m
B.
1m
C.
0m
D.
2m
Câu
289:
Tìm tất cả giá trị thực
m
để hàm số
3 2 3
31
22
y x mx m
có cực đại, cực tiểu đối xứng nhau qua
đường thẳng
yx
?
A.
2m
B.
3m
C.
1m
D.
2m
Câu
290:
Biết rằng đồ thị hàm số
4 2 2
2 x 3 2y x m m m
có
3
điểm cực trị. Tìm tất cả giá trị
m
để
3
điểm cực trị đó tạo thành một tam giác có diện tích bằng 32.
A.
4m
B.
2m
C.
4m
D.
2m
Câu
291:
Tìm tất cả giá trị thực
m
để hàm số
32
1
1
3
m
y x mx mx
đạt cực tiểu tại
1
x
, cực đại tại
2
x
sao
cho
12
11xx
?
A.
1
1
4
m
B.
01m
C.
0, 1mm
D.
1
,m 1
4
m
Câu
292:
Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
32
3 +2 4033 1y x mx m m
có hai điểm
cực đại, cực tiểu nằm trên đường thẳng
2017 2018yx
.
A.
1
2
m
B.
1
2017,
2
mm
C.
2017m
D.
Không có giá trị
của m.
Câu
293:
Biết rằng hàm số
32
1
34
3
y x ax ax
đạt cực trị tại
1
x
,
2
x
. Tìm giá trị thực của
a
thoả mãn điều
kiện
2
2
12
22
21
29
2
29
x ax a
a
a x ax a
A.
4a
B.
0a
C.
2a
D.
6a
1
m
0
m
01
m

SDT: 0946798489 42
Câu
294:
Tìm tất cả giá trị thực của tham số
m
để điểm
1; 6I
là điểm cực đại của đồ thị hàm số
32
– 3 – 9 1y x mx x
?
A.
m = - 1
B.
m = 1
C.
m =
1
D.
m = 2
Câu
295:
Biết rằng hàm số
42
( 1) 1y x m x
có
3
điểm cực trị
,,A Oy B C
tạo thành một tam giác có bán
kính đường tròn ngoại tiếp bằng
1
. Tất cả giá trị nguyên tham số
m
bằng :
A.
25m
B.
25m
C.
1m
hoặc
25m
D.
1m
Câu
296:
Tìm tất cả giá trị thực
m
để hàm số
3 2 2
22f x x mx m x
đạt cực tiểu tại
1x
?
A.
1m
B.
1;3m
C.
3m
D.
1; 3m
Câu
297:
Tìm tất cả giá trị thực của tham số
m
để đồ thị hàm số
3
31y x mx
có 2 điểm cực trị A, B sao
cho tam giác OAB vuông tại O (với O là gốc tọa độ ).
A.
4m
B.
2m
C.
3m
D.
1
2
m
Câu
298:
Tìm tất cả giá trị thực của tham số
m
để hàm số
32
y x x mx m
có cực trị?
A.
1
3
m
B.
1
3
m
C.
1
3
m
D.
1
3
m
Câu
299:
Tìm tất cả các giá trị thực của m để hàm số
42
1
1 1 2017
2
y m x m x
đạt cực tiểu tại
0
0x
?
A.
1m
B.
1m
C.
1m
hoặc
1m
D.
Không tồn tại giá
trị m
Câu
300:
Tìm tất cả giá trị thực
m
để đồ thị hàm số
3
2
5
3
x
y mx
có cực trị và hai điểm cực trị nằm ở hai
phía khác nhau so với đường thẳng
1x
?
A.
0m
B.
1m
C.
0m
D.
1
2
m
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 43
Câu
301:
Tìm tất cả giá trị thực của tham số
m
để hàm số
3 2 2
1
1 3 2 5
3
y x m x m m x
đạt cực đại
tại
0?x
A.
m = 6
B.
m = 2
C.
m = 1
D.
m = 1 hoặc m = 2
Câu
302:
Tìm tất cả giá trị thực
m
để hàm số
32
36 3f x x mx m x
không có cực trị ?
A.
9 12m
B.
9m
hoặc
12m
C.
9m
hoặc
12m
D.
9 12m
Câu
303:
Tìm tất cả các giá trị thực của m để đồ thị hàm số
32
3y x x m
có 2 điểm cực trị A, B sao cho
góc
0
60AOB
, trong đó O là gốc tọa độ.
A.
12 12
3
m
B.
12 12
3
m
C.
0m
D.
0m
hoặc
12 12
3
m
Câu 304
:
Tìm tất cả giá trị thực của tham số
m
để hàm số
32
31y x mx mx
có hai điểm cực trị?
A.
1
0
3
m
B.
0m
hoặc
1
3
m
C.
0m
hoặc
1
3
m
D.
0m
hoặc
1
3
m
Câu 305
:
Tìm tất cả giá trị thực
m
để đồ thị hàm số
2
1
x x m
y
x
có cực đại và cực tiểu?
A.
2m
B.
2m
C.
2m
D.
2m
Câu 306
:
Tìm tất cả giá trị thực
m
để đồ thị hàm số
32
1
11
3
y x mx m x m
có hai điểm cực đại, cực
tiểu cách đều trục tung?
A.
Không tồn tại giá
trị m.
B.
2
C.
1
D.
0
Câu 307
:
Tìm tất cả giá trị thực
m
để đồ thị hàm số
32
3 3 1y x mx m
có điểm cực đại và điểm cực tiểu
đối xứng nhau qua đường thẳng
: 8 74 0d x y
?
SDT: 0946798489 44
A.
1m
B.
2m
C.
1m
D.
2m
Câu 308
:
Tìm tất cả giá trị thực của tham số
m
để hàm số
42
1 2 1
2
42
mm
y x x
có 2 cực đại và 1 cực
tiểu?
A.
1
2
m
B.
1
1
2
m
C.
1
2
m
D.
1m
Câu 309
:
Tìm tất cả giá trị thực
m
để đồ thị hàm số
4 2 2
21y x m x
có ba điểm cực trị là ba đỉnh của một
tam giác vuông cân?
A.
1m
B.
1m
C.
1m
D.
2m
Câu 310
:
Biết rằng hàm số
4 2 2 4
21y x m x m
có
3
điểm cực trị
,,A Oy B C
sao cho bốn điểm
cùng nằm trên
1
đường tròn ?. Tất cả giá trị tham số
m
bằng :
A.
1m
B.
0m
C.
1m
D.
1m
Câu 311
:
Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
32
11
x 2 1
32
y x m m m
có hai cực trị
nằm phía trên trục hoành là:
A.
mR
B.
1;m
C.
;1 1;m
D.
Không có giá trị
của m.
Câu 312
:
Biết rằng hàm số
32
1
82
3
y x mx x
có 2 cực trị
12
;xx
thỏa
12
20xx
thì giá trị thực của m
thích hợp là ?
A.
3m
B.
4m
C.
2m
D.
1m
Câu 313
:
Tìm tất cả giá trị thực của tham số
m
để đường thẳng nối 2 điểm cưc trị của đồ thị hàm số
3
31y x x
vuông góc với đường thẳng
32y mx
A.
1
3
m
B.
1
3
m
C.
1
6
m
D.
7
6
m
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 45
Câu 314
:
Tìm tất cả giá trị thực của tham số
m
để đồ thị hàm số
42
1
( 1) 2 1
4
y x m x m
có cực đại
A
và
cực tiểu
,BC
sao cho
ABIC
là hình thoi với
5
0;
2
I
?
A.
1
B.
22
C.
1
2
D.
3
Câu 315
:
Tìm tất cả giá trị thực
m
để hàm số
32
32y x x mx m
có hai điểm cực trị ?
A.
0m
B.
3m
C.
3m
D.
0m
Câu 316
:
Tìm tất cả giá trị thực
m
để thích hợp để hàm số
42
2y x mx
có 1 cực trị?
A.
2m
B.
3m
C.
1m
D.
0 m
Câu
317:
Tìm tất cả giá trị thực của tham số
m
để đường thẳng đi qua hai điểm cực trị của hàm số
3
31y x mx
tiếp xúc với đường tròn (T):
22
4
11
5
xy
?
A.
2m
B.
1m
C.
1m
hoặc
1m
D.
1m
Câu 318
:
Tìm tất cả giá trị thực
m
để hàm số
3
22
( 1) ( 3) 1
3
x
y m x m x
đạt cực trị tại
1x
?
A.
0m
B.
0m
hoặc
2m
C.
0m
hoặc
2m
D.
2m
Thầy Lê Văn Đoàn (218 câu)
Câu 1. Cho hàm số
()y f x
xác định, liên tục trên và có bảng biến thiên:
x
0
1
y
0
y
0
1
Khẳng định nào sau đây là khẳng định đúng ?
SDT: 0946798489 46
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng
1.
C. Hàm số có giá trị lớn nhất bằng
0
và giá trị nhỏ nhất bằng
1.
D. Hàm số đạt cực đại tại
0x
và đạt cực tiểu tại
1.x
Câu 2. Cho hàm số
()y f x
có đạo hàm tại
.
o
x
Tìm mệnh đề đúng ?
A. Hàm số đạt cực trị tại
o
x
thì
( ) 0.
o
fx
B. Nếu
( ) 0
o
fx
thì hàm số đạt cực trị tại
.
o
x
C. Hàm số đạt cực trị tại
o
x
thì
()fx
đổi dấu khi qua
.
o
x
D. Nếu hàm số đạt cực trị tại
o
x
thì
( ) 0.
o
fx
Câu 3. Giả sử hàm số
()y f x
có đạo hàm cấp hai. Chọn phát biểu đúng ?
A. Nếu
( ) 0
o
fx
và
( ) 0
o
fx
thì hàm số
()y f x
đạt cực đại tại
.
o
x
B. Nếu
( ) 0
o
fx
và
( ) 0
o
fx
thì hàm số
()y f x
đạt cực tiểu tại
.
o
x
C. Nếu
( ) 0
o
fx
và
( ) 0
o
fx
thì hàm số
()y f x
đạt cực đại tại
.
o
x
D. Nếu
( ) 0
o
fx
thì hàm số
()y f x
đạt cực đại tại
.
o
x
Câu 4. Hàm số bậc ba có thể có bao nhiêu cực trị ?
A.
1
hoặc
2
hoặc
3.
B.
0
hoặc
2.
C.
0
hoặc
1
hoặc
2.
D.
2.
Câu 5. Đồ thị hàm số
42
23y x x
có:
A. Một cực đại và hai cực tiểu. B. Một cực tiểu và hai cực đại.
C. Một cực tiểu và không cực đại. D. Không có cực đại và cực tiểu.
Câu 6. Hàm số nào sau đây không có cực trị:
A.
3
3.y x x
B.
2
21
x
y
x
C.
1
yx
x
D.
42
2.y x x
Câu 7. Hàm số nào sau đây không có cực đại và cực tiểu ?
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 47
A.
42
2.y x x
B.
3
2.y x x
C.
3
.yx
D.
2
2 1.y x x
Câu 8. Cho hàm số
3
3 2.y x x
Khẳng định nào sau đây sai ?
A. Hàm số đạt cực đại tại
1.x
B. Hàm số đạt cực tiểu tại
1.x
C. Hàm số không có cực trị. D. Hàm số có 2 điểm cực trị.
Câu 9. Trong các mệnh đề sau, hãy tìm mệnh đề sai ?
A. Hàm số
1
2
y
x
không có cực trị.
B. Hàm số
32
31y x x
có cực đại và cực tiểu.
C. Hàm số
1
1
yx
x
có hai cực trị.
D. Hàm số
3
2y x x
có cực trị.
Câu 10. Đồ thị hàm số
42
12y x x
có mấy điểm cực trị:
A.
4.
B.
3.
C.
2.
D.
1.
Câu 11. Số điểm cực trị của đồ thị hàm số
3
7
3
x
yx
là:
A.
0.
B.
1.
C.
2.
D.
3.
Câu 12.
Số điểm cực trị của đồ thị hàm số
42
21y x x
là:
A.
0.
B.
1.
C.
2.
D.
3.
Câu 13.
Số điểm cực trị của đồ thị hàm số
43
8 12y x x
là:
A.
0.
B.
1.
C.
2.
D.
3.
Câu 14. Đồ thị hàm số
sinyx
có mấy điểm cực trị ?
A.
3.
B.
2.
C.
1.
D. Vô số.
Câu 15. Hàm số
6
2 4 7y x x
có số điểm cực trị là:
A.
0.
B.
1.
C.
2.
D.
3.
Câu 16. Một hàm số
()fx
có đạo hàm là
32
( ) 2 .f x x x x
Số cực trị của hàm số là:
SDT: 0946798489 48
A.
0.
B.
1.
C.
2.
D.
3.
Câu 17. Một hàm số
()fx
có đạo hàm là
2 3 5
( ) ( 1) ( 2) ( 3) .f x x x x x
Hỏi hàm số này có bao nhiêu
cực trị ?
A.
4.
B.
3.
C.
2.
D.
1.
Câu 18. Số các điểm cực trị của hàm số
53
(2 ) ( 1)y x x
là:
A.
1.
B.
3.
C.
5.
D.
7.
Câu 19. Đồ thị hàm số
2
9yx
có mấy điểm cực trị ?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 20. Hàm số
32
3 9 2y x x x
có điểm cực tiểu tại:
A.
1.x
B.
3.x
C.
1.x
D.
3.x
Câu 21. Hệ thức liên hệ giữa giá trị cực đại
()
CD
y
và giá trị cực tiểu
()
CT
y
của đồ thị hàm số
3
2y x x
là:
A.
2.
CT CD
yy
B.
2 3 .
CT CD
yy
C.
.
CT CD
yy
D.
0.
CT CD
yy
Câu 22. Tìm giá trị cực đại
C
y
Đ
của đồ thị hàm số
3
3 2.y x x
A.
4.
C
y
Đ
B.
1.
C
y
Đ
C.
0.
C
y
Đ
D.
1.
C
y
Đ
Câu 23.
Giá trị cực đại của hàm số
3
34y x x
là:
A.
2.
B.
1.
C.
6.
D.
1.
Câu 24.
Hàm số
1
yx
x
có giá trị cực đại là:
A.
2.
B.
2.
C.
1.
D.
1.
Câu 25. Hàm số
3
3y x x
có giá trị cực tiểu là:
A.
2.
B.
2.
C.
1.
D.
1.
Câu 26. Giá trị cực đại của hàm số
32
3 3 2y x x x
bằng:
A.
3 4 2.
B.
3 4 2.
C.
3 4 2.
D.
3 4 2.
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 49
Câu 27. Giá trị cực đại của hàm số
2
21y x x
là:
A.
2
2
B.
2
2
C.
2
4
D. Không có
.
C
y
Đ
.............................................................................................................................................................
.............................................................................................................................................................
Câu 28. Giá trị cực đại của hàm số
2cosy x x
trên khoảng
(0; )
là:
A.
3.
6
B.
5
3.
6
C.
5
3.
6
D.
3.
6
Câu 29. Hàm số
cos yx
đạt cực đại tại điểm:
A.
, ( ).
2
x k k
B.
2 , ( ).x k k
C.
2 , ( ).x k k
D.
, ( ).x k k
Câu 30. Hàm số
2sin2 3yx
đạt cực tiểu tại:
A.
; ( ).
42
k
xk
B.
; ( ).
4
x k k
C.
; ( ).
2
x k k
D.
; ( ).
4
x k k
Câu 31. Hàm số
3 2cos cos2y x x
đạt cực tiểu tại:
A.
2 , ( ).x k k
B.
, ( ).x k k
C.
2 , ( ).
2
x k k
D.
, ( ).
2
x k k
Câu 32. Cực trị của hàm số
sin cosy x x
là:
A.
, ( ); 2
4
CT CT
x k k y
và
3
2 , ( ); 2.
4
CD CD
x k k y
SDT: 0946798489 50
B.
, ( ); 2
4
CD CD
x k k y
và
3
2 , ( ); 2.
4
CT CT
x k k y
C.
3
, ( ); 2.
4
CT CT
x k k y
D.
, ( ); 2.
4
CD CD
x k k y
Câu 33. Hàm số
2sin 2y x x
đạt cực tiểu tại:
A.
, ( ).
3
x k k
B.
, ( ).
3
x k k
C.
2 , ( ).
3
x k k
D.
2 , ( ).
3
x k k
Câu 34. Cho hàm số
cos2 1, ( ;0)y x x
thì khẳng định nào sau đây sai ?
A. Hàm số đạt cực tiểu tại điểm
7
12
x
B. Hàm số đạt cực đại tại điểm
11
12
x
C. Tại
2
x
hàm số không đạt cực đại.
D. Tại
12
x
hàm số không đạt cực tiểu.
Câu 35. Hàm số
22
3
( 2 )y x x
đạt cực trị tại điểm có hoành độ là:
A.
1.x
B.
0, 1.xx
C.
0, 1, 2.x x x
D. Hàm số không có điểm cực trị.
Câu 36. Hàm số
32
3 4 14y x x x
đạt cực trị tại hai điểm
12
, .xx
Khi đó tích số
12
xx
là:
A.
1
9
B.
1
7
C.
1.
D.
3.
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 51
Câu 37. Cho hàm số
4
3
41
4
x
y x x
. Gọi
12
, xx
là
2
nghiệm của phương trình
0.y
Khi đó
tổng
12
xx
bằng:
A.
1.
B.
2.
C.
0.
D.
1.
Câu 38. Cho hàm số
32
3 4 14.y x x x
Hàm số đạt cực trị tại
2
điểm
12
, .xx
Khi đó tổng
12
xx
có giá trị là:
A.
1
9
B.
1
7
C.
8
9
D.
1.
Câu 39. Cho hàm số
32
5 6 2.y x x x
Hàm số đạt cực trị tại
2
điểm
12
, .xx
Khi đó tổng
12
xx
có giá trị là:
A.
10
3
B.
10
3
C.
1.
D. Đáp án khác.
Câu 40. Cho hàm số
32
1
3.
2
y x x x
Hàm số đạt cực trị tại
2
điểm
12
, .xx
Khi đó tổng
22
12
S x x
có giá trị là:
A.
11
3
B.
13
3
C.
1
2
D.
3
2
Câu 41. Cho hàm số
32
1
3.
2
y x x x
Hàm số đạt cực trị tại
2
điểm
12
, .xx
Khi đó tổng
22
12
S x x
có giá trị là:
A.
12.
B.
12.
C.
18.
D.
20.
Câu 42. Cho hàm số
32
3 21 1.y x x x
Hàm số đạt cực trị tại
2
điểm
12
, .xx
Khi đó tổng
22
12
S x x
có giá trị là:
A.
18.
B.
24.
C.
36.
D.
48.
Câu 43. Cho hàm số
32
3 1.y x x
Tích giá trị cực đại và cực tiểu của đồ thị hàm số là:
A.
6.
B.
3.
C.
0.
D.
3.
SDT: 0946798489 52
Câu 44. Gọi
12
, yy
lần lượt là giá trị cực đại và giá trị cực tiểu của đồ thị hàm số
42
10 9.y x x
Khi đó giá trị của biểu thức
12
T y y
bằng:
A.
7.
B.
9.
C.
25.
D.
2 5.
Câu 45. Cho hàm số
32
2 3 5.y x x
Tổng các giá trị cực trị của hàm số là:
A.
9.
B.
1.
C.
1.
D.
5.
Câu 46. Hàm số
42
25y x x
có các điểm cực trị lần lượt là
1 2 3
, , x x x
thì tích
1 2 3
..x x x
là:
A.
2.
B.
1.
C.
0.
D.
1.
Câu 47. Hàm số
3
1yx
x
có tổng các điểm cực đại và cực tiểu bằng:
A. A.
2.
B.
1.
C.
0.
D.
2.
Câu 48. Hàm số
2
41
1
xx
y
x
có tích các điểm cực đại và cực tiểu bằng:
A.
2.
B.
5.
C.
1.
D.
4.
Câu 49. Cho đồ thị hàm số
2
2
1
yx
x
Khi đó
?
CÐ CT
yy
A.
3 2 2.
B.
3 2 2.
C.
2.
D.
6.
Câu 50. Hàm số
2
33
1
xx
y
x
có tích các giá trị cực đại và cực tiểu bằng:
A.
3.
B.
1.
C.
1.
D.
2.
Câu 51. Khẳng định nào sau đây là đúng về đồ thị hàm số
2
25
1
xx
y
x
:
A.
0.
CÐ CT
yy
B.
4.
CT
y
C.
1.
CÐ
x
D.
3.
CÐ CT
xx
Câu 52. Khoảng cách giữa hai cực trị của đồ thị hàm số
32
33y x x
là:
A.
5.
B.
2 5.
C.
3 5.
D.
8 5.
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 53
Câu 53. Cho hàm số
2
21
1
xx
y
x
Khoảng cách giữa hai điểm cực trị là:
A.
4 5.
B.
4.
C.
8.
D.
5 2.
Câu 54. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số
2
1
x mx m
y
x
bằng:
A.
5.
B.
2 5.
C.
4 5.
D.
5 2.
Câu 55. Biết đồ thị hàm số
42
2y x px q
có một điểm cực trị là
(1;2),M
thế thì khoảng cách giữa
điểm cực tiểu và điểm cực đại là:
A.
26.
B.
5.
C.
2.
D.
2.
Câu 56. Đồ thị hàm số
2
22
1
xx
y
x
có
2
điểm cực trị nằm trên đường thẳng
y ax b
thì giá trị
của tổng
ab
bằng bao nhiêu ?
A.
4.
B.
4.
C.
2.
D.
2.
Câu 57. Đồ thị hàm số
1
1
1
yx
x
có hai điểm cực trị nằm trên đường thẳng
y ax b
thì tích
.ab
bằng:
A.
0.
B.
2.
C.
4.
D.
2.
Câu 58. Hàm số
4
2
21
4
x
yx
đạt cực đại tại:
A.
2.x
B.
2.x
C.
0.x
D.
2.x
Câu 59. Hàm số
3
2
2 3 5
3
x
y x x
đạt cực tiểu tại:
A.
1.x
B.
3.x
C.
1.x
D.
3.x
Câu 60. Hàm số
2
33
2
xx
y
x
đạt cực đại tại:
A.
1.x
B.
2.x
C.
3.x
D.
0.x
SDT: 0946798489 54
Câu 61.
Hàm số
42
1
23
2
y x x
đạt cực đại tại
x
bằng:
A.
0.
B.
2.
C.
2.
D.
2.
Câu 62. Hàm số
3
34y x x
đạt cực tiểu tại
x
bằng:
A.
1.
B.
1.
C.
3.
D.
3.
Câu 63. Hàm số
32
(1 )y x x
đạt cực đại tại:
A.
1.x
B.
1.x
C.
3
5
x
D. Đáp án khác.
Câu 64.
Điểm cực đại của đồ thị hàm số
32
2 3 2y x x
là:
A.
(0; 2).M
B.
(2;2).N
C.
(1; 3).P
D.
( 1; 7).Q
Câu 65. Tọa độ điểm cực tiểu của đồ thị hàm số
42
2y x x
là:
A.
(0;0).M
B.
(1;1).N
C.
( 1;1).P
D.
( 1;0).Q
Câu 66. Tọa độ điểm cực đại của đồ thị hàm số
32
12
23
33
y x x x
là:
A.
(1;3).M
B.
(1;0).N
C.
(1;2).P
D.
(3;1).Q
Câu 67. Điểm cực tiểu của đồ thị hàm số
32
33y x x
là:
A.
(1;1).M
B.
( 2;1).N
C.
(0;3).P
D.
(1; 6).Q
Câu 68. Điểm cực đại của đồ thị hàm số
42
6 8 1y x x x
là:
A.
( 2;24).M
B.
( 2;25).N
C.
(7;3).P
D.
(1; 6).Q
Câu 69. Điểm cực tiểu của đồ thị hàm số
42
65y x x
là:
A.
( 3;0).
B.
( 3; 4).
C.
( 3;4).
D.
(0;2).
Câu 70. Hàm số nào sau đây đạt cực tiểu tại
3
2
x
?
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 55
A.
1
2
x
y
x
B.
2
3 2.y x x
C.
2
4 12 8.y x x
D.
4 3 2
1
3.
2
y x x x x
Câu 71. Điểm cực tiểu của đồ thị hàm số
43
41y x x
là:
A.
(2; 15).M
B.
(1;2).N
C.
( 2;11).P
D.
(4; 6).Q
Câu 72. Cho hàm số
2
3 2 .y x x
Trong các điểm sau, điểm nào có tọa độ sau đây là điểm cực trị
của hàm số đã cho:
A.
( 1;2).M
B.
( 3;0).N
C.
(1;0).P
D.
( 2; 3).Q
Câu 73. Điểm cực tiểu của đồ thị hàm số
2
4y x x
là:
A.
( 2;2).M
B.
( 2;1).N
C.
( 2; 2).P
D.
( 2;2).Q
Câu 74. Xét tính cực trị của đồ thị hàm số
2
25
;
1
xx
y
x
ta có:
A.
( 3; 4)M
là điểm cực tiểu. B.
(1; 4)N
là điểm cực đại.
C.
( 3; 4)P
là điểm cực đại. D. Hàm số không có cực trị.
Câu 75. Cho hàm số
43
3 4 .y x x
Khẳng định nào sau đây đúng ?
A. Hàm số không có cực trị. B. Điểm
là điểm cực tiểu.
C. Hàm số đạt cực đại tại gốc tọa độ. D. Hàm số đạt cực tiểu tại gốc tọa độ.
Câu 76. Với giá trị nào của tham số
m
thì đường thẳng
:d y x m
đi qua trung điểm của đoạn thẳng
nối hai điểm cực trị của đồ thị hàm số
32
6 9 ?y x x x
A.
0.m
B.
1.m
C.
2.m
D.
3.m
Câu 77. Hàm số nào sau đây chỉ có cực đại mà không có cực tiểu ?
A.
32
3 2.y x x
B.
1
2
x
y
x
SDT: 0946798489 56
C.
4
2
1.
2
x
yx
D.
2
1
x
y
x
Câu 78. Cho hàm số
4 3 2
1 4 7
2 1.
4 3 2
y x x x x
Khẳng định nào sau đây đúng ?
A. Hàm số không có cực trị. B. Hàm số có cực tiểu, không có cực đại.
C. Hàm số có 1 cực đại và 2 cực tiểu. D. Hàm số có 1 cực tiểu và 2 cực đại.
Câu 79. Hàm số
23
32y x x
đạt cực trị tại:
A.
1; 0.
CD CT
xx
B.
1; 0.
CD CT
xx
C.
0; 1.
CD CT
xx
D.
0; 1.
CD CT
xx
Câu 80. Gọi
, AB
lần lượt là
2
điểm cực trị của đồ thị hàm số
32
3 4.y x x
Khi đó diện tích tam
giác
,OBC
(với O là gốc tọa độ) có giá trị bằng bao nhiêu ?
A.
2.
B.
4.
C.
2 5.
D.
8.
Câu 81. Gọi
, AB
lần lượt là
2
điểm cực trị của đồ thị hàm số
32
3 2.y x x
Khi đó diện tích tam
giác
,ABC
với
(1;1)C
có giá trị bằng bao nhiêu ?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 82. Gọi
, AB
lần lượt là
2
điểm cực trị của đồ thị hàm số
32
2 3 36 10.y x x x
Khi đó diện
tích của tam giác
,ABC
với
(2;3)C
có giá trị bằng bao nhiêu ?
A.
78.
B.
87
3
C.
287
2
D.
285
2
Câu 83. Gọi
, AB
lần lượt là
2
điểm cực trị của đồ thị hàm số
2
( 1) (2 ).y x x
Khi đó diện tích của
tam giác
,ABC
với
(1; 3)C
có giá trị bằng bao nhiêu ?
A.
3
5
B.
8
3
C.
7.
D. Đáp án khác.
Câu 84. Gọi
, , A B C
là ba điểm cực trị của đồ thị hàm số
42
2 4 1.y x x
Hỏi diện tích tam giác
ABC
là bao nhiêu ?
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 57
A.
4.
B.
2.
C.
1.
D.
3
2
Câu 85. Cho hàm số
2 1 4 1.y x x
Tìm mệnh đề đúng trong các mệnh đề sau ?
A. Giá trị cực đại bằng
1
2
B. Điểm cực tiểu có tọa độ là
1
;1
2
M
C. Điểm cực tiểu là
11
;
42
N
D. Hàm số không có cực trị.
Câu 86. Cho hàm số
32
2 3 2.y x x
Câu nào sau đây sai ?
A. Hàm số đạt cực tiểu trên
11
;
22
B. Hàm số đạt cực đại trên
1
;2
2
C. Hàm số có 2 cực trị trên
1
;2
2
D. Hàm số có 2 cực trị trên
1
;3
3
Câu 87. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
3
2
2 3 5 :
3
x
y x x
A. Song song với đường thẳng
1.x
B. Song song với trục hoành.
C. Có hệ số góc dương. D. Có hệ số góc bằng
1.
Câu 88. Tiếp tuyến tại điểm cực trị của đồ thị hàm số
42
, 0y ax bx c a
có gì đặc biệt
A. Song song với trục tung. B. Có hệ số góc dương.
C. Song song với trục hoành. D. Luôn đi qua gốc tọa độ.
Câu 89. Phương trình tiếp tuyến của đồ thị hàm số
42
21y x x
tại điểm cực tiểu là:
A.
1 0.y
B.
0.y
C.
1 0.xy
D.
.yx
Câu 90. Khoảng cách từ điểm cực đại của đồ thị hàm số
3
31y x x
đến đường phân giác góc phần
tư thứ hai trong hệ trục
Oxy
là:
A.
1.
B.
2.
C.
2.
D.
3.
SDT: 0946798489 58
Câu 91. Đồ thị hàm số
2
3
2
x x m
y
x
nhận điểm
(0;3)A
làm cực trị thì phương trình của hàm số
có dạng là:
A.
2
36
2
xx
y
x
B.
2
31
2
xx
y
x
C.
2
36
2
xx
y
x
D.
2
3
2
xx
y
x
Dạng toán 2. Phương trình đường thẳng nối hai điểm cực trị
Câu 92. Phương trình đường thẳng nào sau đây là phương trình đường thẳng đi qua hai điểm cực trị của
đồ thị hàm số
32
6 9 ?y x x x
A.
2 6.yx
B.
2 6.yx
C.
6 2 .yx
D.
3.yx
Câu 93. Phương trình đường thẳng nào sau đây là phương trình đường thẳng đi qua hai điểm cực trị của
đồ thị hàm số
32
3 2 ?y x x
A.
2.yx
B.
2.yx
C.
2 2 .yx
D.
2 2.yx
Câu 94. Đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số
3
35y x x
có hệ số góc là
A.
2.
B.
1.
C.
2.
D.
5.
Câu 95. Cho hàm số
3 2 2 3
3 3( 1) .y x mx m x m m
Phương trình đường thẳng nối hai điểm
cực trị của đồ thị hàm số có dạng:
A.
2 0.xy
B.
3 0.mx y
C.
2
2.y x m
D.
.y x m
Câu 96. Phương trình đường thẳng
d
đi qua điểm cực đại và điểm cực tiểu của đồ thị hàm số
32
2 5 1y x x x
có dạng:
A.
: 3 9 2 0.d x y
B.
: 4 5.d y x
C.
: 38 9 19 0.d x y
D.
: 17 11.d y x
Câu 97. Đồ thị hàm số
32
3y x x mx m
có đường thẳng đi qua hai điểm cực trị song song với
đường thẳng
: 2 1d y x
khi:
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 59
A.
B.
C.
6.m
D.
Câu 98. Đồ thị hàm số
32
32y x x mx
có đường thẳng đi qua hai điểm cực trị song song với
đường thẳng
: 4 3 0d x y
khi:
A.
1.m
B.
2.m
C.
3.m
D.
4.m
Câu 99. Đồ thị hàm số
32
3( 1) 6( 2) 1y x m x m x
có đường thẳng đi qua hai điểm cực trị
song song với đường thẳng
: 1 4d y x
khi:
A.
1.m
B.
3.m
C.
1m
hoặc
3.m
D.
3m
hoặc
1.m
Câu 100. Đồ thị hàm số
32
2 3( 1) 6y x m x mx
có hai điểm cực trị
, .AB
Với giá trị nào của tham
số
m
thì đường thẳng
:2d y x
vuông góc với đường thẳng
?AB
A.
0.m
B.
2.m
C.
0m
hoặc
2.m
D.
0m
hoặc
2.m
Câu 101. Đồ thị hàm số
2
55
22
xx
y
x
có hai điểm cực trị
, AB
nằm trên đường thẳng
.d
Hệ số góc
của đường thẳng
d
là:
A.
1.
B.
1.
C.
3.
D.
5.
Câu 102. Đồ thị hám số
2
35
2
xx
y
x
có hai điểm cực trị
, AB
nằm trên đường thẳng
d
có phương
trình
y ax b
thì giá trị của
T a b
là:
A.
1.
B.
1.
C.
3.
D.
5.
Câu 103. Đồ thị hám số
2
24
2
xx
y
x
có hai điểm cực trị
, AB
nằm trên đường thẳng
d
có phương
trình
y ax b
thì giá trị của
T a b
là:
A.
1.
B.
0.
C.
1.
D.
2.
Dạng toán 3. Tìm tham số
m
để hàm số có
n
cực trị, có cực trị tại
.
o
xx
Câu 104. Tìm
m
để hàm số
32
32y x mx x
đạt cực tiểu tại
2x
?
SDT: 0946798489 60
A.
15
4
m
B.
4
15
m
C.
4
15
m
D.
15
4
m
Câu 105. Tìm
m
để hàm số
32
3 12 2y mx x x
đạt cực đại tại
2x
?
A.
2.m
B.
3.m
C.
0.m
D.
1.m
Câu 106. Hàm số
32
3y x x mx
đạt cực tiểu tại
2x
khi:
A.
0.m
B.
0.m
C.
0.m
D.
0.m
Câu 107. Hàm số
3 2 2
1
( 1) 1
3
y x mx m m x
đạt cực đại tại điểm
1x
khi:
A.
1m
hoặc
2.m
B.
1.m
C.
2.m
D.
m
tùy ý.
Câu 108. Hàm số
3
( 1) 1y x m x
đạt cực tiểu tại điểm
2x
khi:
A.
13.m
B.
13.m
C.
1.m
D.
.m
Câu 109. Hàm số
3 2 2
6 (4 1) 2y x mx m x
đạt cực đại tại điểm
2x
khi:
A.
0.m
B.
11
2
m
C.
4.m
D.
4.m
Câu 110. Hàm số
32
21y x x mx
đạt cực tiểu tại
1x
khi:
A.
1.m
B.
1.m
C.
2.m
D. Không có
.m
Câu 111. Hàm số
3 2 2
1
2 3 3
3
y x mx m x m
đạt cực tiểu tại
1x
khi:
A.
1.m
B.
1.m
C.
D.
1
3
m
Câu 112. Hàm số
32
( 1) 2y x m x m
đạt cực đại tại điểm
2x
khi:
A.
0.m
B.
11
2
m
C.
4.m
D.
4.m
Câu 113. Hàm số
3 2 2
2 2y x mx m x
đạt cực tiểu tại điểm
1x
khi:
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 61
A.
1.m
B.
1.m
C.
2.m
D.
2.m
Câu 114. Hàm số
32
1
( 1)
32
m
y x x m x
đạt cực đại tại
1x
khi:
A.
2.m
B.
2.m
C.
2.m
D.
.m
Câu 115. Hàm số
32
( 3) 2y x m x mx m
đạt cực tiểu tại điểm
2x
khi:
A.
0.m
B.
11
2
m
C.
4.m
D.
4.m
Câu 116. Hàm số
3 2 2
1
( 1) ( 3 2) 5
3
y x m x m m x
đạt cực trị tại
0x
khi:
A.
1.m
B.
2.m
C. A, B đều đúng. D. A, B đều sai.
Câu 117. Hàm số
3 2 2
1
( 1) 1
3
y x mx m m x
đạt cực trị tại
1x
khi:
A.
0.m
B.
1.m
C.
2.m
D.
3.m
Câu 118. Hàm số
4 2 2
25y x m x
đạt cực tiểu tại
1x
khi:
A.
1.m
B.
1.m
C. A, B đều đúng. D. A, B đều sai.
Câu 119. Hàm số
42
2( 2) 3y x m x m
đạt cực đại tại điểm
1x
khi:
A.
3.m
B.
5.m
C.
3.m
D.
5.m
Câu 120. Hàm số
42
31y x mx
đạt cực tiểu tại điểm
2x
khi:
A.
8
3
m
B.
C.
3.m
D.
8.m
Câu 121. Hàm số
42
1
4
y x ax b
có cực trị tại
1x
và giá trị cực trị tương ứng bằng
2
thì giá trị
của
, ab
lần lượt là:
A.
19
;
24
ab
B.
19
;
24
ab
C.
19
;
24
ab
D.
19
;
24
ab
Câu 122. Đồ thị hàm số
42
y ax bx c
đạt cực đại tại
(0; 3),A
đạt cực tiểu tại
( 1; 5)B
thì sẽ có
giá trị của
, , a b c
lần lượt là:
SDT: 0946798489 62
A.
2; 4; 3.
B.
3; 1; 5.
C.
2; 4; 3.
D.
2; 4; 3.
Câu 123. Hàm số
32
5y ax x x b
đạt cực tiểu tại
1x
và giá trị cực tiểu bằng
2
khi:
A.
1, 5.ab
B.
1, 5.ab
C.
1, 5.ab
D.
1, 1.ab
Câu 124. Hàm số
32
2 4 2016y x ax bx
đạt cực đại tại
1.x
Khi đó tổng
ab
là:
A.
4
3
B.
4
3
C.
3
4
D.
3
4
Câu 125. Hàm số
1
.sin sin 3
3
y m x x
đạt cực trị tại điểm
3
x
khi:
A.
2.m
B.
0.m
C.
2.m
D.
3.m
Câu 126. Hàm số
2
1x mx
y
xm
đạt cực tiểu tại
1x
khi:
A.
2.m
B.
2m
hoặc
0.m
C.
0.m
D. Không có
m
thỏa yêu cầu bài toán.
Câu 127. Cho hàm số
32
1
(2 1) 1.
3
y x m x m x
Mệnh đề nào sau đây là sai ?
A.
thì hàm số có cực đại và cực tiểu.
B.
1m
thì hàm số có hai điểm cực trị.
C.
1m
thì hàm số có cực trị.
D. Hàm số luôn có cực đại và cực tiểu.
Câu 128. Đồ thị hàm số
42
, ( 0)y ax bx c a
có ba điểm cực trị khi và chỉ khi:
A.
0.b
B.
0.ab
C.
0.ab
D.
0.ab
Câu 129. Đồ thị hàm số
42
, ( 0)y ax bx c a
có một điểm cực trị khi và chỉ khi:
A.
0.b
B.
0.ab
C.
0.ab
D.
0.b
Câu 130. Đồ thị hàm số
42
, ( 0)y ax bx c a
có
1
điểm cực đại và
2
điểm cực tiểu khi và chỉ khi:
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 63
A.
0
0
a
b
B.
C.
0
0
a
b
D.
0
0
a
b
Câu 131. Đồ thị hàm số
42
, ( 0)y ax bx c a
có
1
điểm cực tiểu và
2
điểm cực đại khi và chỉ khi:
A.
0
0
a
b
B.
0
0
a
b
C.
0
0
a
b
D.
0
0
a
b
Câu 132. Đồ thị hàm số
32
, ( 0)y ax bx cx d a
có hai điểm cực trị khi và chỉ khi:
A.
2
4 12 0.b ac
B.
2
4 12 0.a bc
C.
2
4 12 0.b ac
D.
2
4 12 0.b ac
Câu 133. Đồ thị hàm số
32
, ( 0)y ax bx cx d a
không có điểm cực trị khi và chỉ khi:
A.
2
4 12 0.b ac
B.
2
4 12 0.a bc
C.
2
4 12 0.b ac
D.
2
4 12 0.b ac
Câu 134. Điều kiện của tham số
m
để hàm số
32
3 3 2y x x mx m
có cực trị là:
A.
1.m
B.
1.m
C.
1.m
D.
1.m
Câu 135. Với giá trị nào của tham số
m
để hàm số
32
11
21
32
y x mx x
có cực trị là:
A.
0.
B.
3.
C.
4.
D. Cả A, B, C.
Câu 136. Điều kiện của
m
để hàm số
32
32y x x mx m
có
2
điểm cực trị là:
A.
3.m
B.
3.m
C.
.m
D.
.m
Câu 137. Hàm số
3
1y x mx
có
2
cực trị khi:
A.
0.m
B.
0.m
C.
0.m
D.
0.m
Câu 138. Với giá trị nào của
m
thì hàm số
32
3 2 1y x mx x m
có cực đại, cực tiểu ?
A.
( 3;3).m
B.
( ; 3) (3; ).m
C.
3;3 .m
D.
; 3 3; .m
Câu 139. Tìm tham số
m
để hàm số
3 2 2
33y x mx m
có
2
điểm cực trị ?
A.
0.m
B.
0.m
C.
0.m
D.
0.m
SDT: 0946798489 64
Câu 140. Hàm số
32
( 1) 2y x m x x
có cực đại, cực tiểu khi:
A.
1 3 1 3.m
B.
1 3 1 3.m
C.
13m
hoặc
1 3.m
D.
13m
hoặc
1 3.m
Câu 141. Hàm số
3 2 2 2
3 3( ) 2 1y x mx m m x m
có
2
điểm cực trị khi:
A.
0.m
B.
0.m
C.
1.m
D.
m
tùy ý.
Câu 142. Tìm
m
để hàm số
3 2 2
1
( 1) ( ) 2
3
y x m x m m x
có cực đại và cực tiểu:
A.
2.m
B.
1
3
m
C.
2
3
m
D.
1.m
Câu 143. Hàm số
32
1
( 2) 1
3
y x m x mx
có cực đại, cực tiểu khi:
A.
0.m
B.
.m
C.
.m
D.
1.m
Câu 144. Hàm số
3 2 2
1
( 1) (3 4 1)
3
y x m x m m x m
có cực đại, cực tiểu khi:
A.
0 1.m
B.
0 1.m
C.
0.m
D.
1.m
Câu 145. Hàm số
32
(3 ) 2 2y x m x mx
có cực đại và cực tiểu khi:
A.
3.m
B.
6 3 3 6 3 3.m
C.
6 3 3 hay 6 3 3.mm
D.
6 3 3 hay 6 3 3.mm
Câu 146. Giá trị của tham số
m
để hàm số
3
( 2) 3y m x mx
không có cực trị là:
A.
0
2
m
m
B.
2.m
C.
0
2
m
m
D.
0 2.m
Câu 147. Đồ thị hàm số
32
3 3 3 4y x mx mx m
không có cực trị khi:
A.
0.m
B.
1.m
C.
0 1.m
D.
0 1.m
Câu 148. Đồ thị hàm số
32
2 ( 2) (6 3 ) 1y x m x m x m
không có cực trị khi:
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 65
A.
16.m
B.
2.m
C.
16 2.m
D.
16 2.m
Câu 149. Đồ thị hàm số
32
3 ( 1) 1y mx mx m x
không có cực trị khi:
A.
1
0
4
m
B.
1
0
4
m
C.
0.m
D.
Câu 150. Đồ thị hàm số
3 3 3
( ) ( )y x a x b x
có cực đại, cực tiểu khi:
A.
. 0.ab
B.
. 0.ab
C.
. 0.ab
D.
. 0.ab
Câu 151. Tìm tham số
m
để đồ thị hàm số
4 2 2 2
2( 3)y x m x m
có
3
điểm cực trị ?
A.
0.m
B.
0.m
C.
0.m
D.
0.m
Câu 152. Tìm tham số
m
để đồ thị hàm số
42
3y x mx
có
3
điểm cực trị ?
A.
0.m
B.
0.m
C.
0.m
D. Không có
.m
Câu 153. Tìm tham số
m
để đồ thị hàm số
42
2 2 1y x mx m
có
3
điểm cực trị ?
A.
2.
B.
1.
C.
0.
D.
1.
Câu 154. Tìm tham số
m
để đồ thị hàm số
4 2 2
3y x m x
có
3
điểm cực trị ?
A.
0.m
B.
0.m
C.
0.m
D.
.m
Câu 155. Tìm tham số
m
để đồ thị hàm số
42
2( 1) 3y x m x
có
3
điểm cực trị ?
A.
0.m
B.
1.m
C.
1.m
D.
0.m
Câu 156. Tìm tham số
m
để đồ thị hàm số
42
( 1) 2 1y x m x m
có
3
điểm cực trị ?
A.
1.m
B.
1.m
C.
1.m
D.
1.m
Câu 157. Tìm tham số
m
để đồ thị hàm số
4 2 4
22y x mx m m
có
3
điểm cực trị ?
A.
2.m
B.
1.m
C.
0.m
D.
2.m
Câu 158. Tìm tham số
m
để đồ thị hàm số
42
2( 1)y x m x m
có
3
điểm cực trị ?
A. Không có
.m
B.
1.m
C.
1.m
D.
1.m
Câu 159. Tìm tham số
m
để đồ thị hàm số
4 2 2
2( 2) 5 5y x m x m m
có
3
điểm cực trị ?
A.
2.m
B.
2.m
C.
1.m
D.
1.m
SDT: 0946798489 66
Câu 160. Tìm tham số
m
để đồ thị hàm số
42
2( 1) 1y x m x m
có đúng
1
cực trị ?
A.
1.m
B.
1.m
C. A, B đều đúng. D. A, B đều sai.
Câu 161. Đồ thị hàm số
42
2(2 1) 3y x m x
có đúng một điểm cực trị khi:
A.
1
2
m
B.
1
2
m
C.
1
2
m
D.
1
2
m
Câu 162. Đồ thị hàm số
42
2(3 ) 2y x m x
có đúng
1
điểm cực trị khi:
A.
3.m
B.
3.m
C.
3.m
D.
3.m
Câu 163. Đồ thị hàm số
42
( ) (: 2 2 1 3)C y x m x
có đúng 1 điểm cực trị khi:
A.
B.
1
2
m
C.
1
2
m
D.
1
2
m
Câu 164. Đồ thị hàm số
42
( 1) 1
4
m
y x m x m
có đúng
1
điểm cực trị khi:
A.
0 1.m
B.
1.m
C.
0.m
D.
;0 1; .m
Câu 165. Đồ thị hàm số
42
2(1 ) 2y x m x
có cực tiểu mà không có cực đại khi:
A.
1.m
B.
1.m
C.
1.m
D.
1.m
Câu 166. Đồ thị hàm số
42
2(5 ) 2y x m x
có cực đại mà không có cực tiểu khi:
A.
5.m
B.
5.m
C.
5.m
D.
5.m
Câu 167. Đồ thị hàm số
42
15
22
m
y x mx
có cực đại mà không có cực tiểu khi:
A.
1;0 .m
B.
1;0 .m
C.
1;0 .m
D.
( 1;0).m
Câu 168. Đồ thị hàm số
42
(2 4)y x m x m
có
2
cực đại,
1
cực tiểu khi:
A.
2.m
B.
2.m
C.
2.m
D.
2.m
Câu 169. Đồ thị hàm số nào sau đây chỉ có 1 điểm cực trị ?
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 67
A.
42
2 4 2.y x x
B.
2 4 2
( 4) 9 1.y m x x
C.
42
2 1.y x x
D.
4 2 2
( 1) 1.y x m x
Câu 170. Tìm tham số
m
để đồ thị hàm số
42
(1 ) 2 1y m x mx m
có đúng
1
cực trị ?
A.
.m
B.
0.m
C.
0 1.m
D.
\ (0;1).
Câu 171. Hàm số
2
2 2 1
21
x mx m
y
x
có hai điểm cực trị khi:
A.
1.m
B.
1.m
C.
1.m
D.
m
tùy ý.
Câu 172. Hàm số
2
1x mx
y
xm
luôn có cực trị khi:
A.
0.m
B.
1.m
C.
.m
D.
.m
Câu 173. Đồ thị hàm số
32
y ax bx cx d
có hai điểm cực trị
(0;0), (1;1)AB
thì các hệ số
, , , a b c d
có giá trị lần lượt là:
A.
2, 0, 0, 3.a b c d
B.
0, 0, 2, 3.a b c d
C.
2, 0, 3, 0.a b c d
D.
2, 3, 0, 0.a b c d
Dạng toán 3. Tìm tham số m để hàm số có n cực trị thỏa mãn điều kiện K.
Nhóm 1. Điều kiện
K
liên quan đến định lí Viét
Câu 174. Hàm số
3
()f x x ax b
với
, ab
có hai cực trị là
12
, .xx
Hỏi kết luận nào sau đây là
đúng về hàm này ?
A. Đường thẳng nối hai điểm cực trị qua gốc tọa độ
.O
B. Phương trình đường thẳng nối hai điểm cực trị có dạng
.y ax b
C. Tổng hai giá trị cực trị là
.b
D. Hai điểm cực trị của đồ thị hàm số nằm về hai phía so với trục tung.
Câu 175. Hàm số
32
( 1) 2y x m x x
có
2
điểm cực trị
12
, xx
thỏa mãn điều kiện
12
3( ) 2xx
khi:
A.
2.m
B.
1.m
C.
1.m
D.
2.m
SDT: 0946798489 68
Câu 176. Hàm số
32
1
( 2) 2
3
y x x m x
có
2
điểm cực trị
12
, xx
thỏa mãn điều kiện
12
10 0xx
khi:
A.
12.m
B.
8.m
C.
8.m
D.
12.m
Câu 177. Đồ thị hàm số
32
1
(2 1) 3
3
y x mx m x
có hai điểm cực trị với hoành độ
12
, xx
thỏa
mãn
12
. 6,xx
thì giá trị
m
sẽ là:
A.
B.
C.
D.
1.m
Câu 178. Đồ thị hàm số
2
( )( 2 1)y x m x x m
có hai điểm cực trị với hoành độ
12
, xx
thỏa mãn
12
. 1,xx
thì giá trị của tham số
m
sẽ là:
A.
2.m
B.
3.m
C.
4.m
D. Cả A và C.
Câu 179. Với giá trị nào của
m
thì hàm số
3 2 2
2
2(1 3 ) 1
3
y x mx m x
có
2
điểm cực trị với
hoành độ
12
, xx
thỏa mãn:
1 2 1 2
2( ) 1 ?x x x x
A.
0m
hoặc
B.
C.
0.m
D. Không tồn tại
.m
Câu 180. Với giá trị nào của
m
thì hàm số
3 2 2
11
(2 1) ( 2) 1
32
y x m x m x
có
2
điểm cực trị
với hoành độ
12
, xx
thỏa mãn:
1 2 1 2
3 5( ) 7 0x x x x
?
A.
B.
2.m
C.
4.m
D.
8.m
Câu 181. Tìm tham số
m
để hàm số
32
31y x x mx
có
2
điểm cực trị
12
, xx
thỏa mãn điều
kiện:
22
12
3 ?xx
A.
1.m
B.
C.
D.
1.m
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 69
Câu 182. Hàm số
32
3( 1) 9y x m x x m
có
2
điểm cực trị
12
, xx
thỏa mãn điều kiện
22
12
10xx
khi:
A.
2m
hoặc
0.m
B.
0m
hoặc
2.m
C.
2.m
D.
0.m
Câu 183. Với giá trị nào của
m
thì hàm số
3 2 2
11
(2 1) ( 2)
32
y x m x m x m
có
2
điểm cực trị
với hoành độ
12
, xx
thỏa mãn:
22
12
8( ) 81xx
?
A.
B.
C.
4.m
D.
8.m
Câu 184. Với giá trị nào của
m
thì hàm số
32
1
3
y x mx x
có
2
điểm cực trị với hoành độ
12
, xx
thỏa mãn:
22
1 2 1 2
7x x x x
?
A.
1.m
B.
2.m
C.
3.m
D.
4.m
Câu 185. Với giá trị nào của
m
thì hàm số
3 2 2 5 2
3 3( 1) 3y x mx m x m m
có
2
điểm cực trị
với hoành độ
12
, xx
thỏa mãn:
22
1 2 1 2
7x x x x
?
A.
2.m
B.
2.m
C.
2.m
D.
2.m
Câu 186. Với giá trị nào của
m
thì đồ thị hàm số
32
1
( 1) ( 2) ( 3) 1
3
y m x m x m x
có
2
điểm
cực trị với hoành độ
12
, xx
thỏa mãn:
12
(4 1)(4 1) 18xx
?
A.
1.m
B.
4.m
C.
7.m
D.
8.m
Câu 187. Nếu gọi
12
, xx
lần lượt là hoành độ các điểm cực trị của đồ thị hàm số:
32
( ) (2 3 2 1 6 1 2)y x m x m m x
thì giá trị
21
T xx
là:
A.
1.Tm
B.
1.Tm
C.
.Tm
D.
1.T
Câu 188. Với giá trị nào của tham số
m
thì đồ thị hàm số
32
43y x mx x
có
2
điểm cực trị với
hoành độ
12
, xx
thỏa mãn:
12
40xx
?
SDT: 0946798489 70
A.
9
2
m
B.
3
2
m
C.
1
2
m
D.
0.m
Câu 189. Với giá trị nào của
m
thì đồ thị hàm số
32
(1 2 ) (2 ) 2y x m x m x m
có
2
điểm
cực trị với hoành độ
12
, xx
thỏa mãn:
21
3 2xx
?
A.
3.m
B.
1 97
8
m
C.
1 97 1 97
;;
88
m
D.
1 97
;3
8
m
Câu 190. Với giá trị nào của
m
thì hàm số
32
11
( 3) 2( 1) 1
32
y x m x m x
có các điểm cực đại,
cực tiểu với hoành độ lớn hơn
1
?
A.
[2; ).m
B.
( ; 7 4 2].m
C.
( 7 4 2;2).m
D.
[ 7 4 2;2].m
Câu 191. Với giá trị nào của
m
thì hàm số
3 2 2 3
3 3( 1)y x mx m x m m
có các điểm cực đại,
cực tiểu thỏa mãn:
2
CD CT
xx
?
A.
0.m
B.
0
3
m
m
C.
3.m
D.
0
3
m
m
Câu 192. Đồ thị hàm số
32
y ax bx cx d
đạt cực trị tại
12
, xx
nằm về hai phía so với trục tung khi
và chỉ khi:
A.
0, 0, 0.a b c
B.
a
và
c
trái dấu.
C.
2
12 0.b ac
D.
2
12 0.b ac
Câu 193. Với giá trị nào của tham số
m
thì đồ thị hàm số
3 2 2
( 3 ) 4y x x m m x
có các điểm
cực đại, điểm cực tiểu nằm về hai phía của trục tung ?
A.
0 3.m
B.
0 3.m
C.
3.m
D.
0.m
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 71
Câu 194. Với giá trị nào của
m
thì đồ thị hàm số
3 2 2
21
(3 1) ( 6)
32
y x m x m m x
có các điểm
cực đại, điểm cực tiểu nằm về hai phía của trục tung ?
A.
2 m 3.
B.
2 m 1.
C.
m 2.
D.
m 4.
Câu 195. Với giá trị nào của
m
thì đồ thị hàm số
3 2 2 3
1
(2 1) ( 1)
3
y mx m x m x m
có các điểm
cực đại, điểm cực tiểu nằm về hai phía so với trục tung ?
A.
1.m
B.
0 1.m
C.
0.m
D.
( ;0) (1; ).m
Câu 196. Với giá trị nào của tham số
m
thì đồ thị hàm số
32
1
( 1) 3
3
y x x m x
có các điểm cực
đại, điểm cực tiểu nằm cùng một phía so với trục tung ?
A.
1 2.m
B.
1 2.m
C.
1 2.m
D.
1 2.m
Câu 197. Với giá trị nào của tham số
m
thì đồ thị hàm số
32
6 3( 2) 6y x x m x m
có hai điểm
cực trị với hoành độ cùng dấu ?
A.
2 2.m
B.
2 2.m
C.
2 2.m
D.
1 3.m
Nhóm 2. Điều kiện K liên quan đến tính chất hình học
Câu 198. Tìm các giá trị thực của tham số
m
sao cho đồ thị hàm số
42
4 3 2y x mx m
có ba điểm
cực trị tạo thành một tam giác nhận
5
0;
3
G
làm trọng tâm ?
A.
1.m
B.
8.m
C.
1m
hoặc
D.
Câu 199. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
42
2y x mx
có ba điểm cực
trị tạo thành một tam giác vuông ?
A.
0.m
B.
2.m
C.
0.m
D.
3.m
Câu 200. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
42
21y x mx
có ba điểm
cực trị tạo thành một tam giác vuông cân ?
SDT: 0946798489 72
A.
3
1
9
m
B.
1.m
C.
3
1
9
m
D.
1.m
Câu 201. Với giá trị nào của tham số
m
thì đồ thị hàm số
4 2 2
2 2016y x m x
có ba điểm cực trị tạo
thành một tam giác vuông cân ?
A.
2016.m
B.
1.m
C.
2.m
D. Đáp án khác.
Câu 202. Với giá trị nào của tham số
m
thì đồ thị hàm số
4 2 2
2( 2) 5 5y x m x m m
có ba
điểm cực trị tạo thành một tam giác vuông cân ?
A.
1.m
B.
1.m
C.
1.m
D.
2.m
Câu 203. Với giá trị nào của tham số
m
thì đồ thị hàm số
4 2 2
2( 2) 5 5y x m x m m
có ba
điểm cực trị tạo thành một tam giác đều ?
A.
2 3.m
B.
2 3.m
C.
3
2 3.m
D.
3
2 3.m
Câu 204. Với giá trị nào của tham số
m
thì đồ thị hàm số
4 2 2
2y x mx m m
có ba điểm cực trị
tạo thành một tam giác có một góc bằng
0
120
?
A.
0m
hoặc
3
1
3
m
B.
0m
hoặc
3
1
3
m
C.
0.m
D.
3
1
3
m
Câu 205. Với giá trị nào của tham số
m
thì đồ thị hàm số
42
21y x mx m
có ba điểm cực trị tạo
thành một tam giác có bán kính đường tròn ngoại tiếp bằng
1
?
A.
1m
hoặc
15
2
m
B.
1m
hoặc
15
2
m
C.
1m
hoặc
15
2
m
D.
1m
hoặc
15
2
m
Câu 206. Với giá trị nào của tham số
m
thì đồ thị hàm số
42
22y x mx
có ba điểm cực trị tạo thành
một tam giác có đường tròn ngoại tiếp đi qua điểm
39
; ?
55
D
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 73
A.
2.m
B.
1.m
C.
1.m
D.
Câu 207. Với giá trị nào của tham số
m
thì đồ thị hàm số
4 2 2
2(1 ) 1y x m x m
có ba điểm cực
trị tạo thành một tam giác có diện tích lớn nhất ?
A.
2.m
B.
2.m
C.
0.m
D.
2.m
Câu 208. Với giá trị nào của tham số
m
thì đồ thị hàm số
42
1
(3 1) 2 2
4
y x m x m
có ba điểm
cực trị tạo thành một tam giác có trọng tâm là gốc tọa độ
?O
A.
2
3
m
B.
2
3
m
hoặc
1
3
m
C.
2
3
m
hoặc
D.
Câu 209. Với giá trị nào của tham số
m
thì đồ thị hàm số
42
(3 1) 3y x m x
có ba điểm cực trị tạo
thành tam giác cân sao cho độ dài cạnh đáy bằng
2
3
độ dài cạnh bên ?
A.
B.
5
3
m
C.
D.
3
5
m
Câu 210. Với giá trị nào của tham số
m
thì đồ thị hàm số
4 2 2 2
21y x m x m
có ba điểm cực trị
, , A B C
sao cho bốn điểm
, , , A B C O
là bốn đỉnh một hình thoi với
O
là gốc tọa độ ?
A.
2.m
B.
2.m
C.
2.m
D.
2
2
m
Câu 211. Với giá trị nào của tham số
m
thì đồ thị hàm số
4 2 4
22y x mx m m
có ba điểm cực trị
tạo thành một tam giác nội tiếp đường tròn có bán kính nhỏ nhất ?
A.
2.m
B.
3
1
2
m
C.
1
2
m
D.
2
2
m
Câu 212. Với
m
bằng bao nhiêu thì đồ thị hàm số
3
31y x mx
có hai cực trị
, BC
thỏa mãn tam
giác
ABC
vuông tại
(2;2) ?A
SDT: 0946798489 74
A.
2.m
B.
2.m
C.
2.m
D. Đáp án khác.
Câu 213. Với
m
bằng bao nhiêu thì đồ thị hàm số
3 2 3
2 3( 1) 6y x m x mx m
có hai cực trị
, AB
thỏa mãn
2AB
?
A.
0.m
B.
2.m
C.
0m
hoặc
2.m
D.
2.m
hoặc
0.m
Câu 214. Với
m
bằng bao nhiêu thì đồ thị hàm số
32
2y x mx m
có hai cực trị thẳng hàng với gốc
tọa độ
O
?
A.
0.m
B.
3.m
C.
D.
3.m
Câu 215. Với
m
bằng bao nhiêu thì đồ thị hàm số
32
2 3( 3) 11 3y x m x m
có hai cực trị
, AB
thẳng hàng với điểm
(0; 1)C
?
A.
2.m
B.
2.m
C.
4.m
D.
4.m
Câu 216. Với giá trị nào của
m
thì đồ thị hàm số
3 2 2 2
3 3( 1) 3 1y x x m x m
có cực đại, cực
tiểu, đồng thời các điểm đó tạo với gốc tọa độ
O
tam giác vuông tại
O
?
A.
1m
hoặc
6
2
m
B.
1m
hoặc
6
2
m
C.
1m
hoặc
6
2
m
D.
1m
hoặc
6
2
m
Câu 217. Với giá trị nào của tham số
m
thì đồ thị hàm số
32
3 3(1 ) 1 3y x x m x m
có cực
đại, cực tiểu, đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam
giác có diện tích bằng
4 ?
A.
2.m
B.
1.m
C.
1.m
D.
1.m
Câu 218. Đồ thị hàm số
32
3 3 1y x mx m
có điểm cực đại và cực tiểu đối xứng nhau qua đường
thẳng
: 8 74 0d x y
khi:
A.
1.m
B.
2.m
C.
1.m
D.
2.m
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 75
Trung tâm luyện thi Thanh Phương
Câu 539. Hàm số
13
2
xxy
có bao nhiêu điểm cực trị:
A.0 B.2 C.3 D. 1
Câu 540. Hàm số
133
23
xxxy
có bao nhiêu điểm cực trị:
A.3 B.2 C.1 D. 0
Câu 541. Hàm số
13
23
xxy
có bao nhiêu điểm cực trị:
A3. B.1 C.0 D. 2
Câu 542. Hàm số
1
24
xxy
có bao nhiêu điểm cực trị:
A.0 B.1 C.2 D. 3
Câu 543. Hàm số
12
24
xxy
có bao nhiêu điểm cực trị:
A.0 B.3 C.2 D. 1
Câu 544. Hàm số
53
12
x
x
y
có bao nhiêu điểm cực trị:
A.1 B.2 C.3 D. 0
Câu 545. Hàm số
1
32
2
x
xx
y
có bao nhiêu điểm cực trị:
A.1 B.0 C.3 D. 2
Câu 546. Hàm số
34
34
xxy
có bao nhiêu điểm cực trị:
A.2 B.3 C.0 D. 1
Câu 547. Hàm số
1
5
2
x
xx
y
có bao nhiêu điểm cực trị:
A.3 B.2 C.1 D. 0
Câu 548 Hàm số
xxy sin
có bao nhiêu điểm cực trị:
SDT: 0946798489 76
A.1 B.2 C.3 D. 0
Câu 549. Hàm số
xxy ln
có bao nhiêu điểm cực trị:
A.3 B.2 C.1 D. 0
Câu 550 Hàm số
xxy ln.
có bao nhiêu điểm cực trị:
A.3 B.2 C.1 D. 1
Câu 551. Hàm số
)2()1(
2
xxy
có bao nhiêu điểm cực trị:
A.1 B.3 C.0 D. 2
Câu 552. Hàm số
23
23
xxy
đạt cực đại tại x = :
A.2 B.-2 C.1 D. -1
Câu 553. Hàm số
)2()1(
2
xxy
đạt cực tiểu tại x =:
A.-1 B.2 C. -2 D. 1
Câu 554. Hàm số
244
234
xxxy
đạt cực đại tại x =
A1. B 2. C.-2 D. -1
Câu 555. Hàm số
2
84
2
x
xx
y
đạt cực tiểu tại x =
A.2 B.3 C.1 D. 4
Câu 556. Hàm số
x
exy
2
đạt cực đại tại x =
A.1 B.3 C.4 D. 2
Câu 557. Hàm số
103632
23
xxxy
có cực trị là:
A.71 B.-54 C. 71 hoặc- 54 D. 71 và – 54
Câu 558. Hàm số
342
34
xxy
có cực trị là:
A.1 B.24 C.-32 D. -24
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 77
Câu 559. Hàm số
32
24
xxy
có cực trị là:
A.1 B.5 C. -2 D. -3
Câu 560. Hàm số
2
54
2
x
xx
y
có giá trị CĐ, CT lần lượt là:
A2; 2. B. 1;2 C. -2 ;0 D. -2; 2
Câu 561. Điểm cực đại của đồ thị hàm số
32
5 7 3y x x x
là:
A.
1;0
B.
0;1
C.
7 32
;
3 27



D.
7 32
;
3 27



.
Câu 562. Điểm cực tiểu của đồ thị hàm số
32
5 7 3y x x x
là:
A.
1;0
B.
0;1
C.
7 32
;
3 27



D.
7 32
;
3 27



.
Câu 563 : Trong các khẳng định sau về hàm số
42
11
3
42
y x x
, khẳng định nào là đúng?
A. Hàm số đạt cực tiểu tại x = 0; B. Hàm số đạt cực đại tại x = 1;
C. Hàm số đạt cực đại tại x = -1; D. Cả 3 câu trên đều đúng.
Câu 564: Hàm số:
3
34y x x
đạt cực tiểu tại x =
A. -1 B. 1 C. - 3 D. 3
Câu 565 Hàm số:
42
1
23
2
y x x
đạt cực đại tại x =
A. 0 B.
2
C.
2
D.
2
Câu 566: Hàm số
3
1y x mx
có 2 cực trị khi :
A.
0m
B.
0m
C.
0m
D.
0m
SDT: 0946798489 78
Câu 567: Đồ thị hàm số
3
31y x x
có điểm cực tiểu là:
A. ( -1 ; -1 ) B. ( -1 ; 3 ) C. ( -1 ; 1 ) D. ( 1 ; 3 )
Câu 568: Đồ thị hàm số nào sau đây có 3 điểm cực trị:
A.
42
21y x x
B.
42
21y x x
C.
42
2 4 1y x x
D.
42
2 4 1y x x
Câu 569. Cho hàm số y = –x
3
+ 3x
2
– 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số luôn luôn nghịch biến; B. Hàm số luôn luôn đồng biến
C. Hàm số đạt cực đại tại x = 1; D. Hàm số đạt cực tiểu tại x = 1.
Câu 570 : Trong các khẳng định sau về hàm số
42
11
3
42
y x x
, khẳng định nào là đúng?
A. Hàm số có điểm cực tiểu là x = 0; B. Hàm số có hai điểm cực đại là x = 1;
C. Cả A và B đều đúng; D. Chỉ có A là đúng.
Câu 571 : Trong các mệnh đề sau, hãy tìm mệnh đề sai:
A. Hàm số y = –x
3
+ 3x
2
– 3 có cực đại và cực tiểu; B. Hàm số y = x
3
+ 3x + 1 có cực trị;
C. Hàm số
1
21
2
yx
x
không có cực trị; D. Hàm số
1
21
2
yx
x
có hai cực trị.
Câu 572 : Tìm kết quả đúng về giá trị cực đại và giá trị cực tiểu của hàm số
2
21
2
yx
x
:
A. yCĐ = 1 và yCT = 9; B. yCĐ = 1 và yCT = –9;
C. yCĐ = –1 và yCT = 9; D. yCĐ = 9 và yCT = 1.
Câu 573 : Hàm số nào dưới đây không có cực trị:
A.
1
1
3
yx
x
; B.
1
1
3

y
x
; C.
4
3
x
y
x
; D. Cả B và
C.
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 79
Câu 574 :Cho hàm số
32
1
2 1 1
3
y x m x m x
. Mệnh đề nào sau đây là sai?
A.
1m
thì hàm số có cực đại và cực tiểu; B.
1m
thì hàm số có hai điểm cực trị;
C.
1m
thì hàm số có cực trị; D. Hàm số luôn luôn có cực đại và cực tiểu.
Câu 575 : Điểm cực tiểu của hàm số :
3
34y x x
là
A. x = -1 B. x = 1 C. x = - 3 D. x = 3
Câu 576 : Điểm cực đại của hàm số :
42
1
23
2
y x x
là
A. x = 0 B. x =
2
C. x =
2
D. x =
2
Câu 577: Đồ thị của hàm số y=x
4
-6x
2
+3 có số điểm cực trị là
A.0 B.1 C.2 D.3
Câu 578: Cho hàm số
3
2
2
23
33
x
y x x
.Toạ độ điểm cực đại của hàm số là
A.(-1;2) B.(1;2) C.(3; 2/3) D.(1;-2)
Câu 579 Cho hàm số
4 2 2
( 9) 10y mx m x
. Tìm
m
để hàm số có 3 điểm cực trị.
A.
3
03
m
m
B . 1< m < 2 C. m > 2 D. m > -1
Câu 580.,Tìm
m
để hàm số
32
(1 2 ) (2 ) 2y x m x m x m
đạt cực trị tại
12
,xx
sao cho
12
1
3
xx
.
A.
3 29
1;
8
mm
B.
3 29
1.
8
m C m
D.
1m
Câu 581: Cho hàm số
42
21y x mx m
. Tìm
m
để đồ thị của hàm số có 3 điểm cực trịA, B,C
đồng thời các điểm A,B,C tạo thành 3 đỉnh của một tam giác đều.
SDT: 0946798489 80
A.
3
3m
B. m = 0 C. m = 3 D.
0m
Violet
Câu 582: Giá trị của m để hàm số
1)1(
3
1
223
xmxmxy
có 2 cực trị là:
A. -1/3 < m <1 B. m > -1/2 C.
 m
D. m > ½
Câu 583: Giá trị của m để hàm số
3
24
mmxxy
có 3 cực trị là:
A. 0 < m <1 B. m > 1 C. m < 0 D.
Rm
Câu 584: Đồ thị hàm số
352
23
xmxxy
đi qua điểm (1; -1) thì hoành độ điểm cực tiểu là:
A. 1 B. 5/3 C. -1 D. -5/3
Câu 585: Giá trị của m để hàm số
1)(
3
1
223
xmmmxxy
có 1 cực đại và 1 cực tiểu là:
A. -1/2 < m <0 B. 0 < m <1/2 C. m < 0 D. m > 0
Câu 586: Số điểm cực trị của hàm số
24
2)( xxxf
là:
A. 4 B. 2 C. 1 D. 3
Câu 587: Số điểm cực trị của hàm số
42
4
1
)(
24
xxxf
là:
A. 4 B. 3 C. 2 D. 1
Câu 588: Số điểm cực trị của hàm số
4
100yx
là:
A. 0 B. 1 C. 2 D. 3
Câu 589: Cho hàm số
32
32y x x
có điểm cực đại là A(-2;2), Cực tiểu là B(0;-2) thì phương trình
32
32x x m
có hai nghiệm phân biêt khi:
A. m = 2 hoặc m = -2 C. m < -2
B. m > 2 D. -2 < m < 2
Câu 590: Cho hàm số
32
2 3 1y x x
, có đồ thị ( C) . Chọn đáp án sai trong các đáp án sau:
A. Hàm số có 2 cực trị C. Hàm số nghịch biến trên khoảng (0 ; 1)
B. Đồ thị hàm số đi qua điểm A( 2 ; 3) D. Hàm số không có tiệm cận
Câu 591: Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số:
32
1
2 3 5
3
y x x x
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 81
A. song song với đường thẳng x = 1 C. Song song với trục hoành
B. Có hệ số góc dương D. Có hệ số góc bằng -1
Câu 592. Tìm m để hàm số
32
( ) 3 1f x x x mx
có hai điểm cực trị
12
,xx
thỏa
22
12
3xx
A.
1m
B.
2m 
C.
3
2
m
D.
1
2
m
Câu 593. Cho hàm số
32
43y x mx x
. Tìm m để hàm số đã cho có 2 điểm cực trị
12
,xx
thỏa
12
4xx
. Chọn đáp án đúng nhất?
A.
1
2
m 
B.
9
2
m 
C.
0m
D.
3
2
m 
Câu 594. Cho hàm số
3
31y x mx
(1). Cho A(2;3), tìm m để đồ thị hàm số (1) có hai điểm cực trị B
và C sao cho tam giác ABC cân tại A.
A.
1
2
m
B.
3
2
m
C.
D.
1
2
m
Câu 595. Với giá trị nào của m thì hàm số
3 2 2
22y x mx m x
đạt cực đại tại
1x
.
A.
1m 
B.
3m
C.
1m
D.
2m 
Câu 596. Tìm m để hàm số
3
3y x m x
đạt cực tiểu tại
0x
.
A.
1m
B.
2m
C.
2m 
D.
1m 
Câu 597. Cho hàm số
3 2 2 3
3 3 1y x mx m x m m
. Tìm m để hàm số đã cho có hai điểm cực
trị. Gọi
12
,xx
là hai điểm cực trị đó. Tìm m để
22
1 2 1 2
7x x x x
.
A.
1
2
m 
B.
9
2
m 
C.
0m
D.
2m 
Câu 598. Cho hàm số
32
3 3 1y x mx m
. Với giá trị nào của m thì đồ thị hàm số đã cho có cực đại
và cực tiểu đối xứng nhau qua đường thẳng
: 8 74 0d x y
.
A.
1m
B.
2m 
C.
2m
D.
1m 
Câu 599: Hàm số
3
3y x x
có điểm cực đại là :
A. (-1 ; 2) B. ( -1;0) C. (1 ; -2) D. (1;0)
SDT: 0946798489 82
Câu 600: Đồ thị hàm số nào có 3 điểm cực trị
A.
42
21y x x
B.
42
21y x x
C.
42
2 4 1y x x
D.
42
21y x x
Câu 601: Giá trị của m để hàm số f(x) =
1
2
2
mx
mxx
có cực trị là
A. -1<m<1 B. -1<m<0 C. 0<m<1 D. Số khác.
Câu 602: Khẳng định nào sau đây là đúng về hàm số
42
42y x x
:
A. Đạt cực tiểu tại x = 0 B. Có cực đại và cực tiểu
C. Có cực đại và không có cực tiểu D. Không có cực trị.
Câu 603: Khẳng định nào sau đây là đúng về đồ thị hàm số
2
25
1
xx
y
x
:
A.
0
CD CT
yy
B.
4
CT
y 
C.
1
CD
x 
D.
3
CD CT
xx
Câu 604. Giá trị m để hàm số :
32
3 ( 1) 4
y mx mx m x
không có cực trị là :
A.
1
0
4
m

B.
1
0
4
m

C.
04
mm
D.
04
mm
Câu 605. Giá trị m để hàm số : có cực tiểu mà không có cực đại là:
A.
0
m
B.
0
m
C.
0
m
D.
0
m
Câu 606. Cho hàm số : có đồ thị là
()
m
C
.
Giá trị m để
()
m
C
có các điểm cực đại và cực tiểu nằm về hai phía của trục tung là:
A.
12
m

B.
12
m

C.
12
mm
D.
2
m
Câu 607. Cho hàm số
2
1
()
1
xx
fx
x

, mệnh đề sai là:
y x mx
42
13
22
y x m x m m x
3 2 2
(2 1) ( 3 2) 4
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 83
A.
()
fx
đạt cực đại tại
2
x

B.
(0;1)
M
là điểm cực tiểu
C.
()
fx
có giá trị cực đại là
3
D.
( 2; 2)
M

là điểm cực đại
Câu 608. Điểm cực đại của đồ thị hàm số
32
5 7 3y x x x
là:
A.
1;0
B.
0;1
C.
7 32
;
3 27



D.
7 32
;
3 27



.
Câu 609. Điểm cực tiểu của đồ thị hàm số
32
5 7 3y x x x
là:
A.
1;0
B.
0;1
C.
7 32
;
3 27



D.
7 32
;
3 27



.
Câu 610. Điểm cực đại của đồ thị hàm số
32
32y x x x
là:
A.
1;0
B.
3 2 3
1;
29




C.
0;1
D.
3 2 3
1;
29





.
Câu 611. Điểm cực tiểu của đồ thị hàm số
32
32y x x x
là:
A.
1;0
B.
3 2 3
1;
29




C.
0;1
D.
3 2 3
1;
29





.
Câu 612. Điểm cực đại của đồ thị hàm số
32
69y x x x
là:
A.
1;4
B.
3;0
C.
0;3
D.
4;1
.
Câu 613. Điểm cực tiểu của đồ thị hàm số
32
69y x x x
là:
A.
1;4
B.
3;0
C.
0;3
D.
4;1
.
Câu 614. Điểm cực đại của đồ thị hàm số
32
2y x x
là:
A.
2;0
B.
2 50
;
3 27



C.
0;2
D.
50 3
;
27 2



.
Câu 615 . Điểm cực tiểu của đồ thị hàm số
32
2y x x
là:
SDT: 0946798489 84
A.
2;0
B.
2 50
;
3 27



C.
0;2
D.
50 3
;
27 2



.
Câu 616. Điểm cực đại của đồ thị hàm số
3
34y x x
là:
A.
1
;1
2



B.
1
;1
2



C.
1
;1
2




D.
1
;1
2



.
Câu 617. Điểm cực tiểu của đồ thị hàm số
3
34y x x
là:
A.
1
;1
2



B.
1
;1
2



C.
1
;1
2




D.
1
;1
2



.
Câu 618. Điểm cực đại của đồ thị hàm số
3
12 12y x x
là:
A.
B.
2; 4
C.
4;28
D.
2;2
.
Câu 619. Điểm cực tiểu của đồ thị hàm số
3
12 12y x x
là:
A.
B.
2; 4
C.
4;28
D.
2;2
.
Câu 620: Cho hàm số y = –x
3
+ 3x
2
– 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số luôn nghịch biến; B. Hàm số luôn đồng biến;
C. Hàm số đạt cực đại tại x = 1; D. Hàm số đạt cực tiểu tại x = 1.
Câu 621: Trong các khẳng định sau về hàm số
24
1
x
y
x
, hãy tìm khẳng định đúng?
A. Hàm số có một điểm cực trị;
B. Hàm số có một điểm cực đại và một điểm cực tiểu;
C. Hàm số đồng biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên từng khoảng xác định.
Câu 622 : Trong các khẳng định sau về hàm số
42
11
3
42
y x x
, khẳng định nào là đúng?
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 85
A. Hàm số đạt cực tiểu tại x = 0; B. Hàm số đạt cực đại tại x = 1;
C. Hàm số đạt cực đại tại x = -1; D. Cả 3 câu trên đều đúng.
Câu 623: Cho hàm số
32
1
(2 1) 1
3
y x mx m x
. Mệnh đề nào sau đây là sai?
A.
1m
thì hàm số có cực đại và cực tiểu;
B.
1m
thì hàm số có hai điểm cực trị;
C.
1m
thì hàm số có cực trị;
D. Hàm số luôn có cực đại và cực tiểu.
Câu 624: Hàm số:
3
34y x x
đạt cực tiểu tại x =
A. -1 B. 1 C. - 3 D. 3
Câu 625: Hàm số:
42
1
23
2
y x x
đạt cực đại tại x =
A. 0 B.
2
C.
2
D.
2
Câu 626: Cho hàm số
42
1
21
4
y x x
. Hàm số có
A. Một cực đại và hai cực tiểu B. Một cực tiểu và hai cực đại
C. Một cực đại và không có cực tiểu D. Một cực tiểu và một cực đại
Câu 627: Cho hàm số y = x
3
- 3x
2
+ 1. Tích các giá trị cực đại và cực tiểu của hàm số bằng
A. 6 B. -3 C. 0 D. 3
Câu 628: Cho hàm số y = f(x) = ax
3
+ bx
2
+ cx + d, a
0 . Khẳng định nào sau đây sai ?
A. Đồ thị hàm số luôn cắt trục hoành B. Hàm số luôn có cực trị
C.
lim ( )
x
fx


D. Đồ thị hàm số luôn có tâm đối xứng.
Câu 629: Hàm số
3
1y x mx
có 2 cực trị khi :
A.
0m
B.
0m
C.
0m
D.
0m
SDT: 0946798489 86
Câu 630: Đồ thị hàm số
3
31y x x
có điểm cực tiểu là:
A. ( -1 ; -1 ) B. ( -1 ; 3 ) C. ( -1 ; 1 ) D. ( 1 ; 3 )
Câu 631: Đồ thị hàm số nào sau đây có 3 điểm cực trị:
A.
42
21y x x
B.
42
21y x x
C.
42
2 4 1y x x
D.
42
2 4 1y x x
Câu 632: Hàm số
32
3y x x mx
đạt cực tiểu tại x = 2 khi:
A.
0m
B.
0m
C.
0m
D.
0m
Câu 633: Khẳng định nào sau đây là đúng về hàm số
42
42y x x
:
A. Đạt cực tiểu tại x = 0 B. Có cực đại và cực tiểu
C. Có cực đại và không có cực tiểu D. Không có cực trị.
Câu 634: Khẳng định nào sau đây là đúng về đồ thị hàm số
2
25
1
xx
y
x
:
A.
0
CD CT
yy
B.
4
CT
y 
C.
1
CD
x 
D.
3
CD CT
xx
Câu 635: Đồ thị hàm số:
32
1
2 5 17
3
y x x x
có tích hoành độ các điểm cực trị bằng
A. 5 B. 8 C. -5 D. -8
Câu 636:
Số điểm cực trị của hàm số
3
1
7
3
y x x
là
A. 1 B. 0 C. 3 D. 2
Câu 637:
Số điểm cực đại của hàm số
4
100yx
là
A. 0 B. 1 C. 2 D. 3
Câu 638: Hàm số
3
1y x mx
có 2 cực trị khi
A.
0m
B.
0m
C.
0m
D.
0m
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 87
Câu 639: Số cực trị của hàm số
42
33y x x
là:
A. 4 B. 2 C. 3 D. 1
Câu 640: Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số
32
34y x x
là:
A.
25
B.
45
C.
65
D.
85
Câu 641: Hàm số
32
3 3 2 3y x mx x m
không có cực đại, cực tiểu với m
A.
1m
B.
1m
C.
11m
D.
11mm
Câu 642: Hàm số
42
3 2 1y mx m x m
chỉ có cực đại mà không có cực tiểu với m:
A.
3m
B
0m
C.
30m
D.
03mm
Câu 643: Hàm số
32
3 1 1y x mx m x
đạt cực đại tại x = 1 với m bằng :
A. m = - 1 B.
3m 
C.
3m 
D. m = - 6
Câu 645. Điểm cực đại của đồ thị hàm số
32
2y x x
là:
A.
2;0
B.
2 50
;
3 27



C.
0;2
D.
50 3
;
27 2



.
Câu 646: Cho hàm số
32
1
2 1 1
3
y x m x m x
. Mệnh đề nào sau đây là sai?
A.
1m
thì hàm số có hai điểm cực trị; B.
1m
thì hàm số có cực đại và cực tiểu;
C. Hàm số luôn có cực đại và cực tiểu. D.
1m
thì hàm số có cực trị;
Câu 647: Trong các mệnh đề sau hãy tìm mệnh đề sai. Chọn 1 câu sai
A. Hàm số
13
23
xxy
có cực đại và cực tiểu.
B. Hàm số
23
3
xxy
có cực trị
C. Hàm số
2
1
12
x
xy
không có cực trị
SDT: 0946798489 88
D. Hàm số
1
1
1
x
xy
có hai cực trị
Câu 648: Hàm số
51292
23
xxxy
có mấy điểm cực trị?. Chọn 1 câu đúng.
A. 1 B. 2 C. 3 D. 4
Câu 649: Hàm số
24
xxy
có điểm cực trị bằng. Chọn 1 câu đúng.
A. 0 B. 1 C. 2 D. 3
Câu 650: Giá trị của m để hàm số
5
23
mxxxy
có cực trị là. Chọn 1 câu đúng.
A.
3
1
m
B.
3
1
m
C.
3
1
m
D.
3
1
m
Câu 651: Giá trị của m để hàm số
x
mmxx
y
12
2
có cực trị là. Chọn 1 câu đúng.
A.
2
1
m
B.
2
1
m
C.
2
1
m
D.
2
1
m
Câu 652: Giá trị của m để hàm số
mxxxy
23
2
đạt cực tiểu tại x = - 1 là .
A.
1m
B.
1m
C.
1m
D.
1m
Câu 653: Cho hàm số
133
23
xxxy
. Mệnh đề nào sau đây là đúng? Chọn 1 câu đúng.
A. Hàm số luôn nghịch biến. B. Hàm số luôn đồng biến.
C. Hàm số đạt cực đại tại x = 1. C. Hàm số đạt cực tiểu tại x = 1 .
Câu 654: Cho hàm số
32
3 3 1y x x x
. Mệnh đề nào sau đây là đúng?
A. Hàm số luôn nghịch biến; B. Hàm số luôn đồng biến;
C. Hàm số đạt cực đại tại x = 1; D. Hàm số đạt cực tiểu tại x = 1;
Câu 655: Câu 5: Trong hàm số
42
11
3
42
y x x
, khẳng định nào đúng?
A. Hàm số có điểm cực tiểu là x = 0; B . Hàm số có cực tiểu là x=1 và x=-1
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 89
C. Hàm số có điểm cực đại là x = 0 D. Hàm số có cực tiểu là x=0 và x=
Câu 656 Hàm số
32
3y x x mx
đạt cực tiểu tại x = 2 khi:
A.
0m
B.
04m
C.
04m
D.
4m
Câu 657: Cho hàm số
2
1
()
1
xx
fx
x
. Trong các mệnh đề sau, tìm mệnh đề sai:
A. f(x) đạt cực đại tại
2x
B.
0
(0;1)M
là điểm cực tiểu
C.
0
( 3; 2)N
là điểm cực đại D. f(x) có giá trị cực đại là
3
Câu 658: Hàm số
2
1
()
1
xx
fx
x
có bao nhiêu điểm cực trị ?
A. 0 B. 1 C. 2 D. 3
Câu 659: Hàm số
4
2
( ) 2 6
4
x
f x x
có bao nhiêu điểm cực tiểu ?
A. 0 B. 1 C. 2 D. 3
Câu 660: Hàm số
42
( ) 6 8 1f x x x x
có bao nhiêu điểm cực trị ?
A. 0 B. 1 C. 2 D. 3
Câu 661: Tìm m để hàm số sau đây có cực trị:
2
2
()
1
x mx
fx
mx
A.
0
33
33
m
m
B.
10m
C. 0 < m < 1 D.
m
Câu 662: Cho hàm số:
3 2 2
( ) 3 3( 1)f x x mx m x
. Tìm m để f(x) đạt cực đại tại x
0
= 1
A. m = 2 B. m = 0 C. m = 0 hay m = 2 D.
02m va m
Câu 663: Hàm số
yx
có bao nhiêu điểm cực trị ?
SDT: 0946798489 90
A. 0 B. 1 C. 2 D. 3
Câu 664: Tìm m để hàm số sau đây luôn có một cực đại và một cực tiểu:
2
2
()
1
x x m
fx
x
A.
3m
B.
3m
C.
3m
D.
30m va m
Câu 665: Hàm số:
2
xx
ee
y
có bao nhiêu điểm cực đại ?
A. 0 B. 1 C. 2 D. 3
Câu 666: Hàm số:
4
5
yx
có bao nhiêu điểm cực đại ?
A. 0 B. 1 C. 2 D. 3
Câu 667: Cho hàm số:
32
29y x x x
. Trong các mệnh đề sau, tìm mệnh đề sai:
A. (C) có 1 cực đại và 1 cực tiểu
B. (C) có 1 điểm uốn
C. Điểm uốn là trung điểm của đoạn thẳng nối cực đại và cực tiểu
D. (C) là một đường cong lồi
Câu 668: Cho:
32
4
2(1 sin ) (1 cos2 )
3
y x x x
. Với giá trị nào của x thì hàm số có cực trị:
A.
xk
B.
2
2
xk
C.
2
2
xk
D.
x
Câu 669: Cho đồ thị (C):
42
2y x x
. Trong các mệnh đề sau, mệnh đề nào sai:
A. (C) có 3 điểm cực trị B. (C) có 1 điểm uốn
C. (C) có 1 trục đối xứng D. (C) có 1 tâm đối xứng
Câu 670: Cho đồ thị (C):
42
2y x x
. Trong các mệnh đề sau, mệnh đề nào đúng:
A. (C) có 3 điểm cực trị B. (C) có 1 trục đối xứng
C. (C) có 2 điểm uốn D. (C) có 1 tâm đối xứng
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 91
Câu 671: Cho hàm số:
42
(1 ) 2 1y m x mx m
. Tìm m để đồ thị hàm số có đúng một cực trị
A.
01mm
B.
01mm
C. m < 0 D. m > 1
Câu 672: Đồ thị hàm số:
42
2y x x
có bao nhiêu cực trị:
A. 0 B. 1 C. 2 D. 3
Câu 673: Cho đồ thị (C):
42
21y x x
. Viết phương trình tiếp tuyến với (C) tại điểm cực đại
A. x = 0 B. x = 1 C. y = 1 D. y = 0
Câu 674: Cho đồ thị (C):
42
41y x x
. Viết ph.trình đường thẳng đi qua 2 điểm cực tiểu của (C).
A.
2x
B.
3y
C. y = 1 D.
3x
Câu 675: Với giá trị nào của m thì hàm số sau có cực trị:
2
2
1
x mx
y
mx
A.
0m
B.
11m
C.
11m
D.
11m
và
0m
Câu 676: Với giá trị nào của m thì hàm số
32
x 2 x 3x 1y m m
có cực đại và cực tiểu ?
A.
9
0
4
m
B.
m
C.
0
9
4
m
m
D. m > 2
Câu 677: Hàm số
2
2
1yx
có :
A. chỉ có 1 cực đại B. 1 cực tiểu, 2 cực đại
C. 1 cực đại , 2 cực tiểu D. chỉ có 1 cực tiểu
Câu 678: Hàm số
42
17
3x
22
yx
có bao nhiêu điểm cực trị ?
A. 2 B. 3 C. 1 D. 0
SDT: 0946798489 92
Câu 679: Với tất cả các giá trị nào của m thì hàm số
42
x 1 1 2y m m x m
chỉ có một cực trị ?
A.
1m
B.
0m
C.
01m
D.
0
1
m
m
Câu 680: Hàm số
42
3x 1yx
có :
A. Một cực tiểu duy nhất B. Một cực đại duy nhất
C. Một cực tiểu và hai cực đại D. Một cực đại và hai cực tiểu
Câu 681: Với giá trị nào của m thì hàm số
3
22
x 1 x 1
3
x
y m m m
đạt cực tiểu tại x = 1 ?
A. 1 B. không có m C. 2 D. 3
Câu 682: Đồ thị hàm số nào sau đây không có cực trị ?
A.
2x 2
1
y
x
B.
2
3
2
xx
y
x

C. cả ba câu A, B, C D.
3
2x 1y
Câu 683: Đồ thị của hàm số nào dưới đây có điểm cực tiểu (0; - 2 ) và cắt trục hoành tại hai điểm có hoành
độ x = 1; x = - 1 .
A.
42
2x 1yx
B.
42
2y x x
C.
42
3x 4yx
D.
42
3x 2yx
Câu 684: Đồ thị hàm số
42
1y x x
có bao nhiêu điểm cực trị có tung độ dương ?
A. 2 B. 3 C. 4 D. 1
Câu 685: Cho hàm số
42
2x 2yx
. Khoảng cách giữa hai điểm cực trị của hàm số bằng :
A.
7
B.
3
C.
5
D.
2
Câu 686: Cho hàm số
32
3x 2yx
. Câu nào sau đây đúng ?
A. Hàm số có cực đại và cực tiểu B. Hàm số chỉ có cực tiểu
C. Hàm số không có cực trị. D. Hàm số chỉ có cực đại
Câu 687: Đồ thị hàm số
32
3x 2yx
có khoảng cách giữa hai điểm cực trị bằng :
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 93
A. 4 B. 2 C. 20 D.
25
Câu 688: Với giá trị nào của m thì thì hàm số
3 2 2
1
x 2 1
3
y x m m m x
đạt cực tiểu tại điểm x =
0 ?
A. 0 B. 1 C. – 1 D. 2
Thầy Nguyễn Bảo Vương ( Câu 1 – 59)
Câu 1. Cho hàm số
y x mx m x m m
3 2 2 3 2
3 3(1 )
(1)
Viết phương trình đường thẳng qua hai điểm cực trị của đồ thị hàm số (1).
A.
y x m m
2
21
B.
y x m m
2
2
C.

y x m
2
2
D.
y x m m
2
22
Câu 2. Cho hàm số
y x x mx m
32
32
(m là tham số) có đồ thị là (C
m
).
Xác định m để (C
m
) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành.
A.
m
2
B.
m
3
C.
m
3
D.
m
2
Câu 3. Cho hàm số
y x m x m m x
3 2 2
(2 1) ( 3 2) 4
(m là tham số) có đồ thị là (C
m
).
Xác định m để (C
m
) có các điểm cực đại và cực tiểu nằm về hai phía của trục tung.
A.

m
13
B.
m
12
C.
m
12
D.

m
14
Câu 4. Cho hàm số
y x mx m x
32
1
(2 1) 3
3
(m là tham số) có đồ thị là (C
m
).
Xác định m để (C
m
) có các điểm cực đại, cực tiểu nằm về cùng một phía đối với trục tung.
A.
m
m
1
1
2
B.

m
m
1
1
2
C.

m
m
1
03
D.

m
m
1
1
Câu 5. Cho hàm số
y x x mx
32
32
(m là tham số) có đồ thị là (C
m
).
Xác định m để (C
m
) có các điểm cực đại và cực tiểu cách đều đường thẳng
yx
1
.
SDT: 0946798489 94
A.

m
1
B.
m
1
C.
m
2
D.
m
0
Câu 6. Cho hàm số
y x mx m
3 2 3
34
(m là tham số) có đồ thị là (C
m
).
Xác định m để (C
m
) có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng y = x.
A.
m
2
2

B.
m
0
C.

m
2
4
D.

m
3
2
Câu 7. Cho hàm số
y x mx m
32
3 3 1
.
Với giá trị nào của m thì đồ thị hàm số có điểm cực đại và điểm cực tiểu đối xứng với nhau qua đường
thẳng d:
xy
8 74 0
.
A.
m
2
B.
m
3
C.

m
2
D.

m
3
Câu 8. Cho hàm số
y x x mx
32
3
(1).
Với giá trị nào của m thì đồ thị hàm số (1) có các điểm cực đại và điểm cực tiểu đối xứng với nhau qua
đường thẳng d:
xy
2 5 0
.
A.
1m
B.
2m 
C.
0m
D.
1m 
Câu 9. Cho hàm số
y x m x x m
32
3( 1) 9 2
(1) có đồ thị là (C
m
).
Với giá trị nào của m thì đồ thị hàm số có điểm cực đại và điểm cực tiểu đối xứng với nhau qua đường
thẳng d:
yx
1
2
.
A.

m
1
B.
m
0
C.
m
2
D.
m
1
Câu 10. Cho hàm số
y x m x x m
32
3( 1) 9
, với
m
là tham số thực.
Xác định
m
để hàm số đã cho đạt cực trị tại
xx
12
,
sao cho
xx
12
2
.
A.
m
m
13
13
B.
m
31
C.
m
3 1 3
và
m
1 3 1.
D.
m 
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 95
Câu 11. Cho hàm số
y x m x m x m
32
(1 2 ) (2 ) 2
, với
m
là tham số thực.
Xác định
m
để hàm số đã cho đạt cực trị tại
xx
12
,
sao cho
xx
12
1
3

.
A.

m
m
5
4
1
B.

mm
3 29 3 29
88
C.
mm
3 29
1
8
D.
m 
Câu 12. Cho hàm số
y x mx mx
32
1
1
3
, với
m
là tham số thực.
Xác định
m
để hàm số đã cho đạt cực trị tại
xx
12
,
sao cho
xx
12
8
.
A.
m
m
1 65
2
1 65
2
B.
m 
C.


m
1 65 1 65
22
D.
m
2
Câu 13. Cho hàm số
y x m x m x
32
11
( 1) 3( 2)
33
, với
m
là tham số thực.
Xác định
m
để hàm số đã cho đạt cực trị tại
xx
12
,
sao cho
xx
12
21
.
A.

m
4 34
4
B.
m
0
C.

m
4 34
2
D.

m
6 34
4
Câu 14. Cho hàm số
y x mx x
32
43
.
Tìm m để hàm số có hai điểm cực trị
xx
12
,
thỏa
xx
12
4
.
A.

m
9
2
B.

m
3
2
C.

m
9
4
D.

m
5
2
Câu 15. Cho hàm số
y x ax ax
32
1
34
3
(1) (a là tham số).
SDT: 0946798489 96
Tìm a để hàm số (1) đạt cực trị tại
x
1
,
x
2
phân biệt và thoả mãn điều kiện:
x ax a
a
a x ax a
2
2
12
22
21
29
2
29



A.

a
4
B.

a
2
C.

a
6
D.

a
0
Câu 16. Cho hàm số
y x mx m x
3 2 2
2 9 12 1
(m là tham số).
Tìm các giá trị của m để hàm số có cực đại tại x
CĐ
, cực tiểu tại x
CT
thỏa mãn:
CÑ CT
xx
2
.
A.

m
1
B.
m
2
C.

m
6
D.

m
3
Câu 17. Cho hàm số
y m x x mx
32
( 2) 3 5
, m là tham số.
Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số
dương.
A.
m
32
B.
m
22
C.
m
31
D.
m
32
Câu 18. Cho hàm số
y x mx m x
3 2 2
11
( 3)
32
(1), m là tham số.
A.
m
2
B.
m
14
2
C.

m
14
2
D.

m
14
2
Câu 19. Cho hàm số
y x m x m x m
32
(1 2 ) (2 ) 2
(m là tham số) (1).
Tìm các giá trị của m để đồ thị hàm số (1) có điểm cực đại, điểm cực tiểu, đồng thời hoành độ của
điểm cực tiểu nhỏ hơn 1.
A.

m
57
25
B.

m
57
43
C.

m
57
42
D.
m
57
45

Câu 20. Cho hàm số
m
y x m x m x
32
( 2) ( 1) 2
3
(Cm).
Tìm m để hàm số có cực đại tại x
1
, cực tiểu tại x
2
thỏa mãn
xx
12
1
.
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 97
A.

m
34
43
B.

m
14
43
C.

m
5
2
4
D.

m
54
43
Câu 21. Cho hàm số
32
(1 2 ) (2 ) 2y x m x m x m
(Cm).
Tìm m để hàm số có ít nhất 1 điểm cực trị có hoành độ thuộc khoảng
( 2;0)
.
A.
m
10
1
7
B.
m
2
C.
m
5
1
3
D.
m
5
; 1 2;
3



Câu 22. Cho hàm số
y x x
32
32
(1)
Tìm điểm M thuộc đường thẳng d:
yx
32
sao tổng khoảng cách từ M tới hai điểm cực trị nhỏ nhất.
A.



M
43
;
55
B.
M
42
;
55



C.



M
24
;
35
D.



M
46
;
55
Câu 23. Cho hàm số
y x mx m x m m
3 2 2 3
3 3( 1)
(1)
Tìm m để hàm số (1) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa
độ O bằng
2
lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.
A.

m
2
B.

m
m
3 2 2
3 2 2
C.
m
m
3 2 2
3 2 2
D.
m
m
4 2 2
4 2 2
Câu 24. Cho hàm số
y x x mx
32
32
có đồ thị là (C
m
).
Tìm m để (C
m
) có các điểm cực đại, cực tiểu và đường thẳng đi qua các điểm cực trị song song với
đường thẳng d:
yx
43
.
A.

m
2
B.
m
3
C.
m
2
D.

m
3
Câu 25. Cho hàm số
y x mx x
32
73
có đồ thị là (C
m
).
Tìm m để (C
m
) có các điểm cực đại, cực tiểu và đường thẳng đi qua các điểm cực trị vuông góc với
đường thẳng d:
yx
37
.
A.

m
3 10
4
B.

m
10
2
C.
m
3 1 0
2

D.

m
5 10
2
Câu 26. Cho hàm số
y x x mx
32
32
có đồ thị là (C
m
).
SDT: 0946798489 98
Tìm m để (C
m
) có các điểm cực đại, cực tiểu và đường thẳng đi qua các điểm cực trị tạo với đường
thẳng d:
xy
4 5 0
một góc
0
45a
.
A.
m
1
2

B.
m
3 15
2
C.


m
m
39
10
1
2
D.
39
10
m 
Câu 27. Cho hàm số
y x x
32
32
(C).
Tìm m để đường thẳng đi qua hai điểm cực trị của (C) tiếp xúc với đường tròn (S) có phương trình
x m y m
22
( ) ( 1) 5
.
A.

mm
4
2;
3
B.
m
4
3
C.
m
2
D.
m
0
Câu 28. Cho hàm số
m
y x mx C
3
3 2 ( )
.
Tìm m để đường thẳng đi qua điểm cực đại, cực tiểu của
m
C
cắt đường tròn tâm
I
(1;1)
, bán kính bằng
1 tại hai điểm phân biệt A, B sao cho diện tích IAB đạt giá trị lớn nhất .
A.
m
33
2
B.
m
23
4
C.
m
13
2
D.
m
23
2
Câu 29. Cho hàm số
y x mx x m
32
6 9 2
(1), với m là tham số thực.
Tìm m để đồ thị hàm số (1) có hai điểm cực trị sao cho khoảng cách từ gốc toạ độ O đến đường thẳng
đi qua hai điểm cực trị bằng
4
5
.
A.

m
37
8
B.
m
1
C.

m
2
D.
m
0
Câu 30. Cho hàm số
y x x m x m
32
3 ( 6) 2
(1), với m là tham số thực.
Tìm m để đồ thị hàm số (1) có hai điểm cực trị sao cho khoảng cách từ điểm
A
(1; 4)
đến đường thẳng
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 99
đi qua hai điểm cực trị bằng
12
265
A.
m
m
1
1053
12
B.
m
m
1
1053
24
C.
m
m
2
1053
249
D.
m
m
1
1053
249
Câu 31. Cho hàm số
y x x mx
32
31
(1), với m là tham số thực.
Tìm m để đồ thị hàm số (1) có hai điểm cực trị sao cho khoảng cách từ điểm
I
1 1 1
;
24



đến đường thẳng
đi qua hai điểm cực trị là lớn nhất.
A.

m
1
B.
m
0
C.
m
1
D.
m
2
Câu 32. Cho hàm số
y x m x mx m
2 2 3
2 3( 1) 6
.
Tìm m để đồ thị hàm số có hai điểm cực trị A, B sao cho
AB
2
.
A.
m
0
B.
mm
0; 2
C.
m
1
D.
m
2
Câu 33. Cho hàm số
y x mx m x m m
3 2 2 3
3 3( 1) 4 1
(1)
Tìm m để đồ thị của hàm số (1) có hai điểm cực trị A, B sao cho OAB vuông tại O.
A.
m
m
1
2
B.


m
m
1
2
C.

m
m
1
2
D.

m
m
1
2
Câu 34. Cho hàm số
y x m x mx m
2 2 3
2 3( 1) 6
(1)
Tìm m để đồ thị của hàm số (1) có hai điểm cực trị A, B sao cho tam giác ABC vuông tại C, với
C
(4;0)
.
A.
m
1
B.

m
2
C.

m
3
D.
m
1
Câu 35. Cho hàm số
y x x m
32
3
(1)
Xác định m để đồ thị của hàm số (1) có hai điểm cực trị A, B sao cho

AOB
0
120
.
A.

m
12 2 3
5
B.

m
12 2 3
3
C.
m
12 2 3
3
D.

m
12 2 3
3
SDT: 0946798489 100
Câu 36. Cho hàm số
y x x m m
3 2 2
31
(1)
Tìm m để đồ thị hàm số (1) có hai điểm cực đại, cực tiểu là A và B sao cho diện tích tam giác ABC
bằng 7, với điểm C(–2; 4 ).
A.

m
m
3
2
B.


m
m
3
2
C.
m
m
3
2
D.

m
m
3
2
Câu 37. Cho hàm số
y x m x mx m
32
3( 1) 12 3 4
(C)
Tìm m để hàm số có hai cực trị là A và B sao cho hai điểm này cùng với điểm
C
9
1;
2




lập thành tam
giác nhận gốc tọa độ O làm trọng tâm.
A.

m
1
3
B.

m
1
2
C.
m
0
D.

m
3
2
Câu 38. Cho hàm số
y f x x m x m
32
( ) 2 3( 3) 11 3
(
m
C
).
Tìm m để
m
C
()
có hai điểm cực trị
MM
12
,
sao cho các điểm
MM
12
,
và B(0; –1) thẳng hàng.
A.

m
1
B.

m
4
C.
m
1
D.
m
4
Câu 39. Cho hàm số
m
y x mx m x C
3 2 2
1
( 1) 1 ( )
3
.
Tìm m để hàm số có cực đại, cực tiểu và
CÑ CT
yy
2
.
A.
m
m
10
1
B.
1m
C.
10m
D.
1m 
Câu 40. Cho hàm số
y x m x m
3 2 3
14
( 1) ( 1)
33
(1) (m là tham số thực).
Tìm m để các điểm cực đại và cực tiểu của đồ thị (1) nằm về 2 phía (phía trong và phía ngoài) của
đường tròn có phương trình (C):
x y x
22
4 3 0
.
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 101
A.
m
1
B.
m
33
22
C.
m
3
D.
m
11
22
Câu 41. Cho hàm số
m
y x mx x m C
32
1
1 ( )
3
.
Tìm m để đồ thị (Cm) có 2 điểm cực trị và khoảng cách giữa 2 điểm cực trị là nhỏ nhất
A.
m
1
B.
m
0
C.

m
1
D.
m
12
Câu 42. Cho hàm số
y x x mx
32
3 2 (1)
.
Tìm m để hàm số (1) có 2 cực trị và đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số tạo với hai
trục toạ độ một tam giác cân.
A.
m
3
2

B.

m
3
4
C.

m
5
2
D.

m
7
2
Câu 43. Cho hàm số : y =
x mx m m x
3 2 2
1
( 1) 1
3
(1).
Tìm m để hàm số có cực trị trong khoảng
( ;1)
.
A.

m
12
B.
m
1
C.
m
0
D.
m
2
Câu 44. Cho hàm số : y =
x mx m m x
3 2 2
1
( 1) 1
3
(1).
Tìm m để hàm số có cực trị trong khoảng
(1; )
.
A.
m
1
B.
m
2
C.
m
1
D.
m
2
Câu 45. Cho hàm số : y =
x mx m m x
3 2 2
1
( 1) 1
3
(1).
Tìm m để hàm số có hai cực trị
xx
12
,
thoả mãn
xx
12
1
.
A.
m
12
B.
m
2
C.
m
1
D.
m
m
2
1
SDT: 0946798489 102
Câu 46. Cho hàm số : y =
x mx m m x
3 2 2
1
( 1) 1
3
(1).
Tìm m để hàm số có hai cực trị
xx
12
,
thoả mãn
xx
12
1
.
A.
1m
B.

m
C.
3m
D.

m
13
Câu 47. Cho hàm số : y =
x mx m m x
3 2 2
1
( 1) 1
3
(1).
Tìm m để hàm số có hai cực trị
xx
12
,
thoả mãn
xx
12
1
.
A.
m
3
B.
m
2
C.
m
2
D.
m
3
Câu 48. Cho hàm số
y x m m x m
4 2 2
2( 1) 1
.
Tìm m để đồ thị (C) có khoảng cách giữa hai điểm cực tiểu ngắn nhất.
A.
1
2
m 
B.
1
2
m
C.
3
2
m
D.
3
2
m 
Câu 49. Cho hàm số
y x mx
42
13
22
(1)
Xác định m để đồ thị của hàm số (1) có cực tiểu mà không có cực đại.
A.
m
0
B.
m
0
C.
m
0
D.
m
0
Câu 50. Cho hàm số
y x mx
42
24
m
C
()
.
Tìm các giá trị của m để tất cả các điểm cực trị của
m
C
()
đều nằm trên các trục toạ độ.
A.
m
0
B.
m
2
C.
m
0
D.
0, 2mm
Câu 51. Cho hàm số
y x m x
42
(3 1) 3
(với
m
là tham số).
Tìm tất cả các giá trị của
m
để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác cân sao cho độ
dài cạnh đáy bằng
2
3
lần độ dài cạnh bên.
747 Bài tập trắc nghiệm cực trị hàm số Giáo viên: Nguyễn Bảo Vương
Biên soạn và sưu tầm 103
A.

m
5
3
B.
m
5
3
C.

m
4
3
D.
m
4
3
Câu 52. Cho hàm số
y f x x m x m m
4 2 2
( ) 2( 2) 5 5
m
C
()
.
Tìm các giá trị của m để đồ thị
m
C
()
của hàm số có các điểm cực đại, cực tiểu tạo thành 1 tam giác
vuông cân.
A.
2m
B.
1m
C.
2m 
D.
1m 
Câu 53. Cho hàm số
m
y x m x m m C
4 2 2
2( 2) 5 5
Với những giá trị nào của m thì đồ thị (C
m
) có điểm cực đại và điểm cực tiểu, đồng thời các điểm cực
đại và điểm cực tiểu lập thành một tam giác đều.
A.
m
3
23
B.
m
3
3
1
2

C.

m
3
43
D.
m
3
3
Câu 54. Cho hàm số
y x mx m m
4 2 4
22
có đồ thị (C
m
) .
Với những giá trị nào của m thì đồ thị (C
m
) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành
một tam giác có diện tích
S
4
.
A.
B.
m
3
3
1
2

C.

m
5
1
16
3
D.
m
3
3
Câu 55. Cho hàm số
y x mx m m
4 2 2
2
có đồ thị (C
m
) .
Với những giá trị nào của m thì đồ thị (C
m
) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành
một tam giác có một góc bằng
0
120
.
A.
m
3
1
3

B.

m
3
43
C.
0m
D.
m
3
3
Câu 56. Cho hàm số
y x mx m
42
21
có đồ thị (C
m
) .
Với những giá trị nào của m thì đồ thị (C
m
) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành
một tam giác có bán kính đường tròn ngoại tiếp bằng
1
.
A.


mm
15
2,
2
B.


mm
15
1,
2
C.


mm
15
0,
2
D.
mm
15
1,
2


SDT: 0946798489 104
Câu 57. Cho hàm số
y x mx
42
22
(Cm).
Tìm các giá trị của m để (Cm) có 3 điểm cực trị tạo thành một tam giác có đường tròn ngoại tiếp đi
qua điểm
D
39
;
55



.
A.

m
1
B.
m
1
C.
m
2
D.

m
2
Câu 58. Cho hàm số
y x m x m
4 2 2
2(1 ) 1
(Cm).
Tìm m để đồ thị (Cm) có 3 điểm cực trị tạo thành một tam giác có diện tích lớn nhất.
A.

m
2
B.
m
0
C.

m
1
D.
m
1
Câu 59. Cho hàm số
y x m x m
42
1
(3 1) 2( 1)
4
(Cm).
Tìm m để đồ thị (Cm) có 3 điểm cực trị tạo thành một tam giác có trọng tâm là gốc toạ độ O.
A.
mm
21
;
33
B.
m
1
3
C.
D.
0m
Chúc các bạn học tốt. Tổng tài liệu gòm có 747 câu cực trị….được tôi sưu tầm và biên soạn.
| 1/105
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NGUYỄN BẢO VƯƠNG 747 BÀI TẬP TRẮC
NGHIỆM CỰC TRỊ HÀM SỐ BIÊN SOẠN VÀ SƯU TẦM SDT: 0946798489
Bờ Ngoong – Chư Sê – Gia Lai
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
Thầy Phan Ngọc Chiến
Câu 1: Giá trị cực đại của hàm số 3
y x  3x  4 là A. 2 B. 1 C. 6 D. 1 
Câu 2: Điểm cực đại của đồ thị hàm số 3 2
y  2x  3x  2 là: A. 0; 2 B. 2; 2 C. 1; 3   D.  1  ; 7  
Câu 3 : Điểmcựcđạicủađồthịhàmsố 3 2
y x  3x  2x là:  3 2 3   3 2 3  A. 1;0 B. 1 ;    C. 0  ;1 D. 1 ;     . 3 9   2 9   2 x  3x  3
Câu 4: Hàm số y x  đạt cực đại tại: 2 A. x  1 B. x  2 C. x  3 D. x  0 Câu 5: Hàm số: 3
y  x  3x  4 đạt cực tiểu tại x bằng A. -1 B. 1 C. - 3 D. 3 1 Câu 6: Hàm số: 4 2 y
x  2x  3 đạt cực đại tại x bằng 2 A. 0 B.  2 C.  2 D. 2 Câu 7: Hàm số 3 2
y x  3x  3x  4 có bao nhiêu cực trị? A. 1 B. 2 C.0 D. 3 3 x 2 Câu 8: Cho hàm số 2 y
 2x  3x  . Toạ độ điểm cực đại của đồ thị hàm số là 3 3 Biên soạn và sưu tầm 1  2  A. (-1;2) B. (1;2) C. 3;   D. (1;-2)  3  4 2
Câu 9: Hàm số y  4
x  3x 1 có
A.Một cự đại và hai cực tiểu
B. Một cực tiểu và hai cực đại
C. Một cực đại duy nhất
D. Một cực tiểu duy nhất 3 2
Câu 10: Giá trị cực đại của hàm số y x
 3x  3x  2 bằng A. 3   4 2 B. 3  4 2 C. 3  4 2 D. 3   4 2
Câu 11: Tìm m để hàm số 3 2
y mx  3x 12x  2 đạt cực đại tại x  2 A. m  2  B. m  3  C. m  0 D. m  1 4 x Câu 12: Cho hàm số 3 y
x  4x 1. Gọi x , x là hai nghiệm của phương trình y'  0 . Khi đó, x x 4 1 2 1 2 bằng: A. 1  B. 2 C. 0 D. 1
Câu 13: Tìm m để hàm số 4
y x  m   2 2
1 x  3 có ba cực trị A. m  0 B. m  1 C. m  1 D. m  0 1
Câu 14: Tìm m để hàm số 3 y
x  m   2 1 x   2
m mx  2 có cực đại và cực tiểu 3 1 2 A. m  2  B. m   C. m   D. m  1 3 3
Câu 15: Gọi y , y lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số 4 2
y  x 10x  9 . Khi đó, 1 2
y y bằng: 1 2 A. 7 B. 9 C. 25 D. 2 5 SDT: 0946798489 2
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương Câu 16:Hàm số 3 2
y x  3x mx đạt cực tiểu tại x = 2 khi: A. m  0 B. m  0 C. m  0 D. m  0 VD1 1 Câu 17: Cho hàm số 3 2
y  x  m x  2m  
1 x 1 . Mệnh đề nào sau đây là sai? 3 A. m
 1thì hàm số có cực đại và cực tiểu; B. m
 1thì hàm số có hai điểm cực trị; C. m
 1thì hàm số có cực trị;
D. Hàm số luôn có cực đại và cực tiểu.
Câu 18: Cho hàmsố y=x3-3x2+1. Tích các giá trị cực đại và cực tiểu của đồ thị hàm số bằng A. -6 B. -3 C. 0 D. 3 Câu 19:Hàmsố 3
y x mx 1 có 2 cựctrị khi : A. m  0 B. m  0 C. m  0 D. m  0 VD1 2
x  2x  5
Câu 20:Khẳng định nào sau đây là đúng về đồ thị hàm số y  : x 1 A. yy  0 B. y  4  C. x  1  D. xx  3 CD CT CT CD CD CT
Thầy Nguyễn Việt Dũng 3 x
Câu 21. Số điểm cực trị của hàm số y x 7 là: 3 A.1 B. 0 C. 2 D. 3 3 2
Câu 22. Hàm số y x 3x 9x
2 có điểm cực tiểu tại: A. x 1 B. x 3 C. x 1 D. x 3 Biên soạn và sưu tầm 3 4 3
Câu 23. Số điểm cực trị của hàm số y 3x 4x 5 là: A.1 B.0 C.3 D.2 1
Câu 24. Hàm số y x
có y cực đại là: x A.-2 B. 2 C. 1 D. -1 3
Câu 25. Hàm số y x
3x có y cực tiểu là: A.-2 B. 2 C. 1 D. -1
Câu 26. Hàm số nào sau đây không có cực trị: 3 4 2 1 x 2 A. y x 3x B. y x 2x 1 C. y x D. y x 2x 1 4 3
Câu 27. Cho hàm số y 3x
4x . Khẳng định nào sau đây đúng?
A. Hàm số không có cực trị B. Điểm (
A 1; 1) là điểm cực tiểu
C. Hàm số đạt cực đại tại gốc tọa độ D. Hàm số đạt cực tiểu tại gốc tọa độ 3
Câu 28. Cho hàm số y x 3x
2.Khẳng định nào sau đây sai?
A. Hàm số đạt cực đại tại x
1. B. Hàm số đạt cực tiểu tại x 1.
C. Hàm số không có cực trị
D. Hàm số có 2 điểm cực trị.
Câu 29. Hàm số nào sau đây chỉ có cực đại mà không có cực tiểu? 3 2 x 1 A. y x 3x 2 B. y 2 x 4 x x 2 2 C. y x 1 D. y 2 x 1 SDT: 0946798489 4
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 1 4 7 4 3 2
Câu 30. Cho hàm số y x x x 2x
1.Khẳng định nào sau đây đúng? 4 3 2
A. Hàm số không có cực trị
B. Hàm số chỉ có 1 cực tiểu và không có cực đại
C. Hàm số có 1 cực đại và 2 cực tiểu D. Hàm số có 1 cực tiểu và 2 cực đại 2 3
Câu 31. Hàm số y 3x
2x đạt cực trị tại A. x 1;x 0 B. x 1;x 0 CD CT CD CT C. x 0;x 1 D. x 0;x 1 CD CT CD CT 3 2
Câu 32. Cho hàm số y 2x 3x 2. Câu nào sau đây sai? 1 1  1 
A.Hàm số đạt cực tiểu trên khoảng ;
B. Hàm số đạt cực đại trên khoảng ; 2   2 2  2  1 1
C. Hàm số có 2 cực trị trên khoảng ;2
D. Hàm số có 2 cực trị trên khoảng ; 3 2 3 4 x 2
Câu 33. Hàm số y 2x 1 đạt cực đại taị 4 A. x 2 B. x 2 C. x 0 D. x 2 3 x 2
Câu 34. Hàm số y 2x 3x 5 đạt cực tiểu tại 3 A. x 1 B. x 3 C. x 1 D. x 3 3 x 2
Câu 35. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số y 2x 3x 5 3
A.Song song với đường thẳng x 1
B.Song song với trục hoành C.Có hệ số góc dương D.Có hệ số góc bằng -1 Biên soạn và sưu tầm 5 3 2 2
Câu 36. Tìm m để hàm số y x 3mx
3m có 2 điểm cực trị. A.m 0 B. m 0 C. m 0 D. m 0 3 2
Câu 37. Tìm m để hàm số y x mx 3x
2 đạt cực tiểu tại x 2. 15 4 4 15 A. m B. m C. m D. m 4 15 15 4 3 2
Câu 38. Với giá trị nào của m thì hàm số y x mx 3x
2m 1 có cực đại và cực tiểu? A. m 3; 3 B. m ; 3 3; C. m 3; 3 D. m ; 3 3; 3 2 2 2
Câu 39. Tìm m để hàm số y x 3x mx
1 có 2 điểm cực trị x ,x x x 3 1 2 thỏa 1 2 . 2 3 A. m 1 B. m C. m D. m 1 3 2 2
Câu 40. Với giá trị nào của m thì hàm số y x 2(m 1)x
m có cực trị trên khoảng (0;1)? A. 1 m 0 B. 0 m 1 C. 2 m 1 D. 2 m 0
Thầy Nguyễn Viết Thông
Câu 41. Số điểm cực trị của đồ thị hàm số 4 2
y x  2x 1 là: A. 0 B. 1 C. 2 D. 3 Câu 42. Cho hàm số 3 2 y  2
x  3x 5 . Tổng các giá trị cực trị của hàm số là: A. -9 B. 1 C. -1 D. -5 5 3
Câu 43. Số các điểm cực trị của hàm số y  2  x  x   1 là: A. 1 B. 3 C. 5 D. 7 SDT: 0946798489 6
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương Câu 44. Cho hàm số 2
y  3  2x x . Trong các điểm sau, điểm nào có tọa độ sau đây là điểm cực trị của hàm số đã cho A.  1  ;2 B.  3  ;0 C. 1;0 D.  2  ; 3
Câu 45. Điểm cực trị của đồ thị hàm số 2
y  3  2x x có tọa độ là: A.  1  ;2 B. 0; 3 C. 1;0 D.  3  ;0
Câu 46 .Giá trị của m để hàm số y  m   3
2 x mx  3 không có cực trị là: m  0 m  0 A.  B. m  2 C.  D. 0  m  2 m  2 m  2 Câu 47. Hàm số 6
y  2x  4x  7 có số điểm cực trị là: A. 0 B. 1 C. 2 D. 3 Câu 48. Hàm số 3 2
y x mx   2 m m 2 3 3
x  2m 1 có hai điểm cực trị khi: A. m  0 B. m  0 C. m  1 D. m tùy ý 2
2x mx  2m 1
Câu 49. Hàm số y
có hai điểm cực trị khi: 2x 1 A. m  1  B. m  1  C. m  1  D. m tùy ý
Câu 50. Đồ thị hàm số 1 y x 1   thì tích . a b
x  có hai điểm cực trị nằm trên đường thẳng y ax b 1 bằng: A. 0 B. 2 C. 4 D. -2 2 x  2x 1
Câu 51. Cho hàm số y x
. Khoảng cách giữa hai điểm cực trị là: 1 Biên soạn và sưu tầm 7 A. 4 5 B. 4 C. 8 D. 5 2
Câu 52. Cho hàm số y  2x 1 4x 1 . Tìm mệnh đề đúng trong các mệnh đề sau: 1  1 
A. Giá trị cực đại bằng 
B. Điểm cực tiểu có tọa độ là ; 1    2  2    C. Điể 1 1 m cực tiểu là ;   
D. Hàm số không có cực trị.  4 2 
Câu 53. Trong các đường thẳng sau, đường thẳng nào đi qua hai điểm cực trị của hàm số 3 2
y x  3x  4x  2 1 1
A. y  2x  3 B. y x
C. y  2x 10
D. 2x  3y 10  0 3 3 Câu 54. Hàm số 3
y x  m  
1 x 1 đạt cực tiểu tại điểm x  2 khi: A. m  13 B. m  13 C. m  1 D. m 
Câu 55. Điều kiện của m để hàm số 3 2
y x  3x  3mx m  2 có cực trị là: A. m  1 B. m  1 C. m  1 D. m  1 1 Câu 56. Hàm số 3 2 y
x mx   2 m m  
1 x 1 đạt cực đại tại điểm x  1 khi: 3
A. m  1 hoặc m  2 B. m  1 C. m  2 D. m tùy ý Câu 57. Hàm số 4
y  x  m   2 2
2 x m  3 đạt cực đại tại điểm x  1 thì: A. m  3 B. m  5 C. m  3 D. m  5
Câu 58. Số cực trị của hàm số 2
y x  4x 1 A. 1 B. 2 C. 3 D. 4
Câu 59. Với m bằng bao nhiêu thì đồ thị hàm số 3 2
y x  2mx m có hai cực trị thẳng hàng với gốc tọa độ SDT: 0946798489 8
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 1 A. m  0 B. m  3 C. m  D. m  3 3
Câu 60. Cho hàm số y  cos 2x 1, x  
 ;0 thì khẳng định nào sau đây sai: 7 11
A. Hàm số đạt cực tiểu tại điểm x  
B. Hàm số đạt cực đại tại điểm x   12 12   C. Tại x  
hàm số không đạt cực đại D. Tại x  
hàm số không đạt cực tiểu 2 12
Không biết của ai thành ra của mình :D
Câu 61. Điểm cực đại của hàm số 3 y x 3x 3 có hoành độ là: A. -3 B. -2 C. -1 D. 1 Câu 62. Hàm số: 3
y  x  3x  4 đạt cực tiểu tại: A. -1 B. 1 C. – 3 D. 3 Câu 63. Cho hàm số 3 2
y  x  3x  9x  2 . Hàm số này:
A. Đạt cực tiểu tại x = 3
B. Đạt cực tiểu tại x = 1.
C. Đạt cực đại tại x = -1
D. Đạt cực đại tại x = 3. 1
Câu 64. Hoành độ điểm cực đại của đồ thị hàm số: 4 2 y
x  2x  3 là: 2 A.  2 B. 2 C.  2 D. 0 4 x Câu 65. Cho hàm số 2 f (x) 
 2x  6. Hàm số đạt cực đại tại 4 A. x  2  B. x  2 C. x  0 D. x  1
Câu 66. Các điểm cực tiểu của hàm số 4 2
y x  3x  2 là: Biên soạn và sưu tầm 9 A. x  1  B. x  5 C. x  0
D. x  1, x  2
Câu 67. Số điểm cực trị hàm số 4 2
y x  2x  3 A. 0 B. 1 C. 3 D. 2 3 x 2 Câu 68. Cho hàm số 2 y
 2x  3x  .Toạ độ điểm cực đại của hàm số là 3 3 2 A. (-1;2) B. (3; ) C. (1;-2) D. (1;2) 3
Câu 69. Đồ thi hàm số 3
y x  3x 1 có điểm cực tiểu là: A. ( 1 ; 3 ) B. ( -1 ; -1 ) C. ( -1 ; 3 ) D. ( -1 ; 1 )
Câu 70: Điểm cực đại của đồ thị hàm số 3 2
y x  6x  9x là: A. 1; 4 B. 3;0 C. 0;3 D. 4  ;1 .
Câu 71. Điểm cực tiểu của đồ thị hàm số 3 2
y x  6x  9x là: A. 1; 4 B. 3;0 C. 0;3 D. 4  ;1 .
Câu 72. Điểm cực đại của đồ thị hàm số 3 2
y x x  2 là:  2 50   50 3  A. 2;0 B. ;   C. 0; 2 D. ;   .  3 27   27 2 
Câu 73. Điểm cực tiểu của đồ thị hàm số 3 2
y x x  2 là:  2 50   50 3  A. 2;0 B. ;   C. 0; 2 D. ;   .  3 27   27 2 
Câu 74. Điểm cực đại của đồ thị hàm số 3
y  3x  4x là: SDT: 0946798489 10
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương  1   1   1   1  A. ; 1    B.  ;1   C.  ; 1    D. ;1   .  2   2   2   2 
Câu 75. Điểm cực tiểu của đồ thị hàm số 3
y  3x  4x là:  1   1   1   1  A. ; 1    B.  ;1   C.  ; 1    D. ;1   .  2   2   2   2 
Câu 76. Điểm cực đại của đồ thị hàm số 3
y x 12x 12 là: A.  2  ;28 B. 2; 4   C. 4; 28 D.  2  ;2 .
Câu 17. Điểm cực tiểu của đồ thị hàm số 3
y x 12x 12 là: A.  2  ;28 B. 2; 4   C. 4; 28 D.  2  ;2 .
Câu 78. Điểm cực đại của đồ thị hàm số 3 2
y x  5x  7x  3 là:  7 3  2   7 32  A. 1;0 B. 0  ;1 C. ;   D. ;   .  3 27   3 27 
Câu 79. Điểm cực tiểu của đồ thị hàm số 3 2
y x  5x  7x  3 là:  7 3  2   7 32  A. 1;0 B. 0  ;1 C. ;   D. ;   .  3 27   3 27 
Câu 80. Điểm cực đại của đồ thị hàm số 3 2
y x  3x  2x là:  3 2 3   3 2 3  A. 1;0 B. 1 ;    C. 0  ;1 D. 1 ;     . 2 9   2 9  
Câu 81. Điểm cực tiểu của đồ thị hàm số 3 2
y x  3x  2x là: Biên soạn và sưu tầm 11  3 2 3   3 2 3  A. 1;0 B. 1 ;    C. 0  ;1 D. 1 ;     . 2 9   2 9  
Câu 82. Đồ thị hàm số 3
y x  3x 1 có điểm cực tiểu là: A. (-1; -1) B. (-1; 3) C. (-1; 1) D. (1; 3) Câu 83. Cho hàm số 4 2
y x  2x  2016 . Hàm số có mấy cực trị. A. 1 B. 2 C. 3 D.4 1
Câu 84. Số điểm cực trị của hàm số 3
y   x x  7 là : 3 A. 1 B. 0 C. 3 D. 2
Câu 85. Số điểm cực đại của hàm số 4
y x 100 là : A. 0 B. 1 C. 2 D. 3
Câu 86. Số cực trị của hàm số 4 2
y x  3x  3 là: A. 1 B. 3 C. 2 D. 4
Câu 87. Số điểm cự trị của y = x4 – 2x2 - 3 A. 0 B. 1 C. 3 D. 2 1 Câu 88. Cho hàm số 4 2 y
x  2x 1. Hàm số có 4
A. Một cực đại và hai cực tiểu
B. Một cực tiểu và hai cực đại
C. Một cực đại và không có cực tiểu
D. Một cực tiểu và một cực đại
Câu 89. Cho hàm số y = x3 - 3x2 + 1. Tích các giá trị cực đại và cực tiểu của hàm số bằng A. 6 B. -3 C. 0 D. 3 SDT: 0946798489 12
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
Câu 90. Đồ thị hàm số nào sau đây có 3 điểm cực trị: A. 4 2
y x  2x 1 B. 4 2
y x  2x 1 C. 4 2
y  2x  4x 1 D. 4 2 y  2
x  4x 1
Câu 91. Khẳng định nào sau đây là đúng về hàm số 4 2
y x  4x  2 :
A. Đạt cực tiểu tại x = 0
B. Có cực đại và cực tiểu
C. Có cực đại và không có cực tiểu D. Không có cực trị. 1 1
Câu 92. Trong các khẳng định sau về hàm số 4 2
y   x  x  3 , khẳng định nào là đúng? 4 2
A. Hàm số đạt cực tiểu tại x = 0;
B. Hàm số đạt cực đại tại x = 1;
C. Hàm số đạt cực đại tại x = -1;
D. Cả 3 câu trên đều đúng. 1 Câu 93. hàm số: 3 2 y
x  2x  5x 17 có tích hoành độ các điểm cực trị bằng: 3 A. 5 B. 8 C. -5 D. -8
Câu 94. Đồ thi hàm số nào sau đây có 3 điểm cực trị : A. 4 2
y  2x  4x 1 B. 4 2
y x  2x 1 C. 4 2
y x  2x 1 D. 4 2
y  x  2x 1 1 Câu 95. Cho hàm số 4 2 y
x  2x 1.Hàm số có 4
A. một cực tiểu và một cực đại
B. một cực đại và không có cực tiểu
C. một cực tiểu và hai cực đại
D. một cực đại và hai cực tiểu 4 x Câu 96.Cho hàm số 2 f (x) 
 2x  6. Giá trị cực đại của hàm số là 4 A. f  6 B. f  2 C. f  20 D. f  6  CÐ CÐ CÐ CÐ Biên soạn và sưu tầm 13 Câu 97. Hàm số 4 3
y  x  8x  6 có bao nhiêu cực trị ? A. 3 B. không có cực trị C. 2 D. 1
Câu 98. Hàm số y = x3 – 3x2 + 3x: A. có hai cực trị. B. có một cực trị. C. không có cực trị. D. có ba cực trị. 4 x 5 Câu 99. Hàm số y = 2  3x  có bao nhiêu cực trị ? 2 2 A. 3 cực trị B. Không có cực trị C. 2 cực trị D. 1 cực trị
Câu 100. Hàm số y = x4 + 2x2 + 3: A. có 3 cực trị B. có 1 cực trị C. có 2 cực trị D. không có cực trị
Câu 101. Hàm số nào sau đây nhận x = 1 làm hoành độ độ điểm cực đại: A. y = x3 + 3x - 3 B. y = x3 -3x – 3 C. y = -x3 + 3x – 3 D. y = -x3 – 3x – 3
Câu 102. Cho hàm số y = –x3 + 3x2 – 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số luôn nghịch biến;
B. Hàm số luôn đồng biến;
C. Hàm số đạt cực đại tại x = 1;
D. Hàm số đạt cực tiểu tại x = 1. 2x  4
Câu 103. Trong các khẳng định sau về hàm số y 
, hãy tìm khẳng định đúng? x 1
A. Hàm số có một điểm cực trị;
B. Hàm số có một điểm cực đại và một điểm cực tiểu;
C. Hàm số đồng biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên từng khoảng xác định. SDT: 0946798489 14
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
Câu 104. Trong các hàm số sau hàm số nào có cực đại, cực tiểu và xx ? CT CD A. 3 2
y x  2x  8x  2 B. 3
y  x  3x  2 C. 3 2
y x  9x  3x  5 D. 3 2
y  x  9x  3x  2 Câu 105. Hàm số 4 2
y x 10x  9 đạt cực đại, cực tiểu lần lượt tại x , x . Khi đó, ta có x x bằng: 1 2 1 2 A. 5 B. 4 C. 2 5 D. 5
Câu 106. Trong các hàm số sau, hàm số nào chỉ có 1 cực đại mà không có cực tiểu? 2 4x x  5 2x 1 A. y  B. 3 2
y x  3x  6x 1 C. y  D. 4 2
y  x x  5 x  2 x 1 1
Câu 107. Trong các khẳng định sau về hàm số 4 2
y   x  x  3 , khẳng định nào là đúng? 4 2
A. Hàm số có điểm cực tiểu là x = 0;
B. Hàm số có hai điểm cực đại là x = 1; C. Cả A và B đều đúng; D. Chỉ có A là đúng.
Câu 108. Cho hàm số y = x3 - 3x2 + 1. Tích các giá trị cực đại và cực tiểu của đồ thị hàm số bằng A. -6 B. -3 C. 0 D. 3 2 x  4x 1
Câu 109. Cho hàm số y x
.Hàm số có hai điểm cực trị x1, x2 .Tích x1.x2 bằng 1 A. -4 B. -5 C. -1 D. -2 x 
Câu 110. Số điểm cực trị của hàm số 11 y  là: x  2 A. 1 B. 3 C. 2 D. 0
Câu 111. Số điểm cực trị của hàm số 2 y
x x 1 là: Biên soạn và sưu tầm 15 A. 1 B. 3 C. 2 D. 4
Câu 112. Đồ thị hàm số nào sau đây có 3 điểm cực trị: A. 4 2
y x  2x 1 B. 4 2
y  2x x 1 C. 4 2
y x  3x 1     D. 4 2 y x 2x 1 Câu 113. Hàm 3 2
y x  3x  21x  1 có 2 điểm cực trị x ; x thì tích x .x bằng: 1 2 1 2 A. 7 B. -7 C. 2 D. -2 Câu 114. Hàm số 4 2
y x  2x  3 có
A. 3 cực trị và 1 cực đại
B. 3 cực trị và 1 cực tiểu
C. 2 cực trị và 1 cực đại
D. 2 cực trị và 1 cực tiểu. 1
Câu 115. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số 3 2 y
x  2x  3x  5 3
A. song song với đường thẳng x 1
B. song song với trục hoành C. Có hệ số góc dương
D. Có hệ số góc bằng -1 Câu 116. Hàm số 3 2
f (x)  x  3x  9x 11
A. Nhận điểm x  1  làm điểm cực tiểu
B. Nhận điểm x  3 làm điểm cực đại
C. Nhận điểm x 1 làm điểm cực đại
D. Nhận điểm x  3 làm điểm cực tiểu Câu 117. Hàm số 4 3
y x  4x  5
A. Nhận điểm x  3 làm điểm cực tiểu
B. Nhận điểm x  0 làm điểm cực đại
C. Nhận điểm x  3 làm điểm cực đại
D. Nhận điểm x  0 làm điểm cực tiểu 2 x  3x  6
Câu 118. Số điểm cực trị hàm số y x 1 A. 0 B. 2 C. 1 D. 3 SDT: 0946798489 16
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
Câu 119. Hàm số f có đạo hàm là 2 2
f '(x)  x (x 1) (2x 1) . Số điểm cực trị của hàm số là A. 1 B. 2 C. 0 D. 3
Câu 120. Hàm số y x  sin 2x  3  
A. Nhận điểm x   làm điểm cực tiểu B. Nhận điểm x  làm điểm cực đại 6 2  
C. Nhận điểm x   làm điểm cực đại
D. Nhận điểm x   làm điểm cực tiểu 6 2
Câu 121. Cho hàm số y = –x3 + 3x2 – 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số luôn nghịch biến;
B. Hàm số luôn đồng biến;
C. Hàm số đạt cực đại tại x = 1;
D. Hàm số đạt cực tiểu tại x = 1. 2x  4
Câu 122. Trong các khẳng định sau về hàm số y 
, hãy tìm khẳng định đúng? x 1
A. Hàm số có một điểm cực trị;
B. Hàm số có một điểm cực đại và một điểm cực tiểu;
C. Hàm số đồng biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên từng khoảng xác định. 1 1
Câu 123. Trong các khẳng định sau về hàm số 4 2
y   x  x  3 , khẳng định nào là đúng? 4 2
A. Hàm số đạt cực tiểu tại x = 0;
B. Hàm số đạt cực đại tại x = 1;
C. Hàm số đạt cực đại tại x = -1;
D. Cả 3 câu trên đều đúng.
Câu 124. Khẳng định nào sau đây là đúng về hàm số 4 2
y x  4x  2 :
A. Đạt cực tiểu tại x = 0
B. Có cực đại và cực tiểu Biên soạn và sưu tầm 17
C. Có cực đại và không có cực tiểu D. Không có cực trị. 2
x  2x  5
Câu 125. Khẳng định nào sau đây là đúng về đồ thị hàm số y  : x 1     A. y y 0 y   x   x x CD CT B. 4 CT C. 1 CD D. 3 CD CT 1 Câu 126. hàm số: 3 2 y
x  2x  5x 17 có tích hoành độ các điểm cực trị bằng 3 A. 5 B. 8 C. -5 D. -8
Câu 127. Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số 3 2
y x  3x  4 là: A. 2 5 B. 4 5 C. 6 5 D. 8 5
Câu 128. Hàm số nào sau đây không có cực trị : 2x  2 2 x x  3 A. y = x3 + 2 B. y = D. Cả 3 đều đúng x  C. y = 1 x  2
Câu 129. Hàm số nào sau đây không có cực trị ? 2 x + x - 2 A. y = 2x2 – 6 x + 1 B. y = 2x3 + x2 – x + 5 C. y = x +1 D. y = 1 4 x4 – 2x2 x
Câu 130. Tại điểm x = e, hàm số y = : ln x A. đạt cực tiểu B. đạt cực đại
C. không đạt cực trị D. không xác định
Câu 131: Hàm số y = x – ex tại điểm x = 0 thì : A. đạt cực tiểu B. đạt cực đại C. không xác định D. không đạt cực trị.
Câu 132. Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số 3 2
y x  3x  4 là: SDT: 0946798489 18
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương A. 2 5 B. 4 5 C. 6 5 D. 8 5
Câu 133. Phương trình đường thẳng đi qua các điểm cực trị của đồ thị hàm số 3 2
y  x x  3x 1 là: 2 1 A. Một kết quả khác B. y  7x 6 C. y  20x 6 D. 9 9 1 y  3x   1 9
Câu 134. Hàm số y  sin 2x x  3 :  
A. nhận điểm x   làm điểm cực đại. B. Nhận điểm x  làm điểm cực tiểu 6 2  
C. Nhận điểm x   làm điểm cực tiểu.
D. Nhận điểm x   làm điểm cực đại. 6 2
Câu 135. Trong các mệnh đề sau, hãy tìm mệnh đề sai: A. Hàm số 1 y  2  x 1 y  x   x không có cực trị; B. Hàm số 1 1 có hai cực trị.  2 x 1
C. Hàm số y = –x3 + 3x2 – 3 có cực đại và cực tiểu; D. Hàm số y = x3 + 3x + 1 có cực trị; 2 x  2x  2
Câu 136. Đồ thị hàm số: y  1
có 2 điểm cực trị nằm trên đường thẳng y = ax + b với: a + b = x A. 2 B. 4 C. - 4 D. - 2 2
Câu 137. Cho đồ thị hàm số y  x  2  . Khi đó yy x 1 CD CT A. 6 B. -2 C. -1 / 2 D. 3  2 2
Câu 138. Cho hàm số y x4  x2
2 1 (C). Tiếp tuyến của (C) tại điểm cực đại có phương trình là: A. x  0 B. y  0 C. y  1 D. y  2 Biên soạn và sưu tầm 19
Câu 139. Hàm số y   5 x4 có bao nhiêu điểm cực đại? A. 1 B. 3 C. 0 D. 2 xx e e
Câu 140. hàm số y
có bao nhiêu điểm cực trị ? 2 A. 0 B. 1 C. 2 D. 3 Câu 141. Hàm số 2 y  3
x ax b đạt cực trị bằng 2 tại x = 2 khi và chỉ khi: A. a  1  2,b  6 B. a  1  2,b  1  0
C. a  4,b  2 D. a  1  0,b 12
Câu 142. cho hàm số f(x) = 3 2 2
x  3mx  3(m 1)x . Tìm m để f đạt giá trị cực đại tại x0 =1. A. m=2 B. m = 0 C. m = 0 hay m = 2 D. m  0 và m  2 Câu 143. Hàm số 3 2
y x  3x mx đạt cực tiểu tại x = 2 khi : A. m  0 B. m  0 C. m  0 D. m  0 Câu 144. Hàm số 3
y x mx 1 có 2 cực trị khi A. m  0 B. m  0 C. m  0 D. m  0
Câu 145. Với giá trị nào của m thì hàm số 3 2
y  x  (m 1)x  2m 1 đạt cực đại tại x  2 ? A. m=0 B. m=1 C. m=2 D. m=3   Câu 146. Hàm số 2 3 2
y x x mm x  7  
có cực trị tại x = 1 khi:  3  7 m  2 A. m  B.  C. 1  m  2
D. Không có giá trị m thỏa mãn 9 m   1 1 Câu 147. Hàm số 3 2 2 y
x mx  (m m 1)x  2 có cực đại tại x = 1 khi: 3 SDT: 0946798489 20
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương A. m  1 B. m = 2
C. m  2 và m  1
D. Không có giá trị m thỏa mãn 1 Câu 148. Hàm số 3 2 2 y
x mx  (m m 1)x  2 có cực tiểu tại x = 1 khi: 3 A. m  1 B. m = 2
C. m  2 và m  1
D. Không có giá trị m thỏa mãn 2   Câu 149. Hàm số x x m 1 y
có cực đại tại x = 2 khi: x m A. m  1  B. m  3  C. m  3  và m  1
 D. Không có giá trị m thỏa mãn  2 
Câu 150. Cho hàm số 3 2
y x mx m x  5  
. Tìm m để hàm số đạt cực tiểu tại x 1  3  2 7 3 A. m  B .m  C. m  D. m  0 5 3 7 1 Câu 151. Hàm số 3 2 y
x mx  1 2mx m  2 có cực đại cực tiểu khi và chỉ khi: 3 A. m  1  B. mọi m C. m  1 
D. không có giá trị nào của
Câu 152. Giá trị của m để hàm số y = x3 + 3x2 + (m + 4)x - 2 có cực đại, cực tiểu là: A. m  1  B. m  2 C. m  0 D. m =2
Câu 153. Cho hàm số y = (m + 2)x3 + 3x2 + mx – 5. Tất cả các giá trị của tham số m để hàm số có cực trị là: A. –3 < m < 1
B. –3 < m < 1 và m  –2 C. –3  m  1
D. –3  m  1 và m  –2 Câu 154. Hàm số 3
y x mx 1 có 2 cực trị khi : A. m  0 B. m  0 C. m  0 D. m  0 1 Câu 155. Hàm số 3 2 y
x mx  (m  6)x  (2m 1) có cực trị khi: 3 Biên soạn và sưu tầm 21     A. m 3 m     B. 3 m     C. 2 D. 2 m 3   m  2  m  2  m  3 1 Câu 156. Hàm số 3 2 y
(m  6)x mx x  (2m 1) có 2 cực trị khi: 3 A. m  3 B. m  3
C. m  3 và m  6  D. 2   m  3    m  2  m  2  m  2  2   Câu 157. Hàm số x 2x m y
có cực đại và cực tiểu khi: 4  x A. m  8  B. m  8  C. m  8  và m  2 D. m  8 2 x mx  2
Câu 158. Hàm số y = có cực trị khi: x 1 A. m = -3 B. m < -2 C. m > -3 D. – 3 < m < -2
Câu 159. Có hai giá trị m để hàm số 3 2
y x  (m  2)x  (1 )
m x  3m 1 đạt cực trị tại x1, x2 mà
x x  2 . Tổng hai số đó là: 1 2 A. -7 B. -5 C. -3 D. 1
Câu 160. Biết đồ thị hàm số 4 2
y x  2 px q có một điểm cực trị là (1;2), thế thì khoảng cách giữa
điểm cực tiểu và điểm cực đại là A. 26 B. 5 C. 2 D. 2
Câu 161. Có bao nhiêu giá trị nguyên của m để hàm số 2
y mln(x  2)  x x có hai điểm cực trị trái dấu A. 3 B. 2 C. 1 D. 0 SDT: 0946798489 22
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 3 1
Câu 162. Xác định m để hàm số 3 2 3 y x mx
m có các điểm cực đại , cực tiểu đối xứng nhau qua 2 2 đường thẳng y = x: A. m  2 B. m   2 C. m   2 D. m   3 2
x mx m
Câu 163. Khoảng cách giữa 2 điểm cực trị của đồ thi hàm số y  bằng : x 1 A. 2 5 B. 5 2 C. 4 5 D. 5
Câu 164. Giả sử đồ thị hàm số 3 2
y x  3mx  3(m  6)x 1có hai cực trị. Khi đó đường thẳng qua hai
điểm cực trị có phương trình là: A. 2
y  2x m  6m  1 B. 2 2
y  2(m m  6)x m  6m  1 C. 2 y  2
x m  6m1 D. Tất cả đều sai 1 3 2
Câu 165. Hàm số y x mx  (m  6)x  (2m 1) không có cực trị khi: 3 m  3 m  2  A.  B. 2   m  3 C.  D. 2   m  3 m  2   m   3 Câu 166. Hàm số 4 2 2
y x  2(m  1)x m có 3 điểm cực trị khi: A. m > -1 B. m < -1 C. m  -1 D. m > 1 Câu 167. Hàm số 4 2 2
y x  2(3m m )x m  1 có 3 điểm cực trị khi: m  3 m  0 A. 0  m  3 B.  C.  D. 0  m  3 m   0 m   3 Câu 168. Hàm số 4 2 2
y x  2(3m m )x m 1 có 1 điểm cực trị khi: Biên soạn và sưu tầm 23 m  3 m  3 A. 0  m  3 B.  C.  D. 0  m  3 m   0 m   0 Câu 169. Hàm 3 2
y x  3x mx  1 có 2 điểm cực trị x ; x : 2 2
x x  3 khi: 1 2 1 2 3 2 3 A. m  1 B. m  C. m  D. m   2 3 2 1 Câu 170. Hàm 3 2 y
x  (m 1)x  (m  5)x 1có 2 điểm cực trị trái dấu nhau khi: 3 A. m  5 B. m  5 C. m  5 D. m  5 1 Câu 171. Hàm 3 2 y
x  (m 1)x  (m  5)x 1có 2 điểm cực trị cùng dương khi: 3 A. m  5 B. m  5 C. m  5 D. m  5 Câu 172. Hàm số 3 2
y x  3mx  3x  2m  3 không có cực đại, cực tiểu với m A. m  1 B. m  1 C. 1   m 1 D. m  1   m 1 Câu 173. Hàm số 4
y mx  m   2
3 x  2m 1 chỉ có cực đại mà không có cực tiểu với m: A. m  3 B m  0 C. 3   m  0
D. m  0  m  3 Câu 174. Hàm số 3 2
y x mx  3m  
1 x 1 đạt cực đại tại x = 1 với m bằng : A. m = - 1 B. m  3  C. m  3  D. m = - 6
Câu 175. Hàm số y= x3-3x2+mx-1=0 có 2 điểm cực trị x 2 2 x x  1,x2 thoả mãn 3 khi: 1 2 2 3 3 A. m = 3 B. m = C. m = D. m = - 3 2 2
Câu 176. Hàm số y= x3 - 3x2 + mx - 1 có 2 điểm cực trị x 2 2 x x  1,x2 thoả mãn 3 khi: 1 2 SDT: 0946798489 24
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 3 3 3 A.m < 3 B. m > C. m < D. < m < 3 2 2 2
Câu 177. Hàm số y= x3 - 3x2 + mx - 1 có 2 điểm cực trị x 2 2 x x  1,x2 thoả mãn 3 khi: 1 2 3 3 3 A. m < 3 B. m > C. m < D. < m < 3 2 2 2
Câu 178. Đồ thị hàm số y = x3 - 3mx2 + 1 có 2 điểm trị A,B thoả mãn: AB = 2 5 khi: A. m = 1 B. m = -1 C.m =  1 D. kết quả khác
Câu 179. Đồ thị hàm số y=x3-3mx2+1 có 2 điểm trị A,B thoả mãn : AB>2 5 khi: A. -1< m < 1 B. m  ;    1  ; 1 ( )  C. m < 1 D. m ( ) 1 , 1 \   0
Câu 180. Đồ thị hàm số y = x3 - 3mx2 + 1 có 2 điểm trị A, B thoả mãn trung điểm I của AB thuộc Ox khi: 1 A. m=1 B. m=0 C. m= 3 D. Không có m thoả 2 mãn
Câu 181. Đồ thị hàm số y = x3 - 3mx + 1 có 2 điểm cực trị B, C thoả mãn tam giác ABC cân tại A(2; 3) nếu: 1 1 A. m = 0 hoặc m = B. m = C. m = 0 D. đáp án khác 2 2
Câu 182. Đồ thị hàm số y = x3 - 3mx + 1 có 2 điểm cực trị B,C thoả mãn tam giác ABC vuông tại A(2; 2) nếu A.m = 0 B. m = 1 C. m = -1 D. đáp án khác Biên soạn và sưu tầm 25
Câu 183. Đồ thị hàm số y = x4 - 4mx2 + 3m - 2 có 3 điểm cực trị thoả mãn:Khoảng cách từ điểm cực đại
tới đường thẳng qua 2 điểm cực tiểu bằng 8 khi: A. m =  2 B. m = 2 C. m = - 2 D. đáp án khác
Câu 184. Đồ thị hàm số y = x4 - 4mx2 + 3m - 2 có 3 điểm cực trị lập thành tam giác vuông khi: 1 1 A. m = 1 B. m = 0 hoặc m = C. m = D. đáp án khác 2 2  5
Câu 185. Đồ thị hàm số y = x4 - 4mx2 + 3m - 2 có 3 điểm cực trị lập thành tam giác nhận G(0; ) làm 3 trọng tâm khi: 1 1 A. m = 1 B. m = 1 hoặc m = C. m = D. đáp án khác 8 8
Câu 186. Hàm số y = x3 - (m - 1)x2 + (m - 4)x + 4 có 2 điểm cực trị cùng dương khi: A. m > 1 B. m > 4 C. m < 4 D. m < 1
Câu 187. Hàm số y = x3 - (m - 1)x2 + (m - 4)x + 4 có 2 điểm cực trị cùng âm khi: A. m < 1 B. m > 1 C. m < 4 D. Không có m
Câu 188. Hàm số y = x3 - (m - 1)x2 + (m - 4)x + 4 có 2 điểm cực trị trái dấu khi: A. m > 1 B. m > 4 C. m < 4 D. m < 1
Câu 189. Đồ thị hàm số y = x3 - (m - 1)x2 + (m - 4)x + 4 có 2 điểm cực trị nằm bên phải Oy khi: A. m > 1 B. m > 4 C. m < 4 D. m < 1
Câu 190. Đồ thị hàm số y = x3 - (m - 1)x2 + (m - 4)x + 4 có 2 điểm cực trị nằm bên trái Oy khi: A. m<1 B. m>1 C. m<4 D. Không có m
Câu 191. Hàm số y = x3 - (m - 1)x2 + (m - 4)x + 4 có 2 điểm cực trị nằm 2 phía 0y khi: A. m > 1 B. m > 4 C. m < 4 D. m < 1 SDT: 0946798489 26
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 2 3 2 2 2 Câu 192. Hàm số y = x mx  3 ( 2 m  ) 1 x
có 2 điểm cực trị x1;x2 thoả: x1.x2 + 2(x1 + x2) = 1 khi 3 3 2 2 3 A. m = 0 hoặc m = B. m = C. m = D. Không có m 3 3 2 2 3 2 2 2 Câu 193. Hàm số y = x mx  3 ( 2 m  ) 1 x
có 2 điểm cực trị x1;x2 thoả: x1.x2 + 2(x1 + x2)  1 khi 3 3 2 13 2 2  2 13 2 2  A. m[ , ] B. m[ , 0 ] C. m  ;   D. d,m   0 ;   ;   13 3 3  13 3  3  2 3 2 2 2 Câu 194. Hàm số y=
x mx  2(3m  ) 1 x
có 2 điểm cực trị x1;x2 thoả mãn: x1.x2+2(x1+x2)  1 khi 3 3 2  2  2 13 2 A. m   0 ;   ;   B. m[ , 0 ] C. m  ;  D. m   3  3  13 3    2 13  2    ;  ;     13  3 
Câu 195. Với giá trị nào của m thì đồ thị hsố 4 2 2
y x  2m x 1 có ba cực trị tạo thành tam giác vuông cân A. m  0 B. m  1 C. m  1  D. m  2 
Câu 196. Với giá trị nào của m thì đồ thị hàm số 3 2
y  2x  3(m 1)x  6(m  2)x 1 có cực đại, cực tiểu thỏa mãn |xCĐ+xCT|=2: A. m  1 B. m  2 C. m  1  D. m  2  Câu 197. Hàm số 3
y x mx 1 có 2 cực trị khi : A. m  0 B. m  0 C. m  0 D. m  0 Câu 198. Hàm số 3 2
y x  3mx  3x  2m  3 không có cực đại, cực tiểu với m Biên soạn và sưu tầm 27 A. m  1 B. m  1 C. 1   m 1 D. m  1   m 1 Câu 199. Hàm số 4
y mx  m   2
3 x  2m 1 chỉ có cực đại mà không có cực tiểu với m: A. m  3 B m  0 C. 3   m  0
D. m  0  m  3 Câu 200. Hàm số 3 2
y x mx  3m  
1 x 1 đạt cực đại tại x = 1 với m bằng : A. m = - 1 B. m  3  C. m  3  D. m = - 6
Câu 201. Hàm số y= x3-3x2+mx-1=0 có 2 điểm cực trị x 2 2 x x  1,x2 thoả mãn 3 khi: 1 2 2 3 3 A. m=3 B. m= C. m= D. m=- 3 2 2
Câu 202. Hàm số y= x3-3x2+mx-1=0 có 2 điểm cực trị x 2 2 x x  1,x2 thoả mãn 3 khi: 1 2 3 3 3 A. m < 3 B. m > C. m< D. 2 2 2
Câu 203. Hàm số y= x3-3x2+mx-1=0 có 2 điểm cực trị x 2 2 x x  1,x2 thoả mãn 3 khi: 1 2 3 3 3 A. m<3 B. m > C. m< D. 2 2 2
Câu 204. Đồ thị hàm số y=x3-3mx2+1 có 2 điểm trị A,B thoả mãn : AB=2 5 khi: A. m=1 B. m=-1 C. m=  1 D. kết quả khác
Câu 205. Đồ thị hàm số y = x3 - 3mx2 + 1 có 2 điểm trị A,B thoả mãn AB > 2 5 khi: A. -1B. m  ;    1  ; 1 ( )  C. m<1 D. m ( ) 1 , 1 \   0
Câu 206. Đồ thị hàm số y = x3 - 3mx2 + 1 có 2 điểm trị A, B và trung điểm I của AB thuộc Ox khi: SDT: 0946798489 28
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 1 A. m = 1 B. m = 0 C. m = 3 D. Không có m thoả mãn 2
Câu 207. Đồ thị hàm số y=x3-3mx+1 có 2 điểm cực trị B,C thoả mãn tam giác ABC cân tại A(2,3) nếu: 1 1 A. m=0 hoặc m= B. m= C. m=0 D. đáp án khác 2 2
Câu 208. Đồ thị hàm số y = x3 - 3mx + 1 có 2 điểm cực trị B,C thoả mãn ABC vuông tại A(2,2) nếu A. m=0 B. m=1 C. m=-1 D. đáp án khác
Câu 209. Đồ thị hàm số y = x4 - 4mx2 + 3m - 2 có 3 điểm cực trị thoả mãn khoảng cách từ điểm cực đại
tới đường thẳng qua 2 điểm cực tiểu bằng 8 khi A. m=  2 B. m= 2 C. m=- 2 D. đáp án khác
Câu 210. Đồ thị hàm số y = x4 - 4mx2 + 3m - 2 có 3 điểm cực trị lập thành tam giác vuông khi: 1 1 A. m = 1 B. m = 0 hoặc m = C. m = D. đáp án khác 2 2  5
Câu 211. Đồ thị hàm số y = x4 - 4mx2 + 3m - 2 có 3 điểm cực trị lập thành tam giác nhận G(0; ) làm 3 trọng tâm khi: 1 1 A. m=1 B. m=1 hoặc m= C. m= D. đáp án khác 8 8
Câu 212. Hàm số y = x3 - (m - 1)x2 + (m - 4)x + 4 có 2 điểm cực trị cùng dương khi: A.m>1 B. m>4 C. m<4 D. m<1
Câu 213. Hàm số y=x3-(m-1)x2+(m-4)x+4 có 2 điểm cực trị cùng âm khi: A.m<1 B. m>1 C. m<4 D. Không có m
Câu 214. Hàm số y = x3 - (m - 1)x2 + (m - 4)x + 4 có 2 điểm cực trị trái dấu khi: Biên soạn và sưu tầm 29 A. m>1 B. m>4 C. m<4 C. m<1
Câu 215. Đồ thị hàm số y = x3 - (m - 1)x2 + (m - 4)x + 4 có 2 điểm cực trị nằm bên phải Oy khi: A. m>1 B. m>4 C. m<4 D. m<1
Câu 216. Đồ thị hàm số y = x3 - (m - 1)x2 + (m - 4)x + 4 có 2 điểm cực trị nằm bên trái Oy khi: A. m<1 B. m>1 C. m<4 D. Không có m
Câu 217. Hàm số y = x3 - (m - 1)x2 + (m - 4)x + 4 có 2 điểm cực trị nằm 2 phía 0y khi: A. m>1 B. m>4 C. m<4 D. m<1 2 3 2 2 2 Câu 218. Hàm số y=
x mx  2(3m  ) 1 x
có 2 điểm cực trị x1;x2 thoả mãn: x1.x2+2(x1+x2)  1 khi 3 3 2  2  2 13 2   2 13  2  A, m   0 ;   ;   B. m[ , 0 ] C. m  ;  D.   ;  ;      3  3  13 3   13  3 
Câu 219. Với giá trị nào của m thì đồ thị hàm số 4 2 2
y x  2m x 1 có ba cực trị tạo thành tam giác vuông cân A. m  0 B. m  1 C. m  1  D. m  2 
Câu 220.Với giá trị nào của m thì đồ thị hàm số 3 2
y  2x  3(m 1)x  6(m  2)x 1 có cực đại, cực tiểu thỏa mãn |xCĐ+xCT|=2 A. m = 1 B. m = 2 C. m = -1 D. m = -2 1 Câu 221. Cho hàm số 3 2 y
x mx  (2m 1)x 1 . Mệnh đề nào sau đây là sai? 3 A. m
 1 thì hàm số có cực đại và cực tiểu; B. m
 1 thì hàm số có hai điểm cực trị; C. m
 1 thì hàm số có cực trị;
D. Hàm số luôn có cực đại và cực tiểu.
Nhóm Toán – thầy Nguyễn Phú Khánh SDT: 0946798489 30
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
Câu 222 Trong các hàm số A, ,
B C, D dưới đây, hàm số nào có cực đại, cực tiểu và x x CT CD : A. 3 2 y x 9x 3x 2 B. 3 2 y x 9x 3x 5 C. 3 2 y x 2x 8x 5 D. 3 y x 5x 2 Câu 223 2016 2017
Số điểm cực trị của hàm số 2 y x 1 x 3x 2 là: : A. 2 B. 3 C. 1 D. 0
Câu 224 Gọi M và N lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số 3 y x 3x . Lúc đó, tổng
: 2M 3N bằng: A. -2 B. -4 C. 4 D. 2 Câu 225 Hàm số 4 3 y f (x) x 8x
32 có bao nhiêu điểm cực trị? : A. 3 điểm B. 2 điểm C. 1 điểm D. Không có cực trị Câu 226 4 x
Số các điểm cực tri của hàm số : 2 y 2x 6 là: : 4 A. 1 B. 2 C. 3 D. 4
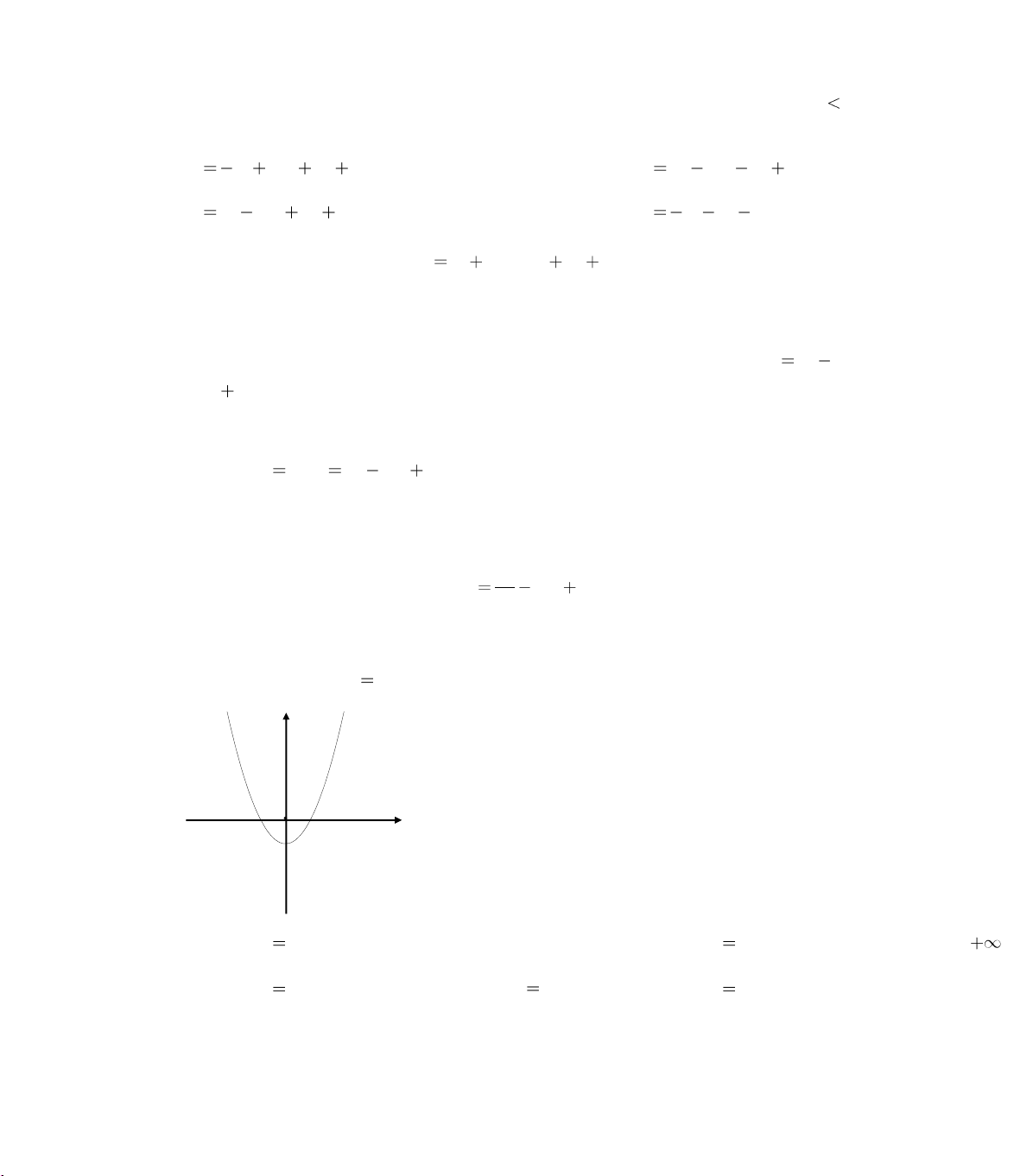
Câu 227 Cho đồ thị hàm số y
f x hình bên. Khẳng định nào là sai : y O x A. Hàm số y
f x có một điểm cực đại. B. Hàm số y
f x luôn đồng biến trên 0; C. Hàm số y
f x có một điểm cực tiểu x 0 D. Hàm số y
f x có một điểm cực trị. Biên soạn và sưu tầm 31
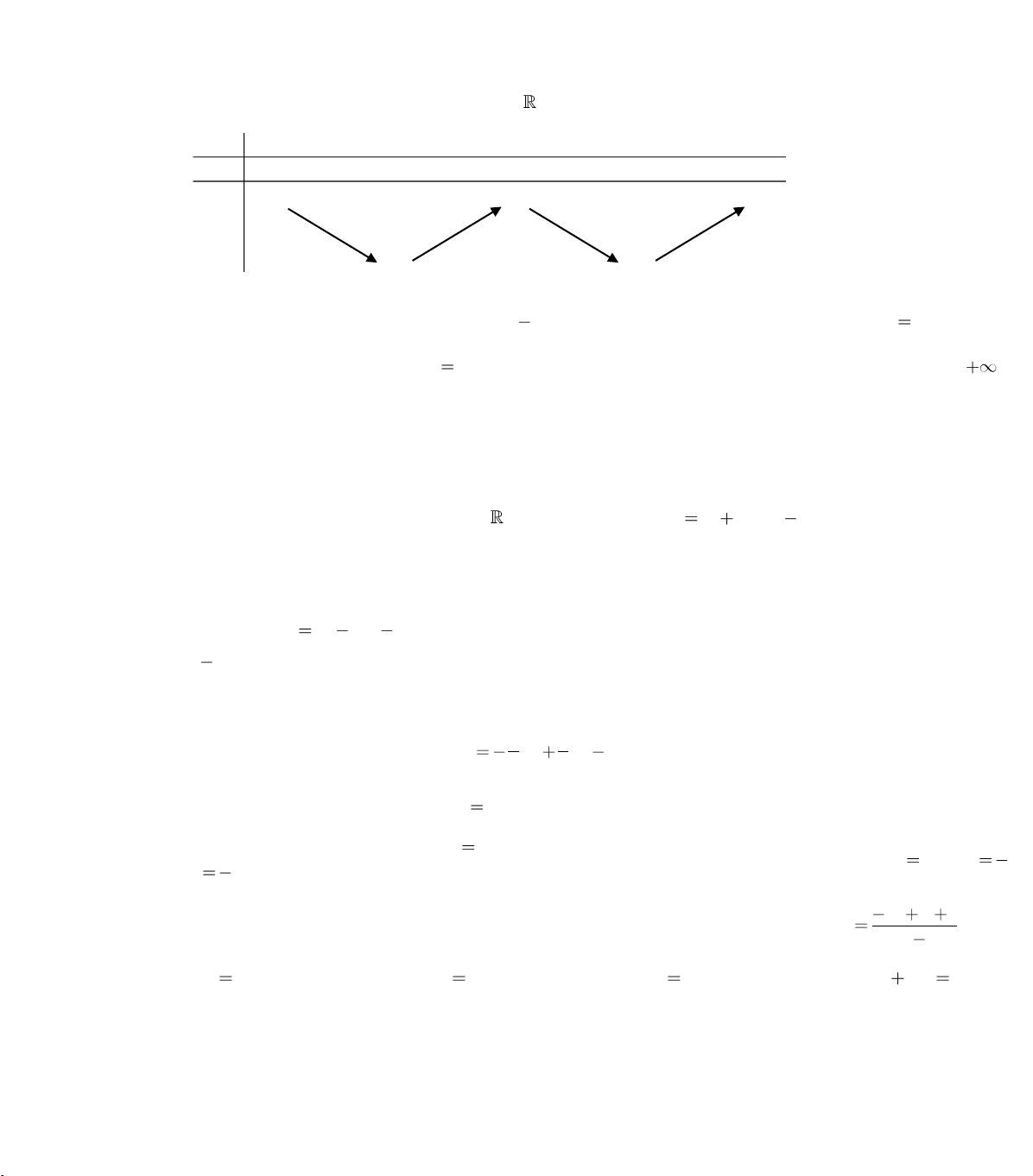
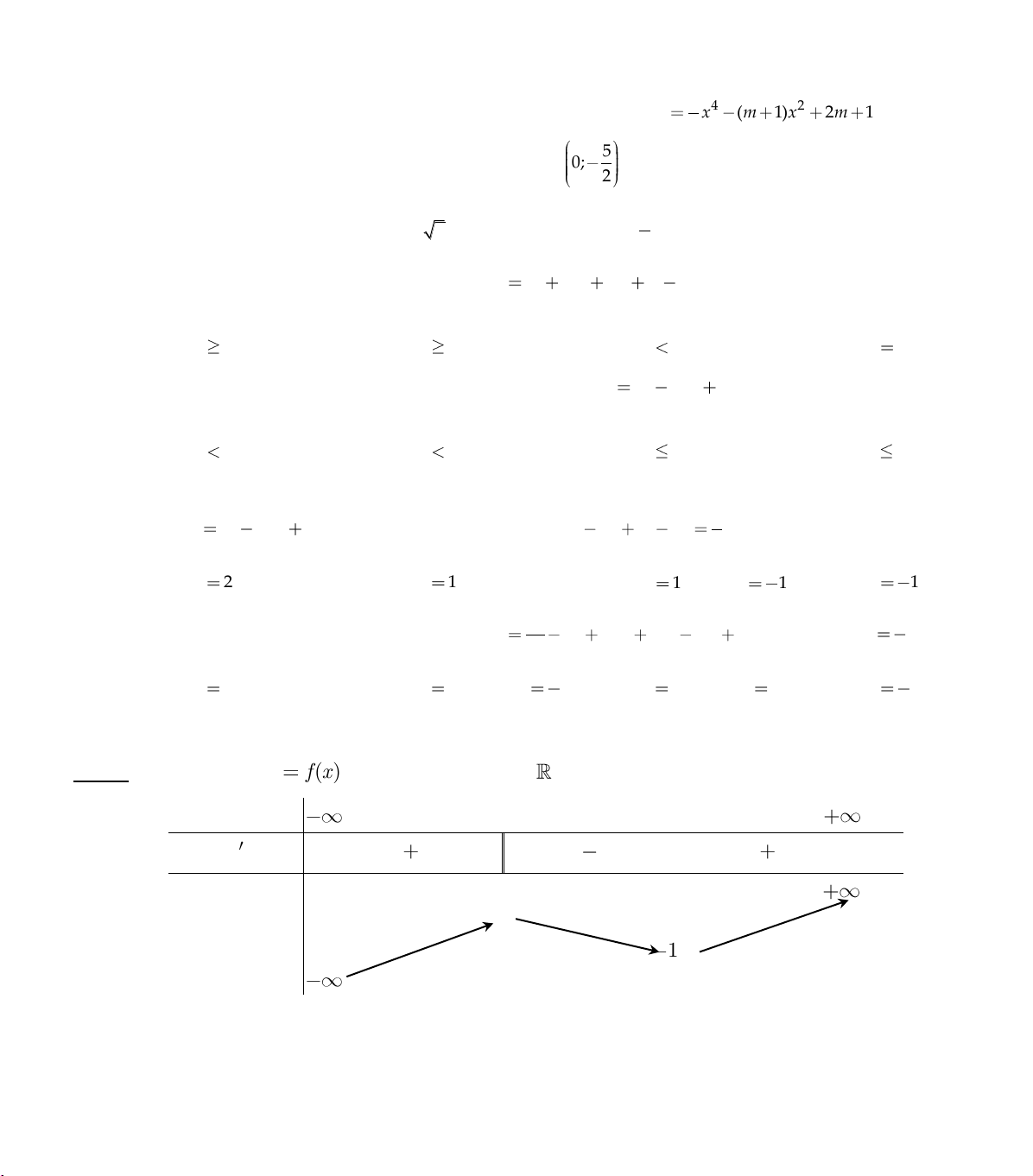
Câu 228 Xét hàm số f x xác định, liên tục trên và có bảng biến thiên: : x –∞ - 1 0 1 +∞ y – 0 + 0 – 0 + +∞ 2 +∞ y 1 1
Mệnh đề nào sau đây là sai.
A. Hàm số f x nghịch biến trên khoảng 1,2
B. Hàm số f x đạt cực tiểu tại x 1
C. Hàm số f x đạt cực đại tại x 0 D.
Hàm số f x đồng biến trên khoảng 1,
Câu 229 Tổng các giá trị cực trị của hàm số là bao nhiêu ? : A. 5 B. 0 C. 6 D. 7
Câu 230 Hàm số f (x) xác định, liên tục trên và có đạo hàm 2 2 f '(x) (x 1) x
4 . Số điểm cực trị của : hàm số là: A. 0 B. 2 C. 3 D. 1 Câu 231 Hàm số 4 2 f x x 2x
3 có giá trị cực đại bằng a và giá trị cực tiểu bằng b. Khi đó giá trị của
: a 2b bằng: A. 4 B. -5 C. 2 D. 5 Câu 232 1 1
Khẳng định nào đúng về hàm số 4 2 y x x 3 ? : 4 2
A. Hàm số chỉ có một điểm cực trị x 0 B.
Hàm số có không có cực trị
Hàm số đạt cực tiểu tại 2 điểm x 1 và C. D.
Hàm số đạt cực đại tại 2 điểm x 1 và x 1 x 1 Câu 233 2 x x 1
Hệ thức liên hệ giữa giá trị cực đại ( y là: : CD y
) và giá trị cực tiểu ( CT y ) của hàm số 2x 4 A. y y y y y y y y CD CT B. 2 3 CT CD C. 5 CD CT D. 0 CD CT SDT: 0946798489 32
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương Câu 234 Hàm số 2 y x
6x 5 có mấy cực trị ? : A. 2 B. 3 C. 1 D. 4
Câu 235 Cho hàm số y
f x là hàm liên tục trên , có đạo hàm 2 2016 f x x x 1 x 1 . Đồ thị hàm số
: có số điểm cực trị là : A. 3 B. 0 C. 2 D. 1 Câu 236 Hàm số 3 2 y 2x 9x
12x 3 có giá trị cực đại là : A. 1 B. 8 C. -1 D. 3
Câu 237 Số cực trị của hàm số 4 2 y x 3x 2 là : : A. 0 B. 1 C. 2 D. 3
Câu 238 Đồ thị hàm số 3 2 y x 3x
2 có số điểm cực trị là: : A. 3 B. 2 C. 0 D. 1
Câu 239 Khẳng định nào đúng về hàm số 3 4 f x 4x x 1? :
A. Nhận điểm x 3 làm điểm cực đại B. Nhận điểm x 0 làm điểm cực đại
C. Nhận điểm x 0 làm điểm cực tiểu D. Nhận điểm x 3 làm điểm cực tiểu
Câu 240 Cho hàm số có đạo hàm 2 3 f '(x)
( x 1) (x 2) (2x 1) . Số cực trị của hàm số là: : A. 0 B. 3 C. 1 D. 2
Câu 241 Hàm số y
x 3 x đạt cực đại tại: : A. x 4 B. x 2 C. x 3 D. x 1 Biên soạn và sưu tầm 33
Câu 242 Trong các hàm số A, ,
B C, D dưới đây, hàm số nào có 3 điểm cực trị ? : 3 2 y x 2x x 1 A. 4 y x 12 B. 4 2 y 2x 5x 12 C. 4 2 y x 2x 12 D. Câu 243 1
Khẳng định nào đúng về hàm số 4 2 y x 2x 1? : 4
A. Một cực đại và hai cực tiểu
B. Một cực tiểu và hai cực đại
C. Một cực đại và không có cực tiểu D.
Một cực tiểu và một cực đại
Câu 244 Điểm cực tiểu của hàm số 3 2 y x 3x 7 là: : A. 3 B. 0 C. 2 D. 7
Câu 245 Đồ thị hàm số 4 2 y x 2x
1 có bao nhiêu điểm cực trị? : A. 3 B. 5 C. 4 D. 6
Câu 246 Khẳng định nào sai về hàm số 4 2 y x 2x 5 ? :
A. Hàm số đã cho đồng biến trên khoảng 1;0 B.
Hàm số đã cho có 2 cực tiểu
Hàm số đã cho nghịch biến trên khoảng C. 1; D.
Hàm số đạt cực đại tại x 0
Câu 247 Toạ độ điểm cực đại của đồ thị hàm số 3 2 y x 6x 9x là: : A. 3,0 B. 1,2 C. 0,0 D. 2,1 Câu 248 Hàm số 4 2 y f x x 2x
1 có giá trị cực tiểu là: : A. -4 B. 0 C. 1 D. 4/3 SDT: 0946798489 34
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
Câu 249 Khẳng định nào đúng về hàm số 2 y x 1 2x 3 ? :
A. Không có cực trị B. Có 1 cực trị C. Có 2 cực trị D. Có 3 cực trị
Câu 250 Giá trị cực đại của hàm số 3 y x 3x 2 là: : A. y 0 y y y cd B. 1 cd C. 2 cd D. 3 cd
Câu 251 Trong các hàm số A, ,
B C, D dưới đây, hàm số nào có hai cực trị thỏa mãn giá trị cực tiểu lớn hơn giá : trị cực đại?. 2x 1 2 x 1 A. y B. 3 y x 3x 2 C. 4 2 y x 2x 3 D. y x 2 x 2 Câu 252 Cho A.hàm số 4 2 y x 2x
1 . Số giao điểm của đồ thị hàm số với trục hoành là: : A. 4 B. 1 C. 3 D. 2 Câu 253 Hàm số 4 2 y x 6x
8x 1 nghịch biến trên khoảng nào sau đây ? : A. (1; ) B. ( 2; ) C. ( ; 2) D. ( 2;1)
Câu 254 Trong các hàm số sau, hàm số nào đồng biến trên ? : 4x 1 A. 4 2 y x x 1 B. y C. 3 y x x 1 D. 2 y x 1 x 2
Câu 255 Lựa chọn mệnh đề sai : A. Hàm số y
f x là đồng biến trên (a;b) nếu có f ' x 0 x ; a b Nếu hàm y
f x có f ' x 0 x ;
a b và f ' x
0 tại một số điểm hữu hạn thì là hàm nghịch B. biến trên (a; b) Biên soạn và sưu tầm 35 C. Nếu hàm y
f x có f ' x 0 x ;
a b thì là hàm nghịch biến trên a;b D. Hàm số y
f x là đồng biến trên (a;b) nếu có f ' x 0 x ; a b Câu 256 Cho hàm số 4 f x x
. Kết luận nào sau đây đúng? : x
A. Hàm số f x nghịch biến trên
B. Hàm số f x đồng biến trên các khoảng ;0 và 0;
C. Hàm số f x đồng biến trên
D. Hàm số f x nghịch biến trên các khoảng ;0 và 0; Câu 257 3 Hàm số 3 2 y x x
18x 5 đồng biến trên : : 2 ; 2 và ; 3 và A. 2;3 B. C. D. 3;3 3; 2;
Câu 258 Hàm số nào sau đây nghịch biến trên khoảng 1;3 ? : 2 1 2x 5 2 x x 1 3 2 y x 4x 6x 10 A. 2 y x 2x 3 B. y C. y D. 3 2 x 1 x 1 Câu 259 Cho hàm số 3 y
3x x . Hàm số đồng biến trên: : A. ( ;0) B. (0; ) C. (0;2) D. (2;3)
Câu 260 Trong các hàm số sau đây, hàm số nào đồng biến trên toàn miền xác định của nó? : 2x 1 2 x 1 A. 3 y x 1 B. y sin x C. y D. y x 1 2 x SDT: 0946798489 36
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương Câu Cho hàm số 2 y
x cos x . Trong các khẳng định sua, khẳng định nào đúng: 261: A. y ' 1 sin 2x B. D 0;
C. Hàm số luôn đồng biến trên D. Hàm số có 1 cực trị. Câu 262 1 1 Hàm số y nghịch biến trên: : x x 2 A. 0;1 B. ;0 C. ;0 và 0;1 D. 0;
Câu 263 Hàm số nào sau đây đồng biến trên tập xác định của nó : x 2 x 2 x 2 x 2 A. y B. y C. y D. y x 2 x 2 x 2 x 2 Câu Hàm số 4 2 y 2x 4x
1 nghịch biến trên khoảng nào sau đây? 264: 3 1 1 A. ; 0; 4 3 B. 1;1 C. 0;2 D. 2 Câu 265 4 Cho hàm số y x
.Phát biểu nào sau đây đúng ? : x 2
Hàm số đồng biến trên từng khoảng ,2 ,
A. Hàm số đồng biến trên R B. 2,
Hàm số nghịch biến trên ,2 ,đồng biến
C. Hàm số đồng biến trên R \ 2 D. trên 2,
Câu 266 Trong các hàm số sau hàm số nào nghịch biến trên 2; : 1 3 1 3 A. 3 2 y x x 2x 1 B. 3 2 y x x 2x 1 3 2 3 2 C. 3 2 y x 6x 9x 2 D. 2 y x 5x 2 Biên soạn và sưu tầm 37 Câu 267 Cho hàm số 3 2 y x 3x
9x 12 trong các mệnh đề sau, mệnh đề nào sai? :
A. Hàm số tăng trên khoảng ; 2
B. Hàm số giảm trên khoảng 1;2
C. Hàm số tăng trên khoảng 5; D.
Hàm số giảm trên khoảng 2;5 Câu 268
Khẳng định dưới đây khẳng định nào sai? : A. Hàm số 2 y x x 8 nghịch biến trên B. Hàm số 2 y x x 8 nghịch biến trên 7 Hàm số 7 6 5 y 9x 7x x 12 đồng biến trên C. Hàm số 2 y x os c x đồng biến trên D. 5 Câu 269 Cho hàm số 3 2 y 2x 3x
2 . Khẳng định nào sau đây là đúng về tính đơn điệu của hàm số? :
A. Hàm số nghịch biến trên khoảng ( ;0) và (1; )
B. Hàm số nghịch biến trên khoảng ( ; 1) và (0; )
C. Hàm số nghịch biến trên khoảng (0;1)
D. Hàm số đồng biến trên khoảng ( ;0) Câu 270 1 Hàm số 3 2 y x x
3x 2 đồng biến trên khoảng nào? : 3 A. 3; B. 3;1 C. 5; 2 D. 4;2 Câu 1
Khoảng nghịch biến của hàm số 4 3 y x x 4x 1 là: 271: 4 A. ( 1; ) B. ( ; 1) C. ( 2; 1) D. ( ;2) Câu 1 1 Cho hàm số (1): 3 2 y x x
2x . Phát biểu nào sau đây đúng ? 272: 3 2
A. Hàm số (1) đồng biến trên khoảng ; 1 B.
Hàm số (1) nghịch biến trên khoảng 2; SDT: 0946798489 38
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
C. Hàm số (1) nghịch biến trên D.
Hàm số (1) đồng biến trên khoảng 1;2 Câu Hàm số 4 y 2x
1 đồng biến trên khoảng: 273: A. ( ,0) B. (1, ) C. ( , ) D. (0, ) Câu Cho hàm số 3 2 y x 3x
1 nghịch biến trên khoảng: 274: A. ;0 B. 1; C. ; D. 0;1 Câu
Tìm tất cả giá trị thực m để đồ thị hàm số 3 y x
3x 1 có 2 điểm cực trị A,B đồng thời A,B, 275: 2 C(m
2; 3m 2) thẳng hàng ? A. m 1 B. m 1 C. m 2 D. m 1 Câu 276
Tìm tất cả các giá trị thực của tham số m để hàm số 4 y mx
2 m 1 x 1 có 3 cực trị? : m 0 A. m 0 B. m m m 1 C. 0 1 D. 2 Câu 277
Tìm tất cả các giá trị của tham số thực m để hàm số 4 2 y x 2 m 1 x 3 có 3 cực trị?. : A. m 0 B. m 1 C. m 0 D. m 1 Câu 278
Biết rằng đồ thị hàm số 4 2 2 y x 2 m 1 x
m có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác
: vuông khi giá trị của tham số m là: A. 3 B. 0 C. 1 D. 2 Câu 279 3 mx
Tìm tất cả giá trị thực m để hàm số 2 y x x
2017 có hai điểm cực trị? : 3 m 1 m 1 A. m m m 0 B. 1 C. m 0 D. 1 Biên soạn và sưu tầm 39 Câu 280 4 x 2 m
Tìm tất cả giá trị thực m để hàm số 3 2 y mx x
m 1 có đúng 1 cực trị? : 4 3 2 A. 0 m 1 B. 0 m 1 C. 0 m 1 D. 0 m 1 Câu 281
Biết rằng đồ thị hàm số 3 2 y x 3x
3mx 3m 4 có điểm cực trị, thì tất cả giá trị thực m nào thích : hợp? A. m 1 B. m 1 C. m 1 D. m 1 Câu 282
Tìm tất cả giá trị thực của tham số m để đồ thị hàm số 3 2 2 3 2 y x 3mx 3 1 m x m m có hai
: điểm cực trị và đường thẳng đi qua hai điểm cực trị này đi qua gốc tọa độ ? A. m 2 B. m 0 hoặc m 1 C. m 0 D. m 1 Câu
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số 4 2 y x 2mx
1 có 3 điểm cực trị tạo
283: thành một tam giác có tâm đường tròn ngoại tiếp trùng với gốc tọa độ O ? 1 5 1 5 A. m 1 hoặc m B. m 1 hoặc m 2 2 1 5 1 5 C. m hoặc m D. m 0 hoặc m 1 2 2 Câu 284 Biết rằng hàm số 3 2 2 2 y x 3x 3 m 1 x 3m 1 có hai cực trị x x 2 . 1 x và x đồng thời 2 1 2
: Giá trị thực m thích hợp có thể là: A. m 2 B. m 1 C. m 4 D. m 3 Câu 285
Tìm tất cả giá trị thực của tham số m để hàm số 4 2 2 y x 2mx m
m có 3 cực trị đồng thời
: khoảng cách hai điểm cực tiểu bằng 2 2 A. 1 B. 2 C. 2 2 D. 3 Câu 286 2 Biết rằng hàm số 3 2 2 y x m 1 x m
4m 3 x có cực trị x ,x . Giá trị lớn nhất của biểu thức : 3 1 2 A x x 2 x x bằng : 1 2 1 2 9 9 A. A B. A C. A 1 D. A 3 2 2 SDT: 0946798489 40
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương Câu 287
Tìm tất cả giá trị thực của tham số m để hàm số 3 2 y x 3mx 3(2m 1)x
1 có cực đại, cực tiểu ? : A. m  1 B. m  0 C. m 1 D. 0  m  1 Câu 1
Tìm tất cả giá trị thực m để hàm số 3 2 2 y x mx (m
1)x 2 đạt cực tiểu tại x 1? 288: 3 A. m 2 B. m 1 C. m 0 D. m 2 Câu 3 1
Tìm tất cả giá trị thực m để hàm số 3 2 3 y x mx
m có cực đại, cực tiểu đối xứng nhau qua 289: 2 2
đường thẳng y x ? A. m 2 B. m 3 C. m 1 D. m 2 Câu
Biết rằng đồ thị hàm số 4 2 2 y x 2 x m 3m
m 2 có 3 điểm cực trị. Tìm tất cả giá trị m để 3
290: điểm cực trị đó tạo thành một tam giác có diện tích bằng 32. A. m 4 B. m 2 C. m 4 D. m 2 Câu m 1
Tìm tất cả giá trị thực m để hàm số 3 2 y x mx
mx 1 đạt cực tiểu tại x , cực đại tại x sao 1 2 291: 3 cho x 1 x 1 ? 1 2 1 1 A. m 1 B. 0 m 1 C. m 0,m 1 D. m ,m 1 4 4 Câu
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 3 2 y x 3mx+2m 4033m 1có hai điểm
292: cực đại, cực tiểu nằm trên đường thẳng y 2017x 2018 . 1 1 Không có giá trị A. m B. m 2017,m C. m 2017 D. 2 2 của m. Câu 1 Biết rằng hàm số 3 2 y x ax 3ax
4 đạt cực trị tại x , x . Tìm giá trị thực của 1 2 a thoả mãn điều 293: 3 2 2 x 2ax 9a a kiện 1 2 2 2 2 a x 2ax 9a 2 1 A. a 4 B. a 0 C. a 2 D. a 6 Biên soạn và sưu tầm 41 Câu
Tìm tất cả giá trị thực của tham số m để điểm I
1; 6 là điểm cực đại của đồ thị hàm số 294: 3 2 y
x – 3mx – 9x 1 ? A. m = - 1 B. m = 1 C. m = 1 D. m = 2 Câu Biết rằng hàm số 4 2 y x (m 1)x
1 có 3 điểm cực trị A O , y ,
B C tạo thành một tam giác có bán
295: kính đường tròn ngoại tiếp bằng 1. Tất cả giá trị nguyên tham số m bằng : m 1 hoặc A. m 2 5 B. m 2 5 C. D. m 1 m 2 5 Câu
Tìm tất cả giá trị thực m để hàm số 3 2 2 f x x 2mx
m x 2 đạt cực tiểu tại x 1? 296: A. m 1 B. m 1;3 C. m 3 D. m 1; 3 Câu
Tìm tất cả giá trị thực của tham số m để đồ thị hàm số 3 y x
3mx 1 có 2 điểm cực trị A, B sao
297: cho tam giác OAB vuông tại O (với O là gốc tọa độ ). 1 A. m 4 B. m 2 C. m 3 D. m 2 Câu
Tìm tất cả giá trị thực của tham số m để hàm số 3 2 y x x mx m có cực trị? 298: 1 1 A. m  1 B. m C. m  1 D. m 3 3 3 3 Câu 1
Tìm tất cả các giá trị thực của m để hàm số 4 2 y m 1 x
1 m x 2017 đạt cực tiểu tại x 0 ? 0 299: 2 Không tồn tại giá A. m 1 B. m 1 C. m 1 hoặc m 1 D. trị m Câu 3 x
Tìm tất cả giá trị thực m để đồ thị hàm số 2 y mx
5 có cực trị và hai điểm cực trị nằm ở hai 300: 3
phía khác nhau so với đường thẳng x 1 ? 1 A. m 0 B. m 1 C. m 0 D. m 2 SDT: 0946798489 42
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương Câu 1
Tìm tất cả giá trị thực của tham số m để hàm số 3 2 2 y x m 1 x m
3m 2 x 5 đạt cực đại 301: 3 tại x 0? m = 1 hoặc m = 2 A. m = 6 B. m = 2 C. m = 1 D. Câu
Tìm tất cả giá trị thực m để hàm số 3 2 f x x mx
m 36 x 3 không có cực trị ? 302: m 9 hoặc m 9 hoặc A. 9 m 12 B. C. D. 9 m 12 m 12 m 12 Câu
Tìm tất cả các giá trị thực của m để đồ thị hàm số 3 2 y x 3x
m có 2 điểm cực trị A, B sao cho 303: góc 0 AOB
60 , trong đó O là gốc tọa độ. m 0 hoặc 12 12 12 12 A. m B. m C. m 0 D. 12 12 3 3 m 3 Câu 304
Tìm tất cả giá trị thực của tham số m để hàm số 3 2 y x 3mx
mx 1 có hai điểm cực trị? : 1 1 1 1 A. 0 m B. m 0 hoặc m C. m 0 hoặc m D. m 0 hoặc m 3 3 3 3 Câu 305 2 x x m
Tìm tất cả giá trị thực m để đồ thị hàm số y
có cực đại và cực tiểu? : x 1 A. m 2 B. m 2 C. m 2 D. m 2 Câu 306 1
Tìm tất cả giá trị thực m để đồ thị hàm số 3 2 y x mx m 1 x
m 1 có hai điểm cực đại, cực : 3
tiểu cách đều trục tung? Không tồn tại giá A. B. 2 C. 1 D. 0 trị m. Câu 307
Tìm tất cả giá trị thực m để đồ thị hàm số 3 2 y x 3mx
3m 1 có điểm cực đại và điểm cực tiểu
: đối xứng nhau qua đường thẳng d : x 8y 74 0 ? Biên soạn và sưu tầm 43 A. m 1 B. m 2 C. m 1 D. m 2 Câu 308 m 1 2m 1
Tìm tất cả giá trị thực của tham số m để hàm số 4 2 y x x
2 có 2 cực đại và 1 cực : 4 2 tiểu? 1 1 1 A. m B. 1 m C. m D. m 1 2 2 2 Câu 309
Tìm tất cả giá trị thực m để đồ thị hàm số 4 2 2 y x 2m x
1 có ba điểm cực trị là ba đỉnh của một
: tam giác vuông cân? A. m 1 B. m 1 C. m 1 D. m 2 Câu 310 Biết rằng hàm số 4 2 2 4 y x 2m x m
1 có 3 điểm cực trị A O , y ,
B C sao cho bốn điểm , A , B C,O
: cùng nằm trên 1 đường tròn ?. Tất cả giá trị tham số m bằng : A. m 1 B. m 0 C. m 1 D. m 1 Câu 311 1 1
Tìm tất cả các giá trị thực của tham số m để hàm số 2 3 2 y x x m m
2m 1có hai cực trị : 3 2
nằm phía trên trục hoành là: Không có giá trị A. m R B. m 1; C. m ;1 1; D. của m. Câu 312 1 Biết rằng hàm số 3 2 y x mx
8x 2 có 2 cực trị x ;x thỏa x 2x
0 thì giá trị thực của m 1 2 1 2 : 3 thích hợp là ? A. m 3 B. m 4 C. m 2 D. m 1 Câu 313
Tìm tất cả giá trị thực của tham số m để đường thẳng nối 2 điểm cưc trị của đồ thị hàm số : 3 y x 3x
1 vuông góc với đường thẳng y 3mx 2 1 1 1 7 A. m B. m C. m D. m 3 3 6 6 SDT: 0946798489 44
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương Câu 314 1
Tìm tất cả giá trị thực của tham số m để đồ thị hàm số 4 2 y x (m 1)x
2m 1 có cực đại A và : 4 5
cực tiểu B,C sao cho ABIC là hình thoi với I 0; ? 2 1 A. 1 B. 2 2 C. D. 3 2 Câu 315
Tìm tất cả giá trị thực m để hàm số 3 2 y x 3x
mx m 2 có hai điểm cực trị ? : A. m 0 B. m 3 C. m 3 D. m 0 Câu 316
Tìm tất cả giá trị thực m để thích hợp để hàm số 4 2 y x mx 2 có 1 cực trị? : A. m 2 B. m 3 C. m 1 D. m 0 Câu
Tìm tất cả giá trị thực của tham số m để đường thẳng đi qua hai điểm cực trị của hàm số 317: 3 y x
3mx 1 tiếp xúc với đường tròn (T): 2 2 4 x 1 y 1 ? 5 A. m 2 B. m 1 C. m 1 hoặc m 1 D. m 1 Câu 318 3 x
Tìm tất cả giá trị thực m để hàm số 2 2 y (m 1)x (m
3)x 1đạt cực trị tại x 1? : 3 A. m 0 B. m 0 hoặc m 2 C. m 0 hoặc m 2 D. m 2
Thầy Lê Văn Đoàn (218 câu) Câu 1. Cho hàm số y
f (x) xác định, liên tục trên và có bảng biến thiên: x 0 1 y 0 0 y 1
Khẳng định nào sau đây là khẳng định đúng ? Biên soạn và sưu tầm 45
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1.
D. Hàm số đạt cực đại tại x
0 và đạt cực tiểu tại x 1. Câu 2. Cho hàm số y
f (x) có đạo hàm tại x . Tìm mệnh đề đúng ? o
A. Hàm số đạt cực trị tại x thì f (x ) 0. o o B. Nếu f (x )
0 thì hàm số đạt cực trị tại x . o o
C. Hàm số đạt cực trị tại x thì f (x) đổi dấu khi qua x . o o
D. Nếu hàm số đạt cực trị tại x thì f (x ) 0. o o Câu 3. Giả sử hàm số y
f (x) có đạo hàm cấp hai. Chọn phát biểu đúng ? A. Nếu f (x ) 0 và f (x ) 0 thì hàm số y
f (x) đạt cực đại tại x . o o o B. Nếu f (x ) 0 và f (x ) 0 thì hàm số y
f (x) đạt cực tiểu tại x . o o o C. Nếu f (x ) 0 và f (x ) 0 thì hàm số y
f (x) đạt cực đại tại x . o o o D. Nếu f (x ) 0 thì hàm số y
f (x) đạt cực đại tại x . o o Câu 4.
Hàm số bậc ba có thể có bao nhiêu cực trị ? A. 1 hoặc 2 hoặc 3. B. 0 hoặc 2. C. 0 hoặc 1 hoặc 2. D. 2. Câu 5. Đồ thị hàm số 4 2 y x 2x 3 có:
A. Một cực đại và hai cực tiểu.
B. Một cực tiểu và hai cực đại.
C. Một cực tiểu và không cực đại.
D. Không có cực đại và cực tiểu. Câu 6.
Hàm số nào sau đây không có cực trị: x 2 1 A. 3 y x 3x. B. y C. y x D. 4 2 y x 2x . 2x 1 x Câu 7.
Hàm số nào sau đây không có cực đại và cực tiểu ? SDT: 0946798489 46
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương A. 4 2 y x 2x . B. 3 y x 2x. C. 3 y x . D. 2 y x 2x 1. Câu 8. Cho hàm số 3 y x 3x
2. Khẳng định nào sau đây sai ?
A. Hàm số đạt cực đại tại x 1.
B. Hàm số đạt cực tiểu tại x 1.
C. Hàm số không có cực trị.
D. Hàm số có 2 điểm cực trị. Câu 9.
Trong các mệnh đề sau, hãy tìm mệnh đề sai ? 1 A. Hàm số y không có cực trị. x 2 B. Hàm số 3 2 y x 3x
1 có cực đại và cực tiểu. 1 C. Hàm số y x có hai cực trị. x 1 D. Hàm số 3 y x x 2 có cực trị.
Câu 10. Đồ thị hàm số 4 2 y x x
12 có mấy điểm cực trị: A. 4. B. 3. C. 2. D. 1. 3 x
Câu 11. Số điểm cực trị của đồ thị hàm số y x 7 là: 3 A. 0. B. 1. C. 2. D. 3.
Câu 12. Số điểm cực trị của đồ thị hàm số 4 2 y x 2x 1 là: A. 0. B. 1. C. 2. D. 3.
Câu 13. Số điểm cực trị của đồ thị hàm số 4 3 y x 8x 12 là: A. 0. B. 1. C. 2. D. 3.
Câu 14. Đồ thị hàm số y
sinx có mấy điểm cực trị ? A. 3. B. 2. C. 1. D. Vô số. Câu 15. Hàm số 6 y 2x 4x
7 có số điểm cực trị là: A. 0. B. 1. C. 2. D. 3.
Câu 16. Một hàm số f (x) có đạo hàm là 3 2 f (x) x 2x
x. Số cực trị của hàm số là: Biên soạn và sưu tầm 47 A. 0. B. 1. C. 2. D. 3.
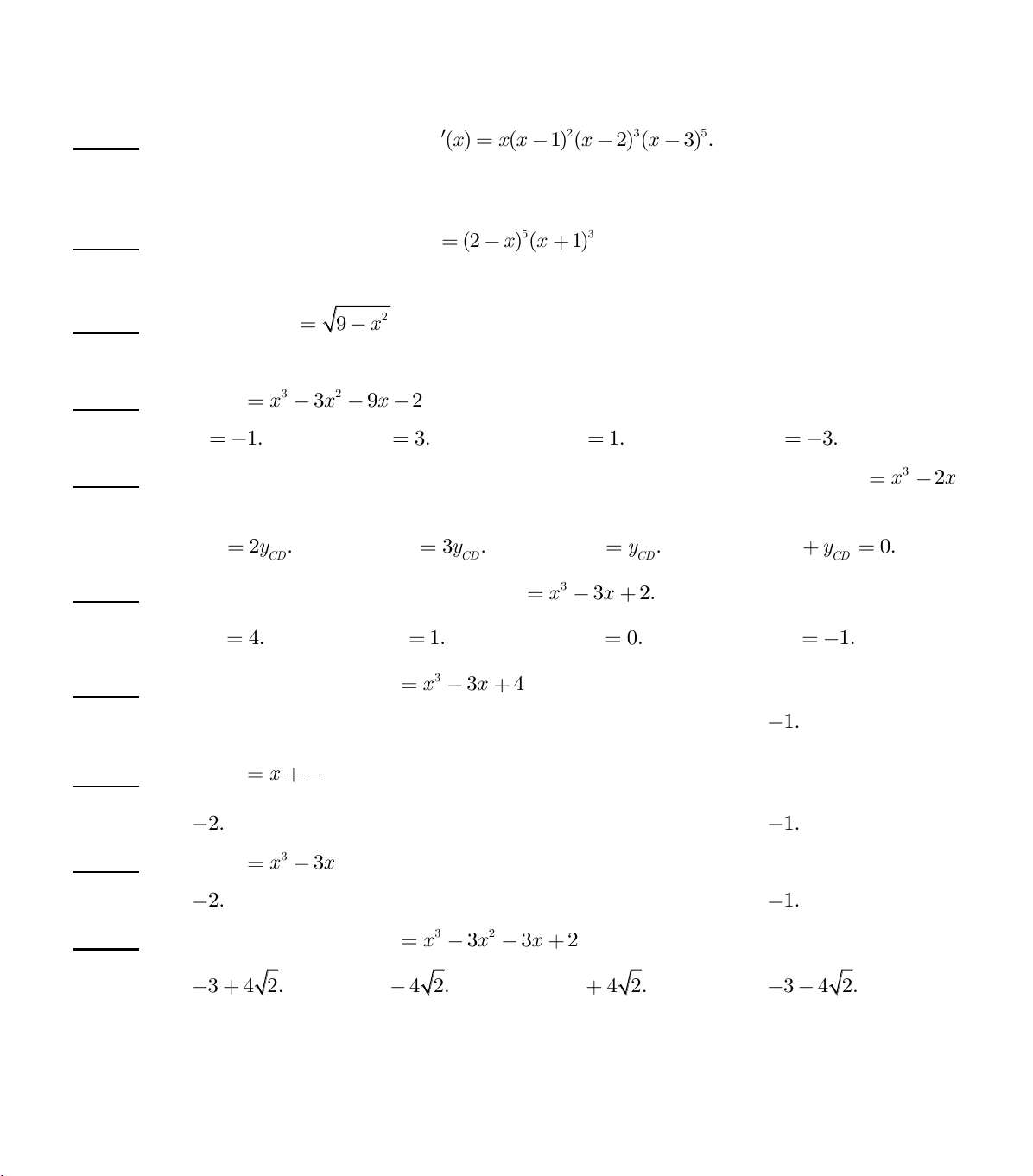
Câu 17. Một hàm số f (x) có đạo hàm là 2 3 5 f (x) x(x 1) (x 2) (x
3) . Hỏi hàm số này có bao nhiêu cực trị ? A. 4. B. 3. C. 2. D. 1.
Câu 18. Số các điểm cực trị của hàm số 5 3 y (2 x) (x 1) là: A. 1. B. 3. C. 5. D. 7.
Câu 19. Đồ thị hàm số 2 y 9
x có mấy điểm cực trị ? A. 0. B. 1. C. 2. D. 3. Câu 20. Hàm số 3 2 y x 3x 9x
2 có điểm cực tiểu tại: A. x 1. B. x 3. C. x 1. D. x 3.
Câu 21. Hệ thức liên hệ giữa giá trị cực đại (y
) và giá trị cực tiểu (y ) của đồ thị hàm số 3 y x 2x CD CT là: A. y 2y . B. 2y 3y . C. y y . D. y y 0. CT CD CT CD CT CD CT CD
Câu 22. Tìm giá trị cực đại y của đồ thị hàm số 3 y x 3x 2. C Đ A. y 4. B. y 1. C. y 0. D. y 1. C Đ C Đ C Đ C Đ
Câu 23. Giá trị cực đại của hàm số 3 y x 3x 4 là: A. 2. B. 1. C. 6. D. 1. 1
Câu 24. Hàm số y x
có giá trị cực đại là: x A. 2. B. 2. C. 1. D. 1. Câu 25. Hàm số 3 y x
3x có giá trị cực tiểu là: A. 2. B. 2. C. 1. D. 1.
Câu 26. Giá trị cực đại của hàm số 3 2 y x 3x 3x 2 bằng: A. 3 4 2. B. 3 4 2. C. 3 4 2. D. 3 4 2. SDT: 0946798489 48
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
Câu 27. Giá trị cực đại của hàm số 2 y x 2x 1 là: 2 2 2 A. B. C. D. Không có y . 2 2 4 C Đ
.............................................................................................................................................................
.............................................................................................................................................................
Câu 28. Giá trị cực đại của hàm số y x
2 cosx trên khoảng (0; ) là: 5 5 A. 3. B. 3. C. 3. D. 3. 6 6 6 6
Câu 29. Hàm số y
cosx đạt cực đại tại điểm: A. x k , (k ). B. x k2 , (k ). 2 C. x k2 , (k ). D. x k , (k ).
Câu 30. Hàm số y 2 sin2x 3 đạt cực tiểu tại: k A. x ; (k ). B. x k ; (k ). 4 2 4 C. x k ; (k ). D. x k ; (k ). 2 4
Câu 31. Hàm số y 3 2 cosx
cos2x đạt cực tiểu tại: A. x k2 , (k ). B. x k , (k ). C. x k2 , (k ). D. x k , (k ). 2 2
Câu 32. Cực trị của hàm số y sinx cosx là: 3 A. x k , (k ); y 2 và x k2 , (k ); y 2. CT 4 CT CD 4 CD Biên soạn và sưu tầm 49 3 B. x k , (k ); y 2 và x k2 , (k ); y 2. CD 4 CD CT 4 CT 3 C. x k , (k ); y 2. D. x k , (k );y 2. CT 4 CT CD 4 CD
Câu 33. Hàm số y x 2 sinx 2 đạt cực tiểu tại: A. x k , ( k ). B. x k , ( k ). 3 3 C. x k2 , ( k ). D. x k2 , ( k ). 3 3
Câu 34. Cho hàm số y cos2x 1, x (
;0) thì khẳng định nào sau đây sai ? 7
A. Hàm số đạt cực tiểu tại điểm x 12 11
B. Hàm số đạt cực đại tại điểm x 12 C. Tại x
hàm số không đạt cực đại. 2 D. Tại x
hàm số không đạt cực tiểu. 12 Câu 35. Hàm số 3 2 2 y (x
2x) đạt cực trị tại điểm có hoành độ là: A. x 1. B. x 0, x 1. C. x 0, x 1, x 2.
D. Hàm số không có điểm cực trị. Câu 36. Hàm số 3 2 y 3x 4x x
14 đạt cực trị tại hai điểm x , x . Khi đó tích số x x là: 1 2 1 2 1 1 A. B. C. 1. D. 3. 9 7 SDT: 0946798489 50
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 4 x Câu 37. Cho hàm số 3 y x 4x
1. Gọi x , x là 2 nghiệm của phương trình y 0. Khi đó 4 1 2 tổng x x bằng: 1 2 A. 1. B. 2. C. 0. D. 1. Câu 38. Cho hàm số 3 2 y 3x 4x x
14. Hàm số đạt cực trị tại 2 điểm x , x . Khi đó tổng x x 1 2 1 2 có giá trị là: 1 1 8 A. B. C. D. 1. 9 7 9 Câu 39. Cho hàm số 3 2 y x 5x 6x
2. Hàm số đạt cực trị tại 2 điểm x , x . Khi đó tổng x x 1 2 1 2 có giá trị là: 10 10 A. B. C. 1. D. Đáp án khác. 3 3 1 Câu 40. Cho hàm số 3 2 y x 3x
x. Hàm số đạt cực trị tại 2 điểm x , x . Khi đó tổng 2 1 2 2 2 S x x có giá trị là: 1 2 11 13 1 3 A. B. C. D. 3 3 2 2 1 Câu 41. Cho hàm số 3 2 y x 3x
x. Hàm số đạt cực trị tại 2 điểm x , x . Khi đó tổng 2 1 2 2 2 S x x có giá trị là: 1 2 A. 12. B. 12. C. 18. D. 20. Câu 42. Cho hàm số 3 2 y x 3x 21x
1. Hàm số đạt cực trị tại 2 điểm x , x . Khi đó tổng 1 2 2 2 S x x có giá trị là: 1 2 A. 18. B. 24. C. 36. D. 48. Câu 43. Cho hàm số 3 2 y x 3x
1. Tích giá trị cực đại và cực tiểu của đồ thị hàm số là: A. 6. B. 3. C. 0. D. 3. Biên soạn và sưu tầm 51
Câu 44. Gọi y , y lần lượt là giá trị cực đại và giá trị cực tiểu của đồ thị hàm số 4 2 y x 10x 9. 1 2
Khi đó giá trị của biểu thức T y y bằng: 1 2 A. 7. B. 9. C. 25. D. 2 5. Câu 45. Cho hàm số 3 2 y 2x 3x
5. Tổng các giá trị cực trị của hàm số là: A. 9. B. 1. C. 1. D. 5. Câu 46. Hàm số 4 2 y x 2x
5 có các điểm cực trị lần lượt là x , x , x thì tích x .x .x là: 1 2 3 1 2 3 A. 2. B. 1. C. 0. D. 1. 3
Câu 47. Hàm số y x 1
có tổng các điểm cực đại và cực tiểu bằng: x A. A. 2. B. 1. C. 0. D. 2. 2 x 4x 1
Câu 48. Hàm số y
có tích các điểm cực đại và cực tiểu bằng: x 1 A. 2. B. 5. C. 1. D. 4. 2
Câu 49. Cho đồ thị hàm số y 2 x Khi đó y y ? x 1 CÐ CT A. 3 2 2. B. 3 2 2. C. 2. D. 6. 2 x 3x 3
Câu 50. Hàm số y
có tích các giá trị cực đại và cực tiểu bằng: x 1 A. 3. B. 1. C. 1. D. 2. 2 x 2x 5
Câu 51. Khẳng định nào sau đây là đúng về đồ thị hàm số y : x 1 A. y y 0. B. y 4. C. x 1. D. x x 3. CÐ CT CT CÐ CÐ CT
Câu 52. Khoảng cách giữa hai cực trị của đồ thị hàm số 3 2 y x 3x 3 là: A. 5. B. 2 5. C. 3 5. D. 8 5. SDT: 0946798489 52
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 2 x 2x 1
Câu 53. Cho hàm số y
Khoảng cách giữa hai điểm cực trị là: x 1 A. 4 5. B. 4. C. 8. D. 5 2. 2 x mx m
Câu 54. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số y bằng: x 1 A. 5. B. 2 5. C. 4 5. D. 5 2.
Câu 55. Biết đồ thị hàm số 4 2 y x 2px
q có một điểm cực trị là M(1;2), thế thì khoảng cách giữa
điểm cực tiểu và điểm cực đại là: A. 26. B. 5. C. 2. D. 2. 2 x 2x 2
Câu 56. Đồ thị hàm số y
có 2 điểm cực trị nằm trên đường thẳng y ax b thì giá trị 1 x của tổng a b bằng bao nhiêu ? A. 4. B. 4. C. 2. D. 2. 1
Câu 57. Đồ thị hàm số y x 1
có hai điểm cực trị nằm trên đường thẳng y ax b thì tích x 1 a.b bằng: A. 0. B. 2. C. 4. D. 2. 4 x Câu 58. Hàm số 2 y 2x 1 đạt cực đại tại: 4 A. x 2. B. x 2. C. x 0. D. x 2. 3 x Câu 59. Hàm số 2 y 2x 3x 5 đạt cực tiểu tại: 3 A. x 1. B. x 3. C. x 1. D. x 3. 2 x 3x 3
Câu 60. Hàm số y đạt cực đại tại: x 2 A. x 1. B. x 2. C. x 3. D. x 0. Biên soạn và sưu tầm 53 1 Câu 61. Hàm số 4 2 y x 2x
3 đạt cực đại tại x bằng: 2 A. 0. B. 2. C. 2. D. 2. Câu 62. Hàm số 3 y x 3x
4 đạt cực tiểu tại x bằng: A. 1. B. 1. C. 3. D. 3. Câu 63. Hàm số 3 2 y
x (1 x) đạt cực đại tại: 3 A. x 1. B. x 1. C. x D. Đáp án khác. 5
Câu 64. Điểm cực đại của đồ thị hàm số 3 2 y 2x 3x 2 là: A. M(0; 2). B. N(2;2). C. P(1; 3). D. ( Q 1; 7).
Câu 65. Tọa độ điểm cực tiểu của đồ thị hàm số 4 2 y x 2x là: A. M(0; 0). B. N(1;1). C. P( 1;1). D. ( Q 1;0). 1 2
Câu 66. Tọa độ điểm cực đại của đồ thị hàm số 3 2 y x 2x 3x là: 3 3 A. M(1; 3). B. N(1; 0). C. P(1;2). D. ( Q 3;1).
Câu 67. Điểm cực tiểu của đồ thị hàm số 3 2 y x 3x 3 là: A. M(1;1). B. N( 2;1). C. P(0; 3). D. ( Q 1; 6).
Câu 68. Điểm cực đại của đồ thị hàm số 4 2 y x 6x 8x 1 là: A. M( 2;24). B. N( 2;25). C. P(7; 3). D. ( Q 1; 6).
Câu 69. Điểm cực tiểu của đồ thị hàm số 4 2 y x 6x 5 là: A. ( 3;0). B. ( 3; 4). C. ( 3;4). D. (0;2). 3
Câu 70. Hàm số nào sau đây đạt cực tiểu tại x ? 2 SDT: 0946798489 54
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương x 1 A. y B. 2 y x 3x 2. x 2 1 C. 2 y 4x 12x 8. D. 4 3 2 y x x x 3x. 2
Câu 71. Điểm cực tiểu của đồ thị hàm số 4 3 y x 4x 1 là: A. M(2; 15). B. N(1;2). C. P( 2;11). D. ( Q 4; 6). Câu 72. Cho hàm số 2 y 3 2x
x . Trong các điểm sau, điểm nào có tọa độ sau đây là điểm cực trị của hàm số đã cho: A. M( 1;2). B. N( 3; 0). C. P(1; 0). D. ( Q 2; 3).
Câu 73. Điểm cực tiểu của đồ thị hàm số 2 y x 4 x là: A. M( 2;2). B. N( 2;1). C. P( 2; 2). D. ( Q 2;2). 2 x 2x 5
Câu 74. Xét tính cực trị của đồ thị hàm số y ; ta có: x 1
A. M( 3; 4) là điểm cực tiểu.
B. N(1; 4) là điểm cực đại.
C. P( 3; 4) là điểm cực đại.
D. Hàm số không có cực trị. Câu 75. Cho hàm số 4 3 y 3x
4x . Khẳng định nào sau đây đúng ?
A. Hàm số không có cực trị. B. Điểm (
A 1; 1) là điểm cực tiểu.
C. Hàm số đạt cực đại tại gốc tọa độ.
D. Hàm số đạt cực tiểu tại gốc tọa độ.
Câu 76. Với giá trị nào của tham số m thì đường thẳng d : y x
m đi qua trung điểm của đoạn thẳng
nối hai điểm cực trị của đồ thị hàm số 3 2 y x 6x 9x ? A. m 0. B. m 1. C. m 2. D. m 3.
Câu 77. Hàm số nào sau đây chỉ có cực đại mà không có cực tiểu ? 1 x A. 3 2 y x 3x 2. B. y 2 x Biên soạn và sưu tầm 55 4 x x 2 C. 2 y x 1. D. y 2 x 1 1 4 7 Câu 78. Cho hàm số 4 3 2 y x x x 2x
1. Khẳng định nào sau đây đúng ? 4 3 2
A. Hàm số không có cực trị.
B. Hàm số có cực tiểu, không có cực đại.
C. Hàm số có 1 cực đại và 2 cực tiểu.
D. Hàm số có 1 cực tiểu và 2 cực đại. Câu 79. Hàm số 2 3 y 3x
2x đạt cực trị tại: A. x 1; x 0. B. x 1; x 0. CD CT CD CT C. x 0; x 1. D. x 0; x 1. CD CT CD CT Câu 80. Gọi ,
A B lần lượt là 2 điểm cực trị của đồ thị hàm số 3 2 y x 3x 4. Khi đó diện tích tam
giác OBC, (với O là gốc tọa độ) có giá trị bằng bao nhiêu ? A. 2. B. 4. C. 2 5. D. 8. Câu 81. Gọi ,
A B lần lượt là 2 điểm cực trị của đồ thị hàm số 3 2 y x 3x 2. Khi đó diện tích tam
giác ABC, với C(1;1) có giá trị bằng bao nhiêu ? A. 1. B. 2. C. 3. D. 4. Câu 82. Gọi ,
A B lần lượt là 2 điểm cực trị của đồ thị hàm số 3 2 y 2x 3x 36x 10. Khi đó diện
tích của tam giác ABC, với C(2; 3) có giá trị bằng bao nhiêu ? 87 287 285 A. 78. B. C. D. 3 2 2 Câu 83. Gọi ,
A B lần lượt là 2 điểm cực trị của đồ thị hàm số 2 y (x 1) (2
x). Khi đó diện tích của
tam giác ABC, với C(1; 3) có giá trị bằng bao nhiêu ? 3 8 A. B. C. 7. D. Đáp án khác. 5 3 Câu 84. Gọi , A ,
B C là ba điểm cực trị của đồ thị hàm số 4 2 y 2x 4x
1. Hỏi diện tích tam giác ABC là bao nhiêu ? SDT: 0946798489 56
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 3 A. 4. B. 2. C. 1. D. 2
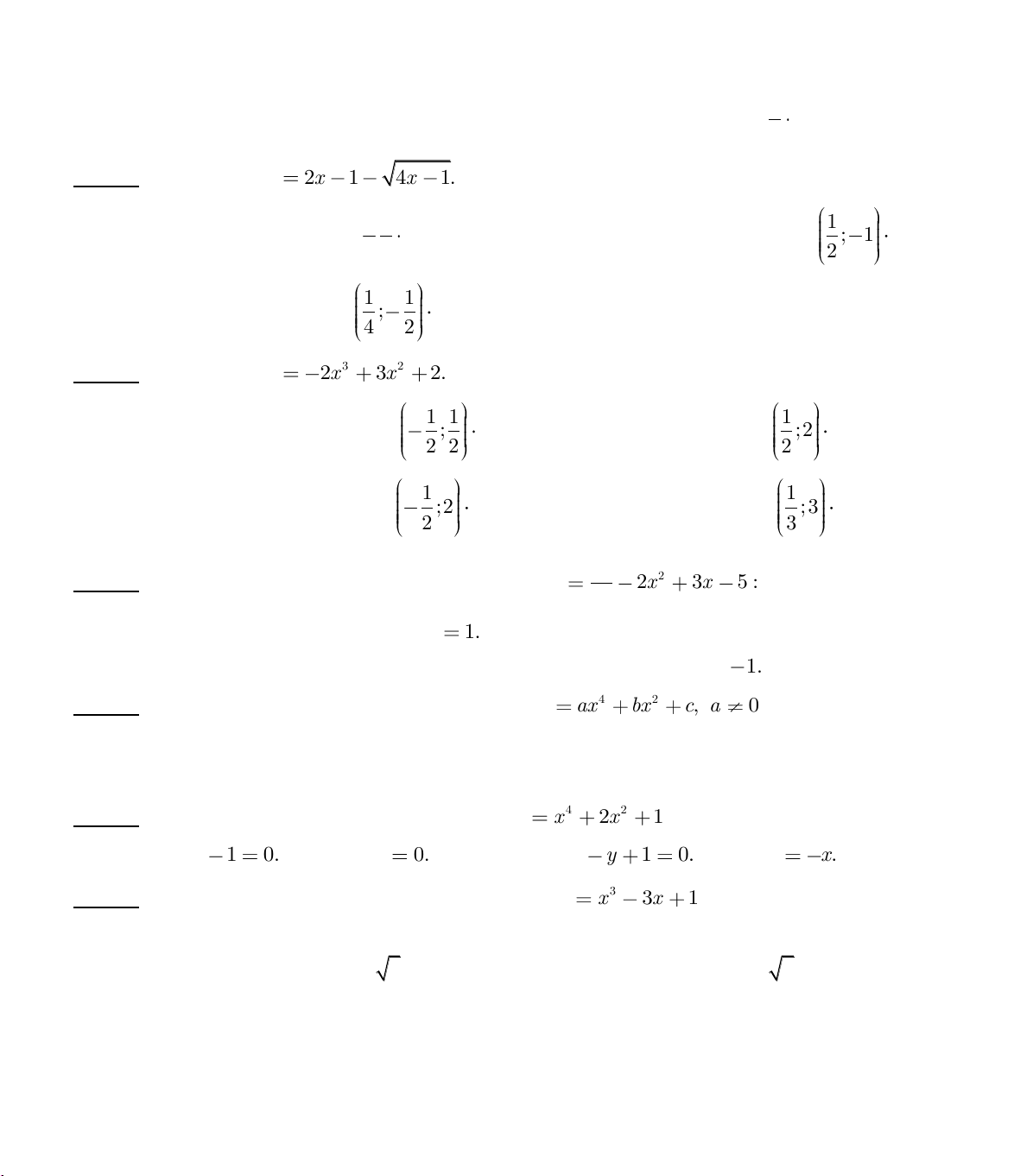
Câu 85. Cho hàm số y 2x 1 4x
1. Tìm mệnh đề đúng trong các mệnh đề sau ? 1 1
A. Giá trị cực đại bằng
B. Điểm cực tiểu có tọa độ là M ; 1 2 2 1 1
C. Điểm cực tiểu là N ;
D. Hàm số không có cực trị. 4 2 Câu 86. Cho hàm số 3 2 y 2x 3x 2. Câu nào sau đây sai ? 1 1 1
A. Hàm số đạt cực tiểu trên ;
B. Hàm số đạt cực đại trên ;2 2 2 2 1 1
C. Hàm số có 2 cực trị trên ;2
D. Hàm số có 2 cực trị trên ; 3 2 3 3 x
Câu 87. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số 2 y 2x 3x 5 : 3
A. Song song với đường thẳng x 1.
B. Song song với trục hoành. C. Có hệ số góc dương.
D. Có hệ số góc bằng 1.
Câu 88. Tiếp tuyến tại điểm cực trị của đồ thị hàm số 4 2 y ax bx , c a 0 có gì đặc biệt
A. Song song với trục tung. B. Có hệ số góc dương.
C. Song song với trục hoành.
D. Luôn đi qua gốc tọa độ.
Câu 89. Phương trình tiếp tuyến của đồ thị hàm số 4 2 y x 2x
1 tại điểm cực tiểu là: A. y 1 0. B. y 0. C. x y 1 0. D. y x.
Câu 90. Khoảng cách từ điểm cực đại của đồ thị hàm số 3 y x 3x
1 đến đường phân giác góc phần
tư thứ hai trong hệ trục Oxy là: A. 1. B. 2. C. 2. D. 3. Biên soạn và sưu tầm 57 2 x 3x m
Câu 91. Đồ thị hàm số y nhận điểm (
A 0;3) làm cực trị thì phương trình của hàm số x 2 có dạng là: 2 x 3x 6 2 x 3x 1 A. y B. y x 2 x 2 2 x 3x 6 2 x 3x C. y D. y x 2 x 2
Dạng toán 2. Phương trình đường thẳng nối hai điểm cực trị
Câu 92. Phương trình đường thẳng nào sau đây là phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2 y x 6x 9x ? A. y 2x 6. B. y 2x 6. C. y 6 2x. D. y 3x.
Câu 93. Phương trình đường thẳng nào sau đây là phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2 y x 3x 2 ? A. y x 2. B. y 2 x. C. y 2 2x. D. y 2x 2.
Câu 94. Đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số 3 y x 3x 5 có hệ số góc là A. 2. B. 1. C. 2. D. 5. Câu 95. Cho hàm số 3 2 2 3 y x 3mx 3(m 1)x m .
m Phương trình đường thẳng nối hai điểm
cực trị của đồ thị hàm số có dạng: A. 2x y 0. B. 3mx y 0. C. 2 y 2x m . D. y x . m
Câu 96. Phương trình đường thẳng d đi qua điểm cực đại và điểm cực tiểu của đồ thị hàm số 3 2 y x 2x 5x 1 có dạng: A. d : 3x 9y 2 0. B. d : y 4x 5. C. d : 38x 9y 19 0. D. d : y 17x 11.
Câu 97. Đồ thị hàm số 3 2 y x 3x mx
m có đường thẳng đi qua hai điểm cực trị song song với
đường thẳng d : y 2x 1 khi: SDT: 0946798489 58
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 1 2 3 A. m B. m C. m 6. D. m 2 3 2
Câu 98. Đồ thị hàm số 3 2 y x 3x mx
2 có đường thẳng đi qua hai điểm cực trị song song với
đường thẳng d : 4x y 3 0 khi: A. m 1. B. m 2. C. m 3. D. m 4.
Câu 99. Đồ thị hàm số 3 2 y x 3(m 1)x 6(m 2)x
1 có đường thẳng đi qua hai điểm cực trị
song song với đường thẳng d : y 1 4x khi: A. m 1. B. m 3. C. m 1 hoặc m 3. D. m 3 hoặc m 1.
Câu 100. Đồ thị hàm số 3 2 y 2x 3(m 1)x
6mx có hai điểm cực trị , A .
B Với giá trị nào của tham
số m thì đường thẳng d : y x
2 vuông góc với đường thẳng AB ? A. m 0. B. m 2. C. m 0 hoặc m 2. D. m 0 hoặc m 2. 2 5x x 5
Câu 101. Đồ thị hàm số y có hai điểm cực trị ,
A B nằm trên đường thẳng d. Hệ số góc 2x 2
của đường thẳng d là: A. 1. B. 1. C. 3. D. 5. 2 3x x 5
Câu 102. Đồ thị hám số y có hai điểm cực trị ,
A B nằm trên đường thẳng d có phương x 2 trình y ax
b thì giá trị của T a b là: A. 1. B. 1. C. 3. D. 5. 2 x 2x 4
Câu 103. Đồ thị hám số y có hai điểm cực trị ,
A B nằm trên đường thẳng d có phương x 2 trình y ax
b thì giá trị của T a b là: A. 1. B. 0. C. 1. D. 2.
Dạng toán 3. Tìm tham số m để hàm số có n cực trị, có cực trị tại x x . o
Câu 104. Tìm m để hàm số 3 2 y x mx 3x
2 đạt cực tiểu tại x 2 ? Biên soạn và sưu tầm 59 15 4 4 15 A. m B. m C. m D. m 4 15 15 4
Câu 105. Tìm m để hàm số 3 2 y mx 3x 12x
2 đạt cực đại tại x 2 ? A. m 2. B. m 3. C. m 0. D. m 1. Câu 106. Hàm số 3 2 y x 3x
mx đạt cực tiểu tại x 2 khi: A. m 0. B. m 0. C. m 0. D. m 0. 1 Câu 107. Hàm số 3 2 2 y x mx (m m 1)x
1 đạt cực đại tại điểm x 1 khi: 3 A. m 1 hoặc m 2. B. m 1. C. m 2. D. m tùy ý. Câu 108. Hàm số 3 y x (m 1)x
1 đạt cực tiểu tại điểm x 2 khi: A. m 13. B. m 13. C. m 1. D. m . Câu 109. Hàm số 3 2 2 y x 6mx (4m 1)x
2 đạt cực đại tại điểm x 2 khi: 11 A. m 0. B. m C. m 4. D. m 4. 2 Câu 110. Hàm số 3 2 y x 2x mx
1 đạt cực tiểu tại x 1 khi: A. m 1. B. m 1. C. m 2. D. Không có . m 1 Câu 111. Hàm số 3 2 2 y x 2mx 3m x
3m đạt cực tiểu tại x 1 khi: 3 1 1 A. m 1. B. m 1. C. m D. m 3 3 Câu 112. Hàm số 3 2 y x (m 1)x m
2 đạt cực đại tại điểm x 2 khi: 11 A. m 0. B. m C. m 4. D. m 4. 2 Câu 113. Hàm số 3 2 2 y x 2mx m x
2 đạt cực tiểu tại điểm x 1 khi: SDT: 0946798489 60
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương A. m 1. B. m 1. C. m 2. D. m 2. 1 m Câu 114. Hàm số 3 2 y x x (m
1)x đạt cực đại tại x 1 khi: 3 2 A. m 2. B. m 2. C. m 2. D. m . Câu 115. Hàm số 3 2 y x (m 3)x mx m
2 đạt cực tiểu tại điểm x 2 khi: 11 A. m 0. B. m C. m 4. D. m 4. 2 1 Câu 116. Hàm số 3 2 2 y x (m 1)x (m 3m 2)x
5 đạt cực trị tại x 0 khi: 3 A. m 1. B. m 2. C. A, B đều đúng. D. A, B đều sai. 1 Câu 117. Hàm số 3 2 2 y x mx (m m 1)x
1 đạt cực trị tại x 1 khi: 3 A. m 0. B. m 1. C. m 2. D. m 3. Câu 118. Hàm số 4 2 2 y x 2m x
5 đạt cực tiểu tại x 1 khi: A. m 1. B. m 1. C. A, B đều đúng. D. A, B đều sai. Câu 119. Hàm số 4 2 y x 2(m 2)x m
3 đạt cực đại tại điểm x 1 khi: A. m 3. B. m 5. C. m 3. D. m 5. Câu 120. Hàm số 4 2 y x 3mx
1 đạt cực tiểu tại điểm x 2 khi: 8 8 A. m B. m C. m 3. D. m 8. 3 3 1 Câu 121. Hàm số 4 2 y x ax
b có cực trị tại x
1 và giá trị cực trị tương ứng bằng 2 thì giá trị 4 của ,
a b lần lượt là: 1 9 1 9 1 9 1 9 A. a ; b B. a ; b C. a ; b D. a ;b 2 4 2 4 2 4 2 4
Câu 122. Đồ thị hàm số 4 2 y ax bx
c đạt cực đại tại (
A 0; 3), đạt cực tiểu tại ( B 1; 5) thì sẽ có giá trị của , a ,
b c lần lượt là: Biên soạn và sưu tầm 61 A. 2; 4; 3. B. 3; 1; 5. C. 2; 4; 3. D. 2; 4; 3. Câu 123. Hàm số 3 2 y ax x 5x
b đạt cực tiểu tại x
1 và giá trị cực tiểu bằng 2 khi: A. a 1, b 5. B. a 1, b 5. C. a 1, b 5. D. a 1, b 1. Câu 124. Hàm số 3 2 y x 2ax 4bx
2016 đạt cực đại tại x 1. Khi đó tổng a b là: 4 4 3 3 A. B. C. D. 3 3 4 4 1
Câu 125. Hàm số y . m sin x
sin 3x đạt cực trị tại điểm x khi: 3 3 A. m 2. B. m 0. C. m 2. D. m 3. 2 x mx 1
Câu 126. Hàm số y
đạt cực tiểu tại x 1 khi: x m A. m 2. B. m 2 hoặc m 0. C. m 0.
D. Không có m thỏa yêu cầu bài toán. 1
Câu 127. Cho hàm số 3 2 y x m x (2m 1)x
1. Mệnh đề nào sau đây là sai ? 3 A. m
1 thì hàm số có cực đại và cực tiểu. B. m
1 thì hàm số có hai điểm cực trị. C. m
1 thì hàm số có cực trị.
D. Hàm số luôn có cực đại và cực tiểu.
Câu 128. Đồ thị hàm số 4 2 y ax bx , c (a
0) có ba điểm cực trị khi và chỉ khi: A. b 0. B. ab 0. C. ab 0. D. ab 0.
Câu 129. Đồ thị hàm số 4 2 y ax bx , c (a
0) có một điểm cực trị khi và chỉ khi: A. b 0. B. ab 0. C. ab 0. D. b 0.
Câu 130. Đồ thị hàm số 4 2 y ax bx , c (a
0) có 1 điểm cực đại và 2 điểm cực tiểu khi và chỉ khi: SDT: 0946798489 62
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương a 0 a 0 a 0 a 0 A. B. C. D. b 0 b 0 b 0 b 0
Câu 131. Đồ thị hàm số 4 2 y ax bx , c (a
0) có 1 điểm cực tiểu và 2 điểm cực đại khi và chỉ khi: a 0 a 0 a 0 a 0 A. B. C. D. b 0 b 0 b 0 b 0
Câu 132. Đồ thị hàm số 3 2 y ax bx cx d, (a
0) có hai điểm cực trị khi và chỉ khi: A. 2 4b 12ac 0. B. 2 4a 12bc 0. C. 2 4b 12ac 0. D. 2 4b 12ac 0.
Câu 133. Đồ thị hàm số 3 2 y ax bx cx d, (a
0) không có điểm cực trị khi và chỉ khi: A. 2 4b 12ac 0. B. 2 4a 12bc 0. C. 2 4b 12ac 0. D. 2 4b 12ac 0.
Câu 134. Điều kiện của tham số m để hàm số 3 2 y x 3x 3mx m 2 có cực trị là: A. m 1. B. m 1. C. m 1. D. m 1. 1 1
Câu 135. Với giá trị nào của tham số m để hàm số 3 2 y x mx 2x 1 có cực trị là: 3 2 A. 0. B. 3. C. 4. D. Cả A, B, C.
Câu 136. Điều kiện của m để hàm số 3 2 y x 3x mx m
2 có 2 điểm cực trị là: A. m 3. B. m 3. C. m . D. m . Câu 137. Hàm số 3 y x mx 1 có 2 cực trị khi: A. m 0. B. m 0. C. m 0. D. m 0.
Câu 138. Với giá trị nào của m thì hàm số 3 2 y x mx 3x 2m
1 có cực đại, cực tiểu ? A. m ( 3;3). B. m ( ; 3) (3; ). C. m 3;3 . D. m ; 3 3; .
Câu 139. Tìm tham số m để hàm số 3 2 2 y x 3mx
3m có 2 điểm cực trị ? A. m 0. B. m 0. C. m 0. D. m 0. Biên soạn và sưu tầm 63 Câu 140. Hàm số 3 2 y x (m 1)x x
2 có cực đại, cực tiểu khi: A. 1 3 m 1 3. B. 1 3 m 1 3. C. m 1 3 hoặc m 1 3. D. m 1 3 hoặc m 1 3. Câu 141. Hàm số 3 2 2 2 y x 3mx 3(m m)x 2m
1 có 2 điểm cực trị khi: A. m 0. B. m 0. C. m 1. D. m tùy ý. 1
Câu 142. Tìm m để hàm số 3 2 2 y x (m 1)x (m m)x
2 có cực đại và cực tiểu: 3 1 2 A. m 2. B. m C. m D. m 1. 3 3 1 Câu 143. Hàm số 3 2 y x (m 2)x mx
1 có cực đại, cực tiểu khi: 3 A. m 0. B. m . C. m . D. m 1. 1 Câu 144. Hàm số 3 2 2 y x (m 1)x (3m 4m 1)x
m có cực đại, cực tiểu khi: 3 A. 0 m 1. B. 0 m 1. C. m 0. D. m 1. Câu 145. Hàm số 3 2 y x (3 m)x 2mx
2 có cực đại và cực tiểu khi: A. m 3. B. 6 3 3 m 6 3 3. C. m 6 3 3 hay m 6 3 3. D. m 6 3 3 hay m 6 3 3.
Câu 146. Giá trị của tham số m để hàm số 3 y (m 2)x mx 3 không có cực trị là: m 0 m 0 A. B. m 2. C. D. 0 m 2. m 2 m 2
Câu 147. Đồ thị hàm số 3 2 y x 3mx 3mx 3m 4 không có cực trị khi: A. m 0. B. m 1. C. 0 m 1. D. 0 m 1.
Câu 148. Đồ thị hàm số 3 2 y 2x (m 2)x (6 3m)x m 1 không có cực trị khi: SDT: 0946798489 64
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương A. m 16. B. m 2. C. 16 m 2. D. 16 m 2.
Câu 149. Đồ thị hàm số 3 2 y mx 3mx (m 1)x 1 không có cực trị khi: 1 1 1 A. 0 m B. 0 m C. m 0. D. m 4 4 4
Câu 150. Đồ thị hàm số 3 3 3 y (x a) (x b)
x có cực đại, cực tiểu khi: A. . a b 0. B. . a b 0. C. . a b 0. D. . a b 0.
Câu 151. Tìm tham số m để đồ thị hàm số 4 2 2 2 y x 2(m 3) x
m có 3 điểm cực trị ? A. m 0. B. m 0. C. m 0. D. m 0.
Câu 152. Tìm tham số m để đồ thị hàm số 4 2 y x mx 3 có 3 điểm cực trị ? A. m 0. B. m 0. C. m 0. D. Không có . m
Câu 153. Tìm tham số m để đồ thị hàm số 4 2 y x 2mx 2m 1 có 3 điểm cực trị ? A. 2. B. 1. C. 0. D. 1.
Câu 154. Tìm tham số m để đồ thị hàm số 4 2 2 y x m x 3 có 3 điểm cực trị ? A. m 0. B. m 0. C. m 0. D. m .
Câu 155. Tìm tham số m để đồ thị hàm số 4 2 y x 2(m 1)x 3 có 3 điểm cực trị ? A. m  0. B. m 1. C. m 1. D. m 0.
Câu 156. Tìm tham số m để đồ thị hàm số 4 2 y x (m 1)x 2m 1 có 3 điểm cực trị ? A. m 1. B. m 1. C. m 1. D. m 1.
Câu 157. Tìm tham số m để đồ thị hàm số 4 2 4 y x 2mx 2m
m có 3 điểm cực trị ? A. m 2. B. m 1. C. m 0. D. m 2.
Câu 158. Tìm tham số m để đồ thị hàm số 4 2 y x 2(m 1)x
m có 3 điểm cực trị ? A. Không có . m B. m 1. C. m 1. D. m 1.
Câu 159. Tìm tham số m để đồ thị hàm số 4 2 2 y x 2(m 2)x m 5m 5 có 3 điểm cực trị ? A. m 2. B. m 2. C. m 1. D. m 1. Biên soạn và sưu tầm 65
Câu 160. Tìm tham số m để đồ thị hàm số 4 2 y x 2(m 1)x m 1 có đúng 1 cực trị ? A. m 1. B. m 1. C. A, B đều đúng. D. A, B đều sai.
Câu 161. Đồ thị hàm số 4 2 y x 2(2m 1)x
3 có đúng một điểm cực trị khi: 1 1 1 1 A. m B. m C. m D. m 2 2 2 2
Câu 162. Đồ thị hàm số 4 2 y x 2(3 m)x
2 có đúng 1 điểm cực trị khi: A. m 3. B. m 3. C. m 3. D. m 3.
Câu 163. Đồ thị hàm số 4 2 (C) : y x ( 2 2m
1)x 3 có đúng 1 điểm cực trị khi: 1 1 1 1 A. m B. m C. m D. m 2 2 2 2 m
Câu 164. Đồ thị hàm số 4 2 y x (m 1)x m
1 có đúng 1 điểm cực trị khi: 4 A. 0 m 1. B. m 1. C. m 0. D. m ;0 1; .
Câu 165. Đồ thị hàm số 4 2 y x 2(1 m)x
2 có cực tiểu mà không có cực đại khi: A. m 1. B. m 1. C. m 1. D. m 1.
Câu 166. Đồ thị hàm số 4 2 y x 2(5 m)x
2 có cực đại mà không có cực tiểu khi: A. m 5. B. m 5. C. m 5. D. m 5. m 1 5
Câu 167. Đồ thị hàm số 4 2 y x mx
có cực đại mà không có cực tiểu khi: 2 2 A. m 1;0 . B. m 1;0 . C. m 1;0 . D. m ( 1;0).
Câu 168. Đồ thị hàm số 4 2 y x (2m 4)x
m có 2 cực đại, 1 cực tiểu khi: A. m 2. B. m 2. C. m 2. D. m 2.
Câu 169. Đồ thị hàm số nào sau đây chỉ có 1 điểm cực trị ? SDT: 0946798489 66
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương A. 4 2 y 2x 4x 2. B. 2 4 2 y (m 4)x 9x 1. C. 4 2 y x 2x 1. D. 4 2 2 y x (m 1)x 1.
Câu 170. Tìm tham số m để đồ thị hàm số 4 2 y (1 m)x mx 2m 1 có đúng 1 cực trị ? A. m . B. m 0. C. 0 m 1. D. \ (0;1). 2 2x mx 2m 1
Câu 171. Hàm số y
có hai điểm cực trị khi: 2x 1 A. m 1. B. m 1. C. m 1. D. m tùy ý. 2 x mx 1
Câu 172. Hàm số y luôn có cực trị khi: x m A. m 0. B. m 1. C. m . D. m .
Câu 173. Đồ thị hàm số 3 2 y ax bx cx
d có hai điểm cực trị ( A 0;0), (
B 1;1) thì các hệ số , a , b ,
c d có giá trị lần lượt là: A. a 2, b 0, c 0, d 3. B. a 0, b 0, c 2, d 3. C. a 2, b 0, c 3, d 0. D. a 2, b 3, c 0, d 0.
Dạng toán 3. Tìm tham số m để hàm số có n cực trị thỏa mãn điều kiện K.
Nhóm 1. Điều kiện K liên quan đến định lí Viét Câu 174. Hàm số 3 f (x) x ax b với , a b
có hai cực trị là x , x . Hỏi kết luận nào sau đây là 1 2 đúng về hàm này ?
A. Đường thẳng nối hai điểm cực trị qua gốc tọa độ O.
B. Phương trình đường thẳng nối hai điểm cực trị có dạng y ax . b
C. Tổng hai giá trị cực trị là . b
D. Hai điểm cực trị của đồ thị hàm số nằm về hai phía so với trục tung. Câu 175. Hàm số 3 2 y x (m 1)x x
2 có 2 điểm cực trị x , x thỏa mãn điều kiện 3(x x ) 2 1 2 1 2 khi: A. m 2. B. m 1. C. m 1. D. m 2. Biên soạn và sưu tầm 67 1 Câu 176. Hàm số 3 2 y x x (m 2)x
2 có 2 điểm cực trị x , x thỏa mãn điều kiện 3 1 2 x x 10 0 khi: 1 2 A. m 12. B. m 8. C. m 8. D. m 12. 1
Câu 177. Đồ thị hàm số 3 2 y x mx (2m 1)x
3 có hai điểm cực trị với hoành độ x , x thỏa 3 1 2 mãn x .x
6, thì giá trị m sẽ là: 1 2 7 1 5 A. m B. m C. m D. m 1. 2 2 2
Câu 178. Đồ thị hàm số 2 y (x m)(x 2x m
1) có hai điểm cực trị với hoành độ x , x thỏa mãn 1 2 x .x
1, thì giá trị của tham số m sẽ là: 1 2 A. m 2. B. m 3. C. m 4. D. Cả A và C. 2
Câu 179. Với giá trị nào của m thì hàm số 3 2 2 y x mx 2(1 3m )x
1 có 2 điểm cực trị với 3
hoành độ x , x thỏa mãn: 2(x x ) x x 1 ? 1 2 1 2 1 2 2 2 A. m 0 hoặc m B. m 3 3 C. m 0. D. Không tồn tại . m 1 1
Câu 180. Với giá trị nào của m thì hàm số 3 2 2 y x (2m 1)x (m 2)x 1 có 2 điểm cực trị 3 2
với hoành độ x , x thỏa mãn: 3x x 5(x x ) 7 0 ? 1 2 1 2 1 2 1 A. m B. m 2. C. m 4. D. m 8. 4
Câu 181. Tìm tham số m để hàm số 3 2 y x 3x mx
1 có 2 điểm cực trị x , x thỏa mãn điều 1 2 kiện: 2 2 x x 3 ? 1 2 2 3 A. m 1. B. m C. m D. m 1. 3 2 SDT: 0946798489 68
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương Câu 182. Hàm số 3 2 y x 3(m 1)x 9x
m có 2 điểm cực trị x , x thỏa mãn điều kiện 1 2 2 2 x x 10 khi: 1 2 A. m 2 hoặc m 0. B. m 0 hoặc m 2. C. m 2. D. m 0. 1 1
Câu 183. Với giá trị nào của m thì hàm số 3 2 2 y x (2m 1)x (m 2)x
m có 2 điểm cực trị 3 2
với hoành độ x , x thỏa mãn: 2 2 8(x x ) 81 ? 1 2 1 2 1 7 A. m B. m C. m 4. D. m 8. 4 4 1
Câu 184. Với giá trị nào của m thì hàm số 3 2 y x mx
x có 2 điểm cực trị với hoành độ x , x 3 1 2 thỏa mãn: 2 2 x x x x 7 ? 1 2 1 2 A. m 1. B. m 2. C. m 3. D. m 4.
Câu 185. Với giá trị nào của m thì hàm số 3 2 2 5 2 y x 3mx 3(m 1)x m
3m có 2 điểm cực trị
với hoành độ x , x thỏa mãn: 2 2 x x x x 7 ? 1 2 1 2 1 2 A. m 2. B. m 2. C. m 2. D. m 2. 1
Câu 186. Với giá trị nào của m thì đồ thị hàm số 3 2 y (m 1)x (m 2)x (m 3)x 1 có 2 điểm 3
cực trị với hoành độ x , x thỏa mãn: (4x 1)(4x 1) 18 ? 1 2 1 2 A. m 1. B. m 4. C. m 7. D. m 8.
Câu 187. Nếu gọi x , x lần lượt là hoành độ các điểm cực trị của đồ thị hàm số: 1 2 3 2 y 2x ( 3 2m ) 1 x 6 ( m m 1 )x 2 thì giá trị T x x là: 2 1 A. T m 1. B. T m 1. C. T . m D. T 1.
Câu 188. Với giá trị nào của tham số m thì đồ thị hàm số 3 2 y 4x mx
3x có 2 điểm cực trị với
hoành độ x , x thỏa mãn: x 4x 0 ? 1 2 1 2 Biên soạn và sưu tầm 69 9 3 1 A. m B. m C. m D. m 0. 2 2 2
Câu 189. Với giá trị nào của m thì đồ thị hàm số 3 2 y x (1 2m)x (2 ) m x m 2 có 2 điểm
cực trị với hoành độ x , x thỏa mãn: 3 x x 2 ? 1 2 2 1 1 97 A. m 3. B. m 8 1 97 1 97 1 97 C. m ; ; D. m ;3 8 8 8 1 1
Câu 190. Với giá trị nào của m thì hàm số 3 2 y x (m 3)x 2(m 1)x
1 có các điểm cực đại, 3 2
cực tiểu với hoành độ lớn hơn 1 ? A. m [2; ). B. m ( ; 7 4 2]. C. m ( 7 4 2;2). D. m [ 7 4 2;2].
Câu 191. Với giá trị nào của m thì hàm số 3 2 2 3 y x 3mx 3(m 1)x m
m có các điểm cực đại, cực tiểu thỏa mãn: 2 x x ? CD CT m 0 m 0 A. m 0. B. C. m 3. D. m 3 m 3
Câu 192. Đồ thị hàm số 3 2 y ax bx cx
d đạt cực trị tại x , x nằm về hai phía so với trục tung khi 1 2 và chỉ khi: A. a 0, b 0, c 0.
B. a và c trái dấu. C. 2 b 12ac 0. D. 2 b 12ac 0.
Câu 193. Với giá trị nào của tham số m thì đồ thị hàm số 3 2 2 y x x (m 3m)x 4 có các điểm
cực đại, điểm cực tiểu nằm về hai phía của trục tung ? A. 0 m 3. B. 0 m 3. C. m 3. D. m 0. SDT: 0946798489 70
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 2 1
Câu 194. Với giá trị nào của m thì đồ thị hàm số 3 2 2 y x (3m 1)x (m m 6)x có các điểm 3 2
cực đại, điểm cực tiểu nằm về hai phía của trục tung ? A. 2 m 3. B. 2 m 1. C. m 2. D. m 4. 1
Câu 195. Với giá trị nào của m thì đồ thị hàm số 3 2 2 3 y mx (2m 1)x (m 1)x m có các điểm 3
cực đại, điểm cực tiểu nằm về hai phía so với trục tung ? A. m 1. B. 0 m 1. C. m 0. D. m ( ;0) (1; ). 1
Câu 196. Với giá trị nào của tham số m thì đồ thị hàm số 3 2 y x x (m 1)x 3 có các điểm cực 3
đại, điểm cực tiểu nằm cùng một phía so với trục tung ? A. 1 m 2. B. 1 m 2. C. 1 m 2. D. 1 m 2.
Câu 197. Với giá trị nào của tham số m thì đồ thị hàm số 3 2 y x 6x 3(m 2)x m 6 có hai điểm
cực trị với hoành độ cùng dấu ? A. 2 m 2. B. 2 m 2. C. 2 m 2. D. 1 m 3.
Nhóm 2. Điều kiện K liên quan đến tính chất hình học
Câu 198. Tìm các giá trị thực của tham số m sao cho đồ thị hàm số 4 2 y x 4mx 3m 2 có ba điểm 5
cực trị tạo thành một tam giác nhận G 0; làm trọng tâm ? 3 A. m 1. B. m 8. 1 1 C. m 1 hoặc m D. m 8 8
Câu 199. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số 4 2 y x
2mx có ba điểm cực
trị tạo thành một tam giác vuông ? A. m 0. B. m 2. C. m 0. D. m 3.
Câu 200. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số 4 2 y x 2mx 1 có ba điểm
cực trị tạo thành một tam giác vuông cân ? Biên soạn và sưu tầm 71 1 1 A. m B. m 1. C. m D. m 1. 3 9 3 9
Câu 201. Với giá trị nào của tham số m thì đồ thị hàm số 4 2 2 y x 2m x
2016 có ba điểm cực trị tạo
thành một tam giác vuông cân ? A. m 2016. B. m 1. C. m 2. D. Đáp án khác.
Câu 202. Với giá trị nào của tham số m thì đồ thị hàm số 4 2 2 y x 2(m 2)x m 5m 5 có ba
điểm cực trị tạo thành một tam giác vuông cân ? A. m 1. B. m 1. C. m 1. D. m 2.
Câu 203. Với giá trị nào của tham số m thì đồ thị hàm số 4 2 2 y x 2(m 2)x m 5m 5 có ba
điểm cực trị tạo thành một tam giác đều ? A. m 2 3. B. m 2 3. C. 3 m 2 3. D. 3 m 2 3.
Câu 204. Với giá trị nào của tham số m thì đồ thị hàm số 4 2 2 y x 2mx m
m có ba điểm cực trị
tạo thành một tam giác có một góc bằng 0 120 ? 1 1 A. m 0 hoặc m B. m 0 hoặc m 3 3 3 3 1 C. m 0. D. m 3 3
Câu 205. Với giá trị nào của tham số m thì đồ thị hàm số 4 2 y x 2mx m
1 có ba điểm cực trị tạo
thành một tam giác có bán kính đường tròn ngoại tiếp bằng 1 ? 1 5 1 5 A. m 1 hoặc m B. m 1 hoặc m 2 2 1 5 1 5 C. m 1 hoặc m D. m 1 hoặc m 2 2
Câu 206. Với giá trị nào của tham số m thì đồ thị hàm số 4 2 y x 2mx
2 có ba điểm cực trị tạo thành 3 9
một tam giác có đường tròn ngoại tiếp đi qua điểm D ; ? 5 5 SDT: 0946798489 72
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 1 A. m 2. B. m 1. C. m 1. D. m 2
Câu 207. Với giá trị nào của tham số m thì đồ thị hàm số 4 2 2 y x 2(1 m )x m 1 có ba điểm cực
trị tạo thành một tam giác có diện tích lớn nhất ? A. m 2. B. m 2. C. m 0. D. m 2. 1
Câu 208. Với giá trị nào của tham số m thì đồ thị hàm số 4 2 y x (3m 1)x 2m 2 có ba điểm 4
cực trị tạo thành một tam giác có trọng tâm là gốc tọa độ O ? 2 2 1 A. m B. m hoặc m 3 3 3 2 1 1 C. m hoặc m D. m 3 3 3
Câu 209. Với giá trị nào của tham số m thì đồ thị hàm số 4 2 y x (3m 1)x
3 có ba điểm cực trị tạo 2
thành tam giác cân sao cho độ dài cạnh đáy bằng độ dài cạnh bên ? 3 5 5 3 3 A. m B. m C. m D. m 3 3 5 5
Câu 210. Với giá trị nào của tham số m thì đồ thị hàm số 4 2 2 2 y 2x m x m 1 có ba điểm cực trị , A ,
B C sao cho bốn điểm , A ,
B C, O là bốn đỉnh một hình thoi với O là gốc tọa độ ? 2 A. m 2. B. m 2. C. m 2. D. m 2
Câu 211. Với giá trị nào của tham số m thì đồ thị hàm số 4 2 4 y x 2mx 2m
m có ba điểm cực trị
tạo thành một tam giác nội tiếp đường tròn có bán kính nhỏ nhất ? 1 1 2 A. m 2. B. m C. m D. m 3 2 2 2
Câu 212. Với m bằng bao nhiêu thì đồ thị hàm số 3 y x 3mx 1 có hai cực trị ,
B C thỏa mãn tam
giác ABC vuông tại ( A 2;2) ? Biên soạn và sưu tầm 73 A. m 2. B. m 2. C. m 2. D. Đáp án khác.
Câu 213. Với m bằng bao nhiêu thì đồ thị hàm số 3 2 3 y 2x 3(m 1)x 6mx
m có hai cực trị , A B thỏa mãn AB 2 ? A. m 0. B. m 2. C. m 0 hoặc m 2. D. m 2. hoặc m 0.
Câu 214. Với m bằng bao nhiêu thì đồ thị hàm số 3 2 y x 2mx
m có hai cực trị thẳng hàng với gốc tọa độ O ? 1 A. m 0. B. m 3. C. m D. m 3. 3
Câu 215. Với m bằng bao nhiêu thì đồ thị hàm số 3 2 y 2x 3(m 3)x
11 3m có hai cực trị , A B
thẳng hàng với điểm C(0; 1) ? A. m 2. B. m 2. C. m 4. D. m 4.
Câu 216. Với giá trị nào của m thì đồ thị hàm số 3 2 2 2 y x 3x 3(m 1)x 3m 1 có cực đại, cực
tiểu, đồng thời các điểm đó tạo với gốc tọa độ O tam giác vuông tại O ? 6 6 A. m 1 hoặc m B. m 1 hoặc m 2 2 6 6 C. m 1 hoặc m D. m 1 hoặc m 2 2
Câu 217. Với giá trị nào của tham số m thì đồ thị hàm số 3 2 y x 3x 3(1 m)x 1 3m có cực
đại, cực tiểu, đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam
giác có diện tích bằng 4 ? A. m 2. B. m 1. C. m 1. D. m 1.
Câu 218. Đồ thị hàm số 3 2 y x 3mx 3m
1 có điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng d : x 8y 74 0 khi: A. m 1. B. m 2. C. m 1. D. m 2. SDT: 0946798489 74
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
Trung tâm luyện thi Thanh Phương Câu 539. Hàm số 2
y x  3x 1 có bao nhiêu điểm cực trị: A.0 B.2 C.3 D. 1 Câu 540. Hàm số 3 y x  3 2
x  3x 1 có bao nhiêu điểm cực trị: A.3 B.2 C.1 D. 0 Câu 541. Hàm số 3 y x  3 2
x 1 có bao nhiêu điểm cực trị: A3. B.1 C.0 D. 2 Câu 542. Hàm số 4 2
y x x 1 có bao nhiêu điểm cực trị: A.0 B.1 C.2 D. 3 Câu 543. Hàm số 4 y x  2 2
x 1 có bao nhiêu điểm cực trị: A.0 B.3 C.2 D. 1 2x 1
Câu 544. Hàm số y
có bao nhiêu điểm cực trị: 3x  5 A.1 B.2 C.3 D. 0 2 2 x x  3
Câu 545. Hàm số y
có bao nhiêu điểm cực trị: x 1 A.1 B.0 C.3 D. 2 Câu 546. Hàm số 4 y x  4 3
x  3 có bao nhiêu điểm cực trị: A.2 B.3 C.0 D. 1 2 x x  5
Câu 547. Hàm số y
có bao nhiêu điểm cực trị: x 1 A.3 B.2 C.1 D. 0
Câu 548 Hàm số y x  sin x có bao nhiêu điểm cực trị: Biên soạn và sưu tầm 75 A.1 B.2 C.3 D. 0
Câu 549. Hàm số y x  ln x có bao nhiêu điểm cực trị: A.3 B.2 C.1 D. 0
Câu 550 Hàm số y x.ln x có bao nhiêu điểm cực trị: A.3 B.2 C.1 D. 1
Câu 551. Hàm số y  (x  )
1 2 (2  x) có bao nhiêu điểm cực trị: A.1 B.3 C.0 D. 2 Câu 552. Hàm số 3 y x  3 2
x  2 đạt cực đại tại x = : A.2 B.-2 C.1 D. -1
Câu 553. Hàm số y  (x  )
1 2 (2  x) đạt cực tiểu tại x =: A.-1 B.2 C. -2 D. 1 Câu 554. Hàm số 4 y x  4 3 x  4 2
x  2 đạt cực đại tại x = A1. B 2. C.-2 D. -1 2 x  4x  8
Câu 555. Hàm số y
đạt cực tiểu tại x = x  2 A.2 B.3 C.1 D. 4 Câu 556. Hàm số 2 x
y x e đạt cực đại tại x = A.1 B.3 C.4 D. 2
Câu 557. Hàm số y  2 3 x  3 2
x  36x 10 có cực trị là: A.71 B.-54 C. 71 hoặc- 54 D. 71 và – 54
Câu 558. Hàm số y  2 4 x  4 3
x  3 có cực trị là: A.1 B.24 C.-32 D. -24 SDT: 0946798489 76
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương Câu 559. Hàm số 4 y x  2 2
x  3 có cực trị là: A.1 B.5 C. -2 D. -3 2 x  4x  5
Câu 560. Hàm số y
có giá trị CĐ, CT lần lượt là: x  2 A2; 2. B. 1;2 C. -2 ;0 D. -2; 2
Câu 561. Điểm cực đại của đồ thị hàm số 3 2
y x  5x  7x  3 là:  7 3  2   7 32  A. 1;0 B. 0  ;1 C. ;   D. ;   .  3 27   3 27 
Câu 562. Điểm cực tiểu của đồ thị hàm số 3 2
y x  5x  7x  3 là:  7 3  2   7 32  A. 1;0 B. 0  ;1 C. ;   D. ;   .  3 27   3 27  1 1
Câu 563 : Trong các khẳng định sau về hàm số 4 2
y   x  x  3 , khẳng định nào là đúng? 4 2
A. Hàm số đạt cực tiểu tại x = 0;
B. Hàm số đạt cực đại tại x = 1;
C. Hàm số đạt cực đại tại x = -1;
D. Cả 3 câu trên đều đúng. Câu 564: Hàm số: 3
y  x  3x  4 đạt cực tiểu tại x = A. -1 B. 1 C. - 3 D. 3 1 Câu 565 Hàm số: 4 2 y
x  2x  3 đạt cực đại tại x = 2 A. 0 B.  2 C.  2 D. 2 Câu 566: Hàm số 3
y x mx 1 có 2 cực trị khi : A. m  0 B. m  0 C. m  0 D. m  0 Biên soạn và sưu tầm 77
Câu 567: Đồ thị hàm số 3
y x  3x 1 có điểm cực tiểu là: A. ( -1 ; -1 ) B. ( -1 ; 3 ) C. ( -1 ; 1 ) D. ( 1 ; 3 )
Câu 568: Đồ thị hàm số nào sau đây có 3 điểm cực trị: A. 4 2
y x  2x 1 B. 4 2
y x  2x 1 C. 4 2
y  2x  4x 1 D. 4 2 y  2
x  4x 1
Câu 569. Cho hàm số y = –x3 + 3x2 – 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số luôn luôn nghịch biến;
B. Hàm số luôn luôn đồng biến
C. Hàm số đạt cực đại tại x = 1;
D. Hàm số đạt cực tiểu tại x = 1. 1 1
Câu 570 : Trong các khẳng định sau về hàm số 4 2
y   x  x  3, khẳng định nào là đúng? 4 2
A. Hàm số có điểm cực tiểu là x = 0;
B. Hàm số có hai điểm cực đại là x = 1; C. Cả A và B đều đúng; D. Chỉ có A là đúng.
Câu 571 : Trong các mệnh đề sau, hãy tìm mệnh đề sai:
A. Hàm số y = –x3 + 3x2 – 3 có cực đại và cực tiểu;
B. Hàm số y = x3 + 3x + 1 có cực trị; C. Hàm số 1 y  2  x 1 không có cực trị; D. Hàm số 1 y   x   có hai cực trị. x 2 1  2 x  2 2
Câu 572 : Tìm kết quả đúng về giá trị cực đại và giá trị cực tiểu của hàm số y  2  x 1 : x  2 A. yCĐ = 1 và yCT = 9; B. yCĐ = 1 và yCT = –9; C. yCĐ = –1 và yCT = 9; D. yCĐ = 9 và yCT = 1.
Câu 573 : Hàm số nào dưới đây không có cực trị: 1 1 x  4 A. y  x 1 ; B. y   ; C. y  ; D. Cả B và x 1  3 x  3 x  3 C. SDT: 0946798489 78
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 1
Câu 574 :Cho hàm số 3 2
y  x  m x  2m  
1 x 1 . Mệnh đề nào sau đây là sai? 3 A. m
 1 thì hàm số có cực đại và cực tiểu; B. m
 1 thì hàm số có hai điểm cực trị; C. m
 1 thì hàm số có cực trị; D. Hàm số luôn luôn có cực đại và cực tiểu.
Câu 575 : Điểm cực tiểu của hàm số : 3
y  x  3x  4 là A. x = -1 B. x = 1 C. x = - 3 D. x = 3 1
Câu 576 : Điểm cực đại của hàm số : 4 2 y
x  2x  3 là 2 A. x = 0 B. x =  2 C. x =  2 D. x = 2
Câu 577: Đồ thị của hàm số y=x4-6x2+3 có số điểm cực trị là A.0 B.1 C.2 D.3 3 x
Câu 578: Cho hàm số 2 2 y
 2x  3x  .Toạ độ điểm cực đại của hàm số là 3 3 A.(-1;2) B.(1;2) C.(3; 2/3) D.(1;-2) 4 2 2
Câu 579 Cho hàm số y mx (m 9)x
10 . Tìm m để hàm số có 3 điểm cực trị. m 3 A. B . 1< m < 2 C. m > 2 D. m > -1 0 m 3
Câu 580.,Tìm m để hàm số 3 2 y x (1 2m)x (2 m)x m
2 đạt cực trị tại x , x 1 2 sao cho 1 x x 1 2 . 3 3 29 3 29 A. m 1; m B. m 1 C.m D. m 1 8 8 4 2
Câu 581: Cho hàm số y x 2mx m
1. Tìm m để đồ thị của hàm số có 3 điểm cực trịA, B,C
đồng thời các điểm A,B,C tạo thành 3 đỉnh của một tam giác đều. Biên soạn và sưu tầm 79 3 A. m 3 B. m = 0 C. m = 3 D. m 0 Violet 1
Câu 582: Giá trị của m để hàm số 3 y x  (m  ) 1 2 2
x m x 1 có 2 cực trị là: 3 A. -1/3 < m <1 B. m > -1/2
C.    m   D. m > ½
Câu 583: Giá trị của m để hàm số 4 2
y x mx m  3 có 3 cực trị là: A. 0 < m <1 B. m > 1 C. m < 0 D. m R
Câu 584: Đồ thị hàm số 3 y x  2 2
mx  5x  3 đi qua điểm (1; -1) thì hoành độ điểm cực tiểu là: A. 1 B. 5/3 C. -1 D. -5/3 1
Câu 585: Giá trị của m để hàm số 3 2 y x mx  ( 2 m  )
m x  1 có 1 cực đại và 1 cực tiểu là: 3 A. -1/2 < m <0 B. 0 < m <1/2 C. m < 0 D. m > 0
Câu 586: Số điểm cực trị của hàm số 4 2
f (x)  x  2x là: A. 4 B. 2 C. 1 D. 3 1
Câu 587: Số điểm cực trị của hàm số f (x) 4  x  2 2 x  4 là: 4 A. 4 B. 3 C. 2 D. 1
Câu 588: Số điểm cực trị của hàm số 4
y x 100 là: A. 0 B. 1 C. 2 D. 3
Câu 589: Cho hàm số 3 2
y x  3x  2 có điểm cực đại là A(-2;2), Cực tiểu là B(0;-2) thì phương trình 3 2
x  3x  2  m có hai nghiệm phân biêt khi: A. m = 2 hoặc m = -2 C. m < -2 B. m > 2 D. -2 < m < 2
Câu 590: Cho hàm số 3 2
y  2x  3x 1 , có đồ thị ( C) . Chọn đáp án sai trong các đáp án sau: A. Hàm số có 2 cực trị
C. Hàm số nghịch biến trên khoảng (0 ; 1)
B. Đồ thị hàm số đi qua điểm A( 2 ; 3)
D. Hàm số không có tiệm cận 1
Câu 591: Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số: 3 2 y
x  2x  3x  5 3 SDT: 0946798489 80
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
A. song song với đường thẳng x = 1
C. Song song với trục hoành B. Có hệ số góc dương
D. Có hệ số góc bằng -1
Câu 592. Tìm m để hàm số 3 2
f (x)  x  3x mx 1 có hai điểm cực trị x , x thỏa 2 2 x x  3 1 2 1 2 3 1 A. m  1 B. m  2  C. m  D. m  2 2
Câu 593. Cho hàm số 3 2
y  4x mx  3x . Tìm m để hàm số đã cho có 2 điểm cực trị x , x 1 2 thỏa x  4
x . Chọn đáp án đúng nhất? 1 2 1 9 3 A. m   B. m   C. m  0 D. m   2 2 2
Câu 594. Cho hàm số 3
y x  3mx 1 (1). Cho A(2;3), tìm m để đồ thị hàm số (1) có hai điểm cực trị B
và C sao cho tam giác ABC cân tại A. 1 3 3  1  A. m  B. m  C. m  D. m  2 2 2 2
Câu 595. Với giá trị nào của m thì hàm số 3 2 2
y x  2mx m x  2 đạt cực đại tại x  1. A. m  1  B. m  3 C. m  1 D. m  2 
Câu 596. Tìm m để hàm số y   x m3  3x đạt cực tiểu tại x  0 . A. m  1 B. m  2 C. m  2  D. m  1 
Câu 597. Cho hàm số 3 2
y x mx   2 m   3 3 3
1 x m m . Tìm m để hàm số đã cho có hai điểm cực
trị. Gọi x , x là hai điểm cực trị đó. Tìm m để 2 2
x x x x  7 . 1 2 1 2 1 2 1 9 A. m   B. m   C. m  0 D. m  2  2 2
Câu 598. Cho hàm số 3 2
y  x  3mx  3m 1. Với giá trị nào của m thì đồ thị hàm số đã cho có cực đại
và cực tiểu đối xứng nhau qua đường thẳng d : x 8y  74  0. A. m  1 B. m  2  C. m  2 D. m  1  Câu 599: Hàm số 3
y x  3x có điểm cực đại là : A. (-1 ; 2) B. ( -1;0) C. (1 ; -2) D. (1;0) Biên soạn và sưu tầm 81
Câu 600: Đồ thị hàm số nào có 3 điểm cực trị A. 4 2
y x  2x 1 B. 4 2
y x  2x 1 C. 4 2
y  2x  4x 1 D. 4 2
y  x  2x 1 2
Câu 601: Giá trị của m để hàm số f(x) = x mx  2 có cực trị là mx 1 A. -1B. -1C. 0D. Số khác.
Câu 602: Khẳng định nào sau đây là đúng về hàm số 4 2
y x  4x  2 :
A. Đạt cực tiểu tại x = 0
B. Có cực đại và cực tiểu
C. Có cực đại và không có cực tiểu D. Không có cực trị. 2
x  2x  5
Câu 603: Khẳng định nào sau đây là đúng về đồ thị hàm số y  : x 1     A. y y 0 y   x   x x CD CT B. 4 CT C. 1 CD D. 3 CD CT
Câu 604. Giá trị m để hàm số : 3 2
y  mx  3mx  (m 1)x  4 không có cực trị là : 1 1 A. 0  m  B. 0  m  C. m  0  m  4 D. m  0  m  4 4 4 1 4 2 3
Câu 605. Giá trị m để hàm số : y 
x  mx  có cực tiểu mà không có cực đại là: 2 2 A. m  0 B. m  0 C. m  0 D. m  0 3 2 2
Câu 606. Cho hàm số : y  x  (2m 1)x  (m  m
3  2)x  4 có đồ thị là (C ) m . Giá trị m để (C )
m có các điểm cực đại và cực tiểu nằm về hai phía của trục tung là: A.1  m  2 B. 1  m  2 C. m  1 m  2 D. m  2 2 x  x  1
Câu 607. Cho hàm số f ( ) x  x  , mệnh đề sai là: 1 SDT: 0946798489 82
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương A. f ( )
x đạt cực đại tại x  2  B. (
M 0;1) là điểm cực tiểu C. f ( )
x có giá trị cực đại là 3  D. ( M 2  ; 2  ) là điểm cực đại
Câu 608. Điểm cực đại của đồ thị hàm số 3 2
y x  5x  7x  3 là:  7 3  2   7 32  A. 1;0 B. 0  ;1 C. ;   D. ;   .  3 27   3 27 
Câu 609. Điểm cực tiểu của đồ thị hàm số 3 2
y x  5x  7x  3 là:  7 3  2   7 32  A. 1;0 B. 0  ;1 C. ;   D. ;   .  3 27   3 27 
Câu 610. Điểm cực đại của đồ thị hàm số 3 2
y x  3x  2x là:  3 2 3   3 2 3  A. 1;0 B. 1 ;    C. 0  ;1 D. 1 ;     . 2 9   2 9  
Câu 611. Điểm cực tiểu của đồ thị hàm số 3 2
y x  3x  2x là:  3 2 3   3 2 3  A. 1;0 B. 1 ;    C. 0  ;1 D. 1 ;     . 2 9   2 9  
Câu 612. Điểm cực đại của đồ thị hàm số 3 2
y x  6x  9x là: A. 1; 4 B. 3;0 C. 0;3 D. 4  ;1 .
Câu 613. Điểm cực tiểu của đồ thị hàm số 3 2
y x  6x  9x là: A. 1; 4 B. 3;0 C. 0;3 D. 4  ;1 .
Câu 614. Điểm cực đại của đồ thị hàm số 3 2
y x x  2 là:  2 50   50 3  A. 2;0 B. ;   C. 0; 2 D. ;   .  3 27   27 2 
Câu 615 . Điểm cực tiểu của đồ thị hàm số 3 2
y x x  2 là: Biên soạn và sưu tầm 83  2 50   50 3  A. 2;0 B. ;   C. 0; 2 D. ;   .  3 27   27 2 
Câu 616. Điểm cực đại của đồ thị hàm số 3
y  3x  4x là:  1   1   1   1  A. ; 1    B.  ;1   C.  ; 1    D. ;1   .  2   2   2   2 
Câu 617. Điểm cực tiểu của đồ thị hàm số 3
y  3x  4x là:  1   1   1   1  A. ; 1    B.  ;1   C.  ; 1    D. ;1   .  2   2   2   2 
Câu 618. Điểm cực đại của đồ thị hàm số 3
y x 12x 12 là: A.  2  ;28 B. 2; 4   C. 4; 28 D.  2  ;2 .
Câu 619. Điểm cực tiểu của đồ thị hàm số 3
y x 12x 12 là: A.  2  ;28 B. 2; 4   C. 4; 28 D.  2  ;2 .
Câu 620: Cho hàm số y = –x3 + 3x2 – 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số luôn nghịch biến;
B. Hàm số luôn đồng biến;
C. Hàm số đạt cực đại tại x = 1;
D. Hàm số đạt cực tiểu tại x = 1. 2x  4
Câu 621: Trong các khẳng định sau về hàm số y 
, hãy tìm khẳng định đúng? x 1
A. Hàm số có một điểm cực trị;
B. Hàm số có một điểm cực đại và một điểm cực tiểu;
C. Hàm số đồng biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên từng khoảng xác định. 1 1
Câu 622 : Trong các khẳng định sau về hàm số 4 2
y   x  x  3 , khẳng định nào là đúng? 4 2 SDT: 0946798489 84
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
A. Hàm số đạt cực tiểu tại x = 0;
B. Hàm số đạt cực đại tại x = 1;
C. Hàm số đạt cực đại tại x = -1;
D. Cả 3 câu trên đều đúng. 1 Câu 623: Cho hàm số 3 2 y
x mx  (2m 1)x 1 . Mệnh đề nào sau đây là sai? 3 A. m
 1 thì hàm số có cực đại và cực tiểu; B. m
 1 thì hàm số có hai điểm cực trị; C. m
 1 thì hàm số có cực trị;
D. Hàm số luôn có cực đại và cực tiểu. Câu 624: Hàm số: 3
y  x  3x  4 đạt cực tiểu tại x = A. -1 B. 1 C. - 3 D. 3 1 Câu 625: Hàm số: 4 2 y
x  2x  3 đạt cực đại tại x = 2 A. 0 B.  2 C.  2 D. 2 1
Câu 626: Cho hàm số 4 2 y
x  2x 1. Hàm số có 4
A. Một cực đại và hai cực tiểu
B. Một cực tiểu và hai cực đại
C. Một cực đại và không có cực tiểu
D. Một cực tiểu và một cực đại
Câu 627: Cho hàm số y = x3 - 3x2 + 1. Tích các giá trị cực đại và cực tiểu của hàm số bằng A. 6 B. -3 C. 0 D. 3
Câu 628: Cho hàm số y = f(x) = ax3 + bx2 + cx + d, a  0 . Khẳng định nào sau đây sai ?
A. Đồ thị hàm số luôn cắt trục hoành
B. Hàm số luôn có cực trị
C. lim f (x)  
D. Đồ thị hàm số luôn có tâm đối xứng. x Câu 629: Hàm số 3
y x mx 1 có 2 cực trị khi : A. m  0 B. m  0 C. m  0 D. m  0 Biên soạn và sưu tầm 85
Câu 630: Đồ thị hàm số 3
y x  3x 1 có điểm cực tiểu là: A. ( -1 ; -1 ) B. ( -1 ; 3 ) C. ( -1 ; 1 ) D. ( 1 ; 3 )
Câu 631: Đồ thị hàm số nào sau đây có 3 điểm cực trị: A. 4 2
y x  2x 1 B. 4 2
y x  2x 1 C. 4 2
y  2x  4x 1 D. 4 2 y  2
x  4x 1 Câu 632: Hàm số 3 2
y x  3x mx đạt cực tiểu tại x = 2 khi: A. m  0 B. m  0 C. m  0 D. m  0
Câu 633: Khẳng định nào sau đây là đúng về hàm số 4 2
y x  4x  2 :
A. Đạt cực tiểu tại x = 0
B. Có cực đại và cực tiểu
C. Có cực đại và không có cực tiểu D. Không có cực trị. 2
x  2x  5
Câu 634: Khẳng định nào sau đây là đúng về đồ thị hàm số y  : x 1     A. y y 0 y   x   x x CD CT B. 4 CT C. 1 CD D. 3 CD CT 1
Câu 635: Đồ thị hàm số: 3 2 y
x  2x  5x 17 có tích hoành độ các điểm cực trị bằng 3 A. 5 B. 8 C. -5 D. -8 1
Câu 636: Số điểm cực trị của hàm số 3
y   x x  7 là 3 A. 1 B. 0 C. 3 D. 2
Câu 637: Số điểm cực đại của hàm số 4
y x 100 là A. 0 B. 1 C. 2 D. 3 Câu 638: Hàm số 3
y x mx 1 có 2 cực trị khi A. m  0 B. m  0 C. m  0 D. m  0 SDT: 0946798489 86
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 4 2
Câu 639: Số cực trị của hàm số y x  3x  3 là: A. 4 B. 2 C. 3 D. 1
Câu 640: Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số 3 2
y x  3x  4 là: A. 2 5 B. 4 5 C. 6 5 D. 8 5 Câu 641: Hàm số 3 2
y x  3mx  3x  2m  3 không có cực đại, cực tiểu với m A. m  1 B. m  1 C. 1   m 1 D. m  1   m 1 Câu 642: Hàm số 4
y mx  m   2
3 x  2m 1 chỉ có cực đại mà không có cực tiểu với m: A. m  3 B m  0 C. 3   m  0
D. m  0  m  3 Câu 643: Hàm số 3 2
y x mx  3m  
1 x 1 đạt cực đại tại x = 1 với m bằng : A. m = - 1 B. m  3  C. m  3  D. m = - 6
Câu 645. Điểm cực đại của đồ thị hàm số 3 2
y x x  2 là:  2 50   50 3  A. 2;0 B. ;   C. 0; 2 D. ;   .  3 27   27 2  1
Câu 646: Cho hàm số 3 2
y  x  m x  2m  
1 x 1 . Mệnh đề nào sau đây là sai? 3 A. m
 1 thì hàm số có hai điểm cực trị; B. m
 1 thì hàm số có cực đại và cực tiểu;
C. Hàm số luôn có cực đại và cực tiểu. D. m
 1 thì hàm số có cực trị;
Câu 647: Trong các mệnh đề sau hãy tìm mệnh đề sai. Chọn 1 câu sai A. Hàm số 3
y  x  3 2
x 1 có cực đại và cực tiểu. B. Hàm số 3
y x  3x  2 có cực trị 1 C. Hàm số y  2  x 1 không có cực trị x  2 Biên soạn và sưu tầm 87 1
D. Hàm số y x 1  có hai cực trị x  1
Câu 648: Hàm số y  2 3 x  9 2
x 12x  5 có mấy điểm cực trị?. Chọn 1 câu đúng. A. 1 B. 2 C. 3 D. 4 Câu 649: Hàm số 4 2
y x x có điểm cực trị bằng. Chọn 1 câu đúng. A. 0 B. 1 C. 2 D. 3
Câu 650: Giá trị của m để hàm số 3 2
y x x mx  5 có cực trị là. Chọn 1 câu đúng. 1 1 1 1 A. m  B. m  C. m  D. m  3 3 3 3
x2  mx  2m 1
Câu 651: Giá trị của m để hàm số y
có cực trị là. Chọn 1 câu đúng. x 1 1 1 1 A. m  B. m  C. m  D. m  2 2 2 2
Câu 652: Giá trị của m để hàm số y  x3  2x2  mx đạt cực tiểu tại x = - 1 là . A. m  1  B. m  1  C. m  1  D. m  1 
Câu 653: Cho hàm số 3
y  x  3 2
x  3x 1. Mệnh đề nào sau đây là đúng? Chọn 1 câu đúng.
A. Hàm số luôn nghịch biến.
B. Hàm số luôn đồng biến.
C. Hàm số đạt cực đại tại x = 1.
C. Hàm số đạt cực tiểu tại x = 1 .
Câu 654: Cho hàm số 3 2
y  x  3x  3x 1. Mệnh đề nào sau đây là đúng?
A. Hàm số luôn nghịch biến;
B. Hàm số luôn đồng biến;
C. Hàm số đạt cực đại tại x = 1;
D. Hàm số đạt cực tiểu tại x = 1; 1 1
Câu 655: Câu 5: Trong hàm số 4 2 y   x
x  3 , khẳng định nào đúng? 4 2
A. Hàm số có điểm cực tiểu là x = 0; B . Hàm số có cực tiểu là x=1 và x=-1 SDT: 0946798489 88
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
C. Hàm số có điểm cực đại là x = 0
D. Hàm số có cực tiểu là x=0 và x= Câu 656 Hàm số 3 2
y x  3x mx đạt cực tiểu tại x = 2 khi: A. m  0 B. 0  m  4 C. 0  m  4 D. m  4 2 x x 1
Câu 657: Cho hàm số f (x)
. Trong các mệnh đề sau, tìm mệnh đề sai: x 1
A. f(x) đạt cực đại tại x 2
B. M (0 ;1) là điểm cực tiểu 0
C. N ( 3 ; 2) là điểm cực đại
D. f(x) có giá trị cực đại là 3 0 2 x x 1
Câu 658: Hàm số f (x)
có bao nhiêu điểm cực trị ? x 1 A. 0 B. 1 C. 2 D. 3 4 x Câu 659: Hàm số 2 f (x) 2x
6 có bao nhiêu điểm cực tiểu ? 4 A. 0 B. 1 C. 2 D. 3 Câu 660: Hàm số 4 2 f (x) x 6x
8x 1 có bao nhiêu điểm cực trị ? A. 0 B. 1 C. 2 D. 3 2 x mx 2
Câu 661: Tìm m để hàm số sau đây có cực trị: f (x) mx 1 m 0 A. 3 3 B. 1 m 0 C. 0 < m < 1 D. m m 3 3
Câu 662: Cho hàm số: 3 2 2 f (x) x 3mx 3(m
1)x . Tìm m để f(x) đạt cực đại tại x0 = 1 A. m = 2 B. m = 0 C. m = 0 hay m = 2 D. m 0 va m 2
Câu 663: Hàm số y
x có bao nhiêu điểm cực trị ? Biên soạn và sưu tầm 89 A. 0 B. 1 C. 2 D. 3 2 x 2x m
Câu 664: Tìm m để hàm số sau đây luôn có một cực đại và một cực tiểu: f (x) x 1 A. m 3 B. m 3 C. m 3 D. m 3 va m 0 x x e e
Câu 665: Hàm số: y
có bao nhiêu điểm cực đại ? 2 A. 0 B. 1 C. 2 D. 3 Câu 666: Hàm số: 5 4 y
x có bao nhiêu điểm cực đại ? A. 0 B. 1 C. 2 D. 3
Câu 667: Cho hàm số: 3 2 y x 2x
x 9 . Trong các mệnh đề sau, tìm mệnh đề sai:
A. (C) có 1 cực đại và 1 cực tiểu
B. (C) có 1 điểm uốn
C. Điểm uốn là trung điểm của đoạn thẳng nối cực đại và cực tiểu
D. (C) là một đường cong lồi 4 Câu 668: Cho: 3 2 y x 2(1 sin )x
(1 cos 2 )x . Với giá trị nào của x thì hàm số có cực trị: 3 A. x k B. x k 2 C. x k 2 D. x 2 2
Câu 669: Cho đồ thị (C): 4 2 y x
2x . Trong các mệnh đề sau, mệnh đề nào sai:
A. (C) có 3 điểm cực trị
B. (C) có 1 điểm uốn
C. (C) có 1 trục đối xứng
D. (C) có 1 tâm đối xứng
Câu 670: Cho đồ thị (C): 4 2 y x x
2 . Trong các mệnh đề sau, mệnh đề nào đúng:
A. (C) có 3 điểm cực trị
B. (C) có 1 trục đối xứng
C. (C) có 2 điểm uốn
D. (C) có 1 tâm đối xứng SDT: 0946798489 90
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương
Câu 671: Cho hàm số: 4 2 y (1 ) m x mx
2m 1. Tìm m để đồ thị hàm số có đúng một cực trị A. m 0 m 1 B. m 0 m 1 C. m < 0 D. m > 1
Câu 672: Đồ thị hàm số: 4 2 y x x 2 có bao nhiêu cực trị: A. 0 B. 1 C. 2 D. 3
Câu 673: Cho đồ thị (C): 4 2 y x 2x
1. Viết phương trình tiếp tuyến với (C) tại điểm cực đại A. x = 0 B. x = 1 C. y = 1 D. y = 0
Câu 674: Cho đồ thị (C): 4 2 y x 4x
1. Viết ph.trình đường thẳng đi qua 2 điểm cực tiểu của (C). A. x 2 B. y 3 C. y = 1 D. x 3 2 x mx 2
Câu 675: Với giá trị nào của m thì hàm số sau có cực trị: y mx 1 A. m 0 B. 1 m 1 C. 1 m 1 D. 1 m 1 và m 0
Câu 676: Với giá trị nào của m thì hàm số 3 2 y  x m  2 x m
 3x 1 có cực đại và cực tiểu ? m  0 9  A. 0  m B. m C. 9 D. m > 2 4 m   4
Câu 677: Hàm số y   x  2 2 1 có :
A. chỉ có 1 cực đại
B. 1 cực tiểu, 2 cực đại
C. 1 cực đại , 2 cực tiểu
D. chỉ có 1 cực tiểu 1 7 Câu 678: Hàm số 4 2 y x  3x 
có bao nhiêu điểm cực trị ? 2 2 A. 2 B. 3 C. 1 D. 0 Biên soạn và sưu tầm 91
Câu 679: Với tất cả các giá trị nào của m thì hàm số 4 y m  m   2 x
1 x 1 2m chỉ có một cực trị ? m  0 A. m  1 B. m  0 C. 0  m 1 D. m 1 Câu 680: Hàm số 4 2
y  x  3x 1 có :
A. Một cực tiểu duy nhất
B. Một cực đại duy nhất
C. Một cực tiểu và hai cực đại
D. Một cực đại và hai cực tiểu 3 x
Câu 681: Với giá trị nào của m thì hàm số 2 y   m   2 x m m  
1 x 1 đạt cực tiểu tại x = 1 ? 3 A. 1 B. không có m C. 2 D. 3
Câu 682: Đồ thị hàm số nào sau đây không có cực trị ? 2x  2 2 x x  3 A. y B. y y    x 1 x C. cả ba câu A, B, C D. 3 2x 1 2
Câu 683: Đồ thị của hàm số nào dưới đây có điểm cực tiểu (0; - 2 ) và cắt trục hoành tại hai điểm có hoành độ x = 1; x = - 1 . A. 4 2
y x  2x 1 B. 4 2
y x x  2 C. 4 2
y x  3x  4 D. 4 2
y x  3x  2
Câu 684: Đồ thị hàm số 4 2
y x x 1 có bao nhiêu điểm cực trị có tung độ dương ? A. 2 B. 3 C. 4 D. 1
Câu 685: Cho hàm số 4 2
y x  2x  2 . Khoảng cách giữa hai điểm cực trị của hàm số bằng : A. 7 B. 3 C. 5 D. 2
Câu 686: Cho hàm số 3 2
y x  3x  2 . Câu nào sau đây đúng ?
A. Hàm số có cực đại và cực tiểu
B. Hàm số chỉ có cực tiểu
C. Hàm số không có cực trị.
D. Hàm số chỉ có cực đại
Câu 687: Đồ thị hàm số 3 2
y x  3x  2 có khoảng cách giữa hai điểm cực trị bằng : SDT: 0946798489 92
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương A. 4 B. 2 C. 20 D. 2 5 1
Câu 688: Với giá trị nào của m thì thì hàm số 3 2 y x  x m   2
m m  2 x 1 đạt cực tiểu tại điểm x = 3 0 ? A. 0 B. 1 C. – 1 D. 2
Thầy Nguyễn Bảo Vương ( Câu 1 – 59) 3 2 2 3 2
Câu 1. Cho hàm số y  x  m
3 x  3(1 m )x  m  m (1)
Viết phương trình đường thẳng qua hai điểm cực trị của đồ thị hàm số (1). A. y  x  m2 2  m 1 B. y  x  m2 2  m C. y  x  m2 2 D. y  x  m2 2  2m 3 2
Câu 2. Cho hàm số y  x  3x  mx  m  2 (m là tham số) có đồ thị là (Cm).
Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành. A. m  2 B. m  3 C. m  3 D. m  2 3 2 2
Câu 3. Cho hàm số y  x  (2m 1)x  (m  m
3  2)x  4 (m là tham số) có đồ thị là (Cm).
Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía của trục tung. A. 1  m  3 B. 1 m  2 C. 1  m  2 D. 1  m  4 1 3 2
Câu 4. Cho hàm số y  x  mx  (2m1)x  3 3
(m là tham số) có đồ thị là (Cm).
Xác định m để (Cm) có các điểm cực đại, cực tiểu nằm về cùng một phía đối với trục tung. m   1 m    1 m  1 m  1 A. m 1 1  B.  C.    m  0  m  3 D. m  1  2  2 3 2
Câu 5. Cho hàm số y  x  3x  mx  2 (m là tham số) có đồ thị là (Cm).
Xác định m để (Cm) có các điểm cực đại và cực tiểu cách đều đường thẳng y  x 1. Biên soạn và sưu tầm 93 A. m  1 B. m  1 C. m  2 D. m  0 3 2 3
Câu 6. Cho hàm số y  x  m
3 x  4m (m là tham số) có đồ thị là (Cm).
Xác định m để (Cm) có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng y = x. A. m 2   m 0 m 2 m 3 2 B.  C.   4 D.   2 3 2
Câu 7. Cho hàm số y  x  m 3 x  m 3 1 .
Với giá trị nào của m thì đồ thị hàm số có điểm cực đại và điểm cực tiểu đối xứng với nhau qua đường
thẳng d: x  8y  74  0 . A. m  2 B. m  3 C. m  2 D. m  3 3 2
Câu 8. Cho hàm số y  x  3x  mx (1).
Với giá trị nào của m thì đồ thị hàm số (1) có các điểm cực đại và điểm cực tiểu đối xứng với nhau qua
đường thẳng d: x  2y 5  0 . A. m  1 B. m  2  C. m  0 D. m  1  3 2
Câu 9. Cho hàm số y  x  3(m 1)x  9x  m  2 (1) có đồ thị là (Cm).
Với giá trị nào của m thì đồ thị hàm số có điểm cực đại và điểm cực tiểu đối xứng với nhau qua đường 1 thẳng d: y  x 2 . A. m  1 B. m  0 C. m  2 D. m  1 3 2
Câu 10. Cho hàm số y  x  3(m 1)x  9x  m , với m là tham số thực.
Xác định m để hàm số đã cho đạt cực trị tại x , x 1 2 sao cho x  x 1 2  2 . m  1 3 A.  B. 3  m  1 C. 3   m  1   3 và 1   3  m 1. D. m   m  1 3 SDT: 0946798489 94
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 3 2
Câu 11. Cho hàm số y  x  (1 2m)x  (2  m)x  m  2 , với m là tham số thực. 1
Xác định m để hàm số đã cho đạt cực trị tại x , x 1 2 sao cho x  x 1 2  3 . m 5  3  29 3  29 3  29 A.  m   m     1   4 B. 8 8 C. m m 8 D. m   m  1 1 3 2
Câu 12. Cho hàm số y  x  mx  mx 1 3
, với m là tham số thực.
Xác định m để hàm số đã cho đạt cực trị tại x , x 1 2 sao cho x  x 1 2  8 .  m 1 65  1 65 1 65 A. 2  B. m   C.  m  m 2  2 2 D.  m 1 65   2 1 3 2 1
Câu 13. Cho hàm số y 
x (m1)x  3(m 2)x  3
3 , với m là tham số thực.
Xác định m để hàm số đã cho đạt cực trị tại x , x 1 2 sao cho x  2x 1 2  1 .       A. m 4 34  m 0 m 4 34  m 6 34  4 B.  C. 2 D. 4 3 2
Câu 14. Cho hàm số y  4x  mx  3x .
Tìm m để hàm số có hai điểm cực trị x , x 1 2 thỏa x  4  x 1 2 . A. m 9   m 3 m 9 m 5 2 B.   2 C.   4 D.   2 1 3 2
Câu 15. Cho hàm số y  x  ax  ax 3  4 3 (1) (a là tham số). Biên soạn và sưu tầm 95
Tìm a để hàm số (1) đạt cực trị tại x1, x2 phân biệt và thoả mãn điều kiện: x 2  2ax  9a a2 1 2   2 a2 x 2  2ax  9a 2 1 A. a  4 B. a  2 C. a  6 D.  a  0 3 2 2
Câu 16. Cho hàm số y  2x  9mx 12m x 1 (m là tham số). 2
Tìm các giá trị của m để hàm số có cực đại tại xCĐ, cực tiểu tại x x  x CT thỏa mãn: CÑ CT . A. m  1 B. m  2  C. m  6 D. m  3 3 2
Câu 17. Cho hàm số y  (m  2)x  3x  mx  5 , m là tham số.
Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương. A. 3  m  2 B. 2  m  2 C. 3  m  1 D. 3  m  2 1 3 1 2 2
Câu 18. Cho hàm số y  x  mx  (m  3)x 3 2 (1), m là tham số. A. m  2 B. m 14  m 14 m 14 2 C.   2 D.   2 3 2
Câu 19. Cho hàm số y  x  (1 2m)x  (2  m)x  m  2 (m là tham số) (1).
Tìm các giá trị của m để đồ thị hàm số (1) có điểm cực đại, điểm cực tiểu, đồng thời hoành độ của
điểm cực tiểu nhỏ hơn 1. 5 7 5 7 5 7 5 7 A.  m  m m   2 5 B.   4 3 C.   4 2 D. m 4 5 m 3 2
Câu 20. Cho hàm số y 
x  (m 2)x  (m1)x  2 3 (Cm).
Tìm m để hàm số có cực đại tại x1, cực tiểu tại x2 thỏa mãn x  x 1 2  1 . SDT: 0946798489 96
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 3 4 1 4 5 5 4 A.  m  m m 2 m 4 3 B.   4 3 C.   4 D.   4 3 Câu 21. Cho hàm số 3 2
y x  (1 2 ) m x  (2  )
m x m  2 (Cm).
Tìm m để hàm số có ít nhất 1 điểm cực trị có hoành độ thuộc khoảng ( 2  ;0) . 10 5   A.   m  1 m 2 m 1 m 5   ; 1      2; 7 B.  C.     3 D.    3  3 2
Câu 22. Cho hàm số y  x  3x  2 (1)
Tìm điểm M thuộc đường thẳng d: y  3x  2 sao tổng khoảng cách từ M tới hai điểm cực trị nhỏ nhất.         A. M 4 3  ;    C. M 2 4  ;  D. M 4 6  ;   5 5 B. M 4 2 ;   5 5   3 5   5 5  3 2 2 3
Câu 23. Cho hàm số y  x  m
3 x  3(m 1)x  m  m (1)
Tìm m để hàm số (1) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa
độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O. m  3  2 2 m  3  2 2 m  4  2 2 A. m  2 B.  C.  D.  m  3  2 2 m  3  2 2 m  4  2 2 3 2
Câu 24. Cho hàm số y  x  3x  mx  2 có đồ thị là (Cm).
Tìm m để (Cm) có các điểm cực đại, cực tiểu và đường thẳng đi qua các điểm cực trị song song với đường thẳng d: y  4  x  3. A. m  2 B. m  3 C. m  2 D. m  3 3 2
Câu 25. Cho hàm số y  x  mx  7x  3 có đồ thị là (Cm).
Tìm m để (Cm) có các điểm cực đại, cực tiểu và đường thẳng đi qua các điểm cực trị vuông góc với
đường thẳng d: y  3x  7 . A. m 3 10   m 10   m 5 10 4 B.   2 C. m 3 10 2 D.   2 3 2
Câu 26. Cho hàm số y  x  3x  mx  2 có đồ thị là (Cm). Biên soạn và sưu tầm 97
Tìm m để (Cm) có các điểm cực đại, cực tiểu và đường thẳng đi qua các điểm cực trị tạo với đường 0
thẳng d: x  4y  5  0 một góc a  45 .  39  m    39 A. m 1    10 2 B. m 3 15 m   2 C.  D. m 1   10  2 3 2
Câu 27. Cho hàm số y  x  3x  2 (C).
Tìm m để đường thẳng đi qua hai điểm cực trị của (C) tiếp xúc với đường tròn (S) có phương trình x  m 2  y m 2 ( ) ( 1)  5 .   A. m  m 4 2;  m 4  m 2 m 0 3 B. 3 C.  D.  3
Câu 28. Cho hàm số y  x  m 3 x  2 ( m C ) .
Tìm m để đường thẳng đi qua điểm cực đại, cực tiểu của Cmcắt đường tròn tâm I(1;1) , bán kính bằng
1 tại hai điểm phân biệt A, B sao cho diện tích IAB đạt giá trị lớn nhất .     A. m 3 3  m 2 3  m 1 3  m 2 3  2 B. 4 C. 2 D. 2 3 2
Câu 29. Cho hàm số y  x  6mx  9x  2m (1), với m là tham số thực.
Tìm m để đồ thị hàm số (1) có hai điểm cực trị sao cho khoảng cách từ gốc toạ độ O đến đường thẳng 4
đi qua hai điểm cực trị bằng . 5 A. m 37     m 2 m 0 8 B. m 1 C.   D.  3 2
Câu 30. Cho hàm số y  x  3x  (m  6)x  m  2 (1), với m là tham số thực.
Tìm m để đồ thị hàm số (1) có hai điểm cực trị sao cho khoảng cách từ điểm A(1; 4
 ) đến đường thẳng SDT: 0946798489 98
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 12
đi qua hai điểm cực trị bằng 265 m  1 m  1 m  2 m  1 A.  1053 B.  1053 C.  1053 D.  1053 m  m  m  m   12  24  249  249 3 2
Câu 31. Cho hàm số y  x  3x  mx 1 (1), với m là tham số thực.  
Tìm m để đồ thị hàm số (1) có hai điểm cực trị sao cho khoảng cách từ điểm I 1 11  ;
2 4  đến đường thẳng  
đi qua hai điểm cực trị là lớn nhất. A. m  1 B. m  0 C. m  1 D. m  2 2 2 3
Câu 32. Cho hàm số y  2x  3(m 1)x  6mx  m .
Tìm m để đồ thị hàm số có hai điểm cực trị A, B sao cho AB  2 . A. m  0 B. m  0; m  2 C. m  1 D. m  2 3 2 2 3
Câu 33. Cho hàm số y  x  m
3 x  3(m 1)x  m  4m1 (1)
Tìm m để đồ thị của hàm số (1) có hai điểm cực trị A, B sao cho OAB vuông tại O. m  1 m  1 m  1 m  1 A. m  2 B. m  2 C. m  2 D. m  2 2 2 3
Câu 34. Cho hàm số y  2x  3(m 1)x  6mx  m (1)
Tìm m để đồ thị của hàm số (1) có hai điểm cực trị A, B sao cho tam giác ABC vuông tại C, với C(4;0) . A. m  1  B. m  2 C. m  3 D. m  1 3 2
Câu 35. Cho hàm số y  x  3x  m (1) 0
Xác định m để đồ thị của hàm số (1) có hai điểm cực trị A, B sao cho AOB  120 .        A. m 12 2 3  m 12 2 3  m 12 2 3  m 12 2 3  5 B. 3 C. 3 D. 3 Biên soạn và sưu tầm 99 3 2 2
Câu 36. Cho hàm số y  x  3x  m  m 1 (1)
Tìm m để đồ thị hàm số (1) có hai điểm cực đại, cực tiểu là A và B sao cho diện tích tam giác ABC
bằng 7, với điểm C(–2; 4 ). m  3 m  3 m  3 m  3 A.   m  2 B. m  2 C. m  2 D. m  2 3 2
Câu 37. Cho hàm số y  x  3(m 1)x 12mx  m 3  4 (C)  
Tìm m để hàm số có hai cực trị là A và B sao cho hai điểm này cùng với điểm C 9 1;    2  lập thành tam  
giác nhận gốc tọa độ O làm trọng tâm. A. m 1   m 1 m 0 m 3 3 B.   2 C.  D.   2 3 2
Câu 38. Cho hàm số y  f (x)  2x  3(m  3)x 11 m 3 ( Cm ). Tìm m để C
( m) có hai điểm cực trị M ,M 1 2 sao cho các điểm M , M 1
2 và B(0; –1) thẳng hàng. A. m  1 B. m  4 C. m  1 D. m  4 1 3 2 2
Câu 39. Cho hàm số y 
x  mx  (m 1)x 1 ( m C ) 3 .
Tìm m để hàm số có cực đại, cực tiểu và C y Ñ  C y T  2. 1 m  0 A.  m  C. 1   m  0 D. m  1  m 1 B. 1 1 3 2 4 3
Câu 40. Cho hàm số y  x  (m1)x  (m1) 3 3 (1) (m là tham số thực).
Tìm m để các điểm cực đại và cực tiểu của đồ thị (1) nằm về 2 phía (phía trong và phía ngoài) của
đường tròn có phương trình (C): x2  y2  4x  3  0 . SDT: 0946798489 100
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương 3 3 1 1 A. m  1  B.   m  m 3    2 2 C.  D. m 2 2 1 3 2
Câu 41. Cho hàm số y  x  mx  x  m1 C ( m) 3 .
Tìm m để đồ thị (Cm) có 2 điểm cực trị và khoảng cách giữa 2 điểm cực trị là nhỏ nhất A. m  1 B. m  0 C. m  1 D. m  12 3 2
Câu 42. Cho hàm số y  x  3x  mx  2 (1) .
Tìm m để hàm số (1) có 2 cực trị và đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số tạo với hai
trục toạ độ một tam giác cân. A. m 3   m 3 m 5 m 7 2 B.   4 C.   2 D.   2 1 3 2 2
Câu 43. Cho hàm số : y =
x  mx  (m  m1)x 1 3 (1).
Tìm m để hàm số có cực trị trong khoảng ( ;  1) . A. 1  m  2 B. m  1 C. m  0 D. m  2 1 3 2 2
Câu 44. Cho hàm số : y =
x  mx  (m  m1)x 1 3 (1).
Tìm m để hàm số có cực trị trong khoảng (1; )  . A. m  1 B. m  2 C. m  1 D. m  2 1 3 2 2
Câu 45. Cho hàm số : y =
x  mx  (m  m1)x 1 3 (1).
Tìm m để hàm số có hai cực trị x , x 1 2 thoả mãn x  1  x 1 2 . m  2 A. 1  m  2 B. m  2 C. 1  m D. m 1 Biên soạn và sưu tầm 101 1 3 2 2
Câu 46. Cho hàm số : y =
x  mx  (m  m1)x 1 3 (1).
Tìm m để hàm số có hai cực trị x , x 1 2 thoả mãn x  x 1 2  1 . A. m  1 B. m  C. m  3 D. 1  m  3 1 3 2 2
Câu 47. Cho hàm số : y =
x  mx  (m  m1)x 1 3 (1).
Tìm m để hàm số có hai cực trị x , x 1 2 thoả mãn 1  x  x 1 2 . A. m  3 B. m  2 C. m  2 D. m  3 4 2 2
Câu 48. Cho hàm số y  x  2(m  m 1)x  m 1 .
Tìm m để đồ thị (C) có khoảng cách giữa hai điểm cực tiểu ngắn nhất. 1 1 3 3 A. m   B. m  C. m  D. m   2 2 2 2 1 4 2 3
Câu 49. Cho hàm số y  x  mx  2 2 (1)
Xác định m để đồ thị của hàm số (1) có cực tiểu mà không có cực đại. A. m  0 B. m  0 C. m  0 D. m  0 4 2
Câu 50. Cho hàm số y  x  2mx  4 C ( m).
Tìm các giá trị của m để tất cả các điểm cực trị của C
( m) đều nằm trên các trục toạ độ. A. m  0 B. m  2 C. m  0
D. m  0, m  2 4 2
Câu 51. Cho hàm số y  x  ( m
3 1)x 3 (với m là tham số).
Tìm tất cả các giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác cân sao cho độ 2
dài cạnh đáy bằng 3 lần độ dài cạnh bên. SDT: 0946798489 102
747 Bài tập trắc nghiệm cực trị hàm số
Giáo viên: Nguyễn Bảo Vương A. m 5   m 5 m 4 m 4 3 B.  3 C.   3 D.  3 4 2 2
Câu 52. Cho hàm số y  f (x)  x  2(m  2)x  m  m 5  5 C ( m).
Tìm các giá trị của m để đồ thị C
( m) của hàm số có các điểm cực đại, cực tiểu tạo thành 1 tam giác vuông cân. A. m  2 B. m  1 C. m  2  D. m  1  4 2 2
Câu 53. Cho hàm số y  x  2(m  2)x  m  m 5  5  m C 
Với những giá trị nào của m thì đồ thị (Cm) có điểm cực đại và điểm cực tiểu, đồng thời các điểm cực
đại và điểm cực tiểu lập thành một tam giác đều. 3 3 A. m 3  2  3 B. m  1 m 3 4 3  2 C.   D. m 3 3 4 2 4
Câu 54. Cho hàm số y  x  2mx  2m  m có đồ thị (Cm) .
Với những giá trị nào của m thì đồ thị (Cm) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành
một tam giác có diện tích S  4 . 3 3 1 A. m 5  16 B. m  1 m 5 16  2 C.   3 D. m 3 3 4 2 2
Câu 55. Cho hàm số y  x  2mx  m  m có đồ thị (Cm) .
Với những giá trị nào của m thì đồ thị (Cm) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành 0
một tam giác có một góc bằng 120 . 1 A. m   m 3 4 3  3 B.   C. m  0 D. m 3 3 3 4 2
Câu 56. Cho hàm số y  x  2mx  m 1 có đồ thị (Cm) .
Với những giá trị nào của m thì đồ thị (Cm) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành
một tam giác có bán kính đường tròn ngoại tiếp bằng 1 .         A. m  m 1 5 2,  m  m 1 5 1,  m  m 1 5 0,    2 B. 2 C. 2 D. m m 1 5 1, 2 Biên soạn và sưu tầm 103 4 2
Câu 57. Cho hàm số y  x  2mx  2 (Cm).
Tìm các giá trị của m để (Cm) có 3 điểm cực trị tạo thành một tam giác có đường tròn ngoại tiếp đi   qua điểm D 3 9  ; 5 5  .   A. m  1 B. m  1 C. m  2 D. m  2 4 2 2
Câu 58. Cho hàm số y  x  2(1 m )x  m 1 (Cm).
Tìm m để đồ thị (Cm) có 3 điểm cực trị tạo thành một tam giác có diện tích lớn nhất. A. m  2 B. m  0 C. m  1 D. m  1 1 4 2
Câu 59. Cho hàm số y  x  ( m 3 1)x  2(m1) 4 (Cm).
Tìm m để đồ thị (Cm) có 3 điểm cực trị tạo thành một tam giác có trọng tâm là gốc toạ độ O. 2 1 A. m   ; m  B. m 1  C. m 2   D. m  0 3 3 3 3
Chúc các bạn học tốt. Tổng tài liệu gòm có 747 câu cực trị….được tôi sưu tầm và biên soạn. SDT: 0946798489 104