







Preview text:
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều CHƯƠNG 5 ĐƯỜNG TRÒN BÀI 1 ĐƯỜNG TRÒN
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN
1. Khái niệm đường tròn
Trong mặt phẳng, đường tròn tâm O bán kính R (với R 0 ) là tập hợp các điểm cách điểm O cố
định một khoảng R , kí hiệu là: O; R R O Chú ý:
Một đường tròn hoàn toàn xác định khi biết tâm và bán kính.
Khi không chú ý đến bán kính của đường tròn O; R , ta cũng có thể kí hiệu đường trònO .
Vị trí tương đối của một điểm đối với đường tròn Nhận xét:
Điểm M nằm trên đường tròn O nếu OM R
Điểm M nằm trong đường tròn O nếu OM R
Điểm M nằm ngoài đường tròn O nếu OM R
2. Tính chất đối xứng của đường tròn
Đường tròn là hình có tâm đối xứng: Tâm của đường tròn là tâm đối
xứng của đường tròn đó A A' O
Đường tròn là hình có trục đối xứng: Bất kì đường kính nào cũng là
trục đối xứng của đường tròn đó.
3. Liên hệ giữa đường kính và dây của đường tròn
Đoạn thẳng nối hai điểm phân biệt thuộc đường tròn được gọi là dây (hay dây cung) của đường tròn.
Dây đi qua tâm là đường kính của đường tròn. Trong các dây của đường tròn, dây lớn nhất là đường
kính của đường tròn đó
https://www.facebook.com/truongngocvy8/ T r an
g 1 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều
4. Vị trí của hai đường tròn
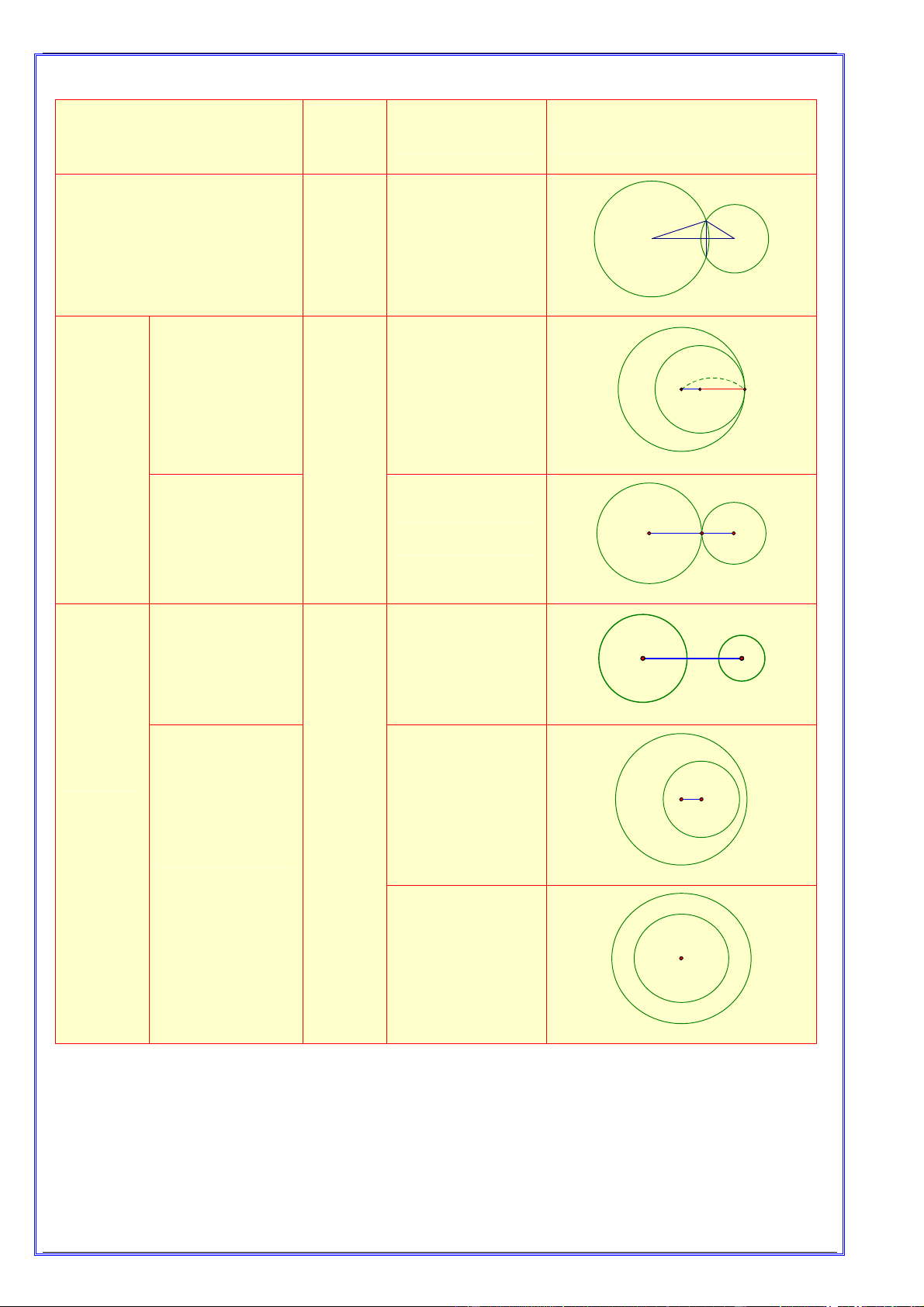
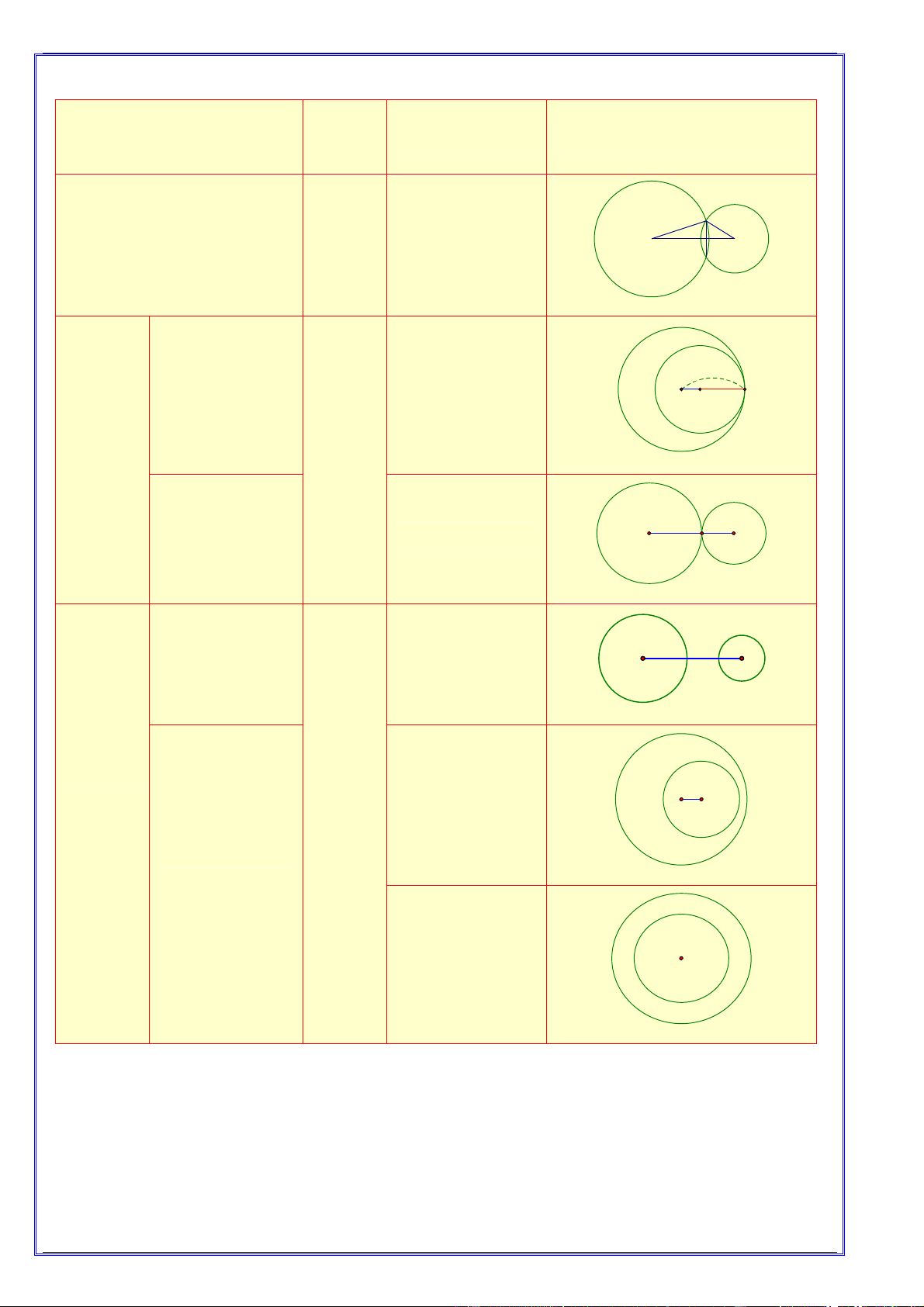
Vị trí tương đối của hai đường Số điểm Hệ thức Hình vẽ
tròn O; R và O '; r R r chung
R r OO ' R r R r Cắt nhau 2 O O' R Tiếp xúc trong
OO ' R r 0 O O' r Tiếp xúc 1 Tiếp xúc ngoài
OO ' R r R r O O' R r Ngoài nhau
OO ' R r Không cắt
0 OO ' R r O O' 0 nhau Đựng nhau O' OO ' O O Chú ý:
Đường nối tâm (đường thẳng đi qua tâm 2 đường tròn) là trục đối xứng của hình tạo bởi hai đường tròn.
Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
Nếu hai đường tròn cắt nhau thì đường nối tâm là đường trung trực của dây chung.
https://www.facebook.com/truongngocvy8/ T r an
g 2 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều DẠNG 1
CHỨNG MINH CÁC ĐIỂM CHO TRƯỚC CÙNG NẰM TRÊN MỘT ĐƯỜNG TRÒN
TÍNH BÁN KÍNH ĐƯỜNG TRÒN Phương pháp
Cách 1: Chứng minh các điểm cho trước cùng cách đều 1 điểm cho trước nào đó. Cách 2: Nếu 0
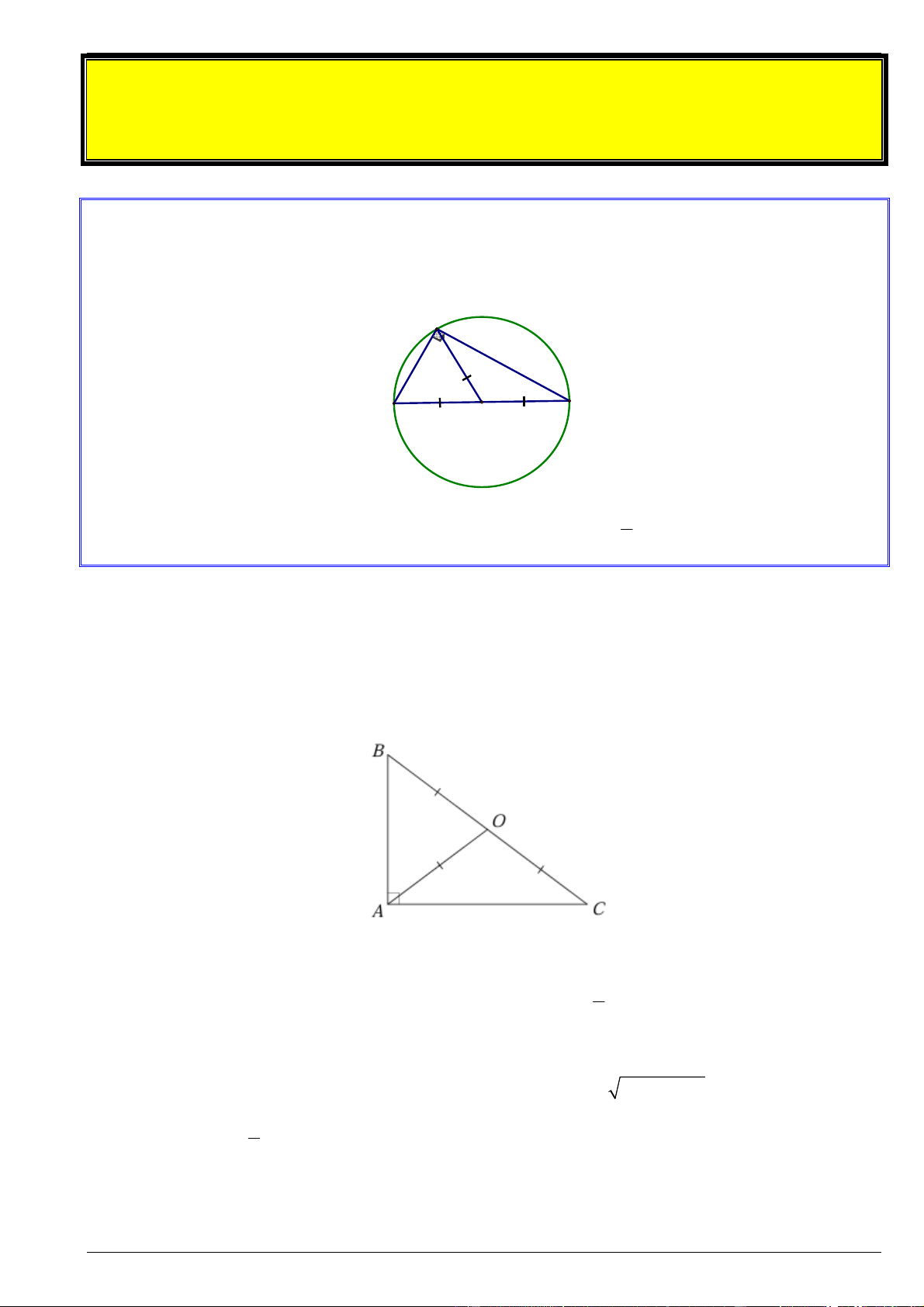
BAC 90 thì A thuộc đường tròn đường kính BC . A C B O 1
Xét tam giác vuông ABC , có AO là đường trung tuyến nên AO BC AO OB OC 2
Bài 1. Cho tam giác ABC vuông ở A có AB 5c , m AC 12cm . a) Chứng minh ba điểm ,
A B,C cùng thuộc một đường tròn.
b) Tính bán kính của đường tròn đó.
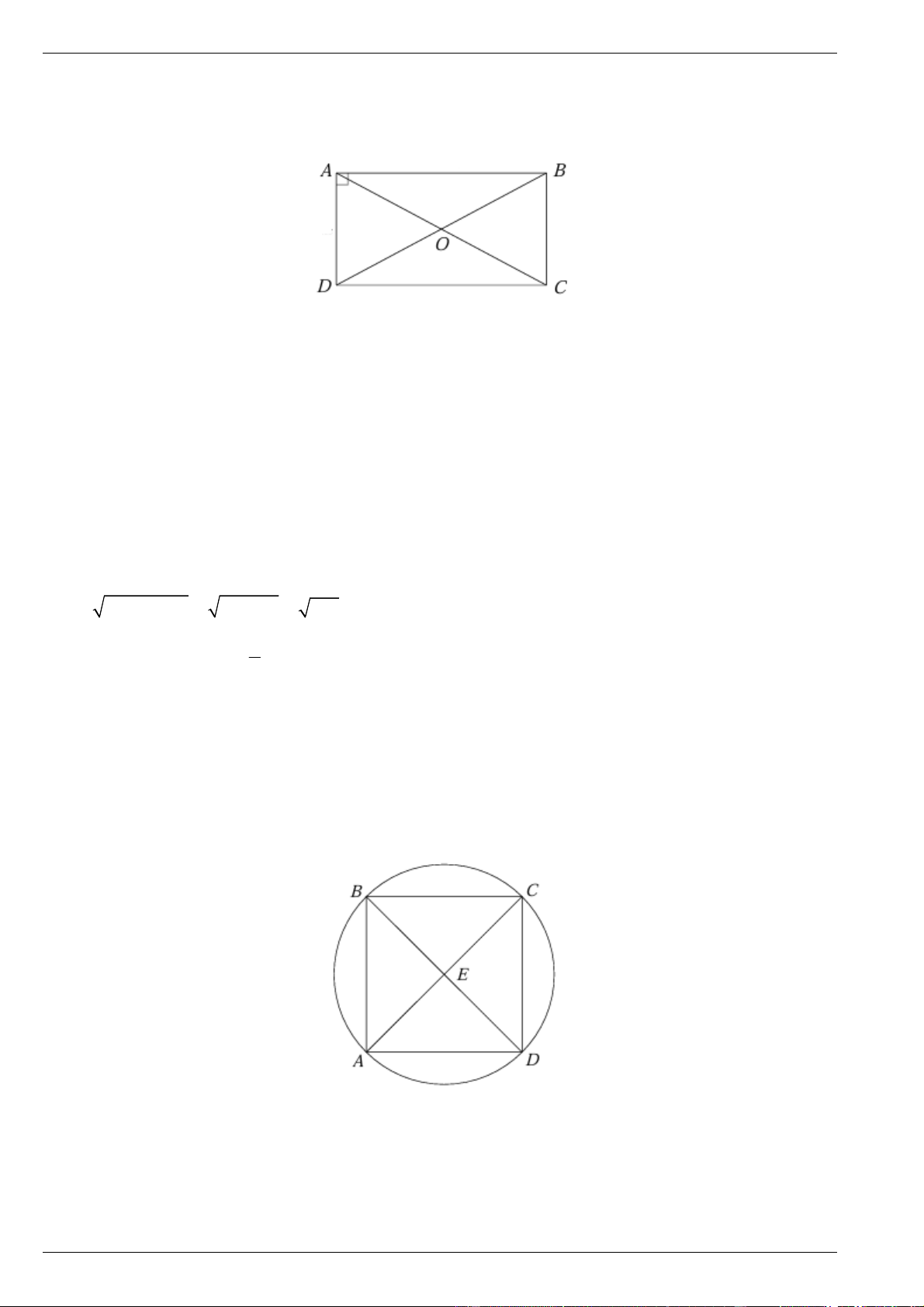
Bài 2. Cho hình chữ nhật ABCD có AB 9c , m BC 12cm .
a) Chứng minh bốn điểm ,
A B,C, D cùng nằm trên một đường tròn.
b) Xác định tâm đối xứng và hai trục đối xứng của đường tròn đó.
c) Tính bán kính đường tròn đó.
Bài 3. Cho hình vuông ABCD cạnh a .
a) Chứng minh bốn điểm ,
A B,C, D cùng nằm trên một đường tròn.
b) Xác định tâm đối xứng và hai trục đối xứng của đường tròn đó.
c) Tính bán kính đường tròn đó theo a .
Bài 4. Cho tam giác đều A
BC cạnh bằng a , các đường cao BM ,CN . Gọi O là trung điểm của BC
a) Chứng minh rằng B, C, M , N cùng thuộc đường tròn (O).
b) Gọi G là giao điểm của BM và CN . Chứng minh điểm G nằm trong, điểm A nằm ngoài đối với
đường tròn đường kính BC .
Bài 5. Cho đường tròn tâm O , đường kính AB và một dây AC bằng bán kính đường tròn.
a) Chứng minh tam giác OAC đều.
b) Tính các góc của A BC .
https://www.facebook.com/truongngocvy8/ T r an
g 3 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều
Bài 6. Cho tứ giác ABCD có 0
BCD ADC 90 và kéo dài AD và BC cắt nhau tại E . Gọi
M , N, P, Q lần lượt là trung điểm của AB, BD, DC,CA .
a) Tam giác ECD là tam giác gì?
b) Chứng minh tứ giác MNPQ là hình chữ nhật.
c) Chứng minh rằng bốn điểm M , N, P, Q cùng nằm trên 1 đường tròn.
BÀI TẬP RÈN LUYỆN
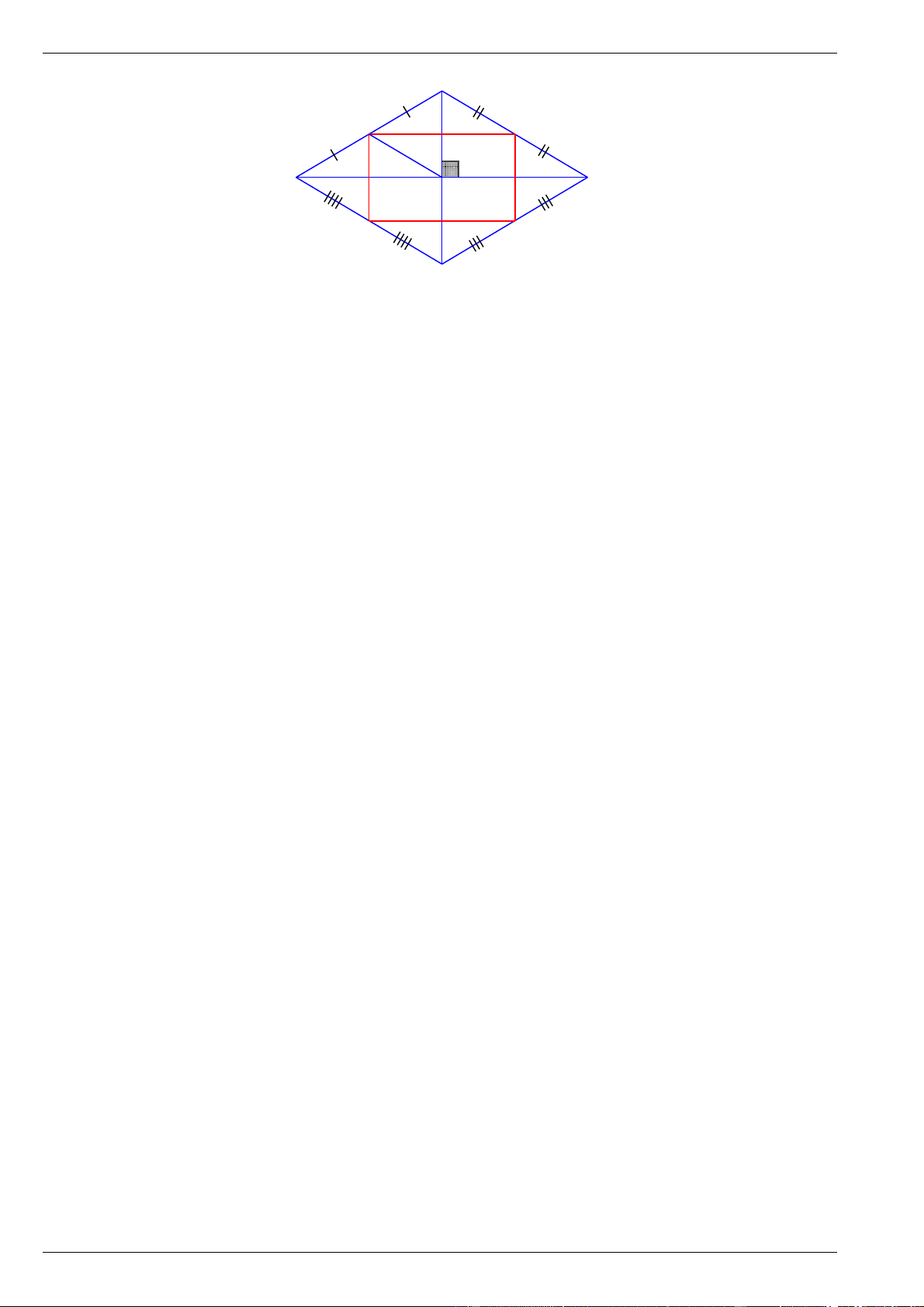
Bài 7. Cho hình thoi ABCD có 0
BAD 60 . Gọi E, F, G, H lần lượt là trung điểm của các cạnh
AB, BC,CD, DA .
a) Chứng minh tứ giác EFGH là hình chữ nhật.
b) Chứng minh rằng 6 điểm E, F, G, H , B, D cùng nằm trên 1 đường tròn
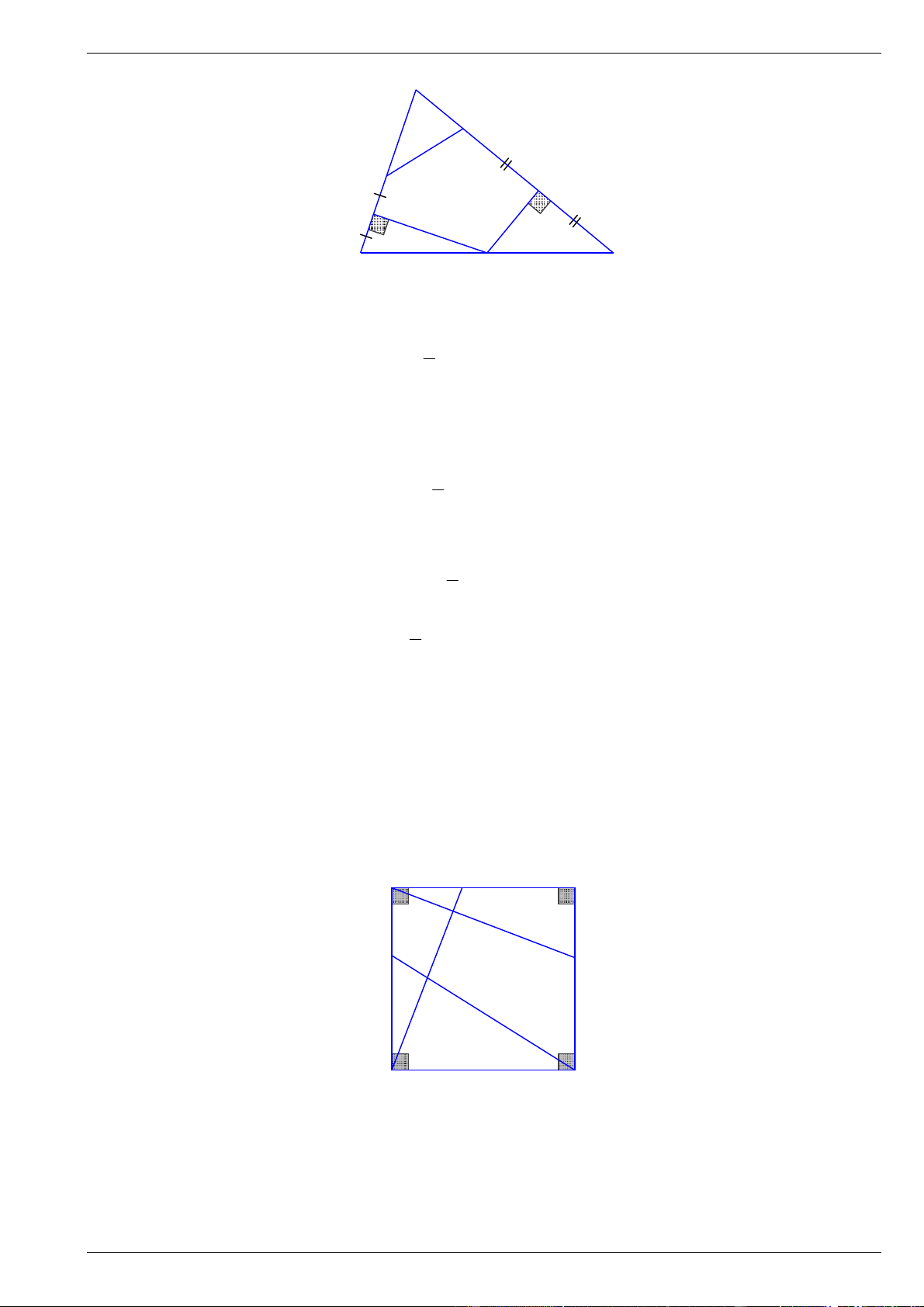
Bài 8. Cho tam giác ABC và điểm M là trung điểm của BC . Hạ MD, ME theo thứ tự vuông góc với
AB, AC . Trên tia đối của tia DB và EC lần lượt lấy các điểm I , K sao cho D là trung điểm của BI , E
là trung điểm của CK . Chứng minh rằng B, I , C, K cùng nằm trên 1 đường tròn.
Bài 9. Gọi I , K theo thứ tự là các điểm nằm trên AB, AD của hình vuông ABCD sao cho AI AK .
Đường thẳng kẻ qua A vuông góc với DI ở P và cắt BC ở Q . Chứng minh rằng C, D, P,Q cùng thuộc 1 đường tròn.
Bài 10. Cho tam giác ABC , ba đường cao AD, BE,CF cắt nhau tại H . Gọi I , J , K, L lần lượt là trung
điểm của AB, AC, HC, HB . Chứng minh rằng 6 điểm I , J , K, L, E, F thuộc 1 đường tròn.
Bài 11. Cho hình vuông ABCD , gọi O là giao điểm hai đường chéo AC và BD . Gọi M , N lần lượt là
trung điểm của OB,CD a) Chứng minh rằng ,
A M , N, D thuộc 1 đường tròn.
b) So sánh AN và DM .
Bài 12. Cho hình vuông ABCD . Gọi M , N lần lượt là trung điểm của AB, BC . Gọi E là giao điểm của CM và DN
a) Tính số đo góc CEN b) Chứng minh , A ,
D E, M cùng nằm trên 1 đường tròn
c) Xác định tâm của đường tròn đi qua 3 điểm B, , D E
Bài 13. Cho nửa đường tròn O; R đường kính BC . A là một điểm thay đổi trên đường tròn sao cho
AB AC . Tia phân giác BAC cắt đường trung trực BC tại D . Hạ DH và DK lần lượt vuông góc với AB và AC .
a) Chứng minh rằng AHDK là hình vuông. b) Chứng minh ,
A B, C
, D cùng thuộc một đường tròn.
Bài 14. Cho ΔABC vuông tại A , đường cao AH .
https://www.facebook.com/truongngocvy8/ T r an
g 4 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều
a) Biết AB 5 c ,
m BC 13 c
m . Tính độ dài cạnh AH và số đo góc BAH
b) Gọi O là trung điểm của AC , K là hình chiếu của O trên BC . Chứng minh 4 điểm ,
A B, O , K
cùng nằm trên một đường tròn.
c) Đường thẳng qua A và vuông góc với BO cắt đường thẳng qua C vuông góc với AC tại M . Chứng
minh ΔABO∽ ΔCAM và ba điểm O, K, M thẳng hàng
Bài 15. Cho ΔABC cân tại A , vẽ hai đường cao BE và CF cắt nhau tại H .
a) Chứng minh rằng bốn điểm B, F, E, C
cùng thuộc một đường tròn và chỉ ra tâm của đường tròn đó.
b) Gọi I , K lần lượt là hai điểm trên BH và CH sao cho HE HI , HF HK . Chứng minh rằng bốn
điểm E, F, I , K cùng thuộc một đường tròn.
c) Gọi M là trung điểm của AH . Tìm điều kiện của ΔABC để điểm M thuộc đường tròn đi qua bốn
điểm E, F, I , K .
https://www.facebook.com/truongngocvy8/ T r an
g 5 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều DẠNG 2
LIÊN HỆ GIỮA ĐƯỜNG KÍNH VÀ DÂY CỦA ĐƯỜNG TRÒN
Bất kì đường kính nào cũng là trục đối xứng của đường tròn đó.
Trong các dây của đường tròn, dây lớn nhất là đường kính của đường tròn đó
Bổ đề 1: Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy
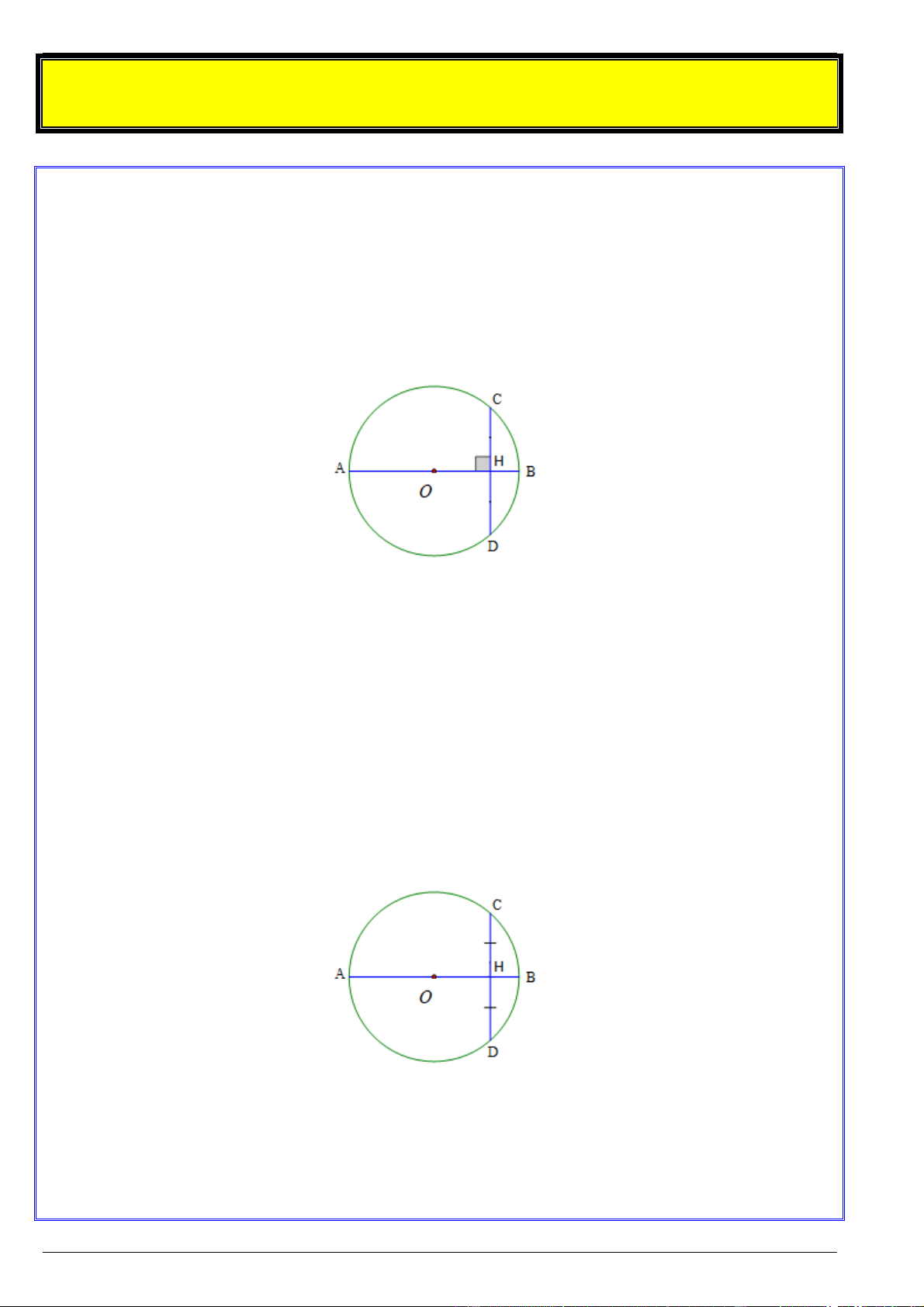
Bài toán: Cho đường tròn tâm O và đường kính AB . Trên đường tròn kẻ dây CD sao cho vuông góc
AB . Chứng minh AB đi qua trung điểm của CD . Chứng minh:
Gọi H là giao điểm của AB và CD .
Xét tam giác COD cân tại O ( OC OD ) và OH là đường cao nên OH là đường trung trực của
đoạn thẳng CD , do đó OH là trung tuyến vì vậy OH đi qua trung điểm CD hay AB đi qua trung điểm của CD .
Bổ đề 2: Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
Bài toán: Cho đường tròn tâm O và đường kính AB . Trên đường tròn kẻ dây CD sao cho AB đi qua
trung điểm của CD . Chứng minh AB vuông góc với CD . Chứng minh:
Gọi H là giao điểm của AB và CD .
Xét tam giác COD cân tại O ( OC OD ) và OH là đường trung tuyến nên OH là đường trung trực
của đoạn thẳng CD , do đó OH vuông góc CD hay AB vuông góc với CD .
Chú ý: Khi dùng 2 bổ đề trên thì phải chứng minh vì trong sách giáo khoa không có nói đến chúng.
https://www.facebook.com/truongngocvy8/ T r an
g 6 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều
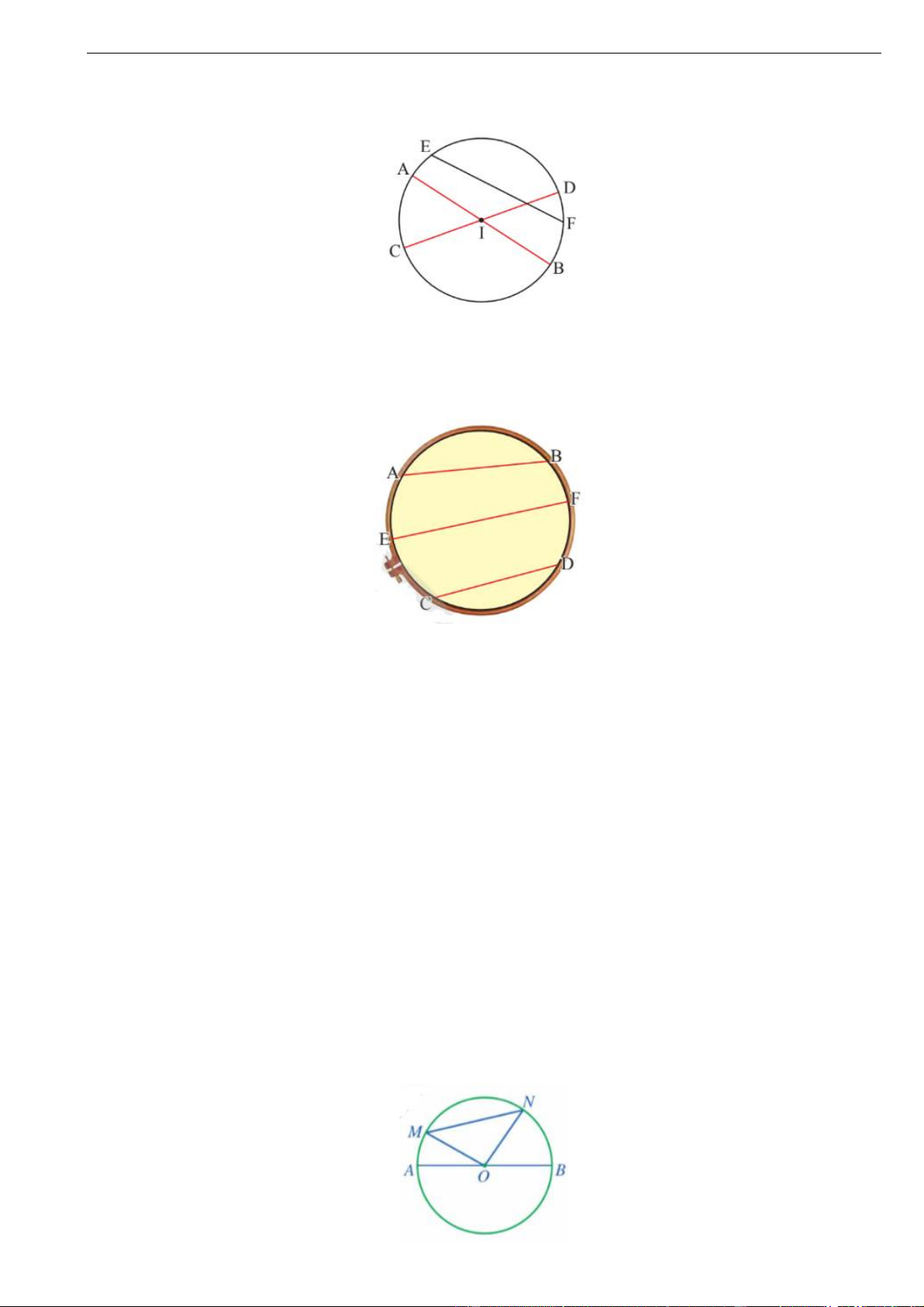
Bài 1. Cho đường tròn I có các dây cung AB,CD, EF . Cho biết AB và CD đi qua tâm I , EF
không đi qua I (như hình vẽ). Hãy so sánh độ dài AB,CD, EF .
Bài 2. Bạn Minh Hiền căng ba đoạn chỉ AB,CD, EF có độ dài lần lượt là 26cm , 24cm và 30cm trên
một khung thêu hình tròn bán kính 15cm (như hình vẽ). Trong ba dây trên, dây nào đi qua tâm của đường tròn? Giải thích.
Bài 3. Cho đường tròn tâm O bán kính 3cm và hai dây AB và AC . Cho biết AB 5cm AC 2cm .
a) Tính khoảng cách từ O đến dây AB .
b) Tính khoảng cách từ O đến dây AC .
Bài 4. Cho đường tròn tâm O; R và một dây cung AB . Gọi I là trung điểm của AB , tia OI cắt cung AB tại M .
a) Cho R 5c ,
m AB 6cm . Tính độ dài dây cung MA
b) Gọi N là điểm đối xứng của M qua O , giả sử MA 5c ;
m AB 6cm . Tính bán kính R .
Bài 5. Cho đường tròn tâm O , hai dây AB và CD vuông góc với nhau ở M . Biết AB 18c , m CD 14c ,
m MC 4cm . Hãy tính khoảng cách từ tâm O đến mỗi dây AB và CD
Bài 6. Cho nửa đường tròn O, đường kính AB và một dây cung CD . Kẻ AE và BF vuông góc với
CD lần lượt tại E và F . Chứng minh CE DF
BÀI TẬP RÈN LUYỆN
Bài 7. Quan sát hình vẽ bên dưới.
https://www.facebook.com/truongngocvy8/ T r an
g 7 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều
a) So sánh MN và OM ON .
b) So sánh MN và AB .
Bài 8. Cho đường tròn O và dây CD . Từ O kẻ tia vuông góc với CD tại M , cắt O tại H . Tính
bán kính R của O biết: CD 16c , m MH 4cm
Bài 9. Cho đường tròn O bán kính OA 11c .
m Điểm M thộc bán kính AO và cách O khoảng 7cm.
Qua M kẻ dây CD có độ dài 18cm. Tính độ dài các đoạn thẳng MC và MD
Bài 10. Cho đường tròn tâm O , đường kính AB . Dây CD cắt AB tại M , biết MC 4c , m MD 12cm . 0
BMD 30 . Hãy tính :
a) Khoảng cách từ O đến CD
b) Bán kính của O
Bài 11. Cho đường tròn O có các dây 0
AB 24cm, AC 20c ,
m BAC 90 và O nằm trong góc BAC .
Gọi M là trung điểm của AC . Khoảng cách từ điểm M đến AB bằng 8cm
a) Chứng minh tam giác ABC cân.
b) Tính bán kính của O
Bài 12. Cho đường tròn tâm O; R , A và B di động trên đường tròn O thỏa mãn 0 AOB 120 . Vẽ
OH AB H
a) Chứng minh H là trung điểm của AB
b) Tính OH , AB và S theo R OAB
c) Tia OH cắt đường tròn O; R tại C . Tứ giác OABC là hình gì? Vì sao
Bài 13. Cho tam giác ABC có trực tâm H và nội tiếp đường tròn O đường kính AD
a) Chứng minh BHCD là hình bình hành
b) Kẻ đường kính OI vuông góc BC tại I . Chứng minh I , H , D thẳng hàng
c) Chứng minh AH 2OI
Bài 14. Cho đường tròn O đường kính AB , dây CD cắt AB tại I . Gọi H , K theo thứ tự là chân
đường vuông góc kẻ từ A và B đến CD . Chứng minh rằng: CH DK
Bài 15. Cho tam giác ABC ( AB AC ) có hai đường cao BD và CE cắt nhau tại trực tâm H . Lấy I là
trung điểm của BC
a) Gọi K là điểm đối xứng của H qua I . Chứng minh tứ giác BHCK là hình bình hành
b) Xác định tâm O của đường tròn qua các điểm ,
A B, K,C
c) Chứng minh: OI / /CH d) Chứng minh rằng: 2
BE.BA C . D CA BC
https://www.facebook.com/truongngocvy8/ T r an
g 8 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều
Bài 16. Cho nửa đường tròn tâm O đường kính AB . Trên đoạn thẳng OA lấy điểm C và trên đoạn
thẳng OB lấy điểm D sao cho OC OD . Từ C và D kẻ hai tia song song cắt nửa đường tròn ở E và
F . Gọi I là trung điểm của EF . Chứng minh rằng: S S EF.OI CEF DEF
Bài 17. Cho đường tròn O; R . Các điểm ,
A B,C, D thuộc O; R . Tìm giá trị lớn nhất của diện tích tứ giác ABCD
https://www.facebook.com/truongngocvy8/ T r an
g 9 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều DẠNG 3
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN Bài 1.
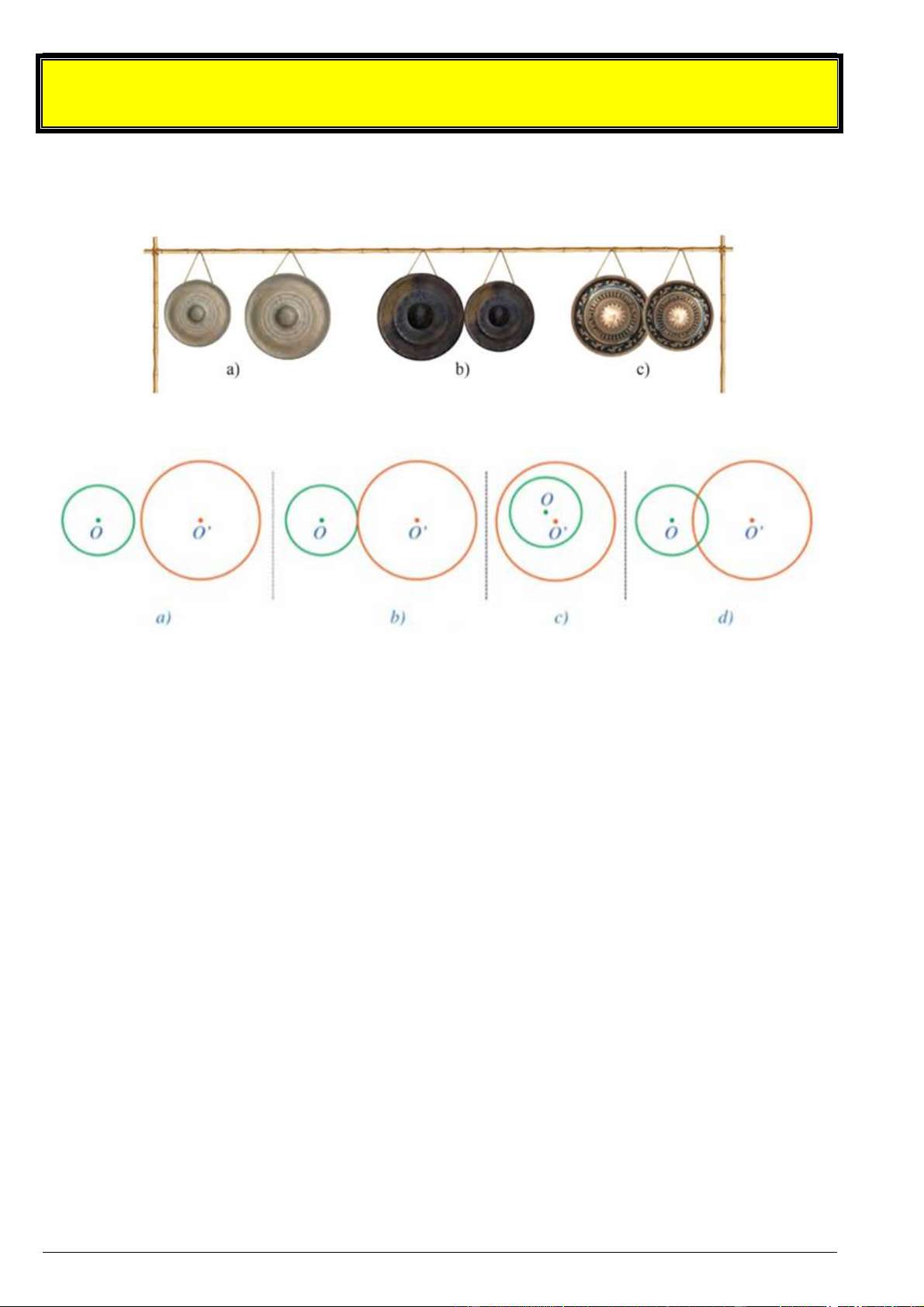
Mô tả vị trí tương đối giữa mỗi cặp đường tròn trong hình chụp bộ cồng chiêng Tây Nguyên
trong hình vẽ bên dưới. Bài 2.
Xác định vị trí tương đối của hai đường tròn O và O trong mỗi hình a, b, c, d: Bài 3.
Xác định vị trí tương đối của O; R và O ; R trong mỗi trường hợp sau:
a) OO 18; R 10; R 6
b) OO 2; R 9; R 3
c) OO 13; R 8; R 5
d) OO 17; R 15; R 4 . Bài 4.
Cho đường tròn O; R và O ; R cắt nhau tại ,
A B . Chứng minh OO ' là đường trung trực của AB .
BÀI TẬP RÈN LUYỆN Bài 5.
Xác định vị trí tương đối của O; R và O ; R trong mỗi trường hợp sau:
a) OO 5; R 3; R 2
b) OO 4; R 11; R 7
c) OO 6; R 9; R 4
d) OO 10; R 4; R 1. Bài 6.
Cho hai đường tròn O và O ' cắt nhau tại ,
A B . Gọi I là trung điểm của OO ' . Qua A vẽ
đường thẳng vuông góc với IA cắt O tại C và cắt O ' tại D . So sánh AC và AD . Bài 7.
Cho hai đường tròn O và đường tròn O ' tiếp xúc ngoài với nhau tại A . Một đường thẳng
qua A cắt O tại B và cắt O ' tại C . Chứng minh rằng OB ∥O 'C . Bài 8.
Cho I là trung điểm của đoạn thẳng AB . Vẽ hai đường tròn I; IA và đường tròn B; BA
a) Hai đường tròn I và B có vị trí như thế nào?
https://www.facebook.com/truongngocvy8/ T r an g
10 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều
b) Kẻ đường thẳng đi qua A , cắt I và B làn lượt tại M và N . So sánh AM và MN . Bài 9.
Cho đường tròn O , đường kính AD R . Vẽ cung tròn tâm D bán kính R cắt O ở B và C
a) Tứ giác OBDC là gì ? vì sao ?
b) Tính số đo các góc
CBD;CBO;OBA
c) Chứng minh rằng tam giác ABC là tam giác đều
https://www.facebook.com/truongngocvy8/ T r an g
11 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều CHƯƠNG 5 ĐƯỜNG TRÒN BÀI 1 ĐƯỜNG TRÒN
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN
1. Khái niệm đường tròn
Trong mặt phẳng, đường tròn tâm O bán kính R (với R 0 ) là tập hợp các điểm cách điểm O cố
định một khoảng R , kí hiệu là: O; R R O Chú ý:
Một đường tròn hoàn toàn xác định khi biết tâm và bán kính.
Khi không chú ý đến bán kính của đường tròn O; R , ta cũng có thể kí hiệu đường trònO .
Vị trí tương đối của một điểm đối với đường tròn Nhận xét:
Điểm M nằm trên đường tròn O nếu OM R
Điểm M nằm trong đường tròn O nếu OM R
Điểm M nằm ngoài đường tròn O nếu OM R
2. Tính chất đối xứng của đường tròn
Đường tròn là hình có tâm đối xứng: Tâm của đường tròn là tâm đối
xứng của đường tròn đó A A' O
Đường tròn là hình có trục đối xứng: Bất kì đường kính nào cũng là
trục đối xứng của đường tròn đó.
3. Liên hệ giữa đường kính và dây của đường tròn
Đoạn thẳng nối hai điểm phân biệt thuộc đường tròn được gọi là dây (hay dây cung) của đường tròn.
Dây đi qua tâm là đường kính của đường tròn. Trong các dây của đường tròn, dây lớn nhất là đường
kính của đường tròn đó
https://www.facebook.com/truongngocvy8/ T r an
g 1 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều
4. Vị trí của hai đường tròn
Vị trí tương đối của hai đường Số điểm Hệ thức Hình vẽ
tròn O; R và O '; r R r chung
R r OO ' R r R r Cắt nhau 2 O O' R Tiếp xúc trong
OO ' R r 0 O O' r Tiếp xúc 1 Tiếp xúc ngoài
OO ' R r R r O O' R r Ngoài nhau
OO ' R r Không cắt
0 OO ' R r O O' 0 nhau Đựng nhau O' OO ' O O Chú ý:
Đường nối tâm (đường thẳng đi qua tâm 2 đường tròn) là trục đối xứng của hình tạo bởi hai đường tròn.
Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
Nếu hai đường tròn cắt nhau thì đường nối tâm là đường trung trực của dây chung.
https://www.facebook.com/truongngocvy8/ T r an
g 2 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều DẠNG 1
CHỨNG MINH CÁC ĐIỂM CHO TRƯỚC CÙNG NẰM TRÊN MỘT ĐƯỜNG TRÒN
TÍNH BÁN KÍNH ĐƯỜNG TRÒN Phương pháp
Cách 1: Chứng minh các điểm cho trước cùng cách đều 1 điểm cho trước nào đó. Cách 2: Nếu 0
BAC 90 thì A thuộc đường tròn đường kính BC . A C B O 1
Xét tam giác vuông ABC , có AO là đường trung tuyến nên AO BC AO OB OC 2
Bài 1. Cho tam giác ABC vuông ở A có AB 5c , m AC 12cm . a) Chứng minh ba điểm ,
A B,C cùng thuộc một đường tròn.
b) Tính bán kính của đường tròn đó. Lời giải
a) Gọi O là trung điểm BC 1
Xét tam giác vuông ABC , có AO là đường trung tuyến nên AO BC AO OB OC 2 Do đó ba điểm ,
A B,C cùng thuộc một đường tròn.
b) Áp dụng định lí Pythagore cho tam giác vuông ABC , ta có: 2 2 BC
AB AC 13cm 1
AO OB OC BC 6,5cm 2
Bài 2. Cho hình chữ nhật ABCD có AB 9c , m BC 12cm .
a) Chứng minh bốn điểm ,
A B,C, D cùng nằm trên một đường tròn.
https://www.facebook.com/truongngocvy8/ T r an
g 3 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều
b) Xác định tâm đối xứng và hai trục đối xứng của đường tròn đó.
c) Tính bán kính đường tròn đó. Lời giải
a) Theo tính chất hình chữ nhật: Hai đường chéo của hình chữ nhật bằng nhau và cắt nhau tại trung điểm của mỗi đường
Gọi O là giao điểm của AC và BD
ABCD là hình chữ nhật, ta có: OA OB OC OD Do đó bốn điểm ,
A B,C, D cùng thuộc một đường tròn O
b) Điểm O là tâm đối xứng của đường tròn đó.
Vì AC và BD đi qua tâm O nên AC và BD là hai trục đối xứng của đường tròn đó.
c) Áp dụng định lí Pythagore cho tam giác vuông ABC , ta có: 2 2 2 2 AC
AB BC 9 12 225 15cm 1
AO OB OC OD AC 7,5cm 2
Bài 3. Cho hình vuông ABCD cạnh a .
a) Chứng minh bốn điểm ,
A B,C, D cùng nằm trên một đường tròn.
b) Xác định tâm đối xứng và hai trục đối xứng của đường tròn đó.
c) Tính bán kính đường tròn đó theo a . Lời giải
a) Theo tính chất hình vuông: Hai đường chéo của hình vuông bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Gọi E là giao điểm của AC và BD
ABCD là hình vuông, ta có: OA OB OC OD
https://www.facebook.com/truongngocvy8/ T r an
g 4 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều Do đó bốn điểm ,
A B,C, D cùng thuộc một đường tròn O
b) Điểm E là tâm đối xứng của đường tròn đó.
Vì AC và BD đi qua tâm E nên AC và BD là hai trục đối xứng của đường tròn đó.
c) Tam giác vuông ABC vuông cân tại B , có cạnh a nên AC a 2 1 a 2
Suy ra EA EB EC ED AC 2 2
Bài 4. Cho tam giác đều A
BC cạnh bằng a , các đường cao BM ,CN . Gọi O là trung điểm của BC
a) Chứng minh rằng B, C, M , N cùng thuộc đường tròn (O).
b) Gọi G là giao điểm của BM và CN . Chứng minh điểm G nằm trong, điểm A nằm ngoài đối với
đường tròn đường kính BC . Lời giải A N M G B a C a) Ta có: 1
Xét tam giác vuông BNC , có NO là đường trung tuyến nên NO BC NO OB OC 2 BC N ; O 2 1
Xét tam giác vuông BMC , có MO là đường trung tuyến nên MO BC MO OB OC 2 BC M ; O 2 BC
Vậy B, C, M , N cùng thuộc 1 đường tròn ; O 2 b) Ta có A
BC đều có G trực tâm đồng thời là trọng tâm 2 a a a 3 Xét 0 2 A
OB(O 90 ), R ON .OA a
R A nằm ngoài đường tròn (O) 2 4 2
https://www.facebook.com/truongngocvy8/ T r an
g 5 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều 1 a 3 Ta lại có: OG OA
R G nằm trong (O). 3 6
Bài 5. Cho đường tròn tâm O , đường kính AB và một dây AC bằng bán kính đường tròn.
a) Chứng minh tam giác OAC đều.
b) Tính các góc của A BC . Lời giải C 1 2 A 1 B O
a) Ta có AC OA OC (giả thiết)
Do đó tam giác OAC có ba cạnh bằng nhau nên là tam giác đều.
b) Tam giác OAC là tam giác đều 0
A C O 60 1 1
Tam giác OAC có OB OC nên cân tại
O B C 2 1
O là góc ngoài của 0 0 OB
C O B C 2B 2C B C
O 30 ACB C C 90 1 1 2 2 2 1 1 2 2 Vậy 0 0 0
A 60 ; B 30 ;C 90
Có thể lí giải như sau: C
AB có trung tuyến CO bằng nửa cạnh đối xứng AB nên vuông tại C 0 0 0
ACB 90 A 60 B 30 0 0 Vậy A BC có 0
C 90 ; A 60 ; B 30
Bài 6. Cho tứ giác ABCD có 0
BCD ADC 90 và kéo dài AD và BC cắt nhau tại E . Gọi
M , N, P, Q lần lượt là trung điểm của AB, BD, DC,CA .
a) Tam giác ECD là tam giác gì?
b) Chứng minh tứ giác MNPQ là hình chữ nhật.
c) Chứng minh rằng bốn điểm M , N, P, Q cùng nằm trên 1 đường tròn. Lời giải
https://www.facebook.com/truongngocvy8/ T r an
g 6 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều E B M A N Q D P C
a) Xét tam giác ECD , ta có: 0
CED BCD ADC 180 0 0 CED 90 180 0 CED 90
Vậy tam giác ECD là tam giác vuông tại E .
b) Xét tam giác ABC , ta có: MQ // BC (vì MQ là đường trung bình của A BC )
Xét tam giác BDC , ta có: NP // BC (vì NP là đường trung bình của B DC )
Suy ra MQ // NP
Xét tam giác ABD , ta có: MN // AD (vì MN là đường trung bình của A BD )
Xét tam giác ACD , ta có: PQ // AD (vì PQ là đường trung bình của A CD )
Suy ra MN // PQ MQ / / NP cmt
Xét tứ giác MNPQ , ta có:
, suy ra MNPQ là hình bình hành MN / /PQ cmt Mà 0
CED 90 hay ED EC MN / / ED Lại có:
MN MQ MNPQ là hình chữ nhật MQ / / EC
c) Vì tứ giác MNPQ là hình chữ nhật nên M , N, P, Q nằm trên 1 đường tròn với tâm là giao điểm của 2
đường chéo của hình chữ nhật, bán kính bằng nửa đường chéo.
BÀI TẬP RÈN LUYỆN
Bài 7. Cho hình thoi ABCD có 0
BAD 60 . Gọi E, F, G, H lần lượt là trung điểm của các cạnh
AB, BC,CD, DA .
a) Chứng minh tứ giác EFGH là hình chữ nhật.
b) Chứng minh rằng 6 điểm E, F, G, H , B, D cùng nằm trên 1 đường tròn Lời giải
https://www.facebook.com/truongngocvy8/ T r an
g 7 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều B 60° E F A C O H G D a) Ta có:
EF // AC (vì EF là đường trung bình của A BC )
HG // AC (vì HG là đường trung bình của A DC )
Suy ra EF // HG
EH // BD (vì EH là đường trung bình của A BD )
FG // BD (vì FG là đường trung bình của B CD )
Suy ra EH // FG EF / /GH cmt
Xét tứ giác EFGH , có:
, suy ra EFGH là hình bình hành EH / / FG cmt
Mà BD AC (đường chéo hình vuông) EH // BD Lại có:
EH EF , suy ra EFGH là hình chữ nhật EF // AC
b) Gọi O là giao điểm của hai đường chéo AC và BD của hình chữ nhật EFGH
OE OF OG OH (1) OE BE
Xét tam giác OBE có: OB
E đều OE OB OD 2 0 B 60
Từ (1) và (2) OE OB OF OG OH OD E, B, F,G, D, H (O)
Bài 8. Cho tam giác ABC và điểm M là trung điểm của BC . Hạ MD, ME theo thứ tự vuông góc với
AB, AC . Trên tia đối của tia DB và EC lần lượt lấy các điểm I , K sao cho D là trung điểm của BI , E
là trung điểm của CK . Chứng minh rằng B, I , C, K cùng nằm trên 1 đường tròn. Lời giải
https://www.facebook.com/truongngocvy8/ T r an
g 8 Trương Ngọc Vỹ 0978 333 093
Hình học 9 - Chương 5: Đường tròn – Tự luận phân dạng có lời giải Cánh Diều A K I E D B M C Cách 1: 1
Ta có: M là trung điểm BC MB MC BC(1) 2
MD là trung trực của BI MI MB(2)
ME là trung trực của CK MC MK (3) 1
Từ (1), (2) và (3) MB MC MI MK BC (đpcm) 2 Cách 2: 1
Ta có: MD là trung trực của BI MI MB
BC BIC vuông tại I I O; BC 2 1
ME là trung trực của CK MK MC
BC BKC vuông tại K K O; BC 2
Vậy: B, I , C, K O; BC .
Bài 9. Gọi I , K theo thứ tự là các điểm nằm trên AB, AD của hình vuông ABCD sao cho AI AK .
Đường thẳng kẻ qua A vuông góc với DI ở P và cắt BC ở Q . Chứng minh rằng C, D, P,Q cùng thuộc 1 đường tròn. Lời giải A I B P K Q 1 D C KD CQ Ta có A
DI BAQ(g c g) AI BQ 0
KDCQ là hình bình hành, mà C 60 KD / /CQ
CDKQ là hình chữ nhật.
https://www.facebook.com/truongngocvy8/ T r an
g 9 Trương Ngọc Vỹ 0978 333 093




