Tuyển tập những bài toán hình học lớp 9 hay và đặc sắc – Bùi Hoàng Nam
Tài liệu gồm 69 trang, được biên soạn bởi tác giả Bùi Hoàng Nam, tuyển tập những bài toán hình học lớp 9 hay và đặc sắc, có đáp án và lời giải chi tiết, giúp học sinh lớp 9 tham khảo khi học chương trình Toán 9 và ôn tập tuyển sinh vào lớp 10.
Chủ đề: Tài liệu chung Toán 9 129 tài liệu
Môn: Toán 9 3.4 K tài liệu
Tác giả:
Preview text:
Bùi Hoàng Nam
THPT Chuyên Trần Phú - Hải Phòng TUYỂN TẬP
NHỮNG BÀI HÌNH HỌC 9 HAY & ĐẶC SẮC 2 Lời nói đầu
Sau một quá trình được ôn luyện và thành công đỗ vào trường THPT Chuyên Trần Phú, với mong
muốn chia sẻ, tác giả mong truyền tải kiến thức của bản thân và tiếp lửa đam mê Toán học tới các
bạn học sinh trên mọi miền tổ quốc. . . .
Toán Học là sự bao hàm của rất nhiều phân môn như: Số học, Giải tích, Hình học, Các phân môn này đều thu hút được sự yêu thích cũng như đam mê của các bạn học sinh. Bằng sự yêu “Tuyển
thích, đam mê và được sự giúp đỡ của các thầy, mình đã quyết định soạn lên file tài liệu
tập những bài hình học 9 Hay & Đặc Sắc” dựa theo quan điểm cũng như đánh giá của cá nhân tác giả.
Tác giả muốn cảm ơn tới gia đình của tác giả đã luôn ủng hộ trong suốt quá trình làm file tài Nguyễn Ngọc Tú Nguyễn Đăng Khoa
liệu này. Tác giả gửi lời cảm ơn tới thầy và thầy là hai người
thầy đã luôn tận tâm và giúp đỡ tác giả tiến bộ lên từng ngày tháng năm cấp 2.
Mặc dù tài liệu đã được tác giả biên soạn khá kĩ lưỡng nhưng sai sót là điều không thể tránh
khỏi. Mong bạn đọc thông cảm và mọi ý kiến đóng góp xin gửi về
buihoangnamila@gmail.com Địa chỉ gmail: Zalo: 0922.330.885 Facebook: Bùi Hoàng Nam (HN)
Tác giả xin chân thành cảm ơn!
Hải Phòng, tháng 01 năm 2025. Bùi Hoàng Nam
Khối 10 Toán 2, K39 THPT Chuyên Trần Phú - Hải Phòng
MỘT SỐ KÝ HIỆU SỬ DỤNG TRONG TÀI LIỆU
1 □ : Hoàn tất bài toán. 2 △ABC ABC . : Tam giác 3 ∠X Y Z X Y Z . : Góc 4 O O. ( ) : Đường tròn tâm > 5 AB AB. : Cung
6 △ABC ∽ △A′B′C ′ ABC △A′B′C ′. : Tam giác đồng dạng với 7 PX X . : Chu vi hình 8 X /S X . [ ] X : Diện tích hình 9 d X⊥AB X AB. ( ) : Đường thẳng qua vuông góc với 10 d X||AB X AB. ( ) : Đường thẳng qua song song với 11 MN MN. (
) : Đường tròn đường kính 12 ABC △ABC . (
) : Đường tròn ngoại tiếp 13 ABC D ABC D. (
) : Đường tròn ngoại tiếp tứ giác
14 || : Song song.
15 ∦: Không song song.
16 ⊥ : Vuông góc.
17 →: Suy ra/Kéo theo.
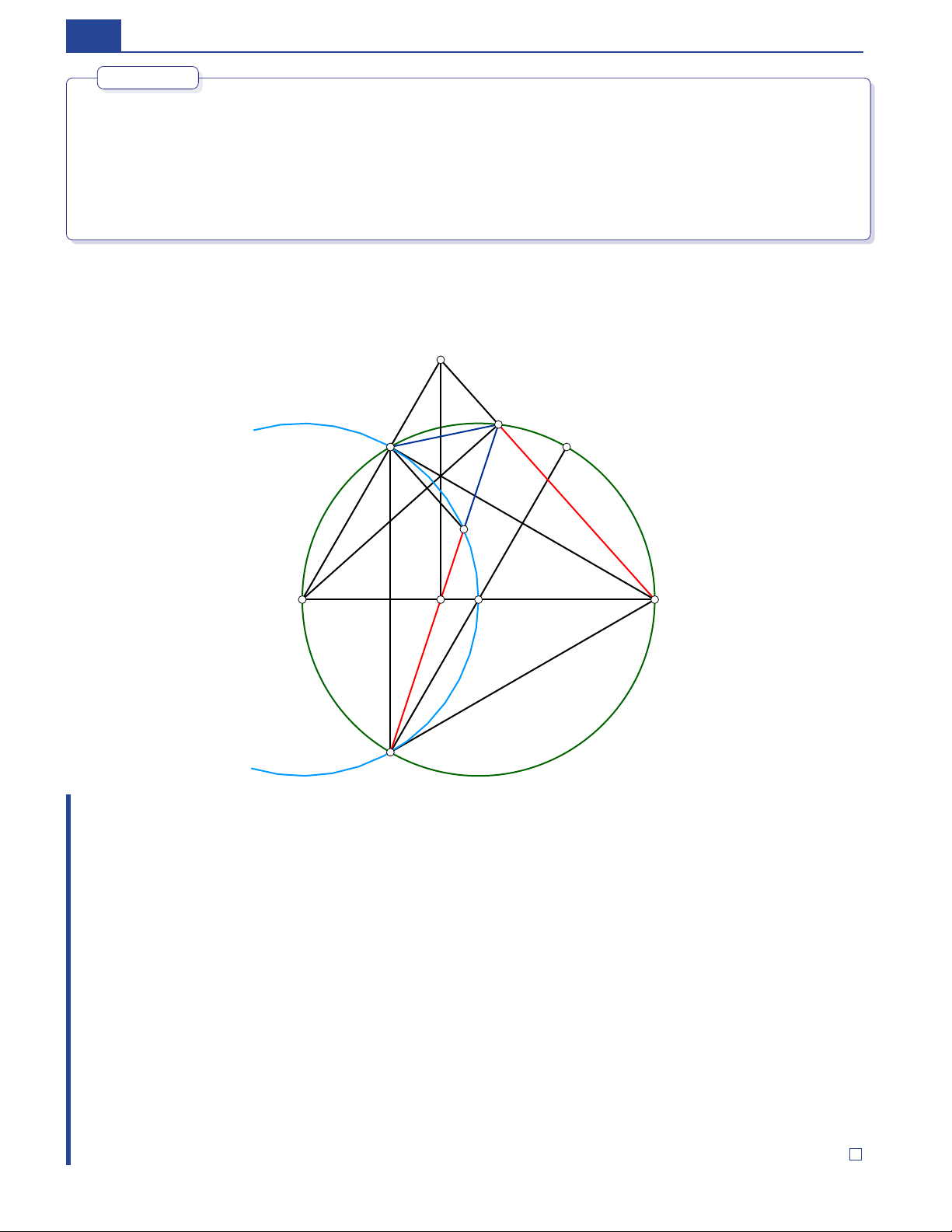
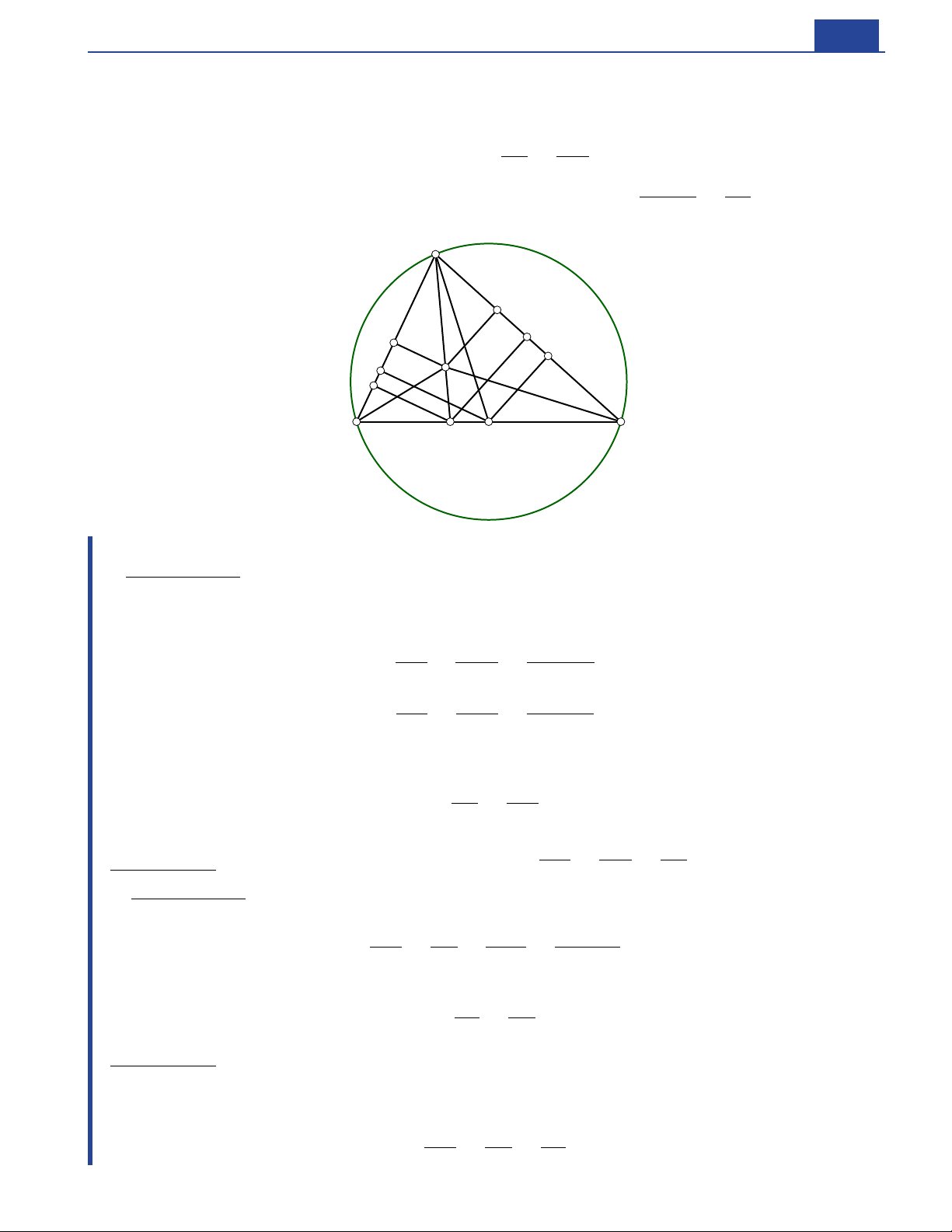
18 ⇔: Tương đương/Khi và chỉ khi. 19 P Q R P Q R ; ; : 3 điểm ; ; thẳng hàng. 1 2 Bài toán 1. O R AB. C O AC R. BC Cho đường tròn ( ; ) đường kính Lấy thuộc ( ) sao cho = Trên cung nhỏ lấy D D B C BD E. AB H. DH O điểm ( khác và ). AC cắt tại Kẻ EH vuông góc với tại Tia cắt ( ) tại F . điểm thứ hai là A, E, D, H (a) Chứng minh 4 điểm
cùng thuộc một đường tròn. ∠DHE ∠DF C △BC F (b) Chứng minh = , từ đó suy ra đều. D ABDC
(c) Xác định vị trí điểm để chu vi tứ giác
đạt giá trị lớn nhất. E D C D′ K A H O B F Chứng minh. a. ∠ADE ∠AHE ◦ AEDH Ta có = = 90 nên tứ giác nội tiếp. b. AEDH AC DF Tứ giác và nội tiếp nên ∠EHD ∠EAD ∠C F D, = = → EH || C F .
mà hai góc này ở đồng vị
EH ⊥ AB → C F ⊥ AB. △BC F B. Lại có Từ đây suy ra cân tại AC OA OC R → △AC O → ∠C AB ◦ → ∠CFB ◦. Vì = = = đều = 60 = 60 △BC F Dẫn đến đều. c. △C OF DF K . F D′ O . Đường tròn ngoại tiếp cắt lại tại Kẻ đường kính của ( ) b F Từ câu , ta suy ra được là điểm cố định. ∠C BF ◦ → ∠COF ◦ → ∠CK F ◦ → ∠CK D ◦. Vì = 60 = 120 = 120 = 60 ∠C DF ∠C BF ◦ → △C DK → C D DK K C . Lại có = = 60 đều = = △K C F △DC B c.g.c → K F DB. Chú ý rằng = ( ) = P AC C D DB BA R DK K F R DF ≤ R F D′ R. Do đó ABDC = + + + = 3 + + = 3 + 3 + = 5 Vậy nên P R. C D || AB. giá trị lớn nhất của ABDC bằng 5 Đẳng thức xảy ra khi 3 Bài toán 2. O R AB C D M Cho ( ; ) có hai đường kính và
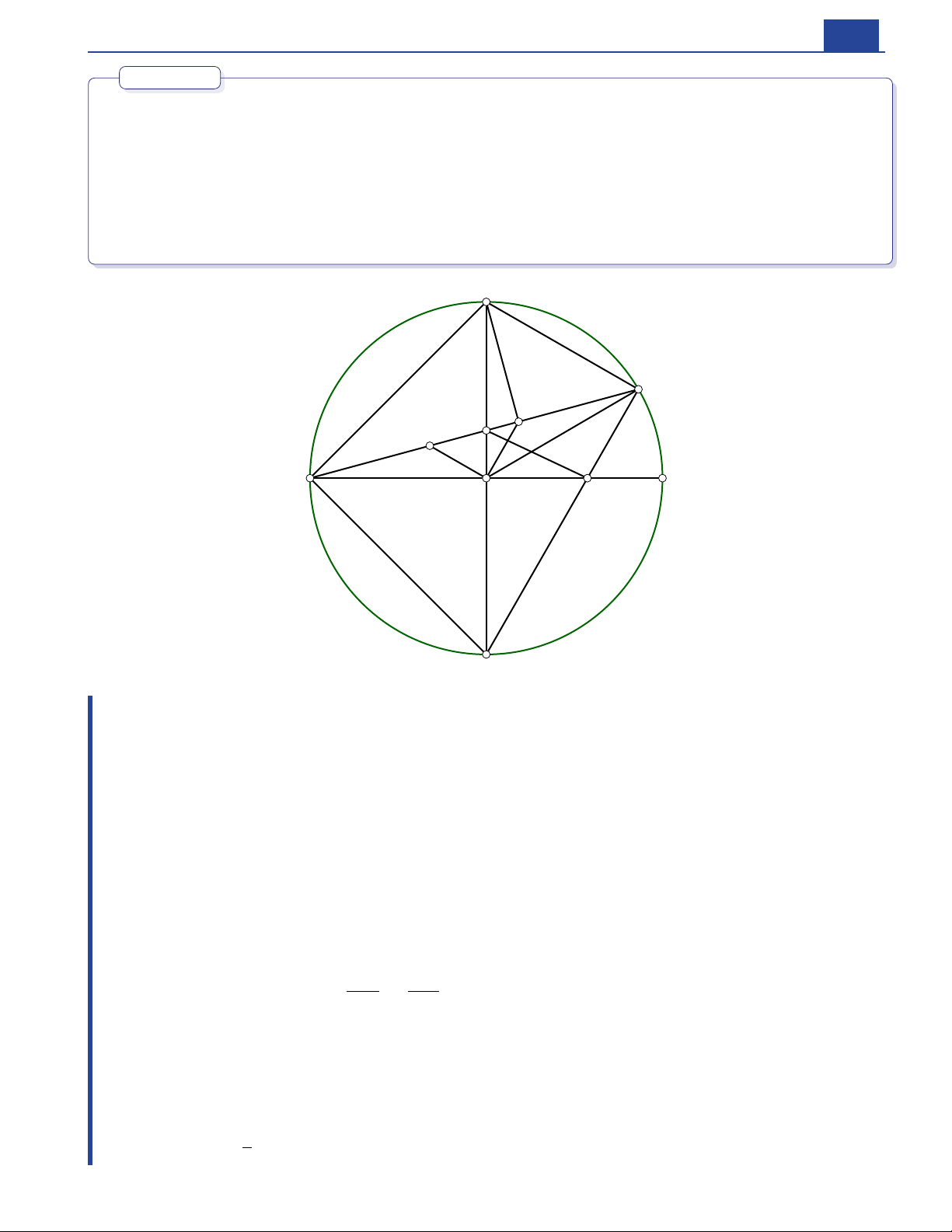
vuông góc với nhau. Một điểm di động trên cung nhỏ BC M C B AM C D N. C H AM H. ( không trùng với và ), cắt tại Kẻ vuông góc với tại Gọi giao DM AB F . điểm của với là a. OAC H Chứng minh tứ giác nội tiếp. b. O OH AM E. OH Qua
kẻ đường thẳng vuông góc với cắt tại Chứng minh rằng song song với DM EN · HM NH · ME. và = c. M BC S Tìm vị trí của trên cung nhỏ để
MNF đạt giá trị lớn nhất. C M H N E A O B F D Chứng minh. a. ∠C HA ∠C OA ◦ OAC H Ta có = = 90 nên tứ giác nội tiếp. b. OAC H AC MD Tứ giác và nội tiếp nên ∠OHN ∠OC A ∠DMN, = = → OH || DM. mà hai góc này đồng vị OAC H, AC MD OH || DM Ta có tứ giác nội tiếp và nên ∠NOH ∠C AM ∠ODM ∠OMD ∠MOH. = = = = OH ∠NOM → OE ∠NOM. Suy ra là phân giác của là phân giác ngoài của
Theo tính chất đường phân giác, ta có HN
EN → EN · HM NH · ME. HM = EM = (∠OAD ∠ODA ◦, c. △OAD O → = = 45 Ta có vuông cân tại AD2 R2. = 2 C MF O AC MD → ∠DF O ∠DC M ∠DAM. Chú ý rằng tứ giác và nội tiếp = =
△DAF ∽ △NDA g.g → AF · DN AD2 R2. Từ đó, ta có ( ) = = 2 S 1 · AF · DN R2 Lại có ANF D = = không đổi, 2 4 S S S S S mà AMD = MNF + ANF D nên
MNF lớn nhất khi và chỉ khi AMD lớn nhất. AD S M Tới đây, ta thấy không đổi nên
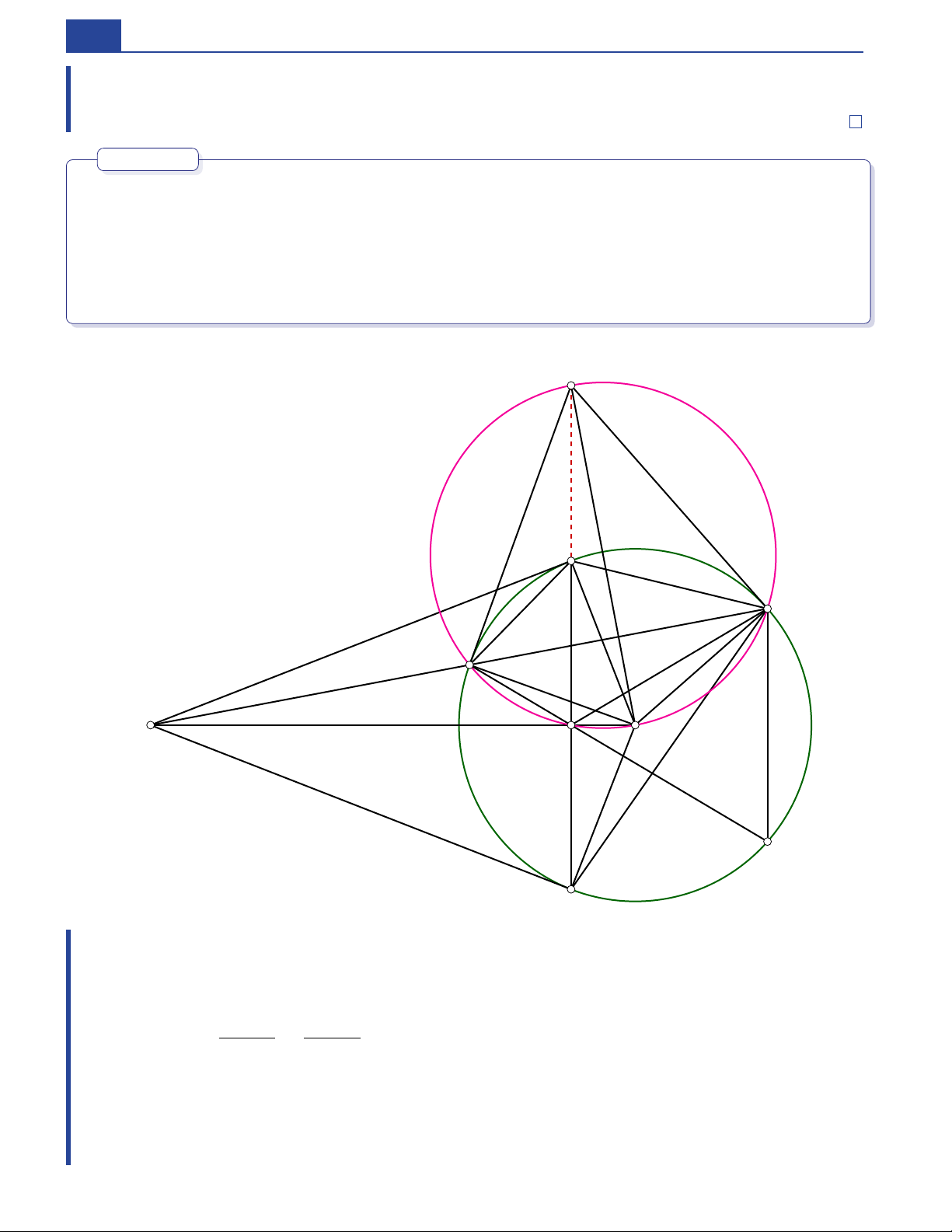
AMD lớn nhất khi và chỉ khi là điểm nằm > BC . chính giữa Bài toán 3. M O MA, MB O A, B Từ điểm nằm ngoài ( ) dựng các tiếp tuyến đến ( ) (
là các tiếp điểm) và dựng MC D MD MA MO. AB MO H. F cát tuyến sao cho tia nằm giữa hai tia và cắt tại Gọi là giao C H O . điểm thứ hai của và ( ) a. DF || AB. Chứng minh rằng b. ∠ADM ∠HDB. Chứng minh rằng = c. C D AB.
Chứng minh tiếp tuyến tại và
cắt nhau tại một điểm thuộc đường thẳng S A D C M H O F B Chứng minh. a. MH · MO MA2 MC · MD → C HOD Ta có = = tứ giác nội tiếp. ∠MHC ∠C DO ∠OC D
∠OHD → ∠C HA ∠DHA. Suy ra = = = = HA ∠C HD. Do đó là phân giác của ∠DOC ∠DHC ∠DF C ∠C HA ∠BHF , Ta có = = = = 2 2 → DF || AB.
mà hai góc này ở vị trí so le trong b. a ∠AHD
∠DF C → ∠BHD ∠C AD, ∠HBD ∠AC D. Từ câu , ta suy ra = = kết hợp với =
△DAC ∽ △DHB g.g → ∠ADM ∠HDB. Suy ra ( ) = c. S C D O . Gọi
là giao điểm của tiếp tuyến tại và của ( ) SC OD C HOD S, C , H, O, D Khi đó tứ giác nội tiếp, mà tứ giác nội tiếp nên 5 điểm 5 SO.
nội tiếp đường tròn đường kính ∠OHS ◦ ∠OHA → S, A, H Từ đó ta suy ra được = 90 = thẳng hàng.
Do đó ta có điều phải chứng minh.
Nhận xét 0.1. Câu b của bài toán, cho ta một tính chất của đường đối trung. Đây là một tính chất
hay để giải quyết được nhiều bài toán hay và khó. Tính chất và cách chứng minh được phát biểu như sau.
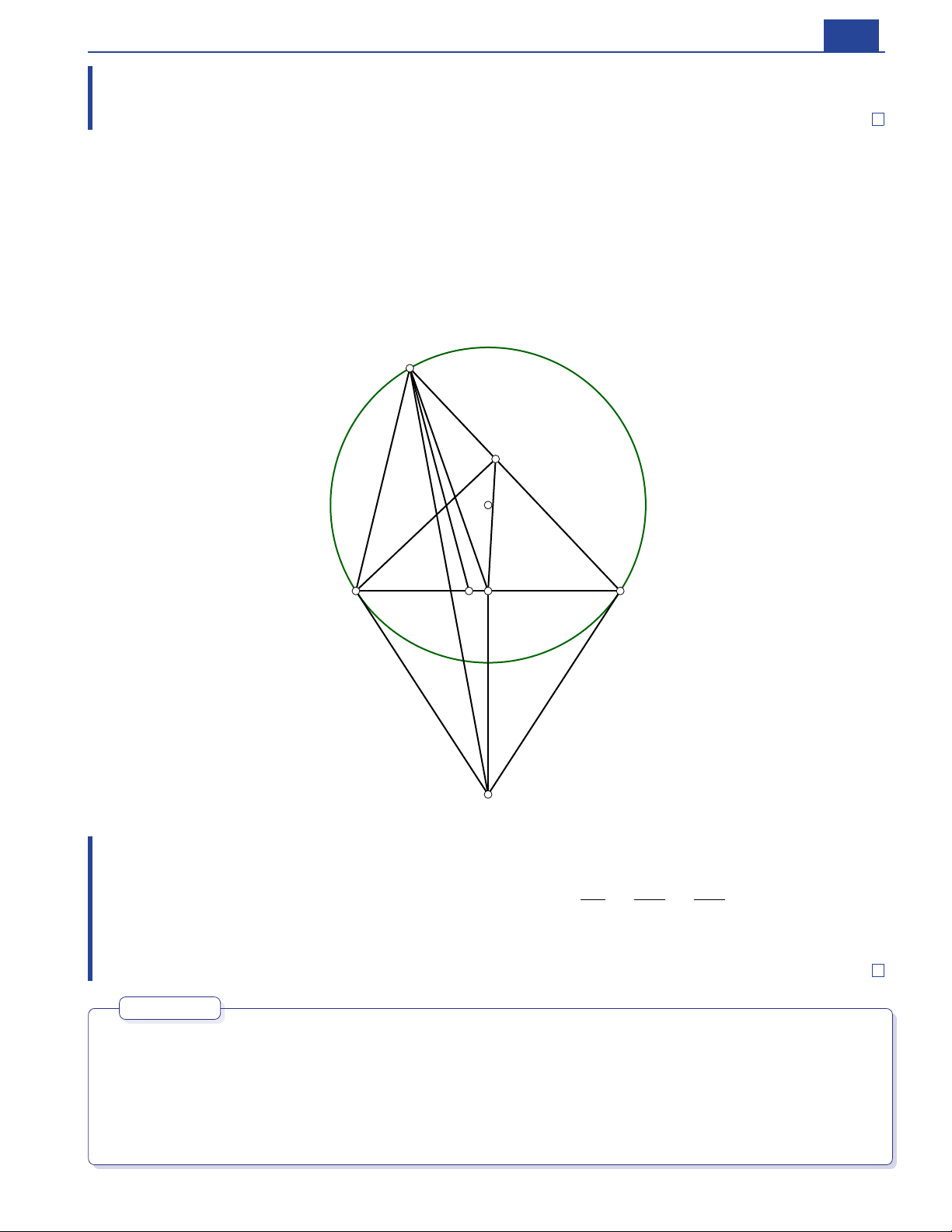
“Cho △ABC nội tiếp O . Tiếp tuyến tại B và C cắt nhau tại T . Gọi M là trung điểm của BC . Khi ( )
đó, AT đối xứng với AM qua phân giác của ∠BAC (AT được gọi là đường đối trung của △ABC .)” A E O M B C D T Chứng minh. AD D ∈ BC ∠BAT ∠MAC . Kẻ phân giác ( ). Ta sẽ đi chứng minh =AB T B T B BE ⊥ AC .
△BMT ∽ △AEB g.g → . Thật vậy, kẻ Khi đó ( )
AE = BM = ME ∠ABT ∠ABC ∠T BC ∠ABC ∠BAC ◦ − ∠ACB ◦ − ∠MEC ∠AEM. Lại có = + = + = 180 = 180 =
△ABT ∽ △AEM g.g . Do đó ( )
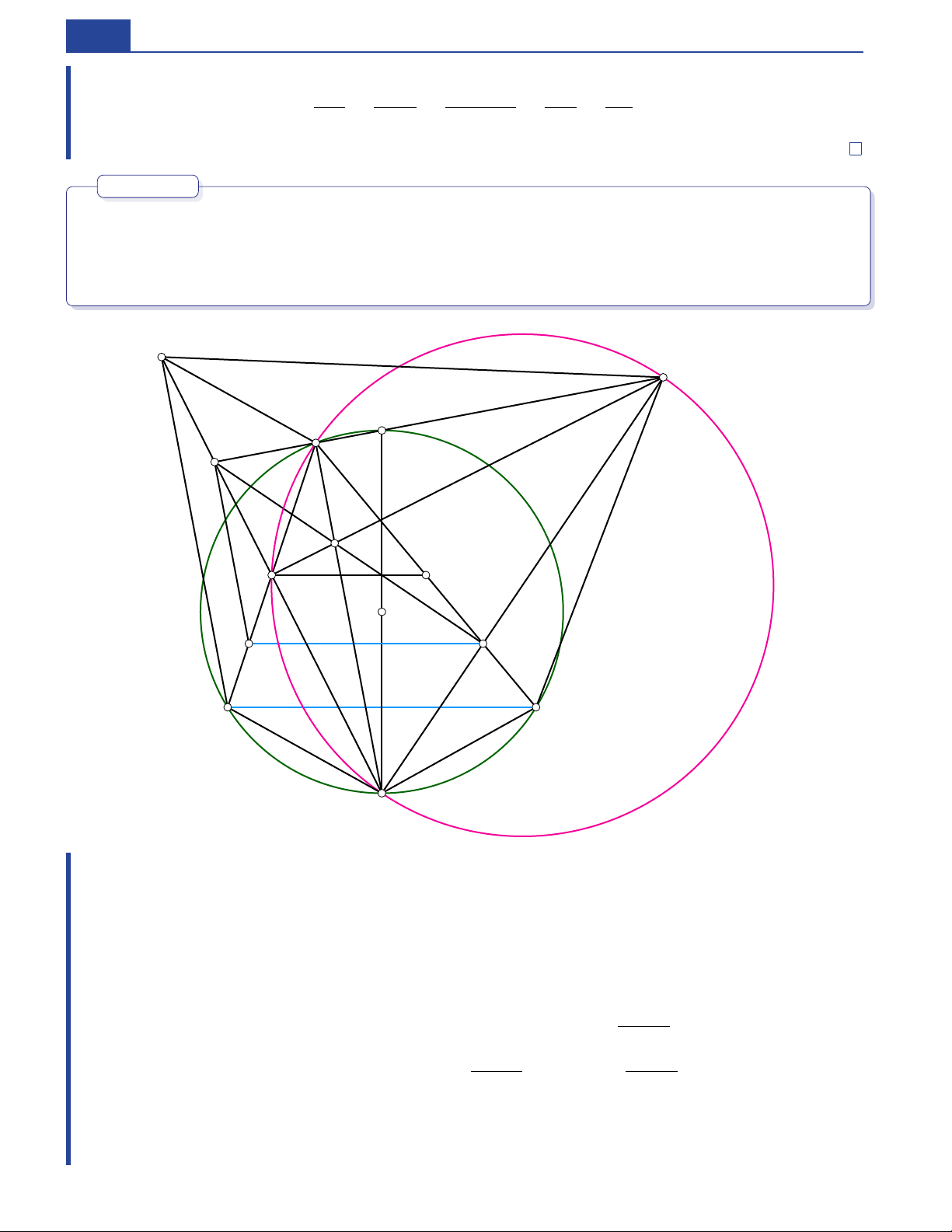
Tới đây, dễ dàng ta đưa tới điều phải chứng minh. Bài toán 4. O BC A BC AB < AC . Cho đường tròn ( ) và dây cố định. Điểm di chuyển trên cung lớn sao cho AD, BE, C F △ABC H. EF BC Ba đường cao của cắt nhau tại Đường thẳng cắt đường thẳng tại P. D EF AB R, AC Q. điểm Qua
kẻ đường thẳng song song với cắt tại cắt tại Chứng minh rằng △PQR A BC . đường tròn ngoại tiếp
luôn đi qua một điểm cố định khi di động trên cung lớn
HSG 9 Hải Phòng 2023 - 2024 6 A E O T Q F H P B C D M R S Chứng minh. M BC → M Gọi là trung điểm của cố định. AS O . T AP O . Kẻ đường kính của ( ) Gọi
là giao điểm thứ hai của với ( ) BHC S → H, M, S Khi đó, tứ giác là hình bình hành thẳng hàng. AT BC EF BC PT · PA PB · PC PF · PE, Ta có tứ giác và nội tiếp nên = = AT F E AF HE dẫn đến tứ giác
nội tiếp, kết hợp với tứ giác nội tiếp. A, T , F , H, E Suy ra 5 điểm
cùng thuộc một đường tròn. ∠AT H ◦, ∠AT S ◦ T ∈ HS. Do đó = 90 mà = 90 nên T , H, M, S Dẫn đến 4 điểm thẳng hàng. △AMP
AD ⊥ MP, MT ⊥ AP → H △AMP Xét có là trực tâm của DP · DM DH · DA. Suy ra = H △ABC → DB · DC DH · DA DP · DM. Lại có là trực tâm của = = QR || PE,
Áp dụng định lý Thalès cho ta có DQ DC , PE = PC (1) DR DB . PF = PB (2) BF EC
Nhân theo vế (1) và (2), kết hợp với tứ giác nội tiếp, ta suy ra DQ · DR
DC · DB → DQ · DR DC · DB.
PE · PF = PC · PB = DQ · DR DP · DM → PRMQ Do đó = tứ giác nội tiếp. △PQR M BC
Tới đây, ta suy ra được đường tròn ngoại tiếp luôn đi qua điểm là trung điểm của A BC . cố định khi di động trên cung lớn
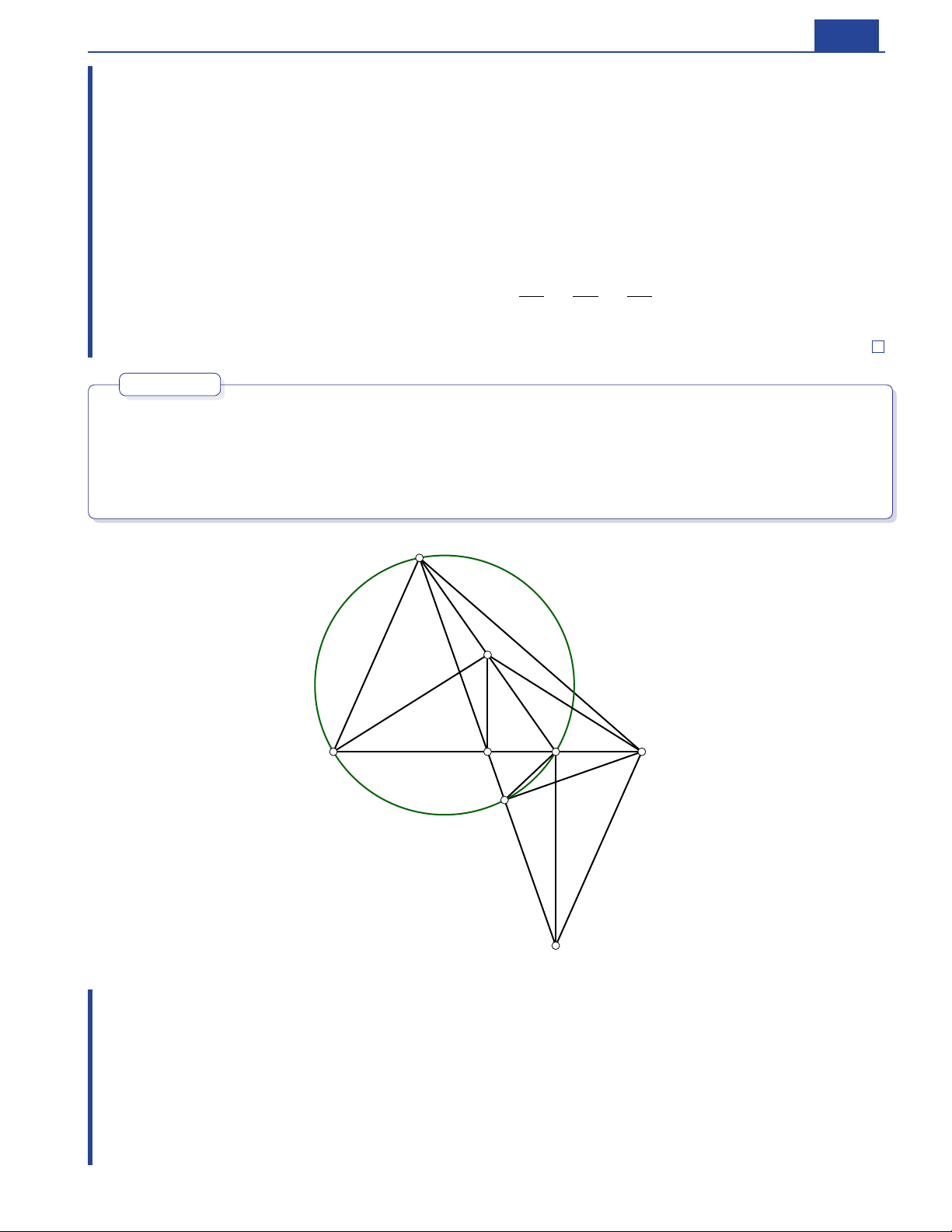
Nhận xét 0.2. Bài toán trên đưa ta đến một tính chất quen thuộc là S, M, H, T thẳng hàng. 7 Bài toán 5. ABC AB < AC , O . M Cho tam giác
nhọn, không cân thỏa mãn nội tiếp đường tròn ( ) Gọi là trung BC . c △ABM AC D. c điểm của Đường tròn 1 ngoại tiếp cắt cạnh tại Đường tròn 2 ngoại tiếp △AC M AB E. c △ADE O K . cắt cạnh tại Đường tròn 3 ngoại tiếp cắt lại ( ) tại a. BE · BA C D · C A. Chứng minh rằng = b.
△K DE ∽ △ABC . Chứng minh rằng c. L ∈ BC ∠BAM ∠C AL. N DE. Lấy điểm sao cho = Gọi là trung điểm của Chứng minh rằng MN || AL.
Thi thử chuyên Lam Sơn - Thanh Hóa A K E N D S L B C M Chứng minh. a. AEMC , ADMB M BC Ta có tứ giác nội tiếp và là trung điểm của nên BE · BA BM · BC C M · BC C D · C A. = = = b.
AK || BC → ∠K ED ∠K AD ∠K BC ∠AC B, Dễ thấy = = = ∠DK E
∠BAC → △K DE ∽ △ABC g.g kết hợp với = ( ) c. K N c S. A, S, L cắt lại ( 3 ) tại Khi đó, dễ thấy thẳng hàng. AK C B → △ABC △K C B Chú ý rằng tứ giác là hình thang cân = . b K N AM Từ câu , ta có và
là hai trung tuyến tương ứng nên K N AM K M ,
K D = AB = K C ∠NK D ∠MAB
∠MK C → △K NM ∽ △K DC c.g.c kết hợp với = = ( ) Từ đó ta suy ra được ∠K NM ∠K DC
∠K EB → ∠SNM ∠AEK ∠ASN, = = = = → MN || AL. mà 2 góc này so le trong 8
Nhận xét 0.3. Nếu gọi giao điểm 2 tiếp tuyến tại B và C của O là R, khi đó ta sẽ có 4 điểm ( )
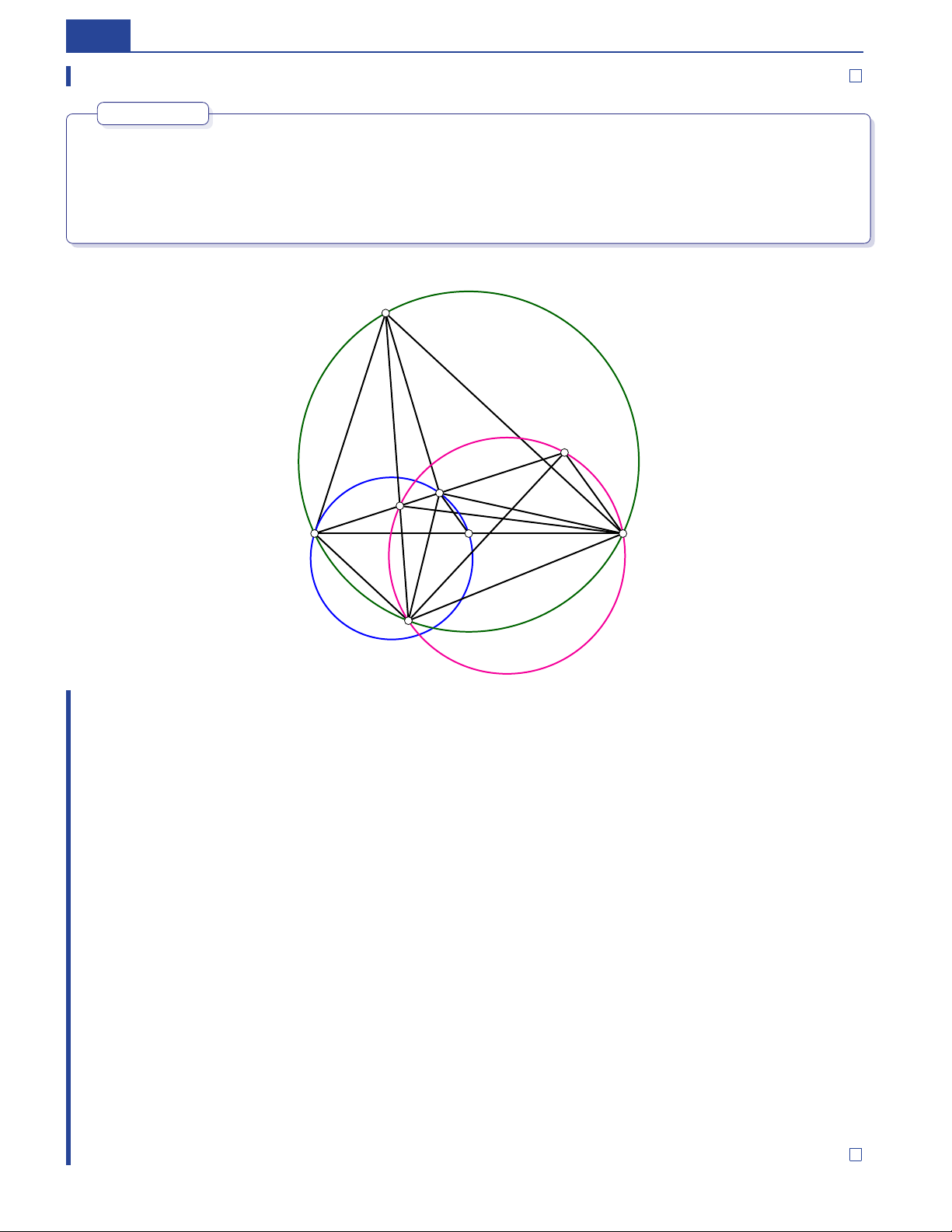
A, S, L, R thẳng hàng. Cách chứng minh sẽ dựa vào bổ đề đường đối trung tác giả đã nêu ở phần Nhận xét 0.1. Bài toán 6. ABC AB < AC . I ABC Cho tam giác nhọn thỏa mãn
Đường tròn ( ) nội tiếp tam giác tiếp xúc với BC , C A, AB D, E, F . M N AI các cạnh lần lượt tại Gọi và
lần lượt là giao điểm của đường thẳng DF AI DE. với và với a. C M ⊥ AI. Chứng minh rằng b. K BC . △K MN Gọi là trung điểm của Chứng minh rằng cân. c. M N K K M S. AS || ID. Tiếp tuyến tại và của ( ; ) cắt nhau tại Chứng minh rằng A E L F I N B H D K C S M Chứng minh. a. Ta có ◦ − ∠ABC ∠BAC ∠AC B ∠IMD
∠BF D − ∠BAI 180 − ∠IC D. = = = = 2 2 2 IDMC → ∠C MA ∠IDC ◦ Suy ra tứ giác nội tiếp = = 90 . C M ⊥ AI. Do đó b. L AC . Gọi là trung điểm của K L △ABC Khi đó
là đường trung bình của nên K L || AB (3) △AC M M, ML ∠LMA ∠LAM ∠BAM, Lại có vuông tại trung tuyến nên = = suy ra ML || AB (4) 9 M, K , L Từ (3) và (4), ta suy ra thẳng hàng. △BF D B MK || BF Ta có cân tại và nên ∠K MD ∠BF D ∠BDF ∠K DM, = = = △K DM K → K M K D. Suy ra cân tại = △K ND K → K N K D,
Bằng cách chứng minh tương tự, ta cũng có cân tại = K M K N → △K MN K . do đó = cân tại c. AH △ABC . Hạ đường cao của a BN ⊥ AM → ANHB Chứng minh tương tự câu , ta suy ra tứ giác nội tiếp. ∠BAC ∠NHK ∠BAM . Suy ra = = 2 ∠BAC ∠AHMC ∠MHC ∠MAC . Lại có tứ giác nội tiếp nên = = 2 Do đó ta có ∠BAC ∠BAC ∠MHN ∠MHK ∠NHK ∠BAC . = + = + = (5) 2 2 Lại có ∠NK C ∠K NM ∠MAC ∠BAC = 2 = 2 = (6) HNK M
Từ (5) và (6), ta suy ra được tứ giác nội tiếp. SNK M Lại có tứ giác nội tiếp. S, H, N, K , M SK → HS ⊥ BC . Nên 5 điểm
cùng thuộc một đường tròn đường kính A, S, H AS ⊥ BC → AS || ID. Dẫn đến 3 điểm thẳng hàng. Nên Bài toán 7. △ABC O . D ∈ AB, E ∈ AC DE || BC . OF ⊥ DE F . Cho nội tiếp ( ) Lấy sao cho Kẻ tại Đường ABE AC D G. tròn ngoại tiếp tam giác
cắt lại đường tròn ngoại tiếp tam giác tại Chứng minh A, F , O, G rằng đồng viên. 10 A O E P D F B C G S Chứng minh.
“Cho △ABC . Gọi T là điểm thuộc cạnh BC .
Trước hết, ta sẽ đi chứng minh 2 bổ đề sau: T B AB2
i. AT là đường đối trung của △ABC khi và chỉ khi . T C = AC 2 d X⊥AB AB
ii. Giả sử AT là đường đối trung của △ABC . X ∈ AT khi và chỉ khi ( ) .” d = X ⊥AC AC ( )
(cách chứng minh sẽ được trình bày ở phần Nhận xét 0.4). Quay lại bài toán.
△BDG ∽ △EC G, DE || BC ii. Chú ý rằng và bổ đề , ta có d G⊥AB BD AB ( ) , d = G⊥AC C E = AC ( ) G △ABC . do đó
thuộc đường đối trung của B C O S → A, G, S Tiếp tuyến tại và của ( ) cắt nhau tại thẳng hàng. P SB ED. Gọi là giao điểm của và ∠BPE ∠SBC ∠BAE → P △ABE. Khi đó, ta có = =
thuộc đường tròn ngoại tiếp OB ⊥ SP OF ⊥ PE OF BP Tuy nhiên, do và nên tứ giác nội tiếp, APBG kết hợp với tứ giác nội tiếp, ta suy ra SF · SO SB · SP SG · SA. = = A, F , O, G Từ đó, ta suy ra 4 điểm đồng viên.
Nhận xét 0.4. Tiếp tục với tính chất về đường đối trung mà tác giả đã nêu ở Nhận xét 0.1, bổ đề 11
của bài toán trên cho ta thêm 2 tính chất nữa của đường đối trung. Sau đây sẽ là cách chứng minh của bổ đề.
“Cho △ABC . Gọi T là điểm thuộc cạnh BC . T B AB2
i. AT là đường đối trung của △ABC khi và chỉ khi . T C = AC 2 d X⊥AB AB
ii. Giả sử AT là đường đối trung của △ABC . X ∈ AT khi và chỉ khi ( ) .” d = X ⊥AC AC ( ) A Y Z P H K Q X B C T M Chứng minh. i. M BC . M Điều kiện cần. Gọi là trung điểm của Qua
kẻ đường thẳng vuông góc với AC , AB AC , AB H K . cắt lần lượt tại và ∠BAT ∠C AM α ∠TAM β. Ta ký hiệu = = ; = Ta có T B SABT AB · AT , C M = S = (7) C AM AC · AM BM SABM AB · AM . T C = S = (8) C AT AC · AT
Nhân dọc theo vế (7) và (8), ta suy ra được T B AB2 . T C = AC 2 T ′B AB2 T B AT ′ △ABC → → T ≡ T ′.
Điều kiện đủ. Kẻ đường đối trung của T ′C = AC = 2 T C ii. Y , Z X AC AB. Điều kiện cần. Gọi
lần lượt là hình chiếu của lên và i. Theo bổ đề , ta suy ra AB2 T B SABX X Z · AB , AC = = 2 T C = SACX X Y · AC hay là AB X Z . AC = X Y AX BC T ′. Điều kiện đủ. cắt tại P, Q T ′ AC AB. Gọi
lần lượt là hình chiếu của lên và X Z || T ′Q X Y || T ′P,
Áp dụng định lý Thalès cho và ta có T ′Q X Z AB .
T ′P = X Y = AC 12 Lại có T ′B SABT′ AB · T ′Q AB2 T B . T ′C = S = = AC T ′
AC · T ′P = AC 2 T C T ≡ T ′. Suy ra Hoàn tất chứng minh. Bài toán 8. ABC O . M BC . MK . Cho tam giác nội tiếp ( )
là điểm chính giữa của cung nhỏ Vẽ đường kính AK AC N. MN AC T . T Đường thẳng qua cắt trung trực tại cắt tại Qua kẻ đường thẳng vuông MN AN H. H HN AB V . góc với cắt tại Qua
kẻ đường thẳng vuông góc với cắt tại Chứng minh V T || BC . rằng R N A K H S P Q O V T B C M Chứng minh. P △AMN AB. Gọi
là giao điểm của đường tròn ngoại tiếp và R M P. Lấy đối xứng với qua APMN ∠MPN ∠MAN ◦. Do tứ giác nội tiếp nên = = 90 NP MR. Dẫn đến
là đường trung trực của △NAR △NC M c.g.c → AY C M BM.
Từ đó dễ dàng suy ra được = ( ) = = Lại có ∠BAC ∠RAP
◦ − ∠RAN − ∠PAM − ∠MAN ◦ − − ∠MC N, = 360 = 270 2 ◦ ∠BAC ∠BAC
− ∠BAC − ∠BC A ∠ABC ∠X BM, = 180 + = + = 2 2 AY || BM.
mà hai góc này ở vị trí so le trong nên ARBM Dẫn đến tứ giác là hình bình hành. P AB. Suy ra là trung điểm của 13 Q AC . S AM HT . Gọi là trung điểm của là giao điểm của và S △HMN → P, S, N Nhận thấy rằng là trực tâm của thẳng hàng. Ta có
△APM ∽ △AST → AP · AT AM · AS, = (9)
△AHS ∽ △AMN → AM · AS AN · AH, = (10)
△AHV ∽ △AQN → AN · AH AQ · AV . = (11) Từ (9),(10),(11), ta suy ra AV AP AB AP · AT AQ · AV → , =
AT = AQ = AC
theo định lý Thalès đảo, ta thu được điều phải chứng minh. Bài toán 9. △ABC M BC . D C AM. Cho nhọn. Gọi là trung điểm của Lấy là hình chiếu của lên Đường tròn △ABD BC E. F ∈ AE F B F C . F ngoại tiếp cắt lại cạnh tại Lấy sao cho = Chứng minh rằng là AE. trung điểm của Hong Kong TST 2024 A F B M C E D S Chứng minh. S A M. Lấy
là điểm đối xứng với qua ABSC Khi đó tứ giác là hình bình hành. Suy ra ∠MSC ∠DAB ∠MED, = = DEC S ∠SEC ∠SDC ◦ → SE ⊥ BC . dẫn đến tứ giác nội tiếp nên = = 90 F B F C MB MC F M ⊥ BC . Lại có = và = nên F M || SE,
Từ đó, ta suy ra ngay được 14 M AS, F AE. kết hợp với là trung điểm của dẫn đến là trung điểm của Bài toán 10. ABC , D △ABC ∠DAC ∠AC B ∠BDC Cho tam giác điểm thuộc miền trong của thỏa mãn = và = ◦ ∠BAC . E BD AE EC . M BC . 90 + Lấy điểm thuộc tia sao cho = Gọi là trung điểm của Chứng AB △BEM. minh rằng
là tiếp tuyến của đường tròn ngoại tiếp USAMO 2024 A P E D B M C Q Chứng minh. AD △ABC Q. Kéo dài
cắt lại đường tròn ngoại tiếp tại P B E. Gọi
là điểm đối xứng của qua Ta có ∠AQC ∠AC B ∠QC B ∠DAC ∠QAB ∠BAC , = + = + = BAC Q suy ra tứ giác là hình thang cân. EA EC E AC → E Do = nên thuộc đường trung trực của cũng thuộc đường trung trực của BQ → EQ EB EP → △BQP Q. = = vuông tại QP ⊥ BQ → QP ⊥ AC Nên . Khi đó, ta có ∠PQC ◦ − ∠ACQ ◦ − ∠BAC ◦ − ∠BDC ∠C DP. = 90 = 90 = 180 = PDQC Suy ra tứ giác nội tiếp. EM △BPC → EM || PC . Chú ý rằng
là đường trung bình của Khi đó, ta có ∠BEM ∠DPC ◦ − ∠DQC ◦ − ∠ABC
◦ − ∠EBM − ∠ABE, = = 180 = 180 = 180 ∠ABE
◦ − ∠EBM − ∠BEM ∠EMB. = 180 = AB △BEM.
Tới đây, ta suy ra ngay rằng
là tiếp tuyến của đường tròn ngoại tiếp 15 Bài toán 11. ABC AB < AC I BC , C A, AB Cho tam giác nhọn (
) có đường tròn ( ) nội tiếp, tiếp xúc với lần lượt D, E, F . AH BC H. DM I . ∠AEI tại Kẻ vuông góc với tại Kẻ đường kính của ( ) Tia phân giác của AI G. MG AH K . cắt tại cắt tại a. AK AE. Chứng minh = b. MK I P, AP I L. D, K , L Gọi cắt lại ( ) tại cắt lại ( ) tại Chứng minh rằng thẳng hàng. c. K I BC Q. AQ I . cắt tại
Chứng minh rằng đường tròn đường kính tiếp xúc với ( ) A M x L E G F K N I S P B H C D Q Chứng minh. a. AK || IM
Áp dụng định lý Thalès cho
và áp dụng tính chất đường phân giác cho phân EG △AEI, giác của ta có AK AG AE ,
IM = IG = IE IM IE, AK AE. với chú ý rằng = ta suy ra ngay = b. AL · AP AE2 AK 2, ∠K AP
△AK L ∽ △APK . Ta có = = kết hợp với chung, suy ra ∠AK L ∠LPM ∠LDM, Do đó = = AK || DM D, K , L mà nên ta có thẳng hàng. c. N LP. → IN ⊥ LP. Gọi là trung điểm của P LP. SP || NI. Qua
vẽ đường thẳng vuông góc với Khi đó
△K LP ∽ △K MD g.g K N K I Lại có ( ) có và
là 2 trung tuyến tương ứng nên ∠SNP ∠LNK ∠MIK ∠QID, = = = ∠SPN ∠QDI ◦,
△SPN ∽ △QDI g.g . kết hợp với = = 90 ta có ( ) Do đó SN NP LP K N ,
QI = ID = MD = K I NI || SQ.
nên theo định lý Thalès đảo, suy ra S, P, Q Dẫn đến 3 điểm thẳng hàng. Px P AQ. Kẻ là tiếp tuyến tại
của đường tròn đường kính K PHD Chú ý rằng tứ giác nội tiếp nên ∠LPx ∠AHP ∠LDP, = = 16 Px I . suy ra là tiếp tuyến của ( )
Tới đây, dễ dàng để suy ra ngay được điều phải chứng minh. Bài toán 12. I O △ABC . S Gọi và
lần lượt là tâm đường tròn nội tiếp và tâm đường tròn ngoại tiếp của Vẽ a ∠BAC . I IO, BC S P là phân giác ngoài của Đường thẳng qua vuông góc với cắt và a lần lượt tại Q. IP IQ. và Chứng minh rằng = 2 Balkan MO 2021 Q A N S R M I O B C P Chứng minh.
Trong bài toán này, bạn đọc cần biết đến bổ đề bắn và định lý con bướm trong tứ giác nội tiếp.
Cách chứng minh sẽ được đề cập tại phần Nhận xét 0.5. > > M N AB, AC △ABC . Gọi và
lần lượt là điểm chính giữa của
của đường tròn ngoại tiếp MN AI IQ R S. cắt và lần lượt tại và NA NI MA MI, MN AI.
Áp dụng bổ đề bắn, có = và = nên
là đường trung trực của R AI, RS || AQ. S IQ. Do đó là trung điểm của kết hợp với Suy ra là trung điểm của IQ IS. Dẫn đến = 2 BMNC , IP IS.
Áp dụng định lý con bướm cho tứ giác nội tiếp có = IQ IP IS. Điều đó chứng tỏ = 2 = 2 Nhận xét 0.5.
i. Bổ đề bắn (Shooting lemma)
“Cho tam giác ABC nội tiếp đường tròn O . Điểm M là điểm chính giữa cung BC nhỏ. Gọi I là tâm ( )
đường tròn nội tiếp △ABC . MI cắt BC tại D. Khi đó MB MI MC và MI2 MD · MA.” = = = 17 A I B C D M Chứng minh.
Theo tính chất góc ngoài, ta có ∠MIB ∠IAB ∠IBA ∠MAC ∠IBD ∠IBD ∠C BM ∠IBM, = + = + = + = MI MB MC . do đó = = ∠MBD ∠MAC ∠MAB, ∠BMA
△MBD ∽ △MAB g.g Ta có = = kết hợp với chung, nên ( ) MD · MA MB2 MI2. Dẫn đến = =
ii. Định lý con bướm (Butterfly theorem)
“Cho tứ giác ABC D nội tiếp đường tròn O . Gọi M là giao điểm của AC và BD. Đường thẳng qua ( )
M vuông góc với MO cắt AD và BC lần lượt tại P và Q. Khi đó M là trung điểm của PQ.” Chứng minh. E F AD BC . Gọi và
lần lượt là trung điểm của và
△MAD ∽ △MBC , ME MF Chú ý rằng có và
là 2 trung tuyến tương ứng nên ∠MED ∠MF C . = MEPO MQF O Lại có tứ giác và nội tiếp nên ∠OPM ∠DEM ∠MF Q ∠MOQ. = = = △OPQ O. Từ đó suy ra cân tại M PQ. Do đó là trung điểm của 18 B A O F P E M Q C D Bài toán 13. ABC O I. BE C F Cho tam giác nội tiếp đường tròn (
) và tâm đường tròn nội tiếp Phân giác và O P, Q. cắt lại ( ) tại a. A O EF , PQ
Chứng minh rằng tiếp tuyến tại của ( ) và đồng quy. b. I IO BC , EF K , L. IK IL. Đường thẳng qua vuông góc với cắt lần lượt tại Chứng minh rằng = 2 A P N M Q L E I F O R T B K C Chứng minh. > a. P AC . Ta có
là điểm chính giữa của PI PE PI − PE IE PI2 PA2 PE · PB → ,
Nên theo bổ đề bắn, ta có = =
PB = PI = PB − PI = IB EI IB . suy ra EP = IP