Ứng dụng của đạo hàm và khảo sát đồ thị hàm số – Trần Thông Toán 12

Ứng dụng của đạo hàm và khảo sát đồ thị hàm số – Trần Thông Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

108 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
TRẦN THÔNG Facebook: hội toán bắc trung nam
MỖI THÁNG MỘT CHỦ ĐỀ
CHUYÊN ĐỀ:
ỨNG DỤNG CỦA ĐẠO HÀM VÀ
KHẢO SÁT ĐỒ THỊ HÀM SỐ
Quảng Nam, tháng 11 năm 2016
1
TRẦN THÔNG Facebook: hội toán bắc trung nam
Mở đầu
Hàm số là một trong những khái niệm cơ bản của toán học, đóng vai trò quan trọng trong
chương trình toán phổ thông và là nền tảng của nhiều lĩnh vực khác nhau của toán học nói riêng
và khoa học tự nhiên nói chung. Để bạn đọc có được cái nhìn tổng quát hơn về hàm số, trong bài
viết tháng 11/2016 của hội toán bắc trung nam tôi xin trình bày một số vấn đề cơ bản về hàm số.
Bài viết được chia làm ba phần chính:
Phần 1: Giới thiệu một số khái niệm cơ bản như tính đơn điệu, cực trị, tiệm cận…
Phần 2: Trình bày sơ đồ khảo sát và vẽ đồ thị một số hàm số quen thuộc.
Phần 3: Khái quát một số dạng toán quen thuộc về hàm số và các ứng dụng.
Lưu ý bạn đọc: Trước khi đọc hiểu bài viết này, bạn đọc cần nắm vững định nghĩa, các
tính chất cơ bản của đạo hàm cùng với bảng đạo hàm các hàm số sơ cấp được trình bày chi tiết
trong chương trình toán THPT hiện hành.
Với hệ thống bài tập tự luận và trắc nghiệm phong phú, hi vọng bài viết này sẽ giúp ích
cho bạn đọc, đặc biệt là các bạn thí sinh trong kỳ thi THPT quốc gia sắp tới khi tìm hiểu về hàm
số. Tuy vậy do nhiều nguyên nhân khác nhau, bài viết không tránh khỏi những khiếm khuyết, tác
giả rất mong nhận được những ý kiến đóng góp của quý độc giả đề chuyên đề ngày một hoàn
thiện hơn. Mọi ý kiến đóng góp, quý độc giả vui lòng gửi về địa chỉ email: thongqna@gmail.com
hoặc trang cá nhân facebook: https://www.facebook.com/thong.tranvan.5203.
Quảng Nam, ngày 15 tháng 11 năm 2016
TRẦN THÔNG
2
TRẦN THÔNG Facebook: hội toán bắc trung nam
PHẦN 1: KIẾN THỨC CHUẨN BỊ
1.Tính đơn điệu của hàm số.
a.Định nghĩa: Cho hàm số
()y f x
xác định trên D, với D là một khoảng, một đoạn hoặc nửa
khoảng.
1.Hàm số
()y f x
được gọi là đồng biến trên D nếu
1 2 1 2 1 2
, , ( ) ( )x x D x x f x f x
2.Hàm số
()y f x
được gọi là nghịch biến trên D nếu
1 2 1 2 1 2
, , ( ) ( )x x D x x f x f x
b.Điều kiện cần để hàm số đơn điệu: Giả sử hàm số
()y f x
có đạo hàm trên khoảng D
1.Nếu hàm số
()y f x
đồng biến trên D thì
'( ) 0,f x x D
2.Nếu hàm số
()y f x
nghịch biến trên D thì
'( ) 0,f x x D
c.Điều kiện đủ để hàm số đơn điệu:
1.Định lý 1. Nếu hàm số
()y f x
liên tục trên đoạn
và có đạo hàm trên khoảng (a,b) thì
tồn tại ít nhất một điểm
( , )c a b
sao cho:
( ) ( ) '( )( )f b f a f c b a
2.Định lý 2. Giả sử hàm số
()y f x
có đạo hàm trên khoảng D
1.Nếu
'( ) 0,f x x D
và
'( ) 0fx
chỉ tại một số hữu hạn điểm thuộc D thì hàm số đồng
biến trên D
2.Nếu
'( ) 0,f x x D
và
'( ) 0fx
chỉ tại một số hữu hạn điểm thuộc D thì hàm số nghịch
biến trên D
3.Nếu
'( ) 0,f x x D
thì hàm số không đổi trên D
2.Cực trị
a.Định nghĩa: Cho hàm số
()y f x
xác định trên
RD
và
0
xD
1.
0
x
được gọi là một điểm cực đại của hàm số
()y f x
nếu tồn tại một (a,b) chứa điểm
0
x
sao cho
( , )a b D
và
00
( ) ( ), ( , )\f x f x x a b x
. Khi đó
0
()fx
được gọi là già trị cực đại của
hàm số và
00
( ; ( ))M x f x
được gọi là điểm cực đại của hàm số .
3
TRẦN THÔNG Facebook: hội toán bắc trung nam
2.
0
x
được gọi là một điểm cực tiểu của hàm số
()y f x
nếu tồn tại một (a,b) chứa điểm
0
x
sao cho
( , )a b D
và
00
( ) ( ), ( , )\f x f x x a b x
. Khi đó
0
()fx
được gọi là già trị cực tiểu
của hàm số và
00
( ; ( ))M x f x
được gọi là điểm cực tiểu của hàm số .
3.Giá trị cực đại và giá trị cực tiểu được gọi chung là cực trị của hàm số
b.Điều kiện cần để hàm số có cực trị : Giả sử hàm số
()y f x
có cực trị tại
0
x
.Khi đó, nếu
()y f x
có đạo hàm tại điểm
0
x
thì
0
'( ) 0fx
.
c.Điều kiện đủ để hàm số có cực trị :
1.Định lý 1. (Dấu hiệu 1 để tìm cực trị của hàm số )
Giả sử hàm số
()y f x
liên tục trên khoảng (a,b) chứa điểm
0
x
và có đạo hàm trên các
khoảng
00
( , ) và ( , )a x x b
. Khi đó :
+ Nếu f’(x) đổi dấu từ âm sang dương khi x qua điểm
0
x
thì hàm số đạt cực tiểu tại
0
x
+ Nếu f’(x) đổi dấu từ dương sang âm khi x qua điểm
0
x
thì hàm số đạt cực đại tại
0
x
2.Định lý 2. (Dấu hiệu 2 để tìm cực trị của hàm số )
Giả sử hàm số
()y f x
có đạo hàm trên khoảng (a,b) chứa điểm
0
x
,
0
'( ) 0fx
và f(x) có
đạo hàm cấp hai khác 0 tại điểm
0
x
. Khi đó:
+ Nếu
0
''( ) 0fx
thì hàm số đạt cực đại tại điểm
0
x
+ Nếu
0
''( ) 0fx
thì hàm số đạt cực tiểu tại điểm
0
x
3.Tiệm cận
a.Đường tiệm cận đứng .
Đường thẳng (d):
0
xx
được gọi là đường tiệm cận đứng của đồ thị (C) của hàm số
()y f x
nếu
0
lim ( )
xx
fx

hoặc
0
lim ( )
xx
fx

hoặc
0
lim ( )
xx
fx

hoặc
0
lim ( )
xx
fx

b.Đường tiệm cận ngang .
Đường thẳng (d):
0
yy
được gọi là đường tiệm cận ngang của đồ thị (C) của hàm số
()y f x
nếu
0
lim ( )
x
f x y

hoặc
0
lim ( )
x
f x y

4.Sự tương giao
a.Giao điểm của hai đồ thị. Cho hàm số
()y f x
có đồ thị
1
()C
và hàm số
()y g x
có đồ thị
2
()C
4
TRẦN THÔNG Facebook: hội toán bắc trung nam
+ Hai đồ thị
1
()C
và
2
()C
cắt nhau tại điểm
0 0 0 0
( ; ) ( ; )M x y x y
là nghiệm của hệ
phương trình
()
()
y f x
y g x
+Hoành độ giao điểm của hai đồ thị
1
()C
và
2
()C
là nghiệm của phương trình
( ) ( )f x g x
(1)
+Phương trình (1) được gọi là phương trình hoành độ giao điểm của
1
()C
và
2
()C
+Số nghiệm của phương trình (1) bằng số giao điểm của
1
()C
và
2
()C
b.Sự tiếp xúc của hai đường cong. Cho hai hàm số
()y f x
và
()y g x
có đồ thị lần lượt
là
1
()C
và
2
()C
và có đạo hàm tại điểm
0
x
.
+Hai đồ thị
1
()C
và
2
()C
tiếp xúc với nhau tại một điểm chung
00
( , )M x y
nếu tại điểm
đó chúng có chung cùng một tiếp tuyến . Khi đó điểm M được gọi là tiếp điểm.
+Hai đồ thị
1
()C
và
2
()C
tiếp xúc với nhau khi và chỉ khi hệ phương trình sau có
nghiệm
( ) ( )
'( ) '( )
f x g x
f x g x
Nghiệm của hệ phương trình trên là hoành độ của tiếp điểm.
PHẦN 2: SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
I.Hàm số bậc 3:
32
0y ax bx cx d a
1.Tập xác định
D
2. Sự biến thiên
2.1. Xét sự biến thiên của hàm số
+ Tính đạo hàm
2
32y ax bx c
+ Giải phương trình
2
0 3 2 0y ax bx c
(lưu ý phải tính nghiệm chính xác không được
tìm nghiệm gần đúng)
+ Xét dấu đạo hàm và suy ra chiều biến thiên của hàm số (hàm số đồng biến,nghịch biến trên
những khoảng nào?)
2.2. Tìm cực trị
2.3. Tính giới hạn tại vô cùng (
x 
)
5
TRẦN THÔNG Facebook: hội toán bắc trung nam
Chú ý:
2.4. Lập
bảng biến thiên
Thể hiện đầy đủ, chính xác các giá trị trên bảng biến thiên
3. Đồ thị
-Giao với trục Oy:
0 0,x y d d
-Giao với trục Ox:
32
0 0 ?y ax bx cx d x
(trong trường hợp nghiệm lẻ có thể bỏ
qua bước này)
-Các điểm cực trị
- Một số hình dạng đồ thị hàm bậc 3
Nếu a>0
Nếu a<0
Phương trình
y’ = 0
có hai
nghiệm
phân biệt
* Nếu a > 0
32
lim lim ( )y ax bx cx d
xx

 
32
lim lim ( )y ax bx cx d
xx

 
* Nếu a < 0


)(limlim
23
dcxbxaxy
xx


)(limlim
23
dcxbxaxy
xx
6
TRẦN THÔNG Facebook: hội toán bắc trung nam
Phương trình
y’ = 0
có nghiệm
kép
Phương trình
y’ = 0
vô nghiệm
Ví dụ minh họa:
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x
3
+ 3x
2
– 4
* Tập xác định:
RD
* Sự biến thiên:
Chiều biến thiên:
xxy 63'
2
Giải phương trình:
0'y
063
2
xx
2
0
x
x
Dấu của y’
x
-
-2
0
+
y’
+
0
-
0
+
Đồ thị hàm số đồng biến trên khoảng:
);0()2;( 
và nghịch biến trên khoảng (- 2; 0).
- Cực trị:
7
TRẦN THÔNG Facebook: hội toán bắc trung nam
- Giới hạn:


)43(limlim
23
xxy
xx


)43(limlim
23
xxy
xx
- Bảng biến thiên:
x
-
-2
0
+
y’
+
0
-
0
+
y
-
0
-4
+
* Đồ thị:
- Giao điểm với Oy:
Cho x = 0
y = -4
- Giao với Ox:
Cho y = 0 giải phương
trình:
x
3
+ 3x
2
– 4 = 0
2
1
x
x
Bảng giá trị:
x
-3 1
y
-4 0
Ví dụ 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x
3
+ 3x
2
+ 3x + 2
* Tập xác định:
RD
* Sự biến thiên:
- Chiều biến thiên:
363'
2
xxy
Giải phương trình:
0'y
0363
2
xx
phương trình có nghiệm kép:
1
21
xx
y’ > 0 với mọi giá trị của x và y’(-1) = 0.
Hàm số luôn đồng biến trên D
- Hàm số không có cực trị.
- Giới hạn:
8
TRẦN THÔNG Facebook: hội toán bắc trung nam


)233(limlim
23
xxxy
xx


)233(limlim
23
xxxy
xx
- Bảng biến thiên:
x
-
-1
+
y’
+
0
+
y
-
1
+
* Đồ thị:
- Giao điểm của đồ thị với trục tung: cho x = 0
y = 2
- Bảng giá trị
x
-2 -3
y
0 -7
-Vẽ đồ thị
Ví dụ 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = - x
3
+ 3x
2
- 4x +2
* Tập xác định:
RD
* Sự biến thiên:
- Chiều biến thiên:
4 -6x -3x'
2
y
Giải phương trình : y’= 0
-3x
2
+6x – 4 = 0
Phương trình vô nghiệm.
9
TRẦN THÔNG Facebook: hội toán bắc trung nam
y’< 0
Dx
Hàm số luôn nghịch biến trên D
- Hàm số không có cực trị
-Giới hạn


)243(limlim
23
xxxy
xx


)243(limlim
23
xxxy
xx
- Bảng biến thiên:
x
-
+
y’
-
y
+
-
* Đồ thị:
- Giao điểm của đồ thị với trục tung: cho x = 0
y = 2
- Bảng giá
trị:
x
2
y
-2
- Vẽ đồ
thị:
Bài tập luyện thi
Khảo sát và vẽ đồ thị các hàm số sau:
10
TRẦN THÔNG Facebook: hội toán bắc trung nam
1.
3
3x 2yx
2.
32
31y x x
3.
32
6 9x 4y x x
4.
2
1 2x 2y x x
5.
32
1
1
3
y x x x
6.
32
1
1
3
y x x
II.Hàm số trùng phương:
42
0y ax bx c a
1.Tập xác định
D
2. Sự biến thiên
2.1. Xét sự biến thiên của hàm số
+ Tính đạo hàm
3
4 . 2 .y a x b x

+ Giải phương trình
32
2
0
0 4a 2 0 2 2a 0 ......
2a
x
y x bx x x b
b
x
(lưu ý phải
tính nghiệm chính xác không được tìm nghiệm gần đúng)
+ Xét dấu đạo hàm và suy ra chiều biến thiên của hàm số(hàm số đồng biến,nghịch biến trên
những khoảng nào?)
2.2. Tìm cực trị
2.3. Tính giới hạn tại vô cùng (
x 
)
Chú ý
2.4. Lập bảng biến thiên
Thể hiện đầy đủ, chính xác các giá trị trên bảng biến thiên
3. Đồ thị
* Nếu a > 0


)(limlim
24
cbxaxy
xx
* Nếu a < 0


)(limlim
24
cbxaxy
xx
11
TRẦN THÔNG Facebook: hội toán bắc trung nam
-Giao với trục Oy:
0 0,cx y c
-Giao với trục Ox:
42
0 0 ?y ax bx c x
(trong trường hợp nghiệm lẻ có thể bỏ qua
bước này)
-Các điểm cực trị
-Tìm thêm một số điểm(nếu cần)
- Một số hình dạng đồ thị hàm trùng phương
a>0
a<0
Phương trình
y’ = 0
có ba nghiệm
phân biệt
Phương trình
y’ = 0
có một nghiệm
Ví dụ minh họa:
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x
4
- 2x
2
+ 2
* Tập xác định:
RD
* Sự biến thiên:
- Chiều biến thiên:
4x 4x'
3
y
giải phương trình:
12
TRẦN THÔNG Facebook: hội toán bắc trung nam
0'y
04x 4x
3
4x(x
2
- 1) = 0
0
1
x
x
Bảng dấu của y’:
x
-
-1
0
1
+
y’
-
0
+
0
-
0
+
Đồ thị hàm số đồng biến trên khoảng:
)(1;0) (-1; 
và nghịch biến trên khoảng:
)1(0;1)- ;(-
Hàm số đạt cực đại tại: x = 0
2
CĐ
y
Hàm số đạt cực tiểu tại:
11
CT
yx
Giới hạn:


)22(limlim
24
xxy
xx


)22(limlim
24
xxy
xx
- Bảng biến thiên:
x
- -1 0 1 +
y’
- 0 + 0 - 0 +
y
+ 2 +
1 1
* Đồ thị:
Giao với trục tung:
Cho x = 0
y = 2
Bảng giá trị:
x
-2 2
y
10 10
O
13
TRẦN THÔNG Facebook: hội toán bắc trung nam
Ví dụ 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y= -
2
4
x
-x
2
+
2
3
* Tập xác định:
RD
* Sự biến thiên:
- Chiều biến thiên:
)1-2x(x2x x2-'
23
y
00)1-2x(x0'
2
xy
Ta có bảng dấu của y’:
x
-
0
+
y’
+
0
-
Hàm số đồng biến trên (-
;0) và nghịch biến trên (0; +
)
Hàm số đạt cực đại tại x = 0
2
3
CĐ
y
; hàm số không có cực tiểu
Giới hạn:



)
2
3
2
(limlim
2
4
x
x
y
x
x
Bảng biến thiên:
x
-
0
+
y’
+
0
-
y
-
2
3
-
* Đồ thị:
- Giao với trục tung: cho x = 0
y=
2
3
- Giao với trục hoành: cho y = 0 giải phương trình: -
2
4
x
-x
2
+
2
3
= 0
032
4
xx
đặt
2
xt
(t
0)Ta có phương trình:
032
2
tt
)(3
1
loait
t
x
11
2
x
14
TRẦN THÔNG Facebook: hội toán bắc trung nam
- Bảng giá trị:
x
-2 2
y
2
21
2
21
- Vẽ đồ thị
Bài tập luyện thi
Khảo sát và vẽ đồ thị các hàm số sau:
1.
42
2y x x
2.
42
41y x x
3.
22
12y x x
4.
2
1 2x 2y x x
5.
42
13
3
22
y x x
6.
42
15
2
22
y x x
III.Hàm số nhất biến:
ax b
y
cx d
1.Tập xác định
\
d
D
c



2. Sự biến thiên
2.1. Xét sự biến thiên của hàm số
15
TRẦN THÔNG Facebook: hội toán bắc trung nam
+ Tính đạo hàm
2
x
ad bc
y
cd
+
y
không xác định tại
d
c
và luôn dương hoặc luôn âm với mọi
d
x
c
+ Hàm số đồng biến (nghịch biến) trên các khoảng
;
d
c




và
;
d
c




.
2.2. Tìm cực trị: Hàm số không có cực trị
2.3. Tìm tiệm cận (Tính giới hạn tại vô cùng) (
x 
)
+Ta có
lim lim
xx
ax b a
y
cx d c
 

nên là tiệm cận đứng của đồ thị.
+Lại có
lim lim
dd
xx
cc
ax b
y
cx d




và
lim lim
dd
xx
cc
ax b
y
cx d




nên là tiệm cận ngang của
đồ thị
2.4. Lập bảng biến thiên: Thể hiện đầy đủ, chính xác các giá trị trên bảng biến thiên
3. Đồ thị
-Giao với trục Oy:
0 0,
bb
xy
dd



-Giao với trục Ox:
0 0 ,0
ax b b b
y ax b x
cx d a a



-Tìm thêm một số điểm(nếu cần)
-Hình dạng đồ thị
0 bcadE
0 bcadE
16
TRẦN THÔNG Facebook: hội toán bắc trung nam
Ví dụ minh họa:
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y =
1
42
x
x
* Tập xác định:
1\ RD
* Sự biến thiên:
- Chiều biến thiên:
2
)1(
2
'
x
y
> 0
Dx
Hàm số đồng biến trên D
- cực trị : Không có
- Giới hạn và tiệm cận :
lim 2;lim 2
xx
yy
 
đường thẳng y = -2 là tiệm cận ngang của đồ thị.
11
lim ;lim
xx
yy



đường thẳng x = -1 là tiệm cận đứng của đồ thị.
- Bảng biến thiên:
x
-
1
+
y’
+
+
y
-2
+
-
-2
* Đồ thị:
17
TRẦN THÔNG Facebook: hội toán bắc trung nam
- Vẽ tiệm cận đứng: x = -1 và tiệm cận ngang: y=-2
- Giao với trục tung:
Cho x=0
y=-4
- Giao với trục
hoành:
Cho y = 0 giải
phương trình:
1
42
x
x
=0
x=-
2
- bảng giá trị:
x
1 2
y
-3 -8/3
Vẽ nhánh bên phải
đường tiệm cận
đứng. nhánh còn lại
lấy đối xứng qua tâm
I(-1;-2)
Ví dụ 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y =
2
3
x
x
* Tập xác định:
2\RD
* Sự biến thiên:
- Chiều biến thiên:
2
)2(
1
'
x
y
< 0
Hàm số nghịch biến trên D
- cực trị : Không có
- Giới hạn và tiệm cận :
lim 1;lim 1
xx
yy
 
đường thẳng y = -1là tiệm cận ngang của đồ thị.
22
lim ;lim
xx
yy



đường thẳng x = 2 là tiệm cận đứng của đồ thị.
- Bảng biến thiên:
18
TRẦN THÔNG Facebook: hội toán bắc trung nam
x
-
2
+
y’
-
-
y
-1
-
+
-1
* Đồ thị:
- Vẽ tiệm cận đứng x = 2; tiệm cận ngang: y = -1
- Giao điểm của đồ thị với trục tung: cho x = 0
y = -
2
3
- Vẽ nhánh bên phải đường tiệm cận đứng. nhánh còn lại lấy đối xứng qua tâm I(-1;-2)
- Giao điểm của
đồ thị với trục
hoành: cho y = 0
giải phương
trình:
0
2
3
x
x
x = 3
x
-1 1
y
-4/3 -2
Bài tập luyện thi
Khảo sát và vẽ đồ thị các hàm số sau:
1.
21
2
x
y
x
2.
21x
y
x
3.
1
1
x
y
x
19
TRẦN THÔNG Facebook: hội toán bắc trung nam
4.
22
2
x
y
x
5.
1
2
1
y
x

6.
2
1
x
y
x

PHẦN 3: MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN HÀM SỐ
Dạng 1: Sự đơn điệu của hàm số.
Bài toán 1: Xét chiều biến thiên của hàm số.
Bước 1. Tìm tập xác định
Bước 2.Tính đạo hàm
y
.Tìm các điểm mà tại đó y = 0 hoặc y không tồn tại.
Bước 3. Lập bảng biến thiên và kết luận các khoảng đơn điệu của hàm số.
Ví dụ minh họa
Ví dụ 1: Tìm các khoảng đơn điệu của hàm số
32
31y x x
.
Tập xác định:
D
.
2
36y x x
;
2
0
0 3 6 0
2
x
y x x
x
Giới hạn:
lim , lim
xx
yy
 

Bảng biến thiên:
Hàm số đồng biến trên (0; 2); hàm số nghịch biến trên
( ;0)
và
(2; )
.
Ví dụ 2:Cho hàm số
42
3x 1yx
. Tìm các khoảng đơn điệu của hàm số.
Tập xác định:
D
.
CĐ
CT
2
0
-1
0
0
3
y
y'
x
20
TRẦN THÔNG Facebook: hội toán bắc trung nam
3
46y x x
;
3
0
0 4 6 0
6
2
x
y x x
x
Giới hạn:
lim , lim
xx
yy
 

Bảng biến thiên
Hàm số đồng biến trên
6
;
2




và
6
0;
2



; nghịch biến trên
6
;0
2



và
6
;
2




.
Ví dụ 3: Cho hàm số
1
x
y
x
. Tìm các khoảng đơn điệu và cực trị của hàm số.
GIẢI
Tập xác định
\1D
.
Đạo hàm
2
1
0,
1
y x D
x
.
Giới hạn:
lim lim 1
xx
yy
;
11
lim ; lim
xx
yy
.
Bảng biến thiên
Hàm số nghịch biến trên các khoảng
;1
và
1; 
.
Hàm số không có cực trị
Bài toán 2: Tìm điều kiện của tham số để hàm số đồng biến (nghịch biến) trên
.
Phương pháp giải:
Bước 1: Tính đạo hàm
CĐ
CT
0
0
CĐ
1
y
y'
x
0
0
y
y'
x
1
1
1
21
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bước 2: Hàm số đồng biến (nghịch biến) khi và chỉ khi y’ luôn đương(luôn âm). Từ đó tìm ra điều
kiện của tham số.
Chú ý: Quy tắc xét dấu tam thức bậc 2:
1. Tam thức
2
ax bx c
luôn âm khi và chỉ khi
0
0
a

2. Tam thức
2
ax bx c
luôn dương khi và chỉ khi
0
0
a

Ví dụ minh họa
Ví dụ 1: Cho hàm số
32
3 3(2 1) 1y x mx m x
. Tìm m để hàm số đồng biến trên R.
Tập xác định:
.D
Đạo hàm
2
' 3 6 3(2 1)y x mx m
Hàm số đồng biến trên R khi
' 0,yx
2
2
3 6 3(2 1) 0,
10
' 2 1 0
1
x mx m x
a
mm
m


Vậy m = 1 thỏa yêu cầu bài toán.
Ví dụ 2: Cho hàm số
32
(2 1) ( 2) 2y mx m x m x
. Tìm m để hàm số luôn nghịch biến.
Tập xác định:
.D
Đạo hàm
2
' 3 2(2 1) 2y mx m x m
Trường hợp 1:
0 ' 2 2m y x
Hàm số nghịch biến khi
2 2 0 1xx
Suy ra m = 0 không thỏa yêu càu bài toán
Trường hợp 2:
0m
Hàm số nghịch biến trên R khi
' 0,yx
22
TRẦN THÔNG Facebook: hội toán bắc trung nam
2
2
30
' (2 1) 3 ( 2) 0
0
2 1 0
0
1
1
am
m m m
m
mm
m
m
m


Vậy
1m
thỏa yêu cầu bài toán.
Ví dụ 3: Cho hàm số
2 3 2
1
( 1) ( 1) 3 5
3
y m x m x x
. Tìm m để hàm số đồng biến trên R.
Tập xác định:
.D
Đạo hàm
22
' ( 1) 2( 1) 3y m x m x
Trường hợp 1:
2
1 0 1mm
*
1 ' 4 3m y x
Hàm số đồng biến khi
3
4 3 0
4
xx
Suy ra m = 1 không thỏa yêu cầu bài toán
*
1 ' 3 0my
m = - 1 thỏa yêu cầu bài toán
Trường hợp 2:
2
1 0 1mm
Hàm số đồng biến trên R khi
' 0,yx
22
2
2
( 1) 2( 1) 3 0
10
2 2 4 0
12
m x m x
m
mm
mm

Vậy: Với
12mm
thỏa mãn yêu cầu bài toán
Bài toán 3: Tìm điều kiện của tham số để hàm số đồng biến và nghịch biến trên khoảng đoạn.
Phương pháp giải:
Bước 1: Tính đạo hàm
Bước 2: Hàm số đồng biến (nghịch biến) khi và chỉ khi y’ luôn dương (luôn âm). Từ đó tìm ra
điều kiện của tham số.
23
TRẦN THÔNG Facebook: hội toán bắc trung nam
Chú ý:So sánh các nghiệm x
1
, x
2
của tam thức bậc hai với số 0
12
0
00
0
x x S
P

12
0
00
0
x x S
P

12
00x x P
(hay ac < 0)
Chú ý:
1.
, min
xI
f x m x I m f x
2.
, min
xI
f x m x I m f x
3.
, max
xI
f x m x I m f x
4.
, max
xI
f x m x I m f x
Ví dụ minh họa
Ví dụ 1:Tìm m để hàm số
32
11
( 1) 3( 2)
33
y mx m x m x
đồng biến trong khoảng
(2; )
.
Tập xác định:
.D
Đạo hàm
2
' 2( 1) 3( 2)y mx m x m
Trường hợp 1:
0 ' 2 6 0 3m y x x
nên không thỏa yêu cầu bài toán
Trường hợp 2:
0m
Điều kiện bài toán được thỏa khi
2
' 0, 2 2( 1) 3( 2) 0, 2y x mx m x m x
2
26
,2
23
x
mx
xx


Xét hàm số
2
2 2 2
2 6 2 12 6
( ) '( )
2 3 ( 2 3)
x x x
g x g x
x x x x
36
'( ) 0
36
x
gx
x



Bảng biến thiên
x

36
2
36

g’(x)
+ 0 -
- 0 +
2
()g x ax bx c
24
TRẦN THÔNG Facebook: hội toán bắc trung nam
g(x)
2
3
0
6
3 2 6
Dựa vào bảng biến thiên ta thấy điều kiện bài toán được thỏa khi
2
3
m
.
Ví dụ 2: Tìm m để hàm số
32
11
(1 3 ) (2 1)
33
y mx m x m x
nghịch biến trên [1; 5].
Tập xác định:
.D
Đạo hàm
2
' 2(1 3 ) 2 1y mx m x m
Trường hợp 1:
1
0 ' 2 1 0
2
m y x x
nên không thỏa yêu cầu bài toán
Trường hợp 2:
0m
Hàm số nghịch biến trên [1; 5] khi
2
' 2(1 3 ) 2 1 0, [1;5]y mx m x m x
2
21
( ), [1;5]
62
x
m g x x
xx

[1;5]
ax ( )m m g x
Ta có:
2
22
1 21
(n)
2( 5)
2
'( ) 0
( 6 2)
1 21
(l)
2
x
xx
gx
xx
x




Lại có
1 21 11 11
1 1; ; 5 .
2 3 3
g g a g





Suy ra
[1;5]
11
max ( )
3
gx
.
Vậy
[1;5]
11
max ( )
3
m g x
thỏa yêu cầu bài toán.
Ví dụ 3: Cho hàm số
32
3y x x mx m
(1), (m là tham số). Tìm m để hàm số (1) nghịch
biến trên đoạn có độ dài bằng 1.
25
TRẦN THÔNG Facebook: hội toán bắc trung nam
Tập xác định:
.D
Đạo hàm
2
' 3 6y x x m
Ta có
2
' 3 6y x x m
có
93m

.
+ Nếu m ≥ 3 thì
0,y x R
; hàm số đồng biến trên
m ≥ 3 không thoả mãn.
+ Nếu m < 3 thì
y 0
có 2 nghiệm phân biệt
1 2 1 2
, ( )x x x x
. Hàm số nghịch biến trên đoạn
12
;xx
với độ dài
12
l x x
.
Áp dụng định lý vi-ét đảo:
1 2 1 2
2;
3
m
x x x x
.
Hàm số (1) nghịch biến trên đoạn có độ dài bằng 1
12
1xx
2
1 2 1 2
( ) 4 1x x x x
9
4
m
.
Bài tập tương tự
Bài 1: Cho hàm số
2 3 2
1
( 1) ( 1) 3 5
3
y m x m x x
. Tìm m để hàm số nghịch biến trên R.
Bài 2: Cho hàm số
3 2 2
35y x x mx m
. Tìm m để hàm số nghịch biến trên
1,3
.
Dạng 2: Bài toán cực trị
Bài toán 1:Tìm cực trị của hàm số
Phương pháp giải bài toán:
Bước 1. Tìm tập xác định
Bước 2.Tính đạo hàm
y
. Giải phương trình
0y
(tìm điểm dừng). Giả sử có n nghiệm
12
; ;...;
n
x x x
.
Bước 3. Lập bảng biến thiên và kết luận cực trị của hàm số.
Ví dụ minh họa
Ví dụ 1: Tìm các cực trị của hàm số
32
31y x x
.
Tập xác định:
D
.
2
36y x x
;
2
0
0 3 6 0
2
x
y x x
x
Giới hạn:
lim , lim
xx
yy
 

26
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bảng biến thiên:
Hàm số đạt cực đại tại x = 2, y
CĐ
= 3; hàm số đạt cực tiểu tại x = 0,
1
CT
y
.
Ví dụ 2:Cho hàm số
42
3x 1yx
. Tìm các khoảng đơn điệu và cực trị của hàm số.
Tập xác định:
D
.
3
46xxy
;
3
0
0 4 6 0
6
2
x
y x x
x
Giới hạn:
lim , lim
xx
yy
 

Bảng biến thiên
Hàm số đạt cực đại tại
6
2
x 
, , Hàm số đạt cực tiểu tại x = 0,
1
CT
y
Bài toán 2:Tìm điều kiện để hàm số có cực trị
Phương pháp giải bài toán:
Bước 1. Tìm tập xác định
Bước 2.Tính đạo hàm
y
.
Bước 3. Hàm số có cực trị khi và chỉ khi phương trình
0y
có nghiệm. Từ đó suy ra điều kiện
của tham số.
Chú ý: Đối với cực trị hàm số bậc 3
32
.y ax bx cx d
ta thường sử dụng định lý viét và các
định lý về dấu của tam thức bậc 2 để tìm tìm ra điều kiện của tham số m.
Chú ý: Một số tính chất đặc biệt của cực trị hàm số trùng phương
42
.y ax bx c
CĐ
CT
2
0
-1
0
0
3
y
y'
x
CĐ
CT
0
0
CĐ
1
y
y'
x
0
0
CĐ
27
TRẦN THÔNG Facebook: hội toán bắc trung nam
Xét hàm số
42
0y ax bx c a
trên R .
Tính đạo hàm
3
4 . 2 .y a x b x

Giải phương trình
32
2
0
0 4a 2 0 2 2a 0 ......
2a
x
y x bx x x b
b
x
Đồ thị hàm số
42
y ax bx c
có ba điểm cực trị phân biệt khi và chỉ khi y
’
=0 có ba điểm phân
biệt hay phương trình (1) có hai nghiệm phân biệt khác 0
0ab
(*)
Với điều kiện (*) ,đồ thị hàm số có ba điểm cực trị là
0,Ac
,
2
,
24
bb
Bc
aa





,
2
,
24
bb
Cc
aa




.
Khi đó
4
2
8
16
b ab
AB AC
a

và
2b
BC
a
.
Sau đậy là một số tính chất thường gặp của các điểm cực trị này .
1) Điều kiện để ba cực trị A,B,C tạo thành ba đỉnh của một ta giác vuông
Vì AB=AC nên tam giác ABC cân tại A .suy ra ABC là tam giác vuông khi và chỉ khi
0
90ABC
hay tam giác ABC vuông cân tại A.Khi đó
22
22BC AB BC AB
2
3
2
28
2. 8 0
16
b b ab
ba
aa
Tính chất 1.Đồ thị hàm số
42
y ax bx c
có ba điểm cực trị tạo thành ba đỉnh của một tam
giác vuông khi và chỉ khi
0ab
và
3
80ba
.
2)Điều kiện để ba cực trị A,B,C tạo thành ba đỉnh của một tam giác đều
Ta có ABC là tam giác đều khi và chỉ khi
22
AB AC BC AC BC
4
82
3
24 0
2
16
b ab b
ba
a
a

28
TRẦN THÔNG Facebook: hội toán bắc trung nam
Tính chất 2.Đồ thị hàm số
42
y ax bx c
có ba điểm cực trị tạo thành ba đỉnh của một tam
giác đều khi và chỉ khi
0ab
và
3
24 0ba
.
3) Điều kiện để ba cực trị A,B,C tạo thành ba đỉnh của một tam giác cân có một góc
cho trước
Trường hợp 1.
90
Khi đó ABC là tam giác tù .Vì tam giác ABC cân tại A nên
ABC
.
Áp dụng định lí côsin vào tam giác ABC ta có
2 2 2
22
4
2
3
33
2 . .cos
2 2 . .cos
28
2. (1 cos )
16
16 8 (1 cos )
8 8 cos 0
BC AB AC AB AC
BC AB AB AC
b b ab
aa
a b a
b a b a
Trường hợp 2.
90
(trường hợp này đã trình bày ở tính chất 1)
Trường hợp 3.
90
+)Ta có
BC

thì
180 2A

,suy ra
cos cos(180 2 ) cos2 .A

Áp dụng định lí côsin cho tam giác ABC có
2 2 2
22
4
2
3
33
2 . .cos2
2 2 . .cos2
28
2. (1 cos2 )
16
16 8 (1 cos2 )
8 8 cos2 0
BC AB AC AB AC
BC AB AB AC
b b ab
aa
a b a
b a b a
+ Nếu
A
thì tương tự trường hợp 1, ta có
33
8 8 cos2 0b a b a
.
Tính chất 3.Đồ thị hàm số
42
y ax bx c
có ba điểm cực trị A,B,C tạo thành ba đỉnh của một
tam giác cân cân có một góc
cho trước khi và chỉ khi
0ab
và
Hoặc
33
8 8 cos 0b a b a
nếu
90
29
TRẦN THÔNG Facebook: hội toán bắc trung nam
Hoặc
3
80ba
nếu
90
Hoặc
33
8 8 cos2 0b a b a
nếu
90
.
4) Điều kiện để ba cực trị A,B,C thỏa mãn BC=OA (với O là gốc tọa độ)
Ta có
2 2 2 2
2
20
b
BC OA BC OA c b ac
a
.
Tính chất 4. Đồ thị hàm số
42
y ax bx c
có ba điểm cực trị A,B,C thảo mãn điều kiện =OA
(với O là gốc tọa độ) khi và chỉ khi
0ab
và
2
20b ac
.
5) Điều kiện để ba cực trị A,B,C tạo thành ba đỉnh của một tam giác và tính diện tích tam giác
đó
Gọi H là giao điểm của BC với trục Oy thì AH là đường cao của tam giác ABC .Khi đó
2
0,c
4
b
H
a



. Suy ra
22
44
bb
AH
aa

.
Vậy
25
3
12
..
2 4 32
ABC
b b b
S
a a a
.
Tính chất 5. Đồ thị hàm số
42
y ax bx c
có ba cực trị A,B,C tạo thành ba đỉnh của một tam
giác có diện tích là S cho trước khi và chỉ khi
0ab
và
5
3
32
b
S
a

.
6) Điều kiện để ba cực trị A,B,C tạo thành ba đỉnh của một tam giác và tính bán kính đường tròn
ngoại tiếp tam giác ABC
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC và H là giao điểm của BC với trục Oy .
Khi đó
2
0,c
4
b
H
a



.Suy ra
22
44
bb
AH
aa

.
Từ tam giác vuông AHC ,ta có :
sin .
AH AH
ACH
AC AB

Áp dụng định lí Sin vào tam giác ABC được
24
22
4
8
2.
16
sin
a
AB AB b ab
R
AH a b
ACH
suy ra
3
8
.
8
ba
R
ab
30
TRẦN THÔNG Facebook: hội toán bắc trung nam
Tính chất 6. Đồ thị hàm số
42
y ax bx c
có ba cực trị A,B,C tạo thành ba đỉnh của một tam
giác có bán kính đường tròn ngoại tiếp là R khi và chỉ khi
0ab
và
3
8
.
8
ba
R
ab
Lưu ý :Các tính chất trên không được thừa nhận trong quá trình giải bài tập.
Ví dụ minh họa
Ví dụ 1: Tìm m để hàm số
y x mx x
32
73
có cực trị
Ta có:
yxmx
2
' 3 72
. Hàm số có CĐ, CT
y 0
có 2 nghiệm phân biệt
xx
12
,
.
mm
2
' 21 0 21
(*)
vậy khi
21m
hàm số
y x mx x
32
73
có cực trị
Ví dụ 2: Tìm m để đồ thị của hàm số
y x mx m x m m
3 2 2 3
3 3( 1) 4 1
có hai điểm cực trị
A, B sao cho OAB vuông tại O.
Ta có:
y x mx m
22
3 6 3( 1)
;
Suy ra
x m y m
y
x m y m
13
0
11

A m m( 1; 3)
,
B m m( 1; 1)
OA m m( 1; 3)
,
OB m m( 1; 1)
.
Mà
OAB vuông tại O
OAOB.0
m
mm
m
2
1
2 2 4 0
2

.
Ví dụ 3: Tìm tất cả các giá trị của
m
để đồ thị hàm số
y x m x
42
(3 1) 3
có ba điểm cực trị tạo
thành một tam giác cân sao cho độ dài cạnh đáy bằng
2
3
lần độ dài cạnh bên.
Ta có:
y x m x
3
' 4 2(3 1)
;
m
y x x
2
31
' 0 0,
2
.
Đồ thị hàm số có ba điểm cực trị
y 0
có 3 nghiệm phân biệt
m
1
3
(*).
Ba điểm cực trị là:
A(0; 3)
;
mm
B
2
3 1 (3 1)
;3
24



;
mm
C
2
3 1 (3 1)
;3
24




ABC
cân tại
A
;
2 m m m
BC AB
3
4
3 1 3 1 (3 1)
9.4 4
2 2 16






m
5
3
, thoả (*).
31
TRẦN THÔNG Facebook: hội toán bắc trung nam
Ví dụ 4: Với những giá trị nào của m thì đồ thị hàm số
y x mx m m
4 2 4
22
có điểm cực đại và
điểm cực tiểu, đồng thời các điểm cực đại và điểm cực tiểu lập thành một tam giác có diện tích
S 4
.
Ta có
x
y x mx
g x x m
3
2
0
' 4 4 0
( ) 0
Hàm số có 3 cực trị
y'0
có 3 nghiệm phân biệt
g
mm00
(*)
Với điều kiện (*), phương trình
y 0
có 3 nghiệm
x m x x m
1 2 3
; 0;
Hàm số đạt cực trị
tại
x x x
1 2 3
;;
. Gọi
A m m B m m m m C m m m m
4 4 2 4 2
(0;2 ); ; 2 ; ; 2
là 3 điểm cực trị của
(C
m
) .
Ta có:
AB AC m m BC m ABC
2 2 4 2
;4
cân đỉnh A
Gọi M là trung điểm của BC
M m m m AM m m
4 2 2 2
(0; 2 )
Vì
ABC
cân tại A nên AM cũng là đường cao, do đó:
ABC
S AM BC m m m m m
5
25
5
2
11
. . . 4 4 4 16 16
22
.
Vậy
m
5
16
.
Ví dụ 5: Cho hàm số
y x x mx
32
32
(m là tham số) có đồ thị là (C
m
). Xác định m để (C
m
) có
các điểm cực đại và cực tiểu cách đều đường thẳng
yx1
.
Ta có:
y x x m
2
' 3 6
.
Hàm số có CĐ, CT
y x x m
2
' 3 6 0
có 2 nghiệm phân biệt
xx
12
;
mm' 9 3 0 3
(*)
Gọi hai điểm cực trị là
A x B xyy
1212
; ; ;
Thực hiện phép chia y cho y
ta được:
mm
y x y x
1 1 2
' 2 2
3 3 3 3
m m m m
xxy y x y y x
121122
22
2 2 ; 2 2
3 3 3
))
3
((


Phương trình đường thẳng đi qua 2 điểm cực trị là
:
mm
yx
2
22
33



32
TRẦN THÔNG Facebook: hội toán bắc trung nam
Các điểm cực trị cách đều đường thẳng
yx1
xảy ra 1 trong 2 trường hợp:
TH1: Đường thẳng đi qua 2 điểm cực trị song song hoặc trùng với đường thẳng
yx1
m
m
29
21
32
(không thỏa (*))
TH2: Trung điểm I của AB nằm trên đường thẳng
yx1
II
x
mm
x x x x
m
y
m
y
y
m
x
x
2
1 2 1 2
1 2 1
2
2 2 2 2
33
2
1
2 .2 2
1
2
2
00
33
2


Vậy các giá trị cần tìm của m là:
m 0
.
Ví dụ 6: Cho hàm số
y x m m x m
4 2 2
2( 1) 1
. Tìm m để đồ thị (C) có khoảng cách giữa hai
điểm cực tiểu ngắn nhất.
Ta có
y x m m x
32
4 4( 1)
;
x
y
x m m
2
0
0
1

.
Khoảng cách giữa các điểm cực tiểu: d =
m m m
2
2
13
2 1 2
24



dmin 3
m =
1
2
.
Bài toán 3: Tìm điều kiện để hàm số đạt cực trị tại
0
x
Phương pháp giải bài toán:
Bước 1. Tìm tập xác định
Bước 2.Tính đạo hàm
,.yy
Bước 3.Từ điều kiện cần
0
0yx
và
0
yx

để tìm tham số .
Bước 4 .Thử lại và kết luận
Chú ý: Trong trường hợp bài toán yêu cầu tìm điều kiện để hàm số đạt cực tiểu (cực đại) tại
0
x
khi
00
0; 0y x y x

(tương ứng
00
0; 0y x y x

). Sau khi tìm được tham số cần kiểm
tra lại trước khi kết luận.
Ví dụ minh họa
33
TRẦN THÔNG Facebook: hội toán bắc trung nam
Ví dụ 1: Cho hàm số:
3 2 2
1
11
3
y x mx m m x
. Tìm m để hàm số đạt cực đại tại
điểm
1x
.
Ta có
22
21y x mx m m
và
22y x m
Hàm số đạt cực đại tại
1x
2
10
12
3 2 0
2
1
10
2 2 0
y
mm
mm
m
m
y
m
Thử lại với
2m
ta thấy hàm số
32
1
2 3 1
3
y x x x
đạt cực đại tại
1x
.
Vậy khi
2m
hàm số đạt cực đại tại
1x
.
Ví dụ 2: Cho hàm số:
3
3y x m x
. Tìm m để hàm số đạt cực tiểu tại điểm
0.x
Tập xác định:
.D
Ta có
2
33y x m
và
66y x m
Hàm số đạt cực đại tại
0.x
2
00
11
3 3 0
1.
0
00
60
y
mm
m
m
m
y
m
Thử lại với
1m
ta thấy hàm số
32
31y x x
đạt cực đại tại
0.x
Vậy khi
1m
hàm số đạt cực đại tại
0.x
Bài tập tương tự
Bài 1: Tìm m để hàm số
32
2 x 2y x m m
có cực trị
Bài 2: Tìm m để hàm số
4
3 x 2y x m m
có 1 cực trị
Bài 3: Tìm m để hàm số
42
3 1 x 2 5y x m m
có 3 cực trị
Bài 4: Tìm m để hàm số
3
3 1 x 2 5y x m m
đạt cực đại tại
Bài 5: Tìm m để hàm số
4 2 2 2
3 1 x 2 1y x m m
đạt cực tiểu tại
Bài 6: Cho hàm số có đồ thị (C
m
) .
y x mx m
42
21
34
TRẦN THÔNG Facebook: hội toán bắc trung nam
1. Với những giá trị nào của m thì đồ thị (C
m
) có ba điểm cực trị, đồng thời ba điểm cực trị
đó lập thành một tam giác có bán kính đường tròn ngoại tiếp bằng .
2. Với những giá trị nào của m thì đồ thị (C
m
) có ba điểm cực trị, đồng thời ba điểm cực trị
đó lập thành một tam giác đều.
3. Với những giá trị nào của m thì đồ thị (C
m
) có ba điểm cực trị, đồng thời ba điểm cực trị
đó lập thành một tam giác vuông cân.
4. Với những giá trị nào của m thì đồ thị (C
m
) có ba điểm cực trị, đồng thời ba điểm cực trị
đó lập thành một tam giác có diện tích là 1.
5. Với những giá trị nào của m thì đồ thị (C
m
) có ba điểm cực trị, đồng thời ba điểm cực trị
đó lập thành một tam giác có một góc bằng .
6. Với những giá trị nào của m thì đồ thị (C
m
) có ba điểm cực trị, đồng thời hoành độ ba điểm
cực trị đó lập thành một cấp số cộng.
Bài 7: Cho hàm số , với là tham số thực.
1. Xác định để hàm số đã cho đạt cực trị tại sao cho .
2. Xác định để hàm số đã cho đạt cực trị tại sao cho .
3. Với giá trị nào của m thì đồ thị hàm số có điểm cực đại và điểm cực tiểu đối xứng với nhau
qua đường thẳng d: .
4. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ
là các số dương.
5. Tìm các giá trị của m để đồ thị hàm số (1) có điểm cực đại, điểm cực tiểu, đồng thời hoành
độ của điểm cực tiểu nhỏ hơn 1.
6. Tìm m để hàm số (1) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số
đến gốc tọa độ O bằng lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc
tọa độ O.
7. Xác định để hàm số đã cho đạt cực trị tại sao cho
12
12
11
xx
xx

.
Bài 8: Tìm cực trị của hàm số :
sin2 2y x x
.
Bài 9: Cho hàm số
42
5y x mx m
có đồ thị là (C
m
), m là tham số. Xác định m để đồ thị
(C
m
) của hàm số đã cho có ba điểm cực trị.
Bài 10: Cho hàm số
296
23
xxxy
(C). Viết phương trình đường thẳng đi qua điểm
1;1A
và vuông góc với đường thẳng đi qua hai điểm cực trị của (C).
Bài 11: Cho hàm số:
4 2 2
2( 1) 1 (1)y x m x
Tìm các giá trị của tham số m để hàm số
(1) có 3 điểm cực trị thỏa mãn giá trị cực tiểu đạt giá trị lớn nhất.
Bài 12: Tìm tham số để hàm số:
3 2 2
3 3 1y x mx m x m
đạt cực đại tại
2x
.
1
0
120
y x m x m x m
32
(1 2 ) (2 ) 2
m
m
xx
12
,
xx
12
1
3

m
xx
12
,
xx
12
21
xy8 74 0
2
m
xx
12
,
35
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 13: Tìm cực trị của các hàm số:
2y x x
Bài 14: Cho các hàm số
32
32y x mx
(C
m
) Tìm các giá trị của m để (C
m
) có hai điểm cực trị và
khoảng cách từ điểm cực tiểu của (C
m
) đến đường thẳng
d : 2yx
bằng
2
.
Bài 15: Tìm cực trị của các hàm số:
3y x x
Bài 16: Cho hàm số
42
21y x mx m
. Tìm m để đồ thị hàm số có ba điểm cực trị tạo thành
tam giác sao cho trục Ox chia tam giác đó thành hai phần có diện tích bằng nhau.
Bài 17: Cho hàm số
32
3y x x
(C). Tìm m để đường thẳng đi qua 2 điểm cực trị của đồ thị (C)
tạo với đường thẳng
: 3 0x my
một góc biết
4
cos
5
.
Bài 18: Cho hàm số
32
. ( 1) ( 2) 5
3
m
y x m x m x
. Tìm m để hàm số có 2 cực trị, đồng
thời 2 điểm cực trị này nằm về hai phía so với trục hoành
Ox
.
Bài 19: Cho hàm số
3 2 2 2
3 1 3 7 1 1y x m x m m x m
. Tìm m để hàm số có
điểm cực tiểu tại một điểm có hoành độ nhỏ hơn 1.
Bài 20: Cho hàm số
32
4y x mx
. Tìm m để hàm số có 2 cực trị là A và B thỏa:
2
2
900
729
m
AB
Bài 21: Cho hàm số
32
1
1
3
y x mx x m
. Tìm m để hàm số có cực đại và cực tiểu, đồng
thời khoảng cách giữa hai điểm ấy là ngắn nhất.
Bài 22: Cho hàm số
32
1
1
3
y x x m x m
. Tìm m để hàm số có hai điểm cực trị A, B
sao cho tam giác ABO vuông cân với O là gốc tọa độ.
Bài 23: Cho hàm số
3 2 3
34y x mx m
. Tìm m để hàm số có cực đại và cực tiểu đối xứng
nhau qua đường phân giác thứ nhất.
Bài 24: Cho hàm số
2
( ) 3 1y x m x x m
. Tìm m để hàm số có cực đại và cực tiểu
thỏa:
.1
CÐ CT
xx
.
Bài 25: Cho hàm số
3 2 2
1
1
33
m
y mx mx m x
. Tìm m để hàm số có 2 cực trị thỏa:
2
1 1 2
. 5 12x x x
.
36
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 26: Cho hàm số
32
1
1
3
y x mx x m
. Tìm m để hàm số có cực đại và cực tiểu, đồng
thời khoảng cách giữa hai điểm ấy là ngắn nhất.
Bài 27: Tìm
m
để đồ thị hàm số
32
32y x x C
có điểm cực đại và điểm cực tiểu của đồ
thị
C
nằm về hai phía khác nhau của một đường tròn (phía trong đường tròn và phía ngoài đường
tròn):
2 2 2
: 2 4 5 1 0
m
C x y mx my m
.
Bài 28: Cho hàm số
3 2 2 2
2 1 2 1 1y x m x m m x m
(m là tham số). Tìm m để (C)
cắt trục hoành tại 3 điểm phân biệt A, B, C (với A là điểm cố định) sao cho
1 2 1 2
2 k k x x
, trong
đó
12
,kk
lần lượt là hệ số góc của tiếp tuyến của (C) tại B, C và
là hoành độ các điểm cực
trị của (C).
Bài 29: Cho hàm số
32
1 3 1
6
2 4 2
y x x mx
.Tìm các số thực m để hàm số có 2 điểm cực đại,
cực tiểu trên
1;1
.
Bài 30: Cho hàm số
4 2 2
2y x mx m m
. Tìm m để đồ thị hàm số (1) có 3 điểm cực trị sao cho
trong mp tọa độ 0xy đường tròn đi qua 3 điểm cực trị này cũng đi qua gốc tọa độ O.
Bài 31: Cho hàm số
42
4y x mx m
. Tìm m để hàm số có 3 điểm cực trị là A, B, C và
tam giác ABC nhận gốc tọa độ O làm trọng tâm
Bài 32: Cho hàm số
2
32
3
2
m
y x x
. Tìm m để hàm số có cực đại A, cực tiểu B và tạo với C(–
2; 3) thành tam giác ABC đều.
Bài 33: Tìm giá trị của tham số
;ab
để hàm số
42
33y x a b x a b
đạt giá trị cực
tiểu bằng 1 tại
0x
.
Bài 34: Tìm giá trị của tham số
;ab
để hàm số
42
3
3 2 2
4
y x a b x a b
có giá trị cực trị
bằng 0 khi
0x
. Khi đó hàm số đạt cực tiểu hay cực đại.
Bài 35: Chứng minh rằng hàm số
32
2 3 2 1 6 1 1y x m x m m x
luôn đạt cực trị tại
12
,xx
với mọi giá trị
m
và biểu thức
21
xx
không phụ thuộc vào
m
.
Bài 36: Cho
3
22
2
2 1 7
33
x
y mx m x m
. Tìm m để hàm số có hai điểm cực trị với hoành
độ
12
,xx
thỏa mãn
12
11
0
11xx


Bài 37: Cho hàm số:
32
3y x x m
()
m
C
. Định giá trị của
m
để hàm số có 2 điểm cực trị
A,B sao cho
0
120AOB
37
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 38: Cho hàm số:
32
3y x x m
()
m
C
. Định giá trị của
m
để hàm số có 2 điểm cực tiểu
sao cho diện tích hình phẳng giới hạn bởi đồ thị
()
m
C
và đường thẳng đi qua hai điểm cực tiểu là
1.
Bài 39:Cho
1).2cos1()sin1(2.
3
4
23
xaxaxy
. Tìm m để hàm số có hai điểm cực trị với
hoành độ
12
,xx
thỏa mãn
1
2
2
2
1
xx
Bài 40: Tìm cực trị của các hàm số:
xg
x
x
y .cot2
sin
cos
3
Bài 41: Tìm cực trị của các hàm số:
xxxy 3cos.
3
1
2cos.
2
1
cos1
Bài 42: Cho hàm số
3 2 2 3
3 3( 1)y x mx m x m m
(1). Chứng minh rằng hàm số (1) luôn có
cự đại,cực tiểu với mọi m.Tìm m để các điểm cự trị của hàm số (1) cùng với điểm I(1;1), tạo thành
một tam giác có bán kính đường tròn ngoại tiếp bằng
5
.
Bài 43: Cho hàm số
1)1(3)2(
2
3
23
xmxmxy
(1), m là tham số. Tìm
0m
để đồ thị hàm
số (1) có giá trị cực đại, giá trị cực tiểu lần lượt là
CTCĐ
yy ,
thỏa mãn
42
CTCĐ
yy
.
Bài 44: Tìm
m
để đồ thị hàm số
42
22y x mx
có ba điểm cực trị tạo thành tam giác nhận gốc
tọa độ làm trực tâm.
Bài 45: Tìm
m
để đồ thị hàm số
3 2 3
33y x mx m
có hai điểm cự trị
,AB
sao cho tam giác
OAB
có diện tích bằng 48.
Bài 46: Cho hàm số có đồ thị (C
m
). Với những giá trị nào của m thì đồ
thị (C
m
) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có một góc bằng
.
Bài 47: Cho hàm số
3
31y x mx
. Tìm
m
để đồ thị của hàm số (1) có 2 điểm cực trị
,AB
sao cho tam giác
OAB
vuông tại
O
( với
O
là gốc tọa độ ).
Bài 48: Cho hàm số
3 2 2 3
3 3( 1)y x mx m x m m
(1). Chứng minh rằng hàm số (1) luôn có
cự đại,cực tiểu với mọi m.Tìm m để các điểm cự trị của hàm số (1) cùng với điểm I(1;1), tạo thành
một tam giác có bán kính đường tròn ngoại tiếp bằng
5
.
Bài 49: Tìm
m
để đồ thị hàm số
42
22y x mx
có ba điểm cực trị tạo thành tam giác nhận
gốc tọa độ làm trực tâm.
Bài 50: Tìm
m
để đồ thị hàm số
32
2 3( 1) 6y x m x mx
có hai điểm cự trị
,AB
sao cho đường
thẳng
AB
vuông góc với đường thảng
2yx
.
Bài 51: Cho hàm số
4 2 2 2
2 1 (1)y x m x m
(m là tham số).Tìm tất cả các giá trị của m để
đồ thị của hàm số (1) có ba điểm cực trị
,,A B C
sao cho bốn điểm O,
,,A B C
là bốn đỉnh của
một hình thoi (với
O
là gốc tọa độ).
Bài 52: Cho hàm số
y x m x m
4 2 2
2(1 ) 1
(Cm).Tìm m để đồ thị (Cm) có 3 điểm cực trị tạo
y x mx m m
4 2 2
2
0
120
38
TRẦN THÔNG Facebook: hội toán bắc trung nam
thành một tam giác có diện tích lớn nhất.
Bài 53: Cho hàm số
y x m x m
42
1
(3 1) 2( 1)
4
(Cm).
Tìm m để đồ thị (Cm) có 3 điểm cực trị tạo thành một tam giác có trọng tâm là gốc toạ độ O.
Bài 54: Cho hàm số
4 2 2
2 2 4 y x mx m
. (m là tham số thực)
Tìm tất cả các giá trị của m để đồ thị hàm số
()
m
C
có 3 điểm cực trị tạo thành một tam giác cân
có góc ở đỉnh của tam giác đó bằng
với
22
1
2
tan
.
Bài 55: Cho hàm số
.)1(12
24
mmxxy
Tìm các giá trị của tham số m để đồ thị hàm số
(1) có ba điểm cực trị tạo thành một tam giác sao cho trục Ox chia tam giác đó thành hai phần có
diện tích bằng nhau
Bài 56: Cho hàm số
y x m x m
42
1
(3 1) 2( 1)
4
(Cm).Tìm m để đồ thị (Cm) có 3 điểm cực trị
tạo thành một tam giác có trọng tâm là gốc toạ độ O.
Bài 57:Tìm m để đồ thị (Cm)
y x m x m
4 2 2
2(1 ) 1
có 3 điểm cực trị tạo thành một tam
giác có diện tích lớn nhất.
Bài 58: Cho hàm số
y x mx
42
22
(Cm).Tìm các giá trị của m để (Cm) có 3 điểm cực trị tạo
thành một tam giác có đường tròn ngoại tiếp đi qua điểm
D
39
;
55



.
Bài 59: Cho hàm số
y x mx m x m
3 2 2 3
3 3( 1)
(C
m
)Chứng minh rằng (C
m
) luôn có điểm cực
đại và điểm cực tiểu lần lượt chạy trên mỗi đường thẳng cố định.
Bài 60: Cho hàm số
y x m x m
3 2 3
14
( 1) ( 1)
33
(1) (m là tham số thực).Tìm m để các điểm cực
đại và cực tiểu của đồ thị (1) nằm về 2 phía (phía trong và phía ngoài) của đường tròn có phương
trình (C):
x y x
22
4 3 0
.
Dạng 3: Bài toán giá trị lớn nhất nhỏ nhất trên
,ab
Phương pháp giải toán
Cho hàm số
y f x
liên tục trên đoạn
,ab
. Để tìm giá trị lớn nhất (max) và giá trị nhỏ nhất
(min) của
fx
trên đoạn [a; b] ta thực hiện các bước sau:
Bước 1. Nhận xét : Hàm số
fx
liên tục trên đoạn
,ab
.
Bước 2. Giải phương trình
0fx
(tìm điểm dừng). Giả sử có n nghiệm
12
; ;...;
n
x x x
thuộc
đoạn
,ab
(ta loại các nghiệm nằm ngoài đoạn
,ab
).
Bước 3. Tính
12
; ; ;...; ;
n
f a f x f x f x f b
.
39
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bước 4. Giá trị lớn nhất, nhỏ nhất trong các giá trị đã tính ở trên là các giá trị tương ứng cần tìm.
Ví dụ minh họa
Ví dụ 1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số
4
f x x
x

trên đoạn
1,3 .
Ta thấy hàm số
1
f x x
x

liên tục trên đoạn
1,3 .
Hơn nữa,
2
4
1fx
x

nên
2
2(n)
4
10
2(l)
x
fx
x
x

Lại có
13
1 5; 2 4; 3 .
3
f f f
Suy ra
1,3
1,3
max 1 5;min 2 4.
x
x
f x f f x f
Vậy giá trị lớn nhất và nhỏ nhất của hàm số
4
f x x
x

trên đoạn
1,3
là 5 và 4.
Ví dụ 2: Tìm giá trị lớn nhất và nhỏ nhất của hàm số
2
sin 1
sin sin 1
x
y
xx

Đặt t = sinx, điều kiện
1 1.t
Bài toán quy về tìm GTNN, GTLN của hàm số
2
1
()
1
t
ft
tt

trên đoạn
1;1
.
Bảng biến thiên của hàm số f(t) trên đoạn
1;1
như sau:
t
-1 0
1

f
’
(t)
+ 0 -
1
f(t)
0
3
2
Từ bảng biến thiên suy ra GTNN, GTLN của hàm số f(t) trên đoạn
1;1
lần lượt là 0 (khi và chỉ
khi t = -1) và 1 (khi và chỉ khi t = 0).
40
TRẦN THÔNG Facebook: hội toán bắc trung nam
Từ đó có: Maxy = 1 đạt được khi và chỉ khi:
xk
, Miny = 0 khi và chỉ khi:
2
2
k

.
Chú ý: Nếu biểu thức xác định của hàm số có thể phân chia thành các nhóm số hạng và giữa
chúng có một mối liên hệ cho bởi các hệ thức toán học cho phép biểu diễn chúng qua nhau thì ta
có thể đưa bài toán đó về bài toán đơn giản hơn bằng phương pháp đổi biến số. Mối liên hệ giữa
các nhóm số hạng trong biểu thức xác định hàm số ở ví dụ trên là rõ ràng dễ thấy, điều này giúp
ta phát hiện cách đổi biến số không mấy khó khăn, tuy nhiên có những trường hợp mối liên hệ
giữa các nhóm số hạng được ẩn kín bên trong, đòi hỏi nhiều phép biến đổi và có cách nhìn tinh
mới phát hiện ra được. Trong phép đổi biến số cần chú ý cần phải tìm điều kiện cho biến để tránh
khỏi sai lầm khi giải toán. Chẳng hạn xét lại ví dụ 2 ta thấy:
Đặt t = sinx, ta có hàm số theo t:
2
1
()
1
t
ft
tt

.
Ta có:
2
'
22
2
()
( 1)
tt
ft
tt


, f
’
(t) = 0
0
2
t
t

;
lim ( ) 0
x
fx

.
Bảng biến thiên của hàm số f(t) như sau:
t

-2 0

f
’
(t)
- 0 + 0 -
f(t)
0 1
1
3
0
Từ BBT suy ra:
1
minf( ) ( 2)
3
tf
;
1)0()( ftMaxf
.
Từ đó có GTNN, GTLN của hàm số ban đầu lần lượt là
3
1
và 1.
Theo lời giải trên thì hàm số f(x) nhận GTNN là
3
1
khi: sinx = -2, điều này không xảy ra.Mặc
dù đã lựa chọn biến mới: t = sinx hợp lí nhưng chưa tìm điều kiện cho nó dẫn đến bài toán tìm
GTNN, GTLN của hàm số theo biến số mới
2
1
()
1
t
ft
tt

không tương thích với bài toán ban
đầu (ngoài ví dụ đang xét thì trong các ví dụ sau đều phải lưu ý điều này).
Ví dụ 3: Cho
2
5 4 .y f x x x mx
Tìm các giá trị của m sao cho
Min 1y
.
41
TRẦN THÔNG Facebook: hội toán bắc trung nam
Ta có
2
1
2
2
5 4 ; x 1 4:
5 4 ; 1 4 :
x m x x P
fx
x m x x P
Gọi (P) là đồ thị của y = f(x)
(P) = (P
1
)
(P
2
) khi đó (P) có 1 trong các hình dạng đồ thị
sau đây
Hoành độ giao điểm (P
1
), (P
2
) x
A
= 1; x
B
= 4 ; Hoành độ đỉnh (P
1
):
5
2
C
m
x
.
Nhìn vào đồ thị ta xét các khả năng sau:
Nếu x
C
[x
A
, x
B
]
m
[
3, 3] thì Minf(x) = Min
f(1), f(4)
.
Khi đó Minf(x) > 1
33
(1) 1
(4) 4 1
m
fm
fm


1 < m
3 (1)
Nếu x
C
[x
A
, x
B
]
m
[
3, 3] thì Minf(x) =
11
5
2
C
m
f x f



=
2
10 9
4
mm
Khi đó Minf(x) > 1
2
[ 3,3]
3 5 2 3
10 13 0
m
m
mm

(2)
Kết luận
:
Từ (1) và (2) suy ra Minf(x) > 1
325m1
Bài tập tương tự
Bài 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
32
91
y x 3x x
44
trên đoạn
[ 1; 1]
.
A
B
C
P
2
P
1
A
B
C
P
2
P
1
A
B
C
P
1
P
2
42
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
42
y x 2x 1
trên đoạn
[ 1; 3]
.
Bài 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
x1
y
x2
trên đoạn
[ 1; 2]
.
Bài 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
f(x) x 4x 5
trên đoạn
[ 2; 3]
.
Bài 5: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
22
22f x x x
trên đoạn
1
;2
2



.
Bài 6: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
3
62
41y x x
trên đoạn
1;1
.
Bài 7: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
2
2
x
y f x
x
trên đoạn
5; 3
.
Bài 8: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
2
32y f x x x
trên đoạn
10;10
.
Bài 9: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
32
31y x x
trên đoạn
2;1
.
Bài 10: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
2
1 3 6 9y x x x
trên
1;3
.
Bài 11: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
32
3 9 1y x x x
trên đoạn
[– 2; 2].
Bài 12: Tìm giá trị lớn nhất và nhỏ nhất của hàm số :
32
24
xxy
trên đoạn
4;0
.
Bài 13: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
()
x
f x e x
trên đoạn
1;1
.
Bài 14: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
32
( ) 3 1f x x x
trên đoạn
3
1;
2



.
43
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 15: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
22
( ) ( 2).
x
f x x e
trên đoạn
[–1 ; 2].
Bài 16: Tìm giá trị lớn nhất và nhỏ nhất của hàm số
4
3
1
f x x
x
trên đoạn
2;5
Bài 17: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2lny x x
trên
1; e
.
Bài 18: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
ln 1 2 y f x x x
trên
đoạn
1;0
.
Bài 19: Tìm giá trị lớn nhất, nhỏ nhất của hàm số
2
21
x
y
x
trên đoạn
.
Bài 20: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2 2 8
1
xx
y
x

trên đoạn
2;0
Bài 21: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
ln 2
2
x
f x x x
trên đoạn
1
;3
3



Bài 22: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số
2
4y x x
.
Bài 23: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( ) 5 4f x x
trên đoạn
1;1
Bài 24: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
4
( ) 2
1
f x x
x
trên đoạn
Bài 25: Tìm giá trị lớn nhất, nhỏ nhất của hàm số
22
1
4
4
y x x x x
Bài 26: Tìm giá trị lớn nhất và nhỏ nhất của hàm số
2
11
4
x
y x x
Bài 27: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
( ) 2 7
x
f x x x e
trên đoạn
0,3
Bài 28: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( ) ln 1 2f x x x
trên đoạn
0,1
Bài 29: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
( ) 4ln 3
2
x
f x x
trên đoạn
2,1
24


;
44
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 30: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
16
()f x x
x

trên đoạn
1
,4
3



.
Bài 31: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
22
3 3 4 3 3 4
( ) 4 4
x x x x
fx

trên đoạn
1,2
.
Bài 32: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
( ) lnf x x
x

trên đoạn
1
,1
e



Bài 33: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
2
1 2 2 2 4y x x x
trên
1;2
.
Bài 34: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
1
sin cos
y
xx
Bài 35: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
1 sin 1 cosy x x
Bài 36: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
2
32y x x
Bài 37: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
x
y
x 2 1
.
Bài 38: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
x
sinx+2cos
2
( ) , 0; .
x
2
cosx+2sin
2
f x x




Bài 39: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
44
2 2 2 6 2 6y x x x x
Bài 40: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
( ) cos x, 0; .
4
f x x x



Bài 41: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
)cos1(sin xxy
Bài 42: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
xx
y
cos4
1
sin4
1
Bài 43: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
( ) log 2, 2; .
x
f x x x e



Bài 44: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x)=5cosx–cos5x,
.
44
x

Bài 45: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
22
1 1, 1;1y x x x x x
Bài 46: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
22
4 21 3 10y x x x x
45
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 47: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
4 2 2
22
2 1 1 1 3
()
1 1 1
x x x
fx
xx
Bài 48: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
)8cos4(cos
2
1
)4cos2sin1(2 xxxxy
Bài 49: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
cos
sin (2cos sin )
x
y
x x x
, với
0.
3
x

Bài 50: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Dạng 4: Bài toán tiếp tuyến
Bài toán 1: Viết phương trình tiếp tuyến của (C):
y f x
tại điểm
00
;.M x f x
Phương pháp giải toán
Bước 1: Nếu cho
0
x
thì tìm
00
()y f x
.Nếu cho
0
y
thì tìm
0
x
là nghiệm của phương trình
0
f x y
.
Bước 2: Tính
y f x()

. Suy ra
00
( ) ( )y x f x

Bước 3: Phương trình tiếp tuyến là:
0 0 0
– ( ).( – )y y f x x x
.
Ví dụ minh họa
Ví dụ 1: Cho hàm số
3
32y x x
(C)
a. Viết phương trình tiếp tuyến của (C) tại điểm
2;4M
.
b. Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ
1
2
x
.
c. Viết phương trình của (C) tại các điểm có tung độ là 0.
Hướng dẫn
a.Ta có
2
33yx

Suy ra hệ số góc của tiếp tuyến tại điểm
M 2;4
là
y' 2 9
.
Phương trình tiếp tuyến của (C) tại điểm M là
y 9x 14
.
b. Điểm thuộc đồ thị hàm số có hoành độ
0
1
x
2
, có tung độ
0
1
y
2
Ta có
2
33yx

Suy ra hệ số góc của tiếp tuyến tại tiếp điểm
11
;
22



là
19
y'
24




46
TRẦN THÔNG Facebook: hội toán bắc trung nam
Phương tình tiếp tuyến của (C) tại điểm
11
;
22



là
9 13
yx
48
.
c.Điểm thuộc (C) có tung độ
0
y0
, có hoành độ
01
x2
hoặc
02
x1
.
Ta có
2
33yx

Hệ số góc của tiếp tuyến tại điểm
2;0
là
y' 2 9
.
Phương tình tiếp tuyến của (C) tại điểm
2;0
là
y 9x 18
.
Hệ số góc của tiếp tuyến tại điểm
1;0
là
' 1 0y
.
Phương tình tiếp tuyến của (C) tại điểm
1;0
là
y0
.
Phương trình của hai tiếp tuyến của (C) tại điểm có tung độ bằng 0 là
y 9x 18
và
y0
.
Ví dụ 2: Cho hàm số
42
2y x x
(C). Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có
tung độ
8.y
Điểm thuộc đồ thị hàm số có tung độ
0
y8
, có hoành độ
0
x2
.
Ta có
3
44y x x

nên hệ số góc của tiếp tuyến tại tiếp điểm
2;8
và
2;8
lần lượt là
y' 2 24
,
y' 2 24
.
Suy ra phương tình tiếp tuyến của (C) tại điểm
2;8
là
y 24x 56
và tại điểm
2;8
là
y 24x 40
.
Bài toán 2: Viết phương trình tiếp tuyến của (C):
y f x()
, biết có hệ số góc k cho trước.
Phương pháp giải 1: Tìm toạ độ tiếp điểm.
Bước 1: Gọi
M x y
00
( ; )
là tiếp điểm. Tính
fx
0
()
.
Bước 2: có hệ số góc k nên
0
( ) kfx
Bước 3: Giải phương trình (1), tìm được
x
0
và tính
y f x
00
()
. Từ đó viết phương trình của .
Phương pháp giải 2: Dùng điều kiện tiếp xúc.
Bước 1: Phương trình đường thẳng có dạng:
y kx m
.
Bước 2: tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:
*
f x kx m
f x k

Bước 3: Giải hệ (*), tìm được m. Từ đó viết phương trình của .
Chú ý: Hệ số góc k của tiếp tuyến có thể được cho gián tiếp như sau:
+ tạo với trục hoành một góc thì
tanka
.
+ song song với đường thẳng d:
y ax b
thì
ka
.
47
TRẦN THÔNG Facebook: hội toán bắc trung nam
+ vuông góc với đường thẳng
,0y ax b a
thì
1
k
a

.
+ tạo với đường thẳng
y ax b
một góc thì
tan
1
ka
ka
.
Ví dụ minh họa
Ví dụ 1: Cho hàm số
21
1
x
y
x
(C). Viết phương trình tiếp tuyến của (C) , biết hệ số góc của
tiếp tuyến
4.k
Ta có
2
1
.
1
y
x
Điểm
00
M x ;y
thuộc đồ thị (C), có hệ số góc của tiếp tuyến tại M là
0
y' x 4
.
Khi đó, ta có:
0 01
2
0
1 1 1
4 x 1 x
22
x1
hoặc
02
3
x
2

.
Tung độ của điểm M là
01
1
y0
2




hoặc
01
3
y4
2




.
Vậy có hai tiếp tuyến có phương trình là
y 4x 2
và
y 4x 10
.
Ví dụ 2: Cho hàm số
42
2y x x
(C). Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến
song song với đường thẳng
24 2017yx
.
Ta có
3
44y x x

Vì tiếp tuyến song song với đường thẳng
24 2017yx
nên hệ số góc của tiếp tuyến bằng 24 .
Điểm
00
M x ;y
thuộc (C) có hệ số góc tiếp tuyến tại M là
0
y' x 24
.
Khi đó, ta có:
32
0 0 0 0 0 0
4x 4x 24 0 x 2 4x 8x 12 0 x 2
Lúc này tung độ của M là
0
y8
.
Phương trình tiếp tuyến của (C) tại điểm M là
y 24x 56
.
Ví dụ 3: Cho hàm số
42
2y x x
(C). Trên (C) lấy hai điểm phân biệt A và B có hoành độ lần
lượt là a và b. Tìm điều kiện đối với a và b để hai tiếp tuyến của (C) tại A và B song song với
nhau.
Ta có:
f x x x
3
'( ) 4 4
Hệ số góc tiếp tuyến của (C) tại A và B là
AB
k f a a a k f b b b
33
'( ) 4 4 , '( ) 4 4
Tiếp tuyến tại A, B lần lượt có phương trình là:
y f a x a f a y f a x f a af a( )( ) ( ) ( ) ( ) ( )
48
TRẦN THÔNG Facebook: hội toán bắc trung nam
y f b x b f b y f b x f b bf b( )( ) ( ) ( ) ( ) ( )
Hai tiếp tuyến của (C) tại A và B song song hoặc trùng nhau khi và chỉ khi:
33
AB
k k a a = 4b b a b a ab b
22
4 4 4 ( )( 1) 0
(1)
Vì A và B phân biệt nên
ab
, do đó (1)
a ab b
22
10
(2)
Mặt khác hai tiếp tuyến của (C) tại A và B trùng nhau khi và chỉ khi:
a ab b
a ab b
ab
a a b b
f a af a f b bf b
22
22
4 2 4 2
10
10
()
3 2 3 2
( ) ( ) ( ) ( )



Giải hệ này ta được nghiệm là
ab( ; ) ( 1;1)
hoặc
ab( ; ) (1; 1)
, hai nghiệm này tương ứng với
cùng một cặp điểm trên đồ thị là
( 1; 1)
và
(1; 1)
Vậy điều kiện cần và đủ để hai tiếp tuyến của (C) tại A và B song song với nhau là:
a ab b
a a b
22
10
1;
Bài toán 3: Viết phương trình tiếp tuyến của (C):
()y f x
, biết đi qua điểm
( ; )
AA
A x y
Phương pháp giải 1: Tìm toạ độ tiếp điểm.
Bước 1: Gọi
00
( ; )M x y
là tiếp điểm. Khi đó
0 0 0 0
( ), ( ) ( )y f x y x f x


.
Bước 2: Phương trình tiếp tuyến tại M:
0 0 0
– ( ).( – )y y f x x x
Bước 3: đi qua
( ; )
AA
A x y
nên:
0 0 0
– ( ).( ) **–
AA
y y f x x x
.
Bước 4: Giải phương trình (**), tìm được
x
0
. Từ đó viết phương trình của .
Phương pháp giải 2: Dùng điều kiện tiếp xúc.
Bước 1: Phương trình đường thẳng đi qua
( ; )
AA
A x y
và có hệ số góc k:
– ( – )
AA
y y k x x
.
Bước 2: tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:
***
AA
f x k x x y
f x k
Bước 3: Giải hệ (***), tìm được x,k. Từ đó viết phương trình của .
Ví dụ minh họa
49
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài toán 4: Viết phương trình tiếp tuyến của (C):
()y f x
, biết cắt hai trục toạ độ tại A
và B sao cho tam giác OAB vuông cân hoặc có diện tích S cho trước.
Phương pháp giải:
Bước 1: Gọi
00
( ; )M x y
là tiếp điểm. Khi đó:
0 0 0 0
( ), ( ) ( )y f x y x f x


.
Bước 2: Xử lý giả thuyết
+ OAB vuông cân tạo với Ox một góc
0
45
và O .(a)
+
. 2S
OAB
S S OAOB
. (b)
Bước 3: Giải (a) hoặc (b) tìm được
0
x
. Từ đó viết phương trình tiếp tuyến .
Ví dụ minh họa
Ví dụ 1: Cho hàm số
2
.1
23
x
y
x
Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp
tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại
gốc tọa độ O.
Gọi là toạ độ của tiếp điểm
OAB cân tại O nên tiếp tuyến
song song với đường thẳng (vì tiếp tuyến có hệ số góc
âm). Nghĩa là:
+ Với
: (loại)
+ Với
: (nhận)
Vậy phương trình tiếp tuyến cần tìm là: .
Ví dụ 2: Cho hàm số có đồ thị (C). Gọi I là giao điểm của hai tiệm cận. Tìm điểm M
thuộc (C) sao cho tiếp tuyến của (C) tại M cắt 2 tiệm cận tại A và B với chu vi tam giác IAB đạt
giá trị nhỏ nhất.
Giao điểm của 2 tiệm cận là . Gọi M
(C).
xy
00
( ; )
yx
x
0
2
0
1
( ) 0
(2 3)

yx
yx
x
0
2
0
1
( ) 1
(2 3)
xy
xy
00
00
11
20
xy
00
1; 1
y x y x1 ( 1)
xy
00
2; 0
y x y x0 ( 2) 2
yx2
1
12
x
x
y
I(1;2)
1
3
2;
0
0
x
x
50
TRẦN THÔNG Facebook: hội toán bắc trung nam
PTTT tại M có dạng:
Toạ độ các giao điểm của tiếp tuyến với 2 tiệm cận: A , B
Ta có: (đvdt)
IAB vuông có diện tích không đổi
chu vi
IAB đạt giá trị nhỏ nhất khi IA= IB
Vậy có hai điểm M thỏa mãn điều kiện , .Khi đó chu vi
AIB = .
Chú ý: Với 2 số dương a, b thoả ab = S (không đổi) thì biểu thức P = nhỏ nhất
khi và chỉ khi a = b.Thật vậy: P =
.Dấu "=" xảy ra
a = b.
Ví dụ 3: Cho hàm số
23
.
2
x
yC
x
Cho M là điểm bất kì trên (C). Tiếp tuyến của (C) tại M cắt
các đường tiệm cận của (C) tại A và B. Gọi I là giao điểm của các đường tiệm cận. Tìm toạ độ
điểm M sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất.
Giả sử ,
Phương trình tiếp tuyến (
) với ( C) tại M:
Toạ độ giao điểm A, B của (
) với hai tiệm cận là:
Ta thấy , suy ra M là trung điểm của
AB.
y x x
x
x
0
2
0
0
33
( ) 2
1
( 1)
1
6
2;1
0
x
x
0
(2 1;2)
IAB
S IAIB x
x
0
0
1 1 6
. 2 1 2.3 6
22
1
31
31
12
1
6
0
0
0
0
x
x
x
x
M
1
1 3;2 3
M
2
1 3;2 3
6234
a b a b
22
a b a b
22
ab ab ab S2 2 (2 2) (2 2)
x
M x x
x
0
00
0
23
; , 2
2




yx
x
0
2
0
1
'( )
2
x
y x x
x
x
0
0
2
0
0
23
1
()
2
2
x
A B x
x
0
0
0
22
2; ; 2 2;2
2




AB
M
x x x
xx
0
0
2 2 2
22
AB
M
y y x
y
x
0
0
23
22


51
TRẦN THÔNG Facebook: hội toán bắc trung nam
Mặt khác I(2; 2) và
IAB vuông tại I nên đường tròn ngoại tiếp tam giác IAB có diện tích
S =
Dấu “=” xảy ra khi
Do đó điểm M cần tìm là M(1; 1) hoặc M(3; 3).
Bài toán 5: Tìm những điểm trên đường thẳng d mà từ đó có thể vẽ được 1, 2, 3, ... tiếp tuyến
với đồ thị (C):
y f x()
.
Phương pháp giải:
Bước 1: Giả sử
d ax by c:0
,
MM
M x y d(;)
.
Bước 2: Phương trình đường thẳng qua M có hệ số góc k:
MM
y k x x y(– )
tiếp xúc với (C) khi hệ sau có nghiệm:
( ) ( ) (1)
'( ) (2)
MM
f x k x x y
f x k
Thế k từ (2) vào (1) ta được:
M M M
f x x f x yx( ) )( – . ( )

(3)
Bước 3: Số tiếp tuyến của (C) vẽ từ M = Số nghiệm x của (3)
Ví dụ minh họa
Ví dụ 1: Cho hàm số
y x x
3
3
(C).Tìm trên đường thẳng (d):
yx
các điểm M mà từ đó kẻ
được đúng 2 tiếp tuyến phân biệt với đồ thị (C).
Gọi
M m m d( ; )
. PT đường thẳ ạng:
y k x m m()
.
là tiếp tuyến của (C)
hệ PT sau có nghiệm:
x x k x m m
xk
3
2
3 ( ) (1)
3 3 (2)

(*)
Thay (2) vào (1) ta được:
x mx m
32
2 3 4 0
x
m
x
3
2
2
34
(**)
Từ M kẻ được đúng 2 tiếp tuyến với (C)
(**) có 2 nghiệm phân biệt
Xét hàm số
x
fx
x
3
2
2
()
34
. Tập xác định
DR
2 3 2 3
\;
33




x
IM x x
x
x
2
2 2 2
0
00
2
0
0
23
1
( 2) 2 ( 2) 2
2
( 2)












x
x
x
x
2
0
0
2
0
0
1
1
( 2)
3
( 2)
52
TRẦN THÔNG Facebook: hội toán bắc trung nam
xx
fx
x
42
22
6 24
()
(3 4)
;
x
fx
x
0
( ) 0
2


Dựa vào BBT, (**) có 2 nghiệm phân biệt
m
m
2
2

. Vậy:
M( 2;2)
hoặc
M(2; 2)
.
Ví dụ 2: Cho hàm số
y x x m x m
32
2 ( 1) 2
(Cm). Tìm m để từ điểm
M(1;2)
kẻ được đúng 2
tiếp tuyến với (Cm).
PT đường thẳng
qua M có dạng:
y k x( 1) 2
.
là tiếp tuyến của (Cm)
hệ PT sau có
nghiệm:
x x m x m k x
x x m k
32
2
2 ( 1) 2 ( 1) 2
3 4 1
f x x x x m
32
( ) 2 5 4 3( 1) 0
(*)
Để qua M kẻ được đúng hai tiếp tuyến đến (Cm) thì (*) có đúng 2 nghiệm phân biệt
Ta có
f x x x f x x x
2
2
( ) 6 10 4 ( ) 0 1;
3

Các điểm cực trị của (Cm) là:
A m B m
2 109
(1;4 3 ), ; 3
3 27




.
Do đó (*) có đúng 2 nghiệm phân biệt
m
A Ox
B Ox
m
4
3
109
81
.
Bài toán 6: Tìm những điểm trên đường thẳng d mà từ đó có thể vẽ được 1, 2, 3, ... tiếp tuyến
với đồ thị (C):
y f x()
.
Phương pháp giải:
Bước 1: Gọi
MM
M x y(;)
. Phương trình đường thẳng qua M có hệ số góc k:
MM
y k x x y(– )
Bước 2: tiếp xúc với (C) khi hệ sau có nghiệm:
MM
f x k x x y
f x k
( ) ( ) (1)
'( ) (2)
Thế k từ (2) vào (1) ta được:
M M M
f x x f x yx( ) )( – . ( )

(3)
Qua M vẽ được 2 tiếp tuyến với (C) (3) có 2 nghiệm phân biệt
x x
12
,
.
Bước 3: Hai tiếp tuyến đó vuông góc với nhau
f x f x
12
( ). ( ) –1

.Từ đó tìm được M.
Ví dụ minh họa
53
TRẦN THÔNG Facebook: hội toán bắc trung nam
Ví dụ 1: Cho hàm số
y f x mx m x m x
32
1
( ) ( 1) (4 3 ) 1
3
có đồ thị là (C
m
).Tìm các giá trị m
sao cho trên đồ thị (C
m
) tồn tại một điểm duy nhất có hoành độ âm mà tiếp tuyến tại đó vuông góc
với đường thẳng (d):
xy2 3 0
.
(d) có hệ số góc
1
2
tiếp tuyến có hệ số góc
k 2
. Gọi x là hoành độ tiếp điểm thì:
f x mx m x m mx m x m
22
'( ) 2 2( 1) (4 3 ) 2 2( 1) 2 3 0
(1)
YCBT
(1) có đúng một nghiệm âm.
+ Nếu
m 0
thì (1)
xx2 2 1
(loại)
+ Nếu
m 0
thì dễ thấy phương trình (1) có 2 nghiệm là
m
x hay x=
m
23
1
Do đó để (1) có một nghiệm âm thì
m
m hoaëc m
m
2 3 2
00
3
Vậy
m hay m
2
0
3

.
Ví dụ 2: Cho hàm số
y x mx m
3
1
(Cm). Tìm m để tiếp tuyến của đồ thị (Cm) tại điểm M
có hoành độ
x 1
cắt đường tròn (C) có phương trình
xy
22
( 2) ( 3) 4
theo một dây cung có
độ dài nhỏ nhất.
Ta có:
y x m
2
3

ym( 1) 3
;
ym( 1) 2 2
. (C) có tâm
I(2;3)
, R = 2.
PTTT d tại
Mm( 1;2 2)
:
y m x m(3 ) 1
m x y m(3 ) 1 0
mm
m
d I d R
m m m
2
2 2 2
1 (3 ) 2. (3 ) 1
4
( , ) 2
(3 ) 1 (3 ) 1 (3 ) 1
Dấu "=" xảy ra
m 2
. Dó đó
d I d( , )
đạt lớn nhất
m 2
Tiếp tuyến d cắt (C) tại 2 điểm A, B sao cho AB ngắn nhất
d I d( , )
đạt lớn nhất
m 2
Khi đó: PTTT d:
yx3
.
Bài tập luyện thi
Bài 1: Cho hàm số
32
31y f x x x
có đồ thị là C.
a. Viết phương trình tiếp tuyến của C tại điểm có hoành độ bằng 0.
b. Viết phương trình tiếp tuyến của C tại điểm có tung độ bằng 1.
c. Viết phương trình tiếp tuyến của C biết nó có hệ số góc bằng -3.
54
TRẦN THÔNG Facebook: hội toán bắc trung nam
d. Viết phương trình tiếp tuyến của C biết nó song song với đường thẳng
9x 1y
.
e. Viết phương trình tiếp tuyến của C biết nó vuông góc với đường thẳng
1
x1
9
y
.
f. Viết phương trình tiếp tuyến của C nó biết hợp với trục 0x góc 45 độ .
g. Viết phương trình tiếp tuyến của C tại những điểm giao với đường thẳng y=1.
Bài 2: Cho hàm số
42
21y f x x x
có đồ thị là C.
a. Viết phương trình tiếp tuyến của C tại điểm có hoành độ bằng 2.
b. Viết phương trình tiếp tuyến của C tại điểm có tung độ bằng 2.
c. Viết phương trình tiếp tuyến của C biết nó có hệ số góc bằng -24.
d. Viết phương trình tiếp tuyến của C biết nó song song với đường thẳng
24x 12y
e. Viết phương trình tiếp tuyến của C biết nó vuông góc với đường thẳng
1
x1
24
y 
.
f. Viết phương trình tiếp tuyến của C biết nó hợp với trục 0x góc 45 độ .
g. Viết phương trình tiếp tuyến của C tại những điểm giao với đường thẳng y=-1.
Bài 3: Cho hàm số
2
21
x
y f x
x

có đồ thị là C.
a. Viết phương trình tiếp tuyến của C tại điểm có hoành độ bằng 1.
b. Viết phương trình tiếp tuyến của C tại điểm có tung độ bằng 2.
c. Viết phương trình tiếp tuyến của C biết nó có hệ số góc bằng 2.
d. Viết phương trình tiếp tuyến của C biết nó song song với đường thẳng
8x-2016y
e. Viết phương trình tiếp tuyến của C biết nó vuông góc với đường thẳng
1
18
yx
.
f. Viết phương trình tiếp tuyến của C biết nó hợp với trục 0x góc 45 độ .
g. Viết phương trình tiếp tuyến của C biết nó cắt hai trục toạ độ tại A và B sao cho tam giác
OAB vuông cân .
h. Viết phương trình tiếp tuyến của C biết nó cắt hai đường tiệm cận tại A và B sao cho tam
giác OAB vuông cân .
i. Lập phương trình tiếp tuyến của đồ thị (C) tại những điểm thuộc đồ thị có khoảng cách đến
đường thẳng
d x y:3 4 2 0
bằng 2.
Bài 3:Cho hàm số
32
1
2 3 1 1
3
y x x x
. Viết phương trình tiếp tuyến của đồ thị hàm số (1)
biết tiếp tuyến song song với đường thẳng
31yx
.
55
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 4: Cho hàm số
21
x
y
x
(C). Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng
2
3
.
Bài 5: : Cho hàm số :
32
34y x x
. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có
hệ số góc.
Bài 6: Cho hàm số:
32
31y x x
có đồ thị là (C). Viết phương trình tiếp tuyến của đồ thị (C)
tại điểm
(1;5)A
. Gọi B là giao điểm của tiếp tuyến với đồ thị (C) (B A). Tính diện tích tam giác
OAB, với O là gốc tọa độ.
Bài 7: Cho hàm số
32
3 3 2y x x x
có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị
(C) tại giao điểm của (C) với trục tung.
Bài 8: Cho hàm số :
)(
1
32
C
x
x
y
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có
tung độ bằng 1.
Bài 9: Khảo sát sự biến thiên và vẽ đồ thị
()C
của hàm số
3
32y x x
.Viết phương trình
tiếp tuyến của đồ thị
()C
tại điểm có hoành độ
0
x
thỏa mãn phương trình
0
" 12yx
.
Bài 10: : Cho hàm số
1
12
x
x
y
(C). Viết phương trình tiếp tuyến của (C) tại điểm A là giao
điểm của (C) với trục hoành.
Bài 11: Cho hàm số
32
34y x x
.(C) Viết phương trình tiếp tuyến của (C), biết tiếp tuyến đó
có hệ số góc bằng 9.
Bài 12: Viết phương trình tiếp tuyến của đồ thị
( ): 3 2C y x
tại điểm M có hoành độ x
0
= 1.
Bài 13: Cho hàm số
4
2
5
3
22
x
yx
(C). Cho điểm M thuộc
()C
có hoành độ
1
M
x
. Viết
phương trình tiếp tuyến của
()C
tại M.
Bài 14: Cho hàm số
23
2
x
y
x
(C). Tìm m để đường thẳng
:2d y x m
cắt (C) tại hai
điểm phân biệt và tiếp tuyến của (C) tại hai điểm đó song song với nhau.
Bài 15: Cho hàm số
32
3 y x x C
. Lập phương trình tiếp tuyến của (C) tại các giao điểm
của đồ thị với trục hoành.
56
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 16: Viết phương trình tiếp tuyến của đồ thị hàm số
1
()fx
x
. Biết tiếp tuyến có hệ số góc là
1
4
.
Bài 17: Viết phương trình tiếp tuyến d của đồ thị hàm số
21
1
x
y
x
biết d có hệ số góc bằng – 1.
Bài 18: Cho hàm số
32
32y x x
. Viết phương trình tiếp tuyến với đồ thị
()C
biết tiếp tuyến
vuông góc với đường thẳng
có phương trình:
2016 0x
.
Bài 19: Cho hàm số
21
1
x
y
x
. Xác định tọa độ giao điểm của đồ thị
()C
với đường thẳng
7yx
và viết phương trình tiếp tuyến của
()C
tại các giao điểm ấy.
Bài 20: Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của nó với
trục tung.
Bài 21: Cho hàm số
33
31y x x
(1). Viết phương trình tiếp tuyến của đồ thị (C) tại giao
điểm của (C) với đường thẳng
: 2 7d y x
.
Bài 22: Cho hàm số
3
2
x
y
x
có đồ thị (C). Viết phương trình tiếp tuyến với (C) biết hình chiếu
vuông góc của hai điểm A(1;1), B(0;-3) lên tiếp tuyến trùng nhau
Bài 23: Cho hàm số
32
6 9 4y x x x
(C). Viết pttt với (C), biết tiếp tuyến song song với y =
9x – 4.
Bài 24: Cho hàm số
32
6 9 2y x x x
(C).Viết pttt với (C), biết hoành độ tiếp điểm của tiếp
tuyến là nghiệm của pt
''( ) 18fx
Bài 25: Cho hàm số
3
32y x x
Viết pttt của (C) tại giao điểm của (C) và d: y = - x – 2, biết
tiếp điểm có hoành độ dương.
Bài 26: Cho hàm số
32
32y x x
. Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của
(C) với đường thẳng
:3d y x
.
Bài 27: Cho hàm số
42
21y x x
(1). Viết pttt của (C) biết tiếp tuyến đi qua M(0;-1).
Bài 28: Cho hàm số: (C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến song
song với đường thẳng .
3
43y x x
x2
y
2x 1
d : y 5x 2
57
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 29: Khảo sát và vẽ đồ thị (C) của hàm số
3
32y x x
Tìm tọa độ của điểm M trên (C) sao
cho tiếp tuyến của (C) tại M song song với đường thẳng (d): 9x – y - 18 = 0
Bài 30: Cho hàm số:
2x 1
y
x1
(H). Viết phương trình tiếp tuyến của (H), biết nó cắt đồ thị tại
hai điểm A,B sao cho tam giác ABC đều trong đó
C 2,5
.
Bài 31: Cho hàm số
21
1
2
m
xm
yC
x

. Viết phương trình tiếp tuyến của đồ thị
m
C
tại
giao điểm của
m
C
với trục tung, biết khoảng cách từ gốc tọa độ O đến tiếp tuyến đó bằng
2
5
.
Bài 32: Tìm
m
để tiếp tuyến của đồ thị
3
: 1 1C x m x
tại điểm
C
có
0
C
x
và chắn
hai trục tọa độ một tam giác có diện tích
8S
.
Bài 33: Cho hàm số Xác định tọa độ các giao điểm của và đường
thẳng . Viết phương trình tiếp tuyến của tại các giao điểm đó.
Bài 34: Tính diện tích tam giác chắn hai trục tọa độ bởi tiếp tuyến của đồ thị
2
: 27 26C y x x
tại điểm
B
có
2
B
x
.
Bài 35: Cho
32
41
: 2 1 2
33
m
C y x m x m x
.Gọi A là giao điểm của
m
C
và trục
Oy. Tìm m để tiếp tuyến tại A tạo với hai trục tọa độ một tam giác có diện tích bằng
1
.
3
Bài 36: Cho A,B,C là ba điểm thẳng hàng nằm trên đồ thị hàm số
32
32y x x C
.Tiếp tuyến
của
C
tại A,B,C cắt đồ thị
C
tại
', ', 'A B C
. Chứng minh
', ', 'A B C
thẳng hàng.
Bài 37: Viết phương trình tiếp tuyến của đồ thị hàm số
32
1y x x
biết nó tạo với các trục tọa
độ tam giác cân.
Bài 38: Cho
21
1
x
yC
x
có I là giao điểm hai đường tiệm cận. M là điểm bất kỳ trên
C
.
Tiếp tuyến của
C
tại M cắt các đường tiệm cận tại các điểm A,B. Chứng minh M là trung
điểm AB và diện tích tam giác IAB không đổi. Tìm M thuộc (C) sao cho chu vi của tam giác
IAB đạt giá trị nhỏ nhất.
Bài 39: Cho
21
1
x
yC
x
có I là giao điểm hai đường tiệm cận. M là điểm bất kỳ trên
C
.Tìm
tọa độ điểm M để tiếp tuyến tại M vuông góc với IM.
42
41y x x C
C
1y
C
58
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 40: Cho hàm số:
2
1
x
yC
x
.Viết phương trình tiếp tuyến của
C
biết rằng nó cắt hai
đường tiệm cận tại hai điểm phân biệt A,B sao cho bán kính đường tròn nội tiếp tam giác OAB
nhỏ nhất
Bài 41: Cho hàm số
1
2
x
y
x
(C) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến cắt
hai đường tiệm cận của (C) lần lượt tại A và B sao cho tam giác ABI có bán kính đường tròn nội
tiếp bằng
22
, với I là giao điểm của hai đường tiệm cận.
Bài 42: Viết phương trình tiếp tuyến của đồ thị (C) hàm số :
2
2
x
y
x
biết tiếp tuyến cắt trục Ox,
Oy lần lượt tại
,AB
sao cho
2AB OA
.
Bài 43: Tìm tọa độ điểm
,AB
thuộc đồ thị (C) hàm số:
1
2
x
y
x

sao cho tiếp tuyến của (C) tại
A
song song tiếp tuyến của (C) tại
B
và
22AB
.
Bài 44: Chứng minh đường thẳng
y x m
cắt đồ thị (C) hàm số
1
21
x
y
x

tại hai điểm phân
biệt
,AB
. Gọi
12
,kk
lần lượt là hệ số góc tiếp tuyến của (C) tại
,AB
. Tìm
m
để
12
kk
đạt giá
trị lớn nhất.
Bài 45: Cho hàm số:
32
1
1 4 3 1
3
y mx m x m x
()
m
C
. Định giá trị của
m
để đồ
thị hàm số
()
m
C
tồn tại duy nhất một điểm có hoành độ âm sao cho tiếp tuyến tại đó vuông góc
với đường thẳng
2 3 0xy
.
Dạng 6: Sự tương giao giửa đồ thị
Bài toán 1: Biện luận số nghiệm phương trình
Phương pháp giải bài toán: Dựa vào các điểm đặc biệt của đồ thị (thường là các điểm cực trị ,các
đường tiệm cận) và sự tương giao của đồ thị và đường thẳng nằm ngang để tìm ra điều kiện của
tham số.
Ví dụ minh họa
Ví dụ 1: Dựa vào đồ thị hàm số:
42
43y x x
tìm các giá trị của tham số thực m để phương
trình
42
4 3 2 0x x m
có hai nghiệm phân biệt.
Ta có
4 2 4 2
4 3 2 0 4 3 2x x m x x m
(*)
Suy ra số nghiệm pt (*) bằng số giao điểm của
42
( ) : 4 3C y x x
và
59
TRẦN THÔNG Facebook: hội toán bắc trung nam
d: y = 2m.
Dựa vào đồ thị tìm được : 2m = 1 hoặc 2m < –3 hay
13
;.
22
mm

Vậy khi
3
2
m
hoặc
1
2
m
phương trình
42
4 3 2 0x x m
có hai nghiệm phân biệt.
Ví dụ 2: Dựa vào đồ thị hàm số:
32
y x 6x 9x 1
tìm các giá trị của tham số thực m để
phương trình

2
x(x 3) m
có ba nghiệm phân biệt.
Ta có

2
x(x 3) m
32
x 6x 9x 1 m 1
. (*)
Suy ra số nghiệm pt (*) bằng số giao điểm của
xx
32
( ) : 6 9 1C y x
và
d: y = m-1.
Dựa vào đồ thị tìm được :
1 m 1 3 0 m 4
Vậy khi
0 m 4
phương trình

2
x(x 3) m
có hai nghiệm phân biệt.
Ví dụ 3: Tìm
k
để phương trình
*
3 2 3 2
3 3 0x x k k
có
3
nghiệm phân biệt.
Phương trình
*
tương đương với
3 2 3 2
33x x k k
.
Nếu đặt
32
3f x x x
thì phương trình trở thành
f x f k
.
*
có ba nghiệm phân biệt
đường thẳng
y f k
có ba điểm chung với đồ thị hàm số
y f x
40fk
.
Từ đồ thị hàm số
y f k
, ta thấy điều kiện
40fk
tương đương với
1;3 \ 0;2k 
.
Bài toán 2:Sự tương giao giữa 2 đồ thị
Cho
y f x
1
C
và
y g x
2
C
. Để tìm giao điểm của
1
C
và
2
C
, ta làm như sau:
Bước 1: Tìm hoành độ giao điểm. Hoành độ giao điểm của
1
C
và
2
C
là nghiệm của phương
trình
f x g x
*
.Phương trình
*
được gọi là phương trình hoành độ giao điểm của
1
C
và
2
C
.
60
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bước 2: Tìm giao điểm. Nếu
0
x
là một hoành độ giao điểm thì
00
;x f x
(
00
;x g x
) là một
giao điểm của
1
C
và
2
C
.
Chú ý. Để giải các bài toán loại này, ta rất hay sử dụng định lý Vi-ét đảo:
Nếu
1
x
,
2
x
là các nghiệm của phương trình bậc hai
2
0ax bx c
(
0a
) thì
12
12
.
b
xx
a
c
xx
a

.
Ví dụ minh họa
Ví dụ 1: Cho hàm số có đồ thị . Tìm m để cắt trục hoành
tại 3 điểm phân biệt có tổng bình phương các hoành độ lớn hơn 15.
cắt trục hoành tại 3 điểm phân biệt có tổng bình phương các hoành độ lớn hơn 15.
(*) có 3 nghiệm phân biệt thỏa .
Ta có: (*)
Do đó: YCBT
có 2 nghiệm phân biệt khác 1 và thỏa .
Vậy thỏa yêu cầu bài toán.
Ví dụ 2: Cho hàm số , trong đó là tham số thực. Tìm tất cả các giá trị
của tham số để đồ thị hàm số đã cho cắt trục hoành tại 3 điểm phân biệt có hoành độ lập thành
cấp số cộng.
Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt có hoành độ lập thành cấp số cộng
Phương trình có 3 nghiệm phân biệt lập thành cấp số cộng
Phương trình có 3 nghiệm phân biệt lập thành cấp số cộng
Đường thẳng đi qua điểm uốn của đồ thị (C)
Vậy thỏa yêu cầu bài toán.
32
12
33
y x mx x m
m
C()
m
C()
m
C()
x mx x m
32
12
0
33
xxx
222
1 2 3
15
x x m x m
2
( 1)( (1 3 ) 2 3 ) 0
x
g x x m x m
2
1
( ) (1 3 ) 2 3 0
gx( ) 0
xx
12
,
xx
22
12
14
m 1
mxxxy 93
23
m
m
32
3 9 0 x x x m
32
39x x x m
ym
.11 11mm
61
TRẦN THÔNG Facebook: hội toán bắc trung nam
Ví dụ 3: Cho hàm số . Viết phương trình đường thẳng d qua điểm và cắt đồ thị
(C) tại hai điểm M, N sao cho I là trung điểm của đoạn MN.
Phương trình đường thẳng
d cắt (C) tại 2 điểm phân biệt M, N có 2 nghiệm phân biệt khác .
có 2 nghiệm phân biệt khác
Mặt khác: I là trung điểm MN với .
Phương trình đường thẳng cần tìm là với .
Ví dụ 4: Cho hàm số có đồ thị là (C). Định m để đường thẳng
cắt đồ thị (C) tại ba điểm phân biệt.
PT hoành độ giao điểm của (C) và (d):
(d) cắt (C) tại ba điểm phân biệt
PT có 2 nghiệm phân biệt khác 2
Bài toán 3:Bài toán điểm trên đồ thị.
1) Khoảng cách giữa hai điểm A, B: AB =
B A B A
x x y y
22
( ) ( )
2) Khoảng cách từ điểm
M x y
00
( ; )
đến đường thẳng :
ax by c 0
:
ax by c
d M d
ab
00
22
( , )

Đặc biệt: + Nếu :
xa
thì
d M x a
0
( , )

+ Nếu :
yb
thì
d M y b
0
( , )

+ Tổng các khoảng cách từ M đến các trục toạ độ là:
xy
00
.
3
1
x
y
x
( 1;1)I
: 1 1d y k x
3
1
1
x
kx k
x
1
2
( ) 2 4 0 f x kx kx k
1
0
4 0 0
( 1) 4 0
k
kk
f
22
M N I
x x x
0k
1y kx k
0k
y x x x
32
6 9 6
d y mx m( ): 2 4
x x x mx m
32
6 9 6 2 4
x x x m
2
( 2)( 4 1 ) 0
x
g x x x m
2
2
( ) 4 1 0
gx( ) 0
m 3
62
TRẦN THÔNG Facebook: hội toán bắc trung nam
3) Diện tích tam giác ABC: S =
AB AC A AB AC AB AC
2
22
11
. .sin . .
22

4) Các điểm A, B đối xứng nhau qua điểm I
IA IB 0
A B I
A B I
x x x
y y y
2
2


5) Các điểm A, B đối xứng nhau qua đường thẳng
AB
I
(I là trung điểm AB).
Đặc biệt: + A, B đối xứng nhau qua trục Ox
BA
BA
xx
yy

+ A, B đối xứng nhau qua trục Ox
BA
BA
xx
yy

6) Khoảng cách giữa đường thẳng với đường cong (C) bằng khoảng cách nhỏ nhất giữa một
điểm M và một điểm N (C).
7) Điểm
M x y( ; )
được gọi là có toạ độ nguyên nếu
xy,
đều là số nguyên.
Ví dụ minh họa
Ví dụ 1: Cho hàm số (C). Tìm 2 điểm trên đồ thị hàm số sao cho chúng đối xứng
nhau qua tâm M(–1; 3).
Gọi , là điểm đối xứng với A qua điểm
Vậy 2 điểm cần tìm là: và
Ví dụ 2: Cho hàm số . Tìm trên (C) hai điểm đối xứng nhau qua đường thẳng MN
biết M(–3; 0) và N(–1; –1).
Phương trình MN: .
3
32y x x
A x y
00
;
B
M( 1;3)
B x y
00
2 ;6
A B C, ( )
y x x
y x x
3
0 0 0
3
0 0 0
32
6 ( 2 ) 3( 2 ) 2
x x x x x x
3
32
0 0 0 0 0 0
6 3 2 2 3 2 2 6 12 6 0
xy
00
10
1;0
1;6
x
y
x
24
1
MN (2; 1)
xy2 3 0
63
TRẦN THÔNG Facebook: hội toán bắc trung nam
Phương trình đường thẳng (d)
MN có dạng: .
Phương trình hoành độ giao điểm của (C) và (d):
(1)
(d) cắt (C) tại hai điểm phân biệt A, B
(2)
Khi đó với là các nghiệm của (1)
Trung điểm của AB là
(theo định lý Vi-et)
A, B đối xứng nhau qua MN
I MN
Suy ra (1)
A(0; –4), B(2; 0).
Ví dụ 3: Cho hàm số . Tìm trên đồ thị (C) hai điểm B, C thuộc hai nhánh sao cho tam
giác ABC vuông cân tại đỉnh A với A(2; 0).
Ta có . Gọi với .
Gọi H, K lần lượt là hình chiếu của B, C lên trục Ox.
Ta có:
và:
Hay: .
Vậy
Ví dụ 4: Cho hàm số (C). Tìm 2 điểm trên đồ thị hàm số sao cho chúng đối xứng
nhau qua đường thẳng d: .
Gọi thuộc (C) là hai điểm đối xứng qua đường thẳng d
y x m2
x
xm
x
24
2
1

x mx m x
2
2 4 0 ( 1)
mm
2
– 8 – 32 0

A x x m B x x m
1 1 2 2
( ;2 ), ( ;2 )
xx
12
,
xx
I x x m
12
12
;
2




mm
I ;
42



m 4
x
xx
x
2
0
2 4 0
2
2
1
x
y
x
Cy
x
2
( ) : 2
1

B b C c
bc
22
;2 , ;2
11


bc1
AB AC BAC CAK BAH CAK ACK BAH ACK
00
; 90 90
AH CK
BHA CKA ABH CAK
HB AK
0
90

b
b
c
c
c
b
2
22
1
1
2
3
22
1

BC( 1; 1), (3;3)
3
32y x x
xy2 – 2 0
1 1 2 2
; ; ;M x y N x y
H
K
B
A
C
64
TRẦN THÔNG Facebook: hội toán bắc trung nam
I là trung điểm của AB nên , ta có
Có:
Lại có:
- Xét
- Xét vô nghiệm
Vậy 2 điểm cần tìm là
7 1 7 7 1 7
;2 ; ;2
2 2 2 2 2 2
.
Ví dụ 5: Cho hàm số
y x x x
32
15
3
33
.
Gọi A, B là các giao điểm của (C) với trục Ox. Chứng minh rằng trên đồ thị (C) tồn tại hai điểm
cùng nhìn đoạn AB dưới một góc vuông.
PT hoành độ giao điểm của (C) với trục hoành:
x
x x x
x
32
15
1
30
5
33

AB( 5;0), (1;0)
. Gọi
M a a a a C M A B
32
15
; 3 ( ), ,
33



AM a a a a
32
15
5; 3
33


,
BM a a a a
32
15
1; 3
33


AM BM AM BM.0
a a a a
24
1
( 5)( 1) ( 5) ( 1) 0
9
aa
3
1
1 ( 1) ( 5) 0
9
a a a a
4 3 2
2 12 14 4 0 (*)
1 2 1 2
;
22
x x y y
I




Id
33
1 1 2 2
1 2 1 2
3 2 3 2
2. 2
2 2 2
x x x x
y y x x

3
12
1 2 1 2 1 2 1 2 1 2
22
1 1 2 2
0
3 3 2
1

xx
x x x x x x x x x x
x x x x
2 1 2 1
.1 .2 0MN d x x y y
2 2 2 2
2 1 2 1 1 1 2 2 1 1 2 2
7
7 2 0
2
x x x x x x x x x x x x
12
0xx
12
77
;
22
xx
22
22
12
1 1 2 2
22
1 1 2 2
12
9
1
4
7
5
2
4
xx
x x x x
x x x x
xx





65
TRẦN THÔNG Facebook: hội toán bắc trung nam
Đặt
y a a a a
4 3 2
2 12 14 4 0
, có tập xác định D = R.
y a a a
32
4 6 12 14
;
y 0
có 1 nghiệm thực
ay
00
7 2043
2 16
Dựa vào BBT ta suy ra (*) luôn có 2 nghiệm khác 1 và –5.
Vậy luôn tồn tại 2 điểm thuộc (C) cùng nhìn đoạn AB dưới một góc vuông.
Ví dụ 6: Cho hàm số
y x x
42
21
.Tìm toạ độ hai điểm P, Q thuộc (C) sao cho đường thẳng PQ
song song với trục hoành và khoảng cách từ điểm cực đại của (C) đến đường thẳng PQ bằng 8.
Điểm cực đại của (C) là
A(0;1)
. PT đường thẳng PQ có dạng:
y m m( 0)
.
Vì
d A PQ( , ) 8
nên
m 9
. Khi đó hoành độ các điểm P, Q là nghiệm của phương trình:
x x x
42
2 8 0 2
.
Vậy:
PQ( 2;9), (2;9)
hoặc
PQ(2;9), ( 2;9)
.
Bài tập luyện thi
Bài 1: Biện luận theo tham số m số nghiệm phương trình
32
31x x m
Bài 2: Biện luận theo tham số m số nghiệm phương trình
42
2x x m
Bài 3: Biện luận theo tham số m số nghiệm phương trình
2
1
x
m
x
Bài 4: Tìm m để phương trình
32
32x x m
có 3 nghiệm phân biệt
Bài 5: Tìm m để phương trình
2 2 1x m x
vô nghiệm
Bài 6: Tìm m để phương trình
4 2 2
2x x m
có 2 nghiệm phân biệt.
Bài 7: Cho hàm số
42
1
y x 2x 3
4
. Tìm m để phương trình
42
8x x m
có 4 nghiệm phân
biệt.
Bài 8: Dựa vào đồ thị, hãy tìm m để phương trình
42
2 1 0x x m
có 4 nghiệm phân biệt.
Bài 9: Cho hàm số:
32
31y x x
có đồ thị là
()C
Dựa vào đồ thị
()C
, hãy tìm điều kiện
của tham số k để phương trình sau đây có 3 nghiệm phân biệt:
32
30x x k
.
Bài 10: Cho hàm số
32
2( 2) (8 5 ) 5y x m x m x m
có đồ thị (C
m
) và đường thẳng
:1d y x m
. Tìm m để d cắt (C
m
) tại 3 điểm phân biệt có hoành độ tại x
1
, x
2
, x
3
thỏa mãn:
222
1 2 3
20xxx
.
66
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 11: Cho hàm số
32
31y x x
(C). Tìm m để đường thẳng
:1d y mx
cắt đồ thị (C) tại
ba điểm phân biệt.
Bài 12: Cho hàm số
32
( 1) ( 1) 1 (1)y x m x m x
. Tìm các giá trị của m để đồ thị của
hàm số (1) cắt trục Ox tại ít nhất một điểm có hoành độ thuộc đoạn
1
;2
2



.
Bài 13: : Cho hàm số
3 2 2 2
2 1 2 1 1y x m x m m x m
(m là tham số). Tìm m để (C)
cắt trục hoành tại 3 điểm phân biệt A, B, C (với A là điểm cố định) sao cho
1 2 1 2
2 k k x x
, trong
đó
12
,kk
lần lượt là hệ số góc của tiếp tuyến của (C) tại B, C và
là hoành độ các điểm cực
trị của (C).
Bài 14: Cho hàm số y =
21
1
x
x
có đồ thị (C). Tìm m để đường thẳng
:2 3 0y x m
cắt đồ thị
(C) tại hai điểm phân biệt A, B sao cho độ dài 4AB
2
= 13.
Bài 15:Cho hàm số
1
1
x
y
x
.Viết phương trình đường thẳng d song song với d’ : x + y + 2= 0
sao cho d cắt (C) tại hai điểm phân biệt A,B và diện tích tam giác IAB bằng
23
(I là giao điểm
hai đường tiệm cận).
Bài 16: Cho hàm số
23
2
x
y
x
. Tìm m để phương trình
2y x m
cắt đồ thị (C) tại hai điểm
phân biệt.
Bài 17: Cho hàm số
3
2 3 1y x x
, có đồ thị là (C). Gọi (d
k
) là đường thẳng đi qua A(0; –1) và
có hệ số góc bằng k. Tìm k để đường thẳng d
k
cắt (C) tại 3 điểm phân biệt, trong đó hai điểm có
hoành độ dương .
Bài 18: Cho hàm số
21
2
x
y
x
Tìm
m
để đường thẳng
y x m
cắt (C) tại hai điểm phân biệt
A,B
sao cho
AB 4 2.
Bài 19: Cho hàm số
2
1
x
y
x
(C).Lập phương trình đường thẳng qua
M 0, 11
cắt (C) tại hai
điểm A,B sao cho
OAB OMB
S 2S
.
Bài 20: Tìm mọi giá trị của m để đường thẳng
:d y x m
cắt đồ thị
2
1
x
yC
x
tại hai điểm
phân biệt. Khi nào có ít nhất một trong hai giao điểm có tọa độ nguyên ?
67
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 21: Cho hàm số
23
1
x
y
x
có đồ thị (C). Gọi (d) là đường thẳng qua H(3; 3) và có hệ số góc
k. Tìm k để (d) cắt (C) tại 2 điểm phân biệt M, N sao cho tam giác MAN vuông tại A(2; 1).
Bài 22: Cho hàm số
21
2
x
y
x
Tìm m để đường thẳng
:d y x m
cắt đồ thị (C) tại hai điểm
phân biệt A, B sao cho
4 2.AB
Bài 23: Cho hàm số
32
3x 2y x C
Tìm m để đường thẳng
: 2 2d y m x
cắt (C) tại
3 điểm phân biệt
2;2 , ,A B C
sao cho tích các hệ số góc của tiếp tuyến với (C) tại B, C đạt giá
trị nhỏ nhất.
Bài 24: Cho hàm số
32
11
1 2 1 1
32
y x m x m x
. Tìm m để hàm số (1) có hai điểm
cực trị A, B đồng thời hai điểm cực trị đó cùng với điểm
7
3;
2
D



và gốc tọa độ O tạo thành hình
bình hành OADB.
Bài 25: Cho hàm số
3
32y x x C
. Gọi (d) là đường thẳng đi qua điểm
0;2I
có hệ số
góc m. Tìm m để (d) cắt (C) tại 3 điểm phân biệt I, A, B. Chứng minh rằng I là trung điểm của
AB.
Bài 26: Cho hàm số
2
2 -1
x
yC
x
. Tìm m để đường thẳng
:d y x m
cắt (C) tại hai điểm A,
B phân biệt sao cho trọng tâm G của tam giác OAB cách d một khoảng bằng
2
(O là gốc tọa
độ).
Bài 27: Cho hàm số
21
1
x
yC
x
. Tìm tất cả các giá trị của m để đường thẳng
2y mx
cắt
đồ thị (C) tại hai điểm phân biệt A, B sao cho tam giác OAB vuông tại gốc tọa độ O.
Bài 28: Cho hàm số có đồ thị . Gọi là đường thẳng đi qua điểm và có
hệ số góc . Tìm tham số để cắt tại 2 điểm phân biệt A, B sao cho I là trung điểm của
đoạn thẳng AB.
Bài 29:
Cho hàm số:
3 2 2
3( 1) 2( 4 1) 4 ( 1)y x m x m m x m m
()
m
C
. Định giá trị
của
m
để hàm số cắt
Ox
tại 3 điểm phân biệt có hoành độ đều lớn hơn 1.
Bài 30: Cho . Tìm m để cắt trục hoành tại ba điểm
phân biệt có hoành độ và thỏa mãn điều kiện: .
21
1
x
y
x
C
2, 0I
m
m
C
32
12
:
33
m
C y x mx x m
m
C
1 2 3
,,x x x
222
123
15xxx
68
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 31: Cho hàm số:
2
2
x
y
x
C
CMR
d
:
y x m
luôn cắt
C
tại 2 điểm P và Q thuộc
2 nhánh khác nhau của đồ thị. Tìm
m
để
OPQ
vuông tại O.
Bài 32: Cho hàm số:
1
x
yC
x
và đường thẳng d
y m x
.Tìm m để d cắt
C
tại hai điểm
phân biệt A,B sao cho bán kính đường tròn ngoại tiếp tam giác OAB là
22
.
Bài 33: Cho hàm số:
21
3
x
yC
x
và đường thẳng d
y m x
. Tìm m để d cắt
C
tại hai
điểm phân biệt A,B sao cho
22
3AB IA
với I là giao điểm hai đường tiệm cận của
C
Bài 34: Cho hàm số:
2
1
x
yC
x
.Viết phương trình tiếp tuyến của
C
biết rằng nó cắt hai
đường tiệm cận tại hai điểm phân biệt A,B sao cho bán kính đường tròn nội tiếp tam giác OAB
nhỏ nhất.
Bài 35: Cho hàm số
1
2
x
y
x
. Gọi (d) là đường thẳng qua
2;0M
có hệ số góc k. Tìm k để (d)
cắt (C) tại hai điểm phân biệt A, B sao cho M nằm giữa A, B và
2MA MB
.
Bài 36: Cho hàm số
1
2
x
y
x
(C) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến cắt
hai đường tiệm cận của (C) lần lượt tại A và B sao cho tam giác ABI có bán kính đường tròn nội
tiếp bằng
22
, với I là giao điểm của hai đường tiệm cận.
Bài 37: Cho hàm số
21
1
x
y
x
. Viết phương trình đường thẳng
đi qua điểm
(0;1)I
và cắt đồ
thị
()C
tại hai điểm phân biệt
,AB
sao cho diện tích tam giác
OAB
bằng
3
(O là gốc tọa độ).
Bài 38: Tìm
k
để đường thẳng
: 2 1d y kx k
cắt đồ thị hàm số (C):
3
2
x
y
x
tại hai điểm
phân biệt
,AB
sao cho khoảng cách từ A và B đến trục hoành bằng nhau.
Bài 39: Tìm
m
để đồ thị hàm số
32
2 (1 )y x x m x m
cắt trục Ox taị 3 điểm phân biệt có
hoành độ
1 2 3
,,x x x
đều lớn hơn
1
2
.
Bài 40: Chứng minh mọi đường thẳng đi qua điểm
(1;2)I
với hệ số góc
( 3)kk
đều cắt đồ thị
hàm số
32
34y x x
tại ba điểm phân biệt
,,I A B
đồng thời
I
là trung điểm của đoạn
.AB
69
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài 41: Cho hàm số Tìm để đồ thị hàm số cắt trục
hoành tại 3 điểm phân biệt có hoành độ thỏa mãn điều kiện .
Bài 42: Cho hàm số Chứng minh rằng mọi đường thẳng đi qua điểm
với hệ số góc đều cắt đồ thị hàm số tại ba điểm phân biệt I, A, B, đồng
thời I là trung điểm của đoạn thẳng AB.
Bài 43: Cho hàm số có đồ thị là
m
C
, điểm , đường
thẳng
d
có phương trình . Tìm các giá trị của
m
để đường thẳng
d
cắt
m
C
tại 3
điểm
0,2 , ,A B C
sao cho tam giác MBC có diện tí c
h bằng
26
Bài 44: Cho hàm số:
3 2 2
3( 1) 2( 4 1) 4 ( 1)y x m x m m x m m
()
m
C
. Định giá trị
của
m
để hàm số cắt
Ox
tại 3 điểm phân biệt có hoành độ đều lớn hơn 1.
Bài 45: Cho hàm số:
3
3
3
x
yx
C
và đường thẳng Tìm
m
để
C
và
: ( 3)d y m x
có
giao điểm là A, B, C với A cố định và
OA OC
,
42BC
.
Bài 46: Cho hàm số y =
32
6 9 3mx x mx
(1) Xác định m để đường thẳng d: y =
9
3
4
x
cắt
đồ thị hàm số (1) tại 3 điểm phân biệt A(0,– 3), B, C thỏa điều kiện B nằm giữa A và C đồng thời
AC = 3AB.
Bài 47: Tìm m để đồ thị (C) của hàm số
32
28y mx x x m
Cắt trục hoành tại ba điểm phân
biệt có hoành độ thỏa x > 1.
Bài 48: Cho (C) là đồ thị hầm số
4 2 2
(3 1)y x m x m
. Tìm m để (C) cắt trục hoành tại bốn
điểm phân biệt có hoành độ lập thành cấp số cộng.
Bài 49: Tìm tham số thực
m
để
d
đi qua
A 1;0
và có hệ số góc là m cắt
C
:
2
1
x
y
x
tại hai điểm
M,N
thuộc hai nhánh của
C
(
M
thuộc nhánh trái ,
N
thuộc nhánh phải )sao cho
AN 2AM
.
Bài 50: Cho hàm số
2
22
x
y
x
có đồ thị là
C
. Tìm tất cả các giá trị tham số
m
để đường
thẳng
d : y x m
cắt đồ thị
C
tại
2
điểm phân biệt
A, B
sao cho
22
37
OA OB .
2

Dạng 7: Đồ thị hàm số chứa dấu giá trị tuyệt đối
32
2 1 1y x x m x m
m
1
1 2 3
,,x x x
222
123
4xxx
32
34y x x C
1,2I
3kk
C
32
2 3 1 2y x mx m x
3,1M
20xy
70
TRẦN THÔNG Facebook: hội toán bắc trung nam
Để vẽ đồ thị hàm số chứa dấu giá trị tuyệt đối, ta sử dụng ba nguyên tắc sau đây:
Nguyên tắc 1. (về sự phân chia đồ thị hàm số) Đồ thị hàm số
là hợp của
n
đồ thị hàm số
k
y f x
với
k
xD
(
1,2, ,kn
).
Nguyên tắc 2. (về sự đổi dấu hàm số) Đồ thị hàm số
y f x
,
xD
và đồ thị hàm số
y f x
,
xD
đối xứng nhau qua
Ox
.
Nguyên tắc 3. (về đồ thị hàm chẵn) Đồ thị của hàm chẵn nhận
Oy
làm trục đối xứng.
Hai trường hợp hay gặp:
-Đồ thị hàm số
y f x
Vì
0
y f x
f x f x x
là hàm chẳn nên đồ thị hàm số
y f x
gồm hai phần:
+) Phần 1 là phần đồ thị hàm số
y f x
nằm bên phải
Oy
;
+) Phần 2 đối xứng với phần 1 qua
Oy
.
-Đồ thị hàm số
y f x
Vì
,0
,0
f x f x
fx
f x f x

nên đồ thị hàm số
y f x
gồm hai phần:
+) Phần 1 là phần Đồ thị hàm số
y f x
nằm phía trên trục hoành;
+) Phần 2 đối xứng với phần Đồ thị hàm số
y f x
ở phía dưới trục hoành qua
trục hoành.
Ví dụ minh họa
Ví dụ 1. Vẽ các đồ thị hàm số
11
22
,
,
...
,
nn
f x x D
f x x D
y f x
f x x D

71
TRẦN THÔNG Facebook: hội toán bắc trung nam
1)
1
1
1
x
fx
x
1
C
;
2)
2
1
1
x
fx
x
2
C
;
3)
3
1
1
x
fx
x
3
C
;
4)
4
1
1
x
fx
x
4
C
;
5)
5
1
1
x
fx
x
5
C
.
Giải. Trước hết, ta vẽ đồ thị
C
của hàm số
1
1
x
fx
x
(hình 0);
1) Ta có
1
0
0
f x khi f x
f x f x
f x khi f x


. Do đó đồ thị
1
C
gồm hai phần (hình 1):
Phần 1: là phần đồ thị
C
nằm trên
Ox
;
Phần 2: đối xứng với phần đồ thị
C
nằm dưới
Ox
qua
Ox
.
2) Ta có
2
f x f x
là hàm chẵn, đồ thị nhận
Oy
làm trục đối xứng. Lại có
2
f x f x
với mọi
0x
. Do đó đồ thị
2
C
gồm hai phần (hình 2):
Phần 1: là phần đồ thị
C
nằm bên phải
Oy
;
Phần 2: đối xứng với phần 1 qua
Oy
.
3) Ta có
22
32
22
0
0
f x khi f x
f x f x
f x khi f x


. Do đó đồ thị
3
C
gồm hai phần (hình 3):
Phần 1: là phần đồ thị
2
C
nằm trên
Ox
;
Phần 2: đối xứng với phần đồ thị
2
C
nằm dưới
Ox
qua
Ox
.
4) Ta có
4
1
1
f x khi x
fx
f x khi x

. Do đó đồ thị
4
C
gồm hai phần (hình 4):
Phần 1: là phần đồ thị
C
ứng với
1x
;
Phần 2: đối xứng với phần đồ thị
C
ứng với
1x
qua
Ox
.
72
TRẦN THÔNG Facebook: hội toán bắc trung nam
5) Ta có
5
1
1
f x khi x
fx
f x khi x

. Do đó đồ thị
5
C
gồm hai phần (hình 5):
Phần 1: là phần đồ thị
C
ứng với
1x 
;
Phần 2: đối xứng với phần đồ thị
C
ứng với
1x 
qua
Ox
.
Hình 0
Hình 1
Hình 2
Hình 3
x
y
-1
1
-1
O
1
x
y
-1
-1
1
O
1
x
y
-1
1
-1
O
1
x
y
-1
1
-1
O
1
73
TRẦN THÔNG Facebook: hội toán bắc trung nam
Hình 4
Hình 5
Ví dụ 2: Tìm
m
để phương trình
3
2
2 9 12x x x m
có
6
nghiệm phân biệt.
Giải. Đặt
32
2 9 12f x x x x
. Phương trình đã cho tương đương với
f x m
.
Trước hết ta vẽ đồ thị
C
của hàm số
32
2 9 12f x x x x
. Hàm
fx
là hàm chẵn,
f x f x
0x
. Do đó, đồ thị
'C
của hàm số
fx
gồm hai phần
Phần 1: là phần
C
nằm ở bên phải
Oy
;
Phần 2: đối xứng với phần 1 qua
Oy
.
Vậy phương trình đã cho có
6
nghiệm phân biệt
đường thẳng
ym
có
6
điểm chung với
'C
45m
.
x
y
-1
1
-1
O
1
x
y
-1
1
-1
O
1
(C)
y
x
9
5
4
3
2
1
O
y = m
-1
-2
-3
(C')
y
x
9
5
4
3
2
1
O
74
TRẦN THÔNG Facebook: hội toán bắc trung nam
Bài tập luyện thi
Bài 1: Vẽ đồ thị các hàm số sau đây
1)
2
3 3 5y x x x
2)
11y x x
3)
2
35y x x
4)
2
35y x x
5)
2
35y x x
6)
22
1
3
31y x x x x
7)
32
1
3
31y x x x
8)
22
1
3
31y x x x x
9)
32
1
18
3 24 26y x x x
10)
3
2
1
18
3 24 26y x x x
11)
3
2
1
18
3 24 26y x x x
12)
2
1
18
1 2 26y x x x
13)
42
43y x x
14)
22
13y x x
15)
22
31y x x
16)
32
1 3 3y x x x x
17)
42
54y x x
18)
32
1 4 4y x x x x
19)
32
1 4 4y x x x x
20)
32
2 2 2y x x x x
21)
32
2 2 2y x x x x
22)
22
41y x x
23)
22
14y x x
24)
22
22y x x x x
25)
22
22y x x x x
26)
1
2
x
y
x
27)
1
2
x
y
x
28)
1
2
x
y
x
29)
1
2
x
y
x
30)
1
2
x
y
x
Bài 2: Với những giá trị nào của
m
, phương trình
22
2x x m
có đúng
6
nghiệm phân biệt.
Bài 3: Tìm
k
để phương trình
2
3
41
40
3 3 2
k
x
x
k
có
3
nghiệm phân biệt.
Bài 4: Từ đồ thị (C):
xxy 3
3
suy ra đồ thị hàm số
3
3y x x
.
Bài 5: Với giá trị nào của a thì phương trình sau có 6 nghiệm phân biệt:
.log12
2
24
axx
Bài 6: Dùng đồ thị (C) của hàm số
42
23y x x
đề biện luận theo m số nghiệm của phương
trình:
4 2 4 2
22x x m m
.
Bài 7: Cho hàm số
x
y
x
34
2
(C). Dựa vào đồ thị C) , tìm các giá trị của m để phương trình
x x m ( x x
6 6 4 4
sin cos sin cos )
có 2 nghiệm trên đoạn
2
0;
3



.
Bài 8: Khảo sát và vẽ đồ thị hàm số
3
3y x x
từ đó suy ra đồ thị hàm số
3
3y x x
75
TRẦN THÔNG Facebook: hội toán bắc trung nam
BÀI TẬP TRẮC NGHIỆM
1. Hàm số
32
y x mx m
đồng biến trên (1;2) thì m thuộc tập nào sau đây:
A.
;3
B.
; 3
C.
;



3
3
2
D.
;




3
2
2. Hàm số
32
1
3
1 32
3
m
y x m x mx 
đồng biến trên
;2
thì m thuộc tập nào sau
đây:
A.
;m



2
3
B.
;m





26
2
C.
;m



2
3
D.
;m  1
3. Trong các hàm số sau, hàm số nào đồng biến trên khoảng
; 1
.
A.
32
3
1
3
x xyx
B.
lnyx
C.
xx
ye
2
2
D.
43
4
3
y x x
4. Hàm số
42
21y x x
đồng biến trên khoảng nào sau đây:
A.
( ; 1);(0;1)
B.
( 1;0);(0;1)
C.
( 1;0);(1; ) 
D. Đồng biến trên R
5. Hàm số
32
1
2 3
3
1y x x x 
đồng biến trên:
A.
;2
B.
;13
C.
;; 13
D.
;13
6. Hàm số
y x x 24
nghịch biến trên:
A.
;34
B.
;23
C.
;23
D.
7. Cho hàm số
mx x m
y
mx

2
1
(với m là tham số). Giá trị của m để hàm số đồng biến trên khoảng
;0
là:
A.
;m 12
B.
;m55
C.
;m 01
D.
;m 01
8. Cho hàm số
()
x
fx
x

31
1
. Trong các mệnh đề sau, tìm mệnh đề đúng:
A.
()fx
tăng trên
; ; ; 11
B.
()fx
giảm trên
; ; ; 11
C.
()fx
đồng biến trên R D.
()fx
liên tục trên
9. Hàm số
lny x x
nghịch biến trên:
A.
;e 
B.
;04
C.
;4
D.
10. Trong các hàm số sau, hàm số nào nghịch biến trên :
A.
cosyx
B.
y x x x
32
2 10
C.
y x x
42
1
D.
x
y
x
2
3
76
TRẦN THÔNG Facebook: hội toán bắc trung nam
11. Trong các hàm số sau, hàm số nào nghịch biến trên khoảng (1; 3):
A.
y x x x
32
2
4 6 9
3
B.
y x x
2
1
23
2
C.
xx
y
x

2
1
1
D.
x
y
x
25
1
12. Hàm số
2
1
x
y
x
đồng biến trên các khoảng
A.
( ;1)
và (1;2) B.
( ;1)
và
(2; )
C.(0;1) và (1;2) D.
( ;1)
và
(1; )
13. Hàm số nào sau đây là hàm số đồng biến trên R?
A.
2
1
x
y
x
B.
2
2
1 3 2y x x
C.
1
x
y
x
D. y = tanx
14. Cho hàm số
1
y 4x 1
x1
và các khoảng
(I)
3
;
2




(II)
3
;1
2




(III)
1
1;
2




(IV)
1
;
2




Hàm số trên đồng biến trên các khoảng
A.(I) và (II) B. (II) và (III) C. (III) và (IV) D.(IV) và (I)
15. Cho hàm số
1
3
2
3
xmx
x
y
giá trị nào của m thì hàm số luôn đồng biến trên tập xác
định của nó
A.
11 m
B.m< -1 hoặc m> 1 C.- 2 < m < 2 D. m >2
16. Hàm số y=
mx
mx
1
A. luôn luôn đồng biến với mọi m. B. luôn luôn đồng biến nếu m
0
C. luôn luôn đồng biến nếu
m
>1 D.đồng biến trên từng khoảng xác định của nó.
17. Cho hàm số
3
54
4
1
53
x
y x x
. Nhận định nào dưới đây là đúng.
A. Nghịch biến trên R B. Nghịch biến trên khoảng
;1
và đồng biến trên khoảng
1; 
C. Đồng biến trên R D. Đồng biến trên khoảng
;1
và nghịch biến trên khoảng
1; 
18. Giá trị của m để hàm số y =
3
1
x
3
– 2mx
2
+ (m + 3)x – 5 + m đồng biến trên R là:
A.
1m
B.
4
3
m
C.
1
4
3
m
D.
1
4
3
m
77
TRẦN THÔNG Facebook: hội toán bắc trung nam
19. Xác định m để hàm số y =
631
3
1
23
xmxmx
nghịch biến trên R?
A.
1m
hoặc
2m
B.
21 m
C.
12 m
D.
2m
hoặc
1m
20. Tìm m để hàm số y =
2
3
x
mx
giảm trên từng khoảng xác định của nó?
A.
2
3
m
B.
2
3
m
C.
2
3
m
D.
2
3
m
21. Hàm số y =
1
2
2
x
mmxx
đồng biến trên từng khoảng xác định của nó khi:
A.
1m
B.
1m
C.
1m
D.
1m
22. Hàm số y =
mx
mx
1
nghịch biến trên khoảng ( -
; 0) khi :
A.m > 0 B.
01 m
C. m < - 1 D. m > 2
23. Hàm số y = ax
3
+ bx
2
+ cx + d đồng biến trên R khi nào?
A.
03,0
0,0
2
acba
cba
C.
03,0
0,0
2
acba
cba
B...
03
0,0
2
acb
cba
D.
03,0
0
2
acba
cba
24. Tìm m lớn nhất để hàm số y =
334
3
1
23
xmmxx
đồng biến trên R.
A.m =3 B. m = 1 C. m = 2 D. m=4
25. Hàm số y =
2
2 xx
nghịch biến trên khoảng:
A.
2;
2
1
B.
2
1
;1
C.
;2
D.
2;1
26. Hàm số nào sau đây là hàm số đồng biến trên R?
A.
2
2
1 3 2y x x
B.
2
1
x
y
x
C.
1
x
y
x
D. y=tanx
27. Cho hàm số
x
yx
(
0x
). Hoành độ điểm cực tiểu của đồ thị hàm số là:
A.
1
x
e
B.
x 1
C.
xe
D.
xe
28. Cho hàm số
y x x
42
21
(C). Tiếp tuyến của (C) tại điểm cực đại có phương trình là:
A.
x 0
B.
y 0
C.
y 1
D.
y 2
29. Cho hàm số
x
y m x m x m
3
2
2 4 8 1
3
. Để hàm số đạt cực trị tại
1
x
,
2
x
thỏa mãn
12
2xx
thì
78
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.
26m
B.
m
3
2
2
C.
2m
hoặc
6m
D.
m
3
2
30. Giả sử hàm số
32
3y x x mx m
nghịch biến trên khoảng có độ dài bằng 1. Khi đó, giá
trị của m là:
A.
3
2
B.
9
2
C.
9
4
D.
3
4
31. Giả sử hàm số
sin 1
2sin
x
y
xm
đồng biến trên khoảng
3
,
2



. Khi đó, các giá trị m thõa
mản bài toán là:
A.
3m 
B.
2m 
C.
0m
D.
2m 
32. Cho hàm số
32
y ax bx cx d
và giả sử có cực trị. Mệnh đề nào dưới đây là đúng.
A. Cả 3 phương án kia đều sai B. Hàm số chỉ có một cực tiểu
C. Hàm số có hai cực đại D. Hàm số chỉ có một cực đại
33. Cho hàm số
n
n
y x c x
,
c 0
,
n 2
. Hoành độ điểm cực tiểu của đồ thị hàm số là:
A.
c1
B.
2c
C.
2
3
c
D.
2
c
34. Cho đường cong
32
3y x x
. Gọi
là đường thẳng nối liền cực đại và cực tiểu của nó. Mệnh
đề nào dưới đây là đúng .
A.
đi qua điểm M(-1; -2) B.
đi qua điểm M(1; -2)
C.
song song với trục hoành D.
không đi qua gốc toạ độ
35. Cho hàm số
432
1y x x x x
. Mệnh đề nào dưới đây là đúng.
A. Hàm số luôn luôn nghịch biến
x
B. Đồ thị hàm số có ít nhất một điểm cực trị
C. Cả 3 phương án kia đều sai D. Hàm số luôn luôn đồng biến
x
36. Cho hàm số
yx
. Mệnh đề nào dưới đây là đúng.
A. Cả hai phương án kia đều đúng B. Cả ba phương án kia đều sai
C. Hàm số đạt giá trị nhỏ nhất trên R tại
0x
D. Hàm số đạt cực tiểu tại
0x
37. Tìm m để hàm số sau đây có cực trị:
()
x mx
fx
mx
2
1
.
A. -1 < m < 0 B. 0 C.
m
D. -1 < m< 1
38. Hàm số
yx
4
5
có bao nhiêu điểm cực đại?
79
TRẦN THÔNG Facebook: hội toán bắc trung nam
A. 1 B. 3 C. 0 D. 2
39. Số điểm cực trị của đồ thị hàm số
y x x
3
1
7
3
là:
A. 1 B. 0 C. 3 D. 2
40. Số điểm cực trị của đồ thị hàm số
yx
4
100
là:
A. 0 B. 1 C. 2 D. 3
41. Đồ thi hàm số nào sau đây có 3 điểm cực trị.
A.
42
2 4 1y x x
B.
42
21y x x
C.
42
21y x x
D.
42
21y x x
42. Đồ thi hàm số
2
22x mx
y
xm

đạt cực đại tại x = 2 khi :
A.Không tồn tại m B. m = -1 C. m = 1 D.
1m 
43. Hàm số
32
3y x x mx
đạt cực tiểu tại x = 2 khi :
A.
0m
B.
0m
C.
0m
D.
0m
44. Cho hàm số
2
41
1
xx
y
x

.Hàm số có hai điểm cực trị x
1
, x
2
.Tích x
1
.x
2
bằng
A. -4 B.-5 C. -1 D. -2
45. Hàm số
42
1
23
2
y x x
đạt cực đại tại
x
A.
2
B.
2
C.
2
D. 0
46. Khẳng định nào sau đây là đúng về đồ thị hàm số
2
25
1
xx
y
x
:
A.
1
CD
x 
B.
4
CT
y 
C.
0
CD CT
yy
D.
3
CD CT
xx
47. Cho hàm số
32
1
2 1 1
3
y x m x m x
Mệnh đề nào sau đây là sai?
A.
1m
thì hàm số có hai điểm cực trị B.Hàm số luôn luôn có cực đại và cực tiểu
C.
1m
thì hàm số có cực đại và cực tiểu D.
1m
thì hàm số có cực trị
48. Cho hàm số
3
2
2
23
33
x
y x x
.Toạ độ điểm cực đại của hàm số là
A. (-1;2) B. (3;
2
3
) C. (1;-2) D.(1;2)
49. Trong các mệnh đề sau, hãy tìm mệnh đề sai:
A. Hàm số
1
21
2
yx
x
không có cực trị;
B. Hàm số
1
1
1
yx
x
có hai cực trị.
80
TRẦN THÔNG Facebook: hội toán bắc trung nam
C. Hàm số y = –x
3
+ 3x
2
– 3 có cực đại và cực tiểu;
D Hàm số y = x
3
+ 3x + 1 có cực trị;
50. Hàm số
2
36
1
xx
y
x

có giá trị cực đại là
A.3 B. -5 C.-1 D. 3
51. Hàm số
186)(
24
xxxxf
có bao nhiêu điểm cực trị
A.0 B. 1 C. 2 D. 3
52. Hàm số
32
2 3 1 6 1 1y x m x m x
có cực đại và cực tiểu nằm trong khoảng
2,3
. Khi
đó, giá trị m là
A.
1,3m
B.
1,4m
C.
3,4m
D.
1,3 3,4m
53. Hàm số
sin cos 0 2y a x b x x x
đạt cực trị tại
,
3
xx

. Khi đó, tổng có giá
trị là:
A.3 B.
3
1
3
C.
31
D.
31
54. Hàm số
sin cos 0 2y a x b x x x
có hai cực trị thõa mãn giá trị cực tiểu đạt giá trị
lớn nhất. Khi đó, giá trị m là:
A.
3m
B.
1m
C.
1m
D.
0m
55. Hàm số
32
3 1 9y x m x x m
có hai cực trị
12
,xx
thõa mãn
12
2.xx
Khi đó, giá
trị m là:
A.
3, 1 3 1 3,1m


B.
1,3m
C.
1, 1 3 1,1 3m


D.
, 1 3 1 3,m  
56. Hàm số
32
11
32
y x x mx m
có hai cực trị
12
,xx
cùng lớn hơn giá trị tham số m. Khi
đó, giá trị m là:
A.
2m 
B.
2m 
C.
1
2
m 
D.
0m
hoặc
2m 
57. Đồ thị hàm số
42
21y x m x m
có ba điểm cực trị tạo thành tam giác vuông .Khi đó,
giá trị m là:
A.
0m
B.
1m
C.
2m
D.
1m
58. Hàm số nào dưới đây có cực tiểu mà không có cực đại.
A.
1
yx
x

B.
3 cos cos2y x x
C.
2
1y x x
D.
3xx
59. Hàm số nào dưới đây có hai cực trị thõa mãn giá trị cực tiểu lớn hơn giá trị cực đại.
A.
42
32y x x
B.
3
31y x x
C.
2
1
2
x
y
x
D.
1
2
x
y
x
60. Hàm số nào dưới đây có cực đại mà không có cực tiểu.
81
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.
32
32y x x
B.
2
32
4
xx
y
x

C.
2
1y x x
D.
cos cos2y x x
61. Đồ thị hàm số
32
y x x ax b
có điểm cực tiểu là
1,2A
. Giá trị biểu thức
2ab
là:
A.0 B.4 C.5 D.-5
62. Cho hàm số
32
43y x mx x
đạt cực trị tại
12
,xx
sao cho
12
40xx
. Giá trị m thõa mãn
yêu cầu bài toán là:
A.
0m
B.
9
2
m 
C.
1
2
m 
D.
3
2
m 
63. Giả sử hàm số
42
0f x ax bx c a
có 3 cực trị. Khẳng định nào dưới đây là đúng.
A.Đồ thị hàm số
fx
có ba điểm cực trị B.Đồ thị hàm số
fx
có năm điểm cực trị
C.Đồ thị hàm số
fx
có năm điểm cực trị D.Đồ thị hàm số
fx
có ba điểm cực trị
64. Giả sử đồ thị hàm số
32
0f x ax bx cx d a
có 2 điểm cực trị nằm về hai phía của
trục Oy. Khẳng định nào dưới đây là đúng.
A.Đồ thị hàm số
fx
có ba điểm cực trị B.Đồ thị hàm số
fx
có năm điểm cực trị
C.Đồ thị hàm số
fx
có năm điểm cực trị D.Đồ thị hàm số
fx
có ba điểm cực trị.
65. Cho hàm số
y f x
xác định trên miền D và
0
xD
Mệnh đề nào dưới đây là đúng
A.Hàm số đạt giá trị lớn nhất tại
0
x
thì đạt cực đại tại
0
x
.
B.Hàm số đạt giá trị nhỏ nhất tại
0
x
thì đạt cực tiểu tại
0
x
.
C.Hàm số đạt cực đại tại
0
x
thì
0
0fx
và
0
0fx

.
D. Hàm số đạt cực tiểu tại
0
x
thì tồn tại
sao cho
00
0
,
min
x x h x h
f x f x
.
66. Cho hàm số
y f x
xác định trên miền D và
0
xD
Mệnh đề nào dưới đây là đúng
A.Hàm số đạt cực trị tại
0
x
thì tồn tại
sao cho
00
00
,
,
max min .
x x h x h
x x h x h
f x f x
B.Hàm số đạt cực đại tại
0
x
thì tồn tại
0h
sao cho
00
0
,
max
x x h x h
f x f x
.
C.Hàm số đạt cực đại tại
0
x
thì với mọi
ta có
00
0
,
max
x x h x h
f x f x
.
D.Hàm số đạt cực tiểu tại
0
x
thì với mọi
ta có
00
0
,
min
x x h x h
f x f x
.
67. Giả sử hàm số
42
0f x ax bx c a
có 3 cực trị sao cho giá trị cực tiểu
0,
CT
y
giá trị
cực đại
0.
CD
y
Đồ thị hàm số
y f x
có số điểm cực trị là:
A.2 B.3 C.4 D.5
68. Giả sử hàm số
42
0f x ax bx c a
có 3 cực trị sao cho giá trị cực tiểu
0.
CT
y
và giá
trị cực đại
0.
CD
y
Đồ thị hàm số
y f x
có số điểm cực trị là:
82
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.7 B.3 C.4 D.5
69. Giả sử hàm số
42
0f x ax bx c a
có 3 cực trị sao cho giá trị cực tiểu
0.
CT
y
Đồ
thị hàm số
y f x
có số điểm cực trị là:
A.2 B.3 C.4 D.5
70. Giả sử hàm số
32
0f x ax bx cx d a
không có cực trị . Khẳng định nào dưới đây
là đúng.
A.Đồ thị hàm số
fx
có ba điểm cực trị B.Đồ thị hàm số
fx
có một điểm cực trị
C.Đồ thị hàm số
fx
có năm điểm cực trị D.Đồ thị hàm số
fx
có ba điểm cực trị.
71. Cho hàm số
y f x
liên tục trên tập xác định
,,D a b a b
. Hai số thực phân biệt
12
,,x x a b
thỏa mãn
1 1 1
,,f x f x x x h x h
và
2 2 2
,,f x f x x x h x h
với
h
đủ bé. Khẳng định nào dưới đây là đúng.
A.Giá trị lớn nhất của hàm số là, giá trị nhỏ nhất của hàm số là
B.Điểm
11
,x f x
là điểm cực đại của hàm số, điểm
22
,x f x
là điểm cực tiểu của hàm số
C.Hàm số có tối đa hai cực trị.
D.Hàm số đạt cực đại tại
1
x
, đạt cực tiểu tại
2
x
.
72. Hàm số
fx
liên tục trên và có đạo hàm là
2016 2017
1 2 .f x x x x
Đồ thị hàm số
có số điểm cực trị là:
A.1 B.2 C.3 D.4
73. Đồ thị hàm số
3
2
3 , 0
,0
x x x
fx
xx

có số điểm cực trị là:
A.1 B.2 C.3 D.0
74. Hàm số
3
f x x bx c
đạt cực trị tại
12
,xx
. Nhận xét nào dưới đây là đúng.
A.
12
.x x b
B.
12
.x x c
C.
12
x x b
D.
12
x x c
75. Gọi A,B,C lần lượt là các điểm cực trị của đồ thị hàm số
42
2 4 1y x x
. Tam giác ABC có
diện tích là:
A.4 B.2 C.1 D.
3
2
76. Hàm số
32
2 3 2 1 6 1 1f x x m x m m x
đạt cực trị tại
12
,xx
sao cho
12
1xx
.
Khi đó, giá trị m thõa mãn yêu cầu bài toán là:
A.
0m
B.
0m
C.
5m
D.
m
77. Hàm số
32
2 3 2 1 6 1 1f x x m x m m x
đạt cực trị tại
12
,xx
.Khi m thay đổi, điểm
cực đại di động trên đường cong nào dưới đây.
A.
32
2 3 1y x x
B.
32
2 3 1y x x
C.
32
3 2 1y x x
D.
32
3 2 1y x x
83
TRẦN THÔNG Facebook: hội toán bắc trung nam
78. Đồ thị hàm số
2
2 , 0
2 , 1 0
3 5, 1
x x x
f x x x
xx

có số điểm cực trị là:
A.1 B.2 C.3 D.0
79. Hàm số
32
2 3 1 6 2 1f x x m x m x
đạt cực trị tại
12
,xx
sao cho
12
2xx
. Khi
đó, giá trị m thõa mãn yêu cầu bài toán là:
A.
1m
B.
2m
C.
1m
D.
2m 
80. Giả sử hàm số
42
0f x ax bx c a
có một cực trị. Khi đó, giá trị a và b thỏa mãn yêu
cầu nào dưới đây.
A.
0, 0ab
B.
0,0ab
C.
0, 0ab
D.
0,0ab
81. Giả sử đồ thị hàm số
m
y x mx x m C
32
1
1 ( )
3
có có 2 điểm cực trị và khoảng cách giữa
2 điểm cực trị là nhỏ nhất. Khi đó, giá trị của m là :
A.
1m
B.
0m
C.
1
3
m 
D.
1m
82. Nhận xét nào dưới đây là đúng khi nói về tích chất của các điểm cực trị hàm số
32
34y x x
A.Các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác vuông tại O.
B.Các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam đều.
C. Các điểm cực đại và cực tiểu đối xứng với nhau qua gốc tọa độ O .
D.Các điểm cực đại và cực tiểu đối xứng với nhau qua trục Oy .
83. Cho hàm số:
3 2 2
1
11
3
y x mx m m x
. Để hàm số đạt cực đại tại điểm
1x
thì giá trị của m là:
A.
0m
B.
1m
C.
1m 
D.
2m
84. Số giá trị nguyên của
m
để hàm số
2
ln( 2)y m x x x
có 2 điểm cực trị trái dấu là:
A.0 B.1 C.2 D.3
85. Cho hàm số
y f x x a x b x c
có đồ thị (C) với
,,abc
và
.abc
Hàm
số có hai điểm cực trị có hoành độ
12
,xx
với
12
xx
. Khi đó khẳng định nào dưới đây là đúng ?
A.
12
x x a
B.
12
a x b x c
C.
12
c x x
D.
12
x b x
86. Hàm số
32
3 2 2f x x m x m m x
đạt cực trị tại
12
,xx
sao cho
1 2 1 2
6 4 0x x x x
. Khi đó, giá trị m thõa mãn yêu cầu bài toán là:
A.
3 2 3 2
22
m
B.
12m
hoặc
2m
C.
2m
D.
12m
87. Hàm số
2 sinf x x x
đạt cực tiểu tại
A.
3
x k k
B.
3
x k k
84
TRẦN THÔNG Facebook: hội toán bắc trung nam
C.
2
3
x k k
D.
2
3
x k k
88. Hàm số
lnf x x x
đạt cực tiểu tại
A.
0
B.1 C.
2
1
e
D.
2
e
89. Giá trị cực đại
CD
y
của hàm số
2
1y x x
là:
A.
2
CD
y
B.
1
2
CD
y
C.
1
CD
y 
D.
1
CD
y
90. Giả sử hàm số
32
x 2 x 3x 1y m m
có cực đại và cực tiểu. Khi đó, giá trị m thõa mãn yêu
cầu bài toán là:
A.
9
0
4
m
B.
m
C.
0
9
4
m
m
D. m > 2
91. Giả sử hàm số
42
x 1 1 2y m m x m
chỉ có một cực trị. Khi đó, giá trị m thõa mãn yêu
cầu bài toán là:
A.
1m
B.
0m
C.
01m
D.
0
1
m
m
92. Giả sử hàm số
3
22
x 1 x 1
3
x
y m m m
đạt cực tiểu tại x = 1. Khi đó, giá trị m thõa
mãn yêu cầu bài toán là:
A.
1m
B.
2m
C.
3m
D.không tồn tại m
93. Số điểm cực trị có tung độ dương của đồ thị hàm số
42
1y x x
là:
A.1 B.2 C.3 D.4
94. Cho hàm số
42
2x 2yx
. Khoảng cách giữa hai điểm cực trị của hàm số bằng :
A.
7
B.
5
C.
3
D.
2
95. Để hàm số
32
6x 3 2 6y x m x m
có cực trị tại hai điểm
1
x
và
2
x
sao cho
12
1xx
thì giá trị m là :
A.
1m
B.
1m
C.
1m
D.
1m 
96. Giả sử hàm số
2 3 2
y (m 5m)x 6mx 6x 5
đạt cực trị tại
1x
. Khi đó, giá trị m
thõa mãn yêu cầu bài toán là:
A.
1m
B.
1m 
C.
D.
2m
97. Giả sử đồ thị hàm số
42
21y x mx
có có ba điểm cực trị A,B,C sao cho
, 1.A Oy BC
Khi đó, giá trị m thõa mãn yêu cầu bài toán là:
85
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.9 B.4 C.1 D.
1
4
98. Đồ thị hàm số
2
21f x x x
có số điểm cực trị là:
A.0 B.1 C.2 D.3
99. Tọa độ các điểm cực trị của đồ thị hàm số
23
3f x x x
là:
A.
0,1
và
2,3
B.
0,3
và
2,1
C.
và
1,2
D.
0,0
và
2,2
100. Hàm số
3 2 2
12
2 1 7
33
f x x mx m x m
đạt cực trị tại
12
,xx
sao
cho
33
12
26xx
. Khi đó, giá trị m thõa mãn yêu cầu bài toán là:
A.
1m 
B.
0m
C.
D.
2m
101. Hàm số
32
2 3 2 1 6 1 5 7f x x m x m m x m
đạt cực trị tại
12
,xx
sao cho
31
CD CT
xx
. Khi đó, giá trị m thõa mãn yêu cầu bài toán là:
A.
1m 
B.
0m
C.
1m
D.
2m
102. Hàm số
3 2 2
2
1 4 3
3
f x x m x m m x
đạt cực trị tại
12
,xx
sao
cho biểu thức
1 2 1 2
2x x x x
đạt giá trị nhỏ nhất. Khi đó, giá trị m thõa mãn yêu cầu bài toán
là:
A.
4m 
B.
0m
C.
4m
D.
1m
103. Xét hàm số
fx
xác định,liên tuc tại mọi
x
có bảng biến thiên:
x
- -1 0 1
+
y’
- 0 + 0 - 0 +
y
+ 2 +
1 1
Mệnh đề nào dưới đây là sai.
A.Hàm số đạt cực đại tại
0x
. B. Hàm số đạt cực tiểu tại
1x
.
C.Đồ thị hàm số có 3 điểm cực trị. D. Đồ thị hàm số có 2 điểm cực đại.
104. Đồ thị hàm số
2
35
x
y e x x
có số điểm cực trị là:
A.2 B.3 C.4 D.5
105. Tiệm cận đứng của đồ thị hàm số
21
1
x
y
x
là
86
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.
1x
B.
1y
C.
D.
2y
106. Tiệm cận ngang của đồ thị hàm số
21
1
x
y
x
là
A.
1x
B.
1y
C.
D.
2y
107. Cho hàm số
31
21
x
y
x
.Mệnh đề nào sau đây đúng.
A. Đồ thị hàm số có tiệm cận ngang là
3
2
y
B. Đồ thị hàm số có tiệm cận đứng là
3
2
y
C. Đồ thị hàm số không có tiệm cận D. Đồ thị hàm số có tiệm cận đứng là
1x
108. Số đường tiệm cận của đồ thị hàm số
31
4
x
y
x
là:
A.1 B.2 C.3 D.4
109. Đồ thị hàm số
2
1
x
y
x
có tiệm cận đứng và tiệm cận ngang lần lượt là
và
yb
.
Khi đó, giá trị biểu thức
a b ab
là:
A.2 B.1 C.3 D.0
110. Gọi a,b,c lần lượt là số tiệm cận của đồ thị các hàm số
42
3
2 , , 1
21
x
y x x y y x
x
.
Nhận xét nào dưới đây là đúng.
A.
ab
B.
ac
C.
a c b
D.
a c b
111. Số tiệm cận của đồ thị hàm số
2
2
9
x
y
x
là:
A.1 B.2 C.3 D.4
112. Số tiệm cận của đồ thị hàm số
2
2
32
23
xx
y
xx


là:
A.1 B.2 C.3 D.4
113. Số tiệm cận của đồ thị hàm số
2
5
y
x
là:
A.1 B.2 C.3 D.4
114. Cho hàm số
2
2
2 3 2
23
xx
y
xx


. Mệnh đề nào sau đây đúng.
A. Đồ thị hàm số có tiệm cận ngang là
2x
B. Đồ thị hàm số có tiệm cận đứng là
2y
C. Đồ thị hàm số không có tiệm cận đứng D. Đồ thị hàm số có hai tiệm cận đứng là
1, 3.xx
115. Số tìm cận của đồ thị hàm số
2
76
1
xx
y
x
là:
A.1 B.2 C.3 D.4
87
TRẦN THÔNG Facebook: hội toán bắc trung nam
116. Đồ thị hàm số
2 2 1xm
y
xm

có tiệm cận đứng của đồ thị hàm số đi qua điểm M( 3; 1).
Giá trị m là:
A.1 B.3 C.-3 D.-1
117. Đồ thị hàm số
3
2
1
mx x
y
x
có tiệm cận đứng là
1x 
. Giá trị m là:
A.
2m
B.
2m 
C.
2m
D.
2m 
118. Đồ thị hàm số
2
2 2 1
1
xm
y
mx

có tiệm cận đứng của đồ thị hàm số đi qua điểm
1,1M
.
Giá trị m là:
A.
1m
B.
2m
C.
D.
119. Cho hàm số
fx
có
lim lim 2
xx
f x f x
 

.Mệnh đề nào dưới đây là đúng.
A. Đồ thị hàm số
fx
có tiệm cận ngang là
2x
B. Đồ thị hàm số
fx
có tiệm cận đứng là
C. Đồ thị hàm số
fx
có tiệm cận ngang là
2y
D. Đồ thị hàm số
fx
có tiệm cận đứng là
2y
120. Cho hàm số
fx
có
22
lim , lim .
xx
f x f x


 
Mệnh đề nào dưới đây là đúng.
A. Đồ thị hàm số
fx
có tiệm cận ngang là
B. Đồ thị hàm số
fx
có tiệm cận đứng là
C. Đồ thị hàm số
fx
có tiệm cận ngang là
2y
D. Đồ thị hàm số
fx
có tiệm cận đứng là
2y
121. Cho hàm số
fx
liên tục trên có
lim 3, lim 2
xx
f x f x
 

.Đồ thị hàm số có số tiệm
cận là:
A.2 B.3 C.4 D.5
122. Cho hàm số
fx
liên tục trên
\2
có
lim 3, lim 2
xx
f x f x
 

.Đồ thị hàm số có số
tiệm cận ngang là:
A.2 B.3 C.1 D.5
123. Giả sử đồ thị hàm số
1
23
mx
y
x
có tiệm cận đứng . Khi đó, giá trị m là:
A.
2
3
m
B.
2
3
m 
C.
3
2
m
D.
3
2
m
124. Giả sử đồ thị hàm số
2
62
2
mx x
y
x

không có tiệm cận. Khi đó, giá trị m là:
88
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.
7
2
m
B.
7
2
m
C.
0m
D.
0m
125. Giả sử đồ thị hàm số
3
2
1
32
mx
y
xx

có một tiệm cận đứng và một tiệm cận ngang. Khi đó,
giá trị m là:
A.
1, 8mm
B.
1
1,
8
mm
C.
1, 8mm
D.
1
1,
8
mm
126. Số tiệm cận của đồ thị hàm số
1, 1
2
,1
1
xx
y
x
x
x
là:
A.1 B.2 C.3 D.4
127. Số tiệm cận của đồ thị hàm số
3
2
1
1
x
y
x
là:
A.1 B.2 C.3 D.4
128. Số tiệm cận ngang của đồ thị hàm số
2
1
1
x
y
x
là:
A.1 B.2 C.3 D.4
129. Cho hàm số
3
32y x x
, chọn phương án đúng trong các phương án sau:
A.
2;0 2;0
max 2,min 0yy


B.
2;0 2;0
max 4,min 0yy


C.
2;0 2;0
max 4,min 1yy

D.
2;0 2;0
max 2,min 1yy

130. Cho hàm số
32
32y x x
. Chọn phương án đúng trong các phương án sau
A.
1;1 1;1
max 0,min 2yy

B.
1;1 1;1
max 2,min 0yy


C.
1;1 1;1
max 2,min 2yy

D.
1;1 1;1
max 2,min 1yy

131. Giá trị lớn nhất của hàm số
2
1 xxy
là:
A.
2
B.
5
C.2 D.1
132. Giá trị lớn nhất của hàm số
xxy cos2
trên đoạn
2
;0
là:
A.
2
B.
5
C.
D.
2
133. Giá trị nhỏ nhất của hàm số
2sin2cossin
3
xxxy
trên khoảng
2
;
2
là:
89
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.
23
27
B.
1
27
C.5 D.1
134. Giá trị nhỏ nhất của hàm số
x
x
y
1
12
trên đoạn
2,3
là:
A.0 B.-2 C.1 D.-5
135. Giá trị lớn nhất của hàm số
1
3
2
x
xx
y
trên đoạn
0,3
là
A.0 B.1 C.2 D.3
136. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
sin 2cos 2y f x x x
lần lượt là :
A.4 và 1 B.3 và c.4 và 0 D.1 và 0
137. Giá trị lớn nhất của hàm số
22
( ) ( 1) (4 ) 5f x x x m m
trên đoạn [2;5] bằng 8, thì giá trị
của m là:
A. m = 1 hoặc m = 4 B. m = 2 hoặc m = 4 C. m = 1 hoặc m = -4 D. m = -1 hoặc m = 2
138. Cho hàm số
2
()
1
ax b
fx
x
có giá trị lớn nhất bằng 4 và giá trị nhỏ nhất bằng -1. Khi đó,
khẳng định nào sau đây là đúng.
A.
22
5ab
B.
22
10ab
C.
22
13ab
D.
22
25ab
139. Một chủ hộ kinh doanh có 50 phòng trọ cho thuê. Biết giá cho thuê mỗi tháng là
2,000,000đ/1 phòng trọ, thì không có phòng trống. Nếu cứ tăng giá mỗi phòng trọ thêm
50,000đ/tháng, thì sẽ có 2 phòng bị bỏ trống. Hỏi chủ hộ kinh doanh sẽ cho thuê với giá là bao
nhiêu để có thu nhập mỗi tháng cao nhất.
A. 2,200,000đ B. 2,250,000đ C. 2,300,000đ D. 2,500,000đ
140. Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí
nguyên liệu làm vỏ lon là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể
tích khối trụ đó bằng 2 và diện tích toàn phần phần hình trụ nhỏ nhất thì bán kính đáy gần số nào
nhất
A.0.6 B.0,7 C.0,8 D.0,5
141. Người ta cắt một tờ giấy hình vuông cạnh bằng
52
để gấp thành một hình chóp tứ giác
đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối
chóp để thể tích lớn nhất.
A.4 B.2 C.
22
D.1
142. Trong một cuộc thi làm đồ dùng học tập do trường phát động, bạn An đã nhờ bố làm một
hình chóp tứ giác đều bằng cách lấy một mảnh tôn hình vuông ABCD có cạnh bằng a, cắt mảnh
tôn theo các tam giác cân AEB; BFC; CGD và DHA; sau đó gò các tam giác AEH; BEF; CFG;
DGH sao cho 4 đỉnh A;B;C;D trùng nhau (Như hình).
90
TRẦN THÔNG Facebook: hội toán bắc trung nam
Thể tích lớn nhất của khối tứ diện đều tạo được là:
A.
3
36
a
B.
3
24
a
C.
3
54
a
D.
3
48
a
143. Gọi
M
và
N
lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số
3
3y x x
. Lúc
đó, tổng
23MN
bằng
A.2 B.-2 C.4 D.-4
144. Cho hàm số
42
( ) sin cosf x x x
. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số là:
A.
5
4
B.
1
4
C.2 D.0
145. Một hành lang giữa hai nhà có hình dạng của 1 lăng trụ đứng như hình vẽ. Hai mặt bên
ABB’A và ACC’A’ là hai tấm kính hình chữ nhật dài 20m, rộng 5m. Gọi x (mét) là độ dài của
cạnh BC. Tìm x để lăng trụ có thể tích lớn nhất.
A.
5
B.
52
C.
25
D.
32
146. Một công ty chuyên sản xuất container muốn thiết kế các thùng gỗ đừng hàng bên trong
dạng hình hộp chữ nhật không nắp, đáy là hình vuông, có thể tích là 62,
3
5m
. Hỏi các cạnh hình
hộp và cạnh đáy là bao nhiêu để tổng diện tích xung quanh và diện tích mặt đáy là nhỏ nhất.
A. Cạnh bên 2,5m. cạnh đáy 5m B. Cạnh bên 4m. cạnh đáy
5 10
4
m
A
C
D
B
E
F
G
H
C'
B'
A'
5
x
A
C
B
91
TRẦN THÔNG Facebook: hội toán bắc trung nam
C. Cạnh bên 3m, cạnh đáy
5 30
6
D. Cạnh bên 5m,cạnh đáy
52
2
147. Một giáo viên đang đau đầu về việc lương thấp và phân vân xem có nên tạm dừng niềm đam
mê với con chữ để chuyển hẳn sang kinh doanh đồ uống trà sữa hay không. Ước tính nếu giá 1 ly
trà sữa là 20(ngàn đồng) thì trung bình hàng tháng có khoảng 1000 lượt khách tới uống nước tại
quán,trung bình mỗi khách lại trả thêm 10(ngàn đồng) tiền bánh tráng trộn để ăn kèm. Nay nguời
giáo viên muốn tăng thêm mỗi ly trà sữa 5(ngàn đồng) thì sẽ mất khoảng 100 khách trong tổng
số trung bình. Hỏi giá 1 ly trà sữa
148. nên là bao nhiêu để tổng thu nhập lớn nhất (giả sử tổng thu chưa trừ vốn)
A. Giảm 15 ngàn đồng B. Tăng 5 ngàn đồng
C. Giữ nguyên không tăng giá D. Tăng thêm 2,5 ngàn đồng
149. Gọi
,MN
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số :
ln ln5y x x x
trên
1,5
. Giá trị M,N lần lượt là:
A.
5
0,MN
e

B.
5
1,MN
e

C.
5
0,
2
MN
e

D.
4
1,MN
e

150. Do nhu cầu sử dụng, người ta cần tạo ra một lăng trụ đứng có đáy là hình vuông cạnh a và
chiều cao h, có thể tích
3
1m
. Với a, h như thế nào để đỡ tốn nhiêu vật liệu nhất.
A.
1, 1ah
B.
11
,
22
ah
C.
2, 2ah
D.
11
,
33
ah
151. Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng
3
500
m
3
. Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ
là
500.000
đồng/m
2
. Hãy xác định kích thước của hồ nước sao cho chi phí thuê nhân công thấp
nhất. Chi phí đó là ?
A. 74 triệu đồng B. 75 triệu đồng C. 76 triệu đồng D. 77 triệu đồng
152. Hình thang cân ABCD có đáy nhỏ AB,
2AB AD BC
. Giá trị của góc
ADC BCD

để hình thang có diện tích lớn nhất là ?
A.
0
30
B.
0
45
C.
0
60
D.
0
90
153. Số giờ có ánh sáng mặt trời của TPHCM năm không nhuận được cho bởi
4 sin ( 60) 10
178
yx
với
1 365x
là số ngày trong năm. Ngày
25/5
của năm thì số giờ có
ánh sáng mặt trời của TPHCM gần với con số nào nhất ?.
A.2h B.12h C.13h30 D.14h
A
B
C
D
92
TRẦN THÔNG Facebook: hội toán bắc trung nam
154. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
62
41y x x
trên
đoạn [-1; 1]. Khi đó, giá trị
M
m
là:
A.4 B.
1
9
C.
14
9
D.9
155. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
sin cosy x x
. Khi
đó
Mm
bằng:
A.
22
B.
2
C
2
D.
0
156. Một đường dây đẫn điện được nối từ một nhà máy điện ở A đến một hòn đảo tại C. Khoảng
cách ngắn nhất từ C đến B là 1km. Khoảng cách ngắn nhất từ A đến B là 4km. Mổi km dây dẫn
đặt trên mặt đất tốn chi phí 3000 triệu đồng, còn đặt dưới nước mất 5000 triệu đồng.S là vị trị
nào đó nằm trên bờ sao cho chi phí lắp đặt đường dây dẫn điện từ A sang C là thấp nhất. Vị trí
của S cách A bao nhiêu km ?
A,1 B. 4 C.
3
4
D.
13
4
157. Một màn ảnh hình chử nhật cao 1,4m đặt ở độ cao 1,8m so với tầm mắt (tính từ mép dưới
của màn ảnh). Để nhìn rỏ màn hình cần phải chọn vị trí đứng sao cho góc nhìn là lớn nhất. Vị trí
đó cách màng ảnh bao nhiêu m?
A.2,4 B.1,4 C.3,2 D.0,4
158. Từ một khúc gỗ hình trụ, người ta cần xẻ thành một chiếc xà có tiết diện ngang là hình
vuông và bốn miếng phụ là hình chử nhật như hình vẽ. Xác định kích thước chiều rộng của
miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất.
93
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.
16
2334
B.
34 3 2
16
C.
D.
34
16
159. Chi phí nguyên liệu của một tàu chở hàng được chi làm hai phần. Trong đó phần thứ nhất
phụ thuộc vào vận tốc và bằng 480 ngàn đồng/ giờ, phần thứ hai tỷ lệ với lập phương vận tốc,
khi vận tốc là thì chi phí phần thứ hai là 30 ngàn đồng/giờ. Vận tốc để tổng chi phí nguyên liệu
đi trên 1km đường là nhỏ nhất là:
A.15km/h B.30km/h C.50km/h D.10km/h
160. Với một đĩa tròn bằng thép trắng, người ta muốn làm một cái phểu bằng cách cắt đi một
hình quạt của đĩa tròn và gấp phần còn lại thành một hình nón.Cung tròn của hình quạt bị cắt đi
phải bằng bao nhiêu độ để thể tích hình quạt là lớn nhất.(13)
A.
0
65
B.
0
295
C.
0
125
D.
0
57
161. Từ cảng A dọc theo đường sắt AB cần phải xác định một trạm trung chuyển C và xây dựng
một con đường từ C đến cảng D. Biết rằng vận tốc khi đi trên đường sắt là
1
v
và trên đường bộ
là
2
v
12
vv
. Hãy xác định phương án chọn vị trí điểm C sao cho thời gian chuyển hàng từ
cảng A đến cảng D là ngắn nhất.
A.C cách A một khoảng là
1
2
.
v
lh
v
B.C cách A một khoảng là
2
1
.
v
lh
v
C. C cách A một khoảng là
1
2
.
v
lh
v
D. C cách A một khoảng là
2
1
.
v
lh
v
162. Cần phải xây dựng một hố ga hình hộp chử nhật có thể tích là
3
Vm
.Hãy xác định các
kích thước của đáy để chi phí vật liệu xây dựng là thấp nhất biết k cho trước là tỷ số chiều cao
của hố và chiều rộng của đáy.
A.Chiều dài là
3
2
1
2
k
yV
k
, chiều rộng là
3
2
4
( 1)
kV
x
k
B. Chiều dài là
3
2
4
( 1)
kV
y
k
, chiều rộng là
3
2
V
k2
1k
x
94
TRẦN THÔNG Facebook: hội toán bắc trung nam
C. Chiều dài là
3
( 1)
2
k k V
y
, chiều rộng là
3
2
4
( 1)
kV
x
k
D. Chiều dài là
3
( 1)
2
k k V
y
, chiều rộng là
3
2
4
( 1)
kV
x
k
163. Hai con tàu cách nhau 5 hải lý. Cả hai con tàu khởi hành cùng lúc, một tàu chạy theo hướng
nam với vận tốc 6 hải lý/giờ; tàu còn lại chạy theo hướng về vị trí hiện tại của tàu thứ nhất với
vận tốc 7 hải lý/giờ. Thời điểm mà khoảng cách giửa hai tàu lớn nhất là:
A.
16
17
B.
1
17
C.
6
17
D.
7
17
164. Cần phải dùng thuyền để vượt sang bờ đối diện của một dòng sông chảy siết với vận tốc
nước chảy
nc
v
lớn hơn vận tốc của thuyền
t
v
. Hướng đi của thuyền phải như thế nào để độ dời
do dòng chảy gây ra là thấp nhất tức là hướng di chuyển hợp với phương ngang góc
thỏa:
A.
cos
nc
t
v
v
B.
cos
t
nc
v
v
C.
sin
nc
t
v
v
D.
sin
t
nc
v
v
165. Một người làm nhiệm vụ cứu hộ gần bờ, cần phải cứu một người bị đuối nước ở giửa hồ.
Nếu biết rõ vận tốc của người cứu hộ là
1
v
và vận tốc của người bị đuối nước là
2
v
. Người cứu
hộ phải chọn đường đi sao cho thời gian tới vị trí người cứu hộ là ngắn nhất. Qủy đạo đường đi
của người cứu hộ phải thỏa mãn điều kiện gì?
95
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.
1
2
sin
sin
v
v
B.
2
1
sin
sin
v
v
C.
21
2
sin
sin
vv
v
D.
1
21
sin
sin
v
vv
166. Hãy xác định độ dài cánh tay nâng của cần cẩu bánh hơi có thể dùng được để xây dựng tòa
nhà có chiều cao H và chiều rộng
2l
(Biết rằng cần cẩu thỏa mãn yêu cầu sau đây: có thể xê
xích chiếc cần cẩu cũng như góc nghiêng của tay nâng để sao cho điểm cuối của tay nâng chiếu
xuống theo phương thẳng đứng thì trùng với trung điểm của bề rộng. Ta giả sử ngôi nhà xây
dựng trên miếng đất rộng,cần cẩu có thể di chuyển thoải mái) .
A.
22
33
11
l H h
AC H h l
H h l
B.
22
33
11
l H h
AC H h l
H h l
C.
22
33
11
l H h
AC
H h l
D.
22
33
11
l H h
AC H h l
H h l
167. Cấu tạo của một hộp diêm gồm một nắp, hai đáy, bốn mặt bên và hai đầu như hình vẽ. Gọi
x,y,z lần lượt là chiều cao chiều rộng chiều dài của hộp diêm Tỷ lệ x,y,z phải như thế nào để với
thể tích
V
cố định khi chế tạo chi phí dành cho vật liệu sản suất là ít nhất.
96
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.
: : 3: 4:2x y z
B.
: : 4:3:2x y z
C.
: : 2:3:4x y z
D.
: : 3: 2:4x y z
168. Cần làm một cái cửa số mà phía trên là hình bán nguyệt, phía dưới là hình chử nhật có chu
vi là a(m) (a là chu vi cửa sổ tức là chu vi hình bán nguyệt cộng với chu vi hình chử nhật trừ độ
dài cạnh hình chử nhật là dây cung hình bán nguyệt ). Kích thước của hình chử nhật để diện tích
cửa sổ lớn nhất là:
A. Chiều cao là
4
a
, chiều rộng là
4
a2
B. Chiều cao là
4
a
, chiều rộng là
4
a
C. Chiều cao là
4
a2
, chiều rộng là
4
a2
D. Chiều cao là
4
a2
, chiều rộng là
4
a
169. Tiếp tuyến của đồ thi hàm số
x
y
2
1
tại điểm A(
2
1
; 1) có phương trình là:
A.
2 2 1 0xy
B.
2 2 1 0xy
C.
2 2 3 0xy
D.
2 2 3 0xy
170. Số đường thẳng đi qua điểm A (0;3) và tiếp xúc với đồ thi hàm số
42
23y x x
là:
A.0 B.1 C.2 D.3
171. Cho hàm số
32
1
2 3 1
3
y x x x
.Tiếp tuyến tại điểm uốn của đồ thị hàm số ,có phương
trình là:
A.
11
3
yx
B.
1
3
yx
C.
11
3
yx
D.
1
3
yx
172. Tiếp tuyến của đồ thị hàm số
1
3
x
y
x
tại giao điểm của đồ thị với trục hoành có phương
trình:
A.
11
44
yx
B.
44yx
C.
11
44
yx
D.
11
43
yx
173. Trong các tiếp tuyến tại các điểm trên đồ thị hàm số
32
32y x x
, tiếp tuyến có hệ số góc
nhỏ nhất bằng:
97
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.-3 B.3 C.4 D.0
174. Cho hàm số
.2
3
1
23
xxy
Phương trình tiếp tuyến tại điểm có hoành độ là nghiêm của
phương trình y’’ = 0 là:
A.
3
7
xy
B.
3
7
xy
C.
3
7
xy
D.
xy
3
7
175. Cho đường cong
133
23
xxxy
có đồ thị (C). Phương trình tiếp tuyến của (C) tại
giao điểm của (C) với trục tung là:
A.
18 xy
B.
13 xy
C.
13 xy
D.
13 xy
176. Gọi M là giao điểm của đồ thị hàm số
21
2
x
y
x
với trục Oy. Phương trình tiếp tuyến với
đồ thị trên tại điểm M là: Chọn 1
A.
31
22
yx
B.
31
22
yx
C.
31
22
yx
D.
31
22
yx
177. Hệ số góc của tiếp tuyến của đồ thị hàm số
42
1
42
xx
y
tại điểm có hoành độ x
0
= - 1
bằng:
A. -2 B. 2 C. 0 D. Đáp số khác
178. Tiếp tuyến của đồ thị hàm số
4
1
y
x
tại điểm có hoành đo x
0
= - 1 có phương trình là:
A. y = - x - 3 B. y = - x + 2 C. y = x -1 D. y = x + 2
179. Cho đồ thị hàm số
32
22y x x x
có đồ thị ( C ) . Gọi
12
,xx
là hoành độ các điểm M,
N trên ( C ), mà tại đó tiếp tuyến của ( C ) vuông góc với đường thẳng
2017yx
. Khi đó
21
xx
bằng :
A.
4
3
B.
4
3
C.
1
3
D. -1
180. Tiếp tuyến của đồ thị hàm số
3
2
32
3
x
yx
có hệ số góc k = - 9 ,có phương trình là:
A. y +16 = - 9(x + 3) B. y – 16 = - 9(x – 3) C. y – 16 = - 9(x +3) D. y = - 9(x +
3)
181. Số tiếp tuyến đi qua điểm A ( 1 ; - 6) của đồ thị hàm số
3
31y x x
là:
A. 1 B. 0 C. 2 D. 3
182. Tiếp tuyến tại điểm cực tiểu của hàm số
532
3
1
23
xxxy
. Mệnh đề nào dưới đây là
đúng.
A. Song song với đường thẳng x = 1 B. Song song với trục hoành
C. Có hệ số góc dương D. Có hệ số góc bằng – 1
98
TRẦN THÔNG Facebook: hội toán bắc trung nam
183. Cho hàm số
33
23
xxy
có đồ thị (C). Số tiếp tuyến của (C) vuông góc với đường
thẳng
2017
9
1
xy
là:
A. 1 B. 2 C. 3 D. 0
184. H
185. Số đường thẳng đi qua điểm A(2 ; 0) và tiếp xúc với đồ thị của hàm số
24
2xxy
là:
A. 0 B. 1 C. 2 D. 3
186. Cho hàm số:
21
1
x
yC
x

Phương trình tiếp tuyến của
()C
tại điểm có hoành độ bằng 2 là:
12
.:
33
A d y x
1
.:
3
B d y x
1
. : 1
3
C d y x
11
.
33
D y x
187. Gọi
21
( ) :
1
x
M C y
x

có tung độ bằng
5
. Tiếp tuyến của
()C
tại M cắt các trục tọa độ
,Ox
Oy
lần lượt tại A và B. Diện tích tam giác
OA B
là:
A.
121
6
B.
119
6
C.
123
6
D.
125
6
188. Hệ số góc của tiếp tuyến của đồ thì hàm số
1
1
x
y
x
tại giao điểm của đồ thị hàm số với
trục tung bằng.
A.-2 B.2 C.1 D.-1
189. Đường thẳng
3y x m
là tiếp tuyến của đường cong
3
2yx
khi m bằng
A. 1 hoặc -1 B. 4 hoặc 0 C. 2 hoặc -2 D. 3 hoặc -3
190. M là điểm thuộc đồ thị hàm số
1
2
x
x
y
, biết tiếp tuyến với đồ thị hàm số tại điểm M đó
tạo với hai trục tọa độ một tam giác có diện tích bằng
4
1
. Tọa độ M là:
A.
1;10;0 MvàM
.
B.
4;21;1 MvàM
.
C.
3
2
;
2
1
2;
2
1
MvàM
D.
2;
2
1
1;1 MvàM
191. Cho hàm số
32
32y x x
có đồ thị
()C
. Đường thẳng nào sau đây là tiếp tuyến của
()C
và có hệ số góc nhỏ nhất?
A.
33yx
B.
3yx
C.
5 10yx
D.
33yx
192. Cho hàm số
32
1
2 3 1
3
y x x x
có đồ thị
()C
. Trong các tiếp tuyến với
()C
, tiếp tuyến
có hệ số góc lớn nhất bằng:
A.
3k
B.
2k
C.
1k
D.
99
TRẦN THÔNG Facebook: hội toán bắc trung nam
193. Cho hàm số
2
1
1
xx
y
x

có đồ thị
()C
. Phương trình tiếp tuyến của
()C
đi qua điểm
( 1;0)A
là:
A.
3
4
yx
B.
3
( 1)
4
yx
C.
3( 1)yx
D.
31yx
194. Qua điểm
(0;2)A
có thể kẻ được bao nhiêu tiếp tuyến với đồ thị
()C
của hàm số
42
22y x x
?
A.0 B.1 C.2 D.3
195. Phương trình tiếp tuyến với đồ thị hàm số
1
1
x
y
x
song song với đường thẳng
:2 1 0xy
là:
A.
2 7 0xy
B.
2 7 0xy
C.
20xy
D.
2 1 0xy
196. Cho đường cong
42
( ): 4 2C y x x
và điểm
(0; )Aa
. Nếu qua
A
kẻ được 4 tiếp tuyến
với
()C
thì
a
phải thoả mãn điều kiện:
A.
10
3
a
B .
10
2
3
a
C.
2
10
3
a
a
D.
2a
197. Giả sử để tiếp tuyến của đồ thị hàm số
3
y x mx m 1
tại điểm có hoành độ bằng 1 cắt
đường tròn
22
1
(x 2) (y 3)
5
theo một dây cung có độ dài nhỏ nhất. Khi đó giá trị m là :
A.
1m
hoặc
5
2
m
B.
5
2
m
hoặc
2m
C.
3
2
m
hoặc
2m
D.
hoặc
2m
198. Cho hàm số
x2
y.
x1
Tiếp tuyến bất kì của đồ thị hàm số tại M cắt hai đường tiệm cận lần
lượt tại hai điểm A va B. Khi đó
MA kMB
, giá trị của k bằng:
A.1 B.2 C.
1
2
D.
3
2
199. Số đường tiếp tuyến vẽ từ
M 1; 9
đến
C
:
32
y 4x 6x 1
là:
A.0 B.1 C.2 D.3
200. Cho hàm số
32
1
2 3 1
3
y x x x
(1)
. Phương trình tiếp tuyến của đồ thị hàm số (1) song
song với đường thẳng
31yx
có dạng
y ax b
( với a,b đã tối giản ). Giá trị S=a+b là:
A.
29
3
B.
20
3
C.
20
3
D.
19
3
201. Đồ thị hàm số
32
( ) +axf x x bx c
cắt trục tung tại điểm có tung độ là 2 và tiếp xúc với
đường thẳng
1y
tại điểm có hoành độ
1x 
. Hệ số a,b,c là:
A.
3, 3, 2abc
B.
3, 3, 2a b c
C.
3, 3, 2a b c
D.
3, 3, 2abc
100
TRẦN THÔNG Facebook: hội toán bắc trung nam
202. Đồ thị hàm số
1
ax b
y
x
cắt trục tung tại điểm A(0;1) và tiếp tuyến tại A có hệ số góc bằng
-3. Giá trị a,b là:
A.
4, 1ab
B.
2, 1ab
C.
4, 1ab
D.
4, 1ab
203. Cho hàm số
21
1
x
y
x
có đồ thị
.C
Các cặp tiếp tuyến song song của
C
sao cho khoảng
cách giữa chúng lớn nhất là:
A.
3 2 3 yx
và
3 2 3 yx
B.
3 2 3yx
và
3 2 3yx
C.
3 2 3yx
và
3 2 3 yx
D.
3 2 3 yx
và
3 2 3yx
204. Số tiếp tuyến đến đồ thị hàm số y=
32
9 17 2x x x
qua A(-2 ;5) là :
A.1 B.2 C.3 D.4
205. Cho hàm số . Tọa độ điểm M sao cho khoảng cách từ điểm tới tiếp
tuyến của (C) tại M là lớn nhất là:
A.
7 3 3 7 3 3
( 3; ); (1 3; )
22
MM

B.
2 3 2 2 3 2
(1 2; ); (1 3; )
22
MM
C.
(1 3; 4 3 3); (1 3; 4 3 3)MM
D.
;
206. Cho hàm số
23
2
x
y
x
đồ thị (C). Tiếp tuyến d tại điểm M thuộc (C) cắt tiệm cận đứng và
tiệm cận ngang tại A, B sao cho
4
cos
17
BAI
,với I là giao 2 tiệm cận là. Tọa độ M là:
A.
53
;4 , ;0
22
MM
B.
53
;4 , ;0
22

MM
C.
35
0; , 4;
22
MM
D.
35
0; , 4;
22

MM
207. Cho hàm số
42
21y x x C
. Điểm
M Oy
sao cho từ M vẽ được 3 tiếp tuyến với (C).
Tọa độ M là:
A.
0; 2M
B.
0; 1M
C.
0;2M
D.
0;1M
208. Cho hàm số
31
1
x
y
x
có đồ thị
C
. Tiếp tuyến của đồ thị
()C
cắt trục hoành, trục tung
lần lượt tại hai điểm phân biệt
,AB
. Tam giác
OAB
có cạnh huyền gấp
5
lần cạnh góc vuông
thì một phương trình tuyến tuyến đó là:
21
1
x
y
x
( 1;2)I
1 3;2 3M
1 3;2 3M
101
TRẦN THÔNG Facebook: hội toán bắc trung nam
(I)
2yx
; (II)
21yx
; (III)
1 11
22
yx
; (IV)
13
22
yx
A. Chỉ có (II), (III), (IV) đúng B. (I), (II), (III), (IV) đều đúng
C. Chỉ có (I), (II), đúng D. Chỉ có (III), (IV), đúng
209. Biết rằng đường thẳng
2yx
cắt đồ thị hàm số
3
32y x x
tại ba điểm có tọa độ lần
lượt là
1 1 2 2 3 3
, , , , , .x y x y x y
Khi đó, giá trị biểu thức
1 1 2 2 3 3
. . .x y x y x y
là:
A. 12 B. 4 C. 0 D. 8
210. Cho đồ thị
1
( ):
2
x
Cy
x
và đường thẳng
:d y x m
. Khi
d
cắt
()C
tại 2 điểm phân biệt
và tiếp tuyến với
()C
tại hai điểm này song song với nhau thì giá trị
m
là:
A.
1m
B.
2m
C.
1m
D.
2m 
211. Tìm m để đường thẳng (d): y = mx – 2m + 4 cắt đồ thị (C) của hàm số
32
6 12 4y x x x
tại ba điểm phân biệt
A.
3m 
B. m > 0 C. m < 0 D.
1m
212. Đường thẳng y = m cắt đồ thị hàm số
3
32y x x
tại 3 điểm phân biệt khi :
A.
04m
B.m < - 2 C.
04m
D. -2< m < 4
213. Cho hàm số
42
24
xxy
. Tìm m để phương trình:
mxx 3)2(
22
có hai nghiệm
phân biệt? Chọn 1 câu đúng.
A.
23 mm
B.
3m
C.
23 mm
D.
2m
214. Cho hàm số
196
23
xxxy
. Tìm m để phương trình:
1)3(
2
mxx
có ba nghiệm
phân biệt? Chọn 1 câu đúng.
A.
1m
B.
51 m
C.
23 mm
D.
5m
215. Cho hàm số
xxy 8
3
. Số giao điểm của đồ thị hàm số cới trục hoành là: Chọn 1 câu
đúng
A. 0 B. 1 C. 2 D. 3
216. Số giao điểm của đường cong
12
23
xxxy
và đường thẳng y = 1 – 2x là:
A. 1 B. 2 C. 3 D. 0
217. Gọi M và N là giao điểm của đường cong
2
67
x
x
y
và đường thẳng y = x + 2 . Khi đó
hoành độ trung điểm I của đoạn MN bằng: Chọn 1 câu đúng
A. 7 B. 3 C.
2
7
D.
2
7
218. Số giao điểm của đồ thị hàm số
2
32
1
xx
y
x

và trục hoành là:
A.0 B.1 C.2 D.3
102
TRẦN THÔNG Facebook: hội toán bắc trung nam
219. Gọi
00
A,xy
là giao điểm của đồ thị hàm số
2
32
1
xx
y
x

và đường thẳng
1yx
.
Khi đó, giá trị
00
xy
là:
A.-1 B.1 C.3 D.-3
220. Tọa độ giao điểm của đồ thị hàm số
21
2
x
y
x
và đường thẳng
2yx
là:
A.
1, 1 , 0, 2
B.
1, 3 , 3,1
C.
1, 3 , 0, 2
D.
1, 1 , 3,1
221. Phương trình
3
3 1 0x x m
có ba nghiệm phân biệt khi:
A.
1m
B.
1
1
m
m

C.
1m
D.
11m
222. Phương trình
3
4 3 0x x m
có hai nghiệm phân biệt khi:
A.
1
1
m
m

B.
1
0
m
m
C.
2
2
m
m

D.
0
2
m
m

223. Phương trình
42
4 3 0x x m
có ba nghiệm phân biệt khi:
A.
12m
B.
12m
C.
31m
D.
13m
224. Đồ thị hàm số
3
3y x m x
cắt trục hoành tại ba điểm phân biệt khi:
A.
3m
B.
3 m
C.
1m
D.
225. Giả sử đồ thị hàm số
32
21y x x m x m
cắt trục hoành tại ba điểm phân biệt có
hoành độ
1 2 3
,,x x x
thỏa mãn
222
1 2 3
4xxx
. Khi đó, giá trị m là:
A.
,1m 
B.
1
,1 \ 0
4
m




C.
1
,1
4
m




D.
1
,1
4
m



226. Đồ thị hàm số
32
1y x mx m
cắt trục hoành tại ba điểm phân biệt khi:
A.
,1 2,3m 
B.
, 3 1,m 
C.
, 1 1,m  
D.
,0 1,m  
227. Đồ thị hàm số
32
2y x mx m
cắt trục hoành tại ba điểm phân biệt khi:
A.
0m
B.
3 6 3 6
22
m
C.
5 6 5 6
22
m
D.
7 6 7 6
22
m
228. Giả sử đồ thị hàm số
32
39y x x x m
cắt trục hoành tại ba điểm phân biệt có hoành độ
1 2 3
,,x x x
tạo thành cấp số cộng. Khi đó, giá trị m là:
A.
1m
B.
12m
C.
2m
D.
11m
229. Giả sử đồ thị hàm số
32
2 1 9y x m x x
cắt trục hoành tại ba điểm phân biệt có hoành
độ
1 2 3
,,x x x
tạo thành cấp số cộng. Khi đó, khoảng chứa giá trị m là:
A.
2,3m
B.
1,0m
C.
1,2m
D.
2, 1m
103
TRẦN THÔNG Facebook: hội toán bắc trung nam
230. Giả sử đồ thị hàm số
32
5 6 5 6y x m x m x m
cắt trục hoành tại ba điểm phân
biệt có hoành độ
1 2 3
,,x x x
tạo thành cấp số nhân. Khi đó, số giá trị m thỏa mãn yêu cầu bài toán
là:
A.1 B.2 C. 3 D. 4
231. Đồ thị
C
của hàm số
3
62y x x
cắt đường thẳng
:1d y mx m
tại ba điểm
phân biệt A,B,C sao cho tổng hệ số góc các tiếp tuyến của
C
tại A,B,C bằng -6. Giá trị m thỏa
mãn đề bài là
A.
3m 
B.
1m 
C.
1m
D.
2m
232. Đồ thị hàm số
1
1
x
y
x
cắt đường thẳng
y x m
tại hai điểm phân biệt khi:
A.
22m 
B.
22m 
C.
2 2 2 2m
D.
22m 
233. Giả sử đồ thị hàm số
1
1
x
y
x
cắt đường thẳng
y x m
tại hai điểm phân biệt A,B sao
cho tiếp tuyến của tại A và B song song với nhau. Giá trị m là:
A.
1m
B.
2m 
C.
2m
D.
0m
234. Cho đồ thị
C
của hàm số
3
62y x x
và đường thẳng
:.d y mx
Đường thẳng
d
cắt
C
tại ba điểm phân biệt khi:
A.
9
, \ 1
4
m




B.
9
, \ 0
4
m




C.
3
, \ 1
2
m




D.
3
, \ 0
2
m




235. Đồ thị
C
của hàm số
23
2
x
y
x
cắt đường thẳng
:2d y x m
tại hai điểm phân biệt
A,B thỏa mãn biểu thức
2018 2018
12
kk
đạt giá trị nhỏ nhất (lần lượt là các hệ số góc tiếp tuyến của
đồ thị
C
tại A,B). Giá trị m là:
A.
2m
B.
2m 
C.
3m 
D.
1m
236. Đồ thị hàm số
2
1
x
y
x
cắt đường thẳng
1
2
y x m
tại hai điểm phân biệt nằm về hai
phía của trục tung khi:
A.
1m
B.
2m
C.
3m
D.
4m
237. Đồ thị
C
của hàm số
32
2 1 1y x m x m
cắt đường thẳng
: 2 1d y mx m
tại
ba điểm phân biệt. Giá trị m thỏa mãn đề bài là
A.
0
1
2
m
m
B.
1
2
m 
C.
3
2
m
D.
3
4
m
238. Đồ thị
C
của hàm số
23
2
x
y
x
cắt đường thẳng
:2d y x m
tại hai điểm phân biệt
A,B sao cho độ dài đoạn thẳng AB ngắn nhất. Giá trị m là:
104
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.
1
2
m
B.
3
2
m
C.
5
2
m
D.
7
2
m
239. Đồ thị
C
của hàm số
22
1
x
y
x
cắt đường thẳng
:2d y x m
tại hai điểm phân biệt
A,B sao cho độ dài đoạn thẳng
5AB
. Giá trị m là:
A.
3m 
B.
2m 
C.
10
2
m
m


D.
2
1
m
m


240. Đồ thị
C
của hàm số
21
1
x
y
x
cắt đường thẳng
:d y x m
tại hai điểm phân biệt A,B
sao cho độ dài đoạn thẳng
OAB
vuông cân (với O là gốc tọa độ). Giá trị m là:
A.
1m 
B.
2m 
C.
2
3
m
D.
2
3
m 
241. Đồ thị
C
của hàm số
1
12
x
y
x
cắt đường thẳng
:d y x m
tại hai điểm phân biệt A,B
sao cho độ dài đoạn thẳng
AB OA OB
vuông cân (với O là gốc tọa độ). Giá trị m là:
A.
1m
B.
2m 
C.
2
1
m
m


D.
3
1
m
m


242. Đồ thị
C
của hàm số
23
1
x
y
x
cắt đường thẳng
:d y x m
tại hai điểm phân biệt
A,B sao cho tiếp tuyến của đồ thị
C
tại A và B song song với nhau. Giá trị m là:
A.
1m
B.
2m
C.
1m
D.
2m 
243. Đồ thị hàm số
4 2 2
2y x mx m m
cắt trục hoành tại bốn điểm phân biệt khi:
A.
1
1
2
m
B.
3
1
2
m
C.
3
1
2
m
D.
1
0
2
m
244. Đường thẳng
:1dy
cắt đồ thị hàm số
42
3 2 3y x m x m
trục hoành tại bốn
điểm phân biệt có hoành độ
1 2 3 4
, , ,x x x x
thỏa mãn
2222
1 2 3 4 1 2 3 4
4x x x x x x x x
. Giá trị m là:
A.
4m
B.
4m 
C.
1
9
m
D.
1
9
m 
245. Đồ thị hàm số
42
44y x x m
cắt trục hoành tại bốn điểm A,B,C,D phân biệt có hoành
độ tăng dần và
2AD BC
. Giá trị m là:
A.
1
1
2
m
B.
3
1
2
m
C.
3
1
2
m
D.
1
0
2
m
105
TRẦN THÔNG Facebook: hội toán bắc trung nam
246. Tiếp tuyến của đồ thị hàm số
42
1
:1
4
m
C y x m x m
tại điểm có hoành độ bằng 1 cắt
đồ thị
m
C
tại ba điểm A,B,C sao cho
4BC
. Giá trị m là:
A.
4m
B.
0m
C.
D.
1m 
247. Đường thẳng
1
:
3
d y mx
cắt đồ thị hàm số
32
11
23
33
y x x x
tại ba điểm A,B,C
trong đó A là điểm cố định và diện tích tam giác OBC gấp 2 lần diện tích tam giác OAB . Giá trị
m là:
A.
3
4
m
B.
3
4
m 
C.
1
9
m
D.
1
9
m 
248. Đường thẳng
d
đi qua
2,0M
có hệ số góc là k cắt đồ thị hàm số
1
2
x
y
x
tại hai điểm
A,B sao
2MA MB
. Giá trị k là:
A.
3
4
k
B.
3
4
k 
C.
2
3
k
D.
2
3
k 
249. M là điểm thuộc đồ thị của hàm số
21
1
x
y
x
sao cho khoảng cách từ M đến tiệm cận đứng
bằng khoảng cách từ M đến tiệm cận ngang. Tọa độ điểm M là:
A.
2,1
4,3
M
M
B.
0, 1
4,3
M
M
C.
0, 1
3,2
M
M
D.
2,1
3,2
M
M
250. M là điểm thuộc đồ thị của hàm số
21
1
x
y
x
sao cho khoảng cách từ M đến tiệm cận
ngang bằng 5 lần khoảng cách từ M đến tiệm cận đứng. Số điểm M thỏa mãn yêu cầu bài toán là:
A.1 B. 2 C. 3 D. 4
251. M,N là điểm thuộc đồ thị của hàm số
32
32y x x
đối xứng với nhau qua
2,18I
. Số
cặp điểm M,N thỏa mãn yêu cầu bài toán là:
A.1 B. 2 C. 3 D. 4
252. Đồ thị của hàm số
42
1y x mx m
luôn đi qua các điểm cố định có tọa độ lần lượt là:
A.
1,0 , 1,0
B.
0,1 , 1,0
C.
2,1 , 2,3
D.
2,1 , 0,1
253. Số điểm có tọa độ nghiêng trên đồ thị của hàm số
27
2
x
y
x
là:
A.4 B. 5 C. 6 D. 7
254. M là điểm thuộc đồ thị của hàm số
42
11
1
42
y x x
và d là tổng khoảng cách từ M đến các
trục tọa độ. Giá trị nhỏ nhất của d là:
106
TRẦN THÔNG Facebook: hội toán bắc trung nam
A.1 B. 2 C.
3
2
D.
1
2
255. Cho hàm số
32
6 9 1 1y x x x
và các mệnh đề:
(1) Hàm số
1
liên tục trên
.
(2) Hàm số đạt cực đại tại
3x
(3) Giá trị cực đại của hàm số
1
là
1
CD
y 
(4) Tiếp tuyến của đồ thị hàm số tại điểm
1x
có hệ số góc là
(5) Đường thẳng
1y 
cắt đồ thị hàm số tại 2 điểm phân biệt
Số mệnh đề đúng trong các mệnh đề trên là:
A.2 B.3 C.4 D.5
256. Cho hàm số
42
4 3 1y x x
và các mệnh đề:
(1) Hàm số
1
có 3 cực trị
(2) Đồ thị hàm số
1
cắt trục hoành tại 1 điểm duy nhất
(3) Tập giá trị của hàm số
1
là
.T
(4) Đồ thị hàm số
1
có một tiệm cận đứng
(5) Tiếp tuyến của đồ thị hàm số
1
tại điểm có hoành độ bằng 1 song song với đường
thẳng
41yx
Các mệnh đề đúng trong các mệnh đề trên là:
A.(1),(3),(5) B. (1),(3),(4) C. (2),(3),(5) D. (1),(2),(5)
107
TRẦN THÔNG Facebook: hội toán bắc trung nam
108
| 1/108
| | Tải xuống

Có thể bạn quan tâm:

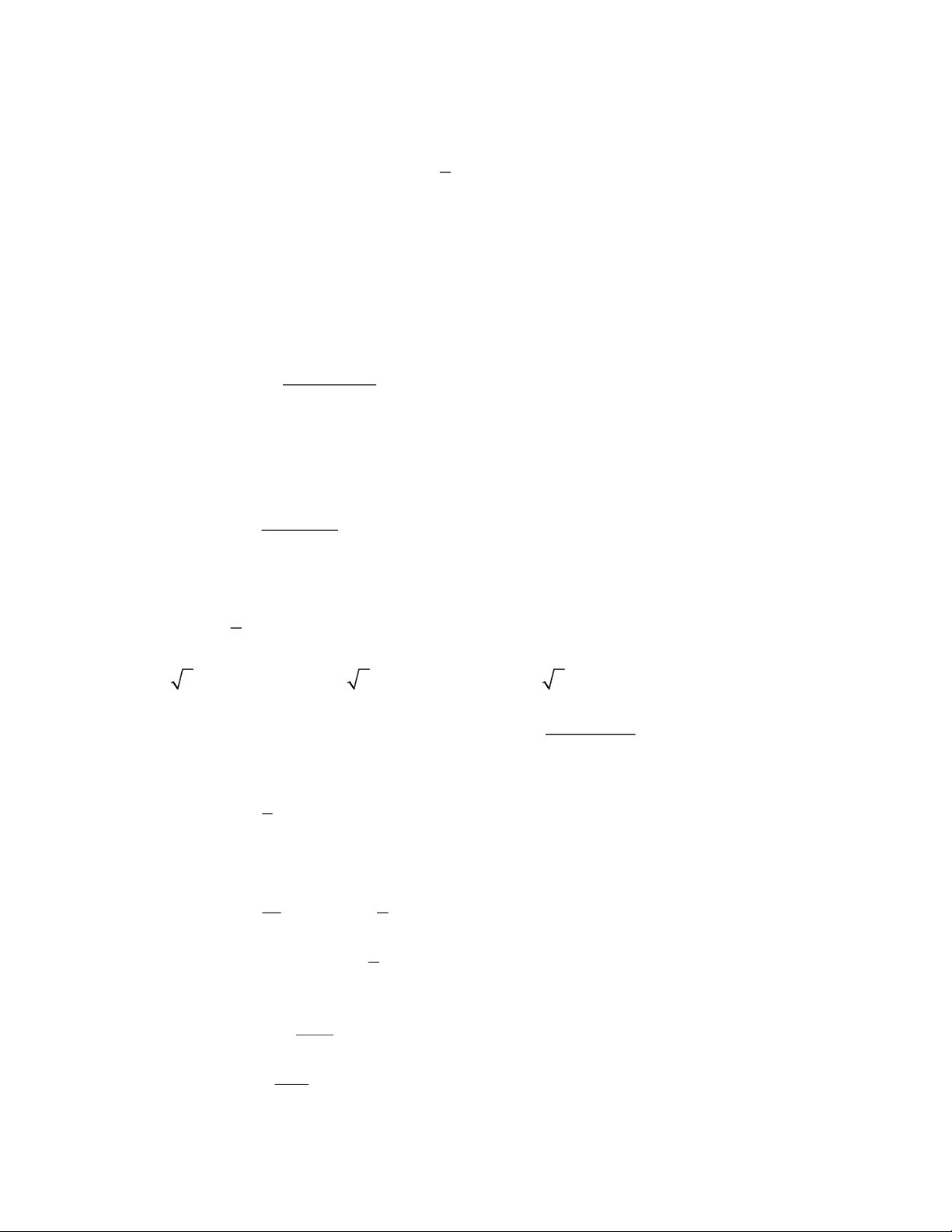
Preview text:


MỖI THÁNG MỘT CHỦ ĐỀ CHUYÊN ĐỀ:
ỨNG DỤNG CỦA ĐẠO HÀM VÀ
KHẢO SÁT ĐỒ THỊ HÀM SỐ
Quảng Nam, tháng 11 năm 2016 TRẦN THÔNG
Facebook: hội toán bắc trung nam 1 Mở đầu
Hàm số là một trong những khái niệm cơ bản của toán học, đóng vai trò quan trọng trong
chương trình toán phổ thông và là nền tảng của nhiều lĩnh vực khác nhau của toán học nói riêng
và khoa học tự nhiên nói chung. Để bạn đọc có được cái nhìn tổng quát hơn về hàm số, trong bài
viết tháng 11/2016 của hội toán bắc trung nam tôi xin trình bày một số vấn đề cơ bản về hàm số.
Bài viết được chia làm ba phần chính:
Phần 1: Giới thiệu một số khái niệm cơ bản như tính đơn điệu, cực trị, tiệm cận…
Phần 2: Trình bày sơ đồ khảo sát và vẽ đồ thị một số hàm số quen thuộc.
Phần 3: Khái quát một số dạng toán quen thuộc về hàm số và các ứng dụng.
Lưu ý bạn đọc: Trước khi đọc hiểu bài viết này, bạn đọc cần nắm vững định nghĩa, các
tính chất cơ bản của đạo hàm cùng với bảng đạo hàm các hàm số sơ cấp được trình bày chi tiết
trong chương trình toán THPT hiện hành.
Với hệ thống bài tập tự luận và trắc nghiệm phong phú, hi vọng bài viết này sẽ giúp ích
cho bạn đọc, đặc biệt là các bạn thí sinh trong kỳ thi THPT quốc gia sắp tới khi tìm hiểu về hàm
số. Tuy vậy do nhiều nguyên nhân khác nhau, bài viết không tránh khỏi những khiếm khuyết, tác
giả rất mong nhận được những ý kiến đóng góp của quý độc giả đề chuyên đề ngày một hoàn
thiện hơn. Mọi ý kiến đóng góp, quý độc giả vui lòng gửi về địa chỉ email: thongqna@gmail.com
hoặc trang cá nhân facebook: https://www.facebook.com/thong.tranvan.5203.
Quảng Nam, ngày 15 tháng 11 năm 2016 TRẦN THÔNG TRẦN THÔNG
Facebook: hội toán bắc trung nam 2
PHẦN 1: KIẾN THỨC CHUẨN BỊ
1.Tính đơn điệu của hàm số.
a.Định nghĩa: Cho hàm số y f (x) xác định trên D, với D là một khoảng, một đoạn hoặc nửa khoảng.
1.Hàm số y f (x) được gọi là đồng biến trên D nếu x  , x  ,
D x x f (x )  f (x ) 1 2 1 2 1 2
2.Hàm số y f (x) được gọi là nghịch biến trên D nếu x  , x  ,
D x x f (x )  f (x ) 1 2 1 2 1 2
b.Điều kiện cần để hàm số đơn điệu: Giả sử hàm số y f (x) có đạo hàm trên khoảng D
1.Nếu hàm số y f (x) đồng biến trên D thì f '(x)  0, x   D
2.Nếu hàm số y f (x) nghịch biến trên D thì f '(x)  0, x   D
c.Điều kiện đủ để hàm số đơn điệu:
1.Định lý 1. Nếu hàm số y f (x) liên tục trên đoạn a,b và có đạo hàm trên khoảng (a,b) thì
tồn tại ít nhất một điểm c  (a, b) sao cho: f (b)  f (a)  f '(c)(b a)
2.Định lý 2. Giả sử hàm số y f (x) có đạo hàm trên khoảng D
1.Nếu f '(x)  0, x
  D và f '(x)  0 chỉ tại một số hữu hạn điểm thuộc D thì hàm số đồng biến trên D
2.Nếu f '(x)  0, x
  D và f '(x)  0 chỉ tại một số hữu hạn điểm thuộc D thì hàm số nghịch biến trên D
3.Nếu f '(x)  0, x
  D thì hàm số không đổi trên D 2.Cực trị
a.Định nghĩa: Cho hàm số y f (x) xác định trên D R và x D 0
1. x được gọi là một điểm cực đại của hàm số y f (x) nếu tồn tại một (a,b) chứa điểm x 0 0
sao cho (a, b)  D và f (x)  f (x ), x  ( , a ) b \ x
. Khi đó f (x ) được gọi là già trị cực đại của 0  0 0
hàm số và M (x ; f (x )) được gọi là điểm cực đại của hàm số . 0 0 TRẦN THÔNG
Facebook: hội toán bắc trung nam 3
2. x được gọi là một điểm cực tiểu của hàm số y f (x) nếu tồn tại một (a,b) chứa điểm x 0 0
sao cho (a, b)  D và f (x)  f (x ), x  ( , a ) b \ x
. Khi đó f (x ) được gọi là già trị cực tiểu 0  0 0
của hàm số và M (x ; f (x )) được gọi là điểm cực tiểu của hàm số . 0 0
3.Giá trị cực đại và giá trị cực tiểu được gọi chung là cực trị của hàm số
b.Điều kiện cần để hàm số có cực trị : Giả sử hàm số y f (x) có cực trị tại x .Khi đó, nếu 0
y f (x) có đạo hàm tại điểm x thì f '(x )  0 . 0 0
c.Điều kiện đủ để hàm số có cực trị :
1.Định lý 1. (Dấu hiệu 1 để tìm cực trị của hàm số )
Giả sử hàm số y f (x) liên tục trên khoảng (a,b) chứa điểm x và có đạo hàm trên các 0
khoảng (a, x ) và (x ,b) . Khi đó : 0 0
+ Nếu f’(x) đổi dấu từ âm sang dương khi x qua điểm x thì hàm số đạt cực tiểu tại x 0 0
+ Nếu f’(x) đổi dấu từ dương sang âm khi x qua điểm x thì hàm số đạt cực đại tại x 0 0
2.Định lý 2. (Dấu hiệu 2 để tìm cực trị của hàm số )
Giả sử hàm số y f (x) có đạo hàm trên khoảng (a,b) chứa điểm x , f '(x )  0 và f(x) có 0 0
đạo hàm cấp hai khác 0 tại điểm x . Khi đó: 0
+ Nếu f ' (x )  0 thì hàm số đạt cực đại tại điểm x 0 0
+ Nếu f ' (x )  0 thì hàm số đạt cực tiểu tại điểm x 0 0 3.Tiệm cận
a.Đường tiệm cận đứng .
Đường thẳng (d): x x được gọi là đường tiệm cận đứng của đồ thị (C) của hàm số y f (x) 0
nếu lim f (x)   hoặc lim f ( x)   hoặc lim f (x)   hoặc lim f ( x)       x    0 x x 0 x x 0 x x 0 x
b.Đường tiệm cận ngang .
Đường thẳng (d): y y được gọi là đường tiệm cận ngang của đồ thị (C) của hàm số y f (x) 0
nếu lim f (x)  y hoặc lim f ( ) x y 0 0 x x 4.Sự tương giao
a.Giao điểm của hai đồ thị. Cho hàm số y f (x) có đồ thị (C ) và hàm số y g(x) có đồ thị 1 (C ) 2 TRẦN THÔNG
Facebook: hội toán bắc trung nam 4
+ Hai đồ thị (C ) và (C ) cắt nhau tại điểm M (x ; y )  (x ; y ) là nghiệm của hệ 1 2 0 0 0 0 phương trình
y f (x) 
y g(x)
+Hoành độ giao điểm của hai đồ thị (C ) và (C ) là nghiệm của phương trình 1 2
f (x)  g(x) (1)
+Phương trình (1) được gọi là phương trình hoành độ giao điểm của (C ) và (C ) 1 2
+Số nghiệm của phương trình (1) bằng số giao điểm của (C ) và (C ) 1 2
b.Sự tiếp xúc của hai đường cong. Cho hai hàm số y f (x) và y g(x) có đồ thị lần lượt
là (C ) và (C ) và có đạo hàm tại điểm x . 1 2 0
+Hai đồ thị (C ) và (C ) tiếp xúc với nhau tại một điểm chung M (x , y ) nếu tại điểm 1 2 0 0
đó chúng có chung cùng một tiếp tuyến . Khi đó điểm M được gọi là tiếp điểm.
+Hai đồ thị (C ) và (C ) tiếp xúc với nhau khi và chỉ khi hệ phương trình sau có 1 2
f (x)  g(x) nghiệm 
f '(x)  g '(x)
Nghiệm của hệ phương trình trên là hoành độ của tiếp điểm.
PHẦN 2: SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ I.Hàm số bậc 3: 3 2
y ax bx cx d a  0
1.Tập xác định D
2. Sự biến thiên
2.1. Xét sự biến thiên của hàm số + Tính đạo hàm 2
y  3ax  2bx c + Giải phương trình 2
y  0  3ax  2bx c  0 (lưu ý phải tính nghiệm chính xác không được tìm nghiệm gần đúng)
+ Xét dấu đạo hàm và suy ra chiều biến thiên của hàm số (hàm số đồng biến,nghịch biến trên những khoảng nào?) 2.2. Tìm cực trị
2.3. Tính giới hạn tại vô cùng ( x   ) TRẦN THÔNG
Facebook: hội toán bắc trung nam 5 Chú ý: 3 2 lim y
lim (ax bx cx d )   x x * Nếu a > 0  3 2 lim y
lim (ax bx cx d )   x x lim y  lim ( 3 ax  2
bx cx d )   x x * Nếu a < 0  lim y  lim ( 3 ax  2
bx cx d )   x x 2.4. Lập bảng biến thiên
Thể hiện đầy đủ, chính xác các giá trị trên bảng biến thiên 3. Đồ thị
-Giao với trục Oy: x  0  y d  0, d  -Giao với trục Ox: 3 2
y  0  ax bx cx d  0   x  ? (trong trường hợp nghiệm lẻ có thể bỏ qua bước này) -Các điểm cực trị
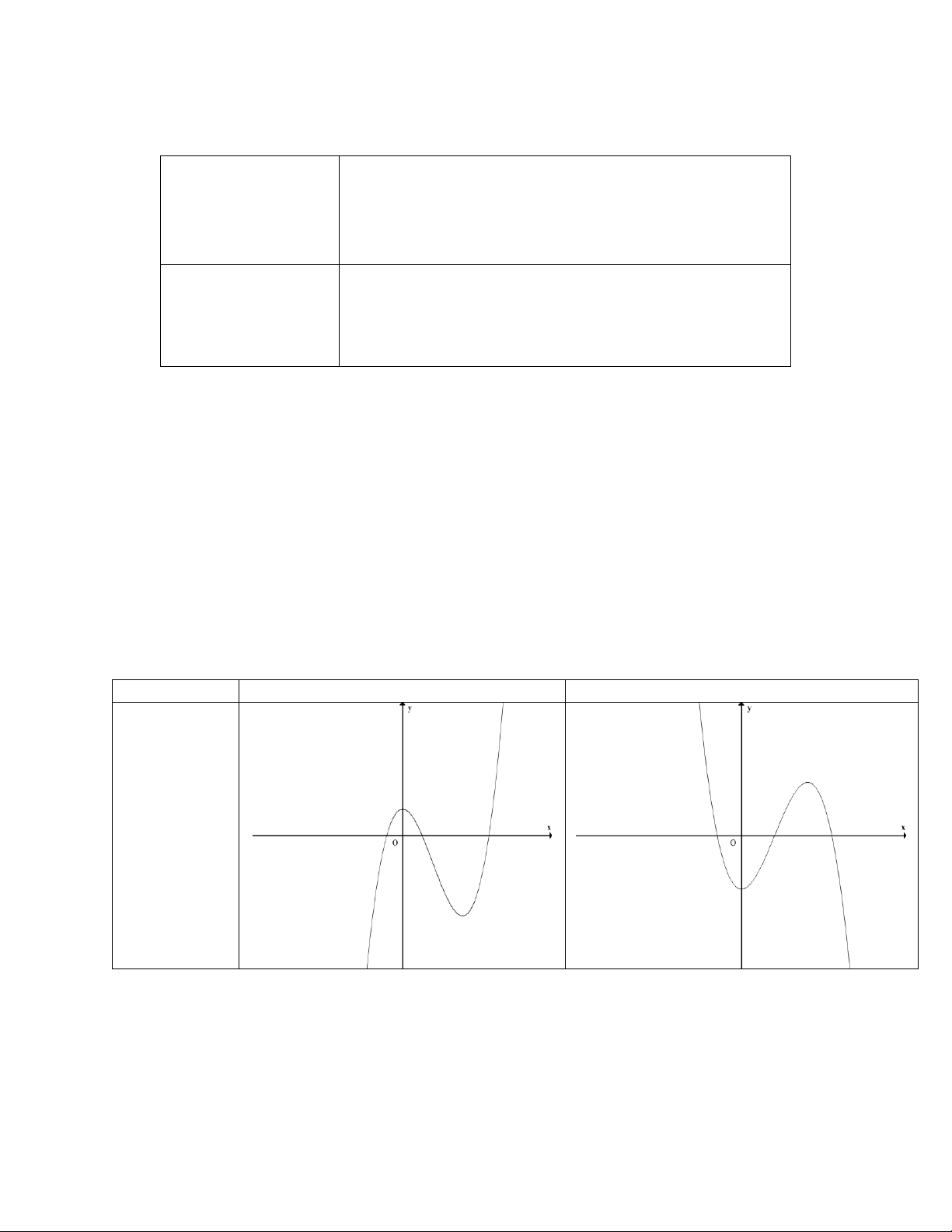
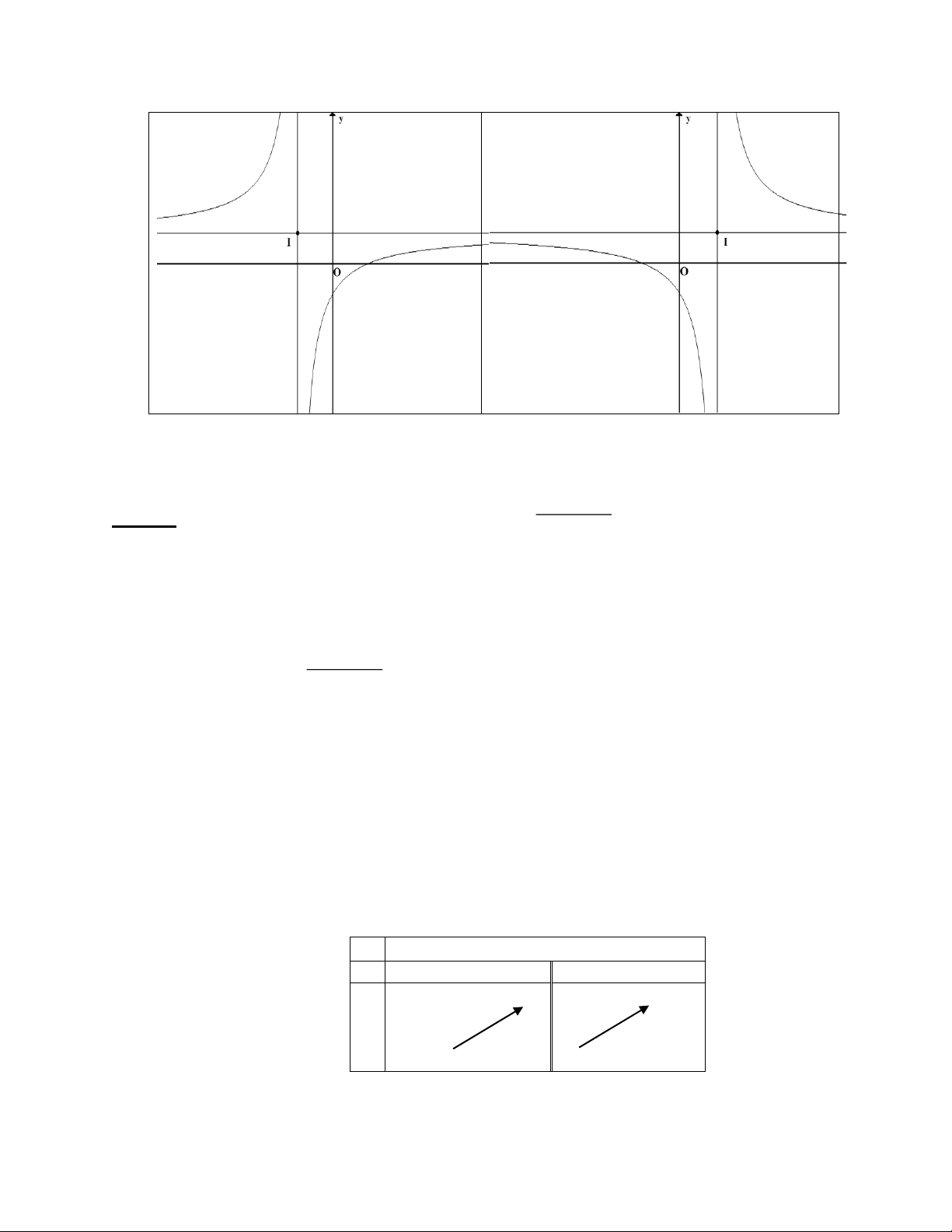
- Một số hình dạng đồ thị hàm bậc 3 Nếu a>0 Nếu a<0 Phương trình y’ = 0 có hai nghiệm phân biệt TRẦN THÔNG
Facebook: hội toán bắc trung nam 6 Phương trình y’ = 0 có nghiệm kép Phương trình y’ = 0 vô nghiệm Ví dụ minh họa:
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x3 + 3x2 – 4
* Tập xác định: D R * Sự biến thiên: 2
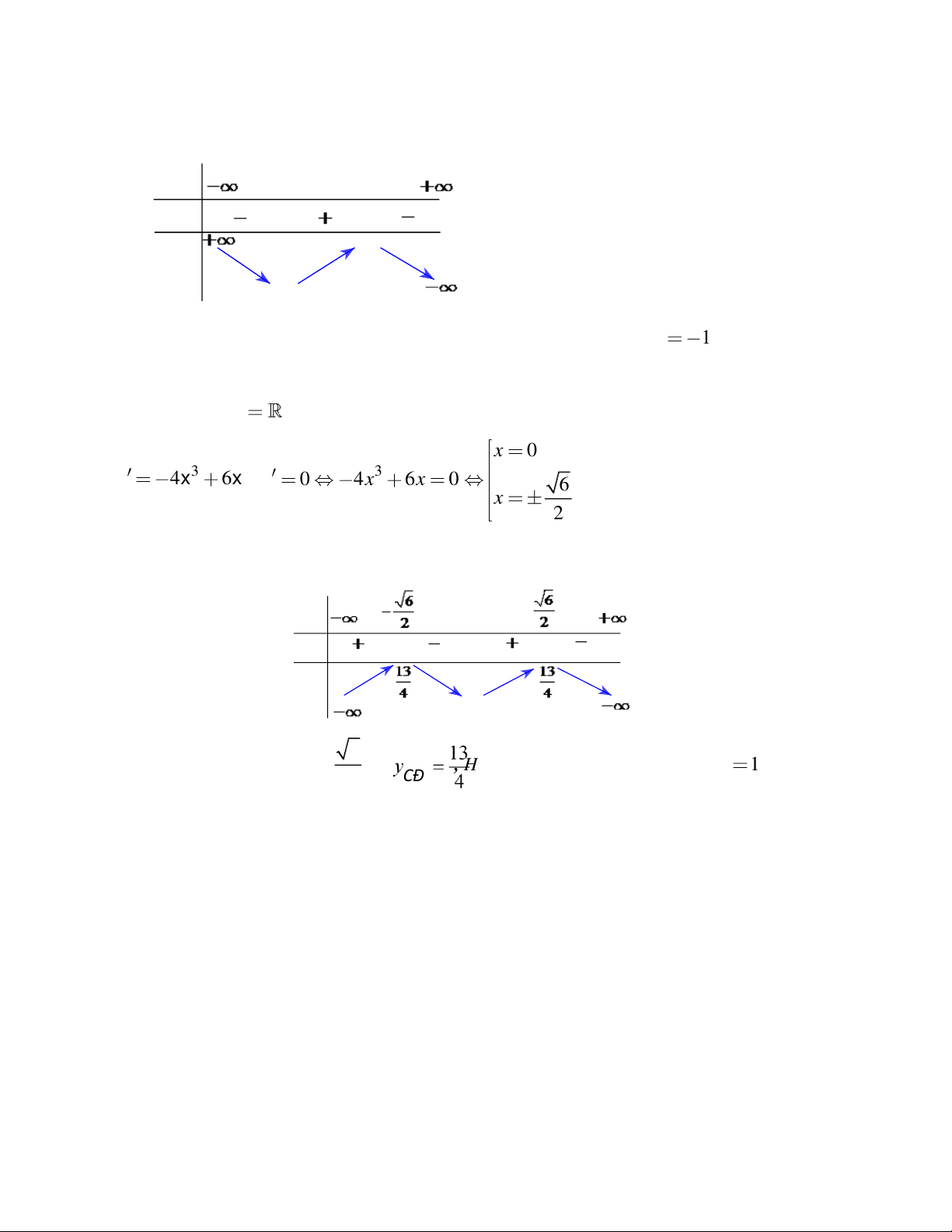
Chiều biến thiên: y'  3x  6x x   0
Giải phương trình: y'  0  3 2 x  6x  0   x  2 Dấu của y’ x -  -2 0 +  y’ + 0 - 0 +
Đồ thị hàm số đồng biến trên khoảng: (;2)  ( ;
0 ) và nghịch biến trên khoảng (- 2; 0). - Cực trị: TRẦN THÔNG
Facebook: hội toán bắc trung nam 7 - Giới hạn: lim y  lim ( 3 x  3 2 x  )
4   lim y  lim ( 3 x  3 2 x  ) 4   x x x x
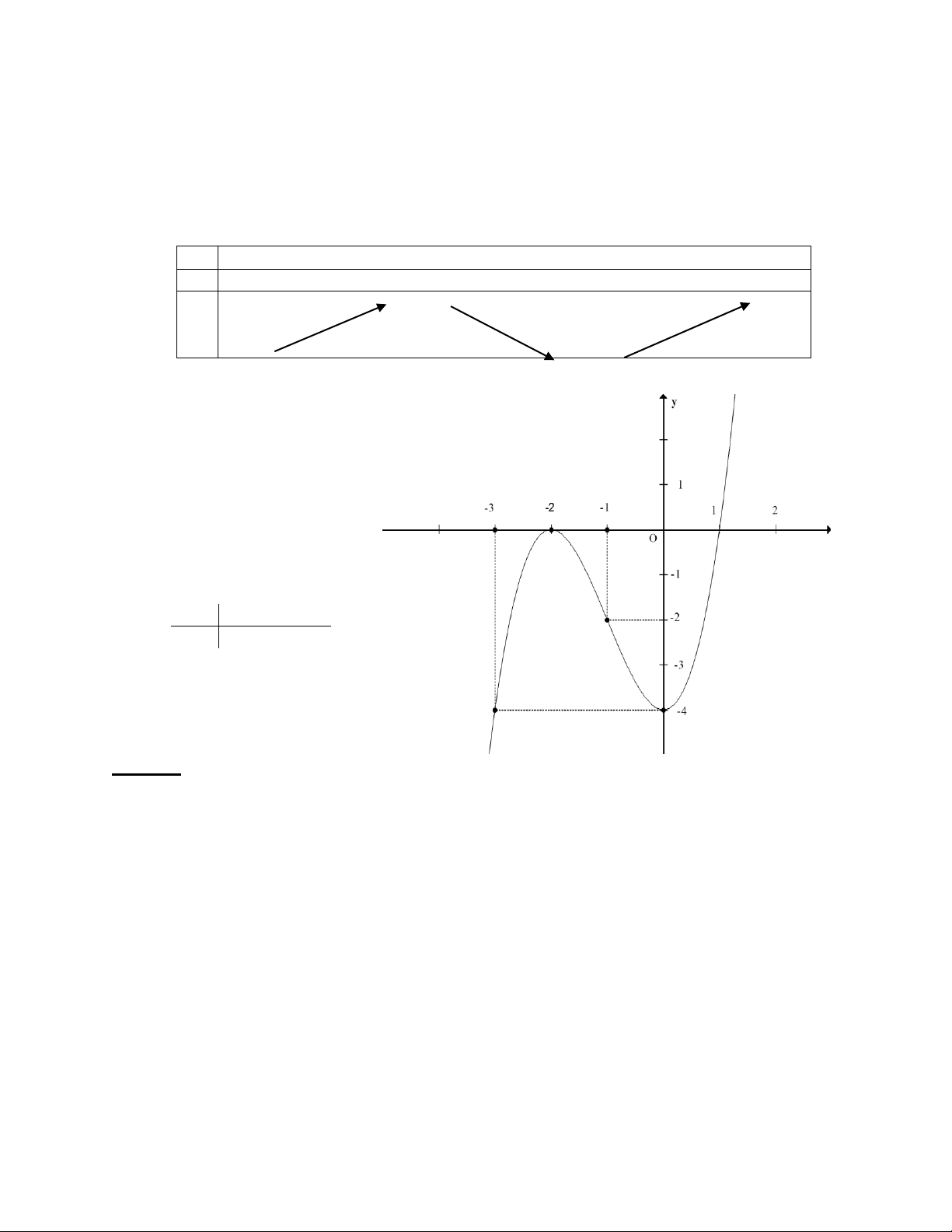
- Bảng biến thiên: x -  -2 0 +  y’ + 0 - 0 + 0 +  y -  -4 * Đồ thị: - Giao điểm với Oy:
Cho x = 0 y = -4 - Giao với Ox: Cho y = 0 giải phương trình: x3 + 3x2 – 4 = 0  x  1  x  2 Bảng giá trị: x -3 1 y -4 0
Ví dụ 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x3 + 3x2 + 3x + 2
* Tập xác định: D R * Sự biến thiên: 2
- Chiều biến thiên: y'  3x  6x  3
Giải phương trình: y'  0  3 2
x  6x  3  0  phương trình có nghiệm kép: x x  1  1 2
y’ > 0 với mọi giá trị của x và y’(-1) = 0. Hàm số luôn đồng biến trên D
- Hàm số không có cực trị. - Giới hạn: TRẦN THÔNG
Facebook: hội toán bắc trung nam 8 lim y  lim ( 3 x  3 2 x  3x  )
2   lim y  lim ( 3 x  3 2 x  3x  ) 2   x x x x - Bảng biến thiên: -  -1 + x  y’ + 0 + +  y 1 -  * Đồ thị:
- Giao điểm của đồ thị với trục tung: cho x = 0 y = 2 - Bảng giá trị x -2 -3 y 0 -7 -Vẽ đồ thị
Ví dụ 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = - x3 + 3x2 - 4x +2
* Tập xác định: D R * Sự biến thiên: 2
- Chiều biến thiên: y'  -3x  6x 4 -
Giải phương trình : y’= 0 -3x2 +6x – 4 = 0  Phương trình vô nghiệm. TRẦN THÔNG
Facebook: hội toán bắc trung nam 9  y’< 0 x
  D Hàm số luôn nghịch biến trên D
- Hàm số không có cực trị -Giới hạn lim y  lim ( 3 x  3 2 x  4x  ) 2   x x lim y  lim ( 3 x  3 2 x  4x  ) 2   x x - Bảng biến thiên: x -  +  y’ - +  y -  * Đồ thị:
- Giao điểm của đồ thị với trục tung: cho x = 0 y = 2 - Bảng giá trị: x 2 y -2 - Vẽ đồ thị: Bài tập luyện thi
Khảo sát và vẽ đồ thị các hàm số sau: TRẦN THÔNG
Facebook: hội toán bắc trung nam 10 3
1. y x  3x  2 3 2
2. y x  3x 1 3 2
3. y x  6x  9x  4
4. y   x   2 1 x  2x  2 1 5. 3 2 y
x x x 1 3 1 6. 3 2 y x x 1 3
II.Hàm số trùng phương: 4 2
y ax bx c a  0
1.Tập xác định D
2. Sự biến thiên
2.1. Xét sự biến thiên của hàm số + Tính đạ 3 o hàm y  4 . a x  2 . b x x  0 + Giải phương trình 3  
y  0  4ax  2bx  0  2x  2
2ax b  0  b
  ...... (lưu ý phải 2 x   2a
tính nghiệm chính xác không được tìm nghiệm gần đúng)
+ Xét dấu đạo hàm và suy ra chiều biến thiên của hàm số(hàm số đồng biến,nghịch biến trên những khoảng nào?) 2.2. Tìm cực trị
2.3. Tính giới hạn tại vô cùng ( x   ) Chú ý 4 2 * Nếu a > 0 
lim y  lim (ax bx c)   x x 4 2 * Nếu a < 0 
lim y  lim (ax bx c)   x x
2.4. Lập bảng biến thiên
Thể hiện đầy đủ, chính xác các giá trị trên bảng biến thiên 3. Đồ thị TRẦN THÔNG
Facebook: hội toán bắc trung nam 11
-Giao với trục Oy: x  0  y c  0,c -Giao với trục Ox: 4 2
y  0  ax bx c  0   x  ? (trong trường hợp nghiệm lẻ có thể bỏ qua bước này) -Các điểm cực trị
-Tìm thêm một số điểm(nếu cần)
- Một số hình dạng đồ thị hàm trùng phương a>0 a<0 Phương trình y’ = 0 có ba nghiệm phân biệt Phương trình y’ = 0 có một nghiệm Ví dụ minh họa:
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x4 - 2x2 + 2
* Tập xác định: D R * Sự biến thiên: 3
- Chiều biến thiên: y'  4x  4x giải phương trình: TRẦN THÔNG
Facebook: hội toán bắc trung nam 12 x  1 y'  0  4x3  4x 
0  4x(x2 - 1) = 0   x  0
Bảng dấu của y’: x -  -1 0 1 +  y’ - 0 + 0 - 0 +
Đồ thị hàm số đồng biến trên khoảng: (-1;0)
 (1;) và nghịch biến trên khoảng: (- - ; 1)  (0; ) 1
Hàm số đạt cực đại tại: x = 0 y  2 CĐ
Hàm số đạt cực tiểu tại: x  1   y  1 CT lim y  lim ( 4 x  2 2 x  )
2   lim y  lim ( 4 x  2 2 x  ) 2   Giới hạn: x x x x
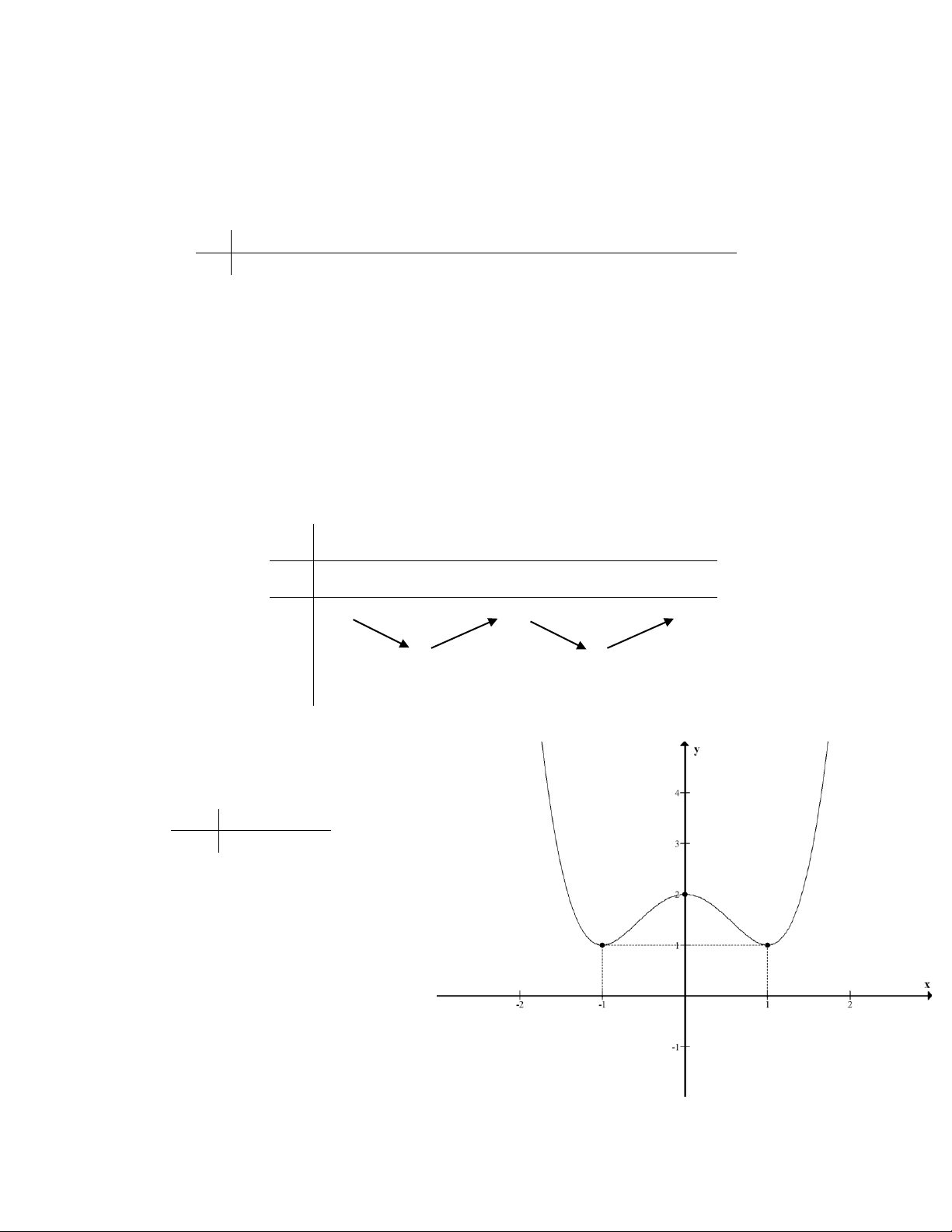
- Bảng biến thiên: x - -1 0 1 + y’ - 0 + 0 - 0 + + 2 + y 1 1 * Đồ thị: Giao với trục tung:
Cho x = 0 y = 2 Bảng giá trị: x -2 2 y 10 10 O TRẦN THÔNG
Facebook: hội toán bắc trung nam 13 4 x 3
Ví dụ 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y= - -x 2 + 2 2
* Tập xác định: D R * Sự biến thiên: 3 2
- Chiều biến thiên: y'  2 - x  2x  -2x(x  ) 1
y'  0  -2x(x2  ) 1  0  x  0
Ta có bảng dấu của y’: x -  0 +  y’ + 0 -
Hàm số đồng biến trên (-  ;0) và nghịch biến trên (0; +  ) 3
Hàm số đạt cực đại tại x = 0yCĐ
; hàm số không có cực tiểu 2 4 x 2 3
Giới hạn: lim y  lim (  x  )   x x 2 2 Bảng biến thiên: x - 0 + y’ + 0 - 3 2 y - - * Đồ thị: 3
- Giao với trục tung: cho x = 0 y= 2 4 x 3
- Giao với trục hoành: cho y = 0 giải phương trình: - -x 2 + = 0 2 2 4 2  x
 2x  3  0 đặt t x (t 0)Ta có phương trình: t  1 2 2 t
 2t  3  0    x  1  x  1  t   ( 3 loa ) i TRẦN THÔNG
Facebook: hội toán bắc trung nam 14 - Bảng giá trị: x -2 2 21  21  y 2 2 - Vẽ đồ thị Bài tập luyện thi
Khảo sát và vẽ đồ thị các hàm số sau: 4 2
1. y x  2x 4 2
2. y  x  4x 1 3. y   2 x   2 1 x  2
4. y   x   2 1 x  2x  2 1 3 5. 4 2 y x  3x  2 2 1 5 6. 4 2 y   x  2x  2 2 ax b
III.Hàm số nhất biến: y cx d d
1.Tập xác định D  \    c
2. Sự biến thiên
2.1. Xét sự biến thiên của hàm số TRẦN THÔNG
Facebook: hội toán bắc trung nam 15  + Tính đạ ad bc o hàm y   c d 2 x dd
+ y không xác định tại
và luôn dương hoặc luôn âm với mọi x c c  d   d
+ Hàm số đồng biến (nghịch biến) trên các khoảng ;    và ;    .  c   c
2.2. Tìm cực trị: Hàm số không có cực trị
2.3. Tìm tiệm cận (Tính giới hạn tại vô cùng) ( x   ) ax b a +Ta có lim y  lim
 nên là tiệm cận đứng của đồ thị. x
x cx d c   +Lại có ax b ax b lim y  lim
  và lim y  lim
  nên là tiệm cận ngang của      dd cx ddd cx d xxxxc c c c đồ thị
2.4. Lập bảng biến thiên: Thể hiện đầy đủ, chính xác các giá trị trên bảng biến thiên 3. Đồ thị bb
-Giao với trục Oy: x  0  y   0,   dd ax b b   b  
-Giao với trục Ox: y  0 
 0  ax b x   , 0   cx d aa
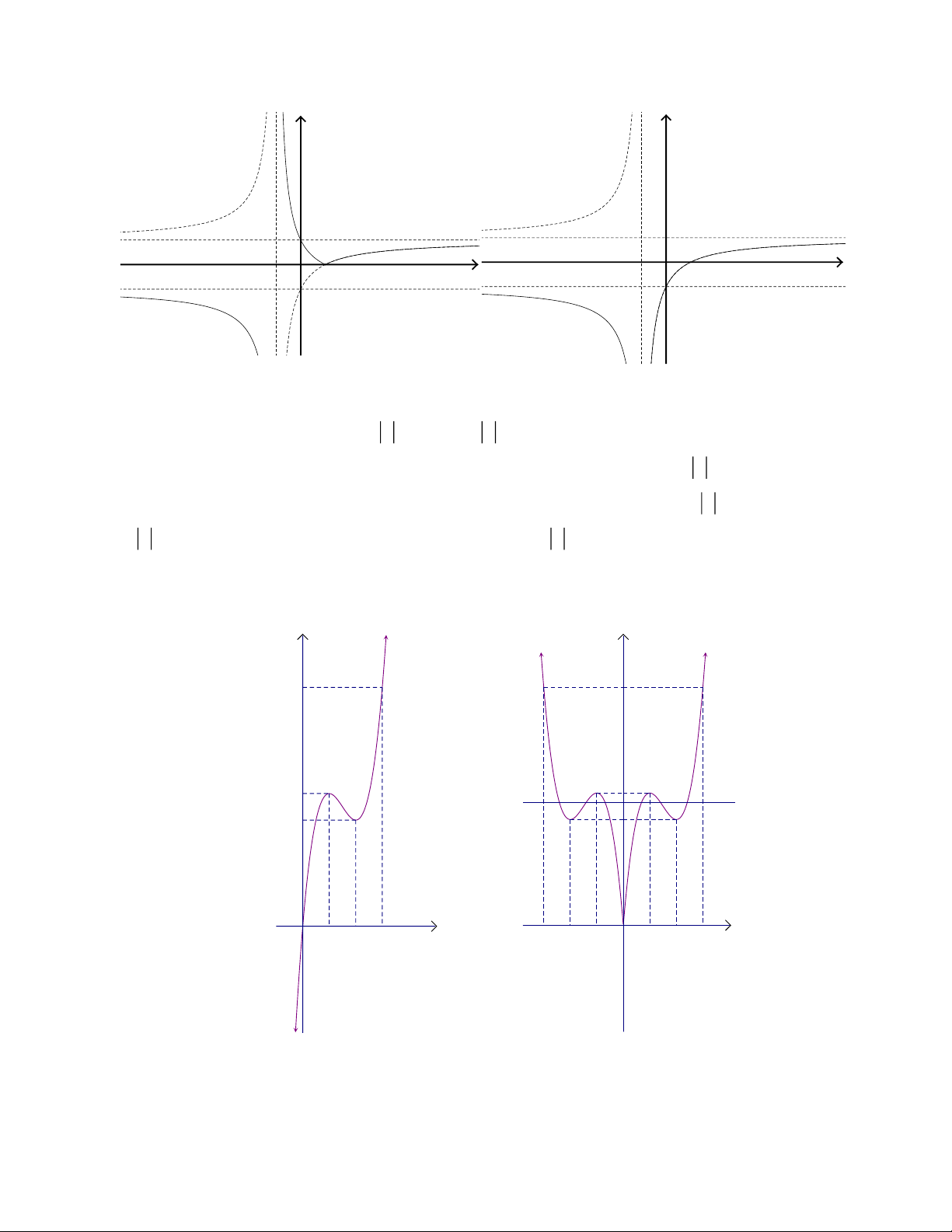
-Tìm thêm một số điểm(nếu cần) -Hình dạng đồ thị
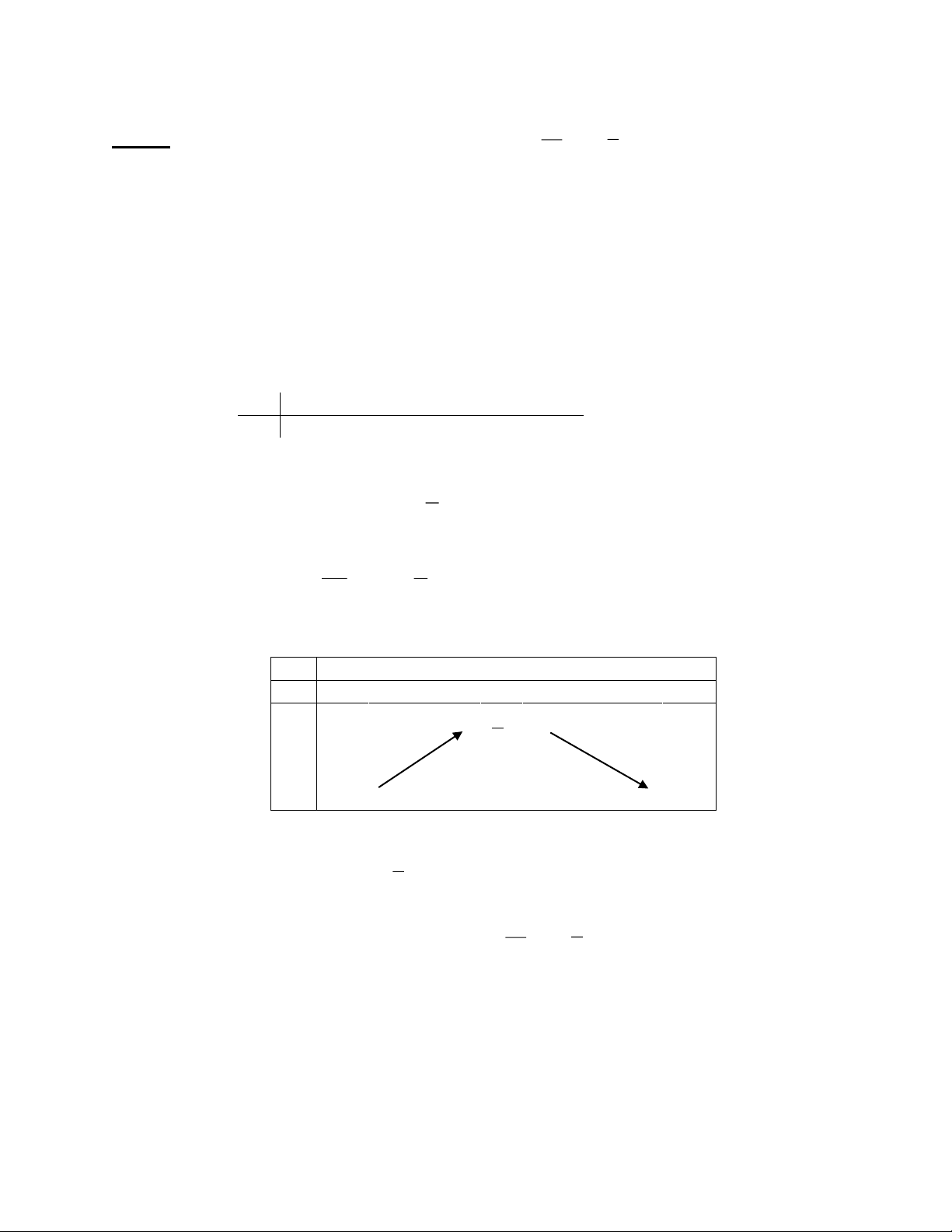
E ad bc  0
E ad bc  0 TRẦN THÔNG
Facebook: hội toán bắc trung nam 16 Ví dụ minh họa:  2x  4
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x  1
* Tập xác định: D R \   1 * Sự biến thiên: 2
- Chiều biến thiên: y'  > 0 x
  D  Hàm số đồng biến trên D 2 (x  ) 1 - cực trị : Không có
- Giới hạn và tiệm cận :
lim y  2; lim y  2 đường thẳng y = -2 là tiệm cận ngang của đồ thị. x x lim y   ;
 lim y      đường thẳng x = -1 là tiệm cận đứng của đồ thị.   x 1  x 1  - Bảng biến thiên: x -  1 +  y’ + + +  -2 y -2 -  * Đồ thị: TRẦN THÔNG
Facebook: hội toán bắc trung nam 17
- Vẽ tiệm cận đứng: x = -1 và tiệm cận ngang: y=-2 - Giao với trục tung: Cho x=0 y=-4 - Giao với trục hoành: Cho y = 0 giải phương trình:
 2x  4 =0x=- x  1 2 - bảng giá trị: x 1 2 y -3 -8/3 Vẽ nhánh bên phải đường tiệm cận đứng. nhánh còn lại lấy đối xứng qua tâm I(-1;-2) 3  x
Ví dụ 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x  2
* Tập xác định: D R \   2 * Sự biến thiên: 1
- Chiều biến thiên: y' 
< 0  Hàm số nghịch biến trên D 2 (x  ) 2 - cực trị : Không có
- Giới hạn và tiệm cận :
lim y  1; lim y  1 đường thẳng y = -1là tiệm cận ngang của đồ thị. x x lim y   ;
 lim y    đường thẳng x = 2 là tiệm cận đứng của đồ thị.   x2 x2 - Bảng biến thiên: TRẦN THÔNG
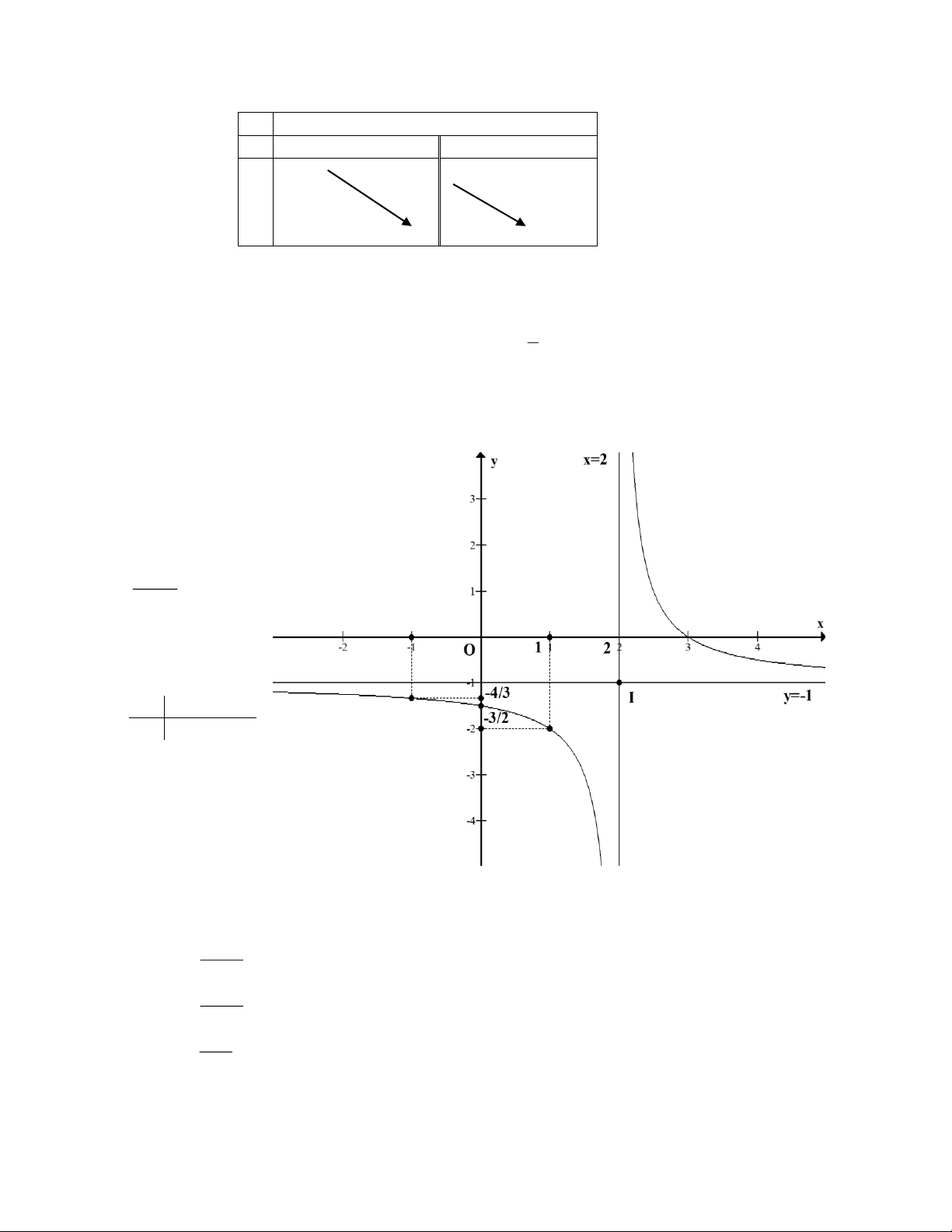
Facebook: hội toán bắc trung nam 18 x -  2 +  y’ - - -1 +  y -  -1 * Đồ thị:
- Vẽ tiệm cận đứng x = 2; tiệm cận ngang: y = -1 3
- Giao điểm của đồ thị với trục tung: cho x = 0  y = - 2
- Vẽ nhánh bên phải đường tiệm cận đứng. nhánh còn lại lấy đối xứng qua tâm I(-1;-2) - Giao điểm của đồ thị với trục hoành: cho y = 0 giải phương trình: 3  x  0 x  2 x = 3 x -1 1 y -4/3 -2 Bài tập luyện thi
Khảo sát và vẽ đồ thị các hàm số sau: x  1. 2 1 y x  2 x  2. 2 1 y x x  3. 1 y x 1 TRẦN THÔNG
Facebook: hội toán bắc trung nam 19  x 4. 2 2 y x  2 5. 1 y  2  x  1 x  6. 2 y x 1
PHẦN 3: MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN HÀM SỐ
Dạng 1: Sự đơn điệu của hàm số.
Bài toán 1: Xét chiều biến thiên của hàm số.
Bước 1. Tìm tập xác định
Bước 2.Tính đạo hàm y .Tìm các điểm mà tại đó y = 0 hoặc y không tồn tại.
Bước 3. Lập bảng biến thiên và kết luận các khoảng đơn điệu của hàm số. Ví dụ minh họa
Ví dụ 1: Tìm các khoảng đơn điệu của hàm số 3 2
y  x  3x 1. Tập xác định: D . 2 x y 3x 6x ; 2 0 y 0 3x 6x 0 x 2
Giới hạn: lim y   , 
lim y   x x
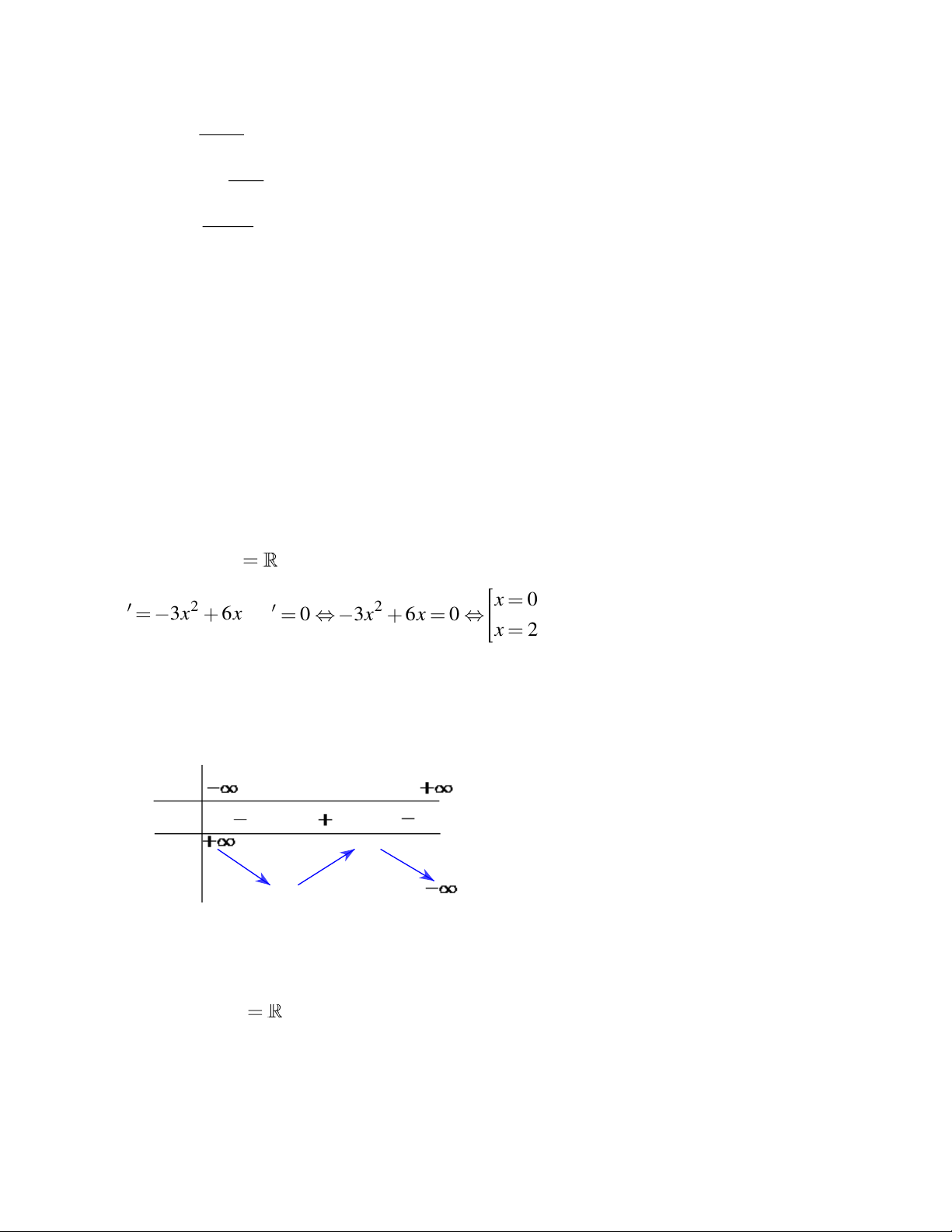
Bảng biến thiên: x 0 2 y' 0 0 3 y -1 CĐ CT
Hàm số đồng biến trên (0; 2); hàm số nghịch biến trên ( ;  0) và(2; )  .
Ví dụ 2:Cho hàm số 4 2
y  x  3x 1 . Tìm các khoảng đơn điệu của hàm số.
Tập xác định: D . TRẦN THÔNG
Facebook: hội toán bắc trung nam 20 x 0 3 y 4x 6x ; 3 y 0 4x 6x 0 6 x 2
Giới hạn: lim y   , 
lim y   x x Bảng biến thiên x 0 y' 0 0 0 1 y CT CĐ CĐ  6   6   6   6 
Hàm số đồng biến trên   ;    và 0;
; nghịch biến trên   ;0 và  ;   . 2   2   2   2   x
Ví dụ 3: Cho hàm số y x  . Tìm các khoảng đơn điệu và cực trị của hàm số. 1 GIẢI
Tập xác định D  \   1 . 1 Đạo hàm y 0, x D . 2 x 1
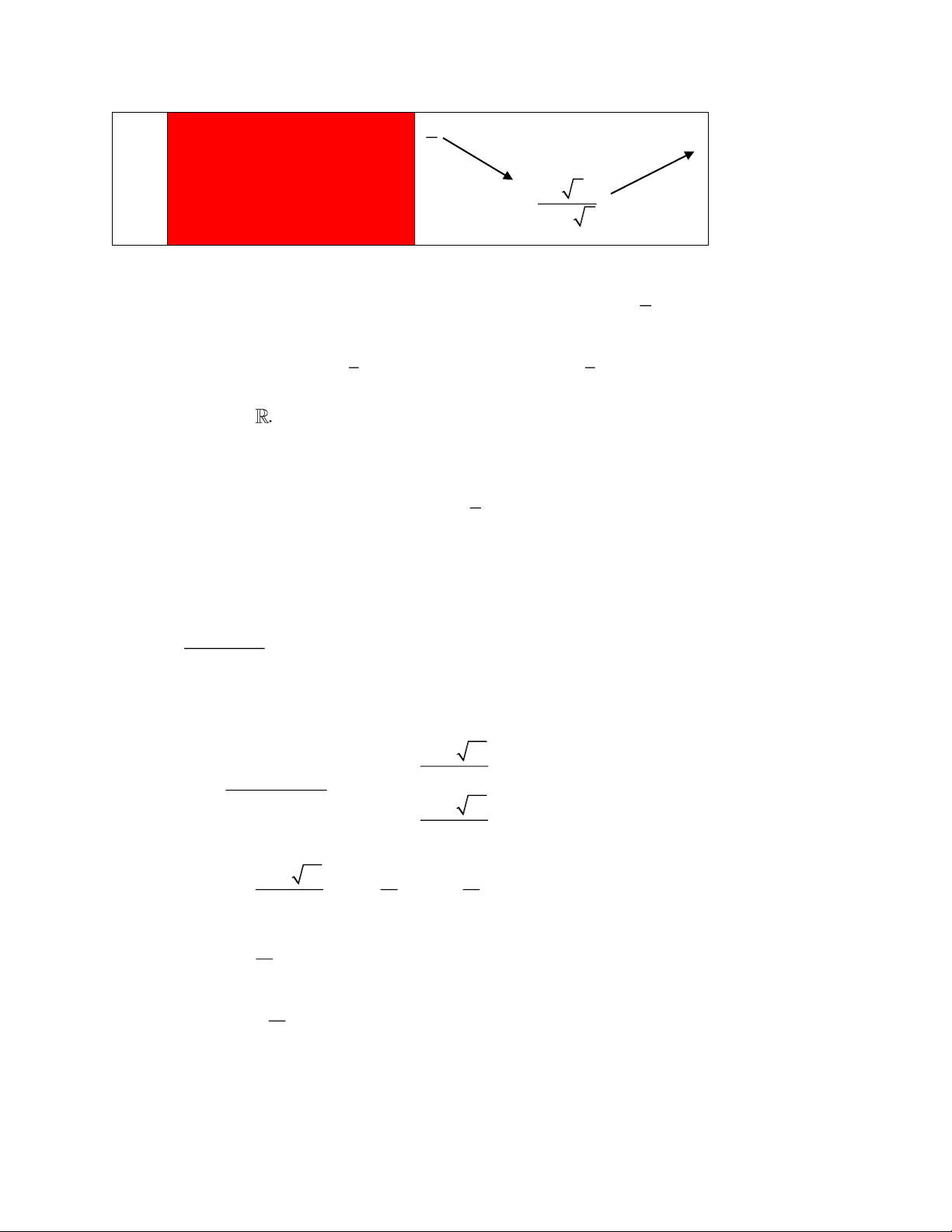
Giới hạn: lim y lim y 1; lim y ; lim y . x x x 1 x 1 Bảng biến thiên x 1 y' 1 y 1
Hàm số nghịch biến trên các khoảng  ;1
  và 1;  .
Hàm số không có cực trị
Bài toán 2: Tìm điều kiện của tham số để hàm số đồng biến (nghịch biến) trên . Phương pháp giải:
Bước 1: Tính đạo hàm TRẦN THÔNG
Facebook: hội toán bắc trung nam 21
Bước 2: Hàm số đồng biến (nghịch biến) khi và chỉ khi y’ luôn đương(luôn âm). Từ đó tìm ra điều
kiện của tham số.
Chú ý: Quy tắc xét dấu tam thức bậc 2: a  0 1. Tam thức 2
ax bx c luôn âm khi và chỉ khi    0 a  0 2. Tam thức 2
ax bx c luôn dương khi và chỉ khi    0 Ví dụ minh họa
Ví dụ 1: Cho hàm số 3 2
y x  3mx  3(2m 1)x 1. Tìm m để hàm số đồng biến trên R.
Tập xác định: D  . Đạo hàm 2
y '  3x  6mx  3(2m 1)
Hàm số đồng biến trên R khi y '  0, x 2
 3x  6mx  3(2m 1)  0, x  a  1  0   2
 '  m  2m 1  0  m  1
Vậy m = 1 thỏa yêu cầu bài toán.
Ví dụ 2: Cho hàm số 3 2
y mx  (2m 1)x  (m  2)x  2 . Tìm m để hàm số luôn nghịch biến.
Tập xác định: D  . Đạo hàm 2
y '  3mx  2(2m 1)x m  2 Trường hợp 1:
m  0  y '  2x  2  Hàm số nghịch biến khi 2x  2  0  x 1
Suy ra m = 0 không thỏa yêu càu bài toán
Trường hợp 2: m  0
Hàm số nghịch biến trên R khi y '  0, x TRẦN THÔNG
Facebook: hội toán bắc trung nam 22
a  3m  0   2
 '  (2m 1)  3m(m  2)  0 m  0   2
m  2m 1  0 m  0  m  1  m  1  Vậy m  1
thỏa yêu cầu bài toán. 1
Ví dụ 3: Cho hàm số 2 3 2 y
(m 1)x  (m 1)x  3x  5 . Tìm m để hàm số đồng biến trên R. 3
Tập xác định: D  . Đạo hàm 2 2
y '  (m 1)x  2(m 1)x  3 Trường hợp 1: 2
m 1  0  m  1  3 
* m  1  y '  4x  3  Hàm số đồng biến khi 4x  3  0  x 4
Suy ra m = 1 không thỏa yêu cầu bài toán * m  1
  y '  3  0  m = - 1 thỏa yêu cầu bài toán Trường hợp 2: 2
m 1  0  m  1 
Hàm số đồng biến trên R khi y '  0, x 2 2
 (m 1)x  2(m 1)x  3  0 2 m 1 0   2
  2m  2m  4  0
m  1 m  2 Vậy: Với m  1
  m  2 thỏa mãn yêu cầu bài toán
Bài toán 3: Tìm điều kiện của tham số để hàm số đồng biến và nghịch biến trên khoảng đoạn. Phương pháp giải:
Bước 1: Tính đạo hàm
Bước 2: Hàm số đồng biến (nghịch biến) khi và chỉ khi y’ luôn dương (luôn âm). Từ đó tìm ra
điều kiện của tham số. TRẦN THÔNG
Facebook: hội toán bắc trung nam 23
Chú ý:So sánh các nghiệm x 2   
1, x2 của tam thức bậc hai ( g x) ax bx c với số 0   0   0   
x x  0  S  0 x x  0  S  0  x  0  x P  0 (hay ac < 0) 1 2 1 2   1 2 P  0   P 0  Chú ý:
1. f x  , m x
  I m  min f x x I
2. f x  , m x
  I m  min f x x I
3. f x  , m x
  I m  max f x x I
4. f x  , m x
  I m  max f x x IVí dụ minh họa 1 1
Ví dụ 1:Tìm m để hàm số 3 2 y
mx  (m 1)x  3(m  2)x
đồng biến trong khoảng (2; ) . 3 3
Tập xác định: D  . Đạo hàm 2
y '  mx  2(m 1)x  3(m  2)
Trường hợp 1: m  0  y '  2x  6  0  x  3 nên không thỏa yêu cầu bài toán
Trường hợp 2: m  0
Điều kiện bài toán được thỏa khi 2 y '  0, x
  2  mx  2(m 1)x  3(m  2)  0, x   2 2  x  6  m  , x   2 2 x  2x  3 2 2  x  6 2x 12x  6
Xét hàm số g(x)   g '(x)  2 2 2 x  2x  3 (x  2x  3) x  3 6
g '(x)  0   x  3 6 Bảng biến thiên x
 3  6 2 3  6  g’(x) + 0 - - 0 + TRẦN THÔNG
Facebook: hội toán bắc trung nam 24 2 0 3 g(x)  6 3  2 6 2
Dựa vào bảng biến thiên ta thấy điều kiện bài toán được thỏa khi m . 3 1 1
Ví dụ 2: Tìm m để hàm số 3 2 y
mx  (1 3m)x  (2m 1)x
nghịch biến trên [1; 5]. 3 3
Tập xác định: D  . Đạo hàm 2
y '  mx  2(1 3 )
m x  2m 1 Trườ 1
ng hợp 1: m  0  y '  2x 1  0  x  
nên không thỏa yêu cầu bài toán 2
Trường hợp 2: m  0
Hàm số nghịch biến trên [1; 5] khi 2
y '  mx  2(1 3 )
m x  2m 1  0, x  [1;5] 2x 1  m  
g(x), x  [1;5] 2 x  6x  2  m  a
m x g(x) [1;5]  1   21 x  (n) 2 2(x x  5) 2
Ta có: g '(x)   0   2 2 (x  6x  2)  1   21 x  (l)  2  1   21  11 11 Lại có g   1  1; g    a  ; g 5  .   2 3 3   11
Suy ra max g(x)  . [1;5] 3 11
Vậy m  max g(x) 
thỏa yêu cầu bài toán. [1;5] 3
Ví dụ 3: Cho hàm số 3 2
y x  3x mx m (1), (m là tham số). Tìm m để hàm số (1) nghịch
biến trên đoạn có độ dài bằng 1. TRẦN THÔNG
Facebook: hội toán bắc trung nam 25
Tập xác định: D  . Đạo hàm 2
y '  3x  6x m Ta có 2
y '  3x  6x m có   9  3m.
+ Nếu m ≥ 3 thì y  0, x
  R ; hàm số đồng biến trên m ≥ 3 không thoả mãn.
+ Nếu m < 3 thì y  0 có 2 nghiệm phân biệt
. Hàm số nghịch biến trên đoạn 1 x , 2 x ( 1 x 2 x )  với độ dài   . 1 x ; 2 x l 1 x 2 x m
Áp dụng định lý vi-ét đảo:     1 x 2 x 2; 1 x 2 x . 3
Hàm số (1) nghịch biến trên đoạn có độ dài bằng 1      1 x 2 x 1 2 ( 1 x 2 x ) 4 1 x 2 x 1  9 m . 4
Bài tập tương tự 1 Bài 1: Cho hàm số 2 3 2 y
(m 1)x  (m 1)x  3x  5 . Tìm m để hàm số nghịch biến trên R. 3 Bài 2: Cho hàm số 3 2 2
y x  3x mx  5  m . Tìm m để hàm số nghịch biến trên 1,3 .
Dạng 2: Bài toán cực trị
Bài toán 1:Tìm cực trị của hàm số
Phương pháp giải bài toán:
Bước 1. Tìm tập xác định
Bước 2.Tính đạo hàm y . Giải phương trình y  0 (tìm điểm dừng). Giả sử có n nghiệm
x ; x ;...; x . 1 2 n
Bước 3. Lập bảng biến thiên và kết luận cực trị của hàm số. Ví dụ minh họa
Ví dụ 1: Tìm các cực trị của hàm số 3 2
y  x  3x 1. Tập xác định: D . 2 x y 3x 6x ; 2 0 y 0 3x 6x 0 x 2
Giới hạn: lim y   , 
lim y   x x TRẦN THÔNG
Facebook: hội toán bắc trung nam 26
Bảng biến thiên: x 0 2 y' 0 0 3 y -1 CĐ CT
Hàm số đạt cực đại tại x = 2, yCĐ = 3; hàm số đạt cực tiểu tại x = 0, 1 CT y .
Ví dụ 2:Cho hàm số 4 2
y  x  3x 1 . Tìm các khoảng đơn điệu và cực trị của hàm số.
Tập xác định: D . x 0 3 y 4x 6x ; 3 y 0 4x 6x 0 6 x 2
Giới hạn: lim y   , 
lim y   x x Bảng biến thiên x 0 y' 0 0 0 1 y CT CĐ CĐ 6
Hàm số đạt cực đại tại x  
, , Hàm
số đạt cực tiểu tại x = 0, 1 CT y 2 CĐ
Bài toán 2:Tìm điều kiện để hàm số có cực trị
Phương pháp giải bài toán:
Bước 1. Tìm tập xác định
Bước 2.Tính đạo hàm y .
Bước 3. Hàm số có cực trị khi và chỉ khi phương trình y  0 có nghiệm. Từ đó suy ra điều kiện của tham số.
Chú ý: Đối với cực trị hàm số bậc 3 3 2
y ax bx cx d. ta thường sử dụng định lý viét và các
định lý về dấu của tam thức bậc 2 để tìm tìm ra điều kiện của tham số m.
Chú ý: Một số tính chất đặc biệt của cực trị hàm số trùng phương 4 2
y ax bx  . c TRẦN THÔNG
Facebook: hội toán bắc trung nam 27 Xét hàm số 4 2
y ax bx c a  0 trên R . Tính đạ 3 o hàm y  4 . a x  2 . b x x  0
Giải phương trình 3  
y  0  4ax  2bx  0  2x  2
2ax b  0  b   ...... 2 x   2a Đồ thị hàm số 4 2
y ax bx c có ba điểm cực trị phân biệt khi và chỉ khi y’=0 có ba điểm phân
biệt hay phương trình (1) có hai nghiệm phân biệt khác 0 ab  0 (*) 2  bb
Với điều kiện (*) ,đồ thị hàm số có ba điểm cực trị là A0,c , B   , c     , 2a 4a   2  bb C  , c     . 2a 4a   4   Khi đó b 8ab 2b AB AC và BC . 2 16a a
Sau đậy là một số tính chất thường gặp của các điểm cực trị này .
1) Điều kiện để ba cực trị A,B,C tạo thành ba đỉnh của một ta giác vuông
Vì AB=AC nên tam giác ABC cân tại A .suy ra ABC là tam giác vuông khi và chỉ khi 0 ABC  90
hay tam giác ABC vuông cân tại A.Khi đó 2 2
BC AB 2  BC  2AB 2 2b b  8ab 3    2.
b  8a  0 2 a 16a
Tính chất 1.Đồ thị hàm số 4 2
y ax bx c có ba điểm cực trị tạo thành ba đỉnh của một tam
giác vuông khi và chỉ khi ab  0 và 3
b  8a  0 .
2)Điều kiện để ba cực trị A,B,C tạo thành ba đỉnh của một tam giác đều
Ta có ABC là tam giác đều khi và chỉ khi 2 2
AB AC BC AC BC 4 b  8ab 2b 3       b 24a 0 2 16 a a TRẦN THÔNG
Facebook: hội toán bắc trung nam 28
Tính chất 2.Đồ thị hàm số 4 2
y ax bx c có ba điểm cực trị tạo thành ba đỉnh của một tam
giác đều khi và chỉ khi ab  0 và 3
b  24a  0 .
3) Điều kiện để ba cực trị A,B,C tạo thành ba đỉnh của một tam giác cân có một góc  cho trước Trường hợp 1.    90
Khi đó ABC là tam giác tù .Vì tam giác ABC cân tại A nên ABC   .
Áp dụng định lí côsin vào tam giác ABC ta có 2 2 2
BC AB AC  2 . AB AC.cos 2 2
BC  2AB  2 . AB AC.cos 4 2b b  8ab    2. (1 cos ) 2 a 16a  16a   3
b  8a(1 cos ) 3
b  8a   3
b  8acos  0 Trường hợp 2. 
  90 (trường hợp này đã trình bày ở tính chất 1) Trường hợp 3.    90
+)Ta có B C   thì A  180  2 ,suy ra cos A  cos(180  2 )   cos 2.
Áp dụng định lí côsin cho tam giác ABC có 2 2 2
BC AB AC  2 . AB AC.cos 2 2 2
BC  2AB  2 . AB AC.cos 2 4 2b b  8ab    2. (1 cos 2 ) 2 a 16a  16  a   3
b  8a(1 cos 2 ) 3
b  8a   3
b  8acos 2  0
+ Nếu A   thì tương tự trường hợp 1, ta có 3
b a   3 8
b  8acos 2  0 .
Tính chất 3.Đồ thị hàm số 4 2
y ax bx c có ba điểm cực trị A,B,C tạo thành ba đỉnh của một
tam giác cân cân có một góc  cho trước khi và chỉ khi ab  0 và Hoặc 3
b a   3 8
b  8acos  0 nếu    90 TRẦN THÔNG
Facebook: hội toán bắc trung nam 29 Hoặc 3
b  8a  0 nếu    90 Hoặc 3
b a   3 8
b  8acos 2  0 nếu    90 .
4) Điều kiện để ba cực trị A,B,C thỏa mãn BC=OA (với O là gốc tọa độ) 2b Ta có 2 2 2 2
BC OA BC OA  
c  2b ac  0 . a
Tính chất 4. Đồ thị hàm số 4 2
y ax bx c có ba điểm cực trị A,B,C thảo mãn điều kiện =OA
(với O là gốc tọa độ) khi và chỉ khi ab  0 và 2
2b ac  0 .
5) Điều kiện để ba cực trị A,B,C tạo thành ba đỉnh của một tam giác và tính diện tích tam giác đó
Gọi H là giao điểm của BC với trục Oy thì AH là đường cao của tam giác ABC .Khi đó 2  b  2 2 bb H  0,c  . Suy ra AH   .  4a  4a 4 a 2 5 1 2b b b     Vậy S . . ABC 3 . 2 a 4 a 32a
Tính chất 5. Đồ thị hàm số 4 2
y ax bx c có ba cực trị A,B,C tạo thành ba đỉnh của một tam 5 b
giác có diện tích là S cho trước khi và chỉ khi ab  0 và S   . 3 32a
6) Điều kiện để ba cực trị A,B,C tạo thành ba đỉnh của một tam giác và tính bán kính đường tròn ngoại tiếp tam giác ABC
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC và H là giao điểm của BC với trục Oy . 2   2 2  Khi đó b b b H  0,c  .Suy ra AH   .  4a  4a 4 a
Từ tam giác vuông AHC ,ta có : AH AH sin ACH   . AC AB
Áp dụng định lí Sin vào tam giác ABC được 2 4 AB AB
b  8ab 4 a 3 b  8a 2R    . suy ra R  . 2 2 sin ACH AH 16a b 8 a b TRẦN THÔNG
Facebook: hội toán bắc trung nam 30
Tính chất 6. Đồ thị hàm số 4 2
y ax bx c có ba cực trị A,B,C tạo thành ba đỉnh của một tam 3  giác có bán kính đườ b 8a
ng tròn ngoại tiếp là R khi và chỉ khi ab  0 và R  . 8 a b
Lưu ý :Các tính chất trên không được thừa nhận trong quá trình giải bài tập. Ví dụ minh họa
Ví dụ 1: Tìm m để hàm số y x3  mx2  x 7  3 có cực trị Ta có: y x2 ' 3  m
2 x  7. Hàm số có CĐ, CT y  0 có 2 nghiệm phân biệt x , x . 1 2    m2 '
 21 0  m  21 (*)
vậy khi m  21 hàm số y x3  mx2  x 7  3 có cực trị
Ví dụ 2: Tìm m để đồ thị của hàm số y x3  mx2  m2  x m3 3 3( 1)  m
4 1 có hai điểm cực trị
A, B sao cho OAB vuông tại O.
Ta có: y  x2  mx m2 3 6 3( 1);
x m1 y m 3
Suy ra y  0   x
  m1 y m1
A(m1;m3), B(m1;m1) OA  (m1;m 3) , OB  (m1;m1). 2 m 1 
Mà OAB vuông tại O OAO
. B  0 m 2  m 2  4  0   . m   2
Ví dụ 3: Tìm tất cả các giá trị của m để đồ thị hàm số y x4  mx2 (3 1)
 3 có ba điểm cực trị tạo 2
thành một tam giác cân sao cho độ dài cạnh đáy bằng
lần độ dài cạnh bên. 3 mTa có: y x3 ' 4  2( m
3 1)x ; y   x x2 3 1 ' 0 0,   . 2
Đồ thị hàm số có ba điểm cực trị  1
y  0 có 3 nghiệm phân biệt m  (*). 3
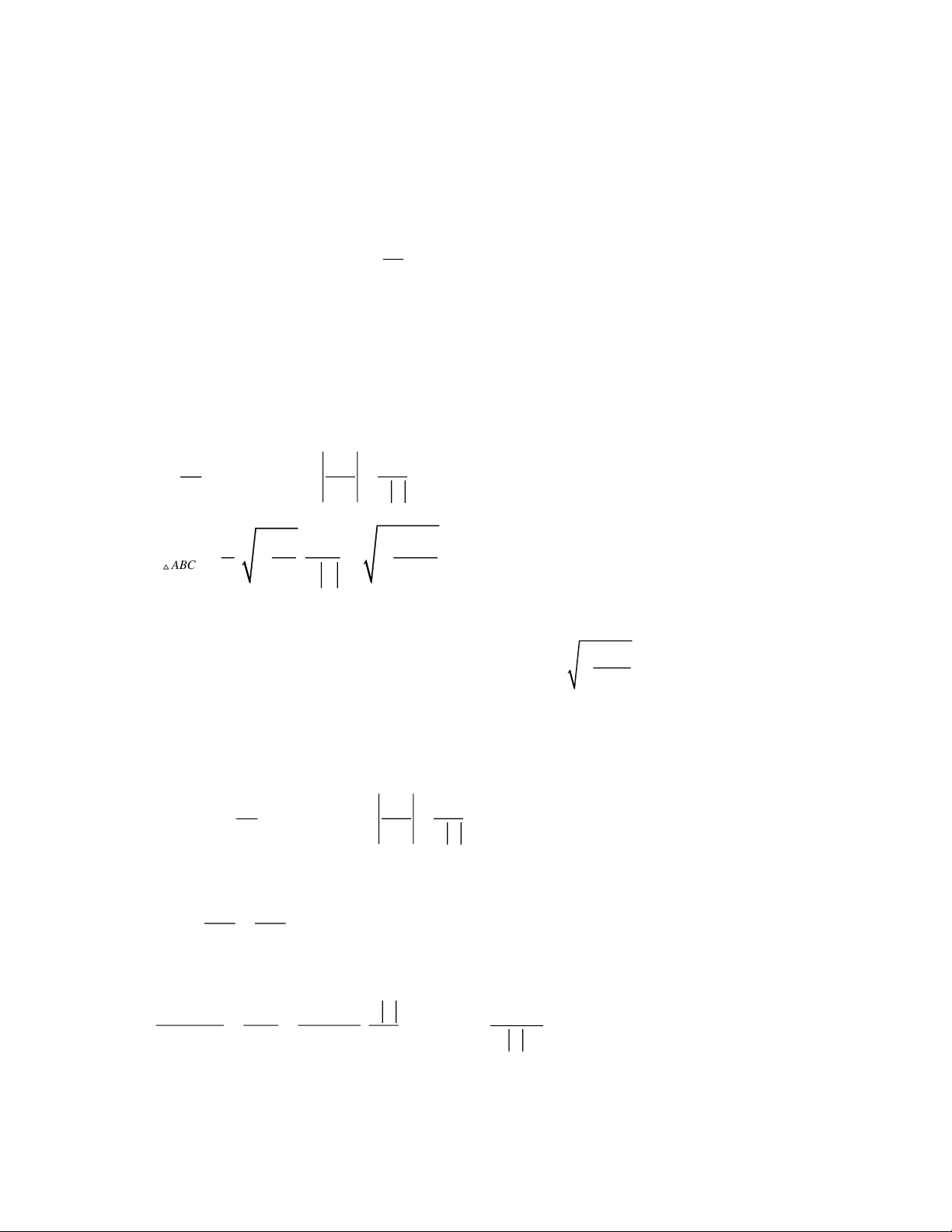
Ba điểm cực trị là: m m 2 3 1 (3 1)       m m 2 3 1 (3 1)      A(0; 3  ) ; B ;  3 ; C  ;  3  2 4   2 4  4        2 m 3 1  m 3 1 m (3  1) 5
ABC cân tại A; BC AB  9.4   4 
m   , thoả (*). 3  2   2 16  3 TRẦN THÔNG
Facebook: hội toán bắc trung nam 31
Ví dụ 4: Với những giá trị nào của m thì đồ thị hàm số y x4  mx2  mm4 2 2 có điểm cực đại và
điểm cực tiểu, đồng thời các điểm cực đại và điểm cực tiểu lập thành một tam giác có diện tích S  4 . x  0
Ta có y'  4x3  m 4 x  0   g(x) 
x2  m  0
Hàm số có 3 cực trị y'  0 có 3 nghiệm phân biệt    m  0  m  0 (*) g
Với điều kiện (*), phương trình y  0 có 3 nghiệm x   m; x  0; x m Hàm số đạt cực trị 1 2 3
tại x ; x ; x . Gọi A
mm4 Bm m4  m2  
m C m m4  m2 (0;2 ); ; 2 ; ;  2 
m là 3 điểm cực trị của 1 2 3 (Cm) .
Ta có: AB2  AC2  m4  m BC2 ;  m
4  ABC cân đỉnh A
Gọi M là trung điểm của BC M
m4  m2  m AM m2  m2 (0; 2 )
Vì ABC cân tại A nên AM cũng là đường cao, do đó: 5 1 1 S AM B . C m2 . . m 4 4 m 4 m5 16 m 5 2 16           . ABC 2 2 Vậy m 5  16 .
Ví dụ 5: Cho hàm số y x3  x2 3
mx  2 (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có
các điểm cực đại và cực tiểu cách đều đường thẳng y x 1. Ta có: y x2 ' 3  6x m.
Hàm số có CĐ, CT y x2 ' 3
 6x m 0 có 2 nghiệm phân biệt x ; x 1 2
 '  9  m 3  0  m 3  (*)
Gọi hai điểm cực trị là Ax ;y ; ; 1  Bx y 1 2 2   1 1   m 2   m
Thực hiện phép chia y cho y ta được: y x y'  2 x  2         3 3   3   3   m 2  mm 2  m
y y(x ) 
 2 x  2  ; y y(x )   2 x  2  1 1   1 2 2   2  3  3  3  3    m 2 m
Phương trình đường thẳng đi qua 2 điểm cực trị là : y   2 x  2     3  3 TRẦN THÔNG
Facebook: hội toán bắc trung nam 32
Các điểm cực trị cách đều đường thẳng y x 1  xảy ra 1 trong 2 trường hợp:
TH1: Đường thẳng đi qua 2 điểm cực trị song song hoặc trùng với đường thẳng y x 1 m 2 9
 2  1 m (không thỏa (*)) 3 2
TH2: Trung điểm I của AB nằm trên đường thẳng y x 1 y y x xm 2   m  y x 1 2 1 2 1  1   2 x   x  2 2
    x x  2 I I  1 2  1 2 2 2  3   3  m 2   m    2 .2   2 2
    0  m  0  3   3 
Vậy các giá trị cần tìm của m là: m  0 .
Ví dụ 6: Cho hàm số y x4 
m2  mx2 2( 1)
m1. Tìm m để đồ thị (C) có khoảng cách giữa hai
điểm cực tiểu ngắn nhất.
Ta có y  x3  m2 4 4(  m1)x ; x  0 y  0   . x
   m2  m1 2  
Khoảng cách giữa các điểm cực tiểu: d = m2 1 3 2
m1  2  m    2  4  1
mind  3 m = . 2
Bài toán 3: Tìm điều kiện để hàm số đạt cực trị tại x 0
Phương pháp giải bài toán:
Bước 1. Tìm tập xác định
Bước 2.Tính đạo hàm y , y.
Bước 3.Từ điều kiện cần y x  0 và y x để tìm tham số . 0  0 
Bước 4 .Thử lại và kết luận
Chú ý: Trong trường hợp bài toán yêu cầu tìm điều kiện để hàm số đạt cực tiểu (cực đại) tại x0
khi y x  0; yx  0 (tương ứng y x  0; yx  0 ). Sau khi tìm được tham số cần kiểm 0   0 0   0
tra lại trước khi kết luận. Ví dụ minh họa TRẦN THÔNG
Facebook: hội toán bắc trung nam 33 1
Ví dụ 1: Cho hàm số: 3 2 2 y x mx m m 1 x
1. Tìm m để hàm số đạt cực đại tại 3 điểm x 1. Ta có 2 2 y x 2mx m m 1 và y 2x 2m
Hàm số đạt cực đại tại x 1 2 y 1 0 m 3m 2 0 m 1 m 2 m 2 y 1 0 2 2m 0 m 1 1 Thử lại với m 2 ta thấy hàm số 3 2 y x 2x 3x
1đạt cực đại tại x 1. 3 Vậy khi m
2 hàm số đạt cực đại tại x 1. 3
Ví dụ 2: Cho hàm số: y x m
3x . Tìm m để hàm số đạt cực tiểu tại điểm x 0.
Tập xác định: D  . 2 Ta có y 3 x m 3 và y 6x 6m
Hàm số đạt cực đại tại x 0. 2 y 0 0 3m 3 0 m 1 m 1 m 1. y 0 0 6m 0 m 0 3 2 Thử lại với m 1 ta thấy hàm số y x 3x
1đạt cực đại tại x 0. Vậy khi m
1 hàm số đạt cực đại tại x 0.
Bài tập tương tự
Bài 1: Tìm m để hàm số 3
y x   2
m  2 x  2m có cực trị
Bài 2: Tìm m để hàm số 4 y x  3 x
m  2m có 1 cực trị
Bài 3: Tìm m để hàm số 4
y x  m   2 3
1 x  2m  5 có 3 cực trị
Bài 4: Tìm m để hàm số 3
y x  3m  
1 x  2m  5 đạt cực đại tại x  2
Bài 5: Tìm m để hàm số 4
y x   2 m   2 2 3
1 x  2m 1 đạt cực tiểu tại x  0
Bài 6: Cho hàm số y x4  mx2 2
m1 có đồ thị (Cm) . TRẦN THÔNG
Facebook: hội toán bắc trung nam 34
1. Với những giá trị nào của m thì đồ thị (Cm) có ba điểm cực trị, đồng thời ba điểm cực trị
đó lập thành một tam giác có bán kính đường tròn ngoại tiếp bằng 1 .
2. Với những giá trị nào của m thì đồ thị (Cm) có ba điểm cực trị, đồng thời ba điểm cực trị
đó lập thành một tam giác đều.
3. Với những giá trị nào của m thì đồ thị (Cm) có ba điểm cực trị, đồng thời ba điểm cực trị
đó lập thành một tam giác vuông cân.
4. Với những giá trị nào của m thì đồ thị (Cm) có ba điểm cực trị, đồng thời ba điểm cực trị
đó lập thành một tam giác có diện tích là 1.
5. Với những giá trị nào của m thì đồ thị (Cm) có ba điểm cực trị, đồng thời ba điểm cực trị
đó lập thành một tam giác có một góc bằng 0 120 .
6. Với những giá trị nào của m thì đồ thị (Cm) có ba điểm cực trị, đồng thời hoành độ ba điểm
cực trị đó lập thành một cấp số cộng.
Bài 7: Cho hàm số y x3   m x2 (1 2 )
 (2 m)x m 2 , với m là tham số thực. 1
1. Xác định m để hàm số đã cho đạt cực trị tại x , x sao cho x x  . 1 2 1 2 3
2. Xác định m để hàm số đã cho đạt cực trị tại x , x sao cho x  2x  1. 1 2 1 2
3. Với giá trị nào của m thì đồ thị hàm số có điểm cực đại và điểm cực tiểu đối xứng với nhau
qua đường thẳng d: x y 8  74  0 .
4. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương.
5. Tìm các giá trị của m để đồ thị hàm số (1) có điểm cực đại, điểm cực tiểu, đồng thời hoành
độ của điểm cực tiểu nhỏ hơn 1.
6. Tìm m để hàm số (1) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số
đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O. 1 1
7. Xác định m để hàm số đã cho đạt cực trị tại x , x sao cho   x x . 1 2 1 2 x x 1 2
Bài 8: Tìm cực trị của hàm số : y x  sin 2x  2 . Bài 9: Cho hàm số 4 2
y x mx m  5 có đồ thị là (Cm), m là tham số. Xác định m để đồ thị
(Cm) của hàm số đã cho có ba điểm cực trị. Bài 10: Cho hàm số 3 y x  6 2
x  9x  2 (C). Viết phương trình đường thẳng đi qua điểm  A  1 ;
1  và vuông góc với đường thẳng đi qua hai điểm cực trị của (C).
Bài 11: Cho hàm số: 4 2 2
y x  2(m  1)x  1 (1) Tìm các giá trị của tham số m để hàm số
(1) có 3 điểm cực trị thỏa mãn giá trị cực tiểu đạt giá trị lớn nhất.
Bài 12: Tìm tham số để hàm số: 3 2 2 y x 3mx 3 m 1 x
m đạt cực đại tại x 2 . TRẦN THÔNG
Facebook: hội toán bắc trung nam 35
Bài 13: Tìm cực trị của các hàm số: y x x 2
Bài 14: Cho các hàm số 3 2
y x  3mx  2 (Cm) Tìm các giá trị của m để (Cm) có hai điểm cực trị và
khoảng cách từ điểm cực tiểu của (Cm) đến đường thẳng d : y  x  2 bằng 2 .
Bài 15: Tìm cực trị của các hàm số: y x 3 x Bài 16: Cho hàm số 4 2
y x  2mx 1 m . Tìm m để đồ thị hàm số có ba điểm cực trị tạo thành
tam giác sao cho trục Ox chia tam giác đó thành hai phần có diện tích bằng nhau. Bài 17: Cho hàm số 3 2
y x  3x (C). Tìm m để đường thẳng đi qua 2 điểm cực trị của đồ thị (C) 4
tạo với đường thẳng  : x my  3  0 một góc  biết cos  . 5 m 3 2
Bài 18: Cho hàm số y .x (m 1)x (m 2)x
5 . Tìm m để hàm số có 2 cực trị, đồng 3
thời 2 điểm cực trị này nằm về hai phía so với trục hoành Ox . Bài 19: Cho hàm số 3 2 2 2 y x 3 m 1 x 3m 7m 1 x m
1 . Tìm m để hàm số có
điểm cực tiểu tại một điểm có hoành độ nhỏ hơn 1. 3 2
Bài 20: Cho hàm số y x mx
4 . Tìm m để hàm số có 2 cực trị là A và B thỏa: 2 900m 2 AB 729 1 Bài 21: Cho hàm số 3 2 y x mx x
1 m . Tìm m để hàm số có cực đại và cực tiểu, đồng 3
thời khoảng cách giữa hai điểm ấy là ngắn nhất. 1 Bài 22: Cho hàm số 3 2 y x x m 1 x
m . Tìm m để hàm số có hai điểm cực trị A, B 3
sao cho tam giác ABO vuông cân với O là gốc tọa độ. 3 2 3
Bài 23: Cho hàm số y x 3mx
4m . Tìm m để hàm số có cực đại và cực tiểu đối xứng
nhau qua đường phân giác thứ nhất. Bài 24: Cho hàm số 2 y (x m) x 3x m
1 . Tìm m để hàm số có cực đại và cực tiểu thỏa: x .x 1 CÐ CT . 1 m Bài 25: Cho hàm số 3 2 2 y mx mx m 1 x
. Tìm m để hàm số có 2 cực trị thỏa: 3 3 2 x x . x 5 12 1 1 2 . TRẦN THÔNG
Facebook: hội toán bắc trung nam 36 1 Bài 26: Cho hàm số 3 2 y x mx x
1 m . Tìm m để hàm số có cực đại và cực tiểu, đồng 3
thời khoảng cách giữa hai điểm ấy là ngắn nhất.
Bài 27: Tìm m để đồ thị hàm số 3 2 y x 3x
2 C có điểm cực đại và điểm cực tiểu của đồ
thị C nằm về hai phía khác nhau của một đường tròn (phía trong đường tròn và phía ngoài đường tròn): 2 2 2 C : x y 2mx 4my 5m 1 0 . m
Bài 28: Cho hàm số 3
y x   m   2 x   2 m m   2 2 1 2
1 x m 1 (m là tham số). Tìm m để (C)
cắt trục hoành tại 3 điểm phân biệt A, B, C (với A là điểm cố định) sao cho 2k k x x , trong 1 2  1 2
đó k , k lần lượt là hệ số góc của tiếp tuyến của (C) tại B, C và x , x là hoành độ các điểm cực 1 2 1 2 trị của (C). 1 3 1 Bài 29: Cho hàm số 3 2 y x x  6mx
.Tìm các số thực m để hàm số có 2 điểm cực đại, 2 4 2 cực tiểu trên  1  ;  1 . Bài 30: Cho hàm số 4 2 2
y x  2mx m m . Tìm m để đồ thị hàm số (1) có 3 điểm cực trị sao cho
trong mp tọa độ 0xy đường tròn đi qua 3 điểm cực trị này cũng đi qua gốc tọa độ O. Bài 31: Cho hàm số 4 2 y x mx 4
m . Tìm m để hàm số có 3 điểm cực trị là A, B, C và
tam giác ABC nhận gốc tọa độ O làm trọng tâm 2 3m Bài 32: Cho hàm số 3 2 y x
x . Tìm m để hàm số có cực đại A, cực tiểu B và tạo với C(– 2
2; 3) thành tam giác ABC đều.
Bài 33: Tìm giá trị của tham số a;b để hàm số 4 2 y x a 3b x 3a
b đạt giá trị cực tiểu bằng 1 tại x 0 . 3
Bài 34: Tìm giá trị của tham số a;b để hàm số 4 2 y x 3a 2b x a
2b có giá trị cực trị 4 bằng 0 khi x
0 . Khi đó hàm số đạt cực tiểu hay cực đại.
Bài 35: Chứng minh rằng hàm số 3 2 y 2x 3 2m 1 x 6m m 1 x
1 luôn đạt cực trị tại
x ,x với mọi giá trị m và biểu thức x
x không phụ thuộc vào m 1 2 2 1 . 3 x 2 Bài 36: Cho 2 y   mx   2 2m   1 x  7m
. Tìm m để hàm số có hai điểm cực trị với hoành 3 3 độ 1 1
x , x thỏa mãn   0 1 2 x 1 x 1 1 2
Bài 37: Cho hàm số: 3 2 y x 3x
m (C ). Định giá trị của m để hàm số có 2 điểm cực trị m A,B sao cho 0 AOB  120 TRẦN THÔNG
Facebook: hội toán bắc trung nam 37
Bài 38: Cho hàm số: 3 2 y x 3x
m (C ). Định giá trị của m để hàm số có 2 điểm cực tiểu m
sao cho diện tích hình phẳng giới hạn bởi đồ thị (C ) và đường thẳng đi qua hai điểm cực tiểu là m 1. 4
Bài 39:Cho y  . 3 x  1 ( 2  sin a) 2 x  1
(  cos2a).x  1 . Tìm m để hàm số có hai điểm cực trị với 3
hoành độ x , x thỏa mãn 2 2 x x  1 1 2 1 2 cos x
Bài 40: Tìm cực trị của các hàm số: y   2cot g.x sin3 x 1 1
Bài 41: Tìm cực trị của các hàm số: y  1  cos x  .cos2x  .cos3x 2 3 Bài 42: Cho hàm số 3 2 2 3
y x  3mx  3(m 1)x m m (1). Chứng minh rằng hàm số (1) luôn có
cự đại,cực tiểu với mọi m.Tìm m để các điểm cự trị của hàm số (1) cùng với điểm I(1;1), tạo thành
một tam giác có bán kính đường tròn ngoại tiếp bằng 5 . 3 3
Bài 43: Cho hàm số y x  (m  ) 2 2 x  ( 3 m  )
1 x 1 (1), m là tham số. Tìm m  0 để đồ thị hàm 2
số (1) có giá trị cực đại, giá trị cực tiểu lần lượt là y , thỏa mãn 2 y   4 . CĐ yCT CĐ yCT
Bài 44: Tìm m để đồ thị hàm số 4 2
y x  2mx  2 có ba điểm cực trị tạo thành tam giác nhận gốc
tọa độ làm trực tâm.
Bài 45: Tìm m để đồ thị hàm số 3 2 3
y x  3mx  3m có hai điểm cự trị , A B sao cho tam giác
OAB có diện tích bằng 48.
Bài 46: Cho hàm số y x4  mx2  m2 2
m có đồ thị (Cm). Với những giá trị nào của m thì đồ
thị (Cm) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có một góc bằng 0 120 . Bài 47: Cho hàm số 3
y  x  3mx 1. Tìm m để đồ thị của hàm số (1) có 2 điểm cực trị , A B
sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ ). Bài 48: Cho hàm số 3 2 2 3
y x  3mx  3(m 1)x m m (1). Chứng minh rằng hàm số (1) luôn có
cự đại,cực tiểu với mọi m.Tìm m để các điểm cự trị của hàm số (1) cùng với điểm I(1;1), tạo thành
một tam giác có bán kính đường tròn ngoại tiếp bằng 5 .
Bài 49: Tìm m để đồ thị hàm số 4 2
y x  2mx  2 có ba điểm cực trị tạo thành tam giác nhận
gốc tọa độ làm trực tâm.
Bài 50: Tìm m để đồ thị hàm số 3 2
y  2x  3(m 1)x  6mx có hai điểm cự trị , A B sao cho đường
thẳng AB vuông góc với đường thảng y x  2 . Bài 51: Cho hàm số 4 2 2 2
y  2x m x m 1
(1) (m là tham số).Tìm tất cả các giá trị của m để
đồ thị của hàm số (1) có ba điểm cực trị ,
A B, C sao cho bốn điểm O, ,
A B, C là bốn đỉnh của
một hình thoi (với O là gốc tọa độ).
Bài 52: Cho hàm số y x4   m2 x2 2(1 )
m1(Cm).Tìm m để đồ thị (Cm) có 3 điểm cực trị tạo TRẦN THÔNG
Facebook: hội toán bắc trung nam 38
thành một tam giác có diện tích lớn nhất. 1
Bài 53: Cho hàm số y x4  ( m
3  1)x2  2(m1) (Cm). 4
Tìm m để đồ thị (Cm) có 3 điểm cực trị tạo thành một tam giác có trọng tâm là gốc toạ độ O. Bài 54: Cho hàm số 4 2 2
y x  2mx  2m  4 (C ) . (m là tham số thực) m
Tìm tất cả các giá trị của m để đồ thị hàm số (C ) có 3 điểm cực trị tạo thành một tam giác cân m  1
có góc ở đỉnh của tam giác đó bằng  với tan  . 2 2 2 Bài 55: Cho hàm số 4 y x  2 2 mx m  1 ) 1 (
. Tìm các giá trị của tham số m để đồ thị hàm số
(1) có ba điểm cực trị tạo thành một tam giác sao cho trục Ox chia tam giác đó thành hai phần có diện tích bằng nhau 1
Bài 56: Cho hàm số y x4  ( m
3  1)x2  2(m1) (Cm).Tìm m để đồ thị (Cm) có 3 điểm cực trị 4
tạo thành một tam giác có trọng tâm là gốc toạ độ O.
Bài 57:Tìm m để đồ thị (Cm) y x4   m2 x2 2(1 )
m1 có 3 điểm cực trị tạo thành một tam
giác có diện tích lớn nhất.
Bài 58: Cho hàm số y x4  mx2 2
 2 (Cm).Tìm các giá trị của m để (Cm) có 3 điểm cực trị tạo  3 9
thành một tam giác có đường tròn ngoại tiếp đi qua điểm D  ;  .  5 5
Bài 59: Cho hàm số y x3  mx2  m2  x m3 3 3( 1)
(Cm)Chứng minh rằng (Cm) luôn có điểm cực
đại và điểm cực tiểu lần lượt chạy trên mỗi đường thẳng cố định. 1 4
Bài 60: Cho hàm số y
x3  (m1)x2  (m 3
1) (1) (m là tham số thực).Tìm m để các điểm cực 3 3
đại và cực tiểu của đồ thị (1) nằm về 2 phía (phía trong và phía ngoài) của đường tròn có phương
trình (C): x2  y2  4x  3  0 .
Dạng 3: Bài toán giá trị lớn nhất nhỏ nhất trên a,b
Phương pháp giải toán
Cho hàm số y f x liên tục trên đoạn a,b . Để tìm giá trị lớn nhất (max) và giá trị nhỏ nhất
(min) của f x trên đoạn [a; b] ta thực hiện các bước sau:
Bước 1. Nhận xét : Hàm số f x liên tục trên đoạn a,b .
Bước 2. Giải phương trình f  x  0 (tìm điểm dừng). Giả sử có n nghiệm x ; x ;...; x thuộc 1 2 n
đoạn a,b (ta loại các nghiệm nằm ngoài đoạn a,b ).
Bước 3. Tính f a; f x ; f x ;...; f x ; f b . 1   2  n   TRẦN THÔNG
Facebook: hội toán bắc trung nam 39
Bước 4. Giá trị lớn nhất, nhỏ nhất trong các giá trị đã tính ở trên là các giá trị tương ứng cần tìm. Ví dụ minh họa
Ví dụ 1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số   4 f x x  trên đoạn 1,  3 . x Ta thấy hàm số   1 f x x
liên tục trên đoạn 1,  3 . x 4 x  2(n) Hơn nữ 4
a, f  x  1
nên f  x  1  0   2 x 2 xx  2(l  ) Lại có f    f    f   13 1 5; 2 4; 3  . 3
Suy ra max f x  f  
1  5; min f x  f 2  4. x   1,  3 x   1,  3
Vậy giá trị lớn nhất và nhỏ nhất của hàm số   4 f x x
trên đoạn 1,  3 là 5 và 4. x sin x 1
Ví dụ 2: Tìm giá trị lớn nhất và nhỏ nhất của hàm số y  2
sin x  sin x  1
Đặt t = sinx, điều kiện 1   t 1. t 1
Bài toán quy về tìm GTNN, GTLN của hàm số f (t)  trên đoạn  1  ;  1 . 2 t t 1
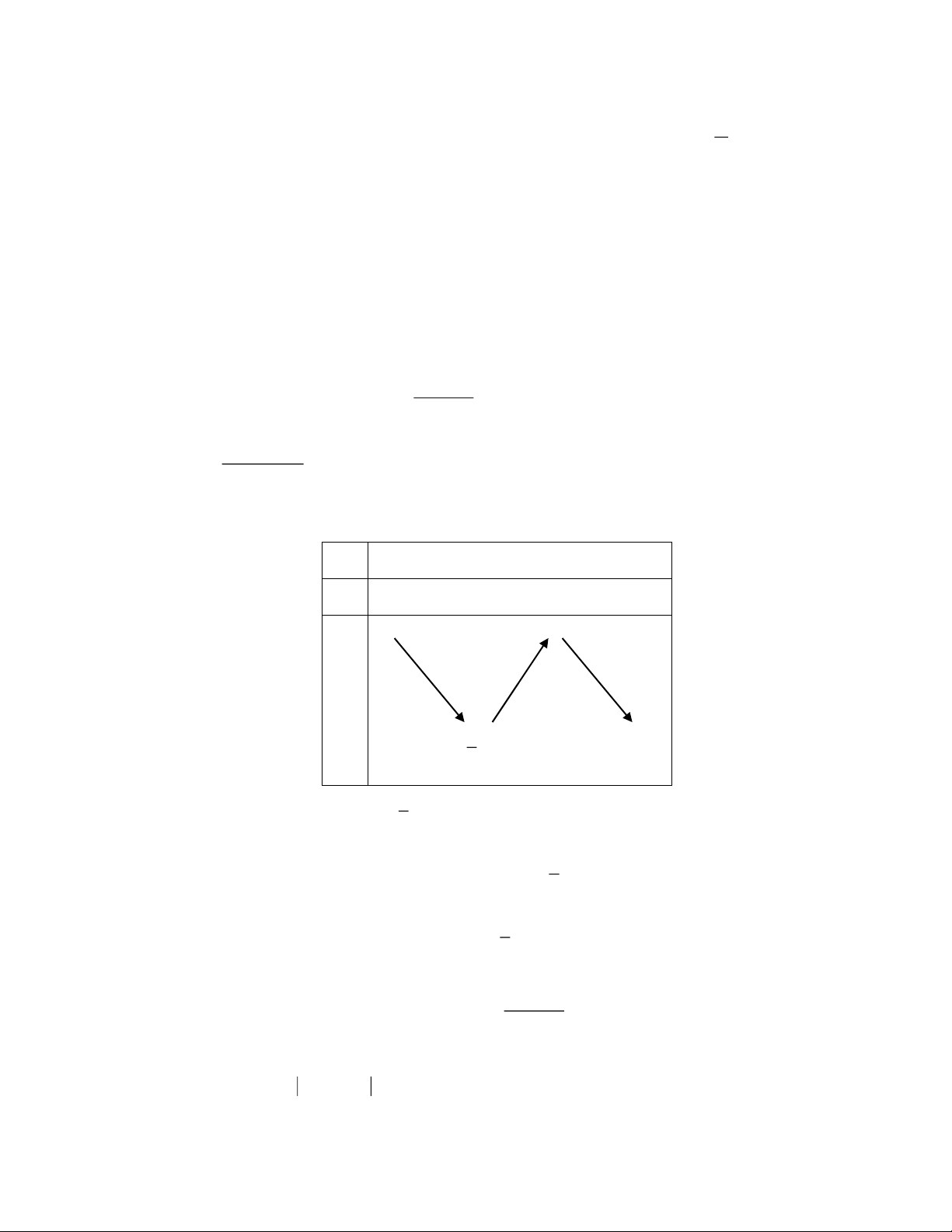
Bảng biến thiên của hàm số f(t) trên đoạn  1  ;  1 như sau: t -1 0 1  f’(t) + 0 - 1 f(t) 2 0 3
Từ bảng biến thiên suy ra GTNN, GTLN của hàm số f(t) trên đoạn  1  ; 
1 lần lượt là 0 (khi và chỉ
khi t = -1) và 1 (khi và chỉ khi t = 0). TRẦN THÔNG
Facebook: hội toán bắc trung nam 40 
Từ đó có: Maxy = 1 đạt được khi và chỉ khi: x k, Miny = 0 khi và chỉ khi:   k2 . 2
Chú ý: Nếu biểu thức xác định của hàm số có thể phân chia thành các nhóm số hạng và giữa
chúng có một mối liên hệ cho bởi các hệ thức toán học cho phép biểu diễn chúng qua nhau thì ta
có thể đưa bài toán đó về bài toán đơn giản hơn bằng phương pháp đổi biến số. Mối liên hệ giữa
các nhóm số hạng trong biểu thức xác định hàm số ở ví dụ trên là rõ ràng dễ thấy, điều này giúp
ta phát hiện cách đổi biến số không mấy khó khăn, tuy nhiên có những trường hợp mối liên hệ
giữa các nhóm số hạng được ẩn kín bên trong, đòi hỏi nhiều phép biến đổi và có cách nhìn tinh
mới phát hiện ra được. Trong phép đổi biến số cần chú ý cần phải tìm điều kiện cho biến để tránh
khỏi sai lầm khi giải toán. Chẳng hạn xét lại ví dụ 2 ta thấy: t 1
Đặt t = sinx, ta có hàm số theo t: f (t)  2t t  . 1 2 t   2tt  Ta có: ' f (t)  , f ’(t) = 0  0 
; lim f (x)  0 . 2 2 (t t 1)
t  2 x
Bảng biến thiên của hàm số f(t) như sau: t  -2 0  f’(t) - 0 + 0 - 0 1 f(t) 1  0 3 1
Từ BBT suy ra: m inf(t)  f ( 2)
   ; Maxf (t)  f ( ) 0  1. 3 1
Từ đó có GTNN, GTLN của hàm số ban đầu lần lượt là  và 1. 3 1
Theo lời giải trên thì hàm số f(x) nhận GTNN là 
khi: sinx = -2, điều này không xảy ra.Mặc 3
dù đã lựa chọn biến mới: t = sinx hợp lí nhưng chưa tìm điều kiện cho nó dẫn đến bài toán tìm t 1
GTNN, GTLN của hàm số theo biến số mới f (t)  2
t t  không tương thích với bài toán ban 1
đầu (ngoài ví dụ đang xét thì trong các ví dụ sau đều phải lưu ý điều này).
Ví dụ 3: Cho y f x 2
x 5x  4  m .
x Tìm các giá trị của m sao cho Min y  1 . TRẦN THÔNG
Facebook: hội toán bắc trung nam 41 2
x  m  5 x  4 ; x 1  x  4:  P1
Ta có f x   2
x  m  5 x  4 ; 1 x  4 :  P2 
Gọi (P) là đồ thị của y = f(x) (P) = (P1) (P2) khi đó (P) có 1 trong các hình dạng đồ thị sau đây P1 A P2 A P1 P1 A P2 P2 B B B C C C Hoành độ 5 m giao điểm (P
1), (P2) xA = 1; xB = 4 ; Hoành độ đỉnh (P1): x . C 2
Nhìn vào đồ thị ta xét các khả năng sau:
Nếu xC [xA, xB] m[ 3, 3] thì Minf(x) = Minf(1), f(4).  3   m  3 
Khi đó Minf(x) > 1 f (1)  m 1 1 < m 3 (1)
f (4)  4m 1    2     5 m m 10m 9
Nếu xC [xA, xB] m[ 3, 3] thì Minf(x) = f xf = 1  C  1    2  4 m[ 3  ,3]
Khi đó Minf(x) > 1  
 3  m  5  2 3 (2) 2
m 10m 13  0 
Kết luận: Từ (1) và (2) suy ra Minf(x) > 1 1  m  5  2 3
Bài tập tương tự 9 1 3 2
Bài 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y x 3x x trên đoạn 4 4 [ 1; 1]. TRẦN THÔNG
Facebook: hội toán bắc trung nam 42 4 2
Bài 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y x 2x 1 trên đoạn [ 1; 3]. x 1
Bài 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y trên đoạn [ 1; 2]. x 2 2
Bài 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) x 4x 5 trên đoạn [ 2; 3] . 2 2
Bài 5: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x   x  2   x  2  trên đoạn  1   ;2   .  2  3
Bài 6: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số 6 2 y x 4 1 x trên đoạn 1;1 . 2 x
Bài 7: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số y f x trên đoạn 5; 3 x 2 .
Bài 8: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số 2 y f x x 3x 2 trên đoạn 10;10 .
Bài 9: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số 3 2 y x 3x 1 trên đoạn 2;1 .
Bài 10: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số 2 y x 1 3x 6x 9 trên 1;3 . 3 2
Bài 11: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y x  3x  9x  1 trên đoạn [– 2; 2].
Bài 12: Tìm giá trị lớn nhất và nhỏ nhất của hàm số : 4 y x  2 2
x  3 trên đoạn  4 ; 0  .
Bài 13: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số ( ) x
f x e x trên đoạn  1  ;  1 .  3 
Bài 14: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3 2
f (x)  x  3x 1 trên đoạn 1  ;   .  2  TRẦN THÔNG
Facebook: hội toán bắc trung nam 43 2 2
Bài 15: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số ( )  (  2). x f x x e trên đoạn [–1 ; 2].
Bài 16: Tìm giá trị lớn nhất và nhỏ nhất của hàm số f x 4  x  3 
trên đoạn 2;5 x 1
Bài 17: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y x  2ln x trên 1;e .
Bài 18: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f x 2
x  ln 1 2x trên đoạn  1  ;0. x  2
Bài 19: Tìm giá trị lớn nhất, nhỏ nhất của hàm số y  trên đoạn [0;3] . 2x 1 2 2x  2x  8
Bài 20: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên đoạn  2  ;0 x 1 x
Bài 21: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x    2
ln x x  2 trên đoạn 2  1   ;3    3 
Bài 22: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số 2 y
4  x x .
Bài 23: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) 
5  4x trên đoạn  1  ;  1 4
Bài 24: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x)  x  2  2;4   x  trên đoạn 1 1
Bài 25: Tìm giá trị lớn nhất, nhỏ nhất của hàm số 2 2 y
x x  4x x 4 2 x
Bài 26: Tìm giá trị lớn nhất và nhỏ nhất của hàm số y
x 1  x 1  4
Bài 27: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số   2 ( )  2  7 x f x x x
e trên đoạn 0,  3
Bài 28: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x)  x  ln 1 2x trên đoạn 0,  1 2 x
Bài 29: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x) 
 4ln 3 x trên đoạn  2  ,  1 2 TRẦN THÔNG
Facebook: hội toán bắc trung nam 44 16 1 
Bài 30: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
f (x)  x  trên đoạn , 4   . x 3  2 2     
Bài 31: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3x 3x 4 3x 3x 4 f (x)  4  4 trên đoạn  1  ,  2 . 2 1 
Bài 32: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x) 
 ln x trên đoạn ,1   xe
Bài 33: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số 2 y x 1 2 2x 2x 4 trên 1;2 . 1
Bài 34: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số y sin x cos x
Bài 35: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số y 1 sin x 1 cos x
Bài 36: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số 2 y 3 2x x x
Bài 37: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y . 2 x 2 1 x s inx+2cos
Bài 38: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2    f (x)  , x  0; . x    2  cosx+2sin 2
Bài 39: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4 4
y  2x  2x  2 6  x  2 6  x   
Bài 40: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
f (x)  x  cos x, x  0; .    4 
Bài 41: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  sin x 1 (  cos x) 1 1
Bài 42: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y   4  sin x 4  cos x
Bài 43: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
f (x)  x log 2, x  2;e . x    
Bài 44: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x)=5cosx–cos5x,   x  . 4 4
Bài 45: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2 2
y x x 1 
x x 1, x 1;  1
Bài 46: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2 2
y  x  4x  21  x  3x 10 TRẦN THÔNG
Facebook: hội toán bắc trung nam 45
Bài 47: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4 2 2
2 1 x  1 x  1 x  3 f (x)  2 2
1 x  1 x 1
Bài 48: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 1 y  1 ( 2
 sin 2x cos4x)  (cos4x  cos8x) 2 cos x
Bài 49: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  , với 0  x  . 2
sin x(2 cos x  sin x) 3
Bài 50: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Dạng 4: Bài toán tiếp tuyến
Bài toán 1: Viết phương trình tiếp tuyến của (C): y f x tại điểm M x ; f x . 0  0
Phương pháp giải toán
Bước 1: Nếu cho x thì tìm y f (x ) .Nếu cho y thì tìm x là nghiệm của phương trình 0 0 0 0 0
f x y . 0 
Bước 2: Tính y  f (x) . Suy ra y (   0 x ) f ( 0 x )
Bước 3: Phương trình tiếp tuyến  là: y – y f (x ).(x – . 0 0 0 x ) Ví dụ minh họa
Ví dụ 1: Cho hàm số 3
y x  3x  2 (C)
a. Viết phương trình tiếp tuyến của (C) tại điểm M 2;4 . 1
b. Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x  . 2
c. Viết phương trình của (C) tại các điểm có tung độ là 0. Hướng dẫn a.Ta có 2
y  3x  3
Suy ra hệ số góc của tiếp tuyến tại điểm M 2; 4 là y '  2  9 .
Phương trình tiếp tuyến của (C) tại điểm M là y  9x 14. 1 1
b. Điểm thuộc đồ thị hàm số có hoành độ x 
, có tung độ y  0 2 0 2 Ta có 2
y  3x  3  1 1   1  9
Suy ra hệ số góc của tiếp tuyến tại tiếp điểm ;   là y '      2 2   2  4 TRẦN THÔNG
Facebook: hội toán bắc trung nam 46   9 13 Phương tình tiế 1 1
p tuyến của (C) tại điểm ; 
là y   x  .  2 2  4 8
c.Điểm thuộc (C) có tung độ y  0 , có hoành độ x  2
hoặc x  1. 0 01 02 Ta có 2
y  3x  3
Hệ số góc của tiếp tuyến tại điểm  2  ;  0 là y '  2  9 .
Phương tình tiếp tuyến của (C) tại điểm  2  ; 
0 là y  9x 18.
Hệ số góc của tiếp tuyến tại điểm 1;0 là y '  1  0 .
Phương tình tiếp tuyến của (C) tại điểm 1;0 là y  0.
Phương trình của hai tiếp tuyến của (C) tại điểm có tung độ bằng 0 là y  9x 18 và y  0 .
Ví dụ 2: Cho hàm số 4 2
y x  2x (C). Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có tung độ y  8.
Điểm thuộc đồ thị hàm số có tung độ y  8 , có hoành độ x  2  . 0 0 Ta có 3
y  4x  4x nên hệ số góc của tiếp tuyến tại tiếp điểm 2;8 và 2;  8 lần lượt là
y '2  24, y'  2  24 .
Suy ra phương tình tiếp tuyến của (C) tại điểm 2; 
8 là y  24x  56 và tại điểm 2;  8 là y  24x  40.
Bài toán 2: Viết phương trình tiếp tuyến của (C): y f (x) , biết có hệ số góc k cho trước.
Phương pháp giải 1: Tìm toạ độ tiếp điểm.
Bước 1: Gọi M(x ;y ) ( ) 0
0 là tiếp điểm. Tính f x0 .
Bước 2:  có hệ số góc k nên f (  0 x ) k
Bước 3: Giải phương trình (1), tìm được x  ( ) 0 và tính y f x 0
0 . Từ đó viết phương trình của .
Phương pháp giải 2: Dùng điều kiện tiếp xúc.
Bước 1: Phương trình đường thẳng  có dạng: y kx m.  f
  x  kx m
Bước 2:  tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:     f    x *  k
Bước 3: Giải hệ (*), tìm được m. Từ đó viết phương trình của .
Chú ý: Hệ số góc k của tiếp tuyến  có thể được cho gián tiếp như sau:
+  tạo với trục hoành một góc  thì k  tan a .
+  song song với đường thẳng d: y ax b thì k a . TRẦN THÔNG
Facebook: hội toán bắc trung nam 47 1
+ vuông góc với đường thẳng y ax  ,
b a  0 thì k   . a k a
+  tạo với đường thẳng y ax b một góc  thì  tan . 1  ka Ví dụ minh họa 2x  1
Ví dụ 1: Cho hàm số y x  (C). Viết phương trình tiếp tuyến của (C) , biết hệ số góc của 1
tiếp tuyến k  4. 1 Ta có y   x   . 2 1
Điểm Mx ; y thuộc đồ thị (C), có hệ số góc của tiếp tuyến tại M là y'x  4 . 0  0 0  3 Khi đó, ta có: 1 1 1            4 x 1 x hoặc x . 02 x 1 2 2 2 0 2 0 01     Tung độ 1 3 của điểm M là y   0 hoặc y   4 . 01      2  01  2 
Vậy có hai tiếp tuyến có phương trình là y  4x  2 và y  4x 10 . 4 2
Ví dụ 2: Cho hàm số y x  2x (C). Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến
song song với đường thẳng y  24x  2017 . 3
Ta có y  4x  4x
Vì tiếp tuyến song song với đường thẳng y  24x  2017 nên hệ số góc của tiếp tuyến bằng 24 .
Điểm Mx ; y thuộc (C) có hệ số góc tiếp tuyến tại M là y'x  24 . 0  0 0  Khi đó, ta có: 3
4x  4x  24  0  x  2 2 4x
8x 12  0  x  2 0 0 0 0 0  0
Lúc này tung độ của M là y  8 0 .
Phương trình tiếp tuyến của (C) tại điểm M là y  24x  56 . 4 2
Ví dụ 3: Cho hàm số y x  2x (C). Trên (C) lấy hai điểm phân biệt A và B có hoành độ lần
lượt là a và b. Tìm điều kiện đối với a và b để hai tiếp tuyến của (C) tại A và B song song với nhau.
Ta có: f x x3 '( ) 4  4x
Hệ số góc tiếp tuyến của (C) tại A và B là k f a a3  a k f b b3 '( ) 4 4 , '( ) 4  b 4 A B
Tiếp tuyến tại A, B lần lượt có phương trình là: y f (
a)(x a)  f (a)  y f (a)x f (a)  af (a) TRẦN THÔNG
Facebook: hội toán bắc trung nam 48 y f (
b)(x b)  f (b)  y f (b)x f (b)  bf (b)
Hai tiếp tuyến của (C) tại A và B song song hoặc trùng nhau khi và chỉ khi: 3 3
k k a a = 4b b a b a2  ab b2 4 4 4 ( )( 1)  0 (1) A B 2 2
Vì A và B phân biệt nên a b , do đó (1) a ab b 1 0 (2)
Mặt khác hai tiếp tuyến của (C) tại A và B trùng nhau khi và chỉ khi:  2 2 2 2            a ab b 1 0 a ab b 1 0  
(a b)   f (a) 
af (a)  f (b)  bf (b)  a4 3  a2 2   b4 3  b2 2
Giải hệ này ta được nghiệm là (a;b)  ( 1
 ;1) hoặc (a;b)  (1; 1
 ) , hai nghiệm này tương ứng với
cùng một cặp điểm trên đồ thị là ( 1  ; 1  ) và (1; 1  )
Vậy điều kiện cần và đủ để hai tiếp tuyến của (C) tại A và B song song với nhau là: 2 2      a ab b 1 0  a   1  ; a b
Bài toán 3: Viết phương trình tiếp tuyến của (C): y f (x) , biết đi qua điểm (
A x ; y ) A A
Phương pháp giải 1: Tìm toạ độ tiếp điểm.
Bước 1: Gọi M (
là tiếp điểm. Khi đó y f (x ), y (
x )  f (x ) . 0 x ; 0 y ) 0 0 0 0
Bước 2: Phương trình tiếp tuyến  tại M: y – y f (x ).(x – 0 0 0 x )
Bước 3:  đi qua (
A x ; y ) nên: y – y f (  x ).(x – A 0 0 A 0 x )**. A A
Bước 4: Giải phương trình (**), tìm được x0 . Từ đó viết phương trình của .
Phương pháp giải 2: Dùng điều kiện tiếp xúc.
Bước 1: Phương trình đường thẳng  đi qua (
A x ; y ) và có hệ số góc k: y – y k(x – . A A x ) A A
Bước 2:  tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:  f
  x  k x x y A A     f    x ***  k
Bước 3: Giải hệ (***), tìm được x,k. Từ đó viết phương trình của . Ví dụ minh họa TRẦN THÔNG
Facebook: hội toán bắc trung nam 49
Bài toán 4: Viết phương trình tiếp tuyến của (C): y f (x) , biết cắt hai trục toạ độ tại A
và B sao cho tam giác OAB vuông cân hoặc có diện tích S cho trước. Phương pháp giải:
Bước 1: Gọi M (
là tiếp điểm. Khi đó:     . 0 x ; 0 y ) 0 y f ( 0 x ), y ( 0 x ) f ( 0 x )
Bước 2: Xử lý giả thuyết 0
+ OAB vuông cân   tạo với Ox một góc 45 và O  .(a) + S S O . A OB 2S O     . (b) AB
Bước 3: Giải (a) hoặc (b) tìm được 0
x . Từ đó viết phương trình tiếp tuyến . Ví dụ minh họa x  2
Ví dụ 1: Cho hàm số y  .  1 2x
Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp 3
tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. 1
Gọi (x ; y ) là toạ độ của tiếp điểm y (  x )   0 0 0 0 (2x 2  3) 0
OAB cân tại O nên tiếp tuyến song song với đường thẳng y  x (vì tiếp tuyến có hệ số góc
x  1 y  1 âm). Nghĩa là: 1 0 0 y (  x )   1 0 (2x 2  3)
x  2  y  0 0  0 0 + Với x  1
 ; y  1 : y 1 (
x 1)  y  x (loại) 0 0 + Với x  2
 ; y  0 : y  0  (
x  2)  y  x  2 (nhận) 0 0
Vậy phương trình tiếp tuyến cần tìm là: y  x  2 . 2x  1
Ví dụ 2: Cho hàm số y
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận. Tìm điểm M x 1
thuộc (C) sao cho tiếp tuyến của (C) tại M cắt 2 tiệm cận tại A và B với chu vi tam giác IAB đạt giá trị nhỏ nhất.  3 
Giao điểm của 2 tiệm cận là I (1;2) . Gọi M  x ;2  0   (C). x 1 0  TRẦN THÔNG
Facebook: hội toán bắc trung nam 50 3 3
PTTT tại M có dạng: y
(x x )  2  0 2  x x 1 ( 1) 0 0  6 
Toạ độ các giao điểm của tiếp tuyến với 2 tiệm cận: A  2 ; 1  , B (2x 1;2)   0  x 1 0  1 1 6 Ta có: S IA I . B 2 x 1 2.3 6         (đvdt) IAB 2 2 x 0 1 0
IAB vuông có diện tích không đổi chu vi IAB đạt giá trị nhỏ nhất khi IA= IB  6 x  1  3 0  2 x 1  0  x 1 0 x  1 3 0 M 1 3; 2  3 M 1 3; 2  3
Vậy có hai điểm M thỏa mãn điều kiện , .Khi đó chu vi 1 2
AIB = 4 3  2 6 . 2 2
Chú ý: Với 2 số dương a, b thoả ab = S (không đổi) thì biểu thức P = a b a b nhỏ nhất
khi và chỉ khi a = b.Thật vậy: P = a b a2 b2     2 ab a
2 b  (2  2) ab  (2  2) S
.Dấu "=" xảy ra a = b. 2x  3
Ví dụ 3: Cho hàm số y  C. x
Cho M là điểm bất kì trên (C). Tiếp tuyến của (C) tại M cắt 2
các đường tiệm cận của (C) tại A và B. Gọi I là giao điểm của các đường tiệm cận. Tìm toạ độ
điểm M sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất.  2x  3  1 
Giả sử M x 0 ;
, x  2, y'(x )   0 x  0  2  0 2 0  x 2 0  1  2x  3
Phương trình tiếp tuyến () với ( C) tại M: y  (x x 0 )     0 2 x x 2 2 0 0  2x  2 
Toạ độ giao điểm A, B của () với hai tiệm cận là: A 0 2;
; B2x  2;2   0  x  2  0  x x 2  2x  2 y y 2x  3 Ta thấy A B 0   x x , A B 0 
y suy ra M là trung điểm của 0 M 2 2 M 2 x  2 0 AB. TRẦN THÔNG
Facebook: hội toán bắc trung nam 51
Mặt khác I(2; 2) và IAB vuông tại I nên đường tròn ngoại tiếp tam giác IAB có diện tích 2    2x     2  2 3 0  2 1
S = IM   (x  2)  
 2   (x  2)    2 0   x  0  2     (x 2   0 2)  0    1 x  1
Dấu “=” xảy ra khi (x 2 0  2)    0 2 x x  3 (  2)  0 0
Do đó điểm M cần tìm là M(1; 1) hoặc M(3; 3).
Bài toán 5: Tìm những điểm trên đường thẳng d mà từ đó có thể vẽ được 1, 2, 3, ... tiếp tuyến
với đồ thị (C): y f (x) . Phương pháp giải:
Bước 1: Giả sử d : ax by c  0, M(x ;y )d . M M
Bước 2: Phương trình đường thẳng  qua M có hệ số góc k: y k(x – x )  y M M
 tiếp xúc với (C) khi hệ sau có nghiệm:
f x k x xy  ( ) ( ) (1) M M f '(x)  k (2)
Thế k từ (2) vào (1) ta được: f (x)  (x – x ). f (
x )  y (3) M M M
Bước 3: Số tiếp tuyến của (C) vẽ từ M = Số nghiệm x của (3) Ví dụ minh họa
Ví dụ 1: Cho hàm số y x x3 3
(C).Tìm trên đường thẳng (d): y  x các điểm M mà từ đó kẻ
được đúng 2 tiếp tuyến phân biệt với đồ thị (C).
Gọi M(m;m) d . PT đường thẳ
ạng: y k(x m)  m.    x
3  x3  k(x m)  m (1)
là tiếp tuyến của (C) hệ PT sau có nghiệm: (*) 3   x2 3  k (2) 3
Thay (2) vào (1) ta đượ 2x c: x3  mx2 2 3  m 4  0 m (**) x2 3  4
Từ M kẻ được đúng 2 tiếp tuyến với (C) (**) có 2 nghiệm phân biệt 2x3  2 3 2 3
Xét hàm số f (x) 
. Tập xác định D R \  ;  x2 3  4  3 3  TRẦN THÔNG
Facebook: hội toán bắc trung nam 52 6x4  24x2 x  0 f (  x)  ; f (  x)  0   ( x2 2 3  4) x   2  m 2 
Dựa vào BBT, (**) có 2 nghiệm phân biệt . Vậy: M( 2  ;2) hoặc M(2; 2  ) . m   2
Ví dụ 2: Cho hàm số y x3  x2 2
 (m1)x m 2
(Cm). Tìm m để từ điểm M(1;2) kẻ được đúng 2
tiếp tuyến với (Cm).
PT đường thẳng qua M có dạng: y k(x 1)  2 . là tiếp tuyến của (Cm) hệ PT sau có
x3  2x2  (m1)x m 2
k(x 1)  2 nghiệm: x2 3 
 4x m1 k
f x x3  x2 ( ) 2 5
 4x  3(m1)  0 (*)
Để qua M kẻ được đúng hai tiếp tuyến đến (Cm) thì (*) có đúng 2 nghiệm phân biệt
Ta có f x x2 2 ( ) 6
10x  4  f (x)  0  x  1; x 3   2 109 
Các điểm cực trị của (Cm) là: A(1;4  m 3 ), B ;  m 3  .  3 27   4 m   
Do đó (*) có đúng 2 nghiệ AOx
m phân biệt 3    . B  Ox 109 m  81
Bài toán 6: Tìm những điểm trên đường thẳng d mà từ đó có thể vẽ được 1, 2, 3, ... tiếp tuyến
với đồ thị (C): y f (x) . Phương pháp giải:
Bước 1: Gọi M(x ; y ) . Phương trình đường thẳng  qua M có hệ số góc k: y k(x – x )  y M M M M
Bước 2:  tiếp xúc với (C) khi hệ sau có nghiệm:
f (x)  k(x x )  y (1) M Mf '(x)   k (2)
Thế k từ (2) vào (1) ta được: f (x)  (x – x ). f (
x )  y (3) M M M
Qua M vẽ được 2 tiếp tuyến với (C)  (3) có 2 nghiệm phân biệt x , x . 1 2
Bước 3: Hai tiếp tuyến đó vuông góc với nhau  f (
x ).f (x )  –1.Từ đó tìm được M. 1 2 Ví dụ minh họa TRẦN THÔNG
Facebook: hội toán bắc trung nam 53 1
Ví dụ 1: Cho hàm số y f (x)  mx3  m ( 1 x2 )  (4 m 3 x
) 1 có đồ thị là (Cm).Tìm các giá trị m 3
sao cho trên đồ thị (Cm) tồn tại một điểm duy nhất có hoành độ âm mà tiếp tuyến tại đó vuông góc
với đường thẳng (d): x y 2  3  0 . 1
(d) có hệ số góc tiếp tuyến có hệ số góc k  2 . Gọi x là hoành độ tiếp điểm thì: 2
f x   mx2  mx
m   mx2 '( ) 2 2( 1) (4 3 ) 2
 2(m1)x  2 m 3  0 (1)
YCBT (1) có đúng một nghiệm âm.
+ Nếu m  0 thì (1)   x 2  2
  x  1 (loại) 2  m 3
+ Nếu m  0 thì dễ thấy phương trình (1) có 2 nghiệm là x  1 hay x= mDo đó để 2 m 3 2
(1) có một nghiệm âm thì
 0  m 0 hoaëc m m 3 2
Vậy m  0 hay m . 3
Ví dụ 2: Cho hàm số y x3  mx m1 (Cm). Tìm m để tiếp tuyến của đồ thị (Cm) tại điểm M
có hoành độ x  1
 cắt đường tròn (C) có phương trình x 2   y 2 ( 2)
(  3)  4 theo một dây cung có độ dài nhỏ nhất.
Ta có: y  x2 3
m y (1)  3 m; y( 1  )  m
2  2 . (C) có tâm I (2;3) , R = 2. PTTT d tại M( 1  ; m
2  2) : y  (3 m)x m1 (3 m)x y m1 0 4  m 1 (3 m) 2. (3 m 2 ) 1
d(I ,d)     2  R (3 m 2 ) 1 (3 m 2 ) 1 (3 m 2 )  1
Dấu "=" xảy ra m  2 . Dó đó d(I ,d) đạt lớn nhất m  2
Tiếp tuyến d cắt (C) tại 2 điểm A, B sao cho AB ngắn nhất d(I ,d) đạt lớn nhất m  2
Khi đó: PTTT d: y x  3. Bài tập luyện thi
Bài 1: Cho hàm số y f x 3 2
x  3x 1có đồ thị là C.
a. Viết phương trình tiếp tuyến của C tại điểm có hoành độ bằng 0.
b. Viết phương trình tiếp tuyến của C tại điểm có tung độ bằng 1.
c. Viết phương trình tiếp tuyến của C biết nó có hệ số góc bằng -3. TRẦN THÔNG
Facebook: hội toán bắc trung nam 54
d. Viết phương trình tiếp tuyến của C biết nó song song với đường thẳng y  9  x 1 . 1
e. Viết phương trình tiếp tuyến của C biết nó vuông góc với đường thẳng y   x  1 . 9
f. Viết phương trình tiếp tuyến của C nó biết hợp với trục 0x góc 45 độ .
g. Viết phương trình tiếp tuyến của C tại những điểm giao với đường thẳng y=1.
Bài 2: Cho hàm số y f x 4 2
x  2x 1có đồ thị là C.
a. Viết phương trình tiếp tuyến của C tại điểm có hoành độ bằng 2.
b. Viết phương trình tiếp tuyến của C tại điểm có tung độ bằng 2.
c. Viết phương trình tiếp tuyến của C biết nó có hệ số góc bằng -24.
d. Viết phương trình tiếp tuyến của C biết nó song song với đường thẳng y  24  x 12 1
e. Viết phương trình tiếp tuyến của C biết nó vuông góc với đường thẳng y  x  1 . 24
f. Viết phương trình tiếp tuyến của C biết nó hợp với trục 0x góc 45 độ .
g. Viết phương trình tiếp tuyến của C tại những điểm giao với đường thẳng y=-1. x
Bài 3: Cho hàm số y f x 2  có đồ thị là C. 2x 1
a. Viết phương trình tiếp tuyến của C tại điểm có hoành độ bằng 1.
b. Viết phương trình tiếp tuyến của C tại điểm có tung độ bằng 2.
c. Viết phương trình tiếp tuyến của C biết nó có hệ số góc bằng 2.
d. Viết phương trình tiếp tuyến của C biết nó song song với đường thẳng y  8x-2016 1
e. Viết phương trình tiếp tuyến của C biết nó vuông góc với đường thẳng y x . 18
f. Viết phương trình tiếp tuyến của C biết nó hợp với trục 0x góc 45 độ .
g. Viết phương trình tiếp tuyến của C biết nó cắt hai trục toạ độ tại A và B sao cho tam giác OAB vuông cân .
h. Viết phương trình tiếp tuyến của C biết nó cắt hai đường tiệm cận tại A và B sao cho tam giác OAB vuông cân .
i. Lập phương trình tiếp tuyến của đồ thị (C) tại những điểm thuộc đồ thị có khoảng cách đến
đường thẳng d : x 3  y 4  2  0 bằng 2. 1 Bài 3:Cho hàm số 3 2 y
x  2x  3x  1 
1 . Viết phương trình tiếp tuyến của đồ thị hàm số (1) 3
biết tiếp tuyến song song với đường thẳng y  3x  1. TRẦN THÔNG
Facebook: hội toán bắc trung nam 55 x
Bài 4: Cho hàm số y  2x  (C). Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng 1 2 . 3
Bài 5: : Cho hàm số : 3 2
y  x  3x  4 . Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc. Bài 6: Cho hàm số: 3 2
y x  3x  1 có đồ thị là (C). Viết phương trình tiếp tuyến của đồ thị (C) tại điểm (
A 1;5) . Gọi B là giao điểm của tiếp tuyến với đồ thị (C) (BA). Tính diện tích tam giác
OAB, với O là gốc tọa độ. Bài 7: Cho hàm số 3 2
y x  3x  3x  2 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị
(C) tại giao điểm của (C) với trục tung. 2x  3
Bài 8: Cho hàm số : y
(C) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có x  1 tung độ bằng 1.
Bài 9: Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số 3
y  x  3x  2 .Viết phương trình
tiếp tuyến của đồ thị (C) tại điểm có hoành độ x thỏa mãn phương trình y " x  12 . 0  0 2x  1
Bài 10: : Cho hàm số y
(C). Viết phương trình tiếp tuyến của (C) tại điểm A là giao x  1
điểm của (C) với trục hoành. Bài 11: Cho hàm số 3 2
y x  3x  4.(C) Viết phương trình tiếp tuyến của (C), biết tiếp tuyến đó
có hệ số góc bằng 9.
Bài 12: Viết phương trình tiếp tuyến của đồ thị (C) : y
3  2x tại điểm M có hoành độ x0 = 1. 4 x 5 Bài 13: Cho hàm số 2 y
 3x  (C). Cho điểm M thuộc (C) có hoành độ x 1. Viết 2 2 M
phương trình tiếp tuyến của (C) tại M. 2x  3
Bài 14: Cho hàm số y d
y x m cắt (C) tại hai x
(C). Tìm m để đường thẳng   : 2 2
điểm phân biệt và tiếp tuyến của (C) tại hai điểm đó song song với nhau. Bài 15: Cho hàm số 3 2
y  x  3x C  . Lập phương trình tiếp tuyến của (C) tại các giao điểm
của đồ thị với trục hoành. TRẦN THÔNG
Facebook: hội toán bắc trung nam 56 1
Bài 16: Viết phương trình tiếp tuyến của đồ thị hàm số f (x) 
. Biết tiếp tuyến có hệ số góc là x 1  . 4 2x 1
Bài 17: Viết phương trình tiếp tuyến d của đồ thị hàm số y x  biết d có hệ số góc bằng – 1. 1 Bài 18: Cho hàm số 3 2
y x  3x  2. Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến
vuông góc với đường thẳng  có phương trình: x  2016  0 . 2x 1
Bài 19: Cho hàm số y
. Xác định tọa độ giao điểm của đồ thị (C) với đường thẳng x  1
y x  7 và viết phương trình tiếp tuyến của (C) tại các giao điểm ấy.
Bài 20: Viết phương trình tiếp tuyến của đồ thị hàm số 3
y x  4x  3 tại giao điểm của nó với trục tung. Bài 21: Cho hàm số 3 3
y  x  3x 1 (1). Viết phương trình tiếp tuyến của đồ thị (C) tại giao
điểm của (C) với đường thẳng d : y  2x  7 . x  3
Bài 22: Cho hàm số y x  có đồ thị (C). Viết phương trình tiếp tuyến với (C) biết hình chiếu 2
vuông góc của hai điểm A(1;1), B(0;-3) lên tiếp tuyến trùng nhau Bài 23: Cho hàm số 3 2
y x  6x  9x  4 (C). Viết pttt với (C), biết tiếp tuyến song song với y = 9x – 4. Bài 24: Cho hàm số 3 2
y  x  6x  9x  2 (C).Viết pttt với (C), biết hoành độ tiếp điểm của tiếp
tuyến là nghiệm của pt f ' (x)  18 Bài 25: Cho hàm số 3
y  x  3x  2 Viết pttt của (C) tại giao điểm của (C) và d: y = - x – 2, biết
tiếp điểm có hoành độ dương. Bài 26: Cho hàm số 3 2
y x  3x  2 . Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của
(C) với đường thẳng d : y  x  3 . Bài 27: Cho hàm số 4 2
y x  2x 1 (1). Viết pttt của (C) biết tiếp tuyến đi qua M(0;-1). x  2
Bài 28: Cho hàm số: y 
(C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến song 2x 1
song với đường thẳng d : y  5x  2 . TRẦN THÔNG
Facebook: hội toán bắc trung nam 57
Bài 29: Khảo sát và vẽ đồ thị (C) của hàm số 3
y x  3x  2 Tìm tọa độ của điểm M trên (C) sao
cho tiếp tuyến của (C) tại M song song với đường thẳng (d): 9x – y - 18 = 0 2x 1
Bài 30: Cho hàm số: y
(H). Viết phương trình tiếp tuyến của (H), biết nó cắt đồ thị tại x 1
hai điểm A,B sao cho tam giác ABC đều trong đó C 2,5 . 2x m 1
Bài 31: Cho hàm số y  C   1 C tại x
. Viết phương trình tiếp tuyến của đồ thị  m  2 m 2
giao điểm của C với trục tung, biết khoảng cách từ gốc tọa độ O đến tiếp tuyến đó bằng . m  5
Bài 32: Tìm m để tiếp tuyến của đồ thị 3 C : x 1 m x
1 tại điểm C có x 0 và chắn C
hai trục tọa độ một tam giác có diện tích S 8 . Bài 33: Cho hàm số 4 2 y x 4x
1 C Xác định tọa độ các giao điểm của C và đường thẳng y
1. Viết phương trình tiếp tuyến của C tại các giao điểm đó.
Bài 34: Tính diện tích tam giác chắn hai trục tọa độ bởi tiếp tuyến của đồ thị 2 C : y x 27x
26 tại điểm B có x 2 . B 4 1
Bài 35: Cho C y x m x m x
.Gọi A là giao điểm của C và trục m m  3 : 2  2 1  2 3 3 Oy. Tìm m để 1
tiếp tuyến tại A tạo với hai trục tọa độ một tam giác có diện tích bằng . 3
Bài 36: Cho A,B,C là ba điểm thẳng hàng nằm trên đồ thị hàm số 3 2
y x  3x  2C .Tiếp tuyến
của C tại A,B,C cắt đồ thị C tại A', B ',C ' . Chứng minh A', B ',C ' thẳng hàng.
Bài 37: Viết phương trình tiếp tuyến của đồ thị hàm số 3 2
y x x 1 biết nó tạo với các trục tọa độ tam giác cân. 2x 1
Bài 38: Cho y
Ccó I là giao điểm hai đường tiệm cận. M là điểm bất kỳ trên C. x 1
Tiếp tuyến của C tại M cắt các đường tiệm cận tại các điểm A,B. Chứng minh M là trung
điểm AB và diện tích tam giác IAB không đổi. Tìm M thuộc (C) sao cho chu vi của tam giác
IAB đạt giá trị nhỏ nhất. 2x 1
Bài 39: Cho y
Ccó I là giao điểm hai đường tiệm cận. M là điểm bất kỳ trên C.Tìm x 1
tọa độ điểm M để tiếp tuyến tại M vuông góc với IM. TRẦN THÔNG
Facebook: hội toán bắc trung nam 58 x 2
Bài 40: Cho hàm số: y
C .Viết phương trình tiếp tuyến của C biết rằng nó cắt hai x 1
đường tiệm cận tại hai điểm phân biệt A,B sao cho bán kính đường tròn nội tiếp tam giác OAB nhỏ nhất x 1
Bài 41: Cho hàm số y x  (C) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến cắt 2
hai đường tiệm cận của (C) lần lượt tại A và B sao cho tam giác ABI có bán kính đường tròn nội
tiếp bằng 2  2 , với I là giao điểm của hai đường tiệm cận. 2x
Bài 42: Viết phương trình tiếp tuyến của đồ thị (C) hàm số : y x  biết tiếp tuyến cắt trục Ox, 2 Oy lần lượt tại ,
A B sao cho AB  2OA . x 1
Bài 43: Tìm tọa độ điểm ,
A B thuộc đồ thị (C) hàm số: y x  sao cho tiếp tuyến của (C) tại 2
A song song tiếp tuyến của (C) tại B và AB  2 2 . x 1
Bài 44: Chứng minh đường thẳng y x m cắt đồ thị (C) hàm số y  2x  tại hai điểm phân 1 biệt ,
A B . Gọi k , k lần lượt là hệ số góc tiếp tuyến của (C) tại ,
A B . Tìm m để k k đạt giá 1 2 1 2 trị lớn nhất. 1
Bài 45: Cho hàm số: 3 2 y mx m 1 x 4 3m x
1 (C ). Định giá trị của m để đồ 3 m
thị hàm số (C ) tồn tại duy nhất một điểm có hoành độ âm sao cho tiếp tuyến tại đó vuông góc m
với đường thẳng x  2 y  3  0 .
Dạng 6: Sự tương giao giửa đồ thị
Bài toán 1: Biện luận số nghiệm phương trình
Phương pháp giải bài toán: Dựa vào các điểm đặc biệt của đồ thị (thường là các điểm cực trị ,các
đường tiệm cận) và sự tương giao của đồ thị và đường thẳng nằm ngang để tìm ra điều kiện của tham số. Ví dụ minh họa
Ví dụ 1: Dựa vào đồ thị hàm số: 4 2 y x 4x
3 tìm các giá trị của tham số thực m để phương trình 4 2 x 4x 3 2m
0 có hai nghiệm phân biệt. Ta có 4 2 4 2 x 4x 3 2m 0 x 4x 3 2m (*)
Suy ra số nghiệm pt (*) bằng số giao điểm của 4 2 (C) : y x 4x 3 và TRẦN THÔNG
Facebook: hội toán bắc trung nam 59 d: y = 2m. 1 3 
Dựa vào đồ thị tìm được : 2m = 1 hoặc 2m < –3 hay m  ;m  . 2 2 3 1 Vậy khi m hoặc m phương trình 4 2 x 4x 3 2m
0 có hai nghiệm phân biệt. 2 2 3 2
Ví dụ 2: Dựa vào đồ thị hàm số: y  x  6x  9x  1 tìm các giá trị của tham số thực m để phương trình  2
x(x 3)  m có ba nghiệm phân biệt. 2 3 2
Ta có x(x  3)  m  x  6x  9x  1  m  1. (*)
Suy ra số nghiệm pt (*) bằng số giao điểm của 3 C y x x2 ( ) : 6 9x 1 và d: y = m-1.
Dựa vào đồ thị tìm được : 1  m  1  3  0  m  4 2
Vậy khi 0  m  4 phương trình x(x  3)  m có hai nghiệm phân biệt.
Ví dụ 3: Tìm k để phương trình   * 3 2 3 2
x  3x k  3k  0 có 3 nghiệm phân biệt. Phương trình  
* tương đương với 3 2 3 2
x  3x k  3k .
Nếu đặt f x 3 2
x 3x thì phương trình trở thành
f x  f k .  
* có ba nghiệm phân biệt đường thẳng y f k có ba điểm chung với đồ thị hàm số
y f x 4
  f k  0 .
Từ đồ thị hàm số y f k , ta thấy điều kiện 4
  f k  0 tương đương với k  1  ;3 \0;  2 .
Bài toán 2:Sự tương giao giữa 2 đồ thị
Cho y f x C và y g x C . Để tìm giao điểm của C và C , ta làm như sau: 2  1  2  1 
Bước 1: Tìm hoành độ giao điểm. Hoành độ giao điểm của C và C là nghiệm của phương 2  1 
trình f x  g x   * .Phương trình  
* được gọi là phương trình hoành độ giao điểm của C 1  và C . 2  TRẦN THÔNG
Facebook: hội toán bắc trung nam 60
Bước 2: Tìm giao điểm. Nếu x là một hoành độ giao điểm thì x ; f x (  x ; g x ) là một 0  0 0  0 0
giao điểm của C và C . 2  1 
Chú ý. Để giải các bài toán loại này, ta rất hay sử dụng định lý Vi-ét đảo:  b x x    1 2  a
Nếu x , x là các nghiệm của phương trình bậc hai 2
ax bx c  0 ( a  0 ) thì  . 1 2 cx .x   1 2  a Ví dụ minh họa 1 2
Ví dụ 1: Cho hàm số 3 2 y
x mx x m có đồ thị C (
) . Tìm m để C ( ) cắt trục hoành 3 3 m m
tại 3 điểm phân biệt có tổng bình phương các hoành độ lớn hơn 15. C (
) cắt trục hoành tại 3 điểm phân biệt có tổng bình phương các hoành độ lớn hơn 15. m  1 2 2 2 2
x3  mx2  x m
 0 (*) có 3 nghiệm phân biệt thỏa x x x  15. 3 3 1 2 3   1
Ta có: (*) x x2 ( 1)(  (1 m 3 )x  2  m 3 )  x 0
g(x)  x2  (1 m 3 )x  2  m 3  0 Do đó: YCBT  2 2
g(x)  0 có 2 nghiệm x , x phân biệt khác 1 và thỏa x x  14 . 1 2 1 2
m  1
Vậy thỏa yêu cầu bài toán.
Ví dụ 2: Cho hàm số y x3  3x2  9x m , trong đó m là tham số thực. Tìm tất cả các giá trị
của tham số m để đồ thị hàm số đã cho cắt trục hoành tại 3 điểm phân biệt có hoành độ lập thành cấp số cộng.
Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt có hoành độ lập thành cấp số cộng Phương trình 3 2
x  3x  9x m  0 có 3 nghiệm phân biệt lập thành cấp số cộng Phương trình 3 2
x  3x  9x  m có 3 nghiệm phân biệt lập thành cấp số cộng
Đường thẳng y  m đi qua điểm uốn của đồ thị (C) m   1  1 m 1 . 1
Vậy thỏa yêu cầu bài toán. TRẦN THÔNG
Facebook: hội toán bắc trung nam 61 x  3
Ví dụ 3: Cho hàm số y
. Viết phương trình đường thẳng d qua điểm I ( 1  ;1) và cắt đồ thị x 1
(C) tại hai điểm M, N sao cho I là trung điểm của đoạn MN.
Phương trình đường thẳng d : y k x   1 1 x  3
d cắt (C) tại 2 điểm phân biệt M, N
kx k 1 có 2 nghiệm phân biệt khác 1. x 1  2 f ( )
x kx  2kx k  4  0 có 2 nghiệm phân biệt khác 1 k  0     4
k  0  k  0 f ( 1  )  4  0  Mặt khác: xx  2
  2x I là trung điểm MN với k   0 . M N I
Phương trình đường thẳng cần tìm là y kx k 1 với k  0 .
Ví dụ 4: Cho hàm số y x3  x2 6
 9x  6 có đồ thị là (C). Định m để đường thẳng
(d) : y mx m
2  4 cắt đồ thị (C) tại ba điểm phân biệt.
PT hoành độ giao điểm của (C) và (d): x3  x2 6  x
9  6  mx m 2  4    2 x x2 ( 2)(
 4x 1 m)  x 0
g(x)  x2  4x 1 m  0
(d) cắt (C) tại ba điểm phân biệt PT g(x)  0 có 2 nghiệm phân biệt khác 2 m 3 
Bài toán 3:Bài toán điểm trên đồ thị.
1) Khoảng cách giữa hai điểm A, B: AB =
x x 2  y y 2 ( ) ( ) B A B A
2) Khoảng cách từ điểm M(x ; y ) đến đường thẳng : ax by c  0: 0 0
ax by c d(M,d 0 0 )  a2  b2
Đặc biệt: + Nếu : x a thì d(M,)  x a 0
+ Nếu : y b thì d(M,)  y b 0
+ Tổng các khoảng cách từ M đến các trục toạ độ là: x y . 0 0 TRẦN THÔNG
Facebook: hội toán bắc trung nam 62 2 1 1
3) Diện tích tam giác ABC: S =
AB.AC.sin A
AB2.AC2   AB.AC 2 2    4) Các điểm A, B đố x x 2x
i xứng nhau qua điểm I  IAIB  0  A B I
y y y 2  A B I 5) Các điểm A, B đố AB  
i xứng nhau qua đường thẳng    (I là trung điểm AB). I     Đặ x x
c biệt: + A, B đối xứng nhau qua trục OxB Ay  yB Ax x
+ A, B đối xứng nhau qua trục OxB Ay  yB A
6) Khoảng cách giữa đường thẳng  với đường cong (C) bằng khoảng cách nhỏ nhất giữa một
điểm M   và một điểm N  (C).
7) Điểm M(x;y) được gọi là có toạ độ nguyên nếu x,y đều là số nguyên. Ví dụ minh họa
Ví dụ 1: Cho hàm số 3
y  x  3x  2 (C). Tìm 2 điểm trên đồ thị hàm số sao cho chúng đối xứng nhau qua tâm M(–1; 3).
Gọi Ax ; y B M( 1  ;3)  B 2
  x ;6 y 0 0  0 0  ,
là điểm đối xứng với A qua điểm 3    3  2 A, By x x C ( ) 0 0 0  6   y  (  2   x 3 )  3( 2   x )  2  0 0 0 3
 6  x3  x 3  2 2    3 2    2  6 12  6  0 0 0  x0   x0  x2 x 0 0 x  1
  y  0 0 0
Vậy 2 điểm cần tìm là:  1  ;  0 và  1  ;  6 2x  4
Ví dụ 2: Cho hàm số y
. Tìm trên (C) hai điểm đối xứng nhau qua đường thẳng MN x 1
biết M(–3; 0) và N(–1; –1). MN  (2; 1
 ) Phương trình MN: x  2y  3  0 . TRẦN THÔNG
Facebook: hội toán bắc trung nam 63
Phương trình đường thẳng (d) MN có dạng: y  2x m.
Phương trình hoành độ giao điểm của (C) và (d):
2x  4  2xm x2 2
mx m 4  0 (x  1  ) (1) x 1 2
(d) cắt (C) tại hai điểm phân biệt A, B   m – m 8 – 32  0 (2)
Khi đó A(x ;2x m), B(x ;2x m) với x , x là các nghiệm của (1) 1 1 2 2 1 2  x x   m m
Trung điểm của AB là I 1 2 
; x x m  I   ;
(theo định lý Vi-et) 1 2 2    4 2 
A, B đối xứng nhau qua MN I MN m 4  2 x  0
Suy ra (1) 2x  4x  0 
A(0; –4), B(2; 0). x  2 2x
Ví dụ 3: Cho hàm số y
. Tìm trên đồ thị (C) hai điểm B, C thuộc hai nhánh sao cho tam x 1
giác ABC vuông cân tại đỉnh A với A(2; 0). 2  2   2  Ta có C ( ) : y  2 
. Gọi Bb; 2 
, Cc;2 
với b1 c . x 1  b  1  c  1
Gọi H, K lần lượt là hình chiếu của B, C lên trục Ox.
Ta có: AB AC BAC 0   CAK BAH 0 ; 90
 90  CAK ACK BAH ACK C BHA CKA 0 90 ABH C       AK  AH CK và: HB AK B  2 2  b  2   H A K c  1 b  1  Hay:   . 2 c3  2   c  2  b  1 Vậy B( 1
 ;1), C(3;3)
Ví dụ 4: Cho hàm số 3
y  x  3x  2 (C). Tìm 2 điểm trên đồ thị hàm số sao cho chúng đối xứng
nhau qua đường thẳng d: 2x – y  2  0 .
Gọi M x ; y ; N x ; y 1 1 
 2 2 thuộc (C) là hai điểm đối xứng qua đường thẳng d TRẦN THÔNG
Facebook: hội toán bắc trung nam 64
x x y y
I là trung điểm của AB nên 1 2 1 2 I ; 
, ta có I d  2 2  y y  3
x  3x  2   3
x  3x  2  1 1 2 2  x x Có: 1 2 1 2   2.  2 2 2 2 x x  0 3 1 2
   x x
 3x x x x  3 x x  2 x x   1 2  1 2  1 2   1 2  1 2 2 2
x x x x  1  1 1 2 2
Lại có: MN d   x x .1 y y .2  0 2 1   2 1 7
 7  x x   2 x x  2 2
x x x x  2 2
 0  x x x x  2 1 2 1 1 1 2 2 1 1 2 2 2 7 7
- Xét x x  0  x   ; x 1 2 1 2 2 2  9 2 2 2 2
x x x x 1 x x  1 1 2 2  1 2   4 - Xét     vô nghiệm 7 2 2
x x x x  5   1 1 2 2 2 x x   1 2  4  7 1 7   7 1 7 
Vậy 2 điểm cần tìm là  ; 2  ;  ; 2       . 2 2 2 2 2 2     1 5
Ví dụ 5: Cho hàm số y
x3  x2  x 3  . 3 3
Gọi A, B là các giao điểm của (C) với trục Ox. Chứng minh rằng trên đồ thị (C) tồn tại hai điểm
cùng nhìn đoạn AB dưới một góc vuông. 1 3 2 5 x  1
PT hoành độ giao điểm của (C) với trục hoành: x x x 3   0   3 3 x   5   1 5 A( 5
 ;0), B(1;0) . Gọi M a; a3  a2  a 3   C
( ), M A,B  3 3  1 5  1 5
AM  a 5; a3  a2  a
3   , BM   a1; a3  a2  a 3    3 3   3 3 1
AM BM AM B
. M  0 (a  5)(a 1)  (a 2  5) (a 4 1)  0 9 1 1 (a 3
1) (a 5)  0 a4  a3  a2 2 12 1 a 4  4  0 (* ) 9 TRẦN THÔNG
Facebook: hội toán bắc trung nam 65
Đặt y a4  a3  a2 2 12 1 a
4  4  0 , có tập xác định D = R. 7 2043
y  a3  a2 4 6 1 a
2 14; y  0 có 1 nghiệm thực a    y   0 0 2 16
Dựa vào BBT ta suy ra (*) luôn có 2 nghiệm khác 1 và –5.
Vậy luôn tồn tại 2 điểm thuộc (C) cùng nhìn đoạn AB dưới một góc vuông.
Ví dụ 6: Cho hàm số y x4  x2 2
1.Tìm toạ độ hai điểm P, Q thuộc (C) sao cho đường thẳng PQ
song song với trục hoành và khoảng cách từ điểm cực đại của (C) đến đường thẳng PQ bằng 8.
Điểm cực đại của (C) là A(0;1) . PT đường thẳng PQ có dạng: y m (m 0) .
Vì d(A,PQ)  8 nên m  9 . Khi đó hoành độ các điểm P, Q là nghiệm của phương trình: x4  x2 2  8  0  x  2  . Vậy: P( 2
 ;9), Q(2;9) hoặc P(2;9), Q( 2  ;9) . Bài tập luyện thi
Bài 1: Biện luận theo tham số m số nghiệm phương trình 3 2
x  3x 1  m
Bài 2: Biện luận theo tham số m số nghiệm phương trình 4 2
x  2x m x  2
Bài 3: Biện luận theo tham số m số nghiệm phương trình  m x  1
Bài 4: Tìm m để phương trình 3 2
x  3x m  2 có 3 nghiệm phân biệt
Bài 5: Tìm m để phương trình 2x  2  mx   1 vô nghiệm
Bài 6: Tìm m để phương trình 4 2 2
x  2x m có 2 nghiệm phân biệt. 1 Bài 7: Cho hàm số 4 2 y 
x  2x  3 . Tìm m để phương trình 4 2
x  8x m có 4 nghiệm phân 4 biệt.
Bài 8: Dựa vào đồ thị, hãy tìm m để phương trình 4 2
x  2x m 1  0 có 4 nghiệm phân biệt. 3 2
Bài 9: Cho hàm số: y x 3x
1 có đồ thị là (C ) Dựa vào đồ thị (C ) , hãy tìm điều kiện
của tham số k để phương trình sau đây có 3 nghiệm phân biệt: 3 2 x 3x k 0 . Bài 10: Cho hàm số 3 2
y x  2(m  2)x  (8  5 )
m x m  5 có đồ thị (Cm) và đường thẳng
d : y x m 1. Tìm m để d cắt (Cm) tại 3 điểm phân biệt có hoành độ tại x1, x2 , x3 thỏa mãn: 2 2 2
x x x  20. 1 2 3 TRẦN THÔNG
Facebook: hội toán bắc trung nam 66 Bài 11: Cho hàm số 3 2
y x  3x 1 (C). Tìm m để đường thẳng d : y mx 1 cắt đồ thị (C) tại
ba điểm phân biệt. Bài 12: Cho hàm số 3 2
y x  (m 1)x  (m 1)x 1 (1) . Tìm các giá trị của m để đồ thị của 1 
hàm số (1) cắt trục Ox tại ít nhất một điểm có hoành độ thuộc đoạn ; 2   . 2 
Bài 13: : Cho hàm số 3
y x   m   2 x   2 m m   2 2 1 2
1 x m 1 (m là tham số). Tìm m để (C)
cắt trục hoành tại 3 điểm phân biệt A, B, C (với A là điểm cố định) sao cho 2k k x x , trong 1 2  1 2
đó k , k lần lượt là hệ số góc của tiếp tuyến của (C) tại B, C và x , x là hoành độ các điểm cực 1 2 1 2 trị của (C). 2x  1
Bài 14: Cho hàm số y =
có đồ thị (C). Tìm m để đường thẳng  : 2y  3x m  0 cắt đồ thị x 1
(C) tại hai điểm phân biệt A, B sao cho độ dài 4AB2 = 13. x 1
Bài 15:Cho hàm số y
.Viết phương trình đường thẳng d song song với d’ : x + y + 2= 0 x 1
sao cho d cắt (C) tại hai điểm phân biệt A,B và diện tích tam giác IAB bằng 2 3 (I là giao điểm
hai đường tiệm cận). 2x  3
Bài 16: Cho hàm số y
y x m cắt đồ thị (C) tại hai điểm x
. Tìm m để phương trình 2 2 phân biệt. Bài 17: Cho hàm số 3
y  2x  3x 1 , có đồ thị là (C). Gọi (dk) là đường thẳng đi qua A(0; –1) và
có hệ số góc bằng k. Tìm k để đường thẳng dk cắt (C) tại 3 điểm phân biệt, trong đó hai điểm có hoành độ dương . 2x 1
Bài 18: Cho hàm số y
Tìm m để đường thẳng y x m cắt (C) tại hai điểm phân biệt x  2 A, B sao cho AB 4 2. x  2
Bài 19: Cho hàm số y x  (C).Lập phương trình đường thẳng qua M 0, 11 cắt (C) tại hai 1 điểm A,B sao cho S 2S . OAB OMB x  2
Bài 20: Tìm mọi giá trị của m để đường thẳng d : y  x m cắt đồ thị y  Cx  tại hai điểm 1
phân biệt. Khi nào có ít nhất một trong hai giao điểm có tọa độ nguyên ? TRẦN THÔNG
Facebook: hội toán bắc trung nam 67 2x  3
Bài 21: Cho hàm số y
có đồ thị (C). Gọi (d) là đường thẳng qua H(3; 3) và có hệ số góc x  1
k. Tìm k để (d) cắt (C) tại 2 điểm phân biệt M, N sao cho tam giác MAN vuông tại A(2; 1). 2x 1
Bài 22: Cho hàm số y
Tìm m để đường thẳng d : y x m cắt đồ thị (C) tại hai điểm x  2
phân biệt A, B sao cho AB  4 2. Bài 23: Cho hàm số 3 2
y  x  3x  2C  Tìm m để đường thẳng d : y m2  x  2 cắt (C) tại
3 điểm phân biệt A2;2, B,C sao cho tích các hệ số góc của tiếp tuyến với (C) tại B, C đạt giá trị nhỏ nhất. 1 1 Bài 24: Cho hàm số 3 y x  m   2
1 x  m  2 x 1 
1 . Tìm m để hàm số (1) có hai điểm 3 2  7 
cực trị A, B đồng thời hai điểm cực trị đó cùng với điểm D 3; 
 và gốc tọa độ O tạo thành hình  2  bình hành OADB. Bài 25: Cho hàm số 3
y  x  3x  2C . Gọi (d) là đường thẳng đi qua điểm I 0;2 có hệ số
góc m. Tìm m để (d) cắt (C) tại 3 điểm phân biệt I, A, B. Chứng minh rằng I là trung điểm của AB. x  2
Bài 26: Cho hàm số y
C. Tìm m để đường thẳng d : y x m cắt (C) tại hai điểm A, 2x-1
B phân biệt sao cho trọng tâm G của tam giác OAB cách d một khoảng bằng 2 (O là gốc tọa độ). 2x 1
Bài 27: Cho hàm số y
C. Tìm tất cả các giá trị của m để đường thẳng y mx  2 cắt x 1
đồ thị (C) tại hai điểm phân biệt A, B sao cho tam giác OAB vuông tại gốc tọa độ O. 2x 1
Bài 28: Cho hàm số y
có đồ thị C . Gọi
là đường thẳng đi qua điểm I 2, 0 và có x 1
hệ số góc m . Tìm tham số m để
cắt C tại 2 điểm phân biệt A, B sao cho I là trung điểm của đoạn thẳng AB.
Bài 29: Cho hàm số: 3 2 2 y x 3(m 1)x 2(m 4m 1)x 4 (
m m 1) (C ). Định giá trị m
của m để hàm số cắtOx tại 3 điểm phân biệt có hoành độ đều lớn hơn 1. 1 2 Bài 30: Cho 3 2 C : y x mx x m
. Tìm m để Cm cắt trục hoành tại ba điểm m 3 3
phân biệt có hoành độ x ,x ,x 2 2 2 x x x 15 1 2
3 và thỏa mãn điều kiện: 1 2 3 . TRẦN THÔNG
Facebook: hội toán bắc trung nam 68 x 2
Bài 31: Cho hàm số: y
C CMR d : y x
m luôn cắt C tại 2 điểm P và Q thuộc x 2
2 nhánh khác nhau của đồ thị. Tìmm để OPQ vuông tại O. x
Bài 32: Cho hàm số: y
C và đường thẳng d y m x .Tìm m để d cắt C tại hai điểm x 1
phân biệt A,B sao cho bán kính đường tròn ngoại tiếp tam giác OAB là 2 2 . 2x 1
Bài 33: Cho hàm số: y
C và đường thẳng d y m x . Tìm m để d cắt C tại hai x 3
điểm phân biệt A,B sao cho 2 2
AB  3IA với I là giao điểm hai đường tiệm cận của C x 2
Bài 34: Cho hàm số: y
C .Viết phương trình tiếp tuyến của C biết rằng nó cắt hai x 1
đường tiệm cận tại hai điểm phân biệt A,B sao cho bán kính đường tròn nội tiếp tam giác OAB nhỏ nhất. x 1
Bài 35: Cho hàm số y
M 2;0 có hệ số góc k. Tìm k để (d)
x  . Gọi (d) là đường thẳng qua   2
cắt (C) tại hai điểm phân biệt A, B sao cho M nằm giữa A, B và MA  2MB . x 1
Bài 36: Cho hàm số y x  (C) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến cắt 2
hai đường tiệm cận của (C) lần lượt tại A và B sao cho tam giác ABI có bán kính đường tròn nội
tiếp bằng 2  2 , với I là giao điểm của hai đường tiệm cận. 2x 1
Bài 37: Cho hàm số y I và cắt đồ x
. Viết phương trình đường thẳng  đi qua điểm (0;1) 1
thị (C) tại hai điểm phân biệt ,
A B sao cho diện tích tam giác OAB bằng 3 (O là gốc tọa độ). x  3
Bài 38: Tìm k để đường thẳng d : y kx  2k 1 cắt đồ thị hàm số (C): y x  tại hai điểm 2 phân biệt ,
A B sao cho khoảng cách từ A và B đến trục hoành bằng nhau.
Bài 39: Tìm m để đồ thị hàm số 3 2
y x  2x  (1 m)x m cắt trục Ox taị 3 điểm phân biệt có 1
hoành độ x , x , x đều lớn hơn . 1 2 3 2
Bài 40: Chứng minh mọi đường thẳng đi qua điểm I (1; 2) với hệ số góc k (k  3
 ) đều cắt đồ thị hàm số 3 2
y x  3x  4 tại ba điểm phân biệt I , ,
A B đồng thời I là trung điểm của đoạn . AB TRẦN THÔNG
Facebook: hội toán bắc trung nam 69 3 2
Bài 41: Cho hàm số y x 2x 1 m x
m 1 Tìm m để đồ thị hàm số 1 cắt trục
hoành tại 3 điểm phân biệt có hoành độ x ,x ,x 2 2 2 x x x 4 1 2 3 thỏa mãn điều kiện 1 2 3 . 3 2
Bài 42: Cho hàm số y x 3x
4 C Chứng minh rằng mọi đường thẳng đi qua điểm
I 1,2 với hệ số góc k k
3 đều cắt đồ thị hàm số C tại ba điểm phân biệt I, A, B, đồng
thời I là trung điểm của đoạn thẳng AB. 3 2
Bài 43: Cho hàm số y x 2mx 3 m 1 x
2 có đồ thị là C , điểm M 3,1 , đường m
thẳng d có phương trình x y 2
0 . Tìm các giá trị của m để đường thẳng d cắt C tại 3 m điểm A 0,2 , ,
B C sao cho tam giác MBC có diện tí c h bằng 2 6 Bài 44: Cho hàm số: 3 2 2 y x 3(m 1)x 2(m 4m 1)x 4 ( m m
1) (C ). Định giá trị m
của m để hàm số cắtOx tại 3 điểm phân biệt có hoành độ đều lớn hơn 1. 3 x
Bài 45: Cho hàm số: y
3x C và đường thẳng Tìm m để C và d : y m(x 3) có 3
giao điểm là A, B, C với A cố định và OA OC , BC 42 . 9
Bài 46: Cho hàm số y = 3 2
mx  6x  9mx  3 (1) Xác định m để đường thẳng d: y = x  3 cắt 4
đồ thị hàm số (1) tại 3 điểm phân biệt A(0,– 3), B, C thỏa điều kiện B nằm giữa A và C đồng thời AC = 3AB.
Bài 47: Tìm m để đồ thị (C) của hàm số 3 2
y mx x  2x  8m Cắt trục hoành tại ba điểm phân
biệt có hoành độ thỏa x > 1.
Bài 48: Cho (C) là đồ thị hầm số 4 2 2
y x  (3m 1)x m . Tìm m để (C) cắt trục hoành tại bốn
điểm phân biệt có hoành độ lập thành cấp số cộng.
Bài 49: Tìm tham số thực m để  x  2
d đi qua A 1; 0 và có hệ số góc là m cắt C : y
tại hai điểm M,N thuộc hai nhánh của x 1
C (M thuộc nhánh trái , N thuộc nhánh phải )sao cho AN  2A  M . x  2
Bài 50: Cho hàm số y
có đồ thị là C . Tìm tất cả các giá trị tham số m để đường 2x  2 thẳng d : y
 x  m cắt đồ thị C tại 2 điểm phân biệt A, B sao cho 2 2 37 OA  OB  . 2
Dạng 7: Đồ thị hàm số chứa dấu giá trị tuyệt đối TRẦN THÔNG
Facebook: hội toán bắc trung nam 70
Để vẽ đồ thị hàm số chứa dấu giá trị tuyệt đối, ta sử dụng ba nguyên tắc sau đây:
Nguyên tắc 1. (về sự phân chia đồ thị hàm số) Đồ thị hàm số
f x , x D 1   1   
y f xf x ,x D 2   2  ...   f
  x , x D n n
là hợp của n đồ thị hàm số y f
x với x D ( k  1, 2,, n ). k   k
Nguyên tắc 2. (về sự đổi dấu hàm số) Đồ thị hàm số y f x , xD và đồ thị hàm số y   f x
, xD đối xứng nhau qua Ox .
Nguyên tắc 3. (về đồ thị hàm chẵn) Đồ thị của hàm chẵn nhận Oy làm trục đối xứng.
Hai trường hợp hay gặp:
-Đồ thị hàm số y f x   y f   x  Vì 
là hàm chẳn nên đồ thị hàm số y f x  gồm hai phần:  f
  x   f xx   0
+) Phần 1 là phần đồ thị hàm số y f x nằm bên phải Oy ;
+) Phần 2 đối xứng với phần 1 qua Oy .
-Đồ thị hàm số y f x  f
x, f x  0
Vì f x  
nên đồ thị hàm số y f x gồm hai phần:  f
x , f x  0
+) Phần 1 là phần Đồ thị hàm số y f x nằm phía trên trục hoành;
+) Phần 2 đối xứng với phần Đồ thị hàm số y f x ở phía dưới trục hoành qua trục hoành. Ví dụ minh họa
Ví dụ 1. Vẽ các đồ thị hàm số TRẦN THÔNG
Facebook: hội toán bắc trung nam 71 x 1 x 1  1) x 1 f x
C ; 2) f x  C ;  2  2   1  1   3) f xC ; 3  3   x 1 x 1 x 1 x 1 x 1 4) f x
C ; 5) f x  C . 5  5   4  4   x1 x 1 x
Giải. Trước hết, ta vẽ đồ thị C của hàm số f x 1  (hình 0); x 1  f   x
khi f x  0
1) Ta có f x f x  
. Do đó đồ thị C gồm hai phần (hình 1): 1  1     f
xkhi f x  0
Phần 1: là phần đồ thị C nằm trên Ox ;
Phần 2: đối xứng với phần đồ thị C nằm dưới Ox qua Ox . 2) Ta có f x f
x là hàm chẵn, đồ thị nhận Oy làm trục đối xứng. Lại có f x f x 2     2    
với mọi x  0 . Do đó đồ thị C gồm hai phần (hình 2): 2 
Phần 1: là phần đồ thị C nằm bên phải Oy ;
Phần 2: đối xứng với phần 1 qua Oy . f x khi f x  0  2   2   3) Ta có f x f x  
. Do đó đồ thị C gồm hai phần (hình 3): 3  3   2 
 f x khi f x 0  2   2  
Phần 1: là phần đồ thị C nằm trên Ox ; 2 
Phần 2: đối xứng với phần đồ thị C nằm dưới Ox qua Ox . 2   f   xkhi x  1 4) Ta có f x  
. Do đó đồ thị C gồm hai phần (hình 4): 4  4   f
xkhi x 1
Phần 1: là phần đồ thị C ứng với x 1;
Phần 2: đối xứng với phần đồ thị C ứng với x 1 qua Ox . TRẦN THÔNG
Facebook: hội toán bắc trung nam 72  f   xkhi x  1  5) Ta có f x  
. Do đó đồ thị C gồm hai phần (hình 5): 5  5   f
xkhi x  1 
Phần 1: là phần đồ thị C ứng với x  1  ;
Phần 2: đối xứng với phần đồ thị C ứng với x  1  qua Ox . y y 1 1 O O -1 1 x -1 1 x -1 -1 Hình 0 Hình 1 y y 1 1 O O -1 1 x -1 1 x -1 -1 Hình 2 Hình 3 TRẦN THÔNG
Facebook: hội toán bắc trung nam 73 y y 1 1 O O -1 1 x -1 1 x -1 -1 Hình 4 Hình 5
Ví dụ 2: Tìm m để phương trình 3 2
2 x  9x 12 x m có 6 nghiệm phân biệt.
Giải. Đặt f x 3 2
 2x 9x 12x . Phương trình đã cho tương đương với f x   m .
Trước hết ta vẽ đồ thị C của hàm số f x 3 2
 2x 9x 12x . Hàm f x là hàm chẵn,
f x   f x x
  0. Do đó, đồ thị C ' của hàm số f x gồm hai phần
Phần 1: là phần C nằm ở bên phải Oy ;
Phần 2: đối xứng với phần 1 qua Oy . y y (C) (C') 9 9 5 5 y = m 4 4 x x O 1 2 3 -3 -2 -1 O 1 2 3
Vậy phương trình đã cho có 6 nghiệm phân biệt đường thẳng y m có 6 điểm chung với
C ' 4 m5. TRẦN THÔNG
Facebook: hội toán bắc trung nam 74 Bài tập luyện thi
Bài 1: Vẽ đồ thị các hàm số sau đây 1) 2
y x x x  3   3  5 2)
y  1 1 x x 3) 2
y x  3x  5 4) 2
y x  3 x  5 5) 2
y x  3 x  5 6) 1 2 2
y x x x  3 x 1 7) 3 2 1 y
x x  3x 1 8) 1 2 2
y x x x  3 x 1 3 3 3 9) 3 2 1 y
x  3x  24x  26 3 2 1     18 10) y x 3x 24 x 26 18   3 2 11) 2 1 y
x  3x  24 x  26 12) 1 y
x 1 x  2x  26 18   18 13) 4 2
y x  4x  3 14) 2
y x   2 1 x   3 15) 2
y x   2 3 x   1
16) y x   3 2
1 x x  3x   3 17) 4 2
y x  5x  4
18) y x   3 2
1 x x  4x  4
19) y x   3 2
1 x x  4x  4
20) y x   3 2
2 x  2x x  2
21) y x   3 2
2 x  2x x  2 22) 2 y x   2 4 x   1 23) 2
y x   2 1 x  4 24) 2
y x x   2
2 x x  2 25) 2
y x x   2
2 x x  2 x 1  xx 1  x 1  x 26) y y   30) 1 y  2 27) 1 x 2 x 28) y   2 x 29) y x 2 x 2
Bài 2: Với những giá trị nào của m , phương trình 2 2
x x  2  m có đúng 6 nghiệm phân biệt.   2 3 4 k x   1
Bài 3: Tìm k để phương trình  4x  
 có 3 nghiệm phân biệt.  k  0 3 3 2
Bài 4: Từ đồ thị (C): y  x3  3x suy ra đồ thị hàm số 3
y  x  3x .
Bài 5: Với giá trị nào của a thì phương trình sau có 6 nghiệm phân biệt: 4 x  2 2 x 1  log . a 2
Bài 6: Dùng đồ thị (C) của hàm số 4 2
y  x  2x  3 đề biện luận theo m số nghiệm của phương trình: 4 2 4 2
x  2x m  2m . x 3  4
Bài 7: Cho hàm số y
(C). Dựa vào đồ thị C) , tìm các giá trị của m để phương trình x  2    6 2 x 6  x m ( 4 x 4 sin cos sin
 cos x) có 2 nghiệm trên đoạn 0;   .  3  3
Bài 8: Khảo sát và vẽ đồ thị hàm số 3
y  x  3x từ đó suy ra đồ thị hàm số y   x  3 x TRẦN THÔNG
Facebook: hội toán bắc trung nam 75
BÀI TẬP TRẮC NGHIỆM 1. Hàm số 3 2
y  x mx m đồng biến trên (1;2) thì m thuộc tập nào sau đây:  3   3  A.  ; 3  B.  ;  3 C.  ;3  D.  ;    2   2  m 1 2. Hàm số 3 y
x  m   2
1 x  3m  2 x  đồng biến trên  ;
2  thì m thuộc tập nào sau 3 3 đây: 2   2  6   2  A. m  ;   B. m   ;   C. m  ;   D. m  ;  1 3   2   3 
3. Trong các hàm số sau, hàm số nào đồng biến trên khoảng  ; 1  . 1 4 A. 3 2 y
x x  3x B. y  ln x C. x x y e   2 2 D. 4 3 y  x x 3 3 4. Hàm số 4 2
y x  2x 1 đồng biến trên khoảng nào sau đây: A. ( ;  1  );(0;1) B. ( 1  ;0);(0;1) C. ( 1
 ;0);(1;) D. Đồng biến trên R 1 5. Hàm số 3 2 y
x  2x  3x 1 đồng biến trên: 3 A.  ; 2  B.  ; 1 3 C.  ;   1   ; 3  D.  ; 1 3   2  4  6. Hàm số y x
x nghịch biến trên: A.  ; 3 4 B.  ; 2 3 C.  2;3 D.  ; 2 4
mx2  x m
7. Cho hàm số y
(với m là tham số). Giá trị của m để hàm số đồng biến trên khoảng mx  1  ; 0  là: A. m  ; 1 2 B. m ; 5  5 C. m  ; 0 1 D. m  ; 0  1 3x  1
8. Cho hàm số f (x) 
. Trong các mệnh đề sau, tìm mệnh đề đúng: x  1
A. f (x) tăng trên  ;   1 ; ; 1 
B. f (x) giảm trên  ;   1 ; ; 1 
C. f (x) đồng biến trên R
D. f (x) liên tục trên   9. Hàm số y x
ln x nghịch biến trên: A.  ; e  B.  ; 0 4 C.  ; 4  D.  ; 0 e
10. Trong các hàm số sau, hàm số nào nghịch biến trên : x  2 A. y  cos x
B. y  x3  x2
2 10x C. y  x4  x2 1 D. y x  3 TRẦN THÔNG
Facebook: hội toán bắc trung nam 76
11. Trong các hàm số sau, hàm số nào nghịch biến trên khoảng (1; 3): 2 1 A. y
x3  4x2  6x  9 B. y x2  2x  3 3 2 x2  x  1 2x  5 C. y  D. y x  1 x  1 2 x
12. Hàm số y
đồng biến trên các khoảng 1 x A. ( ;  1) và (1;2) B. ( ;
 1) và (2;) C.(0;1) và (1;2) D. ( ;  1) và (1;)
13. Hàm số nào sau đây là hàm số đồng biến trên R? x x A. y
B. y   x  2 2
1  3x  2 C. y  D. y = tanx 2 x 1 x 1 1
14. Cho hàm số y  4x  1 và các khoảng x  1  3   3   1   1  (I)  ;     (II)  ;1   (III) 1;   (IV)  ;    2   2   2   2 
Hàm số trên đồng biến trên các khoảng A.(I) và (II) B. (II) và (III) C. (III) và (IV) D.(IV) và (I) 3 x 15. Cho hàm số 2 y
mx x 1 giá trị nào của m thì hàm số luôn đồng biến trên tập xác 3 định của nó
A. 1 m 1 B.m< -1 hoặc m> 1 C.- 2 < m < 2 D. m >2 mx  1 16. Hàm số y= x m
A. luôn luôn đồng biến với mọi m. B. luôn luôn đồng biến nếu m  0
C. luôn luôn đồng biến nếu m >1 D.đồng biến trên từng khoảng xác định của nó. 3 4 x 17. Cho hàm số 5 4 y x x
1. Nhận định nào dưới đây là đúng. 5 3
A. Nghịch biến trên R
B. Nghịch biến trên khoảng   ;1
 và đồng biến trên khoảng 1;
C. Đồng biến trên R D. Đồng biến trên khoảng   ;1
 và nghịch biến trên khoảng 1; 1
18. Giá trị của m để hàm số y =
x3 – 2mx2 + (m + 3)x – 5 + m đồng biến trên R là: 3 3 3 3
A. m  1 B. m   C. 
m  1 D.   m  1 4 4 4 TRẦN THÔNG
Facebook: hội toán bắc trung nam 77 1
19. Xác định m để hàm số y = 3
x  m   1 2
x  m  
3 x  6 nghịch biến trên R? 3 A. m  1
 hoặc m  2 B. 1 m  2 C.  2  m 1 D. m  2  hoặc m  1 mx  3
20. Tìm m để hàm số y =
giảm trên từng khoảng xác định của nó? x  2 3 3 3 3 A. m  B. m  C. m  D. m  2 2 2 2 2
x  2mx m 21. Hàm số y =
đồng biến trên từng khoảng xác định của nó khi: x 1
A. m  1 B. m  1 C. m  1 D. m  1  mx  1 22. Hàm số y =
nghịch biến trên khoảng ( -  ; 0) khi : x m
A.m > 0 B. 1  m  0 C. m < - 1 D. m > 2
23. Hàm số y = ax3 + bx2 + cx + d đồng biến trên R khi nào? a b  , 0 c  0 a b  , 0 c  0 A.  C.  a  , 0 2 b  3ac  0 a  , 0 2 b  3ac  0 a b  , 0 c  0
a b c  0 B...  D.   2 b  3ac  0 a  , 0 2 b  3ac  0 1
24. Tìm m lớn nhất để hàm số y = 3 2
x mx  4m  3x  3 đồng biến trên R. 3
A.m =3 B. m = 1 C. m = 2 D. m=4 25. Hàm số y = 2
2  x x nghịch biến trên khoảng:  1   1  A.  ; 2 B.  1;
 C. 2;   D.  ; 1 2  2   2 
26. Hàm số nào sau đây là hàm số đồng biến trên R? x x
A. y  x  2 2 1
 3x  2 B. y  C. y  D. y=tanx 2 x 1 x  1 x
27. Cho hàm số y
x ( x  0). Hoành độ điểm cực tiểu của đồ thị hàm số là: 1 x  A. e B. x 1 C. x  e D. x e
28. Cho hàm số y x4  x2
2 1 (C). Tiếp tuyến của (C) tại điểm cực đại có phương trình là: A. x  0 B. y  0 C. y  1 D. y  2 x3 y
 m   x2 2
 4m  8 x m 1 29. Cho hàm số 3
. Để hàm số đạt cực trị tại x , x thỏa mãn 1 2 x  2   x thì 1 2 TRẦN THÔNG
Facebook: hội toán bắc trung nam 78 3  m  2 m  3 A. 2  m  6 B. 2
C. m  2 hoặc m  6 D. 2
30. Giả sử hàm số 3 2
y x  3x mx m nghịch biến trên khoảng có độ dài bằng 1. Khi đó, giá trị của m là: 3 9 9 3 A. 2 B. 2 C. 4 D. 4 sin x 1  3 
31. Giả sử hàm số y
đồng biến trên khoảng  , 
 . Khi đó, các giá trị m thõa 2sin x m  2  mản bài toán là: A. m  3  B. m  2  C. m  0 D. m  2  32. Cho hàm số 3 2
y ax bx cx d và giả sử có cực trị. Mệnh đề nào dưới đây là đúng.
A. Cả 3 phương án kia đều sai
B. Hàm số chỉ có một cực tiểu
C. Hàm số có hai cực đại
D. Hàm số chỉ có một cực đại 33. Cho hàm số     n n y x c
x , c  0 , n  2 . Hoành độ điểm cực tiểu của đồ thị hàm số là: 2c c A. c 1 B. 2c C. 3 D. 2 34. Cho đường cong 3 2
y x  3x . Gọi  là đường thẳng nối liền cực đại và cực tiểu của nó. Mệnh
đề nào dưới đây là đúng .
A.  đi qua điểm M(-1; -2)
B.  đi qua điểm M(1; -2)
C.  song song với trục hoành
D.  không đi qua gốc toạ độ 35. Cho hàm số 4 3 2
y x x x x 1. Mệnh đề nào dưới đây là đúng.
A. Hàm số luôn luôn nghịch biến x  
B. Đồ thị hàm số có ít nhất một điểm cực trị
C. Cả 3 phương án kia đều sai
D. Hàm số luôn luôn đồng biến x  
36. Cho hàm số y x . Mệnh đề nào dưới đây là đúng.
A. Cả hai phương án kia đều đúng
B. Cả ba phương án kia đều sai
C. Hàm số đạt giá trị nhỏ nhất trên R tại x  0 D. Hàm số đạt cực tiểu tại x  0 x2  mx
37. Tìm m để hàm số sau đây có cực trị: f (x)  . mx 1 A. -1 < m < 0 B. 0 C. m   D. -1 < m< 1
38. Hàm số y   5 x4 có bao nhiêu điểm cực đại? TRẦN THÔNG
Facebook: hội toán bắc trung nam 79 A. 1 B. 3 C. 0 D. 2 1
39. Số điểm cực trị của đồ thị hàm số y  
x3  x  7 là: 3 A. 1 B. 0 C. 3 D. 2
40. Số điểm cực trị của đồ thị hàm số y x4  100 là: A. 0 B. 1 C. 2 D. 3
41. Đồ thi hàm số nào sau đây có 3 điểm cực trị. A. 4 2
y  2x  4x 1 B. 4 2
y x  2x 1 C. 4 2
y x  2x 1 D. 4 2
y  x  2x 1 2 x  2mx  2
42. Đồ thi hàm số y
đạt cực đại tại x = 2 khi : x m A.Không tồn tại m B. m = -1 C. m = 1 D. m  1  43. Hàm số 3 2
y x  3x mx đạt cực tiểu tại x = 2 khi : A. m  0 B. m  0 C. m  0 D. m  0 2 x  4x 1
44. Cho hàm số y
.Hàm số có hai điểm cực trị x1, x2 .Tích x1.x2 bằng x 1 A. -4 B.-5 C. -1 D. -2 1 45. Hàm số 4 2 y
x  2x  3 đạt cực đại tại x  2 A.  2 B. 2 C.  2 D. 0 2
x  2x  5
46. Khẳng định nào sau đây là đúng về đồ thị hàm số y  : x 1 A. x  1  B. y  4  C. yy  0 D. xx  3 CD CT CD CT CD CT 1 47. Cho hàm số 3 2 y
x m x  2m  
1 x 1 Mệnh đề nào sau đây là sai? 3 A. m
 1 thì hàm số có hai điểm cực trị
B.Hàm số luôn luôn có cực đại và cực tiểu C. m
  1 thì hàm số có cực đại và cực tiểu D. m
 1 thì hàm số có cực trị 3 x 2 48. Cho hàm số 2 y
 2x  3x  .Toạ độ điểm cực đại của hàm số là 3 3 2 A. (-1;2) B. (3; ) C. (1;-2) D.(1;2) 3
49. Trong các mệnh đề sau, hãy tìm mệnh đề sai: 1 A. Hàm số y  2  x 1 không có cực trị; x  2 1 B. Hàm số y  x 1 có hai cực trị. x 1 TRẦN THÔNG
Facebook: hội toán bắc trung nam 80
C. Hàm số y = –x3 + 3x2 – 3 có cực đại và cực tiểu;
D Hàm số y = x3 + 3x + 1 có cực trị; 2 x  3x  6
50. Hàm số y
có giá trị cực đại là x 1 A.3 B. -5 C.-1 D. 3
51. Hàm số f (x) 4  x  6 2
x  8x  1 có bao nhiêu điểm cực trị A.0 B. 1 C. 2 D. 3 52. Hàm số 3
y x  m   2 2 3
1 x  6m  
1 x 1 có cực đại và cực tiểu nằm trong khoảng  2  ,  3 . Khi đó, giá trị m là
A. m 1,3 B. m 1, 4 C. m 3, 4 D. m 1,3  3,4 
53. Hàm số y a sin x b cos x x 0  x  2  đạt cực trị tại x
, x   . Khi đó, tổng có giá 3 trị là: 3 A.3 B. 1 C. 3 1 D. 3 1 3
54. Hàm số y a sin x b cos x x 0  x  2  có hai cực trị thõa mãn giá trị cực tiểu đạt giá trị
lớn nhất. Khi đó, giá trị m là:
A. m  3 B. m 1 C. m  1  D. m  0 55. Hàm số 3
y x  m   2 3
1 x  9x m có hai cực trị x , x thõa mãn x x  2. Khi đó, giá 1 2 1 2 trị m là:
A. m  3, 1 3   1 3,1 B. m  1  ,  3
C. m  1, 1 3  1,1 3
D. m  ,1 3  1 3, 1 1 56. Hàm số 3 2 y x
x mx m   có hai cực trị x , x cùng lớn hơn giá trị tham số m. Khi 3 2 1 2 đó, giá trị m là: 1 A. m  2  B. m  2
 C. m   D. m  0 hoặc m  2  2
57. Đồ thị hàm số 4
y x  m   2 2
1 x m có ba điểm cực trị tạo thành tam giác vuông .Khi đó, giá trị m là: A. m  0
B. m 1 C. m  2 D. m  1 
58. Hàm số nào dưới đây có cực tiểu mà không có cực đại. 1 A. y x
B. y  3  cos x  cos 2 x C. 2 y
x x 1 D.  x  3 x x
59. Hàm số nào dưới đây có hai cực trị thõa mãn giá trị cực tiểu lớn hơn giá trị cực đại. 2 x 1 x 1 A. 4 2
y x  3x  2 B. 3
y  x  3x 1 C. y  D. y x  2 x  2
60. Hàm số nào dưới đây có cực đại mà không có cực tiểu. TRẦN THÔNG
Facebook: hội toán bắc trung nam 81 2 x  3x  2 A. 3 2
y x  3x  2 B. y  C. 2 y x x 1
D. y  cos x  cos 2x x  4
61. Đồ thị hàm số 3 2
y x x ax b có điểm cực tiểu là A1,2 . Giá trị biểu thức a  2b là: A.0 B.4 C.5 D.-5 62. Cho hàm số 3 2
y  4x mx  3x đạt cực trị tại x , x sao cho x  4x  0 . Giá trị m thõa mãn 1 2 1 2 yêu cầu bài toán là: 9 1 3 A. m  0 B. m   C. m   D. m   2 2 2
63. Giả sử hàm số f x 4 2
ax bx ca  0có 3 cực trị. Khẳng định nào dưới đây là đúng.
A.Đồ thị hàm số f x có ba điểm cực trị B.Đồ thị hàm số f x có năm điểm cực trị
C.Đồ thị hàm số f x  có năm điểm cực trị D.Đồ thị hàm số f x  có ba điểm cực trị
64. Giả sử đồ thị hàm số f x 3 2
ax bx cx d a  0 có 2 điểm cực trị nằm về hai phía của
trục Oy. Khẳng định nào dưới đây là đúng.
A.Đồ thị hàm số f x có ba điểm cực trị
B.Đồ thị hàm số f x có năm điểm cực trị
C.Đồ thị hàm số f x  có năm điểm cực trị D.Đồ thị hàm số f x  có ba điểm cực trị.
65. Cho hàm số y f x xác định trên miền D và x D Mệnh đề nào dưới đây là đúng 0
A.Hàm số đạt giá trị lớn nhất tại x thì đạt cực đại tại x . 0 0
B.Hàm số đạt giá trị nhỏ nhất tại x thì đạt cực tiểu tại x . 0 0
C.Hàm số đạt cực đại tại x thì f  x  0 và f   x  0 . 0  0  0
D. Hàm số đạt cực tiểu tại x thì tồn tại h  0 sao cho min
f x  f x . 0  0 x     0 x h, 0 x h
66. Cho hàm số y f x xác định trên miền D và x D Mệnh đề nào dưới đây là đúng 0
A.Hàm số đạt cực trị tại x thì tồn tại h  0 sao cho max f x  min f x. 0 x
x h,x h
xx h,x h 0 0   0 0 
B.Hàm số đạt cực đại tại x thì tồn tại h  0 sao cho max
f x  f x . 0  0 x     0 x h, 0 x h
C.Hàm số đạt cực đại tại x thì với mọi h  0 ta có max
f x  f x . 0  0 x     0 x h, 0 x h
D.Hàm số đạt cực tiểu tại x thì với mọi h  0 ta có min
f x  f x . 0  0 x     0 x h, 0 x h
67. Giả sử hàm số f x 4 2
ax bx ca  0có 3 cực trị sao cho giá trị cực tiểu y  0, giá trị CT cực đại y
 0. Đồ thị hàm số y f x có số điểm cực trị là: CD A.2 B.3 C.4 D.5
68. Giả sử hàm số f x 4 2
ax bx ca  0có 3 cực trị sao cho giá trị cực tiểu y  0. và giá CT trị cực đại y
 0. Đồ thị hàm số y f x có số điểm cực trị là: CD TRẦN THÔNG
Facebook: hội toán bắc trung nam 82 A.7 B.3 C.4 D.5
69. Giả sử hàm số f x 4 2
ax bx ca  0có 3 cực trị sao cho giá trị cực tiểu y  0. Đồ CT
thị hàm số y f x có số điểm cực trị là: A.2 B.3 C.4 D.5
70. Giả sử hàm số f x 3 2
ax bx cx d a  0 không có cực trị . Khẳng định nào dưới đây là đúng.
A.Đồ thị hàm số f x có ba điểm cực trị
B.Đồ thị hàm số f x có một điểm cực trị
C.Đồ thị hàm số f x  có năm điểm cực trị D.Đồ thị hàm số f x  có ba điểm cực trị.
71. Cho hàm số y f x liên tục trên tập xác định D  a,b,a b . Hai số thực phân biệt
x , x a,b thỏa mãn f x f x , x   x  ,
h x h và f x f x , x   x  , h x h 2     2 2  1     1 1  1 2  
với h đủ bé. Khẳng định nào dưới đây là đúng.
A.Giá trị lớn nhất của hàm số là, giá trị nhỏ nhất của hàm số là
B.Điểm x , f x là điểm cực đại của hàm số, điểm x , f x là điểm cực tiểu của hàm số 2  2 1  1
C.Hàm số có tối đa hai cực trị.
D.Hàm số đạt cực đại tại x , đạt cực tiểu tại x . 1 2 2016 2017
72. Hàm số f x liên tục trên
và có đạo hàm là f  x  xx   1
x 2 . Đồ thị hàm số
có số điểm cực trị là: A.1 B.2 C.3 D.4 3
x 3x, x  0
73. Đồ thị hàm số f x  
có số điểm cực trị là: 2
x , x  0 A.1 B.2 C.3 D.0 74. Hàm số   3
f x x bx c đạt cực trị tại x , x . Nhận xét nào dưới đây là đúng. 1 2
A. x .x b
B. x .x c
C. x x b
D. x x  c 1 2 1 2 1 2 1 2
75. Gọi A,B,C lần lượt là các điểm cực trị của đồ thị hàm số 4 2
y  2x  4x 1. Tam giác ABC có diện tích là: 3 A.4 B.2 C.1 D. 2
76. Hàm số f x 3
x   m   2 2 3 2
1 x  6mm  
1 x 1đạt cực trị tại x , x sao cho x x  1. 1 2 1 2
Khi đó, giá trị m thõa mãn yêu cầu bài toán là: A. m  0 B. m  0 C. m  5 D. m
77. Hàm số f x 3
x   m   2 2 3 2
1 x  6mm  
1 x 1đạt cực trị tại x , x .Khi m thay đổi, điểm 1 2
cực đại di động trên đường cong nào dưới đây. A. 3 2
y  2x  3x 1 B. 3 2
y  2x  3x 1 C. 3 2
y  3x  2x 1 D. 3 2
y  3x  2x 1 TRẦN THÔNG
Facebook: hội toán bắc trung nam 83 2
x  2x, x  0 
78. Đồ thị hàm số f x  2x, 1
  x  0 có số điểm cực trị là:  3
x  5, x  1   A.1 B.2 C.3 D.0
79. Hàm số f x 3
x  m   2 2 3
1 x  6m  2 x 1đạt cực trị tại x , x sao cho x x  2 . Khi 1 2 1 2
đó, giá trị m thõa mãn yêu cầu bài toán là: A. m 1 B. m  2 C. m  1  D. m  2 
80. Giả sử hàm số f x 4 2
ax bx ca  0có một cực trị. Khi đó, giá trị a và b thỏa mãn yêu cầu nào dưới đây.
A. a  0,b  0
B. a  0, 0  b
C. a  0,b  0
D. a  0, 0  b 1
81. Giả sử đồ thị hàm số y x3  mx2  x m1 C (
) có có 2 điểm cực trị và khoảng cách giữa m 3
2 điểm cực trị là nhỏ nhất. Khi đó, giá trị của m là : 1
A. m 1 B. m  0 C. m   D. m  1  3
82. Nhận xét nào dưới đây là đúng khi nói về tích chất của các điểm cực trị hàm số 3 2
y  x  3x  4
A.Các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác vuông tại O.
B.Các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam đều.
C. Các điểm cực đại và cực tiểu đối xứng với nhau qua gốc tọa độ O .
D.Các điểm cực đại và cực tiểu đối xứng với nhau qua trục Oy . 1 83. Cho hàm số: 3 2 2 y x mx m m 1 x
1. Để hàm số đạt cực đại tại điểm x 1 3
thì giá trị của m là: A. m  0 B. m 1 C. m  1  D. m  2
84. Số giá trị nguyên của m để hàm số 2
y m ln(x  2)  x x có 2 điểm cực trị trái dấu là: A.0 B.1 C.2 D.3
85. Cho hàm số y f x   x a x b x c có đồ thị (C) với a, , b c
và a b  . c Hàm
số có hai điểm cực trị có hoành độ x , x với x x . Khi đó khẳng định nào dưới đây là đúng ? 1 2 1 2
A. x x a
B. a x b x c
C. c x x
D. x b x 1 2 1 2 1 2 1 2
86. Hàm số f x 3
 x  m   2
3 x mm  2 x  2 đạt cực trị tại x , x sao cho 1 2
x x  6 x x  4  0 . Khi đó, giá trị m thõa mãn yêu cầu bài toán là: 1 2  1 2 3 2 3 2 A.   m
B. m 12 hoặc m  2 C. m  2 D. m 12 2 2
87. Hàm số f x  x  2  sin x đạt cực tiểu tại   A. x  
k k   B. x   k k   3 3 TRẦN THÔNG
Facebook: hội toán bắc trung nam 84   C. x  
k2 k   D. x   k2 k   3 3
88. Hàm số f x  x ln x đạt cực tiểu tại 1 2 A. 0 B.1 C. D.  2 e e
89. Giá trị cực đại y của hàm số 2
y x  1 x là: CD 1 A. y  2 B. y  C. y  1  D. y  1 CD CD CD CD 2
90. Giả sử hàm số 3 2 y  x m  2 x m
 3x 1 có cực đại và cực tiểu. Khi đó, giá trị m thõa mãn yêu cầu bài toán là: m  0 9  A. 0  m B. m C. 9 D. m > 2 4 m   4
91. Giả sử hàm số 4 y m  m   2 x
1 x 1 2m chỉ có một cực trị. Khi đó, giá trị m thõa mãn yêu cầu bài toán là: m  0
A. m 1 B. m  0 C. 0  m 1 D.  m  1 3 x
92. Giả sử hàm số 2 y   m   2 x m m  
1 x 1 đạt cực tiểu tại x = 1. Khi đó, giá trị m thõa 3
mãn yêu cầu bài toán là: A. m 1 B. m  2 C. m  3 D.không tồn tại m
93. Số điểm cực trị có tung độ dương của đồ thị hàm số 4 2
y x x 1là: A.1 B.2 C.3 D.4 94. Cho hàm số 4 2
y x  2x  2 . Khoảng cách giữa hai điểm cực trị của hàm số bằng : A. 7 B. 5 C. 3 D. 2 95. Để hàm số 3 2
y x  6x  3m  2 x m  6 có cực trị tại hai điểm x và x sao cho 1 2
x  1  x thì giá trị m là : 1 2 A. m 1 B. m 1 C. m  1  D. m  1 
96. Giả sử hàm số 2 3 2
y  (m  5m)x  6mx  6x  5 đạt cực trị tại x 1. Khi đó, giá trị m
thõa mãn yêu cầu bài toán là: A. m 1 B. m  1  C. m 1 D. m  2
97. Giả sử đồ thị hàm số 4 2
y x  2mx  1 có có ba điểm cực trị A,B,C sao cho A Oy, BC  1.
Khi đó, giá trị m thõa mãn yêu cầu bài toán là: TRẦN THÔNG
Facebook: hội toán bắc trung nam 85 1 A.9 B.4 C.1 D. 4
98. Đồ thị hàm số f x 2
x  2x 1 có số điểm cực trị là: A.0 B.1 C.2 D.3
99. Tọa độ các điểm cực trị của đồ thị hàm số f x 2 3
 3x x là: A. 0  ,1 và 2,3 B. 0,3 và 2  ,1
C. 0,3 và 1, 2 D. 0,0 và 2, 2 1 2 100.
Hàm số f x 3 2
x mx   2 2m   1 x  7m
đạt cực trị tại x , x sao 3 3 1 2 cho 3 3
x x  26 . Khi đó, giá trị m thõa mãn yêu cầu bài toán là: 1 2 A. m  1  B. m  0 C. m 1 D. m  2 101.
Hàm số f x 3
  x   m   2 2 3 2
1 x  6mm  
1 x  5m  7 đạt cực trị tại
x , x sao cho x
 3x 1. Khi đó, giá trị m thõa mãn yêu cầu bài toán là: 1 2 CD CT A. m  1  B. m  0 C. m  1  D. m  2 2 102.
Hàm số f x 3
x  m   2 1 x   2
m  4m  3 x đạt cực trị tại x , x sao 3 1 2
cho biểu thức x x  2 x x
đạt giá trị nhỏ nhất. Khi đó, giá trị m thõa mãn yêu cầu bài toán 1 2  1 2 là: A. m  4  B. m  0 C. m  4 D. m  1 
103. Xét hàm số f x xác định,liên tuc tại mọi x có bảng biến thiên: x - -1 0 1 + y’ - 0 + 0 - 0 + + 2 + y 1 1
Mệnh đề nào dưới đây là sai.
A.Hàm số đạt cực đại tại x  0 .
B. Hàm số đạt cực tiểu tại x 1.
C.Đồ thị hàm số có 3 điểm cực trị.
D. Đồ thị hàm số có 2 điểm cực đại.
104. Đồ thị hàm số x y e  2
x  3x  5 có số điểm cực trị là: A.2 B.3 C.4 D.5 2x  1
105. Tiệm cận đứng của đồ thị hàm số y x  là 1 TRẦN THÔNG
Facebook: hội toán bắc trung nam 86 A. x 1 B. y  1 C. x  2 D. y  2 2x  1
106. Tiệm cận ngang của đồ thị hàm số y x  là 1 A. x 1 B. y  1 C. x  2 D. y  2 3x 1
107. Cho hàm số y
.Mệnh đề nào sau đây đúng. 2x 1 3 3
A. Đồ thị hàm số có tiệm cận ngang là y  B. Đồ thị hàm số có tiệm cận đứng là y  2 2
C. Đồ thị hàm số không có tiệm cận D. Đồ thị hàm số có tiệm cận đứng là x 1 3x 1
108. Số đường tiệm cận của đồ thị hàm số y  là: x  4 A.1 B.2 C.3 D.4 x
109. Đồ thị hàm số 2 y
có tiệm cận đứng và tiệm cận ngang lần lượt là x a và y b . x 1
Khi đó, giá trị biểu thức a b ab là: A.2 B.1 C.3 D.0 x  3
110. Gọi a,b,c lần lượt là số tiệm cận của đồ thị các hàm số 4 2
y x  2x , y
, y x 1 . 2x 1
Nhận xét nào dưới đây là đúng. A. a b B. a c
C. a c b
D. a c b x  2
111. Số tiệm cận của đồ thị hàm số y  là: 2 x  9 A.1 B.2 C.3 D.4 2 x  3x  2
112. Số tiệm cận của đồ thị hàm số y  là: 2 x  2x  3 A.1 B.2 C.3 D.4 2
113. Số tiệm cận của đồ thị hàm số y  là: 5  x A.1 B.2 C.3 D.4 2 2x  3x  2
114. Cho hàm số y
. Mệnh đề nào sau đây đúng. 2 x  2x  3
A. Đồ thị hàm số có tiệm cận ngang là x  2 B. Đồ thị hàm số có tiệm cận đứng là y  2
C. Đồ thị hàm số không có tiệm cận đứng D. Đồ thị hàm số có hai tiệm cận đứng là
x  1, x  3. 2 x 7x 6
115. Số tìm cận của đồ thị hàm số y là: x 1 A.1 B.2 C.3 D.4 TRẦN THÔNG
Facebook: hội toán bắc trung nam 87 2x  2m 1
116. Đồ thị hàm số y x
có tiệm cận đứng của đồ thị hàm số đi qua điểm M( 3; 1). m Giá trị m là: A.1 B.3 C.-3 D.-1 3 mx  2x
117. Đồ thị hàm số y
x   . Giá trị m là: x  có tiệm cận đứng là 1 1 A. m  2 B. m  2  C. m  2 D. m  2  2 2x  2m 1
118. Đồ thị hàm số y M 1,1 . mx
có tiệm cận đứng của đồ thị hàm số đi qua điểm   1 Giá trị m là: A. m 1 B. m  2 C. m 1 D. m 1
119. Cho hàm số f x có lim f x  lim f x  2 .Mệnh đề nào dưới đây là đúng. x x
A. Đồ thị hàm số f x có tiệm cận ngang là x  2
B. Đồ thị hàm số f x có tiệm cận đứng là x  2
C. Đồ thị hàm số f x có tiệm cận ngang là y  2
D. Đồ thị hàm số f x có tiệm cận đứng là y  2
120. Cho hàm số f x có lim f x   ,
 lim f x   .
 Mệnh đề nào dưới đây là đúng.   x 2  x 2 
A. Đồ thị hàm số f x có tiệm cận ngang là x  2
B. Đồ thị hàm số f x có tiệm cận đứng là x  2
C. Đồ thị hàm số f x có tiệm cận ngang là y  2
D. Đồ thị hàm số f x có tiệm cận đứng là y  2
121. Cho hàm số f x liên tục trên
có lim f x  3, lim f x  2 .Đồ thị hàm số có số tiệm x x cận là: A.2 B.3 C.4 D.5
122. Cho hàm số f x liên tục trên \  
2 có lim f x  3, lim f x  2 .Đồ thị hàm số có số x x tiệm cận ngang là: A.2 B.3 C.1 D.5 mx 1
123. Giả sử đồ thị hàm số y
có tiệm cận đứng . Khi đó, giá trị m là: 2x  3 2 2 3 3 A. m  B. m   C. m  D. m  3 3 2 2 2 mx  6x  2
124. Giả sử đồ thị hàm số y
không có tiệm cận. Khi đó, giá trị m là: x  2 TRẦN THÔNG
Facebook: hội toán bắc trung nam 88 7 7 A. m  B. m  C. m  0 D. m  0 2 2 3 mx 1
125. Giả sử đồ thị hàm số y
có một tiệm cận đứng và một tiệm cận ngang. Khi đó, 2 x  3x  2 giá trị m là: 1 1
A. m  1, m  8
B. m  1, m  C. m  1  ,m  8
D. m  1, m   8 8 x 1,x 1
126. Số tiệm cận của đồ thị hàm số y 2x là: ,x 1 x 1 A.1 B.2 C.3 D.4 3 x 1
127. Số tiệm cận của đồ thị hàm số y là: 2 x 1 A.1 B.2 C.3 D.4 x 1
128. Số tiệm cận ngang của đồ thị hàm số y là: 2 x 1 A.1 B.2 C.3 D.4 129. Cho hàm số 3
y x  3x  2 , chọn phương án đúng trong các phương án sau:
A. max y  2, min y  0
B. max y  4, min y  0  2  ;0  2  ;0  2  ;0  2  ;0
C. max y  4, min y  1 D. max y  2, min y  1   2  ;0 2; 0  2  ;0  2  ;0 130. Cho hàm số 3 2
y x  3x  2 . Chọn phương án đúng trong các phương án sau
A. max y  0, min y  2 
B. max y  2, min y  0  1  ;  1  1  ;  1  1  ;  1  1  ;  1
C. max y  2, min y  2 
D. max y  2, min y  1   1  ;  1  1  ;  1  1  ;  1  1  ;  1
131. Giá trị lớn nhất của hàm số 2
y x  1  x là: A. 2 B. 5 C.2 D.1   
132. Giá trị lớn nhất của hàm số y x  2 cos x trên đoạn 0;  là:  2    A. 2 B. 5 C. 1 D. 4 2    
133. Giá trị nhỏ nhất của hàm số y  sin3 x  cos2x  sin x  2 trên khoảng   ;  là:  2 2  TRẦN THÔNG
Facebook: hội toán bắc trung nam 89 23 1 A. B. C.5 D.1 27 27 2x  1
134. Giá trị nhỏ nhất của hàm số y  trên đoạn 2,  3 là: 1  x A.0 B.-2 C.1 D.-5 2 x  3x
135. Giá trị lớn nhất của hàm số y  trên đoạn 0,  3 là x  1 A.0 B.1 C.2 D.3
136. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f x 2
 sin x  2cos x  2 lần lượt là : A.4 và 1 B.3 và c.4 và 0 D.1 và 0
137. Giá trị lớn nhất của hàm số 2 2
f (x)  (x 1) (4  x)  m  5m trên đoạn [2;5] bằng 8, thì giá trị của m là:
A. m = 1 hoặc m = 4
B. m = 2 hoặc m = 4
C. m = 1 hoặc m = -4 D. m = -1 hoặc m = 2 ax b
138. Cho hàm số f (x)  2
x  có giá trị lớn nhất bằng 4 và giá trị nhỏ nhất bằng -1. Khi đó, 1
khẳng định nào sau đây là đúng. A. 2 2 a b  5 B. 2 2 a b  10 C. 2 2 a b  13 D. 2 2 a b  25
139. Một chủ hộ kinh doanh có 50 phòng trọ cho thuê. Biết giá cho thuê mỗi tháng là
2,000,000đ/1 phòng trọ, thì không có phòng trống. Nếu cứ tăng giá mỗi phòng trọ thêm
50,000đ/tháng, thì sẽ có 2 phòng bị bỏ trống. Hỏi chủ hộ kinh doanh sẽ cho thuê với giá là bao
nhiêu để có thu nhập mỗi tháng cao nhất. A. 2,200,000đ B. 2,250,000đ C. 2,300,000đ D. 2,500,000đ
140. Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí
nguyên liệu làm vỏ lon là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể
tích khối trụ đó bằng 2 và diện tích toàn phần phần hình trụ nhỏ nhất thì bán kính đáy gần số nào nhất A.0.6 B.0,7 C.0,8 D.0,5
141. Người ta cắt một tờ giấy hình vuông cạnh bằng 5 2 để gấp thành một hình chóp tứ giác
đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối
chóp để thể tích lớn nhất. A.4 B.2 C. 2 2 D.1
142. Trong một cuộc thi làm đồ dùng học tập do trường phát động, bạn An đã nhờ bố làm một
hình chóp tứ giác đều bằng cách lấy một mảnh tôn hình vuông ABCD có cạnh bằng a, cắt mảnh
tôn theo các tam giác cân AEB; BFC; CGD và DHA; sau đó gò các tam giác AEH; BEF; CFG;
DGH sao cho 4 đỉnh A;B;C;D trùng nhau (Như hình). TRẦN THÔNG
Facebook: hội toán bắc trung nam 90 B E F A C H G D
Thể tích lớn nhất của khối tứ diện đều tạo được là: 3 a 3 a 3 a 3 a A. B. C. D. 36 24 54 48 3
143. Gọi M và N lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số y x 3x . Lúc đó, tổng 2M 3N bằng A.2 B.-2 C.4 D.-4 144. Cho hàm số 4 2 f (x) sin x
cos x . Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số là: 5 1 A.  B.  C.2 D.0 4 4
145. Một hành lang giữa hai nhà có hình dạng của 1 lăng trụ đứng như hình vẽ. Hai mặt bên
ABB’A và ACC’A’ là hai tấm kính hình chữ nhật dài 20m, rộng 5m. Gọi x (mét) là độ dài của
cạnh BC. Tìm x để lăng trụ có thể tích lớn nhất. A' 5 B' C' A C x B A. 5 B. 5 2 C. 2 5 D. 3 2
146. Một công ty chuyên sản xuất container muốn thiết kế các thùng gỗ đừng hàng bên trong
dạng hình hộp chữ nhật không nắp, đáy là hình vuông, có thể tích là 62, 3
5m . Hỏi các cạnh hình
hộp và cạnh đáy là bao nhiêu để tổng diện tích xung quanh và diện tích mặt đáy là nhỏ nhất.
A. Cạnh bên 2,5m. cạnh đáy 5m
B. Cạnh bên 4m. cạnh đáy 5 10 m 4 TRẦN THÔNG
Facebook: hội toán bắc trung nam 91
C. Cạnh bên 3m, cạnh đáy 5 30
D. Cạnh bên 5m,cạnh đáy 5 2 6 2
147. Một giáo viên đang đau đầu về việc lương thấp và phân vân xem có nên tạm dừng niềm đam
mê với con chữ để chuyển hẳn sang kinh doanh đồ uống trà sữa hay không. Ước tính nếu giá 1 ly
trà sữa là 20(ngàn đồng) thì trung bình hàng tháng có khoảng 1000 lượt khách tới uống nước tại
quán,trung bình mỗi khách lại trả thêm 10(ngàn đồng) tiền bánh tráng trộn để ăn kèm. Nay nguời
giáo viên muốn tăng thêm mỗi ly trà sữa 5(ngàn đồng) thì sẽ mất khoảng 100 khách trong tổng
số trung bình. Hỏi giá 1 ly trà sữa
148. nên là bao nhiêu để tổng thu nhập lớn nhất (giả sử tổng thu chưa trừ vốn) A. Giảm 15 ngàn đồng B. Tăng 5 ngàn đồng
C. Giữ nguyên không tăng giá
D. Tăng thêm 2,5 ngàn đồng
149. Gọi M , N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số : y x ln x x ln 5 trên
1,5. Giá trị M,N lần lượt là: 5 5 5 4
A. M  0, N
B. M  1, N
C. M  0, N
D. M  1, N e e 2e e
150. Do nhu cầu sử dụng, người ta cần tạo ra một lăng trụ đứng có đáy là hình vuông cạnh a và
chiều cao h, có thể tích 3
1m . Với a, h như thế nào để đỡ tốn nhiêu vật liệu nhất. 1 1 1 1
A. a  1, h  1 B. a  , h
C. a  2, h  2 D. a  , h  2 2 3 3
151. Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng 500 3
m . Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ 3
là 500.000 đồng/m2. Hãy xác định kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất. Chi phí đó là ? A. 74 triệu đồng B. 75 triệu đồng C. 76 triệu đồng D. 77 triệu đồng
152. Hình thang cân ABCD có đáy nhỏ AB, AB AD BC  2 . Giá trị của góc
  ADC  BCD để hình thang có diện tích lớn nhất là ? A B D C A. 0 30 B. 0 45 C. 0 60 D. 0 90
153. Số giờ có ánh sáng mặt trời của TPHCM năm không nhuận được cho bởi y 4 sin (x 60)
10 với 1 x 365 là số ngày trong năm. Ngày 25/5 của năm thì số giờ có 178
ánh sáng mặt trời của TPHCM gần với con số nào nhất ?. A.2h B.12h C.13h30 D.14h TRẦN THÔNG
Facebook: hội toán bắc trung nam 92
154. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y x    x 3 6 2 4 1 trên đoạ M
n [-1; 1]. Khi đó, giá trị là: m 1 14 A.4 B. C. D.9 9 9
155. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
sin x cos x . Khi đó M m bằng: A. 2 2 B.  2 C 2 D. 0
156. Một đường dây đẫn điện được nối từ một nhà máy điện ở A đến một hòn đảo tại C. Khoảng
cách ngắn nhất từ C đến B là 1km. Khoảng cách ngắn nhất từ A đến B là 4km. Mổi km dây dẫn
đặt trên mặt đất tốn chi phí 3000 triệu đồng, còn đặt dưới nước mất 5000 triệu đồng.S là vị trị
nào đó nằm trên bờ sao cho chi phí lắp đặt đường dây dẫn điện từ A sang C là thấp nhất. Vị trí
của S cách A bao nhiêu km ? 3 13 A,1 B. 4 C. D. 4 4
157. Một màn ảnh hình chử nhật cao 1,4m đặt ở độ cao 1,8m so với tầm mắt (tính từ mép dưới
của màn ảnh). Để nhìn rỏ màn hình cần phải chọn vị trí đứng sao cho góc nhìn là lớn nhất. Vị trí
đó cách màng ảnh bao nhiêu m? A.2,4 B.1,4 C.3,2 D.0,4
158. Từ một khúc gỗ hình trụ, người ta cần xẻ thành một chiếc xà có tiết diện ngang là hình
vuông và bốn miếng phụ là hình chử nhật như hình vẽ. Xác định kích thước chiều rộng của
miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất. TRẦN THÔNG
Facebook: hội toán bắc trung nam 93 34  3 2 34  3 2 3 2 34 A. B. C. D. 16 16 16 16
159. Chi phí nguyên liệu của một tàu chở hàng được chi làm hai phần. Trong đó phần thứ nhất
phụ thuộc vào vận tốc và bằng 480 ngàn đồng/ giờ, phần thứ hai tỷ lệ với lập phương vận tốc,
khi vận tốc là thì chi phí phần thứ hai là 30 ngàn đồng/giờ. Vận tốc để tổng chi phí nguyên liệu
đi trên 1km đường là nhỏ nhất là: A.15km/h B.30km/h C.50km/h D.10km/h
160. Với một đĩa tròn bằng thép trắng, người ta muốn làm một cái phểu bằng cách cắt đi một
hình quạt của đĩa tròn và gấp phần còn lại thành một hình nón.Cung tròn của hình quạt bị cắt đi
phải bằng bao nhiêu độ để thể tích hình quạt là lớn nhất.(13) A. 0 65 B. 0 295 C. 0 125 D. 0 57
161. Từ cảng A dọc theo đường sắt AB cần phải xác định một trạm trung chuyển C và xây dựng
một con đường từ C đến cảng D. Biết rằng vận tốc khi đi trên đường sắt là v và trên đường bộ 1
là v v v . Hãy xác định phương án chọn vị trí điểm C sao cho thời gian chuyển hàng từ 1 2  2
cảng A đến cảng D là ngắn nhất. v v
A.C cách A một khoảng là 1 l  . h
B.C cách A một khoảng là 2 l  . h v v 2 1 v v
C. C cách A một khoảng là 1 l  . h
D. C cách A một khoảng là 2 l  . h v v 2 1
162. Cần phải xây dựng một hố ga hình hộp chử nhật có thể tích là  3
V m  .Hãy xác định các
kích thước của đáy để chi phí vật liệu xây dựng là thấp nhất biết k cho trước là tỷ số chiều cao
của hố và chiều rộng của đáy. k 1 4kV A.Chiều dài là 3 y
V , chiều rộng là x  3 2 2k 2 (k 1) 4kV k  1
B. Chiều dài là y   3 , chiều rộng là 3 x V 2 (k 1) 2 2k TRẦN THÔNG
Facebook: hội toán bắc trung nam 94
k(k 1)V 4kV C. Chiều dài là 3 y
, chiều rộng là x  3 2 2 (k 1)
k(k 1)V 4kV D. Chiều dài là 3 y
, chiều rộng là x  3 2 2 (k 1)
163. Hai con tàu cách nhau 5 hải lý. Cả hai con tàu khởi hành cùng lúc, một tàu chạy theo hướng
nam với vận tốc 6 hải lý/giờ; tàu còn lại chạy theo hướng về vị trí hiện tại của tàu thứ nhất với
vận tốc 7 hải lý/giờ. Thời điểm mà khoảng cách giửa hai tàu lớn nhất là: 16 1 6 7 A. B. C. D. 17 17 17 17
164. Cần phải dùng thuyền để vượt sang bờ đối diện của một dòng sông chảy siết với vận tốc
nước chảy v lớn hơn vận tốc của thuyền v . Hướng đi của thuyền phải như thế nào để độ dời nc t
do dòng chảy gây ra là thấp nhất tức là hướng di chuyển hợp với phương ngang góc thỏa: v v v v A. cos nc   B. cos t   C. sin nc   D. sin t   v v v v t nc t nc
165. Một người làm nhiệm vụ cứu hộ gần bờ, cần phải cứu một người bị đuối nước ở giửa hồ.
Nếu biết rõ vận tốc của người cứu hộ là v và vận tốc của người bị đuối nước là v . Người cứu 1 2
hộ phải chọn đường đi sao cho thời gian tới vị trí người cứu hộ là ngắn nhất. Qủy đạo đường đi
của người cứu hộ phải thỏa mãn điều kiện gì? TRẦN THÔNG
Facebook: hội toán bắc trung nam 95 sin v sin v sin v v sin v A. 1  B. 2  C. 2 1  D. 1  sin  v sin  v sin  v sin  v v 2 1 2 2 1
166. Hãy xác định độ dài cánh tay nâng của cần cẩu bánh hơi có thể dùng được để xây dựng tòa
nhà có chiều cao H và chiều rộng 2l (Biết rằng cần cẩu thỏa mãn yêu cầu sau đây: có thể xê
xích chiếc cần cẩu cũng như góc nghiêng của tay nâng để sao cho điểm cuối của tay nâng chiếu
xuống theo phương thẳng đứng thì trùng với trung điểm của bề rộng. Ta giả sử ngôi nhà xây
dựng trên miếng đất rộng,cần cẩu có thể di chuyển thoải mái) . 2 2  l   H h
A. AC   H h 3 3 1  l 1      H h   l  2 2  l   H h
B. AC   H h 3 3 1  l 1      H h   l  2 2  l   H h  C. 3 3 AC  1  1      H h   l  2 2  l   H h
D. AC   H h 3 3 1  l 1      H h   l
167. Cấu tạo của một hộp diêm gồm một nắp, hai đáy, bốn mặt bên và hai đầu như hình vẽ. Gọi
x,y,z lần lượt là chiều cao chiều rộng chiều dài của hộp diêm Tỷ lệ x,y,z phải như thế nào để với
thể tích V cố định khi chế tạo chi phí dành cho vật liệu sản suất là ít nhất. TRẦN THÔNG
Facebook: hội toán bắc trung nam 96
A. x : y : z  3 : 4 : 2
B. x : y : z  4 : 3 : 2
C. x : y : z  2 : 3 : 4
D. x : y : z  3 : 2 : 4
168. Cần làm một cái cửa số mà phía trên là hình bán nguyệt, phía dưới là hình chử nhật có chu
vi là a(m) (a là chu vi cửa sổ tức là chu vi hình bán nguyệt cộng với chu vi hình chử nhật trừ độ
dài cạnh hình chử nhật là dây cung hình bán nguyệt ). Kích thước của hình chử nhật để diện tích cửa sổ lớn nhất là: a 2a A. Chiều cao là , chiều rộng là 4   4   a a B. Chiều cao là , chiều rộng là 4   4   2a 2a C. Chiều cao là , chiều rộng là 4   4   2a a D. Chiều cao là , chiều rộng là 4   4   1 1
169. Tiếp tuyến của đồ thi hàm số y  tại điểm A( ; 1) có phương trình là: 2x 2
A. 2x  2 y 1  0
B. 2x  2 y 1  0
C. 2x  2 y  3  0 D.
2x  2 y  3  0
170. Số đường thẳng đi qua điểm A (0;3) và tiếp xúc với đồ thi hàm số 4 2
y x  2x  3 là: A.0 B.1 C.2 D.3 1 171. Cho hàm số 3 2 y
x  2x  3x 1.Tiếp tuyến tại điểm uốn của đồ thị hàm số ,có phương 3 trình là: 11 1 11 1
A. y  x
B. y  x  C. y x  D. y x  3 3 3 3 1 x
172. Tiếp tuyến của đồ thị hàm số y
tại giao điểm của đồ thị với trục hoành có phương x  3 trình: 1 1 1 1 1 1 A. y x  B. y  4  x  4
C. y   x
D. y   x  4 4 4 4 4 3
173. Trong các tiếp tuyến tại các điểm trên đồ thị hàm số 3 2
y x  3x  2 , tiếp tuyến có hệ số góc nhỏ nhất bằng: TRẦN THÔNG
Facebook: hội toán bắc trung nam 97 A.-3 B.3 C.4 D.0 1 174. Cho hàm số 3 2 y
x x  2. Phương trình tiếp tuyến tại điểm có hoành độ là nghiêm của 3
phương trình y’’ = 0 là: 7 7 7 7
A. y  x  B. y x
C. y  x  D. y x 3 3 3 3
175. Cho đường cong 3 y x  3 2
x  3x  1 có đồ thị (C). Phương trình tiếp tuyến của (C) tại
giao điểm của (C) với trục tung là:
A. y  8x  1
B. y  3x  1
C. y  3x  1
D. y  3x  1 2x 1
176. Gọi M là giao điểm của đồ thị hàm số y
với trục Oy. Phương trình tiếp tuyến với x  2
đồ thị trên tại điểm M là: Chọn 1 3 1 3 1 3 1 3 1 A. y   x  B. y x  C. y   x  D. y x  2 2 2 2 2 2 2 2 4 2 x x
177. Hệ số góc của tiếp tuyến của đồ thị hàm số y  
1 tại điểm có hoành độ x0 = - 1 4 2 bằng:
A. -2 B. 2 C. 0 D. Đáp số khác 4
178. Tiếp tuyến của đồ thị hàm số y
tại điểm có hoành đo x0 = - 1 có phương trình là: x 1
A. y = - x - 3 B. y = - x + 2 C. y = x -1 D. y = x + 2
179. Cho đồ thị hàm số 3 2
y x  2x  2x có đồ thị ( C ) . Gọi x , x là hoành độ các điểm M, 1 2
N trên ( C ), mà tại đó tiếp tuyến của ( C ) vuông góc với đường thẳng y  x  2017 . Khi đó
x x bằng : 1 2 4 4 1 A. B. C. D. -1 3 3 3 3 x
180. Tiếp tuyến của đồ thị hàm số 2 y
3x  2 có hệ số góc k = - 9 ,có phương trình là: 3
A. y +16 = - 9(x + 3) B. y – 16 = - 9(x – 3) C. y – 16 = - 9(x +3) D. y = - 9(x + 3)
181. Số tiếp tuyến đi qua điểm A ( 1 ; - 6) của đồ thị hàm số 3
y x  3x 1 là: A. 1 B. 0 C. 2 D. 3 1
182. Tiếp tuyến tại điểm cực tiểu của hàm số 3 y x  2 2
x  3x  5 . Mệnh đề nào dưới đây là 3 đúng.
A. Song song với đường thẳng x = 1
B. Song song với trục hoành C. Có hệ số góc dương
D. Có hệ số góc bằng – 1 TRẦN THÔNG
Facebook: hội toán bắc trung nam 98 183. Cho hàm số 3
y  x  3 2
x  3 có đồ thị (C). Số tiếp tuyến của (C) vuông góc với đường 1 thẳng y x  2017 là: 9 A. 1 B. 2 C. 3 D. 0 184. H
185. Số đường thẳng đi qua điểm A(2 ; 0) và tiếp xúc với đồ thị của hàm số 4 2
y  x  2x là: A. 0 B. 1 C. 2 D. 3 2x  1
186. Cho hàm số: y
C Phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng 2 là: x  1 1 2 1 1 1 1 .
A d : y x  .
B d : y x  .
C d : y   x  1 . D y x  3 3 3 3 3 3 2x  1
187. Gọi M  (C) : y
C tại M cắt các trục tọa độ x
có tung độ bằng 5 . Tiếp tuyến của ( ) 1
Ox, Oy lần lượt tại A và B. Diện tích tam giác OAB là: 121 119 123 125 A. B. C. D. 6 6 6 6 x
188. Hệ số góc của tiếp tuyến của đồ thì hàm số 1 y
tại giao điểm của đồ thị hàm số với x 1 trục tung bằng. A.-2 B.2 C.1 D.-1
189. Đường thẳng y  3x m là tiếp tuyến của đường cong 3
y x  2 khi m bằng
A. 1 hoặc -1 B. 4 hoặc 0 C. 2 hoặc -2 D. 3 hoặc -3 2x
190. M là điểm thuộc đồ thị hàm số y
, biết tiếp tuyến với đồ thị hàm số tại điểm M đó x  1 1
tạo với hai trục tọa độ một tam giác có diện tích bằng . Tọa độ M là: 4 A. M  0 ; 0  và M  ; 1  1 . B. M  ; 1  1 và M  ; 2 4.  1   1 2   1 
C. M   ;  2 và M  ;  D. M  ; 1 
1 và M   ;  2  2   2 3   2  191. Cho hàm số 3 2
y x  3x  2 có đồ thị (C) . Đường thẳng nào sau đây là tiếp tuyến của (C)
và có hệ số góc nhỏ nhất?
A. y  3x  3
B. y  x  3 C. y  5  x 10
D. y  3x  3 1 192. Cho hàm số 3 2 y  
x  2x  3x 1 có đồ thị (C) . Trong các tiếp tuyến với (C) , tiếp tuyến 3
có hệ số góc lớn nhất bằng:
A. k  3 B. k  2 C. k 1 D. k  0 TRẦN THÔNG
Facebook: hội toán bắc trung nam 99 2 x x 1
193. Cho hàm số y
có đồ thị (C) . Phương trình tiếp tuyến của (C) đi qua điểm x 1 ( A 1; 0) là: 3 3 A. y x B. y  (x 1)
C. y  3(x 1)
D. y  3x 1 4 4 194. Qua điểm (
A 0; 2) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị (C) của hàm số 4 2
y x  2x  2 ? A.0 B.1 C.2 D.3 x 1
195. Phương trình tiếp tuyến với đồ thị hàm số y
song song với đường thẳng x 1
 : 2x y 1  0 là:
A. 2x y  7  0
B. 2x y  7  0
C. 2x y  0 D. 2
x y 1  0
196. Cho đường cong 4 2
(C) : y x  4x  2 và điểm (
A 0; a) . Nếu qua A kẻ được 4 tiếp tuyến
với (C) thì a phải thoả mãn điều kiện: a  2 10 10 A. a B . 2  a C.  10 D. a  2 3 3 a   3
197. Giả sử để tiếp tuyến của đồ thị hàm số 3
y  x  mx  m 1 tại điểm có hoành độ bằng 1 cắt đường tròn 2 2 1 (x  2)  (y  3) 
theo một dây cung có độ dài nhỏ nhất. Khi đó giá trị m là : 5 5 5 3
A. m 1 hoặc m  B. m  hoặc m  2 C. m
hoặc m  2 D. m 1 hoặc m  2 2 2 2 x  2
198. Cho hàm số y 
. Tiếp tuyến bất kì của đồ thị hàm số tại M cắt hai đường tiệm cận lần x 1
lượt tại hai điểm A va B. Khi đó MA kMB , giá trị của k bằng: 1 3 A.1 B.2 C. D. 2 2
199. Số đường tiếp tuyến vẽ từ M  1  ; 9   đến C : 3 2 y  4x  6x 1 là: A.0 B.1 C.2 D.3 1 200. Cho hàm số 3 2 y
x  2x  3x 1 (1) . Phương trình tiếp tuyến của đồ thị hàm số (1) song 3
song với đường thẳng y  3x 1có dạng y ax b ( với a,b đã tối giản ). Giá trị S=a+b là: 29 20 20 19 A.  B.  C. D.  3 3 3 3
201. Đồ thị hàm số 3 2 f ( )
x x +ax  bx c cắt trục tung tại điểm có tung độ là 2 và tiếp xúc với
đường thẳng y  1 tại điểm có hoành độ x  1
 . Hệ số a,b,c là:
A. a  3,b  3, c  2 B. a  3,b  3, c  2
C. a  3,b  3, c  2 D. a  3  ,b  3  ,c  2 TRẦN THÔNG
Facebook: hội toán bắc trung nam 100 
202. Đồ thị hàm số ax b
y x  cắt trục tung tại điểm A(0;1) và tiếp tuyến tại A có hệ số góc bằng 1
-3. Giá trị a,b là:
A. a  4,b  1
B. a  2,b  1
C. a  4,b  1 D. a  4  ,b  1  x 203. Cho hàm số 2 1 y
có đồ thị C . Các cặp tiếp tuyến song song của C sao cho khoảng x 1
cách giữa chúng lớn nhất là:
A. y x   y x   3 2 3 và 3 2 3 B.         y x 3 2 3 và y x 3 2 3 C.    y x   y x 3 2 3 và 3 2 3
D. y x      3 2 3 và y x 3 2 3
204. Số tiếp tuyến đến đồ thị hàm số y= 3 2
x  9x 17x  2 qua A(-2 ;5) là : A.1 B.2 C.3 D.4 2x 1
205. Cho hàm số y
. Tọa độ điểm M sao cho khoảng cách từ điểm I  tới tiếp x  ( 1; 2) 1
tuyến của (C) tại M là lớn nhất là: 7  3 3 7  3 3 A. M ( 3; ); M (1 3; ) 2 2 2  3 2 2   3 2 B. M (1 2;  ); M (1 3; ) 2 2 C. M (1 3; 4
 3 3); M(1 3; 4  3 3) D. M  1
  3;2  3 ; M  1   3;2  3 2x  3
206. Cho hàm số y
đồ thị (C). Tiếp tuyến d tại điểm M thuộc (C) cắt tiệm cận đứng và x  2 4
tiệm cận ngang tại A, B sao cho cos BAI
,với I là giao 2 tiệm cận là. Tọa độ M là: 17  5   3   5   3  A. M ; 4 , M ; 0    
B. M  ; 4 , M  ; 0      2   2   2   2   3   5   3   5  C. M 0; , M 4;     D. M 0;  , M 4;       2   2   2   2  207. Cho hàm số 4 2
y x  2x  
1 C  . Điểm M Oy sao cho từ M vẽ được 3 tiếp tuyến với (C). Tọa độ M là: A. M 0; 2   B. M 0;   1 C. M 0;2 D. M 0  ;1 3x 1
208. Cho hàm số y
có đồ thị C . Tiếp tuyến của đồ thị (C) cắt trục hoành, trục tung x 1
lần lượt tại hai điểm phân biệt ,
A B . Tam giác OAB có cạnh huyền gấp 5 lần cạnh góc vuông
thì một phương trình tuyến tuyến đó là: TRẦN THÔNG
Facebook: hội toán bắc trung nam 101 1 11 1 3
(I) y  2x ; (II) y  2
x 1; (III) y   x  ; (IV) y   x  2 2 2 2
A. Chỉ có (II), (III), (IV) đúng
B. (I), (II), (III), (IV) đều đúng
C. Chỉ có (I), (II), đúng
D. Chỉ có (III), (IV), đúng
209. Biết rằng đường thẳng y x  2 cắt đồ thị hàm số 3
y x  3x  2 tại ba điểm có tọa độ lần
lượt là x , y , x , y , x , y .Khi đó, giá trị biểu thức x .y x .y x .y là: 1 1   2 2   3 3  1 1 2 2 3 3 A. 12 B. 4 C. 0 D. 8 x 1
210. Cho đồ thị (C) : y
và đường thẳng d : y x m . Khi d cắt (C) tại 2 điểm phân biệt x  2
và tiếp tuyến với (C) tại hai điểm này song song với nhau thì giá trị m là: A. m 1 B. m  2 C. m  1  D. m  2  211.
Tìm m để đường thẳng (d): y = mx – 2m + 4 cắt đồ thị (C) của hàm số 3 2
y x  6x 12x  4 tại ba điểm phân biệt A. m  3  B. m > 0 C. m < 0 D. m 1
212. Đường thẳng y = m cắt đồ thị hàm số 3
y  x  3x  2 tại 3 điểm phân biệt khi : A. 0  m  4
B.m < - 2 C. 0  m  4 D. -2< m < 4 213. Cho hàm số 4 y x  2 2
x  4 . Tìm m để phương trình: x 2 (x2  )
2  3  m có hai nghiệm
phân biệt? Chọn 1 câu đúng.
A. m  3  m  2 B. m  3 C. m  3  m  2 D. m  2 214. Cho hàm số 3 y x  6 2
x  9x  1. Tìm m để phương trình: x(x  )
3 2  m 1 có ba nghiệm
phân biệt? Chọn 1 câu đúng.
A. m  1 B. 1  m  5 C. m  3  m  2 D. m  5
215. Cho hàm số y x3  8x . Số giao điểm của đồ thị hàm số cới trục hoành là: Chọn 1 câu đúng A. 0 B. 1 C. 2 D. 3
216. Số giao điểm của đường cong 3 y x  2 2
x x 1 và đường thẳng y = 1 – 2x là: A. 1 B. 2 C. 3 D. 0 7x  6
217. Gọi M và N là giao điểm của đường cong y
và đường thẳng y = x + 2 . Khi đó x  2
hoành độ trung điểm I của đoạn MN bằng: Chọn 1 câu đúng 7 7 A. 7 B. 3 C.  D. 2 2 2 x  3x  2
218. Số giao điểm của đồ thị hàm số y  và trục hoành là: x 1 A.0 B.1 C.2 D.3 TRẦN THÔNG
Facebook: hội toán bắc trung nam 102 2 x  3x  2
219. Gọi A  x , y là giao điểm của đồ thị hàm số y
và đường thẳng y x 1. 0 0  x 1
Khi đó, giá trị x y là: 0 0 A.-1 B.1 C.3 D.-3 2x 1
220. Tọa độ giao điểm của đồ thị hàm số y
và đường thẳng y x  2 là: x  2 A. 1,   1 ,0, 2   B.  1  , 3  ,3,  1 C.  1  , 3  ,0, 2   D. 1,   1 ,3,  1 221. Phương trình 3
x  3x 1 m  0 có ba nghiệm phân biệt khi: m 1 A. m 1 B.  C. m 1 D. 1   m 1 m  1  222. Phương trình 3
4x  3x m  0 có hai nghiệm phân biệt khi: m 1 m  1 m  2 m  0 A.  B.  C.  D.  m  1  m  0 m  2 m  2 223. Phương trình 4 2
x  4x  3 m  0 có ba nghiệm phân biệt khi: A.1 m  2 B. 1   m  2 C. 3   m 1 D.1 m  3
224. Đồ thị hàm số 3
y x  3  mx cắt trục hoành tại ba điểm phân biệt khi: A. m  3 B. 3  m C. m 1 D.1 m
225. Giả sử đồ thị hàm số 3 2
y x  2x  1 mx m cắt trục hoành tại ba điểm phân biệt có
hoành độ x , x , x thỏa mãn 2 2 2
x x x  4 . Khi đó, giá trị m là: 1 2 3 1 2 3  1   1   1  A. m   ,1 B. m   ,1 \     0 C. m   ,1   D. m  ,1    4   4   4 
226. Đồ thị hàm số 3 2
y x mx m 1 cắt trục hoành tại ba điểm phân biệt khi: A. m  ,   1  2,3 B. m  ,  3  1, C. m  ,    1  1, D. m  ,  01,
227. Đồ thị hàm số 3 2
y x mx  2m cắt trục hoành tại ba điểm phân biệt khi: 3 6 3 6 5 6 5 6 7 6 7 6 A. m  0 B.   m  C.   m  D.   m  2 2 2 2 2 2
228. Giả sử đồ thị hàm số 3 2
y x  3x  9x m cắt trục hoành tại ba điểm phân biệt có hoành độ
x , x , x tạo thành cấp số cộng. Khi đó, giá trị m là: 1 2 3 A. m 1 B. m 12 C. m  2 D. m 11
229. Giả sử đồ thị hàm số 3
y x   m   2 2
1 x  9x cắt trục hoành tại ba điểm phân biệt có hoành
độ x , x , x tạo thành cấp số cộng. Khi đó, khoảng chứa giá trị m là: 1 2 3 A. m  2,3 B. m  1  ,0 C. m 1, 2 D. m  2  ,  1 TRẦN THÔNG
Facebook: hội toán bắc trung nam 103
230. Giả sử đồ thị hàm số 3
y x    m 2 5
x  6  5mx  6m cắt trục hoành tại ba điểm phân
biệt có hoành độ x , x , x tạo thành cấp số nhân. Khi đó, số giá trị m thỏa mãn yêu cầu bài toán 1 2 3 là: A.1 B.2 C. 3 D. 4
231. Đồ thị C của hàm số 3
y  x  6x  2 cắt đường thẳng d  : y mx m 1 tại ba điểm
phân biệt A,B,C sao cho tổng hệ số góc các tiếp tuyến của C tại A,B,C bằng -6. Giá trị m thỏa mãn đề bài là A. m  3  B. m  1  C. m 1 D. m  2 x 1
232. Đồ thị hàm số y
cắt đường thẳng y  x m tại hai điểm phân biệt khi: x 1 A. m  2  2 B. m  2  2
C. 2  2  m  2  2 D. m  2  2 x 1
233. Giả sử đồ thị hàm số y
cắt đường thẳng y  x m tại hai điểm phân biệt A,B sao x 1
cho tiếp tuyến của tại A và B song song với nhau. Giá trị m là: A. m 1 B. m  2  C. m  2 D. m  0
234. Cho đồ thị C của hàm số 3
y  x  6x  2 và đường thẳng d  : y m .
x Đường thẳng d
cắt C tại ba điểm phân biệt khi:  9   9   3   3  A. m   ,  \    
1 B. m   ,  \     0 C. m  , \     1 D. m  , \     0  4   4   2   2  2x  3
235. Đồ thị C của hàm số y
cắt đường thẳng d  : y  2
x m tại hai điểm phân biệt x  2
A,B thỏa mãn biểu thức 2018 2018 kk
đạt giá trị nhỏ nhất (lần lượt là các hệ số góc tiếp tuyến của 1 2
đồ thị C tại A,B). Giá trị m là: A. m  2 B. m  2  C. m  3  D. m  1  x  2 1
236. Đồ thị hàm số y
cắt đường thẳng y  
x m tại hai điểm phân biệt nằm về hai x 1 2 phía của trục tung khi: A. m 1 B. m  2 C. m  3 D. m  4
237. Đồ thị C của hàm số 3
y x   m   2 2
1 x m 1 cắt đường thẳng d  : y  2mx m 1 tại
ba điểm phân biệt. Giá trị m thỏa mãn đề bài là m  0  1 3 3 A. 1  B. m   C. m  D. m m  2 2 4  2 2x  3
238. Đồ thị C của hàm số y
cắt đường thẳng d  : y  2
x m tại hai điểm phân biệt x  2
A,B sao cho độ dài đoạn thẳng AB ngắn nhất. Giá trị m là: TRẦN THÔNG
Facebook: hội toán bắc trung nam 104 1 3 5 7 A. m  B. m  C. m  D. m  2 2 2 2 2x  2
239. Đồ thị C của hàm số y
cắt đường thẳng d  : y  2x m tại hai điểm phân biệt x 1
A,B sao cho độ dài đoạn thẳng AB  5 . Giá trị m là: m  10  m  2 A. m  3  B. m  2  C.  D.  m  2  m  1 2x 1
240. Đồ thị C của hàm số y
cắt đường thẳng d  : y x m tại hai điểm phân biệt A,B x 1
sao cho độ dài đoạn thẳng O
AB vuông cân (với O là gốc tọa độ). Giá trị m là: 2 2 A. m  1  B. m  2  C. m  D. m   3 3 x 1
241. Đồ thị C của hàm số y
cắt đường thẳng d  : y x m tại hai điểm phân biệt A,B 1 2x
sao cho độ dài đoạn thẳng AB OA OB vuông cân (với O là gốc tọa độ). Giá trị m là: m  2 m  3 A. m  1  B. m  2  C.  D.  m  1 m  1 2x  3
242. Đồ thị C của hàm số y
cắt đường thẳng d  : y  x m tại hai điểm phân biệt x 1
A,B sao cho tiếp tuyến của đồ thị C tại A và B song song với nhau. Giá trị m là: A. m 1 B. m  2 C. m  1  D. m  2 
243. Đồ thị hàm số 4 2 2
y  x  2mx m m cắt trục hoành tại bốn điểm phân biệt khi: 1 3 3 1 A. 1  m   B. 1  m  C. 1   m  D.   m  0 2 2 2 2
244. Đường thẳng d  : y  1
 cắt đồ thị hàm số 4
y x   m   2 3
2 x  3m trục hoành tại bốn
điểm phân biệt có hoành độ x , x , x , x thỏa mãn 2 2 2 2
x x x x x x x x  4 . Giá trị m là: 1 2 3 4 1 2 3 4 1 2 3 4 1 1 A. m  4 B. m  4  C. m  D. m   9 9
245. Đồ thị hàm số 4 2
y  x  4x  4m cắt trục hoành tại bốn điểm A,B,C,D phân biệt có hoành
độ tăng dần và AD  2BC . Giá trị m là: 1 3 3 1 A. 1  m   B. 1  m  C. 1   m  D.   m  0 2 2 2 2 TRẦN THÔNG
Facebook: hội toán bắc trung nam 105 1
246. Tiếp tuyến của đồ thị hàm số C y x m
x m tại điểm có hoành độ bằng 1 cắt m  4 :   2 1 4
đồ thị C tại ba điểm A,B,C sao cho BC  4 . Giá trị m là: m  A. m  4 B. m  0 C. m 1 D. m  1  1 1
247. Đường thẳng d  1 : y mx  cắt đồ thị hàm số 3 2 y
x  2x  3x  tại ba điểm A,B,C 3 3 3
trong đó A là điểm cố định và diện tích tam giác OBC gấp 2 lần diện tích tam giác OAB . Giá trị m là: 3 3 1 1 A. m  B. m   C. m  D. m   4 4 9 9 x 1
248. Đường thẳng d  đi qua M 2,0 có hệ số góc là k cắt đồ thị hàm số y  tại hai điểm x  2
A,B sao MA  2MB . Giá trị k là: 3 3 2 2 A. k  B. k   C. k  D. k   4 4 3 3 2x 1
249. M là điểm thuộc đồ thị của hàm số y
sao cho khoảng cách từ M đến tiệm cận đứng x 1
bằng khoảng cách từ M đến tiệm cận ngang. Tọa độ điểm M là: M 2  ,1 M 0,  1 M 0,  1 M 2  ,1 A.  B.  C.  D.  M  4,3 M  4,3 M  3,2 M  3,2 2x 1
250. M là điểm thuộc đồ thị của hàm số y
sao cho khoảng cách từ M đến tiệm cận x 1
ngang bằng 5 lần khoảng cách từ M đến tiệm cận đứng. Số điểm M thỏa mãn yêu cầu bài toán là: A.1 B. 2 C. 3 D. 4
251. M,N là điểm thuộc đồ thị của hàm số 3 2
y x  3x  2 đối xứng với nhau qua I 2,18 . Số
cặp điểm M,N thỏa mãn yêu cầu bài toán là: A.1 B. 2 C. 3 D. 4
252. Đồ thị của hàm số 4 2
y x mx 1 m luôn đi qua các điểm cố định có tọa độ lần lượt là: A.  1  ,0,1,0 B. 0,  1 ,1,0 C.  2  ,  1 , 2  ,3 D. 2,  1 ,0,  1 2x  7
253. Số điểm có tọa độ nghiêng trên đồ thị của hàm số y  là: x  2 A.4 B. 5 C. 6 D. 7 1 1
254. M là điểm thuộc đồ thị của hàm số 4 2 y x
x 1và d là tổng khoảng cách từ M đến các 4 2
trục tọa độ. Giá trị nhỏ nhất của d là: TRẦN THÔNG
Facebook: hội toán bắc trung nam 106 3 1 A.1 B. 2 C. D. 2 2 255. Cho hàm số 3 2
y x  6x  9x   1  1 và các mệnh đề: (1) Hàm số   1 liên tục trên .
(2) Hàm số đạt cực đại tại x  3
(3) Giá trị cực đại của hàm số   1 là y  1  CD
(4) Tiếp tuyến của đồ thị hàm số tại điểm x 1 có hệ số góc là k  0
(5) Đường thẳng y  1 cắt đồ thị hàm số tại 2 điểm phân biệt
Số mệnh đề đúng trong các mệnh đề trên là: A.2 B.3 C.4 D.5 256. Cho hàm số 4 2
y x  4x  3  1 và các mệnh đề: (1) Hàm số   1 có 3 cực trị
(2) Đồ thị hàm số  
1 cắt trục hoành tại 1 điểm duy nhất
(3) Tập giá trị của hàm số   1 là T  .
(4) Đồ thị hàm số  
1 có một tiệm cận đứng
(5) Tiếp tuyến của đồ thị hàm số  
1 tại điểm có hoành độ bằng 1 song song với đường thẳng y  4  x 1
Các mệnh đề đúng trong các mệnh đề trên là: A.(1),(3),(5) B. (1),(3),(4) C. (2),(3),(5) D. (1),(2),(5) TRẦN THÔNG
Facebook: hội toán bắc trung nam 107 TRẦN THÔNG
Facebook: hội toán bắc trung nam 108