Xét tính đơn điệu của hàm số dựa vào công thức Toán 12

Xét tính đơn điệu của hàm số dựa vào công thức Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Môn:

Toán 12 3.9 K tài liệu

Thông tin:
75 trang 1 năm trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Xét tính đơn điệu của hàm số dựa vào công thức Toán 12

Xét tính đơn điệu của hàm số dựa vào công thức Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

50 25 lượt tải Tải xuống

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số 375 tài liệu

Môn: Toán 12 3.9 K tài liệu

Thông tin:

75 trang 1 năm trước

Tác giả:

Profile Mai Nguyệt
–
– Email:
1
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
– Email:
2
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
– Email:
3
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
– Email:
4
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
– Email:
5
–
–
–
–
–
–
–
–
–
–
–
–
–
– Email:
6
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
– Email:
7
–
2
5 2
3
x x
y
x
\ 3
; 3 3; 
; 3
3; 
2
5 2
3
x x
y
x
\ 3D
2
2
2
2 2 2
6 9 4
3 4
6 13
0,
3 3 3
x x
x
x x
y x D
x x x
; 3
3; 
–
–
– Email:
8
–
–
,
n
p x
y
q x
,p x g x x
n
p x
y
q x
1
2 1
. . . . . . .
n n
n n
p x q x n p x q x q x p x q x n p x q x
y
q x q x
1
.
n
y q x x
1n
n
x X
p x
d
q x
dx
q x
r
100
100x
1 2
1 2 1 0
...
k k
k k
f x a x a x a x a x a
1n
f x
y
q x
n
p x
y
q x
2
2
5 2
3
3
x X
d x x
x
dx x
r
100X 10613
–
– Email:
9
2
2
6.100
100
10613 10000 600 13 6 13, 100x x x
2
2
6 13
3
x x
y
x
–
2
2
ax bx c
y
a x b x c
w5
2
2
ax bx c
y
a x b x c
2 2
2
2
2 . . 2ax b a x b x c ax bx c a x b
y
a x b x c
2
2
2
2 2 2
2 2 2
2
2
2
a b c a b c
x x
a b c a b c
ab a b x a c ac x bc b c
mx nx p
y
a x b x c a x b x c a x b x c
; ; , ; ;u a b c v a b c
, ; ; ; ;
b c c a a b
u v bc b c a c ac ab a b
b c c a a b
; ;p n m
,u v
w5
VctA ; ;a b c
, ,a b c
–
– Email:
10
VctB ; ;a b c
, ,a b c
C T3
T3
VctA
OT4
VctB
=
, ,m n p
T5
VctA 1;5;2 , VctB 0;1;3
T5131=5=2=
T1230=1=3=’
T3T3OT4=
13
3
1
p
n
m
2
2
6 13
3
x x
y
x
–
3
507 506y x x
3
507 506y x x
–
– Email:
11
3
507 506y x x
; 13
13;
3
507 506y x x
15
3
507 506y x x
13;13
3
507 506y x x
26
0 1 2 3
3
507 506y x x
3
23 1
507 506 0
22
x
x x
x
23;1 22;D

2
3
13
3 507
0
13
2 507 506
x
x
y
x
x x
23; 13
22;
13;1
1 13 14l
–
– Email:
12
–
y f x
2
4y f x
0; 7
7;
0;
7;0
2
2 . 4y x f x
2
4y f x
2 2
2 . 4 0 . 4 0x f x x f x
2
2
2
2
2
2
0
0
7
0
4 3
7
4 0
3 4 5
7 7
4 7
0
4 0
0
0
5 4 7
x
x
x
x
x
x
f x
x
x
x
x
x
f x
x
x
x
x
7
0 7
x
x
2
4y f x
0; 7
7;
2
4y f x
0;
0;
2
4y f x
0y
" "
7x
–
y f x
–
– Email:
13
3 2
3 2 6 63 2022y f x x x x
; 3
3; 9
3; 9
;7
3 2
3 2 6 63 2022y f x x x x
2
3 2 3 12 63y f x x x
3 2
3 2 6 63 2022y f x x x x
2
3 2 3 12 63 0y f x x x
2
2
2 4 21 0 2 2 25 0 *f x x x f x x
2t x
2
* 25 0f t t
2
0
25 0
f t
t
3
3 5
5 2 5 3
7
7 2 7 9
5
5
t
t
t x x
t
t x x
t
t
–
– Email:
14
–
3
2
2021
2 21
3 2022
x
y x x
7; 3
3;7
; 7
3;
–
3 2
3 9 2022y x x x
1;2
3;1
; 3
1; 
–
3
2 6 2022y x x
0;2
1;1
0;1
; 1
–
3 2
4 5 5y x x x
5
1;
3
1;1
5
;
3

; 1
–
2
2 lny x x x
1 3
0;
2
1 3
0;
2
1 3
;0
2
1 3
;0
2
–
3 2
5 3 1y x x x
x
2
1
3 10 3; 0
3
3
x
y x x y
x
–
– Email:
15
3 2
5 3 1y x x x
1
; 3;
3
 
1
; 3
3
–
3 sin 5 2y x
3;3D
6 cos 5 2 ;y x
10 2
0 5 2 ,
2 4
k
y x k x k
–
– Email:
16
3 sin 5 2y x
10 3 10
;
4 4
k k
10 3 10
;
4 4
k k
–
1
x
x
e
y
e
\ 0D
2
0,
1
x
x
e
y x D
e
1
x
x
e
y
e
1
x
x
e
y
e
; 0
0;
–
4 2
2y f x x x
0;1
; 1

;1
0;1
–
3
3 4y x x
–
– Email:
17
; 1
1;
1;1
; 1
1;
–
2022
y x
1
;
2

; 0
1
;
2

0;
–
2 3
1
x
y
x
;2
; 
0;
–
; 
4 2
3 2 1.y x x x
1
.
2 2
x
y
x
3 2
2 1.y x x x
3
3.y x
–
3
logy x
2
3
logy x
4
x
e
y
2
5
x
y
–
1
1
x
y
x
2 1
3
x
y
x
2
2 1
x
y
x
3
2
x
y
x
–
4 2 3
1 1
; ; 3 1; 3 1
1 2
x x
f x g x h x x x k x x x
x x
0 1 2 3
–
–
– Email:
18
2
3
1 3
2
2
2
; 2 ; log ;
3
x
x
f x g x h x x k x x
x
0 1 2 3
–
2
2
log 2 1 .y x x
1
;
2

1;
1
;
2

1;
1
;
2

1; 
1
;
2

1;
–
3 2
2 1y x x x
1;
1
;1
3
1
;
3

1
;1
3
–
4 2
2 2y x x
2;
2;
–
– Email:
19
; 0
;0
–
y f x
2
5 4f x x x
1;4
3;
; 3
1;4
–
5 3
3 5y x x
; 1
1;
; 
; 1
1;
1;1
–
m
4 3 2
4 2y x x mx
;0
9
4
m
9
2
m
9
2
m
9
4
m
–
2 3 2
1
1 1 3 5
3
y m x m x x
m
1 2m 1 2m
2
1
m
m
2
1
m
m
–
2 1
,
x
y m
x m
m
–
– Email:
20
1
;1 ?
2
1
1
2
m
1
2
m
1m
1
2
m
–
m
2 sin 1
sin
x
y
x m
0;
2
1
2
m
1
0
2
m
1m
1
0
2
m
1m
1
2
m
–
m
1;1
6
2 1
mx
y
x m
4 3m
4 3
1 3
m
m
1 4m
4 3
1 3
m
m
–
m
2
2
1
x
y x mx
x
1; .
5.m 5.m 5.m 5.m
–
y f x
2
2 2 1f x x x x m
x
m
2
g x f x
1;
5 2 3 4
–
f x
, ,g x f mx n m n
–
– Email:
21
g x
5
3 2m n
5
.
13
5
16
5
4
–
y f x
f x
1 2 2018f x x x g x
0, .g x x
1 2018 2019y f x x
1;
.
0; 3
.
;3
3;
–
5
3 . 2
2018
2019
x x
e m e
y
. , , ,
b
m a e c a b c
2;5
S a b c
7S
9S 8S 10S
–
,y f x y g x
y g x
1 1h x f x g x
1
;1
2
1
1;
2
1;
2;
–
m
2
ln 1 2018y x mx
; 
; 1 1;1
; 1

1;

–
– Email:
22
–
3
sinh x x x x
2 1k x x
.
3 2
6 15 3g x x x x
.
2
2 5
1
x x
f x
x
.
–
.y f x
y f x
2 2 0f f
.
2
3g x f x
2; 1
.
1;2
.
2;5
.
5;
.
–
y f x
.
y f x
2
1
2
x
g x f x x
3;1
2;0
3
1;
2
1; 3
–
–
– Email:
23
.y f x
y f x
2
3g x f x
2;3
.
2; 1
.
0;1
.
1;0
.
–
y f x
f x
m
2
2
480
1
2
g x f x x
m x x
0;1
4 6
7
8
–
y f x
y f x
2
2
1
2 2
2
h x f x xf x x
.
–
– Email:
24
y h x
1; 0M
.
y h x
y h x
1;2N
.
y h x
1; 0M
.
–
f x
2
2 1 ,f x f x x x
.
m
3 . 1 1y x f x m x
.
m
.
10
3
m
.
1m
.
1m
.
–
y f x
.
y f x
1 2g x f x
1; 0 .
;0 .
0;1 .
1; .
–
f x
.
f x
1;3
1
2
x
g x f x
4; 2
.
2; 0
.
0;2
.
2;4
.
–
– Email:
25
–
m
5;5
1
x
e m x
5 6
7
10
–
3 34 2 2 2 2
2 1 1 1x x m x x x m
m
m 1x
.
1m
.
1m
.
5
4
m
5
4
m
.
–
y f x
3
2 1g x f x x m
.
m
0;1
max 10g x
.
13m
.
12m
.
1m
.
3m
.
–
.y f x
y f x
1 1,f
1
2.f
e
lnf x x m
1
1;x
e
–
– Email:
26
2m
2m
3m
3m
–
2 2
3 6 18 3 1x x x x m m
m
m
5; 5
3;6x
3
.
5
.
9
.
10
.
–
y f x
0 0f
0, 1;2f x x
–
f x
2
2
1 2f x x x x
x
.
2
2 2g x f x x
2
.
1
.
3
2
.
3
–
– Email:
27
–
3
2
2021
2 21
3 2022
x
y x x
7; 3
3;7
; 7
3;
3
2
2021
2 21
3 2022
x
y x x
2
4 21y x x
3
2
2021
2 21
3 2022
x
y x x
0y
2
4 21 0 7 3x x x
w8
10 10
10 10 1
End Begin 1
45 45
w8a[^3$$3$+2[d
p21[+a2021$2022
=p10
=10=
(10p(p10)+1)P45=
–
– Email:
28
10; 7
x
3;10
x
4x 6x
4x
qya[^3$$3$+2[dp2
1[+a2021$2022$$p4
6x
qya[^3$$3$+2[dp2
1[+a2021$2022$$p6
6x
0y
6x
–
– Email:
29
–
3 2
3 9 2022y x x x
1;2
3;1
; 3
1;
3 2
3 9 2022y x x x
2
3 6 9y x x
3 2
3 9 2022y x x x
0y
2
3 6 9 0 3 1x x x
w8
10 10
10 10 1
End Begin 1
45 45
w8p[^3$p3[d+9[+2022
=p10
=10=
(10p(p10)+1)P45=
–
– Email:
30
10; 3
x
1;2
x
1,5x
1, 5x
qyp[^3$p3[d+9[+2022
1, 5x
0y
1, 5x
–
3
2 6 2022y x x
0;2
1;1
0;1
; 1
3
2 6 2022y x x
2
6 6y x
3
2 6 2022y x x
0y
2
6 6 0 1 1x x
–
– Email:
31
w8
3 2
2 3 1
End Begin 1
45 45
w82[^3$p6[p2022
=p3=
=2=
(2p(p3)+1)P45=
3; 1
x
1;2
x
0;1 1;1
1;1
x
–
– Email:
32
4; 0,5; 0,5x x x
1,5x
4x
qy2[^3$p6
[p2022$$p4
0, 5x
qyw82[^3$p6
[p2022$$p0.5
0,5x
qyw82[^3$p
6[p2022$$0.5
1;0
1, 5x
qyw82[^3$p
6[p2022$$1.5
–
– Email:
33
1, 5x
0y
1,5x
–
3
2 6 2022y x x
0;2
21
;1
20
0;1
; 1
21
; 1
20
–
3 2
4 5 5y x x x
5
1;
3
1;1
5
;
3

; 1
3 2
4 5 5y x x x
2
3 8 5y x x
3 2
4 5 5y x x x
0y
2
5
3 8 5 0 1
3
x x x
–
– Email:
34
w8
10 10
10 10 1
End Begin 1
45 45
w8p[^3$+4[dp5[p5
=p10
=10=
(10p(p10)+1)P45=
10;1
x
5
;10
3
x
5; 0x x
5x
5x
–
– Email:
35
qyp[^3$+4[
dp5[p5$$p5
0x
qyp[^3$+4
[dp5[p5$$0
5x
qyw82[^3$
p6[p2022$$5
–
2
2 lny x x x
1 3
0;
2
1 3
0;
2
1 3
;0
2
1 3
;0
2
2
2 lny x x x
0;D 
–
– Email:
36
2
1 2 2 1
2 2
x x
y x
x x
2
2 lny x x x
0y
2
1 3
2 2 1
2
0
1 3
0
2
x
x x
x
x
1 3
0
2
x
0x
–
3 2
5 3 1y x x x
x
2
1
3 10 3; 0
3
3
x
y x x y
x
3 2
5 3 1y x x x
1
; 3;
3
 
1
;3
3
–
– Email:
37
3 2
5 3 1y x x x
D
–
3 sin 5 2y x
3;3D
6 cos 5 2 ;y x
10 2
0 5 2 ,
2 4
k
y x k x k
–
– Email:
38
3 sin 5 2y x
10 3 10
;
4 4
k k
10 3 10
;
4 4
k k
3;3T
D
–
1
x
x
e
y
e
\ 0D
2
0,
1
x
x
e
y x D
e
1
x
x
e
y
e
1
x
x
e
y
e
; 0
0;
\ 0D
;0 0;D  
–
– Email:
39
–
4 2
2y f x x x
0;1
; 1

;1
0;1
4 2
2y f x x x
3
1
4 4 0 0
1
x
f x x x x
x
x

1
'
f x

1
1
0
0
f x


1
– –
0;1
0.5x
0.5x
qyp[^4$+
–
– Email:
40
2[d$p0.5=
–
3
3 4y x x
; 1
1;
1;1
; 1
1;
D
2
1
' 3 3, ' 0
1
x
y x y
x
1;1
2, 0, 2x x x
2x
qyp[^3$+
3[p4$p2=
–
– Email:
41
0x
qyp[^3$
+3[p4$0=
2x
qyp[^3$
+3[p4$2=
–
2022
y x
1
;
2

; 0
1
;
2

0;
2021
2022y x
0x
0y
0x
0y
( ;0)
0.4, 1, 2x x x
–
– Email:
42
1x
qy[^2022$p1=
0.4x
qy[^2022$0.4=
0.4x

2021
2021
2022 2021
2 2 2022
2022 0.4 0
5 5
y x y x y y
0
0.4x
qy[^2022$2=

2022 2021 2021
2022 2 2022.2y x y x y CASIO CAPACITY
2x
–
– Email:
43
–
2 3
1
x
y
x
;2
; 
0;
2
1
0, 1
1
y x
x
;1
1;
\ 1D
–
; 
4 2
3 2 1.y x x x
1
.
2 2
x
y
x
3 2
2 1.y x x x
3
3.y x
; 
3 2
2 1y x x x
D
2
2
1 5
3 2 2 3 0,
3 9
y x x x x
–
– Email:
44
;
3
3y x
D
2
3 0y x
; 
4 3 2
, 0y ax bx cx dx e a
3 2
4 3 2y ax bx cx d
0a


 
0 0
lim 0
; 0
lim 0
x
x
y
x y x
y
0
x x
2
0
x x
0
x x
0 0
x x
0
x x
0
x x
0a


 
0 0
lim 0
; 0
lim 0
x
x
y
x y x
y
0
x x
2
0
x x
0
x x
0 0
x x
0
x x
0
x x
–
–
– Email:
45
–
3
logy x
2
3
logy x
4
x
e
y
2
5
x
y
3
logy x
0;D 
2
3
logy x
\ 0D
2 5
5 2
x x
y
5
1
2
4
x
e
y
1
4
e
–
1
1
x
y
x
2 1
3
x
y
x
2
2 1
x
y
x
3
2
x
y
x
1
1
x
y
x
2
2
0, 1
1
y x
x
1
1
x
y
x
2x 1
3
y
x
2
7
0 3
3
y x
x
2x 1
3
y
x
2
2 1
x
y
x
2
3 1
0,
2
2 1
y x
x
–
– Email:
46
2
2 1
x
y
x
3
2
x
y
x
2
1
0, 2
2
y x
x
3
2
x
y
x
–
4 2 3
1 1
; ; 3 1; 3 1
1 2
x x
f x g x h x x x k x x x
x x
0 1 2 3
1
2
x
f x
x
1
2
x
g x
x
4 2
3 1h x x x
3
3 1k x x x
3
3 1k x x x
\
d
D
c

;
d
c

;
d
c
–
2
3
1 3
2
2
2
; 2 ; log ;
3
x
x
f x g x h x x k x x
x
–
– Email:
47
0 1 2 3
2
3
x
f x
x
2
5
0, 3
3
f x x
x
2
1
2
x
f x
2
1
2 .2 .ln 2
x
f x x
2
1
0, 2 .2 .ln2 0
x
x x
2
1
2
x
f x
;0
3
2 2
log 3 logf x x x
0;D 
3
0,
.ln 2
f x x D
x
3
2
f x x
0;D 
1
2
3
0,
2
f x x x D
–
2
2
log 2 1 .y x x
1
;
2

1; 
1
;
2

1;
1
;
2

1;
–
– Email:
48
1
;
2

1;
1
; 1; .
2
D
 
2
4 1 1
; 0
4
2 1 ln 2
x
y y x
x x
1; 0x y

1
; 0
2
x y

1
;
2

1; .
–
3 2
2 1y x x x
1;
1
;1
3
1
;
3

1
;1
3
2
3 4 1y x x
1
0
1
3
x
y
x
–
– Email:
49
1
;1
3
–
4 2
2 2y x x
2;
2;
; 0
;0
3
1
4 4 0 0
1
x
y x x x
x
1 0
2 0
a
ab
W
; 1
0;1
1; 0
1;
2; 1;
2;
–
y f x
2
5 4f x x x
1;4
3;
; 3
–
– Email:
50
1; 4
2
0 5 4 0 1 4f x x x x
1; 4
–
5 3
3 5y x x
; 1
1;
; 
; 1
1;
1;1
4 2 2 2
15 15 15 1y x x x x
2
1
0 1 0
1
x
y x
x
; 1
1;
1;1
–
m
4 3 2
4 2y x x mx
;0
9
4
m
9
2
m
9
2
m
9
4
m
;0
3 2
4 12 2y x x mx
; 0
0, ;0y x

–
– Email:
51
3 2 2
4 12 2 0 2 6 0, ;0x x mx x x m x 
2
2 6 , ;0m x x x 
;0
minm f x

2
2 6f x x x
2
2 6f x x x
3
4 6 0
2
f x x x
;0
9
min .
2
f x

9
2
m
–
2 3 2
1
1 1 3 5
3
y m x m x x
m
1 2m 1 2m
2
1
m
m
2
1
m
m
D
2 2
1 2 1 3y m x m x
2 2
0, 1 2 1 3 0,y x y m x m x x
2
1 0 1m m
–
– Email:
52
3
1 4 3; 0
4
m y x y x
1 3 0m y
1m
2
1 0 1m m
2
2
2
2
1
1
1 0
1
0 2
1
0 1
2
1 3 1 0
2 2 4 0
1
m
m
m
m
a m
m
m
m
m m
m m
m
2
1
m
m
m m
a
a m
0a 0a
–
2 1
,
x
y m
x m
m
1
;1 ?
2
1
1
2
m
1
2
m
1m
1
2
m
\D m
2
1 2m
y
x m
1
;1
2
1 2 0
1
0, ;1
2
1
1
1
2
;1
1
2
m
y x
m
m
m
m
–
– Email:
53
m m
–
m
2 sin 1
sin
x
y
x m
0;
2
1
2
m
1
0
2
m
1m
1
0
2
m
1m
1
2
m
0;
2
sin 0 1
x
t x t
2 1t
y
t m
0;1t
\D m
2
2 1m
y
t m
0,
0;1
0;1
y x D
m
1
2 1 0
1
2
0
0
2
0
1
1
1
m
m
m
m
m
m
m
m
f g x
K
t g x
K
g x
K
K
–
m
1;1
6
2 1
mx
y
x m
–
– Email:
54
4 3m
4 3
1 3
m
m
1 4m
4 3
1 3
m
m
1
\
2
m
D
2
2
12
2 1
m m
y
x m
1;1
0, 1;1
1
1;1
2
y x
m
2
4 3
12 0
4 3
1
1 2
1 3
3
1 2
m
m m
m
m
m
m
m
m
–
m
2
2
1
x
y x mx
x
1; .
5.m 5.m 5.m 5.m
1;
2
1
2
1
y x m
x
1; 
0, 1;y x
2 2
1 1
2 0, 1; 2 , 1;
1 1
x m x m x x
x x

1;
minm f x

2
1
2
1
f x x
x
2
1
2
1
f x x
x
1;
–
– Email:
55
3
3
3 3
2 1 1
2
2 ; 0 1 1 1 1 2
1 1
x
f x f x x x x
x x
1;
min 5f x

5 5m m
–
y f x
2
2 2 1f x x x x m
x
m
2
g x f x
1;
5 2 3 4
2
2 2 2 2
2 2 1f x x x x m
2
2g x xf x
g x
1; 
2
0, 1; 2 0, 1;g x x xf x x
 
2
2 2 2
2 . 2 2 1 0, 1;x x x x m x
2
2 1 0, 1;x m x 
2
2 1, 1;m x x 
2
2 1h x x
1; 
4 ; 0 0h x x h x x
–
– Email:
56
1; 3m
3; 2; 1m m
–
f x
, ,g x f mx n m n
g x
5
3 2m n
5
.
13
5
16
5
4
3 2 2
, 0 3 2f x ax bx cx d a f x ax bx c
2;3 , 0; 1
3 2
2 3
8 4 2 3 1
0 1 1 3
3 1
12 4 0 0
' 2 0
0 1
' 0 0
f
a b c d a
f d b
f x x x
a b c c
f
c d
f
3 2
0 3 1g f n n n
0 1g
3 2 3 2 2
1
3 1 1 3 2 0 1 2 2 0
1 3
n
n n n n n n n
n
n
1n
–
– Email:
57
g x f mx n
5
h x g x f mx n
5
f x
0;2
h x g mx n
2
;
n n
m m
0m
2 2 2
5 5
5
n n
m
m m
m
0m
2 16
3 2 3. 2.1
5 5
m n
y f x
k
f x
1 2
;x x
2 1
x x k
y f x
;a b
, 0y f mx n m
;
a n b n
m m
y f x
;a b
, 0y f mx n m
;
b n a n
m m
–
y f x
f x
1 2 2018f x x x g x
0, .g x x
1 2018 2019y f x x
1;
.
0; 3
.
;3
3;
1 2018 2019 1 2018y g x f x x g x f x
1 1 . 1 2 . 1 2018 2018g x x x g x
3 1g x x x g x
3
0 3 0
0
x
g x x x
x
1 0,g x x
–
– Email:
58
y g x
3;
y f u x
.y u x f u x
–
5
3 . 2
2018
2019
x x
e m e
y
. , , ,
b
m a e c a b c
2;5
S a b c
7S
9S 8S 10S
5
3 . 2
5
2018 2018
3 . 2 . . ln
2019 2019
x x
e m e
x x
y e m e
.
5
3 . 2
5
2018 2018
5 3 . . .ln
2019 2019
x x
e m e
x x
y e m e
2;5
0y
2;5x
.
5
5 3 . 0
x x
e m e
2;5x
4
5 3
x
m e
2;5 1x
4
5 3
x
f x e
2;5
4
20 0
x
f x e
2;5x
f x
2;5
2 5f f x f
1
8
2 5 3m f e
5
8
3
a
b
c
10S a b c
m f x
x D
max
D
m f x
–
,y f x y g x
y g x
–
– Email:
59
1 1h x f x g x
1
;1
2
1
1;
2
1;
2;
1 , 1f x g x
,f x g x
1
1 1h x f x g x
h x
0 1 1h x f x g x
ñoà thò môùi
1
1; 1;2
2
x
.
y f x a
y f x
a
0a
a
0a
y f x a
y f x
a
0a
a
0a
–
m
2
ln 1 2018y x mx
; 
; 1 1;1
; 1

1;

–
– Email:
60
; 
0, y x
2 2 2
2 2 2
0, , min
1 1 1
x x x
m x m x m
x x x
2
2
1
x
f x
x
2
2
2
1
2 2
0
1
1
x
x
f x
x
x
lim 0
1 1 min
1 1 max
lim 0
x
x
f x
f f x
f f x
f x


1m
–
3
sinh x x x x
2 1k x x
.
3 2
6 15 3g x x x x
.
2
2 5
1
x x
f x
x
.
2 2 2
3 1 cos 3 2 sin 0
2
x
h x x x x
x
h x
2 0k x
x
k x
2
2 2
3 12 15 3 4 5 3 2 3 0g x x x x x x
x
g x
6
1
1
f x x
x
2
6
1 0
1
f x
x
1x
f x
–
– Email:
61
h x
g x
k x
f x
–
.y f x
y f x
2 2 0f f
.
2
3g x f x
2; 1
.
1;2
.
2;5
.
5;
.
,f x
f x
0, f x x
.
2 3 . 3g x f x f x
.
2 3 1
3 0 2 5
3 2
0 3 . 3 0
1
3 0
3 2
x
f x x
x
g x f x f x
x
f x
x
.
–
– Email:
62
g x
;1 ,
2;5
–
y f x
.
y f x
2
1
2
x
g x f x x
3;1
2;0
3
1;
2
1; 3
1 1g x f x x
.
0 1 1g x f x x
1t x
f t t
.
y x
f x
3; 1; 3x x x
–
– Email:
63
3 1 3 4
1 3 1 1 3 2 0
t x x
f t t
t x x
.
–
.y f x
y f x
2
3g x f x
2;3
.
2; 1
.
0;1
.
1;0
.
2
2 . 3g x x f x
.
g x
2
2
2
22
2
0
0
3 6
1 3 2
3 0
00
6 3 13 0
3 2
x
x
x
x
f x
xx
xf x
x
2
2
2
2
0
3
0
3
9
3
1 2
1 4
1
2 1
0
0
4 9
2 3
1
3 2
1 1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
2
3 2
1 0
x
x
–
– Email:
64
2 2
3 2 . 3 0g x f x g x x f x
.
2 2
2 2
2 2
0 0
0
3 6 9
3
2
3 1 4
1
3 2 1
x x
x
x x
x
x
x x
x
x x
–
y f x
f x
m
2
2
480
1
2
g x f x x
m x x
0;1
4 6
7
8
g x
0;1
0, 0;1g x x
.
–
– Email:
65
2
2
2
480
2 1 1 0, 0;1
2
x f x x x
m x x
2
2 2
480
2 . 1 , 0;1x x f x x x
m
2
2
1
480
3 . , 1;1 .
t x x
t f t t
m
2
2
0 4
, 1;1 3 . 64, 1;1
2 3 16
f t
t t f t t
t
.
480 15
64
2
m
m
.
–
y f x
y f x
2
2
1
2 2
2
h x f x xf x x
.
y h x
1;0M
.
y h x
y h x
1;2N
.
y h x
1;0M
.
2 2 4h x f x f x f x xf x x
–
– Email:
66
2
0 2 2 2 0
2
f x x
h x f x f x x f x
f x
.
•
0f x
x
.
2 0f x
x
.
•
2f x x
1x
–
y h x
1;0M
.
–
f x
2
2 1 ,f x f x x x
.
m
3 . 1 1y x f x m x
.
m
.
10
3
m
.
1m
.
1m
.
x
1x
2
2 1 1f x f x x
.
2
2
2
2 1
3 2 1
2 1 2 1
f x f x x
f x x x
f x f x x x
.
3 2 2
2 2 1 3 4 2y x x m x y x x m
0
10
0, 4 3 2 0
3 0
3
y x m m
a
–
–
– Email:
67
y f x
.
y f x
1 2g x f x
1;0 .
;0 .
0;1 .
1; .
1
0
1 2
x
f x
x
.
2 1 2g x f x
.
1
1 2 1
0 1 2 0
1
1 1 2 2
0
2
x
x
g x f x
x
x
g x
1
;0
2
1;
–
f x
.
f x
1;3
1
2
x
g x f x
4; 2
.
2; 0
.
0;2
.
2; 4
.
–
– Email:
68
1
1 1
2 2
x
g x f
0 1 2
2
x
g x f
.
1 2 2 1 3 4 2
2 2
x x
f x
.
4; 2
1 2 1 1 0 2 2 2 4
2 2
x x
f a a x
2 2 ; 4a
2; 4
.
1
2
x
g x f x
4; 2 .
–
m
5;5
1
x
e m x
5 6
7
10
0
x
e
0m
1
x
e m x
1 1
x
x
m
e
1
1
x
x e f x
m
1
x
f x x e
' 0 0
x
f x xe x
–
– Email:
69
1
1
0
1 1
0
m
m
m
m
5;5
5; 4; 3; 2; 1;1
m
m
m
x
y e
0
x
y e
x
C
0m
1y m x
1; 0
:
x
C y e
0m
0
x
y e
0m
: 1y m x
C
1
x
x
e m x
e m
0
1
1
x
m
m
–
3 34 2 2 2 2
2 1 1 1x x m x x x m
m
m
1x
.
–
– Email:
70
1m
.
1m
.
5
4
m
5
4
m
.
3 4 2
3 3 4 2
3 2
1
2 1
a x x m
a b x x m
b x
.
3 3 3 3
0a b a b a a b b a b
.
3 3 4 2
1a b x x m
.
4 2
1f x x x
1;
.
3 2
4 2 2 2 1 0, 1f x x x x x x
.
f x
1;

1;
.
1;
min 1 1m f x f

1m
.
–
y f x
3
2 1g x f x x m
.
m
0;1
max 10g x
.
13m
.
12m
.
1m
.
3m
.
3
2 1t x x x
0;1x
.
2
6 1 0, 0;1t x x x
.
t x
0;1 1;2x t
.
–
– Email:
71
1;2 1; 2
max 3 max 3f t f t m m
.
3 10 13m m
.
–
.y f x
y f x
1 1,f
1
2.f
e
lnf x x m
1
1;x
e
2m
2m
3m
3m
lnm f x x
1
1;x
e
1
1;
max
e
m g x
lng x f x x
1
g x f x
x
1
0, 1;
1
0, 1;
1 1
0, 1;
f x x
e
g x x
e
x
x e
g x
1
1;
e
1
1;
e
1
1;
1
max 3.
e
g x g
e
–
–
– Email:
72
2 2
3 6 18 3 1x x x x m m
m
m
5;5
3;6x
3
.
5
.
9
.
10
.
3 6t x x
.
2 2
9 2 18 3t x x
.
1 1 1 1 3
; 0 0 3;6
2
2 3 2 6 2 3 2 6
t t x
x x x x
.
3; 3 2t
.
2 2
2 2
9 2 9
1 1
2 2
t t t
t m m m m
.
2
2 9
2
t t
f t
3; 3 2t
.
1 0 3; 3 2f t t t
.
f t
3; 3 2
3;3 2
max 3 3f t f
.
2 2 2
3;3 2
2
1 max 1 3 2 0
1
m
m m f t m m m m
m
.
–
y f x
0 0f
0, 1;2f x x
–
– Email:
73
0, 1;2f x x
y f x
1;2
y f x
x
f x
f x
1f
2
f
0 0, 1; 0
0 0, 0;2
f x f x
f x f x
y f x
1; 0
0;2
0x
y f x
;
o o
K x h x h
K
0
\K x
0h
–
– Email:
74
0, ;
o o
f x x x h x
0, ;
o o
f x x x x h
o
x
y f x
0, ;
o o
f x x x h x
0, ;
o o
f x x x x h
o
x
y f x
–
f x
2
2
1 2f x x x x
x
.
2
2 2g x f x x
2
.
1
.
3
2
.
3
2
2 1 2 2g x x f x x
2 2
2 2 2
5 4
2 1 2 2 1 2 2 2 2 2
2 1 1 1 .
x x x x x x x
x x
5 4
0 1
2 1 1 1 0
2
x
x x
x
.
0;1 ,
2;
3
g x
.
–
– Email:
75
| 1/75

Tài liệu khác của Toán 12

Preview text:

– – Email: – – – – – – – – – – – – – – – – – – – – 1 – – Email: – – – – – – – – – – – – – – – – – – – – – – – – – – – – 2 – – Email: – – – – – – – – – – – – – – – – – – – – 3 – – Email: – – – – – – – – – – – – – – 4 – – Email: – – – – – – – – – – – – 5 – – Email: – – – – – – – – – – – – – – 6 – – Email: – 2 x  5x  2 y  x  3   \   3  ;    3  3;  ;   3 3; 2 x  5x  2 y  x  3 D   \   3
x  6x  13 x  6x   9  4 x  2 2 2 3  4 y     0, x  D x  2 3 x  32 x  2 3  ;   3 3;   – 7 – – Email: – – px y  q x, n
px,gx   x   px y  nq x
px. nq xn.px n 1
.q  x.qx px.qxn.px.qx y   2n q x n 1 q  x 1 . n
yq  x   x       qxn 1 d p  x         r 100 n dx q  xxX x  100 f x f x k k 1  2  a x a x  . . a x a x a y  k k 1  2 1 0 n 1 q  x px y  n q x    x   2 2 d x 5x 2 3    
dx  x  3 xX r X  100 10613 8 – – Email: 10613   10000   2
600  13  x  6x  13,x  10 0 2 100 6.100 2 x  6x 13 y  x  23 – 2 ax bx c y  w5 2 ax bx c 2 ax bx c y  2 ax bx c 2ax b. 2
a x b x c 2
ax bx c.2a x b y 
a x b x c2 2 a b c a b c    ab a b x x
x  2a c acx bc b c 2 2 2 a b c a b c 2 mx 2nx  p y   
a x b x c2
a x b x c2
a x b x c2 2 2 2  
u  a;b;c, v  a ;b ;c       b c c a a b  u,v   ; ;        
    bc b ;ca c ac ;ab a b b c c a a b        ; p n;m u,v     w5 VctA a; ;bc    , a ,bc 9 – – Email:
VctB  a ;b ;c   , a ,bc C T3 T3 VctA OT4 VctB = , m , n p T5 VctA 1;5;2, VctB 0;1;3       T5131=5=2= T1230=1=3=’ T3T3OT4= p  13 n  3 m   1  2 x  6x 13 y  x  23 – 3 y  x 507x  506 3 y  x 507x  506 1 0 – – Email: 3 y  x 507x  506  ;  13 13; 3 y  x 507x  506 15 3 y  x 507x  506 13;13 3 y  x 507x  506 26 0 1 2 3 3 y  x  507x  506 23  x  1 3 x 507x 506 0      x  22 
D  23;1  22;         2 3x  507 x  13 y   0    3 x  13 2 x  507x  506 
23;13 22; 13; 1 l  11  3  14 1 1 – – Email: – y  f x y  f  2 4 x  0; 7  7; 0;  7;0 y   x f  2 2 . 4 x  y  f  2 4 x   x f  2 x    x f  2 2 . 4 0 . 4 x   0  x   0  x   0               x  7 2 x 0   4  x  3      f       2 x    2 x   7 4  0    3  4 x  5   x    7         2     7  x  7  x  0 4  x  7      0  x  7         2 4    0  x f x      x   0      2 x   0 5   4 x  7      x    y  f  2 4 x  0; 7  7; y  f  2 4 x  0;   0; y  f  2 4 x  y  0 "  " x  7 – y  f x 1 2 – – Email: y  f x   3 2 3 2  x  6x  63x 2022  ;   3  3  ; 9 3; 9  ;  7 y  f x   3 2 3 2  x  6x  63x 2022 y  f x   2 3 2  3x 12x  63 y  f x   3 2 3 2  x  6x  63x 2022 y  f x   2 3 2  3x  12x  63  0
f x  x  x    f x  x  2 2 2 4 21 0 2 2  25  0  * t  x 2    f t 2 * t  25  0 f   t  0  2  t   25  0  t  3   3  t  5  t  5 x 2  5 x  3  t  7     
t  7  x  2  7  x  9 t  5    t 5  1 3 – – Email: – 3 x 2 2021 y   2x  21x  3 2022   7  ; 3  3  ;7  ;  7 3; – 3 2 y  x  3x  9x 2022  1; 2 3; 1  ;   3 1;   – 3 y  2x 6x 2022 0;2 1; 1 0; 1  ;   1 – 3 2 y  x   4x  5x 5  5   1  ;  5       1; 1 ;   ;   1  3 3  – 2 y  2x  lnx x  1 3         1  3 1 3  1 3  0;        0;  ;0 ;0    2      2        2     2    – 3 2 y  x  5x  3x 1 x    1  2
  3 10  3;   0 x y x x y    3 x  3  1 4 – – Email:   3 2 y  x  5x  3x 1  1   ;       3;    3 1   ;3 3  – y  3 sin52x D  3;3   y  6cos5 2x;  10  k2 y 0 5 2x k x             ,k   2 4 1 5 – – Email:     y  3 sin5 2x 10 3 10   k ;    k  4 4  103 10     k ;    k  4 4  – x e y  xe 1 D   \   0 x e y     0, x  D  xe  21 x e y  xe 1 x e y   ;  0 0; x e 1 – y  f x 4 2  x   2x 0;1    ;  1    ;  1 0; 1 – 3 y  x   3x  4 1 6 – – Email:  ;   1 1;   1; 1  ;   1 1;   – 2022 y  x  1     ;    1        ;  0 ;  0;  2 2  – 2x  3 y  x 1  ;  2  ;   0;   –  ;     4 2 y  x   3x 2x 1. x 1 y  . 2x  2 3 2 y  x   x 2x 1. 3 y  x  3. –  x   x    y   3 log x  2 y  log x e y     2 y     3 4 5 – x 1 y  2x 1 y  x 2 y  x  3 y  x 1 x  3 2x 1 x 2 – f x x 1  g x x 1 ;  ; h x 4 2  x  3x 1; k x 3  x  3x 1 x 1 x  2 0 1 2 3 – 1 7 – – Email: f x x 2  ; g x 3 2 x 1  2  ; h x 3  log x ; k x 2  x 2 x  3 0 1 2 3 – y  log  2 2x x 1 . 2   1   ;      1;    2  1   ;      1;     2  1   ;      1;    2  1   ;      1;    2 – 3 2 y  x 2x  x 1 1;   1   ;1 3   1   ;     3 1   ;1 3  – 4 2 y  x 2x  2 2; 2;   1 8 – – Email:  ;   0  ;   0 – y  f x  f x 2  x  5x  4 1;4 3;    ;  3 1;4 – 5 3 y  3x  5x  ;   1 1;    ;      ;   1 1;   1; 1 – m 4 3 2 y  x   4x mx 2  ;   0 9 m  9 m   9 m   9 m   4 2 2 4 – 1 y   2 m   3 1 x  m   2 1 x  3x  5  3 m m   2 m   2 1  m  2 1  m  2   m   1    m  1  – 2x 1 y  , m m x m 1 9 – – Email: 1   ;1  ? 2  1 m 1 1 m  m  1 1 m  2 2 2 –   m 2 sinx 1 y  0;  sinx m  2 1 m   1   m  0 m  1 2 2 1   m  0 m  1 1 m   2 2 – m 1; 1 mx  6 y  2x m 1 4  m  3 4  m  3 4  m  3   1  m  3 1  m  4    1  m  3  – m 2 x 2 y  x  mx  1;   . x 1 m  5. m  5. m  5. m  5. – y  f x
f x  x x  2 2 2x m  1 x   m    2 g x f x  1;   5 2 3 4 – f x
g x  f mx n,  , m n   2 0 – – Email: g x 5 3m  2n 5  13 .  16 4 5 5 – y  f x  f x
f x  1xx   2 g x2018 g x  0,x  . 
y  f 1x2018x  2019 1;   . 0; 3. ; 3 3;   – 5x    3. x e m e 2 2018    y      b 
m  a.e  ,c a, ,bc   2019 2; 5 S  a b c S  7 S  9 S  8 S  10 –
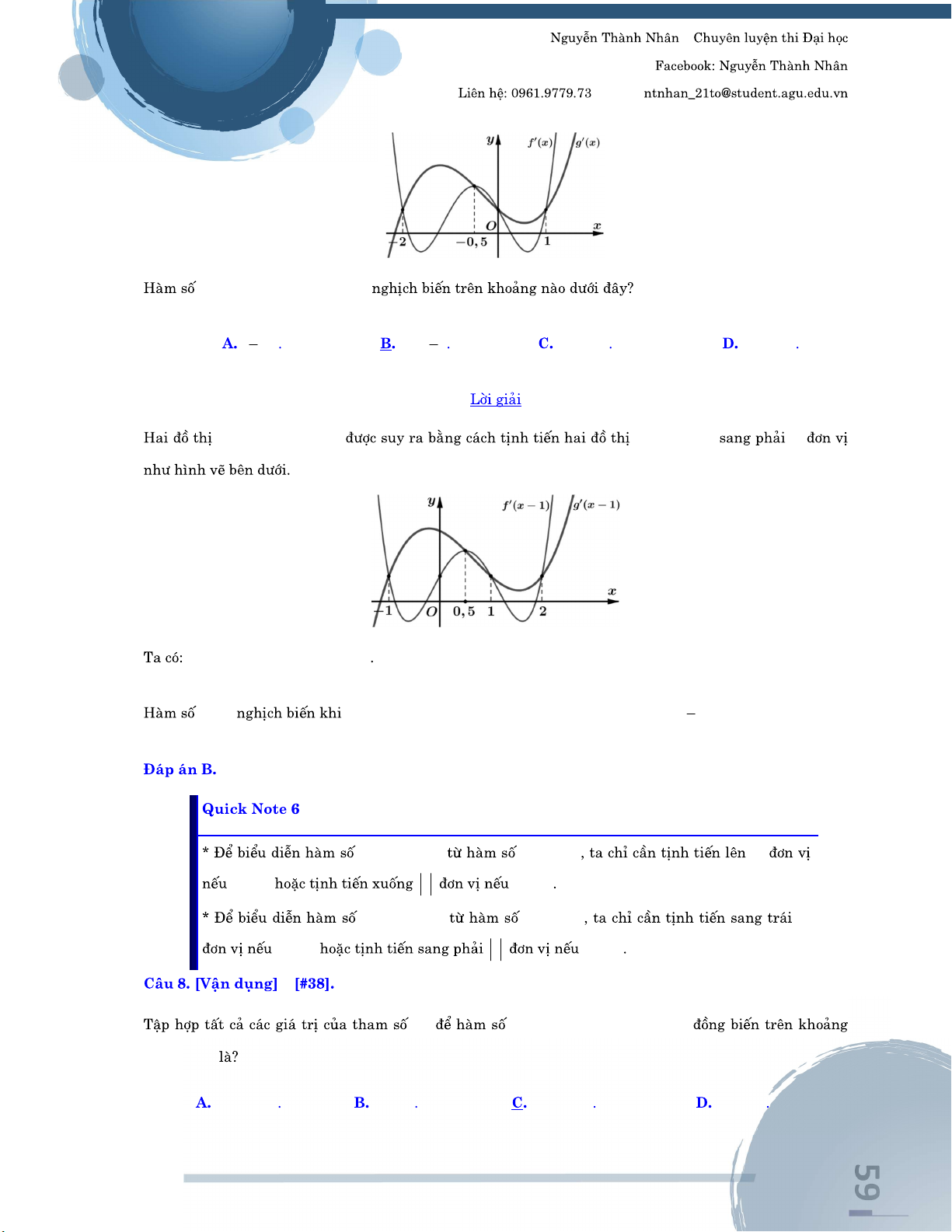
y  f x, y  gx  y  gx
h x  f x  1gx  1 1     ;1  1      1; 1;   2;   2   2 – m y   2 ln x  1mx 2018  ;    ;   1 1;1      ;  1 1;   2 1 – – Email: – h x 3  x  x  sinx k x  2x 1. g x 3 2  x  6x 15x  3 . f x 2 x  2x  5  . x 1 – y  f x. y  f x
f  2  f  2  0 . g x f  x2 3      2; 1. 1; 2. 2; 5. 5;   . – y  f x  . y  f x       2 1 x g x f x   x 2  3 3; 1 2; 0     1;    1;   3  2 – 2 2 – – Email: y  f x. y  f x g x  f  2 3  x  2; 3. 2; 1. 0; 1. 1; 0. – y  f x f x m
g x  f  2x  x   480 1  0; 1 m  2x x  2 4 6 7 8 – y  f x  y  f x h x 1  2 2 f x    2xf x   2x . 2 2 3 – – Email: y  h x M 1;  0 . y  h x y  h x N 1;2 . y  h x M 1; 0. – f x
f x f  x  2 2 1 x , x   . m
y  3x.f xm  1x 1  . m   . m  10 . m  1 . m  1 . 3 – y  f x. y  f x g x  f 12x 1;0.  ;  0. 0; 1. 1;   . – f x  . f x 1;3        1  x g x f        x  2 4; 2. 2; 0. 0; 2. 2;4. 2 4 – – Email: – m 5;5  x   e  m x  1 5 6 7 10 – 3 4 2 3 2 2
x  x  m  x   x  2 2 1 x  1  1m m m x  1 . m  1 . m  1 . m  5 m  5 . 4 4 – y  f x  g x  f  3 2x  x  1m . m max g x  10 . 0;     1 m  13 . m  12 . m  1. m  3 . – y  f x. y  f x     f  1  1,  1 f      1    2.       f x  ln x  m x 1;  e  e 2 5 – – Email: m  2 m  2 m  3 m  3 – 2 2
3  x  6 x  18  3x x  m m 1 m m 5;5       x  3;6   3 . 5 . 9 . 10 . – y  f x  f 0  0
f x  0,x  1;2 – f x
f x  x  2  2 1 x 2x x   .
g x  f  2x 2x 2 2 3 . 1 . . 3 2 2 6 – – Email: – 3 x 2 2021 y   2x  21x  3 2022   7  ; 3  3  ;7  ;  7 3;   3 x 2 2021 y   2x  21x  2 y  x  4x 21 3 2022 3 x 2 2021 y   2x 21x  y  0 3 2022 2 x  4x  21  0  7   x  3 w8 1  0 10
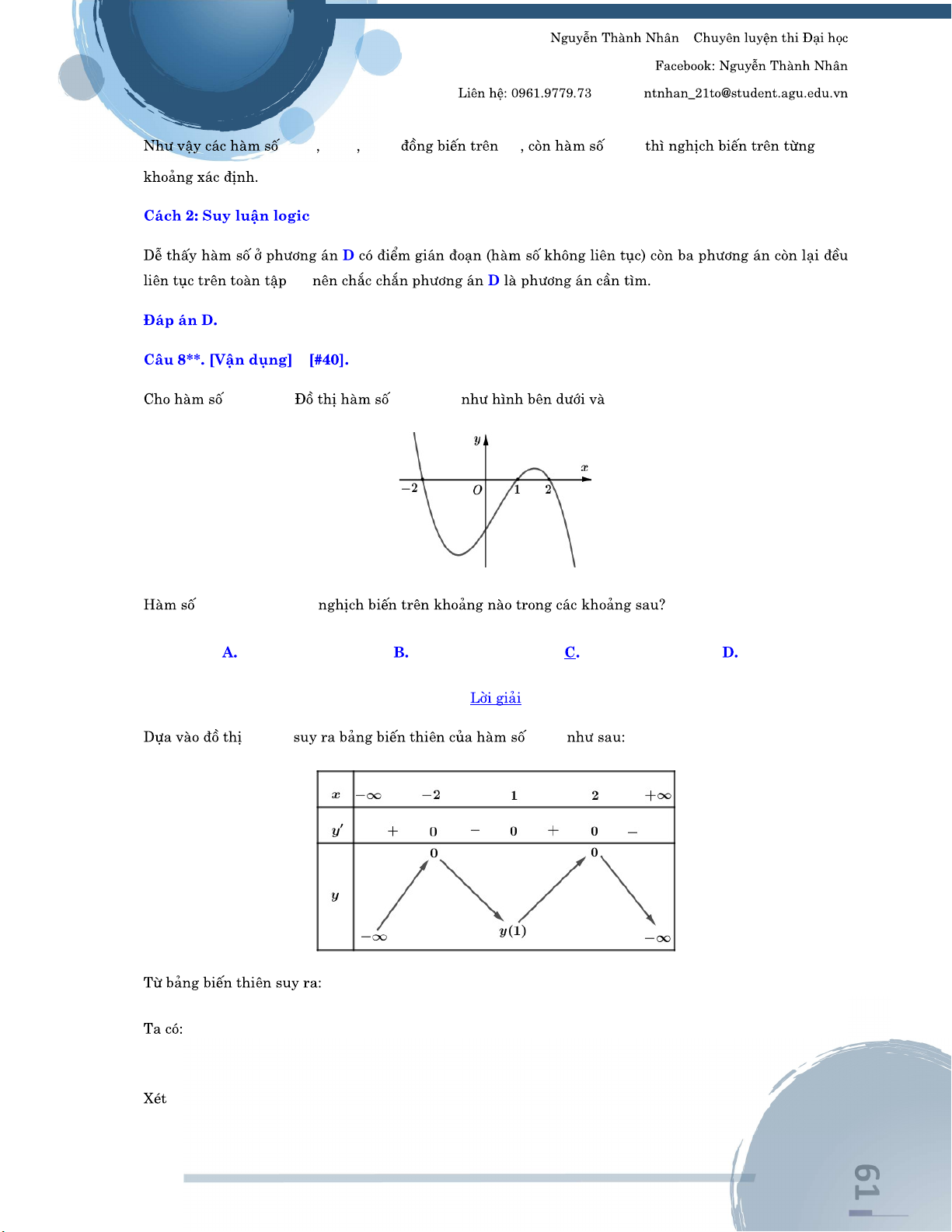
End  Begin  1 10  1   0  1  45 45 w8a[^3$$3$+2[d p21[+a2021$2022 =p10 =10= (10p(p10)+1)P45= 2 7 – – Email: 10;7 x 3;1 0 x x  4  x  6 x  4  qya[^3$$3$+2[dp2 1[+a2021$2022$$p4 x  6 qya[^3$$3$+2[dp2 1[+a2021$2022$$p6 x  6 y  0 x  6 2 8 – – Email: – 3 2 y  x   3x  9x  2022  1; 2 3; 1  ;   3 1;   3 2 y  x   3x  9x  2022 2 y  3  x  6x  9 3 2 y  x   3x  9x  2022 y  0 2
3x  6x  9  0  3  x  1 w8 1  0 10
End  Begin  1 10  1   0  1  45 45 w8p[^3$p3[d+9[+2022 =p10 =10= (10p(p10)+1)P45= 2 9 – – Email:  1  0; 3 x 1; 2 x x  1,5 x  1,5 qyp[^3$p3[d+9[+2022 x  1,5 y  0 x  1,5 – 3 y  2x 6x 2022 0; 2 1; 1 0; 1  ;   1 3 y  2x  6x 2022 2 y  6x 6 3 y  2x 6x 2022 y  0 2
6x  6  0  1  x  1 3 0 – – Email: w8 3  2
End  Begin 1 2   3 1  45 45 w82[^3$p6[p2022 =p3= =2= (2p(p3)+1)P45= 3; 1 x 1; 2 x 0; 1 1; 1 1; 1 x 3 1 – – Email:
x  4; x  0,5; x  0,5 x  1,5 x  4  qy2[^3$p6 [p2022$$p4 x  0  ,5 qyw82[^3$p6 [p2022$$p0.5 x  0,5 qyw82[^3$p 6[p2022$$0.5  1  ; 0 x  1,5 qyw82[^3$p 6[p2022$$1.5 3 2 – – Email: x  1,5 y  0 x  1,5 – 3 y  2x 6x 2022    0;  2  21   ;1  0;   1  ;   1  20   21    ;1  20  – 3 2 y  x   4x 5x 5  5   1  ;  5       1; 1 ;   ;   1  3 3  3 2 y  x   4x 5x 5 2 y  3  x  8x  5 3 2 y  x   4x  5x  5 y  0 2 5
3x  8x  5  0  1  x  3 3 3 – – Email: w8 1  0 10
End  Begin  1 10  1   0  1  45 45 w8p[^3$+4[dp5[p5 =p10 =10= (10p(p10)+1)P45= 10; 1 x 5   ;10  x 3  x  5; x  0 x  5 x  5  3 4 – – Email: qyp[^3$+4[ dp5[p5$$p5 x  0 qyp[^3$+4 [dp5[p5$$0 x  5 qyw82[^3$ p6[p2022$$5 – 2 y  2x  lnx x  1 3         1  3 1 3  1 3  0;        0;  ;0 ;0      2   2       2   2    2 y  2x  lnx x D  0;   3 5 – – Email: 2 1 2  2 1   2   2 x x y x  x x 2 y  2x  lnx x y  0  1 3 2 2   2 1 x x x    0   2 x  1  3 0  x   2 1 3 0 x    2 x  0 – 3 2 y  x  5x  3x 1 x    1  2
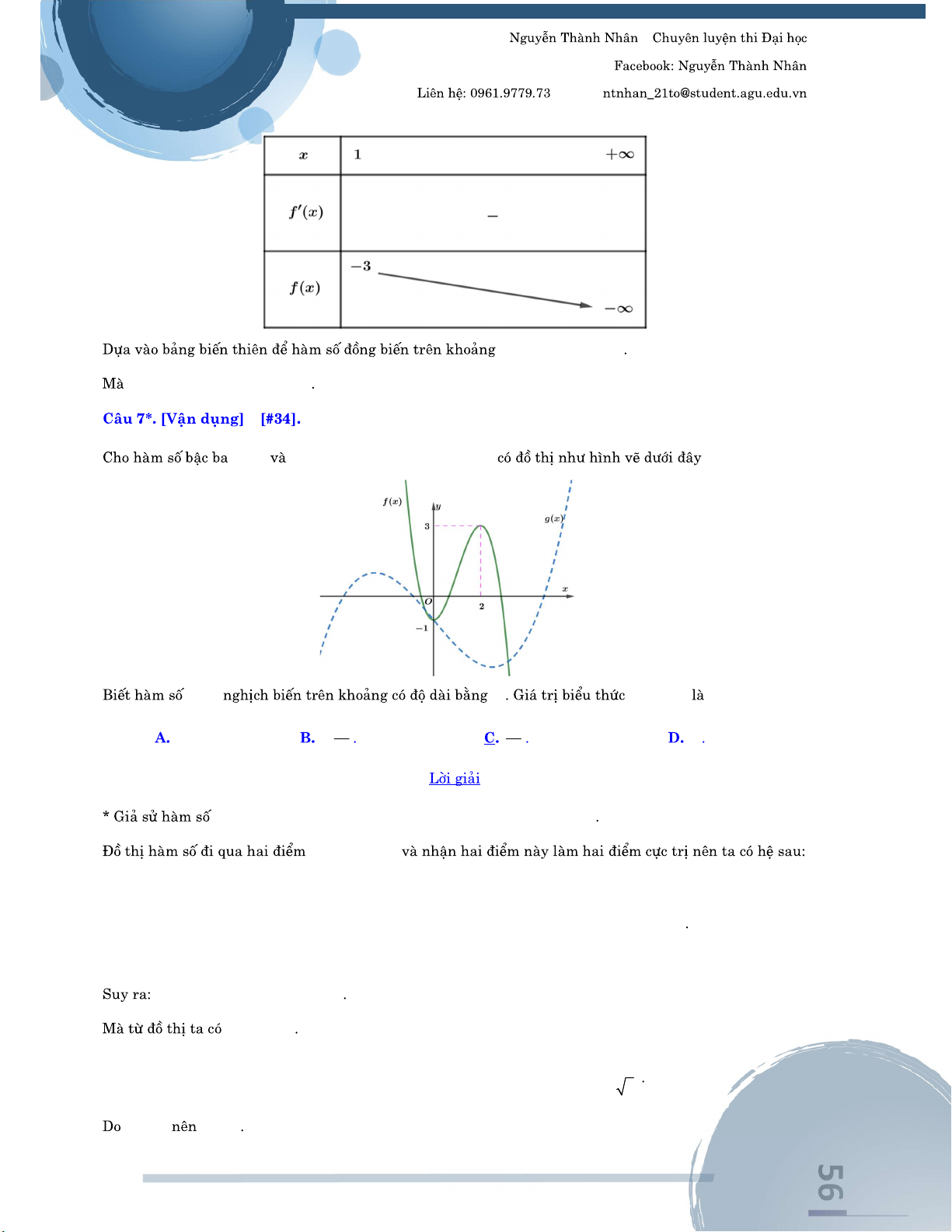
  3 10  3;   0 x y x x y    3 x  3      3 2 y  x  5x  3x 1  1   ;    1     3;      ;3  3 3  3 6 – – Email: 3 2 y  x  5x  3x 1 D   – y  3 sin52x D  3;3   y  6cos5 2x;  10  k2 y 0 5 2x k x             ,k   2 4 3 7 – – Email:     y  3 sin5 2x 10 3 10   k ;    k  4 4  103 10     k ;    k  4 4  T  3;3   D   – x e y  xe 1 D   \   0 x e y     0, x  D  xe  21 x e y  xe 1 x e y   ;  0 0; x e 1 D   \   0 D   ;   0  0; 3 8 – – Email: – y  f x 4 2  x   2x 0;1    ;  1  ;  1 0; 1 y  f x 4 2  x   2x x  1  f x 3 4x 4x 0        x  0 x  1  x  1 0 1  f 'x  0  0  0  1 1 f x 0   – – 0; 1 x  0.5 x  0.5 qyp[^4$+ 3 9 – – Email: 2[d$p0.5= – 3 y  x   3x  4  ;   1 1;   1; 1  ;   1 1;   D   x  1 2 y ' 3x 3,y ' 0       x  1  1; 1 x  2, x  0, x  2 x  2 qyp[^3$+ 3[p4$p2= 4 0 – – Email: x  0 qyp[^3$ +3[p4$0= x  2 qyp[^3$ +3[p4$2= – 2022 y  x  1     ;    1    ;      0;  0 ;   2 2  2021 y  2022x x  0 y  0 x  0 y  0 ( ;  0) x  0.4, x  1, x  2 4 1 – – Email: x  1 qy[^2022$p1= x  0.4 qy[^2022$0.4= x  0.4 2021 2021 y  2022 x  y  2021 2022x  y0.4 2    y  2 2022             0 0 5    5    x  0.4 qy[^2022$2= y  2022 x  y  2021 x  y   2021 2022 2 2022.2 CASIO CAPACITY x  2 4 2 – – Email: – 2x  3 y  x 1  ;  2  ;     0;   1 y   0, x  1 x  21  ;  1 1;   D   \   1 –  ;     4 2 y  x   3x 2x 1. x 1 y  . 2x  2 3 2 y  x   x 2x 1. 3 y  x  3.  ;     3 2 y  x   x 2x 1 D   2     2    1 5
y  3x  2x 2  3 x          0, x     3 9   4 3 – – Email:  ;     3 y  x  3 D   2 y  3x  0  ;    y  4 ax  3 bx  2 cx dx  ,e a  0 y  3 ax  2 4 3bx  2cx  d a  0  lim y   0 x   x   lim y ; y x 0 0      0    0 x x  x0 2 x  x  x  x x  x  0 0 0 0 x  x x  x 0 0   a  0  lim y   0 x    x   lim y ; y x 0 0      0    0 x   x  x0 2 x  x  x  x x  x  0 0 0 0 x  x x  x 0 0   – 4 4 – – Email: –  x   x    y   3 log x  2 y  log x e y     2 y     3 4 5 y   3 log x  D  0;   y  log  2x D   \   0 3   2 x        5 x y         5 1 5   2 2  x e y     e    1  4 4 – x 1 y  2x 1 y  x 2 y  x  3 y  x 1 x  3 2x 1 x 2 x 1 y  2 y   0, x  1 x  1 x  21 x 1 y  x 1 2x 1 y  7 y   0 x  3 x  3 x  2 3 2x 1 y  x 3 x 2 y  3 1 y   0, x  2x 1  x  2 2 2 1 4 5 – – Email: x 2 y  2x 1 x  3 y  1 y   0, x  2 x  2 x  2 2 x  3 y  x 2 – f x x 1  g x x 1 ;  ; h x 4 2  x  3x  1; k x 3  x  3x  1 x 1 x  2 0 1 2 3 f x x 1  x 2 g x x 1  x  2 h x 4 2  x  3x  1  k x 3  x  3x  1  k x 3  x  3x  1   d   D   \     c     d     d    ;        ;     c     c  – f x x 2  ; g x 3 2 x 1  2  ; h x 3  log x ; k x 2  x 2 x  3 4 6 – – Email: 0 1 2 3 f x x 2  f x 5   0, x  3 x  3 x  2 3   2 1 2x f x   f x 2 x 1 2x.2    .ln2 2 x 1 x 0, 2x.2    .ln2  0   2 1 2x f x    ;   0 f x 3  log x  3 log x D  0;   2 2 f x 3   0, x  D x.ln2   32 f x  x D  0;   f x 1 3 2  x  0, x  D 2 – y  log  2 2x x 1 . 2   1   ;      1;    2  1   ;      1;    2  1   ;      1;     2 4 7 – – Email:  1   ;      1;    2  1 D    ;        1;   .  2 4x 1 1 y   ;y  0  x  2 2x  x  1ln2 4   x  1;    y  0  1 x    ;        y  0  2  1   ;      1;   .  2 – 3 2 y  x 2x  x 1 1;   1   ;1 3   1   ;     3 1   ;1 3  2 y  3x  4x 1 x  1  y  0   1 x   3 4 8 – – Email: 1   ;1 3  – 4 2 y  x 2x  2 2; 2;  ;   0  ;   0 x  1  3 y 4x 4x 0       x  0 x  1  a   1  0 ab  20 W   ; 1 0; 1  1  ; 0 1;   2;    1;   2; – y  f x  f x 2  x  5x  4 1;4 3;    ;  3 4 9 – – Email: 1;4 f x 2
 0  x  5x  4  0  1  x  4 1;4 – 5 3 y  3x 5x  ;   1 1;    ;      ;   1 1;   1; 1 4 2 2 y  x  x  x  2 15 15 15 x  1 x  1 2 y  0  x 1  0   x 1   ;   1 1;   1; 1 – m 4 3 2 y  x   4x mx 2  ;   0 9 m  9 m   9 m   9 m   4 2 2 4  ;   0 3 2 y  4x 12x  2mx  ;  0 y  0, x   ;  0 5 0 – – Email: 3 2 2
 4x 12x  2mx  0  2x  6x  m  0, x   ;  0 2
 m  2x  6x, x   ;  0  m  min f x f x 2  2x  6x  ;  0 f x 2  2x  6x  f x 3
 4x  6  0  x   2 f x 9 min   . 9 m    ;  0 2 2 – 1 y   2 m   3 1 x  m   2 1 x  3x  5  m 3 m   2 m   2 1  m  2 1  m  2   m   1    m  1  D   y   2 m   2 1 x  2m  1x  3   y  x     y   2 m   2 0,
1 x  2m  1x  3  0, x    2 m 1  0  m  1 5 1 – – Email: 3
m  1  y  4x  3;y  0  x     4
m  1  y  3  0    m  1  2 m 1  0  m  1    m   1         2 m 1 a  0 m   1  0   m   1      m   2       m       0       m   21 3   1 2 m  1  0   m   2 m   1  2
2m  2m  4  0   m   1   m   2 m  1   m m a a m a  0 a  0 – 2x 1 y  , m m x m 1   ;1  ? 2  1 m 1 1 m  m  1 1 m  2 2 2 D   \ m 12m y  xm2 1   ;1 2      1  1  2m  0 y  0, x   ;1         2     1    m    m  1    1         2 m ;1         m     1 2     5 2 – – Email: m m –   m 2 sinx 1 y  0  ;  sinx m  2 1 m   1   m  0 m  1 2 2 1   m  0 m  1 1 m   2 2   x   0;  2 t sinx    0  t  1 2t 1 y  t  0; 1 t m D   \ m 2m 1 y  tm2
  y  0, x D 0;1   m    0; 1   1 2  m  1  0  m     1     2   m  0   m  0   m  0   2  m   1  m      1   m  1   f gx K t  g x K g x K   K – m 1; 1 mx  6 y  2x m 1 5 3 – – Email: 4  m  3 4  m  3 4  m  3   1  m  3 1  m  4    1  m  3   m  1 D  \    2      2 m  m  y  12 2x m  21 y  
  0, x  1;  1 1; 1  m  1     1  ; 1  2 2 m
 m 12  0 4 m  3    4  m  3  m  1  2    m   1     1     m  3  m  1  2  m   3    – m 2 x 2 y  x  mx  1;   . x 1 m  5. m  5. m  5. m  5. 1;   1
y  2x  m  x 21 1;  
y  0, x  1;   1 1  2x  m   0, x  1;  m   2x  , x   1; 2   2   x  1 x  1  m   min f x f x 1  2x  1;   x  2 1 f x 1  2x  1;   x  2 1 5 4 – – Email: 2 x 3 1 1    f x 2  2     
; f  x  0  x 1  1  x 1  1  x  2 3 3    3 x  1 x  1 min f x  5 1;     m   5  m  5 – y  f x
f x  x x  2 2 2x m  1 x   m     2 g x f x  1;   5 2 3 4
f x   x x  2 2 2 2  2 2 2x  m  1 gx  xf  2 2 x  g x 1;    gx  x        xf  2 0, 1; 2 x   0, x   1;    x x x  2 2 2  2 2 .
2 2x  m  1  0,x  1;   2
 2x  m  1  0, x  1; 2
 m  2x 1, x  1; h x 2  2  x 1 1;   hx  4
 x; hx  0  x  0 5 5 – – Email: 1;    m  3 m 
   m  3;2;  1 – f x
g x  f mx n,  , m n   g x 5 3m  2n 5  13 .  16 4 5 5 f x 3 2
 ax bx cx  d a    f x 2 , 0  3ax  2bx c 2; 3, 0; 1 f  2  3 8
 a  4b  2c d  3 a   1       f    0  1 d   1 b   3         f x  x   x  f '      3 2 3 1 2  0 1  2a  4b c  0 c   0      f '    0  0 c  0 d     1    g    f n 3 2 0  n  3n  1 g 0  1 n   1 3 2 3 2  n 3n 1 1 n 3n 2 0 n 1 2n 2n 2 0           
    n 1 3  n   n  1 5 6 – – Email:
g x  f mx n 5  h x  g
 x  f mx n 5 f x 0; 2 h x  g mx n  n  2    ; n   m  0  m m  2 n n  2 2    5   5  m  m  0 m m m 5 2 16 3m  2n  3.  2.1  5 5 y  f x k f x x ;x x x  k 1 2  2 1 y  f x a;b    
y  f mx n, m  0 a n  ;b n  m m  y  f x a;b    
y  f mx n, m  0 b n  ;a n  m m  – y  f x  f x
f x  1xx   2 g x 2018 g x  0,x  . 
y  f 1x 2018x  2019 1;   . 0; 3. ; 3 3;  
y  g x  f 1x 2018x 2019  gx  f 1x 2018
 gx   1
 1x. 1x 
2.g1x20182018
 gx  x x  3g1x  
gx   x x   x 3 0 3  0    g 1x x  0  0, x    5 7 – – Email: y  g x 3;   y  f ux
y  ux.f ux – 5x    3. x e m e 2 2018 y      b 
m  a.e  ,c a, ,bc   2019 2; 5 S  a b c S  7 S  9 S  8 S  10 5x     3. x e m e 2     5x y   e   
m   x  2018    2018 3 .e 2 .    .ln     . 2019   2019 5x      3 . x e m e 2       5x y    e   m   x 2018   2018 5 3 .e .  .ln    2019   2019
2;5 y  0 x 2; 5.  5 5 x    3. x e m
e  0 x  2; 5  4  5 x m e  3 x   2; 5  1   4  5 x f x e  3 2;5   4  20 x f x e  0 x  2;  5 f x
2; 5 f  2 f x f  5  1  m  f   8 2  5e  3 a   5 b  8   S  a b c  10 c   3 
m  f x x  D  m  max f x D   –
y  f x, y  gx  y  gx 5 8 – – Email:
h x  f x  1g x  1 1     ;1  1     1;   1;  2;   2   2
f x  1, gx  1 f x, gx 1
hx  f x  1gx  1   h x
hx  0  f x  1  gx  1  ñoà t  hò m  ôùi 1 x     1;     1;  2  .  2 y  f xa y  f x a a  0 a a  0 y  f x a y  f x a a  0 a a  0 – m y   2 ln x  1mx 2018  ;    ;   1 1;1      ;  1 1;   5 9 – – Email:  ;     y  0, x    2x 2x  2     0,      ,      min x m x m x m    2 2   2 x 1 x  1 x 1   2x f x   2 x 1  lim f x  x     0      
f  1  1  min f  x f x 2 2x 2 x 1   0      x  2 2 x  1 1  f    1  1  max f  x  lim f x  x     0  m  1 – h x 3  x  x  sinx k x  2x 1. g x 3 2  x  6x 15x  3 . f x 2 x  2x  5  . x 1   2 2 2
 3 1 cos  3  2sin x h x x x x  0 x    h x  2
kx  2  0 x   k x 
gx  x  x   x  x    x  2 2 2 3 12 15 3 4 5 3 2  3  0 x   g x  f x 6  x  1   f x 6  1  0 x  1 f x x 1 x  2 1 6 0 – – Email: h x gx k x  f x  – y  f x. y  f x
f  2  f  2  0 . g x f  x2 3      2; 1. 1; 2. 2; 5. 5;   . f x, f x
f x  0,  x   .
gx  2f 3x.f 3x.    2  3  x  1 gx f 3 x 0 2 x 5
 0  f 3 x.f 3x               0   .  3 x 2 f 3 x         0  x    1 3  x  2   6 1 – – Email: g x  ;  1, 2; 5 – y  f x  . y  f x       2 1 x g x f x   x 2  3 3; 1 2; 0     1;    1;   3  2
gx  f 1xx 1 .
gx  0  f 1x  x 1 t  1  x f t  t . y  x  f x
x  3; x  1; x  3 6 2 – – Email: f t t  3 1x  3 x     4  t       . 1  t  3 1  1 x  3 2  x     0 – y  f x. y  f x g x  f  2 3  x  2; 3. 2; 1. 0; 1. 1; 0.
gx   x f   2 2 . 3 x . x   0    x  0    3  2 x    6 f   2 2  3  x    0    1  3 x  2 g x       x  0 x    0 f   2 2  3  x    0  6  3 x      1
3 2x   2   x   0      x  x  0  3      x 3 2        x  9    x    3 1 x 2  2     
1  x  4  1  x    2     2  x  1       x    0    3  x  2    x 0  2       4  x  9      1  x  0    2  x    3 2  x  1      3  x    2 1x   1   6 3 – – Email:
g x  f   2x  gx   x f   2 3 2 . 3 x   0 . x  0 x  0 x     0  2  2  3 x  6 x    9 x    3  2   2   3 x  1 x  4 x  2  2  2  3 x  2 x  1 x      1 – y  f x f x m
g x  f  2x  x   480 1  0; 1 m  2x x  2 4 6 7 8 g x 0; 1
gx  0, x  0; 1. 6 4 – – Email:       x  f  2 480 2 2   2 x  x   480 2 1 1    0, x  0;1 
 x x  2 .f x x  1, x 0; 1 2     m  2x x  m  2  2 tx x    t  2 1 480
3 .f t, t  1; 1. m 0  f   t 4 2  .  2 , t 1;1 t 3 .f t 64, t 1;1 2   t  
              3  16  480   m  15 64 . m 2 – y  f x  y  f x h x 1  2 2 f x    2xf x   2x . 2 y  h x M 1;  0 . y  h x y  h x N 1;2 . y  h x M 1; 0.
hx  f xf x2f x2xf x 4x 6 5 – – Email:    f x 2x
h x  0  f xf   x   2 2x f    x      2  0     . f   x  2 • f x  0 x . f x2  0 x . • f x  2x x  1 – y  h x M 1;0. – f x
f x f  x  2 2 1 x , x   . m
y  3x.f xm  1x 1  . m   . m  10 . m  1 . m  1 . 3 x x 1
f  x f x  x  2 2 1 1 .  2
2f x  f 1 x  x  2 .  f  3f x x 2x 1 2 1 x f x 2        x 2x   1 y  3 x  2
x  m  x  y  2 2 2 1 3x  4x  m  2    0  y   x    10 0, 
 4  3m  2  0 m  a  3   0 3 – 6 6 – – Email: y  f x. y  f x g x  f 12x 1; 0.  ;  0. 0; 1. 1;   . f x x    1  0   . 1  x   2
gx  2f 12x.   x  1 gx 1 2x 1  0  f 12x       0    1  12x  2  1    x    0  2   g x  1   ;0  1;    2  – f x  . f x 1;3        1  x g x f        x  2 4; 2. 2; 0. 0; 2. 2;4. 6 7 – – Email: gx 1  x    f   1      1 2  2 gx  x   0  f   1     .  2  2  x  x  f   1  
  2  2  1  3  4  x   .  2  2 2 4; 2   x  x  f 1       2  1
  1  a  0  2  2 2a  x  4  2 2 22a;4 2;4.      1  x g x f        x  4; 2.  2 – m 5;5  x   e  m x  1 5 6 7 10 x e  0 m  0 x e  m x  1 1 x  1   1  1 x x e     f x x m e m        1 x f x x e '     x f x xe  0  x  0 6 8 – – Email:  1   1  m   0 m   1  m   1   0  m m
m  5;4;3;2;1;1 m5;5      x y  e  x y  e  0 x   C  m  0 y  m x  1  1;0  : x C y  e  m  0 x y  e  0  m  0  : y  m x  1  x e   m  x  1 x  0 C        m  1 x e   m  m   1 – 3 4 2 3 2 2
x  x  m  x   x  2 2 1 x  1  1m m m x  1 . 6 9 – – Email: m  1 . m  1 . m  5 m  5 . 4 4 a  3 4x  2x   m   3 a  3 b  4 x  2 x  m  .  1 b  3 2 2x   1 3 3 3 3
ab a b  0  a  a  b b   a  b .  3 a  3 b  4 x  2 x 1  m . f x 4 2  x x 1 1;   . f x  3 x  x  x  2 4 2
2 2x  1  0,  x  1 . f x 1;       1; .  m
  min f x  f 1  1 m  1 . 1;       – y  f x  g x  f  3 2x  x  1m . m max g x  10 . 0; 1     m  13 . m  12 . m  1. m  3 . t x 3  2x  x 1   x  0; 1 . tx 2    6x  1  0,  x  0; 1. t x     x  0;1 t      1; 2 . 7 0 – – Email:  
max f t  3  max f t  m  3  m .       1;2 1;2           
3  m  10  m  13 . – y  f x. y  f x     f  1  1,  1 f      1    2.       f x  ln x  m x 1;  e  e m  2 m  2 m  3 m  3   m  f x ln x    1 x   1  ;     e  m  max g x
g x  f x lnx    1  1  ;   e        1 g x f x x f 1  x      0, x    1;        e 1  g  x x 1  1        0,     1;         e    0, x    1;      x  e        g x  1  1  ;    1  1          1; max g      x  g 3.  e  e   1    1  ;  e  e   – 7 1 – – Email: 2 2
3  x  6 x  18  3x x  m m 1 m m  5  ;5       x  3;6   3 . 5 . 9 . 10 . t  x  3  6 x . 2 t    x  2 9 2 18 3 x . t  1  1 t   1  1   x  3 ; 0 0  3;   6 . 2 x  3 2 6 x 2 x  3 2 6 x 2   t  3;3 2   . 2 t  9  2 2 t  2t  t   m m   9 1  2 m m 1. 2 2 f t 2 t   2t  9    t  3;3 2 . 2     f t     t  1  0  t  3;3 2   . f t 3;3 2   max f t  f 3  3 .         3;3 2   m  2 2 2 2 
 m m  1  max f t  m m 1  3  m m  2  0  .      3;3 2 m  1    – y  f x  f  0  0
f  x  0,x  1; 2 7 2 – – Email:
f x  0,x  1;  2 y  f x 1; 2 y  f x x f x f  1 f x f   2 f   x  f  
0  0, x  1; 0  y  f x 1; 0 f x  f   0  0, x   0; 2 0; 2 x  0 y  f x K  x h;x h o o  K K \ x h  0 0  7 3 – – Email: f x  0, x   x h;x
f x  0,x  x ;x h x o o  o o  o y  f x
f x  0,x  x h;x
f x  0,x  x ;x h x o o  o o  o y  f x – f x
f x  x  2  2 1 x 2x x   .
g x  f  2x 2x  2 2 3 . 1 . . 3 2
gx  x  f  2 2 1 x  2x  2   
 2x  1 x 2x 2  21 x 2x   2 2 2
2  2 2x 2x  2   2x 5 1 x 4 1 1     .   x 5  0 x 1 2 1  x 4       1  1  0    .   x   2 0; 1, 2;   3 g x. 7 4 – – Email: 7 5