











Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI HUYỆN Môn: Toán 9
Thời gian làm bài: 150 phút Đề gồm 01 trang Bài 1: (6,0 điểm) 1) Cho biểu thức 3 3 x 3 Q = + + +1 2 3 x x 3 3 x 27 3 x + + −
a/ Tìm điều kiện của Q và rút gọn Q b/ Tính giá trị của Q khi x = 4 + 7 − 4 − 7
2) Chứng minh rằng A = 13 + 23 + 33 + ...+ 1003 chia hết cho B = 1 + 2 + 3 + ... + 100 Bài 2: (4,0 điểm)
1) Giải phương trình: x − 2013 + 4x − 8052 = 3 2) Cho abc = 1.Tính S = 1 1 1 + +
1+ a + ab 1+ b + bc 1+ c + ac Bài 3: (3,0 điểm)
1) Tìm nghiệm nguyên của phương trình: x2 + 2y2 + 2xy + 3y – 4 = 0
2) Biết rằng a,b là các số thoả mãn a > b > 0 và a.b = 1 Chứng minh : 2 2 a + b 2 2 a − b Bài 3: (6,0 điểm)
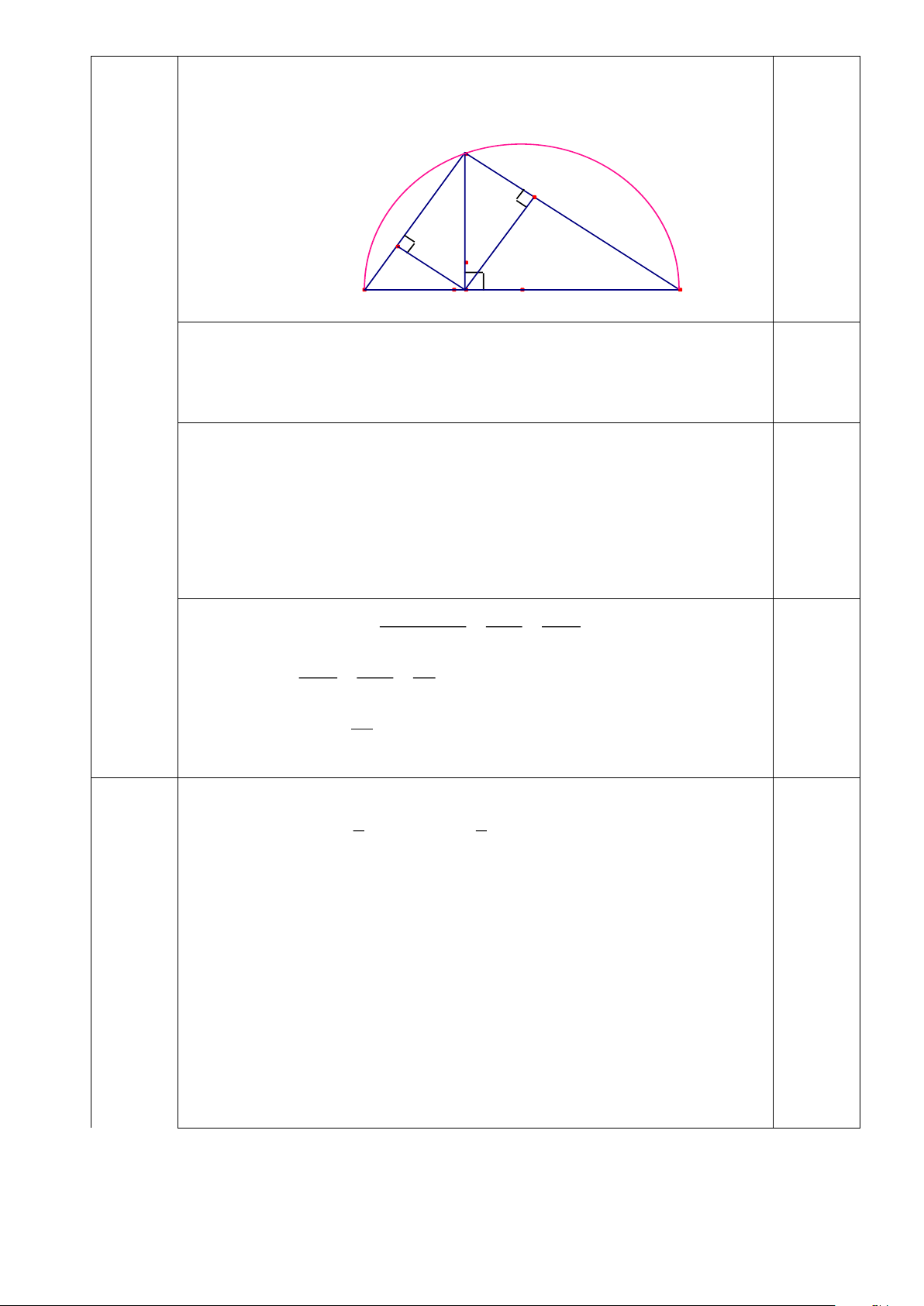
Cho nửa đường tròn đường kính BC = 2R, tâm O cố định. Điểm A di động trên
nửa đường tròn. Gọi H là hình chiếu của điểm A lên BC. Gọi D và E lần lượt là
hình chiếu của H lên AC và AB.
a) Chứng minh tam giác ABC vuông
b)Chứng minh: AB . EB + AC . EH = AB2
c) Xác định tam giác ABC sao cho tứ giác AEHD có diện tích lớn nhất? Tính d/
tích lớn nhất đó theo R. Bài 5: (1,0 điểm)
Tìm nghiệm nguyên dương của phương trình: 2(x + y) +16 = 3xy
HƯỚNG DẪN CHẤM THI HỌC SINH GIỎI LỚP 9 Bài
Tóm tắt lời giải Điểm 0,5 1.a) ĐKXĐ: x 0; x 3 Bài 1 Câu 1a 3 3 x 3 (2đ) Q = + + +1 2 3 x + x 3 + 3 x − 27 3 x 0,5 Trang 1 3 3
x2 + x 3 + 3 Q = + 2 2
x + x 3 + 3 (x − 3)(x + x 3 + ) 3 3x 0,5 (x − 3) 3 + 3
x2 + x 3 + 3 = 2
(x − 3)(x + x 3 + ) 3 3x 0,5 1 = x − 3
1.b) Ta có: x = 4 + 7 − 4 − 7 8 + 2 7 8 − 2 7 0,5 x = − 2 2 ( 1 + 7 )2 (1− 7)2 Bài 1 x = − 2 2 0,5 Câu 1b (2 đ) 1 + 7 7 −1 x = − 2 2 0,5 x = 2 Thay x = 2 vào Q ta có: 0,5 1 Q = = − 2 − 3 2 − 3
2. Ta có: B = (1 + 100) + (2 + 99) + ...+ (50 + 51) = 101. 50 0,5
Bài 1 Để chứng minh A chia hết cho B ta chứng minh A chia hết cho 50 0,25 Câu 2 và 101 (2 đ)
Ta có: A = (13 + 1003) + (23 + 993) + ... +(503 + 513) 0,25
= (1 + 100)(12 + 100 + 1002) + (2 + 99)(22 + 2. 99 + 992) + ... + 0,25
(50 + 51)(502 + 50. 51 + 512) = 101(12 + 100 + 1002 + 22 + 2. 99 + 0,25
992 + ... + 502 + 50. 51 + 512) chia hết cho 101 (1)
Lại có: A = (13 + 993) + (23 + 983) + ... + (503 + 1003) 0,25
Mỗi số hạng trong ngoặc đều chia hết cho 50 nên A chia hết cho 0,25 50 (2) 0,25
Từ (1) và (2) suy ra A chia hết cho 101 và 50 nên A chi hết cho B Bài 2
x − 2013 + 4x − 8052 = 3;Ð K : x 2013 0,5 (1,5 đ) 1.
3 x − 2013 = 3 x = 2014(TMÐ K ) 1,0 1
2. Cho abc = 1. ab = c 0.5 1 1 1 S = + +
1+ a + ab 1+ b + bc 1+ c + ac Trang 2 1 1 1 (2,5 đ) + + = 1 + + 1 0,5 1 abc b bc + c + ac + a + c c 1 1 = + +
c + ac +1 b(ac +1+ c) 1+ c + ac 0,5 bc +1+ b =
b(1+ c + ac) 0,5
b (c + ac + ) 1 = =
b (c + ac + ) 1 1 0,5 Bài 3
1. Tìm nghiệm nguyên của phương trình: (1,5đ)
x2 + 2y2 + 2xy + 3y – 4 = 0 (1)
(1) (x2 + 2xy + y2) + (y2 + 3y – 4) = 0 0,25
(x + y)2 + (y - 1)(y + 4) = 0 0,25
(y - 1)(y + 4) = - (x + y)2 (2) 0,25
Vì - (x + y)2 0 với mọi x, y nên: (y - 1)(y + 4) 0 - 4 y 1 0,25 Vì y nguyên nên y 4 − ;− 3;− 2;−1; 0; 1 0,25
Thay các giá trị nguyên của y vào (2) ta tìm được các cặp nghiệm
nguyên (x; y) của PT đã cho là: (4; -4), (1; -3), (5; -3), ( -2; 0), (-1; 1). 0,25
(1,5 đ) 2. - Vì a.b = 1 nên a + b (a − b)2 2 2 + 2ab = 0,25 a − b a − b (a − b)2 + 2 = = (a − b) 2 + 0,25 a − b a − b
- Do a > b > 0 nên áp dụng BĐT Cô Si cho 2 số dương 0,25
Ta có : (a −b) 2 + (a −b) 2 2 a − b a − b 0,5 2 2 Vậy a + b 2 2 a − b 0,25 Bài 4 6đ 0,5 Trang 3 A E D C B H O
a) Chứng minh tam giác ABC vuông 0,25 Ta có: OA= OB = OC = R 0,25
=> Tam giác ABC vuông tại A (theo đl đảo)
b) Chứng minh: AB . EB + AC . EH = AB2
Chứng minh tứ giác ADHE là hình chữ nhật 0,5 AB . EB = HB2 0,5
AC . EH = AC . AD = AH2 0,5
Ta có: AB2 = AH2 + HB2 (định lý Pi ta go) 0,5 => Đpcm 0,5 2 2 2 2 b) S AD + AE DE AH (ADHE)= AD.AE = = 1,0 2 2 2 S AH AO R (ADHE) 2 2 2 = 2 2 2 0,5 2 Vậy Max S R (ADHE)= Khi AD = AE hay AB = AC 0,5 2 0,5
<=> Tam giác ABC vuông cân tại A Bài 5
Ta có 2(x + y) +16 = 3xy 3xy − 2x − 2y =16 (1,0đ) 2 4 0,25
y(3x − 2) − (3x − 2) =16 + (3x − 2)(3y − 2) = 52 3 3
Giả sử: x y khi đó 1 3x − 2 3y − 2 và 52 = 1.52 = 2.26 = 4.13 ta 0,25 có các trường hợp sau: 3 x − 2 =1 3 x − 2 = 2 3 x − 2 = 4 0,25 ; ; (loại) ; 3 y − 2 = 52 3 y − 2 = 26 3 y − 2 =13
=> nghiệm nguyên dương của PT là: ( 1; 18);( 18; 1); ( 2; 5); ( 5; 2) 0,25 Trang 4
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI HUYỆN HUYỆN PHÙ MỸ Môn: Toán 9
Thời gian làm bài: 150 phút Đề gồm 01 trang Bài 1: (3,5 điểm)
Chứng minh rằng với mọi số tự nhiên n ta có:
A = 7.52n + 12.6n chia hết cho 19 Bài 2: (2,5 điểm)
Tìm số tự nhiên n sao cho: n + 24 và n – 65 là hai số chính phương Bài 3: (3,0 điểm)
Cho a, b > 0 và a + b = 1. 2 2 1 1
Chứng minh rằng : a + + b + 12,5 a b Bài 4: (3,0 điểm)
Cho x, y là hai số dương thỏa mãn : x2 + y2 = 4. 2 2 1 1
Tìm giá trị nhỏ nhất của biểu thức : E = x + + y + y x Bài 5: (4,0 điểm)
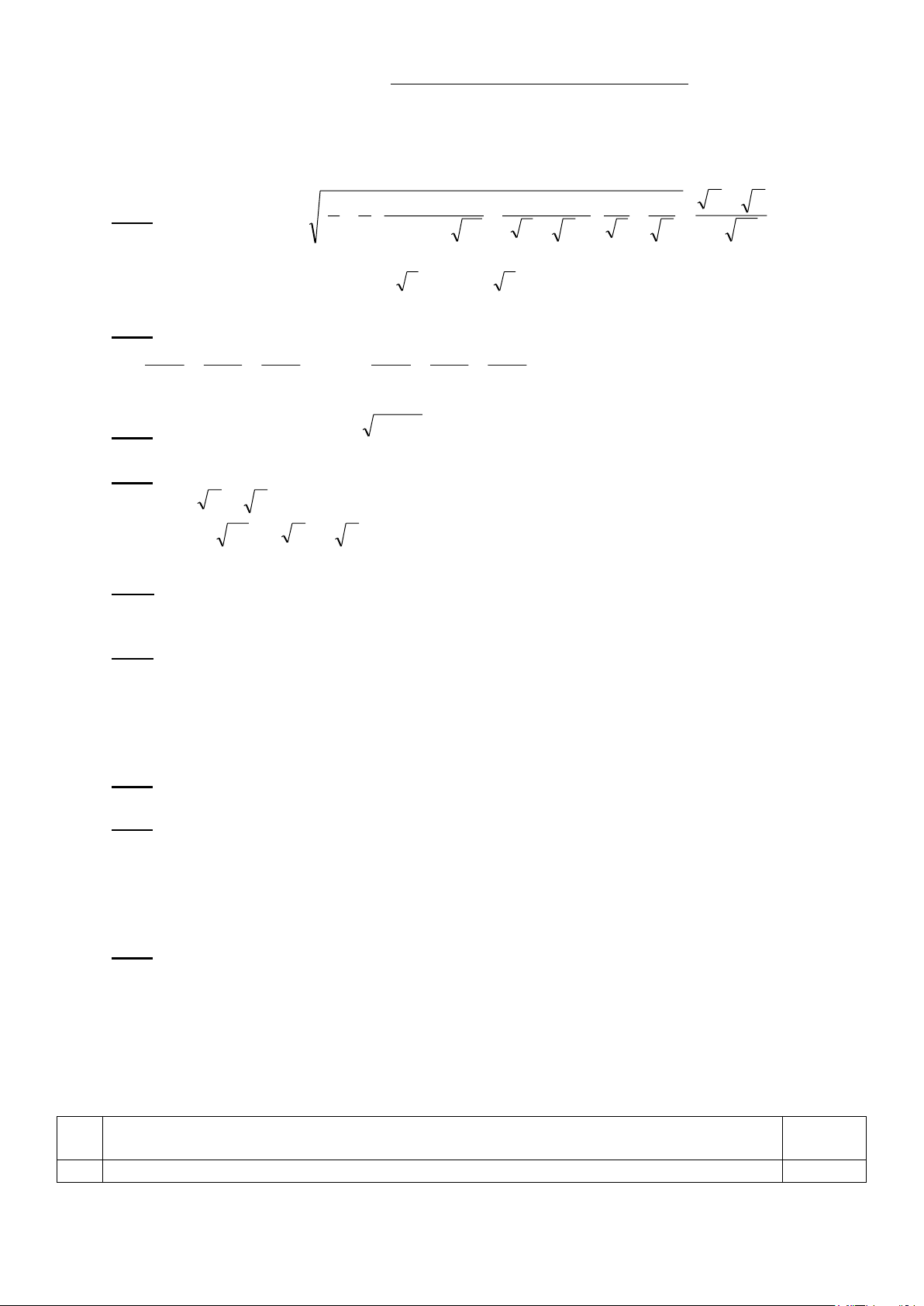
Cho tam giác ABC có D là trung điểm cạnh BC, điểm M nằm trên trung
tuyến AD. Gọi I, K lần lượt là các trung điểm tương ứng của MB, MC và P, Q
là các giao điểm tương ứng của các tia DI, DK với các cạnh AB, AC. Chứng minh: PQ // IK. Bài 6: (4,0 điểm)
Cho tam giác ABC có BC = a , CA = b , AB = c. Gọi đường cao hạ từ
các đỉnh A,B,C xuống các cạnh BC , CA và AB tương ứng là ha , hb , hc . Gọi O
là một điểm bất kỳ trong tam giác đó và khoảng cách từ O xuống ba cạnh BC ,
CA và AB tương ứng là x , y và z . Tính x y z M = + + h h h a b c Trang 5 HƯỚNG DẪN CHẤM
ĐỀ THI HSG LỚP 9 CẤP HUYỆN - MÔN TOÁN
Bài 1 Với n = 0 ta có A(0) = 19 19 0,5
(3,5đ) Giả sử A chia hết cho 19 với n = k nghĩa là: A(k) = 7.52k + 12.6k 19 0,75
Ta phải chứng minh A chia hết cho 19 với n = k + 1 nghĩa là phải chứng minh: 0,75
A(k + 1) = 7.52(k + 1) + 12.6k + 1 19
Ta có: A(k + 1) = 7.52(k + 1) + 12.6k + 1 = 7.52k.52 + 12.6n. 6
= 7.52k.6 + 7.52k .19 + 12.6n. 6 = 6.A(k) + 7.52k .19 19 1,0
Vậy theo nguyên lý quy nạp thì A = 7.52n + 12.6n chia hết cho 19 với mọi số tự nhiên n 0,5 Bài 2 (2,5đ) n + 24 = 2 k Ta có: 0,5 n − 65 = 2 h 1 2 2 k − 24 = h + 65 0,5
(k − h)(k + h) = 89 = . 1 89 0,5 k + h = 89 k = 45 Vậy: 0,5 k − h = 1 h = 44 n = 452 – 24 = 2001 0,5
Bài 3 Nhận xét rằng với mọi x,y ta có: (3,0đ) (x − y)2 2 2
0 x + y 2xy 2( 2 2 x + y ) 2 2
x + y + 2xy ( x + y)2 2 2 x + y 0,5 2 1 1 Đặt a + = x ; b + = y ta được : a b 0,5 2 2 2 2 2 1 1 1 1 1 1 a + b 1 1 a + + b + a + + b + = a + b + = 1+ a b 2 a b 2 ab 2 ab 0,75 Vì = (a + b)2 1 1
4ab ab 4 0,5 2 2 2 1 1 1 1 1 1 Do đó : a + + b + 1+ 1+ =12,5 0,75 a b 2 ab 2 1 4 Trang 6 Bài 4 1 1 x y 0,5 (3,0đ) Ta có 2 2
E = (x + y ) + + + 2 + 2 2 x y y x 1 1 4 Áp dụng BĐT: + vôùi a > 0; b > 0. 1,0 a b a + b 1 1 4 1 1 Ta có + + 1 2 2 2 2 2 2 x
y x + y x y a b 1,0
Áp dụng BĐT: + 2 vôùi a > 0; b > 0. b a 0,5 x y x y Ta có + 2 2 + 4 y x y x
Vậy giá trị nhỏ nhất của biểu thức E = 9 . Dấu “=” xảy ra khi x = y = 2 Bài 5
- Vẽ hình đúng 0,5 (4,0đ)
- Gọi E là trung điểm của AM, chứng minh được: 1,5
IK // BC, EI // AB, EK // AC
- Áp dụng định lý Ta-lét vào các tam giác DPA, DAQ. Suy ra: 1,5 DI DE DK = = DP DA DQ
- Áp dụng định lý Ta-lét đảo vào tam giác DPQ, suy ra: 0,5 PQ // IK
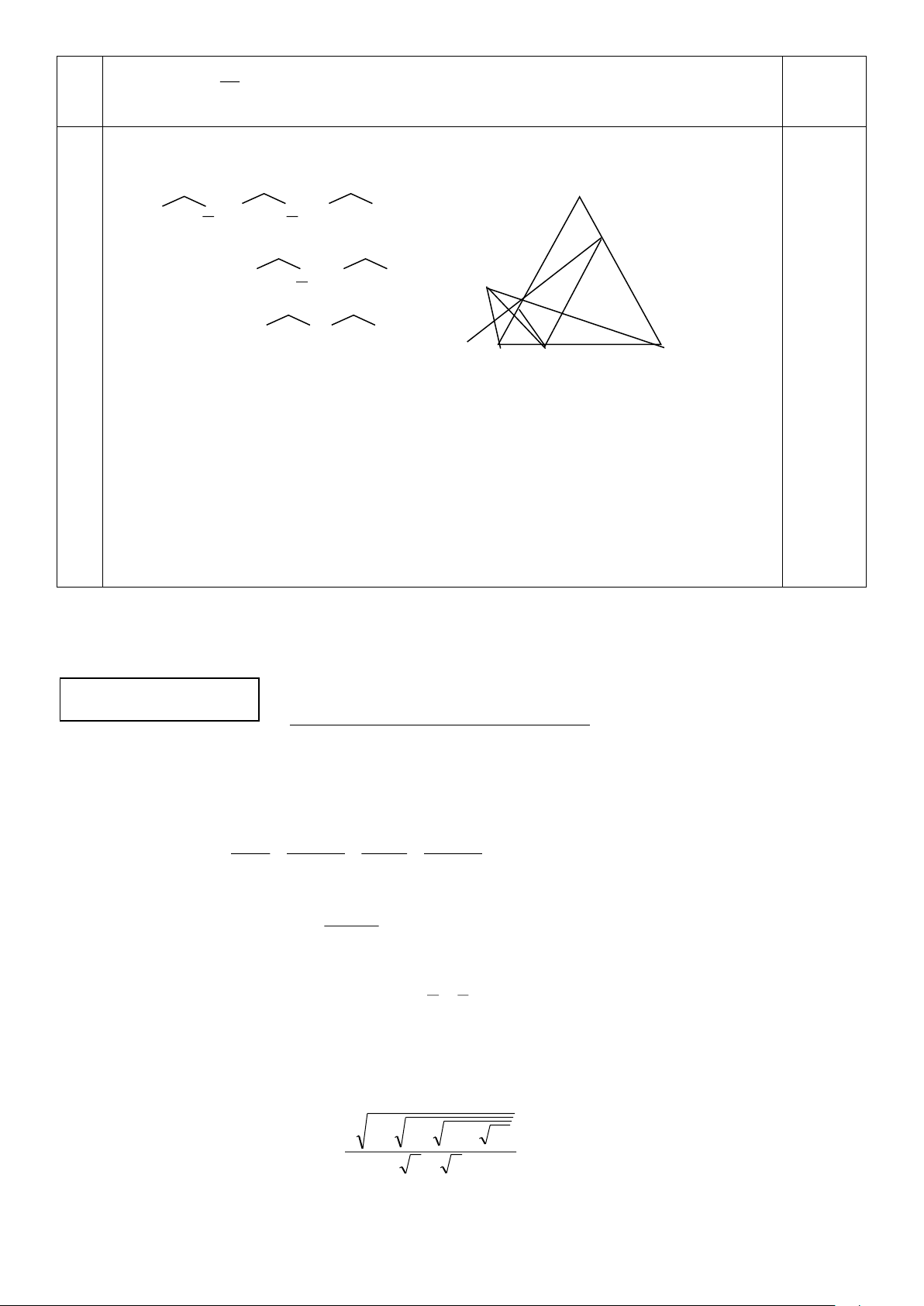
Bài 6 Vẽ hình đúng 0,5 A (4,0đ) ha x B C
Xét hai tam giác ABC và OBC ta có : 1 SABC = BC h . (1) a 2 0,5 1
SOBC = BC..x (2) 2 x S Từ (1)và (2) ta suy ra : OBC = 1,0 h S a ABC y S COA = h S 0,5 Tương tự ta có : b ABC z S AOB = 0,5 h S c ABC S + S + S S Từ đó tính được : BOC COA AOB ABC M = = =1 S S 1,0 ABC ABC Trang 7
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI HUYỆN HUYỆN ĐÔNG SƠN Môn: Toán 9
Thời gian làm bài: 150 phút Đề gồm 01 trang 1 1 1 2 1 1
x − y
Bài 1: Cho biểu thức: A = ( + ). + .( + ) : x
y x + y + 2 xy ( x + y )3 x y xy xy
a, Rút gọn biểu thức A.
b, Tính giá trị biểu thức A khi x = 3 + 5 ; y = 3 - 5
Bài 2: Cho 3 số a, b, c 0 thỏa mãn: a b c và a3+b3 +c3 = 3abc.
a − b
b − c
c − a c a b P = + + ; Q = + + c a c
a − b
b − c
c − a
Chứng minh rằng : P.Q = 9.
Bài 3: Giải phơng trình : (4x – 1) x2 + 1 = 2(x2+1) + 2x -1.
Bài 4: Giải hệ phương trình sau:
x − y + x = y
x + y + 18 xy = 4 x + 3 y + 13
Bài 5: Cho 3 số x,y,z thỏa mãn x + y + z = 3 và x4+y4+z4 =3xyz. Hãy tính giá trị của biểu
thức M = x2006 + y2006 + z2006
Bài 6: Cho Parabol (P) có phương trình y = x2 và điểm A(3;0) ; Điểm M thuộc (P) có hoành độ a.
a) Xác định a để đoạn thẳng AM có độ dài ngắn nhất .
b) Chứng minh rằng khi AM ngắn nhất thì đường thẳng AM vuông góc với tiếp tuyến của (P) tại điểm M.
Bài 7: Tìm nghiệm nguyên của phương trình : x3 + x2 + x +1 = 2003y
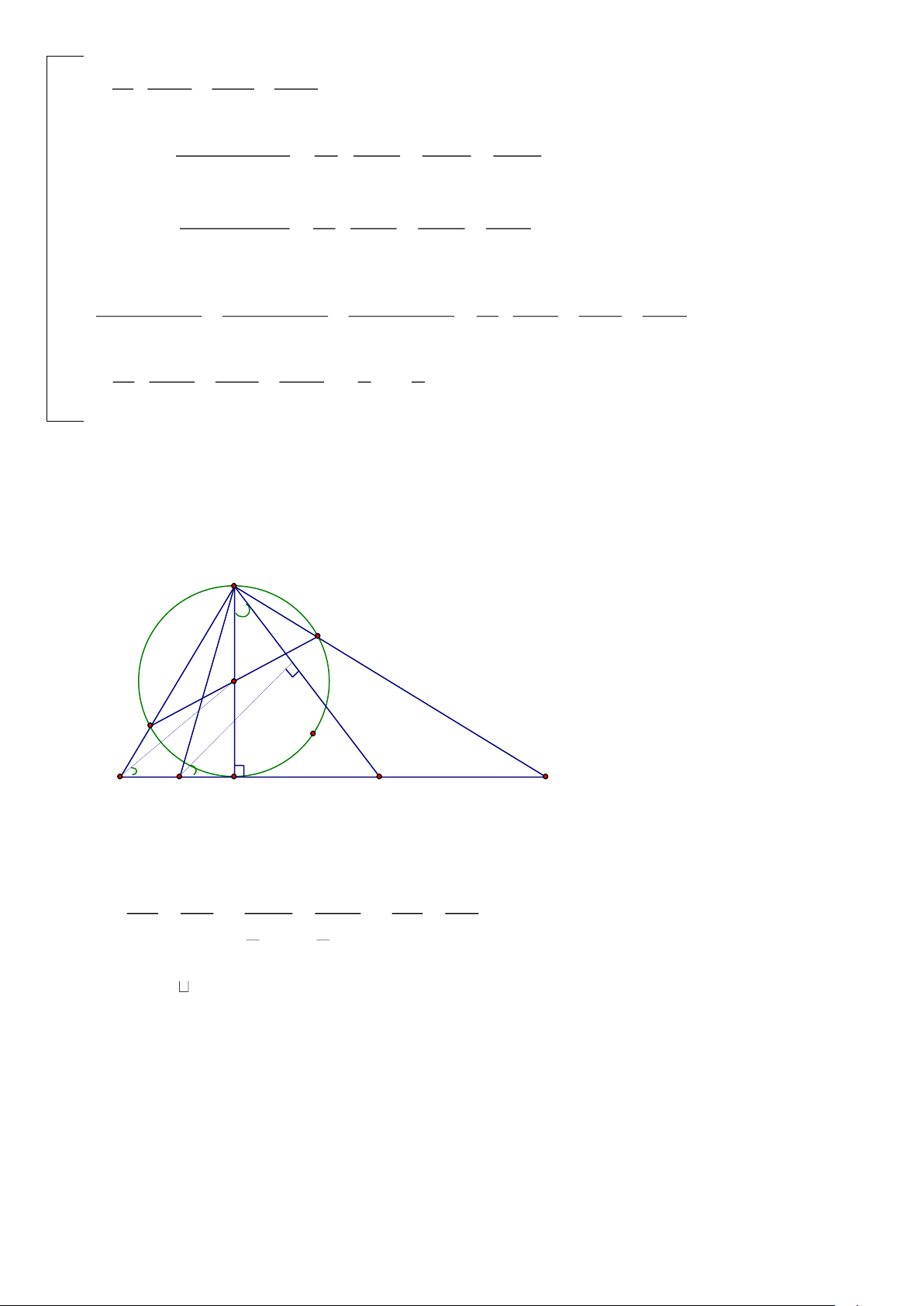
Bài 8: Cho tam giác ABC vuông ở A. I là trung điểm của cạnh BC, D là một điểm bất kỳ
trên cạnh BC. Đường trung trực của AD cắt các đường trung trực của AB, AC theo thứ tự tại E và F.
a) Chứng minh rằng: 5 điểm A,E,I,D,F cùng thuộc một đường tròn.
b) Chứng minh rằng: AE.AC = AF.AB.
c) Cho AC = b; AB = c. Hãy tìm giá trị nhỏ nhất của diện tích tam giác AEF theo b, c
Bài 9: Cho tam giác ABC cân tại A. Một điểm P di động trên BC. Qua P vẽ PQ//AC
(QAB) và PR//AB (RAC). Tìm quỹ tích các điểm D đối xứng với P qua QR.
Hướng dẫn chấm thi học sinh giỏi lớp 9 Môn : Toán Bài Lời giải Biểu điểm
1 a ) ĐKXĐ : x >0 ; y>0 ; x y 0,25 Trang 8 1 1 1 2 1 1
x − y A = ( + ). + .( + ) : x
y x + y + 2 xy
( x + y )3 x y xy xy
x + y
2( x + y ) xy xy = + .
xy.( x + y )2
( x + y )3 .( x . y )
x − y
x + y + 2 xy xy xy = . 2
xy( x + y )
x − y 1 xy xy xy 0,75 = . = xy
x − y
x − y
b) Với x= 3 + 5 Và y = 3 - 5 ta có : x >y do đó 0,25 xy A = 0
x − y ( xy )2
[( 3 + 5 ).( 3 − 5 ) ] 2 42 Mà A2 = = = = 8 0,75
x + y − 2 xy 2 2
6 − 2.2
( 3 + 5 ) + ( 3 − 5 ) − 2. 3 − ( 5 )
Vậy : A = 8 = 2 2
Ta có : a3 + b3 + c3 = 3abc a3 + b3 + c3 -3abc = 0
(a + b + c ) ( a2 + b2 + c2 – ab – ac – bc ) = 0 (1) 1
Mà a2 + b2 + c2 - ab – ac –bc = [(a –b )2 + (b – c)2 +(c-a)2 ] 0 2 ( Do a b c ) 0,5
Do đó:(1) a +b +c = 0 a +b = - c ; a +c = -b ; b +c = -a (2) Mặt khác :
a − b
b − c
c − a (
ab b − a ) + bc( b − c ) + ac( c − a ) P = + + = c a b abc (
ab a − b ) + b2c − bc2 + ac2 − a2c
( a − b )( b − c )( a − c ) P = = (3) 0,5 abc abc Hơn nữa :
a − b = z
x − y = a + b − 2c = −3c
Đặt b − c = x Ta có y − z = b + c − 2a = −3a (do (2) ) 2
c − a = y
z − x = a + c − 2b = −3b Vì thế : c a b
1 x − y
y − z
z − x Q = + + = − ( + + )
a − b
b − c
c − a 3 z x y
1 ( x − y ).( y − z ).( x − z ) = - .
( Biến đổi tương tự rút gọn P ) 3 xyz
1 ( −3c ).( −3a ).[ −( −3b )] = - .
3 ( a − b ).( b − c c
). − a ) − 9abc = (4) 0,75
( a − b )( b − c )( c − a )
( a − b ).( b − c ).( a − c ) − 9abc Từ (3) và (4) ta có : P.Q= . = 9 abc
( a − b ).( b − c ).( c − a ) 0,25 Vậy P.Q = 9 Trang 9
(4x – 1) x2 + 1 = 2(x2 +1) +2x -1 (5) Đặt
x2 + 1 = y ( y 1) Ta có : 0,25
(5) (4x -1).y = 2y2 + 2x – 1 2y2 - 4xy +2x + y -1 = 0
(2y2 – 4xy +2y ) – ( y -2x + 1) = 0 1,0
2y (y -2x + 1) – ( y -2x + 1) = 0
y = 2 x − 1 3
(y-2x + 1 ) (2y- 1) = 0 1 y = (
1 lo¹i ) 2
x2 + 1 = 2x -1 0,75 x2 + 1 = 4x2 – 4x + 1
x = 0
x(3x – 4) = 0
x = 4 3
x − y + x = y( a ) (I ) (ĐKXĐ : x 0; y 0 )
x + y + 18 xy = 4 x + 3 y + ( 13 b ) Ta có :
( a) ( x − y )( x + y + 1 ) = 0 x − y =0 x = y 1,0
x = y thế vào (b) ta đợc :
2x +18x = 4 x + 3 x + 13 20x - 7 x -13 = 0 (6) 4
Đặt x = t (t 0 ) ta có :
t = 1
( 6) 20 t2 – 7t – 13 = 0 − = 13 t
0( lo¹i ) 20 1,0
x = 1 x = 1
Vậy hệ (I) có nghiệm duy nhất (x,y) = (1, 1) 4
x + 4 y 4 4
x .y = 2 2 x y 2 4
y + 4 z Theo BĐT Cô si ta có : 4 4 y z . = 2 2 y z 2 4
z + 4 x 4 4
z .x = 2 2 x z 2 0,75
x4 + y4 +z4 x2y2 + y2z2 +x2z2 ( 7 ) 5
Mặt khác : x2y2 + y2z2 +x2z2 xy2z + xyz2 +x2yz (C/M tương tự quá trình trên)
x2y2 + y2z2 +x2z2 xyz (x +y +z)
x2y2 + y2z2 +x2z2 3xyz (8) (do x +y z =3 )
Do đó : x4 +y4 + z4 3xyz (9) 0,75 Dấu “ = “xảy ra 4
x = 4 4
y ; y = 4 4
z ;z = 4 x x = y = z (10) 2 2
x y = 2 2 2 2
y z ; y z = 2 2 2 2
z x ;z x = 2 2 x y Hơn nữa x + y +z =3 (11)
Từ (10 ) và (11) 3x = 3 x = 1 y = z =1 Trang 10
x2006 + y2006 + z2006 = 1 + 1 +1 = 3 0,5 Vậy : M = 3
a)Ta có : A (3; 0) và M(a; a2 ) do đó :
AM2 = (a – 3)2 +(a2 – 0)2 = a4 + a2 – 6a +9
= (a4 -2a2 +1 ) +3 ( a2 – 2a +1 ) +5
= ( a2 -1)2 + 3(a-1)2 + 5 5 AM 5 1.0
Min AM = 5 khi và chỉ khi a = 1
b) Theo câu a : AM có độ dài ngắn nhất a = 1 ,Khi đó M(1;1) 1 3
Do đó phương trình đường thẳng AM là: y = - x + 2 2 0,25 (do A(3;0)) ( c )
Gọi phương trình đường thẳng đi qua điểm M (1;1) và tiếp xúc với ( P) tại điểm M là (d)
: y = ax +b ta có : a .1 + b = 1 (12) (Do M(1;1) (d) ) 6
và phương trình : x2 = ax +b có nghiệm kép (13) (do (d) tiếp xúc với (P) )
Mà : x2 = ax + b x2 – (ax + b ) = 0 (14)
Phương trình (14 ) có = (-a)2 – 4.1.(-b) = a2 + 4b
Nên : (13) a2 + 4b = 0 (15)
Từ (12) và (15 ) ta có hệ phương trình:
a + b = 1
a2 + 4( 1 − a ) = 0
a = 2
a2 + 4b = 0
b = 1 − a
b = −1
Vì thế phương trình đường thẳng đi qua điểm M(1;1) và tiếp xúc với
( P ) tại M là : y = 2x -1 (d) 0,5 1
Từ (c ) và ( d) (d) AM (do - . 2 = -1 ) 2
Vậy : Khi AM ngắn nhất thì AM vuông góc với tiếp tuyến của (P) tạiM 0,25
+)Nhận thấy (0;0) là nghiệm nguyên của phương trình : 3
x + x2 +x +1 = 2003 (16) 0,5
+) Với y< 0 ta có : 2003y Z mà x3 +x2 +x +1 Z
(Với x Z ) Phương trình (16) không có nghiệm nguyên thỏa mãn y < 0 0,25 +) Với y >0 ta có :
(16) (x +1)(x2 +1) = 2003y (*)
Từ (*) x +1 >0 (do x2 +1 > 0 và 2003y > 0 )
Đặt ƯCLN ( x + 1; x2 +1 ) = d ta có : 7
(x+1) d và (x2 + 1) d [ x2 +1 + (x +1) (1 - x)] d 2 d d =1 (**) y Ho n nòa (*) tõ 2003 d
Mặt khác : 2003 là số nguyên tố ,nên các ớc của 2003y chỉ có thể là 1 hoặc 2003m (m N* ) (***)
x + 1 = 1
Từ (*) , (**) và (***) x = 0 y = 0 (loại)
x2 + 1 = 1
phương trình (16) cũng không có nghiệm nguyên thỏa mản y > 0 1,0
Vậy : Phương trình có nghiệm nguyên duy nhất ( 0; 0) 0,25 Trang 11
a) Ta có : E là giao điểm
của 2 đường trung trực A F của 2 cạnh AD,AB
Nên E là tâm đường tròn ngoại tiếp ABD.
Tương tự ta có: F là tâm M
đường tròn ngoại tiếp ACD 0,5 E C Do đó : B H I D 1 +ABD = AED AED = 2 B 2 1 +ACD = AFD AFD = 2 C 2
AED + AFD = 2 (B +C) =1800 AEDF Nội tiếp (17) 1 0,5 Lại có : AI =
BC = BI ABC cân tại I 2 0,5
BAI = B AID = 2 B AID + AFD = 1800
Tứ Giác AIDF nội tiếp (18)
Từ (17 ) ; (18 ) 5 điểm A , E , I , D , F cùng thuộc đường tròn
b)Ta có EF là đường trung trực của AD nên : AE = ED ; FA =FD
AEF = DEF ( c. c.c ) 0,5 1 1
+ )AEF = DEF = AED = . 2 B = B 2 2 8 + ) Tương tự AEF = C Suy ra AEF ABC (g.g) AE AF = AE.AC = AE. AB AB AC
c) Theo câu b) Ta ccó : AEF ABC AE AF =
= k ( k là tỉ số đồng dạng) AB AC AE =kc ; AF = kb .
Ta có : AEF vuông tại A (do ABC vuông tại A và AEF ABC ) 1
Nên diện tích AEF là S = AE.AF 2S = k2 bc (19) 2 1
Mặt khác S = AM.EF 2S = AM . EF 4S2 = AM2 .EF2 2 AD 4S2 = ( 2 ) . (k2b2 + k2c2 ) (20) 2
AD2 b2 + c2 2 2 b + c Từ (19) và (20) 2S = . S = 2 .AD (21) 4 bc 8bc
Do đó : S nhỏ nhất AD nhỏ nhất
Mà AD AH ( AH BC , H BC ) . AB AC bc bc Lại có AH = = AD (22) 2 2 2 2 BC b + c b + c 2 2 b + c (bc)2 bc Từ (21) ; (22) S . = 8 2 2 bc b + c 8 Trang 12 bc Vậy Min S = ( Khi D H ) 8 a) Phần thuận
Giả sử D là điểm đối xứng với P qua QR ta có :
* QP = QB = QD P, B , D thuộc đường tròn (Q) A 1 1 BDP = BQP = BAC (23) 2 2 R 1
* Tương tự : CDP = BAC (24) D 2 Q 1,0
Từ (23) ;(24) BDC = BAC 9
điểm D thuộc cung BAC B P C
(Của đường tròn ngoại tiếp tam giác ABC ) b) Phần đảo
Lấy điểm D” thuộc cung BAC ( D’ B, C) , Gọi Q’ là giao điểm của AB với đường
trung trực của D’B ; qua Q’ kẻ Q’P’ // AC qua P’ kẻ P’R’ // AB ta có Q’R’ là đường trung trực của D’P’
Vậy qũy tích các điểm D là cung BAC của đường tròn ngoại tiếp tam giác ABC (trừ 2 1,0 điểm B,C ) PHÒNG GD-ĐT CAM LỘ
KÌ THI HỌC SINH GIỎI VĂN HÓA ĐỀ THI MÔN: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút Câu 1:(1 điểm)
Phân tích đa thức sau thành nhân tử : 4 x +2009 2 x +2008 x +2009
Câu 2:(1 điểm) Giải phương trình sau:
x + 2 2x + 45 3x + 8 4x + 69 + = + 13 15 37 9
Câu 3: (2 điểm) 4 4 a + b a/ Chứng minh rằng 3 3 2 2
ab + a b − a b 2
b/ Cho hai số dương a,b và a=5-b. 1 1
Tìm giá trị nhỏ nhất của tổng P= + a b
Câu 4:(2 điểm)
a/ Cho a và b là hai số thực dương thõa mãn điều kiện : 2006 2006 2007 2007 2008 2008 a + b = a + b = a + b Hãy tính tổng: S= 2009 2009 a + b 2 3 + 5 − 13 + 48 b/ Chứng minh rằng :A= là số nguyên 6 + 2 Trang 13
Câu 5: (1 điểm) Tìm các số nguyên dương x,y thõa mãn phương trình sau: xy-2x-3y+1=0 Câu 6: (3điểm)
Cho tam giác ABC vuông tại A có cạnh AC>AB ,đường cao AH (H thuộc BC).Trên tia HC
lấy điểm D sao cho HD=HA.Đường vuông góc với với BC tại D cắt AC tại E.
a)Chứng minh hai tam giác BEC và ADC đồng dạng
b)Chứng minh tam giác ABE cân.
c)Gọi M là trung điểm của BE và vẽ tia AM cắt BC tại G. Chứng minh rằng: GB HD = BC AH + HC PHÒNG GD-ĐT CAM LỘ
KÌ THI HỌC SINH GIỎI VĂN HÓA
HƯỚNG DẪN CHẤM MÔN: TOÁN ĐỀ CHÍNH THỨC Câu 1: (1 điểm) 4 x +2009 2 x +2008 x +2009 = ( 4 x + 2 x +1) +2008( 2
x + x +1) 0,25 đ = ( 2 x + x +1)( 2
x - x +1)+ 2008( 2
x + x +1) 0.5 đ = ( 2 x + x +1)( 2
x - x +2009) 0,25 đ Câu 2: ( 1 điểm)
x + 2 2x + 45 3x + 8 4x + 69 + = + 13 15 37 9 x + 2 2x + 45 3x + 8 4x + 69 ( +1)+( -1)=( +1)+( -1) 0,25đ 13 15 37 9 x +15 ( 2 x + ) 15 ( 3 x + ) 15 ( 4 x + ) 15 + = + 0,25đ 13 15 37 9 1 2 3 4 (x + )( 15 + − − ) = 0 0,25 đ 13 15 37 9 x=-15 0,25 đ Câu 3: (2 điểm) a/ (1 điểm) 4 4 a + b 3 3 2 2
ab + a b − a b 2 4 a + 4 b 3 3 2 2
2ab + 2a b − 2a b 0,25 đ 4 a + 4 b − 3 3 2 2
2ab − 2a b + 2a b 0 0,25 đ ( 4 a − 2 3 2 2
a b + a b ) + ( 4 b − 2 3 2 2
ab + a b ) 0,25 đ Trang 14 ( 2 a − ab)2 + ( 2
b − ab)2 0 0,25 đ b/ (1 điểm) 1 1 a + b 5 P= + = = 0,25 đ a b ab ab 20 20 4 P= = 0,5 đ 2 4ab (a + b) 5 4 5
Vậy giá trị nhỏ nhất của P là khi a=b= 0,25 đ 5 2 Câu 4 (2 điểm) a/ (1 điểm) Ta có: 2008 a + 2008 b = ( 2007 2007 a + b
)(a + b) − ab( 2006 2006 a + b ) 0,25 đ
1= a + b − ab 0,25 đ 1 ( − a 1 )( − b) = 0 0,25 đ a = , 1 b = 1 Vậy S=1+1=2 0,25 đ b/ (1 điểm) 2 3 + 5 − 13 + 48 A= 6 + 2 2 3 + 5 − (2 3 + ) 1 2 A= 0,25 đ 6 + 2 2 3 + ( 3 − ) 1 2 = 0,25 đ 6 + 2 2 2 + 3 ( 6 + 2)2 = = 0,25 đ 6 + 2 6 + 2 =1 Z 0,25 đ Câu 5 (1 điểm) xy-2x-3y+1=0 xy-3y=2x-1 y(x-3)=2x-1 0,25 đ
Ta thấy x=3 không thõa mãn,với x 3 thì 5 y=2+ 0,25 đ x − 3
Để y nguyên thì x-3 phải là ước của 5 0,25 đ
Suy ra: (x,y) là (4,7) ;(8,3) 0,25 đ Trang 15 Câu 6 (3 điểm) a) (1đ điểm)
Tam giác ADC và tam giác BEC: CD CA = ( vì hai tam giác CE CB CDE và CAB đồng dạng) Góc C: chung 0,75 đ
Suy ra: Tam giác ADC đồng dạng với tam giác BEC (c-g-c) 0,25 đ
b)(1 điểm) Theo câu ta suy ra: BEC = ADC có: 0
ADC = EDC + ADE = 135 Suy ra: 0 BEC = 135 0,5 đ Suy ra: 0 AEB = 45 0,25 đ
Do đó: Tam giác ABE cân( tam giác vuông có một góc bằng 45 0 ) 0,25 đ c)(1 điểm)
Tam giác ABE cân tại E nên AM còn là phân giác của góc BAC GB AB AB ED AH HD Suy ra: = , mà = ( A BC D EC) = (ED // AH ) = 0,5 đ GC AC AC DC HC HC GB HD GB HD GB HD Do đó: = = = 0,5 đ GC HC GB + GC HD + HC BC AH + HC
PHÒNG GD&ĐT THANH OAI
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) Đề thi gồm có: 01 trang Câu 1: (6 điểm) x x + 3 x + 2 x + 2 a) Cho M = 1 ( − ) : ( + + ) x +1 x − 2 3 − x x − 5 x + 6 1. Rút gọn M
2. Tìm giá trị nguyên của x để biểu thức M nhận giá trị là số nguyên
b) Tính giá trị của biểu thức P P = 3 2013 x + 5 2011 x
+ 2006 với x = 6 + 2 2. 3 − 2 + 2 3 + 18 − 8 2 − 3
Câu 2: (4 điểm) Giải phương trình x + x + x + x + = a) ( )( 3 )( 4 )( 5 ) 6 24 2 2
b) 2x − x −1 = 2x − x −1 Câu 3: (4 điểm)
a/ Cho hai số dương x, y thoả mãn x + y = 1. Trang 16 1 1
Tìm giá trị nhỏ nhất của biểu thức: 2 2 M = x + y + 2 2 y x 1 1 1
b/ Cho x, y, z là các số dương thoả mãn + + = 6 . x + y y + z z + x 1 1 1 3 Chứng minh rằng: + + .
3x + 3y + 2z 3x + 2y + 3z 2x + 3y + 3z 2 Câu 4: (5 điểm)
Cho đường tròn (O; R) và hai đường kính AB và CD sao cho tiếp tuyến tại A của đường tròn
(O; R) cắt các đường thẳng BC và BD tại hai điểm tương ứng là E và F. Gọi P và Q lần lượt
là trung điểm của các đoạn thẳng AE và AF.
1. Chứng minh rằng trực tâm H của tam giác BPQ là trung điểm của đoạn thẳng OA.
2. Gọi α là số đo của góc BFE. Hai đường kính AB và CD thoả mãn điều kiện gì thì biểu 6 6
thức P = sin + cos . Đạt giá trị nhỏ nhất? tìm giá trị nhỏ nhất đó. 3 BE CE
3. Chứng minh các hệ thức sau: CE.DF.EF = CD3 và = . 3 BF DF Câu 5: (1 điểm)
Tìm nN* sao cho: n4 +n3+1 là số chính phương. - Hết -
Lưu ý: Cán bộ coi thi không giải thích gì thêm!
PHÒNG GD&ĐT THANH OAI
HƯỚNG DẪN CHẤM THI CHỌN HỌC SINH GIỎI LỚP 9 Môn: Toán Câu 1: (6 điểm) a) (4,5đ) ĐKXĐ: x ; 0 x ; 4 x 9 (*)
1)Rút gọn M : Với x ; 0 x ; 4 x 9 (0,5đ)
x +1− x x + 3 x + 2 x + 2 M = : − + x +1 x − 2 x − 3
( x − 2)( x − ) 3 1 ( x + )( 3 x − )
3 − ( x − 2)( x + 2) + ( x + 2) = : x +1
( x − 2)( x − ) 3 1
x − 9 − (x − 4) + x + 2 = : x +1
( x − 2)( x − ) 3 x − 2 = x +1 x − 2 Vậy M = (với x ; 0 x ;
4 x 9 ) (*) (2,5đ) x +1 Trang 17 x − 2 x +1− 3 x +1 3 3 2) M = = = − = 1− (0,75đ) x +1 x +1 x +1 x +1 x +1
Biểu thức M có giá trị nguyên khi và chỉ khi: 3 x +1 x +1U ) 3 ( Ư(3) ; 1 3
Vì x 0 x 0 x +11 Nên x +1 3 ;
1 Xảy ra các trường hợp sau: (0,5đ)
. x +1 = 1 x = 0 x = 0 (TMĐK (*) )
. x +1 = 3 x = 2 x = 4 (không TMĐK (*) loại ) (0,25đ)
Vậy x = 0 thì M nhận giá trị nguyên. b_ x = 6 + 2 2. 3 − 2 + 2 3 + 18 − 8 2 . − 3
Có 18 − 8 2 = (4 − 2)2 = 4 − 2 = 4 − 2 (0,5đ)
2 + 2 3 + 4 − 2 = 2 3 + 4 = ( 3 + ) 1 2 = 3 +1 (0,25đ)
x = 6 + 2 2. 3 − 3 −1 − 3 = 6 + 2 2. 2 − 3 − 3 = 6 + 2 4 − 2 3 − 3 x = 6 + 2 ( 3 − )
1 2 − 3 = 6 + 2 3 −1 − 3 = 4 + 2 3 − 3 x = ( 3 + )
1 2 − 3 = 3 +1 − 3 = 3 +1− 3 = 1 (0,75đ)
Với x = 1.Ta có P = 1 . 3 2013 + 1 .
5 2011 + 2006 = 3 + 5 + 2006 = 2014
Vậy với x = 1 thì P = 2014 Câu 2: (4 điểm) a. ( x + )( 3 x + )( 6 x + )( 4 x + ) 5 = 24 0,25 đ ( 2 x + 9x +18)( 2
x + 9x + 20) = 24 (1) 0,25 đ 0,5 đ
Đặt x2 + 9x +19 = y 0,5 đ
(1) ( y + 1)(y – 1 ) – 24 = 0 0,25 đ y2 – 25 = 0 0,5 đ ( 2 x + 9x + 24)( 2 x + 9x +14) = 0 0,5 đ (x + )( 2 x + 7)( 2
x + 9x + 24) = 0 Chứng tỏ 2
x + 9x + 24 0 0,25 đ
Vậy nghiệm của phương trình : x = − ; 2 x = 7 − 0,25 đ b. Ta có 2 2
x − x −1 = −( 2 x − 2x + ) 1 = −(x − ) 1 2 0 0,5 đ pt trở thành : 2 2 x − x −1 2 = x − 2x +1 0,25 đ x = 1 Câu 3: (4 điểm) Trang 18
a Cho hai số dương thỏa mãn: x + y =1. 2đ 1 1
Tìm GTNN của biểu thức: M = 2 2 x + y + 2 2 y x 1 1 4 4 2 2 1 x y + 2x y +1 2 2 M = 2 2 x + y + = x y +1+1+ = 2 2 y x 2 2 2 2 x y x y ( 2 2 x y + )2 2 2 2 2 1 0,5 x y +1 1 = = = xy + 2 2 x y xy xy 0, 5 1 1 15 Ta có: xy + = xy + + xy 16xy 16xy 1 1 1 1 * Ta có: xy + 2 x . y = 2. = (1) * 16xy 16xy 4 2 x + y 1 1 1 1 4 1 15 15 xy = xy 4 = (2) 0,5 2 2 4 xy 16xy 16 4 16xy 4 1 1 15 1 15 17
Từ (1) và (2) xy + = xy + + + = 0,25 xy
16xy 16xy 2 4 4 2 2 1 17 289 Vậy M = xy + = xy 4 16 0,25 1 1 xy = xy = 1 Dấu “=” xảy ra 16xy 4 x = y = 2 (Vì x, y > 0) x = y x = y 289 1 0,5
Vậy min M = 16 tại x = y = 2 b 1 1 1 2đ + + = 6
Cho x, y là các số dương thỏa mãn: x + y y + z z + x 1 1 1 3 + +
Chứng minh rằng: 3x + 3y + 2z
3x + 2y + 3z 2x + 3y + 3z 2 1 1 4 + 0.5 Áp dụng BĐT a b
a + b (với a, b > 0) 1 1 1 1 + a + b 4 a b 1 1 1 1 1 = +
3x + 3y + 2z
(2x + y + z)+(x + 2y + z) 4 2x + y + z x + 2y + z Ta có: 1 1 1 1 1 1 1 1 1 + + + +
4 (x + y) +(x + z) (x + y) +( y + z) 4 4
x + y x + z x + y y + z 0,5 Trang 19 1 2 1 1 + +
16 x + y x + z y + z 1 1 2 1 1 + +
3x + 2y + 3z 16 x + z x + y y + z Tương tự: 1 1 2 1 1 + + 0,5
2x + 3y + 3z 16 y + z x + y x + z
cộng vế theo vế, ta có: 0,5 1 1 1 1 4 4 4 + + + +
3x + 3y + 2z 3x + 2y + 3z 2x + 3y + 3z 16 x + y x + z y + z 4 1 1 1 1 3 + + = .6 =
16 x + y x + z y + z 4 2 0,5 Caai 4: (5 điểm) B 1 D I 0,25 O C H 1 . E F P Q A 0,75đ.
BA là đường cao của tam giác BPQ suy ra H thuộc BA
Nối OE, BEF vuông tại B; BA ⊥ EF nên AB2 = AE. AF AE AB AE AB E A AB = = = AB AF 1 1 0,75đ. AB AF OA AQ 2 2
Vậy AEO ABQ(c.g.c). Suy ra ABQ = E
A O mà ABQ = P (góc có các cạnh tương 0,25đ 1
ứng vuông góc) nên AEO = P , mà hai góc đồng vị => PH // OE. . 1
Trong AEO có PE = PA (giả thiết); PH// OE suy ra H là trung điểm của OA. 2. Ta cã: 0,75đ. P = + = ( )3 +(co )3 6 6 2 2 sin cos sin s P = ( 2 2 + ) 4 2 2 4 sin cos
sin − sin cos + cos 0,5đ Trang 20




