9 phương pháp giải phương trình mũ và phương trình lôgarit

------------O0O------------
Phƣơng pháp 1: GIẢI PHƢƠNG TRÌNH CƠ BẢN f ( x) a
 b  f (x)  log b ; log f (x)  b  f (x) b  a . a a
Ví dụ 1. Giải các phƣơng trình: 2 a) x 5  x4 3
 81 ; b) log (3x  4)  3. 2 Giải: 2   a) x 5x 4 2 2 4 3
 81 x  5x  4  log 81 x  5x  4  log 3 3 3 x  2 2
 x  5x  4  4  x  5x  0  x(x  5)  0 0   . x  5
Vậy phương trình đã cho có hai nghiệm x = 0 và x = 5.
b) log (3x  4)  3. 2 ĐK: 4
3x  4  0  x  . 3 3
log (3x  4)  3  l3x  4  2  3x  4  8  3x 12  x  4 . 2
Vậy phương trình đã cho có nghiệm x = 4. Page 1
Phƣơng pháp 2: ĐƢA VỀ CÙNG CƠ S Ố
1) Đối với phương trình mũ: biến đổi phương trình về dạng f (x) g ( x) a  a .
- Nếu cơ số a là một số dương khác 1 thì f (x) g ( x) a  a
 f (x)  g(x) . a  0
- Nếu cơ số a thay đổi thì f (x) g ( x) a  a   . (a 1) 
 f (x)  g(x) 0
2) Đối với phương trình logarit: biến đổi phương trình về dạng 0  a 1 
log f (x)  log g(x)   f (x)  0 a a
 f (x)  g(x) 
Ví dụ 1. Giải các phƣơng trình: 2 a) x 5  x4 3
 81 ; b) log (3x  4)  3. 2 Giải: 2 2 a) x 5  x4 x 5  x4 4 2 3  81 3
 3  x  5x  4  4 x  2
 x  5x  0  x(x  5)  0 0   . x  5
Vậy phương trình đã cho có hai nghiệm x = 0 và x = 5. b) ĐK: 4
3x  4  0  x  . 3 3 3
log (3x  4)  3  log (3x  4)  log 2  3x  4  2  3x  4  8 2 2 2
 3x 12  x  4 .
Vậy phương trình đã cho có nghiệm x = 4. Page 2
Ví dụ 2. Giải các phƣơng trình: 2 a) x x 8  1 3 3
 9  x ; b) x 1 x 1 2 2    2x  28. 2 2 2 2 2 2 c) x 3  x 3 2.5 5.2   ; d) x 1  x x 1  x 2 2  3  3  2 . Giải: 2 2       a) x x 8 1 3x x x 8 2(1 3x) 2 3  9  3  3
 x  x  8  2(1 3 ) x x   2
 x  5x  6  0  2  . x  3 
Vậy phương trình đã cho có hai nghiệm x = - 2 và x = - 3.       b) x 1 x 1 x 2 x 1 x 1 x 1 x 1 2 2
 2  2  28  2 .2  2  2.2  28  2 (2 1 2)  28 x 1  x 1  2
 2  4  2  2  x 1 2  x  3.
Vậy phương trình đã cho có nghiệm x = 3. 2 2 x 3 1 x 3 2 2     x  x  5 5 5 5 c) 3 3 2.5  5.2         2 x 3 2  2  2   2  2 2
 x  3 1  x  4  x  2  .
Vậy phương trình đã cho có hai nghiệm x = - 2 và x = 2. 2 2 2 2 2 2 2 2 d) x 1  x x 1  x 2 x 1  x 1  x 1  3 x 1 2 3 3 2 2 3.3 3 2 .2         2 2 2 2 2 2 x 1  3 x 1  x 1  x 1  x 1  3 x 1 2 2 .2 3 3.3 2 (1 2 ) 3         (1 3) 2 2 x 1  x 1  2 2 2      x  x   2 4 2 2 1 1 2  2 .9  3 .4      x 1 2        3  9  3   3  2
 x  3  x   3 .
Vậy phương trình đã cho có hai nghiệm x = - 3 và x = 3 . Page 3
Ví dụ 3. Giải các phƣơng trình: a) 2
lg x  lg x  lg 4x ; b) log x  log x  log x  log x . 2 3 4 5 Giải: b) ĐK: x  0 . 2
lg x  lg x  lg 4x  lg x  2lg x  lg 4  lg x  2lg x  lg 4 x  2 2
 2lg x  lg2  lg x  lg2  x  2   . x  2 
Do x  0 nên nghiệm của phương trình là x  2. b) ĐK: x  0 .
log x  log x  log x  log x  log x  log 2.log x  log 2.log x  log 2.log x 2 3 4 5 2 3 2 4 2 5 2  log .
x (1 log 2  log 2  log 2)  0  log x  0  x 1. 2 3 4 5 2
Vậy phương trình đã cho có nghiệm x = 1.
Phƣơng pháp 3: BIẾN ĐỔI ĐƢA VỀ PHƢƠNG TRÌNH TÍC H
Ví dụ 1. Giải các phƣơng trình: a) x x x 1 12.3 3.15 5   
 20 ; b) log (3x  4).log x  log x . 2 2 2 Giải: a) x x x 1 12.3 3.15 5   
 20 12.3x  3.3 .x5x  5.5x  20  0
3.3x (4 5x ) 5(5x 4) 0 (5x 4)(3.3x         5)  0 5x  4  0   x 5 5    3   x  log . 3   3.3x  5  0 3  3  Page 4  5 
Vậy phương trình đã cho có nghiệm x  log . 3    3  3  x  4  0 b) ĐK: 4   x  . x  0 3
log (3x  4).log x  log x  log x log (3x  4) 1  0 2 2 2 2  2  log x  0 log x  0 x 1 x 1 2   2      
log (3x  4) 1  0  log (3x  4)  1 3   x  4  2 x  2 2 2 4 Do x 
nên nghiệm của phương trình là x  2. 3
Phƣơng pháp 4: LÔGARIT HÓA, MŨ HÓA
Ví dụ 1. Giải các phƣơng trình: 2 x x log x a) 3 .2 1 ; b) 2 3  x  2. Giải:
a) Lấy lô garit hai vế với cơ số 2, ta được log  2 3 . x 2x  2 x x 2
 log 1 log 3  log 2  0  .
x log 3  x .log 2  0 2 2 2 2 2 2 x  0 x  0 2  .
x log 3  x  0  x log 3  x  0   . 2  2    log 3  x  0 x  log 3  2  2
Vậy phương trình đã cho có hai nghiệm x = 0 và x = log 3. 2 b) ĐK: x  0 . Đặt log    2t x t x
ta thu được phương trình mũ theo biến t : 2 Page 5 3t 2t   2 (*).
Vế trái của (*) là hàm số đồng biến, vế phải là hàm hằng nên phương trình (*)
nếu có nghiệm thì có nhiều nhất là một nghiệm. Mà t  0 là một nghiệm của (*)
nên đó là nghiệm duy nhất của (*).
 log x  0  x 1. 2
Vậy phương trình đã cho có nghiệm x = 1.
Phƣơng pháp 5: DÙNG ẨN PHỤ 2 2
Ví dụ 1. Giải phƣơng trình: 2x 1 x x 2x 2 2 9.2 2 0
Giải: Chia cả 2 vế phương trình cho 2x 2 2 0 ta được: 2 2 x x x x 1 2 x x 9 2 2 2 1 2 2 2 2 2 9.2 1 0 .2 .2x x 1 0 2 4 2 2 2x 2 2.2 x 9.2x x 4 0 2 Đặt 2x x t
điều kiện t > 0. Khi đó phương trình tương đương với : 2 t 4 x x 2 2 2 2 x x 2 x 1 2 2t 9t 4 0 1 2 2 t x x 1 x x 1 x 2 2 2 2
Vậy phương trình có 2 nghiệm x = - 1, x = 2. Page 6 x x
Ví dụ 2. Giải phƣơng trình: 7 4 3 3 2 3 2 0 2
Giải: Nhận xét rằng: 7 4 3 2 3 ; 2 3 2 3 1 x x 1 x Do đó nếu đặt t 2
3 điều kiện t > 0, thì: 2 3 và 2 7 4 3 t t
Khi đó phương trình tương đương với: t 1 3 2 3 2 t 2 0 t 2t 3 0 t 1 t t 3 0 2 t t t 3 0 x t 1 2 3 1 x 0.
Vậy phương trình có nghiệm x = 0.
Ví dụ 3. Giải phƣơng trình: 2 3 x 2x 9 .3x 9.2x 0 Giải: Đặt 3x t
, điều kiện t > 0. Khi đó phương trình tương đương với: 2 2x 9 9.2x t t 0 2 2 t 9 2x 9 4.9.2x 2x 9 . t 2x Khi đó : + Với 9 3x t 9 x 2 x x x x 3 + Với t 2 3 2 1 x 0 2
Vậy phương trình có 2 nghiệm x = 2, x = 0. Page 7
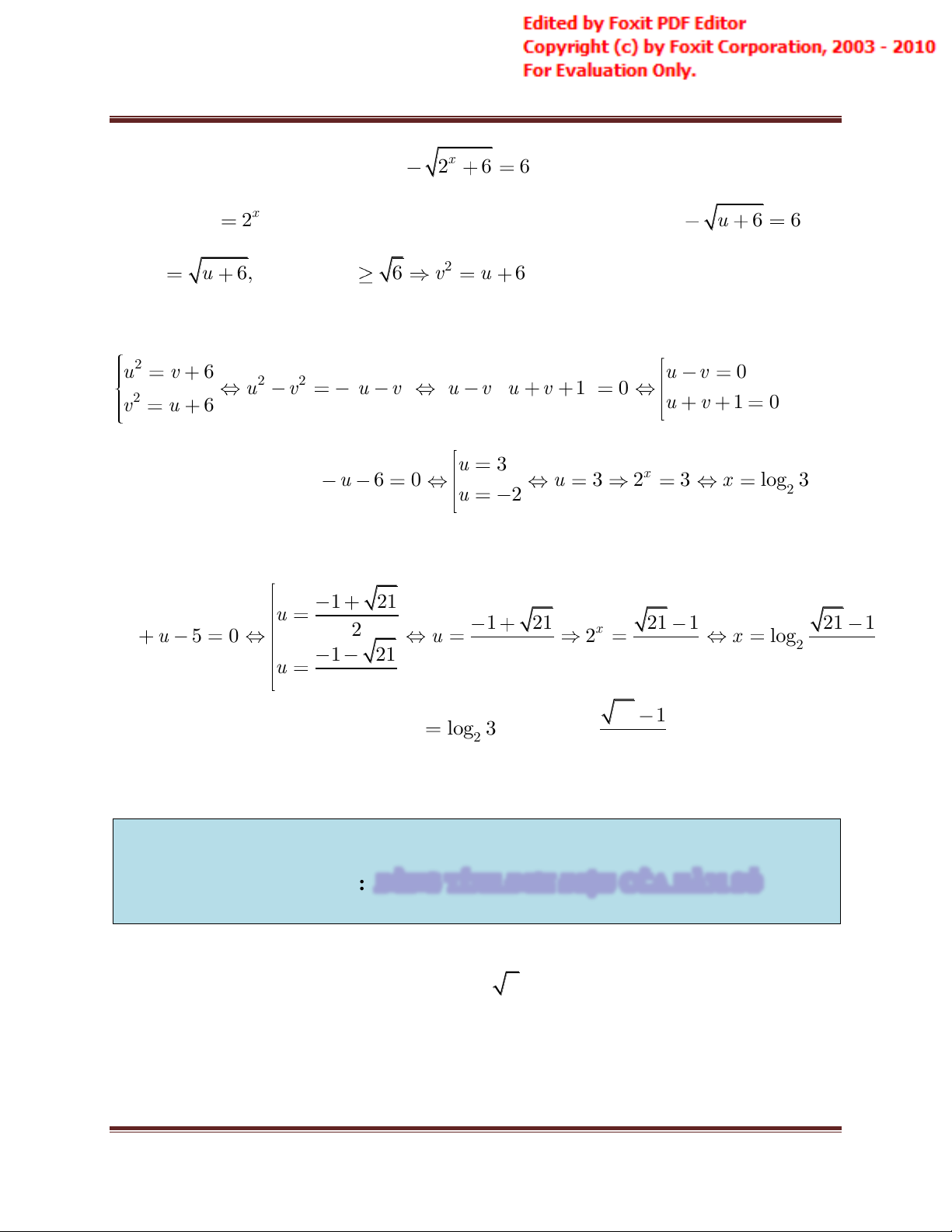
Ví dụ 4. Giải phƣơng trình: 2 2 x 2x 6 6 Giải: Đặt 2x u
, điều kiện u > 0. Khi đó phương trình thành: 2 u u 6 6 Đặt v u 6,điều kiện 2 v 6 v u 6
Khi đó phương trình được chuyển thành hệ: 2 u v 6 u v 0 2 2 u v u v u v u v 1 0 2 v u 6 u v 1 0 u 3 + Với u = v ta được: 2 u u 6 0 u 3 2x 3 x log 3 2 u 2
+ Với u + v + 1 = 0 ta được : 1 21 u 2 1 21 x 21 1 21 1 2 u u 5 0 u 2 x log2 1 21 2 2 2 u 2 21 1
Vậy phương trình có 2 nghiệm là x log 3 log . 2 và x = 2 2
Phƣơng pháp 6: DÙNG TÍNH ĐƠN ĐIỆU CỦA HÀM S Ố
Ví dụ 1. Giải phƣơng trình: log x  log ( x  2) . 7 3
Giải: ĐK : x  0 . Đặt t = log   7t x x
. Khi đó phương trình trở thành : 7 Page 8 t  7   1 t
 log ( 7t  2)  3t  7t t  2   2.      1 (*). 3 3    3 
Vế trái của (*) là hàm số nghịch biến, vế phải là hàm hằng nên phương trình (*)
nếu có nghiệm thì có nhiều nhất là một nghiệm. Mà t  2 là một nghiệm của (*)
nên đó là nghiệm duy nhất của (*).
 log x  2  x  49. 7
Vậy phương trình có nghiệm x = 49.
Ví dụ 2. Giải phƣơng trình: x 1
7   6log (6x  5) 1 7 5
Giải: ĐK : 6x  5  0  x  . 6
Đặt y 1 log 6x  5 . Khi đó, ta có hệ phương trình 7   x 1 7   6   y   x 1  x 1 1 1 7  6y  5 7   6y  5  x 1  y 1        x    y . y 1 log  6x 5 7 6 7 6 y 1  y 1 7  6x  5 7   6x  5  7 t  5
Xét hàm số f t  t 1 7  
 6t . f 't 1
 7 .ln 7  6  0, t
  nên f t là hàm số 6 đồ   ng biến trên 5 x ;  
 . Mà f  x  f  y  x  y . Khi đó: 1 7
 6x  5  0 . Xét  6   hàm số  x
gx  7x 1
  6x  5 . g x x 1 '
 7 ln7  6 . g x   2 1 ' 7 ln 7  0. Suy ra,  5 
g ' x là hàm số đồng biến trên D  ; 
 , do đó phương trình g 'x  0có  6 
nhiều nhất một nghiệm. Suy ra, phương trình g  x  0 nếu có nghiệm thì có nhiều nhất là hai nghiệm.
Nhẩm nghiệm ta được 2 nghiệm của phương trình là: x = 1, x = 2. Sài Gòn, 10/2013 Page 9
Ví dụ 3. Giải phƣơng trình: 3x  4x  2  7x (*). Giải:
Vế trái của (*) là hàm số đồng biến, vế phải của (*) là hàm số nghịch biến nên
phương trình (*) nếu có nghiệm thì có nhiều nhất là một nghiệm. Mà x  0 là một
nghiệm của (*) nên đó là nghiệm duy nhất của (*).
Phƣơng pháp 7: PHƢƠNG PHÁP ĐÁNH GIÁ 
Ví dụ 1. Giải phƣơng trình: 2 x 1 2  2  x .
Giải: ĐK : x  0 . 2   Ta có x 1 0 1 VT  2
 2  2 và VP  2  x  2  0  2 . Suy ra VT VP , dấu bằng xảy ra khi x  0 .
Vậy x  0 là nghiệm duy nhất của phương trình đã cho.  
Ví dụ 2. Giải phƣơng trình: x x 1 1 4  2
 2x  2 x . Giải:    Ta có x x 1 1 4  2
 2x  2 x  2  (4x  2.2x 1)  2x  2 x  x 2
 2  (2 1)  2x  2 x . x 2  
VT  2  (2 1)  2  0  2 và
 2x  2 x  2 2 .x2 x VP
 2. Suy ra VT VP, dấu 2x 1  0 bằng xảy ra khi   x  0 . 2x  2x Page 10
Vậy x  0 là nghiệm duy nhất của phương trình đã cho.
Ví dụ 3. Giải phƣơng trình: log 9  x 1  log  2
x  2x  5 . 3 2  Giải: x 1 0 x 1 x 1      ĐK : 9
  x 1  0  9   x 1  x 82  x1;82  .    2
x  2x  5  0    x   2 1  4  0   x 1  2 4 0 Ta có :
VT  log 9  x 1  log 9  2 và 3   3
VP  log x  2x  5  log x  2 2 1  4  log 4  2  , dấu bằng 2 2 2   . Suy ra VT VP  x 1  0 xảy ra khi   x  1.
 x 12  0
Vậy x  1 là nghiệm duy nhất của phương trình đã cho.
Phƣơng pháp 8: PHƢƠNG PHÁP QUAN NIỆM HẰNG SỐ LÀ ẨN
Ví dụ 1. Giải phƣơng trình: x x 1  x2 16  4  2 16 . Giải: Ta có x x 1  x2 2 x x 1  16  4  2 16  4  2 .4  4 16x  0 (*).
Xét phương trình ẩn t sau đây 2 x x 1   2  4 16x t t
 0 (**). Giả sử (*) đúng với giá trị
x nào đó thì phương trình ẩn t sau có nghiệm t = 4: 2  0 x 0 x 1 0  2  4 16x t t  0 . 0 Page 11 2 Biệt thức     0 2x   4 0x 1 0 4 16x  0  4.16x  0 . 0 x 0 2  4.16x 0 x 0 2  4.16x Suy ra t  4  ; t  4  . 2 2    x 1 65   x x 2 (n) 2 2  4.16 TH1: 4 
 2x  2.4x  8  2.2x  0 0 0 x 4 0 0 0 0  2  8  0   2    x 1 65 0 2  (l)  4  1   65   . 0 x log2     4   0 x 0 x 2 2  4.16 TH2: 0 x 0 4 
 2  2.4x  8  2. 0 2x  0
 2x  8  0 (pt vô nghiệm) 2    
Vậy phương trình đã cho có nghiệm 1 65 x  log . 2     4  
Phƣơng pháp 9: SỬ DỤNG ĐỊNH LÍ LAGRANGE
Ví dụ 1. Giải phƣơng trình: 5x 4x 2x 7x    (1). Giải: Giả sử 0
x là một nghiệm của (1), hay ta có: 0 x 0 x 0 x 0 x 0 x 0 x 0 x 0 5 4 2 7 5 2 7 4x        (*). x Xét hàm số     0 0 ( ) 3 x f t t
 t trên đoạn 2;4 thì f (t) là hàm số liên tục và có
đạo hàm trên đoạn 2;4 . Áp dụng định lí lagrange thì có số k 2;4 sao cho Page 12     f
 0x 0x  0x 0 7 4 5 2x f (4) (2)  x 1   f '(k)  
 0 (do (*)) mà f '(t)  x t  3 0 0 x 1  0 0 x t 4  2 4  2    x  x t  3 0 1 0 x 1  t  0   . x  0 x  0  0 0 x 1 
Suy ra x k  3 0 0 x 1  k   0     0    x   x   k  3 0 1 x 1  k  0 k  3 0 1 0 0 x 1  k x  0 0  x  0 x  0 0 0  0 x 1   k 3       . 1 x 1  0 x  1    0  0  k 
Thay x  0; x 1 vào (1) ta thấy chúng đều thỏa mãn.
Vậy phương trình đã cho có hai nghiệm x  0; x 1. Page 13