
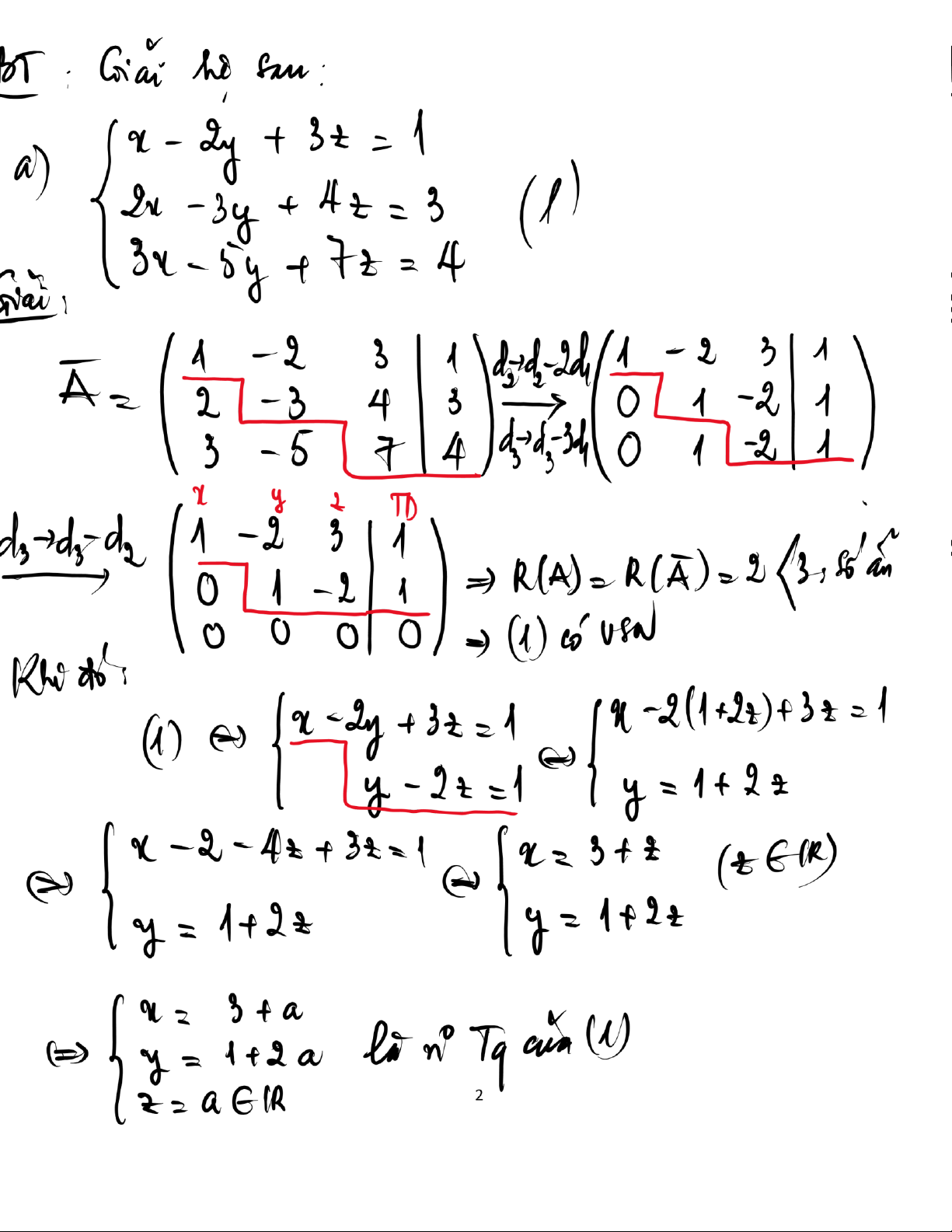
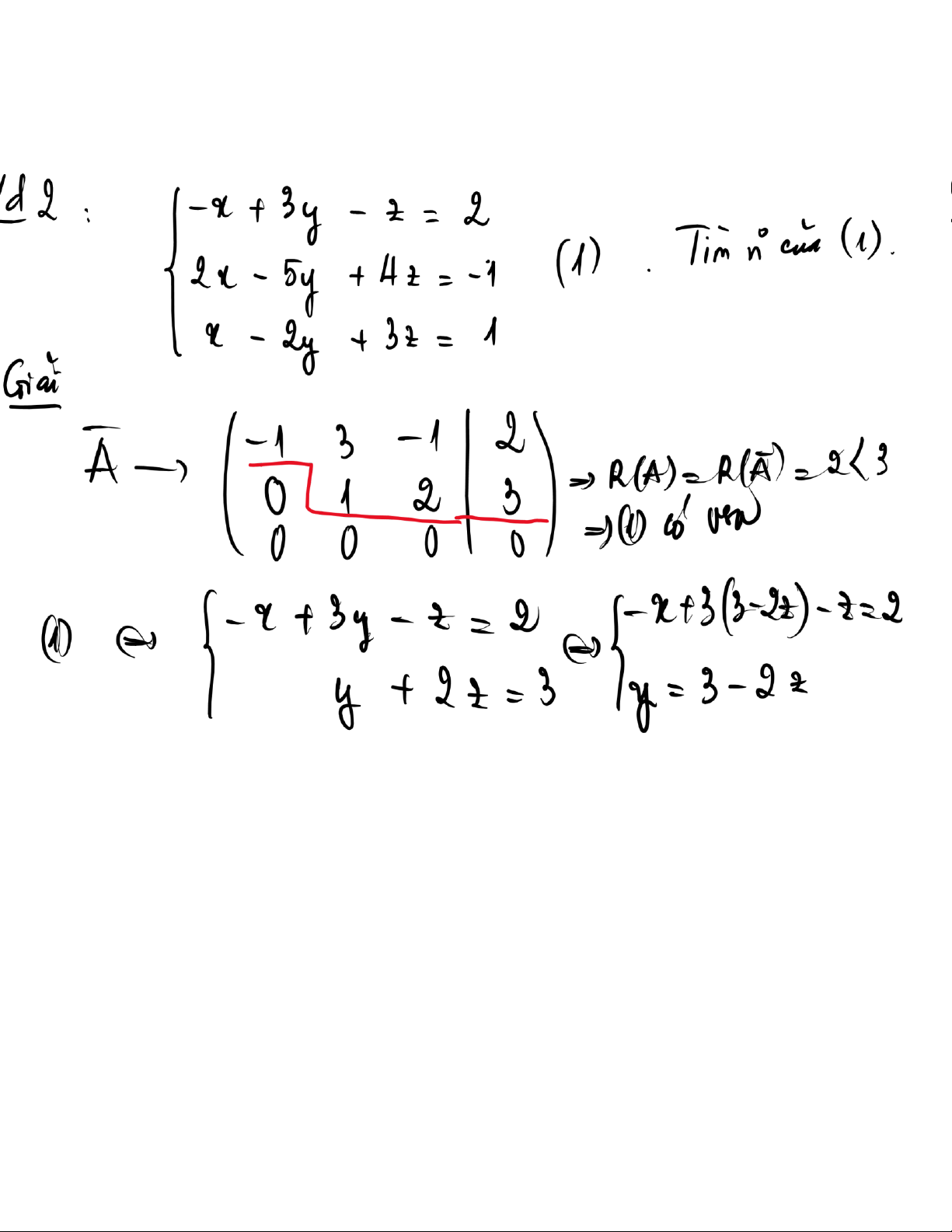
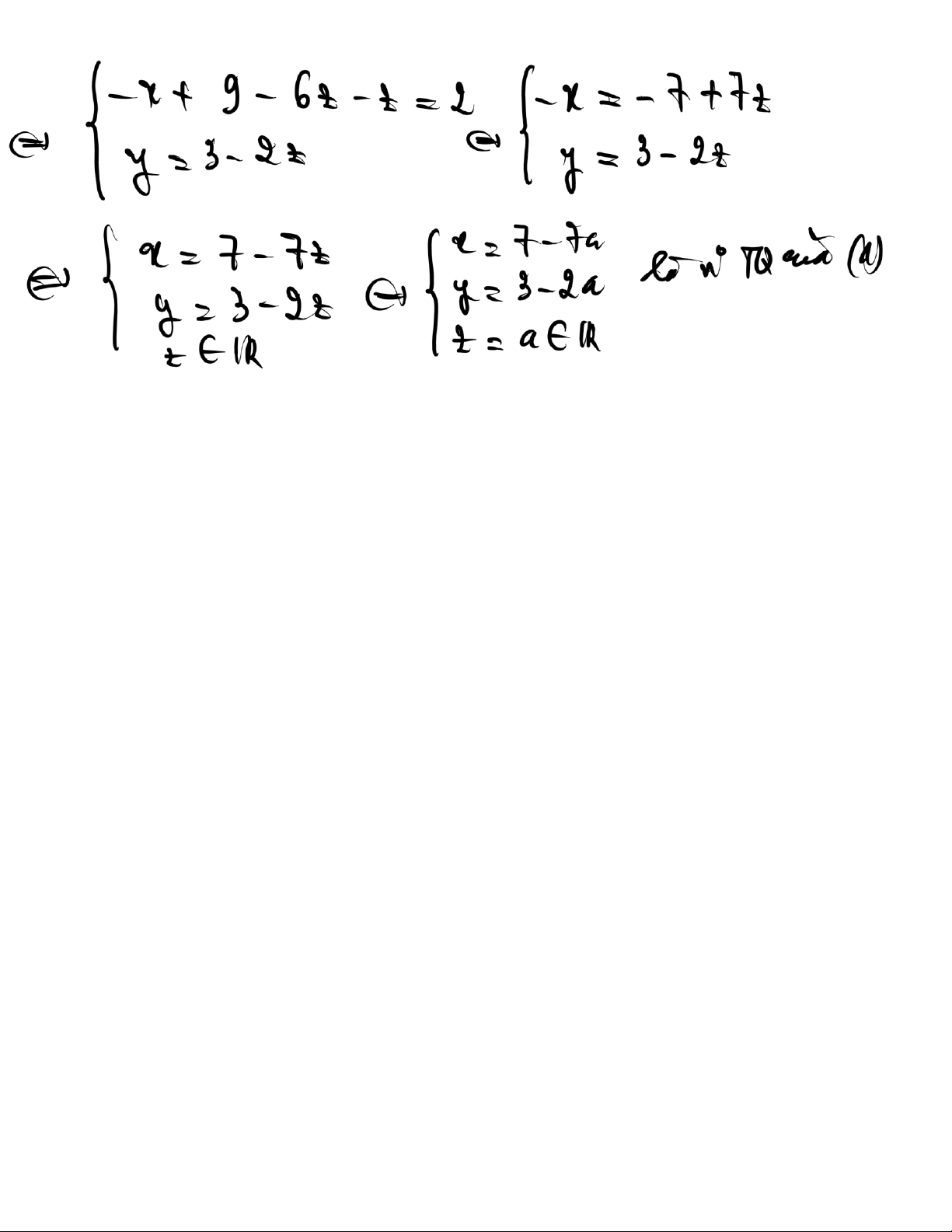
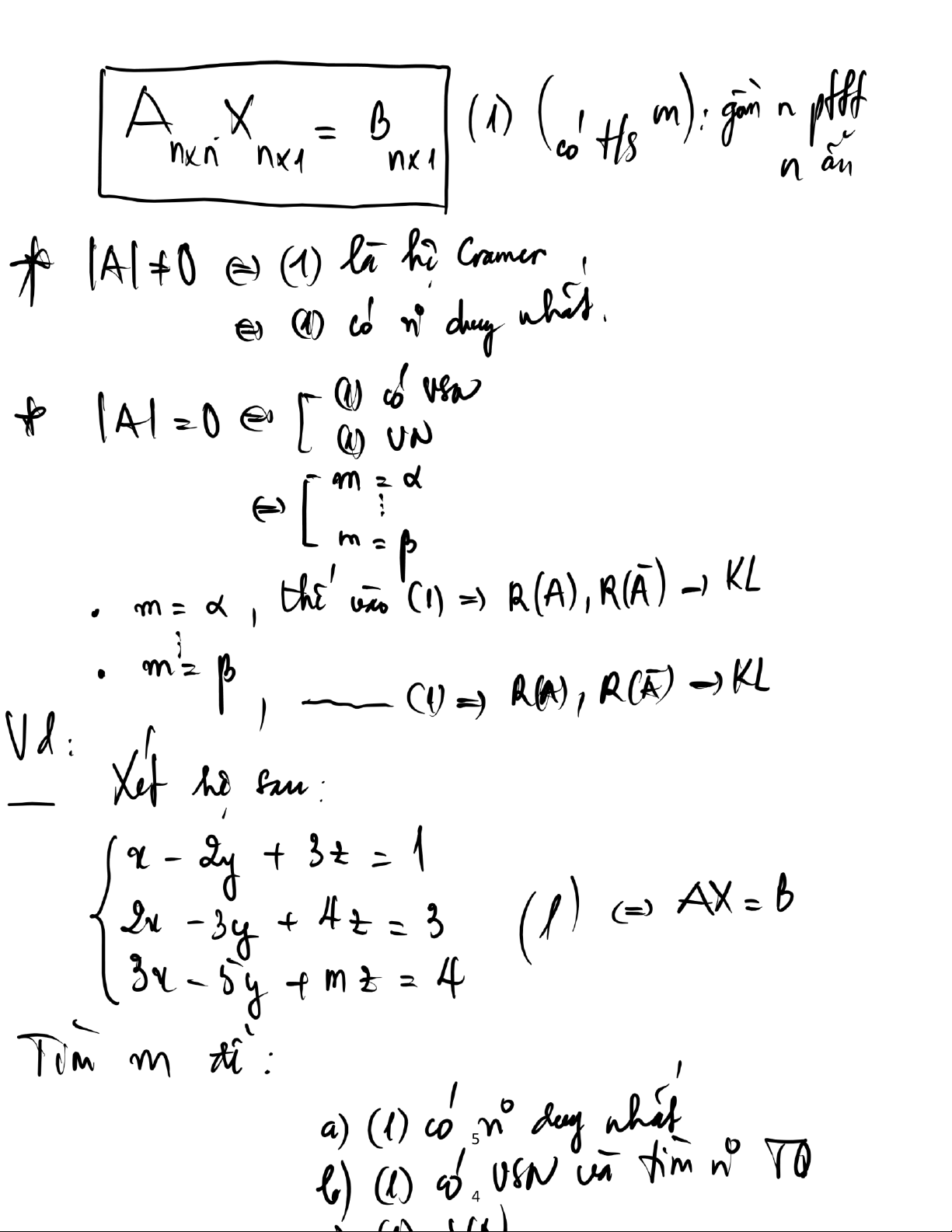
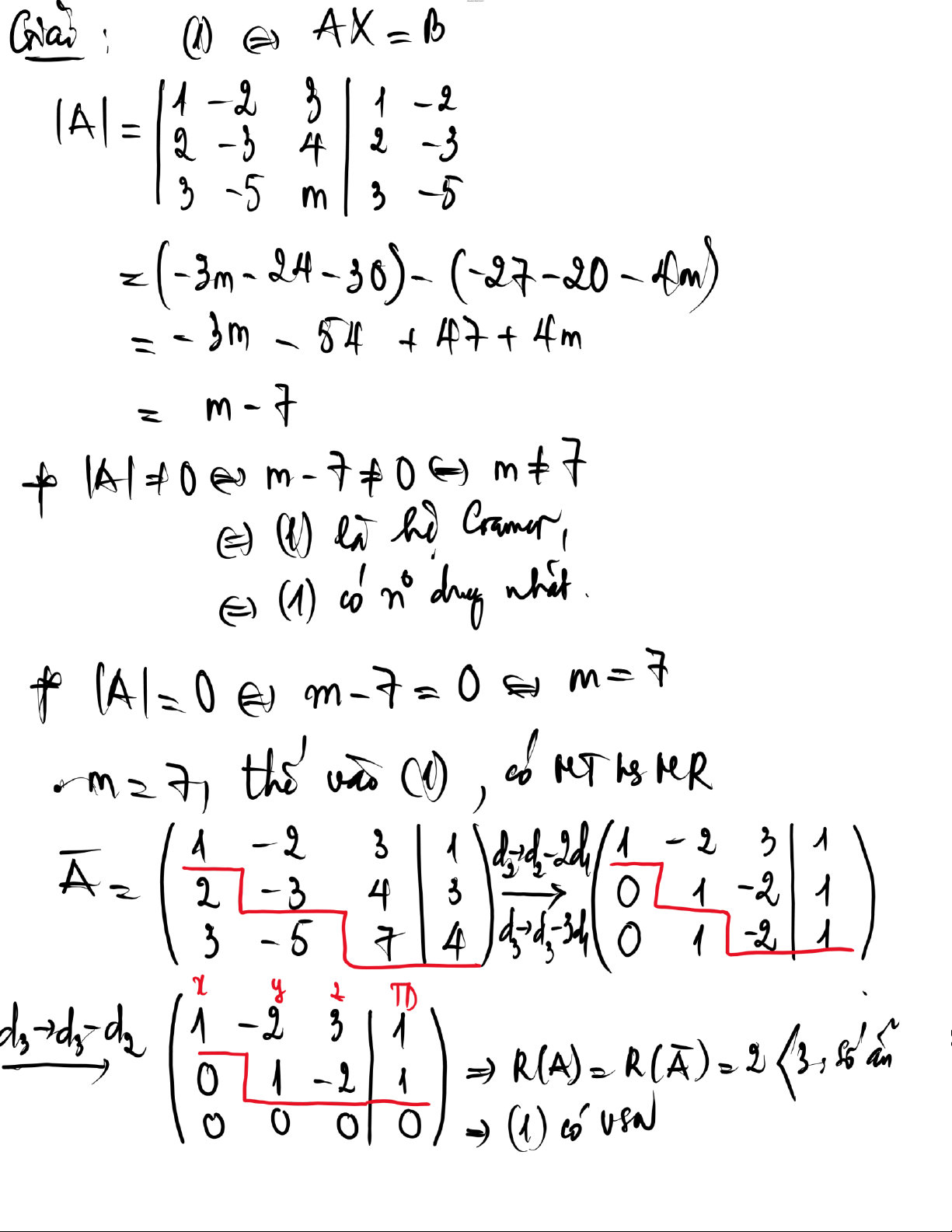
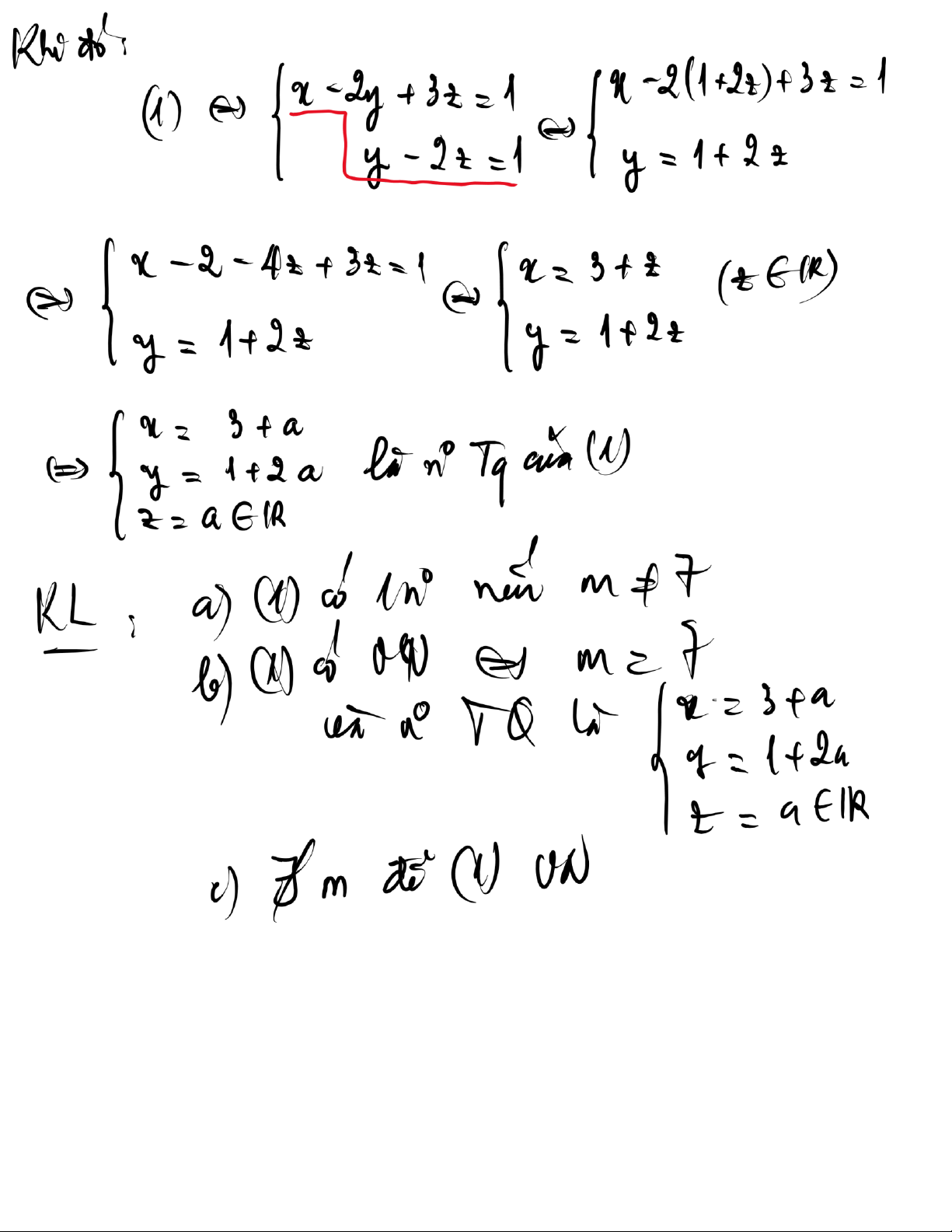

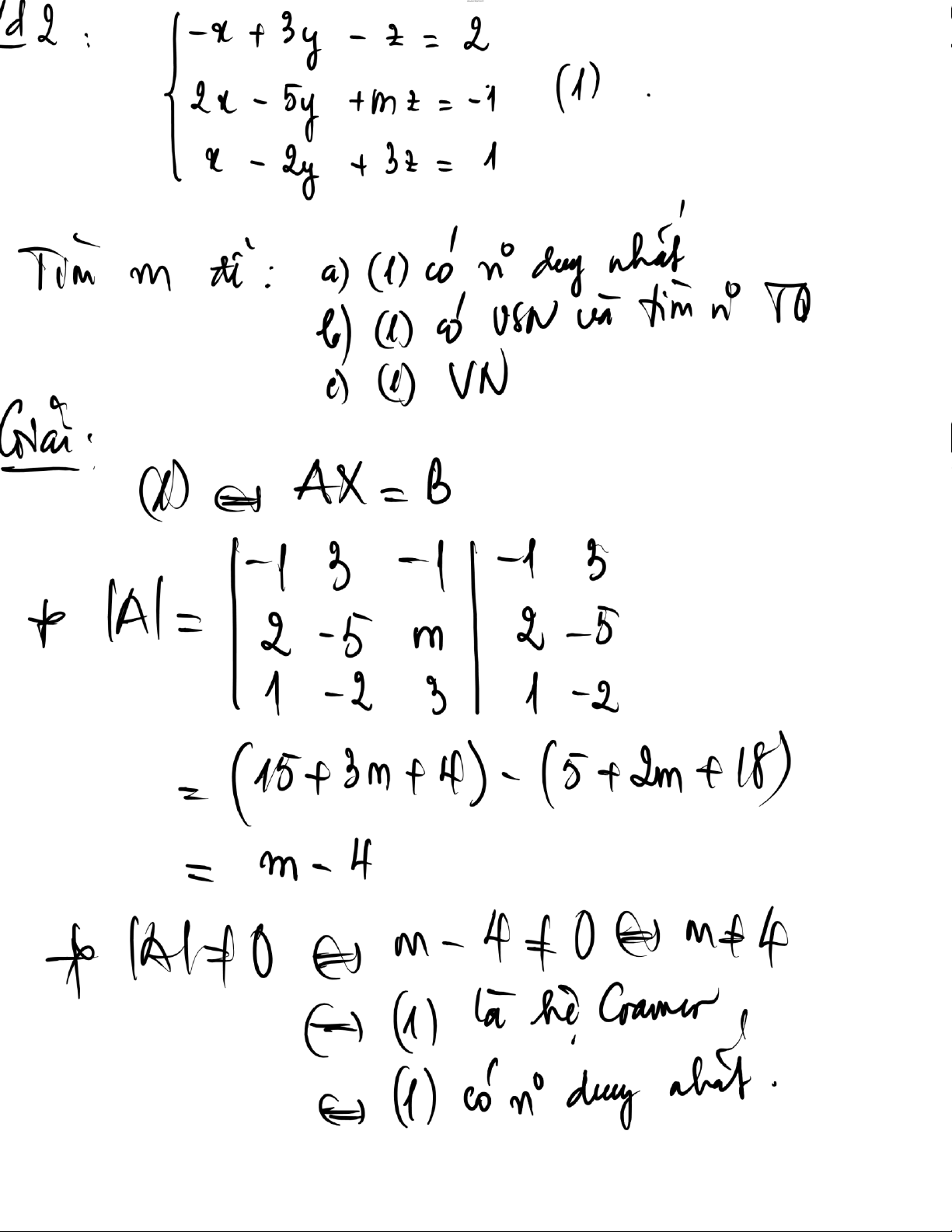

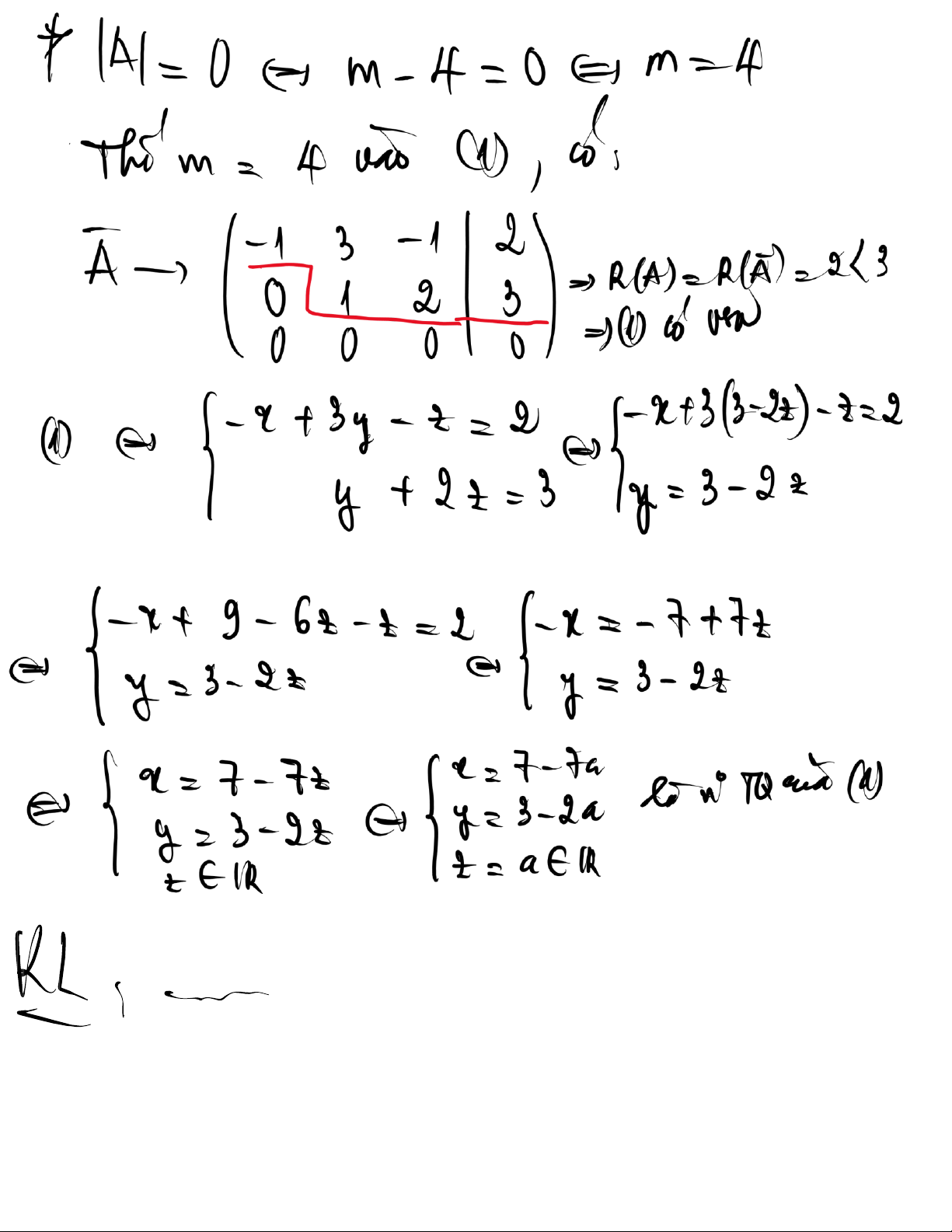







Preview text:
lOMoAR cPSD| 47206071 1 lOMoAR cPSD| 47206071 lOMoAR cPSD| 47206071 3 lOMoAR cPSD| 47206071 lOMoAR cPSD| 47206071 5 lOMoAR cPSD| 47206071 lOMoAR cPSD| 47206071 7 lOMoAR cPSD| 47206071 8 lOMoAR cPSD| 47206071 9 lOMoAR cPSD| 47206071 10 lOMoAR cPSD| 47206071 11 lOMoAR cPSD| 47206071
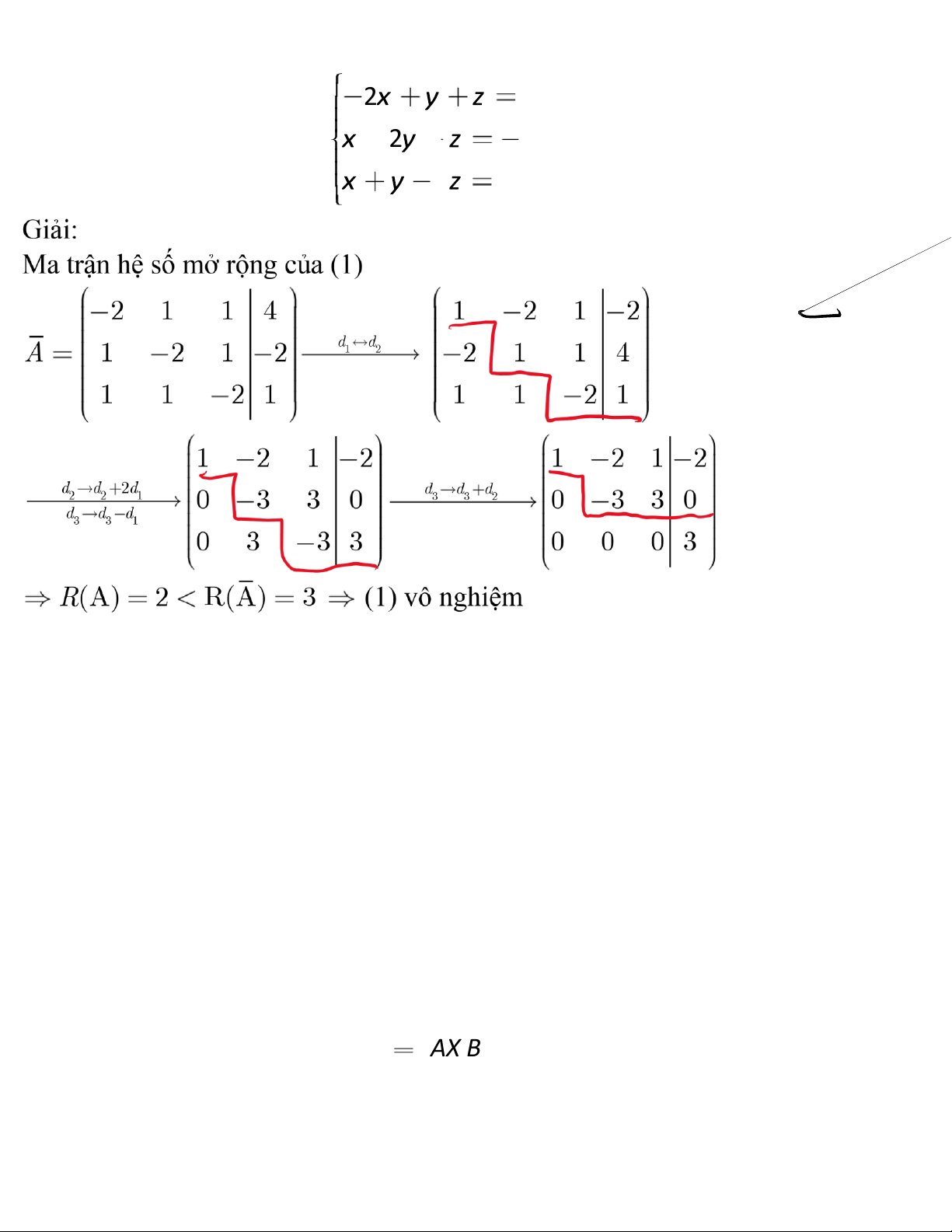
B i tập 1. Giải hệ phương trình sau: 2 4 2 2 1 2 (1) Ch ý:
X t hệ gồm n phương trình tuyến t nh n ẩn dạng
AX B (1) (c chứa tham số m) 12 lOMoAR cPSD| 47206071
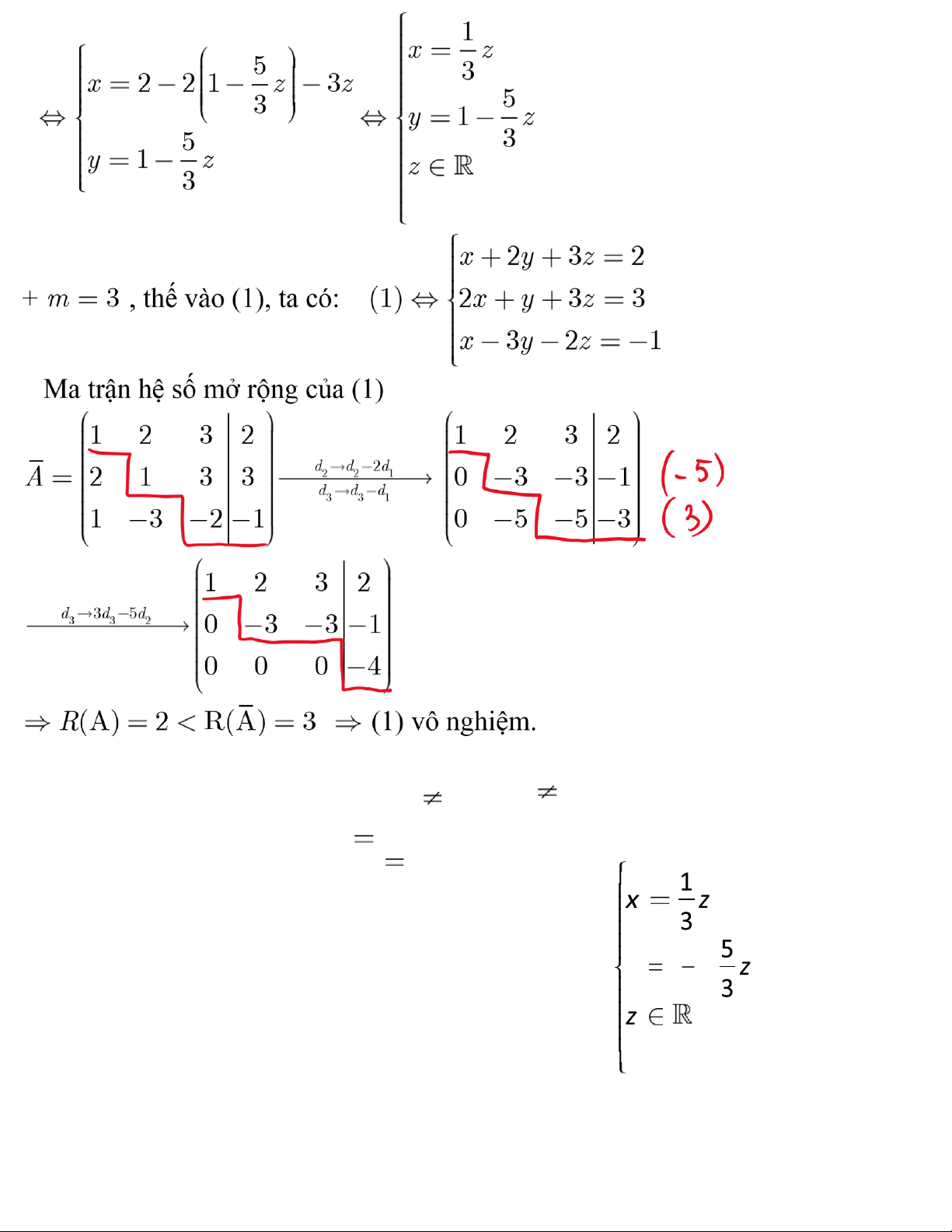
(1) c nghiệm duy nhất (tìm ược bằng qt Gramer) (1) c VSN hay (1) v nghiệm R(A),R(A) kết luận …. + m , thế v o (1) R(A),R(A) kết luận
B i tập 2. Cho hệ phương trình
x m (1) (với m l tham số) T m m ể: a) (1) c nghiệm duy nhất. b) (1) v nghiệm.
c) (1) c v số nghiệm v t m nghiệm tổng quát trong trường hợp ó. 13 lOMoAR cPSD| 47206071 (m 14 lOMoAR cPSD| 47206071 Kết luận:
a) (1) c nghiệm duy nhất khi m 1 v m 2.
b) (1) c v nghiệm khi m 2. c)
(1) c v số nghiệm khi m 1 v nghiệm tổng qu t : y .
B i tập 3. Cho hệ phương trình 15 lOMoAR cPSD| 47206071 x 2y z 2 2x 3y 4z
m (1) (với m l tham số) x y mz 1 T m m ể: a) (1) c nghiệm duy nhất. b) (1) v nghiệm.
c) (1) c v số nghiệm v t m nghiệm tổng quát trong trường hợp ó. Giải: (1) AX B • A m 3
A 0 m 3 0 m 3 (1) l hệ Gramer (1) c nghiệm duy nhất
• A 0 m 3 0 m 3 16 lOMoAR cPSD| 47206071
b) Kh ng tồn tại m ể (1) v nghiệm. . c)
(1) c v số nghiệm khi m 3 v nghiệm tổng qu t :
B i tập 4. Cho hệ phương trình x 2y 3z 2 2x y mz
m (1) (với m l tham số) x my 2z 1 T m m ể: a) (1) c nghiệm duy nhất. b) (1) v nghiệm.
c) (1) c v số nghiệm v t m nghiệm tổng quát trong trường hợp ó. 17 lOMoAR cPSD| 47206071 18 lOMoAR cPSD| 47206071 Kết luận:
a) (1) c nghiệm duy nhất khi m 1 v m 3.
b) (1) c v nghiệm khi m 3. z z . z
c) (1) c v số nghiệm khi m 1 v nghiệm tổng qu t : y 1 19 lOMoAR cPSD| 47206071 20




