Bài giảng chương 1: Hàm số, giới hạn và liên tục | Môn toán cao cấp

lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
BÀI 1: HÀM SỐ, GIỚI HẠN VÀ LIÊN TỤC Thời lượng Mục tiêu
Bạn nên học và làm bài tập của bài này
• Hiểu ược khái niệm hàm số, giới hạn, sự
trong hai tuần, mỗi tuần khoảng 3 ến 4 liên tục giờ ồng hồ.
• Giải ược các bài tập về hàm số, giới hạn, tính liên tục
• Áp dụng phần mềm toán ể tính toán với hàm số, giới hạn Nội dung
Trên cơ sở các kiến thức của chương trình phổ thông, mục ích của bài này là ôn tập, hệ thống
hóa và nâng cao các kiến thức về hàm số một biến số: Giới hạn, tính liên tục của hàm số. Hướng dẫn học
• Đây là bài học nhằm ôn tập và hệ thống hóa lại các kiến thức toán học ã học trong chương
trình phổ thông nên bạn cần ọc kỹ lại các lý thuyết về hàm số, giới hạn.
• Sau khi ọc kỹ lý thuyết bạn cần làm bài tập càng nhiều càng tốt ể củng cố và nâng cao kiến thức. 1.1.
Hàm số một biến số lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
1.1.1. Định nghĩa hàm số một biến số
Cho X là tập hợp khác rỗng của . Ta gọi ánh xạ f :X x y f x
là hàm số một biến số trên tập hợp X , trong ó x là biến số ộc lập, y là ại lượng phụ
thuộc hay hàm số của x.
Tập hợp X gọi là miền xác ịnh của hàm số f .
Tập hợp f(X) {y ,y f(x): x X} gọi là miền giá trị của f
Nếu hàm số một biến số cho trong dạng biểu thức: y f(x) mà không nói gì thêm thì
ta hiểu miền xác ịnh của hàm số là tập hợp những giá trị thực của biến số x làm cho biểu thức có nghĩa. Ví dụ 1:
Biểu thức y 1 x2 xác ịnh khi : 1 x2 0 x 1 1 x 1.
Do ó miền xác ịnh của hàm số y 1 x2 là 1,1 .
Dễ dàng thấy rằng miền giá trị của hàm y là [0,1].
Miền xác ịnh của một hàm số có thể gồm nhiều tập con rời nhau, trên mỗi tập con ó
lại có một quy tắc riêng ể xác ịnh giá trị của hàm số. Hàm số có thể ược xác ịnh bởi
nhiều công thức khác nhau tùy thuộc vào giá trị của biến. Ví dụ 2: x2 1 khi x 0 f(x) 1 2x khi x 0
Hàm f(x) là một hàm số xác ịnh trên . Nếu x không âm thì giá trị của hàm số ược
tính theo công thức: f(x) x2 1. Nếu x âm, giá trị của hàm số ược tính bởi: f(x) 1 2x.
1.1.2. Đồ thị của hàm số
Giả sử hàm số y = f(x) có miền xác ịnh là X
. Ứng với mỗi giá trị x0 X ta có giá trị y 0
f(x )0 của hàm số. Trong hệ trục tọa ộ Đề-các vuông góc, xét iểm M 0
(x ,y0 0 ) . Khi x thay ổi và “quét” hết tập xác ịnh X thì 0 M cũng thay ổi 0
theo và vạch nên một ường cong trong mặt phẳng tọa ộOxy. Đường cong này ược gọi
là ồ thị của hàm số y = f(x). lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
Như vậy, ồ thị của hàm số y = f(x) là tập hợp những iểm trong mặt phẳng có tọa ộM
x;y , ở ó y = f(x), x thuộc miền xác ịnh X. 2 CHÚ Ý:
Đồ thị của hàm số có thể là tập hợp các iểm rời rạc, cũng có thể gồm một số cung liền
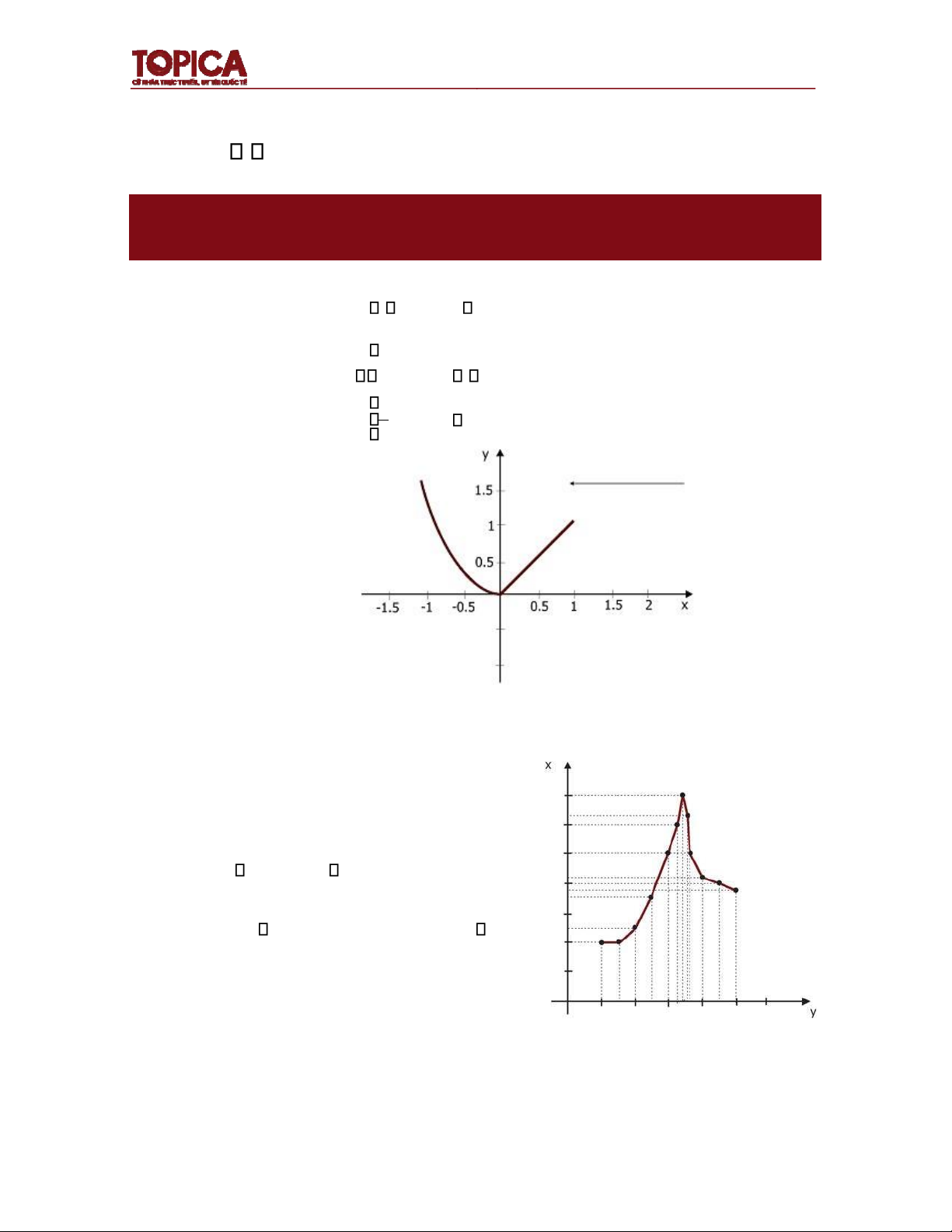
Ví dụ 3: x2 khi x 0 Đồ thị của hàm số y
x khi 0 x 1 ược biểu diễn như sau: 3 khi x 1 2 Hình 1.1
Việc vẽ phác họa ồ thị của hàm số f với miền xác ịnh là một khoảng số thực
thường ược xác ịnh theo trình tự như sau: y
Lấy các số x ,x ,...,x từ miền xác ịnh 1 2 n của
hàm số (càng nhiều iểm và các iểm càng gần nhau càng tốt).
• Tính các giá trị tương ứng của hàm số y1 f(x ),...,y 1 n f(x )n • Xác ịnh các iểm • M 1 (x ,y ),...,M1 (x ,y 1 n n n)
• Nối các iểm ã xác ịnh nói trên ta có hình
ảnh phác họa của ồ thị hàm số. x
Cách vẽ như trên không hoàn toàn chính xác
mà chỉ cho hình dáng của ồ thị hàm số.
Đồ thị của hàm số ược dùng ể minh họa Hình 1.2
các ặc trưng cơ bản, sự phụ thuộc của giá trị của hàm số và biến số. Nhìn vào ồ thị có
thể dễ dàng quan sát xu hướng thay ổi của giá trị hàm số khi biến ộc lập thay ổi. lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục 1.1.3.
Hàm số ơn iệu. Hàm số chẵn, lẻ, tuần hoàn
1.1.3.1. Hàm số ơn iệu
Hàm số f(x) xác ịnh trong khoảng (a,b)
• Được gọi là ơn iệu tăng trong khoảng (a,b) nếu với mọi x ,x 1 2 (a,b),x1 x2 kéo theo: f(x ) 1 f(x )2 . lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
(Nếu iều kiện trên vẫn úng khi bỏ dấu ẳng thức, tức là: x ,x 1 x f(x ) f(x ) 2 (a,b),x1 2 1 2
thì ta nói hàm f tăng ngặt (hay ồng biến) trên (a,b)).
• Được gọi là ơn iệu giảm trong khoảng (a,b) nếu với mọi x ,x 1 2 (a,b),x1 x2 kéo theo: f(x ) 1 f(x )2 .
(Nếu iều kiện trên vẫn úng khi bỏ dấu ẳng thức: x ,x 1 2
(a,b),x1 x2 f(x )1 f(x )2 thì ta nói
hàm f giảm ngặt (hay nghịch biến) trên (a,b)).
Hàm số f ược gọi là ơn iệu trên (a,b) nếu nó chỉ ơn iệu tăng hoặc chỉ ơn iệu giảm trong khoảng này.
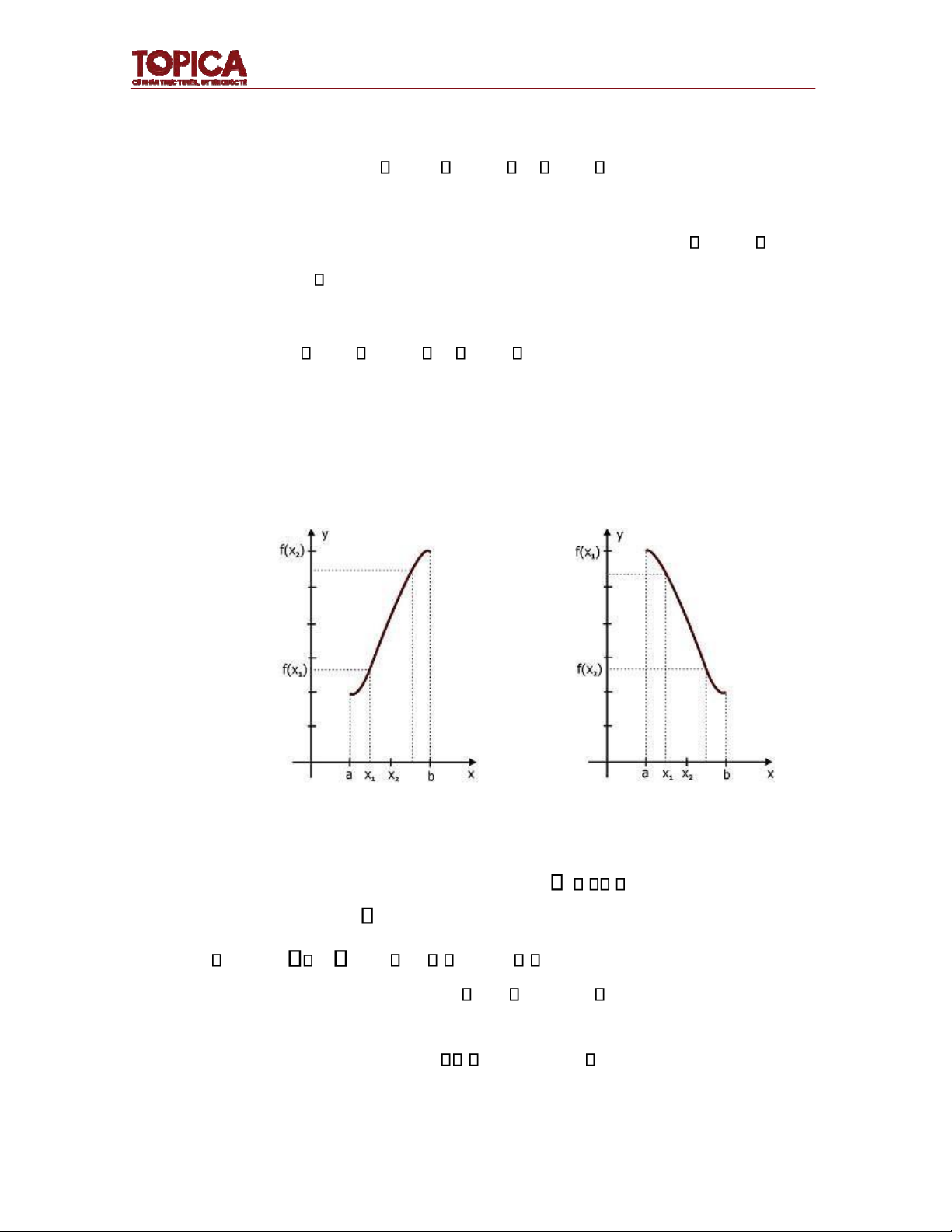
Đồ thị của hàm số tăng là một ường “ i lên”, ngược lại ồ thị hàm số giảm là ường
“ i xuống” nếu nhìn từ trái sang phải. Hình 1.3
1.1.3.2. Hàm số chẵn, hàm số lẻ
Hàm số f xác ịnh trên một tập hợp D ối xứng x D x D , chẳng hạn khoảng ( l,l) , oạn
a,a , tập ( b, a )(a,b)(0 a b),…
• Được gọi là hàm chẵn nếu: f(x) f( x) với mọi x D .
Nói một cách ơn giản khi x ổi dấu thì yvẫn không thay ổi.
• Được gọi là hàm lẻ nếu: f(x) f( x) với mọi x D .
Nói một cách ơn giản khi x ổi dấu thì ycũng ổi dấu. Ví dụ 4: lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
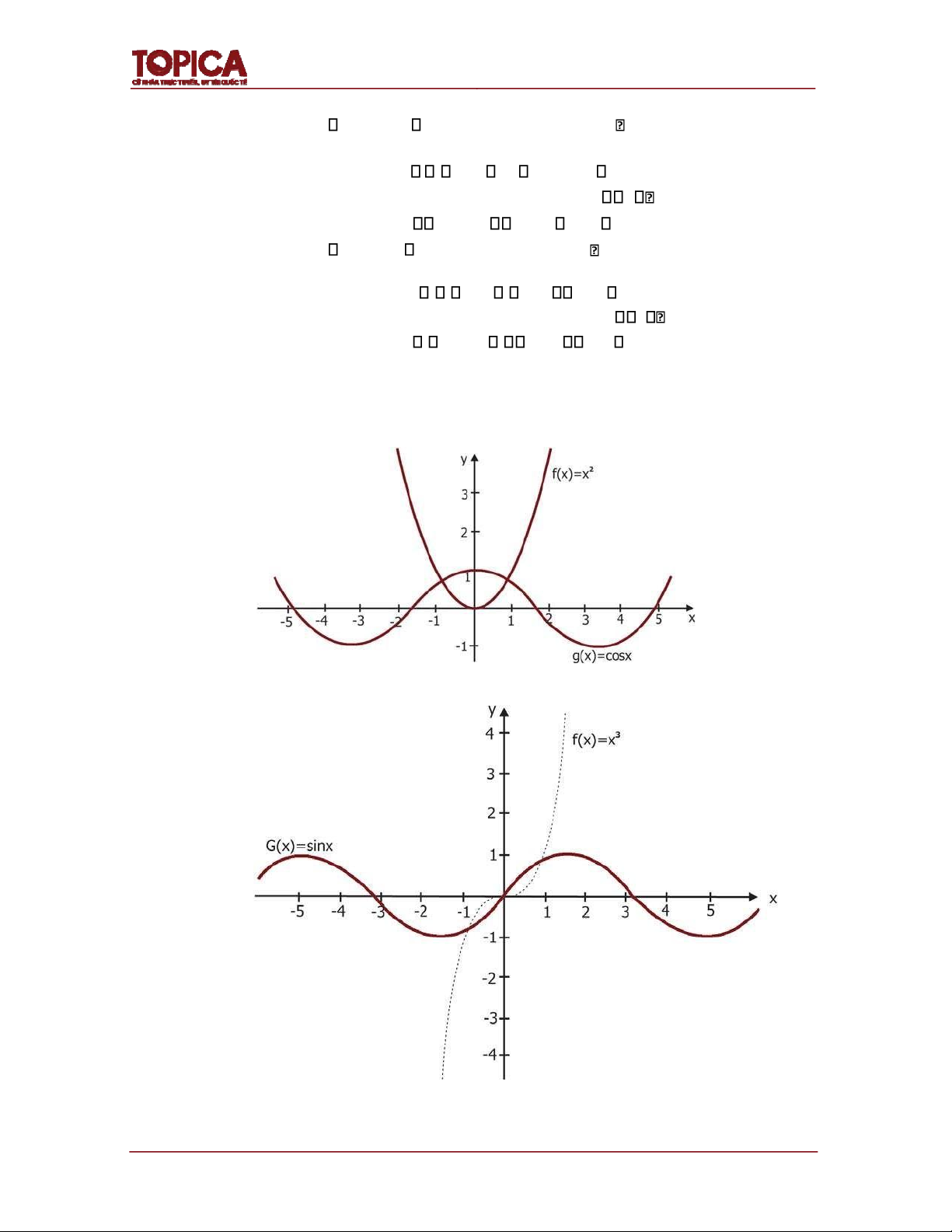
Các hàm số f(x) x , g(x)2 cosx là các hàm chẵn trên vì: f( x) ( x)2 x2 f(x) x g( x) cos( x) cosx g(x)
còn hàm số h(x) x ,k(x)3 sin x là các hàm lẻ trên vì: h( x) ( x)3 ( x)3 h(x) x ฀ k( x) sin( x) sin x k(x)
Đồ thị của hàm chẵn nhận trục Oy làm trục ối xứng, còn ồ thị hàm lẻ nhận gốc tọa ộ
O làm tâm ối xứng (hình 1.4) Hàm chẵn: Hàm lẻ:
1.1.3.3. Hàm số tuần hoàn 6 MAT101_Bài 1_v2.3013101225 lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục Định nghĩa:
Hàm số f ược gọi là tuần hoàn trên miền xác ịnh D (thông thường xét D ) nếu tồn
tại số thực p 0 sao cho:
x D thì x p D và f(x p) f(x).
Số p gọi là chu kỳ của hàm f .
Nếu trong các số p nói trên, tồn tại một số dương nhỏ nhất – ký hiệu bởi T – thì T ược
gọi là chu kỳ cơ bản của f . Ví dụ 5:
Các hàm sin x,cosx ều tuần hoàn với chu kỳ 2 vì:
sin(x 2 ) sin x,cos(x 2 )cosx x
Các hàm tgx,cotgx ều tuần hoàn với chu kỳ vì: tg x tgx, x k ;cotg(x )cotgx, x k 2
Hơn nữa các chu kỳ nói trên ều là các chu kỳ cơ bản. Thật vậy, chẳng hạn xem xét
hàm y sin x , giả sử tồn tại số dương T 2 ể: sin x T sinx x .
Khi ó với x 0 ta phải có: sinT sin0 0 T k (k ) mà T 2 nên T . 2 sin 2, hay 1 1. Khi ó với x thì sin 2
Về mặt hình học, ồ thị của hàm tuần hoàn là một họ ường lặp i lặp lại trong từng
khoảng có ộ dài bằng chu kỳ. Do ó ể vẽ ồ thị của hàm tuần hoàn, ta chỉ cần vẽ ồ thị
trong một chu kỳ cơ bản T, sau ó thực hiện liên tiếp các phép tịnh tiến theo các vectơ
song song với trục hoành và có ộ dài bằng T. lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
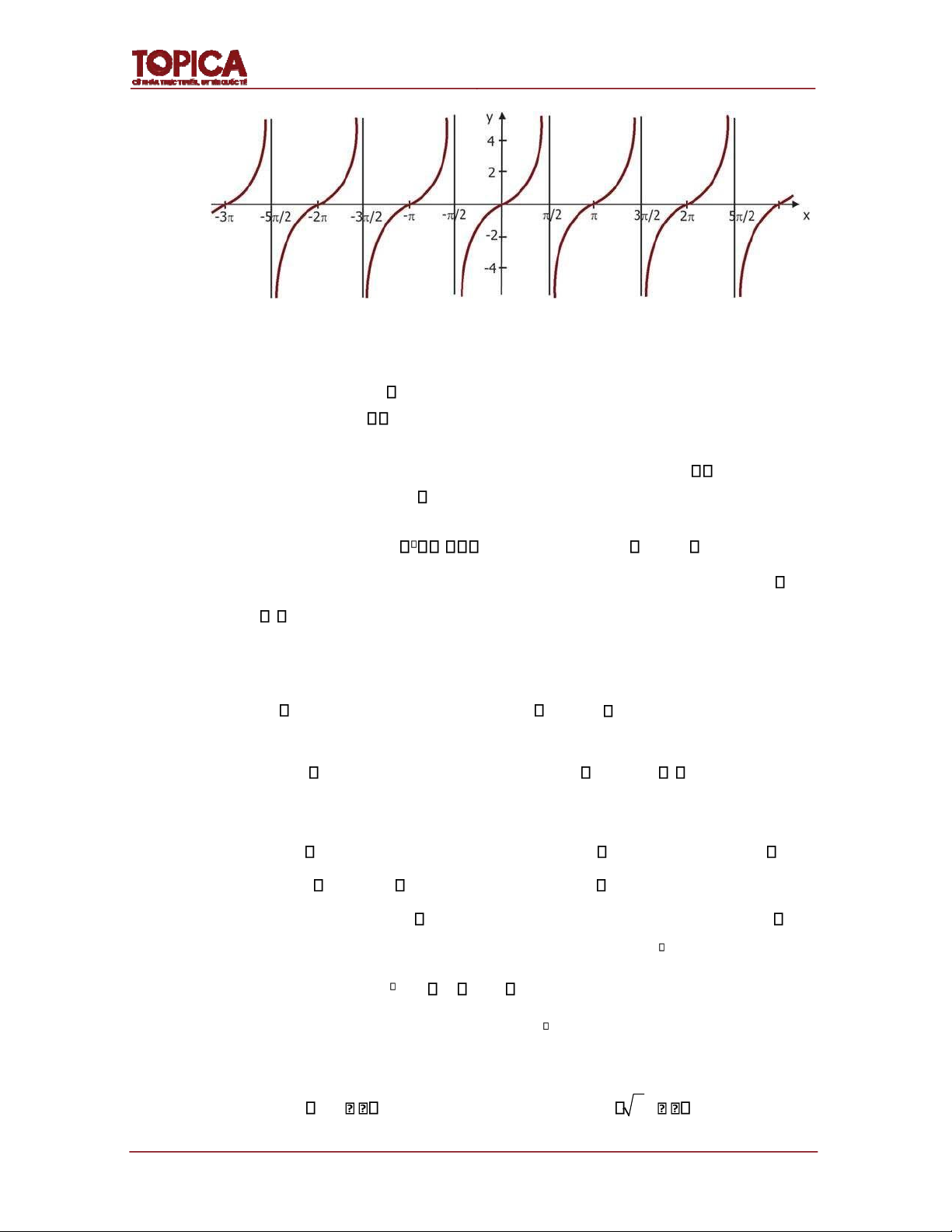
Hình 1.5: Đồ thị hàm số y = tgx
1.1.4. Hàm số hợp
Giả sử ta có hai hàm số y f(u) biểu diễn sự phụ thuộc của y theo u u (x) biểu diễn sự phục thuộc của u theo x.
Thêm vào ó, khi x thay ổi trong miền X , các giá trị của hàm số u (x) luôn thuộc
vào miền xác ịnh của hàm y f(u). Khi ó mỗi giá trị của biến x ược cho tương ứng
với duy nhất một giá trị của biến y theo quy tắc: x u f y , hay y f( (x)) .
Hàm số g biến x thành y theo quy tắc trên gọi là (hàm số) hợp của hai hàm f và . Ký
hiệu: g f( (x)) . (Nhớ rằng trong cách ký hiệu trên, hàm nào ứng sau lại có tác ộng trước ến biến x). Ví dụ 6:
Hàm số y sin x5 là hàm hợp của hai hàm y u5 và u sinx .
Cách nói sau cũng ược chấp nhận:
“Hàm số g(x) sin x5 là hàm hợp của hai hàm f(x) x5 và (x) sin x”.
1.1.5. Hàm số ngược
Xét hàm số y f(x) có miền xác ịnh X , miền giá trị Y f(X) . Nếu với mỗi y0 Y tồn tại duy nhất x 0
X ể f(x )0 y0 (hay phương trình f(x) y0 có nghiệm duy nhất trong
X ) thì quy tắc biến mỗi số y Y thành nghiệm duy nhất của phương trình f(x) y là
một hàm số i từ Y ến X gọi là hàm ngược của hàm f , ký hiệu f 1 f 1(y) x f(x) y. 1.
Khi ó, dễ dàng thấy rằng f là hàm ngược của f Ví dụ 7: • Hàm số y x3 (
) có hàm ngược là hàm số x 3 y ( ) vì: 8 MAT101_Bài 1_v2.3013101225 lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục y x3 x 3 y •
Hàm số y ax a 0,a 1 ( + *
) có hàm ngược là hàm số x log ya ( * ) vì: y ax x log x.a
• Các hàm lượng giác quen thuộc ều có hàm ngược với cùng một cách ký hiệu: o Hàm số y sin x ฀ 2 2, [ 1,1]
có hàm ngược, ta ký hiệu hàm ngược ó là: x arcsin y [ 1,1]฀ 2 2, . o Hàm số y cosx 0,
[ 1,1] có hàm ngược, ta ký hiệu hàm ngược ó là: x arccosy [ 1,1] 0, . o Hàm số y tgx ฀ 2 2,
có hàm ngược, ta ký hiệu hàm ngược ó là: x arctgy  2 2, . o Hàm số y cotgx 0,
có hàm ngược, ta ký hiệu hàm ngược ó là: lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục x a rccotgy  0. , 0 CHÚ Ý :
Do thường ký hiệu x ể chỉ biến ộc lập và y ể chỉ biến phụ thuộc nên khi biểu diễn hàm ngược thay vì 1 x f ( y ) có viết 1 y f ( x ) .
Chẳng hạn y l og x là hàm ngược của hàm: x y a a
Đồ thị của hai hàm ngược nhau không
thay ổi như khi ổi vai trò x,y cho nhau
thì nó ối xứng nhau qua ường phân giác thứ nhất.
Thật vậy, gọi (C) và (C’) lần lượt là ồ thị của hai hàm f(x) và 1 f (x) t hì theo ịnh nghĩa: M ( x,y ) ( C ) M' ( y,x ) ( C' )
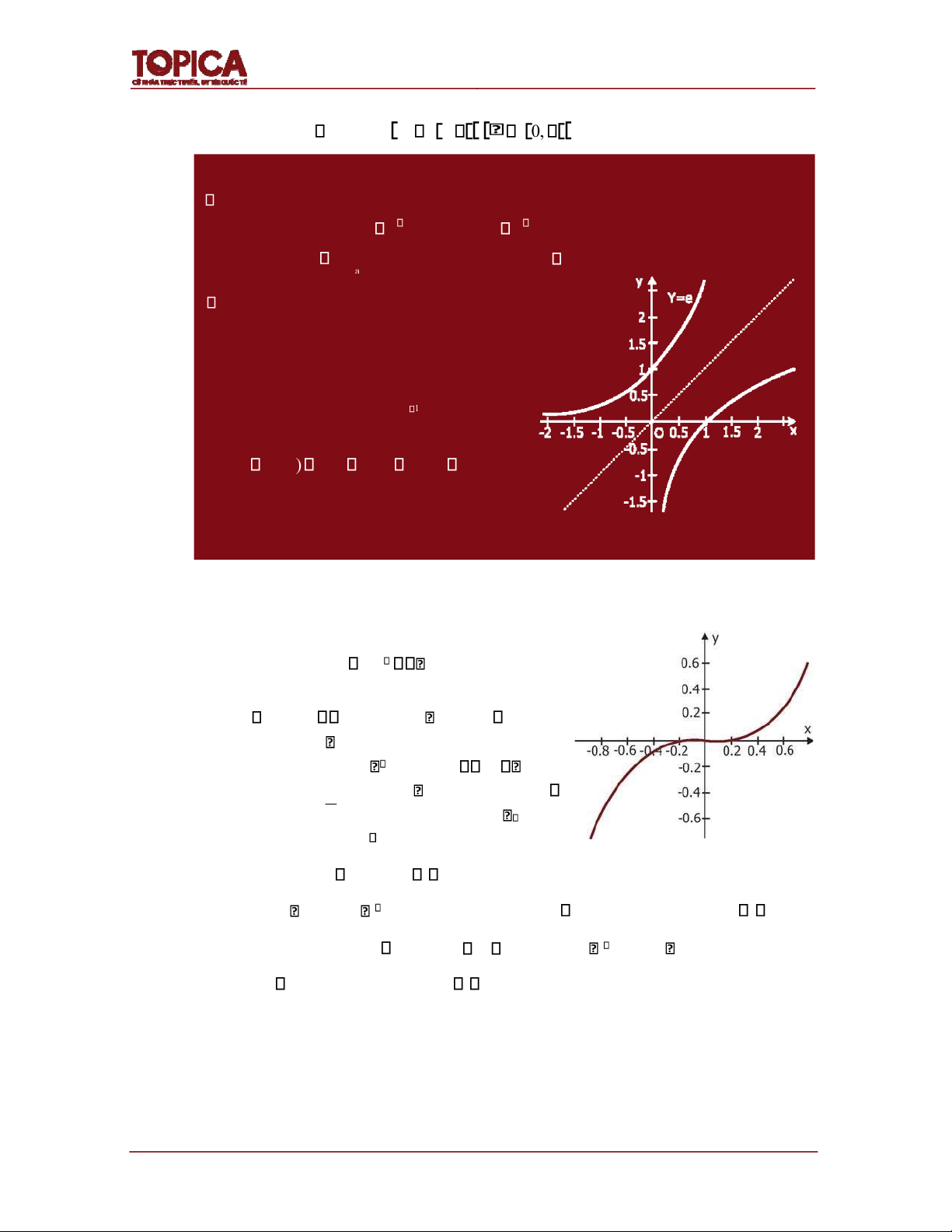
Hình 1.6: Hàm mũ, hàm logarit
1.1.6. Các hàm số sơ cấp
1.1.6.1. Các hàm số sơ cấp cơ bản • Hàm lũy thừa y x ( )
Miền xác ịnh (MXĐ) của hàm phụ thuộc vào số . o Nếu
0, MXĐ là . o Nếu nguyên âm. MXĐ là \{0}. o 1 * thì MXĐ là nếu Nếu ,p
p p chẵn và nếu p lẻ. o Nếu vô tỷ,
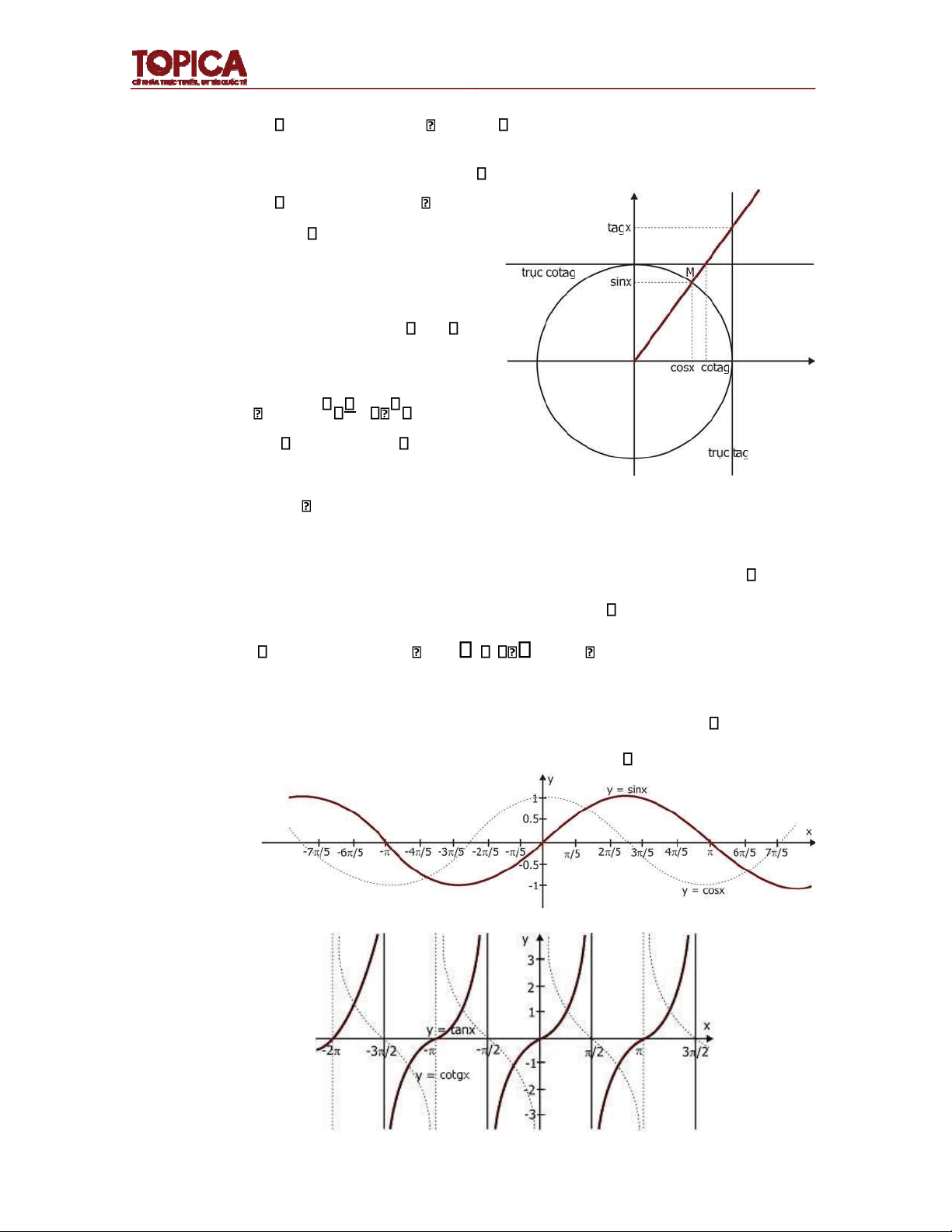
MXĐ ược quy ước là . Hình
1.7: Đồ thị hàm số y x3 • Hàm mũ: f(x) a (0x a 1)
MXĐ: , MGT: * ; Hàm số ồng biến nếu a 1 và nghịch biến nếu 0 a 1.
• Hàm số lôgarit: f(x) log x a (0
a 1) o MXĐ: * , MGT: ; Hàm số ồng biến
nếu a 1 và nghịch biến nếu 0 a 1. • Hàm lượng giác 10 MAT101_Bài 1_v2.3013101225 lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục o
y sin x : Có MXĐ là , MGT [ 1,1]; cho tương ứng mỗi số thực x với tung
ộ iểm biểu diễn cung x radian trên ường tròn lượng giác. Hàm sin là hàm lẻ,
tuần hoàn với chu kỳ cơ bản 2 . o
y cosx: Có MXĐ là ,
MGT [ 1,1]; cho tương ứng mỗi
số thực x với hoành ộ iểm biểu diễn
cung x radian trên ường tròn lượng
giác. Hàm cos là hàm chẵn, tuần
hoàn với chu kỳ cơ bản 2 . o y tgx: Có MXĐ là \ (2k+1) ,k , 2 MGT ; cho tương ứng mỗi
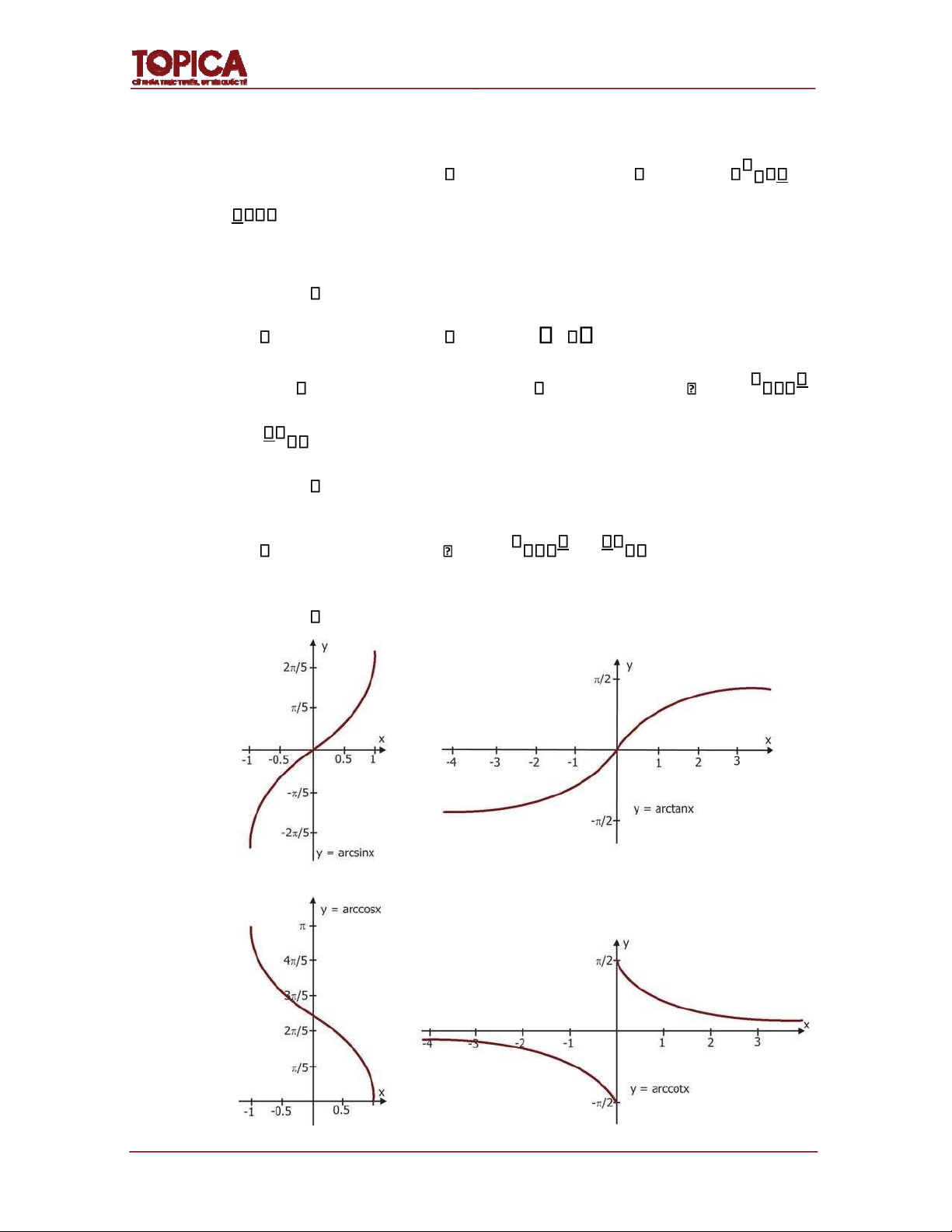
Hình 1.8: Quy tắc xác ịnh các hàm lượng giác số
thực x với tung ộ của giao iểm tia OM (M là iểm biểu diễn cung x radian trên
ường tròn lượng giác) với trục tan là ường thẳng có phương trình: x 1 .
Hàm tgx là hàm lẻ, tuần hoàn với chu kỳ cơ bản . o y cotgx: Có MXĐ là \ k ,k
, MGT ; cho tương ứng mỗi số thực x
với hoành ộ của giao iểm tia OM (M là iểm biểu diễn cung x radian trên ường
tròn lượng giác) với trục cotg là ường thẳng có phương trình y 1.
Hàm cotgx là hàm lẻ, tuần hoàn với chu kỳ cơ bản . lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
Hình 1.9: Đồ thị các hàm số lượng giác
• Hàm lượng giác ngược o y arcsin x: Có MXĐ là [ 1,1], MGT 2 2,
là hàm ngược của hàm sin.
Hàm y arcsin x là hàm lẻ, ồng biến. o
y arccosx : Có MXĐ là [ 1,1], MGT 0,
là hàm ngược của hàm cos. o
Hàm y arccosx là hàm nghịch biến. o y arctgx: Có MXĐ là , MGT 2 2,
là hàm ngược của hàm tg.
Hàm y arctgx là hàm lẻ, ồng biến. o
y arccotgx : Có MXĐ là , MGT 2 2, là hàm ngược của hàm cotgx.
Hàm y arccotgx là hàm lẻ, nghịch biến. 12 MAT101_Bài 1_v2.3013101225 lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
Hình 1.10: Đồ thị các hàm lượng giác ngược
1.1.6.2. Định nghĩa
Hàm số sơ cấp là một hàm số ược thành lập từ các hàm số sơ cấp cơ bản và hàm hằng
cùng với một số hữu hạn các phép toán số học (cộng, trừ, nhân chia) và các phép toán lấy hàm hợp. Ví dụ 8:
Các hàm số sau ều là các hàm sơ cấp:
• Hàm bậc nhất: y ax b .
• Hàm bậc hai: y ax2 bx c. • Hàm lôgarit: loga x x2 1 . • Hàm lượng giác: y arctg(2x 3) .
• Hàm phân thức hũu tỷ: y x 2 . 1 x 1.2.
Dãy số và giới hạn của dãy số 1.2.1. Khái niệm 1.2.1.1. Dãy số
Ta gọi dãy số là một tập hợp các số (gọi là các số hạng) ược viết theo một thứ tự, hay
ược ánh số bằng các số tự nhiên.
Để cho một dãy số, người ta có thể dùng các cách thức như liệt kê, công thức tổng quát và công thức truy hồi.
• Liệt kê: Viết tất cả các số hạng theo úng thứ tự (nếu không viết ược hết thì dùng
dấu “…” ể biểu thị dãy còn tiếp tục).
• Công thức tổng quát: Chỉ rõ cách xác ịnh một số hạng bất kỳ chỉ cần biết thứ tự
của số hạng ó trong dãy.
• Công thức truy hồi: Chỉ rõ cách xác ịnh một số hạng khi biết các số hạng liền trước nó trong dãy.
• Liệt kê chỉ có ý nghĩa mô tả và thích hợp nhất với dãy hữu hạn, có thể xem là cách
biểu diễn bằng quy nạp không hoàn toàn. Còn hai cách kia ảm bảo có thể tìm ược
số hạng với thứ tự bất kỳ trong dãy. Ví dụ 9:
Dãy Fibonacci và 3 cách biểu diễn nêu trên
Liệt kê: 1, 1, 2, 3, 5, 8, 13, 21, 34, …
• Công thức tổng quát: Số hạng thứ n là: lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục 1 5 n 1 5 n 2 2
• Công thức truy hồi: Hai số hạng ầu tiên ề bằng 1, tiếp ó, số hạng sau ược tính bằng
tổng hai số hạng liền trước.
Công thức tổng quát của dãy số là cách biểu diễn tốt nhất ể có thể ịnh nghĩa dãy số.
Nhờ nó, dãy số ược ịnh nghĩa một cách hết sức ơn giản mà chặt chẽ. Định nghĩa:
Dãy số là một ánh xạ (hàm số) có miền xác ịnh là  (hoặc một tập con các số tự nhiên
liên tiếp của ) và lấy giá trị trong tập các số thực .
Ta thường ký hiệu dãy số bởi xn n 1 hay gọn hơn xn . Ví dụ 10: 1 (A) 1, 1 1, ,..., 1 ,... n n 1 2 3 n (B) ( 1) n n 1 1,1, 1,...,( 1) ,... n (C) n2 n 1 1,4,9,...,n ,...2 (D) n n 1 2 3, , ,..., ,... n 1 n 1 2 3 4 n 1
1.2.1.2. Dãy tăng, dãy giảm, dãy bị chặn Dãy xn gọi là • Dãy tăng nếu x n xn 1 n  • Dãy giảm nếu x n xn 1 n 
• Dãy ơn iệu nếu nó là dãy tăng hoặc dãy giảm.
• Bị chặn trên nếu tồn tại số M sao cho x n
M, n  Bị chặn dưới nếu tồn tại số m sao cho x n m, n 
• Bị chặn nếu vừa bị chặn trên, vừa bị chặn dưới. Trong ví dụ 10 14 MAT101_Bài 1_v2.3013101225 lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
• Dãy (A) là dãy số giảm, bị chặn dưới bởi 0 và bị chặn trên bởi 1.
• Dãy (B) không ơn iệu, bị chặn dưới bởi 1 và bị chặn trên bởi 1.
• Dãy (C) là dãy tăng, bị chặn dưới bởi 1 không bị chặn trên nên không bị chặn.
Dãy (D) là dãy tăng, bị chặn dưới bởi 0 và bị chặn trên bởi 1.
1.2.2. Giới hạn của dãy số Xét dãy số xn 1n 1 , 12 ,..., 1n ,...
. Khoảng cách giữa x và n0 là: 2 n 1 2 2 2 xn 0 1n 2
Ta thấy: Cho trước một số
0 bé tùy ý thì sẽ tìm ược một số N sao cho n> N thì
khoảng cách giữa xn và 0 sẽ bé hơn số ó. 1
Chẳng hạn, cho trước khoảng
0,05 thì chỉ cần n 8 thì x n 0 0,05. 256
Ta nói dãy xn dần tới 0 khi n tiến tới vô cùng. Định nghĩa:
Dãy xn có giới hạn a hữu hạn khi n tiến tới vô cùng nếu với mọi số 0 cho trước
(bé tùy ý), tồn tại số tự nhiên n sao cho với mọi 0 n n0 thì xn a . Ta viết: lim xn a hay x n a khi n . n
Dãy xn ược gọi là dãy hội tụ nếu tồn tại số a ể lim xn n a . Trong trường hợp
ngược lại, ta nói dãy phân kỳ.
Trong ịnh nghĩa trên, số n 0 phụ thuộc vào nên ta viết n0 n ( )0 . Ví dụ 11: 1 lim 0. n n Thật vậy, ta có: 1 x n 0 . lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục n Với mỗi
0 bất kỳ chỉ cần chọn n 1 0 1 thì khi n n0 có ngay x n 0 n1 11 . Định nghĩa:
Dãy xn ược nói là có giới hạn khi n tiến tới vô cùng nếu với mọi số M 0 cho
trước (lớn tùy ý), tồn tại số tự nhiên n sao cho với mọi 0 n n0 thì xn M ; ta cũng viết lim xn và là dãy phân kỳ. n
Trên ây chỉ phát biểu ịnh nghĩa giới hạn vô cùng nói chung, ta có thể phát biểu chi tiết hơn về giới hạn , .
1.2.3. Tiêu chuẩn tồn tại giới hạn
1.2.3.1. Tính duy nhất của giới hạn Định lý:
Nếu một dãy có giới hạn (hữu hạn)
thì Dãy ó là dãy bị chặn . Giới hạn là duy nhất.
1.2.3.2. Nguyên lý giới hạn kẹp
Nếu có ba dãy số xn , y n , z n thỏa mãn: • x n yn zn • lim x limz n n
n a (a có thể hữu hạn, hoặc
) thì yn có giới hạn và n lim yn a . n
1.2.3.3. Định lý Weierstrass
Dãy số tăng và bị chặn trên (hoặc giảm và bị chặn dưới) thì hội tụ. 1.2.4.
Các ịnh lý về giới hạn của dãy số 16 MAT101_Bài 1_v2.3013101225 lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
Cho xn , y n là các dãy có giới hạn hữu hạn. Dùng ịnh nghĩa có thể chứng minh các kết quả sau:
lim(xn n y )n nlim x n nlim y n
lim(x y )n n lim x lim y n n n n n xn lim xn n (khi lim yn 0). lim n yn nlim y n n
Chú ý rằng khi cả xn , y n có các giới hạn vô cực thì nhìn chung không sử dụng 0
ược các kết quả nói trên. Các dạng vô ịnh thường gặp là , , ,0. . Khi ó ta 0
phải dùng các phép biến ổi ể khử dạng vô ịnh. Ví dụ 12: 1 2 n2 n 2 1
:nlim 2n2 1 nlim 2n n12n2 12. 2 ( ): lim n2 3n 2 n lim 2 3n3n 22 n nlim 1 3n3 nn22 1 32. n n n 1.3.
Giới hạn và sự liên tục của hàm số 1.3.1. Định nghĩa
1.3.1.1. Định nghĩa (giới hạn hàm số)
Giả sử hàm số f(x) xác ịnh ở lân cận iểm x (có thể trừ tại 0 x ). Ta nói hàm số 0 f(x) có
giới hạn là A khi x dần tới x nếu: 0 lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục Với mọi số
0 cho trước, ều tồn tại một số 0 sao cho khi: x x0 thì f(x) A . Kí hiệu là: lim f(x) 0 A hay f(x) A khi x a . x x
Một cách tương ương ta có thể ịnh nghĩa f x có giới hạn là A khi x x0 khi và chỉ khi với mọi xn x0 ta có f x n A .
1.3.1.2. Định nghĩa (giới hạn một phía)
Trong ịnh nghĩa nêu trên, chúng ta xét quá trình x x0 không phân biệt x x0 hay x
x0 . Khi xem xét giới hạn, nhiều khi ta phải xét riêng hai quá trình này với kí hiệu như sau:
• Quá trình x tiến ến x0 về phía bên phải, tức là x x0 với iều kiện x x0, ược kí
hiệu là: x x0 0 hoặc ơn giản hơn là x x0
• Quá trình x tiến ến x về phía bên trái, tức là 0 x x0 với iều kiện x x0 , ược kí
hiệu là: x x0 0 hoặc ơn giản hơn là x x0
• Giới hạn của hàm số f(x) khi x x0 hoặc khi x x0 ược gọi tương ứng là giới
hạn bên phải và giới hạn bên trái của hàm số tại iểm x . 0
• Giới hạn bên phải: lim f(x) lim f(x). x x0 x x ,x x0 0
• Giới hạn bên trái: lim f(x) lim f(x). x x0 x x ,x x0 0
Từ ịnh nghĩa trên ta suy ra: Định lý:
Điều kiện cần và ủ ể lim f(x) L là: lim f(x) lim f(x) L. x x 0 x x 0 x x 0 1.3.2. Tính chất
1.3.2.1. Tính chất các hàm có giới hạn
Giới hạn của hàm số cũng có một số tính chất tương tự như giới hạn của dãy số Định lý:
Nếu hàm số f(x) có giới hạn khi x a thì giới hạn ó là duy nhất. Định lý: 18 MAT101_Bài 1_v2.3013101225 lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
Nếu hàm số f(x) có giới hạn hữu hạn khi x a thì nó bị chặn trong miền X x : 0
x a , với là một số dương ủ nhỏ. Định lý:
Nếu limf(x) L và L b (L b) thì, với là một số dương ủ nhỏ ta cũng có x a f(x) b (f(x) b) x x : 0 x a . Định lý:
Nếu f(x) g(x) f(x) g(x) với mọi x x : 0 x a và cả hai hàm số
f(x),g(x) có giới hạn hữu hạn khi x a thì limf(x) limg(x) . x a x a
1.3.2.2. Các quy tắc tính giới hạn
Sử dụng ịnh nghĩa giới hạn của hàm số bằng ngôn ngữ dãy số và các quy tắc tương
ứng về giới hạn của dãy số ta dễ dàng chứng minh ược các quy tắc sau ây: Định lý:
Nếu khi x a các hàm số f(x) và g(x) lần lượt có giới hạn là các số thực L và 1 L thì: 2 • lim f(x) a g(x) L1 L 2 x • lim kf(x) a kL1 x • lim f(x)g(x) a L L1 2 x • lim a g(x)f(x) LL12 khi L 2 0. x Định lý:
Giả sử (x) và f(u) thỏa mãn các iều kiện:
lim (x) a b và limf(u)u b f b L x • tồn tại số 0 sao cho khi x (a ;a ) và x a ta luôn có: u (x) b thì: limf a (x) L. x lOMoAR cPSD| 49519085
Bài 1: Hàm số, giới hạn và liên tục
Định lý: Nếu hàm số sơ cấp f(x) xác ịnh trong khoảng chứa iểm x a thì limf(x) f(a) . x a Định lý: Nếu tồn tại số
0 sao cho u(x) f(x) v(x) với mọi x x :0 x a và
limu(x) limv(x) b thì limf(x) b. x a x a x a Định lý:
Giả sử các hàm số f(x) và g(x) có giới hạn hữu hạn khi x a : limf(x) a b 0, limg(x)x . Khi ó: lim f(x) g(x) b . x a x a Ví dụ 13: 3x lim 2xx 11 x 5 23 8, do limx 2xx 11 2 và limx x3 x5 3. x
Định lý: Nếu limf(x) 0 và g(x) là một hàm số bị chặn thì limf(x).g(x) 0 . x a x a Ví dụ: limx sin2
1 0 vì limx2 0 và sin 1 là hàm bị chặn. x 0 x x 0 x
1.3.3. Vô cùng lớn, vô cùng bé 1.3.3.1. Khái niệm
• Đại lượng f(x) gọi là một vô cùng bé (viết tắt là VCB) khi x a nếu limf(x) 0. x a
Ở ây, a có thể là hữu hạn hay vô cùng. Từ ịnh nghĩa giới hạn của hàm số, ta suy ra rằng nếu: f(x) A khi x a thì f(x) A (x)
Trong ó (x) là một VCB khi x a
• Đại lượngF(x) gọi là một vô cùng lớn (viết tắt là VCL) khi x a nếu lim F(x) x a 20 MAT101_Bài 1_v2.3013101225