Bài giảng chương 2: Some expended problems of Functions of one variable | Môn toán cao cấp

lOMoAR cPSD| 47207194
Department of Mathematics, Faculty of Basic
Science, Foreign Trade University
------------------------------------------------------------------------------------- Part II, Calculus Chapter 2:
Some expended problems of Functions of one variable lOMoAR cPSD| 47207194 Instructor Dr. Son Lam CONTENTS
--------------------------------------------------------------------------------------------------------------------------- I – Taylor Series Formula II – L’Hôpital’s Rule lOMoAR cPSD| 47207194
I – Taylor Series Formula Theorem lOMoAR cPSD| 47207194
The function f(x) is assumed to possess derivatives to the nth order.
The Taylor series expansion of the function f(x) in a neighborhood
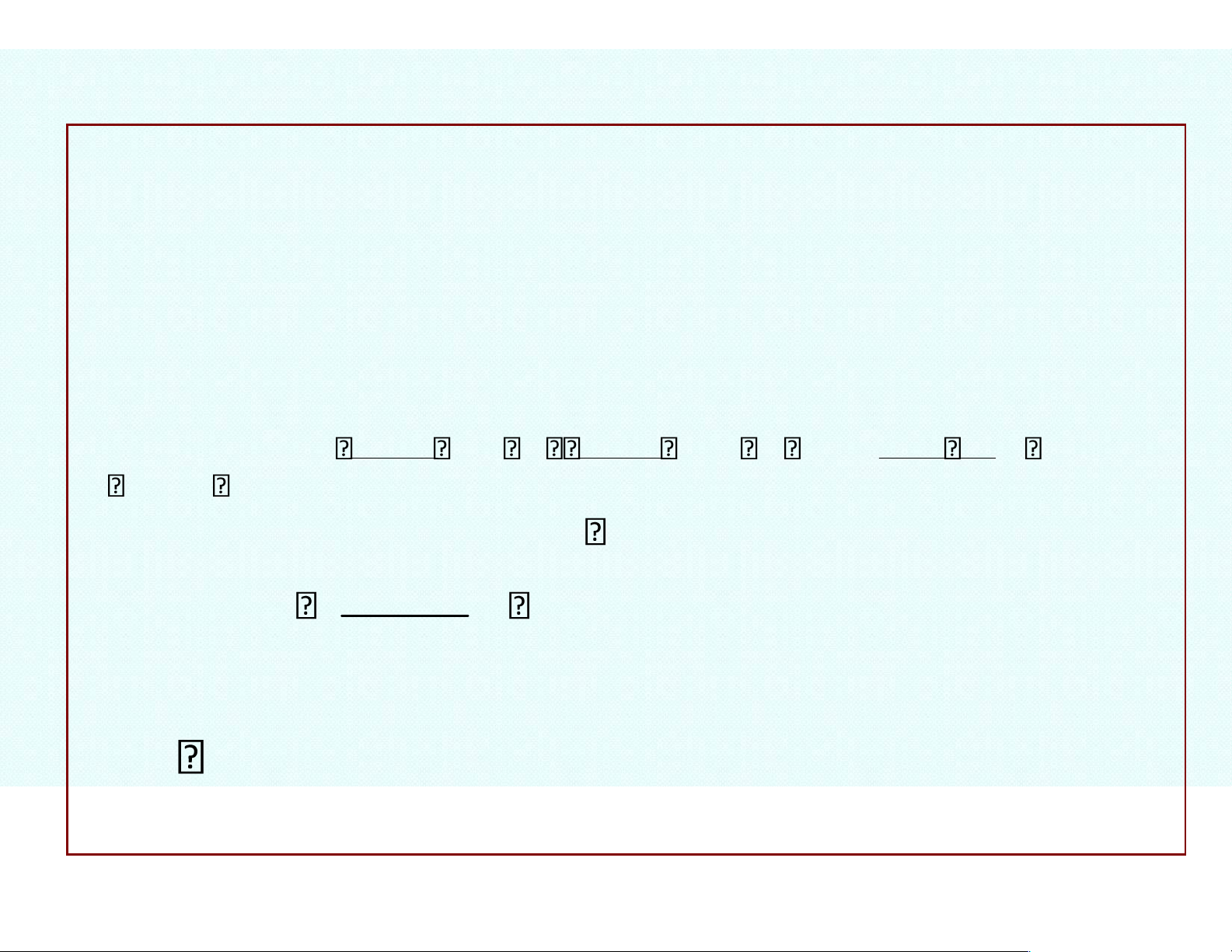
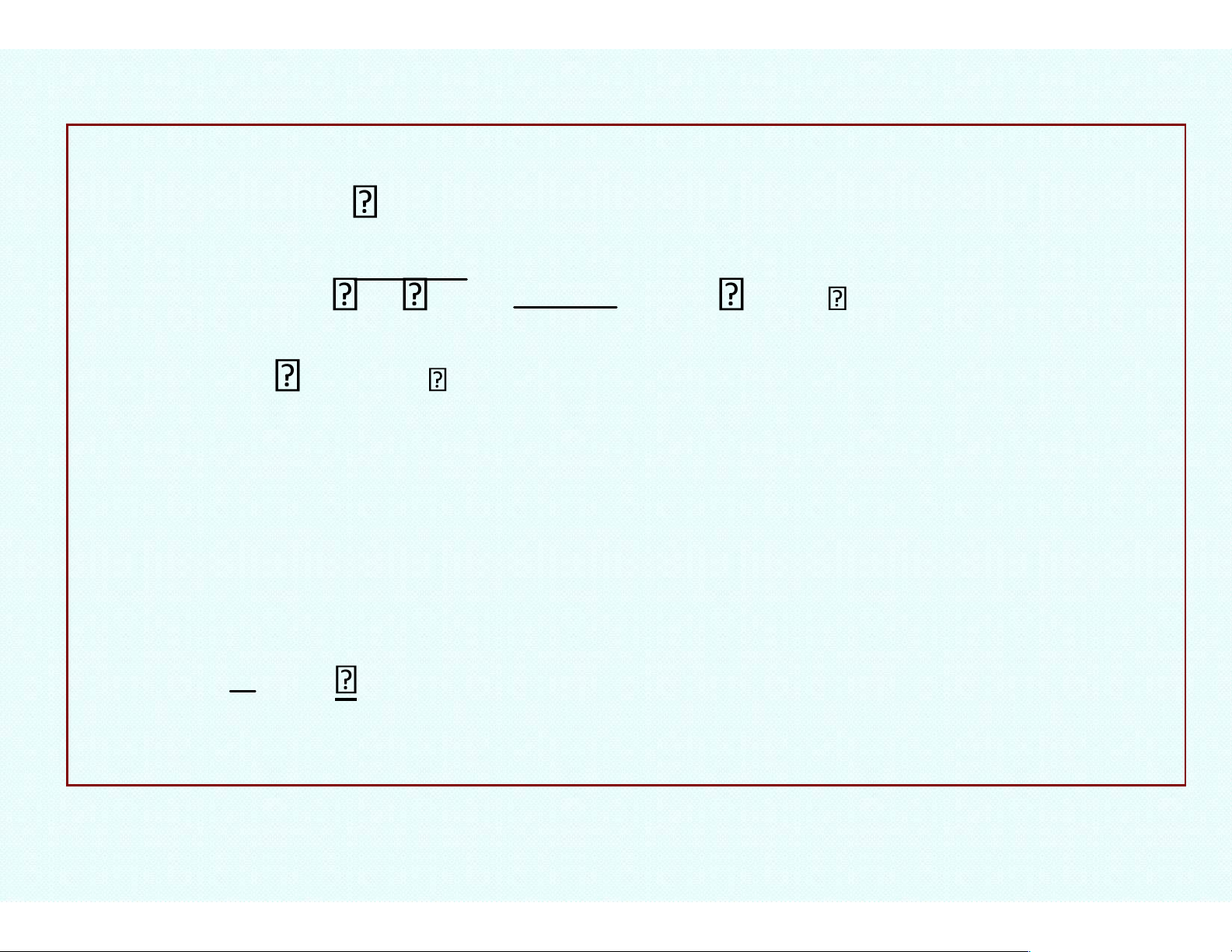
of the value x0 in the remainder formula is: f (x0)(x x0) f
(x0)(x x0)2 ... f ( )n (x0)(x x0)n Rn f x( ) f x( 0) 1! 2! n! f ( )n ( ) n where Rn (x x0) n! and lies between x and x0 R lOMoAR cPSD| 47207194 Note: x xlim 0 x x n0 n 0 lOMoAR cPSD| 47207194
I – Taylor Series Formula Theorem
The function f(x) is assumed to possess derivatives to the nth order.
The Maclaurin series expansion of the function f(x) in a
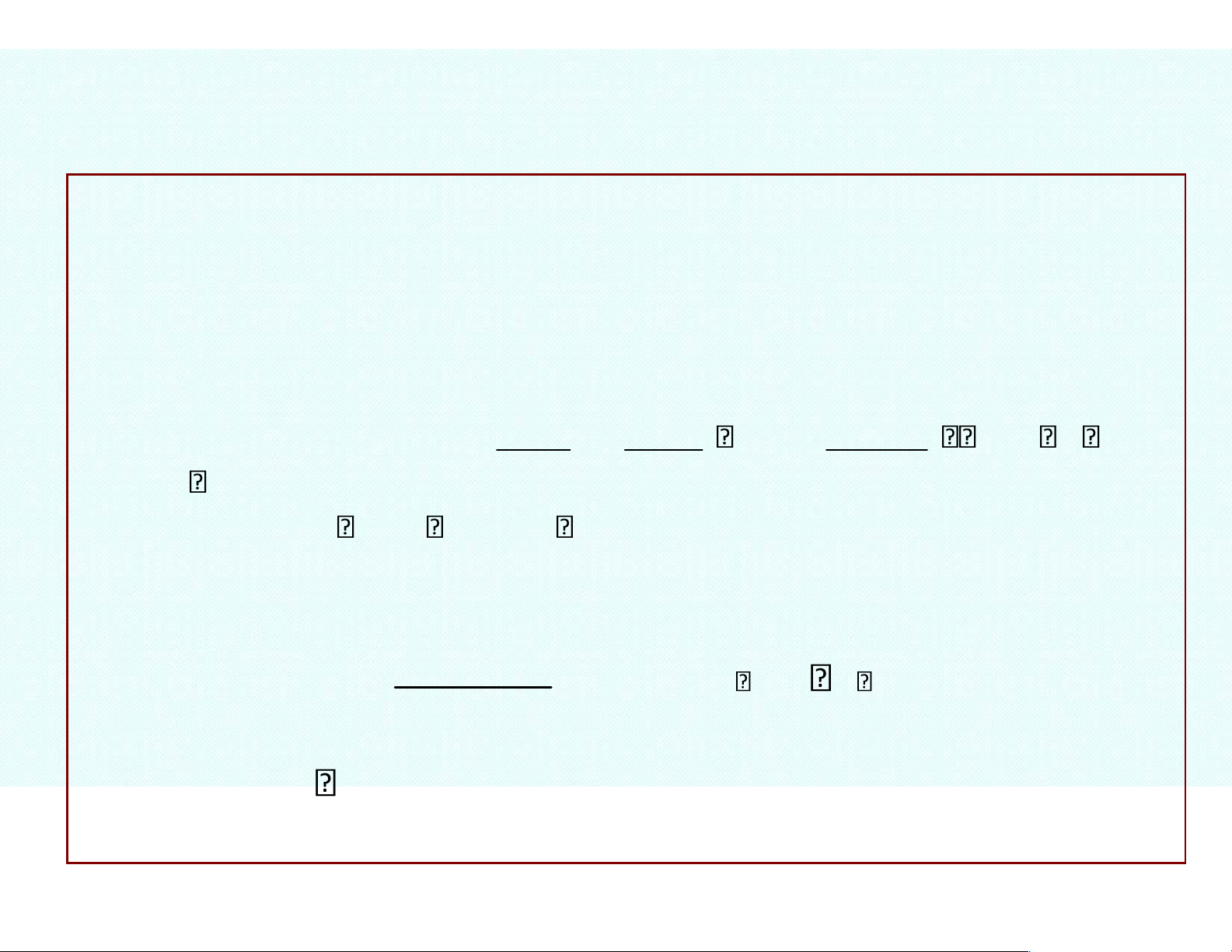
neighborhood of the value x0 in the remainder formula is: f (0) f (0) 2 ... f ( )n (0) xn Rn f x( ) f (0) x x 1! 2! n! f (n 1)( ) n 1 (Lagrange residual) where Rn x lOMoAR cPSD| 47207194 (n 1)! and lies between x and 0. R lim Note: n x 0 n 0 (Peano residual) x lOMoAR cPSD| 47207194 lOMoAR cPSD| 47207194 I – Taylor Series Formula Example
Find the Maclaurin series expansion for the function : f x( ) ex x2
f ( )k ( )x ex f ( )k (0) 1,k 1,2,... lOMoAR cPSD| 47207194 I – Taylor Series Formula e x 1 x x2 ...xn Rn 1! 2! n! Example
Find the Maclaurin series expansion for the function : f x( ) ex x 1 x x2 ... xn Rn lOMoAR cPSD| 47207194 I – Taylor Series Formula e 1! 2! n! ex 1 x x2!2 ... xnn! ... xnn! 1! n 1 lOMoAR cPSD| 47207194 I – Taylor Series Formula 1 1 1 1 1 e 1 2,716666 1! 2! 3! 4! 5! Example
Find the Maclaurin series expansion for the function : f x( ) ex x 1 x x2 ... xn Rn lOMoAR cPSD| 47207194 I – Taylor Series Formula e 1! 2! n! x ex1 R1 1! ex 1 x x2 R2 1! 2! Example lOMoAR cPSD| 47207194 I – Taylor Series Formula
Find the Taylor series expansion for the function : a. f x( ) sin x b. g x( ) cosx Example
Find the Taylor series expansion for the following function at the point x0=1. P x( ) x5 2x4 x3 x2 2x 1 lOMoAR cPSD| 47207194 I – Taylor Series Formula P x( ) x5 2x4 x3 x2 2x 1 lOMoAR cPSD| 47207194 II – L’Hôpital’s Rule Theorem lOMoAR cPSD| 47207194 II – L’Hôpital’s Rule f ( )x f x( ) lim L lim L x x 0 g x ( ) x x g x( ) 0
This rule, which is more an application of differentiation than a rule
for finding derivatives, is useful for finding the limiting value of the
ratio of functions at a point (x = x0) where that value is undefined, such as 0 or lOMoAR cPSD| 47207194 II – L’Hôpital’s Rule 0 lOMoAR cPSD| 47207194 II – L’Hôpital’s Rule Example lOMoAR cPSD| 47207194 II – L’Hôpital’s Rule 2x - x2 2x - 22 x2 2 lim x 2lim x - 2 x 2lim x - 22 x 2 x - 2 22ln2 4 2x - x2 0 lim 0 x 2 x - 2 2x - x2 2xln2 - 2x