lOMoAR cPSD| 46836766 BÀI 2
BÀI TOÁN QUY HOẠCH TUYẾN TÍNH Hướng dẫn học
Để học tốt bài này, sinh viên cần làm tốt các việc sau:
• Học úng lịch trình của môn học theo tuần, làm các bài luyện tập ầy ủ và
tham gia thảo luận trên diễn àn. • Đọc tài liệu:
o Trần Việt Lâm, Giáo trình Phương pháp tối ưu trong kinh doanh
( chương 2 ) , Nhà xuất bản Đại học Kinh tế quốc dân, 2009
o Trần Túc , Quy hoạch tuyến tính, Đại học Kinh tế quốc dân, 2001
o Trần Vũ Thiệu, Giáo trình tối ưu tuyến tính , Nhà xuất bản Đại học quốc gia Hà Nội, 2004
• Sinh viên làm việc theo nhóm và trao ổi với giảng viê
n trực tiếp tại lớp học hoặc qua email. • Trang Web môn học. Nội dung
• Giới thiệu khái quát bài toán quy hoạch tuyến tính
• Phương pháp ơn hình giải bài toán quy hoạch tuyến tính
• Ứng dụng bài toán quy hoạch tuyến tính trong kinh doanh Mục tiêu
• Giúp sinh viên hiểu ược các dạng của bài toán quy hoạch tuyến tính, các khái
niệm phương án, phương án cực biên và phương án tối ư
u của bài toán quy hoạch tuyến tính;
• Giúp sinh viên hiểu và sử dụng ược phương pháp ơn hìn h giải bài toán quy hoạch tuyến tính;
• Giúp sinh viên nắm rõ
việc sử dụng bài toán quy hoạch tuyến tính ể giải quyết các vấn ề trong kinh doanh. 1 lOMoAR cPSD| 46836766
Tình huống dẫn nhập
• Nhu cầu của khách hàng ối với sản phẩm của doanh nghiệp ở các tháng khác nhau là
khác nhau. Năng lực sản xuất sản phẩm của doanh nghiệp, chi phí sản xuất, chi phí
lưu kho cho 1 sản phẩm ở những tháng khác nhau cũng là khác nhau. Nhà quản
trị phải lập kế hoạch iều ộ sản xuất trong các tháng như thế nào ể áp ứng ược
nhu cầu của khách hàng song với tổng chi phí sản xuất, chi phí lưu kho của cả năm là nhỏ nhất?
• Doanh nghiệp cần pha cắt những tấm vật liệu với kích thước cố ịnh thành những
tấm vật liệu nhỏ hơn có kích thước khác nhau ể phục vụ cho kế hoạch sản xuất sản
phẩm. Số lượng những tấm vật liệu có kích thức nhỏ hơn ã ược xác ị nh. Nhà
quản trị phải xác ịnh cách pha cắt những tấm vật liệu như thế nào ể ảm bảo ủ
số lượng những tấm vật liệu có kích thước nhỏ hơn phục vụ cho kế hoạch sản xuất
song với phần dư thừa là nhỏ nhất?
1. Sử dụng bài toán quy hoạch tuyến tính ể mô tả các vấn ề cần giải
quyết trong kinh doanh như thế nào?
2. Tìm phương án tối ưu của bài toán quy hoạch tuyến tính và sử dụng
phương án này ể ra quyết ịnh trong kinh doanh như thế nào? 2 lOMoAR cPSD| 46836766 Chương 2
Bài toán quy hoạch tuyến tính
2.1. Giới thiệu khái quát bài toán quy hoạch tuyến tính
2.1.1. Phát biểu bài toán quy hoạch tuyến tính
Bài toán quy hoạch tuyến tính là bài toán tối ưu có ứng dụng rộng rãi trong thực
tế vì , thứ nhất, về mặt lý thuyết nó ã ược giải quyết trọn vẹn, thứ hai, mô hình
tuyến tính là mô hình ơn giản, thường ược sử dụng ể mô hình hoá các vấn ề thực
tế. Bài toán quy hoạch tuyến tính có thể trình bày ở 3 dạng, dạng tổng quát, dạng
chuẩn tắc và dạng chính tắc.
Bài toán quy hoạch tuyến tính dạng tổng quát ược phát biểu như sau:
tìm các số x1,x2,...,xn sao cho f (x1,x2,....,xn ) =
n c j x j → Max(Min) j=1 với iều kiện
n aij x j ( ,=, ) bi i =1,2,,m j=1
x j 0 j = 1,2,,n.
Hàm mục tiêu f (x1,x2,....,xn ) là hàm số tuyến tính của các biến x1,x2,...,xn . m ràng
buộc của bài toán có thể là các phương trình hoặc bất phương trình.
Bài toán quy hoạch tuyến tính tổng quát có thể viết dưới dạng ma trận như sau:
tìm véc tơ X sao cho f (X) = C, X → Max(Min) A X ( ,=, ) B 3 lOMoAR cPSD| 46836766 X 0 . x 1 c1 b1 x 2 c2 b2 . ở ây . . X = , C , B và ma trận . . . x. n c.n b.m 4 lOMoAR cPSD| 46836766
Bài toán quy hoạch tuyến tính dạng chính tắc ược phát biểu như sau :
tìm các số x1,x2,...,xn sao cho
f (x1,x2,....,xn ) = n c j x j → Max(Min) j=1 với iều kiện j = 1 x 0 j = 1 ,2, ,  . j n
Bả ng 1 . Các dạng của bài toán quy hoạch tuyến tính Bài toán dạng Bài toán dạng Bài toán dạng Tổng quát Chuẩn tắc C hính tắc ( , , , f )
X = C X → ( f )
X = C X → ( f )
X = C X → ( Max ) Min ( Max ) Min ( Max ) Min A X ( ,=
, ) B A X ( ) B A X = B X 0 X 0 X 0 . Bi 2.1.2
ến ổi dạng bài toán quy hoạch tuyến tính
Bằng cách thực hiện các phép biến ổi dưới ây, chúng ta có thể c huyển
bài toán quy hoạch tuyến tính từ dạng này sang dạng khác, ch uyển từ bài toán tìm
Max thành bài toán tìm Min và ngược lại.
n aij x j = bi i =1,2,,m 5 lOMoAR cPSD| 46836766
Một bài toán tìm Min f (x1,x2,....,xn ) = n
c j x j → Min j=1
n aij x j ( ,=, ) bi i =1,2,,m j=1
x j 0 j = 1,2,,n.
tương ương với bài toán tìm Max sau ây :
g(x1,x2,...,xn ) = n (−c j ) x j → Max j=1
n aij x j ( ,=, ) bi i =1,2,,m j=1
x j 0 j = 1,2,,n.
Tức là nếu X opt là lời giải của bài toán thứ nhất thì X opt cũng là lời giải của bài
toán thứ hai và fMin = − gMax.
Mỗi ràng buộc bất phương trình n aij x j bi hoặc n aij x j bi có thể j=1 j=1
chuyển thành ràng buộc phương trình nhờ ưa vào một biến mới, gọi là biến bù xn+1
0, hệ số ứng với biến bù trong hàm mục tiêu bằng 0 ể n a +
. Như vậy, với phép biến ổi này ij x j
xn+1 = bi hoặc n aij x j - xn+1 = bi j=1 j=1
chúng ta có thể chuyển bài toán quy hoạch tuyến tính dạng tổng quát về bài toán
quy hoạch tuyến tính dạng chính tắc. 6 lOMoAR cPSD| 46836766
Các ràng buộc x j 0 trong bài toán quy hoạch tuyến tính ược gọi là các
ràng buộc về dấu. Giả sử chúng ta gặp bài toán mà biến x j không có ràng buộc về
dấu, khi ó chúng ta sẽ thay biến + − + − x , ở ây
j bằng hai biến là x j và x j
x j = x j - x j và + − x j 0, x j
0. Như vậy, với phép biến ổi này chúng ta có thể chuyển bài toán ã
cho thành một bài toán quy hoạch tuyến tính tương ương mà tất cả các biến ều có ràng buộc về dấu.
2.1.3. Minh hoạ hình học bài toán quy hoạch tuyến tính
Giải bài toán quy hoạch tuyến tính sau : 7 lOMoAR cPSD| 46836766 f ( ) X = x + 1
3x2 → Max 8 4 16 1 x + x2 4 6 12 1 x + x2 3 x 2 2 0 . 1 x 0 , x2
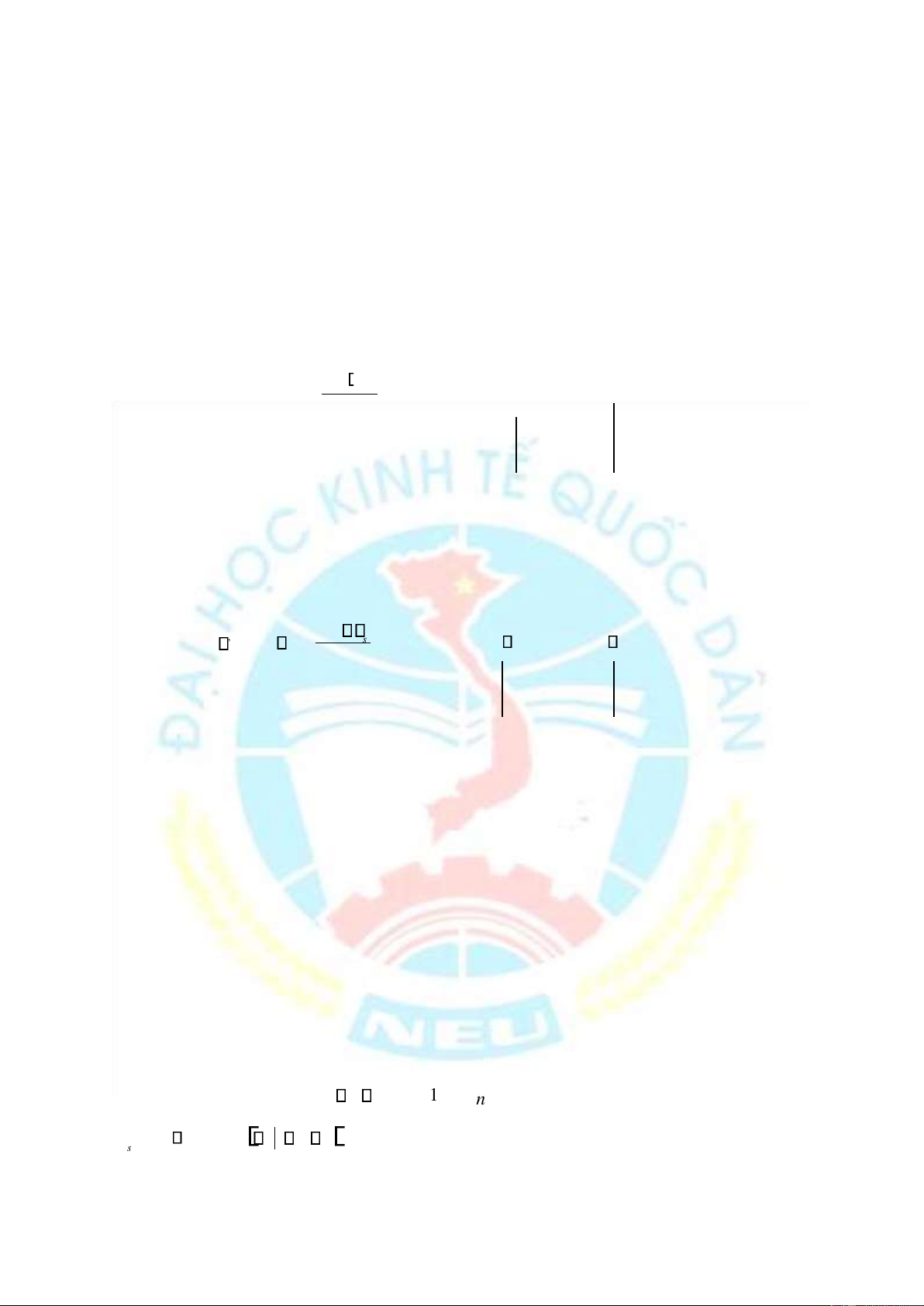
Sau khi vẽ các ường thẳng 3 8 4 = 16 , 4 6 = 12 và = chúng ta 1 x + x2 1 x + x2 x2 2
thấy tập hợp các phương án chấp nhận ược của bài toán chính là toạ ộ của các iểm thuộc a giác OABCD. X 2 4 8 4 = 16 1 x + x2 2 A B x 3 / 2 2 = C 1 4 6 = 12 1 x + x2 O 2 D 3 X 1 1 x + 3 x = 3 2
Chúng ta gọi ường thẳng x + 1
3x2 = tương ứng với một giá trị cụ thể của
là một ường mức (mức ). Mỗi khi thay ổi các ường mức sẽ tịnh tiến song 8 lOMoAR cPSD| 46836766
song với nhau. Trên ồ thị là ường mức x + 1
3x2 = 3 và ường mức ứng với giá trị
lớn nhất chính là ường mức i qua ỉnh B, hay nói cách khác toạ ộ của ỉnh B chính
là lời giải của bài toán quy hoạch tuyến tính.
Toạ ộ mỗi một iểm của a giác OABCD tương ứng với một phương án chấp
nhận ược của bài toán. Trong các phương án chấp nhận ược của bài toán chúng
ta ặc biệt quan tâm ến các phương án tương ứng với các ỉnh của a giác OABCD
và sau này chúng ta sẽ gọi ó là các phương án cực biên. Từ ví dụ này có thể thấy
nếu bài toán quy hoạch tuyến tính có lời giải thì chắc chắn một phương án cực
biên sẽ là lời giải của bài toán. Do số phương án cực biên có hạn nên cần xây
dựng một tiêu chuẩn kiểm tra xem khi nào một phương án cực biên là phương án
tối ưu và nếu phương án cực biên chưa phải là phương án tối ưu thì cần biết cách
chuyển sang một phương án cực biên khác tốt hơn. Chúng ta lại áp tiêu chuẩn ể
kiểm tra tính tối ưu của phương án cực biên mới,...Quá trình cứ tiếp tục như vậy,
sau một số hữu hạn bước hoặc chúng ta tìm ược phương án tối ưu của bài toán
quy hoạch tuyến tính hoặc chúng ta kết luận bài toán quy hoạch tuyến tính không
có lời giải. Đó chính là tư tưởng của phương pháp ơn hình giải bài toán quy hoạch
tuyến tính ược trình bày ở phần sau.
Đưa vào thêm 3 biến x3,x4,x5 chúng ta chuyển bài toán ã cho về dạng chính tắc : f ( ) X = x + + 1
3x2 → Max 8x1 4x2 + x3 = 16 4x + 1
6x2 + x4 = 12
x2 + x5 = x j
0 , j = 1,2,3,4,5 . 9 lOMoAR cPSD| 46836766
Với 5 thành phần dễ dàng xác ịnh ược toạ ộ tương ứng với các ỉnh O, A, B, C, D : O= 0,0,16,12, 3 , A = 0, 3 ,10,3,0 , B = 3 , 3 ,4,0,0 , C = 3 ,1,0,0, 1 2 2 4 2 2 2 , D = 3 2,0,0,4,
. Chúng ta thấy rằng mỗi một phương án của bài toán ứng với 2
các ỉnh O, A, B, C, D ều có 3 thành phần dương (m = 3 ) trong tổng số 5 thành
phần (n = 5) và các véc tơ cột của ma trận A ứng với các thành phần dương này ều
là ộc lập tuyến tính. Đặc iểm này sẽ ược sử dụng ể ịnh nghĩa phương án cực biên.
2.1.4. Phương án, phương án cực biên và phương án tối
ưu của bài toán quy hoạch tuyến tính
Xét bài toán quy hoạch tuyến tính dưới dạng tổng quát. Véc tơ X thỏa mãn
các ràng buộc của bài toán ược gọi là một phương án của bài toán. Phương án
X thỏa mãn ràng buộc thứ i của bài toán với dấu =, tức là n a = ij x j bi thì
j=1 phương án X
ược gọi là thỏa mãn chặt ối với ràng buộc thứ i . Phương án X thỏa mãn ràng buộc
thứ i với dấu hay , tức là n aij x j ( ) bi thì phương j=1
án X ược gọi là thỏa mãn lỏng ối với ràng buộc thứ i .
Xét bài toán quy hoạch tuyến tính dưới dạng chính tắc. Phương án 10 lOMoAR cPSD| 46836766 X = ( )
x1,x2,...,xn của bài toán mà các véc tơ cột Aj của ma trận A ứng với các thành
phần x j 0 là ộc lập tuyến tính ược gọi là phương án cực biên.
Vì ma trận A có m hàng nên ma trận A sẽ có tối a m véc tơ cột ộc lập tuyến
tính, iều ó có nghĩa là một phương án cực biên sẽ có tối a m thành phần dương.
Phương án cực biên có úng m thành phần dương ược gọi là phương án cực biên
không suy biến. Phương án cực biên có ít hơn m thành phần dương ược gọi là
phương án cực biên suy biến .
Nếu kể cả các ràng buộc về dấu thì tổng số các ràng buộc của bài toán quy
hoạch tuyến tính là m+n. Phương án cực biên X sẽ thỏa mãn chặt n ràng buộc ộc
lập tuyến tính trong tổng số m+n ràng buộc của bài toán. Phương án cực biên X
thỏa mãn chặt úng n ràng buộc ộc lập tuyến ược gọi là phương án cực biên không
suy biến, thỏa mãn chặt hơn n ràng buộc ộc lập tuyến ược gọi là phương án cực biên suy biến.
Phương án X mà ứng với nó hàm mục tiêu f (X) nhận giá trị cực ại trong bài toán
tìm Max hoặc nhận giá trị cực tiểu trong bài toán tìm Min ược gọi là phương án tối
ưu và ký hiệu là X opt .
2.1.5. Một số tính chất của bài toán quy hoạch tuyến tính
(1). Điều kiện cần và ủ ể bài toán quy hoạch tuyến tính có phương án tối ưu là
tập hợp các phương án khác rỗng và hàm mục tiêu bị chặn ( hàm mục tiêu bị chặn
có nghĩa là M mà ối với bài toán tìm Min, f (X) M ối với mọi phương án của bài
toán; ối với bài toán tìm Max, f (X) M ối với mọi phương án của bài toán).
(2). Nếu bài toán quy hoạch tuyến tính dạng chính tắc có phương án thì nó
có ít nhất một phương án cực biên.
(3). Số phương án cực biên của bài toán quy hoạch tuyến tính là hữu hạn. 11 lOMoAR cPSD| 46836766
(4). Nếu bài toán quy hoạch tuyến tính dạng chính tắc có phương án tối ưu
thì nó có ít nhất một phương án cực biên là phương án tối ưu.
(5). Tiêu chuẩn ể một phương án cực biên là phương án tối ưu
Xét bài toán quy hoạch tuyến tính dưới dạng chính tắc. Giả sử X = ( )
x1,x2,...,xn là một phương án cực biên không suy biến của bài toán. Không
giảm tính tổng quát chúng ta giả sử m thành phần dương của phương án X là
x1,x2,...,xm (trong trường hợp ngược lại chúng ta ánh số lại các biến), tức là
X = (x1,x2,....,xm,0,0,...,0). Như vậy, các véc tơ cột A1, A2,...,Am của ma trận A là
những véc tơ ộc lập tuyến tính. Mọi véc tơ cột Ak của ma trận A ều có thể biểu diễn
tuyến tính qua m véc tơ này, tức là A . Đối với mỗi véc tơ k = m z jk Aj Ak j=1
(k =1,2,...,n) chúng ta xây dựng số kiểm tra − k , k =
m z jk c j ck . Điều kiện cần j=1
và ủ ể phương án cực biên )
X = (x1,x2,...,xn là phương án tối ưu của bài toán tìm Max
là các số kiểm tra k 0 , k =1,2,....,n. Điều kiện cần và ủ ể phương án cực biên X = ( )
x1,x2,...,xn là phương án tối ưu của bài toán tìm Min là các số
kiểm tra k 0 , k =1,2,....,n.
(6). Cải tiến phương án cực biên
Xét bài toán quy hoạch tuyến tính tìm Max (Min) dưới dạng chính tắc, giả
sử với phương án cực biên )
X = (x1,x2,...,xn tồn tại số kiểm tra k 0 ( k 0), iều ó
chứng tỏ phương án X chưa phải là phương án tối ưu. Phương án X , với các thành
phần ược xác ịnh như sau: 12 lOMoAR cPSD| 46836766 x, = − , = j x j
z jk , j =1,2,,m, xk ,
những thành phần x,j khác bằng 0 . ở ây = x
Min j với j =1,2,m và z jk
0. X , sẽ là một phương án cực biên tốt z jk hơn so với phương án ( )
X , tức là f X , )= f (X k .
Chứng minh các tính chất trên có thể tìm ọc trong [3] trang 36-45 hoặc [4] trang 26-36.
2.2. Phương pháp ơn hình giải bài toán quy hoạch tuyến tính
2.2.1. Xây dựng bảng ơn hình
Xét bài toán quy hoạch tuyến tính tìm Max dưới dạng chính tắc:
f (x1,x2,....,xn ) =
n c j x j → Max 13 lOMoAR cPSD| 46836766 j=1 với iều kiện n
a x = b =1 ,2, , ij j i i  m = j 1 x 0 1 ,2, , . j j =  n Giả sử ( X = x ,
là một phương án cực biên với 1 x ,..., 2 x )
m thành phần dương là n ( x , tức là , . Các véc tơ cột ,1 ,..., 2 1 x ,...., x ,0,0,...,0 x 1 x ,..., 2 x m X = 2 ) m A A của ma trận m A
A ứng với các thành phần dương ược gọi là các véc tơ cơ sở, các véc tơ cột còn
lại của ma trận A ược gọi là các véc tơ phi cơ sở. Mọi véc tơ cột của ma trận A m
ều có thể biểu diễn qua các v
éc tơ cơ sở theo công thức A = k z A jk j j = 1 ( 1 k = ,2,..., )
n . Bảng ơn hình xuất phát có dạng như sau:
Bảng 2. Bảng ơn hình của bài toán quy hoạch tuyến tính 14 lOMoAR cPSD| 46836766
j =1,2,...,n thì phương án X ang xét là phương án tối ưu. Thuật toán kết thúc.
Trường hợp ngược lại, tức là tồn tại ít nhất một số kiểm tra k 0 chúng ta chuyển sang bước 2.
(2). Bước 2, kiểm tra iều kiện hàm mục tiêu bị chặn 15 lOMoAR cPSD| 46836766
Nếu có số kiểm tra k
0 mà mọi phần tử trong bảng ơn hình tương ứng với nó
ều không dương, tức là z jk 0, j =1,2,....,m thì khi ó hàm mục tiêu của bài toán
không bị chặn, bài toán không có lời giải, thuật toán kết thúc. Trường hợp ngược
lại chúng ta chuyển sang bước 3.
(3). Bước 3, tìm véc tơ ưa vào cơ sở
Trong số các số kiểm tra k 0 chúng ta chọn số kiểm tra nhỏ nhất, tức là tìm = s Min k k 0
, cột s của bảng ơn hình tương ứng với s ược gọi là cột xoay,
véc tơ A là véc tơ ược lựa chọn ể ưa vào cơ sở. s
(4). Bước 4, tìm véc tơ ưa ra khỏi cơ sở
Trên cột s của bảng ơn hình, ứng với các phần tử z js 0, j =1,2,,m , chúng ta tính = x j j
và ghi vào cột cuối cùng của bảng ơn hình. Trong các j z js
tính ược chúng ta chọn ra giá trị nhỏ nhất = r Min j
. Hàng r tương ứng với r
của bảng ơn hình ược gọi là hàng xoay, phần tử z ược gọi là phần tử xoay, véc tơ rs
A là véc tơ ược ưa ra khỏi cơ sở. r
(5). Bước 5, xây dựng bảng ơn hình của phương án cực biên mới X ,
Phương án X chưa phải là phương án tối ưu chúng ta cần chuyển sang
phương án cực biên mới X , tốt hơn so với phương án X .
A1,A2,...,Ar−1, As ,Ar+1,...,Am sẽ là hệ véc tơ cơ sở của phương án X , . Bảng ơn hình của
phương án X , ược xây dựng như sau :
• Trong cột hệ số CJ , phần tử cr ược thay bằng cs . Trong cột cơ sở, véc tơ
Ar ược thay bằng véc tơ As ; 16 lOMoAR cPSD| 46836766
• Các phần tử của hàng xoay trong bảng mới bằng các phần tử tương ứng
trong bảng cũ chia cho phần tử xoay zrs ;
• Các phần tử của cột xoay trong bảng mới bằng 0 ngoại trừ phần tử xoay bằng 1;
• Các phần tử còn lại của bảng mới z,jk ược tính theo quy tắc hình chữ nhật như sau : z z , rk js z = − jk z jk z jk z js z rs z z rk rs
• Các s ố ki ể m tra trong b ả ng m ới cũng ượ c tính theo quy t ắ c hình ch ữ nh ật như sau : , = z rk s − k k k s z rs z z rk rs
Sau khi có bảng ơn hình mới của phương án cực biến ,
X chúng ta quay
trở lại bước 1 của thuật toán. Quá trình cứ tiếp tục, sau một số hữu hạn bước hoặc
chúng ta tìm ược lời giải tối ưu của bài toán hoặc i tới kết luận là bài toán không có lời giải. Chú ý
(1) . Đối với bài to án tìm Min thuật toán hoàn toàn tương tự chỉ có tiêu
chuẩn tối ưu ở bước 1 là 0
=1 ,2,..., và ở bước 3 chúng ta sẽ chọn véc tơ j , j n A với = Max , 0
ể ưa vào cơ sở. s s k k 17 lOMoAR cPSD| 46836766
(2). ở bảng ơn hình cuối cùng ứng với phương án tối ưu nếu có số kiểm tra
k = 0 ứng với véc tơ phi cơ sở Ak thì iều ó chứng tỏ nghiệm tối ưu của 18 lOMoAR cPSD| 46836766
bài toán không duy nhất. Thực hiện phép biến ổi, ưa véc tơ Ak vào cơ sở chúng ta
sẽ thu ược nghiệm tối ưu khác của bài toán.
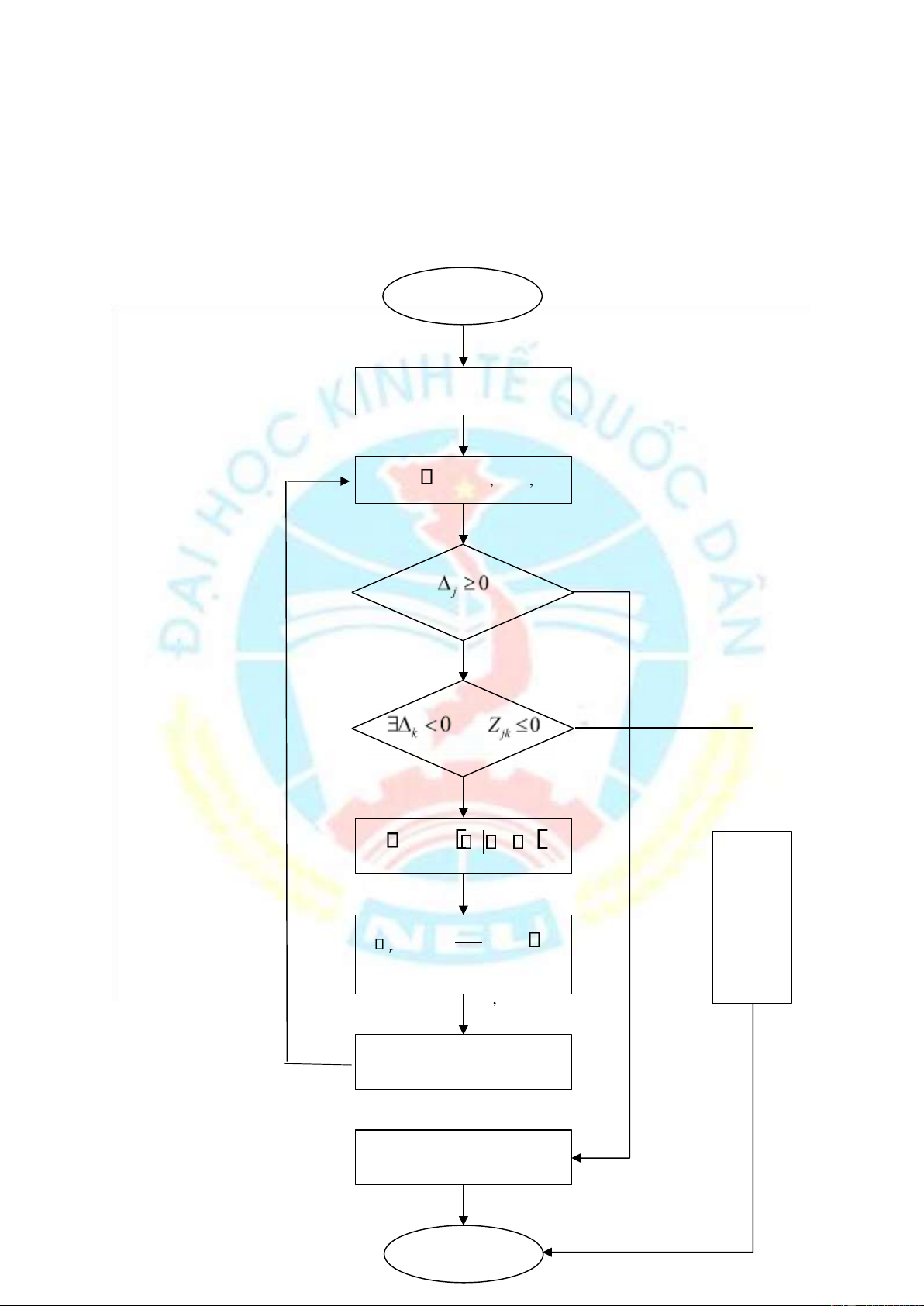
Hình 3. Thuật toán ơn hình giải bài toán tìm Max Bắt ầu
Nhập C , A , X , Z Tính = ,2, 1 ,  j , j n Đ Đ mà S Min 0 s = k k Hàm mục tiêu không x = j Z bị Min , 0 r S js Z js chặn j = 1 ,2, ,  n
Xây dựng X , Z mới X := o X pt 16 Kết thúc
Downloaded by Tr?n Lan Anh (lananh1406@gmail.com) lOMoAR cPSD| 46836766 Ví dụ
Chúng ta giải bài toán quy hoạch tuyến tính ã ược sử dụng ể minh hoạ hình học. ( ) f X = x + 1
3x2 → Max 20
Downloaded by Tr?n Lan Anh (lananh1406@gmail.com)