Bài giảng Hàm nhiều biến | Trường Đại học Nha Trang

BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC NHA TRANG BỘ MÔN TOÁN HÀM NHIỀU BIẾN Nguyễn Quang Tuấn Ngày 14 tháng 10 năm 2024 1. Hàm hai biến 1
Cho ba đại lượng x , y và z phụ thuộc vào nhau. Biểu
diễn đại lượng này qua hai đại lượng kia
z = f (x , y ).
x , y : là các biến số. 2 Một số ví dụ
a) Hàm lợi nhuận: z = f (vốn, nhân công)= f (x , y ).
b) Hàm: z = f (x , y ) = 2x 2y + xy 3 + ex+y+1. 3
Tính giá trị của hàm hai biến (Hàm 2b)
f (0, 1) = 2 × 02 × 1 + 0 × 13 + e0+1+1 = e2. Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 2 / 14
2. Các đạo hàm riêng cấp 1
Cho hàm hai biến z = f (x , y ). 1
Đạo hàm riêng cấp 1 theo biến x ′ ∂f
• Kí hiệu ngắn gọn: f hoặc . x ∂x ′ ∂f
• Kí hiệu đầy đủ: f (x , y ) hoặc (x , y ). x ∂x 2
Đạo hàm riêng cấp 1 theo biến y ′ ∂f
• Kí hiệu ngắn gọn: f hoặc . y ∂y ′ ∂f
• Kí hiệu đầy đủ: f (x , y ) hoặc (x , y ). y ∂y Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 3 / 14
3. Quy tắc thực hành tính đạo hàm riêng
Khi tính đạo hàm riêng theo biến x thì xem y là
hằng số và ngược lại.
Ví dụ 1. Cho hàm z = f (x , y ) = 2x 2y + xy 3 + ex+y+1.
Tính các đạo hàm riêng cấp 1.
Giải. Ta có các đạo hàm riêng cấp 1 là ′
f (x , y ) = 4xy + y 3 + ex+y+1, x ′
f (x , y ) = 2x 2 + 3xy 2 + ex+y+1. y Ví dụ 2. Cho hàm
z = f (x , y ) = x 2y + xy + 2x − 3y + ln(x 2 + y 2 + 1) + 2024.
Tính các đạo hàm riêng cấp 1. Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 4 / 14
4. Các đạo hàm riêng cấp 2
Cho hàm z = f (x , y ). Có 4 đạo hàm riêng cấp 2 sau ′ ′′ ′ 1 f = f
: Lần thứ nhất đạo hàm riêng theo biến x xx x x
và lần thứ hai đạo hàm riêng theo biến x . ′ ′′ ′ 2 f = f
: Lần thứ nhất đạo hàm riêng theo biến x xy x y
và lần thứ hai đạo hàm riêng theo biến y . ′ ′′ ′ 3 f = f
: Lần thứ nhất đạo hàm riêng theo biến y yx y x
và lần thứ hai đạo hàm riêng theo biến x . ′ ′′ ′ 4 f = f
: Lần thứ nhất đạo hàm riêng theo biến y yy y y
và lần thứ hai đạo hàm riêng theo biến y . Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 5 / 14
4. Các đạo hàm riêng cấp 2 - Ví dụ
Ví dụ 1. Cho hàm z = f (x , y ) = 2x 2y + xy 3 + ex+y+1.
Tính các đạo hàm riêng cấp 2.
Giải. Ta có các đạo hàm riêng cấp 1 là ′
f (x , y ) = 4xy + y 3 + ex+y+1, x ′
f (x , y ) = 2x 2 + 3xy 2 + ex+y+1. y
Các đạo hàm riêng cấp 2 là ′′
f (x , y ) = 4y + ex+y+1, xx ′′
f (x , y ) = 4x + 3y 2 + ex+y+1, xy ′′
f (x , y ) = 4x + 3y 2 + ex+y+1, yx ′′
f (x , y ) = 6xy + ex+y+1 yy Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 6 / 14
5. Các yêu cầu của buổi học 1
Giải các Bài tập 2, 3, 4 và 5. 2
Tính các đạo hàm riêng cấp 1 và cấp 2 ở Bài tập 6. 3
Giải các hệ phương trình  ′ f = 0  x ′  = 0 fy trong Bài tập 6.
(Hướng dẫn: Tính các đạo hàm riêng cấp 1 và
giải một hệ phương trình theo hai biến x và y ). Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 7 / 14
6. Bài toán cực trị tự do
6.1. Phát biểu bài toán
Tìm cực trị của hàm z = f (x , y ). 6.2. Các bước làm ′ ′
Bước 1. Tính các đạo riêng cấp 1 là f (x , y ) và f (x , y ). x y  ′
f (x , y ) = 0 
Bước 2. Giải hệ pt x → Nghiệm. ′  ( f x , y ) = 0 y
Giả sử các nghiệm là M0(x0, y0), M1(x1, y1), ...(các điểm
nghi ngờ đạt cực trị). ′′ ′′
Bước 3. Tính các đạo riêng cấp 2 là f (x , y ), f (x , y ) xx xy ′′ và f (x , y ). yy Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 8 / 14 6.2. Các bước làm
Bước 4. Xét tại điểm M0(x0, y0). Đặt và tính ′′ A = f (x xx
0, y0) (là một số) ′′ B = f (x xy
0, y0) (là một số) ′′ C = f (x yy
0, y0) (là một số)
và ∆ = B2 − AC (là một số).
Tính các số A, B, C giống như tính giá trị của một hàm
hai biến tại một điểm. Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 9 / 14 6.2. Các bước làm
Bước 5. So sánh số ∆ với số 0. 1
Trường hợp 1. Nếu ∆ > 0 thì hàm z = f (x , y )
không đạt cực trị tại M0(x0, y0). 2
Trường hợp 2. Nếu ∆ < 0 thì hàm z = f (x , y ) đạt
cực trị tại M0(x0, y0).
• Nếu A > 0 thì hàm z = f (x , y ) đạt cực tiểu.
• Nếu A < 0 thì hàm z = f (x , y ) đạt cực đại. 3
Trường hợp 3. Nếu ∆ = 0 thì chưa có kết luận về
điểm đang xét M0(x0, y0). Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 10 / 14
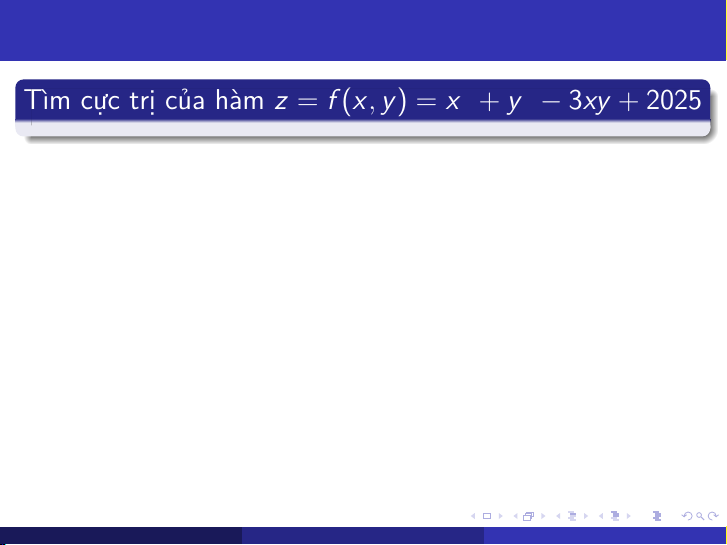
6.3 Ví dụ về bài toán cực trị tự do
Tìm cực trị của hàm z = f (x , y ) = x 3 + y 3 − 3xy + 2025
Giải. Các đạo hàm riêng cấp 1 là ′
f (x , y ) = 3x 2 − 3y , x ′
f (x , y ) = 3y 2 − 3x . y Giải hệ phương trình   x = 0   (M  ′   0)
f (x , y ) = 0
3x 2 − 3y = 0  y = 0  x   ⇐⇒ ⇐⇒  ′     ( 3  f x , y ) = 0 y 2 − 3x = 0 x = 1 y     (M  1)  y = 1 Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 11 / 14
Các đạo hàm riêng cấp 2 là ′′ ′′ ′′
f (x , y ) = 6x ,
f (x , y ) = −3,
f (x , y ) = 6y xx xy yy
• Xét tại M0(0, 0). Đặt ′′
A = f (0, 0) = 6 × 0 = 0, xx ′′
B = f (0, 0) = −3, xy ′′
C = f (0, 0) = 6 × 0 = 0. yy
và ∆ = B2 − AC = (−3)2 − 0 × 0 = 9.
Do ∆ = 9 > 0 nên hàm z = f (x , y ) không đạt cực trị tại M0(0, 0) Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 12 / 14
• Xét tại M1(1, 1). Đặt ′′
A = f (1, 1) = 6 × 1 = 6, xx ′′
B = f (1, 1) = −3, xy ′′
C = f (1, 1) = 6 × 1 = 6. yy
và ∆ = B2 − AC = (−3)2 − 6 × 6 = −27.
Do ∆ = −27 < 0 nên hàm z = f (x , y ) đạt cực trị tại M1(1, 1).
Hơn nữa, do A = 6 > 0 nên hàm đạt cực tiểu tại M1(1, 1) và
fmin = 13 + 13 − 3 × 1 × 1 + 2025 = 2024. Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 13 / 14
7. Luyện tập về Bài toán cực trị tự do 1
Thực hiện giải Bài tập 6. (Giáo trình) 2
Thực hiện giải các Bài tập bổ sung.
(Tải file bài tập từ Elearning) Nguyễn Quang Tuấn HÀM NHIỀU BIẾN Ngày 14 tháng 10 năm 2024 14 / 14