Bài giảng Phương trình vi phân | Trường Đại học Nha Trang

BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC NHA TRANG BỘ MÔN TOÁN PHƯƠNG TRÌNH VI PHÂN Nguyễn Quang Tuấn Ngày 14 tháng 10 năm 2024
1. Một số khái niệm 1
Phương trình vi phân là một phương trình có chứa
biến x, hàm y = y(x) và các đạo hàm của nó ′ ′′
F (x , y , y , y , . . . , y (n)) = 0. (1) 2
Nghiệm tổng quát của phương trình vi phân là họ các
hàm y = y(x, C1, C2, . . . , Cn) sao cho khi thay vào
phương trình (1) thì thoả mãn. 3
Nghiệm riêng của phương trình vi phân (1) là nghiệm
ứng với các giá trị C1, C2, . . . , Cn cụ thể. Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 2 / 23
2. Các loại phương trình vi phân sẽ học 1
Phương trình vi phân cấp 1 ′
• Dạng: F (x, y, y ) = 0.
• Nghiệm tổng quát y = y(x, C) hoặc φ(x, y, C) = 0.
• Nghiệm riêng thoả mãn y(x0) = a.
(Tìm C tương ứng với điều kiện này). 2
Phương trình vi phân cấp 2 ′ ′′
• Dạng: F (x, y, y , y ) = 0. • Nghiệm tổng quát:
y = y (x , C1, C2) hoặc φ(x , y , C1, C2) = 0. ′
• Nghiệm riêng thoả mãn y(x0) = a và y (x0) = b.
(Tìm C1, C2 tương ứng với hai điều kiện này). Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 3 / 23 3. Một số ví dụ 1
Mô hình toán học và phương trình vi phân:
• Nhiều vấn đề vật lý và thực tiễn liên quan đến các
đại lượng thay đổi theo thời gian.
• Để phân tích, ta chuyển bài toán sang ngôn ngữ
toán học và xây dựng mô hình toán học.
• Quá trình này thường dẫn đến phương trình vi
phân, mô tả sự thay đổi thông qua đạo hàm. 2
Một mô hình toán học tốt cần:
• Đủ đơn giản để có thể giải được.
• Mô tả sát thực tế để dự đoán được và kiểm chứng bằng dữ liệu. Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 4 / 23
Ví dụ 1: Mô hình tăng trưởng dân số Từ thực tế:
Dân số tăng nhanh khi tài nguyên dồi dào.
Khi dân số lớn, tài nguyên hạn chế → tốc độ tăng giảm dần.
Mô hình Malthus (tăng trưởng mũ): dP = rP dt
Mô hình Verhulst (Logistic): dP = P rP 1 − dt K
Ý nghĩa các tham số:
P(t) — dân số tại thời điểm t
r — tốc độ tăng trưởng nội tại (intrinsic growth rate)
K — sức chứa môi trường (carrying capacity) Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 5 / 23
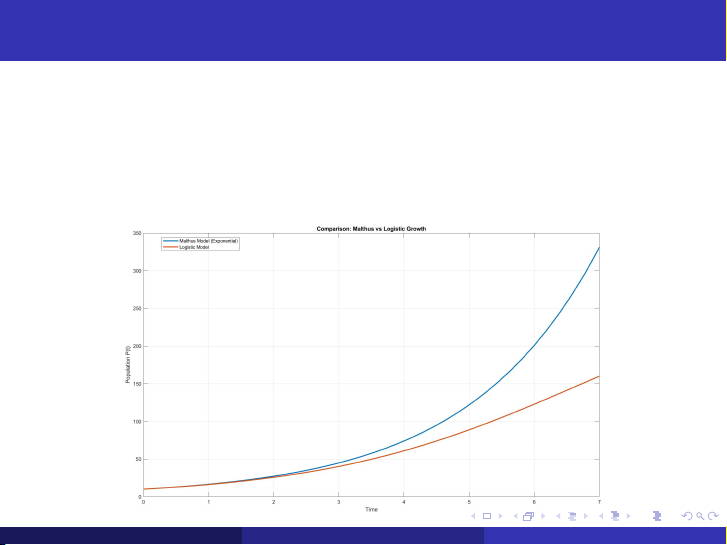
So sánh Mô hình Malthus và Logistic
- Malthus: tăng trưởng không giới hạn, dân số tiếp tục tăng theo hàm mũ.
- Logistic: tăng trưởng bị giới hạn bởi sức chứa môi trường K. Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 6 / 23
Ví dụ 2: Newton’s Law of Cooling
Thực tế: Một vật nóng đặt trong môi trường mát - Nhiệt độ vật
thay đổi theo thời gian - Tốc độ thay đổi nhiệt độ tỷ lệ với hiệu số
nhiệt độ giữa vật và môi trường. Mô hình toán học:
dT = −k(T − Tmôi trường) dt
Ý nghĩa các tham số:
T (t) — nhiệt độ của vật tại thời điểm t
Tmôi trường — nhiệt độ môi trường
k > 0 — hằng số làm mát (cooling rate)
Nghiệm của phương trình: T (t) = T + ( ) môi trường
T0 − Tmôi trường e−kt Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 7 / 23
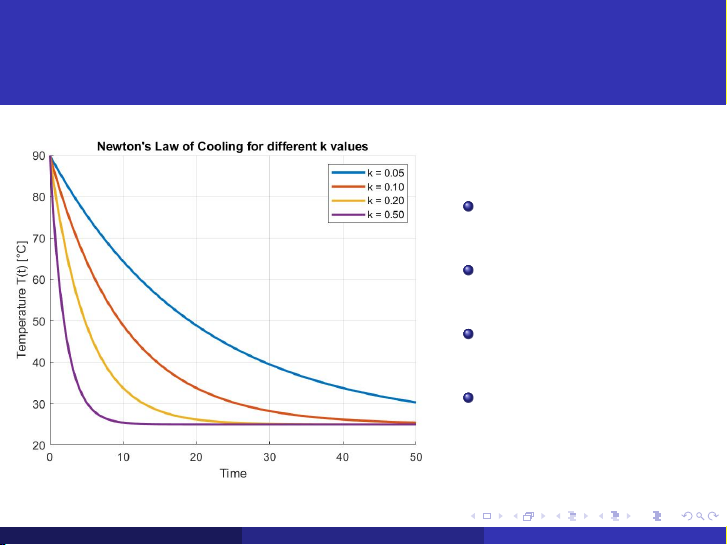
Newton’s Law of Cooling: So sánh các hằng số làm mát
Chú thích các tham số:
T (t) — nhiệt độ vật tại thời điểm t
Tmôi trường — nhiệt độ môi trường T = 90◦ 0 C — nhiệt độ ban đầu của vật
k — hằng số làm mát:
giá trị lớn → vật mát nhanh hơn Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 8 / 23
Ví dụ 3: Mô hình Tiền gửi tiết kiệm
Thực tế: Số dư tài khoản thay đổi theo thời gian nhờ lãi
suất - Lãi suất có thể hằng số hoặc thay đổi theo thời gian. Mô hình toán học: dS = rS dt
Nghiệm (lãi suất hằng số):
S(t) = S0ert
Ý nghĩa các tham số:
S(t) — số dư tài khoản tại thời điểm t
S0 — số tiền ban đầu
r — lãi suất liên tục Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 9 / 23
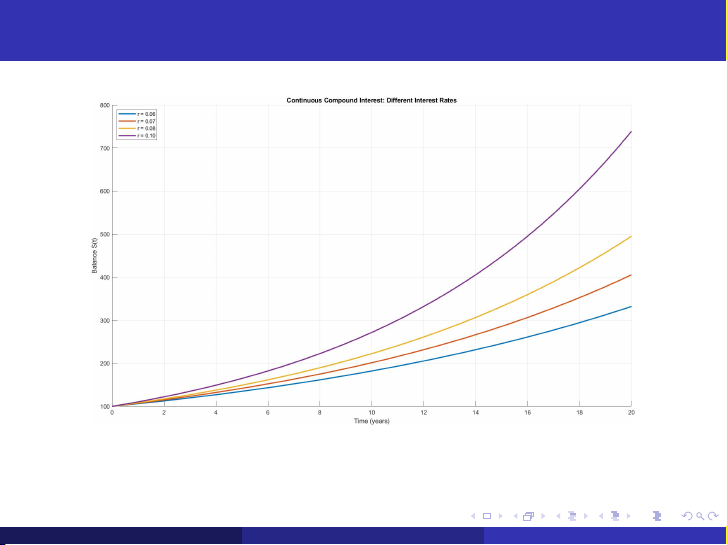
Tiền gửi tiết kiệm: So sánh lãi suất khác nhau
Chú thích: S(t) — số dư tài khoản tại thời điểm t ;S0 — số tiền
ban đầu ; r — lãi suất liên tục: giá trị lớn → số dư tăng nhanh hơn. Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 10 / 23
4. Phương trình vi phân tuyến tính cấp 1 ′ 1
Dạng: y + p(x)y = f (x). 2 Nghiệm tổng quát R
y = Z f (x )e p(x)dx dx + C e− R p(x)dx . (2) 3
Nghiệm riêng: Tìm C thoả mãn điều kiện y(x0) = a. Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 11 / 23 Các bước làm
Xác định p(x) = . . . và f (x) = . . .. Tính tích phân Z Z
p(x )dx = . . .
và suy ra − p(x)dx = . . . Tính R
e p(x)dx = . . .
và e−R p(x)dx = . . .
Vậy nghiệm tổng quát của phương trình đã cho là R
y = Z f (x )e p(x)dx dx + C e− R p(x)dx .
Nếu bài toán cho điều kiện y(x0) = a thì tìm C và
kết luận: Vậy nghiệm riêng của hệ là... Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 12 / 23
Ví dụ về giải ptvp tuyến tính cấp 1
Giải phương trình vi phân: ′
y + 2xy = 2xe−x2 (Bài 2a)
Giải. Ta có p(x ) = 2x và f (x ) = 2xe−x2. Tính các tích phân Z
p(x )dx = Z 2xdx = x 2, và Z Z −
p(x )dx = −
2xdx = −x2. Suy ra R
e p(x)dx = ex2
và e−R p(x)dx = e−x2. Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 13 / 23
Vậy nghiệm tổng quát của phương trình đã cho là R
y = Z f (x )e p(x)dx dx + C e− R p(x)dx = Z 2
xe−x2ex2dx + C e−x2 = Z 2
xdx + C e−x2 =
x 2 + C e−x2,
C là hằng số.
Chú ý. Nếu có thêm điều kiện y (x0) = a thì thay vào giải
tìm C. Kết luận nghiệm riêng của hệ là... Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 14 / 23 Luyện tập
Bài 1. Xác định p(x), f (x) cho các phương trình sau a) ′
y + 2y = x 3e−2x . b) ′
y + 4y = e−4x thoả mãn y (1) = 3.
Bài 2. Giải các phương trình vi phân ở Bài 1. Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 15 / 23
5. Phương trình vi phân tuyến tính cấp 2
hệ số hằng với vế phải có dạng đặc biệt Dạng: ′′ ′
y + py + qy = Pn(x )eαx trong đó
p, q, α là các hằng số đã biết (cho trong đề bài).
Pn(x ) = a0 + a1x + a2x 2 + · · · + anx n là đa thức bậc
n đã biết (cho trong đề bài).
Các kiến thức cũ cần nắm 1
Giải phương trình bậc 2: ax2 + bx + c = 0. 2
Kỹ năng tính đạo hàm của hàm 1 biến. Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 16 / 23 Các bước làm
Bước 1. Phương trình thuần nhất tương ứng là ′′ ′
y + py + qy = 0,
có phương trình đặc trưng là  k  1 =
k2 + pk + q = 0 ⇔ k2 =
Vậy nghiệm tổng quát của phương trình thuần nhất là y = . . .
(Tra vào bảng trong file .pdf đã upload trên E - Learning
của hệ thống NTU để xác định y ). Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 17 / 23 Bước 2.
Tìm một nghiệm riêng y∗ của phương trình không thuần nhất có dạng. Số α
Dạng của nghiệm riêng y ∗
α ̸= k1, k2
y ∗ = A0 + A1x + A2x 2 + · · · + Anx n eαx α = k hoặc + 1 α = k2 y ∗ = A0
A1x + A2x 2 + · · · + Anx n .x .eαx
α = k1 = k2
y ∗ = A0 + A1x + A2x 2 + · · · + Anx n .x 2.eαx
trong đó các số A0, A1, A2, . . . , An cần được xác định ở Bước 3.
Bước 3. Tìm các số A0, A1, A2, . . . , An và xác định y ∗.
Tính các đạo hàm (y∗)′ và (y∗)′′.
Thay y∗, (y∗)′ và (y∗)′′ vào phương trình không thuần nhất
⇒ rút gọn hai vế cho thừa số eαx ⇒ so sánh hai đa thức
⇒ hệ phương trình theo A0, A1, A2, . . . ⇒ Giải hệ này.
Thay các số A0, A1, A2, . . . tìm được ở trên vào biểu thức của y∗. Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 18 / 23
Bước 4. Nghiệm tổng quát của phương trình không thuần nhất là
Y = y + y ∗.
Giải phương trình vi phân: ′′ ′
y + 3y − 4y = (6x + 1)e2x .
• Phương trình thuần nhất tương ứng là ′′ ′
y + 3y − 4y = 0,
có phương trình đặc trưng là  k  1 = 1
k2 + 3k − 4 = 0 ⇔ .  k2 = −4
Nghiệm tổng quát của phương trình thuần nhất là
y = C1ex + C2e−4x . Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 19 / 23
• Do α = 2 ̸= k1, k2 và Pn(x) = 6x + 1(n = 1) nên một
nghiệm riêng y∗ của phương trình không thuần nhất có dạng
y ∗ = (A + Bx )e2x . • Ta có
(y∗)′ = (2A + B + 2Bx) e2x
(y∗)′′ = (4A + 4B + 4Bx) e2x
Thay y∗, (y∗)′ và (y∗)′′ vào phương trình không thuần nhất, ta được Nguyễn Quang Tuấn PHƯƠNG TRÌNH VI PHÂN Ngày 14 tháng 10 năm 2024 19 / 23