lOMoAR cPSD| 47305584
TRƯỜNG ĐẠI HỌC CÔNG NGHIỆP
THÀNH PHỐ HỒ CHÍ MINH
KHOA KHOA HỌC CƠ BẢN
Giảng viên: Ngô Quốc Nhàn BÀI GIẢNG TOÁN CAO CẤP 1
Thời lượng giảng dạy: 30 tiết
TP. HỒ CHÍ MINH – 2021 LƯU HÀNH NỘI BỘ MỤC LỤC lOMoAR cPSD| 47305584
Chương 1. GIỚI HẠN – SỰ LIÊN TỤC CỦA HÀM SỐ MỘT BIẾN SỐ ......................... 4
Bài 1. GIỚI HẠN HÀM SỐ .......................................................................................... 4
1.1. Bổ túc về hàm số ................................................................................................. 4
1.2. Dãy số ................................................................................................................ 8
1.3. Giới hạn của hàm số .......................................................................................... 11
Bài 2. ĐẠI LƯỢNG VÔ CÙNG BÉ ............................................................................ 16
3.1. Đại lượng vô cùng bé ........................................................................................ 16
3.2. Tính chất ........................................................................................................... 17
3.3. Quy tắc ngắt bỏ vô cùng bé cấp cao .................................................................. 17
Bài 3. HÀM SỐ LIÊN TỤC ........................................................................................ 18
2.1. Hàm số liên tục ................................................................................................. 18
2.2. Các ịnh lý ........................................................................................................ 19
BÀI TẬP CHƯƠNG 1................................................................................................. 21
Chương 2. PHÉP TÍNH VI PHÂN HÀM SỐ MỘT BIẾN ............................................... 24
Bài 1. ĐẠO HÀM VÀ VI PHÂN ................................................................................ 24
1.1. Các ịnh nghĩa .................................................................................................. 24
1.2. Quy tắc ạo hàm ............................................................................................... 25
Bài 2. ĐỊNH LÝ GIÁ TRỊ TRUNG BÌNH VÀ QUY TẮC L’HOSPITAL ................... 28
2.1. Định lý giá trị trung bình (tham khảo) ............................................................... 28
2.2. Quy tắc L’Hospital ............................................................................................ 28
Bài 3. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT ................................................ 29
3.1. Cực trị ịa phương ............................................................................................ 29
3.2. Giá trị lớn nhất – Giá trị nhỏ nhất ...................................................................... 30
BÀI TẬP CHƯƠNG 2................................................................................................. 32
Chương 3. PHÉP TÍNH TÍCH PHÂN HÀM SỐ MỘT BIẾN .......................................... 33
Bài 1. TÍCH PHÂN BẤT ĐỊNH .................................................................................. 33
1.1. Định nghĩa ........................................................................................................ 33
1.2. Phương pháp ổi biến ....................................................................................... 34
1.3. Phương pháp tích phân từng phần ..................................................................... 37
Bài 2. TÍCH PHÂN XÁC ĐỊNH .................................................................................. 38
2.1. Định nghĩa ........................................................................................................ 38
2.2. Công thức Newton – Leibnitz ........................................................................... 39
Bài 3. TÍCH PHÂN SUY RỘNG ................................................................................. 41
3.1. Tích phân suy rộng loại 1 .................................................................................. 41
3.2. Tích phân suy rộng loại 2 .................................................................................. 44
BÀI TẬP CHƯƠNG 3................................................................................................. 46
Chương 4. LÝ THUYẾT CHUỖI .................................................................................... 48
Bài 1. KHÁI NIỆM CƠ BẢN VỀ CHUỖI SỐ ............................................................. 48
1.1. Định nghĩa ........................................................................................................ 48
2.2. Điều kiện cần ể chuỗi số hội tụ ........................................................................ 49 2 lOMoAR cPSD| 47305584
2.3. Tính chất ........................................................................................................... 49
Bài 2. CHUỖI SỐ DƯƠNG ......................................................................................... 50
2.1. Định nghĩa ........................................................................................................ 50
2.2. Các ịnh lý so sánh ........................................................................................... 50
2.3. Các tiêu chuẩn hội tụ ......................................................................................... 51
Bài 3. CHUỖI SỐ CÓ DẤU TÙY Ý ........................................................................... 52
3.1. Chuỗi số có dấu tùy ý ........................................................................................ 52
3.2. Chuỗi số an dấu .............................................................................................. 53
BÀI TẬP CHƯƠNG 4................................................................................................. 54
Chương 5. HÀM SỐ NHIỀU BIẾN SỐ ........................................................................... 56
Bài 1. CÁC KHÁI NIỆM CƠ BẢN ............................................................................. 56
1.1. Tập hợp trong Rn ............................................................................................... 56
1.2. Hàm số nhiều biến ............................................................................................ 57
Bài 2. ĐẠO HÀM RIÊNG – VI PHÂN ....................................................................... 58
2.1. Đạo hàm riêng .................................................................................................. 58
2.2. Vi phân ............................................................................................................. 60
Bài 3. CỰC TRỊ CỦA HÀM SỐ HAI BIẾN ................................................................ 63
3.1. Cực trị ịa phương ............................................................................................ 63
3.2. Cực trị tự do ...................................................................................................... 64
3.3. Cực trị có iều kiện ........................................................................................... 66
BÀI TẬP CHƯƠNG 5................................................................................................. 67
Chương 1. GIỚI HẠN – SỰ LIÊN TỤC CỦA HÀM SỐ MỘT BIẾN SỐ
Bài 1. GIỚI HẠN HÀM SỐ
1.1. Bổ túc về hàm số 1.1.1. Định nghĩa
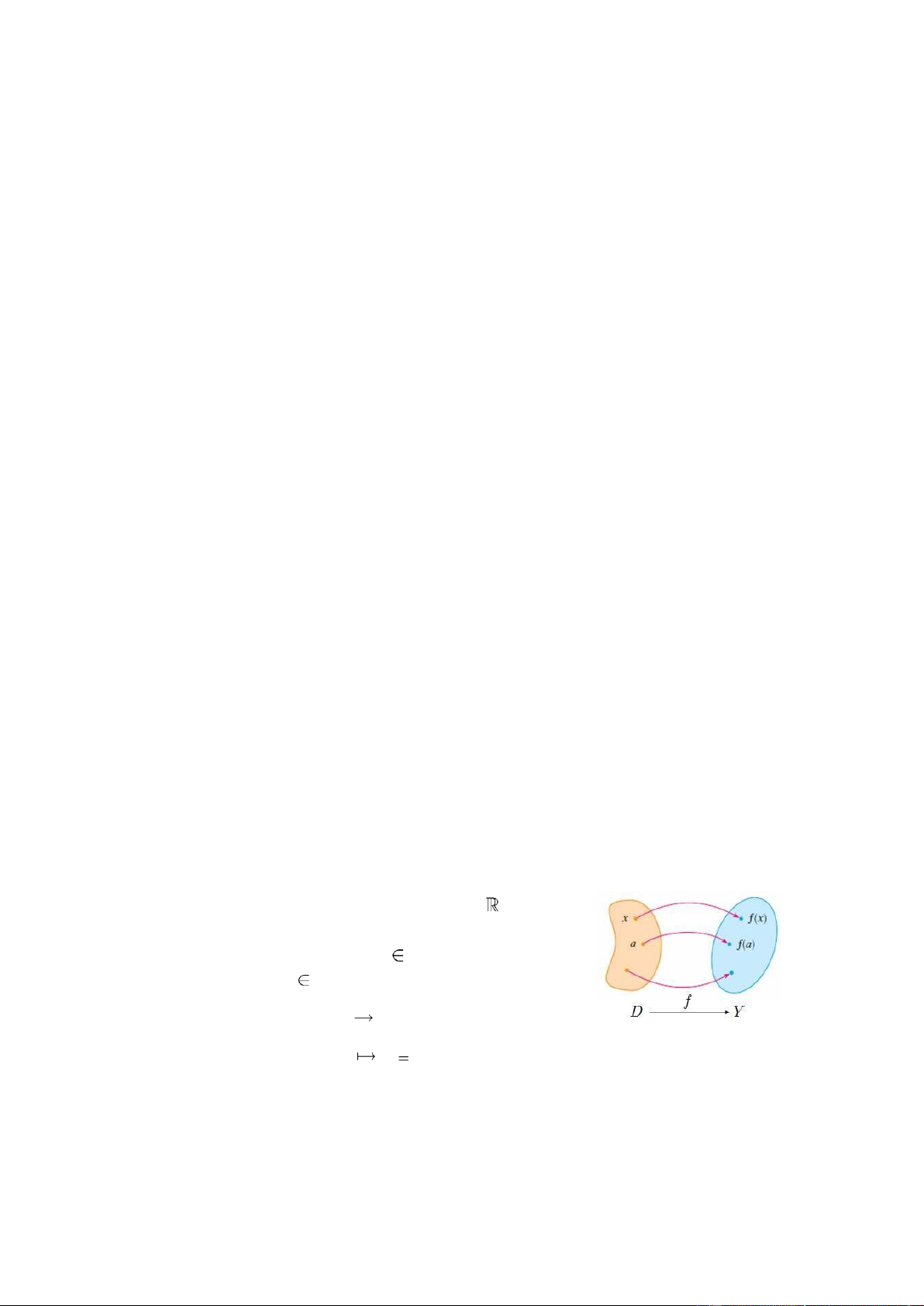
Xét hai tập con khác rỗng D và Y của . Hàm số f
là một quy tắc (hay ánh xạ) cho tương ứng mỗi
phần tử x D với duy nhất một phần tử y Y , ký hiệu là f x( ) f D: Y x y f x( )
• Tập D ược gọi là miền xác ịnh (MXĐ - domain) của hàm số f , ký hiệu là D . f 3 lOMoAR cPSD| 47305584
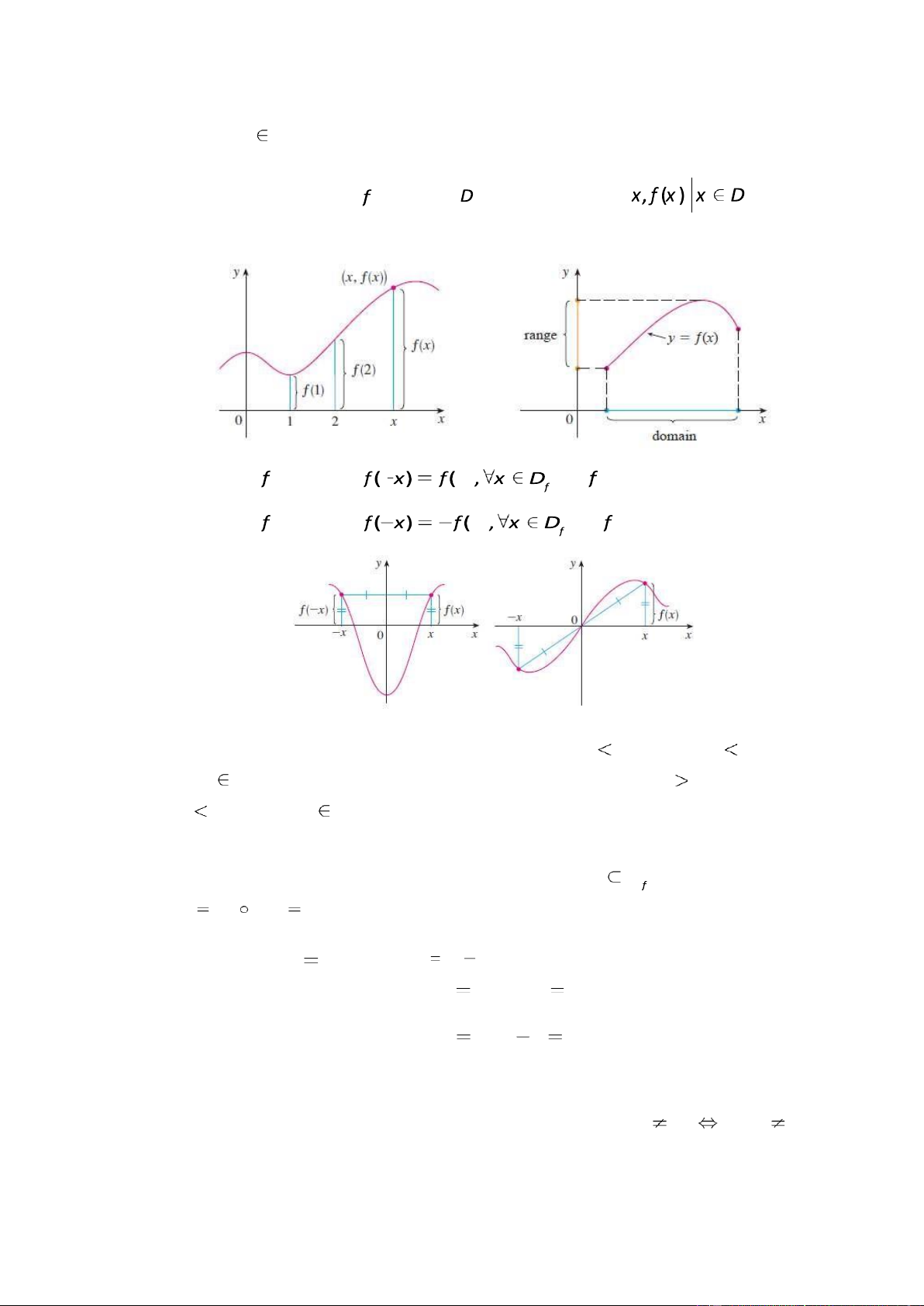
• Tập f D( f ) { ( )f x |x Df } ược gọi là miền giá trị (range) của hàm f . phẳng Oxy .
• Đồ th ị (graph) c ủ a hàm có MXĐ là t ậ p h ợp iể m trên m ặ t • Nế u hàm th ỏ a mãn thì
ượ c g ọ i là hàm s ố ch ẵ n . • Nế u hàm th ỏ a mãn thì
ượ c g ọ i là hàm s ố l ẻ .
• Hàm f ược gọi là ồng biến trên (a b; ) nếu f x( ) với
1 f x( 2) khi x1 x2
x x1, 2 (a b; ); f
ược gọi là nghịch biến trên (a b; ) nếu f x( ) với
1 f x( 2) khi x1 x2
x x1, 2 (a b; ). 1.1.2. Hàm số hợp
Giả sử hai hàm số f và g thỏa mãn G ó, hàm số g D . Khi h x( ) (f g
x)( ) f g x( ( )) ược gọi là hàm số hợp của f và g .
Ví dụ 1. Xét f x( ) 3x2 và g x( ) x 1, ta có:
• Hàm số hợp của f và g là f g x( ( )) 3( ( ))g x 2 3x2 6x 3.
• Hàm số hợp của g và f là g f x( ( )) f x( ) 1 3x2 1.
1.1.3. Hàm số ngược
• Hàm số f ược gọi là song ánh (one-to-one function) nếux1 x2 f x( )1 f x( 2) 4 lOMoAR cPSD| 47305584 .
• Xét hàm song ánh f có MXĐ D và miền giá trị G . Khi ó, hàm số ngược của f , ký
hiệu là f , có MXĐ
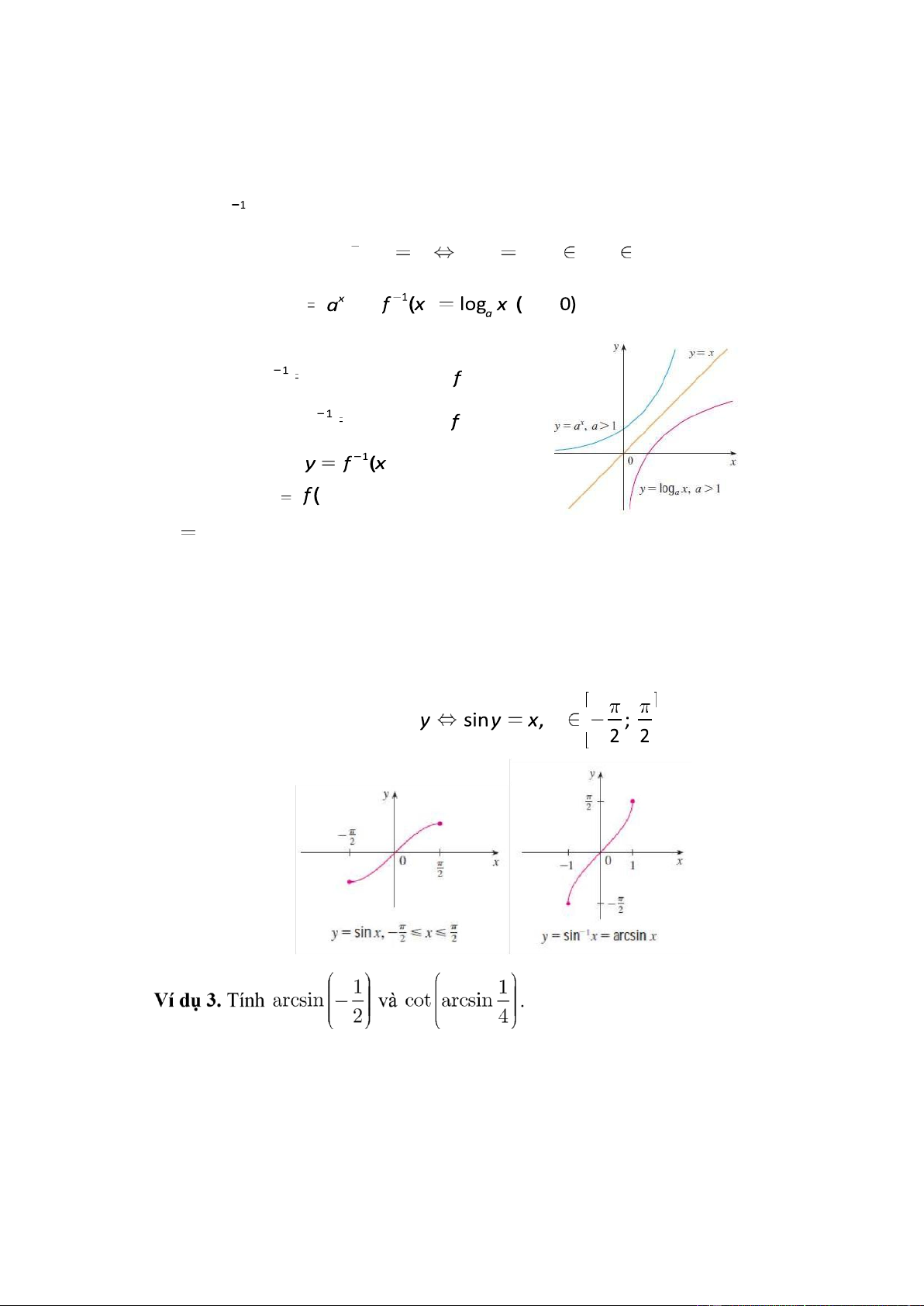
G và miền giá trị D ược ịnh nghĩa f 1( )y x f x( ) y x( D y, G). Ví dụ 2. thì . Nếu f x( ) Chú ý • MXĐ của f
mi ề n giá tr ị c ủ a , và miền giá MXĐ củ a . trị của f • Đồ thị của ố i x ứ ng v ới ồ hàm thị của hàm qua ườ ng th ẳ ng y y x .
1.1.4. Hàm số Lượng giác ngược
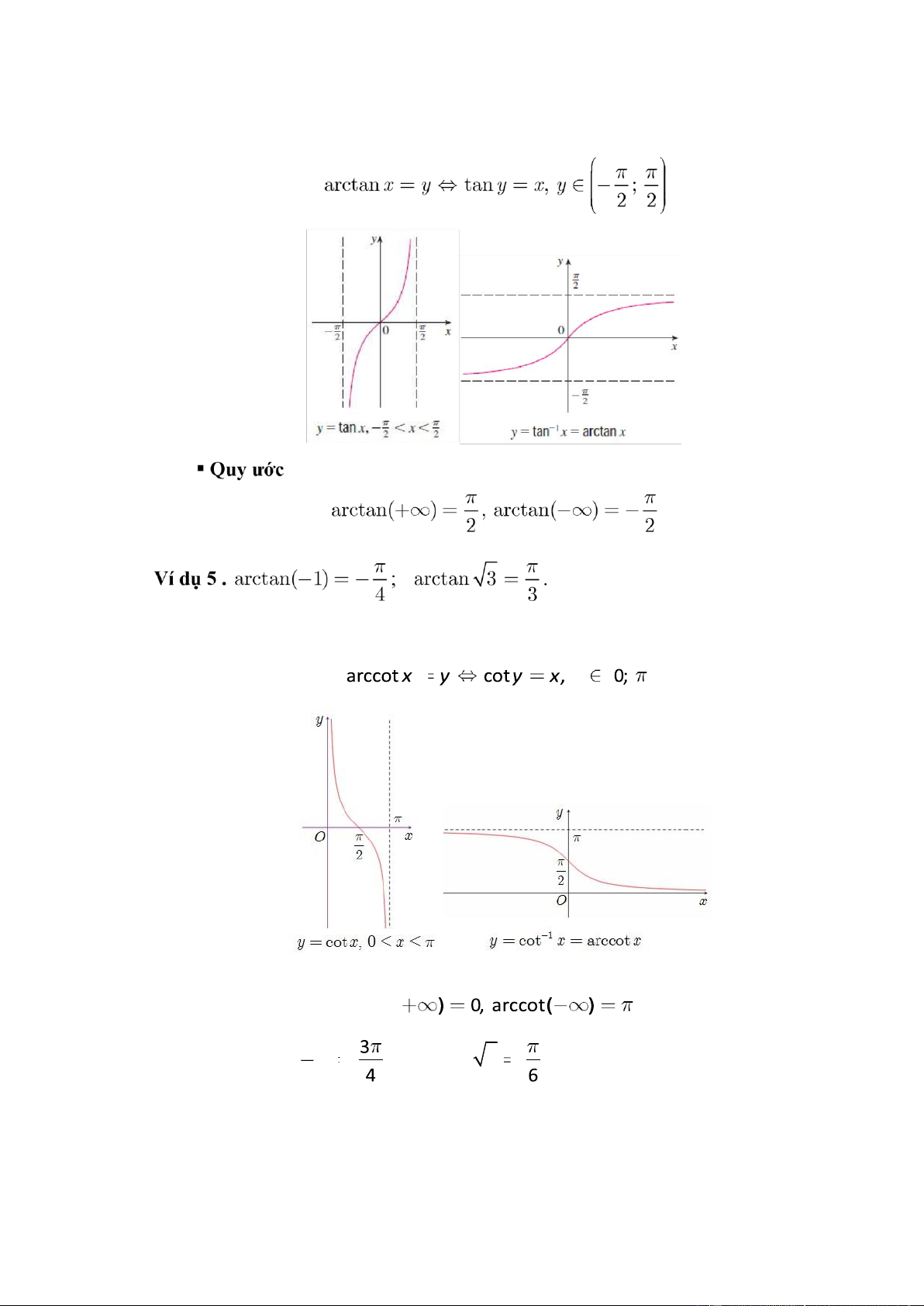
1.1.4.1. Hàm số y = arcsin x arcsinx Giải. 5 lOMoAR cPSD| 47305584
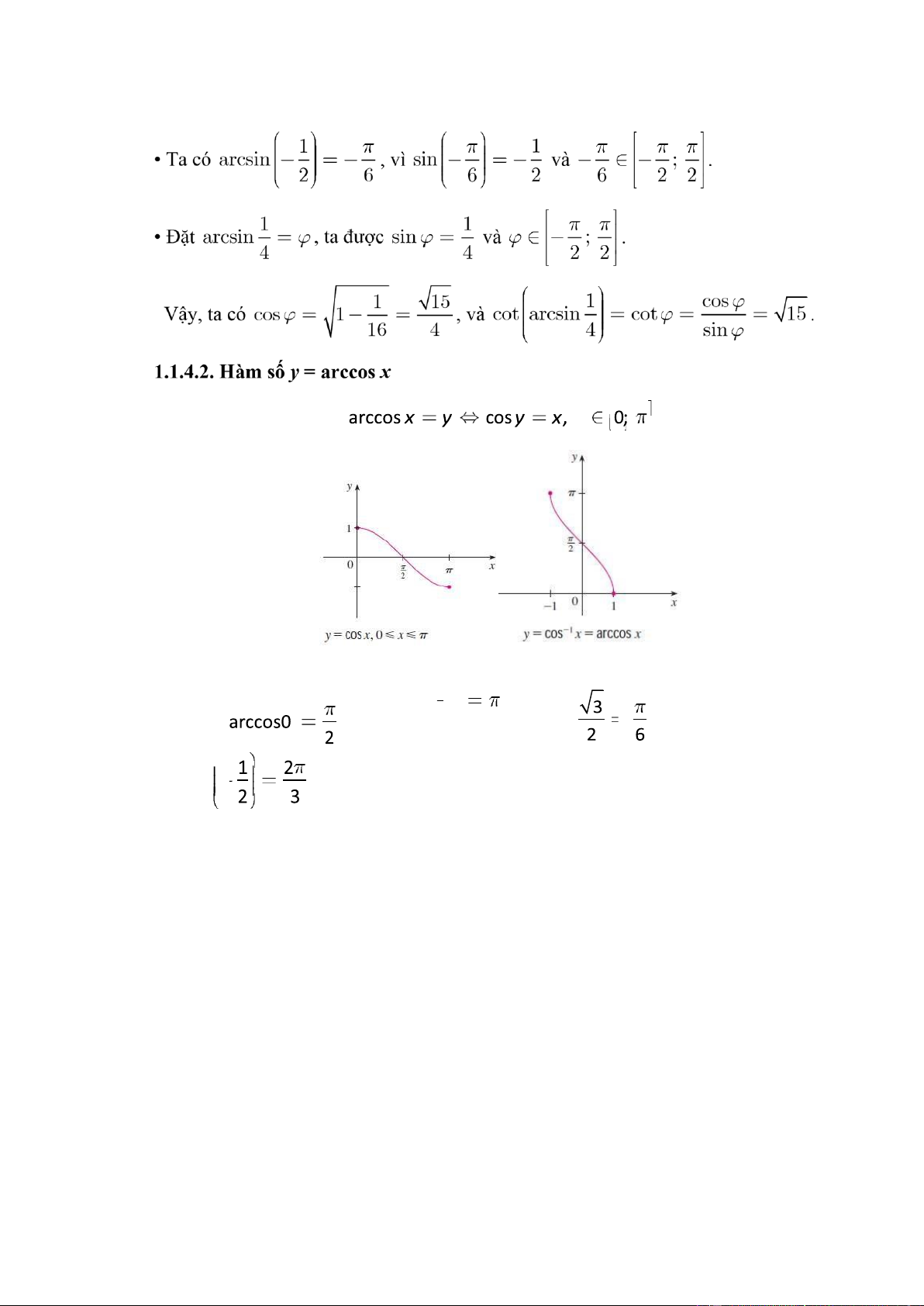
Ví d ụ 4. ; arccos( 1) ; arccos ; arccos 6 lOMoAR cPSD| 47305584
1.1.4.3. Hàm số y = arctan x
1.1.4.4. Hàm số y = arccot x ▪ Quy ước arccot( Ví dụ 6.arccot( 1) ; arccot 3 . 1.2. Dãy số 7 lOMoAR cPSD| 47305584
1.2.1 Định nghĩa. Dãy số là một ánh xạ từ vào . x: → n x( )n =xn =1 Ví dụ 1. xn
, n=1,2,3, …; xn = sinn n
Định nghĩa 1. Cho dãy số xn . a ược gọi là giới hạn của dãy xn nếu:
0, N0 N : n N0 xn −a .
Ký hiệu: a = lim→ xn. n Ví dụ 2 .lim 1 = 0 n→ n M n M
Định nghĩa 2. Dãy số x ( )
n gọi là bị chặn trên (dưới ) nếu xn n , n .
Dãy số xn gọi là bị chặn nếu dãy bị chặn trên và bị chặn dưới.
Ví dụ 3. Dãy số an ,an = sinn bị chặn vì an 1, n.
Dãy số bn = +n2 1 không bị chặn .
Định nghĩa 3. Dãy số an gọi là tăng nếu an an+1, n.
Dãy an gọi là giảm nếu an an+1, n .
Dãy số tăng hay giảm gọi chung là ơn iệu.
Ví dụ 4. Dãy số a an , n = +n 1 là dãy số tang;
Dãy số a an , n =
2n+1 là dãy số giảm. 3n 8 lOMoAR cPSD| 47305584
1.2.2 Định lý. Dãy số có giới hạn thì bị chặn . Ví dụ 5 . Dãy số 1 1
có giới hạn là 0 nên bị chặn . Dễ dàng thấy 1 n. n +1 n+1
Chú ý: Dãy số bị chặn nhưng có thể không có giới hạn . Ví dụ 6. an=(-1)n
Định lý. Cho an , bn là hai dãy số và tồn tại lima , . Ta có: n limbn n→ n→
i) lim→ (an +bn) = ii)lim ak = n kliman→ n,
limn→ an+limn→ bn ; n k n→ lim a iii) lim→ (a a
n.bn) = nlim→ an n .limn→ bn ;
iv) lim n = n→ ,bn 0; lim bn 0 bn lim b n n n→ n→ n→
Ví dụ 7.Tính giới hạn : lim n→ 3 1 = lim
lim→ 2n33n+2n−21+1n→ n3n(23(+ +n3 1n− n13n1)3) = nlim→ nlim(→ (2+ +n 1n− n3n1)3 ) = =02 0 n Tương tự, ta có: Ví dụ 8. lim = = n→
Định nghĩa. Dãy số an gọi là có giới hạn () nếu : 9 lOMoAR cPSD| 47305584
M 0, n0 : n n0 an M liman =+
M 0, n0 : n n0 an M n→ liman =−
m 0, n0 : n n0an m n→
Ký hiệu: liman = ( ) n→
Ví dụ 9. limn2 =+ ; lim(−n3) =− . n→ n→
1.2.3 Một số kết quả cần nhớ: i) limC = C ;
ii) nlim→+ an = 0 nlim→+ n→ an = 1 iii) limn→ iv) liman = 0 ; a 1 np = 0 ; p 0; n→ 1
v) lim nn=1 ;lim an=1,a 0 n→ n→
Ví dụ 10.Tính lim(3 n3 −2n2 +1−n) n→ 10 lOMoAR cPSD| 47305584 lim( ( ) ( )
3 n3 −2n2 +1−n)=lim 3 − 23 n3
2 2n 32 +231−n3 2 −2 1 + = = 2
n→ n→ n ( −2 1+ ) 3 23 3 2 +
−2n +1 + n −2n +1 2 − 1 2 + 2 → 2 2 2 1 2 1 3 3 (
.n+n2 n→ 1− + 3 + 1− + + 1 3 )
3 n −2n +1 .n+n2 = =
Định lý. Cho các dãy số xn , yn , zn thỏa: xn yn zn, n
Nếu limxn = limzn = a thì lim yn = a.
n→ n→ n→ nsin(n!)
Ví dụ 11.Tính: limn 2 . → n +1
Ta có: −2 n nsin(2 n!) 2n và lim 2n = lim n =0. n +1 n +1 n +1 n→ n +1 n→ n2(1+ 12 ) n nsin(n!) Ta có: lim 2 = 0 n +1 11 lOMoAR cPSD| 47305584 n→
Định lý. Dãy số ơn iệu và bị chặn thì hội tụ. 1
Ví dụ 12. Cho dãy số an có an = 1 + 1 + 1 + +... . Chứng minh 1.2 2.3 3.4 n n( +1)
dãy số an hội tụ. Ta có: an+1 = 1 + 1 +...+ 1 + 1 =an + 1 an 1.2 2.3
n(n+1) (n+1)(n+ 2) (n+1)(n+ 2)
(an) là dãy số ơn iệu tăng. Mặt khác, ta có:
an =1− 1 + 1 − 1 + 1 +...+ 1 − 1 =1− 1 1, n 2 2 3 3 n n−1 n−1 Vậy (a ) n nhội tụ
Chú ý:Từ trên ta thấy lim an =lim(1− 1 ) =1 n→ n+1 n→
Định nghĩa. lim(1+ 1)n =e 2,718281828... n n→ Tổng quát ta cólim 1+ s n =es n→ n
1.3. Giới hạn của hàm số
1.3.1. Giới hạn tổng quát 12 lOMoAR cPSD| 47305584
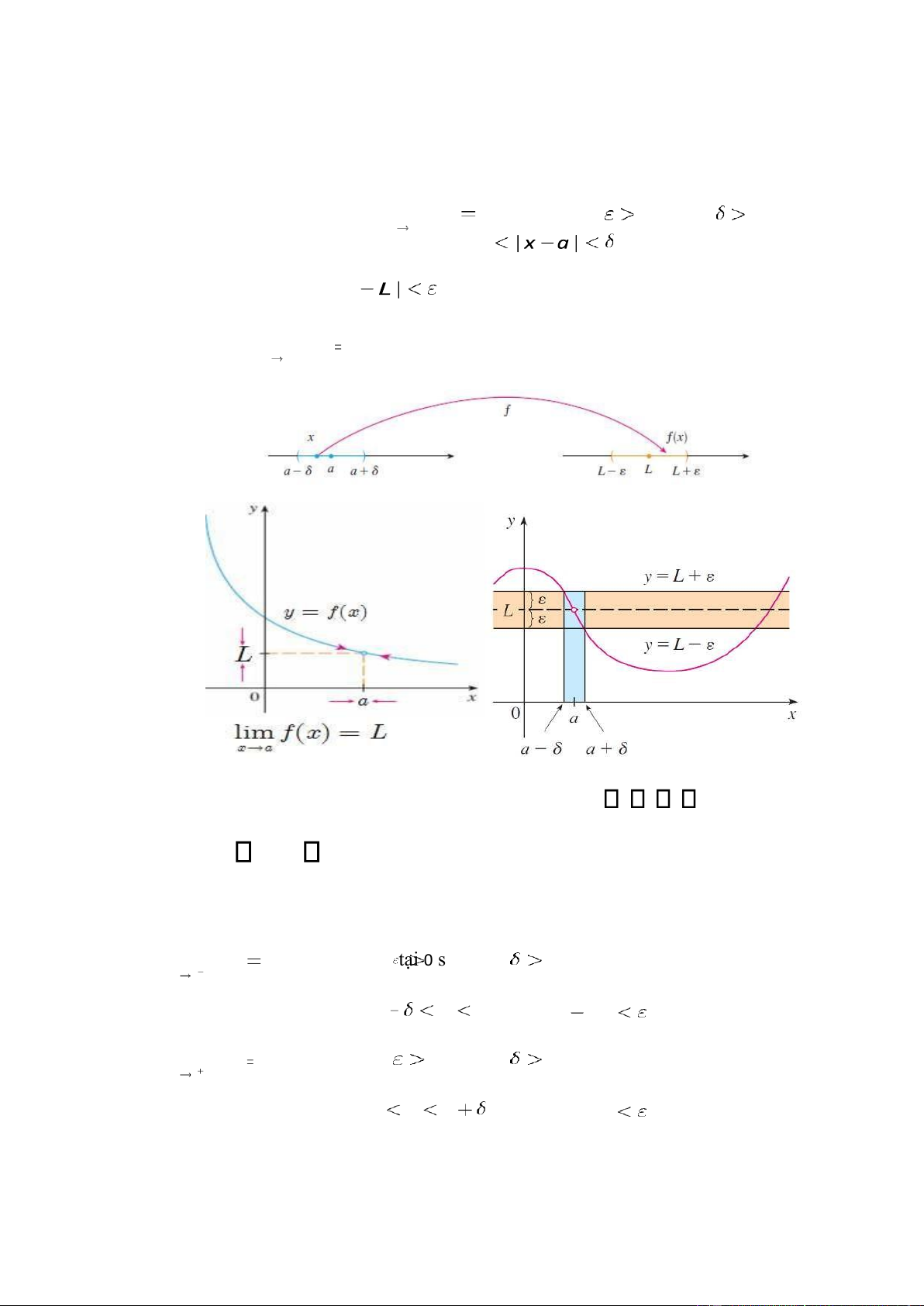
Định nghĩa
Xét hàm f xác ịnh trên khoảng chứa iểm a . Ta nói rằng giới hạn của f x( ) khi x tiến
ến a là L , và ta viết lim ( )f x L nếu với mọi 0 tồn tại 0 sao cho: x a nếu 0 thì | ( )f x .
Kí hiệu là lim ( )f x
L và ọc là “giới hạn củaf x( ), khi x tiến ến a , bằngL ” x a
Định lý. lim ( )x a→ f x = L khi và chỉ khi với mọi dãy xn , xn hội tụ
về a thì f x( ) n hội tụ về L .
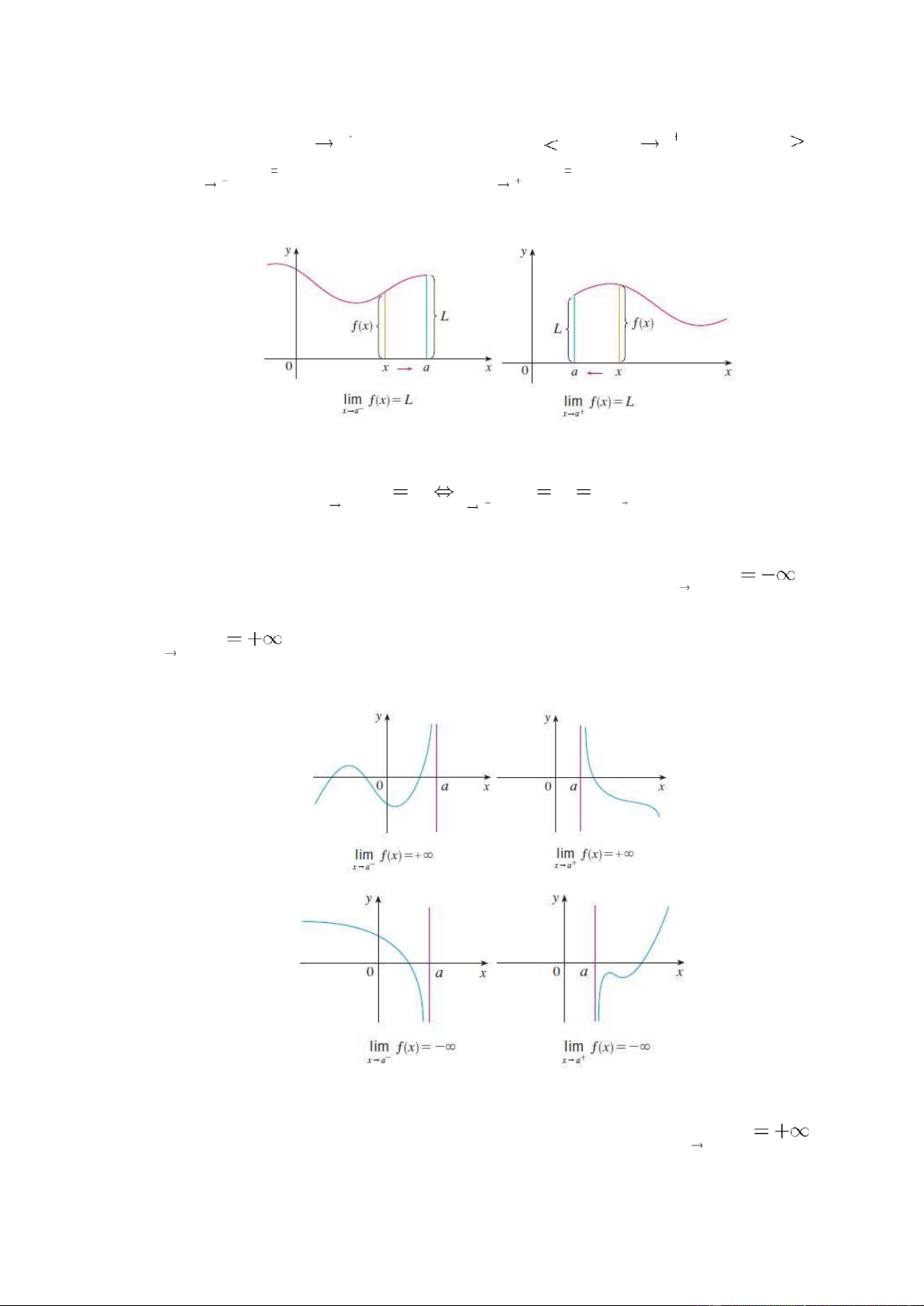
1.3.2. Giới hạn một phía Định nghĩa
• lim ( )f x L nếu với mọi 0 tồn tại 0 sao cho: x a nếu a
x a thì | ( )f x L | .
• lim ( )f x L nếu với mọi 0 tồn tại 0 sao cho: x a nếu a x a thì | ( )f x L | . 13 lOMoAR cPSD| 47305584
Chú ý: Ký hiệu “x
a ” nghĩa là ta chỉ xét x a , và “x
a ” nghĩa là x a . lim ( )f x
L gọi là giới hạn trái; lim ( )f x
L gọi là giới hạn phải x a x a
Định lý lim ( )f x L lim ( )f x L lim ( )f x x a x a x a
1.3.3. Giới hạn vô cùng
Xét hàm f x( ) xác ịnh trên khoảng chứa iểm a . Khi ó, lim ( )f x hay x a lim ( )f x
có nghĩa là giá trị tuyệt ối của f x( ) vô cùng lớn khi x tiến ến a x
a nhưng khác a . Có 4 dạng sau: Định nghĩa
• Giả sử hàm số f xác ịnh trên khoảng chứa iểm a . Khi ó lim ( )f x có x a 14 lOMoAR cPSD| 47305584
nghĩa là với mọi giá trị dương M tồn tại sao cho: nếu 0 thì f x( ) M .
• Giả sử hàm số f xác ịnh trên khoảng chứa iểm a . Khi ó lim ( )f x có x a
nghĩa là với mọi giá trị âm N tồn tại sao cho: nếu 0 thì f x( ) N .
1.3.4. Quy tắc giới hạn
Giả sử k là hằng số và lim ( )f x , lim ( )g x tồn tại hữu hạn. Khi ó x a x a 1) lim[ . ( )]k f x k.lim ( )f x x a x a
2) lim[ ( )f x g x( )] lim ( )f x lim ( )g x x a x a x a
3) lim[ ( ) ( )]f x g x lim ( ).lim ( )f x g x x a x a x a
4) lim f x( ) lim ( )x a f x nếu lim ( )g x 0 x a g x( ) lim ( )g x x a x a lim ( )g x 5)lim [ ( )]f x g x( ) lim ( )f x x a
nếu lim ( )f x 0 x a x a x a
Chú ý: Các quy tắc trên vẫn úng nếu lim ( )f x , lim ( )g x x a x a
ngoại trừ 7 trường hợp sau gọi là 7 dạng vô ịnh. 0 0 0 ; , − ;0. ,1 ,0 , 0 Định lý Nếu f x( )
g x( ) khi x tiến ến a (x a ) và lim ( )f x , lim ( )g x tồn tại thì 15 lOMoAR cPSD| 47305584 x a x a lim ( )f x lim ( )g x . x a x a
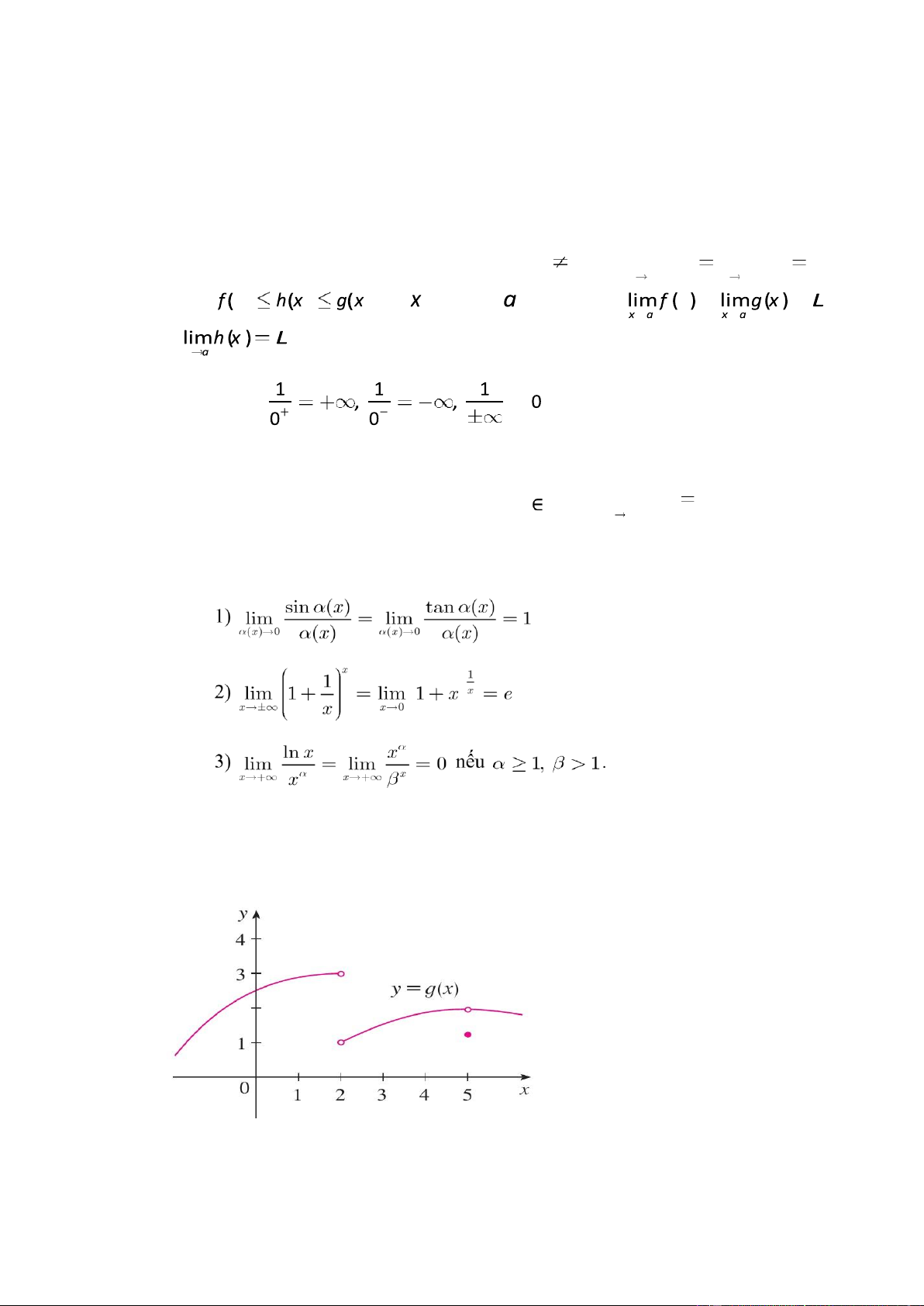
Định lý (giới hạn kẹp) N ế u khi ti ến ế n ( x ) và a thì Chú ý: x Định lý
Nếu f(x) là hàm sơ cấp xác ịnh trên D, x0 D thì xlim ( )x f x f x( ) 0 0
▪ Một số kết quả giới hạn cần nhớ
1.3.5. Một số ví dụ
Ví dụ 1. Cho hàm y = g x( ) có ồ thị như hình bên dưới. 16 lOMoAR cPSD| 47305584
Tìm xlim→2+ g x( );limx→2− g x( );limx→5+ g x( );limx→5− g x( ). Từ ó suy ra limx→2 g x(
),limx→5 g x( ), nếu có. Ví dụ 2. Cho hàm f x( ) , xét sự tồn tại của lim ( )f x . x 2 Ví dụ 3. Chứng tỏ Ví dụ 4.
Chứng tỏ rằng limx sin Ví dụ 5. Tính L Ví dụ 6. Tính L Ví dụ 7. Tính L Ví dụ 8. Tính L Ví dụ 9. Tính L Ví dụ 10. Tính L .
Ví dụ 11. Tính L
Bài 2. ĐẠI LƯỢNG VÔ CÙNG BÉ 17 lOMoAR cPSD| 47305584
3.1. Đại lượng vô cùng bé 3.1.1. Định nghĩa 1
Đại lượng ( )x ược gọi là vô cùng bé (viết tắt là VCB) khi x tiến ến a nếu . Ví d ụ 1. là VCB khi ; là VCB khi .
Định nghĩa 1.1 1
Đại lượng ( )x ược gọi là vô cùng lớn (VCL) khi x→x0 nếu là vô cùng ( )x
bé khi x→x0 .
Khi ó, ta viết lim v x( ) = ( ) x x→ 0 Ví dụ 1.1. ; ( )x x3 2021 là VCL khi x 2 ln x là VCL khi x 0 .
3.1.2. Định nghĩa 2
Giả sử ( )x , ( )x là hai vô cùng bé khi x tiến ến a . Xét ( )x . lim k x a ( )x Ta có:
• ( )x là vô cùng bé bậc cao hơn ( )x , ký hiệu là ( )x O( ( ))x , nếu k = 0.
• ( )x là vô cùng bé bậc thấp hơn ( )x , nếu k
• ( )x là vô cùng bé cùng bậc với ( )x nếu 0 k .
• ( )x là vô cùng bé tương ương với ( )x , ký hiệu là ( )x ( )x , nếu k 1. Ví dụ 2. 18 lOMoAR cPSD| 47305584 , vì •
1 cosx là vô cùng bé cùng bậc vớix2 khi x .
Ví dụ 3. tan (2 x 1) khi x 1. 3.2. Tính chất
Giả sử ( )x , ( ), ( ),x x
( )x là các vô cùng bé khix tiến ến a . Ta có: 1) ( )x ( )x ( )x ( )x O( ( ))x
2) Nếu ( )x ( )x và ( )x ( )x thì ( )x ( )x 3) Nếu ( )x ( )x và ( )x ( )x
thì ( ) ( )x x ( ) ( )x x 4) Nếu ( )x O( ( ))x thì ( )x ( )x ( )x .
3.3. Quy tắc ngắt bỏ vô cùng bé cấp cao
Nếu ( )x và ( )x là tổng của những vô cùng bé khác cấp khi x → a thì
bằng giới hạn tỉ số của vô cùng bé cấp thấp nhất của ( )x và ( )x . x3 cosx 1 Ví dụ 4. Tính lim L x 0 4 2 . x x
Ghi nhớ. Khi x→0, ta có các công thức vô cùng bé tương ương sau: 1) sinx 2) tanx x 3) arcsinx 4) arctanx x 5) 1 cosx x2 /2 6) e x 1 x 7) ln(1
8) n 1 x 1 x n/ Chú ý x 1)
Nếu u x( ) là vô cùng bé khi x→x0 thì ta có thể thay bởi u x( ) trong 8 công thức trên. 2)
Các công thức vô cùng bé tương ương trên không áp dụng ược cho hiệu hoặc
tổng của các vô cùng bé nếu chúng làm triệt tiêu tử hoặc mẫu của phân thức. 19 lOMoAR cPSD| 47305584 Ví d ụ 5. (sai !). K ế t qu ả úng là (xem bài quy t
ắc L’Hospital ở chương 2). Ví d ụ 6. Tính .
Ví dụ 7. Tính L limx 0 3 x 31 arctan2 x 1 . cos x cosx 2x
Ví dụ 8. Cho hàm số y
f x( ) ược xác ịnh bởi x 2t t và y . x2 Khi x
0, chứng minh rằng f x( ) . 4 Ví dụ 9. Tìm giá trị của a ể hàm số sau ây liên tục tại x f x( ) f x( ) 20